中考压轴题专题训练

中考压轴题专题训练：“四点共圆”典型问题50练一．选择题（共9小题）1．如图，在等腰Rt△ABC中，∠ABC＝90°，AB＝BC＝4，D是BC中点，∠CAD＝∠CBE，则AE＝（）A．4B．3C．2D．2．在圆内接四边形ABCD中，∠BAD、∠ADC的角平分线交于点E，过E作直线MN平行于BC，与AB、CD交于M、N，则总有MN＝（）A．BM+DN B．AM+CN C．BM+CN D．AM+DN3．如图，已知（1）已知△ABC的两条中线BD、CE交于点M，A、D、M、E四点共圆，BC＝8，则AM 的长为（）A．2B．C．D．34．如图，在△ABC中，∠B＝75°，∠C＝45°，BC＝6﹣2，点P是BC上一动点，PE⊥AB于E，PD ⊥AC于D．无论P的位置如何变化，线段DE的最小值为（）A．3﹣3B．C．4﹣6D．25．如图①，若BC是Rt△ABC和Rt△DBC的公共斜边，则A、B、C、D在以BC为直径的圆上，则叫它们“四点共圆”．如图②，△ABC的三条高AD、BE、CF相交于点H，则图②中“四点共圆”的组数为（）A．2B．3C．4D．66．如图，在四边形ABCD中，AC、BD为对角线，点M、E、N、F分别为AD、AB、BC、CD边的中点，下列说法：①当AC＝BD时，M、E、N、F四点共圆．②当AC⊥BD时，M、E、N、F四点共圆．③当AC＝BD且AC⊥BD时，M、E、N、F四点共圆．其中正确的是（）A．①②B．①③C．②③D．①②③7．如图放置的两个正方形，大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），M在BC边上，且BM＝b，连接AM，MF，MF交CG于点P，将△ABM绕点A旋转至△ADN，将△MEF绕点F旋转至△NGF，给出以下五个结论：①∠MAD＝∠AND；②CP＝b﹣；③△ABM≌△NGF；④S四边形AMFN ＝a2+b2；⑤A，M，P，D四点共圆，其中正确的个数是（）A．2B．3C．4D．58．如图，已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M，过D任作一条与直线BC不重合的直线l，直线l分别与直线MB、MC交于点P、Q，下列判断错误的是（）A．无论直线l的位置如何，总有直线PM与△ABD的外接圆相切B．无论直线l的位置如何，总有∠PAQ＞∠BACC．直线l选取适当的位置，可使A、P、M、Q四点共圆D．直线l选取适当的位置，可使S△APQ＜S△ABC9．如图，一副直角三角板满足∠ACB＝∠EDF＝90°，AC＝BC，AB＝DF，∠EFD＝30°，将三角板DEF 的直角顶点D放置于三角板ABC的斜边AB上，再将三角板DEF绕点D旋转，并使边DE与边AC交于点M，边DF与边BC于点N．当∠EDF在△ABC内绕顶点D旋转时有以下结论：①点C，M，D，N四点共圆；②连接CD，若AD＝DB，则△ADM∽△CDN；③若AD＝DB，则DN•CM＝BN•DM；④若AD＝DB，则CM+CN＝AD；⑤若DB＝2AD，AB＝6，则2≤S△DMN≤4．其中正确结论的个数是（）A．2B．3C．4D．5二．填空题（共14小题）10．若一个圆经过梯形ABCD的四个顶点，则这个梯形是梯形．11．已知AB为圆O的一条弦（非直径），OC⊥AB于C，P为圆O上任意一点，直线PA与直线OC相交于点M，直线PB与直线OC相交于点N．以下说法正确的有．①O，M，B，P四点共圆；②A，M，B，N四点共圆；③A，O，P，N四点共圆．12．已知△ABC中，∠BAC≠90°，AD⊥BC，BE⊥AC，且AD、BE交于点H，连接CH，则∠ACH+∠BAE＝．13．已知△ABC为等腰直角三角形，∠C为直角，延长CA至D，以AD为直径作圆，连BD与圆O交于点E，连CE，CE的延长线交圆O于另一点F，那么的值等于．14．已知二次函数y1＝a1（x﹣1）2﹣2012，其图象顶点为M，且与x轴交于A（x1，0），B（x2，0）两点，又知二次函数y2＝a2（x﹣1）2+1的顶点为N，若A，B，M，N四点共圆，则x1x2﹣x1﹣x2＝．15．如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，∠ABD＝72°，则∠CAD的度数为．16．已知：AB＝2，AC平分∠DAB，∠DAB+∠DCB＝180°，∠DCB＝120°，当∠ABD＝∠CBF时，则AC＝．17．在四边形ABCD中，∠DAC＝98°，∠DBC＝82°，∠BCD＝70°，BC＝AD，则∠ACD＝．18．如图，在等腰△ABC中，∠ABC＝90°，点D为BC的中点，点E在AC边上，以DE为腰作等腰Rt △DEF，连接CF，BF．若CE＝1，△CDF的面积为7.5，则BF的长为．19．如图，线段AB、CD相交于E，AE＝AC，DE＝DB，点M、F、G分别为线段AD、CE、EB的中点，如果∠MAE＝25°，∠AMF＝40°，那么∠MFG的度数为．20．如图，点O为等边△ABC内一点，OA＝2，OC＝，连接BO并延长交AC于点D，且∠DOC ＝30°，过点B作BF⊥BD交CO延长线于点F，连接AF，过点D作DE⊥AF于点E，则DE＝．21．如图，正方形ABCD的边长为2，对角线AC、BD交于点O，E为DC上一点，∠DAE＝30°，过D 作DF⊥AE于F点，连接OF．则线段OF的长度为．22．如图，ABCD、CEFG是正方形，E在CD上，且BE平分∠DBC，O是BD中点，直线BE、DG交于H．BD，AH交于M，连接OH，则OH＝，BM＝．23．如图放置的两个正方形，大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），M在BC边上，且BM＝b，连接AM，MF，MF交CG于点P，将△ABM绕点A旋转至△ADN，将△MEF绕点F旋转至△NGF，给出以下五个结论：①∠MAD＝∠AND；②CP＝a﹣；③△ABM≌△NGF；④S四边形AMFN＝a2+b2；⑤A，M，P，D四点共圆，其中正确的序号为．三．解答题（共27小题）24．设梯形ABCD中，AB∥CD，E，F分别在腰AD和BC上，若A，B，F，E四点共圆，证明C，D，E，F也必四点共圆．25．已知四边形ABCD为菱形，点E、F、G、H分别为各边中点，判断E、F、G、H四点是否在同一个圆上，如果在同一圆上，找到圆心，并证明四点共圆；如果不在，说明理由．26．如图，在△ABC中，AB＜AC，AD平分∠BAC，BM＝CM，K为AM上一点，且∠BKC＝180°﹣∠BAC．求证：∠BKD＝∠CKD．27．如图，O为△ABC外心，D为BC上一点，BD中垂线交AB于F，CD中垂线交AC于E，求证：A、F、O、E四点共圆．28．如图，点E，F分别在线段AC，BC上运动（不与端点重合），而且CE＝BF，AC＝BC，O是△ABC 的外心，证明C，E，O，F四点共圆．29．如图，点F是△ABC外接圆的中点，点D、E在边AC上，使得AD＝AB，BE＝EC．证明：B、E、D、F四点共圆．30．如图，AB是⊙O的直径，AC是⊙O的切线，BC交⊙O于点D，点E是AC的中点，连接OD．（1）求证：OD⊥DE；（2）求证：O、A、E、D四点共圆．（3）△ABC满足什么条件时，经过O、A、E、D的圆与BC相切？并说明理由．31．如图，在锐角三角形ABC中，AB＝AC，∠ACB的平分线交AB于点D．过△ABC的外心O作直线OG⊥CD交AC于点E，交CD于点G，过点E作EF∥AB交CD于F．（1）求证：C，E，O，F四点共圆；（2）求证：A，O，F三点共线；（3）求证：EA＝EF．32．在学习《圆》这一单元时，我们学习了圆周角定理的推论：圆内接四边形的对角互补；事实上，它的逆命题：对角互补的四边形的四个顶点共圆，也是一个真命题．在图形旋转的综合题中经常会出现对角互补的四边形，那么，我们就可以借助“对角互补的四边形的四个顶点共圆”，然后借助圆的相关知识来解决问题，例如：已知：△ABC是等边三角形，点D是△ABC内一点，连接CD，将线段CD绕C逆时针旋转60°得到线段CE，连接BE，DE，AD，并延长AD交BE于点F．当点D在如图所示的位置时：（1）观察填空：①与△ACD全等的三角形是；②∠AFB的度数为；（2）利用题干中的结论，证明：C，D，F，E四点共圆；（3）直接写出线段FD，FE，FC之间的数量关系．33．如图，四边形ABCD中，∠ACB＝∠ADB＝90°，自对角线AC、BD的交点N作NM⊥AB于点M，线段AC、MD交于点E，BD、MC交于点F，P是线段EF上的任意一点．证明：点P到线段CD的距离等于点P到线段MC、MD的距离之和．34．如图，在△ABC中，过A作BC的垂线，垂足为D，O为AD的中点，以AD为直径的⊙O分别与边AB、AC交于点E、F．试求证：（1）BC是⊙O的切线；（2）B、C、F、E四点共圆吗？说明理由．35．如图，圆O内接四边形ABCD的对边AD，BC延长线交于点P，对角线AC，BD交于点Q，设△PDB 的外接圆交直线PQ与P和另一个点K，求证：（1）OK⊥PQ（2）C，D，O，K四点共圆；（3）三条直线AB，OK，DC交于一点．36．如图，已知锐角三角形ABC，过点A作BC的垂线与以BC为直径的⊙O1分别交于点D，E．过点B 作CA的垂线与以CA为直径的⊙O2分别交于点F，G．求证：E，F，D，G四点共圆，并确定圆心的位置．37．已知△ABC中，∠A＝60°，E、F分别为AB、AC延长线上的点，且BE＝CF＝BC，△ACE的外接圆与EF交于不同于E的点K，设BF与CE交于点T．（1）证明：A、B、T、C四点共圆；（2）证明：点K在∠BAC的角平分线上．38．已知半径为r的⊙O1与半径为R的⊙O2外离，直线DE经过O1切⊙O2于点E并交⊙O1于点A和点D，直线CF经过O2切⊙O1于点F并交⊙O2于点B和点C，连接AB、CD，（1）[以下ⅰ、ⅱ两小题任选一题]（ⅰ）求四边形ABCD的面积（ⅱ）求证：A、B、E、F四点在同一个圆上（2）求证：AB∥DC．39．已知：AB是⊙O的直径，C为AB延长线上的一点，过点C作⊙O的割线，与⊙O交于D、E两点，OF是△BOD的外接圆O1的直径，连接CF并延长交⊙O1于点G．求证：O、A、E、G四点共圆．40．如图，四边形ABCD为⊙O的内接四边形，对边BC，AD交于点F，AB、DC交于点E，△ECF的外接圆与⊙O的另一交点为H，AH与EF交于点M，MC与⊙O交于点C．证明：（1）M为EF的中点；（2）A、G、E、F四点共圆．41．已知：AB∥DF，它们之间的距离等于AB；AC∥DE，它们之间的距离等于AC；CB∥EF，它们之间的距离等于BC，求证：A1、B1、C1、A2、B2、C2六点共圆．42．设△ADE内接于圆O，弦BC分别交AD、AE边于点F、G，且AB＝AC，求证：F、D、E、G四点共圆．43．若以圆内接四边形ABCD的各边为弦作任意圆，求证：这些圆相交的四点共圆．44．如图，PQ为两圆的公共弦，M为PQ上一点，AB、CD分别是两圆的弦且它们相交于M，求证：A、C、B、D四点共圆．45．如图，⊙O1与⊙O2相交于P、Q两点，过P点作两圆的割线分别交于⊙O1与⊙O2于A、B，过A、B 分别作两圆的切线相交于T，求证：T、A、Q、B四点共圆．46．如图所示，两圆交于A、B两点，过B的直线交两圆于C、D，两圆外有一点P，连接PC，PD，分别交两圆于E，F．求证：P、E、A、F四点共圆．47．如图，⊙O是以等腰Rt△ABC的斜边AB为直径的圆，点P是BA的延长线上的一点，过点P作⊙O 的一条切线，切点为点Q，∠QPB的平分线交AC、BC于点E、F．（1）求证：P、A、E、Q四点共圆．（2）若AE＝a，BF＝b，求EF的长．48．如图，四边形ABCD内接于⊙O，P、Q、R分别是AB、BC、AD的中点，连接PQ与DA的延长线交于S，连接PR与CB延长线交于T，求证：S、T、Q、R四点共圆．49．如图，两圆T1、T2相交于A、B两点，过点B的一条直线分别交圆T1、T2于点C、D，过点B的另一条直线分别交圆T1、T2于点E、F，直线CF分别交圆T1、T2于点P、Q，设M、N分别是弧PB、弧QB的中点，求证：若CD＝EF，则C、F、M、N四点共圆．50．如图，D是△ABC的BC边上的一点，O1、O2和O3分别为△ABC、△ADB和△ADC外接圆的圆心，求证：A、O2、O1、O3四点共圆．中考压轴题专题训练：“四点共圆”典型问题50练参考答案与试题解析一．选择题（共9小题）1．如图，在等腰Rt△ABC中，∠ABC＝90°，AB＝BC＝4，D是BC中点，∠CAD＝∠CBE，则AE＝（）A．4B．3C．2D．【分析】如图，连接DE，由等腰直角三角形的性质可求∠C＝∠BAC＝45°，AC＝AB＝4，由∠CAD＝∠CBE，可证点A，点B，点D，点E四点共圆，可得∠ABD＝∠DEC＝90°，由等腰直角三角形的性质可求DE＝，即可求解．【解答】解：如图，连接DE，∵∠ABC＝90°，AB＝BC＝4，∴∠C＝∠BAC＝45°，AC＝AB＝4，∵D是BC中点，∴CD＝BC＝2，∵∠CAD＝∠CBE，∴点A，点B，点D，点E四点共圆，∴∠ABD＝∠DEC＝90°，∴∠C＝∠EDC＝45°，∴DE＝CE＝CD＝，∴AE＝AC﹣CE＝3，故选：B．2．在圆内接四边形ABCD中，∠BAD、∠ADC的角平分线交于点E，过E作直线MN平行于BC，与AB、CD交于M、N，则总有MN＝（）A．BM+DN B．AM+CN C．BM+CN D．AM+DN【分析】在NM上截取NF＝ND，连结DF，AF，由A，B，C，D四点共圆，得出∠MND+∠MAD＝180°，由MN∥BC，得出∠AMN+∠ADN＝180°，可得到A，D，N，M四点共圆，再由AE，DE分别平分∠BAD，∠CDA，A，F，E，D四点共圆，由∠MAF＝180°﹣∠DAF﹣∠MND＝180°﹣∠DEN﹣∠MND ＝∠EDN＝∠ADE＝∠AFM，可得出MA＝MF，即得出MN＝MF+NF＝MA+ND．【解答】解：如图，在NM上截取NF＝ND，连结DF，AF∴∠NFD＝∠NDF，∵A，B，C，D四点共圆，∴∠ADC+∠B＝180°，∵MN∥BC，∴∠AMN＝∠B，∴∠AMN+∠ADN＝180°，∴A，D，N，M四点共圆，∴∠MND+∠MAD＝180°，∵AE，DE分别平分∠BAD，∠CDA，∴∠END+2∠DFN＝∠END+2∠DAE＝180°，∴∠DFN＝∠DAE，∴A，F，E，D四点共圆，∴∠DEN＝∠DAF，∠AFM＝∠ADE，∴∠MAF＝180°﹣∠DAF﹣∠MND＝180°﹣∠DEN﹣∠MND＝∠EDN＝∠ADE＝∠AFM，∴MA＝MF，∴MN＝MF+NF＝MA+ND．故选：D．3．如图，已知（1）已知△ABC的两条中线BD、CE交于点M，A、D、M、E四点共圆，BC＝8，则AM 的长为（）A．2B．C．D．3【分析】延长AM交BC于F，连接ED，根据三角形中位线定理得出ED∥BC，即可求得∠DBC＝∠MDE，根据四点共圆，可得∠MDE＝∠BAF，由题意可得M是三角形的重心，则F是BC的中点，AM＝2FM，证得△ABF∽△MBF，可得＝，得出AF•FM＝BF2＝16，根据条件化成AM2＝16，即可求得结论．【解答】解：延长AM交BC于F，连接ED，∵BD、CE是△ABC的两条中线，∴ED∥BC，∴∠DBC＝∠MDE，∵A、D、M、E四点共圆，∴∠MDE＝∠BAF，∵△ABC的两条中线BD、CE交于点M，∴BF＝FC＝BC＝4，∴M为三角形的重心，∴AM＝2FM，∵∠BAF＝∠MBF，∠AFB＝∠BFM，∴△ABF∽△MBF，∴＝，∴AF•FM＝BF2＝16，（AM+AM）•AM＝16，∴AM2＝16，∴AM＝．故选：C．4．如图，在△ABC中，∠B＝75°，∠C＝45°，BC＝6﹣2，点P是BC上一动点，PE⊥AB于E，PD ⊥AC于D．无论P的位置如何变化，线段DE的最小值为（）A．3﹣3B．C．4﹣6D．2【分析】下面介绍两种解法：解法一：当AP⊥BC时，线段DE的值最小，利用四点共圆的判定可得：A、E、P、D四点共圆，且直径为AP，得出∠AED＝∠C＝45°，有一公共角，根据两角对应相等两三角形相似得△AED∽△ACB，则，设AD＝2x，表示出AE和AC的长，求出AE与AC的比，代入比例式中，可求出DE的值．解法二：先通过四点共圆同理得到：△EFD为顶角为120°的等腰三角形，所以当AP⊥BC时，线段DE的值最小，再作辅助线，求AP的长，从而得EF的长，由等腰三角形三线合一及勾股定理得DE的值．【解答】解：解法一：当AP⊥BC时，线段DE的值最小，如图1，∵PE⊥AB，PD⊥AC，∴∠AEP＝∠ADP＝90°，∴∠AEP+∠ADP＝180°，∴A、E、P、D四点共圆，且直径为AP，在Rt△PDC中，∠C＝45°，∴△PDC是等腰直角三角形，∠APD＝45°，∴△APD也是等腰直角三角形，∴∠PAD＝45°，∴∠PED＝∠PAD＝45°，∴∠AED＝45°，∴∠AED＝∠C＝45°，∵∠EAD＝∠CAB，∴△AED∽△ACB，∴，设AD＝2x，则PD＝DC＝2x，AP＝2x，如图2，取AP的中点O，连接EO，则AO＝OE＝OP＝x，∵∠EAP＝∠BAC﹣∠PAD＝60°﹣45°＝15°，∴∠EOP＝2∠EAO＝30°，过E作EM⊥AP于M，则EM＝x，cos30°＝，∴OM＝x•＝x，∴AM＝x+x＝x，由勾股定理得：AE＝，＝，＝（+1）x，∴＝，∴ED＝．则线段DE的最小值为；解法二：如图3，取AP的中点F，连接EF、DF，有EF＝DF＝AP，∠EFD＝120°，∴△EFD为顶角为120°的等腰三角形，∴当AP⊥BC时，线段DE的值最小，如图4，作AB的中垂线，交AP于一点O，交AB于G，连接OB，设OA＝OB＝2x，∵∠BOP＝2∠BAO＝30°，∴BP＝x，OP＝x，∴AP＝PC＝（2+）x，∵BC＝6﹣2，∴x+2x+x＝6﹣2，x＝4﹣2，∴AP＝（2+）x＝（2+）（4﹣2）＝2，∴EF＝FD＝1，如图5，过F作FH⊥ED于H，∴EH＝DH，∵∠FED＝30°，∴FH＝，∴EH＝DH＝，∴DE＝；故选：B．5．如图①，若BC是Rt△ABC和Rt△DBC的公共斜边，则A、B、C、D在以BC为直径的圆上，则叫它们“四点共圆”．如图②，△ABC的三条高AD、BE、CF相交于点H，则图②中“四点共圆”的组数为（）A．2B．3C．4D．6【分析】根据两个直角三角形公共斜边时，四个顶点共圆，结合图形求解可得．【解答】解：如图，以AH为斜边的两个直角三角形，四个顶点共圆（A、F、H、E），以BH为斜边的两个直角三角形，四个顶点共圆（B、F、H、D），以CH为斜边的两个直角三角形，四个顶点共圆（C、D、H、E），以AB为斜边的两个直角三角形，四个顶点共圆（A、E、D、B），以BC为斜边的两个直角三角形，四个顶点共圆（B、F、E、C），以AC为斜边的两个直角三角形，四个顶点共圆（A、F、D、C），共6组．故选：D．6．如图，在四边形ABCD中，AC、BD为对角线，点M、E、N、F分别为AD、AB、BC、CD边的中点，下列说法：①当AC＝BD时，M、E、N、F四点共圆．②当AC⊥BD时，M、E、N、F四点共圆．③当AC＝BD且AC⊥BD时，M、E、N、F四点共圆．其中正确的是（）A．①②B．①③C．②③D．①②③【分析】连接EM、MF、FN、NE，连接EF、MN，交于点O，利用三角形中位线定理可证到四边形ENFM 是平行四边形；然后根据条件判定四边形ENFM的形状，就可知道M、E、N、F四点是否共圆．【解答】解：连接EM、MF、FN、NE，连接EF、MN，交于点O，如图所示．∵点M、E、N、F分别为AD、AB、BC、CD边的中点，∴EM∥BD∥NF，EN∥AC∥MF，EM＝NF＝BD，EN＝MF＝AC．∴四边形ENFM是平行四边形．①当AC＝BD时，则有EM＝EN，所以平行四边形ENFM是菱形．而菱形的四个顶点不一定共圆，故①不一定正确．②当AC⊥BD时，由EM∥BD，EN∥AC可得：EM⊥EN，即∠MEN＝90°．所以平行四边形ENFM是矩形．则有OE＝ON＝OF＝OM．所以M、E、N、F四点共圆，故②正确．③当AC＝BD且AC⊥BD时，同理可得：四边形ENFM是正方形．则有OE＝ON＝OF＝OM．所以M、E、N、F四点共圆，故③正确．故选：C．7．如图放置的两个正方形，大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），M在BC边上，且BM＝b，连接AM，MF，MF交CG于点P，将△ABM绕点A旋转至△ADN，将△MEF绕点F旋转至△NGF，给出以下五个结论：①∠MAD＝∠AND；②CP＝b﹣；③△ABM≌△NGF；④S四边形AMFN ＝a2+b2；⑤A，M，P，D四点共圆，其中正确的个数是（）A．2B．3C．4D．5【分析】①根据正方形的性质得到∠BAD＝∠ADC＝∠B＝90°，根据旋转的性质得到∠NAD＝∠BAM，∠AND＝∠AMB，根据余角的性质得到∠DAM+∠NAD＝∠NAD+∠AND＝∠AND+∠NAD＝90°，等量代换得到∠DAM＝∠AND，故①正确；②根据正方形的性质得到PC∥EF，根据相似三角形的性质得到CP＝b﹣；故②正确；③根据旋转的性质得到GN＝ME，等量代换得到AB＝ME＝NG，根据全等三角形的判定定理得到△ABM ≌△NGF；故③正确；④由旋转的性质得到AM＝AN，NF＝MF，根据全等三角形的性质得到AM＝NF，推出四边形AMFN＝AM2是矩形，根据余角的想知道的∠NAM＝90°，推出四边形AMFN是正方形，于是得到S四边形AMFN＝a2+b2；故④正确；⑤根据正方形的性质得到∠AMP＝90°，∠ADP＝90°，得到∠ABP+∠ADP＝180°，于是推出A，M，P，D四点共圆，故⑤正确．【解答】解：①∵四边形ABCD是正方形，∴∠BAD＝∠ADC＝∠B＝90°，∴∠BAM+∠DAM＝90°，∵将△ABM绕点A旋转至△ADN，∴∠NAD＝∠BAM，∠AND＝∠AMB，∴∠DAM+∠NAD＝∠NAD+∠AND＝∠AND+∠NAD＝90°，∴∠DAM＝∠AND，故①正确；②∵四边形CEFG是正方形，∴PC∥EF，∴△MPC∽△EMF，∴，∵大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），BM＝b，∴EF＝b，CM＝a﹣b，ME＝（a﹣b）+b＝a，∴，∴CP＝b﹣；故②正确；③∵将△MEF绕点F旋转至△NGF，∴GN＝ME，∵AB＝a，ME＝a，∴AB＝ME＝NG，在△ABM与△NGF中，，∴△ABM≌△NGF；故③正确；④∵将△ABM绕点A旋转至△ADN，∴AM＝AN，∵将△MEF绕点F旋转至△NGF，∴NF＝MF，∵△ABM≌△NGF，∴AM＝NF，∴四边形AMFN是矩形，∵∠BAM＝∠NAD，∴∠BAM+DAM＝∠NAD+∠DAN＝90°，∴∠NAM＝90°，∴四边形AMFN是正方形，∵在Rt△ABM中，a2+b2＝AM2，＝AM2＝a2+b2；故④正确；∴S四边形AMFN⑤∵四边形AMFN是正方形，∴∠AMP＝90°，∵∠ADP＝90°，∴∠AMP+∠ADP＝180°，∴A，M，P，D四点共圆，故⑤正确．故选：D．8．如图，已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M，过D任作一条与直线BC不重合的直线l，直线l分别与直线MB、MC交于点P、Q，下列判断错误的是（）A．无论直线l的位置如何，总有直线PM与△ABD的外接圆相切B．无论直线l的位置如何，总有∠PAQ＞∠BACC．直线l选取适当的位置，可使A、P、M、Q四点共圆D．直线l选取适当的位置，可使S△APQ＜S△ABC【分析】本题要求选出错误的命题，只需找到一个命题，说明该命题是假命题即可．可采用反证法判断C是错误的，运用相交弦定理可得DA•DM＝DP•DQ，DA•DM＝DB•DC，可得DP•DQ＝DB•DC，即＝，从而可得△DBP∽△DQC，则有∠BPD＝∠QCD．由AM平分∠BAC可得∠BAM＝∠MAC，根据圆周角定理可得∠MBC＝∠MAC，∠MCB＝∠BAM，即可得到∠MBC＝∠MCB，从而有∠BPD＝∠MBC，与三角形外角的性质∠MBC＝∠BPD+∠BDP矛盾，故假设不成立，即选择C错误．【解答】解：假设A、P、M、Q四点共圆，根据相交弦定理可得：DA•DM＝DP•DQ，∵A、B、M、C四点共圆，∴根据相交弦定理可得：DA•DM＝DB•DC，∴DP•DQ＝DB•DC，即＝，∵∠BDP＝∠QDC，∴△DBP∽△DQC，∴∠BPD＝∠QCD，∵AM平分∠BAC，∴∠BAM＝∠MAC，∵∠MBC＝∠MAC，∠MCB＝∠BAM，∴∠MBC＝∠MCB，∴∠BPD＝∠MBC．与∠MBC＝∠BPD+∠BDP矛盾，故假设不成立，因而命题C错误，故选：C．9．如图，一副直角三角板满足∠ACB＝∠EDF＝90°，AC＝BC，AB＝DF，∠EFD＝30°，将三角板DEF 的直角顶点D放置于三角板ABC的斜边AB上，再将三角板DEF绕点D旋转，并使边DE与边AC交于点M，边DF与边BC于点N．当∠EDF在△ABC内绕顶点D旋转时有以下结论：①点C，M，D，N四点共圆；②连接CD，若AD＝DB，则△ADM∽△CDN；③若AD＝DB，则DN•CM＝BN•DM；④若AD＝DB，则CM+CN＝AD；⑤若DB＝2AD，AB＝6，则2≤S△DMN≤4．其中正确结论的个数是（）A．2B．3C．4D．5【分析】①正确，如图1中，只要证明∠MCN+∠MDN＝180°．②正确，可以证明△ADM与△DCN全等．③正确，如图3中，只要证明△ADM≌△CDN，推出AM＝CN，DM＝DN，因为AC＝BC，推出CM＝BN，即可证明．④正确，如图4中，作DH⊥AC于H，DG⊥BC于G．只要证明四边形CHDG是正方形，△DHM≌△DGN，推出MH＝NG，推出CM+CN＝CH+MH+CG﹣NG＝2CH，又因为AD＝CD＝CH，由此即可证明．⑤正确，如图5中，由△DHM∽△DGN，推出＝＝，设DM＝x，则DG＝2x，推出S△DMN＝•2x•x＝x2，当DM⊥AC时，DM的值最小，此时DM＝DH＝，△DMN的面积最小值为2，当DM ⊥AB时，DM的值最大，此时DM＝AD＝2，△DMN的面积的最大值为4，由此即可判断．【解答】解：①正确．理由如下：如图1中，∵∠ACB＝90°，∠EDF＝90°，∴∠MCN+∠MDN＝180°，∴点C，M，D，N四点共圆．②正确．理由如下：如图2中，连接CD．∵AC＝BC．AD＝DB．∴CD⊥AB，CD＝AD＝DB，∴∠ADC＝∠MDN＝90°，∴∠ADM＝∠CDN，在△ADM和△CDN中，，∴△ADM≌△CDN．故②正确．③正确．理由如下：如图3中∵CA＝CB，∠ACB＝90°，AD＝DB，∴CD＝AD＝DB，CD⊥AB，∠A＝∠ACD＝∠DCN＝45°，∴∠ADC＝∠EDF＝90°，∴∠ADM＝∠CDN，在△ADM和△CDN中，，∴△ADM≌△CDN，∴AM＝CN，DM＝DN，∵AC＝BC，∴CM＝BN，∴DN•CM＝BN•DM④正确．理由如下：如图4中，作DH⊥AC于H，DG⊥BC于G．∵∠ACD＝∠BCD＝45°，∴DH＝DG，∵∠DHC＝∠HCG＝∠CGD＝90°，∴四边形CHDG是矩形，∵DH＝DG，∴四边形CHDG是正方形，∴∠HDG＝∠MDN＝90°，CH＝CG，∴∠MDH＝∠GDN，在△DHM和△DGN中，，∴△DHM≌△DGN，∴MH＝NG∴CM+CN＝CH+MH+CG﹣NG＝2CH，∵AD＝CD＝CH，∴CM+CN＝AD．如图5中，作DH⊥AC于H，DG⊥BC于G．∵AB＝6，BD＝2AD，∴AD＝2，BD＝4，∴AH＝DH＝，DG＝GB＝2，∵∠DHC＝∠HCG＝∠CGD＝90°，∴四边形CHDG是矩形，∴∠HDG＝∠MDN，∴∠MDH＝∠NDG，∵∠DHM＝∠DGN＝90°，∴△DHM∽△DGN，∴＝＝，设DM＝x，则DG＝2x，＝•2x•x＝x2，∴S△DMN当DM⊥AC时，DM的值最小，此时DM＝DH＝，△DMN的面积最小值为2，当DM⊥AB时，DM的值最大，此时DM＝AD＝2，△DMN的面积的最大值为4，≤4．∴2≤S△DMN故选：D．二．填空题（共14小题）10．若一个圆经过梯形ABCD的四个顶点，则这个梯形是等腰梯形．【分析】由四点共圆和平行线的性质证出∠B＝∠C，根据在同一底上的两角相等的梯形是等腰梯形就能求出答案．【解答】解：∵圆经过梯形ABCD的四个顶点，∴∠A+∠C＝180°，∵AD∥BC，∴∠A+∠B＝180°，∴∠B＝∠C，∴梯形ABCD是等腰梯形．故答案为：等腰．11．已知AB为圆O的一条弦（非直径），OC⊥AB于C，P为圆O上任意一点，直线PA与直线OC相交于点M，直线PB与直线OC相交于点N．以下说法正确的有①③．①O，M，B，P四点共圆；②A，M，B，N四点共圆；③A，O，P，N四点共圆．【分析】首先按照题意画出示意图，然后根据四点共圆的判定定理进行判断．①验证∠BPM＝∠BOC 即可；②由图形可知明显错误；③推导∠AOP+∠ANP＝180°即可．【解答】解：如图，∵OC⊥AB于C，∴∠BOC＝∠AOC＝∠AOB，NA＝NB，∵∠BPM＝∠AOB，∴∠BPM＝∠BOC，∴O、M、B、P四点共圆，∴①正确．∵四边形AMBN为凹四边形．∴A、M、B、N不共圆，∴②错误．∵NA＝NB，∴∠NAB＝∠NBA，∵∠NAB+∠NBA+∠ANP＝180°，∴∠ANP+2∠NBA＝180°∵∠AOP＝2∠NBA，∴∠AOP+∠ANP＝180°，∴A、O、P、N四点共圆，∴③正确．故答案为：①③12．已知△ABC中，∠BAC≠90°，AD⊥BC，BE⊥AC，且AD、BE交于点H，连接CH，则∠ACH+∠BAE＝90°．【分析】根据题意可知，点A、B、D、E共圆，点H是△ABC的垂心．过点A作⊙O的切线AF交BC 的延长线BC于点F．根据切线的性质可知△ABF是直角三角形、由平行线的判定与性质可知∠HCA＝∠CAF；最后由图形可知∠BAF＝∠FAC+∠CAB＝90°，即∠BAC+∠HCA＝90°．【解答】解：∵△ABC中，∠BAC≠90°，AD⊥BC，BE⊥AC，∴点A、B、D、E在以AB为直径的⊙O上；过点A作⊙O的切线AF交BC的延长线BC于点F，则AF⊥AB．∵点H是三角形ABC的垂心，∴CH⊥AB，∴CH∥AF，∴∠HCA＝∠CAF（两直线平行，内错角相等）；又∵∠BAF＝∠FAC+∠CAB＝90°，∴∠BAC+∠HCA＝90°．故答案是：90°．13．已知△ABC为等腰直角三角形，∠C为直角，延长CA至D，以AD为直径作圆，连BD与圆O交于点E，连CE，CE的延长线交圆O于另一点F，那么的值等于．【分析】连接AE，AF，DF，根据AD为直径，可证A、C、B、E四点共圆，则∠ACF＝∠ABD，又∠AFC＝∠ADB，可证△AFC∽△ADB，则＝，而∠FAD＝∠FED＝∠BEC＝∠BAC＝45°，根据＝求解．【解答】解：如图，连接AE，AF，DF，∵AD为直径，∴∠AED＝∠AEB＝∠ACB＝90°，∴A、C、B、E四点共圆，∴∠ACF＝∠ABD，又∵∠AFC＝∠ADB，∴△AFC∽△ADB，∴＝，∵∠FAD＝∠FED＝∠BEC＝∠BAC＝45°，在Rt△ADF中，＝＝＝．故答案为：．14．已知二次函数y1＝a1（x﹣1）2﹣2012，其图象顶点为M，且与x轴交于A（x1，0），B（x2，0）两点，又知二次函数y2＝a2（x﹣1）2+1的顶点为N，若A，B，M，N四点共圆，则x1x2﹣x1﹣x2＝﹣2013．【分析】不妨设A在B的左边，设MN与AB的交点为H，易证△AHM∽△NHA，从而可求出AH，进而得到x1，同理可求出x2，然后代入所求代数式就可解决问题．【解答】解：不妨设A在B的左边，设MN与AB的交点为H，由题可知：M（1，﹣2012），N（1，1），则MH＝2012，NH＝1．根据抛物线的对称性可得MN垂直平分AB，故MN为四边形AMBN外接圆的直径，根据圆周角定理可得∠NAM＝∠NBM＝90°，∴∠NAH+∠MAH＝90°，∠HMA+∠MAH＝90°，∴∠NAH＝∠HMA．∵∠AHN＝∠MHA＝90°，∴△AHM∽△NHA，∴＝，∴AH2＝MH•NH＝2012，∴AH＝＝2，∴1﹣x1＝2，∴x1＝1﹣2．同理x2＝1+2，∴x1x2﹣x1﹣x2＝（1﹣2（1+2）﹣（1﹣2）﹣（1+2）＝1﹣2012﹣1+2﹣1﹣2＝﹣2013．故答案为﹣2013．15．如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，∠ABD＝72°，则∠CAD的度数为18°．【分析】通过证明点A，点B，点C，点D四点共圆，可得∠ABD＝∠ACD＝72°，由直角三角形的性质可求解．【解答】解：∵∠ABC＝∠ADC＝90°，∴点A，点B，点C，点D四点共圆，∴∠ABD＝∠ACD＝72°，∴∠CAD＝90°﹣∠ACD＝18°，故答案为：18°．16．已知：AB＝2，AC平分∠DAB，∠DAB+∠DCB＝180°，∠DCB＝120°，当∠ABD＝∠CBF时，则AC＝+1．【分析】先证明A、B、C、D四点共圆，由圆周角定理得出∠ABD＝∠ACD，再由已知条件和圆内接四边形的性质得出∠ACD＝∠ADC，由三角形内角和定理求出∠ACD＝∠ADC＝75°，得出∠ACB＝45°，作BM⊥AC于M，则∠AMB＝∠CMB＝90°，由含30°角的直角三角形的性质和勾股定理得出BM＝AB＝1，AM＝，得出△CBM是等腰直角三角形，因此CM＝BM＝1，即可得出AC的长．【解答】解：∵∠DAB+∠DCB＝180°，∴A、B、C、D四点共圆，∠DAB＝180°﹣∠DCB＝60°，∴∠ABD＝∠ACD，∵∠ABD＝∠CBF，∴∠ACD＝∠CBF，∵∠CBF＝∠ADC，∴∠ACD＝∠ADC，∵AC平分∠DAB，∴∠DAC＝∠BAC＝30°，∴∠ACD＝∠ADC＝75°，∴∠ACB＝120°﹣75°＝45°，作BM⊥AC于M，如图所示：则∠AMB＝∠CMB＝90°，∴BM＝AB＝1，△CBM是等腰直角三角形，∴AM＝BM＝，CM＝BM＝1，∴AC＝AM+CM＝+1；故答案为：+1．17．在四边形ABCD中，∠DAC＝98°，∠DBC＝82°，∠BCD＝70°，BC＝AD，则∠ACD＝28°．【分析】以CD为对称轴作△CDE与△CBD对称，可得∠DEC＝∠DBC＝82°，CE＝CB，然后由∠DAC＝98°可得∠DEC+∠DAC＝180°，得出A、D、E、C四点共圆，然后可得CE＝AD，继而得出∠DCA＝∠CDE＝∠CDB，由∠BCD和∠DBC的度数可求出∠BCD的度数，即可求出∠ACD的度数．【解答】解：以CD为对称轴作△CDE与△CBD对称，则∠DEC＝∠DBC，CE＝CB，∵∠DAC＝98°，∠DBC＝82°，∴∠DEC＝82°，∴∠DEC+∠DAC＝180°，∴A、D、E、C四点共圆，∵BC＝AD，CE＝CB，∴CE＝AD，∴∠DCA＝∠CDE＝∠CDB，∵∠BCD＝70°，∠DBC＝82°，∴∠BDC＝180°﹣∠BCD﹣∠DBC＝28°，∴∠ACD＝∠BDC＝28°．故答案为：28°．18．如图，在等腰△ABC中，∠ABC＝90°，点D为BC的中点，点E在AC边上，以DE为腰作等腰Rt△DEF，连接CF，BF．若CE＝1，△CDF的面积为7.5，则BF的长为．【分析】作DN⊥AC，DM⊥FC，FK⊥BC，垂足分别为N，M，K，如图所示．易证∠DFE＝∠ACB═45°，可得D、E、C、F四点共圆，从而可证到∠DEN＝∠DFM，进而可得△DNE≌△DMF，则有DN ＝DM，NE＝MF．易证四边形DNCM是正方形，设正方形DNCM的边长为x，根据△CDF的面积为7.5建立关于x的方程，求出x，从而可求出FC、KC、BK，然后根据勾股定理就可求出BF的长．【解答】证明：作DN⊥AC，DM⊥FC，FK⊥BC，垂足分别为N，M，K，如图所示．∵△ABC和△DEF都是等腰直角三角形，∴∠DFE＝∠ACB＝45°，∴D、E、C、F四点共圆，∴∠EDF+∠ECF＝180°，∠DEC+∠DFC＝180°，∠DCF＝∠DEF＝45°．∵∠DEN+∠DEC＝180°，∴∠DEN＝∠DFM．在△DNE和△DMF中，．∴△DNE≌△DMF，∴DN＝DM，NE＝MF．∵∠DNC＝∠NCM＝∠DMC＝90°，∴四边形DNCM是矩形．∵DN＝DM，∴矩形DNCM是正方形．设正方形DNCM的边长为x，则NC＝MC＝DM＝DN＝x，∴MF＝NE＝NC﹣EC＝x﹣1，∴FC＝MC+FM＝x+（x﹣1）＝2x﹣1．∵△CDF的面积为7.5，∴x（2x﹣1）＝7.5．解得：x1＝﹣2.5（舍去），x2＝3．∴BD＝DC＝＝3，FC＝5，∴KF＝FC•sin45°＝．同理：KC＝，∴BK＝BC﹣KC＝6﹣＝，∴BF＝＝．故答案为：．19．如图，线段AB、CD相交于E，AE＝AC，DE＝DB，点M、F、G分别为线段AD、CE、EB的中点，如果∠MAE＝25°，∠AMF＝40°，那么∠MFG的度数为45°．【分析】如图，连接AF，DG，由等腰三角形的性质可得∠AFD＝∠AGD＝90°，可得点A，点F，点G，点D四点共圆，可得∠DFG＝∠GAD＝25°，由直角三角形的性质和等腰三角形的性质可求∠DFM ＝20°，即可求解．【解答】解：如图，连接AF，DG，∵AE＝AC，DE＝DB，点F，点G是CE，BE的中点，∴AF⊥CE，DG⊥BE，∴∠AFD＝∠AGD＝90°，∴点A，点F，点G，点D四点共圆，∴∠DFG＝∠GAD＝25°，∵∠AFD＝90°，点M是AD中点，∴AM＝FM＝DM，∴∠DFM＝∠FDM，且∠AMF＝∠FDM+∠DFM＝40°，∴∠DFM＝20°，∴∠MFG＝∠MFD+∠DFG＝45°，故答案为45°．20．如图，点O为等边△ABC内一点，OA＝2，OC＝，连接BO并延长交AC于点D，且∠DOC＝30°，过点B作BF⊥BD交CO延长线于点F，连接AF，过点D作DE⊥AF于点E，则DE＝．【分析】过点C作CM⊥CF交BD延长线于点M，连接AM，由∠BMC＝∠BAC＝∠BFC＝60°知A、F、B、C、M五点共圆，证∠AMB＝60°、OM＝OA＝2得△AOM是等边三角形，由∠AOM＝60°＝∠OMC知MC∥AO，得＝＝＝，从而有OD＝OM＝、DM＝OM＝，由A、F、B、M四点共圆证△ODG是等边三角形，得AG＝OA﹣OG＝OM﹣OD＝DM＝、EG＝AG＝，根据DE＝DG+EG＝OD+EG得出答案．【解答】解：过点C作CM⊥CF交BD延长线于点M，连接AM，∵∠DOC＝30°，∴∠BMC＝∠BAC＝∠BFC＝60°，∴A、F、B、C、M五点共圆，∴∠AMB＝∠ACB＝60°，∵OC＝、∠COD＝30°，∴OM＝＝2＝OA，∴△AOM是等边三角形，∴∠AOM＝60°，∵∠AOM＝60°＝∠OMC，∴MC∥AO，∴＝＝＝，∴OD＝OM＝，DM＝OM＝，∵A、F、B、M四点共圆，∴∠FAM＝180°﹣∠FBM＝90°，∴∠EAG＝∠FAM﹣∠OAM＝30°，∴∠OGD＝∠AGE＝60°，∴△ODG是等边三角形，∴AG＝OA﹣OG＝OM﹣OD＝DM＝，∴EG＝AG＝，∴DE＝DG+EG＝OD+EG＝，故答案为：．21．如图，正方形ABCD的边长为2，对角线AC、BD交于点O，E为DC上一点，∠DAE＝30°，过D作DF⊥AE于F点，连接OF．则线段OF的长度为﹣．【分析】作OG⊥DF于G，连接OG．易证A、O、F、D四点共圆，从而有∠OFG＝∠DAO＝45°，则有OG＝FG．设GF＝GO＝x，则有DG＝1+x，OF＝x．然后先求出OD，再在Rt△OGD中运用勾股定理求出x，就可得到OF的长．【解答】解：作OG⊥DF于G，连接OG，如图所示．∵四边形ABCD是正方形，∴∠DAC＝45°，∠AOD＝90°．∵DF⊥AE，即∠AFD＝90°，∴∠AOD＝∠AFD．∴A、O、F、D四点共圆．∴∠OFG＝∠DAO＝45°．∵OG⊥DF，即∠OGF＝90°，∴∠FOG＝45°＝∠OFG．∴OG＝FG．∵∠AFD＝90°，∠DAE＝30°，AD＝2，∴DF＝1．设GF＝GO＝x，则有DG＝DF+FG＝1+x，OF＝＝x．在Rt△AOD中，OD＝AD•sin∠DAO＝2×＝．在Rt△OGD中，∵∠OGD＝90°，∴OG2+DG2＝OD2．∴x2+（1+x）2＝（）2．解得：x1＝﹣+，x2＝﹣﹣（舍去）．所以OF＝x＝﹣．故答案为：﹣．22．如图，ABCD、CEFG是正方形，E在CD上，且BE平分∠DBC，O是BD中点，直线BE、DG交于H．BD，AH交于M，连接OH，则OH＝AB，BM＝AB．【分析】易得△BCE≌△DCG，得到∠1＝∠2，B，C，H，D四点共圆，得出OH＝BD＝AB，由E关于BD的对称E′，得到△BEE′是等腰三角形，BM⊥E′E于M，由角平分线到角两边的距离相等得出BM＝AB．【解答】解：如图，设EE′与BD交于点M′，∵AD＝CD∴AE′＝CE＝EF，∵∠E′AM′＝∠EFM′，∠AM′E′＝∠FM′F，∴△AM′E′≌△FM′E（AAS），∴EM′＝E′M′，∵ME′＝ME∴M与M′重合，∵BC＝DC，EC＝CG，∠BCE＝∠DCG，在△BCE和△DCG中，，∴△BCE≌△DCG（SAS），∴∠1＝∠2，∴B，C，H，D四点共圆，∴OH＝BD＝AB，∵E关于BD的对称E′，∵∠3＝∠4，BE＝BE′，∴△BEE′是等腰三角形，∴BM⊥E′E于M，∴BM＝AB．故答案为：AB，AB．23．如图放置的两个正方形，大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），M在BC边上，且BM＝b，连接AM，MF，MF交CG于点P，将△ABM绕点A旋转至△ADN，将△MEF绕点F旋转至△NGF，给出以下五个结论：①∠MAD＝∠AND；②CP＝a﹣；③△ABM≌△NGF；④S四边形AMFN＝a2+b2；⑤A，M，P，D四点共圆，其中正确的序号为①③④⑤．【分析】①由正方形的性质得∠BAD＝∠ADC＝∠B＝90°，由旋转的性质得∠NAD＝∠BAM，∠AND ＝∠AMB，由余角的性质进而得∠DAM＝∠AND，①正确；②由正方形的性质得PC∥EF，由相似三角形的性质得到CP＝b﹣，②错误；③由旋转的性质得GN＝ME，则AB＝ME＝NG，证出△ABM≌△NGF（SAS）；③正确；＝AM2＝a2+b2；④正确；得到S四边形AMFN⑤由正方形的性质得∠AMP＝90°，∠ADP＝90°，得∠ABP+∠ADP＝180°，推出A，M，P，D四点共圆，⑤正确．【解答】解：①∵四边形ABCD是正方形，∴∠BAD＝∠ADC＝∠B＝90°，∴∠BAM+∠DAM＝90°，∵将△ABM绕点A旋转至△ADN，∴∠NAD＝∠BAM，∠AND＝∠AMB，∴∠DAM+∠NAD＝∠NAD+∠AND＝∠AND+∠NAD＝90°，∴∠DAM＝∠AND，故①正确；②∵四边形CEFG是正方形，∴PC∥EF，∴△MPC∽△MFE，∴＝，∵大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），BM＝b，∴EF＝b，CM＝a﹣b，ME＝（a﹣b）+b＝a，∴＝，∴CP＝b﹣；故②错误；③∵将△MEF绕点F旋转至△NGF，∴GN＝ME，∵AB＝a，ME＝a，∴AB＝ME＝NG，在△ABM与△NGF中，，∴△ABM≌△NGF（SAS）；故③正确；④∵将△ABM绕点A旋转至△ADN，∴AM＝AN，∵将△MEF绕点F旋转至△NGF，∴NF＝MF，∵△ABM≌△NGF，。

一、中考数学压轴题1．如图，在平面直角坐标系中，点O 为坐标原点，直线y =-x + m 交 y 轴的正半轴于点A ，交x 轴的正半轴于点B ，过点A 的直线AF 交x 轴的负半轴于点F ，∠AFO=45°． （1）求∠FAB 的度数；（2）点 P 是线段OB 上一点，过点P 作 PQ ⊥OB 交直线 FA 于点Q ，连接 BQ ，取 BQ 的中点C ，连接AP 、AC 、CP ，过点C 作 CR ⊥AP 于点R ，设 BQ 的长为d ，CR 的长为h ，求d 与 h 的函数关系式（不要求写出自变量h 的取值范围）；（3）在（2）的条件下，过点 C 作 CE ⊥OB 于点E ，CE 交 AB 于点D ，连接 AE ，∠AEC=2∠DAP ，EP=2，作线段 CD 关于直线AB 的对称线段DS ，求直线PS 与直线 AF 的交点K 的坐标．2．已知：如图，在平面直角坐标系中，点O 为坐标原点，()2,0C ．直线26y x =+与x 轴交于点A ，交y 轴于点B ．过C 点作直线AB 的垂线，垂足为E ，交y 轴于点D ． （1）求直线CD 的解析式；（2）点G 为y 轴负半轴上一点，连接EG ，过点E 作EH EG ⊥交x 轴于点H ．设点G 的坐标为()0,t ，线段AH 的长为d ．求d 与t 之间的函数关系式（不要求写出自变量的取值范围）（3）过点C 作x 轴的垂线，过点G 作y 轴的垂线，两线交于点M ，过点H 作HN GM ⊥于点N ，交直线CD 于点K ，连接MK ，若MK 平分NMB ∠，求t 的值．3．如图1，抛物线2(0)y ax bx c a =++≠的顶点为C （1，4），交x 轴于A 、B 两点，交y 轴于点D ，其中点B 的坐标为（3，0）．（1）求抛物线的解析式；（2）如图2，点E 是BD 上方抛物线上的一点，连接AE 交DB 于点F ，若AF=2EF ，求出点E 的坐标．（3）如图3，点M 的坐标为（32，0），点P 是对称轴左侧抛物线上的一点，连接MP ，将MP 沿MD 折叠，若点P 恰好落在抛物线的对称轴CE 上，请求出点P 的横坐标．4．如图，在梯形ABCD 中，AD//BC ，AB=CD=AD=5，cos 45B =，点O 是边BC 上的动点，以OB 为半径的O 与射线BA 和边BC 分别交于点E 和点M ，联结AM ，作∠CMN=∠BAM ，射线MN 与边AD 、射线CD 分别交于点F 、N ．（1）当点E 为边AB 的中点时，求DF 的长；（2）分别联结AN 、MD ，当AN//MD 时，求MN 的长；（3）将O 绕着点M 旋转180°得到'O ，如果以点N 为圆心的N 与'O 都内切，求O 的半径长．5．如图，在平面直角坐标系中，直线6y x =+与x 轴交于点A ，与y 轴交于点B ，点C 在x 轴正半轴上，2ABC ACB ∠=∠．（1）求直线BC 的解析式；（2）点D 是射线BC 上一点，连接AD ，设点D 的横坐标为t ，ACD ∆的面积为S ()0S ≠，求S 与t 的函数解析式，并直接写出自变量t 的取值范围；（3）在（2）的条件下，AD 与y 轴交于点E ，连接CE ，过点B 作AD 的垂线，垂足为点H ，直线BH 交x 轴于点F ，交线段CE 于点M ，直线DM 交x 轴于点N ，当:7:12NF FC =时，求直线DM 的解析式．6．在梯形ABCD 中，//AD BC ，90B ∠=︒，45C ∠=︒，8AB =，14BC =，点E 、F 分别在边AB 、CD 上，//EF AD ，点P 与AD 在直线EF 的两侧，90EPF ∠=︒，PE PF =，射线EP 、FP 与边BC 分别相交于点M 、N ，设AE x =，MN y =．（1）求边AD 的长；（2）如图，当点P 在梯形ABCD 内部时，求关于x 的函数解析式，并写出定义域； （3）如果MN 的长为2，求梯形AEFD 的面积．7．如图，已知正方形ABCD 中，4,BC AC BD =、相交于点O ，过点A 作射线AM AC ⊥，点E 是射线AM 上一动点，连接OE 交AB 于点F ，以OE 为一边，作正方形OEGH ，且点A 在正方形OEGH 的内部，连接DH ．（1）求证：EDO EAO ∆≅∆；（2）设BF x =，正方形OEGH 的边长为y ，求y 关于x 的函数关系式，并写出定义域；（3）连接AG ，当AEG ∆是等腰三角形时，求BF 的长．8．问题提出（1）如图①，在ABC 中，42,6,135AB AC BAC ==∠=，求ABC 的面积．问题探究（2）如图②，半圆O 的直径10AB =，C 是半圆AB 的中点，点D 在BC 上，且2CD BD =，点P 是AB 上的动点，试求PC PD +的最小值．问题解决（3）如图③，扇形AOB 的半径为20,45AOB ∠=在AB 选点P ，在边OA 上选点E ，在边OB 上选点F ，求PE EF FP ++的长度的最小值．9．如图，在ABC ∆中，14AB =，45B ∠=︒，4tan 3A =，点D 为AB 中点．动点P 从点D 出发，沿DA 方向以每秒1个单位长度的速度向终点A 运动，点P 关于点D 对称点为点Q ，以PQ 为边向上作正方形PQMN ．设点P 的运动时间为t 秒．（1）当t =_______秒时，点N 落在AC 边上．（2）设正方形PQMN 与ABC ∆重叠部分面积为S ，当点N 在ABC ∆内部时，求S 关于t 的函数关系式．（3）当正方形PQMN 的对角线所在直线将ABC ∆的分为面积相等的两部分时，直接写出t 的值．10．对于平面直角坐标系xOy 中的任意点()P x y ，，如果满足x y a += (x ≥0，a 为常数)，那么我们称这样的点叫做“特征点”．（1）当2≤a ≤3时，①在点(1,2),(1,3),(2.5,0)A B C 中，满足此条件的特征点为__________________；②⊙W 的圆心为(,0)W m ，半径为1，如果⊙W 上始终存在满足条件的特征点，请画出示意图，并直接写出m 的取值范围；（2）已知函数()10Z x x x=+>，请利用特征点求出该函数的最小值．11．如图，在平面直角坐标系中，点(1,2)A ，(5,0)B ，抛物线22(0)y ax ax a =->交x 轴正半轴于点C ，连结AO ，AB ．（1）求点C 的坐标；（2）求直线AB 的表达式； （3）设抛物线22(0)y ax ax a =->分别交边BA ，BA 延长线于点D ，E ．①若2AE AO =，求抛物线表达式；②若CDB △与BOA △相似，则a 的值为 ．（直接写出答案）12．如图1，在平面直角坐标系中，抛物线239334y x x =--x 轴交于A B 、两点（点A 在点B 的左侧），与y 轴交于点C ． （1）过点C 的直线5334y x =-x 轴于点H ，若点P 是第四象限内抛物线上的一个动点，且在对称轴的右侧，过点P 作//PQ y 轴交直线CH 于点Q ，作//PN x 轴交对称轴于点N ，以PQ PN 、为邻边作矩形PQMN ，当矩形PQMN 的周长最大时，在y 轴上有一动点K ，x 轴上有一动点T ，一动点G 从线段CP 的中点R 出发以每秒1个单位的速度沿R K T →→的路径运动到点T ，再沿线段TB 以每秒2个单位的速度运动到B 点处停止运动，求动点G 运动时间的最小值：（2）如图2， 将ABC ∆绕点B 顺时针旋转至A BC ''∆的位置， 点A C 、的对应点分别为A C ''、，且点C '恰好落在抛物线的对称轴上，连接AC '．点E 是y 轴上的一个动点，连接AE C E '、， 将AC E ∆'沿直线C E '翻折为A C E ∆''， 是否存在点E ， 使得BAA ∆'为等腰三角形?若存在，请求出点E 的坐标；若不存在，请说明理由．13．（1）如图1，A 是⊙O 上一动点，P 是⊙O 外一点，在图中作出PA 最小时的点A ． （2）如图2，Rt △ABC 中，∠C ＝90°，AC ＝8，BC ＝6，以点C 为圆心的⊙C 的半径是3.6，Q 是⊙C 上一动点，在线段AB 上确定点P 的位置，使PQ 的长最小，并求出其最小值． （3）如图3，矩形ABCD 中，AB ＝6，BC ＝9，以D 为圆心，3为半径作⊙D ，E 为⊙D 上一动点，连接AE ，以AE 为直角边作Rt △AEF ，∠EAF ＝90°，tan ∠AEF ＝13，试探究四边形ADCF 的面积是否有最大或最小值，如果有，请求出最大或最小值，否则，请说明理由．14．（问题探究）课堂上老师提出了这样的问题：“如图①，在ABC 中，108BAC ∠=︒，点D 是BC 边上的一点，7224BAD BD CD AD ∠=︒==，，，求AC 的长”．某同学做了如下的思考：如图②，过点C 作CE AB ∥，交AD 的延长线于点E ，进而求解，请回答下列问题：（1）ACE ∠=___________度；（2）求AC 的长．（拓展应用）如图③，在四边形ABCD 中，12075BAD ADC ∠=︒∠=︒，，对角线AC BD 、相交于点E ，且AC AB ⊥，22EB ED AE ==，，则BC 的长为_____________．15． 在平面直角坐标系中，点O 为坐标原点，直线y ＝﹣x+4与x 轴交于点A ，过点A 的抛物线y ＝ax 2+bx 与直线y ＝﹣x+4交于另一点B ，且点B 的横坐标为1．（1）该抛物线的解析式为；（2）如图1，Q 为抛物线上位于直线AB 上方的一动点（不与B 、A 重合），过Q 作QP ⊥x 轴，交x 轴于P ，连接AQ ，M 为AQ 中点，连接PM ，过M 作MN ⊥PM 交直线AB 于N ，若点P 的横坐标为t ，点N 的横坐标为n ，求n 与t 的函数关系式；在此条件下，如图2，连接QN 并延长，交y 轴于E ，连接AE ，求t 为何值时，MN ∥AE ．（3）如图3，将直线AB 绕点A 顺时针旋转15度交抛物线对称轴于点C ，点T 为线段OA 上的一动点（不与O 、A 重合），以点O 为圆心、以OT 为半径的圆弧与线段OC 交于点D ，以点A 为圆心、以AT 为半径的圆弧与线段AC 交于点F ，连接DF ．在点T 运动的过程中，四边形ODFA 的面积有最大值还是有最小值？请求出该值．16．如图，抛物线25y ax bx =+-交x 轴于点A 、B （A 在B 的左侧），交y 轴于点C ，且OB OC =，()2,0A -．（1）求抛物线的解析式；（2）点P 为第四象限抛物线上一点，过点P 作y 轴的平行线交BC 于点D ，设P 点横坐标为t ，线段PD 的长度为d ，求d 与t 的函数关系式．（不要求写出t 的取值范围） （3）在（2）的条件下，F 为BP 延长线上一点，且45PFC ∠=︒，连接OF 、CP 、PB ，FOB ∆的面积为3600169，求PBC ∆的面积．17．如图①，△ABC是等腰直角三角形，在两腰AB、AC外侧作两个等边三角形ABD和ACE，AM和AN分别是等边三角形ABD和ACE的角平分线，连接CM、BN，CM与AB交于点P．（1）求证：CM＝BN；（2）如图②，点F为角平分线AN上一点，且∠CPF＝30°，求证：△APF∽△AMC；（3）在（2）的条件下，求PFBN的值．18．如图，在⊙O中，直径AB＝10，tanA＝3．（1）求弦AC的长；（2）D是AB延长线上一点，且AB＝kBD，连接CD，若CD与⊙O相切，求k的值；（3）若动点P以3cm/s的速度从A点出发，沿AB方向运动，同时动点Q以32cm/s的速度从B点出发沿BC方向运动，设运动时间为t （0＜t＜103），连结PQ．当t为何值时，△BPQ为Rt△？19．如图，在矩形ABCD中，点E为BC的中点，连接AE，过点D作DF AE⊥于点F，过点C作CN DF⊥于点N，延长CN交AD于点M．（1）求证：AM MD=（2）连接CF，并延长CF交AB于G①若2AB=，求CF的长度；②探究当ABAD为何值时，点G恰好为AB的中点．20．在一次数学课上，李老师让同学们独立完成课本第23页第七题选择题（2）如图 1，如果 AB∥CD∥EF，那么∠BAC+∠ACE+∠CEF＝（）A．180° B．270° C．360° D．540°（1）请写出这道题的正确选项；（2）在同学们都正确解答这道题后，李老师对这道题进行了改编：如图2，AB∥EF，请直接写出∠BAD，∠ADE，∠DEF之间的数量关系．（3）善于思考的龙洋同学想：将图1平移至与图2重合（如图3所示），当AD，ED分别平分∠BAC，∠CEF时，∠ACE与∠ADE之间有怎样的数量关系？请你直接写出结果，不需要证明．（4）彭敏同学又提出来了，如果像图4这样，AB∥EF，当∠ACD=90°时，∠BAC、∠CDE 和∠DEF之间又有怎样的数量关系？请你直接写出结果，不需要证明．21．如图1，以AB为直径作⊙O，点C是直径AB上方半圆上的一点，连结AC，BC，过点C作∠ACB的平分线交⊙O于点D，过点D作AB的平行线交CB的延长线于点E．（1）如图1，连结AD，求证：∠ADC＝∠DEC．（2）若⊙O的半径为5，求CA•CE的最大值．（3）如图2，连结AE，设tan∠ABC＝x，tan∠AEC＝y，①求y关于x的函数解析式；②若CBBE＝45，求y的值．22．发现来源于探究．小亮进行数学探究活动，作边长为a的正方形ABCD和边长为b的正方形AEFG（a>b），开始时，点E在AB上，如图1．将正方形AEFG绕点A逆时针方向旋转．（1）如图2，小亮将正方形AEFG 绕点A 逆时针方向旋转，连接BE 、DG ，当点G 恰好落在线段BE 上时，小亮发现DG ⊥BE ，请你帮他说明理由．当a=3，b=2时，请你帮他求此时DG 的长．（2）如图3，小亮旋转正方形AEFG ，点E 在DA 的延长线上，连接BF 、DF ．当FG 平分∠BFD 时，请你帮他求a ：b 及∠FBG 的度数．（3）如图4，BE 的延长线与直线DG 相交于点P ，a=2b ．当正方形AEFG 绕点A 从图1开始，逆时针方向旋转一周时，请你帮小亮求点P 运动的路线长（用含b 的代数式表示）．23．问题探究（1）如图1．在ABC 中，8BC =，D 为BC 上一点，6AD =．则ABC 面积的最大值是_______．（2）如图2，在ABC 中，60BAC ∠=︒，AG 为BC 边上的高，O 为ABC 的外接圆，若3AG =，试判断BC 是否存在最小值？若存在，请求出最小值：若不存在，请说明理由．问题解决：如图3，王老先生有一块矩形地ABCD ，6212AB =，626BC =+，现在他想利用这块地建一个四边形鱼塘AMFN ，且满足点E 在CD 上，AD DE =，点F 在BC 上，且6CF =，点M 在AE 上，点N 在AB 上，90MFN ∠=︒，这个四边形AMFN 的面积是否存在最大值？若存在，求出面积的最大值；若不存在，请说明理由．24．问题一：如图①，已知AC ＝160km ，甲，乙两人分别从相距30km 的A ，B 两地同时出发到C 地．若甲的速度为80km /h ，乙的速度为60km /h ，设乙行驶时间为x （h ），两车之间距离为y （km ）．（1）当甲追上乙时，x ＝ ．（2）请用x 的代数式表示y ．问题二：如图②，若将上述线段AC 弯曲后视作钟表外围的一部分，线段AB 正好对应钟表上的弧AB （1小时的间隔），易知∠AOB ＝30°．（3）分针OD 指向圆周上的点的速度为每分钟转动 km ，时针OE 指向圆周上的点的速度为每分钟转动 °；（4）若从2：00起计时，求几分钟后分针与时针第一次重合？25．在平面直角坐标系中，点O 为坐标原点，抛物线(2)()y a x x m =++与x 轴交于点A C 、（点A 在点C 的左侧），与y 轴正半轴交于点B ，24OC OB ==．（1）如图1，求a m 、的值；（2）如图2，抛物线的顶点坐标是M ，点D 是第一象限抛物线上的一点，连接AD 交抛物线的对称轴于点N ，设点D 的横坐标是t ，线段MN 的长为d ，求d 与t 的函数关系式；（3）如图3，在（2）的条件下，当154d =时，过点D 作DE x 轴交抛物线于点E ，点P 是x 轴下方抛物线上的一个动点，连接PE 交x 轴于点F ，直线211y x b =+经过点D 交EF 于点G ，连接CG ，过点E 作EH CG 交DG 于点H ，若3CFG EGH S S =△△，求点P 的坐标．【参考答案】***试卷处理标记，请不要删除一、中考数学压轴题1．F解析：（1）∠FAB=90°；（2）22d h =；（3）直线PS 与直线AF 的交点K(-2，6)．【解析】【分析】（1）通过直线AB 的解析式可求出点A 、B 的坐标，可知AOB 是等腰直角三角形，再结合已知条件即可确定90FAB ∠=︒；（2）根据已知条件证明CP=AC=QC=BC 从而得出△ACP 是等腰直角三角形，在Rt △CRP 中，利用sin ∠CPR 22CR CP ==，推出2CP CR =，继而得出22BQ CR =，得出答案； （3）过点 A 作AH ⊥CE 交 EC 的延长线于点 H ，延长 CH 到点 G ，使 HG=CH ，连接AG ，证明△AHC ≌△CEP ，设AH CE n ==，得出EG=CE+CH+GH=n+2+2=n+4，再通过角的等量代换，得出∠EAG=∠G ，从而有EG=EA=n+4，在Rt △AHE 中，通过勾股定理AE²=HE²+AH²可求出n 的值为6，从而得出直线AF 的解析式y = x + 8 ，再求出直线PS 的解析式为 y=-x+4，求交点即可．【详解】解：（1）如下图，y = -x + m ，当x=0时，y=m∴A （0，m ），OA=m当y=0时，0=-x+m ，x=m ，∴B （m ，0），OB=m∴OA=OB∴∠OAB=∠OBA=45°∵∠AFO=45°，∠FAB+∠FBA+∠AFB=180°∴∠FAB=90°（2）如下图 ，∵CP 、AC 分别是 Rt △QPB 和 Rt △QAB 的斜边上的中线∴CP= 12QB ，12AC QB =， ∴CP=AC=QC=BC∴∠CAB=∠CBA设∠CAB=∠CBA=α，∴∠CBP=45°+α∴∠CPB=∠CBP=45°+α∴∠PCB=180°-（∠CPB+∠CBP ）=90°-2α∵∠ACB=180°-∠CAB-∠CBA=180°-2α∴∠ACP=∠ACB-∠PCB=180°-2α-（90°-2α）=90°∵AC=CP∴△ACP 是等腰直角三角形∴∠CPA=∠CAP=45°∵CR ⊥AP ，∴∠CRP=90°，在Rt △CRP 中sin ∠CPR 22CR CP == ∴2CP CR =∵12CP BQ =， ∴22BQ CR =即22d h =（3）过点 A 作AH ⊥CE 交 EC 的延长线于点 H ，延长 CH 到点 G ，使 HG=CH ，连接AG ∴∠AHC=∠CEP=90°∴∠HAC+∠HCA=∠PCE+∠HCA∴∠HAC=∠PCE ，∵AC=CP∴△AHC ≌△CEP∴CH=PE=2，AH=CE ，∴GH=CH=2，AH CE n ==∴EG=CE+CH+GH=n+2+2=n+4设∠DAP=β，则∠AEG=2β∴α+β=45°∵∠EBD=∠EDB=∠HDA=∠HAD=45°∴∠CAH=∠HAD-α=45°-α=β∵AH 垂直平分 GC∴AG=AC∴∠GAH=∠CAH=β∴∠G=90°-β 在△EAG 中∠EAG=180°-∠G-∠AEG=180°-（90°-β）-2β =90°-β∴∠EAG=∠G∴EG=EA=n+4在 Rt △AHE 中，AE²=HE²+AH²222(4)(2)n n n +=++126,2n n ==-（舍）∴AH=OE=6，EP=EB=2∴OB=OE+BE=8∴m=8，∴A （0，8）∴OA=OF=8 ， ∴F （-8，0）∴直线 AF 的解析式为 y = x + 8∵CD=CE-DE=CE-BE=6-2=4∵线段 CD 关于直线 AB 的对称线段 DS∴SD=CD=4，∠CDA=∠SDA=45°∴∠CDS=90°，∴SD ∥x 轴过点 S 分别作 SM ⊥x 轴于点 M ，SN ⊥y 轴于点 N∴四边形 OMSN 、SMED 都是矩形∴OM=SN=OE-ME=2，ON=SM=DE=BE=2∴S(2，2)∵OP=OE-EP=6-2=4，∴P(4，0)设直线 PS 的解析式为 y=ax+b∴4022a b a b +=⎧⎨+=⎩，解得：14a b =-⎧⎨=⎩∴直线 PS 的解析式为 y=-x+4设直线PS 与直线AF 的交点K(x ，y)∴48y x y x =-+⎧⎨=+⎩解得26x y =-⎧⎨=⎩∴直线PS 与直线AF 的交点K(-2，6)．【点睛】本题考查的知识点是一次函数与几何图形，将一次函数的图象与几何图形综合在一起的问题，是考查学生综合素质和能力的热点题型，它充分体现了数学解题中的数形结合思想和整体转化思想．本题考查的知识点有一次函数图象与坐标轴的交点问题、等腰直角三角形的判定及性质、三角形内角和定理、全等三角形的判定及性质、矩形的性质、待定系数法求一次函数解析式、线段垂直平分线等．2．C解析：（1）112y x =-+；（2）1d t =-+；（3）6215t -= 【解析】【分析】（1）根据互相垂直两直线斜率积为-1，设出直线CE 的解析式，再将点C 坐标代入即可求解；（2）过点E 作EM ⊥y 轴于点M ，过点E 作EN x ⊥轴于点N ，通过解直角三角形可证EDM ≌EAN ，ENH ≌EMG ，得到AN =DM ，HN =GM ，进而得到AH DG =，再根据CE 解析式求出D 点坐标，即可找出d 与t 之间的函数关系式；（3）过点B 作BT CM ⊥于点T ，在直线BT 上截取TL NK =，证四边形BGMT 与四边形HNMC 均为矩形，得MN MT =，再进一步证明ENH ≌EMG ，利用全等三角形的性质通过角度计算，得出△BML 为等腰三角形且BM BL =，再用含有t 的代数式表示BM ，最后在Rt △BMG 中利用勾股定理建立等式，求出t 的值．【详解】解：（1）∵CE ⊥AB ，∴设直线CE 的解析式为：12y x c =-+， 把点C （2，0）代入上述解析式，得1c =，∴直线CD 的解析式为：112y x =-+； （2）过点E 作EM ⊥y 轴于点M ，过点E 作EN x ⊥轴于点N ，令26 112y xy x=+⎧⎪⎨=-+⎪⎩，解得22xy=-⎧⎨=⎩，∴()2,2E-，易证EDM≌EAN，ENH≌EMG，∴AN=DM ，HN=GM，∴AH DG=，由直线CE的解析式112y x=-+，可求点D（0，1）∴DG=1—t，∴1d t=-+；（3）过点B作BT CM⊥于点T，在直线BT上截取TL NK=，易证四边形BGMT与四边形HNMC均为矩形，由（2）问可知1tAH GD==-，则6tHC=-∴6tBG MT==-，∴MN MT=，∵90KNM LTM∠=∠=︒，∴ENH≌EMG，∴LNKM∠=∠，设KMNα∠=，则KMB KMNα∠=∠=，∴90NKM α∠=︒-，∴90NKM L α∠=∠=︒-，∵//BL MN ，∴2MBL BMN α∠=∠=，∴18090BML MBL L α∠=︒-∠-∠=︒-，∴BM BL =， ∵1tan 2KCH ∠=， ∴11322KH CH t ==-， ∴133322KN KH HN t t t TL =+=--=-=， ∴352BL BT TL t BM =+=-=， 在Rt BMG △中， 222BM BG GM =+，解得t =（不合题意舍去）或t =故，65t -=． 【点睛】本题一次函数综合题，考查了待定系数法求解析式，一次函数的性质，全等三角形的判定与性质，角平分线的性质，勾股定理等，利用已知条件求相等交，相等线段是解决本题的关键．3．E解析：（1）2y x 2x 3=-++；（2）E （2，3）或（1，4）；（3）P 点横坐标为118【解析】【分析】(1) 抛物线2(0)y ax bx c a =++≠的顶点为C （1，4），设抛物线的解析式为2(1)4y a x =-+，由抛物线过点B,（3，0），即可求出a 的值，即可求得解析式； （2）过点E 、F 分别作x 轴的垂线，交x 轴于点M 、N ，设点E 的坐标为()2,23x xx -++，求出A 、D 点的坐标，得到OM=x ，则AM=x+1，由AF=2EF 得到22(1)33x AN AM +==，从而推出点F 的坐标21210(,)3333x x --+，由23FN EM =，列出关于x 的方程求解即可；（3）先根据待定系数法求出直线DM 的解析式为y=-2x+3，过点P 作PT ∥y 轴交直线DM 于点T ，过点F 作直线GH ⊥y 轴交PT 于点G ，交直线CE 于点H.证明△FGP ≌△FHQ ，得到FG=FH ，PT=45GH.设点P （m ，-m²+2m+3），则T （m ，-2m+3），则PT=m²-4m ，GH=1-m ， 可得m²-4m=45（1-m ），解方程即可. 【详解】（1）∵抛物线的顶点为C （1，4），∴设抛物线的解析式为2(1)4y a x =-+，∵抛物线过点B,（3，0），∴20(31)4a =-+，解得a=-1，∴设抛物线的解析式为2(1)4y x =--+，即2y x 2x 3=-++；（2）如图，过点E 、F 分别作x 轴的垂线，交x 轴于点M 、N ，设点E 的坐标为()2,23x x x -++，∵抛物线的解析式为2y x 2x 3=-++，当y=0时，2023x x =-++，解得x=-1或x=3，∴A （-1.0），∴点D （0,3），∴过点BD 的直线解析式为3y x =-+，点F 在直线BD 上，则OM=x ，AM=x+1，∴22(1)33x AN AM +==， ∴2(1)2111333x x ON AN +=-=-=-， ∴21210(,)3333x x F --+，∴2210332233FN EM x x x +--++==， 解得x=1或x=2， ∴点E 的坐标为（2，3）或（1，4）；（3）设直线DM 的解析式为y=kx+b ，过点D （0,3），M （32，0）， 可得，3023k b b ⎧+=⎪⎨⎪=⎩，解得k=-2，b=3，∴直线DM 的解析式为y=-2x+3，∴32OM =，3OD =， ∴tan ∠DMO=2， 如图，过点P 作PT ∥y 轴交直线DM 于点T ，过点F 作直线GH ⊥y 轴交PT 于点G ，交直线CE 于点H.∵PQ ⊥MT ，∴∠TFG=∠TPF ，∴TG=2GF ，GF=2PG ，∴PT=25GF ， ∵PF=QF ，∴△FGP ≌△FHQ ，∴FG=FH ，∴PT=45GH. 设点P （m ，-m²+2m+3），则T （m ，-2m+3），∴PT=m²-4m ，GH=1-m ，∴m²-4m=45（1-m ）， 解得：1112018m -=，或2112018m +=（不合题意，舍去）， ∴点P 的横坐标为11201-. 【点睛】 本题考查二次函数综合题、平行线分线段成比例定理、轴对称性质等知识，解题的关键是学会用转化的思想思考问题，学会用数形结合的思想解决问题，有一定难度.4．D解析：（1）DF 的长为158；（2）MN 的长为5；（3）O 的半径长为258． 【解析】【分析】（1）作EH BM ⊥于H ，根据中位线定理得出四边形BMFA 是平行四边形，从而利用cos 45B =解直角三角形即可求算半径，再根据平行四边形的性质求FD 即可； （2）先证AMB CNM ∠=∠，再证MAD CNM ∠=∠，从而证明AFM NFD ∆~∆，得到AF MF AF DF NF MF NF DF=⇒=，再通过平行证明AFN DFM ∆~∆，从而得到AF NF AF MF NF DF DF MF=⇒=，通过两式相乘得出AF NF =再根据平行得出NF DF =， 从而得出答案．（3）通过图形得出MN 垂直平分'OO ,从而得出90BAM CMN ∠=∠=︒，再利用cos 45B =解三角函数即可得出答案． 【详解】（1）如图，作EH BM ⊥于H ：∵E 为AB 中点，45,cos 5AB AD DC B ====∴52AE BE ==∴cos 45BH B BE == ∴2BH = ∴2253222EH ⎛⎫=-= ⎪⎝⎭设半径为r ，在Rt OEH ∆中：()222322r r ⎛⎫=-+ ⎪⎝⎭ 解得：2516r =∵,E O 分别为,BA BM 中点 ∴BAM BEO OBE ∠=∠=∠又∵CMN BAM ∠=∠∴CMN OBE ∠=∠∴//MF AB∴四边形BMFA 是平行四边形∴2528AF BM r ===∴2515588FD AD AF =-=-= （2）如图：连接MD AN ，∵,B C BAM CMN ∠=∠∠=∠∴AMB CNM ∠=∠又∵AMB MAD ∠=∠∴MAD CNM ∠=∠又∵AFM NFD ∠=∠∴AFM NFD ∆~∆∴AF MF AF DF NF MF NF DF=⇒=① 又∵//MD AN ∴AFN DFM ∆~∆∴AF NF AF MF NF DF DF MF=⇒=② 由①⨯②得; 22AF NF AF NF =⇒=∴NF DF =∴5MN AD ==故MN 的长为5；（3）作如图：∵圆O 与圆'O 外切且均与圆N 内切设圆N 半径为R ，圆O 半径为r∴'=NO R r NO -=∴N 在'OO 的中垂线上 ∴MN 垂直平分'OO∴90NMC ∠=︒∵90BAM CMN ∠=∠=︒∴A 点在圆上∴54cos 5AB B BM BM === 解得：254BM = O 的半径长为258【点睛】 本题是一道圆的综合题目，难度较大，掌握相似之间的关系转化以及相关线段角度的关系转化是解题关键．5．A解析：（1）6y x =-+；（2）636S t =-，()6t >；（3）5599y x =+ 【解析】【分析】（1）求出点A 、B 的坐标，从而得出△ABO 是等腰直角三角形，再根据2ABC ACB ∠=∠可得△OCB 也是等腰直角三角形，从而可求得点C 的坐标，将点B 、C 代入可求得解析式；（2）存在2种情况，一种是点D 在线段BC 上，另一种是点D 在线段BC 的延长线上，分别利用三角形的面积公式可求得；（3）如下图，先证ACR CAD ∆≅∆，从而推导出//RD AC ，进而得到CF RG =，同理还可得NF DG =，RD CN =，然后利用:7:12NF FC =可得到N 、D 的坐标，代入即可求得．【详解】解：（1）直线6y x =+与x 轴交于点A ，与y 轴交于点B ，(6,0)A ∴-，(0,6)B ．6OA OB ∴==．45BAO ∴∠=︒，180BAO ABC BCO ∠+∠+∠=︒，2ABC ACB ∠=∠，45BCO ∴∠=︒6OC OB ∴==，()6,0C ∴．设直线BC 的解析式为y kx b =+，将B 、C 两点坐标代得606k b b +=⎧⎨=⎩ 解得16k b =-⎧⎨=⎩∴直线BC 的解析式为6y x =-+．（2）点D 是射线BC 上一点，点D 的横坐标为t ，(,6)D t t ∴-+，6(6)12AC =--=．如下图，过点D 作DK AC ⊥于点K ，当点D 在线段BC 上时，6DK t =-+，16362S AC DK t ∴=⋅=-+()06t ≤<； 如下图，当点D 在线段BC 的延长线上时，6DK t =-，636S t ∴=-()6t >．（3）如图，延长CE 交AB 于点R ，连接DR 交BF 于点G ，交y 轴于点P ．45BAO BCO ∠=∠=︒，BA BC ∴=．AO CO =，BO AC ⊥EA EC ∴=，EAC ECA ∴∠=∠．ACR CAD ∴∆≅∆．BAD BCR ∴∠=∠．AR CD ∴=．BR BD ∴=．//RD AC ∴．BH AD ⊥，HBD BAD BCR ∴∠=∠=∠．MB MC ∴=，∠MRB MRB MBR ∠=∠MR MB ∴=．CM MR ∴=．//RD AC ，::1:1CF RG CM RM ∴==．CF RG ∴=．同理NF DG =．RD CN =．∵:7:12NF FC =．:7:12DG RG ∴=．RP PD BP ==，5tan 19PG OF OBF BP OB∴==∠= 6OB ∴=，3019OF ∴=，6OC =，8419CF ∴=． 7RD GN ∴==．1ON ∴=，72PD =．52OP OB BP ∴=-=． (1,0)N ∴-，75,22D ⎛⎫ ⎪⎝⎭． 设直线 DN 的解析式为y ax c =+，将N 、D 两点代入，07522a c a c -+=⎧⎪⎨+=⎪⎩解得5959 ac⎧=⎪⎪⎨⎪=⎪⎩∴直线DM的解析式为5599y x=+．【点睛】本题考查了一次函数与图形的综合，需要用到全等、三角函数和平面直角坐标系的知识，解题关键是想办法确定函数图像上点的坐标．6．D解析：（1）6；（2）y=－3x+10(1≤x＜103)；（2）1769或32【解析】【分析】（1）如下图，利用等腰直角三角形DHC可得到HC的长度，从而得出HB的长，进而得出AD的长；（2）如下图，利用等腰直角三角形的性质，可得PQ、PR的长，然后利用EB=PQ+PR得去x、y的函数关系，最后根据图形特点得出取值范围；（3）存在2种情况，一种是点P在梯形内，一种是在梯形外，分别根y的值求出x的值，然后根据梯形面积求解即可．【详解】（1）如下图，过点D作BC的垂线，交BC于点H∵∠C=45°，DH⊥BC∴△DHC是等腰直角三角形∵四边形ABCD是梯形，∠B=90°∴四边形ABHD是矩形，∴DH=AB=8∴HC=8∴BH=BC－HC=6∴AD=6（2）如下图，过点P作EF的垂线，交EF于点Q，反向延长交BC于点R，DH与EF交于点G∵EF ∥AD,∴EF ∥BC∴∠EFP=∠C=45°∵EP ⊥PF∴△EPF 是等腰直角三角形同理,还可得△NPM 和△DGF 也是等腰直角三角形∵AE=x∴DG=x=GF,∴EF=AD+GF=6+x∵PQ ⊥EF,∴PQ=QE=QF∴PQ=()162x + 同理，PR=12y ∵AB=8，∴EB=8－x∵EB=QR∴8－x=()11622x y ++ 化简得：y=－3x+10 ∵y ＞0，∴x ＜103 当点N 与点B 重合时，x 可取得最小值则BC=NM+MC=NM+EF=－3x+10+614x +=，解得x=1∴1≤x ＜103（3）情况一：点P 在梯形ABCD 内，即（2）中的图形 ∵MN=2，即y=2，代入（2）中的关系式可得：x=83=AE ∴188176662339ABCD S ⎛⎫=⨯++⨯= ⎪⎝⎭梯形 情况二：点P 在梯形ABCD 外，图形如下：与（2）相同，可得y=3x －10则当y=2时，x=4，即AE=4 ∴()16644322ABCD S =⨯++⨯=梯形 【点睛】本题考查了等腰直角三角形、矩形的性质，难点在于第（2）问中确定x 的取值范围，需要一定的空间想象能力． 7．A解析：（1）详见解析；（2）2448x x y -+=（04x <<）；（3）当AEG ∆是等腰三角形时，2BF =或43【解析】【分析】 （1）根据正方形的性质得到∠AOD=90°，AO=OD ，∠EOH=90°，OE=OH ，由全等三角形的性质即可得到结论；（2）如图1，过O 作ON ⊥AB 于N ，根据等腰直角三角形的性质得到122AN BN ON AB ====， 根据勾股定理得到()222222248OF FN ON x x x =+=-+=-+线段成比例定理即可得到结论；（3）①当AE=EG 时，△AEG 是等腰三角形，②当AE=AG 时，△AEG 是等腰三角形，如图2，过A 作AP ⊥EG 于P ③当GE=AG 时，△AEG 是等腰三角形，如图3，过G 作GQ ⊥AE 于Q ，根据相似三角形的性质或全等三角形的性质健即可得到结论．【详解】（1）∵四边形ABCD 是正方形，,OA OD AC BD ∴=⊥，90AOD ∴∠=︒，∵四边形OEGH 是正方形，,90OE OH EOH ∴=∠=︒，AOD EOH ∴∠=∠，AOD AOH EOH AOH ∴∠-∠=∠-∠，即HOD EOA ∠=∠，HDO EAO ∴∆≅∆．（2）如图1，过O 作ON⊥AB 于N ，则122AN BN ON AB ====， ∵BF=x，∴AF=4-x ，∴FN=2-x ， ∴()222222248OF FN ON x x x =+=-+=-+∴248EF y x x =-+ ∵AM⊥AC，∴AE∥OB，∴BF OF AF EF＝， ∴2248448x x x x y x x -+=---+， ∴)24804x x y x x-+≤＝＜； （3）①当AE=EG 时，△AEG 是等腰三角形，则AE=OE ，∵∠EAO=90°，∴这种情况不存在；②当AE=AG 时，△AEG 是等腰三角形，如图2，过A 作AP⊥EG 于P ，则AP∥OE，∴∠PAE=∠AEO，∴△APE∽△EAO，∴PE AE OA OE=，∵AE=AG，∴2421482x xxPE y-+==，()22248xAE yx-=-=，∴()22222224448448xx xxx xx---+=+，解得：x=2，②当GE=AG时，△AEG是等腰三角形，如图3，过G作GQ⊥AE于Q，∴∠GQE=∠EAO=90°，∴∠GEQ+∠EGQ=∠GEQ+∠AEO=90°，∴∠EGQ=∠AEO，∵GE=OE，∴△EGQ≌△OEA（AAS），∴22EQ AO==∴224242()xAE E Q-===∴43x =， ∴BF=2或43． 【点睛】本题考查了四边形的综合题，正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质，等腰三角形的性质，勾股定理，正确的作出辅助线构造全等三角形是解题的关键．8．B解析：（1）12；（2）3）【解析】【分析】（1）如图1中，过点B 作BD CA ⊥，交CA 延长线于点D ，通过构造直角三角形，求出BD 利用三角形面积公式求解即可.（2）如图示，作点D 关于AB 的对称点Q ，交AB 于点H ，连接CQ ，交AB 于点P ，连接PD 、OD 、OC ，过点Q 作QM CO ⊥，交CO 延长线于点M ，确定点P 的位置，利用勾股定理与矩形的性质求出CQ 的长度即为答案.（3）解图3所示，在AB 上这一点作点P 关于OA 的对称点S ，作点P 关于OB 的对称点N ，连接SN ，交OA 于点E ，交OB 于点F ，连接OS ON OP EP FP 、、、、，通过轴对称性质的转化，最终确定最小值转化为SN 的长.【详解】（1）如解图1所示，过点B 作BD CA ⊥，交CA 延长线于点D ，135BAC ∠=，180********BAD BAC ∴∠=-∠=-=，BD CA ⊥，交CA 延长线于点D ，BAD ∴为等腰直角三角形，且90BDA ∠=，BD AD ∴=，在BAD 中，,90BD AD BDA =∠=，222BD AD AB ∴+=，即222BD AB =，4AB =222232BD AB ∴===，解得：4BD =，6AC =，11641222ABC S AC BD ∴=⋅=⨯⨯=．（2）如解图2所示，作点D 关于AB 的对称点Q ，交AB 于点H ，连接CQ ，交AB 于点P ，连接PD 、OD 、OC ，过点Q 作QM CO ⊥，交CO 延长线于点M ， D 关于AB 的对称点Q ，CQ 交AB 于点P ，PD PQ ∴=，PC PD PC PQ CQ ∴+=+=，点P 为AB 上的动点，PC PD CQ ∴+≥，∴当点P 处于解图2中的位置，PC PD +取最小值，且最小值为CQ 的长度， 点C 为半圆AB 的中点，90COB ∴∠=，90BOD COD COB ∠+∠=∠=，11903033BOD COB ∴∠=∠=⨯=， 10AB =，1110522OD AB ∴==⨯=， 在Rt ODH △中，由作图知，90OHD ∠=，且30HOD BOD ∠=∠=， 155,222DH OD QH DH ∴==∴==， 222255352OH OD DH ⎛⎫∴=-=-= ⎪⎝⎭， 由作图知，四边形OMQH 为矩形，553,2OM QH MQ OH ∴==== 515522CM OM OC ∴=+=+=， 222215535322CQ CM MQ ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭，PC PD ∴+的最小值为53．（3）如解图3所示，在AB 上这一点作点P 关于OA 的对称点S ，作点P 关于OB 的对称点N ，连接SN ，交OA 于点E ，交OB 于点F ，连接OS ON OP EP FP 、、、、， 点P 关于OA 的对称点S ，点P 关于OB 的对称点N ，连接SN ，交OA 于点E ，交OB 于点F ，PE SE ∴=，FP FN =，SOA POA ∠=∠，,NOB POB OS OP ON ∠=∠==，．PE EF FP SE EF FN SN ∴++=++=，SOA NOB POA POB ∠+∠=∠+∠，E 为OA 上的点，F 为OB 上的点PE EF FP SN ∴++≥，∴当点E F 、处于解图3的位置时，PE EF FP ++的长度取最小值，最小值为SN 的长度，45POA POB AOB ∠+∠=∠=，45SOA NOB ∴∠+∠=，454590SON SOA AOB NOB ∴∠=∠+∠+∠=+=．扇形AOB 的半径为20，20OS ON OP ∴===，在Rt SON 中，90SON ∠=，20,90OS ON SON ==∠=PE EF FP ∴++的长度的最小值为202【点睛】本题主要考察了轴对称、勾股定理、圆、四边形等相关内容，理解题意，作出辅助线是做题的关键.9．A解析：（1）145；（2）2274,0314971421,2235t tSt t t⎧⎛⎫<≤⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+-<<⎪⎪⎝⎭⎩；（3）t的值为477或727．【解析】【分析】（1）如下图，根据4tan3A=，可得出PN与AP的关系，从而求出t的值；（2）如下图，存在2种情况，一种是点M在△ABC内，另一种是点M在△ABC外部，分别根据正方形和三角形求面积的公式可求解；（3）如下图，存在2种情况，一种是PM所在的直线将△ABC的面积平分，另一种是QN 所在的直线将△ABC的面积平分．【详解】（1）如图1，点N在AC上图1由题意可知：PD=DQ=t ，AP=7－t∴PN=PQ=2t ∵4tan 3A = ∴43NP AP =，即2473t t =- 解得：t=145 （2）①如图2，图2四边形PQMN 是正方形，90BQM ∴∠=︒，45B ∠=︒，BQ MQ ∴=，即72t t -=解得73t =， 故当0t <≤73时，22(2)4S t t ==； ②如图3， 图390BQF ∠=︒，45B ∠=︒，7BQ FQ t ∴==-，45BFQ MFE ∠=∠=︒，则37MF MQ QF t =-=-，90M ∠=︒，37ME MF t ∴==-， 则2221149(2)(37)21222S t t t t =--=-+-71435t ⎛⎫<< ⎪⎝⎭； 综上，2274,0314971421,2235t t S t t t ⎧⎛⎫<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+-<< ⎪⎪⎝⎭⎩． （3）如下图，过点C 作AB 的垂线，交AB 于点G图4∵4tan 3A = ∴设CG=4x ，则AG=3x∵∠B=45°∴△CBG 是等腰直角三角形∴GB=GC=4x∵AB=14∴3x+4x=14，解得：x=2∴1148562ABC S== ∴1282ABCS = 情况一：PM 所在的直线平分△ABC 的面积，如下图，PM 与BC 交于点E图5则28PBES=∵四边形PQMN是正方形，∴∠EPB=45°∵∠B=45°∴△PBE是等腰直角三角形∵1282PBES PE PB==∴PE=PB=214∴PB=47∵PB=AB－PA=14－(7－t)=7+t∴7+t=47t=477-情况二：如下图，QN所在线段平分△ABC的面积，QF交AC于点F，过点F作AB的垂线，交AB于点H图6同理，28AFQS=∵四边形PQMN是正方形，∴∠EQH=45°∴△FHQ是等腰直角三角形∵4 tan3A=∴设FH=4y，则AH=3y，HQ=FH=4y，∴AQ=7y∴174282AFQS y y==，解得：2∵AQ=AB－QB=14－(7－t)=7+t∴2解得：27∴综上得：t的值为477或727．【点睛】本题考查动点问题，解题关键是根据动点的变化情况，适当划分为几种不同的形式分别分析求解．10．A。

中考数学综合压轴题100题（附答案）一、中考压轴题1．在△ABC中，AB＝BC，将△ABC绕点A沿顺时针方向旋转得△A1B1C1，使点C1落在直线BC上（点C1与点C不重合），（1）如图，当∠C＞60°时，写出边AB1与边CB的位置关系，并加以证明；（2）当∠C＝60°时，写出边AB1与边CB的位置关系（不要求证明）；（3）当∠C＜60°时，请你在如图中用尺规作图法作出△AB1C1（保留作图痕迹，不写作法），再猜想你在（1）、（2）中得出的结论是否还成立并说明理由．【分析】（1）AB1∥BC．因为等腰三角形，两底角相等，再根据平行线的判定，内错角相等两直线平行，可证明两直线平行．（2）当∠C＝60°时，写出边AB1与边CB的位置关系也是平行，证明方法同（1）题．（3）成立，根据旋转变换的性质画出图形．利用三角形全等即可证明．【解答】解：（1）AB1∥BC．证明：由已知得△ABC≌△AB1C1，∴∠BAC＝∠B1AC1，∠B1AB＝∠C1AC，∵AC1＝AC，∴∠AC1C＝∠ACC1，∵∠C1AC+∠AC1C+∠ACC1＝180°，∴∠C1AC＝180°﹣2∠ACC1，同理，在△ABC中，∵BA＝BC，∴∠ABC＝180°﹣2∠ACC1，∴∠ABC＝∠C1AC＝∠B1AB，∴AB1∥BC．（5分）（2）如图1，∠C＝60°时，AB1∥BC．（7分）（3）如图，当∠C＜60°时，（1）、（2）中的结论还成立．证明：显然△ABC≌△AB1C1，∴∠BAC＝∠B1AC1，∴∠B1AB＝∠C1AC，∵AC1＝AC，∴∠AC1C＝∠ACC1，∵∠C1AC+∠AC1C+∠ACC1＝180°，∴∠C1AC＝180°﹣2∠ACC1，同理，在△ABC中，∵BA＝BC，∴∠ABC＝180°﹣2∠ACC1，∴∠ABC＝∠C1AC＝∠B1AB，∴AB1∥BC．（13分）【点评】考查图形的旋转，等腰三角形的性质，平行线的判定．本题实质是考查对图形旋转特征的理解，旋转前后的图形是全等的．2．已知：y关于x的函数y＝（k﹣1）x2﹣2kx+k+2的图象与x轴有交点．（1）求k的取值范围；（2）若x1，x2是函数图象与x轴两个交点的横坐标，且满足（k﹣1）x12+2kx2+k+2＝4x1x2．①求k的值；②当k≤x≤k+2时，请结合函数图象确定y的最大值和最小值．【分析】（1）分两种情况讨论，当k＝1时，可求出函数为一次函数，必与x轴有一交点；当k≠1时，函数为二次函数，若与x轴有交点，则△≥0．（2）①根据（k﹣1）x12+2kx2+k+2＝4x1x2及根与系数的关系，建立关于k的方程，求出k 的值；②充分利用图象，直接得出y的最大值和最小值．【解答】解：（1）当k＝1时，函数为一次函数y＝﹣2x+3，其图象与x轴有一个交点．当k≠1时，函数为二次函数，其图象与x轴有一个或两个交点，令y＝0得（k﹣1）x2﹣2kx+k+2＝0．△＝（﹣2k）2﹣4（k﹣1）（k+2）≥0，解得k≤2．即k≤2且k≠1．综上所述，k的取值范围是k≤2．（2）①∵x1≠x2，由（1）知k＜2且k≠1，函数图象与x轴两个交点，∴k＜2，且k≠1．由题意得（k﹣1）x12+（k+2）＝2kx1①，将①代入（k﹣1）x12+2kx2+k+2＝4x1x2中得：2k（x1+x2）＝4x1x2．又∵x1+x2＝，x1x2＝，∴2k•＝4•．解得：k1＝﹣1，k2＝2（不合题意，舍去）．∴所求k值为﹣1．②如图，∵k1＝﹣1，y＝﹣2x2+2x+1＝﹣2（x﹣）2+．且﹣1≤x≤1．由图象知：当x＝﹣1时，y最小＝﹣3；当x＝时，y最大＝．∴y的最大值为，最小值为﹣3．【点评】本题考查了抛物线与x轴的交点、一次函数的定义、二次函数的最值，充分利用图象是解题的关键．3．广安市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售．（1）求平均每次下调的百分率．（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？【分析】（1）根据题意设平均每次下调的百分率为x，列出一元二次方程，解方程即可得出答案；（2）分别计算两种方案的优惠价格，比较后发现方案①更优惠．【解答】解：（1）设平均每次下调的百分率为x，则6000（1﹣x）2＝4860，解得：x1＝0.1＝10%，x2＝1.9（舍去），故平均每次下调的百分率为10%；（2）方案①购房优惠：4860×100×（1﹣0.98）＝9720（元）；方案②可优惠：80×100＝8000（元）．故选择方案①更优惠．【点评】本题主要考查一元二次方程的实际应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解，属于中档题．4．我们学习了利用函数图象求方程的近似解，例如：把方程2x﹣1＝3﹣x的解看成函数y ＝2x﹣1的图象与函数y＝3﹣x的图象交点的横坐标．如图，已画出反比例函数y＝在第一象限内的图象，请你按照上述方法，利用此图象求方程x2﹣x﹣1＝0的正数解．（要求画出相应函数的图象；求出的解精确到0.1）【分析】根据题意可知，方程x2﹣x﹣1＝0的解可看做是函数y＝和y＝x﹣1的交点坐标，所以根据图象可知方程x2﹣x﹣1＝0的正数解约为1.1．【解答】解：∵x≠0，∴将x2﹣x﹣1＝0两边同时除以x，得x﹣1﹣＝0，即＝x﹣1，把x2﹣x﹣1＝0的正根视为由函数y＝与函数y＝x﹣1的图象在第一象限交点的横坐标．如图：∴正数解约为1.1．【点评】主要考查了反比例函数和一元二次方程之间的关系．一元二次方程的解都可化为一个反比例函数和一次函数的交点问题求解．5．如图，在矩形ABCD中，AB＝8，AD＝6，点P、Q分别是AB边和CD边上的动点，点P从点A向点B运动，点Q从点C向点D运动，且保持AP＝CQ．设AP＝x．（1）当PQ∥AD时，求x的值；（2）当线段PQ的垂直平分线与BC边相交时，求x的取值范围；（3）当线段PQ的垂直平分线与BC相交时，设交点为E，连接EP、EQ，设△EPQ的面积为S，求S关于x的函数关系式，并写出S的取值范围．【分析】（1）根据已知条件，证明四边形APQD是矩形，再根据矩形的性质和AP＝CQ 求x即可；（2）连接EP、EQ，则EP＝EQ，设BE＝y，列出等式（8﹣x）2+y2＝（6﹣y）2+x2然后根据函数的性质来求x的取值范围；（3）由图形的等量关系列出方程，再根据函数的性质来求最值．【解答】解：（1）当PQ∥AD时，则∠A＝∠APQ＝90°，∠D＝∠DQP＝90°，又∵AB∥CD，∴四边形APQD是矩形，∴AP＝QD，∵AP＝CQ，AP＝CD＝，∴x＝4．（2）如图，连接EP、EQ，则EP＝EQ，设BE＝y．∴（8﹣x）2+y2＝（6﹣y）2+x2，∴y＝．∵0≤y≤6，∴0≤≤6，∴≤x≤．（3）S△BPE＝•BE•BP＝••（8﹣x）＝，S△ECQ＝＝•（6﹣）•x＝，∵AP＝CQ，∴S BPQC＝，∴S＝S BPQC﹣S△BPE﹣S△ECQ＝24﹣﹣，整理得：S＝＝（x﹣4）2+12（），∴当x＝4时，S有最小值12，当x＝或x＝时，S有最大值．∴12≤S≤．【点评】解答本题时，涉及到了矩形的判定、矩形的性质、勾股定理以及二次函数的最值等知识点，这是一道综合性比较强的题目，所以在解答题目时，一定要把各个知识点融会贯通，这样解题时才会少走弯路．6．九年级（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度CD＝3m，标杆与旗杆的水平距离BD＝15m，人的眼睛与地面的高度EF＝1.6m，人与标杆CD的水平距离DF＝2m，求旗杆AB的高度．【分析】利用三角形相似中的比例关系，首先由题目和图形可看出，求AB的长度分成了2个部分，AH和HB部分，其中HB＝EF＝1.6m，剩下的问题就是求AH的长度，利用△CGE∽△AHE，得出，把相关条件代入即可求得AH＝11.9，所以AB＝AH+HB＝AH+EF＝13.5m．【解答】解：∵CD⊥FB，AB⊥FB，∴CD∥AB∴△CGE∽△AHE∴即：∴∴AH＝11.9∴AB＝AH+HB＝AH+EF＝11.9+1.6＝13.5（m）．【点评】主要用到的解题思想是把梯形问题转化成三角形问题，利用三角形相似比列方程来求未知线段的长度．7．如图，已知△BEC是等边三角形，∠AEB＝∠DEC＝90°，AE＝DE，AC，BD的交点为O．（1）求证：△AEC≌△DEB；（2）若∠ABC＝∠DCB＝90°，AB＝2 cm，求图中阴影部分的面积．【分析】（1）在△AEC和△DEB中，已知AE＝DE，BE＝CE，且夹角相等，根据边角边可证全等．（2）由图可知，在连接EO并延长EO交BC于点F，连接AD之后，整个图形是一个以EF所在直线对称的图形．即△AEO和△DEO面积相等，只要求出其中一个即可，而三角形AEO面积＝•OE•FB，所以解题中心即为求出OE和FB，有（1）中结论和已知条件即可求解．【解答】（1）证明：∵∠AEB＝∠DEC＝90°，∴∠AEB+∠BEC＝∠DEC+∠BEC，即∠AEC＝∠DEB，∵△BEC是等边三角形，∴CE＝BE，又AE＝DE，∴△AEC≌△DEB．（2）解：连接EO并延长EO交BC于点F，连接AD．由（1）知AC＝BD．∵∠ABC＝∠DCB＝90°，∴∠ABC+∠DCB＝180°，∴AB∥DC，AB＝＝CD，∴四边形ABCD为平行四边形且是矩形，∴OA＝OB＝OC＝OD，又∵BE＝CE，∴OE所在直线垂直平分线段BC，∴BF＝FC，∠EFB＝90°．∴OF＝AB＝×2＝1，∵△BEC是等边三角形，∴∠EBC＝60°．在Rt△AEB中，∠AEB＝90°，∠ABE＝∠ABC﹣∠EBC＝90°﹣60°＝30°，∴BE＝AB•cos30°＝，在Rt△BFE中，∠BFE＝90°，∠EBF＝60°，∴BF＝BE•cos60°＝，EF＝BE•sin60°＝，∴OE＝EF﹣OF＝＝，∵AE＝ED，OE＝OE，AO＝DO，∴△AOE≌△DOE．∴S△AOE＝S△DOE∴S阴影＝2S△AOE＝2וEO•BF＝2×××＝（cm2）．【点评】考查综合应用等边三角形、等腰三角形、解直角三角形、直角三角形性质，进行逻辑推理能力和运算能力．8．如图，⊙O是等边△ABC的外接圆，AB＝2，M、N分别是边AB、AC的中点，直线MN交⊙O于E、F两点，BD∥AC交直线MN于点D．求出图中线段DM上已有的一条线段的长．【分析】连接OA交MN于点G，则OA⊥BC，由三角形的中位线的性质可得MN的长，易证得△BMD≌△AMN，有DM＝MN，由相交弦定理得ME•MF＝MA•MB，就可求得EM，DE的值．【解答】解：∵M，N分别是边AB，AC的中点∴MN∥BC，MN＝BC＝1又∵BD∥AC∴∠DBA＝∠A＝60°∵BM＝AM，∠BMD＝∠AMN∴△BMD≌△AMN∴DM＝MN＝1连接OA交MN于点G，则OA⊥BC∴OA⊥EF∴EG＝FG，MG＝FN由相交弦定理得：ME•MF＝MA•MB∴EM（EM+1）＝1解得EM＝（EM＝不合题意，舍去）∴DE＝DM﹣EM＝∴DE（3﹣DE）＝1解得DE＝（DE＝不合题意，舍去）．【点评】本题利用了三角形的中位线的性质，等边三角形的性质，全等三角形的判定和性质，一元二次方程的解法求解．9．如图，有一直径MN＝4的半圆形纸片，其圆心为点P，从初始位置Ⅰ开始，在无滑动的情况下沿数轴向右翻滚至位置Ⅴ，其中，位置Ⅰ中的MN平行于数轴，且半⊙P与数轴相切于原点O；位置Ⅱ和位置Ⅳ中的MN垂直于数轴；位置Ⅲ中的MN在数轴上；位置Ⅴ中的点N到数轴的距离为3，且半⊙P与数轴相切于点A．解答下列问题：（1）位置Ⅰ中的MN与数轴之间的距离为2；位置Ⅱ中的半⊙P与数轴的位置关系是相切；（2）求位置Ⅲ中的圆心P在数轴上表示的数；（3）纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时，求点N所经过路径长及该纸片所扫过图形的面积；（4）求OA的长．[（2），（3），（4）中的结果保留π]．【分析】（1）先求出圆的半径，再根据切线的性质进行解答；（2）根据位置Ⅰ中的长与数轴上线段ON相等求出的长，再根据弧长公式求出的长，进而可得出结论；（3）作NC垂直数轴于点C，作PH⊥NC于点H，连接P A，则四边形PHCA为矩形，在Rt△NPH中，根据sin∠NPH＝＝即可∠NPH、∠MP A的度数，进而可得出的长，【解答】解：（1）∵⊙P的直径＝4，∴⊙P的半径＝2，∵⊙P与直线有一个交点，∴位置Ⅰ中的MN与数轴之间的距离为2；位置Ⅱ中的半⊙P与数轴的位置关系是相切；故答案为：2，相切；（2）位置Ⅰ中的长与数轴上线段ON相等，∵的长为＝π，NP＝2，∴位置Ⅲ中的圆心P在数轴上表示的数为π+2．（3）点N所经过路径长为＝2π，S半圆＝＝2π，S扇形＝＝4π，半⊙P所扫过图形的面积为2π+4π＝6π．（4）如图，作NC垂直数轴于点C，作PH⊥NC于点H，连接P A，则四边形PHCA为矩形．在Rt△NPH中，PN＝2，NH＝NC﹣HC＝NC﹣P A＝1，于是sin∠NPH＝＝，∴∠NPH＝30°．∴∠MP A＝60°．从而的长为＝，于是OA的长为π+4+π＝π+4．【点评】本题考查的是直线与圆的关系、弧长的计算、扇形的面积公式，在解答此题时要注意Ⅰ中的长与数轴上线段ON相等的数量关系．10．已知⊙O1与⊙O2相交于A、B两点，点O1在⊙O2上，C为⊙O2上一点（不与A，B，O1重合），直线CB与⊙O1交于另一点D．（1）如图（1），若AD是⊙O1的直径，AC是⊙O2的直径，求证：AC＝CD；（2）如图（2），若C是⊙O1外一点，求证：O1C丄AD；（3）如图（3），若C是⊙O1内的一点，判断（2）中的结论是否成立？【分析】（1）连接C01，利用直径所对圆周角等于90度，以及垂直平分线的性质得出即可；（2）根据已知得出四边形AEDB内接于⊙O1，得出∠ABC＝∠E，再利用＝，得出∠E＝∠AO1C，进而得出CO1∥ED即可求出；（3）根据已知得出∠B＝∠EO1C，又∠E＝∠B，即可得出∠EO1C＝∠E，得出CO1∥ED，即可求出．【解答】（1）证明：连接C01∵AC为⊙O2直径∴∠AO1C＝90°即CO1⊥AD，∵AO1＝DO1∴DC＝AC（垂直平分线的性质）；（2）证明：连接AO1，连接AB，延长AO1交⊙O1于点E，连接ED，∵四边形AEDB内接于⊙O1，∴∠E+∠ABD＝180°，∵∠ABC+∠ABD＝180°，∴∠ABC＝∠E，又∵＝，∴∠ABC＝∠AO1C，∴∠E＝∠AO1C，∴CO1∥ED，又AE为⊙O1的直径，∴ED⊥AD，∴O1C⊥AD，（3）（2）中的结论仍然成立．证明：连接AO1，连接AB，延长AO1交⊙O1于点E，连接ED，∵∠B+∠AO1C＝180°，∠EO1C+∠AO1C═180°，∴∠B＝∠EO1C，又∵∠E＝∠B，∴∠EO1C＝∠E，∴CO1∥ED，又ED⊥AD，∴CO1⊥AD．【点评】此题主要考查了圆周角定理以及相交两圆的性质和圆内接四边形的性质，根据圆内接四边形的性质得出对应角之间的关系是解决问题的关键．11．如图①，有四张编号为1、2、3、4的卡片，卡片的背面完全相同．现将它们搅匀并正面朝下放置在桌面上．（1）从中随机抽取一张，抽到的卡片是眼睛的概率是多少？（2）从四张卡片中随机抽取一张贴在如图②所示的大头娃娃的左眼处，然后再随机抽取一张贴在大头娃娃的右眼处，用树状图或列表法求贴法正确的概率．【分析】根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．【解答】解：（1）所求概率为；（2）方法①（树状图法）共有12种可能的结果：（1，2），（1，3），（1，4），（2，1），（2，3），（2，4），（3，1），（3，2），（3，4），（4，1），（4，2），（4，3）∵其中有两种结果（1，2），（2，1）是符合条件的，∴贴法正确的概率为，方法②（列表法）1 2 3 4第一次抽取第二次抽取1（2，1）（3，1）（4，1）2（1，2）（3，2）（4，2）3（1，3）（2，3）（4，3）4（1，4）（2，4）（3，4）共有12种可能的结果：（1，2），（1，3），（1，4），（2，1），（2，3），（2，4），（3，1），（3，2），（3，4），（4，1），（4，2），（4，3），∵其中有两种结果（1，2），（2，1）是符合条件的，∴贴法正确的概率为．【点评】此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）＝．12．如图，菱形、矩形与正方形的形状有差异，我们将菱形、矩形与正方形的接近程度称为“接近度”．在研究“接近度”时，应保证相似图形的“接近度”相等．（1）设菱形相邻两个内角的度数分别为m°和n°，将菱形的“接近度”定义为|m﹣n|，于是|m﹣n|越小，菱形越接近于正方形．①若菱形的一个内角为70°，则该菱形的“接近度”等于40；②当菱形的“接近度”等于0时，菱形是正方形．（2）设矩形相邻两条边长分别是a和b（a≤b），将矩形的“接近度”定义为|a﹣b|，于是|a﹣b|越小，矩形越接近于正方形．你认为这种说法是否合理？若不合理，给出矩形的“接近度”一个合理定义．【分析】（1）根据相似图形的定义知，相似图形的形状相同，但大小不一定相同，相似图形的“接近度”相等．所以若菱形的一个内角为70°，则该菱形的“接近度”等于|m﹣n|；当菱形的“接近度”等于0时，菱形是正方形；（2）不合理，举例进行说明．【解答】解：（1）①∵内角为70°，∴与它相邻内角的度数为110°．∴菱形的“接近度”＝|m﹣n|＝|110﹣70|＝40．②当菱形的“接近度”等于0时，菱形是正方形．（2）不合理．例如，对两个相似而不全等的矩形来说，它们接近正方形的程度是相同的，但|a﹣b|却不相等．合理定义方法不唯一．如定义为，越接近1，矩形越接近于正方形；越大，矩形与正方形的形状差异越大；当时，矩形就变成了正方形，即只有矩形的越接近1，矩形才越接近正方形．【点评】正确理解“接近度”的意思，矩形的“接近度”|a﹣b|越小，矩形越接近于正方形．这是解决问题的关键．13．如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（1，0）①画出△ABC关于x轴对称的△A1B1C1；②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2；③△A1B1C1与△A2B2C2成轴对称图形吗？若成轴对称图形，画出所有的对称轴；④△A1B1C1与△A2B2C2成中心对称图形吗？若成中心对称图形，写出所有的对称中心的坐标．【分析】（1）将三角形的各顶点，向x轴作垂线并延长相同长度得到三点的对应点，顺次连接；（2）将三角形的各顶点，绕原点O按逆时针旋转90°得到三点的对应点．顺次连接各对应点得△A2B2C2；（3）从图中可发现成轴对称图形，根据轴对称图形的性质画出对称轴即连接两对应点的线段，做它的垂直平分线；（4）成中心对称图形，画出两条对应点的连线，交点就是对称中心．【解答】解：如下图所示：（3）成轴对称图形，根据轴对称图形的性质画出对称轴即连接两对应点的线段，作它的垂直平分线，或连接A1C1，A2C2的中点的连线为对称轴．（4）成中心对称，对称中心为线段BB2的中点P，坐标是（，）．【点评】本题综合考查了图形的变换，在图形的变换中，关键是找到图形的对应点．14．图（1）是一个10×10格点正方形组成的网格．△ABC是格点三角形（顶点在网格交点处），请你完成下面的两个问题：（1）在图（1）中画出与△ABC相似的格点△A1B1C1和△A2B2C2，且△A1B1C1与△ABC的相似比是2，△A2B2C2与△ABC的相似比是；（2）在图（2）中用与△ABC，△A1B1C1，△A2B2C2全等的格点三角形（每个三角形至少使用一次），拼出一个你熟悉的图案，并为你设计的图案配一句贴切的解说词．【分析】（1）△A1B1C1与△ABC的相似比是2，则让△ABC的各边都扩大2倍就可．△A2B2C2与△ABC的相似比是；△ABC的直角边是2，所以△A2B2C2与的直角边是即一个对角线的长度．斜边为2．依此画图即可；（2）拼图有审美意义即可，答案不唯一．【解答】解：【点评】本题主要考查了相似图形的画法，做这类题时根据的是相似图形的性质，即相似比相等．对应角相等．15．如图所示，AB＝AC，AB为⊙O的直径，AC、BC分别交⊙O于E、D，连接ED、BE．（1）试判断DE与BD是否相等，并说明理由；（2）如果BC＝6，AB＝5，求BE的长．【分析】（1）可通过连接AD，AD就是等腰三角形ABC底边上的高，根据等腰三角形三线合一的特点，可得出∠CAD＝∠BAD，根据圆周角定理即可得出∠DEB＝∠DBE，便可证得DE＝DB．（2）本题中由于BE⊥AC，那么BE就是三角形ABC中AC边上的高，可用面积的不同表示方法得出AC•BE＝CB•AD．进而求出BE的长．【解答】解：（1）DE＝BD证明：连接AD，则AD⊥BC，在等腰三角形ABC中，AD⊥BC，∴∠CAD＝∠BAD（等腰三角形三线合一），∴＝，∴DE＝BD；（2）∵AB＝5，BD＝BC＝3，∴AD＝4，∵AB＝AC＝5，∴S△ABC＝•AC•BE＝•CB•AD，∴BE＝4.8．【点评】本题主要考查了等腰三角形的性质，圆周角定理等知识点的运用，用等腰三角形三线合一的特点得出圆周角相等是解题的关键．16．如图，在Rt△ABC中，∠C＝90°，Rt△BAP中，∠BAP＝90°，已知∠CBO＝∠ABP，BP交AC于点O，E为AC上一点，且AE＝OC．（1）求证：AP＝AO；（2）求证：PE⊥AO；（3）当AE＝AC，AB＝10时，求线段BO的长度．【分析】（1）根据等角的余角相等证明即可；（2）过点O作OD⊥AB于D，根据角平分线上的点到角的两边的距离相等可得CO＝DO，利用“SAS”证明△APE和△OAD全等，根据全等三角形对应角相等可得∠AEP＝∠ADO＝90°，从而得证；（3）设C0＝3k，AC＝8k，表示出AE＝CO＝3k，AO＝AP＝5k，然后利用勾股定理列式求出PE＝4k，BC＝BD＝10﹣4k，再根据相似三角形对应边成比例列式求出k＝1然后在Rt △BDO中，利用勾股定理列式求解即可．【解答】（1）证明：∵∠C＝90°，∠BAP＝90°∴∠CBO+∠BOC＝90°，∠ABP+∠APB＝90°，又∵∠CBO＝∠ABP，∴∠BOC＝∠APB，∵∠BOC＝∠AOP，∴∠AOP＝∠APB，∴AP＝AO；（2）证明：如图，过点O作OD⊥AB于D，∵∠CBO＝∠ABP，∴CO＝DO，∵AE＝OC，∴AE＝OD，∵∠AOD+∠OAD＝90°，∠P AE+∠OAD＝90°，∴∠AOD＝∠P AE，在△AOD和△P AE中，，∴△AOD≌△P AE（SAS），∴∠AEP＝∠ADO＝90°∴PE⊥AO；（3）解：设AE＝OC＝3k，∵AE＝AC，∴AC＝8k，∴OE＝AC﹣AE﹣OC＝2k，∴OA＝OE+AE＝5k．由（1）可知，AP＝AO＝5k．如图，过点O作OD⊥AB于点D，∵∠CBO＝∠ABP，∴OD＝OC＝3k．在Rt△AOD中，AD＝＝＝4k．∴BD＝AB﹣AD＝10﹣4k．∵OD∥AP，∴，即解得k＝1，∵AB＝10，PE＝AD，∴PE＝AD＝4K，BD＝AB﹣AD＝10﹣4k＝6，OD＝3在Rt△BDO中，由勾股定理得：BO＝＝＝3．【点评】本题考查了全等三角形的判定与性质，角平分线上的点到角的两边的距离相等的性质，勾股定理，相似三角形的判定与性质，（2）作辅助线构造出过渡线段DO并得到全等三角形是解题的关键，（3）利用相似三角形对应边成比例求出k＝1是解题的关键．17．如图，AD是⊙O的直径．（1）如图①，垂直于AD的两条弦B1C1，B2C2把圆周4等分，则∠B1的度数是22.5°，∠B2的度数是67.5°；（2）如图②，垂直于AD的三条弦B1C1，B2C2，B3C3把圆周6等分，分别求∠B1，∠B2，∠B3的度数；（3）如图③，垂直于AD的n条弦B1C1，B2C2，B3C3，…，B n∁n把圆周2n等分，请你用含n的代数式表示∠B n的度数（只需直接写出答案）．【分析】根据条件可以先求出圆的各段弧的度数，根据圆周角等于所对弧的度数的一半，就可以求出圆周角的度数．【解答】解：（1）垂直于AD的两条弦B1C1，B2C2把圆周4等分，则是圆的，因而度数是45°，因而∠B1的度数是22.5°，同理的度数是135度，因而，∠B2的度数是67.5°；（2）∵圆周被6等分∴＝＝＝360°÷6＝60°∵直径AD⊥B1C1∴＝＝30°，∴∠B1＝＝15°∠B2＝＝×（30°+60°）＝45°∠B3＝＝×（30°+60°+60°）＝75°；（3）B n∁n把圆周2n等分，则弧BnD的度数是：，则∠B n AD＝，在直角△AB n D中，．【点评】本题是把求圆周角的度数的问题转化为求弧的度数的问题，依据是圆周角等于所对弧的度数的一半．18．下框中是小明对一道题目的解答以及老师的批改．题目：某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1，在温室内，沿前侧内墙保留3m的空地，其他三侧内墙各保留1m的通道，当温室的长与宽各为多少时，矩形蔬菜种植区域的面积是288m2？解：设矩形蔬菜种植区域的宽为xm，则长为2xm，根据题意，得x•2x＝288．解这个方程，得x1＝﹣12（不合题意，舍去），x2＝12所以温室的长为2×12+3+1＝28（m），宽为12+1+1＝14（m）答：当温室的长为28m，宽为14m时，矩形蔬菜种植区域的面积是288m2．我的结果也正确！小明发现他解答的结果是正确的，但是老师却在他的解答中画了一条横线，并打了一个？．结果为何正确呢？（1）请指出小明解答中存在的问题，并补充缺少的过程：变化一下会怎样…（2）如图，矩形A′B′C′D′在矩形ABCD的内部，AB∥A′B′，AD∥A′D′，且AD：AB＝2：1，设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d，要使矩形A′B′C′D′∽矩形ABCD，a、b、c、d应满足什么条件？请说明理由．【分析】（1）根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2：1的理由，所以应设矩形蔬菜种植区域的宽为xm，则长为2xm，然后由题意得，矩形蔬菜种植区域的长与宽之比为2：1，再利用小明的解法求解即可；（2）由使矩形A′B′C′D′∽矩形ABCD，利用相似多边形的性质，可得，即，然后利用比例的性质，即可求得答案．【解答】解：（1）小明没有说明矩形蔬菜种植区域的长与宽之比为2：1的理由．在“设矩形蔬菜种植区域的宽为xm，则长为2xm．”前补充以下过程：设温室的宽为xm，则长为2xm．则矩形蔬菜种植区域的宽为（x﹣1﹣1）m，长为（2x﹣3﹣1）m．∵，∴矩形蔬菜种植区域的长与宽之比为2：1；（2）要使矩形A′B′C′D′∽矩形ABCD，就要，即，即，即2AB﹣2（b+d）＝2AB﹣（a+c），∴a+c＝2（b+d），即．【点评】此题考查了相似多边形的性质．此题属于阅读性题目，注意理解题意，读懂题目是解此题的关键．19．二次函数y＝ax2+bx+c图象的一部分如图所示，则a的取值范围是﹣1＜a＜0．【分析】由抛物线的开口方向判断a的符号，由抛物线与y轴的交点得出c的值，然后根据图象经过的点的情况进行推理，进而推出所得结论．【解答】解：抛物线开口向下，a＜0，图象过点（0，1），c＝1，图象过点（1，0），a+b+c＝0，∴b＝﹣（a+c）＝﹣（a+1）．由题意知，当x＝﹣1时，应有y＞0，∴a﹣b+c＞0，∴a+（a+1）+1＞0，∴a＞﹣1，∴实数a的取值范围是﹣1＜a＜0．【点评】根据开口判断a的符号，根据与x轴，y轴的交点判断c的值以及b用a表示出的代数式．难点是推断出当x＝﹣1时，应有y＞0．20．今年，我国政府为减轻农民负担，决定在5年内免去农业税．某乡今年人均上缴农业税25元，若两年后人均上缴农业税为16元，假设这两年降低的百分率相同．（1）求降低的百分率；（2）若小红家有4人，明年小红家减少多少农业税？（3）小红所在的乡约有16000农民，问该乡农民明年减少多少农业税？【分析】（1）设降低的百分率为x，则降低一次后的数额是25（1﹣x），再在这个数的基础上降低x，则变成25（1﹣x）（1﹣x）即25（1﹣x）2，据此即可列方程求解；（2）每人减少的税额是25x，则4个人的就是4×25x，代入（1）中求得的x的值，即可求解；（3）每个人减少的税额是25x，乘以总人数16000即可求解．【解答】解：（1）设降低的百分率为x，依题意有，25（1﹣x）2＝16，解得，x1＝0.2＝20%，x2＝1.8（舍去）；（2）小红全家少上缴税25×20%×4＝20（元）；（3）全乡少上缴税16000×25×20%＝80 000（元）．答：降低的增长率是20%，明年小红家减少的农业税是20元，该乡农民明年减少的农业税是80 000元．【点评】本题考查求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2＝b．21．如图，在矩形ABCD中，AB＝m（m是大于0的常数），BC＝8，E为线段BC上的动点（不与B、C重合）．连接DE，作EF⊥DE，EF与射线BA交于点F，设CE＝x，BF＝y．（1）求y关于x的函数关系式；（2）若m＝8，求x为何值时，y的值最大，最大值是多少？（3）若y＝，要使△DEF为等腰三角形，m的值应为多少？【分析】（1）利用互余关系找角相等，证明△BEF∽△CDE，根据对应边的比相等求函数关系式；（2）把m的值代入函数关系式，再求二次函数的最大值；（3）∵∠DEF＝90°，只有当DE＝EF时，△DEF为等腰三角形，把条件代入即可．【解答】解：（1）∵EF⊥DE，∴∠BEF＝90°﹣∠CED＝∠CDE，又∠B＝∠C＝90°，∴△BEF∽△CDE，∴＝，即＝，解得y＝；（2）由（1）得y＝，将m＝8代入，得y＝﹣x2+x＝﹣（x2﹣8x）＝﹣（x﹣4）2+2，所以当x＝4时，y取得最大值为2；（3）∵∠DEF＝90°，∴只有当DE＝EF时，△DEF为等腰三角形，∴△BEF≌△CDE，∴BE＝CD＝m，此时m＝8﹣x，解方程＝，得x＝6，或x＝2，当x＝2时，m＝6，当x＝6时，m＝2．【点评】本题把相似三角形与求二次函数解析式联系起来，在解题过程中，充分运用相似三角形对应边的比相等，建立函数关系式．22．在△ABC中，AB＝AC，D为BC上一点，由D分别作DE⊥AB于E，DF⊥AC于F．设DE＝a，DF＝b，且实数a，b满足9a2﹣24ab+16b2＝0，并有＝2566，∠A使得方程x2﹣x•sin A+sin A﹣＝0有两个相等的实数根．（1）试求实数a，b的值；（2）试求线段BC的长．【分析】（1）由题意可知：2a2b＝2566，则2a2b＝248，则a2b＝48．化简9a2﹣24ab+16b2＝0得：（3a﹣4b）2＝0，则3a﹣4b＝0，即3a＝4b，则根据，可求得a与b的值；（2）要求BC的长需求出BD和CD的长，知BD、CD分别是直角三角形BDE和直角三角形CDF中的斜边．又知在△ABC中，AB＝AC，则∠B＝∠C，则根据三角函数只要知道∠B或∠C的读数即可，要求∠B或∠C的读数需求的∠A的读数，根据判别式可以求得∠A的读数．【解答】解：（1）由条件有，解得；（2）又由关于x的方程的判别式△＝sin2A﹣sin A+＝（sin A﹣）2＝0，则sin A＝，而∠A为三角形的一个内角，所以∠A1＝60°或∠A2＝120° 2分当∠A＝60°时，△ABC为正三角形，∠B＝∠C＝60°于是分别在Rt△BDE和Rt△CDF中有BD＝，CD＝所以BC＝BD+DC＝．当∠A＝120°时，△ABC为等腰三角形，∠B＝∠C＝30°同上方法可得BC＝14． 3分所以线段BC的长应为或14．【点评】考查了解直角三角形以及判别式的应用．23．某市城建部门经过长期市场调查发现，该市年新建商品房面积P（万平方米）与市场新房均价x（千元/平方米）存在函数关系P＝25x；年新房销售面积Q（万平方米）与市场新房均价x（千元/平方米）的函数关系为Q＝﹣10；（1）如果年新建商品房的面积与年新房销售面积相等，求市场新房均价和年新房销售总额；（2）在（1）的基础上，如果市场新房均价上涨1千元，那么该市年新房销售总额是增加还是减少？变化了多少？结合年新房销售总额和积压面积的变化情况，请你提出一条合理化的建议．（字数不超过50）【分析】（1）根据“新建商品房的面积与年新房销售面积相等”作为相等关系求x的值即可；（2）分别求算出市场新房均价上涨1千元后的新建商品房面积P，年新房销售面积Q再来求算其变化的量和积压的情况．【解答】解：（1）根据题意得：25x＝﹣10，解得x1＝2，x2＝﹣（舍去），则Q＝﹣10＝50万平方米，所以市场新房均价为2千元．则年新房销售总额为2000×500000＝10亿元．。

压轴题1、已知，在平行四边形OABC 中，OA=5，AB=4，∠OCA=90°，动点P 从O 点出发沿射线OA 方向以每秒2个单位的速度移动，同时动点Q 从A 点出发沿射线AB 方向以每秒1个单位的速度移动．设移动的时间为t 秒． （1）求直线AC 的解析式；（2）试求出当t 为何值时，△OAC 与△PAQ 相似； （3）若⊙P 的半径为58，⊙Q 的半径为23；当⊙P 与对角线AC 相切时，判断⊙Q 与直线AC 、BC 的位置关系，并求出Q 点坐标。

解：（1）42033y x =-+ （2）①当0≤t≤2.5时，P 在OA 上，若∠OAQ=90°时， 故此时△OAC 与△PAQ 不可能相似．当t>2.5时，①若∠APQ=90°，则△APQ ∽△OCA ，∵t>2.5，∴符合条件．②若∠AQP=90°，则△APQ ∽△∠OAC ，∵t>2.5，∴符合条件．综上可知，当时，△OAC 与△APQ 相似．（3）⊙Q 与直线AC 、BC 均相切，Q 点坐标为（109,531）。

2、如图，以矩形OABC 的顶点O 为原点，OA 所在的直线为x 轴，OC 所在的直线为y 轴，建立平面直角坐标系．已知OA ＝3，OC ＝2，点E 是AB 的中点，在OA 上取一点D ，将△BDA 沿BD 翻折，使点A 落在BC 边上的点F 处． （1）直接写出点E 、F 的坐标；（2）设顶点为F 的抛物线交y 轴正半轴．．．于点P ，且以点E 、F 、P 为顶点的三角形是等腰三角形，求该抛物线的解析式；（3）在x 轴、y 轴上是否分别存在点M 、N ，使得四边形MNFE 的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．解：（1）(31)E ，；(12)F ，．（2）在Rt EBF △中，90B ∠=， 2222125EF EB BF ∴=+=+=．设点P 的坐标为(0)n ，，其中0n >，顶点(12)F ，， ∴设抛物线解析式为2(1)2(0)y a x a =-+≠．①如图①，当EF PF =时，22EF PF =，221(2)5n ∴+-=．解得10n =（舍去）；24n =．(04)P ∴，．24(01)2a ∴=-+．解得2a =． ∴抛物线的解析式为22(1)2y x =-+（第2题）②如图②，当EP FP =时，22EP FP =，22(2)1(1)9n n ∴-+=-+． 解得52n =-（舍去）．③当EF EP =时，53EP =<，这种情况不存在． 综上所述，符合条件的抛物线解析式是22(1)2y x =-+． （3）存在点M N ，，使得四边形MNFE 的周长最小． 如图③，作点E 关于x 轴的对称点E '，作点F 关于y 轴的对称点F '，连接E F ''，分别与x 轴、y 轴交于点M N ，，则点M N ，就是所求点．(31)E '∴-，，(12)F NF NF ME ME '''-==，，，．43BF BE ''∴==，．FN NM ME F N NM ME F E ''''∴++=++=22345+=．又5EF =，∴55FN NM ME EF +++=+，此时四边形MNFE 的周长最小值是553、如图，在边长为2的等边△ABC 中，A D ⊥BC,点P 为边AB 上一个动点，过P 点作PF//AC 交线段BD 于点F,作PG ⊥AB 交AD 于点E,交线段CD 于点G,设BP=x . （1）①试判断BG 与2BP 的大小关系,并说明理由;②用x 的代数式表示线段DG 的长,并写出自变量x 的取值范围;（2）记△DEF 的面积为S,求S 与x 之间的函数关系式,并求出S 的最大值;（3）以P 、E 、F 为顶点的三角形与△EDG 是否可能相似？如果能相似，请求出BP 的长，如果不能，请说明理由。

2023中考压轴题专题训练-旋转中的相似三角问题姓名： 成绩：模型证明：（1）全等旋转中的相似已知△ABC 顺时针旋转一定角度，得到△DBE ，且k BCAB=，求证：△ABD ∽△CBE ，求它们相似比； 证明：∵∠ABD=∠ABC -∠CBD ∠CBE=∠DBE -∠CBD又∵∠ABC=∠DBE ∴∠ABD=∠CBE ∵AB=DB,BC=BE∴k BEBDBC AB == ∴△ABD ∽△CBE ∴k BEBDBC AB CE AD ===（2）相似旋转中的相似已知△ABC ∽△ADE ， 求证：△ABD ∽△ACE 证明：∵△ABC ∽△ADE∴AC AEAB AD= ∴ACABAEAD = ∴∠DAE=∠BAC∴∠DAE -∠BAE=∠BAC -∠BAE ∴∠BAD=∠CAE ∴△ABD ∽△ACE ∴CEBDAC AB AE AD == 1、（4分）如图，在矩形ABCD 中，将∠ABC 绕点A 按逆时针方向旋转一定角度后，BC 的对应边''C B 交CD 边于点G ．连接B 'B 、'CC ．若AB =3，AD =4，则''BB CC =2、（4分）如图，在Rt△ABC中，∠ACB＝90°，D为AB边上一点，且点D到BC的距离等于点D到AC的距离．将△ABC绕点D旋转得到△A′B′C′，连接BB′，CC′．若＝，则的值为．3、（10分）在四边形ABCD中，对角线AC、BD相交于点O，将△COD绕点O按逆时针方向旋转得到△C1OD1，旋转角为θ（0°＜θ＜90°），连接AC1、BD1，AC1与BD1交于点P．（1）如图1，若四边形ABCD是正方形．①求证：△AOC1≌△BOD1．②请直接写出AC1与BD1的位置关系．（2）如图2，若四边形ABCD是菱形，AC=5，BD=7，设AC1=k BD1．判断AC1与BD1的位置关系，说明理由，并求出k的值．（3）如图3，若四边形ABCD是平行四边形，AC=4，BD=8，连接DD1，设AC1=kBD1．请求出（AC1）2+（kDD1）2的值。

【中考二轮专题训练系列】2024中考物理压轴题型训练专题06 作图题专练训练题01【2022·四川成都·中考真题】知识点（光学-直线传播）“圭表”是我国古代先进的天文观测仪器，根据“表”在“圭”面上形长的变化就能知道时节的更替。

元代天文学家郭守敬改进和创新了“圭表”（如图甲），国乙是其示意图。

他在“表”上方加一根架空的横梁，在“圭”面上放置一个可移动的景符（有小孔的铜片）。

他利用改进后的“圭表”，精确推算出了二十四节气和一回归年天数。

请根据以上资料在图乙中画出横梁通过景符的小孔在“圭”面上所成的影像，并标明两条光线的传播方向。

训练题02【2023·山东日照·中考真题】知识点（光学-光的反射/折射）一个底面镀银的球冠形玻璃球放置在水平桌面上，其横截面如图所示。

一条光线从玻璃球冠上表面的M点通过球心O射到球冠的底面N点。

虚线PN为底面AB的法线。

画出该光线经底面AB反射后在球冠形玻璃球内外的光路图。

训练题03【2023·江苏泰州·中考真题】知识点（光学-平面镜成像）如图所示，请作出物体AB在平面镜MN中所成的像A B''。

训练题04【2023·湖北恩施·中考真题】知识点（光学-凸透镜/凹透镜）如图，一束光经平面镜反射后，平行凹透镜的主光轴射向透镜，请画出平面镜和经过凹透镜后的折射光线。

训练题05【2023·广东深圳·中考真题】知识点（力学-力的示意图）小白同学用斜向右上的拉力拉动物体向右做匀速运动，请在图中：①画出绳子对手的拉力F，②物块受到的摩擦力f。

训练题06【2023·辽宁锦州·中考真题】知识点（力学-杠杆/力臂）如图所示是中医用切刀切药材的示意图，请你在图中画出施加在手柄上A点的最小力F及其力臂L。

训练题07【2023·黑龙江哈尔滨·中考真题】知识点（力学-滑轮）小丽学习了滑轮的知识后，想利用滑轮组设计一个升降装置，自己把物体吊上楼来，请你画出最省力的绕线方式和物体所受重力的示意图。

长沙市近5年数学中考压轴题专题训练1.设a,b 是任意两个不等实数，我们规定：满足不等式a ≤x ≤b 的实数x 的所有取值的全体叫做闭区间，表示为{a,b},对于一个函数，如果它的自变量x 与函数值y 满足：当m ≤x ≤n 时，有m ≤y ≤n,我们就称此函数是闭区间{m,n}上的“闭函数”.（2013·长沙）（1）反比列函数2013y x=是闭区间{1,2013}上的“闭函数”吗？请判断并说明理由； （2）若一次函数y=kx+b(k ≠0)是闭区间{m,n}上的“闭函数”，求此函数的解析式：（3）若二次函数2147555y x x =--是闭区间{a,b}上的“闭函数”，求实数a,b 的值.2.如图，在平面直角坐标系中，直线y=-x+2与x 轴，y 轴分别交于点A,点B,动点P(a,b)在第一象限内，由点P 向x 轴，y 轴所作的垂线PM,PN （垂足为M,N ）分别于直线AB 相交于点E,点F ，当点P(A,B)运动时，矩形PMON 的面积为定值2.（2013·长沙）（1）求∠OAB 的度数； （2）求证△AOF ∽△BEO ；（3）当点E,F 都在线段AB 上时，由三条线段AE,EF,BF 组成一个三角形，记此三角形的外接圆面积为1S △OEF 的面积为2S 试探究： 12S S +是否存在最小值？ 若存在，请求出该最小值：若不存在，请说明理由.3.在平面直角坐标系中，我们把横坐标与纵坐标相等的点称为“梦之点”，例如点（﹣1，﹣1），（0，0），（，），…都是“梦之点”，显然，这样的“梦之点”有无数个．（2014·长沙）（1）若点P（2，m）是反比例函数y=（n为常数，n≠0）的图象上的“梦之点”，求这个反比例函数的解析式；（2）函数y=3kx+s﹣1（k，s是常数）的图象上存在“梦之点”吗？若存在，请求出“梦之点”的坐标；若不存在，请说明理由；（3）若二次函数y=ax2+bx+1（a，b是常数，a＞0）的图象上存在两个不同的“梦之点”A（x1，x1），B（x2，x2），且满足﹣2＜x1＜2，|x1﹣x2|=2，令t=b2﹣2b+，试求出t的取值范围．4.（2014•长沙）如图，抛物线y=ax2+bx+c（a，b，c是常数，a≠0）的对称轴为y轴，且经过（0，0）和（，）两点，点P在该抛物线上运动，以点P为圆心的⊙P总经过定点A（0，2）．（1）求a，b，c的值；（2）求证：在点P运动的过程中，⊙P始终与x轴相交；（3）设⊙P与x轴相交于M（x1，0），N（x2，0）（x1＜x2）两点，当△AMN为等腰三角形时，求圆心P的纵坐标．5.在直角坐标系中，我们不妨将横坐标，纵坐标均为整数的点称之为“中国结”。

中考数学压轴题复习20题1．在平面直角坐标系xO y 中，抛物线y ＝－41 m x2＋45mx ＋m2－3m ＋2与x 轴的交点分别为原点O 和点A ，点B （2，n ）在这条抛物线上．（1）求点B 的坐标；（2）点P 在线段OA 上，从O 点出发向A 点运动，过P 点作x 轴的垂线，与直线OB 交于点E ，延长PE 到点D ，使得ED ＝PE ，以PD 为斜边，在PD 右侧作等腰直角三角形PCD （当P 点运动时，C 点、D 点也随之运动）．①当等腰直角三角形PCD 的顶点C 落在此抛物线上时，求OP 的长；②若P 点从O 点出发向A 点作匀速运动，速度为每秒1个单位，同时线段OA 上另一个点Q 从A 点出发向O 点作匀速运动，速度为每秒2个单位（当Q 点到达O 点时停止运动，P 点也同时停止运动）．过Q 点作x 轴的垂线，与直线AB 交于点F ，延长QF 到点M ，使得FM ＝QF ，以QM 为斜边，在QM 的左侧作等腰直角三角形QMN （当Q 点运动时，M 点、N 点也随之运动）．若P 点运动到t 秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线上，求此刻t 的值．2．在平面直角坐标系中，矩形OACB 的顶点O 在坐标原点，顶点A 、B 分别在x 轴、y 轴的正半轴上，OA ＝3，OB ＝4，D 为边OB 的中点．（Ⅰ）若E 为边OA 上的一个动点，当△CDE 的周长最小时，求点E 的坐标；（Ⅱ）若E 、F 为边OA 上的两个动点，且EF ＝2，当四边形CDEF 的周长最小时，求点E 、F 的坐标．3．在平面直角坐标系中，已知抛物线y ＝－x2＋bx ＋c 与x 轴交于点A 、B （点A 在点B 的左侧），与y 轴的正半轴交于点C ，顶点为E ．（Ⅰ）若b ＝2，c ＝3，求此时抛物线顶点E 的坐标；（Ⅱ）将（Ⅰ）中的抛物线向下平移，若平移后，在四边形ABEC 中满足S △BCE＝S △ABC，求此时直线BC的解析式；（Ⅲ）将（Ⅰ）中的抛物线作适当的平移，若平移后，在四边形ABEC 中满足S △BCE＝2S △AOC，且顶点E 恰好落在直线y ＝－4x ＋3上，求此时抛物线的解析式．4．如图1，在Rt △ABC 中，∠ACB ＝90°，半径为1的圆A 与边AB 相交于点D ，与边AC 相交于点E ，连结DE 并延长，与线段BC 的延长线交于点P ． （1）当∠B ＝30°时，连结AP ，若△AEP 与△BDP 相似，求CE 的长； （2）若CE ＝2，BD ＝BC ，求∠BPD 的正切值；（3）若tan ∠BPD ＝31，设CE ＝x ，△ABC 的周长为y ，求y 关于x 的函数关系式．5．已知：如图①，在平面直角坐标系xO y 中，边长为2的等边△OAB 的顶点B 在第一象限，顶点A 在x 轴的正半轴上．另一等腰△OCA 的顶点C 在第四象限，OC ＝AC ，∠C ＝120°．现有两动点P ，Q 分别从A ，O 两点同时出发，点Q 以每秒1个单位的速度沿OC 向点C 运动，点P 以每秒3个单位的速度沿A →O →B 运动，当其中一个点到达终点时，另一个点也随即停止. （1）求在运动过程中形成的△OPQ 的面积S 与运动的时间t 之间的函数关系，并写出自变量t 的取值范围； （2）在等边△OAB 的边上（点A 除外）存在点D ，使得△OCD 为等腰三角形，请直接写出所有符合条件的点D 的坐标；（3）如图②，现有∠MCN ＝60°，其两边分别与OB ，AB 交于点M ，N ，连接MN ．将∠MCN 绕着C 点旋转（0°＜旋转角＜60°），使得M ，N 始终在边OB 和边AB 上．试判断在这一过程中，△BMN 的周长是否发生变化？若没变化，请求出其周长；若发生变化，请说明理由．6．已知抛物线y ＝ax2＋bx ＋c （a ＞0）的图象经过点B （12，0）和C （0，－6），对称轴为x ＝2． （1）求该抛物线的解析式：（2）点D 在线段AB 上且AD ＝AC ，若动点P 从A 出发沿线段AB 以每秒1个单位长度的速度匀速运动，同时另一动点Q 以某一速度从C 出发沿线段CB 匀速运动，问是否存在某一时刻，使线段PQ 被直线CD 垂直平分？若存在，请求出此时的时间t （秒）和点Q 的运动速度；若不存在，请说明理由；AE C B P D 图2（备用） B PE C D A 图3（备用） A B C P E D 图1图②图①（3）在（2）的结论下，直线x ＝1上是否存在点M ，使△MPQ 为等腰三角形？若存在，请求出所有点M 的坐标；若不存在，请说明理由．7．如图，抛物线y ＝ax2＋bx ＋1与x 轴交于两点A （－1，0），B （1，0），与y 轴交于点C ． （1）求抛物线的解析式；（2）过点B 作BD ∥CA 与抛物线交于点D ，求四边形ACBD 的面积；（3）在x 轴下方的抛物线上是否存在点M ，过M 作MN ⊥x 轴于点N ，使以A 、M 、N 为顶点的三角形与△BCD 相似？若存在，则求出点M 的坐标；若不存在，请说明理由．8．如图，已知抛物线y ＝21x2＋bx ＋c 与y 轴相交于C ，与x 轴相交于A 、B ，点A 的坐标为（2，0），点C 的坐标为（0，－1）．（1）求抛物线的解析式；（2）点E 是线段AC 上一动点，过点E 作DE ⊥x 轴于点D ，连结DC ，当△DCE 的面积最大时，求点D 的坐标；（3）在直线BC 上是否存在一点P ，使△ACP 为等腰三角形，若存在，求点P 的坐标，若不存在，说明理由．9．如图，已知△ABC ∽△A 1B 1C 1，相似比为k （k ＞1），且△ABC 的三边长分别为a 、b 、c （a ＞b ＞c ），△A 1B 1C 1的三边长分别为a 1、b 1、c 1． （1）若c ＝a 1，求证：a ＝kc ；（2）若c ＝a 1，试给出符合条件的一对△ABC 和△A 1B 1C 1，使得a 、b 、c 和a 1、b 1、c 1都是正整数，并加以说明；（3）若b ＝a 1，c ＝b 1，是否存在△ABC 和△A 1B 1C 1，使得k ＝2？请说明理由．10．如图，Rt △ABC 内接于⊙O ，AC ＝BC ，∠BAC 的平分线AD 与⊙O 交于点D ，与BC 交于点E ，延长BD ，与AC 的延长线交于点F ，连结CD ，G 是CD 的中点，连结OG ． （1）判断OG 与CD 的位置关系，写出你的结论并证明； （2）求证：AE ＝BF ； （3）若OG ·DE ＝3(2－2)，求⊙O 的面积．11．已知：抛物线y ＝ax2＋bx ＋c （a ≠0）的对称轴为x ＝－1，与x 轴交于A 、B 两点，与y 轴交于点C ，其中A （－3，0）、C （0，－2）． （1）求这条抛物线的函数表达式．（2）已知在对称轴上存在一点P ，使得△PBC 的周长最小．请求出点P 的坐标．（3）若点D 是线段OC 上的一个动点（不与点O 、点C 重合）．过点D 作DE ∥PC 交x 轴于点E ，连接PD 、PE ．设CD 的长为m ，△PDE 的面积为S ．求S 与m 之间的函数关系式．试说明S 是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．12．（本小题满分12分）如图，BD 是⊙O 的直径，OA ⊥OB ，M 是劣弧上一点，过M 点作⊙O 的切线MP 交OA 的延长线于P 点，MD 与OA 交于N 点． （1）求证：PM ＝PN ； （2）若BD ＝4，P A ＝23AO ，过B 点作BC ∥MP 交⊙O 于C 点，求BC 的长． B C AA 1 a b cB 1C 1 a 1b 1c 1 A C B F D EO G13．如图，在平面直角坐标系中放置一矩形ABCO ，其顶点为A （0，1）、B （－33，1）、C （－33，0）、O （0，0）．将此矩形沿着过E （－3，1）、F （－334，0）的直线EF 向右下方翻折，B 、C 的对应点分别为B ′、C ′．（1）求折痕所在直线EF 的解析式；（2）一抛物线经过B 、E 、B ′三点，求此二次函数解析式；（3）能否在直线EF 上求一点P ，使得△PBC 周长最小？如能，求出点P 的坐标；若不能，说明理由．14．已知：甲、乙两车分别从相距300（km ）的M 、N回，图1、图2分别是它们离各自出发地的距离y （km ）与行驶时间x （h ）之间的函数图象． （1）试求线段AB所对应的函数关系式，并写出自变量的取值范围；（2）当它们行驶到与各自出发地的距离相等时，用了29h ，求乙车的速度； （3）在（2）的条件下，求它们在行驶的过程中相遇的时间．y h图1y h图215．如图1，在△ABC 中，AB ＝BC ，且BC ≠AC ，在△ABC 上画一条直线，若这条直线．．既平分△ABC 的面积，又平分△ABC 的周长，我们称这条线为△ABC 的“等分积周线”． （1）请你在图1中用尺规作图作出一条△ABC 的“等分积周线”；（2）在图1中过点C 能否画出一条“等分积周线”？若能，说出确定的方法；若不能，请说明理由； （3）如图2，若AB ＝BC ＝5cm ，AC ＝6cm ，请你找出△ABC 的所有“等分积周线”，并简要说明确定的方法．16．如图，在Rt △ABC 中，∠C ＝90°，AC ＝3cm ，BC ＝4cm ，点P 以一定的速度沿AC 边由A 向C 运动，点Q 以1cm/s 的速度沿CB 边由C 向B 运动，设P 、Q 同时运动，且当一点运动到终点时，另一点也随之停止运动，设运动时间为t （s ）． （1）若点P 以43cm/s 的速度运动 ①当PQ ∥AB 时，求t 的值；②在①的条件下，试判断以PQ 为直径的圆与直线AB 的位置关系，并说明理由．（2）若点P 以1cm/s 的速度运动，在整个运动过程中，以PQ 为直径的圆能否与直线AB 相切？若能，请求出运动时间t ；若不能，请说明理由．17．青海玉树发生7.1级强震后，为使人民的生命财产损失降到最低，部队官兵发扬了连续作战的作风。

九年级中考数学动点问题压轴题专题训练1.如图1, 在平面直角坐标系中, 四边形OABC各顶点的坐标分别为O(0, 0), A(3, 3 ), B(9, 5 ), C(14, 0). 动点P与Q同时从O点出发, 运动时间为t秒, 点P沿OC方向以1单位长度/秒的速度向点C运动, 点Q沿折线OA－AB－BC运动, 在OA, AB, BC上运动的速度分别为3, , (单位长度/秒). 当P, Q中的一点到达C点时, 两点同时停止运动.(1)求AB所在直线的函数表达式.(2)如图2, 当点Q在AB上运动时, 求△CPQ的面积S关于t的函数表达式及S的最大值.(3)在P, Q的运动过程中, 若线段PQ的垂直平分线经过四边形OABC的顶点, 求相应的t值．图1 图22.如图, 抛物线y=-x2+bx+c与x轴交于A, B两点(A在B的左侧), 与y轴交于点N, 过A点的直线l:y=kx+n与y轴交于点C, 与抛物线y=-x2+bx+c的另一个交点为D, 已知A(-1, 0), D(5, -6), P 点为抛物线y=-x2+bx+c上一动点(不与A, D重合).(1)求抛物线和直线l的解析式;(2)当点P在直线l上方的抛物线上时, 过P点作PE∥x轴交直线l于点E, 作PF ∥y轴交直线l于点F, 求PE+PF的最大值;(3)设M为直线l上的点, 探究是否存在点M, 使得以点N, C, M, P为顶点的四边形为平行四边形.若存在, 求出点M的坐标;若不存在, 请说明理由.3.如图, 在平面直角坐标系中, 抛物线y＝ax2＋bx＋c经过A(－2, －4 )、O(0, 0)、B(2, 0)三点.（1）求抛物线y＝ax2＋bx＋c的解析式；（2）若点M是该抛物线对称轴上的一点, 求AM＋OM的最小值.4.设直线l1: y＝k1x＋b1与l2: y＝k2x＋b2, 若l1⊥l2, 垂足为H, 则称直线l1与l2是点H的直角线.（1）已知直线①；②；③；④和点C(0, 2), 则直线_______和_______是点C的直角线（填序号即可）；（2）如图, 在平面直角坐标系中, 直角梯形OABC的顶点A(3, 0)、B(2, 7)、C(0, 7), P为线段OC上一点, 设过B、P两点的直线为l1, 过A、P两点的直线为l2, 若l1与l2是点P的直角线, 求直线l1与l2的解析式．5.如图①, 在平面直角坐标系xOy中, 已知抛物线y=ax2-2ax-8a与x轴相交于A, B两点(点A在点B的左侧), 与y轴交于点C(0, -4).(1)点A的坐标为, 点B的坐标为, 线段AC的长为, 抛物线的解析式为.(2)点P是线段BC下方抛物线上的一个动点.如果在x轴上存在点Q, 使得以点B, C, P, Q为顶点的四边形是平行四边形, 求点Q的坐标.①6.如图, 已知抛物线（b是实数且b＞2）与x轴的正半轴分别交于点A.B（点A位于点B是左侧）, 与y轴的正半轴交于点C.（1）点B的坐标为______, 点C的坐标为__________（用含b的代数式表示）；（2）请你探索在第一象限内是否存在点P, 使得四边形PCOB的面积等于2b, 且△PBC是以点P为直角顶点的等腰直角三角形？如果存在, 求出点P的坐标；如果不存在, 请说明理由；（3）请你进一步探索在第一象限内是否存在点Q, 使得△QCO、△QOA和△QAB中的任意两个三角形均相似（全等可看作相似的特殊情况）？如果存在, 求出点Q的坐标；如果不存在, 请说明理由．7.如图, 已知A.B是线段MN上的两点, , , . 以A为中心顺时针旋转点M, 以B为中心逆时针旋转点N, 使M、N两点重合成一点C, 构成△ABC, 设.（1）求x的取值范围；（2）若△ABC为直角三角形, 求x的值；（3）探究: △ABC的最大面积？8.如图, 已知抛物线y＝－x2＋bx＋c经过A(0, 1)、B(4, 3)两点.（1）求抛物线的解析式；（2）求tan∠ABO的值；（3）过点B作BC⊥x轴, 垂足为C, 在对称轴的左侧且平行于y轴的直线交线段AB于点N, 交抛物线于点M, 若四边形MNCB为平行四边形, 求点M的坐标.9.在平面直角坐标系中, 反比例函数与二次函数y＝k(x2＋x－1)的图象交于点A(1,k)和点B(－1,－k).（1）当k＝－2时, 求反比例函数的解析式；（2）要使反比例函数与二次函数都是y随x增大而增大, 求k应满足的条件以及x的取值范围；（3）设二次函数的图象的顶点为Q, 当△ABQ是以AB为斜边的直角三角形时, 求k的值．10.如图, 已知抛物线y＝ax2＋bx＋4(a≠0)的对称轴为直线x＝3, 抛物线与x轴相交于A, B两点, 与y轴相交于点C, 已知B点的坐标为(8, 0).(1)求抛物线的解析式；(2)点M为线段BC上方抛物线上的一点, 点N为线段BC上的一点, 若MN∥y 轴, 求MN的最大值；(3)在抛物线的对称轴上是否存在点Q, 使△ACQ为等腰三角形？若存在, 求出符合条件的Q点坐标；若不存在, 请说明理由．11.如图, 直线y＝2x＋6与反比例函数y＝(k＞0)的图象交于点A(m, 8), 与x轴交于点B, 平行于x轴的直线y＝n(0＜n＜6)交反比例函数的图象于点M, 交AB于点N, 连接BM.(1)求m的值和反比例函数的解析式；(2)观察图象, 直接写出当x＞0时不等式2x＋6－＞0的解集；(3)直线y＝n沿y轴方向平移, 当n为何值时, △BMN的面积最大？最大值是多少？12.如图, 在平面直角坐标系xOy中, 顶点为M的抛物线y＝ax2＋bx（a＞0）经过点A和x轴正半轴上的点B, AO＝BO＝2, ∠AOB＝120°.（1）求这条抛物线的表达式；（2）连结OM, 求∠AOM的大小；（3）如果点C在x轴上, 且△ABC与△AOM相似, 求点C的坐标．13.在直角梯形OABC中, CB//OA, ∠COA＝90°, CB＝3, OA＝6, BA＝. 分别以OA.OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.（1）求点B的坐标；（2）已知D.E分别为线段OC.OB上的点, OD＝5, OE＝2EB, 直线DE交x轴于点F. 求直线DE的解析式；（3）点M是（2）中直线DE上的一个动点, 在x轴上方的平面内是否存在另一点N, 使以O、D、M、N为顶点的四边形是菱形？若存在, 请求出点N的坐标；若不存在, 请说明理由．14.如图, 已知一次函数y＝－x＋7与正比例函数的图象交于点A, 且与x轴交于点B. （1）求点A和点B的坐标；（2）过点A作AC⊥y轴于点C, 过点B作直线l//y轴. 动点P从点O出发, 以每秒1个单位长的速度, 沿O—C—A的路线向点A运动；同时直线l从点B出发, 以相同速度向左平移, 在平移过程中, 直线l交x轴于点R, 交线段BA或线段AO于点Q. 当点P到达点A时, 点P和直线l都停止运动. 在运动过程中, 设动点P运动的时间为t秒.①当t为何值时, 以A.P、R为顶点的三角形的面积为8？②是否存在以A、P、Q为顶点的三角形是等腰三角形？若存在, 求t的值；若不存在, 请说明理由．15.如图, 二次函数y＝a(x2－2mx－3m2)（其中a、m是常数, 且a＞0, m＞0）的图像与x轴分别交于A.B（点A位于点B的左侧）, 与y轴交于点C(0,－3), 点D在二次函数的图像上, CD//AB, 联结AD. 过点A作射线AE交二次函数的图像于点E, AB平分∠DAE.（1）用含m的式子表示a；（2）求证: 为定值；（3）设该二次函数的图像的顶点为F．探索：在x轴的负半轴上是否存在点G, 联结GF, 以线段GF、AD、AE的长度为三边长的三角形是直角三角形？如果存在, 只要找出一个满足要求的点G即可, 并用含m的代数式表示该点的横坐标；如果不存在, 请说明理由．16.如图, 二次函数y=-x2+4x+5的图象的顶点为D, 对称轴是直线l, 一次函数y= x+1的图象与x轴交于点A, 且与直线DA关于l的对称直线交于点B.(1)点D的坐标是.(2)直线l与直线AB交于点C, N是线段DC上一点(不与点D, C重合), 点N的纵坐标为n.过点N作直线与线段DA, DB分别交于点P, Q, 使得△DPQ与△DAB 相似.①当n= 时, 求DP的长;②若对于每一个确定的n的值, 有且只有一个△DPQ与△DAB相似, 请直接写出n的取值范围.17.已知直线y＝3x－3分别与x轴、y轴交于点A, B, 抛物线y＝ax2＋2x＋c经过点A, B. （1）求该抛物线的表达式, 并写出该抛物线的对称轴和顶点坐标；（2）记该抛物线的对称轴为直线l, 点B关于直线l的对称点为C, 若点D在y 轴的正半轴上, 且四边形ABCD为梯形．①求点D的坐标；②将此抛物线向右平移, 平移后抛物线的顶点为P, 其对称轴与直线y＝3x－3交于点E, 若, 求四边形BDEP的面积.18.如图, 在平面直角坐标系xOy中, 二次函数y＝－x2＋2x＋8的图象与一次函数y＝－x＋b的图象交于A.B两点, 点A在x轴上, 点B的纵坐标为－7.点P是二次函数图象上A.B两点之间的一个动点(不与点A.B重合), 设点P的横坐标为m, 过点P作x轴的垂线交AB于点C, 作PD ⊥AB于点D.(1)求b及sin∠ACP的值；(2)用含m的代数式表示线段PD的长；(3)连接PB, 线段PC把△PDB分成两个三角形, 是否存在适合的m值, 使这两个三角形的面积之比为1∶2？如果存在, 直接写出m的值；如果不存在, 请说明理由.19.如图, 抛物线与x轴交于A.B两点（点A在点B的左侧）, 与y轴交于点C.（1）求点A.B的坐标；（2）设D为已知抛物线的对称轴上的任意一点, 当△ACD的面积等于△ACB 的面积时, 求点D的坐标；（3）若直线l过点E(4, 0), M为直线l上的动点, 当以A、B、M为顶点所作的直角三角形有且只有三个时, 求直线l的解析式．20.已知平面直角坐标系中两定点A(－1, 0)、B(4, 0), 抛物线y＝ax2＋bx－2（a≠0）过点A.B, 顶点为C, 点P(m, n)（n＜0）为抛物线上一点.（1）求抛物线的解析式和顶点C的坐标；（2）当∠APB为钝角时, 求m的取值范围；（3）若m＞, 当∠APB为直角时, 将该抛物线向左或向右平移t（0＜t＜）个单位, 点C、P平移后对应的点分别记为C′、P′, 是否存在t, 使得顺次首尾连接A、B、P′、C′所构成的多边形的周长最短？若存在, 求t的值并说明抛物线平移的方向；若不存在, 请说明理由．2021中考数学压轴专题训练之动点问题-答案一、解答题（本大题共20道小题）1.【答案】【思维教练】(1)设一次函数解析式, 将已知点A、B的坐标值代入求解即可；(2)S △CPQ＝·CP·Qy, CP＝14－t, 点Q在AB上, Qy即为当x＝t时的y值, 代入化简得出S与t的函数关系式, 化为顶点式得出最值；(3)垂直平分线过顶点需以时间为临界点分情况讨论, 当Q在OA上时, 过点C；当Q在AB上时, 过点A；当Q在BC上时, 过点C和点B, 再列方程并求解．解图1解: (1)把A(3, 3 ), B(9, 5 )代入y＝kx＋b,得, 解得,∴y＝33x＋23；(3分)(2)在△PQC中, PC＝14－t,∵OA＝＝6且Q在OA上速度为3单位长度/s,AB＝＝4 且Q点在AB上的速度为单位长度/s,∴Q在OA上时的横坐标为t, Q在AB上时的横坐标为t,PC边上的高线长为33t＋2 3.(6分)所以S＝(14－t)( t＋2 )＝－t2＋t＋14 (2≤t≤6).当t＝5时, S有最大值为.(7分)解图2(3)①当0＜t ≤2时, 线段PQ 的中垂线经过点C(如解图1). 可得方程(332t )2＋(14－32t )2＝(14－t )2.解得t1＝ , t2＝0(舍去), 此时t ＝ .(8分)解图3②当2＜t ≤6时, 线段PQ 的中垂线经过点A(如解图2).可得方程(33)2＋(t －3)2＝[3(t －2)]2.解得t1＝ , ∵t2＝ (舍去), 此时t ＝ .③当6＜t ≤10时,(1)线段PQ 的中垂线经过点C(如解图3).可得方程14－t ＝25－ t, 解得t ＝ .(10分)解图4(2)线段PQ 的中垂线经过点B(如解图4).可得方程(53)2＋(t －9)2＝[52(t －6)]2.解得t1＝ , t2＝ (舍去).此时t＝38＋2027.(11分)综上所述, t的值为, , , .(12分)【难点突破】解决本题的关键点在于对PQ的垂直平分线过四边形顶点的情况进行分类讨论, 在不同阶段列方程求解.2.【答案】[分析] (1)将点A, D的坐标分别代入直线表达式、抛物线的表达式, 即可求解;(2)设出P点坐标, 用参数表示PE, PF的长, 利用二次函数求最值的方法.求解;(3)分NC是平行四边形的一条边或NC是平行四边形的对角线两种情况, 分别求解即可.解:(1)将点A, D的坐标代入y=kx+n得:解得:故直线l的表达式为y=-x-1.将点A, D的坐标代入抛物线表达式,得解得故抛物线的表达式为:y=-x2+3x+4.(2)∵直线l的表达式为y=-x-1,∴C(0, -1), 则直线l与x轴的夹角为45°, 即∠OAC=45°,∵PE∥x轴, ∴∠PEF=∠OAC=45°.又∵PF∥y轴, ∴∠EPF=90°, ∴∠EFP=45°.则PE=PF.设点P坐标为(x, -x2+3x+4),则点F(x, -x-1),∴PE+PF=2PF=2(-x2+3x+4+x+1)=-2(x-2)2+18,∵-2<0, ∴当x=2时, PE+PF有最大值, 其最大值为18.(3)由题意知N(0, 4), C(0, -1), ∴NC=5,①当NC是平行四边形的一条边时, 有NC∥PM, NC=PM.设点P坐标为(x, -x2+3x+4), 则点M的坐标为(x, -x-1),∴|yM-yP|=5, 即|-x2+3x+4+x+1|=5,解得x=2±或x=0或x=4(舍去x=0),则点M坐标为(2+ , -3- )或(2- , -3+ )或(4, -5);②当NC是平行四边形的对角线时, 线段NC与PM互相平分.由题意, NC的中点坐标为0, ,设点P坐标为(m, -m2+3m+4),则点M(n', -n'-1),∴0= = ,解得:n'=0或-4(舍去n'=0), 故点M(-4, 3).综上所述, 存在点M, 使得以N, C, M, P为顶点的四边形为平行四边形, 点M的坐标分别为:(2+ , -3- ), (2- , -3+ ), (4, -5), (-4, 3).3.【答案】（1）。

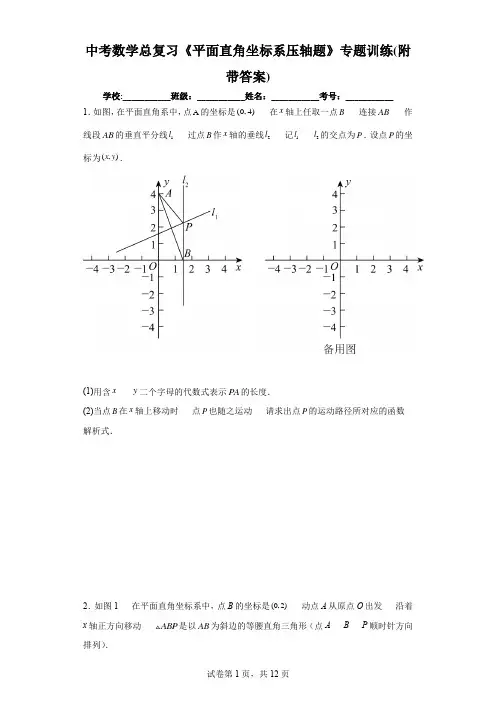
中考数学总复习《平面直角坐标系压轴题》专题训练(附带答案)学校:___________班级：___________姓名：___________考号：___________ 1．如图，在平面直角系中，点A的坐标是(0,4)在x轴上任取一点B连接AB作线段AB的垂直平分线1l过点B作x轴的垂线2l记1l2l的交点为P．设点P的坐x y．标为(,)(1)用含x y二个字母的代数式表示PA的长度．(2)当点B在x轴上移动时点P也随之运动请求出点P的运动路径所对应的函数解析式．2．如图1 在平面直角坐标系中，点B的坐标是(0,2)动点A从原点O出发沿着x轴正方向移动ABP是以AB为斜边的等腰直角三角形（点A B P顺时针方向排列）．(1)当点A 与点O 重合时 得到等腰直角OBC △（此时点P 与点C 重合） 则BC =______．当2OA =时 点P 的坐标是______； (2)设动点A 的坐标为(,0)(0)t t ≥．①点A 在移动过程中，作PM y ⊥轴于M PN OA ⊥于N 求证：四边形PMON 是正方形；①用含t 的代数式表示点P 的坐标为：（______ ______）；(3)在上述条件中，过点A 作y 轴的平行线交MP 的延长线于点Q 如图2 是否存在这样的点A 使得AQB 的面积是AOB 的面积的3倍？若存在 请求出A 的坐标 若不存在 请说明理由．3．如图，在平面直角坐标系中，点O 是坐标原点 直线3y x分别交x 轴 y 轴于点A B ．(1)求ABO ∠的度数；(2)点C 是线段AB 上一点 连接OC 以OC 为直角边作等腰直角OCD 其中OC OD=且点D在第三象限连接AD．设点C的横坐标为t ACD的面积为S 求S与t之间的函数解析式（不要求写出自变量t的取值范围）；(3)在（2）的条件下点E为x轴正半轴上的一点连接BE点F是BE的中点连∥交x轴于点H若接CF并延长交x轴于点G过点D作DH CFCG DH=求点D的坐标．∠-∠=︒345AEB ADH4．如图，在直角平面坐标系中，ABC的边AB在x轴上且3AB=点A的坐标为-点C的坐标为(2,5)．(5,0)(1)求这样的ABC一共几个？并写出符合条件的点B的坐标；(2)试求ABC的面积．5．如图，平面直角坐标系中有点()1，0B 和y 轴上一动点(0,)A a - 其中0a > 以点A 为直角顶点在第四象限内作等腰直角ABC 设点C 的坐标为(,)c d ．(1)当2a =时 点C 的坐标为 ．(2)动点A 在运动的过程中，试判断+c d 的值是否发生变化 若不变 请求出其值；若发生变化 请说明理由．(3)当3a =时 在坐标平面内是否存在一点P （不与点C 重合） 使PAB 与ABC 全等？若存在 请直接写出点P 的坐标；若不存在 请说明理由．6．如图，在平面直角坐标系中，()2,0A - ()0,3B ．(1)如图1 以A 为直角顶点在第二象限内作等腰直角三角形ABE 过点E 作EF x ⊥轴于点F 求点F 的坐标；(2)如图2 点()0,P P y 为y 轴正半轴上一动点 以AP 为直角边作等腰直角三角形APC 点(),C C C x y 在第一象限 90APC ∠=︒ 当点P 运动时 P C y y -的值是否发生变化？若不变 求出其值；若变化 请说明理由．(3)如图3 点P 在y 轴负半轴上 以AP 为直角边作等腰直角三角形APC 90APC ∠=︒ 点C 在第一象限 点H 在AC 延长线上 作HG x ⊥轴于G 当(),2H m 探究线段PH AG OP 之间的数量关系 并证明你的结论．7．已知在平面直角坐标系中，()()4003A B ，，， 以线段AB 为直角边在第一象限内作等腰直角三角形90ABC AB AC BAC =∠=︒，，．(1)直接写出OA OB ⋅的值． (2)求点C 坐标．(3)若点A B ，是x y ，轴正半轴上的动点 BQ AQ ，分别是ABy ∠和BAx ∠的角平分线 交点为Q 求Q ∠的大小．8． 在平面直角坐标系中，点A B ，分别在x 轴负半轴 y 轴正半轴上运动 且满足AB BC = 90ABC ∠=︒ 点C 在第二象限．(1)如图1 当点()()4002A B -，，，时 点C 的坐标为________； (2)以OB 为直角边作等腰直角()90OBD OB BD OBD =∠=︒，△ 如图2 连接AD 和OC 且相交于点P 判断AD 和OC 的数量关系与位置关系 并说明理由；(3)以OB 为直角边作等腰直角()90OBD OB BD OBD =∠=︒，△ 如图3 连接CD 交y 轴于点Q 在点,A B 的运动过程中，判断BQ 与OA 的数量关系 并说明理由．9．在平面直角坐标系中，AOB 为等腰直角三角形 ()4,4A ．(1)直接写出B 点坐标；(2)如图2 若C 为x 轴正半轴上一动点 以AC 为直角边作等腰直角ACD =90ACD ∠︒ 连接OD 求AOD ∠度数；(3)如图3 过点A 作y 轴的垂线交y 轴于E F 为x 轴负半轴上一点 G 在EF 的延长线上 以EG 为直角边作等腰Rt EGH 过A 作x 轴的垂线交EH 于点M 连接FM 等式1AM FMOF-=是否成立？若成立 请证明；若不成立 说明理由．10．如图，在平面直角坐标系中，直线24y x =-+交坐标轴于A B 两点 过x 轴负半轴上一点C 作直线CD 交y 轴正半轴于点D 且AOB DOC △≌△．(1)OC =________ OD =________．(2)点()1,M a -是线段CD 上一点 作ON OM ⊥交AB 于点N 连接MN 求点N 的坐标；(3)若()1,E b 为直线AB 上的点 P 为y 轴上的点 请问：直线CD 上是否存在点Q 使得EPQ △是以E 为直角顶点的等腰直角三角形 若存在 请直接写出此时Q 点的坐标；若不存在 请说明理由．象限内作等腰直角ABC则点b点D在第一象限作等腰直角BDE△c ABO，=∠(1)如图1 点A 关于x 轴的对称点为P 点 则点P 的坐标为________ 当PB 最短时 点B 的坐标为________；（结果均用a 表示）(2)如图2 当AB y ⊥轴 且垂足为点A 时 以OA 为边作正方形ABQO M 在x 轴的正半轴 且OM OA < 以OM 为边在x 轴上方作正方形OMNH 连接AN 若6QM = 两个正方形面积之和为20 求AHN 的面积；(3)如图3 当AB y ⊥轴 且垂足为点A 时 点F 在线段OB 上运动（不与端点重合） 点C 是线段BF 的中点 连接AF AC ， 以A 为直角顶点 AF 为直角边在第二象限内作等腰Rt EAF △ 连接OE 交AC 于点G 探究线段OE 与AC 的关系 并说明理由．13．如图，在平面直角坐标系中，点A B C 都在坐标轴上 08A BO CO BC ===，．(1)点A 坐标为（______ _______）．(2)过点C 作x 轴的垂线l 动点Р从点C 出发 沿着直线①向上运动 若点Р的速度是1个单位/秒 时间是t 连接PA PB ， 请用含t 的式子表示PABS．(3)在（2）的条件下 连接AP 以AP 为斜边 在AP 下方作等腰直角APD △ 连接BD 并延长至点Q 连接PO QC ， 当点D 为BQ 中点时 请判断PCQ △的形状 并说明理由．14．如图，在平面直角坐标系中，(0,2)A (3,0)B 过点B 作直线ly 轴 点P 是直线l 上的动点 以AP 为边在AP 右上侧作等腰直角APQ △ 使90APQ ∠=︒．(1)如图1当点P 落在点B 时 则点Q 的坐标是________； 学生甲认为点Q 的坐标一定跟点P 有关 于是进行了如下探究：(2)如图2 小聪同学画草图时 让点P 落在1P 2P 3P 不同的特殊位置时（1P 在x 轴上 2P A 与x 轴平行 当Q 落在x 轴上时对应点3P ） 画出了几个点对应的1Q 2Q 3Q 三个不同的位置 发现1Q 2Q 3Q 在同一条直线上 请你根据学生甲的猜测及题目条件 求出点Q 所在直线的解析式；(3)在（2）中，虽然求出了点Q 所在直线的解析式 但是小明同学认为几个特殊点确定解析式是一种猜测 当点P 在l 上运动时 所有的Q 点都在一条直线上吗？就解设了点Q 的坐标为(,)x y 希望用一般推理的方式求出x 和y 满足的关系式 请你帮助小明给出解答．15．在平面直角坐标系中，直线AB 与x 轴交于点()6,0A - 与y 轴交于点B 且45ABO ∠=︒．(1)求点B 坐标和ABO 的面积；(2)如图2 点D 为OA 上的一条延长线的一个动点 以BD 为直角边 以点D 为直角顶点 作等腰三角形BDE 求证AB AE ⊥；(3)如图3 AF 平分OAB ∠ 点M 是射线AF 上一动点 点N 是线段AO 上一动点 判断是否存在这样的点M N 使得OM NM +的值最小 若存在 求出此时点N 的坐标 并加以说明；若不存在 则说明理由．参考答案： 1．（1）解：过点A 作2AH l ⊥于点H 如图所示：①点A 的坐标是(0,4) 点P 的坐标为(,)x y①4OA = ||OB x =①||AH OB x == 4BH OA ==①|4|HP y =-根据勾股定理 得()2222224816PA AH HP x y x y y =+=+-=+-+ 即22816PA x y y =+-+；（2）根据题意 可知点B 坐标为(,0)x①点P 在线段AB 的垂直平分线上①PA PB =①222816y x y y =+-+①2128y x =+ 2．（1）解：①OBC △是等腰直角三角形①,90BC AC C =∠=︒①2OB BC =①点B 的坐标是(0,2)①2OB =①22OB BC ==；①OAB是等腰直角三角形∠=∠OAB①ABP是等腰直角三角形ABP∠=∠∠=∠OBP四边形OAPB==BP OA点P的坐标为①ABP是等腰直角三角形∠=APB90∠=∠MPB在BPM△和APN中∠=∠=︒ANP BMP90≌△△BPM APNPMON是正方形；△△BPM≌①2AN t AN +=-①22t AN -=①22t OM ON +==①点P 的坐标为22,22t t ++⎛⎫⎪⎝⎭；故答案为：22t +；22t +（3）解：存在设点A 的坐标为()(),00m m ≥ 则OA m =①11222AOB S OA OB m m =⨯=⨯=由（2）①得：点P 的坐标为22,22m m ++⎛⎫ ⎪⎝⎭ 则22m OM +=根据题意得：90OMP AOB OAQ ∠=∠=∠=︒①四边形OAQM 是矩形①2,2m MQ OA m AQ OM +====①()2112122224ABQ m S AQ OA m m m +=⨯=⨯=+①AQB 的面积是AOB 的面积的3倍①()21234m m m +=解得：10m =或0（舍去）即存在点()10,0A 使得AQB 的面积是AOB 的面积的3倍． 3．（1）解：在3y x 中，当0x =时 3y = 当0y =时 03x =+ 解得3x =-①()30A -, ()0,3B①3OA OB ==①BAO ABO ∠=∠①90AOB ∠=︒①45BAO ABO ∠=∠=︒．（2）解：如图1 过点C 作CR y ⊥轴于点R ．Rt BCR 中，90BCR =︒-∠BR CR t ==-2BC BR =+COD AOB =∠在ACD 中，12S AD =⨯3）解：如图所示①90BOE ∠=︒ BF EF =①OF BF EF ==①FOE FEO ∠=∠设ADH a ∠=①45AEB a ∠=+︒①45FOE FEO a ∠=∠=+︒ 45AHD OAD ADH a ∠=∠-∠=︒- ①DH CG ∥①45CGO AHD a ∠=∠=︒-①454590CFO FOG FGO a a ∠=∠+∠=︒++︒-=︒取OC 的中点K 连接FK 交OB 于点P 过点F 作FL OB ⊥于点L过点K 分别作KM OB ⊥于点M KN FL ⊥交FL 的延长线于点N 连接KL ． ①四边形KMLN 是矩形；①90CFO ∠=︒ CK OK =①FK OK CK ==①BF OF = FL OB ⊥①BL OL =①KL BC ∥①45OLK OBC ∠=∠=︒①904545NLK NLO OLK ∠=∠-∠=︒-︒=︒①KM KN =①Rt Rt KOM KFN ≌△△①KOM KFN ∠=∠又①OPK FPL ∠=∠①90KOM OPK KFN FPL ∠+∠=∠+∠=︒①90OKP ∠=︒①FK OC ⊥①CF OF =①45CFK OFK ∠=∠=︒①45OCF ∠=︒①90COD ∠=︒ OC OD =在Rt ODS △中，()22223910()44OS OD DS =-=-= ①点D 的坐标为93,44⎛⎫-- ⎪⎝⎭． 4．1）解：如图所示 符合条件的ABC 有两个 分别为1AB C 2AB C 其中12(2,0)(8,0)B B --、；（2）点C 的坐标为(2,5)115|2(5)|57.522ABC S ∴=⨯---⨯==△． 5．（1）解：如下图 过点C 作CE y ⊥轴于点E 则CEA AOB ∠=∠①ABC 是等腰直角三角形①,90AC BA BAC =∠︒＝①90ACE CAE BAO CAE ∠+∠=︒=∠+∠①ACE BAO ∠=∠．在ACE △和BAO 中CEA AOB ACE BAO AC BA ∠=∠⎧⎪∠=∠⎨⎪=⎩①ACE BAO≌（AAS）①(0,1),(0,2)B A-①12BO AE AO CE====，①123OE=+=①2,3C-(）；（2）解：动点A在运动的过程中，+c d的值不变．理由如下：由（1）知ACE BAO≌①(0,1)B(0,)A a-①1,BO AE AO CE a====①1OE a=+①(,1)C a a--又①点C的坐标为(,)c d①11c d a a+=--=-即+c d的值不变；（3）解：存在一点P使PAB与ABC全等符合条件的点P的坐标是(4,)1-或(3,2)--或(2,1)-分为三种情况讨论：①如下图过点P作PE x⊥轴于点E则90PBA AOB PEB∠=∠=∠=︒①90,90EPB PBE PBE ABO∠+∠=︒∠+∠=︒①EPB ABO∠=∠在PEB△和BOA△中EPB OBAPEB BOAPB BA∠=∠⎧⎪∠=∠⎨⎪=⎩①PEB BOA△≌△（AAS）①1,3PE BO EB AO ====①314OE =+=即点P 的坐标是(4,)1-①如下图 过点C 作CM x ⊥轴于点M 过点P 作PE x ⊥轴于点E则90CMB PEB ∠=∠=︒．①CAB PAB △≌△①45,PBA CBA BC BP ∠=∠=︒=①90CBP ∠=︒①90,90MCB CBM CBM PBE ∠+∠=︒∠+∠=︒①MCB PBE ∠=∠在CMB 和BEP △中MCB EBP CMB BEP BC PB ∠=∠⎧⎪∠=∠⎨⎪=⎩①CMB BEP △≌△（AAS ）①,PE BM CM BE ==．①3,4),10C B -(（，）①2,413PE OE BE BO ==-=-=即点P 的坐标是(3,2)--；①如下图 过点P 作PE x ⊥轴于点E 则90BEP BOA ∠=∠=︒．①CAB PBA △≌△①,90AB BP CAB ABP =∠=∠=︒①90,90ABO PBE PBE BPE ∠+∠=︒∠+∠=︒①ABO BPE ∠=∠．在BOA △和PEB △中ABO BPE BOA PEB BA PB ∠=∠⎧⎪∠=∠⎨⎪=⎩①BOA PEB △≌△（AAS ）①1,3PE BO BE OA ====①312OE BE BO =-=-=即点P 的坐标是(2,1)-综上所述 符合条件的点P 的坐标是(4,)1-或(3,2)--或(2,1)-． 6．（1）三角形ABE 是等腰直角三角形AE AB ∴= 90EAB ∠=︒90FAE BAO ∴∠+∠=︒．EF x ⊥轴90EFA ∴∠=︒90AEF FAE ∴∠+∠=︒AEF OAB ∴∠=∠．90AOB ∠=︒EFA AOB ∴∠=∠．在AEF △和BAO 中,,,AEF BAO EFA AOBAE BA ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS AEF BAO ∴≌3AF BO ∴==235OF ∴=+=()5,0F ∴-；（2）不变 理由如下：如图2 作CF y ⊥轴于FC y OF ∴=90PFC CFO ∴∠=∠=︒90FPC FCP ∴∠+∠=︒．三角形APC 是等腰直角三角形 90APC ∠=︒ PA PC ∴=90APO OPC ∴∠+∠=︒．APO PCF ∴∠=∠．又90AOP PFC ∠=∠=︒．在AOP 和PFC △中,,,APO PCF AOP PFC PA CP ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS AOP PFC ∴△≌△AO PF ．2P C y y OP OF PF AO ∴-=-===；（3）AG PH OP =+ 证明如下：在OG 上取一点M 使MG OP = 连接HM 并延长交AP 的延长线于N 如图3所示()2,0A -2AO ∴=HG x ⊥轴于G (),2H m2HG ∴=AO HG ∴=90AOP HGM ∠=∠=︒ MG OP =()SAS APO HMG ∴△≌△PAO MHG ∴∠=∠ AP HM =AMN HMG ∠=∠90ANM HGM ∴∠=∠=︒90APC ∠=︒ PC AP =45PAC ∴∠=︒AHN ∴是等腰直角三角形45PAH MHA ∴∠=∠=︒又AP HM = AH HA =()SAS APH HMA ∴△≌△PH MA ∴=AG AM MG =+AG PH OP ∴=+．7．（1）解：()()4003A B ，，，4∴=OA 3OB =4312OA OB ⋅=⨯=∴；（2）解：如图，作CD x ⊥轴于点D 则90AOB CDA ∠=∠=︒90ACD CAD ∴∠+∠=︒90BAC ∠=︒90CAD BAO ∴∠+∠=︒ACD BAO ∴∠=∠在BAO 和ACD 中90AOB CDA ACD BAOAB CA ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()AAS BAO ACD ∴≌3AD OB ∴== 4CD OA ==437OD OA AD ∴=+=+=()74C ∴，；（3）解：如图BQ 平分ABy ∠ AQ 平分BAx ∠12ABQ ABy ∴∠=∠ 12BAQ BAx ∠=∠ABO∠+∴∠=ABy∴∠+ABQ(1180=︒21︒=-180∠+∠Q ABQ ∴∠=Q180 8．（1）解：作①()SAS CBO ABD ≌△△①AD OC = BCO BAD ∠=∠①BCO ABC BAD APC ∠+∠=∠+∠又90ABC ∠=︒①90APC ∠=︒ 即AD OC ⊥；（3）解：2OA BQ = 理由如下：作CF y ⊥轴于点F同理 ()AAS BAO CBF ≌△△ ①CF OB = BF OA =①90OB BD OBD =∠=︒，①=CF BD CF BD ∥①QCF QDB ∠=∠ 90QFC QBD ∠=∠=︒①()ASA QCF QDB ≌△△ ①BQ FQ =①1122BQ BF OA == 即2OA BQ =． 9．（1）解：如图，作AE OB ⊥于点E①()4,4A①4OE =①AOB 为等腰直角三角形 AE OB ⊥①=2=8OB OE①()8,0B ；①ACD 为等腰直角三角形AC DC =即ACF ∠+∠FDC ∠+∠ACF ∠=∠又①DFC ∠①()DFC CEA AAS ≌EC DF = FC =()4,4A4AE OE ===FC OE 即OF +①AOB 为等腰直角三角形45AOB ∠==AOD ∠∠AM FM -①()4,4A ①4AE OE ==又①==90EAN EOF ∠∠︒ AN OF =①()EAN EOF SAS ≌①=OEF AEN ∠∠ EF EN =又①EGH 为等腰直角三角形①45GEH ∠=︒ 即=45OEF OEM ∠+∠︒ ①=45AEN OEM ∠+∠︒又①90AEO ∠=︒①=45=NEM FEM ∠︒∠又①EM EM =①()NEM FEM SAS ≌①MN MF =①==AM MF AM MN AN --①=AM MF OF -即1AM FM OF-=．10．（1）解：把0x =代入24y x =-+得：4y =①点()04B ，①4OB =把0y =代入24y x =-+得：2x =①点()20A ，①2OA =①AOB DOC △≌△①(ASA OBN OCM ≌OM ON =分别过点M N 作ME①OFN OEM ∠=∠①BON COM OM ON ∠=∠=，①()AAS OFN OEM ≌①312OF OE FN EM ====， ①点N 的坐标为312⎛⎫ ⎪⎝⎭，； （3）解：直线CD 上存在点Q 使EPQ △是以E 为直角顶点的等腰三角形． ①()1E b ，为直线AB 上的点①2142b =-⨯+=①()12E ，①当点P 在点B 下方时 如图，连接DE 过点Q 作QM DE ⊥ 交DE 的延长线于M 点①()02D ，①DE y ⊥轴 1DE = 点M 的纵坐标为2 90M EDP ∠=∠=︒ ①EPQ △是以E 为直角顶点的等腰直角三角形①(AAS DEP MQE ≌1MQ DE ==Q 点的纵坐标为3把3y =代入12y x =+点()23Q ，；①()AAS EQM PEN ≌1EM PN ==()12E ，①M 点的纵坐标为1①Q 点的纵坐标为1把1y =代入122y x =+中得：2x =- ①()21Q -，； 综上所述 直线CD 上存在点Q 使得EPQ △是以E 为直角顶点的等腰直角三角形 Q 点的坐标为()23，或()21-，． 11．（1）解：()2430a b -+-= ()240a -≥ 30b -≥ 40a ∴-= 30b -=4a ∴= 3b =()()00A a B b ，、，4∴=OA 3OB =如图，过点C 作CN y ⊥轴于N则90BNC ∠=︒90ABC AOB ∠︒∠==90CBN ABO 90BAO ABO ∠+∠=︒ CBN BAO ∴∠=∠90BNC AOB ∠=∠=︒ BC AB =()AAS BNC AOB ∴≌4BN AO ∴== 3CN BO ==7ON OB BN ∴=+=()37C ∴，故答案为：()37，； （2）证明：如图，过E 作EF x ⊥轴于F 则90EFD ∠=︒a b =OA OB ∴=90AOB ∠=︒OAB ∴是等腰直角三角形45ABO BAO ∴∠=∠=︒BDE 是等腰直角三角形 90BDE ∠=︒BD DE ∴=90EDF BDO ∠+∠=︒ 90DEF EDF ∠+∠=︒ BDO DEF ∴∠=∠90EFD DOB ∠=∠=︒()AAS DEF BDO ∴≌EDF DBO ∴∠=∠ DF OB = EF OD = OB OA =DF OA ∴=DF AD OA OD ∴+=+ 即AF OD =AF EF ∴=AEF ∴是等腰直角三角形45EAF AEF ∴∠=∠=︒45EDF EAF AED AED ∠=∠+∠=︒+∠ 45DBO OBA ABD ABD ∠=∠+∠=︒+∠ ABD AED ∴∠=∠；（3）解：如图，过点D 作DM y ⊥轴于M DH x ⊥轴于H DG BA ⊥交BA 的延长线于G()33D -，3DM DH OM OH ∴====BD 平分ABO ∠ ⊥DM OB DG AB ⊥DM DG ∴=BD BD =()Rt Rt HL BDG BDM ∴≌同理可得：()Rt Rt HL ADH ADG ≌AH AG ∴=OA a = OB b = AB c =a b c OA OB AB ∴-+=-+()()()OH AH BM OM BG AG =+--+-33AH BM BG AG =+-++-6=即6a b c -+=．12．（1）解：①点A 关于x 轴的对称点为P 点 ①点P 的坐标为(0,)a -；由垂线段最短 当PB l ⊥时 PB 最短 过点B 作BD y ⊥轴于D 点 如图①直线l 平分坐标系的第二 四象限①45BOD ∠=︒①PB l ⊥①45BOD OPB ∠=∠=︒①OBP 是等腰直角三角形 OB PB =①BD y ⊥轴 OP a =22⎝⎭a a⎛⎫①()ACF QCB SAS △≌△①QB AF AE == QB AF ∥①180QBA BAF ∠+∠=︒又①90EAF BAO ∠=∠=︒①180BAF EAO ∠+∠=︒①QBA EAO ∠=∠又①BA AO =①(SAS)QBA EAO ≌△△①2OE AQ AC == BAQ AOE ∠=∠①90AOE GAO GAO BAQ ∠+∠=∠+∠=︒ ①90AGO ∠=︒①OE AC ⊥13．（1）OB OC = 8BC =4OB OC ∴==4OA OB ==()0,4A ∴故答案为：0 4；（2）4OC =()4,0C ∴．PC BC ⊥()4,P t ∴4OA OB OC ∴=== PC t =①当08t ≤<时 如图1PAB AOB BCP AOCP S S S S =+-梯形PAB PBC AOB SS S S =--梯形1122BC PC OA OB =⨯-⨯(1118444t =⨯⨯-⨯⨯-PAB S ⎧-⎪=⎨⎪⎩是等腰直角三角形；延长PD 至ADP 是等腰直角三角形AD ∴垂直平分AP AH ∴=90BAC ∠=︒BAH PAC ∴∠=∠在ABH 和ACP △中AH AP BAH CAP AB AC =⎧⎪∠=∠⎨⎪=⎩()SAS ABH ACP ∴≌45ABH ACP ∴∠=∠=︒ BH PC =45ABC ∠=︒∴点H 在BC 上点D 是BD 的中点BD QB ∴=在PDQ 和HDB 中DP DH PDQ HDB BD QD =⎧⎪∠=∠⎨⎪=⎩()SAS PDQ HDB ∴≌PQ BH ∴∥ PQ BH =BH PC =PC PQ ∴=PQ BC ∥ 90BCP ∠=︒90CPQ BCP ∴∠=∠=︒PAQ ∴是等腰直角三角形；14．（1）解：作QG l ⊥于点G①(0,2)A (3,0)B①2AO = 3BO =①AP PQ = 90APQ ∠=︒①90APO APG QPG ∠=︒-∠=∠①APO QPG ≌△△①2QG AO == 3BG BO ==①点Q 的坐标是()53，故答案为：()53，； （2）解：当点Q 在于直线l 上时 如图2223P Q AP OB ===①点2Q 的坐标是()35，由（1）知点1Q 的坐标是()53，设点Q 所在直线的解析式为y kx b =+则5335k b k b +=⎧⎨+=⎩ 解得18k b =-⎧⎨=⎩①点Q 所在直线的解析式为8y x =-+；（3）解：如图，作PM OA ⊥于M QN MP ⊥于N①90APQ ∠=︒①四边形OBPM 是矩形PA PQ = 90APQ ∠=︒①90APM QPN ∠+∠=︒ 90QPN PQN ∠+∠=︒APM PQN ∴∠=∠在PAM △和QPN 中AMP PNQ APM PQN AP PQ ∠=∠⎧⎪∠=∠⎨⎪=⎩PAM QPN ∴≌△△QN PM ∴= AM PN =①点Q 的坐标为(,)x y①MN x = 3PN x =- 3PB y QN y PM y =-=-=- ()2223AM OM PB y =-=-=--①AM PN =①()233y x --=-整理得8y x =-+．15．（1）①()6,0A -①6OA =；①45ABO ∠=︒①6OB OA ==①()0,6B11661822ABO S OA OB ==⨯⨯=． （2）过点E 作EF x ⊥轴①90EDB ∠=︒①90FED ODB FDE ∠=∠=︒-∠①FED ODB EFD DOB ED DB ∠=∠⎧⎪∠=∠⎨⎪=⎩①()AAS EFD DOB ≌①(ASA AGH AOH ≌6AG AO == OH ①O G 是对称点故OM GM =根据垂线段最短故OM NM +最小①()6,0A -①6OA =；①45ABO ∠=︒①6OB OA == 45BAO ∠=︒ ①45AGN ∠=︒①AN GN =①222236AN GN AN +== 解得32,32AN AN ==-（舍去） ①632ON OA AN =-=-． 故()326,0N -．。

中考数学压轴题专题训练-----方程、不等式中的含参问题例1．已知三个非负实数a ，b ，c 满足：3a ＋2b ＋c ＝5和2a ＋b －3c ＝1，若m ＝3a ＋b －7c ，则m 的最小值为__________．同类题型1.1 已知x ＋2y －3z ＝0，2x ＋3y ＋5z ＝0，则＝________．x ＋y ＋z x －y ＋z同类题型 1.2 方程组的解x ，y 满足x ＞y ，则m 的取值范围是{4x ＋3m ＝28x －3y ＝m )（ ）A ．B ．C ．D ．m ＞ 910m ＞ 109m ＞ 1910m ＞ 1019例2．关于x 的方程＋mx －9＝0和＋6m ＝0有公共根，则m 的值为________．x x －3x ＋m 同类题型2.1 已知a 是一元二次方程－2018x ＋1＝0的一个根，则代数式的值是___．x a －2017a ＋ 2018a ＋1同类题型2.2 已知关于x 的方程＋（2k －1）x ＋1＝0有两个不相等的实数根，那么实数k 的取值（k －1）x 范围为_____________．同类题型2.3 已知α、β是方程－2x －4＝0的两个实数根，则＋8β＋6的值为（ ）x αA ．－1 B ．2 C ．22 D ．30例3．已知方程的两根分别为a ，，则方程的根是（ ）x ＋ 1x ＝a ＋ 1a 1a x ＋ 1x －1＝a ＋ 1a －1A ．a ，B ．，a －1C ．，a －1D ．a ，1a －11a －11a a a －1同类题型3.1 若关于x 的方程＝3的解是非负数，则b 的取值范围是________．2x －b x －1同类题型3.2 观察分析下列方程：①＝3；②＝5；③＝7．请利用它们所蕴含的规律，求x ＋ 2x x ＋ 6x x ＋ 12x关于x 的方程＝2n ＋5（n 为正整数）的根，你的答案是_________________．x ＋ n ＋n x －4同类题型 3.3 已知关于x 的方程只有整数解，则整数a 的值为2x －1－ a ＋1x ＋2＝ 3a (x －1)(x ＋2)_____________．例4．[x ]表示不超过x 的最大整数．如，[π]＝3，[2]＝2，[－2.1]＝－3．则下列结论：①[－x ]＝－[x ]；②若[x ]＝n ，则x 的取值范围是n ≤x ＜n ＋1；③当－1＜x ＜1时，[1＋x ]＋[1－x ]的值为1或2；④x ＝－2.75是方程4x －2[x ]＋5＝0的唯一一个解．其中正确的结论有_________（写出所有正确结论的序号）．同类题型4.1 设[x ]表示不大于x 的最大整数，{x }表示不小于x 的最小整数，（x ）表示最接近x 的整数（x ≠n ＋0.5，n 为整数）．例如[3.4]＝3，{3.4}＝4，（3.4）＝3．则不等式8≤2x ＋[x ]＋3{x }＋4（x ）≤14的解为（ ）A ．0.5≤x ≤2B ．0.5＜x ＜1.5或1.5＜x ＜2C ．0.5＜x ＜1.5D ．1.5＜x ＜2同类题型4.2规定：[x ]表示不大于x 的最大整数，（x ）表示不小于x 的最小整数，[x ）表示最接近x 的整数（x ≠n ＋0.5，n 为整数），例如：[2.3]＝2，（2.3）＝3，[2.3）＝2．则下列说法正确的是___________．（写出所有正确说法的序号）①当x ＝1.7时，[x ]＋（x ）＋[x ）＝6；②当x ＝－2.1时，[x ]＋（x ）＋[x ）＝－7；③方程4[x ]＋3（x ）＋[x ）＝11的解为1＜x ＜1.5；④当－1＜x ＜1时，函数y ＝[x ]＋（x ）＋x 的图象与正比例函数y ＝4x 的图象有两个交点．同类题型4.3 如果关于x 的不等式（a ＋b ）x ＋2a －b ＞0的解集是，那么关于x 的不等式（b －a ）x x ＜ 52＋a ＋2b ≤0的解集是____________．同类题型4.4 若关于x 的不等式组解集为x ＜2，则a 的取值范围是___________．{x ＋43＞ x 2＋1x －a ＜0)同类题型4.5 按如图的程序计算，若开始输入的值x 为正数，最后输出的结果为656，则满足条件的x 的不同值最多有___________．参考答案例1．已知三个非负实数a ，b ，c 满足：3a ＋2b ＋c ＝5和2a ＋b －3c ＝1，若m ＝3a ＋b －7c ，则m 的最小值为__________．解：由题意可得，{3a ＋2b ＋c ＝52a ＋b －3c ＝1m ＝3a ＋b －7c )解得－3，，，a ＝7﹒(m ＋2)3b ＝7－11﹒(m ＋2)3c ＝m ＋23由于a ，b ，c 是三个非负实数，∴a ≥0，b ≥0，c ≥0，∴．－111≥m ≥－57所以m _(最小值)＝．－57故本题答案为：－．57同类题型1.1 已知x ＋2y －3z ＝0，2x ＋3y ＋5z ＝0，则＝________．x ＋y ＋z x －y ＋z解：由题意得：，{x ＋2y －3z ＝0①2x ＋3y ＋5z ＝0②)①×2－②得y ＝11z ，代入①得x ＝－19z ，原式．＝x ＋y ＋z x －y ＋z ＝－19z ＋11z ＋z －19z －11z ＋z ＝729同类题型1.2 方程组的解x ，y 满足x ＞y ，则m 的取值范围是（ ）{4x ＋3m ＝28x －3y ＝m )A ．B ．C ．D ．m ＞ 910m ＞ 109m ＞ 1910m ＞ 1019解：{4x ＋3m ＝2①8x －3y ＝m ②)由①得，代入②得，－3y ＝m ，．x ＝2－3m 48×2－3m 4y ＝4－7m 3∵x ＞y ，即，解得．2－3m 4＞4－7m 3m ＞1019选D ．例2．关于x 的方程＋mx －9＝0和＋6m ＝0有公共根，则m 的值为________．x x －3x ＋m 解：设这个公共根为α．则方程＋mx －9＝0的两根为α、－m －α；方程＋6m ＝0的两根为α、3－α，x x －3x ＋m 由根与系数的关系有：α（－m －α）＝－9，＋6m ，α（3－α）＝m 整理得，＋mα＝9①，＋6m ＝0②，αα－3α＋m ②－①得，＋6m －3α－mα＝－9，m 即－α（m ＋3）＝0，（m ＋3）（m ＋3）（m ＋3－α）＝0，所以m ＋3＝0或m ＋3－α＝0，解得m ＝－3或α＝m ＋3，把α＝m ＋3代入①得，＋m （m ＋3）＝9，（m ＋3）＋3m ＝9，m ＋6m ＋9＋m m （2m ＋9）＝0，所以m ＝0或2m ＋9＝0，解得m ＝0或m ＝－4.5，综上所述，m 的值为－3，0，－4.5．同类题型2.1 已知a 是一元二次方程－2018x ＋1＝0的一个根，则代数式的值是___．x a －2017a ＋2018a ＋1解：由题意，把根a 代入－2018x ＋1＝0，可得：－2018a ＋1＝0，x a ∴－2017a －a ＋1＝0，＋1＝2018a ；a a ∴－2017a ＝a －1，a ∴－1a －2017a ＋2018a ＋1＝a －1＋20182018a ＝a ＋1a－1＝a ＋1a －1＝2018a a＝2018－1，＝2017．同类题型2.2 已知关于x 的方程＋（2k －1）x ＋1＝0有两个不相等的实数根，那么实数k 的取值（k －1）x 范围为_____________．解：由题意知，k ≠±1，－1）＝5－4k ＞0△＝（2k －1）－4（k ∴且k ≠±1．k ＜54同类题型2.3 已知α、β是方程－2x －4＝0的两个实数根，则＋8β＋6的值为（ ）x αA ．－1 B ．2 C ．22 D ．30解：∵α、β是方程－2x －4＝0的两个实数根，x ∴α＋β＝2，－2α－4＝0，α∴＝2α＋4α∴＋8β＋6α＋8β＋6＝α﹒α＝α﹒（2α＋4）＋8β＋6＋4α＋8β＋6＝2α＝2（2α＋4）＋4α＋8β＋6＝8α＋8β＋14＝8（α＋β）＋14＝30，故选D ．例3．已知方程的两根分别为a ，，则方程的根是（ ）x ＋ 1x ＝a ＋ 1a 1a x ＋ 1x －1＝a ＋ 1a －1A ．a ，B ．，a －1C ．，a －1D ．a ，1a －11a －11a a a －1解：方程可以写成的形式，x ＋1x －1＝a ＋1a －1x －1＋1x －1＝a －1＋1a －1∵方程的两根分别为a ，，x ＋1x ＝a ＋1a 1a∴方程的两根的关系式为x －1＝a －1，，即方程的根为x ＝a 或x －1＋1x －1＝a －1＋1a －1x －1＝1a －1a a －1，∴方程的根是a ，．x ＋1x －1＝a ＋1a －1a a －1选D ．同类题型3.1 若关于x 的方程＝3的解是非负数，则b 的取值范围是________．2x －b x －1解：去分母得，2x －b ＝3x －3∴x ＝3－b∵x ≥0∴3－b ≥0解得，b ≤3又∵x －1≠0∴x ≠1即3－b ≠1，b ≠2则b 的取值范围是b ≤3且b ≠2．同类题型3.2 观察分析下列方程：①＝3；②＝5；③＝7．请利用它们所蕴含的规律，求x ＋ 2x x ＋ 6x x ＋ 12x关于x 的方程＝2n ＋5（n 为正整数）的根，你的答案是_________________．x ＋ n ＋n x －4解：＝3，解得：x ＝2或x ＝1；x ＋1×2x＝5，解得：x ＝2或x ＝3；x ＋2×3x＝7，解得：x ＝3或x ＝4，x ＋3×4x得到规律＝m ＋n 的解为：x ＝m 或x ＝n ，x ＋mn x所求方程整理得：＝2n ＋1，x －4＋n (n ＋1)x －4根据规律得：x －4＝n 或x －4＝n ＋1，解得：x ＝n ＋4或x ＝n ＋5．同类题型 3.3 已知关于x 的方程只有整数解，则整数a 的值为2x －1－ a ＋1x ＋2＝ 3a (x －1)(x ＋2)_____________．解：方程两边同乘以（x －1）（x ＋2），得：2（x ＋2）－（a ＋1）（x －1）＝3a ，解得：，x ＝2a －51－a ＝－2－31－a∵方程只有整数解，∴1－a ＝3或1或－3或－1，当1－a ＝3，即a ＝－2时，x ＝－2－1＝－3，检验，将x ＝－3代入（x －1）（x ＋2）＝4≠0，故x ＝－3是原分式方程的解；当1－a ＝1，即a ＝0时，x ＝－2－3＝－5，检验，将x ＝－5代入（x －1）（x ＋2）＝18≠0，故x ＝－7是原分式方程的解；当1－a ＝－3，即a ＝4时，x ＝－2＋1＝－1，检验，将x ＝－1代入（x －1）（x ＋2）＝－2≠0，故x ＝－1是原分式方程的解；当1－a ＝－1，即a ＝2时，x ＝1，检验，将x ＝1代入（x －1）（x ＋2）＝0，故x ＝1不是原分式方程的解；∴整数a 的值为：－2，0或4．例4．[x ]表示不超过x 的最大整数．如，[π]＝3，[2]＝2，[－2.1]＝－3．则下列结论：①[－x ]＝－[x ]；②若[x ]＝n ，则x 的取值范围是n ≤x ＜n ＋1；③当－1＜x ＜1时，[1＋x ]＋[1－x ]的值为1或2；④x ＝－2.75是方程4x －2[x ]＋5＝0的唯一一个解．其中正确的结论有_________（写出所有正确结论的序号）．解：①当x ＝－3.5时，[－3.5]＝－4，－[x ]＝－3，不相等，故原来的说法错误；②若[x ]＝n ，则x 的取值范围是n ≤x ＜n ＋1是正确的；③当－1＜x ＜0时，[1＋x ]＋[1－x ]＝0＋1＝1；当x ＝0时，[1＋x ]＋[1－x ]＝1＋1＝2；当0＜x ＜1时，[1＋x ]＋[1－x ]＝1＋0＝1；故当－1＜x ＜1时，[1＋x ]＋[1－x ]的值为1或2是正确的；④x －[x ]的范围为0～1，4x －2[x ]＋5＝0，－5≤2x ＜－7，即－2.5≤x ＜－3.5，x ＝－2.75或x ＝－3.25都是方程4x －2[x ]＋5＝0，故原来的说法错误．故答案为：②③．同类题型4.1 设[x ]表示不大于x 的最大整数，{x }表示不小于x 的最小整数，（x ）表示最接近x 的整数（x ≠n ＋0.5，n 为整数）．例如[3.4]＝3，{3.4}＝4，（3.4）＝3．则不等式8≤2x ＋[x ]＋3{x }＋4（x ）≤14的解为（ ）A ．0.5≤x ≤2B ．0.5＜x ＜1.5或1.5＜x ＜2C ．0.5＜x ＜1.5D ．1.5＜x ＜2解：根据题意得：x ＞0，若x ≥2，则2x ≥4，[x ]≥2，3{x }≥6，4（x ）≥8，不等式不成立．故只需分析0＜x ＜2时的情形即可，①0＜x ≤0.5时，不等式可化为：8≤2x ＋0＋3＋0≤14，解得：2.5≤x ≤5.5，不符合不等式；②当0.5＜x ≤1时，不等式可化为：8≤2x ＋0＋3＋4≤14，解得：0.5≤x ≤3，因此0.5＜x ≤1，符合不等式；③当1＜x ＜1.5时，不等式可化为：8≤2x ＋1＋6＋4≤14，解得：－1.5≤x ≤1.5，因此1＜x ＜1.5，符合不等式；④当1.5＜x ＜2时，不等式可化为：8≤2x ＋1＋6＋8≤14，解得：－3.5≤x ≤－0.5，不符合不等式．故原不等式的解集为：0.5＜x ＜1.5．故选C ．同类题型4.2规定：[x ]表示不大于x 的最大整数，（x ）表示不小于x 的最小整数，[x ）表示最接近x 的整数（x ≠n ＋0.5，n 为整数），例如：[2.3]＝2，（2.3）＝3，[2.3）＝2．则下列说法正确的是___________．（写出所有正确说法的序号）①当x ＝1.7时，[x ]＋（x ）＋[x ）＝6；②当x ＝－2.1时，[x ]＋（x ）＋[x ）＝－7；③方程4[x ]＋3（x ）＋[x ）＝11的解为1＜x ＜1.5；④当－1＜x ＜1时，函数y ＝[x ]＋（x ）＋x 的图象与正比例函数y ＝4x 的图象有两个交点．解：①当x ＝1.7时，[x ]＋（x ）＋[x ）＝[1.7]＋（1.7）＋[1.7）＝1＋2＋2＝5，故①错误；②当x ＝－2.1时，[x ]＋（x ）＋[x ）＝[－2.1]＋（－2.1）＋[－2.1）＝（－3）＋（－2）＋（－2）＝－7，故②正确；③4[x ]＋3（x ）＋[x ）＝11，7[x ]＋3＋[x ）＝11，7[x ]＋[x ）＝8，1＜x ＜1.5，故③正确；④∵－1＜x ＜1时，∴当－1＜x ＜－0.5时，y ＝[x ]＋（x ）＋x ＝－1＋0＋x ＝x －1，当－0.5＜x ＜0时，y ＝[x ]＋（x ）＋x ＝－1＋0＋x ＝x －1，当x ＝0时，y ＝[x ]＋（x ）＋x ＝0＋0＋0＝0，当0＜x ＜0.5时，y ＝[x ]＋（x ）＋x ＝0＋1＋x ＝x ＋1，当0.5＜x ＜1时，y ＝[x ]＋（x ）＋x ＝0＋1＋x ＝x ＋1，∵y ＝4x ，则x －1＝4x 时，得；x ＋1＝4x 时，得；当x ＝0时，y ＝4x ＝0，x ＝－13x ＝13∴当－1＜x ＜1时，函数y ＝[x ]＋（x ）＋x 的图象与正比例函数y ＝4x 的图象有三个交点，故④错误，故答案为：②③．同类题型4.3 如果关于x 的不等式（a ＋b ）x ＋2a －b ＞0的解集是，那么关于x 的不等式（b －a ）x x ＜ 52＋a ＋2b ≤0的解集是____________．解：∵关于x 的不等式（a ＋b ）x ＋2a －b ＞0的解集是，x ＜52∴，x ＜b －2a a ＋b∴，且a ＋b ＜0，b －2a a ＋b ＝52即b ＝－3a ，a ＋b ＜0，∴a －3a ＜0，即a ＞0，∴b －a ＝－4a ＜0，∴关于x 的不等式（b －a ）x ＋a ＋2b ≤0的解集是，x ≥－a －2b b －a∵，－a －2b b －a ＝－a ＋6a －3a －a ＝－54∴关于x 的不等式（b －a ）x ＋a ＋2b ≤0的解集是．x ≥－54同类题型4.4 若关于x 的不等式组解集为x ＜2，则a 的取值范围是___________．{x ＋43＞ x 2＋1x －a ＜0)解：由＋1，得x ＋43＞x 22x ＋8＞3x ＋6，解得x ＜2，由x －a ＜0，得x ＜a ，又因关于x 的不等式组解集为x ＜2，{x ＋43＞x 2＋1x －a ＜0)所以a ≥2．同类题型4.5 按如图的程序计算，若开始输入的值x 为正数，最后输出的结果为656，则满足条件的x 的不同值最多有___________．解：∵最后输出的数为656，∴5x ＋1＝656，得：x ＝131＞0，∴5x ＋1＝131，得：x ＝26＞0，∴5x ＋1＝26，得：x ＝5＞0，∴5x ＋1＝5，得：x ＝0.8＞0；∴5x ＋1＝0.8，得：x ＝－0.04＜0，不符合题意，故x 的值可取131，26，5，0.8共4个．。

冲刺专题6：第12和18题专题训练一、工具法例1.如图，将正方形ABCD折叠，使顶点A与CD边上的一点H重合（H不与端点C，D重合），折痕交AD 于点E，交BC于点F，边AB折叠后与边BC交于点G．设正方形ABCD的周长为m，△CHG的周长为n，则的值为（）A．B． C．D．随H点位置的变化而变化例1 变式1变式1：点P是正方形ABCD边AB上一点（不与A、B重合），连接PD并将线段PD绕点P顺时针旋转90°，得线段PE，连接BE，则∠CBE等于（）A．75° B．60° C．45° D．30°二、极值法例2.若对于任意非零实数a，抛物线y＝a（x+2）（x﹣1）总不经过点P（x0﹣3，x0﹣5），则符合条件的点P（）A．有1个B．有2个C．有3个D．有无穷多个变式2：在平面直角坐标系xOy中，已知点M，N的坐标分别为（﹣1，2），（2，1），若抛物线y＝ax2﹣x+2（a＜0）与线段MN有一个交点，则a的取值范围是（）A．a≤﹣1 B．﹣1＜a＜0 C．a＜﹣1 D．﹣1≤a＜0三、特殊值法例3.若实数a，b满足ab＝1，设M＝，N＝，则M，N的大小关系是（）A．M＞N B．M＝N C．M＜N D．不确定变式3：无论m为何值，二次函数y＝x2+（2﹣m）x+m的图象总经过定点．四、特殊位置法：特殊点，特殊线，特殊角，特殊模型例4.如图，已知点A（12，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD＝AD＝8时，这两个二次函数的最大值之和等于（）变式4：（1）如图，在菱形ABCD和菱形BEFG中，点A、B、E在同一直线上，P是线段DF的中点，连接PG，PC．若∠ABC＝∠BEF＝60°，则＝（）A． B． C． D．（2）如图，E是边长为4的正方形ABCD的对角线BD上一点，且BE＝BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BR于点R，则PQ+PR的值是（）A．2B．2 C．2D．五、排除法例5.如图，△ABC中，∠ACB＝90°，AB＝10，tanA＝．点P是斜边AB上一个动点．过点P作PQ⊥AB，垂足为P，交边AC（或边CB）于点Q，设AP＝x，△APQ的面积为y，则y与x之间的函数图象大致为（）A．B．C．D．例5 变式5变式5：如图，直线y＝kx+b（k≠0）与抛物线y＝ax2（a≠0）交于A，B两点，且点A的横坐标是﹣2，点B的横坐标是3，则以下结论：①抛物线y＝ax2（a≠0）的图象的顶点一定是原点；②x＞0时，直线y＝kx+b（k≠0）与抛物线y＝ax2（a≠0）的函数值都随着x的增大而增大；③AB的长度可以等于5；④△OAB有可能成为等边三角形；⑤当﹣3＜x＜2时，ax2+kx＜b，其中正确的结论是（）A．①②④B．①②⑤C．②③④D．③④⑤六、转化法例6.如图，△ABC中，AB＝AC＝10，tanA＝2，BE⊥AC于点E，D是线段BE上的一个动点，则CD+BD 的最小值是．（1）如图，在△ABC中，∠BAC＝60°，∠ACB＝75°，AB＝2，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB、AC于点E、F，连接EF，则线段EF长度的最小值为．（2）如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A′B′C，M是BC的中点，P是A′B′的中点，连接PM，若BC＝2，∠BAC＝30°，则线段PM的最小值是．例6变式6（1）变式6（2）七、综合分析法例7.已知抛物线y＝ax2+bx+c（b＞a＞0）与x轴最多有一个交点，现有以下四个结论：①该抛物线的对称轴在y轴左侧；②关于x的方程ax2+bx+c+2＝0无实数根；③a﹣b+c≥0；④的最小值为3．其中，正确结论的个数为（）A．1个B．2个C．3个D．4个变式7：如图，正方形ABCD的边长为4，点E、F分别从点A、点D以相同速度同时出发，点E从点A向点D运动，点F从点D向点C运动，点E运动到D点时，E、F停止运动．连接BE、AF相交于点G，连接CG．有下列结论：①AF⊥BE；②点G随着点E、F的运动而运动，且点G的运动路径的长度为π；③线段DG的最小值为2﹣2；④当线段DG最小时，△BCG的面积S＝8+．其中正确的命题有．（填序号）八、特征分析法例8．如图，在平面直角坐标系中，OA＝AB，∠OAB＝90°，反比例函数y＝（x＞0）的图象经过A，B 两点．若点A的坐标为（n，1），则k的值为（）A．B．C．D．变式8：如图，两个反比例函数y＝和y＝﹣的图象分别是l1和l2．设点P在l1上，PC⊥x轴，垂足为C，交l2于点A，PD⊥y轴，垂足为D，交l2于点B，则三角形PAB的面积为（）A．3 B．4 C．D．5例8变式8。

【中考压轴题专题训练】PISA 专题训练（解析版）选择题（本大题有30小题，每小题5分，共150分）下面每小题给出的四个选项中，只有一个是正确的.1．如图，在矩形ABCD 中，AB =2BC ，M 是边CD 的中点，E ，F 分别是边AB ，BC 上的点，且AF ⊥ME ，垂足为点G.若EB =2，BF =1，则GE MG 的值为（ ）A ．13B ．310C ．25D ．12【答案】B【解析】过M 作MH ⊥AB 于H ，如图所示则∠MHE=∠ABF=90°∵ME ⊥AF∴∠FAE+∠GEA=90°又∠HME+∠GEA=90°∴∠FAE=∠HME∴△ABF ∽△MHE∴AB MH =BF EH =AF ME∵AB=2BC ，M 为CD 中点∴设BC=x ，则AB=2x ，CM=BH=AH=x ，MH=BC=x∴2x x =1EH =AF ME解得：EH=12∴BH=BE+EH=52，AE=3在Rt △ABF 中，由勾股定理得：AF=√52+12=√26在Rt △MEH 中，由勾股定理得：ME=√(52)2+(12)2=√262由∠GAE=∠BAF ，∠AGE=∠ABF=90°得：△AEG ∽△AFB∴AE AF =EG BF =AG AB ∴3√26=EG1 解得：EG=3√2626∴MG=ME －EG=5√2613∴GE MG =3√26265√2613=310故答案为：B.2．如图，正方形ABCD 被分成五个面积相等的矩形，若FG=4，则正方形的面积为（ ）A ．64B ．2254C ．49D ．36【答案】B【解析】设KJ=LI=x ，∵正方形ABCD 被分成五个面积相等的矩形，∴IF=JG=KJ=LI=x ，∴EB=2x ，又∵FG=4，∴EB·EL=2x·EL=AE·EK=KJ·FG=4x ，∴EL=2，EK=2+4=6，∴AE=23x ，∴CD=AB=AE+BE=23x+2x=83x ， ∴4x=CG·CD=CG·83x ，∴CG=32，∴BC=EL+FG+GC=2+4+32=152，∴正方形ABCD 的面积=BC 2=（152）2=2254.故答案为：B.3．两个全等的矩形ABCD和矩形BEFG如图放置，且FG恰好过点C. 过点G作MN平行AD交AB，CD于M，N. 知道下列哪个式子的值，即可求出图中阴影部分的面积()A．CF⋅CD B．CF⋅CN C．CF⋅CG D．CF⋅CB【答案】A【解析】如图，作CH⊥BE于点H.阴影部分面积= S矩形ABCD−S矩形BCNM=S矩形ABCD−2S△BCG=S矩形BEFG−S矩形BHCH=S矩形CHEF= CF·EF=CF·CD故答案为： A.4．在矩形ABCD内，将两张边长分别为a和b(a>a)的正方形纸片按图①，图②两种方式放置（图①，图②中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，若图①中阴影部分面积为S1，图②中阴影部分的面积和为S2.则S1−S2的值表示正确的是（）A．BE⋅FG B．MN⋅FG C．BE⋅GD D．MN⋅GD【答案】A【解析】∵S1=（AB-a）•a+（CD-b）（AD-a）=（AB-a）•a+（AB-b）（AD-a），S2=（AB-a）（AD-b）+（AD-a）（AB-b），∴S1-S2=（AB-a）•a+（AB-b）（AD-a）-（AB-a）（AD-b）-（AD-a）（AB-b）=（AB-a ）•a -（AB-a ）（AD-b ）=（AB-a ）•（a-AD+b ）=BE•FG故答案为：A.5．用面积为1，3，4，8的四张长方形纸片拼成如图所示的一个大长方形， 则图中阴影的面积为( )A ．23B ．43C ．1112D ．116【答案】A 【解析】设面积为1的长方形长为a ，宽为b ，则ab=1，∴面积为3的长方形宽为a ，长为3a， ∵面积为4的长方形和面积为8的长方形的长相等，∴它们的宽之比为1：2，∴面积为4的长方形的宽=13×（b+3a ）=ab+33a =43a ，长=443a=3a ， 两个阴影三角形的底=43a-b ， ∴整个阴影部分面积=两个阴影三角形的面积之和=12×（43a -b ）（3a+a ）=23ab=23. 故答案为：A.6．由四个全等的直角三角形和一个小正方形组成的大正方形ABCD 如图所示.作EM ∥NG ∥AD .若GF =2FM ，则MN ：FD 的值为（ ）A ．2√33B ．√52C ．54D ．1【答案】B【解析】连结CF ，设AF=a ，DF=b ，∵ME ∥AD ，∴△FME ∽△FAD ，∴FM FA =FE FD ，即FD FA =FE FM =2FM FM=2， ∴DF=2AF ，∴b=2a ，∵AF=DE=HC=BG=a ，∴FE=GF=GH=EH=AG-AF=2a-a=a ，∴点E 为DF 的中点，∵CE ⊥DF ，∴CF=CD ，∵四边形FGHE 为正方形，∴GF ∥EH ，即MG ∥NE ，又∵ME ∥GM ，∴四边形MGNE 为平行四边形，∴GM=EN ，∵GF=EH ，∴MF=HN=12FG =12a ， ∴NC=CH-HN=a −12a =12a ， ∴MF=CN ，且MF ∥CN ，∴四边形MFCN 为平行四边形，∴MN=FC=DC ，在Rt △AFD 中，AD=√AF 2+DF 2=√a 2+4a 2=√5a ，∴MN=CD=AD=√5a ，∴MN ：DF=√5a ：2a =√5：2=√52.7．如图，图中小正方形的组合图形是棱长为1的正方体一种表面展开图，过小正方形的顶点A ，B ，C ，D 的线段AB ，CD 与经过小正方形的顶点E ，F 的直线交于点M ，N ，则线段MN 的长为（ ）A ．2√2B ．1+√2C ．52D ．74√2 【答案】D 【解析】如图所示，以点A 为原点，AE 所在的直线为x 轴建立平面直角坐标系，则点E 的坐标为（2，0），点D 的坐标为（1，2），点F 的坐标为（3，1），点B 的坐标为（3，-1），点C 的坐标为（4，1），设直线CD 的解析式为y =kx +b ，∴{k +b =24k +b =1， ∴{k =−13b =73， ∴直线CD 的解析式为y =−13x +73， 同理求出直线EF 的解析式为y =x −2，直线AB 的解析式为y =−13x ， 联立{y =−13x y =x −2，解得{x =32y =−12， ∴点M 的坐标为(32，−12) ，联立{y =−13x +73y =x −2，解得{x =134y =54， ∴点N 的坐标为(134，54) ，∴MN =√(32−134)2+(−12−54)2=7√24.8．如图，在Rt△ABC中，∠ACB=90∘，分别以该直角三角形的三边为边，并在直线AB同侧作正方形ABMN，正方形BQPC，正方形ACEF，且点N恰好在正方形ACEF的边EF上.其中S1，S2，S3，S4，S5表示相应阴影部分面积，若S3＝1，则S1+S2+S4+S5=（）A．2B．2√3C．3D．3√52【答案】C【解析】如图，连接MQ，作MG⊥EC于G，设PC交BM于T，MN交EC于W.∵∠ABM＝∠CBQ＝90°，∴∠ABC＝∠MBQ，∵BA＝BM，BC＝BQ，∴△ABC≌△MBQ（SAS），∴∠ACB＝∠BQM＝90°，∵∠PQB＝90°，∴M，P，Q共线，∵四边形CGMP是矩形，∴MG＝PC＝BC，∵∠BCT＝∠MGB＝90°，∴∠BTC＋∠CBT＝90°，∠BWM＋∠CBT＝90°，∴∠BWM＝∠BTC，∴△MGW≌△BCT（AAS），∴MW＝BT，∵MN＝BM，∴NW＝MT，可证△NWE≌MTP，∴S1＋S5＝S3＝1，∵∠F=∠ACB=90°，AF=AC，AN=AB，∴Rt△ANF≌Rt△ABC（HL），∴S2=S3=1，∵AC2＋BC2＝AB2，∴S1＋S2＋S左空＋S右空＋S5＝S3＋S4＋S左空＋S右空，∴S1＋S2＋S5＝S3＋S4，∴S2＝S4=1∴S1+S2+S4+S5=3，故答案为：C9．如图，在Rt△ABC中，∠ACB=90°，分别以AB，AC，BC为边作三个等边三角形：△ABD，△ACE，△BCF，其中∠CAB=15°，AB=2+43√3，BD与CE交于点M，AC与BD交于点N，连结AM，则△AMN的面积为（）A．3+√33B．2+√32C．3+2√33D．√6+√32【答案】B【解析】连接ED，作DF∥BC交EC与F，在AM上截取AG=NG，∵△ABD和△ACE是等边三角形，∴AB=AD，AC=AE，∠DAB=∠EAC=∠AEC=60°，∴∠CAB=∠EAD，∴△AED≌△ACB，∴ED=BC，∠AED=ACB=90°，∴∠DEF=30°，∵DF∥BC，∴∠DFC=FCB=150°，∴∠DEF=∠DFE=30°，∴ED=DF，∴BC=DF，∵∠DMF=∠BMC，∴△DFM≌△BCM，∴BM=DM，∴AM⊥DB，∠MAB=30°，∵AB=2+43√3，∴MB=12AB=1+23√3，MA=BM·tan60°=√3+2，∵∠CAB=15°，∴∠MAN=15°，∵AG=NG，∴∠GAN=∠GNA=15°∴∠MGN=∠GAN+∠GNA=30°设MN=x，则GN=AG=2x，MG=√3x，∴2x+√3x=2+√3，解得，x=1，△AMN的面积为12×(2+√3)×1=2+√3 2.故答案为：B.10．由四个全等的矩形围成了一个大正方形ABCD，如图所示.连结CH，延长EF交CH于点G，作PG⊥CH交AB于点P，若AH=2DH，则APBP的值为（）A．97B．1611C．32D．2【答案】B【解析】如图，∵正方形ABCD中，∴∠D=90°，AD=CD，∵AH=2DH，∴可设小矩形的宽为3x，则长为6x，∵HM∥CR，∴△NMH∽△NRC，∴MNNR=HMRC=3x6x=12，∴MN=2NR=23MR=2x，∴QG=8x，∵FG∥MN，∴△HFG∽△HMN，∴HFHM=FGMN，∴12=FG2x，∴FG=x，∴QG=7x，∵PG⊥CH，∴∠PGQ+∠HGQ=90°，∵∠HFG=90°，∴∠MHN+∠HGQ=90°，∴∠MHN=∠PGQ，∵∠PQG=∠PGQ=90°，∴△NMH∽△PQG，∴MNHM=QPQG，即2x6x=QP7x，∴QP=73x，∴AP=3x+73x=163x，BP=6x−73x=113x，∴APBP=163x113x=1611.故答案为：B.11．如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH.连接EB，EG，延长EG交CD于点M，若∠BEM=90°，则BE：EM的值为（）A．1：2B．3：4C．5：6D．5：12【答案】B【解析】∵四个全等的直角三角形拼成“赵爽弦图”，得正方形ABCD与正方形EFGH，∴∠FEG=45°，∠EFG=∠HEF=90°，∵∠BEM=90°，∴∠BEF=45°，∴∠EBF=45°，∴BF=EF，连接DG，延长BG交CD于N，设EF=x，则BE=EG=√2x，∵DE⊥EF，BG⊥EF，∴DE∥BG，∵DE=BG，∴四边形BEDG是平行四边形，∴DG=BE=√2x，∠HGD=∠EDG=∠EBF=45°，∴∠DGM=90°，∵GN ∥ED ，∴△MNG ∽△MDE ，∴NG DE =GM EM， ∵∠CBG=∠NBC ，∠BGC=∠BCN=90°，∴△CBG ∽△NBC ，∴BC 2=BG ⋅BN ，∵BC =√CG 2+BG 2=√x 2+(2x)2=√5x ，∴BN =BC 2BG =5x 22x =52x ，NG =BN −BG =52x −2x =12x ， ∴12x 2x =GM GM+√2x， 解得GM =√2x 3， ∴EM=EG+GM=√2x +√2x 3=4√2x 3， ∴BE EM =√2x 4√2x 3=34.故答案为：B.12．如图，在△ABC 中，∠BAC ＝90°，以BC 为边向上作正方形BCDE ，以AC 为边作正方形ACFG ，点D 落在GF 上，连结AE ，EG ．若DG ＝2，BC ＝6，则△AEG 的面积为（ ）A ．4B ．6C ．5√2D ．8【答案】D 【解析】过点E 作EH ⊥AG 于点H ，过点E 作EH ⊥EK ，垂足为E ，交FG 的延长线于点K∴∠EHB=∠EHG=90°，∠KEH=90°在正方形BCDE中，BE=DE=BC=CD=6，∠EBC=∠BCD=∠EDC=90°正方形ACFG中，AC=FC=AG，∠ACF=∠CAG=∠AGF=∠F=90°∴∠KGH=180°−∠AGF=90°∴四边形EHGK是矩形在Rt△ABC和Rt△FDC中，∵BC=DC，AC=FC∴Rt△ABC≅Rt△FDC(HL)∴∠1=∠2∵∠2+∠3=180°−∠EDC=90°，∠1+∠4=∠EBC=90°∴∠3=∠4∵∠BAC+∠CAG=180°∴B、A、G三点同在一条直线上，∵四边形EHGK是矩形∴∠K=90°∴∠K=∠EHB△EKD与△EHB中∵∠K=∠EHB，∠3=∠4，DE=BE∴△EKD≅△EHB(AAS)∴EK=EH∴四边形EHGK是正方形设正方形EHGK的边长为x则EK=EH=KG=xRt△EKD，EK2+DK2=ED2∵DK=DG+KG=2+x∴x2+(2+x)2=36x1=√17−1，x2=−√17−1（舍去）∴DK=2+√17−1=√17+1，EH=√17−1∵∠2+∠5=90°，∠2+∠3=90°∴∠3=∠5△EKD与△DFC中∵∠K=∠F=90°，∠3=∠5，ED=DC∴△EKD≅△DFC(AAS)∴KD=FC∴AG=KD=√17+1∴S AEG=12AG⋅EH=12(√17+1)(√17−1)=12×(17−1)=8故答案为：D.13．在数学拓展课上，小华同学将正方形纸片的顶点A，B，C，D与各边的中点E，F，G，H分别连接，形成四边形MNST，直线MS，TN与正方形ABCD各边相交构成一个如图的“风车”图案．若正方形的边长为2√5，则阴影部分面积之和为（）A．43B．2C．3√55D．2√105【答案】A【解析】如图，过点T作TL⊥AB，连接OH，则OH⊥AB，∵四边形ABCD是正方形，E，F，G，H分别为各边中点，∴∠DAH=∠ABE=90°，DA=AB，AH=BE，∴△DAH≌△ABE，∴∠DHA=∠AEB，∠ADH=∠BAE，∴△A TH∽△ABE，∵AB=2√5，∴AH=BE=√5，∴AE=√AB2+BE2=5，∴AT AB=AHAE=THBE，∴AT=2，TH=1，∴TM=AE-AT-ME=AE-AT-TH=2，同理可得ST=NS=NM=2，∵∠ADH+∠DHA=90°，∴∠DHA+∠BAE=90°即∠STM=90°，∴四边形STMN是正方形，∴OT=√2，∵TL⊥AB，OH⊥AB，∴TL∥OH，∵TL∥AD，∴△DAH∽△TLH，∴TH DH=TL DA，∵TL∥OH，∴△TKL∽△OKH，∴TK OK=TL OH，TK TK+√2=2√55√5，∴TK=2√23，OK=2√23+√2=5√23，在Rt△OKH中，KH=√OK2−OH2=√53，∴S△TKH=12×KH×TL=13，∴四个阴影部分的面积为43．故答案为：A.14．将矩形ABCD和矩形CEFG分割成5块图形（如图中①②③④⑤），并把这5块图形重新组合，恰好拼成矩形BEHN.若AM＝1，DE＝4，EF＝3，那么矩形BEHN的面积为（）A．20B．24C．30D．45【答案】C【解析】如图，由题意知AN =EF =3，BC =AD =MN =AN +AM =4∴MD =AD −AM =3∵∠BEH =90°∴∠PED +∠BEC =∠BEC +∠EBC =90°∴∠PED =∠EBC∵BC =DE =4∴△BCE ≌△EDP(AAS)∴PD =EC设HM =EC =PD =x ，MP =3−x ，∵∠HMP =∠EDP =90°，∠HPM =∠EPD∴△HPM ∽△EPD∴MP PD =MH DE 即3−x x =x 4解得x =2∴EC =2，DC =6∴S 矩形BEHN =S 矩形ABCD +S 矩形CEFG=BC ×DC +EC ×EF=4×6+2×3=30故答案为：C.15．如图，在Rt △ABC 中，∠ABC =90°，以AB ，AC 为边分别向外作正方形ABFG 和正方形ACDE ，CG 交AB 于点M ，BD 交AC 于点N.若GM CM =12，则AN CN=（ ）A．12B．34C．2√55D．1【答案】B【解析】如图，过点D作DH⊥BC交BC延长线于点H，延长AC交DH延长线于点Q，∵四边形ABCD是正方形，∴AB∥FG，AB=BF，∴GMMC=FBBC=12，∴ABBC=12，设AB=x，则BC=2x，∵∠ABC=90°，∴AC=√5x，∵四边形ACDE是正方形，∴AC=CD，∠ACD=90°，∴∠1+∠ACB=∠2+∠ACB=90°，∴∠1=∠2，∵DH⊥BH，∴∠CHD=∠ABC=90°，∴△ABC≌△CHD，∴AB=CH=x，DH=BC=2x，∵∠ABC+∠CHD=180°，∴AB∥DQ，∴∠1=∠Q，∵∠ACB=∠QCH，∴△ABC∽△QHC，∴ABQH=BCCH=ACCQ=2，∴QH=12AB=12x，QC=12AC=√52x，∴AQ=AC+CQ=3√52x ，DQ=DH+HQ=52x，∵∠1=∠Q，∠ANB=∠QND，∴△ABN∽△QDN，∴ANNQ=ABDQ=x52x=25，设AN=2a，则NQ=5a，∴AQ=2a+5a=7a=3√52x，∴a=3√514x，∴AN=2a=3√57x，NQ=5a=15√514x，∵CQ=√52x，∴NC=NQ−CQ=4√57x，∴ANCN=34.故答案为：B.16．如图是中国古代数学家赵爽用来证明勾股定理的弦图示意图，它是由四个全等的直角三角形和一个小正方形EFGH组成，恰好拼成一个大正方形ABCD，连结EG并延长交CD于点P.若AE=3EF=3，则DP的长为（）A．207B．209C．3D．157【答案】A【解析】依题意，可得AF=4，即ED=4，在Rt△ADE中，可得AD=√AE2+ED2=5，则正方形ABCD的边长为5，过P作PM⊥CG与M，∵△EGH为等腰直角三角形，∠EGH=45°，∴△GMP为等腰直角三角形，∠MGP=45°，设GM=x，PM=x，CM=3−x，又∠DHC=∠PMC=90°，∠HCD=∠MCP，∴△HCD∽△MCP，∴CH DH=CMPM，即43=3−xx，故x=9 7，故CM=3−97=127，在Rt△PCM中，PC=√PM2+CM2=157，∴DP=5−157=207，故答案为：A.17．如图，两个大小不等的正方形被切割成5部分，且②与⑤的面积之差为8，将这5部分拼接成一个大正方形ABCD，连结AC交DF于点E，若DEEF=43，则大正方形ABCD的面积为（）A．18B．25C．32D．50【答案】D【解析】如图，图2中∵两个大小不等的正方形被切割成5部分，将这5部分拼接成一个大正方形ABCD，∴AD∥BC，AM⊥DF，CN⊥DF，∴△ADE∽△CFE，∴ADCF=DEEF=AMCN=43由④③可知CN=KJ，AM=GT=IH，∴GTKJ=43设GT=QT=HI=4x，KJ=QI=IJ=3x，∴HQ=HI-QI=4x-3x=x，图1中RQ∥JI，∴△HRQ∽△HJI，∴QRIJ=HQHI∴RQ3x=x4x解之：RQ=34x；S②=S梯形HQTG−S△HQR=12(HQ+GT)·TQ+12HQ·QR∴S②=12(x+4x)·4x+12x·34x=778x2；S⑤=12(RQ+IJ)·QI=12(34x+3x)·3x=458x2；∵②与⑤的面积之差为8，∴778x2−458x2=8∵x＞0∴x=√2.∴GT=4x=4√2，QI=3x=3√2，∴正方形ABCD 的面积=GT 2+QI 2=(4√2)2+(3√2)2=32+18=50. 故答案为：D.18．中国古代数学家张爽证明勾股定理的弦图如图所示，它由四个全等的直角三角形和．一个小正方形EFGH 组成，恰好拼成大正方形ABCD ．作直线EG 分别交AD ，BC 于点M ， N ．若图中两个正方形的面积分别是13和1，则MN 的长为（ ）A ．3√2B ．14√25C ．13√25D ．12√25【答案】C【解析】如图，过点F 作FK ∥MN ，交BC 于点K ，根据题意知：∠AEB=90°，BF=AE=CG ，CF=BE=AH ，FG=EF=EH=1，AB=√13， ∴AE=CG ，EG=√2， ∵AE 2+BE 2=AB 2，∴BF 2+（BF+1）2=（√13）2， ∴BF=2或BF=-3（不符合题意）， ∴BF=AE=CG=2，CF=BE=3， ∵FK ∥MN ，∴△CGN ∽△CFK ，△BFK ∽△BEN ， ∴FK GN =CF CG =32，EN FK =BE BF =32， ∴FK=32GN ，∴EG+GN FK =√2+GN FK =32，∴√2+GN32GN =32， ∴GN=4√25，∵∠AME=∠CNG ，∠AEM=∠CGN=45°，AE=CG ， ∴△AEM ≌△CGN ，∴ME=GN=4√25，∴MN=4√25+4√25+√2=13√25.故答案为：C.19．如图，在△ABC 中，∠ACB=90°，以AB 为边向上作正方形ABDE ，以AC 为边作正方形ACFG ，点E 落在GF 上，连结CD ，DF ．若要求出五边形ACDFE 的面积，则只要知道（ ）A ．AB 的长B ．AC 的长 C ．△ABC 的面积D ．△DEF 的面积【答案】B【解析】如图，过点D 作DH ⊥CF 于点H ，∴∠DHB=90°， ∵正方形ABDE ， ∴∠ABD=90°，DB=AB ， 又∵∠ACB=90°， ∴∠DBH=∠BAC ，∴△ACB ≌△BHD （AAS ）， 同理可证：△ACB ≌△AGE ， ∴△ACB ≌△BHD ≌△AGE ， ∴S △ACB =S △BHD =S △AGE ，∴S 五边形ACDFE =S △DCF +S 梯形ACFE =S △AGE +S 梯形ACFE =S 正方形ACFG ， ∴当AC 已知时，可求得S 正方形ACFG ， ∴可求出五边形ACDFE 的面积.故答案为：B.20．如图，在△ABC中，∠ACB＝90°，分别以AC，BC为边向外作正方形ACDE与正方形BCFG，H为EG的中点，连接DH，FH.记△FGH的面积为S1，△CDH的面积为S2，若S1－S2＝6，则AB 的长为（）A．2√6B．3√2C．3√3D．4√2【答案】A【解析】连接AD交EC于点M，连接BF交CG于点N，∵四边形ACDE，BCFG是正方形，∴AD⊥EC，BF⊥CG，AD=EC，BF=CG，DM=12AD，FN=12BF，设AC=a，BC=b，∵∠EAC=90°，AE=AC=a，∴EC=√AE2+AC2=√2a∴AD=√2a，∴DM=12AD=12×√2a=√22a，同理可证：CG=√2b，FN=√22b，∵EG=EC+CG，∴EG=√2(a+b)，∵H为EG的中点，∴HG=EH=12×√2(a+b)=√22(a+b)，∴CH=EH−EC=√22(b−a)，∵S1=SΔFG1H=12⋅HG⋅FN=ab+b24，S2=SΔ(DH=12CH·DM=ab−a24又∵S 1−S 2=6 ， ∴ab+b 24−ab−a 24=6 ，整理得， a 2+b 2=24 ， ∵∠ ACB =90° ，∴AB =√AC 2+BC 2=√24=2√6. 故答案为：A.21．如图，点 H ， F 分别在菱形 ABCD 的边 AD ， BC 上，点 E ， G 分别在 BA ， DC 的延长线上，且 AE =AH =CG =CF .连结 EH ， EF ， GF ， GH ，若菱形 ABCD 和四边形 EFGH 的面积相等，则 AH AD的值为（ ）A ．12B ．√22C ．√32D ．1【答案】D【解析】连接HC 、AF 、HF 、AC ，HF 交AC 于O ，连接EG.∵四边形ABCD 是菱形， ∠D=∠B ，AB=CD=AD=BC ， ∵AE=AH=CG=CF ， ∴DH=BF ，BE=DG ， 在△DHG 和△BFE 中， {DH =BF ∠D =∠B BE =DG， ∴△DHG ≌△BFE ， ∴HG=EF ，∠DHG=∠BFE ， ∵BC ∥AD ，∴∠BFE=∠DKF，∴∠DHG=∠DKG，∴HG∥EF，∴四边形EFGH是平行四边形.∵AH=CF，AH∥CF，∴四边形AHCF是平行四边形，∴AC与HF互相平分，∵四边形EFGH是平行四边形，∴HF与EG互相平分，∴HF、AC、EG互相平分，相交于点O，∵AE=AH，DA=DC，BE∥DC，∴∠EAH=∠D，∴∠AEH=∠AHE=∠DAC=∠DCA，∴EH∥AC，∴S△AEH=S△EHO=S△AHO= 12S△AHC= 14S四边形EFGH= 14S四边形ABCD，∴S△AHC= 12S四边形ABCD=S△ADC，∴AD=AH，∴AH AD=1.故答案为：D.22．如图，正六边形ABCDEF中，点P是边AF上的点，记图中各三角形的面积依次为S1，S2，S3，S4，S5，则下列判断正确的是（）A．S1+S2=2S3B．S1+S4=S3C．S2+S4=2S3D．S1+S5=S3【答案】B【解析】如图，作正六边形ABCDEF的外接圆O，连接BE，DF，记DF与BE的交点为Q，PD，BE的交点为N，过O作OH⊥CD于H，∴∠COD=60°，设正六边形ABCDEF的边长为a，则CO=DO=CD=a，∴CH=DH=12a，OH=√32a，由正六边形的性质可得：∠DEF=120°，EF=DE，BE⊥DF，FQ=DQ，∴∠EFQ=30°，EQ=12a，FQ=√32a，∴DF⊥AF，DF=2OH=√3a，∴S3=12×a×√3a=√32a2，设PF=x，则AP=a−x，∴S1=12AP·FQ=12(a−x)×√32a=√34a2−√34ax，S4=S△PDF+S△DEF−S5=12x×√3a+12×√3a×12a−12x×√32a=√34a2+√34ax∴S1+S4=√34a2−√34ax+√34a2+√34ax=√32a2，S3=12a×√3a=√32a2，∴S1+S4=S3，故B符合题意；由S1+S4=S3，同理可得：S2+S5=S3，∴S1+S2+S4+S5=2S3，故S1+S2=2S3，S2+S4=2S3，S1+S5=S3都错误，故A，C，D都不符合题意；故答案为：B.23．将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内（相邻纸片之间互不重叠也无缝隙），未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为l.若知道l的值，则不需测量就能知道周长的正方形的标号为（）A．①B．②C．③D．④【答案】D【解析】设①、②、③、④四个正方形的边长分别为a、b、c、d，由题意得,（a+d−b−c+b+a+d−b+b−c+c+c）−（a−d+a−d+d+d）=l，整理得，2d=l，则知道l的值，则不需测量就能知道正方形④的周长，故答案为：D.24．如图，以Rt △ABC的各边为边分别向外作正方形，∠BAC=90∘，连接DG，点H为DG的中点，连接HB，HN，若要求出△HBN的面积，只需知道（）A．△ABC的面积B．正方形ADEB的面积C．正方形ACFG的面积D．正方形BNMC的面积【答案】B【解析】如图，延长HA交BC于点P，交MN于点O，连接CE、AN，由题意可得：AB=AD，∠DAG=∠BAC，AC=AG，∴△DAG≌△BAC（SAS），∴∠2=∠4，由题意可得：BE=AB，∠EBC=∠ABN=90°+∠ABC，BN =BC，∴△ABN≌△EBC（SAS），S△ABN=S△EBC，∵点H为DG的中点，∠DAG=90°，∴∠1=∠2，∵∠1+∠3=90°，∴∠3+∠4=90°，∴HA⊥BC，∴BN∥HQ，∴S△HBN=S△ABN，又∵BE∥CD，∴S△EBC=S△EBA=12S正方形ABED，S△HBN=12S正方形ABED.故答案为：B.25．如图，等边△ABC和等边△DEF的边长相等，点A、D分别在边EF，BC上，AB与DF交于G，AC与DE交于H．要求出△ABC的面积，只需已知（）A．△BDG与△CDH的面积之和B．△BDG与△AGF的面积之和C．△BDG与△CDH的周长之和D．△BDG与△AGF的周长之和【答案】C【解析】如图，连接AD，由题意可知：AB=BC=AC=DF=EF=ED，∠B=∠C=∠E=∠F=60°，∴△ABD≌△DFA（SAS），∴BD=AF，∴△AGF≌△BGD（AAS），∴BG=AG=FG=GD，同理可证得：△ACD≌△DEA（SAS），∴AE=DC，∴△AEH≌△CDH（AAS），∴AH=HC=DH=HE，∴BD+BG+DG+CD+DH+CH=BD+CD+BG+AG+AH+CH=BC+AB+AC，∴△ABC的周长=BD+BG+DG+CD+DH+CH=△BGD周长+△CDH周长.故答案为：C.26．如图，点F，G分别在正方形ABCD的边BC，CD上，E为AB中点，连结ED，正方形FGQP 的边PQ恰好在DE上，记正方形ABCD面积为S1，正方形FPQG面积为S2，则S1：S2的值为（）A．10：7B．20：7C．49：10D．49：20【答案】D【解析】∵正方形ABCD，正方形FPQG，∴∠EAD=∠ADG=∠DQG=GCF=90°，AB=AD，QG=GF，∴∠GDQ=∠DEA，∠QGD=∠GFC，∴△ADE∽△DQG，△QGD∽△GFC，∴AE：AD=QD：QG=GC：CF，∵E 为AB 的中点， ∴AD=AB=2AE ，∴QD ：QG=GC ：CF=1：2，设QD=x ，则QG=GF=2x ，GC=y ，则CF=2y ， ∴S 2=QG 2=4x 2，在Rt △DQG 中，由勾股定理得：DG=√x 2+4x 2=√5x ， ∴DC=DG+GC=√5x+y ，在Rt △GCF 中，由勾股定理得：GC 2+CF 2=GF 2， ∴y 2+4y 2=4x 2，∴√5y=2x ，整理得：y=2√55x ，∴DC=7√55x ，∴S 1=DC 2=495x 2，∴S 1：S 2=495x 2：4x 2∴S 1：S 2=49：20. 故答案：D.27．如图是由7个等边三角形拼成的图形，若要求出阴影部分的面积，则只需要知道（ ）A ．⑤和③的面积差B ．③和②的面积差C ．④和②的面积差D ．⑤和②的面积差【答案】C【解析】设7个等边三角形的边长依次为a ，b ，c ，d ，e ，f ，g ，∴S 阴影=12（c-b ）·√32c=√34c·（c-b ），S ④-S ②=12d·√32d-12b·√32b=√34（d 2-b 2）=√34（d+b ）（d-b ），∵a+b=c ，a+c=d ， ∴d+b=2c ，d-b=2a∴S ④-S ②=√34×2c·2a=√3c·a ， 又∵a=c-b ，∴S ④-S ②=√3c·（c-b ），∴S ④-S ②=4S 阴影，∴只要知道④和②的面积之差就能求出阴影部分的面积.故答案为：C.28．如图来自清朝数学家梅文鼎的《勾股举隅》，该图由四个全等的直角三角形围成，延长BC 分别交AG ，HG 于点M ，N ，梅文鼎就是利用这幅图证明了勾股定理．若图中记△MNG 的面积为S ，△GDF 的面积为9S ，则阴影部分的面积为（ ）A ．20SB ．21SC ．22SD ．24S【答案】B 【解析】设直角三角形较短的直角边为a ，较长的直角边为b ，斜边长为c ，∵△MNG 的面积为S ，△GDF 的面积为9S ， ∴12ab=9s ，正方形MNHA 的面积为8S ，S △MNG S △AGH =19=(MG AG )2， ∴MG AM =12， ∴△AMC 的面积为4S ，∴正方形ACNH 的面积为a 2=12S ，∴b 2=(18s a )2=27s ， ∴c 2=a 2+b 2=39s ，∴阴影部分的面积=39s-9s-9s=21s.故答案为：B.29． 如图， 在正△ABC 中， D 、E 分别为边AB 、AC 上的点， BD =2CE ， 过点E 作EF ⊥DE 交BC 于点F ， 连结DF ， 若想求△ABC 的周长， 则只需知道下列哪个三角形的周长? 该 三角形是( )A ．△CEFB ．△BDFC ．△DEFD ．△ADE【答案】B【解析】过点A 作AO ⊥AB ，过点C 作CO ⊥BC 于点C ，连接BO ，延长BC ，使CG=AD ，连接OG ，OE ，∴∠BAO=∠BCO=90°，∵△ABC 是等边三角形，∴AB=BC ，∠ACB=60°，∴∠OCE=90°-60°=30°，在Rt △BAO 和Rt △BCO 中，{BA =BC BO =BO∴Rt △BAO ≌Rt △BCO （HL ），∴OA=OC ，∠ABO=∠CBO=30°，∴OB=2OC∵BD=2CE ，∴BD CE =BO CE=2 ∵∠OCE=∠OBD=30°，∴△OBD ∽△OCE ，∴∠DOB=∠EOC ，OD OE =BO CO=2， ∴∠DEO=90°，∵∠DEF=90°，∴点O ，E ，F 三点在同一直线上，在△OAD 和△OCG 中{OA =OC ∠BAO =∠BCO AD =CG∴△OAD ≌△OCG （SAS ），∴OD=OG ，∠AOD=∠COG ，∴∠DOG=∠DOC+∠COG=∠DOC+∠AOD=∠AOC=120°，∴∠FOG=∠DOG-∠DOF=120°-60°=60°，在△ODF 和△OGF 中{OD=OG ∠DOF=∠GOF OF=OF∴△ODF≌△OGF（SAS），∴DF=FG∴△BDF的周长为：BD+DF+BF=BD+FG+BF=BD+BC+CG=BC+BD+AD=BC+AB=2AB，∴要想求出△ABC的周长，只需知道△BDF的周长.故答案为：B.法二：过点E作EG∥BC，交AB于G，交DF于H，如图：由题意可知：三角形AGE是正三角形；G是BD中点、H是DF中点；EH是DF一半（斜边中线），GH是BF一半△BDF的周长=2（a+b+c）,AG=EG=b+c；AB=AG+BG=a+b+c，∴要想求出△ABC的周长，只需知道△BDF的周长.30．如图，在Rt△ABC中，∠ACB 90°，以其三边为边向外作正方形．P是AE边上一点，连结PC并延长交HI于点Q，连结CG交AB于点K．若PCCQ=34，则CKKG的值为（）A．1225B．34C．1325D．45【答案】A【解析】如图，过点C，作CN⊥FG，分别交AB于点M，交FG于点N，∵Rt△ABC中，∠ACB= 90°，以其三边为边向外作正方形，∴△ CAP=∠CIQ=90°，IC=BC ，AB ∥FG ，BG ⊥FG ，BG= AB ， ∵∠ACP=∠ICQ ，∴△ ACP ∽△ICQ ，∴IC AC =PC CQ =34，设AC= 3p ，则BC=IC=4p ，在Rt △ ABC 中，∴AB=√AC 2+BC 2=5p ，∴AB ∥FG. CN ⊥FG ，∴CM ⊥AB ，∴CM=AC×BC AB =12P 5， ∵CN ⊥FG ，BG ⊥FG ，∴MN ∥BG ，∴AB ∥FG ，CN ⊥FG ，∴四边形MNGB 为矩形，∴MN=BG=5p ，∴CN=CM+MN=37p 5， ∵∠MCK=∠NCG ，CN ⊥FG ，CM ⊥AB ，∴△MCK ∽△NCG ，∴CK CG =CM CN =1237， ∴CK CK+KG =1237， ∴CK KG =1225. 故答案为：A.。

中考数学压轴题100题精选及答案全第一篇：数与代数1.下列各组数中，哪一组数最大？A. \frac{1}{2} ,\frac{2}{3},\frac{3}{4},\frac{4}{5}B. 0.99,0.999,0.9999,0.99999C. \sqrt{2},\sqrt{3},\sqrt{5},\sqrt{7}D. 1,10^2,10^3,10^42. 一个整数，十位数与各位数的和为9，再去掉该整数中的各位数，十位数与剩下的数字的和为40，该整数为__________。

A. 45B. 54C. 63D. 723. 已知 a+b=2, ab=-1，求a^2+b^2的值。

A. 3B. 5C. 7D. 94. 解方程 2x-5=3x+1。

A. x=-3.5B. x=-2C. x=2D. x=3.55. 有两个数，各位数字相同，但顺序颠倒，若它们的和为110，这两个数分别是多少？A. 47,74B. 49,94C. 56,65D. 59,956. 若x-3y=-7，x+4y=1，则y的值为__________。

A. -2B. -1C. 0D. 17. 16÷(a-2)=4，则 a 的值为__________。

A. 6B. 8C. 10D. 128. 若a:b=5:3，b:c=7:4，则a∶b∶c=__________。

A. 35:21:12B. 25:15:12C. 25:21:16D. 35:15:169. 若a+3b=5，3a-5b=7，则 a 的值为__________。

A. -2B. -1C. 0D. 110. 已知x+y=3，xy=2，则y的值为__________。

A. 1B. 2C. 3D. 4第二篇：几何图形11. 已知正方形 ABCD 的边长为6，以 BC 为边，画一个正三角形 BCE，连接 AE，AD，请问△ADE 和正方形 ABCD 的面积之比是多少？A. \frac{2}{9}B. \frac{1}{2}C. \frac{4}{9}D.\frac{5}{6}12. 把一张纸平整地放在桌上，在纸的中央画一个圆形，请问可以用多少个直径为5 厘米的圆去覆盖这个圆形（圆覆盖圆）？A. 1B. 2C. 3D. 413. 已知△ABC 是等腰三角形，AB=AC，E是BC中点，DE∥AC，AE=CD=2，求△ABC 的面积。