概率与统计初步测试题3份
- 格式:doc
- 大小:505.50 KB
- 文档页数:15

《概率论与数理统计初步》试卷试卷共 6 页,请先查看试卷有无缺页,然后答题。
一.选择题(53⨯分)1.设离散型随机变量则(A). 0.2 (B). 0.3 (C). 0.1 (D). 0.52.设总体X 服从正态分布)6,1(N ,125,,,X X X 为X 的样本,记5115i i X X ==∑,则X ~______________(A). )41,1(N (B). )6,1(N (C). 6(1,)5N (D). (0,6)N3.已知总体X ~N(μ,σ2),其中μ未知, σ2已知,n X X X ,,,21 是X 的样本,下列哪个函数不是统计量_____________(A). min(X 1,X 2,…,X n ) (B). ∑=--ni i X X n 12)(11 (C).121n X i i n()-=∑μ (D). Xii n212=∑σ4.某人射击击中的概率为14。
如射击直到击中为止,则射击次数为3的概率为( ) (A ) 343⎪⎭⎫ ⎝⎛ (B )41432⨯⎪⎭⎫ ⎝⎛ (C ) 43412⨯⎪⎭⎫ ⎝⎛(D ) 341⎪⎭⎫⎝⎛5. 21,X X 是总体(,4)N μ的一个样本,,下面四个估计量中,未知参数μ的无偏估计是_________________________(A).121433X X + (B). 121344X X + (C). 214143X X - (D). 215352X X +二. 填空题(53⨯分)1. 若随机变量ξ与η相互独立,且方差D(ξ)=0.5,D(η)=1,则D(2ξ-3η)=______________________.2.设事件A ,B 相互独立,且4.0)(=A P ,0)(=AB P ,则=)(B P _________________________3. 设(X ,Y) ~ N(1, 2, 3, 4, 0),则=XY ρ____________4. 设随机变量X ~)21,4(B ,则=2)]([)(X E X D _________________________5. 设B A ,互不相容,且q B P p A P ==)(,)(,则)(B A P =___________ 二.计算题1. 已知某厂生产的灯泡寿命在1万小时以上的概率为0.8,寿命在2万小时以上的概率为0.2,求已使用1万小时的灯泡能用2万小时的概率。

中职概率与统计初步练习及答案概率与统计初步例1.指出下列事件是必然事件,不可能事件,还是随机事件?①某乒乓球运动员在某运动会上获得冠军。
②掷⼀颗骰⼦出现8点。
③如果0=-b a ,则b a =。
④某⼈买某⼀期的体育彩票中奖。
解析:①④为随机事件,②是不可能事件,③是必然事件。
例2.某活动⼩组有20名同学,其中男⽣15⼈,⼥⽣5⼈,现从中任选3⼈组成代表队参加⽐赛,A 表⽰“⾄少有1名⼥⽣代表”,求)(A P 。
例3.在50件产品中,有5件次品,现从中任取2件。
以下四对事件那些是互斥事件?那些是对⽴事件?那些不是互斥事件?①恰有1件次品和恰有2件次品②⾄少有1件次品和⾄少有1件正品③最多有1件次品和⾄少有1件正品④⾄少有1件次品和全是正品例4.从1,2,3,4,5,6六个数字中任取两个数,计算它们都是偶数的概率。
例5.抛掷两颗骰⼦,求:①总点数出现5点的概率;②出现两个相同点数的概率。
例6.甲、⼄两⼈各进⾏⼀次射击,如果两⼈击中⽬标的概率都是0.6,计算:①两⼈都未击中⽬标的概率;②两⼈都击中⽬标的概率;③其中恰有1⼈击中⽬标的概率;④⾄少有1⼈击中⽬标的概率。
例7.种植某种树苗成活率为0.9,现种植5棵。
试求:①全部成活的概率;②全部死亡的概率;③恰好成活4棵的概率;④⾄少成活3棵的概率。
【过关训练】⼀、选择题1、事件A 与事件B 的和“B A ”意味A 、B 中() A 、⾄多有⼀个发⽣ B 、⾄少有⼀个发⽣ C 、只有⼀个发⽣ D 、没有⼀个发⽣2、在⼀次招聘程序纠错员的考试中,程序设置了依照先后顺序按下h,u,a,n,g 五个键的密码,键盘共有104个键,则破译密码的概率为()A 、51041P B 、51041C C 、1041 D 、1045 3、抛掷两枚硬币的试验中,设事件M 表⽰“两个都是反⾯”,则事件M 表⽰() A 、两个都是正⾯ B 、⾄少出现⼀个正⾯C 、⼀个是正⾯⼀个是反⾯D 、以上答案都不对 4、已知事件A 、B 发⽣的概率都⼤于0,则() A 、如果A 、B 是互斥事件,那么A 与B 也是互斥事件B 、如果A 、B 不是相互独⽴事件,那么它们⼀定是互斥事件 C 、如果A 、B 是相互独⽴事件,那么它们⼀定不是互斥事件D 、如果A 、B 是互斥且B A 是必然事件,那么它们⼀定是对⽴事件5、有5件新产品,其中A 型产品3件,B 型产品2件,现从中任取2件,它们都是A 型产品的概率是()A 、53B 、52C 、103D 、2036、设甲、⼄两⼈独⽴地射击同⼀⽬标,甲击中⽬标的概率为0.9,⼄击中⽬标的概率为98,现各射击⼀次,⽬标被击中的概率为()A 、98109+B 、98109?C 、981081?-D 、90897、⼀个电路板上装有甲、⼄两个保险丝,若甲熔断的概率为0.2,⼄熔断的概率为0.3,⾄少有⼀根熔断的概率为0.4,则两根同时熔断的概率为()A 、0.5B 、0.1C 、0.8D 、以上答案都不对8、某机械零件加⼯有2道⼯序组成,第1道⼯序的废品率为a ,第2道⼯序的废品率为b ,假定这2道⼯序出废品是彼此⽆关的,那么产品的合格率是()A 、1+--b a abB 、b a --1C 、ab -1D 、ab 21-9、某⼚⼤量⽣产某种⼩零件,经抽样检验知道其次品率是1﹪,现把这种零件每6件装成⼀盒,那么每盒中恰好含1件次品的概率是()A 、6)10099(B 、0.01C 、516)10011(1001-CD 、4226)10011()1001(-C 10、某⽓象站天⽓预报的准确率为0.8,计算5次预报中⾄少4次准确的概率是()A 、45445)8.01(84.0--??CB 、55555)8.01(84.0--??C C 、45445)8.01(84.0--??C +55555)8.01(84.0--??C D 、以上答案都不对11、同时抛掷两颗骰⼦,总数出现9点的概率是() A 、41 B 、51 C 、61 D 、91 12、某⼈参加⼀次考试,4道题中解对3道则为及格,已知他的解题准确率为0.4,则他能及格的概率约是()A 、0.18B 、0.28C 、0.37D 、0.48⼆、填空题1、若事件A 、B 互斥,且61)(=A P ,32)(=B P ,则=)(B A P 2、设A 、B 、C 是三个事件,“A 、B 、C ⾄多有⼀个发⽣”这⼀事件⽤A 、B 、C 的运算式可表⽰为3、1个⼝袋内有带标号的7个⽩球,3个⿊球,事件A :“从袋中摸出1个是⿊球,放回后再摸1个是⽩球”的概率是4、在4次独⽴重复试验中,事件A ⾄少出现1次的概率是8180,则事件A 在每次试验中发⽣的概率是5、甲、⼄两射⼿彼此独⽴地射击同⼀⽬标,甲击中⽬标的概率为0.8,⼄击中⽬标的概率为0.9,则恰好有⼀⼈击中⽬标的概率为三、解答题1、甲、⼄两⼈射击,甲击中靶的概率为0.8,⼄击中靶的概率为0.7,现在,两⼈同时射击,并假定中靶与否是相互独⽴的,求:(1)两⼈都中靶的概率;(2)甲中靶⼄不中靶的概率;(3)甲不中靶⼄中靶的概率。

概率与统计的基础练习题在概率与统计学中,练习题是帮助学生巩固知识和提高技能的重要方式。
通过解答练习题,学生可以加深对概率和统计理论的理解,掌握基本的解题方法和技巧。
本文将为您提供一系列概率与统计的基础练习题,帮助您巩固相关知识。
1. 骰子问题假设有一个六面骰子,每个面上的数字分别为1、2、3、4、5和6。
现从中抽取一个骰子,并投掷5次,每次记录下骰子的面数。
请计算以下概率:a) 出现奇数的次数为3次的概率。
b) 至少出现一次6的概率。
c) 第一次出现4的概率。
解答:a) 出现奇数的次数为3次的概率=(投掷出奇数的次数为3次)/(总共投掷的次数为5次)= C(5, 3) * (1/2)^3 * (1/2)^2 = 10/32 = 5/16。
b) 至少出现一次6的概率= 1 - 不出现6的概率= 1 - (5/6)^5 = 1 - 3125/7776 = 4651/7776。
c) 第一次出现4的概率= (第一次投掷出现4,后面四次不出现4)= 1/6 * (5/6)^4 = 625/7776。
2. 选课问题某高中学生共有20门选修课可供选择,但该学生只能选择其中5门课。
假设该学生随机选课,求以下概率:a) 至少选择一门语言课的概率。
b) 选择4门以上的概率。
c) 选课中不包含数学和科学课的概率。
解答:a) 至少选择一门语言课的概率= 1 - 全选非语言课的概率 = 1 - (C(15,5) / C(20, 5)) = 1 - 3003/15504 = 12501/15504。
b) 选择4门以上的概率= (选择4门课的情况数 + 选择5门课的情况数) / 总共的情况数 = (C(20, 4) + C(20, 5)) / C(20, 5) = (4845 + 15504) / 15504 = 20349/15504 = 462/351。
c) 选课中不包含数学和科学课的概率= (C(8, 5) / C(20, 5)) =56/15504。

初二数学下册概率与统计基础练习题概率与统计是数学中重要的分支之一,它研究的是事件发生的可能性以及事件发生后的数据分析。
为加深同学们对概率与统计的理解,下面将给出一些针对初二学生的概率与统计基础练习题。
1. 掷一枚骰子,求出现奇数点数的概率。
2. 一个班级有30名学生,其中20名是男生,10名是女生。
如果从中随机选择两名学生,求选出的两名学生都是男生的概率。
3. 某电子产品的使用寿命服从正态分布,平均寿命为1000小时,标准差为50小时。
问该产品寿命在900小时至1100小时之间的概率是多少?4. 某商场一日活动中,顾客购买3件商品的概率为0.3,购买4件商品的概率为0.4,购买5件商品的概率为0.2。
问购买商品数超过3件的概率是多少?5. 某市区的天气状况可分为晴天、阴天和雨天三种状态。
统计数据显示,晴天的概率为0.4,阴天的概率为0.3,雨天的概率为0.3。
如果明天晴天,两天后仍然是晴天的概率是多少?6. 某班级学生的成绩服从正态分布,平均分为80分,标准差为10分。
选取一个学生,其成绩在70分至90分之间的概率是多少?7. 抛掷一枚均匀硬币,连续抛掷3次,其中至少有两次出现正面的概率是多少?8. 一批商品中有5%存在质量问题,从中随机抽取4件商品,求其中至少有一件存在质量问题的概率。
9. 某校毕业生的薪水数据符合正态分布,平均薪水为5000元,标准差为1000元。
求薪水在6000元以上的毕业生所占的比例。
10. 使用某款手机 App 的用户数量每天都在变化,根据统计数据,用户数量最多的情况出现的概率为0.2,用户数量次多的情况出现的概率为0.3,其他情况出现的概率为0.5。
如果今天用户数量最多,明天用户数量次多的概率是多少?以上是针对初二数学下册概率与统计基础的练习题,涵盖了概率的计算、正态分布、事件概率的计算等内容。
希望同学们通过练习,巩固对这些知识点的理解,并提高解题的能力。
祝大家顺利完成练习!。

概率与统计初步测试《概率与统计初步》单元测试班级姓名成绩一、选择题(每题3分,共30分)1、书架上有6本数学书,8本语文书,3本历史书,从书架上任取一本,不同的选法有() A 、3种 B 、8种 C 、144种 D 、17种2、用0、1、2、3可以组成的两位数有()A 、2个B 、12个C 、16个D 、256个 3、下列现象为确定现象的是()A 、一次数学考试某学生得到的分数B 、测量零件长度产生的误差C 、在标准状态下,水加热到100度会沸腾D 、抛掷一颗骰子掷得的点数 4、下列事件是随机事件的是()A 、测量三角形内角和为180度B 、掷骰子得到点数为0C 、当a 是实数时,a 2<0D 、抛硬币结果正面向上5、从一批产品中取出三件,设A={三件产品都不是次品},B={三件产品都是次品}, C={三件产品不都是次品},则下列结论正确的是( )A 、A 与C 互斥B 、 B 与C 互斥 C 、任两个都互斥D 、任两个均不互斥6、抛一颗骰子,下列事件中是复合事件的是()A 、{点数是1}B 、{点数是2 }C 、{点数是奇数}D 、{点数是5 } 7、同时抛掷两枚质地均匀的硬币,则出现两个正面的的概率是( )A 、21B 、41C 、 31 D 、818、调查13级学生的身高情况,随机抽取50个学生进行测量,这100个小时的身高是() A 、样本 B 、总体 C 、样本容量 D 、个体9、同组8个人要决定周三值日生1人,用怎样的抽样方法合适()A 、随机抽样B 、分层抽样C 、系统抽样D 、以上均可以10、甲,乙两位同学在几次数学测验中,各自的平均成绩都是88分,甲的方差为0.62,乙的方差为0.73,则()A .甲成绩比乙稳定B .乙成绩比甲好C .甲,乙成绩一样D .甲,乙成绩无法比较二、填空题(每空3分,共24分)1、从1,2,…,9共九个数字中任取一个数字,取出数字为偶数的概率为________ ;2、投掷两枚骰子,出现点数之和为3的概率为________;3、班里有男生28人,女生20人,选出男、女生各1人参加会议,共有种选法;4、盒中装有3个白球,2个黑球,从中一次摸出2个球,{取出的3个球是黑色}是事件;5、对于不可能事件A ,P(A)= ,对于必然事件B ,P(B)= ;6、一个射击运动员连续射靶5次所得环数分别为8,6,10,7,9,则这个运动员所得环数的均值为,方差为;三、解答题(共46分)1、用互斥事件的概率加法公式求抛掷一枚骰子,点数小于3的概率。
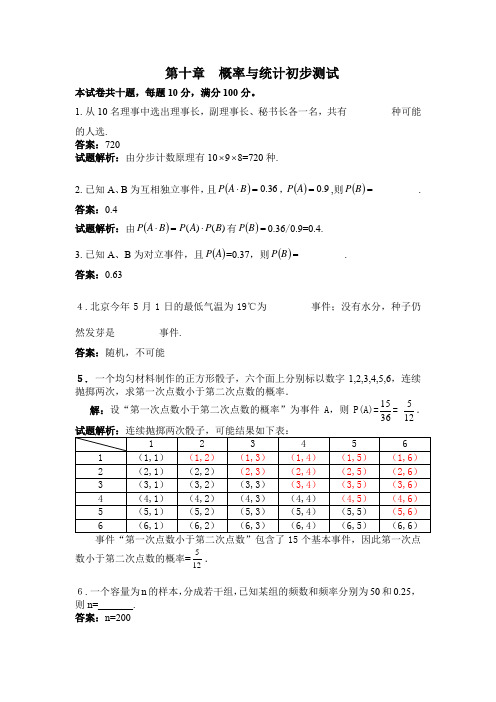
第十章 概率与统计初步测试本试卷共十题,每题10分,满分100分。
1.从10名理事中选出理事长,副理事长、秘书长各一名,共有________种可能的人选.答案:720试题解析:由分步计数原理有10⨯9⨯8=720种.2.已知A 、B 为互相独立事件,且()36.0=⋅B A P ,()9.0=A P ,则()=B P ________. 答案:0.4试题解析:由())()(B P A P B A P ⋅=⋅有()=B P 0.36/0.9=0.4.3.已知A 、B 为对立事件,且()A P =0.37,则()=B P ________.答案:0.634.北京今年5月1日的最低气温为19℃为________事件;没有水分,种子仍然发芽是________事件.答案:随机,不可能5. 一个均匀材料制作的正方形骰子,六个面上分别标以数字1,2,3,4,5,6,连续抛掷两次,求第一次点数小于第二次点数的概率.解:设“第一次点数小于第二次点数的概率”为事件A ,则P(A)=3615= 125.数小于第二次点数的概率=125.6.一个容量为n 的样本,分成若干组,已知某组的频数和频率分别为50和0.25,则n=_______.答案:n=2007.如果x ,y 表示0,1,2,···,10中任意两个不等的数,P(x ,y)在第一象限的个数是( ).A 、72B 、90C 、110D 、121答案:B8.甲、乙、丙三人射击的命中率都是0.5,它们各自打靶一次,那么他们都没有中靶的概率是( ).A 、 0.5B 、0.25C 、 0.3D 、 0.125答案:D9.两个盒子内各有3个同样的小球,每个盒子中的小球上分别标有1,2,3三个数字。
从两个盒子中分别任意取出一个球,则取出的两个球上所标数字的和为3的概率是( ).A 、91B 、92C 、31D 、32 答案:B10.下面属于分层抽样的特点的是( ).A 、从总体中逐个抽样B 、将总体分成几层,分层进行抽取C 、将总体分成几个部分,按事先确定的规则在各部分抽取D 、将总体随意分成几个部分,然后再进行随机选取答案:B。

第十章 概率与统计初步测试本试卷共十题,每题10分,满分100分。
1。
从10名理事中选出理事长,副理事长、秘书长各一名,共有________种可能的人选. 答案:720试题解析:由分步计数原理有10⨯9⨯8=720种。
2。
已知A、B 为互相独立事件,且()36.0=⋅B A P ,()9.0=A P ,则()=B P ________。
答案:0.4试题解析:由())()(B P A P B A P ⋅=⋅有()=B P 0.36/0.9=0。
4. 3.已知A 、B 为对立事件,且()A P =0.37,则()=B P ________. 答案:0.634.北京今年5月1日的最低气温为19℃为________事件;没有水分,种子仍然发芽是________事件. 答案:随机,不可能5. 一个均匀材料制作的正方形骰子,六个面上分别标以数字1,2,3,4,5,6,连续抛掷两次,求第一次点数小于第二次点数的概率.解:设“第一次点数小于第二次点数的概率”为事件A,则P (A)=3615= 125. 试题解析:连续抛掷两次骰子,可能结果如下表:事件“第一次点数小于第二次点数”包含了15个基本事件,因此第一次点数小于第二次点数的概率=125.6。
一个容量为n 的样本,分成若干组,已知某组的频数和频率分别为50和0.25,则n =_______. 答案:n =2007.如果x,y 表示0,1,2,···,10中任意两个不等的数,P(x,y)在第一象限的个数是( ).A 、72B 、90 C、110 D 、121 答案:B8.甲、乙、丙三人射击的命中率都是0.5,它们各自打靶一次,那么他们都没有中靶的概率是( ).A 、 0.5 B、0。
25 C 、 0。
3 D、 0。
125 答案:D9。
两个盒子内各有3个同样的小球,每个盒子中的小球上分别标有1,2,3三个数字。
从两个盒子中分别任意取出一个球,则取出的两个球上所标数字的和为3的概率是( ).A 、91 B、92 C 、31 D 、32答案:B10.下面属于分层抽样的特点的是( )。

第十章 概率统计初步测试题一、选择题1.某商场有4个大门,若从一个门进去,购买商品后再从另一个门出去,不同 的走法共有多少种?( )A. 3B.7C. 12D.16 A. B. C. D. 2.下列事件为随机事件的是( )A. {太阳从西边下山}B.{某人的体温100℃}C. {买康师傅绿茶,得到“再来一瓶”}D.{水往低处走} 3.掷一颗骰子,得到4点的概率( ) A.21 B.41 C. 121 D. 61 4. 已知一个总体含有N 个个体,要从中抽取一个个体,则抽样过程中,每个个体被抽到的概率( )A. 变小B.变大C. 相等D.无法确定 5.关于频率直方图下列说法正确的是( ) A. 直方图的高是表示取某数的频率B. 直方图的高是表示该组上的个体在样本中出现的频率C. 直方图的高是表示该组上的个体在样本中出现的频数与组距的比值D. 直方图的高是表示该组上的个体在样本中出现的频率与组距的比值则第四组的频率是( )A. 0.14B. 0.13C. 0.15D. 0.12 7. 掷两颗骰子,得到和为7点的概率( ) A.21 B.41 C. 121 D. 61 8.一个容量为n 的样本,分成若干组后,已知某数的频数为60,频率为83, 则n 等于( )A. 150B. 160C. 170D. 1809.为考察某市初中毕业生数学考试情况,从中抽取200名学生的成绩,该问题 的样本是( )A. 这200名学生的成绩B. 这200名学生C. 这200名学生的平均成绩D. 这200名学生的数学成绩10.某此普通话比赛,七位评委为一名参赛者打分,参赛者小红表演后,评委 打出的分数为:9.9 9.7 9.7 9.4 9.9 9.5 9.3 9.1按规定去掉一个最高分,去掉一个最低分,将其余分数的平均分数作为参赛者 的最后得分,则小红最后得分为( )A. 9.5B. 9.6C. 9.7D. 9.8二、填空题1.三个人性别各不相同,这个事件是________________2.从12个同类产品(其中10个正品,2个次品)中,任意抽出2个,抽到1 个次品的概率是_____________________________三、解答题1.判断下列事件哪个是必然事件,哪个是不可能事件,哪个是随机事件?(1)上抛一个物体,经过一段时间后,物体落在地面上(2)标准大气压下,水在20℃时结冰(3)从一副扑克牌中任取一张,得到红桃K2.甲班有三好学生8人,乙班有三好学生8人,丙班有三好学生9人:(1)由这三个班中任选1名三好学生,出席三好学生表彰会,有多少种不同的选法?(2)由这三个班中各选1名三好学生,出席三好学生表彰会,有多少种不同的选法?若取组距为7cm,(1)根据上面数据列出频率分布表,(2)画出频率分布直方图课后反思:。

概率与统计初步例1.指出下列事件是必然事件,不可能事件,还是随机事件? ①某乒乓球运动员在某运动会上获得冠军。
②掷一颗骰子出现8点。
③如果0=-b a ,则b a =。
④某人买某一期的体育彩票中奖。
解析:①④为随机事件,②是不可能事件,③是必然事件。
例2.某活动小组有20名同学,其中男生15人,女生5人,现从中任选3人组成代表队参加比赛,A 表示“至少有1名女生代表”,求)(A P 。
例3.在50件产品中,有5件次品,现从中任取2件。
以下四对事件那些是互斥事件?那些是对立事件?那些不是互斥事件?①恰有1件次品和恰有2件次品 ②至少有1件次品和至少有1件正品 ③最多有1件次品和至少有1件正品 ④至少有1件次品和全是正品例4.从1,2,3,4,5,6六个数字中任取两个数,计算它们都是偶数的概率。
例5.抛掷两颗骰子,求:①总点数出现5点的概率;②出现两个相同点数的概率。
例6.甲、乙两人各进行一次射击,如果两人击中目标的概率都是0.6,计算: ①两人都未击中目标的概率; ②两人都击中目标的概率;③其中恰有1人击中目标的概率; ④至少有1人击中目标的概率。
例7.种植某种树苗成活率为0.9,现种植5棵。
试求: ①全部成活的概率; ②全部死亡的概率; ③恰好成活4棵的概率; ④至少成活3棵的概率。
【过关训练】一、选择题1、事件A 与事件B 的和“B A Y ”意味A 、B 中( ) A 、至多有一个发生 B 、至少有一个发生 C 、只有一个发生 D 、没有一个发生2、在一次招聘程序纠错员的考试中,程序设置了依照先后顺序按下h,u,a,n,g 五个键的密码,键盘共有104个键,则破译密码的概率为( )A 、51041P B 、51041C C 、1041 D 、1045 3、抛掷两枚硬币的试验中,设事件M 表示“两个都是反面”,则事件M 表示( ) A 、两个都是正面 B 、至少出现一个正面C 、一个是正面一个是反面D 、以上答案都不对 4、已知事件A 、B 发生的概率都大于0,则( ) A 、如果A 、B 是互斥事件,那么A 与B 也是互斥事件B 、如果A 、B 不是相互独立事件,那么它们一定是互斥事件C 、如果A 、B 是相互独立事件,那么它们一定不是互斥事件D 、如果A 、B 是互斥且B A Y 是必然事件,那么它们一定是对立事件5、有5件新产品,其中A 型产品3件,B 型产品2件,现从中任取2件,它们都是A 型产品的概率是( )A 、53B 、52C 、103D 、2036、设甲、乙两人独立地射击同一目标,甲击中目标的概率为0.9,乙击中目标的概率为98,现各射击一次,目标被击中的概率为( )A 、98109+B 、98109⨯C 、981081⨯-D 、90897、一个电路板上装有甲、乙两个保险丝,若甲熔断的概率为0.2,乙熔断的概率为0.3,至少有一根熔断的概率为0.4,则两根同时熔断的概率为( )A 、0.5B 、0.1C 、0.8D 、以上答案都不对8、某机械零件加工有2道工序组成,第1道工序的废品率为a ,第2道工序的废品率为b ,假定这2道工序出废品是彼此无关的,那么产品的合格率是( )A 、1+--b a abB 、b a --1C 、ab -1D 、ab 21-9、某厂大量生产某种小零件,经抽样检验知道其次品率是1﹪,现把这种零件每6件装成一盒,那么每盒中恰好含1件次品的概率是( )A 、6)10099(B 、0.01C 、516)10011(1001-CD 、4226)10011()1001(-C 10、某气象站天气预报的准确率为0.8,计算5次预报中至少4次准确的概率是( )A 、45445)8.01(84.0--⨯⨯CB 、55555)8.01(84.0--⨯⨯C C 、45445)8.01(84.0--⨯⨯C +55555)8.01(84.0--⨯⨯C D 、以上答案都不对11、同时抛掷两颗骰子,总数出现9点的概率是( )A 、41B 、51C 、61D 、9112、某人参加一次考试,4道题中解对3道则为及格,已知他的解题准确率为0.4,则他能及格的概率约是( )A 、0.18B 、0.28C 、0.37D 、0.48二、填空题1、若事件A 、B 互斥,且61)(=A P ,32)(=B P ,则=)(B A P Y 2、设A 、B 、C 是三个事件,“A 、B 、C 至多有一个发生”这一事件用A 、B 、C 的运算式可表示为3、1个口袋内有带标号的7个白球,3个黑球,事件A :“从袋中摸出1个是黑球,放回后再摸1个是白球”的概率是4、在4次独立重复试验中,事件A 至少出现1次的概率是8180,则事件A 在每次试验中发生的概率是5、甲、乙两射手彼此独立地射击同一目标,甲击中目标的概率为0.8,乙击中目标的概率为0.9,则恰好有一人击中目标的概率为三、解答题1、甲、乙两人射击,甲击中靶的概率为0.8,乙击中靶的概率为0.7,现在,两人同时射击,并假定中靶与否是相互独立的,求:(1)两人都中靶的概率; (2)甲中靶乙不中靶的概率; (3)甲不中靶乙中靶的概率。

概率与统计初步测试题姓 名:一、选择题:(本题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.同时向上抛100个铜板,落地时100个铜板朝上的面都相同,你认为对这100个铜板下面情况更可能正确的是A.这100个铜板两面是一样的 B.这100个铜板两面是不同的 C.这100个铜板中有50个两面是一样的,另外50个两面是不相同的 D.这100个铜板中有20个两面是一样的,另外80个两面是不相同的2.口袋内装有一些大小相同的红球、白球和黒球,从中摸出1个球,摸出红球的概率是0.42,摸出白球的概率是0,28,那么摸出黒球的概率是 A .0.42 B .0.28 C .0.3 D .0.73.某单位有老年人28人,中年人54人,青年人81人.为了调查他们的身体状况,需从他们中抽取一个容量为36的样本,最适合抽取样本的方法是( ). A .简单随机抽样 B .系统抽样C .分层抽样D .先从老年人中剔除一人,然后分层抽样 4.10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,4.设其平均数为a ,中位数为b ,众数为c ,则有( ).A .a>b>cB .b>c>aC .c>a>bD .c>b>a 5.下列说法错误的是( ).A .在统计里,把所需考察对象的全体叫作总体B .一组数据的平均数一定大于这组数据中的每个数据C .平均数、众数与中位数从不同的角度描述了一组数据的集中趋势D .一组数据的方差越大,说明这组数据的波动越大6.从甲、乙两班分别任意抽出10名学生进行英语口语测验,其测验成绩的方差分别为S12= 13.2,S22=26.26,则( ).A .甲班10名学生的成绩比乙班10名学生的成绩整齐B .乙班10名学生的成绩比甲班10名学生的成绩整齐C .甲、乙两班10名学生的成绩一样整齐D .不能比较甲、乙两班10名学生成绩的整齐程度 7.下列说法正确的是( ).A .根据样本估计总体,其误差与所选择的样本容量无关B .方差和标准差具有相同的单位C .从总体中可以抽取不同的几个样本D .如果容量相同的两个样本的方差满足21S < 22S ,那么推得总体也满足21S <22S 是错的8.先后抛掷硬币三次,则至少一次正面朝上的概率是A .81B . 83C . 85D . 879.在一次数学测验中,某小组14名学生分别与全班的平均分85分的差是:2,3,-3,-5,12,12,8,2,-1,4,-10,-2,5,5,那么这个小组的平均分是( ) A .97.2 B .87.29 C .92.32 D .82.86 10.如果一组数中每个数减去同一个非零常数,则这一组数的( ). A .平均数不变,方差不变 B .平均数改变,方差改变 C .平均数不变,方差改变 D .平均数改变,方差不变 二、填空题:(本题共5小题,每小题5分,共25分,请把答案填写在答题纸上) 11.在20瓶墨水中,有5瓶已经变质不能使用,从这20瓶墨水中任意选出1瓶,取出的墨水是变质墨水的概率为________.12. 从1,2,3,4,5五个数字中,任意有放回地连续抽取三个数字,则三个数字完全不同的概率是_________.13. 从1,2,3,…,9这9个数字中任取2个数字.(1)2个数字都是奇数的概率为_____;14.一个公司共有240名员工,下设一些部门,要采用分层抽样方法从全体员工中抽取一个容量为20的样本.已知某部门有60名员工,那么从这一部门抽取的员工人数是 。

第十章概率与统计初步测验题第十章概率与统计初步测验题班级学号姓名分数一、选择题(每小题3分,共30分)1. 从5名男生和5名女生中任选1人参加校合唱队,那么不同的选法有( )A.1种B. 5种C.10种D.25种2.下列事件中,概率为1的是( )A.随机事件B.必然事件C.不可能事件D.对立事件3.下列现象不是随机现象的是( )A.掷一枚硬币着地时反面朝上B.明天下雨C.三角形的内角和为180°D.买一张彩票中奖4. 先后抛掷两枚硬币,出现“一正一反”的概率是( )A. 1/2 B. 1/3C. 1/4D. 3/45.书架上有语文、英语、数学、物理、化学共5本不同的书,现从中任抽一本,则没有抽到物理书的概率是( )A. 1/5 B. 2/5 C. 3/5 D. 4/56. 某职业学校高一有15个班,为了了解学生的课外兴趣爱好,对每班的5号进行问卷调查.这里运用的抽样方法是( )A.分层抽样 B. 抽签法C.随机数表法D.系统抽样7. 从全班45名学生中抽取5名学生进行体能测试,下列说法正确的是( )A.总体是45B.个体是每个学生C.样本是5名学生D.样本容量是58. 一个样本的容量为n,分组后某一组的频数和频率分分别是40,0.25,则n是( ) A.10 B. 40 C.100 D.1609、在对100个数据进行整理后的频数分布表中,各组的频率之和与频数之和分别是( )A. 100,1 B. 100,100 C. 1,100 D. 1,110.7名男选手和8名女选手组成乒乓球混合双打队,不同的组合方式有()种A 15种B 1 种C 49 种D 56种二、填空题(每空3分,共30分)1. 给出5个数90,92,94,90,94,则这5个数的平均值和方差分别是,。
2.某工厂生产A、B、C三种不同型号的仪器,数量之比是2:3:5,现采用分层抽样的方法抽取一容量为50的样本,则样本中这三种不同型号的仪器分别有件件件。

第十章《概率与统计初步》过关试题一、选择题:(每小题5分,共计50分)1. A,B,C,D,E五种不同的商品要在货架上排成一排,其中A,B两种商品必须排在一起,而C,D两种商品不能排在一起,则不同的排法共有( )种种种种2. 从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是( )A.{至少有一个白球},{都是白球}B.{至少有一个白球},{至少有一个红球}C.{恰有1个白球},{恰有2个白球}D.{至少有1个白球},{都是红球}3. 从1,2,……,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是( )A.59B.49C.1121D.10214. 同一天内,甲地下雨的概率是,乙地下雨的概率是,假定在这天两地是否下雨相互之间没有影响,那么甲、乙两地都不下雨的概率是( )某射手射击1次,击中目标的概率是.他连续射击4次,且各次射击是否击中目标相互之间没有影响.有下列结论:①他第3次击中目标的概率是;②他恰好击中目标3次的概率是×;③他至少击中目标1次的概率是1—.其中正确结论的是( )A.①③B.①②C.③D.①②③6. 从某年级500名学生中抽取60名学生进行体重的统计分析,下列说法正确的是()名学生是总体B.每个被抽查的学生是样本C.抽取的60名学生的体重是一个样本D.抽取的60名学生的体重是样本容量7. 为了让人们感知丢弃塑料袋对环境造成的影响,某班环保小组的六名同学记录了自己家中一周内丢的塑料袋的数量,结果如下(单位:个):33、25、28、26、25、31.如果该班有45名学生,那么根据提供的数据估计本周全班同学各家共丢弃塑料袋( )个个个个8. 从甲、乙两种玉米苗中各抽10株,测得它们的株高分别如下:(单位:cm)根据以上数据估计( )A.甲种玉米比乙种不仅长得高而且长得整齐B.乙种玉米比甲种不仅长得高而且长得整齐C.甲种玉米比乙种长得高但长势没有乙整齐D.乙种玉米比甲种长得高但长势没有甲整齐9. 某公司甲、乙、丙、丁四个地区分别有150 个、120个、180个、150个销售点.公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其收入和售后服务等情况,记这项调查为②.则完成①、②这两项调查宜采用的抽样方法依次是()A.分层抽样法,系统抽样法B.分层抽样法,简单随机抽样法C.系统抽样法,分层抽样法D.简单随机抽样法,分层抽样法10. 实验测得四组()x y,的值为(12)(23)(34)(45),,,,,,,,则y与x之间的回归直线方程为( )A.1y x=+ B.2y x=+C.21y x=+ D.1y x=-二、填空题:(每小题5分,共计25分)11. 8名同学争夺3项冠军,获得冠军的可能性有种.12. 有1元、2元、5元、50元、100元的人民币各一张,取其中的一张或几张,能组成不同的币值的种数是 .13. 同时掷四枚均匀硬币,恰有两枚“正面向上”的概率是 .14. 某学校共有教师490人,其中不到40岁的有350人,40岁及以上的有140人.为了了解普通话在该校中的推广普及情况,用分层抽样的方法,从全体教师中抽取一个容量为70人的样本进行普通话水平测试,其中在不到40岁的教师中应抽取的人数为______. 15. 有下列关系:(1)人的年龄与他(她)拥有的财富之间的关系(2)曲线上的点与该点的坐标之间的关系(3)苹果的产量与气候之间的关系(4)森林中的同一种树木,其断面直径与高度之间的关系(5)学生与他(她)的学号之间的关系其中,具有相关关系的是.三、解答题:(16-19每小题12分,20题13分,21题14分,共计75分)16. 用0,1,2,3,4,5这六个数字:(1)可组成多少个无重复数字的自然数(2)可组成多少个无重复数字的四位偶数(3)组成无重复数字的四位数中比4023大的数有多少17. 解答下列各题:(1)一个口袋内装有相同的7个白球和3个黑球,从中任意摸出两个,得到1个白球和1个黑球的概率是多少(2)有发芽率分别为与的两批种子,在两批种子中各任取1粒,求恰有1粒种子发芽的概率18. 5人并排坐在一起照像,计算:(1)甲恰好坐在正中间的概率;(2)甲、乙两人恰好坐在一起的概率;(3)甲、乙两人恰好坐在两端的概率;(4)甲坐在中间、乙坐在一端的概率.19. 盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率:(1)取到的2只都是次品;(2)取到的2只中正品、次品各一只;(3)取到的2只中至少有一只正品.20. 某港口为了加强货运管理,缩短货物候船日期,从去年的原始资料中随机地抽出10份,得出关于货物候船日期如下:(单位:日)15 20 11 7 910 16 13 1118试估计该港口去年货物候船日期的均值和标准差.21. 某医院用光电比色计检验尿汞时,得尿汞含量(毫克/升)与消光系数如下表:(1)如果y与x之间具有线性相关关系,求回归直线方程;(2)估计尿汞含量为9毫克/升时的消光系数.。

概率、统计、统计案例、算法初步一、选择题(本题共12小题,每小题5分,共60分)1.在如图所示的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(圆中阴影部分)中的概率是( )A.41 B .81 C.4πD.8π解析:选D 设正方形的边长为2,则豆子落在正方形内切圆的上半圆中的概率为4π×12=8π.2.(2012·中山模拟)为了检查某超市货架上的饮料是否含有塑化剂,要从编号依次为1到50的塑料瓶装饮料中抽取5瓶进行检验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的5瓶饮料的编号可能是( )A .5,10,15,20,25B .2,4,8,16,32C .1,2,3,4,5D .7,17,27,37,47解析:选D 利用系统抽样,把编号分为5段,每段10个,每段抽取一个,号码间隔为10.3.一块各面均涂有油漆的正方体被锯成1 000个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,则任意取出一个正方体其三面涂有油漆的概率是( )A.121B.101C.253D.1251解析:选D 小正方体三面涂油漆的有8种情况,所求概率为1 0008=1251.4.(文科)在三棱锥的六条棱中任选两条,则这两条棱所在直线为异面直线的概率是( ) A.61 B.51 C.41D.31解析:选B 由已知得基本事件总数为15,其中互为异面直线的对数为3,故所求的概率为P =153=51.5.(2012·山东高考)执行右面的程序框图,如果输入a =4,那么输出的n 的值为( ) A .2 B .3 C .4 D .5解析:选B 逐次计算结果是P =1,Q =3,n =1;P =5,Q =7,n =2;P =21,Q =15,n =3,退出循环,故输出结果是n =3.6.(2012·湖北模拟)一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,收集数据如下:设回归方程为^y=bx +a ,则点(a ,b )在直线x +45y -10=0的( ) A .左上方 B .左下方 C .右上方D .右下方解析:选C 依题意得,=81×(10+20+30+40+50+60+70+80)=45,=81×(62+68+75+81+89+95+102+108)=85.则85=45b +a ,a +45b -10=75>0,因此点(a ,b )必位于直线x +45y -10=0的右上方.7.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为x 、y ,则log 2x y =1的概率为( )A.61B.365C.121D.21解析:选C 由log 2x y =1⇒2x =y ,x ∈{1,2,3,4,5,6},y ∈{1,2,3,4,5,6},∴x =1,y =2或x =2,y =4或x =3,y =6,共3种情况,∴P =6×63=121.8.某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单元:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )A .90B .75C .60D .45解析:选A 产品净重小于100克的频率为(0.050+0.100)×2=0.300,设样本容量为n ,则n 36=0.300,所以n =120,净重大于或等于98克并且小于104克的产品的频率为(0.100+0.150+0.125)×2=0.75,所以样本中净重大于或等于98克并且小于104克的产品的个数是120×0.75=90.9.(2012·陕西高考)如图是计算某年级500名学生期末考试(满分为100分)及格率q 的程序框图,则图中空白框内应填入( )A .q =M NB .q =N MC .q =M +N ND .q =M +N M解析:选D 程序执行的过程是如果输入的成绩不小于60分即及格,就把变量M 的值增加1,即变量M 为成绩及格的人数,否则,由变量N 统计不及格的人数,但总人数由变量i 进行统计,不超过500就继续输入成绩,直到输入完500个成绩停止循环,输出变量q ,变量q 代表的含义为及格率,也就是总人数及格人数=M +N M.10. (2012.泉州质检)为了调查某校学生喜欢数学课的人数比例,采用如下调查方法: (1)在该校中随机抽取100名学生,并编号为1,2,3, (100)(2)在箱内放置两个白球和三个红球,让抽取的100名学生分别从箱中随机摸出一球,记住其颜色并放回;(3)请下列两类学生举手:①摸到白球且号数为偶数的学生,②摸到红球且不喜欢数学课的学生.如果总共有26名学生举手,那么用概率与统计的知识估计该校学生中喜欢数学课的人数比例大约是( )A .88%B .90%C .92%D .94%解析:选B 100名学生中大约有40人摸出白球,60人摸出红球;摸出白球且号数为偶数的大约有20人,因此摸到红球且不喜欢数学课的大约有26-20=6(人),摸到红球且喜欢数学课的大约有60-6=54(人),由此估计该校学生中喜欢数学课的大约占6054=90%.11.(2012·湖北模拟)在区间[0,1]上任取三个数a ,b ,c ,若向量m =(a ,b ,c ),则|m |≤1的概率是( )A.24πB.12πC.323πD.6π解析:选D 依题意得,实数a ,b ,c 满足0≤c ≤1,0≤b ≤1,这样的点(a ,b ,c )可视为在空间直角坐标系下的单位正方体区域(其中原点是该正方体的一个顶点)内的点,其中满足|m |≤1,即≤1,a 2+b 2+c 2≤1,这样(a ,b ,c )可视为在空间直角坐标系下的单位正方体区域内且其还在以原点为球心、1为半径的球形区域内的点,该部分的体积恰好等于该球体积的81,因此|m |≤1的概率等于13π×13=6π.12. (2012·临沂模拟)若在区间[-5,5]内任取一个实数a ,则使直线x +y +a =0与圆(x -1)2+(y +2)2=2有公共点的概率为( )A.52B.52C.53D.102解析:选B 若直线与圆有公共点,则圆心到直线的距离d =2|1-2+a|=2|a -1|≤,解得-1≤a ≤3.又a ∈[-5,5],故所求概率为104=52.二、填空题(本题有4小题,每小题5分,共20分)13.某校开展“爱我青岛,爱我家乡”摄影比赛,9位评委为参赛作品A 给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x )无法看清,若记分员计算无误,则数字x 应该是________.解析:当x ≥4时,789+89+92+93+92+91+94=7640≠91,∴x <4,则789+89+92+93+92+91+x +90=91,∴x =1.答案:114. (2012·河南模拟)2012年的NBA 全明星赛于美国当地时间2012年2月26日在佛罗里达州奥兰多市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是________.解析:依题意得,甲、乙两人这几场比赛得分的中位数分别是28、36,因此甲、乙两人这几场比赛得分的中位数之和是64.答案:6415.(2012·苏州模拟)甲、乙两名射击运动员参加某大型运动会的预选赛,他们分别射击了5次,成绩如下表(单位:环):如果甲、乙两人中只有1人入选,则入选的最佳人选应是________.解析:甲=乙=9,s 甲2=51×[(9-10)2+(9-8)2+(9-9)2+(9-9)2+(9-9)2]=52, s 乙2=51×[(9-10)2+(9-10)2+(9-7)2+(9-9)2+(9-9)2]=56>s 甲2,故甲更稳定.答案:甲16. (2012·福州模拟)在圆x 2+y 2=4所围成的区域内随机取一个点P (x ,y ),则|x |+|y |≤2的概率为________.解析:不等式|x |+|y |≤2表示的平面区域如图中的阴影部分所示,则|x |+|y |≤2的概率为P =π×2222=π2.答案:π2三、解答题(本题有6小题,共70分)17.(11分)(2012·东北三校联考)一次数学模拟考试,共12道选择题,每题5分,共计60分,每道题有四个可供选择的答案,仅有一个是正确的.学生小张只能确定其中10道题的正确答案,其余2道题完全靠猜测回答.小张所在班级共有40人,此次考试选择题得分情况统计表:现采用分层抽样的方法从此班抽取20人的试卷进行选择题质量分析. (1)应抽取多少张选择题得60分的试卷?(2)若小张选择题得60分,求他的试卷被抽到的概率.解:(1)得60分的人数40×10%=4.设抽取x 张选择题得60分的试卷,则2040=x 4, 则x =2,故应抽取2张选择题得60分的试卷.(2)设小张的试卷为a 1,另三名得60分的同学的试卷为a 2,a 3,a 4,所有抽取60分试卷的方法为:(a 1,a 2),(a 1,a 3),(a 1,a 4),(a 2,a 3),(a 2,a 4),(a 3,a 4)共6种,其中小张的试卷被抽到的抽法共有3种,故小张的试卷被抽到的概率为P =63=21.18.(11分)某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗的生长情况,在这批树苗中随机测量了其中50棵树苗的高度(单位:厘米),并把所得数据列成了如下表所示的频数分布表:(1)在这批树苗中任取一棵,其高度在85厘米以上的概率大约是多少?(2)这批树苗的平均高度大约是多少?(计算时可以用组中值代替各组数据的平均值) (3)为了进一步获得研究资料,若从[40,50)组中移出1棵树苗,从[90,100]组中移出2棵树苗进行试验研究,则[40,50)组中的树苗A 和[90,100]组中的树苗C 同时被移出的概率是多少?解:(1)因为[80,90)的组中值是85,所以高度在85厘米以上的树苗棵数约为6+4=10. 所以在这批树苗中任取一棵,其高度在85厘米以上的概率大约是5010=51=0.2. (2)树苗的平均高度约为5045×2+55×3+65×14+75×15+85×12+95= 503 690=73.8(厘米).(3)记[40,50)组中的树苗为A ,B ,[90,100)组中的树苗为C ,D ,E ,F ,则事件“从[40,50)组中移出1棵树苗,从[90,100]组中移出2棵树苗”中所包含的基本事件是(A ,C ,D ),(A ,C ,E ),(A ,C ,F ),(A ,D ,E ),(A ,D ,F ),(A ,E ,F ),(B ,C ,D ),(B ,C ,E ),(B ,C ,F ),(B ,D ,E ),(B ,D ,F ),(B ,E ,F ),共12个.其中,满足树苗A ,C 同时被移出的事件为(A ,C ,D ),(A ,C ,E ),(A ,C ,F ),共3个.所以树苗A 和树苗C 同时被移出的概率P =123=0.25.19.(12分)(2012·东北三校联考)汽车行业是碳排放量比较大的行业之一.欧盟规定,从2012年开始,将对CO 2排放量超过130 g/km(视为排放量超标)的MI 型新车进行惩罚.某检测单位从甲、乙两类MI 型品牌车中各抽取5辆进行CO 2排放量检测,记录如下(单位:g/km):经检测发现,乙品牌车CO 2排放量的平均值为乙=120 g/km.(1)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆CO 2排放量超标的概率是多少?(2)若90<x <130,试比较甲、乙两类品牌车CO 2排放量的稳定性.解:(1)从被检测的5辆甲类品牌车中任取2辆,其CO 2排放量共有10种不同的结果:80,110;80,120;80,140;80,150;110,120;110,140;110,150;120,140;120,150;140,150.设“至少有一辆CO 2排放量超标”为事件A ,则事件A 包含以下7种不同的结果:80,140;80,150;110,140;110,150;120,140;120,150;140,150.∴P (A )=107=0.7.(2)由题可知,甲=乙=120,x +y =220.5s 甲2=(80-120)2+(110-120)2+(120-120)2+(140-120)2+(150-120)2=3 000, 5s 乙2=(100-120)2+(120-120)2+(x -120)2+(y -120)2+(160-120)2=2 000+(x -120)2+(y -120)2.∵x +y =220,∴5s 乙2=2 000+(x -120)2+(x -100)2, 令x -120=t ,∵90<x <130,∴-30<t <10, ∴5s 乙2=2 000+t 2+(t +20)2,∴5s 乙2-5s 甲2=2t 2+40t -600=2(t +30)(t -10)<0, ∴s 乙2<s 甲2,∴乙类品牌车CO 2排放量的稳定性好.20.(12分)(2012·福建模拟)某种产品的广告费支出x 与销售额y (单位:万元)之间有如下对应数据:(1)求回归直线方程;(2)试预测广告费支出为10万元时,销售额多大?(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.参考数据:x 5i 2=145,y 5i 2=13 500,x 5i y i =1 380解:(1)=52+4+5+6+8=525=5, =530+40+60+50+70=5250=50,又已知x 5i 2=145,x 5i y i =1 380,于是可得:^b =22=145-5×5×51380-5×5×50=6.5,^a =-^b=50-6.5×5=17.5,因此,所求回归直线方程为^y=6.5x +17.5.(2)根据上面求得的回归直线方程,当广告费支出为10万元时,^y=6.5×10+17.5=82.5(万元),即这种产品的销售收入大约为82.5万元. (3)基本事件:(30,40),(30,60),(30,50),(30,70),(40,60),(40,50),(40,70),(60,50),(60,70),(50,70)共10个.两组数据其预测值与实际值之差的绝对值都超过5有(60,50),所以至少有一组数据其预测值与实际值之差的绝对值不超过5的概率为1-101=109. 21.(12分) (2012·深圳调研)通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:(1)从这50名女生中按是否看营养说明采取分层抽样的方法抽取一个容量为5的样本,则样本中看与不看营养说明的女生各有多少名?(2)从(1)中的5名女生样本中随机选取两名作深度访谈,求选到看与不看营养说明的女生各一名的概率;(3)根据以上列联表,问有多大把握认为“性别与在购买食物时是否看营养说明”有关? 参考公式:K 2=(a +b(c +d(a +c(b +d n(ad -bc2,其中n =a +b +c +d .参考数据:解:(1)根据分层抽样可得:样本中看营养说明的女生有505×30=3名,样本中不看营养说明的女生有505×20=2名.(2)记样本中看营养说明的3名女生为a 1,a 2,a 3,不看营养说明的2名女生为b 1,b 2,从这5名女生中随机选取2名,共有10个等可能的基本事件:a 1,a 2;a 1,a 3;a 1,b 1;a 1,b 2;a 2,a 3;a 2,b 1;a 2,b 2;a 3,b 1;a 3,b 2;b 1,b 2.其中事件A “选到看与不看营养说明的女生各一名”包含了6个基本事件:a 1,b 1;a 1,b 2;a 2,b 1;a 2,b 2;a 3,b 1;a 3,b 2.所以所求的概率为P (A )=106=53. (3)根据题中的列联表得K 2=80×30×60×50110×(50×20-30×102=72539≈7.486. 由P (K 2≥6.635)=0.010,P (K 2≥7.879)=0.005可知,有99%的把握认为“性别与在购买食物时是否看营养说明”有关.22.(12分)(2012·石家庄模拟)某班甲、乙两名同学参加100米达标训练,在相同条件下两人10次训练的成绩(单位:秒)如下:(1)请画出适当的统计图;如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论);(2)从甲、乙两人的10次成绩中各随机抽取一次,求抽取的成绩中至少有一个低于12.8秒的概率;(3)经过对甲、乙两位同学的若干次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率.解:(1)甲、乙两人10次训练的成绩的茎叶图:或频率分布直方图如下:从统计图中可以看出,乙的成绩较为集中,差异程度较小,所以选派乙同学代表班级参加比赛更好.(2)设事件A 为:甲的成绩低于12.8秒,事件B 为:乙的成绩低于12.8秒,则甲、乙两人成绩至少有一个低于12.8秒的概率为:1-106×106=2516.(3)设甲同学的成绩为x ,乙同学的成绩为y ,则|x -y |<0.8,得x -0.8<y <0.8+x ,如图,阴影部分面积即为3×3-2.2×2.2=4.16,则P (|x -y |<0.8)=P (x -0.8<y <0.8+x )=3×34.16=225104.选修4-1 几何证明选讲。

数学概率与统计基础练习题及答案1. 概率基础在一个标准的52张扑克牌中,有4种花色(红桃、黑桃、方片和梅花),每个花色有13张牌(A、2至10、J、Q、K)。
现从牌中随机抽取一张牌,计算以下概率:a) 抽到红桃的概率是多少?b) 抽到一个大于10的牌的概率是多少?c) 抽到一个心牌且是红色的概率是多少?答案:a) 红桃有13张,总共有52张牌,所以抽到红桃的概率是13/52,即1/4。
b) 大于10的牌有J、Q和K共12张,总共有52张牌,所以抽到一个大于10的牌的概率是12/52,即3/13。
c) 心牌共有13张,其中红桃为红色,总共有52张牌,所以抽到一个心牌且是红色的概率是13/52,即1/4。
2. 组合与排列a) 有5个人排成一排,请问一共有多少种不同的排列方式?b) 从8个人中选出3个人,请问一共有多少种不同的选法?答案:a) 5个人排成一排有5!= 5 × 4 × 3 × 2 × 1 = 120种不同的排列方式。
b) 从8个人中选出3个人有8个人中选3个的组合数,即C(8, 3) =8! / (3! × (8-3)!) = 56种不同的选法。
3. 条件概率某班级中有40%的学生会打篮球,15%的学生会弹吉他。
已知会打篮球的学生中有70%也会弹吉他,计算:a) 一个随机选中的学生会打篮球且会弹吉他的概率是多少?b) 一个随机选中的学生会打篮球或会弹吉他的概率是多少?答案:a) 会打篮球的学生中会弹吉他的概率是70%,所以一个随机选中的学生会打篮球且会弹吉他的概率是40% × 70% = 28%。
b) 一个随机选中的学生会打篮球或会弹吉他的概率是会打篮球的概率加上会弹吉他的概率减去同时会打篮球且会弹吉他的概率,即40%+ 15% - 28% = 27%。
4. 正态分布某城市的成年男性身高服从正态分布,均值为175厘米,标准差为6厘米。

1.从甲地到乙地,一天内有3班火车,4班汽车开出,则在一天中,不同乘车方法有()A.7种B.12种c .31种D.矿种2.在两个方格里涂红、黄、蓝三种颜色,每个格子只能涂一种颜色,但两个格子颜色可相同也可以不同,则这样的涂法共有(A. 4种B.6种C.8种D.9种3.一次掷甲、乙两枚骰子的实验中,其基本事件的个数是(A. 12B. 24C. 36D.484. 甲、乙、丙三人站成一排,甲站在两头的概率是(l _3 .A 2_3 B 1_5.cl _6.D 5. 从1,2,3,4,5这些数中任取两个不同的数,则取到一奇一偶的概率是(1_3. A1_2 B 、2_5 6.若事件B 与事件E互为对立事件,则P (B)+P CB)等于(A. 1B .』C.1 27.从1,2,3,4,5这五个数字中任取一个,得到偶数的概率是(1·23A.-B .一55C .一58.在100张奖券中有2张中奖,从中任抽一张,则中奖的概率是(11 1 A.—B . -525C .一509.从一副52张扑克牌中,任意抽1张,得到A或K 的概率是(A .213B . ]_26C .1133 D .—5)1 D.一4 )1 D.—2 )1D .一100 )1D .一2 6)))42018-2019学年对口升学班数学(基础模块)单元检测试题(9)概率与统计初步一、选择题(每小题3分,共30分)10.从1,2,3,…,9九个数字中任取两个,则这两个数字都是偶数的概率为()A .了B .』5二、填空题(每小题3分,共24分)11.若事件A 与事件A 互为对立事件,且PCA )= o . 2, 则P(A )=12.某机电班共有42名学生,任选一人是男生的概率为享,则这个班的男生共有名.13.若随机事件A 与随机事件B 为互斥事件,且P(A)+P CB) = O. 5, 则PC A U B) =1_6. c 1_7D 14. 一个笼子里装有3只鸡,5只兔和8只鸭,现从笼子里抓取两只不同种类的动物送人,不同的取法有15.小明,小强和小华三位同学高考的前天晚上被安排在一家宾馆的两个房间住宿,每个房间至多住两人,则共有不同的安排方法种.16.甲、乙、丙三人排成一行,乙站在中间的概率为17.从1,2,3,4,5这些数中任取两个不同的数,则取到两个奇数的概率是11 18. 若事件A,B 相互独立,且P(A)=-,PCB)=—,则P(AB)=3 2 三、计算题(每小题8分,共24分)119.三个运动员练习篮球投篮,每个运动员投进的概率都是—,求2(1)三人都同时是投进的概率;(2)至少有两个人投进的概率.20.将一颗骰子掷两次,求:(1)恰有一次出现6点的概率;.1(2)两次点数之和等于6的概率.21.从含有2件次品的7件产品中,任取2件产品,求以下事件的概率.(1)恰有2件次品的概率P门(2)恰有1件次品的概率P z.四、证明题(每小题6分,共12分)22.10张奖券中有2张中奖券,甲先抽一张,乙再抽一张,证明:两人的中奖的概率相同.23.从含有2件次品的5件产品中,任取2件,事件A"恰有1件次品”事件B"恰有2件次品”,求证:P(A) > P C B).五、综合题(共10分)24.有语文书3本,数学书4本,英语书5本,书都各不相同,要把这些书随机排在书架上.(1)求=利1书各自都必须排在一起的排法有多少种?(2)求英语书不挨着排的概率P.。
测试一一、填空题:(每空4分,共32分)1.设,表示两个随机事件,,分别表示它们对立事件,用,和,表示,恰有一个发生的式子为_________.2.从一批乒乓球中任取4只检验,设表示“取出的4只至少有1只是次品”,则对立事件表示________.3.甲、乙两人同时各掷一枚硬币观察两枚硬币哪面向上。
这个随机试验的样本空间为________.4.掷一颗骰子,出现4点或2点的概率等于________.5.甲、乙两个气象合同时作天气预报,如果它们预报准确的概率分别是0.8和0.7,那么在一次预报中,两个气象台都预报准确的概率是________(设两台独立作预报).6.标准正态变量(0,1)在区间(-2,2)内取值的概率为________.7.作统计推断时,首先要求样本为随机样本,要得到简单随机样本,必须遵从的条件是________.8.已知随机变量的分布列为则()=________.二、选择题:(每小题5分,共25分)9.在掷一颗骰子的试验中,下列事件和事件为互斥事件的选项是().(A)={1,2} ={1,3,5} (B)={2,4,6}={1}(C)={1,5} ={3,5,6} (D)={2,3,4,5}={1,2}10.下面给出的表,可以作为某一随机变量的分布列的是11.对某项试验,重复做了次,某事件出现了次,则下列说法正确的一个是(). (A)就是(B)当很大时,与有较大的偏差(C)随着试验次数的增大,稳定于(D)随着试验次数的无限增大,与的偏差无限变小。
12.总体期望的无偏估计量是().(A)样本平均数(B)样本方差(C)样本标准差(D)样本各数据之和13.表示随机变量取值的平均水平的指标是().(A)样本平均数(B)数学期望(C)方差(D)标准差三、解答题:14.(7分)某射手在相同的条件下对同一目标进行射击5次,已知每次中靶的概率为0.4,求5次射击恰有2次中靶的概率?15.(7分)一个袋内装有红、黄、白三种颜色的球各一只,从中每次任取一只,有放回地取3次,求3只全是红球的概率.16.(9分)某工人同时看管三台机器.已知一个小时内各机器不需要看管的概率分别为是:甲为0.9,乙为0.8,丙为0.85,各机器自动独立工作,求在一个小时内至少有一台机器需要看管的概率.17.(10分)某港口为了加强货运管理,缩短货物候船日期,从去年的原始资料中随机地抽出10份,得出关于货物候船日期如下:(单位:日)15 20 11 7 8 10 16 13 11 18试估计该港口去年货物候船日期的均值和标准差。
18.已知,两变量与有如下试验数据:[考虑到解题所用时间,本题可采取两种方案,一是测试时间多得够用,可用本测试所给条件样式,如果估计时间不够,可直接给出数据计算表(见解答中的表)这样可以省去复杂的计算过程.]求(1)与的回归直线方程.答案、提示和解答:1.+(或).2.全是正品(一只次品都没有,即都是正品).3.{(正,反)(反,正)(正,正)(反,反)}.4..5.0.56. 6.68.3%.7.总体中的每个个体都有被抽到的可能,且每个个体被推到的机会都是相等的.8.0.16. 9.B 10.B 11.C 12.A 13.B14.射手射靶只有中和不中两种对立的可能,每次射击条件相同,即相互独立的,故本题可用独立重复试验模型来作.设一次射击中靶为事件,=0.4问题是求5次独立重复试中,恰发生2次的概率,即.15.设={第次取到红球},=1、2、3.16.设={甲机器不需看管},={乙机器不需看管} ,={丙机器不需看管},{至少有一台机器需要看管}的对立事件是三台都不需要看管,我们先求三台都不需看管的概率,即{至少有一台需要看管}=1-0.612=0.388.17.样本平均数和样本标准差分别是总体均值和总体标准差的无偏估计量,所以我们先求样本平均数和样本标准差,用它们分别估计总体参数。
(15+20+11+7+8+10+16+13+11+18)=12.9,=4.28,所以估计该港口去年货物候船日期的均值为12.9(日),标准差为4.28(日).此题的解是用函数型计算器作的,时间很短即可计算出来。
如果多数学生没有条件用计算器,建议教师教给学生公式:.这也便于教师给出不必由学生在考试时进行计算的结果.如将的数值直接作为已知提供给学生.18.(1)先作散点图.以的取值作横坐标,把的相应取值作为纵坐标,在直角坐标系中作散点图,如图.由散点图可看出呈直线型分布,设所求回归直线方程为,由样本数据列表计算:将表中计算结果代入公式计算,所以所求回归线方程为.测试二一、填空题:(每空4分,共32分)1.设,表示两个随机事件,,分别表示,的对立事件,用,和,表示,不都发生的式子为___________.2.从含有2件次品的10件产品中任取3件,则事件“至少有一件次品”的对立的事件是___________.3.小概率原理内容是______________________.4.甲、乙两人在相同的条件下进行射击,互无影响.甲射中目标的概率是0.8,乙射中目标的概率是0.9,两人各射击一次,则两人都击中目标的概率是_____________________.5.掷两颗骰子,所得点数和为5的概率是_____________________.6.已知的概率密度函数为则在区间内取值的概率为__________7.已知的分布列为则()=__________.8.已知随机变量只取1、2、3、4,这4个值且取各值的概率依次为,2,3,4,则=________.二、选择题:(每小题5分,共25分)9.从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是(). (A){至少有一个白球},{都是白球} (B){至少有一个白球},(至少有一个红球)(C){恰有1个白球},{恰有2个白球} (D){至少有1个白球},{都是红球}10.已知事件的概率=,事件的概率=,则事件,至少有一个发生的概率为().11.频率与概率的关系为().(A)概率依频率的改变而改变(B)频率是概率的稳定值(C)概率是频率的稳定值(D)概率与频率无关12.下列选项中,为总体方差无偏估计量的是(其中是样本值,为样本平均数)().13.在下列命题中,假命题一个是()(A)随机变量的方差表示它的离散程度(B)随机变量的数学期望反映的是它取值的平均水平(C)随机变量的标准差表示它的波动大小(D)随机变量概率密度曲线上横坐标=的点的纵坐标表示随机变量在处取值的概率四、解答题:14.(8分)已知羊群受到某种传染病病菌感染后,发病率为,试求5只已感菌的羊中发病头数不多于2只的概率.15.(7分)一个口袋内装有相同的7个白球和3个黑球,从中任意摸出两个,得到1个白球和1个黑球的概率是多少?16.(8分)有发芽率分别为0.9与0.7的两批种子,在两批种子中各任取1粒,求恰有1粒种子发芽的概率?17.(8分)正常人的脉搏平均为72次/分,现测出10例病人的脉搏为(次/分):54 67 68 78 70 66 67 70 65 69试求这些病人的脉搏与正常人脉搏偏差的数学期望及方差的无偏估计值.18.(12分)某工厂半年中每月产品的总成本(万元)与每月产量(万件)的统计数据如下:[建议本题在试卷上直接给出数据计算表(见解答),这样可以节约时间增加检测需要检测的内容](1)绘出散点图:(2)求与的回归直线方程.答案、提示和解答.1. 2.{3件都是正品}. 3.小概率事件在一次试验中是几乎不可能发生的.4.0.9×0.8=0.72.5.. 6、.7、1.6. 8、. 9.C. 10、D. 11、C. 12、A. 13、D.14.设{一只感染病菌的羊发病}为事件,=,5只已感菌的羊相当于作5次独立重复试验,恰好0、1、2只发病分别为不多于2只发病的概率为.另外也可以用{不多于2只}的对立事件为{多于2只}即发病恰为3只,恰为4只,5恰为5只,求出,再用来解.15、设{从中任意摸出两球,得到1个白球和1个黑球}为事件,则由于等可能性和基本事件总数为,为有限,所以为古典概型,事件所包含的基本事件数为.所以.16.设{从第一批种子中任取1粒,发芽}=,则{从第一批种子中任取1粒,不发芽}=;{从第二批种子中任取1粒,发芽}=,则{从第二批种子中任取1粒,不发芽}=.{从两批种子各取一粒恰有1粒种子发芽}17.根据题意,所求是病人的脉搏与正常人脉搏偏差的数学期望及方差,所以总体为病人的脉搏与正常人的脉搏的偏差,所给样本只是病人脉搏;应该转换成“偏差”的样本,用各数据分别减去72得到需要的样本:―18 ―5 ―4 6 ―2 ―6 ―5 ―2 ―7 ―3样本平均数是总体期望的无偏估计值,样本方差是总体方差的无偏估计值,所以有(-18-5-4+6-2-6-5-2-7-3)=-4.6,=35.156,即得病人脉搏与正常人脉搏偏差的数学期望为-4.6,方差为35.156.18.(1)以的取值为横坐标,把的相应取值作为纵坐标,在直角坐标系中作散点图,如图所示(2)将计算列成表格如下把表中计算结果代入求回归系数, 的公式所求回归直线方程为.测试三一、填空题:(每空4分,共32分)1.设,,表示三个随机事件,,,分别表示它们的对应事件,则,,至少有一个发生可表示为_________.2.从含有2件次品的10件产品中任取3件,则事件{所取3种都是正品}的对立事件为________.3.从含有2件次品的5件产品中任取2件,事件={所取2件恰有1件次品},它有一个互斥的事件为________.4.甲,乙两个射手各自在相同的条件下进行射击,甲击中目标的概率是0.8,乙击中的目标的概率为0.9,两个各射击一次,则两个都没击中目标的概率为________.5.已知,,事件和相互独立,则________.6.已知随机变量的分布列为:则()=________.7.已知随机变量的概率密度函数为:则在区间[1、2]内取值的概率为________.8.已知某批产品的长度~(25,2),那么从该批产品中任取一件,其长度落入区间(21,29)的概率是________.二、选择题(每小题5分,共25分)9.一个口袋里装有2个白球2个红球,把“从中任意摸出一个球,是白球”叫做事件,把“从剩下的3个球中任意摸出一个球是白球”叫做事件,则事件和为().(A)相互独立事件(B)互斥事件(C)互为对立事件(D)既不是相互独立的事件,又不是互斥事件10.两个事件互斥是这两个事件对立的().(A)充分条件,但不必要条件. (B)必要条件,但不是充分条件.(C)充分必要条件. (D)既不充分又不必要的条件.11.下列命题正确的一个是().(A)“,,最多有一个不发生”与“,,至少有一个发生”是互斥事件.(B)“,,至少有一个发生”是“,,至少有一个不发生”的对立事件.(C)“,,都不发生”即“,,不都发生”.(D)“,,至多有两个发生”是“,,都发生”的对立事件.12.下列各选项为随机变量的是().(A)总体期望(B)总体方差(C)样本平均数(D)总体所含个体个数13.要考察某批灯泡的平均使用寿命,那么这个平均使用寿命为().(A)样本均值(B)样本方差(C)总体期望(D)总体方差三、解答题:14.(11分)有一批蚕豆种子的发芽率为90%,点播时每穴3粒,求每穴里发芽种子数的分布列.15.(12分)10张奖券中有2张中奖券,设首先由甲,然后由乙各抽1张,试求:(1)甲,乙都中奖的概率;(2)乙中奖的概率.16.(10分)某地区1984年对双职工家庭收入情况调查,抽查了12户,结果如下(单位:元):1914 1492 1820 1521 1496 16071140 1454 1273 1474 1706 1547求该地区双职工户平均年收入的无偏估计值以及方差的无偏估计值.17.(10分)根据某地区统计资料,商品的年销售额和居民平均每人年收入水平数据如下表:[此题在考试时应该给解答中的计算列成的表作为已知条件.](1)作出散点图;(2)求平均每人年收入与商品年销售额之间的回归直线方程.答案、提示和解答:1..2.{至少有一件是次品}.3.{所取2件都是正品}(或{所取2件都是次品}).4.0.025..6.0.96. 7、. 8、95.4%. 9.D. 10、B. 11、D. 12、C. 13、C.14.设一粒蚕豆种子发芽为事件,则=90%. 种3粒相当于3次独立重复试验,其中恰有一粒种子发芽,即事件恰好发生1次,那么粒种子发芽相当于恰好发生次,于是有所以所求发芽种子数的分布列,用表示发芽的种子数,则有:15.设{甲从10张奖券中任抽一张中奖}=.{乙从剩下的奖券中任抽一张中奖}=.(1)因为甲抽时,10张中每一张被抽到的机会相等,所以.甲,乙都中奖,首先甲中奖,在甲中奖的前提下,剩下9张奖券中只有一张奖券,所以乙从中任抽一张中奖的概率为,因此甲、乙都中奖的概率为.也可以这样理解:甲任抽一张有10种抽法,乙从剩下的任抽一张有9种抽法,所以一共有90种等可能抽法,其中甲抽到奖券且乙也抽到奖券为=2,所以(2)发生包含且仅包含两种情况:发生且发生或不发生且发生,即16.样本平均数和样本方差是总体均值和方差的无偏估计量,所以我们可以由样本平均数和方差分别作为总体均值和方差的无偏估计值.[此题最好用计算器计算,否则应给数据计算列表,表中给出方差式用.]即该地区双职工户平均年收入的无偏估计值为1 537元,方差为45 264(标准差为212.75元).17.(1)以的取值为横坐标,把的相应取值作为纵坐标,在直角标系中作点,得散点图如下:(2)将计算列成表格如下:按表中计算出的有关结果可得:代入求回归系数的公式,有所以得商品年销售额与平均每人年收入的回归直线方程为.。