含参数的一元二次不等式的解法

含参数的一元二次不等式的解法解含参数的一元二次不等式，通常情况下，均需分类讨论，那么如何讨论呢？对含参一元二次不等式常用的分类方法有三种：一、按2x 项的系数a 的符号分类，即0,0,0<=>a a a ;例1 解不等式：()0122>+++x a ax分析：本题二次项系数含有参数，()044222>+=-+=∆a a a ，故只需对二次项 系数进行分类讨论。

二、按判别式∆的符号分类，即0,0,0<∆=∆>∆；例2 解不等式042>++ax x分析 本题中由于2x 的系数大于0,故只需考虑∆与根的情况。

例3解不等式()()R m x x m ∈≥+-+014122三、按方程02=++c bx ax 的根21,x x 的大小来分类，即212121,,x x x x x x <=<； 例4解不等式)0( 01)1(2≠<++-a x a a x 分析：此不等式可以分解为：()0)1(<--a x a x ，故对应的方程必有两解。

本题 只需讨论两根的大小即可。

考向二 含参数的一元二次不等式的解法【例2】►求不等式12x 2－ax ＞a 2(a ∈R )的解集．解含参数的一元二次不等式的一般步骤：(1)二次项若含有参数应讨论是等于0，小于0，还是大于0，然后将不等式转化为二次项系数为正的形式．(2)判断方程的根的个数，讨论判别式Δ与0的关系．(3)确定无根时可直接写出解集，确定方程有两个根时，要讨论两根的大小关系，从而确定解集形式．【训练2】 解关于x 的不等式(1－ax )2＜1.考向三 不等式恒成立问题【例3】►已知不等式ax 2＋4x ＋a ＞1－2x 2对一切实数x 恒成立，求实数a 的取值范围．[审题视点] 化为标准形式ax 2＋bx ＋c ＞0后分a ＝0与a ≠0讨论．当a ≠0时，不等式ax 2＋bx ＋c ＞0的解是全体实数(或恒成立)的条件是当a ＝0时，b ＝0，c ＞0；当a ≠0时，⎩⎨⎧ a ＞0，Δ＜0；不等式ax 2＋bx ＋c ＜0的解是全体实数(或恒成立)的条件是当a ＝0时，b ＝0，c ＜0；当a ≠0时，⎩⎨⎧a ＜0，Δ＜0. 【训练3】 已知f (x )＝x 2－2ax ＋2(a ∈R )，当x ∈[－1，＋∞)时，f (x )≥a 恒成立，求a 的取值范围．规范解答12——怎样求解含参数不等式的恒成立问题【解决方案】解决这类问题的关键是将恒成立问题进行等价转化，使之转化为函数的最值问题.【试一试】设函数f(x)＝ax3－3x＋1，若对于任意x∈[－1,1]，都有f(x)≥0成立，求实数a的值．。

2含参数的一元二次不等式的解法含参一元二次不等式常用的分类方法有三种： 一、按X 2项的系数a 的符号分类，即a 0,a 0,a 0;例1解不等式：ax 2系数进行分类讨论。

例2解不等式ax 2 5ax 6a 0 a 0分析因为a 0 , 0, 所以我们只要讨论二次项系数的正负。

解 a(x 2 5x 6)a x 2 x 3 0当a时,解集为 x | x 2或x 3 ; 当a0时，解集为x | 2 x 3变式：解关于 x 的不等式1、(x 2)(ax 2) 0 ；32、ax -(a + 1)x + 1<0(a € R)二、按判别式的符号分类，即0,0, 0；例3解不等式x 2 ax 4 0分析 本题中由于x 2的系数大于0,故只需考虑 与根的情况。

解：T a 2 16当a 4即厶=0时，解集为 xx R 且x —分析：本题二次项系数含有参数,2a 2 4a a 24 0，故只需对二次项解:4aa 2解得方程 ax 2a 2 a 22a4 —,X 2 2a 2 a 42a 0时，不等式为 2x 10时，解集为 x|「— 或 x2aa 2 a 242a2..a 24x2a 2 2a、a 2 4 •••当 a 4,4 即0时，解集为R ；< 23 m 2m 21当m ...3或m 3，即 0时，解集为R变式：解关于x 的不等式：ax 2 x 1三、按方程ax bx c 0的根x 1, x 2的大小来分类，即 x 1 x 2 ,x 1 x 2, x 1 x 2 ；例5解不等式x 2 (a 1)x 1 0 (a 0)a1分析：此不等式可以分解为： x a (x ) 0，故对应的方程必有两解。

本题a只需讨论两根的大小即可。

11 解：原不等式可化为： x a (x ) 0，令a，可得：a 1aa11•••当a 1或0 a 1时，a，故原不等式的解集为x | a xaa1当a 1或a 1时，a -,可得其解集为a当1 a 0或a1时， a 1,解集为a.1x | x a 。

一元二次不等式是指形如$ax^2 + bx + c > 0$ 或$ax^2 + bx + c < 0$ 的不等式，其中$a,b,c$ 是常数。

解决这种不等式的方法与解决一元二次方程的方法类似，需要先求出方程$ax^2 + bx + c = 0$ 的根。

首先，将不等式中的常数移到右边，得到$ax^2 + bx = -c$。

然后，将左边因式分解，得到$a(x - r_1)(x - r_2) = -c$，其中$r_1$ 和$r_2$ 是方程$ax^2 + bx + c = 0$ 的两个根。

根据分解因式的性质，可以得到以下三种情况：
当$a > 0$ 时，不等式$ax^2 + bx + c > 0$ 的解为$r_1 < x < r_2$，而不等式$ax^2 + bx + c < 0$ 的解为$x < r_1$ 或$x > r_2$。

当$a < 0$ 时，不等式$ax^2 + bx + c > 0$ 的解为$x < r_1$ 或$x > r_2$，而不等式$ax^2 + bx + c < 0$ 的解为$r_1 < x < r_2$。

注意，当$a = 0$ 时，不等式变成一元一次不等式，应使用相应的解法。

含参数的一元二次不等式的解法解含参数的一元二次不等式，通常情况下，均需分类讨论，那么如何讨论呢？对含参一元二次不等式常用的分类方法有三种：一、按2x 项的系数a 的符号分类，即0,0,0<=>a a a ;例1 解不等式：()0122>+++x a ax分析：本题二次项系数含有参数，()044222>+=-+=∆a a a ，故只需对二次项系数进行分类讨论。

解：∵()044222>+=-+=∆a a a解得方程()0122=+++x a ax 两根,24221a a a x +---=aa a x 24222++--=∴当0>a 时,解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+---<++-->a a a x a a a x x 242242|22或当0=a 时，不等式为012>+x ,解集为⎭⎬⎫⎩⎨⎧->21|x x当0<a 时, 解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+---<<++--a a a x a a a x 242242|22练习1 解不等式()00652≠>+-a a ax ax二、按判别式∆的符号分类，即0,0,0<∆=∆>∆；例2 解不等式042>++ax x分析 本题中由于2x 的系数大于0,故只需考虑∆与根的情况。

解：∵162-=∆a ∴当()4,4-∈a 即0<∆时，解集为R ；当4±=a 即Δ＝0时，解集为⎭⎬⎫⎩⎨⎧≠∈2a xR x x 且； 当4>a 或4-<a 即>∆,此时两根分别为21621-+-=a a x ，21622---=a a x ，显然21x x >, ∴不等式的解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧----+->21621622a a x a a x x 〈或练习2 解不等式()()R m x x m∈≥+-+014122三、按方程2=++c bx ax 的根21,x x 的大小来分类，即212121,,x x x x x x <=<；例3 解不等式)0( 01)1(2≠<++-a x aa x分析：此不等式可以分解为：()0)1(<--ax a x ，故对应的方程必有两解。

含参数的一元二次不等式的解法高中数学一元二次不等式是高中数学中重要的内容之一，它与一元二次方程不同，需要通过特定的方法来解决。

当一元二次不等式中出现参数时，解法也会有所不同。

本文将介绍含参数的一元二次不等式的解法。

首先，我们来看一个简单的例子，假设有不等式 f(x) =ax^2+bx+c > 0，其中a、b、c为实数且不为零。

我们的目标是确定x的取值范围使得不等式成立。

步骤一：将不等式化简为标准形式首先，我们需要将不等式化简为标准形式，即形如(ax^2+bx+c)>0的形式。

若不等式已经处于此形式，则可以直接进行下一步。

若不等式不满足此形式，则需要移项合并同类项，将不等式转化为标准形式。

步骤二：确定基本情况下的解法对于标准形式的一元二次不等式，我们可以利用图像法或代数法来解决。

对于a>0和a<0的两种情况，基本的解法如下：1. 当a>0时：- 如果a>0，二次函数的开口朝上，函数图像是一个开口朝上的抛物线。

此时的不等式解集为抛物线上方的实数集。

- 若抛物线与x轴有两个交点，我们可以通过求解对应的一元二次方程，求出两个交点x1和x2。

然后我们可以得到解集: x<x1 或x>x2- 若抛物线与x轴只有一个交点，我们可以求解的结果只有一个交点x0，此时解集为：x<x0 或 x>x0。

2. 当a<0时：- 如果a<0，二次函数的开口朝下，函数图像是一个开口朝下的抛物线。

此时的不等式解集为抛物线下方的实数集。

- 若抛物线与x轴有两个交点，我们可以通过求解对应的一元二次方程，求出两个交点x1和x2。

然后我们可以得到解集: x1<x<x2- 若抛物线与x轴没有交点，则解集为空集：ø步骤三：含参数时的解法当一元二次不等式中存在参数时，解法稍有不同。

我们以一个具体的例子来说明。

例题：对于不等式f(x) = (a+b)x^2+(b+c)x+c>0，其中a，b，c 为实数且不为零。

含参数的一元二次不等式的解法解含参数的一元二次不等式，通常情况下，均需分类讨论，那么如何讨论呢？对含参一元 二次不等式常用的分类方法有三种：一、按2x 项的系数a 的符号分类，即0,0,0<=>a a a ; 例1 解不等式：()0122>+++x a ax分析：本题二次项系数含有参数，()044222>+=-+=∆a a a ，故只需对二次项系数进行分类讨论。

解：∵()044222>+=-+=∆a a a解得方程 ()0122=+++x a ax 两根,24221a a a x +---=aa a x 24222++--=∴当0>a 时,解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+---<++-->a a a x a a a x x 242242|22或当0=a 时，不等式为012>+x ,解集为⎭⎬⎫⎩⎨⎧>21|x x 当0<a 时, 解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+---<<++--a a a x a a a x 242242|22例2 解不等式分析 因为0≠a ，0>∆，所以我们只要讨论二次项系数的正负。

解 ()()032)65(2>--=+-x x a x x a Θ∴当0>a 时，解集为{}32|><x x x 或；当0<a 时，解集为{}32|<<x x二、按判别式∆的符号分类，即0,0,0<∆=∆>∆； 例3 解不等式042>++ax x分析 本题中由于2x 的系数大于0,故只需考虑∆与根的情况。

解：∵162-=∆a∴当()4,4-∈a 即0<∆时，解集为R ； 当4±=a 即Δ＝0时，解集为⎭⎬⎫⎩⎨⎧≠∈2a x R x x 且；当4>a 或4-<a 即0>∆,此时两根分别为21621-+-=a a x ，21622---=a a x ，显然21x x >,∴不等式的解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧----+->21621622a a x a a x x 〈或例4 解不等式()()R m x x m ∈≥+-+014122解 因,012>+m ()()2223414)4(m m -=+--=∆所以当3±=m ，即0=∆时，解集为⎭⎬⎫⎩⎨⎧=21|x x ； 当33<<-m ，即0>∆时，解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+--+-+>1321322222m m x m m x x 〈或； 当33>-<m m 或，即0<∆时，解集为R 。

含参数的一元二次不等式的解法解含参数的一元二次不等式，通常情况下，均需分类讨论，那么如何讨论呢？首先，必需弄清楚，它的解集与哪些因素有关。

一般地，一元二次不等式的解集（以ax 2+bx+c>0为例）常与以下因素有关（1）a ；（2）Δ；（3）两根x 1,x 2的大小。

其中系数a 影响着解集最后的形式，Δ关系到不等式对应的方程是否有解，而两根x 1,x 2的大小关系到解集最后的次序；其次再根据具体情况，合理分类，确保不重不漏。

下面举例说明：例1、解不等式x 2+ax+4>0分析：本题中由于x 2的系数大于0,故只需考虑后两个因素。

解：∵Δ＝a 2 -16∴当()4,4-∈a 时，Δ<0，解集为R ；当4±=a 时，Δ＝0，解集为⎭⎬⎫⎩⎨⎧≠∈2a x R x x 且； 当a>4或a<-4时, Δ>0,此时两根分别为21621-+-=a a x ，21622---=a a x ，显然x 1>x 2, ∴不等式的解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧----+->21621622a a x a a x x 〈或 例2、解不等式)0( 01)1(2≠<++-a x aa x 分析：此不等式可以分解为：()0)1(<--ax a x ，故对应的方程必有两解。

又1>0,所以本题只需讨论两根的大小即可。

解：原不等式可化为：()0)1(<--a x a x ，令a a 1=，可得：1±=a ∴当1-<a 或0<a<1时，a a 1< ，故原不等式的解集为⎭⎬⎫⎩⎨⎧<<a x a x 1|； 当a=1或a=-1时，aa 1=,可得其解集为φ； 当a ∈(0,1)或a<1时, a a 1>,解集为⎭⎬⎫⎩⎨⎧<<a x a x 1|。

例3、解不等式：mx 2 -2x+1>0分析：本题对解集的影响因素较多，若处理不当，不仅要分级讨论，而且极易漏解或重复。

含参数的一元二次不等式的解法含参一元二次不等式常用的分类方法有三种：一、按$x$项的系数$a$的符号分类，即$a>0$，$a=0$，$a<0$。

例1：解不等式$ax+(a+2)x+1>2$分析：本题二次项系数含有参数，$\Delta=(a+2)^2-4a=a+4>0$，故只需对二次项系数进行分类讨论。

解：当$a>0$时，解得方程$ax+(a+2)x+1=0$的两根$x_1=-\frac{a+2+\sqrt{a+4}}{2a}$，$x_2=-\frac{a+2-\sqrt{a+4}}{2a}$，因为$a>0$，所以$x_1x_2$或$x<x_1$，即$x\in\left(-\infty,\frac{a+2-\sqrt{a+4}}{2a}\right)\cup\left(\frac{a+2+\sqrt{a+4}}{2a},+\infty\right)$。

当$a=0$时，不等式为$2x+1>2$，解得$x>\frac{1}{2}$，即解集为$x>\frac{1}{2}$。

当$a<0$时，解得方程$ax+(a+2)x+1=0$的两根$x_1=-\frac{a+2-\sqrt{a+4}}{2a}$，$x_2=-\frac{a+2+\sqrt{a+4}}{2a}$，因为$a<0$，所以$x_1<x_2$。

所以解集为$x_1<x<x_2$，即$x\in\left(\frac{a+2-\sqrt{a+4}}{2a},\frac{a+2+\sqrt{a+4}}{2a}\right)$。

例2：解不等式$ax-5ax+6a>(a\neq0)^2$分析：因为$a\neq0$，$\Delta>0$，所以我们只需讨论二次项系数的正负。

解：当$a>0$时，解得方程$ax-5ax+6a=0$的两根$x_1=2$，$x_2=3$，因为$a>0$，所以$x_13$，即$x\in\left(-\infty,2\right)\cup\left(3,+\infty\right)$。

含参数的一元二次不等式的解法含参一元二次不等式常用的分类办法有三种：一.按2x 项的系数a 的符号分类,即0,0,0<=>a a a ;例1解不等式：()0122>+++x a ax 剖析：本题二次项系数含有参数,()044222>+=-+=∆a a a ,故只需对二次项 系数进行分类评论辩论.解：∵()044222>+=-+=∆a a a 解得方程 ()0122=+++x a ax 两根,24221a a a x +---=a a a x 24222++--=∴当0>a 时,解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+---<++-->a a a x a a a x x 242242|22或 当0=a 时,不等式为012>+x ,解集为⎭⎬⎫⎩⎨⎧>21|x x当0<a 时,解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+---<<++--a a a x a a a x 242242|22 例2 解不等式()00652≠>+-a a ax ax剖析 因为0≠a ,0>∆,所以我们只要评论辩论二次项系数的正负.解()()032)65(2>--=+-x x a x x a ∴当0>a 时,解集为{}32|><x x x 或;当0<a 时,解集为{}32|<<x x变式：解关于x 的不等式 1.0)2)(2(>--ax x ;2.(1－ax )2<1.}2,2|{,1)5(}2|{,1)4(}2,2|{,10)3(}2|{,0)2(}22|{,0)1(><>≠=><<<<=<<<x a x x a x x a ax x x a x x a x ax a 或时当时当或时当时当时当【解】由(1－ax )2<1得a 2x 2－2ax ＋1<1.即ax (ax －2)<0.(1)当a ＝0时，不等式转化为0<0，故原不等式无解．(2)当a <0时，不等式转化为x (ax －2)>0，即x (x －2)<0.}11|{1)5(1)4(}11|{10)3(}1|{0)2(}1,1|{0)1(<<>Φ=<<<<>=><<x ax a a ax x a x x a x ax x a 时，当时，当时，当时，当或时，当3.ax 2－(a ＋1)x ＋1<0(a ∈R)二.按判别式∆的符号分类,即0,0,0<∆=∆>∆;例3解不等式042>++ax x剖析本题中因为2x 的系数大于0,故只需斟酌∆与根的情形. 解：∵162-=∆a∴当()4,4-∈a 即0<∆时,解集为R ; 当4±=a 即Δ＝0时,解集为⎭⎬⎫⎩⎨⎧≠∈2a x R x x 且;当4>a 或4-<a 即0>∆,此时两根分离为21621-+-=a a x ,21622---=a a x ,显然21x x >,∴不等式的解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧----+->21621622a a x a a x x 〈或 例4 解不等式()()R m x x m∈≥+-+014122解 因,012>+m ()()2223414)4(m m -=+--=∆所以当3±=m ,即0=∆时,解集为⎭⎬⎫⎩⎨⎧=21|x x ;当33<<-m ,即0>∆时,解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+--+-+>1321322222m m x m m x x 〈或;当33>-<m m 或,即0<∆时,解集为R.变式：解关于x 的不等式：012<++x axΦ≥-+-<<---<<-<=--->-+-<<时，当时，当时，当或时，当41)4(}24112411|{410)3(}1|{0)2(}2411,2411|{0)1(a aax a a x a x x a aax a a x x a三.按方程02=++c bx ax 的根21,x x 的大小来分类,即212121,,x x x x x x <=<;(3)当a >0时，不等式转化为x (ax －2)<0，又2a >0，∴不等式的解集为{x |0<x <2a }． 综上所述：当a ＝0时，不等式解集为空集；当a <0时，不等式解集为{x |2a<x <0}； 当a >0时，不等式解集为{x |0<x <2a}．例5解不等式)0( 01)1(2≠<++-a x a a x剖析：此不等式可以分化为：()0)1(<--ax a x ,故对应的方程必有两解.本题 只需评论辩论两根的大小即可.解：原不等式可化为：()0)1(<--ax a x ,令a a 1=,可得：1±=a∴当1-<a 或10<<a 时,a a 1<,故原不等式的解集为⎭⎬⎫⎩⎨⎧<<a x a x 1|;当1=a 或1-=a 时,a a 1=,可得其解集为φ;当01<<-a 或1>a 时,a a 1>,解集为⎭⎬⎫⎩⎨⎧<<a x a x 1|. 例6 解不等式06522>+-a ax x ,0≠a剖析 此不等式()0245222>=--=∆a a a ,又不等式可分化为()0)3(2>--a x a x ,故只需比较两根a 2与a 3的大小.解 原不等式可化为：()0)3(2>--a x a x ,对应方程()0)3(2=--a x a x 的两根为a x a x 3,221==,当0a时,即23a a ,解集为{}a x a x x 23|<>或;当0<a 时,即23aa ,解集为{}|23x x a x a ><或变式：1.223()0x aa x a 2.0222<--a ax x解：∵x 2－（a+a 2）x+a 3＝（x －a ）（x －a 2） ∴当a>1,或a<0时,不等式的解为a<x<a 2 当0<a<1时,不等式的解为a 2<x<a 当a ＝0,或a ＝1时,不等式解为φ 课后演习：1.)23(0)3)(2(-≠≠<-+-a a x x ax ，且（分3;32;2><<--<a a a 评论辩论）098.0222222≥=+=∆=--a a a a ax x 的判别式方程.,221a x a x -==得方程的两根为.2,0)3(a x a a -<<<则若ax a a 2,0)1(<<->则若}.2|{,0)3(,0)2(}2|{,0)1(a x a x a a a x a x a -<<<Φ=<<->时当；时当；时当解集为：综上所述，原不等式的Φ<=此时解为则原不等式为若,0,0)2(2x a}3,2|{3)3(}3,2|{32)2(}32,|{2)1(a x x x a x a x x a x a x x a <<-<><<-<<<-<<-<-<或时，当或时，当或时，当2.不等式11<-x ax 的解集为}21|{><x x x ，或,求a 的值. （21=a ） 3.已知}0)1(|{},023|{22≤++-=≤+-=a x a x x B x x x A ,①若AB ,求实数a 的取值规模.;（2>a ）②若A B ⊆,求实数a 的取值规模.;（21≤≤a ）③若B A 为仅含有一个元素的聚集,求a 的值.（1≤a ） 解：A=｛x ｜1≤x ≤2｝,B=｛x ｜(x-1)(x-a)≤0｝ (1)若AB(图甲),应有a ＞2. (2)若BA(图乙),必有1≤a ≤2.(3)若A ∩B 为仅含一个元素的聚集(图丙),必有a ≤1.4.已知}031|{≤--=x x x A ,B B A a x a x x B =≤++-= 且},0)1(|{2,求实数a 的取值规模.（31<≤a ）5.设全集R U =,聚集}3|12||{},01|{<+=≥+-=x x B x ax x A ,若R B A = ,求实数a 的取值规模. （12≤≤-a ）6.已知全集R U =,}034|{},082|{},06|{2222<+-=>-+=<--=a ax x x C x x x B x x x A ,若C B A ⊆)( ,求实数a 的取值规模.（ 21≤≤a ）7.若关于x 的不等式(2x －1)2＜ax 2的解分散的整数恰有3个,求实数a 的取值规模.（]1649925<<a 【解析】 不等式可化为(4－a )x 2－4x ＋1＜0①,因为原不等式的解分散的整数恰有3个,所以⎩⎨⎧>--=∆>-0)4(41604a a ,解得0＜a ＜4,故由①得a x a-<<+2121,又212141<+<a ,所以解分散的3个整数必为1,2,3,所以3＜a -21≤4,解得925＜a ≤1649。

含参数一元二次不等式的解法我们把只含有一个未知数, 并且未知数的最高次数是2的不等式, 称为一元二次不等式.一元二次不等式的一般形式是/ 或/ （其中/ 均为常数, / ）.解含参一元二次不等式的相关问题对于基础薄弱的同学来说是一个难点.为了帮助这些同学解决此类问题, 本文将相关解题方法进行简化、总结, 帮助同学们理解和学习.下面我们通过例举进行具体的分析说明.类型一解二次项前不带参数的一元二次不等式1.对应方程/ （其中/ 均为常数, / ）可以进行因式分解.方法：所求解的一元二次不等式对应的一元二次方程/ 可因式分解为/ （/ 为方程的实数根）的形式, 则分类讨论的关键在于通过比较两根/ 的大小, 确定参数讨论的界限, 进而解出/ 的取值范围.例1 解关于的不等式 .分析: 对应方程/ 可因式分解为/ 的形式, 讨论两根/ 的大小, 即可解出/ 的取值范围.解: 原不等式等价于/ , 所对应方程/ 的两根是/当/ 时, 不等式的解集为/ .当/ 时, 不等式的解集为/ .当/ 时, 不等式的解集为/ .2.对应方程/ （其中/ 均为常数, / ）不能进行因式分解.方法：所求解的一元二次不等式对应的一元二次方程/ 不能进行因式分解, 则分类讨论的关键在于判别式, 此时根据判别式确定参数讨论的界限, 解出/ 的取值范围.例2 解关于的不等式 .分析: 对应方程/ 不能进行因式分解, 此时根据判别式确定参数讨论的界限, 求出/ 的取值范围.解: 原不等式对应方程/ 的判别式为/（1）当/ , / 时, / 的两根为/ 或/ , 不等式的解集为/ .（2）当/ , / 时, / 的根为/ ,不等式的解集为 .1.当/ , / 时, 不等式的解集为/ .综上所述：当/ 时, 不等式的解集为.当/ 时, 不等式的解集为/ .当/ 时, 不等式的解集为/ .类型二解二次项前带参数的一元二次不等式1.对应方程/ （其中/ 均为常数, / ）可以进行因式分解.方法：所求解的一元二次不等式对应的一元二次方程/ 可因式分解为/ （/ 为方程的实数根）的形式，则分类讨论的关键仍然在于通过比较两根/ 的大小确定参数讨论的界限.另外，需要注意的问题是二次项前带参数与二次项前不带参数不同，参数的范围决定对应二次函数/ 的开口方向，影响对应一元二次不等式的解集.例3 解关于的不等式 .分析: 对应方程/ 可因式分解为/ 的形式, 讨论两根/ 的大小, 即可确定参数讨论的界限, 根据参数的不同取值范围, 求出不等式相应解集。

For personal use only in study and research; not for commercialuse含参数的一元二次不等式的解法解含参数的一元二次不等式，通常情况下，均需分类讨论，那么如何讨论呢？对含参一元 二次不等式常用的分类方法有三种：一、按2x 项的系数a 的符号分类，即0,0,0<=>a a a ; 例1 解不等式：()0122>+++x a ax分析：本题二次项系数含有参数，()044222>+=-+=∆a a a ，故只需对二次项系数进行分类讨论。

解：∵()044222>+=-+=∆a a a解得方程 ()0122=+++x a ax 两根,24221a a a x +---=aa a x 24222++--=∴当0>a 时,解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+---<++-->a a a x a a a x x 242242|22或当0=a 时，不等式为012>+x ,解集为⎭⎬⎫⎩⎨⎧>21|x x 当0<a 时, 解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+---<<++--a a a x a a a x 242242|22例2 解不等式()00652≠>+-a a ax ax分析 因为0≠a ，0>∆，所以我们只要讨论二次项系数的正负。

解 ()()032)65(2>--=+-x x a x x a∴当0>a 时，解集为{}32|><x x x 或；当0<a 时，解集为{}32|<<x x二、按判别式∆的符号分类，即0,0,0<∆=∆>∆； 例3 解不等式042>++ax x分析 本题中由于2x 的系数大于0,故只需考虑∆与根的情况。

解：∵162-=∆a∴当()4,4-∈a 即0<∆时，解集为R ； 当4±=a 即Δ＝0时，解集为⎭⎬⎫⎩⎨⎧≠∈2a x R x x 且； 当4>a 或4-<a 即0>∆,此时两根分别为21621-+-=a a x ，21622---=a a x ，显然21x x >,∴不等式的解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧----+->21621622a a x a a x x 〈或例4 解不等式()()R m x x m ∈≥+-+014122解 因,012>+m ()()2223414)4(m m -=+--=∆所以当3±=m ，即0=∆时，解集为⎭⎬⎫⎩⎨⎧=21|x x ； 当33<<-m ，即0>∆时，解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+--+-+>1321322222m m x m m x x 〈或； 当33>-<m m 或，即0<∆时，解集为R 。

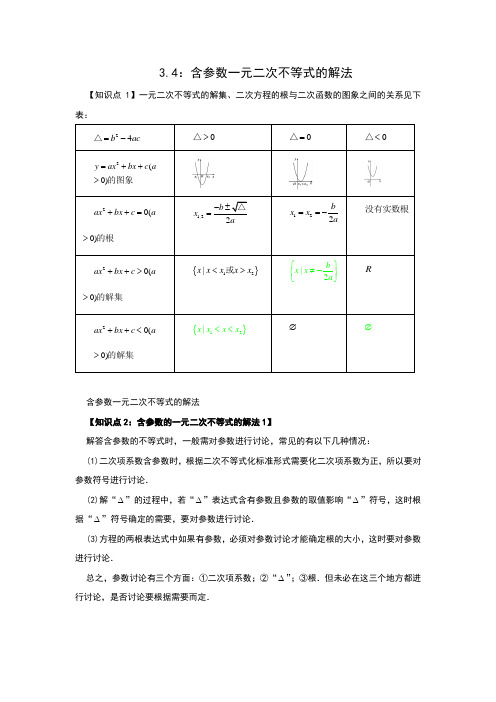
3.4：含参数一元二次不等式的解法【知识点1】一元二次不等式的解集、二次方程的根与二次函数的图象之间的关系见下表：含参数一元二次不等式的解法【知识点2：含参数的一元二次不等式的解法1】解答含参数的不等式时，一般需对参数进行讨论，常见的有以下几种情况：(1)二次项系数含参数时，根据二次不等式化标准形式需要化二次项系数为正，所以要对参数符号进行讨论．(2)解“∆”的过程中，若“∆”表达式含有参数且参数的取值影响“∆”符号，这时根据“∆”符号确定的需要，要对参数进行讨论．(3)方程的两根表达式中如果有参数，必须对参数讨论才能确定根的大小，这时要对参数进行讨论．总之，参数讨论有三个方面：①二次项系数；②“∆”；③根．但未必在这三个地方都进行讨论，是否讨论要根据需要而定．例题：解关于x 的不等式22560.x ax a +-<12(7)(8)0(7)(8)078x a x a a a x a x a x x +-<+-==-=解析：原不等式化为，方程的两根为，，0{|}7800{|}87a aa x x a a aa x x ∴>-<<=∅<<<-时，解集为；时，解集为；时，解集为．【知识点3：含参数一元二次不等式的解法2．分式不等式的解法】 (1)分式不等式分母中含有未知数，且分子、分母都是关于x 的多项式的不等式称为__分式不等式___ (2)等价转化法解分式不等式解分式不等式的基本方法是将其转化为与之同解的__整式__不等式(组)．具体情况见下表：例题：解下列不等式： 42(1)023x -≤+；1(2)3.2x x+≥- (4)(23)0443(1)00|4.23023232x x x x x x x x x x -+≥⎧--⎧⎫≤⇔≥⇔⇔≥<-⎨⎨⎬+≠++⎩⎭⎩解析：或3{|4}2x x x ∴<-≥原不等式的解集为或．114545(2)330002222x x x x x x x x ++--≥⇔-≥⇔≥⇔≤----，(45)(2)05|2.204x x x x x --≤⎧⎧⎫⇔⇔≤<⎨⎨⎬-≠⎩⎭⎩，5{|2}4x x ∴≤<原不等式的解集为．【知识点4：含参数一元二次不等式的解法3．简单的高次不等式的解法】 (1)高次不等式不等式最高次项的次数高于2，这样的不等式称为__高次不等式_ (2)穿根法解高次不等式的步骤 ①将()f x 最高次项系数化为正数；②将()f x 分解为若干个一次因式的积或二次不可分因式的积；③将每一个一次因式的根标在数轴上，自上而下，从右向左依次通过每一点画曲线(注意重根情况，偶次方根穿而不过，奇次方根既穿又过)；④观察曲线显现出的()f x 的值的符号变化规律，写出不等式的解集．例题：解不等式：(2)(1)(1)(2)0.x x x x ++--≤(2)(1)(1)(2)y x x x x =++--解析：设，021,1,2y =--则的根分别是，，将其分别标在数轴上，并画出如图所示的示意图：{|2112}x x x -≤≤-≤≤所以原不等式的解集是，或．点评： (1)大于0的不等式的解，对应着曲线在x 轴上方部分的实数x 的取值集合；反之，对应着x 轴下方部分的实数x 的取值集合．注意端点处值是否取到．(2)穿根法可形象地称为“穿根引线法”，这样的“线”可看成是函数的图象草图，只不过不画y 轴而已．变式1：解关于x 的不等式：22(21)0.x m x m m -+++<22(21)0m m x m x m m -+++= 分析：在上述不等式中含有参数，因此需要先判断参数对方程的解的影响，然后求解．2212(21)01x m x m m x m x m -+++===+ 解析：解法一：方程的解为，，1.m m <+且知 22(21)y x m x m m x ∴=-+++二次函数的图象开口向上，且与轴有两个交点．{|1}x m x m ∴<<+不等式的解集为．2(1)(1)21m m m m m m m -=+++=+解法二：注意到，及，()(1)0x m x m ---<可先因式分解，化为，1 1.m m m x m <+∴<<+ ，{|1}x m x m ∴<<+不等式的解集为． 点评：含参数的不等式的解题步骤为 (1)将二次项系数转化为正数；(2)判断相应方程是否有根(如果可以直接分解因式，可省去此步)；(3)根据根的情况写出相应的解集(若方程有相异根，为了写出解集还要分析根的大小)． 另外，当二次项含有参数时，应先讨论二次项系数是否为0，这决定不等式是否为二次不等式．变式2：当0a >时，解关于x 的不等式2(1)10.ax a x -++<2(1)10(1)(1)0ax a x ax x -++<--<解析：不等式可化为，10(1)(1)0()(1)0a ax x x x a >∴--<--< ，不等式，可化为，1a =当时，不等式无解； 1011a x a <<<<当时，； 11 1.a x a><<当时，101{|1}111{|1}.a x x a aa x x a<<<<=><<综上可知，当时，原不等式的解集为；当时，原不等式的解集为空集；当时，原不等式的解集为变式3： (1)不等式12x x-≥的解集为( A ) A ．[1,0)-B ．[1)-+∞，C ．(1]-∞-，D ．(1](0)-∞-+∞ ，， (2)不等式21134x x ->-的解集为_23|34x x ⎧⎫<<⎨⎬⎩⎭__． ()()0(0)()()f x f xg x g x >< 分析：此类不等式求解，要先移项通分化为的形式再化为或整式不等式．转化必须保持等价．11(1)200x x x x----≥∴≥解析：，，(1)010.0x x x x +≤⎧∴∴-≤<⎨≠⎩，64(2)043x x -<-原不等式化为：，23(64)(43)034x x x ∴--<∴<<，，23|.34x x ⎧⎫∴<<⎨⎬⎩⎭原不等式的解集为变式4：不等式3112x x-≥-的解集是( C ) A ．3|24x x ⎧⎫≤≤⎨⎬⎩⎭ B ．3|24x x x ⎧⎫≤>⎨⎬⎩⎭或C ．3|24x x ⎧⎫≤<⎨⎬⎩⎭D ．{}|2x x <31431022x x x x--≥≥--解析：不等式，化为，32.4x ∴≤<变式5：不等式(2)03x x x +<-的解集为( ) A ．{}|203x x x <-<<，或 B ．{}|223x x x -<<>，或 C ．{}|20x x x <->，或 D ．{}|03x x x <<，或分析：原不等式左端是分式，右端为0，属于0AB<型，可等价转化为0AB <，即(2)(3)0x x x +-<，依次令12302030023x x x x x x =+=-===-=，，得，，，数轴按此三数对应点分成四段，令=(2)(3)y x x x +-列出x 与y 的对应值如表：(2)(3)0(2)(0,3)x x x +-<-∞- 故不等式的解集为，．(2)(3)0.x x x +-<解析：原不等式等价于()结合数轴穿根法如图可知：20 3.x x <-<<或变式6：解不等式：23(1)(1)(2)0.x x x x -+-> (1)(2)010x x x x +->⎧⎨-≠⎩解析：原不等式可化为10210 2.1x x x x x -<<>⎧⇔⇔-<<>⎨≠⎩，或，或{|102}.x x x ∴-<<>原不等式的解集为，或变式7：关于x 的不等式22(1)1m x mx m x x R +++<+∈对成立，求实数m 的取值范围． 分析：首先考虑二次项系数是否为零，化简后，需要对m 对进行讨论．0m ≠时，可利用三个“二次”之间的关系求解．210mx mx m x R ++-<∈解析：原不等式等价于对恒成立，200010m x x x R =⋅+⋅-<∈当时，对恒成立． 0m ≠当时，由题意，得22004(1)0340m m m m m m m <<⎧⎧⇔⎨⎨∆=--<->⎩⎩ 00.403m m m m <⎧⎪⇔⇔<⎨<>⎪⎩，或0.m m ≤综上，的取值范围为点评：一元二次不等式恒成立时满足条件22220(1)0()00(2)0()00(3)0()00(4)0().0a ax bx c R a ax bx c R a ax bx c R a ax bx c R >⎧++>⎨∆<⎩>⎧++≥⎨∆≤⎩<⎧++<⎨∆<⎩<⎧++≤⎨∆≤⎩恒成立或解集为时，满足；恒成立或解集为时，满足；恒成立或解集为时，满足；恒成立或解集为时，满足变式8：已知不等式2(1)10ax a x a +-+-<对于所有的实数x 都成立，求a 的取值范围． 010a x =--<解析：若，则原不等式为，10.x a >-≠即，不合题意．故2()(1)1f x ax a x a =+-+-令，x R ∈ 原不等式对任意都成立．()f x x ∴二次函数的图象在轴的下方．20(1)4(1)0.a a a a ∴<∆=---<且(1)(31)0a a a <⎧⎨-+>⎩即，1.3a ∴<-1()3a -∞-故的取值范围为，．变式9：若函数y R ，则k 的取值范围是_01k ≤≤__． 01k <≤错解：26(8)0kx kx k -++≥由题意知恒成立，201364(8)0k k k k k >⎧∴∴<≤⎨∆=-+≤⎩，， 0 1.k k <≤即的取值范围是206(8)0k kx kx k =-++≥辨析：错解忽视时，也成立，考虑问题不全面导致错误．01k ≤≤正解：26(8)0kx kx k -++≥由题意恒成立．200364(8)0k k k k k >⎧=≠⎨=-+≤⎩当时满足，当时，△010 1.k k ∴≤≤≤＜，综上得。