分式概念及意义
- 格式:doc
- 大小:218.50 KB
- 文档页数:9

分式的意义与性质【知识要点】1.分式的概念:两个整式A 、B 相除,即B A ÷时,可以表示为B A .如果B 中含有字母,那么BA 叫做分式,A 叫做分式的分子,B 叫做分式的分母.注:分式的分子可以含有字母,也可以不含字母,但分母必须含有字母;2.分式有意义:分母不等于零3.分式的值:分式的分母不等于零,且分子等于零时,分式的值为零.4.分式的基本性质(初步约分):分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变. 5. 约分:把一个分式的分子与分母中相同的因式约去的过程,叫做约分。
6. 最简分式:如果一个分式的分子与分母没有相同的因式(1除外),那么这个分式叫做最简分式.7. 代入计算方法(初步求值)【典型例题】例1 判断下列各式,哪些是分式?(1)x 1,(2)21,(3)212+x ,(4)πxy 3,(5)m a 1+,(6)b a 5132-,(7)b a ÷ 例2 (1)x 为何值时,下列分式有意义.(2)x 为何值时,下列分式没有意义.例3 (1)x 为何值时,下列分式的值为零.(2)求满足条件的x 的值.①分式224534x x x x -+-+的值为1; ②分式221x x -+的值为负数; (3)若23+x 的值为整数,求x 的整数值; 例4 (1)填空:22222()()22,2y a ab b xy a b xy a b +-==+-;(2)当x 、y 满足关系式 时,分式3()5()x y x y --的值等于35; (3)若x 、y 同时扩大2倍,则下列分式的值的变化情况为:例5 (1)a 为何值时,下列等式成立:(2)不改变分式的值,把下列分式的分子、分母中的各项系数化为整数.例6 (1)化简下列分式:(2)求下列分式的值: ①12122++-x x x ,其中2005=x ; ②2224200833,1100322a b a b a b -=⎧⎨=-⎩-其中; 例7 (1)已知2=y x ,求22222y x xy y x -++的值; 【大展身手】一.选择题:1. 如果分式063=+-yx y x ,那么x ,y 应满足( ) A. y x 2= B.y x -≠ C. y x y x -≠=且2 D. 02≠=y y x 且2. 若分式1122++x x 无意义,则( )A. 1=xB. 1-=xC. 11-==x x 或D.没有这样的有理数3. 下列分式a c b 4122、x y y x ++2)(5、)(322b a b a ++、b a b a --2422、a b b a --中,最简分式的个数是( ) A.1个 B. 2个 C. 3个 D. 4个4.下列等式成立的是( )其实,任何一门学科都离不开死记硬背,关键是记忆有技巧,“死记”之后会“活用”。
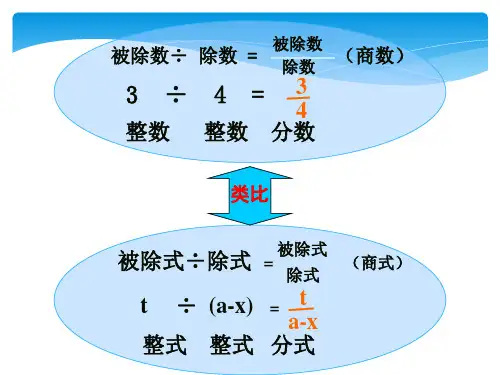

分式的概念与运算分式,也可称为有理数的形式,是表示两个整数之间关系的一种数学表达式。
它由一个分子和一个分母组成,分子表示除法的被除数,分母表示除法的除数。
在数学中,分式广泛应用于各种实际问题的求解与计算中。
本文将介绍分式的概念、基本性质,以及分式的加减乘除运算。
一、分式的概念分式的本质是一个数的表达方式,它可以表示两个整数之间的比例关系。
例如,$\frac{1}{2}$表示整数1与整数2之间的比值,读作“1除以2”。
在分式中,分子和分母可以是任意整数,并且分母不能为零。
当分子为0时,分式的值为0。
二、分式的基本性质1. 分式的值可以是一个整数、一个真分数或带分数。
当分子大于分母时,分式的值大于1;当分子小于分母时,分式的值小于1。
2. 分式可以进行化简。
也就是说,可以约分分式中的分子和分母,将它们的公约数约掉,使得分子和分母互质。
例如,$\frac{2}{4}$可以化简为$\frac{1}{2}$。
3. 分式可以进行扩展。
也就是说,可以将分子和分母同时乘以一个非零整数,得到等价的分式。
例如,$\frac{3}{5}$可以扩展为$\frac{6}{10}$。
三、分式的加减乘除运算1. 分式的加法和减法分式的加法和减法遵循公式:$$\frac{a}{b} \pm \frac{c}{d} = \frac{ad \pm bc}{bd}$$其中$a$、$b$、$c$和$d$为任意整数。
具体来说,对于分式$\frac{a}{b}$和$\frac{c}{d}$,只需将两个分式的分母取公倍数得到新的分母,然后将分子相应操作后得到新的分子,即可得到结果。
示例:$$\frac{3}{5} + \frac{2}{3} = \frac{9}{15} + \frac{10}{15} =\frac{19}{15}$$$$\frac{7}{8} - \frac{1}{4} = \frac{7}{8} - \frac{2}{8} = \frac{5}{8} $$2. 分式的乘法和除法分式的乘法和除法遵循公式:$$\frac{a}{b} \cdot \frac{c}{d} = \frac{ac}{bd}$$$$\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} =\frac{ad}{bc}$$其中$a$、$b$、$c$和$d$为任意整数。

分式的意义和性质一、分式的概念1、用A、B表示两个整式,A÷B可以表示成的形式,其中A叫做分式的分子,B叫做分式的分母,如果除式B中含有字母,式子就叫做分式。
这就是分式的概念。
研究分式就从这里展开。
2、既然除式里含有字母的有理代数式叫做分式,那么,在分式里分母所包含的字母,就不一定可以取任意值。
分式的分子A可取任意数值,但分母B不能为零,因为用零做除数没有意义。
一般地说,在一个分式里,分子中的字母可取任意数值,但分母中的字母,只能取不使分母等于零的值。
3.(1)分式:,当B=0时,分式无意义。
(2)分式:,当B≠0时,分式有意义。
(3)分式:,当时,分式的值为零。
(4)分式:,当时,分式的值为1。
(5)分式:,当时,即或时,为正数。
(6)分式:,当时,即或时,为负数。
(7)分式:,当时或时,为非负数。
三、分式的基本性质:1、学习分式的基本性质应该与分数的基本性质类比。
不同点在于同乘以或同除以同一个不等于零的整式,这个整式可以是数也可以是字母,只要是不为零的整式。
2、这个性质可用式子表示为:(M为不等于零的整式)3、学习基本性质应注意几点:(1)分子与分母同乘或同除的整式的值不能为零;(2)易犯错误是只乘(或只除)分母或只乘(或只除)分子;(3)如果分子或分母是多项式时,必须乘以多项式的每一项。
4、分式变号法则的依据是分式的基本性质。
5、分式的分子,分母和分式的符号,改变其中任何两个,分式的值不变,如下列式子:,。
四、约分:1、约分是约去分子、分母中的公因式。
就是用分式中分子和分母的公因式去除分子和分母,使分式化简为最简分式,最简分式又叫既约分式。
2、约分的理论依据是分式的基本性质。
3、约分的方法:(1)如果分式的分子和分母都是几个因式乘积的形式,就约去分子和分母中相同因式的最低次幂,当分子和分母的系数是整数时,还要约去它们的最大公约数。
例1,请说出下列各式中哪些是整式,那些是分式?(1)(2)(3)(4)(5)a2-a(6)。

分式和分式方程的概念和意义如何理解分式和分式方程?1. 什么是分式?分式是数学中的一个重要概念,它表示为a/b的形式,其中a和b都是整数且b不等于0。
分式也可以表示为小数形式,比如2/3可以表示为0.6667。
2. 分式的意义是什么?分式可以表示部分的概念,比如一块蛋糕被分成4份,每份就可以用1/4来表示。
分式的意义在于它可以准确地表示一个整体被分成若干份时每一份所占的比例。
3. 分式方程又是什么?分式方程就是含有未知数的分式表达式,并且这个未知数不是分式中的参数。
比如(x+1)/3 = 2,这个方程中的未知数是x,方程中含有分式。
4. 分式和分式方程的解的意义?解分式方程可以得到未知数的值,可以帮助我们解决实际生活中的问题,比如工程施工中需要确定某种材料的用量,涉及到分式方程的计算。
5. 个人观点和理解对于分式和分式方程的概念,我认为它们是数学中非常重要且实用的概念。
在现实生活中,我们经常会遇到一些比例和分配的问题,比如商业中的利润分成,生活中食物的配比等等,这些都可以用分式和分式方程来表示和求解。
学好分式和分式方程对于提高解决实际问题的能力是非常有帮助的。
回顾总结通过本次写作,我对分式和分式方程的概念有了更加深入和全面的理解。
我会在以后的学习和工作中更加灵活地运用这些概念,提高数学解决实际问题的能力。
本文总结了分式和分式方程的概念和意义,并对其进行了全面深入的讨论。
希望本文能帮助您更好地理解和应用分式和分式方程。
续写:6. 分式方程的应用分式方程在实际生活中有很多应用。
比如在商业中,我们经常需要解决利润分成的问题,这就可以通过分式方程来表示和求解。
另外,在化学实验中,需要按照一定的比例混合不同的溶液,这也可以用分式方程来描述。
在工程施工中,需要确定材料的用量,也可以通过分式方程来进行计算。
学好分式方程可以帮助我们更好地解决实际生活和工作中的问题。
7. 分式方程的解法解分式方程的方法主要有通分法、分离变量法等。

---------------------------------------------------------------最新资料推荐------------------------------------------------------分式的意义和性质分式的意义和性质一、分式的概念 1、用 A、 B 表示两个整式, AB 可以表示成的形式,其中 A 叫做分式的分子, B 叫做分式的分母,如果除式 B 中含有字母,式子就叫做分式。
这就是分式的概念。
研究分式就从这里展开。
2、既然除式里含有字母的有理代数式叫做分式,那么,在分式里分母所包含的字母,就不一定可以取任意值。
分式的分子 A 可取任意数值,但分母 B 不能为零,因为用零做除数没有意义。
一般地说,在一个分式里,分子中的字母可取任意数值,但分母中的字母,只能取不使分母等于零的值。
3、(1)分式:,当 B=0 时,分式无意义。
(2)分式:,当 B0 时,分式有意义。
(3)分式:,当时,分式的值为零。
(4)分式:,当时,分式的值为 1。
(5)分式:1 / 10,当时,即或时,为正数。
(6)分式:,当时,即或时,为负数。
(7)分式:,当时或时,为非负数。
二、分式的基本性质:1、学习分式的基本性质应该与分数的基本性质类比。
不同点在于同乘以或同除以同一个不等于零的整式,这个整式可以是数也可以是字母,只要是不为零的整式。
2、这个性质可用式子表示为:(M 为不等于零的整式) 3、学习基本性质应注意几点:(1)分子与分母同乘或同除的整式的值不能为零;(2)易犯错误是只乘(或只除)分母或只乘(或只除)分子;(3)如果分子或分母是多项式时,必须乘以多项式的每一项。
4、分式变号法则的依据是分式的基本性质。
5、分式的分子,分母和分式的符号,改变其中任何两个,分式的值不变,如下列式子:,。
三、约分:1、约分是约去分子、分母中的公因式。
就是用分式中分子和分母的公因式去除分子和分母,使分式化简为最简分式,最简分式又叫既约分式。

第17讲分式的意义及基本性质模块一:分式的意义1、分式的概念两个整式、B相除,即A B÷时,可以表示为AB.如果B中含有字母,那么AB叫做分式,叫做分式的分子,B叫做分式的分母.在理解分式的概念时,注意以下三点:(1)分式的分母中必然含有字母;(2)分式的分母的值不为0;(3)分式必然是写成两式相除的形式,中间以分数线隔开.2、分式有意义的条件两个整式相除,除数不能为0,故分式有意义的条件是分母不为0,当分母为0时,分式无意义.例如:分式1211mx x=+--,当1111A B C D时,分式有意义;当1D时,分式无意义.3、分式的值为零分式的值为零时,必须满足分式的分子为零,且分式的分母不能为零,注意是“同时”.【例1】在下列代数式中,哪些是分式?哪些是整式?1t ,(2)3xx +,(42)n +,()3n n ≥,52a .【例2】 x 为何值时,分式2141x x ++无意义?【例3】 x 为何值时,分式2132x x -+有意义?【例4】 当x 为何值时,下列分式的值为0? (1)1x x+;(2)211x x -+;(3)33x x --.【例5】 x 为何值时,分式1122x x+-+有意义?模块二:分式的基本性质1、分式的基本性质:分式的分子与分母同时乘(或除以)一个不等于0的整式,分式的值不变.上述性质用公式可表示为:a am b bm =,a a mb b m ÷=÷(0m ≠).注意:①在运用分式的基本性质时,基于的前提是0m ≠;②强调“同时”,分子分母都要乘以或者除以同一个“非零”的数字或者整式; ③分式的基本性质是约分和通分的理论依据.2、约分:把一个分式的分子与分母中相同的因式约去的过程,叫做约分.3、如果一个分式的分子与分母没有相同的因式(1除外),那么这个分式叫做最简分式.【例6】 填空:(1)()2ab b a = ;(2)()32x x xy x y=++;(3)()2x y x xyxy ++=;(4)()222x y x y x xy y +=--+.【例7】 不改变分式的值,使分子和分母中的最高次项系数都为正数:(1)232645x x x x --+-; (2)23721x x x -+-+-.【例8】 化简:(1)2232x x x-+; (2)22x yx y +- ;(3)23326a a a--;(4)22222m mn n m n-+-.【例9】 若x ,y 的值扩大为原来的3倍,下列分式的值如何变化?(1)2222x y x y +-(2)3323x y(3)223x y xy-【例10】 下列分式中,哪些是最简分式?若不是最简分式,请化为最简分式.(1)22444x x x -+- ;(2)()()6334a a b b a --.1. (2022秋·上海·七年级校考期末)如果分式32xyx y-中的x 、y 的值都扩大为原来的2倍,那么分式的值( ) A .不变B .扩大到原来的2倍C .扩大到原来的4倍D .扩大到原来的6倍2. (2022秋·上海·七年级校考阶段练习)若()()121x x x x -++的值为0,则x 的值一定不是( )A .1-B .2-C .0D .13. (2022秋·上海闵行·七年级校考期末)分式2421x x --中x的取值范围是( )A .2x ≠B .2x ≠-C .12x = D .12x ≠4. (2022秋·上海普陀·七年级校联考期末)下列对于分式1x x+的变形,其中一定成立的是( ) A .121x x x x ++=+ B .221x x x x x ++=C .1212x x x x ++= D .11x x x+= 5. (2022秋·上海·七年级校考阶段练习)如果将分式23x yxy-中的x 和y 都扩大到原来的3倍,那么分式的值( ) A .不变B .扩大到原来的9倍C .缩小到原来的13D .扩大到原来的3倍6. (2022秋·上海闵行·七年级校考期末)下列各式是最简分式的是( ) A .1625xB .22x y xC .22x y x y +-D .222132x x x x -+-+7. (2022秋·上海·七年级校联考期末)分式423xyx y+中,当x 和y 分别扩大3倍时,分式的值( )A .扩大9倍B .扩大6倍C .扩大3倍D .不变8. (2022秋·上海·七年级校联考期末)若分式||22x x --的值为零,则x 的值是( ) A .±2B .2C .﹣2D .09. (2022秋·上海·七年级校联考期末)要使分式32xx -+有意义,则x 的取值范围是_________. 10. (2022秋·上海·七年级上海市民办新复兴初级中学校考期中)如果分式262x x x--+无意义,那么分式231-+x x 的值为______. 11. (2022秋·上海·七年级上海市民办新复兴初级中学校考期中)当x =______时,分式()()2226x x x x +---的值为零;12. (2022秋·上海徐汇·七年级上海市徐汇中学校联考期末)1x =时,分式23x x a+-无意义,则a =_______.13. (2022秋·上海闵行·七年级校考阶段练习)若分式33x x -+的值为0,则x 的值为_______. 14. (2022春·上海·七年级开学考试)分式2314a b 、316a b的最简公分母是______. 15. (2022秋·上海·七年级期末)化简:2232x x x -=-+______.16. (2022秋·上海·七年级校考阶段练习)若分式aba b+中的a 和b 都扩大到10a 和10b ,则分式的值扩大__________倍17. (2022秋·上海闵行·七年级校考期末)计算:11111x y x y ----+-.18. (2022秋·七年级单元测试)约分(1)2244a b ab -(2)22222a ab a b ab -- 19. (2022秋·上海·七年级阶段练习)对于正数x ,规定:()1xf x x =+. 例如:11(1)112f ==+,22(2)213f ==+,111212312f ⎛⎫== ⎪⎝⎭+. (1)填空:()3f =________;13f ⎛⎫= ⎪⎝⎭_______;1(4)4⎛⎫+= ⎪⎝⎭f f _________;(2)猜想:1()⎛⎫+= ⎪⎝⎭f x f x _________,并证明你的结论;(3)求值:111(1)(2)(2019)(2020)202020192⎛⎫⎛⎫⎛⎫+++⋅⋅⋅++++⋅⋅⋅++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭f f ff f f f .1. 当3x =时下列各式中值为0的是( )A .299x x -- B .13x - C .266x x -- D .33x x +- 2. 代数式3459258,,,,-+-b x x y x y a 中,分式的个数是( ) A .1 B .2 C .3 D .43. 化简:2562a a a ++=+____.4. 已知230x y +=,代数式2222x xy y x xy y +-=-+__________. 5. 化简:22x y ax bx ay by--+-6. 阅读下面的解题过程: 已知:2113x x =+,求241x x +的值. 解:由2113x x =+知x ≠0,所以213x x+=,即x +1x =3. 所以421x x +=x 2+21x=(x +1x)2﹣2=32﹣2=7.故241x x +的值为17.该题的解法叫做“倒数法”,请你利用“倒数法”解决下面的题目: 已知:21315x x x =-+,求2421x x x ++的值.。

学好分式三步走:1.分式的概念,分式何时有意义,何时值为零2.分式的基本性质,约分,通分3.分式的加、减、乘、除、乘方运算1.分式的概念,分式何时有意义,何时值为零①分式的定义:一般地,如果A 、B 表示两个整式,并且B 中含有字母,那么式子AB 叫做分式,其中A 叫分子,B 叫分母且B ≠0 。
②分式有意义(或分式存在)的条件:分式的分母不等于零即 B ≠0 。
③分式的值为零的条件:分式的值为零是指分式在有意义的前提下分式的分子为零。
即当A =0且B ≠0时,0AB =。
【例1】 ⑴若分式25x -有意义,则x 的取值范围是( )⑵分式211x x --的值为0,则x 的值为( )2.分式的基本性质,约分,通分①分式的基本性质:分式的分子与分母同乘以(或除以)一个不等于0的整式,分式的值不变。
()0A A M A MM B B M B M ÷==÷×≠×②利用分式的基本性质,约去分子和分母的公因式,但不改变分式的值,这样的分式变形叫做分式的约分。
分子分母中没有公因式的分式叫做最简分式。
③通分:利用分式的基本性质,使分子和分母同乘适当的整式,不改变分式的值,把几个分式变成分母相同的分式。
为了通分,要先确定各分式的公分母,一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母。
【例2】 ⑴化简222a b a ab -+的结果为( )分 式⑵化简2244xy y x x --+的结果为( )3.分式的加、减、乘、除、乘方运算分式的乘法 a c a c b d b d⋅⋅=⋅ 分式的除法 a c a d a d b d b c b c ⋅÷=⋅=⋅分式的乘方 nnn a a b b ⎛⎫= ⎪⎝⎭同分母分式相加减 a b a bc c c ±±=异分母分式相加减 acadbc ad bcb d bd bd bd ±±=±=0指数幂 01(0)a a =≠ 负整数指数幂 1p p a a -= (a ≠0,且p 为正整数)【例3】 化简22226211296x x x x x x x x -++++÷--+-思想方法吐血大总结:1.分式是否有意义、何时值为零以及基本性质都和分数相近。

分式的概念与运算知识点总结分式是数学中常见的一种表示方法,用于表示两个数之间的比例关系或部分关系。
本文将对分式的概念和运算相关的知识点进行总结,以帮助读者更好地理解和运用分式。
一、分式的基本概念1. 分式的定义:分式是由分子和分母组成的表达式,其中分母不能为零。
2. 分式的读法:分子通常读作“分子”,分母读作“分母”。
例如,"3/4 "读作“三分之四”。
3. 分式的意义:分式表示部分与整体的比例关系,可用于表示分数、比率、百分比等概念。
二、分式的基本形式1. 真分式:分子小于分母的分式,如:3/4。
2. 假分式:分子大于等于分母的分式,如:5/4。
3. 整式:分子恒为零的分式,如:0/6。
4. 真分数:分子绝对值小于分母的分式,如:|-2/5|。
5. 假分数:分子绝对值大于等于分母的分式,如:|7/2|。
三、分式的基本运算1. 分式的相等:若两个分式的分子、分母完全相同,则它们相等。
例如,1/2 = 2/4。
2. 分式的加减运算:将两个分式的分母取相同的公倍数,然后将分子相加或相减。
例如,1/3 + 1/4 = 7/12。
3. 分式的乘除运算:将两个分式的分子相乘,分母相除。
例如,2/3 × 4/5 = 8/15。
4. 分式的倒数:将分式的分子与分母互换位置得到的新分式称为原分式的倒数。
例如,倒数为3/4的分式为4/3。
5. 分式的化简:将分式的分子和分母约分,使它们没有公因数。
例如,8/12可以化简为2/3。
四、分式的应用1. 分式在比例问题中的应用:通过设置分式的比例关系来求解问题。
例如,已知一辆车以每小时60公里的速度行驶,求2小时行驶的距离。
2. 分式在百分数问题中的应用:将百分数转化为分式,进行运算。
例如,计算75%的数值为多少。
3. 分式在平均数问题中的应用:通过设置分式的平均数关系来求解问题。
例如,已知某次数学考试的平均分为80分,其中A同学的得分为90分,求B同学的得分。

分式的意义概念分式是数学中常见的一种表示形式,它由分子和分母组成,形式通常为a/b,其中a和b都是整数,b不等于0。
分式可以用来表示比例、比率、部分的整体等概念,也可以用来解决实际问题中的分割、比较、加减乘除等计算问题。
在数学、物理、化学、经济学等领域都有广泛的应用。
首先,分式的意义之一是表示比例和比率。
在日常生活和学习中,我们经常会遇到各种比例和比率的问题。
比如商店打折促销,某种商品的原价是100元,现在打8折,我们可以用分式1/10来表示折扣的比例,即原价的十分之一。
再比如,小明和小华两人合伙做生意,他们的投资比例是3:5,我们可以用分式3/5来表示小明和小华的投资比率。
分式的分子和分母分别表示了两个不同的部分,而它们的比值则表示了两者之间的比例关系,帮助我们更直观地理解和计算比例和比率的问题。
其次,分式还可以表示部分和整体的关系。
在日常生活中,我们常常需要计算一部分占整体的比例。
比如我们想知道全班学生中男生的比例,全班学生有60人,其中男生有30人,我们可以用分式30/60或简化后的1/2来表示男生占全班学生的比例。
再比如一个容器里有300毫升的水,现在倒出了100毫升,我们可以用分式1/3来表示倒出的水占原来水量的比例。
这种表示方法直观清晰地展现了部分和整体的关系,帮助我们更容易地进行计算和理解。
此外,分式还可以用来解决实际问题中的分割、比较、加减乘除等计算问题。
在日常生活和学习中,我们经常会遇到需要分割物品、比较数值大小、对不同比例的物品进行合并等问题。
比如,一块土地被分成3等份,我们想知道其中一份占总土地面积的比例,这时我们就可以用分式1/3来表示;再比如,小明和小华两人分别做了不同的作业题数,我们需要计算他们完成的总题数,这时我们可以用分式相加来表示他们的完成比例。
而乘法和除法运算中,分式同样也发挥着重要的作用,比如在物理学中,力的计算问题中,就需要进行分式的乘除运算。
总的来说,分式是数学中一个非常重要的概念,它在日常生活和各个学科领域中都有广泛的应用。

公因式 如32262464=÷÷=(公因式是2) b a b b b ab b ab 33322=÷÷=(公因式是b )y x y x y x y x y x y x y x y x +-=++-+=+-))(())(()(222最小公倍数=两数的乘积/最大公约(因)数, 解题时要避免和最大公约(因)数问题混淆例子6,9的最小公倍数是6×9÷3=18;4,6的最小公倍数是4×6÷2=12;3,4的最小公倍数是3×4=12 如23,32 通分得693233=⨯⨯,642322=⨯⨯(最小公分母是2×3=6)最小公分母,即分母的最小公倍数 a 3,b 2通分得ab b b a b 33=⨯⨯,aba ab a 22=⨯⨯(最小公分母是a ×b=ab ) d b a 23,mbc 2通分得dm b am md b m a 2233=⨯⨯,dm b cbd bd mb bd c 222=⨯⨯(d mb mb d b 32=⨯,不是最小公分母,d mb 2才是) 22y x x -,2)(y x y -, 注意))((22y x y x y x +-=- ,))(()(2y x y x y x --=-由此可得两式的最小分母是 ))()((y x y x y x +--,即通分得))()(())()(()(2y x y x y x xy x y x y x y x y x x +---=+--- ))()(())()(()(2y x y x y x y xy y x y x y x y x y +--+=+--+ 四、分式的运算1)分式的乘除用到的知识是约分,分式的加减用到的知识是通分 2)分式的加减要通分令分母相同,分子再进行相加减,得出结果后,看能否约分,假如能约分,则需约分,假如不能约分,则不需约分。
分式的定义和有意义的条件一、分式的定义和有意义的条件1、分式的概念一般地,如果$A$,$B$表示两个整式,并且$B$中含有字母,那么式子$\frac{A}{B}$叫做分式。
分式$\frac{A}{B}$中,$A$叫做分子,$B$叫做分母。
2、分式有意义的条件分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0。
即当$B≠0$时,分式$\frac{A}{B}$才有意义。
3、分式的值为0的条件当分式的分子等于0,且分母不等于0时,分式的值为0,即当$A=0$,且$B≠0$时,分式$\frac{A}{B}=0$。
4、分式的基本性质(1)分式的基本性质分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变。
即$\frac{A}{B}=\frac{A·C}{B·C}$,$\frac{A}{B}=\frac{A÷C}{B÷C}$$(C≠0)$,其中$A$,$B$,$C$是整式。
(2)约分:根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分。
(3)约分法则:把一个分式约分,如果分子和分母都是几个因式乘积的形式,约去分子和分母中相同因式的最低次幂;分子与分母的系数约去它们的最大公约数,如果分式的分子、分母是多项式,先分解因式,然后约分。
(4)最简分式:分子与分母没有公因式的分式叫做最简分式。
(5)通分:根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分。
(6)通分法则:把两个或者几个分式通分,① 先求各个分式的最简公分母(即各分母系数的最小公倍数、相同因式的最高次幂与所有不同因式的积)。
② 再利用分式的基本性质,用最简公分母除以原来各分母所得的商分别去乘原来分式的分子、分母,使每个分式变为与原分式的值相等,而且以最简公分母为分母的分式。
③ 若分母是多项式,则先分解因式,再通分。
(7)最简公分母:各分式分母的所有因式的最高次幂的积,叫做最简公分母。
教师姓名学生姓名年级初一上课时间单击此处输入日期。
学科数学课题名称分式的意义与基本性质1、分式的概念与意义:
(1)A、B表示两个整式,A÷B(B≠0)可以表示为A
B
的形式,如果B中含有字母,那么我们把式
子A
B
(B≠0)叫分式,其中A叫分子,B叫分母。
(2)关于分式概念的两点说明:
①分式的分子中可以含有字母,也可以不含字母,但分母中必须含有字母,这是分式与整式的根本
区别。
②分式中的分母不能为零,是分式概念的组成部分,只有分式的分母不为零,分式才有意义,因此,若分式有意义,则分母的值不为零(所谓分母的值不为零,就是分母中字母不能取使分母为零的那些值)反之,分母的值不为零时,分式有意义。
(3)分式的值为零
分式的意义与基本性质
例8、将下列各组分式进行通分。
(1) 223a ,1
6ab
(2)
244x -,21(x 2)x -+ (3)123x +,232x - ,225
49
x x +-
答案:(1)
223a 246b a b = 16ab 26a a b =
(2)24
4x -2(x 2)(x 2)(x 2)x +=-+ 21(x 2)x -+2(x 1)(x 2)(x 2)(x 2)--=-+
(2) 123x +23(23)(2x 3)x x -=+- 232x -2(23)(23)(2x 3)x x -=+- 2
2549x x +-25(23)(2x 3)x x +=+-
1、根据分式的基本性质,分式
a
a b
--可变形为( )。
分式的概念与分式有意义的条件分式是数学中一个重要的概念,它由分子和分母组成,用斜杠"/"或横线"-"表示两者的关系。
分式可以表示两个数的比值,常用于解决问题中的比例、比率、百分比、碰撞问题等。
分式的形式通常为:\(\dfrac{a}{b}\) 或 \(a/b\)其中,a为分子,b为分母。
分子和分母均可以是整数、分数或代数式。
分式有意义的条件包括:1. 分母不能为0:由于除数不能为0,分式的分母必须为非零数。
当分母为0时,分式的数值就没有意义,因此分母必须满足\(b\neq0\)的条件。
2.分母不能为分数:分式的分母不应该是分数,因为这样会导致分式难以化简和计算,并且会增加问题的复杂性。
3.分子和分母应该具有相同的单位:在一些问题中,分子和分母表示的是同一物理量的不同测量值。
在这种情况下,分子和分母应该具有相同的单位,以确保比率的一致性。
4.分子和分母应该为整数:在一些情况下,分式的分子和分母可以是分数或代数式,但在常见的问题中,一般要求分子和分母都是整数,以方便计算和解决问题。
5.分式应当合理存在:分式不能出现不合理的数值,如负数开方、分母含有根号等情况。
在实际问题中,分式所代表的比率或比例应当存在,不能出现意义上的不合理的情况。
分式在实际问题中的应用非常广泛,可以用于解决各种实际问题。
下面以几个实例来说明分式的应用:1.比例问题:分式经常用于解决比例问题,如甲乙丙三个人的年龄比例为3:4:5,且他们的年龄相加为144岁,求甲的年龄。
分子表示甲的年龄,分母表示甲的年龄与整个年龄之间的比例关系。
2.比率问题:分式常用于表示两个相似量之间的比率,如速度与时间的比值,体积与面积的比值等。
分子表示比例中较大的值,分母表示较小的值,比值可以通过分式计算或比例解题方法求解。
3.百分比问题:分式可以用于表示百分比、利率、比率等问题,如计算折扣价格、计算商品的增长率等。
分子表示所占的部分,分母表示总量,分式的值可以通过计算得到。
分式概念及意义分式的意义和性质一、分式的概念1、用A、B表示两个整式,A÷B可以表示成的形式,其中A叫做分式的分子,B叫做分式的分母,如果除式B中含有字母,式子就叫做分式。
这就是分式的概念。
研究分式就从这里展开。
2、既然除式里含有字母的有理代数式叫做分式,那么,在分式里分母所包含的字母,就不一定可以取任意值。
分式的分子A可取任意数值,但分母B不能为零,因为用零做除数没有意义。
一般地说,在一个分式里,分子中的字母可取任意数值,但分母中的字母,只能取不使分母等于零的值。
3.(1)分式:,当B=0时,分式无意义。
(2)分式:,当B≠0时,分式有意义。
(3)分式:,当时,分式的值为零。
(4)分式:,当时,分式的值为1。
(5)分式:,当时,即或时,为正数。
(6)分式:,当时,即或时,为负数。
(7)分式:,当时或时,为非负数。
三、分式的基本性质:1、学习分式的基本性质应该与分数的基本性质类比。
不同点在于同乘以或同除以同一个不等于零的整式,这个整式可以是数也可以是字母,只要是不为零的整式。
2、这个性质可用式子表示为:(M为不等于零的整式)3、学习基本性质应注意几点:(1)分子与分母同乘或同除的整式的值不能为零;(2)易犯错误是只乘(或只除)分母或只乘(或只除)分子;(3)如果分子或分母是多项式时,必须乘以多项式的每一项。
4、分式变号法则的依据是分式的基本性质。
5、分式的分子,分母和分式的符号,改变其中任何两个,分式的值不变,如下列式子:,。
四、约分:1、约分是约去分子、分母中的公因式。
就是用分式中分子和分母的公因式去除分子和分母,使分式化简为最简分式,最简分式又叫既约分式。
2、约分的理论依据是分式的基本性质。
3、约分的方法:(1)如果分式的分子和分母都是几个因式乘积的形式,就约去分子和分母中相同因式的最低次幂,当分子和分母的系数是整数时,还要约去它们的最大公约数。
例1,请说出下列各式中哪些是整式,那些是分式?(1)(2)(3)(4)(5)a2-a(6)。
分式知识点总结一、分式的定义如果 A、B 表示两个整式,并且 B 中含有字母,那么式子 A/B 就叫做分式。
其中 A 叫做分子,B 叫做分母。
需要注意的是,分母 B 的值不能为 0,如果 B=0,那么分式就没有意义了。
例如,分式 1/x,当 x=0 时,这个分式就没有意义。
二、分式的基本性质分式的分子和分母同时乘以(或除以)同一个不为 0 的整式,分式的值不变。
用式子表示为:A/B = A×C/B×C,A/B = A÷C/B÷C(C 为不等于 0 的整式)。
这就像分蛋糕,如果把蛋糕(分式的值)平均分成的份数(分母)和每份的大小(分子)同时扩大或缩小相同的倍数,蛋糕的大小(分式的值)不变。
例如,对于分式 2/3,分子分母同时乘以 2,得到 4/6,分式的值不变。
三、分式的约分把一个分式的分子和分母的公因式约去,叫做分式的约分。
约分的关键是确定分子和分母的公因式。
确定公因式的方法:1、系数:取分子和分母系数的最大公因数。
2、字母:取相同字母的最低次幂。
例如,对于分式 6x/8x²,分子分母的公因式是 2x,约分后得到 3/4x。
四、分式的通分把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分。
通分的关键是确定几个分式的最简公分母。
确定最简公分母的方法:1、取各分母系数的最小公倍数。
2、凡单独出现的字母连同它的指数作为最简公分母的一个因式。
3、同底数幂取次数最高的。
例如,对于分式 1/2x 和 1/3y,最简公分母是 6xy,通分后分别为3y/6xy 和 2x/6xy。
五、分式的运算1、分式的乘法法则:分式乘以分式,用分子的积做积的分子,分母的积做积的分母。
用式子表示为:(A/B)×(C/D) = AC/BD。
例如,(2/3)×(4/5) = 8/15。
2、分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
分式有意义的条件一、引言分式是代数中的一种运算形式,通常用分子和分母表示。
在数学中,分式广泛应用于代数表达式的化简、方程的求解以及解析几何等领域。
在实际生活中,我们也可以发现许多分式的应用,比如用分数表示家庭开销占总收入的比例、用比率表示物品的价格、用百分比表示考试分数等。
二、分式的基本概念分式是指两个整式的商,分为真分式和假分式两种情况。
真分式的分子次数小于分母次数,假分式的分子次数大于等于分母次数。
分式还可以进一步化简,即将分子和分母的公因式约去,得到最简分式。
三、分式的应用1.比例在很多实际问题中,可以用比例关系表示,而比例就可以转化为分式。
比如描述两种物品的价格比、人口比例等。
2.百分比百分比是一种特殊的分式表示方法,分子是百分数,分母是100。
百分比在日常生活中经常用来表示数据的比较和增减。
3.分数运算运用分式进行四则运算是学习分数的基础。
加、减、乘、除分式可以帮助我们解决实际问题。
4.代数式的运算在化简代数式的过程中,常常会涉及到分式的加减乘除,需要熟练掌握分式运算的规则。
四、分式有意义的条件分式在数学和现实生活中都有广泛的应用,但是要让分式有意义,需要满足一定的条件: 1. 分母不为零当分母为零时,分式的值无意义,因为数学运算中除数不能为零。
因此,在使用分式时,分母不可以为零。
2.分子和分母互质为了得到最简分式,分子和分母应该互质,即两者没有除1以外的公因数。
这样可以避免分式的冗余和不必要的复杂性。
3.分数形式表示有些问题中,整式可以转化为分数形式表示更为方便和直观。
比如在几何问题中,可以用分数表示线段的比例关系。
五、结论分式作为一种常见的数学表达形式,具有重要的应用意义。
通过对分式的概念和应用展开讨论,可以更好地理解分式在数学中的作用和意义。
要让分式有意义,需要注意分母不为零、分子和分母互质以及适当选择分数形式表示等条件,这样才能更好地利用分式解决问题。
以上就是关于分式有意义的条件的探讨,希望对读者有所启发和帮助。
分式的意义和性质
一、分式的概念
1、用A、B表示两个整式,A÷B可以表示成的形式,其中A叫做分式的分子,B叫做
分式的分母,如果除式B中含有字母,式子就叫做分式。
这就是分式的概念。
研究分式就从这里展开。
2、既然除式里含有字母的有理代数式叫做分式,那么,在分式里分母所包含的字母,就不
一定可以取任意值。
分式的分子A可取任意数值,但分母B不能为零,因为用零做除数没有
意义。
一般地说,在一个分式里,分子中的字母可取任意数值,但分母中的字母,只能取不使分母等于零的值。
3.〔1〕分式:,当B=0时,分式无意义。
〔2〕分式:,当B≠0时,分式有意义。
〔3〕分式:,当时,分式的值为零。
〔4〕分式:,当时,分式的值为1。
〔5〕分式:,当时,即或时,为正数。
〔6〕分式:,当时,即或时,为负数。
〔7〕分式:,当时或时,为非负数。
三、分式的根本性质:
1、学习分式的根本性质应该与分数的根本性质类比。
不同点在于同乘以或同除以同一个不等于零的整式,这个整式可以是数也可以是字母,只要是不为零的整式。
2、这个性质可用式子表示为:〔M为不等于零的整式〕
3、学习根本性质应注意几点:
〔1〕分子与分母同乘或同除的整式的值不能为零;
〔2〕易犯错误是只乘〔或只除〕分母或只乘〔或只除〕分子;
〔3〕如果分子或分母是多项式时,必须乘以多项式的每一项。
4、分式变号法那么的依据是分式的根本性质。
5、分式的分子,分母和分式的符号,改变其中任何两个,分式的值不变,如以下式子:
,。
四、约分:
1、约分是约去分子、分母中的公因式。
就是用分式中分子和分母的公因式去除分子和分母,使分式化简为最简分式,最简分式又叫既约分式。
2、约分的理论依据是分式的根本性质。
3、约分的方法:
〔1〕如果分式的分子和分母都是几个因式乘积的形式,就约去分子和分母中一样因式的最低次幂,当分子和分母的系数是整数时,还要约去它们的最大公约数。
例1,请说出以下各式中哪些是整式,那些是分式?〔1〕〔2〕〔3〕
〔4〕
〔5〕a2-a〔6〕。
解:根据分式定义知〔1〕、〔2〕、〔3〕是分式,〔4〕、〔5〕、〔6〕是整式。
说明:判断一个代数式是否是分式要紧紧抓住除式中含不含字母。
这里是分式,不能因为==a+b,而认为是整式,a+b是分式的值。
要区分分式的值和分式这两个不同的概念。
另外是整式而不是分式。
虽然分母中有π,但π不是字母而是无理数,是无限不循环小数,因此的除式中不含字母。
例2,在分式〔1〕〔2〕〔3〕中,字母x的值有什么限制?
解:〔1〕在中,当x=2时,使得分母x-2=0,∴x≠2,
〔2〕在中,当x=-2时,使得分母x+2=0, ∴x≠-2,
〔3〕在中,当x=-2或x=3时,使得分母(x+2)(x-3)=0,
∴x≠-2且x≠3。
例3,x为何值时,分式,〔1〕无意义;〔2〕值为零;〔3〕值为1;〔4〕值为非负数。
解:〔1〕∵当分母2x+3=0时分式无意义,∴x=-时,分式无意义。
〔2〕∵当时,分式值为零。
∴,∴x=1时分式值为零。
〔3〕∵当时,分式值为1,∴x=-4时分式值为1。
〔4〕∵当或时,分式值为非负数。
∴或∴x≥1或x<-时分式值为非负数。
例4,当x取何值时,分式〔1〕值为零;〔2〕无意义;〔3〕有意义。
解:〔1〕∵当(x+3)(x-1)≠0时,分式有意义,∴当x≠-3且x≠1时分式有意义。
又∵6-2|x|=0时分式值为零,那么3-|x|=0, ∴|x|=3, ∴x=±3。
∴,∴x=3时分式值为零。
〔2〕∵(x+3)(x-1)=0分式无意义,
即x+3=0或x-1=0,∴x=-3或x=1时分式无意义。
说明:对于〔1〕也可先令分子为零,求出字母的所有可能值为x=±3后,再逐一代入分母验证是否为零,不为零者即为所求。
对于〔2〕当x+3=0或x-1=0时,都会使分式的分母等于零,所以要注意“或〞字的使用。
解:〔3〕∵(x+3)(x-1)≠0时分式有意义。
即x+3≠0且x-1≠0时,∴x≠-3且x≠1时分式有意义,
说明:对于〔3〕分母(x+3)(x-1)只有不为零时,分式有意义,而(x+3)(x-1)≠0,当x+3=0或x-1=0都会使(x+3)(x-1)=0,所以应将x=-3和x=1都同时排除掉,写成x≠-3且x≠1,用“且〞字,而不用“或〞字。
意义为x不能为-3而且还不能为1,即-3和1都不能取。
因为取任何其中一个值,分母(x+3)(x-1)都会为0,而使分式都会无意义。
例5,写出等式中未知的分子或分母:
〔1〕;〔2〕;〔3〕;
〔1〕分析:这类问题要从条件入手,根据分式的根本性质,分析变化的过程,如〔1〕右边分母x2-y2是(x+y)(x-y),而左边分母为x+y,所以需将左式的分子和分母同乘以(x-y)。
解:,∴未知的分子是(x-y)2,
〔2〕分析:左边分子a2-ab=a(a-b),而右边分子是a-b,所以需将左式的分子和分母同除以a。
解:=,未知的分母是b。
〔3〕∵a2+ab=a(a+b)〔将分子因式分解〕
∴〔比拟分子,发现分子、分母同乘以a〕
=,2ab即为所求的分母。
例6,把以下分式的分子和分母中各项的系数都化为整数。
〔1〕;〔2〕;
〔1〕分析:先找到分式中分子和分母中的分母的最小公倍数为15,再据分数根本性质,分子和分母同乘以15。
解:=。
〔2〕解:==
注:必须乘以分子和分母的每一项,防止发生(0.2a+3b)×10=2a+3b这样的错误。
例7,不改变分式的值,使以下分式中分子与分母不含“-〞号,〔1〕-;〔2〕-。
解:根据分式的符号法那么得:
〔1〕-=;〔2〕-=-。
注意:分式、分子和分母的符号中,任意改变其中两个,分式的值不变。
〔1〕中改变分式本身和分母两个负号,〔2〕中改变分子和分母两个负号。
例8,不改变分式的值,依照x的降幂排列,使分子和分母中x的最高项的系数都为正数。
〔1〕;〔2〕-。
解:〔1〕===;
〔2〕-=-=-
=-。
说明:解题可分为三步:〔1〕先将分式的分子和分母都按x的降幂排列,这步只是运用加法交换律,不改变符号。
〔2〕将分子和分母的最高项系数化为正数,只要提取公因式-1即可,提取时注意每项都要变号。
〔3〕运用符号法那么进展变号。
注意:如果分子或分母的首项为负,那么必须先将负号提到括号外面,再使用符号法那么,要注意防止以下的错误:
=。
例9,约分:〔1〕〔2〕。
解:〔1〕===-3yz10。
注意:分母的因式约去后得1,分式变为整式。
假设化简分式时千万不要犯以下错误:
==0。
〔2〕===-。
注意:分母的负号一般要移去。
〔2〕如果分式的分子或分母是多项式,应先分解因式,然后再约分。
例10、约分:〔1〕;〔2〕;〔3〕;〔4〕;〔5〕。
解:〔1〕=。
注意:不要把约成=,也不要将最后结果写成,因为分式的横线表示括号,再写括号就多余了。
〔2〕=。
注:不要将约做,因为这样是分子分母都减a2,不是同除以一样的整式。
〔3〕===x2+1。
注:不要犯下面的错误:=x3-x2。
〔4〕==
==-。
注意:这里应用到了(2-x)3=-(x-2)3的变形。
〔5〕=〔分子按x的降幂排列〕
=〔分子提取公因式-1〕
=〔分子、分母都分解因式〕
=〔约去公因式:x-1〕
=-〔应用分式的符号法那么〕
说明:此题的解法,一方面显示出分式约分的一般步骤,另一方面在解题的右侧的括号内写出运算的算理,平日的化简是不写这些的,但不是它不存在,在思维上它是不可缺少的。
分数的乘除法的关键是约分,而分式乘除法的关键也是约分,就是说,分式乘除法运算的实质是约分,它能使运算的结果化为最简分式。
同分数的约分一样,分式的约分是应用分式的根本性质,把分式的分子、分母同除以它们的公因式,把分式化简,因此约分的关键在于正确寻找到分式分子、分母中的公因式。
附录:
一、本讲教学内容及要求
单元节次知识要点教学要求
二、本讲技能要求
1、了解分式、有理式、最简分式、最简公分母的概念,会利用这些概念进展判断。
2、掌握分式有意义的条件,分式为零的条件及分式的根本性质,掌握分式的变号法那么,能熟练地进展约分。
3、重要数学思想
通过本讲中分式性质及分式约分进一步理解转化思想;
对本章中数、式通性的理解,进一步掌握类比归纳的思维方法。