尺寸链计算方法

尺寸链概率法计算公式
尺寸链是指由不同大小的尺寸组成的链条，通常会按照其中一种规则进行排序，比如从大到小或从小到大。

在实际应用中，尺寸链可以用来描述一系列不同尺寸的物体、事件或数据，比如排行榜、尺码表或者网络结构。

P(x) = P(x1) * P(x2，x1) * P(x3，x2) * ... * P(xn，xn-1)
其中，P(x)表示整个尺寸链的概率，P(xi)表示第i个尺寸的概率，P(xi，xi-1)表示第i个尺寸在已知前一个尺寸的条件下的概率。

1.收集数据：收集尺寸链中各个尺寸的数据，比如物体的大小、事件发生的概率或者数据的分布情况。

2.计算单个尺寸的概率：根据收集到的数据，计算每个尺寸出现的概率。

可以使用频率方法，通过统计尺寸出现的次数来计算概率，也可以使用概率密度方法，通过拟合尺寸的分布来计算概率。

3.计算条件概率：对于每个尺寸，计算它在已知前一个尺寸的条件下的概率。

可以使用条件概率密度方法，通过拟合条件概率分布来计算条件概率。

4.计算尺寸链的概率：根据计算得到的单个尺寸概率和条件概率，使用尺寸链概率计算公式计算整个尺寸链的概率。

尺寸链概率法的应用范围广泛，可以用于各种尺寸链的计算，比如排行榜的排序概率、尺码表的尺寸分布概率或者网络节点的连接概率等。

在实际应用中，需要使用适当的数据收集和计算方法来得到准确的概率值，以提高尺寸链模型的预测能力。

总之，尺寸链概率法是一种基于尺寸链模型的计算方法，通过计算单个尺寸和条件概率来确定整个尺寸链的概率。

它可以用于各种尺寸链的计算，为我们理解和应用尺寸链提供了有力的工具。

尺寸链计算方法及步骤尺寸链计算方法是在工程和设计领域中用来确定产品尺寸的一种方法。

通过尺寸链计算，可以确保产品的各个组成部分之间的尺寸关系符合设计要求，从而实现功能和装配的有效性。

下面将介绍尺寸链计算的具体方法及步骤。

一、确定设计要求在进行尺寸链计算之前，首先需要明确产品的设计要求。

这包括产品的功能要求、装配要求、尺寸公差要求等。

只有明确了这些设计要求，才能够有针对性地进行尺寸链计算。

二、确定尺寸链的起点和终点尺寸链计算中，需要确定尺寸链的起点和终点。

起点是指一个确定的尺寸基准，终点是指产品中的某个关键尺寸。

起点和终点之间的尺寸关系将通过尺寸链计算得出。

三、确定尺寸链的路径确定尺寸链的路径是指确定起点和终点之间的尺寸关系路径。

这个路径通常是通过产品的装配关系来确定的。

在确定路径时，需要考虑产品的功能和装配要求，确保路径的合理性和有效性。

四、确定尺寸链各个环节的尺寸公差尺寸链计算中，每个环节都有一定的尺寸公差。

尺寸公差是指在设计和生产过程中，为了满足产品功能和装配要求而允许的尺寸偏差范围。

确定尺寸链各个环节的尺寸公差需要考虑产品的功能要求和装配要求，确保尺寸链的有效性和可控性。

五、计算尺寸链各个环节的尺寸在确定了尺寸链的路径和尺寸公差之后，就可以开始计算尺寸链各个环节的尺寸了。

计算尺寸时，需要考虑尺寸公差和装配要求，确保尺寸的准确性和一致性。

六、验证尺寸链的有效性计算完成后，需要对尺寸链进行验证，确保其满足设计要求和装配要求。

验证的方法可以采用数值模拟、实验测试等手段。

通过验证，可以判断尺寸链的有效性，及时发现和解决尺寸关系的问题。

七、优化尺寸链在进行尺寸链计算的过程中，可能会发现一些尺寸关系不符合设计要求或装配要求。

在这种情况下，需要对尺寸链进行优化，调整尺寸关系，使其满足要求。

优化尺寸链的方法可以包括调整尺寸公差、改变尺寸关系路径等。

八、更新尺寸链计算结果在完成尺寸链计算和优化之后，需要及时更新尺寸链计算结果。

尺寸链的计算方法尺寸链（Size Chain）是一种用于计算产品尺寸的方法。

它通常应用于制造业中，用于确定产品的尺寸规格和控制尺寸变化的程度。

尺寸链的计算方法通常包括以下几个步骤：1.确定产品的需求和要求：在开始计算尺寸链之前，首先需要明确产品的需求和要求，包括外观和性能等方面。

这包括与客户和设计师沟通，以确保产品尺寸链的计算符合其期望。

2.收集尺寸数据：通过测量和记录产品的关键尺寸数据，包括长度、宽度、高度、深度、直径等。

这些数据将用于计算尺寸链的各个参数。

3. 计算起始尺寸（Baseline）：起始尺寸是指产品的基准尺寸，即在制造过程中不发生任何尺寸变化时的尺寸。

可以根据客户的要求或产品设计文档中的规格来确定起始尺寸。

4.确定各个工序的尺寸变化：对于产品制造过程中涉及尺寸变化的每个工序，需要确定其对产品尺寸的影响程度。

这可以通过实验、模拟或经验来获取相关数据。

例如，在注塑成型过程中，温度、压力和材料流动性等因素都会影响最终产品的尺寸。

5. 计算尺寸链参数：根据各个工序的尺寸变化数据，可以计算出尺寸链的各个参数，包括尺寸链比例（Size Chain Ratio）和尺寸链统计（Size Chain Statistics）等。

尺寸链比例表示每个工序中尺寸变化的幅度与起始尺寸之间的比例关系。

尺寸链统计表示在整个制造过程中尺寸变化的累积情况。

6.分析和优化尺寸链：一旦计算出尺寸链的参数，可以对其进行分析和优化。

通过对尺寸链数据的统计和分析，可以确定影响尺寸变化的主要因素，并采取相应的措施来减小尺寸变化的幅度，提高产品的尺寸一致性和质量稳定性。

7.应用尺寸链于生产控制：尺寸链的计算结果可以应用于产品的生产控制和质量管理中。

例如，在制造过程中可以设置尺寸监测点，对产品进行尺寸测量，并与尺寸链数据进行比较，以确保产品尺寸处于可接受的范围内。

如果发现尺寸偏差过大，可以及时调整制造参数，纠正尺寸偏差，以保证产品质量。

尺寸链（dimension chain）计算是在工程和制造领域中常用的方法，用于计算物体的尺寸或特征之间的关系。

以下是尺寸链计算中常用的四个公式：
1.长度链：长度链用于计算物体的长度或距离之间的关系。

常见的长度链公式如下：
L = L₁ + L₂ + L₃ + … + Ln
其中，L 表示总长度或距离，L₁、L₂、L₃等表示各个部分的长度或距离。

2.半径链：半径链用于计算物体的半径或直径之间的关系。

常见的半径链公式如下：
R = R₁ + R₂ + R₃ + … + Rn
或
D = 2R = 2(R₁ + R₂ + R₃ + … + Rn)
其中，R 表示总半径或直径，R₁、R₂、R₃等表示各个部分的半径或直径。

3.弧长链：弧长链用于计算物体的弧长之间的关系。

通常以角度来度量弧长，常见的弧长链公式如下：
S = S₁ + S₂ + S₃ + … + Sn
其中，S 表示总弧长，S₁、S₂、S₃等表示各个部分的弧长。

4.面积链：面积链用于计算物体的面积之间的关系。

常见的面积链公式如下：
A = A₁ + A₂ + A₃ + … + An
其中，A 表示总面积，A₁、A₂、A₃等表示各个部分的面积。

这些公式表示了尺寸链计算中常见的关系，可用于计算和预测物体的尺寸或特征。

在实际应用中，具体的公式和计算方式可能会根据实际情况和所涉及的几何形状而有所变化。

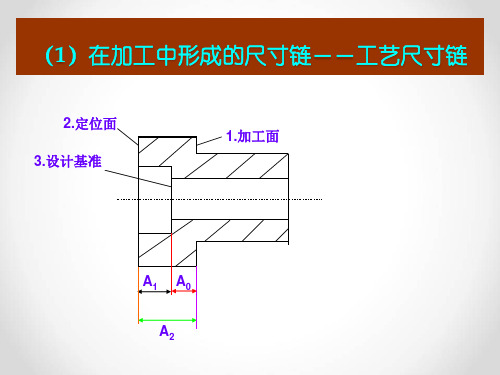
一、尺寸链及尺寸链计算公式1、尺寸链的定义在工件加工和机器装配过程中，由相互联系的尺寸,按一定顺序排列成的封闭尺寸组，称为尺寸链。

尺寸链示例2、工艺尺寸链的组成环：工艺尺寸链中的每一个尺寸称为尺寸链的环。

工艺尺寸链由一系列的环组成。

环又分为：（1）封闭环（终结环）：在加工过程中间接获得的尺寸，称为封闭环。

在图b所示尺寸链中，A0是间接得到的尺寸，它就是图b所示尺寸链的封闭环。

（2）组成环：在加工过程中直接获得的尺寸，称为组成环。

尺寸链中A1与A2都是通过加工直接得到的尺寸，A1、A2都是尺寸链的组成环。

1）增环：在尺寸链中，自身增大或减小，会使封闭环随之增大或减小的组成环，称为增环。

表示增环字母上面用--> 表示。

2）减环：在尺寸链中，自身增大或减小，会使封闭环反而随之减小或增大的组成环，称为减环。

表示减环字母上面用<-- 表示。

3）怎样确定增减环：用箭头方法确定，即凡是箭头方向与封闭环箭头方向相反的组成环为增环，相同的组成环为减环。

在图b所示尺寸链中，A1是增环，A2是减环。

4）传递系数ξi：表示组成环对封闭环影响大小的系数。

即组成环在封闭环上引起的变动量对组成环本身变动量之比。

对直线尺寸链而言，增环的ξi＝1，减环的ξi＝－1。

3.尺寸链的分类4.尺寸链的计算尺寸链计算有正计算、反计算和中间计算等三种类型。

已知组成环求封闭环的计算方式称作正计算；已知封闭环求各组成环称作反计算；已知封闭环及部分组成环，求其余的一个或几个组成环，称为中间计算。

尺寸链计算有极值法与统计法（或概率法）两种。

用极值法解尺寸链是从尺寸链各环均处于极值条件来求解封闭环尺寸与组成环尺寸之间关系的。

用统计法解尺寸链则是运用概率论理论来求解封闭环尺寸与组成环尺寸之间关系的。

5.极值法解尺寸链的计算公式（4）封闭环的中间偏差（5）封闭环公差（6）组成环中间偏差Δi＝(ES i＋EI i)/2（7）封闭环极限尺寸（8）封闭环极限偏差6.竖式计算法口诀：封闭环和增环的基本尺寸和上下偏差照抄；减环基本尺寸变号；减环上下偏差对调且变号。

尺寸链的计算方法
尺寸链是指产品设计、制造、装配和质量控制过程中的一种重要工具，它可以
帮助我们更好地理解产品的尺寸要求，保证产品的质量和性能。

在实际工程中，尺寸链的计算方法是非常关键的，下面我们将详细介绍尺寸链的计算方法。

首先，我们需要明确尺寸链的定义。

尺寸链是指产品各零部件之间的尺寸关系，包括公差、配合、间隙等内容。

在产品设计阶段，我们需要根据产品的功能要求和制造工艺来确定尺寸链，以保证产品的装配性和性能。

其次，尺寸链的计算方法主要包括以下几个步骤，确定尺寸链的起始尺寸、确
定尺寸链的公差、计算尺寸链的累积公差、分析尺寸链的影响。

首先，我们需要根据产品的功能要求和装配工艺确定尺寸链的起始尺寸，即各零部件的基准尺寸。

然后，根据国家标准或行业标准确定各零部件的公差，包括尺寸公差、形位公差等。

接下来，我们需要计算尺寸链的累积公差，即各零部件在装配过程中的尺寸偏差累积值。

最后，我们需要分析尺寸链对产品性能和装配性的影响，以确定是否满足产品设计要求。

在实际工程中，尺寸链的计算方法需要结合产品的具体情况和制造工艺来进行。

我们需要根据产品的功能要求和装配工艺来确定尺寸链的起始尺寸和公差，同时考虑产品的材料特性和加工工艺，以保证产品的质量和性能。

总之，尺寸链的计算方法是产品设计和制造过程中的重要内容，它可以帮助我
们更好地理解产品的尺寸要求，保证产品的质量和性能。

在实际工程中，我们需要根据产品的具体情况和制造工艺来确定尺寸链，以保证产品的装配性和性能。

希望本文对您有所帮助，谢谢阅读！。

尺寸链计算方法及案例详解尺寸链计算方法是指根据产品的尺寸要求和特定的工艺流程，通过一系列的计算和分析来确定产品各个部件的尺寸和配合关系的方法。

尺寸链计算方法主要应用于机械设计、工程制图、零部件加工等领域，是确保产品尺寸精度和装配质量的重要手段。

首先，尺寸链计算方法需要明确产品设计的功能要求和工艺要求，包括产品的使用环境、受力情况、材料特性等。

然后，根据这些要求，确定产品各个部件之间的配合关系和尺寸范围。

接着，通过计算和分析，确定各个部件的尺寸，并建立尺寸链，保证各个部件在装配时能够满足设计要求。

在实际应用中，尺寸链计算方法通常涉及到几个方面的内容，包括尺寸配合计算、公差分配、尺寸链分析等。

在尺寸配合计算中，需要根据配合要求和公差要求，确定配合尺寸的上限和下限。

公差分配则是根据产品功能和装配要求，合理地分配公差，确保产品的性能和装配质量。

尺寸链分析则是通过建立尺寸链图，分析各个部件之间的尺寸关系，找出影响产品尺寸精度的关键因素，从而指导产品设计和加工。

举个简单的案例来说明尺寸链计算方法的应用。

比如，某机械零件的装配要求是要求两个轴承孔的中心距离在一定范围内，并且轴承孔的直径要求在一定的公差范围内。

在这种情况下，就需要通过尺寸链计算方法来确定轴承孔的尺寸和配合关系。

首先根据轴承的尺寸和公差要求，确定轴承孔的上限和下限尺寸。

然后根据轴承孔的位置和受力情况，确定轴承孔中心距离的范围。

最后通过尺寸链计算方法，确定轴承孔的尺寸和配合关系，以保证产品的装配质量和性能。

总之，尺寸链计算方法是一种重要的工程技术方法，通过合理的计算和分析，能够确保产品的尺寸精度和装配质量，对于提高产品的质量和竞争力具有重要意义。