双曲线及其标准方程(1)
- 格式:docx
- 大小:38.02 KB
- 文档页数:7

2.3 双曲线2.3.1 双曲线及其标准方程整体设计教材分析“双曲线及其标准方程”是在讲完了“圆的方程”“椭圆及其标准方程”之后,学习的又一类圆锥曲线知识,也是中学解析几何的学习中最重要的内容之一,它在社会生产、日常生活和科学技术等领域有着广泛的应用,也是大纲中明确要求学生必须熟练掌握的重要内容.双曲线的定义、标准方程与椭圆类似,教科书的处理方法也相仿,也就是说,本小节在数学思想和方法上没有新内容,因此,这一小节的教学可以参照第2.2.1节进行.教学中要着重对比椭圆与双曲线的相同点和不同点,特别是它们的不同点.课时分配本节内容分两课时完成.第1课时讲解双曲线的定义,要求学生类比椭圆标准方程的推导过程推导双曲线的标准方程;第2课时讲解运用双曲线的定义及其标准方程解题.第1课时教学目标知识与技能使学生掌握双曲线的定义,理解双曲线标准方程的推导过程,能根据条件确定双曲线的标准方程.过程与方法在与椭圆的类比中,掌握双曲线的标准方程的推导方法,增强合作学习能力和运用所学知识解决实际问题的能力;培养学生运用类比、数形结合思想解决问题的能力.情感、态度与价值观发挥类比的作用,与椭圆形成对比,激发学生学习数学的兴趣,提高学生的审美情趣,培养学生勇于探索、敢于创新的精神,通过引入b2,使方程形式更对称、简洁,无疑会让学生感到数学的特殊魅力,增强学生学习数学的浓厚兴趣.重点难点教学重点:双曲线的定义和双曲线的标准方程.教学难点:双曲线标准方程的推导.教学过程复习引入1.椭圆的定义平面内与两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.2.椭圆的标准方程(1)焦点在x 轴x 2a 2+y 2b 2=1,(a>b>0); (2)焦点在y 轴y 2a 2+x 2b 2=1,(a>b>0). 3.a 、b 、c 之间有何种关系?a 2=c 2+b 2.探究新知探究:如果把椭圆定义中的“距离的和”改为“距离的差”,那么点的轨迹会发生什么变化?用几何画板演示拉链的轨迹:(A) (B)活动成果:以上两条曲线合起来叫做双曲线,每一条叫做双曲线的一支.下面请同学们思考以下问题:设问:①定点与动点不在同一平面内,能否得到双曲线?②两条曲线中到“两定点的距离的差”有什么关系?③这个常数是否会大于或等于两定点间的距离?(几何画板演示当常数等于|F 1F 2|及常数大于|F 1F 2|时的点的轨迹,帮助学生理解)请学生回答:1.不能.指出必须“在平面内”.2.到两定点的距离的差的绝对值相等,否则只表示双曲线的一支,且到两定点的距离的差的绝对值为一个常数,即||MF 1|-|MF 2||=2a.3.应小于两定点间距离且大于零.当常数等于|F 1F 2|时,轨迹是以F 1、F 2为端点的两条射线;当常数大于|F 1F 2|时,无轨迹.活动设计:小组讨论,实验演示,通过提出问题,让学生讨论问题,并尝试解决问题.让学生了解双曲线的前提条件,并培养学生的全面思考能力.感受曲线,解读演示得到的图形是双曲线(一部分).提出问题:类比椭圆的定义,给出双曲线的定义.活动设计:学生先独立思考,教师加以引导,与椭圆有一个类比,允许学生自愿合作、讨论、交流.学情预测:学生的回答可能不全面、不准确,我们可以用几何画板演示学生的回答,让他们发现问题,然后不断补充、纠正,趋于完善.活动成果:师生共同概括出双曲线的定义:平面内与两个定点F 1,F 2的距离的差的绝对值等于常数(小于|F 1F 2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.(在归纳定义时强调定义要满足三个条件:在平面内、任意一点到两个定点的距离的差的绝对值等于常数、常数小于|F 1F 2|且大于零)下面我们类比椭圆方程的推导,选择适当的坐标系,建立双曲线方程.为今后通过方程研究双曲线的性质做好准备.提出问题:求椭圆方程的步骤是什么?。

双曲线及其标准方程式
双曲线是代数曲线中的一种,其标准方程常用于描述其形状。
标准方程式表示为:
(x^2/a^2) - (y^2/b^2) = 1 (双曲线的方程式)
其中x和y是坐标系中的变量,a和b是正实数,而a>b。
双曲线通常是对称于x轴和y轴的,并且具有两个分支。
当a和b相等时,双曲线变成一个特殊的形状,称为单位双曲线。
单位双曲线的标准方程变为:
(x^2/a^2) - (y^2/a^2) = 1 (单位双曲线的方程式)
双曲线在数学和物理中有广泛的应用,例如在电磁学、光学和力学等领域中描述抛物面、光学器件的形状和物体的运动等。

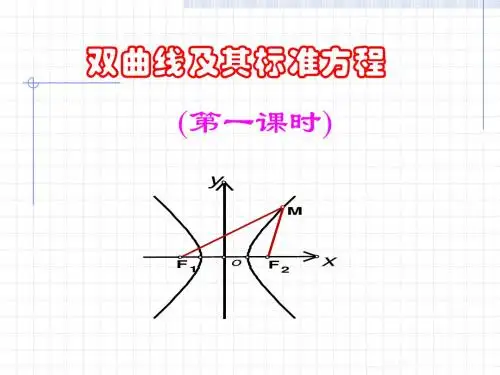






〖人教版高中数学选修2—1〗第二章 圆锥曲线与方程三.双曲线§2.3.1 双曲线及其标准方程第1课时 双曲线及其标准方程(1) 教学过程一.尝试探索、形成概念【探索1】 如果把椭圆定义中的“与两定点距离之和”改为“与两定点距离之差”,那么点的轨迹是怎样的曲线呢?1.画图 演示实验:2.原理分析由于拉链的两边原来是等长的,即||||||221F F MF MF +=,所以拉开或闭拢拉链时,虽然M 点在移动,但||1MF 却总是比||2MF 长出||2F F 这段(即a 2).所以这条曲线上的动点M 满足的条件是:a MF MF 2||||21=-.如果使点M 到点2F 的距离减去到点1F 的距离所得的差等于a 2,就得到另一条曲线, 这条曲线上的动点满足的条件是a MF MF 2||||12=-.这两条曲线合起来叫做双曲线,每一条叫做双曲线的一支.3.概括定义定义:平面内与两定点1F 、2F 的距离的差的绝对值等于常数(小于||21F F )的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距.即, 12||||||2MF MF a -=(常数), 其中,122||a F F >.说明:读完这个定义后,你觉得定义中有哪些关键之处? 双曲线定义中有三个要素: ⑴前提——平面内;⑵条件——①与两定点的距离差的绝对值为常数; ②常数小于||21F F .⑶结论——点的轨迹是双曲线.【讨论】 在上述定义中,⑴当||221F F a =时,动点M 的轨迹是什么? ⑵当||221F F a >时,动点M 的轨迹又是什么?二.双曲线标准方程的推导【探索2】 ⑴用直接法求曲线方程的步骤是什么? ①与椭圆比较,要求双曲线的标准方程,如何建立坐标系?②点M 的轨迹构成的点集是什么?{}12|||||2P M MF MF a =-=±.③列方程: (),0f x y =,即设(), M x y ,且()1, 0F c - 、()2, 0F c ,那么2a =±.④化方程(),0f x y =为最简形式.a =±()()2222244x c y a x c y ++=±-+即 ()()22222222c a x a y c a a --=-, 令()2220b c a b =->,得12222=-b y a x , 这个方程叫做双曲线的标准方程.它表示焦点在x 轴上的双曲线.【思考】 ⑴在双曲线的标准方程中,a 、b 是否需要满足条件0>>b a ?⑵在椭圆中,有222c b a +=.那么在双曲线中,a 、b 、c 的关系如何?⑶如果双曲线的焦点在y 轴上,焦点坐标为()10, F c -、()20, F c ,这时双曲线的方程是什么呢?⑷如何判断双曲线的两种标准方程的焦点位置?说明:⑴比较这两个双曲线的标准方程,所谓“标准”指的是:双曲线的中心在坐标原点,焦点在坐标轴上.⑵方程的特点:①左边是两式的平方差,右边是1; ②a 、b 、c 中c 最大,222c a b =+; ③焦点在哪个轴上,哪个系数为正.三.应用 1. 定义的应用 【例1】 ⑴化简方程2)1()1(2222=+--++y x y x ,得( )A .122=-y x (1-≤x )B .122=-y x (1≥x )C .0=y (1-≤x )D .0=y (1≥x )⑵已知1F 、2F 分别是双曲线2212x y -=的左、右焦点,P ,Q 为双曲线右支上的两点,直线PQ 过2F ,且倾斜角为α,则11||||||PF QF PQ +-的值为( )A .8; B . C .; D .随α的大小而变化.点评:双曲线定义的双向运用⑴判断:符合定义中到两定点距离之差的绝对值为常数(小于两定点的距离)的点的轨迹是双曲线,这是不可忽视限制条件.巧妙利用双曲线的定义求双曲线的轨迹方程,可以提高解题速度,回避大量的运算,具体步骤为:①寻找关系:寻找动点M 与1F ,2F 的关系; ②计算:21||||||2MF MF a -=;③判断:122||a F F <是否成立?并检查是是一支,还是两支.⑵求值:逆向利用双曲线的定义,即双曲线上的任意一点一定满足条件,即——到两定点距离之差的绝对值等于2a .2.标准方程的简单应用【例2】 ⑴【2008年高考宁夏文科】双曲线221102x y -=的焦距为 ( )A .B .C .D .⑵已知方程22121x y k k -=++表示双曲线,则k 的取值范围是 .点评:双曲线标准方程的使用⑴先化为标准方程,确定焦点位置,从而确定2a 和2b 的值. ⑵当焦点位置不确定时,应注意分类讨论.【同步训练】1.“方程22ax by c +=表示双曲线”是“0ab <”的 ( ) A .充分不必要条件; B .必要不充分条件; C .充要条件; D .既不充分又不必要条件. 2.如图,在△ABC中,已知AB =,且三个内角A 、B 、C 满足2sin sin 2sin A C B +=,建立适当的坐标系,求顶点C 的轨迹方程.【解析】以AB 为x 轴,AB 垂直平分线为y 轴,建立直角坐标系.则() 0A -,() 0B . 由2sin sin 2sin A C B +=,根据正弦定理,得2||||2||CB AB CA +=,即1|||||22||2C A C B A B A B-=<, ∴点C 的轨迹为双曲线的右支(除去与x 轴交点).∵a =c =b ==所以,顶点C的轨迹方程(22126x y x -=>.C四.小结1.知识方面:双曲线的定义(注意条件)和标准方程(注意焦点的位置与方程形式的关系);常数a、b、c之间的关系:222b=;会用定义法和待ac+定系数法求双曲线的标准方程.2.能力方面:巩固求曲线方程的方法与步骤,会用动力变化的观点研究问题.3.体会数学知识的和谐美,几何图形的对称美.。

人教版高中数学第二册(上)8.3 双曲线及其标准方程(一)教学目标:(1) 知识与技能:与椭圆定义类比,深刻理解双曲线的定义并能独立推导出双曲线标准方程;(2) 过程与方法:通过定义及标准方程的深刻挖掘与探究 ,使学生进一步体验类比发现及数形结合等思想方法的运用,提高学生的观察与探究能力;(3) 情感态度与价值观:通过教师指导下的学生交流探索活动,发学生的学习兴趣,培养学生用联系的观点认识问题。
教学重点:双曲线的定义、标准方程及其简单应用教学难点:双曲线定义中关于绝对值,2a<2c 的理解授课类型:新授课课时安排:1课时教 具:多媒体 , 一根拉链,小夹子 教学过程: 一、复习提问 师:椭圆定义是什么?生:平面内与两个定点21,F F 的距离之和等于常数(大于||21F F )的点的轨迹叫作椭圆。
(幻灯片展示椭圆图形及其定义)二、新课引入 1、设问师:平面内与两个定点21,F F 的距离之差等于常数的点的轨迹是什么?学生思考(老师在黑板上画出两个点21,F F ,使F 1在左侧,F 2在右侧.记21F F =2c,2c>0)。
师: 在椭圆里到两个定点的距离的和这个常数是正数,那么,平面内到两定点的差这个常数还一定是正数吗生:不一定。
师:可能是什么数呢?(学生甲回答:是正数,负数或零) 师:当常数是零时动点的轨迹是什么?生:是线段F 1F 2的中垂线。
老师做出21,F F 的中垂线。
师:当常数是正数时的点的位置在什么地方? 生:在线段F 1F 2的中垂线的右侧。
师:当常数是负数时的点的位置在什么地方?生:在线段F 1F 2的中垂线的左侧。
师:平面内与两个定点21,F F 的距离之差等于非零常数的点的轨迹到底是是什么呢?我们一起做一个实验来探索。
2、实验:(师生共同完成) 道具:一根拉链具体做法:老师在拉开的拉链两侧各取一点打结(实验前已经测量好,使两结之间的距离小于两定点间的距离),请两位同学协助将两点分别固定在定点F 1,F 2处,使拉链头在21,F F 的上方。
双曲线及其标准方程 (1) 理解双曲线的定义,明确焦点、焦距的意义;能根据定义,按求 曲线方程的步骤
导出双曲线的标准方程, 并能熟练写出两类标准 方程; 培养学生分析问题能力和抽象概括能力。
学会用辩证的观 点从椭圆的定义到双曲线定义的“变化”中认识其“不变”性, 并从中发现数学曲线的简洁美和对称美, 培养学生学习数学的兴 趣。
双曲线的定义和双曲线的标准方程.
( 解决办法:通过一个简单实验得出双曲线,再通过设问给出 双曲线的定
义;对于双曲线的标准方程通过比较加深认识.
双曲线的标准方程的推导 (解决办法:引导学生完成,提醒学生与椭圆标准方程
的推导 类比. )
教学过程:复习椭圆的定义及标准方程 7 新知探索 7
双曲线 7 展示现实生活中的双曲线
7 对定义的思考 7 双曲线标准方程的推导 7 课堂小结 7 作业 7 研究性学习
一、 复习引入:
前面我们已经学习了椭圆的有关知识, 请同学们回忆一下椭圆的定义。
问题 1:椭圆的定义是什么?
(板书)平面内与两定点 F i 、F 2的距离的和等于常数(大于|F I F 2|)的点的 轨迹叫做椭
圆. 这两个定点叫做椭圆的焦点, 两焦点间的距离叫做焦距。
二、新知探索 思考:把椭圆定义中的“距离的和”改为“距离的差”,那么这样 点是否存在?
若存在,轨迹会什么? 2、实物拉链演示:双曲线的形成(请同学参与协助画图) (取一条拉链,拉开它的
一部分,在拉开的两边的长度相等,现将 其中的一边剪掉一段(长为2a ),两端点分别固定在黑板的两个定点 F1、F2上,把粉笔放在拉链关上,随着拉链的逐渐拉开或闭合,粉
教学方法: 启发式
福建师大附中
苏诗圣
教学目标: 教学重点: 教学难点: 数学实验 7 双曲线的定义
7 例与练
1、
笔就画出了一条曲线。
请同学们观察在变化中哪些量在变化,哪些量不变。
进作图工具? 3、对双曲线有了初步的认识,现实生活中的双曲线的实物图
(古代建
筑、现代建筑、冷却塔、北京市区交通图
),这些古今中外与双曲
线有关的图片给人一种对称、简洁、流畅的美的享受。
那么,如何 给双曲线一个科学的定义呢?
4、(请同学回答)双曲线的定义:平面内与两定点 F i 、F 2的距离的差的绝对
值是常数(大于零且小于|F I F 2|)的点的轨迹叫做双曲线.这两个定点 叫做双曲线的焦点,两个焦点之间的距离叫做焦距.
(1) 定义中“平面内”起到什么作用?
如果没有这个条件,点的轨迹将变为一个立体图形。
(2) 将定义中的“绝对值”去掉,动点的轨迹是什么?
双曲线的一支,双曲线有两支,丢掉任意一支都是不完整的。
⑶ 将定义中的常数改为零,动点的轨迹是什么?
F I F 2的中垂线。
(4) 将定义中的 两条射线。
(5) 将定义中的 不存在。
(6) 将定义中的 分类讨论
电脑演示(用几何画板制作课件)以上6种情形,在上述基础上,引导学生再 次理解双曲线的定义。
2、双曲线标准方程的推导
现在我们可以用类似于求椭圆标准方程的方法求双曲线的标准方程, 们思考回忆椭圆标准方程的推导方法,随后引导学生自己推导。
(1) 建系设点
取过焦点F i 、F 2的直线为x 轴,线段F I F 2的垂直平分线为y 轴(如图2-24) 建立直角坐标系. 设M(x , y)为双曲线上任意一点,双曲线的焦距是
2C (C >0),
那么F i 、F 2的坐标分别是(-C , 0)、(C , 0).又设点M 与 F i 、F 2的距离的差的绝对值等于常数
2a .
(2) 点的集合
由定义可知,双曲线就是集合
)思考如何改
F i 、F 2 “小于” 改
为“等于” ,动点的轨迹是什么?
“小于” 改
为“大于” ,动点的轨迹是什么? 动点的轨迹是什么?
|F I F 2| ” 去掉, “小于 请同学
F1
F 曾雷
P={M||MF i|-|MF 2||=2a}={M|MF i|-|MF 2|= ± 2a}.
(3) 代数方程
+ I 亚 I 卡一八汽 J (K + c)2 +5? ■ J(if +y2 = ± 2a.
(4) 化简方程
将这个方程移项,两边平方得:
(£ + + 护=4『+ (;: Y 尸 +y<
cx+a 2 2=± a J (x c)2
y 2
化简整理得:(c 2-a 2)x 2-a 2y 2=a 2(c 2-a 2).
由双曲线定义,2c >2a>0 即c >a>0,所以c 2-a 2>0. 设 c 2-a 2=b 2(b > 0),代入上式得:b 2x 2-
a 2y 2=a 2
b 2.
2
y
E T 1(a 0,b 0) b
这就是双曲线的标准方程.(从以上推导过程中可知,曲线上的每一点的坐 标都满足方程。
若以F I F 2所在的直线为y 轴,F I F 2的中垂线为x 轴建立直角坐标系,只须将
2 2
方程中的X 、y 对调即得务 1
a 2
b 2
2 双曲线标准方程中,a >0, b > 0,但a 不一定大于b ;
2
x
~2
a
(1) 2
x
2 a
2 y b 1(a 0,b 0)表示焦点在 0)、
F 2 (c , 0), 这里 c 2=a 2+b 2。
2 2
⑵ y
2
x 2 1(
a
0,b 0)表示焦点在
a
b
-C )、
冃(0, c ), 这里
2 2 , 2
c =a +b 。
X 轴上的双曲线,焦点是F i (-c ,
y 轴上的双曲线,焦点是 F i (O ,
两种标准方程的比较(引导学生归纳):
取值范围和焦点坐标。
分析:
(0, J 2m 1)
变式三:上述方程是否可以表示椭圆和圆?
2
L 1 (2) 2y
2
-7X 2= -14
2
是(2, 例2(书P105例1):已知双曲线两个焦点 F 1(-5,0) 、F 2(5,0),双曲线上
一
点P 到F 1、F 2的距离差的绝对值等于 6,求双曲线的标准方程。
分析:(1) “定位”
中心是否在原点,焦点在哪个轴上,以便确定是哪个
标准方程;
(2) “定量” 双曲线的标准方程中有两个参数,
必须有两个相互独
立的条件来确定 a 和b ;
0)
是(0,
3)
因此,所求方程是梦率
X 2
例3:(书P107练习2)已知方程——
2
1表示焦点在x 轴上的双
曲线,求m 的取值范围。
分析:(2-m )>0 且
(m+1)>0
2
变式一:已知方程」一
2 m
1表示双曲线,
求m 的取值范围。
分析:(2-m)(m+1)>0
得-1<m<2
2
变式二:已知方程一X —
2 m
1表示焦点在 y 轴上的双曲线,求 m 的
(m 1) (m 2) 2m 1
隹占为
八、、八
分析:2-m>0 且 m+1>0 得-1<m<2時为椭圆。
当 2-m=m+1>0时 得m =l 时,表示圆。
四、 小结
双曲线与椭圆的联系与区别 (图表)。
五、 布置作业
P 108 1、2、3
六、 思考题:将作业第一题改为 “△ ABC —边的两个端点是 B (a ,0)和C (-a ,
0),另两边所在直线的斜率之积为常数 k ”,求顶点A 的轨迹。
七、研
究性问题:平面内到两个定点的距离之积为定值的点的轨迹是什么?
1、 可以进行理论研究
2、 可以利用电脑进行研究
3、 可以利用文曲星自编 BASIC 语言进行研究
4、 进行合作探究,相互学习和交流。
设两定点分别为 A ( -C , 0 )、B ( c , 0 ),
P ( X , y )到两定点的距离的积为
a ,则J (x C )2
y 2
J (x
V X 2 c 2 J a 2 4X 2C 2.
点的轨迹为两个分离的封闭图形,如图 1所
点的轨迹为两个相切的封闭图形,在原点相切,如图
\2 2
C ) y a,
示。
化简得
2
当c >a 当c 2
=a 时,
y
时, 当C 2 <a 时, 3所示。
点的轨迹为一个封闭图形,我们可称其为“花生形” 如图
©
e
图1 图2
厂f
■.
c >0 .平面上任意一点
平面内到两个定点的距离之商为定值K 的点的轨迹是什么?当K>0 且不等于1 时,表示圆,当K 等于1 时,表示中垂线。