七年级(下)数学思维拓展训练试题附答案

一、选择题1. 下列各数中，哪个数是正数？A. -3B. 0C. 3D. -5答案：C解析：正数是大于零的数，故选C。

2. 下列哪个图形是轴对称图形？A. 正方形B. 长方形C. 三角形D. 圆形答案：A解析：轴对称图形是指通过一个轴将图形分成两个完全相同的部分，故选A。

3. 已知一个等边三角形的边长为6cm，求这个三角形的周长。

答案：18cm解析：等边三角形的三条边相等，故周长为3×6=18cm。

4. 下列哪个数是偶数？A. 3B. 4C. 5D. 6答案：B解析：偶数是能被2整除的数，故选B。

5. 已知一个长方形的长为8cm，宽为4cm，求这个长方形的面积。

答案：32cm²解析：长方形的面积等于长乘以宽，故面积为8×4=32cm²。

二、填空题1. 已知一个数的绝对值是5，那么这个数可以是______或______。

答案：5，-5解析：绝对值表示一个数与零的距离，故可以是正数或负数。

2. 下列哪个数是负数？A. -3B. 0C. 3D. -5答案：A解析：负数是小于零的数，故选A。

3. 一个等腰三角形的底边长为6cm，腰长为8cm，求这个三角形的面积。

答案：24cm²解析：等腰三角形的面积等于底边乘以高的一半，高可以用勾股定理求得。

设高为h，则有h²=8²-3²=64-9=55，所以h=√55。

故面积为6×√55/2=3√55≈24cm²。

4. 下列哪个数是奇数？A. 3B. 4C. 5D. 6答案：C解析：奇数是不能被2整除的数，故选C。

5. 已知一个长方形的长为10cm，宽为5cm，求这个长方形的周长。

答案：30cm解析：长方形的周长等于两倍的长加两倍的宽，故周长为2×10+2×5=30cm。

三、解答题1. 已知一个等腰直角三角形的直角边长为3cm，求这个三角形的面积。

答案：9cm²解析：等腰直角三角形的面积等于直角边长乘以直角边长的一半，故面积为3×3/2=9cm²。

1. 下列各数中，不是有理数的是（）A. -2.5B. √2C. 0.1010010001…D. -1/3答案：B解析：有理数是可以表示为两个整数之比的数，包括整数、分数和小数。

选项B的√2是无理数，不能表示为两个整数之比。

2. 若a、b是实数，且a+b=0，则下列各式中，正确的是（）A. a=0B. b=0C. a=-bD. ab=0答案：C解析：由题意知，a+b=0，则a=-b。

3. 下列各式中，正确的是（）A. 3^2 = 9B. (-2)^3 = -8C. 2^0 = 1D. (-3)^2 = 9答案：B解析：A选项中的3^2=9是正确的，B选项中的(-2)^3=-8也是正确的，C选项中的2^0=1是正确的，D选项中的(-3)^2=9也是正确的。

但题目要求选择正确的式子，故选B。

4. 若a、b、c是三角形的三边长，则下列各式中，正确的是（）A. a+b>cB. a-b>cC. a+b>cD. a-b>c答案：C解析：根据三角形的性质，任意两边之和大于第三边，故选C。

5. 下列各式中，正确的是（）A. √9=±3B. √16=4C. √25=5D. √36=6答案：C解析：A选项中的√9=±3是错误的，因为√9=3；B选项中的√16=4是正确的；C 选项中的√25=5是正确的；D选项中的√36=6是正确的。

故选C。

1. 若x^2=9，则x=_________。

答案：±3解析：由平方根的定义可知，若x^2=9，则x=±3。

2. 若a=2，b=-3，则a^2+b^2=_________。

答案：13解析：将a、b的值代入公式，得a^2+b^2=2^2+(-3)^2=4+9=13。

3. 若x=5，则(x+2)^2=_________。

答案：49解析：将x的值代入公式，得(x+2)^2=5+2)^2=49。

4. 若x=3，则|x-2|=_________。

七年级下册数学思维专项训练题（共10套）思维训练题（一）班级______________ 姓名_____________ 一、选择题：1．a 为任意自然数，包括a 在内的三个连续的自然数，可以表示为 （ ）A ．a －2，a －1，aB ．a －3，a －2，a －1C ．a ，a ＋1，a ＋2D ．不同于A 、B 、C 的形式二、计算题：（动动脑筋，可能会有简便的解题方法！）1．____________________56875=⨯2．____________2006200420022000...12108642=+-+-+-+-+- 3．__________________8567785667855678=+++4．()()__________888...6428002...888488868888=++++-++++5．______________125.01712517125625.05.0171251753=⨯-⨯+⨯+ 6．______________12346123451234512345=÷7．_________________31313131=-+-8．_______________99163135115131=++++ 9．_____________20042004...200432004220041=++++10．_____________90197218561742163015201412136121=++++++++三、应用与创新：1．有一高楼，每上一层需要3分钟，每下一层需要1分30秒。

小贤于下午6时15分开始从最底层不断地向上走，到了最顶层后便立即往下走，中途没有停留，他在7时36分返回最底层。

这座高楼共有多少层？2．回答下列各题：（1）用1、2、3、4、5、6、7、8可组成多少个没有重复数字的五位数？（2）在15个连续自然数中最多有多少个质数？最少有多少个质数？（3）以下是一个数列，第一项是1，第二项是4，以后每一项是前两项相乘的积。

一、选择题（每题5分，共25分）1. 小明在计算一道题目时，错误地将一个数的个位和十位数字交换了位置，结果得到的差是18。

请问原来的数是多少？A. 58B. 63C. 78D. 842. 在等差数列1, 4, 7, 10, ...中，第100项是多少？A. 297B. 299C. 301D. 3033. 一个正方体的体积是64立方厘米，如果将其切割成8个相同的小正方体，每个小正方体的棱长是多少厘米？A. 2B. 4C. 6D. 84. 小华有5个连续的自然数，它们的和是45，请问这5个数分别是多少？A. 7, 8, 9, 10, 11B. 8, 9, 10, 11, 12C. 9, 10, 11, 12, 13D. 10, 11, 12, 13, 145. 小明有红球、蓝球和绿球共30个，其中红球和蓝球的总数是绿球的两倍，蓝球和绿球的总数是红球的三倍。

请问每种颜色的球各有多少个？A. 红球10个，蓝球8个，绿球12个B. 红球8个，蓝球10个，绿球12个C. 红球12个，蓝球8个，绿球10个D. 红球12个，蓝球10个，绿球8个二、填空题（每题5分，共25分）6. 一个长方形的长是10厘米，宽是5厘米，如果将其对角线上的点分割成两段，使得两段的比例是3:2，那么这两段对角线的长度分别是多少厘米？7. 在一个等腰三角形中，底边长为10厘米，腰长为8厘米，求这个三角形的面积。

8. 小明有若干个相同的正方体，他将这些正方体排成一排，使得排成的长方体的体积最大。

如果每个正方体的边长为1厘米，那么小明至少需要多少个正方体？9. 一个等差数列的前三项分别是2, 5, 8，求这个数列的第10项。

10. 小华在一条直线上从左到右每隔2米放置一个路灯，如果这条直线长100米，那么至少需要多少个路灯？三、解答题（每题10分，共30分）11. 小明在一条直线上从左到右每隔3米放置一个树，如果这条直线长120米，那么他至少需要多少棵树？请用方程表示并解答。

一、选择题（每题3分，共30分）1. 下列各组数中，互为相反数的是（）A. 3和-5B. 4和-4C. -2和2D. 0和52. 若a > 0，则下列不等式中正确的是（）A. a > 0B. -a < 0C. a < 0D. a² > 03. 下列代数式中，表示负数的是（）A. 2xB. -3xC. 5xD. -2x + 54. 已知函数f(x) = 2x - 1，则f(-1)的值为（）A. -3B. -1C. 1D. 35. 在直角坐标系中，点P(2,3)关于x轴的对称点坐标为（）A. (2, -3)B. (-2, 3)C. (2, -3)D. (-2, -3)6. 若a² = 16，则a的值为（）A. ±4B. ±2C. ±8D. ±17. 下列方程中，解为整数的是（）A. 2x + 3 = 7B. 3x - 4 = 5C. 4x + 2 = 9D. 5x - 3 = 68. 在△ABC中，若∠A = 60°，∠B = 45°，则∠C的度数为（）A. 75°B. 90°C. 105°D. 120°9. 下列数中，是质数的是（）A. 15B. 16C. 17D. 1810. 若a、b是方程2x² - 5x + 3 = 0的两根，则a + b的值为（）A. 5B. 3C. 2D. 4二、填空题（每题5分，共25分）11. 若x + 2 = 0，则x = _______。

12. 已知a² + 2a + 1 = 0，则a = _______。

13. 若函数f(x) = 3x - 4，则f(2) = _______。

14. 在△ABC中，若AB = 5，AC = 6，BC = 7，则△ABC是_______三角形。

15. 若a、b是方程2x² - 5x + 3 = 0的两根，则ab = _______。

七年级下册数学思维题（共10套）思维训练题（一）班级______________ 姓名_____________一、选择题：1．a 为任意自然数，包括a 在内的三个连续的自然数，可以表示为 （ ）A ．a －2，a －1，aB ．a －3，a －2，a －1C ．a ，a ＋1，a ＋2D ．不同于A 、B 、C 的形式二、计算题：（动动脑筋，可能会有简便的解题方法！）1．____________________56875=⨯2．____________2006200420022000...12108642=+-+-+-+-+-3．__________________8567785667855678=+++4．()()__________888...6428002...888488868888=++++-++++5．______________125.01712517125625.05.0171251753=⨯-⨯+⨯+ 6．______________12346123451234512345=÷ 7．_________________31313131=-+-8．_______________99163135115131=++++9．_____________20042004...200432004220041=++++10．_____________90197218561742163015201412136121=++++++++三、应用与创新：1．有一高楼，每上一层需要3分钟，每下一层需要1分30秒。

小贤于下午6时15分开始从最底层不断地向上走，到了最顶层后便立即往下走，中途没有停留，他在7时36分返回最底层。

这座高楼共有多少层？2．回答下列各题：（1）用1、2、3、4、5、6、7、8可组成多少个没有重复数字的五位数？（2）在15个连续自然数中最多有多少个质数？最少有多少个质数？（3）以下是一个数列，第一项是1，第二项是4，以后每一项是前两项相乘的积。

初中数学数学思维拓展练习题及参考答案一、选择题1. 已知正整数a、b满足a/b=2/3，且a的10倍比b的7倍小6，那么a/b等于：A. 2/9B. 4/21C. 8/21D. 6/92. 直角三角形的两条直角边分别是3cm和4cm，求斜边的长。

A. 5cmB. 7cmC. 9cmD. 12cm3. 若正方形的边长为x，则其对角线的长度是：A. xB. x√2C. 2xD. 2x√24. 一辆火车正常行驶时，从一个站到另一个站需要2小时，如果每小时增加10分钟的停站时间，则从一个站到另一个站需要2小时20分钟。

求每个站的停站时间。

A. 6分钟B. 8分钟C. 10分钟D. 12分钟5. 一辆车从A地到B地，全程120公里，前一半路程速度为60km/h，后一半路程速度为80km/h。

那么从A地到B地需要多长时间？A. 2小时B. 2.5小时C. 3小时D. 3.5小时二、填空题1. 已知a:b=5:3， b:c=4:7，求a:b:c的比值为______。

2. 一条铁路上，相邻两个车站的距离为10km，A、B两辆列车同时从两个车站出发，相对速度为30km/h，那么两辆列车相遇需要______分钟。

3. 甲车速率为60km/h，乙车速率为80km/h，两车同时从A地到B 地，甲车先出发，已知甲车比乙车晚1个小时到达B地，从A地到B 地的距离为______公里。

4. 若一个图形的内角和是900°，则这个图形是一个______。

5. 一块边长为12cm的正方形纸板，按照下图所示方式剪下4个边长为xcm的小正方形，则x的值为______。

（图形描述）三、计算题1. 甲乙两个数的和是25，差为3，求这两个数分别是多少。

2. 已知梯形的上底长度为6cm，下底长度为14cm，高度为8cm，求梯形的面积。

3. 如果一个数a加上它自己的2/5再减去它自己的1/2等于15，求这个数a是多少。

4. 一辆车以每小时60km的速度行驶，过了10分钟后又以每小时80km的速度行驶，那么这辆车行驶了多远？5. 甲、乙两位运动员进行百米赛跑，以秒为单位分别记作甲的成绩和乙的成绩，甲跑完全程的速度是乙的4倍，已知甲的成绩比乙的成绩多4秒，求甲、乙两位运动员的成绩。

图4 七（下）数学思维拓展训练时间：45分钟 分值：100分一、选择题（每小题5分，共25分）1.若n 为正整数，且x 2n =3，则(3x 3n )2－4(x 2)2n 的值为( ) （A ）207 （B ）36 （C ）45 （D ）217 2．一个长方形的长是2x 厘米，宽比长的一半少4厘米，若将长方形的长和宽都增加3厘米，则该长方形的面积增加为（ ）(A)9 （B ）2x 2+x －3 （C ）－7x －3 （D ）9x －3 3．若(x-5)·A= x 2+x+B ，则（ ）（A ）A=x+6，B=－30 （B ）A=x －6，B=30 （C ）A=x+4，B=－20 （D ）A=x －4，B=204.已知6141319,27,81===c b a ，则a ，b ，c 大小关系是（ ）（A ）a>c>b （B ）a>b>c （C ）a<b<c （D ）b>c>a5.如图1，直线MN//PQ ，OA ⊥OB ，∠BOQ=30︒.若以点O 为旋转中心，将射线OA 顺时针旋转60︒后，这时图中30︒的角的个数是 （ ）(A) 4个 (B) 3个 (C) 2个 (D) 1个二、填空题（每小题5分，共25分）6.用如图2所示的正方形和长方形卡片若干张，拼成一个边长为a+b 的正方形，需要B 类卡片_______张.7.如图3，AB ∥CD ，M 、N 分别在AB ，CD 上，P 为两平行线间一点，那么∠1+∠2+∠3= ︒.8.如图4，一把矩形直尺沿直线断开并错位，点E 、D 、B 、F 在同一条直线上，若∠ADE ＝125︒, 则∠DBC= ︒.9.三个同学对问题“若方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是34x y =⎧⎨=⎩，求方程组111222325325a x b y c a x b y c +=⎧⎨+=⎩的解．”提出各自的想法．甲说：“这个题目好象条件不够，不能求解”；乙说：“它们的系数有一定的规律，可以试试”；丙说：“能不能把第二个方程组的两个方程的两边都除以5，通过换元替代的方法来解决”．参考他们的讨论，你认为这个题目的解应该是 ． 10. 数学家发明了一个魔术盒，当任意数对()b a ,进入其中时，会得到一个新的数：图1O N M A B P Qa b图2 3 2 C P D 1B N A M 图3()()21--b a .现将数对()1,m 放入其中得到数n ，再将数对()m n ,放入其中后，如果最后得到的数是 .（结果要化简） 三、解答题（每小题10分，共50分）11.计算：(1+2+3+…+2013)(2+3+4+…+2012)－(1+2+3+…+2012) (2+3+4+…+2013)．12.图5是按一定规律排列的方程组集合和它解的集合的对应关系图，若方程组集合中的方程组自左至右依次记作方程组1、方程组2、方程组3、……方程组n ． （1）将方程组1的解填入图中；（2）请依据方程组和它的解变化的规律，将方程组n 和它的解直接填入集合图中； （3）若方程组⎩⎨⎧-=+1my x y x 的解是⎨⎧=10x ，求m 的值，并判断该方程组是否符合（2）中的规律？13.如图6，已知两组直线分别互相平行． （1）若∠1=115º，求∠2，∠3的度数；（2）题（1）中隐含着一个规律，请你根据（1）的结果进行归纳，试用文字表述出来； （3）利用（2）中的结论解答：如果两个角的两边分别平行，其中一个角是另一个角的2倍，求这两个角的大小．方程组图514.下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．解：设x2－4x=y．原式=(y+2) (y +6)+4 ①=y2+8y+16 ②=( y+4)2 ③=(x2－4x+4)2 ④回答下列问题：（1）该同学②到③运用了因式分解的_______.（A）提取公因式（B）平方差公式（C）两数和的完全平方公式（D）两数差的完全平方公式（2）该同学因式分解的结果是否彻底？________（填“彻底”或“不彻底”）；若不彻底，请直接写出因式分解的最后结果_________．（3）请模仿以上方法对多项式（x2－2x）（x2－2x+2）+1进行因式分解．15．如下几个图形是五角星和它的变形．（1）图7中是一个五角星，则∠A+∠B+∠C+∠D+∠E= º．（2）图7中的点A向下移到BE上时，五个角的和（即∠CAD+∠B+∠C+∠D+∠E）有无变化？如图8，说明你的结论的正确性．（3）把图8中的点C向上移到BD上时，五个角的和（即∠CAD+∠B+∠ACE +∠D+∠E）有参考答案 1~5.ADABA6.27.3608.559. 510x y =⎧⎨=⎩ 10. －m 2+2m11.设1+2+3+…+2012=a ，2+3+4+…+2012=b ，则a= b+1．(1+2+3+…+2013)(2+3+4+…+2012)－(1+2+3+…+2012) (2+3+4+…+2013)= (a+2013)b －a(b+2013)=ab+2013b －ab －2013a=2013b －2013a=2013b －2013(b+1)= 2013b －2013 b －2013=－2013．12.（1）直接消元可求出⎩⎨⎧==01y x ；（2）观察第一个方程都是x+y=1，第二个方程x 前面的系数都是1，而y 前面的系数应是－n ，常数项应是n 2，这样第二个方程应是x －ny= n 2，所以第n 个方程组为⎩⎨⎧=-=+21n ny x y x ．其解的规律是x 从1开始依次增1，y 从0开始依次减1，这样第n 个方程组的解为⎩⎨⎧-==n y n x 1；（3）把⎩⎨⎧-==9y 10x 代入方程x －my=16，得m=32．显然不符合(2)中的规律．13.（1）因为两组直线分别互相平行，所以由平行线的性质可得∠2=∠1=115º，∠3+∠2=180º，则∠3=180º－115º=65º；（2）如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补；（3）设其中的一个角为xº，则另一个角为2xº．因为xº+2xº=180º，所以x=60º．故这两个角分别为60º和120º． 14.（1）C（2）不彻底，( x －2)4（3）设x 2－2x=y ．原式=y (y +2)+1= y 2+2y+1=( y+1)2=(x 2－2x+1)2=( x －1)4 ． 15．（1）180º．（2）无变化．因为∠BAC=∠C+∠E ，∠EAD=∠B+∠D ，所以∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠EAD=180º．（3）无变化．因为∠ACB=∠CAD+∠D ，∠ECD=∠B+∠E ，所以∠CAD+∠B+∠ACE +∠D+∠E=∠ACB+∠ACE+∠ECD=180º．。

1. 计算：七年级思维训练80题（含答案），拔高数学思维能力111113355720212023________． 2. 已知20212021202120222022202220232023202320202020+2020202120212021202220222022a b c，，，则abc ________．3. 123499910001001(1)1(1)1(1)1(1) 的值是________．4. 设11112018201920202050M，则1M的整数部分是________． 5.计算：44444444441032422324343244632458324432416324283244032452324 =________．6.已知5555284110133144□，其中□里的数字是________．7.哪些连续正整数之和为1000？试求出所有的解．8.2023减去它的12，再减去余下的13，再减去余下的14，以此类推，一直到最后减去余下的11000，最后的结果为________．9.n个正数的乘积的n次方根称为这n个数的几何平均数．喜羊羊写了4个数，这4个数的几何平均数是2048；美羊羊也写了4个数，这4个数的几何平均数是8．那么，喜羊羊和美羊羊写的这8个数的几何平均数是________．10.有下列三个命题：（1）若α，β是不相等的无理数，则αβ + α – β是无理数；（2）若α，β是不相等的无理数，则是无理数；（3）若α，β是无理数．其中正确的命题个数是________．11. 如果a ，b ，c 是三个任意整数，那么2a b ，2a c ，2b c（ ）． A. 都不是整数B. 至少有两个整数C. 至少有一个整数D. 都是整数12. 有理数m ，n 在数轴上的位置如图所示，在m n ，m n ，n m ，m n 中正数的个数是________．13. 如果实数a ，b ，c 在数轴上的位置如图所示，那么代数式||||a b b c 可以化简为（ ）．A. 2c – aB. 2a – 2bC. –aD. a14. 把4个不同的整数两两相加得到6个和，并且这6个和是5个互不相同的数：23，26，29，32和35．那么这4个整数中最大的是________．15. 从1~26这26个整数中取出两个数，选出的两个数相乘所得的积正好是剩余的24个数之和．选出的两个数分别是________和________．16. 已知a – b = 4，ab + c 2 + 4 = 0，则a + b = ________．17. 已知a 、b 、c 是实数，且13ab a b ，17bc b c ，112ac a c ，则acbc ab abc=________．18. 已知 | x | + x + y =5，x + | y |－y = 10，则 x + y 的值是________．19.________．20. 222 − 4有________个不同的质因数．21. 已知x 是实数，则(x 2－4x +3)(x 2+4x +3)的最小值是________．22. 若实数a ，b ，c 满足等式36b ，96b c ，则c 可能取的最大值为________．23. 已知x ，y 是非负整数，且满足4(2)34x y ，那么满足条件的x + y 的最大值是________．24. 若正整数x ，y ，z 满足11145x y z ，则xyz 的最大值是________．25. 231x x x 的最小值是________．26. 满足24x y y 的整数对（x ，y ）有________个．27. 设a 是整数，关于x 的方程12x a 只有三个不同的整数解，求这三个解．28. 若a 为整数，则关于x 的方程(a – 1) x = a + 1的所有整数解的和是________．29. 已知x 与y 使得x + y ，x – y ，xy ，x y四个数中的三个相等，则这样的数对（x ，y ）有________对．30. 若关于x ，y 的二元一次方程组 132kx y bk x y 有无穷多组解，则22k b 的值为________．31. 若[x ]表示不超过x 的最大整数，且满足方程3x + 5[x ] – 49 = 0，则3x +1=________．32. 如果关于x 的不等式组9080x a x b 的整数解仅有1，2，3，那么整数a ，b 组成的有序数对（a ，b ）共有________对．33. 如果关于x 的不等式组100x x a无解，则a 的取值范围是________．34. 在1~100的自然数中与10互质的自然数共有________个．35. 已知三个质数a ，b ，c 满足133a b c ab bc ac ，则abc ＝________．36.已知三位数abc能被5整除，但不能被6和7整除；三位数cba能被6整除，但不能被5和7整除；三位数cab能被7整除，但不能被5和6整除，则abc ＝________．37.九位数ABCABCBBB能被1~17中的任意整数整除，且A，B，C是不同的数字，则九位数ABCABCBBB是________．38.乘积376×733的个位数字是________．39.四位数aabb是一个整数的平方，aabb=________．p 的不同正因数的个数不超过10，则满足题意的p 40.已知p是质数，且271的个数是________．41.如图所示有4种类型的几何体，每个几何体都是由4个单位正方体组成．选出8个同类型的几何体，把它们组合成一个2×4×4的长方体．可以完成组合的几何体有________种类型．42.已知圆环内直径为a厘米，外直径为b厘米，将50个这样的圆环一个接一个环套地连成一条锁链，那么这条锁链拉直后的长度为________厘米．43.设有一个边长为1的正三角形，记作A1（如图1），将A1的每条边三等分，以中间的线段为一边向形外作正三角形，去掉中间的线段后所得到的图形记作A2（如图2）；将A2的每条边三等分，并重复上述过程，所得到的图形记作A3（如图3）；再将A3的每条边三等分，并重复上述过程，所得到的图形记作A4，那么A4的周长是________．图1 图2 图344. 如图所示，AOB 是一条直线，若1:2:3:41:2:4:5 ，则2 的余角是________度．45. 如图，AB //CD ，那么∠1 –∠2 +∠3 –∠4 +∠5 =________度．46. 如图，∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7=（ ）．A ．450°B ．540°C ．630°D ．720°47.从一个凸n边形的纸板上剪下一个三角形，剩余的是一个内角和为2160°的多边形，则n最大是________．48.一个凸n边形的内角和小于1998°，那么n的最大值是________．49.如果一个凸多边形的内角和等于外角和的3倍，那么这个多边形的边数是（）．A.4B.6C.8D.10E.1250.如图所示，在△ABC中，AC=7，BC=4，D为AB中点，E为AC边上一点，且1902AED C，则CE =________．51.在△ABC中，已知BD和CE分别是两边上的中线，并且BD⊥CE，BD=4，CE=6，那么△ABC的面积是________．52.△ABC中，∠A为最小角，∠B为最大角，且2∠B = 5∠A，若∠B的最大值为m°，∠B的最小值为n°，则m + n =________．53.如图，在锐角△ABC中，高线CD，BE相交于点F，若∠A=55°，则∠BFC的度数是________度．54.如图，PQ=PR=QS，线段PR与QS相互垂直，则∠PRQ与∠PSQ度数之和是________度．55.在平行四边形ABCD中，AD = 2AB，点M是AD的中点，CE⊥AB于E．如果∠CEM = 40°，那么∠DME的值是（）．A．150° B．140° C．135° D．130°56.若长方形内有一点P，点P到各边的距离从小到大依次为1，2，5，6则长方形面积最小为________．57.如图所示的4×5的方格图中，过格点P的直线与方格图上、下边界相交形成的直角梯形ABCD（其中AB<CD）的面积最大是________．58. 如图，CD 是Rt △ABC 斜边AB 上的高，∠BAC 的平分线AE 交CD 于H ，交∠BCD 的平分线CF 于G ．求证：HF ∥BC ．59. 由8个相同的小正方体搭成的一个几何体，俯视图如下，那么这个几何体的左视图一定不是（ ）．60. 若n 个人完成一项工程需要m 天，则（m +n ）个人完成这项工程需要（ ）天． A.nm mnB.m nm nC.m nmnD.2mnm n61. 一个商人用m 元（m 为正整数）买来了n 台（n 为质数）电视机，其中有两台以成本的一半价钱卖给某个慈善机构，其余的电视机在商店出售，每台盈利500元，结果该商人获得利润为5500元，则n 的最小值是________．62. 某商场经销一种商品，由于进货时价格比原进价降低了6.4％，使得利润率增加了8个百分点，那么经销这种商品原来的利润率是________%． （注：100% 销售价进价利润率进价）63. 小倩和小玲每人都有若干面值为整数元的人民币．小倩对小玲说：“你若给我2元，我的钱将是你的n 倍”；小玲对小倩说：“你若给我n 元，我的钱数将是你的2倍”，其中n 为正整数，则n 的最大值是________．64. 图书馆内，在标有号码1，2，3，4的书架上分别有书120，135，142，167本．若干天后，每个书架上都各被借出a 本书，又过了若干天，四个书架又分别被借出0，b ，c ，d 本书，并且四个书架上余下同样本数的书． 若b ，c ，d ≥1，b +c +d =a ，则两次借出书后，1号书架剩有________本书．65.五个不同的数，两两之和依次等于3，4，5，6，7，8，11，12，13，15 则这五个数的平均数是________．66.王明在早晨六点至七点之间外出晨练，锻炼时长不超过一小时，出门和回家的时候，时针与分针的夹角都是110°．则王明晨练的时间为________分钟．67.某人骑车沿直线旅行，先前进了a千米，休息了一段时间，又原路返回b千米（b﹤a），再前进c千米，则此人离起点的距离S与时间t的关系示意图是（）．68.某届运动会的十一天的比赛中，醒狮队拿了16块金牌，其中每天至少拿一枚金牌，则醒狮队拿金牌的不同的情况可能有________种．(假设金牌都是一样的)69.将正方形的每条边8等分，再以这些分点为顶点（不包括正方形的顶点），可以得到不同的三角形的个数是________．70.口袋中装有20个只有颜色不同其他都相同的球，其中白球9个，红球5个，黑球6个．现从中任取10个球，使得白球不少于2个但不多于8个，红球不少于2个，黑球不多于3个，那么这样取法有________种．71.将若干红黑两种颜色的球摆成一行，要求两种颜色的球都要出现，且任意中间夹有5个或10个球的两个球必为同一种颜色的球．按这种要求摆放，最多可以摆放________个球．72.在{1000，1001，1002，…，2000}中有________对相邻的数满足下列条件：每对中的两数相加时不需要进位．73.试求所有满足如下性质的四元实数组（a，b，c，d）：组中的任一数都等于其余三个数中某两个数的乘积．（注：四元实数组中的数相同，顺序不同，算作同一组）74.将三位数A各个数位上的数字重新排列，得出的所有数的算术平均值等于A．这样的三位数A共有________个．75.如图，6个人围成一圈做传球游戏，每个人接到球后传给和他不相邻的某一人(如：A接到球后可以传给C、D或E)，开始时，球在A的手中，若球被传递三次后又回到A，此种情况出现的概率是________．76.如图，△ABC中，D、E分别是边BC、AC的中点，从这8个图形△ABD、△ACD、△ABE、△BCE、△GAB、△GAE、△GBD、四边形CEGD中任取2个图形，取出的2个图形面积相等的概率是________．77.按如图的程序进行操作，规定：程序运行从“输入一个值x”到“结果是否>487？”为一次操作．如果操作进行四次才停止，那么x的取值范围是________．78.如图是一个正方体的平面展开图，若该正方体相对的两个面上的代数式的值相等，则x – y – z的值是________．79. 设)(n f 为正整数n （十进制）的各数位上的数字的平方之和，如14321)123(222 f ．记)()(1n f n f ，))(()(1n f f n f k k ，k =1，2，3……，则2016(2016)f 的值是________．80. 有16枚棋子，都是一面黑色，另一面白色，放在4×4的正方形网格里．最初，所有棋子都是黑面朝上．规定：每次操作，将一个2×2正方形中的4枚棋子都正反面翻转一次．那么，要得到如图所示的排列，至少需要经过________次操作．1.计算：7年级思维训练80题答案1111 13355720212023________．答案：1011 20232.已知202120212021202220222022202320232023 20202020+2020202120212021202220222022 a b c，，，则abc ________．答案：13.123499910001001(1)1(1)1(1)1(1)的值是________．答案：–14.设11112018201920202050M，则1M的整数部分是________．答案：615.计算：4444444444 1032422324343244632458324 432416324283244032452324=________．答案：3736.已知5555284110133144□，其中□里的数字是________．答案：77.哪些连续正整数之和为1000？试求出所有的解．答案：198＋199＋200＋201＋202；55＋56＋...＋70；28＋29＋ (52)8. 2023减去它的12，再减去余下的13，再减去余下的14，以此类推，一直到最后减去余下的11000，最后的结果为________．答案：202310009. n 个正数的乘积的n 次方根称为这n 个数的几何平均数．喜羊羊写了4个数，这4个数的几何平均数是2048；美羊羊也写了4个数，这4个数的几何平均数是8．那么，喜羊羊和美羊羊写的这8个数的几何平均数是________． 答案：12810. 有下列三个命题：（1）若α，β是不相等的无理数，则αβ + α – β是无理数； （2）若α，β是不相等的无理数，则是无理数；（3）若α，β是无理数． 其中正确的命题个数是________． 答案：011. 如果a ，b ，c 是三个任意整数，那么2a b ，2a c ，2b c（ ）． A. 都不是整数B. 至少有两个整数C. 至少有一个整数D. 都是整数答案：C12. 有理数m ，n 在数轴上的位置如图所示，在m n ，m n ，n m ，m n 中正数的个数是________．答案：213. 如果实数a ，b ，c 在数轴上的位置如图所示，那么代数式||||a b b c 可以化简为（ ）．A. 2c – aB. 2a – 2bC. –aD. a答案：C14. 把4个不同的整数两两相加得到6个和，并且这6个和是5个互不相同的数：23，26，29，32和35．那么这4个整数中最大的是________． 答案：1915. 从1~26这26个整数中取出两个数，选出的两个数相乘所得的积正好是剩余的24个数之和．选出的两个数分别是________和________． 答案：15，2116. 已知a – b = 4，ab + c 2 + 4 = 0，则a + b = ________．答案：017. 已知a 、b 、c 是实数，且13ab a b ，17bc b c ，112ac a c ，则acbc ab abc=________．答案：11118. 已知 | x | + x + y =5，x + | y |－y = 10，则 x + y 的值是________．答案：119.________．答案：20. 222 − 4有________个不同的质因数．答案：621. 已知x 是实数，则(x 2－4x +3)(x 2+4x +3)的最小值是________．答案：–1622. 若实数a ，b ，c 满足等式36b ，96b c ，则c 可能取的最大值为________． 答案：223. 已知x ，y 是非负整数，且满足4(2)34x y ，那么满足条件的x + y 的最大值是________． 答案：424. 若正整数x ，y ，z 满足11145x y z，则xyz 的最大值是________． 答案：16025. 231x x x 的最小值是________．答案：526. 满足24x y y 的整数对（x ，y ）有________个．答案：627. 设a 是整数，关于x 的方程12x a 只有三个不同的整数解，求这三个解．答案：–3，1，528. 若a 为整数，则关于x 的方程(a – 1) x = a + 1的所有整数解的和是________．答案：429. 已知x 与y 使得x + y ，x – y ，xy ，x y四个数中的三个相等，则这样的数对（x ，y ）有________对． 答案：230. 若关于x ，y 的二元一次方程组 132kx y bk x y 有无穷多组解，则22k b 的值为________． 答案：531. 若[x ]表示不超过x 的最大整数，且满足方程3x + 5[x ] – 49 = 0，则3x +1=________． 答案：2032. 如果关于x 的不等式组9080x a x b的整数解仅有1，2，3，那么整数a ，b 组成的有序数对（a ，b ）共有________对． 答案：7233. 如果关于x 的不等式组100x x a无解，则a 的取值范围是________．答案：1a34. 在1~100的自然数中与10互质的自然数共有________个．答案：4035. 已知三个质数a ，b ，c 满足133a b c ab bc ac ，则abc ＝________．答案：15436. 已知三位数abc 能被5整除，但不能被6和7整除；三位数cba 能被6整除，但不能被5和7整除；三位数cab 能被7整除，但不能被5和6整除，则abc ＝________． 答案：67537. 九位数ABCABCBBB 能被1~17中的任意整数整除，且A ，B ，C 是不同的数字，则九位数ABCABCBBB 是________． 答案：30630600038. 乘积376 ×733 的个位数字是________．答案：739. 四位数aabb 是一个整数的平方，aabb =________．答案：774440. 已知p 是质数，且271p 的不同正因数的个数不超过10，则满足题意的p的个数是________． 答案：241. 如图所示有4种类型的几何体，每个几何体都是由4个单位正方体组成．选出8个同类型的几何体，把它们组合成一个2×4×4的长方体．可以完成组合的几何体有________种类型．答案：442. 已知圆环内直径为a 厘米，外直径为b 厘米，将50个这样的圆环一个接一个环套地连成一条锁链，那么这条锁链拉直后的长度为________厘米． 答案：49a +b43. 设有一个边长为1的正三角形，记作A 1（如图1），将A 1的每条边三等分，以中间的线段为一边向形外作正三角形，去掉中间的线段后所得到的图形记作A 2（如图2）；将A 2的每条边三等分，并重复上述过程，所得到的图形记作A 3（如图3）；再将A 3的每条边三等分，并重复上述过程，所得到的图形记作A 4，那么A 4的周长是________．图1 图2 图3答案：64944. 如图所示，AOB 是一条直线，若1:2:3:41:2:4:5 ，则2 的余角是________度．答案：6045.如图，AB//CD，那么∠1 –∠2 +∠3 –∠4 +∠5 =________度．答案：046.如图，∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7=（）．A．450° B．540° C．630° D．720°答案：B47.从一个凸n边形的纸板上剪下一个三角形，剩余的是一个内角和为2160°的多边形，则n最大是________．答案：1548.一个凸n边形的内角和小于1998°，那么n的最大值是________．答案：1349.如果一个凸多边形的内角和等于外角和的3倍，那么这个多边形的边数是（）．A.4B.6C.8D.10E.12答案：C50.如图所示，在△ABC中，AC=7，BC=4，D为AB中点，E为AC边上一点，且1902AED C，则CE =________．答案：5.551.在△ABC中，已知BD和CE分别是两边上的中线，并且BD⊥CE，BD=4，CE=6，那么△ABC的面积是________．答案：1652.△ABC中，∠A为最小角，∠B为最大角，且2∠B = 5∠A，若∠B的最大值为m°，∠B的最小值为n°，则m + n =________．答案：17553.如图，在锐角△ABC中，高线CD，BE相交于点F，若∠A=55°，则∠BFC的度数是________度．答案：12554.如图，PQ=PR=QS，线段PR与QS相互垂直，则∠PRQ与∠PSQ度数之和是________度．答案：13555.在平行四边形ABCD中，AD = 2AB，点M是AD的中点，CE⊥AB于E．如果∠CEM = 40°，那么∠DME的值是（）．A．150° B．140° C．135° D．130°答案：A56.若长方形内有一点P，点P到各边的距离从小到大依次为1，2，5，6则长方形面积最小为________．答案：3357.如图所示的4×5的方格图中，过格点P的直线与方格图上、下边界相交形成的直角梯形ABCD（其中AB<CD）的面积最大是________．答案：1258. 如图，CD 是Rt △ABC 斜边AB 上的高，∠BAC 的平分线AE 交CD 于H ，交∠BCD 的平分线CF 于G ．求证：HF ∥BC ．答案：证明：由∠DCB ＝90°－∠B ＝∠BAC ，知∠HCG ＝12∠DCB ＝12∠BAC ＝∠HAD ．而∠CHG ＝∠AHD ，从而∠CGH ＝180°－(∠HCG ＋∠CHG )＝180°－(∠HAD ＋∠AHD )＝90°，知AG ⊥CG ，即AG ⊥CF ．此时，∠FCA ＝90°－∠GAC ＝90°－∠GAF ＝∠CF A ，故AC ＝AF ，即点A 在CF 的垂直平分线AG 上．又H 在AG 上，则HC ＝HF ，即知∠HFC ＝∠FCH ＝∠FCB ，故HF ∥BC ．59. 由8个相同的小正方体搭成的一个几何体，俯视图如下，那么这个几何体的左视图一定不是（ ）．答案：C60. 若n 个人完成一项工程需要m 天，则（m +n ）个人完成这项工程需要（ ）天． A.nm mnB.m nm nC.m nmnD.2mnm n答案：A61. 一个商人用m 元（m 为正整数）买来了n 台（n 为质数）电视机，其中有两台以成本的一半价钱卖给某个慈善机构，其余的电视机在商店出售，每台盈利500元，结果该商人获得利润为5500元，则n 的最小值是________． 答案：1762. 某商场经销一种商品，由于进货时价格比原进价降低了6.4％，使得利润率增加了8个百分点，那么经销这种商品原来的利润率是________%． （注：100% 销售价进价利润率进价）答案：1763. 小倩和小玲每人都有若干面值为整数元的人民币．小倩对小玲说：“你若给我2元，我的钱将是你的n倍”；小玲对小倩说：“你若给我n元，我的钱数将是你的2倍”，其中n为正整数，则n的最大值是________．答案：864.图书馆内，在标有号码1，2，3，4的书架上分别有书120，135，142，167本．若干天后，每个书架上都各被借出a本书，又过了若干天，四个书架又分别被借出0，b，c，d本书，并且四个书架上余下同样本数的书．若b，c，d≥1，b+c+d=a，则两次借出书后，1号书架剩有________本书．答案：3665.五个不同的数，两两之和依次等于3，4，5，6，7，8，11，12，13，15 则这五个数的平均数是________．答案：4.266.王明在早晨六点至七点之间外出晨练，锻炼时长不超过一小时，出门和回家的时候，时针与分针的夹角都是110°．则王明晨练的时间为________分钟．答案：4067.某人骑车沿直线旅行，先前进了a千米，休息了一段时间，又原路返回b千米（b﹤a），再前进c千米，则此人离起点的距离S与时间t的关系示意图是（）．答案：C68.某届运动会的十一天的比赛中，醒狮队拿了16块金牌，其中每天至少拿一枚金牌，则醒狮队拿金牌的不同的情况可能有________种．(假设金牌都是一样的)答案：300369.将正方形的每条边8等分，再以这些分点为顶点（不包括正方形的顶点），可以得到不同的三角形的个数是________．答案：313670.口袋中装有20个只有颜色不同其他都相同的球，其中白球9个，红球5个，黑球6个．现从中任取10个球，使得白球不少于2个但不多于8个，红球不少于2个，黑球不多于3个，那么这样取法有________种．答案：1671.将若干红黑两种颜色的球摆成一行，要求两种颜色的球都要出现，且任意中间夹有5个或10个球的两个球必为同一种颜色的球．按这种要求摆放，最多可以摆放________个球．答案：1572.在{1000，1001，1002，…，2000}中有________对相邻的数满足下列条件：每对中的两数相加时不需要进位．答案：15673.试求所有满足如下性质的四元实数组（a，b，c，d）：组中的任一数都等于其余三个数中某两个数的乘积．（注：四元实数组中的数相同，顺序不同，算作同一组）答案：（0，0，0，0），（1，1，1，1），（－1，－1，1，1），（－1，－1，－1，1）74.将三位数A各个数位上的数字重新排列，得出的所有数的算术平均值等于A ．这样的三位数A 共有________个． 答案：1575. 如图，6个人围成一圈做传球游戏，每个人接到球后传给和他不相邻的某一人(如：A 接到球后可以传给C 、D 或E )，开始时，球在A 的手中，若球被传递三次后又回到A ，此种情况出现的概率是________．答案：22776. 如图，△ABC 中，D 、E 分别是边BC 、AC 的中点，从这 8个图形△ABD 、△ACD 、△ABE 、△BCE 、△GAB 、△GAE 、△GBD 、四边形CEGD 中任取2个图形，取出的2个图形面积相等的概率是________．答案：2777. 按如图的程序进行操作，规定：程序运行从“输入一个值x ”到“结果是否>487？”为一次操作．如果操作进行四次才停止，那么x 的取值范围是________．答案：7＜x ≤1978. 如图是一个正方体的平面展开图，若该正方体相对的两个面上的代数式的值相等，则x – y – z 的值是________．答案：379. 设)(n f 为正整数n （十进制）的各数位上的数字的平方之和，如14321)123(222 f ．记)()(1n f n f ，))(()(1n f f n f k k ，k =1，2，3……，则2016(2016)f 的值是________． 答案：14580. 有16枚棋子，都是一面黑色，另一面白色，放在4×4的正方形网格里．最初，所有棋子都是黑面朝上．规定：每次操作，将一个2×2正方形中的4枚棋子都正反面翻转一次．那么，要得到如图所示的排列，至少需要经过________次操作．答案：6。

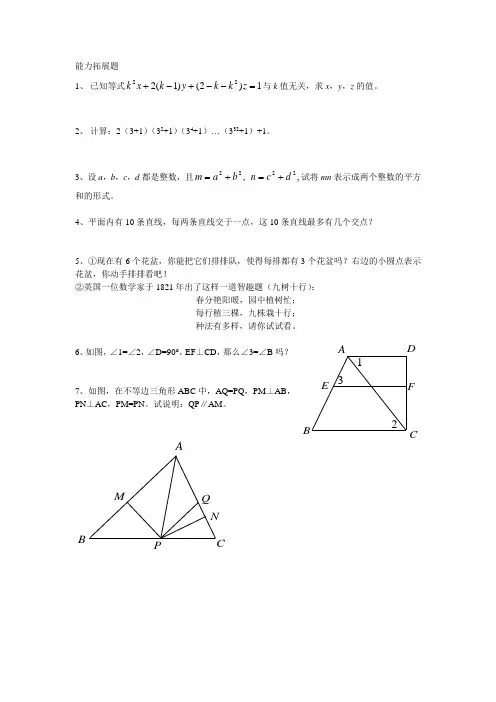
能力拓展题
1、 已知等式1)2()1(222=--+-+z k k y k x k 与k 值无关，求x ，y ，z 的值。

2、 计算：2（3+1）（32+1）（34+1）…（332+1）+1。

3、设a ，b ，c ，d 都是整数，且,,2222d c n b a m +=+=试将mn 表示成两个整数的平方和的形式。

4、平面内有10条直线，每两条直线交于一点，这10条直线最多有几个交点？
5、①现在有6个花盆，你能把它们排排队，使得每排都有3个花盆吗？右边的小圆点表示花盆，你动手排排看吧！
②英国一位数学家于1821年出了这样一道智趣题（九树十行）：
春分艳阳暖，园中植树忙；
每行植三棵，九株栽十行；
种法有多样，请你试试看。

6、如图，∠1=∠2，∠D=90°，EF ⊥CD ，那么∠3=∠B 吗？
7、如图，在不等边三角形ABC 中，AQ=PQ ，PM ⊥AB ，
PN ⊥AC ，PM=PN 。

试说明：QP ∥AM 。

123A B C D E F A B C M N Q。

图4七（下）数学思维拓展训练时间：45分钟 分值：100分一、选择题（每小题5分，共25分）1.若n 为正整数，且x 2n =3，则(3x 3n )2－4(x 2)2n 的值为( )（A ）207 （B ）36 （C ）45 （D ）2172．一个长方形的长是2x 厘米，宽比长的一半少4厘米，若将长方形的长和宽都增加3厘米，则该长方形的面积增加为（ ）(A)9 （B ）2x 2+x －3 （C ）－7x －3 （D ）9x －33．若(x-5)·A= x 2+x+B ，则（ ）（A ）A=x+6，B=－30 （B ）A=x －6，B=30（C ）A=x+4，B=－20 （D ）A=x －4，B=204.已知6141319,27,81===c b a ，则a ，b ，c 大小关系是（ ）（A ）a>c>b （B ）a>b>c （C ）a<b<c （D ）b>c>a5.如图1，直线MN//PQ ，OA ⊥OB ，∠BOQ=30︒.若以点O 为旋转中心，将射线OA 顺时针旋转60︒后，这时图中30︒的角的个数是 （ ）(A) 4个 (B) 3个 (C) 2个 (D) 1个二、填空题（每小题5分，共25分）6.用如图2所示的正方形和长方形卡片若干张，拼成一个边长为a+b 的正方形，需要B 类卡片_______张.7.如图3，AB ∥CD ，M 、N 分别在AB ，CD 上，P 为两平行线间一点，那么∠1+∠2+∠3= ︒.8.如图4，一把矩形直尺沿直线断开并错位，点E 、D 、B 、F 在同一条直线上，若∠ADE ＝125︒, 则∠DBC= ︒.9.三个同学对问题“若方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是34x y =⎧⎨=⎩，求方程组111222325325a x b y c a x b y c +=⎧⎨+=⎩的解．”提出各自的想法．甲说：“这个题目好象条件不够，不能求解”；乙说：“它们的系数有一定的规律，可以试试”；丙说：“能不能把第二个方程组的两个方程的两边都除以5，通过换元替代的方法来解决”．参考他们的讨论，你认为这个题目的解应该是 ．10. 数学家发明了一个魔术盒，当任意数对()b a ,进入其中时，会得到一个新的数：图1 O N M A B P Q aa ab A 类 B 类 C 类 图2()()21--b a .现将数对()1,m 放入其中得到数n ，再将数对()m n ,放入其中后，如果最后得到的数是 .（结果要化简）三、解答题（每小题10分，共50分）11.计算：(1+2+3+…+2013)(2+3+4+…+2012)－(1+2+3+…+2012) (2+3+4+…+2013)．12.图5是按一定规律排列的方程组集合和它解的集合的对应关系图，若方程组集合中的方程组自左至右依次记作方程组1、方程组2、方程组3、……方程组n ．（1）将方程组1的解填入图中；（2）请依据方程组和它的解变化的规律，将方程组n 和它的解直接填入集合图中；（3）若方程组⎩⎨⎧-=+1my x y x 的解是⎨⎧=10x ，求m 的值，并判断该方程组是否符合（2）中的规律？13.如图6，已知两组直线分别互相平行．（1）若∠1=115º，求∠2，∠3的度数；（2）题（1）中隐含着一个规律，请你根据（1）的结果进行归纳，试用文字表述出来；（3）利用（2）中的结论解答：如果两个角的两边分别平行，其中一个角是另一个角的2倍，求这两个角的大小．方程组图514.下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．解：设x2－4x=y．原式=(y+2) (y +6)+4 ①=y2+8y+16 ②=( y+4)2 ③=(x2－4x+4)2 ④回答下列问题：（1）该同学②到③运用了因式分解的_______.（A）提取公因式（B）平方差公式（C）两数和的完全平方公式（D）两数差的完全平方公式（2）该同学因式分解的结果是否彻底？________（填“彻底”或“不彻底”）；若不彻底，请直接写出因式分解的最后结果_________．（3）请模仿以上方法对多项式（x2－2x）（x2－2x+2）+1进行因式分解．15．如下几个图形是五角星和它的变形．（1）图7中是一个五角星，则∠A+∠B+∠C+∠D+∠E= º．（2）图7中的点A向下移到BE上时，五个角的和（即∠CAD+∠B+∠C+∠D+∠E）有无变化？如图8，说明你的结论的正确性．（3）把图8中的点C向上移到BD上时，五个角的和（即∠CAD+∠B+∠ACE +∠D+∠E）参考答案1~5.ADABA6.27.3608.559. 510x y =⎧⎨=⎩ 10. －m 2+2m 11.设1+2+3+…+2012=a ，2+3+4+…+2012=b ，则a= b+1．(1+2+3+…+2013)(2+3+4+…+2012)－(1+2+3+…+2012) (2+3+4+…+2013)= (a+2013)b －a(b+2013)=ab+2013b －ab －2013a=2013b －2013a=2013b －2013(b+1)= 2013b －2013 b －2013=－2013．12.（1）直接消元可求出⎩⎨⎧==01y x ；（2）观察第一个方程都是x+y=1，第二个方程x 前面的系数都是1，而y 前面的系数应是－n ，常数项应是n 2，这样第二个方程应是x －ny= n 2，所以第n 个方程组为⎩⎨⎧=-=+21n ny x y x ．其解的规律是x 从1开始依次增1，y 从0开始依次减1，这样第n 个方程组的解为⎩⎨⎧-==n y n x 1；（3）把⎩⎨⎧-==9y 10x 代入方程x －my=16，得m=32．显然不符合(2)中的规律．13.（1）因为两组直线分别互相平行，所以由平行线的性质可得∠2=∠1=115º，∠3+∠2=180º，则∠3=180º－115º=65º；（2）如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补；（3）设其中的一个角为xº，则另一个角为2xº．因为xº+2xº=180º，所以x=60º．故这两个角分别为60º和120º．14.（1）C（2）不彻底，( x －2)4（3）设x 2－2x=y ．原式=y (y +2)+1= y 2+2y+1=( y+1)2=(x 2－2x+1)2=( x －1)4 ．15．（1）180º．（2）无变化．因为∠BAC=∠C+∠E ，∠EAD=∠B+∠D ，所以∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠EAD=180º．（3）无变化．因为∠ACB=∠CAD+∠D ，∠ECD=∠B+∠E ，所以∠CAD+∠B+∠ACE +∠D+∠E=∠ACB+∠ACE+∠ECD=180º．。

七下思维创新题4
1. 某村去年种植的油菜籽亩产量达150千克，含油率为40﹪。

今年改种新选育的油菜籽后亩产量提高了30千克，含油率提高了10百分点。

今年与去年相比，油菜的种植面积减少了40亩，而村榨油厂用本村所产油菜籽的产油量提高了20﹪。

（1）求今年油菜的种植面积。

设今年油菜的种植面积是x 亩。

完成下表后再列方程解答。

亩产量（千克/亩）
种植面积
（亩）
油菜籽总产量
（千克）
150
x
（2）已知油菜种植成本为200元/亩，菜油收购价为6元/千克。

试比较这个村去今两年种植油菜的纯收入。

2. 如图1，射线OC，OD在∠AOB的内部，且∠AOB=150°，∠COD=30°，射线OM，ON分别平分∠AOD，∠BOC．
（1）若∠AOC=60°，试通过计算比较∠NOD和∠MOC的大小；
（2）如图2，若将图1中∠COD在∠AOB内部绕点O顺时针旋转．
①旋转过程中∠MON的大小始终不变．求∠MON的值；
②如图3，若旋转后OC恰好为∠MOA的角平分线，试探究∠NOD与∠MOC的数量关系.
1。

初中数学数学思维拓展题练习及参考答案2023初中数学是培养学生数学思维的重要阶段。

在此过程中，需要适时进行一些数学思维拓展训练，让学生更好地掌握数学知识，提高数学思维能力。

为此，我们编制了一些初中数学思维拓展题及参考答案，以供学生参考。

一、综合运用1.设计一个图形，使其中既包含一个等边三角形，又包含一个等腰直角三角形。

2.某校运动会上，甲、乙两人比赛。

甲比乙多走50米，但用的时间比乙少5秒。

已知甲的速度是每秒6米，求乙的速度是多少？3.某校有一个1500元的集资活动，已经筹集到1000元，还差多少钱才能圆满完成？二、实际应用1.甲、乙两人在赛场上相距80米，它们同时起跑，甲的速度是每秒9米，乙的速度是每秒8米，那么它们第一次相遇在多少秒后？2.某超市进行特惠活动，原价15元的商品8折出售。

如果你有100元，可以买多少件该商品？3.某学生用40分钟完成一项作业，如果他有30分钟时间再做作业，那么他能提高多少完成度？若他能提高40%的完成度，还需要多长时间？三、数学证明1.如下图所示，AC ⊥ BD，且AC = BD。

证明：三角形ABC与三角形DCB全等。

2.已知a，b都是正整数，证明：若(a+b)是一个奇数，那么(a-b)一定是一个奇数。

3.如下图，AC = BC，角ACD = 60°，角DBC = 75°。

求角BDC的度数。

参考答案：一、综合运用1.如图所示，图形中ABC为等边三角形，ACD为等腰直角三角形。

2.设乙用时t秒，则甲用时t+5秒。

由v = s/t，得甲走的距离为6(t+5)，乙走的距离为vt。

因为题目中已经提示甲比乙多走了50米，所以可以列出以下方程：6(t+5) = vt + 50将v = 8带入方程中，可以解得t = 20秒。

3.筹集到的资金已经是：(1000元 / 1500元) × 100 % = 66.67 %。

还差的资金是 33.33%，即未筹100 %的资金。

人教版七年级下册思维特训（二十）方案问题与二元一次方程（组）(355)1.某企业在“蜀南竹海”收购毛竹，如果直接销售，每吨可获利100元；如果进行粗加工，每天可加工8吨，每吨可获利800元；如果对毛竹进行精加工，每天可加工1吨，每吨可获利4000元．由于受条件限制，每天只能采用一种方式加工，要求在一月内(30天)将这批毛竹93吨全部销售完毕．为此企业厂长召集职工开会，让职工讨论如何加工销售更合算．甲说：将毛竹全部进行粗加工后销售；乙说：30天都进行精加工，未加工的毛竹直接销售．丙说：30天中可用几天进行粗加工，再用几天进行精加工后销售．那么厂长应按照哪位说的方案做，获利最大？2.某体育彩票经销商计划用45 000元从省体彩中心购进彩票20扎，每扎1000张，已知体彩中心有A、B、C三种不同价格的彩票，进价分别是A彩票每张 1.5元，B彩票每张2元，C彩票每张 2.5元.(1)若经销商同时购进两种不同型号的彩票20扎，用去45000元，请你设计进票方案；(2)若销售A型彩票一张获得手续费0.2元，B型彩票一张获得手续费0.3元，C型彩票一张获得手续费0.5元.在购进两种彩票的方案中，为使销售完时获得手续费最多，你选择哪种进票方案？(3)若经销商准备用45000元同时购进A、B、C三种彩票20扎，请你设计进票方案.3.小明家需要用钢管做防盗窗，按设计要求，其中需要长为0.8m，2.5m且粗细相同的钢管分别为100根、32根，并要求这些用料不能是焊接而成的．现钢材市场的这种规格的钢管每根为6m．(1)那么一根6m长的钢管有哪些裁剪方法呢？请填写在下面(余料作废)：方法①：当只裁剪长为0.8m的用料时，最多可剪根；方法②：当先剪下1根2.5m的用料时，余下部分最多能剪0.8m长的用料根；方法③：当先剪下2根2.5m的用料时，余下部分最多能剪0.8m长的用料根(2)分别用(1)中的方法②和方法③各裁剪多少根6m长的钢管，才能刚好得到所需要的相应数量的材料？(3)试探究：除(2)中的方案外，在(1)中还有哪两种方法联合，所需要6m长的钢管与(2)中的根数相同？4.某商场计划拨款9万元从厂家购进50台电视机．已知该厂家生产三种不同型号的电视机，出厂价分别为甲种每台1500元，乙种每台2100元，丙种每台2500元．(1)若商场同时购进其中两种不同型号的电视机共50台，用去9万元，请研究一下商场的进货方案；(2)若商场销售一台甲种电视机可获利150元，销售一台乙种电视机可获利200元，销售一台丙种电视机可获利250元．在同时购进两种不同型号电视机的方案中，为使销售时获利最多，你选择哪种进货方案？(3)若商场准备用9万元同时购进三种不同型号的电视机共50台，请你设计进货方案5.某牛奶加工厂现有鲜奶9吨，若在市场上直接销售鲜奶，每吨可获利润500元，制成酸奶销售，每吨可获利润1200元，制成奶片销售，每吨可获利润2000元．该厂的生产能力如下：如制成酸奶，每天可加工3吨，制成奶片，每天可加工1吨，受人员限制，两种加工方式不可同时进行，受气温限制，这批牛奶需在4天内全部销售或加工完毕．由此该厂设计了两种方案：方案一：尽可能多的制成奶片，其余鲜奶直接销售；方案二：一部分制成奶片，其余制成酸奶销售，并恰好4天完成．你认为选择哪种方案获利最多？6.某地生产一种绿色蔬菜，若在市场上直接销售，每吨利润为1000元；经粗加工后销售，每吨利润可达4500元；经精加工后销售，每吨利润涨至7500元．当地一家农工商公司收获这种蔬菜140吨，该公司加工厂的生产能力如下：如果对蔬菜进行粗加工，每天可加工16吨；如果进行精加工，每天可加工6吨，但两种加工方式不能同时进行．受季节条件的限制，该公司必须在15天之内将这批蔬菜全部销售或加工完毕，为此该公司研制了三种加工方案．方案一：将蔬菜全部进行粗加工;方案二：尽可能多的对蔬菜进行精加工，没有来得及加工的蔬菜在市场上全部直接销售；方案三：将部分蔬菜进行精加工，其余蔬菜进行粗加工，并恰好在15天完成．你认为选择哪种方案获利最多，为什么？参考答案1.【答案】:解：①如果将毛竹全部进行粗加工后销售，那么可以获利93×800= 74400(元)；②30天都进行精加工，可加工的数量为30吨，获利30×4000=120000(元)，未加工的毛竹63吨直接销售可获利63×100=6300(元)，因此共获利120000+6300=126300(元)；③设x天粗加工，y天精加工，则{x+y=30，8x+y=93，解得{x=9，y=21，所以9天粗加工的数量为9×8=72(吨)，可获利72×800=57600(元)，21天精加工的数量为21吨，可获利21×4000=84000(元)，因此共获利141600元，因为141600>126300>74400.所以采用丙的方案获利最大2(1)【答案】设经销商从体彩中心购进A种彩票x张，B种彩票y张，C种彩票z张，只购进A种彩票和B种彩票，依题意可列方程组\(\left\{ \begin{array}{l}{x+y=1000\times20 } \\ {1.5x+2y=45000} \end{array} \right.\).解得x<0，所以无解.只购进A种彩票和C种彩票，依题意可列方程组\(\left\{\begin{array}{l}{x+z=1000\times20 } \\ {1.5x+2.5z=45000} \end{array} \right.\).∴\(\left\{ \begin{array}{l}{x=5000 } \\ {z=15000} \end{array}\right.\).只购进B种彩票和C种彩票，依题意可列方程组\(\left\{ \begin{array}{l}{y+z=1000\times20 }\\{2y+2.5z=45000}\en d{array} \right.\).∴\(\left\{ \begin{array}{l}{y=10000 } \\ {z=10000} \end{array} \right.\).综上所述，若经销商同时购进不同型号的彩票，共有两种方案可行，即A种彩票5扎，C种彩票15扎或B种彩票与C种彩票各10扎.【解析】:分三种情况列方程组进行分析即可.(2)【答案】若购进A种彩票5扎，C种彩票15扎，销售完后获手续费为0.2×5000+0.5×15000=8500（元）；若购进B种彩票与C种彩票各10扎，销售完后获手续费为0.3×10000+0.5×10000=8000（元）.∴为使销售完时获得手续费最多选择的方案为A种彩票5扎，C种彩票15扎. 【解析】:根据上一问分别求出每一种情况的手续费，然后进行比较，可以得出结果．(3)【答案】若经销商准备用45000元同时购进A、B、C三种彩票20扎.设购进A种彩票x扎，B种彩票y扎，C种彩票z扎.则\(\left\{ \begin{array}{l}{x+y+z=20 } \\{1.5\times1000x+2\times1000y+2.5\times1000z=45000} \end{array}\right.\).∴\(\left\{ \begin{array}{l}{y=-2x+10 } \\ {z=x+10} \end{array}\right.\).∵x、y都是正数，∴1≤x<5.又∵x为整数，∴共有4种进票方案.A种1扎，B种8扎，C种11扎，或A种2扎，B种6扎，C种12扎，或A种3扎，B种4扎，C种13扎，或A种4扎，B种2扎，C种14扎.【解析】:根据题意列方程组，用含有同一个未知数的代数式去表示另外的两个未知数，然后根据三个未知数的实际意义得到取值范围，进而确定进票方案.3(1)【答案】7；4；1【解析】:①6÷0.8=712，因此当只裁剪长为0.8m的用料时，最多可剪7根．②(6−2.5)÷0.8=438，因此当先剪下1根2.5m的用料时，余下部分最多能剪0.8m长的用料4根．③(6−2.5×2)÷0.8=114，因此当先剪下2根2.5m的用料时，余下部分最多能剪0.8m 长的用料1根(2)【答案】设用方法②裁剪x根，用方法③裁剪y根6m长的钢管．由题意，得{x+2y=32，4x+y=100，解得{x=24，y=4.答：用方法②裁剪24根，用方法③裁剪4根6m长的钢管,才能刚好得到所需要的相应数量的材料(3)【答案】设用方法①裁剪m根，用方法③裁剪n根6m长的钢管．由题意，得{7m+n=100，2n=32，解得{m=12，n=16，∴m+n=28.∵(2)中x+y=24+4=28，∴m+n=x+y，符合题目要求．设用方法①裁剪a根，用方法②裁剪b根6m长的钢管．由题意，得{7a+4b=100，b=32，解得{a=−4，b=32，无意义．∴方法①与方法③联合，所需要6m长的钢管与(2)中的根数相同4(1)【答案】解：分以下三种情况：①若购进甲种电视机和乙种电视机，则{x+y=50，1500x+2100y=90000，解得{x=25，y=25.②若购进乙种电视机和丙种电视机，则{y+z=50，2100y+2500z=90000，解得{y=87.5，z=−37.5.(不合题意，舍去此方案) ③若购进甲种电视机和丙种电视机，则{x+z=50，1500x+2500z=90000，解得{x=35，z=15.综上所述，有以下两种方案成立：①甲、乙两种型号的电视机各购25台；②甲种型号的电视机购35台，丙种型号的电视机购15台(2)【答案】方案①获利：25×150+25×200=8750(元)；方案②获利：35×150+15×250=9000(元)．所以为使销售时获利最多，应选择第②种进货方案,即甲种型号的电视机购35台，丙种型号的电视机购15台(3)【答案】由题意，得z=50−x−y．则1500x+2100y+2500(50−x−y)=90000，化简整理，得5x+2y=175.又因为0<x<50，0<y<50,0<z<50,且x,y,z均为整数，所以上述二元一次方程只有四组解：{x=27，y=20，{x=29，y=15，{x=31，y=10，{x=33，y=5.对应的z值分别为3,6,9,12.因此，有四种进货方案：①购进甲种电视机27台，乙种电视机20台，丙种电视机3台；②购进甲种电视机29台，乙种电视机15台，丙种电视机6台；③购进甲种电视机31台，乙种电视机10台，丙种电视机9台；④购进甲种电视机33台，乙种电视机5台，丙种电视机12台5.【答案】:解：方案一获利：4×2000+5×500=10500(元)． 方案二：设x 吨制成奶片，y 吨制成酸奶，则{x +y =9，x 1+y 3=4， 所以{x =1.5，y =7.5.利润为1.5×2000+7.5×1200=12000元>10500元． 所以选择方案二获利最多6.【答案】:解： 选择方案三获利最多． 理由如下：方案一获利为4500×140=630000(元)．方案二获利为7500×(6×15)+1000×(140−6×15) =675000+50000=725000(元)．方案三：设x 天进行粗加工，y 天进行精加工． 由题意，得{x +y =15，16x +6y =140， 解得{x =5，y =10.所以方案三获利为7500×6×10+4500×16×5=810000(元)． 由于810000>725000>630000，所以选择方案三获利最多． 答：选择方案三获利最多。

最近新都区数学七思维训练试卷（含答案）第Ⅰ卷选择题（共30分）一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）1.有理数6的相反数是( )A.-6B.6C.1/6D.-1/62.平方得16的数是（）A.4B.-4C.4或-4D.163．．．．x2．2xy3．y．1．( )A．．．．．．B．．．．．．C．．．．．．D．．．．．．4.两个三次多项式的和的次数是（）Ａ.六次Ｂ.三次Ｃ.不低于三次Ｄ.不高于三次5.下列判断错误的是（）Ａ、一个正数的绝对值一定是正数；Ｂ、一个负数的绝对值一定是正数；Ｃ、任何数的绝对值一定是正数；D、任何数的绝对值都不是负数；6．下列说法正确的是( ) A．过一点有且仅有一条直线与已知直线平行B．两点之间的所有连线中，线段最短C．相等的角是对顶角D．若AC＝BC，则点C是线段AB的中点7．如图，C，D是线段AB上两点，若CB=4cm，DB=7cm，且D是AC的中点，则AC的长等于……………………………………………………………（）A．3 cm B．6 cm C．11 cm D．14 cmA BCD(第7题)8．．．．．．．．．．．( )A．．．．．．．．．．．．．．．B．．．．．．．．．．．．．．．C．．．．．．．．．．．．．．．．D．．．．．．．．．．．．．9．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．A．．．B．．．C．．．D．．．10．若有理数a、b、c在数轴上的位置如图所示，则将－a、－b、c按从小到大的顺序为( )c a 0 bA．－b<c<－a B．－b<－a<c C．－a<c<－b D．－a<－b<c第Ⅱ卷非选择题（共90分）二、填空题（本大题共5个小题，每小题3分，共15分）11．．．．．．．．．．．．．．．．．．．．．．．．2013．．．+2013．．．．．．．．．．500．．．．．．．．．．．．__________．12.绝对值小于8.9的所有整数的积是_________.13. 已知4x2m y m＋n与－3x6y2是同类项，则m－n＝.14．如图，边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后，剩余部分又剪拼成一个长方形(不重叠无缝隙)，若拼成的长方形一边长为3，则另一边长是（用含m 的代数式表示）．15．跳格游戏：如图，人从格外只能进入第1格；在格中每次可向前跳1格或2格，那么人从格外跳到第6格，可以有________种不同的方法．（第15题）三、解答题 （本大题共8个小题，共75分．解答应写出文字说明、证明过程或演算步骤）16. (1) (－28)÷(―6+4)+(―1)×5 (2) －14－[2―(―3)2]+(－1)4（3）、 33+（-32）+7-（-3） （4）、－｜－32｜÷3×（－）－（－2）317．解方程(1) 3(x －4)＝12； (2) x －x －12 ＝2－x ＋23．18．先化简，再求值5(3a 2b －ab 2)－4(－ab 2＋3a 2b )，其中a ＝12、b ＝－13．19.阅读下面的文字，解答问题： 大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部地写出来，于是小明用 −1来表示 的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：∵＜＜，即2＜＜3，∴的整数部分为2，小数部分为(−2)．请解答：（1）的整数部分是__________，小数部分是__________（2）如果的小数部分为a，的整数部分为b，求a+b−的值；20．．．．．AB．CD．．．．．BD=AB=CD．．．AB．CD．．．E．F．．．．．．14cm．．BD．AC．．．21．．．．．．．．．．．．．．．．．．．．．．．．“．．．．”．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．“．．．．”．．．．．．．．．．．．．．．．．．．．．(a+b)n．n ．．．．．．．．．．．．a．．．．．．．．．．．．．．．．．．．．．．．．．．1．．(a+b)0=1．．．(a+b)1 =a+b．．．．．．．1．1．．．．．．．．．．．．．(a+b)2 =a2+2ab+b2．．．．．．．1．2．1．．．．．．．．．．．．．(a+b)3 =a3+3a2b+3ab2+b3．．．．．．．1．3．3．1．．．．．．．．．．．．．（1）请认真观察此图，写出(a+b)4的展开式，(a+b)4= ．（2）类似地，请你探索并画出(a-b) 0，、(a-b) 1 ，(a-b) 2 ，(a-b) 3 的展开式中按a次幂从大到小排列的项的系数．．对应的三角形．（3）探究解决问题：已知a+b=3，a2+b2=5，求ab的值．22．A．B．．．．1755．．．．．．．．．．．．．A．B．．．．．．．．．．．．．．．．．．．．．．．．．．．9．．．．．5．．．．．．．．． 675．．．．1．．．．．．．．．．．．．．．．．．．．．．2．．5．．．．．．．．．．．．．．．3.5．．．．．．．．．．．．．5.5．．．．．．．．．．．．．．．．．．．．．．．．．．．．23.某工程队承包了某标段全长1755米的过江隧道施工任务，甲、乙两个班组分别从东、西两端同时掘进．已知甲组比乙组平均每天多掘进0.6米，经过5天施工，两组共掘进了45米．（1）求甲、乙两个班组平均每天各掘进多少米？（2）为加快工程进度，通过改进施工技术，在剩余的工程中，甲组平均每天能比原来多掘进0.2米，乙组平均每天能比原来多掘进0.3米．按此旄工进度，能够比原来少用多少天完成任务？。

初一数学思维测试题及答案一、选择题（每题2分，共10分）1. 下列哪个数是最小的正整数？A. 0B. 1C. -1D. 22. 如果一个数的平方等于它本身，那么这个数可能是：A. 1B. -1C. 0D. A和C3. 一个数的绝对值是它本身，这个数是：A. 正数B. 负数C. 非负数D. 非正数4. 以下哪个表达式的结果不是整数？A. \( \frac{7}{2} \)B. \( 5 - 3 \)C. \( 4 \div 2 \)D.\( 3 + 4 \)5. 一个数的相反数是它自己，这个数是：A. 0B. 1C. -1D. 2二、填空题（每题2分，共10分）6. 一个数的平方是16，这个数可能是______。

7. 如果\( a \)和\( b \)互为相反数，那么\( a + b = _______ \)。

8. 一个数的绝对值等于4，这个数可能是______。

9. 一个数的立方等于它自身，这个数可能是______。

10. 如果\( x \)是最小的正整数，那么\( x + 1 \)是______。

三、解答题（每题5分，共20分）11. 已知一个数的立方是-27，求这个数。

12. 一个数的平方加上8等于这个数本身，求这个数。

13. 一个数的绝对值是它自己，这个数可能是哪些？14. 如果\( x \)是最小的正整数，\( y \)是最大的负整数，求\( x- y \)。

四、应用题（每题10分，共30分）15. 一个班级有40名学生，其中一半是男生。

如果班级平均成绩是85分，求男生的平均成绩。

16. 一个长方形的长是宽的两倍，面积是48平方厘米。

求长方形的长和宽。

17. 一个数列的前三项是1, 3, 6，每一项都是前一项的两倍。

求第10项的值。

五、结束语通过以上初一数学思维测试题的练习，同学们可以检验自己的数学基础知识和逻辑思维能力。

希望这些题目能够帮助大家更好地理解和掌握数学概念，提高解题技巧。

数学是一门需要不断练习和思考的学科，希望同学们能够保持好奇心和探索精神，不断挑战自己，享受数学带来的乐趣。

初中数学思维拓展题训练及答案一、选择题1、若一次函数y=kx+1与两坐标轴围成的三角形面积为3，则k 为（C ） A 、16 B 、-16 C 、±16 D 、±132、若11m n -=3，2322m mn nm mn n+---的值是（B ） A 、1.5 B 、35 C 、-2 D 、-753、判断下列真命题有（C ）①任意两个全等三角形可拼成平行四边形②两条对角线垂直且相等的四边形是正方形③四边形ABCD ，AB=BC=CD ，∠A=90°，那么它是正方形④在同一平面内，两条线段不相交就会平行⑤有一条对角线平分一个内角的平行四边形是菱形 A 、②③ B 、①②④ C 、①⑤ D 、②③④4、如图，矩形ABCD 中,已知AB=5,AD=12,P 是AD 上的动点,PE ⊥AC ，E,PF ⊥BD 于F,则PE+PF=（B ） A 、5 B 、6013 C 、245 D 、55125、在直角坐标系中，已知两点A （-8，3）、B （-4，5）以及动点C （0，n ）、D(m,0)，则当四边形ABCD 的周长最小时，比值为 mn（B ）A 、-23B 、-32C 、-34D 、34二、填空题6、当x= 负数 时，||3x x -与3x x-互为倒数。

9、已知x 2-3x+1=0，求（x-1x ）2= 57、一个人要翻过两座山到另外一个村庄，途中的道路不是上山就是下山，已知他上山的速度为v ，下山的速度为v ′，单程的路程为s ．则这个人往返这个村庄的平均速度为 (2vv v v '+')8、将点A （4，0）绕着原点O 顺时针方向旋转30°角到对应点A '，则点A '的坐标是 (23,2)9、菱形ABCD 的一条对角线长为6，边AB 的长是方程(X-3)(X-4)=0的解，则菱形ABCD 的周长为 1610、△ABC 中，∠A=90°，AB=AC ，BD 是△ABC 的中线，△CDB 内以CD 为边的等腰直角三角形周长是 （222AB +或122AB +）11235...11231511211321④③②①11. 如图，边长为6的菱形ABCD 中，∠DAB=60°，AE=BE ，F 是AC•上一动点，EF+BF 的最小值为 (33) 12、如图，边长为3的正方形ABCD 顺时针旋转30°，得上图，交DE 于D ’,阴影部分面积是 (933-)13、如图，已知四边形ABCD 中，AC 和BD 相交于点O ， 且∠AOD ＝90°，若BC ＝2AD ，AB ＝12，CD ＝9，四边形ABCD 的周长是 (215+)14、有这样一组数：1，1，2，3，5…，现以这组数据的数作为正方形边长的长度构造如下正方形；再分别从左到右取2个、3个、4个、5个正方形拼成如下矩形记为①、②、③、④.第⑩个矩形周长是 46615、如图，在直线y=-33x+1与x 轴、y 轴交于点A 、B ，以线段AB 为直角边在第一象限内作等腰直角△ABC ，∠BAC=90°，第二象限内有一点P （a,12 ）,且△ABP 的面积与△ABC 的面积相等，则a= (342-+) 三、解答题16、如图，已知矩形ABCD ，延长CB 到E ，使CE=CA ，连结AE 并取中点F ，连结AE 并取中点F ，连结BF 、DF ，求证BF ⊥DF 。