九年级数学上垂径定理练习题

专题08垂径定理、圆心角、圆周角之六大题型利用垂径定理求值【答案】2【分析】根据垂径定理和勾股定理列方程求解即可．【详解】解：设OC=△中，由勾股定理得，在Rt COE【变式训练】【答案】45cm/4【分析】连接BO，延长22=，即可求解．BC OB OC-【详解】解：如图，连接=，由折叠得：CD CEQ D是OC的中点，\=，CD OD\==，CE CD OD2\==，4OC OE【答案】310【分析】由题意易得【详解】解：连接OD∵AB 是O e 的直径，AB ∴152OD OB AB ===，∵CD AB ^，6CD =，∴13,2DE CD DEO ==Ð∴22OE OD DE =-=垂径定理的实际应用【点睛】本题考查了勾股定理和垂径定理，灵活运用所学知识，掌握垂直于弦的直径平分弦，且平分弦所对的弧，是解决本题的关键．【变式训练】1．（2023上·福建龙岩·九年级统考期末）筒车是我国古代发明的一种水利灌溉工具，彰显了我国古代劳动人民的智慧．如图1，点M 表示筒车的一个盛水桶．如图2，当筒车工作时，盛水桶的运行路径是以轴心O （O 在水面上方）为圆心的圆，且圆O 被水面截得的弦AB 长为8米．若筒车工作时，盛水桶在水面以下的最大深度为2米，则这个圆的半径为（ ）A ．2米B ．3米C ．4米D ．5米【答案】D 【分析】过圆O 作OD AB ^于E ，如图所示，由垂径定理可知4AE BE ==，设圆的半径为r ，再利用勾股定理列方程求解即可得到答案．【详解】解：过圆O 作OD AB ^于E ，如图所示：Q 弦AB 长为8米，\4AE BE ==，Q 盛水桶在水面以下的最大深度为2米，设圆的半径为r ，在Rt AOE △中，90AEO Ð=°，OA r =，4AE =，2OE OD ED r =-=-，则由勾【答案】26【分析】连接AO ，依题意，得出222AO AC CO =+，解方程即可求解．【详解】解：如图所示，连接∵1CD =，10AB =，AB ∴5AC =，设半径为r ，则AO r =在Rt AOC V 中，2AO =利用弧、弦、圆心角的关系求解A．AB OC=C．12ABC BOC Ð+Ð=【答案】D 【变式训练】【答案】80°/80度【分析】利用等腰三角形的性质和三角形内角和计算出即可求出答案．Ð【详解】解：∵OBC半圆（直径）所对的圆周角是直角A．43【答案】B【分析】如图：连接AQ QB=，最后根据勾股定理即可解答．【点睛】本题主要考查了圆周角定理、等腰三角形的判定与性质、勾股定理等知识点，灵活运用勾股定理成为解答本题的关键．【变式训练】【答案】13【分析】连接BD ，先由三角形内角和定理求出求出30ABD Ð=°，即有【详解】解：连接BD∵在ABC V 中，55B Ð=∴60A Ð=°，∵AB 为O e 的直径，∴90ADB CDB Ð=Ð=°Ð的度数；(1)求BAC(2)若点E为OB中点，CE 【答案】(1)45°(2)3590°的圆周角所对的弦是直径例题：（2023上·广东汕头DA DC =，2AB BC ==【答案】32【分析】连接AC ，过点角三角形，勾股定理求得∵90ADC Ð=°，∴AC 是直径，∴90ABC Ð=°【变式训练】1．（2023上·山东济南·九年级统考期末）如图，正方形ABCD 中，4AB =，E 点沿线段AD 由A 向D【答案】2p【分析】连接BD 交EF 于点1222OB OD BD ===，再由∵四边形ABCD 是正方形，∴4BC AB AD ===，EDO Ð∴242BD AB ==，【答案】90°Ð【分析】（1）由ABP （2）首先证明点P理求出OC即可得到则OP OA OB ==，\点P 在以AB 为直径的O e 在Rt BCO V 中，90OBC Ð=225OC BO BC \=+=，532PC OC OP =-=-=，已知圆内接四边形求角度【答案】102°【分析】根据圆内接四边形的性质得出【详解】解：∵四边形∴180A DCB Ð+Ð=°，又180DCE DCB Ð+Ð=°，∴102DCE A ÐÐ==°，故答案为102°．【点睛】本题主要考查了圆内接四边形的性质，熟知圆内接四边形的对角互补是解决此题的关键．【变式训练】【答案】40【分析】根据已知可得»»BCBD =56DAC BAC BAD Ð=Ð+Ð=°，再利用圆内接四边形对角互补以及平角的定义可得56DBE DAC Ð=Ð=°，继而利用角平分线定义及三角形内角和定理即可求解．(1)求证：A AEBÐ=Ð(2)若90Ð=°，点CEDC【答案】(1)见解析e的半径为25 (2)O一、单选题1．（2023上·河北张家口·九年级统考期末）O e 中的一段劣弧»AB 的度数为80o ，则AOB Ð=（ ）A ．10oB ．80oC ．170oD ．180o【答案】B 【分析】根据圆心角、弧、弦之间的关系得出答案即可．【详解】解：Q O e 中的一段劣弧»AB 的度数为80°，80AOB \Ð=°，故选：B ．A ．32°B ．42【答案】A 【分析】先根据同弧所对的圆周角相等得到小即可．【详解】解：∵50A Ð=°，∴50D A Ð=Ð=°，A ．10【答案】D∴12AH BH AB===在Rt BOHV中，OH∴线段OP长的最小值为A．105°B．110【答案】D【分析】先根据圆内接四边形的性质和平角的定义求出求解．A ．1米B ．()35+米C ．3米【答案】D 【分析】连接OC 交AB 于D ，根据圆的性质和垂径定理可知理求得OD 的长，由CD OC OD =-即可求解．则OC AB ^，12AD BD AB ==在Rt OAD △中，3OA =，AD ∴225OD AO AD =-=，【点睛】本题考查圆的性质、垂径定理、勾股定理，熟练掌握垂径定理是解答的关键．【答案】120【分析】过O 点作OD AC ^AD CD =，根据三角形中位线定理可得由折叠可得：12OD OE ==∵AB 是直径，∴90ACB Ð=°，12OD BC =【答案】64°/64度【分析】根据在同圆中，Ð=Ð可推出AOC BOD【详解】解：Q»AE=【答案】3【分析】由圆的性质可得OA后根据中位线的性质即可解答．【答案】45【分析】连接AC ，如图所示，由直径所对的圆周角为直角可知及勾股定理求出AC 【详解】解：连接Q OC AB ^，AB =12AD BD AB \==在Rt AOD V 中，OA 420r \=，解得r【答案】4【分析】如图，连接CD直角三角形斜边上的中线等于斜边的一半可得【点睛】本题考查直径所对的圆周角为直角，直角三角形斜边上的中线等于斜边的一半，勾股定理．掌握直径所对的圆周角为直角是解题的关键．三、解答题e的直径AB垂直于弦CD，垂足为E，11．（2023上·安徽合肥·九年级统考期末）如图，O，．==28AE CD(1)求O e 的半径长；(2)连接 BC ，作OF BC ^【答案】(1)5(2)5在Rt OCE V 中，2OE ∴()22224R R -+=，解得5R =，∴O e 的半径长为5；(1)若这个输水管道有水部分的水面宽半径；OE AB ^Q ，11168cm 22BD AB \==´=(1)连接AD，求证：(2)若52,==CD AB 【答案】(1)详见解析；(2)6Ð相等吗？为什么？(1)BAFÐ和CAD^，垂足为(2)过圆心O作OH AB【答案】(1)相等，理由见解析(2)10【详解】（1）解：连接BF ，Q AF 是O e 的直径，90F BAF \Ð+Ð=°Q AC BD ^，\90CAD BDA Ð+Ð=°，Q F BDA Ð=Ð，\BAF CAD Ð=Ð．（2）解：OH AB ^Q ，AH BH \=，OA OF =Q ，210BF OH \==，BAF CAD Ð=ÐQ ，10CD BF \==．【点睛】本题考查的是圆周角定理，等角的余角相等，圆心角、弦的关系，三角形的中位线性质，垂径定理，掌握圆心角、弦的关系，三角形的中位线性质以及垂径定理是解题的关键．15．（2023上·山东威海·九年级统考期末）【初识模型】如图1，在ABC V 中，,90AB AC BAC =Ð=°．点D 为BC 边上一点，以AD 为边作ADE V ，使=90DAE а，AE AD =，连接CE ，则CE 与BD 的数量关系是__________；【构建模型】如图2，ABC V 内接于,O BC e 为O e 的直径，AB AC =，点E 为弧AC 上一点，连接,,AE BE CE ．若3,9CE BE ==，求AE 的长；【运用模型】如图3，等边ABC V 内接于O e ，点E 为弧AC 上一点，连接,,AE BE CE ．若6,10CE BE ==，求AE 的长．【答案】（1）BD CE =；（2）32；（3）4【分析】（1）只需要利用SAS 证明BAD CAE V V ≌，即可证明BD CE =（2）如图所示，过点A 作AD AE ^交BE 于D ，由BC 是直径，得到明BAD CAE Ð=Ð，再证明45ADE AED Ð=Ð=°，得到AD AE =，即可证明2（3）如图所示，在BE 上取一点∵ABC V 是等边三角形，∴60AB AC ACB ==°，∠，∴60AEB ACB Ð=Ð=°，∴ADE V 是等边三角形，∴60AE DE DAE ==°=，∠∠∴BAC CAD DAE Ð-Ð=Ð-Ð【点睛】本题主要考查了全等三角形的性质与判定，等边三角形的性质与判定，圆周角定理，勾股定理等等，正确作出辅助线构造全等三角形是解题的关键．。

2020 九级数学上册圆圆的基本性质-垂径定理课堂测试卷一、选择题：1、如图，⊙O的弦AB=8，M是AB的中点，且OM=3，则⊙O的半径等于（）A.8B.4C.10D.52、如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（）A.CM=DMB.CB=DBC.∠ACD=∠ADCD.OM=MD3、如图，⊙O的半径为5，AB为弦，OC⊥AB，垂足为C，如果OC=3，那么弦AB的长为（）A.4B.6C.8D.104、下列判断正确的是( )A.平分弦的直径垂直于弦B.平分弦的直径必平分弦所对的两条弧C.弦的垂直平分线必平分弦所对的两条弧D.平分一条弧的直线必平分这条弧所对的弦5、如图，⊙O的直径AB垂直于弦CD，垂足为E，∠A=22.5°，OC=4，CD的长为（）A.2B.4C.4D.86、一个隧道的横截面如图所示，它的形状是以点O为圆心，5为半径的圆的一部分，M是⊙O中弦CD的中点，EM经过圆心O交⊙O于点E.若CD=6，则隧道的高（ME的长）为（）A.4B.6C.8D.97、如图，一圆弧过方格的格点A、B、C，在方格中建立平面直角坐标系，使点A的坐标为（﹣3，2），则该圆弧所在圆心坐标是（）A.（0，0）B.（﹣2，1）C.（﹣2，﹣1）D.（0，﹣1）8、如图，⊙O的直径为10，弦AB的长为8，M是弦AB上的动点，则OM的长的取值范围（）A.3≤OM≤5B.4≤OM≤5C.3＜OM＜5D.4＜OM＜59、如图，⊙O的半径为2，弦AB=，点C在弦AB上，AC=AB，则OC的长为（）A. B. C. D.10、如图，AB是⊙O的直径，半径OC⊥AB,点D是弧ACB上的动点（不与A、B、C重合）,DE⊥OC,DF⊥AB,垂足分别是E、F，则EF长度（）A. 变大B. 变小C. 不变D. 无法确定二、填空题:11、如图，AB是⊙O的弦，半径OC⊥AB于点D，且AB=8cm，DC=2cm，则OC= cm.12、如图，C是以AB为直径的⊙O上一点，已知AB=5，BC=3，则圆心O到弦BC的距离是.13、如图，AB为⊙O的直径，CD⊥AB，若AB=10,CD=8，则圆心O到弦CD的距离为.14、如图，AB是⊙O的直径，点C在⊙O上，CD⊥AB，垂足为D，已知CD=4，OD=3，求AB长是.15、一根水平放置的圆柱形输水管道横截面如图所示，其中有水部分水面宽0.8米，最深处水深0.2米，则此输水管道的半径是米.16、如图，AB是⊙O的弦，AB=10，点C是⊙O上的一个动点，且∠ACB=45°，若点M、N分别是AB、BC的中点，则MN长的最大值是 .三、解答题:17、如图，⊙O的半径为5，AB为弦，OC⊥AB，交AB于点D，交⊙O于点C，CD=2，求弦AB的长.18、如图，在以点O为圆心的两个圆中，大圆的弦AB交小圆于点C、D，求证：AC=BD.19、如图，已知AB是⊙O的弦，点C在线段AB上，OC=AC=4，CB=8.求⊙O的半径.20、每位同学都能感受到日出时美丽的景色.右图是一位同学从照片上剪切下来的画面，“图上”太阳与海平线交于A﹑B两点，他测得“图上”圆的半径为5厘米，AB=8厘米，若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟，求“图上”太阳升起的速度.参考答案1、D2、D3、C4、C5、C6、D.7、C8、A9、D10、C11、512、213、答案为：3；14、答案为：10.15、答案为：0.516、答案为：5.17、解：∵OC是⊙O的半径，OC⊥AB于点D，∴AD=BD=AB.∵OC=5，CD=2，∴OD=OC－CD=3.在Rt△AOD中，OA=5，OD=3，∴AD===4，∴AB=2AD=8.18、证明：过圆心O作OE⊥AB于点E，在大圆O中，OE⊥AB，∴AE=BE.在小圆O中，OE⊥CD，∴CE=DE.∴AE﹣CE=BE﹣DE.∴AC=BD.19、连接OA，过点O作OD⊥AB于点D.∵AC=4，CB=8，∴AB=12.∵OD⊥AB，∴AD=DB=6，∴CD=2.在Rt△CDO中，∠CDO=90°，∴OD=2.在Rt△ADO中，∠ADO=90°，由勾股定理,得OA=4，即⊙O的半径是4.20、解：连接OA，过点O作OD⊥AB，∵AB=8厘米，∴AD=AB=4厘米，∵OA=5厘米，∴OD==3厘米，∴海平线以下部分的高度=OA+OD=5+3=8（厘米），∵太阳从所处位置到完全跳出海平面的时间为16分钟，∴“图上”太阳升起的速度==0.5厘米/分钟.。

精品字里行间精品文档成功是必须的垂径定理练习题一一．选择题1、如图2,AB 是⊙O 的直径,弦CD ⊥AB,垂足为E,如果AB=20,CD=16, 那么线段OE 的长为（ ） A 、10 B 、8 C 、6 D 、42．如图，已知⊙O 的半径为5，弦AB =6，M 是AB 上任意一点，则线段OM 的长可能是（ ）A ．2.5B ．3.5C ．4.5D ．5.53．高速公路的隧道和桥梁最多．图3是一个隧道的横截面，若它的形状是以O 为圆心的圆的一部分，路面AB =10米，净高CD =7米，则此圆的半径OA =（ ）A ．5B ．7C ．375D ．3774．如图，圆弧形桥拱的跨度AB ＝12米，拱高CD ＝4米，则拱桥的半径为（ ）A ．6.5米C ．13米D ．15米二．填空题1．工程上常用钢珠来测量零件上小孔的直径，假设钢珠的直径是10mm ，测得钢珠顶端离零件表面的距离为8mm ，如图所示，则这个小孔的直径AB是 mm ．2．如图，⊙O 的半径OA =10cm ，弦AB=16cm ，P 为AB 上一动点，则点P 到圆心O 的最短距离为 cm ． 3．如图，⊙O 的半径为5，弦8AB =，OC AB ⊥于C ，则OC 的长等于 ．4．如图，某花园小区一圆形管道破裂，修理工准备更换一段新管道，现在量得污水水面宽度为80cm ，水面到管道顶部距离为20cm ，则修理工应准备内直径是 cm 的管道．5．如图5，点A B ，是⊙O 上两点，10AB =，点P 是⊙O 上的动点（P 与A B ，不重合）连结AP PB ，，过点O分别作OE AP ⊥于点E ，OF PB ⊥于点F ，则EF = ．三．解答题已知：如图1，30PAC ∠=︒，在射线AC 上顺次截取AD =3cm ，DB =10cm ，以DB 为直径作⊙O 交射线AP 于E 、F 两点，求圆心O 到AP 的距离及EF 的长．垂径定理练习题二1、已知：AB 是⊙O 的直径，弦CD ⊥AB 于点P ，CD ＝10cm ，AP:PB ＝1:5，则⊙O 的半径为_______。

专题24.2 垂径定理的应用【典例1】如图，有一座圆弧形拱桥，桥下水面宽度AB为12m，拱高CD为4m．（1）求拱桥的半径；（2）有一艘宽为5m的货船，船舱顶部为长方形，并高出水面3.4m，则此货船是否能顺利通过此圆弧形拱桥，并说明理由．（1）根据垂径定理和勾股定理求解；（2）连接ON，OB，根据勾股定理即可得到结论．解：（1）如图，连接ON，OB．∵OC⊥AB，∴D为AB中点，∵AB＝12m，∴BD=12AB＝6m．又∵CD＝4m，设OB＝OC＝ON＝r，则OD＝（r﹣4）m．在Rt△BOD中，根据勾股定理得：r2＝（r﹣4）2+62，解得r＝6.5．∴拱桥的半径为6.5m．（2）∵CD＝4m，船舱顶部为长方形并高出水面3.4m，∴CE＝4﹣3.4＝0.6（m），∴OE＝r﹣CE＝6.5﹣0.6＝5.9（m），在Rt△OEN中，EN2＝ON2﹣OE2＝6.52﹣5.92＝7.44，∴EN m）．∴MN＝2EN＝2×≈5.4m＞5m．∴此货船能顺利通过这座拱桥．1．（2022•南海区校级一模）如图，武汉晴川桥可以近似地看作半径为250m的圆弧，桥拱和路面之间用数根钢索垂直相连，其正下方的路面AB长度为300m，那么这些钢索中最长的一根为（ ）A．50m B．45m C．40m D．60m【思路点拨】设圆弧的圆心为O，过O作OC⊥AB于C，交AB于D，连接OA，先由垂径定理得AC＝BC=12AB＝150，再由勾股定理求出OC＝200，然后求出CD的长即可．【解题过程】解：设圆弧的圆心为O，过O作OC⊥AB于C，交AB于D，连接OA，如图所示：则OA＝OD＝250，AC＝BC=12AB＝150，∴OC=200，∴CD＝OD﹣OC＝250﹣200＝50（m），即这些钢索中最长的一根为50m ，故选：A ．2．（2022•旌阳区二模）筒车是我国古代发明的一种水利灌溉工具，如图1，筒车盛水桶的运行轨道是以轴心O 为圆心的圆，如图2，已知圆心O 在水面上方，且⊙O 被水面截得弦AB 长为4米，⊙O 半径长为3米．若点C 为运行轨道的最低点，则点C 到弦AB 所在直线的距离是（ ）A ．1米B ．2米C ．米D ．(3+米【思路点拨】连接OC ，OC 交AB 于D ，由垂径定理得AD ＝BD =12AB ＝2（米），再由勾股定理得OD 后求出CD 的长即可．【解题过程】解：连接OC ，OC 交AB 于D ，由题意得：OA ＝OC ＝3米，OC ⊥AB ，∴AD ＝BD =12AB ＝2（米），∠ADO ＝90°，∴OD ==∴CD＝OC﹣OD＝（3即点C到弦AB所在直线的距离是（3故选：C．3．（2022•宣州区二模）如图所示的是一圆弧形拱门，其中路面AB＝2m，拱高CD＝3m，则该拱门的半径为（ ）A．53m B．2m C．83m D．3m【思路点拨】取圆心为O，连接OA，由垂径定理设⊙O的半径为rm，则OC＝OA＝rm，由拱高CD＝3m，OD＝（3﹣r）m，OD⊥AB，由垂径定理得出AD＝1m，由勾股定理得出方程r2＝12+（3﹣r）2，解得：r=53，得出该拱门的半径为53m，即可得出答案．【解题过程】解：如图，取圆心为O，连接OA，设⊙O的半径为rm，则OC＝OA＝rm，∵拱高CD＝3m，∴OD＝（3﹣r）m，OD⊥AB，∵AB＝2m，∴AD＝BD=12AB＝1m，∵OA2＝AD2+OD2，∴r2＝12+（3﹣r）2，解得：r=5 3，∴该拱门的半径为53 m，故选：A．4．（2021秋•海淀区校级期中）数学活动课上，同学们想测出一个残损轮子的半径，小的解决方案如下：如图，在轮子圆弧上任取两点A，B，连接AB，再作出AB的垂直平分线，交AB于点C，交AB于点D，测出AB，CD的长度，即可计算得出轮子的半径．现测出AB＝40cm，CD＝10cm，则轮子的半径为（ ）A．50cm B．35cm C．25cm D．20cm【思路点拨】由垂径定理，可得出BC的长；连接OB，在Rt△OBC中，可用半径OB表示出OC的长，进而可根据勾股定理求出得出轮子的半径，即可得出轮子的直径长．【解题过程】解：设圆心为O，连接OB．Rt△OBC中，BC=12AB＝20cm，根据勾股定理得：OC2+BC2＝OB2，即：（OB﹣10）2+202＝OB2，解得：OB＝25；故轮子的半径为25cm．故选：C．5．（2021秋•曾都区期中）在圆柱形油槽内装有一些油，油槽直径MN为10分米．截面如图，油面宽AB 为6分米，如果再注入一些油后，当油面宽变为8分米，油面AB上升（ ）A．1分米B．4分米C．3分米D．1分米或7分米【思路点拨】实质是求两条平行弦之间的距离．根据勾股定理求弦心距，作和或差分别求解．【解题过程】解：连接OA．作OG⊥AB于G，则在直角△OAG中，AG＝3分米，因为OA＝5cm，根据勾股定理得到：OG＝4分米，即弦AB的弦心距是4分米，同理当油面宽AB为8分米时，弦心距是3分米，当油面没超过圆心O时，油上升了1分米；当油面超过圆心O时，油上升了7分米．因而油上升了1分米或7分米．故选：D．6．（2021秋•宁波期末）把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF＝CD＝6cm，则球的半径为（ ）A．3cm B．134cm C．154cm D．174cm【思路点拨】设球的平面投影圆心为O，过点O作ON⊥AD于点N，延长NO交BC于点M，连接OF，由垂径定理得：NF＝EN=12EF＝3（cm），设OF＝xcm，则OM＝（4﹣x）cm，再在Rt△MOF中由勾股定理求得OF的长即可．【解题过程】解：设球的平面投影圆心为O，过点O作ON⊥AD于点N，延长NO交BC于点M，连接OF，如图所示：则NF＝EN=12EF＝3（cm），∵四边形ABCD是矩形，∴∠C＝∠D＝90°，∴四边形CDNM是矩形，∴MN＝CD＝6cm，设OF＝xcm，则OM＝OF，∴ON＝MN﹣OM＝（6﹣x）cm，在Rt△ONF中，由勾股定理得：ON2+NF2＝OF2，即：（6﹣x）2+32＝x2，解得：x=15 4，即球的半径长是154cm，故选：C．7．（2022•鄂州）工人师傅为检测该厂生产的一种铁球的大小是否符合要求，设计了一个如图（1）所示的工件槽，其两个底角均为90°，将形状规则的铁球放入槽内时，若同时具有图（1）所示的A、B、E三个接触点，该球的大小就符合要求．图（2）是过球心及A、B、E三点的截面示意图，已知⊙O的直径就是铁球的直径，AB是⊙O的弦，CD切⊙O于点E，AC⊥CD、BD⊥CD，若CD＝16cm，AC＝BD＝4cm，则这种铁球的直径为（ ）A ．10cmB ．15cmC ．20cmD ．24cm【思路点拨】连接OE ，交AB 于点F ，连接OA ，∵AC ⊥CD 、BD ⊥CD ，由矩形的判断方法得出四边形ACDB 是矩形，得出AB ∥CD ，AB ＝CD ＝16cm ，由切线的性质得出OE ⊥CD ，得出OE ⊥AB ，得出四边形EFBD 是矩形，AF =12AB =12×16＝8（cm ），进而得出EF ＝BD ＝4cm ，设⊙O 的半径为rcm ，则OA ＝rcm ，OF ＝OE ﹣EF ＝（r ﹣4）cm ，由勾股定理得出方程r 2＝82+（r ﹣4）2，解方程即可求出半径，继而求出这种铁球的直径．【解题过程】解：如图，连接OE ，交AB 于点F ，连接OA ，∵AC ⊥CD 、BD ⊥CD ，∴AC ∥BD ，∵AC ＝BD ＝4cm ，∴四边形ACDB 是平行四边形，∴四边形ACDB 是矩形，∴AB ∥CD ，AB ＝CD ＝16cm ，∵CD 切⊙O 于点E ，∴OE ⊥CD ，∴OE ⊥AB ，∴四边形EFBD 是矩形，AF =12AB =12×16＝8（cm ），∴EF ＝BD ＝4cm ，设⊙O 的半径为rcm ，则OA ＝rcm ，OF ＝OE ﹣EF ＝（r ﹣4）cm ，在Rt△AOF中，OA2＝AF2+OF2，∴r2＝82+（r﹣4）2，解得：r＝10，∴这种铁球的直径为20cm，故选：C．8．（2022•上海）如图所示，小区内有个圆形花坛O，点C在弦AB上，AC＝11，BC＝21，OC＝13，则这个花坛的面积为　400π　.（结果保留π）【思路点拨】根据垂径定理，勾股定理求出OB2，再根据圆面积的计算方法进行计算即可．【解题过程】解：如图，连接OB，过点O作OD⊥AB于D，∵OD⊥AB，OD过圆心，AB是弦，∴AD＝BD=12AB=12（AC+BC）=12×（11+21）＝16，∴CD＝BC﹣BD＝21﹣16＝5，在Rt△COD中，OD2＝OC2﹣CD2＝132﹣52＝144，在Rt△BOD中，OB2＝OD2+BD2＝144+256＝400，∴S⊙O＝π×OB2＝400π，故答案为：400π．9．（2021秋•溧水区期末）在一个残缺的圆形工件上量得弦BC＝8cm，BC的中点D到弦BC的距离DE＝2cm，则这个圆形工件的半径是　5　cm．【思路点拨】由垂径定理的推论得圆心在直线DE上，设圆心为0，连接OB，半径为R，再由垂径定理得BE＝CE=12 BC＝4（cm），然后由勾股定理得出方程，解方程即可．【解题过程】解：∵DE⊥BC，DE平分弧BC，∴圆心在直线DE上，设圆心为O，半径为Rcm，如图，连接OB，则OD⊥BC，OE＝R﹣DE＝（R﹣2）cm，∴BE＝CE=12BC＝4（cm），在Rt△OEB中，OB2＝BE2+OE2，即R2＝42+（R﹣2）2，解得：R＝5，即这个圆形工件的半径是5cm，故答案为：5．10．（2022•柯桥区一模）《九章算术》是中国传统数学重要的著作之一，奠定了中国传统数学的基本框架．其中卷九中记载了一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”其意思是：如图，AB为⊙O的直径，弦CD⊥AB于点E，BE＝1寸，CD＝1尺，那么直径AB的长为多少寸？（注：1尺＝10寸）根据题意，该圆的直径为　26　寸．【思路点拨】连接OC，由直径AB与弦CD垂直，根据垂径定理得到E为CD的中点，由CD的长求出DE的长，设OC ＝OA＝x寸，则AB＝2x寸，OE＝（x﹣1）寸，由勾股定理得出方程，解方程求出半径，即可得出直径AB 的长．【解题过程】解：连接OC，∵弦CD⊥AB，AB为圆O的直径，∴E为CD的中点，又∵CD＝10寸，∴CE＝DE=12CD＝5寸，设OC＝OA＝x寸，则AB＝2x寸，OE＝（x﹣1）寸，由勾股定理得：OE2+CE2＝OC2，即（x﹣1）2+52＝x2，解得x＝13，∴AB＝26寸，即直径AB的长为26寸，故答案为：26．11．（2021秋•瑞安市期末）某公路上有一隧道，顶部是圆弧形拱顶，圆心为O，隧道的水平宽AB为24m，AB离地面的高度AE＝10 m，拱顶最高处C离地面的高度CD为18m，在拱顶的M，N处安装照明灯，且M，N离地面的高度相等都等于17m，则MN＝　10　m．【思路点拨】根据题意和垂径定理得到CG＝8m，AG＝12m，CH＝1m，根据勾股定理求得半径，进而利用勾股定理求得MH，即可求得MN．【解题过程】解：设CD于AB交于G，与MN交于H，∵CD＝18m，AE＝10m，AB＝24m，HD＝17m，∴CG＝8m，AG＝12m，CH＝1m，设圆拱的半径为r，在Rt△AOG中，OA2＝OG2+AG2，∴r2＝（r﹣8）2+122，解得r＝13，∴OC＝13m，∴OH＝13﹣1＝12m，在Rt△MOH中，OM2＝OH2+MH2，∴132＝122+MH2，解得MH2＝25，∴MH＝5m，∴MN＝10m，故答案为10．12．（2022•荆州）如图，将一个球放置在圆柱形玻璃瓶上，测得瓶高AB＝20cm，底面直径BC＝12cm，球的最高点到瓶底面的距离为32cm，则球的半径为　7.5　cm（玻璃瓶厚度忽略不计）．【思路点拨】设球心为O，过O作OM⊥AD于M，连接OA，设球的半径为rcm，由垂径定理得AM＝DM=12AD＝6（cm）然后在Rt△OAM中，由勾股定理得出方程，解方程即可．【解题过程】解：如图，设球心为O，过O作OM⊥AD于M，连接OA，设球的半径为rcm，由题意得：AD＝12cm，OM＝32﹣20﹣r＝（12﹣r）（cm），由垂径定理得：AM＝DM=12AD＝6（cm），在Rt△OAM中，由勾股定理得：AM2+OM2＝OA2，即62+（12﹣r）2＝r2，解得：r＝7.5，即球的半径为7.5cm，故答案为：7.5．13．（2021秋•温州校级月考）如图是郑州圆形“戒指桥”，其数学模型为如图所示．已知桥面跨径AB＝20米，D为圆上一点，DC⊥AB于点C，且CD＝BC＝14米，则该圆的半径长为　26　米．【思路点拨】过O作ON⊥AB于N，过D作DM⊥ON于M，由垂径定理得AN＝BN=12AB＝10（米），再证四边形DCNM是矩形，则MN＝CD＝14米，DM＝CN＝BC+BN＝24（米），设该圆的半径长为r米，然后由题意列出方程组，解方程组即可．【解题过程】解：过O作ON⊥AB于N，过D作DM⊥ON于M，如图所示：则AN＝BN=12AB＝10（米），∠ONC＝∠DMN＝90°，∵DC⊥AB，∴∠DCN＝90°，∴四边形DCNM是矩形，∴MN＝CD＝14米，DM＝CN＝BC+BN＝24（米），设该圆的半径长为r米，由题意得：ON2=r2−102 OM2=r2−242 OM=ON−14，解得：r=26ON=24 OM=10，即该圆的半径长为26米，故答案为：26．14．（2021秋•金安区校级期末）往直径为680mm的圆柱形油槽内装入一些油以后，截面如图所示，若油面宽AB＝600mm，求油的最大深度．【思路点拨】连接OB，过点O作OC⊥AB于点D，交⊙O于点C，先由垂径定理求出BD的长，再根据勾股定理求出OD 的长，进而可得出CD的长．【解题过程】解：过点O作OC⊥AB于点D，交弧AB于点C．∵OC⊥AB于点D∴BD=12AB=12×600＝300mm，∵⊙O的直径为680mm∴OB＝340mm…（5分）∵在Rt△ODB中，OD=160（mm），∴DC＝OC﹣OD＝340﹣160＝180（mm）；答：油的最大深度为180mm．15．（2021秋•惠城区校级期中）如图，⊙O为水管横截面，水面宽AB＝24cm，水的最大深度为18cm，求⊙O的半径．【思路点拨】由垂径定理可知AD＝12cm，设⊙O的半径为rcm，则OD＝（18﹣r）cm，在Rt△AOd中，再利用勾股定理即可求出r的值．【解题过程】解：作OD⊥AB于D，交⊙O于E，连接OA，∴AD=12AB=12×24＝12cm，设⊙O的半径为rcm，则OD＝ED﹣OE＝（18﹣r）cm，在Rt△AOD中，由勾股定理得：OA2＝OD2+AD2，即r2＝（18﹣r）2+122，解得：r＝13，即⊙O的半径为13cm.16．（2021秋•奈曼旗期中）如图所示，测得AB是8mm，测得钢珠顶端离零件表面的距离为8mm，求这个圆的直径．【思路点拨】过O作OC⊥AB于C，交优弧AB于D，连接AO，由垂径定理得AC＝BC=12AB＝4（mm），设⊙O的半径为rmm，则OC＝CD﹣OD＝（8﹣r）mm，然后在Rt△AOC中，由勾股定理得出方程，解方程即可．【解题过程】解：如图，过O作OC⊥AB于C，交优弧AB于D，连接AO，则AC＝BC=12AB＝4（mm），CD＝8mm，设⊙O的半径为rmm，则OC＝CD﹣OD＝（8﹣r）mm，在Rt△AOC中，由勾股定理得：42+（8﹣r）2＝r2，解得：r＝5，即⊙O的半径为5mm，∴⊙O的直径为10mm．17．（2021秋•阜阳月考）《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就，它的算法体系至今仍在推动着计算机的发展和应用．书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（ED＝1寸），锯道长1尺（AB＝1尺＝10寸）．问这块圆形木材的直径（AC）是多少？”如图所示，请根据所学的知识解答上述问题．【思路点拨】设⊙O的半径为x寸．在Rt△ADO中，AD＝5寸，OD＝（x﹣1）寸，OA＝x寸，则有x2＝（x﹣1）2+52，解方程即可．【解题过程】解：设⊙O的半径为x寸，∵OE⊥AB，AB＝10寸，∴AD＝BD=12AB＝5寸，在Rt△AOD中，OA＝x，OD＝x﹣1，由勾股定理得x2＝（x﹣1）2+52，解得x＝13，∴⊙O的直径AC＝2x＝26（寸），答：这块圆形木材的直径（AC）是26寸．18．（2021秋•高新区期中）某居民小区的一处圆柱形的输水管道破裂，维修人员为更换管道，需要确定管道圆形截面的半径，如图是水平放置的破裂管道有水部分的截面．（1）请你补全这个输水管道的圆形截面图；（要求尺规作图，保留作图痕迹，不写作法）（2）若这个输水管道有水部分的水面宽AB＝32cm，水最深处的地方高度为8cm，求这个圆形截面的半径．【思路点拨】（1）根据尺规作图的步骤和方法做出图即可；（2）先过圆心O作半径OD⊥AB，交AB于点D，设半径为r，得出AD、OD的长，在Rt△AOD中，根据勾股定理求出这个圆形截面的半径．【解题过程】解：（1）如图所示；（2）作OD⊥AB于D，并延长交⊙O于C，则D为AB的中点，∵AB＝32cm，∴AD=12AB＝16．设这个圆形截面的半径为xcm，又∵CD＝8cm，∴OC＝x﹣8，在Rt△OAD中，∵OD2+AD2＝OA2，即（x﹣8）2+162＝x2，解得，x＝20．∴圆形截面的半径为20cm．19．（2021秋•黔西南州期末）如图，在一座圆弧形拱桥，它的跨度AB为60m，拱高PM为18m，当洪水泛滥到跨度只有30m时，就要采取紧急措施，若某次洪水中，拱顶离水面只有4m，即PN＝4m时，试通过计算说明是否需要采取紧急措施．【思路点拨】由垂径定理可知AM＝BM、A′N＝B′N，利用AB＝60，PM＝18，可先求得圆弧所在圆的半径，再计算当PN ＝4时A′B′的长度，与30米进行比较大小即可．【解题过程】解：设圆弧所在圆的圆心为O，连接OA、OA′，设半径为x米，则OA＝OA′＝OP，由垂径定理可知AM＝BM，A′N＝B′N，∵AB＝60米，∴AM＝30米，且OM＝OP﹣PM＝（x﹣18）米，在Rt△AOM中，由勾股定理可得AO2＝OM2+AM2，即x2＝（x﹣18）2+302，解得x＝34，∴ON＝OP﹣PN＝34﹣4＝30（米），在Rt△A′ON中，由勾股定理可得A′N=16（米），∴A′B′＝32米＞30米，∴不需要采取紧急措施．20．（2021秋•余干县期中）如图是某蔬菜基地搭建一座圆弧型蔬菜棚，跨度AB＝3.2米，拱高CD＝0.8米（C为AB的中点，D为弧AB的中点）．（1）求该圆弧所在圆的半径；（2）在距蔬菜棚的一端0.4米处竖立支撑杆EF，求支撑杆EF的高度．【思路点拨】（1）设弧AB所在的圆心为O，D为弧AB的中点，CD⊥AB于C，延长DC至O点，设⊙O的半径为R，利用勾股定理求出即可；（2）利用垂径定理以及勾股定理得出HF的长，再求出EF的长即可．【解题过程】解：（1）设弧AB所在的圆心为O，D为弧AB的中点，CD⊥AB于C，延长DC经过O点，则BC=12AB＝1.6（米），设⊙O的半径为R，在Rt△OBC中，OB2＝OC2+CB2，∴R2＝（R﹣0.8）2+1.62，解得R＝2，即该圆弧所在圆的半径为2米；（2）过O作OH⊥FE于H，则OH＝CE＝1.6﹣0.4＝1.2=65（米），OF＝2米，在Rt△OHF中，HF== 1.6（米），∵HE＝OC＝OD﹣CD＝2﹣0.8＝1.2（米），∴EF＝HF﹣HE＝1.6﹣1.2＝0.4（米），即支撑杆EF的高度为0.4米．21．如图①，圆形拱门屏风是中国古代家庭中常见的装饰隔断，既美观又实用，彰显出中国元素的韵味．图②是一款拱门的示意图，其中C为AB中点，D为拱门最高点，线段CD经过圆心，已知拱门的半径为1.5m，拱门最下端AB＝1.8m．（1）求拱门最高点D到地面的距离；（2）现需要给房间内搬进一个长和宽为2m，高为1.2m的桌子，已知搬桌子的两名工人在搬运时所抬高度相同，且高度为0.5m 2.236）【思路点拨】（1）如图②中，连接AO．利用勾股定理求出OC即可；（2）如图②﹣1，弦EF＝2m，且EF⊥CD，连接OE．求出CJ即可．【解题过程】解：（1）如图②中，连接AO．∵CD⊥AB，CD经过圆心O，∴AC＝CB＝0.9m，∴OC= 1.2（m），∴CD＝OD+PC＝1.5+1.2＝2.7（m），∴拱门最高点D到地面的距离为2.7m；（2）如图②﹣1，弦EF＝2m，且EF⊥CD，连接OE．∵CD⊥EF，CD经过圆心，∴EJ＝JF＝1m，≈1.118，∴OJ=2∴CJ＝1.2﹣1.118＝0.082（m），∵0.5＞0.082，∴搬运该桌子时能够通过拱门．22．（2021秋•姑苏区校级月考）诗句“君到姑苏见，人家尽枕河”所描绘的就是有东方威尼斯之称的水城苏州．小勇要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥，现测得桥下水面AB宽度16m时，拱顶高出水平面4m，货船宽12m，船舱顶部为矩形并高出水面3m．（1）请你帮助小勇求此圆弧形拱桥的半径；（2）小勇在解决这个问题时遇到困难，请你判断一下，此货船能顺利通过这座拱桥吗？说说你的理由．【思路点拨】（1）根据垂径定理和勾股定理求解；（2）连接ON，利用勾股定理求出EN，得出MN的长，即可得到结论．【解题过程】解：（1）如图，连接OB．∵OC⊥AB，∴D为AB中点，∵AB＝16m，∴BD=12AB＝8（m），又∵CD＝4m，设OB＝OC＝r，则OD＝（r﹣4）m．在Rt△BOD中，根据勾股定理得：r2＝（r﹣4）2+82，解得r＝10．答：此圆弧形拱桥的半径为10m．（2）此货船不能顺利通过这座拱桥，理由如下：连接ON，∵CD＝4m，船舱顶部为长方形并高出水面3m，∴CE＝4﹣3＝1（m），∴OE＝r﹣CE＝10﹣1＝9（m），在Rt△OEN中，由勾股定理得：EN∴MN＝2EN＝＜12m．∴此货船B不能顺利通过这座拱桥．。

3.3 垂径定理同步训练2024-2025学年浙教版数学九年级上册一、单选题1．下列说法正确的是（）A．长度相等的弧叫等弧B．平分弦的直径一定垂直于该弦C．三角形的外心是三条角平分线的交点D．不在同一直线上的三个点确定一个圆2．点P是⊙O内一点，过点P的最长弦的长为10cm，最短弦的长为6cm，则OP的长为（）A．7cm B．5cm C．4cm D．3.5cm3．点P为⊙O内一点，且OP=4，若⊙O的半径为6，则过点P的弦长不可能为（）．A．12B．2√30C．8D．10.54．如图，这是一种用于液体蒸馏或分馏物质的玻璃容器——蒸馏瓶，其底部是圆球形．球的半径为5cm，瓶内液体的最大深度CD=3cm，则截面圆中弦AB的长为（）A．√34cm B．8cm C．√21cm D．2√21cm 5．下列说法正确的数量为（）（1）三角形的外心到三角形三顶点距离相等（2）一组对边平行的四边形是梯形（3）垂直平分弦的直径垂直平分弦所对的弧A．0B．1C．2D．36．⊙O的直径是15cm，CD经过圆心O，与⊙O交于C、D两点，垂直弦AB于M，且OM：OC=3 ：5，则AB=（）A．24cm B．12cm C．6cm D．3cm7．已知⊙O的半径为2cm，弦AB长为2cm，则这条弦的中点到弦所对优弧中点的距离为()A．2cm B．√3cm C．(2－√3)cm D．(2＋√3)cm 8．如图，在⊙O中，直径CD垂直弦AB，连接OA，CB，已知⊙O的半径为2√3，AB＝2，则⊙BCD等于A．20°B．30°C．60°D．70°二、填空题9．《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著，与古希腊的《几何原本》并称现代数学的两大源泉．在《九章算术》中记载有一问题“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何？”小辉同学根据原文题意，画出圆材截面图如图所示，已知：锯口深为1寸，锯道AB=1尺（1尺＝10寸），则该圆材的直径为寸．10．一圆柱形排水管的截面如图所示，已知排水管的半径为1m，水面宽AB为1.6m．由于天气干燥，水管水面下降，此时排水管水面宽变为1.2m，则水面下降了m．第1页共6页◎第2页共6页11．如图，AB是⊙O的弦，半径OC⊙AB，AC⊙OB，则⊙BOC的度数为．12．如图，AB为⊙O的弦，半径OC⊥AB，垂足为点D．如果AB=10cm，CD=3cm，那么⊙O的半径是cm．13．如图，C、D是以AB为直径的⊙O上的两个动点（点C、D不与A、B重合），在运动过程中，弦CD的长度始终保持不变，点M是弦CD的中点，过点C作CP⊥AB于点P.若CD=3，AB=5，则PM的最大值是 .三、解答题14．估计如图中三段弧的半径的大小关系，再用圆规检验你的结论．15．如图，是一个高速公路的隧道的横截面，若它的形状是以O为圆心的圆的一部分，路面AB=12米，拱高CD=9米，求圆的半径．16．如图，某储藏室入口的截面是一个半径为1.2米的半圆形，一个长、宽、高分别是1.2m，1m，0.8m的箱子能放进储藏室吗？请说明理由．17．如图，在△ABC中，已知⊙ACB=130°，⊙BAC=20°，BC=2，以点C为圆心，CB 为半径的圆交AB于点D，求弦BD的长18．如图，要把破残的圆片复制完整，已知弧上的三点A、B、C．(1)用尺规作图法，找出弧BC所在圆的圆心O（保留作图痕迹，不写作法）；第3页共6页◎第4页共6页(2)设△ABC是等腰三角形，底边BC=24cm，腰AB=13cm，求圆片的半径R．第5页共6页◎第6页共6页。

九年级数学：垂径定理练习(第2课时)（含答案）1．平分弦(____________)的直径垂直于弦,并且平分弦所对的弧．2．平分弧的直径垂直平分弧所对的弦．3．垂径定理解读：(1)过圆心；(2)平分弦(不是直径)；(3)垂直于弦；(4)平分弦所对的优弧；(5)平分弦所对的劣弧．若一条直线具备这五项中任意两项,则必具备另外三项．A组基础训练1．下列命题正确的有( )①垂直于弦的直径平分弦②平分弦的直径必垂直于弦,并且平分弦所对的两条弧③平分弦的直线必过圆心④弦所对的两条弧的中点连线垂直平分弦A．1个 B．2个 C．3个 D．4个2．如图,⊙O的弦AB＝8,M是AB的中点,且OM＝3,则⊙O的半径等于( )A．8 B．2 C．10 D．5第2题图3．如图,已知⊙O的半径为2cm,弦AB长23cm,则这条弦的中点C到弦所对劣弧的中点D 的距离为( )第3题图A ．1cmB ．2cm C.2cm D.3cm4．如图,一条公路弯道处是一段圆弧AB ︵,点O 是这条弧所在圆的圆心,C 是AB ︵的中点,OC 与AB 相交于点D.已知AB ＝120m ,CD ＝20m ,那么这段弯道的半径为( )第4题图A ．200mB ．2003mC ．100mD ．1003m5．如图,AB 为⊙O 的直径,CD 是弦,AB 与CD 相交于点E.若要得到结论AB⊥CD ,还需添加的条件是________________________________．(不添加其他辅助线)第5题图6.如图,AB ,CD 是⊙O 的直径,D 是AE ︵的中点,AE 与CD 交于点F ,若OF ＝3,则BE 的长为________．第6题图7．如图所示,AB 是半圆的直径,O 是圆心,C 是半圆上一点,E 是AC ︵的中点,OE 交弦AC 于点D.若AC ＝8cm ,DE ＝2cm ,则OD 的长为________．第7题图8.如图,在平面直角坐标系中,点A 的坐标是(10,0),点B 的坐标为(8,0),点C 、D 在以OA 为直径的半圆M 上,且四边形OCDB 是平行四边形,则点C 的坐标为________．第8题图9．如图,⊙O是△ABC的外接圆,且AB＝AC＝13,BC＝24,求⊙O的半径．第9题图10．(绍兴中考)如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB＝40cm,脸盆的最低点C到AB的距离为10cm,求该脸盆的半径．第10题图B组自主提高11．如图所示,某游乐场的摩天轮⊙P的最高处A到地面l的距离是23m,最低处B到地面l的距离是3m,从B处乘摩天轮绕一周需3分钟,小明从B处乘摩天轮一周的过程中,当他到地面l的距离恰好是18m的时候应为第________分钟．第11题图11．如图,AB ,CD 是半径为5的⊙O 的两条弦,AB ＝8,CD ＝6,MN 是直径,AB ⊥MN 于点E ,CD ⊥MN 于点F ,P 为EF 上的任意一点,则PA ＋PC 的最小值为________．第12题图13．已知：如图,A 、B 、C 为⊙O 上三点,点D 、E 分别为AB ︵、AC ︵的中点,连结DE ,分别交AB 、AC 于点F 、G ,求证：AF ＝AG.第13题图C 组 综合运用14．如图,隧道的截面由圆弧AED 和矩形ABCD 构成,矩形的长BC 为12m ,宽AB 为3m ,隧道的顶端E (圆弧AED 的中点)高出道路(BC )7m.(1)求圆弧AED 所在圆的半径；(2)如果该隧道内设双行道,现有一辆超高货运卡车高6.5m ,宽2.3m ,问这辆货运卡车能否通过该隧道．第14题图3．3 垂径定理(第2课时)【课堂笔记】1．不是直径【课时训练】1－4.BDAC5．CE ＝DE 或AC ︵＝AD ︵或BC ︵＝BD ︵6．67．3cm8．(1,3)9．连结OA 交BC 于点D,连结OC,OB,∵AB ＝AC ＝13,∴AB ︵＝AC ︵,∴∠AOB ＝∠AOC ,∵OB ＝OC,∴AO ⊥BC,CD ＝12BC ＝12.在Rt △ACD 中,AC ＝13,CD ＝12,所以AD ＝132－122＝5,设⊙O 的半径为r,则在Rt △OCD 中,OD ＝r －5,CD ＝12,OC ＝r,所以(r －5)2＋122＝r 2,计算得出r ＝16.9.答：⊙O 的半径为16.9.第10题图10．如图,设圆的圆心为O,连结OA,OC,OC 与AB 交于点D,设⊙O 半径为R,∵OC ⊥AB,∴AD ＝DB ＝12AB ＝20,∠ADO ＝90°,在Rt △AOD 中,∵OA 2＝OD 2＋AD 2,∴R 2＝202＋(R －10)2,∴R ＝25,即该脸盆的半径为25cm.11．1或212．7 2第13题图13．连OD、OE,交AB、AC于M、N,∵OD＝OE＝r,∴∠ODE＝∠OED,而D,E分别为弧AB,弧AC的中点,∴OD、OE分别垂直于AB、AC,则有∠DFB＝∠EGC,∴∠AFG＝∠AGF,∴AF＝AG.14．(1)设圆心为点O,半径为R,连结OE交AD于F点,连结OA,OD,由垂径定理,得OF垂直平分AD,AF＝6,OF＝R－(7－3)＝R－4,由勾股定理,得AF2＋OF2＝OA2,即：62＋(R－4)2＝R2,解得R＝6.5米；(2)能通过,但要小心．车宽GH＝2.3,圆的半径OH＝6.5,由勾股定理,得OG＝ 6.52－2.32≈6.08,G点与BC的距离为7－6.5＋6.08＝6.58＞6.5；能通过．第14题图。

专题24.1 垂径定理【典例1】如图，在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于C、D两点．（1）求证：AC＝BD；（2）连接OA、OC，若OA＝6，OC＝4，∠OCD＝60°，求AC的长．（1）过O作OH⊥CD于H，根据垂径定理得到CH＝DH，AH＝BH，即可得出结论；（2）过O作OH⊥CD于H，连接OD，由垂径定理得CH＝DH=12CD，再证△OCD是等边三角形，得CD＝OC＝4，则CH＝2，然后由勾股定理即可解决问题．（1）证明：过O作OH⊥CD于H，如图1所示：∵OH⊥CD，∴CH＝DH，AH＝BH，∴AH﹣CH＝BH﹣DH，∴AC＝BD；（2）解：过O作OH⊥CD于H，连接OD，如图2所示：则CH＝DH=12 CD，∵OC＝OD，∠OCD＝60°，∴△OCD是等边三角形，∴CD＝OC＝4，∴CH＝2，∴OH=∴AH∴AC＝AH﹣CH＝2．1．（2022•芜湖一模）已知⊙O的直径CD＝10，AB是⊙O的弦，AB＝8，且AB⊥CD，垂足为M，则AC 的长为（ ）A．B．C．D．【思路点拨】连接OA，由AB⊥CD，根据垂径定理得到AM＝4，再根据勾股定理计算出OM＝3，然后分类讨论：当如图1时，CM＝8；当如图2时，CM＝2，再利用勾股定理分别计算即可．【解题过程】解：连接OA，∵AB⊥CD，∴AM＝BM=12AB=12×8＝4，在Rt△OAM中，OA＝5，∴OM=3，当如图1时，CM＝OC+OM＝5+3＝8，在Rt△ACM中，AC=当如图2时，CM＝OC﹣OM＝5﹣3＝2，在Rt△ACM中，AC=故选：C．2．（2022春•江夏区校级月考）如图，在⊙O中，弦AB＝5，点C在AB上移动，连结OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为（ ）A．5B．2.5C．3D．2【思路点拨】连接OD，如图，利用勾股定理得到CD，利用垂线段最短得到当OC⊥AB时，OC最小，再求出CD即可．【解题过程】解：连接OD，如图，∵CD⊥OC，∴∠DCO＝90°，∴CD=当OC的值最小时，CD的值最大，而OC⊥AB时，OC最小，此时D、B两点重合，∴CD＝CB=12AB=12×5＝2.5，即CD的最大值为2.5，故选：B．3．（2022•山海关区一模）已知⊙O的直径CD＝10，CD与⊙O的弦AB垂直，垂足为M，且AM＝4.8，则直径CD上的点（包含端点）与A点的距离为整数的点有（ ）A．1个B．3个C．6个D．7个【思路点拨】利用勾股定理得出线段AD和AC的长，根据垂线段的性质结合图形判断即可．【解题过程】解：∵CD是直径，∴OC＝OD=12CD=12×10＝5，∵AB⊥CD，∴∠AMC＝∠AMD＝90°，∵AM＝4.8，∴OM==1.4，∴CM＝5+1.4＝6.4，MD＝5﹣1.4＝3.6，∴AC=8，AD=6，∵AM＝4.8，∴A点到线段MD的最小距离为4.8，最大距离为6，则A点到线段MD的整数距离有5，6，A点到线段MC的最小距离为4.8，最大距离为8，则A点到线段MC的整数距离有5，6，7，8，直径CD上的点（包含端点）与A点的距离为整数的点有6个，故选：C．4．（2022•博山区一模）如图，在平面直角坐标系中，半径为5的⊙E与y轴交于点A（0，﹣2），B（0，4），与x轴交于C，D，则点D的坐标为（ ）A．0)B．(−4+0)C．(−40)D．0)【思路点拨】过O点作EH⊥AB于H，EF⊥CD于F，连接ED，如图，根据垂径定理得到CF＝DF，AH＝BH＝3，所以OH＝1，再利用勾股定理计算出EH＝4，则EF＝1，OF＝4，接着利用勾股定理计算出FD，然后计算出OD，从而得到D点坐标．【解题过程】解：过O点作EH⊥AB于H，EF⊥CD于F，连接ED，如图，则CF＝DF，AH＝BH∵A（0，﹣2），B（0，4），∴AB＝6，∴BH＝3，∴OH＝1，在Rt△BHE中，EH4，∵四边形EHOF为矩形，∴EF＝OH＝1，OF＝EH＝4，在Rt△OEF中，FD==∴OD＝FD﹣OF＝4，∴D（4，0）．故选：B ．5．（2022•新洲区模拟）如图，点A ，C ，D 均在⊙O 上，点B 在⊙O 内，且AB ⊥BC 于点B ，BC ⊥CD 于点C ，若AB ＝4，BC ＝8，CD ＝2，则⊙O 的面积为（ ）A ．125π4B ．275π4C ．125π9D ．275π9【思路点拨】利用垂径定理和勾股定理建立方程求出ON ，再求出半径后，根据圆面积的计算方法进行计算即可．【解题过程】解：如图，连接OA 、OC ，过点O 作OM ⊥CD 于M ，MO 的延长线于AB 延长线交于N ，则四边形BCMN 是矩形，∵OM ⊥CD ，CD 是弦，∴CM ＝DM =12CD ＝1＝BN ，∴AN ＝AB +BN ＝4+1＝5，设ON ＝x ，则OM ＝8﹣x ，在Rt △AON 、Rt △COM 中，由勾股定理得，OA 2＝AN 2+ON 2，OC 2＝OM 2+CM 2，∵OA ＝OC ，∴AN 2+ON 2＝OM 2+CM 2，即52+x 2＝（8﹣x ）2+12，解得x =52，即ON =52，∴OA 2＝52+（52）2=1254，∴S⊙O＝π×OA2=1254π，故选：A．6．（2021秋•延平区校级期末）在Rt△ABC中，∠C＝90°，BC＝3，AC＝4，D、E分别是AC、BC上的一点，且DE＝3，若以DE为直径的圆与斜边AB相交于M、N，则MN的最大值为（ ）A．910B．65C．85D．125【思路点拨】由题意可知，C、O、G三点在一条直线上OG最小，MN最大，再由勾股定理求得AB，然后由三角形面积求得CF，最后由垂径定理和勾股定理即可求得MN的最大值．【解题过程】解：过O作OG⊥AB于G，连接OC、OM，∵DE＝3，∠ACB＝90°，OD＝OE，∴OC=12DE=32，只有C、O、G三点在一条直线上OG最小，∵OM=3 2，∴只有OG最小，GM才能最大，从而MN有最大值，过C作CF⊥AB于F，∴G和F重合时，MN有最大值，∵∠ACB＝90°，BC＝3，AC＝4，∴AB==5，∵12AC•BC=12AB•CF，∴CF=AC×BCAB=4×35=125，∴OG＝CF﹣OC=125−32=910，∴MG===6 5，∴MN＝2MG=12 5，故选：D．7．（2022•吴忠模拟）如图，AB是⊙O的直径，且CD⊥AB于E，若AE＝1，∠D＝30°，则AB＝　4　．【思路点拨】根据含30度角的直角三角形的性质求出AD，根据垂径定理求出AC=AD，求出AC＝AD＝2，根据圆周角定理求出∠ACB＝90°，∠B＝∠D＝30°，再根据含30度角的直角三角形的性质得出AB＝2AC即可．【解题过程】解：∵CD⊥AB，∴∠AED＝90°，∵AE＝1，∠D＝30°，∴AD＝2AE＝2，∠ABC＝∠D＝30°，∵AB⊥CD，AB过圆心O，∴AC=AD，∴AC＝AD＝2，∵AB是⊙O的直径，∴∠ACB＝90°，∴AB＝2AC＝2×2＝4，故答案为：4．8．（2022•烟台模拟）如图，AB是⊙O的直径，弦CD交AB于点P，AP＝4，BP＝12，∠APC＝30°，则CD的长为【思路点拨】过O作OI⊥CD于I，连接OD，求出半径OD＝OA＝8，求出OP，根据含30度角的直角三角形的性质求出OI，根据勾股定理求出DI，根据垂径定理求出DI＝CI，再求出CD即可．【解题过程】解：过O作OI⊥CD于I，连接OD，则∠OID＝∠OIP＝90°，∵AP＝4，BP＝12，∴直径AB＝4+12＝16，即半径OD＝OA＝8，∴OP＝OA﹣AP＝8﹣4＝4，∵∠IPO＝∠APC＝30°，∴OI=12OP=12×4=2，由勾股定理得：DI==∵OI⊥CD，OI过圆心O，∴DI＝CI＝即CD＝DI+CI＝故答案为：9．（2022•桥西区校级模拟）如图，AB是⊙C的弦，直径MN⊥AB于点O，MN＝10，AB＝8，如图以O为原点建立坐标系．我们把横纵坐标都是整数的点叫做整数点，则线段OC长是　3　，⊙C上的整数点有　12　个．【思路点拨】过C作直径UL∥x轴，连接AC，根据垂径定理求出AO＝BO＝4，根据勾股定理求出OC，再得出答案即可．【解题过程】解：过C作直径UL∥x轴，连接CA，则AC=12×10＝5，∵MN过圆心C，MN⊥AB，AB＝8，∴AO＝BO＝4，∠AOC＝90°，由勾股定理得：CO3，∴ON＝5﹣3＝2，OM＝5+3＝8，即A（﹣4，0），B（4，0），M（0，8），N（0，﹣2），同理还有弦QR＝AB＝8，弦WE＝TS＝6，且WE、TS、QR都平行于x轴，Q（﹣4，6），R（4，6），W（﹣3，7），E（3，7），T（﹣3，﹣1），S（3，﹣1），U（﹣5，3），L （5，3），即共12个点，故答案为：3；12．10．（2022•商城县三模）如图所示的网格中，每个小正方形的边长均为1，点A、B、C均在小正方形的顶点上，点C 同时也在AB 上，若点P 是BC 的一个动点，则△ABP 面积的最大值是 −8　．【思路点拨】作AB 的垂直平分线交AB 于D ，交AB 于E ，圆心为0，则点O 在DE 上，连接AE 、BE ，CF ⊥OE 于F ，如图，设⊙O 的半径为r ，OD ＝x ，利用勾股定理得到r 2＝x 2+42①，r 2＝（x +2）2+22②，则利用②﹣①可求出得x ＝2，所以r ＝DE ＝2，然后根据三角形面积公式，点P 点与点E 重合时，△ABP 面积的最大值．【解题过程】解：作AB 的垂直平分线交AB 于D ，交AB 于E ，圆心为0，则点O 在DE 上，连接AE 、BE ，CF ⊥OE 于F ，如图，设⊙O 的半径为r ，OD ＝x ，在Rt △BOD 中，r 2＝x 2+42①，在Rt △OCF 中，r 2＝（x +2）2+22②，②﹣①得4+4x +4﹣16＝0，解得x ＝2，∴OD ＝2，∴r =∴DE ＝OE ﹣OD ＝2，∵点P 是BC 的一个动点，∴点P 点与点E 重合时，△ABP 面积的最大值，最大值为12×8×（2）＝8．故答案为：8．11．（2022春•徐汇区校级期中）如图，AB是⊙O的弦，D为半径OA的中点，过D作CD⊥OA交弦AB于点E，且CE＝CB，若BE＝2AE，CD＝5，那么⊙O的半径为【思路点拨】先证明△AFO和△BCE是等边三角形，设DE＝x，根据CD＝5列方程，求出x得到AD【解题过程】解：如图，记DC与⊙O交于点F，连接AF、OF、OB，过点C作CT⊥AB于点T，连接OE，OT．∵D为半径OA的中点，CD⊥OA，∴FD垂直平分AO，∴FA＝FO，又∵OA＝OF，∴△AOF是等边三角形，∴∠OAF＝∠AOF＝∠AFO＝60°，∵CE＝CB，CT⊥EB，∴ET＝TB，∵BE＝2AE，∴AE＝ET＝BT，∵AD＝OD，∴DE∥OT，∴∠AOT＝∠ADE＝90°，∴OE＝AE＝ET，∵OA＝OB，∴∠OAE＝∠OBT，∵AO＝BO，AE＝BT，∴△AOE≌△BOT（SAS），∴OE＝OT，∴OE＝OT＝ET，∴∠ETO＝60°，∴∠OAB＝∠OBA＝30°，∠AED＝∠CEB＝60°，∴△CEB是等边三角形，∴CE＝CB＝BE，设DE＝x，∴AE＝2x，BE＝CE＝4x，∴CD＝5x＝5，∴x＝1，∴AD∴AO＝故答案为：12．（2022•盐城）证明：垂直于弦AB的直径CD平分弦以及弦所对的两条弧．【思路点拨】先根据已知画图，然后写出已知和求证，再进行证明即可．【解题过程】如图，CD为⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为M．求证：AM＝BM，AC=BC，AD=BD．证明：连接OA、OB，∵OA＝OB，∴△OAB是等腰三角形，∵AB⊥CD，∴AM＝BM，∠AOC＝∠BOC，∴AC=BC，AD=BD．13．（2021秋•鼓楼区校级期末）如图，AB是⊙O的直径，弦CD⊥AB于点E，若BE＝5，CD＝6，求AE 的长．【思路点拨】根据垂径定理和勾股定理求出圆的半径，进而求出AE的长即可．【解题过程】解：如图，连接OC，∵CD⊥AB，AB是直径，∴CE＝DE=12CD＝3，在Rt△COE中，设半径为r，则OE＝5﹣r，OC＝r，由勾股定理得，OE2+CE2＝OC2，即（5﹣r）2+32＝r2，解得r ＝3.4，∴AE ＝AB ﹣BE ＝3.4×2﹣5＝1.8，答：AE 的长为1.8．14．（2021秋•芜湖月考）如图，在△ABC 中AB ＝5，AC ＝4，BC ＝2，以A 为圆心，AB 为半径作⊙A ，延长BC 交⊙A 于点D ，试求CD 的长．【思路点拨】过点A 作AE ⊥BD 于点E ，如图，则DE ＝BE ，利用双勾股得到AC 2﹣CE 2＝AB 2﹣BE 2，即42﹣（BE ﹣2）2＝52﹣BE 2，解方程得到BE =134，然后计算BD ﹣BC 即可．【解题过程】解：过点A 作AE ⊥BD 于点E ，连接AD ，如图，则DE ＝BE ，在Rt △ACE 中，AE 2＝AC 2﹣CE 2，在Rt △ABE 中，AE 2＝AB 2﹣BE 2，∴AC 2﹣CE 2＝AB 2﹣BE 2，即42﹣（BE ﹣2）2＝52﹣BE 2，解得BE =134，∴CD ＝BD ﹣BC ＝2BE ﹣2＝2×134−2=92．答：CD 的长为92．15．（2022•江西开学）如图，在⊙O 中，弦AB ∥CD ，AB ＝8，CD ＝6，AB ，CD 之间的距离为1．（1）求圆的半径．（2）将弦AB 绕着圆心O 旋转一周，求弦AB 扫过的面积．【思路点拨】（1）过点O作OF⊥CD于点F，交AB于点E，连接OA、OD，即可得出DF＝CF＝3，再因为AB∥CD，则可得到OE⊥AB，进而得到AE＝BE＝4，最后根据勾股定理计算即可；（2）先判断出将弦AB绕着圆心O旋转一周，得到的图形，再根据圆面积公式计算即可．【解题过程】解：（1）如图，过点O作OF⊥CD于点F，交AB于点E，连接OA、OD，则DF＝CF＝3，∵AB∥CD，∴OE⊥AB，∴AE＝BE＝4，设OE＝x，则OF＝x+1，根据题意可得：x2+42＝（x+1）2+32，∴x＝3，∴=5；（2）将弦AB绕着圆心O旋转一周，得到的图形是以点O为圆心，以3为半径的圆与以5为半径的圆所围成的环形，故弦AB扫过的面积为π×52﹣π×32＝16π．16．（2021秋•玄武区校级月考）如图，AB是⊙O直径，弦CD⊥AB于点E，过点C作DB的垂线，交AB 的延长线于点G，垂足为点F，连结AC．（1）求证：AC＝CG；（2）若CD＝EG＝8，求⊙O的半径．【思路点拨】（1）利用等角的余角证明∠D＝∠G，再根据圆周角定理得到∠A＝∠D，所以∠A＝∠G，从而得到结论；（2）连接OC，如图，设⊙O的半径为r，根据等腰三角形的性质和垂径定理得到AE＝EG＝8，EC＝ED＝4，则OE＝8﹣r，利用勾股定理得r2＝（8﹣r）2+42，然后解方程即可．【解题过程】（1）证明：∵DF⊥CG，CD⊥AB，∴∠DEB＝∠BFG＝90°，∵∠DBE＝∠GBF，∴∠D＝∠G，∵∠A＝∠D，∴∠A＝∠G，∴AC＝CG；（2）解：连接OC，如图，设⊙O的半径为r．∵CA＝CG，CD⊥AB，∴AE＝EG＝8，EC＝ED＝4，∴OE＝AE﹣OA＝8﹣r，在Rt△OEC中，∵OC2＝OE2+EC2，∴r2＝（8﹣r）2+42，解得r＝5，∴⊙O的半径为5．17．（2022•白云区二模）已知：如图，A，B是半圆O上的两点，CD是⊙O的直径，∠AOD＝80°，B是AD 的中点．（1）在CD上求作一点P，使得AP+PB最短；（2）若CD＝4cm，求AP+PB的最小值．【思路点拨】（1）作出B关于CD的对称点B′，连接AB′，交CD于P点，P就是所求的点；（2）延长AO交圆与E，连接OB′，B′E，可以根据圆周角定理求得∠AOB′的度数，根据等腰三角形的性质求得∠A的度数，然后在直角△AEB′中，解直角三角形即可求解．【解题过程】解：（1）作BB′⊥CD，交圆于B′，然后连接AB′，交CD于P点，P就是所求的点；（2）延长AO交圆于E，连接OB′，B′E．∵BB′⊥CD∴BD=B′D，∵∠AOD＝80°，B是AD的中点，∴∠DOB′=12∠AOD＝40°．∴∠AOB′＝∠AOD+∠DOB′＝120°，又∵OA＝OB′，∴∠A=180°−∠AOB′2=30°．∵AE是圆的直径，∴∠AB′E＝90°，∴直角△AEB′中，B′E=12AE=12×4＝2，∴AB′=．18．（2022•中山市模拟）已知：如图，在⊙O中，AB、AC为互相垂直的两条弦，OD⊥AB，OE⊥AC，D、E 为垂足．（1）若AB＝AC，求证：四边形ADOE为正方形．（2）若AB＞AC，判断OD与OE的大小关系，并证明你的结论．【思路点拨】（1）连接OA，根据垂径定理得出AE＝CE，AD＝BD，根据AB＝AC求出AE＝AD，再根据矩形的判定和正方形的判定推出即可；（2）根据勾股定理得出OE2＝OA2﹣AE2，OD2＝OA2﹣AD2，根据AB＞AC求出AD＞AE，再得出答案即可．【解题过程】（1）证明：连接OA，∵OD⊥AB，OE⊥AC，OD和OE都过圆心O，∴∠OEA＝∠ODA＝90°，AE＝CE，AD＝BD，∵AC＝AB，∴AE＝AD，∵AB、AC为互相垂直的两条弦，∴∠EAD＝90°，即∠OEA＝∠EAD＝∠ODA＝90°，∴四边形EADO是正方形（有一组邻边相等的矩形是正方形）；（2）解：OD＜OE，证明：∵AB＞AC，AE＝CE，AD＝BD，∴AD＞AE，在Rt△ODA和Rt△OEA中，由勾股定理得：OE2＝OA2﹣AE2，OD2＝OA2﹣AD2，∴OD2＜OE2，即OD＜OE．19．（2022•全椒县一模）如图，⊙O中两条互相垂直的弦AB，CD交于点E．（1）OM⊥CD于点M，CD＝24，⊙O的半径长为OM的长．（2）点G在BD上，且AG⊥BD交CD于点F，求证：CE＝EF．【思路点拨】（1）连接OD，由垂径定理和勾股定理可得答案；（2）连接AC，由垂直的定义及等腰三角形的性质可得结论．【解题过程】（1）解：如图，连接OD，∵OM⊥CD，OM过圆心，CD＝24，∴DM＝CM=12CD＝12，∠OMD＝90°，由勾股定理得，OM=4，即OM的长为4；（2）证明：如图，连接AC，∵AG⊥BD，∴∠DGF＝90°，∴∠DFG+∠D＝90°，∵AB⊥CD，∴∠CEA＝90°，∴∠C+∠EAC＝90°，∵∠EAC＝∠D，∠DFG＝∠AFC，∴∠C＝∠AFC，∴AF＝AC，∵AB⊥CD，∴CE＝EF．20．（2022•合肥模拟）如图，在⊙O中，AB，AC为弦，CD为直径，AB⊥CD于E，BF⊥AC于F，BF与CD相交于G．（1）求证：ED＝EG；（2）若AB＝8，OG＝1，求⊙O的半径．【思路点拨】（1）连接BD，容易得到∠GBE和∠DBE相等，利用ASA证明△BGE和△BDE全等即可；（2）连接OA，设OA＝r，则DG＝r+1，根据ED＝EG容易求出OE=r−12，再根据垂径定理求出AE的值，最后在Rt△OAE中根据勾股定理求出r的值即可．【解题过程】（1）证明：如图：连接BD，∵AB⊥CD于E，BF⊥AC于F，∴∠CFG＝∠GEB，∵∠CGF＝∠BGE，∴∠C＝∠GBE，∵∠C＝∠DBE，∴∠GBE＝∠DBE，∵AB⊥CD于E，∴∠GEB＝∠DEB，在△GBE和△DBE中，∠GEB=∠DEBBE=BE∠GBE=∠DBE，∴△BGE≌△BDE（ASA），∴ED＝EG．（2）解：如图：连接OA，设OA＝r，则DG＝r+1，由（1）可知ED＝EG，∴OE=r−1 2，∵AB⊥CD于E，AB＝8，∴AE＝BE＝4，∴在Rt△OAE中，根据勾股定理得：OE2+AE2＝OA2，即（r−12）2+42＝r2，解得：r=13 3，即⊙O的半径为13 3．21．（2021•遵义一模）在《折叠圆形纸片》综合实践课上，小东同学展示了如下的操作及问题：（1）如图1，⊙O1的半径为4cm，通过折叠圆形纸片，使得劣弧AB沿弦AB折叠后恰好过圆心O1，求，AB长；（2）如图2，O2C⊥弦AB，垂足为点C，劣弧AB沿弦AB折叠后经过O2C的中点D，AB＝10cm，求⊙O 的半径．【思路点拨】（1）过点O1作O1F⊥AB于F，得出O1F=12O1F，再根据勾股定理，即可得出结论；（2）同（1）的方法先判断出O2C＝2rcm，再根据勾股定理建立方程求解，即可得出结论．【解题过程】解：（1）如图1，过点O1作O1F⊥AB于F，并延长O1F交虚线劣弧AB于E，∴AB＝2AF，由折叠知，EF＝O1F=12O1E=12×4＝2（cm），连接O1A，在Rt△O1FA中，O1A＝4，根据勾股定理得，AF cm），∴AB＝2AF＝；（2）如图2，延长O2C交虚线劣弧AB于G，由折叠知，CG＝CD，∵D是O2C的中点，∴CD＝O2D，∴CG＝CD＝O2D，设⊙O2的半径为3rcm，则O2C＝2r（cm），∵O2C⊥弦AB，∴AC=12AB＝5（cm），连接O2A，在Rt△ACO2中，根据勾股定理得，（3r）2﹣（2r）2＝25，∴r∴O2A＝3r＝cm），即⊙O2的半径为．22．（2021•浙江自主招生）以O为圆心，1为半径的圆内有一定点A，过A引互相垂直的弦PQ，RS．求PQ+RS的最大值和最小值．【思路点拨】设OA＝a（定值），过O作OB⊥PQ，OC⊥RS，B、C为垂足，设OB＝x，OC＝y，0≤x≤a，（0≤y≤a），由勾股定理得出x，y，a的关系，再由垂径定理PQ和RS，最后由完全平方公式求得最大值和最小值．【解题过程】解：如图，设OA＝a（定值），过O作OB⊥PQ，OC⊥RS，B、C为垂足，设OB＝x，OC＝y，0≤x≤a，（0≤y≤a），且x2+y2＝a2．所以PQ＝2PB＝RS＝所以PQ+RS＝2∴（PQ+RS）2＝4（2﹣a2而x2y2＝x2（a2﹣x2）＝﹣（x2−a22）2+a44．当x2=a22时，（x2y2）最大值=a4 4．此时PQ+RS=当x2＝0或x2＝a2时，（x2y2）最小值＝0，＝2（1+此时（PQ+RS）最小值。

专题24.3 垂径定理【十大题型】【人教版】【题型1 利用垂径定理求线段长度】 (1)【题型2 利用垂径定理求角度】 (2)【题型3 利用垂径定理求最值】 (3)【题型4 利用垂径定理求取值范围】 (4)【题型5 利用垂径定理求整点】 (6)【题型6 利用垂径定理求面积】 (7)【题型7 垂径定理在格点中的运用】 (8)【题型9 垂径定理与分类讨论中的综合运用】 (10)【题型10 垂径定理的应用】 (11)【题型1 利用垂径定理求线段长度】【例1】（2022•雨花区校级开学）如图，⊙O的半径OD⊥弦AB交AB于点C，连接AO并延长交⊙O于点E，连接EC．若AB＝8，EC＝2√13，则CD的长为（）A．1B．3C．2D．4【变式1-1】（2022•宁津县二模）如图，已知圆O的半径为10，AB⊥CD，垂足为P，且AB＝CD＝16，则OP的长为（）A．6B．6√2C．8D．8√2【变式1-2】（2022•建华区二模）如图，⊙O的直径AB与弦CD相交于点E，若AE＝5，EB＝1，∠AEC ＝30°，则CD的长为（）A．5B．2√3C．4√2D．2√2+√3+1【变式1-3】（2022春•徐汇区校级期中）如图，AB是⊙O的弦，D为半径OA的中点，过D作CD⊥OA交弦AB于点E，且CE＝CB，若BE＝2AE，CD＝5，那么⊙O的半径为．【题型2 利用垂径定理求角度】【例2】（2022•泰安模拟）如图，⊙O的半径OA，OB，且OA⊥OB，连接AB．现在⊙O上找一点C，使OA2+AB2＝BC2，则∠OAC的度数为（）A．15°或75°B．20°或70°C．20°D．30°̂上的【变式2-1】（2022秋•天心区期中）如图，已知⊙O半径OA＝4，点B为圆上的一点，点C为劣弧AB一动点，CD⊥OA，CE⊥OB，连接DE，要使DE取得最大值，则∠AOB等于（）A．60°B．90°C．120°D．135°【变式2-2】（2022秋•青田县期末）如图，在⊙O中，半径OC过弦AB的中点E，OC＝2，OE=√2．（1）求弦AB的长；（2）求∠CAB的度数．【变式2-3】（2022秋•开州区期末）如图，在⊙O中，弦BC与半径OA垂直于点D，连接AB、AC．点E为AC的中点，连接DE．（1）若AB＝6，求DE的长；（2）若∠BAC＝100°，求∠CDE的度数．【题型3 利用垂径定理求最值】【例3】（2022•威海模拟）⊙O中，点C为弦AB上一点，AB＝1，CD⊥OC交⊙O于点D，则线段CD的最大值是（）A．12B．1C．32D．2【变式3-1】（2022•河北模拟）如图所示，在⊙O中，AB为弦，OC⊥AB交AB于点D．且OD＝DC．P为⊙O上任意一点，连接P A，PB，若⊙O的半径为1，则S△P AB的最大值为（）A．1B．2√33C．3√34D．3√32【变式3-2】（2022秋•龙凤区校级期末）如图，矩形ABCD中，AB＝20，AD＝15，P，Q分别是AB，AD 边上的动点，PQ＝16，以PQ为直径的⊙O与BD交于点M，N，则MN的最大值为．【变式3-3】（2022秋•延平区校级期末）在Rt△ABC中，∠C＝90°，BC＝3，AC＝4，D、E分别是AC、BC上的一点，且DE＝3，若以DE为直径的圆与斜边AB相交于M、N，则MN的最大值为（）A．910B．65C．85D．125【题型4 利用垂径定理求取值范围】【例4】（2022•包河区校级二模）如图，在⊙O中，直径AB＝10，CD⊥AB于点E，CD＝8．点F是弧BC上动点，且与点B、C不重合，P是直径AB上的动点，设m＝PC+PF，则m的取值范围是（）A．8＜m≤4√5B．4√5＜m≤10C．8＜m≤10D．6＜m＜10【变式4-1】（2022•佛山）如图，⊙O的直径为10cm，弦AB＝8cm，P是弦AB上的一个动点，求OP的长度范围．【变式4-2】（2022秋•盐都区校级月考）如图，点P是⊙O内一定点．（1）过点P作弦AB，使点P是AB的中点（不写作法，保留作图痕迹）；（2）若⊙O的半径为13，OP＝5，①求过点P的弦的长度m范围；②过点P的弦中，长度为整数的弦有条．【变式4-3】（2022秋•天河区校级期中）已知⊙O的半径为5，点O到弦AB的距离OH＝3，点P是圆上一动点，设过点P且与AB平行的直线为l，记直线AB到直线l的距离为d．（1）求AB的长；（2）如果点P只有两个时，求d的取值范围；（3）如果点P有且只有三个时，求连接这三个点所得到的三角形的面积．【题型5 利用垂径定理求整点】【例5】（2022•山海关区一模）已知⊙O的直径CD＝10，CD与⊙O的弦AB垂直，垂足为M，且AM＝4.8，则直径CD上的点（包含端点）与A点的距离为整数的点有（）A．1个B．3个C．6个D．7个【变式5-1】（2022秋•新昌县期末）如图，AB是⊙O的弦，OC⊥AB于点C，连接OB，点P是半径OB上任意一点，连接AP，若OB＝5，OC＝3，则AP的长不可能是（）A．6B．7C．8D．9【变式5-2】（2022•桥西区校级模拟）如图，AB是⊙C的弦，直径MN⊥AB于点O，MN＝10，AB＝8，如图以O为原点建立坐标系．我们把横纵坐标都是整数的点叫做整数点，则线段OC长是3，⊙C上的整数点有个．【变式5-3】（2022秋•肇东市期末）已知⊙O的半径为5，点O到弦AB的距离为3，则⊙O上到弦AB所在直线的距离为2的点有（）A．4个B．3个C．2个D．1个【题型6 利用垂径定理求面积】【例6】（2022•武汉模拟）如图，在半径为1的⊙O中有三条弦，它们所对的圆心角分别为60°，90°，120°，那么以这三条弦长为边长的三角形的面积是（）A．√2B．1C．√32D．√22【变式6-1】（2022秋•黄州区校级月考）如图，矩形MNGH的四个顶点都在⊙O上，顺次连接矩形各边的中点，得到菱形ABCD，若BD＝12，DF＝4，则菱形ABCD的面积为．【变式6-2】（2022秋•西城区校级期中）如图，AB为⊙O直径，过点O作OD⊥BC于点E，交⊙O于点D，CD∥AB．（1）求证：E为OD的中点；（2）若CB＝6，求四边形CAOD的面积．【变式6-3】（2022•新洲区模拟）如图，点A，C，D均在⊙O上，点B在⊙O内，且AB⊥BC于点B，BC ⊥CD于点C，若AB＝4，BC＝8，CD＝2，则⊙O的面积为（）A．125π4B．275π4C．125π9D．275π9【题型7 垂径定理在格点中的运用】【例7】（2022秋•襄都区校级期末）如图所示，一圆弧过方格的格点AB，试在方格中建立平面直角坐标系，使点A的坐标为（0，4），则该圆弧所在圆的圆心坐标是（）A．（﹣1，2）B．（1，﹣1）C．（﹣1，1）D．（2，1）【变式7-1】（2022春•海门市期中）如图所示，⊙P过B、C两点，写出⊙P上的格点坐标．【变式7-2】（2022•商城县三模）如图所示的网格中，每个小正方形的边长均为1，点A、B、C均在小正方形的顶点上，点C同时也在AB̂上，若点P是BĈ的一个动点，则△ABP面积的最大值是．【变式7-3】（2017秋•靖江市校级月考）如图，在单位长度为1的正方形网格中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作（以下结果保留根号）：（1）利用网格作出该圆弧所在圆的圆心D点的位置，并写出D点的坐标为；（2）连接AD、CD，则⊙D的半径为，∠ADC的度数．【题型8 垂径定理在坐标系中的运用】【例8】（2022•博山区一模）如图，在平面直角坐标系中，半径为5的⊙E与y轴交于点A（0，﹣2），B （0，4），与x轴交于C，D，则点D的坐标为（）A．(4−2√6，0)B．(−4+2√6，0)C．(−4+√26，0)D．(4−√26，0)【变式8-1】（2022秋•西林县期末）如图，⊙P与y轴交于点M（0，﹣4），N（0，﹣10），圆心P的横坐标为﹣4．则⊙P的半径为（）A．3B．4C．5D．6【变式8-2】（2022•印江县三模）如图，直线l为y＝x，过点A1（1，0）作A1B1⊥x轴，与直线l交于点B1，以原点O为圆心，OB1长为半径画圆弧交x轴于点A2；再作A2B2⊥x轴，交直线l于点B2，以原点O为圆心，OB2长为半径画圆弧交x轴于点A3；…，按此作法进行下去，则点A2022的坐标为．【变式8-3】（2015•宜春模拟）如图，半径为5的⊙P与y轴交于点M（0，﹣4），N（0，﹣10），函数y ＝﹣2x+m图象过点P，则m＝．【题型9 垂径定理与分类讨论中的综合运用】【例9】（2022秋•化德县校级期末）⊙O的半径为10cm，弦AB∥CD，且AB＝12cm，CD＝16cm，则AB 和CD的距离为（）A．2cm B．14cm C．2cm或14cm D．10cm或20cm【变式9-1】（2022•包河区二模）已知圆O的半径为5，弦AB＝8，D为弦AB上一点，且AD＝1，过点D 作CD⊥AB，交圆O于C，则CD长为（）A．1B．7C．8或1D．7或1【变式9-2】（2022秋•方正县期末）如图，⊙O的弦AB与半径OC垂直，点D为垂足，OD＝DC，AB＝2√3，点E在⊙O上，∠EOA＝30°，则△EOC的面积为．【变式9-3】（2022秋•淮南月考）如图，已知⊙O的半径为2．弦AB的长度为2，点C是⊙O上一动点，若△ABC为等腰三角形，则BC2的长为．【题型10 垂径定理的应用】【例10】（2022秋•武昌区校级期末）某地有一座圆弧形拱桥，它的跨度（弧所对的弦的长）24m，拱高（弧的中点到弦的距离）4米，则求拱桥的半径为（）A．16m B．20m C．24m D．28m【变式10-1】（2022•望城区模拟）《九章算术》是我国古代著名数学经典，其中对勾股定理的论述比西方早一千多年，其中有这样一个问题：“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该材料，锯口深1寸，锯道长1尺．如图，已知弦AB＝1尺，弓形高CD＝1寸，（注：1尺＝10寸）问这块圆柱形木材的直径是（）A．13寸B．6.5寸C．26寸D．20寸【变式10-2】（2022秋•西城区校级期中）京西某游乐园的摩天轮采用了国内首创的横梁结构，风格更加简约．如图，摩天轮直径88米，最高点A距离地面100米，匀速运行一圈的时间是18分钟．由于受到周边建筑物的影响，乘客与地面的距离超过34米时，可视为最佳观赏位置，在运行的一圈里最佳观赏时长为分钟．【变式10-3】（2022•浙江）如图，公园内有一个半径为20米的圆形草坪，A，B是圆上的点，O为圆心，̂，一部分市民为走“捷径”，踩坏了花草，走出了一条小路AB．通∠AOB＝120°，从A到B只有路AB过计算可知，这些市民其实仅仅少走了步（假设1步为0.5米，结果保留整数）．（参考数据：√3≈1.732，π取3.142）。

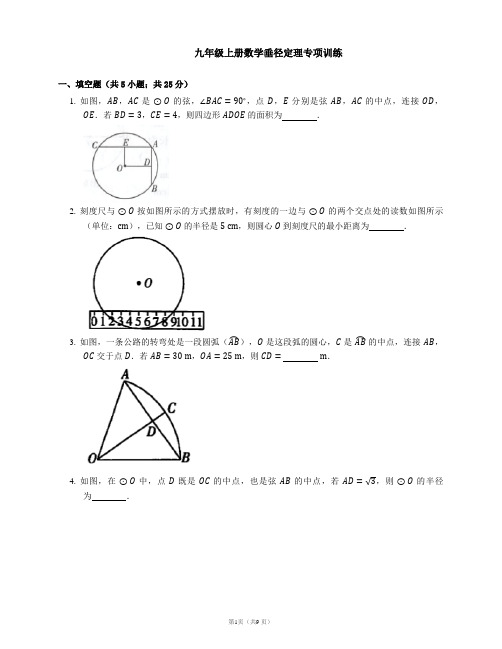
九年级上册数学垂径定理专项训练一、填空题（共5小题；共25分）1. 如图，AB，AC是⊙O的弦，∠BAC=90∘，点D，E分别是弦AB，AC的中点，连接OD，OE．若BD=3，CE=4，则四边形ADOE的面积为．2. 刻度尺与⊙O按如图所示的方式摆放时，有刻度的一边与⊙O的两个交点处的读数如图所示（单位：cm），已知⊙O的半径是5cm，则圆心O到刻度尺的最小距离为．⏜），O是这段弧的圆心，C是AB⏜的中点，连接AB，3. 如图，一条公路的转弯处是一段圆弧（ABOC交于点D．若AB=30m，OA=25m，则CD=m．4. 如图，在⊙O中，点D既是OC的中点，也是弦AB的中点，若AD=√3，则⊙O的半径为．5. 如图，在△ABC中，点O在边AC上，⊙O与△ABC的边BC，AB分别相切于C，D两点，与边AC交于点E点，弦CF与AB平行，与DO的延长线交于点M．若点E是DF⏜的中点，BC= 2，则OC的长为．二、选择题（共25小题；共125分）1. 如图，在⊙O中，半径OC⊥AB于点D，AD=4，则下列说法正确的是( )A. OC=4B. AB=8C. OD=3D. AB垂直平分OC2. 已知圆的半径为R，这个圆的内接正六边形的面积为( )A. 3√34R2 B. 3√32R2 C. 6R2 D. 32R23. 下列判断中正确的是( )A. 弦的垂直平分线必平分弦所对的两条弧B. 平分弦的直线也必平分弦所对的两条弧C. 平分弦的直线垂直于弦D. 平分一条弧的直线必平分这条弧所对的弦4. 如图，已知△ABC（AC<BC），用尺规在BC上确定一点P，使PA+PC=BC，则符合要求的作图痕迹是( )A. B.C. D.5. 如图是一位同学从照片上剪切下来的海上日出时的画面，“图上”太阳与海平线交于A，B两点，他测得“图上”圆的半径为10厘米，AB=16厘米．若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟，则“图上”太阳升起的速度为( )A. 1.0厘米/分B. 0.8厘米/分C. 1.2厘米/分D. 1.4厘米/分6. 下列命题中，正确的是( )A. 平分一条直径的弦必垂直于这条直径B. 平分一条弧的直线垂直于这条弧所对的弦C. 弦的垂线必经过这条弦所在圆的圆心D. 在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心7. 如图，⊙O的半径为10，圆心O到弦AB的距离为6，则AB的长为( )A. 8B. 10C. 12D. 16⏜=AD⏜；②8. 如图，CD是⊙O的弦，AB是⊙O的直径，AB⊥CD于点E，下列结论：①AC⏜；③EO=EB；④EC=ED，其中一定成立的是( )BC⏜=BDA. ①③B. ①④C. ①②④D. ①②③④9. 下列命题中，真命题是( )A. 平分弦的直径垂直于弦B. 垂直平分弦的直线平分这条弦所对的弧C. 在同圆中，相等的弦所对的弧也相等D. 经过半径一端且垂直于这条半径的直线是圆的切线10. 已知⊙O的半径为5，弦AB的长为8，M是弦AB上的动点，则OM的长的最小值为( )A. 2B. 3C. 4D. 511. 如图，⊙O的直径CD=8，AB是⊙O的弦，AB⊥CD，垂足为点M，OM=2，则AB的长为( )A. 2B. 2√3C. 4D. 4√312. 如图，在 ⊙O 中，弦 AB =6 cm ，圆心 O 到 AB 的距离 OC =3 cm ，则 OA 的长度是 ( )A. 3 cmB. 3√2 cmC. 4 cmD. 3√3 cm 13. 如图，⊙O 的直径 CD =20，AB 是 ⊙O 的弦，AB ⊥CD ，垂足为 M ，OM:MC =3:2，则 AB的长为 ( )A. 8B. 12C. 16D. 2√91 14. 如图，AB 为 ⊙O 的直径，AB ，CD 相交于点 E ，且点 E 是弦 CD 的中点，则下列结论中错误的是 ( )A. AB ⊥CDB. BC ⏜=BD ⏜C. AC ⏜=AD ⏜D. OE =BE15. 如图，如果 AB 为 ⊙O 的直径，弦 CD ⊥AB ，垂足为点 E ，那么下面结论中，错误的是 ( )A. CE =DEB. BC ⏜=BD ⏜C. ∠BAC =∠BADD. AC >AD16. 下列命题中，正确的是 ( )A. 圆是轴对称图形，对称轴只有一条B. 在同圆中，互相垂直的两弦不能互相平分C. 直径一定平分弦D. 垂直于弦的直径平分这条弦，并且平分弦所对的两条弧17. 给出下列命题：①垂直于弦的直线平分弦；②平分弦的直径必垂直于弦，并且平分弦所对应的两条弧；③平分弦的直线必过圆心；④弦所对应的两条弧的中点连线垂直平分弦． 其中正确的命题有 ( )A. 1 个B. 2 个C. 3 个D. 4 个 18. 如图，AB ，AC 是圆的两条弦，AD 是圆的一条直径，且 AD 平分 ∠BAC ，下列结论中不一定正确的是 ( )A. AB ⏜=DB ⏜B. BD ⏜=CD ⏜C. BC ⊥ADD. ∠B =∠C19. 如图，CD 是 ⊙O 的直径，CD ⊥AB 于点 E ，则下列结论不一定成立的是 ( )A. EA =EBB. DA ⏜=DB ⏜C. EO =EDD. CA ⏜=CB ⏜ 20. 下列说法：①平分弧的直径垂直平分弧所对的弦；②平分弦的直径平分弦所对的弧；③垂直于弦的直线必过圆心；④垂直于弦的直径平分弦所对的弧． 其中正确的是 ( )A. ②③B. ①③C. ②④D. ①④21. 如图，AB为⊙O的直径，点P在AB的延长线上，PC，PD与⊙O相切，切点分别为C，D．若AB=6，PC=4，则sin∠CAD等于( )A. 35B. 23C. 34D. 4522. 如图，△ABC内接于⊙O，∠BAC=120∘，AB=AC，BD是⊙O的直径，若AD=3，则BC=( )A. 2√3B. 3√3C. 3D. 423. 如图，△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为点F，若⊙O的半径为4√3，∠CDF=15∘，则阴影部分的面积为( )A. 16π−12√3B. 16π−24√3C. 20π−12√3D. 20π−24√324. 正六边形的周长为12，则该正六边形的内切圆的半径为( )A. 1B. √3C. 2D. 325. 一个等腰三角形的底边长是6，腰长是一元二次方程(x−3)(x−5)=0的一根，则此三角形的外接圆的半径是( )A. 3.2B. 258C. 3.5D. 4三、解答题（共6小题；共78分）1. 如图，已知⊙O的半径为10，AB⊥CD，垂足为点P，且AB=CD=16，求OP的长．2. 如图，AB是⊙O的一条弦，CD经过圆心O且与AB交于点E，若AE=BE，AB=2√7，ED=1，求CD的长．⏜的中点，OE交BC于点D．连接AC，若BC=6，3. 如图，AB是⊙O的直径，BC是弦，E是BCDE=1，求AC的长．⏜的中点，AB，OC相交于点M．试4. 如图，在⊙O中，弦AB的长是半径OA的√3倍，C为AB判断四边形OACB的形状，并说明理由．5. 如图，在⊙O中，OC与AB交于点D，D是弦AB的中点，∠CBA=30∘．求证：OA∥BC．。

圆期末复习题垂径定理：1.下列命题中，正确的是（）A．平分一条直径的弦必垂直于这条直径B．平分一条弧的直线垂直于这条弧所对的弦C．弦的垂线必经过这条弦所在圆的圆心D．在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心2.如图，CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=6,则BE的长是（）A.1或9B.9C.1D.4第2题图第3题图第4题图3.如图,圆O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是（）A.23cmB.32cmC.42cmD.43cm4.如图,已知⊙O中弧AB的度数是弧CD度数的2倍,则AB与2CD的关系是( )A.AB＝2CDB.AB＞2CDC.AB＜2CDD.无法确定5.下列说法中，正确的有________．(填序号)①弦是直径；②半圆是弧，但弧不一定是半圆；③半径相等的两个半圆是等弧；④直径是圆中最长的弦．6.如图,已知⊙O的半径是6cm，弦CB=63cm，OD⊥BC，垂足为D，则∠COB=第6题图第7题图第8题图7.如图,直线l与⊙O有两个公共点A，B，O到直线l的距离为5cm，AB=24cm，则⊙O的半径是 cm．8.如图,⊙O的半径是5cm,P是⊙O外一点,PO=8cm,∠P=30º,则AB= cm9.如图,AB是⊙O的直径,且AD∥OC,若弧AD的度数为800.求CD的度数.10.如图，已知等腰△ABC的三个顶点都在半径为5的⊙O上，如果底边BC的长为8，求BC边上的高.11.如图,O的直径AB=4,半径OC AB⊥,D为BC上一点，,⊥⊥ ,垂足分别为E,F，求DE OC DF ABEF的长.12.如图,AD是△ABC的高,AE是△ABC的外接圆的直径.试说明弧BE=弧CF.13.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=300，求弦CD长．14.如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB.（1）求证:AC平分∠DAB；（2）若AC=8,弧AC:弧CD=2:1，试求圆O的半径；（3）若点B为AC的中点,试判断四边形ABCD的形状.15.O是∠MPN的平分线上一点,以O为圆心的圆和PM,PN别交于A、B、C、D四点.求证:∠OBA=∠OCD.16.如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F．（1）求证：CF=BF；（2）若AD=2,⊙O的半径为3,求BC的长．圆心角、圆周角1.如图,等边△ABC的三个顶点都在⊙O上,D是AC上任一点(不与A、C重合),则∠ADC度数是______.第1题图第2题图第3题图2.已知,如图,∠BAC的对角∠BAD=1000,则∠BOC=_______度.3.如图,A、B、C为⊙O上三点，若∠OAB=480,则∠ACB=_______度.4.如图,AB是⊙O的直径, BC BD,∠A=250,则∠BOD的度数为________.第4题图第5题图第6题图第7题图5.如图,已知圆心角∠BOC=1100,则圆周角∠BAC的度数是6.如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为7.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC=1420, ∠CBD 的度数是8.如图,⊙O的直径AB=8cm,∠CBD=300,求弦DC的长.9.如图,AB, AC 是⊙O 的两条弦,且AB=AC.延长CA 到点D ．使AD=AC,连结DB 并延长,交⊙O 于点E.求证：CE 是⊙O 的直径．10.在⊙O 中,弦AB 与DC 相交于E,且AE=EC,求证：AD=BC.11.如图,AB 是⊙O 直径,CD 是⊙O 弦,AB 、CD 的延长线交于E,AB=2DE,∠E=180，求∠C 及∠AOC 的度数．12.已知：如图，AB 为O ⊙的直径，AB=AC,BC 交O ⊙于点D ，AC 交O ⊙于点E,∠BAC=450． （1）求∠EBC 的度数；（2）求证：BD=CD ．13.如图,A 、B 、C 、D 四点都在⊙O 上,AD 是⊙O 的直径,且AD=8cm,若∠ABC=∠CAD,求弦AC 的长.14.如图,在Rt△ABC中,∠ACB=900,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB 交于点E，连接DE.（1）求证：AC=AE；（2）求△ACD外接圆的半径.15.如图,已知O的半径为R,C,D是直径AB同侧圆周上的两点,AC的度数为960,BD的度数为360，动点P在AB上，求PC+PD的最小.数学期末复习题测试题01满分：100分时间：25分钟姓名：得分：1.下列命题中，正确的是（）①顶点在圆周上的角是圆周角；②圆周角的度数等于圆心角度数的一半;③900的圆周角所对的弦是直径；④不在同一条直线上的三个点确定一个圆；⑤同弧所对的圆周角相等A.①②③B.③④⑤C.①②⑤D.②④⑤2.如图,AB是半圆直径,∠BAC=200，D是AC的中点，则∠DAC的度数是（）A.30°B.35°C.45°D.70°3.下列说法中正确的是________．(填序号)①圆是轴对称图形,每一条直径都是它的对称轴;②在同圆或等圆中,如果两条弦相等,那么它所对的两条弧也相等;③平分弦的直径垂直于这条弦;④垂直于弦的直径平分这条弦．4.过⊙O内一点M的最长的弦长为6cm,最短的弦长为4cm,则OM的长等于cm.5.如图,⊙O中OA⊥BC,∠CDA=24o,则∠AOB的度数为_______．第5题图第6题图第7题图6.如图,AB为⊙O的直径,点C、D在⊙O上,∠BAC=46 o,则∠ADC=_______．7.如图,点A、B、C都在⊙O上,连结AB、BC、AC、OA、OB，且∠BAO=250，则∠ACB的大小为________8.如图,⊙O的直径AB垂直于弦CD,垂足为E,若∠COD=1200，OE=3厘米,则CD= 厘米.O图 4E DCB A第8题图 第9题图 第10题图 9.如图,已知AB 是⊙O 的直径,弦CD ⊥AB,E 为垂足,CD=8,OE=1,则AB=_________10.如图,AB 为⊙O 的弦,⊙O 的半径为5,OC ⊥AB 于点D,交⊙O 于点C,且CD=l,则弦AB 的长是11.如图,是一个隧道的截面，如果路面AB 宽为8米，净高CD 为8米，那么这个隧道所在圆的半径OA 是___________米第11题图 第12题图 第13题图 第14题图 12.如图,AB 为半圆直径,O 为圆心,C 为半圆上一点,E 是弧AC 的中点,OE 交弦AC 于点D.若AC=8cm, DE=2cm,则OD 的长为 cm.13.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,AB=16m,OA=10m,则中间柱CD 高度为 m. 14.如图,在直角坐标系中,以点P 为圆心的圆弧与轴交于A 、B 两点,已知P(3，2)和A(1,0)，则点B 的坐标是 ,圆P 的半径为 .15,如图,在△ABC 中,∠ACB=900，以C 为圆心、CB 为半径的圆交AB 于点D. (1)若∠A=400；求∠ACD 的度数；（2）若AC=8，BC=6,求弦BD 长度.B A POyx17.如图,⊙O是△ABC的外接圆,圆心O在这个三角形的高AD上,AB=10,BC=12.求⊙O的半径.18.已知:如图,点P是⊙O外的一点,PB与⊙O相交于点A、B，PD与⊙O相交于C、D，AB=CD．求证：（1）PO平分∠BPD；（2）PA=PC.。

初三数学圆垂径定理的练习题初三数学-圆垂径定理的练习题题一：在平面直角坐标系中，已知圆C的圆心坐标为O(0, 0)，半径为r，点A(a, 0)和点B(0, b)分别是圆上的两个点。

证明：OA⊥OB（即向量OA与向量OB垂直）。

解题思路：要证明向量OA与向量OB垂直，可以利用向量的数量积来进行推导。

首先，根据向量的定义和坐标表示，得到向量OA为OA(a, 0)和向量OB为OB(0, b)。

然后，根据向量的数量积公式有向量OA·向量OB= a·0 + 0·b = 0。

当两个向量的数量积等于0时，可判定这两个向量垂直。

因此，OA⊥OB。

题二：在平面直角坐标系中，已知圆C的直径AB的端点分别为A(3, 4)和B(-5, -12)。

求证：直径AB的中点O在圆C上。

解题思路：根据圆的直径定义，直径AB的中点O为AB的中点。

假设O的坐标为(x₀, y₀)，则中点O的横坐标为(x₁+x₂)/2，纵坐标为(y₁+y₂)/2。

代入A(3, 4)和B(-5, -12)的坐标可得：(x₀, y₀) = ((3-5)/2, (4-12)/2)简化可得，(x₀, y₀) = (-1, -4)。

对比圆心O的坐标和中点O的坐标，可发现它们是相等的，即坐标值完全相同。

所以，可以证明直径AB的中点O在圆C上。

题三：在平面直角坐标系中，已知圆C的圆心坐标为O(2, 3)，点A(6, 1)是圆上的一个点。

设点B(x, y)是圆C上一点，且OA⊥OB。

求点B的坐标。

解题思路：根据题意，需要找到一个点B(x, y)在圆C上，并满足OA⊥OB。

根据圆垂径定理，垂直于直径的线段必然经过圆心。

首先，根据圆心坐标O(2, 3)和点A(6, 1)，可以求得向量OA的坐标差为(6-2, 1-3) = (4, -2)。

根据OA⊥OB，可知向量OA和向量OB的数量积为0，即(4, -2)·(x-2, y-3) = 4(x-2) - 2(y-3) = 0。

浙教新版数学九年级上册：3.3垂径定理同步练习题一．选择题（共7小题）1．过⊙O内一点N的最长弦为6，最短的弦长为4，那么ON的长为（）A．B．2C．D．2．圆的半径为13cm，两弦AB∥CD，AB＝24cm，CD＝10cm，则两弦AB，CD的距离是（）A．7cm B．17cm C．12cm D．7cm或17cm3．如图，已知⊙O的半径为5，弦AB＝7，M是AB上任意一点，则线段OM的长不可能是（）A．3.5B．4.5C．4D．54．在圆柱形油槽内装有一些油，截面如图，油面宽AB为6dm，如果再注入一些油后，油面AB上升ldm，油面宽为8dm，圆柱形油槽直径MN为（）A．6dm B．8dm C．10dm D．12dm5．若P为半径长是6cm的⊙O内一点，OP＝2cm，则过P点的最短的弦长为（）A．12cm B．cm C．cm D．cm6．下列命题中，正确的是（）A．平分弦的直线必垂直于这条弦B．垂直于弦的直线必过圆心C．平分弦的直径必垂直于这条弦，并且平分这条弦所对的两条弧D．垂直平分弦的直线必平分这条弦所对的弧7．如图所示，⊙O的弦AB、AC的夹角为50°，MN分别为弧AB和弧AC的中点，OM、ON分别交AB、AC于点E、F，则∠MON的度数为（）A．110°B．120°C．130°D．100°二．填空题（共10小题）8．秋千长度的长度为3m，秋千向两边摆动时，最大摆角为60度，且两边的摆动角度相同，则它摆置最高处与最低处的高度差为．9．如图，⊙O的半径为5，弦AB的长为8，M是弦AB上的动点，则线段OM长的最小值为，最大值为．10．如图，以点P为圆心的圆弧与x轴交于A，B两点，点P的坐标为（10，5），点A的坐标为（6，0），则点B的坐标为．11．如图，已知在⊙O中，直径MN＝10，四边形ABCD是正方形，并且∠POM＝45°，则AB的长为．12．已知如图，⊙O中直径AB交CD于E，点B是弧CD的中点，CD＝8cm，AE＝8cm，则⊙O的半径为．13．如图，⊙O的弦AB的垂直平分半径OC，⊙O的半径等于8cm，则四边形OACB的面积等于cm2．14．垂直于弦的直径平分这条弦，并且平弦所对的弧．即：如图，若AB⊥CD，则有AP PB，，AD＝．如图，若CD＝10，AB＝8，求PC的长？15．如图，在⊙O中，直径AB⊥CD，若AB＝10cm，OE＝4cm，则CD＝cm．16．如图AB是⊙O的直径CD是弦，且CD⊥AB于点E，BC＝6，AC＝8，则DE＝．17．如图，在⊙O中，AB是弦，∠AOB＝120°，OA＝5cm，那么圆心O到AB的距离是cm，弦AB的长是cm．三．解答题（共8小题）18．直径为80cm的油桶水平放置于地面上，截面图如图所示，油面MN与直径AB交于点C，且最大深度BC为直径的时．（1）求油面的宽度MN（结果保留根号）；（2）若油桶的高为120cm，求油桶中存贮油的体积（结果保留根号）．19．如图，一圆弧形拱桥，跨度AB＝16m，拱高为4m，求半径OA的长．20．如图，已知AB和CD是⊙O的两条弦，且AB⊥CD，连接OC，作∠OCD的平分线交⊙O于P，连接P A、PB，求证：P A＝PB．21．已知：如图，⊙O中，AB＝AC，OD⊥AB于D，OE⊥AC于E．求证：∠ODE＝∠OED．22．如图，有一拱桥为圆弧形，跨度AB＝60米，拱高PM＝18米，当洪水泛滥时，跨度只有30米时要采取紧急措施，测量人员测得水面A1B1到拱顶距离只有4米时，是否采取紧急措施？23．如图所示，AB是⊙O的一条弦（不是直径），点C，D是直线AB上的两点，且AC＝BD．（1）判断△OCD的形状，并说明理由．（2）当图中的点C与点D在线段AB上时（即C，D在A，B两点之间），（1）题的结论还存在吗？24．（综合题）如图所示，⊙O中的弦AB，CD互相垂直于E，AE＝5cm，BE＝13cm，O到AB的距离为2cm，求⊙O的半径及O到CD的距离．25．在直径为1米的圆柱形油槽内装入一些油后，截面如图所示，若油面宽AB＝0.6米，求油的最大深度．浙教新版数学九年级上册：3.3垂径定理同步练习题参考答案一．选择题（共7小题）1．过⊙O内一点N的最长弦为6，最短的弦长为4，那么ON的长为（）A．B．2C．D．【解答】解：如图所示，则直径AB是过点N的最长的弦．过N点作弦CD⊥AB，则CD是过N的最短的弦．连接OC．∵ON⊥CD，∴CN＝CD＝2，又OC＝3，∴ON＝．故选：C．2．圆的半径为13cm，两弦AB∥CD，AB＝24cm，CD＝10cm，则两弦AB，CD的距离是（）A．7cm B．17cm C．12cm D．7cm或17cm【解答】解：作OE⊥CD，∵AB∥CD，∴OE⊥AB，当两弦在圆心的同侧时，已知CD＝10cm，∴由垂径定理得DE＝5．∵OD＝13，∴利用勾股定理可得：OE＝12．同理可求OF＝5，∴EF＝7．当两弦在圆心的两侧时，EF＝OE+OF＝17．故选：D．3．如图，已知⊙O的半径为5，弦AB＝7，M是AB上任意一点，则线段OM的长不可能是（）A．3.5B．4.5C．4D．5【解答】解：连接OA，过点O作OD⊥AB于点D，当点M与点A重合时OM最长，当点M于点D重合时OM最短，∵OD⊥AB，AB＝7，∴AD＝AB＝，∴OD＝＝＝，∴≤OM≤5．∵＞＝3.5，∴A不合题意．故选：A．4．在圆柱形油槽内装有一些油，截面如图，油面宽AB为6dm，如果再注入一些油后，油面AB上升ldm，油面宽为8dm，圆柱形油槽直径MN为（）A．6dm B．8dm C．10dm D．12dm【解答】解：根据题意画出图形，如图所示，EF＝1dm，AB＝6dm，CD＝8dm，设圆的半径为r，∵OE⊥CD，OF⊥AB，∴CE＝DE＝4dm，AF＝BF＝3dm，在Rt△OCE和△OAF中，根据勾股定理得：OE＝＝，OF＝＝，∴OE﹣OF＝1，即﹣＝1，＝+1，两边平方得，r2﹣9＝r2﹣16+2+1，＝3，两边平方得，r2﹣16＝9，r2＝25，解得：r＝5，则圆柱形油槽直径MN为10dm．故选：C．5．若P为半径长是6cm的⊙O内一点，OP＝2cm，则过P点的最短的弦长为（）A．12cm B．cm C．cm D．cm【解答】解：如图，∵OA＝6cm，OP＝2cm，∴AP＝＝＝4cm，∴AB＝8cm，∴过P的最短的弦长等于8cm，故选：D．6．下列命题中，正确的是（）A．平分弦的直线必垂直于这条弦B．垂直于弦的直线必过圆心C．平分弦的直径必垂直于这条弦，并且平分这条弦所对的两条弧D．垂直平分弦的直线必平分这条弦所对的弧【解答】解：A、过弦的中点的直线都是平分线的直线，有无数条，所以平分弦的直线不一定垂直于这条弦；故A 错误．B、垂直于弦的直线有无数条，所以垂直于弦的直线不一定过圆心，垂直平分弦的直线过圆心；故B错误．C、根据垂径定理的推论，平分弦（不是直径）的直径必垂直于这条弦，因为任意两条直径互相平分，但不一定垂直；故C错误．D、垂直平分弦的直线必过圆心，并且平分这条弦所对的弧；故D正确．故选：D．7．如图所示，⊙O的弦AB、AC的夹角为50°，MN分别为弧AB和弧AC的中点，OM、ON分别交AB、AC于点E、F，则∠MON的度数为（）A．110°B．120°C．130°D．100°【解答】解：∵M、N分别为弧AB和弧AC的中点，∴OF⊥AC，OE⊥AB，∴∠OF A＝∠OEA＝90°，∴在四边形OEAF中，∠MON＝360°﹣∠OF A﹣∠OEA﹣∠A＝360°﹣90°﹣90°﹣50°＝130°．故选：C．二．填空题（共10小题）8．秋千长度的长度为3m，秋千向两边摆动时，最大摆角为60度，且两边的摆动角度相同，则它摆置最高处与最低处的高度差为（3﹣）米．【解答】解：∵最大摆角为60度，∴∠BOD＝60°，∴∠BOA＝∠DOA＝30°．∵OB＝OD＝3米，∴BC＝OB＝米，∴OC＝＝＝（米），∴AC＝OA﹣AC＝（3﹣）米．故答案为：（3﹣）米．9．如图，⊙O的半径为5，弦AB的长为8，M是弦AB上的动点，则线段OM长的最小值为3，最大值为5．【解答】解：如图所示，过O作OM′⊥AB，连接OA，∵过直线外一点与直线上的所有连线中垂线段最短，∴当OM于OM′重合时OM最短，∵AB＝8，OA＝5，∴AM′＝×8＝4，∴在Rt△OAM′中，OM′＝＝＝3，∴线段OM长的最小值为3，最大值为5．故答案为：3，5．10．如图，以点P为圆心的圆弧与x轴交于A，B两点，点P的坐标为（10，5），点A的坐标为（6，0），则点B的坐标为（14，0）．【解答】解：过点P作PM⊥AB于M，则M的坐标是（10，0）．又∵A的坐标为（6，0），∴OA＝6，AM＝OM﹣OA＝10﹣6＝4，∵A，B两点一定关于PM对称．∴MB＝AM＝4，∴OB＝OM+MB＝10+4＝14，∴点B的坐标是（14，0）．故答案为：（14，0）．11．如图，已知在⊙O中，直径MN＝10，四边形ABCD是正方形，并且∠POM＝45°，则AB的长为．【解答】解：∵∠POM＝45°，∠DCO＝90°，∴∠DOC＝∠CDO＝45°，∴△CDO为等腰直角三角形，∴CO＝CD．连接OA，则△OAB是直角三角形，∵四边形ABCD是正方形，∴AB＝BC＝CD＝CO，BO＝BC+CO＝BC+CD＝2AB，∴AB2+OB2＝52，即AB2+（2AB）2＝52，∴AB的长为．故答案为：．12．已知如图，⊙O中直径AB交CD于E，点B是弧CD的中点，CD＝8cm，AE＝8cm，则⊙O的半径为5．【解答】解：设⊙O的半径为rcm，∵点B是弧CD的中点，CD＝8cm，AB是直径，∴AB⊥CD，CE＝ED＝CD＝4cm，在Rt△COE中，由勾股定理得：OC2＝CE2+OE2，r2＝42+（8﹣r）2，解得r＝5．故答案为：5．13．如图，⊙O的弦AB的垂直平分半径OC，⊙O的半径等于8cm，则四边形OACB的面积等于cm2．【解答】解：∵AB垂直平分OC，∴OA＝AC，又半径OA＝OC，∴△OAC为等边三角形，四边形OACB为菱形，∵OA＝OC＝8，∴AB＝8，S四边形OACB＝×OC×AB＝×8×8＝32．故答案为：32．14．垂直于弦的直径平分这条弦，并且平弦所对的弧．即：如图，若AB⊥CD，则有AP＝PB，＝，AD＝BD．如图，若CD＝10，AB＝8，求PC的长？【解答】解：∵AB⊥CD，∴由垂径定理，可得AP＝BP，＝，AD＝BD，连接OA，∵AB⊥CD，CD＝10，AB＝8，∴AP＝4，OA＝5，∴由勾股定理得，OP＝3，∴PC＝OC﹣OP＝5﹣3＝2．15．如图，在⊙O中，直径AB⊥CD，若AB＝10cm，OE＝4cm，则CD＝6cm．【解答】解：由题意得：OC＝5，OE＝4∴Rt△OCE中可求得CE＝＝3cm根据垂径定理可得：CD＝2CE＝6cm．16．如图AB是⊙O的直径CD是弦，且CD⊥AB于点E，BC＝6，AC＝8，则DE＝．【解答】解：∵AB是⊙O的直径CD是弦，且CD⊥AB于点E∴CE＝DE，AC⊥BC∵BC＝6，AC＝8∴AB＝10∵S△ABC＝×AC×BC＝×CE×AB∴AC×BC＝CE×AB∴CE＝＝∴DE＝CE＝故此题应该填．17．如图，在⊙O中，AB是弦，∠AOB＝120°，OA＝5cm，那么圆心O到AB的距离是cm，弦AB的长是5 cm．【解答】解：过O作OC⊥AB交AB于C点，如右图所示：由垂径定理可知，OC垂直平分AB，∵OA＝OB，∠AOB＝120°∴∠OAB＝30°∴OC＝OA＝cm∴由勾股定理可得：AC＝cm∴AB＝5cm故此题应该填，5．三．解答题（共8小题）18．直径为80cm的油桶水平放置于地面上，截面图如图所示，油面MN与直径AB交于点C，且最大深度BC为直径的时．（1）求油面的宽度MN（结果保留根号）；（2）若油桶的高为120cm，求油桶中存贮油的体积（结果保留根号）．【解答】解：（1）如图，连接OM，∵AB＝80cm，BC为直径的，∴OM＝OB＝40cm，BC＝20cm，∴OC＝20cm，∴MC＝cm，∴MN＝2CM＝40cm；（2）∵OC＝20cm，OM＝40cm，∴sin∠OMC＝，∴∠OMC＝30°，∴∠MOC＝60°，∴∠MON＝120°，∴阴影部分的面积是：＝，∵油桶的高为120cm，∴油桶中存贮油的体积是：（）×120＝64000π﹣48000，即油桶中存贮油的体积是（64000π﹣48000）cm3．19．如图，一圆弧形拱桥，跨度AB＝16m，拱高为4m，求半径OA的长．【解答】解：∵AB＝16m，OC⊥AB，∴AD＝AB＝8m，设OA＝r，则OD＝r﹣4，在Rt△AOD中，OA2＝AD2+OD2，即r2＝82+（r﹣4）2，解得r＝10m，即半径OA的长是10m．20．如图，已知AB和CD是⊙O的两条弦，且AB⊥CD，连接OC，作∠OCD的平分线交⊙O于P，连接P A、PB，求证：P A＝PB．【解答】证明：∵OC＝OP，∴∠1＝∠2．∵CP平分∠OCD，∴∠2＝∠3，∴∠3＝∠1，∴CD∥OP，∵CD⊥AB，∴OP⊥AB．∴＝，∴P A＝PB．21．已知：如图，⊙O中，AB＝AC，OD⊥AB于D，OE⊥AC于E．求证：∠ODE＝∠OED．【解答】解：连接OA并延长交BC于点F，∵⊙O是△ABC的外接圆，∴点O是△ABC的外心，∵AB＝AC，∴AF是BC的垂直平分线，∴∠BAF＝∠CAF，∵OD⊥AB，OE⊥AC，∴OD、OE分别是AB、AC的垂直平分线，∵AB＝AC，∴AD＝AE，在Rt△AOD与Rt△AOE中，，∴Rt△AOD≌Rt△AOE，∴OD＝OE，∴△ODE是等腰三角形，∴∠ODE＝∠OED．22．如图，有一拱桥为圆弧形，跨度AB＝60米，拱高PM＝18米，当洪水泛滥时，跨度只有30米时要采取紧急措施，测量人员测得水面A1B1到拱顶距离只有4米时，是否采取紧急措施？【解答】解：连接OA、OA1，如下图所示：由题可得：AB＝60m，PM＝18m，PN＝4m，OA＝OA1＝OP＝ROP⊥AB，OP⊥A1B1由垂径定理可得：AM＝MB＝30m在Rt△AMO中，由勾股定理可得：AO2＝AM2+MO2即R2＝302+（R﹣18）2解得R＝34m∵PN＝4m，OP＝R＝34m∴ON＝30m在Rt△ONA1中，由勾股定理可得：A1N2＝A1O2﹣ON2可得A1N＝16m故A1B1＝32m＞30m故不用采取紧急措施．23．如图所示，AB是⊙O的一条弦（不是直径），点C，D是直线AB上的两点，且AC＝BD．（1）判断△OCD的形状，并说明理由．（2）当图中的点C与点D在线段AB上时（即C，D在A，B两点之间），（1）题的结论还存在吗？【解答】解：（1）△OCD是等腰三角形如左图所示，过点O作OM⊥AB，垂足为M，则有MA＝MB又AC＝BD∴AC+MA＝BD+MB即CM＝DM又OM⊥CD，即OM是CD的垂直平分线∴OC＝OD∴△OCD为等腰三角形（2）当点C，D在线段AB上时，如右图所示同（1）题作OM⊥AB，垂足为M由垂径定理，得AM＝BM又AC＝BD∴CM＝AM﹣AC＝BM﹣BD＝MD∴OC＝OD∴△OCD为等腰三角形．24．（综合题）如图所示，⊙O中的弦AB，CD互相垂直于E，AE＝5cm，BE＝13cm，O到AB的距离为2cm，求⊙O的半径及O到CD的距离．【解答】解：AB＝AE+BE＝5+13＝18（cm），连接OB，过O作OM⊥AB，∴AM＝AB＝9（cm），又∵OM＝2（cm），∴在Rt△OBM中，BO＝＝＝＝11cm，ON＝EM＝AM﹣AE＝9﹣5＝4（cm）．25．在直径为1米的圆柱形油槽内装入一些油后，截面如图所示，若油面宽AB＝0.6米，求油的最大深度．【解答】解：连接OA．∵OA＝OD＝0.5米，AC＝AB＝0.3米∴OC2＝OA2﹣AC2∴OC＝＝0.4米∴CD＝OD﹣OC＝0.5﹣0.4＝0.1米故油的最大深度是0.1米．。

3.3　垂径定理第2课时　垂径定理的逆定理基础过关全练知识点1　垂径定理的逆定理11.如图,☉O的直径CD过弦AB的中点E,且CE=2,DE=8,则AB的长为( )A.9B.8C.6D.42.如图,☉O的半径为5,弦AB的长为8,半径OD过弦AB的中点C,则CD的长为 .知识点2　垂径定理的逆定理23.如图,☉O的直径AB与弦CD交于点E,若B为CD的中点,则下列说法错误的是( )A.CB=BDB.OE=BEC.CE=DED.AB⊥CD4.【新独家原创】如图,AB是☉O的直径,点P是BD的中点,若BD=8,BP=25,则AD的长为 .5.如图所示,D、E分别是AB、AC的中点,DE交AB于M,交AC于N,求证:AM=AN.知识点3　垂径定理的逆定理的应用6.【新情境·中国元素】圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.如图所示的是一款拱门的示意图,其中拱门最下端AB=18分米,C为AB的中点,D为拱门最高点,圆心O在线段CD上,CD=27分米,求拱门所在圆的半径.能力提升全练7.下列命题中,正确的个数是( )①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧. A.1 B.2 C.3 D.48.【新考法】如图,AB为☉O的直径,AE为☉O的弦,C为优弧ABE的中点,CD⊥AB,垂足为D.若AE=8,DB=2,则☉O的半径为 .9.【教材变式·P79例3】如图所示的是某蔬菜基地搭建的一座蔬菜棚的截面,其为圆弧形,跨度AB(弧所对的弦)为3.2米,拱高(弧的中点到弦的距离)为0.8米.(1)求该圆弧所在圆的半径;(2)在距蔬菜棚的一端(点B)0.4米处竖立支撑杆EF,求支撑杆EF的长度.10.如图,AB是☉O的直径,AB⊥CD于点E,连结CO并延长交AD于点F,且F恰为AD的中点.求证:E是OB的中点.素养探究全练11.【运算能力】木工师傅经常要测量圆木截面的直径,实际上不易操作,为解决这一难题,小颖设计了一个测圆工具,如图所示,在长为h的木条AB的中点钉另一根木条MN,MN⊥AB,在木条MN上自MN上某一点向N标注刻度,使用时,将A、B置于圆上,读出MN与圆的交点C处的刻度,就可以知道圆的直径,设MC=d d≥(1)用含h,d的式子表示该圆的直径;(2)若h=2,圆木截面的直径为5.2,则MC的长度为多少?答案全解全析基础过关全练1.B　∵CE=2,DE=8,∴CD=10,∴OB=OC=5,∴OE=5-2=3.∵☉O的直径CD过弦AB的中点E,∴CD⊥AB,AE=BE,在Rt△OBE中,∵OE=3,OB=5,∴BE=OB2―OE2=4,∴AB=2BE=8.故选B.2.答案　2解析　连结OA(图略),∵半径OD过弦AB的中点C,∴OD⊥AB,AC=BC,∴∠OCA=90°,∵弦AB的长为8,∴AC=BC=4,∵AO=5,∴由勾股定理得OC=52―42=3,∴CD=OD-OC=5-3=2.3.B　∵B为CD的中点,∴CB=BD,故A选项说法正确,不符合题意;∵AB是☉O的直径,CB=BD,∴CE=DE,AB⊥CD,故C、D选项说法正确,不符合题意;根据题中条件不能证明OE=BE,故B选项说法错误,符合题意.故选B.4.答案　6解析　如图,连结OP交BD于点G,BD=4,∵P是BD的中点,∴OP⊥BD,DG=BG=12在Rt△BPG中,PG=BP2―BG2=(25)2―42=2,设☉O的半径为r,在Rt△OBG中,OB2=OG2+BG2,即r2=(r-2)2+42,解得r=5,∴OG=3,∵OA=OB,DG=BG,∴OG为△ABD的中位线,∴AD=2OG=6.5.证明　如图,连结DO,EO,∵D是AB的中点,E是AC的中点,∴OD⊥AB,OE⊥AC.∵OD=OE,∴∠EDO=∠DEO,∴∠DMB=180°-90°-∠EDO,∠ENC=180°-90°-∠DEO,∴∠DMB=∠ENC.∵∠AMN=∠DMB,∠ANM=∠ENC,∴∠AMN=∠ANM,∴AM=AN.6.解析　如图,连结AO,∵CD过圆心,C为AB的中点,∴CD⊥AB,∵AB=18分米,C为AB的中点,∴AC=BC=9分米,设圆的半径为x分米,则OA=OD=x分米,∵CD=27分米,∴OC=(27-x)分米,在Rt△OAC中,AC2+OC2=OA2,∴92+(27-x)2=x2,∴x=15.答:拱门所在圆的半径是15分米.能力提升全练7.B　平分弧的直径垂直平分弧所对的弦,所以①正确;平分弦(非直径)的直径平分弦所对的弧,所以②错误;垂直平分弦的直线必过圆心,所以③错误;垂直于弦的直径平分弦所对的弧,所以④正确.故选B.8.答案　5解析　如图,连结CO并延长,交AE于点T.∵C为优弧ABE的中点,∴AC=CE,AE=4,∴CT⊥AE,AT=TE=12∵∠ATO=∠CDO=90°,∠AOT=∠COD,AO=CO,∴△AOT≌△COD(AAS),∴CD=AT=4,设☉O的半径为r.在Rt△COD中,OC2=CD2+OD2,∴r2=42+(r-2)2,∴r=5,∴☉O的半径为5.9.解析　(1)如图,设AB所在圆的圆心为O,D为AB的中点,连结OB,OD,OD交AB于点C,∴OD垂直平分AB,由题可知AB=3.2米,CD=0.8米,AB=1.6米,∴BC=12设☉O的半径为R米,则OC=OD-CD=(R-0.8)米,在Rt△OBC中,由勾股定理得OB2=OC2+CB2,即R2=(R-0.8)2+1.62,解得R=2,即该圆弧所在圆的半径为2米.(2)如图,过O作OH⊥EF,交EF的延长线于点H,连结OE,则四边形OHFC是矩形,∴OH=CF=1.6-0.4=1.2(米),∵OE=2米,∴在Rt△OHE中,HE=OE2―OH2=22―1.22=1.6(米),∵HF=OC=OD-CD=2-0.8=1.2(米),∴EF=HE-HF=1.6-1.2=0.4(米),即支撑杆EF的长度为0.4米.10.证明　如图,连结AC,BC,∵AB⊥CD,AB为☉O的直径,∴CE=DE,∴AB垂直平分CD,∴AC=AD,∵F为AD的中点,CF过圆心,∴CF⊥AD,∴CF垂直平分AD,∴AC=CD,∴AC=AD=CD,∴△ACD是等边三角形,∴∠ACD=60°,∵F为AD的中点,∴∠FCD=30°,∴∠COE=60°,∵OC=OB,∴△OCB为等边三角形,∵CE⊥OB,∴OE=BE,即E是OB的中点.素养探究全练11.解析　(1)∵MN⊥AB,M为AB的中点,∴MN 过圆心,设圆心为O ,连结AO ,如图:设AO =x ,在Rt △AOM 中,AO 2=MO 2+AM 2,∴x 2=(d -x )2,∴x 2=d 2-2dx +x 2+ℎ24,∴2dx =d 2+ℎ24,∴2x =d +ℎ24d ,即该圆的直径为d +ℎ24d .(2)当h =2,圆木截面的直径为5.2时,d +224d =5.2,∴d +1d =5.2,∴d 2-5.2d +1=0,解得d =5或d =0.2,∵d ≥ℎ2,∴d ≥1,∴d =0.2不符合题意,舍去,∴d =5,∴MC 的长度为5.。

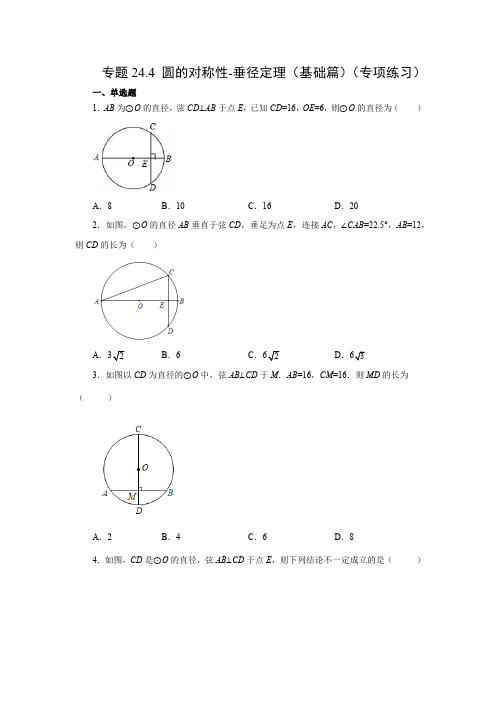
专题24.4 圆的对称性-垂径定理（基础篇）（专项练习）一、单选题1．AB为⊙O的直径，弦CD⊥AB于点E，已知CD=16，OE=6，则⊙O的直径为（ ）A．8B．10C．16D．202．如图，⊙O的直径AB垂直于弦CD，垂足为点E，连接AC，∠CAB=22.5°，AB=12，则CD的长为（ ）A．B．6C．D．3．如图以CD为直径的⊙O中，弦AB⊥CD于M．AB=16，CM=16．则MD的长为（）A．2B．4C．6D．84．如图，CD是⊙O的直径，弦AB⊥CD于点E，则下列结论不一定成立的是（）A ．AE ＝BEB ．OE ＝DEC ．»»AC BC =D ．»»AD BD=5．如图，点A ，B ，C ，D 在圆上，弦AB 和CD 交于点E ，则下列说法正确的是（ ）A ．若CD 平分AB ，则CD AB ^B ．若CD AB ^，则CD 平分ABC ．若CD 垂直平分AB ，则圆心在CD 上D ．若圆心在CD 上，则CD 垂直平分AB 6．如图，CD 是O e 的直径，弦AB CD ^于点E ，连接BC 、BD ，下列结论中不一定正确的是（ ）A ．AE BE =B ．»»AD BD =C ．OE DE =D ．»»AC BC=7．下列命题中假命题是（ ）A ．平分弦的半径垂直于弦B ．垂直平分弦的直线必经过圆心C ．垂直于弦的直径平分这条弦所对的弧D ．平分弧的直径垂直平分这条弧所对的弦8．如图，在⊙O 中，半径OC ⊥AB 于点E ，AE =2，则下列结论正确的是（ ）EC=A．2OE=B．2C．AB垂直平分OC D．OC垂直平分AB9．如图，⊙O的半径为5，弦AB＝8，点C是AB的中点，连接OC，则OC的长为（ ）A．1B．2C．3D．410．如图，在⊙O中，弦AB的长是半径OA C为»AB中点，AB、OC交于点P，则四边形OACB是（）A．平行四边形B．矩形C．菱形D．正方形11．如图，在平面直角坐标系中，点A、B、C的坐标分别为(1,4)，(5,4)，(1,0)，则以A、B、C为顶点的三角形外接圆的圆心坐标是（）A ．(3,2)B ．(2,3)C ．(1,3)D ．(3,1)12．我国古代数学名著《九章算术》中有一个经典的“圆材埋壁”问题： “今有圆材埋壁中，以锯锯之，深一寸，锯道长一尺，问径几何? "意思是： 如图，CD 是⊙O 的直径， 弦 AB ⊥CD 于P ，CP =1寸，AB =10寸，则直径CD 的长是 （ ）寸A ．20B ．23C ．26D ．30二、填空题13．圆的半径为5cm ，圆心到弦AB 的距离为4cm ，则AB =_______cm ．14．如图，OE ⊥AB 于E ，若⊙O 的半径为10，OE ＝6，则AB ＝_______．15．如图，O e 的半径为4，AB ，CD 是O e 的弦，且//AB CD ，4AB =，CD =则AB 和CD 之间的距离为______．16．某隧道口横截面如图所示，上部分是圆弧形，下部分是矩形、已知隧道口最高点E与DC的距离EF为4米，且弧DC所在圆的半径为10米，则路面AB的宽度为_____米．17．如图，CD是⊙O的直径，弦AB⊥CD于点H，若∠D=30°，AD=，则AB=________cm．Ð的度数为18．如图，在⊙O中，弦AB的长为4，圆心O到弦AB的距离为2，则AOC______．19．如图，在平面直角坐标系中，点A，B，C的坐标分别为（1，4），（5，4），（1，﹣2），则△ABC外接圆的圆心坐标是_________．20．如图，一圆弧过方格的格点A、B、C，在方格中建立平面直角坐标系，使点A的坐标为（0，3），则该圆弧所在圆的圆心坐标是______．21．在进行垂径定理的证明教学中，老师设计了如下活动：先让同学们在圆中作了一条直径MN，然后任意作了一条弦（非直径）．如图1，接下来老师提出问题：在保证弦AB长度不变的情况下，如何能找到它的中点？在同学们思考作图验证后，小华说了自己的一种想法：只要将弦AB与直径MN保持垂直关系，如图2，它们的交点就是弦AB的中点，请你说出小华此想法的依据是__．22．如图AB是⊙O的直径，∠BAC=42°，点D是弦AC的中点，则∠DOC的度数是______度．23．如图，某小区的一个圆形管道破裂，修理工人准备更换一段新管道，现在量得污水水面宽度为80cm，水面到管道顶部的距离为20cm，则修理工人应准备的新管道的内直径是______cm．24．已知O e 的半径为2，弦BC =，A 是O e 上一点，且»»AB AC =，直线AO 与BC 交于点D ，则AD 的长为________．三、解答题25．如图，在⊙O 中，直径AB =10，弦AC =8，连接BC ．(1)尺规作图：作半径OD 交AC 于E ，使得点E 为AC 中点；(2)连接AD ，求三角形OAD 的面积．26．《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就，它的算法体系至今仍在推动着计算机的发展和应用.书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（1ED =寸），锯道长1尺（AB =1尺=10寸）．问这块圆形木材的直径（AC ）是多少？”如图所示，请根据所学的知识解答上述问题．27．已知：如图，在O e 中，AB AC 、为互相垂直的两条弦，,OD AB OE AC ^^，D 、E 为垂足．(1)若AB AC =，求证：四边形ADOE 为正方形．(2)若AB AC >，判断OD 与OE 的大小关系，并证明你的结论．28．如图，AB 为⊙O 的直径，弦CD AB ^于点F ，OE AC ^于点E ，若3OE =，OB=，求OF的长．5参考答案1．D【分析】连接OC ，由垂径定理可知，点E 为CD 的中点，且OE ⊥CD ，在Rt △OEC 中，根据勾股定理，即可得出OC ，从而得出直径．解：连接OC ，∵AB 为⊙O 的直径，弦CD ⊥AB 于点E∴CE=12CD=8，∵OE=6．在Rt △OEC 中，由勾股定理得：OC 2=OE 2+EC 2，即OC 2=62+82解得：OC=10∴直径AB=2OC=20．故选D ．【点拨】本题考查垂径定理，勾股定理．熟练掌握定理是解答关键.2．C【分析】连接OC ，求出∠COB =45°，根据垂径定理求出CD =2CE ，根据勾股定理求出CE 即可．解：连接OC ，则OC =12AB =12×12=6， ∵OA =OC ，∠CAB =22.5°，∴∠CAB =∠ACO =22.5°，∴∠COB=∠CAB+∠ACO=45°，∵AB⊥CD，AB为直径，∴CD=2CE，∠CEO=90°，∴∠OCE=∠COB=45°，∴OE=CE，∵CE2+OE2=OC2，∴2CE2=62，解得：CE，即CD=2CE，故选：C．【点拨】本题考查了等腰三角形的性质，勾股定理，三角形的外角性质，垂径定理等知识点，能求出CE=OE是解此题的关键．3．B【分析】连接OA，如图，设⊙O的半径为r，则OA=r，OM=16-r，根据垂径定理得到AM=BM=8，再根据勾股定理得到82+（16-r）2=r2，解方程求出r=10，然后计算CD-CM即可．解：连接OA，如图，设⊙O的半径为r，则OA=r，OM=16-r，∵AB⊥CD，∴AM=BM=12AB=8，在Rt△AOM中，82+（16-r）2=r2，解得r=10，∴MD=CD-CM=20-16=4．故选：B．【点拨】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．4．B【分析】根据垂径定理即可判断．解：CD Q 是O e 的直径，弦AB CD ^于点E ，AE EB \=，»»AC BC =， »»AD BD=．故选：B ．【点拨】本题主要考查垂径定理，掌握垂径定理是解题的关键．5．C【分析】根据垂径定理的内容和垂径定理的推论的内容进行判断．解：A 、平分弦（不是直径）的直径垂直于弦，原说法错误，不符合题意；B 、垂直于弦的直径平分弦，原说法错误，不符合题意；C 、弦的垂直平分线必经过圆心，原说法正确，符合题意；D 、AB 若也是直径，则原说法不符合题意；故选：C ．【点拨】本题考查了垂径定理以及推论，解答时熟悉垂径定理的内容以及推论的内容是关键．6．C【分析】根据垂径定理判断即可；解：∵直径CD 垂直于弦AB 于点E ，则由垂径定理可得，AE BE =，»»AD BD=，»»AC BC=，故选项A ，B ，D 正确；OE DE =无法得出，故C 错误．故选C ．【点拨】本题主要考查了垂径定理的应用，准确分析判断是解题的关键．7．A【分析】根据垂径定理及其推论分别进行判断．解：A、平分弦（非直径）的半径垂直于弦，所以A为假命题；B、垂直平分弦的直线必经过圆心，所以B选项为真命题；C、垂直于弦的直径平分这条弦所对的弧，所以C选项为真命题；D、平分弧的直径垂直平分这条弧所对的弦，所以D选项为真命题．故选：A．【点拨】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理，也考查了垂径定理的性质．8．D【分析】由垂径定理和勾股定理分别对各个选项进行判断即可．解：连接OA，条件不足，不能求出OE和EC的长，故选项A、B不符合题意；∵OC⊥AB于点E，∴OC是线段AB的垂直平分线，故选项D正确，符合题意；选项C不符合题意，故选：D．【点拨】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．9．C【分析】根据垂径定理的推论，勾股定理即可求得OC的长解：OA OBQ点C是AB的中点，=Q ⊙O 的半径为5，弦AB ＝8，1,42OC AB AC BC AB \^===在Rt AOC △中3OC ==故选C【点拨】本题考查了垂径定理，勾股定理，掌握垂径定理是解题的关键．10．C【分析】根据弦AB 的长是半径OA C 为»AB 的中点，判定出四边形OACB 是平行四边形，再由AB OC ^，即可判定四边形OACB 是菱形.解：∵弦AB 的长是半径OA C 为»AB 的中点，OC 为半径，∴12AP AB AO AB OC ==^，，∴1122OP OA OC ===，∴12PC OC =，即OP PC =，∴四边形OACB 是平行四边形，又∵AB OC ^，∴四边形OACB 是菱形.【点拨】本题主要考查了勾股定理，菱形的判定，以及垂径定理的推论，读懂题意是解题的关键．11．A【分析】根据垂径定理的推论“弦的垂直平分线必过圆心”作两条弦的垂直平分线，交点即为圆心．解：如图，作弦AB 、AC 的垂直平分线，∵点A 、B 、C 的坐标分别为(1,4)，(5,4)，(1,0)，所以弦514AB =-=，弦404AC =-=，∴弦AB 的垂直平分线与x 轴相交于点(30)，，弦AC 的垂直平分线与y 轴相交于点(0)2，，∴两条垂直平分线的交点1O即为三角形外接圆的圆心，且1O点的坐标是(3,2)．故选：A．【点拨】本题考查了垂径定理，三角形的外接圆与圆心，熟知垂径定理是解题的关键．12．C【分析】连接OA构成直角三角形，先根据垂径定理，由DP垂直AB得到点P为AB的中点，由AB=6可求出AP的长，再设出圆的半径OA为x，表示出OP，根据勾股定理建立关于x 的方程，解方程直接可得2x的值，即为圆的直径．解：连接OA，∵AB⊥CD，且AB=10寸，∴AP=BP=5寸，设圆O的半径OA的长为x，则OC=OD=x，∵CP=1，∴OP=x-1，在直角三角形AOP中，根据勾股定理得：x2-（x-1）2=52，化简得：x2-x2+2x-1=25，即2x=26，∴CD =26（寸）．故选：C ．【点拨】本题考查了垂径定理和勾股定理，正确作出辅助线构造直角三角形是关键．13．6【分析】根据题意，画出图形，利用垂径定理，可得2AB AC = ，然后利用勾股定理求出3AC cm =，即可求解．解：根据题意画出如下图形，半径5OA cm = ，OC AB ^ ，则4OC cm = ，∵半径5OA cm = ，OC AB ^ ，∴2AB AC = ，在Rt AOC △ 中，由勾股定理得：3A C cm === ，∴26A B A C cm == ．故答案为：6 ．【点拨】本意主要考查了垂径定理，勾股定理，利用垂径定理，得到2AB AC =是解题的关键．14．16【分析】连接OA ，由垂径定理可得2AB AE =，在Rt AOE D 中利用勾股定理即可求得AE 的长，进而求得AB ．解：连接OA ，∵OE ⊥AB 于E ，∴2AB AE =，在Rt AOE D 中，10OA =，OE ＝6，∴8AE ==，∴216AB AE ==，故答案为：16【点拨】本题考查了垂径定理和勾股定理，构造直角三角形是解题的关键．15．±【分析】作OE AB ^于E ，交CD 于F ，连结OA ，OC ，根据平行线的性质等到OF CD ^，再利用垂径定理得到1122AE AB CF CD ==，，再由勾股定理解得OE ，OF 的长，继而分类讨论解题即可．解：作OE AB ^于E ，交CD 于F ，连结OA ，OC ，如图，//AB CDQ OF CD\^11222AE BE AB CF DF CD \======，在Rt OAE △中，42OA AE ==Q ，\==OEV中，在Rt OCFQ，C F4OC==\==OF当圆心O在AB与CD之间时，=+=EF OF OE当圆心O不在AB与CD之间时，=-=-EF OF OE即AB和CD之间的距离为故答案为：【点拨】本题考查勾股定理、垂径定理、分类讨论等知识，是重要考点，难度较易，掌握相关知识是解题关键．16．16【分析】先根据勾股定理CF8=米，根据垂径定理求出DF=CF=8米，然后根据四边形ABCD为矩形，得出AB=DC=16米即可．解：∵EF=4米，OC=OE=10米，∴OF=OE-EF=6米，在Rt△OEC中，CF8=米，∵OF⊥DC，DC为弦，∴DF=CF=8米，∴DC=2×8=16米，∴四边形ABCD为矩形，∴AB=DC=16米，故答案为：16．【点拨】本题考查勾股定理，垂径定理，矩形性质，掌握勾股定理，垂径定理，矩形性质是解题关键．17．【分析】根据∠D =30°，直角三角形中30°角对应的直角边等于斜边的一半计算出AH ，再根据垂直于弦的直径平分弦得到AB =2AH 计算出AB ．解：在Rt AHD V 中，∠D =30°∴2AD AH=∴AH =cm∵弦AB ⊥CD∴2==AB AH故答案为：【点拨】本题考查直角三角形和圆的性质，解题的关键是熟练掌握直角三角形和圆的相关知识．18．45°【分析】先根据垂径定理可得122AC AB ==，再根据等腰直角三角形的判定与性质即可得．解：由题意得：OC AB ^，4AB =，122AC AB \==，2OC =Q ，AC OC \=，Rt AOC \V 是等腰直角三角形，45AOC =\а，故答案为：45°．【点拨】本题考查了垂径定理、等腰直角三角形的判定与性质，熟练掌握垂径定理是解题关键．19．（3，1）【分析】根据垂径定理的推论“弦的垂直平分线必过圆心”，作两条弦的垂直平分线，交点即为圆心．解：根据垂径定理的推论，则作弦AB、AC的垂直平分线，交点D即为圆心，且坐标是（3，1）．故答案为：（3，1）．【点拨】此题考查了垂径定理的推论，能够准确确定一个圆的圆心．20．(1,0)．【分析】直接利用垂径定理推论得出圆心位置，进而利用A点坐标得出原点位置即可得出答案．解：如图示，∵点A的坐标为（0，3），据此建立平面直角坐标系如下图所示，连接AB，AC，作AB，AC的中垂线，交点是点D则，该圆弧所在圆的圆心坐标是：(1,0)．故答案是：(1,0)．【点拨】本题主要考查了垂径定理以及坐标与图形的性质，正确得出圆心位置是解题关键．21．等腰三角形三线合一的性质【分析】连接OA、OB，则△OAB是等腰三角形，依据等腰三角形的性质判断．解：连接OA、OB，则△OAB是等腰三角形，当MN⊥AB时，一定有MB过AB的中点，依据三线合一的性质可得．故答案是：等腰三角形三线合一的性质．【点拨】本题考查了垂径定理，正确转化为等腰三角形的性质解决问题是关键．22．48【分析】根据点D是弦AC的中点，得到OD⊥AC，然后根据∠DOC=∠DOA即可求得答案：解：∵AB是⊙O的直径，∴OA=OC．∵∠A=42°，∴∠ACO=∠A=42°．∵D为AC的中点，∴OD⊥AC．∴∠DOC=90°﹣∠DCO=90°﹣42°=48°．故答案为：48．23．100【分析】由垂径定理和勾股定理计算即可．解：如图所示，作管道圆心O，管道顶部为A点，污水水面为BD，连接AO，AO与BD垂直相交于点C．设AO=OB=r则OC=r-20，BC=140 2BD=有222 OB OC BC=+222(20)40r r =-+化简得r =50故新管道直径为100cm ．故答案为：100．【点拨】本题为垂径定理的实际应用题，主要是通过圆心距，圆的半径及弦长的一半构成直角三角形，并应用勾股定理，来解决问题．24．1或3【分析】根据垂径定理建立直角三角形，再运用勾股定理求得OD ，进而分两种情况讨论即可．解：如图，连接OB ，»»AB AC =Q ，\由垂径定理可知，OA BC ^，BD CD ==则在Rt OBD △中，1OD ==，211AD r OD \=-=-=或213AD r OD =+=+=，故答案为：1或3．【点拨】本题考查了垂径定理，勾股定理计算圆周上点到弦得距离，熟练掌握基本定理，准确分类讨论是解题关键．25．(1)见分析(2)10【分析】（1）过点O 作OD ⊥AC ，交AC 于点E ，交⊙O 于点D ；（2）由题意可得OD =5，由（1）得：OE ⊥AC ，点E 为AC 中点，继而可得118422AE AC ==´=，然后根据三角形的面积公式即可求得答案．(1)解：如图，点E 即为所求；(2)解：如图，连接AD ，∵⊙O 的直径是10，∴OD =5，由（1）得：OE ⊥AC ，点E 为AC 中点，∴118422AE AC ==´=，∴11541022OAD S OD AE =×=´´=V ．【点拨】本题主要考查了垂径定理、三角形的面积公式，熟练掌握垂径定理是解题的关键．26．这块圆形木材的直径（AC ）是26寸【分析】设O e 的半径为x 寸，根据题意可得AD BD =，在Rt AOD △中，OA x =，1OD x =-，勾股定理求解即可．解：设O e 的半径为x 寸，∵OE AB ^，10AB =寸，∴152AD BD AB ===寸，在Rt AOD △中，OA x =，1OD x =-，由勾股定理得()22215x x =-+，解得13x =.∴O e 的直径226AC x ==（寸）.答：这块圆形木材的直径（AC ）是26寸.【点拨】本题考查了垂径定理的应用，掌握垂径定理是解题的关键．27．(1)见分析(2)OD ＜OE【分析】（1）先根据垂径定理，由OD ⊥AB ，OE ⊥AC 得到AD ＝12AB ，AE ＝12AC ，且∠ADO ＝∠AEO ＝90°，加上∠DAE ＝90°，则可判断四边形ADOE 是矩形，由于AB ＝AC ，所以AD ＝AE ，于是可判断四边形ADOE 是正方形；（2）由（1）得四边形ADOE 是矩形，可得OE ＝AD ＝12AB ，OD ＝AE ＝12AC ，又AB ＞AC ，即可得出OE 和OD 的大小关系．(1)证明：∵OD ⊥AB ，OE ⊥AC ，AB ⊥AC ，∴四边形ADOE 为矩形，且OD 平分AB ，OE 平分AC ，∴BD ＝AD ＝12AB ，AE ＝EC ＝12AC ，∵AB ＝AC ，∴AD ＝AE ，∴四边形ADOE 为正方形．(2)解：OD ＜OE ，理由如下：由（1）得四边形ADOE 是矩形，∴OE ＝AD ，OD ＝AE ，∵AD ＝12AB ，AE ＝12AC ，∴OE ＝12AB ，OD ＝12AC ，又∵AB ＞AC ，∴OD ＜OE ．【点拨】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧、也考查了正方形的判定．28．1.4【分析】根据垂径定理得到AE EC =，CF FD =，根据勾股定理求出AE ．设OF x =，再次根据勾股定理得到等式2222AC AF OC OF -=-，代入求值即可解答．解：连接OC ，∵AB CD ^，OE AC ^，∴AE EC =，CF FD =，∵3OE =，5OB =，∴5OB OC OA ===，∴在Rt OAE △中，4AE ===，∴4AE EC ==，∴8AC =，设OF x =，∵在Rt CAF V 中，222CF AC AF =-，在Rt OFC V 中，222CF OC OF =-，∴2222AC AF OC OF -=-，∴()2222855x x -+=-，解得： 1.4x =，即 1.4OF =．【点拨】本题考查了垂径定理、勾股定理知识，关键在于合理运用垂径定理和勾股定理求出边的长度．。

2022-2023学年浙教版九年级数学上册《3.3垂径定理》同步练习题（附答案）一．选择题1．如图，AB是⊙O的直径，OD垂直于弦AC于点D，DO的延长线交⊙O于点E．若AC ＝4，DE＝4，则BC的长是（）A．1B．C．2D．42．过⊙O内一点M的最长弦为20cm，最短弦为16cm，那么OM的长为（）A．3cm B．6cm C．8cm D．9cm3．如图，CD是圆O的弦，直径AB⊥CD，垂足为E，若AB＝12，BE＝3，则四边形ACBD 的面积为（）A．36B．24C．18D．724．工人师傅为检测该厂生产的一种铁球的大小是否符合要求，设计了一个如图（1）所示的工件槽，其两个底角均为90°，将形状规则的铁球放入槽内时，若同时具有图（1）所示的A、B、E三个接触点，该球的大小就符合要求．图（2）是过球心及A、B、E三点的截面示意图，已知⊙O的直径就是铁球的直径，AB是⊙O的弦，CD切⊙O于点E，AC ⊥CD、BD⊥CD，若CD＝16cm，AC＝BD＝4cm，则这种铁球的直径为（）A．10cm B．15cm C．20cm D．24cm5．如图，在⊙O中，直径AB＝8，弦DE⊥AB于点C，若AD＝DE，则BC的长为（）A．B．C．1D．26．如图，在⊙O中，直径CD垂直弦AB于点E，且OE＝DE．点P为上一点（点P不与点B，C重合），连接AP，BP，CP，AC，BC．过点C作CF⊥BP于点F．给出下列结论：①△ABC是等边三角形；②在点P从B→C的运动过程中，的值始终等于．则下列说法正确的是（）A．①，②都对B．①对，②错C．①错，②对D．①，②都错二．填空题7．如图，AB是半圆O的直径，四边形CDMN和DEFG都是正方形，其中C，D，E在AB 上，F、N在半圆上．若则正方形CDMN的面积与正方形DEFG的面积之和是16，则AB 的长为．8．如图，以AB为直径的⨀O中，点C为⨀O上一点，且AC＝BC＝，过点O作OD⊥AC，垂足为D，点P为直线OD上一个动点，则弧BC，PB，PC构成的封闭图形周长最小值为．9．如图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分，如果C是⊙O中弦AB的中点，CD经过圆心O交⊙O于点D，并且AB＝4m，CD＝6m，则⊙O的半径长为m．10．如图，在⊙O中，AD⊥BC，连接AB、CD，当AB＝2，CD＝6时，则⊙O半径长为．11．平面直角坐标系xOy如图所示，以原点O为圆心，以2为半径的⊙O中，弦AB＝，点C是弦AB中点，P（+1，﹣1），连接PC，当弦AB在⊙O上滑动，线段PC扫过的面积为．12．如图，AB是⊙O的直径，弦CD交AB于点P，AP＝4，BP＝12，∠APC＝30°，则CD的长为．13．如图，圆O的半径为4，点P是直径AB上定点，AP＝1，过P的直线与圆O交于C，D两点，则△COD面积的最大值为；作弦DE∥AB，CH⊥DE于H，则CH的最大值为．三．解答题14．如图，在⊙O中，AB，AC为弦，CD为直径，AB⊥CD于E，BF⊥AC于F，BF与CD 相交于G．（1）求证：ED＝EG；（2）若AB＝8，OG＝1，求⊙O的半径．15．石拱桥是我国古代入民勤劳和智慧的结晶（如图1），隋代建造的赵州桥距今约有1400年历史，是我国古代石拱桥的代表．如图2是根据某石拱桥的实物图画出的几何图形，桥的主桥拱是圆弧形，表示为．桥的跨度（弧所对的弦长）AB＝26m，设所在圆的圆心为O，半径OC⊥AB，垂足为D．拱高（弧的中点到弦的距离）CD＝5m．连接OB．（1）直接判断AD与BD的数量关系；（2）求这座石拱桥主桥拱的半径（精确到1m）．16．如图，⊙O中两条互相垂直的弦AB，CD交于点E．（1）OM⊥CD于点M，CD＝24，⊙O的半径长为4，求OM的长．（2）点G在BD上，且AG⊥BD交CD于点F，求证：CE＝EF．17．如图，在⊙O中，AB、AC是互相垂直且相等的两条弦，OD⊥AB，OE⊥AC，垂足分别为D、E．（1）求证：四边形ADOE是正方形；（2）若AC＝2cm，求⊙O的半径．18．如图，线段AB＝10，AC＝8，点D，E在以AB为直径的半圆O上，且四边形ACDE 是平行四边形，过点O作OF⊥DE于点F，求AE的长．19．如图，圆柱形水管内原有积水的水平面宽CD＝20cm，水深GF＝2cm．若水面上升2cm （EG＝2cm），则此时水面宽AB为多少？20．某隧道的截面是由如图所示的图形构成，图形下面是长方形ABCD，上面是半圆形，其中AB＝10米，BC＝2.5米，隧道设双向通车道，中间有宽度为2米的隔离墩，一辆满载家具的卡车，宽度为3米，高度为4.9米，请计算说明这辆卡车是否能安全通过这个隧道？参考答案一．选择题1．解：∵AB是⊙O的直径，∴∠C＝90°，∵OD⊥AC，∴点D是AC的中点，∴OD是△ABC的中位线，∴OD∥BC，且OD＝BC，设OD＝x，则BC＝2x，∵DE＝4，∴OE＝4﹣x，∴AB＝2OE＝8﹣2x，在Rt△ABC中，由勾股定理可得，AB2＝AC2+BC2，∴（8﹣2x）2＝（4）2+（2x）2，解得x＝1．∴BC＝2x＝2．故选：C．2．解：由题意知，最长的弦为直径，最短的弦为垂直于直径的弦，如图所示．直径ED⊥AB于点M，则ED＝20cm，AB＝16cm，由垂径定理知：点M为AB中点，∴AM＝8cm，∵半径OA＝10cm，∴OM2＝OA2﹣AM2＝100﹣64＝36，∴OM＝6cm．故选：B．3．解：如图，连接OC，∵AB＝12，BE＝3，∴OB＝OC＝6，OE＝3，∵AB⊥CD，在Rt△COE中，EC＝，∴CD＝2CE＝6，∴四边形ACBD的面积＝．故选：A．4．解：如图，连接OE，交AB于点F，连接OA，∵AC⊥CD、BD⊥CD，∴AC∥BD，∵AC＝BD＝4cm，∴四边形ACDB是平行四边形，∴四边形ACDB是矩形，∴AB∥CD，AB＝CD＝16cm，∵CD切⊙O于点E，∴OE⊥CD，∴OE⊥AB，∴四边形EFBD是矩形，AF＝AB＝×16＝8（cm），∴EF＝BD＝4cm，设⊙O的半径为rcm，则OA＝rcm，OF＝OE﹣EF＝（r﹣4）cm，在Rt△AOF中，OA2＝AF2+OF2，∴r2＝82+（r﹣4）2，解得：r＝10，∴这种铁球的直径为20cm，故选：C．5．解：∵DE⊥AB，AB过圆心O，∴DC＝CE＝DE，∠ACD＝∠BCD＝90°，∵AD＝DE，∴DC＝AD，∴∠DAC＝30°，∵AB是⊙O的直径，∴∠ADB＝90°，∴BD＝AB＝＝4，∵∠ADB＝90°，∠DAB＝30°，∴∠ABD＝60°，∵∠DCB＝90°，∴∠CDB＝30°，∴BC＝BD＝，故选：D．6．解：如图，作CM⊥AP于M，连接AD．∵AE⊥OD，OE＝DE，∴AO＝AD，∵OA＝OD，∴AO＝AD＝OD，∴△AOD是等边三角形，∴∠D＝∠ABC＝60°，∵CD⊥AB，∴AE＝EB，∴CA＝CB，∴△ABC是等边三角形，故①正确，∵∠CP A＝∠ABC＝60°，∠APB＝∠ACB＝60°，∴∠CPF＝180°﹣60°﹣60°＝60°，∵∠CPM＝∠CPF＝60°，CF⊥PF，CM⊥P A，∴CF＝CM，∵PC＝PC，∠CFP＝∠CMP，∴Rt△CPF≌Rt△CPM（HL），∴PF＝PM，∵AC＝BC，CM＝CF，∠AMC＝∠CFB＝90°，∴Rt△AMC≌Rt△BFC（HL），∴AM＝BF，∴AP﹣PB＝PM+AM﹣（BF﹣PF）＝2PM＝2PF，∴＝，在Rt△CPF中，∵∠CPF＝60°，∠CFP＝90°，∴CF＝PF，∴PF＝CF，∴＝，故②正确，故选：A．二．填空题7．解：连接ON，OF，设正方形CDMN的边长为a，正方形DEFG边长为b，OD＝c，则CN＝CD＝a，DE＝EF＝b，∵四边形CDMN和DEFG都是正方形，∴∠NCD＝90°，∠FED＝90°，设OA＝ON＝OF＝OB＝r，由勾股定理得：NC2+CO2＝ON2，OE2+EF2＝OF2，∴a2+（a+c）2＝r2①，b2+（b﹣c）2＝r2②，①﹣②，得a2+（a+c）2﹣b2﹣（b﹣c）2＝0，（a2﹣b2）+[（a+c）2﹣（b﹣c）2）]＝0，（a+b）（a﹣b）+（a+c+b﹣c）（a+c﹣b+c）＝0，（a+b）（a﹣b）+（a+b）（a﹣b+2c）＝0，（a+b）（a﹣b+a﹣b+2c）＝0，2（a+b）（a﹣b+c）＝0，∵a+b≠0，∴a﹣b+c＝0，即b＝a+c，把b＝a+c代入①，得a2+b2＝r2，∵正方形CDMN的面积与正方形DEFG的面积之和是16，∴a2+b2＝16，∴r2＝16，解得r＝4（负值舍去），∴AB＝2r＝8．故答案为：8．8．解：要使得弧BC，PB，PC构成的封闭图形周长最小，弧BC的值不变，则BP+PC最小即可，∵OD⊥AC，∴点C关于PD的对称点为点A，即当P点与O点重合时，BP+PC最小，即弧BC，PB，PC构成的封闭图形周长最小，连接OC，∵AC＝BC＝，∴∠BOC＝90°，OB＝OC＝BC＝＝1，∴弧BC的长为＝，∴弧BC，PB，PC构成的封闭图形周长最小为：2+．故答案为：2．9．解：连接OA，如图，设⊙O的半径为rm，∵C是⊙O中弦AB的中点，CD过圆心，∴CD⊥AB，AC＝BC＝AB＝2m，在Rt△AOC中，∵OA＝rcm，OC＝（6﹣r）m，∴22+（6﹣r）2＝r2，解得r＝，即⊙O的半径长为m．故答案为：．10．解：如图，连接CO，延长CO交⊙O于H，连接BH，DH，BD．∵CH是直径，∴∠CBH＝∠CDH＝90°，∴CB⊥BH，∵CB⊥AD，∴AD∥BH，∴∠CDB＝∠DBH，∴＝，∴DH＝BA＝2，而CD＝6，根据勾股定理CH＝＝2，故答案为2．11．解：连接OC，OA，如图，∵点C是弦AB中点，∴OC⊥AB，AC＝BC＝AB＝，∴OC＝＝．∵弦AB在⊙O上滑动，∴点C的轨迹为以点O为圆心，以为半径的圆，如图中的虚线⊙O，过点P作该圆的切线PD，PE，连接OD，OE，PO，如上图，则OD＝OE＝．利用勾股定理可求得PO＝，∵PD，PE是虚线⊙O的切线，∴OD⊥PD，OE⊥PE，PD＝PE，∠DPO＝∠EPO．∴∠OPD＝30°，∴∠OPE＝30°，∴∠DOP＝60°，∠EOP＝60°，∴∠DOE＝120°．∵线段PC扫过的面积为四边形DOEP的面积+大扇形ODE的面积，∴线段PC扫过的面积为2×PD•OD+＝+π．故答案为：+π．12．解：过O作OI⊥CD于I，连接OD，则∠OID＝∠OIP＝90°，∵AP＝4，BP＝12，∴直径AB＝4+12＝16，即半径OD＝OA＝8，∴OP＝OA﹣AP＝8﹣4＝4，∵∠IPO＝∠APC＝30°，∴OI＝OP＝＝2，由勾股定理得：DI＝＝＝2，∵OI⊥CD，OI过圆心O，∴DI＝CI＝2，即CD＝DI+CI＝4，故答案为：4．13．解：如图1，∵OC•OD•sin∠COD，∴当∠COD＝90°时，△COD面积有最大值，且最大值＝×4×4×1＝8；设△APO的PO边上的高为h1，△DPO的边PO上的高为h2，如图，∵S△CDO＝S△PCO+S△DPO，∴当△COD面积有最大值时，PO×h1+PO×h2＝8．∴×3×（h1+h2）＝8，∴h1+h2＝．∴CH的最大值为．故答案为：8；．三．解答题14．（1）证明：如图：连接BD，∵AB⊥CD于E，BF⊥AC于F，∴∠CFG＝∠GEB，∵∠CGF＝∠BGE，∴∠C＝∠GBE，∵∠C＝∠DBE，∴∠GBE＝∠DBE，∵AB⊥CD于E，∴∠GEB＝∠DEB，在△GBE和△DBE中，，∴△BGE≌△BDE（ASA），∴ED＝EG．（2）解：如图：连接OA，设OA＝r，则DG＝r+1，由（1）可知ED＝EG，∴OE＝，∵AB⊥CD于E，AB＝8，∴AE＝BE＝4，∴在Rt△OAE中，根据勾股定理得：OE2+AE2＝OA2，即（）2+42＝r2，解得：r＝，即⊙O的半径为．15．解：（1）∵OC⊥AB，∴AD＝BD；（2）设主桥拱半径为R，由题意可知AB＝26，CD＝5，∴BD＝AB＝13，OD＝OC﹣CD＝R﹣5，∵∠ODB＝90°，∴OD2+BD2＝OB2，∴（R﹣5）2+132＝R2，解得R＝19.4≈19，答：这座石拱桥主桥拱的半径约为19m．16．（1）解：如图，连接OD，∵OM⊥CD，OM过圆心，CD＝24，∴DM＝CM＝CD＝12，∠OMD＝90°，由勾股定理得，OM＝＝＝4，即OM的长为4；（2）证明：如图，连接AC，∵AG⊥BD，∴∠DGF＝90°，∴∠DFG+∠D＝90°，∵AB⊥CD，∴∠CEA＝90°，∴∠C+∠EAC＝90°，∵∠EAC＝∠D，∠DFG＝∠AFC，∴∠C＝∠AFC，∴AF＝AC，∵AB⊥CD，∴CE＝EF．17．（1）证明：∵OD⊥AB，OE⊥AC，∴AD＝AB，AE＝AC，∵AB＝AC，∴AD＝AE，∵∠ADO＝∠A＝∠AEO＝90°，∴四边形ADOE是正方形；（2）解：连接OA，∵AC＝2cm，∴AE＝1cm，在Rt△AOE中，OA＝＝（cm），答：⊙O的半径是cm．18．解：过点E作EG⊥AB于点G，连接OE，则OE＝OA＝，∠EGO＝90°，∵四边形ACDE是平行四边形，∴DE＝AC＝8，DE∥AB，∵OF⊥DE，即∠OFE＝90°，∴EF＝＝4，∠FOG＝∠OFE＝90°，∴四边形OFEG是矩形，∴OG＝EF＝4，∴AG＝5﹣4＝1，在Rt△OEG中，EG＝，在Rt△AGE中，AE＝．19．解：连接OA、OC，∵由题意知：AB∥CD，OE⊥AB，OF⊥CD，CD＝20cm，∴CG＝CD＝10cm，在Rt△OGC中，由勾股定理得：OC2＝CG2+OG2，OC2＝102+（OC﹣2）2，解得：OC＝26（cm），则OE＝26cm﹣2cm﹣2cm＝22cm，∵在Rt△OEA中，由勾股定理得：OA2＝OE2+AE2，∴262＝222+AE2，∴AE＝8，∵OE⊥AB，OE过圆心O，∴AB＝2AE＝16cm．20．解：如图，作OM⊥AB于M，交AB于M，图中KN＝3，作KF⊥CD于H，交⊙O于F，连接OF．易知四边形OHKM是矩形，四边形ABCD是矩形，OH＝KM＝4，AB＝CD＝10，OF＝OD＝5，在Rt△OHF中，FH＝＝＝3，∵HK＝BC＝2.5，∴FK＝2.5+3＝5.5，∵5.5＞4.9，∴这辆卡车能安全通过这个隧道．。