集合与函数概念单元测试题经典含答案

集合与函数概念测试题及答案The document was prepared on January 2, 2021新课标高一数学单元测试题一集合与函数概念一、选择题1.已知全集{1,3,5,7,9}U =,集合{5,7}A =,2{1,,||}UA a a =,则a 的值为A ．3B ．3-C ．±3D ．9± 2.已知函数()([,])y f x x a b =∈,那么集合(){(,)|,[,]}x y y f x x a b =∈(){,|}x y x c =所含元素的个数为A ．1个B ．0个C ．0或1个D ．0或1或2个3.设{}{}2|0,|02x M x N y y ≤≤==≤≤,给出的4个图形中能表示集合M 到集合N 的映射的是4.定义域为R 的函数()y f x =的值域为[,]a b ,则函数()y f x c =+的值域为 A ．[,]a c b c ++ B ．[,]a c b c -- C ．[,]a b D ．不确定5.设2()lg2x f x x +=-,则2()()2x f f x+的定义域为 A.(4,0)(0,4)- B.(4,1)(1,4)-- C.(2,1)(1,2)-- D.(4,2)(2,4)-- 6.设()f x 是R 上的任意函数,则下列叙述正确的是 A ()()f x f x -是奇函数 B ()()f x f x -是奇函数C ()()f x f x --是偶函数D ()()f x f x +-是偶函数B.D.A.7. 定义在R 上的奇函数()f x 为减函数,若0m n +≥,给出下列不等式： 1()()0f m f m ⋅-≤ 2()()()()f m f n f m f n +≥-+- 3()()0f n f n ⋅-≥ 4()()()()f m f n f m f n +≤-+- 其中正确的是A ．1和4B ．2和 3C ．1和3D ．2和48.已知函数()()22403f x ax ax a =++<<,若12x x <,120x x +=,则 ． A ．()()12f x f x < B ．()()12f x f x >C ．()()12f x f x =D ．()1f x 与()2f x 大小关系不确定9.函数1,[1,4]y x x=∈的最小值为A ．74B ．74-C ．12D ．010．设()f x 为定义在R 上的偶函数,且()()()()00,11f f x f x f x =++-=则下列说法正确的是A ．()0f x =有惟一实根0x =B ．()0f x =有两个实根1x =或0x =C ．()0f x =有3个实根1x =±或0x =D ．()0f x =有无数多个实根 11．函数()()||0f x x x px p =+>的定义域为R ,则函数()f x 是 A ．既是偶函数也是增函数 B ．既是偶函数也是减函数 C ．既是奇函数也是增函数 D ．既是奇函数也是减函数12．把函数()y f x =的图像沿着直线0x y +=的方向向右下方移动位,得到的图形恰好是函数2log y x =的图像,则()f x 是 A ．()()lg 22f x x =++ B ．()()lg 22f x x =-+ C ．()()lg 22f x x =+- D ．()()lg 22f x x =-- 二、填空题13．已知集合{}{}2|1,|1A x x B x ax ====,若B A ⊆,则实数a 的集合为-________________．14．设函数()f x 满足()211log x 2f x f ⎛⎫=+⋅ ⎪⎝⎭,则()2f =___________．15．已知定义在R 上的奇函数()f x ,当0x >时()2x f x x =+,则当0x ≤时()f x 的表达式为__________________．16. 设集合{}R t t t A ∈≤≤=,41|,A 到坐标平面上的映射为()t t t f 22log 2,log :-→,集合()()(){}r G t f A t t f B ∈∈=都有对任意的,|,()(){}0,|,222>≤+=r r y x y x r G ,则满足()r G B ⊆的r 的最小值是________________. 三、解答题17．设函数()f x 为奇函数,且对任意x 、y R ∈都有()()()f x f y f x y -=-,当0x <时()()0,15f x f >=-,求()f x 在[2,2]-上的最大值．18．已知()23g x x =--,()f x 是二次函数,()()g x f x +是奇函数,且当[1,2]x ∈-时,()f x 的最小值是1,求()f x 的表达式．19．设a R ∈,函数2()22.f x ax x a =--若()0f x >的解集为A,{}|13,B x x A B φ=<<≠,求实数a 的取值范围.20．已知函数()()110,0f x x a a x=->>, 1判断()f x 在定义域上的单调性,并证明；2若()f x 在[,]m n 上的值域是[,]m n ()0m n <<求a 的取值范围和相应的m 、n 的值．参考答案1．答案：C 2．答案：C 3．答案：D 4．答案：C 5．答案：B 6．答案：D 7．答案：A8．答案：A 提示：由条件知120x x <<,抛物线对称轴为1x =-,画出大致图像容易知选A ．9．答案：D 提示：函数1y x=-在[1,4]上递增,∴当1x =时min 1101y =-=．10．答案：D 11．答案：C12．答案：A 提示：此平移可分解为把()y f x =的图像向右平移2个单位再向下平移2个单位,即可得到2log y x =． 13．答案：{}1,0,1- 14．答案：32 提示：令12x =,则21111log 222f f ⎛⎫⎛⎫=+⋅ ⎪ ⎪⎝⎭⎝⎭,1122f⎛⎫∴= ⎪⎝⎭；令2x =,则()211321log 21222f f ⎛⎫=+⋅=+= ⎪⎝⎭．15．答案：()0,02,0xx f x x x -=⎧=⎨-<⎩ 16．答案：2 提示: ()t f 为⎩⎨⎧-==ty tx 22log 2log ,满足222r y x ≤+,则()()22222log 2log r t t ≤-+,即求左端的最大值为4.17．解：设1222x x -≤≤≤,则120x x -<()()()12120f x f x f x x ∴-=-> ()()12f x f x ∴>从而()f x 在[2,2]-上递减()()()max 22f x f f ∴=-=-在()()()f x f y f x y -=-中,令2,1x y ==得()()()2121f f f -=-()()22110f f ∴==- ()max 10f x ∴=18．解：设()()20f x ax bx c a =++≠,则()()()213,f x g x a x bx c +=-++-又()()f x g x +为奇函数, ()()221313a x bx c a x bx c ∴--+-=----+对x R ∈恒成立, 1133a a c c -=-+⎧∴⎨-=-+⎩,解得13a c =⎧⎨=⎩, ()23f x x bx ∴=++,其对称轴为2b x =-．（1） 当12b-<-即2b ≥时,()()min 141,3f x f b b =-=-=∴=；（2） 当122b-≤-≤即42b -≤≤时,()22min31242b bb f x f ⎛⎫=-=-+= ⎪⎝⎭,解得b =-b = ；（3）当22b->即4b <-时,()()min 2721,3f x f b b ==+=∴=-舍,综上知()233f x x x =++或()23f x x =-． 19．解：由fx 为二次函数知0a ≠令fx ＝0解得其两根为1211x x a a == 由此可知120,0x x <>i 当0a >时,12{|}{|}A x x x x x x =<⋃>A B φ⋂≠的充要条件是23x <,即13a +<解得67a >ii 当0a <时,12{|}A x x x x =<<A B φ⋂≠的充要条件是21x >,即11a +>解得2a <- 综上,使A B φ⋂=成立的a 的取值范围为6(,2)(,)7-∞-⋃+∞20．解：1此函数为增函数, 设120x x >>,则()()1212121211x x f x f x x x x x --=-+=, 1212120,0,0x x x x x x >>∴>->()()12f x f x ∴>()f x ∴在()0,+∞上是增函数． 2()f x 在[,]m n 上是增函数()(),f m m f n n ∴==即：1111,m n a m a n-=-=故m 、n 是关于x 的方程11x a x-=的两个不相等的正实根,即为20ax x a -+=有两个不相等的正实根,()221401010a m n a mn ⎧∆=-->⎪⎪∴+=>⎨⎪=>⎪⎩,1120,212m a a n a⎧=⎪⎪∴<<⎨⎪=⎪⎩。

⾼中数学必修⼀第⼀章《集合与函数概念》单元测试题（含答案）《集合与函数概念》单元测试题(第⼀章)(120分钟150分)⼀、选择题(本⼤题共12⼩题,每⼩题5分,共60分.在每⼩题给出的四个选项中,只有⼀项是符合题⽬要求的)1.集合A={0,1,2},B={x|-1A.{0}B.{1}C.{0,1}D.{0,1,2}2.设集合M={2,0,x},集合N={0,1},若N?M,则x的值为( )A.2B.0C.1D.不确定3.在下列由M到N的对应中构成映射的是( )4.已知函数f(x)=ax3+bx(a≠0),满⾜f(-3)=3,则f(3)= ( )A.2B.-2C.-3D.3【补偿训练】已知y=f(x)是偶函数,且f(4)=5,那么f(4)+f(-4)的值为( ) A.5 B.10C.8D.不确定5.已知⼀次函数y=kx+b为减函数,且kb<0,则在直⾓坐标系内它的⼤致图象是( )6.若f(x)=则f的值为( )A.-B.C.D.7.若f(g(x))=6x+3,且g(x)=2x+1,则f(x)= ( )A.3B.3xC.6x+3D.6x+18.下列四个图形中,不是以x为⾃变量的函数的图象是( )9.已知集合A={x|x2+x+1=0},若A∩R=?,则实数m的取值范围是( )A.m<4B.m>4C.0D.0≤m<410.函数f(x)=|x|和g(x)=x(2-x)的单调递增区间分别是( )A.(-∞,0]和(-∞,1]B.(-∞,0]和[1,+∞)C.[0,+∞)和(-∞,1]D.[0,+∞)和[1,+∞)11.对于任意两个正整数m,n,定义某种运算“※”如下:当m,n都为正偶数或正奇数时,m※n=m+n;当m,n中⼀个为正偶数,另⼀个为正奇数时,m※n=mn.则在此定义下,集合M={(a,b)|a※b=12,a∈N*,b∈N*}中的元素个数是( )A.10个B.15个C.16个D.18个12.设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则使<0的x的取值范围为( )A.(-1,0)∪(1,+∞)B.(-∞,-1)∪(0,1)C.(-∞,-1)∪(1,+∞)D.(-1,0)∪(0,1)⼆、填空题(本⼤题共4⼩题,每⼩题5分,共20分.请把正确答案填在题中横线上)13.已知集合A={x|1≤x<2},B={x|x14.已知a是实数,若集合{x|ax=1}是任何集合的⼦集,则a的值是.15.已知f(x)为偶函数,则f(x)=x1,1x0, ______,0x 1.+-≤≤≤≤16.定义在R上的奇函数f(x)为减函数,若a+b≤0,给出下列不等式:①f(a)f(b)≤0;②f(a)+f(b)≤f(-a)+f(-b);③f(b)f(-b)≤0;④f(a)+f(b)≥f(-a)+f(-b).其中正确的是.(把你认为正确的不等式的序号全写上).三、解答题(本⼤题共6⼩题,共70分.解答时应写出必要的⽂字说明、证明过程或演算步骤)17.(10分)设全集为R,集合A={x|3≤x<6},B={x|2(1)分别求A∩B,(eB)∪A.R(2)已知C={x|a18.(12分)已知函数f(x)=.(1)判断点(3,14)是否在f(x)的图象上.(2)当x=4时,求f(x)的值.(3)当f(x)=2时,求x的值.19.(12分)若函数f(x)=x2+4x+a的定义域和值域均为[-2,b](b>-2),求实数a,b的值.20.(12分)(2015·烟台⾼⼀检测)已知函数f(x)=ax+b,且f(1)=2,f(2)=-1.(1)求f(m+1)的值.(2)判断函数f(x)的单调性,并⽤定义证明..【拓展延伸】定义法证明函数单调性时常⽤变形技巧(1)因式分解:当原函数是多项式函数时,作差后的变形通常进⾏因式分解.(2)通分:当原函数是分式函数时,作差后往往进⾏通分,然后对分⼦进⾏因式分解.(3)配⽅:当原函数是⼆次函数时,作差后可考虑配⽅,便于判断符号.21.(12分)已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,⼜f(1)=-2.(1)判断f(x)的奇偶性.(2)求证:f(x)为R上的减函数.(3)求f(x)在区间[-3,3]上的值域.22.(12分)定义在(-1,1)上的函数f(x)满⾜:①对任意x,y∈(-1,1),都有f(x)+f(y)=f;②f(x)在(-1,1)上是单调递减函数,f=-1.(1)求f(0)的值.(2)求证:f(x)为奇函数.(3)解不等式f(2x-1)<1.《集合与函数概念》单元测试题参考答案(第⼀章)(120分钟150分)。

第⼀章__《集合与函数概念》单元测试题（含答案）《集合与函数概念》单元测试题⼀、选择题：1、在“①⾼⼀数学课本中的难题；②所有的正三⾓形；③⽅程220x +=的实数解”中，能够表⽰成集合的是( )（A ）②（B ）③（C ）②③（D ）①②③2、若{{}|0,|12A x x B x x =<<=≤<，则A B ?= ( )（A ）{}|0x x ≤ （B ）{}|2x x ≥（C ）{0x ≤≤ （D ）{}|02x x <<3、若{}{}0,1,2,3,|3,A B x x a a A ===∈，则A B ?= ( )（A ）{}1,2 （B ）{}0,1（C ）{}0,3 （D ）{}34、在映射中B A f →:，},|),{(R y x y x B A ∈==，且),(),(:y x y x y x f +-→，则与A 中的元素)2,1(-对应的B 中的元素为（）（A ）)1,3(- （B ）)3,1( （C ）)3,1(-- （D ）)1,3(5、下列各组函数)()(x g x f 与的图象相同的是（）（A ）2)()(,)(x x g x x f == （B ）22)1()(,)(+==x x g x x f（C ）0)(,1)(x x g x f == （D ）?-==x x x g x x f )(|,|)( )0()0(<≥x x 6、已知集合2{40}A x x =-=，集合{1}B x ax ==，若B A ?，则实数a 的值是（）A ．0B ．12±C ．0或12±D ．0或127、已知集合{(,)2}A x y x y =+=，{(,)4}B x y x y =-=，则A B = （）A ．{3,1}x y ==-B ．(3,1)-C ．{3,1}-D ．{(3,1)}-8、设A 、B 为两个⾮空集合，定义{(,),}A B a b a A b B ⊕=∈∈，若{1,2,3}A =，{2,3,4}B =，则A B ⊕中的元素个数为（）A ．3B ．7C ．9D ．129、已知集合2{1}A y y x ==+，集合2{26}B x y x ==-+，则A B = （）A ．{(,)1,2}x y x y ==B ．{13}x x ≤≤C ．{13}x x -≤≤D ．?10、如图所⽰，阴影部分的⾯积S 是h 的函数()H h ≤≤0。

新课标高一数学必修1第一章集合与函数概念单元测试题一、 选择题2． 设集合{}|43A x x =-<<，{}|2B x x =≤，则A B = （ ）A ．(4,3)-B ．(4,2]-C ．(,2]-∞D ．(,3)-∞3．已知()5412-+=-x x x f ，则()x f 的表达式是（ ）A ．x x 62+B ．782++x xC ．322-+x xD ．1062-+x x5．下列四个函数：①3y x =-；②211y x =+；③2210y x x =+-；④(0)1(0)x x y x x⎧-≤⎪=⎨->⎪⎩. 其中值域为R 的函数有 （ ）A ．1个B ．2个C ．3个D ．4个7．下列函数中，定义域为[0，∞）的函数是 （ ）A ．x y =B ．22x y -=C ．13+=x yD ．2)1(-=x y8．若R y x ∈,，且)()()(y f x f y x f +=+，则函数)(x f （ ） A ． 0)0(=f 且)(x f 为奇函数 B ．0)0(=f 且)(x f 为偶函数C ．)(x f 为增函数且为奇函数D ．)(x f 为增函数且为偶函数9（A ） (B) (C )(D)二、 填空题11．若{}{}0,1,2,3,|3,A B x x a a A ===∈，则A B = ．12．已知集合M={(x ，y )|x ＋y =2}，N={(x ，y )|x －y =4}，那么集合M∩N ＝ ．14．某班50名学生参加跳远、铅球两项测试，成绩及格人数分别为40人和31人，两项测试均不及格的人数是4人，两项测试都及格的有 人．15．已知函数f(x)满足f(xy)=f(x)+f(y),且f(2)=p,f(3)=q ，那么f(36)= ．解答题16．已知集合A={}71<≤x x ，B={x|2<x<10}，C={x|x<a }，全集为实数集R ． （Ⅰ）求A ∪B ，(C R A)∩B ；（Ⅱ）如果A ∩C ≠φ，求a 的取值范围．17．集合A ＝｛x ｜x 2－ax ＋a 2－19＝0｝，B ＝｛x ｜x 2－5x ＋6＝0｝，C ＝｛x ｜x 2＋2x －8＝0｝．（Ⅰ）若A ＝Ｂ，求a 的值；（Ⅱ）若∅A ∩B ，A ∩C ＝∅，求a 的值．19．已知函数2()21f x x =-．（Ⅰ）用定义证明()f x 是偶函数；（Ⅱ）用定义证明()f x 在(,0]-∞上是减函数；（Ⅲ）作出函数()f x 的图像，并写出函数()f x 当[1,2]x ∈-时的最大值与最小值．20．设函数1)(2++=bx ax x f （0≠a 、R b ∈），若0)1(=-f ，且对任意实数x （R x ∈）不等式)(x f ≥0恒成立．（Ⅰ）求实数a 、b 的值；（Ⅱ)当∈x [－2，2]时，kx x f x g -=)()(是单调函数，求实数k 的取值范围．一、选择题 CBACB AAACB二、填空题 11. {}0,3 12. {(3，－1)} 13. 0 14. 25 15. 2()p q +三、解答题16．解：（Ⅰ）A ∪B={x|1≤x<10}(C R A)∩B={x|x<1或x ≥7}∩{x|2<x<10}={x|7≤x<10}（Ⅱ）当a >1时满足A ∩C ≠φ17．解： 由已知，得B ＝｛2，3｝，C ＝｛2，－4｝(Ⅰ)∵A ＝B 于是2，3是一元二次方程x 2－ax ＋a 2－19＝0的两个根， 由韦达定理知：⎩⎨⎧-=⨯=+1932322a a 解之得a ＝5.(Ⅱ)由A ∩B ∅A ⇒∩≠B Φ，又A ∩C ＝∅，得3∈A ，2∉A ，－4∉A ，由3∈A ，得32－3a ＋a 2－19＝0，解得a ＝5或a =－2当a =5时，A ＝｛x ｜x 2－5x ＋6＝0｝＝｛2，3｝，与2∉A 矛盾； 当a =－2时，A ＝｛x ｜x 2＋2x －15＝0｝＝｛3，－5｝，符合题意.∴a ＝－2.19．（Ⅰ）证明：函数()f x 的定义域为R ，对于任意的x R ∈，都有22()2()121()f x x x f x -=--=-=，∴()f x 是偶函数． （Ⅱ）证明：在区间(,0]-∞上任取12,x x ，且12x x <，则有22221212121212()()(21)(21)2()2()()f x f x x x x x x x x x -=---=-=-⋅+， ∵12,(,0]x x ∈-∞，12x x <，∴12120,x x x x -<0,+< 即1212()()0x x x x -⋅+>∴12()()0f x f x ->，即()f x 在(,0]-∞上是减函数． （Ⅲ）解：最大值为(2)7f =，最小值为(0)1f =-．20．解：（Ⅰ）∵0)1(=-f ∴01=+-b a∵任意实数x 均有)(x f ≥0成立∴⎩⎨⎧≤-=∆>0402a b a 解得：1=a ，2=b（Ⅱ）由（1）知12)(2++=x x x f∴1)2()()(2+-+=-=x k x kx x f x g 的对称轴为22-=k x ∵当∈x [－2，2]时，)(x g 是单调函数 ∴222-≤-k 或222≥-k ∴实数k 的取值范围是),6[]2,(+∞--∞ ．。

下一数教集中与函数尝试题 之阳早格格创做 一、 采用题（每题5分，共60分）1、下列各组对于象：○12008年北京奥运会上所有的角逐名目；○2《下中数教》必建1中的所有易题；○3所有量数；○4仄里上到面(1,1)的距离等于5的面的部分；○5正在数轴上与本面O 非常近的面.其中能形成集中的有（ ）A ．2组B ．3组C ．4组D ．5组2、下列集中中与集中{21,}x x k k N +=+∈没有相等的是（ ）A ．{23,}x x k k N =+∈B ．{41,}x x k k N +=±∈C ．{21,}x x k k N =+∈D ．{23,3,}x x k k k Z =-≥∈3、设221()1x f x x -=+，则(2)1()2f f 等于（ ） A ．1 B ．1- C ．35 D ．35- 4、已知集中2{40}A x x =-=，集中{1}B x ax ==，若B A ⊆，则真数a 的值是（ ）A ．0B ．12±C ．0或者12±D ．0或者125、已知集中{(,)2}A x y x y =+=，{(,)4}B x y x y =-=，则AB =（ ） A ．{3,1}x y ==- B ．(3,1)-C ．{3,1}-D ．{(3,1)}-6、下列各组函数)()(x g x f 与的图象相共的是（ ）（A ）2)()(,)(x x g x x f == （B ）22)1()(,)(+==x x g x x f（C ）0)(,1)(x x g x f ==（D ）⎩⎨⎧-==x x x g x x f )(|,|)()0()0(<≥x x7、是定义正在上的删函数,则没有等式的解集是（ ） (A)(0 ,+∞) (B)(0 , 2) (C) (2 ,+∞) (D) (2 ,716) 8、已知齐集U R =，集中{12}A x x x =><-或，集中{10}B x x =-≤<， 则()U A C B =（ ）A ．{10}x x x <-≥或B ．{11}x x x <->或C ．{21}x x x <->或D ．{20}x x x <-≥或9、设A 、B 为二个非空集中，定义{(,),}A B a b a A b B ⊕=∈∈，若{1,2,3}A =，{2,3,4}B =，则A B ⊕中的元素个数为（ ）A ．3B ．7C ．9D ．1210、已知集中2{1}A yy x ==+，集中2{26}B x y x ==-+，则A B =（ ）A ．{(,)1,2}x y x y ==B ．{13}x x ≤≤C ．{13}x x -≤≤D ．∅11、若偶函数()x f 正在[]3,1上为删函数，且有最小值0，则它正在[]1,3--上（ ）A.是减函数，有最小值0B.是删函数，有最小值0C.是减函数，有最大值0D.是删函数，有最大值012、若{}21,,0,,b a a a b a ⎧⎫=+⎨⎬⎩⎭，则20052005a b +的值为( ) （A ）0 （B ）1（C ）1- （D ）1或者1- 二、 挖空题（每题4分，共16分）13、已知)(x f y =为偶函数，当0≥x 时)1()(x x x f -=，则当0≤x 时， 则=)(x f 14、函数1()1111f x x =++的定义域为15、12)(2++=x x x f ，]2,2[-∈x 的最大值是16、偶函数()f x 谦脚：①()f x 正在(0,)+∞内单调递加；②(1)0f =；则没有等式()0xf x >的解集为：；三、 解问题（共44分 10+10+12+12）17、设集中A 为圆程220x x p ++=的解集，集中B 为圆程2220x qx ++=的解集， 1{}2A B =，供A B . 18、设集中{34}A x C x =∈-≤≤，集中{121}B x m x m =+≤<-.（1）当C 为自然数集N 时，供A 的真子集的个数；（2）当C 为真数集R 时，且A B =∅，供m 的与值范畴.19、已知集中2{10,,}A x ax bx a R b R =++=∈∈，供（1）当2b =时，A 中至多惟有一个元素，供a 的与值范畴；（2）当2b =-时，A 中起码有一个元素，供a 的与值范畴； 20、已知函数f （x ）=xx 1+. (1)推断f （x ）正在（0，+∞）上的单调性并加以说明；（2）供f （x ）的定义域、值域；临浑二中下一数教尝试题（第一章）集中与函数（问案）一采用题（每题5分，共50分）二挖空题（每题4分，共16分） 13、x(1+x)； 14、10,1,2x x ⎧⎫≠--⎨⎬⎩⎭； 15、9 ； 16、}{}{11>⋃-<x x x x三解问题（共54分 10+10+10+12+12）17、解：将21分别代进二个圆程中得：111,5,{,1},{,2}22p q A B =-=-=-= 19、（1）52131-=；2、解：（1）当B =∅时，121m m +≥-；所以2m ≤当3m >时，（2）B ≠∅，且A B =∅则{121213m m m +<-⎧⎪⎨-≤-⎪⎩或者{12114m m m +<-⎧⎪⎨+>⎪⎩解出3m >综上：2m ≤或者3m >20、解：（1）当0a =时，1{}2A =-创造，（2）当0a ≠时，有一个根0∆=坐即1a =，{1}A =-；无根0∆<坐即1a >，A =∅.综上：1a ≥或者0a =（2） 当0a =时，1{}2A =-创造，当0a ≠有一个根0∆=坐即1a =，{1}A =-；有二个根0∆>即1a <；综上：1a ≤或者0a =21、（1）令+∞<<<210x x ，则 012>-x x ，当1021≤<<x x 时，012121<-x x x x ，0)()(12<-x f x f ，函数单调递减当+∞<<<211x x 时，012121>-x x x x ，0)()(12>-x f x f ，函数单调递加 （2）又题意可知，f(x)定义域为{}0,≠∈x R x x 且 当+∞<<x 0时，由（1）可知，当x=1时，f （x ）有最小值2，故f （x ）正在{}+∞<<x x 0的值域为[)+∞,2 共理，当0<<∞-x 时，当x=-1时，f （x ）有最大值-2， 故f （x ）正在{}0<<∞-x x 的值域为(]2,-∞- 综上得，f （x ）的值域为(]2,-∞-⋃(]2,-∞-。

高一数学必修1《集合与函数概念》测试卷(含答案)第一章（一）《集合与函数概念》测试卷考试时间：120分钟满分：150分一.选择题（本大题共12小题，每小题5分，共60分）1.下列叙述正确的是（）A.函数的值域就是其定义中的数集BB.函数y=f(x)的图像与直线x=m至少有一个交点C.函数是一种特殊的映射D.映射是一种特殊的函数2.如果A={x|x>-1}，则下列结论正确的是（）A.XXXB.{}⊆AC.{}∈AD.∅∈A3.设f(x)=(2a-1)x+b在R上是减函数，则有（）A.a≥1/2B.a≤1/2C.a>1/2D.a<1/24.定义在R上的偶函数f(x)，对任意x1,x2∈[0,+∞)(x1≠x2)，有|x1-x2|<π/2，则有（）A.f(3)<f(-2)<f(1)B.f(1)<f(-2)<f(3)C.f(-2)<f(1)<f(3)D.f(3)<f(1)<f(-2)5.若奇函数f(x)在区间[1,3]上为增函数，且有最小值，则它在区间[-3,-1]上（）A.是减函数，有最小值0B.是增函数，有最小值0C.是减函数，有最大值0D.是增函数，有最大值06.设f:x→x是集合A到集合B的映射，若A={-2,0,2}，则AB等于（）A.{}B.{2}C.{0,2}D.{-2,0}7.定义两种运算：a⊕b=ab，a⊗b=a²+b²，则函数f(x⊗3-3)为（）A.奇函数B.偶函数C.既不是奇函数又不是偶函数D.既是奇函数又是偶函数8.若函数f(x)是定义域在R上的偶函数，在(-∞,0)上是减函数，且f(-2)=1/4，则使f(x)<1/4的x的取值范围为（）A.(-2,2)B.(-2,0)∪(0,2)C.(-∞,-2)∪(2,+∞)D.(-∞,-2]∪[2,+∞)9.函数f(x)=x+(x|x|)的图像是（）10.设f(x)是定义域在R上的奇函数，f(x+2)=-f(x)，当|x|<1时，f(x)=x，则f(7.5)的值为（）A.-0.5B.0.5C.-5.5D.7.511.已知f(-2x+1)=x²+1，且-1/2≤x≤1/2，则f(x)的值域为（）A.[1,5/4]B.[1/4,5/4]C.[0,5/4]D.[1/4,2]12.设f(x)是定义在R上的奇函数，且f(x)在[-2,2]上单调递增，则f(x)在(-∞,-2)∪(2,+∞)上（）A.单调递减B.单调不增也不减C.单调递增D.无法确定第一章（一）《集合与函数概念》测试卷考试时间：120分钟满分：150分一、选择题（本大题共12小题，每小题5分，共60分）1.下列叙述正确的是（）A。

必修1第一章综合检测一、选择题（每小题5分，共10个小题）1．如图是集合的知识结构图，如果要加入“全集”，则应该放在（ ）A ．“集合的概念”的下位B ．“集合的表示”的下位C ．“基本关系”的下位D ．“基本运算”的下位 2．已知集合32A x x Z Z x ⎧⎫=∈∈⎨⎬-⎩⎭且，则集合A 中的元素个数为（ ） A.2 B.3 C.4 D.5 3．已知定义在（－1,1）上的奇函数()f x 为减函数，且(1)(2)0f a f a -+<，则a 的取值范围（ ） A. (,1)-∞- B.（1,-+∞） C. （11,22-） D.（10,2） 4．设全集}02|},51|{,2=--∈=≤≤∈==x x R x B x N x A R U ，则图中阴影表示的集合为（ ）A ．{－1}B ．{2}C ．{3，4，5}D ．{3，4}5．若a 是常数，函数()f x 对于任何的非零实数x 都有1()()1f af x x x=--，且(1)1f =，则不等式()0f x x -≥的解集为（ ） A ．1(,](0,1]5-∞- B ．1(,][1,)5-∞-+∞ C ． 1[,0)(0,1]5-D ．1[,0)[1,)5-+∞6．设集合}5,4,3,2,1{},1,0,2{=-=N M ，映射N M f →:使得对任意的M x ∈，都有)()(x xf x f x ++是奇数，则这样的映射f 的个数是（ ）A ．45B ．27C ．15D ．11 7．设U 为全集，M , P 是U 的两个子集，且P P M C U = )(，则=P M （ ）A ． MB ． PC ． P C UD ． φ8．设，则函数的图像大致形状是（ ）9．已知()f x 为偶函数，当0x ≥时，()()211f x x =--+，则满足()12f f a ⎡⎤=⎣⎦的实数a 的个数为（ ）． A ．2 B ．4 C ．6 D ．8xyOa xyOaxyOaxyOaAB CD()y x x a =-0a >AMEPDCB N F 10．对于函数()y f x =，如果存在区间[,]m n ，同时满足下列条件：①()f x 在[,]m n 内是单调的；②当定义域是[,]m n 时，()f x 的值域也是[,]m n ，则称[,]m n 是该函数的“和谐区间”．若函数11()(0)a f x a a x+=->存在“和谐区间”，则a 的取值范围是（ ） A ．(0,1) B ． (0,2) C ．15(,)22D ．(1,3)二、填空题（每小题5分，共5个小题）11．对于集合B A ,，我们把集合},|{B x A x x ∉∈且叫做集合A 与B 的差集，记作B A -.若集合B A ,都是有限集，设集合B A -中元素的个数为)(B A f -，则对于集合},1{},3,2,1{a B A ==，有=-)(B A f __________ 12．将一张坐标纸折叠一次，使点（10，0）与（－6，8）重合，则与点（－4，2）重合的点是 . 13．如图，已知边长为8米的正方形钢板有一个角锈蚀，其中4AE =米，6CD =米. 为了合理利用这块钢板,将在五边形ABCDE 内截取一个矩形块BNPM ，使点P 在边DE 上. 则矩形BNPM 面积的最大值为____14．若对于任意的[]3,1∈x , 02)1(2≥+--+a x a x 恒成立, 则实数a 的取值范围是 . 15.已知函数()f x 满足：(1)f =41，4()()()().(,)f x f y f x y f x y x y R ⋅=++-∈.则(2010)f =_________ 三、解答题（共6个小题）16．已知集合{}{}(2)(1)0,(1)()0A x x x B x ax x a =++≤=-+>，,A B a ⊆且求的范围．17．已知函数2()1xf x x =+，()1,1x ∈-（1）判断此函数的奇偶性；（2）判断函数的单调性，并加以证明.(3)解不等式()()10f x f x -->18．随着机构改革工作的深入进行，各单位要减员增效，有一家公司现有职员2a 人（140＜2a ＜420，且a 为偶数)，每人每年可创利10万元．据评估，在经营条件不变的前提下，若裁员x 人，则留岗职员每人每年多创利0.1x 万元，但公司需付下岗职员每人每年4万元的生活费，并且该公司正常运转情况下，所裁人数不超过50人，为获得最大的经济效益，该公司应裁员多少人？19．设bx ax x f +=2)(，求满足下列条件的实数a 的值：至少有一个正实数b ，使函数)(x f 的定义域和值域相同。

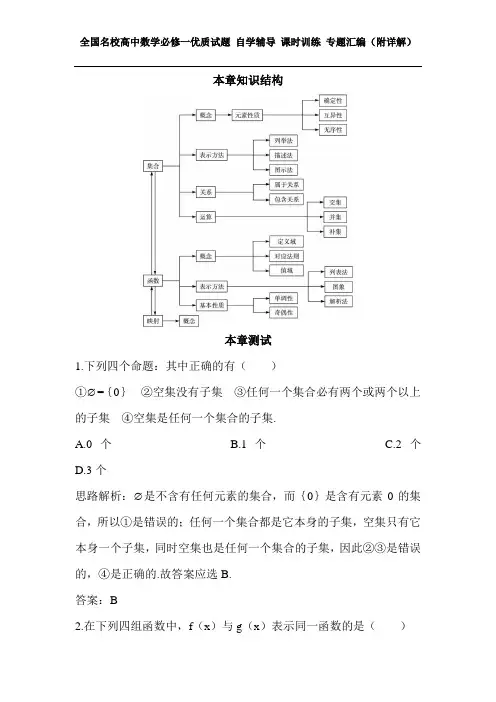
本章知识结构本章测试1.下列四个命题：其中正确的有（）①∅=｛0｝②空集没有子集③任何一个集合必有两个或两个以上的子集④空集是任何一个集合的子集.A.0个B.1个C.2个D.3个思路解析：∅是不含有任何元素的集合，而｛0｝是含有元素0的集合，所以①是错误的；任何一个集合都是它本身的子集，空集只有它本身一个子集，同时空集也是任何一个集合的子集，因此②③是错误的，④是正确的.故答案应选B.答案：B2.在下列四组函数中，f（x）与g（x）表示同一函数的是（）A.f （x ）=x-1，g （x ）=112+-x x B.f （x ）=｜x+1｜，g （x ）=⎩⎨⎧-<---≥+.1,1,1,1x x x x C.f （x ）=x+1，x ∈R ，g （x ）=x+1，x ∈ZD.f （x ）=x ，g （x ）=（x ）2思路解析：选项A 、C 、D 两个函数的定义域不同，所以不是同一个函数，应选B.答案：B3.已知M=｛x 2，2x-1，-x-1｝，N=｛x 2+1，-3，x+1｝，且M ∩N=｛0，-3｝，则x 的值为（ ）A.-1B.1C.-2D.2思路解析：∵M ∩N=｛0，-3｝，可知N 中有元素0，由于x 2+1≠0，故只能是x+1=0，解得x=-1，此时M={1,-3,0},N={2,-3,0}，符合题意.应选A.答案：A4.y=f （x ）（x ∈R ）是奇函数，则它的图象必经过点（ ）A.（-a ，-f （-a ））B.（a ，-f （a ））C.（a ，f （1a ））D.（-a ，-f （a ））思路解析：由函数解析式的含义可知函数f （x ）的图象经过点（a ，f（a ）），又因为y=f （x ）（x ∈R ）是奇函数，所以有f （-a ）=-f （a ），即函数图象经过点 （-a ，-f （a ）），应选D.答案：D5.拟定从甲地到乙地通话m分钟的电话费由f（m）=1.06×（0.5·［m］+1）（元）决定，其中m＞0，［m］是小于或等于m的最大整数，则从甲地到乙地通话时间为6.5分钟的电话费为（）A.3.71元B.3.97元C.4.24元D.4.77元思路解析：根据题意知m=6.5，［m］=6，所以f（m）=1.06×（0.5·［m］+1）=1.06×4=4.24元，应选C.答案：C6.已知集合M、P、S，满足M∪P=M∪S，则（）A.P=SB.M∩P=M∩SC.M∩（P∪S）=M∩（P∩S）D.（S∪M）∩P=（P∪M）∩S思路解析：特例法，举M={1,2}，P={3}，S={1,2,3},满足M∪P=M∪S，而P≠S，M∩P≠M∩S，M∩（P∪S）={1,2}，M∩（P∩S）= ，所以A、B、C均是错误的，故正确答案应该为D.答案：D7.已知集合P={x∈N|1≤x≤10},集合Q={x∈R|x2+x-6≤0},则P∩Q等于( )A.{2}B.{1,2}C.{2,3}D.{1,2,3}思路解析：P=｛1,2,3,4,5,6,7,8,9,10｝,Q=｛-3,2｝,P∩Q=｛2｝.答案：A8.函数y=ax 2+a 与y=xa（a ≠0）在同一坐标系中的图象可能是（ ）思路解析：从A 中的反比例图象可以看出a>0，此时y=ax 2+a 应是开口向上，且与x 轴没有交点的抛物线，故A 、B 、C 均是错误的；而对于D 可知a ＜0，y=ax 2+a 应是开口向下，且与x 轴没有交点的抛物线，所以D 是正确的.答案：D9.已知集合M=｛x ｜x ≥2或x ≤-1｝，N=｛x ｜x —a ≤0｝，若M ∩N ≠∅，则a 的取值范围是（ ）A.（-∞，2）B.（-1，+∞）C.(-∞，1) D(-∞，1]思路解析：由题意知M=｛x ｜-1＜x ＜2=，N={x ｜x ≤-a}，若M ∩N ≠∅，根据数轴，可得-a>-1即a ＜1，故选C.答案：C10.函数y=2)1(20++--x x x 的定义域为( )A.（-1， 2）B.（-1，1）∪（1，2）C.(-∞，1)∪（1，+∞）D.［-1，1］∪（1，2] 思路解析：要使函数有意义，则⎩⎨⎧>++-≠.02,12x x x 解得（-1，1）∪（1，2）.答案：B11.函数f（x）=-x2+2（a-1）x+3在（-∞，4）上是增函数，则a的范围是（）A.a≥5B.a≥3C.a≤3D.a ≤-5思路解析：本题作出函数f（x）=-x2+2（a-1）x+3的图象，可知此函数图象的对称轴是x=a-1，由图象可知，当a-1≥4，即当a≥5时，函数f（x）=-x2+2（a-1）x+2在（-∞，4）上是增函数．答案：A12.已知集合A=｛x｜y=x2-2x-3，x∈R｝，B=｛y｜y=x2-2x+2，x∈R｝，则A∩B=_________.思路解析：集合A=｛x｜y=x2-2x-3，x∈R｝表示函数y=x2?x-3的定义域，所以A=R；而B=｛y｜y=x2-2x+2，x∈R｝表示函数y=x2-2x+2的值域，应有B=｛y｜y≥1｝，因此A∩B=｛y｜y≥1｝.答案：｛y｜y≥1｝13.如右图，有一块边长为a的正方形铁皮，将其四个角各截去一个边长为x的小正方形，然后折成一个无盖的盒子，写出体积V以x 为自变量的函数式是_____________，这个函数的定义域为___________________.思路解析：围成的几何体是一个长方体，它的底面积为(a-2x)2,高为x ，所以体积V=x(a-2x)2，而x 满足a-2x ＞0且x ＞0，所以0＜x ＜2a . 答案：V=x （a-2x ）2 {x|0＜x ＜2a }14.给定映射f ：（x ，y ）→（x ，x+y ），在映射f 下象（2，12）的原象是（a ，b ），则函数f （x ）=ax 2+bx 的顶点坐标是____________________.思路解析：根据题意有a=2，a+b=12，解得a=4，b=8，所以函数f(x)=4x 2+8x=4(x+1)2-4，其顶点坐标为(-1,-4).答案：(-1,-4)15.函数f （x ）=x 2-2｜x ｜的单调减区间是____________________. 思路解析：因为f （-x ）=x 2-2｜x ｜=f （x ），所以f(x)是偶函数，我们可先考虑x ＞0的情况，当x ＞0时，f(x)=x 2-2x ，函数在(0,1)上为减函数，在［1,+∞)上为增函数；由于偶函数的图象关于y 轴对称，故函数在(-1,0)上为增函数，在(-∞,-1)上为减函数.答案：(0,1)和(-∞,-1]16.设A={x|x 2-x-12=0} ，B={x|x 2-2ax+b=0}，若B ≠ ,且A ∪B=A,求a 、b 的值.思路解析：分别将每一个集合化简，再利用集合的运算进行求解. 解：∵A={x|x 2-x-12=0}={-3,4},若B ≠∅,且A ∪B=A ，则B ⊆A,当A=B 时，a=21,b=-12；当B={-3}时，a=-3,b=9；当B={4}时，a=4,b=16.因此，a=21,b=-12或A=-3,b=9或 a=4,b=16.17.设g(x)=⎩⎨⎧>≤,0,ln ,0,x x x e x 则g ［g(21)］=__________________. 解：依题可知g(21)=ln 21=-ln2＜0所以,g ［g （21）］=g(-ln2)=21ln e =21. 18.已知函数f(x)=ax 2+2ax+4(0＜a ＜3＝,若x 1＜x 2,x 1+x 2=1-a,则（ ）A.f(x 1)＜f(x 2)B.f(x 1)=f(x 2)C.f(x 1)＞f(x 2)D.f(x 1)与f(x 2)的大小不能确定思路解析：由f(x)=ax 2+2ax+4(0＜a ＜3＝，得f(x)为二次函数，且对称轴为x 0=-1,∵x 1+x 2=1-a,∴221x x +=21a -,即x 1,x 2中点横坐标为21a -,又∵0＜a ＜3,∴21a -＞-1.∵x 1＜x 2, 如右图∴x1离对称轴的距离小于x2离对称轴的距离，∴f(x1)＜f(x2).答案：A19.快艇和轮船分别从A地和C地同时开出，各沿箭头方向航行，如右图所示，快艇和轮船的速度分别是45千米/时和15千米/时，已知AC=150千米，经过多少时间后，快艇和轮船之间的距离最短？思路解析：解决有关函数的应用题，关键在于审清题意，正确列出函数模型.解：设经过x小时后快艇和轮船之间的距离最短，距离设为y，10）,y=22)(xx+-（0＜x≤4515150()3可求得当x=3时，y有最小值．答：经过3小时后，快艇和轮船之间的距离最短.20.设f（x）是定义在R上的增函数，f（xy）=f（x）+f（y），f（3）=1，求解不等式f（x）+f（x-2）＞1.思路解析：对抽象不等式，常把常数看成某些变量的函数值，再利用函数的性质去“外层包装”，取出x，化成一元一次或二次不等式求解.解：由条件可得f（x）+f（x-2）=f［x（x-2）］，1=f（3）．所以f［x（x-2）］＞f（3），又f（x）是定义在R上的增函数，所以有x （x-2）＞3，可解得x ＞3或x ＜-1．答案：x ＞3或x ＜-121.已知函数f （x ）=x+xm ，且f （1）=2. （1）求m ；（2）判断f （x ）的奇偶性；（3）判断函数f （x ）在［1，2］上的单调性，并求函数f （x ）在［1，2］上的最值.思路解析：判断函数的奇偶性，首先观察函数的定义域是否关于原点对称，然后判断 f （-x ）与f(x)的关系；而证明在某一区间上的单调性，常用定义进行证明，由于单调函数在闭区间内肯定有最值，可根据单调性求出最值.解：（1）f （1）=1+m=2，解得m=1．（2）f （x ）=x+x 1，f （-x ）=-x-x 1=-f （x ），∴f （x ）是奇函数．（3）设x 1、x 2是［1，2］上的任意两个实数，且x 1＜x 2，则 f （x 1）-f （x 2）=x 1+11x -（x 2+21x ）=x 1-x 2+（11x -21x ）=x 1-x 2-2121x x x x -=（x 1-x 2）21211x x x x -． 当1≤x 1＜x 2≤2时，x 1x 2＞1，x 1x 2-1＞0，从而f （x 1）-f （x 2）＜0， 即f （x 1）＜f （x 2）．∴函数f （x ）=x1+x 在［1，2］上为增函数，其最小值为 f （1）=2，最大值为f （2）=25.。

Equation Chapter 1 Section 1【1】第一章集合与函数概念测试题 一：选择题 1、下列集合中与集合{21,}x x k k N +=+∈不相等的是（ ）A ．{23,}x x k k N =+∈B ．{41,}x x k k N +=±∈C ．{21,}x x k k N =+∈D ．{23,3,}x x k k k Z =-≥∈2、图中阴影部分所表示的集合是（）A.B∩［CU(A ∪C)］B.(A ∪B) ∪(B ∪C)C.(A ∪C)∩(CUB)D.［C U(A∩C)］∪B3、已知集合2{1}A y y x ==+，集合2{26}B x y x ==-+，则A B =（ ）A ．{(,)1,2}x y x y ==B ．{13}x x ≤≤C ．{13}x x -≤≤D ．∅4、已知集合2{40}A x x =-=，集合{1}B x ax ==，若B A ⊆，则实数a 的值是（ ）A ．0B ．12±C ．0或12±D ．0或125、已知集合{1,2,3,}A a =，2{3,}B a =，则使得Φ=B A C U )(成立的a 的值的个数为（ ）A ．2B ．3C ．4D ．56、设A 、B 为两个非空集合，定义{(,),}A B a b a A b B ⊕=∈∈，若{1,2,3}A =，{2,3,4}B =，则A B ⊕中的元素个数为 （ ）A ．3B ．7C ．9D ．127、已知A 、B 两地相距150千米，某人开汽车以60千米/小时的速度从A 地到达B 地，在B 地停留1小时后再以50千米/小时的速度返回A 地，把汽车离开A 地的距离x 表示为时间t （小时）的函数表达式是（ ）A ．x=60tB ．x=60t+50C ．x=⎩⎨⎧>-≤≤)5.3(,50150)5.20(,60t t t tD ．x=⎪⎩⎪⎨⎧≤<--≤<≤≤)5.65.3(),5.3(50150)5.35.2(,150)5.20(,60t t t t t 8、已知g(x)=1-2x,f[g(x)]=)0(122≠-x x x ,则f(21)等于（ ） A ．1B ．3C ．15D ．309、函数y=xx ++-1912是（ ） A ．奇函数 B ．偶函数 C ．既是奇函数又是偶函数 D ．非奇非偶数10、设函数f (x)是（－∞，+∞）上的减函数，又若a ∈R ，则（ ）A ．f(a)>f(2a)B ．f(a2)<f(a)C ．f(a2+a)<f(a)D ．f(a2+1)<f(a)二、填空题11、设集合A={23≤≤-x x },B={x 1122-≤≤-k x k },且A ⊇B ，则实数k 的取值范围是.12、已知x ∈[0,1],则函数y=x x --+12的值域是.13、设函数x y 111+=的定义域为___________________;值域为_____________________________.14、设f(x)是定义在R 上的偶函数，在区间（－∞，0）上单调递增，且满足, 22(25)(21)f a a f a a -+-<++求实数a 的取值范围_______________。

集合与函数概念一、选择题1．设全集U ＝{(x ，y )| x ∈R ，y ∈R }，集合M ＝⎭⎬⎫⎩⎨⎧1＝2－3－|),(x y y x ， P ＝{(x ，y )| y ≠x ＋1}，那么C U (M ∪P )等于( )． A ．∅B ．{(2，3)}C ．(2，3)D ．{(x ，y )| y ＝x ＋1}2．假设A ＝{a ，b }，B ⊆A ，则集合B 中元素的个数是( )． A ．0B ．1C ．2D ．0或1或23．函数y ＝f (x )的图象与直线x ＝1的公共点数目是( )． A ．1B ．0C ．0或1D ．1或24．设函数f (x )＝2x ＋3，g (x ＋2)＝f (x )，则g (x )的表达式是( )． A ．2x ＋1B ．2x －1C ．2x －3D ．2x ＋75. 已知函数f (x )＝ax 3＋bx 2＋cx ＋d 的图象如下图，则( )． A ．b ∈(－∞，0) B ．b ∈(0，1) C ．b ∈(1，2)D ．b ∈(2，＋∞)6．设函数f (x )＝⎩⎨⎧00＋＋2 x c x c bx x ，，≤， 假设f (－4)＝f (0)，f (－2)＝－2，则关于x 的方程f (x )＝x 的解的个数为( )．A ．1B ．2C ．3D ．47．设集合A ＝{x | 0≤x ≤6}，B ＝{y | 0≤y ≤2}，以下从A 到B 的对应法则f 不是映射的是( )．A ．f :x →y ＝21x B ．f :x →y ＝31xC ．f :x →y ＝41x D ．f :x →y ＝61x 8．有下面四个命题：①偶函数的图象一定与y 轴相交； ②奇函数的图象一定通过原点； ③偶函数的图象关于y 轴对称；④既是奇函数，又是偶函数的函数一定是f (x )＝0(x ∈R )． 其中正确命题的个数是( )． A ．1B ．2C ．3D ．4(第5题) ＞9．函数y＝x2－6x＋10在区间(2，4)上是()．A．递减函数B．递增函数C．先递减再递增D．先递增再递减10．二次函数y＝x2＋bx＋c的图象的对称轴是x＝2，则有()．A．f(1)＜f(2)＜f(4)B．f(2)＜f(1)＜f(4)C．f(2)＜f(4)＜f(1)D．f(4)＜f(2)＜f(1)二、填空题11．集合{3，x，x2－2x}中，x应满足的条件是．12．假设集合A＝{x | x2＋(a－1)x＋b＝0}中，仅有一个元素a，则a＝___，b＝___．13．建造一个容积为8 m3，深为2 m的长方体无盖水池，如果池底和池壁的造价每平方米分别为120元和80元，那么水池的最低总造价为元．14．已知f(x＋1)＝x2－2x，则f(x)＝；f(x－2)＝．15．y＝(2a－1)x＋5是减函数，求a的取值范围．16．设f(x)是R上的奇函数，且当x∈［0，＋∞)时，f(x)＝x(1＋x3)，那么当x∈(－∞，0］时，f(x)＝．三、解答题17．已知集合A＝{x∈R| ax2－3x＋2＝0}，其中a为常数，且a∈R．①假设A是空集，求a的范围；②假设A中只有一个元素，求a的值；③假设A中至多只有一个元素，求a的范围．18．已知M＝{2，a，b}，N＝{2a，2，b2}，且M＝N，求a，b的值．19．证明f(x)＝x3在R上是增函数．20．判断以下函数的奇偶性： (1)f (x )＝3x 4＋21x ；(2)f (x )＝(x －1)xx－＋11； (3)f (x )＝1－x ＋x －1；(4)f (x )＝12－x ＋21x －第一章 集合与函数概念参考答案一、选择题1．B 2．D 3．C 4．B 5．A 6．C 7．A 8．A 9．C 10．B ． 二、填空题11．x ≠3且x ≠0且x ≠－1．12．a ＝31，b ＝91．13．1 760元．14．f (x )＝x 2－4x ＋3，f (x －2)＝x 2－8x ＋15． 15．(－∞，21)． 16．x (1－x 3)． 三、解答题17．解：①∵A 是空集， ∴方程ax 2－3x ＋2＝0无实数根．∴⎩⎨⎧∆，a a 08－9＝,0 解得a ＞89．②∵A 中只有一个元素，∴方程ax 2－3x ＋2＝0只有一个实数根．当a ＝0时，方程化为－3x ＋2＝0，只有一个实数根x ＝32； 当a ≠0时，令Δ＝9－8a ＝0，得a ＝89，这时一元二次方程ax 2－3x ＋2＝0有两个相等的实数根，即A 中只有一个元素．由以上可知a ＝0，或a ＝89时，A 中只有一个元素． ③假设A 中至多只有一个元素，则包括两种情形：A 中有且仅有一个元素；A 是空集．由①②的结果可得a ＝0，或a ≥89．18．解：根据集合中元素的互异性，有≠ ＜⎩⎨⎧==⎩⎨⎧==ab b a b b a a 2222或解得 或或再根据集合中元素的互异性，得或19．证明：设x 1，x 2∈R 且x 1＜x 2，则f (x 1)－f (x 2)＝31x －32x ＝(x 1－x 2)(21x ＋x 1x 2＋22x )．又21x ＋x 1x 2＋22x ＝(x 1＋21x 2)2＋4322x ． 由x 1＜x 2得x 1－x 2＜0，且x 1＋21x 2与x 2不会同时为0， 否则x 1＝x 2＝0与x 1＜x 2矛盾，所以 21x ＋x 1x 2＋22x ＞0．因此f (x 1)－ f (x 2)＜0，即f (x 1)＜f (x 2)， f (x )＝x 3 在 R 上是增函数．20．解：(1)∵ 函数定义域为{x | x ∈R ，且x ≠0}， f (－x )＝3(－x )4＋21）（－x ＝3x 4＋21x ＝f (x )，∴f (x )＝3x 4＋21x 是偶函数． (2)由xx－＋11≥0⇔⎩⎨⎧≠01－－1＋1x x x ))(( 解得－1≤x ＜1． ∴ 函数定义域为x ∈［－1，1)，不关于原点对称，∴f (x )＝(x －1)xx－11＋为非奇非偶函数．(3)f (x )＝1－x ＋x －1定义域为x ＝1，∴ 函数为f (x )＝0(x ＝1)，定义域不关于原点对称， ∴f (x )＝1－x ＋x －1为非奇非偶函数． (4)f (x )＝1－2x ＋2－1x 定义域为≥ －10≥1－22x x ⇒ x ∈{±1}，∴函数变形为f (x )＝0 (x ＝±1)，∴f (x )=1－2x ＋2－1x 既是奇函数又是偶函数．a ＝0b ＝1 a ＝0b ＝0a ＝41b ＝21 a ＝0b ＝1 a ＝41 b ＝21 ≥0。

高一第一章集合与函数试卷班级 ________座号 _______姓名 _____________第Ⅰ卷 （选择题共 60 分） 一、选择题（本大题共 12 小题，每小题 5 分，共 60 分．在每小题所给的四个答案中有且只有一个答案是正确的． ）1．下列各组对象中，不能形成 集合的是（ ）．．．．A ．连江五中全体学生B ．连江五中的必修课C ．连江五中 2012 级高一学生D ．连江五中全体高个子学生2. 下列从集合 M 到集合 N 的对应 f 是映射的是（）AB CD3．下列关系正确的是（）A ．0 NB ．1 RC ．QD ．3Z4.下列各组函数是同一函数的是（）x 与 y 1x 1,x 1, A ． yB ． y x 1 与 yx, x 1x1C ． y x x 1 与 y 2 x 1D ． yx 3x与 y xx 2 15．已知 f xx 2 1,x1, 则 f2 的值为（）2x 3, x ≥1,A ． 7B ． 2C ． 1D ．56．下列哪个是偶函数的图像（）yyyyOxO x OxOxABC D7．已知集合 Ax2 ≤ x 1 ≤ 2 和 Bx x 2k 1, k N * 的关AB系的 Venn 图如图所示，则阴影部分所示的集合的元素共有（）A ．3 个B ．2 个C ． 1 个D ．无穷多个8．已知函数 f xx 2x 1,x0, 3的最值情况是（）2A ．有最大值3，但无最小值B ．有最小值3，有最大值 144C ．有最小值 1，有最大值19D ．无最大值，也无最小值49．某学生离家去学校，由于怕迟到，所以一开始就匀速跑步，等跑累了再匀速走余下的路程 . 在下图中纵轴表示该生离学校的距离d ，横轴表示出发后的时间 t ，则下图中的四个图形中较符合该学生走法的是（）d d d dOt Ot OtOtABCD 10．已知集合 A {2，3，9} 且 A 中至少有一个奇数，则这样的集合有（）。

第一章集合与函数概念单元测试卷一、选择题（本大题共20小题，共100.0分）1.设集合A={x|x2−4x+3<0}，B={x|2x−3>0}，则A∩B=()A. (−3,−32) B. (−3,32) C. (1,32) D. (32,3)2.已知集合A={1,2，3}，B={x|x2<9}，则A∩B=()A. {−2,−1,0，1，2，3}B. {−2,−1,0，1，2}C. {1,2，3}D. {1,2}3.已知集合A={x|x<1}，B={x|3x<1}，则()A. A∩B={x|x<0}B. A∪B=RC. A∪B={x|x>1}D. A∩B=⌀4.已知集合A={(x,y)|y=x2}，B={(x,y)|2x−y−1=0}，则A∩B=()A. x=1，y=1B. (1,1)C. {1,1}D. {(1,1)}5.已知集合A={x|x≥0}，B={−1,0，1}，则A∩B=()A. {1}B. {0,1}C. {−1,0}D. ⌀6.设集合A={1,2，4}，B={x|x2−4x+m=0}.若A∩B={1}，则B=()A. {1,−3}B. {1,0}C. {1,3}D. {1,5}7.已知全集U={1,2，3，4，5，6}，集合P={1,3，5}，Q={1,2，4}，则(∁U P)∪Q=()A. {1}B. {3,5}C. {1,2，4，6}D. D8.已知集合A={1,2，3，4}，B={y|y=3x−2,x∈A}，则A∩B=()A. {1}B. {4}C. {1,3}D. {1,4}9.设集合A={1,2，3}，B={2,3，4}，则A∪B=()A. {1,2，3，4}B. {1,2，3}C. {2,3，4}D. {1,3，4}10.已知集合M={x|x≥−1}，N={x|−2<x<2}，则M∩N=()A. (−∞,−1]B. [−1,2)C. (−1,2]D. (2,+∞)11.已知集合A={1,2，3，4}，B={2,4，6，8}，则A∩B中元素的个数为()A. 1B. 2C. 3D. 412.已知集合A={x|x−1≥0}，B={0,1，2}，则A∩B=()A. {0}B. {1}C. {1,2}D. {0,1，2}13.已知集合M={x|−1<x<3}，N={x|−2<x<1}，则M∩N=()A. (−2,1)B. (−1,1)C. (1,3)D. (−2,3)14.已知函数f(x)=3x−(13)x，则f(x)()A. 是奇函数，且在R上是增函数B. 是偶函数，且在R上是增函数C. 是奇函数，且在R上是减函数D. 是偶函数，且在R上是减函数15.已知函数f(x)=x+1,x≤02x,x>0，则f(−2)=()A. −1B. 0C. 14D. 416.设f(x)=1,x>00,x=0−1,x<0，g(x)=0,x为无理数1,x为有理数，若f(g(a))=0，则()A. a为无理数B. a为有理数C. a=0D. a=117.函数f(x)=x+2x−2的定义域是()18. 下列图象中，表示y 是x 的函数的个数有( )A. 1个B. 2个C. 3个D. 4个19. 已知定义在R 上的偶函数f (x )在x ∈[0,+∞)上单调递增，则满足f (2x −1)<f (13)的x 的取值范围是( )A. (13,23)B. (−13,23) C. (13,43) D. (−13,43) 20. 设定义在R 上的函数f (x )满足f (x )⋅f (x +2)=13，若f (1)=2，则f (2015)=( )A. 133B. 132C. 13D. 392二、填空题（本大题共10小题，共50.0分）21. 已知集合A ={1,2}，B ={a ,a 2+3}.若A ∩B ={1}，则实数a 的值为______ ． 22. 已知集合A ={1,2，3，4}，集合B ={3,4，5}，则A ∩B =______ ． 23. 已知集合A ={1,2，6}，B ={2,3，6}，则A ∪B =______ ．24. 设全集U =R ，集合A ={x |x 2<1}，B ={x |x 2−2x >0}，则A ∩(∁R B )=______．25. 若全集U =R ，集合M ={x |−2≤x ≤2}，N ={x |x 2−3x ≤0}，则M ∩(∁U N )=______ ． 26. 函数y = 2x +3(x ≤0)x +3(0<x ≤1)−x +5(x >1)的最大值是______ ． 27. 设函数y =e x +1e −a 的值域为A ，若A ⊆[0,+∞)，则实数a 的取值范围是______． 28. 已知函数f (x )= x −x 2,x <0x 2+x ,x≥0，若f (a )>f (2−a )，则a 的取值范围是______ ． 29. 已知函数f (x )= x 2+1,x ≥0 1−x ,x <0，则f (f (−3))=______．30. 已知f (x )是定义在R 上的奇函数，则f (−1)+f (0)+f (1)=______． 三、解答题（本大题共10小题，共120.0分）31. 已知全集U =R ，集合A ={x |x 2−4x ≤0}，B ={x |m ≤x ≤m +2}．(1)若m =3，求∁U B 和A ∪B ；(2)若B ⊆A ，求实数m 的取值范围； (3)若A ∩B =⌀，求实数m 的取值范围．32. 求函数f (x )=1+x −x 2在区间[−2,4]上的最大值和最小值．33.已知函数f(x)=x21+x2，(1)求f(2)+f(12)，f(3)+f(13)的值；(2)求证f(x)+f(1x)是定值．34.已知函数f(x)是定义在R上的奇函数，当x>0时，f(x)=x−3x−2．(1)求函数f(x)的解析式；(2)求函数f(x)的所有零点．35.已知函数f(x)=x+3+1x+2，(1)求函数的定义域；(2)求f(−3),f(23)的值．36.已知函数f(x)=x+4x(其中常数a>0)．(Ⅰ)求证：f(x)在(0,2]上是减函数，在[2,+∞)上是增函数；(Ⅱ)求函数f(x)在区间[2,4]上的值域．37.已知函数f(x)=1−3，x∈[3,5]．x+2(1)利用定义证明函数f(x)单调递增；(2)求函数f(x)的最大值和最小值．38.已知函数f(x)=x+m的图象过点P(1,5)．x(Ⅰ)求实数m的值，并证明函数f(x)是奇函数；(Ⅱ)利用单调性定义证明f(x)在区间[2,+∞)上是增函数．39.证明函数f(x)=x+4在(2,+∞)上是增函数．x40.已知函数g(x)=x+1，f(x)=x+1g(x)．x+2(1)写出函数f(x)的定义域(2)求证.函数f(x)在区间(0,+∞)上是增函数．答案和解析【答案】1. D2. D3. A4. D5. B6. C7. C8. D9. A10. B11. B12. C13. B14. A 15. A16. A17. B18. B19. A20. B21. 122. {3,4}23. {1,2，3，6}24. [0,1)25. {x|−2≤x<0}26. 427. (−∞,2]28. a>129. 530. 031. 解：(1)当m=3时，B={x|3≤x≤5}，集合A={x|x2−4x≤0}={x|0≤x≤4}，…(2分)∴C U B={x|x<3或x>5}，…(4分)A∪B={x|0≤x≤5}.…(6分)(2)∵集合A{x|0≤x≤4}，B={x|m≤x≤m+2}，B⊆A，∴m+2≤4m≥0，…(8分)解得0≤m≤2．∴实数m的取值范围[0,2].…(10分)(3)∵集合A={x|0≤x≤4}，B={x|m≤x≤m+2}．A∩B=⌀，∴m+2<0或m>4，…(12分)解得m<−2或m>4．∴实数m的取值范围(−∞,−2)∪(4,+∞).…(14分)32. 解：f(x)=1+x−x2=−(x−12)2+54，故函数的图象开口向下，对称轴为x=12，f(x)在[−2,12]上递增，在[12,4]上递减，y max=f(12)=54，y min=f(4)=−11．33. 解：(1)∵函数f(x)=x21+x，∴f(2)+f(12)=41+4+141+14=45+15=1，f(3)+f(13)=91+9+191+1=910+110=1．证明：(2)∵f(x)=x21+x2，∴f(x)+f(1=x2+1x2=x2+1=1．34. 解：(Ⅰ)因为f(x)是定义在R上的奇函数，所以f(−x)=−f(x)，且f(0)=0．设x<0，则−x>0，所以f(−x)=−x+3x −2=−f(x)，所以f(x)=x−3x+2．所以函数f(x)的解析式为f(x)=x−3x+2,x<0 0,x=0x−3x−2,x>0(Ⅱ)当x<0时，由x−3x+2=0，解得x=1(舍去)或x=−3；当x>0时，由x−3x−2=0，解得x=−1(舍去)或x=3．所以函数f(x)的零点为−3，0，3.…(12分)35. 解：(1)由题意可得，x+2≠0x+3≥0解不等式可得，{x|x≥−3且x≠−2}故函数的定义域，{x|x≥−3且x≠−2}(2)f(−3)=−1，f(23)=833+92436. 证明：(Ⅰ)设x1>x2≥2，所以x1x2>4，则：f(x1)−f(x2)=x1+4x1−x2−4x2=x1−x2+4x1−4x2=x1−x2−4(x1−x2)x1x2=(x1−x2)(x1x2−4)x1x2>0所以f(x)在[2,+∞)为单调增函数．同理f(x)在(0,2]上是减函数，(Ⅱ)因为：函数f(x)在区间[2,4]上为增函数，f(2)=2+2=4，f(4)=4+1=5，所以：值域为[4,5]．37. 解：(1)证明：令3≤x1<x2≤5，则f(x1)−f(x2)=1−3x1+2−(1−3x2+2)=−3(1x1+2−1x2+2)=−3⋅x2−x1(x1+2)(x2+2)，∵3≤x1<x2≤5，∴x2−x1>0，(x1+2)(x2+2)>0，∴f(x1)<f(x2)，故f(x)在[3,5]递增；(2)由f(x)在[3,5]递增，可得f(3)取得最小值1−35=25；f(5)取得最大值1−37=47．38. 解：(Ⅰ)f(x)=x+mx的图象过点P(1,5)，∴5=1+m，∴m=4…(2分)∴f(x)=x+4x，f(x)的定义域为{x|x≠0}，关于原点对称，…(4分)f(x)=x+4x 又f(−x)=−x−4x∴f(x)=−f(x)，…(6分)则f(x2)−f(x1)=x2−x1+4x2−4x1=(x2−x1)(1−4x1x2)=(x2−x1)x1x2−4x1x2(10分)又x2−x1>0，x1≥2，x2>2，∴x1x2>4…(12分)∴f(x2)−f(x1)>0，∴f(x2)>f(x1)，即f(x)在区间[2,+∞)上是增函数…(15分)39. 证明：设x1>x2>2，则：f(x1)−f(x2)=x1+4x1−x2−4x2=(x1−x2)(1−4x1x2)；∵x1>x2>2；∴x1−x2>0，x1x2>4，1−4x1x2>0；∴(x1−x2)(1−4x1x2)>0；∴f(x1)>f(x2)；∴f(x)在(2,+∞)上是增函数．40. 解：(1)∵函数g(x)=x+1x+2，f(x)=x+1g(x)=x+x+2x+1，∴x+1x+2≠0x+2≠0，解得x≠−1x≠−2，∴函数f(x)的定义域为(−∞,−2)∪(−2,−1)∪(−1,+∞)；…(4分)(2)f(x)=x+x+2x+1=x+1+1x+1任取x1，x2∈(0,+∞)，且x1<x2；则f(x1)−f(x2)=(x1+1+1x1+1)−(x2+1+1x2+1)=(x1−x2)⋅x1x2+x1+x2(x1+1)(x2+1)；∵x1，x2∈(0,+∞)，∴x1−x2<0，x1x2+x1+x2(x1+1)(x2+2)>0，∴f(x1)<f(x2)；∴f(x)在区间(0,+∞)上是增函数.(8分)【解析】1. 【分析】本题考查的知识点是集合的交集及其运算，难度不大，属于基础题.解不等式求出集合A，B，结合交集的定义，可得答案．【解答】解：∵集合A={x|x2−4x+3<0}=(1,3)，B={x|2x−3>0}=(32,+∞)，∴A∩B=(3,3)，2. 解：∵集合A={1,2，3}，B={x|x2<9}={x|−3<x<3}，∴A∩B={1,2}．故选：D．先求出集合A和B，由此利用交集的定义能求出A∩B的值．本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．3. 解：∵集合A={x|x<1}，B={x|3x<1}={x|x<0}，∴A∩B={x|x<0}，故A正确，D错误；A∪B={x|x<1}，故B和C都错误．故选：A．先分别求出集合A和B，再求出A∩B和A∪B，由此能求出结果．本题考查交集和并集求法及应用，是基础题，解题时要认真审题，注意交集、并集定义的合理运用．4. 【分析】联立A与B中两方程组成方程组，求出方程组的解即可确定出两集合的交集.此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．【解答】解：联立得：y=x22x−y−1=0，消去y得：2x−1=x2，即(x−1)2=0，解得：x=1，y=1，则A∩B={(1,1)}，故选D．5. 解：∵A={x|x≥0}，B={−1,0，1}，∴A∩B={0,1}，故选：B．根据集合的基本运算进行求解即可．本题主要考查集合的基本运算，比较基础．6. 解：集合A={1,2，4}，B={x|x2−4x+m=0}．若A∩B={1}，则1∈A且1∈B，可得1−4+m=0，解得m=3，即有B={x|x2−4x+3=0}={1,3}．故选：C．由交集的定义可得1∈A且1∈B，代入二次方程，求得m，再解二次方程可得集合B．本题考查集合的运算，主要是交集的求法，同时考查二次方程的解法，运用定义法是解题的关键，属于基础题．7. ∁U P={2,4，6}，(∁U P)∪Q={2,4，6}∪{1，2，4}={1，2，4，6}．故选C．先求出∁U P，再得出(∁U P)∪Q．本题考查了集合的运算，属于基础题．8. 解：把x=1，2，3，4分别代入y=3x−2得：y=1，4，7，10，即B={1,4，7，10}，∵A={1,2，3，4}，∴A∩B={1,4}，故选：D．把A中元素代入y=3x−2中计算求出y的值，确定出B，找出A与B的交集即可．此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．9. 解：∵A={1,2，3}，B={2,3，4}，∴A∪B={1,2，3，4}集合A={1,2，3}，B={2,3，4}，求A∪B，可用并集的定义直接求出两集合的并集．本题考查并集及其运算，解题的关系是正确理解并集的定义及求并集的运算规则，是集合中的基本概念型题．10. 解：∵集合M={x|x≥−1}，N={x|−2<x<2}，∴M∩N={x|−1≤x<2}=[−1,2)．故选：B．先分别求出集合M，N，由此利用交集定义能求出M∩N．本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．11. 解：∵集合A={1,2，3，4}，B={2,4，6，8}，∴A∩B={2,4}，∴A∩B中元素的个数为2．故选：B．利用交集定义先求出A∩B，由此能求出A∩B中元素的个数．本题考查交集中元素个数的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．12. 解：∵A={x|x−1≥0}={x|x≥1}，B={0,1，2}，∴A∩B={x|x≥1}∩{0,1，2}={1，2}．故选：C．求解不等式化简集合A，再由交集的运算性质得答案．本题考查了交集及其运算，是基础题．13. 解：M={x|−1<x<3}，N={x|−2<x<1}，则M∩N={x|−1<x<1}，故选：B根据集合的基本运算即可得到结论．本题主要考查集合的基本运算，比较基础．)x=3x−3−x，14. 解：f(x)=3x−(13∴f(−x)=3−x−3x=−f(x)，即函数f(x)为奇函数，)x为减函数，又由函数y=3x为增函数，y=(13)x为增函数，故函数f(x)=3x−(13故选：A．)x为减函数，结合“增”−“减”=“增”由已知得f(−x)=−f(x)，即函数f(x)为奇函数，由函数y=3x为增函数，y=(13可得答案．本题考查的知识点是函数的奇偶性，函数的单调性，是函数图象和性质的综合应用，难度不大，属于基础题．2x,x>0，15. 解：∵函数f(x)=x+1,x≤0∴f(−2)=−2+1=−1．故选：A．利用分段函数的性质即可得出．本题考查了分段函数的性质，考查了推理能力与计算能力，属于基础题．16. 解：∵f(g(a))=0，∴g(a)=0，∴a为无理数，故选：A．由f(x)=1,x>00,x=0−1,x<0可知g(a)=0，再由g(x)求得．本题考查了分段函数及复合函数的应用．17. 解：由x−2≠0x+2≥0，解得x≥−2且x≠2．∴函数f(x)=x+2x−2的定义域是[−2,2)∪(2,+∞)．故选：B．由根式内部的代数式大于等于0，分式的分母不为0联立不等式组求解．本题考查函数的定义域及其求法，是基础的计算题．18. 解：由函数的定义可知，A，B表示函数的图象，C，D不能表示函数的图象．故选：B．利用函数的定义判断选项即可．本题考查函数的定义的理解，是基础题．19. 解：∵定义在R上的偶函数f(x)在x∈[0,+∞)上单调递增，∴f(x)在(−∞,0)上单调递减，则由f(2x−1)<f(13)，可得−13<2x−1<13，求得13<x<23，故选：A．由条件利用函数的奇偶性和单调性的关系求得满足f(2x−1)<f(13)的x的取值范围．本题主要考查函数的奇偶性和单调性的应用，属于基础题．20. 解：由函数的关系式可得：f(x)f(x+2)=13，f(x+2)f(x+4)=13，据此有：f(x)=f(x+4)，即函数f(x)是周期为4的函数，据此可得：f(2015)=f(504×4−1)=f(−1)，关系式f(x)f(x+2)=13中，令x=−1可得：f(−1)f(1)=2f(−1)=13，∴f(−1)=132．故选：B．由题意首先确定函数的周期，然后结合周期性和函数的关系式进行计算即可求得最终结果．本题考查了函数的周期性，函数的递推关系，函数值的求解等，重点考查学生对基础概念的理解和计算能力，属于中等题．21. 解：∵集合A={1,2}，B={a,a2+3}.A∩B={1}，∴a=1或a2+3=1，解得a=1．故答案为：1．利用交集定义直接求解．本题考查实数值的求法，是基础题，解题时要认真审题，注意交集定义及性质的合理运用．22. 解：∵集合A={1,2，3，4}，集合B={3,4，5}，∴A∩B={3,4}．故答案为：{3,4}．利用交集定义直接求解．本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．23. 解：∵集合A={1,2，6}，B={2,3，6}，∴A∪B={1,2，3，6}．故答案为：{1,2，3，6}．利用并集定义求解．24. 解：集合A ={x |x 2<1}=(−1,1)，B ={x |x 2−2x >0}=(−∞,0)∪(2,+∞)，即∁R B =[0,2]，故A ∩(∁R B )=[0,1)故答案为：[0,1)．求出集合A ，B ，利用集合的基本运算即可得到结论．本题主要考查集合的基本运算，求出集合A ，B 的元素是解决本题的关键，比较基础．25. 解：全集U =R ，集合M ={x |−2≤x ≤2}，N ={x |x 2−3x ≤0}={x |0≤x ≤3}，∴∁U N ={x |x <0或x >3}，∴M ∩(∁U N )={x |−2≤x <0}．故答案为：{x |−2≤x <0}．化简集合N ，求出∁U N ，即可得出M ∩(∁U N )．本题考查了集合的化简与运算问题，是基础题目．26. 解：x ≤0时，y =2x +3≤3，0<x ≤1时，y =x +3≤4，x >1时，y =−x +5<4综上所述，y 的最大值为4故答案为：4分别求f (x )在x ≤0、0<x ≤1、x >1上的最大值，再取其中最大的即可.也可画出f (x )的图象，由图象求最大值． 本题考查分段函数的最值问题，属基本题，难度不大．27. 解：函数y =e x +1e x −a 的值域为A∵e x +1e ≥2 1e ×e x =2，∴值域为A =[2−a ,+∞)．又∵A ⊆[0,+∞)，∴2−a ≥0，即a ≤2．故答案为：(−∞,2]．利用基本不等式的性质即可求解．本题考查了函数值域的求法.高中函数值域求法有：1、观察法，2、配方法，3、反函数法，4、判别式法；5、换元法，6、数形结合法，7、不等式法，8、分离常数法，9、单调性法，10、利用导数求函数的值域，11、最值法，12、构造法，13、比例法.要根据题意选择． 28. 解：函数f (x )= x −x 2,x <0x 2+x ,x≥0在R 上单调递增，∵f (a )>f (2−a )，∴a >2−a ，∴a >1，故答案为a >1函数f (x )= x −x 2,x <0x 2+x ,x≥0在R 上单调递增，利用f (a )>f (2−a )，可得a >2−a ，即可求出a 的取值范围． 本题考查函数的单调性，考查学生解不等式的能力，属于中档题．29. 解：∵函数f (x )= x 2+1,x ≥0 1−x ,x <0， ∴f (−3)= 1−(−3)= 4=2，f (f (−3))=f (2)=22+1=5．故答案为：5．由题意先求出f (−3)= = 4=2，从而f (f (−3))=f (2)，由此能求出结果．本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．30. 解：∵f(x)是定义在R上的奇函数，∴f(−1)=−f(1)，f(0)=0，即f(−1)+f(0)+f(1)=0，故答案为：0．根据奇函数的定义及性质，可得答案．本题考查的知识点是函数奇偶性的性质，难度不大，属于基础题．31. (1)当m=3时，B={x|3≤x≤5}，集合A={x|x2−4x≤0}={x|0≤x≤4}，由此能求出∁U B和A∪B．(2)由集合A{x|0≤x≤4}，B={x|m≤x≤m+2}，B⊆A，列出不等式组，能求出实数m的取值范围．(3)由集合A={x|0≤x≤4}，B={x|m≤x≤m+2}，A∩B=⌀，得到m+2<0或m>4，由此能求出实数m的取值范围．本题考查补集、并集、实数的范围的求法，考查补集、并集、交集等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．32. 对f(x)进行配方，由图象形状，可判断f(x)在[2,4]上的单调性，据单调性即可求得最值．本题考查二次函数在闭区间上的最值问题，属基础题，数形结合是解决该类问题的强有力工具．33. (1)利用函数表达式，能求出f(2)+f(12)，f(3)+f(13)的值．(2)由f(x)=x21+x ，利用函数性质能证明f(x)+f(1x)是定值1．本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．34. (1)利用函数的奇偶性推出f(0)=0，利用奇函数的性质求解函数f(x)的解析式；(2)利用分段函数，通过x的范围，分别求解方程的根即可．本题考查函数的解析式的求法，函数的奇偶性的性质，函数的零点的求法，考查转化思想以及计算能力．35. (1)根据分式及偶次根式成立的条件可得，x+2≠0x+3≥0，解不等式可求函数的定义域(2)直接把x=−3，x=23代入到函数解析式中可求本题主要考查了函数的定义域的求解，函数值的求解，属于基础试题36. (Ⅰ)设x1>x2≥2，可得：x1x2>4，由于f(x1)−f(x2)>0，即可证明f(x)在[2,+∞)为单调增函数.同理可证f(x)在(0,2]上是减函数，(Ⅱ)函数f(x)在区间[2,4]上为增函数，计算f(2)，f(4)的值即可得解值域．本题的考点是函数单调性的判断与证明及函数的值域的求法，本题采取了定义法证明，考查了转化思想，属于基础题．37. (1)根据函数单调性的定义证明函数的单调性，注意取值、作差、变形和定符号和下结论；(2)运用函数的单调性，从而求出函数的最值．本题考查了函数的单调性的定义，考查求函数的值域问题，是一道基础题．38. (Ⅰ)代入点P，求得m，再由奇函数的定义，即可得证；(Ⅱ)根据单调性的定义，设值、作差、变形、定符号和下结论即可得证．本题考查函数的奇偶性的判断和证明，注意运用定义法，考查推理和运算能力，属于基础题．39. 根据增函数的定义，设任意的x1>x2>2，然后作差，通分，提取公因式x1−x2，从而证明f(x1)>f(x2)即可得出f(x)在(2,+∞)上是增函数．考查增函数的定义，以及根据增函数的定义证明一个函数为增函数的方法和过程，作差的方法比较f(x1)，f(x2)，作差之后是分式的一般要通分，一般要提取公因式x1−x2，不等式的性质．40. (1)根据函数的解析式，求出f(x)的定义域即可；(2)利用单调性的定义即可证明函数f(x)在区间(0,+∞)上是增函数．本题考查了根据函数的解析式求定义域以及利用定义证明函数的单调性问题，是基础题目．。

第一章 《集合与函数概念》单元测试题一、选择题：每小题4分，共40分1、在“①高一数学课本中的难题；②所有的正三角形； ③方程220x +=的实数解”中，能够表示成集合的是( A )（A ）② （B ）③ （C ）②③ （D ）①②③2、若{{}|0,|12A x x B x x =<<=≤<，则A B ⋃= ( D ) （A ）{}|0x x ≤ （B ）{}|2x x ≥ （C）{0x ≤≤ （D ）{}|02x x << 3、若{}{}0,1,2,3,|3,A B x x a a A ===∈，则A B ⋂= ( C )（A ）{}1,2 （B ）{}0,1 （C ）{}0,3 （D ）{}34、在映射中B A f →:，},|),{(R y x y x B A ∈==，且),(),(:y x y x y x f +-→，则与A 中的元素)2,1(-对应的B 中的元素为（ A ）（A ）)1,3(- （B ）)3,1( （C ）)3,1(-- （D ）)1,3(5、下列各组函数)()(x g x f 与的图象相同的是（ D ）（A ）2)()(,)(x x g x x f ==（B ）22)1()(,)(+==x x g x x f （C ）0)(,1)(x x g x f == （D ）⎩⎨⎧-==x x x g x x f )(|,|)( )0()0(<≥x x 6、是定义在上的增函数,则不等式的解集是（ D ） (A)(0 ,+∞) (B)(0 , 2) (C) (2 ,+∞) (D) (2 ,716) 7、若奇函数()x f 在[]3,1上为增函数，且有最小值0，则它在[]1,3--上（ C ）A .是减函数，有最小值0B .是增函数，有最小值0C .是减函数，有最大值0D .是增函数，有最大值08、如图所示，阴影部分的面积S 是h 的函数(h ≤≤0则该函数的图象是（ C ）9、若}1,a ⎧⎨⎩，则20052005a b +的值为( D （A ） （B ）1 （C ）1- （D ）1或1-210、奇函数f (x)在区间[-b, -a]上单调递减，且f (x)>0,(0<a<b),那么| f (x)|在区间[a, b]上是( A )A 单调递增B 单调递减C 不增也不减D 无法判断 二、填空题：每小题4分，共20分11、若{}{}{}0,1,2,,1,2,3,2,3,4A B C ===，则()()A B B C ⋂⋃⋂={}3,2,1 12、已知)(x f y =为奇函数，当0≥x 时)1()(x x x f -=，则当0≤x 时，则=)(x fx(1+x) 14、12)(2++=x x x f ，]2,2[-∈x 的最大值是 915、奇函数()f x 满足：①()f x 在(0,)+∞内单调递增；②(1)0f =；则不等式(1)()0x f x ->的解集为：}{}{101>⋃<<-x x x x ；三、解答题 ：每小题12分，共60分17、已知函数0,{|21,}()1,{|2,}x x x n n Z f x x x x n n Z ∈=+∈⎧=⎨∈=∈⎩，画出它的图象,并求()()3-f f 的值 解：图像略（离散点） 0)3(=-f ∴1)0()3((==-f f f18、已知函数f （x ）=xx 1+. （1）判断f （x ）在（0，+∞）上的单调性并加以证明；（2）求f （x ）的定义域、值域；解：（1）令+∞<<<210x x ，则2121121212112212)()()11()()1()1()()(x x x x x x x x x x x x x x x f x f -+-=-+-=+-+=-)11)((2112x x x x --= 012>-x x ， 当1021≤<<x x 时，01121<-x x ，0)()(12<-x f x f ，函数单调递减 当+∞<<<211x x 时，01121>-x x ，0)()(12>-x f x f ，函数单调递增 （2）又题意可知，f(x)定义域为{}0,≠∈x R x x 且当+∞<<x 0时，由（1）可知，当x=1时，f （x ）有最小值2，故f （x ）在{}+∞<<x x 0的值域为{}+∞,2同理，当0<<∞-x 时，当x=-1时，f （x ）有最大值-2，故f （x ）在{}0<<∞-x x 的值域为{}2,-∞-综上得，f （x ）的值域为{}+∞,2⋃{}2,-∞-19、中山市的一家报刊摊点，从报社买进《南方都市报》的价格是每份0.90元，卖出的价格是每份1.0元，卖不掉的报纸可以以每份0.10元的价格退回报社。

高一数学必修一 集合与函数的概念单元测试 附答案解析(时间：120分钟 满分：150分)一、选择题(本大题共12个小题.每小题5分.共60分．在每小题给出的四个选项中.只有一项是符合题目要求的)1．设集合M ＝{x |x 2＋2x ＝0.x ∈R }.N ＝{x |x 2－2x ＝0.x ∈R }.则M ∪N ＝( ) A ．{0} B ．{0,2} C ．{－2,0} D ．{－2,0,2}2．设f ：x →|x |是集合A 到集合B 的映射.若A ＝{－2,0,2}.则A ∩B ＝( ) A ．{0} B ．{2} C ．{0,2} D ．{－2,0}3．f (x )是定义在R 上的奇函数.f (－3)＝2.则下列各点在函数f (x )图象上的是( ) A ．(3.－2) B ．(3,2) C ．(－3.－2) D ．(2.－3)4．已知集合A ＝{0,1,2}.则集合B ＝{x －y |x ∈A .y ∈A }中元素的个数是( ) A ．1 B ．3 C ．5 D ．95．若函数f (x )满足f (3x ＋2)＝9x ＋8.则f (x )的解析式是( )A ．f (x )＝9x ＋8B ．f (x )＝3x ＋2C ．f (x )＝－3x －4D ．f (x )＝3x ＋2或f (x )＝－3x －46．设f (x )＝⎩⎨⎧x ＋3 x >10，f x ＋5 x ≤10，则f (5)的值为( )A ．16B ．18C ．21D ．247．设T ＝{(x .y )|ax ＋y －3＝0}.S ＝{(x .y )|x －y －b ＝0}.若S ∩T ＝{(2,1)}.则a .b 的值为( )A ．a ＝1.b ＝－1B ．a ＝－1.b ＝1C ．a ＝1.b ＝1D ．a ＝－1.b ＝－18．已知函数f (x )的定义域为(－1,0).则函数f (2x ＋1)的定义域为( ) A ．(－1,1) B.⎝ ⎛⎭⎪⎫－1，－12 C ．(－1,0) D.⎝ ⎛⎭⎪⎫12，19．已知A ＝{0,1}.B ＝{－1,0,1}.f 是从A 到B 映射的对应关系.则满足f (0)>f (1)的映射有( ) A ．3个 B ．4个 C ．5个D ．6个10．定义在R 上的偶函数f (x )满足：对任意的x 1.x 2∈(－∞.0](x 1≠x 2).有(x 2－x 1)[f (x 2)－f (x 1)]>0.则当n ∈N *时.有( )A ．f (－n )<f (n －1)<f (n ＋1)B ．f (n －1)<f (－n )<f (n ＋1)C ．f (n ＋1)<f (－n )<f (n －1)D ．f (n ＋1)<f (n －1)<f (－n ) 11．函数f (x )是定义在R 上的奇函数.下列说法：①f (0)＝0； ②若f (x )在[0.＋∞)上有最小值为－1.则f (x )在(－∞.0]上有最大值为1；③若f (x )在[1.＋∞)上为增函数.则f (x )在(－∞.－1]上为减函数；④若x >0时.f (x )＝x 2－2x .则x <0时.f (x )＝－x 2－2x .其中正确说法的个数是( )A ．1个B ．2个C ．3个D ．4个12．f (x )满足对任意的实数a .b 都有f (a ＋b )＝f (a )·f (b )且f (1)＝2.则f 2f 1＋f 4f 3＋f 6f 5＋…＋f 2014f 2013＝( )A ．1006B ．2014C ．2012D ．1007二、填空题(本大题共4小题.每小题5分.共20分．把答案填在题中横线上)13．函数y ＝x ＋1x 的定义域为________．14．f (x )＝⎩⎨⎧x 2＋1x ≤0，－2x x >0，若f (x )＝10.则x ＝________.15．若函数f (x )＝(x ＋a )(bx ＋2a )(常数a .b ∈R )是偶函数.且它的值域为(－∞.4].则该函数的解析式f (x )＝________.16．在一定范围内.某种产品的购买量y 吨与单价x 元之间满足一次函数关系.如果购买1000吨.每吨为800元.购买2000吨.每吨为700元.那么客户购买400吨.单价应该是________元．三、解答题(本大题共6小题.共70分．解答应写出必要的文字说明、证明过程或演算步骤) 17．(本小题满分10分)已知集合A ＝{x |2≤x ≤8}.B ＝{x |1<x <6}.C ＝{x |x >a }.U ＝R . (1)求A ∪B .(∁U A )∩B ；(2)若A ∩C ≠∅.求a 的取值范围．18．(本小题满分12分)设函数f (x )＝1＋x 21－x 2.(1)求f (x )的定义域； (2)判断f (x )的奇偶性； (3)求证：f ⎝ ⎛⎭⎪⎫1x ＋f (x )＝0.19．(本小题满分12分)已知y ＝f (x )是定义在R 上的偶函数.当x ≥0时.f (x )＝x 2－2x . (1)求当x <0时.f (x )的解析式；(2)作出函数f (x )的图象.并指出其单调区间．20．(本小题满分12分)已知函数f (x )＝2x ＋1x ＋1. (1)判断函数在区间[1.＋∞)上的单调性.并用定义证明你的结论． (2)求该函数在区间[1,4]上的最大值与最小值．21．(本小题满分12分)已知函数f (x )的定义域为(0.＋∞).且f (x )为增函数.f (x ·y )＝f (x )＋f (y )．(1)求证：f ⎝ ⎛⎭⎪⎫x y ＝f (x )－f (y )；(2)若f(3)＝1.且f(a)>f(a－1)＋2.求a的取值范围．22．(本小题满分12分)某商场经销一批进价为每件30元的商品.在市场试销中发现.此商品的销售单价x(元)与日销售量y(件)之间有如下表所示的关系：x 30404550y 6030150(1)在所给的坐标图纸中.根据表中提供的数据.描出实数对(x.y)的对应点.并确定y与x的一个函数关系式．(2)设经营此商品的日销售利润为P元.根据上述关系.写出P关于x的函数关系式.并指出销售单价x为多少元时.才能获得最大日销售利润？1.解析 M ＝{x |x (x ＋2)＝0..x ∈R }＝{0.－2}.N ＝{x |x (x －2)＝0.x ∈R }＝{0,2}.所以M ∪N ＝{－2,0,2}．答案 D2. 解析 依题意.得B ＝{0,2}.∴A ∩B ＝{0,2}．答案 C3. 解析 ∵f (x )是奇函数.∴f (－3)＝－f (3)．又f (－3)＝2.∴f (3)＝－2.∴点(3.－2)在函数f (x )的图象上．答案 A4. 解析 逐个列举可得．x ＝0.y ＝0,1,2时.x －y ＝0.－1.－2；x ＝1.y ＝0,1,2时.x －y ＝1,0.－1；x ＝2.y ＝0,1,2时.x －y ＝2,1,0.根据集合中元素的互异性可知集合B 的元素为－2.－1,0,1,2.共5个．答案 C5. 解析 ∵f (3x ＋2)＝9x ＋8＝3(3x ＋2)＋2.∴f (x )＝3x ＋2.答案 B6. 解析 f (5)＝f (5＋5)＝f (10)＝f (15)＝15＋3＝18.答案 B7. 解析 依题意可得方程组⎩⎨⎧2a ＋1－3＝0，2－1－b ＝0，⇒⎩⎨⎧a ＝1，b ＝1.答案 C8. 解析 由－1<2x ＋1<0.解得－1<x <－12.故函数f (2x ＋1)的定义域为⎝⎛⎭⎪⎫－1，－12.答案 B9. 解析 当f (0)＝1时.f (1)的值为0或－1都能满足f (0)>f (1)；当f (0)＝0时.只有f (1)＝－1满足f (0)>f (1)；当f (0)＝－1时.没有f (1)的值满足f (0)>f (1).故有3个．答案 A10.解析 由题设知.f (x )在(－∞.0]上是增函数.又f (x )为偶函数.∴f (x )在[0.＋∞)上为减函数． ∴f (n ＋1)<f (n )<f (n －1)． 又f (－n )＝f (n ).∴f (n ＋1)<f (－n )<f (n －1)． 答案 C11. 解析 ①f (0)＝0正确；②也正确；③不正确.奇函数在对称区间上具有相同的单调性；④正确． 答案 C12. 解析 因为对任意的实数a .b 都有f (a ＋b )＝f (a )·f (b )且f (1)＝2.由f (2)＝f (1)·f (1).得f (2)f (1)＝f (1)＝2. 由f (4)＝f (3)·f (1).得f (4)f (3)＝f (1)＝2. ……由f (2014)＝f (2013)·f (1). 得f (2014)f (2013)＝f (1)＝2.∴f (2)f (1)＋f (4)f (3)＋f (6)f (5)＋…＋f (2014)f (2013)＝1007×2＝2014. 答案 B13. 解析 由⎩⎨⎧x ＋1≥1，x ≠0得函数的定义域为{x |x ≥－1.且x ≠0}．答案 {x |x ≥－1.且x ≠0}14. 解析 当x ≤0时.x 2＋1＝10.∴x 2＝9.∴x ＝－3.当x >0时.－2x ＝10.x ＝－5(不合题意.舍去)． ∴x ＝－3. 答案 －315. 解析 f (x )＝(x ＋a )(bx ＋2a )＝bx 2＋(2a ＋ab )x ＋2a 2为偶函数.则2a ＋ab ＝0.∴a ＝0.或b ＝－2.又f (x )的值域为(－∞.4].∴a ≠0.b ＝－2.∴2a 2＝4. ∴f (x )＝－2x 2＋4. 答案 －2x 2＋416. 解析 设一次函数y ＝ax ＋b (a ≠0).把⎩⎨⎧x ＝800，y ＝1000，和⎩⎨⎧x ＝700，y ＝2000，代入求得⎩⎨⎧a ＝－10，b ＝9000.∴y ＝－10x ＋9000.于是当y ＝400时.x ＝860.答案 86017. 解 (1)A ∪B ＝{x |2≤x ≤8}∪{x |1<x <6}＝{x |1<x ≤8}． ∁U A ＝{x |x <2.或x >8}． ∴(∁U A )∩B ＝{x |1<x <2}． (2)∵A ∩C ≠∅.∴a <8.18. 解 (1)由解析式知.函数应满足1－x 2≠0.即x ≠±1.∴函数f (x )的定义域为{x ∈R |x ≠±1}． (2)由(1)知定义域关于原点对称. f (－x )＝1＋(－x )21－(－x )2＝1＋x 21－x 2＝f (x )．∴f (x )为偶函数．(3)证明：∵f ⎝ ⎛⎭⎪⎫1x ＝1＋⎝ ⎛⎭⎪⎫1x 21－⎝ ⎛⎭⎪⎫1x 2＝x 2＋1x 2－1.f (x )＝1＋x 21－x 2.∴f ⎝ ⎛⎭⎪⎫1x ＋f (x )＝x 2＋1x 2－1＋1＋x 21－x 2＝x 2＋1x 2－1－x 2＋1x 2－1＝0. 19. 解 (1)当x <0时.－x >0.∴f (－x )＝(－x )2－2(－x )＝x 2＋2x . 又f (x )是定义在R 上的偶函数. ∴f (－x )＝f (x )． ∴当x <0时.f (x )＝x 2＋2x .(2)由(1)知.f (x )＝⎩⎨⎧x 2－2x (x ≥0)，x 2＋2x (x <0).作出f (x )的图象如图所示：由图得函数f (x )的递减区间是(－∞.－1].[0,1]．f (x )的递增区间是[－1,0].[1.＋∞)．20. 解 (1)函数f (x )在[1.＋∞)上是增函数．证明如下：任取x 1.x 2∈[1.＋∞).且x 1<x 2.f (x 1)－f (x 2)＝2x 1＋1x 1＋1－2x 2＋1x 2＋1＝x 1－x 2(x 1＋1)(x 2＋1). ∵x 1－x 2<0.(x 1＋1)(x 2＋1)>0. 所以f (x 1)－f (x 2)<0.即f (x 1)<f (x 2). 所以函数f (x )在[1.＋∞)上是增函数．(2)由(1)知函数f (x )在[1,4]上是增函数.最大值f (4)＝95.最小值f (1)＝32.21. 解 (1)证明：∵f (x )＝f ⎝ ⎛⎭⎪⎫xy·y ＝f ⎝ ⎛⎭⎪⎫x y ＋f (y ).(y ≠0)∴f ⎝ ⎛⎭⎪⎫x y ＝f (x )－f (y )．(2)∵f (3)＝1.∴f (9)＝f (3·3)＝f (3)＋f (3)＝2. ∴f (a )>f (a －1)＋2＝f (a －1)＋f (9)＝f [9(a －1)]．又f (x )在定义域(0.＋∞)上为增函数.∴⎩⎨⎧a >0，a －1>0，a >9(a －1)，∴1<a <98.22. 解 (1)由题表作出(30,60).(40,30).(45,15).(50,0)的对应点.它们近似地分布在一条直线上.如图所示．设它们共线于直线y ＝kx ＋b .则⎩⎨⎧50k ＋b ＝0，45k ＋b ＝15，⇒⎩⎨⎧k ＝－3，b ＝150.∴y ＝－3x ＋150(0≤x ≤50.且x ∈N *).经检验(30,60).(40,30)也在此直线上． ∴所求函数解析式为y ＝－3x ＋150(0≤x ≤50.且x ∈N *)．(2)依题意P ＝y (x －30)＝(－3x ＋150)(x －30)＝－3(x －40)2＋300.∴当x ＝40时.P 有最大值300.故销售单价为40元时.才能获得最大日销售利润．。

第一章测试题（总分100分）一、选择题（每小题2分，共20分）1.设集合M ＝{x |x 2－x －12＝0}，N ＝{x |x 2＋3x ＝0}，则M ∪N 等于（ ） A . ｛－3｝ B .｛0，－3,4｝ C .｛－3，4｝ D .｛0,4｝2.设集合，（ ）A .B .C .D .3.已知全集I ＝｛x |x 是小于9的正整数｝，集合M ＝｛1，2，3｝，集合N ＝｛3，4，5, 6｝，则（C U M ）∩N 等于（ ）A .｛3｝B .｛7，8｝C .｛4，5, 6｝D . {4, 5，6, 7，8}4.设全集U ={（x ,y ）|x ∈R ,y ∈R }，集合M ={（x ,y ）|y ≠x } ，N ={（x ,y ）|y ≠-x }，则集合P ={（x ,y ）|y 2=x 2} 等于（ ）A .（C U M ）∩（C u N ）B .（C U M ）∪NC .（ C U M ）∪（ C u N ）D .M ∪（ C U N ）5.已知函数的定义域为，的定义域为，则（ ）A .B .C .D .6.下列四个函数中，在（0，+∞）上为增函数的是（ ） A . f （x ）＝3－x B . f （x ）＝x 2－3x C . f （x ）＝－｜x ｜D . f （x ）＝－7.如图所示，液体从一圆锥形漏斗漏入一圆柱形桶中，开始时，漏斗盛满液体，经过3分钟漏完.已知圆柱中液面上升的速度是一个常量，H 是圆锥形漏斗中液面下落的距离，则H 与下落时间t （分）的函数关系表示的图象只可能是（ ）{|32}M m m =∈-<<Z {|13}N n n M N =∈-=Z 则，≤≤{}01，{}101-，，{}012，，{}1012-，，，xx f -=21)(M 2)(+=x x g N =⋂N M {}2-≥x x {}2<x x {}22<<-x x {}22<≤-x x 23+xA .B .C .D .8.函数y =是（ ） A .奇函数 B .偶函数 C .既是奇函数又是偶函数 D .非奇非偶数9.函数则的值为（ ）A.1516B . 2716-C . 89D . 1810.定义在R 上的偶函数在[0，7]上是增函数，在[7，+]上是减函数，又，则（ ）A . 在[－7，0]上是增函数，且最大值是6B . 在[－7，0]上是增函数，且最小值是6C . 在[－7，0]上是减函数，且最小值是6D . 在[－7，0]上是减函数，且最大值是6 二、填空题（每小题5分，共20分）11.已知集合U ＝{1，2，3，4，5}，A ＝{2，3，4}，B ＝{4，5}，则A ∩（UB ）＝ . 12.已知集合A ＝－2，3，4－4，集合B ＝3，.若B A ，则实数＝ . 13.已知f （x ）是偶函数，当x ＜0时，f （x ）＝x （2x －1），则当x ＞0时，f （x ）＝_________ .14.已知f （x ）＝,若f （x ）＝10，则x ＝ .三、解答题（每小题15分，共60分） 15.若{}2214-A x x =-，，，}{519=-B x x -，，，}{9B A =，求AB .16.证明函数f （x ）＝在［3,5］上单调递减，并求函数在［3,5］的最大值和最小值.xx ++-19122211()31x x f x x x x ⎧-⎪=⎨-->⎪⎩，，，，≤1(3)f f ⎛⎫⎪⎝⎭∞6)7(=f )(x f {m }{2m }⊆m ⎩⎨⎧>-≤+05062x x x x 13+x17. 如图，已知底角为45︒的等腰梯形ABCD ，底边BC 长为7cm ，腰长为，当一条垂直于底边BC （垂足为F ）的直线l 从左至右移动（与梯形ABCD 有公共点）时，直线l 把梯形分成两部分，令BF ＝x ,试写出左边部分的面积y 与x 的函数解析式.18.判断下列函数的奇偶性.（1）()f x x (1-x ),x ＜0， （2）()f x =x (1+x ),x ＞0；（3）已知函数对任意x y ∈R 、都有.参考答案1. B2. B3. C4. C5. D6. D7. A8. B9. C 10. D 11.{2 , 3} 12.2 13.x （2x ＋1） 14.－215.由，可得或，解得或5.当时，，，集合B 中元素不满足互异性，故舍去.当时，，，满足题意，此时.当时，，，此时，这与矛盾，故舍去.综上知.16.用定义证明即可.f （x ）的最大值为，最小值为 17.解：过点A ,D 分别作AG BC DH BC ⊥⊥，，垂足分别是G ，H .因为ABCD 是等腰梯)(x f )()()(y f x f y x f +=+A ∈992=x 912=-x 3±=x 3=x {}4,5,9-=A {}9,2,2--=B 3=x 3-=x {}4,7,9--=A {}9,4,8-=B {}9,4,8,4,7---=B A 5=x {}4,9,25-=A {}9,4,0-=B {}9,4-=B A {}9=B A 5=x {}9,4,8,4,7---=B A 4321形，底角为45︒，AB =，所以 2cm BG AG DH HC ====，所以AD = GH =3cm .（1）当点F 在BG 上时，即](02x ∈，时，212y x =； （2）当点F 在GH 上时，即](25x ∈，时，2(2)222；y x x =+-=-（3）当点F 在HC 上时，即](5,7x ∈时，=217102-+x -（）. 所以，函数解析式为 ]]]221(02222(251710(57.2-+x x y x x x x ⎧∈⎪⎪⎪=-∈⎨⎪⎪∈⎪⎩，，，，，，（），，18.（1）既是奇函数，又是偶函数；（2）函数的定义域00-+)∞∞（，）（，，当0x >时，0x -<，()(1)()f x x x f x -=-+=-； 当0x <时，0x ->，1-=--=-x f x x x f （）（）（）. 综上，对任意(00+x ∈-∞∞，）（，），()()()f x f x f x -=-，所以是奇函数. （3）定义域是R ,关于原点对称.令y =x =0时，f (0+0)=f (0)+f (0),即f (0)=0.令y =-x ,则f (x -x )=f (x )+f (-x ),即f (0)=f (x )+f (-x ),所以f (-x )=-f (x )所以 f (x )是奇函数.CEF Rt ABCD ABFED S S S y ∆-==梯形五边形。