连续系统离散化处理基本方法
- 格式:doc
- 大小:235.00 KB
- 文档页数:3



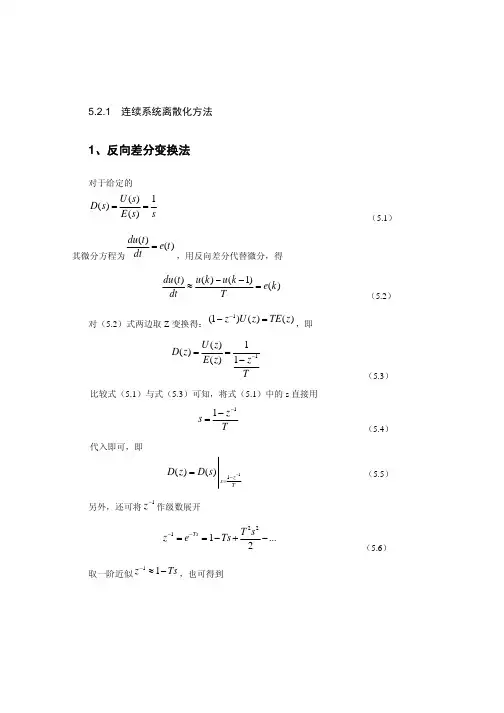
第6章连续系统的离散化方法及近似解在连续系统中,我们经常需要将其离散化为离散系统以便于分析和求解。
离散化方法能够将连续系统的微分方程转化为差分方程,从而得到近似解。
本章将介绍连续系统的离散化方法及近似解的计算。
连续系统的离散化方法有许多种,常见的有Euler方法、Runge-Kutta方法和有限差分方法等。
其中,Euler方法是最简单和最基础的离散化方法,其基本思想是将连续时间轴划分为若干个小时间间隔,并用差分逼近连续系统的导数。
具体地,对于一阶常微分方程:\[\frac{{dy}}{{dt}} = f(y, t)\]可以使用Euler方法将其离散化为:\[y_{n+1} = y_n + h \cdot f(y_n, t_n)\]其中,\(y_n\)是时间点\(t_n\)的近似解,\(h\)是时间步长。
Runge-Kutta方法是一种更精确的离散化方法,其基本思想是利用多个中间步骤来更准确地逼近连续系统的导数。
常见的是四阶Runge-Kutta 方法,其公式为:\[y_{n+1} = y_n + \frac{h}{6} \cdot (k_1 + 2k_2 + 2k_3 +k_4)\]其中\[k_1=f(y_n,t_n)\]\[k_2 = f(y_n + \frac{h}{2}k_1, t_n + \frac{h}{2})\]\[k_3 = f(y_n + \frac{h}{2}k_2, t_n + \frac{h}{2})\]\[k_4 = f(y_n + hk_3, t_n + h)\]这样可以得到更准确的近似解。
有限差分方法是一种常用的离散化方法,其基本思想是将连续的导数用差分逼近。
以二阶偏微分方程为例,该方程的一般形式为:\[\frac{{\partial^2u}}{{\partial x^2}} +\frac{{\partial^2u}}{{\partial y^2}} = f(x, y)\]可以使用中心差分公式将其离散化为:\[\frac{{u_{i+1,j} - 2u_{i,j} + u_{i-1,j}}}{{\Delta x^2}} + \frac{{u_{i,j+1} - 2u_{i,j} + u_{i,j-1}}}{{\Delta y^2}} =f_{i,j}\]其中,\(u_{i,j}\) 是近似解在网格点 \((i, j)\) 处的值,\(\Delta x\) 和 \(\Delta y\) 分别是网格在 \(x\) 和 \(y\) 方向的步长,\(f_{i,j}\) 是离散化后的右侧函数。

连续传递函数离散化的方法与原理连续传递函数离散化是将连续时间域中的传递函数转换为离散时间域中的传递函数的过程。
在控制系统设计中,离散化是非常重要的一步,因为大多数数字控制器本质上只能处理离散的输入和输出信号。
离散化方法的选择对系统的稳定性、性能和可实现性都有很大的影响。
离散化方法分为两大类:时域方法和频域方法。
时域方法根据传递函数的时间响应,或者根据传递函数的微分方程进行转换。
频域方法通过拉普拉斯变换和z变换之间的等价关系进行转换。
时域离散化方法:1. 脉冲响应不变法(Impulse Invariance Method):这是最常用的离散化方法之一、它通过将连续时间系统的脉冲响应对应到离散时间系统的单位冲激响应上来实现离散化。
该方法的原理是保持连续系统和离散系统的单位冲激响应相同,从而尽可能保持系统的动态特性。
2. 零阶保持法(Zero Order Hold Method):这个方法假设连续时间系统在每个采样周期内是恒定的,即将采样周期内的连续时间系统输出等效为一个恒定值。
这个方法的原理是根据离散系统的输出间隔和连续时间系统的采样间隔,使用插值方法得到离散系统的输出值。
3. 一阶保持法(First Order Hold Method):这个方法在零阶保持法的基础上改进,考虑了连续时间系统在每个采样周期内的变化趋势。
它假设连续时间系统在每个采样周期内是线性变化的。
通过插值方法得到离散系统的输出值。
4. 向后微分法(Backward Difference Method):这个方法根据连续时间系统微分方程中的向后差分近似来实现离散化。
它假设离散时间系统输出的变化率等于连续时间系统输出的变化率。
频域离散化方法:1. 频率响应匹配法(Frequency Response Matching Method):这个方法将连续时间系统和离散时间系统的频率响应函数进行匹配,使它们在一定频率范围内的增益和相位相近。
通过频率响应函数的等价性,可以使用拉普拉斯变换和z变换之间的关系得到离散时间系统的传递函数。





连续系统离散化方法连续系统离散化方法是一种常用的数值计算方法,它将连续系统转化为离散系统,从而使得计算机可以进行处理。
本文将从离散化方法的定义、应用、实现以及优缺点等方面进行介绍。
一、离散化方法的定义离散化方法是指将连续系统转化为离散系统的过程。
在计算机中,所有的数值都是离散的,而实际上很多系统是连续的,比如电路、机械系统、化学反应等等。
离散化方法就是将这些连续系统转化为可以在计算机中处理的离散系统。
离散化方法可以通过采样和量化来实现。
二、离散化方法的应用离散化方法在很多领域都有应用,比如电路设计、控制系统设计、信号处理等等。
在电路设计中,离散化方法可以将连续电路转化为数字电路,从而实现数字信号的处理。
在控制系统设计中,离散化方法可以将连续控制器转化为数字控制器,从而实现数字化自动控制。
在信号处理中,离散化方法可以将连续信号转化为数字信号,从而实现对信号的数字处理。
三、离散化方法的实现离散化方法的实现可以通过采样和量化来实现。
采样是指对连续信号进行离散化,将其转化为一系列的采样值。
量化是指对采样值进行离散化,将其转化为一系列的离散数值。
采样和量化的具体实现方式包括正弦采样、脉冲采样、最大值采样、平均值采样等等。
量化的具体实现方式包括线性量化、对数量化、非线性量化等等。
四、离散化方法的优缺点离散化方法的优点是可以将连续系统转化为离散系统,从而可以在计算机中进行处理。
离散系统具有稳定性、可控性、可观性等优点。
离散化方法的缺点是会引入误差,因为离散化过程中会丢失一些信息。
此外,离散化方法需要选取适当的采样周期和量化精度,否则会影响系统的性能。
离散化方法是一种常用的数值计算方法,它将连续系统转化为离散系统,从而使得计算机可以进行处理。
离散化方法的应用广泛,包括电路设计、控制系统设计、信号处理等等。
离散化方法的实现可以通过采样和量化来实现。
离散化方法既有优点,又有缺点,需要在具体应用中对其进行合理的选择和设计。
连续系统离散化方法一、概述连续系统离散化方法是一种将连续系统转化为离散系统的方法,常用于控制系统的设计和分析。
该方法可以将一个无限维度的连续系统转化为有限维度的离散系统,使得控制器设计和分析变得更加简单和可行。
二、连续系统模型在开始进行连续系统离散化的过程中,需要先建立一个连续系统模型。
通常情况下,这个模型可以由微分方程或者差分方程来表示。
三、离散化方法1. 时域离散化方法时域离散化方法是最基本的离散化方法之一。
它通过将时间轴上的信号进行采样,从而将一个连续时间信号转换为一个离散时间信号。
这个过程中需要确定采样周期以及采样点数目等参数。
2. 频域离散化方法频域离散化方法是一种利用傅里叶变换将一个连续时间信号转换为一个频域信号,然后再对该频域信号进行采样得到一个离散时间信号的方法。
这个过程中需要确定采样频率以及采样点数目等参数。
3. 模拟器法模拟器法是一种将连续系统转化为离散系统的方法。
这个方法的核心思想是利用一个数字模拟器来模拟连续系统的行为,从而得到一个离散时间信号。
4. 差分方程法差分方程法是一种将连续系统转化为离散系统的方法。
这个方法的核心思想是利用微分方程在离散时间点上进行近似,从而得到一个差分方程。
四、误差分析在进行离散化过程中,会产生一定的误差。
因此,需要对误差进行分析和评估,以确保离散化后的结果与原始连续系统相近。
五、应用实例1. 机械控制系统机械控制系统中通常需要对连续时间信号进行采样和处理。
通过使用离散化方法,可以将连续信号转换为数字信号,并且可以在数字域上进行控制器设计和分析。
2. 电力电子控制系统电力电子控制系统中通常需要对高频信号进行处理。
通过使用频域离散化方法,可以将高频信号转换为数字信号,并且可以在数字域上进行控制器设计和分析。
六、总结连续系统离散化方法是一种将连续系统转化为离散系统的方法。
通过使用不同的离散化方法,可以将连续时间信号转换为数字信号,并且可以在数字域上进行控制器设计和分析。
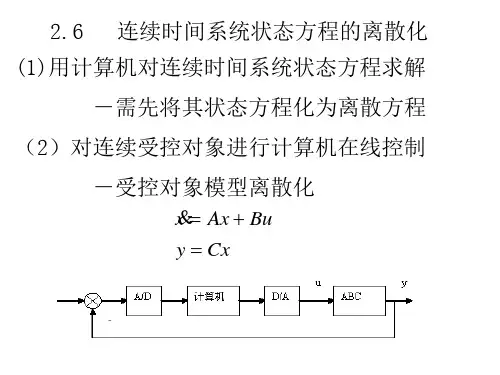
一、概述连续状态空间方程是描述系统状态随时间演化的重要数学模型,在许多领域都有着广泛的应用。
然而,实际系统往往是离散的,为了将连续状态空间方程应用到离散系统中,需要进行离散化处理。
离散化是指将连续系统的状态空间方程转化为离散系统的状态空间方程,以便于在计算机上进行分析和仿真。
二、连续状态空间方程连续状态空间方程可被描述为:dx/dt = f(x,u)y = h(x)其中,x表示系统状态,u表示输入,f(x,u)表示状态方程,h(x)表示输出方程。
连续状态空间方程描述了系统状态随时间的变化规律,是控制系统、信号处理、通信系统等领域的重要数学工具。
三、离散化方法对于离散系统,通常使用下面的方法将连续状态空间方程离散化:1. Euler方法Euler方法是一种简单且常用的数值积分方法,可以用来离散化连续状态空间方程。
通过欧拉方法,可以将连续时间上的状态方程转化为离散时间上的状态更新方程。
2. 隐式Euler方法隐式Euler方法相比于显式Euler方法,具有更好的数值稳定性。
使用隐式Euler方法进行离散化处理,可以有效解决一些数值不稳定的问题。
3. 4阶Runge-Kutta方法4阶Runge-Kutta方法是一种更加精确的数值积分方法,同样可以应用于连续状态空间方程的离散化处理。
相比于Euler方法,Runge-Kutta方法通常能够提供更准确的结果。
四、离散化精度在进行连续状态空间方程的离散化处理时,离散化精度是一个重要的衡量指标。
离散化精度决定了离散系统模型的精确程度,对系统分析和控制设计都具有重要的影响。
1. 离散化步长离散化步长是指在进行离散化处理时,时间或空间上的离散化间隔大小。
步长越小,离散化的精度越高,但计算负荷也越大。
2. 离散化误差离散化误差是指离散系统模型与连续系统模型之间的差距。
通过控制离散化步长和选择合适的离散化方法,可以有效降低离散化误差,提高系统模型的精确度。
五、离散化应用离散化处理后的系统模型可以在计算机上进行仿真和实时控制,应用十分广泛。
在数字计算机上对连续系统进行仿真时,首先遇到的问题是如何解决数字计算机在数值及时间上的离散性与被仿真系统数值及时间上的连续性这一基本问题。
从根本意义上讲,数字计算机所进行的数值计算仅仅是“数字”计算,它表示数值的精度受限于字长,这将引入舍入误差;另一方面,这种计算是按指令一步一步进行的,因而,还必须将时间离散化,这样就只能得到离散时间点上系统性能。
用数字仿真的方法对微分方程的数值积分是通过某种数值计算方法来实现的。
任何一种计算方法都只能是原积分的一种近似。
因此,连续系统仿真,从本质上是对原连续系统从时间、数值两个方面对原系统进行离散化,并选择合适的数值计算方法来近似积分运算,由此得到的离散模型来近似原连续模型。
如何保证离散模型的计算结果从原理上确能代表原系统的行为,这是连续系统数字仿真首先必须解决的问题。
设系统模型为:),,(t u y f y
=&,其中u (t )为输入变量,y (t )为系统变量;令仿真时间间隔为h ,离散化后的输入变量为)(ˆk t u
,系统变量为)(ˆk t y ,其中k t 表示t=kh 。
如果)()(ˆk k t u t u
≈,)()(ˆk k t y t y ≈,即0)()(ˆ)(≈-=k k k u t u t u t e ,0)()(ˆ)(≈-=k k k y t y t y t e (对所有k=0,1,2,…),则可认为两模型等价,这称为相似
原理(参见图)。
实际上,要完全保证0)(,0)(==k y k u t e t e 是很困难的。
进一步分析离散化引的误差,随着计算机技术的发展,由计算机字长引入的舍入误差可以忽略,关键是数值积分算法,也称为仿真建模方法。
相似原理用于仿真时,对仿真建模方法有三个基本要求:
(1)稳定性:若原连续系统是稳定的,则离散化后得到的仿真模型也应是稳定的。
关于稳定性的详细讨论将在节中进行。
(2)准确性:有不同的准确性评价准则,最基本的准则是:
绝对误差准则:δ≤-=)()(ˆ)(k k k y t y t y
t e 相对误差准则:δ≤-=
)(ˆ)()(ˆ)(k k k k y t y
t y t y
t e 其中 规定精度的误差量。
原连续模型
仿真模型
)(≈k y t e
图 相
f (t,y )
f (t 0,y o )
t
t
t 0
t 1
图数值积分法
(3)快速性:如前所述,数字仿真是一步一步推进的,即由某一初始值)(0t y 出发,逐步计算,得到)(,),(),(21k t y t y t y Λ,每一步计算所需时间决定了仿真速度。
若第k 步计算对应的系统时间间隔为,1k k k t t h -=+计算机由)(k t y 计算)(1+k t y 需要的时间为T k ,则,若T k =h k 称为实时仿真,T k h k 称为超实时仿真,而大多数情况是T k h k ,对应于离线仿真。
连续系统数字仿真中离散化最基本的算法是数值积分算法。
对于形如),,(t u y f y
=&的系统,已知系统变量y 的初始条件y t y ()00=,现在要求y 随时间变化的过程y t ()。
计算过程可以这样考虑(参见图):首先求出初始点y t y ()00=的f t y ()00,,微分方程可以写作:
y t y f t y dt t t
()(,)=+⎰00 ()
图所示曲线下的面积就是y t (),由于难以得到f(y,u,t)积分的数值表达式,人们对数值积分方法进行了长期探索,其中欧拉法是最经典的近似方法。
欧拉法用矩形面积近似表示积分结果,也就是当t=t 1时,y t ()1的近似值为y 1 :
y y t y t f t y 11000=≅+⋅()()∆,
重复上述作法,当t t =2时
y y t y t t f t y 2212111=≅+-⋅()()(), 所以,对任意时刻t k+1,有:
y y t y t t f t y κκκκκκκ+++=≅+-⋅111()()(), () 令t t h κκκ+-=1称为第κ步的计算步距。
若积分过程中步距不变h h κ=,可以证明,欧拉法的截断误差正比于h 2。
为进一步提高计算精度,人们提出了“梯形法”。
梯形法近似积分形式如式所示,令:
t t h h κκκ+-=1=已知:t t =κ时y t ()κ的近似值y κ,那么:
y y t y h f t y f t y κκκκκκκ++++=≅+
+11111
2
()[(,)(,)] 可见,梯形法是隐函数形式。
采用这种积分方法最简单的预报校正方法是用欧拉法估计初
值,用梯形法校正,即:
y
y h f t y f t y i i κκκκκκ++++≅++1
11112
()()
[(,)(,)] y y h f t y i κκκκ+≅+⋅1()
(,)
式称作预报公式,采用欧拉法,式为校正公式,采用梯形法。
用欧拉法估计一次y i κ+1()
的值,代入校正公式得到y κ+1的校正值y i κ++11()。
设是规定的足够小正整数,称作允许误差,若i =0, i +1=1
称作第一次校正;i i =+=112,称作第二次校正;通过反复迭代,直到满足y y i i
κκε+++-≤111,
这时y i κ++11()
是满足误差要求的校正值。
上述方法是针对式所示的微分方程在已知初值情况下进行求解,因此也称为微分方程初值问题数值计算法,为统一起见,本书中称为数值积分法。
连续系统数字仿真的离散化方法有两类,它们是数值积分方法和离散相似方法,本文讨论数值积分法。
数值积分方法采用递推方式进行运算,而采用不同的积分方法会引进不同的计算误差,为了提高计算精度,往往会增加运算量。
就同一种积分算法而言,为提高计算精度,减小积分步距h ,计算量增大,影响系统运算速度。
因此,计算精度和速度是连续系统仿真中常迂到的一对矛盾,也是数字仿真中要求解决的问题之一。
也就是说,选择合适的算法、合适的软、硬件环境,在保证计算精度的前提下,考虑怎样提高仿真的速度。