新安江模型介绍

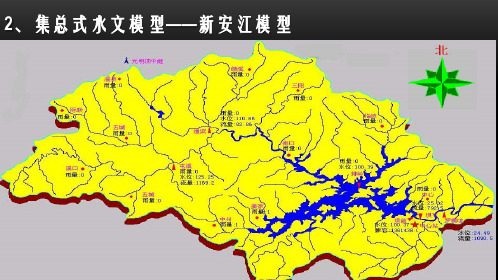
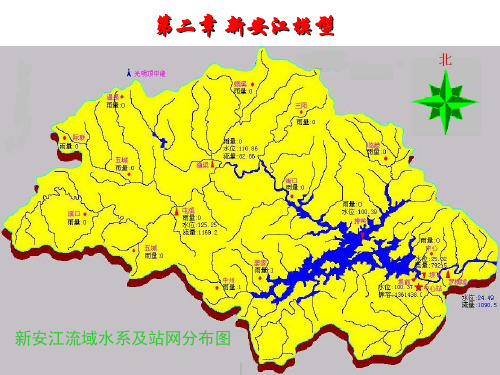
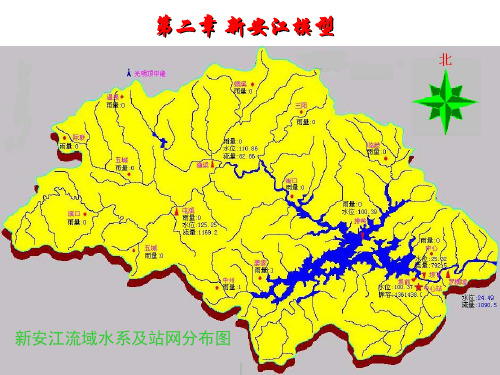
第二章新安江流域水文模型60年代初，河海大学(原华东水利学院)水文系赵人授等开始研究蓄满产流模型，配合一定的汇流计算，将模型应用于水文预报和水文设计。

1973年，他们在对新安江水库做人库流量预报的工作中，把他们的经验归纳成一个完整的降雨径流流域模型——新安江模型。

模型可用于湿润地区和半湿润地区的湿润季节径流模拟和计算。

最初的新安江模型为两水源模型，只能模拟地表径流和地下径流。

80年代初期，模型研制者将萨克拉门托模型与水箱模型中，用线性水库函数划分水源的概念引入新安江模型，提出了三水源新安江模型，模型可以模拟地面径流、壤中流、地下径流。

1984至1986年，又提出了四水源新安江模型，可以模拟地面径流、壤中流、快速地下径流和慢速地下径流。

三水源新安江模型一般应用效果较好，但模拟地下水丰富地区的日径流过程精度不够理想。

在新安江三模型中增加慢速地下水结构就成为四水源新安江模型。

当流域面积较小时，新安江模型采用集总模型，当面积较大时，采用分块模型。

分块模型把流域分成许多块单元流域，对每个单元流域做产、汇计算，得到单元流域的出口流量过程。

再进行出口以下的河道洪水演算，求得流域出口的流量过程。

把每个单元流域的出流过程相加，就求得了流域出口的总出流过程。

划分单元流域的主要目的是处理降雨分布的不均匀性，因此单元流域应当大小适当，使得每块面积上的降雨分布比较均匀．并有一定数目的雨量站。

其次尽可能使单元流域与自然流域相一致，以便于分析与处理问题，并便于利用已有的小流域水文资料。

如果流域内有大中型水库，则水库以上的集水面积即应作为一个单元流域。

因为各单元流域的产汇、流计算方法基本相同，以下只讨论一个单元流域的情况。

2.1新安江两水源模型1．模型结构和参数新安江两水源模型的产流子模型采用蓄满产流模型，蒸发计算采用三层蒸发计算模型。

利用稳定下渗率FC将径流划分为地面径流和地下径流两种水源。

地面径流采用单位线汇流，地下径流采用一次线性水库汇流。

《流域水文模拟》结课报告新安江模型的原理、结构及应用、发展历程The principle, structure, application and development process of Xin anjiang Model作者姓名：孔旭学科、专业：水文学及水资源学号：21506149指导教师：王国利完成日期：2016年8月30日大连理工大学Dalian University of Technology摘要新安江模型是河海大学提出的一个概念性降雨径流模型，具有原创性，是我国为数不多的被国际上广泛认可的水文模型。

新安江水文模型在我国湿润与半湿润地区广为应用，取得了良好的效果。

经过近50年的发展，新安江模型已经从最初的专门从事水库入库洪水预报的单一功能模型发展为适合用于水文预报、水资源管理、水土资源评价、面源污染预测、气候变化和人类活动影响研究的多功能的水文模型；其部分参数已从靠经验率定发展为可以进行物理推求。

总之，新安江模型是一个不断发展的模型体系。

本文主要由三部分构成。

第一部分为新安江模型简介，回顾了新安江模型产生的历史背景和发展历程，介绍了新安江模型的基本原理和结构体系；第二部分讲述了新安江模型参数的物理意义及其率定；第三部分为新安江水文模型在英那河流域防洪规划编制当中的应用。

关键词：水文模型；新安江模型；洪水预报The principle, structure, application and development process of Xinanjiang ModelAbstractXin anjiang Model originally proposed by Hehai University is a conceptual rainfall runoff model and is also one of the few widely recognized international hydrological model in China. Xin anjiang hydrological model was widely used in our humid and semi-humid areas, and achieved good results.After nearly 50 years study, Xin anjiang model has been developed from the single-function of reservoir flood forecasting into multi-purpose model including hydrological forecasting, water resources management, water and soil resources evaluation, non-point source pollution prediction, climate change and human activities versatile hydrological model studies. And part of its parameters can be acquired through physical calculation instead of experience. In short, Xin anjiang model is an evolving model system.This paper consists of three parts. The first part is about the brief introduction of Xin anjiang model, which recalls the historical background and the development, as well as introduces the basic principles and architecture; the second part describes the physical meaning of Xin anjiang model parameters and calibration; the third part is about the application of Xin anjiang model in Ying Na River Basin flood control planning.Key Words: hydrological model; Xin anjiang model; Flood forecasting目 录摘 要 .............................................................. I Abstract .. (II)引 言 (1)1 新安江模型简介 (2)1.1 新安江模型起源 ............................... 错误!未定义书签。

《流域水文模拟》结课报告新安江模型的原理、结构及应用、发展历程The principle, structure, application and development process of Xin anjiang Model作者姓名：孔旭学科、专业：水文学及水资源学号：21506149指导教师：王国利完成日期：2016年8月30日大连理工大学Dalian University of Technology摘要新安江模型是河海大学提出的一个概念性降雨径流模型，具有原创性，是我国为数不多的被国际上广泛认可的水文模型。

新安江水文模型在我国湿润与半湿润地区广为应用，取得了良好的效果。

经过近50年的发展，新安江模型已经从最初的专门从事水库入库洪水预报的单一功能模型发展为适合用于水文预报、水资源管理、水土资源评价、面源污染预测、气候变化和人类活动影响研究的多功能的水文模型；其部分参数已从靠经验率定发展为可以进行物理推求。

总之，新安江模型是一个不断发展的模型体系。

本文主要由三部分构成。

第一部分为新安江模型简介，回顾了新安江模型产生的历史背景和发展历程，介绍了新安江模型的基本原理和结构体系；第二部分讲述了新安江模型参数的物理意义及其率定；第三部分为新安江水文模型在英那河流域防洪规划编制当中的应用。

关键词：水文模型；新安江模型；洪水预报The principle, structure, application and development process of Xinanjiang ModelAbstractXin anjiang Model originally proposed by Hehai University is a conceptual rainfall runoff model and is also one of the few widely recognized international hydrological model in China. Xin anjiang hydrological model was widely used in our humid and semi-humid areas, and achieved good results.After nearly 50 years study, Xin anjiang model has been developed from the single-function of reservoir flood forecasting into multi-purpose model including hydrological forecasting, water resources management, water and soil resources evaluation, non-point source pollution prediction, climate change and human activities versatile hydrological model studies. And part of its parameters can be acquired through physical calculation instead of experience. In short, Xin anjiang model is an evolving model system.This paper consists of three parts. The first part is about the brief introduction of Xin anjiang model, which recalls the historical background and the development, as well as introduces the basic principles and architecture; the second part describes the physical meaning of Xin anjiang model parameters and calibration; the third part is about the application of Xin anjiang model in Ying Na River Basin flood control planning.Key Words: hydrological model; Xin anjiang model; Flood forecasting目 录摘 要 .............................................................. I Abstract .. (II)引 言 (1)1 新安江模型简介 (2)1.1 新安江模型起源 ............................... 错误!未定义书签。

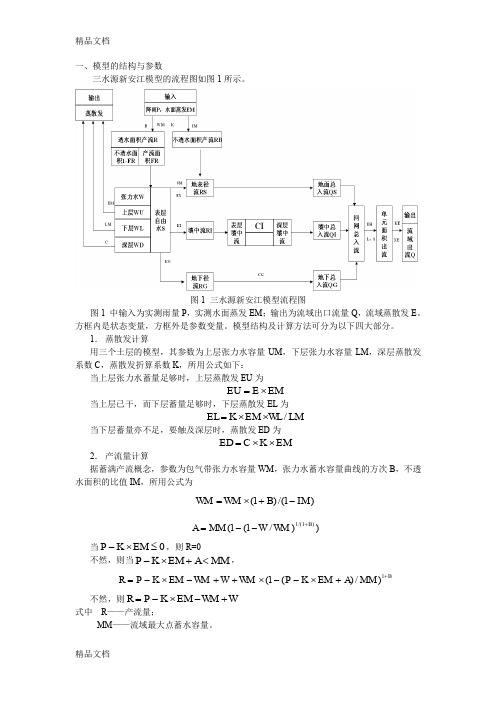
一、模型的结构与参数三水源新安江模型的流程图如图1所示。

图1 三水源新安江模型流程图图1 中输入为实测雨量P ，实测水面蒸发EM ；输出为流域出口流量Q ，流域蒸散发E 。

方框内是状态变量，方框外是参数变量。

模型结构及计算方法可分为以下四大部分。

1． 蒸散发计算用三个土层的模型，其参数为上层张力水容量UM ，下层张力水容量LM ，深层蒸散发系数C ，蒸散发折算系数K ，所用公式如下：当上层张力水蓄量足够时，上层蒸散发EU 为EM E EU ⨯=当上层已干，而下层蓄量足够时，下层蒸散发EL 为LM WL EM K EL /⨯⨯=当下层蓄量亦不足，要触及深层时，蒸散发ED 为EM K C ED ⨯⨯=2． 产流量计算据蓄满产流概念，参数为包气带张力水容量WM ，张力水蓄水容量曲线的方次B ，不透水面积的比值IM ，所用公式为)1/()1(IM B WM WM -+⨯=))/1(1()1/(1B WM W MM A +--=当0≤⨯-EM K P ，则R=0不然，则当MM A EM K P <+⨯-，B MM A EM K P WM W WM EM K P R ++⨯--⨯++-⨯-=1)/)(1(不然，则W WM EM K P R +-⨯-=式中 R ——产流量；MM ——流域最大点蓄水容量。

3． 分水源计算分三种水源，即地面径流RS 、地下径流RG 和壤中流RI 。

参数为表层土自由水蓄水容量SM ，表层自由水蓄水容量曲线的方次EX ，表层自由水蓄量对地下水的出流系数KG 及对壤中流的出流系数KI ，所用公式为SM EX MS ⨯+=)1())/1(1()1/(1EX SM S MS AU +--⨯=)/())((EM K P EM K P IM R FR ⨯-⨯-⨯-=FR KG S RG ⨯⨯=FR KI S RI ⨯⨯=当 0,0=≤⨯-RS EM K P不然，当MS AU EM K P <+⨯-，则FR MS AU EM K P SM S SM EM K P RS EX ⨯+⨯--⨯++-⨯-=+))/)(1((1 当MS AU EM K P ≥+⨯-，则FR SM S EM K P RS ⨯-+⨯-=)(4． 汇流计算地下径流用线性水库模拟，其消退系数为CG ，出流进入河网。

8新安江模型第八章新安江模型8.1 概述新安江模型是由原华东水利学院(现为河海大学)赵人俊教授等(赵人俊，1984)提出来的。

从降雨径流经验相关图研究开始(华东水利学院水文系，1962)，投入了水文预报教研室的十余位教师、研究生和上百的本科生前后经历了约20年才形成了蓄满产流概念、理论及其二水源新安江模型。

之后提出三水源新安江模型(赵人俊，1984)，并开始在水情预报和遥测自动化的实时洪水预报系统中开始大量应用，通过对模型的结构、考虑的因素不断改进和完善，发展至今已形成了理论上具有一定系统性、结构较为完善、应用效果较好的流域水文模型，并被联合国教科文组织列为国际推广模型而广为国内外水文学家所了解和应用。

新安江模型研究概括起来可以分为二水源新安江模型、三水源新安江模型和新安江模型改进研究三个阶段。

8.2 二水源新安江模型二水源新安江模型包括直接径流和地下径流，产流计算用蓄满产流方法，流域蒸发采用二层或三层蒸发，水源划分用的是稳定下渗法，直接径流坡面汇流用单位线法，地下径流坡面汇流用线性水库，河道汇流采用马斯京根分河段演算法。

8.2.1 前期研究降雨径流相关图是径流估计最早使用的方法之一。

考虑前期气候指数的降雨径流相关图是蓄满产流概念形成的基础，见图8-1。

图中为降雨量,为径流深, P为前期气候指PRa,0数。

在实际应用中，要计算一次降雨所产生的洪水径流总量，为配合汇流计算，还需求出逐时段的净雨量。

利用上述相关图推求时段净雨量的具体步骤如下。

P(1)求本次降雨开始时的; a,0(2)按逐时段累积降雨量在关系图上查得累积径流量;图8-1 时段净雨量推求(3)由相邻时段的累积径流量之差得时段净雨量。

在这相关图应用过程中发现两个问题，一是前期气候指数不是一个物理量，二是关系不满足水量平衡方程。

为此，提出由土壤含水量来反应前期气候的W 湿润情况，点关系图，经大量的实践发RfPW,(,)现，在湿润地区曲线簇的上段均接近45?直线，若W点绘成与关系(是扣除雨期蒸发后的PEW，RPE净雨量)，则呈现如图8-2所示的关系。