(完整版)高中数学必修二2.1空间点、直线、平面之间的位置关系课堂练习及详细答案

2.1 空间点、直线、平面之间的位置关系2．1.1 平面预习课本P40～43，思考并完成以下问题[新知初探]1．平面的概念几何里所说的“平面”，是从课桌面、黑板面、海面这样的一些物体中抽象出来的．几何里的平面是无限延展的．2．平面的画法(1)水平放置的平面通常画成一个平行四边形，它的锐角通常画成45°，且横边长等于其邻边长的2倍．如图①.(2)如果一个平面被另一个平面遮挡住，为了增强它的立体感，把被遮挡部分用虚线画出来．如图②.3．平面的表示法图①的平面可表示为平面α、平面ABCD、平面AC或平面BD.[点睛] (1)平面和点、直线一样，是只描述而不加定义的原始概念，不能进行度量；(2)平面无厚薄、无大小，是无限延展的．4．平面的基本性质[点睛] 对公理2必须强调是不共线的三点．[尝试应用](1)空间不同三点确定一个平面( )(2)空间两两相交的三条直线确定一个平面( )(3)和同一直线都相交的三条平行线在同一平面内( )答案：(1)×(2)×(3)√(1)8个平面重叠起来要比6个平面重叠起来厚；(2)有一个平面的长是50 m，宽是20 m；(3)平面是无厚度、可以无限延展的抽象的数学概念．A．0 B．1C．2 D．33．根据右图，填入相应的符号：A__________平面ABC，A________平面BCD，BD________平面ABC，平面ABC∩平面ACD＝________.答案：∈∉⊄AC文字语言、图形语言、符号语言的相互转化[典例] 根据图形用符号表示下列点、直线、平面之间的关系．(1)点P与直线AB；(2)点C与直线AB；(3)点M与平面AC；(4)点A1与平面AC；(5)直线AB与直线BC；(6)直线AB与平面AC；(7)平面A1B与平面AC.[解] (1)点P∈直线AB.(2)点C∉直线AB.(3)点M∈平面AC.(4)点A1∉平面AC.(5)直线AB∩直线BC＝点B.(6)直线AB⊂平面AC.(7)平面A1B∩平面AC＝直线AB.三种语言的转换方法(1)用文字语言、符号语言表示一个图形时，首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何，试着用文字语言表示，再用符号语言表示．(2)根据符号语言或文字语言画相应的图形时，要注意实线和虚线的区别．[活学活用]1．若点M在直线a上，a在平面α内，则M，a，α间的关系可记为( )A．M∈a，a∈αB．M∈a，a⊂αC．M⊂a，a⊂αD．M⊂a，a∈α解析：选B 根据点与线、线与面之间位置关系的符号表示可知B正确．2．用符号语言表示下列语句，并画出图形：(1)三个平面α，β，γ相交于一点P，且平面α与平面β相交于PA，平面α与平面γ相交于PB，平面β与平面γ相交于PC；(2)平面ABD与平面BDC相交于BD，平面ABC与平面ADC相交于AC.解：(1)符号语言表示：α∩β∩γ＝P，α∩β＝PA，α∩γ＝PB，β∩γ＝PC，图形表示：如图(1)．(2)符号语言表示：平面ABD∩平面BDC＝BD，平面ABC∩平面ADC＝AC，图形表示：如图(2)．平面的基本性质的应用1.如图，已知直线a∥b∥c，l∩a＝A，l∩b＝B，l∩c＝C.求证：a，b，c，l共面．证明：∵a∥b，∴a，b确定一个平面α.∵l∩a＝A，l∩b＝B，∴A∈α，B∈α.又∵A∈l，B∈l，∴l⊂α.∵b∥c，∴b，c确定一个平面β.同理可证l⊂β.于是b⊂α，l⊂α，b⊂β，l⊂β，即α∩β＝b，α∩β＝l.又∵b与l不重合，∴α与β重合，∴a，b，c，l共面．点线共面问题是指证明一些点或直线在同一平面内的问题，主要依据是公理1、公理2．解决该类问题通常有三种方法：(1)纳入平面法，先由部分元素确定一个平面，再证其他元素也在该平面内；(2)辅助平面法(平面重合法)，先由有关的点、线确定平面α，再由其余元素确定平面β，最后证明平面α，β重合；(3)反证法．通常情况下采用第一种方法．题点二：点共线问题2.如图，在正方体ABCD­A1B1C1D1中，设线段A1C与平面ABC1D1交于点Q，求证：B，Q，D1三点共线．证明：如图，连接A1B，CD1，显然B∈平面A1BCD1，D1∈平面A1BCD1.∴BD1⊂平面A1BCD1.同理BD1⊂平面ABC1D1.∴平面ABC1D1∩平面A1BCD1＝BD1.∵A1C∩平面ABC1D1＝Q，∴Q∈平面ABC1D1.又∵A1C⊂平面A1BCD1，∴Q∈平面A1BCD1.∴Q在平面A1BCD1与ABC1D1的交线上，即Q∈BD1，∴B，Q，D1三点共线．点共线问题是证明三个或三个以上的点在同一条直线上，主要依据是公理3.解决此类问题常用以下两种方法：(1)首先找出两个平面，然后证明这些点都是这两个平面的公共点，根据公理3知，这些点都在这两个平面的交线上；(2)选择其中两点，确定一条直线，然后证明其他点也在这条直线上．题点三：三线共点问题3．已知：平面α，β，γ两两相交于三条直线l1，l2，l3，且l1，l2不平行．求证：l1，l2，l3相交于一点．证明：如图，α∩β＝l1，β∩γ＝l2，α∩γ＝l3.∵l1⊂β，l2⊂β，且l1，l2不平行，∴l1与l2必相交．设l1∩l2＝P，则P∈l1⊂α，P∈l2⊂γ，∴P∈α∩γ＝l3，∴l1，l2，l3相交于一点P.证明三线共点问题的基本方法是，先确定待证的三线中的两条相交于一点，再证明第三条直线也过该点．常结合公理3，证出该点在不重合的两个平面内，故该点在它们的交线(第三条直线)上，从而证明三线共点．层级一学业水平达标1．下列说法中正确的是( )A．三点确定一个平面B．四边形一定是平面图形C．梯形一定是平面图形D．两个不同平面α和β有不在同一条直线上的三个公共点解析：选C 不共线的三点确定一个平面，故A不正确；四边形有时指空间四边形，故B 不正确；梯形的上底和下底平行，可以确定一个平面，故C正确；两个平面如果相交，一定有一条交线，所有这两个平面的公共点都在这条交线上，故D不正确．故选C.①不共面的四点中，其中任意三点不共线；②若点A，B，C，D共面，点A，B，C，E共面，则点A，B，C，D，E共面；③若直线a，b共面，直线a，c共面，则直线b，c共面；④依次首尾相接的四条线段必共面．A．0 B．1C．2 D．3解析：选B ①假设其中有三点共线，则该直线和直线外的另一点确定一个平面，这与四点不共面矛盾，故其中任意三点不共线，所以①正确；②如图，两个相交平面有三个公共点A，B，C，但A，B，C，D，E不共面；③显然不正确；④不正确，因为此时所得的四边形的四条边可以不在一个平面上，如空间四边形．3．在空间四边形ABCD中，在AB，BC，CD，DA上分别取E，F，G，H四点，如果GH，EF 交于一点P，则( )A．P一定在直线BD上B．P一定在直线AC上C．P在直线AC或BD上D．P既不在直线BD上，也不在AC上解析：选B 由题意知GH⊂平面ADC.因为GH，EF交于一点P，所以P∈平面ADC.同理，P∈平面ABC.因为平面ABC∩平面ADC＝AC，由公理3可知点P一定在直线AC上．4．用一个平面截正方体所得的截面图形不可能是( )A．六边形B．五边形C．菱形D．直角三角形解析：选D 可用排除法，正方体的截面图形可能是六边形、五边形、菱形，故选D.5．下列各图均是正六棱柱，P，Q，R，S分别是所在棱的中点，这四个点不共面的图形是( )解析：选D 在选项A、B、C中，由棱柱、正六边形、中位线的性质，知均有PS∥QR，即在此三个图形中P，Q，R，S共面，故选D.6．用符号表示“点A在直线l上，l在平面α外”为________．答案：A∈l，l⊄α7．如图，看图填空：(1)平面AB1∩平面A1C1＝________；(2)平面A1C1CA∩平面AC＝________.答案：A1B1AC8．已知空间四点中无任何三点共线，那么这四点可以确定平面的个数是________．解析：其中三个点可确定唯一的平面，当第四个点在此平面内时，可确定1个平面，当第四个点不在此平面内时，则可确定4个平面．答案：1或4(1)由点A，O，C可以确定一个平面；(2)由点A，C1，B1确定的平面为平面ADC1B1.解：(1)不正确．因为点A，O，C在同一条直线上，故不能确定一个平面．(2)正确．因为点A，B1，C1不共线，所以可确定一个平面．又因为AD∥B1C1，所以点D∈平面AB1C1.所以由点A，C1，B1确定的平面为平面ADC1B1.10．按照给出的要求，完成图中两个相交平面的作图，图中所给线段AB分别是两个平面的交线．解：以AB为其中一边，分别画出表示平面的平行四边形．如图．层级二 应试能力达标1．如果直线a ⊂平面α，直线b ⊂平面α，M ∈a ，N ∈b ，M ∈l ，N ∈l ，则( ) A ．l ⊂α B ．l ⊄α C ．l ∩α＝MD ．l ∩α＝N解析：选A ∵M ∈a ，a ⊂α，∴M ∈α，同理，N ∈α，又M ∈l ，N ∈l ，故l ⊂α. A ．一条直线和一点确定一个平面 B ．两条相交直线确定一个平面 C ．四点确定一个平面 D ．三条平行直线确定一个平面解析：选B 根据一条直线和直线外的一点确定一个平面，知A 不正确；B 显然正确；C 中四点不一定共面，故C 不正确；三条平行直线可以确定一个平面或三个平面，故D 不正确．故选B.A ．经过正方体任意两条面对角线，有且只有一个平面B ．经过正方体任意两条体对角线，有且只有一个平面C ．经过正方体任意两条棱，有且只有一个平面D ．经过正方体任意一条体对角线与任意一条面对角线，有且只有一个平面解析：选 B 因为正方体的四条体对角线相交于同一点(正方体的中心)，因此经过正方体任意两条体对角线，有且只有一个平面，故选B.4．在正方体ABCD ­A 1B 1C 1D 1中，M ，N 分别是棱DD 1和BB 1上的点，MD ＝13DD 1，NB ＝13BB 1，那么正方体的过点M ，N ，C 1的截面图形是( )A ．三角形B ．四边形C ．五边形D ．六边形解析：选C 在正方体ABCD ­A 1B 1C 1D 1中，M ，N 分别是棱DD 1和BB 1上的点，MD ＝13DD 1，NB ＝13BB 1.如图，延长C 1M 交CD 于点P ，延长C 1N 交CB于点Q ，连接PQ 交AD 于点E ，AB 于点F ，连接NF ，ME ，则正方体的过点M ，N ，C 1的截面图形是五边形．故选C.5．已知α，β是不同的平面，l ，m ，n 是不同的直线，P 为空间中一点．若α∩β＝l，m⊂α，n⊂β，m∩n＝P，则点P与直线l的位置关系用符号表示为________．解析：因为m⊂α，n⊂β，m∩n＝P，所以P∈α且P∈β.又α∩β＝l，所以点P在直线l上，所以P∈l.答案：P∈l6．在长方体ABCD­A1B1C1D1的所有棱中，既与AB共面，又与CC1共面的棱有________条．解析：作图并观察可知既与AB共面，又与CC1共面的棱有CD，BC，BB1，AA1，C1D1，共5条．答案：57.如图所示，AB∩α＝P，CD∩α＝P，A，D与B，C分别在平面α的两侧，AC∩α＝Q，BD∩α＝R.求证：P，Q，R三点共线．证明：∵AB∩α＝P，CD∩α＝P，∴AB∩CD＝P.∴AB，CD可确定一个平面，设为β.∵A∈AB，C∈CD，B∈AB，D∈CD，∴A∈β，C∈β，B∈β，D∈β.∴AC⊂β，BD⊂β，平面α，β相交．∵AB∩α＝P，AC∩α＝Q，BD∩α＝R，∴P，Q，R三点是平面α与平面β的公共点．∴P，Q，R都在α与β的交线上，故P，Q，R三点共线．8.如图，在直四棱柱ABCD­A1B1C1D1中，AD>BC，P，Q，M，N分别为AA1，BB1，CC1，DD1上的点，设PQ与NM的交点为S，AB与DC的交点为R，A1B1与D1C1的交点为G.求证：R，S，G三点共线．证明：因为P，Q，M，N分别为AA1，BB1，CC1，DD1上的点，PQ∩NM＝S，所以S∈MN，MN⊂平面CC1D1D，S∈PQ，PQ⊂平面AA1B1B，所以S∈平面CC1D1D，且S∈平面AA1B1B，所以S在平面AA1B1B与平面CC1D1D的交线上．同理可证：R，G也在平面AA1B1B与平面CC1D1D的交线上，所以R，S，G三点共线．2．1.2 空间中直线与直线之间的位置关系预习课本P44～47，思考并完成以下问题1．空间两直线有哪几种位置关系？2．什么是异面直线？3．什么是异面直线所成的角？4．平行公理的内容是什么？5．等角定理的内容是什么？[新知初探]1．异面直线(1)定义：不同在任何一个平面内的两条直线．(2)异面直线的画法：2．空间两条直线的位置关系位置关系特点相交同一平面内，有且只有一个公共点平行同一平面内，没有公共点异面直线不同在任何一个平面内，没有公共点[点睛] (1)异面直线的定义表明异面直线不具备确定平面的条件．异面直线既不相交，也不平行．(2)不能把异面直线误认为分别在不同平面内的两条直线，如图中，虽然有a⊂α，b⊂β，即a，b分别在两个不同的平面内，但是因为a∩b＝O，所以a与b不是异面直线．3．平行公理(公理4)(1)文字表述：平行于同一条直线的两条直线互相平行．这一性质叫做空间平行线的传递性．a∥b b∥c⇒a∥c.(2)符号表述：}4．等角定理空间中如果两个角的两边分别对应平行，那么这两个角相等或互补．5．异面直线所成的角(1)定义：已知两条异面直线a，b，经过空间任一点O作直线a′∥a，b′∥b，我们把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角)．(2)异面直线所成的角θ的取值范围：0°＜θ≤90°.(3)当θ＝90°时，a与b互相垂直，记作a⊥b.[点睛] (1)异面直线所成角的范围是0°<θ≤90°，所以垂直有两种情况：异面垂直和相交垂直．(2)公理4也称为平行公理，表明空间的平行具有传递性，它在直线、平面的平行关系中得到了广泛的应用．[小试身手](1)两条直线无公共点，则这两条直线平行( )(2)两直线若不是异面直线，则必相交或平行( )(3)过平面外一点与平面内一点的连线，与平面内的任意一条直线均构成异面直线( )(4)和两条异面直线都相交的两直线必是异面直线( )答案：(1)×(2)√(3)×(4)×2．如果两条直线a和b没有公共点，那么a与b的位置关系是( )A．共面B．平行C．异面D．平行或异面解析：选 D 空间中两直线的位置关系有：①相交；②平行；③异面．两条直线平行和两条直线异面都满足两条直线没有公共点，故a与b的位置关系是平行或异面．3．已知AB∥PQ，BC∥QR，若∠ABC＝30°，则∠PQR等于( )A．30° B．30°或150°C．150° D．以上结论都不对解析：选B 由等角定理可知∠PQR与∠ABC相等或互补，故∠PQR＝30°或150°.两直线位置关系的判定[典例] 如图，在长方体ABCD­A1B1C1D1中，(1)直线A1B与直线D1C的位置关系是________；(2)直线A1B与直线B1C的位置关系是________；(3)直线D1D与直线D1C的位置关系是________；(4)直线AB与直线B1C的位置关系是________．[解析] (1)在长方体ABCD­A1B1C1D1中，A1D1綊BC，∴四边形A1BCD1为平行四边形，∴A1B ∥D1C.(2)直线A1B与直线B1C不同在任何一个平面内．(3)直线D1D与直线D1C相交于点D1.(4)直线AB与直线B1C不同在任何一个平面内．[答案] (1)平行(2)异面(3)相交(4)异面(1)判定两条直线平行或相交的方法判定两条直线平行或相交可用平面几何的方法去判断，而两条直线平行也可以用公理4判断．(2)判定两条直线是异面直线的方法①定义法：由定义判断两直线不可能在同一平面内．②重要结论：连接平面内一点与平面外一点的直线，和这个平面内不经过此点的直线是异面直线．用符号语言可表示为A∉α，B∈α，l⊂α，B∉l⇒AB与l是异面直线(如图)．[活学活用]1．在空间四边形ABCD中，E，F分别为对角线AC，BD的中点，则BE与CF( )A．平行B．异面C．相交D．以上均有可能解析：选B 假设BE与CF是共面直线，设此平面为α，则E，F，B，C∈α，所以BF，CE⊂α，而A∈CE，D∈BF，所以A，D∈α，即有A，B，C，D∈α，与ABCD为空间四边形矛盾，所以BE与CF是异面直线，故选B.2．若a，b为异面直线，直线c∥a，则c与b的位置关系是( )A．相交B．异面C．平行D．异面或相交解析：选D 由空间直线的位置关系，知c与b可能异面或相交．平行公理与等角定理的应用[典例] 如图，在正方体ABCD­A1B1C1D1中，M，M1分别是棱AD和A1D1的中点．(1)求证：四边形BB1M1M为平行四边形；(2)求证：∠BMC＝∠B1M1C1.[证明] (1)在正方形ADD1A1中，M，M1分别为AD，A1D1的中点，∴A1M1綊AM，∴四边形AMM1A1是平行四边形，∴A1A綊M1M.又∵A1A綊B1B，∴M1M綊B1B，∴四边形BB1M1M为平行四边形．(2)由(1)知四边形BB1M1M为平行四边形，∴B1M1∥BM.同理可得四边形CC1M1M为平行四边形，∴C1M1∥CM.由平面几何知识可知，∠BMC和∠B1M1C1都是锐角．∴∠BMC＝∠B1M1C1.(1)空间两条直线平行的证明：①定义法：即证明两条直线在同一个平面内没有公共点；②利用公理4找到一条直线，使所证的直线都与这条直线平行．(2)“等角”定理的结论是相等或互补，在实际应用时，一般是借助于图形判断是相等，还是互补，这是两种情况都有可能．[活学活用]如图，已知在棱长为a的正方体ABCD­A1B1C1D1中，M，N分别是棱CD，AD的中点．求证：(1)四边形MNA 1C1是梯形；(2)∠DNM＝∠D1A1C1.证明：(1)如图，连接AC，在△ACD中，∵M ，N 分别是CD ，AD 的中点， ∴MN 是△ACD 的中位线， ∴MN ∥AC ，MN ＝12AC .由正方体的性质得：AC ∥A 1C 1，AC ＝A 1C 1.∴MN ∥A 1C 1，且MN ＝12A 1C 1，即MN ≠A 1C 1，∴四边形MNA 1C 1是梯形． (2)由(1)可知MN ∥A 1C 1.又∵ND ∥A 1D 1，∴∠DNM 与∠D 1A 1C 1相等或互补． 而∠DNM 与∠D 1A 1C 1均为锐角， ∴∠DNM ＝∠D 1A 1C 1.异面直线所成角[典例] 11111111DB 1与EF 所成角的大小．[解] 法一：如图1所示，连接A 1C 1，B 1D 1，并设它们相交于点O ，取DD 1的中点G ，连接OG ，A 1G ，C 1G ，则OG ∥B 1D ，EF ∥A 1C 1，∴∠GOA 1为异面直线DB 1与EF 所成的角(或其补角)． ∵GA 1＝GC 1，O 为A 1C 1的中点， ∴GO ⊥A 1C 1.∴异面直线DB 1与EF 所成的角为90°.图1法二：如图2所示，连接A 1D ，取A 1D 的中点H ，连接HE ，则HE 綊12DB 1，于是∠HEF 为异面直线DB 1与EF 所成的角(或其补角)．连接HF ，设AA 1＝1， 则EF ＝22，HE ＝32，取A 1D 1的中点I ，连接HI ，IF ， 则HI ⊥IF ，∴HF 2＝HI 2＋IF 2＝54，∴HF 2＝EF 2＋HE 2，∴∠HEF ＝90°. ∴异面直线DB 1与EF 所成的角为90°.图2法三：如图3，连接A 1C 1，分别取AA 1，CC 1的中点M ，N ，连接MN . ∵E ，F 分别是A 1B 1，B 1C 1的中点， ∴EF ∥A 1C 1，又MN ∥A 1C 1，∴MN ∥EF . 连接DM ，B 1N ，MB 1，DN ，则B 1N 綊DM ， ∴四边形DMB 1N 为平行四边形， ∴MN 与DB 1必相交，设交点为P ，则∠DPM 为异面直线DB 1与EF 所成的角(或其补角)． 设AA 1＝k (k >0)，则MP ＝22k ，DM ＝52k ，DP ＝32k ， ∴DM 2＝DP 2＋MP 2，∴∠DPM ＝90°. ∴异面直线DB 1与EF 所成的角为90°.法四：如图4，在原正方体的右侧补上一个全等的正方体，连接B 1Q ，易得B 1Q ∥EF ， ∴∠DB 1Q 就是异面直线DB 1与EF 所成的角(或其补角)． 设AA 1＝k (k >0)，则B 1D ＝3k ，DQ ＝5k ，B 1Q ＝2k ， ∴B 1D 2＋B 1Q 2＝DQ 2，∴∠DB 1Q ＝90°. ∴异面直线DB 1与EF 所成的角为90°.(2)证：证明作出的角就是要求的角； (3)计算：求角的值，常利用解三角形得出．可用“一作二证三计算”来概括．同时注意异面直线所成角范围是0°＜θ≤90°. [活学活用] 如图所示，点A 是△BCD 所在平面外一点，AD ＝BC ，E ，F 分别是AB ，CD 的中点，当EF ＝22AD 时，求异面直线AD 和BC 所成的角． 解：如图所示，设G 为AC 的中点，连接EG ，FG . ∵E ，F ，G 分别为AB ，CD ，AC 的中点． ∴EG ∥BC ，且EG ＝12BC ；FG ∥AD ，且FG ＝12AD .又AD ＝BC ，∴EG ＝FG ＝12AD .∴EG 与GF 所成的锐角(或直角)即为AD 与BC 所成的角． 在△EFG 中，∵EG ＝FG ＝12AD ，又EF ＝22AD ，∴EG 2＋FG 2＝EF 2，即EG ⊥FG .∴∠EGF ＝90°.故AD 与BC 所成角为90°.层级一 学业水平达标1．若空间三条直线a ，b ，c 满足a ⊥b ，b ∥c ，则直线a 与c ( ) A ．一定平行 B ．一定相交 C ．一定是异面直线D ．一定垂直解析：选D 因为a ⊥b ，b ∥c ，则a ⊥c ，故选D.2．一条直线与两条平行线中的一条成为异面直线，则它与另一条( ) A ．相交 B ．异面 C ．相交或异面D ．平行解析：选C 如图所示的长方体ABCD ­A 1B 1C 1D 1中，直线AA 1与直线B 1C 1是异面直线，与B 1C 1平行的直线有A 1D 1，AD ，BC ，显然直线AA 1与A 1D 1相交，与BC 异面．3．在正方体ABCD ­A 1B 1C 1D 1中，E ，F 分别是平面AA 1D 1D 、平面CC 1D 1D 的中心，G ，H 分别是线段AB ，BC 的中点，则直线EF 与直线GH 的位置关系是( )A ．相交B ．异面C．平行D．垂直解析：选C 如图，连接AD1，CD1，AC，则E，F分别为AD1，CD1的中点．由三角形的中位线定理，知EF∥AC，GH∥AC，所以EF∥GH，故选C.①若a与b异面，b与c异面，则a与c异面；②若a∥b，a和c相交，则b和c也相交；③若a⊥b，a⊥c，则b∥c.A．0 B．1C．2 D．3解析：选 A ①不正确如图；②不正确，有可能相交也有可能异面；③不正确．可能平行，可能相交也可能异面．5．异面直线a，b，有a⊂α，b⊂β且α∩β＝c，则直线c与a，b的关系是( )A．c与a，b都相交B．c与a，b都不相交C．c至多与a，b中的一条相交D．c至少与a，b中的一条相交解析：选D 若c与a，b都不相交，∵c与a在α内，∴a∥c.又c与b都在β内，∴b∥c.由公理4，可知a∥b，与已知条件矛盾．如图，只有以下三种情况．6.如图，正方体ABCD­A1B1C1D1中，AC与BC1所成角的大小是________．解析：连接AD1，则AD1∥BC1.∴∠CAD1(或其补角)就是AC与BC1所成的角，连接CD1，在正方体ABCD­A1B1C1D1中，AC＝AD1＝CD1，∴∠CAD1＝60°，即AC与BC1所成的角为60°.答案：60°7．如图，点P，Q，R，S分别在正方体的四条棱上，且是所在棱的中点，则直线PQ与RS 是异面直线的一个图是________(填序号)．解析：①中PQ ∥RS ，②中RS ∥PQ ，④中RS 和PQ 相交． 答案：③8.如图，在正方体ABCD ­A 1B 1C 1D 1中，M ，N 分别是棱CD ，CC 1的中点，则异面直线A 1M 与DN 所成的角的大小是________．解析：如图，过点M 作ME ∥DN 交CC 1于点E ，连接A 1E ，则∠A 1ME为异面直线A 1M 与DN 所成的角(或其补角)．设正方体的棱长为a ，则A 1M ＝32a ，ME ＝54a ，A 1E ＝414a ，所以A 1M 2＋ME 2＝A 1E 2，所以∠A 1ME ＝90°，即异面直线A 1M 与DN 所成的角为90°. 答案：90°9.如图所示，E ，F 分别是长方体A 1B 1C 1D 1­ABCD 的棱A 1A ，C 1C 的中点． 求证：四边形B 1EDF 是平行四边形． 证明：设Q 是DD 1的中点，连接EQ ，QC 1. ∵E 是AA 1的中点， ∴EQ 綊A 1D 1.又在矩形A 1B 1C 1D 1中，A 1D 1綊B 1C 1， ∴EQ 綊B 1C 1(平行公理)．∴四边形EQC 1B 1为平行四边形．∴B 1E 綊C 1Q . 又∵Q ，F 是DD 1，C 1C 两边的中点，∴QD 綊C 1F . ∴四边形QDFC 1为平行四边形． ∴C 1Q 綊DF .∴B 1E 綊DF . ∴四边形B 1EDF 为平行四边形．10.如图所示，空间四边形ABCD 中，AB ＝CD ，AB ⊥CD ，E ，F 分别为BC ，AD 的中点，求EF 和AB 所成的角．解：如图所示，取BD 的中点G ，连接EG ，FG . ∵E ，F 分别为BC ，AD 的中点，AB ＝CD ，∴EG ∥CD ，GF ∥AB ，且EG ＝12CD ，GF ＝12AB .∴∠GFE 就是EF 与AB 所成的角，EG ＝GF . ∵AB ⊥CD ，∴EG ⊥GF . ∴∠EGF ＝90°.∴△EFG 为等腰直角三角形．∴∠GFE ＝45°，即EF 与AB 所成的角为45°.层级二 应试能力达标1．在正方体ABCD ­A 1B 1C 1D 1中，E ，F 分别是线段BC ，C 1D 的中点，则直线A 1B 与直线EF 的位置关系是( )A ．相交B ．异面C ．平行D ．垂直解析：选A 如图所示，连接BD 1，CD 1，CD 1与C 1D 交于点F ，由题意可得四边形A 1BCD 1是平行四边形，在平行四边形A 1BCD 1中，E ，F 分别是线段BC ，CD 1的中点，所以EF ∥BD 1，所以直线A 1B 与直线EF 相交，故选A.2．在三棱锥A ­BCD 中，AC ⊥BD ，E ，F ，G ，H 分别是AB ，BC ，CD ，DA 的中点，则四边形EFGH 是( )A ．菱形B ．矩形C ．梯形D ．正方形解析：选B 如图，在△ABD 中，点H ，E 分别为边AD ，AB 的中点，所以HE 綊12BD ，同理GF 綊12BD ，所以HE 綊GF ，所以四边形EFGH 为平行四边形．又AC ⊥BD ，所以HG ⊥HE ，所以四边形EFGH 是矩形，故选B.3．在正三棱柱ABC ­A 1B 1C 1中，若AB ＝2BB 1，则AB 1与BC 1所成的角的大小是( ) A ．60° B ．75° C ．90°D ．105°解析：选C 设BB 1＝1，如图，延长CC 1至C 2，使C 1C 2＝CC 1＝1，连接B 1C 2，则B 1C 2∥BC 1，所以∠AB 1C 2为AB 1与BC 1所成的角(或其补角)．连接AC 2，因为AB 1＝3，B 1C 2＝3，AC 2＝6，所以AC 22＝AB 21＋B 1C 22，则∠AB 1C 2＝90°.4．在正方体ABCD ­A 1B 1C 1D 1中，点P 在线段AD 1上运动，则异面直线CP 与BA 1所成的角θ的取值范围是( )A ．0°<θ<60°B ．0°≤θ<60°C ．0°≤θ≤60°D ．0°<θ≤60°解析：选D 如图，连接CD1，AC，因为CD1∥BA1，所以CP与BA1所成的角就是CP与CD1所成的角，即θ＝∠D1CP.当点P从D1向A运动时，∠D1CP从0°增大到60°，但当点P与D1重合时，CP∥BA1，与CP与BA1为异面直线矛盾，所以异面直线CP与BA1所成的角θ的取值范围是0°<θ≤60°.5.如图所示，正方体ABCD­A1B1C1D1中，E，F分别是棱BC，CC1的中点，则异面直线EF与B1D1所成的角为__________．解析：连接BC1，AD1，AB1，则EF为△BCC1的中位线，∴EF∥BC1.又∵AB綊CD綊C1D1，∴四边形ABC1D1为平行四边形．∴BC1∥AD1.∴EF∥AD1.∴∠AD1B1为异面直线EF和B1D1所成的角或其补角．在△AB1D1中，易知AB1＝B1D1＝AD1，∴△AB1D1为正三角形，∴∠AD1B1＝60°.∴EF与B1D1所成的角为60°.答案：60°6.如图，空间四边形ABCD的对角线AC＝8，BD＝6，M，N分别为AB，CD的中点，并且异面直线AC与BD所成的角为90°，则MN等于________．解析：取AD的中点P，连接PM，PN，则BD∥PM，AC∥PN，∴∠MPN即异面直线AC与BD所成的角，∴∠MPN＝90°，PN＝12AC＝4，PM＝12BD＝3，∴MN＝5.答案：57．在三棱柱ABC­A1B1C1中，AA1与AC，AB所成的角均为60°，∠BAC＝90°，且AB＝AC＝AA1，求异面直线A1B与AC1所成角的余弦值．解：如图所示，把三棱柱补为四棱柱ABDC­A1B1D1C1，连接BD1，A1D1，AD，由四棱柱的性质知BD1∥AC1，则∠A1BD1就是异面直线A1B与AC1所成的角．设AB＝a，∵AA1与AC，AB所成的角均为60°，且AB＝AC＝AA1，∴A1B＝a，BD1＝AC1＝2AA1·cos 30°＝3a.又∠BAC ＝90°，∴在矩形ABCD 中，AD ＝2a ， ∴A 1D 1＝2a ， ∴A 1D 21＋A 1B 2＝BD 21，∴∠BA 1D 1＝90°，∴在Rt △BA 1D 1中，cos ∠A 1BD 1＝A 1B BD 1＝a 3a ＝33.8.正三棱锥S ­ABC 的侧棱长与底面边长都为a ，E ，F 分别是SC ，AB 的中点，求直线EF 和SA 所成的角．解：如图，取SB 的中点G ，连接EG ，GF ，SF ，CF .在△SAB 中，F ，G 分别是AB ，SB 的中点，∴FG ∥SA ，且FG ＝12SA . 于是异面直线SA 与EF 所成的角就是直线EF 与FG 所成的角．在△SAB 中，SA ＝SB ＝a ，AF ＝FB ＝12a ， ∴SF ⊥AB ，且SF ＝32a . 同理可得CF ⊥AB ，且CF ＝32a . 在△SFC 中，SF ＝CF ＝32a ，SE ＝EC ， ∴FE ⊥SC 且FE ＝SF 2－SE 2＝22a . 在△SAB 中，FG 是中位线，∴FG ＝12SA ＝a 2. 在△SBC 中，GE 是中位线，∴GE ＝12BC ＝a 2. 在△EGF 中，FG 2＋GE 2＝a 22＝FE 2， ∴△EGF 是以∠FGE 为直角的等腰直角三角形，∴∠EFG ＝45°.∴异面直线SA 与EF 所成的角为45°.2．1.3&2.1.4 空间中直线与平面之间的位置关系、平面与平面之间的位置关系预习课本P48～50，思考并完成以下问题1．直线与平面的位置关系2．两个平面的位置关系[点睛] (1)判断面面位置关系时，要利用好长方体(或正方体)这一模型．(2)画两个互相平行的平面时，要注意使表示平面的两个平行四边形的对应边平行．[小试身手](1)若两条直线和同一个平面所成的角相等，则这两条直线平行( )(2)若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行( )(3)若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行( )(4)若两个平面都平行于同一条直线，则这两个平面平行( )答案：(1)×(2)×(3)√(4)×2.如图所示，用符号语言可表示为( )A．α∩β＝l B．α∥β，l∈αC．l∥β，l⊄αD．α∥β，l⊂α解析：选D 显然图中α∥β，且l⊂α.3．平面α∥平面β，直线a⊂α，则a与β的位置关系是________．答案：平行直线与平面的位置关系①如果a，b a b②如果直线a和平面α满足a∥α，那么a与平面α内的任何一条直线平行；③如果直线a，b满足a∥α，b∥α，则a∥b；④如果直线a，b和平面α满足a∥b，a∥α，b⊄α，那么b∥α；⑤如果平面α的同侧有两点A，B到平面α的距离相等，则AB∥α.A．0 B．1C．2 D．3[答案] C在判断直线与平面的位置关系时，这三种情形都要考虑到，避免疏忽或遗漏．另外，我们可以借助空间几何图形，把要判断关系的直线、平面放在某些具体的空间图形中，以便于正确作出判断，避免凭空臆断．下列说法：①若直线l平行于平面α内的无数条直线，则l∥α；②若直线a在平面α外，则a∥α；③若直线a∥b，b⊂α，则a∥α；④若直线a∥b，b⊂α，那么直线a平行于平面α内的无数条直线．其中正确的个数为( )A．1 B．2C．3 D．4解析：选A 对于①，∵直线l虽与平面α内无数条直线平行，但l有可能在平面α内，∴l不一定平行于α，①错误；对于②，∵直线a在平面α外包括两种情况：a∥α和a与α相交，∴a和α不一定平行，②错误；对于③，直线a∥b，b⊂α，只能说明a和b 没有公共点，a可能在平面α内，∴a不一定平行于α，③错误；对于④，∵a∥b，b⊂α，那么a⊂α或a∥α，a与平面α内的无数条直线平行，④正确.[典例] α，β是两个不重合的平面，下面说法中正确的是( )A．平面α内有两条直线a，b都与平面β平行，那么α∥βB．平面α内有无数条直线平行于平面β，那么α∥βC．若直线a与平面α和平面β都平行，那么α∥βD．平面α内所有的直线都与平面β平行，那么α∥β[解析] A、B都不能保证α，β无公共点，如图(1)所示；C中当a∥α，a∥β时，α与β可能相交，如图(2)所示；只有D说明α，β一定无公共点，即α∥β.[答案] D1．在底面为正六边形的六棱柱中，互相平行的面视为一组，则共有________组互相平行的面．与其中一个侧面相交的面共有________个．解析：六棱柱的两个底面互相平行，每个侧面与其直接相对的侧面平行，故共有4组互相平行的面．六棱柱共有8个面围成，在其余的7个面中，与某个侧面平行的面有1个，其余6个面与该侧面均为相交的关系．答案：4 62.如图所示，平面ABC与三棱柱ABC­A1B1C1的其他面之间有什么位置关系？解：∵平面ABC与平面A1B1C1无公共点，∴平面ABC与平面A1B1C1平行．∵平面ABC与平面ABB1A1有公共直线AB，∴平面ABC与平面ABB1A1相交．同理可得平面ABC与平面ACC1A1及平面BCC1B1均相交.线面、面面交线问题[典例] 在直三棱柱ABC­A1B1C1中，E，F分别为A1B1，B1C1的中点．求证：平面ACC1A1与平面BEF相交．[证明] ∵在矩形AA1B1B中，E为A1B1的中点，∴AA1与BE不平行，则AA1，BE的延长线相交于一点，设此点为G，∴G∈AA1，G∈BE.又AA1⊂平面ACC1A1，BE⊂平面BEF，∴G∈平面ACC1A1，G∈平面BEF，∴平面ACC1A1与平面BEF相交．判断或证明平面与平面的位置关系时主要考虑平面与平面有无公共点，如果没有公共点，则两平面平行；如果可以找到一个公共点，则两平面相交．[活学活用]如图所示，G是正方体ABCD­A1B1C1D1的棱DD1延长线上的一点，E，F是棱AB，BC的中点．试分别画出过下列各点、直线的平面与正方体表面的交线．(1)过点G及AC；(2)过三点E，F，D1.解：(1)画法：连接GA交A1D1于点M，连接GC交C1D1于点N；连接MN，AC，则MA，CN，MN，AC为所求平面与正方体表面的交线．如图①所示．(2)画法：连接EF交DC的延长线于点P，交DA的延长线于点Q；连接D1P交CC1于点M，连接D1Q交AA1于点N；连接MF，NE，则D1M，MF，FE，EN，ND1为所求平面与正方体表面的交线．如图②所示．。

描述：高中数学必修2(人教A版)知识点总结含同步练习题及答案第二章 点、直线、平面之间的位置关系 2.1 空间点、直线、平面之间的位置关系一、学习任务理解空间点、线、面的位置关系，会用数学语言规范地表述空间点、线、面的位置关系；了解可以作为推理依据的公理和定理，能正确地判断空间线线、线面与面面的位置关系．二、知识清单平面的概念与基本性质 点、线、面的位置关系三、知识讲解1.平面的概念与基本性质平面的概念生活中的一些物体通常呈平面形，课桌面、黑板面、海面都给我们以平面的形象．几何里所说的平面就是从这样的一些物体中抽象出来的，但是几何中的平面是没有厚度、无限延展的．平面的画法我们常常把水平的平面画成一个平行四边形，用平行四边形表示平面，平行四边形的锐角通常画为 ，且横边长等于其邻边长的 倍．如果一个平面被另一个平面遮挡住，为了增强它的立体感，我们常把被遮挡的部分用虚线画出来．平面的表示为了表示平面，常把希腊字母 等等写在代表平面的平行四边形的一个角上，如平面 、平面 ；也可以用代表平面的平行四边形的四个顶点，或者相对的两个顶点的大写英文字母作为这个平面的名称，如图中的平面可以表示为平面 、平面 或者平面 ．集合符号在立体几何中的应用以点作为元素，直线和平面都是由点构成的集合．几何中许多符号的规定都是源于将图形视为点集．例如：点 在平面 内，记作 ；点 不在平面 内，记作 ．直线 在平面 内，记作 ；直线 不在平面 内，记作 ；直线 与 相交于点 ，记作 ；平面 与平面 相交于直线 ，记作 ．平面的基本性质平面的基本性质是由三条公理描述的：公理1 如果一条直线上的两点在一个平面内，那么这条直线在此平面内．45∘2α,β,γαβABCD AC BD A αA ∈αA αA ∉αl αl ⊂αl αl ⊄αl m A l ∩m =A αβa α∩β=a A ∈l A ∈α例题：符号语言：，，且 ，．公理2 过不在一条直线上的三点，有且只有一个平面．推论1 经过一条直线和直线外一点，有且只有一个平面．推论2 经过两条相交直线，有且只有一个平面．推论3 经过两条平行直线，有且只有一个平面．公理3 如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线．符号语言：，且 ，且 ．空间位置关系与几何量的基础平行公理 平行于同一条直线的两条直线互相平行．等角定理 空间中如果两个角的两边分别对应平行，那么这两个角相等或互补．A∈l B∈l A∈αB∈α⇒l⊂αP∈αP∈β⇒α∩β=l P∈l用符号语言表示下列语句．（1）点 在平面 外，点 在平面 内，直线 经过点 ，；（2） 与 交于 ， 与 交于 ．解：（1），，，．（2），．AαBαl A B平面ABD平面BCD BD平面ABC平面ADC ACa∉αB∈αA∈l B∈l平面ABD∩平面BCD=BD平面ABC∩平面ADC=AC如图所示，在四面体 中，、、、 分别是 、、、 上的点，且 ，求证 ，， 三点共线．ABCD E F G H AB AD BC CDEF∩GH=PB D P2.点、线、面的位置关系证明：因为 ，，所以 ，同理，，又，所以 ，，而 ，所以 ，即 ，， 三点共线．E ∈ABF ∈AD EF ⊂平面 ABD GH ⊂平面 BCD EF ∩GH =P P ∈平面 ABD P ∈平面 BCD 平面 ABD ∩平面 BCD =BD P ∈直线BD B D P 已知：如图，，，．求证：直线 ，， 在同一平面内．证法一：（同一法）因为 ，所以 和 确定一个平面 ．　因为 ，所以 ．又因为 ，所以 ．同理可证 ．又 ，，所以 ．因此，直线 ，， 在同一个平面内．证法二：（重合法）因为 ，所以 ， 确定一个平面 ．因为 ，所以 ， 确定一个平面 ．又因为 ，，所以 ．又 ，，所以 ．同理可证得 ，，，．所以不共线的三个点 ，， 在平面 内，又在平面 内．所以平面 和平面 重合，即直线 ，， 在同一平面内．∩=A l 1l 2∩=B l 2l 3∩=C l 1l 3l 1l 2l 3∩=A l 1l 2l 1l 2α∩=B l 2l 3B ∈l 2⊂αl 2B ∈αC ∈αB ∈l 3C ∈l 3⊂αl 3l 1l 2l 3∩=A l 1l 2l 1l 2α∩=B l 2l 3l 2l 3βA ∈l 2⊂αl 2A ∈αA ∈l 2⊂βl 2A ∈βB ∈αB ∈βC ∈αC ∈βA B C αβαβl 1l 2l 3结合空间想象回答下列问题：（1） 个平面可以分空间为______部分；（2） 个平面可以分空间为______部分；（3）正方体的各个面延伸后将空间分成______部分．解：（1），；（2），，，；（3）．对于（1）：当 个平面平行时，分成 部分；当两个面相交时，分成 部分；对于（2）：当 个平面两两平行时，分成 部分；当其中两个平面平行，和另外一个平面相交或者三个平面相交于一条直线时，分成 部分；当 个平面两两相交且交线两两平行时，分成 部分；当 个平面两两相交且交线相交于一点时，分成 部分；对于（3）：首先，将正方体的四个侧面延伸，可知将空间分成 部分，然后，将正方体的上下底面延伸可知将之前部分分成了 层，每层 部分，共 部分 ．233446782723434637389393×9=27若直线 、、 相交于一点，则这 条直线可能确定的平面有（ ）A． 个 B． 个 C．无数个 D． 个或 个解：D当 、、 三线共面时，平面只有 个；当三线不共面时，任意两条可确定一个平面，共 个．a b c 30113a b c 13描述：例题：点与平面的位置关系平面内有无数个点，平面可以看成点的集合．点 在平面 内，记作 ；点 不在平面 内，记作 ．直线与直线的位置关系空间直线与直线的位置关系共有以下两种：共面直线 在同一平面内的两条直线．更进一步，若这两条直线有且只有一个公共点，则称它们是相交直线 ，若这两条直线没有公共点，则称它们是平行直线；异面直线 不同在任何一个平面内的两条直线．直线垂直如果两条直线所成的角是直角，那么我们就说这两条直线互相垂直，记作 ．在空间，两条直线垂直包括两种情形：共面垂直和异面垂直．直线与平面的位置关系空间直线与平面的位置关系共有以下三种：直线在平面内 直线上的所有点都在平面内；直线与平面相交 直线与平面有且仅有一个公共点；直线与平面平行 直线与平面没有公共点．平面与平面的位置关系空间平面与平面的位置关系共有以下两种：平行 两个平面没有公共点，则称这两个平面平行；相交 两个平面有一条公共直线，则称这两个平面相交，此时这条公共直线称为这两个平面的交线．A αA ∈αA αA ∉αa ⊥b 如果在两个平面内分别各有一条直线，这两条直线互相平行，那么这两个平面的位置关系是（）A．平行 B．相交 C．平行或相交 D．垂直相交解：C可根据题意作图判断，如图所示，分别为两个平面平行、相交的情况 ．分别和两条异面直线都相交的两条直线的位置关系是（ ）A．相交 B．异面 C．异面或相交 D．平行解：C如图所示，可能相交，也可能异面，若两直线平行，则此两条直线确定一个平面，且原两条异面直线均在此平面内，故矛盾 ．四、课后作业 （查看更多本章节同步练习题，请到快乐学）若直线 不平行于平面 ，且 ，则（ ）A． 内的所有直线与 异面 B． 内不存在与 平行的直线 C． 内存在唯一的直线与 平行 D． 内的直线与 都相交解：B依题意，设直线 ，如图． 内的直线若经过点 ，则与直线 相交；若不经过点 ，则与直线 是异面直线，但不可能与 平行．l αl ⊄ααl αl αl αl l ∩α=A αA l A l l 答案：解析：1. 如图，在正方体 中， 是底面正方形 的中心， 是 的中点， 是 上的动点，则直线 、 的位置关系是 ．A ．平行B ．相交C ．异面垂直D ．异面不垂直C和点 确定平面 ，且 平面 ， 判定 与平面 的位置关系，只需判定直线 的位置关系即可．ABCD −A 1B 1C 1D 1O ABCD M D D 1N A 1B 1NO AM ()A 1B 1O O A 1B 1NO ⊂O A 1B 1∴MA O A 1B 1NO 、AM 答案：2. 平行六面体 中，既与 共面也与 共面的棱的条数为 A ．B ．C ．D ．C ABCD −A 1B 1C 1D 1AB C C 1()3456答案：3. 正方体 中， 、 、 分别是 、 、 的中点．那么，正方体的过 、 、 的截面图形是 A ．三角形B ．四边形C ．五边形D ．六边形D ABCD −A 1B 1C 1D 1P Q R AB AD B 1C 1P Q R ()4. 下列正方体或正四面体中，，，， 分别是所在棱的中点，这四个点不共面的一个图是 P Q R S ()高考不提分，赔付1万元，关注快乐学了解详情。

第二章点、直线、平面之间的位置关系§2.1空间点、直线、平面之间的位置关系2.1.1平面一、基础过关1．下列命题：①书桌面是平面；②有一个平面的长是50 m，宽是20 m；③平面是绝对的平、无厚度，可以无限延展的抽象数学概念．其中正确命题的个数为() A．1个B．2个C．3个D．0个2．下列图形中，不一定是平面图形的是() A．三角形B．菱形C．梯形D．四边相等的四边形3．空间中，可以确定一个平面的条件是() A．两条直线B．一点和一条直线C．一个三角形D．三个点4．已知平面α与平面β、γ都相交，则这三个平面可能的交线有() A．1条或2条B．2条或3条C．1条或3条D．1条或2条或3条5．给出以下命题：①和一条直线都相交的两条直线在同一平面内；②三条两两相交的直线在同一平面内；③有三个不同公共点的两个平面重合；④两两平行的三条直线确定三个平面．其中正确命题的个数是________．6．已知α∩β＝m，a⊂α，b⊂β，a∩b＝A，则直线m与A的位置关系用集合符号表示为________．7．如图，梯形ABDC中，AB∥CD，AB>CD，S是直角梯形ABDC所在平面外一点，画出平面SBD和平面SAC的交线，并说明理由．8．空间中三个平面两两相交于三条直线，这三条直线两两不平行，证明此三条直线必相交于一点．二、能力提升9．空间不共线的四点，可以确定平面的个数是() A．0 B．1 C．1或4 D．无法确定10．已知α、β为平面，A、B、M、N为点，a为直线，下列推理错误的是() A．A∈a，A∈β，B∈a，B∈β⇒a⊂βB．M∈α，M∈β，N∈α，N∈β⇒α∩β＝MNC．A∈α，A∈β⇒α∩β＝AD．A、B、M∈α，A、B、M∈β，且A、B、M不共线⇒α、β重合11．下列四个命题：①两个相交平面有不在同一直线上的三个公共点；②经过空间任意三点有且只有一个平面；③过两平行直线有且只有一个平面；④在空间两两相交的三条直线必共面．其中正确命题的序号是________．12. 如图所示，四边形ABCD中，已知AB∥CD，AB，BC，DC，AD(或延长线)分别与平面α相交于E，F，G，H，求证：E，F，G，H必在同一直线上．三、探究与拓展13. 如图，在正方体ABCD－A1B1C1D1中，对角线A1C与平面BDC1交于点O，AC、BD交于点M，E为AB的中点，F为AA1的中点．求证：(1)C1、O、M三点共线；(2)E、C、D1、F四点共面．答案1．A 2.D 3.C 4.D5．06．A∈m7. 解很明显，点S是平面SBD和平面SAC的一个公共点，即点S在交线上，由于AB>CD，则分别延长AC和BD交于点E，如图所示．∵E∈AC，AC⊂平面SAC，∴E∈平面SAC.同理，可证E∈平面SBD.∴点E在平面SBD和平面SAC的交线上，连接SE，直线SE是平面SBD和平面SAC的交线．8．证明∵l1⊂β，l2⊂β，l1D∥\l2，∴l1、l2交于一点，记交点为P.∵P∈l1⊂α，P∈l2⊂γ，∴P∈α∩γ＝l3，∴l1，l2，l3交于一点．9．C10.C11．③12．证明因为AB∥CD，所以AB，CD确定平面AC，AD∩α＝H，因为H∈平面AC，H∈α，由公理3可知，H必在平面AC与平面α的交线上．同理F、G、E都在平面AC与平面α的交线上，因此E，F，G，H必在同一直线上．13．证明(1)∵C1、O、M∈平面BDC1，又C1、O、M∈平面A1ACC1，由公理3知，点C1、O、M在平面BDC1与平面A1ACC1的交线上，∴C1、O、M三点共线．(2)∵E，F分别是AB，A1A的中点，∴EF∥A1B.∵A1B∥CD1，∴EF∥CD1.∴E、C、D1、F四点共面．2.1.2空间中直线与直线之间的位置关系一、基础过关1．分别在两个平面内的两条直线间的位置关系是() A．异面B．平行C．相交D．以上都有可能2．若AB∥A′B′，AC∥A′C′，则有() A．∠BAC＝∠B′A′C′B．∠BAC＋∠B′A′C′＝180°C．∠BAC＝∠B′A′C′或∠BAC＋∠B′A′C′＝180°D ．∠BAC ＞∠B ′A ′C ′3．空间四边形的两条对角线相互垂直，顺次连接四边中点的四边形一定是 ( )A ．空间四边形B ．矩形C ．菱形D ．正方形4．“a 、b 为异面直线”是指：①a ∩b ＝∅，且aD \∥b ；②a ⊂面α，b ⊂面β，且a ∩b ＝∅；③a ⊂面α，b ⊂面β，且α∩β＝∅；④a ⊂面α，b ⊄面α；⑤不存在面α，使a ⊂面α，b ⊂面α成立． 上述结论中，正确的是( )A ．①④⑤B ．①③④C ．②④D ．①⑤5．如果两条直线a 和b 没有公共点，那么a 与b 的位置关系是________． 6．已知正方体ABCD —A ′B ′C ′D ′中： (1)BC ′与CD ′所成的角为________； (2)AD 与BC ′所成的角为________．7．如图所示，四边形ABEF 和ABCD 都是直角梯形，∠BAD ＝∠F AB＝90°，BC 綊12AD ，BE 綊12F A ，G 、H 分别为F A 、FD 的中点．(1)证明：四边形BCHG 是平行四边形； (2)C 、D 、F 、E 四点是否共面？为什么？8．如图，正方体ABCD －EFGH 中，O 为侧面ADHE 的中心，求：(1)BE 与CG 所成的角； (2)FO 与BD 所成的角． 二、能力提升9.如图所示，已知三棱锥A －BCD 中，M 、N 分别为AB 、CD 的中点，则下列结论正确的是( )A ．MN ≥12(AC ＋BD )B ．MN ≤12(AC ＋BD )C ．MN ＝12(AC ＋BD )D ．MN <12(AC ＋BD )10．如果两条异面直线称为“一对”，那么在正方体的十二条棱中共有异面直线( )A ．12对B ．24对C ．36对D ．48对11．一个正方体纸盒展开后如图所示，在原正方体纸盒中有如下结论：①AB ⊥EF ；②AB 与CM 所成的角为60°； ③EF 与MN 是异面直线； ④MN ∥CD .以上结论中正确的序号为________．12．已知A 是△BCD 平面外的一点，E ，F 分别是BC ，AD 的中点，(1)求证：直线EF 与BD 是异面直线；(2)若AC ⊥BD ，AC ＝BD ，求EF 与BD 所成的角． 三、探究与拓展13．已知三棱锥A —BCD 中，AB ＝CD ，且直线AB 与CD 成60°角，点M 、N 分别是BC 、AD 的中点，求直线AB 和MN 所成的角．答案1．D 2．C 3．B 4．D 5.平行或异面 6．(1)60° (2)45°7．(1)证明 由已知FG ＝GA ，FH ＝HD ，可得GH 綊12AD .又BC 綊12AD ，∴GH 綊BC ，∴四边形BCHG 为平行四边形．(2)解 由BE 綊12AF ，G 为F A 中点知，BE 綊FG ，∴四边形BEFG 为平行四边形，∴EF ∥BG . 由(1)知BG 綊CH ，∴EF ∥CH ，∴EF 与CH 共面．又D ∈FH ，∴C 、D 、F 、E 四点共面．8．解 (1)如图，∵CG ∥BF ，∴∠EBF (或其补角)为异面直线BE 与CG 所成的角，又△BEF 中，∠EBF ＝45°，所以BE 与CG 所成的角为45°.(2)连接FH ，BD ，FO ，∵HD 綊EA ，EA 綊FB ， ∴HD 綊FB ，∴四边形HFBD 为平行四边形， ∴HF ∥BD ，∴∠HFO (或其补角)为异面直线FO 与BD 所成的角． 连接HA 、AF ，易得FH ＝HA ＝AF ， ∴△AFH 为等边三角形，又依题意知O 为AH 中点，∴∠HFO ＝30°，即FO 与BD 所成的角是30°.9．D 10．B 11．①③12．(1)证明 假设EF 与BD 不是异面直线，则EF 与BD 共面，从而DF 与BE 共面，即AD 与BC 共面，所以A 、B 、C 、D 在同一平面内，这与A 是△BCD 平面外的一点相矛盾．故直线EF 与BD 是异面直线．(2)解 取CD 的中点G ，连接EG 、FG ，则EG ∥BD ，所以相交直线EF 与EG 所成的角，即为异面直线EF 与BD 所成的角．在Rt △EGF 中，由EG ＝FG ＝12AC ，求得∠FEG ＝45°，即异面直线EF 与BD 所成的角为45°.13．解 如图，取AC 的中点P .连接PM 、PN ，则PM ∥AB ，且PM ＝12AB ，PN ∥CD ，且PN ＝12CD ，所以∠MPN 为直线AB 与CD 所成的角(或所成角的补角)． 则∠MPN ＝60°或∠MPN ＝120°， 若∠MPN ＝60°，因为PM ∥AB ，所以∠PMN 是AB 与MN 所成的角(或所成角的补角)． 又因AB ＝CD ，所以PM ＝PN ，则△PMN 是等边三角形， 所以∠PMN ＝60°，即AB 与MN 所成的角为60°.若∠MPN ＝120°，则易知△PMN 是等腰三角形．所以∠PMN ＝30°，即AB与MN所成的角为30°.故直线AB和MN所成的角为60°或30°.2.1.3空间中直线与平面之间的位置关系2.1.4平面与平面之间的位置关系一、基础过关1．已知直线a∥平面α，直线b⊂α，则a与b的位置关系是() A．相交B．平行C．异面D．平行或异面2．直线l与平面α不平行，则() A．l与α相交B．l⊂αC．l与α相交或l⊂αD．以上结论都不对3．如果直线a∥平面α，那么直线a与平面α内的() A．一条直线不相交B．两条直线不相交C．无数条直线不相交D．任意一条直线不相交4．如果平面α外有两点A、B，它们到平面α的距离都是a，则直线AB和平面α的位置关系一定是() A．平行B．相交C．平行或相交D．AB⊂α5．直线a⊂平面α，直线b⊄平面α，则a，b的位置关系是________．6．若a、b是两条异面直线，且a∥平面α，则b与α的位置关系是________．7．平面α内有无数条直线与平面β平行，那么α∥β是否正确？说明理由．8. 如图，直线a∥平面α，a⊂β，α∩β＝b，求证：a∥b.二、能力提升9．下列命题正确的是() A．若直线a在平面α外，则直线a∥αB．若直线a与平面α有公共点，则a与α相交C．若平面α内存在直线与平面β无交点，则α∥βD．若平面α内的任意直线与平面β均无交点，则α∥β10．教室内有一根直尺，无论怎样放置，在地面上总有这样的直线与直尺所在的直线() A．异面B．相交C．平行D．垂直11．若不在同一条直线上的三点A、B、C到平面α的距离相等，且A、B、CD/∈α，则面ABC 与面α的位置关系为________．12. 如图，平面α、β、γ满足α∥β，α∩γ＝a，β∩γ＝b，判断a与b、a与β的关系并证明你的结论．三、探究与拓展13．正方体ABCD—A1B1C1D1中，点Q是棱DD1上的动点，判断过A、Q、B1三点的截面图形的形状．答案1．D2．C3．D4．C5.平行、相交或异面6．b⊂α，b∥α或b与α相交7．解不正确．如图，设α∩β＝l，则在α内与l平行的直线可以有无数条，如a1，a2，…，a n，它们是一组平行线，这时a1，a2，…，a n与平面β平行，但此时α与β不平行，α∩β＝l.8．证明∵直线a∥平面α，∴直线a与平面α无公共点．∵α∩β＝b，∴b⊂α，b⊂β.∴直线a与b无公共点．∵a⊂β，∴a∥b.9．D10.D11.平行或相交12．解由α∩γ＝a知a⊂α且a⊂γ，由β∩γ＝b知b⊂β且b⊂γ，∵α∥β，a⊂α，b⊂β，∴a、b无公共点．又∵a⊂γ且b⊂γ，∴a∥b.∵α∥β，∴α与β无公共点，又a⊂α，∴a与β无公共点，∴a∥β.13．解由点Q在线段DD1上移动，当点Q与点D1重合时，截面图形为等边三角形AB1D1，如图(1)所示；当点Q与点D重合时，截面图形为矩形AB1C1D，如图(2)所示；图(1)图(2)当点Q不与点D，D1重合时，截面图形为等腰梯形AQRB1，如图(3)所示．图(3)。

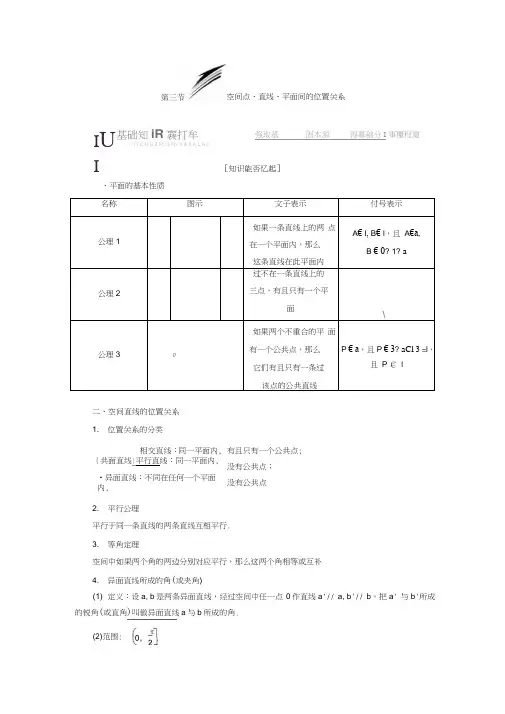
［知识能否忆起］、平面的基本性质 名称图示文子表示 付号表示公理1如果一条直线上的两 点在一个平面内，那么 这条直线在此平面内 A € l , B € l ，且 A €a,B € 0? 1? a公理2过不在一条直线上的 三点，有且只有一个平面\公理3如果两个不重合的平 面有一个公共点，那么 它们有且只有一条过该点的公共直线P € a ，且 P € 3? aCl 3 =l ，且 P € l二、空间直线的位置关系 1. 位置关系的分类相交直线：同一平面内, ｛共面直线|平行直线：同一平面内,•异面直线：不同在任何一个平面内, 2. 平行公理平行于同一条直线的两条直线互相平行. 3. 等角定理空间中如果两个角的两边分别对应平行，那么这两个角相等或互补 4. 异面直线所成的角(或夹角)(1) 定义：设a, b 是两条异面直线，经过空间中任一点 0作直线a '// a, b '// b ，把a ' 与b '所成的锐角(或直角)叫做异面直线a 与b 所成的角.I U I空间点、直线、平面间的位置关系基础知iR 襄打牟11 C H U Z H I $ H I Y A 0 A L A 0强取基 固本源 得募础分I 事覆程廈有且只有一个公共点;没有公共点；没有公共点(2)范围:三、直线与平面的位置关系/亠护¥方位置大糸图示付号表示公共点个数直线1在平面a内1? a无数个直线l与平面a相交八/l Cl a= A一个直线l与平面a平行Z / 1 〃a0个四、平面与平面的位置关系/亠护¥方位置大糸图示付号表示公共点个数两个平面平行\Aall 30个7两个平面相交aC 3= l无数个(这些公共点均在交线1上)1•三个公理的作用(1) 公理1的作用：①检验平面；②判断直线在平面内；③由直线在平面内判断直线上的点在平面内.(2) 公理2的作用：确定平面的依据，它提供了把空间问题转化为平面问题的条件.(3) 公理3的作用：①判定两平面相交；②作两相交平面的交线；③证明多点共线.2. 异面直线的有关问题(1) 判定方法：①反证法；②利用结论即过平面外一点与平面内一点的直线与平面内不过该点的直线是异面直线，如图.(2) 所成的角的求法：平移法.師吾点］学技法］得拔高分| 拿握狸度i**-平面的基本性质及应用■典题导入［例1］（2012湘潭模拟）如图所示，在正方体ABCD —A i B i C i D i中，E为AB的中点，F 为A i A的中点，求证：CE , D i F, DA三线共点.［自主解答］•EF 綊qCD i,•••直线D i F和CE必相交.设D i F n CE = P,••P Pi F 且D i F?平面AA i D i D,••P € 平面AA i D i D.又P €EC且CE?平面ABCD ,••P € 平面ABCD ,即P是平面ABCD与平面AA i D i D的公共点.而平面ABCD n平面AA i D i D = AD.••P 3D.•CE、D i F、DA三线共点.本例条件不变试证明E , C, D i, F四点共面.证明：••E, F分别是AB和AA i的中点，i•'EF 綊2A i B.又A i D i 綊B i C i 綊BC. •四边形A i D i CB为平行四边形. ••A i B CD i，从而EF CD i.•'EF与CD i确定一个平面. ••E, C i, F, D四点共面.占由题悟法i. 证明线共点问题常用的方法是：先证其中两条直线交于一点，再证交点在第三条直线上.2•证明点或线共面问题一般有以下两种途径：①首先由所给条件中的部分线（或点）确定一个平面，然后再证其余线（或点）均在这个平面内；②将所有条件分为两部分，然后分别确定平面，再证平面重合.3以题试法1. （1）（2012江•西模拟）在空间中，下列命题正确的是（）A .对边相等的四边形一定是平面图形B .四边相等的四边形- -定是平面图形C.有一组对边平行的四边形一定是平面图形D .有一组对角相等的四边形一定是平面图形⑵对于四面体ABCD，下列命题正确的是 __________ （写出所有正确命题的编号）.①相对棱AB与CD所在直线异面；②由顶点A作四面体的高，其垂足是△ BCD三条高线的交点；③若分别作△ ABC和厶ABD的边AB上的高，则这两条高所在的直线异面；④分别作三组相对棱中点的连线，所得的三条线段相交于一点.解析：（1）由“两平行直线确定一个平面”知C正确.（2）由四面体的概念可知，AB与CD所在的直线为异面直线，故①正确；由顶点A作四面体的高，只有当四面体ABCD的对棱互相垂直时,其垂足是厶BCD的三条高线的交点，故②错误；当DA = DB , CA= CB时，这两条高线共面，故③错误；设AB , BC, CD , DA的中点依次为E, F, M , N,易证四边形EFMN为平行四边形，所以EM与FN相交于一点，易证另一组对棱中点的连线也过它们的交点，故④正确.答案：（1）C （2）①④异面直线的判定由典题导入[例2] （2012金华模拟）在图中，G, N , M, H分别是正三棱柱的顶点或所在棱的中点,则表示直线GH , MN是异面直线的图形有___________ .（填上所有正确答案的序号）①②③④［自主解答］图①中，直线GH /MN ;图②中，G , H , N三点共面，但M?面GHN ,因此直线GH与MN异面；图③中，连接MG, GM /HN，因此GH与MN共面；图④中，G , M , N共面，但H?面GMN ,因此GH与MN异面.所以图②④中GH与MN异面.［答案］②④石由题悟法1•异面直线的判定常用的是反证法，先假设两条直线不是异面直线，即两条直线平行或相交，由假设的条件出发，经过严格的推理，导出矛盾，从而否定假设肯定两条直线异面. 此法在异面直线的判定中经常用到.2.客观题中，也可用下述结论：过平面外一点和平面内一点的直线，与平面内不过该点的直线是异面直线.&以题试法2. 已知m, n, I为不同的直线，a, B为不同的平面，有下面四个命题：①m, n为异面直线，过空间任一点P, —定能作一条直线I与m, n都相交.②m, n为异面直线，过空间任一点P, —定存在一个与直线m, n都平行的平面.③a丄B, aA 3= I, m? a, n? 3, m, n与I都斜交，则m与n—定不垂直；④m, n是a内两相交直线，则a与3相交的充要条件是m, n至少有一条与3相交.则四个结论中正确的个数为( )A. 1B. 2C. 3D. 4解析：选B①错误，因为过直线m存在一个与直线n平行的平面，当点P在这个平面内且不在直线m上时，就不满足结论；②错误，因为过直线m存在一个与直线n平行的平面，当点P在这个平面内时，就不满足结论；③正确，否则，若m丄n,在直线m上取一点作直线a丄I，由a丄3得a丄n.从而有n丄a,贝U n丄I :④正确.LI 典题导入［例3］ （2012大纲全国卷）已知正方体 ABCD — A 1B 1C 1D 1中，E , F 分别为BB i , CC i 的 中点，那么异面直线 AE 与D 1F 所成角的余弦值为 ___________ .［自主解答］连接DF ，则AE/DF , •••D 1FD 即为异面直线 AE 与D 1F 所成的角. 设正方体棱长为a ,则 D 1D = a , DF = ~25a , D 1F = ~25a ,… 3 ［答案］5-由题悟法求异面直线所成的角一般用平移法，步骤如下： （1） 一作：即找或作平行线，作出异面直线所成的角; ⑵二证：即证明作出的角是异面直线所成的角；（3）三求：解三角形，求出所作的角，如果求出的角是锐角或直角，则它就是要求的角, 如果求出的角是钝角，则它的补角才是要求的角.初以题试法3. （2012唐山模拟）四棱锥P — ABCD 的所有侧棱长都为.5,底面ABCD 是边长为2的 正方形，则CD 与PA 所成角的余弦值为（）D.；解析：选B 如图所示，因为四边形ABCD 为正方形，故CD // AB ,则CD 与PA 所成的角即为 AB 与FA 所成的角/ PAB ，在△ FAB 内，FB = FA = ■.5, AB = 2,利用余弦定理可知:PA 2+ AB 2- PB 2_ 5+ 4— 5 _近 2X FA X AB 2X 2八 55［小题能否全取］A. 2 *5 5B.cos / FAB =1.（教材习题改编）已知a, b是异面直线，直线c平行于直线a，那么c与b（）A .异面B.相交C.不可能平行D.不可能相交解析：选C 由已知直线c与b可能为异面直线也可能为相交直线，但不可能为平行直线，若b // c,贝U a// b.与a, b是异面直线相矛盾.2. （2012东北三校联考）下列命题正确的个数为（）①经过三点确定一个平面；②梯形可以确定一个平面；③两两相交的三条直线最多可以确定三个平面；④如果两个平面有三个公共点，则这两个平面重合.A. 0B. 1C. 2D. 3解析：选C ①④错误，②③正确.3. 已知空间中有三条线段AB, BC和CD，且/ ABC =Z BCD，那么直线AB与CD的位置关系是（）A. AB / CDB. AB与CD异面C. AB与CD相交D. AB / CD或AB与CD异面或AB与CD相交解析：选D 若三条线段共面，如果AB, BC, CD构成等腰三角形，则直线AB与CD相交，否则直线AB与CD平行；若不共面，则直线AB与CD是异面直线.4. （教材习题改编）如图所示，在正方体ABCD —A i B i C i D i中，E,F分别是AB , AD的中点，则异面直线B i C与EF所成的角的大小为解析：连接B i D i, D i C,则B i D i/EF,故ZDi B i C 为所求，又B i D i= B i C= D i C,••』i B i C= 60 °答案：60°5. （教材习题改编）平行六面体ABCD —A i B i C i D i中既与AB共面又与CC i共面的棱的条数为________ .解析：如图，与AB和CC i都相交的棱有BC;与AB相交且与CC i平行的棱有AA i,BB i；与AB平行且与CC i相交的棱有CD , C1D1,故符合条件的棱共有5条.答案：5基础MliR靈扫年J I C H U Z H D S H I YAOIRALAO［知识能否忆起］一、直线与平面平行1. 判定定理文字语言图形语言符号语言判定定理平面外一条直线与此平—面内的一条直线平行, 则直线与此平面平行—a?a、b? a b //a」^ ? a / a2.性质定理文字语言图形语言付号语言性质定理一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行a/ a '卜？ a // baCl 6= b j二、平面与平面平行直线、平面平行的判定及性质1.判定定理判定定理一个平面内的两条相交直线与另一个平面平 行，则这两个平面平行a? a 、 b? aa Ab = P » ? a// a / 3 b / 3' 32.两平面平行的性质定理文字语言图形语言付号语言性质定理如果两个平行平面同时 和第三个平面相交，那 么它们的交线平行a// 3、aA Y a * ? a // b 3A Y b J7，心/IX1.平行问题的转化关系:2.在解决线面、面面平行的判定时，一般遵循从“低维”到“高维”的转化， 即从“线线平行”到“线面平行”，再到“面面平行”；而在性质定理的应用中，其顺序恰好相反， 但也要注意，转化的方向总是由题目的具体条件而定，决不可过于“模式化”.3•辅助线（面）是求证平行问题的关键，注意平面几何中位线，平行四边形及相似中有 关平行性质的应用.由典题导入[例1] （2011福建高考）如图，正方体 ABCD — A i B i C i D i 中，AB = 2, 点E 为AD 的中点，点F 在CD 上•若EF //平面ABQ ,则线段EF 的长 度等于 _______________ .线//线判定判定 ------------- 判定 -------------- 性质 |线/面—质勺面/面性质［自主解答］ 因为直线 EF //平面AB i C , EF?平面ABCD ，且平面 AB i C Q 平面ABCD = AC ,所以EF /AC.又因为点E 是DA 的中点，所以F 是DC 的中点，由中位线定理可得 EF1=2AC.又因为在正方体 ABCD — A i B i C i D i 中，AB = 2,所以AC = 2 2•所以EF = 2.［答案］,2本例条件变为“ E 是AD 中点，F , G , H , N 分别是AA i , A i D i , DD i 与D i C i 的中点,解：如图,••G N //平面AA i C i C , EG //平面 AA i C i C , 又 GN n EG = G ,•••平面EGN //平面AA i C i C.•••当M 在线段EG 上运动时，恒有 MN //平面AA i C i C.呂由题悟法解决有关线面平行、面面平行的基本问题要注意：(i)判定定理与性质定理中易忽视的条件，如线面平行的判定定理中条件线在面外易忽 视.⑵结合题意构造或绘制图形，结合图形作出判断. (3)举反例否定结论或用反证法推断命题是否正确.&以题试法i . (i)(20i2浙江高三调研)已知直线I //平面a, P € a,那么过点P 且平行于直线I 的直 线() A •只有一条，不在平面 a 内 B .有无数条，不一定在平面 a 内C .只有一条，且在平面 a 内D .有无数条，一定在平面a 内解析：选C 由直线I 与点P 可确定一个平面 3,且平面a, B 有公共点，因此它们有若M 在四边形EFGH 及其内部运动”，则M 满足什么条件时，有 MN //平面A i C i CA.一条公共直线,设该公共直线为m ,因为I // a,所以I // m ,故过点P且平行于直线I的直线只有一条，且在平面a内.(2)(2012潍坊模拟)已知m, n, l i, I2表示直线，a, B表示平面.若m? a, n? a, l i? B, 12? B IE 12= M,贝U all B的一个充分条件是()A. m l B且l i l a B • m // B且n// BC. m l B 且n l I2 D . m l l i 且n l I2解析：选D 由定理“如果一个平面内有两条相交直线分别与另一个平面平行，那么这两个平面平行”可得，由选项D可推知al B-直线与平面平行的判定与性质[例2] (2012辽宁高考)如图，直三棱柱ABC —A' B ' C', / BAC= 90° AB= AC =羽，AA' = 1,点M , N 分别为A' B 和B' C'的中点.(1) 证明：MN l 平面A' ACC ';1(2) 求三棱锥A' —MNC的体积.(锥体体积公式V = §Sh,其中S为底面面积，h为高)［自主解答］(1)证明：法一：连接AB'、AC '，因为点M , N 分别是A' B和B' C'的中点，所以点M为AB'的中点.又因为点N为B ' C'的中点,所以MN /AC'又MN?平面A' ACCAC' ?平面A' ACC',因此MN l平面A' ACC'.法二：取A' B '的中点P.连接MP.而点M, N分别为AB '与B ' C'的中点，所以MP/AA ' , PN/A ' C '.所以MP l 平面A ' ACC ' , PN l 平面A ' ACC ' •又MP n PN= P,因此平面MPN l平面A ' ACC ' •而MN?平面MPN ,因此MN //平面A ' ACC(2)法一：连接 BN ，由题意得 A ' N IB ' C '，平面 A B ' C 'Q 平面 B ' BCC '=B 'C '，所以A ' N 丄平面NBC. 又 A ' N = 1B ' C ' = 1 ,吕由题悟法利用判定定理证明线面平行的关键是找平面内与已知直线平行的直线，可先直观判断平面内是否已有，若没有，则需作出该直线，常考虑三角形的中位线、平行四边形的对边或过 已知直线作一平面找其交线.畐以题试法2. (2012淄博模拟)如图，在棱长为2的正方体 ABCD — A 1B 1C 1D 1中，E , F 分别是BD , BB 1的中点.(1) 求证：EF //平面 A 1B 1CD ; (2) 求证：EF 丄 AD 1.解：(1)在正方体ABCD — A 1B 1C 1D 1中，连接B 1D , 在平面BB 1D 内，E , F 分别为BD , BB 1的中点, ••EF BD.又•••B 1D?平面 A 1B 1CD. EF?平面 A 1B 1CD , ••EF //平面A 1B 1CD.⑵'-ABCD — A 1B 1C 1D 1 是正方体,•'AD 1 ^A 1 D , AD 1 JA 1B 1. 又 A 1D n A 1B 1 = A 1, ••AD 1 丄平面 A 1B 1D.故 V A ' - MNC = V N -A ' MC = 2V N -A ' BC = gV A '—NBC = 16.法二：V A ' -MNC = V A-NBC —V M — NBC =1V A '— NBC =••AD1I B1D.又由(1)知,EF B1D , /-EF_LAD1.平面与平面平行的判定与性质i典题导入［例3］如图，已知ABCD —A i B i C i D i是棱长为3的正方体，点E 在AA i 上，点 F 在CC i 上，G 在BB i 上，且AE = FC i = B i G= 1, H 是B i C i的中点.⑴求证：E, B, F , D i四点共面；⑵求证：平面A i GH //平面BED i F.5［自主解答］(i)在正方形AA i B i B中，'•AE = B i G= i,••BG = A i E= 2,••BG 綊A i E.•四边形A i GBE是平行四边形.•■AiG /BE.又C i F 綊B i G,•四边形C i FGB i是平行四边形.••FG 綊C i B i 綊D i A i.•四边形A i GFD i是平行四边形.• A i G 綊D i F.•D i F 綊EB.故E, B, F, D i四点共面.3⑵--H是B i C i的中点，• B i H = 2厂B i G 2又B i G= i, /B1H= 3.又EC = f,且/FCB = /GB i H = 90 ° BC 3•••△i HG s/CBF.•••启i GH = ZCFB = ZFBG.••HG /FB.••GH ?面FBED i, FB?面FBED i ,「GH //面BED i F.由⑴知A i G/BE, A i G?面FBED i, BE?面FBED i,AG //面BED i F.且HG A A i G = G ,•平面A i GH //平面BED i F.占由题悟法常用的判断面面平行的方法(1) 利用面面平行的判定定理；(2) 面面平行的传递性(all 3,训Y all Y；⑶利用线面垂直的性质(I丄a, I丄3? a// 3 .血以题试法3. (20i2北京东城二模)如图，矩形AMND所在的平面与直角梯形MBCN 所在的平面互相垂直，MB // NC , MN丄MB.(1) 求证：平面AMB //平面DNC ;(2) 若MC丄CB，求证：BC丄AC.证明：(i)因为MB /NIC , MB?平面DNC , NC?平面DNC ,所以MB //平面DNC.又因为四边形AMND为矩形，所以MA /DN.又MA?平面DNC, DN?平面DNC.所以MA //平面DNC.又MA A MB = M，且MA, MB?平面AMB ,所以平面AMB //平面DNC.(2)因为四边形AMND是矩形，所以AM丄/IN.因为平面AMND丄平面MBCN，且平面AMND A平面MBCN = MN ,所以AM丄平面MBCN.因为BC?平面MBCN ,所以AM JBC.因为MC _LBC, MC A AM = M , 所以BC丄平面AMC.因为AC? 平面AMC，所以BC JAC.[ 小题能否全取]1．（教材习题改编）下列条件中，能作为两平面平行的充分条件的是（）A •一个平面内的一条直线平行于另一个平面B .一个平面内的两条直线平行于另一个平面C. 一个平面内有无数条直线平行于另一个平面D •一个平面内任何一条直线都平行于另一个平面解析：选D 由面面平行的定义可知，一平面内所有的直线都平行于另一个平面时，两平面才能平行，故D正确.2. 已知直线a, b,平面a,则以下三个命题:①若a// b, b? a,贝U a// a;②若 a / b, a // a,贝U b // a;③若a/ a, b// a,贝U all b.其中真命题的个数是（）A. 0B. 1C. 2D. 3解析：选A 对于命题①，若a// b, b? a ,贝U应有a// a或a? a,所以①不正确;对于命题②，若a// b , a// a ,则应有b// a或b? a,因此②也不正确;对于命题③，若a//a, b // a,则应有a // b或a与b相交或a与b异面，因此③也不正确.3. （教材习题改编）若一直线上有相异三个点A , B , C到平面a的距离相等，那么直线I与平面a的位置关系是（）A . I // a B. I 丄aC. I与a相交且不垂直D. I // a或I? a解析：选D 由于I上有三个相异点到平面a的距离相等，贝U I与a可以平行，I? a时也成立.4. ___________________________________________________________ 平面a//平面3, a? a, b? 3,则直线a, b的位置关系是______________________________________________ 解析：由a//3可知，a, b的位置关系是平行或异面.答案：平行或异面5. （2012衡阳质检）在正方体ABCD —A1B1C1D1中，E是DD 1的中点，则BD i与平面ACE 的位置关系为_________解析：如图.连接AC, BD交于O点，连接OE,因为OE /BD1,而OE?平面ACE,BD1?平面ACE，所以BD1 /平面ACE.答案：平行基础知MW1 I C M U Z H I S H I Y A 0［知识能否忆起］一、直线与平面垂直1. 直线和平面垂直的定义直线I与平面a内的任意一条直线都垂直，就说直线I与平面a互相垂直.2.直线与平面垂直的判定定理及推论文字语言图形语言付号语言判定定理一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直1心k a, b? a] a A b = O.r ? I 丄a1丄aI丄b 」推论如果在两条平行直线中，有一条垂直于平面，那么另一条直线也垂直这个平面ab7 a / b、\? b丄aa丄a_直线、平面垂直的判定与性质3.直线与平面垂直的性质定理文字语言图形语言付号语言性质定理垂直于冋一个平面的两条直线平行a匚—b7a丄ab丄a€ a// b、平面与平面垂直1.平面与平面垂直的判定定理文字语言图形语言付号语言判定定理一个平面过另一个平面的垂线，则这两个平面垂直□a 丄3l丄aa j2.平面与平面垂直的性质定理文字语言图形语言付号语言性质定理a_L 3 、》？ 1丄a ad 3= a1丄a」两个平面垂直，则一个平面内垂直于父线的直线垂直于另一个平面L71•在证明线面垂直、面面垂直时，一定要注意判定定理成立的条件. 同时抓住线线、线面、面面垂直的转化关系，即:线血垂百线线垂直、一…厂：面面垂直-------- 性质---------------2•在证明两平面垂直时，一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决，如有平面垂直时，一般要用性质定理.3•几个常用的结论：(1) 过空间任一点有且只有一条直线与已知平面垂直.(2) 过空间任一点有且只有一个平面与已知直线垂直.垂直关系的基本问题高频考点3EIB美GAOP1N K.AOI>IAN YAOLI典题导入［例1］（2012襄州模拟）若m, n为两条不重合的直线，a, B为两个不重合的平面，给出下列命题：①若m，n都平行于平面a,则m，n—定不是相交直线；②若m、n都垂直于平面a,贝U m, n—定是平行直线；③已知a, B互相垂直，m, n互相垂直，若m丄a,则n丄④m,n在平面a内的射影互相垂直，则m,n互相垂直.其中的假命题的序号是________________ .［自主解答］①显然错误，因为平面a//平面平面a内的所有直线都平行所以3内的两条相交直线可同时平行于a；②正确；如图1所示，若aCl 3= I,且n/,当m丄a时，mln,但n//3,所以③错误；如图2显然当m' Jn'时，m不垂直于n,所以④错误.［答案］①③④-由题悟法解决此类问题常用的方法有：①依据定理条件才能得出结论的，可结合符合题意的图形作出判断；②否定命题时只需举一个反例. ③寻找恰当的特殊模型（如构造长方体）进行筛选.初以题试法1. （2012长春模拟）设a, b是两条不同的直线，a, 3是两个不同的平面，则下列四个命题：①若a丄b, a丄a, b? a,贝U b // a；②若a // a, a丄3贝U a丄3；③若a丄3, a丄3,贝U a// a或a? a；④若a丄b ,a丄a, b丄3,贝U a丄3-其中正确命题的个数为()A. 1B.2C. 3D.4解析：选D对于①,由b不在平面a内知，直线b或者平行于平面a,或者与平面相交，若直线b与平面a相交，则直线b与直线a不可能垂直，这与已知"a丄b”相矛盾, 因此①正确.对于②，由 a // a知，在平面a内必存在直线a1 // a,又a丄3,所以有a j丄3, 所以a丄3,②正确.对于③，若直线a与平面a相交于点A,过点A作平面a 3的交线的垂线m,则m丄3,又a丄3,则有a / m,这与"直线a、m有公共点A”相矛盾，因此③正确.对于④，过空间一点O分别向平面a、3引垂线a1、b1 ,则有a // a1 , b / B ,又a丄b , 所以a1丄b1 ,所以a丄3,因此④正确•综上所述，其中正确命题的个数为 4.直线与平面垂直的判定与性质LI典题导入［例2］(2012广东高考)如图所示，在四棱锥P—ABCD中，AB 丄平面PAD , AB // CD, PD = AD , E 是PB 的中点，F 是DC1上的点且DF = 2AB, PH PAD中AD边上的高.(1)证明：PH丄平面ABCD ;⑵若PH = 1 , AD = 2, FC = 1,求三棱锥E—BCF的体积;(3)证EF丄平面［自主解答］(1)证明：因为AB丄平面FAD, PH?平面FAD ,所以PH JAB.因为PH为APAD中AD边上的高，所以PH 1AD.因为PH?平面ABCD , AB A AD = A, AB,AD?平面ABCD , 所以PH丄平面ABCD.连接EG.⑵如图，连接BH，取BH的中点G,因为E是PB的中点，所以EG PH ,1 1且EG = -PH = 2.因为PH丄平面ABCD , 所以EG丄平面ABCD.因为AB丄平面PAD , AD?平面PAD,所以AB丄\D.所以底面ABCD为直角梯形.所以V E-BCF = 3S Z SCF EG =1• FC AD EG =鲁.(3) 证明：取PA中点M，连接MD , ME.1 因为E是PB的中点，所以ME綊T^AB.1又因为DF綊^AB,所以ME綊DF，所以四边形MEFD是平行四边形，所以EF /MID.因为PD = AD，所以MD _LPA.因为AB丄平面PAD，所以MD 1AB.因为PA A AB = A,所以MD丄平面FAB，所以EF丄平面FAB.呂由题悟法证明直线和平面垂直的常用方法有：(1)利用判定定理.⑵利用判定定理的推论(a// b, a丄a? b丄汰⑶利用面面平行的性质(a丄a, a// 3? a± 3).(4) 利用面面垂直的性质.当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面.EJ以题试法2. (2012启东模拟)如图所示，已知PA丄矩形ABCD所在平面, M , N分别是AB, PC的中点.(1) 求证：MN丄CD ;(2) 若/ PDA = 45°求证：MN丄平面PCD.证明：(1)连接AC, AN, BN,••PA丄平面ABCD , /PA1AC,1在Rt△AC 中，N 为PC 中点，••• AN = ^PC.••PA丄平面ABCD，/PAJBC,又BC _1AB,PA A AB= A,••BC 丄平面PAB./BC1PB.从而在RtAPBC中，BN为斜边PC上的中线，1「BN = ?PC.••AN = BN. •△BN为等腰三角形，又M为AB的中点，• MN _LAB,又TAB CD , AMN JCD.⑵连接PM , MC ,Vz PDA = 45 °PAAAD, A AP = AD.• •四边形ABCD 为矩形，• AD = BC,「AP = BC./?又为AB的中点，••• AM = BM.而/PAM = ZCBM = 90°• △AM 也/CBM .•'PM = CM.又N为PC的中点，• MN JPC.由⑴知，MN _LCD , PC A CD = C，/MN 丄平面PCD.面面垂直的判定与性质［例3］ (2012江苏高考)如图，在直三棱柱ABC —A i B i C i中，"B!=A i C i, D, E分别是棱BC, CC i上的点(点D不同于点C),且AD丄DE , F为B iC i的中点.求证：⑴平面ADE丄平面BCC i B i；(2)直线A i F //平面ADE.ti ［自主解答］(i)因为ABC —A i B i C i是直三棱柱，所以CC i丄平面ABC,又AD?平面ABC，所以CC i L AD.又因为AD IDE , CC i, DE?平面BCC i B i,CC i A DE = E,所以AD丄平面BCC i B i.又AD?平面ADE ,所以平面ADE丄平面BCC i B i.⑵因为A i B i= A i C i, F为B i C i的中点，所以A i F _LBi C i.因为CC i丄平面A i B i C i，且A i F?平面A i B i C i,所以CC il A i F.又因为CC i, B i C i?平面BCC i B i, CC i A B i C i= C i,所以A i F丄平面BCC i B i.由⑴知AD 丄平面BCC i B i ，所以A i F/AD. 又AD?平面ADE , A i F?平面ADE , 所以A i F //平面ADE.呂由题悟法1. 判定面面垂直的方法： （i ）面面垂直的定义.⑵面面垂直的判定定理（a 丄B, a? a a 丄2. 在已知平面垂直时，一般要用性质定理进行转化，转化为线面垂直或线线垂直. 转化方法：在一个平面内作交线的垂线， 转化为线面垂直，然后进一步转化为线线垂直.$以题试法3. （20i2泸州一模）如图，在四棱锥P — ABCD 中，底面ABCD 为 菱形，/ BAD = 60° Q 为AD 的中点.⑴若PA = PD ，求证：平面 PQB 丄平面PAD ;⑵若点M 在线段PC 上，且PM = tPC （t>0），试确定实数t 的值, 使得FA //平面MQB.解：（1）因为FA = PD , Q 为AD 的中点，所以 PQ 丄AD. 连接BD ，因为四边形 ABCD 为菱形，/ BAD = 60° 所以AB = BD. 所以BQ 丄\D.因为BQ?平面PQB , PQ?平面PQB , BQ A PQ = Q , 所以AD 丄平面PQB.因为AD?平面PAD ，所以平面 PQB 丄平面PAD.证明如下:连接AC ,设AC n BQ = O ,连接 OM •在△AOQ 与△COB 中， 因为 AD BC ,所以/OQA=ZOBC,ZOAQ = ZOCB. 所以…。

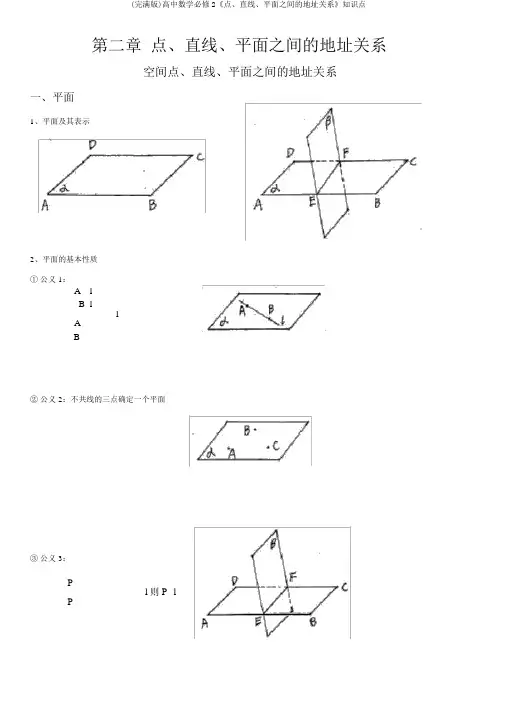
第二章点、直线、平面之间的地址关系空间点、直线、平面之间的地址关系一、平面1、平面及其表示2、平面的基本性质①公义 1：A lB llAB②公义 2：不共线的三点确定一个平面③公义 3：Pl 则P lP二、点与面、直线地址关系1、A1、点与平面有 2 种地址关系2、B1、A l2、点与直线有 2 种地址关系2、 B l三、空间中直线与直线之间的地址关系1、异面直线2、直线与直线的地址关系订交共面平行异面3、公义 4 和定理公义 4：l1 Pl3l1 Pl 2l 2 Pl3定理：空间中若是两个角的两边分别对应平行，那么这两个角相等或互补。

4、求异面直线所成角的步骤：① 作：作平行线获取订交直线；② 证：证明作出的角即为所求的异面直线所成的角；③ 构造三角形求出该角。

提示： 1、作平行线常有方法有：直接平移，中位线，平行四边形。

2、异面直线所的角的范围是00 ,900。

四、空间中直线与平面之间的地址关系地址关系直线 a在平面内直线 a与平面订交直线 a与平面平行公共点有无数个公共点有且只有一个公共点没有公共点符号表示a a I Aa P图形表示五、空间中平面与平面之间的地址关系地址关系两个平面平行两个平面订交公共点没有公共点有一条公共直线符号表示P I a图形表示直线、平面平行的判断及其性质一、线面平行1、判断：ba b Pb Pa（线线平行，则线面平行）2、性质：a PaPa b b（线面平行，则线线平行）二、面面平行1、判断：aba b P Pa Pb P（线面平行，则面面平行）2、性质 1：PI a a PbI b（面面平行，则线面平行）性质 2：Pm Pm（面面平行，则线面平行）说明（ 1）判断直线与平面平行的方法：① 利用定义：证明直线与平面无公共点。

② 利用判判定理：从直线与直线平行等到直线与平面平行。

③ 利用面面平行的性质：两个平面平行，则其中一个平面内的直线必平行于另一个平面。

（2）证明面面平行的常用方法①利用面面平行的定义：此法一般与反证法结合。

第一节空间点、直线、平面的位置关系精讲公理1:如果一条直线的两点在一个平面内，那么这条直线是所有的点都在这个平面内符号语言表示： A 三1, B 三1, Aw 很，B ： = 1 二很公理2：经过不在同一条直线上的三点，有且只有一个平面。

推论：一直线和直线外一点确定一平面；两相交直线确定一平面；两平行直线确定一平面。

公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线公理4:平行于同一条直线的两条直线互相平行1. 空间直线与直线之间的位置关系2. 空间直线与平面之间的位置关系3. 平面与平面之间的位置关系:4. 空间中的平行问题线面平行的判定定理：平面外一条直线与此平面内一条直线平行，则该直线与此平面平行。

线面平行的性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交, 平面与平面平行的判定及其性质两个平面平行的判定定理1. 如果一个平面内的两条相交直线都平行于另一个平面，那么这两个平面平行2. 如果在两个平面内，各有两组相交直线对应平行，那么这两个平面平行。

3. 垂直于同一条直线的两个平面平行，两个平面平行的性质定理1. 如果两个平面平行，那么某一个平面内的直线与另一个平面平行。

2. 如果两个平行平面都和第三个平面相交，那么它们的交线平行。

5. 空间中的垂直问题线面垂直平面和平面垂直垂直关系的判定和性质定理线面垂直判定定理和性质定理判定定理：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直这个平面, 性质定理：如果两条直线同垂直于一个平面，那么这两条直线平行。

面面垂直的判定定理和性质定理判定定理：如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直。

性质定理：如果两个平面互相垂直，那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。

点线面位置关系精炼1. 下列命题中，错误的是............................... ( )A. 平行于同一个平面的两个平面平行B. 平行于同一条直线的两个平面平行C. 一个平面与两个平行平面相交，交线平行D. —条直线与两个平行平面中的一个相交，则必与另一个相交2. 直线a,b,c及平面a , B , Y ,下列命题正确的是.................... ( )A、若a：_ a， b：_ a ,c 丄a, c丄b 贝U c丄aB、若b：_ a , allb贝U all aC 若all a , aAp =b 则allbD 、若a丄a , b 丄a 则allb3. 下列命题中正确的是.......................... ( )A. 如果一个平面内两条直线都平行于另一平面，那么这两个平面平行。

第八章立体几何初步8.4空间点、直线、平面之间的位置关系8.4.2空间点、直线、平面之间的位置关系课后篇巩固提升必备知识基础练1.如图所示,用符号语言可表示为()A.α∩β=lB.α∥β,l∈αC.l∥β,l⊄αD.α∥β,l⊂α2.在长方体ABCD-A1B1C1D1的六个表面与六个对角面(平面AA1C1C、平面ABC1D1、平面ADC1B1、平面BB1D1D、平面A1BCD1及平面A1B1CD)所在的平面中,与棱AA1平行的平面共有()A.2个B.3个C.4个D.5个,结合图形可知AA1∥平面BB1C1C,AA1∥平面DD1C1C,AA1∥平面BB1D1D.3.(多选题)如图所示,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,则以下四个结论正确的是()A.直线AM与CC1是相交直线B.直线AM与BN是平行直线C.直线BN与MB1是异面直线D.直线AM与DD1是异面直线AM与CC1不同在任何一个平面内,直线AM与BN不同在任何一个平面内,故A,B错误;直线BN与MB1不同在任何一个平面内,直线AM与DD1不同在任何一个平面内,故C,D正确.4.如果空间的三个平面两两相交,那么()A.不可能只有两条交线B.必相交于一点C.必相交于一条直线D.必相交于三条平行线,可能相交于一点,也可能相交于一条直线,还可能相交于三条平行线,故选A.5.若两个平面内分别有一条直线,且这两条直线是异面直线,则这两个平面的公共点()A.有有限个B.有无数个C.不存在D.不存在或有无数个,直线AB与直线CC1异面,平面ABCD与平面CDD1C1相交,有无数个公共点;平面ABB1A1与平面CDD1C1平行,没有公共点.6.以下说法正确的是()A.若直线a不平行于平面α,则直线a与平面α相交B.直线a和b是异面直线,若直线c∥a,则c与b一定相交C.若直线a和b都和平面α平行,则a和b也平行D.若点M∈l,点N∈l,N∉α,M∈α,则直线l与平面α相交a不平行于平面α,则直线a与平面α相交,或a⊂α,故A错误;若直线a和b是异面直线,若直线c∥a,则c与b相交或异面,故B错误;若直线a和b都和平面α平行,则a和b可能平行,可能相交,也可能异面,故C错误;若点M,N∈l,N∉α,M∈α,则直线l和平面α相交,故D正确.故选D.7.如图,在正方体ABCD-A1B1C1D1中,所在直线与BD1异面的棱有条.,知在正方体ABCD-A1B1C1D1中,所在直线与BD1异面的棱有CD,A1B1,AD,B1C1,AA1,CC1共6条.8.已知直线a,平面α,β,且a∥α,a∥β,则平面α与β的位置关系是.a∥α,a∥β,所以平面α与β相交(如图①)或平行(如图②).9.过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有条.,与平面ABB1A1平行的直线有6条:D1E1,E1E,ED,DD1,D1E,DE1.10.如图,在长方体ABCD-A1B1C1D1中,面对角线B1D1与长方体的六个面之间的位置关系如何?B1∈平面A1B1C1D1,D1∈平面A1B1C1D1,∴B1D1⊂平面A1B1C1D1.∵B1∈平面BB1C1C,D1∉平面BB1C1C,∴直线B1D1∩平面BB1C1C=B1.同理直线B1D1与平面AA1B1B、平面AA1D1D、平面CC1D1D都相交.在平行四边形B1BDD1中,B1D1∥BD,B1D1与BD无公共点,∴B1D1与平面ABCD无公共点,∴B1D1∥平面ABCD.关键能力提升练11.若a,b是异面直线,且a∥平面α,那么b与平面α的位置关系是()A.b∥αB.b与α相交C.b⊂αD.以上三种情况都有可能a,b是异面直线,且a∥平面α,则根据空间中线面的位置关系可得,b∥a,或b⊂α,或b与α相交.12.(多选题)以下结论中,正确的是()A.过平面α外一点P,有且仅有一条直线与α平行B.过平面α外一点P,有且仅有一个平面与α平行C.过直线l外一点P,有且仅有一条直线与l平行D.过直线l外一点P,有且仅有一个平面与l平行①所示,过点P有无数条直线都与α平行,这无数条直线都在平面β内,过点P有且只有一个平面与α平行,故A错,B正确;如图②所示,过点P只有一条直线与l平行,但有无数个平面与l平行,故C正确,D错.13.(多选题)下列说法中正确的是()A.若直线a不在平面α内,则a∥αB.若直线l上有无数个点不在平面α内,则l∥αC.若l∥α,则直线l与平面α内任何一条直线都没有公共点D.平行于同一平面的两直线可以相交中,直线a也可能与平面α相交,故A错误;B中,直线l与平面α相交时,l上也有无数个点不在平面α内,故B错误;C中,当l∥α时,l与α没有公共点,所以l与α内任何一条直线都没有公共点,故C正确;D中,平行于同一个平面的直线,可以平行也可以相交,也可以是异面直线,故D正确.14.一个正方体的平面展开图如图所示,A,B,C,D为原正方体的顶点,则在原来的正方体中()A.AB∥CDB.AB与CD相交C.AB⊥CDD.AB与CD异面,则在原来的正方体中,由异面直线的定义可知AB与CD异面.故选D.15.下列命题正确的有.(填序号)①若直线与平面有两个公共点,则直线在平面内;②若直线l与平面α相交,则l与平面α内的任意直线都是异面直线;③若直线l与平面α平行,则l与平面α内的直线平行或异面;④若直线a⊂平面α,平面α∩平面β=b,a∥b,则a∥β.显然是正确的;②中,直线l和平面α内过l与α交点的直线都相交而不是异面,所以②是错误的;③中,直线l与平面α没有公共点,所以直线l与平面α内的直线没有公共点,即它们平行或异面,所以③是正确的;因为a∥b,所以a与b无公共点.又因为a⊂α,且α与β的公共点都在直线b上,所以a 与β无公共点,故a与β平行,故④是正确的.16.如图,平面α,β,γ满足α∥β,α∩γ=a,β∩γ=b,判断a与b,a与β的关系,并证明你的结论.∥b,a∥β.证明如下.由α∩γ=a知a⊂α,且a⊂γ,由β∩γ=b知b⊂β,且b⊂γ.∵α∥β,a⊂α,b⊂β,∴a,b无公共点.又∵a⊂γ,且b⊂γ,∴a∥b.∵α∥β,∴α与β无公共点.又a⊂α,∴a与β无公共点,∴a∥β.学科素养创新练17.若直线a不平行于平面α,且a⊄α,则下列结论成立的是()A.平面α内的所有直线与a异面B.平面α内不存在与a平行的直线C.平面α内存在唯一的直线与a平行D.平面α内的直线与a都相交a与平面α相交,则平面α内的直线与a可能相交,也可能异面,不可能平行.故选B.18.(多选题)已知a,b是两条不重合的直线,α,β是两个不重合的平面,则下列说法中正确的是()A.若a∥b,b⊂α,则直线a平行于平面α内的无数条直线B.若α∥β,a⊂α,b⊂β,则a与b是异面直线C.若α∥β,a⊂α,则a∥βD.若α∩β=b,a⊂α,则a,b一定相交中,a∥b,b⊂α,则a∥α或a⊂α,所以不管a在平面内还是平面外,结论都成立,故A正确;B中,直线a与b没有交点,所以a与b可能异面,也可能平行,故B错误;C中,直线a与平面β没有公共点,所以α∥β,故C正确;D中,直线a与平面β有可能平行,所以a,b可能相交,也可能平行,故D错误.。

人教版新课标普通高中◎数学 2 必修（A 版）第二章点、直线、平面之间的位置关系2. 1空间点、直线、平面之间的位置关系教案 A第 1 课时教学内容： 2. 1. 1平面教学目标一、知识与技能1.利用生活中的实物对平面进行描述，掌握平面的表示法及水平放置的直观图；2.掌握平面的基本性质及作用，提高学生的空间想象能力.二、过程与方法在师生的共同讨论中，形成对平面的感性认识.三、情感、态度与价值观通过实例认识到我们所处的世界是一个三维空间，进而增强了学习的兴趣.教学重点、难点教学重点：1.平面的概念及表示；2.平面的基本性质，注意它们的条件、结论、作用、图形语言及符号语言.教学难点：平面基本性质的掌握与运用.教学关键：让学生理解平面的概念，熟记平面的性质及性质的应用，使学生对平面的概念及其性质由感性认识上升到理性认识.教学突破方法：对三个公理要结合图形进行理解，清楚其用途.教法与学法导航教学方法：探究讨论，讲练结合法．学习方法：学生通过阅读教材，联系身边的实物思考、交流，师生共同讨论等，从而较好地完成本节课的教学目标.教学准备教师准备：投影仪、投影片、正（长）方形模型、三角板．学生准备：直尺、三角板．教学过程教学教学内容师生互动设计过程意图创设什么是平面？师：生活中常见的如黑板、情境一些能看得见的平面实桌面等，给我们以平面的印象，形成平导入例 .你们能举出更多例子吗？那么面的概新课平面的含义是什么呢？这就是念我们这节课所要学习的内容 .1教师备课系统──多媒体教案续上表1.平面含义随堂练习判定下列命题是否正确：主题① 书桌面是平面；探究② 8 个平面重叠起来要比合作 6 个平面重叠起来厚；交流③ 有一个平面的长是50m，宽是 20m；④平面是绝对的平，无厚度，可以无限延展的抽象的数学概念 .师：以上实物都给我们以平面的印象，几何里所说加强对知的平面，就是从这样的一些识的理解物体中抽象出来的，但是，培养，自几何里的平面是无限延展觉钻研的的 .学习习惯 . 数形结合，加深理解 .2.平面的画法及表示师：在平面几何中，怎（1）平面的画法：水平放样画直线？（一学生上黑板置的平面通常画成一个平行四画）边形，锐角画成 45°，且横边之后教师加以肯定，解说、画成邻边的 2 倍长（如图）．类比，将知识迁移，得出平面的画法：D CαA B如果几个平面画在一起，主题当一个平面的一部分被另一个探究平面遮住时，应画成虚线或不合作画（打出投影片）．交流（2）平面通常用希腊字母α、β、γ等表示，如平面α、平面β等，也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示，如平面 AC 、平面 ABCD等.（3）平面内有无数个点，平面可以看成点的集合 .点 A 在平面α内，记作：A ∈ α ; 点B 在平面α外，记作： Bα．β通过类比α探索，培养学生知识迁移能β力，加强知识的系统性 .α·B·Aα2续上表人教版新课标普通高中◎数学 2 必修（A 版）3.平面的基本性质公理 1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内．A Bα· C··教师引导学生思考教材P41 的思考题，让学生充分发表自己的见解 .师：把一把直尺边缘上的任意两点放在桌边，可以看到，直尺的整个边缘就落在了桌面上，用事实引导学生归纳出公理主题探究合作交流符号表示为A ∈ LB∈ L? L ? α．A ∈ αB∈ α公理 1：判断直线是否在平面内．公理 2：过不在一条直线上的三点，有且只有一个平面 .A· Bα·L符号表示为： A 、B、C 三点不共线 ? 有且只有一个平面α，使A ∈ α、 B∈ α、 C∈ α.公理 2 作用：确定一个平面的依据 .公理 3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线 .βPα·L符号表示为： P∈ α∩β? α∩β =L，且P∈ L ．公理 3 作用：判定两个平面是否相交的依据 .1．教师引导学生阅读教材P42 前几行相关内容，并加以解析．师：生活中，我们看到三脚架可以牢固地支撑照相机或测量用的平板仪等等．通过类比引导学生归纳出公理探索，培2．养学生知教师用正（长）方形识迁移能模型，让学生理解两个平力，加强面的交线的含义.知识的系注意：（ 1）公理中“有统性 .且只有一个”的含义是：“有”，是说图形存在，“只有一个”，是说图形唯一，“有且只有一个平面”的意思是说“经过不在同一直线上的三个点的平面是有的，而且只有一个”，也即不共线的三点确定一个平面.“ 有且只有一个平面”也可以说成“确定一个平面 . ”引导学生阅读P42 的思考题，从而归纳出公理3．3教师备课系统──多媒体教案续上表拓展 4. 教材 P43 例 1教师及时评价和纠正同创新通过例子，让学生掌握图形学的表达方法，规范画图和巩固应用中点、线、面的位置关系及符号符号表示 .提高．提高的正确使用 .1．平面的概念，画法及表示方法 .培养学2．平面的性质及其作用．生归纳3．符号表示．整合知4．注意事项．学生归纳总结、教师给识能小结力，以予点拨、完善并板书 .及思维的灵活性与严谨性 .课堂作业1.下列说法中，（1）铺得很平的一张白纸是一个平面；（ 2）一个平面的面积可以等于 6cm 2；（ 3）平面是矩形或平行四边形的形状. 其中说法正确的个数为（）．A . 0 B . 1 C. 2 D . 32.若点 A 在直线 b 上，在平面内，则 A， b，之间的关系可以记作（）．A . A b B. A b C. A b D . A b3.图中表示两个相交平面，其中画法正确的是（）．A B C D4.空间中两个不重合的平面可以把空间分成（）部分.答案： 1. A 2. B 3. D 4. 3 或 4第 2 课时教学内容2.1. 2 空间中直线与直线之间的位置关系教学目标一、知识与技能1.了解空间中两条直线的位置关系；4人教版新课标普通高中◎数学 2 必修（A 版）2.理解异面直线的概念、画法，提高空间想象能力；3.理解并掌握公理 4 和等角定理；4.理解异面直线所成角的定义、范围及应用.二、过程与方法1.经历两条直线位置关系的讨论过程，掌握异面直线所成角的基本求法.2.体会平移不改变两条直线所成角的基本思想和方法.三、情感、态度与价值观感受到掌握空间两直线关系的必要性，提高学习兴趣.教学重点、难点教学重点1.异面直线的概念 .2.公理 4 及等角定理 .教学难点异面直线所成角的计算.教学关键提高学生空间想象能力，结合图形来判断空间直线的位置关系，使学生掌握两异面直线所成角的步骤及求法 .教学突破方法结合图形，利用不同的分类标准给出空间直线的位置关系，由两异面直线所成角的定义求其大小，注意两异面直线所成角的范围.教法与学法导航教学方法探究讨论法．学习方法学生通过阅读教材、思考与教师交流、概括，从而较好地完成教学目标.教学准备教师准备投影仪、投影片、长方体模型、三角板．学生准备三角板 .教学过程详见下表 .教学教学内容师生互动设计环节意图创设通过身边实物，相互设疑激情境异面直线的概念：不同在任何一个交流异面直线的概念．趣点出导入平面内的两条直线叫做异面直线.师：空间两条直线有主题．新课多少种位置关系？1. 空间的两条直线的位置关系教师给出长方体模多媒体5教师备课系统──多媒体教案相交直线：同一平面内，有且只有型，引导学生得出空间的演示提一个公共点；两条直线有如下三种关高上课平行直线：同一平面内，没有公共系．效率 .探索点；异面直线：不同在任何一个平面内，教师再次强调异面直新知没有公共点 .线不共面的特点．师生互异面直线作图时通常用一个或两个动，突平面衬托，如下图：破重点 .2. 平行公理师：在同一平面内，例 2 的思考：长方体ABCD-A'B'C'D' 中，如果两条直线都与第三条讲解让BB' ∥AA'， DD' ∥AA'，那么 BB' 与直线平行，那么这两条直学生掌DD' 平行吗？线互相平行 . 在空间中，是握了公否有类似的规律？理 4 的运用．生：是．强调：公理 4 实质上探索是说平行具有传递性，在新知公理 4：平行于同一条直线的两条平面、空间这个性质都适直线互相平行 .用．符号表示为：设a、b、c 是三条直线如果 a//b， b//c，那么 a//c.例 2 空间四边形ABCD 中， E、 F、G、 H 分别是AB 、BC 、 CD 、 DA 的中点．求证：四边形 EFGH 是平行四边形 .续上表3. 思考：在平面上，我们容易证明让学生观察、思考：等角定“如果一个角的两边与另一个角的两边理为异探索分别平行，那么这两个角相等或互补”.面直线新知空间中，结论是否仍然成立呢？所成的等角定理：空间中如果两个角的两角的概边分别对应平行，那么这两个角相等或念作准6人教版新课标普通高中◎数学 2 必修（A 版）互补 .∠ ADC与A'D'C' 、备.∠ ADC与∠ A'B'C'的两边分别对应平行，这两组角的大小关系如何？生：∠ ADC = A'D'C' ，∠ ADC +∠ A'B'C' = 180°4.异面直线所成的角如图，已知异面直线 a、b，经过空探索间中任一点 O 作直线 a'∥ a、b'∥ b，我新知们把 a'与 b'所成的锐角（或直角）叫异面直线 a 与 b 所成的角（夹角）．教师画出更具一般性的图形，师生共同归纳出如下等角定理．师：① a'与 b'所成的角的以教师大小只由 a、b 的相互位置讲授为来确定，与 O 的选择无关，主，师为了简便，点 O 一般取在生共同两直线中的一条上；交流，② 两条异面直线所成的导出异角θ∈（ 0，π）；面直线2所成的③ 当两条异面直线所成角的概探索的角是直角时，我们就说念 .新知这两条异面直线互相垂例 3 让直，记作 a⊥ b；学生掌④ 两条直线互相垂直，有握了如共面垂直与异面垂直两种何求异情形；面直线⑤ 计算中，通常把两条异所成的例 3（投影）面直线所成的角转化为两角，从条相交直线所成的角 .而巩固了所学知识 .续上表充分调动学拓展生动手创新教材 P49 练习 1、 2．生完成练习，教师当的积极应用堂评价 .性，教提高师适时7教师备课系统──多媒体教案给予肯定 .本节课学习了哪些知识内容？小结知2．计算异面直线所成的角应注意什学生归纳，然后老师补识，形小结么？充、完善．成整体思维．课堂作业1. 异面直线是指（）．A.空间中两条不相交的直线B.分别位于两不同平面内的两条直线C.平面内的一条直线与平面外的一条直线D.不同在任何一个平面内的两条直线2.如右图所示，在三棱锥 P-ABC 的六条棱所在的直线中，异面直线共有（）．A. 2 对 B . 3 对 C. 4 对 D. 6 对3.正方体 ABCD-A 1B1C1D1中与棱AA1平行的棱共有（）．A. 1 条 B . 2 条 C. 3 条 D. 4 条4.空间两个角、，且与的两边对应平行，若=60 °，则的大小为（）．.答案： 1. D 2.B 3. C 4. 60 °或 120°第 3 课时教学内容8人教版新课标普通高中◎数学 2 必修（A 版）2. 1. 3 空间中直线与平面之间的位置关系 2. 1. 4 平面与平面之间的位置关系教学目标一、知识与技能1.了解空间中直线与平面的位置关系，了解空间中平面与平面的位置关系；2.提高空间想象能力 .二、过程与方法1.通过观察与类比加深了对这些位置关系的理解、掌握；2.利用已有的知识与经验归纳整理本节所学知识.三、情感、态度与价值观感受空间中图形的基本位置关系，形成严谨的思维品质.教学重点、难点教学重点空间直线与平面、平面与平面之间的位置关系.教学难点用图形表达直线与平面、平面与平面的位置关系.教学关键借助图形，使学生清楚直线与平面，平面与平面的分类标准，并能依据这些标准对直线与平面、平面与平面的位置关系进行分类及判定.教学突破方法恰当地利用图形，用符号语言表述直线与平面、平面与平面的位置关系.教法与学法导航教学方法借助实物，让学生观察事物、思考关系，讲练结合，较好地完成本节课的教学目标.学习方法探究讨论，自主学习法.教学准备教师准备多媒体课件，投影仪，三角板，直尺.学生准备三角板，直尺．教学过程详见下表 .教学教学内容师生互动设计过程意图创设问题1：空间中直线和直线有几生 1：平行、相交、异复习9教师备课系统──多媒体教案情境种位置关系？面；回顾，导入问题 2：一支笔所在的直线和一生 2：有三种位置关系：激发新课个作业本所在平面有几种位置关（1）直线在平面内；学习系？（2）直线与平面相交；兴趣 .（3）直线与平面平行．师肯定并板书，点出主题 .1．直线与平面的位置关系 .师：有谁能讲出这三种（ 1）直线在平面内——有无数位置有什么特点吗？个公共点 .生：直线在平面内时二（ 2）直线与平面相交——有且者有无数个公共点 .仅有一个公共点 .直线与平面相交时，二（ 3）直线在平面平行——没有者有且仅有一个公共点 .公共点 .直线与平面平行时，三其中直线与平面相交或平行的者没有公共点（师板书）．情况，统称为直线在平面外，记作师：我们把直线与平面加强a.相交或直线与平面平行的对知直线 a 在面内的符号语言是情况统称为直线在平面外 .识的a. 图形语言是：师：直线与平面的三种理解位置关系的图形语言、符号培养，主题语言各是怎样的？谁来画自觉探究图表示一个和书写一下 .钻研合作学生上台画图表示 .的学交流直线 a 与面相交的 a∩ = A.师；好 . 应该注意：画习习图形语言是符号语言是：直线在平面内时，要把直线惯，数画在表示平面的平行四边形结形内；画直线在平面外时，合，加应把直线或它的一部分画深理在表示平面的平行四边形解 .外 .直线 a 与面平行的符号语言是a∥. 图形语言是：10人教版新课标普通高中◎数学 2 必修（A 版）续上表2．平面与平面的位置关系师：下面请同学们思考以（ 1）问题 1：拿出两本书，看下两个问题（投影）．作两个平面，上下、左右移动和翻生：平行、相交 .转，它们之间的位置关系有几种？师：它们有什么特点？（ 2）问题 2：如图所示，围成生：两个平面平行时二者长方体 ABCD –没有公共点，两个平面相交A′B′C′D′的六个时，二者有且仅有一条公共直通过面，两两之间的线（师板书）．类比位置关系有几师：下面请同学们用图形探索，种？和符号把平面和平面的位置培养主题关系表示出来⋯⋯学生（ 3）平面与平面的位置关系探究——没有公师：下面我们来看几个例知识平面与平面平行合作子（投影例 1）．迁移共点 .交流能力 .平面与平面相交——有且只有一条公共直线 .加强平面与平面平行的符号语言知识是∥ . 图形语言是：的系统性 .11教师备课系统──多媒体教案续上表拓展创新应用提高例 1 下列命题中正确的个数是（ B ）．①若直线 l 上有无数个点不在平面内，则 l∥ .②若直线l 与平面平行，则l与平面内的任意一条直线都平行 .③如果两条平行直线中的一条与一个平面平行，那么另一条也与这个平面平行 .④若直线 l 与平面平行，则 l 与平面内的任意一条直线没有公共点 .A . 0B . 1 C. 2 D. 3例 2 已知平面∥，直线a，求证 a∥ .证明：假设 a 不平行，则 a在内或 a 与相交 .∴ a 与有公共点 .又 a.∴ a与有公共点，与面∥面矛盾 .∴∥ .学生先独立完成，然后讨例 1 通论、共同研究，得出答案. 教师过示范利用投影仪给出示范 .传授学师：如图，我们借助长方体生一个模型，棱 AA 1所在直线有无数点通过模在平型来研面究问题ABCD的方外，但法，加棱 AA 1深对概所在直线与平面ABCD 相交，所念的理以命题①不正确； A1B1所在直线解. 例 2平行于平面 ABCD ，A1B1显然不目标训平行于 BD，所以命题②不正确；练学生A1 B1∥AB，A1B1所在直线平行于思维的平面 ABCD ，但直线 AB平灵活，面 ABCD ，所以命题③不正确；并加深l 与平面平行，则 l 与无公对面面共点， l与平面内所有直线都平行、没有公共点，所以命题④正确，线面平应选 B .行的理师：投影例2，并读题，先解.让学生尝试证明，发现正面证明并不容易，然后教师给予引导，共同完成，并归纳反证法步骤和线面平行、面面平行的理解 .1．直线与平面、平面与平培养学面的位置关系 .生整合2．“正难到反”数学思想知识能与反证法解题步骤 .学生归纳总结、教师给予点力，以小结拨、完善并板书 .及思维3. “分类讨论”数学思想．的灵活性与严谨性 . 12人教版新课标普通高中◎数学 2 必修（A 版）课堂作业1.直线与平面平行的充要条件是这条直线与平面内的（）．A ．一条直线不相交B．两条直线不相交C．任意一条直线都不相交 D ．无数条直线都不相交【解析】直线与平面平行，则直线与平面内的任意直线都不相交，反之亦然；故应选C.2. “平面内有无穷条直线都和直线l 平行”是“l //”的（）．A．充分而不必要条件 B ．必要而不充分条件C．充分必要条件 D ．即不充分也不必要条件【解析】如果直线在平面内，直线可能与平面内的无穷条直线都平行，但直线不与平面平行，应选 B.3．如图，试根据下列要求，把被遮挡的部分改为虚线：（ 1）AB 没有被平面遮挡；（ 2）AB 被平面遮挡.答案：略4．已知，，直线a，b，且∥，a，b，则直线 a 与直线 b 具有怎样的位置关系？【解析】平行或异面．5．如果三个平面两两相交，那么它们的交线有多少条？画出图形表示你的结论.【解析】三个平面两两相交，它们的交线有一条或三条.6.求证：如果过一个平面内一点的直线平行于与该平面平行的一条直线，则这条直线在这个平面内 .已知： l ∥，点P∈，P∈ m，m∥ l，求证： m.证明：设 l 与 P 确定的平面为，且= m′，则 l ∥ m′.又知 l ∥ m， m m P ，由平行公理可知，m 与 m′重合 .所以 m.13教师备课系统──多媒体教案教案 B第 1 课时教学内容： 2. 1. 1 平面教学目标1.了解平面的概念，掌握平面的画法、表示法及两个平面相交的画法；2.理解公理一、二、三，并能运用它们解决一些简单的问题；3.通过实践活动，感知数学图形及符号的作用，从而由感性认识提升为理性认识，注意区别空间几何与平面几何的不同，多方面培养学生的空间想象力.教学重点：公理一、二、三，实践活动感知空间图形．教学难点：公理三，由抽象图形认识空间模型．学法指导：动手实践操作，由模型到图形，由图形到模型不断感知.教学过程一、引入在平面几何中，我们已经了解了平面图形都是由点和线构成的，我们所做的一切都是在一个无形的平面中进行，请同学谈谈到底平面是什么样子的？可以举实例说明.在平面几何中，我们也知道直线是无限延伸的，我们是怎样表示这种无限延伸的？那么你认为平面是否有边界？你又认为如何去表示平面呢？二、新课以上问题经过学生分小组充分讨论，由各小组代表陈述你这样表示的理由？教师暂不作评判，继续往下进行 .实践活动：1.仔细观察教室，举出空间的点、线、面的实例.2.只准切三刀，请你把一块长方体形状的豆腐切成形状、大小都相同的八块.3.请你准备六根游戏棒，以每根游戏棒为一边，设法搭出四个正三角形.以上这些问题已经走出了平面的限制，是空间问题. 今后我们将研究空间中的点、线、面之间的关系.图 1问题：指出上述活动中几何体的面，并想想如何在一张纸上画出这个几何体？至此我们应感受到画几何体与我们的视角有一定的关系.练习一：试画出下列各种位置的平面.1.水平放置的平面2.竖直放置的平面14人教版新课标普通高中◎数学 2 必修（A 版）图 2（ 1）图2（2）3.倾斜放置的平面图 34.请将以下四图中，看得见的部分用实线描出．图 4（1）图4（2）图4（3）图4（4）小结：平面的画法和表示法.我们常常把水平的平面画成一个平行四边形，用平行四边形表示一个平面，如图 5.平行四边形的锐角通常画成45o，且横边长等于其邻边长的 2 倍.如果一个平面被另一个平面遮挡住，为了增强它的立体感，我们常把被遮挡部分用虚线画出来，如图 6.βFA DA DααB E CB C图 5图 6图 7平面常用希腊字母, ,等表示（写在代表平面的平行四边形的一个角上），如平面、平面；也可以用代表平面的平行四边形的四个顶点，或相对的两个顶点的大写英文字母作为平面的名称，图 5 的平面，也可表示为平面ABCD ，平面 AC 或平面BD .前面我们感受了空间中面与面的关系及画法，现在让我们研究一下点、线与一个平面会有怎样的关系？15教师备课系统──多媒体教案显然，一个点与一个平面有两种位置关系：点在平面内和点在平面外.我们知道平面内有无数个点，可以认为平面是由它内部的所有的点组成的点集，因此点和平面的位置关系可以引用集合与元素之间关系.从集合的角度，点 A 在平面内，记为A；点B在平面外，记为B （如图 7）.再来研究一下直线与平面的位置关系.将学生分成小组，并动手实践操作后讨论：把一把直尺边缘上的任意两点放在桌面上，直尺的整个边缘就落在桌面上吗？请同学们再试着想一下，如何用图形表示直线与平面的这些空间关系？由“两点确定一条直线”这一公理，我们不难理解如下结论：公理 1如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内 .A l ,B l , 且 A, B,l．A l Bα图8例1 分别用符号语言、文字语言描述下列图形．AA aa图 9（ 1）图 9（ 2）图 9（ 3）例 2 识图填空（在空格内分别填上, , ,）．A____ a；A____ α，B____ a； B____ α，Aa____ α；a____ α = B，B bb____ α；B____ b．a图 10图 11问题情景：制作一张桌子，至少需要多少条腿？为什么？公理 2 经过不在同一条直线上的三点，有且只有一个平A面 .CB实践活动：取出两张纸演示两个平面会有怎样的位置关α图 12系，并试着用图画出来 .图 12试问：如图13 是两个平面的另一种关系吗？（相对于同学们得出的关系）由平面的无限延展性，不难理解如下结论：公理 3如果两个不重合平面有一个公共点，那么它们有且只有一条过这个公共点16人教版新课标普通高中◎数学 2 必修（A 版）的直线 .βP l 且P l．αP l图 13例 3如图14用符号表示下列图形中点、直线、平面之间的位置关系.l【分析】根据图形，先判断点、直线、平面之间的位置关系，然后用符号表示出来.【解析】在（1）中，l , a A , a B .l , a, b, a l P , B l P .在（ 2）中，三、巩固练习教材 P43 练习 1— 4.四、课堂小结（1）本节课我们学习了哪些知识内容？（2）三个公理的内容及作用是什么？（3）判断共面的方法 .五、布置作业P51 习题 A 组 1， 2．第 2 课时教学内容： 2. 1. 2 空间中直线与直线之间的位置关系教学目标：一、知识目标1.了解空间中两条直线的位置关系；2.理解异面直线的概念、画法，培养学生的空间想象能力；3.理解并掌握公理 4．二、能力目标1.让学生在观察中培养自主思考的能力；17教师备课系统──多媒体教案2.通过师生的共同讨论培养合作学习的能力.三、情感、态度与价值观让学生感受到掌握空间两直线关系的必要性，提高学生的学习兴趣.教学重点、难点教学重点： 1.异面直线的概念； 2.公理 4.教学难点：异面直线的概念.学法与教学用具1.学法：学生通过观察、思考与教师交流、概括，从而较好地完成本节课的教学目标；2.教学用具：多媒体、长方体模型、三角板．教学过程一、复习引入1．平面内两条直线的位置关系有（相交直线、平行直线）．相交直线（有一个公共点）；平行直线（无公共点）．2．实例 . 十字路口——立交桥．立交桥中，两条路线 AB ， CD 既不平行，又不相交（非平面问题）．六角螺母DCA B二、新课讲解1.异面直线的定义不同在任何一个平面内的两条直线叫做异面直线．练习：在教室里找出几对异面直线的例子．注1：两直线异面的判别一 : 两条直线既不相交、又不平行．两直线异面的判别二 : 两条直线不同在任何一个平面内．合作探究一：分别在两个平面内的两条直线是否一定异面？答：不一定，它们可能异面，可能相交，也可能平行．空间两直线的位置关系：按平面基本性质分（1）同在一个平面内：相交直线、平行直线；（ 2）不同在任何一个平面内：异面直线．按公共点个数分（ 1）有一个公共点 : 相交直线；（ 2）无公共点：平行直线、异面直线．2．异面直线的画法说明：画异面直线时，为了体现它们不共面的特点，常借助一个或两个平面来衬托. 18。

2.1 空间点、直线、平面之间的位置关系2.1.1 平面知识梳理1 平面含义：平面是无限延展的2 三个公理：（1）公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内符号表示为【公理 1 作用】判断直线是否在平面内.（2）公理2：过不在一条直线上的三点，有且只有一个平面。

符号表示为：A、B、C三点不共线=> 有且只有一个平面α，使A∈α、B∈α、C∈α。

公理 2 作】确定一个平面的依据。

3）公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

符号表示为：P∈α∩β => α∩β =L，且P∈L【公理3作用】判定两个平面是否相交的依据知能训练一．选择题1．已知m，n 分别是两条不重合的直线，a，①若m⊥α，n∥b，且α⊥β，则m∥n；③若m∥α，n∥b，且α∥β，则m⊥n；其中真命题的序号是（）2．在下列命题中，不是公理的是（）A．平行于同一个平面的两个平面平行B．过不在同一直线上的三个点，有且只有一个平面C．如果一条直线上的两点在同一个平面内，那么这条直线上所有点都在此平面内D．如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线3．l1，l 2，l 3是空间三条不同的直线，则下列命题正确的是（）A．1 ⊥ l 2，l 2 ⊥ l 3?l 1 ∥ l 3B．1 ⊥ l 2，l 2 ∥l3?l 1⊥ l 3C．1∥ l 2∥l 3? l1，l 2 ，l 3 共面D．l1，l2，l3共点? l1，l2，l 3共面A．①②B．③④C．①④D．②③b 分别垂直于两不重合平面②若m∥a，n∥ b，且α④若m⊥α，n ⊥b，且4．下面四个说法中，正确的个数为（）（1）如果两个平面有三个公共点，那么这两个平面重合（2）两条直线可以确定一个平面（3）若M∈α，M∈β，α∩β =l ，则M∈l（4）空间中，相交于同一点的三直线在同一平面内．A． 1 B． 2 C． 3 D． 4 5．已知空间三条直线l 、m、n．若l 与m异面，且l 与n 异面，则（）A．m 与n 异面B．m与n 相交C．m 与n 平行D．m与n 异面、相交、平行均有可能6．若m、n 为两条不重合的直线，α、β 为两个不重合的平面，则下列命题中的真命题是（）A．若m、n 都平行于平面α，则m、n 一定不是相交直线B．若m、n 都垂直于平面α，则m、n 一定是平行直线C．已知α、β互相垂直，m、n 互相垂直，若m⊥α，n ⊥βD．m、n 在平面α内的射影互相垂直，则m、n 互相垂直7．已知平面α，β，γ，直线m，l ，点A，有下面四个命题，其中正确的命题是（）A．若l ? α，m∩α =A，则l 与m 必为异面直线B ．若l ∥α，l ∥m，则m∥αC ．若l ? α，m?β，l ∥β，m∥α，则α∥βD ．若α⊥γ，γ∩α=m，γ∩β =l ，l⊥m，则l ⊥α8．已知α，β 为互不重合的平面，m，n 为互不重合的直线，给出下列四个命题：①若m⊥α，n⊥α，则m∥n；②若m? α，n? α，m∥β，n∥β，，则α∥β；③若α⊥β，α∩β =m，n? α，n⊥m，则n⊥β；④若m⊥α，α⊥β，m∥ n，则n∥β．其中所有正确命题的序号是（）A．①③B．②④C．①④D．③④二．填空题9．（文）平面上三条直线x+2y-1=0 ，x+1=0，x+ky=0 ，如果这三条直线将平面划分为六部分，则实数k 的所有取值为．（将你认为所有正确的序号都填上）①0 ② 1/2 ③1 ④2 ⑤ 3．10．空间中有7 个点，其中有 3 个点在同一直线上，此外再无任何三点共线，由这7个点最多可确定个平面．三．解答题1．如图，在四边形ABCD中，已知AB∥ CD，直线AB，BC，AD，DC分别与平面α相交于点E，G，H，F．求证：E，F，G，H四点必定共线．2．四面体ABCD中，E、G分别为BC、AB的中点，F 在CD上，H在AD上，且有DF：FC=2：3．DH：HA=2 ：3．（1）证明：点G、E、F、H四点共面；（2）证明：EF、GH、BD交于一点．2.1.2 空间中直线与直线之间的位置关系1 空间的两条直线有如下三种关系：相交直线：同一平面内，有且只有一个公共点；共面直线平行直线：同一平面内，没有公共点；异面直线：不同在任何一个平面内，没有公共点。

数学必修二空间点、直线、平面的位置关系学校：__________ 班级：__________ 姓名：__________ 考号：__________1. 如图，平面不能用( )表示．A.平面αB.平面ABC.平面ACD.平面ABCD2. 已知m，n，l为三条不同的直线，α，β，γ为三个不同的平面，则下列命题中正确的是（）A.若m⊥l，n⊥l，则m // nB.若m // α，n // α，则m // nC.若m⊥α，n⊥α，则m // nD.若α⊥γ，β⊥γ，则α // β3. 对于不同点A、B，不同直线a、b、l，不同平面α，β，下面推理错误的是（）A.若A∈a，A∈β，B∈a，B∈β，则a⊂βB.若A∈α，A∈β，B∈α，B∈β，则α∩β=直线ABC.若l⊄α，A∈l，则A∉αD.a∩b=Φ，a不平行于b，则a、b为异面直线4. 若点B在直线b上，b在平面β内，则B、b、β之间的关系可记作（）A.B∈b∈βB.B∈b⊂βC.B⊂b⊂βD.B⊂b∈β5. 直线a、b为两异面直线，下列结论正确的是（）A.过不在a、b上的任何一点，可作一个平面与a、b都平行B.过不在a、b上的任一点，可作一直线与a、b都相交C.过不在a、b上任一点，可作一直线与a、b都平行D.过a可以并且只可以作一个平面与b平行6. 如图所示，平面α∩平面β=l，点A，B∈α，点C∈β，直线AB∩l=R．设过A，B，C三点的平面为γ，则β∩γ=（）A.直线ACB.直线BCC.直线CRD.以上均不正确7. 一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，则这两个二面角的关系是()A.相等B.互补C.相等或互补D.不确定8. 若点P为两条异面直线a，b外的任意一点，则下列说法一定正确的是( )A.过点P有且仅有一条直线与a，b都平行B.过点P有且仅有一条直线与a，b都垂直C.过点P有且仅有一条直线与a，b都相交D.过点P有且仅有一条直线与a，b都异面9. 在正方体ABCD−A1B1C1D1中，E为棱CC1上一点且CE=2EC1，则异面直线AE与A1B所成角的余弦值为()A.√1144B.√1122C.3√1144D.√111110. 空间中，如果一个角的两边和另一个角的两边分别对应平行，那么这两个角的大小关系为（）A.相等B.互补C.相等或互补D.互余11. 在棱长为2的正方体ABCD−A1B1C1D1中，异面直线AB和CC1的距离为________．12. 如图所示是一个正方体的表面展开图，A，B，C均为棱的中点，D是顶点，则在正方体中，异面直线AB和CD的夹角的余弦值为________．13. 如果一条直线不在平面内，那么这条直线与这个平面的位置关系是________．14. 已知a // β，a⊂α，α∩β=b，则a和b的位置关系是________．15. 设a、b为两条直线，α、β为两个平面，有下列四个命题：①若a⊂α，b⊂β，且a // b，则α // β；②若a⊂α，b⊂β，且a⊥b，则α⊥β；③若a // α，b⊂α，则a // b；④若a⊥α，b⊥α，则a // b；其中正确命题的序号为________．16. 设α，β是空间两个不同的平面，m，n是平面α及β外的两条不同直线．从“①m⊥n；②α⊥β；③n⊥β；④m⊥α”中选取三个作为条件，余下一个作为结论，写出你认为正确的一个命题：________（用代号表示）．17. 在空间直角坐标系O−xyz中，经过A(1, 0, 2)，B(1, 1, −1)，C(2, −1, 1)三个点的平面方程为________．18. 如图，在三棱柱ABC−A1B1C1中，D、E、F分别是A1B1、BC、B1C1的中点，则平面DEF与平面ACC1A1的位置关系是________．19. 如图，正方体的底面与正四面体的底面在同一平面α上，且AB // CD，则直线EF与正方体的六个面所在的平面相交的平面个数为________．20. 给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的一条垂线，那么这两个平面相互垂直；③垂直干同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中真命题是________（写出所有真命题的序号）21. 已知直线a，b，c，且a∩b＝A，a∩c＝B，b和c异面，试画出图形表示它们之间的关系．22. 举几对既不相交也不平行的直线的例子．23. 如图，已知E，F，G，H分别是空间四边形（四条线段首尾相接，且连接点不在同一个平面内，所组成的空间图形叫空间四边形）各边AB，AD，CB，CD上的点，且直线EF和HG交于点P，求证：点B，D，P在同一条直线上．24. 如图，过直线l外一点P，作直线a，b，c分别交直线l于点A，B，C，求证：直线a、b、c共面．25. 如图，已知E、F分别是正方体ABCD−A1B1C1D1的棱AA1和棱CC1上的中点，求证：四边形EBFD1是菱形．26. 在正方体ABCD−A1B1C1D1中，底面ABCD是正方形，若AC1=3,BC1=√5，则异面直线BC1与AD所成的角的正切值为________.27. 在长方体ABCD−A1B1C1D1中，E为DD1的中点．（1）判断BD1与平面AEC的位置关系，并证明你的结论．（2）若AB=BC=√3，CC1=2，求异面直线AE、BD1所成的角的余弦值．28. 如图，长方体ABCD−A1B1C1D1中，AB=AD=2，AA1=3，求异面直线A1B与B1C夹角的余弦值．29. 如图，已知长方体的长宽都是4cm，高为2cm．（1）求BC与A′C′，A′D与BC′所成角的余弦值；（2）求AA′与BC，AA′与CC′所成角的大小．30. 已知m，n是两条不同直线，α，β，γ是三个不同平面（1）若α⊥γ，β⊥γ，则α // β；（2）若m // α，m // β，则α // β；（3）若m // α，n // α，则m // n；（4）若m⊥α，n⊥α，则m // n．上述命题中正确的为________．31. 如图，已知ABCD是空间四边形，AB=AD，CB=CD，求证：BD⊥AC．32. 已知三条直线a、b、c，若这三条直线两两相交，且交点分别为A、B、C，试判断这三条直线是否共面．33. 如图，△ABC中，∠ABC=90∘，SA⊥平面ABC，E、F分别为点A在SC、SB上的射影．（1）求证：BC⊥SB；（2）求证：EF⊥SC．34. 三棱柱ABC−A1B1C1中，侧棱与底面垂直，∠ABC＝90∘，AB＝BC＝BB1＝2，M，N分别是AB，A1C的中点．(Ⅰ)求证：MN // 平面BCC1B1；(Ⅱ)求证：MN⊥平面A1B1C．35. 如图所示的一块木料中，棱BC平行于面A′C′．（1）要经过面A′C′内的一点P和棱BC将木料锯开，应怎样画线？（写出画法步骤，并在图中画出）（2）说明所画的线与平面AC的位置关系．36. 直线a // b，a与平面α相交，判定b与平面α的位置关系，并证明你的结论．37. 如图，在四棱锥P−ABCD中，有同学说平面PAD∩平面PBC=P，这句话对吗？请说明理由．38.（1）如图，对于任一给定的四面体A1A2A3A4，找出依次排列的四个相互平行的α1，α2，α3，α4，使得A i∈αi(i=1, 2, 3, 4)，且其中每相邻两个平面间的距离都相等；（2）给定依次排列的四个相互平行的平面α1，α2，α3，α4，其中每相邻两个平面间的距离都为1，若一个正四面体A1A2A3A4的四个顶点满足：A i∈αi(i=1, 2, 3, 4)，求该正四面体A1A2A3A4的体积．39. 如图，a，b是异面直线，A，C与B，D分别是a，b上的两点，直线a // 平面a，直线b // 平面a，AB∩a=M，CD∩a=N，若AM=BM，求证：CN=DN．40. 如图，已知平面α、β，且α∩β=l．设梯形ABCD中，AD // BC，且AB⊂α，CD⊂β．求证：AB，CD，l共点（相交于一点）．参考答案与试题解析数学必修二空间点、直线、平面的位置关系一、选择题（本题共计 10 小题，每题 3 分，共计30分）1.【答案】B【考点】平面的概念、画法及表示【解析】利用平面的表示方法，对每个选项逐一判断即可.【解答】解：A．平面可用希腊字母α，β，γ表示，故A正确；B．平面不可用平行四边形的某条边表示，故B错误；C．平面可用平行四边形的对角的两个字母表示，故C正确；D．平面可用平行四边形的顶点表示，故D正确.故选B.2.【答案】C【考点】空间中直线与平面之间的位置关系空间中平面与平面之间的位置关系【解析】根据空间线面位置关系的情况举出反例判断或根据性质说明．【解答】对于A，当l⊥α，m⊂α，n⊂α时，显然有m⊥l，n⊥l，单m与n可能平行，也可能相交，故A错误．对于B，若α // β，m⊂β，n⊂β，则m // α，n // α，但m，n可能平行也可能相交，故B错误．对于C，由线面平行的性质“垂直于同一个平面的两条直线平行“可知C正确．对于D，当三个平面α，β，γ两两垂直时，显然结论错误．3.【答案】C【考点】平面的基本性质及推论【解析】在A中，由直线a上有两个点A，B都在β内，知a⊂β；在B中，由不同点A、B分别是两个不同平面α，β的公共点，知α∩β=直线AB；在C中，由l⊄α，A∈l，知A有可能是l与α的交点；在D中，因a∩b=Φ，a不平行于b，知a、b为异面直线．【解答】解：在A中，∵直线a上有两个点A，B都在β内，∴a⊂β，故A正确；在B中，∵不同点A、B分别是两个不同平面α，β的公共点，∴α∩β=直线AB，故B正确；在C中，∵l⊄α，A∈l，∴A有可能是l与α的交点，故C错误；在D中，∵a∩b=Φ，a不平行于b，∴a、b为异面直线，故D正确．故选C．4.【答案】B【考点】平面的概念、画法及表示【解析】由题意，点B在直线b上，b在平面β内，点与面之间的关系是属于关系，线与面之间的关系是包含关系，由此三者之间的关系易得【解答】解：由题意，点B在直线b上，b在平面β内，则B、b、β之间的关系可记作B∈b⊂β故选B5.【答案】D【考点】异面直线的判定【解析】若此点与直线a确定一平面β恰好与直线b平行，可得a⊂β，可判断A的真假；结合空间中直线关系的定义及几何特征，可判断B的真假；依据平行公理，即可判断C的真假；由公理2及其推论，我们可以判断D的真假．【解答】解：A中：若此点与直线a确定一平面β恰好与直线b平行，此时直线a在已知平面上，并非与已知平面平行，故A错误；B中：由①可得，当此点在β平面上时，结论B不成立；C中：若存在这样的直线l，则l // a，l // b，有平行公理知，必有a // b，与已知矛盾，故C错误；D中：在直线a上取A、B点，过A、B分别作直线c、d与直线b平行，c、d可确定平面α，即b平行于α，此时a在α平面上，故D正确；故答案为D6.【答案】C【考点】平面的基本性质及推论【解析】此题暂无解析【解答】解：由题意知，∵AB∩l=R，平面α∩平面β=l，∴ R ∈l ，l ⊂β，R ∈AB ，∴ R ∈β．又∵ A ，B ，C 三点确定的平面为γ，∴ C ∈γ，AB ⊂γ，∴ R ∈γ．又∵ C ∈β，∴ C ，R 是平面β和γ的公共点，∴ β∩γ=CR ．故选C ．7.【答案】D【考点】平行公理【解析】根据题意，可在正方体中，举例说明，得到答案【解答】如图所示，在正方体ABCD −A 1B 1C 1D 1中，二面角D −AA 1−F 与二面角D 1−DC −A 的两个半平面分别对应垂直，但是这两个二面角既不相等，也不互补，所以这两个二面角不一定相等或互补．．AB例如：开门的过程中，门所在平面及门轴所在墙面分别垂直于地面与另一墙面，但门所在平面与门轴所在墙面所成二面角的大小不定，而另一二面角却是90∘，所以这两个二面角不一定相等或互补．8.【答案】B【考点】异面直线的判定【解析】A 通过反证法可以判定；B 由异面直线公垂线的唯一性可以判定；C 、D 利用常见的图形举出反例即可．【解答】解：设过点P 的直线为n ，且{n//a,n//b,， ∴ a // b ，这与a ，b 异面矛盾，选项A 错误；∵ 异面直线a ，b 有唯一的公垂线，∴ 过点P 与公垂线平行的直线有且只有一条，选项B 正确；如图所示的正方体中，设AD 为直线a ，A′B′为直线b ，若点P 在P 1点处，则无法作出直线与两直线都相交， ∴ 选项C 错误；如图所示的正方体中，若P 在P 2点，则由图中可知直线CC′及D′P 2均与a ，b 异面， ∴ 选项D 错误.故选B .9.【答案】B【考点】异面直线及其所成的角【解析】本题考查建立适当的空间直角坐标系，利用向量方法求解即可.【解答】解：建立如图所示空间直角坐标系，如图，设正方体棱长为1，则A(0,0,0)，E (1,1,23)，A 1(0,0,1)，B(1,0,0),∴ AE →=(1,1,23)，A 1B →=(1,0,−1),∴ cos <AE →,A 1B →>=AE →⋅A 1B →|AE||A 1B|=1−2 3√12+12+(23)2⋅√12+(−1)2=√1122.故选B．10.【答案】C【考点】平行公理【解析】根据等角定理：如果一个角的两边和另一个角的两边分别对应平行并且方向相同，那么这两个角的相等，从而易知本题答案．【解答】解：根据等角定理：如果一个角的两边和另一个角的两边分别对应平行并且方向相同，那么这两个角的相等．本题的条件是：一个角的两边和另一个角的两边分别对应平行，由于没有指出角的对应两边的方向情况，故两个角可能相等或互补．故选C．二、填空题（本题共计 10 小题，每题 3 分，共计30分）11.【答案】2【考点】空间中直线与直线之间的位置关系【解析】由题意，异面直线AB和CC1的距离为BC，即可得出结论．【解答】解：由题意，异面直线AB和CC1的距离为BC=2．故答案为：2．12.【答案】√105【考点】异面直线及其所成的角【解析】建立空间坐标系，分别求出两条异面直线的方向向量，利用向量的夹角公式即可得出．【解答】解：如图所示，建立空间坐标坐标系．取正方体的棱长为2．则B(1, 2, 0)，A(2, 2, 1)，D(2, 0, 2)，C(2, 1, 0)．∴ BA →=(1, 0, 1)，CD →=(0, −1, 2)．∴ cos <BA →，CD →>=|BA →|⋅|CD →|˙=2√2⋅√5=√105． ∴ 异面直线AB 和CD 的夹角的余弦值为√105． 故答案为：√105． 13. 【答案】平行或相交【考点】空间中直线与平面之间的位置关系【解析】利用直线与平面的位置关系求解．【解答】解：∵ 直线与平面的位置关系有三种：平行、相交或直线在平面内，∴ 如果一条直线不在平面内，那么这条直线与这个平面的位置关系是平行或相交．故答案为：平行或相交．14.【答案】平行【考点】空间中直线与直线之间的位置关系【解析】根据线面平行的性质定理判断出a // b ．【解答】解：∵ a // β，a ⊂α，α∩β=b ，∴ 由线面平行的性质定理得，a // b ，故答案为：平行．15.【答案】④【考点】空间中平面与平面之间的位置关系空间中直线与直线之间的位置关系【解析】根据空间中面面平行的判定方法，面面垂直的判定方法，线面平行的性质及线面垂直的性质，我们对已知中四个结论逐一进行判断即可得到结论．【解答】解：若a⊂α，b⊂β，且a // b，则α与β可能平行与可能相交，故①错误；若a⊂α，b⊂β，且a⊥b，则α与β可能平行与可能相交，故②错误；若a // α，b⊂α，则a与b可能平行与可能异面，故③错误；若a⊥α，b⊥α，则a // b，故④正确；故答案为：④16.【答案】①③④⇒②（或②③④⇒①）【考点】空间中平面与平面之间的位置关系空间中直线与平面之间的位置关系【解析】分析本题中的条件，四个条件取三个，有四种组合，由于本题是一开放式题答案不唯一，故选取其一即可．【解答】解：观察发现，①③④⇒②与②③④⇒①是正确的命题，证明如下：证①③④⇒②，即证若m⊥n，n⊥β，m⊥α，则α⊥β，因为m⊥n，n⊥β，则m⊂β或m // β，又m⊥α故可得α⊥β，命题正确；证②③④⇒①，即证若n⊥β，m⊥α，α⊥β，则m⊥n，因为m⊥α，α⊥β则m⊂β或m // β，又m⊥α故可得m⊥n，命题正确．故答案为：①③④⇒②（或②③④⇒①）．17.【答案】4x+3y+z＝6【考点】平面的概念、画法及表示【解析】设过A、B、C三点的平面方程为Ax+By+Cz＝D，把点的坐标代入方程求得A、B、C的值，从而求得平面方程．【解答】设过A(1, 0, 2)，B(1, 1, −1)，C(2, −1, 1)三点的平面方程为Ax+By+Cz＝D，则A+2C＝D①，A+B−C＝D②，2A−B+C＝D③，由①②③组成方程组，解得A=2D3，B=D2，C=D6；∴2D3x+D2y+D6z＝D，化简得4x+3y+z＝（6）18.【答案】平行【考点】空间中平面与平面之间的位置关系【解析】根据面面平行的判定定理，判断两个平面平行即可．【解答】解：因为D、E、F分别是A1B1、BC、B1C1的中点，所以BD // A1C1，BE // C1C，所以BD // 面A1B1C1，BE // 面A1B1C1，因为DB∩BE=E，所以平面DEF // ACC1A1．故答案为：平行．19.【答案】4【考点】平面的基本性质及推论【解析】判断EF与正方体表面的关系，即可推出正方体的六个面所在的平面与直线EF相交的平面个数即可．【解答】由题意可知直线EF与正方体的左右两个侧面平行，与正方体的上下底面相交，前后侧面相交，所以直线EF与正方体的六个面所在的平面相交的平面个数为4．20.【答案】②④【考点】平面的基本性质及推论【解析】利用两个平面平行的判断判断出①错；利用两个平面垂直的判断判断出②对；利用垂直于同一条直线的直线的位置关系判断出③错；利用两个平面垂直的性质判断出④对．【解答】解：对于①，若一个平面内的两条相交直线与另一个平面都平行，那么这两个平面相互平行，故①错对于②，若一个平面经过另一个平面的一条垂线，那么这两个平面相互垂直是两个平面垂直的判断定理，故②对对于③，垂直干同一直线的两条直线相互平行、相交或异面，故③错．对于④，若两个平面垂直，那么一个平面内与它们的交线垂直的直线与另一个平面也垂直．故④对故答案为：②④．三、 解答题 （本题共计 20 小题 ，每题 10 分 ，共计200分 ）21.【答案】∵ a ∩b ＝A ，a ∩c ＝B ，b 和c 异面，∴ 画图表示如下：．【考点】异面直线的判定【解析】根据直线a ，b ，c 的关系，画出图形即可．【解答】∵ a ∩b ＝A ，a ∩c ＝B ，b 和c 异面，∴ 画图表示如下：．22.【答案】既不相交也不平行的直线是异面直线，如图，在正方体A 1B 1C 1D 1−ABCD 中，AB 和A 1D 1，B 1C 1都构成异面直线，BC 和A 1B 1，C 1D 1→都构成异面直线．【考点】异面直线的判定【解析】可知，既不相交也不平行的直线是异面直线，可画出一个正方体，找出几对上面的异面直线即可．【解答】既不相交也不平行的直线是异面直线，如图，在正方体A 1B 1C 1D 1−ABCD 中，AB 和A 1D 1，B 1C 1都构成异面直线，BC 和A 1B 1，C 1D 1→都构成异面直线．23.【答案】证明：∵ E ，F ，G ，H 分别是空间四边形ABCD 各边AB ，AD ，CB ，CD 上的点， ∴ 由公理一，得EF ⊂平面ABD ，GH ⊂平面CBD ，∵ 面ABD ∩面CBD =BD ，直线EF 和HG 交于点P ，∴ 由公理三得P ∈BD ，∴ 点B ，D ，P 在同一条直线上．．【考点】平面的基本性质及推论【解析】由公理一，得EF⊂平面ABD，GH⊂平面CBD，由公理三得P∈BD，由此能证明点B，D，P在同一条直线上．．【解答】证明：∵E，F，G，H分别是空间四边形ABCD各边AB，AD，CB，CD上的点，∴由公理一，得EF⊂平面ABD，GH⊂平面CBD，∵面ABD∩面CBD=BD，直线EF和HG交于点P，∴由公理三得P∈BD，∴点B，D，P在同一条直线上．．24.【答案】证明：设直线l与l外一点P确定的平面为α，则P∈平面α，又A∈直线l，∴A∈平面α；又P∈直线a，A∈直线a，∴直线a⊂平面α；同理直线b⊂平面α，直线c⊂平面α，∴直线a、b、c共面．【考点】平面的基本性质及推论【解析】先设直线l与l外一点P确定一个平面α，再证明直线a⊂平面α，同理得出直线b、c⊂平面α即可．【解答】证明：设直线l与l外一点P确定的平面为α，则P∈平面α，又A∈直线l，∴A∈平面α；又P∈直线a，A∈直线a，∴直线a⊂平面α；同理直线b⊂平面α，直线c⊂平面α，∴直线a、b、c共面．25.【答案】证明：取棱BB1中点为G，连C1G、EG，由正方体性质，侧面ABB1A1为正方形，又E、G分别为边AA1、BB1中点，所以EG=A1B1=C1D1，EG // A1B1 // C1D1，从而四边形EGC1D1为平行四边形，∴D1E // C1G，D1E=C1G，又F、G分别为棱CC1、BB1中点，由侧面CBB1C1为正方形，知四边形BGC1F为平行四边形，所以BF // C1G，BF=C1G，又∴D1E // C1G，D1E=C1G，由平行公理可知D1E=BF，D1E // BF，从而四边形EBFD1为平行四边形．由ABCD−A1B1C1D1为正方体，不妨设其棱长为a，易a知BE=BF=√52而由四边形EBFD1为平行四边形，从而即为菱形．【考点】平行公理【解析】根据菱形的定义直接证明即可．【解答】证明：取棱BB1中点为G，连C1G、EG，由正方体性质，侧面ABB1A1为正方形，又E、G分别为边AA1、BB1中点，所以EG=A1B1=C1D1，EG // A1B1 // C1D1，从而四边形EGC1D1为平行四边形，∴D1E // C1G，D1E=C1G，又F、G分别为棱CC1、BB1中点，由侧面CBB1C1为正方形，知四边形BGC1F为平行四边形，所以BF // C1G，BF=C1G，又∴D1E // C1G，D1E=C1G，由平行公理可知D1E=BF，D1E // BF，从而四边形EBFD1为平行四边形．由ABCD−A1B1C1D1为正方体，不妨设其棱长为a，易a知BE=BF=√52而由四边形EBFD1为平行四边形，从而即为菱形．26.【答案】12【考点】异面直线及其所成的角【解析】此题暂无解析【解答】解：设AB=a，因为ABCD是正方形，所以AC=√2a.所以CC1⊥AC,CC1⊥BC，所以CC12=AC12−AC2=BC12−BC2，即9−2a2=5−a2，解得a=2.所以CC1=1，因为AD//BC，所以∠CBC1即异面直线BC1与AD所成的角，tan∠CBC1=CC1BC =12.故答案为：12.27.【答案】解：（1）BD1 // 平面AEC，如图，连结BD交AC于O，则O为BD中点，连结OE；∵E为DD1的中点，∴OE // BD1；∵OE⊂平面AEC，BD1⊄平面AEC；∴BD1 // 平面AEC；（2）∵OE // BD1；∴异面直线AE，BD1所成的角为∠AEO；∵AB=BC=√3，CC1=2；∴EA=EC=2，EO=12BD1=√102；∴EO⊥AC；∴Rt△AEO中，cos∠AEO=EOEA =√104；因此，异面直线AE，BD1所成的角的余弦值为√104．【考点】异面直线及其所成的角空间中直线与平面之间的位置关系【解析】（1）连接BD，设交AC于O，连接EO，便可说明BD1 // OE，由线面平行的判定定理即（2）由上面BD1 // OE即可得到异面直线AE、BD1所成的角为∠AEO，而通过条件可说明OE⊥AC，并且可求出AE，OE，从而根据直角三角形的边角关系cos∠AEO=EOAE，这样即可求出异面直线AE，BD1所成角的余弦值．【解答】解：（1）BD1 // 平面AEC，如图，连结BD交AC于O，则O为BD中点，连结OE；∵E为DD1的中点，∴OE // BD1；∵OE⊂平面AEC，BD1⊄平面AEC；∴BD1 // 平面AEC；（2）∵OE // BD1；∴异面直线AE，BD1所成的角为∠AEO；∵AB=BC=√3，CC1=2；∴EA=EC=2，EO=12BD1=√102；∴EO⊥AC；∴Rt△AEO中，cos∠AEO=EOEA =√104；因此，异面直线AE，BD1所成的角的余弦值为√104．28.【答案】【考点】异面直线及其所成的角【解析】此题暂无解析【解答】此题暂无解答29.【答案】解：（1）∵ 长方体ABCD −A ′B ′C ′D ′中，BC // A′C′∴ ∠A ′C ′B ′就是异面直线BC 与A′C′所成角 Rt △A ′B ′C ′中，A′C′=√42+42=4√2 ∴ cos ∠A ′C ′B ′=B ′C‘A′C′=√22； 连结B ′C ，可得四边形A ′DCB ′是平行四边形，∴ A ′D // CB ′，直线B ′C 与BC ′所成的角就是A′D 与BC′所成的角 矩形BB ′C ′C 中，BC ′=B ′C =√42+22=2√5 设A′D 与BC′所成的角为θ，则由余弦定理得cos θ=2×√5×√5=35综上所述，可得BC 与A′C′，A′D 与BC′所成角的余弦值分别为√22和35； （2）∵ 长方体ABCD −A ′B ′C ′D ′中，AA ′ // BB ′∴ ∠B ′BC （或其补角）就是AA′与BC 所成的角 矩形BB ′C ′C 中，可得∠B ′BC =90∘；又∵ AA′ // CC′，∴ AA′与CC′所成角为0∘综上所述AA′与BC ，AA′与CC′所成角的大小分别为90∘和0∘．【考点】异面直线及其所成的角 【解析】（1）根据长方体的性质，可得∠A ′C ′B ′就是异面直线BC 与A′C′所成角，在Rt △A ′B ′C ′中，利用三角函数的定义可得cos ∠A ′C ′B ′=√22，即为BC 与A′C′所成角的余弦值．同理可得直线B ′C 与BC ′所成的角就是A′D 与BC′所成的角，结合余弦定理加以计算即可得到A′D 与BC′所成角的余弦值；（2）根据长方体的性质可得AA ′ // BB ′，因此矩形BB ′C ′C 中，∠B ′BC =90∘就是AA′与BC 所成的角；再由AA′ // CC′，得到AA′与CC′所成角为0∘． 【解答】解：（1）∵ 长方体ABCD −A ′B ′C ′D ′中，BC // A′C′∴ ∠A ′C ′B ′就是异面直线BC 与A′C′所成角 Rt △A ′B ′C ′中，A′C′=√42+42=4√2 ∴ cos ∠A ′C ′B ′=B ′C‘A′C′=√22； 连结B ′C ，可得四边形A ′DCB ′是平行四边形，∴ A ′D // CB ′，直线B ′C 与BC ′所成的角就是A′D 与BC′所成的角 矩形BB ′C ′C 中，BC ′=B ′C =√42+22=2√5设A′D 与BC′所成的角为θ，则由余弦定理得cos θ=5+5−162×√5×√5=35综上所述，可得BC 与A′C′，A′D 与BC′所成角的余弦值分别为√22和35；（2）∵ 长方体ABCD −A ′B ′C ′D ′中，AA ′ // BB ′ ∴ ∠B ′BC （或其补角）就是AA′与BC 所成的角 矩形BB ′C ′C 中，可得∠B ′BC =90∘；又∵ AA′ // CC′，∴ AA′与CC′所成角为0∘综上所述AA′与BC ，AA′与CC′所成角的大小分别为90∘和0∘． 30.【答案】 （4）． 【考点】空间中平面与平面之间的位置关系 空间中直线与直线之间的位置关系【解析】根据题意，分析4个命题：（1）由α⊥γ，β⊥γ，得α // β，或α∩β； （2）由m // α，m // β，得α // β，或α∩β；（3）由m // α，n // α，得m // n ，或m ∩n ，或m ，n 异面；（4）由m ⊥α，n ⊥α，根据线面垂直的性质，得m // n ．进而可得答案． 【解答】 解：（1）命题不一定成立，因为α⊥γ，β⊥γ时，α，β可能平行，也可能相交； （2）命题不一定成立，因为m // α，m // β时，α，β可能平行，也可能相交； （3）命题不一定成立，因为m // α，n // α时，直线m ，n 可能平行，也可能相交，也可能异面；（4）命题是正确的，因为m ⊥α，n ⊥α时，由垂直于同一平面的两条直线平行，得m // n ．所以，上述正确的命题只有（4）． 31.【答案】证明：取BD 的中点O ，连接AO ，CO ． ∵ AB =AD ，∴ AO ⊥BD ， ∵ CB =CD ，∴ CO ⊥BD ， 又AO ∩CO =O ， ∴ BD ⊥平面ACO ， AC ⊂平面ACO ，∴BD⊥AC．【考点】空间中直线与直线之间的位置关系【解析】取BD的中点O，连接AO，CO．由等腰三角形的三线合一，得到AO⊥BD，CO⊥BD，再由线面垂直的判定定理得到BD⊥平面ACO，运用线面垂直的性质即可得证．【解答】证明：取BD的中点O，连接AO，CO．∵AB=AD，∴AO⊥BD，∵CB=CD，∴CO⊥BD，又AO∩CO=O，∴BD⊥平面ACO，AC⊂平面ACO，∴BD⊥AC．32.【答案】解：如图，三条直线a、b、c两两相交，且交点分别为A、B、C，设a，b确定一个平面α，∵B∈a，C∈a，A∈b，C∈b，∴A∈α，B∈α，又∵A∈c，B∈c，∴c⊂α，∴三条直线a，b，c共面于α．∴这三条直线共面．【考点】空间中直线与直线之间的位置关系【解析】利用设a，b确定一个平面α，由已知条件利用公理二能推导出c⊂α，从而这三条直线a，b，c共面于α．【解答】解：如图，三条直线a、b、c两两相交，且交点分别为A、B、C，设a，b确定一个平面α，∵B∈a，C∈a，A∈b，C∈b，∴A∈α，B∈α，又∵A∈c，B∈c，∴c⊂α，∴三条直线a，b，c共面于α．∴这三条直线共面．33.【答案】证明：（1）∵ SA ⊥面ABC ，BC ⊂平面ABC ， ∴ SA ⊥BC ，又∵ AB ⊥BC ，SA ∩AB =A ， ∴ BC ⊥平面SAB ， ∵ SB ⊂平面SAB ， ∴ BC ⊥SB ；（2）∵ AF ⊂平面SAB ，BC ⊥平面SAB ， ∴ BC ⊥AF ，∵ AF ⊥SB ，且BC ∩SB =B ， ∴ AF ⊥平面SBC ， ∵ SC ⊂平面SBC ，∴ SC ⊥AF ，又AE ⊥SC ，且AF ∩AE =A ， ∴ SC ⊥平面AEF ， ∴ EF ⊥SC ．【考点】空间中直线与直线之间的位置关系 【解析】（1）证明BC ⊥平面SAB ，然后，从而得到BC ⊥SB ；（2）对于EF ⊥SC 的证明，可以先证明SC ⊥平面EF ，然后，很容易得到EF ⊥SC ． 【解答】 证明：（1）∵ SA ⊥面ABC ，BC ⊂平面ABC ， ∴ SA ⊥BC ，又∵ AB ⊥BC ，SA ∩AB =A ， ∴ BC ⊥平面SAB ， ∵ SB ⊂平面SAB ， ∴ BC ⊥SB ；（2）∵ AF ⊂平面SAB ，BC ⊥平面SAB ， ∴ BC ⊥AF ，∵ AF ⊥SB ，且BC ∩SB =B ， ∴ AF ⊥平面SBC ， ∵ SC ⊂平面SBC ，∴ SC ⊥AF ，又AE ⊥SC ，且AF ∩AE =A ， ∴ SC ⊥平面AEF ， ∴ EF ⊥SC ． 34.【答案】证明：(Ⅰ)证明：连接BC 1，AC 1．在△ABC 1中，∵ M ，N 是AB ，A 1C 的中点，∴ MN||BC 1． 又∵ MN ⊄平面BCC 1B 1，∴ MN||平面BCC 1B 1．（2）如图，以B 1为原点建立空间直角坐标系B 1−xyz ．则B 1(0, 0, 0)，C(0, 2, 2)，A 1(−2, 0, 0)，M(−1, 0, 2)，N(−1, 1, 1) ∴ B 1C →=(0, 2, 2)，A 1B 1→=(2,0,0)，NM →=(0,−1,1)． 设平面A 1B 1C 的法向量为n ＝(x, y, z)．{n ⋅B 1C →=0n ⋅A 1B 1→=0⇒{x =0y =−z令z ＝1，则x ＝0，y ＝−1，∴ n ＝(0, −1, 1)． ∴ n =NM →．∴ MN ⊥平面A 1B 1C ．【考点】空间中直线与平面之间的位置关系 【解析】(Ⅰ)欲证MN||平面BCC 1B 1，根据直线与平面平行的判定定理可知只需证MN 与平面BCC 1B 1内一直线平行即可，而连接BC 1，AC 1．根据中位线定理可知MN||BC 1，又MN ⊄平面BCC 1B 1满足定理所需条件；(Ⅱ)以B 1为原点，A 1B 1为x 轴，B 1B 为y 轴，B 1C 1为z 轴建立空间直角坐标系B 1−xyz ，求出平面A 1B 1C 的法向量为n ＝(x, y, z)，而n =NM →，根据法向量的意义可知MN ⊥平面A 1B 1C ． 【解答】证明：(Ⅰ)证明：连接BC 1，AC 1．在△ABC 1中，∵ M ，N 是AB ，A 1C 的中点，∴ MN||BC 1． 又∵ MN ⊄平面BCC 1B 1，∴ MN||平面BCC 1B 1．（2）如图，以B 1为原点建立空间直角坐标系B 1−xyz ．则B 1(0, 0, 0)，C(0, 2, 2)，A 1(−2, 0, 0)，M(−1, 0, 2)，N(−1, 1, 1) ∴ B 1C →=(0, 2, 2)，A 1B 1→=(2,0,0)，NM →=(0,−1,1)． 设平面A 1B 1C 的法向量为n ＝(x, y, z)．{n ⋅B 1C →=0n ⋅A 1B 1→=0 ⇒{x =0y =−z令z ＝1，则x ＝0，y ＝−1，∴ n ＝(0, −1, 1)． ∴ n =NM →．∴ MN ⊥平面A 1B 1C ．35.【答案】解：（1）过点P作B′C′的平行线，交A′B′、C′D′于点E，F，连结BE，CF；作图如右图，（2）易知BE，CF与平面AC的相交，∵BC // 平面A′C′，又∵平面B′C′CB∩平面A′C′=B′C′，∴BC // B′C′，∴EF // BC，又∵EF⊄平面AC，BC⊂平面AC，∴EF // 平面AC．【考点】空间中直线与平面之间的位置关系【解析】（1）注意到棱BC平行于面A′C′，故过点P作B′C′的平行线，交A′B′、C′D′于点E，F，连结BE，CF；（2）易知BE，CF与平面AC的相交，可证EF // 平面AC．【解答】解：（1）过点P作B′C′的平行线，交A′B′、C′D′于点E，F，连结BE，CF；作图如右图，（2）易知BE，CF与平面AC的相交，∵BC // 平面A′C′，又∵平面B′C′CB∩平面A′C′=B′C′，∴BC // B′C′，∴EF // BC，又∵EF⊄平面AC，BC⊂平面AC，∴EF // 平面AC．36.【答案】解：判定b与平面α的位置关系是b∩α=Q，下面给出证明：如图所示，∵a // b，∴可以经过直线a，b确定一个平面β．∵a∩α=P，∴α∩β=l．则b与直线l必然相交，否则b // l，则a // l，与a∩l=P相矛盾．因此b∩l=Q，∴b∩α=Q．【考点】空间中直线与平面之间的位置关系【解析】判定b与平面α的位置关系是b∩α=Q，可用反证法给出证明：如图所示，由于a // b，可以经过直线a，b确定一个平面β．由于a∩α=P，可得α∩β=l．可得b与直线l必然相交，否则b // l，得出矛盾．【解答】解：判定b与平面α的位置关系是b∩α=Q，下面给出证明：如图所示，∵a // b，∴可以经过直线a，b确定一个平面β．∵a∩α=P，∴α∩β=l．则b与直线l必然相交，否则b // l，则a // l，与a∩l=P相矛盾．因此b∩l=Q，∴b∩α=Q．37.【答案】解：由平面与平面的基本性质可知，如果两个平面相交，有且仅有结果该点的公共直线，所以如图，在四棱锥P −ABCD 中，有同学说平面PAD ∩平面PBC =P ，这句话不正确．【考点】平面的基本性质及推论空间中直线与平面之间的位置关系【解析】利用平面的基本性质判断即可．【解答】解：由平面与平面的基本性质可知，如果两个平面相交，有且仅有结果该点的公共直线，所以如图，在四棱锥P −ABCD 中，有同学说平面PAD ∩平面PBC =P ，这句话不正确． 38.【答案】解：（1）如图所示，取A 1A 4的三等分点p 2，p 3，A 1A 3的中点M ，A 2A 4，的中点N ， 过三点A 2，P 2，M ，作平面α2，过三点A 3，P 3，N 作平面α3，因为A 2P 2 // NP 3，A 3P 3 // MP 2，所以平面α2 // α3，再过点A 1，A 4，分别作平面α1，α4，与平面α3平行，那么四个平面α1，α2，α3，α4依次互相平行，由线段A 1A 4被平行平面α1，α2，α3，α4截得的线段相等知，其中每相邻两个平面间的距离相等，故α1，α2，α3，α4为所求平面．（2）：当（1）中的四面体为正四面体，若所得的四个平行平面每相邻两平面之间的距离为1，则正四面体A 1A 2A 3A 4就是满足题意的正四面体．设正四面体的棱长为a ，以△A 2A 3A 4的中心O 为坐标原点，以直线A 4O 为y 轴，直线OA 1为Z 轴建立如图所示的右手直角坐标系，则A 1(0, 0, √63a)，A 2(−a 2, √36a, 0)，A 3(a 2, √36a, 0)，A 4(0, −√33a, 0)． 令P 2，P 3为．A 1A 4的三等分点，N 为A 2A 4的中点，有P 3(0, −2√39a, √69a)，N(−a 4, −√312a, 0)，所以P 3N →=(−a 4, 5√336a, −√69a)，NA 3→=(34a, √34a, 0)，A 4N →=(−a 4, √34a, 0)。

2.1 《空间点、直线、平面之间的位置关系》导学案【学习目标】 1.能够从日常生活实例中抽象出数学中所说的“平面”；2.理解平面的无限延展性；3.理解公理1、2、3、4；4.了解空间中两条直线的位置关系；5.理解异面直线的概念、画法，培养学生的空间想象能力；6.理解并掌握等角定理；7.异面直线所成角的定义、范围及应用；8.了解空间中直线与平面的位置关系；9.了解空间中平面与平面的位置关系.【重点难点】重点：1.异面直线的概念；2.公理4；3.空间直线与平面、平面与平面之间的位置关系难点：用图形表达直线与平面、平面与平面的位置关系；异面直线所成角的计算及等角定理.【学法指导】自主探索与合作交流相结合【知识链接】空间几何体【学习过程】一.预习自学1．平面概述（1）平面的两个特征：①无限延展②没有厚度（2）平面的画法：（3）平面的表示：平面可以看成点的集合，点A在平面错误!未找到引用源。

内，记作，点B不在平面错误!未找到引用源。

内，记作2．三个公理公理1：用数学符号表示为：公理2：公理3：用数学符号表示为：3．空间中直线与直线的位置关系（1）异面直线：（2）空间两条直线的位置关系：相交直线——在同一平面内，；平行直线——在同一平面内，；异面直线——，没有公共点.相交直线和平行直线也称为共面直线.异面直线的画法（3）在平面几何中，平行于同一条直线的两条直线互相平行，这个结论在空间也是成立的.公理4：（平行线的传递性）（4）等角定理:（5）异面直线 a ,b 所成的角（异面直线 a ,b 的夹角）（6）如果两条异面直线 a ,b，那么我们就说异面直线a ,b 互相垂直，记作所以，在空间里说两条直线互相垂直包括相交垂直和异面垂直两种情况.4.空间中直线与平面的位置关系（1）（无数个公共点）；（2）（有且只有一个公共点）；（3）（没有公共点）直线和平面相交或平行统称用图形分别可表示为用符号分别可表示为5．两个平面的位置关系（1）（没有公共点）（2）（有一条公共直线）平面错误!未找到引用源。

一、选择题【共10道小题】1、给出的下列命题中,正确命题的个数是( )①梯形的四个顶点在同一平面内②三条平行直线必共面③有三个公共点的两个平面必重合④每两条都相交且交点各不相同的四条直线一定共面A.1B.2C.3D.4参考答案与解析:思路解析:逐个对各选项分析:梯形是一个平面图形,所以其四个顶点在同一个平面内,①对;两条平行直线是可以确定一个平面的,三条平行直线有可能确定三个平面,②错;三个公共点可以同在两个相交平面的公共直线上,③错;设这四条直线分别为l1、l2、l3、l4,取其中两条相交直线l1和l2,则它们可确定一个平面α,取l3,设其与l1、l2的交点分别为A、B,则由题意知这两点不同,且A∈l1,B∈l2,所以有A、B∈α,从而l3∈α;同理可证明l4∈α.所以每两条都相交且交点各不相同的四条直线一定共面,④对.答案:B主要考察知识点:空间直线和平面2、如图2-1-17,空间四边形SABC中,各边及对角线长都相等,若E、F分别为SC、AB的中点,那么异面直线EF与SA所成的角等于( )A.90°B.60°C.45°D.30°图2-1-17参考答案与解析:思路解析:求EF与SA所成的角,可把SA平移,使其角的顶点在EF上,为此取SB的中点G,连结GE、GF、BE、AE.由三角形中位线定理得GE=BC,GF=SA,且GF∥SA,所以∠GFE就是EF与SA所成的角.若设此空间四边形边长为a,那么GF=GE=a,EA=a,EF=a,因此△EFG为等腰直角三角形,∠EFG=45°,所以EF与SA所成的角为45°.答案:C主要考察知识点:空间直线和平面3、如果直线a∥平面α,那么直线a与平面α内的( )A.一条直线不相交B.两条直线不相交C.无数条直线不相交D.任意一条直线不相交参考答案与解析:思路解析:利用线面平行的定义.直线a∥平面α,则a与α无公共点,与α内的直线当然均无公共点.答案:D主要考察知识点:空间直线和平面4、若点M在直线α上，α在平面α内，则M、a、α间的上述关系可记为( )A.M∈a,a∈αB.M∈a,aαC.M a,aαD.M a,aα参考答案与解析:B主要考察知识点:空间直线和平面5、在空间四边形ABCD的边AB、BC、CD、DA上分别取E、F、G、H四点,如果EF与HG交于点M，则( )A.M一定在直线AC上B.M一定在直线BD上C.M可能在AC上，也可能在BD上D.M不在AC上，也不在BD上参考答案与解析:A主要考察知识点:空间直线和平面6、下列说法正确的是()A.三点确定一个平面B.四边形一定是平面图形C.梯形一定是平面图形D.平面α和平面β有不同在一条直线上的三个交点参考答案与解析:解析：A错,不共点的三点;B错,如空间四边形;D错,两平面的三个交点在同一直线上.答案：C主要考察知识点:空间直线和平面7、若点M在直线a上,a在平面α内，则M，a,α间的上述关系可记为（）A.M∈a,a∈αB.M∈a,C.,D.,参考答案与解析:解析：要明确数学符号语言的表示.答案：B主要考察知识点:空间直线和平面8、异面直线是指()A.空间中两条不相交的直线B.分别位于两个不同平面内的两条直线C.平面内的一条直线与平面外的一条直线D.不同在任何一个平面内的两条直线参考答案与解析:解析：A错,有可能平行；B错,有可能平行或相交；C错,有可能平行或相交；D正确.答案：D主要考察知识点:空间直线和平面9、若a∥α,b∥α,则直线a、b的位置关系是()A.平行B.相交C.异面 D.A、B、C均有可能参考答案与解析:解析：平行、相交、异面都有可能,此题的难点在于可能选平行,易和平行公理混淆.答案：D主要考察知识点:空间直线和平面10、下列命题:①若直线l平行于平面α内的无数条直线,则l∥α;②若直线a在平面α外,则a∥α;③若直线a∥b,直线,则a∥α;④若直线a∥b,bα,那么直线a就平行于平面α内的无数条直线.其中真命题的个数为( )A.1B.2C.3D.4参考答案与解析:解析：对于①,∵直线l虽与平面α内无数条直线平行,但l有可能在平面α内,∴l不一定平行于α.∴①是假命题.对于②,∵直线a在平面α外包括两种情况:a∥α和a与α相交,∴a和α不一定平行.∴②是假命题.对于③,∵直线a∥b, ,则只能说明a和b无公共点,但a可能在平面α内,∴a不一定平行于α.∴③是假命题.对于④,∵a∥b, ,那么aα或a∥α,∴a可以与平面α内的无数条直线平行.∴④是真命题.综上所述,真命题的个数为1.答案：A主要考察知识点:空间直线和平面二、填空题【共4道小题】1、空间三条直线两两相交，点P不在这三条直线上，那么由点P和这三条直线最多可以确定的平面的个数为__________.参考答案与解析:解析：(1)当题中三条直线共点但不共面相交时，可确定3个平面；而P点与每条直线又可确定3个平面，故共确定6个.主要考察知识点:空间直线和平面2、和两条平行直线中的一条是异面直线的直线与另一条直线的位置关系是_______.参考答案与解析:思路解析:由公理4可知不可能平行,只有相交或异面.答案:相交或异面主要考察知识点:空间直线和平面3、看图填空.(1)AC∩BD=_______;(2)平面AB1∩平面A1C1=________；(3)平面A1C1CA∩平面AC=________；(4)平面A1C1CA∩平面D1B1BD=_________;(5)平面A1C1∩平面AB1∩平面B1C=_________；(6)A1B1∩B1B∩B1C1=_________.参考答案与解析:解析：两个面的两个公共点连线即为交线.答案：（1）O（2）A1B1（3）AC（4）OO1（5）B1（6）B1主要考察知识点:空间直线和平面4、已知平面α、β相交,在α、β内各取两点,这四点都不在交线上,这四点能确定平面_______个.参考答案与解析:解析：分类,如果这四点在同一平面内,那么确定一个平面,如果这四点不共面,则任意三点可确定一个平面,可确定四个.答案：1或4主要考察知识点:空间直线和平面三、解答题【共3道小题】1、如图，已知△ABC在平面α外，它的三边所在直线分别交平面α于点P、Q、R，求证：P、Q、R三点共线.参考答案与解析:解析：本题是一个证明三点共线的问题，利用公理3，两平面相交时，有且只有一条公共直线.因此只需证明P、Q、R三点是某两个平面的公共点，即可得这三个点都在两平面的交线上，因此是共线的.证明：设△ABC确定平面ABC，直线AB交平面α于点Q,直线CB交平面α于点P,直线AC 交平面α于点R,则P、Q、R三点都在平面α内，又因为P、Q、R三点都在平面ABC内，所以P、Q、R三点都在平面α和平面ABC的交线上，而两平面的交线只有一条，所以P、Q、R三点共线.主要考察知识点:空间直线和平面2、如图，已知正方体ABCD—A′B′C′D′.①哪些棱所在直线与直线BA′是异面直线？②直线BA′和CC′的夹角是多少？③哪些棱所在的直线与直线AA′垂直？参考答案与解析:解析：①由异面直线的定义可知，棱AD，DC，CC′，DD′，D′C′,B′D′所在直线分别与直线BA′是异面直线.②由BB′∥CC′可知，∠B′BA′为异面直线BA′与CC′的夹角，∠B′BA′=45°，所以BA′与CC′的夹角为45°.③直线AB，BC，CD，DA，A′B′,B′C′,C′D′,D′A′分别与直线AA′垂直.主要考察知识点:空间直线和平面3、已知直线b∥c,且直线a与b、c都相交,求证:直线a,b,c共面.参考答案与解析:证明:∵b∥c,∴不妨设b,c共面于平面α.设a∩b=A,a∩c=B,∴A∈a,B∈a,A∈α,B∈α,即.∴三线共面.主要考察知识点:空间直线和平面一、选择题【共10道小题】1、若两个平面互相平行，则分别在这两个平行平面内的直线( )A.平行B.异面C.相交 D.平行或异面参考答案与解析:解析：两平行平面内的直线可能平行，也可能异面，就是不可能相交.答案：D主要考察知识点:空间直线和平面2、下列结论中，正确的有( )①若aα,则a∥α②a∥平面α,bα则a∥b③平面α∥平面β,aα,bβ,则a∥b④平面α∥β,点P∈α,a∥β,且P∈a，则aαA.1个B.2个C.3个 D.4个参考答案与解析:解析：若aα，则a∥α或a与α相交，由此知①不正确若a∥平面α,bα,则a与b异面或a∥b，∴②不正确若平面α∥β，aα，bβ，则a∥b或a与b异面，∴③不正确由平面α∥β，点P∈α知Pβ过点P而平行平β的直线a必在平面α内，是正确的.证明如下：假设aα，过直线a作一面γ，使γ与平面α相交，则γ与平面β必相交.设γ∩α=b,γ∩β=c,则点P∈b.由面面平行性质知b∥c；由线面平行性质知a∥c,则a∥b,这与a∩b=P矛盾，∴aα.故④正确.答案：A主要考察知识点:空间直线和平面3、在空间四边形ABCD中，E、F分别是AB和BC上的点，若AE∶EB=CF∶FB=1∶3，则对角线AC和平面DEF的位置关系是( )A.平行B.相交C.在内 D.不能确定参考答案与解析:解析：在平面ABC内.∵AE：EB=CF：FB=1：3，∴AC∥EF.可以证明AC平面DEF.若AC平面DEF，则AD平面DEF，BC平面DEF.由此可知ABCD为平面图形，这与ABCD是空间四边形矛盾，故AC平面DEF.∵AC∥EF，EF平面DEF.∴AC∥平面DEF.答案：A主要考察知识点:空间直线和平面4、a，b是两条异面直线，A是不在a，b上的点，则下列结论成立的是( )A.过A有且只有一个平面平行于a,bB.过A至少有一个平面平行于a,bC.过A有无数个平面平行于a,bD.过A且平行a,b的平面可能不存在参考答案与解析:解析：如当A与a确定的平面与b平行时，过A作与a,b都平行的平面不存在.答案：D主要考察知识点:空间直线和平面5、已知直线a与直线b垂直,a平行于平面α,则b与α的位置关系是( )A.b∥αB.bαC.b与α相交D.以上都有可能参考答案与解析:思路解析:a与b垂直,a与b的关系可以平行、相交、异面,a与α平行,所以b与α的位置可以平行、相交、或在α内,这三种位置关系都有可能.答案:D主要考察知识点:空间直线和平面6、下列命题中正确的命题的个数为( )①直线l平行于平面α内的无数条直线，则l∥α;②若直线a在平面α外，则a∥α;③若直线a∥b,直线bα,则a∥α;④若直线a∥b,b平面α，那么直线a就平行于平面α内的无数条直线.A.1B.2C.3D.4参考答案与解析:解析：对于①,∵直线l虽与平面α内无数条直线平行，但l有可能在平面α内(若改为l与α内任何直线都平行，则必有l∥α),∴①是假命题.对于②，∵直线a在平面α外，包括两种情况a∥α和a与α相交，∴a与α不一定平行，∴②为假命题.对于③,∵a∥b,bα,只能说明a与b无公共点，但a可能在平面α内，∴a不一定平行于平面α.∴③也是假命题.对于④,∵a∥b,bα.那么aα,或a∥α.∴a可以与平面α内的无数条直线平行.∴④是真命题.综上，真命题的个数为1.答案：A主要考察知识点:空间直线和平面7、下列命题正确的个数是( )(1)若直线l上有无数个点不在α内，则l∥α(2)若直线l与平面α平行，l与平面α内的任意一直线平行(3)两条平行线中的一条直线与平面平行，那么另一条也与这个平面平行(4)若一直线a和平面α内一直线b平行，则a∥αA.0个B.1个C.2个 D.3个参考答案与解析:解析：由直线和平面平行的判定定理知，没有正确命题.答案：A主要考察知识点:空间直线和平面8、已知m、n是两条不重合的直线，α、β、γ是三个两两不重合的平面，给出下列四个命题：①若m⊥α,m⊥β,则α∥β;②若α⊥γ,β⊥γ,则α∥β;③若mα,nβ,m∥n,则α∥β;④若m、n是异面直线，mα,m∥β,nβ,n∥α,则α∥β.其中真命题是( )A.①和②B.①和③C.③和④ D.①和④参考答案与解析:解析：利用平面平行判定定理知①④正确.②α与β相交且均与γ垂直的情况也成立，③中α与β相交时，也能满足前提条件答案：D主要考察知识点:空间直线和平面9、长方体ABCD-A1B1C1D1中,E为AA1中点,F为BB1中点,与EF平行的长方体的面有()A.1个B.2个C.3个 D.4个参考答案与解析:解析：面A1C1,面DC1,面AC共3个.答案：C主要考察知识点:空间直线和平面10、对于不重合的两个平面α与β，给定下列条件：①存在平面γ，使得α、β都垂直于γ；②存在平面γ，使α、β都平行于γ；③α内有不共线的三点到β的距离相等；④存在异面直线l，M，使得l∥α,l∥β,M∥α,M∥β.其中可以判断两个平面α与β平行的条件有（）A.1个B.2个C.3个 D.4个参考答案与解析:解析：取正方体相邻三个面为α、β、γ，易知α⊥γ，β⊥γ，但是α与β相交，不平行，故排除①，若α与β相交，如图所示，可在α内找到A、B、C三个点到平面β的距离相等，所以排除③.容易证明②④都是正确的.答案：B主要考察知识点:空间直线和平面1、在棱长为a的正方体ABCD—A1B1C1D1中，M、N分别是棱A1B1、B1C1的中点，P是棱AD上一点，AP=,过P、M、N的平面与棱CD交于Q，则PQ=_________.参考答案与解析:解析：由线面平行的性质定理知MN∥PQ(∵MN∥平面AC，PQ=平面PMN∩平面AC，∴MN∥PQ).易知DP=DQ=.故.答案：主要考察知识点:空间直线和平面2、如果空间中若干点在同一平面内的射影在一条直线上，那么这些点在空间的位置是__________.参考答案与解析:共线或在与已知平面垂直的平面内主要考察知识点:空间直线和平面3、若直线a和b都与平面α平行，则a和b的位置关系是__________.参考答案与解析:相交或平行或异面主要考察知识点:空间直线和平面4、正方体ABCD-A1B1C1D1中，E为DD1中点，则BD1与过点A，C，E的平面的位置关系是_________.参考答案与解析:解析：如图所示，连结BD，设BD∩AC=O，连结BD1，在△BDD1中，E 为DD1的中点，O为BD的中点，∴OE为△BDD1的中位线.∴OE∥BD1.又平面ACE，OE平面ACE，∴BD1∥平面ACE.答案：平行主要考察知识点:空间直线和平面1、如图，直线AC，DF被三个平行平面α、β、γ所截.①是否一定有AD∥BE∥CF；②求证：.参考答案与解析:解析：①平面α∥平面β，平面α与β没有公共点，但不一定总有AD∥BE. 同理不总有BE∥CF.②过A点作DF的平行线，交β，γ于G，H两点，AH∥DF.过两条平行线AH，DF的平面，交平面α,β,γ于AD，GE，HF.根据两平面平行的性质定理，有AD∥GE∥HF.AGED为平行四边形.∴AG=DE.同理GH=EF.又过AC，AH两相交直线之平面与平面β,γ的交线为BG，CH.根据两平面平行的性质定理，有BG∥CH.在△ACH中，.而AG=DE，GH=EF，∴.主要考察知识点:空间直线和平面2、如图，ABCD是平行四边形，S是平面ABCD外一点，M为SC的中点.求证：SA∥平面MDB.参考答案与解析:解析：要说明SA∥平面MDB，就要在平面MDB内找一条直线与SA平行，注意到M是SC的中点，于是可找AC的中点，构造与SA平行的中位线，再说明此中位线在平面MDB内，即可得证.证明：连结AC交BD于N，因为ABCD是平行四边形，所以N是AC的中点.又因为M是SC的中点，所以MN∥SA.因为MN平面MDB，所以SA∥平面MDB.主要考察知识点:空间直线和平面3、如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点，P是正方形ABCD 的中心，求证：MN∥平面PB1C.参考答案与解析:证明：如图，连结AC，则P为AC的中点，连结AB1，∵M、N分别是A1A与A1B1的中点，∴MN∥AB1.又∵平面PB1C，平面PB1C，故MN∥面PB1C.一、选择题【共10道小题】1、二面角指的是( )A.两个平面相交所组成的角B.经过同一条直线的两个平面所组成的图形C.一条直线出发的两个半平面组成的图形D.两个平面所夹的不大于90°的角参考答案与解析:解析：根据二面角的定义讨论，故选C.答案：C主要考察知识点:空间直线和平面2、α、β、γ、ω是四个不同平面，若α⊥γ，β⊥γ，α⊥ω，β⊥ω，则( )A.α∥β且γ∥ωB.α∥β或γ∥ωC.这四个平面中可能任意两个都不平行D.这四个平面中至多有一对平面平行参考答案与解析:解析：若α∩β=a.∵α⊥γ,β⊥γ，∴α⊥γ.同理a⊥ω.∴γ∥ω;若α∥β,则γ与ω相交或平行，∴α∥β或γ∥ω.答案：B主要考察知识点:空间直线和平面3、已知直线m、n与平面α、β，给出下列三个命题：①若m∥α,n∥α,则m∥n;②若m∥α,n⊥α，则n⊥m;③若m⊥α,m∥β,则α⊥β.其中真命题的个数是( )A.0B.1C.2D.3参考答案与解析:解析：①m∥α,n∥α不一定有m∥α.②③正确.答案：C主要考察知识点:空间直线和平面4、如图2-3-15,设P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( )图2-3-15A.平面PAB与平面PBC、平面PAD都垂直B.它们两两都垂直C.平面PAB与平面PBC垂直、与平面PAD不垂直D.平面PAB与平面PBC、平面PAD都不垂直参考答案与解析:思路解析:∵PA⊥平面ABCD,∴PA⊥BC.又∵BC⊥AB,PA∩AB=A,∴PC⊥平面PAB,从而平面PBC⊥平面PAB.由AD⊥PA,AD⊥AB,PA∩AB=A得AD⊥平面PAB.∵AD平面PAD,∴平面PAD⊥平面PAB.答案:A主要考察知识点:空间直线和平面5、如图2-3-16,等边三角形ABC的边长为1,BC边上的高为AD,若沿AD折成直二面角,则A 到BC的距离是……()图2-3-16A.1B.C.D.参考答案与解析:思路解析:折叠后BD=DC=,且∠BDC为二面角的平面角,∠BDC=90°,∴BC=.取BC中点E,连结DE,则DE⊥BC,进一步易证AE⊥BC,AE的长为所求距离.∵AD=,DE=BC=,∴AE=.答案:C主要考察知识点:空间直线和平面6、下列命题正确的是( )A.垂直于同一条直线的两直线平行B.垂直于同一条直线的两直线垂直C.垂直于同一个平面的两直线平行D.垂直于同一条直线的一条直线和平面平行参考答案与解析:思路解析:在空间中垂直于同一直线的两条直线,可能平行相交,也可能异面,所以A,B错,垂直于同一直线的直线和平面的位置关系可以是直线在平面内,直线和平面平行,所以D错.答案:C主要考察知识点:空间直线和平面7、空间四边形ABCD的四边相等，则它的两对角线AC、BD的关系是( )A.垂直且相交B.相交但不一定垂直C.垂直但不相交D.不垂直也不相交参考答案与解析:解析：取BD中点E，连结AE、CE.∵AB=AD=BC=CD,∴AE⊥BD,CE⊥BD.∴BD⊥平面AEC.又AC面AEC，∴BD⊥AC.答案：C主要考察知识点:空间直线和平面8、线段AB的长等于它在平面α内射影长的2倍，则AB所在直线与平面α所成的角为（）A.30°B.45°C.60°D.120°参考答案与解析:解析：由直角三角形的边角关系，可知直线与平面α所成的角为60°.答案：C主要考察知识点:空间直线和平面9、设α,β为两个不重合的平面,l,M,n为两两不重合的直线,给出下列四个命题:①若α∥β,,则l∥β;②若, ,M∥β,n∥β，则α∥β；③若l∥α,l⊥β,则α⊥β;④若,,且l⊥M,l⊥n,则l⊥α.其中正确命题的序号是( )A.①③④B.①②③C.①③D.②④参考答案与解析:解析：由面面平行的判定定理,知②错误;由线面垂直的判定定理知④错误.答案：C主要考察知识点:空间直线和平面10、下列说法中正确的是()①过平面外一点有且只有一条直线和已知平面垂直②过直线外一点有且只有一个平面和已知直线垂直③过平面外一点可作无数条直线与已知平面平行④过直线外一点只可作一条直线与已知直线垂直A.①②③B.①②③④C.②③D.②③④参考答案与解析:解析：由线面垂直的性质及线面平行的性质,知①②③正确;④错,过直线外一点作平面与直线垂直,则平面内的所有直线都与该直线垂直.答案：A主要考察知识点:空间直线和平面二、填空题【共4道小题】1、α、β是两个不同的平面，m、n是平面α、β外的两条不同直线，给出四个结论：①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题______.参考答案与解析:解析：假设①③④为条件，即m⊥n,n⊥β,m⊥α成立，如图.过m上一点P 作PB∥N，则PB⊥m，PB⊥β，设垂足为B.又设m⊥α，垂足为A，过PA、PB的平面与α、β的交线l交于点C.∵l⊥PA,l⊥PB,∴l⊥平面PAB.∴l⊥AC，l⊥BC.∴∠ACB是二面角α-l-β的平面角.由m⊥n,显然PA⊥PB，∴∠ACB=90°,∴α⊥β.由①③④②成立.反过来，如果②③④成立，与上面证法类似可得①成立.答案：②③④①或①③④②.主要考察知识点:空间直线和平面2、α、β是两个不同的平面，m、n是平面α、β外的两条不同直线，给出四个结论：①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题______.参考答案与解析:解析：假设①③④为条件，即m⊥n,n⊥β,m⊥α成立，如图.过m上一点P 作PB∥N，则PB⊥m，PB⊥β，设垂足为B.又设m⊥α，垂足为A，过PA、PB的平面与α、β的交线l交于点C.∵l⊥PA,l⊥PB,∴l⊥平面PAB.∴l⊥AC，l⊥BC.∴∠ACB是二面角α-l-β的平面角.由m⊥n,显然PA⊥PB，∴∠ACB=90°,∴α⊥β.由①③④②成立.反过来，如果②③④成立，与上面证法类似可得①成立.答案：②③④①或①③④②.主要考察知识点:空间直线和平面3、设三棱锥P ABC的顶点P在平面ABC上的射影是H，给出下列命题：①若PA⊥BC，PB⊥AC，则H是△ABC的垂心；②若PA、PB、PC两两互相垂直，则H是△ABC的垂心；③若∠ABC=90°，H是AC的中点，则PA=PB=PC；④若PA=PB=PC，则H是△ABC的外心.请把正确命题的序号填在横线上:______________.参考答案与解析:解析：①若P A⊥BC，PB⊥AC，则H为垂心.②∵PA⊥PB，PA⊥PC,∴PA⊥面PBC.∴PA⊥BC.又PH⊥面ABC，∴PH⊥BC.∴BC⊥面PAH.∴AH⊥BC.同理BH⊥AC，∴H为垂心.③∵H为AC中点，∠ABC=90°,∴AH=BH=CH.又PH⊥面ABC，由勾股定理知PA=PB=PC.④∵PA=PB=PC，又PH⊥面ABC，同③可知AH=BH=CH，∴H为外心.答案：①②③④主要考察知识点:空间直线和平面4、如图，P是二面角α-AB-β的棱AB上一点，分别在α、β上引射线PM、PN,截PM=PN，如果∠BPM=∠BPN=45°，∠MPN=60°，则二面角α-AB-β的大小是___________.参考答案与解析:解析：过M在α内作MO⊥AB于点O，连结NO，设PM=PN=a,又∠BPM=∠B PN=45°,∴△OPM≌△OPN.∴ON⊥AB.∴∠MON为所求二面角的平面角.连结MN，∵∠MPN=60°,∴MN=a.又,∴MO2+NO2=MN2.∴∠MON=90°.答案：90°主要考察知识点:空间直线和平面三、解答题【共3道小题】1、如图，在正方体ABCD—A1B1C1D1中，EF⊥A1D，EF⊥AC，求证：EF∥BD1.参考答案与解析:解析：要证明EF∥BD1，可构造与它们都垂直的一个平面.由于A1D，AC 均为各面的对角线，通过对角线的平行性可构造垂直关系.证明：连结A1C1，由于AC∥A1C1，EF⊥AC，∴EF⊥A1C1.又EF⊥A1D，A1D∩A1C1＝A1,∴EF⊥平面A1C1D. ①∵BB1⊥平面A1B1C1D1，A1C1平面A1B1C1D1,∴BB1⊥A1C1.又A1B1C1D1为正方体,∴A1C1⊥B1D1.∵BB1∩B1D1＝B1,∴A1C1⊥平面BB1D1D.而BD1平面BB1D1D,∴BD1⊥A1C1.同理，DC1⊥BD1，DC1∩A1C1＝C1,∴BD1⊥平面A1C1D. ②由①②可知EF∥BD1.主要考察知识点:空间直线和平面2、在长江汽车渡口,马力不足或装货较重的汽车上岸时,采用沿着坡面斜着成S形的方法向上开,这是为什么？你能从数学的角度进行解释吗？参考答案与解析:答案:在汽车马力恒定的情况下,行驶单位路程内,垂直上升高度愈大,汽车愈费“力”,当“力”所不及时,就会发生危险.日常经验告诉我们,走S形可减少这种危险,从数学的角度看,可作如下解释.图2-3-22如图,AB表示笔直向上行走的路线(AB⊥CA),α表示它与水平面所成的交角,CB表示斜着向上行走的路线,β表示它与水平面所成的夹角,它们所达到的高度都是BD.现在的问题就是要研究α和β这两个角哪个大,越大越费力.在Rt△BAD中,sinα=.①在Rt△BCD中,sinβ=.②比较①与②,因为AB、CB分别是直角三角形ABC的直角边和斜边,也就是说AB＜CB,所以＞.又因为α、β都是锐角,所以α＞β.因此汽车沿着CB方向斜着向上开要省力.山区修筑的公路,采取盘山而上的方法,也是这个道理.主要考察知识点:空间直线和平面3、如图，在四面体ABCD中，△ABD、△ACD、△BCD、△ABC都全等，且，BC=2，求以BC为棱、以面BCD和面BCA为面的二面角的大小.参考答案与解析:解:取BC的中点E，连结AE、DE，∵AB=AC，∴AE⊥BC.又∵△ABD≌△ACD，AB=AC，∴DB=DC.∴DE⊥BC.∴∠AE D为二面角A-BC-D的平面角.又∵△ABC≌△DBC,且△ABC为以BC为底的等腰三角形，故△DBC也是以BC为底的等腰三角形，∴.又△ABD≌△BDC，∴AD=BC=2.在Rt△DEB中，，BE=1，∴,同理.在△AE D中，∵AE=DE=,AD=2,∴AD2=AE2+DE2.∴∠AE D=90°.∴以面BCD和面BCA为面的二面角的大小为90°.主要考察知识点:空间直线和平面一、选择题【共12道小题】1、下列说法中正确的是( )A.棱柱的侧面可以是三角形B.正方体和长方体都是特殊的四棱柱C.所有的几何体的表面都能展成平面图形D.棱柱的各条棱都相等参考答案与解析:B主要考察知识点:简单几何体和球2、将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所得的几何体包括( )A.一个圆台、两个圆锥B.两个圆台、一个圆柱C.两个圆台、一个圆柱D.一个圆柱、两个圆锥参考答案与解析:D主要考察知识点:简单几何体和球3、过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为( )A. B. C.D.参考答案与解析:解析：设球半径为R，截面半径为r.+r2=R2,∴r2=.∴.答案：A主要考察知识点:简单几何体和球4、如图所示的直观图是将正方体模型放置在你的水平视线的左上角而绘制的，其中正确的是( )参考答案与解析:解析：由几何体的直观图画法及主体图形中虚线的使用，知A正确.答案：A主要考察知识点:简单几何体和球5、长方体的高等于h，底面积等于S，过相对侧棱的截面面积为S′，则长方体的侧面积等于( )A. B.C. D.参考答案与解析:解析：设长方体的底面边长分别为a、b，过相对侧棱的截面面积S′=①,S=ab②,由①②得：(a+b)2=+2S,∴a+b=,S侧=2(a+b)h=2h.答案：C主要考察知识点:简单几何体和球6、设长方体的对角线长度是4，过每一顶点有两条棱与对角线的夹角都是60°,则此长方体的体积是( )A. B. C.D.参考答案与解析:解析：设长方体的过一顶点的三条棱长为a、b、c，并且长为a、b的两条棱与对角线的夹角都是60°，则a=4cos60°=2,b=4cos60°=2.根据长方体的对角线性质，有a2+b2+c2=42,即22+22+c2=42.∴c=.因此长方体的体积V=abc=2×2×=.答案：B主要考察知识点:简单几何体和球7、棱锥被平行于底面的平面所截，当截面分别平分棱锥的侧棱、侧面积、体积时，相应的截面面积分别为S1、S2、S3，则( )A.S1＜S2＜S3B.S3＜S2＜S1C.S2＜S1＜S3 D.S1＜S3＜S2参考答案与解析:解析：由截面性质可知，设底面积为S.;;可知：S1＜S2＜S3故选A.用平行于底面的平面截棱锥所得截面性质都是一些比例关系：截得面积之比就是对应高之比的平方，截得体积之比，就是对应高之比的立方，所谓“高”，是指大棱锥、小棱锥的高，而不是两部分几何体的高.答案：A主要考察知识点:简单几何体和球8、正四面体的内切球球心到一个面的距离等于这个正四面体高的( )A. B. C.D.参考答案与解析:解析：球心到正四面体一个面的距离即球的半径r，连结球心与正四面体的四个顶点.把正四面体分成四个高为r的三棱锥，所以4×S·r=·S·h,r= h (其中S为正四面体一个面的面积，h为正四面体的高)答案：C主要考察知识点:简单几何体和球9、若圆台两底面周长的比是1∶4，过高的中点作平行于底面的平面，则圆台被分成两部分的体积比是( )A.1∶16B.3∶27C.13∶129D.39∶129参考答案与解析:解析：由题意设上、下底面半径分别为r，4r，截面半径为x，圆台的高为2h，则有,∴x=.∴.答案：D主要考察知识点:简单几何体和球10、在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体，则截去8个三棱锥后，剩下的凸多面体的体积是( )A. B. C.D.。

温馨提示：
此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。

关闭Word文档返回原板块。

课堂10分钟达标练
1.如果直线a∥平面α,b是平面α内的直线,则a与b的位置关系是( )
A.平行
B.相交
C.异面
D.平行或异面
【解析】选D.因为a∥α,b⊂α,故a与b没有公共点,故a与b平行或异面.
2.已知直线a,b与平面α,满足a∥α,b∥α,则a与b的位置关系是________.
【解析】如图长方体中,a∥α,b∥α,a与b相交,
b′∥α,则a与b′异面,
b″∥α,则a与b″平行,
故a与b关系:平行、异面或相交.
答案:平行、异面或相交
3.平面α∥平面β,a⊂α,则a与β的位置关系是________.
【解析】因为α∥β,所以α与β无公共点,又a⊂α,所以a与β无公共点,所以a∥β.
答案:a∥β
4.已知三个平面α,β,γ,如果α∥β,α∩γ=a,β∩γ=b,且c⊂β,c∥b,判断c与a的位置关系,并说明理由.
【解析】因为α∥β,所以α与β无公共点,又α∩γ=a,β∩γ=b,a⊂α,b⊂β,且a,b⊂γ,所以a,b没有公共点,故a∥b,又c∥b,所以c∥a.
关闭Word文档返回原板块。