第二章计算机测控系统组成及类型2.1 计算机测控系统的组成及特点计算机测控系统是应用计算机来实现生产过程的测试、控制的系统。
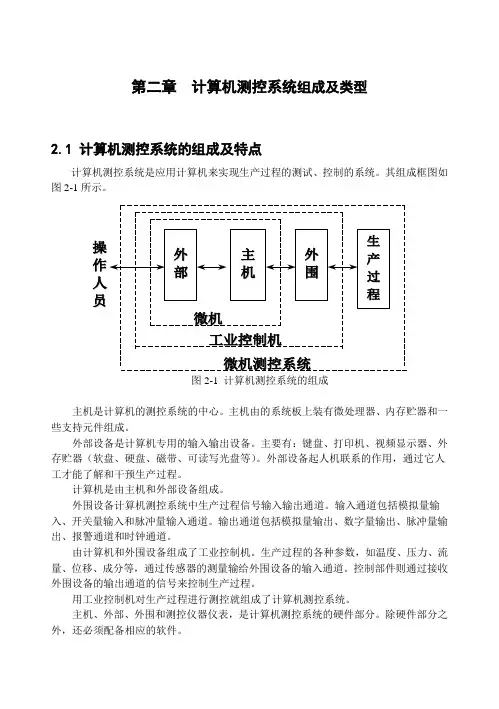
其组成框图如图2-1所示。
操作人员微机测控系统图2-1 计算机测控系统的组成主机是计算机的测控系统的中心。
主机由的系统板上装有微处理器、内存贮器和一些支持元件组成。
外部设备是计算机专用的输入输出设备。
主要有：键盘、打印机、视频显示器、外存贮器（软盘、硬盘、磁带、可读写光盘等）。
外部设备起人机联系的作用，通过它人工才能了解和干预生产过程。
计算机是由主机和外部设备组成。
外围设备计算机测控系统中生产过程信号输入输出通道。
输入通道包括模拟量输入、开关量输入和脉冲量输入通道。
输出通道包括模拟量输出、数字量输出、脉冲量输出、报警通道和时钟通道。
由计算机和外围设备组成了工业控制机。
生产过程的各种参数，如温度、压力、流量、位移、成分等，通过传感器的测量输给外围设备的输入通道。
控制部件则通过接收外围设备的输出通道的信号来控制生产过程。
用工业控制机对生产过程进行测控就组成了计算机测控系统。
主机、外部、外围和测控仪器仪表，是计算机测控系统的硬件部分。
除硬件部分之外，还必须配备相应的软件。
计算机测控系统的软件可分系统软件和应用软件。
系统软件是计算机本身的操作系统和监控程序，它有一定的通用性，由计算机生产厂家提供。
应用软件是实现生产过程测控的应用程序，也称用户程序，它具有专用性，由用户根据具体需要编制。
由常规测控仪器仪表构成的模拟测控系统，虽具有可靠性高、成本低、易于维护操作的优点，但是它难以实现多变量测控、复杂控制规律的控制，如最优控制，自适应控制，时变控制；模拟控制屏越来越长，难以实现集中控制；各分子系统之间不便于进行通讯联系，难以实现多级控制；控制方案的修改比较麻烦。
计算机测控系统则能很好地解决上述问题。
计算机测控系统不仅能完成模拟测控系统的所有功能，而且还具有如下优点：（1）测控的速度和精度高；（2）由于计算机具有分时操作功能，所以一台计算机可以代替多台常规测控装置；（3）由于计算机具有记忆和逻辑判断功能，所以能够综合生产过程各方面的情况，在工艺参数变化时能及时地作出判断，选择最优控制。
