当前位置：文档之家 › 3-(3-4)力矩 转动定律解析

3-(3-4)力矩 转动定律解析

  • 格式：ppt
  • 大小：1.53 MB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

力矩转动定律转动惯量解析课件

力矩转动定律转动惯量解析课件


02
CATALOGUE
转动惯量基础概念
转动惯量的定义
转动惯量
描述刚体绕固定轴转动的惯性大 小的物理量。
定义公式
I = Σ(m * r^2)，其中m为刚体的 质量，r为刚体上任意质点到转动 轴的距离。
转动惯量的性质
转动惯量只与刚体的质量分布 和转动轴的位置有关，与刚体 的运动状态无关。
对于同一刚体，不同的转动轴 位置，其转动惯量可能不同。
力矩转动定律转动 惯量解析课件
contents
目录
• 力矩转动定律概述 • 转动惯量基础概念 • 力矩与转动惯量的关系 • 转动惯量的计算方法 • 转动惯量的应用实例
01
CATALOGUE
力矩转动定律概述
力矩的定义
力矩是描述力的转动效果的物理量，其大小等于力和力臂的乘积。
力矩是一个向量，其大小等于力和力臂的乘积。力臂是从转动轴到力的垂直距离 。在二维平面中，力矩可以表示为M=F×r，其中F是力，r是力臂。
CATALOGUE
转动惯量的应用实例
飞轮的设计与优化
飞轮的设计
飞轮是利用转动惯量储存能量的重要 装置，其设计需要考虑转动惯量的大 小、质量分布、转速等因素。
飞轮的优化
为了提高飞轮的储能效率和稳定性， 需要对飞轮进行优化设计，如采用轻 质高强度的材料、优化飞轮的形状和 尺寸等。
陀螺仪的设计与优化
陀螺仪的设计
陀螺仪是利用角动量守恒原理工作的惯性导 航和姿态测量器件，其设计需要考虑转动轴 的稳定性、转动惯量的大小和分布等因素。
陀螺仪的优化
为了提高陀螺仪的测量精度和稳定性，需要 对陀螺仪进行优化设计，如采用高性能的轴 承材料、减小摩擦力矩等。
电机转子的设计与优化
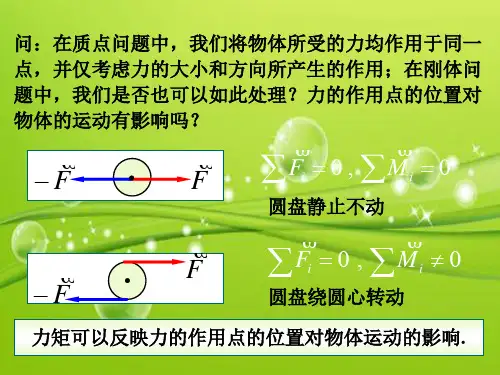
力矩转动定律 PPT

力矩转动定律 PPT

式中：Fit ri 是合外力Fi 的对
Oz轴的力矩；
fit ri是内力 fi 对Oz轴的力矩。
故上式左边为作用在质点i 上
的外力矩与内力矩之和。
对于刚体上所有的质点，可得：
z
f
it
Fit
r O i Δmi
(ri Fit ) (ri fit ) ( miri2 )
i
i
i
M J
转动定律与牛顿第二定律的比较：
转动定律 M
J
牛顿第二定律 a F m
转动定律是解决刚体绕定 牛顿第二定律是解决质点 轴转动问题的基本方程。 运动问题的基本定律。
它们的形式很相似：外力矩M和外力F相对应，角加速 度α与加速度a相对应，转动惯量J 与质量 m 相对应。
10
三 转动惯量 J miri2 国际单位：kg·m2
P96 表4-1列出了一些均匀刚体的转动惯量 .
平行轴定理
质量为m的刚体，如果对 其质心轴的转动惯量为 Jc，则 对任一与该轴平行，相距为d 的转轴的转动惯量
d
C mO
JO JC md 2 （证明略）
例：圆盘对P 轴的转动惯量
JP

1 2
mR2

mR2
3 2
mR2
P R Om
12
哪种握法转动惯量大？
结束21
*P98例4 如图一斜面长 l = 1.5m, 与水平面的夹角θ= 5o.
有两个物体分别静止地位于斜面的顶端, 然后由顶端沿
斜面向下滚动, 一个物体是质量 m1 = 0.65kg、半径为R1 的实心圆柱体, 另一物体是质量为 m2 = 0.13 kg 、半径 R2 = R1 = R 的薄壁圆柱筒. 它们分别由斜面顶端滚到斜 面底部各经历多长时间?
大学物理一复习第四章刚体的转动-文档资料

大学物理一复习第四章刚体的转动-文档资料


mg FT2 ma2

FT1 FT2
R
mg FT1 r
m
a1
J
a1 r
a2 R
FT1 r R
FT1'
A
mg
β
FT2
FT2'
B
mg
mg(R r)
J mR2 mr2
a1

r

J
mgr(R r) mR2 mr2
40 半径减小角速度增加。
（2）拉力作功。请考虑合外力矩为0， 为什么拉力还作功呢？
W


0
Md
在定义力矩作功 时，我们认为只 有切向力作功， 而法向力与位移 垂直不作功。
但在例题中，小 球受的拉力与位 移并不垂直，小 球的运动轨迹为 螺旋线，法向力 要作功。
o
F
r d Fn F
解得
a2

R

mgR(R r) J mR2 mr2
FT1 mg ma1
FT2 mg ma2
例2：光滑斜面倾角为 ，顶端固定一半 径为 R ，质量为 M 的定滑轮，质量为 m 的物体用一轻绳缠在定滑轮上沿斜面 下滑，求:下滑的加速度 a 。
解：物体系中先以
物体 m 研究对象，
A
分别根据牛二定律和转动定律列方程：
角量、线量关系式
解得：
a
mB g
mA mB mC 2
T1

mAmB g
mA mB mC
2
T2

(mA mC 2)mBg mA mB mC 2
如令 mC 0，可得：
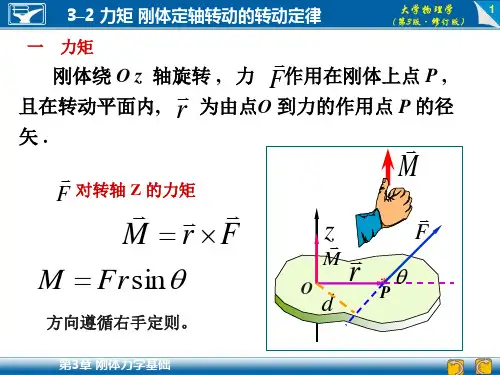
力矩 刚体定轴转动的转动定律解析

力矩 刚体定轴转动的转动定律解析


如图 dS 2 rdr, m , dm dS 2 rdr R2
dJ r2dm 2 r3dr
J
dJ
R
2
r3dr
1
mR2
0
2
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
竿
子
长
些
还
是
短
些
较
安
飞轮的质量为什么
全
大都分布于外轮缘？
？
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
9
例3.1 如图所示，求质量为m，长为l的均匀细棒 的转动惯量：(1)转轴通过棒的中心并与棒垂直； (2)转轴通过棒一端并与棒垂直.
解 (1)转轴通过棒的中心并与棒垂直
m dm dx
l
dJ x2dm x2dx
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
10
整个棒对中心轴的转动惯量为
J
dJ
l
2 l
2
x2dx
1 12
ml 2
(2)转轴通过棒一端并与棒垂直时，整个棒对该轴的 转动惯量为
J l x2dx 1 ml2
0
3
由此看出，同一均匀细棒，转轴位置不同，转动惯 量不同.
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
11
例3.2 设质量为m，半径为R的细圆环和均匀圆盘分 别绕通过各自中心并与圆面垂直的轴转动，求圆环和 圆盘的转动惯量.
第四章 刚体转动
4 – 2 力矩 转动定律 转动惯量
二 刚体定轴转动的转动定律
物理学教程 （第二版）
Fit (mi )ait
3.4 力矩的功 转动动能定理.

3.4 力矩的功 转动动能定理.


1 3g M 2 ， 而 I mL 可得 0 L 3 I
1 2 1 2 I I0 2 2
N
XO
YZ

法三：机械能守恒定律

C
r
mg
1 2 1 2 1 I0 I mgL 2 2 2
A

1 2 I mL 3
3g 可得 L
FN
Z
θ
L
E p E p 2 E p1
L mg 2 L 重力矩的功： A mg 2
mg
可见：刚体重力矩的功 = 刚体重力势能的减少
A E p ( E p 2 E p1 )
二、刚体转动动能定理
力矩的功定义式
dA Md
在定轴转动中，由转动定律，
d d Id dA Md Id I dt
3.4 力矩的功 转动动能定理 一、力矩的功
z
O
r
d
dr
α
F
力矩 M | r F | rF sin dA F dr Fds cos Frd cos
90
0
Frd sin M d
对于任意角度的转动
A dA Md ——力矩的功
任一对内力大小相等、方向相反且作用在 同一直线上。这一对内力对转轴的力矩大小 相等、方向相反，代数和为零。这一对内力 矩的总功必为零。定轴转动刚体上所有内力 矩的总功也必为零。
刚体重力矩的功： 设一细杆的质量为m，长为L，一端支以枢轴 而能自由旋转，设此杆自水平静止释放。求： 当细杆到达铅直位置时重力矩所作的功。 FN 以杆为研究对象 Z L 受力： mg，FN θ
力矩对刚体作的功，等于力矩和角位移的乘积
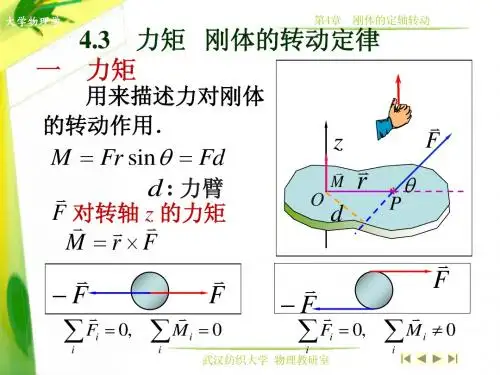
4.3 力矩 转动定律

4.3 力矩 转动定律


v −F v
i
v F
v ∑ Mi ≠ 0
i
∑ F = 0,
i
武汉纺织大学 物理教研室
大学物理学
第4章
刚体的定轴转动
讨论
v 不在转动平面内， （1）若力 F 不在转动平面内，把力分 ）
解为平行和垂直于转轴方向的两个分量
力矩为零， 力矩为零，故 F 对转 轴的力矩
v 其中 Fz 对转轴的 v
v v v F = Fz + F⊥
大学物理学
第4章
刚体的定轴转动
4.3 力矩 刚体的转动定律 一 力矩
用来描述力对刚体 的转动作用． 的转动作用．
M = Fr sin θ = Fd d : 力臂 v F 对转轴 z 的力矩 v v v M = r ×F
z
v M
v F
O
v r
*
d
P
θ
v −F
i
v F
v ∑ Mi = 0
i
v ∑ Fi = 0,
M = I β , β 与 M 方向相同． 方向相同．
(2) 为瞬时关系． ) 为瞬时关系． (3) 转动中 M = I β 与平动中F = ma ) 地位相同． 地位相同．
武汉纺织大学 物理教研室
大学物理学
第4章
刚体的定轴转动
质量为m 的物体A 例2 质量为 A的物体 静止在光滑水 平面上，和一质量不计的绳索相连接， 平面上，和一质量不计的绳索相连接，绳 索跨过一半径为R、质量为m 索跨过一半径为 、质量为 C的圆柱形滑轮 C，并系在另一质量为 B 的物体 上，B 竖 ，并系在另一质量为m 的物体B上 直悬挂．滑轮与绳索间无滑动， 直悬挂．滑轮与绳索间无滑动， 且滑轮与 轴承间的摩擦力可略去不计． ) 轴承间的摩擦力可略去不计．(1)两物体的 线加速度为多少？ 线加速度为多少？ 水平和竖直两段绳索的 张力各为多少？ ) 张力各为多少？(2) 物体 B 从静止落下距 其速率是多少？ 离 y 时，其速率是多少？
4-3转动定律

4-3转动定律


[例2]有一均质细直杆在一个粗糙的水平 例 有一均质细直杆在一个粗糙的水平 面上可绕一条通过其一端的竖直轴旋转， 面上可绕一条通过其一端的竖直轴旋转，它 与平面之间的摩擦系数为µ 。设杆子质量为 m,长度为 l ，其初始转速为ω0 。试求当它 长度为 的转速为原来的一半时所用的时间。 的转速为原来的一半时所用的时间。 o l o´
结束
返回
4. J 和转轴有关。同一个物体对不同转 和转轴有关。 轴的转动惯量是不同的。 轴的转动惯量是不同的。 o o´ 1 ml J = 12
2
o o´ 1 ml J= 3
o 1 mr 2 J= 4 o´
o 1 mr 2 J= 2 o´
结束
返回
5*. 回转半径：假想将物体的质量集中在 回转半径： 的细圆环上， 半径为 rc 的细圆环上，而保持转动惯量不 回转半径。 称这圆环半径为物体的回转半径 变，称这圆环半径为物体的回转半径。即任 何物体的转动惯量为： 何物体的转动惯量为： J = mrc o
ห้องสมุดไป่ตู้结束
1 µ 1 ml 2 d ω mg l = dt 2 3 3µ g dt = d ω 2l 3µ g t ∫ 0 dt = 2l
∫ω dω
2 0
ω0
3µ g ω ω t= 2 2l
0
0
∴
ωl t= 3µ g
0 结束
返回
[例3]有一高为 ，宽为 ，质量为 的 例 有一高为 有一高为h，宽为b 质量为m 均质平板可绕一条通过其一端的竖直轴旋转， 均质平板可绕一条通过其一端的竖直轴旋转， 板上面元所受到的阻力和面元的大小与面元 的速度平方乘积成正比，比例系数为k 。板 的速度平方乘积成正比，比例系数为 的初始角速度为ω0 。 试求其角速度变化规律。 试求其角速度变化规律。 o b m
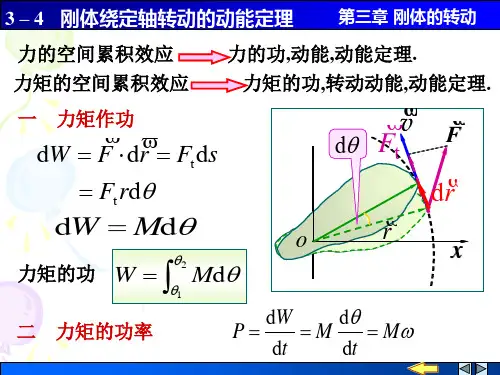
大学物理3_4 刚体绕定轴转动的动能定理

大学物理3_4 刚体绕定轴转动的动能定理

t 3 3 3 5 3 2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
例3 留声机的转盘绕通过盘心垂直盘面的轴以角速度 作匀速转动.放上唱片后,唱片将在摩擦力作用下随转盘一 起转动.设唱片的半径为 R 、质量为 m ,它与转盘间的摩 擦系数为 .求(1)唱片与转盘间的摩擦力矩;(2)唱片达到 角速度 需要多长时间;(3)在这段时间内,转盘的驱动力 矩作了多少功? 解 (1)如图所示,在唱片上取长为 dl 宽为 dr 的面积元 dS dldr ,该面 积元所受的摩擦力为:
1 2 1 2 1 1 1 2 2 2 2 W J J0 mR 0 mR 2 2 2 2 4
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 例3-11 一长为 l , 质量为 m0 的均质细竿可绕支点O自 由转动 . 一质量为 m、速率为 v0 的子弹射入竿内一端， 使竿的偏转角为30º 问子弹的初速率为多少 ? .
加速度
力 质量
dr v dt dv a dt
F
d 角速度 dt d 角加速度 dt
力矩

M
m
转动惯量 J
动量
P mv
角动量
L J
r
dm
2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动
EPB EkB EPA EkA
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 1 2 4 2 2 J J1 J 2 ml ml ml 3 3
取A点的重力势能为零,即 则有 而
EPA 0
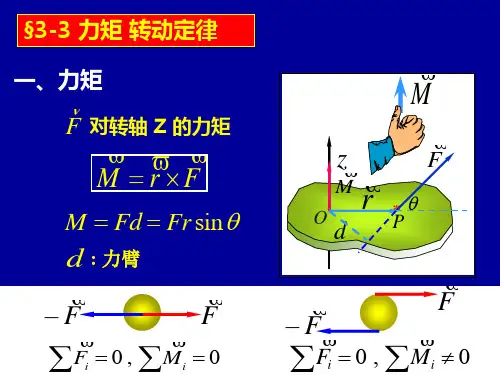
3-3,4力矩的功

3-3,4力矩的功


R,I
m
0 x x
例2 ：
方法一：转动定律＋ 方法一：转动定律＋牛顿定律 方法二： 方法二：机械能守恒
2mgh − kh2 v= m+ I 2 R
F
R,I
T T’ m mg
0 x x
例3 ： 求物体从弹簧原长时开始下落到h距离时的速度？ 求物体从弹簧原长时开始下落到h距离时的速度？
m R,I
m
0 x x
方法二： 方法二：转动动能定理 方法三： 方法三：机械能守恒
mg
例1 ： 1.当杆下落到 处时的角速度和A处法向加速度； 当杆下落到θ 1.当杆下落到θ处时的角速度和A处法向加速度； 2.当杆转到铅直位置时的转动动能、 当杆转到铅直位置时的转动动能 2.当杆转到铅直位置时的转动动能、角加速度及 轴上的作用力是多少？ 轴上的作用力是多少？
例1 ： 设一细杆OA的质量为m 长为L OA的质量为 设一细杆OA的质量为m，长为L，一端支以枢轴而 能自由旋转。 端固定一质量为m的小球（ 能自由旋转。在A端固定一质量为m的小球（可看 作质点），设细杆由水平静止释放。 ），设细杆由水平静止释放 作质点），设细杆由水平静止释放。求： 1.当杆下落到θ处时的角速度和A处法向加速度； 1.当杆下落到θ处时的角速度和A处法向加速度； 当杆下落到 2.当杆转到铅直位置时的转动动能、 当杆转到铅直位置时的转动动能 2.当杆转到铅直位置时的转动动能、角加速度及 轴上的作用力是多少？ 轴上的作用力是多少？ N A L O θ 方法一： 方法一：转动定律
dA = Mω 3. 力矩的功率 N = dt
类比质点中N = Fv
如：设一细杆的质量为m，长为L，一端支以枢 设一细杆的质量为m 长为L 轴而能自由旋转，设此杆自水平静止释放。 轴而能自由旋转，设此杆自水平静止释放。求： 当杆到达铅直位置时重力矩所作的功 时重力矩所作的功。 当杆到达铅直位置时重力矩所作的功。 Z α mg L 以杆为研究对象 mg， 受力： 受力： ，FN
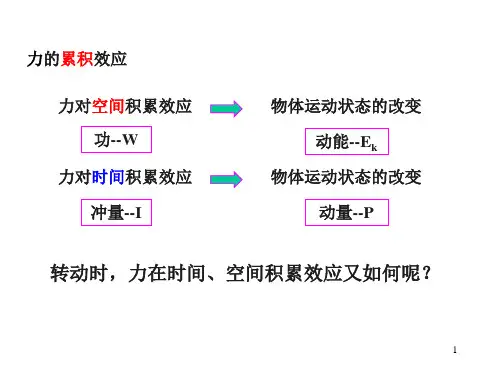
3-(3-4)力矩 转动定律解析

3-(3-4)力矩 转动定律解析


Fr sin d Md
其中：θ是刚体在力矩的作用下转过的角度。
力矩的功：
A Md
24
二 重力矩的功
设一细杆的质量为 m，长为L，一端支以枢轴而能自由旋 转，设此杆自水平静止释放。求：当杆到达铅直位置时重力 矩所作的功 以杆为研究对象 受力分析 MN=0 N Z L dM gxdxsinα
29
例1 设一细杆的质量为m，长为L，一端支以枢轴而能自由旋转， 设此杆自水平静止释放。求：当杆过铅直位置时的角加速度、 角速度以及此时A和C点的线速度量值。 N 解法一： Y Z L X O
C mg 建立坐标系 A
30
(1) 以杆为研究对象 受力 分析 mg和N， N不产生对轴的力矩
建立XYZ坐标系（并以Z轴为转动量的正方向） N L Y M mg sin Z L 2 X O
M M1 M2 M3
5
(2) 若刚体受N个外力作用时的力矩，
M 合 M i ＝r1 F1 r2 F2 rN FN
F1 , F2 ,, FN
ri Fi
i
i
力不连续
“牛二”定律
转动定律
M I
F ma
mI
12
定轴转动定律：绕某定轴转动的刚体，所受合外力的力矩在该 轴上的分量等于刚体对该轴的转动惯量与角加速度的乘积。
M I
或
M I
说明：
(1) 定轴转动定律是瞬时对应关系； (2) M, I, β应是对同一轴而言的。
M dM
m rg 2 2rdr R
R0Fra bibliotekm 2 2 g 2 2r dr gmR R 3
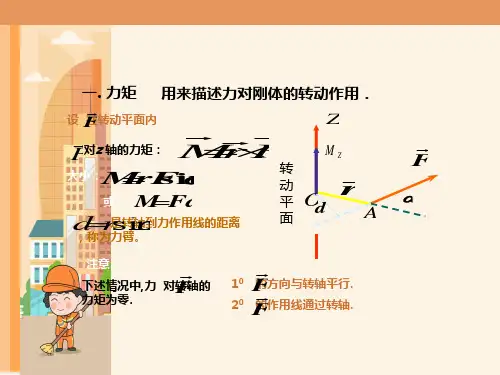
力矩转动定律转动惯量

力矩转动定律转动惯量

有
解 (1) 用隔离法分别对各物体作受力分析，取如图所示坐标系．
A
B
C
O
O
O
O
解得：
如令 ，可得
B由静止出发作匀加速直线运动，下落的速率
稳定平衡状态，当其受到微小扰动时，细杆将在重力作用下由静止开始绕铰链O 转动．试计算细杆转动到与竖直线成 角时的角加速度和角速度．
同一刚体,转轴位置不同,J 就不相同
质量离散分布
J 的计算方法
质量连续分布
：质量元
：体积元
例.求长L,质量m均匀细棒的转动惯量. (1)O轴通过棒一端且与棒垂直;(2)O'轴通过棒中点且与棒垂直.
x
dx
O
O'
解： 取轴为坐标原点, 取长度微元如图
dm=dx,
=m/L
例3 一长为 l 、质量为 m 匀质细杆竖直放置，其下端与一固定铰链O相接，并可绕其转动．由于此竖直放置的细杆处于非
m,l
O
mg
θ
解 细杆受重力和铰链对细杆的约束力 作用，由转动定律得
式中
得
m,l
O
mg
θ
由角加速度的定义
对上式积分，利用初始条件，
m,l
O
mg
θ
解得：
dJ=r2dm
=x2dx
(1)过棒的一端O
=L3/3
=mL2/3
(2)过棒的中点O'
=x3/3
=L3/12
=mL2/12
结果表明： 同一刚体对不同位置的转轴，转动惯量并不相同。
例题 求圆盘对于通过中心并与盘面垂直的转轴的 转动惯量。设圆盘的半径为R，质量为m，密度均匀。
r
R

3.3 力矩 转动定律解读


r
转动平面
转轴
(3) 若刚体受N个外力作用， F1 , F2 , , FN
ri Fi M i i i 注意: (a) M 合 ri Fi
i i
M 合 M i＝r1 F1 r2 F2 rN FN
T2 T1 ' m3 g T ' 2 a1 m1 m2 m1g a m2 g 2
M+ M0
求：（t）=？ I M1 解： 1）以刚体为研究对象； 2）分析受力矩 3）建立轴的正方向； 4）列方程：
M 0 M1 I
解：4）列方程：
M1=–a M 0 M 1 M 0 a I I d M 0 a M 0 a 1 t (ln ) dt I a M0 I 分离变量： at d dt M a 0 e I M 0 a I M0
M 0 M1 I
M+ M0
d t dt 0 M a 0 I 0

1 M 0 (1 e a

at I
)
例6. 质量分别为 m1、m2 的物体，通过轻绳挂在质量为 m3半径为 r 的圆盘形滑轮上。求物体 m1 、m2 运动的加 速度以及绳子的张力T1, T2（绳子质量不计）。 ,
m1g - T= m1a….(1)
列方程：
T’r=I
a=r
…(2)
…(3)
1 2 I mr 2
T=T’ …(4)
+ r T m2 T’
m1
N
r
T’
m1g - T= m1a….(1) T’r=I…(2) a = r …(3) T=T’ …(4) 1 2 I mr 2 m1gr = m1r2+ 1 m2r2 2 2m1g = (2m1+m2)r 2m1g a=r= 2m1+m2

3力矩转动定律(大学物理 - 刚体部分)



F
二、转动定律
刚体作定轴转动时，合外力矩等于 刚体的转动惯量与角加速度的乘积。 M Jβ
注意几点
1. 是矢量式 2. 具有瞬时性。 3. M、J、是对同一轴而言的。
§5.力矩、转动定律 / 二、转动定律
三. 解题方法及应用举例
M Jβ
1.确定研究对象。
2.受力分析（只考虑对转动有影响的力矩）。
M J
l 1 2 mg cos ml 2 3 3 g cos 2l
习题课 / 例3
m,l
mg

3 g cos 2l
60时
0时
3 g 4l 3 g 2l
m,l
mg

习题课 / 例3
3.列方程求解(平动物体列牛顿定律方程，转 动刚体列转动定律方程和角量与线量关系)。
§5.力矩、转动定律 / 三、解题方法及应用举例
例1：如图所示，两个同心圆盘结合在一 起可绕中心轴转动，大圆盘质量为 m1、 半径为 R，小圆盘质量为 m2、半径为 r， 两圆盘都用力 F 作用，求角加速度。
解：以 m1、 m2 为研 究对象，它们有共同 的角加速度，只有 F、 F 产生力矩。 FR Fr ( J1 J 2 )
第三节
力矩 转动定律
一、力矩
力与力臂的乘积。
O d
M
r
P r M dF r sin F M rF sin 根据矢量乘积法则： A B AB sin 用矢量方法表示力矩： M r F 单位：牛顿· 米， N ·m 方向：从r沿小于角右旋到F，大拇指指向。
§5.力矩、转动定律 / 一、力矩
m2 r
R
m1

§4.3 力矩 转动定律(打印稿)

1 M = mgl cosθ 2
)θ
M = Jα = 1 ml 2 ⋅ dω⋅ dθ dθ dt 3
3g ωdω = cosθ dθ 2l
ω
l 2
θ
m、 、 l C
mg
3g 3g ∫ ωdω = ∫ 2l cosθ dθ ∴ ω= l sinθ 0 0
θ
(解毕)
10 ·
Chapter 4. 刚体的转动
i=1 i i
n
Mz = Jα
( 转动定律 )
5·
Chapter 4. 刚体的转动
§4. 3 力矩 转动定律
明确几点
1. Mz = Jα 反映了力矩 Mz与角加速度 α 间的 间的瞬时关系。 。 2. 矢量关系（但在定轴转动中力矩 （但在定轴转动中力矩只有两个方向）。 ）。 3. Mz、J、α皆对同一轴而言。 而言。 4. 综合解题时，除了考虑运用牛顿定律外, 还需考 综合解题时，除了考虑运用牛顿定律外, 虑刚体的转动定律。 虑刚体的 。
m1 g −T1 = m1a
m2
T2
T2 = m2a (T −T2 )R = Jα = 1 M α R 1 2 a= Rα
2
T2 M, R T 1
a
T 1
m1
2g a= 4+ M / m
{
( 2 + M / m) T1 = mg 4+ M / m 2mg T2 = (解毕) 4+ M / m
m1 g
Chapter 4. 刚体的转动
§4. 3 力矩 转动定律
§4.3 力矩
转动定律
1·
Chapter 4. 刚体的转动
§4. 3 力矩 转动定律
一、作用在刚体上的力矩

大学物理-力矩-转动定律-转动惯量


F
p
18
2 – 5 刚体的定轴转动
第二章 动力学基础
解 (1) Fr J
Fr 98 0.2 39.2 rad/s2
J 0.5
mg T ma
(2) Tr J
a r
两者区别?
rO
F T
T


J
mgr mr 2

98 0.2 0.5 10 0.22
i
J r2dm
9
2 – 5 刚体的定轴转动
第二章 动力学基础
四. J 的计算
质量连续分布刚体的转动惯量
J mjrj2 r2dm dm ：质量元 j
对质量线分布的刚体： dm dl
：质量线密度
对质量面分布的刚体：
：质量面密度
对质量体分布的刚体：
在圆规迹切线方向
mk ak mk rk Fk fk
两边乘以rk，并对整个刚体求和
第二章 动力学基础
z
o

vk
mk
( mk rk2 ) Fk rk fk rk
k
k
k
5
2 – 5 刚体的定轴转动
第二章 动力学基础
( mk rk2 ) Fk rk fk rk
17
2 – 5 刚体的定轴转动
第二章 动力学基础
四、转动定律的应用举例
例1 一轻绳绕在半径 r =20 cm 的飞轮边缘， 在绳端施以F=98 N 的拉力，飞轮的转动惯量 J=0.5 kg·m2,飞轮与转轴间的摩擦不计 。
rO
求: (1) 飞轮的角加速度。
(2) 如以重量P =98 N的物体挂在 绳端,试计算飞轮的角加速度。

3-3 转动定理的积分形式-力矩对时间和空间的累积效应


4、刚体绕定轴转动的动能定理 、
设在合外力矩M的作用下，刚体绕定轴转过的角位移为 设在合外力矩 的作用下， 的作用下 dθ，合外力矩对刚体所作的元功为 ，
dW = Mdθ
dω M = Jα = J dt
dω dθ dW = J dθ ＝ J dω ＝ Jω d ω dt dt ω 刚体绕定轴转动的动能 W＝∫ dW = J ∫ ω dω ＝ 定理： 定理：合外力矩对绕定 ω0 轴转动的刚体所作的功 等于刚体的转动动能的 1 1 2 2 W＝ Jω － Jω 0 增量。 增量。 2 2
h = R∆ θ v = Rω
解上述方程， 解上述方程，可得
m v= 2 gh ( M / 2) + m
（2）公式 ）
dW dθ P= ＝M = Mω dt dt
功率一定时，转速越大，力矩越小； 功率一定时，转速越大，力矩越小； 转速越小，力矩越大。 转速越小，力矩越ห้องสมุดไป่ตู้。 （3）意义 ）
表示力矩对刚体作功的快慢
3、刚体的转动动能 、
刚体以角速度ω作定轴转动，取一质元 刚体以角速度 作定轴转动，取一质元∆mi，距转轴 ri，则 作定轴转动 此质元的速度为v 此质元的速度为 i=riω，动能为 ，
二、 刚体定轴转动的功能关系
1、力矩的功 、
刚体在外力F 的作用下， 刚体在外力 的作用下，绕转轴 转过的角位移为dθ，这时力F的作 转过的角位移为 ，这时力 的作 用点位移的大小为dr=rdθ。力F在 用点位移的大小为 。 在 这段位移内所作的功为
v v v π dW = F dr = F dr cos − ϕ = Frdθ sin ϕ 2
1 1 2 2 2 E ki = ∆m i v i = ∆m i ri ω 2 2

大学物理—力矩


已知：mi
v Fi :
: p点质量 rvi :
p 点所受外力
p
点对 o
点位矢
(o
Z
p)

d : p点绕轴转过的角位移
dsvi : :
i :
p 点元位移
dsvi 与
rvi 与
v Fi 的夹角 v Fi 的夹角
v
O d dsvi
Fi
rvi
i
P

求证： A Md 0
dsi rid
1、公式： Ep mghc
不太大刚体的势能
2、证： Ep Vmi ghi g Vmihi mghc
刚体不太大，g一定
质心hc
mi hi m
6
对刚体绕轴转动不起作用
力
v F 对于转轴
F2
oz
:与转轴垂直
v
的力矩= F2对
O
起作用 点的力矩
v Mz

rv
v F2
大小： M z F2r sin F2d
方向：
v Mz
方向:
OZ
3、总力矩的大小= 所有外力力矩的代数和
v M
z
正方向的规定：促进转动的力矩为正
1
§3-3 力矩 刚体定轴转动定律
二、F定v=轴m转a动v 定律m dvv
dt
v dpv
F=
dt
牛二
类比法
Mz
已知：
都在与轴 垂直的平 面内
J
rvvmi :i :
Fvi : F′i :
i :
i :
J dw
dt
p 点质量
Mz

dLz dt
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

M I
M
M
14
纸风车
电风扇
没事！
疼吗？
15
例1 一质量m1为的物体绕在一半径为 r质量为m2的圆盘上，开始 时静止，求重物的加速度、绳中的张力和 t 时刻重物下降多高？ (绳的质量与轴上的磨擦力不计)。 m2
r
+ T m1
T
T’ m1g
N
解：建立转动轴的正方向， 加速度的正方向。 r T’ 隔离物体分析力：
“牛二”定律
转动定律
M I
F ma
mI
12
定轴转动定律：绕某定轴转动的刚体，所受合外力的力矩在该 轴上的分量等于刚体对该轴的转动惯量与角加速度的乘积。
M I
或
M I
说明：
(1) 定轴转动定律是瞬时对应关系； (2) M, I, β应是对同一轴而言的。
i
mi (dmi ), ri 受力：合内力 F内与 ri 成 i 角 i
外力 F 与 ri 成 i 角 i
P
Fi F内i＝mi ai mi (ain ai )
用 ri 左叉乘(1)式：
10
用 ri 左叉乘(1)式：
(mi )ri (ain ai )
M
z
r
d
M
F

F 对转轴 Z 的力矩
O
M r F
大小 方向
P
-- 力臂
M Fr sin Fd rF
米·牛顿
d
单位
3
M r F
大小 方向
M Fr sin Fd rF
F
Mi 0
F
F
2 ri Fi (mi )ri
11
对整个刚体，求和
对整个刚体，求和
z
O
2 ri Fi (mi )ri
I (mi )ri
i 2
F内 i
ri
i
Fi
i
P
M 合外力 ri Fi I
i
M rF sin
合力矩等于各分力矩的矢量和。
M M1 M2 M3
5
(2) 若刚体受N个外力作用时的力矩，
M 合 M i ＝r1 F1 r2 F2 rN FN
F1 , F2 ,, FN
大小：M
r 0
M r F
C）力的方向与转轴平行
F
投影为零
以上情况力矩M=0
F
向心力的力矩为零
7
例1 长为L均匀细杆，质量为m，在平面内以角速度ω转动， 求M摩擦力。 解：建立坐标系 力是连续的 受力分析
M 合 r dF
方向： 向下
dm
O
x
T ' r I
…(2)
…(3) …(4) …(5)
m2g
a+
m1 g T m1a ….(1)
T ' r I
…(2) …(3) …(4) …(5)
线量和角量关系：
列方程：
T T'
a r
a r
1 I mr 2 2
16
r
m2
N
+ T’ T m1 m 1g a+ m2g
T
r
m1 g T m1a ….(1)
力的累积效应
力对空间积累效应 功--W 力对时间积累效应 物体运动状态的改变 动能--Ek 物体运动状态的改变
冲量--I
动量--P
转动时，力在时间、空间积累效应又如何呢？
1
3-3 力矩 转动定律
竿 子 较长 安些 全还 ？是 短 些
2
一 力矩
刚体绕 OZ 轴旋转，力 F 作用在刚
体上点P，且在转动平面内， 为由点O到力的作用点P的位矢。 r
ri ( Fi F内i )
z
O
F内 i
(mi )(ri ain ri ai ) ri F内i 0
ri
i
Fi
i
P
ri ain 0
i
方向在一条直线上
ai ri 0 2 ri ai ri
Mi 0
F
Fi 0
Mi ?
4
讨论
(1) 若力 F 不在转动平面内，把
力分解为平行和垂直于转轴方向 的两个分量
z
转轴
M
O
Fz 对转轴的力矩 为零 ？ F 对转轴的力矩:
F Fz F
Fz
r

F F
Mk r F
M dM
m rg 2 2rdr R

R
0
m 2 2 g 2 2r dr gmR R 3
9
二 转动定律
要揭示转动惯量的物理意义， 实际上是要找到一个类似于牛顿 定律的规律 -- 转动定律。 刚体可看成是由许多质元 组成，任取一质元P点， O
z
ri
F内 i
i
Fi
F
M合
X
dF gdm
m g dx l
8
rdF
l
1 1 mg xdx mgL 0 l 2
例2 现有一圆盘在平面内以角速度 ω 转动，求摩擦力产生的 力矩（μ 、m、R）。 解： 取细圆环为质元 dr
ω
r
m 2rdr dm ds 2 R
dM rf rgdm
ri Fi
i
i
力不连续
力是连续的
M ri Fi
i
M 合 ri Fi
i i
M 合 r dF
6
(3) 当 F 0）力的方向与矢径的方向在同一直线上。 方向： r F sin 0
如何求力对轴的力矩呢？ 如图可将力分解为两个力， 只求那个垂直于轴的力的力矩 就可以了。
z
M
O
Fz
r

F F
13
(3) 转动定律说明了I 是物体转动惯性大小的量度。 M一定时
I
I
即： I 越大的物体，转动惯性就越大，保持原有转动状态的 能力就越强；反之， I 越小，越容易改变状态，保持原有状 态的能力越弱，或者说转动惯性越小。 如一个外径和质量相同的实心圆柱与 空心圆筒，若受力和力矩一样，谁转 动得快些呢？