历年全国理科数学高考试题立体几何部分含答案

2023年高考数学立体几何真题练习（含答案解析）1．（2022·北京·高考真题）已知正三棱锥−P ABC 的六条棱长均为6，S 是ABC 及其内部的点构成的集合．设集合{}5T Q S PQ =∈≤，则T 表示的区域的面积为（ ） A ．34πB ．πC ．2πD ．3π【答案】B 【解析】设顶点P 在底面上的投影为O ，连接BO ，则O 为三角形ABC 的中心，且263BO =⨯=PO 因为5PQ =，故1OQ =，故S 的轨迹为以O 为圆心，1为半径的圆，而三角形ABC 内切圆的圆心为O ，半径为2364136=>⨯， 故S 的轨迹圆在三角形ABC 内部，故其面积为π 故选：B2．（2022·浙江·高考真题）如图，已知正三棱柱1111,ABC A B C AC AA −=，E ，F 分别是棱11,BC AC 上的点．记EF 与1AA 所成的角为α，EF 与平面ABC 所成的角为β，二面角F BC A −−的平面角为γ，则（ ）A ．αβγ≤≤B ．βαγ≤≤C ．βγα≤≤D ．αγβ≤≤【答案】A【解析】如图所示，过点F 作FP AC ⊥于P ，过P 作PM BC ⊥于M ，连接PE ，则EFP α=∠，FEP β=∠，FMP γ=∠， tan 1PE PE FP AB α==≤，tan 1FP AB PE PE β==≥，tan tan FP FPPM PEγβ=≥=， 所以αβγ≤≤， 故选：A ．3．（多选题）（2022·全国·高考真题）如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，,2FB ED AB ED FB ==∥，记三棱锥E ACD −，F ABC −，F ACE −的体积分别为123,,V V V ，则（ ）A ．322V V =B ．31V V =C ．312V V V =+D ．3123V V =【答案】CD 【解析】设22AB ED FB a ===，因为ED ⊥平面ABCD ，FB ED ，则()2311114223323ACDV ED Sa a a =⋅⋅=⋅⋅⋅=， ()232111223323ABCV FB Sa a a =⋅⋅=⋅⋅⋅=，连接BD 交AC 于点M ，连接,EM FM ，易得BD AC ⊥，又ED ⊥平面ABCD ，AC ⊂平面ABCD ，则ED AC ⊥，又ED BD D =，,ED BD ⊂平面BDEF ，则AC ⊥平面BDEF ，又12BM DM BD ===，过F 作FG DE ⊥于G ，易得四边形BDGF 为矩形，则,FG BD EG a ===，则,EM FM ==，3EF a =，222EM FM EF +=，则EM FM ⊥，212EFMSEM FM =⋅，AC =， 则33123A EFM C EFM EFMV V V AC S a −−=+=⋅=，则3123V V =，323V V =，312V V V =+，故A 、B 错误；C 、D 正确. 故选：CD.4．（多选题）（2022·全国·高考真题）已知正方体1111ABCD A B C D −，则（ ） A ．直线1BC 与1DA 所成的角为90︒ B ．直线1BC 与1CA 所成的角为90︒ C ．直线1BC 与平面11BB D D 所成的角为45︒ D ．直线1BC 与平面ABCD 所成的角为45︒【答案】ABD【解析】如图，连接1B C 、1BC ，因为11//DA B C ，所以直线1BC 与1B C 所成的角即为直线1BC与1DA 所成的角，因为四边形11BB C C 为正方形，则1B C ⊥1BC ，故直线1BC 与1DA 所成的角为90︒，A 正确；连接1AC ，因为11A B ⊥平面11BB C C ，1BC ⊂平面11BB C C ，则111A B BC ⊥， 因为1B C ⊥1BC ，1111A B B C B =，所以1BC ⊥平面11A B C ，又1AC ⊂平面11A B C ，所以11BC CA ⊥，故B 正确； 连接11AC ，设1111ACB D O =，连接BO ，因为1BB ⊥平面1111D C B A ，1C O ⊂平面1111D C B A ，则11C O B B ⊥， 因为111C O B D ⊥，1111B D B B B ⋂=，所以1C O ⊥平面11BB D D ， 所以1C BO ∠为直线1BC 与平面11BB D D 所成的角，设正方体棱长为1，则1C O =1BC =1111sin 2C O C BO BC ∠==， 所以，直线1BC 与平面11BB D D 所成的角为30，故C 错误；因为1C C ⊥平面ABCD ，所以1C BC ∠为直线1BC 与平面ABCD 所成的角，易得145C BC ∠=，故D 正确. 故选：ABD5．（多选题）（2021·全国·高考真题）在正三棱柱111ABC A B C -中，11AB AA ==，点P 满足1BP BC BB λμ=+，其中[]0,1λ∈，[]0,1μ∈，则（ ）A ．当1λ=时，1AB P △的周长为定值B ．当1μ=时，三棱锥1P A BC −的体积为定值C ．当12λ=时，有且仅有一个点P ，使得1A P BP ⊥ D ．当12μ=时，有且仅有一个点P ，使得1A B ⊥平面1AB P 【答案】BD 【解析】易知，点P 在矩形11BCC B 内部（含边界）．对于A ，当1λ=时，11=BP BC BB BC CC μμ=++，即此时P ∈线段1CC ，1AB P △周长不是定值，故A 错误；对于B ，当1μ=时，1111=BP BC BB BB B C λλ=++，故此时P 点轨迹为线段11B C ，而11//B C BC ，11//B C 平面1A BC ，则有P 到平面1A BC 的距离为定值，所以其体积为定值，故B 正确．对于C ，当12λ=时，112BP BC BB μ=+，取BC ，11B C 中点分别为Q ，H ，则BP BQ QH μ=+，所以P 点轨迹为线段QH ，不妨建系解决，建立空间直角坐标系如图，1A ⎫⎪⎪⎝⎭，()0,0P μ,，10,,02B ⎛⎫⎪⎝⎭，则112A P μ⎛⎫=−− ⎪ ⎪⎝⎭，10,,2BP μ⎛⎫=− ⎪⎝⎭，()110A P BP μμ⋅=−=，所以0μ=或1μ=．故,H Q 均满足，故C 错误； 对于D ，当12μ=时，112BP BC BB λ=+，取1BB ，1CC 中点为,M N ．BP BM MN λ=+，所以P 点轨迹为线段MN ．设010,,2P y ⎛⎫ ⎪⎝⎭，因为0,0A ⎫⎪⎪⎝⎭，所以01,2AP y ⎛⎫=− ⎪ ⎪⎝⎭，11,122A B ⎛⎫=−− ⎪ ⎪⎝⎭，所以00311104222y y +−=⇒=−，此时P 与N 重合，故D 正确． 故选：BD ．6．（2020·海南·高考真题）已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2，∠BAD =60°．以1DBCC 1B 1的交线长为________．【答案】2. 【解析】如图：取11B C 的中点为E ，1BB 的中点为F ，1CC 的中点为G ，因为BAD ∠=60°，直四棱柱1111ABCD A B C D −的棱长均为2，所以△111D B C 为等边三角形，所以1D E =111D E B C ⊥，又四棱柱1111ABCD A B C D −为直四棱柱，所以1BB ⊥平面1111D C B A ，所以111BB B C ⊥， 因为1111BB B C B =，所以1D E ⊥侧面11B C CB ，设P 为侧面11B C CB 与球面的交线上的点，则1D E EP ⊥，1D E =||EP =所以侧面11B C CB 与球面的交线上的点到E因为||||EF EG ==11B C CB 与球面的交线是扇形EFG 的弧FG ， 因为114B EFC EG π∠=∠=，所以2FEG π∠=，所以根据弧长公式可得22FG π==..。

高考数学理数立体几何大题训练(含答案)1.（2020·新课标Ⅲ·理）在长方体中，点P、Q分别在棱AB、CD上，且AP=CQ.（1）证明：点PQ平分长方体的体对角线；（2）若PQ在平面BCFE内，求二面角的正弦值．2.（2020·新课标Ⅱ·理）如图，已知三棱柱ABC-A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M、N分别为BC、B1C1的中点，P为AM上一点，过B1C1和P的平面交AB于E，交AC于F.（1）证明：AA1∥MN，且平面A1AMN⊥EB1C1F；（2）设O为△A1B1C1的中心，若AO∥平面EB1C1F，且AO=AB，求直线B1E与平面A1AMN 所成角的正弦值.3.（2020·新课标Ⅰ·理）如图，D为圆锥的顶点，O是圆锥底面的圆心，底面是内接正三角形ABC，P为上一点，AP为底面直径，DP⊥底面．（1）证明：DP平分∠ADC；（2）求二面角平面APD与平面ABC的余弦值．4.（2020·新高考Ⅰ）如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．5.（2020·天津）如图，在三棱柱ABC-A1B1C1中，点P、Q分别在棱AB、A1B1上，且AP=A1Q，平面PQC1为棱BC1的中垂面，M为棱AC的中点．（Ⅰ）求证：PM∥B1Q，且PM=B1Q；（Ⅱ）求二面角平面PQC1与直线PM所成角的正弦值；（Ⅲ）求直线B1Q与平面PQC1所成角的正弦值．6.（2020·江苏）在三棱锥ABCD中，已知CB=CD=1，AC=2，BD=2，O为BD的中点，AO⊥平面BCD，AO=2，E为AC上一点，DE⊥平面BCD，DE=1.（1）求直线AB与DE所成角的余弦值；（2）若点F在BC上，满足BF=BC，设二面角F-DE-C的大小为θ，求sinθ的值．7.（2020·北京）如图，正方体ABCD-EFGH中，E为AD的中点，P为BF上一点．（Ⅰ）求证：PE∥CG；（Ⅱ）求直线PE与平面CGH所成角的正弦值．8.（2020·浙江）如图，三棱台DEF-ABC中，面ADFC⊥面ABC，∠ACB=∠ACD=45°，XXX．（Ⅰ）证明：EF⊥DB；（Ⅱ）求DF与面DBC所成角的正弦值．9.（2020·扬州模拟）如图，在等边三角形ABC的三棱锥ABCD中，D为底面的中点，E为线段AD上一动点，记DE=λAD.（1）当λ=1时，求证：DE与平面ABC垂直；（2）当λ=2时，求直线BE与平面ACD所成角的正弦值．求证：直线AD与平面BCD垂直；2）若平面ABD与平面ACD所成二面角为，求二面角ABC与平面BCD所成二面角的正弦值。

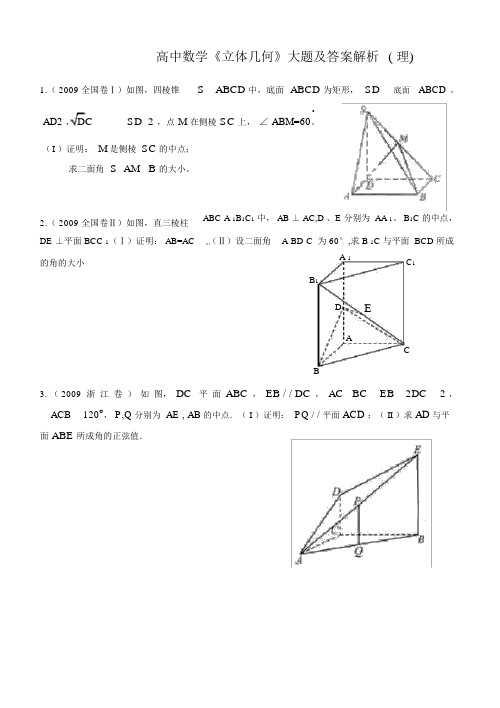
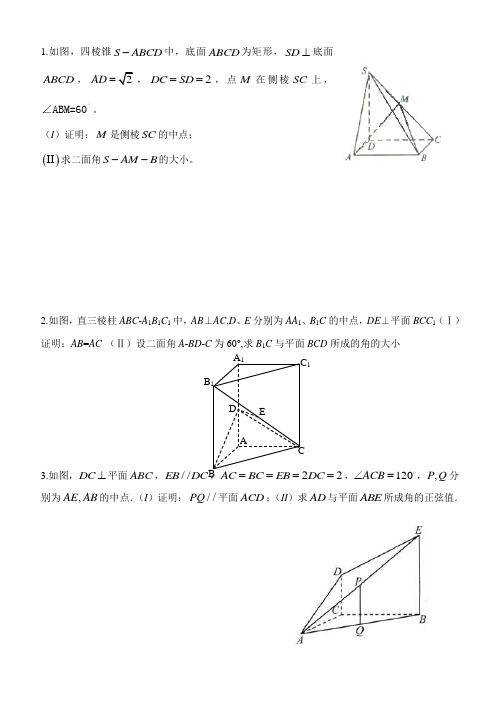
高中数学《立体几何》大题及答案解析( 理)1.（ 2009 全国卷Ⅰ）如图，四棱锥S ABCD 中，底面 ABCD 为矩形， SD底面ABCD，AD2 ，DCo SD 2 ，点 M 在侧棱 SC 上，∠ABM=60。

（I ）证明：M是侧棱SC的中点；求二面角 S AM B 的大小。

2.（ 2009 全国卷Ⅱ）如图，直三棱柱DE ⊥平面 BCC 1（Ⅰ）证明： AB=AC 的角的大小ABC-A 1B1C1中， AB ⊥ AC,D 、E 分别为 AA 1、 B1C 的中点，（Ⅱ）设二面角A-BD-C 为 60°,求 B 1C 与平面 BCD 所成A 1 C1B1D EACB3. （ 2009浙江卷）如图，DC平面ABC，EB / / DC，AC BC EB 2DC 2 ，ACB 120o， P,Q 分别为 AE , AB 的中点．（I）证明： PQ / / 平面ACD；（II）求AD与平面 ABE 所成角的正弦值．4.（ 2009 北京卷）如图，四棱锥P ABCD 的底面是正方形，PD 底面 ABCD ，点E在棱PB上.（Ⅰ）求证：平面AEC 平面 PDB ；（Ⅱ）当 PD2AB 且E为PB的中点时，求 AE 与平面 PDB 所成的角的大小.5.（ 2009 江西卷）如图，在四棱锥P ABCD 中，底面 ABCD 是矩形， PA平面ABCD，PA AD 4 ， AB 2 ．以 BD 的中点 O 为球心、 BD 为直径的球面交PD 于点 M ．（1）求证：平面ABM⊥平面PCD；（2）求直线PC与平面ABM所成的角；（3）求点O到平面ABM的距离．PMA DOBC6（. 2009 四川卷）如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△ ABE 是等腰直角三角形，AB AE , FA FE , AEF 45 （I）求证： EF 平面 BCE ；（ II ）设线段 CD 、 AE 的中点分别为 P 、 M ，求证： PM ∥平面BCE （ III ）求二面角 F BD A 的大小。

专题25 立体几何中综合问题考纲解读明方向分析解读 1.能运用共线向量、共面向量、空间向量基本定理及有关结论证明点共线、点共面、线共面及线线、线面的平行与垂直问题;会求线线角、线面角;会求点点距、点面距等距离问题,从而培养用向量法思考问题和解决问题的能力.2.会利用空间向量的坐标运算、两点间距离公式、夹角公式以及相关结论解决有关平行、垂直、长度、角、距离等问题,从而培养准确无误的运算能力.3.本节内容在高考中延续解答题的形式,以多面体为载体,求空间角的命题趋势较强,分值约为12分,属中档题.2018年高考全景展示1．【2018年理数天津卷】如图，且AD =2BC ，,且EG =AD ，且CD =2FG ，，DA =DC =DG =2（I ）若M 为CF 的中点，N 为EG 的中点，求证：；（II ）求二面角的正弦值；（III ）若点P 在线段DG 上，且直线BP 与平面ADGE 所成的角为60°，求线段DP 的长.【答案】(Ⅰ)证明见解析；(Ⅱ)；(Ⅲ).详解：依题意，可以建立以D为原点，分别以，，的方向为x轴，y轴，z轴的正方向的空间直角坐标系（如图），可得D（0，0，0），A（2，0，0），B（1，2，0），C（0，2，0），E（2，0，2），F（0，1，2），G（0，0，2），M（0，，1），N（1，0，2）．（Ⅰ）依题意=（0，2，0），=（2，0，2）．设n0=(x，y，z)为平面CDE的法向量，则即不妨令z=–1，可得n0=（1，0，–1）．又=（1，，1），可得，又因为直线MN平面CDE，所以MN∥平面CDE．（Ⅱ）依题意，可得=（–1，0，0），，=（0，–1，2）．设n=（x，y，z）为平面BCE的法向量，则即不妨令z=1，可得n=（0，1，1）．设m=（x，y，z）为平面BCF的法向量，则即不妨令z=1，可得m=（0，2，1）．因此有cos<m，n>=，于是sin<m，n>=．所以，二面角E–BC–F的正弦值为．（Ⅲ）设线段DP的长为h（h∈［0，2］），则点P的坐标为（0，0，h），可得．易知，=（0，2，0）为平面ADGE的一个法向量，故，由题意，可得=sin60°=，解得h=∈［0，2］．所以线段的长为.点睛：本题主要考查空间向量的应用，线面平行的证明，二面角问题等知识，意在考查学生的转化能力和计算求解能力.2．【2018年理北京卷】如图，在三棱柱ABC-中，平面ABC，D，E，F，G分别为，AC，，的中点，AB=BC=，AC==2．（Ⅰ）求证：AC⊥平面BEF；（Ⅱ）求二面角B-CD-C1的余弦值；（Ⅲ）证明：直线FG与平面BCD相交．【答案】(1)证明见解析(2) B-CD-C1的余弦值为(3)证明过程见解析【解析】分析：（1）由等腰三角形性质得，由线面垂直性质得,由三棱柱性质可得，因此，最后根据线面垂直判定定理得结论，（2）根据条件建立空间直角坐标系E-ABF，设立各点坐标，利用方程组解得平面BCD一个法向量，根据向量数量积求得两法向量夹角，再根据二面角与法向量夹角相等或互补关系求结果，（3）根据平面BCD一个法向量与直线F G方向向量数量积不为零，可得结论. 详解：解：（Ⅰ）在三棱柱ABC-A1B1C1中，∵CC1⊥平面ABC，∴四边形A1ACC1为矩形．又E，F分别为AC，A1C1的中点，∴AC⊥EF．∵AB=BC．∴AC⊥BE，∴AC⊥平面BEF．（Ⅱ）由（I）知AC⊥EF，AC⊥BE，EF∥CC1．又CC1⊥平面ABC，∴EF⊥平面ABC．∵BE平面ABC，∴EF⊥BE．如图建立空间直角坐称系E-xyz．由题意得B（0，2，0），C（-1，0，0），D （1，0，1），F（0，0，2），G（0，2，1）．∴，设平面BCD的法向量为，∴，∴，令a=2，则b=-1，c=-4，∴平面BCD的法向量，又∵平面CDC1的法向量为，∴．由图可得二面角B-CD-C1为钝角，所以二面角B-CD-C1的余弦值为．（Ⅲ）平面BCD的法向量为，∵G（0，2，1），F（0，0，2），∴，∴，∴与不垂直，∴GF与平面BCD不平行且不在平面BCD内，∴GF与平面BCD相交．点睛：垂直、平行关系证明中应用转化与化归思想的常见类型.(1)证明线面、面面平行，需转化为证明线线平行.(2)证明线面垂直，需转化为证明线线垂直.(3)证明线线垂直，需转化为证明线面垂直.3．【2018年江苏卷】如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，点P，Q分别为A1B1，BC的中点．（1）求异面直线BP与AC1所成角的余弦值；（2）求直线CC1与平面AQC1所成角的正弦值．【答案】（1）（2）【解析】分析：（1）先建立空间直角坐标系，设立各点坐标，根据向量数量积求得向量的夹角，再根据向量夹角与异面直线所成角的关系得结果；（2）利用平面的方向量的求法列方程组解得平面的一个法向量，再根据向量数量积得向量夹角，最后根据线面角与所求向量夹角之间的关系得结果.详解：如图，在正三棱柱ABC−A1B1C1中，设AC，A1C1的中点分别为O，O1，则OB⊥OC，OO1⊥OC，OO1⊥OB，以为基底，建立空间直角坐标系O−xyz．因为AB=AA1=2，所以．（1）因为P为A1B1的中点，所以，从而，故．因此，异面直线BP与AC1所成角的余弦值为．点睛：本题考查空间向量、异面直线所成角和线面角等基础知识，考查运用空间向量解决问题的能力.利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”. 4．【2018年江苏卷】在平行六面体中，．求证：（1）；（2）．【答案】答案见解析【解析】分析：（1）先根据平行六面体得线线平行，再根据线面平行判定定理得结论；（2）先根据条件得菱形ABB1A1，再根据菱形对角线相互垂直，以及已知垂直条件，利用线面垂直判定定理得线面垂直，最后根据面面垂直判定定理得结论.详解：证明：（1）在平行六面体ABCD-A 1B1C1D1中，AB∥A1B1．因为AB平面A1B1C，A1B1平面A1B1C，所以AB∥平面A1B1C．（2）在平行六面体ABCD-A1B1C1D1中，四边形ABB1A1为平行四边形．又因为AA1=AB，所以四边形ABB1A1为菱形，因此AB1⊥A1B．又因为AB1⊥B1C1，BC∥B1C1，所以AB1⊥BC．又因为A1B∩BC=B，A1B平面A1BC，BC平面A1BC，所以AB1⊥平面A1BC．因为AB1平面ABB1A1，所以平面ABB1A1⊥平面A1BC．点睛：本题可能会出现对常见几何体的结构不熟悉导致几何体中的位置关系无法得到运用或者运用错误，如柱体的概念中包含“两个底面是全等的多边形，且对应边互相平行，侧面都是平行四边形”，再如菱形对角线互相垂直的条件，这些条件在解题中都是已知条件，缺少对这些条件的应用可导致无法证明. 5．【2018年理新课标I卷】如图，四边形为正方形，分别为的中点，以为折痕把折起，使点到达点的位置，且.（1）证明：平面平面；（2）求与平面所成角的正弦值.【答案】(1)证明见解析.(2) .【解析】分析：(1)首先从题的条件中确定相应的垂直关系，即BF⊥PF，BF⊥EF，又因为，利用线面垂直的判定定理可以得出BF⊥平面PEF，又平面ABFD，利用面面垂直的判定定理证得平面PEF⊥平面ABFD.(2)结合题意，建立相应的空间直角坐标系，正确写出相应的点的坐标，求得平面ABFD的法向量，设DP与平面ABFD所成角为，利用线面角的定义，可以求得，得到结果.详解：（1）由已知可得，BF⊥PF，BF⊥EF，又，所以BF⊥平面PEF.又平面ABFD，所以平面PEF⊥平面ABFD.点睛：该题考查的是有关立体几何的问题，涉及到的知识点有面面垂直的证明以及线面角的正弦值的求解，属于常规题目，在解题的过程中，需要明确面面垂直的判定定理的条件，这里需要先证明线面垂直，所以要明确线线垂直、线面垂直和面面垂直的关系，从而证得结果；对于线面角的正弦值可以借助于平面的法向量来完成，注意相对应的等量关系即可.6．【2018年全国卷Ⅲ理】如图，边长为2的正方形所在的平面与半圆弧所在平面垂直，是上异于，的点．（1）证明：平面平面；（2）当三棱锥体积最大时，求面与面所成二面角的正弦值．【答案】（1）见解析（2）【解析】分析：（1）先证平面CMD,得,再证，进而完成证明。

立体几何高考题及答案【篇一：新课标近三年立体几何高考题(解析版)】ss=txt>1、（2011.8．)在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧视图可以为（Ｄ）2、（2011.18．）（本小题满分12分）如图，四棱锥p?abcd中，底面abcd为平行四边形，?dab?60?，ab?2ad，pd?底面abcd．（i）证明：pa?bd；（ii）设pd=ad=1，求棱锥d-pbc的高．解：（Ⅰ）因为?dab?60?,ab?2ad，由余弦定理得bd?从而bd2+ad2= ab2，故bd?ad又pd?底面abcd，可得bd?pd所以bd?平面pad. 故 pa?bd故bc?平面pbd，bc?de。

则de?平面pbc。

由题设知，pd=1，则bd=，pb=2，即棱锥d—pbc的高为. 24、（2012.19）（本小题满分12分）12的中点(Ｉ)证明：平面bdc1⊥平面bdc（Ⅱ）平面bdc1分此棱柱为两部分，求这两部分体积的比。

（Ⅰ）由题设知bc⊥cc1,bc⊥ac，cc1?ac?c,∴bc?面acc1a1, 又∵dc1?面acc1a1，0∴dc1?bc,由题设知?a1dc1??adc?45,∴?cdc1=90,即dc1?dc,又∵dc?bc?c,∴dc1⊥面bdc,∵dc1?面bdc1，∴面bdc⊥面bdc1；（Ⅱ）设棱锥b?dacc1的体积为v1，ac=1，由题意得，v1=?由三棱柱abc?a1b1c1的体积v=1，∴(v?v1):v1=1:1，∴平面bdc1分此棱柱为两部分体积之比为1:1.5、(2013课标全国Ⅰ，文11)某几何体的三视图如图所示，则该几何体的体积为( d )．6．(2013课标全国Ⅰ，文15)已知h是球o的直径ab上一点，ah∶0111?2?1?1=， 232(1)证明：ab⊥a1c；(2)若ab＝cb＝2，a1c，求三棱柱abc－a1b1c1的体积．(1)证明：取ab的中点o，连结oc，oa1，a1b. 因为ca＝cb，所以oc⊥ab.故△aa1b为等边三角形，所以oa1⊥ab.因为oc∩oa1＝o，所以 ab⊥平面oa1c.又a1c?平面oa1c，故ab⊥a1c.(2)解：由题设知△abc与△aa1b都是边长为2的等边三角形，所以oc＝oa1又a1ca1c＝oc＋oa12， 22故oa1⊥oc.因为oc∩ab＝o，所以oa1⊥平面abc，oa1为三棱柱abc－a1b1c1的高．又△abc的面积s△abcx解：(1)f′(x)＝e(ax＋a＋b)－2x－4.由已知得f(0)＝4，f′(0)＝4.故b＝4，a＋b＝8.从而a＝4，b＝4.x2(2)由(1)知，f(x)＝4e(x＋1)－x－4x，【篇二：2015年高考题立体几何汇编】lass=txt>1.（15北京理科）设?，?是两个不同的平面，m是直线且m??．“m∥?”是“?∥?”的a．充分而不必要条件 c．充分必要条件【答案】b 【解析】b．必要而不充分条件 d．既不充分也不必要条件?是两个不同的平面，试题分析：因为?，若“m∥?”，则平面?、?m是直线且m??．可能相交也可能平行，不能推出?//?，反过来若?//?，m“m∥?”是“?∥?”的必要而不充分条件.考点：1.空间直线与平面的位置关系；2.充要条件.2.（15北京理科）某三棱锥的三视图如图所示，则该三棱锥的表面积是侧(左)视图??，则有m∥?，则俯视图a．2? b．4 c．2? d．5 【答案】c 【解析】试题分析：根据三视图恢复成三棱锥p-abc，其中pc?平面abc，取ab棱的中点d，d连接cd、pd，有pad=bd=1,pc=1,?abcd,ab?，底面abc为等腰三角形底边ab上的高cd为2，pd?s?abc?11?2?2?2,,s?pab??2??22ac?bc?，s?pac?s?pbc?1??1?,三棱锥表面积s表??2. 22考点：1.三视图；2.三棱锥的表面积.3.（15北京理科）如图，在四棱锥a?efcb中，△aef为等边三角形，平面aef?平面efcb，ef∥bc，bc?4，ef?2a，?ebc??fcb?60?，o为ef的中点． (Ⅰ) 求证：ao?be；(Ⅱ) 求二面角f?ae?b的余弦值；(Ⅲ) 若be?平面aoc，求a的值． afceb【答案】(1)证明见解析，（2）?【解析】4，（3）a?3试题分析：证明线线垂直可寻求线面垂直，利用题目提供的面面垂直平面aef?平面efcb，借助性质定理证明ao?平面efcb，进而得出线线垂直，第二步建立空间直角坐标系，写出相关点的坐标，平面aef的法向量易得，只需求平面aeb的法向量，设平面aeb的法向量，利用线线垂直，数量积为零，列方程求出法向量，再根据二面角公式求出法向量的余弦值；第三步由于ao?be，要想be?平面aoc，只需be?oc，利用向量be、oc的坐标，借助数量积为零，求出a的值，根据实际问题予以取舍.试题解析：(Ⅰ)由于平面aef?平面efcb，△aef为等边三角形，o为ef的中点，则ao?ef，根据面面垂直性质定理，所以ao?平面efcb，又be?平面efcb，则ao?be.(Ⅱ)取cb的中点d，连接od,以o为原点，分别以oe、od、oa为x、y、z轴建立空间直角坐标系，a)，e(a,0,0),b?,0),ae?(a,0,)，eb?(2?a?,0)，由于平面aef与y轴垂直，则设平面aef的法向量为n1?(0,1,0)，设平面aeb的法向量n2?(x,y,1)，n2?ae,ax?0,x?n2?eb,(2?a)x??)y?0,y??1，则n2??1,1)，二面角f?ae?b的余弦值cos?n1,n2??n1?n2n1?n2?1??，5由二面角f?ae?b为钝二面角，所以二面角f?ae?b的余弦值为?. （Ⅲ）有（1）知ao?平面efcb，则ao?be，若be?平面aoc，只需be?oc，eb?(2?a,?,0)，又oc?(??,0)，2be?oc??2(2?a)??)?0，解得a?2或a?44，由于a?2，则a?. 33考点：1.线线垂直的证明；2.利用法向量求二面角；3.利用数量积解决垂直问题.4.（15北京文科）某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为（） a．1bc．2【答案】c 【解析】试题分析：四棱锥的直观图如图所示：由三视图可知，sc?平面abcd，sa是四棱锥最长的棱，sa???.考点：三视图.6.（15年广东理科）若空间中n个不同的点两两距离都相等，则正整数n的取值 a．大于5 b. 等于5 c. 至多等于4 d. 至多等于3 【答案】c．【考点定位】本题考查空间想象能力、推理能力，属于中高档题． 7.（15年广东理科）如图2，三角形pdc所在的平面与长方形abcd所在的平面垂直，pd=pc=4，ab=6，bc=3.点e是cd边的中点，点f、g分别在线段ab、bc上，且af=2fb，cg=2gb.图2（1）证明：pe?fg；（2）求二面角p-ad-c的正切值；（3）求直线pa与直线fg所成角的余弦值.【答案】（1）见解析；（2（3．【解析】（1）证明：∵ pd?pc且点e为cd的中点，∴pe?dc，又平面pdc?平面abcd，且平面pdc面pdc，∴ pe?平面abcd，又fg?平面abcd，∴ pe?fg；（2）∵ abcd是矩形，∴ ad?dc，又平面pdc?平面abcd，且平面pdc面abcd，∴ ad?平面pcd，又cd、pd?平面pdc，∴ ad?dc，ad?pd，∴?pdc即为二面角p?ad?c的平面角，在rt?pde中，pd?4，de?fec平面abcd?cd，pe?平平面abcd?cd，ad?平1ab?3，pe? 2∴ tan?pdc?pe?即二面角p?ad?c； de（3）如下图所示，连接ac，【篇三：立体几何(2013年高考题汇编)】ass=txt>一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的1 ．（2013广东（理））设m,n是两条不同的直线,?,?是两个不同的平面,下列命题中正确的是（）a．若???,m??,n??,则m?n b．若?//?,m??,n??,则m//n c．若m?n,m??,n??,则??? d．若m??,m//n,n//?,则???【答案】d2.（2013年高考大纲卷（文））已知正四棱锥abcd?a1b1c1d1中，aa1?2ab,则cd与平面bdc1所成角的正弦值等于a．213bc．3d．3【答案】a3．（2013浙江（理））在空间中,过点a作平面?的垂线,垂足为b,记b?f?(a).设?,?是两个不同的平面,对空间任意一点p,q1?f?[f?(p)],q2?f?[f?(p)],恒有 pq1?pq2,则a．平面?与平面?垂直 b．平面?与平面?所成的(锐)二面角为450 c．平面?与平面?平行d．平面?与平面?所成的(锐)二面角为600【答案】a4 ．（2013上海春季高考）若两个球的表面积之比为1:4,则这两个球的体积之比为a．1:2b．1:4 c．1:8 d．1:16【答案】c5 ．（2013广东（理））某四棱台的三视图如图所示,则该四棱台的体积是）））（（（正视图侧视图俯视图第5题图1416a．4b．3 c．3d．6【答案】b6．（2013山东数（理））已知三棱柱abc?a1b1c1的侧棱与底面垂直,体积为4,底面是边长.若p为底面a1b1c1的中心,则pa与平面abc所成角的大小为 5????a．12b．3 c．4 d．6【答案】b7．（2013年高考辽宁卷（文））已知三棱柱abc?a1b1c1的6个顶点都在球o的球面上,若ab?3，ac?4,ab?ac,aa1?12,则球o的半径为a．2b．c．132d．【答案】c8 （2013新课标Ⅱ（理））已知m,n为异面直线,m?平面?,n?平面?.直线l满足l?m,l?n,l??,l??,则a．?//?,且l//?b．???,且l??c．?与?相交,且交线垂直于ld．?与?相交,且交线平行于l【答案】d9．（2013辽宁（理））已知三棱柱abc?a1b1c1的6个顶点都在球o的球面上,若））））（（（（ab?3，ac?4,ab?ac,aa1?12,则球o的半径为（）a．2b．c．132d．【答案】c10．（2013江西（理））如图,正方体的底面与正四面体的底面在同一平面?上,且ab?cd,正方体的六个面所在的平面与直线ce,ef相交的平面个数分别记为m,n,那么m?n?a．8b．9 c．10 d．11【答案】a11．（2013新课标Ⅱ（理））一个四面体的顶点在空间直角坐标系o?xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zox平面为投影面,则得到正视图可以为a．b． c． d．【答案】a12．（2013安徽（理））在下列命题中,不是公理．．的是 a．平行于同一个平面的两个平面相互平行b．过不在同一条直线上的三点,有且只有一个平面c．如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 d．如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线【答案】a二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上．13．（2013北京（文））某四棱锥的三视图如图所示,该四棱锥的体积为__________.）））（（（【答案】314．（2013上海（理））在xoy平面上,将两个半圆弧(x?1)2?y2?1(x?1)和(x?3)2?y2?1(x?3)、两条直线y?1 和y??1围成的封闭图形记为d,如图中阴影部分.记d绕y轴旋转一周而成的几何体为?,过(0,y)(|y|?1)作?的水平截面,所得截面面积为48?,试利用祖暅原理、一个平放的圆柱和一个长方体,得出?的体积值为__________【答案】2?2?16?.15．（2013陕西（理））某几何体的三视图如图所示, 则其体积为_______.【答案】?316．（2013上海（文科））已知圆柱?的母线长为l,底面半径为r,o 是上地面圆心,a、b是下底面圆周上两个不同的点,bc是母线,如图.若直线oa与bc所成角的大小为则1?________. r【答案】三、解答题：本大题共6小题，共70分,解答应写出文字说明、证明过程或演算步骤17．（2013江西（文））如图,直四棱柱abcd – a1b1c1d1中,ab//cd,ad⊥ab,ab=2,ad=,aa1=3,e为cd上一点,de=1,ec=3 (1) 证明:be⊥平面bb1c1c; (2) 求点b1 到平面ea1c1 的距离【答案】解.(1)证明:过b作cd的垂线交cd于f,则bf?ad?ef?ab?de?1,fc?2在rt?bfe中，be，rt?bfc中，bc 在?bce中，因为be?bc＝9＝ec,故be?bc 由bb1?平面abcd，得be?bb1，所以be?平面bb1c1c(2)三棱锥e?a1b1c1的体积v＝aa1?s?a1b1c122213在rt?a1d1c1中，a1c1,ea1同理,ec1，因此s?a1c1e?.设点b1到平面eac11的体积11的距离为d,则三棱锥b1?eac1v＝?d?s?a1ec1,?d?318．（2013重庆（理））如图,四棱锥p?abcd中,pa?底面abcd,bc?cd?2,ac?4,?acb??acd?点,af?pb.(1)求pa的长; (2)求二面角b?af?d的正弦值.?3,f为pc的中。

1、（2015年1卷18题）如图，四边形ABCD 为菱形，∠ABC=120°，E ，F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE=2DF ，AE ⊥EC.试题解析：（Ⅰ）连接BD ，设BD∩AC=G，连接EG ，FG ，EF ，在菱形ABCD 中，不妨设GB=1，由∠ABC=120°，可得AG=GC=3. 由BE ⊥平面ABCD ，AB=BC 可知，AE=EC ， 又∵AE ⊥EC ，∴EG=3，EG ⊥AC ，在Rt △EBG 中，可得BE=2，故DF=22. 在Rt △FDG 中，可得FG=62. 在直角梯形BDFE 中，由BD=2，BE=2，DF=22可得EF=322， ∴222EG FG EF +=，∴EG ⊥FG ， ∵AC∩FG=G，∴EG ⊥平面AFC ，∵EG ⊂面AEC ，∴平面AFC ⊥平面AEC.（Ⅱ）如图，以G 为坐标原点，分别以,GB GC 的方向为x 轴，y 轴正方向，||GB 为单位长度，建立空间直角坐标系G-xyz ，由（Ⅰ）可得A （030），E （2），F （－1,0，22），C （030），∴AE =（132），CF =（-1，3，22）.…10分故cos ,3||||AE CF AE CF AE CF ⋅<>==-. 所以直线AE 与CF 所成的角的余弦值为3. 2、（2016年1卷18题）如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD ,90AFD ∠=,且二面角D -AF -E 与二面角C -BE -F 都是60．（I ）证明：平面ABEF ⊥平面EFDC ； （II ）求二面角E -BC -A 的余弦值．试题解析：（I ）由已知可得F DF A ⊥,F F A ⊥E ,所以F A ⊥平面FDC E ． 又F A ⊂平面F ABE ,故平面F ABE ⊥平面FDC E ．（II ）过D 作DG F ⊥E ,垂足为G ,由（I ）知DG ⊥平面F ABE ．以G 为坐标原点,GF 的方向为x 轴正方向,GF 为单位长度,建立如图所示的空间直角坐标系G xyz -．由（I ）知DF ∠E 为二面角D F -A -E 的平面角,故DF 60∠E =,则DF 2=,DG 3=,可得()1,4,0A ,()3,4,0B -,()3,0,0E -,(D ． 由已知,//F AB E ,所以//AB 平面FDC E ． 又平面CDAB 平面FDC DC E =,故//CD AB ,CD//F E ．由//F BE A ,可得BE ⊥平面FDC E ,所以C F ∠E 为二面角C F -BE -的平面角,C F 60∠E =．从而可得(C -．所以(C E =,()0,4,0EB =,(C 3,A =--,()4,0,0AB =-． 设(),,n x y z =是平面C B E 的法向量,则C 00n n⎧⋅E =⎪⎨⋅EB =⎪⎩,即40x y ⎧+=⎪⎨=⎪⎩, 所以可取(3,0,n =．CABDEF设m 是平面CD AB 的法向量,则C 00m m ⎧⋅A =⎪⎨⋅AB =⎪⎩,同理可取()0,3,4m =．则219cos ,19n m n m n m ⋅==-． 故二面角C E -B -A 的余弦值为21919-．3（2016年2卷19题）（本小题满分12分）如图，菱形ABCD 的对角线AC 与BD 交于点O ，5AB =，6AC =，点E ，F 分别在AD ，CD 上，54AE CF ==，EF 交BD 于点H .将△DEF 沿EF 折到△D EF '的位置10OD '=.（I ）证明：D H '⊥平面ABCD ； （II ）求二面角B D A C '--的正弦值.【解析】⑴证明：∵54AE CF ==，∴AE CF AD CD=，∴EF AC ∥． ∵四边形ABCD 为菱形，∴AC BD ⊥，∴EF BD ⊥，∴EF DH ⊥，∴EF DH'⊥．∵6AC =，∴3AO =；又5AB =，AO OB ⊥， ∴4OB =，∴1AE OH OD AO=⋅=，∴3DH D H '==，∴222'OD OH D H '=+， ∴'D H OH ⊥．又∵OH EF H =，∴'D H ⊥面ABCD ．⑵建立如图坐标系H xyz -．()500B ，，，()130C ，，，()'003D ，，，()130A -，，， ()430AB =，，，()'133AD =-，，，()060AC =，，，设面'ABD 法向量()1n x y z =，，，由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩，取345x y z =⎧⎪=-⎨⎪=⎩， ∴()1345n =-，，．同理可得面'AD C 的法向量()2301n =，，， ∴12129575cos 255210n n n n θ⋅+===⋅，∴295sin 25θ=4、（2017年1卷18题）如图，在四棱锥P ABCD -中，AB CD ∥中，且90BAP CDP ∠=∠=︒．（1）证明：平面PAB ⊥平面PAD ；（2）若PA PD AB DC ===，90APD ∠=︒，求二面角A PB C --的余弦值． 【解析】（1）证明：∵90BAP CDP ∠=∠=︒∴PA AB ⊥，PD CD ⊥又∵AB CD ∥，∴PD AB ⊥又∵PD PA P =，PD 、PA ⊂平面PAD ∴AB ⊥平面PAD ，又AB ⊂平面PAB ∴平面PAB ⊥平面PAD（2）取AD 中点O ，BC 中点E ，连接PO ，OE ∵AB CD∴四边形ABCD 为平行四边形 ∴OE AB由（1）知，AB ⊥平面PAD∴OE ⊥平面PAD ，又PO 、AD ⊂平面PAD ∴OE PO ⊥，OE AD ⊥ 又∵PA PD =，∴PO AD ⊥ ∴PO 、OE 、AD 两两垂直∴以O 为坐标原点，建立如图所示的空间直角坐标系O xyz - 设2PA =，∴()002D -，，、()220B ，，、()002P ，，、()202C -，，， ∴()022PD =--，，、()222PB =-，，、()2200BC =-，，设()n x y z =,,为平面PBC 的法向量由00n PB n BC ⎧⋅=⎪⎨⋅=⎪⎩，得2220220x y z x ⎧+-=⎪⎨-=⎪⎩令1y =，则2z =，0x =，可得平面PBC 的一个法向量()012n =,, ∵90APD ∠=︒，∴PD PA ⊥又知AB ⊥平面PAD ，PD ⊂平面PAD ∴PD AB ⊥，又PA AB A = ∴PD ⊥平面PAB即PD 是平面PAB 的一个法向量，()022PD =--,, ∴23cos 323PD n PD n PD n⋅-===-⋅, 由图知二面角A PB C --为钝角，所以它的余弦值为33-5．（2018年1卷18题）如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点P 的位置，且PF BF ⊥． ⑴证明：平面PEF ⊥平面ABFD ； ⑵求DP 与平面ABFD 所成角的正弦值．解答：（1）,E F 分别为,AD BC 的中点，则//EF AB ，∴EF BF ⊥，又PF BF ⊥，EF PF F ⋂=，∴BF ⊥平面PEF ， BE ⊂平面ABFD ，∴平面PEF ⊥平面ABFD . （2）PF BF ⊥，//BF ED ，∴PF ED ⊥，又PF PD ⊥，ED DP D ⋂=，∴PF ⊥平面PED ，∴PF PE ⊥， 设4AB =，则4EF =，2PF =，∴23PE =， 过P 作PH EF ⊥交EF 于H 点， 由平面PEF ⊥平面ABFD ，∴PH ⊥平面ABFD ，连结DH ，则PDH ∠即为直线DP 与平面ABFD 所成的角， 由PE PF EF PH ⋅=⋅，∴23234PH ⋅==， 而4PD =，∴3sin 4PH PDH PD ∠==， ∴DP 与平面ABFD 所成角的正弦值34. 6.(2018年新课标Ⅱ理)如图,在三棱锥P -ABC 中,AB ＝BC ＝22,P A ＝PB ＝PC ＝AC ＝4,O 为AC 的中点.（1）求证:PO ⊥平面ABC ；（2）若点M 在棱BC 上,且二面角M -P A -C 为30°,求PC 与平面P AM 所成角的正弦值.【解析】（1）证明:∵AB ＝BC ＝22,AC ＝4,∴AB 2＋BC 2＝AC 2,即△ABC 是直角三角形. 又O 为AC 的中点,∴OA ＝OB ＝OC . ∵P A ＝PB ＝PC ,∴△POA ≌△POB ≌△POC . ∴∠POA ＝∠POB ＝∠POC ＝90°.∴PO ⊥AC ,PO ⊥OB ,OB ∩AC ＝0,∴PO ⊥平面ABC .（2）以O 坐标原点,OB ,OC ,OP 所在直线分别为x ,y ,z 轴建立空间直角坐标系如图所示.易知A (0,－2,0),P (0,0,23),C (0,2,0),B (2,0,0),BC →＝(－2,2,0). 设BM →＝λBC →＝(－2λ,2λ,0),0＜λ＜1,则AM →＝BM →－BA →＝(－2λ,2λ,0)－(－2,－2,0)＝(2－2λ,2λ＋2,0), 则平面P AC 的一个法向量为m ＝(1,0,0).设平面MP A 的法向量为n ＝(x ,y ,z ),则PA →＝(0,－2,23), 则n ·PA →＝－2y －23z ＝0,n ·AM →＝(2－2λ)x ＋(2λ＋2)y ＝0. 令z ＝1,则y ＝－3,x ＝(λ＋1)31－λ,即n ＝⎝ ⎛⎭⎪⎫(λ＋1)31－λ，－3，1.∵二面角M -P A -C 为30°,∴cos 30°＝m ·n |m ||n |＝32,即(λ＋1)3λ－1⎝ ⎛⎭⎪⎫(λ＋1)31－λ2＋1＋3×1＝32,解得λ＝13或λ＝3(舍去). ∴n ＝(23,－3,1),PC →＝(0,2,－23).PC 与平面P AM 所成角的正弦值sin θ＝|cos 〈PC →,n 〉|＝⎪⎪⎪⎪⎪⎪－23－2316·16＝4316＝34.18．（2019年1卷18题）（12分）如图，直四棱柱ABCD ﹣A 1B 1C 1D 1的底面是菱形，AA 1＝4，AB ＝2，∠BAD ＝60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点．（1）证明：MN ∥平面C 1DE ； （2）求二面角A ﹣MA 1﹣N 的正弦值．解答】（1）证明：如图，过N作NH⊥AD，则NH∥AA1，且，又MB∥AA1，MB＝，∴四边形NMBH为平行四边形，则NM∥BH，由NH∥AA1，N为A1D中点，得H为AD中点，而E为BC中点，∴BE∥DH，BE＝DH，则四边形BEDH为平行四边形，则BH∥DE，∴NM∥DE，∵NM⊄平面C1DE，DE⊂平面C1DE，∴MN∥平面C1DE；（2）解：以D为坐标原点，以垂直于DC得直线为x轴，以DC所在直线为y轴，以DD1所在直线为z轴建立空间直角坐标系，则N（，，2），M（，1，2），A1（，﹣1，4），，，设平面A1MN的一个法向量为，由，取x＝，得，又平面MAA1的一个法向量为，∴cos＜＞＝＝＝．∴二面角A﹣MA1﹣N的正弦值为．8．（12分）(2019年新课标Ⅱ理）如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1. （1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，求二面角B –EC –C 1的正弦值.解：（1）由已知得，11B C ⊥平面11ABB A ，BE ⊂平面11ABB A ，故11B C ⊥BE ．又1BEEC ⊥，所以BE ⊥平面11EB C ．（2）由（1）知190BEB ∠=︒．由题设知11Rt Rt ABE A B E ≅△△，所以45AEB ∠=︒，故AE AB =，12AA AB =．以D 为坐标原点，DA 的方向为x 轴正方向，||DA 为单位长，建立如图所示的空间直角坐标系D -xyz ，则C （0，1，0），B （1，1，0），1C （0，1，2），E （1，0，1），(1,1,1)CE =-，1(0,0,2)CC =．设平面EBC 的法向量为n =（x ，y ，x ），则0,0,CB CE ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0,x x y z =⎧⎨-+=⎩ 所以可取n =(0,1,1)--.设平面1ECC 的法向量为m =（x ，y ，z ），则10,0,CC CE ⎧⋅=⎪⎨⋅=⎪⎩m m 即20,0.z x y z =⎧⎨-+=⎩ 所以可取m =（1，1，0）． 于是1cos ,||||2⋅<>==-n m n m n m ．所以，二面角1B EC C --3．。

1.在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的俯视图可以为2.已知矩形ABCD的顶点都在半径为4的球O的球面上，且6,==,则棱锥AB BC-的体积为。

O ABCD3.如图，四棱锥P—ABCD中，底面ABCD为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD.(Ⅰ)证明：PA⊥BD；(Ⅱ)若PD=AD，求二面角A-PB-C的余弦值。

1.D2.3. 解：（Ⅰ）因为60,2DAB AB AD ∠=︒=，由余弦定理得BD =从而BD 2+AD 2= AB 2，故BD ⊥AD 又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面PAD. 故 PA ⊥BD（Ⅱ）如图，以D 为坐标原点，AD 的长为单位长，射线DA 为x 轴的正半轴建立空间直角坐标系D-xyz ，则()1,0,0A，()0B，()C -，()0,0,1P 。

(1),(1,0,0)AB PB BC =-=-=-uu u v uu v uu u v设平面PAB 的法向量为n=（x ，y ，z ），则0,0,{n AB n PB ⋅=⋅=u u u r u u u r00z =-=因此可取n=设平面PBC 的法向量为m ，则m 0,m 0,{PB BC ⋅=⋅=u u u ru u u r可取m=（0，-1， cos ,m n == 故二面角A-PB-C 的余弦值为1. 正方体ABCD-1111A B C D 中，B 1B 与平面AC 1D 所成角的余弦值为C 232. 已知圆O 的半径为1，PA 、PB 为该圆的两条切线，A 、B 为俩切点，那么PA PB ∙的最小值为(A) 4- (B)3-+ (C) 4-+3-+3. 已知在半径为2的球面上有A 、B 、C 、D 四点，若AB=CD=2,则四面体ABCD 的体积的最大值为(C)4. 如图，四棱锥S-ABCD 中，SD ⊥底面ABCD ，AB//DC ，AD ⊥DC ，AB=AD=1，DC=SD=2，E 为棱SB 上的一点，平面EDC ⊥平面SBC .（Ⅰ）证明：SE=2EB ；（Ⅱ）求二面角A-DE-C 的大小 .1. D2. D3. B4. 解法一：(Ⅰ)连接BD,取DC 的中点G ，连接BG,由此知 1,DG GC BG ===即ABC ∆为直角三角形，故BC BD ⊥. 又ABCD,BC SD SD ⊥⊥平面故,所以，BC ⊥⊥平面BDS,BC DE .作BK ⊥EC,EDC SBC K ⊥为垂足，因平面平面，故,BK EDC BK DE DE ⊥⊥平面，与平面SBC 内的两条相交直线BK 、BC 都垂直 DE ⊥平面SBC ，DE ⊥EC,DE ⊥SBSB =SD DB DE SB ==-EB SE SB EB ====所以，SE=2EB(Ⅱ) 由1,2,,SA AB SE EB AB SA ===⊥知1,AD=1AE ==又.故ADE ∆为等腰三角形.取ED 中点F,连接AF ,则,AF DE AF ⊥==. 连接FG ，则//,FG EC FG DE ⊥.所以，AFG ∠是二面角A DE C --的平面角.连接AG,A G=,3FG ==, 2221cos 22AF FG AG AFG AF FG +-∠==-,所以，二面角A DE C --的大小为120°. 解法二：以D 为坐标原点，射线DA 为x 轴的正半轴，建立如图所示的直角坐标系D xyz -， 设A(1,0,0)，则B(1,1,0),C(0,2,0),S(0,0,2)（Ⅰ）(0,2,-2),(-1,1,0)SC BC ==设平面SBC 的法向量为n=(a, b, c) 由,n SC n BC ⊥⊥，得0,0n SC n BC == 故2b-2c=0,-a+b=0令a=1，则b=c,c=1,n=(1,1,1) 又设SE EB λ= (0)λ>，则2(,,)111E λλλλλ+++ 2(,,),(0,2,0)111DE DC λλλλλ==+++设平面CDE 的法向量m=(x,y,z) 由,m DE m DC ⊥⊥,得0m DE ⊥=，0m DC ⊥= 故20,20111x y zy λλλλλ++==+++. 令2x =，则(2,0,)m λ=-.由平面DEC ⊥平面SBC 得m ⊥n,0,20,2m n λλ=-== 故SE=2EB（Ⅱ）由（Ⅰ）知222(,,)333E ，取DE 的中点F ，则111211(,,),(,,)333333F FA =--，故0FA DE =，由此得FA DE ⊥ 又242(,,)333EC =--，故0EC DE =，由此得EC DE ⊥， 向量FA 与EC 的夹角等于二面角A DE C --的平面角 于是 1cos(,)2||||FA EC FA EC FA EC ==-所以，二面角A DE C --的大小为120（三）1. 已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（ ）（A （B （C (D) 342. 已知二面角l αβ--为60o，动点P 、Q 分别在面α、β内，P 到β，Q 到α的距离为则P 、Q 两点之间距离的最小值为（ ）(A) (B)2 (C) 3. 直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===, 120BAC ∠=︒，则此球的表面积等于 。

高考数学-立体几何（含22年真题讲解）1．【2022年全国甲卷】如图，网格纸上绘制的是一个多面体的三视图，网格小正方形的边长为1，则该多面体的体积为（）A．8B．12C．16D．20【答案】B【解析】【分析】由三视图还原几何体，再由棱柱的体积公式即可得解.【详解】由三视图还原几何体，如图，×2×2=12.则该直四棱柱的体积V=2+42故选：B.2．【2022年全国甲卷】在长方体ABCD−A1B1C1D1中，已知B1D与平面ABCD和平面AA1B1B 所成的角均为30°，则（）A．AB=2AD B．AB与平面AB1C1D所成的角为30°C．AC=CB1D．B1D与平面BB1C1C所成的角为45°【解析】 【分析】根据线面角的定义以及长方体的结构特征即可求出． 【详解】 如图所示：不妨设AB =a,AD =b,AA 1=c ，依题以及长方体的结构特征可知，B 1D 与平面ABCD 所成角为∠B 1DB ，B 1D 与平面AA 1B 1B 所成角为∠DB 1A ，所以sin30∘=cB 1D=bB 1D ，即b =c ，B 1D =2c =√a 2+b 2+c 2，解得a =√2c ．对于A ，AB =a ，AD =b ，AB =√2AD ，A 错误；对于B ，过B 作BE ⊥AB 1于E ，易知BE ⊥平面AB 1C 1D ，所以AB 与平面AB 1C 1D 所成角为∠BAE ，因为tan∠BAE =c a=√22，所以∠BAE ≠30∘，B 错误；对于C ，AC =√a 2+b 2=√3c ，CB 1=√b 2+c 2=√2c ，AC ≠CB 1，C 错误； 对于D ，B 1D 与平面BB 1C 1C 所成角为∠DB 1C ，sin∠DB 1C =CDB 1D=a2c =√22，而0<∠DB 1C <90∘，所以∠DB 1C =45∘．D 正确． 故选：D ．3．【2022年全国甲卷】甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为2π，侧面积分别为S 甲和S 乙，体积分别为V 甲和V 乙．若S 甲S 乙=2，则V 甲V 乙=（ ）A ．√5B ．2√2C ．√10D ．5√104【答案】C 【解析】设母线长为l ，甲圆锥底面半径为r 1，乙圆锥底面圆半径为r 2，根据圆锥的侧面积公式可得r 1=2r 2，再结合圆心角之和可将r 1,r 2分别用l 表示，再利用勾股定理分别求出两圆锥的高，再根据圆锥的体积公式即可得解. 【详解】解：设母线长为l ，甲圆锥底面半径为r 1，乙圆锥底面圆半径为r 2，则S 甲S 乙=πr 1l πr 2l =r1r 2=2， 所以r 1=2r 2， 又2πr 1l+2πr 2l=2π，则r 1+r 2l=1，所以r 1=23l,r 2=13l ，所以甲圆锥的高ℎ1=√l 2−49l 2=√53l ，乙圆锥的高ℎ2=√l 2−19l 2=2√23l ， 所以V 甲V 乙=13πr 12ℎ113πr 22ℎ2=49l 2×√53l 19l ×2√23l =√10.故选：C.4．【2022年全国乙卷】在正方体ABCD −A 1B 1C 1D 1中，E ，F 分别为AB,BC 的中点，则（ ） A ．平面B 1EF ⊥平面BDD 1 B ．平面B 1EF ⊥平面A 1BD C ．平面B 1EF//平面A 1AC D ．平面B 1EF//平面A 1C 1D【答案】A 【解析】 【分析】证明EF ⊥平面BDD 1，即可判断A ；如图，以点D 为原点，建立空间直角坐标系，设AB =2，分别求出平面B 1EF ，A 1BD ，A 1C 1D 的法向量，根据法向量的位置关系，即可判断BCD . 【详解】解：在正方体ABCD −A 1B 1C 1D 1中， AC ⊥BD 且DD 1⊥平面ABCD ， 又EF ⊂平面ABCD ，所以EF ⊥DD 1，因为E,F 分别为AB,BC 的中点， 所以EF ∥AC ，所以EF ⊥BD ， 又BD ∩DD 1=D ， 所以EF ⊥平面BDD 1， 又EF ⊂平面B 1EF ，所以平面B 1EF ⊥平面BDD 1，故A 正确；如图，以点D 为原点，建立空间直角坐标系，设AB =2，则B 1(2,2,2),E (2,1,0),F (1,2,0),B (2,2,0),A 1(2,0,2),A (2,0,0),C (0,2,0)， C 1(0,2,2)，则EF ⃑⃑⃑⃑⃑ =(−1,1,0),EB 1⃑⃑⃑⃑⃑⃑⃑ =(0,1,2)，DB ⃑⃑⃑⃑⃑⃑ =(2,2,0),DA 1⃑⃑⃑⃑⃑⃑⃑⃑ =(2,0,2)，AA 1⃑⃑⃑⃑⃑⃑⃑ =(0,0,2),AC ⃑⃑⃑⃑⃑ =(−2,2,0),A 1C 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ =(−2,2,0),设平面B 1EF 的法向量为m ⃑⃑ =(x 1,y 1,z 1)， 则有{m ⃑⃑ ⋅EF ⃑⃑⃑⃑⃑ =−x 1+y 1=0m ⃑⃑ ⋅EB 1⃑⃑⃑⃑⃑⃑⃑ =y 1+2z 1=0 ，可取m ⃑⃑ =(2,2,−1)，同理可得平面A 1BD 的法向量为n 1⃑⃑⃑⃑ =(1,−1,−1)， 平面A 1AC 的法向量为n 2⃑⃑⃑⃑ =(1,1,0)， 平面A 1C 1D 的法向量为n 3⃑⃑⃑⃑ =(1,1,−1)， 则m ⃑⃑ ⋅n 1⃑⃑⃑⃑ =2−2+1=1≠0，所以平面B 1EF 与平面A 1BD 不垂直，故B 错误； 因为m ⃑⃑ 与n 2⃑⃑⃑⃑ 不平行，所以平面B 1EF 与平面A 1AC 不平行，故C 错误； 因为m ⃑⃑ 与n 3⃑⃑⃑⃑ 不平行，所以平面B 1EF 与平面A 1C 1D 不平行，故D 错误， 故选：A.5．【2022年全国乙卷】已知球O的半径为1，四棱锥的顶点为O，底面的四个顶点均在球O 的球面上，则当该四棱锥的体积最大时，其高为（）A．13B．12C．√33D．√22【答案】C【解析】【分析】先证明当四棱锥的顶点O到底面ABCD所在小圆距离一定时，底面ABCD面积最大值为2r2，进而得到四棱锥体积表达式，再利用均值定理去求四棱锥体积的最大值，从而得到当该四棱锥的体积最大时其高的值.【详解】设该四棱锥底面为四边形ABCD，四边形ABCD所在小圆半径为r，设四边形ABCD对角线夹角为α，则S ABCD=12⋅AC⋅BD⋅sinα≤12⋅AC⋅BD≤12⋅2r⋅2r=2r2（当且仅当四边形ABCD为正方形时等号成立）即当四棱锥的顶点O到底面ABCD所在小圆距离一定时，底面ABCD面积最大值为2r2又r2+ℎ2=1则VO−ABCD =13⋅2r2⋅ℎ=√23√r2⋅r2⋅2ℎ2≤√23√(r2+r2+2ℎ23)3=4√327当且仅当r2=2ℎ2即ℎ=√33时等号成立，故选：C6．【2022年新高考1卷】南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔148．5m 时，相应水面的面积为140．0km 2；水位为海拔157．5m 时，相应水面的面积为180．0km 2，将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148．5m 上升到157．5m 时，增加的水量约为（√7≈2.65）（ ） A ．1.0×109m 3 B ．1.2×109m 3 C ．1.4×109m 3 D ．1.6×109m 3【答案】C 【解析】 【分析】根据题意只要求出棱台的高，即可利用棱台的体积公式求出． 【详解】依题意可知棱台的高为MN =157.5−148.5=9(m)，所以增加的水量即为棱台的体积V ． 棱台上底面积S =140.0km 2=140×106m 2，下底面积S ′=180.0km 2=180×106m 2， ∴V =13ℎ(S +S ′+√SS ′)=13×9×(140×106+180×106+√140×180×1012) =3×(320+60√7)×106≈(96+18×2.65)×107=1.437×109≈1.4×109(m 3)．故选：C ．7．【2022年新高考1卷】已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上.若该球的体积为36π，且3≤l ≤3√3，则该正四棱锥体积的取值范围是（ ） A ．[18,814]B ．[274,814]C ．[274,643]D ．[18,27]【答案】C 【解析】 【分析】设正四棱锥的高为ℎ，由球的截面性质列方程求出正四棱锥的底面边长与高的关系，由此确定正四棱锥体积的取值范围. 【详解】∵ 球的体积为36π，所以球的半径R =3, 设正四棱锥的底面边长为2a ，高为ℎ， 则l 2=2a 2+ℎ2，32=2a 2+(3−ℎ)2, 所以6ℎ=l 2，2a 2=l 2−ℎ2所以正四棱锥的体积V =13Sℎ=13×4a 2×ℎ=23×(l 2−l 436)×l 26=19(l 4−l 636)， 所以V ′=19(4l 3−l 56)=19l 3(24−l 26)，当3≤l ≤2√6时，V ′>0，当2√6<l ≤3√3时，V ′<0， 所以当l =2√6时，正四棱锥的体积V 取最大值，最大值为643， 又l =3时，V =274，l =3√3时，V =814,所以正四棱锥的体积V 的最小值为274， 所以该正四棱锥体积的取值范围是[274，643]. 故选：C.8．【2022年新高考2卷】已知正三棱台的高为1，上、下底面边长分别为3√3和4√3，其顶点都在同一球面上，则该球的表面积为（ ） A ．100π B ．128π C ．144π D ．192π【答案】A 【解析】 【分析】根据题意可求出正三棱台上下底面所在圆面的半径r 1,r 2，再根据球心距，圆面半径，以及球的半径之间的关系，即可解出球的半径，从而得出球的表面积． 【详解】设正三棱台上下底面所在圆面的半径r 1,r 2，所以2r 1=3√3sin60∘,2r 2=4√3sin60∘，即r 1=3,r 2=4，设球心到上下底面的距离分别为d 1,d 2，球的半径为R ，所以d 1=√R 2−9，d 2=√R 2−16，故|d 1−d 2|=1或d 1+d 2=1，即|√R 2−9−√R 2−16|=1或√R 2−9+√R 2−16=1，解得R2=25符合题意，所以球的表面积为S=4πR2=100π．故选：A．9．【2022年北京】已知正三棱锥P−ABC的六条棱长均为6，S是△ABC及其内部的点构成的集合．设集合T={Q∈S|PQ≤5}，则T表示的区域的面积为（）A．3π4B．πC．2πD．3π【答案】B【解析】【分析】求出以P为球心，5为半径的球与底面ABC的截面圆的半径后可求区域的面积.【详解】设顶点P在底面上的投影为O，连接BO，则O为三角形ABC的中心，且BO=23×6×√32=2√3，故PO=√36−12=2√6.因为PQ=5，故OQ=1，故S的轨迹为以O为圆心，1为半径的圆，而三角形ABC内切圆的圆心为O，半径为2×√34×363×6=√3>1，故S的轨迹圆在三角形ABC内部，故其面积为π故选：B10．【2022年浙江】某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（）A．22πB．8πC．223πD．163π【答案】C【解析】【分析】根据三视图还原几何体可知，原几何体是一个半球，一个圆柱，一个圆台组合成的几何体，即可根据球，圆柱，圆台的体积公式求出．【详解】由三视图可知，该几何体是一个半球，一个圆柱，一个圆台组合成的几何体，球的半径，圆柱的底面半径，圆台的上底面半径都为1cm，圆台的下底面半径为2cm，所以该几何体的体积V=12×43π×13+π×12×2+13×2×(π×22+π×12+√π×22×π×12)=22π3cm3．故选：C．11．【2022年浙江】如图，已知正三棱柱ABC−A1B1C1,AC=AA1，E，F分别是棱BC,A1C1上的点．记EF与AA1所成的角为α，EF与平面ABC所成的角为β，二面角F−BC−A的平面角为γ，则（）A．α≤β≤γB．β≤α≤γC．β≤γ≤αD．α≤γ≤β【答案】A【解析】【分析】先用几何法表示出α，β，γ，再根据边长关系即可比较大小．【详解】如图所示，过点F作FP⊥AC于P，过P作PM⊥BC于M，连接PE，则α=∠EFP，β=∠FEP，γ=FMP，tanα=PEFP =PEAB≤1，tanβ=FPPE=ABPE≥1，tanγ=FPPM≥FPPE=tanβ，所以α≤β≤γ，故选：A．12．【2022年新高考1卷】（多选）已知正方体ABCD−A1B1C1D1，则（）A．直线BC1与DA1所成的角为90°B．直线BC1与CA1所成的角为90°C．直线BC1与平面BB1D1D所成的角为45°D．直线BC1与平面ABCD所成的角为45°【答案】ABD【解析】【分析】数形结合，依次对所给选项进行判断即可. 【详解】如图，连接B 1C 、BC 1，因为DA 1//B 1C ，所以直线BC 1与B 1C 所成的角即为直线BC 1与DA 1所成的角，因为四边形BB 1C 1C 为正方形，则B 1C ⊥ BC 1，故直线BC 1与DA 1所成的角为90°，A 正确；连接A 1C ，因为A 1B 1⊥平面BB 1C 1C ，BC 1⊂平面BB 1C 1C ，则A 1B 1⊥BC 1， 因为B 1C ⊥ BC 1，A 1B 1∩B 1C =B 1，所以BC 1⊥平面A 1B 1C ， 又A 1C ⊂平面A 1B 1C ，所以BC 1⊥CA 1，故B 正确； 连接A 1C 1，设A 1C 1∩B 1D 1=O ，连接BO ，因为BB 1⊥平面A 1B 1C 1D 1，C 1O ⊂平面A 1B 1C 1D 1，则C 1O ⊥B 1B ， 因为C 1O ⊥B 1D 1，B 1D 1∩B 1B =B 1，所以C 1O ⊥平面BB 1D 1D ， 所以∠C 1BO 为直线BC 1与平面BB 1D 1D 所成的角，设正方体棱长为1，则C 1O =√22，BC 1=√2，sin∠C 1BO =C 1O BC 1=12，所以，直线BC 1与平面BB 1D 1D 所成的角为30∘，故C 错误；因为C 1C ⊥平面ABCD ，所以∠C 1BC 为直线BC 1与平面ABCD 所成的角，易得∠C 1BC =45∘，故D 正确. 故选：ABD13．【2022年新高考2卷】（多选）如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，FB ∥ED,AB =ED =2FB ，记三棱锥E −ACD ，F −ABC ，F −ACE 的体积分别为V 1,V 2,V 3，则（ ）A．V3=2V2B．V3=V1C．V3=V1+V2D．2V3=3V1【答案】CD【解析】【分析】直接由体积公式计算V1,V2，连接BD交AC于点M，连接EM,FM，由V3=V A−EFM+V C−EFM计算出V3，依次判断选项即可.【详解】设AB=ED=2FB=2a，因为ED⊥平面ABCD，FB∥ED，则V1=13⋅ED⋅S△ACD=13⋅2a⋅12⋅(2a)2=43a3，V2=13⋅FB⋅S△ABC=13⋅a⋅12⋅(2a)2=23a3，连接BD交AC于点M，连接EM,FM，易得BD⊥AC，又ED⊥平面ABCD，AC⊂平面ABCD，则ED⊥AC，又ED∩BD=D，ED,BD⊂平面BDEF，则AC⊥平面BDEF，又BM=DM=12BD=√2a，过F作FG⊥DE于G，易得四边形BDGF为矩形，则FG=BD=2√2a,EG=a，则EM=√(2a)2+(√2a)2=√6a,FM=√a2+(√2a)2=√3a，EF=√a2+(2√2a)2=3a，EM2+FM2=EF2，则EM⊥FM，S△EFM=12EM⋅FM=3√22a2，AC=2√2a，则V3=V A−EFM+V C−EFM=13AC⋅S△EFM=2a3，则2V3=3V1，V3=3V2，V3=V1+V2，故A、B错误；C、D正确.故选：CD.14．【2022年全国甲卷】小明同学参加综合实践活动，设计了一个封闭的包装盒，包装盒如图所示：底面ABCD是边长为8（单位：cm）的正方形，△EAB,△FBC,△GCD,△HDA均为正三角形，且它们所在的平面都与平面ABCD垂直．(1)证明：EF//平面ABCD；(2)求该包装盒的容积（不计包装盒材料的厚度）．【答案】(1)证明见解析；(2)6403√3．【解析】【分析】（1）分别取AB,BC的中点M,N，连接MN，由平面知识可知EM⊥AB,FN⊥BC，EM=FN，依题从而可证EM⊥平面ABCD，FN⊥平面ABCD，根据线面垂直的性质定理可知EM//FN，即可知四边形EMNF为平行四边形，于是EF//MN，最后根据线面平行的判定定理即可证出；（2）再分别取AD,DC中点K,L，由（1）知，该几何体的体积等于长方体KMNL−EFGH的体积加上四棱锥B−MNFE体积的4倍，即可解出．(1)如图所示：，分别取AB,BC 的中点M,N ，连接MN ，因为△EAB,△FBC 为全等的正三角形，所以EM ⊥AB,FN ⊥BC ，EM =FN ，又平面EAB ⊥平面ABCD ，平面EAB ∩平面ABCD =AB ，EM ⊂平面EAB ，所以EM ⊥平面ABCD ，同理可得FN ⊥平面ABCD ，根据线面垂直的性质定理可知EM//FN ，而EM =FN ，所以四边形EMNF 为平行四边形，所以EF//MN ，又EF ⊄平面ABCD ，MN ⊂平面ABCD ，所以EF//平面ABCD ． (2)如图所示：，分别取AD,DC 中点K,L ，由（1）知，EF//MN 且EF =MN ，同理有，HE//KM,HE =KM ，HG//KL,HG =KL ，GF//LN,GF =LN ，由平面知识可知，BD ⊥MN ，MN ⊥MK ，KM =MN =NL =LK ，所以该几何体的体积等于长方体KMNL −EFGH 的体积加上四棱锥B −MNFE 体积的4倍．因为MN =NL =LK =KM =4√2，EM =8sin60∘=4√3，点B 到平面MNFE 的距离即为点B 到直线MN 的距离d ，d =2√2，所以该几何体的体积V =(4√2)2×4√3+4×13×4√2×4√3×2√2=128√3+2563√3=6403√3．15．【2022年全国甲卷】在四棱锥P−ABCD中，PD⊥底面ABCD,CD∥AB,AD=DC=CB=1 ,AB=2,DP=√3．(1)证明：BD⊥PA；(2)求PD与平面PAB所成的角的正弦值．【答案】(1)证明见解析；(2)√55.【解析】【分析】（1）作DE⊥AB于E，CF⊥AB于F，利用勾股定理证明AD⊥BD，根据线面垂直的性质可得PD⊥BD，从而可得BD⊥平面PAD，再根据线面垂直的性质即可得证；（2）以点D为原点建立空间直角坐标系，利用向量法即可得出答案.(1)证明：在四边形ABCD中，作DE⊥AB于E，CF⊥AB于F，因为CD//AB,AD=CD=CB=1,AB=2，所以四边形ABCD为等腰梯形，所以AE=BF=12，故DE=√32，BD=√DE2+BE2=√3，所以AD2+BD2=AB2，所以AD⊥BD，因为PD⊥平面ABCD，BD⊂平面ABCD，所以PD⊥BD，又PD∩AD=D，所以BD ⊥平面PAD ， 又因PA ⊂平面PAD ， 所以BD ⊥PA ；(2)解：如图，以点D 为原点建立空间直角坐标系， BD =√3，则A(1,0,0),B(0,√3,0),P(0,0,√3)，则AP⃑⃑⃑⃑⃑ =(−1,0,√3),BP ⃑⃑⃑⃑⃑ =(0,−√3,√3),DP ⃑⃑⃑⃑⃑ =(0,0,√3)， 设平面PAB 的法向量n⃑ =(x,y,z)， 则有{n →⋅AP →=−x +√3z =0n →⋅BP →=−√3y +√3z =0，可取n ⃑ =(√3,1,1)， 则cos〈n ⃑ ,DP ⃑⃑⃑⃑⃑ 〉=n ⃑ ⋅DP ⃑⃑⃑⃑⃑⃑|n ⃑ ||DP ⃑⃑⃑⃑⃑⃑ |=√55， 所以PD 与平面PAB 所成角的正弦值为√55.16．【2022年全国乙卷】如图，四面体ABCD 中，AD ⊥CD,AD =CD,∠ADB =∠BDC ，E 为AC 的中点．(1)证明：平面BED⊥平面ACD；(2)设AB=BD=2,∠ACB=60°，点F在BD上，当△AFC的面积最小时，求三棱锥F−ABC 的体积．【答案】(1)证明详见解析(2)√34【解析】【分析】（1）通过证明AC⊥平面BED来证得平面BED⊥平面ACD.（2）首先判断出三角形AFC的面积最小时F点的位置，然后求得F到平面ABC的距离，从而求得三棱锥F−ABC的体积.(1)由于AD=CD，E是AC的中点，所以AC⊥DE.由于{AD=CDBD=BD∠ADB=∠CDB，所以△ADB≅△CDB，所以AB=CB，故AC⊥BD，由于DE∩BD=D，DE,BD⊂平面BED，所以AC⊥平面BED，由于AC⊂平面ACD，所以平面BED⊥平面ACD.(2)依题意AB=BD=BC=2，∠ACB=60°，三角形ABC是等边三角形，所以AC=2,AE=CE=1,BE=√3，由于AD=CD,AD⊥CD，所以三角形ACD是等腰直角三角形，所以DE=1. DE2+BE2=BD2，所以DE⊥BE，由于AC∩BE=E，AC,BE⊂平面ABC，所以DE⊥平面ABC.由于△ADB ≅△CDB ，所以∠FBA =∠FBC ， 由于{BF =BF∠FBA =∠FBC AB =CB ，所以△FBA ≅△FBC ，所以AF =CF ，所以EF ⊥AC ，由于S △AFC =12⋅AC ⋅EF ，所以当EF 最短时，三角形AFC 的面积最小值. 过E 作EF ⊥BD ，垂足为F ，在Rt △BED 中，12⋅BE ⋅DE =12⋅BD ⋅EF ，解得EF =√32，所以DF =√12−(√32)2=12,BF =2−DF =32，所以BF BD =34.过F 作FH ⊥BE ，垂足为H ，则FH //DE ，所以FH ⊥平面ABC ，且FHDE =BFBD =34， 所以FH =34,所以V F−ABC =13⋅S △ABC ⋅FH =13×12×2×√3×34=√34.17．【2022年全国乙卷】如图，四面体ABCD 中，AD ⊥CD,AD =CD,∠ADB =∠BDC ，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设AB =BD =2,∠ACB =60°，点F 在BD 上，当△AFC 的面积最小时，求CF 与平面ABD 所成的角的正弦值．【答案】(1)证明过程见解析(2)CF 与平面ABD 所成的角的正弦值为4√37【解析】 【分析】（1）根据已知关系证明△ABD ≌△CBD ，得到AB =CB ，结合等腰三角形三线合一得到垂直关系，结合面面垂直的判定定理即可证明；（2）根据勾股定理逆用得到BE ⊥DE ，从而建立空间直角坐标系，结合线面角的运算法则进行计算即可. (1)因为AD =CD ，E 为AC 的中点，所以AC ⊥DE ；在△ABD 和△CBD 中，因为AD =CD,∠ADB =∠CDB,DB =DB ，所以△ABD ≌△CBD ，所以AB =CB ，又因为E 为AC 的中点，所以AC ⊥BE ； 又因为DE,BE ⊂平面BED ，DE ∩BE =E ，所以AC ⊥平面BED ， 因为AC ⊂平面ACD ，所以平面BED ⊥平面ACD . (2)连接EF ，由（1）知，AC ⊥平面BED ，因为EF ⊂平面BED ， 所以AC ⊥EF ，所以S △AFC =12AC ⋅EF ， 当EF ⊥BD 时，EF 最小，即△AFC 的面积最小. 因为△ABD ≌△CBD ，所以CB =AB =2， 又因为∠ACB =60°，所以△ABC 是等边三角形， 因为E 为AC 的中点，所以AE =EC =1，BE =√3， 因为AD ⊥CD ，所以DE =12AC =1,在△DEB 中，DE 2+BE 2=BD 2，所以BE ⊥DE .以E 为坐标原点建立如图所示的空间直角坐标系E −xyz ，则A (1,0,0),B(0,√3,0),D (0,0,1)，所以AD ⃑⃑⃑⃑⃑ =(−1,0,1),AB ⃑⃑⃑⃑⃑ =(−1,√3,0)， 设平面ABD 的一个法向量为n⃑ =(x,y,z )， 则{n ⃑ ⋅AD ⃑⃑⃑⃑⃑ =−x +z =0n ⃑ ⋅AB⃑⃑⃑⃑⃑ =−x +√3y =0，取y =√3，则n ⃑ =(3,√3,3)，又因为C (−1,0,0),F (0,√34,34)，所以CF⃑⃑⃑⃑⃑ =(1,√34,34)， 所以cos⟨n ⃑ ,CF ⃑⃑⃑⃑⃑ ⟩=n ⃑ ⋅CF⃑⃑⃑⃑⃑|n ⃑ ||CF⃑⃑⃑⃑⃑ |=√21×√74=4√37，设CF 与平面ABD 所成的角的正弦值为θ(0≤θ≤π2)， 所以sinθ=|cos⟨n ⃑ ,CF⃑⃑⃑⃑⃑ ⟩|=4√37， 所以CF 与平面ABD 所成的角的正弦值为4√37.18．【2022年新高考1卷】如图，直三棱柱ABC −A 1B 1C 1的体积为4，△A 1BC 的面积为2√2．(1)求A 到平面A 1BC 的距离；(2)设D 为A 1C 的中点，AA 1=AB ，平面A 1BC ⊥平面ABB 1A 1，求二面角A −BD −C 的正弦值． 【答案】(1)√2 (2)√32【解析】 【分析】（1）由等体积法运算即可得解；（2）由面面垂直的性质及判定可得BC ⊥平面ABB 1A 1，建立空间直角坐标系，利用空间向量法即可得解. (1)在直三棱柱ABC −A 1B 1C 1中，设点A 到平面A 1BC 的距离为h ， 则V A−A 1BC =13S △A 1BC ⋅ℎ=2√23ℎ=V A 1−ABC =13S △ABC ⋅A 1A =13V ABC−A 1B 1C 1=43，解得ℎ=√2，所以点A 到平面A 1BC 的距离为√2； (2)取A 1B 的中点E ,连接AE ,如图，因为AA 1=AB ，所以AE ⊥A 1B , 又平面A 1BC ⊥平面ABB 1A 1，平面A 1BC ∩平面ABB 1A 1=A 1B ， 且AE ⊂平面ABB 1A 1，所以AE ⊥平面A 1BC ， 在直三棱柱ABC −A 1B 1C 1中，BB 1⊥平面ABC ，由BC ⊂平面A 1BC ，BC ⊂平面ABC 可得AE ⊥BC ，BB 1⊥BC ， 又AE,BB 1⊂平面ABB 1A 1且相交，所以BC ⊥平面ABB 1A 1，所以BC,BA,BB 1两两垂直，以B 为原点，建立空间直角坐标系，如图，由（1）得AE =√2，所以AA 1=AB =2，A 1B =2√2，所以BC =2， 则A(0,2,0),A 1(0,2,2),B(0,0,0),C(2,0,0),所以A 1C 的中点D(1,1,1)， 则BD⃑⃑⃑⃑⃑⃑ =(1,1,1)，BA ⃑⃑⃑⃑⃑ =(0,2,0),BC ⃑⃑⃑⃑⃑ =(2,0,0), 设平面ABD 的一个法向量m ⃑⃑ =(x,y,z)，则{m ⃑⃑ ⋅BD ⃑⃑⃑⃑⃑⃑ =x +y +z =0m ⃑⃑ ⋅BA ⃑⃑⃑⃑⃑ =2y =0，可取m⃑⃑ =(1,0,−1)，设平面BDC 的一个法向量n ⃑ =(a,b,c)，则{m ⃑⃑ ⋅BD ⃑⃑⃑⃑⃑⃑ =a +b +c =0m ⃑⃑ ⋅BC ⃑⃑⃑⃑⃑ =2a =0， 可取n⃑ =(0,1,−1)， 则cos〈m ⃑⃑ ,n ⃑ 〉=m⃑⃑⃑ ⋅n ⃑ |m ⃑⃑⃑ |⋅|n ⃑ |=√2×√2=12， 所以二面角A −BD −C 的正弦值为√1−(12)2=√32.19．【2022年新高考2卷】如图，PO 是三棱锥P −ABC 的高，PA =PB ，AB ⊥AC ，E 是PB 的中点．(1)证明：OE//平面PAC ；(2)若∠ABO =∠CBO =30°，PO =3，PA =5，求二面角C −AE −B 的正弦值． 【答案】(1)证明见解析 (2)1113 【解析】 【分析】（1）连接BO 并延长交AC 于点D ，连接OA 、PD ，根据三角形全等得到OA =OB ，再根据直角三角形的性质得到AO =DO ，即可得到O 为BD 的中点从而得到OE //PD ，即可得证； （2）过点A 作Az //OP ，如图建立平面直角坐标系，利用空间向量法求出二面角的余弦值，再根据同角三角函数的基本关系计算可得； (1)证明：连接BO 并延长交AC 于点D ，连接OA 、PD ，因为PO 是三棱锥P −ABC 的高，所以PO ⊥平面ABC ，AO,BO ⊂平面ABC ， 所以PO ⊥AO 、PO ⊥BO ，又PA =PB ，所以△POA ≅△POB ，即OA =OB ，所以∠OAB =∠OBA ，又AB ⊥AC ，即∠BAC =90°，所以∠OAB +∠OAD =90°，∠OBA +∠ODA =90°， 所以∠ODA =∠OAD所以AO =DO ，即AO =DO =OB ，所以O 为BD 的中点，又E 为PB 的中点，所以OE //PD ，又OE ⊄平面PAC ，PD ⊂平面PAC ， 所以OE //平面PAC(2)解：过点A 作Az //OP ，如图建立平面直角坐标系， 因为PO =3，AP =5，所以OA =√AP 2−PO 2=4，又∠OBA =∠OBC =30°，所以BD =2OA =8，则AD =4，AB =4√3，所以AC =12，所以O(2√3,2,0)，B(4√3,0,0)，P(2√3,2,3)，C (0,12,0)，所以E (3√3,1,32)， 则AE ⃑⃑⃑⃑⃑ =(3√3,1,32)，AB ⃑⃑⃑⃑⃑ =(4√3,0,0)，AC ⃑⃑⃑⃑⃑ =(0,12,0)， 设平面AEB 的法向量为n ⃑ =(x,y,z )，则{n ⃑ ⋅AE ⃑⃑⃑⃑⃑ =3√3x +y +32z =0n ⃑ ⋅AB ⃑⃑⃑⃑⃑ =4√3x =0 ，令z =2，则y =−3，x =0，所以n ⃑ =(0,−3,2)；设平面AEC 的法向量为m⃑⃑ =(a,b,c )，则{m ⃑⃑ ⋅AE ⃑⃑⃑⃑⃑ =3√3a +b +32c =0m ⃑⃑ ⋅AC ⃑⃑⃑⃑⃑ =12b =0 ，令a =√3，则c =−6，b =0，所以m ⃑⃑ =(√3,0,−6)；所以cos⟨n⃑ ,m⃑⃑ ⟩=n⃑ ⋅m⃑⃑⃑|n⃑ ||m⃑⃑⃑ |=√13×√39=−4√313设二面角C−AE−B为θ，由图可知二面角C−AE−B为钝二面角，所以cosθ=−4√313，所以sinθ=√1−cos2θ=1113故二面角C−AE−B的正弦值为1113；20．【2022年北京】如图，在三棱柱ABC−A1B1C1中，侧面BCC1B1为正方形，平面BCC1B1⊥平面ABB1A1，AB=BC=2，M，N分别为A1B1，AC的中点．(1)求证：MN∥平面BCC1B1；(2)再从条件①、条件②这两个条件中选择一个作为已知，求直线AB与平面BMN所成角的正弦值．条件①：AB⊥MN；条件②：BM=MN．注：如果选择条件①和条件②分别解答，按第一个解答计分．【答案】(1)见解析(2)见解析【解析】【分析】（1）取AB的中点为K，连接MK,NK，可证平面MKN//平面CBB1C1，从而可证MN//平面CB B1C1.（2）选①②均可证明BB1⊥平面ABC，从而可建立如图所示的空间直角坐标系，利用空间向量可求线面角的正弦值.(1)取AB的中点为K，连接MK,NK，由三棱柱ABC −A 1B 1C 1可得四边形ABB 1A 1为平行四边形， 而B 1M =MA 1,BK =KA ，则MK //BB 1，而MK ⊄平面CBB 1C 1，BB 1⊂平面CBB 1C 1，故MK //平面CBB 1C 1， 而CN =NA,BK =KA ，则NK //BC ，同理可得NK //平面CBB 1C 1， 而NK ∩MK =K,NK,MK ⊂平面MKN ，故平面MKN //平面CBB 1C 1，而MN ⊂平面MKN ，故MN //平面CBB 1C 1， (2)因为侧面CBB 1C 1为正方形，故CB ⊥BB 1， 而CB ⊂平面CBB 1C 1，平面CBB 1C 1⊥平面ABB 1A 1， 平面CBB 1C 1∩平面ABB 1A 1=BB 1，故CB ⊥平面ABB 1A 1， 因为NK //BC ，故NK ⊥平面ABB 1A 1， 因为AB ⊂平面ABB 1A 1，故NK ⊥AB ，若选①，则AB ⊥MN ，而NK ⊥AB ，NK ∩MN =N ， 故AB ⊥平面MNK ，而MK ⊂平面MNK ，故AB ⊥MK ，所以AB ⊥BB 1，而CB ⊥BB 1，CB ∩AB =B ，故BB 1⊥平面ABC ，故可建立如所示的空间直角坐标系，则B(0,0,0),A(0,2,0),N(1,1,0),M(0,1,2)， 故BA ⃑⃑⃑⃑⃑ =(0,2,0),BN ⃑⃑⃑⃑⃑⃑ =(1,1,0),BM ⃑⃑⃑⃑⃑⃑ =(0,1,2)， 设平面BNM 的法向量为n⃑ =(x,y,z)， 则{n ⃑ ⋅BN ⃑⃑⃑⃑⃑⃑ =0n ⃑ ⋅BM ⃑⃑⃑⃑⃑⃑ =0，从而{x +y =0y +2z =0，取z =−1，则n⃑ =(−2,2,−1)， 设直线AB 与平面BNM 所成的角为θ，则 sinθ=|cos〈n ⃑ ,AB ⃑⃑⃑⃑⃑ 〉|=42×3=23. 若选②，因为NK //BC ，故NK ⊥平面ABB 1A 1，而KM ⊂平面MKN ， 故NK ⊥KM ，而B 1M =BK =1,NK =1，故B 1M =NK ， 而B 1B =MK =2，MB =MN ，故△BB 1M ≅△MKN ， 所以∠BB 1M =∠MKN =90°，故A 1B 1⊥BB 1， 而CB ⊥BB 1，CB ∩AB =B ，故BB 1⊥平面ABC ，故可建立如所示的空间直角坐标系，则B(0,0,0),A(0,2,0),N(1,1,0),M(0,1,2)， 故BA⃑⃑⃑⃑⃑ =(0,2,0),BN ⃑⃑⃑⃑⃑⃑ =(1,1,0),BM ⃑⃑⃑⃑⃑⃑ =(0,1,2)， 设平面BNM 的法向量为n⃑ =(x,y,z)，则{n ⃑ ⋅BN ⃑⃑⃑⃑⃑⃑ =0n ⃑ ⋅BM ⃑⃑⃑⃑⃑⃑ =0，从而{x +y =0y +2z =0，取z =−1，则n ⃑ =(−2,2,−1)， 设直线AB 与平面BNM 所成的角为θ，则 sinθ=|cos〈n ⃑ ,AB⃑⃑⃑⃑⃑ 〉|=42×3=23.21．【2022年浙江】如图，已知ABCD 和CDEF 都是直角梯形，AB//DC ，DC//EF ，AB =5，DC =3，EF =1，∠BAD =∠CDE =60°，二面角F −DC −B 的平面角为60°．设M ，N 分别为AE,BC 的中点．(1)证明：FN ⊥AD ；(2)求直线BM 与平面ADE 所成角的正弦值． 【答案】(1)证明见解析； (2)5√714．【解析】 【分析】（1）过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点G 、H ，由平面知识易得FC =BC ，再根据二面角的定义可知，∠BCF =60∘，由此可知，FN ⊥BC ，FN ⊥CD ，从而可证得FN ⊥平面ABCD ，即得FN ⊥AD ；（2）由（1）可知FN ⊥平面ABCD ，过点N 做AB 平行线NK ，所以可以以点N 为原点，NK ，NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N −xyz ，求出平面ADE 的一个法向量，以及BM ⃑⃑⃑⃑⃑⃑ ，即可利用线面角的向量公式解出． (1)过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点交于点G 、H ．∵四边形ABCD 和EFCD 都是直角梯形，AB//DC,CD//EF,AB =5,DC =3,EF =1，∠BAD =∠CDE =60°，由平面几何知识易知，DG =AH =2,∠EFC =∠DCF =∠DCB =∠ABC =90°，则四边形EFCG 和四边形DCBH 是矩形，∴在Rt △EGD 和Rt △DHA ，EG =DH =2√3， ∵DC ⊥CF,DC ⊥CB ，且CF ∩CB =C ，∴DC ⊥平面BCF,∠BCF 是二面角F −DC −B 的平面角，则∠BCF =60∘， ∴△BCF 是正三角形，由DC ⊂平面ABCD ，得平面ABCD ⊥平面BCF ，∵N 是BC 的中点，∴ FN ⊥BC ，又DC ⊥平面BCF ，FN ⊂平面BCF ，可得FN ⊥CD ，而BC ∩CD =C ，∴FN ⊥平面ABCD ，而AD ⊂平面ABCD ∴FN ⊥AD ． (2)因为FN ⊥平面ABCD ，过点N 做AB 平行线NK ，所以以点N 为原点， NK ，NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N −xyz ，设A(5,√3,0),B(0,√3,0),D(3,−√3,0),E(1,0,3)，则M (3,√32,32)，∴BM ⃑⃑⃑⃑⃑⃑ =(3,−√32,32),AD ⃑⃑⃑⃑⃑ =(−2,−2√3,0),DE⃑⃑⃑⃑⃑ =(−2,√3,3) 设平面ADE 的法向量为n⃑ =(x,y,z) 由{n ⃑ ⋅AD ⃑⃑⃑⃑⃑ =0n ⃑ ⋅DE ⃑⃑⃑⃑⃑ =0 ，得{−2x −2√3y =0−2x +√3y +3z =0 ，取n ⃑ =(√3,−1,√3)，设直线BM 与平面ADE 所成角为θ， ∴sinθ=|cos〈n⃑ ,BM ⃑⃑⃑⃑⃑⃑ 〉|=|n⃑ ⋅BM ⃑⃑⃑⃑⃑⃑⃑ ||n⃑ |⋅BM ⃑⃑⃑⃑⃑⃑⃑ |=|3√3+√32+3√32|√3+1+3⋅√9+34+94=√3√7⋅2√3=5√714．1．（2022·全国·模拟预测）已知正方体中1111ABCD A B C D -，E ，G 分别为11A D ，11C D 的中点，则直线1A G ，CE 所成角的余弦值为（ ）A B C D 【答案】C 【解析】 【分析】根据异面直线所成角的定义，取AB 的中点F ，则∠ECF （或其补角）为直线1A G 与CE 所成角，再解三角形即可得解． 【详解】如图所示：，取AB 的中点F ，连接EF ，CF ，易知1A G CF ∥，则∠ECF （或其补角）为直线1A G 与CE 所成角．不妨设2AB =，则CF =EF =3EC =，由余弦定理得cosECF ∠==，即直线1A G 与CE 故选：C ．2．（2022·全国·模拟预测（理））如图，在三棱台111ABC A B C -中，1AA ⊥平面ABC ，90ABC ∠=︒，111111AA A B B C ===，2AB =，则AC 与平面11BCC B 所成的角为（ ）A ．30B ．45︒C ．60︒D ．90︒【答案】A 【解析】 【分析】将棱台补全为棱锥，利用等体积法求A 到面11BCC B 的距离，结合线面角的定义求AC 与平面11BCC B 所成角的大小. 【详解】将棱台补全为如下棱锥D ABC -，由90ABC ∠=︒，111111AA A B B C ===，2AB =，易知：2DA BC ==，AC = 由1AA ⊥平面ABC ，,AB AC ⊥平面ABC ，则1AA AB ⊥，1AA AC ⊥，所以BD =CD =222BC BD CD +=，所以122BCD S =⨯⨯=△A 到面11BCC B 的距离为h ，又D ABC A BCD V V --=，则111222323h ⨯⨯⨯⨯=⨯h = 综上，AC 与平面11BCC B 所成角[0,]2πθ∈，则1sin 2h AC θ==，即6πθ=. 故选：A3．（2022·浙江湖州·模拟预测）如图，已知四边形ABCD ，BCD △是以BD 为斜边的等腰直角三角形，ABD △为等边三角形，2BD =，将ABD △沿对角线BD 翻折到PBD △在翻折的过程中，下列结论中不正确．．．的是（ ）A ．BD PC ⊥B ．DP 与BC 可能垂直C ．直线DP 与平面BCD 所成角的最大值是45︒ D ．四面体PBCD 【答案】C 【解析】 【分析】对于A ，取BD 的中点M ，即可得到BD ⊥面PMC ，A 选项可判断对于B ，采用反证法，假设DP BC ⊥，则BC ⊥面PCD ，再根据题目所给的长度即可判断；对于C ，当面PBD ⊥面BCD 时，此时直线DP 与平面BCD 所成角有最大值，判断即可；对于D ，当面PBD ⊥面BCD 时，此时四面体PBCD 的体积有最大值，计算最大体积判断即可 【详解】如图所示，取BD 的中点M ，连接,PM CMBCD △是以BD 为斜边的等腰直角三角形,BD CM ∴⊥ABD △为等边三角形,BD PM ∴⊥BD ∴⊥面PMC ,BD PC ∴⊥ ,故A 正确 对于B ，假设DP BC ⊥，又BC CD ⊥BC ∴⊥面PCD ，BC PC ∴⊥，又2,PB BC ==1PC ⎤⎦，故DP 与BC 可能垂直，故B 正确当面PBD ⊥面BCD 时，此时PM ⊥面BCD ，PDB ∠即为直线DP 与平面BCD 所成角 此时60PDB ︒∠=，故C 错误当面PBD ⊥面BCD 时，此时四面体PBCD 的体积最大，此时的体积为：111(332BCDV S PM ==⨯=，故D 正确 故选：C4．（2022·河南安阳·模拟预测（理））已知球O 的体积为125π6，高为1的圆锥内接于球O ，经过圆锥顶点的平面α截球O 和圆锥所得的截面面积分别为12,S S ，若125π8S =，则2S =（ ）A ．2BCD ．【答案】C 【解析】 【分析】根据给定条件，求出球O 半径，平面α截球O 所得截面小圆半径，圆锥底面圆半径，再求出平面α截圆锥所得的截面等腰三角形底边长及高即可计算作答. 【详解】球O 半径为R ，由34π125π36R =得52R =，平面α截球O 所得截面小圆半径1r ，由21128π5πS r ==得1r =因此，球心O 到平面α的距离1d r ===，而球心O 在圆锥的轴上，则圆锥的轴与平面α所成的角为45，因圆锥的高为1，则球心O 到圆锥底面圆的距离为132d =，于是得圆锥底面圆半径2r =，令平面α截圆锥所得截面为等腰PAB △，线段AB 为圆锥底面圆1O 的弦，点C 为弦AB 中点，依题意，145CPO ∠=，111CO PO ==，PC =AB ==所以212AB S PC =⋅=. 故选：C 【点睛】关键点睛：解决与球有关的内切或外接问题时，关键是确定球心的位置，再利用球的截面小圆性质求解.5．（2022·浙江·模拟预测）如图，矩形BDEF 所在平面与正方形ABCD 所在平面互相垂直，2,1BD DE ==，点P 在线段EF 上，给出下列命题：①存在点P ，使得直线//DP 平面ACF ②存在点P ，使得直线DP ⊥平面ACF③直线DP 与平面ABCD 所成角的正弦值的取值范围是⎤⎥⎣⎦④三棱锥A CDE -的外接球被平面ACF 所截取的截面面积是98π 其中所有真命题的序号是（ ） A ．①③ B ．①④C ．②④D ．①③④ 【答案】D 【解析】 【分析】取EF 中点推理判断①；假定DP ⊥平面ACF ，分析判断②；确定直线DP 与平面ABCD 所成角，求出临界值判断③；求出ACF 外接圆面积判断④作答.令AC BD O =，连接,FO DF ，令EF 中点为G ，连DG ，如图，依题意，O 是,BD AC 的中点，对于①，在矩形BDEF 中，//DO FG ，DO FG =，四边形DOFG 是平行四边形，直线//DG OF ，OF ⊂平面ACF ，DG ⊄平面ACF ，则//DG 平面ACF ，当P 是线段EF 中点G 时，直线//DP 平面ACF ，①正确；对于②，假定直线DP ⊥平面ACF ，由①知，DP OF ⊥，DP DG ⊥，当点P 在线段EF 上任意位置（除点G 外），PDG ∠均为锐角，即DP 不垂直于DG ，也不垂直于OF ，因此，不存在点P ，使得直线DP ⊥平面ACF ，②不正确；对于③，平面BDEF ⊥平面ABCD ，DP 在平面ABCD 内射影在直线BD 上，直线DP 与平面ABCD 所成角为PDB ∠，当点P 由点E 运动到点F 的过程中，PDB ∠逐渐减小，当P 与E 重合时，PDB ∠最大，为90EDB ∠=，max (sin )1PDB ∠=，当P 与F 重合时，PDB ∠最小，为FDB ∠，min (sin )BF PDB DF ∠==所以直线DP 与平面ABCD 所成角的正弦值的取值范围是⎤⎥⎣⎦，③正确；对于④，在ACF 中，2AC =，|AF CF ==FO sin OF FAC AF ∠==由正弦定理得ACF 外接圆直径2sin FC r FAC ==∠半径r =圆面积为298S r ππ==，三棱锥A CDE -的外接球被平面ACF 所截取的截面是ACF 外接圆， 因此三棱锥A CDE -的外接球被平面ACF 所截取的截面面积是98π，④正确, 所以所有真命题的序号是①③④. 故选：D6．（2022·四川省泸县第二中学模拟预测（文））已知1O 是正方体1111ABCD A B C D -的中心O 关于平面1111D C B A 的对称点，则下列说法中正确的是（ ）A ．11O C 与1A C 是异面直线B ．11OC ∥平面11A BCD C ．11O C AD ⊥ D ．11O C ⊥平面11BDD B【答案】B 【解析】 【分析】根据正方体的性质、空间直线与平面的位置关系，即可对选项做出判断. 【详解】连接1A C 、1AC ，交于点O ，连接11A C 、11B D ，交于点P . 连接AC 、BD 、1A B 、1D C 、1O O .由题可知，1O 在平面11A C CA 上，所以11O C 与1A C 共面，故A 错误；在四边形11OO C C 中，11//O O C C 且11O O C C =，所以四边形11OO C C 为平行四边形. 11//O C OC ∴.OC ⊂平面11A BCD ，11O C ⊄平面11A BCD ，11O C ∴∥平面11A BCD ，故B 正确；由正方体的性质可得1111AC B D ⊥，因为1111O B O D =，所以111O P B D ⊥，又111O P AC P =，11B D ∴⊥平面111O AC ， 1111B D O C ∴⊥，又11//B D BD ， 11BD O C ∴⊥，而AD 与BD 所成角为45︒，所以显然11O C 与AD 不垂直，故C 错误；显然11O C 与11O B 不垂直，而11O B ⊂平面11BDD B ，所以11O C 与平面11BDD B 不垂直，故D 错误. 故选：B.7．（2022·北京·北大附中三模）已知平面,,αβγ，直线m 和n ，则下列命题中正确的是（ ） A ．若,m m αβ⊥⊥，则αβ∥ B ．若,αγβγ⊥⊥，则αβ∥ C ．若,m n m α⊥⊥，则n α∥ D ．若,m n αα∥∥，则m n ∥ 【答案】A 【解析】 【分析】对于A 选项，垂直于同一条直线的两个平面互相平行；对于B 选项，垂直于同一个平面的两个平面有可能相交，也有可能互相平行； 对于C 选项，由线面垂直的性质即可判断；对于D 选项，平行于同一个平面的两条直线有可能相交、平行或异面. 【详解】选项A 正确，因为垂直于同一直线的两个平面互相平行； 选项B 错误，平面α和β也可以相交； 选项C 错误，直线n 可能在平面α内； 选项D 错误，直线m 和n 还可能相交或者异面. 故选：A.8．（2022·云南师大附中模拟预测（理））已知正方形ABCD 的边长为ABC 沿对角线AC 折起，使得二面角B AC D --的大小为90°.若三棱锥B ACD -的四个顶点都在球O 的球面上，G 为AC 边的中点，E ，F 分别为线段BG ，DC 上的动点（不包括端点），且BE ，当三棱锥E ACF -的体积最大时，过点F 作球O 的截面，则截面面积的最小值为（ ）A ．B ．2πC ．32πD ．89π【答案】D 【解析】 【分析】根据面面垂直的判定定理得BG ⊥平面ACD ，继而表示出三棱锥E ACF -的体积，求出x =V 取得最大值，在∠GCF 中，由余弦定理，得GF =当GF 垂直于截面时，截面圆的面积最小，继而得解. 【详解】因为正方形ABCD 的边长为4AC =.如图，由于平面ABC ⊥平面ACD ，平面ABC 平面ACD AC =，又G 为AC 边的中点，则有BG AC ⊥，所以BG ⊥平面ACD ．设CF x =(0x <<，则BE =，所以三棱锥E ACF -的体积13ACF V S EG ==△2111122sin 4(22))323223AC CF ACF EG x x x ⨯∠=⨯⨯-=-，当x =时，V 取得最大值．由于GA GB GC GD ===，则球O 的球心即为G ，且球O 的半径2R =．又在△GCF中，由余弦定理，得cos GF GC CF ACF =∠=。

2012-2021十年全国高考数学真题分类汇编立体几何客观题（精解精析版）一、选择题1．(2021年高考全国乙卷理科)在正方体1111ABCD A B C D -中，P 为11B D 的中点，则直线PB 与1AD 所成的角为()A ．π2B ．π3C ．π4D ．π6【答案】D解析：如图，连接11,,BC PC PB ，因为1AD ∥1BC ，所以1PBC ∠或其补角为直线PB 与1AD 所成的角，因为1BB ⊥平面1111D C B A ，所以11BB PC ⊥，又111PC B D ⊥，1111BB B D B ⋂=，所以1PC ⊥平面1P B B ，所以1PC PB ⊥，设正方体棱长为2，则111112BC PC D B ===1111sin 2PC PBC BC ∠==，所以16PBC π∠=．故选：D2．(2021年高考全国甲卷理科)在一个正方体中，过顶点A 的三条棱的中点分别为E ，F ，G ．该正方体截去三棱锥A EFG -后，所得多面体的三视图中，正视图如图所示，则相应的侧视图是()()A．B．C．D．【答案】D解析：由题意及正视图可得几何体的直观图，如图所示，所以其侧视图为故选：D3．(2021年高考全国甲卷理科)已如A．B．C是半径为1的球O的球面上的三个点，且,1AC BC AC BC⊥==，则三棱锥O ABC-的体积为()A．212B．312C．24D．34【答案】A解析：,1AC BC AC BC ⊥== ，ABC ∴ 为等腰直角三角形，AB ∴=，则ABC 外接圆的半径为22，又球的半径为1，设O 到平面ABC 的距离为d ，则22d =，所以1112211332212O ABC ABC V S d -=⋅=⨯⨯⨯⨯=．故选：A ．【点睛】关键点睛：本题考查球内几何体问题，解题的关键是正确利用截面圆半径、球半径、球心到截面距离的勾股关系求解．4．(2020年高考数学课标Ⅰ卷理科)已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC 的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为()A ．64πB ．48πC ．36πD ．32π【答案】A【解析】设圆1O 半径为r ，球的半径为R ，依题意，得24,2r r ππ=∴=， ABC 为等边三角形，由正弦定理可得2sin 60AB r =︒=，1OO AB ∴==，根据球的截面性质1OO ⊥平面ABC ，11,4OO O A R OA ∴⊥====，∴球O 的表面积2464S R ππ==．故选：A【点睛】本题考查球的表面积，应用球的截面性质是解题的关键，考查计算求解能力，属于基础题．5．(2020年高考数学课标Ⅰ卷理科)埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为()()A ．514-B ．512-C ．514+D ．512+【答案】C【解析】如图，设,CD a PE b ==，则22224a PO PE OEb =-=-，由题意212PO ab =，即22142a b ab-=，化简得24()210b b a a -⋅-=，解得154b a =（负值舍去）．故选：C ．【点晴】本题主要考查正四棱锥的概念及其有关计算，考查学生的数学计算能力，是一道容易题．6．(2020年高考数学课标Ⅱ卷理科)已知△ABC 是面积为934的等边三角形，且其顶点都在球O 的球面上．若球O 的表面积为16π，则O 到平面ABC 的距离为()A ．3B ．32C ．1D ．32【答案】C解析：设球O 的半径为R ，则2416R ππ=，解得：2R =．设ABC 外接圆半径为r ，边长为a ，ABC 是面积为934的等边三角形，21393224a ∴⨯=，解得：3a =，22229933434a r a ∴=-=-=，∴球心O 到平面ABC 的距离22431d R r =-=-=．故选：C ．【点睛】本题考查球的相关问题的求解，涉及到球的表面积公式和三角形面积公式的应用；解题关键是明确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面．7．(2020年高考数学课标Ⅱ卷理科)如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为()()A ．EB ．FC ．GD ．H【答案】A解析：根据三视图，画出多面体立体图形，14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N,∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E ．故选：A【点睛】本题主要考查了根据三视图判断点的位置，解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法，考查了分析能力和空间想象，属于基础题．8．(2020年高考数学课标Ⅲ卷理科)下图为某几何体的三视图，则该几何体的表面积是()()A ．6+4B ．C ．D ．【答案】C解析：根据三视图特征，在正方体中截取出符合题意的立体图形根据立体图形可得：12222ABC ADC CDB S S S ===⨯⨯=△△△根据勾股定理可得：AB AD DB ===∴ADB △是边长为的等边三角形根据三角形面积公式可得：211sin 60222ADB S AB AD =⋅⋅︒=⋅=△∴该几何体的表面积是：632=⨯++．故选：C ．【点睛】本题主要考查了根据三视图求立体图形的表面积问题，解题关键是掌握根据三视图画出立体图形，考查了分析能力和空间想象能力，属于基础题．9．(2019年高考数学课标Ⅲ卷理科)如图，点N 为正方形ABCD 的中心，ECD △为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则()A ．BM EN =，且直线,BM EN 是相交直线B ．BM EN ≠，且直线,BM EN 是相交直线C ．BM EN =，且直线,BM EN 是异面直线D ．BM EN ≠，且直线,BM EN 是异面直线【答案】B 【解析】取DC 中点E ，如图连接辅助线，在BDE △中，N 为BD 中点，M 为DE 中点，所以//MN BE ，所以BM ，EN 共面相交，选项C ，D 错误． 平面CDE ⊥平面ABCD ，EF CD ⊥，EF ∴⊥平面ABCD ，又DC CD ⊥,∴DC ⊥平面DCE ，从而EF FN ⊥，BC MC ⊥．所以MCB △与EFN△均为直角三角形．不妨设正方形边长为2，易知3,1MC EF NF ===，所以22(3)27BM =+=，22(3)12EN =+=,BM EN ∴≠，故选B ．【点评】本题比较具有综合性，既考查了面面垂直、线面垂直等线面关系，还考查了三角形中的一些计算问题，是一个比较经典的题目．10．(2019年高考数学课标全国Ⅱ卷理科)设α、β为两个平面，则αβ//的充要条件是()()A ．α内有无数条直线与β平行B ．α内有两条相交直线与β平行C ．α，β平行于同一条直线D ．α，β垂直于同一平面【答案】B【解析】由面面平行的判定定理知：α内两条相交直线都与β平行是αβ//的充分条件，由面面平行性质定理知，若αβ//，则α内任意一条直线都与β平行，所以α内两条相交直线都与β平行是αβ//的必要条件，故选B .【点评】本题考查了空间两个平面的判定与性质及充要条件，渗透直观想象、逻辑推理素养，利用面面平行的判定定理与性质定理即可作出判断．面面平行的判定问题要紧扣面面平行判定定理，最容易犯的错误为定理记不住，凭主观臆断，如：“若,,//a b a b αβ⊂⊂，则//αβ”此类的错误．11．(2019年高考数学课标全国Ⅰ卷理科)已知三棱锥P ABC -的四个顶点在球O 的球面上，PA PB PC ==，ABC △是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，90CEF ∠=︒，则球O 的体积为()A ．B ．C ．D 【答案】D解析：三棱锥P ABC -为正三棱锥，取AC 中点M ，连接,PM BM ，则,AC PM AB BM ⊥⊥，PM BM M = ，可得AC ⊥平面PBM ，从而AC PB ⊥，又//,PB EF EF CE ⊥，可得PB CE ⊥，又AC CE C = ，所以PB ⊥平面PAC ，从而,PB PA PB PC ⊥⊥，从而正三棱锥P ABC -的三条侧棱,,PA PB PC 两两垂直，且PA PB PC ===,,PA PB PC 为棱的正方体，正方体的体对角线即为球O 的直径，即22R R ==，所以球O 的体积为343V R π==．12．(2018年高考数学课标Ⅲ卷（理）)设,,,A B C D 是同一个半径为4的球的球面上四点，ABC △为等边三角形且其面积为，则三棱锥D ABC -体积的最大值为()A．B．C．D．【答案】B解析：设ABC △的边长为a，则21sin 6062ABC S a a =︒=⇒=△，此时ABC △外接圆的半径为112sin 60232a r =⋅=⨯︒，故球心O 到面ABC2==，故点D 到面ABC 的最大距离为26R +=，此时11633D ABC ABC D ABC V S d --=⋅=⨯=△，故选B．点评：本题主要考查三棱锥的外接球，考查了勾股定理，三角形的面积公式和三棱锥的体积公式，判断出当DM ⊥平面ABC 时，三棱锥D ABC -体积最大很关键，由M 为三角形ABC 的重心，计算得到23BM BE ==，再由勾股定理得到OM ，进而得到结果，属于较难题型．13．(2018年高考数学课标Ⅲ卷（理）)中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫，凹进部分叫卯眼，图中木构件右边的小长方体是榫头，若如图摆放的木构件与某一带卯眼的木构件咬合成长方体．则咬合时带卯眼的木构件的俯视图可以是()()【答案】A解析：依题意，结合三视图的知识易知，带卯眼的木构件的俯视图可以是A 图．14．(2018年高考数学课标Ⅱ卷（理）)在长方体1111ABCD A B C D -中，1AB BC ==，1AA =线1AD 与1DB 所成角的余弦值为()A ．15B ．56C ．55D ．22【答案】C解析：以D 为坐标原点，1,,DA DC DD DA 为,,x y z 轴建立空间直角坐标系，则11(0,0,0),(1,0,0),(1,1,3),(0,0,3)D A B D ，所以11(1,0,3),(1,1,3)AD DB =-=因为111111135cos ,5||||25AD DB AD DB AD DB ⋅-+<>===⋅⨯所以异面直线1AD 与1DB 所成角的余弦值为55，故选C ．15．(2018年高考数学课标卷Ⅰ（理）)已知正方体的校长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面而积的最大值为()A ．334B ．233C ．324D ．32【答案】A【解析一】根据题意，平面α与正方体对角线垂直，记正方体为111ABCD A B C D -不妨设平面α与1AC 垂直，且交于点M ．平面ABD 与平面11B D C 与1AC 分别交于,P Q ．正方体中心为O ,则容易证明当M 从A 运动到P 时，截面为三角形且周长逐渐增大:当M 从P 运动到Q 时，截面为六边形且周长不变;当M 从Q 运动到1C 时，截面为三角形且周长还渐减小。

专题05立体几何（选择题、填空题）1．【2021·浙江高考真题】某几何体的三视图如图所示，则该几何体的体积是（）A ．32B ．3C．2D．【答案】A【分析】根据三视图可得如图所示的几何体，根据棱柱的体积公式可求其体积.【解析】几何体为如图所示的四棱柱1111ABCD A B C D -，其高为1，底面为等腰梯形ABCD ，，下底为12=，故1111131222ABCD A B C D V -=⨯+⨯⨯=，故选：A.2．【2021·北京高考真题】某四面体的三视图如图所示，该四面体的表面积为（）A ．332+B ．4C ．33D ．2【答案】A【分析】根据三视图可得如图所示的几何体（三棱锥），根据三视图中的数据可计算该几何体的表面积.【解析】根据三视图可得如图所示的几何体-正三棱锥O ABC -，其侧面为等腰直角三角形，底面等边三角形，由三视图可得该正三棱锥的侧棱长为1，故其表面积为213333112242+⨯⨯⨯+⨯=，故选：A.3．【2021·浙江高考真题】如图已知正方体1111ABCD A B C D -，M ，N 分别是1A D ，1D B 的中点，则（）A ．直线1A D 与直线1DB 垂直，直线//MN 平面ABCD B ．直线1A D 与直线1D B 平行，直线MN ⊥平面11BDD BC ．直线1AD 与直线1D B 相交，直线//MN 平面ABCD D ．直线1A D 与直线1D B 异面，直线MN ⊥平面11BDD B 【答案】A【分析】由正方体间的垂直、平行关系，可证1//,MN AB A D ⊥平面1ABD ，即可得出结论.【解析】连1AD ，在正方体1111ABCD A B C D -中，M 是1A D 的中点，所以M 为1AD 中点，又N 是1D B 的中点，所以//MN AB ，MN ⊄平面,ABCD AB ⊂平面ABCD ，所以//MN 平面ABCD .因为AB 不垂直BD ，所以MN 不垂直BD 则MN 不垂直平面11BDD B ，所以选项B,D 不正确；在正方体1111ABCD A B C D -中，11AD A D ⊥，AB ⊥平面11AA D D ，所以1AB A D ⊥，1AD AB A ⋂=，所以1A D ⊥平面1ABD ，1D B ⊂平面1ABD ，所以11A D D B ⊥，且直线11,A D D B 是异面直线，所以选项B 错误，选项A 正确.故选：A.【点睛】关键点点睛：熟练掌握正方体中的垂直、平行关系是解题的关键，如两条棱平行或垂直，同一个面对角线互相垂直，正方体的对角线与面的对角线是相交但不垂直或异面垂直关系.4．【2021·全国高考真题（理）】已如A ，B ，C 是半径为1的球O 的球面上的三个点，且,1AC BC AC BC ⊥==，则三棱锥O ABC -的体积为（）A ．212B ．312C ．24D ．34【答案】A【分析】由题可得ABC 为等腰直角三角形，得出ABC 外接圆的半径，则可求得O 到平面ABC 的距离，进而求得体积.【解析】,1AC BC AC BC ⊥== ，ABC ∴ 为等腰直角三角形，AB ∴=，则ABC 外接圆的半径为22，又球的半径为1，设O 到平面ABC 的距离为d ，则2d ==，所以1112211332212O ABC ABC V S d -=⋅=⨯⨯⨯⨯=.故选：A.【点睛】关键点睛：本题考查球内几何体问题，解题的关键是正确利用截面圆半径、球半径、球心到截面距离的勾股关系求解.5．【2021·全国高考真题（理）】在正方体1111ABCD A B C D -中，P 为11B D 的中点，则直线PB 与1AD 所成的角为（）A ．π2B ．π3C ．π4D ．π6【答案】D【分析】平移直线1AD 至1BC ，将直线PB 与1AD 所成的角转化为PB 与1BC 所成的角，解三角形即可.【解析】如图，连接11,,BC PC PB ，因为1AD ∥1BC ，所以1PBC ∠或其补角为直线PB 与1AD 所成的角，因为1BB ⊥平面1111D C B A ，所以11BB PC ⊥，又111PC B D ⊥，1111BB B D B ⋂=，所以1PC ⊥平面1P B B ，所以1PC PB ⊥，设正方体棱长为2，则111112BC PC D B ===1111sin 2PC PBC BC ∠==，所以16PBC π∠=.故选：D6．【2021·全国高考真题】已知圆锥的底面半径为，其侧面展开图为一个半圆，则该圆锥的母线长为（）A ．2B．C ．4D．【答案】B【分析】设圆锥的母线长为l ，根据圆锥底面圆的周长等于扇形的弧长可求得l 的值，即为所求.【解析】设圆锥的母线长为l，由于圆锥底面圆的周长等于扇形的弧长，则2l ππ=解得l =.故选：B.7．【2021·北京高考真题】定义：24小时内降水在平地上积水厚度（mm ）来判断降雨程度．其中小雨（10mm <），中雨（10mm 25mm -），大雨（25mm 50mm -），暴雨（50mm 100mm -），小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级（）A ．小雨B ．中雨C ．大雨D ．暴雨【答案】B【分析】计算出圆锥体积，除以圆面的面积即可得降雨量，即可得解.【解析】由题意，一个半径为()200100mm 2=的圆面内的降雨充满一个底面半径为()20015050mm 2300⨯=，高为()150mm 的圆锥，所以积水厚度()22150150312.5mm 100d ππ⨯⨯==⨯，属于中雨.故选：B.8．【2021·全国高考真题】在正三棱柱111ABC A B C -中，11AB AA ==，点P 满足1BP BC BB λμ=+，其中[]0,1λ∈，[]0,1μ∈，则（）A ．当1λ=时，1AB P △的周长为定值B ．当1μ=时，三棱锥1P A BC -的体积为定值C ．当12λ=时，有且仅有一个点P ，使得1A P BP ⊥D ．当12μ=时，有且仅有一个点P ，使得1A B ⊥平面1AB P 【答案】BD【分析】对于A ，由于等价向量关系，联系到一个三角形内，进而确定点的坐标；对于B ，将P 点的运动轨迹考虑到一个三角形内，确定路线，进而考虑体积是否为定值；对于C ，考虑借助向量的平移将P 点轨迹确定，进而考虑建立合适的直角坐标系来求解P 点的个数；对于D ，考虑借助向量的平移将P 点轨迹确定，进而考虑建立合适的直角坐标系来求解P 点的个数．【解析】易知，点P 在矩形11BCC B 内部（含边界）．对于A ，当1λ=时，11=BP BC BB BC CC μμ=++，即此时P ∈线段1CC ，1AB P △周长不是定值，故A 错误；对于B ，当1μ=时，1111=BP BC BB BB B C λλ=++，故此时P 点轨迹为线段11B C ，而11//B C BC ，11//B C 平面1A BC ，则有P 到平面1A BC 的距离为定值，所以其体积为定值，故B 正确．对于C ，当12λ=时，112BP BC BB μ=+，取BC ，11B C 中点分别为Q ，H ，则BP BQ QH μ=+，所以P 点轨迹为线段QH ，不妨建系解决，建立空间直角坐标系如图，13,0,12A ⎛⎫ ⎪ ⎪⎝⎭，()0,0P μ,，10,,02B ⎛⎫⎪⎝⎭，则13,0,12A P μ⎛⎫=-- ⎪ ⎪⎝⎭，10,,2BP μ⎛⎫=- ⎪⎝⎭ ，()110A P BP μμ⋅=-=，所以0μ=或1μ=．故,H Q 均满足，故C 错误；对于D ，当12μ=时，112BP BC BB λ=+ ，取1BB ，1CC 中点为,M N ．BP BM MN λ=+ ，所以P 点轨迹为线段MN ．设010,,2P y ⎛⎫ ⎪⎝⎭，因为0,02A ⎛⎫ ⎪ ⎪⎝⎭，所以01,22AP y ⎛⎫= ⎪ ⎪⎝⎭，11,,122A B ⎛⎫=-- ⎪ ⎪⎝⎭，所以00311104222y y +-=⇒=-，此时P 与N 重合，故D 正确．故选：BD ．【点睛】本题主要考查向量的等价替换，关键之处在于所求点的坐标放在三角形内．9．【2021·全国高考真题（理）】以图①为正视图，在图②③④⑤中选两个分别作为侧视图和俯视图，组成某三棱锥的三视图，则所选侧视图和俯视图的编号依次为_________（写出符合要求的一组答案即可）．【答案】③④（答案不唯一）【分析】由题意结合所给的图形确定一组三视图的组合即可.【解析】选择侧视图为③，俯视图为④，如图所示，长方体1111ABCD A B C D -中，12,1AB BC BB ===，,E F 分别为棱11,BC BC 的中点，则正视图①，侧视图③，俯视图④对应的几何体为三棱锥E ADF -.故答案为：③④.【点睛】三视图问题解决的关键之处是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系.10．【2020年高考全国Ⅰ卷理数】埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为A ．514-B ．512-C ．514D ．512+【答案】C【解析】如图，设,CD a PE b ==，则22224a PO PE OEb =-=-由题意得212PO ab =，即22142a b ab-=，化简得24()210b b a a -⋅-=，解得14b a +=（负值舍去）.故选C ．【点晴】本题主要考查正四棱锥的概念及其有关计算，考查学生的数学计算能力，是一道容易题.11．【2020年高考全国Ⅱ卷理数】如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为A ．EB ．FC ．GD ．H【答案】A【解析】根据三视图，画出多面体立体图形，14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N,∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E .故选A.【点睛】本题主要考查了根据三视图判断点的位置，解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法，考查了分析能力和空间想象，属于基础题.12．【2020年高考全国II 卷理数】已知△ABC 是面积为934O 的球面上.若球O 的表面积为16π，则O 到平面ABC 的距离为A 3B ．32C ．1D ．32【答案】C【解析】设球O 的半径为R ，则2416R π=π，解得：2R =.设ABC △外接圆半径为r ，边长为a ，ABC △是面积为934的等边三角形，21393224a ∴⨯=，解得：3a =，22229933434a r a ∴=-=⨯-，∴球心O 到平面ABC 的距离22431d R r =-=-=.故选：C ．【点睛】本题考查球的相关问题的求解，涉及到球的表面积公式和三角形面积公式的应用；解题关键是明确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.13．【2020年高考全国Ⅲ卷理数】如图为某几何体的三视图，则该几何体的表面积是A ．2B ．4+42C ．3D ．4+23【答案】C 【解析】根据三视图特征，在正方体中截取出符合题意的立体图形根据立体图形可得：12222ABC ADC CDB S S S ===⨯⨯=△△△根据勾股定理可得：22AB AD DB ===∴ADB △是边长为的等边三角形根据三角形面积公式可得：2113sin 60222ADB S AB AD =⋅⋅︒=⋅=△∴该几何体的表面积是：632=⨯++.故选：C ．【点睛】本题主要考查了根据三视图求立体图形的表面积问题，解题关键是掌握根据三视图画出立体图形，考查了分析能力和空间想象能力，属于基础题.14．【2020年高考全国Ⅰ卷理数】已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC △的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为A ．64πB ．48πC ．36πD ．32π【答案】A【解析】设圆1O 半径为r ，球的半径为R ，依题意，得24,2r r π=π=∴， ABC 为等边三角形，由正弦定理可得2sin 60AB r =︒=，1OO AB ∴==，根据球的截面性质1OO ⊥平面ABC ，11,4OO O A R OA ∴⊥====，∴球O 的表面积2464S R ππ==.故选：A.【点睛】本题考查球的表面积，应用球的截面性质是解题的关键，考查计算求解能力，属于基础题.15．【2020年高考天津】若棱长为为A ．12πB ．24πC ．36πD ．144π【答案】C【解析】这个球是正方体的外接球，其半径等于正方体的体对角线的一半，即3R ==，所以，这个球的表面积为2244336S R πππ==⨯=.故选：C ．【点睛】本题考查正方体的外接球的表面积的求法，求出外接球的半径是本题的解题关键，属于基础题.求多面体的外接球的面积和体积问题，常用方法有：（1）三条棱两两互相垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再根据勾股定理求球的半径；（3）如果设计几何体有两个面相交，可过两个面的外心分别作两个面的垂线，垂线的交点为几何体的球心.16．【2020年高考北京】某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为A ．6+B ．6+C ．12+D ．12+【答案】D 【解析】由题意可得，三棱柱的上下底面为边长为2的等边三角形，侧面为三个边长为2的正方形，则其表面积为：()1322222sin 60122S ⎛⎫=⨯⨯+⨯⨯⨯⨯︒=+⎪⎝⎭故选：D ．【点睛】(1)以三视图为载体考查几何体的表面积，关键是能够对给出的三视图进行恰当的分析，从三视图中发现几何体中各元素间的位置关系及数量关系．(2)多面体的表面积是各个面的面积之和；组合体的表面积应注意重合部分的处理．(3)圆柱、圆锥、圆台的侧面是曲面，计算侧面积时需要将这个曲面展为平面图形计算，而表面积是侧面积与底面圆的面积之和．17．【2020年高考浙江】某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：cm 3）是A ．73B ．143C ．3D ．6【答案】A 【解析】由三视图可知，该几何体是上半部分是三棱锥，下半部分是三棱柱，且三棱锥的一个侧面垂直于底面，且棱锥的高为1，棱柱的底面为等腰直角三角形，棱柱的高为2，所以几何体的体积为11117211212232233⎛⎫⎛⎫⨯⨯⨯⨯+⨯⨯⨯=+=⎪ ⎪⎝⎭⎝⎭.故选：A【点睛】本小题主要考查根据三视图计算几何体的体积，属于基础题.18．【2020年高考浙江】已知空间中不过同一点的三条直线l ，m ，n ．“l ，m ，n 共面”是“l ，m ，n 两两相交”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】B【解析】依题意,,m n l 是空间不过同一点的三条直线，当,,m n l 在同一平面时，可能////m n l ，故不能得出,,m n l 两两相交.当,,m n l 两两相交时，设,,m n A m l B n l C ⋂=⋂=⋂=，根据公理2可知,m n 确定一个平面α，而,B m C n αα∈⊂∈⊂，根据公理1可知，直线BC 即l α⊂，所以,,m n l 在同一平面.综上所述，“,,m n l 在同一平面”是“,,m n l 两两相交”的必要不充分条件.故选：B【点睛】本小题主要考查充分、必要条件的判断，考查公理1和公理2的运用，属于中档题.19．【2020年新高考全国Ⅰ卷】日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O )，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40°，则晷针与点A 处的水平面所成角为A ．20°B ．40°C ．50°D ．90°【答案】B 【解析】画出截面图如下图所示，其中CD 是赤道所在平面的截线；l 是点A 处的水平面的截线，依题意可知OA l ⊥；AB 是晷针所在直线.m 是晷面的截线，依题意依题意,晷面和赤道平面平行，晷针与晷面垂直，根据平面平行的性质定理可得可知//m CD 、根据线面垂直的定义可得AB m ⊥..由于40,//AOC m CD ∠=︒，所以40OAG AOC ∠=∠=︒，由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒，所以40BAE OAG ∠=∠=︒，也即晷针与点A 处的水平面所成角为40BAE ∠=︒.故选：B.【点睛】本小题主要考查中国古代数学文化，考查球体有关计算，涉及平面平行，线面垂直的性质，属于中档题.20．【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上，PA =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF =90°，则球O 的体积为A ．B ．C ．D 【答案】D【解析】解法一：,PA PB PC ABC == △为边长为2的等边三角形，P ABC ∴-为正三棱锥，PB AC ∴⊥，又E ，F 分别为PA ，AB 的中点，EF PB ∴∥，EF AC ∴⊥，又EF CE ⊥，,CE AC C EF =∴⊥ 平面PAC ，∴PB ⊥平面PAC ，APB PA PB PC ∴∠=90︒,∴===，P ABC ∴-为正方体的一部分，2R ==364466,π2338R V R =∴=π=⨯=，故选D ．解法二：设2PA PB PC x ===，,E F 分别为,PA AB 的中点，EF PB ∴∥，且12EF PB x ==，ABC △为边长为2的等边三角形，CF ∴=又90CEF ∠=︒，12CE AE PA x ∴===，AEC △中，由余弦定理可得()2243cos 22x x EAC x +--∠=⨯⨯，作PD AC ⊥于D ，PA PC = ，D \为AC 的中点，1cos 2AD EAC PA x ∠==，2243142x x x x+-+∴=，221221222x x x ∴+=∴==，，，PA PB PC ∴===，又===2AB BC AC ，,,PA PB PC ∴两两垂直，2R ∴==，62R ∴=，34466338V R ∴=π=π⨯=，故选D.【名师点睛】本题主要考查学生的空间想象能力，补体法解决外接球问题．可通过线面垂直定理，得到三棱两两互相垂直关系，快速得到侧棱长，进而补体成正方体解决．21．【2019年高考全国Ⅱ卷理数】设α，β为两个平面，则α∥β的充要条件是A ．α内有无数条直线与β平行B ．α内有两条相交直线与β平行C ．α，β平行于同一条直线D ．α，β垂直于同一平面【答案】B【解析】由面面平行的判定定理知：α内两条相交直线都与β平行是αβ∥的充分条件，由面面平行性质定理知，若αβ∥，则α内任意一条直线都与β平行，所以α内两条相交直线都与β平行是αβ∥的必要条件，故选B ．【名师点睛】本题考查了空间两个平面的判定与性质及充要条件，渗透直观想象、逻辑推理素养，利用面面平行的判定定理与性质定理即可作出判断．面面平行的判定问题要紧扣面面平行判定定理，最容易犯的错误为定理记不住，凭主观臆断，如：“若,,a b a b αβ⊂⊂∥，则αβ∥”此类的错误．22．【2019年高考全国Ⅲ卷理数】如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则A ．BM =EN ，且直线BM ，EN 是相交直线B ．BM ≠EN ，且直线BM ，EN 是相交直线C ．BM =EN ，且直线BM ，EN 是异面直线D ．BM ≠EN ，且直线BM ，EN 是异面直线【答案】B【解析】如图所示，作EO CD ⊥于O ，连接ON ，BD ，易得直线BM ，EN 是三角形EBD 的中线，是相交直线.过M 作MF OD ⊥于F ，连接BF ，平面CDE ⊥平面ABCD ，,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，MF ⊥平面ABCD ，MFB ∴△与EON △均为直角三角形．设正方形边长为2，易知12EO ON EN ===,，5,,22MF BF BM ==∴=BM EN ∴≠，故选B ．【名师点睛】本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形.解答本题时，先利用垂直关系，再结合勾股定理进而解决问题．23．【2019年高考浙江卷】祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V柱体=Sh，其中S是柱体的底面积，h是柱体的高．若某柱体的三视图如图所示（单位：cm），则该柱体的体积（单位：cm3）是A．158B．162C．182D．324【答案】B【解析】由三视图得该棱柱的高为6，底面可以看作是由两个直角梯形组合而成的，其中一个上底为4，下底为6，高为3，另一个的上底为2，下底为6，高为3，则该棱柱的体积为2646336162 22++⎛⎫⨯+⨯⨯=⎪⎝⎭.故选B.【名师点睛】本题首先根据三视图，还原得到几何体——棱柱，根据题目给定的数据，计算几何体的体积，常规题目.难度不大，注重了基础知识、视图用图能力、基本计算能力的考查.易错点有二，一是不能正确还原几何体；二是计算体积有误.为避免出错，应注重多观察、细心算.24．【2019年高考浙江卷】设三棱锥V–ABC的底面是正三角形，侧棱长均相等，P是棱VA 上的点（不含端点）．记直线PB与直线AC所成的角为α，直线PB与平面ABC所成的角为β，二面角P–AC–B的平面角为γ，则A．β<γ，α<γB．β<α，β<γC．β<α，γ<αD．α<β，γ<β【答案】B【解析】如图，G 为AC 中点，连接VG ，V 在底面ABC 的投影为O ，则P 在底面的投影D 在线段AO 上，过D 作DE 垂直于AC 于E ，连接PE ，BD ，易得PE VG ∥，过P 作PF AC ∥交VG 于F ，连接BF ，过D 作DH AC ∥，交BG 于H ，则,,BPF PBD PED αβγ=∠=∠=∠，结合△PFB ，△BDH ，△PDB 均为直角三角形，可得cos cos PF EG DH BD PB PB PB PB αβ===<=，即αβ>；在Rt △PED 中，tan tan PD PD ED BD γβ=>=，即γβ>，综上所述，答案为B.【名师点睛】本题以三棱锥为载体，综合考查异面直线所成的角、直线与平面所成的角、二面角的概念，以及各种角的计算.解答的基本方法是通过明确各种角，应用三角函数知识求解，而后比较大小.而充分利用图形特征，则可事倍功半.常规解法下易出现的错误有，不能正确作图得出各种角，未能想到利用“特殊位置法”，寻求简便解法.25．【2020年高考全国Ⅱ卷理数】设有下列四个命题：p 1：两两相交且不过同一点的三条直线必在同一平面内．p 2：过空间中任意三点有且仅有一个平面．p 3：若空间两条直线不相交，则这两条直线平行．p 4：若直线l ⊂平面α，直线m ⊥平面α，则m ⊥l ．则下述命题中所有真命题的序号是__________．①14p p ∧②12p p ∧③23p p ⌝∨④34p p ⌝∨⌝【答案】①③④【解析】对于命题1p ，可设1l 与2l 相交，这两条直线确定的平面为α；若3l 与1l 相交，则交点A 在平面α内，同理，3l 与2l 的交点B 也在平面α内，所以，AB α⊂，即3l α⊂，命题1p 为真命题；对于命题2p ，若三点共线，则过这三个点的平面有无数个，命题2p 为假命题；对于命题3p ，空间中两条直线相交、平行或异面，命题3p 为假命题；对于命题4p ，若直线m ⊥平面α，则m 垂直于平面α内所有直线，直线l ⊂平面α，∴直线m ⊥直线l ，命题4p 为真命题.综上可知，，为真命题，，为假命题，14p p ∧为真命题，12p p ∧为假命题，23p p ⌝∨为真命题，34p p ⌝∨⌝为真命题.故答案为：①③④.【点睛】本题考查复合命题的真假，同时也考查了空间中线面关系有关命题真假的判断，考查推理能力，属于中等题.26．【2020年高考全国Ⅲ卷理数】已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为_________．【答案】23【解析】易知半径最大球为圆锥的内切球，球与圆锥内切时的轴截面如图所示，其中2,3BC AB AC ===，且点M 为BC 边上的中点，设内切圆的圆心为O ，由于223122AM =-=，故1222222S =⨯⨯=△ABC 设内切圆半径为r ，则：ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯()1332222r =⨯++⨯=解得：22r =，其体积：34233V r =π=π.故答案为：23π.【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.27．【2020年高考浙江】已知圆锥的侧面积（单位：cm 2）为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径（单位：cm ）是_______．【答案】1【解析】设圆锥底面半径为r ，母线长为l ，则21222r l r l ππππ⨯⨯=⎧⎪⎨⨯⨯=⨯⨯⨯⎪⎩，解得1,2r l ==.故答案为：1【点睛】本小题主要考查圆锥侧面展开图有关计算，属于基础题.28．【2020年高考江苏】如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2cm ，高为2cm ，内孔半轻为0.5cm ，则此六角螺帽毛坯的体积是▲cm.【答案】2π【解析】正六棱柱体积为2624⨯⨯⨯，圆柱体积为21()222ππ⋅=，所求几何体体积为2π.故答案为：2π-【点睛】本题考查正六棱柱体积、圆柱体积，考查基本分析求解能力，属基础题.29．【2020年新高考全国Ⅰ卷】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2，∠BAD =60°．以1D 为球心，为半径的球面与侧面BCC 1B 1的交线长为________．【答案】22π.【解析】如图：取11B C 的中点为E ，1BB 的中点为F ，1CC 的中点为G ，因为BAD ∠=60°，直四棱柱1111ABCD A B C D -的棱长均为2，所以△111D B C 为等边三角形，所以1D E =111D E B C ⊥，又四棱柱1111ABCD A B C D -为直四棱柱，所以1BB ⊥平面1111D C B A ，所以111BB B C ⊥，因为1111BB B C B = ，所以1D E ⊥侧面11B C CB ，设P 为侧面11B C CB 与球面的交线上的点，则1D E EP ⊥，，1D E =，所以||EP ===，所以侧面11B C CB 与球面的交线上的点到E ，因为||||EF EG ==11B C CB 与球面的交线是扇形EFG 的弧 FG ，因为114B EF C EG π∠=∠=，所以2FEG π∠=，所以根据弧长公式可得 22FGπ==.故答案为：22π.【点睛】本题考查了直棱柱的结构特征，考查了直线与平面垂直的判定，考查了立体几何中的轨迹问题，考查了扇形中的弧长公式，属于中档题.30．【2019年高考全国Ⅲ卷理数】学生到工厂劳动实践，利用3D 打印技术制作模型.如图，该模型为长方体1111ABCD A B C D -挖去四棱锥O —EFGH 后所得的几何体，其中O 为长方体的中心，E ，F ，G ，H 分别为所在棱的中点，16cm 4cm AB =BC =, AA =，3D 打印所用原料密度为0.9g/cm 3，不考虑打印损耗，制作该模型所需原料的质量为___________g.【答案】118.8【解析】由题意得，214642312cm 2EFGH S =⨯-⨯⨯⨯=四边形，∵四棱锥O −EFGH 的高为3cm ，∴3112312cm 3O EFGH V -=⨯⨯=．又长方体1111ABCD A B C D -的体积为32466144cm V =⨯⨯=，所以该模型体积为3214412132cm O EFGH V V V -=-=-=，其质量为0.9132118.8g ⨯=．【名师点睛】本题考查几何体的体积问题，理解题中信息联系几何体的体积和质量关系，从而利用公式求解．根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积，再求出模型的质量即可.31．【2019年高考北京卷理数】某几何体是由一个正方体去掉一个四棱柱所得，其三视图如图所示．如果网格纸上小正方形的边长为1，那么该几何体的体积为__________．【答案】40【解析】如图所示，在棱长为4的正方体中，三视图对应的几何体为正方体去掉棱柱1111MPD A NQC B -之后余下的几何体，则几何体的体积()3142424402V =-⨯+⨯⨯=.【名师点睛】本题首先根据三视图，还原得到几何体，再根据题目给定的数据，计算几何体的体积.属于中等题.(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；(2)若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．32．【2019年高考北京卷理数】已知l ，m 是平面α外的两条不同直线．给出下列三个论断：①l ⊥m ；②m ∥α；③l ⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．【答案】如果l ⊥α，m ∥α，则l ⊥m .【解析】将所给论断，分别作为条件、结论，得到如下三个命题：（1）如果l ⊥α，m ∥α，则l ⊥m ，正确；（2）如果l ⊥α，l ⊥m ，则m ∥α，不正确，有可能m 在平面α内；（3）如果l ⊥m ，m ∥α，则l ⊥α，不正确，有可能l 与α斜交、l ∥α.故答案为：如果l ⊥α，m ∥α，则l ⊥m.【名师点睛】本题主要考查空间线面的位置关系、命题、逻辑推理能力及空间想象能力.将所给论断，分别作为条件、结论加以分析即可.33．【2019年高考天津卷理数】2的正方形，5若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为_____________．【答案】π4【解析】由题意，的正方形，借助勾股定理，2=.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，一个底面的圆心为四棱锥底面的中心，故圆柱的高为1，圆柱的底面半径为12，故圆柱的体积为21ππ124⎛⎫⨯⨯= ⎪⎝⎭.【名师点睛】根据棱锥的结构特点，确定所求的圆柱的高和底面半径.注意本题中圆柱的底面半径是棱锥底面对角线长度的一半、不是底边棱长的一半.34．【2019年高考江苏卷】如图，长方体1111ABCD A B C D -的体积是120，E 为1CC 的中点，则三棱锥E −BCD 的体积是▲.【答案】10【解析】因为长方体1111ABCD A B C D -的体积为120，所以1120AB BC CC ⋅⋅=，因为E 为1CC 的中点，所以112CE CC =，由长方体的性质知1CC ⊥底面ABCD ，所以CE 是三棱锥E BCD -的底面BCD 上的高，所以三棱锥E BCD -的体积1132V AB BC CE =⨯⋅⋅=111111201032212AB BC CC =⨯⋅⋅=⨯=.【名师点睛】本题蕴含“整体和局部”的对立统一规律.在几何体面积或体积的计算问题中，往往需要注意理清整体和局部的关系，灵活利用“割”与“补”的方法解题.由题意结合几何体的特征和所给几何体的性质可得三棱锥的体积.35．【2019年高考全国Ⅱ卷理数】中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．（本题第一空2分，第二空3分．）【答案】261【解析】由图可知第一层（包括上底面）与第三层（包括下底面）各有9个面，计18个面，第二层共有8个面，所以该半正多面体共有18826+=个面．如图，设该半正多面体的棱长为x ，则AB BE x ==，延长CB 与FE 的延长线交于点G ，延长BC 交正方体的棱于H ，由半正多面体对称性可知，BGE △为等腰直角三角形，22,21)122BG GE CH x GH x x x ∴===∴=⨯+=+=，1x ∴=1．。

1. 在一个几何体的三视图中，正视图和俯视图女口右图所示，则相应的俯视图可以为2. 已知矩形ABCD的顶点都在半径为4的球0的球面上，且AB 6,BC 2・.3,则棱锥O ABCD的体积为____________ 。

3. 如图，四棱锥P-ABCD中,底面ABCD为平行四边形，/ DAB=60,AB=2AD,PDL底面ABCD.(I )证明：PA! BD;(H )若PD=AD,求二面角A-PB-C的余弦值71.D2.8.33.解：(I)因为 DAB 60 ,AB 2AD ,由余弦定理得BD , 3AD 从而 BD 2+AD 2= AB 2，故 BD AD 又PD 底面ABCD,可得BD PD 所以BD 平面PAD.故PA BD(H)如图，以D 为坐标原点，AD 的长为单位长，射线 DA 为X 轴的正半轴建立空间直角坐标系D-xyz ，则A 1,0,0 ,B 0,301,.'3,0 , P 0,0,1。

uuu m PB 0, uuu m BC 0,uuv - uuvAB ( 1, 3,0), PB(0, ■ 3,uuv1),BC ( 1,0,0)设平面PAB 的法向量为 n= (x , y , z ),则{： uuu ABuu u PB0, 0,即因此可取n=(,3,1, 3)可取 m= (0, -1, .3)cos m, n4 2.72.7 7故二面角A-PB-C 的余弦值为2.7设平面PBC 的法向量为 m ，则1.正方体ABCD-A BQD !中，B B l 与平面AC D i 所成角的余弦值为A -2B -2C 2D _63 3 3 3uuv uuv2.已知圆0的半径为1, PA 、PB 为该圆的两条切线，A B 为俩切点，那么 PA?PB 的最小值为(A)4 2(B)3 2 (C)4 2 2 (D)3 2、22的球面上有 A 、B 、C D 四点，若AB=CD=2则四面体ABCD 勺体积的最大值为4.如图，四棱锥 S-ABCD 中, SD 底面 ABCD AB//DC , AD DC=SD=2 E 为棱SB 上的一点，平面 EDC 平面SBC .(I)证明：SE=2EB(n)求二面角 A-DE-C 的大小.(A )223(B)2,3(D)8.3 33.已知在半径为 DC AB=AD=11. D2. D3. B4.解法一：(I )连接BD,取DC 的中点G,连接BG,由此知 DG GC BG 1,即 ABC 为直角三角形，故 BC BD .又SD 平面 ABCD,故 BC SD , 所以， BC 平面 BDS,BC DE . 作BKEC,K 为垂足，因平面 EDC 平面SBC ,故BK 平面EDC , BK DE,DE 与平面SBC 内的两条相交直线 BK BC 都垂直 DE !平面 SBC DEL EC,DE ± SB故ADE 为等腰三角形..SD 2 DB 2SDgDB 2 SB3.DB 2- DE 2SE=2EBSD 2 AD 2SB DEEB所以, .6 (,SE SB-EB32EB,AB SA,知1,又 AD=1取ED 中点F,连接AF ,则AFDE,AF 「AD 2 DF 2 f所以，AFG是二面角A DE C的平面角连接FG，则FG //EC, FG DE . 连接AG,AG=、2, FG DG"DF2寸,cos AFG AF2 FG2 AG2 2gAF gFG解法以D 为坐标原点，射线 DA 为x 轴的正半轴，建立如图所示的直角坐标系 D xyz ,故 SE=2EB2 2 2 1 1 1 uur 2 11(□)由(【)知 E(—,,)，取 DE 的中点 F ,则 F(-，, ), FA (一，,3 3 3 3 3 3 3 3 3uuu uuir故FAgDE 0，由此得FA DEuuu 2 4 2 uuu uuu又 EC (,,)，故 ECgDE 0，由此得 EC DE ,3 3 3uuu uuu向量FA 与EC 的夹角等于二面角 A DE C 的平面角uur uuu… ，出u uu 、 FA (EC 1 于是cos(FA, EC) ULU ^Eiuu -|FA||EC| 2设 A(1,0,0)，贝U B(1,1,0),C(0,2,0),S(0,0,2)uur uuu (I) SC (0,2,-2), BC (-1,1,0)设平面SBC 的法向量为n=(a, b, c)uur uuu uuu uuu 由 n SC, n BC ，得 ngSC 0, ngBC故 2b-2c=0,-a+b=0 uir uuu 又设SEEB (0），则2 、E(— J .J .)1 1 1uuu2 uurDE (1‘1,1 -),DC (0,2,0)设平面 CDE 的法向量m=(x,y,z)由mDE,mDC,得m DE 0 , mDC 0故x y2z 0,2y 0111令x 2 ,则m (2,0,).令 a=1，贝U由平面 DECL 平面 SBC 得 ml n, mgn 0,2 0,2)1. 已知三棱柱 ABC A \B i C i 的侧棱与底面边长都相等,A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与CC !所成的角的余弦值为（面积等于 _______________ 。

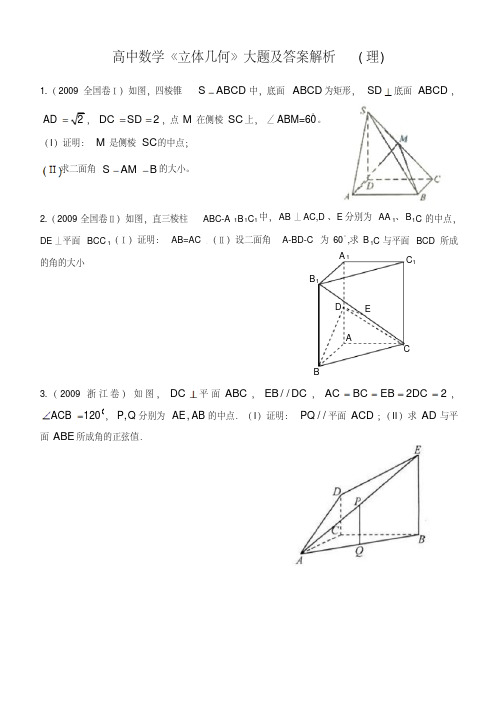
06 立体几何（解答题）（理科专用）1．【2022年全国甲卷】在四棱锥P−ABCD中，PD⊥底面ABCD,CD∥AB,AD=DC=CB=1 ,AB=2,DP=√3．(1)证明：BD⊥PA；(2)求PD与平面PAB所成的角的正弦值．【答案】(1)证明见解析；(2)√5.5【解析】【分析】（1）作DE⊥AB于E，CF⊥AB于F，利用勾股定理证明AD⊥BD，根据线面垂直的性质可得PD⊥BD，从而可得BD⊥平面PAD，再根据线面垂直的性质即可得证；（2）以点D为原点建立空间直角坐标系，利用向量法即可得出答案.(1)证明：在四边形ABCD中，作DE⊥AB于E，CF⊥AB于F，因为CD//AB,AD=CD=CB=1,AB=2，所以四边形ABCD为等腰梯形，所以AE=BF=1，2，BD=√DE2+BE2=√3，故DE=√32所以AD2+BD2=AB2，所以AD⊥BD，因为PD⊥平面ABCD，BD⊂平面ABCD，所以PD⊥BD，又PD∩AD=D，所以BD⊥平面PAD，又因PA⊂平面PAD，所以BD⊥PA；(2)解：如图，以点D 为原点建立空间直角坐标系， BD =√3，则A(1,0,0),B(0,√3,0),P(0,0,√3)，则AP⃗⃗⃗⃗⃗ =(−1,0,√3),BP ⃗⃗⃗⃗⃗ =(0,−√3,√3),DP ⃗⃗⃗⃗⃗ =(0,0,√3)， 设平面PAB 的法向量n⃗ =(x,y,z)， 则有{n →⋅AP →=−x +√3z =0n →⋅BP →=−√3y +√3z =0，可取n ⃗ =(√3,1,1)， 则cos〈n ⃗ ,DP⃗⃗⃗⃗⃗ 〉=n⃗ ⋅DP ⃗⃗⃗⃗⃗⃗ |n ⃗ ||DP ⃗⃗⃗⃗⃗⃗ |=√55， 所以PD 与平面PAB 所成角的正弦值为√55.2．【2022年全国乙卷】如图，四面体ABCD 中，AD ⊥CD,AD =CD,∠ADB =∠BDC ，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设AB =BD =2,∠ACB =60°，点F 在BD 上，当△AFC 的面积最小时，求CF 与平面ABD 所成的角的正弦值． 【答案】(1)证明过程见解析 (2)CF 与平面ABD 所成的角的正弦值为4√37【解析】 【分析】（1）根据已知关系证明△ABD ≌△CBD ，得到AB =CB ，结合等腰三角形三线合一得到垂直关系，结合面面垂直的判定定理即可证明；（2）根据勾股定理逆用得到BE ⊥DE ，从而建立空间直角坐标系，结合线面角的运算法则进行计算即可. (1)因为AD =CD ，E 为AC 的中点，所以AC ⊥DE ；在△ABD 和△CBD 中，因为AD =CD,∠ADB =∠CDB,DB =DB ，所以△ABD ≌△CBD ，所以AB =CB ，又因为E 为AC 的中点，所以AC ⊥BE ； 又因为DE,BE ⊂平面BED ，DE ∩BE =E ，所以AC ⊥平面BED ， 因为AC ⊂平面ACD ，所以平面BED ⊥平面ACD . (2)连接EF ，由（1）知，AC ⊥平面BED ，因为EF ⊂平面BED ， 所以AC ⊥EF ，所以S △AFC =12AC ⋅EF ， 当EF ⊥BD 时，EF 最小，即△AFC 的面积最小. 因为△ABD ≌△CBD ，所以CB =AB =2， 又因为∠ACB =60°，所以△ABC 是等边三角形， 因为E 为AC 的中点，所以AE =EC =1，BE =√3， 因为AD ⊥CD ，所以DE =12AC =1,在△DEB 中，DE 2+BE 2=BD 2，所以BE ⊥DE . 以E 为坐标原点建立如图所示的空间直角坐标系E −xyz ，则A (1,0,0),B(0,√3,0),D (0,0,1)，所以AD ⃗⃗⃗⃗⃗ =(−1,0,1),AB ⃗⃗⃗⃗⃗ =(−1,√3,0)， 设平面ABD 的一个法向量为n⃗ =(x,y,z )， 则{n ⃗ ⋅AD ⃗⃗⃗⃗⃗ =−x +z =0n ⃗ ⋅AB⃗⃗⃗⃗⃗ =−x +√3y =0 ，取y =√3，则n ⃗ =(3,√3,3)，又因为C (−1,0,0),F (0,√34,34)，所以CF⃗⃗⃗⃗⃗ =(1,√34,34)，所以cos⟨n ⃗ ,CF ⃗⃗⃗⃗⃗ ⟩=n ⃗ ⋅CF⃗⃗⃗⃗⃗ |n ⃗ ||CF⃗⃗⃗⃗⃗ |=√21×√74=4√37，设CF 与平面ABD 所成的角的正弦值为θ(0≤θ≤π2)， 所以sinθ=|cos⟨n ⃗ ,CF⃗⃗⃗⃗⃗ ⟩|=4√37， 所以CF 与平面ABD 所成的角的正弦值为4√37.3．【2022年新高考1卷】如图，直三棱柱ABC −A 1B 1C 1的体积为4，△A 1BC 的面积为2√2．(1)求A 到平面A 1BC 的距离；(2)设D 为A 1C 的中点，AA 1=AB ，平面A 1BC ⊥平面ABB 1A 1，求二面角A −BD −C 的正弦值．【答案】(1)√2 (2)√32【解析】 【分析】（1）由等体积法运算即可得解；（2）由面面垂直的性质及判定可得BC ⊥平面ABB 1A 1，建立空间直角坐标系，利用空间向量法即可得解. (1)在直三棱柱ABC −A 1B 1C 1中，设点A 到平面A 1BC 的距离为h ， 则V A−A 1BC =13S △A 1BC ⋅ℎ=2√23ℎ=V A 1−ABC =13S △ABC ⋅A 1A =13V ABC−A 1B 1C 1=43，解得ℎ=√2，所以点A 到平面A 1BC 的距离为√2； (2)取A 1B 的中点E ,连接AE ,如图，因为AA 1=AB ，所以AE ⊥A 1B , 又平面A 1BC ⊥平面ABB 1A 1，平面A 1BC ∩平面ABB 1A 1=A 1B ， 且AE ⊂平面ABB 1A 1，所以AE ⊥平面A 1BC ， 在直三棱柱ABC −A 1B 1C 1中，BB 1⊥平面ABC ，由BC ⊂平面A 1BC ，BC ⊂平面ABC 可得AE ⊥BC ，BB 1⊥BC ， 又AE,BB 1⊂平面ABB 1A 1且相交，所以BC ⊥平面ABB 1A 1，所以BC,BA,BB 1两两垂直，以B 为原点，建立空间直角坐标系，如图，由（1）得AE =√2，所以AA 1=AB =2，A 1B =2√2，所以BC =2， 则A(0,2,0),A 1(0,2,2),B(0,0,0),C(2,0,0),所以A 1C 的中点D(1,1,1)， 则BD⃗⃗⃗⃗⃗⃗ =(1,1,1)，BA ⃗⃗⃗⃗⃗ =(0,2,0),BC ⃗⃗⃗⃗⃗ =(2,0,0), 设平面ABD 的一个法向量m ⃗⃗ =(x,y,z)，则{m ⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ =x +y +z =0m ⃗⃗ ⋅BA ⃗⃗⃗⃗⃗ =2y =0，可取m⃗⃗ =(1,0,−1)， 设平面BDC 的一个法向量n ⃗ =(a,b,c)，则{m ⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ =a +b +c =0m ⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =2a =0， 可取n⃗ =(0,1,−1)， 则cos〈m ⃗⃗ ,n ⃗ 〉=m⃗⃗⃗ ⋅n ⃗ |m ⃗⃗⃗ |⋅|n ⃗ |=√2×√2=12，所以二面角A −BD −C 的正弦值为√1−(12)2=√32.4．【2022年新高考2卷】如图，PO 是三棱锥P −ABC 的高，PA =PB ，AB ⊥AC ，E 是PB 的中点．(1)证明：OE//平面PAC ；(2)若∠ABO =∠CBO =30°，PO =3，PA =5，求二面角C −AE −B 的正弦值． 【答案】(1)证明见解析 (2)1113 【解析】 【分析】（1）连接BO 并延长交AC 于点D ，连接OA 、PD ，根据三角形全等得到OA =OB ，再根据直角三角形的性质得到AO =DO ，即可得到O 为BD 的中点从而得到OE//PD ，即可得证； （2）过点A 作Az//OP ，如图建立平面直角坐标系，利用空间向量法求出二面角的余弦值，再根据同角三角函数的基本关系计算可得； (1)证明：连接BO 并延长交AC 于点D ，连接OA 、PD ，因为PO 是三棱锥P −ABC 的高，所以PO ⊥平面ABC ，AO,BO ⊂平面ABC ， 所以PO ⊥AO 、PO ⊥BO ，又PA =PB ，所以△POA ≅△POB ，即OA =OB ，所以∠OAB =∠OBA ，又AB ⊥AC ，即∠BAC =90°，所以∠OAB +∠OAD =90°，∠OBA +∠ODA =90°， 所以∠ODA =∠OAD所以AO =DO ，即AO =DO =OB ，所以O 为BD 的中点，又E 为PB 的中点，所以OE//PD ， 又OE ⊄平面PAC ，PD ⊂平面PAC ， 所以OE//平面PAC(2)解：过点A 作Az//OP ，如图建立平面直角坐标系， 因为PO =3，AP =5，所以OA =√AP 2−PO 2=4，又∠OBA =∠OBC =30°，所以BD =2OA =8，则AD =4，AB =4√3，所以AC =12，所以O(2√3,2,0)，B(4√3,0,0)，P(2√3,2,3)，C (0,12,0)，所以E (3√3,1,32)， 则AE ⃗⃗⃗⃗⃗ =(3√3,1,32)，AB ⃗⃗⃗⃗⃗ =(4√3,0,0)，AC ⃗⃗⃗⃗⃗ =(0,12,0)， 设平面AEB 的法向量为n ⃗ =(x,y,z )，则{n ⃗ ⋅AE ⃗⃗⃗⃗⃗ =3√3x +y +32z =0n ⃗ ⋅AB ⃗⃗⃗⃗⃗ =4√3x =0 ，令z =2，则y =−3，x =0，所以n ⃗ =(0,−3,2)；设平面AEC 的法向量为m⃗⃗ =(a,b,c )，则{m ⃗⃗ ⋅AE ⃗⃗⃗⃗⃗ =3√3a +b +32c =0m ⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =12b =0 ，令a =√3，则c =−6，b =0，所以m ⃗⃗ =(√3,0,−6)； 所以cos ⟨n ⃗ ,m ⃗⃗ ⟩=n⃗ ⋅m ⃗⃗⃗ |n ⃗ ||m ⃗⃗⃗ |=√13×√39=−4√313设二面角C −AE −B 为θ，由图可知二面角C −AE −B 为钝二面角， 所以cosθ=−4√313，所以sinθ=√1−cos 2θ=1113故二面角C −AE −B 的正弦值为1113；5．【2021年甲卷理科】已知直三棱柱111ABC A B C -中，侧面11AA B B 为正方形，2AB BC ==，E ，F 分别为AC 和1CC 的中点，D 为棱11A B 上的点．11BF A B ⊥（1）证明：BF DE ⊥；（2）当1B D 为何值时，面11BB C C 与面DFE 所成的二面角的正弦值最小? 【答案】（1）证明见解析；（2）112B D = 【解析】 【分析】（1）方法二：通过已知条件，确定三条互相垂直的直线，建立合适的空间直角坐标系，借助空间向量证明线线垂直；（2）方法一：建立空间直角坐标系，利用空间向量求出二面角的平面角的余弦值最大，进而可以确定出答案； 【详解】（1）[方法一]：几何法 因为1111,//BFA B A B AB ⊥，所以BF AB ⊥．又因为1AB BB ⊥，1BF BB B ⋂=，所以AB ⊥平面11BCC B ．又因为2AB BC ==，构造正方体1111ABCG A B C G -，如图所示，过E 作AB 的平行线分别与AG BC ，交于其中点,M N ，连接11,A M B N ， 因为E ，F 分别为AC 和1CC 的中点，所以N 是BC 的中点， 易证1Rt Rt BCF B BN ≅，则1CBF BB N ∠=∠．又因为1190BB N B NB ∠+∠=︒，所以1190CBF B NB BF B N ∠+∠=︒⊥，． 又因为111111,BFA B B N A B B ⊥=，所以BF ⊥平面11A MNB ．又因为ED ⊂平面11A MNB ，所以BF DE ⊥． [方法二] 【最优解】：向量法因为三棱柱111ABC A B C -是直三棱柱，1BB ∴⊥底面ABC ，1BB AB ∴⊥11//A B AB ，11BF A B ⊥，BF AB ∴⊥，又1BB BF B ⋂=，AB ∴⊥平面11BCC B ．所以1,,BA BC BB 两两垂直．以B 为坐标原点，分别以1,,BA BC BB 所在直线为,,x y z 轴建立空间直角坐标系，如图．()()()0,0,0,2,0,0,0,2,0,B A C ∴()()()1110,0,2,2,0,2,0,2,2B A C ，()()1,1,0,0,2,1E F ．由题设(),0,2D a （02a ≤≤）． 因为()()0,2,1,1,1,2BF DE a ==--，所以()()0121120BF DE a ⋅=⨯-+⨯+⨯-=，所以BF DE ⊥．[方法三]：因为11BF A B ⊥，11//A B AB ，所以BF AB ⊥，故110BF A B ⋅=，0BF AB ⋅=，所以()11BF ED BF EB BB B D ⋅=⋅++()11=BF B D BF EB BB ⋅+⋅+1BF EB BF BB =⋅+⋅11122BF BA BC BF BB ⎛⎫=--+⋅ ⎪⎝⎭11122BF BA BF BC BF BB =-⋅-⋅+⋅112BF BC BF BB =-⋅+⋅111cos cos 2BF BC FBC BF BB FBB =-⋅∠+⋅∠1=2202-=，所以BF ED ⊥．（2）[方法一]【最优解】：向量法 设平面DFE 的法向量为(),,m x y z =， 因为()()1,1,1,1,1,2EF DE a =-=--，所以00m EF m DE ⎧⋅=⎨⋅=⎩，即()0120x y z a x y z -++=⎧⎨-+-=⎩．令2z a =-，则()3,1,2m a a =+-因为平面11BCC B 的法向量为()2,0,0BA =， 设平面11BCC B 与平面DEF 的二面角的平面角为θ， 则cos m BA m BAθ⋅=⋅==当12a =时，2224a a -+取最小值为272， 此时cos θ=所以()minsin θ=112B D =． [方法二] ：几何法如图所示，延长EF 交11A C 的延长线于点S ，联结DS 交11B C 于点T ，则平面DFE平面11BB C C FT =．作1B H FT ⊥，垂足为H ，因为1DB ⊥平面11BB C C ，联结DH ，则1DHB ∠为平面11BB C C 与平面DFE 所成二面角的平面角．设1,B D t =[0,2],t ∈1B T s =，过1C 作111//C G A B 交DS 于点G ． 由111113C S C G SA A D ==得11(2)3C G t =-． 又1111BD B T C G C T=，即12(2)3t s s t =--，所以31ts t =+．又111B H B TC F FT =，即11B H =1B H =所以DH === 则11sin B D DHB DH∠===所以，当12t =时，()1min sin DHB ∠= [方法三]：投影法 如图，联结1,FB FN ，DEF 在平面11BB C C 的投影为1B NF ，记面11BB C C 与面DFE 所成的二面角的平面角为θ，则1cos B NF DEFS Sθ=．设1(02)B D t t =≤≤，在1Rt DB F中，DF =在Rt ECF中，EF D作1B N 的平行线交MN 于点Q ．在Rt DEQ △中，DE =在DEF 中，由余弦定理得222cos 2DF EF DE DFE DF EF+-∠=⋅sin DFE ∠=1sin 2DFESDF EF DFE =⋅∠13,2B NFS = 1cos B NF DFES Sθ==，sin θ=当12t =，即112B D =，面11BBC C 与面DFE 【整体点评】第一问，方法一为常规方法，不过这道题常规方法较为复杂，方法二建立合适的空间直角坐标系，借助空间向量求解是最简单，也是最优解；方法三利用空间向量加减法则及数量积的定义运算进行证明不常用，不过这道题用这种方法过程也很简单，可以开拓学生的思维. 第二问：方法一建立空间直角坐标系，利用空间向量求出二面角的平面角是最常规的方法，也是最优方法；方法二：利用空间线面关系找到，面11BB C C 与面DFE 所成的二面角，并求出其正弦值的最小值，不是很容易找到；方法三：利用面DFE 在面11BB C C 上的投影三角形的面积与DFE △面积之比即为面11BB C C 与面DFE 所成的二面角的余弦值，求出余弦值的最小值，进而求出二面角的正弦值最小，非常好的方法，开阔学生的思维．6．【2021年乙卷理科】如图，四棱锥P ABCD -的底面是矩形，PD ⊥底面ABCD ，1PD DC ==，M 为BC 的中点，且PB AM ⊥．（1）求BC ；（2）求二面角A PM B --的正弦值． 【答案】（1（2【解析】【分析】（1）以点D 为坐标原点，DA 、DC 、DP 所在直线分别为x 、y 、z 轴建立空间直角坐标系，设2BC a =，由已知条件得出0PB AM ⋅=，求出a 的值，即可得出BC 的长； （2）求出平面PAM 、PBM 的法向量，利用空间向量法结合同角三角函数的基本关系可求得结果. 【详解】（1）[方法一]：空间坐标系+空间向量法PD ⊥平面ABCD ，四边形ABCD 为矩形，不妨以点D 为坐标原点，DA 、DC 、DP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系D xyz -，设2BC a =，则()0,0,0D 、()0,0,1P 、()2,1,0B a 、(),1,0M a 、()2,0,0A a ， 则()2,1,1PB a =-，(),1,0AM a =-，PB AM ⊥，则2210PB AM a ⋅=-+=，解得a =2BC a == [方法二]【最优解】：几何法+相似三角形法如图，连结BD ．因为PD ⊥底面ABCD ，且AM ⊂底面ABCD ，所以PD AM ⊥． 又因为PB AM ⊥，PBPD P =，所以AM ⊥平面PBD ．又BD ⊂平面PBD ，所以AM BD ⊥．从而90ADB DAM ∠+∠=︒．因为90∠+∠=︒MAB DAM ，所以∠=∠MAB ADB ． 所以∽ADB BAM ，于是=AD BAAB BM．所以2112BC =．所以BC = [方法三]：几何法+三角形面积法 如图，联结BD 交AM 于点N ．由[方法二]知⊥AM DB ．在矩形ABCD 中，有∽DAN BMN ，所以2==AN DA MN BM，即23AN AM =．令2(0)=>BC t t ，因为M 为BC 的中点，则BM t =，DB AM由1122=⋅=⋅DABSDA AB DB AN ，得=t ，解得212t =，所以2==BC t（2）[方法一]【最优解】：空间坐标系+空间向量法设平面PAM 的法向量为()111,,m x y z =，则AM ⎛⎫= ⎪ ⎪⎝⎭，()AP =-， 由111120220m AMy m AP z ⎧⋅=-+=⎪⎨⎪⋅=-+=⎩，取1x =()2,1,2m =，设平面PBM 的法向量为()222,,n x yz =，BM ⎛⎫=- ⎪ ⎪⎝⎭，()1,1BP =--，由222220220n BM n BP y z ⎧⋅=-=⎪⎨⎪⋅=--+=⎩，取21y =，可得()0,1,1n =，3cos ,7m n m n m n ⋅===⋅⨯ 所以，270sin ,1cos ,14m n m n =-=， 因此，二面角A PM B --[方法二]：构造长方体法+等体积法如图，构造长方体1111ABCD A B C D -，联结11,AB A B ，交点记为H ，由于11AB A B ⊥，1AB BC ⊥，所以AH ⊥平面11A BCD ．过H 作1D M 的垂线，垂足记为G ．联结AG ，由三垂线定理可知1⊥AG D M ， 故AGH ∠为二面角A PM B --的平面角．易证四边形11A BCD 的正方形，联结1D H ，HM ． 111111111,2D HMD HMD A HHBMMCD A BCD SD M HG S S SSS=⋅=---正方形，由等积法解得=HG在Rt AHG 中，==AH HG =AG所以，sin AH AGH AG ∠==A PMB -- 【整体点评】（1）方法一利用空坐标系和空间向量的坐标运算求解；方法二利用线面垂直的判定定理，结合三角形相似进行计算求解，运算简洁，为最优解；方法三主要是在几何证明的基础上，利用三角形等面积方法求得.（2）方法一，利用空间坐标系和空间向量方法计算求解二面角问题是常用的方法，思路清晰，运算简洁，为最优解；方法二采用构造长方体方法+等体积转化法，技巧性较强，需注意进行严格的论证.7．【2021年新高考1卷】如图，在三棱锥A BCD -中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点.（1）证明：OA CD ⊥；（2）若OCD 是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D --的大小为45︒，求三棱锥A BCD -的体积.【答案】(1)证明见解析；【解析】 【分析】(1)由题意首先证得线面垂直，然后利用线面垂直的定义证明线线垂直即可；(2)方法二：利用几何关系找到二面角的平面角，然后结合相关的几何特征计算三棱锥的体积即可. 【详解】（1）因为AB AD =，O 是BD 中点，所以OA BD ⊥， 因为OA ⊂平面ABD ，平面ABD ⊥平面BCD ， 且平面ABD ⋂平面BCD BD =，所以OA ⊥平面BCD ． 因为CD ⊂平面BCD ，所以OA CD ⊥. （2）[方法一]：通性通法—坐标法如图所示，以O 为坐标原点，OA 为z 轴，OD 为y 轴，垂直OD 且过O 的直线为x 轴，建立空间直角坐标系O xyz -，则1,0),(0,1,0),(0,1,0)2C D B -，设12(0,0,),(0,,)33A m E m ,所以4233(0,,),(,,0)3322EB m BC =--=，设(),,n x y z =为平面EBC 的法向量，则由00EB n EC n ⎧⋅=⎨⋅=⎩可求得平面EBC 的一个法向量为2(3,1,)n m =--．又平面BCD 的一个法向量为()0,0,OA m=，所以cos ,2n OA ==，解得1m =．又点C 到平面ABD112132A BCD C ABD V V--==⨯⨯⨯=， 所以三棱锥A BCD - [方法二]【最优解】：作出二面角的平面角 如图所示，作EGBD ⊥，垂足为点G ．作GF BC ⊥，垂足为点F ，连结EF ，则OA EG ∥．因为OA ⊥平面BCD ，所以EG ⊥平面BCD ，EFG 为二面角E BC D --的平面角．因为45EFG ∠=︒，所以EG FG =． 由已知得1OB OD ==，故1OB OC ==．又30OBC OCB ∠=∠=︒，所以BC =因为24222,,,,133333GD GB FG CD EG OA ======，111122(11)13332A BCD BCDBOCV SO SOA A -==⨯⨯=⨯⨯⨯⨯⨯=[方法三]：三面角公式考虑三面角B EDC -，记EBD ∠为α，EBC ∠为β，30DBC ∠=︒， 记二面角E BC D --为θ．据题意，得45θ=︒． 对β使用三面角的余弦公式，可得cos cos cos30βα=⋅︒，化简可得cos βα=．①使用三面角的正弦公式，可得sin sin sin αβθ=，化简可得sin βα=．② 将①②两式平方后相加，可得223cos 2sin 14αα+=，由此得221sin cos 4αα=，从而可得1tan 2α=±．如图可知π(0,)2α∈，即有1tan 2α=，根据三角形相似知，点G 为OD 的三等分点，即可得43BG =， 结合α的正切值，可得2,13EG OA ==从而可得三棱锥A BCD -【整体点评】(2)方法一：建立空间直角坐标系是解析几何中常用的方法，是此类题的通性通法，其好处在于将几何问题代数化，适合于复杂图形的处理；方法二：找到二面角的平面角是立体几何的基本功，在找出二面角的同时可以对几何体的几何特征有更加深刻的认识，该法为本题的最优解.方法三：三面角公式是一个优美的公式，在很多题目的解析中灵活使用三面角公式可以使得问题更加简单、直观、迅速.8．【2021年新高考2卷】在四棱锥Q ABCD -中，底面ABCD 是正方形，若2,3AD QD QA QC ====．（1）证明：平面QAD ⊥平面ABCD ； （2）求二面角B QD A --的平面角的余弦值． 【答案】（1）证明见解析；（2）23. 【解析】 【分析】（1）取AD 的中点为O ，连接,QO CO ，可证QO ⊥平面ABCD ，从而得到面QAD ⊥面ABCD . （2）在平面ABCD 内，过O 作//OT CD ，交BC 于T ，则OT AD ⊥，建如图所示的空间坐标系，求出平面QAD 、平面BQD 的法向量后可求二面角的余弦值. 【详解】（1）取AD 的中点为O ，连接,QO CO . 因为QA QD =，OA OD =，则QO ⊥AD ，而2,AD QA ==2QO ==.在正方形ABCD 中，因为2AD =，故1DO =，故CO =因为3QC =，故222QC QO OC =+，故QOC 为直角三角形且QO OC ⊥， 因为OCAD O =，故QO ⊥平面ABCD ，因为QO ⊂平面QAD ，故平面QAD ⊥平面ABCD .（2）在平面ABCD 内，过O 作//OT CD ，交BC 于T ，则OT AD ⊥， 结合（1）中的QO ⊥平面ABCD ，故可建如图所示的空间坐标系.则()()()0,1,0,0,0,2,2,1,0D Q B -，故()()2,1,2,2,2,0BQ BD =-=-. 设平面QBD 的法向量(),,n x y z =，则00n BQ n BD ⎧⋅=⎨⋅=⎩即220220x y z x y -++=⎧⎨-+=⎩，取1x =，则11,2y z ==，故11,1,2n ⎛⎫= ⎪⎝⎭.而平面QAD 的法向量为()1,0,0m =，故12cos ,3312m n ==⨯.二面角B QD A --的平面角为锐角，故其余弦值为23.9．【2020年新课标1卷理科】如图，D 为圆锥的顶点，O 是圆锥底面的圆心，AE 为底面直径，AE AD =．ABC 是底面的内接正三角形，P 为DO上一点，PO ．（1）证明：PA ⊥平面PBC ； （2）求二面角B PC E --的余弦值． 【答案】（1）证明见解析；（2. 【解析】 【分析】（1）要证明PA ⊥平面PBC ，只需证明PA PB ⊥，PA PC ⊥即可；（2）方法一：过O 作ON ∥BC 交AB 于点N ，以O 为坐标原点，OA 为x 轴，ON 为y 轴建立如图所示的空间直角坐标系，分别算出平面PCB 的一个法向量n ，平面PCE 的一个法向量为m ，利用公式cos ,||||n mm n n m ⋅<>=计算即可得到答案. 【详解】（1）[方法一]：勾股运算法证明由题设，知DAE △为等边三角形，设1AE =， 则DO =，1122CO BO AE===，所以PO ==PC PB PA ====又ABC 为等边三角形，则2sin 60BA OA =，所以BA = 22234PA PB AB +==，则90APB ∠=，所以PA PB ⊥， 同理PA PC ⊥，又PC PB P =，所以PA ⊥平面PBC ；[方法二]：空间直角坐标系法 不妨设AB =4sin 60==︒=ABAE AD ，由圆锥性质知DO ⊥平面ABC ，所以==DO ==PO O 是ABC 的外心，因此AE BC ⊥．在底面过O 作BC 的平行线与AB 的交点为W ，以O 为原点，OW 方向为x 轴正方向，OE 方向为y 轴正方向，OD 方向为z 轴正方向，建立空间直角坐标系O xyz -，则(0,2,0)A -，B ，(C ，(0,2,0)E ，P ．所以(0,AP =，(=--BP ，(3,=-CP ． 故0220⋅=-+=AP BP ，0220⋅=-+=AP CP ． 所以AP BP ⊥，AP CP ⊥．又BP CP P =，故AP ⊥平面PBC ．[方法三]：因为ABC 是底面圆O 的内接正三角形，且AE 为底面直径，所以AE BC ⊥． 因为DO （即PO ）垂直于底面，BC 在底面内，所以PO BC ⊥． 又因为PO ⊂平面PAE ，AE ⊂平面PAE ，PO AE O =，所以BC ⊥平面PAE ．又因为PA ⊂平面PAE ，所以PA BC ⊥．设AE BC F =，则F 为BC 的中点，连结PF ．设DO a =，且PO ，则AF =，PA =，12PF a =． 因此222+=PA PF AF ，从而PA PF ⊥． 又因为PFBC F =，所以PA ⊥平面PBC ．[方法四]：空间基底向量法如图所示，圆锥底面圆O 半径为R ，连结DE ，AE AD DE ==，易得OD =，因为=PO ，所以=PO ． 以,,OA OB OD 为基底，OD ⊥平面ABC ，则66=+=-+AP AO OP OA OD ， 66=+=-+BP BO OP OB OD ，且212OA OB R ⋅=-，0OA OD OB OD ⋅=⋅=所以6666⎛⎫⎛⎫⋅=-+⋅-+= ⎪ ⎪⎝⎭⎝⎭AP BP OA OD OB OD26610666⋅-⋅-⋅+=OA OB OA OD OB OD OD ． 故0AP BP ⋅=．所以AP BP ⊥，即AP BP ⊥． 同理AP CP ⊥．又BP CP P =，所以AP ⊥平面PBC ． （2）[方法一]：空间直角坐标系法过O 作ON ∥BC 交AB 于点N ，因为PO ⊥平面ABC ，以O 为坐标原点，OA 为x 轴，ON 为y 轴建立如图所示的空间直角坐标系，则111(,0,0),((,244E PB C ---，1(,44PC =--，1()44PB =-，1(,0,24PE =--，设平面PCB 的一个法向量为111(,,)n x y z =，由00n PC n PB ⎧⋅=⎨⋅=⎩，得11111100x x ⎧-=⎪⎨-=⎪⎩，令1x 111,0z y =-=，所以(2,0,1)n =-，设平面PCE 的一个法向量为222(,,)m x y z =由00m PC m PE ⎧⋅=⎨⋅=⎩，得22222020x x ⎧-=⎪⎨-=⎪⎩，令21x =，得22z y ==所以3(1,3m =故2cos ,||||3n mmn n m ⋅<>===⋅⨯设二面角B PC E --的大小为θ，由图可知二面角为锐二面角，所以cos θ=[方法二]【最优解】：几何法 设=BCAE F ，易知F 是BC 的中点，过F 作∥FG AP 交PE 于G ，取PC 的中点H ，联结GH ，则∥HF PB ．由PA ⊥平面PBC ，得FG ⊥平面PBC ． 由（1）可得，222BC PB PC =+，得PB PC ⊥． 所以FH PC ⊥，根据三垂线定理，得GH PC ⊥． 所以GHF ∠是二面角B PC E --的平面角． 设圆O 的半径为r ，则3sin602︒==AF AB r ，2AE r =，12=EF r ，13EF AF =，所以14=FG PA ，1122==FH PB PA ，12=FG FH ． 在Rt GFH 中，1tan 2∠==FG GHF FH ，cos ∠=GHF ． 所以二面角B PC E --．[方法三]：射影面积法如图所示，在PE 上取点H ，使14HE PE =，设BC AE N =，连结NH ．由（1）知14NE AE =，所以∥NH PA ．故NH ⊥平面PBC ． 所以，点H 在面PBC 上的射影为N ．故由射影面积法可知二面角B PC E --的余弦值为cos PCN PCHS θS=．在PCE中，令==PC PE 1CE =，易知=PCES ．所以335416PCH PCES S ==．又1328PCNPBCSS ==，故3cos PCN PCHS θS ===所以二面角BPC E --．【整体点评】本题以圆锥为载体，隐含条件是圆锥的轴垂直于底面，（1）方法一：利用勾股数进行运算证明，是在给出数据去证明垂直时的常用方法；方法二：选择建系利用空间向量法，给空间立体感较弱的学生提供了可行的途径；方法三：利用线面垂直，结合勾股定理可证出；方法四：利用空间基底解决问题，此解法在解答题中用的比较少；（2）方法一：建系利用空间向量法求解二面角，属于解答题中求角的常规方法；方法二：利用几何法，通过三垂线法作出二面角，求解三角形进行求解二面角，适合立体感强的学生；方法三：利用射影面积法求解二面角，提高解题速度.10．【2020年新课标2卷理科】如图，已知三棱柱ABC -A 1B 1C 1的底面是正三角形，侧面BB 1C 1C 是矩形，M ，N 分别为BC ，B 1C 1的中点，P 为AM 上一点，过B 1C 1和P 的平面交AB 于E ，交AC 于F .（1）证明：AA 1∥MN ，且平面A1AMN ⊥EB 1C 1F ；（2）设O 为△A 1B 1C 1的中心，若AO ∥平面EB 1C 1F ，且AO =AB ，求直线B 1E 与平面A 1AMN 所成角的正弦值.【答案】（1）证明见解析；（2【解析】 【分析】（1）由,M N 分别为BC ，11B C 的中点，1//MN CC ，根据条件可得11//AA BB ，可证1MN AA //，要证平面11EB C F ⊥平面1A AMN ，只需证明EF ⊥平面1A AMN 即可；（2）连接NP ，先求证四边形ONPA 是平行四边形，根据几何关系求得EP ，在11B C 截取1B Q EP =，由（1）BC ⊥平面1A AMN ，可得QPN ∠为1B E 与平面1A AMN 所成角，即可求得答案. 【详解】 （1）,M N 分别为BC ，11B C 的中点，1//MN BB ∴，又11//AA BB ， 1//MN AA ∴，在ABC 中，M 为BC 中点，则BC AM ⊥， 又侧面11BB C C 为矩形， 1BC BB ∴⊥， 1//MN BB ，MN BC ⊥，由MN AM M ⋂=，,MN AM ⊂平面1A AMN ， ∴BC ⊥平面1A AMN ，又11//B C BC ，且11B C ⊄平面ABC ，BC ⊂平面ABC ，11//B C ∴平面ABC ，又11B C ⊂平面11EB C F ，且平面11EB C F ⋂平面ABC EF =11//B C EF ∴ ，//EF BC ∴，又BC ⊥平面1A AMN ， ∴EF ⊥平面1A AMN ，EF ⊂平面11EB C F ， ∴平面11EB C F ⊥平面1A AMN .(2)[方法一]：几何法如图，过O 作11B C 的平行线分别交1111,A B AC 于点11,E F ，联结11,,,AE AO AF NP ， 由于//AO 平面11EB C F ，11//E F 平面11EB C F ，11=AOE F O ，AO ⊂平面11AE F ，11E F ⊂平面11AE F ，所以平面11//AE F 平面11EB C F ．又因平面11AE F 平面111=AA B B AE ，平面11EB C F ⋂平面111=AA B B EB ，所以11∥EB AE ．因为111B C A N ⊥，11B C MN ⊥，1A N MN N =，所以11B C ⊥面1AA NM ．又因1111∥E F B C ，所以11⊥E F 面1AA NM ， 所以1AE 与平面1AA NM 所成的角为1∠E AO ．令2AB =，则11=NB ，由于O 为111A B C △的中心，故112233==OE NB ． 在1Rt AE O 中，122,3===AO AB OE ，由勾股定理得1==AE所以111sin ∠==E O E AO AE 由于11∥EB AE ，直线1B E 与平面1A AMN[方法二]【最优解】：几何法 因为//AO 平面11EFC B ，平面11EFC B 平面1=AMNA NP ，所以∥AO NP ．因为//ON AP ，所以四边形OAPN 为平行四边形．由（Ⅰ）知EF ⊥平面1AMNA ，则EF 为平面1AMNA 的垂线． 所以1B E 在平面1AMNA 的射影为NP ． 从而1B E 与NP 所成角的正弦值即为所求．在梯形11EFC B 中，设1EF =，过E 作11EG B C ⊥，垂足为G ，则3==PN EG ． 在直角三角形1B EG中，1sin ∠==B EG [方法三]：向量法由（Ⅰ）知，11B C ⊥平面1A AMN ，则11B C 为平面1A AMN 的法向量．因为∥AO 平面11EB C F ，AO ⊆平面1A AMN ，且平面1A AMN ⋂平面11EB C F PN =， 所以//AO PN ．由（Ⅰ）知11,=∥AA MN AA MN ，即四边形APNO 为平行四边形，则==AO NP AB ． 因为O 为正111A B C △的中心，故13==AP ON AM ． 由面面平行的性质得111111,33=∥EF B C EF B C ，所以四边形11EFC B 为等腰梯形．由P ，N 为等腰梯形两底的中点，得11PN B C ⊥，则11110,⋅==++=PN B C EB EP PN NB 111111111623+-=-B C PN B C PN B C ． 设直线1B E 与平面1A AMN 所成角为θ，AB a ，则21111111sin θ⋅===aEB B C EB B C a 所以直线1B E 与平面1A AMN[方法四]：基底法不妨设2===AO AB AC ，则在直角1AA O 中，1AA =以向量1,,AA AB AC 为基底， 从而1,2π=AA AB ，1,2π=AA AC ，,3π=AB AC ．1111123=++=+EB EA AA A B AB AA ，BC AC AB =-， 则12103=EB ，||2BC =． 所以112()3⎛⎫⋅=+⋅-= ⎪⎝⎭EB BC AB AA AC AB 2224333⋅-=-AB AC AB ．由（Ⅰ）知BC ⊥平面1A AMN ，所以向量BC 为平面1A AMN 的法向量． 设直线1B E 与平面1A AMN 所成角θ，则11110sin cos ,10||θ⋅===EB BC EB BC EB BC 故直线1B E 与平面1A AMN 所成角的正弦值为sin θ= 【整体点评】(2)方法一：几何法的核心在于找到线面角，本题中利用平行关系进行等价转化是解决问题的关键；方法二：等价转化是解决问题的关键，构造直角三角形是求解角度的正弦值的基本方法； 方法三：利用向量法的核心是找到平面的法向量和直线的方向向量，然后利用向量法求解即可；方法四：基底法是立体几何的重要思想，它是平面向量基本定理的延伸，其关键之处在于找到平面的法向量和直线的方向向量.11．【2020年新课标3卷理科】如图，在长方体1111ABCD A B C D -中，点,E F 分别在棱11,DD BB 上，且12DE ED =，12BF FB =．（1）证明：点1C 在平面AEF 内；（2）若2AB =，1AD =，13AA =，求二面角1A EF A --的正弦值．【答案】（1）证明见解析；（2. 【解析】 【分析】（1）方法一:连接1C E 、1C F ，证明出四边形1AEC F 为平行四边形，进而可证得点1C 在平面AEF 内；（2）方法一：以点1C 为坐标原点，11C D 、11C B 、1C C 所在直线分别为x 、y 、z 轴建立空间直角坐标系1C xyz -，利用空间向量法可计算出二面角1A EF A --的余弦值，进而可求得二面角1A EF A --的正弦值. 【详解】（1）［方法一］【最优解】：利用平面基本事实的推论在棱1CC 上取点G ，使得112C G CG =，连接DG 、FG 、1C E 、1C F ，如图1所示.在长方体1111ABCD A B C D -中，//,BF CG BF CG =，所以四边形BCGF 为平行四边形，则//,BC FG BC FG =，而,//BC AD BC AD =，所以//,AD FG AD FG =，所以四边形DAFG 为平行四边形，即有//AF DG ，同理可证四边形1DEC G 为平行四边形，1//C E DG ∴，1//C E AF ∴，因此点1C 在平面AEF 内.［方法二］：空间向量共线定理以11111,,C D C B C C 分别为x 轴，y 轴，z 轴，建立空间直角坐标系，如图2所示． 设11111,,3C D a C B b C C c ===，则1(0,0,0),(,0,2),(0,,),(,,3)C E a c F b c A a b c ．所以1(,0,2),(,0,2)C E a c FA a c ==．故1C E FA =．所以1AF C E ∥，点1C 在平面AEF 内． ［方法三］：平面向量基本定理同方法二建系，并得1(0,0,0),(,0,2),(0,,),(,,3)C E a c F b c A a b c ， 所以111(,0,2),(0,,),(,,3)C E a c C F b c C A a b c ===．故111C A C E C F =+．所以点1C 在平面AEF 内． ［方法四］：根据题意，如图3，设11111,2,3A D a A B b A A c ===．在平面11A B BA 内，因为12BF FB =，所以1111133B F B B A A ==．延长AF 交11A B 于G ，AF ⊂平面AEF ，11A B ⊂平面1111D C B A ．11,G AF G A B ∈∈，所以G ∈平面,AEF G ∈平面1111D C B A ①．延长AE 交11A D 于H ，同理H ∈平面,AEF H ∈平面1111D C B A ②． 由①②得，平面AEF平面1111A B C D GH =．连接11,,GH GC HC ，根据相似三角形知识可得11,2GB b D H a ==．在11Rt C B G 中，1C G =同理，在11Rt C D H 中，1C H =如图4，在1Rt A GH 中，GH = 所以11GH C G C H =+，即G ，1C ，H 三点共线． 因为GH ⊂平面AEF ，所以1C ⊂平面AEF ，得证． ［方法五］：如图5，连接11,,DF EB DB ，则四边形1DEB F 为平行四边形，设1DB 与EF 相交于点O ，则O 为1,EF DB 的中点．联结1AC ，由长方体知识知，体对角线交于一点，且为它们的中点，即11AC B D O =，则1AC 经过点O ，故点1C 在平面AEF 内．（2）［方法一］【最优解】：坐标法以点1C 为坐标原点，11C D 、11C B 、1C C 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系1C xyz -，如图2.则()2,1,3A 、()12,1,0A 、()2,0,2E 、()0,1,1F ，()0,1,1AE =--，()2,0,2AF =--，()10,1,2A E =-，()12,0,1A F =-，设平面AEF 的一个法向量为()111,,m x y z =，由00m AE m AF ⎧⋅=⎨⋅=⎩，得11110220y z x z --=⎧⎨--=⎩取11z =-，得111x y ==，则()1,1,1m =-，设平面1A EF 的一个法向量为()222,,n x y z =，由1100n A E n A F ⎧⋅=⎪⎨⋅=⎪⎩，得22222020y z x z -+=⎧⎨-+=⎩，取22z =，得21x =，24y =，则()1,4,2n =，3cos ,3m n m n m n⋅<>===⨯⋅ 设二面角1A EF A--的平面角为θ，则cos θ=sin7θ∴=. 因此，二面角1A EF A--. ［方法二］：定义法在AEF 中，AE AF EF ====即222AE EF AF +=，所以AE EF ⊥．在1A EF 中，11A E A F =6，设,EF AF 的中点分别为M ，N ，连接11,,A M MN A N ，则1,A M EF MN EF ⊥⊥，所以1AMN ∠为二面角1A EFA --的平面角．在1AMN 中，1122MN A M A N ====所以1175cos A MN+-∠==1sin A MN∠==［方法三］：向量法由题意得11AE AF AF AE EF==，由于222AE EF AF+=，所以AE EF⊥．如图7，在平面1A EF内作1A G EF⊥，垂足为G，则EA与1GA的夹角即为二面角1A EF A--的大小．由11AA AE EG GA=++，得22221111222AA AE EG GA AE EG EG GA AE GA=++++⋅⋅+⋅．其中，1EG AG==11AE GA⋅=，1cos,AE GA〉〈=所以二面角1A EF A--．［方法四］：三面角公式由题易得，11EA FA FE EA FA===所以2221111cos2EA EA AAAEAEA EA+-∠===⋅．222cos0,sin12EA EF AFAEF AEFEA EF+-∠===∠=⋅．22211111cos2EA EF A FA EF A EFEA EF+-∠===∠=⋅设θ为二面角1A EF A--的平面角，由二面角的三个面角公式，得111cos cos cos cos sin sin AEA AEF A EF AEF A EF θ∠-∠⋅∠==∠⋅∠sin θ=【整体点评】（1）方法一：通过证明直线1//C E AF ，根据平面的基本事实二的推论即可证出，思路直接，简单明了，是通性通法，也是最优解；方法二：利用空间向量基本定理证明；方法三：利用平面向量基本定理；方法四：利用平面的基本事实三通过证明三点共线说明点在平面内；方法五：利用平面的基本事实以及平行四边形的对角线和长方体的体对角线互相平分即可证出． （2）方法一：利用建立空间直角坐标系，由两个平面的法向量的夹角和二面角的关系求出；方法二：利用二面角的定义结合解三角形求出；方法三：利用和二面角公共棱垂直的两个向量夹角和二面角的关系即可求出，为最优解；方法四：利用三面角的余弦公式即可求出． 12．【2020年新高考1卷（山东卷）】如图，四棱锥P -ABCD 的底面为正方形，PD ⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知PD =AD =1，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值． 【答案】（1）证明见解析；（2【解析】 【分析】（1）利用线面垂直的判定定理证得AD ⊥平面PDC ，利用线面平行的判定定理以及性质定理，证得//AD l ，从而得到l ⊥平面PDC ；（2）方法一：根据题意，建立相应的空间直角坐标系，得到相应点的坐标，设出点(,0,1)Q m ，之后求得平面QCD 的法向量以及向量PB 的坐标，求得cos ,n PB <>的最大值，即为直线PB 与平面QCD 所成角的正弦值的最大值. 【详解】 （1）证明：在正方形ABCD 中，//AD BC ，因为AD ⊄平面PBC ，BC ⊂平面PBC ， 所以//AD 平面PBC ，又因为AD ⊂平面PAD ，平面PAD 平面PBC l =，所以//AD l ，因为在四棱锥P ABCD -中，底面ABCD 是正方形，所以,,AD DC l DC ⊥∴⊥且PD ⊥平面ABCD ，所以,,AD PD l PD ⊥∴⊥因为CD PD D =，所以l ⊥平面PDC ．（2）［方法一］【最优解】：通性通法因为,,DP DA DC 两两垂直，建立空间直角坐标系D xyz -，如图所示：因为1PD AD ==，设(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)D C A P B ， 设(,0,1)Q m ，则有(0,1,0),(,0,1),(1,1,1)DC DQ m PB ===-， 设平面QCD 的法向量为(,,)n x y z =，则00DC n DQ n ⎧⋅=⎨⋅=⎩，即00y mx z =⎧⎨+=⎩，令1x =，则z m =-，所以平面QCD 的一个法向量为(1,0,)n m =-，则 1cos ,3n PB n PB n PB⋅+<>==根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线PB 与平面QCD 所成角的正弦值等于|cos ,|n PB <>====当且仅当1m =时取等号，所以直线PB 与平面QCD ［方法二］：定义法如图2，因为l ⊂平面PBC ，Q l ∈，所以Q ∈平面PBC ．。

新课标卷高考真题1、（2016 年全国I 高考）如图，在以A，B，C，D，E，F 为顶点的五面体中，面ABEF 为正方形，AF=2FD，∠AFD = 90 ，且二面角D -AF -E 与二面角C -BE - F 都是60 ．（I）证明：平面ABEF ⊥平面EFDC；（II）求二面角E - BC - A 的余弦值．10 2、（ 2016 年全国 II 高考） 如图， 菱形 ABCD 的对角线 AC 与 BD 交于点 O ，AB = 5, AC = 6 ， 点 E , F 分别在 AD , CD 上， AE = CF = 5 ， EF 交 BD 于点 H4．将∆DEF 沿 EF 折到∆D 'EF 位置， OD ' = ．（Ⅰ）证明： D 'H ⊥ 平面 ABCD ；（Ⅱ）求二面角 B - D 'A - C 的正弦值．3【2015 高考新课标 1，理 18】如图，四边形ABCD 为菱形，∠ABC=120°，E，F 是平面ABCD 同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC.（Ⅰ）证明：平面AEC⊥平面AFC；（Ⅱ）求直线AE 与直线CF 所成角的余弦值.4、[2014·新课标全国卷Ⅱ] 如图1-3，四棱锥P-ABCD 中，底面ABCD 为矩形，PA⊥平面ABCD，E 为PD 的中点．(1)证明：PB∥平面AEC；(2)设二面角D-AE-C 为60°，AP＝1，AD＝ 3，求三棱锥E-ACD 的体积．图1-35、[2014·新课标全国卷Ⅰ] 如图1-5，三棱柱ABC -A1B1C1中，侧面BB1C1C 为菱形，AB⊥B1C.图1-5(1)证明：AC＝AB1；(2)若AC⊥AB1，∠CBB1＝60°，AB＝BC，求二面角A -A1B1­C1的余弦值．6、（2017•新课标Ⅱ）如图，四棱锥P﹣ABCD 中，侧面PAD 为等边三角形且垂直于底面ABCD，AB=BC= AD，∠BAD=∠ABC=90°，E 是PD 的中点．（Ⅰ）证明：直线CE∥平面PAB；（Ⅱ）点M 在棱PC 上，且直线BM 与底面ABCD 所成角为45°，求二面角M﹣AB﹣D 的余弦值．7（、2017•新课标Ⅲ）如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形，∠ABD= ∠CBD，AB=BD．（Ⅰ）证明：平面ACD⊥平面ABC；（Ⅱ）过AC 的平面交BD 于点E，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角D﹣AE﹣C 的余弦值．8、（2017•新课标Ⅰ卷）如图，在四棱锥P﹣ABCD 中，AB∥CD，且∠BAP=∠CDP=90°．（12分）(1)证明：平面PAB⊥平面PAD；(2)若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C 的余弦值．m n ⋅ -4 3 + 1 ⋅ 3 + 16 m 1 1 1 m 1【解析】⑴ ∵ ABEF 为正方形∴ AF ⊥ EF ∵ ∠AFD = 90︒∴ AF ⊥ DF ∵ D F EF =F∴ AF ⊥ 面 EFDC AF ⊥ 面 ABEF∴平面 ABEF ⊥ 平面 EFDC⑵ 由⑴知∠DFE = ∠CEF = 60︒∵ AB ∥ EF AB ⊄ 平面 EFDCEF ⊂ 平面 EFDC ∴ AB ∥平面 ABCDAB ⊂ 平面 ABCD∵面 ABCD 面 EFDC = CD∴ AB ∥CD ,∴ CD ∥ EF∴四边形 EFDC 为等腰梯形以 E 为原点， 如图建立坐标系，FD = aE (0 ，0 ，0)B (0 ，2a ，0)C ⎛ a ，0 ， 3 a ⎫ A (2a ，2a ，0)2 2 ⎪ ⎝ ⎭ ⎛ a3 ⎫EB = (0 ，2a ，0) ， BC = 2 ，- 2a ， 2 a ⎪ ， AB = (-2a ，0 ，0)⎝ ⎭设面 BEC 法向量为= ( x ，y ，z ) . ⎧ ⎧2a ⋅ y 1 = 0 ⎪m ⋅ EB = 0 ，即⎪ ⎨ ⋅ = 0 ⎨ a ⋅ x - 2ay + 3 a ⋅ z = 0 ⎪⎩m BC ⎪⎩ 2 1 1 2 1x = 3 ，y = 0 ，z = -1 = ( 3 ，0 ，- 1)设面 ABC 法向量为 = ( x ，y ，z ) ⎧ n 2 2 2 ⎧ a ⎪n ⋅ BC =0 .即⎪ x 2 - 2ay 2 + az 2 = 0 x = 0 ，y = 3 ，z = 4 ⎨ ⎨ 2 22 2 2⎪⎩n ⋅ AB = 0⎪⎩2ax 2 = 0 n = (0 ， 3 ，4)设二面角 E - BC - A 的大小为. cos =∴二面角 E - BC - A 的余弦值为-2 19 19 m ⋅ n = = - 2 19 19 3u r u u r n 1 ⋅ n 2 u r u u r n 1 n 2 7 5 2 95 ⋅ ' ⎩ ⎩ 2【解析】⑴证明：∵ AE = CF = 5 ，∴AE = CF ， 4 AD CD∴ EF ∥ AC ．∵四边形 ABCD 为菱形，∴ AC ⊥ BD ， ∴ EF ⊥ BD ，∴ EF ⊥ DH ，∴ EF ⊥ D 'H ．∵ AC = 6 ，∴ AO = 3 ；又 AB = 5 ， AO ⊥ OB ，∴ OB = 4 ， ∴ O H = AE⋅ OD = 1 ，∴ D H = D 'H = 3 ，∴ OD ' 2 = O H 2 + D ' H 2 ，∴ D ' H ⊥ O H AO ．又∵ OH I EF = H ，∴ D ' H ⊥ 面 ABCD ．⑵建立如图坐标系 H - xyz ．B (5 ， 0 ， 0) ，C (1， 3，0) ， D '(0 ， 0 ， 3) ， A (1， - 3， 0) ，AB = (4 ， 3， 0) ， AD ' = (-1， 3，3) ， AC = (0 ， 6 ， 0) ，设面 ABD ' 法向量n 1 = ( x ，y ，z ) ，⎧ ⎧x = 3 由⎪n 1 ⋅ AB = 0 得⎧4x + 3y = 0 ，取⎪ y = -4 ，∴ n = (3， - 4 ， 5) ． ⎨ ⎪⎩n 1 A D = 0 ⎨-x + 3y + 3z = 0 ⎨ 1 ⎪z = 5同理可得面 AD 'C 的法向量n 2 = (3， 0 ， 1) ，∴ cos= = = ，∴ s in = ． 25 253，【答案】（Ⅰ）见解析（Ⅱ） 339 + 5 5 2 ⋅ 103 2 2 32 GB , G C又∵AE ⊥EC ，∴EG = ，EG ⊥AC ， 在 Rt △EBG 中，可得 BE = ，故 DF =2 .2在 Rt △FDG 中，可得 FG =6 .2在直角梯形 BDFE 中，由 BD =2，BE = ，DF = 2可得 EF = 3 2， 2 2 ∴ EG 2 + FG 2 = EF 2 ，∴EG ⊥FG ， ∵AC ∩FG=G ，∴EG ⊥平面 AFC ， ∵EG ⊂ 面 AEC ，∴平面 AFC ⊥平面 AEC .……6 分（Ⅱ）如图，以 G 为坐标原点，分别以 的方向为 x 轴，y 轴正方向，| GB |为单位长度，建立空间直角坐标系 G-xyz ，由（Ⅰ）可得 A （0，－ ，0），E (1,0,)，F （－1,0， ），C （0， ，0），∴ AE =（1， ， ）， C F =（-1，- 2 ， 2 ）.…10 分 23 2 3 2 33 3 3 33 AE ,C F >= •1AP |为单位长，建立空间直角坐标系 A -xyz ，则 D (0， 3，0)，E 0， 2 ， 2，AE ＝ 0 2 ， 2 = - { 即 故cos < AE CF 3 . | AE || C F | 3 所以直线 AE 与 CF 所成的角的余弦值为3 .……12 分3 4，解：(1)证明：连接 BD 交 AC 于点 O ，连接 EO .因为 ABCD 为矩形，所以 O 为 BD 的中点． 又 E 为 PD 的中点，所以 EO ∥PB .因为 EO ⊂平面 AEC ，PB ⊄平面 AEC ，所以 PB ∥平面 AEC . (2)因为 PA ⊥平面 ABCD ，ABCD 为矩形， 所以 AB ，AD ，AP 两两垂直．如图，以 A→ AD ，AP 的方向为 x 轴、y 轴、z 轴的正方向，| 为坐标原点，AB ， →( 1)→ (， 1).设 B (m ，0，0)(m >0)，则 C (m ，3，0) →(m ，3，0)．，AC ＝ 设 n 1＝(x ，y ，z )为平面 ACE 的法向量，→ n 1·AC ＝0，则 → ) {m x ＋ 3y ＝0，)n 1·AE ＝0， 2 y ＋ z ＝0，可取 n 1＝(2，－1， ).又 n 2＝(1，0，0)为平面 DAE 的法向量，1由题设易知|cos 〈n 1，n 2〉|＝ ，即2 13 ＝ ，解得 m ＝ .22 1因为 E 为 PD 的中点，所以三棱锥 E -ACD 的高为 .三棱锥 E -ACD 的体积 V ＝21 1 3 1 × × 3× × ＝ . 3 22 2 83m 3 3＋4m 233 3 3 3 1(( )B 1C 1＝BC ＝ －1，－ 3，0 . {{335 解：(1)证明：连接 BC 1，交 B 1C 于点 O ，连接 AO ，因为侧面 BB 1C 1C 为菱形，所以 B 1C ⊥BC 1，且 O 为 B 1C 及 BC 1 的中点．又 AB ⊥B 1C ，所以 B 1C ⊥平面 ABO . 由于 AO ⊂平面 ABO ，故 B 1C ⊥AO . 又 B 1O ＝CO ，故 AC ＝AB 1.(2)因为 AC ⊥AB 1，且 O 为 B 1C 的中点，所以 AO ＝CO .又因为 AB ＝BC ，所以△BOA ≌ △BOC .故 OA ⊥OB ，从而 OA ，OB ，OB 1 两两垂直．以 O 为坐标原点，OB 的方向为 x 轴正方向，|OB |为单位长，建立如图所示的空间直角坐标系 O ­ xyz .(3)因为∠CBB 1＝60°，所以△CBB 1 为等边三角形，又 AB ＝BC ，则 A 0，0， 3 ，B (1，0，0)，B (0， 3，0)，C (0，－ 3，0).→ AB 1＝ 0， 3 ，－ 3)3 → 3 ，A 1B 1＝AB ＝1，0，－ ， 3 3 3→ ( )设 n ＝(x ，y ，z )是平面 AA 1B 1 的法向量，则n ·AB 1＝0，3 y － z ＝0，)→n ·A 1B 1＝0，)即所以可取 n ＝(1，3， 3)．x － z ＝0.{设m 是平面A1B1C1的法向量，→m·A1B1＝0，则→m·B1C1＝0，)同理可取m＝(1，－3， 3)．n·m 1则cos〈n，m〉＝＝.|n||m| 71所以结合图形知二面角 A -A1B1­ C1的余弦值为.76、【答案】（Ⅰ）证明：取PA 的中点F，连接EF，BF，因为E 是PD 的中点，所以EF AD，AB=BC= AD，∠BAD=∠ABC=90°，∴BC∥ AD，∴BCEF 是平行四边形，可得CE∥BF，BF⊂平面PAB，CF✪平面PAB，∴直线CE∥平面PAB；（Ⅱ）解：四棱锥P﹣ABCD 中，侧面PAD 为等边三角形且垂直于底面ABCD，AB=BC= AD，∠BAD=∠ABC=90°，E 是PD 的中点．取AD 的中点O，M 在底面ABCD 上的射影N 在OC 上，设AD=2，则AB=BC=1，OP= ，∴∠PCO=60°，直线BM 与底面ABCD 所成角为45°，可得：BN=MN，CN= MN，BC=1，可得：1+ BN2=BN2 ，BN= ，MN= ，作NQ⊥AB 于Q，连接MQ，所以∠MQN 就是二面角M﹣AB﹣D 的平面角，MQ== ，二面角M﹣AB﹣D 的余弦值为： = ．7、【答案】（Ⅰ）证明：如图所示，取AC 的中点O，连接BO，OD．∵△ABC 是等边三角形，∴OB⊥AC．△ABD 与△CBD 中，AB=BD=BC，∠ABD=∠CBD，∴△ABD≌△CBD，∴AD=CD．∵△ACD 是直角三角形，∴AC 是斜边，∴∠ADC=90°．∴DO= AC．∴DO2+BO2=AB2=BD2 ．∴∠BOD=90°．∴OB⊥OD．又DO∩AC=O，∴OB⊥平面ACD．又OB⊂平面ABC，∴平面ACD⊥平面ABC．（Ⅱ）解：设点D，B 到平面ACE 的距离分别为h D，h E．则= ．∵平面AEC 把四面体ABCD 分成体积相等的两部分，∴ = = =1．∴点E 是BD 的中点．建立如图所示的空间直角坐标系．不妨设AB=2．则O（0，0，0），A（1，0，0），C（﹣1，0，0），D（0，0，1），B（0，，0），E ．=（﹣1，0，1），= ，=（﹣2，0，0）．设平面ADE 的法向量为=（x，y，z），则，即，取= ．同理可得：平面ACE 的法向量为=（0，1，）．∴cos = = =﹣．∴二面角D﹣AE﹣C 的余弦值为．8、【答案】（1）证明：∵∠BAP=∠CDP=90°，∴PA⊥AB，PD⊥CD，∵AB∥CD，∴AB⊥PD，又∵PA∩PD=P，且PA⊂平面PAD，PD⊂平面PAD，∴AB⊥平面PAD，又AB⊂平面PAB，∴平面PAB⊥平面PAD；（2）解：∵AB∥CD，AB=CD，∴四边形ABCD 为平行四边形，由（1）知AB⊥平面PAD，∴AB⊥AD，则四边形ABCD 为矩形，在△APD 中，由PA=PD，∠APD=90°，可得△PAD 为等腰直角三角形，设PA=AB=2a，则AD= ．取AD 中点O，BC 中点E，连接PO、OE，以O 为坐标原点，分别以OA、OE、OP 所在直线为x、y、z 轴建立空间直角坐标系，则：D（），B（），P（0，0，），C（）．，，．设平面PBC 的一个法向量为，由，得，取y=1，得．∵AB⊥平面PAD，AD⊂平面PAD，∴AB⊥AD，又PD⊥PA，PA∩AB=A，∴PD⊥平面PAB，则为平面PAB 的一个法向量，．∴cos＜＞= =．由图可知，二面角A﹣PB﹣C为钝角，∴二面角A﹣PB﹣C 的余弦值为．。

立体几何大题1.空间中的平行关系（1）线线平行（2）线面平行的判定定理：平面外一直线与平面内一直线平行，则线面平行（3）线面平行的性质定理若线面平行，经过直线的平面与该平面相交，则直线与交线平行（4）面面平行的判定定理判定定理1：一个平面内有两条相交直线分别平行于另一个平面，则面面平行判定定理2：一个平面内有两条相交直线分别于另一个平面内两条相交直线平行，则面面平行（5）面面平行的性质定理性质定理1：两平面互相平行，一个平面内任意一条直线平行于另一个平面性质定理2：两平面互相平行，一平面与两平面相交，则交线互相平行6.空间中的垂直关系（1）线线垂直（2）线面垂直的判定定理一直线与平面内两条相交直线垂直，则线面垂直（3）线面垂直的性质定理性质定理1：一直线与平面垂直，则这条直线垂直于平面内的任意一条直线性质定理2：垂直于同一个平面的两条直线平行（4）面面垂直的判定定理一个平面内有一条直线垂直于另一个平面，则两个平面垂直(或：一个平面经过另一个平面的垂线，则面面垂直)（5）面面垂直的性质定理两平面垂直，其中一个平面内有一条直线与交线垂直，则这条直线垂直于另一个平面6.异面直线所成角cos θ=cos a ,b =|a ⋅b ||a |⋅|b |=|x 1x 2+y 1y 2+z 1z 2|x 12+y 12+z 12⋅x 22+y 22+z 22(其中θ(0°<θ≤90°)为异面直线a ,b 所成角，a ,b 分别表示异面直线a ,b 的方向向量)7.直线AB 与平面所成角，sin β=AB ⋅m |AB ||m |(m 为平面α的法向量).8.二面角α-l -β的平面角cos θ=m ⋅n |m ||n |(m ，n 为平面α，β的法向量).9.点B 到平面α的距离d =|AB ⋅n | (n 为平面α的法向量，AB 是经过面α的一条斜线，A ∈α).2024届高考数学专项立体几何大题含答案模拟训练一、解答题1(22·23下·湖南·二模)如图，在直三棱柱ABC -A B C 中，∠ABC =120°,AB =BC =2,AC =BB ，点D 为棱BB 的中点，AE =13AC ．(1)求DE 的长度；(2)求平面CDE 与平面BDE 夹角的余弦值．2(22·23下·绍兴·二模)如图，在多面体ABCDE 中，DE ⊥平面BCD ,△ABC 为正三角形，△BCD 为等腰Rt △,∠BDC =90°,AB =2,DE =2.(1)求证：AE ⊥BC ；(2)若AE ⎳平面BCD ，求直线BE 与平面ABC 所成的线面角的正弦值.3(22·23·张家口·三模)如图，在三棱柱ABC-A1B1C1中，侧面BB1C1C为菱形，∠CBB1=60°，AB= BC=2，AC=AB1=2.(1)证明：平面ACB1⊥平面BB1C1C；(2)求平面ACC1A1与平面A1B1C1夹角的余弦值.4(22·23·湛江·二模)如图1，在五边形ABCDE中，四边形ABCE为正方形，CD⊥DE，CD=DE，如图2，将△ABE沿BE折起，使得A至A1处，且A1B⊥A1D．(1)证明：DE⊥平面A1BE；(2)求二面角C-A1E-D的余弦值．5(22·23下·长沙·三模)如图，在多面体ABCDE 中，平面ACD ⊥平面ABC ，BE ⊥平面ABC ，△ABC 和△ACD 均为正三角形，AC =4，BE =3，点F 在AC 上.(1)若BF ⎳平面CDE ，求CF ；(2)若F 是AC 的中点，求二面角F -DE -C 的正弦值.6(22·23下·湖北·二模)如图，S 为圆锥的顶点，O 是圆锥底面的圆心，△ABC 内接于⊙O ,AC ⊥BC ,AC =BC =322，AM =2MS ,AS =3,PQ 为⊙O 的一条弦，且SB ⎳平面PMQ .(1)求PQ 的最小值；(2)若SA ⊥PQ ，求直线PQ 与平面BCM 所成角的正弦值.7(22·23·深圳·二模)如图，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD,PA= AD=2AB，点M是PD的中点.(1)证明：AM⊥PC；(2)设AC的中点为O，点N在棱PC上(异于点P，C)，且ON=OA，求直线AN与平面ACM所成角的正弦值.8(22·23下·温州·二模)已知三棱锥D-ABC中，△BCD是边长为3的正三角形，AB=AC=AD, AD与平面BCD所成角的余弦值为33．(1)求证：AD⊥BC；(2)求二面角D-AC-B的平面角的正弦值．9(22·23下·浙江·二模)如图，四面体ABCD,AD⊥CD,AD=CD,AC=2,AB=3,∠CAB=60°，E为AB上的点，且AC⊥DE,DE与平面ABC所成角为30°，(1)求三棱锥D-BCE的体积；(2)求二面角B-CD-E的余弦值.10(22·23下·襄阳·三模)如图，在三棱柱ABC-A1B1C1中，侧面BB1C1C为矩形，∠BAC=90°，AB= AC=2，AA1=4，A1在底面ABC的射影为BC的中点N，M为B1C1的中点.(1)求证：平面A1MNA⊥平面A1BC；(2)求平面A1B1BA与平面BB1C1C夹角的余弦值.11(22·23·唐山·二模)如图，在三棱柱ABC-A1B1C1中，△ABC是等边三角形，侧面ACC1A1⊥底面ABC，且AA1=AC，∠AA1C1=120°，M是CC1的中点．(1)证明：A1C⊥BM．(2)求二面角A1-BC-M的正弦值．12(22·23下·盐城·三模)如图，该几何体是由等高的半个圆柱和14个圆柱拼接而成，点G为弧CD的中点，且C，E，D，G四点共面.(1)证明：平面BDF⊥平面BCG；(2)若平面BDF与平面ABG所成二面角的余弦值为155，且线段AB长度为2，求点G到直线DF的距离.13(22·23下·江苏·三模)如图，圆锥DO中，AE为底面圆O的直径，AE=AD，△ABC为底面圆O的内接正三角形，圆锥的高DO=18，点P为线段DO上一个动点.(1)当PO=36时，证明：PA⊥平面PBC；(2)当P点在什么位置时，直线PE和平面PBC所成角的正弦值最大.14(22·23下·镇江·三模)如图，四边形ABCD是边长为2的菱形，∠ABC=60°，四边形PACQ为矩形，PA=1，从下列三个条件中任选一个作为已知条件，并解答问题(如果选择多个条件分别解答，按第一个解答计分).①BP,DP与平面ABCD所成角相等；②三棱锥P-ABD体积为33；③cos∠BPA=55(1)平面PACQ⊥平面ABCD；(2)求二面角B-PQ-D的大小；(3)求点C到平面BPQ的距离.15(22·23下·江苏·一模)在三棱柱ABC -A 1B 1C 1中，平面A 1B 1BA ⊥平面ABC ，侧面A 1B 1BA 为菱形，∠ABB 1=π3，AB 1⊥AC ，AB =AC =2，E 是AC 的中点.(1)求证：A 1B ⊥平面AB 1C ；(2)点P 在线段A 1E 上(异于点A 1，E )，AP 与平面A 1BE 所成角为π4，求EP EA 1的值.16(22·23下·河北·三模)如图，四棱锥P -ABCD 的底面ABCD 是菱形，其对角线AC ,BD 交于点O ，且PO ⊥平面ABCD ,OC =1,OD =OP =2,M 是PD 的中点，N 是线段CD 上一动点．(1)当平面OMN ⎳平面PBC 时，试确定点N 的位置，并说明理由；(2)在(1)的前提下，点Q 在直线MN 上，以PQ 为直径的球的表面积为214π．以O 为原点，OC ,OD ,OP 的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系O -xyz ，求点Q 的坐标．17(22·23·汕头·三模)如图，圆台O1O2的轴截面为等腰梯形A1ACC1，AC=2AA1=2A1C1=4,B为底面圆周上异于A,C的点.(1)在平面BCC1内，过C1作一条直线与平面A1AB平行，并说明理由；(2)若四棱锥B-A1ACC1的体积为23，设平面A1AB∩平面C1CB=l,Q∈l，求CQ的最小值.18(19·20下·临沂·二模)如图①，在Rt△ABC中，B为直角，AB=BC=6，EF∥BC，AE=2，沿EF将△AEF折起，使∠AEB=π3，得到如图②的几何体，点D在线段AC上．(1)求证：平面AEF⊥平面ABC；(2)若AE⎳平面BDF，求直线AF与平面BDF所成角的正弦值．19(22·23下·广州·三模)如图，四棱锥P-ABCD的底面为正方形，AB=AP=2，PA⊥平面ABCD，E,F分别是线段PB,PD的中点，G是线段PC上的一点.(1)求证：平面EFG⊥平面PAC；(2)若直线AG与平面AEF所成角的正弦值为13，且G点不是线段PC的中点，求三棱锥E-ABG体积.20(22·23下·长沙·一模)斜三棱柱ABC-A1B1C1的各棱长都为2，∠A1AB=60°，点A1在下底面ABC 的投影为AB的中点O．(1)在棱BB1(含端点)上是否存在一点D使A1D⊥AC1若存在，求出BD的长；若不存在，请说明理由；(2)求点A1到平面BCC1B1的距离．21(22·23下·长沙·三模)如图，三棱台ABC -A 1B 1C 1，AB ⊥BC ，AC ⊥BB 1，平面ABB 1A 1⊥平面ABC ，AB =6,BC =4，BB 1=2，AC 1与A 1C 相交于点D ，AE =2EB，且DE ∥平面BCC 1B 1.(1)求三棱锥C -A 1B 1C 1的体积；(2)平面A 1B 1C 与平面ABC 所成角为α，CC 1与平面A 1B 1C 所成角为β，求证：α+β=π4.22(22·23·衡水·一模)如图所示，A ,B ,C ,D 四点共面，其中∠BAD =∠ADC =90°，AB =12AD ，点P ,Q 在平面ABCD 的同侧，且PA ⊥平面ABCD ，CQ ⊥平面ABCD .(1)若直线l ⊂平面PAB ，求证：l ⎳平面CDQ ；(2)若PQ ⎳AC ，∠ABP =∠DAC =45°，平面BPQ ∩平面CDQ =m ，求锐二面角B -m -C 的余弦值.23(22·23下·湖北·三模)已知平行六面体(底面是平行四边形的四棱柱)ABCD-A1B1C1D1的各条棱长均为2，且有∠AA1D1=∠AA1B1=∠D1A1B1=60°．(1)求证：平面AA1C1C⊥平面A1B1C1D1；(2)求直线B1D与平面AA1C1C所成角的正弦值．24(22·23下·武汉·三模)如图，在四棱锥P-ABCD中，底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，E为线段PB的中点，F为线段BC上的动点.(1)求证：平面AEF⊥平面PBC；(2)求平面AEF与平面PDC夹角的最小值.25(22·23下·黄冈·三模)如图1，在四边形ABCD中，BC⊥CD，AE∥CD,AE=BE=2CD=2,CE =3．将四边形AECD沿AE折起，使得BC=3，得到如图2所示的几何体．(1)若G为AB的中点，证明：DG⊥平面ABE；(2)若F为BE上一动点，且二面角B-AD-F的余弦值为63，求EFEB的值．26(22·23·德州·三模)图1是直角梯形ABCD，AB⎳CD，∠D=90°，AD=3，AB=2，CD=3，四边形ABCE为平行四边形，以BE为折痕将△BCE折起，使点C到达C1的位置，且AC1=6，如图2．(1)求证：平面BC1E⊥平面ABED；(2)在线段BE上存在点P使得PA与平面ABC1的正弦值为365，求平面BAC1与PAC1所成角的余弦值．27(22·23·山东·二模)如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AB⎳CD，AB⊥BC，PA =AB=BC=2，CD=4．(1)证明：AD⊥PC；(2)若M为线段PB的靠近B点的四等分点，判断直线AM与平面PDC是否相交？如果相交，求出P到交点H的距离，如果不相交，说明理由．28(22·23·黄山·三模)如图，在直角梯形ABCD中，AD⎳BC，AD⊥CD，四边形CDEF为平行四边形，对角线CE和DF相交于点H，平面CDEF⊥平面ABCD，BC=2AD，∠DCF=60°，G是线段BE上一动点(不含端点)．(1)当点G为线段BE的中点时，证明：AG⎳平面CDEF；(2)若AD=1,CD=DE=2，且直线DG与平面CDEF成45°角，求二面角E-DG-F的正弦值．29(22·23·菏泽·三模)已知在直三棱柱ABC-A1B1C1中，其中AA1=2AC=4,AB=BC,F为BB1的中点，点E是CC1上靠近C1的四等分点，A1F与底面ABC所成角的余弦值为2 2．(1)求证：平面AFC⊥平面A1EF；(2)在线段A1F上是否存在一点N，使得平面AFC与平面NB1C1所成的锐二面角的余弦值为277，若存在，确定点N的位置，若不存在，请说明理由．30(22·23·福州·三模)如图，在三棱锥P-ABC中，PA⊥底面ABC，PA=2，AB=AC=1，将△PAB绕着PA逆时针旋转π3到△PAD的位置，得到如图所示的组合体，M为PD的中点.(1)当∠BAC为何值时，该组合体的体积最大，并求出最大值；(2)当PC⎳平面MAB时，求直线PC与平面PBD所成角的正弦值.31(22·23·福州·二模)如图1，在△ABC 中，AB =AC =2,∠BAC =2π3,E 为BC 的中点，F 为AB 上一点，且EF ⊥AB .将△BEF 沿EF 翻折到△B EF 的位置，如图2.(1)当AB =2时，证明：平面B AE ⊥平面ABC ；(2)已知二面角B -EF -A 的大小为π4，棱AC 上是否存在点M ，使得直线B E 与平面B MF 所成角的正弦值为1010？若存在，确定M 的位置；若不存在，请说明理由.32(22·23·三明·三模)如图，平面五边形ABCDE 由等边三角形ADE 与直角梯形ABCD 组成，其中AD ∥BC ，AD ⊥DC ，AD =2BC =2，CD =3，将△ADE 沿AD 折起，使点E 到达点M 的位置，且BM =a .(1)当a =6时，证明AD ⊥BM 并求四棱锥M -ABCD 的体积；(2)已知点P 为棱CM 上靠近点C 的三等分点，当a =3时，求平面PBD 与平面ABCD 夹角的余弦值.33(22·23·宁德·一模)如图①在平行四边形ABCD 中，AE ⊥DC ，AD =4，AB =3，∠ADE =60°，将△ADE 沿AE 折起，使平面ADE ⊥平面ABCE ，得到图②所示几何体．(1)若M 为BD 的中点，求四棱锥M -ABCE 的体积V M -ABCE ；(2)在线段DB 上，是否存在一点M ，使得平面MAC 与平面ABCE 所成锐二面角的余弦值为235，如果存在，求出DMDB的值，如果不存在，说明理由．34(22·23·龙岩·二模)三棱柱ABC -A 1B 1C 1中，AB ⊥AC ，AB =AC =2，侧面A 1ACC 1为矩形，∠A 1AB =2π3，三棱锥C 1-ABC 的体积为233．(1)求侧棱AA 1的长；(2)侧棱CC 1上是否存在点E ，使得直线AE 与平面A 1BC 所成角的正弦值为55？若存在，求出线段C 1E 的长；若不存在，请说明理由．35(22·23下·浙江·二模)如图，在多面体ABC-A1B1C1中，AA1⎳BB1⎳CC1，AA1⊥平面A1B1C1，△A1B1C1为等边三角形，A1B1=BB1=2，AA1=3，CC1=1，点M是AC的中点．(1)若点G是△A1B1C1的重心，证明；点G在平面BB1M内；(2)求二面角B1-BM-C1的正弦值．36(22·23下·浙江·三模)如图，三棱台ABC-A1B1C1中，A1C1=4，AC=6，D为线段AC上靠近C的三等分点.(1)线段BC上是否存在点E，使得A1B⎳平面C1DE，若不存在，请说明理由；若存在，请求出BEBC的值；(2)若A1A=AB=4，∠A1AC=∠BAC=π3，点A1到平面ABC的距离为3，且点A1在底面ABC的射影落在△ABC内部，求直线B1D与平面ACC1A1所成角的正弦值.37(22·23下·苏州·三模)如图，在三棱锥P-ABC中，△ABC是边长为62的等边三角形，且PA= PB=PC=6，PD⊥平面ABC，垂足为D,DE⊥平面PAB，垂足为E，连接PE并延长交AB于点G.(1)求二面角P-AB-C的余弦值；(2)在平面PAC内找一点F，使得EF⊥平面PAC，说明作法及理由，并求四面体PDEF的体积.38(22·23·沧州·三模)如图，该几何体是由等高的半个圆柱和14个圆柱拼接而成.C,E,D,G在同一平面内，且CG=DG.(1)证明：平面BFD⊥平面BCG；(2)若直线GC与平面ABG所成角的正弦值为105，求平面BFD与平面ABG所成角的余弦值.39(23·24上·永州·一模)如图所示，在四棱锥P-ABCD中，底面ABCD为矩形，侧面PAD为正三角形，且AD=2AB=4,M、N分别为PD、BC的中点，H在线段PC上，且PC=3PH．(1)求证：MN⎳平面PAB；(2)当AM⊥PC时，求平面AMN与平面HMN的夹角的余弦值．40(22·23·潍坊·三模)如图，P为圆锥的顶点，O是圆锥底面的圆心，AC为底面直径，△ABD为底面圆O的内接正三角形，且边长为3，点E在母线PC上，且AE=3，CE=1．(1)求证：PO∥平面BDE；(2)求证：平面BED⊥平面ABD(3)若点M为线段PO上的动点．当直线DM与平面ABE所成角的正弦值最大时，求此时点M到平面ABE的距离．立体几何大题1.空间中的平行关系（1）线线平行（2）线面平行的判定定理：平面外一直线与平面内一直线平行，则线面平行（3）线面平行的性质定理若线面平行，经过直线的平面与该平面相交，则直线与交线平行（4）面面平行的判定定理判定定理1：一个平面内有两条相交直线分别平行于另一个平面，则面面平行判定定理2：一个平面内有两条相交直线分别于另一个平面内两条相交直线平行，则面面平行（5）面面平行的性质定理性质定理1：两平面互相平行，一个平面内任意一条直线平行于另一个平面性质定理2：两平面互相平行，一平面与两平面相交，则交线互相平行6.空间中的垂直关系（1）线线垂直（2）线面垂直的判定定理一直线与平面内两条相交直线垂直，则线面垂直（3）线面垂直的性质定理性质定理1：一直线与平面垂直，则这条直线垂直于平面内的任意一条直线性质定理2：垂直于同一个平面的两条直线平行（4）面面垂直的判定定理一个平面内有一条直线垂直于另一个平面，则两个平面垂直(或：一个平面经过另一个平面的垂线，则面面垂直)（5）面面垂直的性质定理两平面垂直，其中一个平面内有一条直线与交线垂直，则这条直线垂直于另一个平面6.异面直线所成角cos θ=cos a ,b =|a ⋅b ||a |⋅|b |=|x 1x 2+y 1y 2+z 1z 2|x 12+y 12+z 12⋅x 22+y 22+z 22(其中θ(0°<θ≤90°)为异面直线a ,b 所成角，a ,b 分别表示异面直线a ,b 的方向向量)7.直线AB 与平面所成角，sin β=AB ⋅m |AB ||m |(m 为平面α的法向量).8.二面角α-l -β的平面角cos θ=m ⋅n |m ||n |(m ，n 为平面α，β的法向量).9.点B 到平面α的距离d =|AB ⋅n | (n 为平面α的法向量，AB 是经过面α的一条斜线，A ∈α).模拟训练一、解答题1(22·23下·湖南·二模)如图，在直三棱柱ABC -A B C 中，∠ABC =120°,AB =BC =2,AC =BB ，点D 为棱BB 的中点，AE =13AC ．(1)求DE 的长度；(2)求平面CDE 与平面BDE 夹角的余弦值．【答案】(1)393(2)34【分析】(1)在△ABC 中，用余弦定理可得到AC =23，在△ABE 中，用余弦定理可得BE =233，即可求得DE =DB 2+BE 2=393；(2)以B 为原点，分别以BE ,BC ,BB 所在的直线为x ,y ,z 轴建立空间直角坐标系，求出平面CDE 与平面BDE 的法向量，即可求解【详解】(1)因为在直三棱柱ABC -A B C 中，∠ABC =120°,AB =BC =2，在△ABC 中，由余弦定理得cos ∠ABC =AB 2+BC 2-AC 22AB ⋅BC=22+22-AC 22×2×2=-12，解得AC =23，则AE =13AC =233，在△ABE 中，由余弦定理得cos ∠BAE =AB 2+AE 2-BE 22AB ⋅AE =22+233 2-BE 22×2×233=32，解得BE =233，又AC =BB =23，所以BD =12BB =3，因为BB ⊥平面ABC ，BE ⊂平面ABC ，所以BB ⊥BE ，在直角三角形DBE 中，DE =DB 2+BE 2=(3)2+233 2=393；(2)因为AE =BE =233，所以∠ABE =∠BAE =30°，则∠CBE =∠ABC -∠ABE =120°-30°=90°，则BE ,BC ,BB 两两互相垂直，以B 为原点，分别以BE ,BC ,BB 所在的直线为x ,y ,z 轴建立如下图所示的空间直角坐标系：设平面CDE 的法向量为n =x ,y ,z ，由n ⋅CD =x ,y ,z ⋅0,-2,3 =-2y +3z =0n ⋅CE =x ,y ,z ⋅233,-2,0 =233x -2y =0 ，得z =233y x =3y，令y =3，得平面CDE 的一个法向量为n =3,3,2 ；平面BDE 的一个法向量为m =0,1,0 ．设平面CDE 与平面BDE 夹角的大小为θ，则cos θ=m ⋅n m n =0,1,0 ⋅3,3,2 1×4=34，故平面CDE 与平面BDE 夹角的余弦值为34．2(22·23下·绍兴·二模)如图，在多面体ABCDE 中，DE ⊥平面BCD ,△ABC 为正三角形，△BCD 为等腰Rt △,∠BDC =90°,AB =2,DE =2.(1)求证：AE ⊥BC ；(2)若AE ⎳平面BCD ，求直线BE 与平面ABC 所成的线面角的正弦值.【答案】(1)证明见解析(2)63【分析】(1)由线面垂直的性质定理和判定定理即可证明；(2)法一：由分析可知，∠EBH 就是直线BE 与平面ABC 所成的线面角，设∠AFD =α，当α<90°时，O 与D 重合，可得A ,E 两点重合，不符合题意，当α>90°时，求出EH ,BE ，即可得出答案；法二：建立空间直角坐标系，求出直线BE 的方向向量与平面ABC 的法向量，由线面角的向量公式代入即可得出答案.【详解】(1)设F 为BC 中点，连接AF ,EF ，则由△ABC 为正三角形，得AF ⊥BC ；DE ⊥平面BCD ，且△BCD 为等腰直角三角形，计算可得：BE =CE =2,∴EF ⊥BC .EF ∩AF =F ,EF ,AF ⊂面AEF ，于是BC ⊥面AEF ，AE ⊂面AEF ，从而BC ⊥AE .(2)法一：由(1)可知，过点E 作EH ⊥AF ，垂足为H ，则∠EBH 就是直线BE 与平面ABC 所成的线面角.当AE ⎳平面BCD 时，可得A 到平面BCD 的距离为 2.设∠AFD =α，所以AF ⋅sin α=2，可得sin α=63，当α<90°时，cos α=33，不妨设A 在底面BCD 射影为O ，则FO =1，此时O 与D 重合，可得A ,E 两点重合，不符合题意，舍去；当α>90°时，FO =1，此时O 在DF 的延长线上，作EH ⊥AF ，由于AODE 为矩形，可得AE =DO =2,AE ∥OD ，可得sin ∠EAH =63，可得EH =263.于是sin ∠EBH =EH BE=63.法二：建立如图坐标系，可得F 0,0,0 ,B 1,0,0 ，C -1,0,0 ,D 0,1,0 ,E 0,1,2 ,A 0,a ,b由AF =3，解得a 2+b 2=3，又∵AE ⎳平面BCD ，令n =0,0,1 ，可得AB ⋅n =0，解得b =2,a =±1.当a =1时A ,E 重合，所以a =-1，此时A 0,-1,2 .不妨设平面ABC 的法向量为m =x ,y ,z ，则CB ⋅m =0CA ⋅m =0代入得x -y +2z =02x =0 ，令z =1，则y =2，所以m =0,2,1 .由于BE =-1,1,2 ，不妨设所成角为θ，则sin θ=∣cos BE ,m |=63.3(22·23·张家口·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面BB 1C 1C 为菱形，∠CBB 1=60°，AB =BC =2，AC =AB 1=2.(1)证明：平面ACB 1⊥平面BB 1C 1C ；(2)求平面ACC 1A 1与平面A 1B 1C 1夹角的余弦值.【答案】(1)证明见解析；(2)57.【分析】(1)利用面面垂直的判定定理进行证明；(2)利用垂直关系建立空间直角坐标系，用向量法进行求解.【详解】(1)如图，连接BC 1，交B 1C 于O ，连接AO .因为侧面BB 1C 1C 为菱形，所以B 1C ⊥BC 1，且O 为BC 1的中点.又AC =AB 1=2，故AO ⊥B 1C .又AB =BC =2，且∠CBB 1=60°，所以CO =1,BO =3，所以AO =AC 2-CO 2=1.又AB =2，所以AB 2=BO 2+AO 2，所以AO ⊥BO .因为BO ,CB 1⊂平面BB 1C 1C ，BO ∩CB 1=O ，所以AO ⊥平面BB 1C 1C .又AO ⊂平面ACB 1，所以平面ACB 1⊥平面BB 1C 1C .(2)由(1)知，OA ,OB ,OB 1两两互相垂直，因此以O 为坐标原点，OB ,OB 1,OA 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系O -xyz ，则A (0,0,1)，B (3,0,0)，C (0,-1,0)，C 1(-3,0,0).故CC 1 =(-3,1,0)，CA =(0,1,1)，CB =(3,1,0).设n =(x 1,y 1,z 1)为平面ACC 1A 1的一个法向量，则有n ⋅CC 1 =0n ⋅CA =0 ，即-3x 1+y 1=0y 1+z 1=0 ，令x 1=1，则n =(1,3,-3).设m =(x 2,y 2,z 2)为平面ABC 的一个法向量，则有m ⋅CA =0m ⋅CB =0，即y 2+z 2=03x 2+y 2=0 ，令x 2=1，则m =(1,-3,3).因为平面A 1B 1C 1∥平面ABC ，所以m =(1,-3,3)也是平面A 1B 1C 1的一个法向量.所以cos <n ,m > =n ⋅m n m=1-3-3 7×7=57.所以平面ACC 1A 1与平面A 1B 1C 1夹角的余弦值57. 4(22·23·湛江·二模)如图1，在五边形ABCDE 中，四边形ABCE 为正方形，CD ⊥DE ，CD =DE ，如图2，将△ABE 沿BE 折起，使得A 至A 1处，且A 1B ⊥A 1D ．(1)证明：DE ⊥平面A 1BE ；(2)求二面角C -A 1E -D 的余弦值．【答案】(1)证明见解析(2)63【分析】(1)由已知易得DE ⊥BE ，即可证明线面垂直；(2)建立空间直角坐标系，用坐标公式法求解即可．【详解】(1)由题意得∠BEC =∠CED =π4，∠BED =π2，DE ⊥BE ，又A 1B ⊥A 1D ，A 1E ∩A 1D =A 1,A 1E ,A 1D ⊂面A 1ED ，所以A 1B ⊥面A 1ED ，又DE ⊂面A 1ED ，则DE ⊥A 1B ，又DE ⊥BE ，A 1B ∩BE =B ，A 1B ⊂平面A 1BE ，BE ⊂平面A 1BE ，所以DE ⊥平面A 1BE ．(2)取BE 的中点O ，可知BE =2CD ,OE =CD ，由DE ⊥BE ，且CD ⊥DE 可得OE ⎳CD ，所以四边形OCDE 是平行四边形，所以CO ∥DE ，则CO ⊥平面A 1BE ，设BE =2，以点O 为坐标原点，OB ,OC ,OA 1所在直线为坐标轴建立空间直角坐标系，如图，则A 1(0,0,1),E (-1,0,0),B (1,0,0),C (0,1,0),D (-1,1,0)，EA 1 =(1,0,1),EC =(1,1,0),ED =(0,1,0)，设平面A 1EC 的一个法向量为n 1 =(x 1,y 1,z 1)，则n 1 ⋅EA 1 =0n 1 ⋅EC =0 ，即x 1+z 1=0x 1+y 1=0 ，取x 1=1，则n 1 =(1,-1,-1)，设平面A 1ED 的一个法向量为n 2 =(x 2,y 2,z 2)，则n 2 ⋅E 1A =0n 2 ⋅ED =0 ，即x 2+z 2=0y 2=0 ，取x 2=1，则n 2 =(1,0,-1)，所以cos n 1 ,n 2 =n 1 ⋅n 2 n 1 n 2=63，由图可知，二面角C -A 1E -D 为锐角，所以面角C -A 1E -D 的余弦值为63．5(22·23下·长沙·三模)如图，在多面体ABCDE 中，平面ACD ⊥平面ABC ，BE ⊥平面ABC ，△ABC 和△ACD 均为正三角形，AC =4，BE =3，点F 在AC 上.(1)若BF ⎳平面CDE ，求CF ；(2)若F 是AC 的中点，求二面角F -DE -C 的正弦值.【答案】(1)CF =1(2)8517【分析】(1)记AC 中点为M ，连接DM 、BM ，依题意可得DM ⊥AC ，根据面面垂直的性质得到DM ⊥平面ABC ，如图建立空间直角坐标系，求出平面CDE 的法向量，设F a ,0,0 ，a ∈2,-2 ，依题意可得BF ⋅n =0求出a 的值，即可得解；(2)依题意点F 与点M 重合，利用空间向量法计算可得.【详解】(1)记AC 中点为M ，连接DM 、BM ，△ACD 为正三角形，AC =4，则DM ⊥AC ，且DM =2 3.所以DM ⊥平面ABC ，又△ABC 为正三角形，所以BM ⊥AC ，所以BM =23，如图建立空间直角坐标系，则B 0,23,0 ，C -2,0,0 ，D 0,0,23 ，E 0,23,3 ，所以CD =2,0,23 ，CE =2,23,3 ，设平面CDE 的法向量为n =x ,y ,z ，则n ⋅CD =2x +23z =0n ⋅CE =2x +23y +3z =0，令x =3，则z =-3，y =-32，则n =3,-32,-3 ，设F a ,0,0 ，a ∈-2,2 ，则BF =a ,-23,0 ，因为BF ⎳平面CDE ，所以BF ⋅n =3a +-23 ×-32+0×-3 =0，解得a =-1，所以F 为CM 的中点，此时CF =1.(2)若F 是AC 的中点，则点F 与点M 重合，则平面FDE 的一个法向量可以为m =1,0,0 ，设二面角F -DE -C 为θ，显然二面角为锐角，则cos θ=m ⋅n m ⋅n=332+-32 2+-3 2=651，所以sin θ=1-cos 2θ=1-651 2=8517，所以二面角F -DE -C 的正弦值为8517.6(22·23下·湖北·二模)如图，S 为圆锥的顶点，O 是圆锥底面的圆心，△ABC 内接于⊙O ,AC ⊥BC ,AC =BC =322，AM =2MS ,AS =3,PQ 为⊙O 的一条弦，且SB ⎳平面PMQ .(1)求PQ 的最小值；(2)若SA ⊥PQ ，求直线PQ 与平面BCM 所成角的正弦值.【答案】(1)22(2)3010【分析】(1)作出辅助线，找到符合要求的PQ ，并利用垂径定理得到最小值；(2)在第一问基础上，得到当PQ 取得最小值时，SA ⊥PQ ，并建立空间直角坐标系，利用空间向量求解线面角.【详解】(1)过点M 作MH ⎳SB 交AB 于点H ，过点H 作PQ ⊥AB ，此时满足SB ⎳平面PMQ ，由平面几何知识易知，PQ =2r 2-d 2，当弦心距d 最大时，d =OH ，弦长最短，即PQ 取得最小值，因为AM =2MS ,AS =3，所以AH =2HB ，因为AC ⊥BC ,AC =BC =322，由勾股定理得AB =322⋅2=3，故AH =2,HB =1，连接OQ ，则OQ =32，由勾股定理得HQ =OQ 2-OH 2=94-14=2，所以PQ =2HQ =22；(2)连接OS ，则OS ⊥平面ACB ，因为PQ ⊂平面ACB ，故OS ⊥PQ ，而SA ⊥PQ ，OS ∩SA =S ，所以PQ ⊥平面AOS ，即有PQ ⊥AB .以O 为坐标原点，过点O 且平行PQ 的直线为x 轴，OB 所在直线为y 轴，OS 所在直线为z 轴，建立空间直角坐标系，则P -2,12,0 ,Q 2,12,0 ,B 0,32,0 ,C 32,0,0 ,M 0,-12,3 ，设平面BCM 的法向量为m =x ,y ,z ，则m ⋅CB =x ,y ,z ⋅-32,32,0 =-32x +32y =0m ⋅MB =x ,y ,z ⋅0,2,-3 =2y -3z =0，令x =1，则y =1,z =233，故m =1,1,233，设直线PQ 与平面BCM 所成角的大小为θ，则sin θ=cos PQ ,m =PQ ⋅m PQ ⋅m =22,0,0 ⋅1,1,233 22×1+1+43=3010.故直线PQ与平面BCM所成角的正弦值为30 10.7(22·23·深圳·二模)如图，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD,PA= AD=2AB，点M是PD的中点.(1)证明：AM⊥PC；(2)设AC的中点为O，点N在棱PC上(异于点P，C)，且ON=OA，求直线AN与平面ACM所成角的正弦值.【答案】(1)证明见解析(2)1510【分析】(1)由等腰三角形的性质可得AM⊥PD，由面面垂直的性质可得CD⊥平面PAD，则CD⊥AM，所以由线面垂直的判定可得AM⊥平面PCD，从而可得结论；(2)以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系，利用空间向量求解即可.【详解】(1)证明：因为PA=AD，点M是PD的中点，所以AM⊥PD.因为PA⊥平面ABCD,PA⊂平面PAD，所以平面PAD⊥平面ABCD，因为四边形ABCD为矩形，所以CD⊥AD，因为平面PAD∩平面ABCD=AD，CD⊂平面ABCD，所以CD⊥平面PAD，所以CD⊥AM，因为PD∩CD=D，PD,CD⊂平面PCD，所以AM⊥平面PCD，因为PC⊂平面PCD，所以AM⊥PC.(2)解：由题意可得AB,AD,AP两两垂直，设AB=1，如图，以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系，则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,2)，22所以AM =0,22,22 ,AC =1,2,0 ，设平面ACM 的法向量为n =x ,y ,z ，则AM ⋅n =22y +22z =0AC ⋅n =x +2y =0，令y =-1可得x =2,z =1，所以平面ACM 的一个法向量n =2,-1,1 .PC =1,2,-2 ，设N x N ,y N ,z N ,PN =λPC =λ,2λ,-2λ (0<λ<1)，即x N ,y N ,z N -2 =λ,2λ,-2λ ，所以N λ,2λ,2-2λ .又O 12,22,0 ,ON =OA =32，所以λ-12 2+2λ-22 2+(2-2λ)2=34，化简得5λ2-7λ+2=0，解得λ=25或λ=1(舍去).所以AN =25,225,325，设直线AN 与平面ACM 所成的角为θ，则sin θ=n ⋅AN n ⋅AN=3252+1+1×425+825+1825=1510，所以直线AN 与平面ACM 所成角的正弦值为1510.8(22·23下·温州·二模)已知三棱锥D -ABC 中，△BCD 是边长为3的正三角形，AB =AC =AD ,AD 与平面BCD 所成角的余弦值为33．(1)求证：AD ⊥BC ；(2)求二面角D -AC -B 的平面角的正弦值．【答案】(1)证明见解析(2)223【分析】(1)取BC 的中点E ，连接AE ,DE ，证明BC ⊥平面ADE ，即可得证；(2)取正三角形BCD 的中心O ，连接OA ，从而可得OA ⊥平面BCD ，则∠ODA 即为AD 与平面BCD 所成角的平面角，进而可得AB =AC =AD =3，取AC 中点为H ，连接DH ,BH ，则DH ⊥AC ,BH ⊥AC ，故∠BHD 即为二面角D -AC -B 的平面角，解△BDH 即可得解.【详解】(1)取BC 的中点E ，连接AE ,DE ，因为△BCD 是边长为3的正三角形，所以DE ⊥BC ，又AE ∩DE =E ,AE ,DE ⊂平面ADE ，所以BC ⊥平面ADE ，因为AD ⊂平面ADE ，所以AD ⊥BC ；(2)取正三角形BCD 的中心O ，连接OA ，则点O 在DE 上，且OD =23DE ，由AB =AC =AD ，△BCD 是正三角形，得三棱锥A -BCD 为正三棱锥，则OA ⊥平面BCD ，故∠ODA 即为AD 与平面BCD 所成角的平面角，又AD 与平面BCD 所成角的余弦值为33，所以OD AD =3×32×23AD=33，即AB =AC =AD =3，即三棱锥A -BCD 是正四面体，取AC 中点为H ，连接DH ,BH ，则DH ⊥AC ,BH ⊥AC ，故∠BHD 即为二面角D -AC -B 的平面角，在△BDH 中，BH =DH =332,BD =3，则cos ∠BHD =BH 2+DH 2-BD 22⋅BH ⋅DH =274+274-92×332×332=13，所以sin ∠BHD =1-cos 2∠BHD =223，所以二面角D -AC -B 的平面角的正弦值223．9(22·23下·浙江·二模)如图，四面体ABCD ,AD ⊥CD ,AD =CD ,AC =2,AB =3,∠CAB =60°，E 为AB 上的点，且AC ⊥DE ,DE 与平面ABC 所成角为30°，(1)求三棱锥D -BCE 的体积；(2)求二面角B -CD -E 的余弦值.【答案】(1)答案见解析；(2)答案见解析．【分析】(1)取AC 中点F ，可证明AC ⊥平面DEF ，得平面ABC ⊥平面DEF ，DE 在平面ABC 内的射影就是直线EF ，∠DEF 是DE 与平面ABC 所成的角，即∠DEF =30°，由正弦定理求得∠FDE ，有两个解，在∠FDE =60°时可证DF ⊥平面ABC ，在∠FDE =120°时，取FE 中点H 证明DH ⊥平面ABC ，然后由棱锥体积公式计算体积；(2)建立如图所示的空间直角坐标系，用空间向量法求二面角．【详解】(1)取AC 中点F ，连接FE ,FD ，因为AD =CD ，所以DF ⊥AC ，又AC ⊥DE ，DE ∩DF =D ，DE ,DF ⊂平面DEF ，所以AC ⊥平面DEF ，而FE ⊂平面DEF ，所以AC ⊥FE ，由AC ⊥平面DEF ，AC ⊂平面ABC 得平面ABC ⊥平面DEF ，因此DE 在平面ABC 内的射影就是直线EF ，所以∠DEF 是DE 与平面ABC 所成的角，即∠DEF =30°，AD =CD ,AC =2，因此DF =12AC =1，在△DEF 中，由正弦定理EF sin ∠FDE =DF sin ∠DEF 得1sin30°=3sin ∠FDE ，sin ∠FDE =32，∠FDE 为△DEF 内角，所以∠FDE =60°或120°，S △ABC =12AB ×AC ×sin ∠BAC =12×3×2×sin60°=333，S △CBE =BE BAS △ABC =3-23×332=32，若∠FDE =60°，则∠DFE =90°，即DF ⊥FE ，AC ∩FE =F ，AC ,FE ⊂平面ABC ，所以DF ⊥平面ABC ，V D -BCE =13S △BCE ⋅DF =13×32×1=36；若∠FDE =120°，则∠DFE =30°，DF =DE =1，取EF 中点H ，连接DH ，则DH ⊥EF ，因为平面ABC ⊥平面DEF ，平面ABC ∩平面DEF =EF ，而DH ⊂平面DEF ，所以DH ⊥平面ABC ，DH =DF sin ∠DFE =1×sin30°=12，所以V D -BCE =13S △BCE ⋅DF =13×32×12=312；(2)若∠FDE =60°，以FA ,FE ,FD 为x ,y ,z 轴建立如图所示的空间直角坐标系F -xyz ，则D (0,0,1)，C (-1,0,0)，A (1,0,0)，E (0,3,0)，AE =(-1,3,0)，EB =12AE =-12,32,0 ，所以B 点坐标为-12,332,0 ，CD =(1,0,1)，CB =12,332,0 ，CE =(1,3,0)，设平面DBC 的一个法向量是m =(x 1,y 1,z 1)，则m ⋅CD =x 1+z 1=0m ⋅CB =12x 1+332y 1=0，取y 1=-1，则x 1=33，z 1=-33，即m =(33,-1,-33)，设平面DEC 的一个法向量是n =(x 2,y 2,z 2)，则n ⋅CD =x 2+z 2=0n ⋅CE =x 2+3y 2=0，取y 2=-1，则x 2=3，z 2=-3，即m =(3,-1,-3)，cos m ,n =m ⋅n m n =9+1+955×7=19385385，所以二面角B -CD -E 的余弦值是19385；若∠FDE =120°，以FA 为x 轴，FE 为y 轴，过F 且平行于HD 的直线为z 轴建立如图所示的空间直角坐标系F -xyz ，FH =12FE =32，则D 0,32,12 ，C (-1,0,0)，A (1,0,0)，E (0,3,0)，AE =(-1,3,0)，EB =12AE =-12,32,0 ，所以B 点坐标为-12,332,0 ，CD =1,32,12 ，CB =12,332,0 ，CE =(1,3,0)，设平面DBC 的一个法向量是m =(x 1,y 1,z 1)，则m ⋅CD =x 1+32y 1+12z 1=0m ⋅CB =12x 1+332y 1=0，取y 1=-1，则x 1=33，z 1=-53，即m =(33,-1,-53)，设平面DEC 的一个法向量是n =(x 2,y 2,z 2)，则n ⋅CD =x 2+32y 2+12z 2=0n ⋅CE =x 2+3y 2=0，取y 2=-1，则x 2=3，z 2=-3，即m =(3,-1,-3)，cos m ,n =m ⋅n m n =9+1+15103×7=25721721，所以二面角B -CD -E 的余弦值是25721721．10(22·23下·襄阳·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面BB 1C 1C 为矩形，∠BAC =90°，AB =AC =2，AA 1=4，A 1在底面ABC 的射影为BC 的中点N ，M 为B 1C 1的中点.(1)求证：平面A 1MNA ⊥平面A 1BC ；(2)求平面A 1B 1BA 与平面BB 1C 1C 夹角的余弦值.【答案】(1)证明见解析(2)23015【分析】(1)利用线面垂直和面面垂直的判定定理证明；(2)利用空间向量的坐标运算求面面夹角的余弦值.【详解】(1)如图，∵A 1N ⊥面ABC ，连AN ，则AN ⊥A 1N ，又AB =AC =2，∴AN ⊥BC ，又AN ∩BC =N ，A 1N ⊂面A 1BC ，BC ⊂面A 1BC ，于是AN ⊥面A 1BC ，又AN ⊂面A 1MN ，，所以面A 1BC ⊥面A 1MNA .(2)由(1)可得，以NA ,NB ,NA 1 为x ,y ,z 轴，建系如图，∠BAC =90°，AB =AC =2，BC =22则A (2,0,0),B (0,2,0),C (0,-2,0),因为AA 1=4,AN =2,所以A 1N =14,则A 1(0,0,14),因为NB 1 =NB +BB 1 =NB +AA 1 =0,2,0 +-2,0,14 =-2,2,14 ,所以B 1-2,2,14 ,设平面A 1BB 1的一个法向量为m =(x ,y ,z )，因为A 1B =(0,2,-14),B 1B =(2,0,-14),所以A 1B ⋅m =2y -14z =0B 1B ⋅m =2x -14z =0 ，令y =7，则x =7,z =1，所以m =(7,7,1)，设平面BCC 1B 1的一个法向量为n =(a ,b ,c )，因为BC =(0,-22,0),BB 1 =(-2,0,14),所以BC ⋅n =-22b =0BB 1 ⋅n =-2a +14c =0，令a =7，则b =0,c =1，所以n =(7,0,1)，设平面A 1BB 1与平面BCC 1B 1夹角为θ，则cos θ=cos <m ,n >=m ⋅n m n=7+0+17+7+1×7+0+1=23015，所以平面A 1BB 1与平面BCC 1B 1夹角的余弦值为23015.11(22·23·唐山·二模)如图，在三棱柱ABC -A 1B 1C 1中，△ABC 是等边三角形，侧面ACC 1A 1⊥底面ABC ，且AA 1=AC ，∠AA 1C 1=120°，M 是CC 1的中点．(1)证明：A 1C ⊥BM ．(2)求二面角A 1-BC -M 的正弦值．【答案】(1)证明见解析(2)45【分析】(1)根据菱形的性质、结合面面垂直的性质，线面垂直的判定定理进行证明即可；(2)建立空间直角坐标系，运用空间向量夹角公式进行求解即sk .【详解】(1)取AC 的中点O ，连接OM ，OB ，AC 1．在三棱柱ABC -A 1B 1C 1中，由AA 1=AC ，得四边形ACC 1A 1为菱形，所以A 1C ⊥AC 1，易知OM ∥AC 1，则A 1C ⊥OM ．由△ABC 是等边三角形，知OB ⊥AC ，又平面ACC 1A 1⊥平面ABC ，平面ACC 1A 1∩平面ABC =AC ，OB ⊂平面ABC ，知OB ⊥平面ACC 1A 1，则OB ⊥A 1C ，又OB ∩OM =O ,OB ,OM ⊂平面OBM ，得A 1C ⊥平面OBM ，又BM ⊂平面OBM ，故A 1C ⊥BM ．.(2)连接OA 1，因为侧面ACC 1A 1为菱形，∠AA 1C 1=120°，则∠A 1AC =60°，则△A 1AC 为等边三角形，所以A 1O ⊥AC ，又由(1)易知OA 1，OB ，AC 两两垂直，故以O 为坐标原点，分别以OB ，OC ，OA 1 的方向为x 轴、y 轴、z 轴的正方向，建立空间直角坐标系．不妨设AB =2，则O 0,0,0 ，B 3,0,0 ，C 0,1,0 ，A 10,0,3 ，C 10,2,3 ，BA 1 =-3,0,3 ，BC =-3,1,0 ，CC 1 =0,1,3 ，。

1.在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的俯视图可以为2.已知矩形ABCD的顶点都在半径为4的球O的球面上，且6,23==,则棱锥AB BC-的体积为。

O ABCD3.如图，四棱锥P—ABCD中，底面ABCD为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD.(Ⅰ)证明：PA⊥BD；(Ⅱ)若PD=AD，求二面角A-PB-C的余弦值。

1.D2.833. 解：（Ⅰ）因为60,2DAB AB AD ∠=︒=， 由余弦定理得3BD AD =从而BD 2+AD 2= AB 2，故BD ⊥AD 又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面PAD. 故 PA ⊥BD（Ⅱ）如图，以D 为坐标原点，AD 的长为单位长，射线DA 为x 轴的正半轴建立空间直角坐标系D-xyz ，则()1,0,0A ，()03,0B ，，()1,3,0C -，()0,0,1P 。

(1,3,0),(0,3,1),(1,0,0)AB PB BC =-=-=- 设平面PAB 的法向量为n=（x ，y ，z ），则0,0,{n AB n PB ⋅=⋅=即 3030x y y z -+=-=因此可取n=(3,1,3)设平面PBC 的法向量为m ，则m 0,m 0,{PB BC ⋅=⋅=可取m=（0，-1，3-） 27cos ,727m n ==- 故二面角A-PB-C 的余弦值为 27-1. 正方体ABCD-1111A B C D 中，B 1B 与平面AC 1D 所成角的余弦值为A23 B 33 C 23D 632. 已知圆O 的半径为1，PA 、PB 为该圆的两条切线，A 、B 为俩切点，那么PA PB •的最小值为(A) 42-+ (B)32-+ (C) 422-+ (D)322-+3. 已知在半径为2的球面上有A 、B 、C 、D 四点，若AB=CD=2,则四面体ABCD 的体积的最大值为(A)23 (B)43 (C) 23 (D) 83 4. 如图，四棱锥S-ABCD 中，SD ⊥底面ABCD ，AB//DC ，AD ⊥DC ，AB=AD=1，DC=SD=2，E 为棱SB 上的一点，平面EDC ⊥平面SBC .（Ⅰ）证明：SE=2EB ；（Ⅱ）求二面角A-DE-C 的大小 .1. D2. D3. B4. 解法一：(Ⅰ)连接BD,取DC 的中点G ，连接BG,由此知 1,DG GC BG ===即ABC ∆为直角三角形，故BC BD ⊥. 又ABCD,BC SD SD ⊥⊥平面故,所以，BC ⊥⊥平面BDS,BC DE .作BK ⊥EC,EDC SBC K ⊥为垂足，因平面平面，故,BK EDC BK DE DE ⊥⊥平面，与平面SBC 内的两条相交直线BK 、BC 都垂直 DE ⊥平面SBC ，DE ⊥EC,DE ⊥SB226SB SD DB =+=3SD DB DE SB == 22626-,-EB DB DE SE SB EB ==== 所以，SE=2EB (Ⅱ) 由225,1,2,,SA SD AD AB SE EB AB SA =+===⊥知22121,AD=133AE SA AB ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭又.故ADE ∆为等腰三角形.取ED 中点F,连接AF ,则226,AF DE AF AD DF ⊥=-=. 连接FG ，则//,FG EC FG DE ⊥.所以，AFG ∠是二面角A DE C --的平面角. 连接AG,A G=2,2263FG DG DF =-=, 2221cos 22AF FG AG AFG AF FG +-∠==-,所以，二面角A DE C --的大小为120°. 解法二：以D 为坐标原点，射线DA 为x 轴的正半轴，建立如图所示的直角坐标系D xyz -， 设A(1,0,0)，则B(1,1,0),C(0,2,0),S(0,0,2) （Ⅰ）(0,2,-2),(-1,1,0)SC BC ==设平面SBC 的法向量为n=(a, b, c) 由,n SC n BC ⊥⊥，得0,0n SC n BC == 故2b-2c=0,-a+b=0令a=1，则b=c,c=1,n=(1,1,1) 又设SE EB λ= (0)λ>，则2(,,)111E λλλλλ+++ 2(,,),(0,2,0)111DE DC λλλλλ==+++设平面CDE 的法向量m=(x,y,z) 由,m DE m DC ⊥⊥,得0m DE ⊥=，0m DC ⊥= 故20,20111x y zy λλλλλ++==+++. 令2x =，则(2,0,)m λ=-.由平面DEC ⊥平面SBC 得m ⊥n,0,20,2m n λλ=-== 故SE=2EB（Ⅱ）由（Ⅰ）知222(,,)333E ，取DE 的中点F ，则111211(,,),(,,)333333F FA =--，故0FA DE =，由此得FA DE ⊥又242(,,)333EC =--，故0EC DE =，由此得EC DE ⊥， 向量FA 与EC 的夹角等于二面角A DE C --的平面角 于是 1cos(,)2||||FA EC FA EC FA EC ==-所以，二面角A DE C --的大小为120（三）1. 已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（ ）（A 3（B 5（C 7 (D) 342. 已知二面角l αβ--为60，动点P 、Q 分别在面α、β内，P 3，Q 到α的距离为3则P 、Q 两点之间距离的最小值为（ ） (A) (B)2 (C) 33. 直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===, 120BAC ∠=︒，则此球的表面积等于 。

第8讲 立体几何中的向量方法（二）一、选择题1．两平行平面α，β分别经过坐标原点O 和点A (2,1,1)，且两平面的一个法向量n ＝(－1,0,1)，则两平面间的距离是( )A.32B.22 C.3 D ．3 2 解析 两平面的一个单位法向量n 0＝⎝ ⎛⎭⎪⎫－22，0，22，故两平面间的距离d＝|OA →·n 0|＝22.答案 B2．已知向量m ，n 分别是直线l 和平面α的方向向量、法向量，若cos 〈m ，n 〉＝－12，则l 与α所成的角为( )．A ．30°B ．60°C ．120°D ．150°解析 设l 与α所成的角为θ，则sin θ＝|cos 〈m ，n 〉|＝12，∴θ＝30°. 答案 A3．长方体ABCD －A 1B 1C 1D 1中，AB ＝AA 1＝2，AD ＝1，E 为CC 1的中点，则异面直线BC 1与AE 所成角的余弦值为( )．A.1010B.3010C.21510D.31010解析 建立坐标系如图，则A (1,0,0)，E (0,2,1)，B (1,2,0)，C 1(0，2,2)． BC 1→＝(－1,0,2)，AE →＝(－1,2,1)， cos 〈BC 1→，AE →〉＝BC 1→·AE →|BC 1→||AE →|＝3010.所以异面直线BC 1与AE 所成角的余弦值为3010. 答案 B4．已知直二面角α­l ­β，点A ∈α，AC ⊥l ，C 为垂足，点B ∈β，BD ⊥l ，D 为垂足，若AB ＝2，AC ＝BD ＝1，则CD ＝( )．A ．2 B. 3 C. 2 D ．1 解析 如图，建立直角坐标系D ­xyz ，由已知条件B (0,0,1)，A (1，t,0)(t ＞0)， 由AB ＝2解得t ＝ 2. 答案 C5．如图，在四面体ABCD 中，AB ＝1，AD ＝23，BC ＝3，CD ＝2.∠ABC ＝∠DCB ＝π2，则二面角A －BC －D 的大小为( )．A.π6 B.π3 C.5π3D.5π6解析 二面角A －BC －D 的大小等于AB 与CD 所成角的大小.AD →＝AB →＋BC →＋CD →.而AD →2＝AB →2＋CD →2＋BC →2－2|AB →|·|CD →|·cos 〈AB →，CD →〉，即12＝1＋4＋9－2×2cos 〈AB →，CD →〉，∴cos 〈AB →，CD →〉＝12，∴AB 与CD 所成角为π3，即二面角A －BC －D 的大小为π3.故选B. 答案 B6．如图，在直三棱柱ABC －A 1B 1C 1中，∠ACB ＝90°，2AC ＝AA 1＝BC ＝2.若二面角B 1－DC －C 1的大小为60°，则AD 的长为( )A. 2B. 3 C ．2D.22解析 如图，以C 为坐标原点，CA ，CB ，CC 1所在的直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，则C (0,0,0)，A (1,0,0)，B 1(0,2,2)，C 1(0,0,2)，D (1,0,1)设AD ＝a ，则D 点坐标为(1,0，a )，CD ＝(1,0，a )，1CB ＝(0,2,2)，设平面B 1CD 的一个法向量为m ＝(x ，y ，z )． 则⎩⎪⎨⎪⎧m ·1CB ＝0m ·CD ＝0⇒⎩⎨⎧2y ＋2z ＝0x ＋az ＝0，令z ＝－1，得m ＝(a,1，－1)，又平面C 1DC 的一个法向量为n (0,1,0)，则由cos60°＝m·n |m ||n |，得1a 2＋2＝12，即a ＝2，故AD ＝ 2. 答案 A 二、填空题7．若平面α的一个法向量为n ＝(4,1,1)，直线l 的一个方向向量为a ＝(－2，－3,3)，则l 与α所成角的正弦值为________． 解析 cos 〈n ，a 〉＝n ·a |n ||a |＝－832×22＝－41133.又l 与α所成角记为θ，即sin θ＝|cos 〈n ，a 〉|＝41133. 答案41133.8．若向量a ＝(1，λ，2)，b ＝(2，－1,2)且a 与b 的夹角的余弦值为89，则λ＝________.解析 由已知得89＝a·b |a ||b |＝2－λ＋45＋λ2·9， ∴8 5＋λ2＝3(6－λ)，解得λ＝－2或λ＝255. 答案 －2或2559．已知点E 、F 分别在正方体ABCD －A 1B 1C 1D 1的棱BB 1，CC 1上，且B 1E ＝2EB ，CF ＝2FC 1，则面AEF 与面ABC 所成的二面角的正切值为________． 解析 如图，建立直角坐标系D －xyz ，设DA ＝1由已知条件A (1,0,0)，E ⎝ ⎛⎭⎪⎫1，1，13，F ⎝ ⎛⎭⎪⎫0，1，23，AE →＝⎝ ⎛⎭⎪⎫0，1，13，AF →＝⎝ ⎛⎭⎪⎫－1，1，23，设平面AEF 的法向量为n ＝(x ，y ，z )， 面AEF 与面ABC 所成的二面角为θ， 由⎩⎪⎨⎪⎧n ·AE →＝0，n ·AF →＝0得⎩⎪⎨⎪⎧y ＋13z ＝0，－x ＋y ＋23z ＝0.令y ＝1，z ＝－3，x ＝－1，则n ＝(－1,1，－3) 平面ABC 的法向量为m ＝(0,0，－1) cos θ＝cos 〈n ，m 〉＝31111，tan θ＝23. 答案 2310．在三棱锥O －ABC 中，三条棱OA ，OB ，OC 两两垂直，且OA ＝OB ＝OC ，M 是AB 边的中点，则OM 与平面ABC 所成角的正切值是________． 解析 如图所示建立空间直角坐标系，设OA ＝OB ＝OC ＝1，则A (1,0,0)，B (0，1,0)，C (0,0,1)，M ⎝ ⎛⎭⎪⎫12，12，0，故AB →＝(－1,1,0)，AC →＝(－1,0,1)，OM →＝⎝ ⎛⎭⎪⎫12，12，0. 设平面ABC 的法向量为n ＝(x ，y ，z )， 则由⎩⎪⎨⎪⎧n ⊥AB →，n ⊥AC →，得⎩⎨⎧－x ＋y ＝0，－x＋z ＝0，令x ＝1，得n ＝(1,1,1)．故cos 〈n ，OM →〉＝13×22＝63， 所以OM 与平面ABC 所成角的正弦值为63，其正切值为 2. 答案2三、解答题11．如图，四面体ABCD 中，AB 、BC 、BD 两两垂直，AB ＝BC ＝BD ＝4，E 、F 分别为棱BC 、AD 的中点． (1)求异面直线AB 与EF 所成角的余弦值； (2)求E 到平面ACD 的距离；(3)求EF 与平面ACD 所成角的正弦值．解 如图，分别以直线BC 、BD 、BA 为x 、y 、z 轴建立空间直角坐标系，则各相关点的坐标为A (0,0,4)、C (4,0，0)、D (0,4，0)，E (2,0,0)、F (0，2,2)． (1)∵AB →＝(0,0，－4)，EF →＝(－2,2,2)， ∴|cos 〈AB →，EF →〉|＝⎪⎪⎪⎪⎪⎪－84×23＝33， ∴异面直线AB 与EF 所成角的余弦值为33. (2)设平面ACD 的一个法向量为n ＝(x ，y,1)， 则⎩⎪⎨⎪⎧n ·AC →＝0，n ·CD →＝0，∵AC →＝(4,0，－4)，CD →＝(－4,4,0)，∴⎩⎨⎧4x －4＝0，－4x ＋4y ＝0， ∴x ＝y ＝1，∴n ＝(1,1,1，)．∵F ∈平面ACD ，EF →＝(－2,2,2)，∴E 到平面ACD 的距离为d ＝|n ·EF →||n |＝23＝233.(3)EF 与平面ACD 所成角的正弦值为|cos 〈n ，EF →〉|＝23×23＝1312．如图，在底面为直角梯形的四棱锥P －ABCD 中，AD ∥BC ，∠ABC ＝90°，P A ⊥平面ABCD ，P A ＝3，AD ＝2，AB ＝23，BC ＝6. (1)求证：BD ⊥平面P AC ；(2)求二面角P －BD －A 的大小． (1)证明 如图，建立空间直角坐标系， 则A (0,0,0)，B (23，0,0)， C (23，6,0)，D (0,2,0)，P (0,0,3)，∴AP →＝(0,0,3)，AC →＝(23，6,0)， BD →＝(－23，2,0)．∴BD →·AP →＝0，BD →·AC →＝0.∴BD ⊥AP ，BD ⊥AC . 又∵P A ∩AC ＝A ，∴BD ⊥面P AC .(2)解 设平面ABD 的法向量为m ＝(0,0,1)， 设平面PBD 的法向量为n ＝(x ，y ，z )， 则n ·BD →＝0，n ·BP →＝0.∵BP →＝(－23，0,3)，∴⎩⎨⎧－23x ＋2y ＝0，－23x ＋3z ＝0解得⎩⎨⎧y ＝3x ，z ＝233x .令x ＝3，则n ＝(3，3,2)，∴cos 〈m ，n 〉＝m·n |m||n |＝12.∴二面角P －BD －A 的大小为60°.13．如图，直三棱柱ABC －A 1B 1C 1中，AC ＝BC ＝12AA 1，D 是棱AA 1的中点，DC 1⊥BD . (1)证明：DC 1⊥BC .(2)求二面角A 1－BD －C 1的大小．(1)证明 由题设知，三棱柱的侧面为矩形．由于D 为AA 1的中点， 故DC ＝DC 1.又AC ＝12AA 1，可得DC 21＋DC 2＝CC 21，所以DC 1⊥DC . 而DC 1⊥BD ，DC ∩BD ＝D ，所以DC 1⊥平面BCD . 因为BC ⊂平面BCD ，所以DC 1⊥BC .(2)解 由(1)知BC ⊥DC 1，且BC ⊥CC 1，则BC ⊥平面ACC 1A 1，所以CA ，CB ，CC 1两两相互垂直．以C 为坐标原点，CA →的方向为x 轴的正方向，|CA →|为单位长，建立如图所示的空间直角坐标系 C －xyz .由题意知A 1(1,0,2)，B (0,1,0)，D (1,0,1)，C 1(0,0,2)．则A 1D →＝(0,0，－1)，BD →＝(1，－1,1)，DC 1→＝(－1,0,1)． 设n ＝(x ，y ，z )是平面A 1B 1BD 的法向量，则 ⎩⎪⎨⎪⎧n ·BD →＝0，n ·A 1D →＝0，即⎩⎨⎧x －y ＋z ＝0，z ＝0，可取n ＝(1,1,0)． 同理，设m ＝(x ，y ，z )是平面C 1BD 的法向量，则 ⎩⎪⎨⎪⎧m ·BD →＝0，m ·DC 1→＝0，即⎩⎨⎧x －y ＋z ＝0，－x ＋z ＝0，可取m ＝(1,2,1)． 从而cos 〈n ，m 〉＝n ·m |n |·|m |＝32. 故二面角A 1－BD －C 1的大小为30°.14．如图，已知AB ⊥平面ACD ，DE ⊥平面ACD ，△ACD 为等边三角形，AD ＝DE ＝2AB ，F 为CD 的中点． (1)求证：AF ∥平面BCE ；(2)求证：平面BCE⊥平面CDE；(3)求直线BF和平面BCE所成角的正弦值．解方法一：(1)证法一：取CE的中点G，连接FG、BG.∵F为CD的中点，∴GF∥DE且GF＝12 DE，∵AB⊥平面ACD，DE⊥平面ACD，∴AB∥DE，∴GF∥AB.又AB＝12DE，∴GF＝AB.又DE＝2AB，∴四边形GFAB为平行四边形，则AF∥BG. ∵AF⊄平面BCE，BG⊂平面BCE，∴AF∥平面BCE.证法二：取DE的中点M，连接AM、FM，∵F为CD的中点，∴FM∥CE.∵AB⊥平面ACD，DE⊥平面ACD，∴DE∥AB.又AB＝12DE＝ME，∴四边形ABEM为平行四边形，则AM∥BE. ∵FM、AM⊄平面BCE，CE、BE⊂平面BCE，∴FM∥平面BCE，AM∥平面BCE.又FM∩AM＝M，∴平面AFM∥平面BCE.∵AF⊂平面AFM，∴AF∥平面BCE.(2)证明：∵△ACD 为等边三角形，F 为CD 的中点， ∴AF ⊥CD .∵DE ⊥平面ACD ，AF ⊂平面ACD ，∴DE ⊥AF . 又CD ∩DE ＝D ，故AF ⊥平面CDE . ∵BG ∥AF ，∴BG ⊥平面CDE . ∵BG ⊂平面BCE ， ∴平面BCE ⊥平面CDE .(3)在平面CDE 内，过F 作FH ⊥CE 于H ，连接BH ， ∵平面BCE ⊥平面CDE ，∴FH ⊥平面BCE . ∴∠FBH 为BF 和平面BCE 所成的角．设AD ＝DE ＝2AB ＝2a ，则FH ＝CF sin45°＝22a ，BF ＝AB 2＋AF 2＝a 2＋3a2＝2a ，在Rt △FHB 中，sin ∠FBH ＝FH BF ＝24. ∴直线BF 和平面BCE 所成角的正弦值为24. 方法二：设AD ＝DE ＝2AB ＝2a ，建立如图所示的坐标系A －xyz ，则A (0,0,0)，C (2a,0,0)，B (0,0，a )，D (a ，3a,0)，E (a ，3a,2a )．∵F 为CD 的中点，∴F ⎝ ⎛⎭⎪⎫32a ，32a ，0.(1)证明：AF →＝⎝ ⎛⎭⎪⎫32a ，32a ，0，BE →＝(a ，3a ，a )，BC →＝(2a,0，－a )，∵AF →＝12(BE →＋BC →)，AF ⊄平面BCE ，∴AF ∥平面BCE .(2)证明：∵AF →＝⎝ ⎛⎭⎪⎫32a ，32a ，0，CD →＝(－a ，3a,0)，ED →＝(0,0，－2a )，∴AF →·CD →＝0，AF →·ED →＝0，∴AF →⊥CD →，AF →⊥ED →. ∴AF →⊥平面CDE ，又AF ∥平面BCE ， ∴平面BCE ⊥平面CDE .(3)设平面BCE 的法向量为n ＝(x ，y ，z )，由n ·BE →＝0，n ·BC →＝0可得x ＋3y ＋z ＝0,2x －z ＝0，取n ＝(1，－3，2)．又BF →＝⎝ ⎛⎭⎪⎫32a ，32a ，－a ，设BF 和平面BCE 所成的角为θ，则sin θ＝|BF →·n ||BF →|·|n |＝2a 2a ·22＝24.∴直线BF 和平面BCE 所成角的正弦值为24.。