Wilcoxon符号秩检验-吴喜之例子
- 格式:docx
- 大小:26.61 KB
- 文档页数:8

Wilcoxon 秩和检验Wilcoxon 符号秩检验是由威尔科克森(F·Wilcoxon)于1945年提出的.该方法是在成对观测数据的符号检验基础上发展起来的,比传统的单独用正负号的检验更加有效。
1947年,Mann 和Whitney 对Wilcoxon 秩和检验进行补充,得到Wilcoxon —Mann-Whitney 检验,由后续的Mann-Whitney 检验又继而得到Mann —Whitney-U 检验。
一、 两样本的Wilcoxon 秩和检验由Mann ,Whitney 和Wilcoxon 三人共同设计的一种检验,有时也称为Wilcoxon 秩和检验,用来决定两个独立样本是否来自相同的或相等的总体.如果这两个独立样本来自正态分布和具有相同方差时,我们可以采用t 检验比较均值。
但当这两个条件都不能确定时,我们常替换t 检验法为Wilcoxon 秩和检验。
Wilcoxon 秩和检验是基于样本数据秩和。
先将两样本看成是单一样本(混合样本)然后由小到大排列观察值统一编秩.如果原假设两个独立样本来自相同的总体为真,那么秩将大约均匀分布在两个样本中,即小的、中等的、大的秩值应该大约均匀被分在两个样本中。
如果备选假设两个独立样本来自不相同的总体为真,那么其中一个样本将会有更多的小秩值,这样就会得到一个较小的秩和;另一个样本将会有更多的大秩值,因此就会得到一个较大的秩和。
设两个独立样本为:第一个x 的样本容量为1n ,第二个y 样本容量为2n ,在容量为21n n n +=的混合样本(第一个和第二个)中,x 样本的秩和为x W ,y 样本的秩和为y W ,且有2)1(21+=+++=+n n n W W y x (1)我们定义 2)1(111+-=n n W W x (2) 2)1(222+-=n n W W y (3)以x 样本为例,若它们在混合样本中享有最小的1n 个秩,于是2)1(11+=n n W x ,也是x W 可能取的最小值;同样y W 可能取的最小值为2)1(22+n n 。


SAS讲义_第二十七课符号检验和Wilcoxon符号秩检验第二十七课符号检验和Wilcoxon 符号秩检验在统计推断和假设检验中,传统的检验统计量都叫做参数检验,因为它们都依赖于确定的概率分布,这个分布带有一组自由的参数。
参数检验被认为是依赖于分布假定的。
通常情况下,我们对数据进行分析时,总是假定误差项服从正态分布,这是人们易于接受的事实,因为正态分布的原始出发点就是来自于误差分布,至于当样本相当大时,数据的正态近似,这是由于大样本理论所保证的。
但有些资料不一定满足上述要求,或不能测量具体数值,其观察结果往往只有程度上的区别,如颜色的深浅、反应的强弱等,此时就不适用参数检验的方法,而只能用非参数统计方法(non-parametric statistical analysis )来处理。
这种方法对数据来自的总体不作任何假设或仅作极少的假设,因此在实用中颇有价值,适用面很广。
一、单样本的符号检验符号检验(sign test )是一种最简单的非参数检验方法。
它是根据正、负号的个数来假设检验。
首先需要将原始观察值按设定的规则,转换成正、负号,然后计数正、负号的个数作出检验。
该检验可用于样本中位数和总体中位数的比较,数据的升降趋势的检验,特别适用于总体分布不服从正态分布或分布不明的配对资料,有时当配对比较的结果只能定性的表示,如试验前后比较结果为颜色从深变浅、程度从强变弱,成绩从一般变优秀,即不能获得具体数字,也可用符号检验,例如用正号表示颜色从深变浅,用负号表示颜色从浅变深。
用于配对资料时,符号检验的计算步骤为:首先定义成对数据指定正号或负号的规则,然后计数正号的个数+S 及负号的个数-S ,由于在具体比较配对资料时,可能存在配对资料的前后没有变化,或等于假设中的中位数,此时仅需要将这些观察值从资料中剔除,当然样本大小n 也随之减少,故修正样本大小-++=S S n 。
当样本n 较小时,应使用二项分布确切概率计算法,当样本n 较大时,常利用二项分布的正态近似。

wilcoxon符号秩检验例题假设有两组数据A和B,每组数据有10个观测值。
现在要进行Wilcoxon符号秩检验来判断两组数据是否来自同一分布。
以下是示例数据:组 A:12, 15, 18, 20, 22, 25, 28, 30, 32, 35组 B:10, 13, 15, 18, 20, 23, 24, 25, 29, 34首先,对A组和B组数据求差值,得到:2, 2, 3, 2, 2, 2, 4, 5, 3, 1然后,对这些差值按绝对值大小进行排序,得到:1, 2, 2, 2, 2, 2, 3, 3, 4, 5为每个差值找到它在排序后的序列中的秩次,即为:1, 2.5, 2.5, 2.5, 2.5, 2.5, 7, 7, 9, 10接下来,计算差值的积和,分别为:S+ = 1 + 2.5 + 2.5 + 2.5 + 2.5 + 2.5 + 7 + 7 + 9 + 10 = 46根据Wilcoxon符号秩检验的原假设,两组数据来自同一分布,因此预期差值和为0。
然后,计算Wilcoxon秩和的标准误差,使用以下公式计算:标准误差 = sqrt(n * (n+1) * (2n+1) / 6)其中,n为样本数量,对本例,n = 10,代入公式得到:标准误差= sqrt(10 * (10+1) * (2*10+1) / 6) ≈ 7.18最后,计算z统计量,使用以下公式计算:z = (S+ - n(n+1)/4) / 标准误差代入数据得到:z = (46 - 10(10+1)/4) / 7.18 ≈ 1.29由于样本数量较小(n=10),可以使用标准正态分布的临界值来判断结果的显著性。
对于双侧检验,若|z| > 1.96,则认为结果是显著的。
在本例中,|z| < 1.96,因此不能拒绝原假设,即认为两组数据来自同一分布。
请注意,这只是一个示例,Wilcoxon符号秩检验可以应用于更多情况和不同的数据。


吴喜之《非参数统计》第35页例子现在用一个例子来说明如何应用Wilcoxon符号秩检验,并表明它和符号检验在解决同样的位置参数检验问题时的不同。
下面是亚洲十个国家1966年的每1000新生儿中的(按从小到大次序排列)死亡数(按世界银行:“世界发展指标”,1998)国家每1000新生儿中的死亡数日本 4以色列 6韩国9斯里兰卡15叙利亚31中国33伊朗36印度65孟加拉国77巴基斯坦88这里想作两个检验作为比较。
一个是H0:M≥34H1:M<34,另一个是H0:M≤16H1:M>16。
之所以作这两个检验是因为34和16在这一列数中的位置是对称的,如果用符号检验,结果也应该是对称的。
现在来看Wilcoxon符号秩检验和符号检验有什么不同,先把上面的步骤列成表:上面的Wilcoxon 符号秩检验在零假设下的P-值可由n 和W 查表得到,该P-值也可以由计算机统计软件把数据和检验目标输入后直接得到。
从上面的检验结果可以看出,在符号检验中,两个检验的p-值都是一样的(等于0.3770)不能拒绝任何一个零假设。
而利用Wilcoxon 符号秩检验,不能拒绝H 0:M ≥34,但可以拒绝H 0:M ≤16。
理由很明显。
34和16虽然都是与其最近端点间隔4个数(这也是符号检验结果相同的原因),但34到它这边的4个数的距离(秩)之和(为W=29)远远大于16到它那边的4个数的距离之和(为W=10)。
所以说Wilcoxon 符号秩检验不但利用了符号,还利用了数值本身大小所包含的信息。
当然,Wilcoxon 符号秩检验需要关于总体分布的对称性和连续性的假定。
详细计算过程Wilcoxon 符号秩检验亚洲十国,每千人婴儿中的死亡数为:4、6、9、15、33、31、36、65、77、88 假设检验:16:0=D M H ;16:<-D M H手算xD=x-16D 的绝对值D 的秩符号 4 -12 12 4 - 6 -10 10 3 - 9 -7 7 2 - 15 -1 1 1 - 31 15 15 5 + 33 17 17 6 + 36 20 20 7 + 65 49 49 8 + 77 61 61 9 + 88 727210+由D 的符号和D 绝对值的秩可以算得:101234=+++=-T 451098756=+++++=+T根据n=10,45=+T 查表得到+T 的右尾概率为P=0.042,由于P<0.05,因此拒绝0H 。

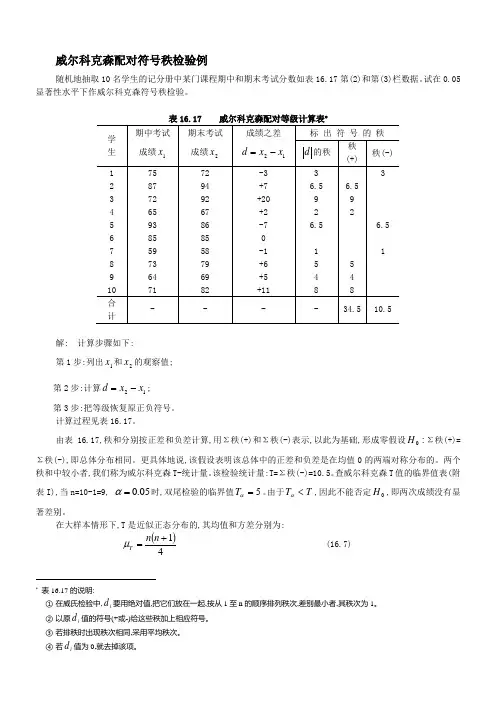
威尔科克森配对符号秩检验例随机地抽取10名学生的记分册中某门课程期中和期末考试分数如表16.17第(2)和第(3)栏数据。
试在0.05显著性水平下作威尔科克森符号秩检验。
表16.17 威尔科克森配对等级计算表*解: 计算步骤如下:第1步:列出1x 和2x 的观察值; 第2步:计算12x x d -=; 第3步:把等级恢复原正负符号。
计算过程见表16.17。
由表16.17,秩和分别按正差和负差计算,用Σ秩(+)和Σ秩(-)表示,以此为基础,形成零假设:0H Σ秩(+)=Σ秩(-),即总体分布相同。
更具体地说,该假设表明该总体中的正差和负差是在均值0的两端对称分布的。
两个秩和中较小者,我们称为威尔科克森T-统计量。
该检验统计量:T=Σ秩(-)=10.5。
查威尔科克森T 值的临界值表(附表I),当n=10-1=9, 05.0=α时,双尾检验的临界值5=αT 。
由于T T <α,因此不能否定0H ,即两次成绩没有显著差别。
在大样本情形下,T 是近似正态分布的,其均值和方差分别为:()41+=n n T μ (16.7)*表16.17的说明:① 在威氏检验中,i d 要用绝对值,把它们放在一起,按从1至n 的顺序排列秩次,差别最小者,其秩次为1。
② 以原i d 值的符号(+或-)给这些秩加上相应符号。
③ 若排秩时出现秩次相同,采用平均秩次。
④ 若i d 值为0,就去掉该项。
()()241212++=n n n T σ (16.8)因此,我们可以计算: TTT T z σμ-= (16.9)。

W i l c o o n符号秩检验吴喜之例子文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]吴喜之《非参数统计》第35页例子现在用一个例子来说明如何应用Wilcoxon符号秩检验,并表明它和符号检验在解决同样的位置参数检验问题时的不同。
下面是亚洲十个国家1966年的每1000新生儿中的(按从小到大次序排列)死亡数(按世界银行:“世界发展指标”,1998)这里想作两个检验作为比较。
一个是H0:M≥34?H1:M<34,另一个是H0:M≤16?H1:M>16。
之所以作这两个检验是因为34和16在这一列数中的位置是对称的,如果用符号检验,结果也应该是对称的。
现在来看Wilcoxon符号秩检验和符号检验有什么不同,先把上面的步骤列成表:上面的Wilcoxon符号秩检验在零假设下的P-值可由n和W查表得到,该P-值也可以由计算机统计软件把数据和检验目标输入后直接得到。
从上面的检验结果可以看出,在符号检验中,两个检验的p-值都是一样的(等于)不能拒绝任何一个零假设。
而利用Wilcoxon符号秩检验,不能拒绝H0:M≥34,但可以拒绝H0:M≤16。
理由很明显。
34和16虽然都是与其最近端点间隔4个数(这也是符号检验结果相同的原因),但34到它这边的4个数的距离(秩)之和(为W=29)远远大于16到它那边的4个数的距离之和(为W=10)。
所以说Wilcoxon符号秩检验不但利用了符号,还利用了数值本身大小所包含的信息。
当然,Wilcoxon 符号秩检验需要关于总体分布的对称性和连续性的假定。
详细计算过程Wilcoxon 符号秩检验亚洲十国,每千人婴儿中的死亡数为:4、6、9、15、33、31、36、65、77、88 假设检验:16:0=D M H ;16:<-D M H手算由D 的符号和D 绝对值的秩可以算得:根据n=10,45=+T 查表得到+T 的右尾概率为P=,由于P<,因此拒绝0H 。


第二节Wilcoxon符号秩检验Wilcoxon符号秩检验符号检验只用了差的符号,但没有利用差值的大小。
12 3Wilcoxon符号秩检验(Wilcoxon signed-rank test) 把差的绝对值的秩分别按照不同的符号相加作为其检验统计量。
显然,相比较于符号检验,Wilcoxon符号秩检验利用了更多的信息。
Wilcoxon符号秩检验:条件u Wilcoxon符号秩检验需要一点总体分布的性质;它要求假定样本点来自连续对称总体分布;而符号检验不需要知道任何总体分布的性质。
u在对称分布中,总体中位数和总体均值是相等的;因此,对于总体中位数的检验,等价于对于总体均值的检验。
u Wilcoxon符号秩检验实际是对对称分布的总体中位数(或均值)的检验。
Wilcoxon符号秩检验:基本原理u计算差值绝对值的秩。
u分别计算出差值序列里正数的秩和(W+)以及负数的秩和(W-)。
u如果原假设成立,W+与W-应该比较接近。
如果W+和W-过大或过小,则说明原假设不成立。
u将正数的秩和或者负数的秩作为检验统计量,根据其统计分布计算p值,从而可以得出检验的结论。
具体步骤设定原假设和备择假设。
分别计算出差值序列中正数的秩和W+以及负数的秩和W-。
根据W+和W-建立检验统计量,计算p值并得出检验的结论。
在双侧检验中检验统计量可以取为W=min(W+,W-)。
显然,如果原假设成立,W+与W-应该比较接近。
如果二者过大或过小,则说明原假设不成立。
秩的计算注意问题计算差值绝对值的秩时,注意差值等于0值不参与排序。
下面一行R i就是上面一行数据Z i的秩。
Z i159183178513719 R i75918426310数据中相同的数值称为“结”。
结中数字的秩为它们所占位置的平均值Z i159173178513719 R i758.518.5426310关于P值u有了检验统计量W,我们就可根据其统计分布计算p值了,双侧检验的p值等于,式中w为检验统计量的样本观测值。
威尔科克森符号秩检验计算公式威尔科克森符号秩检验是一种非参数检验方法,常用于比较两组相关样本的中位数是否存在显著差异。
它的计算公式包括了多个步骤,涉及到符号的排序、秩次的计算和统计量的计算等。
在本文中,我将按照你提供的要求,从深度和广度两个方面来全面评估威尔科克森符号秩检验的计算公式,并进行详细的阐述和分析。
让我们来探讨威尔科克森符号秩检验的计算公式。
威尔科克森符号秩检验的计算公式主要包括以下几个步骤:1. 符号的确定:对样本数据进行两两比较,根据差值的正负情况确定符号,即正差记为“+”,负差记为“-”,零差记为“0”。
2. 符号排序:对确定的符号进行排序,然后依次给符号排名,得到符号的秩次。
3. 统计量的计算:根据得到的符号秩次,计算出用于检验的统计量,进而进行假设检验。
在这个过程中,每一个步骤都凝聚着丰富的统计学原理和实际应用背景,需要我们对统计学原理和计算方法有较为全面的理解。
通过对计算公式的深入分析,我们可以更好地理解威尔科克森符号秩检验方法的原理和应用,为进一步的研究和实践提供坚实的基础。
接下来,我们将以“威尔科克森符号秩检验计算公式”为主题,深入探讨其理论和实践应用,并按照从简到繁、由浅入深的方式来展开阐述。
1. 理论基础:威尔科克森符号秩检验的理论基础是非参数统计学中的重要内容,包括了符号的秩次计算、秩和的比较、假设检验等基本理论。
这一部分将围绕着统计学中的基本概念展开,帮助读者建立起对理论基础的全面理解。
2. 计算公式:在理论基础的基础上,我们将详细介绍威尔科克森符号秩检验的计算公式,并通过实例进行演示,以帮助读者深入理解每一步计算的具体方法和意义。
这一部分将包括符号的排序方法、秩次的计算公式以及统计量的计算方法等内容。
3. 实践应用:我们将结合实际案例,以及你的个人观点和理解,探讨威尔科克森符号秩检验的实践应用。
这一部分将帮助读者将理论知识与实际问题相结合,为他们在实际工作中灵活运用威尔科克森符号秩检验方法提供参考和指导。
Wilcoxon秩和检验在审计推理中的应用研究杨玲玲【摘要】为了在有限时间内以合理的成本完成审计工作,审计抽样应运而生,同时也制造出了统计与审计学科间互相渗透的机缘.在实质性测试阶段,审计人员常常需要对被审计单位某类交易或账户余额是否存在错报作出判断,这时,统计分析方法便有其用武之地.本文针对被审计单位账面金额与审定金额间的差异提出一种非参数检验方法—Wilcoxon秩和检验.非参数检验不涉及描述总体分布的有关参数,仅从样本数据的秩特征来推断总体情况.本文在介绍秩和检验方法之余,通过实例分析秩和检验方法在审计推断中的应用,以期提高审计人员的工作效率,防范审计风险.【期刊名称】《中国注册会计师》【年(卷),期】2013(000)007【总页数】6页(P82-87)【关键词】Wilcoxon秩和检验;审计推断;审计风险;审计效率【作者】杨玲玲【作者单位】天津财经大学【正文语种】中文国内现有关于审计抽样的研究多注重于统计抽样方法的介绍及样本规模的确定,对于如何进行总体推断也主要是运用参数估计的方法,关于将统计中的检验方法应用于审计抽样工作的研究并不多,如王芳、王景东(2010)就曾研究将统计假设检验应用于审计抽样工作,这样的研究对于学科间的交叉渗透有重要意义,值得相关学者们继续探讨。
统计中的假设检验可以应用于检验审计人员关于错报存在与否的判断是否正确,但一般意义上的假设检验通常都需要这样的前提,即总体分布相关参数已知,如均值或方差等。
而实际工作中在评价总体之前很多时候并不能确切获得关于总体分布的信息,这种情况下若仍采用这样的假设检验来判断未免有失公允。
因此本文引入Wilcoxon秩和检验这一非参数检验方法,即使总体分布情况未知,也可以通过样本信息来把握总体情况。
在整理和分析被审计单位数据资料时,审计人员常常会用到统计分析方法。
审计抽样是指审计人员对具有审计相关性的总体中低于百分之百的项目实施审计程序,使所有抽样单元都有被选取的机会,为审计人员针对总体得出结论提供合理基础。
吴喜之《非参数统计》第35页例子
现在用一个例子来说明如何应用Wilcoxon符号秩检验,并表明它和符号检验在解决同样的位置参数检验问题时的不同。
下面是亚洲十个国家1966年的每1000新生儿中的(按从小到大次序排列)死亡数(按世界银行:“世界发展指标”,1998)
:M≥34?H1:M<34,
这里想作两个检验作为比较。
一个是H
另一个是H
:M≤16?H1:M>16。
之所以作这两个检验是因为34和16在这一列数中的位置是对称的,如果用符号检验,结果也应该是对称的。
现在来看Wilcoxon符号秩检验和符号检验有什么不同,先把上面的步骤列成表:
上面的Wilcoxon符号秩检验在零假设下的P-值可由n和W查表得到,该P-值也可以由计算机统计软件把数据和检验目标输入后直接得到。
从上面的检验结果可以看出,在符号检验中,两个检验的p-值都是一样的(等于0.3770)不能
:M≥34,但可拒绝任何一个零假设。
而利用Wilcoxon符号秩检验,不能拒绝H
:M≤16。
理由很明显。
34和16虽然都是与其最近端点间隔4个数(这以拒绝H
也是符号检验结果相同的原因),但34到它这边的4个数的距离(秩)之和(为W=29)远远大于16到它那边的4个数的距离之和(为W=10)。
所以说Wilcoxon 符号秩检验不但利用了符号,还利用了数值本身大小所包含的信息。
当然,Wilcoxon符号秩检验需要关于总体分布的对称性和连续性的假定。
详细计算过程
Wilcoxon符号秩检验
亚洲十国,每千人婴儿中的死亡数为:4、6、9、15、33、31、36、65、77、88
假设检验:16:0=D M H ;16:<-D M H 手算
由D 的符号和D 绝对值的秩可以算得:
根据n=10,45=+T 查表得到+T 的右尾概率为P=0.042,由于P<0.05,因此拒绝0H 。
SPSS
Ranks
N
Mean Rank
Sum of Ranks
死亡数 - 常数 Negative Ranks
4a 2.50 10.00 Positive Ranks 6b
7.50
45.00
Ties
0c Total
10
a. 死亡数 < 常数
b. 死亡数 > 常数
Ranks
N Mean Rank Sum of Ranks 死亡数- 常数Negative Ranks 4a 2.50 10.00 Positive Ranks 6b7.50 45.00
Ties
0c
Total
10
a. 死亡数< 常数
c. 死亡数= 常数
Test Statistics b
死亡数- 常数
Z -1.784a
Asymp. Sig. (2-tailed) .074
Exact Sig. (2-tailed) .084
Exact Sig. (1-tailed) .042
Point Probability .010
a. Based on negative ranks.
b. Wilcoxon Signed Ranks Test
P值为0.042小于显着性水平0.05,故拒绝
H。
SAS
data a;
input id x;
cards;
1 4
2 6
3 9
4 15
5 31
6 33
7 36
8 65
9 77
10 88
run;
proc univariate mu0=16;
var x;
run;
UNIVARIATE 过程
变量: x
矩
N 10 权重总和10
均值36.4 观测总
和364
标准偏差30.4638219 方差928.044444
偏度峰度-0.9927987
未校平方和21602 校正平方和8352.4
变异系数83.6918184 标准误
差均值
基本统计测度
位置
变异性
均值36.40000 标准偏差30.46382
中位数32.00000 方差928.04444
众数. 极差
84.00000
四分位极差56.00000
位置检验: Mu0=16
检验--统计量--- -------P 值-------
学生t t 2.117609 Pr > |t| 0.0633
符号M 1 Pr >= |M| 0.7539
符号秩S 17.5
Pr >= |S| 0.0840
分位数(定义5)
分位数估计值
100% 最大值
88.0
99%
88.0
95%
88.0
90%
82.5
75% Q3
65.0
50% 中位数
32.0
25% Q1
9.0
10%
5.0
5%
4.0
1%
4.0
0% 最小值
4.0
极值观测
---最小值--- ---最大值---
值观测值
观测
4 1 33
6
6 2 36
7
9 3 65
8
15 4 77
9
31 5 88 10
得到符号秩检验的双侧概率为0.0840,则单侧概率P=0.0420,,小于显着性水平0.05,故拒绝
H
Wilcoxon检验
亚洲十国新生儿死亡率的Wilcoxon符号秩检验:
在这里假定亚洲十国新生儿死亡率是对称性分布。
建立假设组为:
:M≥34?H1:M<34
H
为做出判定,需要计算T+、T-,计算过程见下表
T+=2+8+9+10=29
T-=10(10+1)/2-29=26
根据n=10,T+=29查表,得到T+的右尾概率为0.461>0.05,因此数据支持了原假设,即亚洲十国新生儿死亡率可以认为是千分之34. 下面是SPSS输出结果:
Ranks
N Mean Rank Sum of Ranks
X - M0 Negative Ranks 6a 4.33 26.00
Positive Ranks 4b7.25 29.00
Ties
0c
Total
10
a. X < M0
b. X > M0
c. X = M0
Test Statistics b
X - M0
Z -.153a
Asymp. Sig. (2-tailed) .878
Exact Sig. (2-tailed) .922
Exact Sig. (1-tailed) .461
Point Probability .038
a. Based on negative ranks.
b. Wilcoxon Signed Ranks Test
R程序:
x<-c(4,6,9,15,33,31,36,65,77,88)
wilcox.test(x, mu=34, alternative="greater",exact=TRUE,correct=FALSE,
conf.int=TRUE)
R输出结果:
Wilcoxon signed rank test
data: x
V = 29, p-value = 0.4609
alternative hypothesis: true location is greater than 34
95 percent confidence interval:
17.5 Inf
sample estimates:
(pseudo)median
34.5
SAS输出结果:
data x;
input x;
cards;
-30
-28
-25
-19
-1
-3
2
31
43
54
;
run;
proc univariate data=x;
var x;
run;
[文档可能无法思考全面,请浏览后下载,另外祝您生活愉快,工作顺利,万事如意!]。