力的分解公开课讲解
- 格式:ppt
- 大小:1.56 MB
- 文档页数:19



《力的分解》讲义一、什么是力的分解在我们的日常生活和物理学的研究中,经常会遇到一个力产生多个效果的情况。
为了更清晰地理解和分析这种现象,就引入了力的分解这一重要概念。
力的分解,简单来说,就是将一个已知力按照特定的要求分解为两个或多个分力。
这些分力的合力应该等于原来的那个已知力。
比如说,一个斜向上拉物体的力,可以分解为一个水平方向的力和一个竖直方向的力。
这两个分力共同的作用效果,与那个斜向上的拉力是相同的。
二、力的分解的原则力的分解并不是随意进行的,而是遵循一定的原则。
1、平行四边形定则这是力的分解最基本的原则。
如果已知一个力 F 作为平行四边形的对角线,那么从力 F 的作用点出发,就可以作出两个邻边,这两个邻边就代表了力 F 的两个分力 F1 和 F2 。
2、按照实际效果分解根据力所产生的实际效果来确定分力的方向。
比如,放在斜面上的物体受到的重力,可以分解为沿斜面下滑的力和垂直斜面压斜面的力,因为重力在斜面上产生了这两个实际的效果。
三、力的分解的方法1、正交分解法这是一种非常常用的方法。
先建立一个直角坐标系,然后将已知力沿着坐标轴分解为相互垂直的两个分力。
通常选择让较多的力落在坐标轴上,这样可以简化计算。
例如,一个物体受到多个力的作用,我们可以将这些力分别投影到x 轴和 y 轴上,然后分别计算 x 轴和 y 轴上的合力。
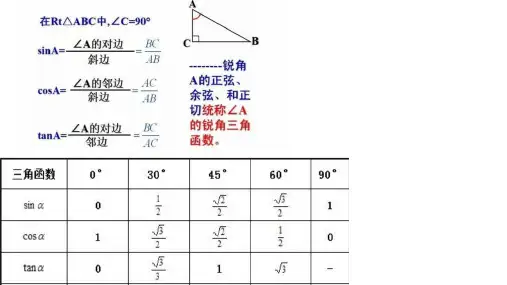
2、按角度分解当已知力与某一方向的夹角时,可以利用三角函数来分解力。
比如,已知力 F 与水平方向的夹角为θ ,那么水平方向的分力 Fx =F cosθ ,竖直方向的分力 Fy =F sinθ 。
四、力的分解的应用1、桥梁设计在桥梁的建设中,需要考虑桥梁所承受的各种力,如重力、车辆的压力等。
通过力的分解,可以计算出桥梁各个部分所承受的力的大小和方向,从而确保桥梁的结构安全。
2、机械运动分析在分析机械的运动和受力情况时,力的分解起着关键作用。
比如,对于一个在斜面上运动的物体,通过力的分解可以知道物体所受的合力,进而分析它的加速度和运动状态。




公开课《力的分解》在我们的日常生活中,力无处不在。
从抬起一杯水到推动一辆汽车,从运动员的跳跃到起重机吊起重物,力的作用影响着我们的一举一动。
而要深入理解力的作用效果,就不得不提到力的分解这一重要的物理概念。
让我们先来想象这样一个场景:一个重物被一根绳子悬挂在天花板上,静止不动。
此时,绳子对重物施加了一个向上的拉力。
那么,这个拉力的效果仅仅是向上提起重物吗?其实不然,从力的分解的角度来看,这个拉力可以被分解为两个相互垂直的分力。
力的分解,简单来说,就是将一个已知力按照我们的需求分解为两个或多个分力。
为什么要进行力的分解呢?这是因为在很多实际问题中,一个力的作用效果往往比较复杂,直接研究这个力不太方便。
通过分解,我们可以将其转化为几个更简单、更易于分析和处理的分力,从而更好地理解和解决问题。
那如何进行力的分解呢?这就需要遵循一定的原则。
通常情况下,我们会按照力的实际作用效果来进行分解。
比如,在刚才提到的重物悬挂的例子中,我们可以将绳子的拉力沿着水平和竖直方向分解。
竖直方向的分力与重物的重力相平衡,使重物保持静止;水平方向的分力则使绳子产生了拉伸的趋势。
再来看一个例子,一个人在斜面上拉着一个物体向上运动。
在这个情境中,拉力的作用效果不仅是向上拉动物体,还有使物体沿斜面方向前进的效果。
我们可以将拉力分解为一个沿斜面向上的分力和一个垂直于斜面的分力。
沿斜面向上的分力克服物体与斜面之间的摩擦力和重力沿斜面方向的分力,从而使物体能够向上运动;垂直于斜面的分力则影响物体对斜面的压力大小。
在力的分解过程中,我们还需要用到一些数学知识,比如三角函数。
通过三角函数的关系,我们可以计算出各个分力的大小。
假设已知一个力的大小为 F,与某一方向的夹角为θ,那么在这个方向上的分力大小就可以通过Fcosθ 来计算,与之垂直方向上的分力大小则为Fsinθ 。
力的分解在实际生活中的应用非常广泛。
比如,在建筑施工中,工人使用起重机吊起重物时,就需要考虑力的分解,以确保起重机的钢索能够承受住重物的重量,并且保证吊起的过程平稳安全。


人教版《物理》(必修一)第三章相互作用第五节力的分解2019.11教材分析:力的分解与力的合成是解决物理问题的一种方法,平行四边形定则(或三角形定则)是矢量运算的工具,它们是高中物理的基石。
本节内容介绍力的分解同样遵守平行四边形定则。
通过例题让学生知道一个已知力可根据实际作用效果来进行分解,最后指出矢量相加的法则—平行四边形定则或三角形定则。
教学对象分析:对刚进入高中的学生,仍处于从形象思维向抽象逻辑思维的过渡时期,分析能力、概括能力、作图能力、运用数学知识解决物理问题的能力有待培养。
学生对于本节内容的困惑主要有:分力是否真实存在?如何正确分解一个已知力?学生对物理量的矢量意识还有待加强。
教学目标:知识与技能1.了解分力的概念,明白力的分解是力的合成的逆运算。
2.会用平行四边形定则作图并能计算。
3.能用力的分解分析生产生活中的问题。
过程与方法1.强化“等效替代”的思想。
2.掌握根据力的作用效果进行分解的方法。
情感态度与价值观培养学生观察、分析、概括能力。
培养学生将所学知识应用于生产实践的意识和习惯。
课时安排1课时教学重点、难点1.理解力的分解是力的合成的逆运算,利用平行四边形进行力的分解。
2.根据力的作用效果来确定分力。
如何判断力的作用效果?依据如下:学生在物理情境变化时,不能自觉应用“等效思想”解决问题。
虽然已学“力的合成”,但对“分力是否真实存在?如何正确分解一个已知力?”会感到困惑。
因此在“等效思想”上理解力的分解是力的合成的逆运算应是教学重点。
按力的作用效果来分解一个力学生往往感到抽象,如何判断力的作用效果这是教学难点。
教学策略与手段首先以提起木块简要复习力的合成,通过一个小游戏引入新课,激发起学生学习新课的兴趣。
由于学生初次接触力的分解知识,引入从学生熟悉的直观事例—拉橡皮筋出发,使学生在已有的合力、力的合成基础上学习分力和力的分解,通过知识的前后比较,更容易接受和理解分力、合力的等效性。