(完整word版)小学奥数解题方法大全

小学奥数解题方法小学奥数解题方法奥数解题方法1有甲、乙、丙三种货物。

如果买甲3件，乙7件，丙1件，共花去3.15元;如果买甲4件，乙10件，丙1件，共花去4.20元。

现在买甲、乙、丙各1件，需要花多少钱？买甲3件，乙7件，丙1件，花3.15元①买甲4件，乙10件，丙1件，花4.20元②要想求出买甲1件，乙1件，丙1件，共需花多少钱，必须使上述①与②中对应的“件数”相差1。

为此，可转化已知条件：将条件①中的每个量都扩大3倍，得：买甲9件，乙21件，丙3件，花9.45元③将条件②中的每个量都扩大2倍，得：买甲8件，乙20件，丙2件，花8.40元④所以，买甲、乙、丙各一件，共需要花的钱数为9.45—8.40=1.05（元）小学奥数解题方法2深圳小学奥数解题方法2——化大为小找规律对于一些较复杂或数目较大的问题，如果一时感到无从下手，我们不妨把问题尽量简单化，在不改变问题性质的前提下，考虑问题最简单的情况(化大为小)，从中分析探寻出问题的规律，以获得问题的答案。

这就是解数学题常用的一种方法，叫做归纳，我们也可以叫做“化大为小找规律”。

10条直线最多可把一个长方形分成多少块?提示：先不考虑10条直线，而是先看1条、2条、3条直线能把一个长方形分成几块?10条直线最多可把一个长方形分成多少块?第一条直线：分成 2 块第二条直线：分成 2+2=4 块第三条直线：分成 2+2+3=7 块10条直线最多可把一个长方形分成多少块?我们发现这样的规律：=2+(2+3+4+5+6+7+8+9+10)=2+54=56(块)这就是说，10条直线可把长方形分为56块。

小学奥数解题方法3小学奥数解题方法——分类分类是一种很重要的数学思考方法，特别是在计数、数个数的问题中，分类的方法是很常用的。

可分为这样几类：(1)以A为左端点的线段共4条，分别是：AB，AC，AD，AE;(2)以B为左端点的线段共3条，分别是：BC，BD，BE;(3)以C为左端点的线段共2条，分别是：CD，CE;(4)以D为左端点的线段有1条，即DE。

奥数解题方法总结
1、形象化画图法：解奥数题时，如果可以科学合理的、科学合理的、巧妙地依靠点、线、面、图、表将小学奥数难题形象化形象的展示出来，将抽象的数量关系具象化，可让学生们非常容易弄清数量关系，沟通交流“”与“”的联系，把握住问题的本质，快速答题
2、倒推法：从题目上述的最后结果考虑，运用标准一步一步向前反推，直至题目中难题及时解决。

3、枚举法：奥数题中常常出现一些数量关系十分特殊题目，用普通的办法难以列式解释，有时候压根列出不来对应的式子来。

人们用枚举法，依据题目的需求，一一列举压根符合要求的数据信息，随后从这当中筛出符合要求的回答。

4、正难那样反：有一些数学题目假如你从标准正脸考虑考虑到有困难，那么你可以更改思考的方位，从结论或问题的背面考虑来考虑事情，使难题及时解决。

5、恰当转化：在解奥数题时，经常要提醒自己，碰到的新问题能不能转化成旧解决问题，化新为旧，通过表面，把握住难题的实质，把问题转化成自身熟悉的难题去解释。

转化的种类有条件转化、难题转化、关联转化、图形转化等。

整体掌握：有一些奥数题，从细节上考虑到，很复杂，也没有必要，如果可以从整体上掌握，宏观上考虑到，根据研究问题的整体方式、整体结构、一部分与整体的相互关系，“只看见山林，看不到花草树木”，来求取问题的解决。

小学奥数解题方法完整版一、引言小学奥数是培养孩子数学思维和解题能力的重要途径。

在面对各种题型和难度的奥数题目时，学生需要了解正确的解题方法。

本文将介绍小学奥数常见的解题方法，帮助学生更好地应对奥数考试。

二、奥数解题方法1. 四则运算四则运算是小学奥数题目中最基本的类型。

在解题时，需要掌握加法、减法、乘法和除法的运算规则。

此外，学生还需了解运算顺序，即先乘除后加减。

2. 分数运算分数运算在小学奥数中也是常见的题型。

在解决分数运算题时，可以使用找最小公倍数、通分、约分等方法来简化计算过程。

同时，还需要熟练掌握分数的加减乘除规则。

3. 算式变换奥数题目中常会涉及算式的变换。

在解题时，可以通过交换律、结合律、分配律等运算法则，将原始算式转化为更简单的形式。

这样能够加快解题速度，提高解题效率。

4. 排列组合排列组合是奥数中的重要概念。

当遇到排列组合问题时，可以运用阶乘、组合数等数学方法来求解。

同时，可以通过画图、列式等方式辅助理解问题，找到更简洁的解题方法。

5. 逻辑推理逻辑推理题目在小学奥数中也经常出现。

解决这类题目时，学生需要运用逻辑思维和分析能力。

可以通过分情况讨论、排除法等方式来找到正确答案。

6. 图形推理图形推理题是小学奥数中较为复杂的题型之一。

解决这类题目需要运用几何知识和图形分析能力。

学生可以通过观察图形的形状、对称性、旋转等特点，找到规律并推理出正确答案。

三、解题技巧除了上述的解题方法外，还有一些解题技巧可以帮助学生更好地解决奥数题目。

1. 多做题目做更多的奥数题目有助于提高解题能力和熟练度。

通过大量练习，学生可以熟悉各类题型的解题方法，掌握常用的技巧和思路。

2. 学会总结每次做完一道题目后，及时总结解题过程中使用的方法和思路。

这样可以帮助学生记住解题思路并且提高解题能力。

3. 理解题意在解题过程中，要仔细阅读题目，理解其中的条件和要求。

只有正确理解题意，才能有针对性地运用相应的解题方法。

【导语】解奥数题时，如果能合理的、科学的、巧妙的借助点、线、⾯、图、表将奥数问题直观形象的展⽰出来，将抽象的数量关系形象化，可使同学们容易搞清数量关系，沟通“已知”与“未知”的联系，抓住问题的本质，迅速解题。

以下是整理的《⼩学⽣奥数解题⽅法⼤全》相关资料，希望帮助到您。

⼩学⽣奥数解题⽅法篇⼀ 尝试法： 解应⽤题时，按照⾃⼰认为可能的想法，通过尝试，探索规律，从⽽获得解题⽅法，叫做尝试法。

尝试法也叫“尝试探索法”。

⼀般来说，在尝试时可以提出假设、猜想，⽆论是假设或猜想，都要⽬的明确，尽可能恰当、合理，都要知道在假设、猜想和尝试过程中得到的结果是什么，从⽽减少尝试的次数，提⾼解题的效率。

在9只规格相同的⼿镯中混有1只较重的假⼿镯。

在⼀架没有砝码的天平上，最多只能称两次，你能把假⼿镯找出来吗？（适于三年级程度） 解：先把9只⼿镯分成A、B、C三组，每组3只。

①把A、B两组放在天平左右两边的秤盘上，如果平衡，则假的1只在C组⾥；若不平衡，则哪组较重，假的就在哪组⾥。

②再把有假⼿镯的那组中的两只分别放在天平的左右秤盘上。

如果平衡，余下的1只是假的；若不平衡，较重的那只是假的。

⼩学⽣奥数解题⽅法篇⼆ 观察法： 在解答数学题时，第⼀步是观察。

观察是基础，是发现问题、解决问题的⾸要步骤。

⼩学数学教材，特别重视培养观察⼒，把培养观察⼒作为开发与培养学⽣智⼒的第⼀步。

观察法，是通过观察题⽬中数字的变化规律及位置特点，条件与结论之间的关系，题⽬的结构特点及图形的特征，从⽽发现题⽬中的数量关系，把题⽬解答出来的⼀种解题⽅法。

观察要有次序，要看得仔细、看得真切，在观察中要动脑，要想出道理、找出规律。

看每⼀⾏的前三个数，想⼀想接下去应该填什么数。

（适于⼆年级程度）6、16、26、____、____、____、____。

9、18、27、____、____、____、____。

80、73、66、____、____、____、____。

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==小学数学奥数题解题技巧小学数学奥数题的解题方法有很多，掌握这些有效的方法，我们在小学数学奥数考试中就能有更好的表现。

因此，我们在复习小学数学奥数时，对这些重要方法一定要认真进行了解。

一起来看看吧。

1、直观画图法：解小学数学奥数题时，如果能合理的、科学的、巧妙的借助点、线、面、图、表将奥数问题直观形象的展示出来，将抽象的数量关系形象化，可使同学们容易搞清数量关系，沟通“已知”与“未知”的联系，抓住问题的本质，迅速解题。

2、倒推法：从题目所述的最后结果出发，利用已知条件一步一步向前倒推，直到题目中问题得到解决。

3、枚举法：奥数题中常常出现一些数量关系非常特殊的题目，用普通的方法很难列式解答，有时根本列不出相应的算式来。

我们可以用枚举法，根据题目的要求，一一列举基本符合要求的数据，然后从中挑选出符合要求的答案。

4、正难则反：有些数学问题如果你从条件正面出发考虑有困难，那么你可以改变思考的方向，从结果或问题的反面出发来考虑问题，使问题得到解决。

5、巧妙转化：在解奥数题时，经常要提醒自己，遇到的新问题能否转化成旧问题解决，化新为旧，透过表面，抓住问题的实质，将问题转化成自己熟悉的问题去解答。

转化的类型有条件转化、问题转化、关系转化、图形转化等。

6、整体把握：有些奥数题，如果从细节上考虑，很繁杂，也没有必要，如果能从整体上把握，宏观上考虑，通过研究问题的整体形式、整体结构、局部与整体的内在联系，“只见森林，不见树木”，来求得问题的解决。

第10讲假设法解题（一）一、知识要点假设法解体的思考方法是先通过假设来改变题目的条件，然后再和已知条件配合推算。

有些题目用假设法思考，能找到巧妙的解答思路。

运用假设法时，可以假设数量增加或减少，从而与已知条件产生联系；也可以假设某个量的分率与另一个量的分率一样，再根据乘法分配律求出这个分率对应的和，最后依据它与实际条件的矛盾求解。

二、精讲精练【例题1】甲、乙两数之和是185，已知甲数的1/4与乙数的1/5的和是42，求两数各是多少？【思路导航】假设将题中“甲数的1/4”、“乙数的1/5”与“和为42”同时扩大4倍，则变成了“甲数与乙数的4/5的和为168”，再用185减去168就是乙数的1/5。

解：乙：（185－42×4）÷（1－1/5×4）＝85答：甲数是100，乙数是85。

练习1：1．甲、乙两人共有钱150元，甲的1/2与乙的1/10的钱数和是35元，求甲、乙两人各有多少元钱？2．甲、乙两个消防队共有338人。

抽调甲队人数的1/7，乙队人数的1/3，共抽调78人，甲、乙两个消防队原来各有多少人？3．海洋化肥厂计划第二季度生产一批化肥，已知四月份完成总数的1/3多50吨，五月份完成总数的2/5少70吨，还有420吨没完成，第二季度原计划生产多少吨？【例题2】彩色电视机和黑白电视机共250台。

如果彩色电视机卖出1/9，则比黑白电视机多5台。

问：两种电视机原来各有多少台？【思路导航】从图中可以看出：假设黑白电视机增加5台，就和彩色电视机卖出1/9后剩下的一样多。

黑白电视机增加5台后，相当于彩色电视机的（1－1/9）＝ 8/9。

（250+5）÷（1+1－1/9）＝135（台）250－125＝115（台）答：彩色电视机原有135台，黑白电视机原有115台。

练习2：1．姐妹俩养兔120只，如果姐姐卖掉1/7，还比妹妹多10只，姐姐和妹妹各养了多少只兔？2．学校有篮球和足球共21个，篮球借出1/3后，比足球少1个，原来篮球和足球各有多少个？3．小明甲养的鸡和鸭共有100只，如果将鸡卖掉1/20，还比鸭多17只，小明家原来养的鸡和鸭各有多少只？【例题3】师傅与徒弟两人共加工零件105个，已知师傅加工零件个数的3/8与徒弟加工零件个数的4/7的和为49个，师、徒各加工零件多少个？【思路导航】假设师、徒两人都完成了4/7，一个能完成（105×4/7）＝60个，和实际相差（60－49）＝11个，这11个就是师傅完成将零件的3/8与完成加工零件的4/7相差的个数。

小学奥数11种解题方法1、对照法如何正确地理解和运用数学概念？小学数学常用的方法就是对照法。

根据数学题意，对照概念、性质、定律、法则、公式、名词、术语的含义和实质，依靠对数学知识的理解、记忆、辨识、再现、迁移来解题的方法叫做对照法。

这个方法的思维意义就在于，训练学生对数学知识的正确理解、牢固记忆、准确辨识。

例1：三个连续自然数的和是18，则这三个自然数从小到大分别是多少？对照自然数的概念和连续自然数的性质可以知道：三个连续自然数和的平均数就是这三个连续自然数的中间那个数。

例2：判断题：能被2除尽的数一定是偶数。

这里要对照“除尽”和“偶数”这两个数学概念。

只有这两个概念全理解了，才能做出正确判断。

2公式法运用定律、公式、规则、法则来解决问题的方法。

它体现的是由一般到特殊的演绎思维。

公式法简便、有效，也是小学生学习数学必须学会和掌握的一种方法。

但一定要让学生对公式、定律、规则、法则有一个正确而深刻的理解，并能准确运用。

例3：计算59×37+12×59+5959×37+12×59+59＝59×(37+12+1)…………运用乘法分配律＝59×50…………运用加法计算法则＝(60-1)×50…………运用数的组成规则＝60×50－1×50…………运用乘法分配律＝3000-50…………运用乘法计算法则＝2950…………运用减法计算法则3比较法通过对比数学条件及问题的异同点，研究产生异同点的原因，从而发现解决问题的方法，叫比较法。

比较法要注意：(1)找相同点必找相异点，找相异点必找相同点，不可或缺，也就是说，比较要完整。

(2)找联系与区别，这是比较的实质。

(3)必须在同一种关系下(同一种标准)进行比较，这是“比较”的基本条件。

(4)要抓住主要内容进行比较，尽量少用“穷举法”进行比较，那样会使重点不突出。

(5)因为数学的严密性，决定了比较必须要精细，往往一个字，一个符号就决定了比较结论的对或错。

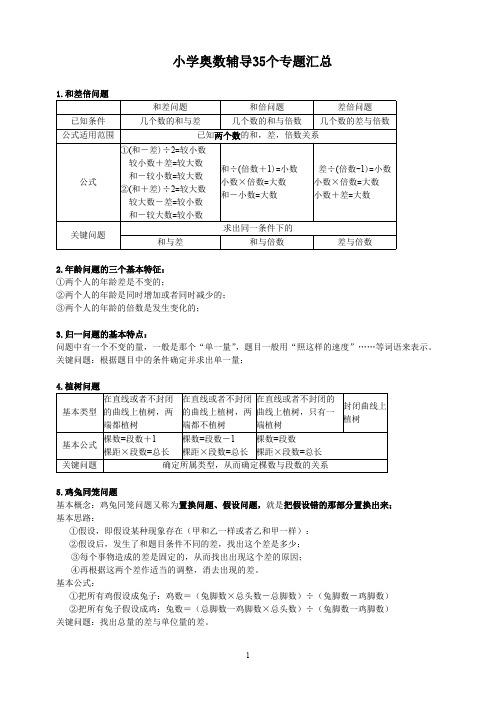
6.盈亏问题基本概念：一定量的对象，按照某种标准分组，产生一种结果：按照另一种标准分组，又产生一种结果，由于分组的标准不同，造成结果的差异，由它们的关系求对象分组的组数或对象的总量．基本思路：先将两种分配方案进行比较，分析由于标准的差异造成结果的变化，根据这个关系求出参加分配的总份数，然后根据题意求出对象的总量．基本题型：①一次有余数，另一次不足；基本公式：总份数＝（余数＋不足数）÷两次每份数的差②当两次都有余数；基本公式：总份数＝（较大余数一较小余数）÷两次每份数的差③当两次都不足；基本公式：总份数＝（较大不足数一较小不足数）÷两次每份数的差基本特点：对象总量和总的组数是不变的。

关键问题：确定对象总量和总的组数。

7.牛吃草问题基本思路：假设每头牛吃草的速度为“1”份，根据两次不同的吃法，求出其中的总草量的差；再找出造成这种差异的原因，即可确定草的生长速度和总草量。

基本特点：原草量和新草生长速度是不变的；关键问题：确定两个不变的量。

基本公式：生长量=（较长时间×长时间牛头数-较短时间×短时间牛头数）÷（长时间-短时间）；总草量=较长时间×长时间牛头数-较长时间×生长量；8.周期循环与数表规律周期现象：事物在运动变化的过程中，某些特征有规律循环出现。

周期：我们把连续两次出现所经过的时间叫周期。

关键问题：确定循环周期。

闰年：一年有366天；①年份能被4整除；②如果年份能被100整除，则年份必须能被400整除；平年：一年有365天。

①年份不能被4整除；②如果年份能被100整除，但不能被400整除；9.平均数基本公式：①平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量÷平均数②平均数=基准数＋每一个数与基准数差的和÷总份数基本算法：①求出总数量以及总份数，利用基本公式①进行计算.②基准数法：根据给出的数之间的关系，确定一个基准数；一般选与所有数比较接近的数或者中间数为基准数；以基准数为标准，求所有给出数与基准数的差；再求出所有差的和；再求出这些差的平均数；最后求这个差的平均数和基准数的和，就是所求的平均数，具体关系见基本公式②10.抽屉原理抽屉原则一：如果把（n+1）个物体放在n个抽屉里，那么必有一个抽屉中至少放有2个物体。

小学奥数解题方法大全100道及答案(完整版)题目1：计算1 + 2 + 3 + 4 + …+ 100 的和。

解题方法：使用等差数列求和公式，首项为1，末项为100，公差为1，项数为100。

求和公式为：（首项+ 末项）×项数÷2 。

答案：(1 + 100) ×100 ÷2 = 5050题目2：鸡兔同笼，共有30 个头，88 只脚，求鸡兔各有多少只？解题方法：假设全是鸡，共有脚30×2 = 60 只，比实际少88 - 60 = 28 只。

因为每把一只兔当成鸡，就少算4 - 2 = 2 只脚，所以兔有28÷2 = 14 只，鸡有30 - 14 = 16 只。

答案：鸡16 只，兔14 只。

题目3：一条路长100 米，从头到尾每隔10 米栽1 棵梧桐树，共栽多少棵树？解题方法：因为两端都栽树，所以棵数= 间隔数+ 1 ，间隔数为100÷10 = 10 ，则棵数为10 + 1 = 11 棵。

答案：11 棵。

题目4：某班有40 名学生，其中有15 人参加数学小组，18 人参加航模小组，有10 人两个小组都参加。

那么有多少人两个小组都不参加？解题方法：参加数学或航模小组的人数为15 + 18 - 10 = 23 人，所以两个小组都不参加的人数为40 - 23 = 17 人。

答案：17 人。

题目5：甲乙两数的和是32，甲数的3 倍与乙数的5 倍的和是122，求甲、乙二数各是多少？解题方法：设甲数为x，乙数为y，则x + y = 32 ，3x + 5y = 122 。

将第一个式子乘以3 得到3x + 3y = 96 ，用第二个式子减去这个式子得到2y = 26 ，y = 13 ，则x = 19 。

答案：甲数19，乙数13 。

题目6：一列火车通过530 米的桥需40 秒钟，以同样的速度穿过380 米的山洞需30 秒钟。

求这列火车的速度是每秒多少米？车长多少米？解题方法：火车40 秒走的路程= 桥长+ 车长，30 秒走的路程= 山洞长+ 车长。

小学奥数解题方法大全一、加减法解题方法在小学奥数中，加减法是最基础也是最常见的题型。

以下是几种常用的解题方法：1. 竖式计算法竖式计算法是最常用的加减法解题方法，适用于任何数值大小的计算。

先将两个数竖式排列，逐位相加或相减，并按进位或借位的要求进行计算。

2. 寻找相反数法有时候，我们可以通过寻找相反数的方法来简化计算。

例如，对于一个加法题目3 + 7，我们可以通过找到7的相反数-7，然后用3 - 7的方式进行计算，得到的结果再取相反数即可。

3. 进退相等法进退相等法适用于一些特殊的加减法题目。

当两个数相差一致（如8和9）时，我们可以采用进退相等法来计算。

比如计算8 + 9，我们可以将9退1，变成8 + 8 = 16，然后再加上1，即可得到17。

二、乘法解题方法乘法是小学奥数中较为复杂的题型。

以下是几种常用的解题方法：1. 分解因数法对于一个较大的乘法题目，我们可以将其中一个数拆分成多个因数的乘积，然后再进行计算。

例如，计算36 × 4，我们可以将36分解成6 × 6，然后计算6 × 4 × 6 = 144。

2. 组合乘法法则组合乘法法则适用于一些特殊的乘法题目。

例如，计算12 × 7，我们可以将12拆分成10 + 2，然后计算(10 × 7) + (2 × 7) = 70 + 14 = 84。

3. 巧用倍数关系在一些乘法题目中，我们可以巧妙地运用倍数关系来简化计算。

例如，计算8 × 25，我们可以将8拆分成2 × 4，然后计算(2 × 25) × 4 =50 × 4 = 200。

三、除法解题方法除法是小学奥数中较为复杂的题型之一。

以下是几种常用的解题方法：1. 精确除法精确除法是最常用的除法解题方法。

根据除法的定义，将被除数除以除数，得到的商和余数就是精确除法的结果。

2. 简化除法有时候，我们可以通过简化运算来进行除法计算。

目录第一讲奇妙的幻方 (3)练习卷 (9)第二讲可能性的大小（游戏与对策） (10)练习卷 (12)第三讲图形的面积（一） (13)第四讲认识分数 (17)练习卷 (21)第五讲行程中的相遇（相遇问题） (22)练习卷 (26)第六讲公因数与公倍数 (27)综合演练 (31)第一讲幻方（第一课时）【知识概述】在一个n×n的正方形方格中，填入一些连续的数字，使得所有的横、竖、斜列所加之和都相等，这样的正方形方格叫做幻方。

幻方一般分为奇数幻方和偶数幻方。

（n 是几就表示为几阶幻方）。

本讲，我们将来学习这方面的知识。

例题讲学例1在一个3×3的表格内，填入1-9九个数，（不能重复，不能遗漏），使得3个横列、3个竖列和2个斜列所加之和都相等。

可以怎样填？【和为15】【思路分析】这样的3×3幻方，在填写时有一定的规律和口诀：二、四为肩，六、八为足，左七右三，戴九履一，五为中央。

【注：戴指头，履指脚。

】试试填一填吧！幻方 （第二课时）知识概述：上一讲中，我们讲述了如何填写3×3的幻方，其实在幻方的知识世界里，像3×3、5×5、7×7……像这样幻方，称之为奇数幻方，这一讲我们将来学习如何填写五阶幻方。

例题：在一个5×5的方格中，填入1-25这25个数字，使5个横列、5个竖列、2个斜列所加之和都相等。

先试试看！看 样 子 ，要 想 顺 利 填 写 好 这 么 多 的 表格，还真 的 不容易，没有 口诀 真 的 不行，下 面这 个 口诀 要 记 牢：一居首行正中央，依次斜向右上方，右出框时左边写，上出框时下边放，双出占位写下方。

你能按顺序继续写下去吗？试试看吧！幻方（第三课时）根据上讲中的方法，把口诀运用到所有的奇数幻方中，可以继续填写七阶幻方、九阶幻方、十一阶幻方……，本讲，我们继续试着填写七阶幻方和九阶幻方。

【思路点拨】再来重温一下口诀吧！一居首行正中央，依次斜向右上方，右出框时左边写，上出框时下边放，双出占位写下方。

小学奥数21类难题汇总，附解题思路题型一：归一问题【含义】在解题时先求出一份是多少（即单一量），然后以单一量为标准，求出所要求的数量。

【数量关系】总量÷份数=单一量单一量×所占份数=所求几份的数量或总量A÷（总量B÷份数B）=份数A【解题思路】先求出单一量，以单一量为标准，求出所要求的数量。

【例】买5支铅笔需要0.6元钱，买同样的铅笔16支，需要多少钱？解：先求出一支铅笔多少钱——0.6÷5=0.12（元）再求买16支铅笔需要多少钱——0.12×16=1.92（元）综合算式：0.6÷5×16=0.12×16=1.92（元）题型二：归总问题【含义】解题时先找出“总数量”，再根据已知条件解决问题的题型。

所谓“总数量”可以指货物总价、几天的工作量、几亩地的总产量、几小时的总路程等。

【数量关系】1份数量×份数=总量总量÷一份数量=份数【解题思路】先求出总数量，再解决问题。

【例】服装厂原来做一套衣服用布3.2米，改进剪裁方法后，每套衣服用布2.8米。

问原来做791套衣服的布，现在可以做多少套衣服？解：先求这批布总共多少米——3.2×791=2531.2（米）再求现在可以做多少套——2531.2÷2.8=904（套）综合算式：3.2×791÷2.8=904（套）题型三：和差问题【含义】已知两个数量的和与差，求这两个数量各是多少。

【数量关系】大数=（和+差）÷2小数=（和－差）÷2【解题思路】简单题目直接套用上述公式，复杂题目变通后再套用公式。

【例】甲乙两班共有学生98人，甲班比乙班多6人，求两班各有多少人？解：直接套用公式——甲班人数=（98+6）÷2=52（人）乙班人数=（98-6）÷2=46（人）题型四：和倍问题【含义】已知两个数的和及“大数是小数的几倍（或小数是大数的几分之几）”，求这两个数各是多少。

专题三组合图形的面积计算1.等量代换法一个量可以用它的等量来代替；被减数和减数都增加（或减少）同一个数，它们的差不变。

前者是等量公理，后者是减法的差不变性质。

这两个性质在解几何题时有很重要的作用，它能将求一个图形的面积转化为求另一个图形的面积，或将两个图形的面积差转化为另两个图形的面积差，从而使隐蔽的关系明朗化，找到解题思路。

例1小两个正方形组成下图所示的组合图形。

已知组合图形的周长是52厘米，DG=4厘米，求阴影部分的面积。

例2两个相同的直角三角形如下图所示（单位：厘米）重叠在一起，求阴影部分的面积。

例3 下页上图中，ABCD是7×4的长方形，DEFG是10×2的长方形，求三角形BCO与三角形EFO的面积之差。

例4在右图中，AB=8厘米，CD=4厘米，BC=6厘米，三角形AFB比三角形EFD的面积大18厘米2。

求ED的长。

例5左下图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC的面积。

2.割补法在组合图形中，除了多边形外，还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形，为了计算它们的面积，常常需要变动图形的位置或对图形进行分割、旋转、拼补，使它变成可以计算出面积的规则图形。

就是在多边形的组合图形中，为了计算面积，有时也要用到割补的方法。

、例6求下列各图中阴影部分的面积：例7如左下图所示，在一个等腰直角三角形中，削去一个三角形后，剩下一个上底长5厘米、下底长9厘米的等腰梯形（阴影部分）。

求这个梯形的面积。

例8下图中，甲、乙两个正方形的边长的和是20厘米，甲正方形比乙正方形的面积大40厘米2。

求乙正方形的面积。

作业：1.左下图中，等腰直角三角形ABC的腰为10厘米，以C为圆心、CF为半径画弧线EF，组成扇形CEF。

如果图中甲、乙两部分的面积相等，那么扇形所在的圆的面积是多少？2.右上图（单位：厘米）是两个相同的直角梯形重叠在一起，求阴影部分的面积。

小学奥数21类难题汇总，附解题思路题型一：归一问题【含义】在解题时先求出一份是多少（即单一量），然后以单一量为标准，求出所要求的数量。

【数量关系】总量÷份数=单一量单一量×所占份数=所求几份的数量或总量A÷（总量B÷份数B）=份数A【解题思路】先求出单一量，以单一量为标准，求出所要求的数量。

【例】买5支铅笔需要0.6元钱，买同样的铅笔16支，需要多少钱？解：先求出一支铅笔多少钱——0.6÷5=0.12（元）再求买16支铅笔需要多少钱——0.12×16=1.92（元）综合算式：0.6÷5×16=0.12×16=1.92（元）题型二：归总问题【含义】解题时先找出“总数量”，再根据已知条件解决问题的题型。

所谓“总数量”可以指货物总价、几天的工作量、几亩地的总产量、几小时的总路程等。

【数量关系】1份数量×份数=总量总量÷一份数量=份数【解题思路】先求出总数量，再解决问题。

【例】服装厂原来做一套衣服用布3.2米，改进剪裁方法后，每套衣服用布2.8米。

问原来做791套衣服的布，现在可以做多少套衣服？解：先求这批布总共多少米——3.2×791=2531.2（米）再求现在可以做多少套——2531.2÷2.8=904（套）综合算式：3.2×791÷2.8=904（套）题型三：和差问题【含义】已知两个数量的和与差，求这两个数量各是多少。

【数量关系】大数=（和+差）÷2小数=（和－差）÷2【解题思路】简单题目直接套用上述公式，复杂题目变通后再套用公式。

【例】甲乙两班共有学生98人，甲班比乙班多6人，求两班各有多少人？解：直接套用公式——甲班人数=（98+6）÷2=52（人）乙班人数=（98-6）÷2=46（人）题型四：和倍问题【含义】已知两个数的和及“大数是小数的几倍（或小数是大数的几分之几）”，求这两个数各是多少。