《天利38套高考模拟试题汇编》数学(理)

天利38套高三高考能力提升卷（四）（基础必刷）一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题如图所示，劲度系数为的轻弹簧下端固定在倾角为的光滑斜面底端，上端连接物块Q，Q同时与平行于斜面的轻绳相连，轻绳跨过定滑轮O与套在足够长的光滑竖直杆上的物块P连接，图中O、B两点等高，间距。

初始时在外力作用下，P在A点静止不动，A、B间距离，此时轻绳中张力大小为。

已知P的质量为，Q的质量为，P、Q均可视为质点。

现将P由静止释放（不计滑轮大小及摩擦，重力加速度取，，，弹簧始终处于弹性限度内），下列说法正确的是（）A．物块P上升的最大高度为B．物块P上升至B点时，其速度大小为C．在物块P由A点运动到B点的过程中，弹簧对物块Q一直做正功D．在物块P由A点运动到B点的过程中，物块P机械能守恒第(2)题传感器是一种检测装置，能感受到被测量的信息，并能将感受到的信息，按一定规律变换成为电信号或其他所需形式的信息输出，以满足信息的传输、处理、存储、显示、记录和控制等要求，它是实现自动检测和自动控制的首要环节。

如图所示是测定液面高度h的电容式传感器示意图，E为电源，G为灵敏电流计，A为固定的导体芯，B为导体芯外面的一层绝缘物质，C为导电液体。

已知电流从灵敏电流计左边接线柱流进电流计，指针向左偏。

如果在导电液体的深度h发生变化时观察到指针正向左偏转，则（ ）A．导体芯A所带电荷量在增加，液体的深度h在增大B．导体芯A所带电荷量在减小，液体的深度h在增大C．导体芯A所带电荷量在增加，液体的深度h在减小D．导体芯A所带电荷量在减小，液体的深度h在减小第(3)题激光陀螺仪是很多现代导航仪器中的关键部件，广泛应用于民航飞机等交通工具。

激光陀螺仪的基本元件是环形激光器，其原理结构比较复杂，我们简化为如图所示模型：由激光器发出的A、B两束激光，经完全对称的两个通道（图中未画出）在光电探测器处相遇，产生干涉条纹。

高考数学(理科)模拟试题含答案(一)精编版高考理科数学模拟试题精编(一)注意事项：1.作答选择题时，在答题卡上涂黑对应选项的答案信息点。

如需改动，先擦干净再涂其他答案。

不得在试卷上作答。

2.非选择题用黑色钢笔或签字笔作答，写在答题卡指定区域内。

如需改动，先划掉原答案再写新答案。

不得用铅笔或涂改液。

不按要求作答无效。

3.答题卡需整洁无误。

考试结束后，交回试卷和答题卡。

第Ⅰ卷一、选择题(本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项符合题目要求。

)1.设全集Q={x|2x²-5x≤0，x∈N}，且P⊆Q，则满足条件的集合P的个数是()A。

3B。

4C。

7D。

82.若复数z=m(m-1)+(m-1)i是纯虚数，其中m是实数，则z=()A。

iB。

-iC。

2iD。

-2i3.已知等差数列{an}的公差为5，前n项和为Sn，且a1，a2，a5成等比数列，则S6=()A。

80B。

85C。

90D。

954.XXX每天上学都需要经过一个有交通信号灯的十字路口。

已知十字路口的交通信号灯绿灯亮的时间为40秒，黄灯5秒，红灯45秒。

如果XXX每天到路口的时间是随机的，则XXX上学时到十字路口需要等待的时间不少于20秒的概率是()A。

4/5B。

3/4C。

2/3D。

3/56.已知p：a=±1，q：函数f(x)=ln(x+a²+x²)为奇函数，则p 是q成立的()A。

充分不必要条件B。

必要不充分条件C。

充分必要条件D。

既不充分也不必要条件7.(省略了一个选项) 327.(1+x²+4x)²的常数项为()A。

120B。

160C。

200D。

2408.我们可以用随机模拟的方法估计π的值，如图所示的程序框图表示其基本步骤(函数RAND是产生随机数的函数，它能随机产生(0,1)内的任何一个实数)，若输出的结果为521，则由此可估计π的近似值为()A。

3.119B。

2023年高考数学模拟考试卷及答案解析（理科）第Ⅰ卷一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．1．已知复数z 满足()()()1i 12i 1z z +=+-，则复数z 的实部与虚部的和为（）A ．1B ．1-C ．15D ．15-【答案】D【分析】根据复数的运算法则求出复数43i 55z -+=，则得到答案.【详解】(1i)(2i 1)(2i 1)z z +=-+-(2i)2i 1z -=-，2i 1(2i 1)(2i)43i 43i 2i 5555z --+-+====-+-，故实部与虚部的和为431555-+=-，故选：D.2．已知()f x =A ，集合{12}B x ax =∈<<R ∣，若B A ⊆，则实数a 的取值范围是（）A ．[2,1]-B ．[1,1]-C ．(,2][1,)-∞-+∞ D ．(,1][1,)∞∞--⋃+【答案】B【分析】先根据二次不等式求出集合A ，再分类讨论集合B ，根据集合间包含关系即可求解.【详解】()f x =A ，所以210x -≥，所以1x ≥或1x ≤-，①当0a =时，{102}B x x =∈<<=∅R∣,满足B A ⊆，所以0a =符合题意；②当0a >时，12{}B x x a a=∈<<R∣，所以若B A ⊆，则有11a≥或21a≤-，所以01a <≤或2a ≤-（舍）③当0<a 时，21{}B x x aa=∈<<R ∣，所以若B A ⊆，则有11a≤-或21a≥（舍），10a -≤<，综上所述，[1,1]a ∈-，故选：B.3．在研究急刹车的停车距离问题时，通常假定停车距离等于反应距离（1d ，单位：m ）与制动距离（2d ，单位：m ）之和.如图为某实验所测得的数据，其中“KPH”表示刹车时汽车的初速度v （单位：km/h ）.根据实验数据可以推测，下面四组函数中最适合描述1d ，2d 与v 的函数关系的是（）A ．1d v α=，2d =B ．1d v α=，22d v β=C ．1d =，2d v β=D ．1d =，22d vβ=【答案】B【分析】设()()1d v f v =，()()2d v g v =，根据图象得到函数图象上的点，作出散点图，即可得到答案.【详解】设()()1d v f v =，()()2d v g v =.由图象知，()()1d v f v =过点()40,8.5，()50,10.3，()60,12.5，()70,14.6，()80,16.7，()90,18.7，()100,20.8，()110,22.9，()120,25，()130,27.1，()140,29.2，()150,31.3，()160,33.3，()170,35.4，()180,37.5.作出散点图，如图1.由图1可得，1d 与v 呈现线性关系，可选择用1d v α=.()()2d v g v =过点()40,8.5，()50,16.2，()60,23.2，()70,31.4，()80,36，()90,52，()100,64.6，()110,78.1，()120,93，()()140,123，()150,144.1，()160,164.3，()170,183.6，()180,208.作出散点图，如图2.由图2可得，2d 与v 呈现非线性关系，比较之下，可选择用22d v β=.故选：B.4．已知函数()ln ,0,e ,0,x xx f x x x x ⎧>⎪=⎨⎪≤⎩则函数()1y f x =-的图象大致是（）A ．B．C ．D ．【答案】B【分析】分段求出函数()1y f x =-的解析式，利用导数判断其单调性，根据单调性可得答案.【详解】当10x ->，即1x <时，ln(1)(1)1x y f x x-=-=-，221(1)ln(1)1ln(1)1(1)(1)x x x x y x x -⋅-+--+--'==--，令0'>y ，得1e x <-，令0'<y ，得1e 1x -<<，所以函数()1y f x =-在(,1e)-∞-上为增函数，在(1e,1)-上为减函数，由此得A 和C 和D 不正确；当10x -≤，即1x ≥时，1(1)(1)e x y f x x -=-=-，()11(1)e (1)e x x y x x --'''=-+-11e (1)e x x x --=---=1e (2)xx ---，令0'>y ，得2x >，令0'<y ，得12x ≤<，所以函数()1y f x =-在(2,)+∞上为增函数，在[1,2)上为减函数，由此得B 正确；故选：B5．若函数()f x 存在一个极大值()1f x 与一个极小值()2f x 满足()()21f x f x >，则()f x 至少有（）个单调区间.A ．3B ．4C ．5D ．6【答案】B【分析】根据单调性与极值之间的关系分析判断.【详解】若函数()f x 存在一个极大值()1f x 与一个极小值()2f x ，则()f x 至少有3个单调区间，若()f x 有3个单调区间，不妨设()f x 的定义域为(),a b ，若12a x x b <<<，其中a 可以为-∞，b 可以为+∞，则()f x 在()()12,,,a x x b 上单调递增，在()12,x x 上单调递减，（若()f x 定义域为(),a b 内不连续不影响总体单调性），故()()21f x f x <，不合题意，若21a x x b <<<，则()f x 在()()21,,,a x x b 上单调递减，在()21,x x 上单调递增，有()()21f x f x <，不合题意；若()f x 有4个单调区间，例如()1f x x x =+的定义域为{}|0x x ≠，则()221x f x x-'=，令()0f x ¢>，解得1x >或1x <-，则()f x 在()(),1,1,-∞-+∞上单调递增，在()()1,0,0,1-上单调递减，故函数()f x 存在一个极大值()12f -=-与一个极小值()12f =，且()()11f f -<，满足题意，此时()f x 有4个单调区间，综上所述：()f x 至少有4个单调区间.故选：B.6．已知实数x 、y 满足10101x y x y y +-≤⎧⎪-+≥⎨⎪≥-⎩，则918222y x z x y --=+--的最小值为（）A ．132B ．372C ．12D ．2【答案】A【分析】由约束条件作出可行域，求出22y t x -=-的范围，再由91821922y x z t x y t --=+=+--结合函数的单调性求得答案．【详解】解：令22y t x -=-，则91821922y x z t x y t --=+=+--，由10101x y x y y +-≤⎧⎪-+≥⎨⎪≥-⎩作出可行域如图，则()()()2,12,1,0,1A B C ---，设点()(),2,2P x y D ，，其中P 在可行域内，2=2PD y t k x -∴-=，由图可知当P 在C 点时，直线PD 斜率最小，min 121=022CD t k -==-∴当P 在B 点时，直线PD 斜率不存在，∴1,2t ⎡⎫∈+∞⎪⎢⎣⎭∵19z t t =+在1,2t ⎡⎫∈+∞⎪⎢⎣⎭上为增函数，∴当12t =时min 132z =．故选：A ．7．在正方体1111ABCD A B C D -中，点P 在正方形11BCC B 内，且不在棱上，则（）A ．在正方形11DCC D 内一定存在一点Q ，使得PQ AC ∥B ．在正方形11DCCD 内一定存在一点Q ，使得PQ AC⊥C ．在正方形11DCC D 内一定存在一点Q ，使得平面1PQC ∥平面ABC D ．在正方形11DCC D 内一定存在一点Q ，使得AC ⊥平面1PQC 【答案】B【分析】对于A ，通过作辅助线，利用平行的性质，推出矛盾，可判断A;对于B ，找到特殊点，说明在正方形11DCC D 内一定存在一点Q ，使得PQ AC ⊥，判断B;利用面面平行的性质推出矛盾，判断C;利用线面垂直的性质定理推出矛盾，判断D.【详解】A 、假设在正方形11DCC D 内一定存在一点Q ，使得PQ AC ∥，作,PE BC QF CD ⊥⊥,垂足分别为,E F ,连接,E F ，则PEFQ 为矩形，且EF 与AC 相交，故PQ EF ∥,由于PQ AC ∥，则AC EF ∥，这与,AC EF 相交矛盾，故A 错误；B 、假设P 为正方形11BCC B 的中心，Q 为正方形11DCC D 的中心，作,PH BC QG CD ⊥⊥,垂足分别为,H G ,连接,H G ，则PHGQ 为矩形，则PQ HG ∥,且,H G 为,BC CD 的中点，连接,GH BD ,则GH BD ∥,因为AC BD ⊥，所以GH AC ⊥,即PQ AC ⊥，故B 正确；C 、在正方形11DCC D 内一定存在一点Q ，使得平面1PQC ∥平面ABC ，由于平面ABC ⋂平面11DCC D CD =,平面1PQC 平面111DCC D C Q =,故1CD C Q ∥,而11C D CD ∥,则Q 在11C D 上，这与题意矛盾，C 错误；D 、假设在正方形11DCC D 内一定存在一点Q ，使得AC ⊥平面1PQC ，1C Q ⊂平面1PQC ,则1AC C Q ⊥,又1CC ⊥平面,ABCD AC Ì平面ABCD ，故1C C AC ⊥,而11111,C C C Q C C C C Q =⊂ ，平面11DCC D ，故AC ⊥平面11DCC D ，由于AD ⊥平面11DCC D ,故,C D 重合，与题意不符，故D 错误，故选∶B8．对于平面上点P 和曲线C ，任取C 上一点Q ，若线段PQ 的长度存在最小值，则称该值为点P 到曲线C 的距离，记作(,)d P C .若曲线C 是边长为6的等边三角形，则点集{(,)1}D Pd P C =≤∣所表示的图形的面积为（）A ．36B ．36-C ．362π-D ．36π-【答案】D【分析】根据题意画出到曲线C 的距离为1的边界，即可得到点集的区域，即可求解.【详解】根据题意作出点集(){}|1D P d P C =≤，的区域如图阴影所示，其中四边形ADEC ，ABKM ，BCFG 为矩形且边长分别为1,6，圆都是以1为半径的，过点I 作IN AC ⊥于N ，连接A I ,则1NI =，30NAI ∠= ，所以AN =则HIJ 是以6-为边长的等边三角形，矩形ABKM 的面积1166S =⨯=，2π3DAM ∠=，扇形ADM 的面积为212ππ1233S =⨯⨯=，21sin 602ABC S AB =⨯⋅ 21622=⨯⨯，21sin 602HIJ S HI =⨯⋅ (21622=⨯-18=-，所以()1233ABC HIJ S S S S S =++- ()π363183=⨯+⨯+--36π=-.故选：D.9．一个宿舍的6名同学被邀请参加一个节目，要求必须有人去，但去几个人自行决定．其中甲和乙两名同学要么都去，要么都不去，则该宿舍同学的去法共有（）A ．15种B ．28种C ．31种D ．63种【答案】C【分析】满足条件的去法可分为两类，第一类甲乙都去，第二类甲乙都不去，再进一步通过分类加法原理求出各类的方法数，将两类方法数相加即可.【详解】若甲和乙两名同学都去，则去的人数可能是2人，3人，4人，5人，6人，所以满足条件的去法数为0123444444C +C C +C C 16++=种；若甲和乙两名同学都不去，则去的人数可能是1人，2人，3人，4人，则满足条件去法有12344444C C +C C 15++=种；故该宿舍同学的去法共有16+15=31种．故选：C.10．已知椭圆C 的焦点为12(0,1),(0,1)F F -，过2F 的直线与C 交于P ，Q 两点，若22143,||5PF F Q PQ QF ==，则椭圆C 的标准方程为（）A ．2255123x y +=B ．2212y x +=C ．22123x y +=D ．22145x y +=【答案】B【分析】由已知可设22,3F Q m PF m ==可求出所有线段用m 表示，在12PF F △中由余弦定理得1290F PF ︒∠=从而可求.【详解】如图，由已知可设22,3F Q m PF m ==，又因为114||55PQ QF QF m =∴=根据椭圆的定义212,62,3QF QF a m a a m +=∴=∴=，12223PF a PF a a a m=-=-==在12PF F △中由余弦定理得222222111116925cos 02243PQ PF QF m m m F PQ PQ PF m m+-+-∠===⋅⋅⋅⋅，所以190F PQ ︒∠=22222211229943213PF PF F F m m m a m b ∴+=⇒+=∴===⇒=故椭圆方程为：2212y x +=故选：B11．已知函数()π2sin 26f x x ⎛⎫=+ ⎪⎝⎭，对于任意的)3,1a ⎡∈-⎣，方程()()0f x a x m =<≤恰有一个实数根，则m 的取值范围为（）A ．7π3π,124⎛⎤⎥⎝⎦B ．π5π,26⎡⎫⎪⎢⎣⎭C ．π5π,26⎛⎤⎥⎝⎦D ．7π3π,124⎡⎫⎪⎢⎣⎭【答案】D【分析】将方程的根的问题转化为函数()y f x =的图象与直线y a =有且仅有1个交点，画出图象，数形结合得到不等式组，求出m 的取值范围.【详解】方程()()0f x a x m =<≤恰有一个实数根，等价于函数()y f x =的图象与直线y a =有且仅有1个交点．当0x m <≤得：πππ22666x m ⎛⎤+∈+ ⎥⎝⎦，结合函数()y f x =的图象可知，π4π5π2633m ⎡⎫+∈⎪⎢⎣⎭，解得：7π3π,124m ⎡⎫∈⎪⎢⎣⎭.故选：D12．已知0.40.7e ,eln1.4,0.98a b c ===，则,,a b c 的大小关系是（）A ．a c b >>B ．b a c >>C ．b c a >>D ．c a b>>【答案】A【分析】构造函数()1=ln ef x x x -，0x >，利用导函数得到其单调性，从而得到ln 1ex x ≤，当且仅当e x =时等号成立，变形后得到22ln2ex x ≤，当x =0.7x =后得到b c <；再构造()1=e x g x x --，利用导函数得到其单调性，得到1e x x -≥，当且仅当1x =时，等号成立，变形后得到21e 2x x ->，当0.5x =时，等号成立，令0.7x =得到a c >，从而得到a cb >>.【详解】构造()1=ln ef x x x -，0x >，则()11=ef x x '-，当0e x <<时，()0f x ¢>，当e x >时，()0f x '<，所以()1=ln ef x x x -在0e x <<上单调递增，在e x >上单调递减，所以()()e =lne 10f x f ≤-=，故ln 1ex x ≤，当且仅当e x =时等号成立，因为20x >，所以222222(2)2ln 2ln ln ln2e e 2e 2e ex x x x x x x x x ≤⇒≤⇒≤⇒≤=，当x =当0.7x =时，220.98ln1.4(0.7)eln1.40.98ee<⨯=⇒<，所以b c <构造()1=e x g x x --，则()1e 1=x g x -'-，当1x >时，()0g x '>，当1x <时，()0g x '<，所以()1=ex g x x --在1x >单调递增，在1x <上单调递减，故()()10g x g ≥=，所以1e x x -≥，当且仅当1x =时，等号成立，故121e e 2x x x x --≥⇒≥，当且仅当0.5x =时，等号成立，令0.7x =，则0.40.4e 1.40.7e 0.98>⇒>，所以a c >，综上:a c b >>，故选：A【点睛】构造函数比较函数值的大小，关键在于观察所给的式子特点，选择合适的函数进行求解.第Ⅱ卷二、填空题：本题共4小题，每小题5分，共20分．13．设i ，j 是x ，y 轴正方向上的单位向量，23a b i j -=- ，3119a b i j +=+，则向量a，b的夹角为______．【答案】π4【分析】分别求出a ，b 的表达式，利用定义求出a ，b 的夹角即可.【详解】23a b i j -=-①，3119a b i j +=+②,3⨯+①②得714,2a i a i =∴=，2-⨯+②①得72121,33b i j b i j -=--∴=+ ，()22·33666a b i i j i i j ⋅=+=+⋅=2,a b ==cos ,2a b a b a b ⋅∴==⋅π,4a b ∴=14．已知双曲线2222:1(0,0)x y C a b a b -=>>的焦距为2c ，过C 的右焦点F 的直线l 与C 的两条渐近线分别交于,A B 两点，O 为坐标原点，若cos b c AFO =∠且3FB FA =，则C 的渐近线方程为__________.【答案】y =【分析】根据题设条件确定AB OA ⊥，进而可确定OA a FA b ==，，从而在直角△AOB 中，()2tan tan π2bAOB aα∠=-=，结合正切的二倍角公式求解.【详解】因为3FB FA =，画出示意图如图，设AOF α∠=，因为cos b c AFO =∠，则cos b AFO c∠=，所以222sin a AFO c∠=，则sin a AFO c ∠=，所以tan aAFO b ∠=.又tan b a α=，所以π2AFO α∠+=，所以AB OA ⊥，根据sin ,cos OA FA a bAFO AFO c c c c ∠==∠==，所以OA a FA b ==，.又因为3FB FA，所以2AB b =.在直角△AOB 中，()2tan tan π2bAOB aα∠=-=，所以222222tan tan21tan 1bb a b a aααα=-==--，化简得：222b a =，所以b a =则渐近线方程为：y =，故答案为:y =.15．已知数列{}n a 满足首项11a =，123n n na n a a n ++⎧=⎨⎩，为奇数，为偶数，则数列{}n a 的前2n 项的和为_____________．【答案】4344n n ⨯--【分析】当n 为奇数时，由递推关系得()21332n n n a a a ++==+，构造{}3n a +为等比数列，可求出通项，结合12n n a a +=+即可分组求和.【详解】当n 为奇数时，()21332n n n a a a ++==+，即()2333n n a a ++=+，此时{}3n a +为以134a +=为首项，公比为3的等比数列，故()123212413333343333n nn n n n a a a a a a a a ----++++=创创+=+++，即12433n n a -=´-.()()()2123421211332121222n n n n n S a a a a a a a a a a a a ---=++++++=+++++++++ ()()01113212224334334332n n a a a n n--=++++=´-+´-++´-+ ()03132432434413nnn n n 骣-琪=´-+=´--琪琪-桫.故答案为：4344n n ⨯--【点睛】本题解题关键是根据题意找到相邻奇数项或偶数项之间的递推关系，从而求出当n 为奇数或n 为偶数时的通项公式，再通过相邻两项的关系求出前2n 项的和．16．在三角形ABC 中，2BC =，2AB AC =，D 为BC 的中点，则tan ADC ∠的最大值为___________.【答案】43##113【分析】设出AC x =，则2AB x =，由πADB ADC ∠+∠=得到cos cos 0ADB ADC ∠+∠=，结合余弦定理得到22512AD x =-，从而得到cos ADC ∠关系得到223x <<，换元后得到cos ADC ∠，由基本不等式求出最小值，结合()cos f x x =在π0,2⎛⎫ ⎪⎝⎭上单调递减，()tan g x x =在π0,2⎛⎫ ⎪⎝⎭单调递增，可求出tan ADC ∠的最大值.【详解】设AC x =，则2AB x =，因为D 为BC 的中点，2BC =，所以1BD DC ==，由三角形三边关系可知：22x x +>且22x x -<，解得：223x <<，在三角形ABD 中，由余弦定理得：()2212cos 2AD x ADB AD+-∠=，在三角形ACD 中，由余弦定理得：221cos 2AD x ADC AD+-∠=，因为πADB ADC ∠+∠=，所以()2222121cos cos 022AD x AD x ADB ADC ADAD+-+-∠+∠=+=，解得：22512AD x =-，由余弦定理得：225112cos x x ADC -+-∠=223x <<，令2511,929x t ⎛⎫-=∈ ⎪⎝⎭，则3cos 5ADC ∠=，当且仅当1t t=，即1t =时，等号成立，此时25112x -=，解得：x =因为3cos 05ADC ∠≥>，故π0,2ADC ⎛⎫∠∈ ⎪⎝⎭，由于()cos f x x =在π0,2⎛⎫ ⎪⎝⎭上单调递减，()tan g x x =在π0,2⎛⎫ ⎪⎝⎭单调递增，故当cos ADC ∠取得最小值时，tan ADC ∠取得最大值，此时4sin 5ADC ∠=，4tan 3ADC ∠=.故答案为：43.【点睛】三角形中常用结论，()sin sin A B C +=，()cos cos A B C +=-，()tan tan A B C +=-，本题中突破口为由πADB ADC ∠+∠=得到cos cos 0ADB ADC ∠+∠=，结合余弦定理得到22512AD x =-，进而利用基本不等式求最值.三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．17．（12分）数列{}n a 满足35a =，点()1,n n P a a +在直线20x y -+=上，设数列{}n b 的前n 项和为n S ，且满足233n n S b =-，*n ∈N ．(1)求数列{}n a 和{}n b 的通项公式；(2)是否存在*k ∈N ，使得对任意的*n ∈N ，都有n kn ka ab b ≤．【答案】(1)21n a n =-；3nn b =(2)存在1k =，2，使得对任意的*n ∈N ，都有n k n ka ab b ≤【分析】（1）根据等差数列的定义可得{}n a 为等差数列，由,n n S b 的关系可得{}n b 为等比数列，进而可求其通项，（2）根据数列的单调性求解最值即可求解.【详解】（1）点()1,n n P a a +在直线20x y -+=上，所以12n n a a +-=又35a =，∴11a =，则数列{}n a 是首项为1，公差为2的等差数列．∴21n a n =-又当1n =时，11233S b =-得13b =，当2n ≥，由233n n S b =-①，得11233n n S b --=-②由①－②整理得：13n n b b -=，∵130b =≠，∴10n b -≠∴13nn b b -=，∴数列{}n b 是首项为3，公比为3的等比数列，故3nn b =（2）设213nn n na n cb -==，由111121212163443333+++++-+-+--=-==n n n n n n n n n n nc c当1n =时，12c c =，当2n ≥时，1n n c c +<，所以当1n =或2时，n c 取得最大值，即nna b 取得最大所以存在1k =，2，使得对任意的*n ∈N ，都有n kn ka ab b≤18．（12分）如图，将等边ABC 绕BC 边旋转90︒到等边DBC △的位置，连接AD．(1)求证：AD BC ⊥；(2)若M 是棱DA 上一点，且两三角形的面积满足2BMD BMA S S = ，求直线BM 与平面ACD 所成角的正弦值．【答案】(1)证明见解析(2)10【分析】（1）取BC 中点为O ，证明BC ⊥平面AOD 即可；（2）建立空间直角坐标系，利用向量法求得直线BM 与平面ACD 所成角的正弦值．【详解】（1）设O 是BC 的中点，连接AO ，DO ，由题知：AB AC =，DB DC =，则BC AO ⊥，BC DO ⊥，又AO DO O ⋂=，,AO DO ⊂平面AOD ，所以BC ⊥平面AOD ，又AD ⊂平面AOD ，所以AD BC ⊥．（2）由题知，OA 、BC 、OD 两两垂直，以O 为原点，,,OA OB OD方向分别为x ，y ，z 轴的正方向建立空间直角坐标系，如图所示，因为2BMD BMA S S = ，所以13AM AD =，设2AB a =，则OA OD ==，则),0,0A，()0,,0B a ，()0,,0C a -，()D，33M ⎛⎫⎪ ⎪⎝⎭．所以),,0CA a =，),0,DA =，,BM a ⎫=-⎪⎪⎝⎭，设平面ACD 的法向量为(),,n x y z =r，则00n CA ay n DA ⎧⋅=+=⎪⎨⋅=-=⎪⎩ ，取1x =，可得()1,n = ，设直线BM 与平面ACD 所成的角为θ，则sin cos ,BM n θ=BM n BM n⋅==⋅所以直线BM 与平面ACD.19．（12分）甲、乙两位选手参加一项射击比赛，每位选手各有n 个射击目标，他们击中每一个目标的概率均为12，且相互独立．甲选手依次对所有n 个目标进行射击，且每击中一个目标可获得1颗星；乙选手按规定的顺序依次对目标进行射击，击中一个目标后可继续对下一个目标进行射击直至有目标未被击中时为止，且每击中一个目标可获得2颗星．(1)当5n =时，分别求甲、乙两位选手各击中3个目标的概率；(2)若累计获得星数多的选手获胜，讨论甲、乙两位选手谁更可能获胜．【答案】(1)516,116；(2)当1,2,3n =时，乙更可能获胜；当4n ≥时，甲更可能获胜.【分析】（1）根据独立重复试验可计算甲击中3个目标的概率，由相互独立事件的概率计算公式可得乙击中3个目标的概率；（2）设X 为甲累计获得的星数，Y 为乙累计获得的星数，分别计算期望，分别讨论1,2,3n =及4n ≥的(),()E X E Y ，得出结论.【详解】（1）当5n =时，甲击中3个目标的概率为33215115C ()()2216P =⨯⨯=，乙击中3个目标，则前3个目标被击中，第4个目标未被击中，其概率为32111()2216P =⨯=.（2）设X 为甲累计获得的星数，则0,1,2,,X n = ，设Y 为乙累计获得的星数，则0,2,4,,2Y n = ，设击中了m 个目标，其中0m n ≤≤，则甲获得星数为m 的概率为C 11()C ()()222m m m n m nnn P X m -===，所以甲累计获得星数为0120C 1C 2C C ()2nn n n nnn E X ⋅+⋅+⋅++⋅= ;记01010C 1C C C (1)C 0C n n n n n n n n n S n n n =⋅+⋅++⋅=⋅+-⋅++⋅ ，所以0112(C C C )2,2n n n n n n n n S n n S n -=+++=⋅=⋅ ，所以12()22n n n nE X -⋅==,乙获得星数为2(01)m m n ≤≤-的概率为1111(2)()222m m P Y m +==⋅=，当m n =时，1(2)2nP Y m ==，所以乙累计获得星数为230242(1)2()22222n n n n E Y -=+++++ ，记230242(1)2222n n n T -=++++ ，则121242(1)20222n n n T --=++++ ，所以12111112(1)122()222222n n n n n n n n T T T ---+=-=+++-=- ，11()22n E Y -=-，当1n =时，1()()12E X E Y =<=，当2n =时，3()1()2E X E Y =<=，当3n =时，37()()24E X E Y =<=，当4n ≥时，()2()E X E Y ≥>所以当1,2,3n =时，乙更可能获胜；当4n ≥时，甲更可能获胜.20．（12分）已知抛物线2y =的焦点与椭圆()2222:10x y a b a bΩ+=>>的右焦点重合，直线1:1x y l a b+=与圆222x y +=相切．(1)求椭圆Ω的方程；(2)设不过原点的直线2l 与椭圆Ω相交于不同的两点A ，B ，M 为线段AB 的中点，O 为坐标原点，射线OM 与椭圆Ω相交于点P ，且O 点在以AB 为直径的圆上，记AOM ，BOP △的面积分别为1S ，2S ，求12S S 的取值范围．【答案】(1)22163x y +=(2)⎣⎦【分析】（1）根据条件建立关于,a b 的方程组，即可求解椭圆方程；（2）根据数形结合可知12AOM BOP OMS S S S OP==△△，分直线斜率不存在，或斜率为0，以及斜率不为0，三种情况讨论12S S 的值或范围.【详解】（1）∵抛物线2y =的焦点为)，∴c =从而223a b =+①，∵直线1:1x yl a b+=与圆222x y +==②，由①②得：ab ，∴椭圆Ω的方程为：22163x y +=（2）∵M 为线段AB 的中点，∴12AOM BOP OMS S S S OP==△△，（1）当直线2l 的斜率不存在时，2l x ⊥轴，由题意知OA OB ⊥，结合椭圆的对称性，不妨设OA 所在直线的方程为y x =，得22Ax =，从而22Mx =，26P x =，123M P OM x S S OP x ∴===（2）当直线2l 的斜率存在时，设直线()2:0l y kx m m =+≠，()11,A x y ，()22,B x y 由22163y kx mx y =+⎧⎪⎨+=⎪⎩可得：()222214260k x kmx m +++-=，由()()222216421260k m k m ∆=-+->可得：22630k m -+>（*）∴122421km x x k +=-+，21222621m x x k -=+，∵O 点在以AB 为直径的圆上，∴0OA OB ⋅=，即12120x x y y +=，∴()()221212121210x x y y k x x km x x m +=++++=，即()22222264102121m km k km m k k -⎛⎫+⨯+-+= ⎪++⎝⎭，2222,m k ⇒=+（**）满足（*）式．∴线段AB 的中点222,2121kmm M k k ⎛⎫- ⎪++⎝⎭，若0k =时，由（**）可得：22m =，此时123OM S S OP ∴===，若0k ≠时，射线OM 所在的直线方程为12y x k=-，由2212163y x k x y ⎧=-⎪⎪⎨⎪+=⎪⎩可得：2221221P k x k =+，12M POM x S S OP x ∴===随着2k 的增大而减小，∵0k ≠，∴20k >，∴1233S S ⎛∈ ⎝⎭综上，1233S S ∈⎣⎦【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下：（1）设直线方程，设交点坐标为()()1122,,,x y x y ；（2）联立直线与圆锥曲线的方程，得到关于x （或y ）的一元二次方程，必要时计算∆；（3）列出韦达定理；（4）将所求问题或题中的关系转化为12x x +、12x x （或12y y +、12y y ）的形式；（5）代入韦达定理求解.21．（12分）已知函数()e xf x ax a=--(1)当1a =时，证明:()0f x ≥.(2)若()f x 有两个零点()1212,x x x x <且22112,e 1x x +⎡⎤∈⎣⎦+，求12x x +的取值范围.【答案】(1)见解析；(2)243ln 22,e 1⎡⎤-⎢⎥-⎣⎦【分析】（1）()e 1x f x x =--，求导得min ()(0)0f x f ==，则()0f x ；（2）由题得11e x ax a =+，22e xax a =+，则21211e1x x x x -+=+，()1212e e 2x x a x x +=++，()2121e e x x a x x -=-，则()()212121121e 2e1x x x x x x x x ---+++=-，从而设21[ln 2,2]t x x =-∈，得到()121e 2e 1t tt x x +++=-，利用导数研究函数()1e ()e 1ttt g t +=-的值域，则得到12x x+的范围.【详解】（1）证明:当1a =时,()e 1x f x x =--,则()e 1x f x '=-.当(,0)x ∈-∞时,()0f x '<,当,()0x ∈+∞时,()0f x '>,所以()f x 在(,0)-∞上单调递减,在()0,∞+上单调递增,则min ()(0)0f x f ==,故()0f x .（2）由题意得1212e e 0x xax a ax a --=--=，则11e x ax a =+，22e xax a =+，从而21211e 1x xx x -+=+，()1212e e 2x x a x x +=++，()2121e e x x a x x -=-，故()()()()12212121212112e e 1e 2e ee1xx x x x x x x x x x x x x ---+-+++==--，因为22112,e 1x x +⎡⎤∈⎣⎦+，所以212e 2,e x x -⎡⎤∈⎣⎦，即[]21ln 2,2x x -∈，设21[ln 2,2]t x x =-∈,则()121e 2e 1t t t x x +++=-.设()1e ()e 1t tt g t +=-,则()22e 2e 1()e1t t tt g t --'=-.设2()e 2e 1t t h t t =--,则()()2e e 1t th t t '=--，由（1）可知()()2e e 10t th t t '=--在R 上恒成立,从而2()e 2e 1t t h t t =--在[ln 2,2]上单调递增,故min ()(ln 2)44ln 210h t h ==-->,即()0g t '>在[]ln 2,2上恒成立,所以()g t 在[ln 2,2]上单调递增,所以()212221e 23ln 2,e 1x x ⎡⎤+⎢⎥++∈-⎢⎥⎣⎦,即12243ln 22e 1,x x ⎡⎤+∈-⎢⎣-⎥⎦,即12x x +的取值范围为243ln 22,e 1⎡⎤-⎢⎥-⎣⎦.【点睛】关键点睛：本题的关键是通过变形用含21x x -的式子表示出122x x ++，即()()212121121e 2e1x x x x x x x x ---+++=-，然后整体换元设21[ln 2,2]t x x =-∈，则得到()121e 2e 1t t t x x +++=-，最后只需求出函数()1e ()e 1tt t g t +=-在[ln 2,2]t ∈上值域即可.（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．22．[选修4-4：坐标系与参数方程]（10分）在直角坐标系xOy 中，直线l的参数方程为cos sin x t y t αα⎧=+⎪⎨=⎪⎩（t 为参数）．以坐标原点为极点，x 轴的正半轴为极轴建立坐标系，曲线C 的极坐标方程为2853cos 2ρθ=-，直线l 与曲线C 相交于A ，B两点，)M．(1)求曲线C 的直角坐标方程；(2)若2AM MB =，求直线l 的斜率．【答案】(1)2214x y +=(2)2±【分析】（1）根据极坐标与直角坐标直角的转化222cos sin x y x y ρθρθρ=⎧⎪=⎨⎪=+⎩，运算求解；（2）联立直线l 的参数方程和曲线C 的直角坐标方程，根据参数的几何意义结合韦达定理运算求解.【详解】（1）∵()()222222288453cos 2cos 4sin 5cos sin 3cos sin ρθθθθθθθ===-++--，则2222cos 4sin 4ρθρθ+=，∴2244x y +=，即2214x y +=，故曲线C 的直角坐标方程为2214x y +=.（2）将直线l的参数方程为cos sin x t y t αα⎧=+⎪⎨=⎪⎩（t 为参数）代入曲线C 的直角坐标方程为2214x y +=，得)()22cos sin 14t t αα+=，整理得()()222cos 4sin 10t t ααα++-=，设A ，B 两点所对应的参数为12,t t ，则1212221cos 4sin t t t t αα+==-+，∵2AM MB =，则122t t =-，联立1212222cos 4sin t t t t ααα=-⎧⎪⎨+=-⎪+⎩，解得122222cos 4sin cos 4sin t t αααααα⎧=-⎪⎪+⎨⎪=⎪+⎩，将12,t t 代入12221cos 4sin t t αα=-+得2222221cos 4sin cos 4sin cos 4sin αααααααα⎛⎫⎛⎫-=- ⎪⎪ ⎪⎪+++⎝⎭⎝⎭，解得2223tan 4k α==，故直线l的斜率为2±.23．[选修4-5：不等式选讲]（10分）设a 、b 、c 为正数，且b c c a a ba b c+++≤≤.证明：(1)a b c ≥≥；(2)()()()2324a b b c c a abc +++≥.【答案】(1)证明见解析(2)证明见解析【分析】（1）由不等式的基本性质可得出111abc≤≤，利用反比例函数在()0,∞+上的单调性可证得结论成立；（2）利用基本不等式可得出a b +≥，2b c +≥3c a +≥等式的基本性质可证得结论成立.【详解】（1）证明：因为a 、b 、c 为正数，由b c c a a ba b c +++≤≤可得a b c a b c a b ca b c++++++≤≤，所以，111a b c≤≤，因为函数1y x =在()0,∞+上为增函数，故a b c ≥≥.（2）证明：由基本不等式可得a b +≥，2b c b b c +=++≥()322c a c a a a +=++≥+≥=由不等式的基本性质可得()()()2171131573362244412232424a b b c c a a b b c a c a b c+++≥=11764122424ab a b c abc ⎛⎫=≥ ⎪⎝⎭，当且仅当a b c ==时，等号成立，故()()()2324a b b c c a abc +++≥.。

高考理科数学模拟试卷(含答案)高考理科数学模拟试卷（含答案）本试卷共分为选择题和非选择题两部分，第Ⅰ卷（选择题）在1至2页，第Ⅱ卷（非选择题）在3至4页，共4页，满分150分，考试时间为120分钟。

注意事项：1.答题前，请务必填写自己的姓名和考籍号。

2.答选择题时，请使用2B铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，请使用橡皮擦擦干净后再选涂其他答案标号。

3.答非选择题时，请使用0.5毫米黑色签字笔，在答题卡规定位置上书写答案。

4.所有题目必须在答题卡上作答，在试题卷上答题无效。

5.考试结束后，请只将答题卡交回。

第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合A={-1.0.1.2.3.4}，B={y|y=x,x∈A}，则A2B=A){0.1.2}B){0.1.4}C){-1.0.1.2}D){-1.0.1.4}2.已知复数z=1/(1+i)，则|z|=A)2B)1C)2D)23.设函数f(x)为奇函数，当x>0时，f(x)=x-2，则f(f(1))=A)-1B)-2C)1D)24.已知单位向量e1，e2的夹角为π/2，则e1-2e2=A)3B)7C)3D)75.已知双曲线2x^2-y^2=1(a>0,b>0)的渐近线方程为y=±3x，则双曲线的离心率是A)10B)10/10C)10D)3/96.在等比数列{an}中，a1>0，则“a1<a4”是“a3<a5”的A)充分不必要条件B)必要不充分条件C)充要条件D)既不充分也不必要条件7.如图所示的程序框图，当其运行结果为31时，则图中判断框①处应填入的是A)i≤6?B)i≤5?C)i≤4?D)i≤3?8.已知a、b为两条不同直线，α、β、γ为三个不同平面，则下列命题中正确的是①若α//β，α//γ，则β//γ；②若a//α，a//β，则α//β；③若α⊥γ，β⊥γ，则α⊥β；④若a⊥α，XXXα，则a//b。

2024年高考第三次模拟考试高三数学（理科）（考试时间：120分钟试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．写在本试卷上无效．3．回答第Ⅱ卷时，将答案写在答题卡上．写在本试卷上无效．4．测试范围：高考全部内容5．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若集合{}24A x x =-≤≤，{}260B x x x =-≥，则A B = （）A ．[]2,0-B ．[]0,4C ．[]2,6-D ．[]4,62．已知3i 2z a =（R a ∈，i 是虚数单位），若21322z =，则=a （）A ．2B ．1C ．12D ．143．如图，已知AM 是ABC 的边BC 上的中线，若AB a=，AC b = ，则AM 等于（）A ．()12a b- B ．()12a b-- C ．()12a b+ D ．()12a b-+ 4．已知函数()()πtan 0,02f x x ωϕωϕ⎛⎫=+><< ⎝⎭的最小正周期为2π，直线π3x =是()f x 图象的一条对称轴，则()f x 的单调递减区间为（）A ．()π5π2π,2πZ 66k k k ⎛⎤-+∈ ⎥⎝⎦B ．()5π2π2π,2πZ 33k k k ⎛⎤--∈ ⎥⎝⎦C ．()4ππ2π,2πZ 33k k k ⎛⎤--∈ ⎥⎝⎦D ．()π2π2π,2πZ 33k k k ⎛⎤-+∈ ⎥⎝⎦5．已知直线l 过点()1,1A 交圆22:4O x y +=于,C D 两点，则“CD =l 的斜率为0”的（）A ．必要而不充分条件B ．充分必要条件C ．充分而不必要条件D ．即不充分也不必要条件6．甲、乙、丙、丁、戊共5名同学进行唱歌比赛，决出第一名到第五名．丙和丁去询问成绩，回答者对丙说：很遗憾，你和丁都没有得到冠军，对丁说：你当然不会是最差的从这两个回答分析，5人的名次排列方式共有（）A ．24种B ．54种C ．96种D ．120种7．函数()πln sin 2x x f x x⎛⎫⋅- ⎪⎝⎭=的部分图象大致为（）A ．B ．C．D．8．祖暅是我国南北朝时期伟大的数学家．祖暅原理用现代语言可以描述为“夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的面积总相等，那么这两个几何体的体积相等”．例如，可以用祖暅原理推导半球的体积公式，如图，底面半径和高都为R 的圆柱与半径为R 的半球放置在同一底平面上，然后在圆柱内挖去一个半径为R ，高为R 的圆锥后得到一个新的几何体，用任何一个平行于底面的平面α去截这两个几何体时，所截得的截面面积总相等，由此可证明半球的体积和新几何体的体积相等．若用平行于半球底面的平面α去截半径为R 的半球，且球心到平面α的距离为2R ，则平面α与半球底面之间的几何体的体积是（）A3R B3R C3R D3R9．已知函数()21e 3ln ,ln ,ln ,ln 222f x x a f b f c f ⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则（）A ．a b c <<B ．b a c <<C ．c<a<bD ．a c b<<10．已知数列{}n a 满足1,231,nn n n n a a a a a +⎧⎪=⎨⎪+⎩当为偶数时当为奇数时，若81a =，1a 的所有可能取值构成集合M ，则M 中的元素的个数是（）A ．7个B ．6个C ．5个D ．4个11．如图，已知双曲线2222:1(0,0)x y C a b a b -=>>的左、右焦点分别为1(,0)F c -，2(,0)F c ，点A 在C 上，点B 在y 轴上，A ，2F ，B 三点共线，若直线1BF1AF的斜率为，则双曲线C 的离心率是（）AB ．32CD ．312．已知()f x ，()g x 都是定义在R 上的函数，对任意x ，y 满足()()()()()f x y f x g y g x f y -=-，且()()210f f -=≠，则下列说法正确的是（）A ．()01f =B ．函数()21g x +的图象关于点()1,0对称C ．()()110g g +-=D ．若()11f =，则()202311n f n ==∑第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分13．已知数列{}n a 的前n 项和2n S n n =+，当9n nS a +取最小值时，n =.14．若函数()sin 1f x x x ωω=-在[]0,2π上恰有5个零点，且在ππ[,415-上单调递增，则正实数ω的取值范围为.15．已知52345012345(23)x a a x a x a x a x a x +=+++++，则123452345a a a a a -+-+=．（用数字作答）16．已知定义在R 上的函数()f x 满足()4()0f x f x '+>，且(01f =），则下列说法正确的是.①()f x 是奇函数；②(0,),()0x f x ∃∈+∞>；③41(1)e f >；④0x ∀>时，41()e xf x <三、解答题：本大题共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．（12分）已知()sin ,5sin 5sin m B A C =+ ，()5sin 6sin ,sin sin n B C C A =--垂直，其中A ，B ，C 为ABC的内角．(1)求cos A 的大小；(2)若BC =ABC 的面积的最大值．18．（12分）2016年10月“蓝瘦香菇”等网络新词突然在网络流行，某社区每月都通过问卷形式进行一次网上调查，现从社区随机抽取了60名居民进行调查．已知上网参与问卷调查次数与参与人数的频数分布如下表：参与调查问卷次数[)0,2[)2,4[)4,6[)6,8[)8,10[]10,12参与调查问卷人数814814106(1)若将参与调查问卷不少于4次的居民称为“关注流行语居民”，请你根据频数分布表，完成22⨯列联表，据此调查你是否有99%的把握认为在此社区内“关注流行语与性别有关”？男女合计关注流行语8不关注流行语合计40(2)从被调查的人中按男女比例随机抽取6人，再从选取的6人中选出3人参加政府听证会，求选出的3人为2男1女的概率．附：参考公式()()()()()22n ad bc K a b c d a c b d -=++++及附表()2P K k ≥0.1000.0500.0100.001k2.7063.8416.63510.82819．（12分）在几何体中，底面ABC 是边长为2的正三角形．⊥AE 平面ABC ，若,5,4,3AE CD BF AE CD BF ===∥∥．(1)求证：平面DEF ⊥平面AEFB ；(2)是否在线段AE 上存在一点P ，使得二面角P DF E --的大小为π3．若存在，求出AP 的长度，若不存在，请说明理由．20．（12分）已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ，点31,2P ⎛⎫ ⎪⎝⎭在椭圆C 上，且PF 垂直于x 轴．(1)求椭圆C 的方程；(2)直线l 斜率存在，交椭圆C 于,A B 两点，,,A B F 三点不共线，且直线AF 和直线BF 关于PF 对称．（ⅰ）证明：直线l 过定点；（ⅱ）求ABF △面积的最大值．21．（12分）已知函数()2,0eax x f x a =>．(1)当2a =时，求函数()f x 的单调区间和极值；(2)当0x >时，不等式()()2cos ln ln 4f x f x a x x ⎡⎤-≥-⎣⎦恒成立，求a 的取值范围．（二）选考题：共10分．请考生在22、23题中任选一题作答，如果多做，则按所做的第一题计分．选修4-4：坐标系与参数方程22．在平面直角坐标系xOy 中，曲线C 的参数方程为12cos 2sin x y αα=+⎧⎨=⎩（α为参数）.以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为sin 42πρθ⎛⎫-= ⎪⎝⎭.(1)求C 的普通方程和l 的直角坐标方程；(2)设直线l 与x 轴相交于点A ，动点B 在C 上，点M 满足AM MB =，点M 的轨迹为E ，试判断曲线C与曲线E 是否有公共点.若有公共点，求出其直角坐标；若没有公共点，请说明理由.选修4-5：不等式选讲23．已知()2122f x x x x =-+-+.(1)求()2f x ≥的解集；(2)记()f x 的最小值为t ，且2(0,0)3a b t a b +=>>，求证：11254a b a b ⎛⎫⎛⎫++≥ ⎪⎪⎝⎭⎝⎭.。

38套专题训练：数列大题1、（宁波期末）（本题满分15分）如果数列{}n a 同时满足以下两个条件：（1）各项均不为0；（2）存在常数k ，对任意*n N Î，212n n n a a a k ++=+都成立。

则称这样的数列{}n a 为“k 类等比数列”。

（I ）若数列{}n a 满足31n a n =+，证明数列{}n a 为“k 类等比数列”，并求出相应的k ； （II ）若数列{}n a 为“3类等比数列”，且满足121,2a a ==，问是否存在常数l ，使得21n n n a a a l +++=对于任意*n N ∈都成立？若存在，求出l ；若不存在，请举出反例。

2、（杭州检测）设数列{}n a 的前n 项和为n S ，若n S +n a =n （*N n ∈）.（I ）求数列{}n a 的通项公式； （II ）求证：221...21212133221＜nn a a a a ++++. 3、（绍兴期末）20、（本小题满分14分）数列{}n a 是公差不为零的等差数列，56a =．数列{}n b 满足：13b =，11231n n b bb b b +=⋅⋅⋅+．()I 当2n ≥时，求证：111n n n b b b +-=-； ()II 当31a >且3a *∈N 时，3a ，5a ，1k a ，2k a ，⋅⋅⋅，n k a ，⋅⋅⋅为等比数列．()i 求3a ；()ii 当3a 取最小值时，求证：1231231111111141111n n k k k k b b b b a a a a ⎛⎫+++⋅⋅⋅+>+++⋅⋅⋅+ ⎪ ⎪----⎝⎭．4、（温州一）19．（本题满分15分）对于任意的n ∈N *，数列{a n }满足1212121212121n na n a a n ---+++=++++ .(Ⅰ) 求数列{a n }的通项公式；(Ⅱ) 求证：对于n≥2，231222112nn ++++<- 5、（台州期末）18．（15分）已知数列{a n }的前n 项和S n ，a 1=t （t ≠﹣1），S n +2a n+1+n+1=0，且数列{a n +1}为等比数列． （1）求实数t 的值；（2）设T n 为数列{b n }的前n 项和，b 1=1，且．若对任意的n ∈N *，使得不等式+…≥恒成立，求实数m 的最大值．6、（湖州期末）20、（本小题满分14分）已知数列{}n a 的前n 项和记为n S ，且满足21n n a S -=．()I 求数列{}n a 的通项公式； ()II 设()1nn n b a =--，记12111n nb b b T =++⋅⋅⋅+，求证：2n T <． 7、（诸暨期末）8、（衢州期末）19. （本题满分14分）已知数列{n a }是公差不为0的等差数列，其前n 项和为n S ，124,,a a a成等比数列，5328a S =+ （Ⅰ）求数列{n a }的通项公式；（Ⅱ）若数列{n a }的前n 项和31n n n T a =+，对任意2n ≥且*n N ∈，不等式n b ＜n kT 恒成立，求实数k 的取值范围.9、（五校联考）21．（本题满分15分）已知数列{}n a 的前n 项和n S 满足2n n S a n =-．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设1n nn a b a +=，记数列{}n b 的前n 和为n T ，证明：1032n nT -<-<．10、（金华十校）11、（金丽衢1）设数列{}n a 的前n 项的和为n S ，且⎭⎬⎫⎩⎨⎧n S n 是等差数列，已知,11=a 12432432=++S S S . （Ⅰ）求{}n a 的通项公式n a ；（Ⅱ）当2≥n 时，1401-≥++λλnn a a 恒成立，求λ的取值范围.12、（杭州2）13、（嘉兴一模）在数列{}n a 中，13a =，n a =2n n b a =-，2n =，3，⋅⋅⋅．()I 求2a ，3a ，判断数列{}n a 的单调性并证明；()II 求证：11224n n a a --<-（2n =，3，⋅⋅⋅）； ()III 是否存在常数M ，对任意2n ≥，有23n b b b ⋅⋅⋅≤M ？若存在，求出M 的值；若不存在，请说明理由． 14、（嘉兴检测2）19．（本题满分15分）如图，在平面直角坐标系xOy 中，设21=a ，有一组圆心在x 轴正半轴上的圆nA （ ,2,1=n ）与x 轴的交点分别为)0,1(0A 和)0,(11++n n a A ．过圆心n A 作垂直于x 轴的直线n l ，在第一象限与圆n A 交于点),(n n n b aB ．（Ⅰ）试求数列}{n a 的通项公式；（Ⅱ）设曲边形11++n n n B B A （阴影所示）的m S S S n≤+++11121 恒成立，试求实数m 的取值范围．15、（宁波二模）19.（本题满分15分）已知m 为实数，且29-≠m ，数列{}n a 的前n 项和S n 满足m a S nn n +⨯+=32134 （Ⅰ）求证：数列{}13+-n n a 为等比数列，并求出公比q ；（Ⅱ）若15≤n a 对任意正整数n 成立，求证：当m 取到最小整数时，对于n ≥4，n ∈N ，都有 4811...n++>-16、（温州二模）20．（本小题14分）已知数列{}n a 满足：2,121==a a ，且1123(2,)n n n a a a n n *+-=+≥∈N ．（I ）设1()n n n b a a n *+=+∈N ，求证{}n b 是等比数列；（II ）（i ）求数列{}n a 的通项公式；（ii ）求证：对于任意*∈N n 都有47111121221<++++-n n a a a a 成立． 17、（绍兴质检）18、（台州调研）19、（诸暨毕业班）20、（衢州二模）19.（本题满分15分）设各项均为正数的等比数列{}n a 的公比为q ，[]n a 表示不超过实数n a 的最大整数（如[]1.21=），设[]n n b a =，数列{}n b 的前n 项和为n T ，{}n a 的前n 项和为n S . （Ⅰ）若114,2a q ==，求n S 及n T ； （Ⅱ）若对于任意不超过2015的正整数n ,都有21n T n =+ ，证明:12013213q ⎛⎫<< ⎪⎝⎭．21、（杭二中）18．已知数列{a n }中，111,1,33,n n na n n a a a n n +⎧+⎪==⎨⎪-⎩为奇数为偶数， （Ⅰ）求证：数列23{}2n a -是等比数列；（Ⅱ）设n S 是数列{}n a 的前n 项和，求满足0n S >的所有正整数n ．22、（学军中学）19.（15分）已知数列{a n }，{b n }中，a 1=1，22111(1)n n n n a b a a ++=-⋅，n ∈N *，数列{b n }的前n 项和为S n ．（1）若12n n a -=，求S n ；（2）是否存在等比数列{a n }，使2n n b S +=对任意n ∈N *恒成立？若存在，求出所有满足条件的数列{a n }的通项公式；若不存在，说明理由；（3）若{a n }是单调递增数列，求证：S n ＜2．23、（镇海中学）19.（本题满分15分）P 在曲线C : ()11y x x=>上，曲线C 在点P 处的切线与直线y = 4x 交于点A ， 与x 轴交于点B .设点A ， B 的横坐标分别为,A B x x ，记()A B f t x x =.正数数列{n a }满足()1n n a f a -=*(,2)n N n ∈≥,1a a =. (Ⅰ)写出1,n n a a -之间的关系式；(Ⅱ)若数列{n a }为递减数列，求实数a 的取值范围； (Ⅲ)若2a =,34n n b a =-，设数列{n b }的前n 项和为n S ，求证：()*32n S n N <∈． 24、（绍兴一中）18. （本小题满分15分）已知正项数列{}n a 的前n 项和为11,,2n S a =且满足1241()n n S S n N *+=+∈．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）当1i n ≤≤，1j n ≤≤（,,i j n 均为正整数）时，求i a 和j a 的所有可能的乘积i j a a 之和.25、（五校2）20．（本小题满分14分）已知数列{}n a （*N n ∈，146n ≤≤）满足1a a =， 1,115,1,1630,1,3145,n n d n a a n n d+⎧⎪⎪-=⎨⎪⎪⎩≤≤≤≤≤≤其中0d ≠，*N n ∈．（1）当1a =时，求46a 关于d 的表达式，并求46a 的取值范围； （2）设集合{|,,,,116}i j k M b b a a a i j k i j k *==++∈<<N ≤≤．①若13a =，14d =，求证：2M ∈；②是否存在实数a ，d ，使18，1，5340都属于M ？若存在，请求出实数a ，d ；若不存在，请说明理由．26、19．（六校联考）已知数列{a n }的前n 项和为S n ，S n *3()2n a n n N =-∈．（I ）求证{a n +1}是等比数列，并求数列{a n }的通项公式；（II ）证明：27、（金华十校）18．（本题满分15分） 设S n 为等差数列{a n }的前n 项和，其中a 1=1，且1nn nS a a λ+=( n ∈N *)．(Ⅰ)求常数λ的值，并写出{a n }的通项公式； (Ⅱ)记3nn na b =，数列{b n }的前n 项和为T n ，若对任意的n k ≥(k ∈N *)，都有3144nT n -<，求常数k 的最小值.28、（宁波十校）已知数列{}n a 满足11a =，点()1,n n a a +在直线21y x =+上．数列{}n b 满足11b a =,121111()n n n b a a a a -=+++ （2n ≥且*n N ∈）． (I)(i)求{}n a 的通项公式 ;(ii) 证明111n n n n b ab a +++=（2n ≥且*n N ∈）； (II)求证：12111101113n b b b ⎛⎫⎛⎫⎛⎫+++< ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭ . 29、（稽阳联谊）20．已知数列{a n }的前n 项和为S n ，满足a 1=2，S n +2=2a n ，n ∈N +， （Ⅰ）求a n ；（Ⅱ）求证+…+（Ⅲ）设b 1，b 2，…，b 2015是数列a 1，a 2，…，a 2015的任意一个排列，求（）的最大值，并说明何时取到等号．30、（金丽衢2）20. （本题满分１４分）在单调递增数列}{n a 中，12a =，24a =，且12212,,+-n n n a a a 成等差数列，22122,,++n n n a a a 成等比数列， ,3,2,1=n ．（Ⅰ）（ⅰ）求证：数列}{2n a 为等差数列； （ⅱ）求数列}{n a 的通项公式.（Ⅱ）设数列}1{na 的前n 项和为n S ，证明：43(3)n n S n >+，*n ∈N ．。

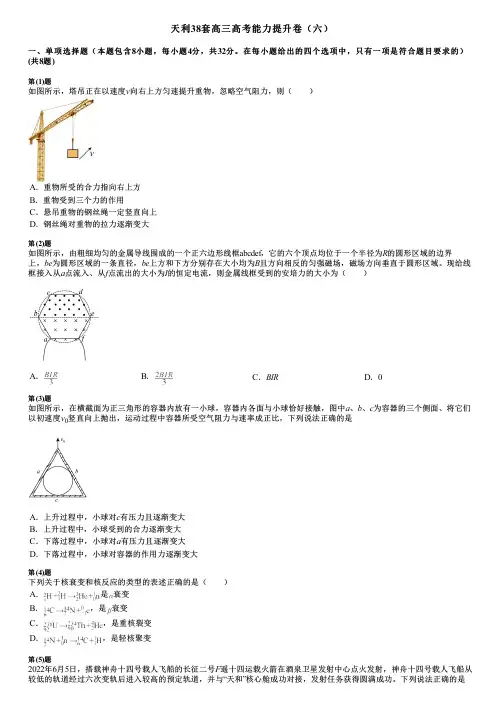
天利38套高三高考能力提升卷（六）一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题如图所示，塔吊正在以速度v向右上方匀速提升重物，忽略空气阻力，则（ ）A．重物所受的合力指向右上方B．重物受到三个力的作用C．悬吊重物的钢丝绳一定竖直向上D．钢丝绳对重物的拉力逐渐变大第(2)题如图所示，由粗细均匀的金属导线围成的一个正六边形线框abcdef，它的六个顶点均位于一个半径为R的圆形区域的边界上，be为圆形区域的一条直径，be上方和下方分别存在大小均为B且方向相反的匀强磁场，磁场方向垂直于圆形区域。

现给线框接入从a点流入、从f点流出的大小为I的恒定电流，则金属线框受到的安培力的大小为（ ）A．B．C．BIR D．0第(3)题如图所示，在横截面为正三角形的容器内放有一小球，容器内各面与小球恰好接触，图中a、b、c为容器的三个侧面、将它们以初速度v0竖直向上抛出，运动过程中容器所受空气阻力与速率成正比，下列说法正确的是A．上升过程中，小球对c有压力且逐渐变大B．上升过程中，小球受到的合力逐渐变大C．下落过程中，小球对a有压力且逐渐变大D．下落过程中，小球对容器的作用力逐渐变大第(4)题下列关于核衰变和核反应的类型的表述正确的是（ ）A．是衰变B．，是衰变C．，是重核裂变D．，是轻核聚变第(5)题2022年6月5日，搭载神舟十四号载人飞船的长征二号F遥十四运载火箭在酒泉卫星发射中心点火发射，神舟十四号载人飞船从较低的轨道经过六次变轨后进入较高的预定轨道，并与“天和”核心舱成功对接，发射任务获得圆满成功。

下列说法正确的是（ ）A．神舟十四号与“天和”核心舱对接后，“天和”核心舱的运行周期不变B．变轨之前，神舟十四号的向心加速度小于“天和”核心舱的向心加速度C．若已知“天和”核心舱的运行周期和轨道半径，则可求出地球的密度D．返回舱落地前的减速过程，其中的宇航员处于失重状态第(6)题彩虹是太阳光经过球形雨滴发生两次折射和一次反射形成的，彩虹成因的简化示意图如图所示。

天利三十八套数学答案天利38套数学答案（一）:急用.高一天利38套单元专题数学,专题6,函数的图像,题实在太难了大题要详细的选择填空直接答案就行名字是天利38套单元专题专题6 函数的图像每个年级都有几个版本的天利,你说的是哪个版本的》天利这练习很好,很强大,我在高中时全校都是用的天利,天利38套数学答案（二）:2010天利38套英语答案1-5张的答案只有一到三套单选：（一）ABBBA DDDCC CDACB（二）ACCBD BDACB BDCBA （三）ACDBC BBBCD CBAA【天利38套数学答案】天利38套数学答案（三）:天利38套2011语文答案11-13张一套一套的在百度上收,因为是中考题所以有答案,但你要检查一下是不是你哪一套.天利38套数学答案（四）:天利38套单元专题7函数的概念与图像7A答案找度娘 == 天利38套数学答案（五）:天利38套六年级英语13完形填空和14阅读理解的答案【天利38套数学答案】(1)亲爱的老师,几年来是您带领我在知识的海洋中遨游;是您引领我放飞理想,我想对您说一声,“老师,您辛苦了!" (2)三年的时光如云般飘过,时间的天使不苟地将时针拨向离别.在这临别之际,我们的心情如大海的波涛汹涌澎湃.曾记得,我们刚进校门时,还是蹦蹦跳跳的少年,多么幼稚、多么天真!而如今,我们已长大,脸上写满了成熟曾记得,我们刚进校门时,还只会加减乘除,多么无知,多么贫乏.而如今,我们似乎上通天文,下明地理,洋洋洒洒,满腹经伦三年的阳光雨露,三年的辛勤耕耘,花儿开放了,姹紫嫣红；果实成熟了,硕果累累.花儿翩翩起舞,是在感谢这片沃土；果实频频点声,是在报答辛勤的园丁风筝飞得再高,它的线仍牵着您的手；游子走得再远,他的心仍挂着母亲.不管走向哪里,我们都不会忘记您——老师；我们会努力学习,用优异的成绩献给您——老师敬爱的老师,是您给了我健飞的翅膀,是您给了我青春的光亮,您是漆黑夜空中的恒星,将照亮我的一生.(3)光阴似箭,日月如梭,转眼间,美好的小学生活将要结束,我的心中不免掠过一丝莫名的忧伤,寻找这忧伤的源头,原来是不忍与您分别.您平易近人,和蔼可亲,您对我们的爱像暖流一样温暖着学生的心,也像熊熊热火,照亮我学习的前程.不知在以后的学习生涯中,我还会不会再一次幸运的遇到您这么优秀的老师,在这里,我想对您说谢谢您对我的教育,老师,您辛苦了.(4)老师你如一位园丁,每天浇灌这我们这些祖国的花朵,你浇灌的是太阳水肥料,也是知识.(5) 一句轻柔的的表扬,心里是那么的甘甜；一句亲切的鼓励,浑身充满了力量……至今铭记也许不仅仅是老师无意间说的话,没有您的话语不会有我今天的收获.老师!我会带着这些话踏入中学的大门.一股流水,不分昼夜滋润一方土地,流过后也不怨辛劳.永远都是那么流啊流,浇灌着一批批花草.今年流到了我们这批花草.亲爱的水!(6)我在绿荫下为你祝福,老师!我们就像这棵树上的叶子,马上就要离你而去,请相信我们一定会在一个云淡风轻的午后,捎上祝福,静静地在你四周撑起一片阴凉.我在花朵旁为你祝福,老师!我们就像这朵花的花瓣,马上就要离你而去,请相信我们一定会在一个风和日丽的早上,捎上成绩,静静地在你四周散出一阵芬芳.我在小河边为你祝福,老师!我们就像这条河里的水珠,马上就要离你而去,请相信我们一定会在一个清风鸣蝉的夜晚,捎上谢意,静静地在你四周撒下一滴清凉.天利38套数学答案（六）:关于数学的动点问题的典型例题以及解析动点题,那种基本图形是四边形的,在平行四边形、矩形、菱形、正方形、等腰梯形等等中所出现的动点问题.另一种可能是抛物线与动点相结合的,你可以看其他省市的中考题,象天利38套等带答案的那种,自己看几道同类型的答案,你就知道动点题怎么做了. 总之,动点问题的解题思路是动中取定（或说动中取静都可以）,多画几个图形,通常一种情况画出一个图形,就可以把动点转化成一般的几何证明了. 希望会对你有所帮助,祝你中考取得好成绩!例:在平行四边形ABCD中,DA=4cm,角A=60度,BD垂直AD,以动点P从A出发,以每秒1cm的速度沿A到B到C的路线匀速运动,过点P作直线PM,使PM垂直AD（1）当点P运动2秒,设直线PM与AD相交于点E,求三角形APE的面积（2）当点P运动2秒时,另一动点Q也从A出发沿A到B到C的路线运动,且在AB上以每秒1cm的速度匀速运动,在BC上以每秒2cm的速度匀速运动,过Q作直线QN,使QN平行PM,设点Q运动速度为t秒（t大于等于0,小于等于10）,直线PM与QN截平行四边形ABCD所得图形的面积为scm^2 1.求s关于t的函数关系式（1）答案是(√3)/2 这一问很简单,就不写过程了. （2）当0≤t≤6时,截面为梯形（开始是三角形）,过Q作QO⊥PM,垂足为O,易求QO为1. 因为QA=tcm,在Rt三角形QAN中,因为角A=60度,所以QN等于QA/2=(√3t)/2,PM=OM+PO=(√3t)/2+√3S=(QN+PM)_QO/2=(√3t+√3)/2 当6＜t≤8时,截面为六边形S ＝S平行四边形ABCD－S三角形AQN－S三角形CPM＝-(5√3)/8_(t-8)^2+6√3 当8天利38套数学答案（七）:谁有初三下册数学第二章二次函数那一部分的习题（带答案）啊,最好稍微难一点的.我建议你去买《天利38套》或《五三中考数学版》天利38套数学答案（八）:一个概率统计题从某自动包装机包袋的食盐中,随机抽取20袋作为样本,按各袋的质量（单位：g）分成四组,[490,495),[495,500),[500,505),[505,510],相应的样本频率分布直方图如图所示,(Ⅰ)估计样本的中位数是多少?落入[500,505)的频数是多少?(Ⅱ)现从这台自动包装机包袋的大批量食盐中,随机抽取3袋,记{表示食盐质量属于[500,505)的袋数,依样本估计总体的统计思想,求ξ的分布列及其期望.题目我会做,但是我只想知道 1 最后一问为什么要强调“大批量”?2 C （k,n）P的n-k次方（1-P）的k次方有什么使用条件么?我做天利38套题为什么有的题目答案用此公式有时又不用?强调“大批量”,是使实验的次数足够多,从而使实验结果的频率等于其概率.独立重复实验才能用此公式.即每次实验的结果对下一次实验没有影响.比如取球的问题,只有有放回地取球才是独立重复实验,如果无放回地取球,则不能用这个公式.天利38套数学答案（九）:交流发电机和直流发电机的原理都是“电磁感应”?为什么《2010年的物理中考天利38套》上的第32套安徽省的22题答案是直流发电机的原理是磁场对通电导体有力的作用?直流发电机的工作原理就是把电枢线圈中感应产生的交变电动势,靠换向器配合电刷的换向作用,使之从电刷端引出时变为直流电动势的原理. 交流发电机和直流发电机的原理是一样的,都是通过电磁感应来发电.直流发电机只是将交流发电机滑环用换向器代替,从而使线圈产生交流电而供给外部的电流方向不变,所以产生的是直流电,没有换向器产生的是交流电!可以看图会发现输出的那个滑片有所不同 . 交流发电机是利用电磁感应原理,将发动机带动发电机轴转动的机械能转变为交流电电能输出的发电机.其构造的一般原则是：用适当的导磁和导电材料构成互相进行电磁感应的磁路和电路,以产生电磁功率,达到能量转换的目的.直流发电机的工作原理就是把电枢线圈中感应产生的交变电动势,靠换向器配合电刷的换向作用,使之从电刷端引出时变为直流电动势的原理.天利38套数学答案(共9篇)。

全国普通高等学校高考数学模拟试卷（理科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的•1. （5 分）已知集合A={x| - x2+4x> 0},片&|占<3玄丈歼} , C=（x|x=2n, n€81N}，贝U（A U B）n C=（）A. {2，4}B. {0，2}C. {0，2，4}D. {x|x=2n, n € N}2. （5分）设i是虚数单位，若-- ' ― ，x，y€ R，则复数x+yi的共轭复数2^1是（）A. 2 - iB.- 2 - iC. 2+iD.- 2+i3. （5分）已知等差数列{a n}的前n项和是S h，且％+a5+a6+a z=18，贝U下列命题正确的是（）A. a5是常数B. S5是常数C. a i0是常数D. Si o是常数4. （5分）七巧板是我们祖先的一项创造，被誉为东方魔板”它是由五块等腰直角三角形（两块全等的小三角形、一块中三角形和两块全等的大三角形）、一块正方形和一块平行四边形组成的.如图是一个用七巧板拼成的正方形中任取一点，贝吐匕点取自黑色部分的概率是（）BCD2 25. （5分）已知点F为双曲线C: = 一一（a>0，b>0）的右焦点，直线x=aa b与双曲线的渐近线在第一象限的交点为A,若AF的中点在双曲线上，贝U双曲线的离心率为（）A. "B. I ■:C. I」订D. - % -6. （5分）已知函数f&）二sinx, K E [-冗50]诋(0t i]A . 7 .nJTD.——-74 一（5分）执行如图所示的程序框图，则输出的S的值为（）2+ n B. C.盒2*出£产〔筠棗）*>201A.二7B. 「」C.. - 厂D. +-8 （5分）已知函数f仗）二sin 3葢X^\/3C^OS23(3> 0) 的相邻两个零点差的绝对值为二，则函数f （x）的图象（4A . 可由函数（X）=cos4x的图象向左平移个单位而得B. 可由函数（X）=cos4x的图象向右平移C. 可由函数（X）=cos4x的图象向右平移D . 可由函数（X）=cos4x的图象向右平移丄个单位而得24丄个单位而得245兀个单位而得9. （5 分）（羽-3）（1的展开式中剔除常数项后的各项系数和为（A . —73 B.—61 C.—55 D.—6310. （5分）某几何体的三视图如图所示，其中俯视图中六边形ABCDEF是边长为1的正六边形，点G为AF的中点，则该几何体的外接球的表面积是（nanA . 317£~6~B.31兀C.481K D丑価兀. ■:6411. （5分）已知抛物线C: y 2=4x 的焦点为F ,过点F 分别作两条直线l i , I 2，直 线l i 与抛物线C 交于A 、B 两点，直线12与抛物线C 交于D 、E 两点，若l i 与12 的斜率的平方和为1,则|AB|+| DE 的最小值为（ ）A . 16 B. 20 C. 24 D . 3212. （5分）若函数y=f （x ）, x € M ，对于给定的非零实数a ,总存在非零常数T , 使得定义域M 内的任意实数x ,都有af （x ） =f （x+T ）恒成立，此时T 为f （x ） 的类周期，函数y=f （x ）是M 上的a 级类周期函数.若函数y=f （x ）是定义在 区间[0 , + %）内的2级类周期函数，且T=2,当x € [0 , 2 ）时，zg ■-2,，1 ©卄比）二戈函数.若？ X 1€ [6, 8] , ?X 2€L<Y <2’二、填空题（每题5分，满分20分，将答案填在答题纸上） 13 . （ 5分）已知向量, ^占口），-1），且旦丄1,则1)-=为 ______ .15. （5分）在等比数列｛a n ｝中，a 2?a 3=2a 1,且a 4与2a 7的等差中项为17,设b n =a 2n -1- a 2n , n € N*，则数列｛b n ｝的前2n 项和为 ______ .16.（5分）如图，在直角梯形 ABCD 中，AB 丄BC, AD // BC,一二亍「二，点14. （ 5分）已知x , y 满足约束条件（0, +x ）,使g （X 2）- f （X 1）w 0成立，则实数m 的取值范围是（ 的最小值E是线段CD上异于点C, D的动点，EF丄AD于点^将厶DEF沿EF折起到△ PEF 的位置，并使PF丄AF,则五棱锥P-ABCEF勺体积的取值范围为________ .三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. （12分）已知△ ABC的内角A, B, C的对边a, b, c分别满足c=2b=2.2bcosA+acosC+ccosA=Q 又点D 满足■ /（1）求a及角A的大小;18. （12分）在四棱柱ABCD- A i B i C i D i中，底面ABCD是正方形，且匚-:-，/ A1AB=Z A1AD=6C°.（1）求证：BD丄CG;（2）若动点E在棱C1D1上，试确定点E的位置，使得直线DE与平面BDB所成角的正弦值为I .19. （12分）过大年，吃水饺”是我国不少地方过春节的一大习俗.2018年春节前夕，A市某质检部门随机抽取了100包某种品牌的速冻水饺，检测其某项质量指标，(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数「(同一组中的数据用该组区间的中点值作代表)；(2)①由直方图可以认为，速冻水饺的该项质量指标值Z服从正态分布N (卩,d2),利用该正态分布，求Z落在(14.55, 38.45)内的概率；②将频率视为概率，若某人从某超市购买了4包这种品牌的速冻水饺，记这 4 包速冻水饺中这种质量指标值位于(10，30)内的包数为X,求X的分布列和数学期望.附：①计算得所抽查的这100包速冻水饺的质量指标的标准差为^=V142. 75^11-95;②若〜N — b 2 )，贝U P (卩―crV Z< p+ o)=0.6826，P (卩―2 o< Z< (J+2 C)=0.9544.0e030 ・-0-025 ・*0.020 - 0.0150.01010 2030 4050各水饺质量指标丄一，且以两焦点为直20. (12分)已知椭圆C: 亏〔呂0)的离心率为径的圆的内接正方形面积为2.(1)求椭圆C的标准方程；(2)若直线I: y=kx+2与椭圆C相交于A，B两点，在y轴上是否存在点D,使直线AD与BD的斜率之和k AD+k BD为定值？若存在，求出点D坐标及该定值，若不存在，试说明理由.21. (12分)已知函数f (x) =e x- 2 (a- 1) x- b，其中e为自然对数的底数.(1)若函数f (x)在区间［0,1］上是单调函数，试求实数a的取值范围；(2)已知函数g (x) =e x-(a- 1) x2- bx- 1,且g (1) =0,若函数g (x)在区间［0,1］上恰有3个零点，求实数a的取值范围.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.［选修4-4:坐标系与参数方程］22. (10分)在平面直角坐标系xOy中，圆C i的参数方程为\ K-_Uacos® ( 0ty=-l+asin9为参数，a是大于0的常数).以坐标原点为极点，x轴正半轴为极轴建立极坐标系，圆C2的极坐标方程为p =2^2^05 ( .(1)求圆C i的极坐标方程和圆C2的直角坐标方程；(2)分别记直线I： ^吕，P€ R与圆C i、圆C2的异于原点的焦点为A，B,若圆C i与圆C2外切，试求实数a的值及线段AB的长.［选修4-5:不等式选讲］23. 已知函数f (x) =|2x+1| .(1)求不等式f (x)< 10-| x-3|的解集；(2)若正数m，n 满足m+2n=mn，求证：f (m) +f (- 2n)》16.2018年全国普通高等学校高考数学模拟试卷（理科）（一）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的•1. （5 分）已知集合A={x| - x2+4x> 0}, B二丘|丄<罗<27} , C={x|x=2n, n€31N}，贝U（A U B）n C=（）A. {2，4}B. {0，2}C. {0，2，4}D. {x|x=2n, n € N}【解答】解：A={x| - x2+4x> 0} ={x| 0< x< 4}，駐〔兀I去V3y 27} ={x| 3-4v 3x v 33}={x| - 4<x< 3}，oJL则A U B={x| - 4< x<4}，C={x| x=2n, n € N}，可得（A U B）n C={0, 2, 4},故选C.2. （5分）设i是虚数单位，若' ,x, y€ R,则复数x+yi的共轭复数2-1是（）A. 2 - iB.- 2 - iC. 2+iD.- 2+i【解答】解：由一「2-1得x+yi= — -i —-! ■=2+i得x+yi= =2+i，•••复数x+yi的共轭复数是2 -i.3（5分）已知等差数列{a n}的前n项和是S，且a4+a5+a e+a7=18,则下列命题正确的是（）A. a5是常数B. S5是常数C. a10是常数D. Si0是常数故选：A.【解答】解：•••等差数列｛a n ｝的前n 项和是S n ,且a 4+a 5+a 6+a 7=18, 二 a 4+a 5+a 6+a 7=2 (a i +a io ) =18, --a i +a io =9, …Sg 二乎(有十^10)=45- 故选：D .4. （5分）七巧板是我们祖先的一项创造，被誉为 东方魔板”它是由五块等腰 直角三角形（两块全等的小三角形、一块中三角形和两块全等的大三角形） 、- 块正方形和一块平行四边形组成的.如图是一个用七巧板拼成的正方形中任取一点，贝吐匕点取自黑色部分的概率是（）【解答】解：设AB=2,则BC=CD=DE=EF=1V B —订,S 平行四边形EFG 阳2S BC =2 X — , •••所求的概率为口 +S 平行四边形EPGH g 正方形AB5 =2x7故选：A .2 25. （5分）已知点F 为双曲线C : 云丄尹1 （a >0, b >0）的右焦点，直线x=a 与双曲线的渐近线在第一象限的交点为 A ,若AF 的中点在双曲线上，贝U 双曲线 的离心率为（）16BCDA. . 1B. I ■:C.「'.打D. I 口2 2【解答】解：设双曲线C:青冬二1的右焦点F （c, 双曲线的渐近线方程为y丄x,a由x=a代入渐近线方程可得y=b，则A（a，b），可得AF的中点为（誓，寺b）,代入双曲线的方程可得卄J -丄=1，可得4a2- 2ac- c2=0，由e*，可得e2+2e- 4=0，a解得e= !.- 1 （- 1 —汀舍去），故选：D. 0)，6. （5分）已知函数f&）二则.A. 2+ nB. JT T-2J Ql-/dK=/ cOSdt= J 1 址齐t芒1 2+'，J 2开£(只),xE [-TT , 0]2,址© 1]^rcsinx *兀4+ (- COSX：=(2. 故选：D.7. （5分）执行如图所示的程序框图，则输出的 S 的值为（）A ...工7B .C.. -厂 D . m【解答】解：第1次循环后，S=-,不满足退出循环的条件，k=2; 第2次循环后，S= -;，不满足退出循环的条件，k=3; 第3次循环后，S= =2，不满足退出循环的条件，k=4；第n 次循环后，S= ，不满足退出循环的条件，k=n+1 ； 第2018次循环后，S=,3.「儿 不满足退出循环的条件，k=2019第2019次循环后，S==2「|「，满足退出循环的条件， 故输出的S 值为2厂「， 故选：C& （5分）已知函数f （瓷）sin® xug®負7勺（3> 0）的相邻两个 零点差的绝对值为「则函数f （x ）的图象（）A. 可由函数g （x ） =cos4x 的图象向左平移卑匚个单位而得B. 可由函数g （x ） =cos4x 的图象向右平移2二个单位而得24C. 可由函数g （x ） =cos4x 的图象向右平移丄?个单位而得D. 可由函数g （x ） =cos4x 的图象向右平移一个单位而得O【解答】 解：函数 f （7） =sinseesxVsccs5 工=寺 sin7T=sin （2^）-—）（3>0）的相邻两个零点差的绝对值为才?爲=：，二①=2 f (x ) =sin (4x -中=cos[(2 3X )]=cos (4x普）.故把函数g （x ） =cos4x 的图象向右平移竺个单位，可得f （X ）的图象，24 故选：B.9・（5分）©-3）（代/的展开式中剔除常数项后的各项系数和为（ ）A .- 73B .- 61C.- 55D .- 63【解答】解：丄广展开式中所有各项系数和为（2- 3） （1+1） 6=- 64; ⑵-3）（1 丄）社（2x -3） （1忑碍+•••）,工工/其展开式中的常数项为-3+12=9,• ••所求展开式中剔除常数项后的各项系数和为 -64 - 9=- 73.故选：A . 6【解答】解：如图，可得该几何体是六棱锥 P -ABCDEF 底面是正六边形，有一 PAF 侧面垂直底面，且P 在底面的投影为AF 中点，过底面中心N 作底面垂线, 过侧面PAF 的外心M 作面PAF 的垂线，两垂线的交点即为球心 0, 设厶PAF 的外接圆半径为r ，/二（2P ）牛（寺严，解得r #，•価二0昨茅6 （5分）某几何体的三视图如图所示，其中俯视图中六边形ABCDEF 是边长为 1的正六边形，点G 为AF 的中点，则该几何体的外接球的表面积是（）A .B .312Z8 C.鋁1叽64D.48MAS11. (5分)已知抛物线C: y 2=4x 的焦点为F ,过点F 分别作两条直线11, 12，直 线11与抛物线C 交于A 、B 两点，直线12与抛物线C 交于D 、E 两点，若11与12 的斜率的平方和为1,则|AB|+| DE 的最小值为()A . 16 B. 20 C. 24 D . 32【解答】解：抛物线C: y 2=4x 的焦点F (1, 0),设直线11: y=k i (x- 1),直线 12： y=k 2 (x - 1),由题意可知，贝U 叭Jk 『二1,设 A (X 1 , y 1), B (X 2 , y 2),贝 U X 1+X 2= -------k l 4设 D (X 3 , y 3), E (X 4 , y 4),同理可得：X 3+X 4=2+ ° ,k2由抛物线的性质可得：丨AB | =X 1+x 2+p=4+则该几何体的外接球的半径•••表面积是则该几何体的外接球的表面积是7 V4M+1 FS=4冗 R =°*l 兀.64联立丿y=k] (i-lj,整理得：k 12x 2-( 2k 12+4) x+k 12=0,R= I :. 故选：C.C,| DE | =X 3+X 4+pk l=84 ,当且仅当k®目时，上式“我立• ••• | AB|+| DE 的最小值 24, 故选：C.12. (5分)若函数y=f (x ), x € M ，对于给定的非零实数a ,总存在非零常数T , 使得定义域M 内的任意实数x ,都有af (x )=f (x+T )恒成立，此时T 为f (x ) 的类周期，函数y=f (x )是M 上的a 级类周期函数.若函数y=f (x )是定义在区间［0 , + %)内的2级类周期函数，且T=2,当x € ［0 , 2 )时，f(2-Kb 1<X<2(0 , +x),使g (x 2)- f (X 1)w 0成立，贝U 实数m 的取值范围是(【解答】解：根据题意,对于函数f(x ),当x € ［0 , 2)时,f k)弓2fCE-s), Kx<2-2,有最大值f (0)二，最小值f (1)2，当1v x v 2时，f (x ) =f (2 -x ),函数f (x )的图象关于直线x=1对称,则此时 有-一v f (x )v又由函数y=f (x )是定义在区间[0, +7 内的2级类周期函数，且T=2; 则在€ [6, 8) 上, f (x ) =23?f (x -6),则有—12<f (x )w 4,则 f (8) =2f (6) =4f (4) =8f (2) =16f (0) =8,则函数f (x )在区间［6 , 8］上的最大值为8,最小值为-12;A .—] B. (a, 13 ] C. 〔a,32 J2」2」D .[普g| AB|+| DE =8+1 k 24(ki 2+k 2Z ) 8P4、412 J一 _ _ •若？ xi € [ 6, 8] , ? X 2 €函数 =-21nx分析可得：当O w x < 1时，f (x) --=84 ,对于函数山)二-加4^5切,有g'(x) =-Z +X+1」®之-炉1)3切L x x x分析可得：在(0 , 1)上,g (x)v0,函数g (x)为减函数，在(1 , +x)上,g r (x)>0,函数g (x)为增函数，则函数g （x ）在（0, +x ）上，由最小值f （1） =_ +m ,2若？ x i € [6, 8] , ? X 2 €(0, +x ),使 g (X 2)— f (x i )< 0 成立, ，即一+m < 8, ，即m 的取值范围为(-x,必有 g (x ) min < f (x ) max 故选：B. 解可得m 13 2 、填空题（每题5分，满分20分，将答案填在答题纸上） 13. （5 分）已知向重.I _ d •二二「，，| 丄---,且-一、，则！ . I I ]【解答】解：根据题意，向重 丁（2営cgd ），b=（l, -1）， 若；丄卞，则 ^?b=2sin a cos a =0 则有 tan a又由 sin 2 a +COS 2 a=1 则有 则 则 |..|-: 2^5sina=^ a" COS Cl - !_ 亍),或 = sin a 二芈^ 5 n _砸 C0S 或（— 5则崙丄）2=3品2- 21?工半 5故答案为: 14. （5分）已知x , y 满足约束条件 的最小值为L_. 【解答】解：由约束条件作出可行域如图,X = — 22n -4,联立fxWQ ，解得A （2, 4）, J 23<2，令t=5x -3y ,化为y 专富诗,由图可知,当直线宾耳过A 时, 」 J "J 直线在y 轴上的截距最大，t 有最小值为-2. •••目标函数 玄二彳； 的最小值为2~^-^. 故答案为：丄.15. （5分）在等比数列｛a n ｝中，a 2?a 3=2a i ,且a 4与2a 7的等差中项为17,设b n =a 2n -1- a 2n , n € N*，则数列｛b n ｝的前2n 项和为—亠〕/" _.丄ka【解答】解：等比数列｛a n ｝中，a 2?a 3=2a i ，且a 4与2a 7的等差中项为17, 设首项为a 1,公比为q , 则：整理得:+血］<1 二 34解得: 则: 所以：b n =a 2n -1 — a 2n =屯一」116. （5分）如图，在直角梯形 ABCD 中，AB 丄BC, AD // BC,上-二一二-_，点 E 是线段CD 上异于点C , D 的动点，EF 丄AD 于点^将厶DEF 沿 EF 折起到△ PEF 的位置，并使PF 丄AF ,则五棱锥P -ABCEF 的体积的取值范围为【解答】 解：T PF 丄AF , PF 丄EF, AF G EF=F 二PF 丄平面ABCD 设 PF=x 贝U O v x v 1, 且 EF=DF=x•五棱锥P-ABCEF 的体积V 丄 丄(3-x 2) x 设 f (x ) (3x - x 3),贝U f ' (x) — (3 - 3x 2)6 6•••当 O v x v 1 时，f'(x )>0,则：T 2n = I' 1-4 故答案为: 討护）. (0,丄) •五边形ABCEF 的面积为S=S 弟形ABCD - x( 1+2)x 1-—X 2丄(3-x 2). (3x — x 3), (1-x 2),••• f（x）在（0, 1）上单调递增，又f （0）=0, •五棱锥P-ABCEF的体积的范围是（0,丄）.故答案为:三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. （12分）已知△ ABC的内角A, B, C的对边a, b, c分别满足c=2b=2.2bcosA+acosC+ccosA=Q 又点 D 满足 【解答】 解：(1)由2bcosA+acosC+ccosA=0及正弦定理得-2sinBcosA=sinAcos&osAsinC 即—2si nBcosA=si n( A+C ) =s inB, 在厶 ABC 中，sinB >0,所以一”二二. 在厶 ABC 中，c=2b=2,由余弦定理得 a 2=b 2+c 2 - 2bccosA=k J +c 2+bc=7, 18. (12分)在四棱柱ABCD — A i B i C i D i 中，底面ABCD 是正方形，且匚-■-,/ A 1AB=Z A 1AD=6C °.(1) 求证：BD 丄CG ;(2) 若动点E 在棱C 1D 1上，试确定点E 的位置，使得直线DE 与平面BDB 所成 角的正弦值为….又A €(0, n),所以(1)求a 及角A 的大小; C所以一 I【解答】解：（1）连接A i B, A i D, AC,因为AB=AA=AD,/ A i AB=Z A i AD=60,所以△ A i AB和厶A i AD均为正三角形，于是A i B=A i D.设AC与BD的交点为0,连接A i O,则A i O丄BD,又四边形ABCD是正方形，所以AC丄BD, 而A i O n AC=O,所以BD丄平面A i AC.又AA i?平面A i AC,所以BD丄AA i, 又CG // AA i,所以BD丄CG.（2）由，及BDW2AB=2，知A i B丄A i D,结合A i O丄BD, AO n AC=O 得A i O丄底面ABCD, 所以OA、OB、OA i两两垂直.如图，以点O为坐标原点，| &的方向为x轴的正方向，建立空间直角坐标系 -xyz 则A (i, 0, 0), B (0 , i , 0), D (0 , - i , 0), A i (0 , 0 , i) , C(- i , 0 , DB=(O, 2, 0),瓦二瓯二(一1・ 0, 1), D]C[二磋(T, 1；",由i 丨，得Di (- i, - i , i).设：,I- ■：.：'(疋[0 , i]),则(X E+i , y E+i , Z E- i)=入(-i , i , 0),即 E (-入—i,入—i , i), 所以；「―■•亠.设平面B i BD的一个法向量为|• • •'!,O 0),B,从而A i O丄AO,设直线DE 与平面BDB 所成角为9, 则血*k^＜运，（—'—D+oy m 丨申, V2XV X 2+（-1-\）£+1 14 解得二二或•，二丄（舍去）,2 3所以当E 为D i C i 的中点时，直线DE 与平面BDBi 所成角的正弦值为「.19. （ 12分）过大年，吃水饺”是我国不少地方过春节的一大习俗.2018年春节 前夕，A 市某质检部门随机抽取了 100包某种品牌的速冻水饺，检测其某项质量 指标，（1） 求所抽取的100包速冻水饺该项质量指标值的样本平均数■:（同一组中的 数据用该组区间的中点值作代表）；（2） ①由直方图可以认为，速冻水饺的该项质量指标值 Z 服从正态分布N（卩, ；），利用该正态分布，求Z 落在（14.55, 38.45）内的概率；②将频率视为概率，若某人从某超市购买了 4包这种品牌的速冻水饺，记这 4 包速冻水饺中这种质量指标值位于（10, 30）内的包数为X ,求X 的分布列和数 学期望. 附：①计算得所抽查的这100包速冻水饺的质量指标的标准差为②若（卩，^ ）,贝U P （卩―eV Z w p+ o ） =0.6826, P （卩―2 eV Z w （J +2 o ） =0.9544.得n=(l, 0, 1)，n ・ E6=0 ｛十…… n • &B-i =0 L得 产。

天利三十八套2022数学答案1．如图1，抛物线y ＝ax 2−154x +c 交x 轴于A ，B 两点，交y 轴于点C ．直线y =−34x +3经过点B ，C ．（1）求抛物线的解析式；（2）若点P 为直线BC 下方的抛物线上一动点（不与点B ，C 重合），则△PBC 的面积能够等于△BOC 的面积吗？若能，求出相应的点P 的坐标；若不能，请说明理由； （3）如图2，现把△BOC 平移至如图所示的位置，此时三角形水平方向一边的两个端点点O ′与点B ′都在抛物线上，称点O ′和点B ′为△BOC 在抛物线上的一“卡点对”；如果把△BOC 旋转一定角度，使得其余边位于水平方向然后平移，能够得到这个三角形在抛物线上新的“卡点对”．请直接写出△BOC 在已知抛物线上所有“卡点对”的坐标．解：（1）分别把x ＝0，y ＝0代入一次函数表达式得：点C 、B 的坐标分别为（0，3）、（4，0），将点B 、C 的坐标代入二次函数表达式得：{16a −15+c =0c =3，解得：{a =34c =3， 故抛物线的表达式为：y =34x 2−154x +3； （2）直线y =−34x 和直线BC 平行，直线y =−34x 和抛物线的交点就是满足条件的点P ， 则{y =34x 2−154x +3y =−34x ，解得：{x =2y =−32， 即当（2，−32）时，两个三角形面积相同； （3）抛物线的对称轴为：x =52，①当O ′B ′在水平位置时，如图2所示， O ′B ′＝4，则点B ′和O ′的横坐标分别为12、92，将横坐标代入二次函数表达式得：y =2116， 故此时的“卡点对”坐标为（12，2116）和（92，2116）；②当O ′C ′在水平位置时，O ′C ′＝3，则点B ′和O ′的横坐标分别为4、1， 将横坐标代入二次函数表达式得：y ＝0， 故此时的“卡点对”坐标为（1，0）和（4，0）； ③当B ′C ′在水平位置时，同理可得：此时的“卡点对”坐标为（0，3）和（5，3）； 故抛物线上所有“卡点对”的坐标是（12，2116）和（92，2116）、（1，0）和（4，0）、（0，3）和（5，3）．2．定义：对于给定的一次函数y ＝ax +b （a ≠0），把形如y ={ax +b(x ≥0)−ax +b(x ＜0)的函数称为一次函数y ＝ax +b （a ≠0）的衍生函数．已知矩形ABCD 的顶点坐标分别为A （1，0），B （1，2），C （﹣3，2），D （﹣3，0）． （1）已知函数y ＝2x +1．①若点P （﹣1，m ）在这个一次函数的衍生函数图象上，则m ＝ 3 ．②这个一次函数的衍生函数图象与矩形ABCD 的边的交点坐标分别为 （12，2）或（−12，2） ．（2）当函数y ＝kx ﹣3（k ＞0）的衍生函数的图象与矩形ABCD 有2个交点时，k 的取值范围是 1＜k ＜3 ．解：（1）①x ＝﹣1＜0，则m ＝﹣2×（﹣1）+1＝3， 故答案为3；②一次函数的衍生函数图象与矩形ABCD 的边的交点位置在BC 上， 当y ＝2时，2x +1＝2，解得：x =12， 当y ＝2时，﹣2x +1＝2，解得：x =−12， 故答案为（12，2）或（−12，2）；（2）函数可以表示为：y ＝|k |x ﹣3，如图所示当直线在位置①时，函数和矩形有1个交点，当x ＝3时，y ＝|k |x ﹣3＝3|k |﹣3＝0，k ＝±1， k ＞0，取k ＝1当直线在位置②时，函数和图象有3个交点， 同理k ＝3，故在图①②之间的位置，直线与矩形有2个交点，即：1＜k＜3．3．如图，在平面直角坐标系中，直线l：y=−√33x+2√3与x轴、y轴分别交于点A，B，将点B绕坐标原点O顺时针旋转60°得点C，解答下列问题：（1）求出点C的坐标，并判断点C是否在直线l上；（2）若点P在x轴上，坐标平面内是否存在点Q，使得以P、C、Q、A为顶点的四边形是菱形？若存在，请直接写出Q点坐标；若不存在，请说明理由．解：（1）设旋转后OB所在的直线m与直线l交于点C′，直线l：y=−√33x+2√3，令x＝0，则y＝2√3，令y＝0，则x＝6，则点A、B的坐标分别为（6，0）、（0，2√3），则AO＝6，OB＝2√3，tan∠OBA=OAOB=√3，则∠OBA＝60°，∠OAB＝30°，而∠BOC′＝60°，则△OBC′为等边三角形，即：OC′＝OB，即点C′为点B旋转后对应的点，即点C在直线l上，则点C、C′重合，∠AOC′＝90﹣∠BOC′＝30°＝∠OAB，而∠OBA＝∠BOC′＝60°，则OC′＝AC′＝BC′，则OC′是Rt△ABC的中线，则x C′=12OA＝3，y C′=12OB=√3，故点C′（C）的坐标为（3，√3）；（2）存在，理由：点A、C的坐标分别为（6，0）、（3，√3），则AC＝2√3，①当AC是菱形的一条边时，当点Q在x轴上方，当菱形为ACQP时，则AC＝AP＝2√3=CQ，则点Q（3+2√3，√3）；当菱形为ACQ′P′时，点Q′（3﹣2√3，√3）；当点Q在x轴下方，同理可得：点Q″（3，−√3）；②当AC是菱形的对角线时，设点P（s，0），点Q（m，n），则AC的中点即为PQ的中点，且P A＝PC（即：P A2＝PC2），∴s+m＝9，n+0=√3，（s﹣3）2+（√3）2＝（6﹣s）2，解得：m＝5，n=√3，s＝4，故点Q（5，√3）；综上，点Q坐标为：（3+2√3，√3）或（3﹣2√3，√3）或（3，−√3）或（5，√3）．4．如图，AB是⊙O的直径，点C是⊙O上一点（与点A，B不重合），过点C作直线PQ，使得∠ACQ＝∠ABC．（1）求证：直线PQ是⊙O的切线．（2）过点A作AD⊥PQ于点D，交⊙O于点E，若⊙O的半径为2，sin∠DAC=12，求图中阴影部分的面积．解：（1）证明：如图，连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∵OA＝OC，∴∠CAB＝∠ACO．∵∠ACQ＝∠ABC，∴∠CAB+∠ABC＝∠ACO+∠ACQ＝∠OCQ＝90°，即OC⊥PQ，∴直线PQ是⊙O的切线．（2）连接OE，∵sin∠DAC=12，AD⊥PQ，∴∠DAC＝30°，∠ACD＝60°．∴∠ABC＝∠ACD＝60°，∴∠CAB＝90°﹣60°＝30°，∴∠EAO＝∠DAC+∠CAB＝60°，又∵OA＝OE，∴△AEO为等边三角形，∴∠AOE＝60°．∴S阴影＝S扇形﹣S△AEO＝S 扇形−12OA •OE •sin60° =60π360×22−12×2×2×√32 =2π3−√3．∴图中阴影部分的面积为2π3−√3．5．如图，在△ABC 中，∠ACB ＝90°，将△ABC 沿直线AB 翻折得到△ABD ，连接CD 交AB 于点M ．E 是线段CM 上的点，连接BE ．F 是△BDE 的外接圆与AD 的另一个交点，连接EF ，BF ．（1）求证：△BEF 是直角三角形； （2）求证：△BEF ∽△BCA ；（3）当AB ＝6，BC ＝m 时，在线段CM 上存在点E ，使得EF 和AB 互相平分，求m 的值．（1）证明：∵∠ACB ＝90°，将△ABC 沿直线AB 翻折得到△ABD ， ∴∠ADB ＝∠ACB ＝90°，∵∠EFB ＝∠EDB ，∠EBF ＝∠EDF ，∴∠EFB +∠EBF ＝∠EDB +∠EDF ＝∠ADB ＝90°， ∴∠BEF ＝90°， ∴△BEF 是直角三角形．（2）证明：∵BC ＝BD ， ∴∠BDC ＝∠BCD ， ∵∠EFB ＝∠EDB ， ∴∠EFB ＝∠BCD ，∵AC ＝AD ，BC ＝BD ， ∴AB ⊥CD ， ∴∠AMC ＝90°，∵∠BCD +∠ACD ＝∠ACD +∠CAB ＝90°， ∴∠BCD ＝∠CAB ， ∴∠BFE ＝∠CAB ， ∵∠ACB ＝∠FEB ＝90°， ∴△BEF ∽△BCA ．（3）解：设EF 交AB 于J ．连接AE ． ∵EF 与AB 互相平分， ∴四边形AFBE 是平行四边形， ∴∠EF A ＝∠FEB ＝90°，即EF ⊥AD ， ∵BD ⊥AD ， ∴EF ∥BD ， ∵AJ ＝JB ， ∴AF ＝DF ， ∴FJ =12BD =m 2， ∴EF ＝m ，∵△ABC ∽△CBM ， ∴BC ：MB ＝AB ：BC ，∴BM =m 26，∵△BEJ ∽△BME ， ∴BE ：BM ＝BJ ：BE ， ∴BE =m √2， ∵△BEF ∽△BCA ， ∴AC EF=BC BE，即√36−m 2m=mm √2， 解得m ＝2√3（负根已经舍弃）．。

【海淀区高三年级第一学期期末练习】 18．（本小题满分13分）已知(0,2),(3,1)A B 是椭圆G ：22221(0)x y a b a b+=>>上的两点．（Ⅰ）求椭圆G 的离心率；（Ⅱ）已知直线l 过点B ，且与椭圆G 交于另一点C （不同于点A ），若以BC 为直径的圆经过点A ，求直线l 的方程． 19. （本小题满分14分）已知函数()ln 1af x x x=--．（Ⅰ）若曲线()y f x =存在斜率为1-的切线，求实数a 的取值范围； （Ⅱ）求()f x 的单调区间；（Ⅲ）设函数()ln x ag x x+=，求证：当10a -<<时，()g x 在(1,)+∞上存在极小值．20．（本小题满分13分）对于无穷数列{}n a ,{}n b ，若1212max{,,,}min{,,,}(1,2,3,)k k k b a a a a a a k =-=L L L ，则称{}n b 是{}n a 的“收缩数列”．其中，12max{,,,}k a a a L ,12min{,,,}k a a a L 分别表示12,,,k a a a L 中的最大数和最小数．已知{}n a 为无穷数列，其前n 项和为n S ，数列{}n b 是{}n a 的“收缩数列”．(Ⅰ)若21n a n =+，求{}n b 的前n 项和； (Ⅱ)证明：{}n b 的“收缩数列”仍是{}n b ；(Ⅲ)若121(1)(1)22n n n n n n S S S a b +-+++=+L (1,2,3,)n =L ，求所有满足该条件的{}n a ． 【西城区高三年级第一学期期末练习】 18．（本小题满分13分）已知函数()ln sin (1)f x x a x =-⋅-，其中a ∈R ．（Ⅰ）如果曲线()y f x =在1x =处的切线的斜率是1-，求a 的值； （Ⅱ）如果()f x 在区间(0,1)上为增函数，求a 的取值范围 19．（本小题满分14分）已知直线:l x t =与椭圆22:142x y C +=相交于A ，B 两点，M 是椭圆C 上一点．（Ⅰ）当1t =时，求△MAB 面积的最大值；（Ⅱ）设直线MA 和MB 与x 轴分别相交于点E ，F ，O 为原点．证明：||||OE OF ⋅为定值．20．（本小题满分13分）数字1,2,3,,(2)n n L ≥的任意一个排列记作12(,,,)n a a a L ，设n S 为所有这样的排列构成的集合．集合12{(,,,)|n n n A a a a S =∈L 任意整数,,1i j i j n <≤≤，都有}i j a i a j --≤；集合12{(,,,)|n n n B a a a S =∈L 任意整数,,1i j i j n <≤≤，都有}i j a i a j ++≤．（Ⅰ）用列举法表示集合3A ，3B ； （Ⅱ）求集合n n A B I 的元素个数；（Ⅲ）记集合n B 的元素个数为n b ．证明：数列{}n b 是等比数列． 【东城区高三年级第一学期期末练习】 18．设函数．（Ⅰ）若f （0）为f （x ）的极小值，求a 的值；（Ⅱ）若f （x ）＞0对x ∈（0，+∞）恒成立，求a 的最大值． 19．已知椭圆C ：=1（a ＞b ＞0）经过点M （2，0），离心率为．A ，B 是椭圆C 上两点，且直线OA ，OB 的斜率之积为﹣，O 为坐标原点．（Ⅰ）求椭圆C 的方程；（Ⅱ）若射线OA 上的点P 满足|PO|=3|OA|，且PB 与椭圆交于点Q ，求的值．20．已知集合A n ={（x 1，x 2，…，x n ）|x i ∈{﹣1，1}（i=1，2，…，n ）}．x ，y ∈A n ，x=（x 1，x 2，…，x n ），y=（y 1，y 2，…，y n ），其中x i ，y i ∈{﹣1，1}（i=1，2，…，n ）．定义x ⊙y=x 1y 1+x 2y 2+…+x n y n ．若x ⊙y=0，则称x 与y 正交．（Ⅰ）若x=（1，1，1，1），写出A 4中与x 正交的所有元素； （Ⅱ）令B={x ⊙y|x ，y ∈A n }．若m ∈B ，证明：m+n 为偶数；（Ⅲ）若A ⊆A n ，且A 中任意两个元素均正交，分别求出n=8，14时，A 中最多可以有多少个元素．【朝阳区高三年级第一学期期末练习】 18． （本小题满分13分）已知椭圆22:132x y C +=上的动点P 与其顶点(A ,B 不重合． （Ⅰ）求证：直线PA 与PB 的斜率乘积为定值；（Ⅱ）设点M ，N 在椭圆C 上，O 为坐标原点，当//OM PA ,//ON PB 时，求OMN ∆的面积．19．（本小题满分14分）设函数2()ln(1)1f x x ax x =-+++，2()(1)e x g x x ax =-+，R a ∈．（Ⅰ）当1a =时，求函数()f x 在点(2,(2))f 处的切线方程； （Ⅱ）若函数()g x 有两个零点，试求a 的取值范围； （Ⅲ）证明()()f x g x ≤． 20．（本小题满分13分）设(3)m,n m n ≤≤是正整数，数列:m A 12m a ,a ,,a L ，其中(1)i a i m ≤≤是集合{123},,,,n L 中互不相同的元素．若数列m A 满足：只要存在1i,j i j m ≤<≤（）使i j a a n +≤，总存在1k k m ≤≤（）有i j k a a a +=，则称数列m A 是“好数列”． （Ⅰ）当6100m ,n ==时，（ⅰ）若数列6:11789790A ,,x,y,,是一个“好数列”，试写出x,y 的值，并判断数列：11789097,,,x,,y 是否是一个“好数列”？（ⅱ）若数列6:1178A ,,a,b,c,d 是“好数列”，且a b c d <<<，求a,b,c,d 共有多少种不同的取值？（Ⅱ）若数列m A 是“好数列”，且m 是偶数，证明：1212m a a a n m ++++≥L ．【丰台区高三年级第一学期期末练习】 18.（本小题共13分）已知函数()e xf x x =与函数21()2g x x ax =+的图象在点(00)，处有相同的切线. （Ⅰ）求a 的值；（Ⅱ）设()()()()h x f x bg x b =-∈R ，求函数()h x 在[12]，上的最小值. 19.（本小题共13分）已知抛物线C ：22(0)y px p =>的焦点为F ，且经过点(12)，A ，过点F 的直线与抛物线C 交于P ，Q 两点.（Ⅰ）求抛物线C 的方程；（Ⅱ）O 为坐标原点，直线OP ，OQ 与直线2px =-分别交于S ，T 两点，试判断FS FT ⋅uu r uu u r 是否为定值？若是，求出这个定值；若不是，请说明理由. 20.（本小题共13分）已知无穷数列{}n c 满足1112n n c c +=--. （Ⅰ）若117c =，写出数列{}n c 的前4项； （Ⅱ）对于任意101c ≤≤，是否存在实数M ，使数列{}n c 中的所有项均不大于M ？若存在，求M 的最小值；若不存在，请说明理由；（Ⅲ）当1c 为有理数，且10c ≥时，若数列{}n c 自某项后是周期数列，写出1c 的最大值.（直接写出结果，无需证明）【石景山区高三年级第一学期期末练习】 18．（本小题共13分）已知椭圆2222:1(0)x y C a b a b+=>>，点(2,0)在椭圆C 上．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）过点(1,0)P 的直线（不与坐标轴垂直）与椭圆交于A B 、两点，设点B 关于x 轴的对称点为B '．直线B A '与x 轴的交点Q 是否为定点？请说明理由．19．（本小题共14分）已知函数2()11xf x x =++，2()(0)a x g x x e a =<． （Ⅰ）求函数()f x 的单调区间；（Ⅱ）若对任意12,[0,2]x x ∈，12()()f x g x ≥恒成立，求a 的取值范围． 20．（本小题共13分）集合M 的若干个子集的集合称为集合M 的一个子集族．对于集合{1,2,3}n L 的一个子集族D 满足如下条件：若,A D B A ∈⊆，则B D ∈，则称子集族D 是“向下封闭”的． （Ⅰ）写出一个含有集合{1,2}的“向下封闭”的子集族D 并计算此时(1)AA D∈-∑的值（其中A 表示集合A 中元素的个数，约定0φ=；A D∈∑表示对子集族D 中所有成员A 求和）；（Ⅱ）D 是集合{1,2,3}n L 的任一“向下封闭的”子集族，对A D ∀∈,记max k A =，()max (1)AA Df k ∈=-∑（其中max 表示最大值），（ⅰ）求(2)f ；（ⅱ）若k 是偶数，求()f k ． 【通州区高三年级第一学期期末练习】18．（本小题满分13分）设函数()()1kxf x e k R =-∈．（Ⅰ）当k ＝1时，求曲线()y f x =在点))0(0(f ，处的切线方程； （Ⅱ）设函数kx x x f x F -+=2)()(，证明：当x ∈)0(∞+，时，()F x ＞0.19．（本小题满分13分）如图，已知椭圆()2222:10x yCaba b +=>>经过点)23,1(P ，离心率21=e .（Ⅰ）求椭圆C 的标准方程；（Ⅱ）设AB 是经过右焦点F 的任一弦（不经过点P ），直线AB 与直线:4l x =相交于点M ，记PA ，PB ，PM 的斜率分别为1k ，2k ，3k ，求证：1k ，3k ，2k 成等差数列． 20．（本小题满分14分）已知数列对任意的满足：+212n n n+a a a +>，则称数列为“T 数列”.（Ⅰ）求证：数列{}2n 是“T 数列”；（Ⅱ）若212nn a n ⎛⎫=⋅ ⎪⎝⎭，试判断数列{}n a 是否是“T 数列”，并说明理由；（Ⅲ）若数列{}n a 是各项均为正的“T 数列”， 求证：13212421n na a a n a a a n+++++>+++L L . 【昌平区高三年级第一学期期末练习】【大兴区高三年级第一学期期末练习】}{n a *N n ∈}{n a【房山区高三年级第一学期期末练习】18．已知函数f（x）=lnx﹣ax（a∈R）．（Ⅰ）当a=1时，求曲线y=f（x）在点（1，f（1））处的切线方程；（Ⅱ）求函数f（x）的单调区间；（Ⅲ）如果f（x）≥0在[2，3]上恒成立，求a的取值范围．19．在平面直角坐标系xOy中，圆O的参数方程为（θ为参数），已知圆O与y轴的正半轴交于点A，与y轴的负半轴交于点B，点P为直线l：y=4上的动点．直线PA，PB与圆O的另一个交点分别为M，N．（Ⅰ）写出圆O的标准方程；（Ⅱ）若△PAN与△MAN的面积相等，求直线PA的方程；（Ⅲ）求证：直线MN经过定点．20．定义：二阶行列式=ad﹣bc（a，b，c，d∈R）．已知数列{a n}满足a1=1，a2=2，=（﹣1）n+1（n∈N*）．（Ⅰ）求a3，a4，a5；（Ⅱ）求证：a n+2=2a n+1+a n（n∈N*）（Ⅲ）试问该数列任意两个相邻项的平方和仍然是该数列中的一个项吗？如果是，请证明你的结论；如果不是，请说明理由．【北京市101中学高三统测】19．平面直角坐标系xOy 中，椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率是32，抛物线E ：x 2＝2y 的焦点F 是C 的一个顶点． (1)求椭圆C 的方程；(2)设P 是E 上的动点，且位于第一象限，E 在点P 处的切线l 与C 交于不同的两点A ，B ，线段AB 的中点为D .直线OD 与过P 且垂直于x 轴的直线交于点M . ①求证：点M 在定直线上；②直线l 与y 轴交于点G ，记△PFG 的面积为S 1，△PDM 的面积为S 2，求S 1S 2的最大值及取得最大值时点P 的坐标．20. 设集合A 、B 均为实数集R 的子集，记：{|,}A B a b a A b B +=+∈∈；（1）已知{0,1,2}A =，{1,3}B =-，试用列举法表示A B +；（2）设123a =，当*n N ∈，且2n ≥时，曲线2221119x y n n n +=-+-的焦距为n a ，如果 12{,,,}n A a a a =⋅⋅⋅，122{,,}993B =---，设A B +中的所有元素之和为n S ，对于满足3m n k +=，且m n ≠的任意正整数m 、n 、k ，不等式0m n k S S S λ+->恒成立，求实数λ的最大值；（3）若整数集合111A A A ⊆+，则称1A 为“自生集”，若任意一个正整数均为整数集合2A 的某个非空有限子集中所有元素的和，则称2A 为“*N 的基底集”，问：是否存在一个整数集合既是自生集又是*N 的基底集？请说明理由； 【海淀区高三年级第二学期期中练习】 18.（本小题满分13分）已知函数2()24(1)ln(1)f x x ax a x =-+-+，其中实数3a <. （Ⅰ）判断1x =是否为函数()f x 的极值点，并说明理由； （Ⅱ）若()0f x ≤在区间[0,1]上恒成立，求a 的取值范围. 19.（本小题满分14分）已知椭圆G :2212x y +=，与x 轴不重合的直线l 经过左焦点1F ，且与椭圆G 相交于A ，B 两点，弦AB 的中点为M ，直线OM 与椭圆G 相交于C ，D 两点． （Ⅰ）若直线l 的斜率为1，求直线OM 的斜率；（Ⅱ）是否存在直线l ，使得2AM CM DM =⋅成立？若存在，求出直线l 的方程；若不存在，请说明理由．20.（本小题满分13分）已知含有n 个元素的正整数集12{,,,}n A a a a =⋅⋅⋅12(,3)n a a a n <<⋅⋅⋅<≥具有性质P ：对任意不大于()S A (其中12()n S A a a a =++⋅⋅⋅+)的正整数,k 存在数集A 的一个子集，使得该子集所有元素的和等于k . （Ⅰ）写出12,a a 的值；（Ⅱ）证明：“12,,,n a a a L 成等差数列”的充要条件是“(1)()2n n S A +=”； （Ⅲ）若()2017S A =，求当n 取最小值时，n a 的最大值.。

高三年级第一次模拟考试数 学 试 题（理）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，共150分，考试时间120分钟。

第Ⅰ卷（选择题，共40分）一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的，将答案涂在答题卡上．．．．．．．．．。

1．复数23()1i i +-= （ ）A ．-3-4iB ．-3+4iC ．3-4iD ．3+4i2．已知条件:|1|2,:,p x q x a +>>⌝⌝条件且p 是q 的充分不必要条件，则实数a 的取值范围是（ ） A ．1a ≥ B ．1a ≤ C ．1a ≥- D ．3a ≤-3．函数()|2|ln f x x x =--在定义域内零点可能落在下列哪个区间内（ ）A ．（0，1）B ．（2，3）C ．（3，4）D ．（4，5） 4．如右图，是一程序框图，则输出结果为（ ）A ．49B ．511 C ．712 D ．613 5．已知n S 为等差数列{}n a 的前n 项和，若641241,4,S S S S S ==则 的值为（ ）A ．94B ．32C ．54D ．46．要得到函数()sin(2)3f x x π=+的导函数'()f x 的图象，只需将()f x 的图象（ ）A ．向左平移2π个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变）B ．向左平移2π个单位，再把各点的纵坐标缩短到原来的12倍（横坐标不变）C ．向右平移4π个单位，再把各点的纵坐标伸长到原来的12倍（横坐标不变）D ．向右平移4π个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变） 7．过双曲线22221(0,0)x y a b a b-=>>的一个焦点F 引它的渐近线的垂线，垂足为M ，延长FM 交y 轴于E ，若|FM|=2|ME|，则该双曲线的离心率为（ ）A ．3B ．2C ．3D ．28．如图所示的每个开关都有闭合与不闭合两种可能，因此5个开关共有25种可能，在这25种可能中电路从P 到Q 接通的情况有（ ）A ．30种B ．10种C ．24种D ．16种第Ⅱ卷（非选择题，共110分）二、填空题：本大题共6小题，每小题5分，共30分，将答案填写在答题纸上。

天利38套高三高考能力提升卷（六）学校：_______ 班级：__________姓名：_______ 考号：__________（满分：100分时间：75分钟）总分栏题号一二三四五六七总分得分评卷人得分一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题如图所示，泳池底有一个点光源P，只有在锥形范围内的光线才能从水面射出，MN为圆锥底面的一条直径。

已知池水深，圆锥的母线与水平方向所成的角为（），光在空气中的传播速度，下列说法正确的是（ ）A．为水的临界角B．水的折射率为C．水面上亮斑的面积为D．光在水中传播的最短时间为第(2)题如图甲所示，固定的长直导线与固定的圆形闭合金属线框位于同一平面内，长直导线中的电流随时间的变化关系如图乙所示，直导线中电流向下，下列说法正确的是（ ）A．线框中会产生逆时针方向的电流B．线框中会产生顺时针方向的电流C．线框受到的安培力平行于直导线向上D．线框受到的安培力平行于直导线向下第(3)题某同学设计了如图所示的电路来研究电源输出功率随外电阻变化的规律。

已知电源电动势恒定，内电阻，滑动变阻器的最大阻值为，定值电阻，同，电流表和电压表均为理想电表。

则当滑动变阻器的触片从到移动的过程中，电源的输出功率的变化情况为（ ）A．一直增大B．先增大再减小C．先增大再减小再增大D．先增大再减小再增大再减小第(4)题如图所示，质量为M的斜面体放于粗糙的水平面，质量为m的小物块静止在斜面上。

则的受力个数为（ ）A．3个B．4个C．5个D．4个或5个第(5)题某同学用红色光从真空对着一正方体透明玻璃砖的AB边似与法线成角大射，在玻璃砖内AD边的中点发生全反射，如图所示，下列说法正确的是（ ）A．该光线还会在CD边全反射B．该光线不会在CD边全反射，出射光线与开始入射的光线平行C．若角度增大到一定程度，则会在AB边全反射D．若角不变，换用折射率大一点的紫色光入射，则在AD边全反射点下移靠近D点第(6)题物体沿直线运动，一段时间内物体的图像如图所示。