中山大学~线性代数期末总复习
- 格式:ppt
- 大小:2.81 MB
- 文档页数:137

《线性代数》期末复习提纲第一部分:基本要求(计算方面)1. 四阶行列式的计算;2. N 阶特殊行列式的计算(如有行和、列和相等);3. 矩阵的运算(包括加、减、数乘、乘法、转置、逆等的混合运算);4. 求矩阵的秩、逆(两种方法);解矩阵方程;5. 含参数的线性方程组解的情况的讨论;6. 齐次、非齐次线性方程组的求解(包括唯一、无穷多解);7. 讨论一个向量能否用和向量组线性表示;8. 讨论或证明向量组的相关性;9. 求向量组的极大无关组,并将多余向量用极大无关组线性表示;10.将无关组正交化、单位化;11.求方阵的特征值和特征向量;12.讨论方阵能否对角化,如能,要能写出相似变换的矩阵及对角阵;13.通过正交相似变换(正交矩阵)将对称矩阵对角化;14.写出二次型的矩阵,并将二次型标准化,写出变换矩阵;15.判定二次型或对称矩阵的正定性。
第二部分:基本知识一、行列式1.行列式的定义用2n 个元素ij a 组成的记号nnn n n n a a a a a a a a a212222111211称为n 阶行列式。
(1)它表示所有可能的取自不同行不同列的n 个元素乘积的代数和;(2)展开式共有n!项,其中符号正负各半;2.行列式的计算1. 一阶行列式a a =,二、三阶行列式有对角线法则;2. N 阶(n ≥3)行列式的计算:降阶法定理:n 阶行列式的值等于它的任意一行(列)的各元素与其对应的代数余子式乘积的和。
方法:选取比较简单的一行(列),保保留一个非零元素,其余元素化为0,利用定理展开降阶。
3. 特特情况(1) 上、下三角形行列式、对角形行列式的值等于主对角线上元素的乘积;(2)行列式值为0的几种情况:Ⅰ 行列式某行(列)元素全为0;Ⅱ 行列式某行(列)的对应元素相同;Ⅲ 行列式某行(列)的元素对应成比例;Ⅳ 奇数阶的反对称行列式。
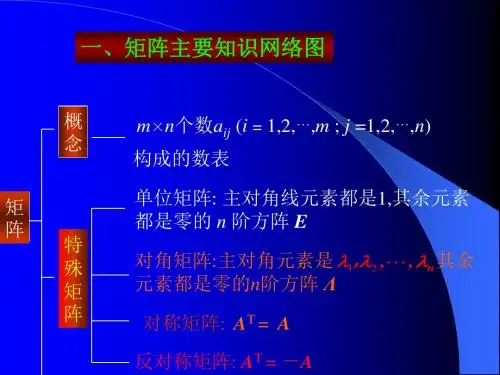
二.矩阵1.矩阵的基本概念(表示符号、一些特殊矩阵――如单位矩阵、对角、对称矩阵等);2.矩阵的运算(1)加减、数乘、乘法运算的条件、结果;(2)关于乘法的几个结论:①矩阵乘法一般不满足交换律(若AB =BA ,称A 、B 是可交换矩阵);②矩阵乘法一般不满足消去律、零因式不存在;③若A 、B 为同阶方阵,则B A AB ⋅=; ④n kA k A =3.矩阵的秩(1)定义 非零子式的最大阶数称为矩阵的秩;(2)秩的求法 一般不用定义求,而用下面结论:矩阵的初等变换不改变矩阵的秩;阶梯形矩阵的秩等于非零行的个数(每行的第一个非零元所在列,从此元开始往下全为0的矩阵称为行阶梯阵)。


行列式1.行列式的性质性质1行列式与它的转置行列式相等TD D =.性质2互换行列式的两行(列),行列式变号.推论1如果行列式有两行(列)的对应元素完全相同,则此行列式的值为零.性质3行列式的某一行(列)中所有的元素都乘以同一数k ,等于用数k 乘此行列式.如111213111213212223212223313233313233a a a a a a ka ka ka k a a a a a a a a a =推论2如果行列式中有两行(列)元素成比例,则此行列式的值为零.性质4若行列式的某一行(列)的元素都是两数之和,则这个行列式等于两个行列式之和.如111213111213111213212122222323212223212223313233313233313233a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a ''''''+++=+性质5把行列式的某一行(列)的各元素乘以同一数然后加到另一行(列)对应的元素上去,行列式的值不变.如111213111213212223212223313233311132123313a a a a a a a a a a a a a a a a ka a ka a ka =+++例1已知,那么()A.-24B.-12C.-6D.12答案B解析2.余子式与代数余子式在n 阶行列式中,把元素ij a 所在的第i 行和第j 列划去后,留下来的n-1阶行列式叫做元素ij a 的余子式,记作ij M ,i jij ij A (1)M +=-叫做元素ij a 的代数余子式.3.行列式按行(列)展开法则定理1行列式的值等于它的任一行(列)的各元素与其对应的代数余子式乘积之和,即1122i i i i in in D a A a A a A =+++ 或 1122j j j j nj njD a A a A a A =+++ ()1,2,,;1,2i n j n ==定理2行列式任一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零,即12120,j j i i jn i n a A a A a A +++= 或,11220.j j j j nj nj a A a A a A i j +++=≠ ()1,2,,;1,2i n j n == 例.设3阶矩阵()ij A a =的行列式12A =,ij A 为ij a 的代数余子式.那么313132323333a A a A a A ++=___12____;213122322333a A a A a A ++=___0___.4.行列式的计算(1)二阶行列式1112112212212122a a a a a a a a =-(3)对角行列式1212n nλλλλλλ=,n(m 1)21212nn(1)λλλλλλ-=- (4)三角行列式1111121n 2122222n1122nnn1n2nnnna a a a a a a a a a a a a a a ==(5)消元法:利用行列式的性质,将行列式化成三角行列式,从而求出行列式的值.(6)降阶法:利用行列式的性质,化某行(列)(一般选择有0元素的行或列)只有一个非零元素,再按该行(列)展开,通过降低行列式的阶数求出行列式的值.(7)加边法:行列式每行(列)所有元素的和相等,将各行(列)元素加到第一列(行),再提出公因式,进而求出行列式的值.例:思路:将有0的第三行化为只有一个非0元素33=1,按该行展开,D=3333,不用忘记B 。



★ 线性代数基本内容、方法及要求第一部分 行列式【主要内容】1、行列式的定义、性质、展开定理、及其应用——克莱姆法则2、排列与逆序3、方阵的行列式4、几个重要公式:(1)TAA =; (2)AA11=-; (3)A kkA n=;(4)1*-=n AA ; (5)B A AB =; (6)B A BA BA ==**0;(7)⎩⎨⎧≠==∑=j i j i A A a ni ijij ,,01; (8)⎩⎨⎧≠==∑=j i j i A A a nj ij ij ,,01(其中B A ,为n 阶方阵,k 为常数)5、行列式的常见计算方法:(1)利用性质化行列式为上(下)三角形;(2)利用行列式的展开定理降阶; (3)根据行列式的特点借助特殊行列式的值【要求】1、了解行列式的定义,熟记几个特殊行列式的值。
2、掌握排列与逆序的定义,会求一个排列的逆序数。
3、能熟练应用行列式的性质、展开法则准确计算3-5阶行列式的值。
4、会计算简单的n阶行列式。
5、知道并会用克莱姆法则。
第二部分矩阵【主要内容】1、矩阵的概念、运算性质、特殊矩阵及其性质。
2、方阵的行列式3、可逆矩阵的定义、性质、求法(公式法、初等变换法、分块对角阵求逆)。
4、n阶矩阵A可逆⇔0A⇔A为非奇异(非退化)的矩阵。
≠⇔n)(⇔A为满秩矩阵。
R=A⇔0AX只有零解=⇔bAX=有唯一解⇔A的行(列)向量组线性无关⇔A的特征值全不为零。
⇔A可以经过初等变换化为单位矩阵。
⇔A可以表示成一系列初等矩阵的乘积。
5、矩阵的初等变换与初等矩阵的定义、性质及其二者之间的关系。
6、矩阵秩的概念及其求法((1)定义法;(2)初等变换法)。
7、矩阵的分块,分块矩阵的运算:加法,数乘,乘法以及分块矩阵求逆。
【要求】1、 了解矩阵的定义,熟悉几类特殊矩阵(单位矩阵,对角矩阵,上、下三角形矩阵,对称矩阵,可逆矩阵,伴随矩阵,正交矩阵)的特殊性质。
2、熟悉矩阵的加法,数乘,乘法,转置等运算法则,会求方阵的行列式。

五、知识复习第一部分线性代数中的最基本概念基础比较好的考生可不必看这部分内容,或者只用本部分的习题对自己进行一次测试.1.矩阵(1)基本概念矩阵是描写事物形态的数量形式的发展.由m⨯n个数排列成的一个m行n列的表格,两边界以圆括号或方括号,就成为一个m⨯n型矩阵.这些数称为它的元素,位于第i行第j列的数称为(i,j)位元素.元素全为0的矩阵称为零矩阵,通常就记作0.两个矩阵A和B相等(记作A=B),是指它的行数相等,列数也相等(即它们的类型相同),并且对应的元素都相等.(2)线性运算和转置加(减)法:两个m⨯n的矩阵A和B可以相加(减),得到的和(差)仍是m⨯n矩阵,记作A+B (A-B),法则为对应元素相加(减).数乘: 一个m⨯n的矩阵A与应该数c可以相乘,乘积仍为m⨯n的矩阵,记作c A,法则为A的每个元素乘c.这两种运算统称为先性运算,它们满足以下规律:①加法交换律:A+B=B+A.②加法结合律:(A+B)+C=A+(B+C).③加乘分配律:c(A+B)=c A+c B.(c+d)A=c A+d A.④数乘结合律: c(d)A=(cd)A.⑤ c A=0⇔ c=0 或A=0.转置:把一个m⨯n的矩阵A行和列互换,得到的n⨯m的矩阵称为A的转置,记作A T(或A').有以下规律:① (A T)T=A.② (A+B)T=A T+B T.③ (c A)T=(c A)T.(3) n阶矩阵几个特殊矩阵行数和列数相等的矩阵称为方阵,行列数都为n的矩阵也常常叫做n阶矩阵.n阶矩阵A的相应的行列式记作|A|,称为A的行列式.把n阶矩阵的从左上到右下的对角线称为它的主对角线.(其上的运算行列号相等.)下面列出几类常用的n阶矩阵,它们但是考试大纲中要求掌握的.对角矩阵: 主对角线外的的元素都为0的n阶矩阵.单位矩阵: 主对角线外的的元素都为1的对角矩阵,记作E(或I).数量矩阵: 主对角线外的的元素都等于一个常数c的对角矩阵,它就是c E.上(下)三角矩阵: 主对角线下(上)的的元素都为0的n阶矩阵.对称矩阵:满足A T=A矩阵.也就是对任何i,j, (i,j)位的元素和(j ,i)位的元素总是相等的n阶矩阵.反对称矩阵:满足A T=-A矩阵.也就是对任何i,j, (i,j)位的元素和(j ,i)位的元素之和总等于0的n阶矩阵.反对称矩阵对角线上的元素一定都是0.(4) 矩阵的初等变换和阶梯形矩阵矩阵的初等行变换有以下三种:①交换两行的上下位置.②用一个非0的常数乘某一行的各元素.③把某一行的倍数加到另一行上.类似地, 矩阵还有三种初等列变换,大家可以模仿着写出它们,这里省略了. 初等行变换与初等列变换统称初等变换.阶梯形矩阵:一个矩阵称为阶梯形矩阵,如果满足:① 如果它有零行,则都出现在下面.② 每个非零行的第一个非0元素所在的列号自上而下严格单调递增.每个矩阵都可以用初等行变换化为阶梯形矩阵.这种运算是在线性代数的各类计算题中频繁运用的基本运算,必须十分熟练.2. 向量 (1)基本概念向量是另一种描述事物形态的数量形式.由n 个数构成的有序数组称为一个n 维向量,称这些数为它的分量.书写中可用矩阵的形式来表示向量,例如分量依次是a 1,a 2,⋯ ,a n 的向量可表示成 a 1(a 1,a 2,⋯ ,a n )或 a 2 , ┆ a n请注意,作为向量它们并没有区别,但是作为矩阵,它们不一样(左边是1⨯n 矩阵,右边n ⨯1是矩阵).习惯上把它们分别称为行向量和列向量.请注意它与矩阵的行向量和列向量的区别.一个m ⨯n 的矩阵的每一行是一个n 维向量,称为它的行向量; 每一列是一个m 维向量, 称为它的列向量.常常用矩阵的列向量组来写出矩阵,例如当矩阵A 的列向量组为α1, α2,⋯ ,αn 时(它们都是表示为列的形式!)可记A =(α1, α2,⋯ ,αn ).矩阵的许多概念也可对向量来规定,如向量的相等,零向量等等.这里从略. (2) 线性运算和线性组合向量也有加减法和数乘这两种线性运算,并且也有完全一样的运算规律,这里也不来复述了.向量组的线性组合:设α1, α2,⋯ ,αs 是一组n 维向量, c 1,c 2,⋯ ,c s 是一组数,则称 c 1α1+ c 2α2+⋯ ,+c s αs 为α1, α2,⋯ ,αs 的(以c 1,c 2,⋯ ,c s 为系数的)线性组合.它也是n 维向量.3.线性方程组(1) 基本概念线性方程组的一般形式为: a 11x 1+a 12x 2+⋯ +a 1n x n =b 1, a 21x 1+a 22x 2+⋯ +a 2n x n =b 2, ⋯ ⋯ ⋯ ⋯a m1x 1+a m2x 2+⋯ +a mn x n =b m ,其中未知数的个数n 和方程式的个数m 不必相等.分别称矩阵a 11 a 12 ⋯ a 1n a 11 a 12 ⋯ a 1nb 1 A = a 21 a 22 ⋯ a 2n 和(A |β)= a 21 a 22 ⋯ a 2n b 2⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ a m1 a m2 ⋯ a mn a m1 a m2 ⋯ a mn b m为方程组的系数矩阵和增广矩阵.如果b 1=b 2=⋯=b m =0,则称为齐次线性方程组.把一个非齐次线性方程组的每个方程的常数项都换成0,所得到的齐次线性方程组称为原方程组的导出齐次线性方程组,简称导出组.线性方程组的解是一个n 维向量(k 1,k 2,⋯ ,k n ),它满足:当每个方程中的未知数x i 都用k i替代时都成为等式.线性方程组的解的情况有三种:无解,唯一解,无穷多解.n 维零向量总是齐次线性方程组的解,因此齐次线性方程组的解情况只有两种:唯一解(即只要零解)和无穷多解(即有非零解).(2) 同解变换与矩阵消元法 线性方程组的同解变换有三种: ① 交换两个方程的上下位置. ② 用一个非0的常数乘某个方程. ③ 把某方程的倍数加到另一方程上.以上变换反映在增广矩阵上就是三种初等行变换.线性方程组的基本求解方法是消元法,用增广矩阵或系数矩阵来进行,称为矩阵消元法:写出方程组的增广矩阵(对齐次方程组用系数矩阵),用初等行变换把它化为阶梯形矩阵,再写出所代表的阶梯形方程组 (它是原方程组的同解方程组),用它求解.第二部分 行列式1. 形式和意义形式:用n 2个数排列成的一个n 行n 列的表格,两边界以竖线,就成为一个n 阶行列式. 如果行列式的列向量组为α1, α2,⋯ ,αn ,则此行列式可表示为|α1, α2,⋯ ,αn |.意义:是一个算式,把n 2个元素按照一定的法则进行运算,得到的数值称为这个行列式的值. 请注意行列式和矩阵在形式和意义上的区别.当两个行列式的值相等时,就可以在它们之间写等号! (不必形式一样,甚至阶数可不同.) 每个n 阶矩阵A 对应一个n 阶行列式,记作|A |.2. 定义(完全展开式)2阶和3阶行列式的计算公式: a 11 a 12a 21 a 22 = a 11a 22-a 12a 21 . a 11 a 12 a 13a 21 a 22 a 23 = a 11a 22a 33+ a 12a 23a 31+ a 13a 21a 32-a 13a 22a 31- a 11a 23a 32+ a 12a 21a 33. a 31 a 32 a 33一般地,一个n 阶行列式 a 11 a 12 ⋯ a 1na 21 a 22 ⋯ a 2n⋯ ⋯ ⋯ a n1 a n2 ⋯ a nn的值是许多项的代数和,每一项都是取自不同行,不同列的n 个元素的乘积,其一般形式为:nnj j j a a a 2121,这里把相乘的n 个元素按照行标的大小顺序排列,它们的列标j 1j 2⋯j n 构成1,2, ⋯,n 的一个全排列(称为一个n 元排列),一共有n!个n 元排列,每个n 元排列对应一项,因此共有n!个项..所谓代数和是在求总和时每项先要乘+1或-1.规定τ(j 1j 2⋯j n )为全排列j 1j 2⋯j n 的逆序数(即小数排列在大数后面的现象出现的个数,例如6元排列231645有4个逆序:21,31,64,65,因此 τ(231645)=4),则所乘的是.)1()(21n j j j τ-于是a 11 a 12 ⋯ a 1na 21 a 22 ⋯ a 2n =.)1(21212121)(n n nnj j j j j j j j j a a a τ-∑⋯ ⋯ ⋯ a n1 a n2 ⋯ a nn这里∑nj j j 21表示对所有n 元排列求和.称上式为n 阶行列式的完全展开式.3.性质行列式有以下性质:① 把行列式转置值不变,即|A T |=|A | . ② 某一行(列)的公因子可提出.③ 对一行或一列可分解,即如果某个行(列)向量α=β+γ ,则原行列式等于两个行列式之和,这两个行列式分别是把原行列式的该行(列)向量α换为β或γ 所得到的行列式.④ 把两个行(列)向量交换, 行列式的值变号.⑤ 如果一个行(列)向量是另一个行(列)向量的倍数,则行列式的值为0.⑥ 如果把一个行(列)向量的倍数加到另一个行(列)向量上,则行列式的值不变.把n 阶行列式的第i 行和第j 列划去后所得到的n-1阶行列式称为(i,j)位元素a ij 的余子式,记作M ij .称A ij =(-1)i+j M ij 为a ij 的代数余子式.⑦ 行列式可对某一行(列)展开,即行列式的值等于该行(列)的各元素与其代数余子式乘积之和.⑧ 某一行(列)的各元素与另一行(列)的对应元素的代数余子式乘积之和=0. ⑨ 如果A 与B 都是方阵(不必同阶),则A * = A O =|A |+|B |. O B * B 范德蒙行列式:形如1 1 1 ⋯ 1 a 1 a2 a3 ⋯ a na 12 a 22 a 32 ⋯ a n 2⋯ ⋯ ⋯a 1n-i a 2n-i a 3n-i ⋯ a n n-i的行列式(或其转置).它由a 1,a 2 ,a 3,⋯,a n 所决定,它的值等于 ).(i j ji a a -∏<因此范德蒙行列式不等于0⇔ a 1,a 2 ,a 3,⋯,a n 两两不同.4.计算行列式的核心问题是值的计算.(1)用完全展开式求行列式的值一般来说工作量很大.只在有大量元素为0,使得只有少数项不为0时,才可能用它作行列式的计算.例如对角行列式,上(下)三角行列式的值就等于主对角线上的元素的乘积,因为其它项都为0.(2)化零降阶法:取定一行(列),先用性质⑥把这行(列)的元素消到只有一个或很少几个不为0,再用⑦,对这行(列)展开.例如设4阶行列式1 1 1 1D= -2 x 3 1 , 2 2 x 4 3 3 4 x取第1行,把第2,3,4行各减去第一行,得到1 0 0 0 x+2 53 x-2 2D= -2 x+2 5 3 = 0 x-2 2 =(x+2) 1 x-3 =(x+2)[(x-2)(x-3)-2]=(x+2)(x-1)(x-4).2 0 x-2 2 0 1 x-33 0 1 x-3(3)利用性质简化计算,主要应用于元素有规律的行列式,包括n阶行列式.5.克莱姆法则克莱姆法则当线性方程组的方程个数等于未知数个数n (即系数矩阵为n阶矩阵)时,如果它的系数行列式不等于0,则方程组有唯一解,这个解为(D1/D, D2/D,⋯,Dn/D),这里D是系数行列式的值, Di是把系数行列式的第i个列向量换成常数列向量所得到的行列式的值.两点说明:①按法则给的公式来求解计算量太大,没有实用价值.因此法则的主要意义在理论上. (实际求解方法:对增广矩阵(A|β)作初等行变换,使得A变为单位矩阵,此时β变为解.)②法则的改进,事实上系数行列式不等于0是唯一解的充分必要条件.练习题一1.计算行列式(1) 2 a a a aa 2 a a aa a 2 a aa a a 2 aa a a a 2 .(2) 1 4 9 164 9 16 259 16 25 3616 25 36 49 .2. (1) a 0⋯0 b (2) a1 0 a20 0 0 b1 0b20 0 c1 0 c2c 0⋯0 d. 0 d1 0 d2.3. 计算n阶行列式(1) 1 2 3 … n-1 n-1 2 3 … n-1 n-1 –2 3 … n-1 n…………-1 –2 –3 … 1-n n .(2) 1 -2 -2 … -2 -2 (3) 1 2 3 … n (4) 1 a10 … 0 02 2 -2 … -2 -2 2 1 2 … n-1 -1 1-a1 a2…0 02 23 … -2 -2 3 2 1 … n-2 0 -1 1-a2…0 0 ……………………………2 2 2 … 2 n . n n-1 n-2 … 1 . 0 0 0 … -1 1-an.4. 设4阶矩阵A=(α, γ1, γ2 ,γ3),B=(β, γ1, γ2 ,γ3),|A|=2, |B|=3 ,求|A+B| .5. 一个三阶行列式的值为8,它的第二行的元素是1,2,a,它们的余子式依次为A21=2,A22=-1,A23=1,则a =( ).6. x3-3 1 -3 2x+2多项式f(x)= -7 5 -2x 1 ,求f(x)的次数,最高次项的系数和常数项.X+3 -1 33x2-29 x3 6 -67. x-2 x-1 x-2 x-3求多项式f(x)= 2x-2 2x-1 2x-2 2x-3 的次数.3x-3 3x-2 4x-5 3x-54x 4x-3 5x-7 4x-38.已知 x-3 a -1 4f(x)= 5 x-8 0 –2 的根为x1, x2, x3, x4,求x1+x2+x3+x4.0 b x+1 12 2 1 x9. 求行列式 0 1 0 0 …… 0 的全部代数余子式的和.0 0 2-1 0 00 0 0 3-1 0…………0 0 0 0 ……(n-1)-1n-1 0 0 0 010. a b c d已知行列式 x -1 -y z+1 的代数余子式A11=-9,A12=3,A13=-1,A14=3,求x,y,z.1 -z x+3 yy-2 x+1 0 z+3参考答案1.(1) 把各列都加到第1列上,提出公因子. 得(4a+2)(a-2)4.(2) 自下而上,各行减去上一行(作两次).得0.2.用换行(列)的方法.得(1) (ad-bc)|B|.(3) (a1c2- a2c1)(b1d2-b2d1).3. (1)提示:把第一行加到其它各行.得2n-1n! .(2) 第3到n行各减第二行.得(n+2)!/4.(3) 提示:自下而上各行减去上行.得(-1)n-12 n-2(n+1) .(4) 提示:从第2行起,自上而下各行加上行.得1 .4. 得40.5. 得8.6. 最高次只出现在下面划线的4个元素的乘积一项中,常数项即f(0).得9 ,6, 0.7. 2.8. 提示:利用特征值的性质.得10.9. 提示:利用伴随矩阵.得(-1)n-1(n+1)/2(n-1)!.10.x=0,y=3,z=-1.第三部分线性方程组1. 线性方程组的形式线性方程组除了通常的写法外,还常用两种简化形式:矩阵式AX=β,(齐次方程组AX=0).向量式 x1α1+ x2α2+⋯ ,+x sαs= β, (齐次方程组x1α1+ x2α2+⋯ ,+x sαs=0).2. 线性方程组解的性质 (1) 齐次方程组AX =0 如果η1, η2,⋯ ,ηs 是齐次方程组AX =0的一组解,则它们的任何线性组合c 1η1+ c 2η2+⋯ + c s ηs也都是解.(2) 非齐次方程组AX =β(≠0)如果ξ1, ξ2,⋯ ,ξs 是AX =β的一组解,则① 它们的线性组合c 1ξ1+ c 2ξ2+⋯ +c s ξs 也是AX =β解的⇔c 1+ c 2+⋯ +c s =1. ② 它们的线性组合c 1ξ1+ c 2ξ2+⋯ +c s ξs 是AX =0的解⇔ c 1+ c 2+⋯ +c s =0.如果ξ0是AX =β的一组解,则n 维向量(n 是未知数的个数) ξ也是解⇔ξ-ξ0是导出齐次方程组AX =0的解.( ξ是ξ0和AX =0的一个解的和.)3. 线性方程组解的情况的判别对于方程组AX =β,判别其解的情况用三个数:未知数个数n,r(A ),r(A |β). ① 无解⇔r(A )<r(A |β).② 有唯一解⇔r(A )=r(A |β)=n.(当A 是方阵时,就推出克莱姆法则.) ③ 有无穷多解⇔r(A )=r(A |β)<n.方程的个数m 虽然在判别公式中没有出现,但它r(A )和r(A |β)的上限,因此当r(A )=m 时, AX =β一定有解. 当m<n 时,一定不是唯一解.对于齐次方程组AX =0,判别解的情况用两个数: n,r(A ).有非零解⇔ r(A )=<n(只有零解⇔r(A)=n).推论 当A 的秩等于列数n 时, A 在矩阵乘法中有左消去律:AB =0⇒ B =0; AB =AC ⇒ B =C .4. 齐次方程组基础解系 线性方程组的通解 (1) 齐次方程组基础解系如果齐次方程组AX =0有非零解,则它的解集(全部解的集合)是无穷集,称解集的每个极大无关组为AX =0的基础解系.于是, 当η1, η2,⋯ ,ηs 是AX =0的基础解系时,向量η是AX =0的解⇔η可用η1, η2,⋯ ,ηs 线性表示.定理 设AX =0有n 个未知数,则它的解集的秩(即基础解系中包含解的个数)等于n-r(A). 于是,判别一组向量η1, η2,⋯ ,ηs 是AX =0的基础解系的条件为 ① η1, η2,⋯ ,ηs 是AX =0的一组解. ② η1, η2,⋯ ,ηs 线性无关.③ s=n-r(A).(2) 线性方程组的通解如果η1, η2,⋯ ,ηs 是齐次方程组AX =0的基础解系,则AX =0的通解(一般解)为 c 1η1+ c 2η2+⋯ + c s ηs , 其中c 1, c 2,⋯ ,c s ,可取任何常数.如果ξ0是非齐次方程组AX =β的解, η1, η2,⋯ ,ηs 是导出组AX =0的基础解系,则AX =β的通解(一般解)为ξ0+c 1η1+ c 2η2+⋯ + c s ηs , 其中c 1, c 2,⋯ ,c s ,可取任何常数.练习题四1. 求齐次方程组的基础解系和通解:3x 1+2x 2+x 3+3x 4+5x 5=0,6x1+4x2 +3x3+5x4+7x5=0,9x1+6x2+5x3+7x4+9x5=0,3x1+2x2+4x4+8x5=0.2. 已知方程组x1+ x2+2x3+3x4=1, x1+3x2 +6x3+x4=3,3x1-x2+k1x3+15x4=3,x1-5x2-10x3+12x4=k2有有无穷多个解,求k1,k2的值,并求此方程组的通解.3.-x1+kx2+2x3=1,已知方程组 x1-x2 +kx3=2,有无穷多个解,求k的值,并求此方程组的通解.-5x1+5x2+4x3=-14. x1+2x2-x3+x4=0,已知齐次方程组 x2+px3+x4=0, 的基础解系含两个解,求p,q的值和方程组的通解.2x1+3x2-x3+qx4=05. (1+a)x1+ x2+x3=3a+a2,a为何值时,线性方程组 x1+(1+a)x2+x3=3a2+a3, 有无穷多解? 写出通解.x1+x2+(1+a)x3=3a3+a46. 1 1 1 1 1设A= 2 1 0 4 ,β= a .已知线性方程组A X=β有解,求a,b, 并写出通解.0 1 2 6 35 4 3 -1 b7. x1+x2+x3=0,已知齐次线性方程组 x1+2x2+px3=0, 有非零解,则p= .x1+4x2+p2x3=08. 设A是m⨯n矩阵,它的列向量组为α1,α 2,…,αn,则(A)如果非齐次方程组A X=β有唯一解,则m=n,并且|A|不为0.(B)如果α1,α 2,…,αn线性相关,则非齐次方程组A X=β有无穷多解.(C)总存在m维向量β ,使得方程组A X=β有无解.(D)如果A X=β有唯一解, 则m≥n.1 2 39.设Q = 2 4 t,矩阵P≠0 ,使得PQ=0 ,则( )3 6 9(A)当t=6r(P; (B)当t=6时,r(P)=2;(C)当t≠6时,r(P)=1; (D)当t≠6时,r(P)=2.10.设η1,η2,η3是齐次方程组A X=0的一个基础解系,则( )也是A X=0的基础解系.(A)η1-η3,η2-η1,η3-η2.(B) η1,η2-η3.(C) η1+η2,η2-η3,η1+η2+η3.(D) η1+η2,η2+η3,η3+η1, η1+η2+η3.11.设ξ1,ξ2,ξ3是3元非齐次线性方程组AX=β的三个无关线性的解,已知r(A)=1, 则( )(A)ξ 1-ξ2,ξ2-ξ3,ξ3-ξ1是A X=0的基础解系.,(B) c(ξ1-2ξ2+ξ3)是A X=0的通解.(C) c 1ξ1+c 2ξ2+c 3ξ3(c 1+c 2+c 3=0) 是A X =0的通解. (D) ξ1,ξ2-ξ3是A X =0的基础解系.12.设A 是m ⨯n 矩阵,非齐次方程组A X =β 有无穷多解,则( )正确. (A) A X =O 有非零解.(B) m <n.(C) n <m .(D) m=n 并且|A |=0.13. 设A 是m ⨯n 矩阵,r(A )=n-2,γ1,γ2,γ3是非齐次方程组A X =β 的三个不同解,则 (A) γ1, γ2,γ3线性相关.(B) γ1-γ2,γ2-γ3是齐次方程组A X =0 的基础解系. (C) 当 γ1,γ2,γ3线性无关时,则{k 1γ1+k 2γ2+k 3γ3,其中k 1,k 2,k 3是满足k 1+k 2+k 3=1的任何数.}是 A X =β 的通解(D) γ1,γ2,γ3的任何线性组合都是A X =β 的解.14.设γ1,γ2,γ3,γ4是非齐次方程组A X =β 的四个不同解,并且a γ1+γ2-b γ3+2γ4也是A X =β 的解,γ1-2b γ2+a γ3-3γ4是A X =0 的解,则a= ,b= . 15. 已知ξ1=(0,1,0)和ξ2=(-3,2,2)都是方程组 x 1-x 2+2x 3=-1, 3x 1+x 2+4x 3=1,ax 1+bx 2+cx 3=d ,求通解.16. 设(Ⅰ)和(Ⅱ)是两个四元齐次线性方程组,(Ⅰ)为 x 1+x 2=0,x 3-x 4=0,(Ⅱ)有一个基础解系(0,1,1,0),(-1,2,2,1).求(Ⅰ)和(Ⅱ)的全部公共解.17.设(Ⅰ)和(Ⅱ)是两个四元齐次线性方程组,(Ⅲ)是将它们合并而得到的方程组.已知(1,0 ,1,1),(-1,0,1,0),(0,1,1,0)是(Ⅰ)的一个基础解系,(0,1,0,1),(1,1,-1,0)是(Ⅱ)的一个基础解系.求(Ⅲ)的通解. 18.已知方程组x 1+2x 2- x 3+ x 4=m x 1 +3x 3 =-2 (Ⅰ) 3x 1+nx 2+3x 3+2x 4=-11 (Ⅱ) x 2-2x 3 =52x 1+2x 2+px 3+ x 4=-4 x 4=-10 同解,求m ,n ,p .19.设B 是3阶非零矩阵,它的每个列向量都是方程组 x 1+2x 2-2x 3=0 2x 1- x 2+kx 3=0 3x 1 +x 2 -x 3=0的解.求k ,并证明|B |=0.20.设(Ⅰ)是有n 个未知数的非齐次线性方程组,系数矩阵的秩为s , 证明:如果(Ⅰ)有解,则⑴ (Ⅰ)有n-s+1个线性无关的解.⑵ (Ⅰ)的任意n-s+2个解都线性相关. 21.设A 是m ⨯n 实矩阵.证明 ⑴ r(A T A )=r(A );⑵ r(A )=n ⇔ A T A 可逆.22.证明n 元非齐次线性方程组AX=β有解⇔ A T Y =0的解都适方程βT Y =0.23. x 1+ x 2+ x 3-x 4=13, 3x 1+mx 2+3x 3+2x 4=h , 已知线性方程组(I) 2x 2-4x 3+x 4=0, 的解都满足方程组(II) x 1+nx 2- x 3+ x 4=k , x 1-x 2+5x 3 =-7 求m,n,h,k,并求(II)的一般解.24.设α1=(1,a,2,-1),α2=(1,3,a,1),α3=(1,2,3,1),α4=(3,6,7,-1),α5=(1,1,3,-1),已知α1,α2,α3, α4线性相关,α5可用α1,α2,α3,α4线性表示,求a,并写出α5用α1,α2,α3, α4线性表示的一般表示式.25.设线性方程组(I)与(II)有公共的非零解,其中(I)为3x1+5x2+2x3-4x4=0,x1+ x2+ x3+x4=0, x1+tx2+2x3 =0(II)有基础解系η1=(1,-1, 1,0),η2=(-2p,p,1,1),求p,t的值和全部公共解.参考答案7. p=1或2.8.(C).1 2 39.设Q = 2 4 t,矩阵P≠0 ,使得PQ=0 ,则( )3 6 9(1)当t=6时,r(P)=1; (2)当t=6时,r(P)=2;(3)当t≠6时,r(P)=1; (4)当t≠6时,r(P)=2.10.(C).11.(B) .12. (A) .13. (C)14. a=-6,b=-4.15. 已知ξ1=(0,1,0)和ξ2=(-3,2,2)都是方程组x 1-x2+2x3=-1,3x1+x2+4x3=1,ax1+bx2+cx3=d的解,求通解.16.设(Ⅰ)和(Ⅱ)是两个四元齐次线性方程组,(Ⅰ)为 x1+x2=0,x 3-x4=0,(Ⅱ)有一个基础解系(0,1,1,0),(-1,2,2,1).求(Ⅰ)和(Ⅱ)的全部公共解.17.设(Ⅰ)和(Ⅱ)是两个四元齐次线性方程组,(Ⅲ)是将它们合并而得到的方程组.已知(1,0 ,1,1),(-1,0,1,0),(0,1,1,0)是(Ⅰ)的一个基础解系,(0,1,0,1),(1,1,-1,0)是(Ⅱ)的一个基础解系.求(Ⅲ)的通解.18.已知方程组x1+2x2- x3+ x4=m x1+3x3=-2(Ⅰ) 3x1+nx2+3x3+2x4=-11 (Ⅱ) x2-2x3=52x1+2x2+px3+ x4=-4 x4=-10同解,求m,n,p.23. x1+ x2+ x3-x4=13, 3x1+mx2+3x3+2x4=h,已知线性方程组(I) 2x2-4x3+x4=0,的解都满足方程组(II) x1+nx2- x3+ x4=k,x1-x2+5x3 =-7求m,n,h,k,并求(II)的一般解.(m=3,n=2,h=-11,k=-2.) 24. a=2, α5=(1+2c)α1-α2+(1+c) α3-c α4.25. p=-2,t=3,c(0,2,-3,1).第四部分n维向量空间向量组的线性关系与秩1. 向量组的线性表示关系如果n 维向量β等于n 维向量组α1, α2,⋯ ,αs 的一个线性组合,就说β可以用α1, α2,⋯ ,αs线性表示.判别“β是否可以用α1, α2,⋯ ,αs 线性表示? 表示方式是否唯一?”就是问:向量方程x 1α1+ x 2α2+⋯ +x s αs =β是否有解?解是否唯一?这个向量方程用分量写出就是以(α1, α2,⋯ ,αs |β)为增广矩阵的线性方程组.设α1, α2,⋯ ,αs 和β1, β2,⋯ , βt 都是n 维向量组,如果每个βi 都可以用α1, α2,⋯ ,αs 线性表示,则说向量组β1, β2,⋯ , βt 可以用α1, α2,⋯ ,αs 线性表示.例如, 乘积矩阵AB 的列向量组可以用A 的列向量组线性组合.反之,如果向量组β1, β2,⋯ , βt 可以用α1, α2,⋯ ,αs 线性表示,则矩阵(β1, β2,⋯ , βt )等于矩阵(α1, α2,⋯ ,αs )和一个s ⨯t 矩阵C 的乘积. C 可以这样构造: 它的第i 个列向量就是βi 对α1, α2,⋯ ,αs 的分解系数.当向量组α1, α2,⋯ ,αs 和β1, β2,⋯ , βt 互相都可以表示时,就说它们互相等价,并记作{α1, α2,⋯ ,αs }≅{β1, β2,⋯ , βt } .向量组的线性表示关系有传递性,从而等价关系也有传递性. 2. 向量组的线性相关性线性相关性是描述向量组内在关系的概念.定义 设α1, α2,⋯ ,αs 是n 维向量组,如果存在不全为0的一组数c 1,c 2,⋯ ,c s 使得c 1α1+ c 2α2+⋯ ,+c s αs =0,则说α1, α2,⋯ ,αs 线性相关,否则(即要使得c 1α1+ c 2α2+⋯ ,+c s αs =0,必须c 1,c 2,⋯ ,c s 全为0)就说它们线性无关.于是, α1, α2,⋯ ,αs “线性相关还是无关”即x 1α1+ x 2α2+⋯ ,+x s αs =0“有还是没有非0解”, 也就是以(α1, α2,⋯ ,αs )为系数矩阵的齐次线性方程组有无非0解.一个向量(s=1)相关(无关)即它是(不是)零向量. 与线性相关性有关的性质:① α1, α2,⋯ ,αs 线性相关⇔至少有一个αi 可以用其它向量线性表示. ② 当向量的个数s 大于维数n 时, α1, α2,⋯ ,αs 一定线性相关. ③ 线性无关向量组的每个部分组都无关(从而每个向量就不是0).④ 如果α1, α2,⋯ ,αs 线性相关,而α1, α2,⋯ ,αs ,β线性相关,则β可用α1, α2,⋯ ,αs 线性表示.⑤ 如果β可用α1, α2,⋯ ,αs 线性表示,则表示方式唯一⇔α1, α2,⋯ ,αs 线性无关. ⑥ 如果β1, β2,⋯ , βt 可以用α1, α2,⋯ ,αs 线性表示,并且t>s,则 β1.β2,⋯,βt 线性相关. 推论 如果两个线性无关的向量组互相等价,则它们包含的向量个数相等. 3.向量组的极大无关组和秩秩是刻画向量组相关“程度”的一个数量概念.它表明向量组可以有多大的线性无关的部分组.定义 设α1, α2,⋯ ,αs 是n 维向量组,(I)是它的一个部分组.如果 ① (I) 线性无关.② (I) 在扩大就线性相关.就称(I)为α1, α2,⋯ ,αs 的一个极大无关组.条件②可换为:任何αI 都可用(I) 线性表示.也就是(I) 与α1, α2,⋯ ,αs 等价.当α1, α2,⋯ ,αs 不全为零向量时, 它就存在极大无关组, 并且任意两个极大无关组都等价,从而包含的向量个数相等,定义 如果α1, α2,⋯ ,αs 不全为零向量,则把它的极大无关组中所包含向量的个数(是一个正整数)称为α1, α2,⋯ ,αs 的秩,记作r(α1, α2,⋯ ,αs ).如果α1, α2,⋯ ,αs 全是零向量,则规定r(α1, α2,⋯ ,αs )=0.秩有以下性质:① α1, α2,⋯ ,αs 线性无关⇔ r(α1, α2,⋯ ,αs )=s.② β可用α1, α2,⋯ ,αs 线性表示⇔r(α1, α2,⋯ ,αs ,β)=r(α1, α2,⋯ ,αs ).(见例3.2) ③ 如果r(α1, α2,⋯ ,αs )=k,则i) α1, α2,⋯ ,αs 的每个含有多于k 个向量的部分组相关.ii) α1, α2,⋯ ,αs 的每个含有k 个向量的无关部分组一定是极大无关组.. ④ 如果β1, β2,⋯ , βt 可以用α1, α2,⋯ ,αs 线性表示,则r(β1, β2,⋯ , βt )≤r(α1, α2,⋯ ,αs ).如果α1, α2,⋯ ,αs 和β1, β2,⋯ , βt 等价,则 r(α1, α2,⋯ ,αs )=r(β1, β2,⋯ , βt ).极大无关组和秩的概念可以推广到向量集合上(即包含的向量的个数不必有限),所有性质仍然成立.4. 有相同线性关系的向量组两个向量数相同的向量组α1, α2,⋯ ,αs 和β1, β2,⋯ , βs 称为有相同线性关系,如果向量方程x 1α1+ x 2α2+⋯ +x s αs =0和x 1β1+ x 2β2+⋯ +x s βs =0同解.(例如,当A 经过初等行变换化为B 时, A 的列向量组和B 的列向量组有相同线性关系.) 当α1, α2,⋯ ,αs 和β1, β2,⋯ , βs 有相同线性关系时, (1)它们的秩相等.(2)它们的极大无关组相对应.(3)它们有相同的内在线性表示关系. 5.矩阵的秩定义 一个矩阵A 的行向量组的秩和列向量组的秩相等,称为此矩阵的秩,记作r(A ). 于是r(A )=0⇔ A =0.如果A 是m ⨯n 矩阵,则r(A )≤Min{m,n},当等号成立时,称A 为满秩的. 如果A 是n 阶矩阵,则A 满秩,即r(A )=n ⇔ A 的行(列)向量组无关⇔|A |≠0⇔A 可逆⇔AX =β有唯一解⇔齐次方程组AX =0只有零解. 命题 ① 初等变换保持矩阵的秩.② 阶梯形矩阵的秩等于它的非零行的个数.矩阵A 的r 阶子式:任取 A 的r 行和r 列,在它们的交叉位置上的元素所构成的行列式.命题 r(A )就是A 的不等于0的子式的阶数的最大值.(即A 的每个阶数大于r(A )的子式都为0,都是A 有阶数等于r(A )非0子式.)在作矩阵的运算中,矩阵的秩有性质: ① r(A T )=r(A ).② 如果c 不为0,则r(c A )=r(A ). ③ r(A ±B )≤r(A )+ r(B ).④ ≤Min{r(A ),r(B )}. ⑤当A (或B )可逆时,r(AB )=r(B )(或r(A )). ⑥ 如果AB =0,n 为A 的列数(B 的行数),则r(A )+r(B )≤n. ⑦ 如果r(A )等于列数,则r(AB )=r(B ).下面给出⑤和⑦在判别向量组的线性相关性和秩的计算问题上的应用.设向量组α1, α2,⋯ ,αs 线性无关,向量组β1, β2,⋯ ,βt 可用α1, α2,⋯ ,αm 线性表示,表示矩阵为C ,则i) r(β1, β2,⋯ ,βt )=r(C ).ii) 如果t=s (此时C是t阶矩阵),则β1, β2,⋯ ,βs线性无关⇔ C可逆.(令A=(α1, α2,⋯,αs),B=(β1, β2,⋯,βt),则B=AC, 并且r(A)=列数s,用⑦得到r(β1, β2,⋯ ,βs)=r(C). t=s时,C可逆⇔r(β1, β2,⋯ ,βs)=r(C)=s⇔β1, β2,⋯ ,βs线性无关.或直接用⑤证明ii): C可逆时r(B)=r(A)=s,从而β1, β2,⋯ ,βs线性无关.如果C不可逆,则r(β1, β2,⋯ ,βs)≤r(C)< s, 从而β1, β2,⋯ ,βs线性相关.)练习题三1.α1,α2,…,αr线性无关⇔ ( ).(A) 存在全为零的实数k1,k2,…,kr,使得k1α1+ k2α2+…+ k rαr=0;(B) 存在不全为零的实数k1,k2,…,kr,使得k1α1+ k2α2+…+ k rαr≠0;(C) 每个αi都不能用其它向量线性表示;有线性无关的部分组.2. 设A是4⨯5矩阵, α1,α2,α3,α4,α5是A的列向量组,r(α1,α2,α3,α4,α5)=3,则( )正确。


线性代数必考的知识点1、行列式1. n 行列式共有2n 个元素,展开后有!n 项,可分解为2n 行列式;2. 代数余子式的性质:①、ij A 和ij a 的大小无关;②、某行(列)的元素乘以其它行(列)元素的代数余子式为0; ③、某行(列)的元素乘以该行(列)元素的代数余子式为A ; 3. 代数余子式和余子式的关系:(1)(1)i j i j ij ij ij ij M A A M ++=-=-4. 设n 行列式D :将D 上、下翻转或左右翻转,所得行列式为1D ,则(1)21(1)n n D D -=-; 将D 顺时针或逆时针旋转90,所得行列式为2D ,则(1)22(1)n n D D -=-;将D 主对角线翻转后(转置),所得行列式为3D ,则3D D =;将D 主副角线翻转后,所得行列式为4D ,则4D D =; 5. 行列式的重要公式:①、主对角行列式:主对角元素的乘积;②、副对角行列式:副对角元素的乘积(1)2(1)n n -⨯ -;③、上、下三角行列式( = ◥◣):主对角元素的乘积; ④、 ◤和 ◢:副对角元素的乘积(1)2(1)n n -⨯ -;⑤、拉普拉斯展开式:A O A C AB CB O B==、(1)m n CA OA AB B OB C==-⑥、德蒙行列式:大指标减小指标的连乘积; ⑦、特征值;6. 对于n 阶行列式A ,恒有:1(1)nn k n k k k E A S λλλ-=-=+-∑,其中k S 为k 阶主子式;7. 证明0A =的方法:①、A A =-; ②、反证法;③、构造齐次方程组0Ax =,证明其有非零解; ④、利用秩,证明()r A n <; ⑤、证明0是其特征值;2、矩阵1.A 是n 阶可逆矩阵:⇔0A ≠(是非奇异矩阵);⇔()r A n =(是满秩矩阵) ⇔A 的行(列)向量组线性无关; ⇔齐次方程组0Ax =有非零解; ⇔n b R ∀∈,Ax b =总有唯一解;⇔A 与E 等价;⇔A 可表示成若干个初等矩阵的乘积; ⇔A 的特征值全不为0; ⇔T A A 是正定矩阵;⇔A 的行(列)向量组是n R 的一组基; ⇔A 是n R 中某两组基的过渡矩阵;2. 对于n 阶矩阵A :**AA A A A E == 无条件恒成立;3.1**111**()()()()()()T T T T A A A A A A ----=== ***111()()()T T TAB B A AB B A AB B A ---===4. 矩阵是表格,推导符号为波浪号或箭头;行列式是数值,可求代数和;5. 关于分块矩阵的重要结论,其中均A 、B 可逆:若12s A A A A ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭,则: Ⅰ、12s A A A A =;Ⅱ、111121s A A A A ----⎛⎫⎪⎪= ⎪ ⎪ ⎪⎝⎭; ②、111A O A O O B O B ---⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭;(主对角分块) ③、111O A O B B O A O ---⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭;(副对角分块) ④、11111A C A A CB O B OB -----⎛⎫-⎛⎫=⎪ ⎪⎝⎭⎝⎭;(拉普拉斯) ⑤、11111A O A O C B B CA B -----⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭;(拉普拉斯) 3、矩阵的初等变换与线性方程组1. 一个m n ⨯矩阵A ,总可经过初等变换化为标准形,其标准形是唯一确定的:r m nE OF OO ⨯⎛⎫=⎪⎝⎭; 等价类:所有与A 等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵; 对于同型矩阵A 、B ,若()()r A r B A B = ⇔ ; 2. 行最简形矩阵:①、只能通过初等行变换获得;②、每行首个非0元素必须为1;③、每行首个非0元素所在列的其他元素必须为0;3. 初等行变换的应用:(初等列变换类似,或转置后采用初等行变换)①、若(,)(,)rA E E X ,则A 可逆,且1X A -=;②、对矩阵(,)A B 做初等行变化,当A 变为E 时,B 就变成1A B -,即:1(,)(,)cA B E A B - ~ ;③、求解线形方程组:对于n 个未知数n 个方程Ax b =,如果(,)(,)rA b E x ,则A 可逆,且1x A b -=; 4. 初等矩阵和对角矩阵的概念:①、初等矩阵是行变换还是列变换,由其位置决定:左乘为初等行矩阵、右乘为初等列矩阵;②、12n ⎛⎫⎪⎪Λ= ⎪ ⎪⎝⎭λλλ,左乘矩阵A ,i λ乘A 的各行元素;右乘,iλ乘A 的各列元素;③、对调两行或两列,符号(,)E i j ,且1(,)(,)E i j E i j -=,例如:1111111-⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭;④、倍乘某行或某列,符号(())E i k ,且11(())(())E i k E i k-=,例如:1111(0)11kk k-⎛⎫⎛⎫⎪⎪ ⎪=≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭; ⑤、倍加某行或某列,符号(())E ij k ,且1(())(())E ij k E ij k -=-,如:11111(0)11k k k --⎛⎫⎛⎫ ⎪ ⎪=≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭;5. 矩阵秩的基本性质:①、0()min(,)m n r A m n ⨯≤≤;②、()()T r A r A =; ③、若AB ,则()()r A r B =;④、若P 、Q 可逆,则()()()()r A r PA r AQ r PAQ ===;(可逆矩阵不影响矩阵的秩) ⑤、max((),())(,)()()r A r B r A B r A r B ≤≤+;(※) ⑥、()()()r A B r A r B +≤+;(※) ⑦、()min((),())r AB r A r B ≤;(※)⑧、如果A 是m n ⨯矩阵,B 是n s ⨯矩阵,且0AB =,则:(※) Ⅰ、B 的列向量全部是齐次方程组0AX =解(转置运算后的结论);Ⅱ、()()r A r B n +≤⑨、若A 、B 均为n 阶方阵,则()()()r AB r A r B n ≥+-;6. 三种特殊矩阵的方幂:①、秩为1的矩阵:一定可以分解为列矩阵(向量)⨯行矩阵(向量)的形式,再采用结合律;②、型如101001a c b ⎛⎫ ⎪⎪ ⎪⎝⎭的矩阵:利用二项展开式;二项展开式:01111110()nnnn m n mmn n n nm m n mnnnnnn m a b C a C a b C ab Ca bC b C a b -----=+=++++++=∑;注:Ⅰ、()n a b +展开后有1n +项;Ⅱ、0(1)(1)!1123!()!--+====-m n n n n n n n m n C C C m m n mⅢ、组合的性质:111102---+-===+==∑nm n mm m m rnr r n n n n nnn n r C C C C C CrC nC ;③、利用特征值和相似对角化: 7. 伴随矩阵:①、伴随矩阵的秩:*()()1()10()1nr A n r A r A n r A n = ⎧⎪==-⎨⎪<-⎩; ②、伴随矩阵的特征值:*1*(,)AAAX X A A A A X X λλλ- == ⇒ =;③、*1A A A -=、1*n A A-=8. 关于A 矩阵秩的描述:①、()r A n =,A 中有n 阶子式不为0,1n +阶子式全部为0;(两句话)②、()r A n <,A 中有n 阶子式全部为0;③、()r A n ≥,A 中有n 阶子式不为0;9. 线性方程组:Ax b =,其中A 为m n ⨯矩阵,则:①、m 与方程的个数相同,即方程组Ax b =有m 个方程;②、n 与方程组得未知数个数相同,方程组Ax b =为n 元方程; 10. 线性方程组Ax b =的求解:①、对增广矩阵B 进行初等行变换(只能使用初等行变换);②、齐次解为对应齐次方程组的解; ③、特解:自由变量赋初值后求得;11. 由n 个未知数m 个方程的方程组构成n 元线性方程:①、11112211211222221122n n n n m m nm n na x a x a xb a x a x a x b a x a x a x b +++= ⎧⎪+++= ⎪⎨⎪⎪+++=⎩; ②、1112111212222212n n m m mn m m a a a x b a a a x b Ax b a a a x b ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪=⇔= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭(向量方程,A 为m n ⨯矩阵,m 个方程,n 个未知数)③、()1212n n x x aa a x β⎛⎫⎪ ⎪= ⎪⎪⎝⎭(全部按列分块,其中12n b b b β⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭); ④、1122n n a x a x a x β+++=(线性表出)⑤、有解的充要条件:()(,)r A r A n β=≤(n 为未知数的个数或维数)4、向量组的线性相关性1.m 个n 维列向量所组成的向量组A :12,,,m ααα构成n m ⨯矩阵12(,,,)m A =ααα;m 个n 维行向量所组成的向量组B :12,,,T TTm βββ构成m n ⨯矩阵12T T T m B βββ⎛⎫⎪ ⎪= ⎪ ⎪ ⎪⎝⎭;含有有限个向量的有序向量组与矩阵一一对应;2. ①、向量组的线性相关、无关 0Ax ⇔=有、无非零解;(齐次线性方程组)②、向量的线性表出 Ax b ⇔=是否有解;(线性方程组) ③、向量组的相互线性表示 AX B ⇔=是否有解;(矩阵方程)3. 矩阵m n A ⨯与l n B ⨯行向量组等价的充分必要条件是:齐次方程组0Ax =和0Bx =同解;(101P 例14)4. ()()T r A A r A =;(101P 例15)5.n 维向量线性相关的几何意义:①、α线性相关⇔0α=; ②、,αβ线性相关 ⇔,αβ坐标成比例或共线(平行);③、,,αβγ线性相关 ⇔,,αβγ共面;6. 线性相关与无关的两套定理:若12,,,s ααα线性相关,则121,,,,s s αααα+必线性相关;若12,,,s ααα线性无关,则121,,,s ααα-必线性无关;(向量的个数加加减减,二者为对偶)若r 维向量组A 的每个向量上添上n r -个分量,构成n 维向量组B :若A 线性无关,则B 也线性无关;反之若B 线性相关,则A 也线性相关;(向量组的维数加加减减) 简言之:无关组延长后仍无关,反之,不确定;7. 向量组A (个数为r )能由向量组B (个数为s )线性表示,且A 线性无关,则r s ≤;向量组A 能由向量组B 线性表示,则()()r A r B ≤;向量组A 能由向量组B 线性表示AX B ⇔=有解;()(,)r A r A B ⇔= 向量组A 能由向量组B 等价()()(,)r A r B r A B ⇔ ==8. 方阵A 可逆⇔存在有限个初等矩阵12,,,l P P P ,使12l A P P P =;①、矩阵行等价:~rA B PA B ⇔=(左乘,P 可逆)0Ax ⇔=与0Bx =同解②、矩阵列等价:~cA B AQ B ⇔=(右乘,Q 可逆); ③、矩阵等价:~A B PAQ B ⇔=(P 、Q 可逆); 9.对于矩阵m n A ⨯与l n B ⨯:①、若A 与B 行等价,则A 与B 的行秩相等;②、若A 与B 行等价,则0Ax =与0Bx =同解,且A 与B 的任何对应的列向量组具有相同的线性相关性; ③、矩阵的初等变换不改变矩阵的秩; ④、矩阵A 的行秩等于列秩; 10.若m s s n m n A B C ⨯⨯⨯=,则:①、C 的列向量组能由A 的列向量组线性表示,B 为系数矩阵;②、C 的行向量组能由B 的行向量组线性表示,T A 为系数矩阵;(转置)11.齐次方程组0Bx =的解一定是0ABx =的解,考试中可以直接作为定理使用,而无需证明; ①、0ABx = 只有零解0Bx ⇒ =只有零解;②、0Bx = 有非零解0ABx ⇒ =一定存在非零解;12. 设向量组12:,,,n r r B b b b ⨯可由向量组12:,,,n s s A a a a ⨯线性表示为:1212(,,,)(,,,)r s b b b a a a K =(B AK =)其中K 为s r ⨯,且A 线性无关,则B 组线性无关()r K r ⇔=;(B 与K 的列向量组具有相同线性相关性) (必要性:()()(),(),()r r B r AK r K r K r r K r ==≤≤∴=;充分性:反证法)注:当r s =时,K 为方阵,可当作定理使用;13. ①、对矩阵m n A ⨯,存在n m Q ⨯,m AQ E = ()r A m ⇔=、Q 的列向量线性无关;②、对矩阵m n A ⨯,存在n m P ⨯,n PA E = ()r A n ⇔=、P 的行向量线性无关; 14. 12,,,s ααα线性相关⇔存在一组不全为0的数12,,,s k k k ,使得11220s s k k k ααα+++=成立;(定义)⇔1212(,,,)0s s x xx ααα⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭有非零解,即0Ax =有非零解;⇔12(,,,)s r s ααα<,系数矩阵的秩小于未知数的个数;15. 设m n ⨯的矩阵A 的秩为r ,则n 元齐次线性方程组0Ax =的解集S 的秩为:()r S n r =-; 16. 若*η为Ax b =的一个解,12,,,n r ξξξ-为0Ax =的一个基础解系,则*12,,,,n r ηξξξ-线性无关;5、相似矩阵和二次型1. 正交矩阵T A A E ⇔=或1T A A -=(定义),性质:①、A 的列向量都是单位向量,且两两正交,即1(,1,2,)0T i j i j a a i j n i j=⎧==⎨≠⎩;②、若A 为正交矩阵,则1T A A -=也为正交阵,且1A =±; ③、若A 、B 正交阵,则AB 也是正交阵; 注意:求解正交阵,千万不要忘记施密特正交化和单位化; 2. 施密特正交化:12(,,,)r a a a11b a =;1222111[,][,]b a b a b b b =-121121112211[,][,][,][,][,][,]r r r r r r r r r b a b a b a b a b b b b b b b b b ----=----;3. 对于普通方阵,不同特征值对应的特征向量线性无关;对于实对称阵,不同特征值对应的特征向量正交; 4. ①、A 与B 等价 ⇔A 经过初等变换得到B ;⇔=PAQ B ,P 、Q 可逆; ()()⇔=r A r B ,A 、B 同型;②、A 与B 合同 ⇔=T C AC B ,其中可逆; ⇔T x Ax 与T x Bx 有相同的正、负惯性指数; ③、A 与B 相似 1-⇔=P AP B ; 5. 相似一定合同、合同未必相似;若C 为正交矩阵,则T C AC B =⇒A B ,(合同、相似的约束条件不同,相似的更严格); 6. A 为对称阵,则A 为二次型矩阵; 7. n 元二次型T x Ax 为正定:A ⇔的正惯性指数为n ;A ⇔与E 合同,即存在可逆矩阵C ,使T C AC E =; A ⇔的所有特征值均为正数; A ⇔的各阶顺序主子式均大于0;0,0ii a A ⇒>>;(必要条件)。
07-08(1) 线性代数总期末考试复习大纲及复习题: 期末考试题型:判断(约占30%)与选择(约占70%) 期末考试形式:开卷 期末复习各章重点第一章 知道行列式的定义并会用定义计算简单的行列式;熟悉并会用行列式的性 质计算行列式,掌握行列式的依行依列展开定理。
第二章掌握向量线性相关与线性无关的定义并会用定义判断向量组相关与无关;会求向量组的极大无关组以及用极大无关组表示其余的向量;熟悉线性方程组解的一般理论,掌握矩阵的初等变换并会用初等变换求解线性方程组;会用初等变换求矩阵的秩.第三章熟悉矩阵的运算性质,特别是矩阵乘法的特殊性(不满足交换律),知道分块矩阵;掌握逆矩阵的定义、伴随矩阵的概念以及关系式E A A A AA ==**,会用伴随矩阵和初等变换求矩阵的逆矩阵;了解初等矩阵及其性质,会解简单的矩阵方程。
第四章 知道向量空间的定义,掌握基变换公式和向量坐标变换公式。
第五章 掌握矩阵的特征值与特征向量的概念以及矩阵能够对角化的条件,会判断一个矩阵能否对角化;掌握相似矩阵的概念及其性质。
第六章 掌握二次型的概念,掌握二次型与矩阵的对应关系,掌握合同矩阵的概念,会判断简单矩阵的合同,掌握二次型正定负定的条件并会判定二次型是否正定。
复习题1.若三阶行列式1231122331232226a a a b a b a b a c c c ---=,则 123123123a a ab b bc c c = 3 (对) 2.若方程组123123123000tx x x x tx x x x tx ++=⎧⎪++=⎨⎪++=⎩有非零解,则t=1或-2 。
(对)3.已知齐次线性方程组32023020x y x y x y z λ+=⎧⎪-=⎨⎪-+=⎩仅有零解,则λ≠ 0(对)4.已知三阶行列式D=123312231,则元素12a =2的代数余子式12A = -1 ;(错)5.若n 阶矩阵A 、B 、C 满足ABC=E (其中E 为n 阶可逆阵),则BCA=E 。
中山大学2018-2019年度 线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1. 若022150131=---x ,则=χ__________。
2.若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,则λ应满足 。
3.已知矩阵n s ij c C B A ⨯=)(,,,满足CB AC =,则A 与B 分别是 阶矩阵。
4.矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5.n 阶方阵A 满足032=--E A A ,则=-1A 。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分)1. 若行列式D 中每个元素都大于零,则0〉D 。
( )2. 零向量一定可以表示成任意一组向量的线性组合。
( )3. 向量组m a a a ,,, 21中,如果1a 与m a 对应的分量成比例,则向量组s a a a ,,, 21线性相关。
( )4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ,则A A =-1。
( ) 5. 若λ为可逆矩阵A 的特征值,则1-A 的特征值为λ。
( )三、单项选择题 (每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分)1. 设A 为n 阶矩阵,且2=A ,则=TA A ( )。
① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα,,, 21(3 ≤ s ≤ n )线性无关的充要条件是( )。
① s ααα,,, 21中任意两个向量都线性无关 ② s ααα,,, 21中存在一个向量不能用其余向量线性表示③ s ααα,,, 21中任一个向量都不能用其余向量线性表示 ④ s ααα,,, 21中不含零向量 3. 下列命题中正确的是( )。
① 任意n 个1+n 维向量线性相关 ② 任意n 个1+n 维向量线性无关 ③ 任意1+n 个n 维向量线性相关 ④ 任意1+n 个n 维向量线性无关4. 设A ,B 均为n 阶方阵,下面结论正确的是( )。
线性代数-期末复习资料单项选择题(每题2分,共20分)1.(学科教研组期末学业水平编写)设n 阶方阵A 、B 、C 满足关系式ABC=E ,其中E 是n 阶单位阵,则必有A.ACE=EB.CBA=EC.BAC=ED.BCA=E2.设A 、B 为n 阶方阵,满足等式AB=0,则必有A .A=0或B=0 B.A+B=0 C.00==B A 或 D. 0=+B A3.设A 是矩阵是矩阵,m n B n m ⨯⨯,则________A.当n m >时,必有行列式0≠ABB.当n m >时,必有行列式0=ABC.当m n >时,必有行列式0≠ABD.当m n >时,必有行列式0=AB4.设A 为n 阶方阵,且A 的行列式,o a A ≠=而*A 是A 的伴随矩阵,则*A = 。
A.a B.a1 C.1-n a D. n a 5.设A 是n 阶可逆矩阵,*A 是A 的伴随矩阵,则 A.1*-=n A A B.A A =* C.nA A =* D.1*-=A A 6.已知 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=96342321t Q ,P 为三阶非零矩阵,且满足PQ=0,则_______ A.t=6时P 的秩必为1 B.t=6时P 的秩必为2C.t ≠6时P 的秩必为1D.t ≠6时P 的秩必为27.设n 元齐次线性方程组O Ax =的系数矩阵A 的秩为r,则O Ax =有非零解的充分必要条件是_______A.n r =B. n r <C. n r ≥D. n r >8.设A 是n 阶矩阵,则A 以0为特征值是A 为奇异矩阵的_______A.充分但不必要条件B.必要但不充分条件C.既非充分有非必要条件D.充分必要条件9.设α是矩阵A 对应于特征值λ的特征向量,则矩阵AP P 1-对应与λ的特征向量是__________A.α1-PB. αPC. αT PD. α10.设n 阶矩阵A 非奇异(2≥n ),*A 是A 的伴随矩阵,则______ A.A AA n 1**)(-= B. A A A n 1**)(+= C.A A A n 2**)(-= D.A A A n 2**)(+= 二、填空题(每题3分,共30分)1.(学科教研组期末学业水平编写)已知()⎪⎭⎫ ⎝⎛==31,21,1,3,2,1βα。