几何体与球的切接问题专项练习
- 格式:docx
- 大小:170.75 KB
- 文档页数:4
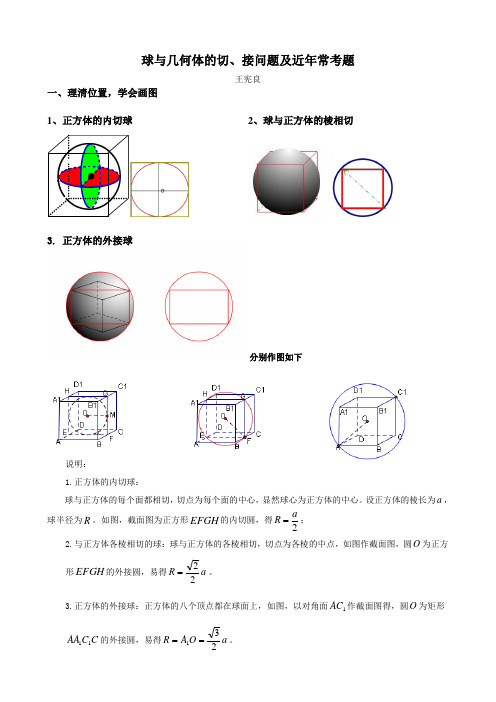
球与几何体的切、接问题及近年常考题王宪良一、理清位置,学会画图1、正方体的内切球2、球与正方体的棱相切3. 正方体的外接球分别作图如下说明:1.正方体的内切球:球与正方体的每个面都相切,切点为每个面的中心,显然球心为正方体的中心。
设正方体的棱长为a ,球半径为R 。
如图,截面图为正方形EFGH 的内切圆,得2aR =; 2.与正方体各棱相切的球:球与正方体的各棱相切,切点为各棱的中点,如图作截面图,圆O 为正方形EFGH 的外接圆,易得a R 22=。
3.正方体的外接球:正方体的八个顶点都在球面上,如图,以对角面1AC 作截面图得,圆O 为矩形C C AA 11的外接圆,易得a O A R 231==。
二、解决球心位置和半径大小的常用方法1. 出现“墙角”结构利用补形知识,联系长方体。
【原理】:长方体中从一个顶点出发的三条棱长分别为c b a ,,,则体对角线长为222c b a l ++=,几何体的外接球直径R 2为体对角线长l 即2222c b a R ++=【例题】:在四面体ABCD 中,共顶点的三条棱两两垂直,其长度分别为3,61,,若该四面体的四个顶点在一个球面上,求这个球的表面积。
解:因为有三条棱两两垂直,所以可补成球内接长方体。
因为:长方体外接球的直径为长方体的体对角线长所以:四面体外接球的直径为AE 的长,即:22224AD AC AB R ++=1663142222=++=R 所以2=R所以球的表面积为ππ1642==R S2. 出现两个垂直关系,利用直角三角形结论。
【原理】:直角三角形斜边中线等于斜边一半。
球心为直角三角形斜边中点。
【例题】:已知三棱锥的四个顶点都在球O 的球面上,BC AB ⊥且7=PA ,5=PB ,51=PC ,10=AC ,求球O 的体积。
解:BC AB ⊥且7=PA ,5=PB ,51=PC ,10=AC ,因为22210517=+ 所以知222PC PA AC +=,所以 PC PA ⊥ 所以可得图形为:在ABC Rt ∆中斜边为AC ; 在PAC Rt ∆中斜边为AC 取斜边的中点O ,在ABC Rt ∆中OC OB OA == 在PAC Rt ∆中OC OB OP ==所以在几何体中OA OC OB OP ===,即O 为该四面体的外接球的球心, 521==AC R 所以该外接球的体积为3500343ππ==R V3. 出现多个垂直关系时建立空间直角坐标系,利用向量知识求解AC【例题】:已知在三棱锥BCD A -中,ABC AD 面⊥,︒∠该棱锥的外接球半径。


第一篇 热点、难点突破篇专题15几何体与球切、接、截的问题(练)【对点演练】一、单选题 1.(2022秋·湖南张家界·高三慈利县第一中学校考阶段练习)如下图是一个正八面体,其每一个面都是正三角形,六个顶点都在球O 的球面上,则球O 与正八面体的体积之比是( )A .πB .4π3C .3π2D .2πAB a ,则R足球赛,比赛于2022年11月21日至12月18日在卡塔尔境内7座城市中的12座球场举行.已知某足球的表面上有四个点A 、B 、C 、P 满足P A =BC =5,PB AC ==PC AB ==则该足球的表面积为( ) A .12π B .8πC .24πD .28π【答案】D【分析】把四面体外接球问题扩展到长方体中,求出长方体外接球半径为R ,进而求出结果. 【详解】因为P A =BC ,PB AC =,PC AB =,所以可以把A ,B ,C ,P 四点放到长方体的则该足球的表面积为四面体A -BCP 外接球的表面积,即为长方体外接球的表面积, 解立方,得两堑堵,斜解堑堵,其一为阳马,其一为鳖臑”,即如图,一个长方体1111ABCD A B C D -,沿对角面11ABC D 分开(图1),得到两个一模一样的堑堵(图2),将其中一个堑堵11ADD BCC -,沿平面1D BC 分开(图2),得到一个四棱锥1D ABCD -称为阳马(图3),和一个三棱锥11D BCC -称为鳖臑(图4). 若鳖臑的体积为4,且4,3AB BC ==,则阳马1D ABCD -的外接球的表面积为( )A .27πB .29πC .31πD .33π23BAC π∠=.若三棱锥-P ABC 的各顶点都在球O 的球面上,则球O 的表面积为( ) A .4πB .8πC .12πD .20π【分析】利用正弦定理求出底面ABC 的外接圆半径,将三棱锥面外接圆中心作垂线,则垂线的中点即为外接球球心,进而即可求解【详解】在ABC 中,设其外接圆半径为由正弦定理可得2,sin 6AB r π=∠解得ABC 补成三棱柱,如图设三棱锥-P ABC 外接球半径为R ,5.(2022·四川广安·广安二中校考模拟预测)已知在Rt ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,且2a =,6A π=.又点A ,B ,C 都在球O 的球面上,且点O 到平面ABC 的O 的体积为______. 【分析】首先求ABC 外接圆的半径,再求球【详解】ABC 中,根据正弦定理所以ABC 外接圆的半径为到平面ABC 的距离为)253=,4π,高为2,上、下底面的圆周在同一球面上,则该圆台外接球的表面积为__________.()2()2长为的正方形,其顶点P到底面ABCD的距离为4.该四棱锥的外接球O的半径为7,若球心O在四棱锥P-ABCD内,则顶点P的轨迹长度为_____________.8.(2022·上海长宁·统考一模)已知1AA 是圆柱的一条母线,AB 是圆柱下底面的直径,C 是圆柱下底面圆周上异于A ,B 的两点,若圆柱的侧面积为4π,则三棱锥1A —ABC 外接球体积的最小值为___________设底面圆半径为r ,圆柱高设为h ,则根据圆柱的侧面积为4π,可得2π4πrh =,解得2rh =.因为ABC 以及2222214ABh r A B ,则224h r ,所以外接球的半径2242hr R.三棱锥—ABC 外接球体积为32244π32hr ,所以要外接球体积最小,只需要224h r 最小即可,又不等式可知2242248r h r rh ,当且仅当12r h ,时成立.故三棱锥外接球体积的最小值为34882ππ323. 故答案为:82π3..(2022秋·江苏南通已知圆台的内切球侧面相切的切点位于圆台高的34______.O 的表面积为______,体积为______.【冲刺提升】一、单选题 1.(2022秋·江苏淮安·高三校考阶段练习)如图,已知三棱柱111ABC A B C 的底面是等腰直角三角形,1AA ⊥底面ABC ,AC =BC =2,14AA =,点D 在上底面111A B C (包括边界)上运动,则三棱锥D -ABC 的外接球表面积的范围为( )A .81π,24π4⎡⎤⎢⎥⎣⎦B .[]9π,24πC .243π,24π16⎡⎤⎢⎥⎣⎦D .243π16⎡⎤⎢⎥⎣⎦因为ABC 为等腰直角三角形,所以ABC 的外接球的截面圆心为,且1AO =1//AA ,所以由球的截面性质可知,(0DE t t =≤OD R ==,所以2814t x =-因为2R =故选:A2.(2022秋·江苏南京·高三南京师大附中校联考阶段练习)四棱锥P ABCD-中,底面ABCD是边长为PAD为正三角形,则其外接球体积最小值为()A B.32 3πC.D.二、多选题3.(2022秋·安徽·高三石室中学校联考阶段练习)已知正四棱台上、下底面的面积分别为2和8,高为()0h h >,则下列结论正确的有( ) A .正四棱台外接球的表面积的最小值为16πB .当(h ∈时,正四棱台外接球球心在正四棱台下底面下方C .正四棱台外接球的半径随h 的增大而增大D .当2h =时,正四棱台存在内切球 1EO B EFB Rt Rt ≌可知O ∠ 2,故可知π2BEC ∠=,,所以1r =,2h =.故D 正确故选:ABD .4.(2022秋·山东潍坊·高三统考阶段练习)截角四面体是一种半正八面体,可由四面体经过适当的截角,即截去四面体的四个顶点处的小棱锥所得的多面体,如图所示,将棱长为3a 的正四面体沿棱的三等分点作平行于底面的截面,得到所有棱长均为a 的截角四面体,则下列说法正确的是( )A 3a B .该截角四面体的体积为312C .该截角四面体的外接球表面积为213π2a D .AEF △外接圆的面积为25π4a【详解】取上下底面的中心为,O O ''',外接球的球心为O ,连接,,,,OC OH CO HO '''如图,.(秋山东高三校联考阶段练习)在棱长为的正方体1111中,点为线段1AD (包含端点)上一动点,则下列选项正确的是( ).A .三棱锥1C BDQ -的体积为定值B .在Q 点运动过程中,存在某个位置使得1AD ⊥平面BQCC .截面三角形BQC 面积的最大值为D .当三棱锥1B B CQ -为正三棱锥时,其内切球半径为66.(2022秋·河北邢台·高三河北南宫中学校考阶段练习)如图,在菱形ABCD 中,π2,,3AB ABC M =∠=为BC 的中点,将ABM 沿直线AM 翻折到1AB M 的位置,连接1B C 和1,B D N 为1B D 的中点,在翻折过程中,则下列结论中正确的是( )A .面1AB M ⊥面1B MCB .线段CN 长度的取值范围为⎡⎣C .直线AM 和CN 所成的角始终为π6D .当三棱锥1B AMD -的体积最大时,点C 在三棱锥1B AMD -外接球的外部B 选项:如图所示,取AD 中点E ,连接EN ,EC ,所以//EC AM ,且EC AM =,又因为,在CEN 中,由余弦,即CN =C 选项:由B 选项得//EN AB ,所以直线AM 和CN 所成角即为与CN 所成角NCE ∠,在AMD 的外接圆内,又AMD 的外接圆在三棱锥1AMD -外接球的内部,故D 选项错误;故选:AC 三、填空题7.(2022秋·江苏·高三校联考阶段练习)已知半径为O 的表面上有A ,B ,C ,D 四点,且满足AD ⊥平面ABC ,BC AB BC =⊥,则四面体D ABC -的体积最大值为_____________;若M 为AD 的中点,当D 到平面MBC 的距离最大时,MBO △的面积为_____________.8.(2022秋·江苏常州·高三统考阶段练习)在正四面体A BCD -中,E 为BC 边的中点,过点E 作该正四面体外接球的截面,记最大的截面面积S ,最小的截面面积为T ,则=T S__________;若记该正四面体内切球和外接球的体积分别为1V 和2V ,则21V V =__________.2面积是___________.【答案】20πAC PC C =,,120APC ∠=所以2O A O P O C '''===,60PO A PO C ''∠=∠=︒.角形的四面体称之为鳖臑.如图,在鳖臑-P ABC 中,PA ⊥平面ABC .已知6AB =,8CB =,10PA AC ==,请写出平面PBC 的直角:_____________;若P ,A ,B ,C 都在球O 的球面上,则球O 的表面积为____________.PAAB A =,,故BC PB ⊥放入长方体中,如图所示:长及对角线BD 的长度均为6,平面ABD ⊥平面CBD ,点M 在AC 上,且2AM MC =,那么ABCD 外接球的半径为______;过点M 作四边形ABCD 外接球的截面.则截面面积最大值与最小值之比为______.【答案】54##1.25 1AE OHCE四、解答题12.(2022秋·安徽·高三校联考阶段练习)如图,长方体1111ABCD A B C D -中,11,2,AB AD AA P ===为棱1DD 的中点.(1)求直线AP 被长方体1111ABCD A B C D -的外接球截得的线段长度;(2)求直线1AC 与平面PAC 所成角的正弦值.()()()()()()10,0,0,1,0,0,0,1,0,0,0,2,0,1,2,0,0,1D A C D C P 设平面PAC 的一个法向量(),,n x y z =因为()()1,1,0,1,0,1AC AP =-=-,00n AC n AP ⎧⋅=⎪⎨⋅=⎪⎩,得,可得()1,1,1n =,又()11,1,2AC =-,设直线1AC 与平面所以()1111,1,1,1,12sin cos ,36AC nAC n AC n θ-⋅====⋅所以直线AC 与平面PAC 所成角的正弦值为。

课时规范练50 球与几何体的切、接问题基础巩固练1.(天津,5)若棱长为2√3的正方体的顶点都在同一球面上,则该球的表面积为( )A.12πB.24πC.36πD.144π2.已知某封闭的直三棱柱各棱长均为2,若三棱柱内有一个球,则该球表面积的最大值为( )A.4π3B.8π3C.4πD.16π33.(浙江余姚模拟)在正四棱锥S-ABCD中,底面是边长为2的正方形,侧面是腰长为√6的等腰三角形,则正四棱锥S-ABCD的外接球的体积为( )A.27π2B.9π C.9π2D.18π4.在三棱锥P-ABC中,已知PA=BC=2√13,AC=PB=√41,PC=AB=√61,则三棱锥P-ABC外接球的表面积为( )A.77πB.64πC.108πD.72π5.《九章算术》卷五《商功》中有如下问题:“今有委粟平地,下周一十二丈,高四丈.”意思是:今将粟放在平地,谷堆下周长12丈,高4丈.将该谷堆模型看作一个圆锥,π取近似值3,则该圆锥外接球的表面积约为( )A.55平方丈B.75平方丈C.110平方丈D.150平方丈6.已知△ABC的顶点都在球O的球面上,且A=60°,BC=√3,球心O到平面ABC的距离为2,则球O的表面积为( )A.12πB.16πC.20πD.25π7.(多选题)正三棱锥P-ABC的底面边长为3,高为√6,则下列结论正确的是( )A.AB⊥PCB.三棱锥P-ABC的表面积为9√3C.三棱锥P-ABC的外接球的表面积为27πD.三棱锥P-ABC的内切球的表面积为3π28.将一个直角边长为2的等腰直角三角形绕其直角边所在的直线旋转一周所得圆锥的内切球的表面积为.9.(陕西汉中模拟)在如图所示的直三棱柱ABC-A1B1C1中,△ABC是直角三角形,AA1=AC=5,AB=3,BC=4,则堑堵ABC-A1B1C1的外接球的体积是.10.SF6(六氟化硫)具有良好的绝缘性,在电子工业上有着广泛的应用,其分子结构如图所示,六个氟原子分别位于正方体六个面的中心,硫原子位于正方体中心,若正方体的棱长为a,记以六个氟原子为顶点的正八面体为T,则T的体积为,T的内切球表面积为.综合提升练11.已知球O的表面积为9π,若球O与正四面体S-ABC的六条棱均相切,则此四面体的体积为( ) A.9 B.3√2C.9√22D.9√2812.已知正三棱锥的外接球半径R为1,则该正三棱锥的体积的最大值为( )A.16√327B.√34C.8√327D.8√3913.(全国甲,文16)在正方体ABCD-A1B1C1D1中,AB=4,O为AC1的中点,若该正方体的棱与球O的球面有公共点,则球O的半径的取值范围是.14.(甘肃二诊)三棱锥P-ABC中,底面为等边三角形,侧棱长相等,∠APB=90°,P到底面ABC的距离为2,则该三棱锥外接球的体积为.创新应用练15.独孤信印信是一枚形状奇特的印信(如图1),它的形状可视为一个26面体,由18个正方形和8个正三角形围成(如图2),已知该多面体的各条棱长均为1,且各个顶点在同一球面上,则此球的半径r= .图1图2课时规范练50 球与几何体的切、接问题1.C 解析这个球是正方体的外接球,其半径等于正方体的体对角线的一半,即R=√(2√3)2+(2√3)2+(2√3)22=3,所以这个球的表面积为S=4πR 2=4π×32=36π.2.A 解析设底面三角形的内切圆的半径为r,则12×(2+2+2)·r=12×2×2sin π3=√3,解得r=√33,小于高的一半1,所以该球的最大半径为√33,所以球的表面积的最大值为4πr 2=4π3.3.C 解析如图所示,不妨设该四棱锥外接球的球心O 在线段SE 上,球心O 在线段SE 的延长线的情况可同理讨论.设球的半径为R.三棱锥的底面中心为E,连接SE,BO,BE.因为在正四棱锥S-ABCD 中,底面是边长为2的正方形,侧面是腰长为√6的等腰三角形,所以BE=√2,SE=√SB 2-BE 2=2.在Rt △OBE 中,OB 2=OE 2+BE 2,即R 2=(2-R)2+(√2)2,解得R=32.球心O 在线段SE 的延长线上时,可得R 2=(R-2)2+(√2)2,解得R=32.所以外接球的体积为V=43πR 3=9π2.4.A 解析因为三棱锥的对棱相等,所以可以把它补成一个长方体.设长方体的同一顶点的三条棱长分别为a,b,c,且长方体的面对角线长为2√13,√41,√61,则√a2+b2=2√13,√c2+b2=√41,√a2+c2=√61,此长方体体对角线为长方体外接球直径,即为该三棱锥外接球的直径,设此外接球半径为R,则2R=√a2+b2+c2=√12×(52+61+41)=√77,R=√772,所以球的表面积为4πR2=77π.5.B 解析设外接球球心为O,底面圆心为O',设底面圆的半径为r,因为谷堆下周长12丈,所以2πr=12,所以r≈2.设外接球半径为R,则OO'=4-R.由勾股定理得(4-R)2+22=R2,解得R=52,所以该圆锥外接球的表面积约为4πR2=25π≈75平方丈,故选B.6.C 解析因为△ABC外接圆的半径r满足2r=BCsinA =√3√32=2,所以r=1,因此球半径R满足R2=r2+d2=1+4=5,所以球O的表面积4πR2=20π,故选C.7.ABD 解析如图,取棱AB的中点D,连接CD,PD.则在正三棱锥P-ABC中,AB⊥CD,AB⊥PD.因为PD,CD⊂平面PCD,且PD∩CD=D,所以AB⊥平面PCD,则AB⊥PC,故A正确;作PH⊥平面ABC,垂足为H,则PH=√6.由正三棱锥的性质可知H在CD上,且CH=2DH.因为AB=3,所以CD=3√32,则CH=√3.因为PH=√6,所以PC=√3+6=3,则三棱锥P-ABC的表面积S=√34×9×4=9√3,故B正确;设三棱锥P-ABC的外接球的球心为O,半径为R,则O在PH上,连接OC,则R2=CH2+OH2=(PH-OH)2,即R2=3+OH2=(√6-OH)2,解得R2=278,则三棱锥P-ABC的外接球的表面积为4πR2=27π2,故C错误;设三棱锥P-ABC的内切球的半径为r,则V P-ABC=13×√34×9×√6=13×9√3r,解得r=√64,从而三棱锥P-ABC的内切球的表面积为4πr2=3π2,故D正确.故选ABD.8.(48-32√2)π解析依题意,作圆锥的轴截面为等腰直角三角形,截得其内切球的大圆是此等腰直角三角形的内切圆,圆锥的底面半径为2,则其母线长为2√2,设圆锥的内切球半径为r,则1 2×2√2r+12×2√2r+12×4×r=12×4×2,所以r=2(√2-1),所以内切球的表面积为4πr2=16(3-2√2)π=(48-32√2)π.9.125√2π3解析将该直三棱柱补为一个长方体,如图,则该直三棱柱的外接球即为长方体的外接球,设长方体的体对角线长为d,则d 2=32+42+52=50,所以d=5√2,所以外接球的体积为43πd 23=125√2π3. 10.a 36πa 23解析正八面体T 可视为两个全等的正四棱锥拼接而成,且该正四棱锥的底面边长为√(a2) 2+(a2) 2=√2a2,高为a 2,所以正八面体的体积为V=2×13×√2a22×a2=a 36.由题图可知,正八面体T 的每个面都是棱长为√2a2的等边三角形,所以正八面体T 的表面积为S=8×√34×√2a 22=√3a 2.设正八面体T 的内切球半径为r,则V=13Sr,所以r=3V S=a 32√3a 2=√3a6,因此正八面体T 的内切球的表面积为4πr 2=4π×√3a 62=πa 23.11.A 解析设球O 的半径是R,由4πR 2=9π,∴R=32.将正四面体放到正方体中,正方体的内切球即与正四面体的六条棱均相切.∵R=32,∴正方体的棱长为3,则正四面体棱长为3√2,底面ABC 上的高h=√(3√2)2-(23×√32×3√2) 2=2√3,∴V=13S △ABC h=13×√34×(3√2)2×2√3=9.12.C 解析如图所示,设该正三棱锥的高为h,底面外接圆的圆心是点O 1,半径为r,底面面积为S,球心是点O.当球心O 在线段SO 1上时,由球的截面圆的性质,可得OA 2=A O 12+O O 12,即R 2=r 2+(h-R)2,同理,当球心O 在线段SO 1的延长线上时,可得R 2=r 2+(R-h)2,解得R=ℎ2+r 22ℎ=1,即r 2=2h-h 2>0,解得0<h<2.这个正三棱锥的体积为V=13Sh=13×3S △O 1BC ·h=13×3×12r 2sin2π3×h=√34r 2h=√34(2h-h 2)h.设f(x)=(2x-x 2)·x=2x 2-x 3(0<x<2),可得f'(x)=4x-3x 2=x(4-3x),当x ∈0,43时,f'(x)>0,f(x)单调递增;当x ∈43,2时,f'(x)<0,f(x)单调递减,所以当x=43时,函数f(x)取得最大值,最大值为f 43=3227,所以正三棱锥体积的最大值为V max =√34×3227=8√327.13.[2√2,2√3] 解析(方法一)第一步,弄清球O 与正方体棱有公共点,球半径最小的球为棱切球(即与棱相切的球),最大的球为外接球.第二步,作对角面ABC 1D 1截正方体与其棱切球、外接球分别得如下矩形和小、大两个圆(如图).第三步,由图可知棱切球半径r 1=12AD 1=12×4√2=2√2,外接球半径r 2=12BD 1=12×4√3=2√3,球O 半径的取值范围是[2√2,2√3]. (方法二)由对称性知,只需考虑球与正方体的棱有公共点,正方体中心O 到一条棱的最短距离即为到棱中点的距离,为2√2,到一条棱的最长距离即为到棱顶点的距离,为2√3,故r ∈[2√2,2√3].14.36π 解析因为三棱锥P-ABC 中,底面为等边三角形,侧棱长相等,所以三个侧面均为全等的等腰三角形.又∠APB=90°,即三个侧面均为全等的等腰直角三角形,所以PA,PB,PC 两两垂直,且PA=PB=PC,所以可将三棱锥P-ABC 补形为正方体,则该三棱锥的外接球即为正方体的外接球,设PA=PB=PC=a,则AB=AC=BC=√2a. 又点P 到底面ABC 的距离为2,所以由13S △ABC ×2=13S △PBC ×PA,即13×√34(√2a)2×2=13×12a×a×a,解得a=2√3,所以正方体的外接球直径2R=√a 2+a 2+a 2= √(2√3)2+(2√3)2+(2√3)2=6,即R=3,所以该三棱锥外接球的体积为V=43πR 3=43π×33=36π.15.√5+2√22解析该多面体可以看作由一个棱长为√2+1的正方体截去8个如①的三棱柱,8个如②的四棱锥和12个如③的三棱柱构成,如图,第11页 共11页 由对称性知,该多面体外接球球心为正方体中心O,它的一个面ABCD 在正方体的上底面内,如图,多面体外接球球心O 到截面ABCD 的距离OO 1=√2+12,正方形ABCD 外接圆半径O 1D=√22,所以多面体外接球半径r=√OO 12+O 1D 2=√(√2+12)2+(√22)2=√5+2√22.。

空间几何体与球的切、接问题1.体积为 8 的正方体的极点都在同一球面上,则该球的表面积为()B.323种类一:三条棱两两垂直可转变为长方体(正方体)2.在三棱锥P ABC中,PA平面ABC , AC BC , AC BC 1, PA3则三棱锥外接球的体积为3.已知球 O 上四点 A、B、C、D,DA平面ABC,AB BC, DA AB BC a ,则球 O 的体积等于圆柱的外接球ORBC2设柱体的高为l ,底面外接圆的半径为r,则有R r2l24.直三棱柱 ABC- A1B1C1的 6 个极点都在球 O 的球面上”,若 AB=3,AC=4,AB⊥AC,AA1= 12,则球 O 的半径为种类二:有一条侧棱垂直于底面可转变为直棱柱5.已知三棱锥 P-ABC 中,三角形 ABC 为等边三角形,且 PA=8,PB=PC= 13 ,AB=3 ,则其外接球的体积为6.在三棱锥 P ABC 中, PA平面ABC , AC1, BC 2, PA 6,ACB 120 ,求三棱锥的外接球的表面积。
圆锥的外接球O O1A设椎体的高为 h, 底面外接圆的半径为 r, 则有R r 22 h R7.正四棱锥的极点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为()A. 81D.27448.在三棱锥 A-BCD中 ACD 与 BCD 都是边长为 2 的正三角形,且平面 ACD 平面BCD,求三棱锥外接球的体积练习 1、在四周体P ABC 中,PC平面ABC,AB=AC=1,BC=2 ,PC= 3 .则该四周体外接球的表面积为.练习 2、正三角形 ABC的边长为 2,将它沿高 AD翻折,使点 B 与点 C 间的距离为2 ,此时四周体ABCD外接球表面积为____________练习 3.已知三棱锥 S-ABC的全部极点都在球 O 的球面上, SC是球 O 的直径。
若平面 SCA⊥平面 SCB,SA=AC,SB=BC,三棱锥 S-ABC的体积为 9,则球 O 的表面积为 ________。

专题层级快练(五十)1.(2017·唐山模拟)正三棱锥的高和底面边长都等于6,则其外接球的表面积为( ) A .64π B .32π C .16π D .8π答案 A解析 如图,作PM ⊥平面ABC 于点M ,则球心O 在PM 上,PM =6,连接AM ,AO ,则OP =OA =R(R 为外接球半径),在Rt △OAM 中,OM =6-R ,OA =R ,又AB =6,且△ABC 为等边三角形,故AM =2362-32=23,则R 2-(6-R)2=(23)2,则R =4,所以球的表面积S =4πR 2=64π.2.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( ) A .16π B .20π C .24π D .32π 答案 C解析 由V =Sh ,得S =4,得正四棱柱底面边长为2.画出球的轴截面可得,该正四棱柱的对角线即为球的直径,所以球的半径为R =1222+22+42= 6.所以球的表面积为S =4πR 2=24π.故选C.3.长方体的三个相邻面的面积分别为2,3,6,若这个长方体的顶点都在同一球面上,则这个球的表面积为( ) A.72π B .56π C .14π D .64π 答案 C解析 设长方体长、宽、高分别为a ,b ,c ,不妨取ab =2,bc =3,ac =6,长方体的体对角线长为a 2+b 2+c 2.而由⎩⎪⎨⎪⎧ab =2,bc =3,ac =6,得⎩⎪⎨⎪⎧a =2,b =1,c =3.∴球的直径d =22+12+32=14.∴r =d 2=142.∴S 球=4πr 2=4π×144=14π.4.若一个正方体的体积是8,则这个正方体的内切球的表面积是( ) A .8π B .6π C .4πD .π答案 C解析 设正方体的棱长为a ,则a 3=8. 因此内切球直径为2,∴S 表=4πr 2=4π.5.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SA ⊥平面ABC ,SA =23,AB =1,AC =2,∠BAC =60°,则球O 的体积为( ) A .4π B.163π C.323π D .12π答案 C解析 如图所示,在△ABC 中,根据余弦定理得BC =3,从而有AB 2+BC 2=AC 2,所以△ABC 是直角三角形,∠ABC =90°,BC ⊥AB.由于SA ⊥平面ABC ,所以SA ⊥BC.因为AB ∩SA =A ,所以BC ⊥平面SAB ,所以BC ⊥SB ,所以△SBC 是直角三角形.取SC 的中点O ′,连接O ′A ,O ′B ,则O ′S =O ′B =O ′C.在Rt △SAC 中,有O ′A =O ′S =O ′C ,所以点O ′为此三棱锥外接球的球心,即O ′与O 重合.在Rt △SAC 中,SC =SA 2+AC 2=4,所以球的半径R =12SC =2,球的体积V =4π3R 3=32π3.6.(2012·课标全国Ⅰ)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为( ) A.26 B.36 C.23D.22 答案 A解析 ∵SC 是球O 的直径,∴∠CAS =∠CBS =90°. ∵BA =BC =AB =1,SC =2,∴AS =BS = 3. 取AB 的中点D ,显然AB ⊥CD ,AB ⊥CS. ∴AB ⊥平面CSD.在△CDS 中,CD =32,DS =112,SC =2,利用余弦定理可得cos ∠CDS =CD 2+SD 2-SC 22CD ·SD =-133.故sin ∠CDS =4233. ∴S △CDS =12×32×112×4233=22,∴V =V B -CDS +V A -CDS =13×S △CDS ×BD +13S △CDS ×AD =13S △CDS ×BA=13×22×1=26.7.(2013·课标全国Ⅰ)如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm ,如果不计容器的厚度,则球的体积为( ) A.500π3 cm 3B.866π3 cm 3C.1 372π3 cm 3D.2 048π3cm 3答案 A解析 设球心为O ,正方体上底面中心为A ,上底面一边的中点为B ,在Rt △OAB 中,|OA|=R -2,|AB|=4,|OB|=R ,由R 2=(R -2)2+42得R =5,∴V 球=43πR 3=5003π(cm 3).故选A.8.(2016·新课标全国Ⅲ)在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( ) A .4π B.9π2 C .6π D.32π3答案 B解析 由题意可得若V 最大,则球与直三棱柱的部分面相切,若与三个侧面都相切,可求得球的半径为2,球的直径为4,超过直三棱柱的高,所以这个球放不进去,则球可与上下底面相切,此时球的半径R =32,此时的体积最大,V max =43πR 3=4π3×278=9π2.9.(2017·郑州质检)四棱锥P -ABCD 的五个顶点都在一个球面上,该四棱锥的三视图如图所示,E ,F 分别是棱AB ,CD 的中点,直线EF 被球面所截得的线段长为22,则该球的表面积为( )A .9πB .3πC .22πD .12π答案 D解析 该几何体的直观图如图所示,该几何体可看作由正方体截得,则正方体外接球的直径即为PC.由直线EF 被球面所截得的线段长为22,可知正方形ABCD 对角线AC 的长为22,可得正方形ABCD 的边长a =2,在△PAC 中,PC =22+(22)2=23,球的半径R =3,∴S 表=4πR 2=4π×(3)2=12π.10.(2017·洛阳统一考试)如图是某几何体的三视图,则该几何体的外接球的表面积为( )A .200πB .150πC .100πD .50π答案 D解析 由三视图知,该几何体可以由一个长方体截去3个角后得到,该长方体的长、宽、高分别为5、4、3,所以其外接球半径R 满足2R =42+32+52=52,所以该几何体的外接球的表面积为S =4πR 2=4π×(522)2=50π,故选D.11.(2014·湖南)一块石材表示的几何体的三视图如图所示.将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )A .1B .2C .3D .4答案 B解析 此几何体为一直三棱柱,底面是边长为6,8,10的直角三角形,侧棱为12,故其最大球的半径为底面直角三角形内切圆的半径,故其半径为r =12×(6+8-10)=2,故选B.12. (2017·张掖模拟)如图是一个空间几何体的三视图,该几何体的外接球的体积记为V 1,俯视图绕斜边所在直线旋转一周形成的几何体的体积记为V 2,则V 1∶V 2=( )A .12 2B .8 2C .6 2D .4 2答案 D解析 三视图复原的几何体如图,它是底面为等腰直角三角形,一条侧棱垂直底面的三棱锥,它的外接球,就是扩展为长方体的外接球,外接球的直径是22,则几何体的外接球的体积V 1=43π×(2)3=823π,V 2=2×(13×12×1×π)=23π,所以V 1∶V 2=823π∶2π3=4 2.13.若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则S 1S 2=________.答案63π解析 设正四面体的棱长为a ,则正四面体的表面积为S 1=4·34·a 2=3a 2,其内切球半径为正四面体高的14,即r =14·63a =612a ,因此内切球表面积为S 2=4πr 2=πa 26,则S 1S 2=3a 2π6a 2=63π. 14.已知一圆柱内接于球O ,且圆柱的底面圆的直径与母线长均为2,则球O 的表面积为________. 答案 8π解析 圆柱的底面圆的直径与母线长均为2,所以球的直径为22+22=8=22,即球半径为2,所以球的表面积为4π×(2)2=8π.15.(2017·衡水中学调研卷)已知正三棱锥P -ABC ,点P ,A ,B ,C 都在半径为3的球面上,若PA ,PB ,PC 两两相互垂直,则球心到截面ABC 的距离为________. 答案33解析 先在一个正方体中找一个满足条件的正三棱锥,再利用正方体的性质解题.如图,满足题意的正三棱锥P -ABC 可以是正方体的一部分,其外接球的直径是正方体的体对角线,且面ABC 与体对角线的交点是体对角线的一个三等分点,所以球心到平面ABC 的距离等于体对角线长的16,故球心到截面ABC 的距离为16×23=33(或用等体积法:V P -ABC =V A -PBC 求解).16. (2017·德州模拟)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,该几何体的体积是________;若该几何体的所有顶点在同一球面上,则球的表面积是________.答案 133π解析 由三视图知该几何体是底面为1的正方形,高为1的四棱锥,故体积V =13×1×1×1=13,该几何体与棱长为1的正方体具有相同的外接球,外接球直径为3,该球表面积S =4π×(32)2=3π,正方体、长方体的体对角线即为外接球的直径.1.(2014·陕西,理)已知底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一个球面上,则该球的体积为( ) A.32π3B .4πC .2π D.4π3答案 D解析 因为该正四棱柱的外接球的半径是四棱柱体对角线的一半,所以半径r =1212+12+(2)2=1,所以V 球=4π3×13=4π3.故选D.2.(2017·人大附中模拟)已知矩形ABCD 的顶点都在半径为R 的球O 的球面上,AB =6,BC =23,棱锥O -ABCD 的体积为83,则球O 的表面积为( ) A .8π B .16π C .32π D .64π答案 D解析 由题意可知矩形ABCD 所在截面圆的半径r =62+(23)22=23,S 矩形ABCD =12 3.设球心O 到平面ABCD 的距离为h ,则13×123×h =83,解得h =2,∴R =r 2+h 2=4,∴S 球O =4πR 2=64π.。

几何体中与球有关的切、接问题球的截面的性质(1)球的任何截面是圆面;(2)球心和截面(不过球心)圆心的连线垂直于截面;(3)球心到截面的距离d 与球的半径R 及截面的半径r 的关系为r =R 2-d 2几个与球有关的切、接常用结论(1)正方体的棱长为a ,球的半径为R ,①若球为正方体的外接球,则2R =3a ;②若球为正方体的内切球,则2R =a ;③若球与正方体的各棱相切,则2R =2a .(2)若长方体的同一顶点的三条棱长分别为a ,b ,c ,外接球的半径为R ,则2R =a 2+b 2+c 2. (3)正四面体的外接球与内切球的半径之比为3∶1. 一、题型选讲题型一 、几何体的外接球解决多面体的外接球问题,关键是确定球心的位置,方法是先选择多面体中的一面,确定此面外接圆的圆心,再过圆心作垂直此面的垂线,则球心一定在此垂线上,最后根据其他顶点确定球心的准确位置.对于特殊的多面体还可采用补成正方体或长方体的方法找到球心位置.例1、【2020年高考全国Ⅰ卷理数】已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为 A .64π B .48πC .36πD .32π例2、【2020年高考天津】若棱长为 A .12π B .24π C .36πD .144π例3、(2020届山东省潍坊市高三上学期统考)已知边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕进行折叠,使折后的2BDC π∠=,则过A ,B ,C ,D 四点的球的表面积为( )A .3πB .4πC .5πD .6π例4、(2020届山东省日照市高三上期末联考)已知四棱锥P ABCD -的体积是ABCD 是正方形,PAB ∆是等边三角形,平面PAB ⊥平面ABCD ,则四棱锥P ABCD -外接球体积为( )A .BCD .例5、(2020届山东省德州市高三上期末)中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知PA ⊥平面ABCE ,四边形ABCD 为正方形,AD =ED =P ADE -的外接球的体积为,则阳马P ABCD -的外接球的表面积等于______.题型二、几何体的内切球求解多面体的内切球的问题,一般是将多面体分割为以球心为顶点,多面体的各面为底面的棱锥,利用多面体的体积等于各棱锥的体积之和求内切球的半径.例6、【2020年高考全国Ⅲ卷理数】已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.例7、(2020届山东省潍坊市高三上期中)如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的表面积为__________;若该六面体内有一小球,则小球的最大体积为___________.二、达标训练1、(2020届山东省泰安市高三上期末)已知正三棱锥S ABC -的侧棱长为6,则该正三棱锥外接球的表面积是( ) A .16πB .20πC .32πD .64π2、【2020年高考全国II 卷理数】已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为A B .32C .1D 3、【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为A .B .C .D4、【2018年高考全国Ⅰ卷理数】设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为D ABC -体积的最大值为A .B .C .D .5、【2020年新高考全国Ⅰ卷】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以1D 半径的球面与侧面BCC 1B 1的交线长为________.6、(2020届山东省滨州市三校高三上学期联考)已知三棱锥S ABC -,SA ⊥平面ABC ,6ABC π∠=,3SA =,1BC =,直线SB 和平面ABC 所成的角大小为3π.若三棱锥S ABC -的四个顶点都在同一球面上,则该球的表面积为________.7、(2020届山东省枣庄、滕州市高三上期末)如图,在三棱锥P -ABC 中,,PA AB ⊥PC BC ⊥,,AB BC ⊥22,AB BC ==PC =,则PA 与平面ABC 所成角的大小为________;三棱锥P -ABC 外接球的表面积是________.8、(2020届山东省烟台市高三上期末)已知三棱锥P ABC -的四个顶点都在球O 的表面上,PA ⊥平面ABC,6PA =,AB =2AC =,4BC =,则:(1)球O 的表面积为__________;(2)若D 是BC 的中点,过点D 作球O 的截面,则截面面积的最小值是__________.9、(2020届山东省滨州市高三上期末)在四面体S ABC -中,2SA SB ==,且SA SB ⊥,BC =,AC=________,该四面体外接球的表面积为________.10、(2020届山东省济宁市高三上期末)下图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形-的外接球的体积为ABCD,现将四边形ABCD沿BD折成直二面角A BD C--,则三棱锥A BCDcm.__________3一、题型选讲题型一 、几何体的外接球解决多面体的外接球问题,关键是确定球心的位置,方法是先选择多面体中的一面,确定此面外接圆的圆心,再过圆心作垂直此面的垂线,则球心一定在此垂线上,最后根据其他顶点确定球心的准确位置.对于特殊的多面体还可采用补成正方体或长方体的方法找到球心位置.例1、【2020年高考全国Ⅰ卷理数】已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为 A .64π B .48πC .36πD .32π【答案】A【解析】设圆1O 半径为r ,球的半径为R ,依题意, 得24,2r r π=π=∴,ABC 为等边三角形,由正弦定理可得2sin 60AB r =︒=,1OO AB ∴==1OO ⊥平面ABC ,11,4OO O A R OA ∴⊥====, ∴球O 的表面积2464S R ππ==.故选:A.本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.例2、【2020年高考天津】若棱长为 A .12π B .24πC .36πD .144π【答案】C【解析】这个球是正方体的外接球,其半径等于正方体的体对角线的一半,即3R ==,所以,这个球的表面积为2244336S R πππ==⨯=. 故选:C .本题考查正方体的外接球的表面积的求法,求出外接球的半径是本题的解题关键,属于基础题.求多面体的外接球的面积和体积问题,常用方法有:(1)三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;(2)直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求球的半径;(3)如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心. 例3、(2020届山东省潍坊市高三上学期统考)已知边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕进行折叠,使折后的2BDC π∠=,则过A ,B ,C ,D 四点的球的表面积为( )A .3πB .4πC .5πD .6π【答案】C【解析】边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕进行折叠,使折后的2BDC π∠=,构成以D 为顶点的三棱锥,且三条侧棱互相垂直,可构造以其为长宽高的长方体,其对角线即为球的直径,三条棱长分别为1,12R ==2452S ππ==,故选C.例4、(2020届山东省日照市高三上期末联考)已知四棱锥P ABCD -的体积是ABCD 是正方形,PAB ∆是等边三角形,平面PAB ⊥平面ABCD ,则四棱锥P ABCD -外接球体积为( )A .BCD .【答案】A【解析】设AB 的中点为Q ,因为PAB ∆是等边三角形,所以PQ AB ⊥,而平面PAB ⊥平面ABCD , 平面PAB ⋂平面ABCD AB =,所以PQ ⊥平面ABCD ,四棱锥P ABCD -的体积是13AB AB PQ =⨯⨯⨯13AB AB AB =⨯⨯,所以边长6AB =,PQ =OH x =,OM x =,()(222222R OA OM AM x==+=+,2222223R OP OH PH x ==+=+,x =2212321R =+=343V R π==球.故选:A.例5、(2020届山东省德州市高三上期末)中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知PA ⊥平面ABCE ,四边形ABCD 为正方形,AD =ED =P ADE -的外接球的体积为,则阳马P ABCD -的外接球的表面积等于______.【答案】20π 【解析】四边形ABCD 是正方形,AD CD ∴⊥,即AD CE ⊥,且AD =ED =,所以,ADE ∆的外接圆半径为122AE r ===设鳖臑P ADE -的外接球的半径1R ,则3143R π=,解得12R =.PA ⊥平面ADE ,1R ∴=2PA ==PA ∴=正方形ABCD 的外接圆直径为22r AC ==22r ∴=,PA ⊥平面ABCD ,所以,阳马P ABCD -的外接球半径2R ==因此,阳马P ABCD -的外接球的表面积为22420R ππ=.故答案为:20π. 题型二、几何体的内切球求解多面体的内切球的问题,一般是将多面体分割为以球心为顶点,多面体的各面为底面的棱锥,利用多面体的体积等于各棱锥的体积之和求内切球的半径.例6、【2020年高考全国Ⅲ卷理数】已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.【解析】易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示, 其中2,3BC AB AC ===,且点M 为BC 边上的中点, 设内切圆的圆心为O ,由于AM ==122S =⨯⨯=△ABC 设内切圆半径为r ,则:ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯()13322r =⨯++⨯=解得:2r,其体积:343V r =π=.故答案为:3. 与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.例7、(2020届山东省潍坊市高三上期中)如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的表面积为__________;若该六面体内有一小球,则小球的最大体积为___________.【解析】(1)因为16(12S =⨯⨯=. (2)由图形的对称性得,小球的体积要达到最大,即球与六个面都相切时,每个三角形面积是4,六面体体积是正四面体的2倍,所以六面体体积是6. 由于图像的对称性,内部的小球要是体积最大,就是球要和六个面相切,连接球心和五个顶点,把六面体分成了六个三棱锥,设球的半径为R ,所以16()6349R R =⨯⨯⨯⇒=,所以球的体积334433V R ππ===.故答案为:. 二、达标训练1、(2020届山东省泰安市高三上期末)已知正三棱锥S ABC -的侧棱长为6,则该正三棱锥外接球的表面积是( ) A .16π B .20πC .32πD .64π【答案】D【解析】如图所示,因为正三棱锥S ABC -的侧棱长为6,则263AE ==6SE ===, 又由球心O 到四个顶点的距离相等,在直角三角形AOE 中,,6AO R OE SE SO R ==-=-,又由222OA AE OE =+,即222(6)R R =+-,解得4R =, 所以球的表面积为2464S R ππ==, 故选D.2、【2020年高考全国II 卷理数】已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为A B .32C .1D 【答案】C【解析】设球O 的半径为R ,则2416R π=π,解得:2R =.设ABC △外接圆半径为r ,边长为a ,ABC △21224a ∴⨯=,解得:3a =,2233r ∴===,∴球心O 到平面ABC 的距离1d ==.故选:C .本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.3、【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为A .B .C .D【答案】D 【解析】解法一:,PA PB PC ABC ==△为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA ,AB 的中点,EF PB ∴∥,EF AC ∴⊥,又EF CE ⊥,,CEAC C EF =∴⊥平面PAC ,∴PB ⊥平面PAC ,APB PA PB PC ∴∠=90︒,∴===P ABC ∴-为正方体的一部分,2R ==即344π33R V R =∴=π==,故选D .解法二:设2PA PB PC x ===,,E F 分别为,PA AB 的中点,EF PB ∴∥,且12EF PB x ==,ABC △为边长为2的等边三角形,CF ∴=又90CEF ∠=︒,12CE AE PA x ∴===, AEC △中,由余弦定理可得()2243cos 22x x EAC x+--∠=⨯⨯,作PD AC ⊥于D ,PA PC =,D 为AC 的中点,1cos 2AD EAC PA x ∠==,2243142x x x x+-+∴=,22121222x x x ∴+=∴==,,,PA PB PC ∴=== 又===2AB BC AC ,,,PA PB PC ∴两两垂直,2R ∴==R ∴=,34433V R ∴=π==,故选D.本题主要考查学生的空间想象能力,补体法解决外接球问题.可通过线面垂直定理,得到三棱两两互相垂直关系,快速得到侧棱长,进而补体成正方体解决.4、【2018年高考全国Ⅰ卷理数】设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为D ABC -体积的最大值为 A. B . C.D .【答案】B【解析】如图所示,设点M 为三角形ABC 的重心,E 为AC 中点,当点D 在平面ABC 上的射影为M 时,三棱锥D ABC -的体积最大,此时,4OD OB R ===,2ABC S AB ==△,6AB ∴=,点M 为三角形ABC 的重心,23BM BE ∴==,Rt OBM ∴△中,有2OM ==,426DM OD OM ∴=+=+=,()max 163D ABC V -∴=⨯= B.5、【2020年新高考全国Ⅰ卷】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以1D 半径的球面与侧面BCC 1B 1的交线长为________.【答案】2. 【解析】如图:取11B C 的中点为E ,1BB 的中点为F ,1CC 的中点为G ,因为BAD ∠=60°,直四棱柱1111ABCD A B C D -的棱长均为2,所以△111D B C 为等边三角形,所以1D E=111D E B C ⊥,又四棱柱1111ABCD A B C D -为直四棱柱,所以1BB ⊥平面1111D C B A ,所以111BB B C ⊥, 因为1111BB B C B =,所以1D E ⊥侧面11B C CB ,设P 为侧面11B C CB 与球面的交线上的点,则1D E EP ⊥,1D E =,所以||EP ===所以侧面11B C CB 与球面的交线上的点到E ,因为||||EF EG ==11B C CB 与球面的交线是扇形EFG 的弧FG ,因为114B EFC EG π∠=∠=,所以2FEG π∠=,所以根据弧长公式可得22FG π==.. 6、(2020届山东省滨州市三校高三上学期联考)已知三棱锥S ABC -,SA ⊥平面ABC ,6ABC π∠=,3SA =,1BC =,直线SB 和平面ABC 所成的角大小为3π.若三棱锥S ABC -的四个顶点都在同一球面上,则该球的表面积为________. 【答案】13π【解析】如图:SA ⊥平面ABC ,则SBA ∠为直线SB 和平面ABC 所成的角,即3SBA π∠=在Rt SAB ∆中:tan3SA AB π=== 如图,设O 为三棱锥S ABC -外接球的球心,G 为ABC ∆外接圆圆心, 连结,,,,OA OB GA GB OG ,则必有OG ⊥面ABC 在ABC ∆,2222cos 312162AC AB BC AB BC π=+-⋅⋅=+-=, 则1AC = 其外接圆半径122,1sin sin 6AC r r ABC π====∠, 又1322OG SA ==, 所以三棱锥S ABC -外接球半径为R ===该球的表面积为21344134S R πππ==⨯=, 故答案为:13π.7、(2020届山东省枣庄、滕州市高三上期末)如图,在三棱锥P -ABC 中,,PA AB ⊥PC BC ⊥,,AB BC ⊥22,AB BC ==PC =,则PA 与平面ABC 所成角的大小为________;三棱锥P -ABC 外接球的表面积是________.【答案】45︒ 6π【解析】如图,作平行四边形ABCD ,连接PD ,由AB BC ⊥,则平行四边形ABCD 是矩形. 由BC CD ⊥,BC PC ⊥,PCCD C =,∴BC ⊥平面PCD ,而PD ⊂平面PCD ,∴BC PD ⊥,同理可得AB PD ⊥,又AB BC B ⋂=,∴PD ⊥平面ABCD .,PD CD PD AD ⊥⊥,PAD ∠是PA 与平面ABC 所成角.由2,CD AB PC ===1PD =,又1AD BC ==,∴45PAD ∠=︒.∴PA 与平面ABC 所成角是45︒.由,PA AB ⊥PC BC ⊥知PB 的中点到,,,A B C P 的距离相等,PB 是三棱锥P -ABC 外接球的直径.由BC ⊥平面PCD 得BC PC ⊥,PB ===24()62PB S ππ==. 故答案为:45︒;6π.8、(2020届山东省烟台市高三上期末)已知三棱锥P ABC -的四个顶点都在球O 的表面上,PA ⊥平面ABC,6PA =,AB =2AC =,4BC =,则:(1)球O 的表面积为__________;(2)若D 是BC 的中点,过点D 作球O 的截面,则截面面积的最小值是__________. 【答案】52π 4π【解析】(1)由题,根据勾股定理可得AC AB ⊥,则可将三棱锥P ABC -可放入以,,AP AC AB 为长方体的长,宽,高的长方体中,则体对角线为外接球直径,即2r ==则r =,所以球的表面积为224452r πππ=⨯=;(2)由题,因为Rt ABC ,所以D 为底面ABC 的外接圆圆心,当DO ⊥截面时,截面面积最小,即截面为平面ABC ,则外接圆半径为2,故截面面积为224ππ⨯=故答案为:(1)52π;(2)4π9、(2020届山东省滨州市高三上期末)在四面体S ABC -中,2SA SB ==,且SA SB ⊥,BC =,AC =________,该四面体外接球的表面积为________.【答案】68π【解析】因为2SA SB ==,且SA SB ⊥,BC =,AC =AB ==,因此222BC AC AB +=,则AC BC ⊥;取AB 中点为O ,连接OS ,OC ,则OA OB OC OS ====,所以该四面体的外接球的球心为O ,半径为OC=所以该四面体外接球的表面积为248S ππ=⋅=; 又因为SA SB =,所以SO AB ⊥;因为底面三角形ABC 的面积为定值122AC BC ⋅=,SO ,因此,当SO ⊥平面ABC 时,四面体的体积最大,为136ABC V S SO =⋅=.故答案为:(1).6(2). 8π10、(2020届山东省济宁市高三上期末)下图是两个腰长均为10cm 的等腰直角三角形拼成的一个四边形ABCD ,现将四边形ABCD 沿BD 折成直二面角A BD C --,则三棱锥A BCD -的外接球的体积为__________3cm .【答案】 【解析】由题设可将该三棱锥拓展成如图所示的正方体,则该正方体的外接球就是三棱锥的外接球,由于正方体的对角线长为2l R ==即球的半径R =该球的体积343V R π==,应填答案.。

专题十七 几何体与球切、接的问题一、讲高考1.【2020年高考全国Ⅰ卷文数12理数10】已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC ∆的外接圆.若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( ) A .64π B .48π C .36π D .32π【答案】A【思路导引】由已知可得等边ABC ∆的外接圆半径,进而求出其边长,得出1OO 的值,根据球截面性质,求出球的半径,即可得出结论.【解析】设圆1O 半径为r ,球的半径为R ,依题意,得24,2r r π=π∴=,由正弦定理可得2sin60AB r =︒=,1OO AB ∴==1OO ⊥平面ABC ,11,4OO O A R OA ∴⊥====,∴球O 的表面积2464S R =π=π,故选A .【专家解读】本题的特点是多面体与球的位置关系,本题考查了三棱锥的外接球,考查球的表面积公式,考查数学运算、数学直观等学科素养.解题关键是正确应用球的截面性质.2.【2020年高考全国Ⅱ卷文数11理数10】已知ABC ∆是面积为439的等边三角形,且其顶点都在球O 的表面上,若球O 的表面积为16π,则球O 到平面ABC 的距离为( ) A .3B .23C .1D .23 【答案】C 【思路导引】根据球O 的表面积和ABC ∆的面积可求得球O 的半径R 和ABC ∆外接圆半径r ,由球的性质可知所求距离d【解析】设球O 的半径为R ,则2416R π=π,解得:2R =.设ABC ∆外接圆半径为r ,边长为a ,ABC ∆的等边三角形,212a ∴=,解得:3a =,2233r ∴==∴球心O 到平面ABC 的距离1d ==,故选C . 【专家解读】本题的特点是多面体与球的位置关系,本题考查了球的相关问题的求解,考查球的表面积公式,考查数学运算、数学直观等学科素养.解题关键是明确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.3.【2020年高考天津卷5】若棱长为( ) A .12πB .24πC .36πD .144π【答案】C【思路导引】求出正方体的体对角线的一半,即为球的半径,利用球的表面积公式,即可得解.【解析】这个球是正方体的外接球,其半径等于正方体的体对角线的一半,即3R ==,所以这个球的表面积为2244336S R πππ==⨯=,故选C .【专家解读】本题的特点是多面体与球的位置关系,本题考查了正方体的外接球,考查球的表面积公式,考查数学运算、数学直观等学科素养.解题关键是正确作出截面,找到正方体外接球直径与正方体体对角线的关系.【方法总结】求多面体的外接球的面积和体积问题,常用方法有:(1)三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;(2)直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求球的半径;(3)如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心.4.【2020年高考全国Ⅲ卷文数16理数15】已知圆维的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为 .【思路导引】将原问题转化为求解圆锥内切球的问题,然后结合截面确定其半径即可确定体积的值.【解析】解法一:易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,其中2,3BC AB AC ===,且点M 为BC 边上的中点,设内切圆的圆心为O ,由于AM =122S =⨯⨯△ABC r ,则:ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯()13322r =⨯++⨯=解得:2r ,其体积:343V r π==. 解法二:分析知圆锥内半径最大的球的应为该圆锥的内切球,如图,由题可知该圆锥的母线长为3BS =,底面半径为=1BC ,高为SC =BS 切于D 点,令OD OC r ==,则由SOD SBC ∆∆,可得OD BCOS BS =13=,得r =,此时343V r =π. 【专家解读】本题的特点是圆锥与球的位置关系,本题考查了圆锥内切球,考查球的体积公式,考查数学运算、数学直观、数学建模等学科素养.解题关键是认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,正确作出截面,构造直角三角形,应用勾股定理解题.5.【2020年高考山东卷16】已知直四棱柱1111ABCD A B C D -的棱长均为2,60BAD ∠=,以1D 为半径的球面与侧面11BCC B 的交线长为 .【思路导引】根据已知条件易得1D E =1D E ⊥侧面11BC CB ,可得侧面11BC CB 与球面的交线上的点到E11BC CB 与球面的交线是扇形EFG 的弧FG ,再根据弧长公式可求得结果.【解析】解法一:如图,取11B C 的中点为E ,1BB 的中点为F ,1CC 的中点为G ,因为BAD ∠=60°,直四棱柱1111ABCD A BC D -的棱长均为2,所以△111D B C 为等边三角形,所以1D E =111D E B C ⊥,又四棱柱1111ABCD A BC D -为直四棱柱,所以1BB ⊥平面1111D C B A ,所以111BBB C ⊥, 因为1111BB B C B =,所以1D E ⊥侧面11BC CB ,设P 为侧面11BC CB 与球面的交线上的点,则1DE EP ⊥,1D E =,所以||EP ==所以侧面11BC CB 与球面的交线上的点到E 因为||||EF EG ==所以侧面11BC CB 与球面的交线是扇形EFG 的弧FG ,因为114B EF C EG π∠=∠=,所以2FEG π∠=,所以根据弧长公式可得2FG π==. 解法二:在直四棱柱1111ABCD A B C D -中,取11BC 中点为O ,1BB 中点为F ,1CC 中点为E ,由题意易知111D O B C ⊥,又11BB D O ⊥,则1D O ⊥面11BB C C ,在面11BB C C 内取一点P ,使1//OP BB ,且OP =,∴1D P ==,又1D E =,1D F =∴以1D 为半径的球面与侧面11BCC B的交线是以O 为半径的圆弧FPE ,由题意易得2FOE π∠=,故该交线长为2π=.解法三:【专家解读】本题的特点是注重空间中基本计算,本题考查了直棱柱的结构特征,考查了直线与平面垂直的判定,考查了立体几何中的轨迹问题,考查了扇形中的弧长公式,考查数学运算、直观想象等学科素养.解题关键是作出合理的截面解决问题.6.【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为A .B .C .D【答案】D 【解析】解法一:,PA PB PC ABC ==△为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA ,AB 的中点,EF PB ∴∥,EF AC ∴⊥,又EF CE ⊥,,CE AC C EF =∴⊥平面PAC ,∴PB ⊥平面PAC ,APB PA PB PC ∴∠=90︒,∴===,P ABC ∴-为正方体的一部分,2R ==即344π33R V R =∴=π==,故选D . 解法二:设2PA PB PC x ===,,E F 分别为,PA AB 的中点,EF PB ∴∥,且12EF PB x ==,ABC △为边长为2的等边三角形,CF ∴=90CEF ∠=︒,12CE AE PA x ∴===,AEC △中,由余弦定理可得()2243cos 22x x EAC x +--∠=⨯⨯,作PD AC ⊥于D ,PA PC =,D 为AC 的中点,1cos 2AD EAC PA x ∠==,2243142x x x x +-+∴=,2212122x x x ∴+=∴==,,PA PB PC ∴======2AB BC AC ,,,PA PB PC ∴两两垂直,2R ∴=,R ∴=,34433V R ∴=π==,故选D 【名师点睛】本题主要考查学生的空间想象能力,补体法解决外接球问题.可通过线面垂直定理,得到三棱两两互相垂直关系,快速得到侧棱长,进而补体成正方体解决.二、练模拟1.(2021·广西梧州模拟)已知,,在球的球面上,,,,直线与A B C O 120BAC ∠=︒2AC =1AB =OA截面所成的角为,则球的表面积为( )A .B .C .D . 【答案】D【分析】设的外心为,由余弦定理可得,再由正弦定理可得外接圆直径,进而可得球的半径和表面积. 【解析】设的外心为,, ,则. 设球的半径为,由题意可知平面,又直线与截面所成的角为,所以,在中,所以,所以球的表面积为,故选D . 【点睛】关键点点睛:本题考查球的表面积,求出球的半径是关键.本题中利用正余弦定理求出三角形的外接圆半径,再利用线面角,构造直角三角形,求出球半径.考查了学生的运算求解能力和逻辑推理能力,属于中档题目.2.(2021·安徽安庆市·高三一模(文))四面体中,,,,且面,则四面体的外接球表面积为( )A .B .C .D . 【答案】D【分析】由面,构造一个直三棱柱,设,分别为上下两个底面的外接圆圆心,易得球心为的中点,然后分别在中求得外接圆的半径,进而中求得球的半径即可.【解析】根据题意,构造一个直三棱柱,如图,ABC 60︒O 43π163π563π1123πABC 1O BC12sin120BC O A ==︒ABC 1O 2222cos BC AB AC AB AC BAC =+-⋅∠2212212cos1207=+-⨯⨯︒=BC=12sin120BC O A ==︒R 1OO ⊥ABC OA ABC 60︒160OAO ∠=︒1RtAOO 12R OA O A ===O 2281124433S R πππ==⨯=A BCD -2AB CD ==1BC =23BCD π∠=AB ⊥BCD A BCD -36π9π1243π403πAB ⊥BCD 1O 2O O 12O O BCD △2BOO,分别为上下两个底面的外接圆圆心,根据球的性质,球心必为的中点,所以球的半径为,设为,的外接圆半径设为,在中,,,,由余弦定理得, 由正弦定理可得,在中,, 所以球的表面积,故选D . 【点睛】关键点睛:解决本题的关键在于利用正弦定理求出的外接圆的半径,结合勾股定理得出三棱锥的外接球的半径.3.(2021·江西上饶模拟)设为等腰三角形,,,为边上的高,将沿翻折成,若四面体,则线段的长度为( )A .B .1 CD【答案】C【分析】由题意画出图形,结合已知求出三角形的外接圆的半径,再由正弦定理求解得答案.【解析】如图,1O 2O O 12O O OB R BCD △r BCD △2AB CD ==1BC =23BCD π∠=214122172BD ⎛⎫=+-⨯⨯⨯-= ⎪⎝⎭2sin BD r BCD ===∠2BOO 221013R r =+=24043S R ππ==BCD △ABC 2AB AC ==3A π∠=AD BC ADC AD ADC 'ABC D 'BC '2BDC '设等腰三角形的外心为,四面体的外接球的球心为,连接,则平面, 由已知求得, ,即等腰三角形又由已知可得,由正弦定理可得,得可得,则,故选C .【点睛】方法点睛:求几何体的外接球的半径常用的方法有:(1)直接法;(2)模型法;(3)解三角形法.要根据已知条件灵活选择方法求解.4.(多选题)( 2021福清西山学校高三期中)已知的等边三角形,且其顶点都在球的球面上.若球的表面积为,则( )A .B .与平面所成的角为C .到平面的距离为1D .二面角的大小为 【答案】ABC【分析】过作平面于点,则点是等边的中心,也是外心、重心,、即可判断选项A ;因为平面于点,所以即为与平面所成的角,在直角三角形中,求即可判断选项B ;求的长即可判断选项C ;取的中点连接,可得即为二面角的平面角,求出即可判断选项D ,进而可得正确选项.【解析】如图,因为的顶点都在球的球面上,且是等边三角形,过作平面于点,则点是等边的中心,也是外心,重心 因为, BDC 'G ABC D 'O GO OG ⊥BDC 'AD =ABC D 'DG ∴=BDC '1BD DC ==1sin DBC =∠sin DBC ∠=45DBC DCB ∠=∠=︒BC 'ABC O O 16πOA BC ⊥OA ABC 30O ABC O AB C --60︒O OH ⊥ABC H H ABC OH BC ⊥AD BC ⊥OH ⊥ABC H OAH ∠OA ABC AHO OAH ∠OA AB M ,OM HM OMH ∠O AB C --OMH ∠ABC O ABC O OH ⊥ABC H H ABCABC 2AB =3AB =延长交于点,则点是的中点,因为,所以,又因为平面,平面,所以,因为,所以平面,又因为平面,所以,故选项A 正确;因为球的表面积为,即,所以,即,因为等边中,,所以,在直角三角形中,,所以到平面的距离为1,故选项C 正确;因为平面于点,所以即为与平面所成的角,在直角三角形中,,,所以,所以,故选项B 正确; 取的中点连接,因为,所以,因为平面,平面,所以,因为,所以平面,所以,结合,可得即为二面角的平面角,由,,所以,,所以,所以,故选项D 不正确,故选ABC .【点睛】方法点睛:求空间中直线与平面所成角的常见方法为(1)定义法:直接作平面的垂线,找到线面成角;(2)等体积法:不作垂线,通过等体积法间接求点到面的距离,距离与斜线长的比值即线面成角的正弦值;(3)向量法:利用平面法向量与斜线方向向量所成的余弦值的绝对值,即是线面成角的正弦值. AH BC D D BC AB AC =AD BC ⊥OH ⊥ABC BC ⊂ABC OH BC ⊥AD OH H ⋂=BC ⊥AOH AO ⊂AOH OA BC ⊥O 16π2416R ππ=2R =2OA=ABC 3AB =33cos30AD AB ==23AH AD ==AHO 1OH=O ABC OH ⊥ABC H OAH ∠OA ABC AHO 1OH =2OA =1sin 2OHOAH OA ∠==30OAH ∠=AB M ,OM HM OA OB =OM AB ⊥OH ⊥ABC AB ABC OH AB ⊥OM OH O ⋂=AB ⊥OHM HM AB ⊥OM AB ⊥OMH ∠O AB C --2OA =32AM =OM ==1OH =sin OH OMH OM ∠==≠60OMH ∠≠5.(多选题)( 2021双峰县第一中学高三月考)已知正方体的棱长为2,,分别是,的中点,过,的平面与该正方体的每条棱所成的角均相等,以平面截该正方体得到的截面为底面,以为顶点的棱锥记为棱锥,则( )A .正方体的外接球的体积为B .正方体的内切球的表面积为C .棱锥的体积为3D .棱锥的体积为【答案】AC【分析】根据正方体外接球的直径为正方体体对角线可知其直径为再根据正方体内切球球心为正方体中心,半径为棱长一半,可求得其内切球表面积;根据题干做出该正方体图形,可知棱锥的正六边形,可求得该锥体体积.【解析】因为正方体的棱长为2,所以正方体,内切球的半径为1,所以正方体的外接球的体积为,内切球的表面积为,故A 正确,B 错误.如图,分别是棱的中点.因为在同一个平面内,并且该平面与正方体的各条棱所成的角均相等,所以平面被此正方体所截得的截面图形为正六边形. 因为正六边形的面积,到平面所以棱锥的体积为.故正确,D 错误,故选AC . 1111ABCD A BC D -E F 1AA1CC E F αα1B Ω1111ABCD A BC D -1111ABCD A BC D -43πΩΩ32Ω1111ABCD A BC D -1111ABCD A BC D -=1111ABCD A BC D -343π⨯=2414ππ⨯=,,,M N S T 1111,,,AB BC C D A D EMNFST αEMNFST EMNFST 1623S π=⨯=1B α=Ω13⨯3=C【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.6.(2021·黑龙江哈尔滨市·哈尔滨三中高三月考(文))沿正三角形的中线翻折,使点与点间的距离,则四面体外接球表面积为_______.【答案】【分析】由题意分析:四面体可补形为长方体,只需要找长方体的外接球即可.【解析】如图示,∵为正三角形的中线,∴,又,∴,∵∴,∴,∴四面体可扩充为长方体.则四面体外接球即为长方体的外接球.设四面体外接球的半径为R,则,∴∴四面体外接球表面积.【点睛】多面体的外接球问题解题关键是找球心和半径,求半径的方法有:(1)公式法;(2) 多面体几何性质法;(3)补形法;(4)寻求轴截面圆半径法;(5)确定球心位置法.7.(2021·新疆高三模拟(理))三棱锥的底面是边长为的等边三角形,二面角为,则三棱锥的外接球的表面积为___________.【答案】ABC AD B CABCD5πABCDAD ABC,AD BD AD CD⊥⊥=BD CD D AD BCD⊥1BC BD CD==,222=BC BD CD+BD CD⊥ABCDABCDABCD()22222R BD CD AD=++2R=ABCD245S Rππ==S ABC-12SB SC==S BC A--60S ABC-208π【分析】设为中点,为正外心,可得是二面角的平面角为,作底面,垂足为,在上,设外接球球心,则,作于,设,利用,由已知线段长及二面角的大小求出图形中各线段长,然后利用勾股定理求得(以图中位置计算出值,如果,说明在平面上方,如果,则在平面正方).然后可得外接球半径,从而得球面积.【解析】如图,设为中点,为正外心,依题意有,,∴,∴,则易证为二面角的平面角,,设在底面的射影为,则可证在上,则,,,,,设为三棱锥的外接球球心,可证,过点在面内作,为垂足,则,,设求半径为,,则,,解得,.则球心在底面的下方,事实上当在底面的下方时 解得,.三棱锥的外接球的表面积为.【点睛】本题考查求三棱锥外接球的表面积,解题关键是找到球心位置,求出球的半径.三棱锥的外接球球心一定在过各面外心与此面垂直的直线上.8.(2021·湖北高三月考)已知球的半径为点均在球面上,若为等边三角形,且其面积则三棱锥的最大体积是___________. D BC G ABC SDA ∠S BC A --60︒SE ⊥ABC E E AD O //OG SE OF SE ⊥F OG d =OS OA R ==d d 0d >O ABC 0d <O ABC D BC G ABC 6BD DC ==SB SC ==SD BC ⊥6SD =SDA ∠S BC A --60SDA ∠=S ABC E E AD 3ED =SE =GD =AG =3GE =O //OG SE O SAD OF SE ⊥F 3OF GE ==AG =R OG d =222R OA OS ==22223))d d +=+2d =-252R =O ABC O ABC 22223))d d +=+2d =252R =S ABC -208πO 4,3,,,A B C D ABC D ABC -【分析】根据三角形面积求出边长,即可求出三角形外接圆半径,继而可求出高的最大值,求出体积.【解析】设外接圆的圆心为由解得,则 当三棱棱锥体积最大时,球心在上,因此有 所以的最大值为,三棱锥的最大体积为故.三、练原创1.已知圆锥的高为3积等于( )A .B .C .D . 【答案】B 【解析】如图:设球心到底面圆心的距离为,则球的半径为,由勾股定理得解得,故半径, 故选. ABC 1,O ABC 21sin603,2AB ⋅⋅=2AB =1122sin60AB O B =⨯=D ABC -O 1DO 12,3OO ==1DO 42233+=D ABC -111233ABC V S DO =⋅⋅==83π323π16π32πx 3x -()2233x x +=-1x =2r =343233V r ππ==球B2.(2021·江西九校联考)已知三棱锥A -BCD 中,侧面ABC ⊥底面BCD ,三角形ABC 是边长为3的正三角形,三角形BCD 是直角三角形,且∠BCD =90°,CD =2,则此三棱锥外接球的体积等于( )A .B .C .16πD .32π【答案】A【分析】把三棱锥放入长方体中,根据长方体的结构特征求出三棱锥外接球的半径,再计算三棱锥外接球的体积.【解析】三棱锥中,侧面底面,把该三棱锥放入长方体中,如图所示;设三棱锥外接球的球心为,取BC 的中点M ,BD 的中点N ,三角形ABC 的重心G ,连接OG ,则,,, 所以三棱锥外接球的半径为,所以三棱锥外接球的体积为,故选A . 3.(多选题)(2021湖南长沙市·长郡中学高三月考)已知球是正三棱锥(底面为正三角形,点在底面的射影为底面中心)的外接球,,点在线段上,且,过点作球的截面,则所得截面圆的面积可能是( )A .B .C .D .【答案】BCD【分析】依题意首先求出外接球的半径,即可求出截面圆的面积最大值,设过且垂直的截面圆的半径为323π643πA BCD -ABC ⊥BCD O AM ==2233AG AM ===112OG CD ==2R OA ==3344232333R V πππ⨯===O A BCD -3BC =AB =E BD 6BD BE =E O π2π3π4πE OE,即可求出截面圆的面积最小值,从而得解;【解析】如下图所示,其中是球心,是等边三角形的中心,可得,,设球的半径为,在三角形中,由,即,解得,故最大的截面面积为,在三角形中,,,由余弦定理得, 在三角形中,,设过且垂直的截面圆的半径为,,故最小的截面面积为,所以过点作球的截面,所以截面圆面积的取值范围是,故选.【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径. 4.(2021·江苏南通一模)已知在圆柱内有一个球O ,该球与圆柱的上、下底面及母线均相切.过直线的平面截圆柱得到四边形,其面积为8.若P 为圆柱底面圆弧的中点,则平面与球O 的交线长为___________.r O O 'BCD O B O D BC ''===3AO '=R ODO '222OO DO OD ''+=()2223R R -+=2R =24=R ππBEO '1162BE BD ==6EBO π'∠=2O E '==OO E 'OE ==E OE r 222115444r R OE =-=-=254r ππ=E O 5,44ππ⎡⎤⎢⎥⎣⎦BCD 12O O 12O O ABCD CD PAB【分析】先根据球与圆柱的上、下底面及母线均相切,可得四边形为正方形,由,求出球的半径r ;由题意分析出平面与球O 的交线为一个圆,利用垂径定理,计算出圆的半径,求出周长即可.【解析】设球的半径为r ,则,而,∴作于H ,∵⊥底面,∴⊥AB .∵P 为圆柱底面圆弧的中点,∴AP =BP ,又为AB 中点,∴⊥AB ,又,∴,∴,又且,∴,∵,, ∴,∴∴平面与球O 的交线为一个圆,其半径,圆周长为. 【点睛】(1)多面体的外接球(内切球)问题解题关键是找球心和半径,求半径的方法有:①公式法;②多面体几何性质法;③补形法;④寻求轴截面圆半径法;⑤确定球心位置法;(2)一个平面与球相交,所得的截面为一个圆.5.(2021·盐城市伍佑中学高三期末)已知三个顶点都在球的表面上,且,,ABCD 8ABCD S =PAB 2r =2AB BC r ==248ABCD S AB BC r ===r =2OH O P ⊥12O O 12O O CD 2O 2O P 1222OO PO O =12AB O O P ⊥AB OH ⊥2OH O P ⊥22AB PO O =OH ABP ⊥122OO r ==1O P =121OO O P ⊥2O P 1122si n O P O O P O P ∠===12255sin O O O O H O P =⨯∠==PAB 2r ===222l r ππ===ABC O 1AC BC ==AB =是球面上异于、、的一点,且平面,若球的表面积为,则球心到平面的距离为____________.【答案】 【分析】根据题中的垂直关系,确定球心,再根据球的表面积公式计算,再求点到平面的距离.【解析】由,,并且平面,平面,,且 平面,,是直角三角形和的公共斜边,取的中点,根据直角三角形的性质可知,所以点是三棱锥外接球的球心,设,则则三棱锥外接球的表面积,,解得:,点到平面的距离.【点睛】方法点睛:本题考查了球与几何体的综合问题,考查空间想象能力以及化归和计算能力,(1)当三棱锥的三条侧棱两两垂直时,并且侧棱长为,那么外接球的直径(2)当有一条侧棱垂直于底面时,先找底面外接圆的圆心,过圆心做底面的垂线,球心在垂线上,根据垂直关系建立的方程.(3)而本题类型,是两个直角三角形的公共斜边的中点是外接球的球心. S A B C SA ⊥ABC O 16πO ABC 2O SA O ABC 222AC BC AB +=AC BC ∴⊥SA ⊥ABC BC ⊂ABC SA BC ∴⊥AC SA A ⋂=BC ∴⊥SAC BC SC ∴⊥SB ∴SBC SAB SB O OA OB OC OS ===O S ABC -SA x =12r SB ==S ABC -2416S r ππ==()21264x +=x =O ABC 122d SA ==,,a b c 2R R。

球与几何体的切接问题整理人:元丽丽【相关知识】一、长方体的外接球1、球心:体对角线的交点;2、半径:()为长方体的长、宽、高c b a c b a r ,,2222++=. 二、正方体的外接球、内切球及与各条棱相切的球:1、外接球:(1)球心:正方体的中心; (2)半径:()为正方体的棱长a a r 23=; 2、内切球:(1)球心:正方体的中心; (2)半径:()为正方体的棱长a a r 2=; 3、与各条棱都相切的球:(1)球心:正方体的中心; (2)半径:()为正方体的棱长a a r 22=. 三、正四面体的外接球与内切球(正四面体可以看作正方体的一部分)1、外接球:(1)球心:正四面体的中心; (2)半径:()为正四面体的棱长a a r 46=; 2、内切球:(1)球心:正四面体的中心; (2)半径:()为正四面体的棱长a a r 126=. 题型一 几何体的外接球1、棱长为1的正四面体外接球的体积为 .2、正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为 .3、如图是某几何体的三视图,其中正视图是一个正三角形,则这个几何体的外接球的表面积为 .4、若棱长为3的正方体的顶点都在同一个球面上,则该球的表面积为 .5、已知三棱柱111C B A ABC -的底面是边长为6的正三角形,侧棱垂直于底面,且该三棱柱的外接球的表面积为12π,则该三棱柱的体积为 .6、已知直三棱柱111C B A ABC -的6个顶点都在球O 的球面上,若AB=3,AC=4,1AA =12,则球O 的半径为 .7、已知三棱锥ABC S -的所有顶点都在球O 的球面上,32=⊥SA ABC SA ,平面, 6021=∠==BAC AC AB ,,,则球O 的体积为 .题型二 几何体的内切球1、半径为R 的球的外切圆柱(球与圆柱的侧面、两底面都相切)的表面积为 ,体积为 .2、若正四面体的棱长为a ,则其内切球的半径为 .3、如图,已知球O 的棱长为1的正方体1111D C B A ABCD -的内切球,则平面1ACD 截球O 的截面面积为 .3、在封闭的直三棱柱111C B A ABC -内有一个体积为V 的球.若,6,=⊥AB BC AB 8=BC ,31=AA ,则V 的最大值为 .4、一块石材表示的几何体的三视图如图所示,将该石材切削,打磨,加工成球,则能得到的最大球的半径为 .5、如图是某几何体的三视图,则该几何体的外接球的表面积为6、一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,该几何体的体积为;若该几何体的所有顶点在同一球面上,则球的表面积为 .。

空间几何体的外接球与内切球问题目录一、必备秘籍二、典型题型题型一:内切球等体积法题型二:内切球独立截面法题型三:外接球公式法题型四:外接球补型法题型五:外接球单面定球心法题型六:外接球双面定球心法三、专项训练一、必备秘籍1.球与多面体的接、切定义1;若一个多面体的各顶点都在一个球面上,则称这个多面体是这个球的内接多面体,这个球是多面体的外接球。
定义2;若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是多面体的内切球。
类型一球的内切问题(等体积法)例如:在四棱锥P-ABCD中,内切球为球O,求球半径r.方法如下:V P-ABCD=V O-ABCD+V O-PBC+V O-PCD+V O-PAD+V O-PAB即:V P-ABCD=13S ABCD⋅r+13S PBC⋅r+13S PCD⋅r+13S PAD⋅r+13S PAB⋅r,可求出r.类型二球的外接问题1、公式法正方体或长方体的外接球的球心为其体对角线的中点2、补形法(补长方体或正方体)①墙角模型(三条线两个垂直)题设:三条棱两两垂直(重点考察三视图)②对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(AB=CD,AD=BC,AC=BD) 3、单面定球心法(定+算)步骤:①定一个面外接圆圆心:选中一个面如图:在三棱锥P-ABC中,选中底面ΔABC,确定其外接圆圆心O1(正三角形外心就是中心,直角三角形外心在斜边中点上,普通三角形用正弦定理定外心2r=asin A);②过外心O1做(找)底面ΔABC的垂线,如图中PO1⊥面ABC,则球心一定在直线(注意不一定在线段PO1上)PO1上;③计算求半径R:在直线PO1上任取一点O如图:则OP=OA=R,利用公式OA2=O1A2+OO12可计算出球半径R.4、双面定球心法(两次单面定球心)如图:在三棱锥P-ABC中:①选定底面ΔABC,定ΔABC外接圆圆心O1②选定面ΔPAB,定ΔPAB外接圆圆心O2③分别过O1做面ABC的垂线,和O2做面PAB的垂线,两垂线交点即为外接球球心O.二、典型题型题型一:内切球等体积法1(22·23·全国·专题练习)正三棱锥P-ABC的三条棱两两互相垂直,则该正三棱锥的内切球与外接球的半径之比为()A.1:3B.1:3+3C.3+1 :3D.3-1 :32(22·23下·朔州·阶段练习)正四面体的内切球、棱切球(与各条棱均相切的球)及外接球的半径之比为.3(23·24上·萍乡·期末)已知球O 是棱长为1的正四面体的内切球,AB 为球O 的一条直径,点P 为正四面体表面上的一个动点,则PA ⋅PB的取值范围为.4(22·23上·张家口·期中)球O 为正四面体ABCD 的内切球,AB =4,PQ 是球O 的直径,点M 在正四面体ABCD 的表面运动,则MP ⋅MQ的最大值为.5(22·23上·河南·阶段练习)已知正四面体ABCD 的棱长为12,球O 内切于正四面体ABCD ,E ,F 是球O 上关于球心O 对称的两个点,则AE ⋅BF的最大值为.6(22·23上·扬州·期中)中国古代数学名著《九章算术》中将底面为矩形且有一条侧棱垂直于底面的四棱锥称为“阳马”.现有一“阳马”的底面是边长为3的正方形,垂直于底面的侧棱长为4,则该“阳马”的内切球表面积为,内切球的球心和外接球的球心之间的距离为.题型二:内切球独立截面法1(23·24上·淮安·开学考试)球M 是圆锥SO 的内切球,若球M 的半径为1,则圆锥SO 体积的最小值为()A.43π B.423π C.83π D.4π2(22·23下·咸宁·期末)已知球O 内切于圆台(即球与该圆台的上、下底面以及侧面均相切),且圆台的上、下底面半径r 1:r 2=2:3,则圆台的体积与球的体积之比为()A.32B.1912C.2D.1963(22·23·全国·专题练习)若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为1,当该圆锥体积取最小值时,该圆锥体积与其内切球体积比为.4(23·24上·佛山·开学考试)若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的体积为4π3,当该圆锥体积取最小值时,该圆锥的表面积为.5(22·23下·成都·阶段练习)已知圆锥的底面半径为2,高为42,则该圆锥的内切球表面积为.题型三:外接球公式法1(16·17·全国·单元测试)若长方体从一个顶点出发的三条棱长分别为3,4,5,则该长方体的外接球表面积为 ()A.50πB.100πC.150πD.200π2(22·23·全国·专题练习)设球O 是棱长为4的正方体的外接球,过该正方体的棱的中点作球O 的截面,则最小截面的面积为()A.3πB.4πC.5πD.6π3(14·15上·佛山·阶段练习)正方体的外接球(正方体的八个顶点都在球面上)与其内切球(正方体的六个面都与球相切)的体积之比是.题型四:外接球补型法1(23·24上·成都·开学考试)在三棱锥P -ABC 中,PA =PB =PC =2,PA ⊥PB ,PA ⊥PC ,PB ⊥PC ,则该三棱锥的外接球的表面积为()A.43πB.12πC.48πD.323π2(22·23下·揭阳·期中)在三棱锥S -ABC 中,SA =BC =5,SB =AC =41,SC =AB =34,则该三棱锥的外接球表面积是()A.50πB.100πC.150πD.200π3(23·24上·成都·开学考试)已知四面体ABCD 满足AB =CD =3,AD =BC =5,AC =BD =2,且该四面体ABCD 的外接球的表面积是()A.2πB.6πC.6π11D.4π4(22·23下·黔西·阶段练习)正三棱锥P -ABC 的三条棱两两互相垂直,则该正三棱锥的内切球与外接球的半径之比为.5(22·23下·黔西·期中)如图,已知在三棱锥P -ABC 中,PA ⊥PB ,PB ⊥PC ,PC ⊥PA ,且PA =2PB =2PC =2,求该三棱锥外接球的表面积是.题型五:外接球单面定球心法1(23·24上·汉中·模拟预测)如图,在三棱锥P -ABC 中,PA ⊥平面ABC ,PA =6,BC =3,∠CAB =π6,O为△ABC 外接圆的圆心,O 为三棱锥P -ABC 外接球的球心,OQ ⊥PA ,则三棱锥P -ABC 的外接球O 的表面积为.2(23·24上·秦皇岛·开学考试)三棱锥P-ABC中,AB⊥BC,P在底面的射影O为△ABC的内心,若AB=4,BC=3,PO=5,则四面体PABC的外接球表面积为.3(22·23下·石家庄·阶段练习)已知球O是正四面体P-ABC的外接球,E为棱PA的中点,F是棱PB上的一点,且FC=2EF,则球O与四面体P-EFC的体积比为.4(22·23下·淄博·期末)已知四棱锥P-ABCD的底面ABCD是矩形,侧面PAD为等边三角形,平面PAD⊥平面ABCD,其中AD=2,AB=3,则四棱锥P-ABCD的外接球表面积为.题型六:外接球双面定球心法1(22·23上·抚州·期中)已知菱形ABCD的各边长为2,∠D=60°.如图所示,将△ACD沿AC折起,使得点D到达点S的位置,连接SB,得到三棱锥S-ABC,此时SB=3.若E是线段SA的中点,点F在三棱锥S-ABC的外接球上运动,且始终保持EF⊥AC则点F的轨迹的面积为.2(22·23·赣州·模拟预测)如图,正三角形ABC中,D,E分别为边AB,AC的中点,其中AB=4,把△ADE沿着DE翻折至△A DE的位置,得到四棱锥A -BCED,则当四棱锥A -BCED的体积最大时,四棱锥A -BCED外接球的球心到平面A BC的距离为.3(22·23下·湖南·期末)为加强学生对平面图形翻折到空间图形的认识,某数学老师充分利用习题素材开展活动,现有一个求外接球表面积的问题,活动分为三个步骤,第一步认识平面图形:如图(一)所示的四边形PABC中,AB=BC=2,PA=PC,∠ABC=60°,PA⊥PC.第二步:以AC为折痕将△PAC折起,得到三棱锥P-ABC,如图(二).第三步:折成的二面角P-AC-B的大小为120°,则活动结束后计算得到三棱锥P-ABC外接球的表面积为.三、专项训练一、单选题1(22·23下·河南·模拟预测)已知直六棱柱的所有棱长均为2,且其各顶点都在同一球面上,则该球的表面积为( ).A.16πB.20πC.24πD.25π2(22·23下·宁德·期中)正四面体ABCD的外接球的半径为2,过棱AB作该球的截面,则截面面积的最小值为()A.2π3B.4π3C.8π3D.3π3(23·24上·河北·开学考试)长方体的一个顶点上三条棱长是3,4,5,且它的八个顶点都在同一球面上,这个球的体积是()A.12523π B.1252π C.50π D.125π4(22·23下·临夏·期末)已知四棱锥P-ABCD的体积为83,侧棱PA⊥底面ABCD,且四边形ABCD是边长为2的正方形,则该四棱锥的外接球的表面积为()A.12πB.8πC.4πD.2π5(23·24上·广东·阶段练习)如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△AED,△BEF,△DCF分别沿DE,EF,DF折起,使得A,B,C三点重合于点A ,若三棱锥A -EFD的所有顶点均在球O的球面上,则球O的表面积为()A.2πB.3πC.6πD.8π6(23·24上·安徽·开学考试)在封闭的等边圆锥(轴截面为等边三角形)内放入一个球,若球的最大半径为1,则该圆锥的体积为()A.3πB.6πC.9πD.12π7(23·24上·莆田·阶段练习)三棱锥P-ABC中,△ABC是边长为23的正三角形,PA=4,PA⊥AB,D为BC中点且PD=5,则该三棱锥外接球的表面积为()A.16πB.32πC.48πD.64π8(22·23·九江·一模)三棱锥A-BCD中,△ABD与△BCD均为边长为2的等边三角形,若平面ABD ⊥平面BCD,则该三棱锥外接球的表面积为()A.8π3B.20π3C.8πD.20π二、填空题9(23·24·柳州·模拟预测)已知圆锥的底面直径为23,轴截面为正三角形,则该圆锥内半径最大的球的体积为.10(22·23·唐山·二模)已知某圆台的上、下底面的圆周在同一球的球面上,且圆台上底面半径为1,下底面半径为2,轴截面的面积为3,则该圆台的外接球的体积为.11(22·23·大同·模拟预测)四个面都为直角三角形的四面体称之为鳌臑.在鳌臑P-ABC中,PA⊥平面ABC,PA=4,AB=BC=2,鳌臑P-ABC的四个顶点都在同一个球面上,则该球的表面积是.12(23·24上·辽宁·阶段练习)已知圆锥的底面半径为2,侧面展开图的面积为8π,则该圆锥的内切球的体积为.13(23·24上·成都·阶段练习)已知三棱锥S-ABC底面ABC是边长为2的等边三角形,平面SAB⊥底面ABC,SA=SB=2,则三棱锥S-ABC的外接球的表面积为.14(23·24上·遂宁·阶段练习)已知正三棱柱ABC-A1B1C1的六个顶点在球O1上,又球O2与此三棱柱的5个面都相切,则球O1与球O2的表面积之比为.15(22·23下·赣州·阶段练习)已知圆锥的内切球半径为1,若圆锥的侧面展开图恰好为一个半圆,则该圆锥的体积为.。

7.1.2空间几何体的截面、球的切接问题-专项训练【原卷版】1.体积为8的正方体的顶点都在同一球面上,则该球的表面积为()πA.12πB.323C.8πD.4π2.一个圆柱的内切球的表面积为36π,则这个圆柱的表面积为()A.45πB.27πC.54πD.36π3.鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,6根等长的正四棱柱体分成3组,经90°榫卯起来.若正四棱柱的高为8,底面正方形的边长为2,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积至少为(容器壁的厚度忽略不计,结果保留π)()A.96πB.84πC.42πD.16π4.如图,在正四棱柱ABCDA1B1C1D1中,AB=1,AA1=3,点E为AB上的动点,则D1E+CE的最小值为()A.22B.10C.5+1D.2+25.已知正方体ABCDA1B1C1D1的边长为2,边AB的中点为M,过点M且垂直BD1的平面被正方体所截的截面面积为()B.3A.32C.23D.336.(多选)用一个平面截一个正方体,截面图形可以是()A.三角形B.等腰梯形C.五边形D.正六边形7.(多选)已知球O的半径为62,则下列结论正确的是()A.球O的表面积为6πB.球O的内接正方体的棱长为1C.球O的外切正方体的棱长为43D.球O的内接正四面体的棱长为28.在一个棱长为3+22的正方体内部有一个大球和小球,大球与正方体的六个面都相切,小球可以在正方体和大球之间的空隙自由滑动,则小球的表面积最大值是________.9.已知正三棱锥SABC的侧棱长为43,底面边长为6,则该正三棱锥外接球的表面积是________.10.如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,求所得三棱锥体积(单位:cm3)的最大值.11.已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为()A.64πB.48πC.36πD.32π解析:A如图所示,设球O的半径为R,⊙O1的半径为r,因为⊙O1的面积为4π,所以4π=πr2,解得r=2,又AB=BC=AC=OO1,所以AB=2r,解得AB=23,故OO1=23,所以R2=OO21+r2=(23)2sin60°+22=16,所以球O的表面积S=4πR2=64π.故选A.12.在四面体ABCD中,若AB=CD=3,AC=BD=2,AD=BC=5,则四面体ABCD 的外接球的表面积为()A.2πB.4πC.6πD.8π13.在半径是13cm的球面上有A,B,C三点,且AB=BC=CA=12cm,则球心到经过这三点的截面的距离为________.射影,PO=6,Q是AC上的一点,过点Q且与PA,BD都平行的截面为五边形EFGHL,求该截面面积的最大值.15.(多选)在南方不少地区,经常看到一种用木片、竹篾或苇蒿等称为“灯罩斗笠”,不同型号的斗笠大小经常用帽坡长(母线长)和帽底宽(底面圆直径长)两个指标进行衡量,现有一个“灯罩斗笠”,帽坡长20厘米,帽底宽203厘米,关于此斗笠,下列说法正确的是()A.斗笠轴截面(过顶点和底面中心的截面图形)的顶角为120°B.过斗笠顶点和斗笠侧面上任意两母线的截面三角形的最大面积为1003平方厘米C.若此斗笠顶点和底面圆上所有点都在同一个球上,则该球的表面积为1600π平方厘米D.此斗笠放在平面上,可以盖住的球(保持斗笠不变形)的最大半径为203-30厘米16.多面体欧拉定理是指对于简单多面体,其各维对象数总满足一定面数)-E(棱长数)=2.在数学上,富勒烯的结构都是以正五边形和正六边形面组成的凸多面体,例如富勒烯C60(结构图如图)是单纯用碳原子组成的稳定分子,具有60个顶点和32个面,其中12个面为正五边形,20个面为正六边形.除C60外具有封闭笼状结构的富勒烯还可能有C28,C32,C50,C70,C84,C240,C540等,则C84结构含有正六边形的个数为()A.12B.24C.30D.327.1.2空间几何体的截面、球的切接问题-专项训练【解析版】1.体积为8的正方体的顶点都在同一球面上,则该球的表面积为()πA.12πB.323C.8πD.4π解析:A设正方体的棱长为a,则a3=8,解得a=2.设球的半径为R,则2R=23,即R=3.所以球的表面积S=4πR2=12π.2.一个圆柱的内切球的表面积为36π,则这个圆柱的表面积为()A.45πB.27πC.54πD.36π解析:C设圆柱的内切球的半径为r,则4πr2=36π,可得r=3,所以该圆柱的底面圆半径为R=3,圆柱的高为h=2r=6,因此该圆柱的表面积为S=2πRh+2πR2=2π×3×6+2π×32=54π.故选C.3.鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,6根等长的正四棱柱体分成3组,经90°榫卯起来.若正四棱柱的高为8,底面正方形的边长为2,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积至少为(容器壁的厚度忽略不计,结果保留π)()A.96πB.84πC.42πD.16π解析:B若球形容器表面积最小,则正四棱柱与球内接,此时球体的直径等于一组正四棱柱的体对角线长,即2R=82+(2+2)2+22=221,所以R=21,球形容器的表面积S=4πR2=84π.故选B.4.如图,在正四棱柱ABCDA1B1C1D1中,AB=1,AA1=3,点E为AB上的动点,则D1E+CE的最小值为()A.22B.10C.5+1D.2+2解析:B如图,连接D1A,C1B并分别延长至F,G,使得AF=AD,BG=BC,连接EG ,FG ,∵四棱柱ABCD A 1B 1C 1D 1为正四棱柱,∴AB ⊥平面ADD 1A 1,AB ⊥平面BCC 1B 1,∴AB ⊥AF ,AB ⊥BG ,又AB =AD =AF ,∴四边形ABGF 为正方形,∴EG =BE 2+BG 2=BE 2+BC 2=CE ,∴D 1E +CE 的最小值为D 1G ,又D 1G =D 1F 2+FG 2=9+1=10,∴D 1E +CE 的最小值为10.5.已知正方体ABCD A 1B 1C 1D 1的边长为2,边AB 的中点为M ,过点M 且垂直BD 1的平面被正方体所截的截面面积为()A .32B .3C .23D .33解析:A如图,连接AC ,CB 1,AB 1,BC 1,易知CB 1⊥BC 1,CB 1⊥D 1C 1,又BC 1∩D 1C 1=C 1,BC 1,D 1C 1⊂平面BD 1C 1,所以CB 1⊥平面BC 1D 1.因为BD 1⊂平面BD 1C 1,故CB 1⊥BD 1,同理可证CA⊥平面BDD 1,则BD 1⊂平面BDD 1,则CA ⊥BD 1,又CA ∩CB 1=C ,CA ,CB 1⊂平面CAB 1,故BD 1⊥平面ACB 1.取BC 的中点E ,BB 1的中点F ,连接ME ,EF ,MF ,易知平面MEF ∥平面ACB 1,所以BD 1⊥平面MEF ,即△MEF 为所求的截面.易知△MEF 为正三角形,边长ME =BM 2+BE 2=2,故S △MEF =12×2×2×32=32.故选A .6.(多选)用一个平面截一个正方体,截面图形可以是()A .三角形B .等腰梯形C .五边形D .正六边形解析:ABCD 如图所示.用一个平面去截正方体,截面可能是三角形、等腰梯形、五边形、正六边形,故选A 、B 、C 、D .7.(多选)已知球O 的半径为62,则下列结论正确的是()A .球O 的表面积为6πB .球O 的内接正方体的棱长为1C .球O 的外切正方体的棱长为43D .球O 的内接正四面体的棱长为2解析:AD 球的表面积为4π=4π×64=6π,A 正确.正方体的体对角线长为2×62=6,棱长为63=2,B 错误.球的外切正方体的棱长为2×62=6,C 错误.将正四面体补形为正方体如图所示A B 1CD 1,正方体的体对角线长为2×62=6,棱长为63=2,所以正四面体的棱长为2×2=2,D 正确.故选A 、D .8.在一个棱长为3+22的正方体内部有一个大球和小球,大球与正方体的六个面都相切,小球可以在正方体和大球之间的空隙自由滑动,则小球的表面积最大值是________.解析:如图所示,为组合体的中截面,易知当小球的表面积最大时大球半径R 和小球半径r 满足2R =R +r +2r ,2R =3+22,解得r =12,故小球表面积的最大值为π.答案:π9.已知正三棱锥S ABC 的侧棱长为43,底面边长为6,则该正三棱锥外接球的表面积是________.解析:如图,过点S 作SE ⊥平面ABC 于点E ,记球心为O .∵在正三棱锥S ABC 中,底面边长为6,侧棱长为43,∴BE =23×32×6=23,∴SE =SB 2-BE 2=6.∵球心O 到四个顶点的距离相等,均等于该正三棱锥外接球的半径R ,∴OB =R ,OE =6-R .在Rt △BOE 中,OB 2=BE 2+OE 2,即R 2=12+(6-R )2,解得R =4,∴外接球的表面积为S =4πR 2=64π.答案:64π10.如图,圆形纸片的圆心为O ,半径为5cm ,该纸片上的等边三角形ABC 的中心为O .D ,E ,F 为圆O 上的点,△DBC ,△ECA ,△FAB 分别是以BC ,CA ,AB 为底边的等腰三角形.沿虚线剪开后,分别以BC ,CA ,AB 为折痕折起△DBC ,△ECA ,△FAB ,使得D ,E ,F 重合,得到三棱锥.当△ABC 的边长变化时,求所得三棱锥体积(单位:cm 3)的最大值.解:如图,连接OD ,交BC 于点G ,由题意,知OD ⊥BC ,OG =36BC .设OG =x ,则BC =23x ,DG =5-x ,三棱锥的高h =DG 2-OG 2=25-10x +x 2-x 2=25-10x ,S △ABC =12×23x ×3x =33x 2,则三棱锥的体积V =13S △ABC ·h =3x 2·25-10x =3·25x 4-10x 5.令f (x )=25x 4-10x 5,x ∈0,52,则f ′(x )=100x 3-50x 4.令f ′(x )=0得x =2.当x ∈(0,2)时,f ′(x )>0,f (x )单调递增,当x ∈2,52时,f ′(x )<0,f (x )单调递减,故当x =2时,f (x )取得最大值80,则V ≤3×80=415.所以三棱锥体积的最大值为415cm 3.11.已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1,则球O 的表面积为()A .64πB .48πC .36πD .32π解析:A 如图所示,设球O 的半径为R ,⊙O 1的半径为r ,因为⊙O 1的面积为4π,所以4π=πr 2,解得r =2,又AB =BC =AC =OO 1,所以AB sin 60°=2r ,解得AB =23,故OO 1=23,所以R 2=OO 21+r 2=(23)2+22=16,所以球O 的表面积S =4πR 2=64π.故选A .12.在四面体ABCD 中,若AB =CD =3,AC =BD =2,AD =BC =5,则四面体ABCD 的外接球的表面积为()A .2πB .4πC .6πD .8π解析:C 由题意可采用割补法,考虑到四面体ABCD 的四个面为全等的三角形,所以可在其每个面补上一个以3,2,5为三边的三角形作为底面,分别以x ,y ,z 为侧棱长的三棱锥,如图所示,从而可得到一个长、宽、高分别为x ,y ,z 的长方体,并且x 2+y 2=3,x 2+z 2=5,y 2+z 2=4,则有(2R )2=x 2+y 2+z 2=6(R 为球的半径),得2R 2=3,所以球的表面积为S =4πR 2=6π.13.在半径是13cm 的球面上有A ,B ,C 三点,且AB =BC =CA =12cm ,则球心到经过这三点的截面的距离为________.解析:由题意知问题实际上是在一个底面是边长为12的正三角形,三条侧棱长度都是13的正三棱锥S ABC 中,求顶点S 到底面ABC 的距离,如图,过顶点向底面作垂线,垂足是O ,连接AO ,根据三角形的重心性质,AO =23×12sin 60°=43,根据在直角三角形中已知的斜边长是SA =13,一条直角边长是AO =43,则要求的直角边长是SO =SA 2-AO 2=132-(43)2=11,即球心到经过这三个点的截面的距离是11cm .答案:11cm14.已知正四棱锥P ABCD 的底面正方形的边长是3,O 是P 在底面上的射影,PO =6,Q 是AC 上的一点,过点Q 且与PA,BD 都平行的截面为五边形EFGHL ,求该截面面积的最大值.解:如图,连接AC ,BD ,设截面与正四棱锥P ABCD 的底面相交于EL ,AC 与EL 相交于点Q ,由BD ∥截面EFGHL ,得LE ∥BD ,由AP ∥截面EFGHL ,得AP ∥QG ,则EL 必定分别与AB,AD 相交于E ,L ,否则,截面将是三角形,则AP ∥EF ,AP ∥LH .在正四棱锥P ABCD 中,BD ⊥AP ,由LE ∥BD,AP ∥QG ,知∠GQE 是异面直线BD 与PA 所成的角,则QG ⊥EL ,所以平面GFEQ 和平面GHLQ 是两个全等的直角梯形.设AE =x (0<x <3),则AP=92.由AP ∥EF ,得EF 92=3-x 3,故EF =32(3-x ),且AQ =x 2,由AP ∥QG ,得QG 92=32-x232,故QGS 五边形EFGHL =2+32(3-x )x 2=-94x 2+9x =-94(x -2)2+9,所以当x =2时,截面EFGHL 的面积取得最大值9.15.(多选)在南方不少地区,经常看到一种用木片、竹篾或苇蒿等材料制作的斗笠,用来遮阳或避雨,其中有一种外形为圆锥形的斗笠,称为“灯罩斗笠”,不同型号的斗笠大小经常用帽坡长(母线长)和帽底宽(底面圆直径长)两个指标进行衡量,现有一个“灯罩斗笠”,帽坡长20厘米,帽底宽203厘米,关于此斗笠,下列说法正确的是()A .斗笠轴截面(过顶点和底面中心的截面图形)的顶角为120°B .过斗笠顶点和斗笠侧面上任意两母线的截面三角形的最大面积为1003平方厘米C .若此斗笠顶点和底面圆上所有点都在同一个球上,则该球的表面积为1600π平方厘米D .此斗笠放在平面上,可以盖住的球(保持斗笠不变形)的最大半径为203-30厘米解析:ACD对A 选项,设顶角为θ,则sin θ2=10320=32,得θ2=60°,所以顶角为θ=120°,A 正确;对B 选项,因为顶角为θ=120°,则截面三角形的最大面积为12×202sin 90°=200平方厘米,B 错误;对C 选项,因为顶角为θ=120°,则θ2=60°,所以外接球半径等于圆锥母线长,即R =20,则该球的表面积为4πR 2=1600π平方厘米,C 正确;对D 选项,如图,设球的最大半径为r ,因为顶角为120°,则∠OCD =15°,所以r =CD ·tan 15°=103·tan 45°-tan 30°1+tan 45°·tan 30°=203-30,D 正确.故选A 、C 、D .16.多面体欧拉定理是指对于简单多面体,其各维对象数总满足一定的数量关系,在三维空间中,多面体欧拉定理可表示为:V (顶点数)+F (表面数)-E (棱长数)=2.在数学上,富勒烯的结构都是以正五边形和正六边形面组成的凸多面体,例如富勒烯C 60(结构图如图)是单纯用碳原子组成的稳定分子,具有60个顶点和32个面,其中12个面为正五边形,20个面为正六边形.除C 60外具有封闭笼状结构的富勒烯还可能有C 28,C 32,C 50,C 70,C 84,C 240,C 540等,则C 84结构含有正六边形的个数为()A .12B .24C .30D .32解析:D 在富勒烯多面体C 84中,连结每一个顶点的棱都是3,并且每条棱都连结2个顶点,因此可由顶点数V =84求得棱数E =3×842=126.设分子中形状为正五边形和正六边形的面的个数分别为x ,y ,由欧拉公式V +F -E =2,可得84+x +y -126=2,即x +y =44.又由多边形的边数可表示C 84的棱数,即(5x +6y )÷2=3×84÷2,即5x +6y =252,由+y =44,x +6y =252,=12,=32.故C 84结构含有正六边形的个数为32.。

立体几何----与球有关的切、接问题提高练【答题技巧】1.“切”“接”问题的处理规律(1)“切”的处理:球的内切问题主要是球内切于多面体或旋转体.解答时要找准切点,通过作截面来解决.(2)“接”的处理:把一个多面体的顶点放在球面上即球外接于该多面体.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.2.当球的内接多面体为共顶点的棱两两垂直的三棱锥、共顶点的三个侧面两两垂直的三棱锥或三组对棱互相垂直的三棱锥时,常构造长方体或正方体以确定球的直径.3.与球有关的组合体的常用结论 (1)长方体的外接球: ①球心:体对角线的交点;②半径:,,r a b c =为长方体的长、宽、高). (2)正方体的外接球、内切球及与各条棱都相切的球:①外接球:球心是正方体的中心,半径(r a =为正方体的棱长); ②内切球:球心是正方体的中心,半径(2ar a =为正方体的棱长);③与各条棱都相切的球:球心是正方体的中心,半径r =(a 为正方体的棱长). (3)正四面体的外接球与内切球(正四面体可以看作是正方体的一部分):①外接球:球心是正四面体的中心,半径(r a =为正四面体的棱长);②内切球:球心是正四面体的中心,半径(r a =为正四面体的棱长). 【练习】1.在三棱锥P-ABC 中,△ABC 的内切圆圆O 的半径为2,PO ⊥平面ABC ,且三棱锥P-ABC 的三个侧面与底面所成角都为60°,则该三棱锥的内切球的体积为( )C.16π3D.4π32.已知在三棱锥P-ABC 中,△ABC 是以A 为直角的三角形,AB=AC=2,△PBC 是正三角形,且PC 与底面ABC所成角的正弦值为34,则三棱锥P-ABC外接球的半径为( )A.43B.32C.133D.2233.张衡是中国东汉时期伟大的天文学家、数学家等,他曾经得出圆周率的平方除以十六等于八分之五.已知三棱锥A-BCD的每个顶点都在球O的表面上,AB⊥底面BCD,BC⊥CD,且AB=CD=3,BC=2,利用张衡的结论可得球O的表面积为( )A.30B.1010C.33D.12104.已知三棱锥P-ABC中,PA PB PC ABC==,是边长为42的正三角形,D,E分别是PA,AB上靠近点A 的三等分点,DE PC⊥,则三棱锥P-ABC的内切球的表面积为( )A.(5763203)π-B.(2881603)π-C.(64323)π-D.(64323)π-5.取两个相互平行且全等的正n边形,将其中一个旋转一定角度,连接这两个多边形的顶点,使得侧面均为等边三角形,我们把这种多面体称作“n角反棱柱”.当6n=时,得到如图所示棱长均为2的“六角反棱柱”,则该“六角反棱柱”外接球的表面积等于( )A.(53)π+ B.(1243)π+ C.(2553)π+ D.(2843)π+6.已知在菱形ABCD中,23AB BD==ABCD沿对角线BD折起,得到三棱锥A BCD-,且使得棱33AC=A BCD-的外接球的表面积为( )A.7πB.14πC.28πD.35π7.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有仓,广三丈,袤四丈五尺,容粟一万斛.问高几何?”其意思为:“今有一个长方体的粮仓,宽3丈,长4丈5尺,可装粟10 000斛,问该粮仓的高是多少?”已知1斛粟的体积为2.7立方尺,一丈为10尺,则该粮仓的外接球的体积是( )A.133π4立方丈 B.133π48立方丈 C.133133π4立方丈 D.133133π48立方丈 8.已知正方形ABCD 中,E ,F 分别是AB ,BC 的中点,沿DE ,DF ,EF 折起得到如图所示的空间几何体,若2AB =,则此几何体的内切球的体积为( )A.3π2B.π4C.π48D.π169.在平面四边形ABCD 中,2,2AB AD BC CD DB =====,现将ABD 沿BD 折起,使二面角A BD C --的大小为60︒.若,,,A B C D 四点在同一个球的球面上,则球的表面积为( ) A.13π3B.14π3C.52π9D.56π910.已知三棱锥S-ABC 的顶点都在球O 的球面上,且该三棱锥的体积为23,SA ⊥平面,4,120ABC SA ABC =∠=︒,则球O 的体积的最小值为_________.11.如图,已知长方体1111ABCD A B C D -的底面ABCD 为正方形,P 为棱11A D 的中点,且6PA AB ==,则四棱锥P ABCD -的外接球的体积为_________________.12.设正四面体的内切球半径为r ,外接球半径为R ,则rR=___________. 13.已知底面为正方形的四棱锥P ABCD -的五个顶点在同一个球面上,,2,1PD BC AB PC ⊥==,3PD =则四棱锥P ABCD -外接球的体积为________.14.已知有两个半径为2的球记为12,O O ,两个半径为3的球记为34,O O ,这四个球彼此相外切,现有一个球O 与这四个球1234,,,O O O O 都相内切,则球O 的半径为____________.15.在三棱锥P-ABC 中,PA ⊥平面,,12ABC AB BC PA AB AC ⊥===,三棱锥P-ABC 的所有顶点都在球O 的表面上,则球O 的半径为__________;若点M 是ABC 的重心,则过点M 的平面截球O 所得截面的面积的最小值为__________.16.已知正三棱柱111ABC A B C -,底面边长为3,高为2,P 为上底面三角形111A B C 中线上一动点,则三棱锥P ABC -的外接球表面积的取值范围是_____________.17.如图,已知边长为1的正方形ABCD 与正方形BCFE 所在平面互相垂直,P 为EF 的中点,Q 为线段FC 上的动点,当三棱锥P-ABQ 的体积最大时,三棱锥P-ABQ 的外接球的表面积为_________________.答案以及解析1.答案:A解析:设三棱锥P ABC -的内切球的半径为R ,过O 作OD AC ⊥于点,D OE BC ⊥于点,E OF AB ⊥于点F ,则2OD OE OF ===.连接PD ,易证PD AC ⊥,因为三棱锥P-ABC 的三个侧面与底面所成角都为60°,所以60PDO ∠=︒,则22tan 6023,4cos60PO PD ===︒=︒.由题意可知三棱锥P-ABC 的内切球的球心'O 在线段PO 上,在Rt POD 中,sin OD RDPO PD PO R∠==-,即2423R =-,解得23R =.所以该三棱锥的内切球的体积为334423323πππ33R ⎛⎫== ⎪ ⎪⎝⎭,故选A. 2.答案:C解析:如图,不妨令二面角P BC A --为钝二面角,取BC 的中点D ,连接AD , 因为2AB AC ==,90BAC ∠=︒,所以2BC =,且D 为ABC 外接圆的圆心.作PH ⊥平面ABC 于H ,易知H 在直线AD 上,连接,HC HA ,则PCH ∠为PC 与底面ABC 所成角, 则3sin 4PH PCH PC ∠==,又2PC BC ==,所以32PH =,又3PD =,则332sin 3PH PDH PD ∠===. 设1O 为PBC 的外心,O 为三棱锥P ABC -外接球的球心,连接1,OO OD ,则1OO ⊥平面PBC ,OD ⊥平面133,,cos ABC O D PDO =∠=,则12cos 3O D OD PDO ==∠,设外接球的半径为R ,则222413131,99R OD DA R =+=+==,故选C.3.答案:B解析:因为BC CD ⊥,所以7BD 又AB ⊥底面BCD ,所以10AD O 的球心为侧棱AD 的中点,从而球O 10利用张衡的结论2π5168=,可得π10=所以球O 的表面积为2104π10π1010==⎝⎭故选B.4.答案:C解析:因为PA PB PC ==,ABC 是边长为42的正三角形,所以三棱锥P ABC -为正三棱锥, 由正棱锥对棱垂直可知PB AC ⊥.又D ,E 分别是PA ,AB 上靠近点A 的三等分点,所以//DE PB , 所以DE AC ⊥.又,DE PC PC AC C ⊥⋂=,所以DE ⊥平面PAC ,所以PB ⊥平面PAC ,所以90APB ∠=︒,所以4PA PB PC ===,所以,,PA PB PC 两两互相垂直. 设三棱锥P ABC -的内切球的半径为r ,则由等体积法可得,()1133PABPACPBCABCPACSSSSr S PB ⋅+++=⋅,即11(88883)8433r ⨯+++=⨯⨯,解得2(33)r -=,故三棱锥P ABC -的内切球的表面积为222(33)(64323)π4π4πS r ⎡⎤--==⨯=⎢⎥⎣⎦.故选C. 5.答案:B解析:如图,设上、下正六边形的中心分别为1O ,2O ,连接12O O ,则其中点O 即为所求外接球的球心. 连接2O C ,取棱AB 的中点M ,作2MN O C ⊥于点N ,连接1O M ,MC ,则13O M MC ==.而22O C =, 则22212NC O C O N O C O M =-=-=-3,222123(23)231O O MN MC NC ∴==-=--=-,则131OO -.连接OA ,1O A ,设所求外接球的半径为R ,则有2222211(31)233R OA OO O A ==+=+=+∴该“六角反棱柱”外接球的表面积24π(1243)πS R ==+.故选B.6.答案:C解析:由题意可知,ABD BCD 为等边三角形.如图所示,设外接球的球心为O ,等边三角形BCD 的中心为,O '取BD 的中点F ,连接,,,AF CF OO ',,,OB O B OA '由AB AD BC BD DC ====,得,,AF BD CF BD ⊥⊥又AF CF F ⋂=,所以BD ⊥平面AFC ,且可求得AF =3,CF =而33,AC =所以AFC ∠=120.︒在平面AFC 中过点A 作CF 的垂线,与CF 的延长线交于点E ,由BD ⊥平面AFC 得.BD AE ⊥又,,AE EC BD EC F ⊥⋂=所以AE ⊥平面BCD .过点O 作OG AE ⊥于点G ,则四边形O EGO '是矩形. 又2sin 6023O B BC '︒=⨯=,所以13331.sin 60,sin3022O F O B AE AF EF AF ''︒︒======. 设外接球的半径为,,R OO x '=则由222222,OO O B OB OA AG GO ''+==+, 得2222223332,1,2x R x R ⎛⎫⎛⎫+=-++= ⎪ ⎪ ⎪⎝⎭⎝⎭解得23,7,x R == 故三棱锥A BCD -外接球的表面积24π28π.S R ==故选C.7.答案:D解析:由题意可得粮仓的高2723 4.5h ==⨯(丈),设外接球的半径为R , 则2222133133(2)23 4.533.25,4R R =++==该粮仓的外接球的体积是34133133133π3⨯⨯⎝⎭(立方丈),选D. 8.答案:C解析:在等腰DEF 中,2222215,112DE DF EF ==+=+=D 到EF 的距离为h , 则22293(5)2222h ⎛⎫-= ⎪ ⎪⎝⎭令该几何体的内切球的球心为O ,且球心O 到三个面的距离均为半径r .又因为,DP PE DP PF ⊥⊥,且PE PF P ⋂=,所以DP ⊥平面PEF .由等体积法知O PEF O PFD O PDE O DEF D PEF V V V V V -----+++=,即11113111121212211232323232232r r r r ⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯⨯,解得14r =, 则3 441πππ336448O V r ==⨯⨯=球,故选C.9.答案:C解析:如图所示,设M 为BD 的中点,连接,MA MC ,依题意,折起后AMC ∠是二面角A BD C --的平面角,则60AMC ∠=︒.易知,四面体ABCD 的外接球的球心O 在平面MCA 上,于是点O 在底面BCD 上的射影是正BCD的中心,设为点Q,而点O在侧面ABD上的射影是M,易得3MQ=,又30OMQ∠=︒,因此13OQ=,进而22221231333R OC OQ QC⎛⎫⎛⎫==+=+=⎪⎪ ⎪⎝⎭⎝⎭,所以球O的表面积为21352π4π9⎛⎫⨯=⎪⎪⎝⎭,故选C.10.4010π解析:由题意得,三棱锥S ABC-的体积11342332S ABCV AB BC-=⨯⋅=,则6AB BC⋅=,、当球O 的体积最小时,ABC外接圆的半径最小,即AC最小,在ABC中,由余弦定理和基本不等式得222123182AC AB BC AB BC AB BC⎛⎫=+-⋅⨯-⋅=⎪⎝⎭,当且仅当6AB BC=取等号,则min32AC=,此时ABC外接圆的直径min32226sin1203ACr===O的半径22210R r=+=O的体积的最小值为344010ππ3R=.11.答案:2821π解析:解法一由题意知PAD为正三角形,取AD的中点M,PAD的中心N,记AC BD F⋂=,连接,PM FM,过,N F分别作平面11AA D D与平面ABCD的垂线,两垂线交于点O,则点O为四棱锥P ABCD-的外接球球心.由题意知22362333PN PM===132ON MF AB===,所以四棱锥P ABCD-的外接球半径22223(23)21R ON PN++所以四棱锥P ABCD-的外接球的体积34π2821π3V R==.解法二连接1111,,,AC BD AC B D,记1111,AC BD F AC B D E⋂=⋂=,连接EF,易知四棱锥P ABCD-的外接球的球心O在线段EF上.取AD的中点G,连接PG,设OF x=,球O的半径为R,易知1122AF AC==⨯36232,633PG==则22222(32)(33)3R x x =+=-+,得3x =,则21R =, 所以四棱锥P ABCD -的外接球的体积34π2821π3V R ==. 12.答案:13解析:如图,在正四面体PABC 中,D ,E 分别为BC ,AC 的中点,连接AD ,BE 交于点F ,则点F 为正三角形ABC 的外心,连接PF ,则PF ⊥底面ABC ,且正四面体PABC 的外接球球心与内切球球心为同一点,应在线段PF 上,记作点O ,如图所示.不妨设正四面体PABC 的棱长为a ,则在ABC 中,22233sin 60333AF AD AC ==⋅⋅==°. PF ⊥底面,ABC AF ⊂底面,ABC PF AF ∴⊥,2222363PF AP AF a a ⎛⎫∴=-=-= ⎪ ⎪⎝⎭. 正四面体PABC 的外接球、内切球球心均为O ,,OP OA R OF r ∴===.OF PF OP =-,且在Rt AFO 中有222AF OF OA +=,22236R R ⎫⎫∴+-=⎪⎪⎪⎪⎝⎭⎝⎭, 6666,R r ∴==-=,611236r R a ∴==. 13.答案:82π3. 解析:由题意知,BC DC BC PD ⊥⊥,所以BC ⊥平面PCD ,而BC ⊂平面ABCD ,则平面PCD ⊥平面ABCD .由条件知222CD PC PD =+,所以PC PD ⊥.如图,取CD 的中点G ,连接,AC BD ,交于点O , 则O 为正方形ABCD 的中心,过点G 作平面CDP 的垂线,则点O 在该垂线上, 所以O 为四棱锥P ABCD -外接球的球心,由于2AO , 所以四棱锥P ABCD -外接球的体积为3482ππ(2)3=.14.答案:6解析:由题意可得121314234,O O O O O O O O ====24345,6O O O O ==.如图,取12O O 的中点34,M O O 的中点N ,连接1234,,,,,MN O N O N O M O M 则12O O ⊥3124,.O M O O O M ⊥ 又3412,O M O M M O O ⋂=∴⊥平面34.O O M 同理可证34O O ⊥平面2,.O O N 平面12O O N ⋂平面34,O O M MN =∴球心O 在线段MN 上. 设球O 的半径为R ,则142442, 3.5,3,OO R OO R O O O N =-=-==2222222114,23,O N MN O N O M OM OO O M ∴==-==-=222244(2)4,(3)9R ON OO O N R --=-=--.,MN OM ON =+即22(2)4(3)923,R R --+--=解得6R =.故球O 的半径为6.15.答案:3;4π9解析:(1)PA ⊥平面,ABC BC ⊂平面ABC ,,PA BC ∴⊥又AB BC ⊥,且,PA AB A BC ⋂=∴⊥平面,PAB PB ⊂平面,PAB BC PB ∴⊥,所以PC 是两个直角三角形PAC 和PBC 的斜边,取PC 的中点O ,点O到四点P ,A ,B ,C 的距离相等,即点O 是三棱锥P ABC -的外接球的球心,2231(2)3,PC R =+==(2)当点M 是截面圆的圆心时,此时圆心到截面的距离最大,那么截面圆的半径最小,即此时的面积最小,点N 是AC 的中点,M 是ABC 的重心,112,366MN BN AC ON ∴====1122PA =,所以22116OM ON MN =+=,截面圆的半径222()3r R OM =-=,所以2min 4ππ9S r ==16.答案:25π,8π4⎡⎤⎢⎥⎣⎦解析:如图,设正三棱柱111ABC A B C -上、下底面中心分别为1,O O ,点P 是111A B C 中线1C D 上一点,G 是三棱锥P ABC -的外接球的球心.因为A ,B ,C 在球面上,所以球心在线段1O O 上,点P 也在球面上, 设三棱锥P ABC -外接球的半径为R ,ABC 外接圆的半径为r ,由正弦定理有260sin 32==r ,所以1r =,设11,O P x O G y ==,则OG =2,y PG CG R -==,在1Rt PGO 中,222R x y =+,在Rt CGO 中,2221(2)R y =+-,于是2221x y +=+2(2)y -,解得254.x y =-因为点P 是111A B C 中线1C D 上一点,所以10≤≤x ,于是451≤≤y ,所以222222554(2)1,216R x y y y y ⎡⎤=+=-+=-+∈⎢⎥⎣⎦,所以外接球的表面积225π4π,8π4S R ⎡⎤=∈⎢⎥⎣⎦球.17.答案:41π16解析:如图,由题意知三棱锥P-ABQ 的体积最大时,点Q 与点C 重合,即求三棱锥P-ABC 外接球的表面积.因为正方形ABCD 与正方形BCFE 的边长均为1,点P 为EF 的中点,所以51,2,AB BC AC BP PC =====.过点P 作PG BC ⊥,垂足为G ,由正方形ABCD 与正方形BCFE 所在平面互相垂直,得PG ⊥平面ABC .设三棱锥P-ABC 外接球的球心为O ,AC 的中点为1O ,连接1OO , 则1OO ⊥平面ABC.延长1O O 到点H ,使1O H PG =.连接PH ,OP ,OA ,设1OO x =, 则2222211,(1)22OH x x x ⎛⎫⎛⎫=-+=+- ⎪ ⎪ ⎪⎝⎭⎝⎭,解得38x =, 设三棱锥P-ABC 外接球的半径为R ,则2221314128264R x ⎛⎫=+=+= ⎪⎝⎭.故所求表面积241414π4ππ6416S R ==⨯=.。

与球有关的切、接问题1.球的表面积公式:S =4πR 2;球的体积公式V =43πR 3 2.与球有关的切、接问题中常见的组合: (1)正四面体与球:如图,设正四面体的棱长为a ,内切球的半径为r ,外接球的半径为R ,取AB 的中点为D ,连接CD ,SE 为正四面体的高,在截面三角形SDC 内作一个与边SD 和DC 相切,圆心在高SE 上的圆.因为正四面体本身的对称性,内切球和外接球的球心同为O .此时,CO =OS =R ,OE =r ,SE = 23a ,CE =33a ,则有R +r = 23a ,R 2-r 2=|CE |2=a 23,解得R =64a ,r =612a . (2)正方体与球:①正方体的内切球:截面图为正方形EFHG 的内切圆,如图所示.设正方体的棱长为a ,则|OJ |=r =a 2(r 为内切球半径). ②与正方体各棱相切的球:截面图为正方形EFHG 的外接圆,则|GO |=R =22a . ③正方体的外接球:截面图为正方形ACC 1A 1的外接圆,则|A 1O |=R ′=32a . (3)三条侧棱互相垂直的三棱锥的外接球:①如果三棱锥的三条侧棱互相垂直并且相等,则可以补形为一个正方体,正方体的外接球的球心就是三棱锥的外接球的球心.即三棱锥A 1-AB 1D 1的外接球的球心和正方体ABCD -A 1B 1C 1D 1的外接球的球心重合.如图,设AA 1=a ,则R =32a . ②如果三棱锥的三条侧棱互相垂直但不相等,则可以补形为一个长方体,长方体的外接球的球心就是三棱锥的外接球的球心.R 2=a 2+b 2+c 24=l 24(l 为长方体的体对角线长). 角度一:正四面体的内切球1.(2015·长春模拟)若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则S 1S 2=________.解析:设正四面体棱长为a ,则正四面体表面积为S 1=4·34·a 2=3a 2,其内切球半径为正四面体高的14,即r =14·63a =612a ,因此内切球表面积为S 2=4πr 2=πa 26,则S 1S 2=3a 2π6a 2=63π. 角度二:直三棱柱的外接球2.(2015·唐山统考)如图,直三棱柱ABC -A 1B 1C 1的六个顶点都在半径为1的半球面上,AB =AC ,侧面BCC 1B 1是半球底面圆的内接正方形,则侧面ABB 1A 1的面积为( )A .2B .1 C. 2 D.22解析:选C 由题意知,球心在侧面BCC 1B 1的中心O 上,BC 为截面圆的直径,∴∠BAC =90°,△ABC 的外接圆圆心N 是BC 的中点,同理△A 1B 1C 1的外心M 是B 1C 1的中心.设正方形BCC 1B 1的边长为x ,Rt △OMC 1中,OM =x 2,MC 1=x 2,OC 1=R =1(R 为球的半径),∴⎝⎛⎭⎫x 22+⎝⎛⎭⎫x 22=1,即x =2,则AB =AC =1,∴S 矩形ABB 1A 1=2×1= 2.角度三:正方体的外接球3.一个正方体削去一个角所得到的几何体的三视图如图所示(图中三个四边形都是边长为2的正方形),则该几何体外接球的体积为________.解析:依题意可知,新的几何体的外接球也就是原正方体的外接球,要求的直径就是正方体的体对角线;∴2R =23(R 为球的半径),∴R =3,∴球的体积V =43πR 3=43π. 答案:43π角度四:四棱锥的外接球4.(2014·大纲卷)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )A.81π4 B .16π C .9π D.27π4解析:选A 如图所示,设球半径为R ,底面中心为O ′且球心为O ,∵正四棱锥P -ABCD中AB =2,∴AO ′= 2.∵PO ′=4,∴在Rt △AOO ′中,AO 2=AO ′2+OO ′2,∴R 2=(2)2+(4-R )2,解得R=94,∴该球的表面积为4πR 2=4π×⎝⎛⎭⎫942=81π4,故选A. [类题通法]“切”“接”问题的处理规律1.“切”的处理解决与球的内切问题主要是指球内切多面体与旋转体,解答时首先要找准切点,通过作截面来解决.如果内切的是多面体,则作截面时主要抓住多面体过球心的对角面来作.2.“接”的处理把一个多面体的几个顶点放在球面上即为球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.[牛刀小试]1.(2015·云南一检)如果一个空间几何体的正视图、侧视图、俯视图都是半径等于5的圆,那么这个空间几何体的表面积等于( )A .100π B.100π3 C .25π D.25π3解析:选A 易知该几何体为球,其半径为5,则表面积为S =4πR 2=100π.2.(2014·陕西高考)已知底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )A.32π3 B .4π C .2π D.4π3解析:选D 因为该正四棱柱的外接球的半径是四棱柱体对角线的一半,所以半径r =1212+12+(2)2=1,所以V 球=4π3×13=4π3.故选D. 3.已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的底面边长为6时,其高的值为( )A .3 3 B.3 C .2 6 D .2 3解析:选D 设正六棱柱的高为h ,则可得(6)2+h 24=32,解得h =2 3. 4.(2015·山西四校联考)将长、宽分别为4和3的长方形ABCD 沿对角线AC 折起,得到四面体A -BCD ,则四面体A -BCD 的外接球的体积为________.解析:设AC 与BD 相交于O ,折起来后仍然有OA =OB =OC =OD ,∴外接球的半径r =32+422=52,从而体积V =4π3×⎝⎛⎭⎫523=125π6. 5.一个圆锥过轴的截面为等边三角形,它的顶点和底面圆周在球O 的球面上,则该圆锥的体积与球O 的体积的比值为________.解析:设等边三角形的边长为2a ,则V 圆锥=13·πa 2·3a =33πa 3;又R 2=a 2+(3a -R )2,所以R =233a ,故 V 球=4π3·⎝⎛⎭⎫233a 3=323π27a 3,则其体积比为932. [高考全国课标卷真题追踪]1.(15课标1理)已知,A B 是球O 的球面上两点,090AOB ∠=,C 为该球面上的动点,若O ABC -三棱锥体积的最大值为36,则球O 的表面积为( C )(A)36π (B)64π (C)144π (D)256π2.(13课标1理)如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的体积为( A )(A )3cm 3500π (B )3cm 3866π (C )3cm 31372π (D )3cm 32048π 3.(12课标理)已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( A )(A)26 (B)36 (C)23 (D )224.(12课标文)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为 ( B )(A )6π (B )43π (C )46π (D )63π5.(10新课标理)设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为( B )(A) 2a π (B) 273a π (C) 2113a π (D) 25a π 6.(10新课标文)设长方体的长、宽、高分别为2,,a a a ,其顶点都在一个球面上,则该球的表面积为( B )(A )23a π (B )26a π (C )212a π (D )224a π 7.(07新课标文)已知三棱锥S ABC -的各顶点都在一个半径为r 的球面上,球心O 在AB 上,SO ⊥底面ABC ,2AC r =,则球的体积与三棱锥体积之比是(D)A.π B.2π C.3π D.4π8.(13新课标2文)已知正四棱锥O ABCD -的体积为322,底面边长为3,则以O 为球心,OA 为半径的球的表面积为24π。

几何体与球的切接1.已知侧棱与底面垂直的三棱柱ABC−A1B1C1满足AA1=2AB=2BC=4,∠ABC=90∘,则其外接球的表面积为______.2.正四棱锥P−ABCD的侧棱和底面边长都等于2√2,则它的外接球的表面积是()A. 16πB. 64πC. 16π3D. 64π33、在△ABC中,AB=8,BC=6,AC=10,P为△ABC外一点,满足PA=PB=PC= 5√5,则三棱锥P−ABC的外接球的半径为______.4、如图所示,在三棱锥P−ABC中,PA⊥底面ABC,AC=1,AB=3,BC=√7,PA=√63,则该三棱锥外接球的表面积为______.5.已知正四面体的棱长为4,则此四面体的外接球的表面积是( )A. 24πB. 18πC. 12πD.6π6、已知四棱锥的顶点都在球O的球面上,底面ABCD是矩形,平面PAD⊥底面ABCD,ΔPAD为正三角形,AB=2AD=4,则球O的表面积为( )A. 56π3B. 64π3C. 24πD. 80π37.三棱锥P−ABC的一条棱长为m,其余棱长均为2,当三棱锥P−ABC的体积最大时,它的外接球的表面积为()A. 21π4B. 20π3C. 5π4D. 5π38、已知三棱锥S−ABC的三条侧棱SA.SB.SC两两互相垂直,且AC=√13,此三棱锥的外接球的表面积为14π,设AB=m,BC=n,则m+n的最大值为()A. √30B. 4√2C. √35D. 3√59.在正三棱锥S−ABC中,M,N分别是SC,BC的中点,且MN⊥AM,若侧棱SA=2√2,则正三棱锥S−ABC外接球的体积是()A. 8√6πB. 12πC. 24πD. 4√6π10.已知三棱锥D−ABC的体积为2,△ABC是边长为2的等边三角形,且三棱锥D−ABC的外接球的球心O恰好是CD的中点,则球O的表面积为A. 52π3B. 40π3C. 25π3D. 24π11.在三棱锥A−SBC中,AB=√10,∠ASC=∠BSC=π4,AC=AS,BC=BS,若该三棱锥的体积为√153,则三棱锥S−ABC外接球的体积为A. πB. 4√3πC. √5πD. π312、如图,求一个棱长为√2的正四面体的体积,可以看成一个棱长为1的正方体截去四个角后得到,类比这种方法,一个三对棱长相等的四面体ABCD ,其三对棱长分别为AB =CD =√5,AD =BC =√13,AC =BD =√10,则此四面体的体积为_______13.三棱锥中成异面直线的一对棱称为相对的棱,已知三棱锥A −BCD 中三组相对的棱分别相等,AB =5,BC =√41,且所有顶点都在一个半径为5√22的球面上,则三棱锥A −BCD 的体积为________.14、已知如图所示的几何体是由一个半球与一个圆锥组合而成的,其中半球的大圆面与圆锥的底面重合,且圆锥的母线长与底面直径均为2,若在该几何体内部放入一球,则此球半径的最大值为( )A. 1B. √22C. √3+13D. √3+1215、已知一个高为1的三棱锥,各侧棱长都相等,底面是边长为边长为2的等边三角形,内有一个体积为V 的球,则V 的最大值为( )A. 4 π 81B. C. D.1、【答案】24π解:由题意,直三棱柱ABC −A 1B 1C 1的底面ABC 为等腰直角三角形, 把直三棱柱ABC −A 1B 1C 1补成正四棱柱, 则正四棱柱的体对角线是其外接球的直径,所以外接球半径为R =√4+4+162=√6,表面积为S =4π⋅6=24π.故答案为24π. 2.【答案】A解:如图,设正四棱锥底面的中心为O 1,设外接球的球心为O , 则O 在正三棱锥的高PO 上. 在直角三角形ABC 中,AC =√2AB =√2×2√2=4,AO 1=2,则高PO 1=√AP 2−AO 12=√(2√2)2−22=√8−4=√4=2,则OO 1=PO 1−R =2−R ,OA =R ,在直角三角形AO 1O 中,R 2=(2−R)2+22,解得R =2,即O 与O 1重合, 即正四棱锥外接球的球心是它的底面的中心O 1,且球半径R =2, 球的表面积S =4πr 2=16π 3、【答案】52解:在△ABC 中,AB =8,BC =6,AC =10,所以AB 2+BC 2=AC 2, P 为△ABC 外一点,满足PA =PB =PC =5√5,则PD ⊥平面ABC , 球心O 为PD 上一点,如图所示:所以:PD =√(PA)2−(PD)2=10, 设球的半径为R ,所以R 2=52+(10−R)2, 解得:R =52.故答案为:52 4、【答案】10π解:在底面△ABC 中,AC =b =1,AB =c =3,BC =a =√7, 由余弦定理,可得;cosA =b 2+c 2−a 22bc =1+9−72×1×3=12,即A =60°,由正弦定理可得,2r =asinA =√7√32,∴r =√213.∵PA ⊥底面ABC ,∴球心与圆心的距离为12AP =√66,∵球心与圆心的接线垂直,构成直角三角形,∴R 2=r 2+(√66)2,∴R 2=156,该三棱锥外接球的表面积S =4πR 2=10π.故答案为10π.5.【答案】A 解:如图所示∵正四面体A −BCD ,棱长AD =4, ∴此三棱锥一定可以放在正方体中, 将正四面体补成一个正方体,则正方体的棱长为2√2,正方体的对角线长为2√6,∵正四面体的外接球的直径为正方体的对角线长,外接球的半径为:√6, ∴外接球的表面积的值为4π·(√6)2=24π. 6、【答案】B解:令△PAD 所在圆的圆心为O 1,则圆O 1的半径,因为平面PAD ⊥底面ABCD , 所以OO 1=12AB =2, 所以球O 的半径R =(2√33)=4√3,所以球O 的表面积=4πR 2=64π3.7、【答案】B解:由题意,三棱锥P −ABC 的一条棱长为m ,其余棱长均为2,可看成是菱形PABC , 即PA =PC =AB =AC =BC =2,PD =m .以AC 对折可得;当面ACP ⊥ABC 时,可得三棱锥P −ABC 的体积最大, 此时高为√3.底面为△ABC ,其外接圆半径r =√3,设外接球的半径为R ,球心与圆心的距离为x ,可得:(√3−x)2+(√33)2=R 2……①x 2+r 2=R 2……② 由①②解得:R 2=53 外接球的表面积S =4πR 2=20π3.8、【答案】A解:三棱锥S −ABC 的三条侧棱SA.SB.SC 两两互相垂直, 则此三棱锥的外接球为以SA ,SB ,SC 为棱的长方体的外接球,设SA =a ,SB =b ,SC =c ,外接球的半径为r ,则a 2+b 2+c 2=(2r )2=4r 2, 又因为外接球的表面积为,所以,解得r 2=72,所以a 2+b 2+c 2=4r 2=14,则{a 2+b 2=m 2b 2+c 2=n 2a 2+c 2=(√13)2,化简整理可得:a 2+b 2+c 2=12(m 2+n 2+13)=14, 则m 2+n 2=15,所以由基本不等式的性质:当m >0,n >0时,(m+n 2)2≤m 2+n 22=152,所以m +n ≤30,当且仅当m =n 时,取等号, 故选A . 9、【答案】A解:∵M ,N 分别是棱SC 、BC 的中点, ∴MN//SB ,MN ⊥AM ,可得SB ⊥AM , 由正三棱锥的性质可得SB ⊥AC , ∴SB ⊥平面SAC ⇒SB ⊥SA 且SB ⊥AC , ∵三棱锥S −ABC 是正三棱锥,∴SA 、SB 、SC 三条侧棱两两互相垂直.侧棱SA =2√2, ∴正三棱锥S −ABC 的外接球的直径为:2R =√(2√2)2+(2√2)2+(2√2)2=2√6,R =√6, 故正三棱锥S −ABC 外接球的体积是43πR 3=8√6π, 10、【答案】A解:设球O 的半径为R ,球心O 到平面ABC 的距离为d , 由三棱锥D −ABC 的外接球的球心O 恰好是CD 的中点, 得V D−ABC =2V O−ABC =23×12×22×√32d =2,解得d =√3,所以R 2=(√3)2+(2√33)2=133,所以球O 的表面积为4πR 2=52π3,11、【答案】B解:如图,设SC 的中点为O ,AB 的中点为D ,连接OA ,OB ,OD . 因为,AC =AS ,BC =BS ,所以∠SAC =SBC =90°,所以OA =OB =OC =OS =R . 又OD ⊥AB ,且AB =√10,所以AD =DB =√102,OD =√R 2−52,则S ▵OAB =12⋅AB ⋅OD =12√10R 2−25.SC ⊥OA,SC ⊥OB,OA ∩OB =O ,则SC ⊥平面OAB ,所以V A−SBC =13×12√10R 2−25×2R =√153,解得R =√3.所以外接球的体积V =4π3⋅(√3)3=4√3π.11、【答案】B解:如图,设SC 的中点为O ,AB 的中点为D ,连接OA ,OB ,OD .因为,AC =AS ,BC =BS ,所以∠SAC =SBC =90°, 所以OA =OB =OC =OS =R .又OD ⊥AB ,且AB =√10,所以AD =DB =√102,OD =√R 2−52,则S ▵OAB =12⋅AB ⋅OD =12√10R 2−25.SC ⊥OA,SC ⊥OB,OA ∩OB =O ,则SC ⊥平面OAB , 所以V A−SBC =13×12√10R 2−25×2R =√153,解得R =√3.所以外接球的体积V =4π3⋅(√3)3=4√3π.12.【答案】2解:设四面体ABCD 所在长方体的棱长分别为a ,b ,c , 则{a 2+b 2=5a 2+c 2=13b 2+c 2=10,解得{a 2=4b 2=1c 2=9, ∴四面体的体积V =abc −13×12abc ×4=13abc =13√a 2b 2c 2=213.【答案】20解:由题意, 构造长方体,其面上的对角线构成三棱锥A −BCD , 设长方体的长,宽,高分别为a ,b ,c ,则{2+b 2=25a 2+c 2=41a 2+b 2+c 2=50,解得a =4,b =3,c =5. 所以三棱锥A −BCD 的体积V =4×3×5−4×13×12×4×3×5=20. 14、【答案】C解:当球与圆锥母线相切,且与半球球面相切时,球的半径最大,其正投影如图,设放入球的半径为r ,则(√3+1)−r =2r , 解得r =√3+13,故选C .15、【答案】A 解:如图所示:设底面三角形ABC 的中心为G , 由△ABC 是边长为2的正三角形, 得AG =23√22−12=2√33,又PG =1,∴PA =(2√33)=√213,即三棱锥侧棱长为√213,∴斜面底边上的高为ℎ=2√33,则一个侧面三角形的面积为12×2×2√33=2√33,设三棱锥内切球的半径为r ,则13×12×2×√3×1=(13×12×2×√3+3×13×12×2×2√33)r ,解得r =13,∴V 的最大值为43π×(13)3=4π81.故选A .。

第 1 页共 2页 球与几何体的的切接问题考试核心:性质的应用22212r R OO d -==,构造直角三角形建立三者之间的关系。
类型一:有公共底边的等腰三角形,借助余弦定理求球心角。
(两题互换条件形成不同的题)1.如图球O 的半径为2,圆1O是一小圆,1OO ,A 、B 是圆1O 上两点,若A ,B 两点间的球面距离为23π,则1AO B ∠= .)2..如图球O 的半径为2,圆1O是一小圆,1OO ,A 、B 是圆1O 上两点,若1AO B ∠=2π,则A,B 两点间的球面距离为类型二:球内接多面体,利用圆内接多边形的性质求出小圆半径,通常用到余弦定理求余弦值,通过余弦值再利用正弦定理得到小圆半径r Cc 2sin =,从而解决问题。
3.. 直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===, 120BAC ∠=︒,则此球的表面积等于 。
4.正三棱柱111ABC A B C -内接于半径为2的球,若,A B 两点的球面距离为π,则正三棱柱的体积为 .5.已知球的直径SC =4,A ,B 是该球球面上的两点,AB =3, 30=∠=∠BSC ASC ,则棱锥S —ABC 的体积为 A .33B .32C .3D .16.已知,,,S A B C 是球O 表面上的点,SA ABC ⊥平面,AB BC ⊥,1SA AB ==,BC =O 表面积等于(A )4π (B )3π (C )2π (D )π类型三:通过线线角、线面角、面面角之间的平面的转化,构造勾股定理处理问题。
7.设OA 是球O 的半径,M 是OA 的中点,过M 且与OA 成45°角的平面截球O 的表面得到圆C 。
若圆C 的面积等于74π,则球O 的表面积等于 .9.如果把地球看成一个球体,则地球上的北纬060纬线长和赤道长的比值为第 2 页共 2页 (A )0.8 (B )0.75 (C )0.5 (D )0.25类型四:球内接多面体的相关元素之间的联系。

专题19 几何体中与球有关的切、接问题球的截面的性质(1)球的任何截面是圆面;(2)球心和截面(不过球心)圆心的连线垂直于截面;(3)球心到截面的距离d 与球的半径R 及截面的半径r 的关系为r =R 2-d 2几个与球有关的切、接常用结论(1)正方体的棱长为a ,球的半径为R ,①若球为正方体的外接球,则2R =3a ;②若球为正方体的内切球,则2R =a ;③若球与正方体的各棱相切,则2R =2a .(2)若长方体的同一顶点的三条棱长分别为a ,b ,c ,外接球的半径为R ,则2R =a 2+b 2+c 2.(3)正四面体的外接球与内切球的半径之比为3∶1.一、题型选讲题型一 、几何体的外接球解决多面体的外接球问题,关键是确定球心的位置,方法是先选择多面体中的一面,确定此面外接圆的圆心,再过圆心作垂直此面的垂线,则球心一定在此垂线上,最后根据其他顶点确定球心的准确位置.对于特殊的多面体还可采用补成正方体或长方体的方法找到球心位置.例1、【2020年高考全国Ⅰ卷理数】已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为A .64πB .48πC .36πD .32π例2、【2020年高考天津】若棱长为A .12πB .24πC .36πD .144π 例3、(2020届山东省潍坊市高三上学期统考)已知边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕进行折叠,使折后的2BDC π∠=,则过A ,B ,C ,D 四点的球的表面积为( ) A .3π B .4π C .5π D .6π例4、(2020届山东省日照市高三上期末联考)已知四棱锥P ABCD -的体积是ABCD 是正方形,PAB ∆是等边三角形,平面PAB ⊥平面ABCD ,则四棱锥P ABCD -外接球体积为( )A .B C D .例5、(2020届山东省德州市高三上期末)中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知PA ⊥平面ABCE ,四边形ABCD 为正方形,AD =ED =P ADE -的外接球的体积为,则阳马P ABCD -的外接球的表面积等于______.题型二、几何体的内切球求解多面体的内切球的问题,一般是将多面体分割为以球心为顶点,多面体的各面为底面的棱锥,利用多面体的体积等于各棱锥的体积之和求内切球的半径.例6、【2020年高考全国Ⅲ卷理数】已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.例7、(2020届山东省潍坊市高三上期中)如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的表面积为__________;若该六面体内有一小球,则小球的最大体积为___________.二、达标训练1、(2020届山东省泰安市高三上期末)已知正三棱锥S ABC -的侧棱长为6,则该正三棱锥外接球的表面积是( )A .16πB .20πC .32πD .64π2、【2020年高考全国II 卷理数】已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为A B .32 C .1 D 3、【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为A .B .C . D4、【2018年高考全国Ⅰ卷理数】设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为D ABC -体积的最大值为A .B .C .D .5、【2020年新高考全国Ⅰ卷】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以1D 半径的球面与侧面BCC 1B 1的交线长为________.6、(2020届山东省滨州市三校高三上学期联考)已知三棱锥S ABC -,SA ⊥平面ABC ,6ABC π∠=,3SA =,1BC =,直线SB 和平面ABC 所成的角大小为3π.若三棱锥S ABC -的四个顶点都在同一球面上,则该球的表面积为________.7、(2020届山东省枣庄、滕州市高三上期末)如图,在三棱锥P -ABC 中,,PA AB ⊥PC BC ⊥,,AB BC ⊥22,AB BC ==PC =,则PA 与平面ABC 所成角的大小为________;三棱锥P -ABC 外接球的表面积是________.8、(2020届山东省烟台市高三上期末)已知三棱锥P ABC -的四个顶点都在球O 的表面上,PA ⊥平面ABC,6PA =,AB =2AC =,4BC =,则:(1)球O 的表面积为__________;(2)若D 是BC 的中点,过点D 作球O 的截面,则截面面积的最小值是__________.9、(2020届山东省滨州市高三上期末)在四面体S ABC -中,2SA SB ==,且SA SB ⊥,BC =AC=________,该四面体外接球的表面积为________.10、(2020届山东省济宁市高三上期末)下图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形-的外接球的体积为ABCD,现将四边形ABCD沿BD折成直二面角A BD C--,则三棱锥A BCDcm.__________3。
4. 一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形.则该几
何体的表面积为()
练习:【2017课标II,文15】长方体的长、宽、高分别为3,2,1,其顶点都在球O的球空间几何体的三视图与球专项练习(A) 60 (B) 30 (C) 20 (D) 10
A.-
B.
C.
D. 面上,则球O的表面积为 ___________
8
(2)三棱柱、圆柱与外接
球
①正(直)三棱柱、圆柱外接球球心为两底外接圆圆心连线的中点
3.【2017北京,文6】某三棱锥的三视图如图所示,则该三棱锥的体积为()
A
OA2 OE2 AE2 ,其中OA=R
2 2 .
3 3 5
AE - AD AB AB
3 3 2 3
求三角形ABC外接圆半径R:正弦定理
a
sin A
b
sin B
c
si nC
2R
专题一.空间几何体的三视图
1. 某几何体的三视图如图所示,其俯视图是由一个半圆与其直径组成的图形,贝U该几何
体的体积是___________ 表面积是____________
A. 88 .158
专题二.几何体及它的外接球
1.柱体外接球
(1)长方体与外接球
2. 一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩
2 2.2 2 (2R) a b c
余部分体积的比值为()
2.【2017课标3,理8】已知圆柱的高为1,它的两个底面的圆周在直径为 2的同一个 球的球面上,则该圆柱的体积为( ) A.n
B. 3n
C. -
D.-
4 2 4
②底面有一角为直角的直三棱柱外接球求法 方法一:由①可知球心在AB 的中点,半径算法同
①
方法二:如图所以,将三棱柱补成长方体,半径 算法与长
方体半径算法相同
练习:1.求棱长为a 的正四面体外接球的半径.(正四面体外接球半径是高的
2.正四棱锥的顶点都在同一球面上,若该棱锥的高为 4,底面边长为2,求该球的表面
积.
练习:已知S,代B,C 是球0表面上的点, SA 平面ABC , AB BC , SA AB 1 , BC '.2,则球O 的表面积等于(
)
求三角形ABC 内切圆半径r :面积法S
ABC
(a b c) r = absinC
2 2
2.锥体外接球
练习:1.设三棱柱的侧棱垂直于底面,所有棱的长都为 a ,顶点都在一个球面上,则该
(1)正棱锥与圆锥外接球
球的表面积为()
OB 2 R 2 (PH R)2 AH 2
(A ) 4 (B ) 3
(C ) 2
(D )
3
3)
(1) 试探究如何切割可以得到一个棱长为 .2的正四面体
(2) 求出这个正四面体的外接球的半径.
(2)底面为直角三角形,一侧棱与底面垂直的三棱锥:补成长方体
练习:1.已知三棱锥S-ABC 从S 点出发的三条棱两两垂直且 SA=1, SB=2 SC=3则该
三棱锥的外接球的半径为(
)
1
练习:求棱长为a 的正四面体内切球的半径.(正四面体内切球半径是高的-)
思考:已知一个棱长为1的正方体,
2.网格纸上的小正方形边长是1,粗实线画出的是某四棱锥的三视图,则该四棱锥的外 接球的表面积为( )
n
n
n
n
球的大圆与底面多边形的内切圆全等,且柱 体的高度与球的直接相等
专题三.几何体及它的内切球
1.正三棱柱,直三棱柱,圆柱内切球
2.棱锥的内切球:等体积法,
V 1S
表面
j
r ( r
为内切球半径)
:0
f
1_卄
P
A
B
H
求法:利用轴截面结合平面几何知识求解
r
1
sin
或S PAB -周长
PH r 2
r 为内切球半径,周长为三角形 PAB 周
长
练习:1.已知三棱锥S
专题练习
ABC 的所有顶点都在球0的求面上,
ABC 是边长为1的正三
角
形,SC 为球0的直径,且SC 2 ;则此棱锥的体积为(
(A
V
(C)
于
(D)上
2
上、下面及母线均相切•记圆柱r O 1.O 2的体积为V 1 ,球O 的体积为V 2,则生的值是
•
V 2
4. 已知OA 为球O 的半径,过OA 的中点M 且垂直于OA 的平面截球面得到圆M ,若圆M
的面积为3,则球O 的表面积等于 ______________________ .
5. 某圆锥的截面为边长为2的正三角形,则该圆锥的内切球的表面积为 ___________
6. (2013年高考课标I 卷(文))已知H 是球O 的直径AB 上一点.AH : HB 1:2. AB 平面.H 为垂足.截球O 所得截面的面积为 .则球O 的表面积为 ________________ .
7. 已知三棱锥A — BCD 勺所有棱长都为灵,则该三棱锥的外接球的表面积为 __________ •
8. 直三棱柱ABC A 1B 1C 1的各顶点都在同一球面上,若
AB AC AA 2. BAC 120,则此球的表面积等于 ______________________
"01已知直三昨心-斗芍q ・ 杠面是边长为五的正三角形,為为込 若它的六
顼点都在球G 的阵而上* SWO 的体积为
(C)
迟
3.【2017江苏,6】 如图,在圆柱01; 02内有一个球O ,该球与圆柱。