判断是否为线性系统例题

线性系统和⾮线性系统⼀、线性和⾮线性的区别？线形指量与量之间按⽐例、成直线的关系，在空间和时间上代表规则和光滑的运动；飞线性则指不按⽐例、不成直线的关系代表不规则的运动和突变。

⼆、如何判断⼀个系统是线形还是⾮线性系统？如果从系统状态空间表达式来观察，线性系统和⾮线性系统最明显的区别⽅式就是线性系统符合叠加原理，⽽⾮线性系统不然。

换句话说线性系统只有状态变量的⼀次项。

⾼次、三⾓函数以及常数项都没有，只要有任意⼀个⾮线性环节就是⾮线性系统。

三、⾮线性系统有⼀种⽅式是局部转化成线性系统才能控制？⾮线性系统不是不能控制⽽是不能掌控设想⼀下汽车的油门是⾮线性控制，如果踩⼀⼩点速度猛然上升，这种现象在现实中不希望看到，现实中需要缓慢的线性变化，⽽不是突变的⾮线性变化。

线形系统具有规律可循，只要找到系统的⼀部分就可以推算出其他部分，⾮线性系统⽆规律可循，于是将⾮线性系统近似为线性系统也是飞线性系统的⼀种计算⽅式。

四、⾮线性系统和线性系统相⽐具有什么特点？（1）线性系统的稳定性和输出特性，只取决于本⾝的结构和参数。

⽽⾮线性系统的稳定性和输出动态过程。

不仅与本⾝的结构和参数有关，⽽且还与系统的初始条件和输⼊信号⼤⼩有关。

（2）⾮线性系统的平衡运动状态，除平衡点外还可能有周期解。

周期解有稳定和不稳定两类，前者观察不到，后者是实际可观察到的。

因此在某些⾮线性系统中，即使没有外部输⼊作⽤也会产⽣有⼀定振幅和频率的振荡，称为⾃激振荡，相应的相轨线为极限环。

改变系统的参数可以改变⾃激振荡的振幅和频率。

这种特性可⽤于实际⼯程问题，以达到某种技术⽬的。

例如根据温度来影响⾃激振荡，可以构成双位式温度调节器。

（3）线性系统的输⼊为正弦函数时，其输出的稳态过程也是同频率的正弦函数，两者仅在相位和幅值上不同。

但⾮线性系统的输⼊为正弦函数时，其输出则包含有⾼次谐波的⾮正弦周期函数，即输出会产⽣倍频、分频、频率。

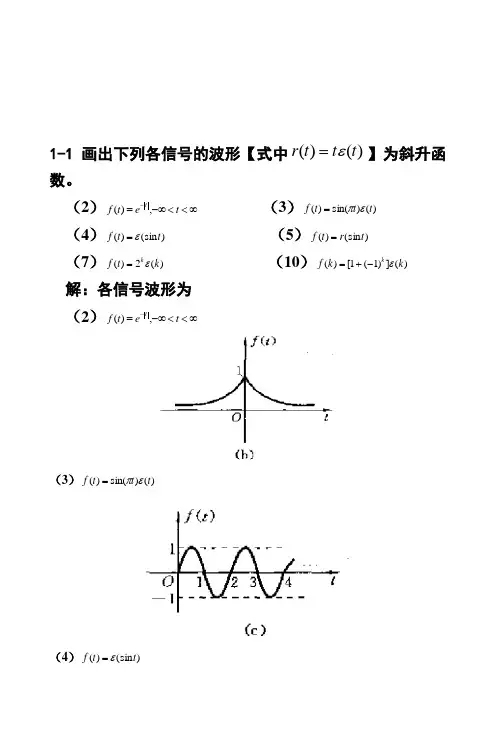
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)f=rt)(sin(t （7）)t(k=f kε)(2（10）)f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）)63cos()443cos()(2ππππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。

x-2 -10 1/扼 1 2 x -6 0 0.385 0 -0.3850 6 x1121211当x(0)》1时，系统发散；x (0) < -1x ~ x 平面上任意分布。

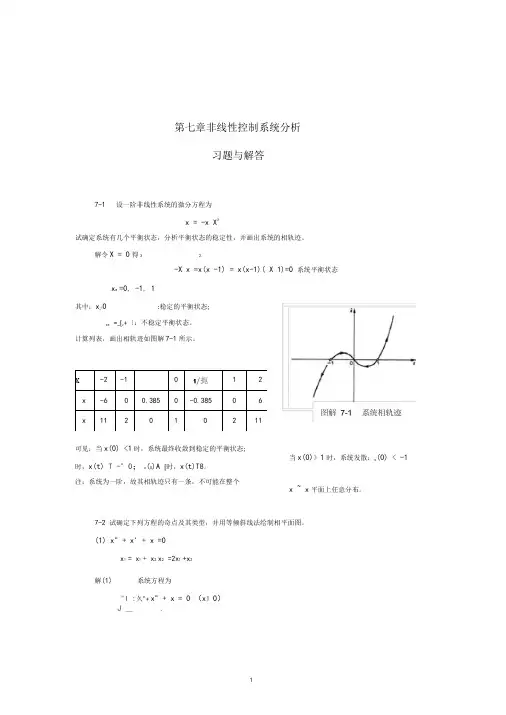
第七章非线性控制系统分析习题与解答7-1 设一阶非线性系统的微分方程为x = -x X 3试确定系统有几个平衡状态，分析平衡状态的稳定性，并画出系统的相轨迹。

解令X = 0得 32-X x =x(x -1) = x(x-1)( X 1)=0 系统平衡状态x e =0, -1, 1其中：x e=0:稳定的平衡状态;xe=_[,+〔：不稳定平衡状态。

计算列表，画出相轨迹如图解 7-1所示。

可见：当x(0) <1时，系统最终收敛到稳定的平衡状态;时，x(t) T -°0； x (0)A [时，x(t)T8。

注：系统为一阶，故其相轨迹只有一条，不可能在整个7-2 试确定下列方程的奇点及其类型，并用等倾斜线法绘制相平面图。

(1) x" + x' + x =0x 1 = x 1 + x 2 x 2 =2x 1 +x 2解(1)系统方程为"I :久”+ x" + x = 0 （x 》0）J __ .]I : X + X _x = 0 （x < 0）令x” = x =0，得平衡点：桅=0。

系统特征方程及特征根：' 2 i 73 」I : s + s +1 = 0, s1 2= ———j —（稳正的焦点）2II： s +s—1=0, §,2=—1.618, 和.618 （鞍点）x = f （x, x） = _x — x , 坚艾=一父一乂dxdx |x| . -1x =E|xCt - 一一1 一. , x -dx x 1 +a' 1I ：0（= —1 -它（x》0）i 1!II： a =— -1 （x <0）用等倾斜线法绘制系统相平面图如图解7-2 ( a )所示。

1.判断下列系统的线性、时不变性、因果性和记忆性。

（解析P7） ①()10()()dy t y t f t dt += ②()()(10)dy t y t f t dt+=+ ③2()()()dy t t y t f t dt+= ④2()(10)()y t f t f t =++2.判断下列系统的线性、时不变性和因果性。

（解析P7） ①20()()sin ()y t y t t at f t =+ ②()()()y t f t f t b =⋅-3.某系统，当输入为()tδτ-时，输出为()()(3)h t u t u t ττ=---，问该系统是否为因果系统？是否为时不变系统？说明理由。

4.下列信号属于功率信号的是（解析P6） ①cos ()tu t ②()teu t - ③()t te u t - ④te-5. 画出函数波形图：2()(1)f t u t =-（指导P12）6.已知()()2(1)(2)(2),f t tu t u t t u t =--+--画出()f t 波形。

（指导P13） 7.根据1.10图中(32)f t -+的波形，画出()f t 波形。

（指导P18） 8.已知()f t 波形波形如例1.11图所示，试画出1(2)2f t --的波形。

（指导P19） 9.已知(52)f t -的波形如图例1.12图所示，求()f t 波形。

（指导P20） 10.求下列函数值 ①432'(652)(1)t t t t dt δ∞+++-⎰②3'()te d τδττ--∞⎰ ③'2(9)t dt δ+∞-∞-⎰ （指导P24）11.求信号0.20.3()j n j n x n ee ππ-=+的周期。

（指导P36） 12.设()x t 是复指数信号：0()j tx t eΩ=，其角频率为0Ω，基本周期为02T π=Ω。

如果离散时间序列是通过对()x t 以取样间隔s T 进行均匀取样的结果，即00()()s j nT j n s x n x nT e e ωΩ===。

《数字信号处理》复习思考题、习题（一）一、选择题1．信号通常是时间的函数，数字信号的主要特征是：信号幅度取 ；时间取 。

A.离散值；连续值B.离散值；离散值C.连续值；离散值D.连续值；连续值2．一个理想采样系统，采样频率Ωs =10π，采样后经低通G(j Ω)还原，⎪⎩⎪⎨⎧≥Ω<Ω=Ωππ5 05 51)(j G ；设输入信号：t t x π6cos )(=，则它的输出信号y(t)为： 。

A ．t t y π6cos )(=； B. t t y π4cos )(=；C ．t t t y ππ4cos 6cos )(+=； D. 无法确定。

3．一个理想采样系统，采样频率Ωs =8π，采样后经低通G(j Ω)还原，G j ()ΩΩΩ=<≥⎧⎨⎩14404 ππ；现有两输入信号：x t t 12()cos =π，x t t 27()cos =π，则它们相应的输出信号y 1(t)和y 2(t)： 。

A ．y 1(t)和y 2(t)都有失真； B. y 1(t)有失真，y 2(t)无失真；C ．y 1(t)和y 2(t)都无失真； D. y 1(t)无失真，y 2(t)有失真。

4．凡是满足叠加原理的系统称为线性系统，亦即： 。

A. 系统的输出信号是输入信号的线性叠加B. 若输入信号可以分解为若干子信号的线性叠加，则系统的输出信号是这些子信号的系统输出信号的线性叠加。

C. 若输入信号是若干子信号的复合，则系统的输出信号是这些子信号的系统输出信号的复合。

D. 系统可以分解成若干个子系统，则系统的输出信号是这些子系统的输出信号的线性叠加。

5．时不变系统的运算关系T[·]在整个运算过程中不随时间变化，亦即 。

A. 无论输入信号如何，系统的输出信号不随时间变化B. 无论信号何时输入，系统的输出信号都是完全一样的C. 若输入信号延时一段时间输入，系统的输出信号除了有相应一段时间延时外完全相同。

一．离散信号及系统1 .已知线性移不变系统的输入为)n (x ,系统的单位抽样响应为)n (h ,试求系统的输出)n (y ,并画图。

)(5.0)(,)1(2 )()4()(5.0)(,)2( )()3()()(,)( )()2()()(,)( )()1(3435n u n h n u n x n R n h n n x n R n h n R n x n R n h n n x n n n =--==-=====δδ2 .已知 10,)1()(<<--=-a n u a n h n，通过直接计算卷积和的办法，试确定单位抽样响应为 )(n h 的线性移不变系统的阶跃响应。

3. 判断下列每个序列是否是周期性的,若是周期性的,试确定其周期：)6()( )( )n 313sin()( )()873cos()( )(ππππ-==-=n j e n x c A n x b n A n x a )()(*)()( )1( 5n R n h n x n y ==解：}1,2,3,3,2,1{)(*)()( )2(==n h n x n y )2(5.0)(5.0*)2()( )3(323-=-=-n R n R n n y n n δ)(5.0)( )1(2)( )4(n u n h n u n x n n =--=n mm m n n y n ---∞=-⋅==≥∑23125.0)( 01当nm nm m n n y n 23425.0)( 1⋅==-≤∑-∞=-当aa a n y n a a an y n n h n x n y a n u a n h n u n x m m nnm mn -==->-==-≤=<<--==∑∑--∞=---∞=--1)(11)(1)(*)()(10,)1()()()(:1时当时当解。

周期为是周期的解：14, 31473/2/2 )873cos()()( 0∴==-=ππωπππn A n x a。

信号与系统（程耕国）下册课后习题答案6.2 精选例题例 1 设一个LTI 离散系统的初始状态不为零，当激励为)()(1n u n f =时全响应为)(121)(1n u n y n ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛=，当激励为)()(2n u n f -=时全响应为)(121)(2n u n y n ⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛-=。

（1）当系统的初始状态保持不变，且激励为)(4)(3n u n f =时，求系统的全响应)(3n y 。

（2）当系统的初始状态增加一倍，且激励为)2(4)(4-=n u n f 时，求系统的全响应)(4n y 。

（3）求该系统的单位序列响应)(n h 。

解：设系统的初始状态保持不变，当激励为)()(1n u n f =时系统的零输入响应和零状态响应分别为)(n y x 、)(n y f 。

依题意，有：)(121)()()(1n u n y n y n y n f x ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛=+= ○1根据LTI 系统的性质，当激励为)()(2n u n f -=时全响应为)(121)(()(2n u n y n y n y n f x ⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛-=-=） ○2联立式○1、○2，可解得：⎪⎪⎩⎪⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=++++)(12121)()(2121(1111n u n y n u n y n n f n n x ）同样，根据LTI 系统的基本性质，不难得到：（1）当系统的初始状态保持不变，且激励为)(4)(3n u n f =时，系统的全响应为：)(4)()(3n y n y n y f x +=)(121214)(21211111n u n u n n n n ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=++++)(421321511n u n n ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛=++（2）当系统的初始状态增加一倍，且激励为)2(4)(4-=n u n f 时，系统的全响应为：)2(4)(2)(4-+=n y n y n y f x)2(121214)(21211111-⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=--++n u n u n n n n（3）由于)1()()(--=n u n u n δ，所以该系统的单位序列响应为：)1()()(--=n y n y n h f f)1(12121)(1212111-⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛=++n u n u n n n n 例2 一个LTI 连续系统对激励)(sin )(t tu t f =的零状态响应)(t y f 如例2图所示，求该系统的冲激响应)(t h 。

第十章非线性系统§ 10.1与线性系统的差异线性系统与非线性系统的不同之处在于：1 •非线性系统的运动是由一个非线性微分方程控制的，但是很多非线性方程都不存在精确解。

2. 一个非线性系统可能不只一个平衡点，而平衡点可能是稳定的，也可能是不稳定的。

3. 非线性系统是否存在稳态运动取决于初始条件。

4. 非线性系统的自由振动周期由初始条件决定，这就意味着自由振动的频率依赖于自由振动的振幅。

5. 非线性系统的共振出现在激发频率不同于系统的线性固有频率处，在一个三维非线性系统中，当激发频率为系统线性固有频率的1/3时，产生超频共振；当激发频率为系统线性固有频率近三倍时，就产生亚频共振。

6. 线性叠加原理不能用来分析受多频激励的非线性系统，共振的组合是对应于激发频率的近似组合。

7. 对应于固有频率的近似组合，在多自由度的连续系统中存在内共振。

8. 在非线性系统中，周期激励可能会引起非周期响应，由于一些特定的参数值，这种混沌运动出现在很多非线性系统中。

§10.1定性分析状态平面或相位平面是速度和位移在整个运动过程中的尖系曲线，通过在平衡点的邻域内将控制微分方程线性化，可以检验平衡点的性质及其稳定性（见题10.2），平衡点的各种类型如图10.1所示图 10.1§ 10.3达芬方程达芬方程是一个无量纲方程。

它作为一个模型可用于求解三维非线性系统。

如果 ；为正， 则表示一个硬弹簧的响应；如果；为负，则表示一个软弹簧系统的响应。

一个系统自 由振动的振幅尖系由达分方程决定，它可以用扰动方法近似表示为：3 A 2 0( 2) 8 其中㊂是固有频率的无量纲化(对于线性系统®=1), A 是振幅，分析共振附近 达芬方程的受迫响应可以设：：：；,2」；彳=F sin rt(10.1)(10.2)稳定节点(a)不稳定焦点2)(10.3)则稳态振幅的定义方程就可近似表示为4A2〔」2—叭2〔二F2(10.4)I 8丿」方程(70・4在图10.2中的尖系曲线表示为；• 0时中枢曲线和跳跃现象，对于给定的二值，方程(704有三个正实解，因为A2引起了三种可能的稳态运动，中间解是不稳定的，引起跳跃现象。

数字信号处理绪论1.模拟信号，离散信号，数字信号的定义；模拟信号：信号随时间（空间）连续变化，并且幅度值取自连续数据域。

自然界中大部分信号时模拟信号。

离散信号: 信号随时间（空间）以一定规律离散变化，幅度值取自连续数据域。

自然界中这样的信号很少，一般通过对模拟信号的采样形成，数字信号：信号随时间（空间）以一定规律离散变化，并且幅度值取自以二进制编码的离散数据域，一般通过对离散信号进行量化得到。

2.数字信号处理的组成；数字信号处理系统并不是孤立的数字系统，一般以数字处理系统为核心，结合A/D和D/A（数字-模拟）转换器、滤波器和放大器等子系统组成，前置低通滤波器将信号中大于1/2采样频率的高频分量过滤掉，防止采样是出现频谱混叠现象，A/D转换包含采样和量化，采样得倒离散信号，量化后每个离散信号将被数字编码形成数字信号，经过D/A转化后形成跳变的模拟信号必须通过拼花滤波器将信号变成平滑的连续信号。

3.数字信号处理的优点；1.软件可实现：纯粹的模拟信号必须完全通过硬件实现，而数字化处理则不仅可以通过微处理器、专用数字器件实现，而且可以通过程序的方式实现。

软件可实现特性带来的出处之一就是处理系统能进行大规模的复杂处理，而且暂用空间极小2.灵活性强：模拟信号处理系统调试和修改不便，而数字处理系统的系统参数一般保存在寄存器或存储器中，修改这些参数对系统进行调试非常简单，软件实现尤其如此。

由于数字器件以及软件的特点，数字信号处理系统的复制也非常容易，便于大规模生产。

3.可靠性高：模拟器件容易受电磁波、环境温度等因素影响，模拟信号连续变化，稍有干扰立即反映。

而数字器件是逻辑器件，一定范围的干扰不会引起数字值得变化，因此数字信号处理系统抗干扰性能强，可靠性高，数据也能永久保存。

4.精度高：模拟器件的数据表示精度低。

第一章．离散时间信号与系统1.奈奎斯特定理定义若要从采样后的信号频谱中不失真的恢复信号，则采样频率Ωs必须大于等于两倍的原信号频谱的最好截止频率Ωc，即Ωs≥2Ωc或f s≥2f c。

1．自动控制中的基本的控制方式有开环控制、闭环控制和复合控制。

正确2．系统的动态性能指标主要有调节时间和超调量，稳态性能指标为稳态误差。

正确3．如果系统的输出端和输入端之间不存在反馈回路，输出量对系统的控制作用没有影响时，这样的系统就称为开环控制系统。

正确4．凡是系统的输出端与输入端间存在反馈回路，即输出量对控制作用能有直接影响的系统，叫做闭环系统。

正确5．无静差系统的特点是当被控制量与给定值不相等时，系统才能稳定。

错误6．对于一个闭环自动控制系统，如果其暂态过程不稳定，系统可以工作。

错误7．叠加性和齐次性是鉴别系统是否为线性系统的根据。

正确8．线性微分方程的各项系数为常数时，称为定常系统。

正确1． 传递函数只与系统结构参数有关，与输出量、输入量无关。

正确2．对于非线性函数的线性化方法有两种：一种方法是在一定条件下，忽略非线性因素。

另一种方法就是切线法，或称微小偏差法。

正确3．在自动控制系统中，用来描述系统内在规律的数学模型有许多不同的形式，在以单输入、单输出系统为研究目标的经典控制理论中，常用的模型有微分方程、传递函数、动态结构图、频率特性等。

正确4. 控制系统的稳态误差大小取决于系统结构参数和外输入。

正确5．传递函数是复变量s 的有理真分式，分母多项式的次数n 高于分子多项式的次数m ，而且其所有系数均为实数。

正确6．在复数平面内，一定的传递函数有一定的零，极点分布图与之相对应。

正确7．传递函数是物理系统的数学模型，但不能反映物理系统的性质，因而不同的物理系统不能有相同的传递函数。

（错误 ）8．自然界中真正的线性系统是不存在的。

许多机电系统、液压系统、气动系统等，在变量之间都包含着非线性关系。

正确9．实际的物理系统都是线性的系统。

（ 错误10． 某环节的输出量与输入量的关系为()()t Kx t y =，K 是一个常数，则称其为惯性环节错误11.惯性环节的时间常数越大，则系统的快速性越好。

《信号与系统》2005 年期末试题A 卷班级姓名学号成绩一一 30 分二二 30 分三三 26 分分四四 14 分分1 2 3 4 5 1 2 3 1 2 3一、共 5 5 小题，总分为 0 30 分1 、试判断下列式子代表的系统是否为线性系统，并说明理由（其中 y t为系统响应， 0 y 为初始条件， f t为系统输入）（8 分）201 0 2ty t y f d2 0 cos5 0 y t y t y f t2 33 3 0 y t y t f t3 2 2245 2d y t d y t d f ty t f tdt dt dt2、、试确定信号 1 cos 1000 sin 2000 x t t t 的奈奎斯特频率。

（3 分）3 、已知描述系统的方程为4 4 2y t y t y t f t ，初始条件为 0 0 2 y y 。

求（1 ）系统传递算子 H p；；（2 ）系统零输入响应 xy t。

（7 分）4 、已知系统的单位冲击响应 2h t t ，当系统输入为142f t t t t 时，用时域分析法求系统零状态响应 fy t。

（6 分）5 、已知 f t的波形如下图，求 F j 。

（6 分）二、共 3 3 小题，总分为 0 30 分1 、系统的微分方程为 5 62 8y t y t y t f t f t ，，激励 tf t e t ，利用复频域分析法求系统的零状态响应。

（7 分）2 、系统传递函数为 N sH sD s ，试分析下列系统是否渐近稳定。

（9 分）21 1 2D s s s s 5 3 22 4 3 2 9 D s s s s s 5 4 3 23 2 3 4 11 8 D s s s s s s 3 、作出下列系统直接实现形式的模拟框图和信号流图。

（注假定系统为零状态）（14 分）113sH ss 2423 2sH ss s 三、共 3 3 小题，总分为 6 26 分1 、系统信号流图如下图所示，求系统的传递函数 H s。