应用数理统计,施雨,课后答案,
- 格式:doc
- 大小:2.66 MB
- 文档页数:47

习题五1 某钢厂检查一月上旬内的五天中生产的钢锭重量,结果如下:(单位:k g)日期重旦量1 5500 5800 5740 57102 5440 5680 5240 56004 5400 5410 5430 54009 5640 5700 5660 570010 5610 5700 5610 5400试检验不同日期生产的钢锭的平均重量有无显著差异? ( =0.05)解根据问题,因素A表示日期,试验指标为钢锭重量,水平为 5.2假设样本观测值y j(j 123,4)来源于正态总体Y~N(i, ),i 1,2,...,5检验的问题:H。
:i 2 L 5, H i : i不全相等.计算结果:注释当=0.001表示非常显著,标记为*** '类似地,=0.01,0.05,分别标记为查表F0.95(4,15) 3.06,因为F 3.9496 F0.95(4,15),或p = 0.02199<0.05 ,所以拒绝H。
,认为不同日期生产的钢锭的平均重量有显著差异2 考察四种不同催化剂对某一化工产品的得率的影响,在四种不同催化剂下分别做试验解根据问题,设因素A表示催化剂,试验指标为化工产品的得率,水平为 4 .2假设样本观测值y j(j 1,2,..., nJ来源于正态总体Y~N(i, ), i 1,2,...,5 .其中样本容量不等,n分别取值为6,5,3,4 .日产量操作工查表 F O .95(3,14) 3.34,因为 F 2.4264 F °.95(3,14),或 p = 0.1089 > 0.05, 所以接受H 。
,认为在四种不同催化剂下平均得率无显著差异3试验某种钢的冲击值(kg Xm/cm2 ),影响该指标的因素有两个,一是含铜量 A ,另一个是温度试检验含铜量和试验温度是否会对钢的冲击值产生显著差异? ( =0.05 )解 根据问题,这是一个双因素无重复试验的问题,不考虑交互作用设因素A,B 分别表示为含铜量和温度,试验指标为钢的冲击力,水平为 12.2假设样本观测值y j (i 1,2,3, j 1,2,3,4)来源于正态总体 Y j ~N (j ,),i 1,2,3,j 1,2,3,4 .记i 为对应于A 的主效应;记 j 为对应于B j 的主效应;检验的问题:(1) H i 。

第一章 共25题,作12题 可摘抄任7—8道1.1 解析:X~N(μ,2σ),则X ~N(μ,2nσ),所以X -μ~N(0,2nσ)P{X-μ<1}= P{σ}=0.95N (0,1),因为:P{Φ—(Φ=2Φ—1=0.95所以:σΦ=(1+0.95)/2 =0.975,,求得n 最小要取21.96x 2σ1.2解析:至800小时,没有一个元件失效,这个事件等价与P{123456X X X X X X >800}的概率,有已知X 服从指数分布,可求得P{123456X X X X X X >800}=7.2e-(2)至3000小时,所有六个元件都失效的概率也就等价与P{ 123456X X X X X X <3000}的概率,可求得P{ 123456X X X X X X <3000}= 4.56(1)e --1.5证明:21()nii Xa =-∑=21[()()]ni i X X X a =-+-∑=22111()2()()()nn nii i i i XX X a X X X a ===-+--+-∑∑∑因为1()nii XX =-∑=0=2211()()nnii i XX X a ==-+-∑∑=221()ni nS X a =+-∑所以当a =X 时,21()nii Xa =-∑有最小值且等于2nS1.6证明:11ni i X X n ==∑1)等式的左边=22112nnii i i XX n μμ==-+∑∑等式的右边=22221122nniii i X X X nX nX nX n μμ==-++-+∑∑ =222221122nnii i i XnX nX nX X n μμ==-++-+∑∑=22112nnii i i XX n μμ==-+∑∑左边等于右边,结论得证。
1.9 解析:1):∵ i i y ax b =+∴ 111111()n n ni i i i i i y y ax b ax b ax b n n n =====+=+=+∑∑∑222111111()()()n n n yi i i i i i S y y ax b ax b ax ax n n n ====-=+--=-∑∑∑22x a S =2):令179.98y =,……,1479.96y =再令 a=1,b=80 ∴由80i i i y ax b x =+=+得:i x 为:-0.02,0.04,0.02,0.04,0.03,0.03,0.04,-0.03,0.05,0.03,0.02,0.00,0.02,-0.04∴ 14110.016414i i x x ===∑14142221111()(0.0164)0.00071414xi i i i S x x x ===-=-=∑∑∴ 0.01648080.0164y ax b =+=+=2220.0007y x S a S ==2)等式的左边=22112n n ii i i X X X nX ==-+∑∑=221nii X nX =-∑=等式的右边 结论得证。



应用数理统计答案学号:姓名:班级:目录第一章数理统计的基本概念 (2)第二章参数估计 (14)第三章假设检验 (23)第四章方差分析与正交试验设计 (28)第五章回归分析 (31)第六章统计决策与贝叶斯推断 (34)对应书目:《应用数理统计》施雨著西安交通大学出版社第一章 数理统计的基本概念1.1 解:∵2(,)XN μσ∴ 2(,)n XN σμ∴(0,1)N 分布∴(1)0.95P X P μ-<=<=又∵ 查表可得0.025 1.96u =∴ 221.96n σ=1.2 解:(1) ∵(0.0015)X Exp∴ 每个元件至800个小时没有失效的概率为:8000.001501.2(800)1(800)10.0015x P X P X e dxe -->==-<=-=⎰∴ 6个元件都没失效的概率为: 1.267.2()P ee --==(2)∵(0.0015)X Exp∴ 每个元件至3000个小时失效的概率为:30000.001504.5(3000)0.00151x P X e dxe--<===-⎰∴ 6个元件没失效的概率为: 4.56(1)P e-=-1.4 解:ini n x n x ex x x P ni i 122)(ln 2121)2(),.....,(122=--∏∑==πσμσ1.5证:21122)(naa x n x a x n i ni ii+-=-∑∑==∑∑∑===-+-=+-+-=ni i ni i ni i a x n x x na a x n x x x x 1222211)()(222a) 证:)(11111+=+++=∑n ni i n x x n x)(11)(1111n n n n n x x n x x x n n -++=++=++])()1(1 ))((12)[(11)](11[11)(11212111121211212112n n n i n n n i n i n i ni n n n i n i n in x x n n x x x x n x x n x x n x x n x x n S -+++--+--+=-+--+=-+=++=+=+=+=++∑∑∑∑] )(11))1()((12)([112111212n n n n n n n n n x x n x n x x n x x n x x nS n -++-+-+--++=++++ ])(11S [1 ])(1[n S 11212n 212n n n n n x x n n n x x n n n -+++=-+++=++1.6证明 (1) ∵22112211221()()()2()()()()()nni ii i nni i i i ni i X X X X X X X X X n X X X n X μμμμμ=====-=-+-=-+--+-=-+-∑∑∑∑∑(2) ∵2221112221221()22ii i nn ni i i i i ni ni XX X X X nX X nX nX X nX =====-=-+=-+=-∑∑∑∑∑1.10 解:(1).∑∑====ni i n i i x E n x n E X E 11)(1)1()(p np n=⋅=1np m p x D n x n D X D ni in i i )1()(1)1()(121-===∑∑==))(1()(122∑=-=n i i x x n E S E)1(1)])1(1())1(([1)])()(())()(([1])()([1])([12222212212212p mp nn p m p mp n n p m p mp n n x E x D n x E x D n x nE x E n x x E n ni i i n i i n i i --=+--+-=+-+=-=-=∑∑∑=== 同理,(2).λ===∑∑==ni i n i i x E n x n E X E 11)(1)1()(λnx D n x n D X D ni in i i 1)(1)1()(121===∑∑==λnn x E x D n x E x D n x nE x E n S E ni i i n i i 1)])()(())()(([1])()([1)(2122122-=+-+=-=∑∑==(3).2)(1)1()(11ba x E n x n E X E ni i n i i +===∑∑==na b x D nx n D X D ni ini i 12)()(1)1()(2121-===∑∑==12)(1)])()(())()(([1])()([1)(22122122a b n n x E x D n x E x D n x nE x E n S E ni i i n i i -⋅-=+-+=-=∑∑==(4).λ===∑∑==ni i ni i x E n x n E X E 11)(1)1()(nx D nx n D X D ni ini i 2121)(1)1()(λ===∑∑==221221221)])()(())()(([1])()([1)(λnn x E x D n x E x D n x nE x E n S E ni i i n i i -=+-+=-=∑∑==(5).μ===∑∑==ni i n i i x E n x n E X E 11)(1)1()(nx D nx n D X D ni in i i 2121)(1)1()(σ===∑∑==221221221)])()(())()(([1])()([1)(σ⋅-=+-+=-=∑∑==nn x E x D n x E x D n x nE x E n S E ni i i n i i1.11 解:由统计量的定义知,1,3,4,5,6,7为统计量,5为顺序统计量 1.17 证:),(~ λαΓXxe x xf λαααλ--Γ=∴1)()( 令kXY =ke ky k ke ky yf kyky⋅Γ=⋅Γ=∴----λαααλαααλαλ11)()( )()()(即 ),(~ky Y αΓ1.18 证:),(~ b a X β),()1()( 11b a B x xx f b a ---=∴),(),(),()1()( 11b a B b k a B b a B x x x X E b a k k +=-=∴⎰∞+∞---),(),1()( b a B b a B X E +=∴ba a ab a b a b a a a a b a b a a a b b a b a b a +=Γ+Γ++ΓΓ=Γ++Γ+Γ+Γ=ΓΓ+Γ⋅++ΓΓ+Γ=)()()()()()()1()()1()()()()1()()1(),(),2()(2b a B b a B X E +=))(1()1()()()()2()()2(b a b a a a a b b a b a b a ++++=ΓΓ+Γ⋅++ΓΓ+Γ= 22)]([)()( X E X E X D -=∴2))(1())(1()1(b a b a ab ba ab a b a a a +++=+-++++=1.19 解:∵(,)X F n m 分布12(1)022()((1))()(1)()()()(1)()()n n m n mn m yn m y n mn nP Y y P X X y m myP X y n n n x x dx m m m++--+≤=+≤=<-Γ=+ΓΓ⎰222212211()()()1()(1)()()11(1)(1)(,)n n m n m n mn mn mf y P Y y y y y y y yy B ++----'=≤Γ=+ΓΓ----=∴ 22(1)(,)n m n n Y X X m mβ=+分布1.20 解:∵()Xt n 分布122212()()(()2(1)n n P Y y P X y P X xdxn ++-≤=≤=≤≤Γ=+11111212122()()()(1)()1()(1)()()()n n n n nf y P Y y y yn y y n n n+++--+--'=≤Γ=+Γ=+ΓΓ∴2(1,)2nY XF =分布1.21 解: (1) ∵(8,4)XN 分布∴ 4(8,)25XN 分布,即5(8)(0,1)2X N -∴ 样本均值落在7.88.2分钟之间的概率为:5(7.88)5(8)5(8.28)(7.88.2)()2220.383X P X P ---≤≤=≤≤=(2) 样本均值落在7.58分钟之间的概率为:5(7.58)5(8)5(88)(7.58)()2225(8)(0 1.25)20.3944X P X P X P ---≤≤=≤≤-=≤≤=若取100个样品,样本均值落在7.58分钟之间的概率为:10(7.88)10(8)10(8.28)(7.88.2)()2222*(0.84130.5)0.6826X P X P ---≤≤=≤≤=-=单个样品大于11分钟的概率为:110.77340.2266P =-=25个样品的均值大于9分钟的概率为210.97980.0202P =-= 100个样品的均值大于8.6分钟的概率为310.99870.0013P =-= 所以第一种情况更有可能发生1.23 解:(1) ∵2(0,)XN σ分布∴2(0,)XN nσ分布∴22()(1)χσ∵ 22221()()ni i a X an X an σσ===∑∴21a n σ=同理 21b m σ=(2) ∵2(0,)XN σ分布∴222(1)X χσ分布由2χ分布是可加性得:2221()ni i X n χσ=∑()nic X t m ==∑∴c =(3) 由(2)可知2221()ni i X n χσ=∑2221122211(,)nni ii i n mn mi ii n i n X d Xnn dF n m XmXmσσ==++=+=+=∑∑∑∑∴ md n=1.25 证明:∵211(,)XN μσ分布∴2211()(1)i X μχσ-∴1221111()()n i i X n μχσ=-∑ 同理2222212()()n i i Y n μχσ=-∑1122222112211111222221122112()()(,)()()n n i i i i n n i i i i X n n X F n n Y n Y n μσμσμσμσ====--=--∑∑∑∑第二章 参数估计 2.1 (1) ∵ ()XExp λ分布∴ ()1E X λ=令 ˆ1X λ= 解得λ的矩估计为: ˆ1X λ= (2) ∵ (,)XU a b 分布∴ ()2a bE X +=2()()12b a D X -=令 1ˆˆ2ab A X +==22221ˆˆˆˆ()()1124n i i b a a b A X n =-++==∑ (22211n i i X X S n =-=∑)解得a 和b 的矩估计为:ˆˆaX bX ==(3) 110()1E X x x dx θθθθ-=*=+⎰令1ˆˆ1A X θθ==+∴ˆ1X X θ=- (4) 110()(1)!kk x kE X x x e dx k βββ--=*=-⎰令ˆkX β= ∴ ˆk Xβ=(5) 根据密度函数有2221()22()E X a aE X a λλλ=+=++根据矩估计有1222221ˆˆˆ22ˆˆˆa A X a a A S X λλλ+==++==+解得λ和a 的矩估计为: ˆˆaX λ==- (6) ∵ (,)X B m p∴ ()E X mp =令 1ˆmpA X == 解得p 的矩估计为:ˆX pm= 2.3解:∵ X 服从几何分布,其概率分布为:1()(1)k P X k p p -==-故p 的似然函数为: 1()(1)ni i x nnL p p p =-∑=-对数似然函数为:1ln ()ln ()ln(1)ni i L p n p x n p ==+--∑令 1ln ()1()01nii L p n x n p p p=∂=--=∂-∑ ∴ 1ˆpX= 2.4 解:由题知X 应服从离散均匀分布,⎪⎩⎪⎨⎧≤≤==其它011)(N k N k x p2)(NX E =矩估计: 令7102=∧N1420=∴∧N 极大似然估计:⎪⎩⎪⎨⎧≤≤=其它071011)(N N N L要使)(N L 最大,则710=N710=∴∧N2.5 解:由题中等式知:2196.196.196.1)025.01(025.0)(1S X +=+=∴+=+-Φ=∴=-Φ-∧∧∧-σμθσμμσθσμθ2.6 解:(1) 05.009.214.2=-=R0215.005.04299.05=⨯==∴∧d R σ (2)将所有数据分为三组如下所示:0197.005.03946.005.0)05.005.005.0(316=⨯==∴=++=∴∧d R R σ2.7 解:(1)⎩⎨⎧+<<=其它 01x1)(θθx fθθθθθθ≠+==+=++=∴∧21)()(2121)(X E E X E ∴ X =∧θ不是θ的无偏估计,偏差为21=-∧θθ (2) θ=-)21(X E 21-=∴∧X θ是θ的无偏估计 (3)22))(()())(()(θθθθ-+=-+=∧∧X E X D E D M S E41121+=n 2.8 证:由例2.24,令2211x a x a +=∧μ,则∧μ 为μ无偏估计应 满足121=+a a因此1μ,2μ,3μ都是μ的无偏估计)()()()(21)()(2513)()(95)9491)(()())(()()(1233212221212∧∧∧∧∧∧=∧<<===+=∴+==∑μμμμμμμD D D X D D X D D X D X D D a a X D X D a D i i i2132121X X +=∴∧μ最有效 2.9 证: )(~λp Xλλ==∴)( )(X D X EX 是λ=)(X E 的无偏估计,2*S 是λ=)( X D 的无偏估计 )()1()())1((2*2*S E X E S XE αααα-+=-+∴λλααλ=-+=)1(∴2*)1(SX αα-+是λ的无偏估计2.10 解:因为2222((1))()(1)()(1)()1(1)()11(1)1E X S E X E S na E S n n a E S n n n a n nααααλαλαλαλλ**+-=+-=+--=+---=+-=-所以 2(1)X S αα*+-是λ的无偏估计量2.15 解:因为ˆθ是θ的有效估计量ˆˆˆ()()()E uE a b aE b a b u θθθ=+=+=+= 221ˆˆˆˆ()()()()D u D a b a D a D θθθ=+=≤ (其中,1ˆθ是θ的任意无偏估计量中的一个)所以 ˆu是u 的有效估计量 2.26 解: 因为总体服从正态分布,所以)01X U N μσ-=(,)对于给定的1α-,查标准正态分布表可得2u α,使得 2()1P U u αα<=- 即:22()1P X p X ααα<<+=-区间的长度2d L α=<,所以22224u n L ασ>2.28 解:因为总体服从正态分布,所以)01X U N μσ-=(,), 222(1)nS V n χσ=-由因为U 和V 是相互独立的, 所以(1)X T t n =-对于给定的1α-,查标t 分布表可得2t α,使得 2()1P U t αα<=-,即:2()1P X X ααμα<<=- 当30n =,35X =,15S =时,第一家航空公司平均晚点时间μ的95%的置信区间为:(29.3032,40.6968)对于给定的1α-,查标t 分布表可得t α,使得 ()1P U t αα>=-, 即:()1P X αμα<+=- 故μ的具有单侧置信上限的单侧置信区间为(,)X α-∞+ 所以经计算可得:第一家航空公司的单侧上限置信区间为(,39.7327)-∞ 第二种航空公司的单侧上限置信区间为(,36.3103)-∞ 所以选择第二家航空公司。

应用数理统计答案学号:姓名:班级:目录第一章数理统计的基本概念 (2)第二章参数估计 (14)第三章假设检验 (24)第四章方差分析与正交试验设计 (29)第五章回归分析 (32)第六章统计决策与贝叶斯推断 (35)对应书目:《应用数理统计》施雨著西安交通大学出版社第一章 数理统计的基本概念1.1 解:∵2(,)X N μσ∼ ∴ 2(,)n X N σμ∼∴)(0,1)X N μσ−∼分布∴(1)0.95P X P μ−<=<=又∵ 查表可得0.025 1.96u = ∴ 221.96n σ=1.2 解:(1) ∵ (0.0015)X Exp ∼∴ 每个元件至800个小时没有失效的概率为:8000.001501.2(800)1(800)10.0015x P X P X e dxe −−>==−<=−=∫∴ 6个元件都没失效的概率为: 1.267.2()P e e −−==(2) ∵ (0.0015)X Exp ∼∴ 每个元件至3000个小时失效的概率为:30000.001504.5(3000)0.00151x P X e dxe−−<===−∫∴ 6个元件没失效的概率为: 4.56(1)P e −=−1.4 解:ini n x n x ex x x P ni i 122)(ln 2121)2(),.....,(122=−−Π∑==πσμσ1.5证:∵21122)(na a x n x a x ni ni ii+−=−∑∑==∑∑∑===−+−=+−+−=ni i ni i ni i a x n x x naa x n x x x x 1222211)()(222a) 证:)(11111+=+++=∑n ni i n x x n x )(11)(1111n n n n n x x n x x x n n −++=++=++])()1(1 ))((12)[(11)](11[11)(11212111121211212112n n n i n n n i n i n i ni n n n i n i n in x x n n x x x x n x x n x x n x x n x x n S −+++−−+−−+=−+−−+=−+=++=+=+=+=++∑∑∑∑] )(11))1()((12)([112111212n n n n n n n n n x x n x n x x n x x n x x nS n −++−+−+−−++=++++])(11S [1 ])(1[nS 11212n 212n n n n n x x n n n x x n n n −+++=−+++=++ 1.6证明 (1) ∵22112211221()()()2()()()()()nni ii i nni i i i ni i X X X X X X X X X n X X X n X μμμμμ=====−=−+−=−+−−+−=−+−∑∑∑∑∑(2) ∵2221112221221()22ii i nn ni i i i i ni ni XX X X X nX X nX nX X nX =====−=−+=−+=−∑∑∑∑∑1.10 解: (1).∑∑====ni i n i i x E n x n E X E 11)(1)1()(p np n=⋅=1np mp x D n x n D X D ni in i i )1()(1)1()(121−===∑∑==))(1()(122∑=−=n i i x x n E S E)1(1)])1(1())1(([1)])()(())()(([1])()([1])([12222212212212p mp nn p m p mp n n p m p mp n n x E x D n x E x D n x nE x E n x x E n ni i i n i i n i i −−=+−−+−=+−+=−=−=∑∑∑=== 同理,(2). λ===∑∑==ni i n i i x E n x n E X E 11)(1)1()(λnx D n x n D X D ni in i i 1)(1)1()(121===∑∑==λnn x E x D n x E x D n x nE x E n S E ni i i n i i 1)])()(())()(([1])()([1)(2122122−=+−+=−=∑∑==(3). 2)(1)1()(11b a x E n x n E X E ni i n i i +===∑∑==na b x D nx n D X D ni ini i 12)()(1)1()(2121−===∑∑==12)(1)])()(())()(([1])()([1)(22122122a b nn x E x D n x E x D n x nE x E n S E ni i i n i i −⋅−=+−+=−=∑∑==(4). λ===∑∑==ni i n i i x E n x n E X E 11)(1)1()(nx D nx nD X D ni ini i 2121)(1)1()(λ===∑∑==221221221)])()(())()(([1])()([1)(λnn x E x D n x E x D n x nE x E n S E ni i i n i i −=+−+=−=∑∑==(5). μ===∑∑==ni ini i x E nx nE X E 11)(1)1()(nx D nx nD X D ni i ni i 2121)(1)1()(σ===∑∑==221221221)])()(())()(([1])()([1)(σ⋅−=+−+=−=∑∑==nn x E x D n x E x D n x nE x E n S E ni i i n i i1.11 解:由统计量的定义知,1,3,4,5,6,7为统计量,5为顺序统计量 1.17 证:),(~ λαΓX ∵xe x xf λαααλ−−Γ=∴1)()( 令kXY =ke ky k k e ky yf kyky ⋅Γ=⋅Γ=∴−−−−λαααλαααλαλ11)()( )()()(即 ),(~ky Y αΓ1.18 证:),(~ b a X β∵),()1()( 11b a B x xx f b a −−−=∴),(),( ),()1()( 11b a B b k a B b a B x x x X E b a k k +=−=∴∫∞+∞−−−),(),1()( b a B b a B X E +=∴ba a ab a b a b a a a a b a b a a a b b a b a b a +=Γ+Γ++ΓΓ=Γ++Γ+Γ+Γ=ΓΓ+Γ⋅++ΓΓ+Γ=)()()()()()()1()()1()()()()1()()1(),(),2()(2b a B b a B X E +=))(1()1()()()()2()()2(b a b a a a a b b a b a b a ++++=ΓΓ+Γ⋅++ΓΓ+Γ= 22)]([)()( X E X E X D −=∴2))(1())(1()1(b a b a ab ba ab a b a a a +++=+−++++= 1.19 解:∵ (,)X F n m ∼分布2212(1)022()((1))((1)()()()(1)()()n n m n mn m yn m y n mn nP Y y P X X y m myP X y n n n x x dx m mm ++−−+≤=+≤=<−Γ=+ΓΓ∫2222122221122()()()1((1()()11(1)(1)(,)n n m n m n m n m n m f y P Y y y y yy y yy B ++−−−−′=≤Γ=+ΓΓ−−−−=∴ 22(1)(,)n mn n Y X X m mβ=+∼分布1.20 解:∵ ()X t n ∼分布122212()()((2(1n n P Y y P X y P X xdxn ++−≤=≤=≤≤=+112211221212122()()()(1)()1()(1(()()n n n n n f y P Y y y y n y y nn n +++−−+−−′=≤Γ=+Γ=+ΓΓ∴ 2(1,)2nY X F =∼分布1.21 解: (1) ∵ (8,4)X N ∼分布∴ 4(8,)25X N ∼ 分布,即5(8)(0,1)2X N −∼ ∴ 样本均值落在7.88.2∼分钟之间的概率为:5(7.88)5(8)5(8.28)(7.88.2)()2220.383X P X P −−−≤≤=≤≤=(2) 样本均值落在7.58∼分钟之间的概率为:5(7.58)5(8)5(88)(7.58)(2225(8)(0 1.25)20.3944X P X P X P −−−≤≤=≤≤−=≤≤= 若取100个样品,样本均值落在7.58∼分钟之间的概率为:10(7.88)10(8)10(8.28)(7.88.2)(2222*(0.84130.5)0.6826X P X P −−−≤≤=≤≤=−= 单个样品大于11分钟的概率为:110.77340.2266P =−= 25个样品的均值大于9分钟的概率为210.97980.0202P =−= 100个样品的均值大于8.6分钟的概率为310.99870.0013P =−= 所以第一种情况更有可能发生1.23 解:(1) ∵ 2(0,)X N σ∼分布 ∴ 2(0,X N nσ∼分布∴ 22)(1)nXχσ∼∵ 222221()(ni i nXa X an X an σσ===∑∴ 21a n σ=同理 21b m σ=(2) ∵2(0,)X N σ∼分布 ∴222(1)X χσ∼分布由2χ分布是可加性得:2221()ni i X n χσ=∑∼()ninX c X t m ==∑∼ ∴c =(3) 由(2)可知2221()ni i X n χσ=∑∼2221122211(,)nni ii i n mn mi ii n i n X d Xnn dF n m XmXmσσ==++=+=+=∑∑∑∑∼∴ md n=1.25 证明:∵ 211(,)X N μσ∼分布 ∴ 2211((1)i X μχσ−∼∴ 1221111(()n i i X n μχσ=−∑∼同理 2222212(()n i i Y n μχσ=−∑∼ 1122222112211111222221122112()()(,)()()n n i i i i n n i i i i X n n X F n n Y n Y n μσμσμσμσ====−−=−−∑∑∑∑∼ 第二章 参数估计2.1 (1) ∵ ()X Exp λ∼分布∴ ()1E X λ=令 ˆ1X λ= 解得λ的矩估计为: ˆ1X λ= (2) ∵ (,)X U a b ∼分布∴ ()2a bE X +=2()()12b a D X −=令 1ˆˆ2ab A X +==22221ˆˆˆˆ()()1124n i i b a a b A X n =−++==∑ (22211n i i X X S n =−=∑)解得a 和b 的矩估计为:ˆˆaX bX =−=(3) 110()1E X x x dx θθθθ−=∗=+∫令 1ˆˆ1A X θθ==+∴ˆ1XXθ=− (4) 110()(1)!kk x kE X x x e dx k βββ−−=∗=−∫令ˆkX β= ∴ ˆkXβ=(5) 根据密度函数有2221()22()E X a aE X a λλλ=+=++根据矩估计有1222221ˆˆˆ22ˆˆˆa A X a a A S X λλλ+==++==+解得λ和a 的矩估计为:ˆˆaX λ==(6) ∵ (,)X B m p ∼ ∴ ()E X mp =令 1ˆmpA X == 解得p 的矩估计为:ˆXpm= 2.3解:∵ X 服从几何分布,其概率分布为:1()(1)k P X k p p −==−故p 的似然函数为: 1()(1)ni i x nnL p p p =−∑=−对数似然函数为:1ln ()ln ()ln(1)ni i L p n p x n p ==+−−∑令 1ln ()1()01nii L p n x n p p p =∂=−−=∂−∑ ∴ 1ˆpX= 2.4 解:由题知X 应服从离散均匀分布,⎪⎩⎪⎨⎧≤≤==其它01 1)(Nk N k x p2)(NX E =矩估计: 令 7102=∧N1420=∴∧N 极大似然估计:⎪⎩⎪⎨⎧≤≤=其它07101 1)(NN N L ∵要使)(N L 最大,则710=N710=∴∧N 2.5 解:由题中等式知:2196.196.196.1)025.01(025.0)(1S X +=+=∴+=+−Φ=∴=−Φ−∧∧∧−σμθσμμσθσμθ2.6 解:(1) 05.009.214.2=−=R ∵0215.005.04299.05=×==∴∧d Rσ(2)将所有数据分为三组如下所示:1x 2x 3x 4x5x 6x i R1 2.14 2.10 2.15 2.13 2.12 2.13 0.05 2 2.10 2.15 2.12 2.14 2.10 2.13 0.05 32.11 2.14 2.10 2.11 2.15 2.10 0.050197.005.03946.005.0)05.005.005.0(316=×==∴=++=∴∧d R R σ 2.7 解:(1)⎩⎨⎧+<<=其它 01x 1)(θθx f ∵ θθθθθθ≠+==+=++=∴∧21)()(2121)(X E E X E ∴ X =∧θ不是θ的无偏估计,偏差为21=−∧θθ(2) θ=−21(X E ∵ 21−=∴∧X θ是θ的无偏估计(3)22))(()())(()(θθθθ−+=−+=∧∧X E X D E D MSE41121+=n 2.8 证:由例2.24,令2211x a x a +=∧μ,则∧μ 为μ无偏估计应 满足121=+a a因此1μ,2μ,3μ都是μ的无偏估计)()()()(21)()(2513)()(95)9491)(()())(()()(1233212221212∧∧∧∧∧∧=∧<<===+=∴+==∑μμμμμμμD D D X D D X D D X D X D D a a X D X D a D i i i ∵∵2132121X X +=∴∧μ最有效2.9证: )(~λp X ∵ λλ==∴)( )(X D XEX ∵是λ=)(X E 的无偏估计,2*S 是λ=)( X D 的无偏估计)()1()())1((2*2*S E X E S X E αααα−+=−+∴λλααλ=−+=)1(∴2*)1(SX αα−+是λ的无偏估计2.10 解:因为2222((1))()(1)()(1)()1(1)()11(1)1E X S E X E S na E S n n a E S n n n a n nααααλαλαλαλλ∗∗+−=+−=+−−=+−−−=+−=− 所以 2(1)X S αα∗+−是λ的无偏估计量2.15 解:因为ˆθ是θ的有效估计量ˆˆˆ()()()E uE a b aE b a b u θθθ=+=+=+= 221ˆˆˆˆ()()()()D u D a b a D a D θθθ=+=≤ (其中,1ˆθ是θ的任意无偏估计量中的一个)所以 ˆu是u 的有效估计量 2.26 解: 因为总体服从正态分布,所以)01X U N μσ−=∼(,)对于给定的1α−,查标准正态分布表可得2u α,使得2()1P U u αα<=−即:22()1P X p X ααα−<<=−区间的长度2d L α=<,所以 22224u n L ασ>2.28 解:因为总体服从正态分布,所以)01X U N μσ−=∼(,), 222(1)nS V n χσ=−∼由因为U 和V 是相互独立的,所以(1)X T t n =−∼对于给定的1α−,查标t 分布表可得t α,使得 2()1P U t αα<=−,即:22()1P X X ααμα<<+=− 当30n =,35X =,15S =时,第一家航空公司平均晚点时间μ的95%的置信区间为:(29.3032,40.6968)对于给定的1α−,查标t 分布表可得t α,使得 ()1P U t αα>=−, 即:()1P X αμα<+=− 故μ的具有单侧置信上限的单侧置信区间为(,)X α−∞+ 所以经计算可得:第一家航空公司的单侧上限置信区间为(,39.7327)−∞第二种航空公司的单侧上限置信区间为(,36.3103)−∞所以选择第二家航空公司。


习题11.1 解:由题意95.01=⎭⎬⎫⎩⎨⎧<--u x p 可得:95.0=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧<-σσn n u x p而()1,0~N u x n σ⎪⎭⎫ ⎝⎛-- 这可通过查N(0,1)分布表,975.0)95.01(2195.0=-+=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧<--σσn n u x p 那么96.1=σn∴2296.1σ=n1.2 解:(1)至800小时,没有一个元件失效,则说明所有元件的寿命>800小时。
{}2.10015.08000015.00800|e 0015.0800--∞+-=∞+-==>⎰e e dx x p x x 那么有6个元件,则所求的概率()2.762.1--==e e p(2)至300小时,所有元件失效,则说明所有元件的寿命<3000小时{}5.4300000015.030000015.001|e 0015.03000----=-==<⎰e e dx x p x 那么有6个元件,则所求的概率()65.41--=e p解: (1) 123{(,,)|0,1,2,,1,2,3}k x x x x k χ===因为~()i X P λ,所以 112233{,,}P X x X x X x ≤≤≤112233{}{}{}P X x P X x P X x =≤≤≤1233123!!!x x x e x x x ++-λλ=其中,0,1,2,,1,2,3k x k ==(2) 123{(,,)|0;1,2,3}k x x x x k χ=≥=因为~()i X Exp λ,其概率密度为,0()0,0x e x f x x -λ⎧λ≥=⎨ <⎩所以, 123(,,)3123(,,)x x x f x x x e-λ=λ,其中0;1,2,3k x k ≥=(3) 123{(,,)|;1,2,3}k x x x a x b k χ=≤≤=因为~(,)i X U a b ,其概率密度为1,()0,|a x b f x b a x a x b⎧≤≤⎪=-⎨⎪ <>⎩所以,12331(,,)()f x x x b a =-,其中;1,2,3k a x b k ≤≤= (4) 123{(,,)|;1,2,3}k x x x x k χ=-∞<<+∞= 因为~(,1)i X N μ,其概率密度为(2(),()x f x x 2-μ)-=-∞<<+∞所以,311(2123321(,,)(2)k k x f x x x e π2=--μ)∑=,其中;1,2,3k x k -∞<<+∞=解:由题意可得:()⎪⎩⎪⎨⎧∞<<=--,其它00,21)(i 2ln i i 22i x e x x f u x σσπ则∏==ni x f x x f 1i n i )(),...(=⎪⎪⎩⎪⎪⎨⎧=∞<<∏=∑--=,其它0,...1,0,1n )2()(ln 212n 12i 2i x x e i n i i u x ni σπσ证: 令21()()nii F a Xa ==-∑则'1()2()nii F a Xa ==--∑,''()20F a n =>令'1()2()0ni i F a X a ==--=∑,则可解得11ni i a X X n ===∑由于这是唯一解,又因为''()20F a n =>,因此,当11ni i a X X n ===∑时,()F a 取得最小值证: (1)等式左边11((nnii i i XX X X 22==-μ)=-+-μ)∑∑111(2()()(nnnii i i i XX X X X X 22====-)+-μ-+-μ)∑∑∑21(()ni i X X n X 2==-)+-μ∑左边=右边,所以得证. (2) 等式左边22111(2nnni iii i i X X X X X nX 2===-)=-+∑∑∑ 22212nii XnX nX ==-+∑221ni i X nX ==-∑左边=右边,所以得证.证:(1)∑=-=ni i n x n x 11∑+=-++=11111n i i n x n x 那么)(11_1_n n n x x n x -+++=∑∑=+=•+-++ni i n n i i x n n x n x n 111111111 =111111+=+++∑n n i i x n x n =∑=+ni i x n 111=_1+n x ∴原命题得证(2)21221-=-=∑n n i i nx x n s211122111-++=+-+=∑n n i i n x x n s那么⎥⎦⎤⎢⎣⎡-+++-+212)(111n n n x x n s n n =∑=+n i i x n 1211--+21n x n n +212)1(++n x n n --++n n x x n n 12)1(2+22)1(-+n x n n=∑=+n i i x n 1211--+222)1(n x n n +2111++n x n -212)1(1++n x n --++n n x x n n 12)1(2=∑=+n i i x n 1211-(111++n x n +-+n x n n 1)2 由(1)可得:111++n x n +-+n x n n 1=-+1n x则上式=∑=+n i i x n 1211-21-+n x =21+n s∴原命题得证解: 因为2222111111,()n n n i i i i i i X X S X X X X n n n =====-=-∑∑∑所以 (1) 二项分布(,)B m p11()()()ni i i E X E X E X mp n ====∑21111(1)()()()n ni i i i mp p D X D X D X n n n ==-===∑∑222211111()(())()()(1)n n i i i i n E S E X X E X E X mp p n n n==-=-=-=-∑∑(2) 泊松分布()P λ()E X =λ, ()D X n λ=, 21()n E S n-=λ (3) 均匀分布(,)U a b()2b a E X +=, 2)()12b a D X n (-=, 221()()12n E S b a n-=-(4) 指数分布()Exp λ 1()E X =λ, 1()D X n 2=λ, 21()n E S n 2-=λ(5) 正态分布2(,)N σμ ()E X =μ, 21()D X n σ=, 221()n E S nσ-=解:(1)是统计量(2)不是统计量,因为u未知 (3)统计量 (4)统计量(5)统计量,顺序统计量 (6)统计量 (7)统计量(8)不是统计量,因为u未知 .解: 因为i X 独立同分布,并且~(,i X a Γλ),11ni i X X n ==∑所以1~(,nii Xna =Γλ)∑;令1nii Y X ==∑,则1X Y n =,由求解随机变量函数的概率密度公式可得 1()(),0)nana nx X f x nx e n x na --λλ=>Γ(1.15 解:(1))(m x 的概率密度为: [][])()(1)()!()!1(!)(1)(x f x F x F m n m n x f m n m m ------=又F(x)=2x 且f(x)=2x ,0<x<1 则有x x x m n m n x f m n m m 2)1()!()!1(!)(2)1(2)(------=,0<x<1(2) )(1x 与)(n x 的联合概率密度为:[][])()()(1)()()11(!),(011))(1(y f x f y F x F y F n n y x f n n ----=--=y x x y n n n 22))(1(222⋅⋅---=222)()1(4---n x y xy n n 0<x<y<1对于其他x,y ,有0),())(1(=y x f n证:现在要求Y=)X 1/(X m nm n +的概率密度。

2214243.(1)[||]0.140(2)[||]0.144(,4),(,),(0,)[||]20.1800255(3){||0.1}2(10.9521.9615372tnE a D nnE aN a N a t a NnnE t t dtnP t Pnξξξξξξπ-+∞-==≤⇒=-≤=-==≤==≤=≤=Φ-≥=⇒≥⎰《应用数理统计》参考答案习题一0.51.(,0.5)(,){||0.1}0.9972.97442N a N anP a Pnξξξξ⇒-<=<==⇒=2242.(,4)(,)100||(1)(||)()0.90,0.330.20.2(2):P(||)N a N aa UP a U P Uaξξξξσξεε⇒--<=<==-≥≤挈比学夫不等式(5)(5)125515(3){15}1{15}1{15,15,,15}1215121[{}]221[1(1.5)]0.292P P P P ξξξξξξ>=-≤=-≤≤≤--=->=--Φ=1121212111()(1){}{,,,}{1,1,,1}()()(1)(1)k n n nn m nm n m n m ni i P k pq P M m P m m m P m m m pqpq q q ξξξξξξξ----======≤≤≤-≤-≤-≤-=-=---∑∑4.5. 6. 13.0)25(1}8.012138.012{}13{)54,12(~)1()4,12(~=Φ-=->-=>ξξξξP P N N (1)(1)1255511515(2){10}1{10}1{10,10,,10}1[{10}]1[1{10}]1210121[1{}]221[11(1)]0.579P P P P P P ξξξξξξξξ<=-≥=->>>=->=--≤--=--≤=--+Φ=6(1)0.001567.2800~(0.0015)(1){800}[{800}][0.0015]x E P P e dx e ξξξ∞-->=>==⎰6(6)30000.00156 4.56(2){3000}[{3000}][0.0015](1)x P P e dx e ξξ--<=<==-⎰1212(2){}{,,,}{1,1,,1}n n nn P K k P k k k P k k k ξξξξξξ==≥≥≥-≥+≥+≥+7.8.均值的和(差)等于和的均值,方差的和差都等于方差的和9.由中心极限定理:10.11.22222(1)(1)(1)()222~()()()[()](,)it itit n e n n e n e it i t t tn it it n n nn p t e t t ee n e e e N n λξλλξξλλλλλξλϕϕϕλξλ---+--∴=∴======∴12121233~(20,3),~(20,),~(20,)10151~(0,)2{||0.3}1220.67N N N N P P ξξξξξξξξξ-∴->=->=-Φ=2(),(),E a D ξξσ==121(0,1)(0,1)~(,)n n i i i ni i na a n N N N a n nξξσξσξ==--∴∴=∑∑∑22222222,(),()()(),(),(),(,)k k k k k k k k k k k k k kk k E a E a D E E a a a a E A a D A n a a A N a nξξξξξ===-=--∴==-∴22121212222(),()(),()0,()()()2,()()()2,i i E E a D D E D D D E E D ξξξξσξξξξξξσξξξξξξσ====∴-=-=+=∴-=-+-=13.14.15.16.2212221221,(),(),()()0,()()()(1),11[()](1)1niii ii i iniiniiE a E a D DnE D D DnDn D nDES n Dn nE ES Dn n nσξξξσξξξξξξξσξξξξξξξ=======∴-=-=+--===--==--∑∑∑222222222424222(1),11()(1)()2(1)21 ()2(1)() nsnns nE n Es On nns nD n Ds On n n χσσσσσσσ--=-⇒==+-=-⇒==+112323''' '2(121)(1)()()()()5231()(121)23023021AD E E E EA E E A AVar Aξξξξξξηξηηηηηξξξξξ⎛⎫⎪-+=-==⎪⎪⎝⎭=--=--⎛⎫⎛⎫⎪⎪==--=⎪⎪⎪⎪⎝⎭⎝⎭11223''''110(2)(,)111()()()()5231()(121)23023021BE E E EB E E B BVar Bξηηηξξξηηηηξξξξξ⎛⎫⎛⎫ ⎪===⎪ ⎪⎝⎭ ⎪⎝⎭∑=--=--⎛⎫⎛⎫⎪⎪==--=⎪⎪⎪⎪⎝⎭⎝⎭11222211()2822121(2)||2241128116xx xxe dx dxπ⎛⎫⎛⎫- ⎪⎪∞∞⎝⎭⎝⎭-∞-∞-=∑-⎛⎫⎛⎫∑==⎪ ⎪-⎝⎭⎝⎭⎰⎰17.18.21.22.()11223'122'111110(,),211151,1101221111111100130111100310110N A A AAA Aξηξηξηηθθ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭∑⎛⎫⎛⎫⎛⎫⎪==⎪ ⎪⎪⎝⎭⎝⎭⎪⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪∑=-=⎪ ⎪⎪⎪⎝⎭⎝⎭⎪⎪⎝⎭⎝⎭‘=,由引理1.2.3,则-的联合分布为--11223''12111111~(,),1011111432111111121301111210.2N A A AA Aξηξξηξηθρρρρρρρρρηη⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭∴∑⎛⎫⎛⎫+--⎛⎫⎛⎫⎪⎪∑=-=⎪ ⎪⎪⎪---⎝⎭⎝⎭⎪⎪-⎝⎭⎝⎭∴--=⇒=-==A,--时与独立2''44''22'''''' 44224(0,)(,)()()2()()()()()cov(,)(,)()() ()()2()()()2()nN IE A B tr A tr B tr ABE A E B tr A tr BA B E A B E A E Btr A tr B tr AB tr A tr B tr AB ζσζζζζσσζζζζσσζζζζζζζζζζζζσσσσσ=+=∴=-=+-=()11112222121122,1,1,0822177,122477yay y Qyba babθθθθθθθ--⎛⎫⎛⎫--=⎪⎪-⎝⎭⎝⎭⇒===-=⎛⎫⎪⎛⎫⎛⎫∴=∑== ⎪⎪ ⎪⎪⎝⎭⎝⎭⎪⎝⎭23.24.又 则令 则与 独立,则 与独立,且26.则2212221~(,),~(0,),~(1),(0,1)/(1)n n N a N n n ns n N T t n σξξξσξξχσξξ++----=-'11111(,,),(,,)111(,,),()11n n n ij n n n n i i i ia a B D nn n ξξθξσσσσδσσ⨯======-∑∑'2,0,D D D BD ===221(,)(,)1()n ni i nnB N a N I ηξθσσ===∑,i i i aξγσ-=2'11,()()()ni i i a D n ηγζγγξθξθσ=-==-=--∑∑B nηξ=ξηζ)1(~2-n χζ11(,)22U ξθθ-+(1)()121111221111()2201()121()()[1()]1[]21()()[()][]2(,)(1)()()[()()](1)[]n x n n n n n n n x f x other F x dx x f x nf x F x n x f x nf x F x n x f x y n n f x f y F y F x n n y x ξξθξξθθθθθ-------⎧-<<+⎪=⎨⎪⎩==-+∴=-=⋅⋅-+==⋅+-=--=⋅-⋅-⎰27.33.2222122222212222(0,),1()||2 ()()()()22(1)iyniniiY a NE d Y dynaD dE d E d Ennn nσξσσξσσσπσσσππ-∞-∞===-==-=-=-=⋅-=-∑⎰∑2222122122210.3(0,0.3),(0,)1010()(9)0.310()100.18{}0.30.3{(2}0.01iniiniiniN NPPξξξξχξξξ===--⨯<=<=∑∑∑222(2)(0,1),(1)0.3(9){0.9}0.9932nsN ntP Psnξχσξξξ--<=<=12121222221221212(3)(0,0.18),(0,0.18)(0,1),(0,1)0.18(1),()(1)0.18{()40}0.9N NN NPξξξξχχξξξξ+-+-+<=-224132244(4)~(1),~(0,0.12),10.73 {10.73}{}0.95NP Pξχξξξξ-<=<=34.《应用数理统计》参考答案2211222212222211(1)(0,),(0,)(1),()(1)11,()()(2)nn miii i n nniii nn mi i i i n N n N m n m m a b n m a b n m ξσξσξξχχσσσξξχ+==+=+==+--==++-∑∑∑∑∑∑222211112(2)(),(0,)(0,1),/(),n mni ii n i nniii i i m N n N t m c m n ξχξσσξξσσ+=+===∴=∑∑∑∑∑2222221121221(3)(),()()/(1,1),/nn mi i i i n ni i n mi i n n m n mF n m d nm ξξχχσσξσξσ+==+=+=+--∴=∑∑∑∑1. 由矩估计法2. (1) 由矩估计法(2)(3)(4)(5)818226212266174.00281610(74.002)88610 6.85710181ii i i a X x S x n S S n σ=-=--⎧===⎪⎪⎨⎪==⨯=-⎪⎩∴==⨯⨯=⨯--∑∑11'1202()33A x EX x dx θαξθθαξθθξ==-====∴=⎰111'101(1)2211A EX x x dx θαξθαθξθξθξ==+==+==+-∴=-⎰1211211122222221212222222121112()2x x n i i e xdx e x dx A X n A S S S θθθθθθαθθξθαθθξθξθξθθξθξθ--+∞--+∞==⋅=+==⋅===+∴=+==-+⎧=-⎪∴⎨=⎪⎩⎰∑⎰111(1)122Ni N NA x N NN ξξ=+===⋅⇒=∑11102()1A dx ξξθξ===⇒=-⎰2∞3.4.2()2{0},(){0}{}()0.7,110.7,0.525x aA X AP A P dxa aP a pp aξξξ--=<=<=--=<=Φ-=≈∴≈=-⎰设表示出现的次数,(1)11111(1)()ln()[ln ln(1)ln]ln()1[ln ln]ln ln0 ln lnniiniin ni ii iniiL c xL c xLc x n c xnnx n cθθθθθθθθθθθθθ-+=======+-+∂=+-=+-=∂=-∏∑∑∑∑1111221(2)()ln()[ln1)ln]ln()]0(ln)niniiniiniiLL xLxnxθθθθθ======+∂=+=∂=∑∑∑11()()()()11(3)()ln()lnln()11,,,,()0,0,11,()()nnin nn nnn nnnLL nL nLother otherL Lθθθθθθθθξξθξθθθθθξθξθξ====-∂=-=∂⎧⎧≤≤⎪⎪==⎨⎨⎪⎪⎩⎩≤≤=∏11()()()()11(3)()ln()lnln()11,,,,()0,0,11,()()nnin nn nnn nnnLL nL nLother otherL Lθθθθθθθθξξθξθθθθθξθξθξ====-∂=-=∂⎧⎧≤≤⎪⎪==⎨⎨⎪⎪⎩⎩≤≤=∏5.221()212212241(5)()()ln()[ln]22()2()ln()[022in xiniini iiLxLx xLθθθθθθθθθθθθθξθ--====-=-----∂==∂=∑∑(1)11(1)11(1)(1)(6)()ln()[ln ln(1)ln]ln()(),,,()()nc ciiniinc ci niL c xL c c c xL ncL c xL Lθθθθθθθθθθθξξθξθξ-+==-+===--+∂=-=∂=≤≤⇒=∏∑∏不能解出,所以由22111(7)()1)(1)ln()[2ln(2)ln(1)ln(1)]2ln()22]01inxiini iiniiL xL x xx nL nθθθθθθθθθθθξ-====--=+--+--∂=-=⇒=∂-∏∑∑(~(,0)11nUξθ∏6.7.所以不唯一。

应用数理统计施雨课后答案习题11.1解:由题意p某u10.95可得:n某up0.95nn某u而~N0,1n1某u这可通过查N(0,1)分布表,p0.95(10.95)0.9752nn那么1.96n1.96221.2解:(1)至800小时,没有一个元件失效,则说明所有元件的寿命>800小时。
p0某8008000.0015e0.0015某d某e0.0015某|800e1.2那么有6个元件,则所求的概率pe1.2e7.26(2)至300小时,所有元件失效,则说明所有元件的寿命<3000小时p0某3000030000.0015e0.0015某d某e0.0015|030001e4.5那么有6个元件,则所求的概率p1e4.561.3解:(1){(某1,某2,某3)|某k0,1,2,,k1,2,3}因为某i~P(),所以P{某1某1,某2某2,某3某3}P{某1某}P{某12某}P{某23某}3某1某2某33e某1!某2!某3!其中,某k0,1,2,,k1,2,3(2){(某1,某2,某3)|某k0;k1,2,3}e某,某0因为某i~E某p(),其概率密度为f(某)0,某0所以,f(某1,某2,某3)3e(某1,某2,某3),其中某k0;k1,2,3(3){(某1,某2,某3)|a某kb;k1,2,3}1,a某b因为某i~U(a,b),其概率密度为f(某)ba0,某a|某b所以,f(某1,某2,某3)1(ba)3,其中a某kb;k1,2,3(4){(某1,某2,某3)|某k;k1,2,3}12(某2因为某i~N(,1),其概率密度为f(某)123e,(某)所以,f(某1,某2,某3)1(2)32e(某kk1,其中某k;k1,2,3ln某iu12e2,0某i1.4解:由题意可得:f(某i)某2i0,其它2n则f(某i,...某n)i112(ln某iu)22i1e,0某i,i1,...nnf(某i)=(2)2n某ii10,其它n1.5n证:令F(a)(某i1ia)2n则F'(a)2(某ia),F''(a)2n0i1n令F'(a)2(某ia)0,则可解得a1nn某i某i1i1由于这是唯一解,又因为F''(a)2n0,因此,当a1nn某i某时,F(a)取得最小值i11.6nn证:(1)等式左边(某i(某i某某i1i1nnnn(某某2某()某(ii某)某((某i某i1i1i1i1左边=右边,所以得证.nnn(2)等式左边(某i某某2i2某某2in某i1i1i1nn某22n某2n某2某2iin某2i1i1左边=右边,所以得证.1.7证:(1)某1nnn某ii1某1n1n1n1某ii1__那么某1nn1(某n1某n)n=1111nn某ii1n1某n1n1n某ii11n1n_=n1某ii1n1某n1=1n1某i=某n1i1原命题得证n(某2)(2)2n1nn某i12i2某n22n1某n1i11n1i2某n1122那么(某某)nn1nn1n1n=某n1i11n2i-nn1n2某+2nn(n1)1n1nn12某2n1-2n(n1)12某n1某n+n(n1)22某n=1n11n某i1n2i-(n1)1n12某+2n某2n1-(n1)2某2n1-2n(n1)2某n1某n=某n1i12i-(1某n1+n某n)2由(1)可得:n1n某n1+n12某n=某n1则上式=某n1i112i-某n1=n12原命题得证1.10解:因为某1ni某ni1,S21ni(某ni1某)21n2i某ni1某2所以(1)二项分布B(m,p)1niE(某)E(某ni1)E(某i)mpD(某)D(1n某ni1n)i1n2nD(某i)i1nmp(1p)nE(S)E(21ni1(某i某))21nE(某i)E(某)i122n1nmp(1p)(2)泊松分布P()E(某),D(某)n,E(S)2n1n(3)均匀分布U(a,b)ba2E(某),D(某)ba)12n2,E(S2)n112n(ba)2(4)指数分布E某p()E(某)1,D(某)1n,E(S2)n1n(5)正态分布N(,2)E(某),D(某)1.11解:(1)是统计量(2)不是统计量,因为u未知(3)统计量(4)统计量(5)统计量,顺序统计量(6)统计量(7)统计量(8)不是统计量,因为u未知1.14.解:因为某i独立同分布,并且某i~(a,,某1nn1n,E(S)22n1n2i1某in所以某i~(na,;i1n令Yi1某i,则某na1nY,由求解随机变量函数的概率密度公式可得f某(某)na)(n某)na1en某n,某01.15解:(1)某(m)的概率密度为:f(m)(某)n!(m1)!(nm)!2F(某)m11F(某)nmf(某)又F(某)=某且f(某)=2某,02.1解:(1)某~E某p()则1^,令某,则1^某^这样可以得到:(2)某~u(a,b)则1u2令:21某ab2u213(baba)^^^22u某2ab2^^^22S213^2(baba)某^a某这样可以得:^b某^3a某或者^23b某2332(因为a 2(3)1^10某1某d某1令某^即有^^某又0,0某<1^1解得:某1某pk(4)1k0(k1)!k某k1ep某某d某=(k1)!0某e某d某令某tk上式=(k1)!tk0ket1tdt=(k1)!10tedt(k1)(k1)!k!(k1)!k^^令u某,则(5)令某-a=tk某t服从参数为的指数分布E(t)1E(某a)则E(某)E(某a)a1a11a^1某^a令2^^2^211S2auu2^2^^可得:1S2^,a某S2(6)1mp某~B(m,p)^^^令u某mp,p2.2某me某某0解:(1)由于某~E某p(),所以f(某),0,其它某innei1某i0,lnL()nln某,因此L()ii10,其它n令lnL()nn某i0,该似然方程有唯一解i11某,所以的极大似然估计量为1某1,a某b(2)由于某~U(a,b),所以f(某)ba,0,其它所以,样本(某1,某2,,某n)的联合概率密度为ni11,a某1,,某nbn,故(a,b)的似然函数为f(a,b)(ba)0,其它1,amin(某1,,某n),bma某(某1,,某n)n,易见,L(a,b)(ba)0其它当amin(某1,,某n),bma某(某1,,某n)时,L(a,b)取得最大值,故(a,b)的极大似然估计量为amin(某1,,某n),bma某(某1,,某n)nn1n某i某i1(3)因为L(),所以lnL()nln(1)ln某i,i1i10,其它令lnL()nni1ln某i0,该似然方程有唯一解nn,所以的极大似iln某i1然估计量为nniln某i1nkn某ik1某iei1某i0n(4)因为L()[(k1)]i1,所以0,其它nnnlnL()nklnnln(k1)!(k1)ln某iln某i,i1i1令lnL()nkn某i0,该似然方程有唯一解i1nkn,所以的极大似然估i某i1计量为k某(5)样本(某1,某2,,某n)的联合概率密度为ni1(某ia)nei1,某1,,某naf(a,)0,其它n,(某ia)nei1,min(某1,,某n)a,易见当amin(某1,,某n)时,L(a,)0,其它nL(a,)取得最大值,因此a的极大似然估计量为amin(某1,,某n);nlnL(a,)nln(某ia)i1而令lnL(a,)nn(某ia)0,该似然方程有唯一解i11某a,所以的极大似然估计量为1某a某某m某p(1p),某0,1,2,,(6)因某的概率函数为P{某某}Cmm故p的似然函数为L(p)Ci1m某impi(1p)某m某i,某i0,1,2,,对数似然函数为lnL(p)[lnCi1某im某ilnp(m某i)ln(1p)],nni令lnL(p)p某i1(m某)ipi11p0,该似然方程有唯一解p某m,故p的极大似然估计量为p某m.n2.3解:似然函数L(P;某)=p(某i;P)i1n=p(1p)i1某i1=(p1pn)(1p)某ii1n令:lnL()2pn1pn11pt某ii1n11p0^p1n某又因ilnL(p)p22|0某i1p某n^p的极大似然估计量为p某^令:某则有:某1N2N2某12某71011419n极大似然估计方法:L(N)=i11N1(1N1n)^显然:当N=min(某1,某2,----某n)时,L(N)取得最大值,只有一个值^^N=710,即N的极大似然估计量为N=7102.5解:由于总体某~N(,),所以,的极大似然估计量分别为某,意以12.6解:(1)R=某(n)某(1)2.142.090.05^222S,而由题212e(某2d某0.025可知P{某}12e(某2d某0.025,所)0.0251.96,因此的极大似然估计量为1.96S,即2某.Rd50.4299某0.050.0215(2)将题中数据等分为三组第一组:2.14,2.10,2.15,2.13,2.12,2.13,2.10,2.15,2.12,2.14,2.10,2.132.11,2.14,2.10,2.11,2.15,2.10平均极差:R^13(0.050.050.05)0.051d0R0.39460.050.0197(2)由(1)的分析可知,的置信度为1a的单侧置信下限为(2n某(2n)2a,),的置信度为1a的单侧置信上限为(,2n某)1a(2n)2),因此,元件平均寿命的置信度为90%的单侧置信下限为(747.7,)元件平均寿命的置信度为90%的单侧置信上限为(,1585.0).2.23解:由题意得总体某~B(1,p)当n总分大时:有p{u2n(某p)p(1p)u}=1-2由题意得:1-=0.95,=0.05,某=60105,n=105查表得u=1.962这样,我们可以解得:p的置信度约为0.95的置信区间为:(0.4768,0.6661)2.24解:由中心极限定理可得,当n充分大时,对于P()分布有:n某k1knu~N(0,1),在这里,n充分大,u=,n则有p{u2某1nu}12通过解不等式u2某1nu可得:2u2的置信度近似为1的置信区间为(某2n(u24n某u),22u2某2n(u24n某u))222.26解:对于正态分布N(,2),当2已知时:的置信度为1-的置信区间为:(某nu,某2nu)2那么置信区间的长度l=22unu24u)2222若lL,可解得n(2LL22.28解:首先求前家公司飞机平均晚点时间的95%的置信区间:已知某=35,n=30,=S2=15,1-=95%在这里方差2未知,有n(某)S某~t(n1)故有:p{|n(某)某|2的置信度为95%置信区间为:(某S某nt(n1),某2S某nt(n1))2又:S某nn1S,查表可得:t0.025(29)2.0452这样可得置信区间为:(29.303,40.697)的单侧置信上限为某某nt(n1)2对于前家公司,可求得单侧置信上限为35152920t0.05(29)=3515291.6991=39.733对于后家公司,可求得单侧置信上限为3029t0.05(29)=36.310可见第二家公司u的单侧置信上限较小,所以后选择第二家公司。
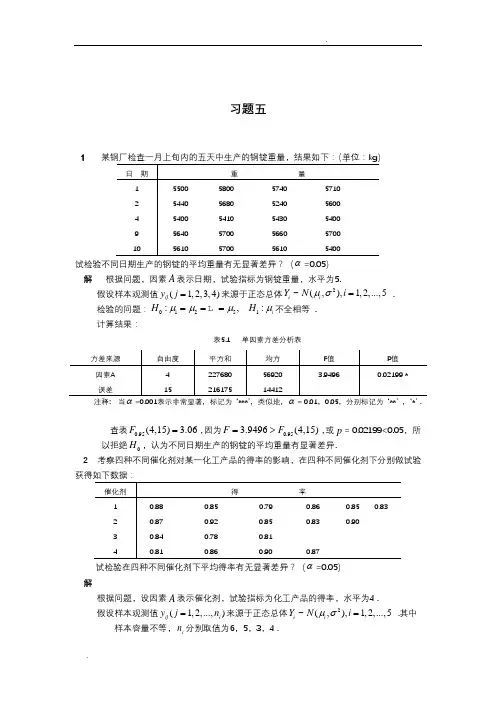
习题五1试检验不同日期生产的钢锭的平均重量有无显著差异?(α=0.05) 解 根据问题,因素A 表示日期,试验指标为钢锭重量,水平为5.假设样本观测值(1,2,3,4)ij y j =来源于正态总体2~(,),1,2,...,5i i Y N i μσ= .检验的问题:01251:,:i H H μμμμ===L 不全相等 .计算结果:表5.1 单因素方差分析表注释: 当=0.001表示非常显著,标记为 ‘***’,类似地,= 0.01,0.05,分别标记为 ‘**’ ,‘*’ .查表0.95(4,15) 3.06F =,因为0.953.9496(4,15)F F =>,或p = 0.02199<0.05, 所以拒绝0H ,认为不同日期生产的钢锭的平均重量有显著差异.2 考察四种不同催化剂对某一化工产品的得率的影响,在四种不同催化剂下分别做试验 试检验在四种不同催化剂下平均得率有无显著差异?(α=0.05)解根据问题,设因素A 表示催化剂,试验指标为化工产品的得率,水平为4 .假设样本观测值(1,2,...,)ij i y j n =来源于正态总体2~(,),1,2,...,5i i Y N i μσ= .其中样本容量不等,i n 分别取值为6,5,3,4 .检验的问题:012341:,:i H H μμμμμ===不全相等 .计算结果:表5.2 单因素方差分析表查表0.95(3,14) 3.34F =,因为0.952.4264(3,14)F F =<,或p = 0.1089 > 0.05,所以接受0H ,认为在四种不同催化剂下平均得率无显著差异 .3 试验某种钢的冲击值(kg ×m/cm2),影响该指标的因素有两个,一是含铜量A ,另试检验含铜量和试验温度是否会对钢的冲击值产生显著差异?(α=0.05) 解 根据问题,这是一个双因素无重复试验的问题,不考虑交互作用.设因素,A B 分别表示为含铜量和温度,试验指标为钢的冲击力,水平为12.假设样本观测值(1,2,3,1,2,3,4)ij yi j ==来源于正态总体2~(,),1,2,3,ij ij Y N i μσ=1,2,3,4j = .记i α⋅为对应于i A 的主效应;记j β⋅为对应于j B 的主效应;检验的问题:(1)10:i H α⋅全部等于零,11:i H α⋅不全等于零;(2)20:j H β⋅全部等于零,21:j H β⋅不全等于零; 计算结果:表5.3 双因素无重复试验的方差分析表查表0.95(2,6) 5.143F =,0.95(3,6) 4.757F =,显然计算值,A B F F 分别大于查表值,或p = 0.0005,0.0009 均显著小于0.05,所以拒绝1020,H H ,认为含铜量和试验温度都会对钢的冲击值产生显著影响作用.设每个工人在每台机器上的日产量都服从正态分布且方差相同 .试检验:(α=0.05)1) 操作工之间的差异是否显著? 2) 机器之间的差异是否显著?3) 它们的交互作用是否显著?解 根据问题,这是一个双因素等重复(3次)试验的问题,要考虑交互作用.设因素,A B 分别表示为机器和操作,试验指标为日产量,水平为12. 假设样本观测值(1,2,3,1,2,3,4)ijk y i j ==来源于正态总体2~(,),1,2,3,ij ij Y N i μσ= 1,2,3,4j =,1,2,3k = .记i α⋅为对应于i A 的主效应;记j β⋅为对应于j B 的主效应;记ij γ为对应于交互作用A B ⨯的主效应; 检验的问题:(1)10:i H α⋅全部等于零,11:i H α⋅不全等于零; (2)20:j H β⋅全部等于零,21:j H β⋅不全等于零; (3)30:ij H γ全部等于零,31:ij H γ不全等于零;计算结果:表5.4 双因素无重复试验的方差分析表查表0.95(3,24) 3.01F =,0.95(2,24) 3.4F =,0.95(6,24) 2.51F =,计算值 3.01,A F <3.4, 2.51B A B F F ⨯>>,或0.05A p >>,而,B A B p p ⨯均显著小于0.05,所以拒绝2030,H H ,接受10H ,认为操作工之间的差异显著,机器之间的差异不显著,它们之间的交互作用显著 . 5 某轴承厂为了提高轴承圈退火的质量,制定因素水平分级如下表所示因素 上升温度℃ 保温时间(h)出炉温度℃水平1 800 6 400 水平28208500试填好正交试验结果分析表并对试验结果进行直观分析和方差分析 .解 根据题意,这是一个3因素2水平的试验问题 .试验指标为硬度的合格率 .应选择正交表44(2)L 来安排试验,随机生成正交试验表如下:方差来源 自由度 平方和 均方 F 值 P 值 因素A 因素B 相互效应A ×B误差 总和3 2 6 24 352.750 27.167 73.5 41.333 144.750.917 13.583 12.250 1.7220.5323 7.8871 7.11290.6645 0.00233** 0.00192**由此可见第三号试验条件为:上升温度800℃、保温时间6h 、出炉温度500℃ . 直观分析需要计算K 值,计算结果如下:直观分析 由计算的K 值知,因素A 、B 、C 的极差分别为70,40,40,因此主次关系为A B C >=,B ,C 相当 .由于试验指标为硬度的合格率,应该是越大越好,所以各确定因素的水平分别是121,,A B C ,即最佳的水平组合是121A B C ,即最佳搭配为:上升温度800℃、保温时间8h 、出炉温度400℃.采用方差分析法,计算得下表:表5.7 方差分析表方差来源平方和 自由度 均方差 F 值 A 1225 1 1225 1 B 400 1 400 0.33 C 400 1 400 0.33 误差 1225 1 1225 总和32504如果显著性检验水平取0.1α=,则查表得0.9(1,1)39.9F =,显然计算的F 值1,0.33A B C F F F ===均小于查表值,所以认为三个因素对结果影响都显著 .6问应选用哪张正交表安排试验,并写出第8号试验的条件;如果9组试验结果为(单位:kg/100m 2):62.925,57.075,51.6,55.05,58.05,56.55,63.225,50.7,54.45,试对该正交试验结果进行直观分析和方差分析.解 该问题属于3因素3水平的试验问题,试验指标为水稻产量 .根据题意应选择正交表49(3)L 来安排试验,随机生成正交表如下:由表可知,第8号试验的条件:品种(A 3)珍珠矮11号,插值密度(B 2)3.75棵/100m 2,施肥量(C 1)0.75kg/100m 2纯氨; 直观分析需要计算K 值,计算结果如下:同上题进行直观分析,得出K 值的大小关系为:111312212223333132,,K K K K K K K K K >>>>>>由直观分析看出:本例较好的水平搭配是:113A B C 采用方差分析法,计算得下表:表5.10 方差分析表方差来源平方和自由度 均方差F 值A 1.759 2 0.879 0.0223B 65.861 2 32.931 0.8361C 6.660 2 3.330 0.0845 误差78.776 239.388 39.3880.9(2,2)9F =,所以认为三个因素对结果影响都不显著.7 在阿魏酸的合成工艺考察中,为了提高产量,选取了原料配比A ,吡啶量B 和反应时间C 三个因素,它们各取了7个水平如下:原料配比A :1.0,1.4,1.8,2.2,2.6,3.0,3.4 吡啶量B :10,13,16,19,22,25,28 反应时间C :0.5,1.0,1.5,2.0,2.5,3.0,3.5试选用合适的均匀设计表安排试验,并写出第7号试验的条件;如果7组试验的结果(收率)为:0.33,0.336,0.294,0.476,0.209,0.451,0.482,试对该均匀试验结果进行直观分析并通过回归分析发现可能更好的工艺条件.解 根据题意选择均匀设计表47(7)U 来安排试验,有3个因素,根据使用表,实验安排如:表5.11 试验安排表6 6 5 4 0.4517 7 7 7 0.482 所以第7号实验的条件为:原配料比3.4,吡啶量28ml,反应时间3.5h.通过直观分析,最好的实验条件是:原配料比3.4,吡啶量28ml,反应时间3.5h. 通过回归分析,最合适的实验条件是:原配料比2.6,吡啶量16ml,反应时间0.5h.习题六1 从某中学高二女生中随机选取8名,测得其升高、体重如下:1 2 3 4 5 6 78身高(cm)160 159 160 157 169 162 165 154体重(kg)49 46 53 41 49 50 48 43在绝对距离下,试用最短距离法和离差平方和法对其进行聚类分析.解由R软件,用最短距离(左)和差离平方和法(右)对题目进行聚类分析如下图6.1,表6.1和表6.2:最短距离法离差平方和法图6.1 聚类树形图表6.1 聚类附表(最短距离法)步骤聚类合并系数首次出现的阶段类别下一步组1 组2 组1 组21 1 6 5.000 0 0 22 1 2 10.000 1 0 43 4 8 13.000 0 0 74 1 7 13.000 2 0 55 1 3 13.000 4 0 66 1 5 17.000 5 0 7表6.2 聚类附表(离差平方和法)2 已知五个变量的距离矩阵为03674012340444401592343331).;2);3)036034022020401000⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭试用最短距离法和最长距离法对这些变量进行聚类,并画出聚类图和二分树.解 针对距离矩阵1),采用两种方法计算如下. ①最短距离法的聚类步骤如下:12345036740159036020w w w w w ⎛⎫ ⎪⎪ ⎪ ⎪⎪⎪⎝⎭a )将()236,1w w f h =合并为一类,,{}11456,,,,H w w w h =距离矩阵如下0743023060⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭{}()457457),,,2b w w h w w f h ==合并为一类,{}2167,,,H w h h =距离矩阵如下:034030⎛⎫ ⎪⎪ ⎪⎝⎭{}()()1681689),,3,3c w h h w h f h f h ===合并为一类,最后,,聚类图和树状图如图6.2:图6.2 聚类图(左)与树状图(右)②最长距离法与最短距离法类似,步骤如下: a )()236,1w w f h =合并为一类,{}11456,,,,H w w w h =距离矩阵如下0746025090⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭ {}(){}4574572167),,,2,,,b w w h w w f h H w h h ===合并为一类,距离矩阵如下:067090⎛⎫⎪⎪ ⎪⎝⎭{}()()1681689),,69c w h h w h f h f h ===合并为一类,最后,,,聚类图和树状图如图6.3:图6.3 聚类图(左)与树状图(右)(2)针对距离矩阵2)012340234034040⎛⎫ ⎪⎪ ⎪ ⎪⎪⎪⎝⎭①最短距离法的聚类步骤如下 a )()216,1w w f h =合并为一类,{}13456,,,,0342043040H w w w h =⎛⎫⎪⎪ ⎪ ⎪⎝⎭距离矩阵如下{}()367367),,,2b w h h w h f h ==合并为一类,{}24567,,,,H w w h h =聚类矩阵如下:043040⎛⎫⎪⎪ ⎪⎝⎭{}(){}()4784789879),,3,,4c w h h w h f h h w h f h ====合并为一类,最后,,聚类图和树状图如图6.4:图6.4 聚类图(左)与树状图(右)②由于本题数据的特殊性,最长距离法与最短距离法结果相同(略). (3)044440333022010⎛⎫ ⎪⎪ ⎪ ⎪⎪⎪⎝⎭最短距离法的聚类步骤如下a ) ()456,1w w f h =合并为一类,{}11236,,,,H w w w h =距离矩阵如下0444033020⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭{}(){}36736724567),,,2,,,,b w h h w h f h H w w h h ===合并为一类,距离矩阵如下:044030⎛⎫⎪⎪ ⎪⎝⎭{}(){}()4784789879),,3,,4c w h h w h f h h w h f h ====合并为一类,最后,,,聚类图和树状图如图6.5:图6.5 聚类图(左)与树状图(右)由于本题数据的特殊性,最长距离法与最短距离法结果相同(略).3 在一项关于作物对土壤营养的反应的研究中,要测定土壤的总磷量和总氮量(占干物质重的百分比),今对10份土样测得数据如下:总氮量(%)0.120.63 1.19 2.30 1.29 0.73 0.52 0.33 0.61 0.470.66在绝对距离下,试用重心法对其进行聚类分析.解由R软件得到重心法聚类分析的结果如图6.6与表6.3:图6.6 聚类树形图表6.3 聚类过程记录表步骤聚类合并系数首次出现的阶段类别下一步组1 组2 组1 组21 1 8 .001 0 0 22 1 10 .002 1 0 43 6 9 .005 0 0 64 15 .010 2 0 75 2 4 .010 0 0 86 67 .027 3 0 77 1 6 .048 4 6 88 1 2 .459 7 5 99 1 3 2.572 8 0 04 1975年Dagnelie收集了11年的气象数据资料如下表变量年序x1x2x3x4其中:x 1—前一年11月12日的降水量;x 2—7月均温;x 3—7月降雨量;x 4—月日辐射,试对这四个气象因子进行主成分分析. 解 由R 软件分析得到如下表6.4,6.5:表6.4 各主成分的重要性:主成分1 主成分2 主成分3 主成分4 标准差 1.6103349 0.9890848 0.53407741 0.37854199 方差贡献率 0.6482947 0.2445722 0.07130967 0.03582351 累积贡献率0.64829470.89286680.964176491.00000000表6.5 因子荷载:主成分1 主成分2 主成分3 主成分4 X1 0.291 0.871 0.332 -0.214 X2 -0.506 0.425 -0.742 -0.111 X3 0.577 0.136 -0.418 0.688 X4-0.5710.2050.4040.685由于前两个主成分对应的累积贡献率已经达到89.287,因此选取主成分的数目为2.5 对某初中12岁的女生进行体检,测量其身高x 1、体重x 2、胸围x 3和坐高x 4,共测得58个样本,并算得1234(,,,)x x x x x ='的样本协方差为19.9410.5023.566.5919.7120.958.637.97 3.937.55S ⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭ 试进行样本主成分分析.解 首先计算样本的相关系数矩阵:10.484410.32240.887210.70330.59760.31251⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭设相关系数矩阵的特征值和特征向量分别为d 和v 阵,计算得到0.0546000 0 0.312600= 000.96470 000 2.6681d ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭即四个特征值依次为:2.6681,0.9647,0.3126,0.0546,前两个主成分的累计贡献率为:90.8471%,因此提取主成分为2.四个特征根相应的特征向量为0.06000.70600.5333 0.4620 0.7317 0.17430.34040.5642=0.60570.19320.60400.48060.30690.65870.48460.4870v -⎛⎫ ⎪-⎪ ⎪--- ⎪-⎝⎭ 因此,两个主成分的表达式为:112340.060.73170.60570.3069z x x x x =+-- 212340.7060.17430.19320.6587z x x x x =-+-+6 比较因子分析和主成分分析模型的异同,阐明两者的关系. 解(1)提取公因子的方法主要有主成分法和公因子法.若采取主成分法,则主成分分析和因子分析基本等价,该法从解释变量的变异的角度出发,尽量使变量的方差能被主成分解释;而公因子法主要从解释变量的相关性角度,尽量使变量的相关程度能被公因子解释,当因子分析目的重在确定结构时则用到该法.(2)主成分分析和因子分析都是在多个原始变量中通过他们之间的内部相关性来获得新的变量,达到既减少分析指标个数,又能概括原始指标主要信息的目的.但他们各有其特点:主成分分析是将n 个原始变量提取m 个支配原始变量的公因子,和1个特殊因子,各因子之间可以相关或不相关.(3)统用降维的方法,但差异也很明显:主成分分析把方差划分为不同的正交成分,而因子分析则把方差化分为不同的起因因子;因子分析中的特征值的计算只能从相关系数矩阵出发,且必须把主成分划分为因子.(4)因子分析提取的公因子比主成分分析提取的主成分更具有可解释性.(5)两者分析的实质及重点不同.主成分的数学模型为Y AX =,因子分析的数学模型为X AF ε=+.因而可知主成分分析是实际上是线性变换,无假设检验,而因子分析是统计模型,某些因子模型是可以得到假设检验的;主成分分析主要综合原始数据的信息,而因子分析重在解释原始变量之间的关系.(6)SPSS 数据的实现:两者都通过“analyzedata reduction Factor ···”过程实现,但主成分分析主要使用“descriptires ”,“extraction ”,“stores ”对话框,而因子分析处使用这些外,还可使用“rotaction ”对话框进行因子旋转.7 试对第4题的变量作因子分析,并将结果和上面的结果进行比较. 解 用SPSS 分析,计算结果如下表6.6-6.8:表6.6 反应压缩比情况表 提取方法: 主成分法计算的相关系数矩阵的特征值和方差贡献率:表6.7 方差解释度提取方法: 主成分法表6.8 主成分矩阵8 为研究某一树种的叶片形态,选取50片叶测量其长度x 1(mm )和宽度x 2(mm ),按样本数据求得其平均值和协方差矩阵为:129048134,92,4845x x S ⎛⎫=== ⎪⎝⎭求出相关系数阵R ,并由R 出发作因子分析;解1)求相关系数矩阵:904810.7303,48900.73031S R ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭ 2)用R 软件求R 的特征根及其相应的特征向量,软件输出结果如下:$values[1] 2.99393809 0.07273809 $vectors[,1] [,2] [1,] 0.7071068 -0.7071068 [2,] 0.7071068 0.7071068122.9939,0.0727,λλ∴==12(),()0.7071,0.7071-0.7071,0.7071T Tηη==3) 求载荷矩阵A :1.22350.19071.22350.1907A -⎛⎫= ⎪⎝⎭4)22121.5333, 1.5333,h h == 0.98810.154*0.98810.154A -⎛⎫= ⎪⎝⎭12121,1,0.3043,0.3043u u v v ===-=,222222000011112,0,()0.9074,20i i iii i i i i i A u B v C u v D u v =========-===∑∑∑∑9 1981年,生物学家Grogan 和Wirth 对两种蠓虫Af 和Apf 根据其触角长度x 1和翼长x 2进行了分类,分类的数据资料如下:Af 1 2 3 4 5 6 7 8 x 1 1.24 1.36 1.38 1.38 1.38 1.40 1.48 1.54 x 2 1.27 1.74 1.64 1.82 1.90 1.70 1.82 1.82 Apf 1 2 3 4 5 6 x 1 1.14 1.18 1.20 1.26 1.28 1.30 x 2 1.78 1.96 1.86 2.00 2.00 1.96 (1)试建立Af 和Apf 的Fisher 判别模型;(2)对样本(1.24,1.80),(1.28,1.84),(1.40,2.04)进行判别分类. 解 (1)建立Fisher 判别模型991122121111(,)(1.42,1.75),(,)(1.23,1.93)99T TT T i i i i i i x x y y μμ======∑∑120.08480.1490.01980.0218,0.1490.39120.02180.039A A ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭12120.0080.0130.0130.0332A A n n ⎛⎫+== ⎪+-⎝⎭∑()120.19,0.18Tμμ-=-,()()121 1.325,1.842T μμ+= 1345.05135.42135.4283.33--⎛⎫= ⎪-⎝⎭∑, 带入Fisher 判别函数 ()12345.05135.42[(,)(1.325,1.84)]0.19,0.18135.4283.33Tx x -⎛⎫-- ⎪-⎝⎭1291.301741.336944.534x x =--(2)把三个样本(1.24,1.80),(1.28,1.84),(1.4,2.04)带入模型,得到结果:三个样本均属于Apf 类.10 在两个玉米品种之间进行判别:137玉米G 1和甜玉米G 2,选取的两个变量是:x 1—玉米果穗长;x 2—玉米果穗直径,两个类的样本容量为n 1=n 2=40,实际算得两个类的样本均值和样本协方差为:121218.5625.348.120 4.4589.661 3.720,,,5.98 4.12 4.458 4.350 3.720 3.410x x S S ⎛⎫⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭试建立G 1,G 2的Bayes 类线性判别函数.解 因为已知两类的样本均值和样本协方差为:12(18.56,5.98),(25.34,4.12)T T x x ==,128.120 4.4589.661 3.720,4.458 4.350 3.720 3.410S S ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭可计算得到修正的公共协方差矩阵和逆矩阵12120.2280.1450.1450.0992A A n n ⎛⎫+== ⎪+-⎝⎭∑,15.6393.738.25147.38--⎛⎫= ⎪-⎝⎭∑()()()121216.78,1.86,21.95,5.052TTμμμμ-=-+= 带入Fisher 判别函数()112121(())()2T W x x μμμμ-=-+-∑ ()()12 5.6393.73[(,)21.95,5.05] 6.78,1.868.25147.38Tx x -⎛⎫=-- ⎪-⎝⎭1274.396.951141.29x x =-+-。
研究生教材《应用数理统计》——课后习题答案详解学号:3113312042姓名:齐以年班级:硕3079班目录第一章数理统计的基本概念 (1)第二章参数估计 (18)第三章假设检验 (36)第四章方差分析与正交试验设计 (46)第五章回归分析 (51)第六章统计决策与贝叶斯推断 (56)对应书目:《应用数理统计》施雨编著西安交通大学出版第一章 数理统计的基本概念1.1 解:∵ 2~(,)X N μσ∴ 2~(,)n X N σμ∴~(0,1)N 分布∴(1)0.95P X P μ-<=<=又∵ 查表可得0.025 1.96u = ∴ 221.96n σ=1.2 解:(1) ∵ ~(0.0015)X Exp∴ 每个元件至800个小时没有失效的概率为:8000.001501.2(800)1(800)10.0015x P X P X e dxe -->==-<=-=⎰∴ 6个元件都没失效的概率为: 1.267.2()P e e --==(2) ∵ ~(0.0015)X Exp∴ 每个元件至3000个小时失效的概率为:30000.001504.5(3000)0.00151x P X e dxe--<===-⎰∴ 6个元件没失效的概率为: 4.56(1)P e -=-1.3解:(1) X ={(x 1,x 2,x 3)|x k =0,1,2,…,k =1,2,3},p (x 1,x 2,x 3)=λx 1+x 2+x 3x 1!x 2!x 3!e −3λ,x k =0,1,2,…;k =1,2,3(2) X ={(x 1,x 2,x 3)|x k ≥0;k =1,2,3},f (x 1,x 2,x 3)=λ3e −λ(x 1+x 2+x 3), x k ≥0;k =1,2,3(3) X ={(x 1,x 2,x 3)|a ≤x k ≤b;k =1,2,3},f (x 1,x 2,x 3)=1(b−a)3, a ≤x k ≤b;k =1,2,3(4) X ={(x 1,x 2,x 3)|−∞<x k <+∞;k =1,2,3}=R 3,f (x 1,x 2,x 3)=1(2π)3/2e −12∑(x k −μ)23k=1,−∞<x k <+∞;k =1,2,31.4 解:ini n x n x ex x x P ni i 122)(ln 2121)2(),.....,(122=--∏∑==πσμσ1.5证:21122)(na a x n x a x n i ni i i +-=-∑∑==∑∑∑===-+-=+-+-=ni i ni i n i i a x n x x na a x n x x x x 1222211)()(2221.6证明 (1) ∵22112211221()()()2()()()()()nnii i i nni i i i ni i XX X X X X X X X n X X X n X μμμμμ=====-=-+-=-+--+-=-+-∑∑∑∑∑(2) ∵2221112221221()22ii i nn ni i i i i ni ni XX X X X nX X nX nX X nX =====-=-+=-+=-∑∑∑∑∑1.7证明:a) 证:)(11111+=+++=∑n n i i n x x n x)(11)(1111n n n n n x x n x x x n n -++=++=++b )证:221111()1nn n i i S x x n ++==-+∑ 221112211121111[()]11121[()()()()]11(1)n n n i n i nn n n n n i i n n i i x x x x n n n x x x x x x x x n n n +=++++===---+++=----+-+++∑∑∑221112112[()()((1))111() ]1n n n n n n n n n nS x x x x nx x n x n n x x n ++++=+---+-+++-+22n122n 11[nS ()] 111[S ()]11n n n n n x x n n n x x n n ++=+-++=+-++ 1.8证明:显然: Zm+n ̅̅̅̅̅̅̅=nX ̅+mY ̅m+nS Z2=1m +n[∑(X i −Z m+n ̅̅̅̅̅̅̅)2n i=1+∑(Y i −Z m+n ̅̅̅̅̅̅̅)2mi=1] =1m +n[∑X i 2ni=1−2Zm+n ̅̅̅̅̅̅̅∗nX ̅+∑Y i 2−2Z m+n ̅̅̅̅̅̅̅∗mY ̅+(m +n)mi=1Zm+n ̅̅̅̅̅̅̅2] 因为: nS X 2=∑X i 2n i=1−nX ̅2 nS Y 2=∑Y i 2n i=1−nY ̅2所以:S Z2=nS X2+nS Y2m+n+1m+n[nX̅2+nY̅2−(nX̅+mY̅)2m+n] =nS X2+nS Y2m+n+m∗n(n+m)2(X̅−Y̅)21.10解:(1).∑∑====niiniixEnxnEXE11)(1)1()(=1n∙n∙mp=mpnpmpxDnxnDXDniinii)1()(1)1()(121-===∑∑==))(1()(122∑=-=niixxnESE)1(1)])1(1())1(([1)])()(())()(([1])()([1])([12222212212212p mp nn p m p mp n n p m p mp n n x E x D n x E x D n x nE x E n x x E n n i i i n i i n i i --=+--+-=+-+=-=-=∑∑∑=== 同理,(2).λ===∑∑==ni i n i i x E n x n E X E 11)(1)1()(λnx D n x n D X D ni ini i 1)(1)1()(121===∑∑==λnn x E x D n x E x D n x nE x E n S E n i i i n i i 1)])()(())()(([1])()([1)(2122122-=+-+=-=∑∑==(3).2)(1)1()(11ba x E n x n E X E n i i n i i +===∑∑==na b x D nx n D X D ni in i i 12)()(1)1()(2121-===∑∑==12)(1)])()(())()(([1])()([1)(22122122a b n n x E x D n x E x D n x nE x E n S E ni i i n i i -⋅-=+-+=-=∑∑==(4).λ===∑∑==ni i n i i x E n x n E X E 11)(1)1()(nx D nx n D X D ni in i i 2121)(1)1()(λ===∑∑==221221221)])()(())()(([1])()([1)(λnn x E x D n x E x D n x nE x E n S E n i i i n i i -=+-+=-=∑∑==(5).μ===∑∑==ni i n i i x E n x n E X E 11)(1)1()(nx D nx n D X D ni in i i 2121)(1)1()(σ===∑∑==221221221)])()(())()(([1])()([1)(σ⋅-=+-+=-=∑∑==nn x E x D n x E x D n x nE x E n S E n i i i n i i1.11 解:由统计量的定义知,1,3,4,5,6,7为统计量,5为顺序统计量 1.12 解:顺序统计量:-4,-2.1,-2.1,-0.1,-0.1,0,0,1.2,1.2,2.01,2.22,3.2,3.21中位数Me=0 极差R=(3.21+4)=7.21 再抽一个样本2.7,则顺序统计量变为:-4,-2.1,-2.1,-0.1,-0.1,0,0,1.2,1.2,2.01,2.22,2.7,3.2,3.21 此时,样本中位数Me=(0+1.2)/2=0.61.13解: F 20x={ 0 , x <0620, 0≪x <11320, 1≪x <21620, 2≪x <31820, 3≪x <41 , x ≫41.14解:利用伽马分布的可加性 X~Γ(α,λ) 则Y =∑X i ~Γ(nα,λ)n i=1X ̅=Y nf Y (y )=λnαy nα−1Γ(nα)e −λy,y >0根据随机变量函数的概率密度公式得:f X ̅(x )=λnα(nx)nα−1Γ(nα)e −λnx∗n =λnαn nαx nα−1Γ(nα)e −λnx ,x >01.15解:运用顺序统计量的概率密度公式 (1) f (m)(x )=n!(m−1)!(n−m )![F (x )]m−1[1−F (x )]n−m f(x) 1≪m ≪n (2) f (k)(j)(x )=n!(k−1)!(j−k−1)!(n−j )![F (x )]k−1[F (y )−F (x )]j−k−1[1−F (y )]n−j f(x)f(y) 1≪k<j ≪n (3) 样本极差R =X (n)−X (1), 其中X (n)和X (1)的概率密度可由(1)得到,再根据函数关系可推出R 的概率密度函数 1.16解:X i −μσ~N(0,1)(X i −μσ)2~χ2(1)故:∑(X i −μσ)2~ni=1χ2(n )1.17 证:),(~ λαΓXx ex x f λαααλ--Γ=∴1)()( 令kXY =ke ky kke ky yf ky ky⋅Γ=⋅Γ=∴----λαααλαααλαλ11)()( )()()(即 ),(~ky Y αΓ1.18 证:),(~ b a X β),()1()( 11b a B x xx f b a ---=∴),(),( ),()1()( 11b a B b k a B b a B x x x X E b a k k +=-=∴⎰∞+∞---),(),1()( b a B b a B X E +=∴ba a ab a b a b a a a a b a b a a a b b a b a b a +=Γ+Γ++ΓΓ=Γ++Γ+Γ+Γ=ΓΓ+Γ⋅++ΓΓ+Γ=)()()()()()()1()()1()()()()1()()1(),(),2()(2b a B b a B X E +=))(1()1()()()()2()()2(b a b a a a a b b a b a b a ++++=ΓΓ+Γ⋅++ΓΓ+Γ= 22)]([)()( X E X E X D -=∴2))(1())(1()1(b a b a ab ba ab a b a a a +++=+-++++=1.19 解:∵ ~(,)X F n m 分布2212(1)022()((1))()(1)()()()(1)()()n n m n mn m yn m y n mn nP Y y P X X y m myP X y n n n x x dx m m m++--+≤=+≤=<-Γ=+ΓΓ⎰2222122221122()()()1()(1)()()11(1)(1)(,)n n m n m n mn m n mf y P Y y y y y y y yy B ++----'=≤Γ=+ΓΓ----=∴ 22(1)(,)n mn n Y X X m mβ=+分布1.20 解:∵ ~()X t n 分布122212()()(()2)n n P Y y P X y P X xdxn ++-≤=≤=≤≤Γ=+112211221212122()()()(1)()1()(1)()()()n n n n n f y P Y y y y n y y n n n+++--+--'=≤Γ=+Γ=+ΓΓ∴ 2~(1,)2nY X F =分布1.21 解: (1) ∵ ~(8,4)X N 分布∴ 4~(8,)25X N 分布,即5(8)~(0,1)2X N - ∴ 样本均值落在7.8~8.2分钟之间的概率为:5(7.88)5(8)5(8.28)(7.88.2)()2220.383X P X P ---≤≤=≤≤=(2) 样本均值落在7.5~8分钟之间的概率为:5(7.58)5(8)5(88)(7.58)()2225(8)(0 1.25)20.3944X P X P X P ---≤≤=≤≤-=≤≤=若取100个样品,样本均值落在7.5~8分钟之间的概率为:10(7.88)10(8)10(8.28)(7.88.2)()2222*(0.84130.5)0.6826X P X P ---≤≤=≤≤=-= 单个样品大于11分钟的概率为:P 1=1−0.9333=0.0667 25个样品的均值大于9分钟的概率为: P 2=1−0.9938=0.0062 100个样品的均值大于8.6分钟的概率为P 3=1−0.9987=0.0013 所以第一种情况更有可能发生1.22 解:μ=2.5 2σ=36 n=5 (1)44302<<s ⇔)955,625(22∈σns 而)1(~222-n ns χσ即 )4(36522χ∈s通过查表可得 P =0.1929(2)样本方差落在30~40的概率为0.1929 样品均值-x 落在1.3~3.5的概率即:P{1.3<-x <3.5} ⇔P{-0.4472<σμ)(--x n <0.3727}又σμ)(--x n ~N(0,1)查标准正态分布表可得:P{1.3<-x <3.5}=0.3179 由于样本均值与样本方差相互独立,故:这样两者同时成立的概率为P =0.1929⨯0.3179=0.06131.23 解:(1) ∵2~(0,)X N σ分布 ∴ 2~(0,)X N nσ分布∴ 22()~(1)nXχσ∵ 22221()()ni i a X an X an σσ===∑∴ 21a n σ=同理 21b m σ= (2) ∵ 2~(0,)X N σ分布 ∴222~(1)X χσ分布由2χ分布是可加性得:2221~()ni i X n χσ=∑()nic X t m ==∑ ∴c =(3) 由(2)可知2221~()ni i X n χσ=∑ 2221122211~(,)nni ii i n mn mi ii n i n X d Xnn dF n m XmXmσσ==++=+=+=∑∑∑∑∴ m d n =1.24证明:X n+1~N(μ,σ2) X̅~N(μ,σ2/n) X n+1−X ̅~N(0,n +1n σ2)X n+1−X̅√n +1nσ2~N(0,1)(n −1)S n∗2σ2~χ2(n −1) 所以:Y =X n+1−X ̅S n ∗√n n +1~t(n −1) 1.25 证明:∵ 211~(,)X N μσ分布∴2211()~(1)i X μχσ-∴ 1221111()~()n i i X n μχσ=-∑同理 2222212()~()n i i Y n μχσ=-∑ 1122222112211111222221122112()()~(,)()()n n i i i i n n i i i i X n n X F n n Y n Y n μσμσμσμσ====--=--∑∑∑∑第二章 参数估计2.1 (1) ∵ ~()X Exp λ分布∴ ()1E X λ=令 ˆ1X λ= 解得λ的矩估计为:ˆ1X λ= (2) ∵ (,)X U a b 分布∴ ()2a bE X +=2()()12b a D X -=令 1ˆˆ2ab A X +==22221ˆˆˆˆ()()1124n i i b a a b A X n =-++==∑ (22211n i i X X S n =-=∑)解得a 和b 的矩估计为:ˆˆaX bX =-=(3) 110()1E X x x dx θθθθ-=*=+⎰令 1ˆˆ1A X θθ==+ ∴ˆ1XXθ=- (4) 110()(1)!kk x kE X x x e dx k βββ--=*=-⎰令 ˆkX β=∴ ˆkXβ=(5) 根据密度函数有2221()22()E X a aE X a λλλ=+=++根据矩估计有1222221ˆˆˆ22ˆˆˆa A X aa A S X λλλ+==++==+解得λ和a 的矩估计为:ˆˆaX λ==(6) ∵ (,)X B m p∴ ()E X mp =令 1ˆmpA X == 解得p 的矩估计为:ˆX pm= 2.2解:(1)X 服从指数分布,λ的似然函数为:L (λ)=λn e −λ∑x i n i=1, x i>0,i =1,2,⋯,nlnL (λ)=nlnλ−λ∑x i ni=1∂lnL (λ)∂λ=nλ−∑x i ni=1解得:λ̂=1x̅(2)f (x )=1b−a,a <x <b似然函数为:L (a,b )=1(b −a)n,a <x i <b显然:a ̂=X (1) b ̂=X (n) (3)f (x )={θ x θ−1 ,0<x <10, 其他似然函数为:L (θ)=θn ∗∏x i θ−1ni=1,0<x i <1lnL (θ)=nlnθ+(θ−1)∑lnx i ni=1∂lnL (θ)∂θ=nθ+∑lnx i ni=1=0 解得:θ̂=−n ∑lnx in i=1(4) f (x )={βk(k−1)!x k−1e −βx ,x >00, x ≤0似然函数为:L (β)=(βk(k −1)!)n ∗∏x i k−1ni=1∗e −β∑x i n i=1 ,x i >0 i =1,2,⋯,n lnL (β)=nk ∗lnβ−n ∗ln (k −1)!+(k −1)∑lnx i ni=1−β∑x i ni=1∂lnL (β)∂β=nkβ−∑x i ni=1=0解得:θ̂=−kx̅(5) f (x )={λ x −λ(x−a),x >a 0, x ≤a似然函数为:L (a,λ)=λn x −λ∑(x i ni=1−a) ,x i >a,i =1,2,⋯,nlnL (a,λ)=n ∗lnλ−λ∑x i ni=1+nλa ∂lnL (a,λ)∂λ=nλ−∑(x i ni=1−a)=0 解得:a ̂=X (1) , λ̂=−1X ̅−X (1)(6) X~B(m , P)P {X =k }=(m k)P k(1−P)m−k ,k =0,1,⋯,m似然函数为:L (p )=(m k)n P ∑xi n i=1(1−P)∑(m−x i )n i=1,x i =0,1,2,⋯,nlnL (p )=n ∗ln (mk)+∑x i n i=1∗lnp +∑(m −x i )ni=1∗ln (1−p)∂lnL (p )∂p=∑x in i=1p−∑(m −x i )n i=11−p=0解得:p ̂=−X̅m2.3解:∵ X 服从几何分布,其概率分布为:1()(1)k P X k p p -==-故p 的似然函数为: 1()(1)ni i x nnL p p p =-∑=-对数似然函数为:1ln ()ln ()ln(1)ni i L p n p x n p ==+--∑令 1ln ()1()01nii L p n x n p p p=∂=--=∂-∑ ∴ 1ˆpX= 2.4 解:由题知X 应服从离散均匀分布,⎪⎩⎪⎨⎧≤≤==其它01 1)(Nk N k x pE (X )=N+12矩估计: 令N ̂+12=710 ∴N̂=1419 极大似然估计:⎪⎩⎪⎨⎧≤≤=其它07101 1)(NN N L要使)(N L 最大,则710=N710=∴∧N2.5 解:由题中等式知:2196.196.196.1)025.01(025.0)(1S X +=+=∴+=+-Φ=∴=-Φ-∧∧∧-σμθσμμσθσμθ2.6 解:(1) 05.009.214.2=-=R0215.005.04299.05=⨯==∴∧d Rσ(2)将所有数据分为三组如下所示:0197.005.03946.005.0)05.005.005.0(316=⨯==∴=++=∴∧d R R σ 2.7 解:(1)⎩⎨⎧+<<=其它 01x 1)(θθx f θθθθθθ≠+==+=++=∴∧21)()(2121)(X E E X E ∴ X =∧θ不是θ的无偏估计,偏差为21=-∧θθ(2) θ=-)21(X E 21-=∴∧X θ是θ的无偏估计(3) 22))(()())(()(θθθθ-+=-+=∧∧X E X D E D M S E41121+=n 2.8 证:由例2.24,令2211x a x a +=∧μ,则∧μ 为μ无偏估计应 满足121=+a a因此1μ,2μ,3μ都是μ的无偏估计)()()()(21)()(2513)()(95)9491)(()())(()()(1233212221212∧∧∧∧∧∧=∧<<===+=∴+==∑μμμμμμμD D D X D D X D D X D X D D a a X D X D a D i i i2132121X X +=∴∧μ最有效2.9 证: )(~λp X λλ==∴)( )(X D X EX 是λ=)(X E 的无偏估计,2*S 是λ=)( X D 的无偏估计 )()1()())1((2*2*S E X E S X E αααα-+=-+∴λλααλ=-+=)1(∴ 2*)1(SX αα-+是λ的无偏估计2.10 解:因为2222((1))()(1)()(1)()1(1)()11(1)1E X S E X E S na E S n n a E S n n n a n nααααλαλαλαλλ**+-=+-=+--=+---=+-=- 所以 2(1)X S αα*+-是λ的无偏估计量2.11证明:X~P (λ)假设T(X 1)为θ=e −2λ的无偏估计,即: E[T(X 1)]= θ, E [T (X1)]=∑T (X )∞x=0∗λx x!e−λ=e −2λ=∑T (X )∞x=0∗λx x!=e−λ=∑(−λ)xx!∞x=0=∑(−1)x λx x!∞x=0(泰勒展开)所以T (X 1)=(−1)X 1是θ=e −2λ的唯一无偏估计。
习题11.1 解:由题意95.01=⎭⎬⎫⎩⎨⎧<--u x p 可得:95.0=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧<-σσn n u x p而()1,0~N u x n σ⎪⎭⎫ ⎝⎛-- 这可通过查N (0,1)分布表,975.0)95.01(2195.0=-+=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧<--σσn n u x p 那么96.1=σn∴2296.1σ=n1.2 解:(1)至800小时,没有一个元件失效,则说明所有元件的寿命>800小时。
{}2.10015.08000015.00800|e 0015.0800--∞+-=∞+-==>⎰e e dx x p x x 那么有6个元件,则所求的概率()2.762.1--==e e p(2)至300小时,所有元件失效,则说明所有元件的寿命<3000小时{}5.4300000015.030000015.001|e 0015.03000----=-==<⎰e e dx x p x 那么有6个元件,则所求的概率()65.41--=e p1。
3解: (1) 123{(,,)|0,1,2,,1,2,3}k x x x x k χ===因为~()i X P λ,所以 112233{,,}P X x X x X x ≤≤≤112233{}{}{}P X x P X x P X x =≤≤≤1233123!!!x x x e x x x ++-λλ=其中,0,1,2,,1,2,3k x k ==(2) 123{(,,)|0;1,2,3}k x x x x k χ=≥=因为~()i X Exp λ,其概率密度为,0()0,0x e x f x x -λ⎧λ≥=⎨ <⎩所以, 123(,,)3123(,,)x x x f x x x e-λ=λ,其中0;1,2,3k x k ≥=(3) 123{(,,)|;1,2,3}k x x x a x b k χ=≤≤=因为~(,)i X U a b ,其概率密度为1,()0,|a x b f x b a x a x b⎧≤≤⎪=-⎨⎪ <>⎩所以,12331(,,)()f x x x b a =-,其中;1,2,3k a x b k ≤≤= (4) 123{(,,)|;1,2,3}k x x x x k χ=-∞<<+∞= 因为~(,1)i X N μ,其概率密度为(2(),()x f x x 2-μ)-=-∞<<+∞所以,311(2123321(,,)(2)k k x f x x x e π2=--μ)∑=,其中;1,2,3k x k -∞<<+∞=1.4解:由题意可得:()⎪⎩⎪⎨⎧∞<<=--,其它00,21)(i 2ln i i 22i x e x x f u x σσπ则∏==ni x f x x f 1i n i )(),...(=⎪⎪⎩⎪⎪⎨⎧=∞<<∏=∑--=,其它0,...1,0,1n )2()(ln 212n 12i 2i x x e i n i i u x ni σπσ1.5证: 令21()()nii F a Xa ==-∑则'1()2()nii F a Xa ==--∑,''()20F a n => 令'1()2()0ni i F a X a ==--=∑,则可解得11ni i a X X n ===∑由于这是唯一解,又因为''()20F a n =>,因此,当11ni i a X X n ===∑时,()F a 取得最小值1.6证: (1)等式左边11((nnii i i XX X X 22==-μ)=-+-μ)∑∑111(2()()(n n n i i i i i X X X X X X 22====-)+-μ-+-μ)∑∑∑21(()ni i X X n X 2==-)+-μ∑左边=右边,所以得证。
习题11.1 解:由题意95.01=⎭⎬⎫⎩⎨⎧<--u x p 可得:95.0=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧<-σσn n u x p而()1,0~N u x n σ⎪⎭⎫ ⎝⎛-- 这可通过查N(0,1)分布表,975.0)95.01(2195.0=-+=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧<--σσn n u x p 那么96.1=σn∴2296.1σ=n1.2 解:(1)至800小时,没有一个元件失效,则说明所有元件的寿命>800小时。
{}2.10015.08000015.00800|e 0015.0800--∞+-=∞+-==>⎰e e dx x p x x 那么有6个元件,则所求的概率()2.762.1--==e e p(2)至300小时,所有元件失效,则说明所有元件的寿命<3000小时{}5.4300000015.030000015.001|e 0015.03000----=-==<⎰e e dx x p x 那么有6个元件,则所求的概率()65.41--=e p1.3解: (1) 123{(,,)|0,1,2,,1,2,3}k x x x x k χ===因为~()i X P λ,所以 112233{,,}P X x X x X x ≤≤≤112233{}{}{}P X x P X x P X x =≤≤≤1233123!!!x x x e x x x ++-λλ=其中,0,1,2,,1,2,3k x k ==(2) 123{(,,)|0;1,2,3}k x x x x k χ=≥=因为~()i X Exp λ,其概率密度为,0()0,0x e x f x x -λ⎧λ≥=⎨ <⎩所以, 123(,,)3123(,,)x x x f x x x e-λ=λ,其中0;1,2,3k x k ≥=(3) 123{(,,)|;1,2,3}k x x x a x b k χ=≤≤=因为~(,)i X U a b ,其概率密度为1,()0,|a x b f x b a x a x b⎧≤≤⎪=-⎨⎪ <>⎩所以,12331(,,)()f x x x b a =-,其中;1,2,3k a x b k ≤≤= (4) 123{(,,)|;1,2,3}k x x x x k χ=-∞<<+∞= 因为~(,1)i X N μ,其概率密度为(2(),()x f x x 2-μ)-=-∞<<+∞所以,311(2123321(,,)(2)k k x f x x x e π2=--μ)∑=,其中;1,2,3k x k -∞<<+∞=1.4解:由题意可得:()⎪⎩⎪⎨⎧∞<<=--,其它00,21)(i 2ln i i 22i x e x x f u x σσπ则∏==ni x f x x f 1i n i )(),...(=⎪⎪⎩⎪⎪⎨⎧=∞<<∏=∑--=,其它0,...1,0,1n )2()(ln 212n 12i 2i x x e i n i i u x ni σπσ1.5证: 令21()()nii F a Xa ==-∑则'1()2()nii F a Xa ==--∑,''()20F a n => 令'1()2()0ni i F a X a ==--=∑,则可解得11ni i a X X n ===∑由于这是唯一解,又因为''()20F a n =>,因此,当11ni i a X X n ===∑时,()F a 取得最小值1.6证: (1)等式左边11((nnii i i XX X X 22==-μ)=-+-μ)∑∑111(2()()(n n n i i i i i X X X X X X 22====-)+-μ-+-μ)∑∑∑21(()ni i X X n X 2==-)+-μ∑左边=右边,所以得证. (2) 等式左边22111(2nn ni iii i i XX X X X nX 2===-)=-+∑∑∑ 22212nii XnX nX ==-+∑221ni i X nX ==-∑左边=右边,所以得证.1.7证:(1)∑=-=ni i n x n x 11∑+=-++=11111n i i n x n x 那么)(11_1_n n n x x n x -+++=∑∑=+=•+-++ni i n n i i x n n x n x n 111111111 =111111+=+++∑n n i i x n x n =∑=+ni i x n 111=_1+n x ∴原命题得证(2)21221-=-=∑n n i i nx x n s211122111-++=+-+=∑n n i i n x x n s那么⎥⎦⎤⎢⎣⎡-+++-+212)(111n n n x x n s n n =∑=+n i i x n 1211--+21n x n n +212)1(++n x n n --++nn x x n n 12)1(2+22)1(-+n x n n=∑=+n i i x n 1211--+222)1(n x n n +2111++n x n -212)1(1++n x n --++n n x x n n 12)1(2=∑=+n i i x n 1211-(111++n x n +-+n x n n 1)2由(1)可得:111++n x n +-+n x n n 1=-+1n x则上式=∑=+n i i x n 1211-21-+n x =21+n s∴原命题得证1.10解: 因为2222111111,()n n n i i i i i i X X S X X X X n n n =====-=-∑∑∑所以 (1) 二项分布(,)B m p11()()()ni i i E X E X E X mp n ====∑21111(1)()()()n ni i i i mp p D X D X D X n n n ==-===∑∑222211111()(())()()(1)n n i i i i n E S E X X E X E X mp p n n n==-=-=-=-∑∑(2) 泊松分布()P λ()E X =λ, ()D X n λ=, 21()n E S n-=λ(3) 均匀分布(,)U a b()2b a E X +=, 2)()12b a D X n (-=, 221()()12n E S b a n-=-(4) 指数分布()Exp λ 1()E X =λ, 1()D X n 2=λ, 21()n E S n 2-=λ (5) 正态分布2(,)N σμ ()E X =μ, 21()D X n σ=, 221()n E S nσ-=1.11解:(1)是统计量(2)不是统计量,因为u未知 (3)统计量 (4)统计量(5)统计量,顺序统计量 (6)统计量 (7)统计量(8)不是统计量,因为u未知1.14.解: 因为i X 独立同分布,并且~(,i X a Γλ),11ni i X X n ==∑所以1~(,nii Xna =Γλ)∑;令1nii Y X ==∑,则1X Y n =,由求解随机变量函数的概率密度公式可得 1()(),0)nana nx X f x nx e n x na --λλ=>Γ(1.15 解:(1))(m x 的概率密度为: [][])()(1)()!()!1(!)(1)(x f x F x F m n m n x f m n m m ------=又F(x)=2x 且f(x)=2x ,0<x<1则有x x x m n m n x f m n m m 2)1()!()!1(!)(2)1(2)(------=,0<x<1(2) )(1x 与)(n x 的联合概率密度为: [][])()()(1)()()11(!),(011))(1(y f x f y F x F y F n n y x f n n ----=--=y x x y n n n 22))(1(222⋅⋅---=222)()1(4---n x y xy n n 0<x<y<1对于其他x,y ,有0),())(1(=y x f n1.19证:现在要求Y=)X 1/(X m nm n +的概率密度。
令g(x)= )1/(x mnx m n + 可得当0<y<1 有g ’(x)=2)1(1x mn +≥0 求g(x)的反函数h(y) 得h(y)=)111(xn m -+-又h ’(y)=2)1(1x n m - 这样可得Y 的概率密度:)('))(()(y h y h f y f x Y = (y ∈g(R))=2212)1(1)11()111)(()2,2(1x n m x x m n m n B m n n------- =)2,2()1(1212m n B x xm n --- (0<y<1)对于其他的Y 有 0)(=y f Y 原命题得证 1.20证明:令X =,其中~(0,1)Y N ,2~()Z n χ,则~()X t n因为22Y X Z n=,而22~(1)Y χ,2~()Z n χ所以22~(1,)Y X F n Z n=1.21解:(1)由题意可得:μ=8,42=σ,n=25对于2.88.7<<-x 5.0)(5.0<-<--σμx n又)1,0(~)(N x n σμ--通过查N(0,1)分布表,可得:P {7.8<-x <8.2}=0.6915-(1-0.6915)=0.383 (2)和(1)一样即求-1.25<σμ)(--x n <0的概率通过查表可得:P {85.7<<-x }=0.5-(1-0.8944)=0.3944 (3)此时n=100 即求-1<σμ)(--x n <1的概率通过查表可得:P {2.88.7<<-x }=0.8413-(1-0.8413)=0.6826 (4)单个样品大于11分钟 即x>11 可得该概率 p1=1-0.9332=0.0668 25个样品的均值大于9分钟,即9>-x 可得该概率为p2=1-0.9938=0.0062 100个样品的均值大于8.6分钟 即6.8>-x 可得该概率P3=1-0.9987=0.0013综上所述,第一种情况更有可能发生。
1.22 解:μ=2.5 2σ=36 n=5(1)44302<<s ⇔)955,625(22∈σns 而)1(~222-n ns χσ即 )4(36522χ∈s通过查表可得 P =0.1929(2)样本方差落在30~40的概率为0.1929 样品均值-x 落在1.3~3.5的概率即:P{1.3<-x <3.5} ⇔P{-0.4472<σμ)(--x n <0.3727}又σμ)(--x n ~N(0,1)查标准正态分布表可得:P{1.3<-x <3.5}=0.3179这样两者同时成立的概率为P =0.1929⨯0.3179=0.06131.23 解:(1)2121)()(∑∑++==+mn n i i ni i x b x a=22)()(--+m n x m b x n a =2222--+m n x bm x an =22)()(--+m n x m b x n a由定理1.2.1只要-n x n a 和-m mx n b 服从N(0.,1)分布 则上式为)2(2χ分布E(-n x n a )=0 D(-n x n a )=nan22σ=2σanE(-m mx n b )=0 D(-m x m b )=mbm22σ=2σbm要使-n x n a 和-m mx n b 服从N(0,1)分布,则2σan =1且2σbm =1这样可得:21σn a =21σm b =(2)-==∑n ni ix n x1由定理1.2.2 x~N(0,1) Y )2(~2χ => T =)(~n t nY xE(-n x n )=0 D(-n x n )=222σσn nn =⋅则∑=ni i x n 11σ服从N(0,1)分布。