初高中数学衔接知识点专题word版含答案
- 格式:doc
- 大小:367.04 KB
- 文档页数:6

初高中数学衔接教材乘法公式我们在初中已经学习过了下列一些乘法公式: (1)平方差公式 22()()a b a b a b +-=-;(2)完全平方公式 222()2a b a ab b ±=±+. 我们还可以通过证明得到下列一些乘法公式:(1)立方和公式 2233()()a b a ab b a b +-+=+; (2)立方差公式 2233()()a b a ab b a b -++=-;(3)三数和平方公式 2222()2()a b c a b c ab bc ac ++=+++++; (4)两数和立方公式 33223()33a b a a b ab b +=+++; (5)两数差立方公式 33223()33a b a a b ab b -=-+-. 对上面列出的五个公式,有兴趣的同学可以自己去证明. 例1 计算:22(1)(1)(1)(1)x x x x x x +--+++.例2 已知4a b c ++=,4ab bc ac ++=,求222a b c ++的值.练习1.填空: (1)221111()9423a b b a -=+( );(2)(4m + 22)164(m m =++ );(3 ) 2222(2)4(a b c a b c +-=+++ ).(4)若212x mx k ++是一个完全平方式,则k 等于 ( )(5)不论a ,b 为何实数,22248a b a b +--+的值 ( )(A )总是正数 (B )总是负数 (C )可以是零 (D )可以是正数也可以是负数第一讲 因式分解因式分解的主要方法有:十字相乘法、提取公因式法、公式法、分组分解法,另外还应了解求根法及待定系数法. 1.十字相乘法例1 分解因式:(1)x 2-3x +2; (2)x 2+4x -12; (3)22()x a b xy aby -++; (4)1xy x y -+-.课堂练习一、填空题:1、把下列各式分解因式:(1)=-+652x x ________。

数 学代数部分第一讲 乘法公式一、知识要点1.平方差公式: 22()()a b a b a b +-=-﹒ 2.完全平方公式:222()2a b a ab b ±=±+;2222()222a b c a b c ab bc ac ++=+++++﹒3.立方和公式: 2233()()a b a ab b a b +-+=+﹒ 4.立方差公式: 2233()()a b a ab b a b -++=-﹒ 5.完全立方公式:33223()33a b a a b ab b +=+++;33223()33a b a a b ab b -=-+-﹒二、例题选讲例1、填空(1)=++-)9)(3)(3(2x x x _______________﹒ 解:原式=81)9)(9(422-=+-x x x ﹒ (2)=+--22)2()12(x x ______________﹒解:原式=383)44(144222--=++-+-x x x x x x ﹒ 例2、已知31=+xx ,求下列各式的值: (1)221x x +;(2)331xx +﹒ 解:(1)21112)1(22222++=+⋅⋅+=+xx x x x x x x Θ,7292)1(1222=-=-+=+∴x x xx ﹒ (2) 18)17(3)11)(1(12233=-⨯=+-+=+x x x x x x ﹒例3、已知2x y +=,求代数式336x y xy ++的值. 解:33226()()6x y xy x y x xy y xy ++=+-++2222(3)2()8x xy y xy x y =-++=+=﹒例4、 已知8,9,x y y z -=-=试求代数式222x y z xy yz xz ++---的值. 解:8,9,17x y y z x z -=-=∴-=Q ,2222221(222222)2x y z xy yz xz x y z xy yz xz ∴++---=++---22222211[()()()](8917)21722x y y z x z =-+-+-=++= 三、自我小结:__________________________________________________________________________ __________________________________________________________________________ __________________________________________________________________________ __________________________________________________________________________ 四、巩固练习1.计算=+-++-++-))(())(())((a c a c c b c b b a b a _________. 2.计算22()2()()()x y x y x y x y +-+-+-= . 3.2200620082004-⨯= . 4.已知2510x x -+=,则221x x += . 5.计算16842321)13)(13)(13)(13(⋅-++++= .6.计算222222221234562009201012345620092010----++++++++L +201220112012201122+-﹒7.已知2a c b +=+,则222222a b c ab bc ac ++--+= .8.已知2x y -=,求代数式336x y xy --的值.9.已知1,3x y xy -==,试求下列各式的值: (1)22;x y +(2)33.x y -第二讲 因式分解一、知识要点1.因式分解:把一个整式化为几个整式的乘积形式. 2.因式分解的基本方法:(1)提公因式法 )(c b a m mc mb ma ++=++ (2)运用公式法 常见公式有:①22()()a b a b a b -=+-, ②2222()a ab b a b ±+=±, ③3322()()a b a b a ab b ±=±+m , ④3223333()a a b ab b a b ±+±=±,⑤2222222()a b c ab ac bc a b c +++++=++, (3)十字相乘法:2()()()x a b x ab x a x b +++=++ (4)配方法、添项拆项法,分组分解法 二、例题选讲例1、 因式分解:(1)244x x -+ ;(2)38x -;(3)33)2()2(a y a x ---﹒ 解:(1)244x x -+2(2)x =-(2)38x -3322(2)(24)x x x x =-=-++(3)33)2()2(a y a x ---=)()2()2()2(333y x a a y a x +-=-+-例2 、因式分解(1)256x x -+;(2)2215x x --;(3)26136x x -+﹒ 解:(1)256x x -+(2)(3)x x =--;(2)2215x x --(25)(3)x x =+-; (3)26136x x -+(23)(32)x x =--﹒例3、 因式分解225636x xy y x y -+-+ 解:225636x xy y x y -+-+(2)(3)3(2)x y x y x y =----(2)(33)x y x y =---例4、因式分解523325a ab a b b --+ 解:523325a ab a b b --+233233()()a a b b a b =---3322()()a b a b =-- 222()()()a b a b a ab b =-+++三、自我小结:__________________________________________________________________________ __________________________________________________________________________ __________________________________________________________________________ __________________________________________________________________________ 四、巩固练习1.将下列各式分解因式: (1)32x x y -__________________________________________________________________ (2)44-x__________________________________________________________________ (3)33125x y -__________________________________________________________________ (4)1322+-x x__________________________________________________________________ (5)2(1)x a x a -++__________________________________________________________________(6)32331a a a +++__________________________________________________________________ (7)222221a b ab a b ++--+__________________________________________________________________ (8)22122512x xy y ++__________________________________________________________________ (9)2226x xy y x y ++---__________________________________________________________________ 2.已知25a b -=,346a b +=,求多项式22328a ab b --的值.第三讲 因式定理一、知识要点定理1(因式定理):若a 是一元多项式)(0111是非负整数n a x a x a x a n n n n ++⋅⋅⋅++--的根,即00111=++⋅⋅⋅++--a a a a a a a n n n n ,则多项式0111a x a x a x a n n n n ++⋅⋅⋅++--有一个因式a x -.根据因式定理,找出一元多项式的一次因式的关键是求出该多项式的一个根,对于任意的多项式,求出它的根是没有一般方法的,然而对于整系数多项式常用下面的定理来判定它是否有有理根。

第04讲充分条件与必要条件模块一思维导图串知识模块二基础知识全梳理(吃透教材)模块三核心考点举一反三模块四小试牛刀过关测1.理解充分条件、必要条件的概念,理解充要条件的意义;2.了解充分条件与判定定理、必要条件与性质定理的关系;3.培养逻辑思维能力,能够在复杂情况下运用充分条件与必要条件进行推理,解决数学问题.知识点1充分条件与必要条件1、命题(1)命题的定义:一般地,我们把用语言、符号或式子表达的,可以判断真假的陈述句叫命题.判断为真的语句是真命题,判断为假的语句是假命题.(2)命题的形式:中学数学中的许多命题可以写成“若p,则q”,“如果p,那么q”等形式.其中p 称为命题的条件,q 称为命题的结论.2、充分条件与必要条件(1)一般地,“若p ,则q ”为真命题,是指由条件p 通过推理可以得出结论q .这时,我们就说,由p 可推出q ,记作p q ⇒,并且说,p 是q 的充分条件,q 是p 的必要条件.(2)如果“若p ,则q ”为假命题,那么由条件p 不能推出结论q ,记作p q ¿.这时,我们就说,p 不是q 的充分条件,q 不是p 的必要条件.(3)充分条件与必要条件的关系p 是q 的充分条件反映了p q ⇒,而q 是p 的必要条件也反映了p q ⇒,所以p 是q 的充分条件与q 是p 的必要条件表述的是同一个逻辑关系,只是说法不同.而p 是q 的充分条件只反映了p q ⇒,与q 能否推出p 没有任何关系.3、充要条件(1)充要条件的概念:如果“若p ,则q ”和它的逆命题“若q ,则p ”均为真命题,即既有p q ⇒,又有q p ⇒,就记作p q ⇔.此时,p 既是q 的充分条件,也是q 的必要条件,我们说p 是q 的充分必要条件,简称充要条件.(2)充要条件的含义:若p 是q 的充要条件,则q 也是p 的充要条件,虽然本质上是一样的,但在说法上还是不同的,因为这两个命题的条件与结论不同.(3)充要条件的等价说法:p 是q 的充要条件又常说成是q 成立当且仅当p 成立,或p 与q 等价.4、充分条件与必要条件的传递性(1)若p 是q 的充分条件,q 是s 的充分条件,即p q ⇒,q s ⇒,则有p s ⇒,即p 是s 的充分条件;(2)若p 是q 的必要条件,q 是s 的必要条件,即q p ⇒,s q ⇒,则有s p ⇒,即p 是s 的必要条件;(3)若p 是q 的充要条件,q 是s 的充要条件,即p q ⇔,q s ⇔,则有p s ⇔,即p 是s 的充要条件.5、条件关系判定的常用结论p 与q 的关系结论p q ⇒,但q p ¿p 是q 的充分不必要条件q p ⇒,但p q ¿p 是q 的必要不充分条件p q ⇒且q p ⇒,即p q ⇔p 是q 的充要条件p q ¿且q p¿p 是q 的既不充分也不必要条件知识点2从不同角度理解充分必要性1、从命题的角度充分理解充分必要性若把原命题中的条件和结论分别记作p和q,则原命题与逆命题同p与q之间有如下关系:(1)若原命题是真命题,逆命题是假命题,则p是q的充分不必要条件;(2)若原命题是假命题,逆命题是真命题,则p是q的必要不充分条件;(3)若原命题和逆命题都是真命题,则p和q互为充要条件;(4)若原命题和逆命题都是假命题,则p是q的既不充分也不必要条件.2、从集合的角度理解充分必要性若条件p,q以集合的形式出现,即A={x|p(x)},B={x|q(x)},则由A⊆B可得,p是q的充分条件,(1)若A B,则p是q的充分不必要条件;(2)若A⊇B,则p是q的必要条件;(3)若A B,则p是q的必要不充分条件;(4)若A=B,则p是q的充要条件;(5)若A⊈B且A⊉B,则p是q的既不充分也不必要条件.充分必要条件判断精髓:小集合推出大集合,小集合是大集合的充分不必要条件,大集合是小集合的必要不充分条件;若两个集合范围一样,就是充要条件的关系;知识点3充分、必要、充要条件的证明1、证明“充分不必要条件”“必要不充分条件”,一般先证明一个方面,然后验证另一个方面不成立。

数学学高中数学的几点建议:1、记数学笔记,特别是对概念理解的不同角度和数学规律,老师为备战高考而加的课外知识。
记录下来本章最有价值的思想方法和例题,以及还存在的未解决的问题,以便今后将其补上。
2、建立数学纠错本。
把平时容易出现错误的知识或推理记载下来,以防再犯。
争取做到:找错、析错、改错、防错。
解答问题完整、推理严密。
3、熟记一些数学规律和数学结论,使自己平时的运算技能达到了自动化熟练程度。
4、经常对知识结构进行梳理,形成板块结构,实行“整体集装”,如表格化,使知识结构一目了然;经常对习题进行类化,由一例到一类,由一类到多类,由多类到统一;使几类问题归纳于同一知识方法。
5、及时复习,强化对基本概念知识体系的理解与记忆,进行适当的反复巩固,消灭前学后忘。
6、学会从多角度、多层次地进行总结归类。
如:①从数学思想分类②从解题方法归类③从知识应用上分类等,使所学的知识系统化、条理化、专题化7、经常在做题后进行一定的“反思”,思考一下本题所用的基础知识,数学思想方法是什么,为什么要这样想,是否还有别的想法和解法,本题的分析方法与解法,在解其它问题时,是否也用到过。
初高中数学衔接教材现有初高中数学知识存在以下“脱节”1.立方和与差的公式初中已删去不讲,而高中的运算还在用。
2.因式分解初中一般只限于二次项且系数为“1”的分解,对系数不为“1”的涉及不多,而且对三次或高次多项式因式分解几乎不作要求,但高中教材许多化简求值都要用到,如解方程、不等式等。
3.二次根式中对分子、分母有理化初中不作要求,而分子、分母有理化是高中函数、不等式常用的解题技巧。
4.初中教材对二次函数要求较低,学生处于了解水平,但二次函数却是高中贯穿始终的重要内容。
配方、作简图、求值域、解二次不等式、判断单调区间、求最大、最小值,研究闭区间上函数最值等等是高中数学必须掌握的基本题型与常用方法。
5.二次函数、二次不等式与二次方程的联系,根与系数的关系(韦达定理)在初中不作要求,此类题目仅限于简单常规运算和难度不大的应用题型,而在高中二次函数、二次不等式与二次方程相互转化被视为重要内容,6.图像的对称、平移变换,初中只作简单介绍,而在高中讲授函数后,对其图像的上、下;左、右平移,两个函数关于原点,轴、直线的对称问题必须掌握。
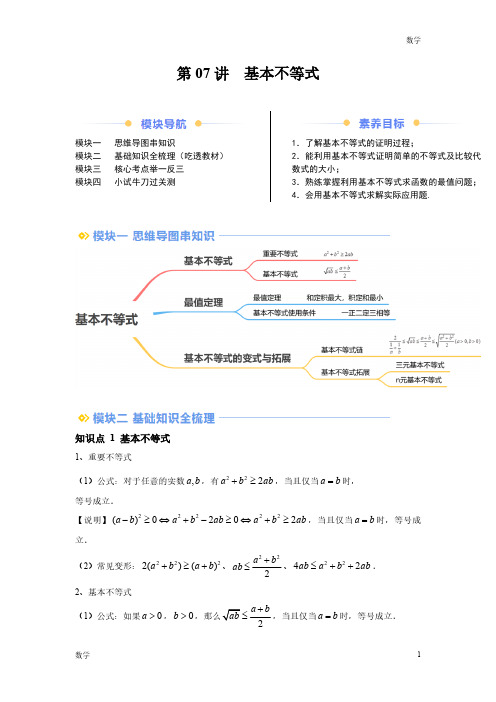
第07讲 基本不等式模块一 思维导图串知识模块二 基础知识全梳理(吃透教材)模块三 核心考点举一反三模块四 小试牛刀过关测1.了解基本不等式的证明过程;2.能利用基本不等式证明简单的不等式及比较代数式的大小;3.熟练掌握利用基本不等式求函数的最值问题;4.会用基本不等式求解实际应用题.知识点 1 基本不等式1、重要不等式(1)公式:对于任意的实数,a b ,有222a b ab +≥,当且仅当a b =时,等号成立.【说明】22222()0202a b a b ab a b ab -≥⇔+-≥⇔+≥,当且仅当a b =时,等号成立.(2)常见变形:2222()()a b a b +≥+、222a b ab +≤、2242ab a b ab ≤++.2、基本不等式(1)公式:如果0a >,0b >2a b+≤,当且仅当a b =时,等号成立.【说明】2ba +叫做正数,ab 的算术平均数,ab 叫做正数,a b 的几何平均数.因此基本不等式表明:两个正数的算术平均数不小于它们的几何平均数.(2)常见变形:a b +≥;2.2a b ab +⎛⎫≤ ⎪⎝⎭(3)常用结论:①2b aa b+≥(,a b 同号),当且仅当a b =时取等号;2b aa b+≤-(,a b 异号),当且仅当a b =-时取等号.②12a a+≥(0a >),当且仅当1a =时取等号;12a a+≤-(0a <),当且仅当1a =-时取等号;知识点 2 最值定理1、最值定理:已知,x y 都是正数,(1)若x +y =s (和s 为定值),则当x=y 时,积xy 有最大值,且这个值为s 24.(2)若xy =p (积p 为定值),则当x=y 时,和x +y 有最小值,且这个值为2p .最值定理简记为:积定和最小,和定积最大.2、在用基本不等式求函数的最值时,要满足三个条件:一正二定三取等.①一正:各项均为正数;②二定:含变数的各项的和或积必须有一个为定值;③三相等:含变数的各项均相等,取得最值.知识点 3 基本不等式的变式与拓展1、基本不等式链20,0)112a b a b a b +≤≤≤>>+或222()(0,0)22a b a b ab a b ++≤≤>>.当且仅当a b =时等号成立.其中,2211aba b a b=++为,a b 的调和平均值,222a b +为,a b 的平方平均值2、基本不等式的拓展(1)三元基本不等式:3a b c ++≥,,a b c 均为正实数),当且仅当a b c ==时等号成立.(2)n元基本不等式:12n a a a n+++ 12,,n a a a 均为正实数),当且仅当12n a a a === 时等号成立.考点一:对基本不等式的理解例1.(22-23高一上·河北邯郸·月考)不等式(x -2y )+12x y-≥2成立的前提条件为( )A .x ≥2yB .x >2yC .x ≤2yD .x <2y【变式1-1】(23-24高一上·西藏林芝·期中)下列命题中正确的是( )A .若0,0a b >>,且16a b +=,则64ab ≤B .若0a ≠,则44a a +≥=C .若,R a b ∈,则2()2a b ab +≥D .对任意,R a b ∈,222,a b ab a b +≥+≥.【变式1-2】(23-24高一上·山西运城·月考)(多选)已知,a b ∈R ,且0ab >,则下列不等式中,恒成立的是( )A.2a b+≥B .()()2222a b a b +≥+C .2b a a b +≥D .114a b a b ⎛⎫⎛⎫++≥ ⎪⎪⎝⎭⎝⎭【变式1-3】(23-24高一上·新疆巴音郭楞·期末)(多选)《几何原本》中的几何代数法是以几何方法研究代数问题,这种方法是数学家处理问题的重要依据,通过这一原理,很多的代数公理或定理都能够通过图形实现证明,也称之为无字证明.现有图形如图所示,C 为线段AB 上的点,且AC a =,BC b =,O 为AB 的中点,以AB 为直径作半圆,过点C 作AB 的垂线交半圆于D ,连接OD 、AD 、BD ,过点C 作OD 的垂线,垂足为E .则该图形可以完成的所有的无字证明为( )A.)0,02a ba b +≥>>B .()2230,0a b ab a b +>>>C()20,011a b a b≥>>+D .()220,022a b a ba b ++≥>>考点二:利用基本不等式比较大小例2. (23-24高一上·甘肃会宁·期中)设n mA m n=+(m 、n 为互不相等的正实数),242B x x =-+-,则A 与B 的大小关系是( )A .A B>B .A B≥C .A B<D .A B≤【变式2-1】(23-24高一上·江苏淮安·期中)已知实数a ,b ,c 满足22c b a a-=+-,2222c b a a a+=++,且0a >,则a ,b ,c 的大小关系是( )A .b c a>>B .c b a>>C .a c b>>D .c a b>>【变式2-2】(23-24高一上·福建莆田·期末)(多选)若170,139a b <<<<,则,a b +22,2a b +中不可能是最大值的是( )A .222a b +B.C.D .a b+【变式2-3】(23-24高一上·全国·专题练习)(多选)若0a b >>,则下列不等式成立的是( )A.2a b+>B .22ab a ba b +<+C .22ab a ba b +>+D 2aba b>+考点三:利用基本不等式求最值例3. (23-24高一下·贵州贵阳·月考)已知02x <<,则()32x x -的最大值是( )A .3-B .3C .1D .6【变式3-1】(23-24高一上·广东韶关·月考)已知100x >>,则2的最小值为( )A .3-B .2-C .1-D .0【变式3-2】(23-24高一下·河南周口·月考)已知正数,a b 满足1ab =,则22(1)(1)T a b =+++的最小值为( )A .4B .6C .8D .16【变式3-3】(23-24高一下·陕西榆林·月考)若正数x ,y 满足44x y +=,则11x y+的最小值为( )A .2B .94C .3D .83【变式3-4】(23-24高一下·广西·开学考试)已知0a >,0b >,且a b ab +=,则27ab a b -+的最小值是( )A .6B .9C .16D .19考点四:利用基本不等式证明不等式例4. (23-24高一上·安徽马鞍山·期中)已知0,0,1a b a b >>+=,求证:(1)114a b+≥;(2)12118a b ⎛⎫⎛⎫++≥+ ⎪⎪⎝⎭⎝⎭.【变式4-1】(23-24高一上·四川雅安·期中)已知0a >,0b >,且1a b +=,证明:(1)22221a b +≥;(2)1916a b+≥.【变式4-2】(23-24高一上·全国·专题练习)设a ,b ,c 均为正数,求证:()11192a b c a b b c a c ⎛⎫++++≥⎪+++⎝⎭.【变式4-3】(23-24高一上·安徽淮南·期中)已知,,a b c 是正实数.(1)证明:a b c ++≥(2)若2a b c ++=,证明:11192a b c ++≥.(3)已知,a b 是正数,且1a b +=,求证:()()ax by bx ay xy ++≥.考点五:基本不等式恒成立问题例5. (23-24高一上·贵州安顺·≥数m 的最大值为( )A .2B .3C .4D .9【变式5-1】(23-24高一上·吉林延边·月考)已知0x >,0y >,且2x y +=.若410x mxy +-≥恒成立,则实数m 的最大值是()A .4B .8C .3D .6【变式5-2】(23-24高一上·广东揭阳·期中)已知0x >,0y >,且9x y xy +=,若不等式a x y ≤+恒成立,则a 的取值范围是( )A .(],6-∞B .(],16-∞C .(],8∞-D .(],9-∞【变式5-3】(23-24高一下·湖南株洲·开学考试)(多选)若对于任意0x >,231xax x ≤++恒成立,则实数a 的取值可以是( )A .15B .110C .12D .13考点六:基本不等式在实际中的应用例6. (23-24高一下·浙江·月考)如图,某灯光设计公司生产一种长方形线路板,长方形()ABCD AB AD >的周长为4,沿AC 折叠使点B 到点B '位置,AB '交DC 于点P .研究发现当ADP △的面积最大时用电最少,则用电最少时,AB 的长度为( )A .54B C .32D 【变式6-1】(23-24高一上·江苏连云港·月考)某工厂建造一个无盖的长方体贮水池,其容积为48003m ,深度为3m .如果池底每平方米的造价为100元,池壁每平方米的造价为80元,怎样设计水池能使总造价最低?最低总造价为多少元?【变式6-2】(23-24高一上·广东佛山·月考)某工厂拟造一座平面图(如图)为长方形且面积为2150m 的三级污水处理池.由于地形限制,该处理池的长、宽都不能超过16 m ,且高度一定.如果四周池壁的造价为400元/2m ,中间两道隔墙的造价为248元/2m ,池底造价为80元/2m ,那么如何设计该处理池的长和宽,才能使总造价最低?(池壁的厚度忽略不计)【变式6-3】(23-24高一上·四川乐山·期中)用篱笆在一块靠墙的空地围一个面积为2的等腰梯形菜园,如图所示,用墙的一部分做下底AD ,用篱笆做两腰及上底,且腰与墙成60︒,当等腰梯形的腰长为多少时,所用篱笆的长度最小?并求出所用篱笆长度的最小值.一、单选题1.(23-24高一上·陕西宝鸡·期中)221x x +取最小值时x 的取值为( )A .1B .1±C .2D .2±2.(23-24高一上·湖南娄底·期末)若0x >,0y >,且1x y +=,则xy 的最大值是( )A .116B .14C .12D .13.(22-23高一上·江苏宿迁·月考)若0x >,则22y x x=+的最小值是( )A .B .C .4D .24.(23-24高一下·云南丽江·开学考试)已知a ,b 为正数,41a b +=,则114a b+的最小值为( )A .1B .2C .4D .85.(23-24高一上·湖南娄底·期末)已知0x >,则24-+x x x 的最小值为( )A .5B .3C .5-D .5-或36.(23-24高一上·山东济南·期末)如图所示,线段AB 为半圆的直径,O 为圆心,,C F 为半圆弧上不与,A B 重合的点,OF AB ⊥.作CD AB ⊥于,D DE OC ⊥于E ,设,AD a BD b ==,则下列不等式中可以直接表示CE DF ≤的是( )A .2aba b≤+B 2a b +≤C .2a b +≤D .2ab a b ≤+二、多选题7.(23-24高一下·云南昆明·期中)下列说法正确的是( )A .1x x+的最小值为2B .(2)x x -的最大值为2C .22x x -+的最小值为2D .2272x x ++最小值为28.(23-24高一上·全国·单元测试)已知,R a b ∈,且0ab ≠,则下列四个不等式中,恒成立的为( )A .222a b ab +≥B .2b a a b+≥C .2a b ab +⎛⎫≤ ⎪⎝⎭2D .22222a b a b ++⎛⎫≤⎪⎝⎭三、填空题9.(23-24高一上·广西百色·期末)若1x >,则2161x x x -+-的最小值为.10.(23-24高一上·北京·期中)某快递公司为提高效率,引进智能机器人分拣系统,以提高分拣效率和降低物流成本.已知购买x 台机器人的总成本为21()150600P x x x =++(单位:万元).若要使每台机器人的平均成本最低,则应买机器人 台.11.(23-24高一上·吉林延边·月考)若x a ∀>,关于x 的不等式225x x a+≥-恒成立,则实数a 的取值范围是.四、解答题12.(23-24高一上·山东菏泽·月考)(1)已知01x <<,则(43)x x -取得最大值时x 的值为?(2)函数22(1)1x y x x +=>- 的最小值为?(3)已知x ,y 是正实数,且4x y +=,求13x y+的最小值.13.(23-24高一上·安徽马鞍山·月考)如图,我国古代的“弦图”是由四个全等的直角三角形围成的.设直角三角形ABC 的直角边长为,a b ,且直角三角形ABC 的周长为2.(已知正实数,x y2x y +≤x y =时等号成立)(1)求直角三角形ABC 面积的最大值;(2)求正方形ABDE 面积的最小值.第07讲 基本不等式模块一 思维导图串知识模块二 基础知识全梳理(吃透教材)模块三 核心考点举一反三模块四 小试牛刀过关测1.了解基本不等式的证明过程;2.能利用基本不等式证明简单的不等式及比较代数式的大小;3.熟练掌握利用基本不等式求函数的最值问题;4.会用基本不等式求解实际应用题.知识点 1 基本不等式1、重要不等式(1)公式:对于任意的实数,a b ,有222a b ab +≥,当且仅当a b =时,等号成立.【说明】22222()0202a b a b ab a b ab -≥⇔+-≥⇔+≥,当且仅当a b =时,等号成立.(2)常见变形:2222()()a b a b +≥+、222a b ab +≤、2242ab a b ab ≤++.2、基本不等式(1)公式:如果0a >,0b >2a b+≤,当且仅当a b =时,等号成立.【说明】2ba +叫做正数,ab 的算术平均数,ab 叫做正数,a b 的几何平均数.因此基本不等式表明:两个正数的算术平均数不小于它们的几何平均数.(2)常见变形:a b +≥;2.2a b ab +⎛⎫≤ ⎪⎝⎭(3)常用结论:①2b aa b+≥(,a b 同号),当且仅当a b =时取等号;2b aa b+≤-(,a b 异号),当且仅当a b =-时取等号.②12a a+≥(0a >),当且仅当1a =时取等号;12a a+≤-(0a <),当且仅当1a =-时取等号;知识点 2 最值定理1、最值定理:已知,x y 都是正数,(1)若x +y =s (和s 为定值),则当x=y 时,积xy 有最大值,且这个值为s 24.(2)若xy =p (积p 为定值),则当x=y 时,和x +y 有最小值,且这个值为2p .最值定理简记为:积定和最小,和定积最大.2、在用基本不等式求函数的最值时,要满足三个条件:一正二定三取等.①一正:各项均为正数;②二定:含变数的各项的和或积必须有一个为定值;③三相等:含变数的各项均相等,取得最值.知识点 3 基本不等式的变式与拓展1、基本不等式链20,0)112a b a b a b +≤≤≤>>+或222()(0,0)22a b a b ab a b ++≤≤>>.当且仅当a b =时等号成立.其中,2211aba b a b=++为,a b 的调和平均值,222a b +为,a b 的平方平均值2、基本不等式的拓展(1)三元基本不等式:3a b c ++≥,,a b c 均为正实数),当且仅当a b c ==时等号成立.(2)n元基本不等式:12n a a a n+++ 12,,n a a a 均为正实数),当且仅当12n a a a === 时等号成立.考点一:对基本不等式的理解例1.(22-23高一上·河北邯郸·月考)不等式(x -2y )+12x y-≥2成立的前提条件为( )A .x ≥2yB .x >2yC .x ≤2yD .x <2y【答案】B【解析】由均值不等式的条件“一正、二定,三相等”,即均值不等式成立的前提条件是各项均为正数,所以不等式()1222x y x y-+≥-成立的前提条件为20x y ->,即2x y >.故选:B.【变式1-1】(23-24高一上·西藏林芝·期中)下列命题中正确的是( )A .若0,0a b >>,且16a b +=,则64ab ≤B .若0a ≠,则44a a +≥=C .若,R a b ∈,则2()2a b ab +≥D .对任意,R a b ∈,222,a b ab a b +≥+≥.【答案】A【解析】A 选项,2642a b ab +⎛⎫≤= ⎪⎝⎭,当且仅当8a b ==时等号成立,A 选项正确.B 选项,当a<0时,40a a+<,所以B 选项错误.C 选项,当0,0a b ><时,()20,02a b ab +<≥,所以C 选项错误.D 选项,当0,0a b <<时,0a b +<,a b +≥不成立,所以D 选项错误. 故选:A【变式1-2】(23-24高一上·山西运城·月考)(多选)已知,a b ∈R ,且0ab >,则下列不等式中,恒成立的是( )A .2a b+≥B .()()2222a b a b +≥+C .2b a a b +≥D .114a b a b ⎛⎫⎛⎫++≥ ⎪⎪⎝⎭⎝⎭【答案】BCD【解析】对于A ,当,a b 为负数时不成立,故A 错误,对于B ,()()22222()0a b a b a b +-+=-≥,则()()2222a b a b +≥+,故B 正确,对于C ,0ab >,则,b aa b 都为正数,2b a a b +≥,当且仅当b a ab=,即a b =时等号成立,故C 正确,对于D ,111224b a a b ab a b ab a b ⎛⎫⎛⎫++=+++≥+= ⎪⎪⎝⎭⎝⎭,当且仅当1ab ab =和b aa b=同时成立,即1a b ==±时等号成立,故D 正确,故选:BCD 【变式1-3】(23-24高一上·新疆巴音郭楞·期末)(多选)《几何原本》中的几何代数法是以几何方法研究代数问题,这种方法是数学家处理问题的重要依据,通过这一原理,很多的代数公理或定理都能够通过图形实现证明,也称之为无字证明.现有图形如图所示,C 为线段AB 上的点,且AC a =,BC b =,O 为AB 的中点,以AB 为直径作半圆,过点C 作AB 的垂线交半圆于D ,连接OD 、AD 、BD ,过点C 作OD 的垂线,垂足为E .则该图形可以完成的所有的无字证明为( )A.)0,02a ba b +≥>>B .()2230,0a b ab a b +>>>C()20,011a b a b≥>>+D .()220,022a b a ba b ++≥>>【答案】AC【解析】由题意可知AB AC BC a b =+=+,2a bOA OB OD +===,因为90CBD CAD ADC ∠=-∠=∠ ,90ACD DCB ∠=∠= ,则Rt Rt ACD DCB ∽ ,所以,CD ACBC CD= ,即2CD AC BC ab =⋅=,所以CD =在Rt OCD △中,OD CD >,即)0,02a ba b +>>当OD AB ⊥时,O 、C 点重合,a b =,此时)0,02a ba b +=>>,则)0,02a ba b +≥>>,所以A 正确;对于C 选项,在Rt OCD △中,CE OD ⊥,则90DCE CDE DOC ∠=-∠=∠ ,又因为90DEC DCO ∠=∠= ,所以,Rt Rt DEC DCO ∽ ,可得CD DE DO CD=,即2CD DE OD =⋅,所以222112CD ab ab DE a b OD a b a b====+++,由于CD DE >111a b >+,当a b =时,CD DE =111a b=+,()20,011a ba b>>+,所以C正确;由于22a b+在该图中没有相应的线段与之对应,故BD中的不等式无法通过这种几何方法来证明,故选:AC.考点二:利用基本不等式比较大小例2. (23-24高一上·甘肃会宁·期中)设n mAm n=+(m、n为互不相等的正实数),242B x x=-+-,则A与B的大小关系是()A.A B>B.A B≥C.A B<D.A B≤【答案】A【解析】m、n为互不相等的正实数,则m nn m≠,所以2n mAm n=+>=,2242(2)22B x x x=-+-=--+≤,=2x时,max2B=,所以A B>.故选:A.【变式2-1】(23-24高一上·江苏淮安·期中)已知实数a,b,c满足22c b aa-=+-,2222c b a aa+=++,且0a>,则a,b,c的大小关系是()A.b c a>>B.c b a>>C.a c b>>D.c a b>>【答案】B【解析】因为0a>,由基本不等式得22220c b aa-=+-≥=>,故c b>,因为2222c b a aa+=++,22c b aa-=+-,两式相减得,2222222222a a a aabaa++-=-+++=,故2112a ab+=+,所以220141151216ab aa a⎛⎫-⎪-+-+⎝=⎭=>,故b a>,所以c b a>>.故选:B【变式2-2】(23-24高一上·福建莆田·期末)(多选)若170,139a b <<<<,则,a b +22,2a b +中不可能是最大值的是( )A .222a b +B .C .D .a b+【答案】ABC【解析】由于170,139a b <<<<,则a b ¹,故a b +>222a b +>,则不可能是最大值,B ,C 符合题意;由于22221132)2()()428(a b a b a b ++=--+--,当170,139a b <<<<时,221112()2(0448a -<-=,22111()(1224b -<-=,故221131132((0428848a b -+--<+-=,即222a b a b +<+,故222a b +不可能是最大值,A 符合题意,故选:ABC【变式2-3】(23-24高一上·全国·专题练习)(多选)若0a b >>,则下列不等式成立的是( )A .2a b+>B .22ab a ba b +<+C .22ab a ba b +>+D 2aba b>+【答案】ABD【解析】对于选项A ,因为0a b >>,则20>,所以2a b+A 正确;因为0a b >>,所以0a b +>,0ab >,又2a b +>,得到01<<故22ab a ba b +<<+,所以选项B 和D 正确,对于选项C ,取2,1a b ==,满足0a b >>,但243322ab a ba b +=<=+,所以C 错误,故选:ABD.考点三:利用基本不等式求最值例3. (23-24高一下·贵州贵阳·月考)已知02x <<,则()32x x -的最大值是( )A .3-B .3C .1D .6【答案】B【解析】()32x x -()213234x x ⎡⎤≤⨯+-=⎣⎦,当且仅当2x x =-,即1x =取得等号,满足题意.故选:B.【变式3-1】(23-24高一上·广东韶关·月考)已知100x >>,则2的最小值为( )A .3-B .2-C .1-D .0【答案】A【解析】因为100x >>,故()10x x +-≥5,当且仅当5x =时,等号成立,所以2253≥-=-.故选:A.【变式3-2】(23-24高一下·河南周口·月考)已知正数,a b 满足1ab =,则22(1)(1)T a b =+++的最小值为( )A .4B .6C .8D .16【答案】C【解析】因为()2222228T a b a b ab =++++≥++=,当且仅当1a b ==时取等号,所以T 的最小值为8.故选:C.【变式3-3】(23-24高一下·陕西榆林·月考)若正数x ,y 满足44x y +=,则11x y+的最小值为( )A .2B .94C .3D .83【答案】B【解析】由正数x ,y 满足44x y +=,得111111419(4)()(5)5)4444y x x y x y x y x y +=++=++≥=,当且仅当4y x x y =,即23x =,43y =时取等号,所以11x y +的最小值为94.故选:B【变式3-4】(23-24高一下·广西·开学考试)已知0a >,0b >,且a b ab +=,则27ab a b -+的最小值是( )A .6B .9C .16D .19【答案】C【解析】因为a b ab +=且0a >,0b >,所以111a b+=,则()1192722799101016b a ab a b a a b b a b a b a b a b ⎛⎫-+=-++=+=++=++≥+= ⎪⎝⎭,当且仅当9111b aa ba b ⎧=⎪⎪⎨⎪+=⎪⎩时,即当4a =,43b =时,等号成立.因此,27ab a b -+的最小值是16.故选:C.考点四:利用基本不等式证明不等式例4. (23-24高一上·安徽马鞍山·期中)已知0,0,1a b a b >>+=,求证:(1)114a b+≥;(2)12118a b ⎛⎫⎛⎫++≥+ ⎪⎪⎝⎭⎝⎭.【答案】(1)证明见解析;(2)证明见解析【解析】(1)0,0,1a b a b >>+= ,()1111224b a a b a b a b a b ⎛⎫∴+=++=++≥+= ⎪⎝⎭,当且仅当ba a b=,即12a b ==时等号成立.(2)0,0,1a b a b >>+= ,12212212()1111a b a b b a ab b a ab +⎛⎫⎛⎫∴++=+++=+++⎪⎪⎝⎭⎝⎭21223434111()a b b a a b a b a b ⎛⎫=++++=++=+++ ⎪⎝⎭3434134888b a b a a b a b =++++=++≥+=+当且仅当34b a ba =时,即3,4ab ==-时等号成立.【变式4-1】(23-24高一上·四川雅安·期中)已知0a >,0b >,且1a b +=,证明:(1)22221a b +≥;(2)1916a b+≥.【答案】(1)证明见解析;(2)证明见解析【解析】(1)因为1a b +=,所以()222212a b a b ab ab +=+-=-,因为0a >,0b >,所以2124a b ab +⎛⎫≤= ⎪⎝⎭,当且仅当12a b ==时,等号成立,所以11121242ab -≥-⨯=,即2212a b +≥,故22221a b +≥;(2)因为1a b +=,所以()1919910b aa b a b a b a b ⎛⎫+=++=++ ⎪⎝⎭,因为0a >,0b >,所以0b a>,90a b >,所以96b a a b +≥,当且仅当9b a a b =,即334b a ==时,等号成立,则91016b aa b ++≥,即1916a b+≥.【变式4-2】(23-24高一上·全国·专题练习)设a ,b ,c 均为正数,求证:()11192a b c a b b c a c ⎛⎫++++≥⎪+++⎝⎭.【答案】证明见解析【解析】∵a ,b ,c 均为正数,∴()()()0a b b c c a +++++≥>,当且仅当a b b c a c +=+=+,即a b c ==时,等号成立.1110a b b c a c ++≥>+++,当且仅当111a b b c a c==+++,即a b c ==时,等号成立.∴()11129a b c a b b c a c ⎛⎫++++≥= ⎪+++⎝⎭,故()11192a b c a b b c a c ⎛⎫++++≥ ⎪+++⎝⎭,当且仅当a b c ==时,等号成立.【变式4-3】(23-24高一上·安徽淮南·期中)已知,,a b c 是正实数.(1)证明:a b c ++≥(2)若2a b c ++=,证明:11192a b c ++≥.(3)已知,a b 是正数,且1a b +=,求证:()()ax by bx ay xy ++≥.【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.【解析】(1)由222()()()a b c a b b c a c ++=+++++≥++,当且仅当a b c ==时等号成立,即a b c ++≥.(2)由11111()(3)22a b c a b c a b c b c a c a ba b c a b c a a b b c c++++++++=⋅++=⋅++++++119(3(3222)222≥++=⋅+++=,当且仅当23a b c ===时等号成立,则11192a b c ++≥,得证.(3)由222222()()()()(2)()ax by bx ay ab x y xy a b ab xy xy a b ++=+++≥++2()xy a b xy =+=,当且仅当x y =时等号成立,不等式得证.考点五:基本不等式恒成立问题例5. (23-24高一上·贵州安顺·≥数m 的最大值为( )A .2B .3C .4D .9【答案】Dm ≥恒成立,即5m +≥恒成立.又559≥+=,当且仅当a b =时取等号.故实数m 的最大值为9.故选:D【变式5-1】(23-24高一上·吉林延边·月考)已知0x >,0y >,且2x y +=.若410x mxy +-≥恒成立,则实数m 的最大值是()A .4B .8C .3D .6【答案】A【解析】由410x mxy +-≥,则41828912222x x x x y m xy xy xy y x++++≤===+()9111991542222222221x y x y y x y x ⎛⎛⎫⎛⎫++==+++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝,当且仅当922x y y x =,即12x =,32y =时,等号成立.故选:A.【变式5-2】(23-24高一上·广东揭阳·期中)已知0x >,0y >,且9x y xy +=,若不等式a x y ≤+恒成立,则a 的取值范围是( )A .(],6-∞B .(],16-∞C .(],8∞-D .(],9-∞【答案】B【解析】9x y xy +=,故911x y +=,()91910x yx y x y x y y x ⎛⎫+=++=++ ⎪⎝⎭,0x >,0y >,故96x y y x +≥=,当且仅当9x y y x=,即12,4x y ==时取等号,故10616x y +≥+=,x y +最小值是16,由不等式a x y ≤+恒成立可得16a ≤.a 的取值范围是(],16-∞,故选:B.【变式5-3】(23-24高一下·湖南株洲·开学考试)(多选)若对于任意0x >,231xax x ≤++恒成立,则实数a 的取值可以是( )A .15B .110C .12D .13【答案】ACD【解析】因为0x >,所以21113153x x x x x =≤=++++,当且仅当1x x=,即1x =时等号成立,由任意0x >,231xa x x ≤++恒成立, 所以15a ≥,符合条件有15,12,13,故A 、C 、D 对;11015<,故B 错;故选:ACD考点六:基本不等式在实际中的应用例6. (23-24高一下·浙江·月考)如图,某灯光设计公司生产一种长方形线路板,长方形()ABCD AB AD >的周长为4,沿AC 折叠使点B 到点B '位置,AB '交DC 于点P .研究发现当ADP △的面积最大时用电最少,则用电最少时,AB 的长度为( )A .54B C .32D 【答案】B【解析】如图,设AB x =,由矩形()ABCD AB AD >的周长为4,可知(2)AD x =-.设PC a =,则()DP x a =-.,90,APD CPB ADP CB P AD CB '''∠=∠∠=∠=︒= ,,Rt ADP Rt CB P AP PC a '∴∴== ≌.在Rt ADP 中,由勾股定理得222AD DP AP +=,即222(2)()x x a a -+-=,解得222x x a x-+=,所以22x DP x a x-=-=.所以ADP △的面积11222(2)322x S AD DP x x x x -⎛⎫=⋅=-⋅=-+ ⎪⎝⎭.所以33S ≤-=-2x x =时,即当x =时,ADP △的面积最大,面积的最大值为3-B .【变式6-1】(23-24高一上·江苏连云港·月考)某工厂建造一个无盖的长方体贮水池,其容积为48003m ,深度为3m .如果池底每平方米的造价为100元,池壁每平方米的造价为80元,怎样设计水池能使总造价最低?最低总造价为多少元?【答案】当水池设计成底面边长为40m 的正方形时,总造价最低,为198400元.【解析】设池底的一边长为()m 0x x >,则另一边长为48001600m=m 3x x,总造价为y 元,则1600160016001003280160000480y x x x x ⎛⎫⎛⎫=⨯++⨯⨯⨯=+⨯+ ⎪ ⎪⎝⎭⎝⎭160000480198400≥+⨯=,当且仅当1600x x=,即40x =时,等号成立,所以当水池设计成底面边长为40m 的正方形时,总造价最低,最低为198400元.【变式6-2】(23-24高一上·广东佛山·月考)某工厂拟造一座平面图(如图)为长方形且面积为2150m 的三级污水处理池.由于地形限制,该处理池的长、宽都不能超过16 m ,且高度一定.如果四周池壁的造价为400元/2m ,中间两道隔墙的造价为248元/2m ,池底造价为80元/2m ,那么如何设计该处理池的长和宽,才能使总造价最低?(池壁的厚度忽略不计)【答案】长为时总造价最低.【解析】设处理池的长和宽分别为x ,y ,高为h ,总造价为z ,则150xy =,(016,016)x y <≤<≤,(22)400224815080(8001296)120001200012000z x y h yh x y h =+⨯+⨯+⨯=++≥+=+,当且仅当8001296x y =,又150xy =,即16x =<,16y 时取到等号,故长为时总造价最低.【变式6-3】(23-24高一上·四川乐山·期中)用篱笆在一块靠墙的空地围一个面积为2的等腰梯形菜园,如图所示,用墙的一部分做下底AD ,用篱笆做两腰及上底,且腰与墙成60︒,当等腰梯形的腰长为多少时,所用篱笆的长度最小?并求出所用篱笆长度的最小值.【答案】当等腰梯形的腰长为10m 时,所用篱笆长度最小,其最小值为30m .【解析】设()()m 0AB a a =>,上底()()m 0BC b b =>,分别过点,B C 作下底的垂线,垂足分别为,E F ,则BE ,2a AE DF ==,则下底22a aAD b a b =++=+,该等腰梯形的面积())22b a b S a b a ++==+=所以()2300a b a +=,则30022a b a =-,所用篱笆长为2l a b =+300222a a a =+-300322a a =+≥30=,当且仅当300322aa =,即()10m a =,()10mb =时取等号.所以,当等腰梯形的腰长为10m 时,所用篱笆长度最小,其最小值为30m .一、单选题1.(23-24高一上·陕西宝鸡·期中)221x x+取最小值时x 的取值为( )A .1B .1±C .2D .2±【答案】B【解析】由题意可知,20x >,∴2212x x +≥=,当且仅当221x x =,即1x =±时,等号成立,即221x x+取最小值时x 的取值为1±.故选:B .2.(23-24高一上·湖南娄底·期末)若0x >,0y >,且1x y +=,则xy 的最大值是( )A .116B .14C .12D .1【答案】B【解析】由题意1x y +=≥,解得14≤xy ,等号成立当且仅当12x y ==.故选:B.3.(22-23高一上·江苏宿迁·月考)若0x >,则22y x x=+的最小值是( )A .B .C .4D .2【答案】C【解析】因为0x >,所以224y x x =+=≥,当且仅当22x x=,即1x =时等号成立,所以22y x x=+的最小值是4.故选:C.4.(23-24高一下·云南丽江·开学考试)已知a ,b 为正数,41a b +=,则114a b+的最小值为( )A .1B .2C .4D .8【答案】C【解析】正数a ,b 满足41a b +=,则11114()2244444)(b a a b a b a a b b +=+=≥++++,当且仅当44b aa b =,即142a b ==时取等号,所以当11,82a b ==时,114a b +取得最小值4.故选:C5.(23-24高一上·湖南娄底·期末)已知0x >,则24-+x x x 的最小值为( )A .5B .3C .5-D .5-或3【答案】B【解析】由0x >,得244113x x x x x -+=+-≥=,当且仅当4x x =,即2x =时等号成立,所以24-+x x x的最小值为3.故选:B.6.(23-24高一上·山东济南·期末)如图所示,线段AB 为半圆的直径,O 为圆心,,C F 为半圆弧上不与,A B 重合的点,OF AB ⊥.作CD AB ⊥于,D DE OC ⊥于E ,设,AD a BD b ==,则下列不等式中可以直接表示CE DF ≤的是( )A .2aba b≤+B 2a b +≤C .2a b +≤D .2ab a b ≤+【答案】D【解析】因为,AD a BD b ==,所以,22a b a b OF OC OD +-===,在Rt DOF △中,DF ==又CD AB ⊥,所以CD ===在Rt CDO △中,DE OC ⊥,故ED OC OD DC ⋅=⋅,得到22a bOD DC ED a b OC -⋅===+所以2abCE a b===+,所以CE DF ≤,即2ab a b +,故选:D.二、多选题7.(23-24高一下·云南昆明·期中)下列说法正确的是( )A .1x x+的最小值为2B .(2)x x -的最大值为2C .22x x -+的最小值为2D .2272x x ++最小值为2【答案】CD【解析】对于选项A ,当=1x -时,12x x+=-,故A 错误;对于选项B ,()()222211x x x x x -=-+=--+,所以()2x x -的最大值为1,故B错误;对于选项C,122222x x x x -+=+≥=,当且仅当122xx=,即0x =时,等号成立,故C 正确.对于选项D ,222277222222x x x x ++=+-≥=-++,当且仅当22722x x+=+,即22x =时,等号成立,故D 正确.故选:CD.8.(23-24高一上·全国·单元测试)已知,R a b ∈,且0ab ≠,则下列四个不等式中,恒成立的为( )A .222a b ab +≥B .2b a a b+≥C .2a b ab +⎛⎫≤ ⎪⎝⎭2D .22222a b a b ++⎛⎫≤⎪⎝⎭【答案】ACD【解析】由,R a b ∈,则222a b ab +≥,得222a b ab +≥,A 正确;由,R a b ∈,取1,2a b =-=,则1202b a a b +=--<,故B 错误;由于,R a b ∈,则22()024a b a b ab +-⎛⎫-=-≤ ⎪⎝⎭,则2a b ab +⎛⎫≤ ⎪⎝⎭,故C 正确;由于2222()0224a b a ba b ++-⎛⎫-=-≤ ⎪⎝⎭,故D 正确,故选:ACD .三、填空题9.(23-24高一上·广西百色·期末)若1x >,则2161x x x -+-的最小值为.【答案】9【解析】由1x >,得10x ->,于是21616161119111x x x x x x x -+=+=-++≥=---,当且仅当1611x x -=-,即5x =时取等号,所以2161x x x -+-的最小值为9.故答案为:910.(23-24高一上·北京·期中)某快递公司为提高效率,引进智能机器人分拣系统,以提高分拣效率和降低物流成本.已知购买x 台机器人的总成本为21()150600P x x x =++(单位:万元).若要使每台机器人的平均成本最低,则应买机器人 台.【答案】300【解析】购买x 台机器人的总成本为21()150600P x x x =++,则平均成本()150112600P x x x x =++≥+=,当且仅当150600x x=,即300x =时,平均成本最低为2万元.故答案为:300.11.(23-24高一上·吉林延边·月考)若x a ∀>,关于x 的不等式225x x a+≥-恒成立,则实数a 的取值范围是 .【答案】1,2⎡⎫+∞⎪⎢⎣⎭【解析】若关于x 的不等式225x x a +≥-恒成立,则min 2(2)5x x a+≥-,因为x a >,故2222()2242x x a a a a x a x a +=-++≥=+--,当且仅当1x a =+时取等,故得425a +≥,解得12a ≥.故答案为:1,2⎡⎫+∞⎪⎢⎣⎭四、解答题12.(23-24高一上·山东菏泽·月考)(1)已知01x <<,则(43)x x -取得最大值时x 的值为?(2)函数22(1)1x y x x +=>- 的最小值为?(3)已知x ,y 是正实数,且4x y +=,求13x y +的最小值.【答案】(1)23;(2)2 ;(3)1+【解析】(1)2113434(43)(3)(43)[3323x x x x x x +--=⨯⨯-≤⨯=,当且仅当343x x =-,即2(0,1)3x =∈时取等号.故(43)x x -取得最大值43时,x 的值为23.(2)2222122311x x x x y x x +-++-+==--2(1)2(1)31x x x -+-+=-3(1)221x x =-++≥+-.(1x >)当且仅当311x x -=-,即1(1,)x =∈+∞时取等号.故函数的最小值为2.(3)x ,R y +∈,()1311313112144y x x y x y x y x y ⎛⎫⎛⎫∴+=++=++≥+= ⎪ ⎪⎝⎭⎝⎭当且仅当y =,即)21x =,(23y =时取等号.∴13x y +的最小值为113.(23-24高一上·安徽马鞍山·月考)如图,我国古代的“弦图”是由四个全等的直角三角形围成的.设直角三角形ABC 的直角边长为,a b ,且直角三角形ABC 的周长为2.(已知正实数数学31,x y2x y +≤x y =时等号成立)(1)求直角三角形ABC 面积的最大值;(2)求正方形ABDE 面积的最小值.【答案】(1)3-;(2)(43-【解析】(1)由题意得:(22a b =+=2≤=6ab ≤-所以132S ab =≤-a b =时,等号成立,所以直角三角形ABC面积的最大值为3-;(2)因为a b +≤所以21a b =+≤)21≥=,所以(2243S a b =+≥-,当且仅当a b =时,等号成立,所以正方形ABDE 面积的最小值为(43-.。

初升高数学衔接带答案一、选择题1. 已知函数\( f(x) = 2x^2 - 3x + 5 \),求\( f(2) \)的值。
A. 7B. 9C. 11D. 13答案:B2. 一个直角三角形的两条直角边分别为3和4,求斜边的长度。
A. 5B. 6C. 7D. 8答案:A3. 一个数列的前三项为1, 2, 3,且每一项都是前一项的两倍加一,求第4项的值。
A. 7B. 8C. 9D. 10答案:A二、填空题1. 计算\( \sqrt{64} \)的值是______。
答案:82. 一个圆的半径为7,求该圆的面积。
面积公式为\( A = \pi r^2 \),所以面积是______。
答案:\( 49\pi \)三、简答题1. 解释什么是二项式定理,并给出一个例子。
答案:二项式定理是代数学中的一个重要定理,它描述了(a+b)^n展开成多项式的形式。
例如,\( (x+y)^2 = x^2 + 2xy + y^2 \)。
2. 给定一个函数\( g(x) = 3x - 4 \),求\( g^{-1}(x) \)。
答案:为了求\( g^{-1}(x) \),我们首先设\( y = g(x) \),即\( y = 3x - 4 \)。
解出x,得到\( x = \frac{y+4}{3} \),所以\( g^{-1}(x) = \frac{x+4}{3} \)。
四、计算题1. 解不等式\( |x - 5| < 2 \)。
答案:解这个绝对值不等式,我们得到两个不等式:\( -2 < x - 5 < 2 \)。
解这两个不等式,我们得到\( 3 < x < 7 \)。
2. 计算\( \int_{0}^{1} (3x^2 + 2x) \, dx \)。
答案:首先找到被积函数的原函数,即\( F(x) = x^3 + x^2 \)。
然后计算定积分:\[ \int_{0}^{1} (3x^2 + 2x) \, dx = F(1) - F(0) = (1^3 + 1^2) - (0^3 + 0^2) = 1 + 1 = 2 \]。

初升高衔接教材—数学2020.8目录1.1 数与式的运算1.1.1绝对值1.1.2. 乘法公式1.1.3.二次根式1.1.4.分式1.2 分解因式2.1 一元二次方程2.1.1根的判别式2.1.2 根与系数的关系(韦达定理)2.2 二次函数2.2.1 二次函数y=ax2+bx+c的图像和性质2.2.2 二次函数的三种表示方式2.2.3 二次函数的简单应用2.3 方程与不等式2.3.1 二元二次方程组解法2.3.2 一元二次不等式解法3.1 相似形3.1.1.平行线分线段成比例定理3.1.2相似形3.2 三角形3.2.1 三角形的“四心”3.2.2 几种特殊的三角形3.3圆3.3.1 直线与圆,圆与圆的位置关系3.3.2 点的轨迹121.1 数与式的运算1.1.1.绝对值绝对值的代数意义:正数的绝对值是它的本身,负数的绝对值是它的相反数,零的绝对值仍是零.即,0,||0,0,,0.a a a a a a >⎧⎪==⎨⎪-<⎩绝对值的几何意义:一个数的绝对值,是数轴上表示它的点到原点的距离. 两个数的差的绝对值的几何意义:b a -表示在数轴上,数a 和数b 之间的距离. 例1 解不等式:13x x -+->4.解法一:由01=-x ,得1=x ;由30x -=,得3x =; ①若1<x ,不等式可变为(1)(3)4x x ---->, 即24x -+>4,解得x <0, 又x <1, ∴x <0;②若12x ≤<,不等式可变为(1)(3)4x x --->, 即1>4,∴不存在满足条件的x ;③若3x ≥,不等式可变为(1)(3)4x x -+->, 即24x ->4, 解得x >4. 又x ≥3, ∴x >4.综上所述,原不等式的解为 x <0,或x >4.解法二:如图1.1-1,1-x 表示x 轴上坐标为x 的点P 到坐标为1的点A 之间的距离|P A |,即|P A |=|x -1|;|x -3|表示x 轴上点P 到坐标为2的点B 之间的距离|PB |,即|PB |=|x -3|.所以,不等式13x x -+->4的几何意义即为 |P A |+|PB |>4. 由|AB |=2,可知点P 在点C (坐标为0)的左侧、或点P 在点D (坐标为4)的右侧.x <0,或x >4.练 习 1.填空:(1)若5=x ,则x =_________;若4-=x ,则x =_________.(2)如果5=+b a ,且1-=a ,则b =________;若21=-c ,则c =________.2.选择题:下列叙述正确的是 ( )(A )若a b =,则a b = (B )若a b >,则a b > (C )若a b <,则a b < (D )若a b =,则a b =± 1A 0 C x|x -1||x -3| 图1.1-133.化简:|x -5|-|2x -13|(x >5).1.1.2. 乘法公式我们在初中已经学习过了下列一些乘法公式:(1)平方差公式 22()()a b a b a b +-=-;(2)完全平方公式 222()2a b a ab b ±=±+. 我们还可以通过证明得到下列一些乘法公式:(1)立方和公式 2233()()a b a ab b a b +-+=+; (2)立方差公式 2233()()a b a ab b a b -++=-;(3)三数和平方公式 2222()2()a b c a b c ab bc ac ++=+++++; (4)两数和立方公式 33223()33a b a a b ab b +=+++; (5)两数差立方公式 33223()33a b a a b ab b -=-+-. 对上面列出的五个公式,有兴趣的同学可以自己去证明. 例1 计算:22(1)(1)(1)(1)x x x x x x +--+++.解法一:原式=2222(1)(1)x x x ⎡⎤-+-⎣⎦=242(1)(1)x x x -++=61x -.解法二:原式=22(1)(1)(1)(1)x x x x x x +-+-++ =33(1)(1)x x +-=61x -.例2 已知4a b c ++=,4ab bc ac ++=,求222a b c ++的值. 解: 2222()2()8a b c a b c ab bc ac ++=++-++=.练 习 1.填空:(1)221111()9423a b b a -=+( ); (2)(4m + 22)164(m m =++ );(3 ) 2222(2)4(a b c a b c +-=+++ ).2.选择题:(1)若212x mx k ++是一个完全平方式,则k 等于 ( ) (A )2m (B )214m (C )213m (D )2116m(2)不论a ,b 为何实数,22248a b a b +--+的值 ( )(A )总是正数 (B )总是负数(C )可以是零 (D )可以是正数也可以是负数1.1.3.二次根式0)a ≥的代数式叫做二次根式.根号下含有字母、且不能够开得尽方的式子称为无理式. 例如32a b21x ++,22x y ++,等是有理式.1.分母(子)有理化把分母(子)中的根号化去,叫做分母(子)有理化.为了进行分母(子)有理化,需要引入有理化因式的概念.两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个代数式互为有理化因式,一般地,b与b互为有理化因式.分母有理化的方法是分母和分子都乘以分母的有理化因式,化去分母中的根号的过程;而分子有理化则是分母和分子都乘以分母的有理化因式,化去分子中的根号的过程在二次根式的化简与运算过程中,二次根式的乘法可参照多项式乘法进行,运算中要运用公0,0)a b=≥≥;而对于二次根式的除法,通常先写成分式的形式,然后通过分母有理化进行运算;二次根式的加减法与多项式的加减法类似,应在化简的基础上去括号与合并同类二次根式.2的意义a==,0,,0.a aa a≥⎧⎨-<⎩例1将下列式子化为最简二次根式:(1(20)a≥;(30)x<.解:(1=(20)a==≥;(3220)x x x==-<.例2(3-.解法一:(3-解法二:(345例3 试比较下列各组数的大小:(1(2. 解: (11===,1===,>.(2)∵1=== 又 4>22,∴6+4>6+22,例4化简:20042005+⋅.解:20042005⋅-=20042004⋅⋅=2004⎡⎤+⋅⋅⎣⎦=20041⋅例 5 化简:(1; (21)x <<. 解:(1)原式===2=2=.(2)原式1x x =-,∵01x <<, ∴11x x>>, 所以,原式=1x x-.6例 6已知x y ==22353x xy y -+的值 . 解:∵2210x y +==+=,1xy ==, ∴22223533()1131011289x xy y x y xy -+=+-=⨯-=.练 习 1.填空: (1=__ ___;(2(x =-x 的取值范围是_ _ ___; (3)=__ ___; (4)若2x ==______ __. 2.选择题:=( ) (A )2x ≠ (B )0x > (C )2x > (D )02x <<3.若b =,求a b +的值.4.比较大小:2-4(填“>”,或“<”).1.1.4.分式1.分式的意义形如A B 的式子,若B 中含有字母,且0B ≠,则称A B 为分式.当M ≠0时,分式AB具有下列性质: A A M B B M⨯=⨯; A A M B B M÷=÷. 上述性质被称为分式的基本性质.2.繁分式7像ab c d+,2m n pm n p +++这样,分子或分母中又含有分式的分式叫做繁分式.例1 若54(2)2x A Bx x x x +=+++,求常数,A B 的值.解: ∵(2)()2542(2)(2)(2)A B A x Bx A B x A x x x x x x x x x ++++++===++++,∴5,24,A B A +=⎧⎨=⎩解得 2,3A B ==.例2 (1)试证:111(1)1n n n n =-++(其中n 是正整数);(2)计算:1111223910+++⨯⨯⨯; (3)证明:对任意大于1的正整数n , 有11112334(1)2n n +++<⨯⨯+. (1)证明:∵11(1)11(1)(1)n n n n n n n n +--==+++,∴111(1)1n n n n =-++(其中n 是正整数)成立.(2)解:由(1)可知1111223910+++⨯⨯⨯ 11111(1)()()223910=-+-++-1110=-=910.(3)证明:∵1112334(1)n n +++⨯⨯+ =111111()()()23341n n -+-++-+=1121n -+,又n ≥2,且n 是正整数,∴1n +1一定为正数,∴1112334(1)n n +++⨯⨯+<12 . 例3 设ce a=,且e >1,2c 2-5ac +2a 2=0,求e 的值.解:在2c 2-5ac +2a 2=0两边同除以a 2,得 2e 2-5e +2=0, ∴(2e -1)(e -2)=0,8∴e =12 <1,舍去;或e =2. ∴e =2.练 习1.填空题:对任意的正整数n ,1(2)n n =+ (112n n -+);2.选择题:若223x y x y -=+,则xy= ( ) (A )1 (B )54 (C )45 (D )653.正数,x y 满足222x y xy -=,求x y x y-+的值.4.计算1111 (12233499100)++++⨯⨯⨯⨯.习题1.1A 组1.解不等式:(1) 13x ->; (2) 327x x ++-< ; (3) 116x x -++>.2.已知1x y +=,求333x y xy ++的值. 3.填空:(1)1819(2(2+-=________;(22=,则a 的取值范围是________; (3=________.B 组1.填空:(1)12a =,13b =,则2223352a ab a ab b -=+-____ ____; (2)若2220x xy y +-=,则22223x xy y x y++=+__ __; 2.已知:11,23x y ==的值.C 组1.选择题:(1=( )(A )a b < (B )a b > (C )0a b << (D )0b a <<(2)计算 ( )9(A(B(C) (D)2.解方程22112()3()10x x x x +-+-=. 3.计算:1111132435911++++⨯⨯⨯⨯. 4.试证:对任意的正整数n ,有111123234(1)(2)n n n +++⨯⨯⨯⨯++<14.1.1.1.绝对值1.(1)5±;4± (2)4±;1-或3 2.D 3.3x -181.1.2.乘法公式1.(1)1132a b - (2)11,24 (3)424ab ac bc --2.(1)D (2)A1.1.3.二次根式1. (12 (2)35x ≤≤ (3)- (4. 2.C 3.1 4.>1.1.4.分式1.12 2.B 3. 1- 4.99100习题1.1 A 组1.(1)2x <-或4x > (2)-4<x <3 (3)x <-3,或x >3 2.1 3.(1)2-(2)11a -≤≤ (31-B 组1.(1)37 (2)52,或-15 2.4.C 组1.(1)C (2)C 2.121,22x x == 3.36554.提示:1111[](1)(2)2(1)(1)(2)n n n n n n n =-+++++1.2 分解因式因式分解的主要方法有:十字相乘法、提取公因式法、公式法、分组分解法,另外还应了解求根法及待定系数法.1.十字相乘法例1 分解因式:(1)x 2-3x +2; (2)x 2+4x -12;10(3)22()x a b xy aby -++; (4)1xy x y -+-.解:(1)如图1.2-1,将二次项x 2分解成图中的两个x 的积,再将常数项2分解成-1与-2的乘积,而图中的对角线上的两个数乘积的和为-3x ,就是x 2-3x +2中的一次项,所以,有x 2-3x +2=(x -1)(x -2).说明:今后在分解与本例类似的二次三项式时,可以直接将图1.2-1中的两个x 用1来表示(如图1.2-2所示).(2)由图1.2-3,得x 2+4x -12=(x -2)(x +6). (3)由图1.2-4,得22()x a b xy aby -++=()()x ay x by -- (4)1xy x y -+-=xy +(x -y )-1=(x -1) (y+1) (如图1.2-5所示). 2.提取公因式法与分组分解法例2 分解因式:(1)32933x x x +++; (2)222456x xy y x y +--+-. 解: (1)32933x x x +++=32(3)(39)x x x +++=2(3)3(3)x x x +++ =2(3)(3)x x ++. 或32933x x x +++=32(331)8x x x ++++=3(1)8x ++=33(1)2x ++=22[(1)2][(1)(1)22]x x x +++-+⨯+ =2(3)(3)x x ++.(2)222456x xy y x y +--+-=222(4)56x y x y y +--+- =22(4)(2)(3)x y x y y +----=(22)(3)x y x y -++-.或222456x xy y x y +--+-=22(2)(45)6x xy y x y +----=(2)()(45)6x y x y x y -+--- =(22)(3)x y x y -++-.3.关于x 的二次三项式ax 2+bx +c (a ≠0)的因式分解.若关于x 的方程20(0)ax bx c a ++=≠的两个实数根是1x 、2x ,则二次三项式2(0)ax bx c a ++≠就可分解为12()()a x x x x --.例3 把下列关于x 的二次多项式分解因式:(1)221x x +-; (2)2244x xy y +-. 解: (1)令221x x +-=0,则解得11x =-21x =-,-1 -2 x x 图1.2-1 -1 -2 1 1 图1.2-2 -2 6 1 1 图1.2-3 -ay -by x x 图1.2-4 -1 1x y图1.2-5∴221x x +-=(1(1x x ⎡⎤⎡⎤-----⎣⎦⎣⎦=(11x x +-++.(2)令2244x xy y +-=0,则解得1(2x y =-+,1(2x y =--,∴2244x xy y +-=[2(1][2(1]x y x y +-++.练 习1.选择题:多项式22215x xy y --的一个因式为 ( ) (A )25x y - (B )3x y - (C )3x y + (D )5x y - 2.分解因式:(1)x 2+6x +8; (2)8a 3-b 3;(3)x 2-2x -1; (4)4(1)(2)x y y y x -++-.习题1.21.分解因式:(1) 31a +; (2)424139x x -+;(3)22222b c ab ac bc ++++; (4)2235294x xy y x y +-++-.2.在实数范围内因式分解:(1)253x x -+ ; (2)23x --;(3)2234x xy y +-; (4)222(2)7(2)12x x x x ---+. 3.ABC ∆三边a ,b ,c 满足222a b c ab bc ca ++=++,试判定ABC ∆的形状. 4.分解因式:x 2+x -(a 2-a ).1.2分解因式1. B 2.(1)(x +2)(x +4) (2)22(2)(42)a b a ab b -++(3)(11x x --+ (4)(2)(22)y x y --+.习题1.21.(1)()()211a a a +-+ (2)()()()()232311x x x x +-+- (3)()()2b c b c a +++ (4)()()3421y y x y -++-2.(1)x x ⎛-- ⎝⎭⎝⎭; (2)(x x -;(3)3x y x y ⎛⎫⎛⎫++ ⎪⎪ ⎪⎪⎝⎭⎝⎭; (4)()3(1)(11x x x x -+--+.3.等边三角形 4.(1)()x a x a -++2.1 一元二次方程2.1.1根的判别式我们知道,对于一元二次方程ax 2+bx +c =0(a ≠0),用配方法可以将其变形为2224()24b b acx a a-+=. ① 因为a ≠0,所以,4a 2>0.于是(1)当b 2-4ac >0时,方程①的右端是一个正数,因此,原方程有两个不相等的实数根x 1,2(2)当b 2-4ac =0时,方程①的右端为零,因此,原方程有两个等的实数根 x 1=x 2=-2b a; (3)当b 2-4ac <0时,方程①的右端是一个负数,而方程①的左边2()2b x a+一定大于或等于零,因此,原方程没有实数根.由此可知,一元二次方程ax 2+bx +c =0(a ≠0)的根的情况可以由b 2-4ac 来判定,我们把b 2-4ac 叫做一元二次方程ax 2+bx +c =0(a ≠0)的根的判别式,通常用符号“Δ”来表示.综上所述,对于一元二次方程ax 2+bx +c =0(a ≠0),有 (1) 当Δ>0时,方程有两个不相等的实数根x 1,2(2)当Δ=0时,方程有两个相等的实数根 x 1=x 2=-2b a; (3)当Δ<0时,方程没有实数根.例1 判定下列关于x 的方程的根的情况(其中a 为常数),如果方程有实数根,写出方程的实数根. (1)x 2-3x +3=0; (2)x 2-ax -1=0; (3) x 2-ax +(a -1)=0; (4)x 2-2x +a =0. 解:(1)∵Δ=32-4×1×3=-3<0,∴方程没有实数根. (2)该方程的根的判别式Δ=a 2-4×1×(-1)=a 2+4>0,所以方程一定有两个不等的实数根1x =, 2x = (3)由于该方程的根的判别式为Δ=a 2-4×1×(a -1)=a 2-4a +4=(a -2)2,所以, ①当a =2时,Δ=0,所以方程有两个相等的实数根 x 1=x 2=1; ②当a ≠2时,Δ>0, 所以方程有两个不相等的实数根 x 1=1,x 2=a -1.(3)由于该方程的根的判别式为Δ=22-4×1×a =4-4a =4(1-a ), 所以①当Δ>0,即4(1-a ) >0,即a <1时,方程有两个不相等的实数根11x = 21x =②当Δ=0,即a =1时,方程有两个相等的实数根 x 1=x 2=1; ③当Δ<0,即a >1时,方程没有实数根.说明:在第3,4小题中,方程的根的判别式的符号随着a 的取值的变化而变化,于是,在解题过程中,需要对a 的取值情况进行讨论,这一方法叫做分类讨论.分类讨论这一思想方法是高中数学中一个非常重要的方法,在今后的解题中会经常地运用这一方法来解决问题.2.1.2 根与系数的关系(韦达定理)若一元二次方程ax 2+bx +c =0(a ≠0)有两个实数根12b x a -+=,22b x a-=,则有1222b bx x a a-+===-;221222(4)42244b b b b ac ac cx x a a a a a-----=⋅===. 所以,一元二次方程的根与系数之间存在下列关系:如果ax 2+bx +c =0(a ≠0)的两根分别是x 1,x 2,那么x 1+x 2=b a -,x 1·x 2=ca.这一关系也被称为韦达定理.特别地,对于二次项系数为1的一元二次方程x 2+px +q =0,若x 1,x 2是其两根,由韦达定理可知x 1+x 2=-p ,x 1·x 2=q ,即 p =-(x 1+x 2),q =x 1·x 2, 所以,方程x 2+px +q =0可化为 x 2-(x 1+x 2)x +x 1·x 2=0,由于x 1,x 2是一元二次方程x 2+px +q =0的两根,所以,x 1,x 2也是一元二次方程x 2-(x 1+x 2)x +x 1·x 2=0.因此有 以两个数x 1,x 2为根的一元二次方程(二次项系数为1)是x 2-(x 1+x 2)x +x 1·x 2=0. 例2 已知方程2560x kx +-=的一个根是2,求它的另一个根及k 的值.分析:由于已知了方程的一个根,可以直接将这一根代入,求出k 的值,再由方程解出另一个根.但由于我们学习了韦达定理,又可以利用韦达定理来解题,即由于已知了方程的一个根及方程的二次项系数和常数项,于是可以利用两根之积求出方程的另一个根,再由两根之和求出k 的值.解法一:∵2是方程的一个根,∴5×22+k ×2-6=0, ∴k =-7.所以,方程就为5x 2-7x -6=0,解得x 1=2,x 2=-35. 所以,方程的另一个根为-35,k 的值为-7. 解法二:设方程的另一个根为x 1,则 2x 1=-65,∴x 1=-35. 由 (-35)+2=-5k,得 k =-7.所以,方程的另一个根为-35,k 的值为-7. 例3 已知关于x 的方程x 2+2(m -2)x +m 2+4=0有两个实数根,并且这两个实数根的平方和比两个根的积大21,求m 的值.分析: 本题可以利用韦达定理,由实数根的平方和比两个根的积大21得到关于m 的方程,从而解得m 的值.但在解题中需要特别注意的是,由于所给的方程有两个实数根,因此,其根的判别式应大于零.解:设x 1,x 2是方程的两根,由韦达定理,得 x 1+x 2=-2(m -2),x 1·x 2=m 2+4. ∵x 12+x 22-x 1·x 2=21, ∴(x 1+x 2)2-3 x 1·x 2=21,即 [-2(m -2)]2-3(m 2+4)=21, 化简,得 m 2-16m -17=0, 解得 m =-1,或m =17.当m =-1时,方程为x 2+6x +5=0,Δ>0,满足题意; 当m =17时,方程为x 2+30x +293=0,Δ=302-4×1×293<0,不合题意,舍去. 综上,m =17. 说明:(1)在本题的解题过程中,也可以先研究满足方程有两个实数根所对应的m 的范围,然后再由“两个实数根的平方和比两个根的积大21”求出m 的值,取满足条件的m 的值即可.(1)在今后的解题过程中,如果仅仅由韦达定理解题时,还要考虑到根的判别式Δ是否大于或大于零.因为,韦达定理成立的前提是一元二次方程有实数根.例4 已知两个数的和为4,积为-12,求这两个数.分析:我们可以设出这两个数分别为x ,y ,利用二元方程求解出这两个数.也可以利用韦达定理转化出一元二次方程来求解.解法一:设这两个数分别是x ,y , 则 x +y =4, ①xy =-12. ② 由①,得 y =4-x , 代入②,得x (4-x )=-12,即 x 2-4x -12=0, ∴x 1=-2,x 2=6.∴112,6,x y =-⎧⎨=⎩ 或226,2.x y =⎧⎨=-⎩因此,这两个数是-2和6.解法二:由韦达定理可知,这两个数是方程 x 2-4x -12=0 的两个根.解这个方程,得x 1=-2,x 2=6. 所以,这两个数是-2和6. 说明:从上面的两种解法我们不难发现,解法二(直接利用韦达定理来解题)要比解法一简捷. 例5 若x 1和x 2分别是一元二次方程2x 2+5x -3=0的两根. (1)求| x 1-x 2|的值;(2)求221211x x +的值; (3)x 13+x 23.解:∵x 1和x 2分别是一元二次方程2x 2+5x -3=0的两根,∴1252x x +=-,1232x x =-.(1)∵| x 1-x 2|2=x 12+ x 22-2 x 1x 2=(x 1+x 2)2-4 x 1x 2=253()4()22--⨯-=254+6=494, ∴| x 1-x 2|=72. (2)22221212122222221212125325()2()3()2113722439()9()24x x x x x x x x x x x x --⨯-+++-+=====⋅-.(3)x 13+x 23=(x 1+x 2)( x 12-x 1x 2+x 22)=(x 1+x 2)[ ( x 1+x 2) 2-3x 1x 2]=(-52)×[(-52)2-3×(32-)]=-2158. 说明:一元二次方程的两根之差的绝对值是一个重要的量,今后我们经常会遇到求这一个量的问题,为了解题简便,我们可以探讨出其一般规律:设x 1和x 2分别是一元二次方程ax 2+bx +c =0(a ≠0),则1x=,2x =, ∴| x 1-x 2|=||||a a ==. 于是有下面的结论:若x 1和x 2分别是一元二次方程ax 2+bx +c =0(a ≠0),则| x 1-x 2|=||a (其中Δ=b 2-4ac ). 今后,在求一元二次方程的两根之差的绝对值时,可以直接利用上面的结论.例6 若关于x 的一元二次方程x 2-x +a -4=0的一根大于零、另一根小于零,求实数a 的取值范围. 解:设x 1,x 2是方程的两根,则x 1x 2=a -4<0, ① 且Δ=(-1)2-4(a -4)>0.② 由①得 a <4,由②得 a <174.∴a 的取值范围是a <4.练 习 1.选择题:(1)方程2230x k -+=的根的情况是 ( ) (A )有一个实数根 (B )有两个不相等的实数根(C )有两个相等的实数根 (D )没有实数根(2)若关于x 的方程mx 2+ (2m +1)x +m =0有两个不相等的实数根,则实数m 的取值范围是( ) (A )m <14 (B )m >-14 (C )m <14,且m ≠0 (D )m >-14,且m ≠02.填空:(1)若方程x 2-3x -1=0的两根分别是x 1和x 2,则1211x x += .(2)方程mx 2+x -2m =0(m ≠0)的根的情况是 . (3)以-3和1为根的一元二次方程是 .3|1|0b -=,当k 取何值时,方程kx 2+ax +b =0有两个不相等的实数根? 4.已知方程x 2-3x -1=0的两根为x 1和x 2,求(x 1-3)( x 2-3)的值.习题2.1 A 组1.选择题:(1)已知关于x 的方程x 2+kx -2=0的一个根是1,则它的另一个根是( ) (A )-3 (B )3 (C )-2 (D )2 (2)下列四个说法:①方程x 2+2x -7=0的两根之和为-2,两根之积为-7; ②方程x 2-2x +7=0的两根之和为-2,两根之积为7;③方程3 x 2-7=0的两根之和为0,两根之积为73-; ④方程3 x 2+2x =0的两根之和为-2,两根之积为0.其中正确说法的个数是 ( ) (A )1个 (B )2个 (C )3个 (D )4个(3)关于x 的一元二次方程ax 2-5x +a 2+a =0的一个根是0,则a 的值是( )(A )0 (B )1 (C )-1 (D )0,或-12.填空:(1)方程kx 2+4x -1=0的两根之和为-2,则k = .(2)方程2x 2-x -4=0的两根为α,β,则α2+β2= .(3)已知关于x 的方程x 2-ax -3a =0的一个根是-2,则它的另一个根是 .(4)方程2x 2+2x -1=0的两根为x 1和x 2,则| x 1-x 2|= .3.试判定当m 取何值时,关于x 的一元二次方程m 2x 2-(2m +1) x +1=0有两个不相等的实数根?有两个相等的实数根?没有实数根?4.求一个一元二次方程,使它的两根分别是方程x 2-7x -1=0各根的相反数.B 组1.选择题:若关于x 的方程x 2+(k 2-1) x +k +1=0的两根互为相反数,则k 的值为( )(A )1,或-1 (B )1 (C )-1 (D )0 2.填空:(1)若m ,n 是方程x 2+2005x -1=0的两个实数根,则m 2n +mn 2-mn 的值等于 .(2)如果a ,b 是方程x 2+x -1=0的两个实数根,那么代数式a 3+a 2b +ab 2+b 3的值是 . 3.已知关于x 的方程x 2-kx -2=0.(1)求证:方程有两个不相等的实数根;(2)设方程的两根为x 1和x 2,如果2(x 1+x 2)>x 1x 2,求实数k 的取值范围. 4.一元二次方程ax 2+bx +c =0(a ≠0)的两根为x 1和x 2.求: (1)| x 1-x 2|和122x x +; (2)x 13+x 23.5.关于x 的方程x 2+4x +m =0的两根为x 1,x 2满足| x 1-x 2|=2,求实数m 的值.C 组1.选择题:(1)已知一个直角三角形的两条直角边长恰好是方程2x 2-8x +7=0的两根,则这个直角三角形的斜边长等于 ( ) (A(B )3 (C )6 (D )9 (2)若x 1,x 2是方程2x 2-4x +1=0的两个根,则1221x x x x +的值为 ( ) (A )6 (B )4 (C )3 (D )32(3)如果关于x 的方程x 2-2(1-m )x +m 2=0有两实数根α,β,则α+β的取值范围为( ) (A )α+β≥12 (B )α+β≤12(C )α+β≥1 (D )α+β≤1 (4)已知a ,b ,c 是ΔABC 的三边长,那么方程cx 2+(a +b )x +4c=0的根的情况是 ( )(A )没有实数根 (B )有两个不相等的实数根(C )有两个相等的实数根 (D )有两个异号实数根 2.填空:若方程x 2-8x +m =0的两根为x 1,x 2,且3x 1+2x 2=18,则m = . 3. 已知x 1,x 2是关于x 的一元二次方程4kx 2-4kx +k +1=0的两个实数根.(1)是否存在实数k ,使(2x 1-x 2)( x 1-2 x 2)=-32成立?若存在,求出k 的值;若不存在,说明理由; (2)求使1221x x x x +-2的值为整数的实数k 的整数值; (3)若k =-2,12xx λ=,试求λ的值.4.已知关于x 的方程22(2)04m x m x ---=. (1)求证:无论m 取什么实数时,这个方程总有两个相异实数根;(2)若这个方程的两个实数根x 1,x 2满足|x 2|=|x 1|+2,求m 的值及相应的x 1,x 2. 5.若关于x 的方程x 2+x +a =0的一个大于1、零一根小于1,求实数a 的取值范围.2.1 一元二次方程练习1. (1)C (2)D2. (1)-3 (2)有两个不相等的实数根 (3)x 2+2x -3=0 3.k <4,且k ≠04.-1 提示:(x 1-3)( x 2-3)=x 1 x 2-3(x 1+x 2)+9习题2.1 A 组1. (1)C (2)B 提示:②和④是错的,对于②,由于方程的根的判别式Δ<0,所以方程没有实数根;对于④,其两根之和应为-23.(3)C 提示:当a =0时,方程不是一元二次方程,不合题意.2. (1)2 (2)174(3)6 (33.当m >-14,且m ≠0时,方程有两个不相等的实数根;当m =-14时,方程有两个相等的实数根;当m <-14时,方程没有实数根. 4.设已知方程的两根分别是x 1和x 2,则所求的方程的两根分别是-x 1和-x 2,∵x 1+x 2=7,x 1x 2=-1,∴(-x 1)+(-x 2)=-7,(-x 1)×(-x 2)=x 1x 2=-1,∴所求的方程为y 2+7y -1=0.B 组1.C 提示:由于k =1时,方程为x 2+2=0,没有实数根,所以k =-1. 2.(1)2006 提示:∵m +n =-2005,mn =-1,∴m 2n +mn 2-mn =mn (m +n -1)=-1×(-2005-1)=2006. (2)-3 提示;∵a +b =-1,ab =-1,∴a 3+a 2b +ab 2+b 3=a 2(a +b )+b 2(a +b )=(a +b )( a 2+b 2)=(a +b )[( a +b ) 2-2ab ]=(-1)×[(-1)2-2×(-1)]=-3.3.(1)∵Δ=(-k )2-4×1×(-2)=k 2+8>0,∴方程一定有两个不相等的实数根. (2)∵x 1+x 2=k ,x 1x 2=-2,∴2k >-2,即k >-1.4.(1)| x 1-x 2|,122x x +=2b a -;(2)x 13+x 23=333abc b a -. 5.∵| x 1-x 2|2==,∴m =3.把m =3代入方程,Δ>0,满足题意,∴m =3.C 组1.(1)B (2)A(3)C 提示:由Δ≥0,得m ≤12,∴α+β=2(1-m )≥1. (4)B 提示:∵a ,b ,c 是ΔABC 的三边长,∴a +b >c ,∴Δ=(a +b )2-c 2>0. 2.(1)12 提示:∵x 1+x 2=8,∴3x 1+2x 2=2(x 1+x 2)+x 1=2×8+x 1=18,∴x 1=2,∴x 2=6,∴m =x 1x 2=12.3.(1)假设存在实数k ,使(2x 1-x 2)( x 1-2 x 2)=-32成立.∵一元二次方程4kx 2-4kx +k +1=0有两个实数根, ∴k ≠0,且Δ=16k 2-16k (k +1)=-16k ≥0,∴k <0. ∵x 1+x 2=1,x 1x 2=14k k+, ∴ (2x 1-x 2)( x 1-2 x 2)=2 x 12-51x 2+2 x 22 =2(x 1+x 2)2-9 x 1x 2=2-9(1)4k k+=-32,即9(1)4k k+=72,解得k =95,与k <0相矛盾,所以,不存在实数k ,使(2x 1-x 2)( x 1-2 x 2)=-32成立.(2)∵1221x x x x +-2=222212121212121212()2()224x x x x x x x x x x x x x x ++-+-=-=- =444(1)44111k k k k k k -+-==-+++, ∴要使1221x xx x +-2的值为整数,只须k +1能整除4.而k 为整数,∴k +1只能取±1,±2,±4.又∵k <0,∴k +1<1, ∴k +1只能取-1,-2,-4,∴k =-2,-3,-5. ∴能使1221x x x x +-2的值为整数的实数k 的整数值为-2,-3和-5.(3)当k =-2时,x 1+x 2=1,① x 1x 2=18, ② ①2÷②,得1221x x x x ++2=8,即16λλ+=,∴2610λλ-+=, ∴3λ=± 4.(1)Δ=22(1)20m -+>;(2)∵x 1x 2=-24m ≤0,∴x 1≤0,x 2≥0,或x 1≥0,x 2≤0.①若x 1≤0,x 2≥0,则x 2=-x 1+2,∴x 1+x 2=2,∴m -2=2,∴m =4.此时,方程为x 2-2x -4=0,∴11x =21x =②若x 1≥0,x 2≤0,则-x 2=x 1+2,∴x 1+x 2=-2,∴m -2=-2,∴m =0.此时,方程为x 2+2=0,∴x 1=0,x 2=-2.5.设方程的两根为x 1,x 2,则x 1+x 2=-1,x 1x 2=a , 由一根大于1、另一根小于1,得(x 1-1)( x 2-1)<0, 即 x 1x 2-(x 1+x 2)+1<0, ∴ a -(-1)+1<0,∴a <-2. 此时,Δ=12-4×(-2) >0, ∴实数a 的取值范围是a <-2.2.2 二次函数2.2.1 二次函数y =ax 2+bx +c 的图像和性质问题1 函数y =ax 2与y =x 2的图象之间存在怎样的关系? 为了研究这一问题,我们可以先画出y =2x 2,y =12x 2,y =-2x 2的图象,通过这些函数图象与函数y =x 2的图象之间的关系,推导出函数y =ax 2与y =x 2的图象之间所存在的关系.先画出函数y =x 2,y =2x 2的图象. 再描点、连线,就分别得到了函数y =x 2,y =2x 2的图象(如图2-1所示)2-1我们可以得到这两个函数图象之间的关系:函数y =2x 2的图象可以由函数的图象各点的纵坐标变为原来的两倍得到.同学们也可以用类似于上面的方法画出函数y =12x 2,y =-2x 2两个函数图象与函数y =x 2的图象之间的关系.通过上面的研究,我们可以得到以下结论:二次函数y =ax 2(a ≠0)的图象可以由y =x 2的图象各点的纵坐标变为原来的a 倍得到.在二次函数y =ax 2(a ≠0)中,二次项系数a 决定了图象的开口方向和在同一个坐标系中的开口的大小.问题2 函数y =a (x +h )2+k 与y =ax 2的图象之间存在怎样的关系? 同样地,我们可以利用几个特殊的函数图象之间的关系来研究它们之间的关系.同学们可以作出函数y =2(x +1)2+1与y =2x 2的图象(如图2-2所示),从函数的同学我们不难发现,只要把函数y =2x 2的图象向左平移一个单位,再向上平移一个单位,就可以得到函数y =2(x +1)2+1的图象.这两个函数图象之间具有“形状相同,位置不同”的特点.类似地,还可以通过画函数y =-3x 2,y =-3(x -1)2+1的图象,研究它们图象之间的相互关系. 通过上面的研究,我们可以得到以下结论:二次函数y =a (x +h )2+k (a ≠0)中,a 决定了二次函数图象的开口大小及方向;h 决定了二次函数图象的左右平移,而且“h 正左移,h 负右移”;k 决定了二次函数图象的上下平移,而且“k 正上移,k 负下移”.由上面结论,我们可以得到研究二次函数y =ax 2+bx +c (a ≠0)的图象的方法:由于y =ax 2+bx +c =a (x 2+b x a )+c =a (x 2+b x a+224b a )+c -24b a 224()24b b ac a x a a -=++,所以,y =ax 2+bx +c (a ≠0)的图象可以看作是将函数y =ax 2的图象作左右平移、上下平移得到的,于是,二次函数y =ax 2+bx +c (a ≠0)具有下列性质:(1)当a >0时,函数y =ax 2+bx +c 图象开口向上;顶点坐标为24(,)24b ac b a a--,对称轴为直线x =-2b a ;当x <2b a -时,y 随着x 的增大而减小;当x >2b a -时,y 随着x 的增大而增大;当x =2b a-时,函数取最小值y =244ac b a-.(2)当a <0时,函数y =ax 2+bx +c 图象开口向下;顶点坐标为24(,)24b ac b a a--,对称轴为直线x =-2b a ;当x <2b a -时,y 随着x 的增大而增大;当x >2b a -时,y 随着x 的增大而减小;当x =2b a-时,函数取最大值y =244ac b a-.上述二次函数的性质可以分别通过图2.2-3和图2.2-4直观地表示出来.1坐标、最大值(或最小值),并指出当x 减小)?并画出该函数的图象.解:∵y =-3x 2-6x +1=-3(x +1)2+4, ∴函数图象的开口向下; 对称轴是直线x =-1;顶点坐标为(-1,4);当x =-1时,函数y 取最大值y =4;当x <-1时,y 随着x 的增大而增大;当x 大而减小;采用描点法画图,选顶点A (-1,4)),与x 和C (,与y 轴的交点为D (0,1),过这五点画出图象(如图2-5所示). 图2.2-3 图2.2-5说明:从这个例题可以看出,根据配方后得到的性质画函数的图象,可以直接选出关键点,减少了选点的盲目性,使画图更简便、图象更精确.例2 某种产品的成本是120元/件,试销阶段每件产品的售价x (元)与产品的日销售量y (件)之间关系元?此时每天的销售利润是多少?分析:由于每天的利润=日销售量y ×(销售价x -120),日销售量y 又是销售价x 的一次函数,所以,欲求每天所获得的利润最大值,首先需要求出每天的利润与销售价x 之间的函数关系,然后,再由它们之间的函数关系求出每天利润的最大值.解:由于y 是x 的一次函数,于是,设y =kx +(B ) 将x =130,y =70;x =150,y =50代入方程,有70130,50150,k b k b =+⎧⎨=+⎩解得 k =-1,b =200.∴ y =-x +200.设每天的利润为z (元),则z =(-x +200)(x -120)=-x 2+320x -24000 =-(x -160)2+1600,∴当x =160时,z 取最大值1600.答:当售价为160元/件时,每天的利润最大,为1600元.例3 把二次函数y =x 2+bx +c 的图像向上平移2个单位,再向左平移4个单位,得到函数y =x 2的图像,求b ,c 的值.解法一:y =x 2+bx +c =(x +2b )224bc +-,把它的图像向上平移2个单位,再向左平移4个单位,得到22(4)224b b y x c =+++-+的图像,也就是函数y =x 2的图像,所以,240,220,4bb c ⎧--=⎪⎪⎨⎪-+=⎪⎩ 解得b =-8,c =14. 解法二:把二次函数y =x 2+bx +c 的图像向上平移2个单位,再向左平移4个单位,得到函数y =x 2的图像,等价于把二次函数y =x 2的图像向下平移2个单位,再向右平移4个单位,得到函数y =x 2+bx +c 的图像. 由于把二次函数y =x 2的图像向下平移2个单位,再向右平移4个单位,得到函数y =(x -4)2+2的图像,即为y =x 2-8x +14的图像,∴函数y =x 2-8x +14与函数y =x 2+bx +c 表示同一个函数,∴b =-8,c =14.说明:本例的两种解法都是利用二次函数图像的平移规律来解决问题,所以,同学们要牢固掌握二次函数图像的变换规律.这两种解法反映了两种不同的思维方法:解法一,是直接利用条件进行正向的思维来解决的,其运算量相对较大;而解法二,则是利用逆向思维,将原来的问题等价转化成与之等价的问题来解,具有计算量小的优点.今后,我们在解题时,可以根据题目的具体情况,选择恰当的方法来解决问题.例4 已知函数y =x 2,-2≤x ≤a ,其中a ≥-2,求该函数的最大值与最小值,并求出函数取最大值和最小值时所对应的自变量x 的值.分析:本例中函数自变量的范围是一个变化的范围,需要对a 的取值进行讨论. 解:(1)当a =-2时,函数y =x 2的图象仅仅对应着一个点(-2,4),所以,函数的最大值和最小值都是4,此时x =-2;(2)当-2<a <0时,由图2.2-6①可知,当x =-2时,函数取最大值y =4;当x =a 时,函数取最小值y =a 2;(3)当0≤a <2时,由图2.2-6②可知,当x =-2时,函数取最大值y =4;当x =0时,函数取最小值y =0;(4)当a ≥2时,由图2.2-6③可知,当x =a 时,函数取最大值y =a 2;当x =0时,函数取最小值y =0.说明:在本例中,利用了分类讨论的方法,对a 的所有可能情形进行讨论.此外,本例中所研究的二次函数的自变量的取值不是取任意的实数,而是取部分实数来研究,在解决这一类问题时,通常需要借助于函数图象来直观地解决问题. 练 习 1.选择题:(1)下列函数图象中,顶点不在坐标轴上的是 ( ) (A )y =2x 2 (B )y =2x 2-4x +2 (C )y =2x 2-1 (D )y =2x 2-4x(2)函数y =2(x -1)2+2是将函数y =2x 2 ( )(A )向左平移1个单位、再向上平移2个单位得到的 (B )向右平移2个单位、再向上平移1个单位得到的 (C )向下平移2个单位、再向右平移1个单位得到的 (D )向上平移2个单位、再向右平移1个单位得到的 2.填空题(1)二次函数y =2x 2-mx +n 图象的顶点坐标为(1,-2),则m = ,n = .(2)已知二次函数y =x 2+(m -2)x -2m ,当m = 时,函数图象的顶点在y 轴上;当m = 时,函数图象的顶点在x 轴上;当m = 时,函数图象经过原点.(3)函数y =-3(x +2)2+5的图象的开口向 ,对称轴为 ,顶点坐标为 ;当x= 时,函数取最 值y = ;当x 时,y 随着x 的增大而减小.3.求下列抛物线的开口方向、对称轴、顶点坐标、最大(小)值及y 随x 的变化情况,并画出其图象. (1)y =x 2-2x -3; (2)y =1+6 x -x 2.4.已知函数y =-x 2-2x +3,当自变量x 在下列取值范围内时,分别求函数的最大值或最小值,并求当函数取最大(小)值时所对应的自变量x 的值:(1)x ≤-2;(2)x ≤2;(3)-2≤x ≤1;(4)0≤x ≤3.2.2.2 二次函数的三种表示方式通过上一小节的学习,我们知道,二次函数可以表示成以下两种形式: 1.一般式:y =ax 2+bx +c (a ≠0);2.顶点式:y =a (x +h )2+k (a ≠0),其中顶点坐标是(-h ,k ).除了上述两种表示方法外,它还可以用另一种形式来表示.为了研究另一种表示方式,我们先来研究二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交点个数.当抛物线y =ax 2+bx +c (a ≠0)与x 轴相交时,其函数值为零,于是有ax 2+bx +c =0. ①①图2.2-6②③并且方程①的解就是抛物线y =ax 2+bx +c (a ≠0)与x 轴交点的横坐标(纵坐标为零),于是,不难发现,抛物线y =ax 2+bx +c (a ≠0)与x 轴交点个数与方程①的解的个数有关,而方程①的解的个数又与方程①的根的判别式Δ=b 2-4ac 有关,由此可知,抛物线y =ax 2+bx +c (a ≠0)与x 轴交点个数与根的判别式Δ=b 2-4ac 存在下列关系:(1)当Δ>0时,抛物线y =ax 2+bx +c (a ≠0)与x 轴有两个交点;反过来,若抛物线y =ax 2+bx +c (a ≠0)与x 轴有两个交点,则Δ>0也成立.(2)当Δ=0时,抛物线y =ax 2+bx +c (a ≠0)与x 轴有一个交点(抛物线的顶点);反过来,若抛物线y =ax 2+bx +c (a ≠0)与x 轴有一个交点,则Δ=0也成立.(3)当Δ<0时,抛物线y =ax 2+bx +c (a ≠0)与x 轴没有交点;反过来,若抛物线y =ax 2+bx +c (a ≠0)与x 轴没有交点,则Δ<0也成立.于是,若抛物线y =ax 2+bx +c (a ≠0)与x 轴有两个交点A (x 1,0),B (x 2,0),则x 1,x 2是方程ax 2+bx +c =0的两根,所以x 1+x 2=b a -,x 1x 2=c a, 即 b a =-(x 1+x 2), ca=x 1x 2.所以,y =ax 2+bx +c =a (2b c x x a a++)= a [x 2-(x 1+x 2)x +x 1x 2]=a (x -x 1) (x -x 2).由上面的推导过程可以得到下面结论: 若抛物线y =ax 2+bx +c (a ≠0)与x 轴交于A (x 1,0),B (x 2,0)两点,则其函数关系式可以表示为y =a (x -x 1) (x -x 2) (a ≠0). 这样,也就得到了表示二次函数的第三种方法:3.交点式:y =a (x -x 1) (x -x 2) (a ≠0),其中x 1,x 2是二次函数图象与x 轴交点的横坐标.今后,在求二次函数的表达式时,我们可以根据题目所提供的条件,选用一般式、顶点式、交点式这三种表达形式中的某一形式来解题.例1 已知某二次函数的最大值为2,图像的顶点在直线y =x +1上,并且图象经过点(3,-1),求二次函数的解析式.分析:在解本例时,要充分利用题目中所给出的条件——最大值、顶点位置,从而可以将二次函数设成顶点式,再由函数图象过定点来求解出系数a .解:∵二次函数的最大值为2,而最大值一定是其顶点的纵坐标,∴顶点的纵坐标为2.又顶点在直线y =x +1上, 所以,2=x +1,∴x =1. ∴顶点坐标是(1,2).设该二次函数的解析式为2(2)1(0)y a x a =-+<, ∵二次函数的图像经过点(3,-1), ∴21(32)1a -=-+,解得a =-2. ∴二次函数的解析式为22(2)1y x =--+,即y =-2x 2+8x -7.说明:在解题时,由最大值确定出顶点的纵坐标,再利用顶点的位置求出顶点坐标,然后设出二次函数的顶点式,最终解决了问题.因此,在解题时,要充分挖掘题目所给的条件,并巧妙地利用条件简捷地解决问题.例2 已知二次函数的图象过点(-3,0),(1,0),且顶点到x 轴的距离等于2,求此二次函数的表达式.。

第24讲同角三角函数的基本关系模块一思维导图串知识模块二基础知识全梳理(吃透教材)模块三核心考点举一反三模块四小试牛刀过关测1.理解并掌握同角三角函数基本关系式的推导及应用;2.会利用同角三角函数的基本关系进行化简、求值与恒等式证明.知识点1同角三角函数的基本关系1、同角三角函数的基本关系基本关系基本关系式语言描述平方关系22sin cos 1αα+=同一个角的正弦、余弦的平方和等于1商数关系sin tan cos ααα=同一个角的正弦、余弦的商等于角的正切2、基本关系式的要点剖析(1)“同角”有两层含义,一是“角相同”;二是对“任意”一个角(在使函数有意义的前提下)关系式都成立,即与角的表达形式无关,如22sin 3cos 31αα+=成立,但是22sin cos 1αβ+=就不一定成立.(2)2sin α是2(sin )α的简写,读作“sin α的平方”,不能将2sin α写成2sin α,前者是α的正弦的平方,后者是2α的正弦,两者是不同的,要弄清它们的区别,并能正确书写.(3)注意同角三角函数的基本关系式都是对于使它们有意义的角而言的,22sin cos 1αα+=对一切R α∈恒成立,而sin tan cos ααα=仅对()2k k Z παπ≠+∈成立.知识点2关系式的常用等价变形1、2222222sin 1cos cos 1sin sin cos 1sin cos (sin cos )12sin cos αααααααααααα⎧=-⎪=-⎪⎪+=⇒=⎨⎪=⎪⎪+=±⎩2、sin tan cos sin tan sin cos cos tan ααααααααα=⎧⎪=⇒⎨=⎪⎩【注意】使用变形公式sin α=,cos α=时,“±”由α的终边所在的象限来确定,而对于其他形式的变形公式则不必考虑符号问题.知识点3基本关系式常用解题方法1、已知某个三角函数值求其余三角函数值的步骤第一步:由已知三角函数的符号,确定其角终边所在的象限;第二步:依据角的终边所在象限分类讨论;第三步:利用同角三角函数关系及其变形公式,求出其余三角函数值。

衔接点04一元二次方程1、能用配方法,公式法,因式分解法解一元二次方程2、会用一元二次方程根的判别式判别方程是否有实根3、能根据现实情境理解方程的意义,能针对具体问题列出方程,理解方程解的意义。
1、一元二次方程根的判别式一元二次方程20(0)ax bx c a ++=≠(c b a 、、均为常数)的判别式ac b 42-=∆.(1)0>∆时,20ax bx c ++=(0≠a )有两个不相等的实数根;(2)0=∆时,20ax bx c ++=(0≠a )有两个相等的实数根;(3)0<∆时,20ax bx c ++=(0≠a )没有实数根.注意:(1)在使用根的判别式之前,应将一元二次方程化成一般式;(2)在确定一元二次方程待定系数的取值范围时,必须检验二次项系数0≠a (3)证明ac b 42-=∆恒为正数的常用方法:把△的表达式通过配方化成“完全平方式+正数”的形式.2、一元二次方程根与系数的关系(韦达定理)对点特训一:利用根的判别式判断一元二次方程根的个数典型例题例题1.(2024·安徽·三模)关于x 的一元二次方程222420x mx m -+=的根的情况为()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.无法确定【答案】B【分析】本题主要考查了一元二次方程根的判别式,对于一元二次方程()200ax bx c a ++=≠,若240b ac ∆=->,则方程有两个不相等的实数根,若240b ac ∆=-=,则方程有两个相等的实数根,若24<0b ac ∆=-,据此求解即可.【详解】解:由题意得,()2244220m m ∆=--⨯⋅=,∴原方程有两个相等的实数根,故选:B.例题2.(2024·四川泸州·一模)关于x 的一元二次方程240x mx --=的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根D.没有实数根【答案】A【分析】本题考查根的判别式,解题的关键是掌握一元二次方程20(0)ax bx c a ++=≠的根与24b ac ∆=-有如下关系:①当0∆>时,方程有两个不相等的两个实数根;②当Δ0=时,方程有两个相等的两个实数根;③当Δ0<时,方程无实数根.判断出判别式的值,可得结论.【详解】解:对于一元二次方程240x mx --=,()2241(4)160m m ∆=--⨯⨯-=+>,∴方程有两个不相等的实数根.故选:A .精练1.(23-24八年级下·安徽安庆·期中)已知a ,b ,c 为常数,0ac <,则关于x 的一元二次方程20ax bx c ++=的根的情况为()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.无法判定【答案】A【分析】本题主要考查了一元二次方程根的判别式,对于一元二次方程()200ax bx c a ++=≠,若240b ac ∆=->,则方程有两个不相等的实数根,若240b ac ∆=-=,则方程有两个相等的实数根,若24<0b ac ∆=-,则方程没有实数根,据此求解即可.【详解】解:由题意得,24b ac ∆=-,∵0ac <,∴40ac ->,∴240b ac ∆=->,∴原方程有两个不相等的实数根,故选:A.2.(23-24九年级下·湖南郴州·期中)方程()()22226250x x x x ++++=不相等的实数根的个数为()A.1B.2C.3D.4【答案】A【分析】本题考查解一元二次方程,将22x x +作为一个整体,解方程,再根据根的判别式,进行判断,即可得出结果.【详解】解:∵()()22226250x x x x ++++=,∴()()2221250x x x x ++++=,∴2210x x ++=或2250x x ++=,当2210x x ++=时,440∆=-=,方程由两个相等的实数根;当2250x x ++=时,445160∆=-⨯=-<,方程没有实数根;故选A.对点特训二:根据根的个数求参数典型例题例题1.(2024·北京大兴·一模)若关于x 的一元二次方程220x x m +-=有两个不相等的实数根,则实数m 的取值范围是()对点特训三:解一元二次方程角度1:直接开平方法(2)根据立方根得定义求出2x+的值,然后再求x的值即可.【详解】(1)解:2x-=,1691000整理得:2169100x=角度2:配方法角度3:因式分解法典型例题角度4:利用求根公式求解角度5:换元法求解故原方程的解为:13x =-,22x =.精练1.(23-24八年级下·安徽亳州·阶段练习)解高次方程的思想就是“降次”,将含未知数的某部分用低次项替换,例如解四次方程42280x x +-=时,可设2y x =,则原方程可化为2280y y +-=,先解出y ,将y 的值再代入2y x =中解x 的值,由此高次方程得解.解高次方程也可以将方程中某个部分看作一个整体,例如上述方程中,可将2x 看作一个整体,得()222280x x +-=,解出2x 的值,再进一步求解即可.根据上述方法,完成下列问题:(1)若()()22222232237x y x y +-++=,则22x y +的值为___________;(2)解方程:()22234120y y y y --+=.【答案】(1)2(2)1y =-或4y =或0y =或3y =【分析】本题考查了换元法解一元二次方程,注意,解方程时要解完整.(1)根据题意,设22+=x y k ,然后解关于k 的一元二次方程,再根据220≥+x y 取值即可;(2)设23y y t -=,然后解关于t 的一元二次方程,然后再来求关于y 的一元二次方程.【详解】(1)解:设22+=x y k ,原方程为:()()222223237x y x y ⎡⎤⎡⎤+-++=⎣⎦⎣⎦,即()()23237k k -+=,2497k -=,24k =,2k ∴=或2k =-,220≥+x y ,2k ∴=,∴222x y +=,故答案为:2;(2)解:设23y y t -=,原方程为:()()2223430y y y y ---=,即240t t -=,()40t t -=,0t ∴=或4t =,当0=t 时,230y y -=,()30y y -=,对点特训四:利用根与系数的关系(韦达定理)求参数对点特训五:利用根与系数的关系(韦达定理)求对称式的值26912m m m =++-269m m =-+()23m =-,∵()230m -≥,∴240b ac -≥,∴无论m 取任何实数,方程总有实数根;(2)解:∵123x x m +=+,123x x m ⋅=,12127x x x x +-=,∴337m m +-=,解得2m =-,故m 的值为2-.精练(1)由题意知()()26410k ∆=---≥,计算求解即可;(2)由题意知,126x x +=,121x x k ⋅=-,由221212324x x x x ++=,可得()2121224x x x x ++=,即26124k +-=,计算求解即可.【详解】(1)解:∵2610x x k -+-=,∴()()26410k ∆=---≥,解得,10k ≤;(2)解:由题意知,126x x +=,121x x k ⋅=-,∵221212324x x x x ++=,∴()2121224x x x x ++=,∴26124k +-=,解得,11k =-,∴k 的值为11-.对点特训六:根的判别式和韦达定理综合应用典型例题例题1.(2024·天津和平·一模)已知1x ,2x 是一元二次方程220x x c ++=(c 是常数)的两个不相等的实数根.(1)求c 的取值范围;(2)若8c =-,求一元二次方程的根;(3)若123x x =-,则c 的值为______.【答案】(1)1c <(2)12x =,24x =-(3)3-【分析】(1)根据题意,由一元二次方程根的判别式,解不等式即可得到答案;(2)将8c =-代入原方程得到2280x x +-=,因式分解法解一元二次方程即可得到答案;(3)根据题意,由一元二次方程根与系数的关系直接求解即可得到答案.【详解】(1)解:∵220x x c ++=有两个不相等的实数根,∴224240b ac c ∆=-=->,∴1c <;(2)解:∵8c =-,∴2280x x +-=,因式分解得()()240x x -+=,∴20x -=或40x +=,解得12x =,24x =-;(3)解: 1x ,2x 是一元二次方程220x x c ++=(c 是常数)的两个不相等的实数根,∴123x x c ==-,故答案为:3-.【点睛】本题考查一元二次方程综合,涉及一元二次方程根的判别式、解不等式、因式分解法解一元二次方程、一元二次方程根与系数的关系等知识,熟练掌握一元二次方程性质与解法是解决问题的关键.例题2.(23-24九年级下·江苏泰州·阶段练习)对于代数式2ax bx c ++,若存在实数n ,当x n =时,代数式的值也等于n ,则称n 为这个代数式的不变值.例如:对于代数式2x ,当0x =时,代数式等于0;当1x =时,代数式等于1,我们就称0和1都是这个代数式的不变值.在代数式存在不变值时,该代数式的最大不变值与最小不变值的差记作A .特别地,当代数式只有一个不变值时,则0A =.(1)代数式22x x -的不变值是________,A =_______.(2)已知代数式2x bx b -+,①若0A =,求b 的值;②若12A ≤≤,b 为整数,求所有整数b 的和.【答案】(1)0,3;3(2)①1;②4(是常数)是“一、单选题1.(2024·上海普陀·二模)下列方程中,有两个不相等的实数根的是()C.()22001160x +=D.()22001160x -=【答案】D 【分析】本题主要考查了一元二次方程的应用.设该商品平均每次降价的百分率为x ,第一次降价后的价格是200(1)x -,第二次后的价格是2200(1)x -,据此即可列方程求解.【详解】解:根据题意得:()22001160x -=,故选:D.7.(23-24八年级下·安徽淮北·期中)若关于x 的一元二次方程()22410k x x --+=有实数根,则实数k 的值可能是()A.10B.8C.5D.2【答案】D【分析】本题考查的是一元二次方程根的判别式,根据题意列出关于k 的不等式是解答此题的关键.若一元二次方程没有实数根,则根的判别式240b ac ∆=-≥,建立关于k 的不等式,求出k 的取值范围.还要注意二次项系数不为0.【详解】解: 关于x 的一元二次方程()22410k x x --+=有实数根,∴0∆≥且20k -≠,即()244(2)0k ∆=---≥且2k ≠,6k ∴≤,且2k ≠故选:D.8.(23-24七年级下·湖南岳阳·期中)问题:聪明的你知道代数式245x x -+的最小值为多少吗?解:因为()222224544142121x x x x x x x -+=-++=-++=-+,又因为()220x -≥,所以()2211x -+≥,所以245x x -+的最小值为1.请用上述方法,解决代数式266x x ++的最小值为()A.3B.3-C.6D.6-【答案】B 【分析】本题考查了配方法的应用,模仿题意的解题过程,进行变形作答即可.【详解】解:依题意,()222266663369333x x x x x x x ++=+++-=++-=+-,∵()230x +≥,∴()2333x +-≥-,∴所以266x x ++的最小值为3-,故选:B.二、填空题9.(23-24八年级下·黑龙江哈尔滨·阶段练习)已知关于x 的方程()23120x k x --+=的一个根是1,则另。

第03讲集合的基本运算,并能够运用这些语言解决集合运算知识点1并集1、并集的概念自然语言一般地,由所有属于集合A 或属于集合B 的元素组成的集合称为A 与B 的并集,记作A ∪B ,读作“A 并B ”符号语言A ∪B ={x |x ∈A 或x ∈B }图形语言2、并集的运算性质性质定义A B B A = 满足交换律A A A = 任何集合与其本身的并集等于这个集合本身A A A∅=∅= 任何集合与空集的并集等于这个集合本身()()A B C A B C = 多个集合的并集满足结合律()A A B ⊆ ,()B A B ⊆ 任何集合都是该集合与另一个集合并集的子集A B ⊆⇔A B B= 任何集合与它子集的并集都是它本身,反之亦然知识点2交集1、交集的概念自然语言由所有属于集合A 且属于集合B 的元素组成的集合,称为集合A 与B 的交集,记作A ∩B ,读作“A 交B ”符号语言A ∩B ={x |x ∈A 且x ∈B }图形语言2、交集的运算性质性质定义A B B A = 满足交换律A ∅=∅ 空集与任何集合的交集都是空集A A A= 集合与集合本身的交集仍为集合本身()()A B C A B C = 多个集合的交集满足结合律()()()A B C A C B C = 多个集合的综合运算满足分配律()()()A B C A C B C = 若A B A = ,则A B⊆交集关系与子集关系的转化()(),A B A A B B⊆⊆ 两个集合的交集是其中任一集合的子集知识点3全集与补集1、全集的概念自然语言一般地,如果一个集合包含所研究问题中涉及的所有元素,那么就称这个集合为全集,通常记为U .符号语言若,,,A U B U C U ⊆⊆⊆ ,则U 为全集.图形语言2、补集的概念自然语言若集合A 是全集U 的一个子集,由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集,记作U A ð.符号语言{}U A x x U x A =∈∉且ð图形语言3、补集的运算性质性质定义()U A A U= ð任何集合与其补集的并集为全集()U A A =∅ ð任何集合与其补集的交集为空集()UUA A=痧任何集合补集的补集为集合本身,U U U U=∅∅=痧全集的补集为空集,空集的补集为全集知识点4德摩根律与容斥原理1、德摩根定律:设集合U 为全集,A 、B 为U 的子集,则有(1)()()()U U U A B A B = 痧(2)()()()U U U A B A B = 痧2、容斥原理:在部分有限集中,我们经常遇到有关集合中元素的个数问题,常用Venn 图表示两集合的交、并、补。

初升高数学衔接题及答案【题目一:代数基础】题目:求解方程 \( x^2 - 5x + 6 = 0 \) 的根。
【答案】首先,我们可以通过因式分解来解这个方程:\( x^2 - 5x + 6 = (x - 2)(x - 3) = 0 \)。
因此,方程的根是 \( x = 2 \) 和 \( x = 3 \)。
【题目二:几何基础】题目:在直角三角形ABC中,角C是直角,AB是斜边,如果AC=6,BC=8,求斜边AB的长度。
【答案】根据勾股定理,直角三角形的斜边平方等于两直角边的平方和,即:\( AB^2 = AC^2 + BC^2 \)。
代入已知值:\( AB^2 = 6^2 + 8^2 = 36 + 64 = 100 \)。
因此,斜边AB的长度为 \( AB = \sqrt{100} = 10 \)。
【题目三:函数基础】题目:如果函数 \( f(x) = 2x - 3 \),求 \( f(5) \) 的值。
【答案】将 \( x = 5 \) 代入函数 \( f(x) = 2x - 3 \) 中,我们得到:\( f(5) = 2 \cdot 5 - 3 = 10 - 3 = 7 \)。
所以,\( f(5) \) 的值为7。
【题目四:不等式基础】题目:解不等式 \( 3x - 5 < 10 \)。
【答案】首先,我们将不等式两边加上5:\( 3x - 5 + 5 < 10 + 5 \),得到 \( 3x < 15 \)。
然后,我们将不等式两边除以3:\( \frac{3x}{3} < \frac{15}{3} \),得到 \( x < 5 \)。
所以,不等式的解为 \( x < 5 \)。
【题目五:概率基础】题目:一个袋子里有5个红球和3个蓝球,随机取出一个球,求取出红球的概率。
【答案】总共有 \( 5 + 3 = 8 \) 个球。
取出红球的概率为红球数量除以总球数,即:\( P(\text{红球}) = \frac{5}{8} \)。
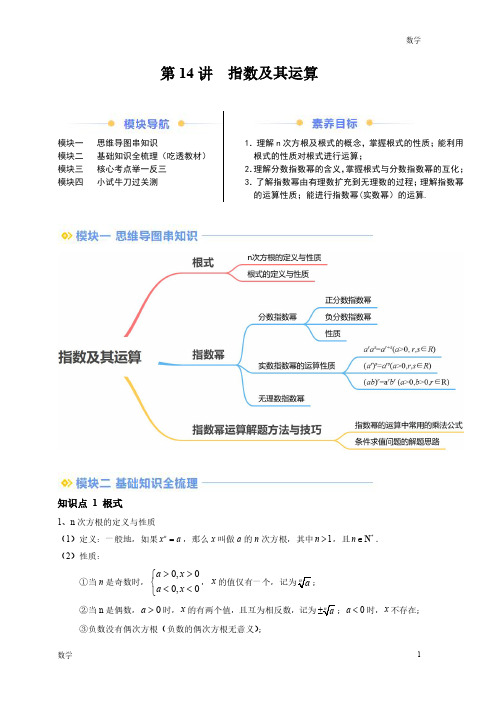
第14讲指数及其运算模块一思维导图串知识模块二基础知识全梳理(吃透教材)模块三核心考点举一反三模块四小试牛刀过关测1.理解n 次方根及根式的概念,掌握根式的性质;能利用根式的性质对根式进行运算;2.理解分数指数幂的含义,掌握根式与分数指数幂的互化;3.了解指数幂由有理数扩充到无理数的过程;理解指数幂的运算性质;能进行指数幂(实数幂)的运算.知识点1根式1、n 次方根的定义与性质(1)定义:一般地,如果n x a =,那么x 叫做a 的n 次方根,其中1n >,且*n ∈N .(2)性质:①当n 是奇数时,0,00,0>>⎧⎨<<⎩a x a x ,x②当n 是偶数,0>a 时,x 的有两个值,且互为相反数,记为;0<a 时,x 不存在;③负数没有偶次方根(负数的偶次方根无意义);④0的任何次方根都是00(,1)n N n +=∈>.2、根式的定义与性质(1n 叫做根指数,a 叫做被开方数.(2)性质:(1n >,且n *∈N)n=a;,,,.⎧⎪=⎨⎪⎩为奇数为偶数na n a n 知识点2指数幂1、分数指数幂(1)正分数指数幂:规定:mn a=()0,,,1a m n n *>∈>N (2)负分数指数幂:规定:1mn m naa-==()0,,,1a m n n *>∈>N (3)性质:0的正分数指数幂等于0,0的负分数指数幂没有意义.【要点辨析】分数指数幂的注意事项:①分数指数幂是指数概念的又一推广,分数指数幂m na 不可理解为mn个a 相乘,它是根式的一种新的写法.在这样的规定下,根式与分数指数幂是表示相同意义的量,只是形式不同而已.化成分数指数幂的形式时,不要轻易对mn进行约分.③在保证相应的根式有意义的前提下,负数也存在分数指数幂,如()235-=有意义,但()345-=就没有意义.2、实数指数幂的运算性质①(0,,)+=>∈r s r s a a a a r s R .②()=sra rs a (0,,)a r s >∈R .③()=r ab r r a b (0,0,)a b r >>∈R .3、无理数指数幂一般地,无理数指数幂a α(0a >,α为无理数)是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.【注意】(1)对于无理数指数幂,我们只需要了解两点:①它是一个确定的实数;②它是有理数指数幂无限逼近的结果.(2)定义了无理数指数幂之后,幂的指数就由原来的有理数范围扩充到了实数范围.知识点3指数幂运算解题方法与技巧1、指数幂的运算中常用的乘法公式(1)完全平方公式:222()2a b a ab b -=-+;222()2a b a ab b +=++;(2)平方差公式:22()()a b a b a b -=-+;(3)立方差公式:3322()()a b a b a ab b -=-++;(4)立方和公式:3322()()a b a b a ab b +=+-+;(5)完全立方公式:33223()33a b a a b ab b -=-+-;33223()33a b a a b ab b +=+++.2、条件求值问题的解题思路(1)将条件中的式子用待求式表示出来,进而代入化简得出结论;(2)当直接代入不易时,可以从总体上把握已知式和所求式的特点,从而巧妙求解,一般先利用平方差、立方和(差)以及完全平方公式对其进行化简,再用整体代入法来求值;(3)适当应用换元法,能使公式的使用更加清晰,过程更简洁.考点一:根式的概念及辨析例1.(23-24高一上·全国·专题练习)若a 是实数,则下列式子中可能没有意义的是()AB C D 【变式1-1】(23-24高一上·全国·课后作业)R a ∈,下列各式一定有意义的是()A .2a -B .14a C .23a D .0a【变式1-2】(2023高一·江苏·a 的取值范围是()A .0a ≥B .1a ≥C .2a ≥D .Ra ∈【变式1-3】(223-24高一下·贵州遵义·月考)若34(12)x --有意义,则实数x 的取值范围为考点二:利用根式的性质化简求值例2.(23-24高一上·北京·期中)下列各式正确的是()A3=-Bx=C2=D .01a =【变式2-1】(23-24高一上·贵州贵阳·月考)若0ab <,则化简)A .-1B .0C .1D .2【变式2-2】(23-24高一上·全国·;【变式2-3】(23-24高一上·甘肃兰州·期中)(多选)若412x<-,3的结果可能为()A .210x -B .46x -C .24x -+D .410x --考点三:根式与分数指数幂互化例3.(23-24高一上·湖南株洲·月考)下列关于nm a -(),m n *∈N 的形式的运算正确的是()A.538-=B.538-=C.538-=D .()328--=【变式3-1】(23-24高一上·浙江杭州·期中)(多选)下列各式正确的是()A .46a=B 5=-C.(36=D .23a -=【变式3-2】(23-24高一上·江西新余·期中)(多选)下列根式与分数指数幂的互化中正确的有()A .)130xx -=≠B()120aa =≥C.21320,0)x y x y ->>D .3142(0)x x ⎤=->【变式3-3】(23-24高一上·广东广州·期中)用分数指数幂表示并计算下列各式(式中字母均正数),写出化简步骤.(2)154m⋅考点四:利用指数幂运算性质化简例4.(23-24高一上·全国·专题练习)下列等式一定成立的是()A .1332a a a⋅=B .11220⋅=a a C .329()a a =D .111362a a a ÷=【变式4-1】(23-24高一上·广东江门·期中)102x =,103y =,则10x y +=.【变式4-2】(23-24高一上·河南·期中)若a b =()2312222a ab ---⎡⎤=⎢⎥⎣⎦.【变式4-3】(23-24高一上·江西九江·期中)化简或计算下列各式.(1)121121332a b a b ---⎛⎫ ⎪;(2)()10.52332770.02721259-⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭.考点五:解简单的指数方程例5.(23-24高一·全国·专题练习)方程11416x -=的解为()A .2B .﹣2C .﹣1D .1【变式5-1】(22-23高一上·河北沧州·期中)关于x 的方程112250x x +--+=的解的个数为()A .0B .1C .2D .4【变式5-2】(23-24高一上·北京顺义·期中)关于x 的方程422x x -=的解为.【变式5-3】(22-23高三·全国·对口高考)方程(2522xx x -+=的解为.考点六:整体换元法解决条件求值例6.(23-24高一下·辽宁抚顺·开学考试)已知12a a+=,则1122a a -+等于()A .2B .4C .2±D .4±【变式6-1】(23-24高一上·全国·专题练习)已知11223a a -+=,则33221122a a a a--++的值为.【变式6-2】(23-24高一上·全国·专题练习)已知11223x x-+=,计算:22111227x x x x x x---+-+++.【变式6-3】(23-24高一上·湖南娄底·期末)已知11223a a -+=,求下列各式的值:(1)1a a -+;(2)33222232a a a a --+-+-.一、单选题1.(23-24高一上·青海海南·期中)已知R a ∈,则下列各式一定有意义的是()A .2a -B .13a C .12a D .0a 2.(23-24高一上·陕西咸阳·期末)化简32的结果为()A .5BC .5-D.3.(23-24高一上·北京大兴·月考)已知0a >=()A .12a B .32a C .2a D .3a 4.(23-24高一上·安徽淮南·月考)下列根式与分数指数幂的互化错误的是()A()120a a =>B.)340xx -=>C.)21320,0x y x y -=>>D .()32140x x =>5.(23-24高一上·江苏泰州·期中)已知14x x -+=,则22x x -+等于()A .6B .12C .14D .166.(23-24高一上·四川德阳·月考)010.256371.586-⎛⎫⨯-++= ⎪⎝⎭()A .110B .109C .108D .100二、多选题7.(23-24高一上·四川成都·期中)以下运算结果等于2的是()AB .C .D 8.(23-24高一上·浙江·月考)已知0a >,0b >,则下列各式正确的是()A π3=-B1=C.mna-=D .121133332463b ab a b ---⎛⎫÷-=- ⎪⎝⎭三、填空题9.(22-23高一上·上海奉贤·期末)化简()222a b ⋅=(其中0a >,0b >).10.(23-24高一上·全国·单元测试)方程2129240x x +-⋅+=的解集是.11.(23-24高一上·重庆沙坪坝·期中)已知12102α-=,131032β=,则314210βα+=(填数值)四、解答题12.(23-24高一上·安徽马鞍山·期中)化简求值:(1)()120120.344⎛⎫+ ⎪⎝⎭(2)20.5231103522216274--⎛⎫⎛⎫⎛⎫-⨯-⨯÷ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭;13.(23-24高一上·辽宁丹东·期中)已知正实数a 满足11221a a --=.(1)求1a a -+的值;(2)求33221122a a a a---+的值.第14讲指数及其运算模块一思维导图串知识模块二基础知识全梳理(吃透教材)模块三核心考点举一反三模块四小试牛刀过关测1.理解n 次方根及根式的概念,掌握根式的性质;能利用根式的性质对根式进行运算;2.理解分数指数幂的含义,掌握根式与分数指数幂的互化;3.了解指数幂由有理数扩充到无理数的过程;理解指数幂的运算性质;能进行指数幂(实数幂)的运算.知识点1根式1、n 次方根的定义与性质(1)定义:一般地,如果n x a =,那么x 叫做a 的n 次方根,其中1n >,且*n ∈N .(2)性质:①当n 是奇数时,0,00,0>>⎧⎨<<⎩a x a x ,x②当n 是偶数,0>a 时,x 的有两个值,且互为相反数,记为;0<a 时,x 不存在;③负数没有偶次方根(负数的偶次方根无意义);④0的任何次方根都是00(,1)n N n +=∈>.2、根式的定义与性质(1n 叫做根指数,a 叫做被开方数.(2)性质:(1n >,且n *∈N)n=a;,,,.⎧⎪=⎨⎪⎩为奇数为偶数na n a n 知识点2指数幂1、分数指数幂(1)正分数指数幂:规定:mn a=()0,,,1a m n n *>∈>N (2)负分数指数幂:规定:1mn m naa-==()0,,,1a m n n *>∈>N (3)性质:0的正分数指数幂等于0,0的负分数指数幂没有意义.【要点辨析】分数指数幂的注意事项:①分数指数幂是指数概念的又一推广,分数指数幂m na 不可理解为mn个a 相乘,它是根式的一种新的写法.在这样的规定下,根式与分数指数幂是表示相同意义的量,只是形式不同而已.化成分数指数幂的形式时,不要轻易对mn进行约分.③在保证相应的根式有意义的前提下,负数也存在分数指数幂,如()235-=有意义,但()345-=就没有意义.2、实数指数幂的运算性质①(0,,)+=>∈r s r s a a a a r s R .②()=sra rs a (0,,)a r s >∈R .③()=r ab r r a b (0,0,)a b r >>∈R .3、无理数指数幂一般地,无理数指数幂a α(0a >,α为无理数)是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.【注意】(1)对于无理数指数幂,我们只需要了解两点:①它是一个确定的实数;②它是有理数指数幂无限逼近的结果.(2)定义了无理数指数幂之后,幂的指数就由原来的有理数范围扩充到了实数范围.知识点3指数幂运算解题方法与技巧1、指数幂的运算中常用的乘法公式(1)完全平方公式:222()2a b a ab b -=-+;222()2a b a ab b +=++;(2)平方差公式:22()()a b a b a b -=-+;(3)立方差公式:3322()()a b a b a ab b -=-++;(4)立方和公式:3322()()a b a b a ab b +=+-+;(5)完全立方公式:33223()33a b a a b ab b -=-+-;33223()33a b a a b ab b +=+++.2、条件求值问题的解题思路(1)将条件中的式子用待求式表示出来,进而代入化简得出结论;(2)当直接代入不易时,可以从总体上把握已知式和所求式的特点,从而巧妙求解,一般先利用平方差、立方和(差)以及完全平方公式对其进行化简,再用整体代入法来求值;(3)适当应用换元法,能使公式的使用更加清晰,过程更简洁.考点一:根式的概念及辨析例1.(23-24高一上·全国·专题练习)若a 是实数,则下列式子中可能没有意义的是()AB C D 【答案】D【解析】A.R a ∈有意义;B.R a ∈有意义;C.R a ∈有意义;D.a<0无意义;故选:D【变式1-1】(23-24高一上·全国·课后作业)R a ∈,下列各式一定有意义的是()A .2a -B .14a C .23a D .0a 【答案】C【解析】对于A ,当0a =时,2a -无意义,A 不是;对于B ,当a<0时,14a 无意义,B 不是;对于C ,23a =C 是;对于D ,当0a =时,0a 无意义,D 不是.故选:C【变式1-2】(2023高一·江苏·a 的取值范围是()A .0a ≥B .1a ≥C .2a ≥D .Ra ∈【答案】B102R a a -≥⎧⎨-∈⎩,解得1a ≥,所以a 的取值范围是1a ≥.故选:B【变式1-3】(223-24高一下·贵州遵义·月考)若34(12)x --有意义,则实数x 的取值范围为【答案】1(,2-∞【解析】由34(12)x --120x ->,解得12x <,故答案为:1(,2-∞.考点二:利用根式的性质化简求值例2.(23-24高一上·北京·期中)下列各式正确的是()A3=-B x =C 2=D .01a =【答案】C【解析】A 3=,故A 错误;B x =,故B 错误;C2=,故C 正确;D :01a =,当0a ≠时成立,故D 错误;故选:C.【变式2-1】(23-24高一上·贵州贵阳·月考)若0ab <,则化简)A .-1B .0C .1D .2【答案】B【解析】+==a b a b ⎛=+ ⎝因为0ab <,所以,a b 异号,0a b a b +=,所以0a b a b a b a b a b++==,所以,0+=.故选:B.【变式2-2】(23-24高一上·全国·;【答案】6-=6(446-++=-.【变式2-3】(23-24高一上·甘肃兰州·期中)(多选)若412x<-,3的结果可能为()A .210x -B .46x -C .24x -+D .410x --【答案】AC 【解析】由题意知412x <-,即4102x-<-,即202x x +>-,故(2)(2)0,2x x x +->∴<-或2x >,3|2|3x =+-3523210,23523352324,2x x x x x x x x x x ----=->⎧=--+-=⎨-+++-=-+<-⎩,故选:AC考点三:根式与分数指数幂互化例3.(23-24高一上·湖南株洲·月考)下列关于nm a -(),m n *∈N 的形式的运算正确的是()A.538-=B.538-=C.538-=D .()328--=【答案】A【解析】由于5353818-==,A 正确,B ,C 错误;()328--=D 错误,故选:A【变式3-1】(23-24高一上·浙江杭州·期中)(多选)下列各式正确的是()A .46a=B 5=-C.(36=D .23a -=【答案】AC【解析】对于A:4263a a ==A正确;对于B 5=,故B 错误;对于C:(2636===,故C 正确;对于D:23231aa-==D 错误.故选:AC【变式3-2】(23-24高一上·江西新余·期中)(多选)下列根式与分数指数幂的互化中正确的有()A .)130xx -=≠B()120a a =≥C.21320,0)x y x y ->>D .3142(0)x x ⎤=->【答案】BC【解析】对选项A:)130xx -=≠,错误;对选项B()1313220a a a ⎛⎫==≥ ⎪⎝⎭,正确;对选项C22133212(0,0)y x y x y x-==>>,正确;对选项D :33214432(0)x x x ⎛⎫==> ⎪⎝⎭,错误;故选:BC【变式3-3】(23-24高一上·广东广州·期中)用分数指数幂表示并计算下列各式(式中字母均正数),写出化简步骤.(2)154m⋅【答案】(1)14b ;(2)1【解析】(1111224b b ⎛⎫=== ⎪⎝⎭.(2)154m⋅111115324023651641m m m mm m m-⋅⋅====⋅.考点四:利用指数幂运算性质化简例4.(23-24高一上·全国·专题练习)下列等式一定成立的是()A .1332a a a ⋅=B .11220⋅=a a C .329()a a =D .111362a a a ÷=【答案】D【解析】对于A :11311333262a a a a +⋅==,故A 错误;对于B :11212221+⋅==a a a a ,故B 错误;对于C :326()a a =,故C 错误;对于D :1111132362a a a a -÷==,故D 正确;故选:D【变式4-1】(23-24高一上·广东江门·期中)102x =,103y =,则10x y +=.【答案】6【解析】102x =Q ,103y =,101010236x y x y +∴=⋅=⨯=,故答案为:6.【变式4-2】(23-24高一上·河南·期中)若a b =()2312222a ab ---⎡⎤=⎢⎥⎣⎦.【答案】1【解析】由题意,0,0a b >>,所以()()231222232246a b ab a b a b -----⎡==⎤⎢⎥⎣⎦,又11322,2a b --===,所以原式6411223222221----⎛⎫⎛⎫=⋅=⋅= ⎪ ⎪⎝⎭⎝⎭.故答案为:1.【变式4-3】(23-24高一上·江西九江·期中)化简或计算下列各式.(1)121121332a b a b ---⎛⎫ ⎪;(2)()10.52332770.02721259-⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭.【答案】(1)1a;(2)0.09【解析】(1)原式2111111111532322132623615661ab a baba aa b⎛⎫--⎪⎝⎭-+--⋅====.(2)原式22333273550.0910001033⨯⎛⎫⎛⎫==+-= ⎪⎪⎝⎭⎝⎭.考点五:解简单的指数方程例5.(23-24高一·全国·专题练习)方程11416x -=的解为()A .2B .﹣2C .﹣1D .1【答案】C 【解析】∵1214416x --==,∴x ﹣1=﹣2,∴x =﹣1.故选:C .【变式5-1】(22-23高一上·河北沧州·期中)关于x 的方程112250x x +--+=的解的个数为()A .0B .1C .2D .4【答案】B【解析】解:原方程即222502x x ⨯-+=,化简可得()2225220x x ⨯+⨯-=,令2(0)x t t =>,可得22520t t +-=,该方程有且只有一个正根,由于2x t =单调递增,所以t 与x 一一对应,即原方程只有一个解.故选:B .【变式5-2】(23-24高一上·北京顺义·期中)关于x 的方程422x x -=的解为.【答案】1x =【解析】由422x x -=可得()22220x x --=,即()()21220x x+-=,因为20x >,可得22x =,故1x =.所以,方程关于x 的方程422x x -=的解为1x =.故答案为:1x =.【变式5-3】(22-23高三·全国·对口高考)方程(2522xx x -+=的解为.【答案】5x =或12x =【解析】由题意可得(2599222222xxx x x -+⎛⎫=== ⎪⎝⎭,所以25922x x x -+=,即221150x x -+=,解得5x =或12x =,故答案为:5x =或12x =考点六:整体换元法解决条件求值例6.(23-24高一下·辽宁抚顺·开学考试)已知12a a+=,则1122a a -+等于()A .2B .4C .2±D .4±【答案】A【解析】112221()2224a a a a-+=++=+=,所以11222a a -+=.故选:A.【变式6-1】(23-24高一上·全国·专题练习)已知11223a a -+=,则33221122a a a a--++的值为.【答案】6【解析】因为11223a a-+=,所以2112223a a -⎛⎫+= ⎪⎝⎭,即129a a -++=,所以17a a -+=,所以3333112222a aa a --⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭22111111222222a a a a a a ---⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥=+-⋅+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦()()11122371181a a a a --⎛⎫=++=⨯- ⎝-=⎪⎭,所以332211221863a a a a--+==+.【变式6-2】(23-24高一上·全国·专题练习)已知11223x x -+=,计算:22111227x x x x x x---+-+++.【答案】4【解析】因为11223x x-+=,所以211229x x -⎛⎫+= ⎪⎝⎭,所以129x x -++=,所以17x x -+=,所以()2127x x -+=,即22249x x -++=,所以2247x x -+=,所以22111227477473x x x x x x---+--==++++.【变式6-3】(23-24高一上·湖南娄底·期末)已知11223a a -+=,求下列各式的值:(1)1a a -+;(2)33222232a a a a --+-+-.【答案】(1)7;(2)13【解析】(1)由题意11223a a-+=,所以21112222327a a a a --⎛⎫+=+-=-= ⎪⎝⎭.(2)由题意11223a a -+=,所以()()1111212233222222213371331512744534a a a a a a a a a a a a ------⎛⎫⎛⎫- ⎪⎪⨯--+-⎝⎭⋅⎝⎭==-==+--+++-.一、单选题1.(23-24高一上·青海海南·期中)已知R a ∈,则下列各式一定有意义的是()A .2a -B .13a C .12a D .0a 【答案】B【解析】对于A ,由221aa -=可知,0a =时表达式无意义;对于B ,根据幂函数性质可知,R a ∈时,表达式13a 恒有意义;对于C,易知12a =a<0时,表达式无意义;对于D ,当0a =时,0a 无意义;故选:B2.(23-24高一上·陕西咸阳·期末)化简32的结果为()A .5BC .5-D.【答案】A【解析】332232232332555⨯⎛⎫=== ⎪⎝⎭=,故选:A3.(23-24高一上·北京大兴·月考)已知0a >=()A .12a B .32a C .2a D .3a 【答案】A12a =,故选:A4.(23-24高一上·安徽淮南·月考改编)下列根式与分数指数幂的互化错误的是()A()120aa =>B.)340xx -=>C.)21320,0x y x y -=>>D .()32140x x =>【答案】B【解析】对于A()1313220a a a ⎛⎫==> ⎪⎝⎭,故A 正确;对于B选项,)334410xx x -⎛⎫=> ⎪⎝⎭,故B 错误;对于C,)21321210,0x y x y x-=>>,故C 正确;对于D,)()33321444320x x x ⎛⎫⎤===> ⎪⎝⎭,故D 正确.故选:B .5.(23-24高一上·江苏泰州·期中)已知14x x -+=,则22x x -+等于()A .6B .12C .14D .16【答案】C【解析】由14x x -+=可得:()2122216x x x x --+=++=,则2214x x -+=.故选:C.6.(23-24高一上·四川德阳·月考)010.256371.586-⎛⎫⨯-++= ⎪⎝⎭()A .110B .109C .108D .100【答案】A【解析】原式()11133333112344131442222223221083331210810231-⎛⎫=+=+= ⎪⎝⎭⎛⎫⎛⎫⎛⎫⨯+⨯+⨯-=⨯+- ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选:A.二、多选题7.(23-24高一上·四川成都·期中)以下运算结果等于2的是()A B .C .D 【答案】BCD【解析】对于A π44π=-=-,不合题意;对于B ,2=,符合题意;对于C ,()22=--=,符合题意;对于D 22=-=,符合题意.故选:BCD8.(23-24高一上·浙江·月考)已知0a >,0b >,则下列各式正确的是()A π3=-B 1=C .mna-=D .121133332463b ab a b ---⎛⎫÷-=- ⎪⎝⎭【答案】ABD【解析】A 选项:由π30->π3=-,A 选项正确;B ()11111123612312600222221a b b a ab a b ⎛⎫⎛⎫-⨯-+⨯ ⎪ ⎪--⎝⎭⎝⎭⎡⎤====⎢⎥⎣⎦,B 选项正确;C 选项:m na-C 选项错误;D 选项:112121101333333331246663b ab a a b a b b ⎛⎫⎛⎫------- ⎪ ⎪⎝⎭⎝⎭⎛⎫÷-=-=-=- ⎪⎝⎭,D 选项正确;故选:ABD.三、填空题9.(22-23高一上·上海奉贤·期末)化简()222a b ⋅=(其中0a >,0b >).【答案】4ab【解析】()((4222222a b ab a b +-⋅=⋅=.故答案为:4ab .10.(23-24高一上·全国·单元测试)方程2129240x x +-⋅+=的解集是.【答案】{1,2}-【解析】令2x t =,则0t >,方程可化为22940t t -+=,解得12t =或4t =,所以,122x =或24x =,解得=1x -或2x =.所以,方程的解集为{1,2}-.故答案为:{1,2}-.11.(23-24高一上·重庆沙坪坝·期中)已知12102α-=,131032β=,则314210βα+=(填数值)【答案】2【解析】()()31131113113142513422342242101010=322222αβα⎛⎫⎛⎫⨯⨯+-⨯+- ⎪⎝⎭⎝⎭⎛⎫⎛⎫=⨯⨯=== ⎪ ⎪⎝⎭⎝⎭.故答案为:2四、解答题12.(23-24高一上·安徽马鞍山·期中)化简求值:(1)()120120.344⎛⎫+ ⎪⎝⎭(2)20.52031103522216274--⎛⎫⎛⎫⎛⎫-⨯-⨯÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;【答案】(1)52;(2)0【解析】(1)()120120.344⎛⎫+ ⎪⎝⎭1293511422⎛⎫=+=+= ⎪⎝⎭.(2)20.52031103522216274--⎛⎫⎛⎫⎛⎫-⨯-⨯÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2222364493322220273444-⎛⎫⎛⎫⎛⎫⎛⎫⨯-÷=-⨯-⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭13.(23-24高一上·辽宁丹东·期中)已知正实数a 满足11221a a --=.(1)求1a a -+的值;(2)求33221122a a a a ---+的值.【答案】(1)3;(2)5【解析】(1)将11221a a --=两边平方得121a a -+-=,所以13a a -+=.(2)因为a 是正实数,令1122(0)a a x x -+=>,则2125x a a -=++=,所以x 可得()33111222214a a a a a a ---⎛⎫-=-++= ⎪⎝⎭,所以332211225a a a a ---==+.。

第06讲 等式性质与不等式性质模块一 思维导图串知识模块二 基础知识全梳理(吃透教材)模块三 核心考点举一反三模块四 小试牛刀过关测1.通过用不等式(组)表示实际问题,提升数学抽象与数学建模素养;2.通过比较两个实数的大小、不等式性质的应用,提升逻辑推理、数学运算素养;3.运用不等式的性质解决有关问题.知识点 1 不等关系与不等式1、不等式的概念(1)用数学符号“≠”“>”“<”“≥”“≤”连接两个数或代数式,以表示它们之间的不等式关系,含有这些不等式号的式子,叫做不等式.(2)用“<”或“>”连接的不等式叫严格不等式;用“≤”或“≥”连接的不等式叫非严格不等式.2、常见文字语言与符号语言之间的对应关系文字语言大于、高于、超过小于、低于、少于大于或等于、至少、不低于小于或等于、至多、不多于、不超过符号语言><≥≤3、用不等式组表示不等式关系当问题情境中包含两个或两个以上的不等式关系时,需要用不等式组来表示不等关系.知识点 2 等式性质性质文字表述性质内容注意1对称性a b b a=⇔=可逆2传递性,a b b c a c==⇒=同向3可加、减性a b a c b c =⇔±=±可逆4可乘性a b ac bc=⇒=同向5可除性,0a b a b c c c=≠⇒=同向知识点 3 不等式性质性质别名性质内容注意1对称性a >b ⇔b <a 可逆2传递性a >b ,b >c ⇒a >c 同向3可加性a >b ⇔a +c >b +c 可逆4可乘性a >b ,c >0⇒ac >bc a >b ,c <0⇒ac <bc c 的符号5同向可加性a >b ,c >d ⇒a +c >b +d 同向6正数同向可乘性a >b >0,c >d >0⇒ac >bd 同向7正数乘方性a >b >0⇒a n >b n (n ∈N ,n ≥2)同正知识点 4 比较大小的方法1、作差法、作商法是比较两个实数(或代数式)大小的基本方法.①作差法的步骤:作差、变形、判断差的符号、得出结论.②作商法的步骤:作商、变形、判断商与1的大小、得出结论.2、介值比较法也是比较大小的常用方法,其实质是不等式的传递性:若a >b ,b >c ,则a >c ;若a <b ,b <c ,那么a <c .其中b 是介于a 与c 之间的值,此种方法的关键是通过恰当的放缩,找出一个比较合适的中介值.3、平方法:对两式先平方,再比较大小.【注意】(1)比较代数式的大小通常采用作差法,如果含有根式,也可以先平方再作差,但此时一定要保证代数式大于零;(2)作差时应该对差式进行恒等变形(如配方、因式分解、有理化、通分等),直到能明显看出其正负号为止;(3)作商法适合于幂式、积式、分式间的大小比较,作商后应变形为能与“1”比较大小的式子,要注意营养函数的有关性质.考点一:用不等式(组)表示不等式关系例1.(23-24高一上·广东深圳·月考)公司运输一批木材,总重600吨,车队有两种货车,A 型货车载重量30吨,B 型货车载重量24吨,设派出A 型货车x 辆,B 型货车y 辆,则运输方案应满足的关系式是( )A .54100x y +<B .54100x y +≥C .54100x y +>D .54100x y +≤【变式1-1】(23-24高一上·贵州遵义·月考)持续的高温干燥天气导致某地突发山火,现需将物资运往灭火前线.从物资集散地到灭火前线-共40km ,其中靠近灭火前线5km 的山路崎岖,需摩托车运送,其他路段可用汽车运送.已知在可用汽车运送的路段,运送的平均速度为60km h ,设需摩托车运送的路段平均速度为km h x ,为使物资能在1小时内到达灭火前线,则x 应该满足的不等式为( ).A .40160x>+B .40160x<+C .355160x+>D .355160x+<【变式1-2】(22-23高一上·甘肃酒泉·期末)铁路总公司关于乘车行李规定如下:乘坐动车组列车携带品的外部尺寸长、宽、高之和不超过130cm ,且体积不超过372000cm ,设携带品外部尺寸长、宽、高分别记为a ,b ,c (单位:cm ),这个规定用数学关系式可表示为( )A .130a b c ++<且72000abc <B .130a b c ++>且72000abc >C .130a b c ++≤且72000abc ≤D .130a b c ++≥且72000abc ≥【变式1-3】(22-23高一上·四川眉山·月考)将一根长为5m 的绳子截成两段,已知其中一段的长度为x m ,若两段绳子长度之差不小于1m ,则x 所满足的不等关系为( )A .25005x x ->⎧⎨<<⎩B .251x -≥或521x -≥C .52105x x -≥⎧⎨<<⎩D .25105x x ⎧-≥⎨<<⎩考点二:比较实数(代数式)的大小例2. (23-24高一上·河南洛阳·期末)今年某地因天气干旱导致白菜价格不稳定,假设第一周、第二周的白菜价格分别为a 元/斤、b 元/斤()a b ≠,王大妈每周购买10元的白菜,李阿姨每周购买8斤白菜,王大妈和李阿姨两周买白菜的平均价格分别记为1m ,2m ,则1m 与2m 的大小关系为( )A .12m m =B .12m m >C .12m m <D .无法确定【变式2-1】(23-24高一上·江苏常州·期末)设a ,b ,m 都是正数,且a b <,记,a m ax y b m b +==+,则( )A .x y >B .x y=C .x y< D .x 与y 的大小与m的取值有关【变式2-2】(23-24高一上·陕西榆林·月考)设0a b >>,比较2222a b a b -+与a b a b -+的大小【变式2-3】(23-24高一上·山东青岛·月考)已知0a >,0b >的大小;考点三:利用不等式的性质判断命题真假例3. (23-24高一上·河北石家庄·月考)若||||a b >,则下列不等式成立的是( )A .0a b ->B .11a b<C .a b >D .22a b >【变式3-1】(23-24高一上·内蒙古呼和浩特·期中)下列说法正确的是( )A .若a b >,则22ac bc >B .若22a bc c >,则a b >C .若a b >,cd >,则ac bd>D .若0b a >>,则a c ab c b+>+【变式3-2】(23-24高一上·吉林延边·月考)(多选)下列结论错误的是()A .若a b >,则ac bc <B .若a b >,则11a b <C .若a b >,则22a b >D .若22ac bc >,则a b>【变式3-3】(23-24高一上·广西贺州·期末)(多选)若0a b >>,0c <,则下列不等关系正确的是( )A .a c b c+>+B .22a bc c >C .ac bc >D .11a b b a+>+考点四:利用不等式的性质求范围例4. (23-24高一上·陕西咸阳·月考)已知23a <<,21b -<<-,则2a b -的取值范围是( )A .[]6,7B .()2,5C .[]4,7D .()5,8【变式4-1】(23-24高一上·江西景德镇·月考)已知3b a b <<-,则ab的取值范围为( )A .03ab<<B .03a b≤<C .3a b >D .13a b<<【变式4-2】(23-24高一上·河北石家庄·期中)已知14a b ≤+≤,12a b -≤-≤,则42a b -的取值范围是( )A .{}410x x -<<B .{}36x x -<<C .{}214x x -<<D .{}210x x -≤≤【变式4-3】(23-24高一上·吉林四平·期中)已知2236x y ≤+≤,3569x y -≤-≤,则113z x y =+的取值范围是( )A .58933z z ⎧⎫≤≤⎨⎬⎩⎭B .5|273z z ⎧⎫≤≤⎨⎬⎩⎭C .8933z z ⎧⎫≤≤⎨⎬⎩⎭D .{}327z z ≤≤考点五:利用不等式的性质证明不等式例5. (23-24高一上·河北保定·月考)设,,a b c ∈R ,0a b c ++=,1abc =.(1)证明:0ab bc ca ++<;(2)若a b >,证明33a b >.【变式5-1】(23-24高一上·陕西榆林·期中)证明下列不等式:(1)已知a b c d >>>,求证:11a db c<--;(2)已知0,0,0a b c d e >><<<,求证:e e a c b d>--.【变式5-2】(23-24高一上·安徽芜湖·月考)(1)已知0b a >>,证明:2a a b b a<+;(2)若a ,b ,c 为三角形的三边长,则2a b cb c a c a b++<+++.【变式5-3】(23-24高一上·云南·月考)证明下列不等式:(1)若0,0a b >>,求证:22a ba b b a++≥;(2)若0a b >>,0c d <<,0e <,求证:()()22eea cb d >--.考点六:不等式性质的实际应用例6. (23-24高一上·四川南充·月考)火车站有某公司待运的甲种货物1530吨,乙种货物1150吨.现计划用A ,B 两种型号的货箱共50节运送这批货物.已知35吨甲种货物和15吨乙种货物可装满一节A 型货箱,25吨甲种货物和35吨乙种货物可装满一节B 型货箱,据此安排A ,B 两种货箱的节数,下列哪个方案不满足:( )A .A 货箱28节,B 货箱22节B .A 货箱29节,B 货箱21节C .A 货箱31节,B 货箱19节D .A 货箱30节,B 货箱20节【变式6-1】(22-23高一上·山东·月考)某化工厂制定明年某产品的生产计划,受下面条件的制约:生产每袋需用4h ;生产此产品的工人不超过200人,每个工人的年工作时间约为2100h ;生产每袋需用原料20kg ,年底库存原料600t ,明年可补充1200t ;此产品今年销售量是60000袋,预计明年的销售量至少在今年的基础上增长13.根据这些数据条件可以预测明年的产量在( )A .70000到75000袋之间B .70000到80000袋之间C .80000到85000袋之间D .80000到90000袋之间【变式6-2】(23-24高一上·全国·专题练习)王老师是高三的班主任,为了更好地督促班上的学生完成作业,王老师特地组建了一个学习小组的钉钉群,群的成员由学生、家长、老师共同组成.已知该钉钉群中男学生人数多于女学生人数,女学生人数多于家长人数,家长人数多于教师人数,教师人数的两倍多于男学生人数.则该钉钉群人数的最小值为( )A .18B .20C .22D .28【变式6-3】(23-24高一上·吉林长春·月考)不等关系是数学中一种最基本的数关系,生活中随处可见.例如.已知b 克糖水中含有a 克糖(0)b a >>,再添加m 克糖(0)m >(假设全部溶解),糖水变甜了.(1)请将这一事实表示为一个不等式.并证明这个不等式成立:(2)利用(1)中的结论证明:若,,a b c 为三角形的三边长,则2a b cb c a c a b++<+++.一、单选题1.(22-23高一上·河北邢台·月考)在开山工程爆破时,已知导火索燃烧的速度是每秒0.5厘米,人跑开的速度为每秒4米,距离爆破点150米以外(含150米)为安全区.为了使导火索燃尽时人能够跑到安全区,导火索的长度x (单位:厘米)应满足的不等式为( )A .41500.5x⨯<B .41500.5x⨯≥C .41500.5x⨯≤D .41500.5x⨯>2.(23-24高一上·云南昆明·期中)设2254M a a =++,(1)(3)N a a =++,则M 与N 的大小关系为( )A .M N>B .M N=C .M N<D .无法确定3.(23-24高一上·广东深圳·期末)已知,,R,a b c a b ∈>,则下列一定成立的是( )A .11a b<B .2ab b >C .b c ba c a+>+D .()()2211a c b c +>+4.(23-24高一上·安徽宣城·自主招生)已知实数a ,b ,则下列选项中正确的是( )A .若a b >,则22a b >B .若a b >,则22a b >C .若a b >,则22a b >D .若a b >,则11a b<5.(23-24高一上·河南驻马店·期末)已知15,31a b -<<-<<,则以下错误的是( )A .155ab -<<B .46a b -<+<C .28a b -<-<D .553ab-<<6.(23-24高一上·山东菏泽·月考)已知11x y -≤+≤,13x y ≤-≤,则32x y -的取值范围是( )A .2328x y ≤-≤B .3328x y ≤-≤C .2327x y ≤-≤D .53210x y ≤-≤二、多选题7.(23-24高一上·山东日照·期末)若实数a ,b ,c 满足()0a b b >≠且0a >,0c >,则下列不等式正确的是( )A .11a b<B .ac bc-<-C .b c ba c a+>+D .22222b a a b+>8.(23-24高一上·四川乐山·期中)下列不等式中,一定成立的是( )A .若0,a b c >>∈R ,则22c ca b<B .若0,a b c >>∈R ,则22ac bc >C .若0a b <<,则22a ab b >>D .若0a b <<,则22a a b b+<+三、填空题9.(23-24高一上·广东韶关·月考)已知x ∈R ,则23x + 2x .(填“<”,“>”,或“=”)10.(23-24高一上·北京西城·期中)已知a ,b ,c 为实数,能说明“若a b c >>,则2a bc >”为假命题的一组a ,b ,c 的值是.11.(23-24高一上·山东菏泽·期中)“双节”遇上亚运会,民宿成为潮流趋势.民宿的改造中,窗户面积与地板面积之比越大,采光效果越好.现有一所地板面积为180平方米的民宿需要同时增加窗户和地板的面积,已知地板增加的面积是窗户增加的面积的2倍,且民宿改造后的采光效果不逊于改造前,则改造前的窗户面积最大为平方米.四、解答题12.(23-24高一上·福建泉州·月考)(1)已知R a ∈,设()21M a a =+,()()21N a a =+-,比较M 与N 的大小;(2)证明:已知a b c >>,且0a b c ++=,求证:c ca cb c>--.13.(23-24高一上·湖北·期中)(1)已知b 克糖水中含有a 克糖(0b a >>),再添加m 克糖(0m >)(假设全部溶解),糖水变甜了.请将这一事实表示为一个不等式,不必证明.利用此结论证明:若,,a b c 为三角形的三边长,则2a b cb c a c a b++<+++.(2)超市里面提供两种糖:白糖每千克1p 元,红糖每千克2p 元()12p p ≠.小东买了相同质量的两种糖,小华买了相同价钱的两种糖.请问谁买的糖的平均价格比较高?请证明你的结论.(物品的平均价格=物品的总价钱÷物品的总质量)第06讲 等式性质与不等式性质模块一 思维导图串知识模块二 基础知识全梳理(吃透教材)模块三 核心考点举一反三模块四 小试牛刀过关测1.通过用不等式(组)表示实际问题,提升数学抽象与数学建模素养;2.通过比较两个实数的大小、不等式性质的应用,提升逻辑推理、数学运算素养;3.运用不等式的性质解决有关问题.知识点 1 不等关系与不等式1、不等式的概念(1)用数学符号“≠”“>”“<”“≥”“≤”连接两个数或代数式,以表示它们之间的不等式关系,含有这些不等式号的式子,叫做不等式.(2)用“<”或“>”连接的不等式叫严格不等式;用“≤”或“≥”连接的不等式叫非严格不等式.2、常见文字语言与符号语言之间的对应关系文字语言大于、高于、超过小于、低于、少于大于或等于、小于或等于、至多、至少、不低于不多于、不超过符号语言><≥≤3、用不等式组表示不等式关系当问题情境中包含两个或两个以上的不等式关系时,需要用不等式组来表示不等关系.知识点 2 等式性质性质文字表述性质内容注意1对称性a b b a=⇔=可逆2传递性,a b b c a c==⇒=同向3可加、减性a b a c b c =⇔±=±可逆4可乘性a b ac bc=⇒=同向5可除性,0a b a b c c c=≠⇒=同向知识点 3 不等式性质性质别名性质内容注意1对称性a >b ⇔b <a 可逆2传递性a >b ,b >c ⇒a >c 同向3可加性a >b ⇔a +c >b +c 可逆4可乘性a >b ,c >0⇒ac >bc a >b ,c <0⇒ac <bc c 的符号5同向可加性a >b ,c >d ⇒a +c >b +d 同向6正数同向可乘性a >b >0,c >d >0⇒ac >bd 同向7正数乘方性a >b >0⇒a n >b n (n ∈N ,n ≥2)同正知识点 4 比较大小的方法1、作差法、作商法是比较两个实数(或代数式)大小的基本方法.①作差法的步骤:作差、变形、判断差的符号、得出结论.②作商法的步骤:作商、变形、判断商与1的大小、得出结论.2、介值比较法也是比较大小的常用方法,其实质是不等式的传递性:若a >b ,b >c ,则a >c ;若a <b ,b <c ,那么a <c .其中b 是介于a 与c 之间的值,此种方法的关键是通过恰当的放缩,找出一个比较合适的中介值.3、平方法:对两式先平方,再比较大小.【注意】(1)比较代数式的大小通常采用作差法,如果含有根式,也可以先平方再作差,但此时一定要保证代数式大于零;(2)作差时应该对差式进行恒等变形(如配方、因式分解、有理化、通分等),直到能明显看出其正负号为止;(3)作商法适合于幂式、积式、分式间的大小比较,作商后应变形为能与“1”比较大小的式子,要注意营养函数的有关性质.考点一:用不等式(组)表示不等式关系例1.(23-24高一上·广东深圳·月考)公司运输一批木材,总重600吨,车队有两种货车,A 型货车载重量30吨,B 型货车载重量24吨,设派出A 型货车x 辆,B 型货车y 辆,则运输方案应满足的关系式是( )A .54100x y +<B .54100x y +≥C .54100x y +>D .54100x y +≤【答案】B【解析】由已知可得,3024600x y +≥,所以有54100x y +≥.故选:B.【变式1-1】(23-24高一上·贵州遵义·月考)持续的高温干燥天气导致某地突发山火,现需将物资运往灭火前线.从物资集散地到灭火前线-共40km ,其中靠近灭火前线5km 的山路崎岖,需摩托车运送,其他路段可用汽车运送.已知在可用汽车运送的路段,运送的平均速度为60km h ,设需摩托车运送的路段平均速度为km h x ,为使物资能在1小时内到达灭火前线,则x 应该满足的不等式为( ).A .40160x>+B .40160x<+C .355160x+>D .355160x+<【答案】D【解析】由题意汽车所用时间加上摩托车所用时间小于1小时,即355160x+<,故选:D .【变式1-2】(22-23高一上·甘肃酒泉·期末)铁路总公司关于乘车行李规定如下:乘坐动车组列车携带品的外部尺寸长、宽、高之和不超过130cm ,且体积不超过372000cm ,设携带品外部尺寸长、宽、高分别记为a ,b ,c (单位:cm ),这个规定用数学关系式可表示为( )A .130a b c ++<且72000abc <B .130a b c ++>且72000abc >C .130a b c ++≤且72000abc ≤D .130a b c ++≥且72000abc ≥【答案】C【解析】由长、宽、高之和不超过130cm 得130a b c ++≤,由体积不超过372000cm 得72000abc ≤.故选:C.【变式1-3】(22-23高一上·四川眉山·月考)将一根长为5m 的绳子截成两段,已知其中一段的长度为x m ,若两段绳子长度之差不小于1m ,则x 所满足的不等关系为( )A .25005x x ->⎧⎨<<⎩B .251x -≥或521x -≥C .52105x x -≥⎧⎨<<⎩D .25105x x ⎧-≥⎨<<⎩【答案】D【解析】由题意,可知另一段绳子的长度为()5m x -.因为两段绳子长度之差不小于1m ,所以()5105x x x ⎧--≥⎪⎨<<⎪⎩,化简得:25105x x ⎧-≥⎨<<⎩.故选:D考点二:比较实数(代数式)的大小例2. (23-24高一上·河南洛阳·期末)今年某地因天气干旱导致白菜价格不稳定,假设第一周、第二周的白菜价格分别为a 元/斤、b 元/斤()a b ≠,王大妈每周购买10元的白菜,李阿姨每周购买8斤白菜,王大妈和李阿姨两周买白菜的平均价格分别记为1m ,2m ,则1m 与2m 的大小关系为( )A .12m m =B .12m m >C .12m m <D .无法确定【答案】C【解析】由题意可得,0a >,0b >,a b ¹,12021010abm a b a b==++,288162a b a b m ++==,()()221224()()0222ab a b ab a b a b m m a b a b a b +-+---=-==<+++ ,12m m ∴<.故选:C .【变式2-1】(23-24高一上·江苏常州·期末)设a ,b ,m 都是正数,且a b <,记,a m ax y b m b +==+,则( )A .x y >B .x y=C .x y< D .x 与y 的大小与m的取值有关【答案】A【解析】由0,0,0a b m >>>,且a b <,即0b a ->,可得()()0m b a a m a b m b x b b m y --=+-=>++,即x y >,故选:A.【变式2-2】(23-24高一上·陕西榆林·月考)设0a b >>,比较2222a b a b -+与a b a b -+的大小【答案】2222a b a ba b a b-->++【解析】00,0a b a b a b >>⇒+>-> ,()()2222220,0a b a b a b a b a b a b a b +---∴=>>+++,222222222()211a b a b ab a b a b a b a b a b-++∴==+>-+++,2222a b a ba b a b--∴>++.【变式2-3】(23-24高一上·山东青岛·月考)已知0a >,0b >的大小;≤a b =时取等号)=()()3322x y x y x xy y +=+-+,可得分子)33a b =+=,a b+==进一步对其分子利用基本不等式可得a b+≥=,且等号成立当且仅当a b =,1≥,≤a b =时取等号).考点三:利用不等式的性质判断命题真假例3. (23-24高一上·河北石家庄·月考)若||||a b >,则下列不等式成立的是( )A .0a b ->B .11a b<C .a b >D .22a b >【答案】D【解析】因为||||a b >,所以22a b >,D 正确;当2,1a b =-=时,满足||||a b >,但是a b <,A,C 不正确;当2,1a b =-=-时,满足||||a b >,但是11a b>,B 不正确;故选:D 【变式3-1】(23-24高一上·内蒙古呼和浩特·期中)下列说法正确的是( )A .若a b >,则22ac bc >B .若22a bc c >,则a b >C .若a b >,c d >,则ac bd >D .若0b a >>,则a c ab c b+>+【答案】B【解析】对于A :当0c =时,2c =0,若a b >,则220ac bc ==,故A 错误;对于B :因为22a b c c>,所以20c ≠,即20c >,所以a b >,故B 正确;对于C :当1a =,0b =,1c =-,2d =-时,满足a b >,c d >,但是ac bd <,故C 错误;对于D :当0c =时,a c ab c b+=+,故D 错误.故选:B 【变式3-2】(23-24高一上·吉林延边·月考)(多选)下列结论错误的是()A .若a b >,则ac bc <B .若a b >,则11a b <C .若a b >,则22a b >D .若22ac bc >,则a b>【答案】AB【解析】取2,2,1a b c ==-=可得,a b >,但22ac bc =>-=,A 错误;取2,2a b ==-可得,a b >,但111122a b=>-=,B错误;因为a b >,又0b ≥,所以22a b >,故22a b >,C 正确;由22ac bc >,可得20c >,所以a b >,D 正确;故选:AB.【变式3-3】(23-24高一上·广西贺州·期末)(多选)若0a b >>,0c <,则下列不等关系正确的是( )A .a c b c +>+B .22a bc c >C .ac bc >D .11a b b a+>+【答案】ABD【解析】对A, 0a b >>,0c <,由不等式性质易知 a c b c +>+,故A 正确;对B, 0a b >>,0c <,则22210,a bc c c >∴>,故B 正确;对C, 0a b >>,0c <,由不等式性质易知ac bc <,故C 错误;对D, 若0a b >>,则()11110⎛⎫⎛⎫+-+=-+> ⎪ ⎪⎝⎭⎝⎭a b a b b a ab , 故D 正确.故选:ABD.考点四:利用不等式的性质求范围例4. (23-24高一上·陕西咸阳·月考)已知23a <<,21b -<<-,则2a b -的取值范围是( )A .[]6,7B .()2,5C .[]4,7D .()5,8【答案】D【解析】由题意可知426a <<,12b <-<,所以528<-<a b ,故选:D【变式4-1】(23-24高一上·江西景德镇·月考)已知3b a b <<-,则ab的取值范围为( )A .03a b<<B .03a b≤<C .3a b >D .13a b<<【答案】B【解析】因为3b a b <<-,所以0b <,则有10b<,将不等式3b a b <<-的两边同时乘1b ,可得31a b-<<,所以03a b ≤<.故选:B .【变式4-2】(23-24高一上·河北石家庄·期中)已知14a b ≤+≤,12a b -≤-≤,则42a b -的取值范围是( )A .{}410x x -<<B .{}36x x -<<C .{}214x x -<<D .{}210x x -≤≤【答案】D【解析】由12a b -≤-≤,14a b ≤+≤,得()()06a b a b ≤-++≤,即026a ≤≤,()224a b -≤-≤,所以()22210a b a -≤-+≤,即24210a b -≤-≤,故选:D【变式4-3】(23-24高一上·吉林四平·期中)已知2236x y ≤+≤,3569x y -≤-≤,则113z x y =+的取值范围是( )A .58933z z ⎧⎫≤≤⎨⎬⎩⎭B .5|273z z ⎧⎫≤≤⎨⎬⎩⎭C .8933z z ⎧⎫≤≤⎨⎬⎩⎭D .{}327z z ≤≤【答案】D【解析】设)231156(3)(x y x x y n y m +=-++,则25)(113(36)x y m n y m n x +++=-,所以2511363m n m n +=⎧⎨-=⎩,解得31m n =⎧⎨=⎩,于是1133(56)23)(x y y x x y +++=-又63(23)18x y ≤+≤,3569x y -≤-≤,所以33(56)2723)(x y x y ++≤-≤,即311327x y ≤+≤.故{}327z z ≤≤.故选:D .考点五:利用不等式的性质证明不等式例5. (23-24高一上·河北保定·月考)设,,a b c ∈R ,0a b c ++=,1abc =.(1)证明:0ab bc ca ++<;(2)若a b >,证明33a b >.【答案】(1)证明见解析;(2)证明见解析【解析】(1)证明:∵()22222220a b c a b c ab ac bc ++=+++++=,∴()22212ab bc ca a b c ++=-++.a ,b ,c 不同时为0,则2220a b c ++>,∴()222102ab bc ca a b c ++=-++<;(2)()()3322a b a b a ab b -=-++.∵222213024a ab b a b b ⎛⎫++=++≥ ⎪⎝⎭,取等号的条件为0a b ==,而a b >,∴等号无法取得,即222213024a b b a ab b ⎛⎫=++> ⎪⎝+⎭+,又a b >,∴()()33220a b a b a ab b -=-++>,∴33a b >.【变式5-1】(23-24高一上·陕西榆林·期中)证明下列不等式:(1)已知a b c d >>>,求证:11a db c<--;(2)已知0,0,0a b c d e >><<<,求证:e e a c b d>--.【答案】(1)证明见解析;(2)证明见解析【解析】(1)a b c d >>>Q ,即,a b d c >->-,0a d b c ∴->->,则11a db c<--.(2)0,0,0a b c d e >><<< ,0c d ∴->->,0,0,0a c b d b a c d ∴->->-<-<,则()()()()()()()()()()0e b d e a c e b d a c e b a c d e ea cb d ac bd a c b d a c b d -----+-+--===>--------,.e ea cb d∴>--【变式5-2】(23-24高一上·安徽芜湖·月考)(1)已知0b a >>,证明:2a a b b a<+;(2)若a ,b ,c 为三角形的三边长,则2a b cb c a c a b++<+++.【答案】(1)证明见解析;(2)证明见解析.【解析】(1)()()()()22a b a ab a a b a ab b a b b a b b a +---==+++,由0b a >>,得0a b -<,而0b >,0b a +>,0a >,则()()0a a b b b a -<+,所以2a ab b a<+.(2),,a b c 为ABC 的三边长,则有0a b c +>>,0a c b +>>,0b c a +>>,由(1)知:c c c a b a b c +<+++,a a a b c a b c +<+++,b b ba c ab c+<+++,将以上不等式左右两边分别相加得:2c a b c c a a b b a b b c a c a b c a b c a b c+++++<++=+++++++++,所以2c a b a b b c c a++<+++.【变式5-3】(23-24高一上·云南·月考)证明下列不等式:(1)若0,0a b >>,求证:22a ba b b a++≥;(2)若0a b >>,0c d <<,0e <,求证:()()22eea cb d >--.【答案】(1)证明见解析;(2)证明见解析【解析】(1)证明:因为()()()2223322a b a b a b a b a b ab a b b a ab ab +-⎛⎫+--+-+== ⎪⎝⎭,又因为0,0a b >>,所以()()20a b a b ab+-≥,所以22a b a b b a++≥.(2)证明:由()()()()()()222222e b d a c eea cb d ac bd ⎡⎤---⎣⎦-=----()()()()()()22e a b c d b a c d a c b d ⎡⎤⎡⎤+-+-+-⎣⎦⎣⎦=--,因为0a b >>,0c d <<,所以0a b +>,0c d +<,0b a -<,0c d -<,所以()()0a b c d +-+>,()()0b a c d -+-<.因为0e <,所以()()()()0e a b c d b a c d ⎡⎤⎡⎤+-+-+->⎣⎦⎣⎦又因为()()220a c b d -->,所以()()220eea cb d ->--,即()()22eea cb d >--.考点六:不等式性质的实际应用例6. (23-24高一上·四川南充·月考)火车站有某公司待运的甲种货物1530吨,乙种货物1150吨.现计划用A ,B 两种型号的货箱共50节运送这批货物.已知35吨甲种货物和15吨乙种货物可装满一节A 型货箱,25吨甲种货物和35吨乙种货物可装满一节B 型货箱,据此安排A ,B 两种货箱的节数,下列哪个方案不满足:( )A .A 货箱28节,B 货箱22节B .A 货箱29节,B 货箱21节C .A 货箱31节,B 货箱19节D .A 货箱30节,B 货箱20节【答案】C【解析】设A 、B 货箱分别有x ,y 节,则503525153015351150x y x y x y +=⎧⎪+≥⎨⎪+≥⎩,A :共50节且352825221530⨯+⨯=,1528352211901150⨯+⨯=>,满足;B :共50节且3529252115401530⨯+⨯=>,1529352111701150⨯+⨯=>,满足;C :共50节且3531251915601530⨯+⨯=>,1531351911301150⨯+⨯=<,不满足;D :共50节且3530252015501530⨯+⨯=>,153035201150⨯+⨯=,满足;故选:C.【变式6-1】(22-23高一上·山东·月考)某化工厂制定明年某产品的生产计划,受下面条件的制约:生产每袋需用4h ;生产此产品的工人不超过200人,每个工人的年工作时间约为2100h ;生产每袋需用原料20kg ,年底库存原料600t ,明年可补充1200t ;此产品今年销售量是60000袋,预计明年的销售量至少在今年的基础上增长13.根据这些数据条件可以预测明年的产量在( )A .70000到75000袋之间B .70000到80000袋之间C .80000到85000袋之间D .80000到90000袋之间【答案】D【解析】设明年的产量为x 袋,则()42002100160000132060012001000x x x ⎧≤⨯⎪⎪⎛⎫≥+⎨ ⎪⎝⎭⎪⎪≤+⨯⎩,所以8000090000x ££,故可以预测明年的产量在80000到90000袋之间,故选:D.【变式6-2】(23-24高一上·全国·专题练习)王老师是高三的班主任,为了更好地督促班上的学生完成作业,王老师特地组建了一个学习小组的钉钉群,群的成员由学生、家长、老师共同组成.已知该钉钉群中男学生人数多于女学生人数,女学生人数多于家长人数,家长人数多于教师人数,教师人数的两倍多于男学生人数.则该钉钉群人数的最小值为( )A .18B .20C .22D .28【答案】C【解析】依题意,设教师、家长、女生、男生人数分别为,,,x y z t ,且,,,N x y z t *∈,于是1,12,123y x z y x t z y x ≥+≥+≥+≥+≥+≥+,则46x y z t x +++≥+,又23x t x >≥+,解得3x >,因此min 4x =,此时22x y z t +++≥,所以当4,5,6,7x y z t ====时,min ()22x y z t +++=,即该钉钉群人数的最小值为22.故选:C【变式6-3】(23-24高一上·吉林长春·月考)不等关系是数学中一种最基本的数关系,生活中随处可见.例如.已知b 克糖水中含有a 克糖(0)b a >>,再添加m 克糖(0)m >(假设全部溶解),糖水变甜了.(1)请将这一事实表示为一个不等式.并证明这个不等式成立:(2)利用(1)中的结论证明:若,,a b c 为三角形的三边长,则2a b cb c a c a b++<+++.【答案】(1)a a mb b m+<+,(0,0)b a m >>>,证明见解析;(2)证明见解析;【解析】(1)糖水变甜了得出不等式a a mb b m+<+,(0,0)b a m >>>.证明:()()()aa ma b m b a m b b m b b m ++-+-==++()()()ab am ba bm m a b b b m b b m +---=++.0,0,0b a a b b >>∴-<> .0,0m b m >∴+> ,()0()m a b b b m -∴<+,a a mb b m+∴<+.(2)设ABC 的三边长分别为,,a b c ,则有,,a b c a c b b c a +>+>+>,由(1)已证不等式可得:c c c a b a b c +<+++,a a a b c a b c +<+++,b b ba c ab c+<+++,将以上不等式左右两边分别相加得:2c a b c c a a b b a b b c a c a b c a b c a b c+++++<++=+++++++++,所以,2c a b a b b c c a++<+++.一、单选题1.(22-23高一上·河北邢台·月考)在开山工程爆破时,已知导火索燃烧的速度是每秒0.5厘米,人跑开的速度为每秒4米,距离爆破点150米以外(含150米)为安全区.为了使导火索燃尽时人能够跑到安全区,导火索的长度x (单位:厘米)应满足的不等式为( )A .41500.5x⨯<B .41500.5x⨯≥C .41500.5x⨯≤D .41500.5x⨯>【答案】B【解析】由题意知导火索的长度x (单位:厘米),故导火索燃烧的时间为0.5x秒,人在此时间内跑的路程为40.5x ⎛⎫⨯ ⎪⎝⎭米,由题意可得41500.5x ⨯≥.故选:B.2.(23-24高一上·云南昆明·期中)设2254M a a =++,(1)(3)N a a =++,则M 与N 的大小关系为( )A .M N >B .M N=C .M N<D .无法确定【答案】A【解析】因为()()()22213254131024M N a a a a a a a ⎛⎫-=++-++=++=++> ⎪⎝⎭,所以M N >.故选:A.3.(23-24高一上·广东深圳·期末)已知,,R,a b c a b ∈>,则下列一定成立的是( )A .11a b<B .2ab b >C .b c ba c a+>+D .()()2211a c b c +>+【答案】D【解析】对于A ,当1,2a b ==-,则11a b>,故A 不正确;对于B ,当0b =时,由a b >可得20ab b ==,故B 不正确;对于C ,当2,1,0a b c ===时,b c ba c a+=+,故C 不正确;对于D ,因为210c +>恒成立,所以由a b >可得()()2211a c b c +>+,故D 正确.故选:D.4.(23-24高一上·安徽宣城·自主招生)已知实数a ,b ,则下列选项中正确的是( )A .若a b >,则22a b >B .若a b >,则22a b >C .若a b >,则22a b >D .若a b >,则11a b<【答案】C【解析】对于A 选项,1,1a b ==-,满足a b >,此时221,1a b ==,不满足22a b >,故A 错误;对于B 选项,1,1a b ==-,满足a b >,此时221,1a b ==,不满足22a b >,故B错误;对于C 选项,0a b >≥,所以222a b b >=,故C 正确;对于D 选项,1,1a b ==-,满足a b >,此时,1111a b==-,不满足11a b <,故D错误,故选:C.5.(23-24高一上·河南驻马店·期末)已知15,31a b -<<-<<,则以下错误的是( )A .155ab -<<B .46a b -<+<C .28a b -<-<D .553ab-<<【答案】D【解析】因为1,153a b -<<-<<,所以13b -<-<,对于A ,1515330a ab b -<<⎧⇒-<<⎨-<<⎩,1500a ab b -<<⎧⇒=⎨=⎩,151501a ab b -<<⎧⇒-<<⎨<<⎩,综上可得155ab -<<,故A 正确;对于B ,314156a b --=-<+<+=,故B 正确;对于C ,112358a b --=-<-<+=,故C 正确;对于D ,当14,2a b ==时,8a b=,故D 错误;故选:D.6.(23-24高一上·山东菏泽·月考)已知11x y -≤+≤,13x y ≤-≤,则32x y -的取值范围是( )A .2328x y ≤-≤B .3328x y ≤-≤C .2327x y ≤-≤D .53210x y ≤-≤【答案】A【解析】设()()()()32x y m x y n x y m n x m n y -=+--=-++,所以32m n m n -=⎧⎨+=-⎩,解得1252m n ⎧=⎪⎪⎨⎪=-⎪⎩,即可得()()153222x y x y x y -=++-,因为11x y -≤+≤,13x y ≤-≤,所以2≤()()153222x y x y x y -=++-8≤,故选:A .二、多选题7.(23-24高一上·山东日照·期末)若实数a ,b ,c 满足()0a b b >≠且0a >,0c >,则下列不等式正确的是( )A .11a b <B .ac bc-<-C .b c ba c a +>+D .22222b a a b+>【答案】BC【解析】对于A ,若1,1a b ==-,则1111a b=>=-,所以A 错误,对于B ,因为a b >,所以a b -<-,因为0c >,所以ac bc -<-,所以B 正确,对于C ,因为a b >,0a >,0c >,所以()0c a b ->,()0a a c +>,所以()()()0()()b c b a b c b a c c a b a c a a a c a a c ++-+--==>+++,所以b c ba c a+>+,所以C 正确,对于D ,若1,1a b ==-,则2222112b a a b+=+=,所以D 错误,故选:BC8.(23-24高一上·四川乐山·期中)下列不等式中,一定成立的是( )A .若0,a b c >>∈R ,则22c ca b<B .若0,a b c >>∈R ,则22ac bc >C .若0a b <<,则22a ab b >>D .若0a b <<,则22a a b b+<+【答案】AC【解析】对于A ,由0a b >>,20c>,知110a b <<,得22c ca b<,故A 正确;对于B ,当0c =时,故B 错误;对于C ,当0a b <<时,由()20a ab a a b -=->,得2a ab >,又()20ab b b a b -=->,则2ab b >,故有22a ab b >>,故C 正确;对于D ,当2a =-,1b =-时,22a a b b +>+,D 中不等式不一定成立,故D 错误.故选:AC.三、填空题9.(23-24高一上·广东韶关·月考)已知x ∈R ,则23x + 2x .(填“<”,“>”,或“=”)【答案】>【解析】()2232120x x x +-=-+>,故232x x +>.故答案为:>.10.(23-24高一上·北京西城·期中)已知a ,b ,c 为实数,能说明“若a b c >>,则2a bc >”为假命题的一组a ,b ,c 的值是.【答案】1a =,1b =-,2c =-(答案不唯一)【解析】当1,1,2a b c ==-=-时,21a =,2bc =,此时满足a b c >>,但是2a bc <.故答案为:1,1,2a b c ==-=-(答案不唯一).11.(23-24高一上·山东菏泽·期中)“双节”遇上亚运会,民宿成为潮流趋势.民宿的改造中,窗户面积与地板面积之比越大,采光效果越好.现有一所地板面积为180平方米的民宿需要同时增加窗户和地板的面积,已知地板增加的面积是窗户增加的面积的2倍,且民宿改造后的采光效果不逊于改造前,则改造前的窗户面积最大为 平方米.【答案】90【解析】设改造前的窗户面积为x ,窗户增加的面积为y ,0,0x y >>,依题意1801802x x yy+≤+,即1802180180,2180,90x xy x y xy y x +≤+≤≤,所以改造前的窗户面积最大为90平方米.故答案为:90四、解答题12.(23-24高一上·福建泉州·月考)(1)已知R a ∈,设()21M a a =+,()()21N a a =+-,比较M 与N 的大小;(2)证明:已知a b c >>,且0a b c ++=,求证:c ca cb c>--.【答案】(1)M N >;(2)证明见解析.【解析】(1)()()()221721212()024M a a a a N a a a ++-=++==+--+>,则M N >;(2)因为a b c >>,且0a b c ++=,则0,0a c ><,则0a c b c ->->,则()()0a c b c -->,则10()()a cbc >--,则11()()0()()()()a c b c a c b c a c b c ⋅->⋅->----,则110b c a c>>--,又0c <则c c a c b c>--.命题得证.13.(23-24高一上·湖北·期中)(1)已知b 克糖水中含有a 克糖(0b a >>),再添加m 克糖。

2020初高中数学衔接教程中考数学与初高中衔接的关系中考起着为高中选拔人才的作用,莘莘学子通过中考这一座桥梁走向高中.初中数学教材难度下降,初中教学跟着中考指挥棒,弱化了很多初高中数学学习中需要一直贯彻的数学思想方法,高中数学内容起点高、难度大、容量多,学生到了高中易衔接不上中考试题除了考察学生对初中知识的掌握程度以外,还为学生适应高中学习做适当的衔接,将会很好地体现“以学生的发展为根本”这一教学理念. 一、延伸高中数学思想方法在初高中数学学习中需要一直贯彻的数学思想方法有函数的思想、数形结合思想、对图形的认识与空间想象能力等例如函数思想,生长点在初中,而发展点在高中,是初高中数学衔接的重要内容初中教材中函数知识的考察重点在于函数的基本性质和如何求函数表达式,而高中数学重视各种函数间的关系、动态问题中融合函数知识等内容.中考试题中对这类问题加以重视,把高中数学思想方法渗入初中的学习,以达到初高中接轨. 例1如图1,在平面直角坐标系x0y 中,四边形ABCD 是菱形,顶点A 、C 、D 均在坐标轴上,且AB=5,4sin 5B =. (1)求过A 、C 、D 三点的抛物线的解析式;(2)记直线AB 的解析式为y 1=mx+n ,(1)中抛物线的解析式为22y ax bx c =++,求当12y y <时,自变量x 的取值范围;(3)设直线AB 与(1)中抛物线的另一个交点为E ,P 点为抛物线上,A ,E 两点之间的一个动点,当P 点在何处时,△PAE 的面积最大?并求出面积的最大值.类似的题型还有结合高中几何不等式考察数形结合思想;利用三视图延伸到高中立体几何,考察空间理解能力;渗透排列组合知识强化概率知识的理解能力等等.学生通过解这一类题目,可以把解题思想延伸到高中,利用高中思维方法解初中函数题,以达到初高中思维方法上的衔接. 二、滲透高中数学概念概念是基础知识的核心.初中概念简单,容易理解,从升学考看,学生只要记准概念公式及教师所讲例题类型,一般均可对号入座取得中考好成绩造成了轻知识形成过程、轻概念理解、重题量的情形.初、高中教师教学方法上的差异中间又缺乏过渡过程,至使高中新生在理解概念时,普遍感到吃力.把高中的概念理解渗透到中考试题,引导学生重视概念理解,正确理解和灵活运用概念,从而增强概念理解能力.例2如图3,对于平面直角坐标系中的任意两点()111,P x y ,()222,P x y ,我们把1212x x y y -+-叫做12,P P 两点间的直角距离记作()12,d P P .(1)已知O 为坐标原点,动点P (x ,y )满足d (O ,P )=1,请写出x 与y 之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P 所组成的图形;(2)设()000,P x y 是一定点,Q (x ,y )是直线上的动点,我们把()0,d P Q 的最小值叫做P 到直线y=ax+b 的直角距离试求点M (2,1)到直线y=x+2的直角距离.类似的题型有以下几种:直接利用高中数学概念解题如直接给出正弦函数、余弦函数解斜三角形;以高中数学概念为背景结合初中知识解题,如射影定理、圆幂定理的应用;或者改编高中概念,使其简单化,在初中背景下应用等这类试题要求学生通过阅读对概念的本质进行理解、概括在新背景下运用新概念,结合初中知识解决问题这类题目能很好地考查学生的数学阅读理解能力数学抽象概括能力和对概念的实际应用能力.三、衔接高中解题技巧高中数学解题有较多技巧,用高中解题技巧解初中数学题,很多时候能事半功倍,展现数学的奥妙之处中考题融人高中解题技巧,能促使师生更新原有的思维方式,为高中后续学习做铺垫.例3为解方程()()2221514x x ---+=0,我们可以将x 2-1视为一个整体然后设x 2-1=y ,则()2221x y -=,原方程化为y 2-5y+4=0 ①,解得121,4y y ==.当y=1时,211,2x x -==当y=4时,214,x x -==所以,原方程的解为1234x x x x ===-解答问题(1)填空:在由原方程得到①过程中,利用法达到了降次的目的,体现了的数学思想;(2)解方程:4260x x --=. 例4观察下列等式: 第1个等式:111111323a ⎛⎫==- ⎪⨯⎝⎭第2个等式111135235⎛⎫==- ⎪⨯⎝⎭ 第3个等式3111157257a ⎛⎫==- ⎪⨯⎝⎭第4个等式4111179279a ⎛⎫==- ⎪⨯⎝⎭请解答下列问题:(1)请按以上规律列出第5个等式:5a = = .(2)用含n 的代数式表示第n 个等式:n a ==.(n 为正整数)(3)求1234100a a a a a +++++的值.四、弥补初中知识层面的不足初中教材知识层面较简单,对能力要求不高,相对来说,高中对数学能力和数学思想的运用要求比较高,初高中知识存在着很多需要衔接的地方,中考题可以在这些方面加以重视.新高一学生的数学知识上看,明显在一元二次方程的解、二次函数根与系数的关系方面知识欠缺,遇到此类问题时,学生表现出思维能力、分析能力等方面的乏力,中考题中,可利用二次函数在开闭区间上的最值,十字相乘法分解因式,元二次不等式的解法等,作为初中数学学习的延伸,高中数学学习的阶梯,并依此为突破口,做好初、高中数学教学的衔接;射影定理,平行线分线段比例定理,圆幂定理等,初中深度不够,高中应用频繁,在考察相似三角形知识的中考题可引用此类知识;初中教材中没有关于含有字母系数的方程的解法和公式变形等内容,进入高中后进行公式推动有困难,这方面中考题可尝试渗透;直线与圆的位置关系的讨论,学生在初中掌握的很肤浅,可在中考题中利用几何法和代数法探讨,作进一步深化;含有参数的函数、方程、不等式,初中教材中同样不作要求,只作定量研究,而在高中,这部分内容被视为重难点,可在中考综合题(如动点问题)中涉及,作为区分度较高的拔高知识点;几何部分很多概念(如重心、垂心、外心、内心等),初中生大都没有学习,而高中教材多常常要涉及,这些也可以作为考察的内容.中考题的多方面、多层次变化,决定了初中教师要站在更高的平台上展望,初高中衔接的中考题,对初中知识和数学思想进行补充、对初中教师的教学起到指导性作用.初中老师在平时的教学中,或初三备考时,不妨多与高中知识、思想方法接轨,以崭新的视角看待中考,以达到中考的真正意义.中考数学与初高中衔接的关系例题答案解析中考起着为高中选拔人才的作用,莘莘学子通过中考这一座桥梁走向高中.初中数学教材难度下降,初中教学跟着中考指挥棒,弱化了很多初高中数学学习中需要一直贯彻的数学思想方法,高中数学内容起点高、难度大、容量多,学生到了高中易衔接不上中考试题除了考察学生对初中知识的掌握程度以外,还为学生适应高中学习做适当的衔接,将会很好地体现“以学生的发展为根本”这一教学理念. 一、延伸高中数学思想方法在初高中数学学习中需要一直贯彻的数学思想方法有函数的思想、数形结合思想、对图形的认识与空间想象能力等例如函数思想,生长点在初中,而发展点在高中,是初高中数学衔接的重要内容初中教材中函数知识的考察重点在于函数的基本性质和如何求函数表达式,而高中数学重视各种函数间的关系、动态问题中融合函数知识等内容.中考试题中对这类问题加以重视,把高中数学思想方法渗入初中的学习,以达到初高中接轨.例1如图1,在平面直角坐标系x0y 中,四边形ABCD 是菱形,顶点A 、C 、D 均在坐标轴上,且AB=5,4sin 5B =. (1)求过A 、C 、D 三点的抛物线的解析式;(2)记直线AB 的解析式为y 1=mx+n ,(1)中抛物线的解析式为22y ax bx c =++,求当12y y <时,自变量x 的取值范围;(3)设直线AB 与(1)中抛物线的另一个交点为E ,P 点为抛物线上,A ,E 两点之间的一个动点,当P 点在何处时,△PAE 的面积最大?并求出面积的最大值.【解答】 如图2,(1)由菱形ABCD 的边长和一角的正弦值,可求出OC ,OD ,OA 的长,进而确定A ,C ,D 三点坐标,通过待定系数法求出抛物线的解析式222433y x x =-++. (2)首先由A ,B 的坐标确定直线AB 的解析式143y x =--83,然后求出直线A 与抛物线的两个交点(-2,0)和285,3⎛⎫- ⎪⎝⎭,然后通过观察图象找出直线y 1在抛物线y 2图象下方的部分,由图可知:当y 1<y 2时,-2<x<5.(3)该题的关键点是确定点P 的位置,△APE 的面积最大,那么12APE S AE h ∆=⨯中h 的值最大,即点P 离直线AE 的距离最远,那么点P 为与直线AB 平行且与抛物线有且仅有的唯一交点的直线上的点. 若设直线4:3L y x b =-+,直线L ∥AB ,当直线L 与抛物线有且只有一个交点P 时,24224333x b x x -+=-++,且0∆=. 求得112b =,即直线411:32L y x =-+;可得点37,22P ⎛⎫⎪⎝⎭. 由(2)得285,3E ⎛⎫ ⎪⎝⎭,则直线11:93PE y x =-+.则点2749,0,1111F AF OA OF ⎛⎫=+=⎪⎝⎭.∴△PAE 的最大值:149211PAE PAF AEF S S S ∆∆∆=+=⨯⨯2873433212⎛⎫+=⎪⎝⎭, 综上所述,当P 为37,22⎛⎫⎪⎝⎭时,△PAE 的面积最大,为34312. 【点评】本题是一道二次函数综合题,初高中衔接性较强,问题(2)在初中求交点方法的基础上拓展了高中数学中直线与抛物线的交点问题,再利用了高中用图象解一元二次不等式的思维方法解题问题(3)突破了常规动点问题的模式,利用直线与抛物线相切找出平行线间的最大距离这一高中常见的数形结合思想解初中动点问题,从而求出三角形的最大面积.类似的题型还有结合高中几何不等式考察数形结合思想;利用三视图延伸到高中立体几何,考察空间理解能力;渗透排列组合知识强化概率知识的理解能力等等.学生通过解这一类题目,可以把解题思想延伸到高中,利用高中思维方法解初中函数题,以达到初高中思维方法上的衔接. 二、滲透高中数学概念概念是基础知识的核心.初中概念简单,容易理解,从升学考看,学生只要记准概念公式及教师所讲例题类型,一般均可对号入座取得中考好成绩造成了轻知识形成过程、轻概念理解、重题量的情形.初、高中教师教学方法上的差异中间又缺乏过渡过程,至使高中新生在理解概念时,普遍感到吃力.把高中的概念理解渗透到中考试题,引导学生重视概念理解,正确理解和灵活运用概念,从而增强概念理解能力.例2如图3,对于平面直角坐标系中的任意两点()111,P x y ,()222,P x y ,我们把1212x x y y -+-叫做12,P P 两点间的直角距离记作()12,d P P .(1)已知O 为坐标原点,动点P (x ,y )满足d (O ,P )=1,请写出x 与y 之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P 所组成的图形;(2)设()000,P x y 是一定点,Q (x ,y )是直线上的动点,我们把()0,d P Q 的最小值叫做P 到直线y=ax+b的直角距离试求点M (2,1)到直线y=x+2的直角距离. 【解答】 如图4,(1)由题意,得|x|+|y|=1,所有符合条件的点P 组成的图形如图所示,(2)(,)|2||d M Q x y =-+-1||2||21|x x =-++-|2||1|x x =-++,∴x 可取一切实数,|x-2|+|x+1|表示数轴上实数x 所对应的点到2和-1所对应的点的距离之和,其最小值为 3.∴点M (2,1)到直线y=x+2的直角距离为3.【点评】本题以高中数学平面两点间距离的知识为背景,将其和初中绝对值知识结合起来,以新概念的形式命题,让学生通过阅读理解“直角距离”这一新概念,转化为自己熟悉的绝对值几何意义,结合绝对值及一次函数的定义灵活结合解题问题(2)还渗透高中“点到直线距离”这一概念,体现初高中概念的紧密联系. 类似的题型有以下几种:直接利用高中数学概念解题如直接给出正弦函数、余弦函数解斜三角形;以高中数学概念为背景结合初中知识解题,如射影定理、圆幂定理的应用;或者改编高中概念,使其简单化,在初中背景下应用等这类试题要求学生通过阅读对概念的本质进行理解、概括在新背景下运用新概念,结合初中知识解决问题这类题目能很好地考查学生的数学阅读理解能力数学抽象概括能力和对概念的实际应用能力.三、衔接高中解题技巧高中数学解题有较多技巧,用高中解题技巧解初中数学题,很多时候能事半功倍,展现数学的奥妙之处中考题融人高中解题技巧,能促使师生更新原有的思维方式,为高中后续学习做铺垫.例3为解方程()()2221514x x ---+=0,我们可以将x 2-1视为一个整体然后设x 2-1=y ,则()2221x y -=,原方程化为y 2-5y+4=0 ①,解得121,4y y ==.当y=1时,211,x x -==当y=4时,214,x x -==所以,原方程的解为1234x x x x ===-解答问题(1)填空:在由原方程得到①过程中,利用 法达到了降次的目的,体现了的数学思想;(2)解方程:4260x x --=. 解:(1)换元法(2)由题意可得:()()22230x x+-=,由于220x +>,故230,x x -==.【点评】本题灵活地运用换元法解高次方程,利用变换思想将数学问题进行有效转化,使解法更加简单、直观,这是高中数学常常用到的解题技巧类似的还有利用换元法进行因式分解、解较复杂的分式方程或无理方程等.例4观察下列等式: 第1个等式:111111323a ⎛⎫==- ⎪⨯⎝⎭第2个等式111135235⎛⎫==- ⎪⨯⎝⎭ 第3个等式3111157257a ⎛⎫==- ⎪⨯⎝⎭第4个等式4111179279a ⎛⎫==- ⎪⨯⎝⎭请解答下列问题:(1)请按以上规律列出第5个等式:5a = = .(2)用含n 的代数式表示第n 个等式:n a ==.(n 为正整数)(3)求1234100a a a a a +++++的值.【解答】 (1)411119112911a ⎛⎫==- ⎪⨯⎝⎭(2)()()1111212122121n a n n n n ⎛⎫==- ⎪-+-+⎝⎭(3)1234100a a a a a +++++11111112335199201⎡⎤⎛⎫⎛⎫⎛⎫=-+-++- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦100201=. 【点评】本题是初中常见的寻找规律题取材于高中数学中的数列结合高中数列求和常用的裂项相消法解题技巧性较强.中考题可渗透韦达定理、参数法数学归纳法反证法解题方法技巧等增加试题的灵活性,提高试题的丰富度这些创新的题型及解法可引导学生平时注重涉足课本以外知识开拓视野发展思维脱离“应试教育”的误区. 四、弥补初中知识层面的不足初中教材知识层面较简单,对能力要求不高,相对来说,高中对数学能力和数学思想的运用要求比较高,初高中知识存在着很多需要衔接的地方,中考题可以在这些方面加以重视.新高一学生的数学知识上看,明显在一元二次方程的解、二次函数根与系数的关系方面知识欠缺,遇到此类问题时,学生表现出思维能力、分析能力等方面的乏力,中考题中,可利用二次函数在开闭区间上的最值,十字相乘法分解因式,元二次不等式的解法等,作为初中数学学习的延伸,高中数学学习的阶梯,并依此为突破口,做好初、高中数学教学的衔接;射影定理,平行线分线段比例定理,圆幂定理等,初中深度不够,高中应用频繁,在考察相似三角形知识的中考题可引用此类知识;初中教材中没有关于含有字母系数的方程的解法和公式变形等内容,进入高中后进行公式推动有困难,这方面中考题可尝试渗透;直线与圆的位置关系的讨论,学生在初中掌握的很肤浅,可在中考题中利用几何法和代数法探讨,作进一步深化;含有参数的函数、方程、不等式,初中教材中同样不作要求,只作定量研究,而在高中,这部分内容被视为重难点,可在中考综合题(如动点问题)中涉及,作为区分度较高的拔高知识点;几何部分很多概念(如重心、垂心、外心、内心等),初中生大都没有学习,而高中教材多常常要涉及,这些也可以作为考察的内容.中考题的多方面、多层次变化,决定了初中教师要站在更高的平台上展望,初高中衔接的中考题,对初中知识和数学思想进行补充、对初中教师的教学起到指导性作用.初中老师在平时的教学中,或初三备考时,不妨多与高中知识、思想方法接轨,以崭新的视角看待中考,以达到中考的真正意义.专题01数与式的运算本专题在初中、高中扮演的角色初中阶段“从分数到分式”,通过观察、分析、类比,找出分式的本质特征,及它们与分数的相同点和不同点,进而归纳得出分式的概念及运算性质,我们已经运用的这些思想方法是高中继续学习的法宝.二次根式是在学习了平方根、立方根等内容的基础上进行的,是对“实数”、“整式”等内容的延伸和补充,对数与式的认识更加完善.二次根式的化简对勾股定理的应用是很好的补充;二次根式的概念、性质、化简与运算是高中学习解三角形、一元二次方程、数列和二次函数的基础.二次根式是初中阶段学习数与式的最后一章,是式的变形的终结章.当两个二次根式的被开方数互为相反数时,可用“夹逼”的方法推出,两个被开方数同时为零.本专题内容蕴涵了许多重要的数学思想方法,如类比的思想(指数幂运算律的推广)、逼近的思想(有理数指数幂逼近无理数指数幂)n的异同.通过与初中所学的知识进行类比,理解分数指数幂的概念,进而学习指数幂的性质,掌握分数指数幂和根式之间的互化,掌握分数指数幂的运算性质高中必备知识点1:绝对值绝对值的代数意义:正数的绝对值是它的本身,负数的绝对值是它的相反数,零的绝对值仍是零.即:,0,||0,0,,0.a a a a a a >⎧⎪==⎨⎪-<⎩绝对值的几何意义:一个数的绝对值,是数轴上表示它的点到原点的距离. 两个数的差的绝对值的几何意义:b a -表示在数轴上,数a 和数b 之间的距离.典型考题【例题】阅读下列材料:我们知道x 的几何意义是在数轴上数x 对应的点与原点的距离,即x =0x -,也就是说,x 表示在数轴上数x 与数0对应的点之间的距离;这个结论可以推广为21x x -表示在数轴上数1x 与数2x 对应的点之间的距离;例1解方程|x |=2.因为在数轴上到原点的距离为2的点对应的数为2±,所以方程|x |=2的解为2±=x . 例2解不等式|x -1|>2.在数轴上找出|x -1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为-1或3,所以方程|x -1|=2的解为x =-1或x =3,因此不等式|x -1|>2的解集为x <-1或x >3.例3解方程|x -1|+|x +2|=5.由绝对值的几何意义知,该方程就是求在数轴上到1和-2对应的点的距离之和等于5的点对应的x 的值.因为在数轴上1和-2对应的点的距离为3(如图),满足方程的x 对应的点在1的右边或-2的左边.若x 对应的点在1的右边,可得x =2;若x 对应的点在-2的左边,可得x =-3,因此方程|x -1|+|x +2|=5的解是x =2或x =-3. 参考阅读材料,解答下列问题: (1)方程|x +2|=3的解为 ; (2)解不等式:|x -2|<6; (3)解不等式:|x -3|+|x +4|≥9; (4)解方程: |x -2|+|x +2|+|x -5|=15.【训练】实数在数轴上所对应的点的位置如图所示:化简.【能力提升】已知方程组的解的值的符号相同.(1)求的取值范围; (2)化简:. 高中必备知识点2:乘法公式我们在初中已经学习过了下列一些乘法公式: (1)平方差公式22()()a b a b a b +-=-;(2)完全平方公式222()2a b a ab b ±=±+. 我们还可以通过证明得到下列一些乘法公式: (1)立方和公式2233()()a b a ab b a b +-+=+; (2)立方差公式2233()()a b a ab b a b -++=-;(3)三数和平方公式2222()2()a b c a b c ab bc ac ++=+++++; (4)两数和立方公式33223()33a b a a b ab b +=+++; (5)两数差立方公式33223()33a b a a b ab b -=-+-.典型考题【例题】(1)计算:203212016(2)(2)2-⎛⎫-++-÷- ⎪⎝⎭(2)化简:2(2)(2)(2)a b a b a b +---【训练】计算:(1)0221( 3.14)(4)()3π--+-- (2)2(3)(2)(2)x x x --+-【能力提升】已知10x =a ,5x =b ,求: (1)50x 的值; (2)2x 的值;(3)20x 的值.(结果用含a 、b 的代数式表示)高中必备知识点3:二次根式一般地,形如0)a ≥的代数式叫做二次根式.根号下含有字母、且不能够开得尽方的式子称为无理式.例如32a b 212x ++,22x y ++等是有理式. 1.分母(子)有理化把分母(子)中的根号化去,叫做分母(子)有理化.为了进行分母(子)有理化,需要引入有理化因式的概念.两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个代数式互为有理化因式,例如与与b 与b 互为有理化因式.分母有理化的方法是分母和分子都乘以分母的有理化因式,化去分母中的根号的过程;而分子有理化则是分母和分子都乘以分母的有理化因式,化去分子中的根号的过程在二次根式的化简与运算过程中,二次根式的乘法可参照多项式乘法进行,运算中要运用公式0,0)a b =≥≥;而对于二次根式的除法,通常先写成分式的形式,然后通过分母有理化进行运算;二次根式的加减法与多项式的加减法类似,应在化简的基础上去括号与合并同类二次根式.2a ==,0,,0.a a a a ≥⎧⎨-<⎩典型考题【例题】计算下面各题.(1)2163)1526(-⨯-;(2时,想起分配律,于是她按分配律完成了下列计算:==她的解法正确吗?若不正确,请给出正确的解答过程.【能力提升】先化简,再求值:(2a ba b-+-ba b-)÷a2ba b-+,其中,.高中必备知识点4:分式1.分式的意义形如AB的式子,若B中含有字母,且0B≠,则称AB为分式.当M≠0时,分式AB具有下列性质:A A MB B M⨯=⨯;A A MB B M÷=÷.上述性质被称为分式的基本性质.2.繁分式像abc d+,2m n pmn p+++这样,分子或分母中又含有分式的分式叫做繁分式.典型考题【例题】先化简,再求值22122()121x x x xx x x x+++-÷--+,其中x满足x2+x﹣1=0.化简:22442x xy y x y-+-÷(4x 2-y 2)【能力提升】已知:112a b-=,则ab b a b ab a 7222+---的值等于多少?专题验收测试题1.如图,若实数m =﹣7+1,则数轴上表示m 的点应落在( )A .线段AB 上B .线段BC 上C .线段CD 上D .线段DE 上2.观察下列各式及其展开式: (a+b )2=a 2+2ab+b 2 (a+b )3=a 3+3a 2b+3ab 2+b 3 (a+b )4=a 4+4a 3b+6a 2b 2+4ab 3+b 4 (a+b )5=a 5+5a 4b+10a 3b 2+10a 2b 3+5ab 4+b 5 …请你猜想(a+b )10的展开式第三项的系数是( ) A .36 B .45C .55D .663.已知1-1x x =,则221x x+等于( ) A .3B .2C .1D .04.设边长为3的正方形的对角线长为a ,下列关于a 的四种说法:① a 是无理数;② a 可以用数轴上的一个点来表示;③ 3<a<4;④ a 是18的算术平方根.其中,所有正确说法的序号是 A .①④B .②③C .①②④D .①③④5.定义一种关于整数n 的“F ”运算:一、当n 为奇数时,结果为3n +5;二、当n 为偶数时,结果为2k n(其中k 是使2kn为奇数的正整数),并且运算重复进行.例如:取n =58,第一次经F 运算是29,第二次经F 运算是92,第三次经F 运算是23,第四次经F 运算是74……,若n =449,求第2020次运算结果是( ) A .1B .2C .7D .86.如图所示,将形状、大小完全相同的“•”和线段按照一定规律摆成下列图形,第1幅图形中“•”的个数为1a ,第2幅图形中“•”的个数为2a ,第3幅图形中“•”的个数为3a ,…,以此类推,则123191111a a a a ++++…的值为( )A .2021B .6184C .589840D .4317607.定义新运算,*(1)a b a b =-,若a 、b 是方程2104x x m -+=(0m <)的两根,则**b b a a -的值为() A .0B .1C .2D .与m 有关8.已知1x ,2x ,…,2019x 均为正数,且满足()()122018232019M x x x x x x =++++++,()()122019232018N x x x x x x =++++++,则M ,N 的大小关系是( )A .M N <B .M N >C .MND .M N ≥9.下列运算正确的是( )A .1a b a b b a -=--B .m n m na b a b --=- C .11b b a a a+-= D .2221a b a b a b a b+-=--- 10.已知a ,b 为实数且满足1a ≠-,1b ≠-,设11=+++a b M a b ,1111=+++N a b .①若1ab =时,M N ;②若1ab >时,M N >;③若1ab <时,M N <;④若0a b +=,则0M N ≤.则上述四个结论正确的有( ) A .1B .2C .3D .411.若11122299919991a +=+,22233399919991b +=+,则a 与b 的大小关系为( ) A .a b >B .a b =C .a b <D .无法确定12.已知实数x ,y ,z 满足1x y ++1y z ++1z x +=76,且z x y x y y z z x+++++=11,则x +y +z 的值为( )A .12B .14C .727D .913.已知226a b ab +=,且a>b>0,则a ba b+-的值为( ) A .2 B .±2C .2D .±214.若a ab+有意义,那么直角坐标系中点A(a,b)在( ) A .第一象限B .第二象限C .第三象限D .第四象限15.已知a 为实数,则代数式227122a a -+的最小值为( ) A .0B .3C .33D .916.已知m 、n 是正整数,若2m +5n是整数,则满足条件的有序数对(m ,n )为( ) A .(2,5)B .(8,20)C .(2,5),(8,20)D .以上都不是17.已知31=3,32=9,33=27,34=81,35=243,36=729,37=2187…….则3+32+33+34+…+32019的末位数字是____.18.如图,将一个正方形分割成11个大小不同的正方形,记图中最大正方形的周长是1C ,最小正方形的周长是2C ,则12C C =_____.19.对于整数a ,b ,c ,d ,定义a dbc =ac ﹣bd ,已知1<1d 4b<3,则b+d 的值为_______. 20. 已知21x y =⎧⎨=⎩,是二元一次方程组81mx ny nx my +=⎧⎨-=⎩的解,则m+3n 的平方根为______.21.若m 35223x y m x y m +--+-199199x y x y =---+m =________.22.若214x x x ++=,则2211x x ++= ________________. 23.已知22143134m n m n =--+,则11m n+的值等于______.24.已知函数1x f x x,那么1f_____.25.先化简,再求值:24211326x x x x -+⎛⎫-÷⎪++⎝⎭,其中1x =+. 26.观察下列等式:1)131====-====回答下列问题:(1;(2;(3….270=(1)求实数,a b 的值;(2的整数部分为x ,小数部分为y ①求2x y +的值;②已知10kx m -=+,其中k 是一个整数,且01m <<,求k m -的值. 28.已知下面一列等式:111122⨯=-;11112323⨯=-;11113434⨯=-;11114545⨯=-;… (1)请你按这些等式左边的结构特征写出它的一般性等式:(2)验证一下你写出的等式是否成立; (3)利用等式计算:11(1)(1)(2)x x x x ++++11(2)(3)(3)(4)x x x x ++++++.29.对有理数a 、b 、c ,在乘法运算中,满足:①交换律:ab ba =;②对加法的分配律:()c a b ca cb +=+.现对a b ⊕这种运算作如下定义,规定:a b a b a b ⊕=⋅++. (1)这种运算是否满足交换律?(2)举例说明:这种运算是否满足对加法的分配律?30.李狗蛋同学在学习整式乘法公式这一节时,发现运用乘法公式在进行一些计算时特别简便,这激发了李狗蛋同学的学习兴趣,他想再探究一些有关整式乘法的公式,便主动查找资料进行学习,以下是他找来的资料题,请你一同跟李狗蛋同学探究一下: (1)探究:()()a b a b -+=____;()()22a b a ab b -++=___;()()3223a b a a b ab b -+++=_____;(2)猜想:()()1221...n n n n a b aa b ab b -----++++=______(n 为正整数,且2n ≥);(3)利用上述猜想的结论计算:98732222...2221-+-+-+-的值.专题01数与式的运算本专题在初中、高中扮演的角色初中阶段“从分数到分式”,通过观察、分析、类比,找出分式的本质特征,及它们与分数的相同点和不同点,进而归纳得出分式的概念及运算性质,我们已经运用的这些思想方法是高中继续学习的法宝.二次根式是在学习了平方根、立方根等内容的基础上进行的,是对“实数”、“整式”等内容的延伸和补充,对数与式的认识更加完善.二次根式的化简对勾股定理的应用是很好的补充;二次根式的概念、性质、化简与运算是高中学习解三角形、一元二次方程、数列和二次函数的基础.二次根式是初中阶段学习数与式的最后一章,是式的变形的终结章.当两个二次根式的被开方数互为相反数时,可用“夹逼”的方法推出,两个被开方数同时为零.本专题内容蕴涵了许多重要的数学思想方法,如类比的思想(指数幂运算律的推广)、逼近的思想(有理数。

数学目录阅读材料:1)高中数学与初中数学的联系2)如何学好高中数学3)熟知高中数学特点是高一数学学习关键4)高中数学学习方法和特点5)怎样培养好对学习的良好的习惯?第一课: 绝对值第二课: 乘法公式第三课: 二次根式(1)第四课: 二次根式(2)第五课: 分式第六课: 分解因式(1)第七课: 分解因式(2)第八课:根的判别式第九课:根与系数的关系(韦达定理)(1)第十课:根与系数的关系(韦达定理)(2)第十一课:二次函数y=ax2+bx+c的图像和性质第十二课:二次函数的三种表示方式第十三课:二次函数的简单应用第十四课:分段函数第十五课: 二元二次方程组解法第十六课: 一元二次不等式解法(1)第十七课: 一元二次不等式解法(2)第十八课:国际数学大师陈省身第十九课: 中华民族是一个具有灿烂文化和悠久历史的民族第二十课: 方差在实际生活中的应用第二十一课: 平行线分线段成比例定理第二十二课:相似形第二十三课:三角形的四心第二十四课:几种特殊的三角形第二十五课:圆第二十六课:点的轨迹1.高中数学与初中数学的联系同学们,首先祝贺你们进入高中数学殿堂继续学习。
在经历了三年的初中数学学习后,大家对数学有了一定的了解,对数学思维有了一定的雏形,在对问题的分析方法和解决能力上得到了一定的训练。
这也是我们继续高中数学学习的基础。
良好的开端是成功的一半,高中数学课即将开始与初中知识有联系,但比初中数学知识系统。
高一数学中我们将学习函数,函数是高中数学的重点,它在高中数学中是起着提纲的作用,它融汇在整个高中数学知识中,其中有数学中重要的数学思想方法;如:函数与方程思想、数形结合思想、分类讨论思想、等价转化思想等,它也是高考的重点,近年来,高考压轴题都以函数题为考察方法的。
高考题中与函数思想方法有关的习题占整个试题的60%以上。
1、有良好的学习兴趣两千多年前孔子说过:“知之者不如好之者,好之者不如乐之者。
”意思说,干一件事,知道它,了解它不如爱好它,爱好它不如乐在其中。
第15讲 指数函数及其性质模块一 思维导图串知识模块二 基础知识全梳理(吃透教材)模块三 核心考点举一反三模块四 小试牛刀过关测1.通过具体实例,了解指数函数的实际意义,理解指数函数的概念;2.能用描点法或借助计算工具画出具体指数函数的图象;3.探索并理解指数函数的单调性与特殊点.知识点 1 指数函数的概念1、定义:一般地,函数x y a =(0a >且1a ≠)叫做指数函数,其中指数x 是自变量,定义域是R ,a 是指数函数的底数.2、指数函数的结构特征指数函数表达式中,需满足:(1)xa 系数必须为1;(2)自变量出现在指数位置上;(3)底数为大于0,且不等于1的常数,不能是自变量;(4)整个式子仅有一项,例如1xy a =+就不是指数函数.3、注意事项:指数函数x y a =的底数规定大于0且不等于1的理由:(1)如果0a =,当0,0,0,.x xx a x a ⎧>⎨≤⎩当时恒等于当时无意义(2)如果0a <,如(4)x y =-,当11,42x =时,在实数范围内函数值不存在.(3)如果1,11x a y ===,是一个常量,对它就没有研究的必要.为了避免上述各种情况,所以规定0a >且1a ≠.知识点 2 指数函数的图象与性质1、指数函数的图象与性质1>a 10<<a 图象定义域R值域),0(+∞过定点)1,0(单调性在R 上是增函数在R 上是减函数性质奇偶性非奇非偶函数2、底数a 对指数函数图象的影响函数2x y =,3x y =,4xy =和1()2xy =,1()3xy =,1(4xy =的图象如图所示.(1)当1a >且0x >时,底数越大,图象越“陡”;当01a <<且0x <时,底数越小,图象越“陡”.(2)在y 轴右侧,图象从上到下相应的底数由大变小,即“底数大图象高”;在y 轴左侧,图象从上到下相应的底数由小变大,即“底数大图象低”.知识点 3 指数函数的图象变换已知指数函数x y a =(0a >且1a ≠)1、平移变换0k k x x y a y a k >=−−−−−−−−→=+向上平移个单位长度();0k k x x y a y a k >=−−−−−−−−→=-向下平移个单位长度();0h h x x h y a y a >+=−−−−−−−−→=向左平移个单位长度();0h h x x h y a y a >-=−−−−−−−−→=向右平移个单位长度().规律总结:上加下减(针对函数值y ),左加右减(针对自变量x ).2、对称变换y x x y a y a -=−−−−−→=关于轴对称;x x x y a y a =−−−−−→=-关于轴对称;x x y a y a -=−−−−−→=-关于原点对称.3、翻折变换xy x y y a y a =−−−−−−−−→=保留轴右侧图象并作其关于轴的对称图形;||x x x x x y a y a =−−−−−−−−−→=保留轴上方图象将轴下方图象翻折到轴上方.知识点 4 常用方法与技巧1、比较指数幂的大小(1)对于底数相同,指数不同的两个幂的大小比较,可以利用指数函数的单调性来判断;(2)对于底数不同,指数相同的两个幂的大小比较,可以利用指数函数图象的变化规律来判断;(3)对于底数不同,且指数也不同的幂的大小比较,可先化为同底的两个幂,或者通过中间值来比较.2、简单指数不等式的解法(1)形如()()>f x g x a a的不等式,可借助=xy a 的单调性求解;(2)形如()>f x a b 的不等式,可将b 化为a 为底数的指数幂的形式,再借助=x y a 的单调性求解;(3)形如>xxa b 的不等式,可借助两函数=x y a ,=xy b 的图象求解。


第21讲 任意角模块一 思维导图串知识模块二 基础知识全梳理(吃透教材)模块三 核心考点举一反三模块四 小试牛刀过关测1.了解任意角的概念,能正确区分正角、零角和负角;2.理解象限角的意义,掌握终边相同的角的意义与表示;3.通过正角和负角理解角的大小、旋转方向,通过角的终边所在的象限的讨论,培养数学抽象与逻辑推理核心素养.知识点 1 角的概念1、角的概念:角可以看成平面内一条射线绕其端点从一个位置旋转到另一个位置形成的图形。
2、角的表示:(1)始边:射线的起始位置OA .(2)终边:射线的终止位置OB .(3)顶点:射线的端点O .(4)记法:图中的角α可记为“角α”或“α∠”或“AOB ∠”.3、角的分类:(1)正角:按逆时针方向旋转形成的角;(2)负角:按顺时针方向旋转形成的角;(3)零角:一条射线没有作任何旋转形成的角。
知识点 2 相等角与角的加减1、相等角:设角α由射线OA 绕端点O 旋转而成,角β由射线O'A'绕端点O'旋转而成,如果他们的旋转方向相同且旋转量相等,那么就称αβ=.2、相反角:把射线OA 绕端点O 按不同方向旋转相同的量所成的两个角叫做互为相反角,角α的相反角记为α-.3、角的加减:记α,β是任意两个角,我们规定:把角α的终边按逆时针旋转角β,这时终边所对应的角是αβ+;按顺时针旋转角β,这时终边所对应的角是αβ-知识点 3 终边相同的角1、终边相同的角的表示:所有与角α终边相同的角,连同角α在内,可构成一个集合S ,它们彼此相差360()k k Z ⋅∈,即{}360,S k k Z ββα==+⋅∈.【要点辨析】相等的角终边一定相同,但终边相同的角却不一定相等,终边相同的角有无数个,它们之间相差360°的整数倍,要注意角的集合的表示形式不是唯一的。
1、象限角:当角的顶点与坐标原点重合,角的始边与x 轴的非负半轴重合,那么角的终边(除端点外)在第几象限,就说这个角是第几象限;象限角集合表示第一象限角{}36036090,⋅<<⋅+∈x k k k Z α第二象限角{}36090360180,⋅+<<⋅+∈x k k k Z α第三象限角{}360180360270,⋅+<<⋅+∈x k k k Z α第四象限角{}360270360360,⋅+<<⋅+∈x k k k Z α3、轴线角:当角的顶点与坐标原点重合,角的始边与x 轴的非负半轴重合,并且角的终边落在坐标轴上时,称这个角为轴线角,这时,这个角不属于任何象限。

202 初高中数学衔接教材初高中数学衔接目录:前言第一讲 数与式的运算(两课时) 第二讲 因式分解(两课时)第三讲 一元二次方程根与系数的关系(一课时) 第四讲 不 等 式(两课时)第五讲 二次函数的最值问题(一课时) 第六讲 简单的二元二次方程组(一课时) 第七讲 分式方程和无理方程的解法(一课时) 第八讲 直线、平面与常见立体图形(一课时) 第九讲 直线与圆,圆与圆的位置关系(一课时)初高中数学衔接教材第一讲 数与式的运算(两课时)在初中,我们已学习了实数,知道字母可以表示数用代数式也可以表示数,我们把实数和代数式简称为数与式.代数式中有整式(多项式、单项式)、分式、根式。
它们具有实数的属性,可以进行运算。
在多项式的乘法运算中,我们学习了乘法公式(平方差公式与完全平方公式),并且知道乘法公式可以使多项式的运算简便。
由于在高中学习中还会遇到更复杂的多项式乘法运算,因此本节中将拓展乘法公式的内容,补充三个数和的完全平方公式、立方和、立方差公式。
在根式的运算中,我们已学过被开方数是实数的根式运算,而在高中数学学习中,经常会接触到被开方数是字母的情形,但在初中却没有涉及,因此本节中要补充。
基于同样的原因,还要补充“繁分式”等有关内容。
一、乘法公式【公式1】ca bc ab c b a c b a 222)(2222+++++=++ 证明:2222)(2)(])[()(c c b a b a c b a c b a ++++=++=++Θca bc ab c b a c bc ac b ab a 222222222222+++++=+++++=203∴等式成立【例1】计算:说明:多项式乘法的结果一般是按某个字母的降幂或升幂排列。
【公式2】3322))((b a b ab a b a +=+-+(立方和公式) 证明: 3332222322))((b a b ab b a ab b a a b ab a b a +=+-++-=+-+ 【例2】计算:))((22b ab a b a ++-【公式3】3322))((b a b ab a b a -=++-(立方差公式)请同学观察立方和、立方差公式的区别与联系,公式1、2、3均称为乘法公式。
初高中数学衔接知识点专题(一)
★ 专题一 数与式的运算
【要点回顾】 1.绝对值
[1]绝对值的代数意义: .即||a = . [2]绝对值的几何意义: 的距离. [3]两个数的差的绝对值的几何意义:a b -表示 的距离. [4]两个绝对值不等式:||(0)x a a <>⇔;||(0)x a a >>⇔
.
2.乘法公式
我们在初中已经学习过了下列一些乘法公式:
[1]平方差公式: ; [2]完全平方和公式: ; [3]完全平方差公式: . 我们还可以通过证明得到下列一些乘法公式: [公式1]2()a b c ++=
[公式2]33a b =+(立方和公式) [公式3]
33a b =- (立方差公式)
说明:上述公式均称为“乘法公式”. 3.根式
[1]
0)a ≥叫做二次根式,其性质如下:
(1) 2
= ;
= ;
= ;
= . [2]平方根与算术平方根的概念: 叫做a
的平方根,记作0)x a =≥,其
(0)a ≥叫做a 的算术平方根.
[3]立方根的概念: 叫做a
的立方根,记为x =4.分式
[1]分式的意义 形如
A B 的式子,若B 中含有字母,且0B ≠,则称A B 为分式.当M ≠0时,分式A
B
具有下列性质: (1) ; (2) . [2]繁分式 当分式
A B 的分子、分母中至少有一个是分式时,A
B
就叫做繁分式,如2m n p m n p
+++,
说明:繁分式的化简常用以下两种方法:(1) 利用除法法则;(2) 利用分式的基本性质. [3]分母(子)有理化
把分母(子)中的根号化去,叫做分母(子)有理化.分母有理化的方法是分母和分子都乘以分母的有理化因式,化去分母中的根号的过程;而分子有理化则是分母和分子都乘以分母的有理化因式,化去分
子中的根号的过程
【例题选讲】
例1 解下列不等式:(1)21x -< (2)13x x -+->4.
例2 计算:
(1)2
2
1()3
x + (2)2211111
()()5225104
m n m mn n -
++
(3)4
2
(2)(2)(416)a a a a +-++ (4)2
2
2
22
(2)()x xy y x xy y ++-+
例3 已知2
310x x -==,求3
3
1
x x +的值.
例4 已知0a b c ++=,求
111111
()()()a b c b c c a a b
+++++的值.
例5 计算(没有特殊说明,本节中出现的字母均为正数):
(1)
(2)1)x ≥
(3) (4)
例6
设x y ==
,求33
x y +的值.
例7 化简:(1)11x
x x x x -+
- (2)222
396127962x x x x x x x x ++-+---+ (1)解法一:原式=22
2(1)1
1(1)1(1)(1)11x x x x x x x x x x x x x x x x x x x x x x x x x ++=====--⋅+-++--+-++ 解法二:原式=22(1)1
(1)(1)111()x x x x x x x x x x x x x x x x x x x x x x x
++====
-⋅-+-++-
-+-⋅ (2)解:原式=2223961161
(3)(39)(9)2(3)3(3)(3)2(3)
x x x x x x x x x x x x x x x ++--+-=---++-+-+--
22(3)12(1)(3)(3)32(3)(3)2(3)(3)2(3)
x x x x x x x x x x +-------===+-+-+
说明:(1) 分式的乘除运算一般化为乘法进行,当分子、分母为多项式时,应先因式分解再进行约分化简;
(2) 分式的计算结果应是最简分式或整式 .
【巩固练习】
1. 解不等式 327x x ++-<
2.
设x y ==,求代数式22x xy y x y +++的值.
3. 当2
2
320(0,0)a ab b a b +-=≠≠,求22
a b a b b a ab
+--的值.
4. 设x
=
,求42
21x x x ++-的值.
5. 计算()()()()x y z x y z x y z x y z +
+-++-++-
6.化简或计算:
(1)
3÷ (2)
(4) ÷+
1
A
C |x -1|
|x -3|
● 各专题参考答案 ●
专题一数与式的运算参考答案
例1 (1)解法1:由20x -=,得2x =;
①若2x >,不等式可变为21x -<,即3x <; ②若2x <,不等式可变为(2)1x --<,即21x -+<,解得:1x >.综上所述,原不等式的解为13x <<.
解法2: 2x -表示x 轴上坐标为x 的点到坐标为2的点之间的距离,所以不等式21x -<的几何意义即为x 轴上坐标为x 的点到坐标为2的点之间的距离小于1,观察数轴可知坐标为x 的点在坐标为3的点的左侧,在坐标为1的点的右侧.所以原不等式的解为13x <<.
解法3:2112113x x x -<⇔-<-<⇔<<,所以原不等式的解为13x <<.
(2)解法一:由10x -=,得1x =;由30x -=,得3x =; ①若1x <,不等式可变为(1)(3)4x x ---->,即24x -+>4,解得x <0,又x <1,∴x <0;②若12x ≤<,不等式可变为(1)(3)4x x --->,即1>4,∴不存在满足条件的x ;
③若3x ≥,不等式可变为(1)(3)4x x -+->,即24x ->4, 解得x >4.又x ≥3,∴x >4. 综上所述,原不等式的解为x <0,或x >4.
解法二:如图,1x -表示x 轴上坐标为x 的点P 到坐标为1的点A 之间的距离|PA |,即|PA |=|x -1|;|x -3|表示x 轴上点P 到坐标为2的点B 之间的距离|PB |,即|PB |=|x -3|. 所以,不等式13x x -+->4的几何意义即为|PA |+|PB |>4.由|AB |可知点P 在点C (坐标为0)的左侧、或点P 在点D (坐标为4)的右侧. 所以原不等式的解为x <0,或
x >4.
例2(1)解:原式=
2
2
1[(
)]3
x +
+222
22
2
1
11()()()2(22()3
33
x x x x =
++++
⨯+⨯⨯
43
281339
x x x =-+-
+ 说明:多项式乘法的结果一般是按某个字母的降幂或升幂排列. (2)原式=3
3
33
1111()()5
2
1258
m n m n -=
-
(3)原式=24222336
(4)(44)()464a a a a a -++=-=-
(4)原式=2
2
22
2
2
2
()()[()()]x y x xy y x y x xy y +-+=+-+3
32
6
3
3
6
()2x y x x y y =+=++ 例3解:
2310x x -== 0x ∴≠ 1
3x x
∴+
= 原式=22
22
1111()(1)()[()3]3(33)18x x x x x x x x
+-+
=++-=-= 例4解:0,,,a b c a b c b c a c a b ++=∴+=-+=-+=-
∴原式=b c a c a b a b c bc ac ab
+++⋅+⋅+⋅
222()()()
a a
b b
c c a b c bc ac ab abc ---++=++=- ① 33223
()[()3](3)3a b a b a b ab c c ab c abc +=++-=--=-+
3333a b c abc ∴++= ②,把②代入①得原式=33abc
abc
-=-
例5解:(1)原式6==- (2)原式=(1)(2)2 3 (2)
|1||2|(1)(2) 1 (1x 2) x x x x x x x x -+-=->⎧-+-=⎨---=≤≤⎩
说明||a =的使用:当化去绝对值符号但字母的范围未知时,要对字母的取值分类讨论.
(3)原式ab =
(4) 原式===
例6解:2
2
(277 14,123x y x y xy ===+=-⇒+==- 原式=2222
()()()[()3]14(143)2702x y x xy y x y x y xy +-+=++-=-=
说明:有关代数式的求值问题:(1)先化简后求值;(2)当直接代入运算较复杂时,可根据结论的结构特点,倒推几步,再代入条件,有时整体代入可简化计算量. 【巩固练习】
1.43x -<< 2. 3.3-或2 4.3-
5.4
4
4
2
2
22
22
222x y z x y x z y z ---+++ 6.()(((13,23,4-。