第一章、电路基础知识2

第一章电路的基础知识1.1电路的组成一、授课章节1.1电路的组成二、学时安排2学时三、教学目标1.了解电路的概念和电路的基本组成，理解各部分的作用；2.理解电路模型的概念；3.能够识别和画出电路图中常用的图形符号；4.能够画出简单电路的电路图。

四、教学重点、难点分析重点：1.电路的基本组成及作用。

2.电路模型的概念。

难点：电路模型的概念。

五、教具演示实验设备、电化教学设备。

六、教学方法讲授法，多媒体课件，理实一体化。

七、教学过程Ⅰ.导入（a）外形（b）分解图图1.1 手电筒外形及其分解图手电筒是人们常用的一种照明工具，手电筒的外形及其分解图如图1.1所示。

1.观察现象，提出问题试用导线将小灯泡、干电池及开关连接起来。

闭合开关，小灯泡就持续发光，如图1.2（a ）所示；断开开关，小灯泡就熄灭了，如图1.2（b ）所示，这是为什么呢？2.分析解决问题小灯泡持续发光，表示有持续电流通过小灯泡的灯丝，这个持续电流是由干电池提供的，像干电池这样能提供持续电流的装置，称为电源。

电源有两个极，一个正极，一个负极。

电源的作用是在电源内部不断地使正极聚集正电荷，负极聚集负电荷，对外持续供电。

从能量转化的角度来看，电源是把其他形式的能量转化为电能的装置。

提问：常见的电源有哪些？归纳总结：干电池、蓄电池→→将化学能转化为电能 发电机→→将机械能转化为电能 Ⅱ.新课 一、电路的组成通过上述观察分析可知：要使小灯泡持续发光，灯丝中就必须有持续电流通过。

因此所谓电路就是电流流通的闭合路径。

提问：通过手电筒电路的实例分析，电路应该由哪几部分组成呢？归纳总结：电路由电源、负载、连接导线、控制和保护装置四部分组成。

（1）电源——向电路提供能量的设备。

它能把其它形式的能转换成电能。

常见的电源有干电池、蓄电池、发电机等。

（a ）开关闭合 （b ）开关断开图1.2 观察手电筒电路的工作状态（2）负载——即用电器，它是各种用电设备的总称。

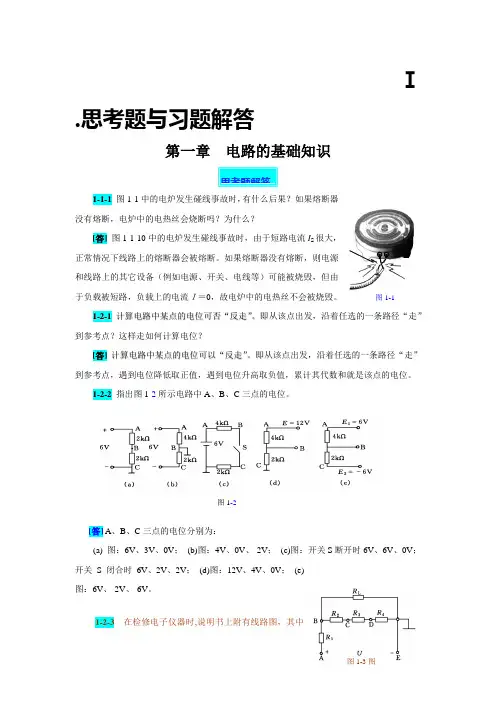
Ⅰ.思考题与习题解答第一章 电路的基础知识 1-1-1 图1-1中的电炉发生碰线事故时，有什么后果？如果熔断器没有熔断，电炉中的电热丝会烧断吗？为什么？[答] 图1-1-10中的电炉发生碰线事故时，由于短路电流I S 很大，正常情况下线路上的熔断器会被熔断。

如果熔断器没有熔断，则电源和线路上的其它设备（例如电源、开关、电线等）可能被烧毁，但由于负载被短路，负载上的电流Ｉ＝0，故电炉中的电热丝不会被烧毁。

1-2-1 计算电路中某点的电位可否“反走”。

即从该点出发，沿着任选的一条路径“走”到参考点？这样走如何计算电位？[答] 计算电路中某点的电位可以“反走”。

即从该点出发，沿着任选的一条路径“走”到参考点，遇到电位降低取正值，遇到电位升高取负值，累计其代数和就是该点的电位。

1-2-2 指出图1-2所示电路中A 、B 、C 三点的电位。

[答] A 、B 、C 三点的电位分别为：(a) 图：6V 、3V 、0V ； (b)图：4V 、0V 、-2V ； (c)图：开关S 断开时6V 、6V 、0V ；开关S 闭合时6V 、2V 、2V ； (d)图：12V 、4V 、0V ； (e)图：6V 、-2V 、-6V 。

1-2-3 在检修电子仪器时,说明书上附有线路图，其中思考题解答图1-2图1-3图图1-1某一局部线路如图1-3所示。

用电压表测量发现ＵAB ＝3V ，ＵBC ＝1V ，ＵCD =0，ＵDE ＝2V ，ＵAE ＝6Ｖ。

试判断线路中可能出现的故障是什么？[答] 由ＵBC ＝1V ，ＵDE ＝2V 可知电阻R 2、R 4支路上有电流通过，而ＵCD =0，故判定电阻R 3短路。

1-2-4 上题的线路故障可否用测量电位的方法进行判断？如何测量？最少需要测量几点电位？ [答] 可以用测量电位的方法进行判断。

只需测出Ｂ、Ｃ、Ｄ三点的电位，就可知R 3支路上有电流，而R 3电阻短路。

1-2-5 在图1-4所示电路中，已知U ＝－10V ，Ｉ＝2A ，试问Ａ、Ｂ两点，哪点电位高？元件Ｐ是电源还是负载？[答] 因U 为负值，电压的实际方向与参考方向相反，故b 点电位高。

第一章 电路基础知识一、电路1、电路的组成：电源+开关+负载+导线二、电流1、电流的方向：正电荷移动的方向2、单位：安培/安，用字母A 表示。

3、分类：直流电【恒流源（a ）、脉动直流电（b ）】、交流电（c ）4、测量：1）交直流分开测；2）必须串联在电路中；3）直流电需注意“+”，“—”；4）注意量程三、电压、电位和电动势1、电压、电位和电动势的单位：均为伏特/伏，用字母V 表示。

*2、电压：任意2点间的电位差。

（电压即电位差）*3、电位：某一点与参考点之间的电压。

（参考点的电位默认为0V ，比如接地时）【重点】4、电位与电压的区别⎩⎨⎧考点无关；电压：两点间电压与参考点的不同而改变；电位：某点的电位随参 【例】：有两块积木，A 和B ，A 在第7块，B 在第3块（类比：A 的电位U A =7V ， B 的电位U B =3V ，而U AB =U A -U B =7-3=4V ）；若将最底的一块积木去掉，则此时A 在第6块，B 在第2块（类比：A 的电位U A =6V ， B 的电位U B =2V ，而U AB =U A -U B =6-2=4V ）【重点】5、电动势与端电压：对电源来说，既有电动势，又有端电压。

由于内阻的存在，电动势比端电压大一点点，只有当电路开路时，两者才相等。

⎩⎨⎧正极方向：从电源负极指向只存在与电源中电动势 ⎩⎨⎧负极方向：从电源正极指向存在于外电路中端电压 6、测量：1）交直流分开测；2）必须并联在电路中；3）直流电需注意“+”，“—”；4）注意量程四、电阻1、电阻概念：对电流的阻碍作用；用R 表示，单位为Ω2、在温度不变的情况下，电阻与材料ρ、长度l 和横截面积S 有关，)()()()(2mm S m l m R ⋅Ω=Ωρ 3、根据导电能力分类：导体、绝缘体和半导体五、欧姆定律1、部分欧姆定律：不考虑电源的一段电路)()()(Ω=R V U A I 2、全欧姆定律：含有电源的闭合电路)()()()(Ω+Ω=r R V U A I 3、电源电动势：内外U U E +=4、电路的三种状态：断路、通路和短路（生活中避免，但有用其他用途）六、电功与电功率1、电功：电流做的功，用W 表示，单位是焦耳（J ）。

1第一章《认识电路》知识要点概括1、电路：电流流过的路径，它由电源（信号源）、用电器（负载）、开关（控制、保护电器）和导线等四部分组成。

2、电路的作用：(1)能实现电能的传输、分配和转换。

(2)信号的产生、传递和处理。

3、电路的三种状态：（1）通路；（2）开路（断路）；（3）短路：短路时电流很大，不允许短路。

4、电路图：用国家规定的统一符号来表示实际电路中各电器元件连接关系的图形。

5、两种电荷：自然界存在两种电荷，正电荷和负电荷：电子带负电，质子带正电。

物体失去电子，带正电，得到电子，带负电。

电荷的单位：库仑，符号为C。

1个电子的电量为1.6×10-19C。

6、电流：电荷的定向运动形成电流，单位时间内通过导体横截面的电量称为电流强度。

定义式：tqI =式中：I——电流强度，单位：安培(A)，其它还有：毫安（mA）、微安（μA）。

换算关系：1A ＝103mA ＝106μA ；q——通过导体横截面的电量，单位：库仑（C）；t——通电时间，单位：秒（S）。

电流的方向：规定正电荷定向移动的方向为电流的方向。

在一个闭合电路中，电池外部，电流是从正极流到负极的；电池内部，是从负极流到正极。

在分析电路时，当无法确定电流的方向时，可任意假定一个参考方向，若电流方向与参考方向相同，电流取正值，否则，取负值。

电流的测量：利用安培表，或万用表的电流档。

测量时电流表要串联在电路中。

7、电压：电压是由电源产生的，电压是使导体中的电荷作定向移动、产生电流的原因。

定义：电路中A、B 两点间的电压等于电场力把单位正电荷从A 点移到B 点所做的功。

即有：qW U AB AB =电压的单位：伏特（V ），其它还有：千伏（KV）、毫伏（mV）。

1V ＝10³mV，1kV ＝10³V 。

电压的方向：正极指向负极，或高电位指向低电位。

电压的测量：用伏特表，或万用表电压档，伏特表应并联在电路中。

8、电源：电源是把其它形式的能转化为电能的装置，它能向用电器提供源源不断的电能。

第一章直流电路基础知识§ 1—1库仑定律本节要求：了解电荷的种类及电荷之间的相互作用力掌握库仑定律。

一、电荷之间的相互作用力当物体受到摩擦等作用时，物体就带了电，或者说带了电荷。

自然界中存在着两种电荷，即正电荷和负电荷。

电荷之间存在相互作用力，同种电荷互相排斥，异种电荷互相吸引。

二、电荷量电荷的多少叫电荷量，用字母Q表示。

在国际单位制中，电荷量的单位名称是库仑，用字母C表示。

三、库仑定律静止的点电荷间的相互作用力所遵循的库仑定律：在真空中两个点电荷q i、q2 间的作用力F的大小跟它们所带电荷量的乘积q i q2成正比，跟它们之间距离r的平方成反比，作用力的方向在它们的连线上。

库仑定律公式为qg2q i、q2――点电荷电荷量，单位是库［仑］,符号为C; r 两个点电荷间的距离，单位是米，符号为m；k——静电恒量，k=9X109 N • m2/C2;F――静电力，单位是牛［顿］,符号为N。

静止的点电荷之间的这种作用力叫静电力或库仑力。

只有当带电体的几何线度(直径)远远小于带电体间的距离时，带电体的形状和大小对相互作用力的影响可以忽略不计，这样的带电体可以看成点电荷。

注意下面两个问题：(1) 只适用于计算两个点电荷间的相互作用力。

(2) 求点电荷间相互作用力时，不用把表示正、负电荷的“+”、“一”符号代人公式中，计算过程中可用绝对值计算，其结果可根据电荷的正、负确定作用力为引力或斥力以及作用力的方向。

例题两个点电荷电荷量q i= —4X10 6C, q2=—1.2X10 6C,在真空中的距离r= 0.4m,求两个点电荷间作用力的大小及方向。

解：根据库仑定律109 ^0 10卫=0.27Nr20.42作用力的方向在两个点电荷的连线上。

因为同带负电荷，所以作用力为斥力。

作业P2 1。

填空题1、22。

计算题1、2§ 1—2 电场和电场强度本节要求：理解电场的特性。

掌握电场强度与电力线的特性。