2019高考数学考点突破——选考系列参数方程学案

坐标系与参数方程【2019年高考考纲解读】高考主要考查平面直角坐标系中的伸缩变换、直线和圆的极坐标方程、参数方程与普通方程的互化、常见曲线的参数方程及参数方程的简单应用．以极坐标、参数方程与普通方程的互化为主要考查形式，同时考查直线与曲线的位置关系等解析几何知识． 【重点、难点剖析】 1．直角坐标与极坐标的互化把直角坐标系的原点作为极点，x 轴正半轴作为极轴，且在两坐标系中取相同的长度单位．设M 是平面内的任意一点，它的直角坐标、极坐标分别为(x ，y )和(ρ，θ)，则⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ，⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝y x x2．直线的极坐标方程若直线过点M (ρ0，θ0)，且极轴到此直线的角为α，则它的方程为：ρsin(θ－α)＝ρ0sin(θ0－α)．几个特殊位置的直线的极坐标方程 (1)直线过极点：θ＝α；(2)直线过点M (a,0)(a >0)且垂直于极轴：ρcos θ＝a ；(3)直线过M ⎝⎛⎭⎪⎫b ，π2且平行于极轴：ρsin θ＝b .3．圆的极坐标方程若圆心为M (ρ0，θ0)，半径为r 的圆方程为： ρ2－2ρ0ρcos(θ－θ0)＋ρ20－r 2＝0. 几个特殊位置的圆的极坐标方程 (1)当圆心位于极点，半径为r ：ρ＝r ；(2)当圆心位于M (r,0)，半径为r ：ρ＝2r cos θ；(3)当圆心位于M ⎝⎛⎭⎪⎫r ，π2，半径为r ：ρ＝2r sin θ.(4)圆心在点M (x 0，y 0)，半径为r的圆的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数，0≤θ≤2π)．圆心在点A (ρ0，θ0)，半径为r 的圆的方程为r 2＝ρ2＋ρ20－2ρρ0cos(θ－θ0)．4．直线的参数方程经过点P 0(x 0，y 0)，倾斜角为α的直线的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．设P 是直线上的任一点，则t 表示有向线段P 0P →的数量． 5．圆的参数方程圆心在点M (x 0，y 0)，半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数，0≤θ≤2π)． 6．圆锥曲线的参数方程(1)椭圆x 2a 2＋y 2b 2＝1的参数方程为⎩⎪⎨⎪⎧x ＝a cos θ，y ＝b sin θ(θ为参数)．(2)双曲线x 2a 2－y 2b 2＝1的参数方程为⎩⎪⎨⎪⎧ x ＝a sec θ，y ＝b tan θ(θ为参数)．(3)抛物线y2＝2px (p >0)的参数方程为⎩⎪⎨⎪⎧x ＝2pt 2，y ＝2pt(t 为参数).【题型示例】题型一 极坐标方程和参数方程【例1】(2018·全国Ⅰ)在直角坐标系xOy 中，曲线C 1的方程为y ＝k |x |＋2.以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ2＋2ρcos θ－3＝0. (1)求C 2的直角坐标方程；【思路方法】(1)先列方程，再进一步转化为参数方程． (2)解出交点，再求得直线方程，最后转化为极坐标方程．【解析】(1)设(x 1，y 1)为圆上的点，在已知变换下变为曲线C 上的点(x ，y )，依题意，得⎩⎪⎨⎪⎧x ＝x 1，y ＝2y 1.由x 21＋y 21＝1，得x 2＋⎝ ⎛⎭⎪⎫y 22＝1，即曲线C 的方程为x 2＋y 24＝1.故C 的参数方程为⎩⎪⎨⎪⎧x ＝cos t ，y ＝2sin t(t 为参数)．【感悟提升】若极坐标系的极点与直角坐标系的原点重合，极轴与x 轴正半轴重合，两坐标系的长度单位相同，则极坐标方程与直角坐标方程可以互化．求解与极坐标方程有关的问题时，可以转化为熟悉的直角坐标方程求解．若最终结果要求用极坐标表示，则需将直角坐标转化为极坐标．题型二 参数方程与普通方程的互化【例2】(2018·全国Ⅲ)在平面直角坐标系xOy 中，⊙O 的参数方程为⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ(θ为参数)，过点(0，－2)且倾斜角为α的直线l 与⊙O 交于A ，B 两点． (1)求α的取值范围；(2)求AB 中点P 的轨迹的参数方程．【解析】 (1)⊙O 的直角坐标方程为x 2＋y 2＝1. 当α＝π2时，l 与⊙O 交于两点．当α≠π2时，记tan α＝k ，则l 的方程为y ＝kx － 2.l 与⊙O 交于两点当且仅当|2|1＋k2<1，解得k <－1或k >1，即α∈⎝ ⎛⎭⎪⎫π2，3π4或α∈⎝ ⎛⎭⎪⎫π4，π2.综上，α的取值范围是⎝ ⎛⎭⎪⎫π4，3π4. (2)l 的参数方程为⎩⎨⎧x ＝t cos α，y ＝－2＋t sin α⎝⎛⎭⎪⎫t 为参数，π4<α<3π4. 设A ，B ，P 对应的参数分别为t A ，t B ，t P ， 则t P ＝t A ＋t B2，且t A ，t B 满足t 2－22t sin α＋1＝0.于是t A ＋t B ＝22sin α，t P ＝2sin α.又点P 的坐标(x ，y )满足⎩⎨⎧x ＝t P cos α，y ＝－2＋t P sin α，所以点P 的轨迹的参数方程是⎩⎪⎨⎪⎧x ＝22sin 2α，y ＝－22－22cos 2α⎝ ⎛⎭⎪⎫α为参数，π4<α<3π4.【感悟提升】(1)将参数方程化为普通方程，需要根据参数方程的结构特征，选取适当的消参方法．常见的消参方法有代入消参法、加减消参法、平方消参法等．(2)将参数方程化为普通方程时，要注意两种方程的等价性，不要增解、漏解，若x ，y 有范围限制，要标出x ，y 的取值范围．【变式探究】 【2017·江苏】[选修4-4：坐标系与参数方程]在平面坐标系中xOy 中,已知直线l 的参考方程为x 82tty =-+⎧⎪⎨=⎪⎩(t 为参数),曲线C的参数方程为22,x s y ⎧=⎪⎨=⎪⎩(s 为参数).设P 为曲线C 上的动点，求点P 到直线l 的距离的最小值.【解析】直线l 的普通方程为. 因为点P 在曲线C 上，设，从而点P 到直线l 的的距离，当s =min 5d =.因此当点P 的坐标为()4,4时，曲线C 上点P 到直线l . 【考点】参数方程化普通方程【变式探究】在直角坐标系x O y 中,曲线C 1的参数方程为（t 为参数,a ＞0）．在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2：ρ=4cos θ. （I ）说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程；（II ）直线C 3的极坐标方程为0θα=,其中0α满足tan 0α=2,若曲线C 1与C 2的公共点都在C 3上,求a ． 【答案】（I ）圆,（II ）1【解析】解：（Ⅰ）消去参数t 得到1C 的普通方程.1C 是以)1,0(为圆心，a 为半径的圆.将代入1C 的普通方程中，得到1C 的极坐标方程为.（Ⅱ）曲线21,C C 的公共点的极坐标满足方程组若0≠ρ，由方程组得，由已知2tan =θ，可得，从而012=-a ，解得1-=a （舍去），1=a .1=a 时，极点也为21,C C 的公共点，在3C 上.所以1=a .【变式探究】在直角坐标系xOy 中，直线C 1：x ＝－2，圆C 2：(x －1)2＋(y －2)2＝1，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系．(1)求C 1，C 2的极坐标方程；(2)若直线C 3的极坐标方程为θ＝π4(ρ∈R )，设C 2与C 3的交点为M ，N ，求△C 2MN 的面积．【变式探究】在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝2cos α，y ＝2＋2sin α(α为参数)，M是C 1上的动点，P 点满足OP →＝2OM →，点P 的轨迹为曲线C 2. (1)求C 2的方程；(2)在以O 为极点，x 轴的正半轴为极轴的极坐标系中，射线θ＝π3与C 1的异于极点的交点为A ，与C 2的异于极点的交点为B ，求AB .【解析】(1)设P (x ，y )，则由条件知M ⎝ ⎛⎭⎪⎫x 2，y 2，由于M 点在C 1上，所以⎩⎪⎨⎪⎧x2＝2cos α，y2＝2＋2sin α，即⎩⎪⎨⎪⎧x ＝4cos α，y ＝4＋4sin α.从而C 2的参数方程为⎩⎪⎨⎪⎧x ＝4cos α，y ＝4＋4sin α(α为参数)．(2)曲线C 1的极坐标方程为ρ＝4sin θ，曲线C 2的极坐标方程为ρ＝8sin θ.射线θ＝π3与C 1的交点A 的极径为ρ1＝4sin π3，射线θ＝π3与C 2的交点B 的极径为ρ2＝8sin π3.所以AB＝|ρ2－ρ1|＝2 3.【规律方法】解决这类问题一般有两种思路，一是将极坐标方程化为直角坐标方程，求出交点的直角坐标，再将其化为极坐标；二是将曲线的极坐标方程联立，根据限制条件求出极坐标．要注意题目所给的限制条件及隐含条件．【变式探究】将圆x 2＋y 2＝1上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C . (1)写出C 的参数方程；(2)设直线l ：2x ＋y －2＝0与C 的交点为P 1，P 2，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求过线段P 1P 2的中点且与l 垂直的直线的极坐标方程． 解 (1)设(x 1，y 1)为圆上的点，在已知变换下变为C 上点(x ，y )，依题意，得1,2,x x y y =⎧⎨=⎩由x 21＋y 21＝1得x 2＋⎝ ⎛⎭⎪⎫y 22＝1， 即曲线C 的方程为x 2＋y 24＝1.故C 的参数方程为cos 2sin x t y t =⎧⎨=⎩(t 为参数)．(2)由解得：1,0x y =⎧⎨=⎩或0,2.x y =⎧⎨=⎩不妨设P 1(1，0)，P 2(0，2)，则线段P 1P 2的中点坐标为⎝ ⎛⎭⎪⎫12，1，所求直线斜率为k ＝12，于是所求直线方程为y －1＝12⎝ ⎛⎭⎪⎫x －12，化为极坐标方程，并整理得 2ρcos θ－4ρsin θ＝－3， 即ρ＝34sin θ－2cos θ.题型三 极坐标 参数方程及其应用【例3】在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝1＋cos α，y ＝sin α(α为参数)，直线l的参数方程为⎩⎪⎨⎪⎧x ＝1－t ，y ＝3＋t (t 为参数)，在以坐标原点为极点，x 轴的正半轴为极轴的极坐标系中，射线m ：θ＝β(ρ>0)． (1)求C 和l 的极坐标方程；(2)设点A 是m 与C 的一个交点(异于原点)，点B 是m 与l 的交点，求|OA ||OB |的最大值．解 (1)曲线C 的普通方程为(x －1)2＋y 2＝1，由⎩⎪⎨⎪⎧ρcos θ＝x ，ρsin θ＝y ，得()ρcos θ－12＋ρ2sin 2θ＝1，化简得C 的极坐标方程为ρ＝2cos θ. 因为l 的普通方程为x ＋y －4＝0，所以极坐标方程为ρcos θ＋ρsin θ－4＝0， 所以l 的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝2 2. (2)设A (ρ1，β)，B (ρ2，β)， 则|OA ||OB |＝ρ1ρ2＝2cos β·sin β＋cos β4＝12(sin βcos β＋cos 2β)＝24sin ⎝⎛⎭⎪⎫2β＋π4＋14，由射线m 与C ，直线l 相交，则不妨设β∈⎝ ⎛⎭⎪⎫－π4，π4， 则2β＋π4∈⎝ ⎛⎭⎪⎫－π4，3π4，所以当2β＋π4＝π2，即β＝π8时，|OA ||OB |取得最大值，即⎝⎛⎭⎪⎫|OA ||OB |max＝2＋14. 【感悟提升】 (1)利用参数方程解决问题，要理解参数的几何意义．(2)在解决直线、圆和圆锥曲线的有关问题时，常常将极坐标方程化为直角坐标方程或将参数方程化为普通方程，有助于认识方程所表示的曲线，从而达到化陌生为熟悉的目的，这是转化与化归思想的应用．【变式探究】在平面直角坐标系中，以原点为极点，以x 轴的正半轴为极轴且取相同的单位长度建立极坐标系，曲线C 1的极坐标方程为ρ＝2cos θ. (1)若曲线C 2的参数方程为⎩⎪⎨⎪⎧ x ＝t cos α，y ＝1＋t sin α(α为参数)，求曲线C 1的直角坐标方程和曲线C 2的普通方程；(2)若曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝1＋t sin α(t 为参数)，A (0,1)，且曲线C 1与曲线C 2的交点分别为P ，Q ，求1|AP |＋1|AQ |的取值范围．【解析】 (1)∵ρ＝2cos θ，∴ρ2＝2ρcos θ，又∵ρ2＝x 2＋y 2，ρcos θ＝x ，∴曲线C 1的直角坐标方程为x 2＋y 2－2x ＝0， 曲线C 2的普通方程为x 2＋(y －1)2＝t 2.(2)将C 2的参数方程⎩⎪⎨⎪⎧x ＝t cos α，y ＝1＋t sin α(t 为参数)代入C 1的方程x 2＋y 2－2x ＝0，得t 2＋(2sinα－2cos α)t ＋1＝0.∵Δ＝(2sin α－2cos α)2－4＝8sin 2⎝ ⎛⎭⎪⎫α－π4－4>0，∴⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π4∈⎝ ⎛⎦⎥⎤22，1，∴sin ⎝ ⎛⎭⎪⎫α－π4∈⎣⎢⎡⎭⎪⎫－1，－22∪⎝ ⎛⎦⎥⎤22，1. t 1＋t 2＝－(2sin α－2cos α)＝－22sin ⎝ ⎛⎭⎪⎫α－π4，t 1t 2＝1>0，∵t 1t 2＝1>0，∴t 1，t 2同号，∴|t 1|＋|t 2|＝|t 1＋t 2|. 由点A 在曲线C 2上，根据t 的几何意义，可得 1|PA |＋1|AQ |＝1|t 1|＋1|t 2|＝|t 1|＋|t 2||t 1||t 2| ＝|t 1|＋|t 2||t 1t 2|＝|t 1＋t 2|1＝22⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π4∈(2,22]．∴1|PA |＋1|AQ |∈(2,22]． 【变式探究】在直角坐标系xOy 中，曲线C 的参数方程为3cos ,sin ,x y θθ=⎧⎨=⎩（θ为参数），直线l的参数方程为.（1）若a =−1，求C 与l 的交点坐标；（2）若C 上的点到l a. 【答案】（1）C 与l 的交点坐标为()3,0， 2124,2525⎛⎫-⎪⎝⎭；（2）8a =或16a =-.【解析】（1）曲线C 的普通方程为2219x y +=. 当1a =-时，直线l 的普通方程为.由解得3{ 0x y ==或2125{ 2425x y =-=.从而C 与l 的交点坐标为()3,0， 2124,2525⎛⎫-⎪⎝⎭. （2）直线l 的普通方程为，故C 上的点到l 的距离为.当4a ≥-时， d=8a =； 当4a <-时， d由题设得，所以16a =-.综上， 8a =或16a =-.【变式探究】在直角坐标系xOy 中，圆C 的方程为．（Ⅰ）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求C 的极坐标方程； （Ⅱ）直线l 的参数方程是cos sin x t y t αα=⎧⎨=⎩（t 为参数）, l 与C 交于,A B两点，||AB =，求l 的斜率． 【答案】（Ⅰ）；（Ⅱ）3±. 【解析】（I ）由可得C 的极坐标方程（II ）在（I ）中建立的极坐标系中，直线l 的极坐标方程为由,A B 所对应的极径分别为12,,ρρ将l 的极坐标方程代入C 的极坐标方程得于是由||AB =得， 所以l的斜率为3或3-. 【变式探究】已知直线l 的参数方程为1,1x t y t =-+⎧⎨=+⎩(t 为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ2cos 2θ＝4⎝⎛⎭⎪⎫ρ＞0，3π4＜θ＜5π4，则直线l 与曲线C 的交点的极坐标为________．解析 直线l 的直角坐标方程为y ＝x ＋2，由ρ2cos 2θ＝4得ρ2(cos 2θ－sin 2θ)＝4，直角坐标方程为x 2－y 2＝4，把y ＝x ＋2代入双曲线方程解得x ＝－2，因此交点为(－2，0)，其极坐标为(2，π)．答案 (2，π)【变式探究】已知直线l的参数方程为⎩⎪⎨⎪⎧ x ＝a －2t ，y ＝－4t (t 为参数)，圆C 的参数方程为⎩⎪⎨⎪⎧ x ＝4cos θ，y ＝4sin θ(θ为参数)．(1)求直线l 和圆C 的普通方程；(2)若直线l 与圆C 有公共点，求实数a 的取值范围．【命题意图】本小题主要考查直线与圆的参数方程等基础知识，意在考查考生的运算求解能力及化归与转化思想．【解题思路】(1)消去参数，即可求出直线l 与圆C 的普通方程．(2)求出圆心的坐标，利用圆心到直线l 的距离不大于半径，得到关于参数a 的不等式，即可求出参数a 的取值范围．【解析】(1)直线l 的普通方程为2x －y －2a ＝0，圆C 的普通方程为x 2＋y 2＝16.(2)因为直线l 与圆C 有公共点，故圆C 的圆心到直线l 的距离d ＝|－2a |5≤4， 解得－25≤a ≤2 5. 【感悟提升】1．将参数方程化为普通方程的过程就是消去参数的过程，常用的消参方法有代入消参、加减消参和三角恒等式消参等，往往需要对参数方程进行变形，为消去参数创造条件．2．在与直线、圆、椭圆有关的题目中，参数方程的使用会使问题的解决事半功倍，尤其是求取值范围和最值问题，可将参数方程代入相关曲线的普通方程中，根据参数的取值条件求解． 【变式探究】在平面直角坐标系xOy 中，圆C 的参数方程为(t 为参数)．在极坐标系(与平面直角坐标系xOy 取相同的长度单位，且以原点O 为极点，以x 轴非负半轴为极轴)中，直线l 的方程为2ρsin ⎝ ⎛⎭⎪⎫θ－π4＝m (m ∈R )． ①求圆C 的普通方程及直线l 的直角坐标方程；②设圆心C 到直线l 的距离等于2，求m 的值．。

第2讲 参数方程板块一 知识梳理·自主学习[必备知识]考点1 参数方程的概念在平面直角坐标系中，如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数⎩⎪⎨⎪⎧x ＝f (t )，y ＝g (t )(*)，如果对于t 的每一个允许值，由方程组(*)所确定的点M (x ，y )都在这条曲线上，那么方程组(*)就叫做这条曲线的参数方程，变数t 叫做参数．考点2 直线和圆锥曲线的参数方程和普通方程[考点自测]1．判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)参数方程⎩⎪⎨⎪⎧x ＝t ＋1，y ＝2－t (t ≥1)表示的曲线为直线．( )(2)直线y ＝x 与曲线⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α(α为参数)的交点个数为1.( )(3)直线⎩⎪⎨⎪⎧x ＝－2＋t cos30°，y ＝1＋t sin150°(t 为参数)的倾斜角α为30°.( )(4)参数方程⎩⎪⎨⎪⎧x ＝2cos θ，y ＝5sin θ⎝ ⎛⎭⎪⎫θ为参数且θ∈⎣⎢⎡⎦⎥⎤0，π2表示的曲线为椭圆．( )答案 (1)× (2)× (3)√ (4)×2．已知圆的参数方程⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2sin θ(θ为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，直线的极坐标方程为3ρcos α－4ρsin α－9＝0，则直线与圆的位置关系是( )A ．相切B ．相离C ．直线过圆心D ．相交但直线不过圆心答案 D解析 圆的普通方程为x 2＋y 2＝4，直线的直角坐标方程为3x －4y －9＝0.圆心(0,0)到直线的距离d ＝|3×0－4×0－9|32＋(－4)2＝95<2，所以直线与圆相交．显然直线不过原点(0,0)，故选D.3．[2018·安徽模拟]以平面直角坐标系的原点为极点，x 轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位．已知直线l 的参数方程是⎩⎪⎨⎪⎧x ＝t ＋1，y ＝t －3(t 为参数)，圆C 的极坐标方程是ρ＝4cos θ，则直线l 被圆C 截得的弦长为( )A.14 B ．214 C. 2 D ．2 2 答案 D解析 由题意得直线l 的方程为x －y －4＝0，圆C 的方程为(x －2)2＋y 2＝4.则圆心到直线的距离d ＝2，故弦长＝2r 2－d 2＝2 2.4．[2018·湖南模拟]在平面直角坐标系xOy中，若直线l ：⎩⎪⎨⎪⎧x ＝t ，y ＝t －a (t 为参数)过椭圆C ：⎩⎪⎨⎪⎧x ＝3cos φ，y ＝2sin φ(φ为参数)的右顶点，则常数a 的值为________．答案 3解析 由题意知在直角坐标系下，直线l 的方程为y ＝x －a ，椭圆的方程为x 29＋y 24＝1，所以其右顶点为(3,0)．由题意知0＝3－a ，所以a ＝3.5．[2018·天津模拟]已知抛物线的参数方程为⎩⎪⎨⎪⎧x ＝2pt 2，y ＝2pt(t 为参数)，其中p >0，焦点为F ，准线为l .过抛物线上一点M 作l 的垂线，垂足为E .若|EF |＝|MF |，点M 的横坐标是3，则p ＝________.答案2解析 由参数方程⎩⎪⎨⎪⎧x ＝2pt 2，y ＝2pt(t 为参数)，p >0，可得曲线方程为y 2＝2px (p >0)． ∵|EF |＝|MF |，且|MF |＝|ME |(抛物线定义)， ∴△MEF 为等边三角形，E 的横坐标为－p2，M 的横坐标为3.∴EM 中点的横坐标为3－p22，与F 的横坐标p2相同．∴3－p22＝p 2，∴p ＝2.6．[2015·湖北高考]在直角坐标系xOy 中，以O 为极点，x 轴的正半轴为极轴建立极坐标系．已知直线l 的极坐标方程为ρ(sin θ－3cos θ)＝0，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝t －1t ，y ＝t ＋1t(t 为参数)，l 与C 相交于A ，B 两点，则|AB |＝________.答案 2 5解析 因为ρ(sin θ－3cos θ)＝0，所以ρsin θ＝3ρcos θ，所以y ＝3x .由⎩⎪⎨⎪⎧x ＝t －1t ，y ＝t ＋1t，消去t 得y 2－x2＝4.由⎩⎪⎨⎪⎧y ＝3x ，y 2－x 2＝4，解得⎩⎪⎨⎪⎧x ＝22，y ＝322或⎩⎪⎨⎪⎧x ＝－22，y ＝－322，不妨令A ⎝⎛⎭⎪⎫22，322，B ⎝ ⎛⎭⎪⎫－22，－322，由两点间的距离公式得|AB |＝⎝ ⎛⎭⎪⎫22＋222＋⎝ ⎛⎭⎪⎫322＋3222＝2 5.板块二 典例探究·考向突破 考向参数方程与普通方程的互化例 1 [2017·全国卷Ⅰ]在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝3cos θ，y ＝sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋4t ，y ＝1－t(t 为参数)．(1)若a ＝－1，求C 与l 的交点坐标； (2)若C 上的点到l 距离的最大值为17，求a . 解 (1)曲线C 的普通方程为x 29＋y 2＝1. 当a ＝－1时，直线l 的普通方程为x ＋4y －3＝0.由⎩⎪⎨⎪⎧x ＋4y －3＝0，x 29＋y 2＝1，解得⎩⎪⎨⎪⎧x ＝3，y ＝0或⎩⎪⎨⎪⎧x ＝－2125，y ＝2425.从而C 与l 的交点坐标为(3,0)，⎝ ⎛⎭⎪⎫－2125，2425.(2)直线l 的普通方程为x ＋4y －a －4＝0，故C 上的点(3cos θ，sin θ)到l 的距离为d ＝|3cos θ＋4sin θ－a －4|17＝|5sin (θ＋φ)－a －4|17⎝ ⎛⎭⎪⎫tan φ＝34，当a ≥－4时，d 的最大值为a ＋917.由题设得a ＋917＝17，所以a ＝8；当a ＜－4时，d 的最大值为－a ＋117. 由题设得－a ＋117＝17，所以a ＝－16.综上，a ＝8或a ＝－16. 触类旁通将参数方程化为普通方程的方法(1)将参数方程化为普通方程，需要根据参数方程的结构特征，选取适当的消参方法．常见的消参方法有：代入消参法、加减消参法、平方消参法等，对于含三角函数的参数方程，常利用同角三角函数关系式消参，如sin 2θ＋cos 2θ＝1等．(2)将参数方程化为普通方程时，要注意两种方程的等价性，不要增解．【变式训练1】 [2018·湖南长郡中学模拟]已知曲线C 1：⎩⎪⎨⎪⎧x ＝－4＋cos t ，y ＝3＋sin t (t 为参数)，C 2：⎩⎪⎨⎪⎧x ＝8cos θ，y ＝3sin θ(θ为参数)．(1)化C 1，C 2的方程为普通方程，并说明它们分别表示什么曲线；(2)若C 1上的点P 对应的参数为t ＝π2，Q 为C 2上的动点，求PQ 的中点M 到直线C 3：⎩⎪⎨⎪⎧x ＝3＋2t ，y ＝－2＋t (t 为参数)距离的最小值．解 (1)C 1：(x ＋4)2＋(y －3)2＝1，C 2：x 264＋y 29＝1，C 1表示圆心是(－4,3)，半径是1的圆，C 2表示中心是坐标原点，焦点在x 轴上，长半轴长是8，短半轴长是3的椭圆．(2)当t ＝π2时，P (－4,4)，又Q (8cos θ，3sin θ)，故M ⎝ ⎛⎭⎪⎫－2＋4cos θ，2＋32sin θ， 又C 3的普通方程为x －2y －7＝0，则M 到C 3的距离d ＝55|4cos θ－3sin θ－13|＝55·|3sin θ－4cos θ＋13|＝55|5sin(θ－φ)＋13|⎝ ⎛⎭⎪⎫其中φ满足tan φ＝43， 所以d 的最小值为855.考向直角坐标方程、参数方程、极坐标方程的互化例 2 [2018·宝鸡模拟]在平面直角坐标系xOy中，已知C 1：⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ(θ为参数)，将C 1上的所有点的横坐标、纵坐标分别伸长为原来的2和2倍后得到曲线C 2.以平面直角坐标系xOy 的原点O 为极点，x 轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线l ：ρ(2cos θ＋sin θ)＝4.(1)试写出曲线C 1的极坐标方程与曲线C 2的参数方程；(2)在曲线C 2上求一点P ，使点P 到直线l 的距离最小，并求此最小值． 解 (1)把C 1：⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ(θ为参数)，消去参数化为普通方程为x 2＋y 2＝1，故曲线C 1的极坐标方程为ρ＝1.再根据函数图象的伸缩变换规律可得曲线C 2的普通方程为⎝ ⎛⎭⎪⎫x 22＋⎝ ⎛⎭⎪⎫y 22＝1，即x 22＋y 24＝1.故曲线C 2的参数方程为⎩⎨⎧x ＝2cos θ，y ＝2sin θ(θ为参数)．(2)直线l ：ρ(2cos θ＋sin θ)＝4，即2x ＋y －4＝0，设点P (2cos θ，2sin θ)，则点P 到直线的距离为d ＝|2cos θ＋2sin θ－4|2＋1＝2⎪⎪⎪⎪⎪⎪2sin ⎝⎛⎭⎪⎫θ＋π4－23，故当sin ⎝ ⎛⎭⎪⎫θ＋π4＝1时，d 取得最小值，此时，θ＝2k π＋π4(k ∈Z )，点P (1，2)，故曲线C 2上有一点P (1，2)满足到直线l 的距离的最小值为433－263.触类旁通参数方程和直角坐标方程及 极坐标方程之间的相互转化(1)把C 1消去参数化为普通方程为x 2＋y 2＝1，再化为极坐标方程．根据函数图象的伸缩变换规律可得曲线C 2的普通方程，再化为参数方程．(2)先求得直线l 的直角坐标方程，设点P (2cos θ，2sin θ)，求得点P 到直线的距离为d ＝2⎪⎪⎪⎪⎪⎪2sin ⎝ ⎛⎭⎪⎫θ＋π4－23，故当sin ⎝ ⎛⎭⎪⎫θ＋π4＝1时，即θ＝2k π＋π4，k ∈Z 时，点P到直线l 的距离最小，从而求得P 的坐标以及此最小值．【变式训练2】 [2018·宜春模拟]在直角坐标系xOy 中，圆C 1和C 2的参数方程分别是⎩⎪⎨⎪⎧x ＝2＋2cos φ，y ＝2sin φ(φ为参数)和⎩⎪⎨⎪⎧x ＝cos φ，y ＝1＋sin φ(φ为参数)，以O 为极点，x 轴的正半轴为极轴建立极坐标系．(1)求圆C 1和C 2的极坐标方程；(2)射线OM ：θ＝α与圆C 1的交点为O 、P ，与圆C 2的交点为O 、Q ，求|OP |·|OQ |的最大值．解 (1)圆C 1⎩⎪⎨⎪⎧x ＝2＋2cos φ，y ＝2sin φ(φ为参数)，转化成直角坐标方程为(x －2)2＋y 2＝4， 即x 2＋y 2－4x ＝0，转化成极坐标方程为ρ2＝4ρcos θ， 即ρ＝4cos θ圆C 2⎩⎪⎨⎪⎧x ＝cos φ，y ＝1＋sin φ(φ为参数)，转化成直角坐标方程为x 2＋(y －1)2＝1， 即x 2＋y 2－2y ＝0转化成极坐标方程为ρ2＝2ρsin θ， 即ρ＝2sin θ.(2)射线OM ：θ＝α与圆C 1的交点为O 、P ，与圆C 2的交点为O 、Q ， 设P ，Q 对应的极径分别为ρ1，ρ2，则|OP |·|OQ |＝ρ1ρ2＝4|sin2α|. ∵(|sin2α|)max ＝1，∴|OP |·|OQ |的最大值为4.考向直线的参数方程例 3 [2018·泉州模拟]已知在平面直角坐标系xOy 中，直线l 的参数方程是⎩⎪⎨⎪⎧x ＝1－t ，y ＝2＋t (t 是参数)，以平面直角坐标系的原点为极点，x 轴的正半轴为极轴建立极坐标系，两种坐标系中取相同的单位长度，曲线C 的极坐标方程为ρ＝42sin ⎝⎛⎭⎪⎫θ＋π4.(1)写出直线l 的普通方程和曲线C 的直角坐标方程；(2)设点P 的直角坐标为(1,2)，直线l 与曲线C 的交点为A ，B ，试求|AB |及|PA |·|PB |的值．解 (1)直线l 的普通方程为x ＋y －3＝0.ρ＝42sin ⎝ ⎛⎭⎪⎫θ＋π4＝4sin θ＋4cos θ，所以ρ2＝4ρsin θ＋4ρcos θ，所以曲线C的直角坐标方程为x 2＋y 2－4x －4y ＝0(或写成(x －2)2＋(y －2)2＝8)．(2)直线l 的参数方程可化为⎩⎪⎨⎪⎧x ＝1－22t ′，y ＝2＋22t ′(t ′是参数)，把直线l 的参数方程代入x 2＋y 2－4x －4y ＝0得，t ′2＋2t ′－7＝0.设A ，B 对应的参数分别为t 1′，t 2′，则t 1′＋t 2′＝－2，t 1′t 2′＝－7，点P (1,2)显然在直线l 上，故|AB |＝|t 1′－t 2′|＝(t 1′＋t 2′)2－4t 1′t 2′＝30，故|PA |·|PB |＝|t 1′t 2′|＝7.触类旁通直线的参数方程的标准形式过定点P 0(x 0，y 0)，倾斜角为α的直线参数方程的标准形式为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t为参数)，t 的几何意义是直线上的点P 到点P 0(x 0，y 0)的数量，即|t |＝|PP 0|时为距离．使用该式时直线上任意两点P 1、P 2对应的参数分别为t 1、t 2，则|P 1P 2|＝|t 1－t 2|，P 1P 2的中点对应的参数为12(t 1＋t 2)．【变式训练3】 [2018·哈尔滨模拟]在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧x ＝2＋t cos φ，y ＝3＋t sin φ⎝ ⎛⎭⎪⎫t 为参数，φ∈⎣⎢⎡⎦⎥⎤0，π3，以坐标原点O 为极点，x 轴的非负半轴为极轴建立极坐标系，已知圆C 的圆心C 的极坐标为⎝⎛⎭⎪⎫2，π3，半径为2，直线l 与圆C 交于M ，N 两点．(1)求圆C 的极坐标方程；(2)当φ变化时，求弦长|MN |的取值范围．解 (1)由已知，得圆心C 的直角坐标为(1，3)，半径为2， ∴圆C 的直角坐标方程为(x －1)2＋(y －3)2＝4， 即x 2＋y 2－2x －23y ＝0，∵x ＝ρcos θ，y ＝ρsin θ，∴ρ2－2ρcos θ－23ρsin θ＝0，故圆C 的极坐标方程为ρ＝4cos ⎝ ⎛⎭⎪⎫π3－θ.(2)由(1)知，圆C 的直角坐标方程为x 2＋y 2－2x －23y ＝0，将直线的参数方程代入圆的直角坐标方程中得，(2＋t cos φ)2＋(3＋t sin φ)2－2(2＋t cos φ)－23(3＋t sin φ)＝0， 整理得，t 2＋2t cos φ－3＝0，设M ，N 两点对应的参数分别为t 1，t 2，则t 1＋t 2＝－2cos φ，t 1·t 2＝－3， ∴|MN |＝|t 1－t 2|＝(t 1＋t 2)2－4t 1·t 2 ＝4cos 2φ＋12，∵φ∈⎣⎢⎡⎦⎥⎤0，π3，∴cos φ∈⎣⎢⎡⎦⎥⎤12，1，∴|MN |∈[13，4]．考向极坐标、参数方程的综合应用例 4 [2018·盐城模拟]已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝2＋t ，y ＝2－2t (t 为参数)，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ＝21＋3cos 2θ.(1)直接写出直线l 的极坐标方程和曲线C 的直角坐标方程；(2)过曲线C 上任意一点P 作与直线l 夹角为π3的直线m ，设直线m 与直线l 的交点为A ，求|PA |的最大值．解 (1)由⎩⎪⎨⎪⎧x ＝2＋t ，y ＝2－2t (t 为参数)，得l 的普通方程为2x ＋y －6＝0，令x ＝ρcos θ，y ＝ρsin θ，得直线l 的极坐标方程为2ρcos θ＋ρsin θ－6＝0，由曲线C 的极坐标方程，知ρ2＋3ρ2cos 2θ＝4，所以曲线C 的直角坐标方程为x 2＋y 24＝1.(2)由(1)，知直线l 的普通方程为2x ＋y －6＝0，设曲线C 上任意一点P (cos α，2sin α)，点P 到直线l 的距离d ＝|2cos α＋2sin α－6|5.由题意得|PA |＝d s in60°＝415⎪⎪⎪⎪⎪⎪2sin ⎝⎛⎭⎪⎫α＋π4－315，∴当sin ⎝ ⎛⎭⎪⎫α＋π4＝－1时，|PA |取得最大值，最大值为415(3＋2)15. 触类旁通极坐标与参数方程综合应用中注意的问题(1)在已知极坐标方程求曲线交点、距离、线段长、切线等几何问题时，如果不能直接用极坐标解决，或用极坐标解决较麻烦时，可将极坐标方程转化为直角坐标方程解决．转化时要注意两坐标系的关系，注意ρ，θ的取值范围，取值范围不同对应的曲线不同．(2)解答参数方程的有关问题时，首先要弄清参数是谁，代表的几何意义是什么；其次要认真观察方程的表现形式，以便于寻找最佳化简途径．【变式训练4】 在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝4t ，y ＝4t 2(t 为参数)，若以O 为极点，x 轴正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρcos θ＋2ρsin θ＋4＝0(ρ≥0)．(1)求曲线C 1的普通方程与曲线C 2的直角坐标方程；(2)若A 是曲线C 1上的任意一点，B 是曲线C 2上的任意一点，求线段AB 的最小值．解 (1)由⎩⎪⎨⎪⎧ x ＝4t ，y ＝4t 2，消去参数t ，得曲线C 1的普通方程为x 2＝4y .将⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ代入到ρcos θ＋2ρsin θ＋4＝0(ρ≥0)中，得x ＋2y ＋4＝0，即曲线C 2的直角坐标方程为x ＋2y ＋4＝0.(2)解法一：因为A 是曲线C 1上的任意一点，B 是曲线C 2上的任意一点，所以线段AB 的最小值，即与曲线C 2平行的直线与曲线C 1相切时，切点到曲线C 2的距离，设切线的方程为x ＋2y ＋m ＝0，由⎩⎪⎨⎪⎧x 2＝4y ，x ＋2y ＋m ＝0，消去y 得x 2＋2x ＋2m ＝0，所以Δ＝22－4×1×2m ＝0，得m ＝12，因此切点为⎝⎛⎭⎪⎫－1，14，其到直线C 2的距离d ＝⎪⎪⎪⎪⎪⎪－1＋2×14＋412＋22＝7510，即|AB |min ＝7510. 解法二：因为A 是曲线C 1上的任意一点，B 是曲线C 2上的任意一点，所以可设点A (4t,4t 2)，线段AB 的最小值即点A 到直线C 2的距离d 的最小值，所以d ＝|4t ＋2×4t 2＋4|12＋22＝4⎪⎪⎪⎪⎪⎪2⎝ ⎛⎭⎪⎫t ＋142＋785， 当t ＝－14时，d min ＝7510，即|AB |min ＝7510.核心规律参数方程与普通方程互化的方法(1)参数方程化为普通方程：化参数方程为普通方程的基本思路是消去参数，常用的消参方法有代入消去法、加减消去法、恒等式(三角的或代数的)消去法．(2)普通方程化为参数方程：化普通方程为参数方程的基本思路是引入参数，即选定合适的参数t ，先确定一个关系x ＝f (t )(或y ＝φ(t ))，再代入普通方程F (x ，y )＝0，求得另一关系y ＝φ(t )(或x ＝f (t ))．满分策略参数方程应用中的注意事项(1)参数方程通过代入消元或加减消元消去参数化为普通方程，要注意普通方程与原参数方程的取值范围保持一致．(2)普通方程化为参数方程需要引入参数，选择的参数不同，所得的参数方程也不一样．一般地，常选择的参数有角、有向线段的数量、斜率，某一点的横坐标(或纵坐标)．(3)常见曲线的参数方程中的参数都有几何意义，注意利用几何意义常能够给解题带来方便.板块三 模拟演练·提能增分[基础能力达标]1．[2017·江苏高考]在平面直角坐标系xOy 中，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－8＋t ，y ＝t 2(t 为参数)，曲线C 的参数方程为⎩⎨⎧x ＝2s 2，y ＝22s(s 为参数)．设P 为曲线C 上的动点，求点P 到直线l 的距离的最小值．解 直线l 的普通方程为x －2y ＋8＝0.因为点P 在曲线C 上，设P (2s 2,22s )， 从而点P 到直线l 的距离d ＝|2s 2－42s ＋8|12＋(－2)2＝2(s －2)2＋45.当s ＝2时，d min ＝455.因此当点P 的坐标为(4,4)时，曲线C 上的点P 到直线l 的距离取到最小值455.2．[2017·全国卷Ⅲ]在直角坐标系xOy中，直线l 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋t ，y ＝kt (t 为参数)，直线l 2的参数方程为⎩⎪⎨⎪⎧x ＝－2＋m ，y ＝mk(m 为参数)．设l 1与l 2的交点为P ，当k 变化时，P 的轨迹为曲线C .(1)写出C 的普通方程；(2)以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设l 3：ρ(cos θ＋sin θ)－2＝0，M 为l 3与C 的交点，求M 的极径．解 (1)消去参数t 得l 1的普通方程l 1：y ＝k (x －2)； 消去参数m 得l 2的普通方程l 2：y ＝1k(x ＋2)．设P (x ，y )，由题设得⎩⎪⎨⎪⎧y ＝k (x －2)，y ＝1k(x ＋2)，消去k 得x 2－y 2＝4(y ≠0)，所以C 的普通方程为x 2－y 2＝4(y ≠0)．(2)C 的极坐标方程为ρ2(cos 2θ－sin 2θ)＝4(0＜θ＜2π，θ≠π)，联立⎩⎨⎧ρ2(cos 2θ－sin 2θ)＝4，ρ(cos θ＋sin θ)－2＝0得cos θ－sin θ＝2(cos θ＋sin θ)．故tan θ＝－13，从而cos 2θ＝910，sin 2θ＝110.代入ρ2(cos 2θ－sin 2θ)＝4得ρ2＝5， 所以交点M 的极径为 5.3．[2018·安阳模拟]已知极坐标系的极点为直角坐标系xOy 的原点，极轴为x 轴的正半轴，两种坐标系中的长度单位相同，圆C 的直角坐标系方程为x 2＋y 2＋2x －2y ＝0，直线l的参数方程为⎩⎪⎨⎪⎧x ＝－1＋t ，y ＝t(t 为参数)，射线OM 的极坐标方程为θ＝3π4.(1)求圆C 和直线l 的极坐标方程；(2)已知射线OM 与圆C 的交点为O ，P ，与直线l 的交点为Q ，求线段PQ 的长． 解 (1)∵圆C 的直角坐标系方程为x 2＋y 2＋2x －2y ＝0， ∴圆C 的极坐标方程为ρ2＋2ρcos θ－2ρsin θ＝0， 化简得ρ＋2cos θ－2sin θ＝0，即ρ＝22sin ⎝ ⎛⎭⎪⎫θ－π4. ∵直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－1＋t ，y ＝t(t 为参数)，消参得：x －y ＋1＝0，∴直线l 的极坐标方程为ρcos θ－ρsin θ＋1＝0， 即ρ＝1sin θ－cos θ.(2)当θ＝3π4时，|OP |＝22sin ⎝ ⎛⎭⎪⎫3π4－π4＝22，故点P 的极坐标为⎝ ⎛⎭⎪⎫22，3π4，|OQ |＝1sin 3π4－cos3π4＝122＋22＝22， 故点Q 的极坐标为⎝⎛⎭⎪⎫22，3π4， |PQ |＝|OP |－|OQ |＝22－22＝322故线段PQ 的长为322.4．[2018·长沙模拟]以直角坐标系的原点O 为极点，x 轴的正半轴为极轴，且两个坐标系取相等的长度单位．已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝t sin φ，y ＝1＋t cos φ(t 为参数，0<φ<π)，曲线C 的极坐标方程为ρcos 2θ＝4sin θ.(1)求直线l 的普通方程和曲线C 的直角坐标方程；(2)设直线l 与曲线C 相交于A ，B 两点，当φ变化时，求|AB |的最小值．解 (1)由⎩⎪⎨⎪⎧x ＝t sin φ，y ＝1＋t cos φ(t 为参数，0<φ<π)，消去t ，得x cos φ－y sin φ＋sin φ＝0，所以直线l 的普通方程为x cos φ－y sin φ＋sin φ＝0. 由ρcos 2θ＝4sin θ，得(ρcos θ)2＝4ρsin θ， 把x ＝ρcos θ，y ＝ρsin θ代入上式，得x 2＝4y ， 所以曲线C 的直角坐标方程为x 2＝4y .(2)将直线l 的参数方程代入x 2＝4y ，得t 2sin 2φ－4t cos φ－4＝0，设A ，B 两点对应的参数分别为t 1，t 2， 则t 1＋t 2＝4cos φsin 2φ，t 1t 2＝－4sin 2φ， 所以|AB |＝|t 1－t 2|＝(t 1＋t 2)2－4t 1t 2 ＝16cos 2φsin 4φ＋16sin 2φ＝4sin 2φ. 当φ＝π2时，|AB |取得最小值，最小值为4.5．[2018·榆林模拟]在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝a cos t ，y ＝2sin t (t 为参数，a >0)．以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，已知直线l 的极坐标方程为ρcos ⎝⎛⎭⎪⎫θ＋π4＝－2 2.(1)设P 是曲线C 上的一个动点，当a ＝2时，求点P 到直线l 的距离的最小值； (2)若曲线C 上的所有点均在直线l 的右下方，求a 的取值范围． 解 (1)由ρcos ⎝ ⎛⎭⎪⎫θ＋π4＝－22，得22(ρcos θ－ρsin θ)＝－22，化成直角坐标方程，得22(x －y )＝－22，即直线l 的方程为x －y ＋4＝0. 依题意，设P (2cos t,2sin t )，则点P 到直线l 的距离d ＝|2cos t －2sin t ＋4|2＝⎪⎪⎪⎪⎪⎪22cos ⎝⎛⎭⎪⎫t ＋π4＋42.当t ＋π4＝2k π＋π，即t ＝2k π＋3π4，k ∈Z 时，d min ＝22－2.故点P 到直线l 的距离的最小值为22－2. (2)∵曲线C 上的所有点均在直线l 的右下方， ∴对∀t ∈R ，有a cos t －2sin t ＋4>0恒成立， 即a 2＋4cos(t ＋φ)>－4⎝ ⎛⎭⎪⎫其中tan φ＝2a 恒成立，∴a 2＋4<4，又a >0，∴0<a <2 3. 故a 的取值范围为(0,23)．6．[2018·豫南九校联考]在直角坐标系xOy 中，设倾斜角为α的直线l ：⎩⎨⎧x ＝2＋t cos α，y ＝3＋t sin α(t 为参数)与曲线C ：⎩⎪⎨⎪⎧x ＝2cos θ，y ＝sin θ(θ为参数)相交于不同的两点A ，B .(1)若α＝π3，求线段AB 的中点M 的直角坐标；(2)若|PA |·|PB |＝|OP |2，其中P (2，3)，求直线l 的斜率．解 (1)将曲线C 的参数方程化为普通方程是x 24＋y 2＝1.当α＝π3时，直线l 的方程为⎩⎪⎨⎪⎧x ＝2＋12t ，y ＝3＋32t (t 为参数)，代入曲线C 的普通方程x 24＋y 2＝1，得13t 2＋56t ＋48＝0，设直线l 上的点A ，B ，M 对应的参数分别为t 1，t 2，t 0. 则t 0＝t 1＋t 22＝－2813，所以点M 的直角坐标为⎝ ⎛⎭⎪⎫1213，－313. (2)设直线l 上的点A ，B 对应的参数分别为t 1，t 2.将⎩⎨⎧x ＝2＋t cos α，y ＝3＋t sin α代入曲线C 的普通方程x 24＋y 2＝1，得(cos 2α＋4sin 2α)t 2＋(83sin α＋4cos α)t ＋12＝0， 因为|PA |·|PB |＝|t 1t 2|＝12cos 2α＋4sin 2α，|OP |2＝7， 所以12cos 2α＋4sin 2α＝7，得tan 2α＝516. 结合Δ＝32cos α(23sin α－cos α)>0可知tan α＝54. 所以直线l 的斜率为54.。

选修4­4 坐标系与参数方程1. （选修44P 11例5改编）在直角坐标系中，点P 的坐标为（－2，－6），求点P 的极坐标.解：ρ＝（－2）2＋（－6）2＝22，tan θ＝－6－2＝3，又点P 在第三象限，得θ＝43π，即P （22，4π3）.2. （选修44P 17习题9改编）在极坐标系中，已知A ，B 两点的极坐标分别为⎝⎛⎭⎪⎫3，π3，⎝ ⎛⎭⎪⎫4，π6，求△AOB（其中O 为极点）的面积. 解：由题意A ，B 两点的极坐标分别为⎝⎛⎭⎪⎫3，π3，⎝ ⎛⎭⎪⎫4，π6，得△AOB 的面积S △AOB ＝12OA ·OB ·sin ∠AOB ＝12×3×4×sin π6＝3.3. 在极坐标系中，求圆ρ＝2cos θ的圆心到直线2ρsin ⎝ ⎛⎭⎪⎫θ＋π3＝1的距离. 解：圆的普通方程为（x －1）2＋y 2＝1，直线的普通方程为3x ＋y －1＝0，∴ 圆心到直线的距离为d ＝3－12.4. （选修44P 19例1改编）在极坐标系中，求过圆ρ＝－2sin θ的圆心，且与极轴平行的直线的极坐标方程.解：由题意，圆ρ＝－2sin θ，可化为ρ2＝－2ρsin θ，化成直角坐标方程为x 2＋y 2＝－2y ，即x 2＋（y ＋1）2＝1，圆心是（0，－1），所求直角坐标方程为y ＝－1，所以其极坐标方程为ρsin θ＝－1.5. 在极坐标系中，求圆ρ＝4上的点到直线ρ（cos θ＋3sin θ）＝8的距离的最大值.解：把ρ＝4化为直角坐标方程为x 2＋y 2＝16，把ρ（cos θ＋3sin θ）＝8化为直角坐标方程为x ＋3y －8＝0，∴ 圆心（0，0）到直线的距离为d ＝82＝4，∴ 直线和圆相切，∴ 圆上的点到直线的最大距离是8.1. 极坐标系是由距离（极径）与方向（极角）确定点的位置的一种方法，由于终边相同的角有无数个且极径可以为负数，故在极坐标系下，有序实数对（ρ，θ）与点不一一对应.这点应与直角坐标系区别开来.2. 在极坐标系中，同一个点M 的坐标形式不尽相同，M （ρ，θ）可表示为（ρ，θ＋2n π）（n∈Z ）.3. 在极坐标系中，极径ρ可以为负数，故M （ρ，θ）可表示为（－ρ，θ＋（2n ＋1）π）（n∈Z ）.4. 特别地，若ρ＝0，则极角θ可取任意角.5. 建立曲线的极坐标方程，其基本思路与在直角坐标系中大致相同，即设曲线上任一点M （ρ，θ），建立等式，化简即得.6. 常见曲线的极坐标方程（1） 过极点，倾斜角为α的直线的极坐标方程为θ＝α（ρ∈R ）或θ＝π＋α（ρ∈R ）；（2） 过点（a ，0）（a ＞0），与极轴垂直的直线的极坐标方程为ρcos θ＝a ；（3） 过点⎝⎛⎭⎪⎫a ，π2，与极轴平行的直线的极坐标方程为ρsin θ＝a ；（4） 圆心在极点，半径为r 的圆的极坐标方程为ρ＝r ； （5） 圆心为（a ，0），半径为a 的圆的极坐标方程为ρ＝2acos θ；（6） 圆心为⎝⎛⎭⎪⎫a ，π2，半径为a 的圆的极坐标方程为ρ＝2asin θ.7. 以平面直角坐标系的原点O 为极点，x 轴的正半轴为极轴，且在两种坐标系中取相同的长度单位，平面内任一点P 的直角坐标（x ，y ）与极坐标（ρ，θ）可以互换，公式是⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ 和⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝y x ., 1 求极坐标或极坐标方程), 1) 在极坐标系中，已知点A ⎝⎛⎭⎪⎫2，π4，圆C 的方程为ρ＝42sin θ（圆心为点C ），求直线AC 的极坐标方程.解：（解法1）以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系xOy.圆C 的平面直角坐标方程为x 2＋y 2＝42y ，即x 2＋（y －22）2＝8，圆心C （0，22）. 点A 的直角坐标为（2，2）.直线AC 的斜率k AC ＝22－20－2＝－1.所以直线AC 的直角坐标方程为y ＝－x ＋22， 极坐标方程为ρ（cos θ＋sin θ）＝22，即ρsin ⎝⎛⎭⎪⎫θ＋π4＝2. （解法2）在直线AC 上任取一点M （ρ，θ），不妨设点M 在线段AC 上.由于圆心为C ⎝⎛⎭⎪⎫22，π2，S △OAC ＝S △OAM ＋S △OCM ， 所以12×22×2sin π4＝12×2×ρsin ⎝ ⎛⎭⎪⎫θ－π4＋12×ρ×22sin ⎝ ⎛⎭⎪⎫π2－θ，即ρ（cos θ＋sin θ）＝22，化简，得直线AC 的极坐标方程为ρsin ⎝⎛⎭⎪⎫θ＋π4＝2. 备选变式（教师专享）在极坐标系中，求曲线ρ＝2cos θ关于直线θ＝π4（ρ∈R ）对称的曲线的极坐标方程.解：（解法1）以极点为坐标原点，极轴为x 轴的正半轴建立直角坐标系，则曲线ρ＝2cos θ的直角坐标方程为（x －1）2＋y 2＝1，且圆心C 的坐标为（1，0），直线θ＝π4的直角坐标方程为y ＝x.因为圆心C （1，0）关于y ＝x 的对称点为（0，1），所以圆C 关于y ＝x 的对称曲线为x 2＋（y －1）2＝1，所以曲线ρ＝2cos θ关于直线θ＝π4对称的曲线的极坐标方程为ρ＝2sin θ.（解法2）设曲线ρ＝2cos θ上任意一点为（ρ′，θ′），其关于直线θ＝π4的对称点为（ρ，θ），则⎩⎪⎨⎪⎧ρ′＝ρ，θ′＝2k π＋π2－θ. 将（ρ′，θ′）代入ρ＝2cos θ，得ρ＝2cos ⎝ ⎛⎭⎪⎫π2－θ，即ρ＝2sin θ， 所以曲线ρ＝2cos θ关于直线θ＝π4（ρ∈R ）对称的曲线的极坐标方程为ρ＝2sinθ., 2 极坐标方程与直角坐标方程的互化), 2) （2017·苏州期中）已知在平面直角坐标系xOy 中，圆C 的参数方程为⎩⎪⎨⎪⎧x ＝rcos θ＋2，y ＝rsin θ＋2（θ为参数，r ＞0）.以直角坐标系的原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为2ρsin ⎝⎛⎭⎪⎫θ＋π4＋1＝0. （1） 求圆C 的圆心的极坐标；（2） 当圆C 与直线l 有公共点时，求r 的取值范围.解：（1） 由C ：⎩⎪⎨⎪⎧x ＝rcos θ＋2，y ＝rsin θ＋2得（x －2）2＋（y －2）2＝r 2，∴ 曲线C 是以（2，2）为圆心，r 为半径的圆，∴ 圆心的极坐标为⎝⎛⎭⎪⎫22，π4. （2） 由直线l ：2ρsin ⎝⎛⎭⎪⎫θ＋π4＋1＝0，得直线l 的直角坐标方程为x ＋y ＋1＝0， 从而圆心（2，2）到直线l 的距离d ＝|2＋2＋1|2＝52 2.∵ 圆C 与直线l 有公共点，∴ d ≤r ，即r≥522.变式训练（2017·苏州期初）自极点O 任意作一条射线与直线ρcos θ＝3相交于点M ，在射线OM 上取点P ，使得OM·OP＝12，求动点P 的轨迹的极坐标方程，并把它化为直角坐标方程.解：设P （ρ，θ），M （ρ′，θ）， ∵ OM ·OP ＝12，∴ ρρ′＝12.∵ ρ′cos θ＝3，∴ 12ρ·cos θ＝3.则动点P 的轨迹的极坐标方程为ρ＝4cos θ. ∵ 极点在此曲线上，∴ 方程两边可同时乘ρ，得ρ2＝4ρcos θ.∴ x 2＋y 2－4x ＝0., 3 曲线的极坐标方程的应用), 3) 在极坐标系中，曲线C ：ρ＝2acos θ（a>0），直线l ：ρcos ⎝⎛⎭⎪⎫θ－π3＝32，C 与l 有且仅有一个公共点. （1） 求a ；（2） O 为极点，A ，B 为C 上的两点，且∠AOB＝π3，求OA ＋OB 的最大值.解：（1） 曲线C 是以（a ，0）为圆心，以a 为半径的圆； 直线l 的直角坐标方程为x ＋3y －3＝0.由直线l 与圆C 相切可得|a －3|2＝a ，解得a ＝1.（2） 不妨设A 的极角为θ，B 的极角为θ＋π3，则OA ＋OB ＝2cos θ＋2cos ⎝⎛⎭⎪⎫θ＋π3 ＝3cos θ－3sin θ＝23cos ⎝⎛⎭⎪⎫θ＋π6， 当θ＝－π6时，OA ＋OB 取得最大值2 3.变式训练在直角坐标系xOy 中，圆C 的方程为（x －3）2＋（y ＋1）2＝9，以O 为极点，x 轴的正半轴为极轴建立极坐标系.（1） 求圆C 的极坐标方程；（2） 直线OP ：θ＝π6（ρ∈R ）与圆C 交于点M ，N ，求线段MN 的长.解：（1） （x －3）2＋（y ＋1）2＝9可化为x 2＋y 2－23x ＋2y －5＝0，故其极坐标方程为ρ2－23ρcos θ＋2ρsin θ－5＝0.（2） 将θ＝π6代入ρ2－23ρcos θ＋2ρsin θ－5＝0，得ρ2－2ρ－5＝0，∴ ρ1＋ρ2＝2，ρ1ρ2＝－5，|MN|＝|ρ1－ρ2|＝（ρ1＋ρ2）2－4ρ1ρ2＝2 6.1. （2017·苏北四市期中）已知曲线C 的极坐标方程为ρsin （θ＋π3）＝3，以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，求曲线C 的直角坐标方程.解：由ρsin ⎝⎛⎭⎪⎫θ＋π3＝3，得12ρsin θ＋32ρcos θ＝3. 又ρcos θ＝x ，ρsin θ＝y ，所以曲线C 的直角坐标方程为3x ＋y －6＝0.2. （2017·苏锡常镇一模）已知圆O 1和圆O 2的极坐标方程分别为ρ＝2，ρ2－22ρcos ⎝⎛⎭⎪⎫θ－π4＝2. （1） 把圆O 1和圆O 2的极坐标方程化为直角坐标方程； （2） 求经过两圆交点的直线的极坐标方程.解：（1） 由ρ＝2⇒ρ2＝4，所以x 2＋y 2＝4.因为ρ2－22ρcos ⎝⎛⎭⎪⎫θ－π4＝2，所以ρ2－22ρ⎝⎛⎭⎪⎫cos θcos π4＋sin θsin π4＝2，所以x 2＋y 2－2x －2y －2＝0.（2） 将两圆的直角坐标方程相减，得经过两圆交点的直线方程为x ＋y ＝1.化为极坐标方程为ρcos θ＋ρsin θ＝1，即ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝22. 3. （2017·苏北三市模拟）在极坐标系中，已知点A ⎝⎛⎭⎪⎫2，π2，点B 在直线l ：ρcos θ＋ρsin θ＝0（0≤θ＜2π）上.当线段AB 最短时，求点B 的极坐标.解：以极点为原点，极轴为x 轴正半轴，建立平面直角坐标系，则点A ⎝⎛⎭⎪⎫2，π2的直角坐标为（0，2），直线l 的直角坐标方程为x ＋y ＝0.AB 最短时，点B 为直线x －y ＋2＝0与直线l 的交点， 由⎩⎪⎨⎪⎧x －y ＋2＝0，x ＋y ＝0，解得⎩⎪⎨⎪⎧x ＝－1，y ＝1. 所以点B 的直角坐标为（－1，1）.所以点B 的极坐标为⎝⎛⎭⎪⎫2，3π4. 4. （2017·常州期末）在平面直角坐标系中，以原点O 为极点，x 轴的正半轴为极轴，建立极坐标系.已知圆ρ＝4sin （θ＋π6）（ρ≥0）被射线θ＝θ0（θ0为常数，且θ0∈⎝ ⎛⎭⎪⎫0，π2）所截得的弦长为23，求θ0的值. 解：圆ρ＝4sin ⎝⎛⎭⎪⎫θ＋π6的直角坐标方程为（x －1）2＋（y －3）2＝4，射线θ＝θ0的直角坐标方程可以设为y ＝kx （x≥0，k ＞0），圆心（1，3）到直线y ＝kx 的距离d ＝|k －3|1＋k2. 根据题意，得24－（k －3）21＋k 2＝23，解得k ＝33， 即tan θ0＝33.又θ0∈⎝⎛⎭⎪⎫0，π2，所以θ0＝π6.1. （2017·南通、扬州、泰州模拟）在极坐标系中，圆C 的圆心在极轴上，且过极点和点⎝⎛⎭⎪⎫32，π4，求圆C 的极坐标方程. 解：（解法1）因为圆C 的圆心在极轴上且过极点， 所以可设圆C 的极坐标方程为ρ＝acos θ.又点⎝⎛⎭⎪⎫32，π4在圆C 上，所以32＝acos π4，解得a ＝6. 所以圆C 的极坐标方程为ρ＝6cos θ.（解法2）点⎝⎛⎭⎪⎫32，π4的直角坐标为（3，3）. 因为圆C 过点（0，0），（3，3）， 所以圆心在直线x ＋y －3＝0上. 又圆心C 在极轴上，所以圆C 的直角坐标方程为（x －3）2＋y 2＝9. 所以圆C 的极坐标方程为ρ＝6cos θ.2. 已知在极坐标系下，圆C ：ρ＝2cos ⎝ ⎛⎭⎪⎫θ＋π2与直线l ：ρsin ⎝⎛⎭⎪⎫θ＋π4＝2，点M 为圆C 上的动点.求点M 到直线l 距离的最大值.解：圆C ：ρ＝2cos ⎝⎛⎭⎪⎫θ＋π2，即 x 2＋y 2＋2y ＝0，x 2＋（y ＋1）2＝1，表示圆心为（0，－1），半径等于1的圆.直线l ：ρsin ⎝⎛⎭⎪⎫θ＋π4＝2，即ρcos θ＋ρsin θ－2＝0，即 x ＋y －2＝0， 圆心到直线l 的距离为|0－1－2|2＝322，故圆上的动点M 到直线l 的距离的最大值等于322＋1.3. 在直角坐标系xOy 中，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，圆C 的极坐标方程为ρ＝4cos θ.（1） 求出圆C 的直角坐标方程；（2） 已知圆C 与x 轴相交于A ，B 两点，若直线l ：y ＝2x ＋2m 上存在点P 使得∠APB ＝90°，求实数m 的最大值.解：（1） 由ρ＝4cos θ得ρ2＝4ρcos θ，即x 2＋y 2－4x ＝0，即圆C 的标准方程为（x －2）2＋y 2＝4.（2） l 的方程为y ＝2x ＋2m ，而AB 为圆C 的直径，故直线l 上存在点P 使得∠APB＝90°的充要条件是直线l 与圆C 有公共点， 故|4＋2m|5≤2，于是实数m 的最大值为5－2.4. 在极坐标系中，已知直线2ρcos θ＋ρsin θ＋a ＝0（a>0）被圆ρ＝4sin θ截得的弦长为2，求a 的值.解：以极点为坐标原点，极轴为x 轴正半轴建立平面直角坐标系，直线的极坐标方程化为直角坐标方程为2x ＋y ＋a ＝0，圆的极坐标方程化为直角坐标方程为x 2＋y 2＝4y ，即x 2＋（y －2）2＝4.因为直线被圆截得的弦长为2，所以圆心（0，2）到直线的距离为4－1＝3， 即|2＋a|5＝3，因为a>0，所以a ＝15－2.1. 极坐标方程与直角坐标方程的互化 （1） 将极坐标或极坐标方程转化为直角坐标或直角坐标方程，直接利用公式x ＝ρcos θ，y ＝ρsin θ即可.常用方法有代入法、平方法，还经常用到同乘（或除以）ρ等技巧.（2） 将直角坐标或直角坐标方程转化为极坐标或极坐标方程，要灵活运用x ＝ρcosθ，y ＝ρsin θ以及ρ＝x 2＋y 2，tan θ＝y x（x≠0），同时要掌握必要的技巧，通常情况下，由tan θ确定角θ时，应根据点P 所在象限取最小正角.在这里要注意：当x≠0时，θ角才能由tan θ＝yx按上述方法确定.当x ＝0时，tan θ没有意义，这时又分三种情况：当x ＝0，y ＝0时，θ可取任何值；当x ＝0，y>0时，可取θ＝π2；当x ＝0，y<0时，可取θ＝3π2.2. 求简单曲线的极坐标方程的方法（1） 设点M （ρ，θ）为曲线上任意一点，由已知条件，构造出三角形，利用正弦定理求解OM 与θ的关系；（2） 先求出曲线的直角坐标方程，再利用极坐标与直角坐标的变换公式，把直角坐标方程化为极坐标方程.[备课札记]第2课时 参 数 方 程（对应学生用书（理）202～205页）1. （选修44P 45例1改编）已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋t 2，y ＝2＋32t（t 为参数），求此直线的倾斜角以及在y 轴上的截距.解：∵ ⎩⎪⎨⎪⎧x －1＝t 2，y －2＝32t ，∴ y －2＝3（x －1）.∴ 此直线的斜率为3，∴ 它的倾斜角为60°.令x ＝0，得它在y 轴上的截距为2－ 3.2. （选修44P 45例2改编）已知点P （3，m ）在以点F 为焦点的抛物线⎩⎪⎨⎪⎧x ＝4t 2，y ＝4t（t 为参数）上，求PF 的值.解：将抛物线的参数方程化为普通方程为y 2＝4x ，则焦点F （1，0），准线方程为x ＝－1，又P （3，m ）在抛物线上，由抛物线的定义知PF ＝3－（－1）＝4.3. （选修44P 57习题3（4））选择适当的参数，将普通方程4x 2＋y 2－16x ＋12＝0化为参数方程.解：由4x 2＋y 2－16x ＋12＝0，得4（x －2）2＋y 2＝4，选择参数θ，令y ＝2sin θ，则x ＝2＋cos θ，故所求曲线的参数方程是⎩⎪⎨⎪⎧x ＝2＋cos θ，y ＝2sin θ.（答案不惟一）4. 在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎨⎧x ＝2cos α＋3，y ＝2sin α（α为参数）.以原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为θ＝π6.若直线l 与曲线C 交于A ，B 两点，求线段AB 的长.解：曲线C 的普通方程为（x －3）2＋y 2＝4，表示以（3，0）为圆心，2为半径的圆.直线l 的直角坐标方程为y ＝33x.所以圆心到直线的距离为32， 所以线段AB 的长为24－⎝ ⎛⎭⎪⎫322＝13. 5. 已知直线l 的极坐标方程为ρsin （θ－π3）＝3，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2sin θ（θ为参数），设P 点是曲线C 上的任意一点，求P 到直线l 的距离的最大值.解：由ρsin ⎝⎛⎭⎪⎫θ－π3＝3，可得ρ（12sin θ－32cos θ）＝3， ∴ y －3x ＝6，即3x －y ＋6＝0.由⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2sin θ，得x 2＋y 2＝4，圆的半径为r ＝2， ∴ 圆心到直线l 的距离d ＝62＝3.∴ P 到直线l 的距离的最大值为d ＋r ＝5.1. 参数方程是用第三个变量（即参数）分别表示曲线上任一点M 的坐标x ，y 的另一种曲线方程的形式，它体现了x ，y 的一种间接关系.2. 参数方程是根据其固有的意义（物理、几何）得到的，要注意参数的取值范围.3. 一些常见曲线的参数方程（1） 过点P 0（x 0，y 0），且倾斜角是α的直线的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋lcos α，y ＝y 0＋lsin α（l 为参数）. l 是有向线段P 0P 的数量.（2） 圆方程（x －a ）2＋（y －b ）2＝r 2的参数方程是⎩⎪⎨⎪⎧x ＝a ＋rcos θ，y ＝b ＋rsin θ（θ为参数）.（3） 椭圆方程x 2a 2＋y2b 2＝1（a>b>0）的参数方程是⎩⎪⎨⎪⎧x ＝acos θ，y ＝bsin θ（θ为参数）.（4） 双曲线方程x 2a －y2b ＝1（a>0，b>0）的参数方程是⎩⎪⎨⎪⎧x ＝a 2⎝ ⎛⎭⎪⎫t ＋1t ，y ＝b 2⎝ ⎛⎭⎪⎫t －1t （t 为参数）.（5） 抛物线方程y 2＝2px （p>0）的参数方程是⎩⎪⎨⎪⎧x ＝2pt 2，y ＝2pt （t 为参数）.4. 在参数方程与普通方程的互化中要注意变量的取值范围.1 参数方程与普通方程的互化1（2017·南京、盐城期末）在平面直角坐标系xOy 中，已知直线l ：⎩⎪⎨⎪⎧x ＝35t ，y ＝45t （t为参数）.现以坐标原点O 为极点，以x 轴正半轴为极轴建立极坐标系.设圆C 的极坐标方程为ρ＝2cos θ，直线l 与圆C 交于A ，B 两点，求弦AB 的长.解：直线l ：⎩⎪⎨⎪⎧x ＝35t ，y ＝45t （t 为参数）化成普通方程为4x －3y ＝0，圆C 的极坐标方程ρ＝2cos θ化成直角坐标方程为（x －1）2＋y 2＝1，则圆C 的圆心到直线l 的距离d ＝|4|42＋（－3）2＝45， 所以AB ＝21－d 2＝65.变式训练在平面直角坐标系xOy 中，已知直线⎩⎪⎨⎪⎧x ＝－1＋55t ，y ＝－1＋255t （t 为参数）与曲线⎩⎪⎨⎪⎧x ＝sin θ，y ＝cos 2θ（θ为参数）相交于A ，B 两点，求线段AB 的长.解：将直线的参数方程化为普通方程，得y ＝2x ＋1 ①. 将曲线的参数方程化为普通方程，得y ＝1－2x 2（－1≤x≤1） ②.由①②，得⎩⎪⎨⎪⎧x ＝－1，y ＝－1或⎩⎪⎨⎪⎧x ＝0，y ＝1，所以A （－1，－1），B （0，1）或A （0，1），B （－1，－1），从而AB ＝（－1－0）2＋（－1－1）2＝ 5. 备选变式（教师专享）已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－1＋22t ，y ＝22t（t 为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ＝2sin θ－2cos θ.若直线l 与曲线C 相交于A ，B 两点，求线段AB 的长.解：由ρ＝2sin θ－2cos θ，可得ρ2＝2ρsin θ－2ρcos θ，所以曲线C 的直角坐标方程为x 2＋y 2＝2y －2x ，标准方程为（x ＋1）2＋（y －1）2＝2.直线l 的方程化成普通方程为x －y ＋1＝0.圆心到直线l 的距离为d ＝|－1－1＋1|2＝22，所求弦长AB ＝22－⎝ ⎛⎭⎪⎫222＝ 6. , 2 求曲线参数方程), 2) 如图，以过原点的直线的倾斜角θ为参数，求圆x 2＋y 2－x ＝0的参数方程.解：设P （x ，y ），则随着θ取值变化，P 可以表示圆上任意一点，由所给的曲线方程x 2＋y 2－x ＝0，即⎝ ⎛⎭⎪⎫x －122＋y 2＝14，表示以⎝ ⎛⎭⎪⎫12，0为圆心，12为半径的圆，可得弦OP ＝1×cosθ，所以⎩⎪⎨⎪⎧x ＝OP·cos θ，y ＝OP·sin θ，从而⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝cos θ·sin θ，故已知圆的参数方程为⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝cos θ·sin θ（θ为参数）.备选变式（教师专享）已知直线C 1：⎩⎪⎨⎪⎧x ＝1＋tcos α，y ＝tsin α（t 为参数），曲线C 2：⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ（θ为参数）. （1） 当α＝π3时，求C 1与C 2的交点坐标；（2） 过坐标原点O 作C 1的垂线，垂足为A ，P 为OA 的中点，当α变化时，求点P 轨迹的参数方程，并指出它是什么曲线.解：（1） 当α＝π3时，C 1的普通方程为y ＝3（x －1），C 2的普通方程为x 2＋y 2＝1，联立构成方程组⎩⎨⎧y ＝3x －3，x 2＋y 2＝1，解得C 1与C 2的交点坐标分别为（1，0），⎝ ⎛⎭⎪⎫12，－32. （2） 依题意，C 1的普通方程为xsin α－ycos α－sin α＝0，则A 点的坐标为（sin 2α，－sin αcos α），故当α变化时，P 点轨迹的参数方程为⎩⎪⎨⎪⎧x ＝12sin 2α，y ＝－12sin αcos α（α为参数），所以点P 轨迹的普通方程为⎝ ⎛⎭⎪⎫x －142＋y 2＝116.故点P 的轨迹是圆心为⎝ ⎛⎭⎪⎫14，0，半径为14的圆. , 3 参数方程的应用), 3) （2017·南通、泰州模拟）在平面直角坐标系xOy 中，已知直线⎩⎪⎨⎪⎧x ＝－32＋22l ，y ＝22l （l 为参数）与曲线⎩⎪⎨⎪⎧x ＝18t 2，y ＝t （t 为参数）相交于A ，B 两点，求线段AB的长.解：（解法1）将曲线⎩⎪⎨⎪⎧x ＝18t 2，y ＝t（t 为参数）化成普通方程为y 2＝8x ，将直线⎩⎪⎨⎪⎧x ＝－32＋22l ，y ＝22l （l 为参数）代入y 2＝8x ，整理得l 2－82l ＋24＝0，解得l 1＝22，l 2＝6 2.则|l 1－l 2|＝42，所以线段AB 的长为4 2.（解法2）将曲线⎩⎪⎨⎪⎧x ＝18t 2，y ＝t（t 为参数）化成普通方程为y 2＝8x ，将直线⎩⎪⎨⎪⎧x ＝－32＋22l ，y ＝22l（l 为参数）化成普通方程为x －y ＋32＝0，由⎩⎪⎨⎪⎧y 2＝8x ，x －y ＋32＝0得⎩⎪⎨⎪⎧x ＝12，y ＝2或⎩⎪⎨⎪⎧x ＝92，y ＝6.所以AB 的长为⎝ ⎛⎭⎪⎫92－122＋（6－2）2＝4 2.备选变式（教师专享）已知直线l ：⎩⎪⎨⎪⎧x ＝tcos α＋m ，y ＝tsin α（t 为参数）恒经过椭圆C ：⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ（φ为参数）的右焦点F.（1） 求m 的值；（2） 设直线l 与椭圆C 交于A ，B 两点，求FA·FB 的最大值与最小值.解：（1） 椭圆的参数方程化为普通方程，得x 225＋y29＝1.因为a ＝5，b ＝3，所以c ＝4，所以点F 的坐标为（4，0）. 因为直线l 经过点（m ，0），所以m ＝4.（2） 将直线l 的参数方程代入椭圆C 的普通方程，并整理得（9cos 2α＋25sin 2α）t 2＋72tcos α－81＝0.设点A ，B 在直线参数方程中对应的参数分别为t 1，t 2，则FA ·FB ＝|t 1t 2|＝819cos 2α＋25sin 2α＝819＋16sin 2α. 当sin α＝0时，FA ·FB 取最大值9；当sin α＝±1时，FA ·FB 取最小值8125., 4 极坐标、参数方程的综合应用), 4) （2017·苏锡常镇二模）在平面直角坐标系xOy 中，以O 为极点，x 轴的正半轴为极轴，取相同的单位长度，建立极坐标系.已知曲线C 1的参数方程为⎩⎨⎧x ＝3＋2cos α，y ＝3＋2sin α（α∈[0，2π]，α为参数），曲线C 2的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π3＝a （a∈R ），若曲线C 1与曲线C 2有且仅有一个公共点，求实数a 的值.解：曲线C 1的方程为（x －3）2＋（y －3）2＝4，圆心坐标为（3，3），半径为2.∵ 曲线C 2的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π3＝a （a∈R ）， ∴ 曲线C 2的直角坐标方程为3x ＋y －2a ＝0.∵ 曲线C 1与曲线C 2有且仅有一个公共点， ∴ |3＋3－2a|2＝2，解得a ＝1或a ＝5.备选变式（教师专享）在平面直角坐标系xOy 中，曲线C ：⎩⎨⎧x ＝6cos α，y ＝2sin α（α为参数）.以原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρ（cos θ＋3sin θ）＋4＝0.求曲线C 上的点到直线l 的最大距离.解：将l 转化为直角坐标方程为x ＋3y ＋4＝0. 在C 上任取一点A （6cos α，2sin α），α∈[0，2π），则点A 到直线l 的距离为d ＝|6cos α＋6sin α＋4|2＝|23sin ⎝ ⎛⎭⎪⎫α＋π4＋4|2＝3sin ⎝⎛⎭⎪⎫α＋π4＋2.当α＝π4时，d 取得最大值，最大值为2＋3，此时A 点为（3，1）.1. 在直角坐标系xOy 中，以O 为极点，x 轴正半轴为极轴建立极坐标系，曲线C 1的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝22a ，曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝－1＋cos t ，y ＝－1＋sin t （t 为参数，0≤t ≤π）.当C 1与C 2有公共点时，求实数a 的取值范围.解：曲线C 1的直角坐标方程为x ＋y ＝a.若C 1与C 2有公共点，则a ＝x ＋y ＝sin t ＋cos t－2在t∈[0，π]上有解，又sin t ＋cos t －2＝2sin ⎝⎛⎭⎪⎫t ＋π4－2，因为t∈[0，π]，所以t ＋π4∈⎣⎢⎡⎦⎥⎤π4，5π4，sin ⎝ ⎛⎭⎪⎫t ＋π4∈⎣⎢⎡⎦⎥⎤－22，1，所以a 的取值范围为[－3，2－2].2. （2017·苏北四市期末）在平面直角坐标系xOy 中，以O 为极点，x 轴的正半轴为极轴建立极坐标系.直线l ：2sin ⎝ ⎛⎭⎪⎫θ－π4＝m （m∈R ），圆C 的参数方程为⎩⎪⎨⎪⎧x ＝1＋3cos t ，y ＝－2＋3sin t （t 为参数）.当圆心C 到直线l 的距离为2时，求m 的值.解：直线l 的直角坐标方程为x －y ＋m ＝0，圆C 的普通方程为（x －1）2＋（y ＋2）2＝9，圆心C 到直线l 的距离为|1－（－2）＋m|2＝2，解得m ＝－1或m ＝－5.3. （2016·江苏卷）在平面直角坐标系xOy 中，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝32t（t 为参数），椭圆C 的参数方程为⎩⎪⎨⎪⎧x ＝cos θ，y ＝2sin θ（θ为参数）.设直线l 与椭圆C 相交于A ，B 两点，求线段AB 的长.解：椭圆C 的普通方程为x 2＋y 24＝1，将直线l 的参数方程⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝32t代入x 2＋y 24＝1，得⎝ ⎛⎭⎪⎫1＋12t 2＋⎝ ⎛⎭⎪⎫32t 24＝1，即7t 2＋16t ＝0，解得t 1＝0，t 2＝－167.所以AB ＝|t 1－t 2|＝167.4. （2017·扬州期末）在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝cos α ，y ＝1＋sin 2α（α为参数），以直角坐标系原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为θ＝π4，试求直线l 与曲线C 的交点的直角坐标.解：将直线l 的极坐标方程化成直角坐标方程为y ＝x ，将曲线C 的参数方程化成普通方程为y ＝2－x 2（－1≤x≤1）. 由⎩⎪⎨⎪⎧y ＝x ，y ＝2－x2得x 2＋x －2＝0，解得x ＝1或x ＝－2. 又－1≤x≤1，所以x ＝1，所以直线l 与曲线C 的交点的直角坐标为（1，1）.1. 在极坐标系中，直线l 的极坐标方程为θ＝π3（ρ∈R ），以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos α，y ＝1＋cos 2α（α为参数），求直线l 与曲线C 的交点P 的直角坐标.解：因为直线l 的极坐标方程为θ＝π3（ρ∈R ），所以直线l 的普通方程为y ＝3x.①又曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos α，y ＝1＋cos 2α（α为参数），所以曲线C 的直角坐标方程为y ＝12x 2（x∈[－2，2]）， ②联立①②解方程组得⎩⎪⎨⎪⎧x ＝0，y ＝0或⎩⎨⎧x ＝23，y ＝6（舍去）.故P 点的直角坐标为（0，0）.2. （2017·苏州期末）在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1－22t ，y ＝2＋22t（t 为参数），以坐标原点O 为极点，x 轴正半轴为极轴的极坐标系中，曲线C 的极坐标方程为ρsin 2θ－4cos θ＝0，已知直线l 与曲线C 相交于A ，B 两点，求线段AB 的长.解：因为曲线C 的极坐标方程为ρsin 2θ－4cos θ＝0，所以ρ2sin 2θ＝4ρcos θ，即曲线C 的直角坐标方程为y 2＝4x.将直线l 的参数方程⎩⎪⎨⎪⎧x ＝1－22t ，y ＝2＋22t代入抛物线方程y 2＝4x ，得⎝ ⎛⎭⎪⎫2＋22t 2＝4⎝⎛⎭⎪⎫1－22t ，即t 2＋82t ＝0，解得t 1＝0，t 2＝－8 2.所以AB ＝|t 1－t 2|＝8 2.3. 在平面直角坐标系xOy 中，已知曲线C ：⎩⎪⎨⎪⎧x ＝s ，y ＝s 2（s 为参数），直线l ：⎩⎪⎨⎪⎧x ＝2＋110t ，y ＝4＋310t （t 为参数）.设曲线C 与直线l 交于A ，B 两点，求线段AB 的长度.解：由⎩⎪⎨⎪⎧x ＝s ，y ＝s 2消去s 得曲线C 的普通方程为y ＝x 2；由⎩⎪⎨⎪⎧x ＝2＋110t ，y ＝4＋310t消去t 得直线l 的普通方程为y ＝3x －2.联立直线l 的方程与曲线C 的方程，即⎩⎪⎨⎪⎧y ＝x 2，y ＝3x －2，解得交点的坐标分别为（1，1），（2，4）.所以线段AB 的长度为（2－1）2＋（4－1）2＝10.4. （2017·南京、盐城模拟）在平面直角坐标系xOy 中，直线l ：⎩⎪⎨⎪⎧x ＝1＋35t ，y ＝45t（t 为参数）与曲线C ：⎩⎪⎨⎪⎧x ＝4k 2，y ＝4k（k 为参数）交于A ，B 两点，求线段AB 的长.解：（解法1）直线l 的参数方程化为普通方程得4x －3y ＝4，将曲线C 的参数方程化为普通方程得y 2＝4x.联立方程组⎩⎪⎨⎪⎧4x －3y ＝4，y 2＝4x ，解得⎩⎪⎨⎪⎧x ＝4，y ＝4或⎩⎪⎨⎪⎧x ＝14，y ＝－1，所以A （4，4），B ⎝ ⎛⎭⎪⎫14，－1或A ⎝ ⎛⎭⎪⎫14，－1，B （4，4）. 所以AB ＝⎝ ⎛⎭⎪⎫4－142＋（4＋1）2＝254. （解法2）将曲线C 的参数方程化为普通方程得y 2＝4x.将直线l 的参数方程代入抛物线C 的方程得⎝ ⎛⎭⎪⎫45t 2＝4⎝ ⎛⎭⎪⎫1＋35t ，即4t 2－15t －25＝0，所以 t 1＋t 2＝154，t 1t 2＝－254.所以AB ＝|t 1－t 2|＝（t 1＋t 2）2－4t 1t 2＝⎝ ⎛⎭⎪⎫1542＋25＝254.1. 在直线的参数方程⎩⎪⎨⎪⎧x ＝x 0＋tcos α，y ＝y 0＋tsin α（t 为参数）中t 的几何意义是表示在直线上过定点P 0（x 0，y 0）与直线上的任一点P （x ，y ）构成的有向线段P 0P 的长度，且在直线上任意两点P 1，P 2的距离为P 1P 2＝|t 1－t 2|＝（t 1＋t 2）2－4t 1t 2.2. 参数方程化为普通方程的关键是消参数：一要熟练掌握常用技巧（如整体代换）；二要注意变量取值范围的一致性，这一点最易忽视.[备课札记]。

2019-2020年高考数学一轮复习参数方程教学案1. 了解参数方程的概念；2. 能够进行参数方程与普通方程的互化；3. 掌握常用曲线的参数方程方程，并能应用.三、 重点难点参数方程与普通方程的互化，常用曲线的参数方程及应用。

四、 知识导学1. 参数方程的含义：.2. 直线的参数方程及参数的几何意义:3. 圆的参数方程及参数的意义:4. 椭圆的参数方程及参数的意义:五、课前自学1．参数方程2x y ⎧⎪⎨⎪=⎩1=t+t （为参数），表示的曲线是 . 2．曲线（为参数）的长为 .3．参数方程()2()t t t t x e e t y e e --⎧=+⎪⎨=-⎪⎩为参数的普通方程为 . 4．经过点，倾斜角为的直线的参数方程为 .5．点是椭圆上的一个动点，则的最大值为 .六、合作、探究、展示例1．已知直线()11cos :sin x t C t y t αα=+⎧⎨=⎩为参数，圆()2cos :sin x C y θθθ=⎧⎨=⎩为参数 。

（1） 当时，求与的交点坐标；（2）过坐标原点O作的垂线，垂足为A，P为OA的中点。

当变化时，求P点的轨迹的参数方程，并指出它是什么曲线。

（xx全国）例2．在椭圆上有动点和定点不同于，以为边作正三角形，求面积的最大值及此时点的坐标.例3．已知曲线22()2x ptt py pt⎧=⎨=⎩为参数,为正常数上的两点对应的参数分别为，，求例4．圆M 的参数方程为03sin 4cos 4222=+--+R Ry Rx y x αα（R>0）.(1) 求该圆的圆心的坐标以及圆M 的半径；（2）当R 固定，变化时，求圆心M 的轨迹.并证明此时不论取什么值，所有的圆M 都外切于一个定圆.七、当堂练习1．直线（t 为参数）的倾斜角是 .2．参数方程（为参数）所表示的曲线是 .3．直线（为参数）截抛物线所得的弦长为 .4．已知P 为半圆()cos :0sin x C y θθθπθ=⎧≤≤⎨=⎩为参数，上的点，点A 的坐标为，0为坐标原点，点M 在射线OP 上，线段OM 与C 的弧的长度均为.（1）以O 为极点，x 轴的正半轴为极轴建立极坐标系，求点M 的极坐标；（2）求直线AM 的参数方程．（xx 辽宁）八、总结反思。

坐标系与参数方程第一节坐标系1．平面直角坐标系中的坐标伸缩变换设点P (x ，y )是平面直角坐标系中的任意一点，在变换 φ：⎩⎪⎨⎪⎧x ′＝λ·x λ＞0 ，y ′＝μ·y μ＞0的作用下，点P (x ，y )对应到点P ′(x ′，y ′)，称φ为平面直角坐标系中的坐标伸缩变换，简称伸缩变换． 2．极坐标系的概念 (1)极坐标系如图所示，在平面内取一个定点O ，叫做极点；自极点O 引一条射线Ox ，叫做极轴；再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向)，这样就建立了一个极坐标系．(2)极坐标①极径：设M 是平面内一点，极点O 与点M 的距离|OM |叫做点M 的极径，记为ρ. ②极角：以极轴Ox 为始边，射线OM 为终边的角xOM 叫做点M 的极角，记为θ. ③极坐标：有序数对(ρ，θ)叫做点M 的极坐标，记为M (ρ，θ)． 一般不作特殊说明时，我们认为ρ≥0，θ可取任意实数． 3．极坐标与直角坐标的互化设M 是平面内任意一点，它的直角坐标是(x ，y )，极坐标是(ρ，θ)，则它们之间的关系为：⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ；⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝y x x ≠0 .4．简单曲线的极坐标方程1．若点P 的直角坐标为(3，－3)，则点P 的极坐标为______．解析：因为点P (3，－3)在第四象限，与原点的距离为23，且OP 与x 轴所成的角为－π6，所以点P 的极坐标为⎝⎛⎭⎪⎫23，－π6.答案：⎝⎛⎭⎪⎫23，－π62．圆ρ＝5cos θ－53sin θ的圆心的极坐标为________． 解析：将方程 ρ＝5cos θ－53sin θ两边都乘以ρ， 得ρ2＝5ρcos θ－53ρsin θ， 化成直角坐标方程为x 2＋y 2－5x ＋53y ＝0. 圆心坐标为⎝ ⎛⎭⎪⎫52，－532，化成极坐标为⎝ ⎛⎭⎪⎫5，5π3.答案：⎝⎛⎭⎪⎫5，5π3(答案不唯一)3．在极坐标系中A ⎝ ⎛⎭⎪⎫2，－π3，B ⎝ ⎛⎭⎪⎫4，2π3两点间的距离为________．解析：法一：(数形结合)在极坐标系中，A ，B 两点如图所示，|AB |＝|OA |＋|OB |＝6.法二：∵A ⎝ ⎛⎭⎪⎫2，－π3，B ⎝ ⎛⎭⎪⎫4，2π3的直角坐标为A (1，－3)，B (－2,23)．∴|AB |＝ －2－1 2＋ 23＋3 2＝6. 答案：64．在极坐标系中，圆ρ＝4sin θ的圆心到直线θ＝π3(θ∈R)的距离是________．解析：设圆心到直线θ＝π3(θ∈R)的距离为d ，因为圆的半径为2, d ＝2·sin π6＝1.答案：1考点一 平面直角坐标系下图形的伸缩变换基础送分型考点——自主练透[考什么·怎么考]高考对平面直角坐标系下图形的伸缩变换要求较低，极少考查，属于基础题. 1．求椭圆x 24＋y 2＝1经过伸缩变换⎩⎪⎨⎪⎧x ′＝12x ，y ′＝y后的曲线方程．解：由⎩⎪⎨⎪⎧x ′＝12x ，y ′＝y得到⎩⎪⎨⎪⎧x ＝2x ′，y ＝y ′.①将①代入x 24＋y 2＝1，得4x ′24＋y ′2＝1，即x ′2＋y ′2＝1.因此椭圆x 24＋y 2＝1经伸缩变换后得到的曲线方程是x 2＋y 2＝1.2．求双曲线C ：x 2－y 264＝1经过φ：⎩⎪⎨⎪⎧x ′＝3x ，2y ′＝y ，变换后所得曲线C ′的焦点坐标．解：设曲线C ′上任意一点P ′(x ′，y ′)， 由上述可知，将⎩⎪⎨⎪⎧x ＝13x ′，y ＝2y ′代入x 2－y 264＝1，得x ′29－4y ′264＝1，化简得x ′29－y ′216＝1，即x 29－y 216＝1为曲线C ′的方程， 可见仍是双曲线，则焦点(－5,0)，(5,0)为所求．3．将圆x 2＋y 2＝1变换为椭圆x 29＋y 24＝1的一个伸缩变换公式为φ：⎩⎪⎨⎪⎧X ＝ax a >0 ，Y ＝by b >0 ，求a ，b 的值．解：由⎩⎪⎨⎪⎧X ＝ax ，Y ＝by得⎩⎪⎨⎪⎧x ＝1aX ，y ＝1b Y ，代入x 2＋y 2＝1中得X 2a 2＋Y 2b2＝1，所以a 2＝9，b 2＝4，即a ＝3，b ＝2.[怎样快解·准解]伸缩变换公式应用时的2个注意点(1)曲线的伸缩变换是通过曲线上任意一点的坐标的伸缩变换实现的，解题时一定要区分变换前的点P 的坐标(x ，y )与变换后的点P ′的坐标(x ′，y ′)，再利用伸缩变换公式⎩⎪⎨⎪⎧x ′＝ax a >0 ，y ′＝by b >0建立联系．(2)已知变换后的曲线方程f (x ，y )＝0，一般都要改写为方程f (x ′，y ′)＝0，再利用换元法确定伸缩变换公式．考点二 极坐标与直角坐标的互化 重点保分型考点——师生共研在极坐标系下，已知圆O ：ρ＝cos θ＋sin θ和直线l ： ρsin ⎝ ⎛⎭⎪⎫θ－π4＝22(ρ≥0,0≤θ＜2π)．(1)求圆O 和直线l 的直角坐标方程；(2)当θ∈(0，π)时，求直线l 与圆O 的公共点的极坐标． [思维路径](1)由ρ＝cos θ＋sin θ及公式⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ，可将等式两边同乘以ρ，得ρ2＝ρcos θ＋ρsin θ，从而可化为直角坐标方程．将ρsin ⎝ ⎛⎭⎪⎫θ－π4＝22利用两角差的正弦公式展开，可得ρsin θ－ρcos θ＝1，从而可化为直角坐标方程．(2)可先求出直线l 与圆O 的公共点，然后将该公共点化为极坐标． 解：(1)圆O ：ρ＝cos θ＋sin θ，即ρ2＝ρcos θ＋ρsin θ， 故圆O 的直角坐标方程为x 2＋y 2－x －y ＝0，直线l ：ρsin ⎝ ⎛⎭⎪⎫θ－π4＝22，即ρsin θ－ρcos θ＝1，则直线l 的直角坐标方程为x －y ＋1＝0. (2)由(1)知圆O 与直线l 的直角坐标方程，将两方程联立得⎩⎪⎨⎪⎧x 2＋y 2－x －y ＝0，x －y ＋1＝0，解得⎩⎪⎨⎪⎧x ＝0，y ＝1，即圆O 与直线l 在直角坐标系下的公共点为(0,1)，将(0,1)转化为极坐标为⎝⎛⎭⎪⎫1，π2即为所求．[解题师说]1．极坐标方程与直角坐标方程的互化方法(1)直角坐标方程化为极坐标方程：将公式x ＝ρcos θ及y ＝ρsin θ直接代入直角坐标方程并化简即可．(2)极坐标方程化为直角坐标方程：通过变形，构造出形如ρcos θ，ρsin θ，ρ2的形式，再应用公式进行代换．其中方程的两边同乘以(或同除以)ρ及方程两边平方是常用的变形技巧．2．极角的确定方法由tan θ确定角θ时，应根据点P 所在象限取最小正角．在这里要注意：当x ≠0时，θ角才能由tan θ＝yx按上述方法确定．当x ＝0时，tan θ没有意义，这时可分三种情况处理：当x ＝0，y ＝0时，θ可取任何值；当x ＝0，y >0时，可取θ＝π2；当x ＝0，y <0时，可取θ＝3π2.[冲关演练]已知圆O 1和圆O 2的极坐标方程分别为ρ＝2，ρ2－22ρ·cos ⎝ ⎛⎭⎪⎫θ－π4＝2.(1)把圆O 1和圆O 2的极坐标方程化为直角坐标方程；(2)求经过两圆交点的直线的极坐标方程． 解：(1)由ρ＝2知ρ2＝4，所以圆O 1的直角坐标方程为x 2＋y 2＝4. 因为ρ2－22ρcos ⎝⎛⎭⎪⎫θ－π4＝2，所以ρ2－22ρ⎝ ⎛⎭⎪⎫cos θcos π4＋sin θsin π4＝2，所以圆O 2的直角坐标方程为x 2＋y 2－2x －2y －2＝0. (2)将两圆的直角坐标方程相减， 得经过两圆交点的直线方程为x ＋y ＝1. 化为极坐标方程为ρcos θ＋ρsin θ＝1， 即ρsin ⎝⎛⎭⎪⎫θ＋π4＝22.考点三 曲线的极坐标方程的应用 重点保分型考点——师生共研(2017·全国卷Ⅱ)在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 1的极坐标方程为ρcos θ＝4.(1)M 为曲线C 1上的动点，点P 在线段OM 上，且满足|OM |·|OP |＝16，求点P 的轨迹C 2的直角坐标方程；(2)设点A 的极坐标为⎝⎛⎭⎪⎫2，π3，点B 在曲线C 2上，求△OAB 面积的最大值．[思维路径](1)可先求点P 在极坐标系中的轨迹方程，然后再化为直角坐标方程．设P (ρ，θ)，则M 点的可设为(ρ1，θ)，利用|OM |·|OP |＝16及相关点可求．(2)由于点O 和点A 都是定点，故△AOB 面积的大小取决于B 点的位置，可设B 点的极坐标为(ρB ，α)，然后利用面积公式S ＝12|OA |·ρB ·sin∠AOB 求解即可．解：(1)设P 的极坐标为(ρ，θ)(ρ＞0)，M 的极坐标为(ρ1，θ)(ρ1＞0)． 由题设知|OP |＝ρ，|OM |＝ρ1＝4cos θ.由|OM |·|OP |＝16，得C 2的极坐标方程ρ＝4cos θ(ρ＞0)． 因此C 2的直角坐标方程为(x －2)2＋y 2＝4(x ≠0)． (2)设点B 的极坐标为(ρB ，α)(ρB ＞0)，由题设知|OA |＝2，ρB ＝4cos α，于是△OAB 的面积 S ＝12|OA |·ρB ·sin∠AOB ＝4cos α·⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π3 ＝2⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2α－π3－32≤2＋ 3.当α＝－π12时，S 取得最大值2＋ 3.所以△OAB 面积的最大值为2＋ 3.[解题师说]1．方法要熟求简单曲线的极坐标方程的方法(1)设点M (ρ，θ)为曲线上任意一点，由已知条件，构造出三角形，利用三角函数及正、余弦定理求解|OM |与θ的关系．(2)先求出曲线的直角坐标方程，再利用极坐标与直角坐标的变换公式，把直角坐标方程化为极坐标方程．2．技巧要会用极坐标系解决问题时要注意题目中的几何关系，如果几何关系不容易通过极坐标表示时，可以先化为直角坐标方程，将不熟悉的问题转化为熟悉的问题加以解决．[冲关演练](2015·全国卷Ⅰ)在直角坐标系xOy 中，直线C 1：x ＝－2，圆C 2：(x －1)2＋(y －2)2＝1，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系．(1)求C 1，C 2的极坐标方程；(2)若直线C 3的极坐标方程为θ＝π4(ρ∈R)，设C 2与C 3的交点为M ，N ，求△C 2MN 的面积．解：(1)因为x ＝ρcos θ，y ＝ρsin θ， 所以C 1的极坐标方程为ρcos θ＝－2，C 2的极坐标方程为ρ2－2ρcos θ－4ρsin θ＋4＝0.(2)将θ＝π4代入ρ2－2ρcos θ－4ρsin θ＋4＝0，得ρ2－32ρ＋4＝0，解得ρ1＝22，ρ2＝ 2. 故ρ1－ρ2＝2，即|MN |＝ 2. 由于C 2的半径为1， 所以△C 2MN 的面积为12.1．在极坐标系中，求直线ρcos ⎝ ⎛⎭⎪⎫θ＋π6＝1与圆ρ＝4sin θ的交点的极坐标． 解：ρcos ⎝ ⎛⎭⎪⎫θ＋π6＝1化为直角坐标方程为3x －y ＝2，即y ＝3x －2.ρ＝4sin θ可化为x 2＋y 2＝4y ， 把y ＝3x －2代入x 2＋y 2＝4y ， 得4x 2－83x ＋12＝0， 即(x －3)2＝0， 所以x ＝3，y ＝1.所以直线与圆的交点坐标为(3，1)，化为极坐标为⎝⎛⎭⎪⎫2，π6.2．在极坐标系中，已知圆C 经过点P ⎝ ⎛⎭⎪⎫2，π4，圆心为直线ρsin ⎝ ⎛⎭⎪⎫θ－π3＝－32与极轴的交点，求圆C 的极坐标方程．解：在ρsin ⎝ ⎛⎭⎪⎫θ－π3＝－32中，令θ＝0，得ρ＝1，所以圆C 的圆心坐标为(1,0)． 因为圆C 经过点P ⎝ ⎛⎭⎪⎫2，π4，所以圆C 的半径|PC |＝2 2＋12－2×1×2cos π4＝1，于是圆C 过极点，所以圆C 的极坐标方程为ρ＝2cos θ.3．设M ，N 分别是曲线ρ＋2sin θ＝0和ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝22上的动点，求M ，N 的最小距离．解：因为M ，N 分别是曲线ρ＋2sin θ＝0和ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝22上的动点，即M ，N分别是圆x 2＋y 2＋2y ＝0和直线x ＋y －1＝0上的动点，要求M ，N 两点间的最小距离，即在直线x ＋y －1＝0上找一点到圆x 2＋y 2＋2y ＝0的距离最小，即圆心(0，－1)到直线x ＋y －1＝0的距离减去半径，故最小值为|0－1－1|2－1＝2－1.4．(2016·全国卷Ⅰ)在直角坐标系xOy中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝a cos t ，y ＝1＋a sin t (t为参数，a >0)．在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ＝4cos θ.(1)说明C 1是哪一种曲线，并将C 1的方程化为极坐标方程；(2)直线C 3的极坐标方程为θ＝α0，其中α0满足tan α0＝2，若曲线C 1与C 2的公共点都在C 3上，求a .解：(1)消去参数t 得到C 1的普通方程为x 2＋(y －1)2＝a 2，则C 1是以(0,1)为圆心，a 为半径的圆．将x ＝ρcos θ，y ＝ρsin θ代入C 1的普通方程中，得到C 1的极坐标方程为ρ2－2ρsin θ＋1－a 2＝0.(2)曲线C 1，C 2的公共点的极坐标满足方程组⎩⎪⎨⎪⎧ρ2－2ρsin θ＋1－a 2＝0，ρ＝4cos θ.若ρ≠0，由方程组得16cos 2θ－8sin θcos θ＋1－a 2＝0， 由已知tan θ＝2，可得16cos 2θ－8sin θcos θ＝0， 从而1－a 2＝0，解得a ＝－1(舍去)或a ＝1. 当a ＝1时，极点也为C 1，C 2的公共点，且在C 3上． 所以a ＝1.5．(2018·洛阳模拟)在直角坐标系xOy 中，圆C 的方程为x 2＋(y －2)2＝4.以O 为极点，x 轴的非负半轴为极轴建立极坐标系．(1)求圆C 的极坐标方程；(2)直线l 的极坐标方程是2ρsin ⎝⎛⎭⎪⎫θ＋π6＝53，射 线OM ：θ＝π6与圆C 的交点为O ，P ，与直线l 的交点为Q ，求线段PQ 的长．解：(1)将x ＝ρcos θ，y ＝ρsin θ代入x 2＋(y －2)2＝4， 得圆C 的极坐标方程为ρ＝4sin θ. (2)设P (ρ1，θ1)，则由⎩⎪⎨⎪⎧ρ＝4sin θ，θ＝π6，解得ρ1＝2，θ1＝π6.设Q (ρ2，θ2)，则由⎩⎪⎨⎪⎧2ρsin ⎝⎛⎭⎪⎫θ＋π6＝53，θ＝π6，解得ρ2＝5，θ2＝π6.所以|PQ |＝ρ2－ρ1＝3.6．在直角坐标系xOy 中，以O 为极点，x 轴正半轴为极轴建立极坐标系．曲线C 的极坐标方程为ρcos ⎝⎛⎭⎪⎫θ－π3＝1，M ，N 分别为C 与x 轴，y 轴的交点． (1)求C 的直角坐标方程，并求M ，N 的极坐标； (2)设MN 的中点为P ，求直线OP 的极坐标方程． 解：(1)由ρcos ⎝⎛⎭⎪⎫θ－π3＝1得ρ⎝ ⎛⎭⎪⎫12cos θ＋32sin θ＝1.从而C 的直角坐标方程为12x ＋32y ＝1，即x ＋3y ＝2.当θ＝0时，ρ＝2，所以M (2,0)． 当θ＝π2时，ρ＝233，所以N ⎝ ⎛⎭⎪⎫233，π2.(2)由(1)知M 点的直角坐标为(2,0)，N 点的直角坐标为⎝⎛⎭⎪⎫0，233.所以P 点的直角坐标为⎝ ⎛⎭⎪⎫1，33，则P 点的极坐标为⎝ ⎛⎭⎪⎫233，π6，所以直线OP 的极坐标方程为θ＝π6(ρ∈R)．7．(2018·福建质检)在直角坐标系xOy 中，曲线C 1的普通方程为(x －2)2＋y 2＝4，在以坐标原点O 为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ＝2sin θ，曲线C 3：θ＝π6(ρ>0)，A (2,0)．(1)把C 1的普通方程化为极坐标方程；(2)设C 3分别交C 1，C 2于点P ，Q ，求△APQ 的面积． 解：(1)因为C 1的普通方程为(x －2)2＋y 2＝4， 即x 2＋y 2－4x ＝0，所以C 1的极坐标方程为ρ2－4ρcos θ＝0，即ρ＝4cos θ. (2)依题意，设点P ，Q 的极坐标分别为⎝ ⎛⎭⎪⎫ρ1，π6，⎝ ⎛⎭⎪⎫ρ2，π6. 将θ＝π6代入ρ＝4cos θ，得ρ1＝23，将θ＝π6代入ρ＝2sin θ，得ρ2＝1，所以|PQ |＝|ρ1－ρ2|＝23－1.依题意，点A (2,0)到曲线θ＝π6(ρ>0)的距离d ＝|OA |sin π6＝1，所以S △APQ ＝12|PQ |·d ＝12×(23－1)×1＝3－12.8．(2018·贵州适应性考试)在以原点O 为极点，x 轴的非负半轴为极轴的极坐标系中，曲线C 1的极坐标方程为ρ＝4cos θ，曲线C 2的极坐标方程为ρcos 2θ＝sin θ.(1)求曲线C 2的直角坐标方程；(2)过原点且倾斜角为α⎝ ⎛⎭⎪⎫π6＜α≤π4的射线l 与曲线C 1，C 2分别相交于A ，B 两点(A ，B 异于原点)，求|OA |·|OB |的取值范围．解：(1)由曲线C 2的极坐标方程为ρcos 2θ＝sin θ， 两边同乘以ρ，得ρ2cos 2θ＝ρsin θ， 故曲线C 2的直角坐标方程为x 2＝y .(2)射线l 的极坐标方程为θ＝α，π6＜α≤π4，把射线l 的极坐标方程代入曲线C 1的极坐标方程得|OA |＝ρ＝4cos α，把射线l 的极坐标方程代入曲线C 2的极坐标方程得|OB |＝ρ＝sin αcos α， ∴|OA |·|OB |＝4cos α·sin αcos 2α＝4tan α. ∵π6＜α≤π4， ∴|OA |·|OB |的取值范围是⎝ ⎛⎦⎥⎤433，4.第二节参数方程1．参数方程一般地，在平面直角坐标系中，如果曲线上任意一点的坐标x ，y 都是某个变数t 的函数：⎩⎪⎨⎪⎧x ＝f t ，y ＝g t ，并且对于t的每一个允许值，由方程组⎩⎪⎨⎪⎧x ＝f t ，y ＝g t所确定的点M (x ，y )都在这条曲线上，那么方程⎩⎪⎨⎪⎧x ＝f t ，y ＝g t 就叫做这条曲线的参数方程，变数t 叫做参变数，简称参数．相对于参数方程而言，直接给出点的坐标间关系的方程叫做普通方程．2．直线、圆、椭圆的参数方程(1)过点M (x 0，y 0)，倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．(2)圆心在点M 0(x 0，y 0)，半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数)．(3)椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的参数方程为⎩⎪⎨⎪⎧x ＝a cos φ，y ＝b sin φ (φ为参数)．(4)双曲线x 2a 2－y 2b2＝1(a >0，b >0)的参数方程为⎩⎪⎨⎪⎧x ＝a 1cos θ，y ＝b tan θ(θ为参数)．1．在平面直角坐标系中，若曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2＋22t ，y ＝1＋22t (t 为参数)，则其普通方程为____________．解析：依题意，消去参数可得x －2＝y －1，即x －y －1＝0. 答案：x －y －1＝02．椭圆C 的参数方程为⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ(φ为参数)，过左焦点F 1的直线l 与C 相交于A ，B 两点，则|AB |min ＝________.解析：由⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ(φ为参数)得，x 225＋y 29＝1，当AB ⊥x 轴时，|AB |有最小值． 所以|AB |min ＝2×95＝185.答案：1853．曲线C的参数方程为⎩⎪⎨⎪⎧x ＝sin θ，y ＝cos 2θ＋1(θ为参数)，则曲线C 的普通方程为____________．解析：由⎩⎪⎨⎪⎧x ＝sin θ，y ＝cos 2θ＋1(θ为参数)消去参数θ，得y ＝2－2x 2(－1≤x ≤1)．答案：y ＝2－2x 2(－1≤x ≤1)4．在平面直角坐标系xOy 中，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝32t(t 为参数)，椭圆C 的方程为x 2＋y 24＝1，设直线l 与椭圆C 相交于A ，B 两点，则线段AB 的长为________________________________________________________________________．解析：将直线l 的参数方程⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝32t代入x 2＋y 24＝1，得⎝ ⎛⎭⎪⎫1＋12t 2＋⎝ ⎛⎭⎪⎫32t 24＝1，即7t 2＋16t ＝0， 解得t 1＝0，t 2＝－167，所以|AB |＝|t 1－t 2|＝167.答案：167考点一 参数方程与普通方程的互化 基础送分型考点——自主练透[考什么·怎么考]参数方程与普通方程的互化是每年高考的热点内容，常与极坐标、直线与圆锥曲线的位置关系综合考查，属于基础题．1．将下列参数方程化为普通方程． (1)⎩⎪⎨⎪⎧x ＝1t ，y ＝1t t 2－1(t 为参数)；(2)⎩⎪⎨⎪⎧x ＝2＋sin 2θ，y ＝－1＋cos 2θ(θ为参数)．解：(1)∵⎝ ⎛⎭⎪⎫1t 2＋⎝ ⎛⎭⎪⎫1tt 2－12＝1，∴x 2＋y 2＝1.∵t 2－1≥0，∴t ≥1或t ≤－1. 又x ＝1t，∴x ≠0.当t ≥1时，0<x ≤1， 当t ≤－1时，－1≤x <0， ∴所求普通方程为x 2＋y 2＝1，其中⎩⎪⎨⎪⎧0<x ≤1，0≤y <1或⎩⎪⎨⎪⎧－1≤x <0，－1<y ≤0.(2)∵y ＝－1＋cos 2θ＝－1＋1－2sin 2θ＝－2sin 2θ，sin 2θ＝x －2， ∴y ＝－2x ＋4，∴2x ＋y －4＝0. ∵0≤sin 2θ≤1，∴0≤x －2≤1，∴2≤x ≤3，∴所求的普通方程为2x ＋y －4＝0(2≤x ≤3)．2.如图，以过原点的直线的倾斜角θ为参数，求圆x 2＋y 2－x ＝0的参数方程．解：圆的半径为12，记圆心为C ⎝ ⎛⎭⎪⎫12，0，连接CP ， 则∠PCx ＝2θ，故x P ＝12＋12cos 2θ＝cos 2θ，y P ＝12sin 2θ＝sin θcos θ(θ为参数)．所以圆的参数方程为⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝sin θcos θ(θ为参数)．3．求直线⎩⎪⎨⎪⎧x ＝2＋t ，y ＝－1－t (t 为参数)与曲线⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α(α为参数)的交点个数．解：将⎩⎪⎨⎪⎧x ＝2＋t ，y ＝－1－t 消去参数t 得直线x ＋y －1＝0；将⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α消去参数α，得圆x 2＋y 2＝9.又圆心(0,0)到直线x ＋y －1＝0的距离d ＝22＜3. 因此直线与圆相交，故直线与曲线有2个交点．[怎样快解·准解]将参数方程化为普通方程的方法将参数方程化为普通方程，需要根据参数方程的结构特征，选取适当的消参方法．常见的消参方法有：代入消参法、加减消参法、平方消参法等，对于含三角函数的参数方程，常利用同角三角函数关系式消参．如sin 2θ＋cos 2θ＝1等．[注意] 将参数方程化为普通方程时，要注意两种方程的等价性，不要增解，如第1题．考点二 参数方程的应用 重点保分型考点——师生共研(2017·全国卷Ⅰ)在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝3cos θ，y ＝sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋4t ，y ＝1－t(t 为参数)．(1)若a ＝－1，求C 与l 的交点坐标； (2)若C 上的点到l 距离的最大值为17，求a . 解：(1)曲线C 的普通方程为x 29＋y 2＝1.当a ＝－1时，直线l 的普通方程为x ＋4y －3＝0，由⎩⎪⎨⎪⎧x ＋4y －3＝0，x 29＋y 2＝1解得⎩⎪⎨⎪⎧x ＝3，y ＝0或⎩⎪⎨⎪⎧x ＝－2125，y ＝2425.从而C 与l 的交点坐标为(3,0)，⎝ ⎛⎭⎪⎫－2125，2425.(2)直线l 的普通方程为x ＋4y －a －4＝0， 故C 上的点(3cos θ，sin θ)到l 的距离为d ＝|3cos θ＋4sin θ－a －4|17.当a ≥－4时，d 的最大值为a ＋917.由题设得a ＋917＝17，解得a ＝8；当a ＜－4时，d 的最大值为－a ＋117. 由题设得－a ＋117＝17，解得a ＝－16.综上，a ＝8或a ＝－16.[解题师说]1．方法要熟(1)解决直线与圆、圆锥曲线的参数方程的应用问题时，一般是先化为普通方程，再根据直线与圆、圆锥曲线的位置关系来解决问题．(2)对于形如⎩⎪⎨⎪⎧x ＝x 0＋at ，y ＝y 0＋bt(t 为参数)的参数方程，当a 2＋b 2≠1时，应先化为标准形式后才能利用t 的几何意义解题．(3)直线参数方程的应用：直线的标准参数方程主要用来解决过定点的直线与圆锥曲线相交时的弦长或距离问题．它可以避免求交点时解方程组的繁琐运算，但应用直线的参数方程时，需先判断是否是标准形式再考虑参数的几何意义．(4)圆、圆锥曲线的参数方程突出了其工具性作用，应用时，把圆、圆锥曲线上的点的坐标设为参数方程的形式，将问题转化为三角函数问题，利用三角函数知识解决问题．2．结论要记根据直线的参数方程的标准式中t 的几何意义，有如下常用结论：过定点M 0的直线与圆锥曲线相交，交点为M 1，M 2，所对应的参数分别为t 1，t 2. (1)弦长l ＝|t 1－t 2|；(2)弦M 1M 2的中点⇒t 1＋t 2＝0； (3)|M 0M 1||M 0M 2|＝|t 1t 2|.[冲关演练]1．(2018·湖南五市十校联考)在直角坐标系xOy 中，设倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x ＝3＋t cos α，y ＝t sin α(t 为参数)，直线l 与曲线C ：⎩⎪⎨⎪⎧x ＝1cos θ，y ＝tan θ(θ为参数)相交于不同的两点A ，B .(1)若α＝π3，求线段AB 的中点的直角坐标；(2)若直线l 的斜率为2，且过已知点P (3,0)，求|PA |·|PB |的值． 解：(1)由曲线C ：⎩⎪⎨⎪⎧x ＝1cos θ，y ＝tan θ (θ为参数)，可得曲线C 的普通方程是x 2－y2＝1.当α＝π3时，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝3＋12t ，y ＝32t (t 为参数)，代入曲线C 的普通方程，得t 2－6t －16＝0， 得t 1＋t 2＝6，所以线段AB 的中点对应的t ＝t 1＋t 22＝3，故线段AB 的中点的直角坐标为⎝ ⎛⎭⎪⎫92，332.(2)将直线l 的参数方程代入曲线C 的普通方程，化简得(cos 2α－sin 2α)t 2＋6cos αt ＋8＝0，则|PA |·|PB |＝|t 1t 2|＝⎪⎪⎪⎪⎪⎪8cos 2α－sin 2α＝⎪⎪⎪⎪⎪⎪8 1＋tan 2α 1－tan 2α，由已知得tan α＝2，故|PA |·|PB |＝403.2．(2018·石家庄质检)在平面直角坐标系xOy 中，圆C 的参数方程为⎩⎨⎧x ＝－5＋2cos t ，y ＝3＋2sin t(t 为参数)，在以原点O 为极点，x 轴的非负半轴为极轴建立的极坐标系中，直线l 的极坐标方程为ρcos ⎝⎛⎭⎪⎫θ＋π4＝－ 2. (1)求圆C 的普通方程和直线l 的直角坐标方程；(2)设直线l 与x 轴，y 轴分别交于A ，B 两点，点P 是圆C 上任意一点，求A ，B 两点的极坐标和△PAB 面积的最小值．解：(1)由⎩⎨⎧x ＝－5＋2cos t ，y ＝3＋2sin t ，消去参数t ，得(x ＋5)2＋(y －3)2＝2，所以圆C 的普通方程为(x ＋5)2＋(y －3)2＝2.由ρcos ⎝ ⎛⎭⎪⎫θ＋π4＝－2，得ρcos θ－ρsin θ＝－2，所以直线l 的直角坐标方程为x －y ＋2＝0.(2)直线l 与x 轴，y 轴的交点分别为A (－2,0)，B (0,2)，化为极坐标为A (2，π)，B ⎝⎛⎭⎪⎫2，π2，设点P 的坐标为(－5＋2cos t,3＋2sin t )， 则点P 到直线l 的距离为d ＝|－5＋2cos t －3－2sin t ＋2|2＝⎪⎪⎪⎪⎪⎪－6＋2cos ⎝ ⎛⎭⎪⎫t ＋π42.所以d min ＝42＝22，又|AB |＝2 2.所以△PAB 面积的最小值是S ＝12×22×22＝4.考点三 极坐标、参数方程的综合应用 重点保分型考点——师生共研在平面直角坐标系xOy 中，以O 为极点，x 轴的非负半轴为极轴建立极坐标系．已知点P 的极坐标为⎝ ⎛⎭⎪⎫23，π6，曲线C 的参数方程为⎩⎨⎧x ＝2cos α，y ＝－3＋2sin α(α为参数)．(1)写出点P 的直角坐标及曲线C 的直角坐标方程；(2)若Q 为曲线C 上的动点，求PQ 中点M 到直线l ：ρcos θ＋2ρsin θ＋1＝0距离的最小值．解：(1)由x ＝ρcos θ，y ＝ρsin θ， 可得点P 的直角坐标为(3，3)，由⎩⎨⎧x ＝2cos α，y ＝－3＋2sin α，得x 2＋(y ＋3)2＝4，∴曲线C 的直角坐标方程为x 2＋(y ＋3)2＝4. (2)直线l 的普通方程为x ＋2y ＋1＝0，曲线C 的参数方程为⎩⎨⎧x ＝2cos α，y ＝－3＋2sin α(α为参数)，设Q (2cos α，－3＋2sin α)，则M ⎝ ⎛⎭⎪⎫32＋cos α，sin α， 故点M 到直线l 的距离d ＝⎪⎪⎪⎪⎪⎪32＋cos α＋2sin α＋112＋22＝⎪⎪⎪⎪⎪⎪5sin α＋φ ＋525≥－5＋525＝52－1⎝⎛⎭⎪⎫tan φ＝12， ∴点M 到直线l 的距离的最小值为52－1. [解题师说]处理极坐标、参数方程综合问题的方法(1)涉及参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解．当然，还要结合题目本身特点，确定选择何种方程．(2)数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用ρ和θ的几何意义，直接求解，能达到化繁为简的解题目的．[冲关演练]1．(2017·全国卷Ⅲ)在直角坐标系xOy中，直线l 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋t ，y ＝kt(t 为参数)，直线l 2的参数方程为⎩⎪⎨⎪⎧x ＝－2＋m ，y ＝mk(m 为参数)．设l 1与l 2的交点为P ，当k 变化时，P 的轨迹为曲线C .(1)写出C 的普通方程；(2)以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设l 3：ρ(cos θ＋sin θ)－2＝0，M 为l 3与C 的交点，求M 的极径．解：(1)消去参数t ，得l 1的普通方程l 1：y ＝k (x －2)， 消去参数m ，得l 2的普通方程l 2：y ＝1k(x ＋2)．设P (x ，y )，由题设得⎩⎪⎨⎪⎧y ＝k x －2 ，y ＝1kx ＋2 .消去k 得x 2－y 2＝4(y ≠0)．所以C 的普通方程为x 2－y 2＝4(y ≠0)．(2)C 的极坐标方程为ρ2(cos 2θ－sin 2θ)＝4(0＜θ＜2π，θ≠π)．联立⎩⎨⎧ρ2 cos 2θ－sin 2θ ＝4，ρ cos θ＋sin θ －2＝0得cos θ－sin θ＝2(cos θ＋sin θ)． 故tan θ＝－13，从而cos 2θ＝910，sin 2θ＝110.代入ρ2(cos 2θ－sin 2θ)＝4得ρ2＝5， 所以交点M 的极径为 5.2．(2018·武昌调研)在直角坐标系xOy 中，曲线C的参数方程为⎩⎪⎨⎪⎧x ＝a cos t ，y ＝2sin t(t为参数，a >0)．以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，已知直线l 的极坐标方程为ρcos ⎝⎛⎭⎪⎫θ＋π4＝－2 2.(1)设P 是曲线C 上的一个动点，当a ＝2时，求点P 到直线l 的距离的最小值； (2)若曲线C 上的所有点均在直线l 的右下方，求a 的取值范围． 解：(1)由ρcos ⎝ ⎛⎭⎪⎫θ＋π4＝－22，得22(ρcos θ－ρsin θ)＝－22， 化成直角坐标方程，得22(x －y )＝－22， 即直线l 的方程为x －y ＋4＝0. 依题意，设P (2cos t,2sin t )， 则点P 到直线l 的距离d ＝|2cos t －2sin t ＋4|2＝⎪⎪⎪⎪⎪⎪22cos ⎝⎛⎭⎪⎫t ＋π4＋42＝22＋2cos ⎝⎛⎭⎪⎫t ＋π4.当cos ⎝⎛⎭⎪⎫t ＋π4＝－1时，d min ＝22－2.故点P 到直线l 的距离的最小值为22－2. (2)∵曲线C 上的所有点均在直线l 的右下方， ∴对∀t ∈R ，有a cos t －2sin t ＋4>0恒成立， 即a 2＋4cos(t ＋φ)>－4⎝ ⎛⎭⎪⎫其中tan φ＝2a 恒成立，∴a 2＋4<4， 又a >0，∴0<a <2 3. 故a 的取值范围为(0,23)．1．已知P为半圆C ：⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ(θ为参数，0≤θ≤π)上的点，点A 的坐标为(1,0)，O 为坐标原点，点M 在射线OP 上，线段OM 与C 的弧AP 的长度均为π3.(1)以O 为极点，x 轴的正半轴为极轴，建立极坐标系，求点M 的极坐标； (2)求直线AM 的参数方程． 解：(1)由已知，点M 的极角为π3，且点M 的极径等于π3，故点M 的极坐标为⎝ ⎛⎭⎪⎫π3，π3. (2)由(1)知点M 的直角坐标为⎝⎛⎭⎪⎫π6，3π6，A (1,0)．故直线AM 的参数方程为⎩⎪⎨⎪⎧x ＝1＋⎝ ⎛⎭⎪⎫π6－1t ，y ＝3π6t(t 为参数)．2．在平面直角坐标系xOy 中，曲线C 1过点P (a,1)，其参数方程为⎩⎨⎧x ＝a ＋2t ，y ＝1＋2t(t为参数，a ∈R)．以O 为极点，x 轴非负半轴为极轴，建立极坐标系，曲线C 2的极坐标方程为ρcos 2θ＋4cos θ－ρ＝0.(1)求曲线C 1的普通方程和曲线C 2的直角坐标方程；(2)已知曲线C 1与曲线C 2交于A ，B 两点，且|PA |＝2|PB |，求实数a 的值．解：(1)∵曲线C 1的参数方程为⎩⎨⎧x ＝a ＋2t ，y ＝1＋2t ，∴其普通方程为x －y －a ＋1＝0.∵曲线C 2的极坐标方程为ρcos 2θ＋4cos θ－ρ＝0， ∴ρ2cos 2θ＋4ρcos θ－ρ2＝0， ∴x 2＋4x －x 2－y 2＝0，即曲线C 2的直角坐标方程为y 2＝4x .(2)设A ，B 两点所对应的参数分别为t 1，t 2，将曲线C 1的参数方程代入曲线C 2的直角坐标方程，化简得2t 2－22t ＋1－4a ＝0. ∴Δ＝(－22)2－4×2(1－4a )>0，即a >0，t 1＋t 2＝2，t 1·t 2＝1－4a2. 根据参数方程的几何意义可知|PA |＝2|t 1|，|PB |＝2|t 2|， 又|PA |＝2|PB |可得2|t 1|＝2×2|t 2|， 即t 1＝2t 2或t 1＝－2t 2.∴当t 1＝2t 2时，有⎩⎪⎨⎪⎧t 1＋t 2＝3t 2＝2，t 1·t 2＝2t 22＝1－4a 2，解得a ＝136，符合题意．当t 1＝－2t 2时，有⎩⎪⎨⎪⎧t 1＋t 2＝－t 2＝2，t 1·t 2＝－2t 22＝1－4a 2，解得a ＝94，符合题意．综上，实数a ＝136或a ＝94.3．(2018·贵阳模拟)在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝4＋3cos t ，y ＝5＋3sin t (t为参数)，以坐标原点O 为极点，x 轴的非负半轴为极轴，建立极坐标系，曲线C 2的极坐标方程为ρ＝2sin θ.(1)求曲线C 1的普通方程和C 2的直角坐标方程；(2)若A ，B 分别为曲线C 1，C 2上的动点，求当AB 取最小值时△AOB 的面积． 解：(1)由⎩⎪⎨⎪⎧x ＝4＋3cos t ，y ＝5＋3sin t(t 为参数)得C 1的普通方程为(x －4)2＋(y －5)2＝9，由ρ＝2sin θ，得ρ2＝2ρsin θ， 将x 2＋y 2＝ρ2，y ＝ρsin θ代入上式， 得C 2的直角坐标方程为x 2＋(y －1)2＝1.(2)如图，当A ，B ，C 1，C 2四点共线，且A ，B 在线段C 1C 2上时，|AB |取得最小值，由(1)得C 1(4,5)，C 2(0,1)，则kC 1C 2＝5－14－0＝1，∴直线C 1C 2的方程为x －y ＋1＝0， ∴点O 到直线C 1C 2的距离d ＝12＝22， 又|AB |＝|C 1C 2|－1－3＝ 4－0 2＋ 5－1 2－4 ＝42－4，∴S △AOB ＝12d |AB |＝12×22×(42－4)＝2－ 2.4．(2018·广州综合测试)在直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝3－t ，y ＝1＋t (t为参数)．在以坐标原点O 为极点，x 轴正半轴为极轴的极坐标系中，曲线C ：ρ＝22cos ⎝⎛⎭⎪⎫θ－π4.(1)求直线l 的普通方程和曲线C 的直角坐标方程； (2)求曲线C 上的点到直线l 的距离的最大值．解：(1)由⎩⎪⎨⎪⎧x ＝3－t ，y ＝1＋t (t 为参数)消去t 得x ＋y －4＝0，所以直线l 的普通方程为x ＋y －4＝0.由ρ＝22cos ⎝ ⎛⎭⎪⎫θ－π4＝22⎝ ⎛⎭⎪⎫cos θcos π4＋sin θsin π4＝2cos θ＋2sin θ， 得ρ2＝2ρcos θ＋2ρsin θ.将ρ2＝x 2＋y 2，ρcos θ＝x ，ρsin θ＝y 代入上式， 得x 2＋y 2＝2x ＋2y ，即(x －1)2＋(y －1)2＝2. 所以曲线C 的直角坐标方程为(x －1)2＋(y －1)2＝2.(2)法一：设曲线C 上的点P (1＋2cos α，1＋2sin α)， 则点P 到直线l 的距离d ＝|1＋2cos α＋1＋2sin α－4|2＝|2 sin α＋cos α －2|2＝⎪⎪⎪⎪⎪⎪2sin ⎝ ⎛⎭⎪⎫α＋π4－22.当sin ⎝⎛⎭⎪⎫α＋π4＝－1时，d max ＝2 2.所以曲线C 上的点到直线l 的距离的最大值为2 2. 法二：设与直线l 平行的直线l ′：x ＋y ＋b ＝0， 当直线l ′与圆C 相切时，|1＋1＋b |2＝2，解得b ＝0或b ＝－4(舍去)， 所以直线l ′的方程为x ＋y ＝0.因为直线l 与直线l ′的距离d ＝|0＋4|2＝2 2.所以曲线C 上的点到直线l 的距离的最大值为2 2. 5．在直角坐标系xOy 中，曲线C 1：⎩⎪⎨⎪⎧x ＝t cos α，y ＝t sin α(t 为参数，t ≠0)，其中0≤α＜π.在以O 为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ＝2sin θ，C 3：ρ＝23cos θ.(1)求C 2与C 3交点的直角坐标；(2)若C 1与C 2相交于点A ，C 1与C 3相交于点B ，求|AB |的最大值． 解：(1)曲线C 2的直角坐标方程为x 2＋y 2－2y ＝0， 曲线C 3的直角坐标方程为x 2＋y 2－23x ＝0.联立⎩⎨⎧x 2＋y 2－2y ＝0，x 2＋y 2－23x ＝0，解得⎩⎪⎨⎪⎧x ＝0，y ＝0或⎩⎪⎨⎪⎧x ＝32，y ＝32.所以C 2与C 3交点的直角坐标为(0,0)和⎝⎛⎭⎪⎫32，32. (2)曲线C 1的极坐标方程为θ＝α(ρ∈R ，ρ≠0)，其中0≤α＜π. 因此A 的极坐标为(2sin α，α)，B 的极坐标为(23cos α，α)． 所以|AB |＝|2sin α－23cos α|＝4⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π3. 当α＝5π6时，|AB |取得最大值，最大值为4.6．已知直线L 的参数方程为⎩⎪⎨⎪⎧x ＝2＋t ，y ＝2－2t(t 为参数)，以原点O 为极点，x 轴的正半轴为极轴，建立极坐标系，曲线C 的极坐标方程为ρ＝21＋3cos 2θ.(1)求直线L 的极坐标方程和曲线C 的直角坐标方程；(2)过曲线C 上任意一点P 作与直线L 夹角为π3的直线l ，设直线l 与直线L 的交点为A ，求|PA |的最大值．解：(1)由⎩⎪⎨⎪⎧x ＝2＋t ，y ＝2－2t (t 为参数)，得L 的普通方程为2x ＋y －6＝0，令x ＝ρcos θ，y ＝ρsin θ，得直线L 的极坐标方程为2ρcos θ＋ρsin θ－6＝0， 由曲线C 的极坐标方程，知ρ2＋3ρ2cos 2θ＝4， 所以曲线C 的直角坐标方程为x 2＋y 24＝1.(2)由(1)，知直线L 的普通方程为2x ＋y －6＝0， 设曲线C 上任意一点P (cos α，2sin α)， 则点P 到直线L 的距离d ＝|2cos α＋2sin α－6|5.由题意得|PA |＝dsinπ3＝415⎪⎪⎪⎪⎪⎪2sin ⎝ ⎛⎭⎪⎫α＋π4－315，所以当sin ⎝⎛⎭⎪⎫α＋π4＝－1时，|PA |取得最大值，最大值为415 3＋2 15.7．(2018·石家庄一模)在平面直角坐标系中，将曲线C 1上的每一个点的横坐标保持不变，纵坐标缩短为原来的12，得到曲线C 2.以坐标原点O 为极点，x 轴的正半轴为极轴，建立极坐标系，已知曲线C 1的极坐标方程为ρ＝2.(1)求曲线C 2的参数方程；(2)过坐标原点O 且关于y 轴对称的两条直线l 1与l 2分别交曲线C 2于A ，C 和B ，D ，且点A 在第一象限，当四边形ABCD 的周长最大时，求直线l 1的普通方程．解：(1)由ρ＝2，得ρ2＝4，所以曲线C 1的直角坐标方程为x 2＋y 2＝4. 故由题意可得曲线C 2的直角坐标方程为x 24＋y 2＝1.所以曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝2cos θ，y ＝sin θ(θ为参数)．(2)设四边形ABCD 的周长为l ，点A (2cos θ，sin θ)，则l ＝8cos θ＋4sin θ＝45sin(θ＋φ)，⎝⎛⎭⎪⎫其中sin φ＝25，cos φ＝15 所以当θ＋φ＝2k π＋π2(k ∈Z)时，l 取得最大值，最大值为45，此时θ＝2k π＋π2－φ(k ∈Z)，所以2cos θ＝2sin φ＝45，sin θ＝cos φ＝15，此时A ⎝ ⎛⎭⎪⎫45，15.所以直线l 1的普通方程为x －4y ＝0.8．(2018·成都诊断)在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos α，y ＝2＋2sin α(α为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝3－32t ，y ＝3＋12t (t 为参数)．在以坐标原点O 为极点，x 轴的正半轴为极轴的极坐标系中，过极点O 的射线与曲线C 相交于不同于极点的点A ，且点A 的极坐标为(23，θ)，其中θ∈⎝ ⎛⎭⎪⎫π2，π.(1)求θ的值；(2)若射线OA 与直线l 相交于点B ，求|AB |的值． 解：(1)由题意知，曲线C 的普通方程为x 2＋(y －2)2＝4，∵x ＝ρcos θ，y ＝ρsin θ，∴曲线C 的极坐标方程为(ρcos θ)2＋(ρsin θ－2)2＝4， 即ρ＝4sin θ. 由ρ＝23，得sin θ＝32， ∵θ∈⎝⎛⎭⎪⎫π2，π，∴θ＝2π3.(2)易知直线l 的普通方程为x ＋3y －43＝0，∴直线l 的极坐标方程为ρcos θ＋3ρsin θ－43＝0. 又射线OA 的极坐标方程为θ＝2π3(ρ≥0)，联立⎩⎪⎨⎪⎧θ＝2π3 ρ≥0 ，ρcos θ＋3ρsin θ－43＝0，解得ρ＝4 3.∴点B 的极坐标为⎝ ⎛⎭⎪⎫43，2π3，∴|AB |＝|ρB －ρA |＝43－23＝2 3.。

参数方程【考点梳理】1．曲线的参数方程一般地，在平面直角坐标系中，如果曲线上任意一点的坐标x ，y 都是某个变数t 的函数⎩⎪⎨⎪⎧x ＝f t ，y ＝g t并且对于t 的每一个允许值，由这个方程组所确定的点M (x ，y )都在这条曲线上，那么这个方程组就叫做这条曲线的参数方程，联系变数x ，y 的变数t 叫做参变数，简称参数．2．参数方程与普通方程的互化通过消去参数从参数方程得到普通方程，如果知道变数x ，y 中的一个与参数t 的关系，例如x ＝f (t )，把它代入普通方程，求出另一个变数与参数的关系y ＝g (t )，那么⎩⎪⎨⎪⎧x ＝f t ，y ＝gt就是曲线的参数方程．在参数方程与普通方程的互化中，必须使x ，y 的取值范围保持一致．3．常见曲线的参数方程和普通方程考点一、参数方程与普通方程的互化【例1】已知曲线C 1：⎩⎪⎨⎪⎧x ＝－4＋cos t ，y ＝3＋sin t(t 为参数)，C 2：⎩⎪⎨⎪⎧x ＝8cos θ，y ＝3sin θ(θ为参数).(1)化C 1，C 2的方程为普通方程，并说明它们分别表示什么曲线；(2)若C 1上的点P 对应的参数为t ＝π2，Q 为C 2上的动点，求PQ 的中点M 到直线C 3：⎩⎪⎨⎪⎧x ＝3＋2t ，y ＝－2＋t (t 为参数)距离的最小值. [解析] (1)由C 1消去参数t ，得曲线C 1的普通方程为(x ＋4)2＋(y －3)2＝1. 同理曲线C 2的普通方程为x 264＋y 29＝1.C 1表示圆心是(－4，3)，半径是1的圆，C 2表示中心是坐标原点，焦点在x 轴上，长半轴长是8，短半轴长是3的椭圆.(2)当t ＝π2时，P (－4，4)，又Q (8cos θ，3sin θ)，故M ⎝⎛⎭⎪⎫－2＋4cos θ，2＋32sin θ，又C 3的普通方程为x －2y －7＝0， 则M 到直线C 3的距离d ＝55|4cos θ－3sin θ－13|＝55|3sin θ－4cos θ＋13| ＝55|5(sin θ－φ)＋13|⎝⎛⎭⎪⎫其中φ满足tan φ＝43，所以d 的最小值为855.【类题通法】1．将参数方程化为普通方程，消参数常用代入法、加减消元法、三角恒等变换消去参数． 2．把参数方程化为普通方程时，要注意哪一个量是参数，并且要注意参数的取值对普通方程中x 及y 的取值范围的影响，要保持同解变形． 【对点训练】在直角坐标系xOy 中，曲线C的参数方程为⎩⎪⎨⎪⎧x ＝3cos θ，y ＝sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋4t ，y ＝1－t (t 为参数).(1)若a ＝－1，求C 与l 的交点坐标； (2)若C 上的点到l 距离的最大值为17，求a .[解析] (1)a ＝－1时，直线l 的普通方程为x ＋4y －3＝0. 曲线C 的标准方程是x 29＋y 2＝1，联立方程⎩⎪⎨⎪⎧x ＋4y －3＝0，x 29＋y 2＝1，解得⎩⎪⎨⎪⎧x ＝3，y ＝0或⎩⎪⎨⎪⎧x ＝－2125，y ＝2425.则C 与l 交点坐标是(3，0)和⎝ ⎛⎭⎪⎫－2125，2425. (2)直线l 的普通方程是x ＋4y －4－a ＝0. 设曲线C 上点P (3cos θ，sin θ).则P 到l 距离d ＝|3cos θ＋4sin θ－4－a |17＝|5sin （θ＋φ）－4－a |17，其中tan φ＝34.又点C 到直线l 距离的最大值为17. ∴|5sin(θ＋φ)－4－a |的最大值为17. 若a ≥0，则－5－4－a ＝－17，∴a ＝8. 若a <0，则5－4－a ＝17，∴a ＝－16. 综上，实数a 的值为a ＝－16或a ＝8.考点二、参数方程的应用【例2】在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2＋2sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1－22t ，y ＝22t (t 为参数).以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系.(1)写出直线l 的普通方程以及曲线C 的极坐标方程；(2)若直线l 与曲线C 的两个交点分别为M ，N ，直线l 与x 轴的交点为P ，求|PM |·|PN |的值.[解析] (1)直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1－22t ，y ＝22t (t 为参数)，消去参数t ，得x ＋y －1＝0.曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2＋2sin θ(θ为参数)，利用平方关系，得x 2＋(y －2)2＝4，则x 2＋y 2－4y ＝0.令ρ2＝x 2＋y 2，y ＝ρsin θ，代入得C 的极坐标方程为ρ＝4sin θ. (2)在直线x ＋y －1＝0中，令y ＝0，得点P (1，0). 把直线l 的参数方程代入圆C 的方程得t 2－32t ＋1＝0， ∴t 1＋t 2＝32，t 1t 2＝1.由直线参数方程的几何意义，|PM |·|PN |＝|t 1·t 2|＝1. 【类题通法】过定点P 0(x 0，y 0)，倾斜角为α的直线参数方程的标准形式为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)，t 的几何意义是P 0P →的数量，即|t |表示P 0到P 的距离，t 有正负之分.对于形如⎩⎪⎨⎪⎧x ＝x 0＋at ，y ＝y 0＋bt (t为参数)，当a 2＋b 2≠1时，应先化为标准形式后才能利用t 的几何意义解题. 【对点训练】在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎨⎧x ＝5cos α，y ＝sin α(α为参数).以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρcos ⎝⎛⎭⎪⎫θ＋π4＝ 2.l 与C交于A ，B 两点.(1)求曲线C 的普通方程及直线l 的直角坐标方程； (2)设点P (0，－2)，求|PA |＋|PB |的值.[解析] (1)由曲线C ：⎩⎨⎧x ＝5cos α，y ＝sin α(α为参数)消去α，得普通方程x 25＋y 2＝1.因为直线l 的极坐标方程为ρcos ⎝ ⎛⎭⎪⎫θ＋π4＝2，即ρcos θ－ρsin θ＝2， 所以直线l 的直角坐标方程为x －y －2＝0.(2)点P (0，－2)在l 上，则l 的参数方程为⎩⎪⎨⎪⎧x ＝22t ，y ＝－2＋22t (t 为参数)，代入x 25＋y 2＝1整理得3t 2－102t ＋15＝0，由题意可得|PA |＋|PB |＝|t 1|＋|t 2|＝|t 1＋t 2|＝1023.考点三、参数方程与极坐标方程的综合应用【例3】在直角坐标系xOy 中，直线l 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋t ，y ＝kt (t 为参数)，直线l 2的参数方程为⎩⎪⎨⎪⎧x ＝－2＋m ，y ＝m k(m 为参数).设l 1与l 2的交点为P ，当k 变化时，P 的轨迹为曲线C .(1)写出C 的普通方程；(2)以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设l 3：ρ(cos θ＋sin θ)－2＝0，M 为与C 的交点，求M 的极径.[解析] (1)由l 1：⎩⎪⎨⎪⎧x ＝2＋t ，y ＝kt (t 为参数)消去t ，化为l 1的普通方程y ＝k (x －2)，① 同理得直线l 2的普通方程为x ＋2＝ky ，② 联立①，②消去k ，得x 2－y 2＝4(y ≠0).所以C 的普通方程为x 2－y 2＝4(y ≠0). (2)将直线l 3化为普通方程为x ＋y ＝2， 联立⎩⎨⎧x ＋y ＝2，x 2－y 2＝4得⎩⎪⎨⎪⎧x ＝322，y ＝－22，∴ρ2＝x 2＋y 2＝184＋24＝5，∴与C 的交点M 的极径为 5.【类题通法】1．参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解．当然，还要结合题目本身特点，确定选择何种方程．2．数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用ρ和θ的几何意义，直接求解，可化繁为简． 【对点训练】已知曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2＋2cos θ，y ＝2sin θ(θ为参数)，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρsin ⎝⎛⎭⎪⎫θ＋π6＝4.(1)写出曲线C 的极坐标方程和直线l 的普通方程；(2)若射线θ＝π3与曲线C 交于O ，A 两点，与直线l 交于B 点，射线θ＝11π6与曲线C交于O ，P 两点，求△PAB 的面积.[解析] (1)由⎩⎪⎨⎪⎧x ＝2＋2cos θ，y ＝2sin θ(θ为参数)，消去θ.普通方程为(x －2)2＋y 2＝4.从而曲线C 的极坐标方程为ρ2－4ρcos θ＝0，即ρ＝4cos θ，因为直线l 的极坐标方程为ρsin ⎝⎛⎭⎪⎫θ＋π6＝4，即32ρsin θ＋12ρcos θ＝4，∴直线l 的直角坐标方程为x ＋3y －8＝0.(2)依题意，A ，B 两点的极坐标分别为⎝⎛⎭⎪⎫2，π3，⎝ ⎛⎭⎪⎫4，π3，联立射线θ＝11π6与曲线C 的极坐标方程得P 点极坐标为⎝ ⎛⎭⎪⎫23，11π6，∴|AB |＝2，∴S △PAB ＝12×2×23sin ⎝ ⎛⎭⎪⎫π3＋π6＝2 3.。

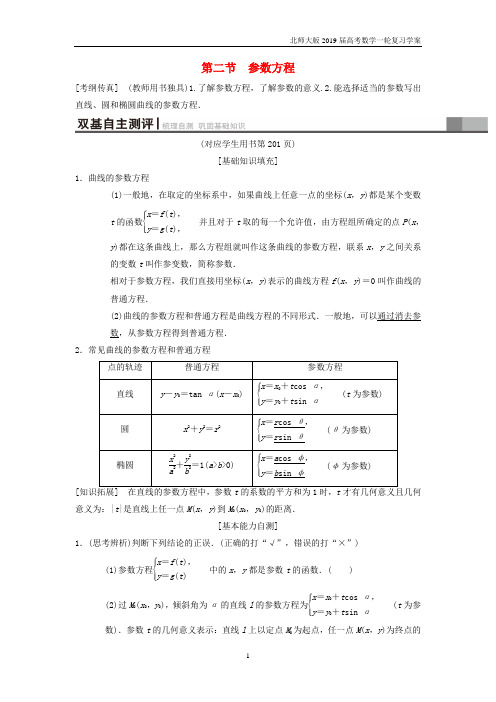
第二节 参数方程[考纲传真] (教师用书独具)1.了解参数方程，了解参数的意义.2.能选择适当的参数写出直线、圆和椭圆曲线的参数方程．(对应学生用书第201页)[基础知识填充]1．曲线的参数方程(1)一般地，在取定的坐标系中，如果曲线上任意一点的坐标(x ，y )都是某个变数t 的函数⎩⎪⎨⎪⎧x ＝f (t )，y ＝g (t )，并且对于t 取的每一个允许值，由方程组所确定的点P (x ，y )都在这条曲线上，那么方程组就叫作这条曲线的参数方程，联系x ，y 之间关系的变数t 叫作参变数，简称参数．相对于参数方程，我们直接用坐标(x ，y )表示的曲线方程f (x ，y )＝0叫作曲线的普通方程．(2)曲线的参数方程和普通方程是曲线方程的不同形式．一般地，可以通过消去参数，从参数方程得到普通方程．2．常见曲线的参数方程和普通方程[意义为：|t |是直线上任一点M (x ，y )到M 0(x 0，y 0)的距离．[基本能力自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)参数方程⎩⎪⎨⎪⎧x ＝f (t )，y ＝g (t )中的x ，y 都是参数t 的函数．( )(2)过M 0(x 0，y 0)，倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．参数t 的几何意义表示：直线l 上以定点M 0为起点，任一点M (x ，y )为终点的有向线段M 0M →的数量．( ) (3)方程⎩⎪⎨⎪⎧x ＝2cos θ，y ＝1＋2sin θ表示以点(0,1)为圆心，以2为半径的圆．( )(4)已知椭圆的参数方程⎩⎪⎨⎪⎧x ＝2cos t ，y ＝4sin t(t 为参数)，点M 在椭圆上，对应参数t＝π3，点O 为原点，则直线OM 的斜率为 3.( ) [答案] (1)√ (2)√ (3)√ (4)×2．(教材改编)曲线⎩⎪⎨⎪⎧x ＝－1＋cos θ，y ＝2＋sin θ(θ为参数)的对称中心( ) A ．在直线y ＝2x 上 B ．在直线y ＝－2x 上 C ．在直线y ＝x －1上D ．在直线y ＝x ＋1上B [由⎩⎪⎨⎪⎧x ＝－1＋cos θ，y ＝2＋sin θ，得⎩⎪⎨⎪⎧cos θ＝x ＋1，sin θ＝y －2，所以(x ＋1)2＋(y －2)2＝1.曲线是以(－1,2)为圆心，1为半径的圆， 所以对称中心为(－1,2)，在直线y ＝－2x 上．] 3．(教材改编)在平面直角坐标系中，曲线C ：⎩⎪⎨⎪⎧x ＝2＋22t ，y ＝1＋22t (t 为参数)的普通方程为________．x －y －1＝0 [由x ＝2＋22t ，且y ＝1＋22t ， 消去t ，得x －y ＝1，即x －y －1＝0.] 4．椭圆C 的参数方程为⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ(φ为参数)，过左焦点F 1的直线l 与C 相交于A ，B ，则|AB |min ＝________.185 [由⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ(φ为参数)，消去参数φ得x 225＋y 29＝1，当AB ⊥x 轴时，|AB |有最小值． 所以|AB |min ＝2×95＝185.]5．(2017·江苏高考)在平面直角坐标系xOy 中，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－8＋t ，y ＝t2(t 为参数)，曲线C 的参数方程为⎩⎨⎧x ＝2s 2，y ＝22s(s 为参数)．设P 为曲线C 上的动点，求点P 到直线l 的距离的最小值．[解] 直线l 的普通方程为x －2y ＋8＝0. 因为点P 在曲线C 上，设P (2s 2,22s )， 从而点P 到直线l 的距离d ＝|2s 2－42s ＋8|12＋(－2)2＝2(s －2)2＋45. 当s ＝2时，d min ＝455.因此当点P 的坐标为(4,4)时，曲线C 上的点P 到直线l 的距离取到最小值455.(对应学生用书第202页)(1)求直线⎩⎪⎨⎪⎧x ＝2＋t ，y ＝－1－t(t 为参数)与曲线⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α(α为参数)的交点个数．(2)在平面直角坐标系xOy中，若直线l ：⎩⎪⎨⎪⎧x ＝t ，y ＝t －a (t 为参数)过椭圆C ：⎩⎪⎨⎪⎧x ＝3cos φ，y ＝2sin φ(φ为参数)的右顶点，求常数a 的值.【导学号：79140389】[解] (1)将⎩⎪⎨⎪⎧x ＝2＋t ，y ＝－1－t消去参数t 得直线x ＋y －1＝0；将⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α消去参数α得圆x 2＋y 2＝9.又圆心(0,0)到直线x ＋y －1＝0的距离d ＝22<3.因此直线与圆相交，故直线与曲线有2个交点． (2)直线l 的普通方程为x －y －a ＝0， 椭圆C 的普通方程为x 29＋y 24＝1，所以椭圆C 的右顶点坐标为(3,0)，若直线l 过(3,0)， 则3－a ＝0，∴a ＝3.法、加减消去法、恒等式三角的或代数的消去法普通方程化为参数方程时，先分清普通方程所表示的曲线类型，图2[解] 圆的半径为12，记圆心为C ⎝ ⎛⎭⎪⎫12，0，连接CP ， 则∠PCx ＝2θ，故x P ＝12＋12cos 2θ＝cos 2θ，y P ＝12sin 2θ＝sin θcos θ(θ为参数)．所以圆的参数方程为⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝sin θcos θ(θ为参数)．(2017·石家庄质检)在平面直角坐标系xOy 中，圆C 的参数方程为⎩⎪⎨⎪⎧x ＝4cos θ，y ＝4sin θ(θ为参数)，直线l 经过点P (1,2)，倾斜角α＝π6.(1)写出圆C 的普通方程和直线l 的参数方程；(2)设直线l 与圆C 相交于A ，B 两点，求|PA |·|PB |的值．[解] (1)由⎩⎪⎨⎪⎧x ＝4cos θ，y ＝4sin θ，消去θ，得圆C 的普通方程为x 2＋y 2＝16. 又直线l 过点P (1,2)且倾斜角α＝π6，所以l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋t cos π6，y ＝2＋t sin π6，即⎩⎪⎨⎪⎧x ＝1＋32t ，y ＝2＋12t (t 为参数)．(2)把直线l 的参数方程⎩⎪⎨⎪⎧x ＝1＋32t ，y ＝2＋12t代入x 2＋y 2＝16，得⎝⎛⎭⎪⎫1＋32t 2＋⎝ ⎛⎭⎪⎫2＋12t 2＝16，t 2＋(3＋2)t －11＝0，所以t 1t 2＝－11，由参数方程的几何意义，|PA |·|PB |＝|t 1t 2|＝11. 解决与圆、圆锥曲线的参数方程有关的综合问题时，要注意普通方程与参数方程的互化公式，主要是通过互化解决与圆、圆锥曲线上与动点有关的问题，如最值、根据直线的参数方程的标准式中过定点M ①弦长l⎩⎪⎨⎪⎧x ＝3cos θ，y ＝sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋4t ，y ＝1－t(t 为参数)．(1)若a ＝－1，求C 与l 的交点坐标； (2)若C 上的点到l 距离的最大值为17，求a . [解] (1)曲线C 的普通方程为x 29＋y 2＝1.当a ＝－1时，直线l 的普通方程为x ＋4y －3＝0.由⎩⎪⎨⎪⎧x ＋4y －3＝0，x 29＋y 2＝1，解得⎩⎪⎨⎪⎧x ＝3，y ＝0或⎩⎪⎨⎪⎧x ＝－2125，y ＝2425.从而C 与l 的交点坐标为(3,0)，⎝ ⎛⎭⎪⎫－2125，2425.(2)直线l 的普通方程为x ＋4y －a －4＝0，故C 上的点(3cos θ，sin θ)到l 的距离为d ＝|3cos θ＋4sin θ－a －4|17.当a ≥－4时，d 的最大值为a ＋917.由题设得a ＋917＝17，所以a ＝8;当a ＜－4时，d 的最大值为－a ＋117. 由题设得－a ＋117＝17，所以a ＝－16.综上，a ＝8或a ＝－16.(2018·石家庄质检(二))在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋a cos β，y ＝a sin β(a >0，β为参数)．以O 为极点，x 轴的正半轴为极轴，建立极坐标系，直线l 的极坐标方程ρcos ⎝⎛⎭⎪⎫θ－π3＝32.(1)若曲线C 与l 只有一个公共点，求a 的值；(2)A ，B 为曲线C 上的两点，且∠AOB ＝π3，求△OAB 的面积最大值．[解] (1)曲线C 是以(a,0)为圆心，以a 为半径的圆， 直线l 的直角坐标方程为x ＋3y －3＝0.由直线l 与圆C 只有一个公共点，则可得|a －3|2＝a ，解得a ＝－3(舍)，a ＝1. 所以a ＝1.(2)法一：曲线C 的极坐标方程为ρ＝2a cos θ(a >0)， 设A 的极角为θ，B 的极角为θ＋π3，则S △OAB ＝12|OA |·|OB |sin π3＝34|2a cos θ|·⎪⎪⎪⎪⎪⎪2a cos ⎝⎛⎭⎪⎫θ＋π3＝3a 2⎪⎪⎪⎪⎪⎪cos θcos ⎝⎛⎭⎪⎫θ＋π3，∵cos θcos ⎝ ⎛⎭⎪⎫θ＋π3＝12cos 2θ－32sin θcos θ ＝12·cos 2θ＋12－34sin 2θ ＝12⎝ ⎛⎭⎪⎫12cos 2θ－32sin 2θ＋14 ＝12cos ⎝⎛⎭⎪⎫2θ＋π3＋14，所以当θ＝－π6时，12cos ⎝ ⎛⎭⎪⎫2θ＋π3＋14取得最大值34.△OAB 的面积最大值为33a24.法二：因为曲线C 是以(a,0)为圆心，以a 为半径的圆，且∠AOB ＝π3，由正弦定理得|AB |sinπ3＝2a ，所以|AB |＝3a .由余弦定理得|AB |2＝3a 2＝|OA |2＋|OB |2－|OA |·|OB | ≥|OA |·|OB |，所以S △OAB ＝12|OA |·|OB |sin π3≤12×3a 2×32＝33a 24， 所以△OAB 的面积最大值为33a 24.涉及参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用意义，直接求解，能达到化繁为简的解题目的[跟踪训练1⎩⎪⎨⎪⎧x ＝2cos φ，y ＝sin φ(其中φ为参数)．以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 2的极坐标方程是ρ(tan α·cos θ－sin θ)＝1(α是常数，0<α<π，且α≠π2)，点A ，B (A 在x 轴的下方)是曲线C 1与C 2的两个不同交点．(1)求曲线C 1的普通方程和C 2的直角坐标方程； (2)求|AB |的最大值及此时点B 的坐标.【导学号：79140390】[解] (1)∵⎩⎪⎨⎪⎧x ＝2cos φ，y ＝sin φ，∴x 24＋y 2＝1，由⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ得曲线C 2的直角坐标方程为y ＝tan α·x －1.(2)由(1)得曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝－1＋t sin α(t 是参数)，设A (t 1cos α，－1＋t 1sin α)，B (t 2cos α，－1＋t 2sin α)，将C 2：⎩⎪⎨⎪⎧x ＝t cos α，y ＝－1＋t sin α，代入x 24＋y 2＝1，整理得t 2(1＋3sin 2α)－8t sin α＝0， ∴t 1＝0，t 2＝8sin α1＋3sin α， ∴|AB |＝|t 1－t 2|＝8|sin α|1＋3sin 2α ＝83|sin α|＋1|sin α|≤823＝433(当且仅当sin α＝33取等号)， 当sin α＝33时，∴0<α<π，且α≠π2， ∴cos α＝±63， ∴B ⎝ ⎛⎭⎪⎫±423，13， ∴|AB |的最大值为433，此时点B 的坐标为⎝ ⎛⎭⎪⎫±423，13.。

Unit 4 Body languageⅠ.单项填空1．(2018·潍坊第一中学高三联考)At the class meeting, some top students introduced several ________ to the study of English.A．approaches B．meansC．methods D．ways解析：approach(es) to……的方法。

means 和 method 表达此意时常和 of 连用；way 可和 of 连用也可接 to do。

答案：A2．—She ________ her back to her friends when they turned to her for help.—That's the reason why she is lonely now.A．won B．turnedC．spy D．consult解析：句意：“当她的朋友们向她求助时，她背信弃义。

”“这就是她现在那么孤独的原因。

”turn one's back to 背对，背弃。

win...back 赢回……，重新获得……；spy 窥视，秘密监视；consult 咨询，请教，商量。

答案： B3．(2018·湖北孝感市统考)Don't blame them any more—this is ________ because they are still young and lack experience.A．exactly B．simplyC．eventually D．generally解析：simply 仅仅。

句意：不要再责备他们了——这只是因为他们年轻，缺乏经验。

exactly 的确；eventually 最终；generally 一般说来。

答案：B4．—Look, John's fallen asleep at work!—Oh, he must have ________ late last night.A．waken up B．put upC．taken up D．stayed up解析：考查动词短语辨析。

第二节参数方程［考纲传真］1. 了解参数方程，了解参数的意义2能选择适当的参数写出直线、圆和椭圆曲线的参数方程.般地，在平面直角坐标系中，如果曲线上任意一点的坐标,都是某个变数的函数|x= f t ,并且对于t的每一个允许值，由这个方程组所确定的点Mx, y）都在这y=g t条曲线上，那么这个方程组就叫做这条曲线的参数方程，联系变数x, y的变数t叫做参变数，简称参数.2•参数方程和普通方程的互化（1）曲线的参数方程和普通方程是曲线方程的不同形式. 一般地，可以通过消去参数从参数方程得到普通方程.（2）如果知道变数x, y中的一个与参数t的关系，例如x = f（t），把它代入普通方程，|x = f t ，求出另一个变数与参数的关系y = g（t），那么就是曲线的参数方程.l y=g t3•常见曲线的参数方程和普通方程温馨提示：在直线的参数方程中，参数t的系数的平方和为1时，t才有几何意义且几何意义为：|t|是直线上任一点M x，y）到M（x o，y o）的距离.［基本能力自测］1. （思考辨析）判断下列结论的正误.（正确的打“V”，错误的打“x”）x= f t ，（1）参数方程F 中的x，y都是参数t的函数.（）i y= g t（2）过M 0（x o,y o ），倾斜角为a 的直线I 的参数方程为y = y o + t sin a 数t 的几何意义表示：直线 I 上以定点M 0为起点，任一点 Mx , y ）为终点的有向线段 MM的数量.（）x = 2cos 0 ,⑶方程表示以点（0,1）为圆心，以2为半径的圆.（）|y = 1 + 2sin 0消去 t ,得 x — y = 1，即 x — y — 1 = 0.] 4.在平面直角坐标系xOy 中，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系.曲线rx 2一 x = t,C 的极坐标方程为 P （cos 0 + sin 0 ） =— 2，曲线G 的参数方程为* 厂 （t 为J= A/2t参数），则C 与C 2交点的直角坐标为 __________ .X = X o + t COS a ,（t 为参数）•参⑷ 已知椭圆的参数方程x = 2cos t , y = 4sin t（t 为参数），点M 在椭圆上，对应参数 点O 为原点，则直线 OM 勺斜率为•. 3.（ ）［答案］ ⑴ V (2) V (3) V ⑷Xx =— 1 + cos 0 ,2.(教材改编)曲线*y = 2 + sin 0A .在直线y = 2x 上C.在直线y = x — 1上（0为参数）的对称中心（B.在直线y = — 2x 上D.在直线y = x + 1上—1 + cosy = 2+ sin 0cos 0 = X + 1 , 得sin 0 = y — 2,所以(x + 1)2+ (y — 2)2= 1.曲线是以（一1,2）为圆心，1为半径的圆, 所以对称中心为（一1,2），在直线y =— 2x 上.]x = 2 + 于，3.（教材改编）在平面直角坐标系中，曲线C <l y = 1 +#（t 为参数）的普通方程x — y — 1 = 0 ［由 x = 2+ t ,（2, —4）[由p （cos 0 + sin 0 ）= —2，得x+ y = — 2.①「X = t 2, 由， 厂 消去t 得y. 8x .② y= 2曲,|x = 2,联立①②得即交点坐标为（2 , - 4）.］5 . （2016 •江苏高考）在平面直角坐标系xOy 中，已知直线I 的参数方程为X = cos 0 ,（t为参数），椭圆C 的参数方程为I = 2sin 0直线I 与椭圆C 相交于A, B 两点，求线段 AB 的长.2［解］椭圆C 的普通方程为x 2+七=1.2分+ 16t = 0,（对应学生用书第162页）参数方程与普通方程的互化卜例H 已知直线l 的参数方程为F = a-2t ， （t 为参数），圆C 的参数方程为 l y =- 4tx = 4cos 0 ,（0为参数）.y = 4s in 0（1） 求直线I 和圆C 的普通方程；（2） 若直线l 与圆C 有公共点，求实数 a 的取值范围. ［解］（1）直线l 的普通方程为2x - y - 2a = 0,2 2圆C 的普通方程为x + y = 16. （2）因为直线l 与圆C 有公共点，（0为参数）.设【导学号：00090372】2代入x 2+y 4=1，得解得t 1= 0,t 2=- 176，所以 AB= |t 1-1216|=〒题型分类突破I将直线l 的参数方程1+$2+10分解得—2 5W a W2 5.故圆C 的圆心到直线 10分l 的距离d =直线与圆的位置关系来解决问题. 2.对于形如,x = + at ， （t 为参数），当a 2 + b 2工1时，应先化为标准形式后才能利用y = y o + bt［规律方法］1.将参数方程化为普通方程，消参数常用代入法、加减消元法、三角恒等变换消去参数.2 •把参数方程化为普通方程时，要注意哪一个量是参数，并且要注意参数的取值对普通 方程中x 及y 的取值范围的影响，要保持同解变形. ［变式训练1］在平面直角坐标系 xOy 中，若直线I : <x =t ， （t 为参数）过椭圆C:y = t — a x = 3cos $ ,（$为参数）的右顶点，求常数y = 2s in $a 的值.［解］ 直线I 的普通方程为x — y — a = 0,2 2椭圆C 的普通方程为牛+ y =1, 所以椭圆C 的右顶点坐标为（3,0）, 若直线I 过椭圆的右顶点（3,0）, 则 3— 0— a = 0，所以 a = 3.10分"■'I（2018 •合肥模拟）已知曲线x = 2 + t , y = 2 — 2t(t 为参数）.（1）写出曲线C 的参数方程，直线I 的普通方程; ⑵过曲线C 上任意一点P 作与I夹角为 30°的直线，交I 于点A 求|PA 的最大值与最小值.x = 2cos［解］（1）曲线C 的参数方程为彳|y = 3si n （0为参数）•直线I 的普通方程为2x + y — 6 = 0.⑵曲线C 上任意一点F （2cos 0 , 3sin的距离为d = #4cos0 + 3sin0 —6| ,则|PA扁—=¥佝n （ 0+a ） —6|，其中a为锐角，且tan当 sin(a ）=— 1时，|PA 取得最大值，最大值为 辛当 sin( a ） = 1时，| PA 取得最小值，最小值为 电2510分 ［规律1.解决直线与圆的参数方程的应用问题时,般是先化为普通方程,再根据t 的几何意义解题.［变式训练 2］ （2017 •石家庄质检）在平面直角坐标系 xOy 中，圆 C 的参数方程为x = 4cos 0 , n<（0为参数），直线I 经过点P （1,2），倾斜角a =—.y = 4sin 06（1） 写出圆C 的普通方程和直线I 的参数方程；（2） 设直线I 与圆C 相交于A , B 两点，求| PA •I PB 的值•【导学号：00090373】x = 4cos 0 ,［解］⑴由*消去0 ,|y = 4sin 0 ,得圆C 的普通方程为x 2+ y 2= 16.2分(nx = 1 + t COS 才, 6所以I 的参数方程为＜；[y = 2 + t sin 青,( y[3 x =1 +即1 y = 2+2t代入 x 2+ y 2= 16,所以 t 1t 2 =— 11 ,由参数方程的几何意义，|PA • PB = |t 1t 2| = 11.10分1■耐— ......................... J参数方程与极坐标方程的综合应用x = 2+ t ,卜（2017 •全国卷川）在直角坐标系xOy 中，直线11的参数方程为1（t 为l y =ktx =— 2+m又直线l 过点R1,2）且倾斜角 （t 为参数）.得 1 + 爭 2+ 2 + 9 2= 16, t 2+ ( 3 + 2)t — 11 = 0,参数），直线I 2的参数方程为（m 为参数）.设11与12的交点为P,当k71（2）把直线l 的参数方程变化时，P的轨迹为曲线C.(1)写出c的普通方程；⑵以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设I 3：p (cos 0 + sin 0 ) —2=0, M为丨3与C的交点，求M的极径.［解］⑴消去参数t得l i的普通方程11: y= k(x —2)；1消去参数m得12的普通方程丨2：y= k(x+ 2).y=k x-2 , 设Rx, y)，由题设得 1 “y=k x+「消去k 得x2—y2= 4( y z 0).所以C的普通方程为x2—y2= 4(y丰0). 4分⑵C 的极坐标方程为p 2(cos 20 —sin 20 ) = 4(0< 0 <2 n , 0 z n ). 5 分f p 2血20 —sin 20 = 4,联立' “厂得(：QS 0 + sin 0 —72= 0L Pcos 0 —sin 0 = 2(cos 0 + sin 0 ). 6 分故tan0 =—1,从而cos20 = 190, sin20 =^代p (cos 0 —sin 0 ) = 4 得p = 5,所以交点M的极径为，5. 10分［规律方法］1.参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解.当然，还要结合题目本身特点，确定选择何种方程.2 .数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用p和0的几何意义，直接求解，可化繁为简.［变式训练3］(2016 •全国卷川)在直角坐标系xOy中，曲线C的参数方程为x = V3cos a ,1 ( a为参数).以坐标原点为极点，以x轴的正半轴为极轴，建立极y = sin a坐标系，曲线C2的极坐标方程为p sin 0 + nn = 2 , 2.(1)写出C的普通方程和C2的直角坐标方程；⑵设点P在C上，点Q在C2上，求| PQ的最小值及此时P的直角坐标.2［解］(1) C的普通方程为号+ y2= 1, 2分由于曲线G的方程为p sin所以p sin 0 + p cos 0 = 4,因此曲线C2的直角坐标方程为x+ y— 4 = 0.⑵由题意，可设点P的直角坐标为(J3C OS a , sin a ). 因为C2是直线，所以I PQ的最小值即为P到C2的距离d( a )的最小值,又d(\ H/3COSa )= ' ---a + sin2^=£sin [当且仅当a = 2k n+青(k € Z)时，d( a )取得最小值，最小值为 .㊁, 2.8分此时P的直角坐标10分。

坐标系与参数方程【2019年高考考纲解读】高考主要考查平面直角坐标系中的伸缩变换、直线和圆的极坐标方程、参数方程与普通方程的互化、常见曲线的参数方程及参数方程的简单应用．以极坐标、参数方程与普通方程的互化为主要考查形式，同时考查直线与曲线的位置关系等解析几何知识． 【重点、难点剖析】 1．直角坐标与极坐标的互化把直角坐标系的原点作为极点，x 轴正半轴作为极轴，且在两坐标系中取相同的长度单位．设M 是平面内的任意一点，它的直角坐标、极坐标分别为(x ，y )和(ρ，θ)，则⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ，⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝y x x2．直线的极坐标方程若直线过点M (ρ0，θ0)，且极轴到此直线的角为α，则它的方程为：ρsin(θ－α)＝ρ0sin(θ0－α)． 几个特殊位置的直线的极坐标方程 (1)直线过极点：θ＝α；(2)直线过点M (a,0)(a >0)且垂直于极轴：ρcos θ＝a ；(3)直线过M ⎝⎛⎭⎪⎫b ，π2且平行于极轴：ρsin θ＝b .3．圆的极坐标方程若圆心为M (ρ0，θ0)，半径为r 的圆方程为： ρ2－2ρ0ρcos(θ－θ0)＋ρ20－r 2＝0. 几个特殊位置的圆的极坐标方程 (1)当圆心位于极点，半径为r ：ρ＝r ；(2)当圆心位于M (r,0)，半径为r ：ρ＝2r cos θ；(3)当圆心位于M ⎝⎛⎭⎪⎫r ，π2，半径为r ：ρ＝2r sin θ.(4)圆心在点M (x 0，y 0)，半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数，0≤θ≤2π)．圆心在点A (ρ0，θ0)，半径为r 的圆的方程为r 2＝ρ2＋ρ20－2ρρ0cos(θ－θ0)． 4．直线的参数方程经过点P 0(x 0，y 0)，倾斜角为α的直线的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．设P 是直线上的任一点，则t 表示有向线段P 0P →的数量． 5．圆的参数方程圆心在点M (x 0，y 0)，半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数，0≤θ≤2π)．6．圆锥曲线的参数方程(1)椭圆x 2a ＋y 2b ＝1的参数方程为⎩⎪⎨⎪⎧x ＝a cos θ，y ＝b sin θ(θ为参数)．(2)双曲线x 2a 2－y 2b 2＝1的参数方程为⎩⎪⎨⎪⎧ x ＝a sec θ，y ＝b tan θ(θ为参数)．(3)抛物线y2＝2px (p >0)的参数方程为⎩⎪⎨⎪⎧x ＝2pt 2，y ＝2pt (t 为参数).【题型示例】题型一 极坐标方程和参数方程【例1】(2018·全国Ⅰ)在直角坐标系xOy 中，曲线C 1的方程为y ＝k |x |＋2.以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ2＋2ρcos θ－3＝0. (1)求C 2的直角坐标方程；【思路方法】(1)先列方程，再进一步转化为参数方程． (2)解出交点，再求得直线方程，最后转化为极坐标方程．【解析】(1)设(x 1，y 1)为圆上的点，在已知变换下变为曲线C 上的点(x ，y )，依题意，得⎩⎪⎨⎪⎧x ＝x 1，y ＝2y 1.由x 21＋y 21＝1，得x 2＋⎝ ⎛⎭⎪⎫y 22＝1，即曲线C 的方程为x 2＋y 24＝1.故C 的参数方程为⎩⎪⎨⎪⎧x ＝cos t ，y ＝2sin t(t 为参数)．【感悟提升】若极坐标系的极点与直角坐标系的原点重合，极轴与x 轴正半轴重合，两坐标系的长度单位相同，则极坐标方程与直角坐标方程可以互化．求解与极坐标方程有关的问题时，可以转化为熟悉的直角坐标方程求解．若最终结果要求用极坐标表示，则需将直角坐标转化为极坐标． 题型二 参数方程与普通方程的互化【例2】(2018·全国Ⅲ)在平面直角坐标系xOy 中，⊙O 的参数方程为⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ(θ为参数)，过点(0，－2)且倾斜角为α的直线l 与⊙O 交于A ，B 两点． (1)求α的取值范围；(2)求AB 中点P 的轨迹的参数方程．【解析】 (1)⊙O 的直角坐标方程为x 2＋y 2＝1. 当α＝π2时，l 与⊙O 交于两点．当α≠π2时，记tan α＝k ，则l 的方程为y ＝kx － 2.l 与⊙O 交于两点当且仅当|2|1＋k 2<1，解得k <－1或k >1，即α∈⎝⎛⎭⎪⎫π2，3π4或α∈⎝ ⎛⎭⎪⎫π4，π2.综上，α的取值范围是⎝ ⎛⎭⎪⎫π4，3π4.(2)l 的参数方程为⎩⎨⎧x ＝t cos α，y ＝－2＋t sin α⎝ ⎛⎭⎪⎫t 为参数，π4<α<3π4. 设A ，B ，P 对应的参数分别为t A ，t B ，t P ，则t P ＝t A ＋t B2，且t A ，t B 满足t 2－22t sin α＋1＝0.于是t A ＋t B ＝22sin α，t P ＝2sin α.又点P 的坐标(x ，y )满足⎩⎨⎧x ＝t P cos α，y ＝－2＋t P sin α，所以点P 的轨迹的参数方程是⎩⎪⎨⎪⎧x ＝22sin 2α，y ＝－22－22cos 2α⎝⎛⎭⎪⎫α为参数，π4<α<3π4.【感悟提升】(1)将参数方程化为普通方程，需要根据参数方程的结构特征，选取适当的消参方法．常见的消参方法有代入消参法、加减消参法、平方消参法等．(2)将参数方程化为普通方程时，要注意两种方程的等价性，不要增解、漏解，若x ，y 有范围限制，要标出x ，y 的取值范围．【变式探究】 【2017·江苏】[选修4-4：坐标系与参数方程]在平面坐标系中xOy 中,已知直线l 的参考方程为x 82t ty =-+⎧⎪⎨=⎪⎩(t 为参数),曲线C的参数方程为22,x s y ⎧=⎪⎨=⎪⎩(s 为参数).设P 为曲线C 上的动点，求点P 到直线l 的距离的最小值.【解析】直线l 的普通方程为. 因为点P 在曲线C 上，设，从而点P 到直线l 的的距离，当s =min d =. 因此当点P 的坐标为()4,4时，曲线C 上点P 到直线l【考点】参数方程化普通方程【变式探究】在直角坐标系x O y 中,曲线C 1的参数方程为（t 为参数,a ＞0）．在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2：ρ=4cos θ. （I ）说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程；（II ）直线C 3的极坐标方程为0θα=,其中0α满足tan 0α=2,若曲线C 1与C 2的公共点都在C 3上,求a ． 【答案】（I ）圆,（II ）1【解析】解：（Ⅰ）消去参数t 得到1C 的普通方程.1C 是以)1,0(为圆心，a 为半径的圆.将代入1C 的普通方程中，得到1C 的极坐标方程为.（Ⅱ）曲线21,C C 的公共点的极坐标满足方程组若0≠ρ，由方程组得，由已知2tan =θ，可得，从而012=-a ，解得1-=a （舍去），1=a .1=a 时，极点也为21,C C 的公共点，在3C 上.所以1=a .【变式探究】在直角坐标系xOy 中，直线C 1：x ＝－2，圆C 2：(x －1)2＋(y －2)2＝1，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系． (1)求C 1，C 2的极坐标方程；(2)若直线C 3的极坐标方程为θ＝π4(ρ∈R )，设C 2与C 3的交点为M ，N ，求△C 2MN 的面积．【变式探究】在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝2cos α，y ＝2＋2sin α(α为参数)，M 是C 1上的动点，P 点满足OP →＝2OM →，点P 的轨迹为曲线C 2.(1)求C 2的方程；(2)在以O 为极点，x 轴的正半轴为极轴的极坐标系中，射线θ＝π3与C 1的异于极点的交点为A ，与C 2的异于极点的交点为B ，求AB .【解析】(1)设P (x ，y )，则由条件知M ⎝ ⎛⎭⎪⎫x 2，y2，由于M 点在C 1上，所以⎩⎪⎨⎪⎧x 2＝2cos α，y2＝2＋2sin α，即⎩⎪⎨⎪⎧x ＝4cos α，y ＝4＋4sin α.从而C 2的参数方程为⎩⎪⎨⎪⎧x ＝4cos α，y ＝4＋4sin α(α为参数)．(2)曲线C 1的极坐标方程为ρ＝4sin θ，曲线C 2的极坐标方程为ρ＝8sin θ.射线θ＝π3与C 1的交点A的极径为ρ1＝4sin π3，射线θ＝π3与C 2的交点B 的极径为ρ2＝8sin π3.所以AB ＝|ρ2－ρ1|＝2 3.【规律方法】解决这类问题一般有两种思路，一是将极坐标方程化为直角坐标方程，求出交点的直角坐标，再将其化为极坐标；二是将曲线的极坐标方程联立，根据限制条件求出极坐标．要注意题目所给的限制条件及隐含条件．【变式探究】将圆x 2＋y 2＝1上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C . (1)写出C 的参数方程；(2)设直线l ：2x ＋y －2＝0与C 的交点为P 1，P 2，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求过线段P 1P 2的中点且与l 垂直的直线的极坐标方程．解 (1)设(x 1，y 1)为圆上的点，在已知变换下变为C 上点(x ，y )，依题意，得1,2,x x y y =⎧⎨=⎩由x 21＋y 21＝1得x 2＋⎝ ⎛⎭⎪⎫y 22＝1，即曲线C 的方程为x 2＋y 24＝1.故C 的参数方程为cos 2sin x t y t =⎧⎨=⎩(t 为参数)．(2)由解得：1,0x y =⎧⎨=⎩或0,2.x y =⎧⎨=⎩不妨设P 1(1，0)，P 2(0，2)，则线段P 1P 2的中点坐标为⎝ ⎛⎭⎪⎫12，1，所求直线斜率为k ＝12，于是所求直线方程为y －1＝12⎝⎛⎭⎪⎫x －12，化为极坐标方程，并整理得 2ρcos θ－4ρsin θ＝－3， 即ρ＝34sin θ－2cos θ.题型三 极坐标 参数方程及其应用【例3】在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝1＋cos α，y ＝sin α(α为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1－t ，y ＝3＋t(t 为参数)，在以坐标原点为极点，x 轴的正半轴为极轴的极坐标系中，射线m ：θ＝β(ρ>0)．(1)求C 和l 的极坐标方程；(2)设点A 是m 与C 的一个交点(异于原点)，点B 是m 与l 的交点，求|OA ||OB |的最大值．解 (1)曲线C 的普通方程为(x －1)2＋y 2＝1，由⎩⎪⎨⎪⎧ρcos θ＝x ，ρsin θ＝y ，得()ρcos θ－12＋ρ2sin 2θ＝1，化简得C 的极坐标方程为ρ＝2cos θ. 因为l 的普通方程为x ＋y －4＝0，所以极坐标方程为ρcos θ＋ρsin θ－4＝0， 所以l 的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝2 2. (2)设A (ρ1，β)，B (ρ2，β)， 则|OA ||OB |＝ρ1ρ2＝2cos β·sin β＋cos β4＝12(sin βcos β＋cos 2β)＝24sin ⎝⎛⎭⎪⎫2β＋π4＋14，由射线m 与C ，直线l 相交，则不妨设β∈⎝ ⎛⎭⎪⎫－π4，π4， 则2β＋π4∈⎝ ⎛⎭⎪⎫－π4，3π4，所以当2β＋π4＝π2，即β＝π8时，|OA ||OB |取得最大值，即⎝⎛⎭⎪⎫|OA ||OB |max＝2＋14. 【感悟提升】 (1)利用参数方程解决问题，要理解参数的几何意义．(2)在解决直线、圆和圆锥曲线的有关问题时，常常将极坐标方程化为直角坐标方程或将参数方程化为普通方程，有助于认识方程所表示的曲线，从而达到化陌生为熟悉的目的，这是转化与化归思想的应用． 【变式探究】在平面直角坐标系中，以原点为极点，以x 轴的正半轴为极轴且取相同的单位长度建立极坐标系，曲线C 1的极坐标方程为ρ＝2cos θ.(1)若曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝1＋t sin α(α为参数)，求曲线C 1的直角坐标方程和曲线C 2的普通方程；(2)若曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝1＋t sin α(t 为参数)，A (0,1)，且曲线C 1与曲线C 2的交点分别为P ，Q ，求1|AP |＋1|AQ |的取值范围． 【解析】 (1)∵ρ＝2cos θ，∴ρ2＝2ρcos θ， 又∵ρ2＝x 2＋y 2，ρcos θ＝x ，∴曲线C 1的直角坐标方程为x 2＋y 2－2x ＝0， 曲线C 2的普通方程为x 2＋(y －1)2＝t 2.(2)将C 2的参数方程⎩⎪⎨⎪⎧x ＝t cos α，y ＝1＋t sin α(t 为参数)代入C 1的方程x 2＋y 2－2x ＝0，得t 2＋(2sin α－2cos α)t＋1＝0.∵Δ＝(2sin α－2cos α)2－4＝8sin 2⎝ ⎛⎭⎪⎫α－π4－4>0，∴⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π4∈⎝ ⎛⎦⎥⎤22，1，∴sin ⎝ ⎛⎭⎪⎫α－π4∈⎣⎢⎡⎭⎪⎫－1，－22∪⎝ ⎛⎦⎥⎤22，1. t 1＋t 2＝－(2sin α－2cos α)＝－22sin ⎝⎛⎭⎪⎫α－π4，t 1t 2＝1>0，∵t 1t 2＝1>0，∴t 1，t 2同号，∴|t 1|＋|t 2|＝|t 1＋t 2|. 由点A 在曲线C 2上，根据t 的几何意义，可得 1|PA |＋1|AQ |＝1|t 1|＋1|t 2|＝|t 1|＋|t 2||t 1||t 2| ＝|t 1|＋|t 2||t 1t 2|＝|t 1＋t 2|1＝22⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π4∈(2,22]．∴1|PA |＋1|AQ |∈(2,22]． 【变式探究】在直角坐标系xOy 中，曲线C 的参数方程为3cos ,sin ,x y θθ=⎧⎨=⎩（θ为参数），直线l 的参数方程为.（1）若a =−1，求C 与l 的交点坐标；（2）若C 上的点到la. 【答案】（1）C 与l 的交点坐标为()3,0， 2124,2525⎛⎫-⎪⎝⎭；（2）8a =或16a =-. 【解析】（1）曲线C 的普通方程为2219x y +=. 当1a =-时，直线l 的普通方程为.由解得3{ 0x y ==或2125{2425x y =-=. 从而C 与l 的交点坐标为()3,0， 2124,2525⎛⎫-⎪⎝⎭. （2）直线l 的普通方程为，故C 上的点到l 的距离为.当4a ≥-时， d=8a =； 当4a <-时， d由题设得，所以16a =-.综上， 8a =或16a =-.【变式探究】在直角坐标系xOy 中，圆C 的方程为．（Ⅰ）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求C 的极坐标方程； （Ⅱ）直线l 的参数方程是cos sin x t y t αα=⎧⎨=⎩（t 为参数）, l 与C 交于,A B两点，||AB =l 的斜率．【答案】（Ⅰ）；（Ⅱ）. 【解析】（I ）由可得C 的极坐标方程（II ）在（I ）中建立的极坐标系中，直线l 的极坐标方程为由,A B 所对应的极径分别为12,,ρρ将l 的极坐标方程代入C 的极坐标方程得于是由||AB =得，所以l【变式探究】已知直线l 的参数方程为1,1x t y t =-+⎧⎨=+⎩(t 为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ2cos 2θ＝4⎝ ⎛⎭⎪⎫ρ＞0，3π4＜θ＜5π4，则直线l 与曲线C 的交点的极坐标为________．解析 直线l 的直角坐标方程为y ＝x ＋2，由ρ2cos 2θ＝4得ρ2(cos 2θ－sin 2θ)＝4，直角坐标方程为x 2－y 2＝4，把y ＝x ＋2代入双曲线方程解得x ＝－2，因此交点为(－2，0)，其极坐标为(2，π)． 答案 (2，π)【变式探究】已知直线l 的参数方程为⎩⎪⎨⎪⎧ x ＝a －2t ，y ＝－4t (t 为参数)，圆C 的参数方程为⎩⎪⎨⎪⎧ x ＝4cos θ，y ＝4sin θ(θ为参数)．(1)求直线l 和圆C 的普通方程；(2)若直线l 与圆C 有公共点，求实数a 的取值范围．【命题意图】本小题主要考查直线与圆的参数方程等基础知识，意在考查考生的运算求解能力及化归与转化思想．【解题思路】(1)消去参数，即可求出直线l 与圆C 的普通方程．(2)求出圆心的坐标，利用圆心到直线l 的距离不大于半径，得到关于参数a 的不等式，即可求出参数a 的取值范围．【解析】(1)直线l 的普通方程为2x －y －2a ＝0，圆C 的普通方程为x 2＋y 2＝16.(2)因为直线l 与圆C 有公共点，故圆C 的圆心到直线l 的距离d ＝|－2a |5≤4， 解得－25≤a ≤2 5. 【感悟提升】1．将参数方程化为普通方程的过程就是消去参数的过程，常用的消参方法有代入消参、加减消参和三角恒等式消参等，往往需要对参数方程进行变形，为消去参数创造条件．2．在与直线、圆、椭圆有关的题目中，参数方程的使用会使问题的解决事半功倍，尤其是求取值范围和最值问题，可将参数方程代入相关曲线的普通方程中，根据参数的取值条件求解． 【变式探究】在平面直角坐标系xOy 中，圆C 的参数方程为(t 为参数)．在极坐标系(与平面直角坐标系xOy 取相同的长度单位，且以原点O 为极点，以x 轴非负半轴为极轴)中，直线l 的方程为2ρsin ⎝ ⎛⎭⎪⎫θ－π4＝m (m ∈R )． ①求圆C 的普通方程及直线l 的直角坐标方程；②设圆心C 到直线l 的距离等于2，求m 的值．。

第一讲 坐标系与参数方程考点一 极坐标方程及应用1．直角坐标与极坐标的互化公式把直角坐标系的原点作为极点，x 轴正半轴作为极轴，并在两坐标系中取相同的长度单位．设M 是平面内任意一点，它的直角坐标是(x ，y )，极坐标是(ρ，θ)，则⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ，⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝y x (x ≠0).2．几个特殊位置的圆的极坐标方程 (1)当圆心位于极点，半径为r ：ρ＝r .(2)当圆心位于M (a,0)，半径为a ：ρ＝2a cos θ.(3)当圆心位于M ⎝⎛⎭⎪⎫a ，π2，半径为a ：ρ＝2a sin θ.3．几个特殊位置的直线的极坐标方程 (1)直线过极点：θ＝θ0和θ＝π＋θ0. (2)直线过点M (a,0)且垂直于极轴：ρcos θ＝a .(3)直线过M ⎝⎛⎭⎪⎫b ，π2且平行于极轴：ρsin θ＝b .[解] (1)设P 的极坐标为(ρ，θ)(ρ>0)，M 的极坐标为(ρ1，θ)(ρ1>0)．由题设知|OP |＝ρ，|OM |＝ρ1＝4cos θ.由|OM |·|OP |＝16得C 2的极坐标方程 ρ＝4cos θ(ρ>0)．因此C 2的直角坐标方程为(x －2)2＋y 2＝4(x ≠0)． (2)设点B 的极坐标为(ρB ，α)(ρB >0)． 由题设知|OA |＝2，ρB ＝4cos α，于是△OAB 面积S ＝12|OA |·ρB ·sin∠AOB＝4cos α·⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π3 ＝2⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2α－π3－32≤2＋ 3.当α＝－π12时，S 取得最大值2＋ 3.所以△OAB 面积的最大值为2＋ 3.解决极坐标问题应关注的两点(1)用极坐标系解决问题时要注意已知的几何关系，如果几何关系不容易通过极坐标表示时，可以先化为直角坐标，将不熟悉的问题转化为熟悉的问题来解决．(2)在极坐标与直角坐标互化的过程中，需要注意当条件涉及“角度”和“距离”时，利用极坐标将会给问题的解决带来很大的便利．[对点训练](2018·福建福州四校联考)在平面直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋cos α，y ＝2＋sin α(α为参数)，直线C 2的方程为y ＝3x .以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系．(1)求曲线C 1和直线C 2的极坐标方程；(2)若直线C 2与曲线C 1交于A ，B 两点，求1|OA |＋1|OB |.[解] (1)由曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋cos α，y ＝2＋sin α(α为参数)，得曲线C 1的普通方程为(x －2)2＋(y －2)2＝1，则C 1的极坐标方程为ρ2－4ρcos θ－4ρsin θ＋7＝0，由于直线C 2过原点，且倾斜角为π3，故其极坐标方程为θ＝π3(ρ∈R )．(2)由⎩⎪⎨⎪⎧ρ2－4ρcos θ－4ρsin θ＋7＝0，θ＝π3得ρ2－(23＋2)ρ＋7＝0，设A ，B 对应的极径分别为ρ1，ρ2，则ρ1＋ρ2＝23＋2，ρ1ρ2＝7，∴1|OA |＋1|OB |＝|OA |＋|OB ||OA |·|OB |＝ρ1＋ρ2ρ1ρ2＝23＋27. 考点二 参数方程及应用1．圆的参数方程以O ′(a ，b )为圆心，r 为半径的圆的参数方程是⎩⎪⎨⎪⎧x ＝a ＋r cos α，y ＝b ＋r sin α，其中α是参数．2．椭圆的参数方程椭圆x 2a 2＋y 2b 2＝1(a >b >0)的参数方程是⎩⎪⎨⎪⎧x ＝a cos φ，y ＝b sin φ，其中φ是参数．3．直线的参数方程(1)经过点P 0(x 0，y 0)，倾斜角为α的直线的参数方程是⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α，其中t 是参数．(2)若A ，B 为直线l 上两点，其对应的参数分别为t 1，t 2，线段AB 的中点为M ，点M 所对应的参数为t 0，则以下结论在解题中经常用到：①t 0＝t 1＋t 22；②|PM |＝|t 0|＝⎪⎪⎪⎪⎪⎪t 1＋t 22；③|AB |＝|t 2－t 1|； ④|PA |·|PB |＝|t 1·t 2|.角度1：参数方程与普通方程的互化[解] (1)曲线C 的普通方程为x 29＋y 2＝1.当a ＝－1时，直线l 的普通方程为x ＋4y －3＝0.由⎩⎪⎨⎪⎧x ＋4y －3＝0，x 29＋y 2＝1解得⎩⎪⎨⎪⎧x ＝3，y ＝0或⎩⎪⎨⎪⎧x ＝－2125，y ＝2425.从而C 与l 的交点坐标为(3,0)，⎝ ⎛⎭⎪⎫－2125，2425. (2)直线l 的普通方程为x ＋4y －a －4＝0，故C 上的点(3cos θ，sin θ)到l 的距离d ＝|3cos θ＋4sin θ－a －4|17.当a ≥－4时，d 的最大值为a ＋917.由题设得a ＋917＝17，所以a ＝8；当a <－4时，d 的最大值为－a ＋117.由题设得－a ＋117＝17，所以a ＝－16.综上，a ＝8或a ＝－16.角度2：直线参数方程中参数几何意义的应用[解] (1)曲线C 的普通方程为x 24＋y 216＝1.当cos α≠0时，l 的普通方程为y ＝tan α·x ＋2－tan α， 当cos α＝0时，l 的普通方程为x ＝1.(2)将l 的参数方程代入C 的普通方程，整理得关于t 的方程(1＋3cos 2α)t 2＋4(2cos α＋sin α)t －8＝0.①因为曲线C 截直线l 所得线段的中点坐标为(1,2)， 所以①有两个解，设为t 1，t 2，则t 1＋t 2＝0. 又由①得t 1＋t 2＝4(2cos α＋sin α)1＋3cos 2α， 故2cos α＋sin α＝0，于是直线l 的斜率k ＝tan α＝－2.解决参数方程问题的3个要点(1)把参数方程化为普通方程，需要根据其结构特征，选取适当的消参方法． (2)把普通方程化为参数方程的关键是选准参数，注意参数的几何意义及变化范围．(3)直线参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(α为倾斜角，t 为参数)，其中|t |＝|PM |，P (x ，y )为动点，M (x 0，y 0)为定点，在解决与点P 有关的弦长和距离的乘积问题时广泛应用．[对点训练]1．[角度1]设直线l 的参数方程为⎩⎪⎨⎪⎧x ＝3＋t cos α，y ＝4＋t sin α(t 为参数，α为倾斜角)，圆C的参数方程为⎩⎪⎨⎪⎧x ＝1＋2cos θ，y ＝－1＋2sin θ(θ为参数)．(1)若直线l 经过圆C 的圆心，求直线l 的斜率；(2)若直线l 与圆C 交于两个不同的点，求直线l 的斜率的取值范围． [解] (1)由已知得直线l 经过的定点是P (3,4)，而圆C 的圆心是C (1，－1)， 所以，当直线l 经过圆C 的圆心时，直线l 的斜率为k ＝52.(2)解法一：由圆C 的参数方程⎩⎪⎨⎪⎧x ＝1＋2cos θ，y ＝－1＋2sin θ，得圆C 的圆心是C (1，－1)，半径为2.由直线l 的参数方程⎩⎪⎨⎪⎧x ＝3＋t cos α，y ＝4＋t sin α(t 为参数，α为倾斜角)，得直线l 的普通方程为y －4＝k (x －3)(斜率存在)，即kx －y ＋4－3k ＝0.当直线l 与圆C 交于两个不同的点时，圆心到直线的距离小于圆的半径， 即|5－2k |k 2＋1<2，解得k >2120.即直线l 的斜率的取值范围为⎝ ⎛⎭⎪⎫2120，＋∞.解法二：将圆C 的参数方程⎩⎪⎨⎪⎧x ＝1＋2cos θ，y ＝－1＋2sin θ化成普通方程为(x －1)2＋(y ＋1)2＝4①，将直线l 的参数方程代入①式，得t 2＋2(2cos α＋5sin α)t ＋25＝0. ②.当直线l 与圆C 交于两个不同的点时，方程②有两个不相等的实根，即Δ＝4(2cos α＋5sin α)2－100>0，即20sin αcos α>21cos 2α，两边同除以20cos 2α，得tan α>2120，即直线l 的斜率的取值范围为⎝ ⎛⎭⎪⎫2120，＋∞. 2．[角度2](2018·郑州一模)已知直线l ：⎩⎪⎨⎪⎧x ＝5＋32t ，y ＝3＋12t (t 为参数)．以坐标原点为极点，x 轴的非负半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ＝2cos θ.(1)将曲线C 的极坐标方程化为直角坐标方程．(2)设点M 的直角坐标为(5，3)，直线l 与曲线C 的交点为A ，B ，求|MA |·|MB |的值． [解] (1)∵ρ＝2cos θ，∴ρ2＝2ρcos θ，∴曲线C 的直线坐标方程为x 2＋y 2＝2x ，即(x －1)2＋y 2＝1. (2)将直线l ：⎩⎪⎨⎪⎧x ＝5＋32t ，y ＝3＋12t (t 为参数)代入曲线C 的直角坐标方程中，化简得t 2＋53t ＋18＝0，且Δ>0.∴t 1t 2＝18.∵点M (5，3)在直线l 上，根据直线参数方程中参数t 的几何意义，得|MA |·|MB |＝|t 1t 2|＝18.考点三 极坐标方程与参数方程的综合应用1．对于参数方程或极坐标方程应用不够熟练的情况下，我们可以先化成直角坐标的普通方程，这样思路可能更加清晰．2．对于一些运算比较复杂的问题，用参数方程或极坐标方程计算会比较简捷．[解] (1)由⎩⎨⎧x ＝－5＋2cos t ，y ＝3＋2sin t消去参数t ，得(x ＋5)2＋(y －3)2＝2，所以圆C 的普通方程为(x ＋5)2＋(y －3)2＝2.由ρcos ⎝ ⎛⎭⎪⎫θ＋π4＝－2，得ρcos θ－ρsin θ＝－2. 可得直线l 的直角坐标方程为x －y ＋2＝0.(2)直线l 与x 轴，y 轴的交点分别为A (－2,0)，B (0,2)，化为极坐标为A (2，π)，B ⎝⎛⎭⎪⎫2，π2，设点P 的坐标为(－5＋2cos t,3＋2sin t )，则点P 到直线l 的距离为d ＝|－5＋2cos t －3－2sin t ＋2|2＝⎪⎪⎪⎪⎪⎪－6＋2cos ⎝ ⎛⎭⎪⎫t ＋π42，所以d min ＝42＝22，又|AB |＝22，所以△PAB 面积的最小值＝12×22×22＝4.解决极坐标与参数方程问题的关键(1)会转化：把直线与圆的参数方程转化为普通方程时，要关注参数的取值范围的限定，还需掌握极坐标与直角坐标的互化公式．(2)懂技巧：合理选择直角坐标形式运算、极坐标形式运算、参数坐标形式运算，利用参数及其几何意义，结合关系式寻找关于参数的方程或函数．[对点训练]在平面直角坐标系xOy中，曲线C 1：⎩⎪⎨⎪⎧x ＝r cos θ，y ＝r sin θ(θ为参数，0<r <4)，曲线C 2：⎩⎨⎧x ＝2＋22cos θ，y ＝2＋22sin θ(θ为参数)，以坐标原点为极点，x 轴的非负半轴为极轴建立极坐标系，射线θ＝α⎝ ⎛⎭⎪⎫0<α<π2与曲线C 1交于点N ，与曲线C 2交于O ，P 两点，且|PN |的最大值为2 2.(1)将曲线C 1与曲线C 2化成极坐标方程，并求r 的值．(2)射线θ＝α＋π4与曲线C 1交于点Q ，与曲线C 2交于O ，M 两点，求四边形MPNQ 面积的最大值．[解] (1)将曲线C 1的参数方程化为普通方程为x 2＋y 2＝r 2. 所以曲线C 1的极坐标方程为ρ＝r .将曲线C 2的参数方程化为普通方程为(x －2)2＋(y －2)2＝8，即x 2＋y 2－4x －4y ＝0. 所以曲线C 2的极坐标方程为ρ－4cos θ－4sin θ＝0，即ρ＝42sin ⎝ ⎛⎭⎪⎫θ＋π4. 因为|PN |max ＝|ρP －ρN |max ＝⎪⎪⎪⎪⎪⎪42sin ⎝ ⎛⎭⎪⎫α＋π4－r max ＝22，所以r ＝22，所以C 1：ρ＝2 2. (2)S四边形MPNQ＝S △OPM －S △ONQ ＝12OP ·OM sin π4－12ON ·OQ ·sin π4＝12×42sin ⎝⎛⎭⎪⎫α＋π4×42sin ⎝ ⎛⎭⎪⎫α＋π2×22－12×22×22×22＝42sin ⎝⎛⎭⎪⎫2α＋π4＋4－2 2.所以当α＝π8时，四边形MPNQ 面积的最大值为4＋2 2.1．(2018·全国卷Ⅰ)在直角坐标系xOy 中，曲线C 1的方程为y ＝k |x |＋2.以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ2＋2ρcos θ－3＝0.(1)求C 2的直角坐标方程；(2)若C 1与C 2有且仅有三个公共点，求C 1的方程．[解] (1)由x ＝ρcos θ，y ＝ρsin θ得C 2的直角坐标方程为 (x ＋1)2＋y 2＝4.(2)由(1)知C 2是圆心为A (－1,0)，半径为2的圆． 由题设知，C 1是过点B (0,2)且关于y 轴对称的两条射线． 记y 轴右边的射线为l 1，y 轴左边的射线为l 2.由于B 在圆C 2的外面，故C 1与C 2有且仅有三个公共点等价于l 1与C 2只有一个公共点且l 2与C 2有两个公共点，或l 2与C 2只有一个公共点且l 1与C 2有两个公共点．当l 1与C 2只有一个公共点时，A 到l 1所在直线的距离为2，所以|－k ＋2|k 2＋1＝2，故k ＝－43或k ＝0，经检验，当k ＝0时，l 1与C 2没有公共点；当k ＝－43时，l 1与C 2只有一个公共点，l 2与C 2有两个公共点．当l 2与C 2只有一个公共点时，A 到l 2所在直线的距离为2，所以|k ＋2|k 2＋1＝2，故k ＝0或k ＝43.经检验，当k ＝0时，l 1与C 2没有公共点；当k ＝43时，l 2与C 2没有公共点．综上，所求C 1的方程为y ＝－43|x |＋2.2．(2018·全国卷Ⅲ)在平面直角坐标系xOy 中，⊙O 的参数方程为⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ(θ为参数)，过点(0，－2)且倾斜角为α的直线l 与⊙O 交于A ，B 两点．(1)求α的取值范围；(2)求AB 中点P 的轨迹的参数方程． [解] (1)⊙O 的直角坐标方程为x 2＋y 2＝1. 当α＝π2时，l 与⊙O 交于两点．当α≠π2时，记tan α＝k ，则l 的方程为y ＝kx － 2.l 与⊙O 交于两点当且仅当⎪⎪⎪⎪⎪⎪21＋k 2<1，解得k <－1或k >1，即α∈⎝ ⎛⎭⎪⎫π4，π2或α∈⎝ ⎛⎭⎪⎫π2，3π4.综上，α的取值范围是⎝ ⎛⎭⎪⎫π4，3π4.(2)l 的参数方程为⎩⎨⎧x ＝t cos α，y ＝－2＋t sin α(t 为参数，π4<α<3π4)．设A ，B ，P 对应的参数分别为t A ，t B ，t P ，则t P ＝t A ＋t B2，且t A ，t B 满足t 2－22t sin α＋1＝0.于是t A ＋t B ＝22sin α，t P ＝2sin α.又点P 的坐标(x ，y )满足⎩⎨⎧x ＝t P cos α，y ＝－2＋t P sin α.所以点P 的轨迹的参数方程是 ⎩⎪⎨⎪⎧x ＝22sin2α，y ＝－22－22cos2α(α为参数，π4<α<3π4)．1.坐标系与参数方程是高考的选考内容之一，高考考查的重点主要有两个方面：一是简单曲线的极坐标方程；二是参数方程、极坐标方程与曲线的综合应用．2．全国课标卷对此部分内容的考查以解答题形式出现，难度中等，备考此部分内容时应注意转化思想的应用．专题跟踪训练(三十二)1．(2018·湖南长沙联考)在直角坐标系xOy 中，直线C 1：x ＝－2，圆C 2：(x －1)2＋(y －2)2＝1，以坐标原点为极点，x 轴的非负半轴为极轴建立极坐标系．(1)求C 1，C 2的极坐标方程．(2)若直线C 3的极坐标方程为θ＝π4(ρ∈R )，设C 2与C 3的交点分别为M ，N ，求△C 2MN的面积．[解] (1)∵x ＝ρcos θ，y ＝ρsin θ， ∴C 1：x ＝－2的极坐标方程为ρcos θ＝－2，C 2：(x －1)2＋(y －2)2＝1的极坐标方程为(ρcos θ－1)2＋(ρsin θ－2)2＝1，化简，得ρ2－(2ρcos θ＋4ρsin θ)＋4＝0.(2)把直线C 3的极坐标方程θ＝π4(ρ∈R )代入圆C 2：ρ2－(2ρcos θ＋4ρsin θ)＋4＝0， 得ρ2－32ρ＋4＝0，解得ρ1＝22，ρ2＝ 2. ∴|MN |＝|ρ1－ρ2|＝ 2.∵圆C 2的半径为1，∴|C 2M |2＋|C 2N |2＝|MN |2， ∴C 2M ⊥C 2N .∴△C 2MN 的面积为12·|C 2M |·|C 2N |＝12×1×1＝12.2．(2018·洛阳联考)在极坐标系中，曲线C 的方程为ρ2＝31＋2sin 2θ，已知点R ⎝ ⎛⎭⎪⎫22，π4.(1)以极点为原点，极轴为x 轴的非负半轴，建立平面直角坐标系，把曲线C 的极坐标方程化为直角坐标方程，R 点的极坐标化为直角坐标．(2)设P 为曲线C 上一动点，以PR 为对角线的矩形PQRS 的一边垂直于极轴，求矩形PQRS 周长的最小值，及此时P 点的直角坐标．[解] (1)∵x ＝ρcos θ，y ＝ρsin θ，x 2＋y 2＝ρ2. ∴曲线C 的直角坐标方程为x 23＋y 2＝1.点R 的直角坐标为(2,2)．(2)设点P (3cos θ，sin θ)，根据题意得Q (2，sin θ)，即可得|PQ |＝2－3cos θ，|QR |＝2－sin θ，∴|PQ |＋|QR |＝4－2sin(θ＋60°)． ∴当θ＝30°时，|PQ |＋|QR |取最小值2， ∴矩形PQRS 周长的最小值为4.此时点P 的直角坐标为⎝ ⎛⎭⎪⎫32，12.3．(2018·安徽皖南八校联考)在平面直角坐标系xOy 中，C 1的参数方程为⎩⎪⎨⎪⎧x ＝1－22t ，y ＝1＋22t (t 为参数)，在以坐标原点为极点，x 轴的非负半轴为极轴的极坐标系中，C 2的极坐标方程为ρ2－2ρcos θ－3＝0.(1)说明C 2是哪种曲线，并将C 2的方程化为直角坐标方程．(2)C 1与C 2有两个公共点A ，B ，定点P 的极坐标⎝⎛⎭⎪⎫2，π4，求线段AB 的长及定点P 到A ，B 两点的距离之积．[解] (1)将⎩⎪⎨⎪⎧x ＝ρcos θ，x 2＋y 2＝ρ2代入C 2的极坐标方程中得C 2的直角坐标方程为(x －1)2＋y 2＝4，所以C 2是圆．(2)将C 1的参数方程⎩⎪⎨⎪⎧x ＝1－22t ，y ＝1＋22t (t 为参数)，代入(x －1)2＋y 2＝4中得⎝ ⎛⎭⎪⎫－22t 2＋⎝⎛⎭⎪⎫1＋22t 2＝4，化简，得t 2＋2t －3＝0.设两根分别为t 1，t 2， 由根与系数的关系得⎩⎨⎧t 1＋t 2＝－2，t 1·t 2＝－3.所以|AB |＝|t 1－t 2|＝(t 1＋t 2)2－4t 1t 2＝2＋12＝14， 定点P 到A ，B 两点的距离之积|PA |·|PB |＝|t 1t 2|＝3.4．(2018·河北衡水中学模拟)在极坐标系中，曲线C 1的极坐标方程是ρ＝244cos θ＋3sin θ，在以极点为原点O ，极轴为x 轴正半轴(两坐标系取相同的单位长度)的直角坐标系xOy 中，曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝cos θy ＝sin θ(θ为参数)．(1)求曲线C 1的直角坐标方程与曲线C 2的普通方程； (2)将曲线C 2经过伸缩变换⎩⎨⎧x ′＝22x ，y ′＝2y后得到曲线C 3，若M 、N 分别是曲线C 1和曲线C 3上的动点，求|MN |的最小值．[解] (1)∵C 1的极坐标方程是ρ＝244cos θ＋3sin θ，∴4ρcos θ＋3ρsin θ＝24， ∴4x ＋3y －24＝0，故C 1的直角坐标方程为4x ＋3y －24＝0.∵曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ，∴x 2＋y 2＝1，故C 2的普通方程为x 2＋y 2＝1. (2)将曲线C 2经过伸缩变换⎩⎨⎧x ′＝22x ，y ′＝2y后得到曲线C 3，则曲线C 3的参数方程为⎩⎨⎧x ′＝22cos α，y ′＝2sin α(α为参数)．设N (22cos α，2sin α)，则点N 到曲线C 1的距离d ＝|4×22cos α＋3×2sin α－24|5＝|241sin (α＋φ)－24|5＝24－241sin (α＋φ)5(其中φ满足tan φ＝423)．当sin(α＋φ)＝1时，d 有最小值24－2415，所以|MN |的最小值为24－2415.百度文库是百度发布的供网友在线分享文档的平台。

12.2 参数方程[知识梳理] 1．曲线的参数方程一般地，在平面直角坐标系中，如果曲线上任意一点的坐标x ，y 都是某个变数t 的函数⎩⎪⎨⎪⎧x ＝f (t )，y ＝g (t )，并且对于t 的每一个允许值，由这个方程组所确定的点M (x ，y )都在这条曲线上，那么这个方程组就叫做这条曲线的参数方程，联系变数x ，y 的变数t 叫做参变数，简称参数．2．常见曲线的参数方程和普通方程提醒：直线的参数方程中，参数t 的系数的平方和为1时，t 才有几何意义且几何意义为：|t |是直线上任一点M (x ，y )到M 0(x 0，y 0)的距离．[诊断自测] 1．概念思辨(1)直线⎩⎪⎨⎪⎧x ＝－2＋t cos30°，y ＝1＋t sin150°(t 为参数)的倾斜角α为30°.( )(2)过M 0(x 0，y 0)，倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．参数t 的几何意义表示：直线l 上以定点M 0为起点，任一点M (x ，y )为终点的有向线段M 0M →的数量．( )(3)方程⎩⎪⎨⎪⎧x ＝2cos θ，y ＝1＋2sin θ表示以点(0,1)为圆心，以2为半径的圆．( )(4)已知椭圆的参数方程⎩⎪⎨⎪⎧x ＝2cos t ，y ＝4sin t (t 为参数)，点M 在椭圆上，对应参数t ＝π3，点O 为原点，则直线OM 的斜率为 3.( )答案 (1)√ (2)√ (3)√ (4)×2．教材衍化(1)(选修A4－4P 39T 1)直线⎩⎪⎨⎪⎧x ＝2t －1，y ＝t ＋1(t 为参数)被圆x 2＋y 2＝9截得的弦长等于( )A.125 B.1255 C.925 D.9105答案 B解析 直线的普通方程为x －2y ＋3＝0. 圆的圆心为(0,0)，半径r ＝3. ∴圆心到直线的距离d ＝35＝355.∴弦长为2r 2－d 2＝1255.故选B.(2)(选修A4－4P 24例2)已知点(x ，y )满足曲线方程⎩⎨⎧x ＝4＋2cos θ，y ＝6＋2sin θ(θ为参数)，则y x的最小值是( )A.32 B.32C. 3 D ．1 答案 D解析 曲线方程⎩⎨⎧x ＝4＋2cos θ，y ＝6＋2sin θ(θ为参数)化为普通方程得(x －4)2＋(y －6)2＝2，∴曲线是以C (4,6)为圆心，以2为半径的圆， ∴y x是原点和圆上的点的连线的斜率，如图，当原点和圆上的点的连线是切线OA 时，y x取最小值，设过原点的切线方程为y ＝kx ，则圆心C (4,6)到切线y ＝kx 的距离： d ＝|4k －6|k 2＋1＝2，即7k 2－24k ＋17＝0， 解得k ＝1或k ＝177，∴yx的最小值是1.故选D. 3．小题热身(1)(2014·安徽高考)以平面直角坐标系的原点为极点，x 轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位．已知直线l 的参数方程是⎩⎪⎨⎪⎧x ＝t ＋1，y ＝t －3(t 为参。

选修4­4 坐标系与参数方程1. （选修44P 11例5改编）在直角坐标系中，点P 的坐标为（－2，－6），求点P 的极坐标.解：ρ＝（－2）2＋（－6）2＝22，tan θ＝－6－2＝3，又点P 在第三象限，得θ＝43π，即P （22，4π3）.2. （选修44P 17习题9改编）在极坐标系中，已知A ，B 两点的极坐标分别为⎝⎛⎭⎪⎫3，π3，⎝ ⎛⎭⎪⎫4，π6，求△AOB（其中O 为极点）的面积.解：由题意A ，B 两点的极坐标分别为⎝⎛⎭⎪⎫3，π3，⎝ ⎛⎭⎪⎫4，π6，得△AOB 的面积S △AOB ＝12OA ·OB ·sin∠AOB ＝12×3×4×sin π6＝3.3. 在极坐标系中，求圆ρ＝2cos θ的圆心到直线2ρsin ⎝ ⎛⎭⎪⎫θ＋π3＝1的距离. 解：圆的普通方程为（x －1）2＋y 2＝1，直线的普通方程为3x ＋y －1＝0，∴ 圆心到直线的距离为d ＝3－12.4. （选修44P 19例1改编）在极坐标系中，求过圆ρ＝－2sin θ的圆心，且与极轴平行的直线的极坐标方程.解：由题意，圆ρ＝－2sin θ，可化为ρ2＝－2ρsin θ，化成直角坐标方程为x 2＋y 2＝－2y ，即x 2＋（y ＋1）2＝1，圆心是（0，－1），所求直角坐标方程为y ＝－1，所以其极坐标方程为ρsin θ＝－1.5. 在极坐标系中，求圆ρ＝4上的点到直线ρ（cos θ＋3sin θ）＝8的距离的最大值.解：把ρ＝4化为直角坐标方程为x 2＋y 2＝16，把ρ（cos θ＋3sin θ）＝8化为直角坐标方程为x ＋3y －8＝0，∴ 圆心（0，0）到直线的距离为d ＝82＝4，∴ 直线和圆相切，∴ 圆上的点到直线的最大距离是8.1. 极坐标系是由距离（极径）与方向（极角）确定点的位置的一种方法，由于终边相同的角有无数个且极径可以为负数，故在极坐标系下，有序实数对（ρ，θ）与点不一一对应.这点应与直角坐标系区别开来.2. 在极坐标系中，同一个点M 的坐标形式不尽相同，M （ρ，θ）可表示为（ρ，θ＋2n π）（n∈Z ）.3. 在极坐标系中，极径ρ可以为负数，故M （ρ，θ）可表示为（－ρ，θ＋（2n ＋1）π）（n∈Z ）.4. 特别地，若ρ＝0，则极角θ可取任意角.5. 建立曲线的极坐标方程，其基本思路与在直角坐标系中大致相同，即设曲线上任一点M （ρ，θ），建立等式，化简即得.6. 常见曲线的极坐标方程（1） 过极点，倾斜角为α的直线的极坐标方程为θ＝α（ρ∈R ）或θ＝π＋α（ρ∈R ）； （2） 过点（a ，0）（a ＞0），与极轴垂直的直线的极坐标方程为ρcos θ＝a ；（3） 过点⎝⎛⎭⎪⎫a ，π2，与极轴平行的直线的极坐标方程为ρsin θ＝a ；（4） 圆心在极点，半径为r 的圆的极坐标方程为ρ＝r ； （5） 圆心为（a ，0），半径为a 的圆的极坐标方程为ρ＝2acos θ；（6） 圆心为⎝⎛⎭⎪⎫a ，π2，半径为a 的圆的极坐标方程为ρ＝2asin θ.7. 以平面直角坐标系的原点O 为极点，x 轴的正半轴为极轴，且在两种坐标系中取相同的长度单位，平面内任一点P 的直角坐标（x ，y ）与极坐标（ρ，θ）可以互换，公式是⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ 和⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝y x ., 1 求极坐标或极坐标方程), 1) 在极坐标系中，已知点A ⎝⎛⎭⎪⎫2，π4，圆C 的方程为ρ＝42sin θ（圆心为点C ），求直线AC 的极坐标方程.解：（解法1）以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系xOy.圆C 的平面直角坐标方程为x 2＋y 2＝42y ，即x 2＋（y －22）2＝8，圆心C （0，22）. 点A 的直角坐标为（2，2）.直线AC 的斜率k AC ＝22－20－2＝－1.所以直线AC 的直角坐标方程为y ＝－x ＋22， 极坐标方程为ρ（cos θ＋sin θ）＝22，即ρsin ⎝⎛⎭⎪⎫θ＋π4＝2. （解法2）在直线AC 上任取一点M （ρ，θ），不妨设点M 在线段AC 上.由于圆心为C ⎝⎛⎭⎪⎫22，π2，S △OAC ＝S △OAM ＋S △OCM ， 所以12×22×2sin π4＝12×2×ρsin ⎝ ⎛⎭⎪⎫θ－π4＋12×ρ×22sin ⎝ ⎛⎭⎪⎫π2－θ，即ρ（cos θ＋sinθ）＝22，化简，得直线AC 的极坐标方程为ρsin ⎝⎛⎭⎪⎫θ＋π4＝2. 备选变式（教师专享）在极坐标系中，求曲线ρ＝2cos θ关于直线θ＝π4（ρ∈R ）对称的曲线的极坐标方程.解：（解法1）以极点为坐标原点，极轴为x 轴的正半轴建立直角坐标系，则曲线ρ＝2cos θ的直角坐标方程为（x －1）2＋y 2＝1，且圆心C 的坐标为（1，0），直线θ＝π4的直角坐标方程为y ＝x.因为圆心C （1，0）关于y ＝x 的对称点为（0，1），所以圆C 关于y ＝x 的对称曲线为x 2＋（y －1）2＝1，所以曲线ρ＝2cos θ关于直线θ＝π4对称的曲线的极坐标方程为ρ＝2sin θ.（解法2）设曲线ρ＝2cos θ上任意一点为（ρ′，θ′），其关于直线θ＝π4的对称点为（ρ，θ），则⎩⎪⎨⎪⎧ρ′＝ρ，θ′＝2k π＋π2－θ. 将（ρ′，θ′）代入ρ＝2cos θ，得ρ＝2cos ⎝ ⎛⎭⎪⎫π2－θ，即ρ＝2sin θ，所以曲线ρ＝2cos θ关于直线θ＝π4（ρ∈R ）对称的曲线的极坐标方程为ρ＝2sin θ., 2 极坐标方程与直角坐标方程的互化), 2) （2017·苏州期中）已知在平面直角坐标系xOy 中，圆C 的参数方程为⎩⎪⎨⎪⎧x ＝rcos θ＋2，y ＝rsin θ＋2（θ为参数，r ＞0）.以直角坐标系的原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为2ρsin ⎝⎛⎭⎪⎫θ＋π4＋1＝0. （1） 求圆C 的圆心的极坐标；（2） 当圆C 与直线l 有公共点时，求r 的取值范围.解：（1） 由C ：⎩⎪⎨⎪⎧x ＝rcos θ＋2，y ＝rsin θ＋2得（x －2）2＋（y －2）2＝r 2，∴ 曲线C 是以（2，2）为圆心，r 为半径的圆，∴ 圆心的极坐标为⎝⎛⎭⎪⎫22，π4. （2） 由直线l ：2ρsin ⎝⎛⎭⎪⎫θ＋π4＋1＝0，得直线l 的直角坐标方程为x ＋y ＋1＝0， 从而圆心（2，2）到直线l 的距离d ＝|2＋2＋1|2＝52 2.∵ 圆C 与直线l 有公共点，∴ d ≤r ，即r≥522.变式训练（2017·苏州期初）自极点O 任意作一条射线与直线ρcos θ＝3相交于点M ，在射线OM 上取点P ，使得OM·OP＝12，求动点P 的轨迹的极坐标方程，并把它化为直角坐标方程.解：设P （ρ，θ），M （ρ′，θ）， ∵ OM ·OP ＝12，∴ ρρ′＝12.∵ ρ′cos θ＝3，∴ 12ρ·cos θ＝3.则动点P 的轨迹的极坐标方程为ρ＝4cos θ. ∵ 极点在此曲线上，∴ 方程两边可同时乘ρ，得ρ2＝4ρcos θ.∴ x 2＋y 2－4x ＝0., 3 曲线的极坐标方程的应用), 3) 在极坐标系中，曲线C ：ρ＝2acos θ（a>0），直线l ：ρcos ⎝⎛⎭⎪⎫θ－π3＝32，C 与l 有且仅有一个公共点.（1） 求a ；（2） O 为极点，A ，B 为C 上的两点，且∠AOB＝π3，求OA ＋OB 的最大值.解：（1） 曲线C 是以（a ，0）为圆心，以a 为半径的圆； 直线l 的直角坐标方程为x ＋3y －3＝0.由直线l 与圆C 相切可得|a －3|2＝a ，解得a ＝1.（2） 不妨设A 的极角为θ，B 的极角为θ＋π3，则OA ＋OB ＝2cos θ＋2cos ⎝⎛⎭⎪⎫θ＋π3 ＝3cos θ－3sin θ＝23cos ⎝⎛⎭⎪⎫θ＋π6， 当θ＝－π6时，OA ＋OB 取得最大值2 3.变式训练在直角坐标系xOy 中，圆C 的方程为（x －3）2＋（y ＋1）2＝9，以O 为极点，x 轴的正半轴为极轴建立极坐标系.（1） 求圆C 的极坐标方程；（2） 直线OP ：θ＝π6（ρ∈R ）与圆C 交于点M ，N ，求线段MN 的长.解：（1） （x －3）2＋（y ＋1）2＝9可化为x 2＋y 2－23x ＋2y －5＝0，故其极坐标方程为ρ2－23ρcos θ＋2ρsin θ－5＝0.（2） 将θ＝π6代入ρ2－23ρcos θ＋2ρsin θ－5＝0，得ρ2－2ρ－5＝0，∴ ρ1＋ρ2＝2，ρ1ρ2＝－5，|MN|＝|ρ1－ρ2|＝（ρ1＋ρ2）2－4ρ1ρ2＝2 6.1. （2017·苏北四市期中）已知曲线C 的极坐标方程为ρsin （θ＋π3）＝3，以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，求曲线C 的直角坐标方程.解：由ρsin ⎝⎛⎭⎪⎫θ＋π3＝3，得12ρsin θ＋32ρcos θ＝3. 又ρcos θ＝x ，ρsin θ＝y ，所以曲线C 的直角坐标方程为3x ＋y －6＝0.2. （2017·苏锡常镇一模）已知圆O 1和圆O 2的极坐标方程分别为ρ＝2，ρ2－22ρcos ⎝ ⎛⎭⎪⎫θ－π4＝2.（1） 把圆O 1和圆O 2的极坐标方程化为直角坐标方程； （2） 求经过两圆交点的直线的极坐标方程.解：（1） 由ρ＝2⇒ρ2＝4，所以x 2＋y 2＝4.因为ρ2－22ρcos ⎝⎛⎭⎪⎫θ－π4＝2，所以ρ2－22ρ⎝⎛⎭⎪⎫cos θcos π4＋sin θsin π4＝2，所以x 2＋y 2－2x －2y －2＝0.（2） 将两圆的直角坐标方程相减，得经过两圆交点的直线方程为x ＋y ＝1.化为极坐标方程为ρcos θ＋ρsin θ＝1，即ρsin ⎝⎛⎭⎪⎫θ＋π4＝22. 3. （2017·苏北三市模拟）在极坐标系中，已知点A ⎝⎛⎭⎪⎫2，π2，点B 在直线l ：ρcos θ＋ρsinθ＝0（0≤θ＜2π）上.当线段AB 最短时，求点B 的极坐标.解：以极点为原点，极轴为x 轴正半轴，建立平面直角坐标系，则点A ⎝⎛⎭⎪⎫2，π2的直角坐标为（0，2），直线l 的直角坐标方程为x ＋y ＝0.AB 最短时，点B 为直线x －y ＋2＝0与直线l 的交点， 由⎩⎪⎨⎪⎧x －y ＋2＝0，x ＋y ＝0，解得⎩⎪⎨⎪⎧x ＝－1，y ＝1.所以点B 的直角坐标为（－1，1）.所以点B 的极坐标为⎝⎛⎭⎪⎫2，3π4. 4. （2017·常州期末）在平面直角坐标系中，以原点O 为极点，x 轴的正半轴为极轴，建立极坐标系.已知圆ρ＝4sin （θ＋π6）（ρ≥0）被射线θ＝θ0（θ0为常数，且θ0∈⎝ ⎛⎭⎪⎫0，π2）所截得的弦长为23，求θ0的值.解：圆ρ＝4sin ⎝⎛⎭⎪⎫θ＋π6的直角坐标方程为（x －1）2＋（y －3）2＝4，射线θ＝θ0的直角坐标方程可以设为y ＝kx （x≥0，k ＞0），圆心（1，3）到直线y ＝kx 的距离d ＝|k －3|1＋k 2. 根据题意，得24－（k －3）21＋k 2＝23，解得k ＝33， 即tan θ0＝33.又θ0∈⎝⎛⎭⎪⎫0，π2，所以θ0＝π6.1. （2017·南通、扬州、泰州模拟）在极坐标系中，圆C 的圆心在极轴上，且过极点和点⎝ ⎛⎭⎪⎫32，π4，求圆C 的极坐标方程. 解：（解法1）因为圆C 的圆心在极轴上且过极点， 所以可设圆C 的极坐标方程为ρ＝acos θ.又点⎝⎛⎭⎪⎫32，π4在圆C 上，所以32＝acos π4，解得a ＝6. 所以圆C 的极坐标方程为ρ＝6cos θ.（解法2）点⎝⎛⎭⎪⎫32，π4的直角坐标为（3，3）. 因为圆C 过点（0，0），（3，3）， 所以圆心在直线x ＋y －3＝0上. 又圆心C 在极轴上，所以圆C 的直角坐标方程为（x －3）2＋y 2＝9. 所以圆C 的极坐标方程为ρ＝6cos θ.2. 已知在极坐标系下，圆C ：ρ＝2cos ⎝ ⎛⎭⎪⎫θ＋π2与直线l ：ρsin ⎝⎛⎭⎪⎫θ＋π4＝2，点M 为圆C 上的动点.求点M 到直线l 距离的最大值.解：圆C ：ρ＝2cos ⎝⎛⎭⎪⎫θ＋π2，即 x 2＋y 2＋2y ＝0，x 2＋（y ＋1）2＝1，表示圆心为（0，－1），半径等于1的圆.直线l ：ρsin ⎝⎛⎭⎪⎫θ＋π4＝2，即ρcos θ＋ρsin θ－2＝0，即 x ＋y －2＝0， 圆心到直线l 的距离为|0－1－2|2＝322，故圆上的动点M 到直线l 的距离的最大值等于322＋1.3. 在直角坐标系xOy 中，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，圆C 的极坐标方程为ρ＝4cos θ.（1） 求出圆C 的直角坐标方程；（2） 已知圆C 与x 轴相交于A ，B 两点，若直线l ：y ＝2x ＋2m 上存在点P 使得∠APB＝90°，求实数m 的最大值.解：（1） 由ρ＝4cos θ得ρ2＝4ρcos θ，即x 2＋y 2－4x ＝0，即圆C 的标准方程为（x －2）2＋y 2＝4.（2） l 的方程为y ＝2x ＋2m ，而AB 为圆C 的直径，故直线l 上存在点P 使得∠APB＝90°的充要条件是直线l 与圆C 有公共点， 故|4＋2m|5≤2，于是实数m 的最大值为5－2.4. 在极坐标系中，已知直线2ρcos θ＋ρsin θ＋a ＝0（a>0）被圆ρ＝4sin θ截得的弦长为2，求a 的值.解：以极点为坐标原点，极轴为x 轴正半轴建立平面直角坐标系，直线的极坐标方程化为直角坐标方程为2x ＋y ＋a ＝0，圆的极坐标方程化为直角坐标方程为x 2＋y 2＝4y ，即x 2＋（y －2）2＝4.因为直线被圆截得的弦长为2，所以圆心（0，2）到直线的距离为4－1＝3， 即|2＋a|5＝3，因为a>0，所以a ＝15－2.1. 极坐标方程与直角坐标方程的互化（1） 将极坐标或极坐标方程转化为直角坐标或直角坐标方程，直接利用公式x ＝ρcos θ，y ＝ρsin θ即可.常用方法有代入法、平方法，还经常用到同乘（或除以）ρ等技巧.（2） 将直角坐标或直角坐标方程转化为极坐标或极坐标方程，要灵活运用x ＝ρcos θ，y＝ρsin θ以及ρ＝x 2＋y 2，tan θ＝y x（x≠0），同时要掌握必要的技巧，通常情况下，由tan θ确定角θ时，应根据点P 所在象限取最小正角.在这里要注意：当x≠0时，θ角才能由tan θ＝yx按上述方法确定.当x ＝0时，tan θ没有意义，这时又分三种情况：当x ＝0，y ＝0时，θ可取任何值；当x ＝0，y>0时，可取θ＝π2；当x ＝0，y<0时，可取θ＝3π2.2. 求简单曲线的极坐标方程的方法（1） 设点M （ρ，θ）为曲线上任意一点，由已知条件，构造出三角形，利用正弦定理求解OM 与θ的关系；（2） 先求出曲线的直角坐标方程，再利用极坐标与直角坐标的变换公式，把直角坐标方程化为极坐标方程.[备课札记]第2课时 参 数 方 程（对应学生用书（理）202～205页）1. （选修44P 45例1改编）已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋t 2，y ＝2＋32t（t 为参数），求此直线的倾斜角以及在y 轴上的截距.解：∵ ⎩⎪⎨⎪⎧x －1＝t 2，y －2＝32t ，∴ y －2＝3（x －1）.∴ 此直线的斜率为3，∴ 它的倾斜角为60°.令x ＝0，得它在y 轴上的截距为2－ 3.2. （选修44P 45例2改编）已知点P （3，m ）在以点F 为焦点的抛物线⎩⎪⎨⎪⎧x ＝4t 2，y ＝4t （t 为参数）上，求PF 的值.解：将抛物线的参数方程化为普通方程为y 2＝4x ，则焦点F （1，0），准线方程为x ＝－1，又P （3，m ）在抛物线上，由抛物线的定义知PF ＝3－（－1）＝4.3. （选修44P 57习题3（4））选择适当的参数，将普通方程4x 2＋y 2－16x ＋12＝0化为参数方程.解：由4x 2＋y 2－16x ＋12＝0，得4（x －2）2＋y 2＝4，选择参数θ，令y ＝2sin θ，则x ＝2＋cos θ，故所求曲线的参数方程是⎩⎪⎨⎪⎧x ＝2＋cos θ，y ＝2sin θ.（答案不惟一）4. 在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎨⎧x ＝2cos α＋3，y ＝2sin α（α为参数）.以原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为θ＝π6.若直线l 与曲线C 交于A ，B 两点，求线段AB 的长.解：曲线C 的普通方程为（x －3）2＋y 2＝4，表示以（3，0）为圆心，2为半径的圆.直线l的直角坐标方程为y ＝33x.所以圆心到直线的距离为32， 所以线段AB 的长为24－⎝ ⎛⎭⎪⎫322＝13. 5. 已知直线l 的极坐标方程为ρsin （θ－π3）＝3，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2sin θ（θ为参数），设P 点是曲线C 上的任意一点，求P 到直线l 的距离的最大值.解：由ρsin ⎝⎛⎭⎪⎫θ－π3＝3，可得ρ（12sin θ－32cos θ）＝3， ∴ y －3x ＝6，即3x －y ＋6＝0.由⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2sin θ，得x 2＋y 2＝4，圆的半径为r ＝2， ∴ 圆心到直线l 的距离d ＝62＝3.∴ P 到直线l 的距离的最大值为d ＋r ＝5.1. 参数方程是用第三个变量（即参数）分别表示曲线上任一点M 的坐标x ，y 的另一种曲线方程的形式，它体现了x ，y 的一种间接关系.2. 参数方程是根据其固有的意义（物理、几何）得到的，要注意参数的取值范围.3. 一些常见曲线的参数方程（1） 过点P 0（x 0，y 0），且倾斜角是α的直线的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋lcos α，y ＝y 0＋lsin α（l 为参数）. l是有向线段P 0P 的数量.（2） 圆方程（x －a ）2＋（y －b ）2＝r 2的参数方程是⎩⎪⎨⎪⎧x ＝a ＋rcos θ，y ＝b ＋rsin θ（θ为参数）.（3） 椭圆方程x 2a 2＋y2b 2＝1（a>b>0）的参数方程是⎩⎪⎨⎪⎧x ＝acos θ，y ＝bsin θ（θ为参数）.（4） 双曲线方程x 2a 2－y2b 2＝1（a>0，b>0）的参数方程是⎩⎪⎨⎪⎧x ＝a 2⎝ ⎛⎭⎪⎫t ＋1t ，y ＝b 2⎝ ⎛⎭⎪⎫t －1t （t 为参数）.（5） 抛物线方程y 2＝2px （p>0）的参数方程是⎩⎪⎨⎪⎧x ＝2pt 2，y ＝2pt（t 为参数）.4. 在参数方程与普通方程的互化中要注意变量的取值范围.1 参数方程与普通方程的互化1（2017·南京、盐城期末）在平面直角坐标系xOy 中，已知直线l ：⎩⎪⎨⎪⎧x ＝35t ，y ＝45t （t 为参数）.现以坐标原点O 为极点，以x 轴正半轴为极轴建立极坐标系.设圆C 的极坐标方程为ρ＝2cos θ，直线l 与圆C 交于A ，B 两点，求弦AB 的长.解：直线l ：⎩⎪⎨⎪⎧x ＝35t ，y ＝45t （t 为参数）化成普通方程为4x －3y ＝0，圆C 的极坐标方程ρ＝2cos θ化成直角坐标方程为（x －1）2＋y 2＝1，则圆C 的圆心到直线l 的距离d ＝|4|42＋（－3）2＝45， 所以AB ＝21－d 2＝65.变式训练在平面直角坐标系xOy 中，已知直线⎩⎪⎨⎪⎧x ＝－1＋55t ，y ＝－1＋255t （t 为参数）与曲线⎩⎪⎨⎪⎧x ＝sin θ，y ＝cos 2θ（θ为参数）相交于A ，B 两点，求线段AB 的长.解：将直线的参数方程化为普通方程，得y ＝2x ＋1 ①. 将曲线的参数方程化为普通方程，得y ＝1－2x 2（－1≤x≤1） ②.由①②，得⎩⎪⎨⎪⎧x ＝－1，y ＝－1或⎩⎪⎨⎪⎧x ＝0，y ＝1，所以A （－1，－1），B （0，1）或A （0，1），B （－1，－1），从而AB ＝（－1－0）2＋（－1－1）2＝ 5. 备选变式（教师专享）已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－1＋22t ，y ＝22t（t 为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ＝2sin θ－2cos θ.若直线l 与曲线C 相交于A ，B 两点，求线段AB 的长.解：由ρ＝2sin θ－2cos θ，可得ρ2＝2ρsin θ－2ρcos θ，所以曲线C 的直角坐标方程为x 2＋y 2＝2y －2x ，标准方程为（x ＋1）2＋（y －1）2＝2.直线l 的方程化成普通方程为x －y ＋1＝0.圆心到直线l 的距离为d ＝|－1－1＋1|2＝22，所求弦长AB ＝22－⎝ ⎛⎭⎪⎫222＝ 6., 2 求曲线参数方程), 2) 如图，以过原点的直线的倾斜角θ为参数，求圆x 2＋y 2－x ＝0的参数方程.解：设P （x ，y ），则随着θ取值变化，P 可以表示圆上任意一点，由所给的曲线方程x 2＋y2－x ＝0，即⎝ ⎛⎭⎪⎫x －122＋y 2＝14，表示以⎝ ⎛⎭⎪⎫12，0为圆心，12为半径的圆，可得弦OP ＝1×cos θ，所以⎩⎪⎨⎪⎧x ＝OP·cos θ，y ＝OP·sin θ，从而⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝cos θ·sin θ， 故已知圆的参数方程为⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝cos θ·sin θ（θ为参数）.备选变式（教师专享）已知直线C 1：⎩⎪⎨⎪⎧x ＝1＋tcos α，y ＝tsin α（t 为参数），曲线C 2：⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ（θ为参数）.（1） 当α＝π3时，求C 1与C 2的交点坐标；（2） 过坐标原点O 作C 1的垂线，垂足为A ，P 为OA 的中点，当α变化时，求点P 轨迹的参数方程，并指出它是什么曲线.解：（1） 当α＝π3时，C 1的普通方程为y ＝3（x －1），C 2的普通方程为x 2＋y 2＝1，联立构成方程组⎩⎨⎧y ＝3x －3，x 2＋y 2＝1，解得C 1与C 2的交点坐标分别为（1，0），⎝ ⎛⎭⎪⎫12，－32.（2） 依题意，C 1的普通方程为xsin α－ycos α－sin α＝0，则A 点的坐标为（sin 2α，－sin αcos α），故当α变化时，P 点轨迹的参数方程为⎩⎪⎨⎪⎧x ＝12sin 2α，y ＝－12sin αcos α（α为参数），所以点P 轨迹的普通方程为⎝ ⎛⎭⎪⎫x －142＋y 2＝116.故点P 的轨迹是圆心为⎝ ⎛⎭⎪⎫14，0，半径为14的圆. , 3 参数方程的应用), 3) （2017·南通、泰州模拟）在平面直角坐标系xOy 中，已知直线⎩⎪⎨⎪⎧x ＝－32＋22l ，y ＝22l （l 为参数）与曲线⎩⎪⎨⎪⎧x ＝18t 2，y ＝t （t 为参数）相交于A ，B 两点，求线段AB 的长.解：（解法1）将曲线⎩⎪⎨⎪⎧x ＝18t 2，y ＝t（t 为参数）化成普通方程为y 2＝8x ，将直线⎩⎪⎨⎪⎧x ＝－32＋22l ，y ＝22l （l 为参数）代入y 2＝8x ，整理得l 2－82l ＋24＝0，解得l 1＝22，l 2＝6 2.则|l 1－l 2|＝42，所以线段AB 的长为4 2.（解法2）将曲线⎩⎪⎨⎪⎧x ＝18t 2，y ＝t（t 为参数）化成普通方程为y 2＝8x ，将直线⎩⎪⎨⎪⎧x ＝－32＋22l ，y ＝22l （l 为参数）化成普通方程为x －y ＋32＝0，由⎩⎪⎨⎪⎧y 2＝8x ，x －y ＋32＝0得⎩⎪⎨⎪⎧x ＝12，y ＝2或⎩⎪⎨⎪⎧x ＝92，y ＝6.所以AB 的长为⎝ ⎛⎭⎪⎫92－122＋（6－2）2＝4 2.备选变式（教师专享）已知直线l ：⎩⎪⎨⎪⎧x ＝tcos α＋m ，y ＝tsin α（t 为参数）恒经过椭圆C ：⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ（φ为参数）的右焦点F.（1） 求m 的值；（2） 设直线l 与椭圆C 交于A ，B 两点，求FA·FB 的最大值与最小值.解：（1） 椭圆的参数方程化为普通方程，得x 225＋y29＝1.因为a ＝5，b ＝3，所以c ＝4，所以点F 的坐标为（4，0）. 因为直线l 经过点（m ，0），所以m ＝4.（2） 将直线l 的参数方程代入椭圆C 的普通方程，并整理得（9cos 2α＋25sin 2α）t 2＋72tcos α－81＝0.设点A ，B 在直线参数方程中对应的参数分别为t 1，t 2，则FA ·FB ＝|t 1t 2|＝819cos 2α＋25sin 2α＝819＋16sin 2α. 当sin α＝0时，FA ·FB 取最大值9；当sin α＝±1时，FA ·FB 取最小值8125., 4 极坐标、参数方程的综合应用), 4) （2017·苏锡常镇二模）在平面直角坐标系xOy 中，以O 为极点，x 轴的正半轴为极轴，取相同的单位长度，建立极坐标系.已知曲线C 1的参数方程为⎩⎨⎧x ＝3＋2cos α，y ＝3＋2sin α（α∈[0，2π]，α为参数），曲线C 2的极坐标方程为ρsin ⎝⎛⎭⎪⎫θ＋π3＝a （a∈R ），若曲线C 1与曲线C 2有且仅有一个公共点，求实数a 的值.解：曲线C 1的方程为（x －3）2＋（y －3）2＝4，圆心坐标为（3，3），半径为2.∵ 曲线C 2的极坐标方程为ρsin ⎝⎛⎭⎪⎫θ＋π3＝a （a∈R ）， ∴ 曲线C 2的直角坐标方程为3x ＋y －2a ＝0.∵ 曲线C 1与曲线C 2有且仅有一个公共点，∴ |3＋3－2a|2＝2，解得a ＝1或a ＝5.备选变式（教师专享）在平面直角坐标系xOy 中，曲线C ：⎩⎨⎧x ＝6cos α，y ＝2sin α（α为参数）.以原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρ（cos θ＋3sin θ）＋4＝0.求曲线C 上的点到直线l 的最大距离.解：将l 转化为直角坐标方程为x ＋3y ＋4＝0. 在C 上任取一点A （6cos α，2sin α），α∈[0，2π），则点A 到直线l 的距离为d ＝|6cos α＋6sin α＋4|2＝|23sin ⎝ ⎛⎭⎪⎫α＋π4＋4|2＝3sin ⎝⎛⎭⎪⎫α＋π4＋2.当α＝π4时，d 取得最大值，最大值为2＋3，此时A 点为（3，1）.1. 在直角坐标系xOy 中，以O 为极点，x 轴正半轴为极轴建立极坐标系，曲线C 1的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝22a ，曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝－1＋cos t ，y ＝－1＋sin t （t 为参数，0≤t ≤π）.当C 1与C 2有公共点时，求实数a 的取值范围.解：曲线C 1的直角坐标方程为x ＋y ＝a.若C 1与C 2有公共点，则a ＝x ＋y ＝sin t ＋cos t －2在t∈[0，π]上有解，又sin t ＋cos t －2＝2sin ⎝ ⎛⎭⎪⎫t ＋π4－2，因为t∈[0，π]，所以t ＋π4∈⎣⎢⎡⎦⎥⎤π4，5π4，sin ⎝ ⎛⎭⎪⎫t ＋π4∈⎣⎢⎡⎦⎥⎤－22，1，所以a 的取值范围为[－3，2－2].2. （2017·苏北四市期末）在平面直角坐标系xOy 中，以O 为极点，x 轴的正半轴为极轴建立极坐标系.直线l ：2sin ⎝ ⎛⎭⎪⎫θ－π4＝m （m∈R ），圆C 的参数方程为⎩⎪⎨⎪⎧x ＝1＋3cos t ，y ＝－2＋3sin t （t 为参数）.当圆心C 到直线l 的距离为2时，求m 的值.解：直线l 的直角坐标方程为x －y ＋m ＝0，圆C 的普通方程为（x －1）2＋（y ＋2）2＝9，圆心C 到直线l 的距离为|1－（－2）＋m|2＝2，解得m ＝－1或m ＝－5.3. （2016·江苏卷）在平面直角坐标系xOy 中，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝32t （t 为参数），椭圆C 的参数方程为⎩⎪⎨⎪⎧x ＝cos θ，y ＝2sin θ（θ为参数）.设直线l 与椭圆C 相交于A ，B 两点，求线段AB 的长.解：椭圆C 的普通方程为x 2＋y 24＝1，将直线l 的参数方程⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝32t代入x 2＋y24＝1，得⎝ ⎛⎭⎪⎫1＋12t 2＋⎝ ⎛⎭⎪⎫32t 24＝1，即7t 2＋16t ＝0，解得t 1＝0，t 2＝－167.所以AB ＝|t 1－t 2|＝167.4. （2017·扬州期末）在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝cos α ，y ＝1＋sin 2α（α为参数），以直角坐标系原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为θ＝π4，试求直线l 与曲线C 的交点的直角坐标. 解：将直线l 的极坐标方程化成直角坐标方程为y ＝x ，将曲线C 的参数方程化成普通方程为y ＝2－x 2（－1≤x≤1）. 由⎩⎪⎨⎪⎧y ＝x ，y ＝2－x 2得x 2＋x －2＝0，解得x ＝1或x ＝－2. 又－1≤x≤1，所以x ＝1，所以直线l 与曲线C 的交点的直角坐标为（1，1）.1. 在极坐标系中，直线l 的极坐标方程为θ＝π3（ρ∈R ），以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos α，y ＝1＋cos 2α（α为参数），求直线l 与曲线C的交点P 的直角坐标.解：因为直线l 的极坐标方程为θ＝π3（ρ∈R ），所以直线l 的普通方程为y ＝3x. ①又曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos α，y ＝1＋cos 2α（α为参数），所以曲线C 的直角坐标方程为y ＝12x 2（x∈[－2，2]）， ②联立①②解方程组得⎩⎪⎨⎪⎧x ＝0，y ＝0或⎩⎨⎧x ＝23，y ＝6（舍去）.故P 点的直角坐标为（0，0）.2. （2017·苏州期末）在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1－22t ，y ＝2＋22t（t 为参数），以坐标原点O 为极点，x 轴正半轴为极轴的极坐标系中，曲线C 的极坐标方程为ρsin 2θ－4cos θ＝0，已知直线l 与曲线C 相交于A ，B 两点，求线段AB 的长.解：因为曲线C 的极坐标方程为ρsin 2θ－4cos θ＝0，所以ρ2sin 2θ＝4ρcos θ，即曲线C 的直角坐标方程为y 2＝4x.将直线l 的参数方程⎩⎪⎨⎪⎧x ＝1－22t ，y ＝2＋22t 代入抛物线方程y 2＝4x ，得⎝ ⎛⎭⎪⎫2＋22t 2＝4⎝ ⎛⎭⎪⎫1－22t ，即t 2＋82t ＝0，解得t 1＝0，t 2＝－8 2.所以AB ＝|t 1－t 2|＝8 2.3. 在平面直角坐标系xOy 中，已知曲线C ：⎩⎪⎨⎪⎧x ＝s ，y ＝s 2（s 为参数），直线l ：⎩⎪⎨⎪⎧x ＝2＋110t ，y ＝4＋310t （t 为参数）.设曲线C 与直线l 交于A ，B 两点，求线段AB 的长度.解：由⎩⎪⎨⎪⎧x ＝s ，y ＝s2消去s 得曲线C 的普通方程为y ＝x 2； 由⎩⎪⎨⎪⎧x ＝2＋110t ，y ＝4＋310t消去t 得直线l 的普通方程为y ＝3x －2.联立直线l 的方程与曲线C 的方程，即⎩⎪⎨⎪⎧y ＝x 2，y ＝3x －2，解得交点的坐标分别为（1，1），（2，4）.所以线段AB 的长度为（2－1）2＋（4－1）2＝10.4. （2017·南京、盐城模拟）在平面直角坐标系xOy 中，直线l ：⎩⎪⎨⎪⎧x ＝1＋35t ，y ＝45t（t 为参数）与曲线C ：⎩⎪⎨⎪⎧x ＝4k 2，y ＝4k （k 为参数）交于A ，B 两点，求线段AB 的长.解：（解法1）直线l 的参数方程化为普通方程得4x －3y ＝4，将曲线C 的参数方程化为普通方程得y 2＝4x.联立方程组⎩⎪⎨⎪⎧4x －3y ＝4，y 2＝4x ，解得⎩⎪⎨⎪⎧x ＝4，y ＝4或⎩⎪⎨⎪⎧x ＝14，y ＝－1，所以A （4，4），B ⎝ ⎛⎭⎪⎫14，－1或A ⎝ ⎛⎭⎪⎫14，－1，B （4，4）. 所以AB ＝⎝ ⎛⎭⎪⎫4－142＋（4＋1）2＝254. （解法2）将曲线C 的参数方程化为普通方程得y 2＝4x.将直线l 的参数方程代入抛物线C 的方程得⎝ ⎛⎭⎪⎫45t 2＝4⎝ ⎛⎭⎪⎫1＋35t ，即4t 2－15t －25＝0，所以 t 1＋t 2＝154，t 1t 2＝－254.所以AB ＝|t 1－t 2|＝（t 1＋t 2）2－4t 1t 2＝⎝ ⎛⎭⎪⎫1542＋25＝254.1. 在直线的参数方程⎩⎪⎨⎪⎧x ＝x 0＋tcos α，y ＝y 0＋tsin α（t 为参数）中t 的几何意义是表示在直线上过定点P 0（x 0，y 0）与直线上的任一点P （x ，y ）构成的有向线段P 0P 的长度，且在直线上任意两点P 1，P 2的距离为P 1P 2＝|t 1－t 2|＝（t 1＋t 2）2－4t 1t 2.2. 参数方程化为普通方程的关键是消参数：一要熟练掌握常用技巧（如整体代换）；二要注意变量取值范围的一致性，这一点最易忽视.[备课札记]。

坐标系与参数方程【2019年高考考纲解读】高考主要考查平面直角坐标系中的伸缩变换、直线和圆的极坐标方程、参数方程与普通方程的互化、常见曲线的参数方程及参数方程的简单应用．以极坐标、参数方程与普通方程的互化为主要考查形式，同时考查直线与曲线的位置关系等解析几何知识． 【重点、难点剖析】 1．直角坐标与极坐标的互化把直角坐标系的原点作为极点，x 轴正半轴作为极轴，且在两坐标系中取相同的长度单位．设M 是平面内的任意一点，它的直角坐标、极坐标分别为(x ，y )和(ρ，θ)，则⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ，⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝y x x2．直线的极坐标方程若直线过点M (ρ0，θ0)，且极轴到此直线的角为α，则它的方程为：ρsin(θ－α)＝ρ0sin(θ0－α)． 几个特殊位置的直线的极坐标方程 (1)直线过极点：θ＝α；(2)直线过点M (a,0)(a >0)且垂直于极轴：ρcos θ＝a ；(3)直线过M ⎝⎛⎭⎪⎫b ，π2且平行于极轴：ρsin θ＝b .3．圆的极坐标方程若圆心为M (ρ0，θ0)，半径为r 的圆方程为： ρ2－2ρ0ρcos(θ－θ0)＋ρ20－r 2＝0. 几个特殊位置的圆的极坐标方程 (1)当圆心位于极点，半径为r ：ρ＝r ；(2)当圆心位于M (r,0)，半径为r ：ρ＝2r cos θ；(3)当圆心位于M ⎝⎛⎭⎪⎫r ，π2，半径为r ：ρ＝2r sin θ.(4)圆心在点M (x 0，y 0)，半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数，0≤θ≤2π)．圆心在点A (ρ0，θ0)，半径为r 的圆的方程为r 2＝ρ2＋ρ20－2ρρ0cos(θ－θ0)． 4．直线的参数方程经过点P 0(x 0，y 0)，倾斜角为α的直线的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．设P 是直线上的任一点，则t 表示有向线段P 0P →的数量． 5．圆的参数方程圆心在点M (x 0，y 0)，半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数，0≤θ≤2π)．6．圆锥曲线的参数方程(1)椭圆x 2a 2＋y 2b 2＝1的参数方程为⎩⎪⎨⎪⎧x ＝a cos θ，y ＝b sin θ(θ为参数)．(2)双曲线x 2a 2－y 2b 2＝1的参数方程为⎩⎪⎨⎪⎧ x ＝a sec θ，y ＝b tan θ(θ为参数)．(3)抛物线y2＝2px (p >0)的参数方程为⎩⎪⎨⎪⎧x ＝2pt 2，y ＝2pt (t 为参数).【题型示例】题型一 极坐标方程和参数方程【例1】(2018·全国Ⅰ)在直角坐标系xOy 中，曲线C 1的方程为y ＝k |x |＋2.以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ2＋2ρcos θ－3＝0. (1)求C 2的直角坐标方程；【思路方法】(1)先列方程，再进一步转化为参数方程． (2)解出交点，再求得直线方程，最后转化为极坐标方程．【解析】(1)设(x 1，y 1)为圆上的点，在已知变换下变为曲线C 上的点(x ，y )，依题意，得⎩⎪⎨⎪⎧x ＝x 1，y ＝2y 1.由x 21＋y 21＝1，得x 2＋⎝ ⎛⎭⎪⎫y 22＝1，即曲线C 的方程为x 2＋y 24＝1.故C 的参数方程为⎩⎪⎨⎪⎧x ＝cos t ，y ＝2sin t(t 为参数)．【感悟提升】若极坐标系的极点与直角坐标系的原点重合，极轴与x 轴正半轴重合，两坐标系的长度单位相同，则极坐标方程与直角坐标方程可以互化．求解与极坐标方程有关的问题时，可以转化为熟悉的直角坐标方程求解．若最终结果要求用极坐标表示，则需将直角坐标转化为极坐标． 题型二 参数方程与普通方程的互化【例2】(2018·全国Ⅲ)在平面直角坐标系xOy 中，⊙O 的参数方程为⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ(θ为参数)，过点(0，－2)且倾斜角为α的直线l 与⊙O 交于A ，B 两点． (1)求α的取值范围；(2)求AB 中点P 的轨迹的参数方程．【解析】 (1)⊙O 的直角坐标方程为x 2＋y 2＝1. 当α＝π2时，l 与⊙O 交于两点．当α≠π2时，记tan α＝k ，则l 的方程为y ＝kx － 2.l 与⊙O 交于两点当且仅当|2|1＋k 2<1，解得k <－1或k >1，即α∈⎝⎛⎭⎪⎫π2，3π4或α∈⎝ ⎛⎭⎪⎫π4，π2.综上，α的取值范围是⎝ ⎛⎭⎪⎫π4，3π4.(2)l 的参数方程为⎩⎨⎧x ＝t cos α，y ＝－2＋t sin α⎝ ⎛⎭⎪⎫t 为参数，π4<α<3π4. 设A ，B ，P 对应的参数分别为t A ，t B ，t P ，则t P ＝t A ＋t B2，且t A ，t B 满足t 2－22t sin α＋1＝0.于是t A ＋t B ＝22sin α，t P ＝2sin α.又点P 的坐标(x ，y )满足⎩⎨⎧x ＝t P cos α，y ＝－2＋t P sin α，所以点P 的轨迹的参数方程是⎩⎪⎨⎪⎧x ＝22sin 2α，y ＝－22－22cos 2α⎝⎛⎭⎪⎫α为参数，π4<α<3π4.【感悟提升】(1)将参数方程化为普通方程，需要根据参数方程的结构特征，选取适当的消参方法．常见的消参方法有代入消参法、加减消参法、平方消参法等．(2)将参数方程化为普通方程时，要注意两种方程的等价性，不要增解、漏解，若x ，y 有范围限制，要标出x ，y 的取值范围．【变式探究】 【2017·江苏】[选修4-4：坐标系与参数方程]在平面坐标系中xOy 中,已知直线l 的参考方程为x 82t ty =-+⎧⎪⎨=⎪⎩(t 为参数),曲线C的参数方程为22,x s y ⎧=⎪⎨=⎪⎩(s 为参数).设P 为曲线C 上的动点，求点P 到直线l 的距离的最小值.【答案】5【解析】直线l 的普通方程为. 因为点P 在曲线C 上，设，从而点P 到直线l 的的距离，当s =min d =. 因此当点P 的坐标为()4,4时，曲线C 上点P 到直线l. 【考点】参数方程化普通方程【变式探究】在直角坐标系x O y 中,曲线C 1的参数方程为（t 为参数,a ＞0）．在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2：ρ=4cos θ. （I ）说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程；（II ）直线C 3的极坐标方程为0θα=,其中0α满足tan 0α=2,若曲线C 1与C 2的公共点都在C 3上,求a ． 【答案】（I ）圆,（II ）1【解析】解：（Ⅰ）消去参数t 得到1C 的普通方程.1C 是以)1,0(为圆心，a 为半径的圆.将代入1C 的普通方程中，得到1C 的极坐标方程为.（Ⅱ）曲线21,C C 的公共点的极坐标满足方程组若0≠ρ，由方程组得，由已知2tan =θ，可得，从而012=-a ，解得1-=a （舍去），1=a .1=a 时，极点也为21,C C 的公共点，在3C 上.所以1=a .【变式探究】在直角坐标系xOy 中，直线C 1：x ＝－2，圆C 2：(x －1)2＋(y －2)2＝1，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系． (1)求C 1，C 2的极坐标方程；(2)若直线C 3的极坐标方程为θ＝π4(ρ∈R )，设C 2与C 3的交点为M ，N ，求△C 2MN 的面积．【变式探究】在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝2cos α，y ＝2＋2sin α(α为参数)，M 是C 1上的动点，P 点满足OP →＝2OM →，点P 的轨迹为曲线C 2.(1)求C 2的方程；(2)在以O 为极点，x 轴的正半轴为极轴的极坐标系中，射线θ＝π3与C 1的异于极点的交点为A ，与C 2的异于极点的交点为B ，求AB .【解析】(1)设P (x ，y )，则由条件知M ⎝ ⎛⎭⎪⎫x 2，y2，由于M 点在C 1上，所以⎩⎪⎨⎪⎧x 2＝2cos α，y2＝2＋2sin α，即⎩⎪⎨⎪⎧x ＝4cos α，y ＝4＋4sin α.从而C 2的参数方程为⎩⎪⎨⎪⎧x ＝4cos α，y ＝4＋4sin α(α为参数)．(2)曲线C 1的极坐标方程为ρ＝4sin θ，曲线C 2的极坐标方程为ρ＝8sin θ.射线θ＝π3与C 1的交点A的极径为ρ1＝4sin π3，射线θ＝π3与C 2的交点B 的极径为ρ2＝8sin π3.所以AB ＝|ρ2－ρ1|＝2 3.【规律方法】解决这类问题一般有两种思路，一是将极坐标方程化为直角坐标方程，求出交点的直角坐标，再将其化为极坐标；二是将曲线的极坐标方程联立，根据限制条件求出极坐标．要注意题目所给的限制条件及隐含条件．【变式探究】将圆x 2＋y 2＝1上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C . (1)写出C 的参数方程；(2)设直线l ：2x ＋y －2＝0与C 的交点为P 1，P 2，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求过线段P 1P 2的中点且与l 垂直的直线的极坐标方程．解 (1)设(x 1，y 1)为圆上的点，在已知变换下变为C 上点(x ，y )，依题意，得1,2,x x y y =⎧⎨=⎩由x 21＋y 21＝1得x 2＋⎝ ⎛⎭⎪⎫y 22＝1，即曲线C 的方程为x 2＋y 24＝1.故C 的参数方程为cos 2sin x t y t =⎧⎨=⎩(t 为参数)．(2)由解得：1,0x y =⎧⎨=⎩或0,2.x y =⎧⎨=⎩不妨设P 1(1，0)，P 2(0，2)，则线段P 1P 2的中点坐标为⎝ ⎛⎭⎪⎫12，1，所求直线斜率为k ＝12，于是所求直线方程为y －1＝12⎝⎛⎭⎪⎫x －12，化为极坐标方程，并整理得 2ρcos θ－4ρsin θ＝－3， 即ρ＝34sin θ－2cos θ.题型三 极坐标 参数方程及其应用【例3】在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝1＋cos α，y ＝sin α(α为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1－t ，y ＝3＋t(t 为参数)，在以坐标原点为极点，x 轴的正半轴为极轴的极坐标系中，射线m ：θ＝β(ρ>0)．(1)求C 和l 的极坐标方程；(2)设点A 是m 与C 的一个交点(异于原点)，点B 是m 与l 的交点，求|OA ||OB |的最大值．解 (1)曲线C 的普通方程为(x －1)2＋y 2＝1，由⎩⎪⎨⎪⎧ρcos θ＝x ，ρsin θ＝y ，得()ρcos θ－12＋ρ2sin 2θ＝1，化简得C 的极坐标方程为ρ＝2cos θ. 因为l 的普通方程为x ＋y －4＝0，所以极坐标方程为ρcos θ＋ρsin θ－4＝0， 所以l 的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝2 2. (2)设A (ρ1，β)，B (ρ2，β)， 则|OA ||OB |＝ρ1ρ2＝2cos β·sin β＋cos β4＝12(sin βcos β＋cos 2β)＝24sin ⎝⎛⎭⎪⎫2β＋π4＋14，由射线m 与C ，直线l 相交，则不妨设β∈⎝ ⎛⎭⎪⎫－π4，π4， 则2β＋π4∈⎝ ⎛⎭⎪⎫－π4，3π4，所以当2β＋π4＝π2，即β＝π8时，|OA ||OB |取得最大值，即⎝⎛⎭⎪⎫|OA ||OB |max＝2＋14. 【感悟提升】 (1)利用参数方程解决问题，要理解参数的几何意义．(2)在解决直线、圆和圆锥曲线的有关问题时，常常将极坐标方程化为直角坐标方程或将参数方程化为普通方程，有助于认识方程所表示的曲线，从而达到化陌生为熟悉的目的，这是转化与化归思想的应用． 【变式探究】在平面直角坐标系中，以原点为极点，以x 轴的正半轴为极轴且取相同的单位长度建立极坐标系，曲线C 1的极坐标方程为ρ＝2cos θ.(1)若曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝1＋t sin α(α为参数)，求曲线C 1的直角坐标方程和曲线C 2的普通方程；(2)若曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝1＋t sin α(t 为参数)，A (0,1)，且曲线C 1与曲线C 2的交点分别为P ，Q ，求1|AP |＋1|AQ |的取值范围． 【解析】 (1)∵ρ＝2cos θ，∴ρ2＝2ρcos θ， 又∵ρ2＝x 2＋y 2，ρcos θ＝x ，∴曲线C 1的直角坐标方程为x 2＋y 2－2x ＝0， 曲线C 2的普通方程为x 2＋(y －1)2＝t 2.(2)将C 2的参数方程⎩⎪⎨⎪⎧x ＝t cos α，y ＝1＋t sin α(t 为参数)代入C 1的方程x 2＋y 2－2x ＝0，得t 2＋(2sin α－2cos α)t＋1＝0.∵Δ＝(2sin α－2cos α)2－4＝8sin 2⎝ ⎛⎭⎪⎫α－π4－4>0，∴⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π4∈⎝ ⎛⎦⎥⎤22，1，∴sin ⎝ ⎛⎭⎪⎫α－π4∈⎣⎢⎡⎭⎪⎫－1，－22∪⎝ ⎛⎦⎥⎤22，1. t 1＋t 2＝－(2sin α－2cos α)＝－22sin ⎝⎛⎭⎪⎫α－π4，t 1t 2＝1>0，∵t 1t 2＝1>0，∴t 1，t 2同号，∴|t 1|＋|t 2|＝|t 1＋t 2|. 由点A 在曲线C 2上，根据t 的几何意义，可得 1|PA |＋1|AQ |＝1|t 1|＋1|t 2|＝|t 1|＋|t 2||t 1||t 2| ＝|t 1|＋|t 2||t 1t 2|＝|t 1＋t 2|1＝22⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π4∈(2,22]．∴1|PA |＋1|AQ |∈(2,22]． 【变式探究】在直角坐标系xOy 中，曲线C 的参数方程为3cos ,sin ,x y θθ=⎧⎨=⎩（θ为参数），直线l 的参数方程为.（1）若a =−1，求C 与l 的交点坐标；（2）若C 上的点到la. 【答案】（1）C 与l 的交点坐标为()3,0， 2124,2525⎛⎫-⎪⎝⎭；（2）8a =或16a =-. 【解析】（1）曲线C 的普通方程为2219x y +=. 当1a =-时，直线l 的普通方程为.由解得3{ 0x y ==或2125{ 2425x y =-=. 从而C 与l 的交点坐标为()3,0， 2124,2525⎛⎫-⎪⎝⎭. （2）直线l 的普通方程为，故C 上的点到l 的距离为.当4a ≥-时， d=8a =； 当4a <-时， d由题设得，所以16a =-.综上， 8a =或16a =-.【变式探究】在直角坐标系xOy 中，圆C 的方程为．（Ⅰ）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求C 的极坐标方程； （Ⅱ）直线l 的参数方程是cos sin x t y t αα=⎧⎨=⎩（t 为参数）, l 与C 交于,A B两点，||AB =，求l 的斜率．【答案】（Ⅰ）；（Ⅱ）3±. 【解析】（I ）由可得C 的极坐标方程（II ）在（I ）中建立的极坐标系中，直线l 的极坐标方程为由,A B 所对应的极径分别为12,,ρρ将l 的极坐标方程代入C 的极坐标方程得于是由||AB =得，所以l的斜率为3或3-. 【变式探究】已知直线l 的参数方程为1,1x t y t =-+⎧⎨=+⎩(t 为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ2cos 2θ＝4⎝ ⎛⎭⎪⎫ρ＞0，3π4＜θ＜5π4，则直线l 与曲线C 的交点的极坐标为________．解析 直线l 的直角坐标方程为y ＝x ＋2，由ρ2cos 2θ＝4得ρ2(cos 2θ－sin 2θ)＝4，直角坐标方程为x 2－y 2＝4，把y ＝x ＋2代入双曲线方程解得x ＝－2，因此交点为(－2，0)，其极坐标为(2，π)． 答案 (2，π)【变式探究】已知直线l 的参数方程为⎩⎪⎨⎪⎧ x ＝a －2t ，y ＝－4t (t 为参数)，圆C 的参数方程为⎩⎪⎨⎪⎧ x ＝4cos θ，y ＝4sin θ(θ为参数)．(1)求直线l 和圆C 的普通方程；(2)若直线l 与圆C 有公共点，求实数a 的取值范围．【命题意图】本小题主要考查直线与圆的参数方程等基础知识，意在考查考生的运算求解能力及化归与转化思想．【解题思路】(1)消去参数，即可求出直线l 与圆C 的普通方程．(2)求出圆心的坐标，利用圆心到直线l 的距离不大于半径，得到关于参数a 的不等式，即可求出参数a 的取值范围．【解析】(1)直线l 的普通方程为2x －y －2a ＝0，圆C 的普通方程为x 2＋y 2＝16.(2)因为直线l 与圆C 有公共点，故圆C 的圆心到直线l 的距离d ＝|－2a |5≤4， 解得－25≤a ≤2 5. 【感悟提升】1．将参数方程化为普通方程的过程就是消去参数的过程，常用的消参方法有代入消参、加减消参和三角恒等式消参等，往往需要对参数方程进行变形，为消去参数创造条件．2．在与直线、圆、椭圆有关的题目中，参数方程的使用会使问题的解决事半功倍，尤其是求取值范围和最值问题，可将参数方程代入相关曲线的普通方程中，根据参数的取值条件求解． 【变式探究】在平面直角坐标系xOy 中，圆C 的参数方程为(t 为参数)．在极坐标系(与平面直角坐标系xOy 取相同的长度单位，且以原点O 为极点，以x 轴非负半轴为极轴)中，直线l 的方程为2ρsin ⎝ ⎛⎭⎪⎫θ－π4＝m (m ∈R )． ①求圆C 的普通方程及直线l 的直角坐标方程；②设圆心C 到直线l 的距离等于2，求m 的值．。

坐标系与参数方程【年高考考纲解读】高考主要考查平面直角坐标系中的伸缩变换、直线和圆的极坐标方程、参数方程与普通方程的互化、常见曲线的参数方程及参数方程的简单应用．以极坐标、参数方程与普通方程的互化为主要考查形式，同时考查直线与曲线的位置关系等解析几何知识．【重点、难点剖析】．直角坐标与极坐标的互化把直角坐标系的原点作为极点，轴正半轴作为极轴，且在两坐标系中取相同的长度单位．设是平面内的任意一点，它的直角坐标、极坐标分别为(，)和(ρ，θ)，则(\\(＝ρθ，＝ρθ，)) (\\(ρ＝＋，θ＝().))．直线的极坐标方程若直线过点(ρ，θ)，且极轴到此直线的角为α，则它的方程为：ρ(θ－α)＝ρ(θ－α)．几个特殊位置的直线的极坐标方程()直线过极点：θ＝α；()直线过点()(>)且垂直于极轴：ρθ＝；()直线过且平行于极轴：ρθ＝.．圆的极坐标方程若圆心为(ρ，θ)，半径为的圆方程为：ρ－ρρ(θ－θ)＋ρ－＝.几个特殊位置的圆的极坐标方程()当圆心位于极点，半径为：ρ＝；()当圆心位于()，半径为：ρ＝θ；()当圆心位于，半径为：ρ＝θ.()圆心在点(，)，半径为的圆的参数方程为(\\(＝＋θ，＝＋θ))(θ为参数，≤θ≤π)．圆心在点(ρ，θ)，半径为的圆的方程为＝ρ＋ρ－ρρ(θ－θ)．．直线的参数方程经过点(，)，倾斜角为α的直线的参数方程为(\\(＝＋α，＝＋α))(为参数)．设是直线上的任一点，则表示有向线段的数量．．圆的参数方程圆心在点(，)，半径为的圆的参数方程为(\\(＝＋θ，＝＋θ))(θ为参数，≤θ≤π)．．圆锥曲线的参数方程()椭圆＋＝的参数方程为(\\(＝θ，＝θ))(θ为参数)．()双曲线－＝的参数方程为(\\(＝θ，＝θ))(θ为参数)．()抛物线＝(>)的参数方程为(\\(＝，＝))(为参数).【题型示例】题型一极坐标方程和参数方程【例】(·全国Ⅰ)在直角坐标系中，曲线的方程为＝＋.以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为ρ＋ρθ－＝.()求的直角坐标方程；【思路方法】()先列方程，再进一步转化为参数方程．()解出交点，再求得直线方程，最后转化为极坐标方程．【解析】()设(，)为圆上的点，在已知变换下变为曲线上的点(，)，依题意，得(\\(＝，＝.))由＋＝，得＋＝，即曲线的方程为＋＝.故的参数方程为(\\(＝，＝ ))(为参数)．【感悟提升】若极坐标系的极点与直角坐标系的原点重合，极轴与轴正半轴重合，两坐标系的长度单位相。

【2019年高考考纲解读】高考主要考查平面直角坐标系中的伸缩变换、直线和圆的极坐标方程、参数方程与普通方程的互化、常见曲线的参数方程及参数方程的简单应用．以极坐标、参数方程与普通方程的互化为主要考查形式，同时考查直线与曲线的位置关系等解析几何知识． 【重点、难点剖析】 1．直角坐标与极坐标的互化把直角坐标系的原点作为极点，x 轴正半轴作为极轴，且在两坐标系中取相同的长度单位．设M 是平面内的任意一点，它的直角坐标、极坐标分别为(x ，y )和(ρ，θ)，则⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ，⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝yx x2．直线的极坐标方程若直线过点M (ρ0，θ0)，且极轴到此直线的角为α，则它的方程为：ρsin(θ－α)＝ρ0sin(θ0－α)． 几个特殊位置的直线的极坐标方程 (1)直线过极点：θ＝α；(2)直线过点M (a,0)(a >0)且垂直于极轴：ρcos θ＝a ； (3)直线过M ⎝⎛⎭⎫b ，π2且平行于极轴：ρsin θ＝b . 3．圆的极坐标方程若圆心为M (ρ0，θ0)，半径为r 的圆方程为： ρ2－2ρ0ρcos(θ－θ0)＋ρ20－r 2＝0. 几个特殊位置的圆的极坐标方程 (1)当圆心位于极点，半径为r ：ρ＝r ； (2)当圆心位于M (r,0)，半径为r ：ρ＝2r cos θ； (3)当圆心位于M ⎝⎛⎭⎫r ，π2，半径为r ：ρ＝2r sin θ. (4)圆心在点M (x 0，y 0)，半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数，0≤θ≤2π)．圆心在点A (ρ0，θ0)，半径为r 的圆的方程为r 2＝ρ2＋ρ20－2ρρ0cos(θ－θ0)．4．直线的参数方程经过点P 0(x 0，y 0)，倾斜角为α的直线的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．设P 是直线上的任一点，则t 表示有向线段P 0P →的数量． 5．圆的参数方程圆心在点M (x 0，y 0)，半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数，0≤θ≤2π)．6．圆锥曲线的参数方程(1)椭圆x 2a 2＋y 2b 2＝1的参数方程为⎩⎪⎨⎪⎧x ＝a cos θ，y ＝b sin θ(θ为参数)．(2)双曲线x 2a 2－y 2b 2＝1的参数方程为⎩⎪⎨⎪⎧x ＝a sec θ，y ＝b tan θ(θ为参数)．(3)抛物线y 2＝2px (p >0)的参数方程为⎩⎪⎨⎪⎧x ＝2pt 2，y ＝2pt (t 为参数). 【题型示例】题型一 极坐标方程和参数方程【例1】(2018·全国Ⅰ)在直角坐标系xOy 中，曲线C 1的方程为y ＝k |x |＋2.以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ2＋2ρcos θ－3＝0. (1)求C 2的直角坐标方程；【思路方法】(1)先列方程，再进一步转化为参数方程． (2)解出交点，再求得直线方程，最后转化为极坐标方程．【解析】(1)设(x 1，y 1)为圆上的点，在已知变换下变为曲线C 上的点(x ，y )，依题意，得⎩⎪⎨⎪⎧x ＝x 1，y ＝2y 1. 由x 21＋y 21＝1，得x 2＋⎝⎛⎭⎫y 22＝1， 即曲线C 的方程为x 2＋y 24＝1.故C 的参数方程为⎩⎪⎨⎪⎧x ＝cos t ，y ＝2sin t(t 为参数)．【感悟提升】若极坐标系的极点与直角坐标系的原点重合，极轴与x 轴正半轴重合，两坐标系的长度单位相同，则极坐标方程与直角坐标方程可以互化．求解与极坐标方程有关的问题时，可以转化为熟悉的直角坐标方程求解．若最终结果要求用极坐标表示，则需将直角坐标转化为极坐标． 题型二 参数方程与普通方程的互化【例2】(2018·全国Ⅲ)在平面直角坐标系xOy 中，⊙O 的参数方程为⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ(θ为参数)，过点(0，－2)且倾斜角为α的直线l 与⊙O 交于A ，B 两点． (1)求α的取值范围；(2)求AB 中点P 的轨迹的参数方程．【解析】 (1)⊙O 的直角坐标方程为x 2＋y 2＝1. 当α＝π2时，l 与⊙O 交于两点．当α≠π2时，记tan α＝k ，则l 的方程为y ＝kx － 2.l 与⊙O 交于两点当且仅当|2|1＋k 2<1，解得k <－1或k >1，即α∈⎝⎛⎭⎫π2，3π4或α∈⎝⎛⎭⎫π4，π2. 综上，α的取值范围是⎝⎛⎭⎫π4，3π4. (2)l 的参数方程为⎩⎨⎧x ＝t cos α，y ＝－2＋t sin α⎝⎛⎭⎫t 为参数，π4<α<3π4. 设A ，B ，P 对应的参数分别为t A ，t B ，t P ， 则t P ＝t A ＋t B2，且t A ，t B 满足t 2－22t sin α＋1＝0.于是t A ＋t B ＝22sin α，t P ＝2sin α.又点P 的坐标(x ，y )满足⎩⎨⎧x ＝t P cos α，y ＝－2＋t P sin α，所以点P 的轨迹的参数方程是⎩⎨⎧x ＝22sin 2α，y ＝－22－22cos 2α⎝⎛⎭⎫α为参数，π4<α<3π4.【感悟提升】(1)将参数方程化为普通方程，需要根据参数方程的结构特征，选取适当的消参方法．常见的消参方法有代入消参法、加减消参法、平方消参法等．(2)将参数方程化为普通方程时，要注意两种方程的等价性，不要增解、漏解，若x ，y 有范围限制，要标出x ，y 的取值范围．【变式探究】 【2017·江苏】[选修4-4：坐标系与参数方程]在平面坐标系中xOy 中,已知直线l 的参考方程为x 82t ty =-+⎧⎪⎨=⎪⎩(t 为参数),曲线C的参数方程为22,x s y ⎧=⎪⎨=⎪⎩(s 为参数).设P 为曲线C 上的动点，求点P 到直线l 的距离的最小值.【解析】直线l 的普通方程为. 因为点P 在曲线C 上，设，从而点P 到直线l 的的距离，当s =min d =. 因此当点P 的坐标为()4,4时，曲线C 上点P 到直线l的距离取到最小值5. 【考点】参数方程化普通方程【变式探究】在直角坐标系x O y 中,曲线C 1的参数方程为（t 为参数,a ＞0）．在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2：ρ=4cos θ.（I ）说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程；（II ）直线C 3的极坐标方程为0θα=,其中0α满足tan 0α=2,若曲线C 1与C 2的公共点都在C 3上,求a ． 【答案】（I ）圆,（II ）1【解析】解：（Ⅰ）消去参数t 得到1C 的普通方程.1C 是以)1,0(为圆心，a 为半径的圆.将代入1C 的普通方程中，得到1C 的极坐标方程为.（Ⅱ）曲线21,C C 的公共点的极坐标满足方程组若0≠ρ，由方程组得，由已知2tan =θ，可得，从而012=-a ，解得1-=a （舍去），1=a .1=a 时，极点也为21,C C 的公共点，在3C 上.所以1=a .【变式探究】在直角坐标系xOy 中，直线C 1：x ＝－2，圆C 2：(x －1)2＋(y －2)2＝1，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系． (1)求C 1，C 2的极坐标方程；(2)若直线C 3的极坐标方程为θ＝π4(ρ∈R )，设C 2与C 3的交点为M ，N ，求△C 2MN 的面积．【变式探究】在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝2cos α，y ＝2＋2sin α(α为参数)，M 是C 1上的动点，P点满足OP →＝2OM →，点P 的轨迹为曲线C 2. (1)求C 2的方程；(2)在以O 为极点，x 轴的正半轴为极轴的极坐标系中，射线θ＝π3与C 1的异于极点的交点为A ，与C 2的异于极点的交点为B ，求AB .【解析】(1)设P (x ，y )，则由条件知M ⎝⎛⎭⎫x 2，y 2，由于M 点在C 1上，所以⎩⎨⎧x2＝2cos α，y2＝2＋2sin α，即⎩⎪⎨⎪⎧x ＝4cos α，y ＝4＋4sin α. 从而C 2的参数方程为⎩⎪⎨⎪⎧x ＝4cos α，y ＝4＋4sin α(α为参数)．(2)曲线C 1的极坐标方程为ρ＝4sin θ，曲线C 2的极坐标方程为ρ＝8sin θ.射线θ＝π3与C 1的交点A 的极径为ρ1＝4sin π3，射线θ＝π3与C 2的交点B 的极径为ρ2＝8sin π3.所以AB ＝|ρ2－ρ1|＝2 3.【规律方法】解决这类问题一般有两种思路，一是将极坐标方程化为直角坐标方程，求出交点的直角坐标，再将其化为极坐标；二是将曲线的极坐标方程联立，根据限制条件求出极坐标．要注意题目所给的限制条件及隐含条件．【变式探究】将圆x 2＋y 2＝1上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C . (1)写出C 的参数方程；(2)设直线l ：2x ＋y －2＝0与C 的交点为P 1，P 2，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求过线段P 1P 2的中点且与l 垂直的直线的极坐标方程．解 (1)设(x 1，y 1)为圆上的点，在已知变换下变为C 上点(x ，y )，依题意，得1,2,x x y y =⎧⎨=⎩由x 21＋y 21＝1得x 2＋⎝⎛⎭⎫y 22＝1，即曲线C 的方程为x 2＋y 24＝1.故C 的参数方程为cos 2sin x t y t =⎧⎨=⎩(t 为参数)．(2)由解得：1,0x y =⎧⎨=⎩或0,2.x y =⎧⎨=⎩。

参数方程【考点梳理】1．曲线的参数方程一般地，在平面直角坐标系中，如果曲线上任意一点的坐标x ，y 都是某个变数t 的函数⎩⎪⎨⎪⎧x ＝f t ，y ＝g t并且对于t 的每一个允许值，由这个方程组所确定的点M (x ，y )都在这条曲线上，那么这个方程组就叫做这条曲线的参数方程，联系变数x ，y 的变数t 叫做参变数，简称参数．2．参数方程与普通方程的互化通过消去参数从参数方程得到普通方程，如果知道变数x ，y 中的一个与参数t 的关系，例如x ＝f (t )，把它代入普通方程，求出另一个变数与参数的关系y ＝g (t )，那么⎩⎪⎨⎪⎧x ＝f t ，y ＝gt就是曲线的参数方程．在参数方程与普通方程的互化中，必须使x ，y 的取值范围保持一致．3．常见曲线的参数方程和普通方程考点一、参数方程与普通方程的互化【例1】已知曲线C 1：⎩⎪⎨⎪⎧x ＝－4＋cos t ，y ＝3＋sin t(t 为参数)，C 2：⎩⎪⎨⎪⎧x ＝8cos θ，y ＝3sin θ(θ为参数).(1)化C 1，C 2的方程为普通方程，并说明它们分别表示什么曲线；(2)若C 1上的点P 对应的参数为t ＝π2，Q 为C 2上的动点，求PQ 的中点M 到直线C 3：⎩⎪⎨⎪⎧x ＝3＋2t ，y ＝－2＋t (t 为参数)距离的最小值. [解析] (1)由C 1消去参数t ，得曲线C 1的普通方程为(x ＋4)2＋(y －3)2＝1.同理曲线C 2的普通方程为x 264＋y 29＝1.C 1表示圆心是(－4，3)，半径是1的圆，C 2表示中心是坐标原点，焦点在x 轴上，长半轴长是8，短半轴长是3的椭圆.(2)当t ＝π2时，P (－4，4)，又Q (8cos θ，3sin θ)，故M ⎝ ⎛⎭⎪⎫－2＋4cos θ，2＋32sin θ， 又C 3的普通方程为x －2y －7＝0， 则M 到直线C 3的距离d ＝55|4cos θ－3sin θ－13|＝55|3sin θ－4cos θ＋13| ＝55|5(sin θ－φ)＋13|⎝⎛⎭⎪⎫其中φ满足tan φ＝43，所以d 的最小值为855.【类题通法】1．将参数方程化为普通方程，消参数常用代入法、加减消元法、三角恒等变换消去参数． 2．把参数方程化为普通方程时，要注意哪一个量是参数，并且要注意参数的取值对普通方程中x 及y 的取值范围的影响，要保持同解变形． 【对点训练】在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝3cos θ，y ＝sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋4t ，y ＝1－t (t 为参数).(1)若a ＝－1，求C 与l 的交点坐标； (2)若C 上的点到l 距离的最大值为17，求a .[解析] (1)a ＝－1时，直线l 的普通方程为x ＋4y －3＝0. 曲线C 的标准方程是x 29＋y 2＝1，联立方程⎩⎪⎨⎪⎧x ＋4y －3＝0，x 29＋y 2＝1，解得⎩⎪⎨⎪⎧x ＝3，y ＝0或⎩⎪⎨⎪⎧x ＝－2125，y ＝2425.则C 与l 交点坐标是(3，0)和⎝ ⎛⎭⎪⎫－2125，2425.(2)直线l 的普通方程是x ＋4y －4－a ＝0.设曲线C 上点P (3cos θ，sin θ).则P 到l 距离d ＝|3cos θ＋4sin θ－4－a |17＝|5sin （θ＋φ）－4－a |17，其中tan φ＝34.又点C 到直线l 距离的最大值为17. ∴|5sin(θ＋φ)－4－a |的最大值为17. 若a ≥0，则－5－4－a ＝－17，∴a ＝8. 若a <0，则5－4－a ＝17，∴a ＝－16. 综上，实数a 的值为a ＝－16或a ＝8.考点二、参数方程的应用【例2】在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2＋2sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1－22t ，y ＝22t (t 为参数).以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系.(1)写出直线l 的普通方程以及曲线C 的极坐标方程；(2)若直线l 与曲线C 的两个交点分别为M ，N ，直线l 与x 轴的交点为P ，求|PM |·|PN |的值.[解析] (1)直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1－22t ，y ＝22t (t 为参数)，消去参数t ，得x ＋y －1＝0.曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2＋2sin θ(θ为参数)，利用平方关系，得x 2＋(y －2)2＝4，则x 2＋y 2－4y ＝0.令ρ2＝x 2＋y 2，y ＝ρsin θ，代入得C 的极坐标方程为ρ＝4sin θ. (2)在直线x ＋y －1＝0中，令y ＝0，得点P (1，0). 把直线l 的参数方程代入圆C 的方程得t 2－32t ＋1＝0，∴t 1＋t 2＝32，t 1t 2＝1.由直线参数方程的几何意义，|PM |·|PN |＝|t 1·t 2|＝1. 【类题通法】过定点P 0(x 0，y 0)，倾斜角为α的直线参数方程的标准形式为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)，t 的几何意义是P 0P →的数量，即|t |表示P 0到P的距离，t 有正负之分.对于形如⎩⎪⎨⎪⎧x ＝x 0＋at ，y ＝y 0＋bt (t为参数)，当a 2＋b 2≠1时，应先化为标准形式后才能利用t 的几何意义解题. 【对点训练】在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎨⎧x ＝5cos α，y ＝sin α(α为参数).以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρcos ⎝⎛⎭⎪⎫θ＋π4＝ 2.l 与C 交于A ，B 两点.(1)求曲线C 的普通方程及直线l 的直角坐标方程； (2)设点P (0，－2)，求|PA |＋|PB |的值.[解析] (1)由曲线C ：⎩⎨⎧x ＝5cos α，y ＝sin α(α为参数)消去α，得普通方程x 25＋y 2＝1.因为直线l 的极坐标方程为ρcos ⎝ ⎛⎭⎪⎫θ＋π4＝2，即ρcos θ－ρsin θ＝2， 所以直线l 的直角坐标方程为x －y －2＝0.(2)点P (0，－2)在l 上，则l 的参数方程为⎩⎪⎨⎪⎧x ＝22t ，y ＝－2＋22t (t 为参数)，代入x 25＋y 2＝1整理得3t 2－102t ＋15＝0，由题意可得|PA |＋|PB |＝|t 1|＋|t 2|＝|t 1＋t 2|＝1023.考点三、参数方程与极坐标方程的综合应用【例3】在直角坐标系xOy 中，直线l 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋t ，y ＝kt (t 为参数)，直线l 2的参数方程为⎩⎪⎨⎪⎧x ＝－2＋m ，y ＝m k(m 为参数).设l 1与l 2的交点为P ，当k 变化时，P 的轨迹为曲线C .(1)写出C 的普通方程；(2)以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设l 3：ρ(cos θ＋sin θ)－2＝0，M 为与C 的交点，求M 的极径.[解析] (1)由l 1：⎩⎪⎨⎪⎧x ＝2＋t ，y ＝kt (t 为参数)消去t ，化为l 1的普通方程y ＝k (x －2)，① 同理得直线l 2的普通方程为x ＋2＝ky ，② 联立①，②消去k ，得x 2－y 2＝4(y ≠0). 所以C 的普通方程为x 2－y 2＝4(y ≠0). (2)将直线l 3化为普通方程为x ＋y ＝2， 联立⎩⎨⎧x ＋y ＝2，x 2－y 2＝4得⎩⎪⎨⎪⎧x ＝322，y ＝－22，∴ρ2＝x 2＋y 2＝184＋24＝5，∴与C 的交点M 的极径为 5.【类题通法】1．参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解．当然，还要结合题目本身特点，确定选择何种方程．2．数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用ρ和θ的几何意义，直接求解，可化繁为简． 【对点训练】已知曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2＋2cos θ，y ＝2sin θ(θ为参数)，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρsin ⎝⎛⎭⎪⎫θ＋π6＝4.(1)写出曲线C 的极坐标方程和直线l 的普通方程；(2)若射线θ＝π3与曲线C 交于O ，A 两点，与直线l 交于B 点，射线θ＝11π6与曲线C交于O ，P 两点，求△PAB 的面积.[解析] (1)由⎩⎪⎨⎪⎧x ＝2＋2cos θ，y ＝2sin θ(θ为参数)，消去θ.普通方程为(x －2)2＋y 2＝4.从而曲线C 的极坐标方程为ρ2－4ρcos θ＝0，即ρ＝4cos θ，因为直线l 的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π6＝4，即32ρsin θ＋12ρcos θ＝4，∴直线l 的直角坐标方程为x ＋3y －8＝0.(2)依题意，A ，B 两点的极坐标分别为⎝⎛⎭⎪⎫2，π3，⎝ ⎛⎭⎪⎫4，π3， 联立射线θ＝11π6与曲线C 的极坐标方程得P 点极坐标为⎝ ⎛⎭⎪⎫23，11π6，∴|AB |＝2，∴S △PAB ＝12×2×23sin ⎝ ⎛⎭⎪⎫π3＋π6＝2 3.。