(精品)初中数学讲义反比例函数(学生版)
- 格式:doc
- 大小:147.00 KB
- 文档页数:4

《反比例函数》讲义一、反比例函数的定义一般地,如果两个变量 x、y 之间的关系可以表示成 y = k/x(k 为常数,k≠0)的形式,那么称 y 是 x 的反比例函数。
例如,速度 v 一定时,路程 s 与时间 t 的关系为 s = vt,当路程一定时,即 s 为常数时,那么时间 t 与速度 v 的关系就可以表示为 t =s/v,此时 t 是 v 的反比例函数。
需要注意的是,反比例函数中,自变量 x 不能等于 0,因为分母不能为 0。
同时,反比例函数的表达式还可以写成 xy = k 或 y = kx^(-1) 的形式。
二、反比例函数的图像反比例函数的图像是双曲线。
当 k>0 时,双曲线的两支分别位于第一、三象限,在每一象限内 y 随 x 的增大而减小;当 k<0 时,双曲线的两支分别位于第二、四象限,在每一象限内 y 随 x 的增大而增大。
例如,函数 y = 2/x,因为 k = 2>0,所以它的图像在第一、三象限,在每个象限内,y 随 x 的增大而减小。
我们可以通过列表、描点、连线的方法来画出反比例函数的图像。
在列表时,要选取一些具有代表性的点,比如 x 取 1、2、-1、-2 等等,然后计算出对应的 y 值,再描点连线。
三、反比例函数的性质1、对称性反比例函数的图像既是轴对称图形,又是中心对称图形。
它的对称轴有两条,分别是直线 y = x 和直线 y = x。
对称中心是坐标原点(0,0)。
2、增减性前面我们提到了,当k>0 时,在每一象限内y 随x 的增大而减小;当 k<0 时,在每一象限内 y 随 x 的增大而增大。
需要注意的是,这里说的增减性是在每个象限内,而不是在整个定义域内。
3、渐近线反比例函数的图像无限接近坐标轴,但永远不会与坐标轴相交。
当 x 趋近于正无穷大或负无穷大时,y 趋近于 0;当 y 趋近于正无穷大或负无穷大时,x 趋近于 0。
四、反比例函数中 k 的几何意义设 P(x,y)是反比例函数 y = k/x 图像上的任意一点,过点 P 作x 轴、y 轴的垂线 PM、PN,垂足分别为 M、N,则矩形 PMON 的面积S = PM·PN =|xy| =|k|。

模型介绍考点1一点一垂线模型【模型讲解】反比例函数图象上一点关于坐标轴的垂线、另一坐标轴上一点(含原点)围成的三角形面积等于12|k|.【示例】拓展:【例1】.如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=(x >0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会()A.越来越小B.越来越大C.不变D.先变大后变小解:如图,过点B作BC⊥PA于点C,则BC=OA,设点P(x,),=PA•BC=••x=3,则S△P AB当点A的横坐标逐渐增大时,△PAB的面积将会不变,始终等于3,故选:C.变式训练【变1-1】.如图,点A、B在反比例函数的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是4,则k的值为﹣.解:设OM=a,则OM=MN=NC=a,∵点A、B在反比例函数y=的图象上,AM⊥OC、BN⊥OC,∴AM=,BN=,=S△AOM+S四边形AMNB+S△BNC,∵S△AOC∴﹣×3a×=﹣k+4﹣×a×,解得k=﹣,故答案为:﹣.【变1-2】.如图,在第一象限内,点P(2,3),M(a,2)是双曲线y=(k≠0)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为()A.B.C.2D.解:把P(2,3),M(a,2)代入y=得k=2×3=2a,解得k=6,a=3,设直线OM的解析式为y=mx,把M(3,2)代入得3m=2,解得m=,所以直线OM的解析式为y=x,当x=2时,y=×2=,所以C点坐标为(2,),所以△OAC的面积=×2×=.故选:B.考点2一点两垂线模型【模型讲解】反比例函数图象上一点与坐标轴的两条垂线所围成的矩形面积等于|k |.【示例】ABCD S k【例2】.双曲线与在第一象限内的图象如图所示,作一条平行于y 轴的直线分别交双曲线于A 、B 两点,连接OA 、OB ,则△AOB 的面积为()A .1B .2C .3D .4解:设直线AB 与x 轴交于点C .∵AB ∥y 轴,∴AC ⊥x 轴,BC ⊥x 轴.∵点A 在双曲线y =的图象上,∴△AOC 的面积=×10=5.∵点B 在双曲线y =的图象上,∴△COB的面积=×6=3.∴△AOB的面积=△AOC的面积﹣△COB的面积=5﹣3=2.故选:B.变式训练【变2-1】.如图,函数y=(x>0)和(x>0)的图象分别是l1和l2.设点P在l2上,PA∥y轴交l1于点A,PB∥x轴交l1于点B,△PAB的面积为.解:设点P(x,),则点B(,),A(x,),∴BP=x﹣=,AP=﹣=,==,∴S△ABP故答案为:.【变2-2】.如图,直线AB∥x轴,分别交反比例函数y=图象于A、B两点,若S△AOB=2,则k2﹣k1的值为4.解:设A(a,b),B(c,d),代入得:k1=ab,k2=cd,=2,∵S△AOB∴cd﹣ab=2,∴cd﹣ab=4,∴k2﹣k1=4,故答案为:4.【变2-3】.如图,在平面直角坐标系中,M为y轴正半轴上一点,过点M的直线l∥x轴,l分别与反比例函数y=和y=的图象交于A、B两点,若S△AOB=3,则k的值为﹣2.解:∵直线l∥x轴,∴AM⊥y轴,BM⊥y轴,=|k|,S△BOM=×4=2,∴S△AOM=3,∵S△AOB=1,∴S△AOM∴|k|=2,∵k<0,∴k=﹣2,故答案为:﹣2.考点3两曲一平行模型【模型讲解】两条双曲线上的两点的连线与一条(或两条)坐标轴平行,求这两点与原点或坐标轴上的点围成的图形面积,过这两点作坐标轴的垂线,结合k的几何意义求解.类型1两条双曲线的k值符号相同【示例】【例3】.如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=(k为常数,k ≠0)的图象上,正方形ADEF的面积为16,且BF=2AF,则k值为()A.﹣8B.﹣12C.﹣24D.﹣36解:设A(x,0).∵正方形ADEF的面积为16,∴ADEF的边长为4,∴E(x﹣4,4),∵BF=2AF,∴BF=2×4=8,∴B(x,12).∵点B、E在反比例函数y=(k为常数,k≠0)的图象上,∴4(x﹣4)=12x,解得x=﹣2,∴B(﹣2,12),∴k=﹣2×12=﹣24,故选:C.变式训练【变3-1】.若正方形OABC的顶点B和正方形ADEF的顶点E都在函数的图象上.若正方形OABC的面积为1,则k的值为1;点E的坐标为(+,﹣).解:∵正方形OABC和正方形AEDF各有一个顶点在一反比例函数图象上,且正方形OABC的边长为1.∴B点坐标为:(1,1),设反比例函数的解析式为y=;∴xy=k=1,设正方形ADEF的边长为a,则E(1+a,a),代入反比例函数y=(x>0)得:1=(1+a)a,又a>0,解得:a=﹣.∴点E的坐标为:(+,﹣).【变3-2】.如图,A、B两点在双曲线y=上,分别经过A、B两点向坐标轴作垂线段,已知S=1.7,则S1+S2等于 4.6.阴影解:如图,∵A、B两点在双曲线y=上,=4,S四边形BDOC=4,∴S四边形AEOF∴S1+S2=S四边形AEOF+S四边形BDOC﹣2×S阴影,∴S1+S2=8﹣3.4=4.6故答案为:4.6.【变3-3】.如图,在反比例函数(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为1,2,3,4,….分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,则S1+S2+S3+…+S n=.(用n的代数式表示,n为正整数)解:当x=1时,P1的纵坐标为2,当x=2时,P2的纵坐标1,当x=3时,P3的纵坐标,当x=4时,P4的纵坐标,当x=5时,P5的纵坐标,…则S1=1×(2﹣1)=2﹣1;S2=1×(1﹣)=1﹣;S3=1×(﹣)=﹣;S4=1×(﹣)=﹣;…S n=﹣;S1+S2+S3+…+S n=2﹣1+1﹣+﹣+﹣+…+﹣=2﹣=.故答案为:.考点4两点一垂线模型【模型讲解】反比例函数与正比例函数图象的交点及由交点向坐标轴所作垂线围成的三角形面积等于|k|,反比例函数与一次函数图象的交点及坐标轴上任一点构成三角形的面积,等于坐标轴所分的两个三角形面积之和.【示例】【例4】.如图,正比例函数y=kx与反比例函数y=﹣相交于A,C两点,点A的横坐标为﹣4,过点A作x轴的垂线交x轴于B点,连接BC,下列结论:①k=﹣;②不等式kx<﹣的解集为﹣4<x<0或x>4;③△ABC的面积等于16.其中正确的结论个数为()A.0B.1C.2D.3解:将x=﹣4代入y=﹣得y=﹣=2,∴点A坐标为(﹣4,2),将(﹣4,2)代入y=kx得2=﹣4k,解得k=﹣,∴①正确.由反比例函数及正比例函数的对称性可得点C坐标为(4,﹣2),∴当﹣4<x<0或x>4时,kx<﹣,∴②正确.=S△AOB+S△BOC=OB•y A+OB•(﹣y C)=BO(y A﹣y C)=×(2+2)∵S△AOC=8,∴③错误.故选:C.变式训练【变4-1】.如图所示,一次函数y=kx(k<0)的图象与反比例函数y=﹣的图象交于A,B两点,过点B作BC⊥y轴于点C,连接AC,则△ABC的面积为4.解:∵BC⊥y轴于点C,=|﹣4|=2,∴S△COB∵正比例函数y=kx(k>0)与反比例函数y=﹣的图象均关于原点对称,∴OA=OB,=S△COB=2,∴S△AOC=S△AOB+S△BOC=2+2=4,∴S△ABC故答案为:4.【变4-2】.如图,过点O的直线与反比例函数y=的图象交于A、B两点,过点A作AC⊥x轴于点C,连接BC,则△ABC的面积为.解:∵点A反比例函数y=的图象上,过点A作AC⊥x轴于点C,=|k|=,∴S△AOC∵过点O的直线与反比例函数y=的图象交于A、B两点,∴OA=OB,=S△AOC=∴S△BOC=2S△ACO=,∴S△ABC故答案为:.【变4-3】.如图,函数y=x与y=的图象交于A、B两点,过点A作AC垂直于y轴,垂=3,则k=3.足为C,连接BC,若S△ABC解:设A(a,a)(a>0),∵函数y=x与y=的图象的中心对称性,∴B(﹣a,﹣a),=•a•2a=a2=3,∴S△ABC∴a=,∴A(,),把A(,)代入y=得k==3.故答案为:3.考点5两点两垂线模型【模型讲解】反比例函数与正比例函数图象的交点及由交点向坐标轴所作两条垂线围成的图形面积等于2|k|.【示例】【例5】.如图,正比例函数y=kx与反比例函数y=﹣的图象交于A,C两点,过点A作AB⊥x轴于点B,过点C作CD⊥x轴于点D,则△ABD的面积为4.解:∵点A在反比例函数y=﹣上,且AB⊥x轴,∴=2,∵A,C是反比例函数与正比例函数的交点,且CD⊥x轴,∴O是BD的中点,=2S△ABO=4.∴S△ABD故答案为:4.变式训练【变5-1】.如图,一次函数y=kx与反比例函数上的图象交于A,C两点,AB∥y轴,BC∥x轴,若△ABC的面积为4,则k=﹣2.解:设AB交x轴于点D,的面积为,由反比例函数系数的几何意义可得S△ADO由函数的对称性可得点O为AC中点,即DO为△ABC中位线,∴=,=4S△ADO=2|k|=4,∴S△ABC∵k<0,∴k=﹣2.故答案为:﹣2.【变5-2】.如图,正比例函数y=kx(k>0)与反比例函数y=的图象交于A,C两点,过点A作x轴的垂线,交x轴于点B,过点C作x轴的垂线,交x轴于点D,连接AD,BC,则四边形ABCD的面积为2.解:∵A、C是两函数图象的交点,∴A、C关于原点对称,∵CD⊥x轴,AB⊥x轴,∴OA=OC,OB=OD,=S△BOC=S△DOC=S△AOD,∴S△AOB又∵A点在反比例函数y=的图象上,=S△BOC=S△DOC=S△AOD×1=,∴S△AOB=4S△AOB=4×=2,∴S四边形ABCD故答案为:2.【变5-3】.如图,直线分别与反比例函数y=﹣和y=的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x轴交于点D,则四边形ABCD的面积是5.解:过点A作AF⊥y轴,垂足于点F;过点B作BE⊥y轴,垂足为点E.∵点P是AB中点.∴PA=PB.又∵∠APF=∠BPE,∠AFP=∠BEP=90°,∴△APF≌△BPE.=S△BPE.∴S△APF=S四边形ACOF+S四边形EODB=|﹣2|+|3|=5.∴S四边形ABCD故答案为:5.考点6反比例函数上两点和外一点模型【模型讲解】反比例函数与一次函数图象的交点和原点所围成的三角形面积,若两交点在同一分支上,用减法.【示例】方法一:S △AOB =S △COD -S △AOC -S △BOD .方法二:作AE ⊥x 轴于点E ,交OB 于点M ,BF ⊥x 轴于点F ,则S △OAM =S 四边形MEFB (划归到模型一),则S △AOB =S 直角梯形AEFB .【拓展】方法一:当BE CE 或BFFA=m 时,则S 四边形OFBE =m |k |.方法二:作EM ⊥x 轴于M ,则S △OEF =S 直角梯形EMAF (划归到上一个模型示例).【例6】.如图,一次函数y =ax +b 的图象与反比例函数y =的图象交于A ,B 两点,则S△AOB=()A.B.C.D.6解:把A(﹣4,1)代入y=的得:k=﹣4,∴反比例函数的解析式是y=﹣,∵B(1,m)代入反比例函数y=﹣得:m=﹣4,∴B的坐标是(1,﹣4),把A、B的坐标代入一次函数y=ax+b得:,解得:a=﹣1,b=﹣3,∴一次函数的解析式是y=﹣x﹣3;把x=0代入一次函数的解析式是y=﹣x﹣3得:y=﹣3,∴D(0,﹣3),=S AOD+S△BOD=×3×(1+4)=.∴S△AOB故选:A.变式训练【变6-1】.如图,直线AB经过原点O,且交反比例函数的图象于点B,A,点C在x=12,则k的值为()轴上,且.若S△BCAA.12B.﹣12C.﹣6D.6解:作AD⊥x轴于D,BE⊥x轴于E,∵点A、B在反比例函数的图象上,直线AB经过原点,∴OA=OB=AB,=12,∵,S△BCA=S△BCA=6,∴OB=BC,S△BCO∵BE⊥OC,∴OE=CE,=S△BCO=3,∴S△OBE∵BE⊥x轴于E,=|k|,∴S△OBE∴|k|=6,∵k<0,∴k=﹣6.故选:C.【变6-2】.如图,在平面直角坐标系中,反比例函数y=与直线y=交于A,B,x轴的正半轴上有一点C 使得∠ACB =90°,若△OCD 的面积为25,则k 的值为48.解:设点A 坐标为(3a ,4a ),由反比例函数图象与正比例函数图象的对称性可得点B 坐标为(﹣3a ,﹣4a ),∴OA =OB ==5a ,∵∠ACB =90°,O 为AB 中点,∴OC =OA =OB =5a ,设直线BC 解析式为y =kx +b ,将(﹣3a ,﹣4a ),(5a ,0)代入y =kx +b 得,解得,∴y =x ﹣a ,∴点D 坐标为(0,﹣a ),∴S △OCD =OC •OD =5a ×a =25,解得a =2或a =﹣2(舍),∴点A 坐标为(6,8),∴k =6×8=48.故答案为:48.【变6-3】.如图,正比例函数y =﹣x 与反比例函数y =的图象交于A ,B 两点,点C 在x 轴上,连接AC ,BC .若∠ACB =90°,△ABC 的面积为10,则该反比例函数的解析式是y =﹣.解:设点A 为(a ,﹣a ),则OA ==﹣a ,∵点C 为x 轴上一点,∠ACB =90°,且△ACB 的面积为20,∴OA =OB =OC =﹣a ,∴S △ACB =×OC ×(y A +|y B |)=×(﹣a )×(﹣a )=10,解得,a =±(舍弃正值),∴点A 为(﹣,2),∴k =﹣×2=﹣6,∴反比例函数的解析式是y =﹣,故答案为:y =﹣.考点7反比例函数上两点和原点模型【模型讲解】反比例函数与一次函数图象的交点和原点所围成的三角形面积,若两交点分别在两个分支上,用加法.【示例】方法一:S △AOB =12OD ·|x B -x A |=12OC ·|y A -y B |.方法二:S △AOB =S △AOC +S △OCD +S △OBD .方法三:作AE ⊥y 轴于点E ,BF ⊥x 轴于点F ,延长AE 与BF 相交于点N ,则S △AOB =S △ABN -S △AOE -S △OBF -S 矩形OENF .【例7】.如图,直线AB 交双曲线于A 、B ,交x 轴于点C ,B 为线段AC 的中点,过=12.则k的值为8.点B作BM⊥x轴于M,连接OA.若OM=2MC,S△OAC解:过A作AN⊥OC于N,∵BM⊥OC∴AN∥BM,∵,B为AC中点,∴MN=MC,∵OM=2MC,∴ON=MN=CM,设A的坐标是(a,b),则B(2a,b),=12.∵S△OAC∴•3a•b=12,∴ab=8,∴k=ab=8,故答案为:8.变式训练【变7-1】.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且四边形ODBE的面积为21,则k=7.解:设D点的横坐标为x,则其纵坐标为,∵BD=3AD,∴点B点的坐标为(4x,),点C的坐标为(4x,0)=21,∵S四边形ODBE﹣S△OCE﹣S△OAD=21,∴S矩形ABCD即:4x•﹣﹣=21解得:k=7.故答案为:7.【变7-2】.如图,点是直线AB与反比例函数图象的两个交点,AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.(1)求反比例函数和直线AB的解析式;(2)△ABC和△ABD的面积分别为S1,S2,求S2﹣S1.解:(1)由点A(,4)在反比例函数y=(x>0)图象上,∴n=×4=6,∴反比例函数的解析式为y=(x>0),将点B(3,m)代入y=(x>0)并解得m=2,∴B(3,2),设直线AB的表达式为y=kx+b,∴,解得,∴直线AB的表达式为y=﹣x+6;(2)由点A坐标得AC=4,则点B到AC的距离为3﹣=,∴S1==3,设AB与y轴的交点为E,则点E(0,6),如图:∴DE=6﹣1=5,由点A(,4),B(3,2)知,点A,B到DE的距离分别为,3,∴S2=S△BDE﹣S△AED=﹣=,∴S2﹣S1=﹣3=.考点8两双曲线k值符号不同模型【模型讲解】两条双曲线上的两点的连线与一条(或两条)坐标轴平行,求这两点与原点或坐标轴上的点围成的图形面积,过这两点作坐标轴的垂线,结合k的几何意义求解.类型1两条双曲线的k值符号相同【示例】【例8】.如图,在平面直角坐标系中,函数y=kx与的图象交于A、B两点,过A作y轴的垂线,交函数的图象于点C,连接BC,则△ABC的面积为()A.2B.3C.5D.6解:∵正比例函数y=kx与反比例函数y=﹣的图象交点关于原点对称,∴设A点坐标为(x,﹣),则B点坐标为(﹣x,),C(﹣2x,﹣),=×(﹣2x﹣x)•(﹣﹣)=×(﹣3x)•(﹣)=6.∴S△ABC故选:D.变式训练【变8-1】.如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=(x>0)和y=﹣(x>0)的图象交于B、A两点.若点C是y轴上任意一点,则△ABC的面积为()A.3B.6C.9D.解:设P(a,0),a>0,则A和B的横坐标都为a,将x=a代入反比例函数y=﹣中得:y=﹣,故A(a,﹣);将x=a代入反比例函数y=中得:y=,故B(a,),∴AB=AP+BP=+=,=AB•x P的横坐标=××a=,则S△ABC故选:D.【变8-2】.如图,点A和点B分别是反比例函数y=(x>0)和y=(x>0)的图象上=2,则m﹣n的值为4.的点,AB⊥x轴,点C为y轴上一点,若S△ABC解:连接AO.CO,∵AB⊥x轴,点C为y轴上一点,∴AB∥y轴,=S△ABO=2,∴S△ABC∴=2.∴=2,即m﹣n=4.故答案为:4.1.如图,Rt△ABC的顶点A在双曲线y=的图象上,直角边BC在x轴上,∠ABC=90°,∠ACB=30°,OC=4,连接OA,∠AOB=60°,则k的值是()A.4B.﹣4C.2D.﹣2解:∵∠ACB=30°,∠AOB=60°,∴∠OAC=∠AOB﹣∠ACB=30°,∴∠OAC=∠ACO,∴OA=OC=4,在△AOB中,∠ABC=90°,∠AOB=60°,OA=4,∴∠OAB=30°,∴OB=OA=2,∴AB=OB=2,∴A点坐标为(﹣2,2),把A(﹣2,2)代入y=得k=﹣2×2=﹣4.故选:B.2.如图,平行四边形OABC的顶点B,C在第一象限,点A的坐标为(3,0),点D为边AB的中点,反比例函数y=(x>0)的图象经过C,D两点,若∠COA=α,则k的值等于()A.8sin2αB.8cos2αC.4tanαD.2tanα解:方法一:过点C作CE⊥OA于点E,过点D作DF⊥OA交OA的延长线于点F,设C点横坐标为:a,则:CE=a•tanα,∴C点坐标为:(a,a•tanα),∵平行四边形OABC中,点D为边AB的中点,∴D点纵坐标为:a•tanα,设D点横坐标为x,∵C,D都在反比例函数图象上,∴a×a•tanα=x×a•tanα,解得:x=2a,则FO=2a,∴FE=a,∵∠COE=∠DAF,∠CEO=∠DFA,∴△COE∽△DAF,∴==2,∴AF=,∴AO=OF﹣AF=a,∵点A的坐标为(3,0),∴AO=3,∴a=3,解得:a=2,∴k=a×a•tanα=2×2tanα=4tanα.方法二:∵C(a,a tanα),A(3,0),∴B(a+3,a tanα),∵D是线段AB中点,∴D(,a tanα),即D(,a tanα).∵反比例函数过C,D两点,∴k=a•a tanα=(a+6)•a tanα,解得a=2,∴k=4tanα.故选:C.3.如图,在直角坐标系xOy中,点A,B分别在x轴和y轴,=.∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是()A.2B.3C.5D.7解:设OA=3a,则OB=4a,∴A(3a,0),B(0,4a).设直线AB的解析式是y=kx+b,则根据题意得:,解得:,则直线AB的解析式是y=﹣x+4a,直线CD是∠AOB的平分线,则OD的解析式是y=x.根据题意得:,解得:则D的坐标是(,),OA的中垂线的解析式是x=,则C的坐标是(,),将C点坐标代入反比例函数y=,则k=.设OA的垂直平分线交x轴于点F,过点D作DE⊥x轴于点E,如图,则OF=CF=,OE=DE=a,∵∠DOA=45°,∴△COF和△DOE为等腰直角三角形,∴OC=OF=a,OD=OE=a,∴CD=OD﹣OC=()=(﹣)=a.∵以CD为边的正方形的面积为,∴=,则a2=,∴k=×=7.故选:D.4.如图,已知第一象限内的点A在反比例函数y=的图象上,第二象限内的点B在反比例函数y=的图象上,且OA⊥OB,cos A=,则k的值为()A.﹣3B.﹣4C.﹣D.﹣2解:过A作AE⊥x轴,过B作BF⊥x轴,∵OA⊥OB,∴∠AOB=90°,∴∠BOF+∠EOA=90°,∵∠BOF+∠FBO=90°,∴∠EOA=∠FBO,∵∠BFO=∠OEA=90°,∴△BFO∽△OEA,在Rt△AOB中,cos∠BAO==,设AB=,则OA=1,根据勾股定理得:BO=,∴OB:OA=:1,:S△OEA=2:1,∴S△BFO∵A在反比例函数y=上,=1,∴S△OEA=2,∴S△BFO则k=﹣4.故选:B.5.如图,反比例函数y=(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是()A.B.C.D.解:如图,∵点A坐标为(﹣1,1),∴k=﹣1×1=﹣1,∴反比例函数解析式为y=﹣,∵OB=AB=1,∴△OAB为等腰直角三角形,∴∠AOB=45°,∵PQ⊥OA,∴∠OPQ=45°,∵点B和点B′关于直线l对称,∴PB=PB′,BB′⊥PQ,∴∠B′PQ=∠OPQ=45°,∠B′PB=90°,∴B′P⊥y轴,∴点B′的坐标为(﹣,t),∵PB=PB′,∴t﹣1=|﹣|=,整理得t2﹣t﹣1=0,解得t1=,t2=(不符合题意,舍去),∴t的值为.故选:A.6.如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(﹣3,2),若反比例函数y=(x>0)的图象经过点A,则k的值为()A.﹣6B.﹣3C.3D.6解:∵A与C关于OB对称,∴A的坐标是(3,2).把(3,2)代入y=得:2=,解得:k=6.故选:D.7.如图,直线y=与双曲线y=(k>0,x>0)交于点A,将直线y=向上平移4个单位长度后,与y轴交于点C,与双曲线y=(k>0,x>0)交于点B,若OA=3BC,则k的值为()A.3B.6C.D.解:∵将直线y=向上平移4个单位长度后,与y轴交于点C,∴平移后直线的解析式为y=x+4,分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,设A(3x,x),∵OA=3BC,BC∥OA,CF∥x轴,∴△BCF∽△AOD,∴CF=OD,∵点B在直线y=x+4上,∴B(x,x+4),∵点A、B在双曲线y=上,∴3x•x=x•(x+4),解得x=1,∴k=3×1××1=.故选:D.8.如图,已知四边形ABCD是平行四边形,BC=2AB.A,B两点的坐标分别是(﹣1,0),(0,2),C,D两点在反比例函数y=(k<0)的图象上,则k等于﹣12.解:设点C坐标为(a,),(k<0),点D的坐标为(x,y),∵四边形ABCD是平行四边形,∴AC与BD的中点坐标相同,∴(,)=(,),则x=a﹣1,y=,代入y=,可得:k=2a﹣2a2①;在Rt△AOB中,AB==,∴BC=2AB=2,故BC2=(0﹣a)2+(﹣2)2=(2)2,整理得:a4+k2﹣4ka=16a2,将①k=2a﹣2a2,代入后化简可得:a2=4,∵a<0,∴a=﹣2,∴k=﹣4﹣8=﹣12.故答案为:﹣12.方法二:因为ABCD是平行四边形,所以点C、D是点B、A分别向左平移a,向上平移b得到的.故设点C坐标是(﹣a,2+b),点D坐标是(﹣1﹣a,b),(a>0,b>0),∴﹣a(2+b)=b(﹣1﹣a),整理得2a+ab=b+ab,解得b=2a.过点D作x轴垂线,交x轴于H点,在直角三角形ADH中,由已知易得AD=2,AH=a,DH=b=2a.AD2=AH2+DH2,即20=a2+4a2,得a=2.所以D坐标是(﹣3,4)所以k=﹣12.9.如图,点E,F在函数y=(x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是2,△OEF的面积是(用含m的式子表示)解:作EC⊥x轴于C,FD⊥x轴于D,FH⊥y轴于H,如图,∵△OEP的面积为1,∴|k|=1,而k>0,∴k=2,∴反比例函数解析式为y=,∵EP⊥y轴,FH⊥y轴,∴EP∥FH,∴△BPE∽△BHF,∴==,即HF=mPE,设E点坐标为(t,),则F点的坐标为(tm,),+S△OFD=S△OEC+S梯形ECDF,∵S△OEF=S△OEC=1,而S△OFD=S梯形ECDF=(+)(tm﹣t)∴S△OEF=(+1)(m﹣1)=.故答案为:2,.10.如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=(k≠0)的图象经过圆心P,则k=.解:设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,如图所示.则有PD⊥OA,PE⊥AB.设⊙P的半径为r,∵AB=5,AC=1,=AB•PE=r,S△APC=AC•PD=r.∴S△APB∵∠AOB=90°,OA=4,AB=5,∴OB=3.=AC•OB=×1×3=.∴S△ABC=S△APB+S△APC,∵S△ABC∴=r+r.∴r=.∴PD=.∵PD⊥OA,∠AOB=90°,∴∠PDC=∠BOC=90°.∴PD∥BO.∴△PDC∽△BOC.∴=.∴PD•OC=CD•BO.∴×(4﹣1)=3CD.∴CD=.∴OD=OC﹣CD=3﹣=.∴点P的坐标为(,).∵反比例函数y=(k≠0)的图象经过圆心P,∴k=×=.故答案为:.11.如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=和y=的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①=;②阴影部分面积是(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是①④(把所有正确的结论的序号都填上).解:作AE⊥y轴于E,CF⊥y轴于F,如图,∵四边形OABC是平行四边形,∴S△AOB=S△COB,∴AE=CF,∴OM=ON,∵S△AOM=|k1|=OM•AM,S△CON=|k2|=ON•CN,∴=,故①正确;∵S△AOM=|k1|,S△CON=|k2|,∴S阴影部分=S△AOM+S△CON=(|k1|+|k2|),而k1>0,k2<0,∴S阴影部分=(k1﹣k2),故②错误;当∠AOC=90°,∴四边形OABC是矩形,∴不能确定OA与OC相等,而OM=ON,∴不能判断△AOM≌△CNO,∴不能判断AM=CN,∴不能确定|k1|=|k2|,故③错误;若OABC是菱形,则OA=OC,而OM=ON,∴Rt△AOM≌Rt△CNO,∴AM=CN,∴|k1|=|k2|,∴k1=﹣k2,∴两双曲线既关于x轴对称,也关于y轴对称,故④正确.故答案为:①④.12.如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y=,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,A n,…记点A n的横坐标为a n,若a1=2,则a2=﹣,a2013=﹣;若要将上述操作无限次地进行下去,则a1不可能取的值是0、﹣1.解:当a1=2时,B1的纵坐标为,B1的纵坐标和A2的纵坐标相同,则A2的横坐标为a2=﹣,A2的横坐标和B2的横坐标相同,则B2的纵坐标为b2=﹣,B2的纵坐标和A3的纵坐标相同,则A3的横坐标为a3=﹣,A3的横坐标和B3的横坐标相同,则B3的纵坐标为b3=﹣3,B3的纵坐标和A4的纵坐标相同,则A4的横坐标为a4=2,A4的横坐标和B4的横坐标相同,则B4的纵坐标为b4=,即当a1=2时,a2=﹣,a3=﹣,a4=2,a5=﹣,b1=,b2=﹣,b3=﹣3,b4=,b5=﹣,∵=671,∴a2013=a3=﹣;点A1不能在y轴上(此时找不到B1),即x≠0,点A1不能在x轴上(此时A2,在y轴上,找不到B2),即y=﹣x﹣1≠0,解得:x≠﹣1;综上可得a1不可取0、﹣1.故答案为:﹣;﹣;0、﹣1.13.如图,一次函数y=x+1的图象与反比例函数y=(x>0)的图象交于点A(a,3),与y轴交于点B.(1)求a,k的值;(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.①求△ABC的面积;②点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.解:(1)把x=a,y=3代入y=x+1得,,∴a=4,把x=4,y=3代入y=得,3=,∴k=12;(2)∵点A(4,3),D点的纵坐标是0,AD=AC,∴点C的纵坐标是3×2﹣0=6,把y=6代入y=得x=2,∴C(2,6),①如图1,作CF⊥x轴于F,交AB于E,当x=2时,y==2,∴E(2,2),∵C(2,6),∴CE=6﹣2=4,∴x A==8;②如图2,当AB是对角线时,即:四边形APBQ是平行四边形,∵A(4,3),B(0,1),点Q的纵坐标为0,∴y P=1+3﹣0=4,当y=4时,4=,∴x=3,∴P(3,4),当AB为边时,即:四边形ABQP是平行四边形(图中的▱ABQ′P′),﹣y B=y P′﹣y A得,由y Q′0﹣1=y P′﹣3,=2,∴y P′当y=2时,x==6,∴P′(6,2),综上所述:P(3,4)或(6,2).14.在平面直角坐标系中,已知一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,且与反比例函数y2=的图象在第一象限内交于P,K两点,连接OP,△OAP的面积为.(1)求一次函数与反比例函数的解析式.(2)当y2>y1时,求x的取值范围.(3)若C为线段OA上的一个动点,当PC+KC最小时,求△PKC的面积.解:(1)∵一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,∴,解得.∴一次函数的解析式为:y1=﹣x+.∵△OAP的面积为,∴•OA•y P=,∴y P=,∵点P在一次函数图象上,∴令﹣x+=.解得x=4,∴P(4,).∵点P在反比例函数y2=的图象上,∴k2=4×=2.∴一次函数的解析式为:y1=﹣x+.反比例函数的解析式为:y2=.(2)令﹣x+=,解得x=1或x=4,∴K(1,2),由图象可知,当y2>y1时,x的取值范围为:0<x<1或x>4.(3)如图,作点P关于x轴的对称点P′,连接KP′,线段KP′与x轴的交点即为点C,∵P(4,).∴P′(4,﹣).∴PP′=1,∴直线KP′的解析式为:y=﹣x+.令y=0,解得x=.∴C(,0).=•(x C﹣x K)•PP′∴S△PKC=×(﹣1)×1=.∴当PC+KC最小时,△PKC的面积为.15.如图,一次函数y=x+1与反比例函数y=的图象相交于A(m,2),B两点,分别连接OA,OB.(1)求这个反比例函数的表达式;(2)求△AOB的面积;(3)在平面内是否存在一点P,使以点O,B,A,P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.解:(1)∵一次函数y=x+1经过点A(m,2),∴m+1=2,∴m=1,∴A(1,2),∵反比例函数y=经过点(1,2),∴k=2,∴反比例函数的解析式为y=;(2)由题意,得,解得或,∴B(﹣2,﹣1),∵C(0,1),=S△AOC+S△BOC=×1×2+×1×1=1.5;∴S△AOB(3)有三种情形,如图所示,满足条件的点P的坐标为(﹣3,﹣3)或(﹣1,1)或(3,3).16.已知A(3,0)、B(0,4)是平面直角坐标系中两点,连接AB.(1)如图①,点P在线段AB上,以点P为圆心的圆与两条坐标轴都相切,求过点P 的反比例函数表达式;(2)如图②,点N是线段OB上一点,连接AN,将△AON沿AN翻折,使得点O与线段AB上的点M重合,求经过A、N两点的一次函数表达式.解:(1)作PC⊥x轴于C,PD⊥y轴于D,则四边形OCPD是矩形,∵以点P为圆心的圆与两条坐标轴都相切,∴PC=PD,∴矩形OCPD是正方形,设PD=PC=x,∵A(3,0)、B(0,4),∴OA=3,OB=4,∴BD=4﹣x,∵PD∥OA,∴△PDB∽△AOB,∴,∴,解得x=,∴P(,),设过点P的函数表达式为y=,∴k=xy==,∴y=;(2)方法一:∵将△AON沿AN翻折,使得点O与线段AB上的点M重合,∴ON=NM,MN⊥AB,由勾股定理得,AB=5,=S△AON+S△ABN,∴S△AOB∴=+,解得,ON=,∴N(0,),设直线AN的函数解析式为y=mx+,则3m+=0,∴m=﹣,∴直线AN的函数解析式为y=﹣x+.方法二:利用△BMN∽△BOA,求出BN的长度,从而得出ON的长度,。



《反比例函数》讲义一、反比例函数的定义一般地,如果两个变量 x、y 之间的关系可以表示成 y = k/x(k 为常数,k≠0)的形式,那么称 y 是 x 的反比例函数。
例如,当路程 s 一定时,速度 v 与时间 t 之间的关系可以表示为 v= s/t,此时速度 v 就是时间 t 的反比例函数。
需要注意的是,反比例函数中自变量 x 的取值范围是x≠0,因为在分数中分母不能为 0。
二、反比例函数的表达式反比例函数常见的表达式有以下三种形式:1、 y = k/x(k 为常数,k≠0),这是最基本的形式。
2、 xy = k(k 为常数,k≠0),通过变形可以得到 y = k/x。
3、 y = kx^(-1)(k 为常数,k≠0),其中 x^(-1)表示 1/x。
三、反比例函数的图象反比例函数的图象是双曲线。
当 k>0 时,双曲线的两支分别位于第一、三象限,在每一象限内 y 随 x 的增大而减小;当 k<0 时,双曲线的两支分别位于第二、四象限,在每一象限内 y 随 x 的增大而增大。
以函数 y = 2/x 为例,我们可以通过列表、描点、连线的方法来画出它的图象。
选取一些 x 的值,计算出相应的 y 值:当 x = 1 时,y = 2;当 x = 2 时,y = 1;当 x =-1 时,y =-2;当 x =-2 时,y =-1 等等。
然后在平面直角坐标系中描出这些点,并用平滑的曲线连接起来,就得到了反比例函数 y = 2/x 的图象。
四、反比例函数图象的性质1、对称性反比例函数的图象既是轴对称图形,又是中心对称图形。
对称轴是直线 y = x 和直线 y = x,对称中心是坐标原点。
2、渐近线双曲线无限接近坐标轴,但永远不会与坐标轴相交。
3、增减性在每个象限内,当 k>0 时,y 随 x 的增大而减小;当 k<0 时,y 随 x 的增大而增大。
但不能说在整个定义域内 y 随 x 的增大而增大或减小,因为它是在不同的象限内有不同的增减性。
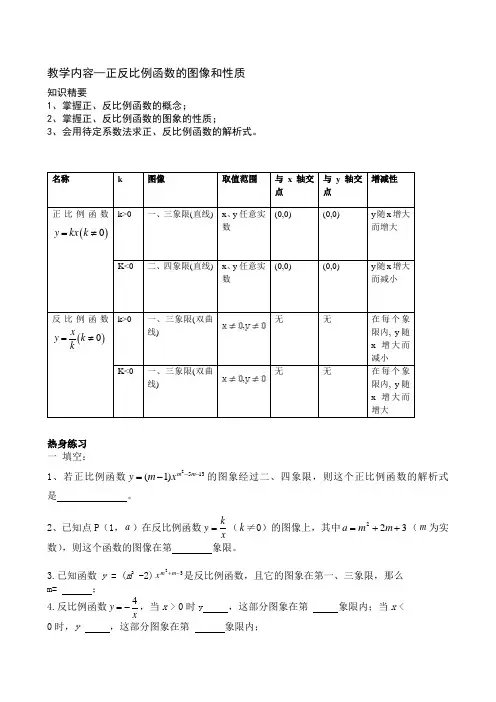
教学内容—正反比例函数的图像和性质知识精要1、掌握正、反比例函数的概念;2、掌握正、反比例函数的图象的性质;3、会用待定系数法求正、反比例函数的解析式。
热身练习 一 填空:1、若正比例函数1352)1(---=m m x m y 的图象经过二、四象限,则这个正比例函数的解析式是 。
2、已知点P (1,a )在反比例函数xky =(k ≠0)的图像上,其中322++=m m a (m 为实数),则这个函数的图像在第 象限。
3.已知函数y = (m 2 -2)32-+m m x 是反比例函数,且它的图象在第一、三象限,那么m= ;4.反比例函数4y x=-,当x > 0时y ,这部分图象在第 象限内;当x <0时,y ,这部分图象在第 象限内;名称k图像取值范围与x 轴交点 与y 轴交点 增减性正比例函数()0y kx k =≠k>0一、三象限(直线) x 、y 任意实数 (0,0)(0,0)y 随x 增大而增大K<0二、四象限(直线) x 、y 任意实数(0,0) (0,0)y 随x 增大而减小反比例函数()0xy k k=≠ k>0一、三象限(双曲线),无 无在每个象限内, y 随x 增大而减小 K<0一、三象限(双曲线),无 无在每个象限内, y 随x 增大而增大5.如图,正比例函数kx y =(k >0)与反比例函数xy 3=的图像交于A 、C 两点,AB ⊥x 轴于B ,CD ⊥x 轴于D ,则ABCD S 四边形= 。
yx例1图O DCBA精解名题例1近视眼镜的度数y (度)与焦距x (m )成反比例,已知400•度近视眼镜镜片 的焦距为0.25m .(1) 试求眼镜度数y 与镜片焦距x 之间的函数关系式(2) 求1 000度近视眼镜镜片的焦距.例2如图所示,是某一蓄水池每小时的排水量V (m 3/h )与排完水池中的水所用的时间 t (h )之间的函数关系图象.(1)请你根据图象提供的信息求出此蓄水池的蓄水量; (2)写出此函数的解析式;(3)若要6h 排完水池中的水,那么每小时的排水量应该是多少?(4)如果每小时排水量是5 000m 3,那么水池中的水将要多少小时排完?巩固练习1、下列命题中:①函数x y 3=(25x ≤≤)的图像是一条直线;②若y 与z 3-成反比例,z 与x 成正比例,则y 与x 成反比例;③如果一条双曲线经过点(a -,b ),那么它一定同时经过点(b -,a );④如果P 1(1x ,1y ),P 2(2x ,2y ),是双曲线x y 4-=同一分支上的两点,那么当1x >2x时,1y >2y 。

模型介绍一、反比例函数k 的几何意义1.反比例函数k 的几何意义:如图,在反比例函数图象上任选一点,向两坐标轴作垂线,垂线与坐标轴所围成矩形的面积为k 。
如图二,所围成三角形的面积为2k二、利用k 的几何意义进行面积转化1.如图,直线AB 与反比例函数k y x=(0k ≠)交于A 、B 两点,与x 、y 轴的交点分别为C 、D ,那么OAB OCD OBD OAC S S S S ∆∆∆∆=--,此方法是绝大部分学生选用的方法。
但是,从效率来讲,就比较低2.如图,过点A 、B 作x 轴的垂线,垂足分别为E 、F ,则根据k 的几何意义可得,OBF OAE S S ∆∆=,而OBF OAB OAE ABFE S S S S ∆∆∆+=+梯形,所以OAB ABFE S S ∆=梯形,此方法的好处,在于方便,快捷,不易出错。
【例1】.如图,反比例函数y=在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,则△AOB的面积是8.过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,∴x=2时,y=3;x=6时,y=1,=S△OBD=3,故S△ACOS四边形AODB=×(3+1)×4+3=11,故△AOB的面积是:11﹣3=8.故答案为:8.变式训练【变1-1】.如图,点A在反比例函数(x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若,△AOB的面积为12,则k的值为()A.4B.6C.10D.12解:如图,过点A作AD⊥x轴,垂足为D,∵OC∥AD,,∴,∴,k>0,∴k=12,故选:D.【变1-2】.如图,反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E,F两点,=4,则k的值为16.若E是AB的中点,S△BEF解:设E(a,),则B纵坐标也为,∵E是AB中点,∴F点坐标为(2a,),∴BF=BC﹣FC=﹣=,=4,∵S△BEF∴a•=4,∴k=16.故答案是:16.【例2】.如图,平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为6,4,反比例函数y=(x>0)的图象经过A,B两点,若菱形ABCD的面积为2,则k的值为12.解:解法一:过点A作x轴的垂线,交CB的延长线于点E,∵BC∥x轴,∴AE⊥BC,∵A,B两点在反比例函数y=(x>0)的图象,且纵坐标分别为6,4,∴A(,6),B(,4),∴AE=2,BE=﹣=,∵菱形ABCD的面积为2,∴BC×AE=2,即BC=,∴AB=BC=,在Rt△AEB中,BE===1,∴k=1,∴k=12.解法二:同理知:BE=1,设A(a,6),则B(a+1,4),∴6a=4(a+1),∴a=2,∴k=2×6=12.故答案为12.变式训练【变2-1】.如图,点A、B在反比例函数y=的图象上,A、B的纵坐标分别是3和6,连接OA、OB,则△OAB的面积是()A.9B.8C.7D.6解:∵点A、B在反比例函数y=的图象上,A、B的纵坐标分别是3和6,∴A(4,3),B(2,6),作AD⊥y轴于D,BE⊥y轴于E,=S△BOE=×12=6,∴S△AOD=S△AOD+S梯形ABED﹣S△BOE=S梯形ABED,∵S△OAB=(4+2)×(6﹣3)=9,∴S△AOB故选:A.【变2-2】.如图,在直角坐标系中,O为坐标原点,函数y=与y=(a>b>0)在第一象限的图象分别为曲线C1,C2,点P为曲线C1上的任意一点,过点P作y轴的垂线交C2于点A,作x轴的垂线交C2于点B,则阴影部分的面积S△AOB=a﹣.(结果用a,b表示)解:设B(m,),A(,n),则P(m,n),∵点P为曲线C1上的任意一点,∴mn=a,=mn﹣b﹣b﹣(m﹣)(n﹣)∴阴影部分的面积S△AOB=mn﹣b﹣(mn﹣b﹣b+)=mn﹣b﹣mn+b﹣=a﹣.故答案为:a﹣.1.如图,在△ABC中,AB=AC,点A在反比例函数y=(k>0,x>0)的图象上,点B,C在x轴上,OC=OB,延长AC交y轴于点D,连接BD,若△BCD的面积等于1,则k的值为()A.3B.2C.D.4解:作AE⊥BC于E,连接OA,∵AB=AC,∴CE=BE,∵OC=OB,∴OC=BC=×2CE=CE,∵AE∥OD,∴△COD∽△CEA,∴=()2=4,∵△BCD的面积等于1,OC=OB,=S△BCD=,∴S△COD=4×=1,∴S△CEA∵OC=CE,=S△CEA=,∴S△AOC=+1=,∴S△AOE=k(k>0),∵S△AOE∴k=3,故选:A.2.如图,OC交双曲线y=于点A,且OC:OA=5:3,若矩形ABCD的面积是8,且AB ∥x轴,则k的值是()A.18B.50C.12D.解:延长DA、交x轴于E,∵四边形ABCD是矩形,且AB∥x轴,∴∠CAB=∠AOE,∴DE⊥x轴,CB⊥x轴,∴∠AEO=∠ABC∴△AOE∽△CAB,∴=()2,∵矩形ABCD的面积是8,OC:OA=5:3,∴△ABC的面积为4,AC:OA=2:3,∴=()2=,=9,∴S△AOE∵双曲线y=经过点A,=|k|=9,∴S△AOE∵k>0,∴k=18,故选:A.3.如图,已知点A,B分别在反比例函数y1=﹣和y2=的图象上,若点A是线段OB 的中点,则k的值为()A.﹣8B.8C.﹣2D.﹣4解:设A(a,b),则B(2a,2b),∵点A在反比例函数y1=﹣的图象上,∴ab=﹣2;∵B点在反比例函数y2=的图象上,∴k=2a•2b=4ab=﹣8.故选:A.4.如图,点A(m,n),B(4,)在双曲线y=上,且0<m<n.若△AOB的面积为,则m+n=()A.7B.C.D.3解:∵点A(m,n),B(4,)在双曲线y=上,∴mn=4×=k,∴mn=k=6,∴双曲线为y=,∴n=,作AD⊥x轴于D,BE⊥x轴于E,=S△AOD+S梯形ADEB﹣S△BOE=S梯形ADEB,∵S△AOB∴(+)(4﹣m)=,解得m1=1,m2=﹣16,∵0<m<n.∴m=1,∴n=6,∴m+n=7,故选:A.5.如图,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴=3,则S△于点C,BD⊥x轴于点D,连接OA、BC,已知点C(2,0),BD=3,S△BCDAOC为()A.2B.3C.4D.6解:在Rt△BCD中,∵×CD×BD=3,∴×CD×3=3,∴CD=2,∵C(2,0),∴OC=2,∴OD=4,∴B(4,3),∵点B是反比例函数y=(x>0)图象上的点,∴k=12,∵AC⊥x轴,==6,∴S△AOC故选:D.6.如图,平行于y轴的直线分别交y=与y=的图象(部分)于点A、B,点C是y 轴上的动点,则△ABC的面积为()A.k1﹣k2B.(k1﹣k2)C.k2﹣k1D.(k2﹣k1)解:由题意可知,AB=﹣,AB边上的高为x,=×(﹣)•x=(k1﹣k2),∴S△ABC故选:B.7.已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线y=与边BC交于点D、与对角线OB交于中点E,若△OBD的面积为10,则k的值是()A.10B.5C.D.解:设E点的坐标是(x,y),∵E是OB的中点,∴B点的坐标是(2x,2y),则D点的坐标是(,2y),∵△OBD的面积为10,∴×(2x﹣)×2y=10,解得,k=,故选:D.8.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=()A.6B.9C.D.解:∵四边形OCBA是矩形,∴AB=OC,OA=BC,设B点的坐标为(a,b),∵BD=3AD,∴D(,b)∵D、E在反比例函数的图象上,∴=k,设E的坐标为(a,y),∴ay=k∴E(a,),=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=ab﹣k﹣k﹣••(b﹣)=12,∵S△ODE∴4k﹣k﹣+=12k=故选:D.9.如图,一直线经过原点O,且与反比例函数y=(k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k=8.解:∵反比例函数与正比例函数的图象相交于A、B两点,∴A、B两点关于原点对称,∴OA=OB,∴△BOC的面积=△AOC的面积=8÷2=4,又∵A是反比例函数y=图象上的点,且AC⊥y轴于点C,∴△AOC的面积=|k|,∴|k|=4,∵k>0,∴k=8.故答案为8.10.如图,若反比例函数y=的图象经过等边三角形POQ的顶点P,则△POQ的边长为2.解:如图,过点P作x轴的垂线于M,∵△POQ为等边三角形,∴OP=OQ,OM=QM=OQ,∵反比例函数的图象经过点P,∴设P(a,)(a>0),则OM=a,OQ=OP=2a,PM=,在Rt△OPM中,PM===a,∴=a,∴a=1(负值舍去),∴OQ=2a=2,故答案为:2.11.如图,A(4,3)是反比例函数y=在第一象限图象上一点,连接OA,过A作AB∥x 轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=的图象于点P.则△OAP 的面积为5.解:过P作MN⊥x轴于M,交AB于N,过A作AD⊥x轴于D,∵A(4,3),∴AD=3,OD=4,∴AO==5,∵AB=AO,∴AB=5,∵AB∥x轴,点B的横坐标是4+5=9,纵坐标是3,即点B的坐标是(9,3),设直线OB的解析式是y=ax,把B点的坐标(9,3)代入得:3=9a,解得:a=,即y=x,∵AB∥x轴,∴MN⊥AB,把A(4,3)代入y=,得k=12,即y=,解方程组得:或,∵点P在第一象限,∴点P的坐标是(6,2),∵A(4,3),AB∥x轴,P(6,2),∴MN=AD=3,PN=3﹣2=1,﹣S△APB=3﹣=5,∴△OAP的面积是S△ABO故答案为:5.12.如图,直线y=x+m与双曲线y=相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC 面积的最小值为6.解:方法一:设A(a,),B(b,),则C(a,).将y=x+m代入y=,得x+m=,整理,得x2+mx﹣3=0,则a+b=﹣m,ab=﹣3,∴(a﹣b)2=(a+b)2﹣4ab=m2+12.=AC•BC∵S△ABC=(﹣)(a﹣b)=••(a﹣b)=(a﹣b)2=(m2+12)=m2+6,∴当m=0时,△ABC的面积有最小值6.故答案为6.方法二:因为y=x+m斜率为1,且BC∥x轴,AC∥y轴,∴∠ABC=∠BAC=45°,∴△ABC为等腰直角三角形,∴AC=BC=AB,=AC•BC=AB2,∴S△ABC当AB最小时,m=0,直线为y=x,联立方程,解得或,∴A(,),B(﹣,﹣),AB=×2=2,=×4×6=6.∴S△ABC最小故答案为:6.13.如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO =AB,点C为斜边OB的中点,反比例函数y=(k>0,x>0)的图象过点C,且交线=6,则k的值为8.段AB于点D,连接CD,OD.若S△OCD解:根据题意设B(m,m),则A(m,0),∵点C为斜边OB的中点,∴C(,),∵反比例函数y=(k>0,x>0)的图象过点C,∴k=•=,∵∠OAB=90°,∴D的横坐标为m,∵反比例函数y=(k>0,x>0)的图象过点D,∴D的纵坐标为,作CE⊥x轴于E,=S△AOD,∵S△COES△OCD=S△COE+S梯形ADCE﹣S△AOD=S梯形ADCE,S△OCD=6,∴(AD+CE)•AE=6,即(+)•(m﹣m)=6,∴m2=32,∴k==8,故答案为:8.解法二:作CE⊥OA于E,∵C为AB的中点,OA=AB,∠OAB=90°,=S△AOD=k,S△AOB=2k,∴S△OEC=k,∴S△BOD∵C为斜边OB的中点,=S△BCD=S△BOD=6,∴S△OCD∴×k=6,∴k=8.故答案为:8.14.如图,在平面直角坐标系中,▱OABC的顶点A,B在第一象限内,顶点C在y轴上,经过点A的反比例函数y=(x>0)的图象交BC于点D.若CD=2BD,▱OABC的面积为15,则k的值为18.解:过点D作DN⊥y轴于N,过点B作BM⊥y轴于M,设OC=a,CN=2b,MN=b,∵▱OABC的面积为15,∴BM=,∴ND=BM=,∴A,D点坐标分别为(,3b),(,a+2b),∴•3b=(a+2b),∴b=a,∴k=•3b=•3×a=18,故答案为:18.15.如图,点A在双曲线y=的第一象限的那一支上,AB垂直于y轴于点B,点C在x 轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为.解:连DC,如图,∵AE=3EC,△ADE的面积为3,∴△CDE的面积为1,∴△ADC的面积为4,设A点坐标为(a,b),则AB=a,OC=2AB=2a,而点D为OB的中点,∴BD=OD=b,=S△ABD+S△ADC+S△ODC,∵S梯形OBAC∴(a+2a)×b=a×b+4+×2a×b,∴ab=,把A(a,b)代入双曲线y=,∴k=ab=.故答案为:.16.如图,已知反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8),B(﹣4,m)两点.(1)求k1,k2,b的值;(2)求△AOB的面积;(3)请直接写出不等式x+b的解.解:(1)∵反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8)、B(﹣4,m),∴k1=8,B(﹣4,﹣2),解方程组,解得;(2)由(1)知一次函数y=k2x+b的图象与y轴的交点坐标为(0,6),=×6×4+×6×1=15;∴S△AOB(3)﹣4≤x<0或x≥1.17.如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB=,反比例函数y=的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为.(1)求反比例函数的解析式;(2)求直线EB的解析式;.(3)求S△OEB解:(1)∵A点的坐标为(a,6),AB⊥x轴,∴AB=6,∵cos∠OAB==,∴,∴OA=10,由勾股定理得:OB=8,∴A(8,6),∴D(8,),∵点D在反比例函数的图象上,∴k=8×=12,∴反比例函数的解析式为:y=;(2)设直线OA的解析式为:y=bx,∵A(8,6),∴8b=6,b=,∴直线OA的解析式为:y=x,则,x=±4,∴E(﹣4,﹣3),设直线BE的解式为:y=mx+n,把B(8,0),E(﹣4,﹣3)代入得:,解得:,∴直线BE的解式为:y=x﹣2;=OB•|y E|=×8×3=12.(3)S△OEB18.如图,直线y=x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=.(1)求反比例函数的解析式;(2)求点B的坐标;.(3)求S△OAB解:(1)∵直线y=x与反比例函数的图象交于点A(3,a),∴a=×3=4,∴点A的坐标为(3,4),∴k=3×4=12,∴反比例函数解析式y=.(2)∵点B在这个反比例函数图象上,设点B坐标为(x,),∵tanα=,∴=,解得:x=±6,∵点B在第一象限,∴x=6,∴点B的坐标为(6,2).(3)设直线OB为y=kx,(k≠0),将点B(6,2)代入得:2=6k,解得:k=,∴OB直线解析式为:y=x.过A点做AC⊥x轴,交OB于点C,如图所示:则点C坐标为(3,1),∴AC=3.S△OAB的面积=S△OAC的面积+S△ACB的面积=×|AC|×6=9.∴△OAB的面积为9.19.已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比=4.例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB (1)求该反比例函数的解析式和直线AB的解析式;(2)若直线AB与双曲线的另一交点为D点,求△ODB的面积.=•|x A|•y B,解:(1)由题意得:S△AOB即×2×y B=4,y B=4,∴B(2,4),设反比例函数的解析式为:y=,把点B的坐标代入得:k=2×4=8,∴y=,设直线AB的解析式为:y=ax+b,把A(﹣2,0)、B(2,4)代入得:,解得:,∴y=x+2;(2)由题意得:x+2=,解得:x1=﹣4,x2=2,∴D(﹣4,﹣2),=S△OAD+S△OAB=×2×2+4=6.∴S△ODB20.如图,在平行四边形OABC中,,点A在x轴上,点D是AB 的中点,反比例函数的图象经过C,D两点.(1)求k的值;(2)求四边形OABC的面积.解:(1)过点C作CE⊥x轴于E,∵∠AOC=45°,∴OE=CE,∴OE2+CE2=OC2∵OC=2,∴OE=CE=2,∴C(2,2),∵反比例函数的图象经过点C点,∴k=2×2=4;(2)过点D作DF⊥x轴于F,∵四边形OABC是平行四边形,∴AB=OC=2,∠DAF=∠AOC=45°,又∵点D是AB的中点,∴AD=,AF=DF,∴AF2+DF2=AD2,∴AF=DF=1,∴D点的纵坐标为1,∵反比例函数的图象过点D点,∴D(4,1),∴OF=4,OA=OF﹣AF=4﹣1=3,∴平行四边形OABC的面积S=OA•CE=3×2=6.21.如图,直线y=6x与双曲线y=(k≠0,且x>0)交于点A,点A的横坐标为2.(1)求点A的坐标及双曲线的解析式;(2)点B是双曲线上的点,且点B的纵坐标是6,连接OB,AB,求△AOB的面积.解:(1)将x=2代入y=6x,得:y=12,∴点A的坐标为(2,12),将A(2,12)代入y=,得:k=24,∴反比例函数的解析式为y=;(2)在y=中y=6时,x=4,∴点B(4,6),而A(2,12),如图,过A作AC⊥y轴,BD⊥x轴,交于点E,则OD=4,OC=12,BD=6,AC=2,AE=2,BE=6,=S矩形OCED﹣S△AOC﹣S△BOD﹣S△ABE∴S△AOB=4×12﹣×2×12﹣×4×6﹣×2×6=48﹣12﹣12﹣6=18.22.如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数的图象的两个交点.(1)求反比例函数和一次函数的表达式;(2)求△AOB的面积;(3)若D(x,0)是x轴上原点左侧的一点,且满足,求x的取值范围.解:(1)∵B(2,﹣4)在反比例函数y=的图象上,∴m=﹣8,∴反比例函数的表达式为y=﹣.∵A(﹣4,n)在y=﹣的图象上,∴n=2,∴A(﹣4,2).∵y=kx+b经过A(﹣4,2)和B(2,﹣4),∴,解得∴一次函数的表达式为y=﹣x﹣2.(2)当y=﹣x﹣2=0时,解得x=﹣2.∴点C(﹣2,0),∴OC=2,=S△AOC+S△COB∴S△AOB=×2×2+×2×4=6.(3)根据函数的图象可知:若D(x,0)是x轴上原点左侧的一点,当﹣4<x<0时,满足kx+b﹣<0.23.如图,一次函数y=k1x+b的图象与反比例函数y=(x<0)的图象相交于点A(﹣1,2)、点B(﹣4,n).(1)求此一次函数和反比例函数的表达式;(2)求△AOB的面积;(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.解:(1)∵反比例函数y=(x<0)的图象经过点A(﹣1,2),∴k2=﹣1×2=﹣2,∴反比例函数表达式为:y=﹣,∵反比例y=﹣的图象经过点B(﹣4,n),∴﹣4n=﹣2,解得n=,∴B点坐标为(﹣4,),∵直线y=k1x+b经过点A(﹣1,2),点B(﹣4,),∴,解得:,∴一次函数表达式为:y=+.(2)设直线AB与x轴的交点为C,如图1,当y=0时,x+=0,x=﹣5;∴C点坐标(﹣5,0),∴OC=5.S△AOC=•OC•|y A|=×5×2=5.S△BOC=•OC•|y B|=×5×=.S△AOB=S△AOC﹣S△BOC=5﹣=;(3)如图2,作点A关于x轴的对称点A′,连接A′B,交x轴于点P,此时△PAB的周长最小,∵点A′和A(﹣1,2)关于x轴对称,∴点A′的坐标为(﹣1,﹣2),设直线A′B的表达式为y=ax+c,∵经过点A′(﹣1,﹣2),点B(﹣4,)∴,解得:,∴直线A′B的表达式为:y=﹣x﹣,当y=0时,则x=﹣,∴P点坐标为(﹣,0).24.如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=(x>0)的图象经过线段OC的中点A(3,2),交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.(1)求反比例函数和直线EF的解析式;(2)求△OEF的面积;(3)请结合图象直接写出不等式k2x+b>0的解集.解:(1)∵四边形DOBC是矩形,且D(0,4),B(6,0),∴C点坐标为(6,4),∵A点坐标为(3,2),∴k1=3×2=6,∴反比例函数解析式为y=;把x=6代入y=得x=1,则F点的坐标为(6,1);把y=4代入y=得x=,则E点坐标为(,4),把F(6,1)、E(,4)代入y=k2x+b,得,解得,,∴直线EF的解析式为y=﹣x+5;﹣S△ODE﹣S△OBF﹣S△CEF(2)△OEF的面积=S矩形BCDO=4×6﹣×4×﹣×6×1﹣×(6﹣)×(4﹣1)=;(3)由图象得:不等式k2x+b﹣>0的解集为<x<6.25.如图,已知反比例函数y=(m≠0)的图象经过点(1,4),一次函数y=﹣x+b的图象经过反比例函数图象上的点Q(﹣4,n).(1)求反比例函数与一次函数的表达式;(2)一次函数的图象分别与x轴、y轴交于A、B两点,与反比例函数图象的另一个交点为P,连结OP、OQ.求△OPQ的面积.解:(1)反比例函数y=(m≠0)的图象经过点(1,4),解得m=4,故反比例函数的表达式为y=.一次函数y=﹣x+b的图象与反比例函数的图象相交于点Q(﹣4,n),所以,解得n=﹣1,b=﹣5.∴一次函数的表达式y=﹣x﹣5;(2)由,解得或.∴点P(﹣1,﹣4),在一次函数y=﹣x﹣5中,令y=0,得﹣x﹣5=0,解得x=﹣5,故点A(﹣5,0),S△OPQ=S△OP A﹣S△OAQ=×5×4−×5×1=7.5.26.如图,在平面直角坐标系中,边长为4的等边△OAB的边OB在x轴的负半轴上,反比例函数y=(x<0)的图象经过AB边的中点C,且与OA边交于点D.(1)求k的值;(2)连接OC,CD,求△OCD的面积;(3)若直线y=mx+n与直线CD平行,且与△OAB的边有交点,直接写出n的取值范围.解:(1)∵等边△OAB,∴AB=BO=AO=4,∠ABO=∠BOA=∠OAB=60°,∵点C是AB的中点,∴BC=AC=2,过点C作CM⊥OB,垂足为M,在Rt△BCM中,∠BCM=90°﹣60°=30°,BC=2,∴BM=1,CM=,∴OM=4﹣1=3,∴点C 的坐标为(﹣3,),代入y =得:k =﹣3答:k 的值为﹣3;(2)过点A 作AN ⊥OB ,垂足为N ,由题意得:AN =2CM =2,ON =OB =2,∴A (﹣2,2),设直线OA 的关系式为y =kx ,将A 的坐标代入得:k =﹣,∴直线OA 的关系式为:y =﹣x ,由题意得:,解得:舍去,,∴D (﹣,3)过D 作DE ⊥OB ,垂足为E ,S △OCD =S CMED +S △DOE ﹣S △COM =S CMED =(+3)×(3﹣)=3,答:△OCD 的面积为3.(3)①当与直线CD 平行的直线y =mx +n 过点O 时,此时y =mx +n 的n =0,②当与直线CD 平行的直线y =mx +n 经过点A 时,设直线CD 的关系式为y =ax +b ,把C 、D 坐标代入得:,解得:a =1,b =3+∴直线CD 的关系式为y =x +3+,∵y =mx +n 与直线y =x +3+平行,∴m =1,把A (﹣2,2)代入y =x +n 得:n =2+2因此:0≤n ≤2+2且n .答:n 的取值范围为:0≤n ≤2+2且n ≠3+.。



变式1 如果y 是m 的反比例函数,m 是x 的反比例函数,那么y 是x 的( ) A .反比例函数 B .正比例函数 C .一次函数 D .反比例或正比例函数 变式2 若函数11-=m xy (m 是常数)是反比例函数,则m =________,解析式为________.题型二:反比例函数解析式例3 已知A (﹣1,m )与B (2,m ﹣3)是反比例函数图象上的两个点.则m 的值 .例4 已知y 与2x -3成反比例,且41=x 时,y =-2,求y 与x 的函数关系式.变式3已知y 与x 成反比例,当x =2时,y =3.(1)求y 与x 的函数关系式;(2)当y =-23时,求x 的值.变式4 已知函数12y y y =-,其中1y 与x 成正比例, 2y 与x 成反比例,且当x =1时,y =1;x =3时,y =5.求:(1)求y 关于x 的函数解析式; (2)当x =2时,y 的值.1、反比例函数的图像(1)形状与位置:反比例函数的图像是双曲线,它有两个分支,这两个分支分别位于第一、三象限,或第二、四象限,它们关于原点对称。
(2)变化趋势:由于反比例函数中自变量x ≠0,函数y ≠0,所以,它的图像与x 轴、y 轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴。
2、反比例函数的性质(1)对称性:反比例函数的图像是关于原点对称的中心对称图形,同时也是轴对称图形,有两条对称轴,分别是一、三象限和二、四象限的角平分线,即直线y x =±。
(注:过原点的直线与双曲线的两个交点关于原点对称)(2)双曲线的位置:当k>0时,双曲线位于一、三象限(x ,y 同号);当k<0时,双曲线位于二、四象限(x ,y 同号异号),反之也成立。
(3)增减性: 当k>0时,双曲线走下坡路,在同一象限内,y 随x 的增大而减小;当k<0时,双曲线走上坡路,在同一象限内,y 随x 的增大而增大。
x
y
P
G
F
E
C
B
A
O
反比例函数
1、正比例函数y=x与反比例函数1yx的图像相交于A、C两点,过A作AB垂直于x
轴于B,CD垂直于x轴于D,则四边形ABCD的面积是( )
A 1 B 32 C 2 D 52
2、点P是x正半轴上一个动点,过点P作x轴的垂线交双曲线1yx于点Q,连接OQ,
当点P沿x轴的正方向运动时,RtQOP的面积大小是否发生变化?如果不变,请求出
RtQOP的面积;如果改变,请说明理由。
3、已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,
点B在函数kyx(k0,x0)的图像上。点P(m,n)是函数kyx(k0,x0)
的图像上任意一点,过点P分别作x轴,y轴的垂线,垂足分别为E、F,并设矩形OEPF
和正方形OABC不重合部分的面积为S。
(1 )求点B的坐标及k的值;
(2)当S=4.5时,求点P的坐标;
(3)写出S关于m的函数关系式。
4、已知点(1,3)在函数kyx (x0)的图像上,矩形ABCD的边BC在x轴上,E是
x
y
E
D
C B
A
O
x
y
S
M
R
H
Q
P
B
A
O
对角线BD的中点,函数kyx (x0)又经过A、E两点,点E的横坐标为m。
(1)求k值;
(2)求点C的横坐标(用m表示)
(3)当045ABD时,求m的值。
5、“三等分角”是数学史上一个著名问题,即仅用尺规不可能“三等分角”。下面是数学
家帕普斯借助函数给出一个“三等分锐角”的方法:将给定的锐角AOB置于直角坐标
系中,边OB在x轴上、边OA与函数1yx的图像交与点P,以P为圆心,2OP为半径
作弧交1yx图像于R,过点P和R分别作x轴和y轴的平行线,两直线相交于点M,
连结OM得到MOB,则MOB=13AOB。要明白帕普斯方法,请研究以下问题:
(1)设P(a,1a)、R(b,1b),求直线OM对应的函数表达式(用a、b的代数
式表示);
(2)分别过点P和R作y轴和x轴的平行线,两直线相交于点Q,请说明点Q在
直线OM上,并据此证明MOB=13AOB;
(3)应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明)。
x
y
E
D
C
B
A
O
6、矩形AOCB的两边OC,OA分别位于x轴,y轴上,点B的坐标为(20-3,5),D是
AB边上一点。将ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点
E在一反比例函数的图像上,求该函数的解析式。
7、 边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限。将
OAB绕点O顺时针旋转030后,恰好点A落在双曲线 kyx(x0
)上。
(1)求双曲线 kyx(x0)的解析式;
(2)等边三角形OAB继续按顺时针旋转多少度后,A点再次落在该双曲线上?
x
y
B'
A'
B
A
O