河北省定州中学2017届高三(高补班)上学期期中考试数学试卷Word版含答案.doc

河北省定州中学2017届高三(高补班)上学期期中考试数学试题doc定州中学XX年第一学期高四数学期中考试试题时间：120分钟总分：150分I卷一、选择题：本大题共12个小题，每小题5分,共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若集合B?{y|y?2x,x?R}，且A?B?A则集合A可能是A. ?1,2? B . xx?1C. ??1,0,1?D . R 2.函数y?x|x|?px , x?RA .是偶函数B.是奇函数 C.不具有奇偶性D .奇偶性与p有关3.复数z???i的共轭复数在复平面上对应的点在1?iA .第一象限B.第二象限C.第三象限D.第四象限4.为了得到y?cos2x，只需将y?sin(2x??3) 作如下变换A .向右平移?3 个单位B.向右平移?6 个单位C .向左平移?? 个单位 D.向右平移个单位12125. 已知平面向量a,b满足a?(a?b)?5，且a?2,b?1，则向量a与b夹角的余弦值为A .1133 B . ? C. D. ?22222??6. 已知函数f(x)?sin(x??) ,且|?|?,又?3f(x)dx?0 ，贝U函数f(x)的图象的一02 条对称轴是A .x??5?7?? B.x? C.x? D.x? 612367.已知？？(？？,), a?(cos?)cos? , b?(sin?)cos? , c?(cos?)sin?则42A . a?b?cB.a?c?b C. b?a?c D. c?a?b8. 已知函数f(x)的定义域为R 当x?0 时，f(x)?x3?1当?1?x?1 时，f(?x)??f(x) ；当x?111)? 时，f(x?)?f(x?) ,f(2016222A . ?2 B . ?1 C . 0 D .9. 已知定义在R上的奇函数y?f(x)满足f(x)?2 ,不等式f(x?1)?ln(x?2)?2?ex?1?3x 的解集为A . (?2,?1)B . (?1,??) C. (?1,2) D . (2,??)12201612x4?x2sinx?4f()?f()??f()?10. 已知函数f(x?)?，则… 42017201720172x?2A . 2017 B . 2016 C. 4034 D . 4032 11.已知函数f(x)?? 不可能为A . 2个B . 3个C . 4个D . 5个12 .函数f(x)?Asin(2x??)(???log5(1?x)(x?1)??(x?2)?2(x?1)2 ，则关于x的方程f(x)?a(a?R)实根个数?2,A?0) 部分图象如图所示，且f(a)?f(b)?0 ,对不同的x1,x2??a,b?，若f(x1)?f(x2)，有f(x1?x2)?3 , 则5??,) 上是减函数A . f(x)在(?1212B . f(x)在(?y 2 5??,) 上是增函数1212a C . f(x)在(?5?3,6)上是减函数O b x D . f(x)在(?5?3,6)上是增函数□卷二、填空题13. 已知tan(???)??12? , tan(??)?，贝U tan(??)的值为544414. 在?ABC 中，？A??2,AB?2,AC?4,AF?111AB,CE?CA,BD?BC 贝U224DE?DF 的值为.15. 在?ABC中，边AB的垂直平分线交边AC于D若C??3,BC?8,BD?7,贝U?ABC的面积为.g(x1)f(x2)x2?1x,g(x)?x ,对任意x1,x2?(0,??),不等式16.设函数f(x)?恒？kk?1xe成立，则正数k的取值范围是.三、解答题17. ( 本小题满分10分)已知平面上三个向量a,b,c的模均为1,他们之间的夹角均为120。

河北定州中学2016-2017学年第一学期高四第3次月考数学试卷一、选择题1．直线1=x 的倾斜角和斜率分别是（ ）．A ．45,1︒B ．1，1C ．90︒，不存在D ．180︒，不存在2．要得到函数R x x x x f ∈=,cos sin 2)(，只需将函数R x x x g ∈-=,1cos 2)(2的图像（ ）A ．向左平移2π个单位 B ．向右平移2π个单位 C ．向左平移4π个单位 D ．向右平移4π个单位 3．等差数列{}n a 中，n S 为其前n 项和，且945672S a a a =+++，则37a a +=（ ） A ．22 B ．24 C ．25 D ．264．若集合{}|128xP x =≤<，{}1,2,3Q =，则P Q = （ ）A ．{}1,2B ．{}1C ．{}2,3D ．{}1,2,35．已知两个不相等的非零向量,a b ，两组向量12345,,,,x x x x x 和12345,,,,y y y y y 均由2个a 和3个b 排成一列而成．记1122334455min ,S x y x y x y x y x y S =⋅+⋅+⋅+⋅+⋅表示S 所有可能取值中的最小值，则下列正确的是（ ）A ．22min 22S a a b b =+⋅+B ．22min 23S a b =+C ．若a b ⊥，则min S 与a 无关D ．S 有5个不同的值6．设ABC ∆中的内角A,B,C 所对的边长分别是c b a ,,若A a B c C b sin cos cos =+,则ABC ∆的形状为（ ）A.锐角三角形B.直角三角形C.钝角三角形D.不确定 7．已知等差数列{a n }的公差为2，若a 1，a 3，a 4成等比数列，则a 2=（ ） A ．﹣4 B ．﹣6 C ．﹣8 D ．﹣10 8．若4tan 3,tan 3αβ==，则tan()αβ-等于（ ）A ．-3B ．13-C ．3D ．139．已知函数||2()x f x e x =+（其中常数 2.71828e = ），则使得()(21)f x f x >-成立的x 的取值范围是（ ）A ．1(,1)3B ．1(,)(1,)3-∞-+∞C ．1(,1)3-D ．11(,)(,)33-∞-+∞10．已知函数y=f （x ）是定义在R 上的偶函数，且当x ＞0时，不等式若则之间的大小关系为（ ）A ．a ＞c ＞bB ．c ＞a ＞bC ．b ＞a ＞cD ．c ＞b ＞a 11．函数1lg(2)y x x =++-的定义域是（ ）A.B.C.[)1,2 D.12．定义区间12[,]x x 的长度为21x x -（21x x >），函数22()1()(,0)a a x f x a R a a x+-=∈≠的定义域与值域都是[,]()m n n m >，则区间[,]m n 取最大长度时实数a 的值为（ ）A ．233B ．-3C ．1D ．3 二、填空题13．在区间(0,1)中随机地取出两个数，则两数的平方和不大于14的概率_____.14．（2015秋•宁德期末）已知方程3﹣x+1﹣|lgx|=0的两根为x 1，x 2，且x 1＞x 2，则x 1，，的大小关系为 ．（用“＜”号连接）15．变量,x y 满足约束条件0220x x y y ≥⎧⎪-≤⎨⎪≤⎩，当目标函数2z x y =-取得最大值时，其最优解为 ．16．已知圆()()22:341C x y -+-=和两点()()(),0,,00A m B m m ->，若圆上存在点P ，使得90APB ∠=︒，则m 的取值范围是 ．三、解答题17．选修4-4：坐标系与参数方程已知圆E 的极坐标方程为4sin ρθ=．以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系，取相同单位长度（其中(),ρθ，0ρ≥，[)0,2θπ∈）． （1）直线l 过原点，且它的倾斜角34πα=，求l 与圆E 的交点A 的极坐标（点A 不是坐标原点）； （2）直线m 过线段OA 中点M ，且直线m 交圆E 于B ，C 两点，求C MB -M 的最大值． 18．如图，空间几何体ADE BCF -中，四边形ABCD 是梯形，四边形CDEF 是矩形，且平面ABCD ⊥平面CDEF ，,2,4AD DC AB AD DE EF ⊥====，M 是线段AE 上的动点．（1）试确定点M 的位置，使//AC 平面MDF ，并说明理由；（2）在（1）的条件下，平面MDF 将几何体ADE BCF -分成两部分，求空间几何体M DEF -与空间几何体ADM BCF -的体积之比；19．正项数列{}n a 的前n 项和n S 满足 ()()22210n n S n n S n n -+--+=.（1）求数列{}n a 的通项公式； （2）设()2212n n n b n a +=+，数列{}n b 的前n 项和n T ，证明：对于任意的n N *∈，都有564n T <. 20．已知曲线C 的参数方程是为参数）θθθ(sin 2cos 2⎩⎨⎧==y x ，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，B A 、的极坐标分别为)34,2(),2(ππB A 、. （1）求直线AB 的直角坐标方程；（2）设M 为曲线C 上的动点的，求点M 到直线AB 距离的最大值. 21．已知椭圆C 的中心在原点，焦点在x 轴上，焦距为2，离心率为21． （1）求椭圆C 的方程；（2）设直线l 经过点M （0，1），且与椭圆C 交于A ，B 两点，若253=AB ，求直线l 的方程．[22．已知定义在R 上的函数()f x 满足()()4f x f x +=，当[]0,4x ∈时，()2x m f x n -=+，且()26f =． （Ⅰ）求,m n 的值；（Ⅱ）当[]0,4x ∈时，关于x 的方程()20xf x a -⋅=有解，求a 的取值范围．23．在△ABC 中，内角,,A B C 的对边分别为,,a b c ，已知b a c B C A -=-2cos cos 2cos ，且43sin =A ，角C为锐角．（1）求角C 的大小； （2）若7=c ，且△ABC 的面积为233，求22b a +的值． 24．已知命题p ：方程表示焦点在y 轴上的椭圆，命题q ：关于x 的方程x 2+2mx+2m+3=0无实根，⑴若命题p 为真命题，求实数m 的取值范围；⑵若“p ∧q ”为假命题，“p ∨q ”为真命题，求实数m 的取值范围．参考答案CDBAC BBDAD 11．D 12．D 13．16π 14．x 2＜＜．15．(2,0). 16．[]4,6 17．（1）322,4π⎛⎫⎪⎝⎭；（2）22． （1） 直线l 的倾斜角34πα=，∴直线l 上的点的极角34πθ=或74πθ=，代入圆E 的极坐标方程为4sin ρθ=得22ρ=或22ρ=-（舍去），∴直线l 与圆E 的交点A 的极坐标为：322,4π⎛⎫ ⎪⎝⎭． （2）由（1）知线段OA 的中点M 的极坐标为32,4π⎛⎫ ⎪⎝⎭， ∴M 的直角坐标为()1,1-，又圆E 的极坐标方程为4sin ρθ=， 圆E 的直角坐标方程2240x y y +-=．设直线m 的参数方程为1cos 1sin x t y t αα=-+⎧⎨=+⎩（t 为参数），代入2240x y y +-=得()22sin cos 20t t αα-+-=，()24sin cos 80αα∆=++>．设B ，C 点的参数分别为1t ，2t ，则()122sin cos t t αα+=+，122t t ⋅=-，∴1212C 2sin cos 22sin 4t t t t πααα⎛⎫MB -M =-=-=+=+ ⎪⎝⎭，∴maxC22MB -M =，此时直线m 的倾斜角4πα=．18．（1）当M 是线段AE 的中点时，//AC 平面MDF ， 证明如下：连结CE 交DF 于N ，连结MN ，由于M N 、分别是AE CE 、的中点，所以//MN AC ，又MN 在平面MDF 内， 所以//AC 平面MDF ． （2）将几何体ADE BCF -补成三棱柱ADE B CF '-，三棱柱ADE B CF '-的体积为122482ADE V S CD ∆==⨯⨯⨯=， 则几何体ADE BCF -的体积11208(22)2323ADE BCF ADE B CF F BB C V V V ''---=-=-⨯⨯⨯⨯=三棱柱， 又三棱锥F DEM -的体积114241323F DEM V -=⨯⨯⨯⨯=三棱柱（）， ∴两几何体的体积之比为42041)3334-=：(．19．（1）由()()22210n n S n n S n n -+--+=，得()()210n n S n n S ⎡⎤-++=⎣⎦，由于{}n a 是正项数列，所以10n S +>,所以()2n S n n =+.当2n ≥时，12n n n a S S n -=-=；当1n =时，112a S ==适合上式,2n a n ∴= （2）由2n a n =，得()()()22222211111162242n n n n b n n a n n n ⎡⎤++===-⎢⎥++⋅+⎢⎥⎣⎦. 则()()()22222222211111111111...1632435112n T n n n n ⎡⎤=-+-+-++-+-⎢⎥-++⎢⎥⎣⎦()()22221111115111621626412n n ⎡⎤⎛⎫=+--<+=⎢⎥ ⎪⎝⎭++⎢⎥⎣⎦. 20．（1）0323=++y x ；（2）13232+. 解：（1）将B A 、化为直角坐标为)sin 2,cos 2(ππA 、)34sin 2,34cos2(ππB ， B '即B A 、的直角坐标分别为)0,2(-A 、)3,1(--B ，32103-=+---=AB k ，∴直线AB 的方程为)2(30+-=-x y ，即AB 的方程为0323=++y x .（2）设)sin ,cos 2(θθM ，它到直线AB 距离232)sin(13232sin cos 32++=++=ϕθθθd ，∴23213max +=d . 21．（1） 22143x y += （2） x －2y ＋2＝0或x ＋2y －2＝0 （1）设椭圆方程为22x a＋22y b ＝1（a ＞b ＞0）．因为c ＝1，e ＝c a ＝12，所以a ＝2，b ＝3， 所以椭圆C 的方程为22143x y +=． （2）由题意可知直线l 的斜率存在，设直线l 的方程为y ＝kx ＋1，则由221143y kx x y =+⎧⎪⎨+=⎪⎩，得（3＋4k 2）x 2＋8kx －8＝0，且Δ＞0．设A （x 1，y 1），B （x 2，y 2），则122122834834k x x k x x k -⎧+=⎪⎪+⎨-⎪=⎪+⎩，又2531212=-+=x x k AB得07241624=-+k k解得k 2＝14，k ＝±12． 所以直线l 的方程为y ＝±12x ＋1，即x －2y ＋2＝0或x ＋2y －2＝0． 22．（1）2,5m n ==（2）9,916a ⎡⎤∈⎢⎥⎣⎦（Ⅰ）由已知()()04f f =，可得4224,2mmn n m m m -+=+∴=-∴=又由()26f =可知2226,5n n -+=∴= ．（Ⅱ）方程即为2252x x a -+=⨯在[]0,4有解．当[]0,2x ∈时，()224525222xxx x a a -+=⨯⇒=+，令11,124xt ⎛⎫⎡⎤=∈ ⎪⎢⎥⎝⎭⎣⎦, 则245a t t =+在1,14⎡⎤⎢⎥⎣⎦单增，3,92a ⎡⎤∴∈⎢⎥⎣⎦当(]2,4x ∈时，211252542x xx a a -+=⨯⇒=+⨯，令111,2164xt ⎛⎫⎡⎫=∈ ⎪⎪⎢⎝⎭⎣⎭,则154a t =+，93,162a ⎡⎫∴∈⎪⎢⎣⎭, 综上：9,916a ⎡⎤∈⎢⎥⎣⎦23．（1）3C π=；（2）2213a b +=． （1）由正弦定理得cos 2cos 22sin sin cos sin A C c a C AB b B---==， 即sin cos 2sin cos 2sin cos sin cos B A B C C B A B -=-， 即有sin()2sin()A B B C +=+，即s i n 2s i n C A =, 又3sin 4A =，所以3sin 2C =，因为角C 为锐角，所以3C π=．（2）由（1）得3C π=，所以1333s i n 242S a b C a b ===，所以6ab =，又7c =，由余弦定理可得：2222cos73c a b ab π=+-=，所以2213a b +=．24解：（1）∵方程表示焦点在y 轴上的椭圆，∴，即，即﹣1＜m ＜1，∴若命题p 为真命题，求实数m 的取值范围是（﹣1，1）；（2）若“p∧q”为假命题，“p∨q”为真命题，则p，q为一个真命题，一个假命题，若关于x的方程x2+2mx+2m+3=0无实根，则判别式△=4m2﹣4（2m+3）＜0，即m2﹣2m﹣3＜0，得﹣1＜m＜3．若p真q假，则，此时无解，柔p假q真，则，得1≤m＜3，综上，实数m的取值范围是[1，3）。

河北定州中学2016-2017学年第一学期高四第二次月考数学试题一、选择题1．已知甲、乙两组数据如茎叶图所示，若它们的中位数相同，平均数也相同，则图中的m,n 的比值mn＝（）A．1 B．13C．29D．382．有两排坐位,前排11个坐位,后排12个坐位,现安排2人就坐,规定前排中间的3个坐位不能坐,并且这2人不左右相邻,那么不同排法的种数是( )A.234B.346C.350D.3633．已知函数f(x)=x2+2x+m(m∈R)的最小值为-1,则()21f x dx⎰ =（）A.2B.163C.6D.74．已知双曲线2213xy-=的左，右焦点分别为12,F F，点P在双曲线上，且满足12||||25PF PF+=12PF F的面积为（）531 D.125．计算机中常用的十六进制是逢16进1的计数制，采用数字9~0和字母FA~共16个计数符号，这些符号与十进制的数字的对应关系如下表：十六进制0 1 2 3 4 5 6 7十进制0 1 2 3 4 5 6 7十六进制8 9 A B C D E F十进制8 9 10 11 12 13 14 15例如，用十六进制表示1E D B+=,则=⨯BA（）(A ）6E (B ）72 (C ）5F (D ）0B 6．已知向量a 、b 满足1a =，7a b +=，,3a b π=，则b 等于（ ）A.2B.3C.D.47．箱中装有标号为1，2，3，4，5，6且大小相同的6个球，从箱中一次摸出两个球，记下号码并放回，如果两球号码之积是4的倍数，则获奖．现有4人参与摸奖，恰好有3人获奖的概率是A ．62516 B ．62596 C ．625624 D ．62548．如果函数31()3f x x x =-满足：对于任意的[]12,0,2x x ∈，都有212()()f x f x a -≤恒成立，则a 的取值范围是（）A 33⎡-⎢⎣⎦B 33⎡-⎢⎣⎦C ,33⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎦⎣⎭D ,33⎛⎡⎫-∞-⋃+∞ ⎪⎢ ⎪⎝⎦⎣⎭9．若变量,x y 满足约束条件210x y x y +≤⎧⎪≥⎨⎪≥⎩，则2z x y =+的最大值和最小值分别为 （ ）A ．43和B ．42和C ．32和D ．20和 10．设,a b 是两个非零的平面向量，下列说法正确的是（ ） ①若0a b =，则有+=-a b a b ； ②⋅=a b a b ；③若存在实数λ，使得a ＝λb ，则+=+a b a b ；④若+=-a b a b ，则存在实数λ，使得a ＝λb ． A ．①③ B ．①④ C ．②③ D ．②④11．由直线y ＝x ＋1上的一点向圆(x －3)2＋y 2＝1引切线，则切线长的最小值为A ．1 B．D ．3 12．已知集合，1,2,3}{=A 则满足A B A =⋃的非空集合B 的个数是 A ．1 B ．2 C ．7 D ．8 二、填空题13．如图,正方体1111ABCD A B C D -中,2AB =,点E 为AD 的中点,点F 在CD 上,若//EF 平面1AB C ,则EF =________.14．已知变量x y ,满足约束条件1211x y x y x ⎧-≥-⎪+≥⎨⎪≤⎩，则2z x y =-的最小值为__________．15．已知)3()0)(2()1()0(),1(log )(2f x x f x f x x x f 则⎩⎨⎧>---≤-=的值等于 ▲ 。

一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.己知直线l的斜率为k，它与抛物线y2＝4x相交于A，B两点，F为抛物线的焦点，若错误！未找到引用源。

＝2错误！未找到引用源。

，则|k|＝（）A．2错误！未找到引用源。

B．错误！未找到引用源。

C．错误！未找到引用源。

D．错误！未找到引用源。

【答案】A【解析】考点：直线与抛物线的位置关系.2.在数列错误！未找到引用源。

中，a1＝2，a n＋1＝a n＋ln错误！未找到引用源。

，则a n＝（）A．2＋ln n B．2＋错误！未找到引用源。

ln nC．2＋nln n D．1＋n＋ln n【答案】A【解析】试题分析：错误！未找到引用源。

，由已知错误！未找到引用源。

，所以错误！未找到引用源。

，故选A.考点：数列的递推公式.3.定义在区间错误！未找到引用源。

上的函数错误！未找到引用源。

使不等式错误！未找到引用源。

恒成立，其中错误！未找到引用源。

为错误！未找到引用源。

的导数，则（）A．错误！未找到引用源。

B．错误！未找到引用源。

C．错误！未找到引用源。

D．错误！未找到引用源。

【答案】B【解析】考点：函数与导数.【易错点睛】本题以不等式的为背景考查的是导数综合运用.解答本题的难点是如何建立两个函数值的表达式.本题在解答时借助题设的不等式错误！未找到引用源。

，运用巧妙变形进行构造函数错误！未找到引用源。

，进而通过构造的函数进行合理有效的变形得到两个单调函数错误！未找到引用源。

和函数错误！未找到引用源。

，即错误！未找到引用源。

和函数错误！未找到引用源。

.最后借助单调性使得问题简捷巧妙获解.4.已知错误！未找到引用源。

为正实数，直线错误！未找到引用源。

与曲线错误！未找到引用源。

相切，则错误！未找到引用源。

的最小值为（）A．1 B．错误！未找到引用源。

C．错误！未找到引用源。

D．错误！未找到引用源。

河北定州中学2017-2018学年第一学期高四数学周练试题（四）一、单项选择题1．下列函数中既不是奇函数也不是偶函数的是（ ）A ．||2x y = BC ．22x x y -=+D 2．下列正确的是 ( ) A ．小于 90的角一定是锐角 B ．终边相同的角一定相等C 上的角可以表示为 60360+⋅k ，Z k ∈D ．若Z k k ∈=-,πβα,则角α的正切值等于角β的正切值3．设函数⎩⎨⎧><-=0)(0)(2x x g x x x f ，若()f x 是奇函数，则(2)g 的值是（ ）A ．4-B ．2-C ．2D ．44．符合下列条件的三角形ABC ∆有且只有一个的是（ ）A ．1,30a b A ===B ．1,2,3a b c ===C ．1,45b c B ===D ．1,2,100a b A ===5．设集合{}x y y x A 2sin 2|)(==，，集合{}x y y x B ==|)(，，则（ ）． A ．B A 中有3个元素 B ．B A 中有1个元素 C ．B A 中有2个元素 D ．B A R =6．若二次函数b x a x y +-+=)1(232在区间(,1]-∞上为减函数，那么（ ） A.2a <- B.2a ≥- C.2-≤a D.2->a7，}012|),{(=+-=y x y x Q ，记Q P A =，则集合A 中元素的个数有 ( )A.3个B.0个C.l 个D.2个 8． 函数()=x f ㏑）x x 22cos (sin-的定义域是A 2kπ k ∈Z B 2k π<x <2k π k ∈Z C k πk ∈Z D k π<x <k πk ∈Z9．函数)22sin(π+=x y 的一条对称轴方程（ ）A ．2π-=xB ．4π-=xC ．8π=xD ．=x π4510．已知cos α＝－45，且α∈（2π，π），则tan （4π－α）＝[来（ ）.源:] A ．－17 B ．－7 C ．17D ．711．复数11i +的共轭复数是 （ ）A ．1122i +B ．1122i - C ．1i - D ．1i +12．已知等差数列1，,a b ，等比数列3，2,5a b ++，则该等差数列的公差为 （ ）A ．3或3-B ．3或-2C ．3D ．-2二、填空题13．用若干个大小相同，棱长为1的正方体摆成一个立体模型，其三视图如下根据三视图回答此立体模型共有正方体个数为14．函数3()3f x x mx =-+，若'(1)0f =，则m = . 15．在ABC Rt ∆中，2π=∠A ,BC=4,若点G 是ABC ∆的重心，则=+⋅)(__________.16．若向量a ,b 满足2=a ，1=b ，3=+b a ，则a 与b 的夹角是 。

一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.己知直线l的斜率为k，它与抛物线y2＝4x相交于A，B两点，F为抛物线的焦点，若错误！未找到引用源。

＝2错误！未找到引用源。

，则|k|＝（）A．2错误！未找到引用源。

B．错误！未找到引用源。

C．错误！未找到引用源。

D．错误！未找到引用源。

【答案】A【解析】考点：直线与抛物线的位置关系.2.在数列错误！未找到引用源。

中，a1＝2，a n＋1＝a n＋ln错误！未找到引用源。

，则a n＝（）A．2＋ln n B．2＋错误！未找到引用源。

ln nC．2＋nln n D．1＋n＋ln n【答案】A【解析】试题分析：错误！未找到引用源。

，由已知错误！未找到引用源。

，所以错误！未找到引用源。

，故选A.考点：数列的递推公式.3.定义在区间错误！未找到引用源。

上的函数错误！未找到引用源。

使不等式错误！未找到引用源。

恒成立，其中错误！未找到引用源。

为错误！未找到引用源。

的导数，则（）A．错误！未找到引用源。

B．错误！未找到引用源。

C．错误！未找到引用源。

D．错误！未找到引用源。

【答案】B【解析】考点：函数与导数.【易错点睛】本题以不等式的为背景考查的是导数综合运用.解答本题的难点是如何建立两个函数值的表达式.本题在解答时借助题设的不等式错误！未找到引用源。

，运用巧妙变形进行构造函数错误！未找到引用源。

，进而通过构造的函数进行合理有效的变形得到两个单调函数错误！未找到引用源。

和函数错误！未找到引用源。

，即错误！未找到引用源。

和函数错误！未找到引用源。

.最后借助单调性使得问题简捷巧妙获解.4.已知错误！未找到引用源。

为正实数，直线错误！未找到引用源。

与曲线错误！未找到引用源。

相切，则错误！未找到引用源。

的最小值为（）A．1 B．错误！未找到引用源。

C．错误！未找到引用源。

D．错误！未找到引用源。

2016-2017学年河北省保定市定州中学高三（上）开学数学试卷一、选择题：共12题每题5分共60分1．（5分）（2016春•惠阳区校级期中）平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则球O的表面积为（）A．12πB．12πC．8πD．4π2．（5分）（2014•石景山区一模）已知某个三棱锥的三视图如图所示，其中正视图是等边三角形，侧视图是直角三角形，俯视图是等腰直角三角形，则此三棱锥的体积等于（）A．B．C．D．3．（5分）（2016•柳州模拟）某四面体的三视图如图所示，则该四面体的四个面中，直角三角形的面积和是（）A．4 B．2 C．D．4．（5分）（2016•柳州模拟）如图所示，直四棱柱ABCD﹣A1B1C1D1内接于半径为的半球O，四边形ABCD为正方形，则该四棱柱的体积最大时，AB的长是（）A．1 B．C．D．25．（5分）（2016•柳州模拟）某四面体三视图如图所示，则该四面体的四个面中，直角三角形的面积和是（）A．2 B．4 C．D．6．（5分）（2016秋•定州市校级月考）如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则该四面体的外接球半径为（）A．2 B．C． D．27．（5分）（2016•济宁三模）已知圆C：（x﹣1）2+（y﹣3）2=2被直线y=3x+b所截得的线段的长度等于2，则b等于（）A．±B．±C．±2D．±8．（5分）（2012•山东）圆（x+2）2+y2=4与圆（x﹣2）2+（y﹣1）2=9的位置关系为（）A．内切 B．相交 C．外切 D．相离9．（5分）（2015•长沙校级一模）六个面都是平行四边形的四棱柱称为平行六面体．已知在平行四边形ABCD中（如图1），有AC2+BD2=2（AB2+AD2），则在平行六面体ABCD﹣A1B1C1D1中（如图2），AC12+BD12+CA12+DB12等于（）A．2（AB2+AD2+AA12）B．3（AB2+AD2+AA12）C．4（AB2+AD2+AA12）D．4（AB2+AD2）10．（5分）（2016•安康三模）一直三棱柱的每条棱长都是3，且每个顶点都在球O的表面上，则球O的半径为（）A．B．C．D．311．（5分）（2016•安康三模）若一个四棱锥底面为正方形，顶点在底面的射影为正方形的中心，且该四棱锥的体积为9，当其外接球表面积最小时，它的高为（）A．3 B．2C．2D．3二、填空题：共4题每题5分共20分12．（5分）（2016春•惠阳区校级期中）已知矩形ABCD的顶点都在半径为R的球O的球面上，且AB=6，BC=2，棱锥O﹣ABCD的体积为8，则R=______．13．（5分）（2016•和平区四模）直线y=kx与圆（x﹣2）2+（y+1）2=4相交于A，B两点，若|AB|≥2，则k的取值范围是______．14．（5分）（2015•广西校级学业考试）过点P（1，2）且在x轴，y轴上截距相等的直线方程是______．15．（5分）（2015•扬州二模）如图，在长方体ABCD﹣A1B1C1D1中，AB=3cm，AD=2cm，AA1=1cm，则三棱锥B1﹣ABD1的体积为______cm3．三、解答题：共8题共70分16．（8分）（2014•东莞一模）如图，已知四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，且∠DAB=90°，∠ABC=45°，CB=，AB=2，PA=1（1）求证：AB∥平面PCD；（2）求证：BC⊥平面PAC；（3）若M是PC的中点，求三棱锥C﹣MAD的体积．17．（8分）（2016•湖南校级模拟）如图，在三棱锥P﹣ABC中，△PAB和△CAB都是以AB为斜边的等腰直角三角形．（1）证明：AB⊥PC；（2）若AB=2PC=，求三棱锥P﹣ABC的体积．18．（8分）（2016•济宁三模）如图，在直角梯形ABCD中，AB∥CD，∠BCD=90°，BC=CD=2，AB=4，EC∥FD，FD⊥底面ABCD，M是AB的中点．（1）求证：平面CFM⊥平面BDF；（2）若点N为线段CE的中点，EC=2，FD=3，求证：MN∥平面BEF．19．（8分）（2016•和平区四模）如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AD⊥AB，DC∥AB，PA=1，AB=2，PD=BC=．（1）求证：平面PAD⊥平面PCD；（2）试在棱PB上确定一点E，使截面AEC把该几何体分成的两部分PDCEA与EACB的体积比为2：1；（3）在（2）的条件下，求二面角E﹣AC﹣P的余弦值．20．（8分）（2016春•重庆校级期末）已知动点P（x，y）满足方程xy=1（x＞0）．（Ⅰ）求动点P到直线l：x+2y﹣=0距离的最小值；（Ⅱ）设定点A（a，a），若点P，A之间的最短距离为2，求满足条件的实数a的取值．21．（10分）（2016春•重庆校级期末）已知圆C：（x﹣3）2+（y﹣4）2=4，直线l过定点A（1，0）．（1）若l与圆C相切，求l的方程；（2）若l与圆C相交于P、Q两点，若|PQ|=2，求此时直线l的方程．22．（10分）（2016•成都校级模拟）在如图所示的几何体中，四边形ABCD是平行四边形，∠ABD=90°，EB⊥平面ABCD，EF∥AB，AB=2，EB=，EF=1，BC=，且M是BD的中点．．（1）求证：EM∥平面ADF；（2）求直线DF和平面ABCD所成角的正切值；（3）求二面角D﹣AF﹣B的大小．23．（10分）（2016春•佛山校级期末）如图所示，在长方体ABCD﹣A 1B1C1D1中，BC=2AB=4，，E是A1D1的中点．（Ⅰ）在平面A1B1C1D1内，请作出过点E与CE垂直的直线l，并证明l⊥CE；（Ⅱ）设（Ⅰ）中所作直线l与CE确定的平面为α，求点C1到平面α的距离．2016-2017学年河北省保定市定州中学高三（上）开学数学试卷参考答案与试题解析一、选择题：共12题每题5分共60分1．（5分）（2016春•惠阳区校级期中）平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则球O的表面积为（）A．12πB．12πC．8πD．4π【分析】根据球心到平面的距离结合球的截面圆性质，利用勾股定理算出球半径R的值，再根据球的表面积公式，可得球的表面积．【解答】解：∵平面α截球O的球面所得圆的半径为1，该平面与球心的距离d=，∴球半径R==根据球的表面积公式，得S=4πR2=12π故选：B．【点评】本题给出球小圆半径，并且已知小圆所在平面到球心距离的情况下求球表面积，着重考查了球的截面圆性质和球表面积公式等知识，属于基础题．2．（5分）（2014•石景山区一模）已知某个三棱锥的三视图如图所示，其中正视图是等边三角形，侧视图是直角三角形，俯视图是等腰直角三角形，则此三棱锥的体积等于（）A．B．C．D．【分析】由三视图知几何体是一个侧面与底面垂直的三棱锥，底面是斜边上的高是1的直角三角形，则两条直角边是，斜边是2与底面垂直的侧面是一个边长为2的正三角形，求出面积．【解答】解：由三视图知几何体是一个侧面与底面垂直的三棱锥，底面是斜边上的高是1的直角三角形，则两条直角边是，斜边是2，∴底面的面积是=1，与底面垂直的侧面是一个边长为2的正三角形，∴三棱锥的高是，∴三棱锥的体积是故选B．【点评】本题考查由三视图还原几何体，本题解题的关键是求出几何体中各个部分的长度，特别注意本题所给的长度1，这是底面三角形斜边的高度．3．（5分）（2016•柳州模拟）某四面体的三视图如图所示，则该四面体的四个面中，直角三角形的面积和是（）A．4 B．2 C．D．【分析】由三视图知该几何体一个三棱锥，由三视图求出几何元素的长度、线面的位置关系，由线面垂直的定义判断几何体四个面中的直角三角形，由勾股定理和三角形面积公式求出直角三角形的面积和．【解答】解：根据三视图可知几何体是一个三棱锥，且PB⊥平面ABC，底面是的等腰三角形，底BC=2，BC边上的高为2，∵PB⊥平面ABC，∴PB⊥BC、PB⊥AB，即△PBC、△PAB是直角三角形，∵AB=，∴直角三角形的面积和S==2+故选：D．【点评】本题考查三视图求几何体的表面积，由三视图正确复原几何体是解题的关键，考查空间想象能力．4．（5分）（2016•柳州模拟）如图所示，直四棱柱ABCD﹣A1B1C1D1内接于半径为的半球O，四边形ABCD为正方形，则该四棱柱的体积最大时，AB的长是（）A．1 B．C．D．2【分析】设AB=a，BB1=h，求出a2=6﹣2h2，故正四棱柱的体积是V=a2h=6h﹣2h3，利用导数，得到该正四棱柱体积的最大值，即可得出结论．【解答】解：设AB=a，BB1=h，则OB=a，连接OB1，OB，则OB2+BB12=OB12=3，∴=3，∴a2=6﹣2h2，故正四棱柱的体积是V=a2h=6h﹣2h3，∴V′=6﹣6h2，当0＜h＜1时，V′＞0，1＜h＜时，V′＜0，∴h=1时，该四棱柱的体积最大，此时AB=2．故选：D．【点评】本题考查棱柱、棱锥、棱台的体积，借助导数研究出四棱柱的体积最大，是解题的关键，根据题意建立适当的模型是解决一个实际问题的关键，学习时要注意积累此类题中模型的建立方法．5．（5分）（2016•柳州模拟）某四面体三视图如图所示，则该四面体的四个面中，直角三角形的面积和是（）A．2 B．4 C．D．【分析】根据三视图还原得到原几何体，分析原几何体可知四个面中直角三角形的个数，求出直角三角形的面积求和即可．【解答】解：由三视图可得原几何体如图，∵PO⊥底面ABC，∴平面PAC⊥底面ABC，而BC⊥AC，∴BC⊥平面PAC，∴BC⊥AC．该几何体的高PO=2，底面ABC为边长为2的等腰直角三角形，∠ACB为直角．所以该几何体中，直角三角形是底面ABC和侧面PBC．PC=，∴，，∴该四面体的四个面中，直角三角形的面积和．故选：C．【点评】本题考查了由三视图还原原图形，考查了学生的空间想象能力和思维能力．6．（5分）（2016秋•定州市校级月考）如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则该四面体的外接球半径为（）A．2 B．C． D．2【分析】根据三视图知几何体是三棱锥为棱长为4的正方体一部分，画出直观图，由正方体的性质求出棱长、判断出各面形状，画出三棱锥C﹣ABD以及外接球，由△ABD是等边三角形，判断出球心O在△ABD的射影的位置，判断线与线的位置关系，设出未知数画出平面图形，利用勾股定理列出方程组，求出该四面体的外接球半径．【解答】解：由三视图知几何体是三棱锥A﹣BCD，为棱长为4的正方体一部分，直观图如图所示：由正方体的性质可得，AB=AD=BD=4，AC=BC==2，CD==6，设三棱锥C﹣ABD的外接球球心是O，设半径是R，取AB的中点E，连接CE、DE，如图所示：设OA=OB=OC=OD=R，△ABD是等边三角形，∴O在底面△ABD的射影是△ABD中心F，∵DE⊥BE，BE=2，∴DE==，同理可得，CE=，则满足CE2+DE2=CD2，即CE⊥DE，在RT△CED中，设OF=x，∵F是等边△ABD的中心，∴，，则，∴，解得x=，代入其中一个方程得，R===，∴该四面体的外接球半径是，故选：C．【点评】本题考查由三视图求几何体外接球的表面积，以及三棱锥外接球问题，在三视图与直观图转化过程中，以一个正方体为载体是很好的方式，使得作图更直观，考查空间想象能力．7．（5分）（2016•济宁三模）已知圆C：（x﹣1）2+（y﹣3）2=2被直线y=3x+b所截得的线段的长度等于2，则b等于（）A．±B．±C．±2D．±【分析】先求出圆C的圆心C（1，3），半径r=，再求出圆心C（1，3）到直线y=3x+b的距离d，由此根据圆C：（x﹣1）2+（y﹣3）2=2被直线y=3x+b所截得的线段的长度等于2，由勾股定理，能求出b 的值．【解答】解：圆C：（x﹣1）2+（y﹣3）2=2的圆心C（1，3），半径r=，圆心C（1，3）到直线y=3x+b的距离d==，∵圆C：（x﹣1）2+（y﹣3）2=2被直线y=3x+b所截得的线段的长度等于2，∴由勾股定理，得：，即2=+1，解得b=．故选：B．【点评】本题考查实数值的求法，是基础题，解题时要认真审题，注意圆的性质和点到直线的距离公式的合理运用．8．（5分）（2012•山东）圆（x+2）2+y2=4与圆（x﹣2）2+（y﹣1）2=9的位置关系为（）A．内切 B．相交 C．外切 D．相离【分析】求出两圆的圆心和半径，计算两圆的圆心距，将圆心距和两圆的半径之和或半径之差作对比，判断两圆的位置关系．【解答】解：圆（x+2）2+y2=4的圆心C1（﹣2，0），半径r=2．圆（x﹣2）2+（y﹣1）2=9的圆心C2（2，1），半径R=3，两圆的圆心距d==，R+r=5，R﹣r=1，R+r＞d＞R﹣r，所以两圆相交，故选B．【点评】本题考查圆与圆的位置关系及其判定的方法，关键是求圆心距和两圆的半径．9．（5分）（2015•长沙校级一模）六个面都是平行四边形的四棱柱称为平行六面体．已知在平行四边形ABCD中（如图1），有AC2+BD2=2（AB2+AD2），则在平行六面体ABCD﹣A1B1C1D1中（如图2），AC12+BD12+CA12+DB12等于（）A．2（AB2+AD2+AA12）B．3（AB2+AD2+AA12）C．4（AB2+AD2+AA12）D．4（AB2+AD2）【分析】根据平行六面体的性质，可以得到它的各个面以及它的对角面均为平行四边形，多次使用已知条件中的定理，再将所得等式相加，可以计算出正确结论．【解答】解：如图，平行六面体的各个面以及对角面都是平行四边形，因此，在平行四边形ABCD中，AC2+BD2=2（AB2+AD2）…①；在平行四边形ACC1A1中，A1C2+AC12=2（AC2+AA12）…②；在平行四边形BDD1B1中，B1D2+BD12=2（BD2+BB12）…③；②、③相加，得A1C2+AC12+B1D2+BD12=2（AC2+AA12）+2（BD2+BB12）…④将①代入④，再结合AA1=BB1得，AC12+B1D2+A1C2+BD12=4（AB2+AD2+AA12）故选C．【点评】此题主要考查学生对平行六面体的认识，对平行四边形的性质的理解和掌握，考查学生方程组的处理能力，属于中档题．10．（5分）（2016•安康三模）一直三棱柱的每条棱长都是3，且每个顶点都在球O的表面上，则球O的半径为（）A．B．C．D．3【分析】正三棱柱的两个底面的中心的连线的中点就是球的球心，球心与顶点的连线长就是半径，利用勾股定理求出球的半径．【解答】解：正三棱柱的两个底面的中心的连线的中点就是球的球心，球心与顶点的连线长就是半径，所以，r==．故选：A．【点评】本题是基础题，考查正三棱柱的外接球的半径的求法，明确球心、球的半径与正三棱柱的关系是本题解决的关键．11．（5分）（2016•安康三模）若一个四棱锥底面为正方形，顶点在底面的射影为正方形的中心，且该四棱锥的体积为9，当其外接球表面积最小时，它的高为（）A．3 B．2C．2D．3【分析】由四棱锥的体积为9可得到底面边长a与高h的关系，作出图形，则球心O在棱锥的高或高的延长线上，分两种情况根据勾股定理列出方程，解出球的半径R的表达式，将问题转化为求R何时取得最小值的问题．【解答】解：设底面边长AB=a，棱锥的高SM=h，∵V棱锥S﹣ABCD=•a2•h=9，∴a2=，∵正四棱锥内接于球O，∴O在直线SM上，设球O半径为R，（1）若O在线段SM上，如图一，则OM=SM﹣SO=h﹣R，（2）若O在在线段SM的延长线上，如图二，则OM=SO﹣SM=R﹣h，∵SM⊥平面ABCD，∴△OMB是直角三角形，∴OM2+MB2=OB2，∵OB=R，MB=BD=a，∴（h﹣R）2+=R2，或（R﹣h）2+=R2∴2hR=h2+，即R=+=+=≥3=．当且仅当=取等号，即h=3时R取得最小值．故选：A．【点评】本题考查了正棱锥与其外接球的结构特征，寻找球的半径与棱锥底面边长的关系是解题关键．二、填空题：共4题每题5分共20分12．（5分）（2016春•惠阳区校级期中）已知矩形ABCD的顶点都在半径为R的球O的球面上，且AB=6，BC=2，棱锥O﹣ABCD的体积为8，则R=4．【分析】由题意求出矩形的对角线的长，即截面圆的直径，根据棱锥的体积计算出球心距，进而求出球的半径．【解答】解：由题可知矩形ABCD所在截面圆的半径即为ABCD的对角线长度的一半，∵AB=6，BC=2，∴r==2，由矩形ABCD的面积S=AB•BC=12，则O到平面ABCD的距离为h满足：=8，解得h=2，故球的半径R==4，故答案为：4．【点评】本题是基础题，考查球内几何体的体积的计算，考查计算能力，空间想象能力，常考题型．13．（5分）（2016•和平区四模）直线y=kx与圆（x﹣2）2+（y+1）2=4相交于A，B两点，若|AB|≥2，则k的取值范围是．【分析】由题意求出圆心坐标和半径，由点到直线的距离公式求出圆心直线y=kx的距离，由直线与圆相交的条件列出不等式求出k的范围，结合条件和弦长公式列出不等式求出k的取值范围．【解答】解：由题意得，圆心坐标（2，﹣1）、半径r=2，则圆心到直线y=kx的距离d=＜2，解得k＜，∵所截得的弦|AB|≥2，∴2=2，化简得，3k2+4k≤0，解得，综上可得，k的取值范围是，故答案为：．【点评】本题考查直线与圆的位置关系，弦长公式，以及点到直线的距离公式的应用，属于中档题．14．（5分）（2015•广西校级学业考试）过点P（1，2）且在x轴，y轴上截距相等的直线方程是x+y﹣3=0或2x﹣y=0．【分析】分类讨论：当直线过原点时，可设直线的方程为y=kx，当直线不过原点时，可设直线的方程为=1，代点分别可得k，a的值，可得方程．【解答】解：当直线过原点时，可设直线的方程为y=kx，代点P（1，2）可得k=2，故方程为y=2x，化为一般式可得2x﹣y=0；当直线不过原点时，可设直线的方程为=1，代点P（1，2）可得a=3，故方程为=1，化为一般式可得x+y﹣3=0，综上可得所求直线的方程为：x+y﹣3=0或2x﹣y=0．故答案为：x+y﹣3=0或2x﹣y=0【点评】本题考查直线的截距式方程，涉及分类讨论的思想，解题时易漏解，属易错题．15．（5分）（2015•扬州二模）如图，在长方体ABCD﹣A1B1C1D1中，AB=3cm，AD=2cm，AA1=1cm，则三棱锥B1﹣ABD1的体积为1cm3．【分析】利用=即可得出．【解答】解：由长方体的性质可得：点D1到平面ABB1A1的距离为AD．====1，故答案为：1．【点评】本题考查了三棱锥的体积计算公式、“等体积变形”、线面垂直的判定及其性质，考查了推理能力与计算能力，属于中档题．三、解答题：共8题共70分16．（8分）（2014•东莞一模）如图，已知四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，且∠DAB=90°，∠ABC=45°，CB=，AB=2，PA=1（1）求证：AB∥平面PCD；（2）求证：BC⊥平面PAC；（3）若M是PC的中点，求三棱锥C﹣MAD的体积．【分析】（1）利用线面平行的判定定理证明；（2）利用勾股定理证明BC⊥AC，由PA⊥平面ABCD，可得PA⊥BC．从而可证得BC⊥平面PAC：（3）在直角梯形ABCD中，过C作CE⊥AB于点E，则四边形ADCE为矩形，AE=DC，AD=EC．求得CE，计算△ACD的面积，根据M到平面ADC的距离是P到平面ADC距离的一半，求得棱锥的高，代入体积公式计算．【解答】解：（1）∵底面ABCD是直角梯形，且∠DAB=90°，∠ABC=45°，∴AB∥CD，又AB⊄平面PCD，CD⊂平面PCD，∴AB∥平面PCD．（2）∵∠ABC=45°，CB=，AB=2，∴AC2=AB2+BC2﹣2AB•BC•cos45°==2．则AC2+BC2=AB2，∴BC⊥AC．∵PA⊥平面ABCD，BC⊂平面ABCD，∴PA⊥BC．又PA∩AC=A，∴BC⊥平面PAC．（3）在直角梯形ABCD中，过C作CE⊥AB于点E，则四边形ADCE为矩形，∴AE=DC，AD=EC．在Rt△CEB中，可得BE=BC•cos45°=，CE=BC•sin45°=，∴AE=AB﹣BE=2﹣1=1∴S△ADC===．，∵M是PC的中点，∴M到平面ADC的距离是P到平面ADC距离的一半，∴V C﹣MAD=V M﹣ACD=×S△ACD×（PA）=××=．【点评】本题考查了线面平行的判定，线面垂直的判断，考查了三棱锥的换底性及棱锥的体积公式，涉及知识较多，对学生的推理论证能力有一定的要求．17．（8分）（2016•湖南校级模拟）如图，在三棱锥P﹣ABC中，△PAB和△CAB都是以AB为斜边的等腰直角三角形．（1）证明：AB⊥PC；（2）若AB=2PC=，求三棱锥P﹣ABC的体积．【分析】（1）根据线面垂直的性质定理证明AB⊥平面PCG，然后根据线面垂直的性质即可证明AB⊥PC．（2）根据三棱锥的体积公式先求出底面积和高，进行求解即可．【解答】证明：（1）取AB的中点G，连结PG，CG．∵△PAB和△CAB都是以AB为斜边的等腰直角三角形，∴PG⊥AB，CG⊥AB，∵PG∩CG=G，且PG⊂平面PCG，CG⊂平面PCG，∴AB⊥平面PCG，又∵PC⊂平面PCG，∴AB⊥PC…（6分）解：（2）在等腰直角三角形PAB中，AB=，G是斜边AB的中点，∴PG=AB=，同理CG=，∵PC=，∴△PCG是等边三角形，∴S△PCG=PC•CGsin60°==，∵AB⊥平面PCG，∴V P﹣ABC=S△PCG•AB==…（12分）【点评】本题主要考查线面垂直的性质定理的应用以及三棱锥体积的计算，根据相应的性质定理以及三棱锥的体积公式是解决本题的关键．18．（8分）（2016•济宁三模）如图，在直角梯形ABCD中，AB∥CD，∠BCD=90°，BC=CD=2，AB=4，EC∥FD，FD⊥底面ABCD，M是AB的中点．（1）求证：平面CFM⊥平面BDF；（2）若点N为线段CE的中点，EC=2，FD=3，求证：MN∥平面BEF．【分析】（1）证明四边形BCDM是菱形，对角线BD⊥CM，再证明FD⊥CM，即可证明CM⊥平面BDF，从而得平面CFM⊥平面BDF；（2）过点N作NP∥EF，交DF与点P，连接PM，证明平面PMN∥平面BEF，即可证明MN∥平面BEF．【解答】解：（1）证明：直角梯形ABCD中，AB∥CD，BC=2，AB=4，且M是AB的中点，∴BM=CD，∴四边形BCDM是平行四边形，又BC=CD=2，∴平行四边形BCDM是菱形；∴BD⊥CM，又FD⊥底面ABCD，CM⊂平面BCDM，∴FD⊥CM，且FD∩BD=D，∴CM⊥平面BDF，有CM⊂平面CFM，∴平面CFM⊥平面BDF；（2）过点N作NP∥EF，交DF与点P，连接PM，如图所示；∵EC∥FD，∴四边形EFPN是平行四边形，又点N为线段CE的中点，EC=2，FD=3，∴FP=EC=1，PD=EC=2，∴PE∥CD，且PE=CD，又BM∥CD，且BM=CD，∴BM∥PE，且PE=BM，∴四边形BEPM为平行四边形，∴PM∥BE；又PM⊄平面BEF，BE⊂平面BEF，∴PM∥平面BEF；同理，PM∥平面BEF，又PM∩PN=P，PM⊂平面PMN，PN⊂平面PMN，∴平面PMN∥平面BEF，又MN⊂平面PMN，∴MN∥平面BEF．【点评】本题主要考查了线面平行，面面平行与垂直的应用问题，解题时应熟记空间中的平行关系与垂直关系的相互转化，是中档题目．求解19．（8分）（2016•和平区四模）如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AD⊥AB，DC∥AB，PA=1，AB=2，PD=BC=．（1）求证：平面PAD⊥平面PCD；（2）试在棱PB上确定一点E，使截面AEC把该几何体分成的两部分PDCEA与EACB的体积比为2：1；（3）在（2）的条件下，求二面角E﹣AC﹣P的余弦值．【分析】（1）推导出DC⊥AD，DC⊥PA，由此能证明平面PAD⊥平面PCD．（2）作EF⊥AB于F点，则EF⊥平面ABCD，设EF=h，由V PDCEA：V EACB=2：1，解得h=，从而得到E为PB的中点．（3）连结FC，FD，FD与AC交于点O，连结OE，推导出EF⊥AC，FO⊥AC，EO⊥AC，从而∠EOF 是二面角E﹣AC﹣B的平面角，由二面角E﹣ACB与二面角E﹣AC﹣P互余，能求出二面角E﹣AC﹣P 的余弦值．【解答】证明：（1）∵AD⊥AB，DC∥AB，∴DC⊥AD，∵PA⊥平面ABCD，DC⊂平面ABCD，∴DC⊥PA，∵AD∩PA=A，∴DC⊥平面PAD，∵DC⊂平面PCD，∴平面PAD⊥平面PCD．解：（2）作EF⊥AB于F点，在△ABP中，PA⊥AB，∴EF∥PA，∴EF⊥平面ABCD，设EF=h，AD==1，，则，==，由V PDCEA：V EACB=2：1，得（）：=2：1，解得h=，EF=PA，故E为PB的中点．（3）连结FC，FD，FD与AC交于点O，连结OE，由（2）知EF⊥平面ABCD，∴EF⊥AC，∵ADCF为正方形，∴FO⊥AC，∵FO∩EF=F，∴AC⊥平面EFO，∴EO⊥AC，∴∠EOF是二面角E﹣AC﹣B的平面角，∵PA⊥平面ABCD，∴平面PAC⊥平面ABCD，∴二面角E﹣ACB与二面角E﹣AC﹣P互余，设二面角E﹣AC﹣P的平面角为θ，则cosθ=sin∠EOF，在Rt△EOF中，EF=，FO=，EO=，cosθ=sin，∴二面角E﹣AC﹣P的余弦值为．【点评】本题考查面面垂直的证明，考查二面角的余弦值的求法，考查满足条件的点的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．20．（8分）（2016春•重庆校级期末）已知动点P（x，y）满足方程xy=1（x＞0）．（Ⅰ）求动点P到直线l：x+2y﹣=0距离的最小值；（Ⅱ）设定点A（a，a），若点P，A之间的最短距离为2，求满足条件的实数a的取值．【分析】（Ⅰ）由点到直线的距离公式与基本不等式的性质即可得出．（Ⅱ）设点（x＞0），则，设（t≥2），则，设f（t）=（t﹣a）2+a2﹣2（t≥2），对a与2的大小关系分类讨论即可得出．【解答】解：（Ⅰ）由点到直线的距离公式可得：，当且仅当时距离取得最小值．（Ⅱ）设点（x＞0），则，设（t≥2），则，设f（t）=（t﹣a）2+a2﹣2（t≥2）对称轴为t=a分两种情况：（1）a≤2时，f（t）在区间[2，+∞）上是单调增函数，故t=2时，f（t）取最小值∴，∴a2﹣2a﹣3=0，∴a=﹣1（a=3舍）．（2）a＞2时，∵f（t）在区间[2，a]上是单调减，在区间[a，+∞）上是单调增，∴t=a时，f（t）取最小值，∴，∴（（舍），综上所述，a=﹣1或．【点评】本题考查了函数的性质、两点之间的距离公式、点到直线的距离公式，考查了分类讨论方法、推理能力与计算能力，属于中档题．21．（10分）（2016春•重庆校级期末）已知圆C：（x﹣3）2+（y﹣4）2=4，直线l过定点A（1，0）．（1）若l与圆C相切，求l的方程；（2）若l与圆C相交于P、Q两点，若|PQ|=2，求此时直线l的方程．【分析】（1）分直线的斜率存在和不存在两种情况，分别根据直线和圆相切的性质求得直线的方程，综合可得结论．（2）用点斜式设出直线的方程，利用条件以及点到直线的距离公式，弦长公式求出斜率的值，可得直线的方程．【解答】解：（1）若直线l的斜率不存在，则直线l：x=1，符合题意．若直线l斜率存在，设直线l的方程为y=k（x﹣1），即kx﹣y﹣k=0．由题意知，圆心（3，4）到已知直线l的距离等于半径2，即：=2，解之得k=，此时直线的方程为3x﹣4y﹣3=0．综上可得，所求直线l的方程是x=1或3x﹣4y﹣3=0．（2）直线与圆相交，斜率必定存在，且不为0，设直线方程为kx﹣y﹣k=0，因为|PQ|=2=2=2，求得弦心距d=，即=2，求得k=1或k=7，所求直线l方程为x﹣y﹣1=0或7x﹣y﹣7=0．【点评】本题主要考查直线和圆相交、相切的性质，点到直线的距离公式，弦长公式的应用，属于基础题．22．（10分）（2016•成都校级模拟）在如图所示的几何体中，四边形ABCD是平行四边形，∠ABD=90°，EB⊥平面ABCD，EF∥AB，AB=2，EB=，EF=1，BC=，且M是BD的中点．．（1）求证：EM∥平面ADF；（2）求直线DF和平面ABCD所成角的正切值；（3）求二面角D﹣AF﹣B的大小．【分析】（1）取AD的中点N，连接MN、NF．由三角形中位线定理，结合已知条件，证出四边形MNFE 为平行四边形，从而得到EM∥FN，结合线面平行的判定定理，证出EM∥平面ADF；（2）取AB中点G，连接FG，DG，可得∠FDG为直线DF和平面ABCD所成角，从而可求直线DF和平面ABCD所成角的正切值；（3）求出平面ADF、平面EBAF的一个法向量，利用向量的夹角公式，可求二面角D﹣AF﹣B的大小．【解答】解：（1）取AD的中点N，连接MN，NF．在△DAB中，M是BD的中点，N是AD的中点，∴MN∥AB，MN=AB．又∵EF∥AB，EF=AB，∴MN∥EF且MN=EF，∴四边形MNFE为平行四边形，可得EM∥FN．又∵FN⊂平面ADF，EM⊄平面ADF，∴EM∥平面ADF；（2）取AB中点G，连接FG，DG，则FG∥EB，FG=∵EB⊥平面ABCD，∴FG⊥平面ABCD，∴∠FDG为直线DF和平面ABCD所成角∵BC=，AB=2，∠ABD=90°，∴BD=3∵BG=1，∴DG=∴tan∠FDG===；（3）因为EB⊥平面ABD，AB⊥BD，故以B为原点，建立空间直角坐标系B﹣xyz．由已知可得B（0，0，0），A（0，2，0），D（3，0，0），F（0，1，）∴=（3，﹣2，0），=（0，﹣1，）．设平面ADF的一个法向量是=（x，y，z）．由，得，令y=3，则=（2，3，）因为EB⊥平面ABD，所以EB⊥BD．又因为AB⊥BD，所以BD⊥平面EBAF．∴=（3，0，0）是平面EBAF的一个法向量．∴cos＜＞==∵二面角D﹣AF﹣B为锐角，∴二面角D﹣AF﹣B的大小为60°【点评】本题考查线面平行，考查线面角，考查面面角，考查向量知识的运用，考查学生分析解决问题的能力，属于中档题．23．（10分）（2016春•佛山校级期末）如图所示，在长方体ABCD﹣A 1B1C1D1中，BC=2AB=4，，E是A1D1的中点．（Ⅰ）在平面A1B1C1D1内，请作出过点E与CE垂直的直线l，并证明l⊥CE；（Ⅱ）设（Ⅰ）中所作直线l与CE确定的平面为α，求点C1到平面α的距离．【分析】（Ⅰ）连接B1E，C1E，则直线B1E即为所求直线l，推导出B1E⊥CC1，B1E⊥C1E，能证明l⊥CE．（Ⅱ）连接B1C，则平面CEB1即为平面α，过点C1作C1F⊥CE于F，则C1F⊥平面α，直线CC1和平面α所成角为∠FCC1，由此能求出点C1到平面α的距离．【解答】解：（Ⅰ）如图所示，连接B1E，C1E，则直线B1E即为所求直线l…（3分）∵在长方体ABCD﹣A1B1C1D1中，CC1⊥平面A1B1C1D1∴B1E⊥CC1…（4分）∵B1C1=2A1B1=4，E是A1D1的中点∴B1E⊥C1E…（5分）又CC1∩C1E=C1∴B1E⊥平面CC1E∴B1E⊥CE，即l⊥CE…（6分）（Ⅱ）如图所示，连接B1C，则平面CEB1即为平面α过点C1作C1F⊥CE于F…（7分）由（Ⅰ）知B1E⊥平面CC1E，故B1E⊥C1F∵C1F⊥CE，CE∩B1E=E∴C1F⊥平面CEB1，即C1F⊥平面α…（9分）∴直线CC1和平面α所成角为∠FCC1…（10分）∵在△ECC 1中，，且EC1⊥CC1∴C1F=2…（11分）∴点C1到平面α的距离为2…（12分）【点评】本题考查线面垂直的作法与证明，考查点到平面的距离的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．。

河北定州中学2016-2017学年第一学期高四数学周练试题（五）一、单项选择题1．函数2()log f x x =在区间[1,2]上的最小值是( )A ．1-B ．0C ．1D ．2 2．设全集U ＝{1，2，3，4}，集合S ＝{1，3}，T ＝{4}，则等于( )A 、{2，4}B 、{4}C 、ΦD 、{1，3，4} 3．已知0.6log 0.5a =，ln 0.5b =，0.50.6c =．则（ ）（A ）>>a b c （B ）>>a c b （C ）>>c a b （D ）>>c b a4．已知全集R U =，{}{}1,0)3(-<=<+=x x M x x x N ，则图中阴影部分表示的集合是（ ）A ．{}13-<<-x x Ｂ．{}03<<-x x Ｃ．{}01<≤-x x Ｄ．{}3-<x5．已知函数()f x 是定义在区间[-2，2]上的偶函数，当[0,2]x ∈时，()f x 是减函数，如果不等式(1)()f m f m -<成立，则实数m 的取值范围（ ）A.1[1,)2- B. 1，2 C. (,0)-∞ D.(,1)-∞ 6．计算662log 3log 4+的结果是( )A 、6log 2B 、2C 、6log 3D 、37．已知函数()⎩⎨⎧≤>=030log 2x x x x f x ，，，则⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛41f f 的值是（ ） A ．91-B ．9-C ．91D ．98．定义在R 上的函数()f x 对任意两个不相等实数,a b ，总有()()0f a f b a b->-成立， 则必有（ ）A.()f x 在R 上是增函数B.()f x 在R 上是减函数C.函数()f x 是先增加后减少D.函数()f x 是先减少后增加9．已知ab ＝0.32，0.20.3c =，则a ，b ，c 三者的大小关系是( ) A ．b>c>a B ．b>a>c C ．a>b>c D ．c>b>a 10．满足条件M ∪{1}={1，2，3}的集合M 的个数是（ ） A ．1 B ．2 C ．3 D ．411．等差数列99637419,27,39,}{S a a a a a a a n 项和则前已知中=++=++的值为（ ） A ．66 B ．99 C ．144 D ．297 12．已知2log 3a =，A.c b a >> B ．c a b >> C.a b c >> D.a c b >>二、填空题13．设)(x f 是周期为2的偶函数，当10≤≤x 时, )1(2)(x x x f -=,则=-)25(f 14．已知(0,)2πα∈，4cos 5α=，则sin()πα-=_____________.15．已知函数()y f x =(x R ∈)的图象如图所示，则不等式'()0xf x <的解集为________.16．已知函数1221,1,()log , 1.x x f x x x ⎧-<⎪=⎨⎪⎩≥若关于x 的方程()f x k =有三个不同的实根，则实数k 的取三、解答题17．已知定义在R 上的奇函数)(x f ，当0>x 时，x x x f 2)(2+-=（1）求函数)(x f 在R 上的解析式；（2）若函数)(x f 在区间[]2,1--a 上单调递增，求实数a 的取值范围。

2016-2017学年河北省保定市定州中学高补班高三上学期数学期末试卷一、选择题1．（3分）在一个不透明的袋子里，有三个大小相等小球（两黄一红），现在分别由3个同学无放回地抽取，如果已知第一名同学没有抽到红球，那么最后一名同学抽到红球的概率为（）A．B．C．D．无法确定2．（3分），，则的值为（）A．B．C．D．3．（3分）某服装加工厂某月生产A、B、C三种产品共4000件，为了保证产品质量，进行抽样检验，根据分层抽样的结果，企业统计员制作了如下的统计表格：产品类别A B C由于不小心，表格中A、C产品的有关数据已被污染看不清楚，统计员记得A产品的样本容量比C产品的样本容量多10，根据以上信息，可得C的产品数量是（）A．80B．800C．90D．9004．（3分）α是第四象限角，cosα=，则sinα=（）A．B．C．D．5．（3分）已知变量x，y满足约束条件，则目标函数z=2x+y的最小值是（）A．4B．3C．2D．16．（3分）设集合A={x|x2﹣x﹣2＞0}，B={x||x|＜3}，则A∩B=（）A．{x|﹣3＜x＜﹣1}B．{x|2＜x＜3}C．{x|﹣3＜x＜﹣1或2＜x＜3}D．{x|﹣3＜x＜﹣2或1＜x＜3} 7．（3分）若a、b是任意实数，且a＞b，则下列不等式成立的是（）A．a2＞b2B．C．lg（a﹣b）＞0D．8．（3分）如图为某几何体的三视图，则该几何体的外接球的表面积为（）A．B．27πC．27πD．9．（3分）已知A是△ABC的内角，则“sinA=”是“tanA=”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件．10．（3分）“2a＞2b”是“log2a＞log2b”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件11．（3分）下列各式中，值为的是（）A．sin15°cos15°B．C．D．12．（3分）函数f（x）=（x﹣3）e x的单调递减区间是（）A．（﹣∞，2）B．（0，3）C．（1，4）D．（2，+∞）二、填空题13．（3分）在△ABC中，角A，B，C所对的边分别为a，b，c，A=60°，b=2，S =2，则a=．△ABC14．（3分）已知tanα，tanβ分别是lg（6x2﹣5x+2）=0的两个实根，则tan（α+β）=．15．（3分）函数f（x）=a x﹣2015+2015（a＞0且a≠1）过定点A，则点A的坐标为．16．（3分）已知向量=（x，2），=（2，1），=（3，x），若∥，则向量在向量方向上的投影为．三、解答题17．（10分）已知集合A={1，3，x2}，B={x+2，1}．是否存在实数x，使得B⊆A？若存在，求出集合A，B；若不存在，说明理由．18．如图，已知AB为⊙O的直径，C，F为⊙O上的两点，OC⊥AB，过点F作⊙O的切线FD交AB的延长线于点D，连接CF交AB于点E．求证：DE2=DA•DB．19．已知函数（1）求函数f（x）的最小正周期；（2）求函数f（x）的最大值及取得最大值时x的取值集合；（3）求函数f（x）的单调递增区间．20．四棱锥S﹣ABCD中，底面ABCD为平行四边形，侧面SBC⊥面ABCD，已知∠ABC=45°，AB=2，BC=2，SB=SC=．（1）设平面SCD与平面SAB的交线为l，求证：l∥AB；（2）求证：SA⊥BC；（3）求直线SD与面SAB所成角的正弦值．21．设集合A={x|x2﹣3x+2=0}，B={x|x2+2（a+1）x+（a2﹣5）=0}．（1）若A∩B={2}，求实数a的值；（2）若A∪B=A，求实数a的取值范围．22．已知函数f（x）=﹣x3+ax﹣，g（x）=e x﹣e（其中e为自然对数的底数）（I）若曲线y=f（x）在（0，f（0））处的切线与曲线y=g（x）在（0，g（0））处的切线互相垂直，求实数a的值．（Ⅱ）设函数h（x）=，讨论函数h（x）零点的个数．23．已知函数f（x）=ln（x+1）﹣，a是常数，且a≥1．（Ⅰ）讨论f（x）零点的个数；（Ⅱ）证明：＜ln（1+）＜，n∈N+．24．已知函数f（x）=ln（1+x2）+ax．（a≤0）（1）若f（x）在x=0处取得极值，求a的值；（2）讨论f（x）的单调性；（3）证明：（1+）（1+）…（1+）＜（n∈N*，e为自然对数的底数）．2016-2017学年河北省保定市定州中学高补班高三上学期数学期末试卷参考答案与试题解析一、选择题1．（3分）在一个不透明的袋子里，有三个大小相等小球（两黄一红），现在分别由3个同学无放回地抽取，如果已知第一名同学没有抽到红球，那么最后一名同学抽到红球的概率为（）A．B．C．D．无法确定【解答】解：由题意，由于第一名同学没有抽到红球，问题转化为研究两个人抽取红球的情况，由于无放回的抽样是一个等可能抽样，故此两个同学抽到红球的概率是一样的都是．故选：C．2．（3分），，则的值为（）A．B．C．D．【解答】解：∵，，∴sinαcosα=，∵sin2α+cos2α=1∴（sinα+cosα）2=1+2sinαcosα=，=（cosα+sinα）=cosα+sinα=．故选：D．3．（3分）某服装加工厂某月生产A、B、C三种产品共4000件，为了保证产品质量，进行抽样检验，根据分层抽样的结果，企业统计员制作了如下的统计表格：由于不小心，表格中A、C产品的有关数据已被污染看不清楚，统计员记得A产品的样本容量比C产品的样本容量多10，根据以上信息，可得C的产品数量是（）A．80B．800C．90D．900【解答】解：∵分层抽样是按比抽取，由B产品知比为=，共抽取样本容量是4000×=400，A产品容量比C产品的样本容量多10，400﹣230﹣2x﹣10=0∴得C产品的样本容量为80，∴C产品共有80=800，故选：B．4．（3分）α是第四象限角，cosα=，则sinα=（）A．B．C．D．【解答】解：∵α是第四象限角，∴sinα=，故选：B．5．（3分）已知变量x，y满足约束条件，则目标函数z=2x+y的最小值是（）A．4B．3C．2D．1【解答】解：作出不等式组对应的平面区域如图：由z=2x+y得y=﹣2x+z，平移直线y=﹣2x+z，由图象可知当直线y=﹣2x+z经过点A（0，1）时，直线的截距最小，此时z最小，此时z=0×2+1=1，故选：D．6．（3分）设集合A={x|x2﹣x﹣2＞0}，B={x||x|＜3}，则A∩B=（）A．{x|﹣3＜x＜﹣1}B．{x|2＜x＜3}C．{x|﹣3＜x＜﹣1或2＜x＜3}D．{x|﹣3＜x＜﹣2或1＜x＜3}【解答】解：集合A={x|x2﹣x﹣2＞0}={x|x＜﹣1或x＞2}，B={x||x|＜3}={x|﹣3＜x＜3}，则A∩B={x|﹣3＜x＜﹣1或2＜x＜3}．故选：C．7．（3分）若a、b是任意实数，且a＞b，则下列不等式成立的是（）A．a2＞b2B．C．lg（a﹣b）＞0D．【解答】解：由题意a、b是任意实数，且a＞b，由于0＞a＞b时，有a2＜b2成立，故A不对；由于当a=0时，无意义，故B不对；由于0＜a﹣b＜1是存在的，故lg（a﹣b）＞0不一定成立，所以C不对；由于函数y=是一个减函数，当a＞b时一定有成立，故D正确．综上，D选项是正确选项故选：D．8．（3分）如图为某几何体的三视图，则该几何体的外接球的表面积为（）A．B．27πC．27πD．【解答】解：由已知中的三视图，可得该几何体是以俯视图为底面的四棱锥，其底面是边长为3的正方形，且高为3，其外接球等同于棱长为3的正方体的外接球，所以外接球半径R满足：2R==，所以外接球的表面积为S=4πR2=27π．故选：B．9．（3分）已知A是△ABC的内角，则“sinA=”是“tanA=”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件．【解答】解：在三角形中，若sinA=，则A=或，若tanA=，则A=，则“sinA=”是“tanA=”的必要不充分条件，故选：B．10．（3分）“2a＞2b”是“log2a＞log2b”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【解答】解：2a＞2b⇒a＞b，当a＜0或b＜0时，不能得到log2a＞log2b，反之由log2a＞log2b即：a＞b＞0可得2a＞2b成立．故选：B．11．（3分）下列各式中，值为的是（）A．sin15°cos15°B．C．D．【解答】解：由于sin15°cos15°=sin30°=，故排除A．由于﹣=cos=，故排除B．由于=tan60°=，满足条件．由于=cos15°=cos（45°﹣30°）=cos45°cos30°+sin45°sin30°=，故排除D，故选：C．12．（3分）函数f（x）=（x﹣3）e x的单调递减区间是（）A．（﹣∞，2）B．（03）．（1，4）D．（2，+∞）【解答】解：∵数f（x）=（x﹣3）e x∴f′（x）=（x﹣2）e x，根据单调性与不等式的关系可得：（x﹣2）e x＜0，即x＜2所以函数f（x）=（x﹣3）e x的单调递减区间是（﹣∞，2）故选：A．二、填空题13．（3分）在△ABC中，角A，B，C所对的边分别为a，b，c，A=60°，b=2，S=2，则a=2．△ABC=2，【解答】解：在△ABC中，∵A=60°，b=2，S△ABC∴2=bcsinA=，解得c=4．∴由余弦定理可得：a2=b2+c2﹣2bccosA=4+16﹣2×=12，∴解得：a=2故答案为：2．14．（3分）已知tanα，tanβ分别是lg（6x2﹣5x+2）=0的两个实根，则tan（α+β）=1．【解答】解：由题意lg（6x2﹣5x+2）=0，可得6x2﹣5x+1=0，tanα，tanβ分别是lg（6x2﹣5x+2）=0的两个实根，∴tanα+tanβ=，tanα•tanβ=，∴tan（α+β）===1．故答案为：1．15．（3分）函数f（x）=a x﹣2015+2015（a＞0且a≠1）过定点A，则点A的坐标为（2015，2016）．【解答】解：当x=2015时，f（2015）=a2015﹣2015+2015=a0+2015=2016，∴f（x）=a x﹣2015+2015（a＞0且a≠1）过定点A（2015，2016）．故答案为：（2015，2016）．16．（3分）已知向量=（x，2），=（2，1），=（3，x），若∥，则向量在向量方向上的投影为4．【解答】解：∵=（x，2），=（2，1），∥，∴x=2×2=4，∴=（3，4），∴||=5，=（4，2）•（3，4）=12+8=20，∴向量在向量方向上的投影为==4，故答案为：4．三、解答题17．（10分）已知集合A={1，3，x2}，B={x+2，1}．是否存在实数x，使得B⊆A？若存在，求出集合A，B；若不存在，说明理由．【解答】解：假设存在实数x，使B⊆A，则x+2=3或x+2=x2．（1）当x+2=3时，x=1，此时A={1，3，1}，不满足集合元素的互异性．故x≠1．（2）当x+2=x2时，即x2﹣x﹣2=0，故x=﹣1或x=2．①当x=﹣1时，A={1，3，1}，与元素互异性矛盾，故x≠﹣1．②当x=2时，A={1，3，4}，B={4，1}，显然有B⊆A．综上所述，存在x=2，使A={1，3，4}，B={4，1}满足B⊆A．18．如图，已知AB为⊙O的直径，C，F为⊙O上的两点，OC⊥AB，过点F作⊙O的切线FD交AB的延长线于点D，连接CF交AB于点E．求证：DE2=DA•DB．【解答】证明：连接OF．因为DF切⊙O于F，所以∠OFD=90°．所以∠OFC+∠CFD=90°．因为OC=OF，所以∠OCF=∠OFC．因为CO⊥AB于O，所以∠OCF+∠CEO=90°．（5分）所以∠CFD=∠CEO=∠DEF，所以DF=DE．因为DF是⊙O的切线，所以DF2=DB•DA．所以DE2=DB•DA．（10分）19．已知函数（1）求函数f（x）的最小正周期；（2）求函数f（x）的最大值及取得最大值时x的取值集合；（3）求函数f（x）的单调递增区间．【解答】解：（1）∵∴f（x）===．∵，即函数f（x）的最小正周期为π．（2）当（5分）即时，f（x）取最大值2（7分）因此f（x）取最大值时x的集合是（8分）（3）f（x）=．再由，解得．所以y=f（x）的单调增区间为．（12分）20．四棱锥S﹣ABCD中，底面ABCD为平行四边形，侧面SBC⊥面ABCD，已知∠ABC=45°，AB=2，BC=2，SB=SC=．（1）设平面SCD与平面SAB的交线为l，求证：l∥AB；（2）求证：SA⊥BC；（3）求直线SD与面SAB所成角的正弦值．【解答】证明：（1）∵底面ABCD为平行四边形，∴AB∥CD，∵AB⊊平面SCD，CD⊂平面SCD，∴AB∥平面SCD，又AB⊂平面SAB，平面SCD∩平面SAB=l，∴l∥AB．（2）取BC中点O，连接OS，OA．∵OB=BC=，AB=2，∠ABC=45°，∴OA==．∴OA2+OB2=AB2，∴OA⊥BC．∵SB=SC，O是BC的中点，∴OS⊥BC，又SO⊂平面SOA，OA⊂平面SOA，SO∩OA=O，∴BC⊥平面SOA，∵SA⊂平面SOA，∴BC⊥SA．（3）∵SB=SC，O是BC中点，∴SO⊥BC．∵侧面SBC⊥面ABCD，侧面SBC∩面ABCD=BC，∴SO⊥平面ABCD．以O为原点，以OA，OB，OS为坐标轴建立空间直角坐标系O﹣xyz，如图所示，则A（，0，0），B（0，，0），S（0，0，1），D（，﹣2，0），∴=（，﹣2，﹣1），=（，0，﹣1），=（，﹣，0）．设平面SAB法向量为=（x，y，z），则，∴．令x=1，则y=1，z=，∴=（1，1，）．∴cos＜，＞===．∴直线SD与面SAB所成角的正弦值为．21．设集合A={x|x2﹣3x+2=0}，B={x|x2+2（a+1）x+（a2﹣5）=0}．（1）若A∩B={2}，求实数a的值；（2）若A∪B=A，求实数a的取值范围．【解答】解：由x2﹣3x+2=0得x=1或x=2，故集合A={1，2}（1）∵A∩B={2}，∴2∈B，代入B中的方程，得a2+4a+3=0⇒a=﹣1或a=﹣3；当a=﹣1时，B={x|x2﹣4=0}={﹣2，2}，满足条件；当a=﹣3时，B={x|x2﹣4x+4=0}={2}，满足条件；综上，a的值为﹣1或﹣3；（2）对于集合B，△=4（a+1）2﹣4（a2﹣5）=8（a+3）．∵A∪B=A，∴B⊆A，①当△＜0，即a＜﹣3时，B=∅满足条件；②当△=0，即a=﹣3时，B={2}，满足条件；③当△＞0，即a＞﹣3时，B=A={1，2}才能满足条件，则由根与系数的关系得⇒矛盾；综上，a的取值范围是a≤﹣3．22．已知函数f（x）=﹣x3+ax﹣，g（x）=e x﹣e（其中e为自然对数的底数）（I）若曲线y=f（x）在（0，f（0））处的切线与曲线y=g（x）在（0，g（0））处的切线互相垂直，求实数a的值．（Ⅱ）设函数h（x）=，讨论函数h（x）零点的个数．【解答】解：（Ⅰ）由已知得f′（x）=﹣3x2+a，g′（x）=e x，则f′（0）=a，g′（0）=1，则a=﹣1；（Ⅱ）函数g（x）=e x﹣e在实数集上为单调增函数，且仅在x=1处有一个零点，且x＜1时，g（x）＜0，又f′（x）=﹣3x2+a，①当a≤0时，f′（x）≤0，f（x）在实数集上单调递减，且过点（0，﹣），f（﹣1）=，即f（x）在x≤0时必有一个零点，此时y=h（x）有两个零点；②当a＞0时，令f′（x）=0，得两根，，则是函数f（x）的一个极小值点，是f（x）的一个极大值点．而f（﹣）=﹣，现在讨论极大值的情况：当＜0，即a＜时，函数f（x）在（0，+∞）恒小于0，此时y=h（x）有两个零点；当=0，即a=时，函数f（x）在（0，+∞）上有一解，此时y=h（x）有三个零点；当＞0，即a＞时，函数f（x）在（0，+∞）上有两个解，一个小于，一个大于．若f（1）=﹣1+a﹣＜0，即a＜时，＜1，此时y=h（x）有四个零点；若f（1）=﹣1+a ﹣=0，即a=时，=1，此时y=h（x）有三个零点；若f（1）=﹣1+a ﹣＞0，即a ＞时，＞1，此时y=h（x）有两个零点．综上所述，①或a时，y=h（x）有两个零点；②a=或a=时，y=h（x）有三个零点；③时，y=h（x）有四个零点．23．已知函数f（x）=ln（x+1）﹣，a是常数，且a≥1．（Ⅰ）讨论f（x）零点的个数；（Ⅱ）证明：＜ln（1+）＜，n∈N+．【解答】证明：（Ⅰ），解f′（x）=0得x=0，或x=a2﹣2a①a=1时，，若x∈（﹣1，0），f′（x）＜0，f（x）＞f（0）=0，若x∈（0，+∞），f′（x）＞0，f（x）＞f（0）=0．f（x）有一个零点，②1＜a＜2时，﹣1＜a2﹣2a0，由上表可知，f（x）在区间（a2﹣2a，+∞）有一个零点x=0，f（a2﹣2a）＞f（0）=0，又，任取，，f（x）在区间（t，a2﹣2a）有一个零点，从而f（x）有两个零点，③a=2时，，f（x）在（﹣1，+∞）上单调递增，有一个零点x=0，④a＞2时，a2﹣2a＞0，由上表可知，f（x）在区间（﹣1，a2﹣2a）有一个零点x=0，在区间（a2﹣2a ，+∞）有一个零点，从而f（x ）有两个零点，（Ⅱ）证明：取a=2，由（1）知在（﹣1，+∞）上单调递增，取（n∈N*），则，化简得，取，由（1）知在区间上单调递减，取（n ∈N*），由f（x）＞f（0）得，即（n∈N*），综上，，n∈N*24．已知函数f（x）=ln（1+x2）+ax．（a≤0）（1）若f（x）在x=0处取得极值，求a的值；（2）讨论f（x）的单调性；（3）证明：（1+）（1+）…（1+）＜（n∈N*，e为自然对数的底数）．【解答】解：（1）∵，∵x=0使f（x）的一个极值点，则f'（0）=0，∴a=0，验证知a=0符合条件．（2）∵①若a=0时，∴f（x）在（0，+∞）单调递增，在（﹣∞，0）单调递减；②若得，当a≤﹣1时，f'（x）≤0对x∈R恒成立，∴f（x）在R上单调递减．③若﹣1＜a＜0时，由f'（x）＞0得ax2+2x+a＞0∴再令f'（x）＜0，可得∴上单调递增，在综上所述，若a≤﹣1时，f（x）在（﹣∞，+∞）上单调递减；若﹣1＜a＜0时，上单调递增上单调递减；若a=0时，f（x）在（0，+∞）单调递增，在（﹣∞，0）单调递减．（3）由（2）知，当a=﹣1时，f（x）在（﹣∞，+∞）单调递减当x∈（0，+∞）时，由f（x）＜f（0）=0∴ln（1+x2）＜x，∴ln[（1+）（1+）…（1+）]=ln（1+）+ln（1+）+…+ln（1+）＜++…+==（1﹣）＜，∴（1+）（1+）…（1+）＜=。

河北定州中学2016-2017学年第一学期高四数学周练试题（六）一、单项选择题1．设命题甲：三角形ABC 有一个内角是060,命题乙：三角形ABC三个内角的度数成等差数列，那么（ ） A ．甲是乙的充分条件,但不是必要条件 B ．甲是乙的必要条件，但不是充分条件 C ．甲是乙的充要条件D ．甲既不是乙的充分条件，也不是必要条件 2．已知角α的终边过点(2,1)-，则cos α的值为（ ） A ．55 B ．552 C ．55-D ．552-3．已知全集R U =，集合},12|{},0|{2Z n n x x N x x x M ∈+===-=,则N M 为（ ）A ．{}0B ．}1{C ．｛0，1}D ．φ4．（2015秋•福州校级期末）已知函数f （x ）=x 2+（2a ﹣1）x+b 是偶函数，那么函数的定义域为( ）A ．B ．C ．（0，2]D ．[2，+∞）5．若直线y x b =+与曲线234y x x =-有公共点，则b 的取值范围是（ )A. [122-122+B.[123］C. [122-3］D.［—1，122+6．设数列{}na 的前n 项和为nS ，且121aa ==,(){}2n n nS n a ++为等差数列,则n a =（ ） A ．12n n- B ．1121n n -++ C ．2121n n --D ．112n n ++7．函数2()23f x x ax =--在区间［1，2］上单调，则(）A ．(],1a ∈-∞B ．[)2,a ∈+∞C ．[]1,2a ∈D ．(][),12,a ∈-∞+∞8．设等差数列{}na 的公差为d ，若数列1{2}na a 为递减数列，则（）A ．0d <B ．0d >C ．10a d < D ．10a d > 9．已知12)(-=xx f ，21)(x x g -=,规定：当)(|)(|x g x f ≥时， |)(|)(x f x h =；当)(|)(|x g x f <时,)()(x g x h -=，则)(x h （ ）A ．有最小值1-,最大值1B ．有最大值1,无最小值C ．有最小值1-,无最大值D ．有最大值1-，无最小值10．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且a ＝1,B ＝45°，S △ABC ＝2，则b 等于( ) A ．5 B ．25 C.D ．11．函数)(x f y =的最小正周期为2，且)()(x f x f =-．当]1,0[∈x 时1)(+-=x x f ,那么在区间[]3,4-上，函数1()()()2xG x f x =-的零点个数( ） A ． 5 B ． 6 C ． 7 D ．812．已知双曲线22221,(0,0)x y a b a b-=>>的左，右焦点分别为12,F F ,点P 在双曲线的右支上，且12||4||PF PF =，则此双曲线的离心率e 的最大值为（ )A ．B ．43C ．23D ．53二、填空题13．已知2,,8x 是一个正项等比数列中连续的三项,则x ； 14．由胡克定律知,弹簧伸长所需力的大小与弹簧伸长的长度成正比．现已知10(N)的力能使弹簧伸长0.01(m),则拉力将弹簧拉长0.2(m)所做的功为 焦耳．15．（a+b ）n 展开式中第r 项为16．向面积为S 的△ABC 内任投一点P ，则随机事件“△PBC 的面积小于3S ”的概率为 ．三、计算题 17．（本小题满分10分）2010年3月国家要求一些企业必须停业处理排污问题，于是各企业考虑引进污水处理设备,现有甲、乙两套设备可以引进.每个企业可引进一套，引进两套或都不引进自行研发。

第I 卷（选择题)请点击修改第I 卷的文字说明评卷人得分一、选择题1．已知A 是ABC ∆内角,命题p ：21sin =A ;命题q ：23cos =A ，则q 是p 的( ）A 。

充分不必要条件B 。

必要不充分条件 C.充要条件 D 。

既不充分也不必要条件 【答案】A 【解析】试题分析:A 为ABC ∆的内角,则()π,0∈A ，若命题p ：21sin =A 成立，说明6π=A 或65π；而命题q :23cos =A 成立，说明6π=A ；因此由q 可以推得p 成立,由p不可以推得q 成立，可见p 是q 的充分非必要条件．故选A ． 考点:充分条件、必要条件的判定。

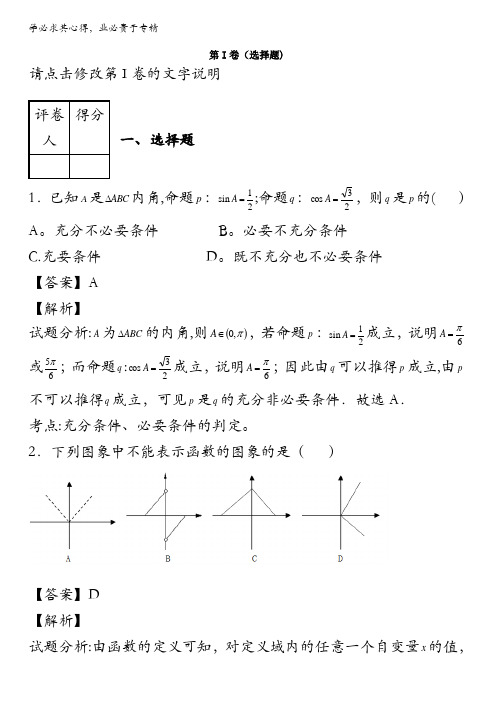
2．下列图象中不能表示函数的图象的是（ ）【答案】D 【解析】试题分析:由函数的定义可知，对定义域内的任意一个自变量x 的值，都有唯一的函数值y 与其对应，故函数的图象与直线a x =至多有一个交点，D 中，当0>a 时，a x =与函数的图象有两个交点，不满足函数的“唯一性",D 不是函数的图象;故选D 。

考点：函数的概念及其构成要素。

3．在ABC ∆中,060A =,a =b = )A ．045B =或0135 B ．0135B =C ．045B = D ．以上答案都不对【答案】C 【解析】试题分析：由正弦定理得B bA a sin sin =，得22342324sin sin =⋅==aA bB ，结合ba >得045B =，故选C ．考点：正弦定理. 4．4()log (1)f x x =+的定义域是（ ）A ．()(]4,11,0B ．[1,1)(1,4]-C ．(1,4)-D ．(1,1)(1,4]-【答案】D 【解析】试题分析：要使函数有意义须满足：⎪⎩⎪⎨⎧>+≠-≥-010104x x x ，解得()(]4,11,1 -∈x ，故选D 。

考点：函数的定义域。

5．函数()()21212-<+=x xx f 的反函数是（ ）A。

河北定州中学2016-2017学年第一学期高四开学考试数学试题一、选择题（共12小题，共60分）1．已知定义在实数集R 的函数()f x 满足()14f =，且()f x 导函数()3f x '<，则不等式()ln 3ln 1f x x >+的解集为（ ）A ．()1,+∞B ．(),e +∞C ．()0,1D ．()0,e2．已知函数()f x 是定义在R 上的奇函数，若22log (1),[0,1)()173,[1,)22x x f x x x x +∈⎧⎪=⎨-+∈+∞⎪⎩，则关于x 的方程()0(01)f x a a +=<<的所有跟之和为（ ）A ．11()2a -B ．1()12a - C ．12a - D ．21a- 3．已知数列{}n a 满足(1)21(1)n n n n a a n +-+=-，n S 是其前n 项和，若20171007S b =--，且10a b >，则112a b+的最小值为（ ） A．3- B ．3 C．．3+4．已知函数|lg |,010()16,102x x f x x x <≤⎧⎪=⎨-+>⎪⎩，若,,a b c 互不相等，且()()()f a f b f c ==，则abc 的取值范围是（ ）A ．(1,10)B ．(5,6)C ．(10,12)D ．(20,24)5．已知()f x 是定义在R 上的增函数，函数(1)y f x =-的图象关于点(1,0)对称，若对任意的,x y R ∈，等式(3)0f y f -+=恒成立，则yx的取值范围是（ ） A．[2 B．[1,2+C．[2D ．[1,3]6．已知双曲线C 1：22221(0,0)x y a b a b-=>>，一条渐近线为l ，抛物线C 2： y 2＝4x 的焦点为F ，点P 为直线l 与抛物线C 2异于原点的交点，则|PF|＝（ ） A ．2 B ．3 C ．4 D ．57．若函数),,,()(2R d c b a cbx ax dx f ∈++=的图象如图所示，则=d c b a :::（ ）A ．1:6:5：（-8）B ．1:6:5:8C ．1：（-6）：5:8D ．1：（-6）：5：（-8） 8．已知集合{}∅=-==B A x y x A ,1，则集合B 不可能是（ ）A ．{}124+<x x x B ．{}1),(-=x y y xC ．{}1-=x yD ．{})12(log 22++-=x x y y 9．设n S 是数列{}n a ()n N+∈的前n 项和，2n ≥时点1(,2)n n a a -在直线21y x =+上，且{}n a 的首项1a 是二次函数223y x x =-+的最小值，则9S 的值为（ ） A ．6 B ．7 C ．36 D ．3210）．2C ．211．已知函数()22,52,x x a f x x x x a+>⎧=⎨++≤⎩，函数()()2g x f x x =-恰有三个不同的零点，则2az =的取值范围是（ ）A ．1,22⎡⎫⎪⎢⎣⎭B ．[]1,4C ．1,44⎡⎫⎪⎢⎣⎭D ．1,42⎡⎫⎪⎢⎣⎭12．已知函数)(x f y =是定义域为R 的偶函数，当0≥x 时，⎪⎩⎪⎨⎧>+≤≤=).1(1)41(),10)(2sin(45)(x x x x f xπ若关于x 的方程)(06)()65()]([52R a a x f a x f ∈=++-有且仅有6个不同实数根，则实数a 的取值范围是（ ）A ．10<<a 或45=a B ．10≤≤a 或45=a C ．10≤<a 或45=a D ．451≤<a 或0=a第II 卷（非选择题）二、填空题（4小题，共20分） 13．已知{}2,M y y x x R==∈，{}222,,N x xy x y R=+=∈，则MN =_____.14．已知函数⎪⎩⎪⎨⎧<-+≥=1),)(2(1,1,ln )(x a x x e x x x f （a 为常数，e 为自然对数的底数）的图象在点A （e,1）处的切线与该函数的图象恰好有三个公共点，则实数a 的取值范围是_____.15．设O 为坐标原点，抛物线C ：x y 42=的准线为l ，焦点为F ，过F 且斜率为3的直线与抛物线C 交于B A ,两点，且||||BF AF >，若直线AO 与l 相交与D ，则=||||BD OF . 16．已知双曲线22221x y a b -=的两条渐近线与抛物线24y x =分别相交于异于原点O 的两点A ，B ，F 为抛物线24y x =的焦点，已知2F 3π∠A B =，则该双曲线的离心率为 ．三、解答题（8小题，共70分）17．已知点(,)x y 是区域2200x y n x y +≤⎧⎪≥⎨⎪≥⎩，*()n N ∈，内的点，目标函数z x y =+，z 的最大值记作nz ，若数列{}n a 的前n 项和为nS ，11a =，且点(,)n n S a 在直线n z x y=+上.（1）证明：数列{2}n a -为等比数列；（2）求数列{}n S 的前n 项和为nT .18．如图，圆C 与x 轴相切于点(2,0)T ，与y 轴正半轴相交于,M N 两点（点M 在点N 的下方），且3MN =.（1）求圆C 的方程；（2）过点M 任作一条直线与椭圆22184x y +=相交于两点,A B ，连接,A N B N ，求证：ANM BNM ∠=∠.19．已知曲线C 的极坐标方程为2cos 4sin ρθθ=-．以极点为原点，极轴为x 轴的正半轴，建立平面直角坐标系，直线l 的参数方程为1cos 1sin x t y t αα=+⎧⎨=-+⎩（t 为参数）．（1）判断直线l 与曲线C 的位置关系，并说明理由； （2）若直线l 和曲线C 相交于,A B两点，且AB =l 的斜率．20．已知函数()()32f x ax x a R =+∈在43x =-处取得最值．（1）确定a 的值； （2）若()()xg x f x e =，讨论()g x 的单调性．21．如图所示，正方形ABCD 所在的平面与三角形CDE 所在的平面交于CD ，且AE ⊥平面CDE.（1）求证：平面ABCD ⊥平面ADE ；（2）已知AB=2AE=2，求三棱锥C-BDE 的高h. 22．已知(),f x x R∈是有界函数，即存在0M >使得()f x M≤恒成立．（1）()()()1F x f x f x =+-是有界函数，则(),f x x R∈是否是有界函数？说明理由；（2）判断()()1224,92323x xx f x f x x x ==-⋅-+是否是有界函数？（3）有界函数(),f x x R ∈满足()()117,,4312f x f x f x f x f x x R⎛⎫⎛⎫⎛⎫+++=++∈ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭是否是周期函数，请说明理由．23．已知函数()()4,3af x xg x kx x =+-=+.（1）当 []3,4a ∈时，函数()f x 在区间[],m 1上的最大值为()f m ，试求实数 m 的取值范围；（2）当[]1,2a ∈时，若不等式()()()()1212f x f x g x g x -<-对任意[]()1212,2,4x x x x ∈<）恒成立，求实数 k 的取值范围．24．设函数2()ln f x ax x =+． （1）若函数()y f x =的图象在点(1,(1))f 处的切线斜率是1-，求a ；（2）已知0a <，若1()2f x ≤-恒成立，求a 的取值范围．参考答案 1．D 【解析】试题分析：设13)()(--=x x f x F ,则03)()(//<-=x f x F ,所以13)()(--=x x f x F 是R 上的单调递减函数,又013)1()1(=--=f F ,因此()ln 3ln 1f x x >+可化为0)(ln >x F ,即)1()(ln F x F >,故由单调性可知1ln <x ,即e x <<0，故应选D.考点：导数和函数性质的综合运用．【易错点晴】导数解决函数问题的重要工具,解答本题时通过借助题设提供的有效信息,巧妙地构造函数13)()(--=x x f x F ,然后运用导数这一重要工具对这个函数求导,凭借题设条件得知函数13)()(--=x x f x F 是R 上的单调递减函数,为下面不等式的求解创造了条件.求解不等式()ln 3ln 1f x x >+时,以x ln 为变量建立不等式,最终通过单调性的定义得到了不等式1ln <x ,使得本题巧妙获解.2．C 【解析】试题分析：因⎪⎩⎪⎨⎧---+--=27321)1(log )(22x x x x f ),1[,]0,1(,+∞∈-∈x x ,故当10<≤x ，0)(=+a x f 的解集为空集,当1>x ,时, 函数273212+-=x x y 的最小值为1-,则方程0)(=+a x f 的解集为},{43x x 且643=+x x .当0<x 且]0,1(-∈x 时,由0)1(log 2=+--a x 可得ax 21-=；当1-<x 时,函数273212---=x x y 的对称轴为3-=x ,因此方程0)(=+a x f 的解集为},{21x x 且621-=+x x ,故该方程的这四个根4321,,,x x x x 的和为4321=+++x x x x ,所以所有根的和为12a-,应选C.考点：分段函数的图象和性质． 【易错点晴】本题考查的是函数的零点问题和函数的性质的综合运用问题.解答本题的关键是搞清楚函数)(x f 的解析式,进而再求其零点,最后求出其和.求解时充分借助函数的奇偶性,先求出当0<x 时的函数解析式为⎪⎩⎪⎨⎧---+--=27321)1(log )(22x x x x f ),1[,]0,1(,+∞∈-∈x x ,在此基础上画出函数的图象,借助函数的图象求出满足题设条件的所有根,并求出其和为12a-.3．B【解析】 试题分析：因2018,2016,,6,4,22018201720162015654321-=+=+⋅⋅⋅-=+=+-=+a a a a a a a a a a ,故2,201620182016-==S S ，则bb S S a --=---=-=302320161007201620172017，进而可得981=b a ,所以由基本不等式可得112a b +38922=⨯≥,应选B.考点：数列的知识和基本不等式的综合运用．4．C 【解析】试题分析：画出函数图象如下图所示，由图可知()1,1,10,12a ab abc c b ===∈，故选C.考点：函数图象与性质.【思路点晴】本题是2010年全国卷第11题.主要的解题思路就是数形结合.有关函数的问题，往往可以先画出函数的图象，然后利用图象与性质来解决.本题分段函数中第一段是对数函数外面加绝对值，我们先画出绝对值里面的函数，然后把x 轴下方的图象向上翻折，就可以得到lg x的图象；第二段是一次函数，图象为直线.5．C 【解析】试题分析：由于“函数(1)y f x =-的图象关于点(1,0)对称”，故()f x 图象关于原点对称，为奇函数，不妨设()f x x=.根据(33)f y x -+-=，得30,3y y -==，作图象如下图所示，故yx 最大值为3.当1,yx y x ==时，过()2,2，由图象可知还不是最小值，不合题意，故选C.考点：1.函数奇偶性与单调性；2.最值问题.【思路点晴】本题考查函数图象与性质，导数与图象等知识.第一个问题就是处理()(),1f x f x -这两个函数图象的关系，()f x 图象向右移1个单位得到()1f x -图象，向左移1个单位得到()1f x +图象.由此可以确定函数是一个奇函数，由于()f x 为增函数，而且为抽象函数，不妨设()f x x=，这样可以简化题目的化简过程.6．D 【解析】试题分析：:l y x =±，则(4,4)P ±，从而415PF =+=,选D.考点：抛物线定义，双曲线渐近线【方法点睛】1.凡涉及抛物线上的点到焦点距离时，一般运用定义转化为到准线距离处理．本题中充分运用抛物线定义实施转化，其关键在于求点P 的坐标．2．若P （x 0，y 0）为抛物线y 2＝2px （p ＞0）上一点，由定义易得|PF|＝x 0＋p 2；若过焦点的弦AB 的端点坐标为A （x 1，y 1），B （x 2，y 2），则弦长为|AB|＝x 1＋x 2＋p ，x 1＋x 2可由根与系数的关系整体求出；若遇到其他标准方程，则焦半径或焦点弦长公式可由数形结合的方法类似地得到．7．D 【解析】试题分析：由图象可知5,1≠x ∴分母上必定可分解为()()51--x x k ，∵在3=x 时，有2=y ，∴k d 8-=，∴()()8:5:61:::--=：d c b a ，故答案为D ． 考点：函数的图象.8．D 【解析】 试题分析：{}{}11≥=-==x x x y x A ，{}{}1)12(log 22≤=++-=y y x x y y ，故选D.考点：（1）函数的定义域及值域；（2）集合的运算.9．C 【解析】试题分析：由已知，1221+=-n n a a ，即211=--n n a a ，可知数列}{n a 为等差数列，且公差为21，又函数223y x x =-+的最小值为2，即21=a ，故3621289299=⨯⨯+⨯=S ．考点：等差数列．10．B 【解析】试题分析：由题意，3=a b 或33，∴2)(12=+=a b e 或332.考点：圆锥曲线的性质．11．D 【解析】试题分析：22()()232x x a g x f x x x x x a-+>⎧=-=⎨++≤⎩，而方程20x -+=的解为2，方程2320x x ++=的解为1-或2-，所以⎪⎩⎪⎨⎧≤-≤-<a a a 212，解得12a -≤<，所以2a z =的取值范围是1,42⎡⎫⎪⎢⎣⎭,故选D.考点：函数的零点．【易错点睛】本题主要考查函数零点的判断.函数零点个数的判断：函数零点的个数即为方程0f(x)=根的个数，可转化为函数f(x)的图象与x 轴交点的个数进行判断，也可转化为两个函数图象的交点个数．利用函数零点的存在性定理判断零点所在的区间时，首先看函数y f(x)=在区间[,]a b 上的图象是否连续不断，再看是否有()0f(a)f b <，若有，则函数y f(x)=在区间(,)a b 内必有零点．12．C 【解析】试题分析：画出函数)(x f y =的图象如图，由)(06)()65()]([52R a a x f a x f ∈=++-，可得()()6,5f x f x a ==，有图象知当()65f x =时，由于65154<<，所以有四个根，x 的方程)(06)()65()]([52R a a x f a x f ∈=++-有且仅有个6不同实数根，所以()f x a =有两个根，由图象知，当10≤<a 或45=a 时，()f x a =有两个根，因此实数a 的取值范围是10≤<a 或45=a ，故选C.考点：1、函数的图象与性质；2、方程的根与函数图象交点的关系.【方法点睛】本题主要考查函数的图象与性质、方程的根与函数图象交点的关系，属于难题.判断方程()0f x =根的个数常用方法：①直接法：可利用判别式的正负直接判定一元二次方程根的个数；②转化法：函数()y f x =零点个数就是方程()0f x =根的个数，结合函数的图象与性质(如单调性、奇偶性、周期性、对称性) 可确定函数的零点个数；③数形结合法： 一是转化为两个函数()(),y g x y h x ==的图象的交点个数问题，画出两个函数的图象，其交点的个数就是函数零点的个数，二是转化为(),y a y g x ==的交点个数的图象的交点个数问题 .本题就利用了方法③.13．⎢⎣【解析】试题分析：因02≥=x y ,而2222≤-=y x ,故22≤≤-x ,所以]2,0[=N M . 考点：集合的交集运算．14．)32,223()223,(+----∞ 【解析】试题分析：当1x ≥时，()1'f x x =,则过(),1A e 的切线斜率为1,k e =故切线方程为()11y x e e -=-，与()()12y x x a e =+-联立后应该有两组解，即消元得到的()2120x a x a +--=有两个的实数解，即()2218610a a a a ∆=-+=++≥，解得)32,223()223,(+----∞ ，故答案为)32,223()223,(+----∞ .考点：1、分段函数的解析式、图象及性质；2、数形结合思想的应用.【方法点睛】本题主要考查分段函数的解析式、图象及性质、数形结合思想的应用，属于难题.数形结合是根据数量与图形之间的对应关系，通过数与形的相互转化来解决数学问题的一种重要思想方法，是中学数学四种重要的数学思想之一，尤其在解决选择题、填空题是发挥着奇特功效，大大提高了解题能力与速度.运用这种方法的关键是将已知函数的性质研究透，这样才能快速找准突破点.本题是通过切线与y =ln x 有一个交点，与1(2)(),1y x x a x e =+-<有两个交点（转化为方程有两个根）解答的.15．43【解析】试题分析：过F 且斜率为3的直线方程为1)y x =-，与抛物线C ：x y 42=联立解得1(3A B ，则直线AO 方程为y =与:1l x =-的交点(1,D -，因此||134||43OF BD ==考点：直线与抛物线位置关系16．3【解析】试题分析：设(,)m n A ，则22244||,4,||b a a n m n m m n a b b ==⇒==，因为2F 3π∠A B =，所以222222244|1|48()4030a a a ab b b b =-⇒-⋅+=222222221313124137a a a a e e b b c c ⇒==⇒==⇒==或或考点：双曲线的离心率【方法点睛】解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于a ，b ，c 的方程或不等式，再根据a ，b ，c 的关系消掉b 得到a ，c 的关系式，建立关于a ，b ，c 的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.17．（1）证明见解析；（2）12212--+-=n n n n T .【解析】 试题分析：（1）借助题设条件和等比数列的定义推证；（2）借助题设条件和等差数列等比数列的求和公式求解.试题解析:（1）由已知当直线过点(2,0)n 时，目标函数取得最大值，故2n z n=，∴方程为2x y n +=. ∵(,)n n S a 在直线n z x y=+上，∴2n n S a n+=①∴112(1),2n n S a n n --+=-≥，②由①-②得，122,2n n a a n --=≥，∴122,2n n a a n -=+≥，∴12(2)2,2n n a a n --=-≥，∵121a -=-，∴数列{2}n a -以-1为首项，12为公比的等比数列. （2）由（1）得：112()2n n a --=-，∴112()2n n a -=-. ∵2n n S a n +=，∴11222()2n n n S n a n -=-=-+. ∴01111[0()][2()][22()]222n n T n -=+++++-+01111[02(22)][()()()]222n n -=+++-++++2111()(22)122()12212nn n n n n ---=+=-+--考点：等差数列等比数列的定义及求和公式等有关知识的运用．18．（1）22525(2)()24x y -+-=；（2）证明见解析.【解析】试题分析：（1）设圆C 的半径为()0>r r ，由3=MN 可得2223()22r =+，从而求圆C 的方程；（2）求出点()1,0M ，()4,0N ，讨论当AB x ⊥轴时与AB 与x 轴不垂直时ANM ∠是否相等BNM ∠，从而证明．试题解析：（1）设圆C 的半径为r （0r >），依题意，圆心坐标为(2,)r .∵3MN =，∴2223()22r =+，解得2254r =. ∴圆C 的方程为22525(2)()24x y -+-=. （2）把0x =代入方程22525(2)()24x y -+-=，解得1y =或4y =，即点(0,1),(0,4)M N . （i ）当AB x ⊥轴时，可知0ANM BNM ∠=∠=.（ii ）当AB 与x 轴不垂直时，可设直线AB 的方程为1y kx =+.联立方程22128y kx x y =+⎧⎨+=⎩，消去y 得，22(12)460k x kx ++-= 设直线AB 交椭圆于1122(,),(,)A x yB x y 两点，则12122246,1212k kx x x x k k --+==++.∴121212124433AN BN y y kx kx k k x x x x ----+=+=+2212121212121223()12120k kkx x x x k k x x x x ---+++===∴ANM BNM ∠=∠.考点：直线与圆的方程的应用.【方法点晴】本题考查了圆的方程的求法及圆锥曲线与直线的交点问题，化简比较复杂，通过根与系数的关系简化运算，要细心，属于中档题．第一问中利用常见的弦长的一半，圆的半径以及圆心到弦的距离构成直角三角形，从而求得圆的方程；第二问中把角相等转化为两直线的斜率之和为0,通过联立直线的方程与椭圆的方程，根据维达定理，利用整体代换得到结果.19．（1）直线l 与曲线C 相交；（2）1±. 【解析】试题分析：（1）利用⎩⎨⎧==θρθρsin cos y x 可把曲线C 的极坐标方程化为直角坐标方程，可得圆心、半径，由于直线l 过点()11-，，求出该点到圆心的距离，与半径半径即可判断出位置关系；（2）利用点到直线的距离公式与弦长公式即可得出．试题解析：（1）∵2cos 4sin ρθθ=-，∴22cos 4sin ρρθρθ=-， ∴曲线C 的直角坐标方程为2224x y x y +=-，即()()22125x y -++=，∵直线l 过点()1,1-，∴直线l 与曲线C 相交．（2）当直线l 的斜率不存在时，直线l过圆心，AB =≠则直线l 必有斜率，设其方程为()11y k x +=-，即10kx y k ---=，圆心到直线l 的距离2d ===，解得1k =±，∴直线l 的斜率为1±．考点：（1）简单曲线的极坐标方程；（2）直线与圆的位置关系；（3）参数方程化成普通方程；【方法点晴】本小题主要考查直线的参数方程及其几何意义、圆的极坐标方程、直线与圆的位置关系、点到直线的距离公式、弦长公式等基础知识；考查运算求解能力；数形结合思想，属于中档题．在极坐标方程两端同时乘以ρ，是把极坐标方程转化为普通方程常用的手段，由直线的参数方程可知：直线恒过定点，并且该点在圆内，故直线与圆相交；第二问主要考查直线与圆相交的情况，利用圆心到直线的距离，弦长的一半以及半径构成直角三角形来解.20．（1）12a =；（2）()g x 在(],4-∞-和[]1,0-上为减函数，在[]4,1--和[)0,+∞上为增函数．【解析】试题分析：（1）求导数，利用()()32f x ax x a R =+∈在43x =-处取得极值，可得043=⎪⎭⎫ ⎝⎛-'f ，即可确定a 的值；（2）由（1）得()xe x x x g ⎪⎭⎫ ⎝⎛+=2321，利用导数的正负可得()x g 的单调性． 试题解析：（1）对()f x 求导得()232f x ax x'=+，因为()f x 在43x =-处取得极值，所以403f ⎛⎫'-= ⎪⎝⎭，即1641683209333a a ⎛⎫⨯+⨯-=-= ⎪⎝⎭，解得12a =． （2）由（1）得()3212x g x x x e ⎛⎫=+ ⎪⎝⎭，()()()32151214222x xg x x x x e x x x e ⎛⎫'=++=++ ⎪⎝⎭．令()0g x '=，解得0,1x x ==-或4x =-．当4x <-时，()0g x '<，故()g x 为减函数；当41x -<<-时，()0g x '>，故()g x 为增函数；当10x -<<时，()0g x '<，故()g x 为减函数；当0x >时，()0g x '>，故()g x 为增函数．综上，知()g x 在(],4-∞-和[]1,0-上为减函数，在[]4,1--和[)0,+∞上为增函数．考点：（1）函数在某点取得极值的条件；（2）利用导数研究函数的单调性.21．（1）证明见解析；（2）h =.【解析】试题分析：（1）由线面垂直AE CD ⊥平面，得线线垂直AE CD ⊥，再由线线垂直，可得线面垂直.CD ADE ⊥平面 再由线面垂直可证得面面垂直；（2）过点B 作//BH AE 且BH AE =，连接,CH HE . 可证C D E H ，，，四点共面. 由等积法BHS h S CDE BDE ⋅=⋅∆∆3131，可得h .试题解析：（1）因为AE ⊥平面CDE ，且CD ⊂平面CDE ，所以AE ⊥CD.又正方形ABCD 中，CD ⊥AD ，且AE ∩AD=A ，AE ，AD ⊂平面ADE ， 所以CD ⊥平面ADE.又CD ⊂平面ABCD ，所以平面ABCD ⊥平面ADE. （2）过点B 作BH ∥AE 且BH=AE ，连接CH ，HE. 由于AE ⊥平面CDE ，所以BH ⊥平面CDE. 四边形AEHB 为平行四边形，所以AB ∥HE. 又四边形ABCD 是正方形，所以CD ∥HE.所以C ，D ，E ，H 四点共面.由（1）知，CD ⊥平面ADE ，所以四边形CDEH 为矩形，所以DE ⊥HE. 又DE ⊥AE ，HE ∩AE=E ，所以DE ⊥平面ABHE ，从而DE ⊥BE.又CDEB BDEC V V --=，所以BH S h S CDE BDE ⋅=⋅∆∆3131，所以552213211322122=+⨯⨯⨯⨯=⋅=∆∆BDE CDE S BH S h .考点：1.线，面之间位置关系的判定与性质；2.三棱锥体积；3.推理与证明. 22．（1）否，（2）()1f x ，有界，()2f x 无界．（3）是【解析】 试题分析：（1）由及时定义，需确定函数值域，值域有上下确界时为有界函数，肯定就需证明，否定只需找个反例：举一个一次函数就行（2）()()()111440,0;0,0,3322x f x x f x x f x x x xx==>=∈<=∈-+-+所以()1f x ∈，有界；()()222923(31)11||0x x x f x f x =-⋅=--≥-⇒≥，无界．（3）由()117,4312f xf x f x f ⎛⎫⎛⎫⎛⎫+++=++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭得()473121212f x f x f x f x ⎛⎫⎛⎫⎛⎫+-=+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 令()4()12h x f x f x ⎛⎫=+- ⎪⎝⎭，则()3()12h x h x +=，因此()(1)h x h x +=，即()()16411212fx f x f x f x ⎛⎫⎛⎫+-=+-+⎪ ⎪⎝⎭⎝⎭，同理可得()()16421212f x f x f x f x ⎛⎫⎛⎫+-=+-+ ⎪ ⎪⎝⎭⎝⎭，因此()()()()121f x f x f x f x +-=+-+，又(),f x x R∈是有界函数，所以必有()()1f x f x =+试题解析：解：（1）否，反例：()()()(),11f x x F x f x f x ==+-=有界，但()f x x=无界．（2）()1f x ∈，有界，()2f x 无界． （3）()47316121212121212f x f x f x f x f x f x ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+-=+-+=+-+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭， ∴()()16411212f x f x f x f x ⎛⎫⎛⎫+-=+-+ ⎪ ⎪⎝⎭⎝⎭， 41851613121212121212f x f x f x f x f x f x ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+-+=+-+=+-+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭， 综上()()13111212f x f x f x f x ⎛⎫⎛⎫+-=+-+ ⎪ ⎪⎝⎭⎝⎭，∴()()()()121f x f x f x f x +-=+-+ ∴()()()()()1f x n f x n f x f x +=++-，∵()f x 有界，∴()()1f x f x =+，是周期函数．考点：及时定义23．（1）4;m ≥（2）6k ≤- 【解析】试题分析：（1）由对勾函数性质知只需满足()()1,f m f ≥得()()max 10,,m m a m a --≥∴≥即4;m ≥（2）构造函数()()()F x f x g x =-，只需F(x)在[2,4]上递增, 按绝对值定义分类讨论：①当224x ⎡∈⎣时，()()11aF x k x x=---+，()()min 221+0(1)6a a F x k k x x '=--≥⇒≤-=-②当()2,4x ∈时，()()17a F x k xx =-+-，类似可得2k ≤试题解析：解：（1）()34,a y f x ≤≤∴=在(上递减，在)∞上递增，又()f x 在区间[]1,m 上的最大值为()f m 。

河北定州中学 2017-2018 学年第一学期高四第一次月考数学试题一、选择题 ( 本题共 12 小题，每题 5 分，共 60 分。

在每题给出的四个选项中，只有一项是切合题目要求的。

)1、已知会集 A { xZ |( x 1)(x 2) 0}，B { x | 2 x 2}，则 ABA 、 { x | 1x 2} B 、 { 1,1} C 、 {0,1, 2} D 、 { 1,0,1} 2、 i 是虚数单位，若2 i a bi ( a, bR) ，则 lg( a b) 的值是1 iA 、 2B 、 1C 、 0D 、123、已知等比数列a n 中，各项都是正数，且a 1 , 1 a 3, 2a 2 成等差数列，则 a 9a10 2 a 7 a 8A 、 1 2B 、322C、 1 2 D 、3224、设 a (7 1( 9 17 ，则 a , b , c 的大小序次是) 4， b) 5， c log 2979A 、 b ac B 、 c a bC 、 c b aD 、 b c a5、已知 m,n 为空间中两条不同样的直线，, 为空间中两个不同样的平面，以下中正确的选项是 A 、若 m //, m // ，则 //B、若 m, m n ，则 n//C 、若 m // ,m // n ，则 n//D 、若 m , m // ，则6、已知菱形 ABCD 边长为2，B3 ，点 P 满足 APAB ，R ．若BD CP3 ，则 的值为A 、1B、1 C、1D、1 22337、函数 f （ x ） =2sin （ ωx+φ ）（ ω＞ 0， ＜φ ＜ ）的部分图象22以以以下图，则ω ， φ 的值分别是 ( )A 、 2,B 、 2,C 、 4,D 、 4,36 6 38、某三棱锥的三视图以以以下图 , 该三棱锥的表面积是A 、28 6 5B 、60 12 5C、56125D、30659、将函数y3cos x sin x x R 的图像向左平移m m0 个单位长度后,所获得的图像关于 y轴对称，则m 的最小值是A、B、C、3D、5612ln 1610、若变量x, y满足x0 ，则y关于 x 的函数图象大体是（）y11、设抛物线C : y2 2 px( p 0) 的焦点为F，点M在C上，MF 5 ，若以MF为直径的圆过点 (0, 2) ，则 C 的方程为A、y24x或y28xB、 y22x或y28xC、y24x或y216xD、 y22x或y216x12、已知函数f ( x)| x1|,7x0x22x ，设 a 为实数，若存在实数ln x, e2x， g(x)m，e使 f （ m）﹣ 2g（ a） =0，则实数a 的取值范围为 ()A、[ 1,)B、 [1,3]C、（,1] U[3,)D、（ ,3]第Ⅱ卷(非选择题)二、填空题( 本题共 4 小题，每题 5 分，共20 分。

河北定州中学2016-2017学年第一学期高四数学周练试题（8）一、单项选择题1．已知中心在原点，焦点在x 轴上的双曲线的离心率1，则此双曲线的方程为( )A ．122=-y x B ．13222=-y xC. 1422=-y x D. 1222=-y x2．已知二次函数()f x 的图象如图所示，则其导函数()'f x 的图象大致形状是（ ）3．某程序框图如图所示，则输出的S= （ ）A ．120B ． 57C ．56D ． 264．如图,半径为R 的圆C 中,已知弦AB 的长为5,则AC AB ⋅=( )A.25 B.225C.25RD.225R5．如图，在长方体1111ABCD A B C D -中，,E H 分别是棱1111,A B D C 上的点（点E 与1B 不重合），且11//EH A D ，过EH 的平面与棱1BB ，1CC 相交，交点分别为,F G ．设122,AB AA a ==EF a =，11B E B F =．在长方体1111ABCD A B C D -内随机选取一点，则该点取自于几何体11A ABFE D DCGH -内的概率为( )A ．1116 B ．34 C ．1316 D ．786．若平面向量b 与34=-()a ，的夹角是180︒，且||10=b ，则=b ( )． A ．34-()， B ．68-()， C ．68-()， D ．86-()， 7．函数()xx x f 1log 2-=的零点所在区间为 A. ⎪⎭⎫ ⎝⎛21,0 B. ⎪⎭⎫⎝⎛1,21 C. ()2,1 D. ()3,28．已知不等式20ax bx c ++>的解集为{}24x x <<，则不等式20cx bx a ++<的解集为 （ ）A ．12x x ⎧⎫>⎨⎬⎩⎭B ．14x x ⎧⎫<⎨⎬⎩⎭C ．1142xx ⎧⎫<<⎨⎬⎩⎭ D ．1124x x x ⎧⎫><⎨⎬⎩⎭或9．参数方程11x y ⎧=+⎪⎨=-⎪⎩t 为参数）表示什么曲线（ ）A ． 一条直线B ． 一个半圆C ． 一条射线D ． 一个圆10．把一枚硬币连续抛两次，记“第一次出现正面”为事件A ，“第二次出现正面”为事件B ，则()|P B A =（ ）A ．12 B ．14 C ．16 D ．1811．数列{}n a 的通项公式为*cos,2n n a n N π=∈，其前n 项和为n S ，则2016S =（ ） A ．1008 B ．-1008 C ．-1 D ．012．在ABC ∆中, 已知向量)72cos ,18(cos 00=, )27cos 2,63cos 2(00=,则BAC ∠cos 的值为( )A ．0B ．21C ．22D ．23二、填空题13．若291010r rC C -=，则实数r 的值为 ；14．对于函数[]sin ,0,2()1(2),(2,)2x x f x f x x π⎧∈⎪=⎨-∈+∞⎪⎩，有下列4个结论： ①任取[)120,x x ∈+∞、，都有12()()2f x f x -≤恒成立； ②()2(2)f x kf x k =+*()k ∈N ，对于一切[)0,x ∈+∞恒成立； ③函数()ln(1)y f x x =--有3个零点； ④对任意0x >，不等式2()f x x≤恒成立． 则其中所有正确结论的序号是 .15．函数()2ln f x x x =-的单调递减区间为 ．16．已知椭圆2222:1x y C a b+=(0)a b >>的左，右焦点分别为12,F F ，点P 是椭圆上异于长轴端点的任意一点，若M 是线段1PF 上一点，且满足122,0MF PM MF OP =⋅=，则椭圆离心率的取值范围为______________. 三、解答题17．已知三个集合：}01|{<-=x ax x A ，}043|{2≤--=x x x B ， }1log |{21>=x x C ，同时满足以下三个条件： 甲：a 为小于6的正整数；乙：A 是B 成立的充分不必要条件；丙：A 是C 成立的必要不充分条件，试确定数a 。

河北定州中学2016-2017学年第一学期高三开学考试数学试题一、选择题（共12小题，共60分）1．已知集合{}0)3(<-=x x x P ，{}2<=x x Q ，则=Q P （ ） A ．)0,2(- B ．)2,0( C ．)3,2( D ．)3,2(-2．已知函数|lg |,010()16,102x x f x x x <≤⎧⎪=⎨-+>⎪⎩，若,,a b c 互不相等，且()()()f a f b f c ==，则abc的取值范围是（ ）A ．(1,10)B ．(5,6)C ．(10,12)D ．(20,24)3．已知a 为实数，函数22()2f x x x ax =---在区间(,1)-∞-和(2,)+∞上单调递增，则a 的取值范围为（ ）A ．[1,8]B ．[3,8]C ．[1,3]D ．[1,8]- 4．平行线3490x y +-=和6820x y ++=的距离是（ ） A ．85 B ．2 C ．115 D ．755．在三棱柱111ABC A B C -中，各棱长相等，侧棱垂直于底面，点D 是侧面11BB C C 的中心，则AD 与平面11BB C C 所成角的大小是（ ）A ．030 B ．045 C ．060 D ．090 6．已知βα,是两个不同的平面，m ，n 是两条不同的直线给出下列命题： ①若,,βα⊂⊥m m 则βα⊥；②若ββαα∥∥n m n m ,,,⊂⊥，则βα∥；③如果n m n m ,,,αα⊄⊂是异面直线，那么n 与α相交； ④若,,,βαβα⊄⊄=n n m n m ，且∥ 则n ∥α且β∥n . 其中的真命题是（ ）A ．①②B ．②③C ．③④D ．①④7．如图，在棱长均为2的正四棱锥P ABCD -中，点E 为PC 中点，则下列命题正确的是（ ）A ．//BE 平面PAD ，且直线BE 到平面PADB ．//BE 平面PAD ，且直线BE 到平面PADC ．BE 不平行于平面PAD ，且BE 到平面PAD 所成角大于30 D ．BE 不平行于平面PAD ，且BE 到平面PAD 所成角小于308．抛掷两个骰子，至少有一个4点或5点出现时，就说这些试验成功，则在10次试验中，成功次数ξ的期望是（ ） A ．103 B ．559 C ．809 D ．5099．有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（ ） A ．13 B ．12 C ．23 D ．3410．从1，2，3，4，5，6，7，8，9中不放回地依次取2个数，事件A=“第一次取到的是奇数”，B=“第二次取到的是奇数”，则P （B|A ）=（ ） A ． B ．C ．D ．11．如图是函数()sin y x ωϕ=A +（0A >，0ω>，2πϕ≤）图象的一部分．为了得到这个函数的图象，只要将sin y x =（R x ∈）的图象上所有的点（ ）A ．向左平移3π个单位长度，再把所有各点的横坐标缩短到原来的12，纵坐标不变B ．向左平移3π个单位长度，再把所有各点的横坐标伸长到原来的2倍，纵坐标不变 C ．向左平移6π个单位长度，再把所有各点的横坐标缩短到原来的12，纵坐标不变D ．向左平移6π个单位长度，再把所有各点的横坐标伸长到原来的2倍，纵坐标不变12．已知()sin cos f x a x b x =-，若()()44f x f x ππ-=+，则直线0ax by c -+=的倾斜角为（ ） A ．4π B ．3π C ．23π D ．34π第II 卷（非选择题）二、填空题（4小题，共20分） 13．函数2sin 26y x π⎛⎫=-⎪⎝⎭（[]0,x π∈）为增函数的区间是 ． 14．一个袋中有12个除颜色外完全相同的球， 2个红球，5个绿球，5个黄球，从中任取一球，不放回后再取一球，则第一次取出红球时第二次取出黄球的概率为 . 15．已知棱长为1的立方体1111ABCD A B C D -，则从顶点A 经过立方体表面到达正方形11CDD C 的心M 的最短路线有______条．16．已知不等式23x -<的解集为A ，函数)1ln(-=x y 的定义域为B ，则图中阴影部分表示的集合为 ．三、解答题（8小题，共70分）17．若关于x 的实系数方程20x ax b ++=有两个根，一个根在区间(0,1)内，另一根在区间(1,3)内，记点(,)a b 对应的区域为S .（1）设2z a b =-，求z 的取值范围；（2）过点(5,1)-的一束光线，射到x 轴被反射后经过区域S ，求反射光线所在直线l 经过区域S 内的整点（即横纵坐标为整数的点）时直线l 的方程.18．已知函数b a x x x x f 3)ln()(2++-+=在0=x 处取得极值0. （1）求实数b a ,的值； （2）若关于x 的方程mx x f +=25)(在区间[]20，上恰有两个不同的实数根，求实数m 的取值范围.19．如图，直角三角形ABC 中，060A =，沿斜边AC 上的高BD ，将ABD ∆折起到PBD ∆的位置，点E 在线段CD 上.（1）求证：PE BD ⊥；（2）过点D 作DM BC ⊥交BC 于点M ，点N 为PB 中点，若//PE 平面DMN ，求DEDC的值.20．选修4-1：几何证明选讲如图，圆O 是ABC ∆的外接圆，D 是弧AC 的中点，BD 交AC 于点E .（1）求证：2CD DE DB =⋅；（2）若CD =O 到AC 的距离为1，求圆O 的半径r .21．某公司的两个部门招聘工作人员，应聘者从1T 、2T 两组试题中选择一组参加测试，成绩合格者可签约．甲、乙、丙、丁四人参加应聘考试，其中甲、乙两人选择使用试题1T ，且表示只要成绩合格就签约；丙、丁两人选择使用试题2T ，并约定：两人成绩都合格就一同签约，否则两人都不签约．已知甲、乙考试合格的概率都是12，丙、丁考试合格的概率都是23，且考试是否合格互不影响． （Ⅰ）求丙、丁未签约的概率；（Ⅱ）记签约人数为X ，求X 的分布列和数学期望EX ．22．为了了解某学段1000名学生的百米成绩情况，随机抽取了若干学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组.按上述分组得到的频率分布直方图如图所示，已知图中从左到右前3个组的频率之比为3:8:19，且第二组的频数为8.（1）将频率当作概率，请估计该学段学生中百米成绩在[16,17)内的人数以及所有抽取学生的百米成绩的中位数（精确到0.01秒）；（2）若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.23．已知函数()22sin cos f x a x x x ωωω=+0a >，0ω>）的最大值为2，且最小正周期为π．（Ⅰ）求函数()f x 的解析式及其对称轴方程； （Ⅱ）若()43f α=，求sin 46πα⎛⎫+ ⎪⎝⎭的值．24．已知向量(3sin,1)4x m =，2(cos ,cos )44x x n =. （1）若1m n ⋅=，求2cos()3x π-的值；（2）记()f x m n =⋅在ABC ∆中角,,A B C 的对边分别为,,a b c ，且满足(2)cos cos a c B b C -=，求()f A 的取值范围.参考答案 1．B 【解析】试题分析：由条件{}|0x 3P x =<<，{}|22Q x x =-<<.则{}|02P Q x x ⋂=<<.故本题答案选B.考点：1.一元二次不等式；2.含绝对值的不等式；3.交集. 2．C 【解析】试题分析：画出函数图象如下图所示，由图可知()1,1,10,12a ab abc c b===∈，故选C.考点：函数图象与性质.【思路点晴】本题是2010年全国卷第11题.主要的解题思路就是数形结合.有关函数的问题，往往可以先画出函数的图象，然后利用图象与性质来解决.本题分段函数中第一段是对数函数外面加绝对值，我们先画出绝对值里面的函数，然后把x 轴下方的图象向上翻折，就可以得到lg x 的图象；第二段是一次函数，图象为直线.3．A 【解析】试题分析：当022≥--a x x 时,2)(+=ax x f 不满足题设,故022<--ax x ,此时22)(2--=ax x x f ,对称轴4a x =,显然24≤a,即8≤a ,所以答案C 被排除.容易验证当0=a 时,函数|2|)(22--=x x x f 在区间(,1)-∞-和(2,)+∞上不满足题设, 答案D 被排除.当1=a 时,函数|2|)(22---=x x x x f 在区间(,1)-∞-和(2,)+∞上也满足题设,当8=a 时,函数|28|)(22---=x x x x f 在区间(,1)-∞-和(2,)+∞上满足题设,故应选答案A. 考点：二次函数的图象和性质．【易错点晴】本题以含绝对值符号的二次函数为背景，考查的是函数中参数的取值范围问题.解答时充分借助函数的解析表达式,运用二次函数的图像等许多有关知识进行合理推理和判断.取值进行判断是解答本题的一大特色.解答时应充分依据题设条件,对题设中提供的几个命题进行分析推断最后作出真假命题的判断.对于假命题,仅举出一个反例,进行了推断从而说明它是假命题.运用反例是否定一个命题是真命题的有效方式和方法. 4．B 【解析】试题分析：由两平行直线之间的距离公式可得210206436|182|==++=d ,故应选B. 考点：两条平行线之间的距离公式． 5．C 【解析】试题分析：如图，取BC 中点E ，连接DE 、AE 、AD ，依题意知三棱柱为正三棱柱，易得⊥AE 平面C C BB 11，故ADE ∠为AD 与平面C C BB 11所成的角．设各棱长为1，则23=AE ，21=DE ，32123tan ===∠DE AE ADE ，∴ 60=∠ADE ．故选C.考点：空间中直线与平面之间的位置关系. 6．D 【解析】试题分析：若,,βα⊂⊥m m 由线面垂直的可得面面垂直，即βα⊥，①正确；若ββαα∥∥n m n m ,,,⊂⊥，由线面垂直与线面平行的相关性质可得，βα⊥，②错误；如果n m n m ,,,αα⊄⊂是异面直线，也可出现n 与α平行，③错误；若,,,βαβα⊄⊄=n n m n m ，且∥ 由线面平行的相关性质可得//n α且β∥n .④正确.故本题答案选D.考点：线面间的位置关系的判定与性质． 7．D 【解析】试题分析：若//BE 平面PAD ，而//BC 平面PAD ，所以平面//PBC 平面PAD ，矛盾，所以,A B 不正确.取PD 中点F ，取AB 中点G ，连接,,EF AF GF ，依题意有1,,E F A F G F =3315cos 2362AFG +-∠==>⋅，故30AFG ∠<，线面角为直线与平面内直线所成角的最小值，故BE 到平面PAD 所成角小于30. 考点：直线与平面的位置关系. 8．D 【解析】试题分析：在10次试验中,成功的次数ξ服从二项分布,每次实验成功的概率为95)32(12=-,故10次试验中,成功次数ξ的数学期望9501095=⨯=ξE ,故应选D. 考点：随机变量的概率分布和数学期望． 9．A 【解析】试题分析：总的方法数有339⋅=种，符合题意的有3种，故概率为13. 考点：概率． 10．D 【解析】试题分析：事件A 共有58⨯种取法，其中第二次取到的是奇数的有54⨯种取法，因此541(|)582P B A ⨯==⨯,选D. 考点：条件概率 11．A 【解析】试题分析：从图象提供的信息可以可以看出π==T A ,1,由此可得2=ω,则)2sin(ϕ+=x y ,将)0,65(π代入可得0)35sin(=+ϕπ,即Z k k ∈=+,35πϕπ,所以3πϕ=,所以)32sin(π+=x y ,故应选A.考点：三角函数的图象及变换． 12．D 【解析】试题分析：由题设可知函数关于直线4π=x 对称,因此)2()0(πf f =,即a b =-,故1-=ba,即1tan -=α,故43πα=，所以应选D. 考点：三角函数的图象和性质及直线的斜率与倾斜角的关系． 13．5,36ππ⎡⎤⎢⎥⎣⎦【解析】试题分析：因为)62sin(2π--=x y ,所以只要求函数)62sin(2π-=x y 的减区间即可.解2326222πππππ+≤-≤+k x k 可得61022322ππππ+≤≤+k x k ,即353ππππ+≤≤+k x k ,所以653ππ≤≤x ,故答案为5,36ππ⎡⎤⎢⎥⎣⎦. 考点：三角函数的图象和基本性质的运用． 【易错点晴】本题以函数2sin 26y x π⎛⎫=-⎪⎝⎭的表达式的单调区间为背景,考查的是三角函数中形如)sin()(ϕω+=x A x f 的正弦函数的图象和性质.解答时先从题设中的条件增函数入手,对函数2sin 26y x π⎛⎫=- ⎪⎝⎭进行变形,将其变形为一般式)62sin(2π--=x y ,将其转化为求函数)62sin(2π-=x y 的减区间.最后将其转化为正弦函数的单调递减区间的求法.通过解不等式使得本题获解. 14．511. 【解析】试题分析：根据题意，第一次取出红球后不放回，剩余球的总个数为11个，黄球的个数为5个，再根据概率公式解答即可，所以其概率为511．故答案为：511. 考点：等可能事件的概率. 15．2 【解析】 试题分析：沿边1DD 或DC 展开将正方形11CDD C 与正方形11ADD A 或正方形ABCD 共面，所以经过边1DD 或DC 时，路线最短，有2条．考点：正方体展开图 16．{}11x x -<≤ 【解析】试题分析：由题设得}1|{},51|{>=<<-=x x B x x A ,则}1|{≤=x x B C R ,则}11|{≤<-=x x B C A R .考点：集合的交集补集运算．17．（1）112z -<<-；（2）4y x =+. 【解析】试题分析：（1）借助题设建立不等式组运用线性规划的知识求解；（2）借助题设条件运用直线的点斜式方程求解. 试题解析: 方程20x a x b ++=的两根在区间(0,1)和(1,3)上的几何意义是：函数2()y f x x ax b ==++与x 轴的两个交点的横坐标分别在区间(0,1)和(1,3)内，由此可得不等式组(0)0(1)0(3)0f f f >⎧⎪<⎨⎪>⎩，即010390b a b a b >⎧⎪++<⎨⎪++>⎩，则在坐标平面aOb 内，点(,)a b 对应的区域S 如图阴影部分所示，易得图中,,A B C 三点的坐标分别为(4,3),(3,0),(1,0)---，（1） 令2z a b =-，则直线2b a z =-经过点A 时，z 取得最小值，经过点C 时z 取得最大值，即min 11z =-，max 2z =-，又,,A B C 三点的值没有取到，所以112z -<<-；（2）过点(5,1)-的光线经x 轴反射后的光线必过点(5,1)--，由图可知，可能满足条件的整点为(3,1),(3,2),(2,2),(2,1)----，再结合不等式知点(3,1)-符合条件， 所以此时直线方程为：1(1)1(5)3(5)y x --+=⋅+---，即4y x =+.考点：线性规划的知识及直线的方程等有关知识的综合运用．【易错点晴】本题以方程的根的分布为背景,考查的是线性约束条件与数形结合的数学思想的综合运用问题.解答时先依据题设条件建立不等式组,然后再构建平面直角坐标系,准确的画出满足题设条件的不等式组010390b a b a b >⎧⎪++<⎨⎪++>⎩所表示的平面区域,然后借助该平面区域所表示的图形,数形结合求出2z a b =-中参数z 的取值范围和满足题设条件的反射光线所在直线l 的方程.18．（1）1,0a b ==（2）1[ln 2,1ln3]2---【解析】试题分析：（1）由极值定义得(0)0(0)0f f '=⎧⎨=⎩，解方程组得1,0a b ==（2）方程根的个数往往转(0,1)上单调递减，在(1,2)上单调递增，因此要有两个零点，须(0)01(1)ln 202(2)1ln 30m m m ϕϕϕ=-≥⎧⎪⎪=---<⎨⎪=--≥⎪⎩，解得m 的取值范围.试题解析：（1）由题设可知1()21f x x x a '=+-+当0x =时，()f x 取得极值0(0)0(0)0f f '=⎧∴⎨=⎩解得1,0a b == 经检验1,0a b ==符合题意（2）由（1）知2()ln(1)f x x x x =+-+，即为令25()ln(1)2x x x x x m ϕ=+-+--则方程()0x ϕ=在区间[0,2]恰有两个不同实数根.13(45)(1)()2122(1)x x x x x x ϕ+-'=--=++，得x 1=1 或 x 2=当(0,1)x ∈时，()0x ϕ'<，于是()x ϕ在(0,1)上单调递减； 当(1,2)x ∈时，()0x ϕ'>，于是()x ϕ在(1,2)上单调递增；依题意有 (0)01(1)ln 202(2)1ln30m m m ϕϕϕ=-≥⎧⎪⎪=---<⎨⎪=--≥⎪⎩考点：极值，利用导数研究函数零点【思路点睛】涉及函数的零点问题、方程解的个数问题、函数图像交点个数问题，一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等，再借助函数的大致图象判断零点、方程根、交点的情况，归根到底还是研究函数的性质，如单调性、极值，然后通过数形结合的思想找到解题的思路. 19．（1）证明见解析；（2）31. 【解析】试题分析：（1）由BD 是AC 边上的高，得出,BD CD BD PD ⊥⊥，由此证明BD ⊥平面PCD ，即可证明PE BD ⊥；（2）连接BE ，交DM 与点F ，由//PE 平面DMN ，得出//PE NF ，证明DEF ∆是等边三角形，再利用直角三角形的边角关系求出DEDC的值即可． 试题解析：（1）因为BD 是AC 边上的高，所以,BD CD BD PD ⊥⊥，又PD CD D =，∴BD ⊥平面PCD .∵PE ⊂平面PCD ，所以PE BD ⊥. （2）连接BE ，交DM 与点F ，//PE平面DMN ，且PE ⊂平面PEB ，平面PEB平面DMN NF =，∴//PE NF ,∴12DF BE EF ==，又000906030BCD ∠=-=，∴DEF ∆是等边三角形设DE a =，则BD =，3DC a ==，∴13DE DC =.考点：（1）直线与平面垂直；（2）直线与平面平行的性质.【方法点晴】本题考查了空间中的平行与垂直关系的应用问题，也考查了空间想象能力与逻辑推理能力的应用问题，是综合性题目．在第一问中主要通过线面垂判定定理得到线面垂直，然后得到线线垂直，线线垂直与线面垂直之间的互化是在证明垂直过程中常用的手段；在第二问中首先根据线面平行性质定理，得到//PE NF ，根据长度与角的关系得到DEF ∆是等边三角形，可得解.20．（1）证明见解析；（2）3r =. 【解析】试题分析：（1）利用同弧所对的圆周相等，可证明BCD CED ∆∆∽,利用相似比可得2CD DE DB =⋅；（2）连接,OD OC ，设OD 交AC 于点F ，由垂径定理有OD AC ⊥，通过解直角三角形可得2221(1)r r =-+-，解得3r =.试题解析：（1）证明：因为ABD CBD ∠=∠，ABD ECD ∠=∠，所以CBD ECD ∠=∠. 又CDB EDC ∠=∠，所以BCD ∆∽CED ∆. 所以DE DCDC DB=，所以2CD DE DB =⋅. （2）连接,OD OC ，设OD 交AC 于点F . 因为点D 是弧AC 的中点，所以OD AC ⊥.在Rt COF ∆中，1OF =，222OC CF OF =+，即221CF r =-. 在Rt CFD ∆中，222DC CF DF =+，所以2221(1)r r =-+-，解得3r =.考点：几何证明选讲. 21．（Ⅰ）95；（Ⅱ）分布列见解析，917. 【解析】试题分析：（Ⅰ）运用对立事件和互斥事件的概率公式求解；（Ⅱ）借助题设条件运用数学期望的公式求解. 试题解析:（Ⅰ）分别记事件甲、乙、丙、丁考试合格为A ，B ，C ，D ．由题意知A ，B ，C ，D 相互独立，且()()12P A =P B =，()()2C D 3P =P =．记事件“丙、丁未签约”为F ， 由事件的独立性和互斥性得：()()F 1CD P =-P2251339=-⨯=（Ⅱ）X 的所有可能取值为0，1，2，3，4．()()()11550F 22936P X ==P AB P =⨯⨯=；()()()()()11551F F 222918P X ==P AB P +P AB P =⨯⨯⨯=；()()()115112212F CD 22922334P X ==P AB +P AB =⨯⨯+⨯⨯⨯=；()()()112223CD CD 222339P X ==P AB +P AB =⨯⨯⨯⨯=；()()112214CD 22339P X ==P AB =⨯⨯⨯=．所以，X 的分布列是：X 的数学期望55121170123436184999EX =⨯+⨯+⨯+⨯+⨯= 考点：对立事件、互斥事件的概率和随机变量的概率分布与数学期望公式的综合运用． 22．（1）15.74；（2）74. 【解析】试题分析：（1）根据频率分步直方图中小正方形的面积是这组数据的频率，用长乘以宽得到面积，即为频率．根据所有的频率之和是1，列出关于x 的方程，解出x 的值，继而求出相应小组的人数，再设中位数为m ，列出关于m 的方程解得即可；（2）本题是一个古典概型，试验发生所包含的事件是从第一、五组中随机取出两个成绩，满足条件的事件是成绩的差的绝对值大于1秒，列举出事件数，根据古典概型概率公式得到结果.试题解析：（1）设前3组的频率依次为x x x 19,8,3，则由题意可得6.008.032.011983=--=++x x x ，由此得：02.0=x ,所以第二组的频率为0.16.因为第二组的频率为8，所以抽取的学生总人数为由此可估计学生中百米成绩在[)1716，内的人数为165032.0=⨯（人）. 设所求中位数为m ，由上述计算可知第一组、第二组、第三组的频率分别为0.380.160.06，，， 则()5.0150.380.160.06=-++m ，解得74.15=m . 故所有抽取学生的百米成绩的中位数为15.74秒. （2）记“两个成绩的差的绝对值大于1秒”为事件A .由（1）可知从第一组抽取的人数为35030.02=⨯⨯，不妨记为c b a ,,， 从第五组抽取的人数为4500.08=⨯，不妨记为4321，，，， 则从第一、五组中随机取出两个成绩有：34,24,23,14,13,12,4,3,2,1,4,3,2,1,,4,3,2,1,,c c c c b b b b bc a a a a ac ab 这21种可能；其中两个成绩的差的绝对值大于1秒的来自不同的组，共有12种. 所以742112)(==A P .故两个成绩的差的绝对值大于1考点：（1）频率分布直方图；（2）古典概型. 23．（Ⅰ）()2sin 23f x x π⎛⎫=+ ⎪⎝⎭,对称轴为122k x ππ=+（k ∈Z ）；（Ⅱ）91-. 【解析】试题分析：（Ⅰ）运用等价转化的方法将问题进行转化与化归；（Ⅱ）借助题设条件将复合命题分类转化进行求解. 试题解析:（Ⅰ）()sin 2f x a x x ωω=， 由题意()f x 的周期为π，所以22ππω=，得1ω=()f x 最大值为22=，又0a >，∴1a =∴()2sin 23f x x π⎛⎫=+⎪⎝⎭令232x k πππ+=+，解得()f x 的对称轴为122k x ππ=+（k ∈Z ）． （Ⅱ）由()43f α=知42sin 233πα⎛⎫+= ⎪⎝⎭，即2sin 233πα⎛⎫+= ⎪⎝⎭，∴sin 4sin 22cos 226323ππππααα⎡⎤⎛⎫⎛⎫⎛⎫+=+-=-+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦222112sin 212339πα⎛⎫⎛⎫=-++=-+⨯=- ⎪ ⎪⎝⎭⎝⎭考点：三角函数的图像和性质及三角变换公式的运用．【易错点晴】本题以函数的最大值和最小正周期为背景,考查的是三角函数中形如)s in()(ϕω+=x A x f 的正弦函数的图象和性质.解答时先从题设中的条件入手,先运用倍角公式将其化简为)sin()(ϕω+=x A x f 的形式,再运用所学知识求出其中的参数ϕω,的值,最后再解决题设中提出的问题即可.需要强调是对称轴的方程是是取得最值的的值,即2ππ±=k x ,学生在求解时很容易错写成22ππ±=k x 从而致错.24．（1）21-；（2）)23,1(. 【解析】试题分析：（1）借助题设条件和向量的数量积公式求解；（2）借助题设条件和正弦定理求解. 试题解析:（1）2()3sincos cos 444x x xf x m n =⋅=+111cos sin()12222262x x x π=++=++=. ∴1sin()262x π+=. ∴21cos()12sin ()3262x x ππ+=-+=. ∴21cos()cos()332x x ππ-=-+=-.（2）(2)cos cos a c B b C -=2sin cos sin()A B B C ⇒=+，∴1cos 2B =，∴3B π=. ∴203A π<<，∴6262A πππ<+<，∴1sin()(,1)262A π+∈. 又∵1()sin()262x f x π=++，∴13()sin()(1,)2622A f A π=++∈.考点：三角函数的图象、正弦定理、向量的数量积等有关知识的综合运用．。