2019年全国各地中考数学试题分类汇编(第三期) 专题35 尺规作图(含解析)

尺规作图一.选择题1.（2019•贵阳•3分）如图，在△ABC中，AB＝AC，以点C为圆心，CB长为半径画弧，交AB于点B和点D，再分别以点B，D为圆心，大于BD长为半径画弧，两弧相交于点M，作射线CM交AB于点E．若AE＝2，BE＝1，则EC的长度是（）A．2 B．3 C．D．【分析】利用基本作图得到CE⊥AB，再根据等腰三角形的性质得到AC＝3，然后利用勾股定理计算CE的长．【解答】解：由作法得CE⊥AB，则∠AEC＝90°，AC＝AB＝BE+AE＝2+1＝3，在Rt△ACE中，CE＝＝．故选：D．【点评】本题考查了作图﹣基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．2. （2019•河北•3分）根据圆规作图的痕迹，可用直尺成功找到三角形外心的是（）A．B．C．D．【解答】解：三角形外心为三边的垂直平分线的交点，由基本作图得到C选项作了两边的垂直平分线，从而可用直尺成功找到三角形外心．故选：C．3. （2019•河南•3分）如图，在四边形ABCD中，AD∥BC，∠D＝90°，AD＝4，BC＝3．分别以点A，C为圆心，大于AC长为半径作弧，两弧交于点E，作射线BE交AD于点F，交AC于点O．若点O是AC的中点，则CD的长为（）A．2B．4 C．3 D．【分析】连接FC，根据基本作图，可得OE垂直平分AC，由垂直平分线的性质得出AF ＝FC．再根据ASA证明△FOA≌△BOC，那么AF＝BC＝3，等量代换得到FC＝AF＝3，利用线段的和差关系求出FD＝AD﹣AF＝1．然后在直角△FDC中利用勾股定理求出CD 的长．【解答】解：如图，连接FC，则AF＝FC．∵AD∥BC，∴∠F AO＝∠BCO．在△FOA与△BOC中，，∴△FOA≌△BOC（ASA），∴AF＝BC＝3，∴FC＝AF＝3，FD＝AD﹣AF＝4﹣3＝1．在△FDC中，∵∠D＝90°，∴CD2+DF2＝FC2，∴CD2+12＝32，∴CD＝2．故选：A．【点评】本题考查了作图﹣基本作图，勾股定理，线段垂直平分线的判定与性质，全等三角形的判定与性质，难度适中．求出CF与DF是解题的关键．二.填空题1.2.3.4.三.解答题1. （2019•江苏无锡•10分）按要求作图，不要求写作法，但要保留作图痕迹．（1）如图1，A为⊙O上一点，请用直尺（不带刻度）和圆规作出⊙O的内接正方形；（2）我们知道，三角形具有性质：三边的垂直平分线相交于同一点，三条角平分线相交于一点，三条中线相交于一点，事实上，三角形还具有性质：三条高所在直线相交于一点．请运用上述性质，只用直尺（不带刻度）作图．①如图2，在▱ABCD中，E为CD的中点，作BC的中点F．②如图3，在由小正方形组成的4×3的网格中，△ABC的顶点都在小正方形的顶点上，作△ABC的高AH．【分析】（1）连结AE并延长交圆E于点C，作AC的中垂线交圆于点B，D，四边形ABCD 即为所求．（2）①连结AC，BD交于点O，连结EB交AC于点G，连结DG并延长交CB于点F，点F即为所求；②结合网格特点和三角形高的概念作图可得．【解答】解：（1）如图1，连结AO并延长交圆O于点C，作AC的中垂线交圆于点B，D，四边形ABCD即为所求．（2）①如图2，连结AC，BD交于点O，连结EB交AC于点G，连结DG并延长交CB 于点F，F即为所求②如图3所示，AH即为所求．【点评】本题主要考查作图﹣应用与设计作图，解题的关键是掌握圆的有关性质和平行四边形的性质及三角形垂心的性质．2. （2019•江苏宿迁•10分）在Rt△ABC中，∠C＝90°．（1）如图①，点O在斜边AB上，以点O为圆心，OB长为半径的圆交AB于点D，交BC于点E，与边AC相切于点F．求证：∠1＝∠2；（2）在图②中作⊙M，使它满足以下条件：①圆心在边AB上；②经过点B；③与边AC相切．（尺规作图，只保留作图痕迹，不要求写出作法）【分析】（1）连接OF，可证得OF∥BC，结合平行线的性质和圆的特性可求得∠1＝∠OFB ＝∠2，可得出结论；（2）由（1）可知切点是∠ABC的角平分线和AC的交点，圆心在BF的垂直平分线上，由此即可作出⊙M．【解答】解：（1）证明：如图①，连接OF，∵AC是⊙O的切线，∴OE⊥AC，∵∠C＝90°，∴OE∥BC，∴∠1＝∠OFB，∵OF＝OB，∴∠OFB＝∠2，∴∠1＝∠2．（2）如图②所示⊙M为所求．①①作∠ABC平分线交AC于F点，②作BF的垂直平分线交AB于M，以MB为半径作圆，即⊙M为所求．证明：∵M在BF的垂直平分线上，∴MF＝MB，∴∠MBF＝∠MFB，又∵BF平分∠ABC，∴∠MBF＝∠CBF，∴∠CBF＝∠MFB，∴MF∥BC，∵∠C＝90°，∴FM⊥AC，∴⊙M与边AC相切．【点评】本题主要考查圆和切线的性质和基本作图的综合应用．掌握连接圆心和切点的半径与切线垂直是解题的关键，3. （2019•江西•6分）在△ABC中，AB=AC，点A在以BC为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图（保留作图痕迹）.（1）在图1中作弦EF，使EF//BC；（2）在图2中以BC为边作一个45°的圆周角.F（1）EF就是所求作的弦；（2）角BCQ或角CBQ就是所求作的角。

2019 年全国中考数学真题分类汇编：尺规作图、选择题1. （2019 年北京市）已知锐角∠ AOB 如图，（1）在射线OA 上取一点C，以点O 为圆心，OC长为半径作弧PQ，交射线OB 于点D，连接CD；2）分别以点C，D 为圆心，CD 长为半径作弧，交弧PQ 于点M，N；3）连接OM，MN ．根据以上作图过程及所作图形，下列结论中错误的是（）A.∠COM= ∠CODB.若 OM=MN ，则∠ AOB=20°C.MN ∥CDD.MN=3CD【考点 】尺规作图【解答 】连接 ON ，由作图可知 △COM ≌△ DON.A. 由△COM ≌△DON.，可得∠ COM= ∠COD ，故 A正确.B. 若 OM=MN ，则 △OMN 为等边三角形，由全等可知∠ COM= ∠COD= ∠DON=2°0 ，故 B 正确180 CODC.由题意， OC=OD ，∴∠ OCD= .设 OC2 180 与 OD 与MN 分别交于 R ，S ，易证△ MOR ≌△ NOS ，则OR=OS ，∴∠ ORS= 2∴∠ OCD= ∠ORS.∴MN ∥CD ，故 C 正确.D.由题意，易证 MC=CD=DN ，∴ MC+CD+DN=3CD. ∵两点之间线段最短 .∴MN < MC+CD+DN=3CD ，故选 D2. （2019 年河南省）如图，在四边形 ABCD 中， AD ∥ BC ，∠D ＝90°，AD ＝4，BC ＝3．分 别以点 A ， C 为圆心，大于 C 长为半径作弧，两弧交于点 交 AC 于点 O ．若点 O 是 AC 的中点，则 CD 的长为（ ）A ．2B ．4C ． 3D ．【考点 】尺规作图、 线段垂直平分线的判定与性质、 勾股定理、 全等三角形的判定与性质【解答 】解：如图，连接 FC ，则 AF ＝FC ．∵AD ∥ BC ，∴∠ FAO ＝∠ BCO ．在 △FOA 与 △BOC 中，COD ，E ，作射线 BE 交 AD 于点F ，A ．正方形B ．矩形C ．梯形D ．菱形考点 】尺规作图、菱形的判定解答 】解：由作图可知： AC ＝ AD ＝BC ＝ BD ，∴四边形ACBD 是菱形，故选： D．通过如下尺规作图，能确定点 D是BC 边中点的是（，∴△ FOA ≌△ BOC （ ASA ），∴AF ＝BC ＝3，∴FC ＝ AF ＝3，FD ＝AD ﹣AF ＝4﹣3＝1． 在△FDC 中，∵∠ D ＝90°， ∴CD 2+DF 2＝FC 2，∴CD 2+12＝32，∴CD ＝2 ．故选： A ．3. （ 2019年湖北省襄阳市）如图，分别以线段 AB 的两个端点为圆心，大于 AB 的一半的长为半径画弧，两弧分别交于 C ，D 两点，连接 AC ，BC ，AD ，BD ，则四边形 ADBC 一定 是（ ）4. （2019 年湖北省宜昌市） C ． D ．考点】尺规作图解答】解：作线段BC 的垂直平分线可得线段BC 的中点．由此可知：选项 A 符合条件，故选： A ．5. （2019年内蒙古包头市）如图，在Rt△ABC 中，∠ B＝90°，以点A为圆心，适当长为半径画弧，分别交AB、AC 于点D，E，再分别以点D、E为圆心，大于DE 为半径画弧，两弧交于点F，作射线AF 交边BC 于点G，若BG＝1，AC＝4，则△ACG 的面积是（）A ．BP 是∠ ABC 的平分线B．AD ＝BDC ．S△CBD：S△ ABD＝1： 3 D．CD＝BD考点】尺规作图-角的平分线A ．1 B．C． 2考点】尺规作图-角的平分线解答】解：由作法得AG 平分∠ BAC，∴G点到AC的距离等于BG 的长，即G 点到AC 的距离为1，所以△ACG 的面积＝×4×1＝2．故选： C ．D．6. （2019 年新疆）如图，在△ ABC 中，∠ C＝90°，∠ A＝30°，以点 B 为圆心，适当长为半径画弧，分别交BA，BC于点M，N；再分别以点M，N 为圆心，大于MN 的长为半径画弧，两弧交于点P，作射线BP 交AC 于点D．则下列说法中不正确的是（）解答】解：由作法得BD 平分∠ ABC，所以 A 选项的结论正确；∵∠ C＝90°，∠ A＝30∴∠ ABC＝60°，∴∠ ABD＝30°＝∠ A，∴AD＝BD，所以 B 选项的结论正确；∵∠ CBD＝∠ ABC＝30°，∴BD＝2CD，所以 D 选项的结论正确；∴AD＝2CD，∴ S△ABD＝2S△CBD，所以 C 选项的结论错误．故选： C ．二、填空题1. （2019 年辽宁省本溪市）如图，BD 是矩形ABCD 的对角线，在BA 和BD 上分别截取BE，BF，使BE＝BF；分别以E，F为圆心，以大于EF的长为半径作弧，两弧在∠ ABD 内交于点G，作射线BG 交AD 于点P，若AP＝3，则点P到BD 的距离为．考点】尺规作图解答】解：结合作图的过程知：BP平分∠ ABD，∵∠ A＝90°，AP＝3，∴点P到BD 的距离等于AP的长，为3，故答案为：3．1. （2019 年山东省菏泽市）如图，四边形ABCD 是矩形．（1）用尺规作线段AC的垂直平分线，交AB于点E，交CD于点F（不写作法，保留作图痕迹）；（2）若BC ＝4，∠ BAC＝30°，求BE 的长．考点】尺规作图、垂直平分线解答】解：（1）如图所示：（2）∵四边形ABCD 是矩形，EF 是线段AC 的垂直平分线，∴ AE＝EC ，∠ CAB ＝∠ ACE＝30°，∴∠ ECB＝60°，∴∠ ECB＝30°，∵BC＝4，∴ BE＝．2. （2019年山东省济宁市）如图，点M 和点N在∠ AOB 内部．（1）请你作出点P，使点P到点M和点N的距离相等，且到∠ AOB 两边的距离也相等（保留作图痕迹，不写作法）；（2）请说明作图理由．考点】作角平分线、作线段垂直平分线解答】解：（1）如图，点P到点M和点N的距离相等，且到∠ AOB两边的距离也相等；（2）理由：角的平分线上的点到角的两边的距离相等、直平分线上的点到线段两端点的3. （2019 年山东省青岛市）请用直尺、圆规作图，不写作法，但要保留作图痕迹．已知：∠α，直线l 及l 上两点A，B．考点】尺规作图解答】解：如图，△ ABC 为所作．4. （2019 年山东省枣庄市）如图，BD 是菱形ABCD 的对角线，∠ CBD＝75°，（1）请用尺规作图法，作AB的垂直平分线EF ，垂足为E，交AD 于F；（不要求写作法，保留作图痕迹）（2）在（1）条件下，连接BF，求∠ DBF 的度数．考点】尺规作图-线段的垂直平分线、菱形的性质解答】解：（1）如图所示，直线EF 即为所求；（2）∵四边形ABCD 是菱形，∴∠ ABD＝∠ DBC＝∠ABC＝75°，DC∥AB，∠ A＝∠C．∴∠ ABC＝150°，∠ ABC+∠C＝180°，∴∠ C＝∠ A＝30°，∵ EF 垂直平分线段AB，∴AF＝FB，∴∠ A＝∠ FBA ＝30°，∴∠ DBF ＝∠ ABD﹣∠ FBE＝455. （2019 年四川省达州市）如图，在Rt△ABC 中，∠ ACB＝90°，AC＝2，BC＝3．1）尺规作图：不写作法，保留作图痕迹．① 作∠ ACB 的平分线，交斜边AB 于点 D ；② 过点 D 作BC 的垂线，垂足为点 E ．（2）在（1）作出的图形中，求DE 的长．考点】尺规作图-角的平分线、相似三角形解答】解：（1）如图，DE 为所作；（2）∵CD 平分∠ ACB，∴∠ BCD＝∠ ACB＝45°，∵DE⊥ BC，∴△CDE 为等腰直角三角形，∴DE＝CE，∵DE∥ AC，∴△ BDE ∽△ BAC ，＝，即＝．6. （2019 年广西贵港市）尺规作图（只保留作图痕迹，不要求写出作法）：如图，已知△ABC，请根据“SAS”基本事实作出△DEF ，使△DEF≌△ABC．△ABC 中，∠ C=900，AC=4, BC=8,（1）用直尺和圆规作AB 的垂直平分线;（保留作图痕迹,不要求写作法）（2）若（1）中所作的垂直平分线交BC 于点D,求BD 的长.解答】解：（1）略；2）由作图可知AD ＝BD，设BD= x，∵∠ C=900，AC=4, BC=8，则CD＝（8- x），∴由勾股定理可得：AC 2+CD 2=AD 2;∴42+x2=（8-x）2;考点】尺规作图-线段的垂直平分线、勾股定理∴DE＝7. （2019 年江苏省泰州市）如图，、全等三角形的判定解得：x＝ 5.∴ BD ＝ 5.8. （2019年陕西省）如图，在△ABC中，AB＝AC，AD是BC边上的高，请用尺规作图法，求作△ ABC 的外接圆．（保留作图痕迹，不写作法）得点M 到AB 和AC 两边的距离相等，并且到点B和点P 的距离相等．（不写作法，保留考点】尺规作图-角平分线解答】解：如图，点M 即为所求，10. （2019 年甘肃省武威市）已知：在△ ABC 中，AB＝AC．（1）求作：△ ABC 的外接圆．（要求：尺规作图，保留作图痕迹，不写作法）（2）若△ ABC的外接圆的圆心O到BC边的距离为4，BC＝6，则S⊙O＝考点】尺规作图-线段的垂直平分线解答】9. 2019 年甘肃省）如图，在△ ABC 中，点P 是AC 上一点，连接BP，求作一点M ，使作图痕迹）考点】尺规作图-角平分线、等腰三角形的性质、三角形的外接圆与外心解答】解：（1）如图⊙O 即为所求．（2）设线段BC 的垂直平分线交BC 于点E．由题意OE＝4，BE＝EC＝3，在Rt△ OBE 中，OB ＝＝5，2∴S 圆O＝π?5 ＝25π．故答案为25π．11. （2019 年内蒙古赤峰市）已知：AC 是? ABCD 的对角线．（1）用直尺和圆规作出线段AC 的垂直平分线，与AD 相交于点E，连接CE．（保留作图痕迹，不写作法）；（2）在（1）的条件下，若AB＝3，BC＝5，求△ DCE的周长．考点】尺规作图-垂直平分线、平行四边形的性质解答】解：（1）如图，CE 为所作；（2）∵四边形ABCD 为平行四边形，∴AD＝BC＝5，CD＝AB＝3，∵点E在线段AC 的垂直平分线上，∴EA＝EC，∴△ DCE 的周长＝CE+DE+CD＝EA+DE+CD＝AD+CD ＝5+3＝8．。

中考数学专题练习《尺规作图》【知识归纳】一）尺规作图1．定义只用没有刻度的和作图叫做尺规作图．2．步骤①根据给出的条件和求作的图形，写出已知和求作部分；②分析作图的方法和过程；③用直尺和圆规进行作图；④写出作法步骤，即作法．二）五种基本作图1．作一条线段等于已知线段；2．作一个角等于已知角；3．作已知角的平分线；4．过一点作已知直线的垂线；5．作已知线段的垂直平分线．三）基本作图的应用1．利用基本作图作三角形(1)已知三边作三角形；(2)已知两边及其夹角作三角形；(3)已知两角及其夹边作三角形；(4)已知底边及底边上的高作等腰三角形；(5)已知一直角边和斜边作直角三角形．2．与圆有关的尺规作图(1)过不在同一直线上的三点作圆(即三角形的外接圆)．(2)作三角形的内切圆．【基础检测】1．如图，在平面直角坐标系中，以O 为圆心，适当长为半径画弧，交x 轴于点M ，交y 轴于点N ，再分别以点M 、N 为圆心，大于MN 的长为半径画弧，两弧在第二象限交于点P ．若点P 的坐标为（2a ，b +1），则a 与b 的数量关系为（ ）A ．a =bB ．2a +b =﹣1C ．2a ﹣b =1D ．2a +b =12.如图，已知△ABC ，以点B 为圆心，AC 长为半径画弧；以点C 为圆心，AB 长为半径画弧，两弧交于点D ，且点A ，点D 在BC 异侧，连结AD ，量一量线段AD 的长，约为（ ）A ．2.5cmB ．3.0cmC ．3.5cmD ．4.0cm3.如图，已知△ABC ，∠BAC=90°，请用尺规过点A 作一条直线，使其将△ABC 分成两个相似的三角形（保留作图痕迹，不写作法）4.如图，在边长为1的正方形网格中，△ABC 的顶点均在格点上，点A 、B 的坐标分别是A （4，3）、B （4，1），把△ABC 绕点C 逆时针旋转90°后得到△A 1B 1C ．（1）画出△A 1B 1C ，直接写出点A 1、B 1的坐标；（2）求在旋转过程中，△ABC 所扫过的面积．5．如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了四边形ABCD 的两条边AB 与BC ，且四边形ABCD 是一个轴对称图形，其对称轴为直线AC ．（1）试在图中标出点D ，并画出该四边形的另两条边；（2）将四边形ABCD 向下平移5个单位，画出平移后得到的四边形A′B′C′D′．6．已知：线段a 及∠ACB ．求作：⊙O ，使⊙O 在∠ACB 的内部，CO=a ，且⊙O 与∠ACB 的两边分别相切．7．如图，OA=2，以点A 为圆心，1为半径画⊙A 与OA 的延长线交于点C ，过点A 画OA 的垂线，垂线与⊙A 的一个交点为B ，连接BC（1）线段BC 的长等于 ； （2）请在图中按下列要求逐一操作，并回答问题：A B C①以点为圆心，以线段的长为半径画弧，与射线BA交于点D，使线段OD的长等于②连OD，在OD上画出点P，使OP得长等于，请写出画法，并说明理由．【达标检测】一、选择题1．如图，在△ABC中，∠B=55°，∠C=30°，分别以点A和点C为圆心，大于AC的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为（）A．65°B．60°C．55°D．45°2.如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹.步骤1：以C为圆心，CA为半径画弧○1；步骤2：以B为圆心，BA为半径画弧○2，将弧○1于点D；步骤3：连接AD，交BC延长线于点H.下列叙述正确的是（）第10题图A．BH垂直分分线段AD B．AC平分∠BAD=BC·AH D．AB=ADC．S△ABC二、填空题3.如图，已知线段AB，分别以点A和点B为圆心，大于AB的长为半径作弧，两弧相交于C、D 两点，作直线CD交AB于点E，在直线CD上任取一点F，连接FA，FB．若FA=5，则FB=．4.如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的是。

2019年中考数学分类汇编（尺规作图）
各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢
一、选择题 1.如图，已知在Rt△ABC 中，∠ABC=90°，点D是BC边的中点，分别以B、C为圆心，大于线段BC长度一半的长为半径圆弧，两弧在直线BC 上方的交点为P，直线PD交AC于点E，连接BE，则下列结论：①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=AB 中，一定正确的是 A.①②③B.①②④C.
①③④D.②③④分析：根据作图过程得到PB=PC，然后利用D为BC的中点，得到PD垂直平分BC，从而利用垂直平分线的性质对各选项进行判断即可. 解：根据作图过程可知：PB=CP，∵D为BC 的中点，∴PD垂直平分BC，∴①ED ⊥BC正确;∵∠ABC=90°，∴PD∥AB，∴E为AC的中点，∴EC=EA，∵EB=EC，
∴②∠A=∠EBA正确;③EB平分∠AED 错误;④ED=AB正确，故正确的有①②④，故选B. 点评：本题考查了基本作图的知识，解题的关键是了解如何作已知线段的垂直平分线，难度中等. 二.填空题1.如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C 均落在格点上.
各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢。

中考尺规作图专题复习（含答案）尺规作图定义：用无刻度的直尺和圆规画图，中考中常见画的图是线段的垂线，垂直平分线，角平分线、画等长的线段，画等角。

1.直线垂线的画法：【分析】：以点C为圆心，任意长为半径画弧交直线与A，B两点，再分别以点A，B为圆心，大于12AB的长为半径画圆弧，分别交直线l两侧于点M，N，连接MN，则MN即为所求的垂线2.线段垂直平分线的画法【分析】：作法如下：分别以点A，B为圆心，大于12AB的长为半径画圆弧，分别交直线AB两侧于点C，D，连接CD，则CD即为所求的线段AB的垂直平分线.3.角平分线的画法【分析】1.选角顶点O为圆心，任意长为半径画圆，分别交角两边A，B点，再分别以A，B为圆心，大于12AB的长为半径画圆弧，交H点，连接OH，并延长，则射线OH即为所求的角平分线.4.等长的线段的画法直接用圆规量取即可。

5.等角的画法【分析】以O为圆心，任意长为半径画圆，交原角的两边为A,B两点，连接AB；画一条射线l，以上面的那个半径为半径，l的顶点K为圆心画圆，交l与L，以L为圆心，AB 为半径画圆，交以K为圆心，KL为半径的圆与M点，连接KM，则角LKM即为所求.备注：1.尺规作图时，直尺主要用作画直线，射线，圆规主要用作截取相等线段和画弧；2.求作一个三角形，其实质是依据三角形全等的基本事实或判定定理来进行的；3.当作图要满足多个要求时，应逐个满足，取公共部分.例题讲解例题1.已知线段a，求作△ABC，使AB=BC=AC=a.解：作法如下:①作线段BC=a；（先作射线BD，BD截取BC=a）.②分别以B、C为圆心，以a半径画弧，两弧交于点A；③连接AB、AC.则△ABC 要求作三角形.例2.已知线段a 和∠α，求作△ABC ，使AB=AC=a ，∠A=∠α.解：作法如下：①作∠MAN=∠α；②以点A 为圆心，a 为半径画弧，分别交射线AM ，AN 于点B ，C. ③连接B ，C.△ABC 即为所求作三角形.例3.(深圳中考)如图，已知△ABC ，AB <BC ，用尺规作图的方法在BC 上取一点P ，使得PA ＋PC ＝BC ，则下列选项中，正确的是(D )【解析】由题意知，做出AB 的垂直平分线和BC 的交点即可。

2019中考数学专题复习之作图问题（附答案详解）类型1 尺规作图1．在数学课本上，同学们已经探究过“经过已知直线外一点作这条直线的垂线”的尺规作图过程：已知：直线l 和l 外一点P.求作：直线l 的垂线，使它经过点P.作法：如图：(1)在直线l 上任取两点A 、B ；(2)分别以点A 、B 为圆心，AP ，BP 长为半径画弧，两弧相交于点Q ；(3)作直线PQ.参考以上材料作图的方法，解决以下问题：(1)以上材料作图的依据是：______________________________________________(2)已知：直线l 和l 外一点P.求作：⊙P ，使它与直线l 相切．(尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔描黑)解：(1)到线段两端点距离相等的点在这条线段的垂直平分线上(2)如图⊙P 即为所求．2．如图，MN 是⊙O 的直径，MN ＝4，点A 在⊙O 上，∠AMN ＝30°，B 为AN ︵的中点，P 是直径MN 上一动点．(1)利用尺规作图，确定当PA ＋PB 最小时P 点的位置(不写作法，但要保留作图痕迹)．(2)求PA ＋PB 的最小值．解：(1)如图1所示，点P 即为所求；(2)由(1)可知，PA ＋PB 的最小值即为A′B 的长，连接OA′、OB 、OA ，∵A′点为点A 关直线MN 的对称点，∠AMN ＝30°，∴∠AON ＝∠A′ON ＝2∠AMN ＝2×30°＝60°，又∵B 为AN ︵的中点，∴AB ︵＝BN ︵，∴∠BON ＝∠AOB ＝12∠AON ＝30°，∴∠A′OB ＝60°＋30°＝90°，又∵MN ＝4，∴OA′＝OB ＝12MN ＝12×4＝2.∴在Rt △A′OB 中，A′B ＝22，∴PA ＋PB 的最小值为2 2.3．如图，已知△ABC ，∠B ＝40°.(1)在图中，用尺规作出△ABC 的内切圆O ，并标出⊙O 与边AB ，BC ，AC 的切点D ，E ，F(保留痕迹，不必写作法)；(2)连接EF ，DF ，求∠EFD 的度数．解：(1)如图1，⊙O 即为所求．(2)如图2，连接OD ，OE ，∴OD ⊥AB ，OE ⊥BC ，∴∠ODB ＝∠OEB ＝90°，∵∠B ＝40°，∴∠DOE ＝140°，∴∠EFD ＝70°.4．小明在“课外新世界”中遇到这样一道题：如图1，已知∠AOB ＝30°与线段a ，你能作出边长为a 的等边三角形△COD 吗？小明的做法是：如图2，以O 为圆心，线段a 为半径画弧，分别交OA ，OB 于点M ，N ，在弧MN 上任取一点P ，以点M 为圆心，MP 为半径画弧，交弧CD 于点C ，同理以点N 为圆心，NP 为半径画弧，交弧CD 于点D ，连结CD ，即△COD 就是所求的等边三角形．(1)请写出小明这种做法的理由；(2)在此基础上请你作如下操作和探究(如图3)：连结MN ，MN 是否平行于CD ？为什么？(3)点P 在什么位置时，MN ∥CD ？请用小明的作图方法在图1中作出图形(不写作法，保留作图痕迹)．解：(1)如图2，连结OP ，由题意可得MC ︵＝MP ︵，∴∠COM ＝∠POM ，PN ︵＝DN ︵，∴∠PON＝∠DON ，∴∠POM ＋∠PON ＝∠COM ＋∠DON ＝30°，∴∠COD ＝2∠MON ＝60°，∴△OCD 是等边三角形；(2)不一定，只有当∠COM ＝15°，CD ∥MN ，理由：∵∠COM ＝15°，∠MON ＝30°，∴∠CON ＝45°，∵∠C ＝60°，∴∠OEC ＝75°，∵ON ＝OM ，∴∠ONM＝∠OMN ＝75°，∴∠OEC ＝∠ONM ，∴CD ∥MN ；(3)当P 是MN ︵的中点时，MN ∥CD ；如图3所示．类型2 网格作图和其他5．如图，在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点)，如果以A 为圆心，r 为半径画圆，选取的格点中除点A 外恰好有3个在圆内，则r 的取值范围为( B )A．22＜r＜17 B.17＜r＜3 2C.17＜r＜5 D．5＜r＜29解：给各点标上字母，如图所示．AB＝22＋22＝22，AC＝AD＝42＋12＝17，AE ＝32＋32＝32，AF＝52＋22＝29，AG＝AM＝AN＝42＋32＝5，∴17＜r＜32时，除点A外恰好有3个在圆内．6．我们约定，若一个三角形(记为△A1)是由另一个三角形(记为△A)通过一次平移，或绕其任一边的中点旋转180°得到的，则称△A1是由△A复制的．以下的操作中每一个三角形只可以复制一次，复制过程可以一直进行下去．如图1，由△A复制出△A1，又由△A1复制出△A2，再由△A2复制出△A3，形成了一个大三角形，记作△B.以下各题中的复制均是由△A开始的，通过复制形成的多边形中的任意相邻两个小三角形(指与△A全等的三角形)之间既无缝隙也无重叠．(1)图1中标出的是一种可能的复制结果，小明发现△A∽△B，其相似比为__1∶2__．在图1的基础上继续复制下去得到△C，若△C的一条边上恰有11个小三角形(指有一条边在该边上的小三角形)，则△C中含有__121__个小三角形；(2)若△A是正三角形，你认为通过复制能形成的正多边形是__正三角形或正六边形__；(3)请你用两次旋转和一次平移复制形成一个四边形，在图2的方框内画出草图，并仿照图1作出标记．解析：(1)△A－△A1是经过旋转所得，△A1－△A2是经过旋转所得，△A2－△A3是经过平移所得．由于△B是由4个△A组成，因此S△B＝4S△A，因此相似比为2∶1.当△C的一条边上有11个小三角形时，那么它们的相似比为11∶1，面积比121∶1，即△C中有121个这样的小三角形；故答案为：1∶2，121.(2)正三角形或正六边形．(3)如图．7．阅读理解：如图①，在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合)，分别连接ED 、EC ，可以把四边形ABCD 分成三个三角形，如果其中有两个三角形相似，我们就把点E 叫做四边形ABCD 的边AB 上的相似点；如果这三个三角形都相似，我们就把点E 叫做四边形ABCD 的边AB 上的强相似点．解决问题：(1)如图①，∠A ＝∠B ＝∠DEC ＝55°，试判断点E 是否是四边形ABCD 的边AB 上的相似点，并说明理由；(2)如图②，在矩形ABCD 中，AB ＝5，BC ＝2，且A ，B ，C ，D 四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上，试在图②中画出矩形ABCD 的边AB 上的一个强相似点E ；拓展探究：(3)如图③，将矩形ABCD 沿CM 折叠，使点D 落在AB 边上的点E 处，若点E 恰好是四边形ABCM 的边AB 上的一个强相似点，试探究AB 和BC 的数量关系．解：(1)点E 是四边形ABCD 的边AB 上的相似点．理由：∵∠A ＝55°，∴∠ADE ＋∠DEA ＝125°，∵∠DEC ＝55°，∴∠BEC ＋∠DEA ＝125°，∴∠ADE ＝∠BEC.∵∠A ＝∠B ，∴△ADE ∽△BEC.∴点E 是四边形ABCD 的AB 边上的相似点．(2)如图如下：(3)∵点E 是四边形ABCD 的边AB 上的一个强相似点，∴△AEM ∽△BCE ∽△ECM ，∴∠BCE ＝∠ECM ＝∠AEM ，由折叠可知：△ECM ≌△DCM ，∴∠ECM ＝∠DCM ，CE ＝CD ，∴∠BCE ＝13∠BCD ＝30°，∴BE ＝12CE ＝12AB.在Rt △BCE 中，tan ∠BCE ＝BE BC＝tan 30°，∴BE BC ＝33，∴AB BC ＝233.。

2019年全国中考试题解析版分类汇编-尺规作图注意事项：认真阅读理解，结合历年的真题，总结经验，查找不足！重在审题，多思考，多理解！【一】选择题1.〔2017•台湾33，4分〕如图，AB为圆O的直径，在圆O上取异于A、B的一点C，并连接BC、AC、假设想在AB上取一点P，使得P与直线BC的距离等于AP长，判断以下四个作法何者正确？〔〕A、作的中垂线，交于P点B、作∠ACB的角平分线，交于P点C、作∠ABC的角平分线，交于D点，过D作直线BC平行线，交于P点D、过A作圆O的切线，交直线BC于D点，作∠ADC的角平分线，交于P点考点：切线的性质；角平分线的性质。

分析：A圆内弦中垂线过原点；角平分线上点到到两边距离相等；角平分线上点到两边距离相等；D角平分线上点到两边距离相等，与切线与过切点的直径垂直、从而判断出来、解答：解：A、圆内弦的中垂线过原点，有圆内弦性质可知，所以交AB于圆点O，故本选项错误；B、作∠ACB的角平分线，那么点P到BC的距离等于点P到AC的距离，而不等于AP，故本选项错误；C、假设过点D作直线BC的平行线交AB于点P，那么点P的距离，等于DP也不等于AP，故本选项错误；D、角平分线DP交直径AB与点P，根据角平分线定理，由PA⊥AD，得到点P到BC的距离等于AP，故正确、点评：此题考查了切线的性质，A考查了圆内弦中垂线过原点；B考查了角平分线上点到到两边距离相等；C考查了角平分线上点到两边距离相等；D考查了角平分线上点到两边距离相等，与切线与过切点的直径垂直、2.〔2017湖北荆州，15，3分〕请将含60°顶角的菱形分割成至少含一个等腰梯形且面积相等的六部分，用实线画出分割后的图形、答案不唯一、考点：作图—应用与设计作图、专题：作图题、分析：整个图形含有36个小菱形，分为面积相等的六部分，那么每一个部分含6个小菱形，由此设计分割方案、解答：解：分割后的图形如下图、此题答案不唯一、点评：此题考查了应用与设计作图、关键是理解题意，根据图形设计分割方案、3.〔2017•西宁〕用直尺和圆规作一个菱形，如图，能得到四边形ABCD是菱形的依据是〔〕A、一组临边相等的四边形是菱形B、四边相等的四边形是菱形C、对角线互相垂直的平行四边形是菱形D、每条对角线平分一组对角的平行四边形是菱形考点：菱形的判定；作图—复杂作图。

（2022•舟山中考）用尺规作一个角的角平分线，下列作法中错误的是（）A．B．C．D．【解析】选D．由图可知，选项A、B、C中的线都可以作为角平分线；选项D中的图作出的是平行四边形，不能保证角中间的线是角平分线.（2022•威海中考）过直线l外一点P作直线l的垂线PQ．下列尺规作图错误的是（）A．B．C．D．【解析】选C．选项A，连接P A，PB，QA，QB，因为P A＝PB，所以点P在线段AB的垂直平分线上，因为QA＝QB，所以点Q在线段AB的垂直平分线上，所以PQ⊥l，故此选项不符合题意；选项B，连接P A，PB，QA，QB，因为P A＝QA，所以点A在线段PQ的垂直平分线上，因为PB＝QB，所以点B在线段PQ的垂直平分线上，所以PQ⊥l，故此选项不符合题意；选项C，无法证明PQ⊥l，故此选项符合题意；选项D，连接P A，PB，QA，QB，因为P A＝QA，所以点A在线段PQ的垂直平分线上，因为PB＝QB，所以点B在线段PQ的垂直平分线上，所以PQ⊥l，故此选项不符合题意．（2022•天津中考）如图，在每个小正方形的边长为1的网格中，圆上的点A，B，C及∠DPF的一边上的点E，F均在格点上．（Ⅰ）线段EF的长等于√10；（Ⅱ）若点M，N分别在射线PD，PF上，满足∠MBN＝90°且BM＝BN．请用无刻度的直尺，在如图所示的网格中，画出点M，N，并简要说明点M，N的位置是如何找到的（不要求【解析】）连接AC，与网格线交于点O，取格点Q，连接EQ交PD于点M，连接BM交⊙O于点⊙，连接GO，延长GO交⊙O于点H，连接BH，延长BH交PF于点N，则点M，N即为所求．【解析】（Ⅰ）EF=√12+32=√10．答案：√10；（Ⅱ）如图，点M，N即为所求．步骤：连接AC，与网格线交于点O，取格点Q，连接EQ交PD于点M，连接BM交⊙O于点⊙，连接GO，延长GO 交⊙O于点H，连接BH，延长BH交PF于点N，则点M，N即为所求．答案：连接AC，与网格线交于点O，取格点Q，连接EQ交PD于点M，连接BM交⊙O于点⊙，连接GO，延长GO 交⊙O于点H，连接BH，延长BH交PF于点N，则点M，N即为所求甲乙丙为定直角．以乙为圆心，以任何半径作丁戊弧；以丁为圆心，以乙丁为半径画弧得交点己；再以戊为圆心，仍以原半径画弧得交点庚；乙与己及庚相连作线．如图2，∠ABC为直角，以点B为圆心，以任意长为半径画弧，交射线BA，BC分别于点D，E；以点D为圆心，以BD长为半径画弧与DÊ交于点F；再以点E为圆心，仍以BD长为半径画弧与DÊ交于点G；作射线BF，BG．（1）根据以上信息，请你用不带刻度的直尺和圆规，在图2中完成这道作图题（保留作图痕迹，不写作法）；（2）根据（1）完成的图，直接写出∠DBG，∠GBF，∠FBE的大小关系．【解析】（1）如图，射线BG，BF即为所求．（2）∠DBG＝∠GBF＝∠FBE．理由：连接DF，EG，则BD＝BF＝DF，BE＝BG＝EG，即△BDF和△BEG均为等边三角形，所以∠DBF＝∠EBG＝60°，因为∠ABC＝90°，所以∠DBG＝∠GBF＝∠FBE＝30°．【解析】（1）如图1中，射线BP即为所求；（2）如图2中，直线l即为所求．（2022•扬州中考）【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积？【初步尝试】如图1，已知扇形OAB，请你用圆规和无刻度的直尺过圆心O作一条直线，使扇形的面积被这条直线平分；【问题联想】如图2，已知线段MN，请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP；【问题再解】如图3，已知扇形OAB，请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧，使扇形的面积被这条圆弧平分．（友情提醒：以上作图均不写作法，但需保留作图痕迹）【解析】【初步尝试】如图1，直线OP即为所求；【问题联想】如图2，三角形MNP即为所求；̂即为所求．【问题再解】如图3中，CD【解析】（1）如图，（2）AE ＝CF ，证明如下：因为四边形ABCD 是矩形，所以AD ∥BC ，所以∠EAO ＝∠FCO ，∠AEO ＝∠CFO ，因为EF 是AC 的垂直平分线，所以AO ＝CO ，在△AOE 和△COF 中，{∠AEO =∠CFO∠EAO =∠FCO AO =CO，所以△AOE ≌△COF （AAS ），所以AE ＝CF.（2022•陕西中考）如图，已知△ABC ，CA ＝CB ，∠ACD 是△ABC 的一个外角．请用尺规作图法，求作射线CP ，使CP ∥AB ．（保留作图痕迹，不写作法）【解析】如图，射线CP 即为所求．（2022•无锡中考）如图，△ABC 为锐角三角形．（1）请在图1中用无刻度的直尺和圆规作图：在AC 右上方确定点D ，使∠DAC ＝∠ACB ，且CD ⊥AD ；（不写作法，保留作图痕迹）（2）在（1）的条件下，若∠B ＝60°，AB ＝2，BC ＝3，则四边形ABCD 的面积为 5 ．【解析】（1）如图1中，点D 即为所求；（2）过点A作AH⊥BC于点H．在Rt△ABH中，AB＝2，∠B＝60°，所以BH＝AB•cos60°＝1，AH＝AB•sin60°=√3，所以CH＝BC﹣BH＝2，因为∠DAC＝∠ACB，所以AD∥BC，因为AH⊥CB，CD⊥AD，所以∠AHC＝∠ADC＝∠DCH＝90°，所以四边形AHCD是矩形，所以AD＝CH＝2，所以S四边形ABCD=12×（2+3）×2＝5，答案：5（2022•仙桃中考）已知四边形ABCD为矩形，点E是边AD的中点，请仅用无刻度的直尺完成下列作图，不写作法，保留作图痕迹．（1）在图1中作出矩形ABCD的对称轴m，使m∥AB；（2）在图2中作出矩形ABCD的对称轴n，使n∥AD．【解析】（1）如图1中，直线m即为所求；（2）如图2中，直线n即为所求；（1）尺规作图：用直尺和圆规作出△ABC内切圆的圆心O．（只保留作图痕迹，不写作法和证明）（2）如果△ABC的周长为14cm，内切圆的半径为1.3cm，求△ABC的面积．【解析】（1）如图，点O即为所求；（2）由题意，△ABC的面积=12×14×1.3＝9.1（cm2）．。

2019中考数学试题分类汇编：考点32 尺规作图一．选择题（共13小题）1．（2019•襄阳）如图，在△ABC中，分别以点A和点C为圆心，大于AC长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E．若AE=3cm，△ABD的周长为13cm，则△ABC的周长为（）A．16cm B．19cm C．22cm D．25cm【分析】利用线段的垂直平分线的性质即可解决问题．【解答】解：∵DE垂直平分线段AC，∴DA=DC，AE=EC=6cm，∵AB+AD+BD=13cm，∴AB+BD+DC=13cm，∴△ABC的周长=AB+BD+BC+AC=13+6=19cm，故选：B．2．（2019•河北）尺规作图要求：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作线段的垂直平分线；Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线．如图是按上述要求排乱顺序的尺规作图：则正确的配对是（）A．①﹣Ⅳ，②﹣Ⅱ，③﹣Ⅰ，④﹣ⅢB．①﹣Ⅳ，②﹣Ⅲ，③﹣Ⅱ，④﹣ⅠC．①﹣Ⅱ，②﹣Ⅳ，③﹣Ⅲ，④﹣ⅠD．①﹣Ⅳ，②﹣Ⅰ，③﹣Ⅱ，④﹣Ⅲ【分析】分别利用过直线外一点作这条直线的垂线作法以及线段垂直平分线的作法和过直线上一点作这条直线的垂线、角平分线的作法分别得出符合题意的答案．【解答】解：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作线段的垂直平分线；Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线．如图是按上述要求排乱顺序的尺规作图：则正确的配对是：①﹣Ⅳ，②﹣Ⅰ，③﹣Ⅱ，④﹣Ⅲ．故选：D．3．（2019•河南）如图，已知▱AOBC的顶点O（0，0），A（﹣1，2），点B在x轴正半轴上按以下步骤作图：①以点O为圆心，适当长度为半径作弧，分别交边OA，OB于点D，E；②分别以点D，E为圆心，大于DE的长为半径作弧，两弧在∠AOB内交于点F；③作射线OF，交边AC于点G，则点G的坐标为（）A．（﹣1，2）B．（，2）C．（3﹣，2）D．（﹣2，2）【分析】依据勾股定理即可得到Rt△AOH中，AO=，依据∠AGO=∠AOG，即可得到AG=AO=，进而得出HG=﹣1，可得G（﹣1，2）．【解答】解：∵▱AOBC的顶点O（0，0），A（﹣1，2），∴AH=1，HO=2，∴Rt△AOH中，AO=，由题可得，OF平分∠AOB，∴∠AOG=∠EOG，又∵AG∥OE，∴∠AGO=∠EOG，∴∠AGO=∠AOG，∴AG=AO=，∴HG=﹣1，∴G（﹣1，2），故选：A．4．（2019•宜昌）尺规作图：经过已知直线外一点作这条直线的垂线，下列作图中正确的是（）A．B．C．D．【分析】根据过直线外一点向直线作垂线即可．【解答】已知：直线AB和AB外一点C．求作：AB的垂线，使它经过点C．作法：（1）任意取一点K，使K和C在AB的两旁．（2）以C为圆心，CK的长为半径作弧，交AB于点D和E．（3）分别以D和E为圆心，大于DE的长为半径作弧，两弧交于点F，（4）作直线CF．直线CF就是所求的垂线．故选：B．5．（2019•潍坊）如图，木工师傅在板材边角处作直角时，往往使用“三弧法”，其作法是：（1）作线段AB，分别以A，B为圆心，以AB长为半径作弧，两弧的交点为C；（2）以C为圆心，仍以AB长为半径作弧交AC的延长线于点D；（3）连接BD，BC．下列说法不正确的是（）A．∠CBD=30°B．S△BDC=AB2C．点C是△ABD的外心D．sin2A+cos2D=1【分析】根据等边三角形的判定方法，直角三角形的判定方法以及等边三角形的性质，直角三角形的性质一一判断即可；【解答】解：由作图可知：AC=AB=BC，∴△ABC是等边三角形，由作图可知：CB=CA=CD，∴点C是△ABD的外心，∠ABD=90°，BD=AB，∴S△ABD=AB2，∵AC=CD，∴S△BDC=AB2，故A、B、C正确，故选：D．6．（2019•郴州）如图，∠AOB=60°，以点O为圆心，以任意长为半径作弧交OA，OB于C，D两点；分别以C，D为圆心，以大于CD的长为半径作弧，两弧相交于点P；以O为端点作射线OP，在射线OP上截取线段OM=6，则M点到OB的距离为（）A．6 B．2 C．3 D．【分析】直接利用角平分线的作法得出OP是∠AOB的角平分线，再利用直角三角形的性质得出答案．【解答】解：过点M作ME⊥OB于点E，由题意可得：OP是∠AOB的角平分线，则∠POB=×60°=30°，∴ME=OM=3．故选：C．7．（2019•台州）如图，在▱ABCD中，AB=2，BC=3．以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于PQ的长为半径画弧，两弧相交于点N，射线CN交BA的延长线于点E，则AE的长是（）A．B．1 C．D．【分析】只要证明BE=BC即可解决问题；【解答】解：∵由题意可知CF是∠BCD的平分线，∴∠BCE=∠DCE．∵四边形ABCD是平行四边形，∴AB∥CD，∴∠DCE=∠E，∠BCE=∠AEC，∴BE=BC=3，∵AB=2，∴AE=BE﹣AB=1，故选：B．8．（2019•嘉兴）用尺规在一个平行四边形内作菱形ABCD，下列作法中错误的是（）A． B．C．D．【分析】根据菱形的判定和作图根据解答即可．【解答】解：A、由作图可知，AC⊥BD，且平分BD，即对角线平分且垂直的四边形是菱形，正确；B、由作图可知AB=BC，AD=AB，即四边相等的四边形是菱形，正确；C、由作图可知AB=DC，AD=BC，只能得出ABCD是平行四边形，错误；D、由作图可知对角线AC平分对角，可以得出是菱形，正确；故选：C．9．（2019•昆明）如图，点A在双曲线y═（x＞0）上，过点A作AB⊥x轴，垂足为点B，分别以点O和点A为圆心，大于OA的长为半径作弧，两弧相交于D，E两点，作直线DE交x轴于点C，交y轴于点F（0，2），连接AC．若AC=1，则k的值为（）A．2 B．C．D．【分析】如图，设OA交CF于K．利用面积法求出OA的长，再利用相似三角形的性质求出AB、OB即可解决问题；【解答】解：如图，设OA交CF于K．由作图可知，CF垂直平分线段OA，∴OC=CA=1，OK=AK，在Rt△OFC中，CF==，∴AK=OK==，∴OA=，由△FOC∽△OBA，可得==，∴==，∴OB=，AB=，∴A（，），∴k=．故选：B．10．（2019•湖州）尺规作图特有的魅力曾使无数人沉湎其中．传说拿破仑通过下列尺规作图考他的大臣：①将半径为r的⊙O六等分，依次得到A，B，C，D，E，F六个分点；②分别以点A，D为圆心，AC长为半径画弧，G是两弧的一个交点；③连结OG．问：OG的长是多少？大臣给出的正确答案应是（）A． r B．（1+）r C．（1+）r D． r【分析】如图连接CD，AC，DG，AG．在直角三角形即可解决问题；【解答】解：如图连接CD，AC，DG，AG．∵AD是⊙O直径，∴∠ACD=90°，在Rt△ACD中，AD=2r，∠DAC=30°，∴AC=r，∵DG=AG=CA，OD=OA，∴OG⊥AD，∴∠GOA=90°，∴OG===r，故选：D．11．（2019•台湾）如图，锐角三角形ABC中，BC＞AB＞AC，甲、乙两人想找一点P，使得∠BPC与∠A 互补，其作法分别如下：（甲）以A为圆心，AC长为半径画弧交AB于P点，则P即为所求；（乙）作过B点且与AB垂直的直线l，作过C点且与AC垂直的直线，交l于P点，则P即为所求对于甲、乙两人的作法，下列叙述何者正确？（）A．两人皆正确B．两人皆错误C．甲正确，乙错误D．甲错误，乙正确【分析】甲：根据作图可得AC=AP，利用等边对等角得：∠APC=∠ACP，由平角的定义可知：∠BPC+∠APC=180°，根据等量代换可作判断；乙：根据四边形的内角和可得：∠BPC+∠A=180°．【解答】解：甲：如图1，∵AC=AP，∴∠APC=∠ACP，∵∠BPC+∠APC=180°∴∠BPC+∠ACP=180°，∴甲错误；乙：如图2，∵AB⊥PB，AC⊥PC，∴∠ABP=∠ACP=90°，∴∠BPC+∠A=180°，∴乙正确，故选：D．12．（2019•安顺）已知△ABC（AC＜BC），用尺规作图的方法在BC上确定一点P，使PA+PC=BC，则符合要求的作图痕迹是（）A．B．C．D．【分析】利用线段垂直平分线的性质以及圆的性质分别分得出即可．【解答】解：A、如图所示：此时BA=BP，则无法得出AP=BP，故不能得出PA+PC=BC，故此选项错误；B、如图所示：此时PA=PC，则无法得出AP=BP，故不能得出PA+PC=BC，故此选项错误；C、如图所示：此时CA=CP，则无法得出AP=BP，故不能得出PA+PC=BC，故此选项错误；D、如图所示：此时BP=AP，故能得出PA+PC=BC，故此选项正确；故选：D．13．（2017•南宁）如图，△ABC中，AB＞AC，∠CAD为△ABC的外角，观察图中尺规作图的痕迹，则下列结论错误的是（）A．∠DAE=∠B B．∠EAC=∠C C．AE∥BC D．∠DAE=∠EAC【分析】根据图中尺规作图的痕迹，可得∠DAE=∠B，进而判定AE∥BC，再根据平行线的性质即可得出结论．【解答】解：根据图中尺规作图的痕迹，可得∠DAE=∠B，故A选项正确，∴AE∥BC，故C选项正确，∴∠EAC=∠C，故B选项正确，∵AB＞AC，∴∠C＞∠B，∴∠CAE＞∠DAE，故D选项错误，故选：D．二．填空题（共7小题）14．（2019•南京）如图，在△ABC中，用直尺和圆规作AB、AC的垂直平分线，分别交AB、AC于点D、E，连接DE．若BC=10cm，则DE= 5 cm．【分析】直接利用线段垂直平分线的性质得出DE是△ABC的中位线，进而得出答案．【解答】解：∵用直尺和圆规作AB、AC的垂直平分线，∴D为AB的中点，E为AC的中点，∴DE是△ABC的中位线，∴DE=BC=5cm．故答案为：5．15．（2019•淮安）如图，在Rt△ABC中，∠C=90°，AC=3，BC=5，分别以点A、B为圆心，大于AB的长为半径画弧，两弧交点分别为点P、Q，过P、Q两点作直线交BC于点D，则CD的长是．【分析】连接AD由PQ垂直平分线段AB，推出DA=DB，设DA=DB=x，在Rt△ACD中，∠C=90°，根据AD2=AC2+CD2构建方程即可解决问题；【解答】解：连接AD．∵PQ垂直平分线段AB，∴DA=DB，设DA=DB=x，在Rt△ACD中，∠C=90°，AD2=AC2+CD2，∴x2=32+（5﹣x）2，解得x=，∴CD=BC﹣DB=5﹣=，故答案为．16．（2019•山西）如图，直线MN∥PQ，直线AB分别与MN，PQ相交于点A，B．小宇同学利用尺规按以下步骤作图：①以点A为圆心，以任意长为半径作弧交AN于点C，交AB于点D；②分别以C，D为圆心，以大于CD长为半径作弧，两弧在∠NAB内交于点E；③作射线AE交PQ于点F．若AB=2，∠ABP=60°，则线段AF的长为2．【分析】作高线BG，根据直角三角形30度角的性质得：BG=1，AG=，可得AF的长．【解答】解：∵MN∥PQ，∴∠NAB=∠ABP=60°，由题意得：AF平分∠NAB，∴∠1=∠2=30°，∵∠ABP=∠1+∠3，∴∠3=30°，∴∠1=∠3=30°，∴AB=BF，AG=GF，∵AB=2，∴BG=AB=1，∴AG=，∴AF=2AG=2，故答案为：2．17．（2019•东营）如图，在Rt△ABC中，∠B=90°，以顶点C为圆心，适当长为半径画弧，分别交AC，BC于点E，F，再分别以点E，F为圆心，大于EF的长为半径画弧，两弧交于点P，作射线CP交AB 于点D．若BD=3，AC=10，则△ACD的面积是15 ．【分析】作DQ⊥AC，由角平分线的性质知DB=DQ=3，再根据三角形的面积公式计算可得．【解答】解：如图，过点D作DQ⊥AC于点Q，由作图知CP是∠ACB的平分线，∵∠B=90°，BD=3，∴DB=DQ=3，∵AC=10，∴S△ACD=•AC•DQ=×10×3=15，故答案为：15．18．（2019•通辽）如图，在△ABC中，按以下步骤作图：①分别以点A和点C为圆心，以大于AC的长为半径作弧，两弧相交于M、N两点；②作直线MN交BC于点D，连接AD．若AB=BD，AB=6，∠C=30°，则△ACD的面积为9．【分析】只要证明△ABD是等边三角形，推出BD=AD=DC，可得S△ADC=S△ABD即可解决问题；【解答】解：由作图可知，MN垂直平分线段AC，∴DA=DC，∴∠C=∠DAC=30°，∴∠ADB=∠C+∠DAC=60°，∵AB=AD，∴△ABD是等边三角形，∴BD=AD=DC，∴S△ADC=S△ABD=×62=9，故答案为9．19．（2019•成都）如图，在矩形ABCD中，按以下步骤作图：①分别以点A和C为圆心，以大于AC 的长为半径作弧，两弧相交于点M和N；②作直线MN交CD于点E．若DE=2，CE=3，则矩形的对角线AC的长为．【分析】连接AE，如图，利用基本作图得到MN垂直平分AC，则EA=EC=3，然后利用勾股定理先计算出AD，再计算出AC．【解答】解：连接AE，如图，由作法得MN垂直平分AC，∴EA=EC=3，在Rt△ADE中，AD==，在Rt△ADC中，AC==．故答案为．20．（2019•湖州）在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．以顶点都是格点的正方形ABCD的边为斜边，向内作四个全等的直角三角形，使四个直角顶点E，F，G，H都是格点，且四边形EFGH为正方形，我们把这样的图形称为格点弦图．例如，在如图1所示的格点弦图中，正方形ABCD的边长为，此时正方形EFGH的而积为5．问：当格点弦图中的正方形ABCD的边长为时，正方形EFGH的面积的所有可能值是13或49或9 （不包括5）．【分析】当DG=，CG=2时，满足DG2+CG2=CD2，此时HG=，可得正方形EFGH的面积为13．当DG=8，CG=1时，满足DG2+CG2=CD2，此时HG=7，可得正方形EFGH的面积为49．当DG=7，CG=4时，满足DG2+CG2=CD2，此时HG=3，可得正方形EFGH的面积为9．【解答】解：当DG=，CG=2时，满足DG2+CG2=CD2，此时HG=，可得正方形EFGH的面积为13．当DG=8，CG=1时，满足DG2+CG2=CD2，此时HG=7，可得正方形EFGH的面积为49．当DG=7，CG=4时，满足DG2+CG2=CD2，此时HG=3，可得正方形EFGH的面积为9．故答案为13或49或9．三．解答题（共21小题）21．（2019•广州）如图，在四边形ABCD中，∠B=∠C=90°，AB＞CD，AD=AB+CD．（1）利用尺规作∠ADC的平分线DE，交BC于点E，连接AE（保留作图痕迹，不写作法）；（2）在（1）的条件下，①证明：AE⊥DE；②若CD=2，AB=4，点M，N分别是AE，AB上的动点，求BM+MN的最小值．【分析】（1）利用尺规作出∠ADC的角平分线即可；（2）①延长DE交AB的延长线于F．只要证明AD=AF，DE=EF，利用等腰三角形三线合一的性质即可解决问题；②作点B关于AE的对称点K，连接EK，作KH⊥AB于H，DG⊥AB于G．连接MK．由MB=MK，推出MB+MN=KM+MN，根据垂线段最短可知：当K、M、N共线，且与KH重合时，KM+MN的值最小，最小值为KH的长；【解答】解：（1）如图，∠ADC的平分线DE如图所示．（2）①延长DE交AB的延长线于F．∵CD∥AF，∴∠CDE=∠F，∵∠CDE=∠ADE，∴∠ADF=∠F，∴AD=AF，∵AD=AB+CD=AB+BF，∴CD=BF，∵∠DEC=∠BEF，∴△DEC≌△FEB，∴DE=EF，∵AD=AF，∴AE⊥DE．②作点B关于AE的对称点K，连接EK，作KH⊥AB于H，DG⊥AB于G．连接MK．∵AD=AF，DE=EF，∴AE平分∠DAF，则△AEK≌△AEB，∴AK=AB=4，在Rt△ADG中，DG==4，∵KH∥DG，∴=，∴=，∴KH=，∵MB=MK，∴MB+MN=KM+MN，∴当K、M、N共线，且与KH重合时，KM+MN的值最小，最小值为KH的长，∴BM+MN的最小值为．22．（2019•广东）如图，BD是菱形ABCD的对角线，∠CBD=75°，（1）请用尺规作图法，作AB的垂直平分线EF，垂足为E，交AD于F；（不要求写作法，保留作图痕迹）（2）在（1）条件下，连接BF，求∠DBF的度数．【分析】（1）分别以A、B为圆心，大于AB长为半径画弧，过两弧的交点作直线即可；（2）根据∠DBF=∠ABD﹣∠ABF计算即可；【解答】解：（1）如图所示，直线EF即为所求；（2）∵四边形ABCD是菱形，∴∠ABD=∠DBC=∠ABC=75°，DC∥AB，∠A=∠C．∴∠ABC=150°，∠ABC+∠C=180°，∴∠C=∠A=30°，∵EF垂直平分线线段AB，∴AF=FB，∴∠A=∠FBA=30°，∴∠DBF=∠ABD﹣∠FBE=45°．23．（2019•安徽）如图，⊙O为锐角△ABC的外接圆，半径为5．（1）用尺规作图作出∠BAC的平分线，并标出它与劣弧的交点E（保留作图痕迹，不写作法）；（2）若（1）中的点E到弦BC的距离为3，求弦CE的长．【分析】（1）利用基本作图作AE平分∠BAC；（2）连接OE交BC于F，连接OC，如图，根据圆周角定理得到=，再根据垂径定理得到OE⊥BC，则EF=3，OF=2，然后在Rt△OCF中利用勾股定理计算出CF=，在Rt△CEF中利用勾股定理可计算出CE．【解答】解：（1）如图，AE为所作；（2）连接OE交BC于F，连接OC，如图，∵AE平分∠BAC，∴∠BAE=∠CAE，∴=，∴OE⊥BC，∴EF=3，∴OF=5﹣3=2，在Rt△OCF中，CF==，在Rt△CEF中，CE==．24．（2019•自贡）如图，在△ABC中，∠ACB=90°．（1）作出经过点B，圆心O在斜边AB上且与边AC相切于点E的⊙O（要求：用尺规作图，保留作图痕迹，不写作法和证明）（2）设（1）中所作的⊙O与边AB交于异于点B的另外一点D，若⊙O的直径为5，BC=4；求DE的长．（如果用尺规作图画不出图形，可画出草图完成（2）问）【分析】（1）作∠ABC的角平分线交AC于E，作EO⊥AC交AB于点O，以O为圆心，OB为半径画圆即可解决问题；（2）作OH⊥BC于H．首先求出OH、EC、BE，利用△BCE∽△BED，可得=，解决问题；【解答】解：（1）⊙O如图所示；（2）作OH⊥BC于H．∵AC是⊙O的切线，∴OE⊥AC，∴∠C=∠CEO=∠OHC=90°，∴四边形ECHO是矩形，∴OE=CH=，BH=BC﹣CH=，在Rt△OBH中，OH==2，∴EC=OH=2，BE==2，∵∠EBC=∠EBD，∠BED=∠C=90°，∴△BCE∽△BED，∴=，∴=，∴DE=．25．（2019•北京）下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程．已知：直线l及直线l外一点P．求作：直线PQ，使得PQ∥l．作法：如图，①在直线l上取一点A，作射线PA，以点A为圆心，AP长为半径画弧，交PA的延长线于点B；②在直线l上取一点C（不与点A重合），作射线BC，以点C为圆心，CB长为半径画弧，交BC的延长线于点Q；③作直线PQ．所以直线PQ就是所求作的直线．根据小东设计的尺规作图过程，（1）使用直尺和圆规，补全图形；（保留作图痕迹）（2）完成下面的证明．证明：∵AB= AP ，CB= CQ ，∴PQ∥l（三角形中位线定理）（填推理的依据）．【分析】（1）根据题目要求作出图形即可；（2）利用三角形中位线定理证明即可；【解答】（1）解：直线PQ如图所示；（2）证明：∵AB=AP，CB=CQ，∴PQ∥l（三角形中位线定理）．故答案为：AP，CQ，三角形中位线定理；26．（2019•白银）如图，在△ABC中，∠ABC=90°．（1）作∠ACB的平分线交AB边于点O，再以点O为圆心，OB的长为半径作⊙O；（要求：不写做法，保留作图痕迹）（2）判断（1）中AC与⊙O的位置关系，直接写出结果．【分析】（1）首先利用角平分线的作法得出CO，进而以点O为圆心，OB为半径作⊙O即可；（2）利用角平分线的性质以及直线与圆的位置关系进而求出即可．【解答】解：（1）如图所示：；（2）相切；过O点作OD⊥AC于D点，∵CO平分∠ACB，∴OB=OD，即d=r，∴⊙O与直线AC相切，27．（2019•无锡）如图，平面直角坐标系中，已知点B的坐标为（6，4）．（1）请用直尺（不带刻度）和圆规作一条直线AC，它与x轴和y轴的正半轴分别交于点A和点C，且使∠ABC=90°，△ABC与△AOC的面积相等．（作图不必写作法，但要保留作图痕迹．）（2）问：（1）中这样的直线AC是否唯一？若唯一，请说明理由；若不唯一，请在图中画出所有这样的直线AC，并写出与之对应的函数表达式．【分析】（1）①作线段OB的垂直平分线AC，满足条件，②作矩形OA′BC′，直线A′C′，满足条件；（2）分两种情形分别求解即可解决问题；【解答】（1）解：如图△ABC即为所求；（2）解：这样的直线不唯一．①作线段OB的垂直平分线AC，满足条件，此时直线的解析式为y=﹣x+．②作矩形OA′BC′，直线A′C′，满足条件，此时直线A′C′的解析式为y=﹣x+4．28．（2019•孝感）如图，△ABC中，AB=AC，小聪同学利用直尺和圆规完成了如下操作：①作∠BAC的平分线AM交BC于点D；②作边AB的垂直平分线EF，EF与AM相交于点P；③连接PB，PC．请你观察图形解答下列问题：（1）线段PA，PB，PC之间的数量关系是PA=PB=PC ；（2）若∠ABC=70°，求∠BPC的度数．【分析】（1）根据线段的垂直平分线的性质可得：PA=PB=PC；（2）根据等腰三角形的性质得：∠ABC=∠ACB=70°，由三角形的内角和得：∠BAC=180°﹣2×70°=40°，由角平分线定义得：∠BAD=∠CAD=20°，最后利用三角形外角的性质可得结论．【解答】解：（1）如图，PA=PB=PC，理由是：∵AB=AC，AM平分∠BAC，∴AD是BC的垂直平分线，∴PB=PC，∵EP是AB的垂直平分线，∴PA=PB，∴PA=PB=PC；故答案为：PA=PB=PC；（2）∵AB=AC，∴∠ABC=∠ACB=70°，∴∠BAC=180°﹣2×70°=40°，∵AM平分∠BAC，∴∠BAD=∠CAD=20°，∵PA=PB=PC，∴∠ABP=∠BAP=∠ACP=20°，∴∠BPC=∠ABP+∠BAC+∠ACP=20°+40°+20°=80°．29．（2019•深圳）已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△CFE中，CF=6，CE=12，∠FCE=45°，以点C为圆心，以任意长为半径作AD，再分别以点A和点D为圆心，大于AD长为半径作弧，交EF于点B，AB ∥CD．（1）求证：四边形ACDB为△FEC的亲密菱形；（2）求四边形ACDB的面积．【分析】（1）根据折叠和已知得出AC=CD，AB=DB，∠ACB=∠DCB，求出AC=AB，根据菱形的判定得出即可；（2）根据相似三角形的性质得出比例式，求出菱形的边长和高，根据菱形的面积公式求出即可．【解答】（1）证明：∵由已知得：AC=CD，AB=DB，由已知尺规作图痕迹得：BC是∠FCE的角平分线，∴∠ACB=∠DCB，又∵AB∥CD，∴∠ABC=∠DCB，∴∠ACB=∠ABC，∴AC=AB，又∵AC=CD，AB=DB，∴AC=CD=DB=BA∴四边形ACDB是菱形，∵∠ACD与△FCE中的∠FCE重合，它的对角∠ABD顶点在EF上，∴四边形ACDB为△FEC的亲密菱形；（2）解：设菱形ACDB的边长为x，∵四边形ABCD是菱形，∴AB∥CE，∴∠FAB=∠FCE，∠FBA=∠E，△EAB∽△FCE则：，即，解得：x=4，过A点作AH⊥CD于H点，∵在Rt△ACH中，∠ACH=45°，∴，∴四边形ACDB的面积为：．30．（2019•贵港）尺规作图（只保留作图痕迹，不要求写出作法）．如图，已知∠α和线段a，求作△ABC，使∠A=∠α，∠C=90°，AB=a．【分析】根据作一个角等于已知角，线段截取以及垂线的尺规作法即可求出答案．【解答】解：如图所示，△ABC为所求作31．（2019•江西）如图，在四边形ABCD中，AB∥CD，AB=2CD，E为AB的中点，请仅用无刻度直尺分别按下列要求画图（保留画图痕迹）．（1）在图1中，画出△ABD的BD边上的中线；（2）在图2中，若BA=BD，画出△ABD的AD边上的高．【分析】（1）连接EC，利用平行四边形的判定和性质解答即可；（2）连接EC，ED，FA，利用三角形重心的性质解答即可．【解答】解：（1）如图1所示，AF即为所求：（2）如图2所示，BH即为所求．32．（2019•青岛）已知：如图，∠ABC，射线BC上一点D．求作：等腰△PBD，使线段BD为等腰△PBD的底边，点P在∠ABC内部，且点P到∠ABC两边的距离相等．【分析】根据角平分线的性质、线段的垂直平分线的性质即可解决问题．【解答】解：∵点P在∠ABC的平分线上，∴点P到∠ABC两边的距离相等（角平分线上的点到角的两边距离相等），∵点P在线段BD的垂直平分线上，∴PB=PD（线段的垂直平分线上的点到线段的两个端点的距离相等），如图所示：33．（2019•宁波）在5×3的方格纸中，△ABC的三个顶点都在格点上．（1）在图1中画出线段BD，使BD∥AC，其中D是格点；（2）在图2中画出线段BE，使BE⊥AC，其中E是格点．【分析】（1）将线段AC沿着AB方向平移2个单位，即可得到线段BD；（2）利用2×3的长方形的对角线，即可得到线段BE⊥AC．【解答】解：（1）如图所示，线段BD即为所求；（2）如图所示，线段BE即为所求．34．（2019•河南）如图，反比例函数y=（x＞0）的图象过格点（网格线的交点）P．（1）求反比例函数的解析式；（2）在图中用直尺和2B铅笔画出两个矩形（不写画法），要求每个矩形均需满足下列两个条件：①四个顶点均在格点上，且其中两个顶点分别是点O，点P；②矩形的面积等于k的值．【分析】（1）将P点坐标代入y=，利用待定系数法即可求出反比例函数的解析式；（2）根据矩形满足的两个条件画出符合要求的两个矩形即可．【解答】解：（1）∵反比例函数y=（x＞0）的图象过格点P（2，2），∴k=2×2=4，∴反比例函数的解析式为y=；（2）如图所示：矩形OAPB、矩形OCDP即为所求作的图形．35．（2019•金华）如图，在6×6的网格中，每个小正方形的边长为1，点A在格点（小正方形的顶点）上．试在各网格中画出顶点在格点上，面积为6，且符合相应条件的图形．【分析】利用数形结合的思想解决问题即可；【解答】解：符合条件的图形如图所示：36．（2019•济宁）在一次数学活动课中，某数学小组探究求环形花坛（如图所示）面积的方法，现有以下工具；①卷尺；②直棒EF；③T型尺（CD所在的直线垂直平分线段AB）．（1）在图1中，请你画出用T形尺找大圆圆心的示意图（保留画图痕迹，不写画法）；（2）如图2，小华说：“我只用一根直棒和一个卷尺就可以求出环形花坛的面积，具体做法如下：将直棒放置到与小圆相切，用卷尺量出此时直棒与大圆两交点M，N之间的距离，就可求出环形花坛的面积”如果测得MN=10m，请你求出这个环形花坛的面积．【分析】（1）直线CD与C′D′的交点即为所求的点O．（2）设切点为C，连接OM，OC．旅游勾股定理即可解决问题；【解答】解：（1）如图点O即为所求；（2）设切点为C，连接OM，OC．∵MN是切线，∴OC⊥MN，∴CM=CN=5，∴OM2﹣OC2=CM2=25，∴S圆环=π•OM2﹣π•OC2=25π．37．（2019•广安）下面有4张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长都是1，请在方格纸中分别画出符合要求的图形，所画图形各顶点必须与方格纸中小正方形的顶点重合，具体要求如下：（1）画一个直角边长为4，面积为6的直角三角形．（2）画一个底边长为4，面积为8的等腰三角形．（3）画一个面积为5的等腰直角三角形．（4）画一个边长为2，面积为6的等腰三角形．【分析】（1）利用三角形面积求法以及直角三角形的性质画即可；（2）利用三角形面积求法以及等腰三角形的性质画出即可．（3）利用三角形面积求法以及等腰直角三角形的性质画出即可；（4）利用三角形面积求法以及等腰三角形的性质画出即可．【解答】解：（1）如图（1）所示：（2）如图（2）所示：（3）如图（3）所示；（4）如图（4）所示．38．（2019•青岛）问题提出：用若干相同的一个单位长度的细直木棒，按照如图1方式搭建一个长方体框架，探究所用木棒条数的规律．问题探究：我们先从简单的问题开始探究，从中找出解决问题的方法．探究一用若干木棒来搭建横长是m，纵长是n的矩形框架（m、n是正整数），需要木棒的条数．如图①，当m=1，n=1时，横放木棒为1×（1+1）条，纵放木棒为（1+1）×1条，共需4条；如图②，当m=2，n=1时，横放木棒为2×（1+1）条，纵放木棒为（2+1）×1条，共需7条；如图③，当m=2，n=2时，横放木棒为2×（2+1））条，纵放木棒为（2+1）×2条，共需12条；如图④，当m=3，n=1时，横放木棒为3×（1+1）条，纵放木棒为（3+1）×1条，共需10条；如图⑤，当m=3，n=2时，横放木棒为3×（2+1）条，纵放木棒为（3+1）×2条，共需17条．问题（一）：当m=4，n=2时，共需木棒22 条．问题（二）：当矩形框架横长是m，纵长是n时，横放的木棒为m（n+1）条，纵放的木棒为n（m+1）条．探究二用若干木棒来搭建横长是m，纵长是n，高是s的长方体框架（m、n、s是正整数），需要木棒的条数．如图⑥，当m=3，n=2，s=1时，横放与纵放木棒之和为[3×（2+1）+（3+1）×2]×（1+1）=34条，竖放木棒为（3+1）×（2+1）×1=12条，共需46条；如图⑦，当m=3，n=2，s=2时，横放与纵放木棒之和为[3×（2+1）+（3+1）×2]×（2+1）=51条，竖放木棒为（3+1）×（2+1）×2=24条，共需75条；如图⑧，当m=3，n=2，s=3时，横放与纵放木棒之和为[3×（2+1）+（3+1）×2]×（3+1）=68条，竖放木棒为（3+1）×（2+1）×3=36条，共需104条．问题（三）：当长方体框架的横长是m，纵长是n，高是s时，横放与纵放木棒条数之和为[m（n+1）+n（m+1）]（s+1）条，竖放木棒条数为（m+1）（n+1）s 条．实际应用：现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架，总共使用了170条木棒，则这个长方体框架的横长是 4 ．拓展应用：若按照如图2方式搭建一个底面边长是10，高是5的正三棱柱框架，需要木棒1320 条．【分析】从特殊到一般探究规律后利用规律即可解决问题；【解答】解：问题（一）：当m=4，n=2时，横放木棒为4×（2+1）条，纵放木棒为（4+1）×2条，共需22条；问题（二）：当矩形框架横长是m，纵长是n时，横放的木棒为 m（n+1）条，纵放的木棒为n（m+1）条；问题（三）：当长方体框架的横长是m，纵长是n，高是s时，横放与纵放木棒条数之和为[m（n+1）+n（m+1）]（s+1）条，竖放木棒条数为（m+1）（n+1）s条．实际应用：这个长方体框架的横长是 s，则：[3m+2（m+1）]×5+（m+1）×3×4=170，解得m=4，拓展应用：若按照如图2方式搭建一个底面边长是10，高是5的正三棱柱框架，横放与纵放木棒条数之和为165×6=990条，竖放木棒条数为66×5=330条需要木棒1320条．故答案为22，m（n+1），n（m+1），[m（n+1）+n（m+1）]（s+1），（m+1）（n+1）s，4，1320；39．（2019•香坊区）如图，在每个小正方形的边长均为1的方格纸中，有线段AB和线段CD，点A、B、C、D均在小正方形的顶点上．（1）在方格纸中画出以AB为斜边的等腰直角三角形ABE，点E在小正方形的顶点上；（2）在方格纸中画出以CD为对角线的矩形CMDN（顶点字母按逆时针顺序），且面积为10，点M、N 均在小正方形的顶点上；（3）连接ME，并直接写出EM的长．【分析】（1）利用等腰直角三角形的性质画出即可；（2）利用矩形的性质画出即可；（3）根据勾股定理解答即可．【解答】解：（1）如图所示；（2）如图所示；（3）如图所示，EM=40．（2019•天门）图①、图②都是由边长为1的小菱形构成的网格，每个小菱形的顶点称为格点．点O，M，N，A，B均在格点上，请仅用无刻度直尺在网格中完成下列画图．（1）在图①中，画出∠MON的平分线OP；（2）在图②中，画一个Rt△ABC，使点C在格点上．【分析】（1）构造全等三角形，利用全等三角形的性质即可解决问题；（2）利用菱形以及平行线的性质即可解决问题；【解答】解：（1）如图所示，射线OP即为所求．（2）如图所示，点C即为所求；41．（2019•哈尔滨）如图，方格纸中每个小正方形的边长均为1，线段AB的两个端点均在小正方形的顶点上．（1）在图中画出以线段AB为一边的矩形ABCD（不是正方形），且点C和点D均在小正方形的顶点上；（2）在图中画出以线段AB为一腰，底边长为2的等腰三角形ABE，点E在小正方形的顶点上，连接CE，请直接写出线段CE的长．【分析】（1）利用数形结合的思想解决问题即可；（2）利用数形结合的思想解决问题即可；【解答】解：（1）如图所示，矩形ABCD即为所求；。

尺规作图1 2BC的长为半径1. .在△ABC中，按以下步骤作图：①分别以B、C为圆心，以大于作弧，两弧相交于两点M、N；②作直线MN交AB于点D，连接CD. 若CD=AC，∠B=250，则∠ACB的度数为 .答案：1050.解析：由①的作图可知CD=BD,则∠DCB=∠B=250,∴∠ADC=500,又∵CD=AC，∴∠A=∠ADC=500,∴∠ACD=800,∴∠ACB==800+250=1050.三、解答题1．（2018•湖南怀化，第21题，10分）两个城镇A、B与两条公路ME，MF位置如图所示，其中ME是东西方向的公路．现电信部门需在C处修建一座信号发射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路ME，MF的距离也必须相等，且在∠FME的内部（1）那么点C应选在何处？请在图中，用尺规作图找出符合条件的点C．（不写已知、求作、作法，只保留作图痕迹）（2）设AB的垂直平分线交ME于点N，且MN=2（+1）km，在M处测得点C位于点M的北偏东60°方向，在N处测得点C位于点N的北偏西45°方向，求点C到公路ME的距离．表示出MD和ND的长，从而求得CD的长即可．∵在Rt△CMD中，=tan∠CMN，∴MD==tan∠CNM，∴ND=∵MN=2（∴MN=MD+DN=CD+CD=22．（2018•江西抚州，第15题，5分）如图，△ABC与△DEF关于直线对称，请用无刻度的直尺，在下面两个图中分别作出直线.解析：利用轴对称性质：对应线段（或延长线）的交于对称轴上一点.如图，直线l 就是所求作的对称轴.3. （2018•浙江杭州，第20题，10分）把一条12个单位长度的线段分成三条线段，其中一条线段成为4个单位长度，另两条线段长都是单位长度的整数倍．（1）不同分段得到的三条线段能组成多少个不全等的三角形？用直尺和圆规作这些三角形（用给定的单位长度，不写作法，保留作图痕迹）；（2）求出（1）中所作三角形外接圆的周长．．三角形为等边三角形，此时外接圆的半径为=（1）用尺规作图作AB边上的中垂线DE，交AC于点D，交AB于点E．（保留作图痕迹，不要求写作法和证明）；（2）连接BD，求证：BD平分∠CBA．一点O为圆心，过A、D两点作⊙O（用尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔加黑）6、（2018•广州,第23题12分）如图6，中，，．（1）动手操作：利用尺规作以为直径的，并标出与的交点，与的交点（保留作图痕迹，不写作法）：（2）综合应用：在你所作的圆中，①求证：；②求点到的距离．【考点】（1）尺规作图；（2）①圆周角、圆心角定理；②勾股定理，等面积法【分析】（1）先做出中点，再以为圆心，为半径画圆.（2）①要求，根据圆心角定理，同圆中圆心角相等所对的弧也相等，只需证出即可，再根据等腰三角形中的边角关系转化.②首先根据已知条件可求出，依题意作出高，求高则用勾股定理或面积法，注意到为直径，所以想到连接，构造直角三角形，进而用勾股定理可求出，的长度，那么在中，求其高，就只需用面积法即可求出高.【答案】（1）如图所示，圆为所求（2）①如图连接，设,又则②连接,过作于,过作于cosC=, 又,又为直径设，则，在和中，有即解得：即又即7．（2018•广东梅州,第16题7分）如图，在Rt△ABC中，∠B=90°，分别以A、C为圆心，大于AC长为半径画弧，两弧相交于点M、N，连接MN，与AC、BC分别交于点D、E，连接AE，则：（1）∠ADE=90 °；（2）AE = EC；（填“=”“＞”或“＜”）（3）当AB=3，AC=5时，△ABE的周长= 7 ．∴BC=。

中考数学专题练习：尺规作图（含答案）1.（·随州)如图，用尺规作图作∠AOC＝∠AOB的第一步是以点O为圆心，以任意长为半径画弧①，分别交OA、OB于点E、F，那么第二步的作图痕迹②的作法是( )A. 以点F为圆心，OE长为半径画弧B. 以点F为圆心，EF长为半径画弧C. 以点E为圆心，OE长为半径画弧D. 以点E为圆心，EF长为半径画弧2.（·河北) 尺规作图要求，Ⅰ.过直线外一点作这条直线的垂线；Ⅱ.做线段的垂直平分线；Ⅲ.过直线上一点作这条直线的垂线．Ⅳ.作角的平分线．如图是按上述要求排乱顺序的尺规作图：则正确的配对是( )A．①—Ⅳ，②—Ⅱ，③—Ⅰ，④—ⅢB．①—Ⅳ，②—Ⅲ，③—Ⅱ，④—ⅠC．①—Ⅱ，②—Ⅳ，③—Ⅲ，④—ⅠD．①—Ⅳ，②—Ⅰ，③—Ⅱ，④—Ⅲ3.（·潍坊) 如图，木工师傅在板材边角处作直角时，往往使用“三弧法”，其作法是：(1)作线段AB，分别以A，B为圆心，以AB长为半径作弧，两弧的交点为C；(2)以C为圆心，仍以AB长为半径作弧交AC的延长线于点D；(3)连接BD，BC.下列说法不正确的是( ) A. ∠CBD＝30°B. S △BDC ＝34AB 2 C. 点C 是△ABD 的外心 D. sin 2A ＋cos 2D ＝14. （·湖州) 尺规作图特有魅力曾使无数人沉湎其中．传说拿破仑通过下列尺规作图考他的大臣：①将半径为r 的⊙O 六等分，依次得到A 、B 、C 、D 、E 、F 六个分点； ②分别以A ，D 为圆心，AC 长为半径画弧，G 是两弧的一个交点； ③连接OG.问：OG 的长是多少？大臣给出的正确答案应是( ) 3rB. (1＋22)r C. (1＋32)rD. 2r5. （·河南) 如图，已知▱AOBC 的顶点O(0，0)，A(－1，2)，点B 在x 轴正半轴上按以下步骤作图：①以点O 为圆心，适当长度为半径作弧，分别交边OA ，OB 于点D ，E ；②分别以点D ，E 为圆心，大于12DE 的长为半径作弧，两弧在∠AOB 内交于点F ；③作射线OF ，交边AC 于点G.则点G 的坐标为( )A．(5－1，2) B. (5，2)C．(3－5，－2) D. (5－2，2)6.（·南通) 如图，Rt△ABC中，∠ACB＝90°，CD平分∠ACB交AB于点D，按下列步骤作图．步骤1：分别以点C和点D为圆心，大于12CD的长为半径作弧，两弧相交于M，N两点；步骤2：作直线MN，分别交AC，BC于点E，F；步骤3：连接DE，DF.若AC＝4，BC＝2，则线段DE的长为( )A. 53B.32C. 2D.437.（·南京) 如图，在△ABC中，用直尺和圆规作AB、AC的垂直平分线，分别交AB、AC于点D、E，连接DE.若BC＝10 cm，则DE＝________cm.8.（·山西) 如图，直线MN∥PQ，直线AB分别与MN，PQ相交于点A，B.小宇同学利用尺规按以下步骤作图：①以点A为圆心，以任意长为半径作弧交AN于点C，交AB于点D；②分别以C，D为圆心，以大于12CD长为半径作弧，两弧在∠NA B内交于点E；③作射线AE交PQ于点F.若AB＝2，∠ABP＝60°，则线段AF的长为______．9.（·创新) 下面是“作一个30°角”的尺规作图过程．已知：平面内一点A.求作：∠A，使得∠A＝30°.作图：如图，(1)作射线AB；(2)在射线AB上取一点O，以O为圆心，OA为半径作圆，与射线AB相交于点C；(3)以C为圆心，OC为半径作弧，与⊙O交于点D，作射线AD，∠DAB即为所求的角．请回答：该尺规作图的依据是__________________________________________________________________________________________________________.10.（·广东) 如图，BD是菱形ABCD的对角线，∠CBD＝75°，(1)请用尺规作图法，作AB的垂直平分线EF，垂足为E，交AD于F；(不要求写作法，保留作图痕迹)(2)在(1)条件下，连接BF，求∠DBF的度数．11.（·福建)求证：相似三角形对应边上的中线之比等于相似比．要求：①根据给出的△ABC及线段A′B′，∠A′(∠A′＝∠A)．以线段A′B′为一边，在给出的图形上用尺规作出△A′B′C′，使得：△A′B′C′∽△ABC.不写作法，保留作图痕迹；②在已有的图形上画出一组对应中线，并据此写出已知、求证和证明过程．12.（·北京) 下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程．已知：直线及直线外一点P.求作：PQ，使得PQ∥l.作法：如图，①在直线上取一点A，作射线PA，以点A为圆心，AP长为半径画弧，交PA的延长线于点B；②在直线上取一点C(不与点A重合)，作射线BC，以点C为圆心，CB长为半径画弧，交BC的延长线于点Q；③作直线PQ.∴直线PQ就是所求作的直线．根据小东设计的尺规作图过程，(1)使用直尺和圆规，补全图形；(保留作图痕迹)(2)完成下面的证明．证明：∵AB＝________，CB＝________，∴PQ∥l(____________________________________)(填推理的依据)．13.（·绥化) 如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，D、E分别是斜边AB、直角边BC上的点，把△ABC沿着直线DE折叠．(1)如图1，当折叠后点B和点A重合时，用直尺和圆规作出直线DE (不写作法和证明，保留作图痕迹)．(2)如图2，当折叠后点B落在AC边上点P处，且四边形PEBD是菱形时，求折痕DE的长．参考答案【基础训练】1．D 2.D 3.D 4.D 5.A 6.D7．5 8.2 39．直径所对的圆周角是直角，等边三角形的每个内角为60°，直角三角形两锐角互余等10．解：(1)如解图所示；(2)∵菱形ABCD，∠CBD＝75°，∴CD＝CB，∠CBD＝∠CDB＝75°，∴∠C＝180°－∠CBD－∠CDB＝180°－75°－75°＝30°，∴∠A＝∠C＝30°，∵EF是AB的垂直平分线，∴∠A＝∠FBA＝30°，∵∠ABD＝∠CBD＝75°，∴∠DBF＝∠ABD－∠FBA＝75°－30°＝45°.11．解：①如解图，△A′B′C′即为所求作的三角形．②已知：△A′B′C′∽△ABC，CD和C′E分别为AB和A′B′边上的中线，求证：CDC′E＝BCB′C′.证明：∵C D和C′E分别为AB和A′B′边上的中线，∴BD＝12AB，B′E＝12A′B′，∴BDAB＝B′EA′B′＝12，∴BDB′E＝ABA′B′，∵△A′B′C′∽△ABC，∴∠CBA＝∠C′B′A′，BCB′C′＝ABA′B′，∴BDB′E＝BCB′C′，∴△B′C′E∽△BCD，∴CDC′E＝BCB′C′.12．解：(1)尺规作图如解图所示：(2)PA，CQ，三角形中位线平行于三角形的第三边．13．解：(1)如解图1，DE为所求作的直线．(2)如解图2，连接BP，∵四边形PEBD是菱形，∴PE＝BE，设CE＝x，则BE＝PE＝4－x，∵PE∥AB，∴△PCE∽△ACB，∴CECB＝PEAB，∴x4＝4－x5，∴x＝169，∴CE＝169，∴BE＝PE＝209，在Rt△PCE中，∵PE＝209，CE＝169，∴PC＝43在Rt△PCB中，∵PC＝43，BC＝4，∴BP＝4310，又∵S菱形PEBD ＝BE·PC＝12DE·BP，∴12×4310DE＝209×43，∴DE＝4910.。

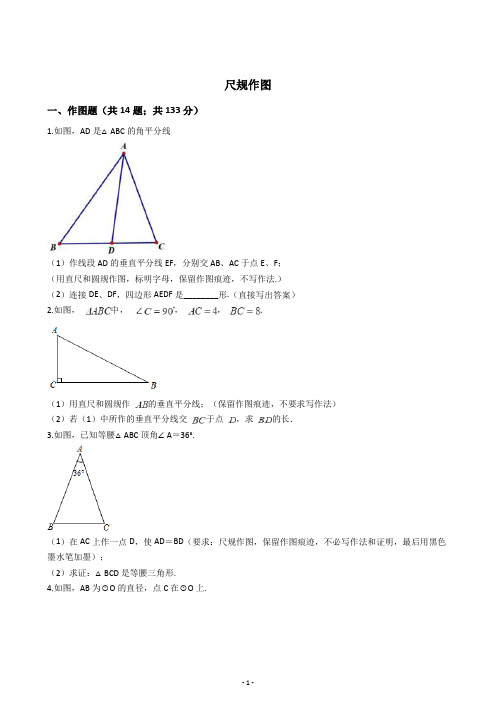
尺规作图一、作图题（共14题；共133分）1.如图，AD是△ABC的角平分线（1）作线段AD的垂直平分线EF，分别交AB、AC于点E、F；（用直尺和圆规作图，标明字母，保留作图痕迹，不写作法.）（2）连接DE、DF，四边形AEDF是________形.（直接写出答案）2.如图，中，，，．（1）用直尺和圆规作的垂直平分线；（保留作图痕迹，不要求写作法）（2）若（1）中所作的垂直平分线交于点，求的长．3.如图，已知等腰△ABC顶角∠A＝36°.（1）在AC上作一点D，使AD＝BD（要求：尺规作图，保留作图痕迹，不必写作法和证明，最后用黑色墨水笔加墨）；（2）求证：△BCD是等腰三角形.4.如图，AB为⊙O的直径，点C在⊙O上.（1）尺规作图：作∠BAC的平分线，与⊙O交于点D；连接OD，交BC于点E（不写作法，只保留作图痕迹，且用黑色墨水笔将作图痕迹加黑）；（2）探究OE与AC的位置及数量关系，并证明你的结论.5.在Rt△ABC中，∠C=90°，∠A=30°，D,E,F分别是AC,AB,BC的中点，连接ED,EF.（1）求证：四边形DEFC是矩形；（2）请用无刻度的直尺在图中作出∠ABC的平分线（保留作图痕迹，不写作法）.6.如图，在中，，，，D、E分别是斜边AB、直角边BC上的点，把沿着直线DE折叠．（1）如图1，当折叠后点B和点A重合时，用直尺和圆规作出直线DE；不写作法和证明，保留作图痕迹（2）如图2，当折叠后点B落在AC边上点P处，且四边形PEBD是菱形时，求折痕DE的长．7.如图，BD是菱形ABCD的对角线，∠CBD=75°，（1）请用尺规作图法，作AB的垂直平分线EF，垂足为E，交AD于F；（不要求写作法，保留作图痕迹）（2）在（1）条件下，连接BF，求∠DBF的度数．8.如图，在△ABC中，∠ABC=90°．（1）作∠ACB的平分线交AB边于点O，再以点O为圆心，OB的长为半径作⊙O；（要求：不写做法，保留作图痕迹）（2）判断（1）中AC与⊙O的位置关系，直接写出结果．9.如图，在中，.（1）作的平分线交边于点，再以点为圆心，的长为半径作；（要求：不写作法，保留作图痕迹）（2）判断（1）中与的位置关系，直接写出结果.10.如图，在中．①利用尺规作图，在BC边上求作一点P，使得点P到AB的距离的长等于PC的长；②利用尺规作图，作出（1）中的线段PD．要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔描黑11.如图，在△ABC中（1）作图，作BC边的垂直平分线分别交于AC，BC于点D，E（用尺规作图法，保留作图痕迹，不要求写作法）（2）在（1）条件下，连接BD，若BD＝9，BC＝12，求∠C的余弦值．12.如图，点D在△ABC的AB边上，且∠ACD=∠A。

完整版)中考数学尺规作图专题复习(含答案)尺规作图是用无刻度的直尺和圆规画图的方法，常见的作图包括线段的垂线、垂直平分线、角平分线、等长线段和等角。

以下是各种作图的具体方法：1.直线垂线的画法：以点C为圆心，任意长为半径画弧交直线与A、B两点，再以点A、B为圆心，大于AB的长为半径画圆弧，分别交直线l两侧于点M、N，连接MN，即可得到所求的垂线。

2.线段垂直平分线的画法：以点A、B为圆心，大于AB的长为半径画圆弧，分别交直线AB两侧于点C、D，连接CD，即可得到线段AB的垂直平分线。

3.角平分线的画法：以角顶点O为圆心，任意长为半径画圆，分别交角两边A、B点，再以A、B为圆心，大于AB的长为半径画圆弧，交点为H，连接OH并延长，即可得到所求的角平分线。

4.等长的线段的画法：直接用圆规量取即可。

5.等角的画法：以O为圆心，任意长为半径画圆，交原角的两边为A、B两点，连接AB；画一条射线l，以上面的半径为半径，l的顶点K为圆心画圆，交l与L，以L为圆心，AB为半径画圆，交以K为圆心，KL为半径的圆与M点，连接KM，则角LKM即为所求。

需要注意的是，直尺主要用于画直线和射线，圆规主要用于截取相等线段和画弧。

在作图时，如果有多个要求，应逐个满足并取公共部分。

例如，对于要求作一个三角形的问题，可以根据三角形全等的基本事实或判定定理来进行作图。

以下是例题解析：例题1：已知线段a，求作△ABC，使AB=BC=AC=a。

作法如下：1.作线段BC=a；2.分别以B、C为圆心，以a半径画弧，两弧交于点A；3.连接AB、AC。

例题2：已知线段a和∠α，求作△ABC，使AB=AC=a，∠A=∠α。

作法如下：1.作∠XXX∠α；2.以点A为圆心，a为半径画弧，分别交射线AM、AN 于点B、C；3.连接B、C。

例题3：已知△ABC，AB<BC，用尺规作图的方法在BC 上取一点P，使得PA+PC=BC。

作法如下：作出AB的垂直平分线，与BC交于点P。

备战2015中考系列：数学2年中考1年模拟第四篇图形的性质专题25 尺规作图☞解读考点知识点名师点晴尺规作图尺规作图概念了解什么是尺规作图五种基本作图1.画一条线段等于已知线段会用尺规作图法完成五种基本作图，了解五种基本作图的理由，会使用精练、准确的作图语言叙述画图过程．2.画一个角等于已知角3.画线段的垂直平分线4.过已知点画已知直线的垂线5.画角平分线会利用基本作图画较简单的图形．1.画三角形会利用基本作图画三角形较简单的图形．2.画圆会利用基本作图画圆．☞2年中考[2014年题组]1. (2014·安顺)用直尺和圆规作一个角等于已知角，如图，能得出∠A′O′B′＝∠AOB的依据是( )A．SAS B．SSS C．ASA D．AAS2.（2014涉县一模）如图，AD为⊙O的直径，作⊙O的内接正三角形ABC，甲、乙两人的作法分别如下：甲：①作OD的垂直平分线，交⊙O于B，C两点．②连接AB，AC.△ABC即为所求作的三角形．乙：①以D为圆心，OD的长为半径作圆弧，交⊙O于B，C两点．②连接AB，BC，CA.△ABC即为所求作的三角形．对于甲、乙两人的作法，可判断( )A．甲、乙均正确 B．甲、乙均错误C．甲正确，乙错误 D．甲错误，乙正确3.(2014·玉林)如图，BC与CD重合，∠ABC＝∠CDE＝90°，△ABC≌△CDE，并且△CDE可由△ABC逆时针旋转而得到．请你利用尺规作出旋转中心O(保留作图痕迹，不写作法，注意最后用墨水笔加黑)，并直接写出旋转角度是．4. （2014•河南）如图，在△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于12BC的长为半径作弧，两弧相交于M，N两点；②作直线MN交AB于点D，连接CD，若CD=AC，∠B=25°，则∠ACB的度数为5. （2014•梅州）如图，在Rt△ABC中，∠B=90°，分别以A、C为圆心，大于12AC长为半径画弧，两弧相交于点M、N，连结MN，与AC、BC分别交于点D、E，连结AE，则：（1）∠ADE= ；（2）AE EC；（填“=”“＞”或“＜”）（3）当AB=3，AC=5时，△ABE的周长=[2013年题组]1. （2013年江苏南通3分）如图，用尺规作出∠OBF=∠AOB，所画痕迹MN是【】A．以点B为圆心，OD为半径的弧B．以点C为圆心，DC为半径的弧C．以点E为圆心，OD为半径的弧D．以点E为圆心，DC为半径的弧2. （2013年山西省8分）如图，在△ABC中，AB=AC，D是BA延长线上的一点，点E是AC的中点。

2019年部分地区中考数学尺规作图试题解析汇编以下是查字典数学网为您推荐的2019年部分地区中考数学尺规作图试题解析汇编，希望本篇文章对您学习有所帮助。

2019年部分地区中考数学尺规作图试题解析汇编7. (2019浙江省绍兴，7，3分)如图，AD为⊙O直径，作⊙O 的内接正三角形ABC，甲、乙两人的作法分别如下：对于甲、乙两人的作法，可判断( )A.甲、乙均正确B.甲、乙均错误C.甲正确，乙错误D.甲错误，乙正确【解析】将圆三等分，依次连结各等分点，即可作出圆内接正三角形 .【答案】A【点评】本题主要考查圆内接正三角形的作法和判定以及圆的有关知识.19.(2019山东德州中考,19,8,)有公路同侧、异侧的两个城镇A，B，如下图.电信部门要修建一座信号发射塔，按照设计要求，发射塔到两个城镇，的距离必须相等，到两条公路，的距离也必须相等，发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点，注明点C的位置.(保留作图痕迹，不要求写出画法)19.【解析】分析此题的条件可知，要想到A、B两点的距离相等，可知点C必在AB的垂直平分线上;要想到两公路的距离相等，必须在两公路夹角的角平分线上.作出二者的交点即为所求.注意两公路夹角的角平分线不止一条.解：根据题意知道，点C应满足两个条件，一是在线段的垂直平分线上;二是在两条公路夹角的平分线上，所以点C应是它们的交点.⑴ 作两条公路夹角的平分线或 ;⑵ 作线段AB的垂直平分线FG;则射线OD，OE与直线FG的交点，就是所求的位置.(8分)注：本题学生能正确得出一个点的位置得6分，得出两个点的位置得8分.【点评】此题综合考查了角平分线的性质和线段垂直平分线的性质，解答此类题不要漏电所有符合条件的点，要注意在角的外部也有符合条件的点.(2)(2019贵州铜仁，19(2)，5分)某市计划在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A、B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A、B、C的位置如图所示，请在原图上利用尺规作图作出音乐喷泉M的位置，(要求：不写已知、求作、作法和结论，保留作图痕迹，必须用铅笔作图)【分析】根据垂直平分线上的点到两个端点的距离相等，连接AB并作AB的垂直平分线，然后以C点为圆心，以AB的长度一半为圆心画弧，与垂直平分线交于一点，即为所求的点M位置【解析】作图1、连结AB2、作出线段AB的垂直平分线3、以C点为圆心，以AB的长度一半为圆心画弧，与垂直平分线交于一点M4、在矩形中标出点M的位置【点评】此题看出来图形设计作图与实际应用，本题主要利用垂直平分线的作法，属于基本作图，应牢固掌握。

尺规作图
一、选择题：
1．（·山东省德州市·3分）如图，在△ABC中，∠B=55°，∠C=30°，分别以点A和点C为圆心，大于AC的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为（）
A．65°B．60°C．55°D．45°[来源学科网]
【考点】线段垂直平分线的性质．
【分析】根据线段垂直平分线的性质得到AD=DC，根据等腰三角形的性质得到∠C=∠DAC，求得∠DAC=30°，根据三角形的内角和得到∠BAC=95°，即可得到结论．
【解答】解：由题意可得：MN是AC的垂直平分线，
则AD=DC，故∠C=∠DAC，
∵∠C=30°，
∴∠DAC=30°，
∵∠B=55°，
∴∠BAC=95°，
∴∠BAD=∠BAC﹣∠CAD=65°，
故选A．
【点评】此题主要考查了线段垂直平分线的性质，三角形的内角和，正确掌握线段垂直平分线的性质是解题关键．2.(河北3分）如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹.
步骤1：以C为圆心，CA为半径画弧○1；
步骤2：以B为圆心，BA为半径画弧○2，将弧○1于点D；
步骤3：连接AD，交BC延长线于点H.
下列叙述正确的是（）。

中考数学专题复习尺规作图一、单选题1.用尺规作图，不能作出唯一直角三角形的是（）A. 已知两条直角边B. 已知两个锐角C. 已知一直角边和直角边所对的一锐角D. 已知斜边和一直角边2.根据已知条件作符合条件的三角形，在作图过程中，主要依据是（）A. 用尺规作一条线段等于已知线段B. 用尺规作一个角等于已知角C. 用尺规作一条线段等于已知线段和作一个角等于已知角D. 不能确定3.用尺规作图，下列条件中可能作出两个不同的三角形的是（）A. 已知三边B. 已知两角及夹边C. 已知两边及夹角D. 已知两边及其中一边的对角4.尺规作图是指（）A. 用直尺规范作图B. 用刻度尺和圆规作图C. 用没有刻度的直尺和圆规作图D. 直尺和圆规是作图工具5.如图，点C在∠AOB的边OB上，用尺规作出了∠BCN=∠AOC，作图痕迹中，弧FG是（）A. 以点C为圆心，OD为半径的弧B. 以点C为圆心，DM为半径的弧C. 以点E为圆心，OD为半径的弧D. 以点E为圆心，DM为半径的弧6. 如图，用尺规作出∠OBF=∠AOB，作图痕迹是（）A. 以点B为圆心，OD为半径的圆B. 以点B为圆心，DC为半径的圆C. 以点E为圆心，OD为半径的圆D. 以点E为圆心，DC为半径的圆7.如图，下面是利用尺规作∠AOB的角平分线OC的作法：①以点O为圆心，任意长为半径作弧，交OA、OB于点D，E；②分别以点D，E为圆心，以大于DE的长为半径作弧，两弧在∠AOB内部交于点C；③作射线OC，则射线OC就是∠AOB的平分线．以上用尺规作角平分线时，用到的三角形全等的判定方法是（）A. SSSB. SASC. ASAD. AAS8.尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA、OB于C、D，再分别以点C、D为圆心，以大于CD长为半径画弧，两弧交于点P，作射线OP，由作法可得△OCP≌△ODP，判定这两个三角形全等的根据是（）A. SASB. ASAC. AASD. SSS9.下列作图语句中，不准确的是（）A. 过点A、B作直线ABB. 以O为圆心作弧C. 在射线AM上截取AB=aD. 延长线段AB到D ，使DB=AB10.如图，点C在∠AOB的OB边上，用尺规作出了CN∥OA，作图痕迹中，是（）A. 以点C为圆心，OD为半径的弧B. 以点C为圆心，DM为半径的弧C. 以点E为圆心，OD为半径的弧D. 以点E为圆心，DM为半径的弧11.如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧在第二象限交于点P．点P关于x轴的对称点P′的坐标为（a，b），则a与b的数量关系为（）A. a+b=0B. a+b＞0C. a﹣b=0D. a﹣b＞012.如图所示的作图痕迹作的是（）A. 线段的垂直平分线B. 过一点作已知直线的垂线C. 一个角的平分线D. 作一个角等于已知角13.下列作图语句正确的是（）A. 作射线AB，使AB=aB. 作∠AOB=∠aC. 延长直线AB到点C，使AC=BCD. 以点O为圆心作弧14.某探究性学习小组仅利用一副三角板不能完成的操作是（）A. 作已知直线的平行线B. 作已知角的平分线C. 测量钢球的直径D. 作已知三角形的中位线15.如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧在第二象限交于点P，若点P的坐标为（m，n﹣3），则m与n的数量关系为（）A. m﹣n=﹣3B. m+n=﹣3C. m﹣n=3D. m+n=316.小明用尺规作图作△ABC边AC上的高BH，作法如下：①分别以点D，E为圆心，大于DE的长为半径作弧，两弧交于F；②作射线BF，交边AC于点H；③以B为圆心，BK长为半径作弧，交直线AC于点D和E；④取一点K，使K和B在AC的两侧；所以，BH就是所求作的高．其中顺序正确的作图步骤是（）A. ①②③④B. ④③②①C. ②④③①D. ④③①②17.已知∠AOB ，求作射线OC ，使OC平分∠AOB作法的合理顺序是（）①作射线OC；②在OA和OB上分别截取OD ，OE ，使OD=OE；③分别以D ，E为圆心，大于DE的长为半径作弧，在∠AOB内，两弧交于C ．A. ①②③B. ②①③C. ②③①D. ③②①二、填空题18.画线段AB；延长线段AB到点C，使BC=2AB；反向延长AB到点D，使AD=AC，则线段CD=________AB．19.已知，∠AOB ．求作：∠A′O′B′，使∠A′O′B′=∠AOB ．作法：①以________为圆心，________为半径画弧．分别交OA ，OB于点C ，D ．②画一条射线O′A′，以________为圆心，________长为半径画弧，交O′A′于点C′，③以点________为圆心________长为半径画弧，与第2步中所画的弧交于点D′．④过点________画射线O′B′，则∠A′O′B′=∠AOB ．20.如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E、F为圆心，大于EF的长为半径画弧，两弧交于点P，作射线AP，交CD于点M．若∠ACD=120°，则∠MAB 的度数为________ ．21.已知△ABC，小明利用下述方法作出了△ABC的一条角平分线．小明的作法：（i）过点B作与AC平行的射线BM；（边AC与射线BM位于边BC的异侧）（ii）在射线BM上取一点D，使得BD=BA；（iii）连结AD，交BC于点E．线段AE即为所求．小明的作法所蕴含的数学道理为________．22.阅读下面材料：在学习《圆》这一章时，老师给同学们布置了一道尺规作图题：尺规作图：过圆外一点作圆的切线．已知：P为⊙O外一点．求作：经过点P的⊙O的切线．小敏的作法如下：如图，（1）连接OP，作线段OP的垂直平分线MN交OP于点C；（2）以点C为圆心，CO的长为半径作圆，交⊙O于A，B两点；（3）作直线PA，PB．所以直线PA，PB就是所求作的切线．老师认为小敏的作法正确．请回答：连接OA，OB后，可证∠OAP=∠OBP=90°，其依据是________ ；由此可证明直线PA，PB都是⊙O 的切线，其依据是________三、解答题23.如图所示，作△ABC关于直线l的对称．24.在△ABC中，F是BC上一点，FG⊥AB，垂足为G.（1）过C点画CD⊥AB，垂足为D；（2）过D点画DE//BC，交AC于E；（3）说明∠EDC=∠GFB的理由.25.如图，△ABC，用尺规作图作角平分线CD．（保留作图痕迹，不要求写作法）四、综合题26.看图、回答问题（1）已知线段m和n，请用直尺和圆规作出等腰△ABC，使得AB=AC，BC=m，∠A的平分线等于n．（只保留作图痕迹，不写作法）（2）若①中m=12，n=8；请求出腰AB边上的高．27.如图，平面内有A、B、C、D四点，按照下列要求画图：（1）顺次连接A、B、C、D四点，画出四边形ABCD；（2）连接AC、BD相交于点O；（3）分别延长线段AD、BC相交于点P；（4）以点C为一个端点的线段有________条；（5）在线段BC上截取线段BM=AD+CD，保留作图痕迹．28.已知不在同一条直线上的三点P，M，N（1）画射线NP；再画直线MP；（2）连接MN并延长MN至点R，使NR=MN；（保留作图痕迹，不写作图过程）（3）若∠PNR比∠PNM大100°，求∠PNR的度数．答案解析部分一、单选题1.【答案】B2.【答案】C3.【答案】D4.【答案】C5.【答案】D6.【答案】D7.【答案】A8.【答案】D9.【答案】B10.【答案】D11.【答案】C12.【答案】B13.【答案】B14.【答案】C15.【答案】D16.【答案】D17.【答案】C二、填空题18.【答案】619.【答案】O；任意长；O′；OC；C ；CD；D′20.【答案】30°21.【答案】等边对等角；两直线平行，内错角相等22.【答案】直径所对的圆周角是90°；经过半径外端，且与半径垂直的直线是圆的切线三、解答题23.【答案】解答：解：如图所示：24.【答案】（1）（2）（3）解：因为DE//BC，所以∠EDC=∠BCD，因为FG⊥AB，CD⊥AB，所以CD//FG，所以∠BCD=∠GFB，所以∠EDC=∠GFB。