专题测定纸带加速度方法共15页
- 格式:ppt
- 大小:2.02 MB
- 文档页数:15

中学物理 V〇1.39 No.052021年3月如何根据紙帑上的点連计算加速皮黄洪才(湖南省长沙市第一中学湖南长沙410005)摘要:根据打点计时器在纸带上打下的点迹计算物体的加速度有三种方法,从计算结果的可信度和准确度两个 方面对三种方法进行了分析,目前广泛采用的方法并非是最合理的方法,进而给出了一种新的、更为合理的方法.关键词:纸带;点迹;加速度;打点计时器中图分类号:G633. 7 文献标识码:B文章编号:丨008-4134(2021 )05 -0057 -02用打点计时器研究物体的运动情况是中学物理 实验中的常用方法.根据打点计时器在纸带上打下的 点迹如何合理地计算物体的加速度?1计算纸带加速度的方法如图1所示,设4、6'、/)、£、厂6是每隔相同的时间r选取的计数点,相邻两计数点之间的间隔依次 为x,、x2、a:3J d%,则计算物体加速度的方法有以 下三种.A B C D E F G參•參*•••*2'*3^4气V、图1方法1 :依次算出5个加速度的值再取平均值,即1 /x2 -xl x3 -x2x4 -x3x5 -x4 x6 -x5\x6 -xla'_5( f+ f+ f+ f+ f5f 方法2:将间隔数分为两组,采取逐差的方法算出 3个加速度的值再取平均值,即1 /x4 -X x x5x6 (x4 +x5 +x6) -(x]+%2+^3) 02~ 3 \3f+ 3f+ 37") _方法3 :依次算出3个加速度的值再取平均值,即1 /x2 -X x x4 -X3x6-^:5\(x2 +x4 +x6)- (%!+x3 +x5) a3~^[f+f+f)~3f2计算结果的可信度分析在上述三种方法中,哪种方法算得的结果更能真 实地反映物体的运动情况?在A、x2、.t:3、;<:4、;c5、x6六个测量数据中,方法1实 际上只用到了 A和%两个数据,难以真实地反映物 体的运动情况,一般不采用这种方法;方法2表面上看来用到了六个测量数据,实际上相当于以37为时 间间隔选取/1、£>、C三个计数点来计算物体的加速度,也难以真实地反映物体的运动情况;方法3用到 了六个测量数据.因此,从所用数据点的个数来看,方 法3算出的加速度具有更高的可信度.3计算结果的准确度分析在实际的实验过程中,^是在刻度尺不移动的情况下直接读取/l、S、C、D、£、f\C各 计数点对应的刻度值逐个相减得到的(如图2),也就 是说、巧、*3、〜、、%不是直接测量的数据.如果用 直接测量的数据表示,方法2和方法3的测量值分 别是~A~B C D E F G~)參••••••/|i i i i|i i l i|i i i i|i i i i|i i i i|m i|i i i i|!i i i|i i i i|i i i i|i i i i|i i i i|m i|i i i i|i i i i|i i i i|pXB XC*〇*£ XF XQ图2- 2x0 +a〇 =-------,----9T^.4 - 2xb + 2*c- 2-^n +2x f: ~2x h~+ xGa,=----------------;--------------假设各计数点对应刻度尺上的刻度值的不确定 度分别为 Ax.t、、A.r f:、A.r,.、A.r c,相邻计 数点时间间隔的不确定度为A7\根据误差理论,方法 2和方法3计算出的加速度的不确定度分别为(采用 算术合成方式)A.r4 + + Axc 2(xa - 2xd x g) ATAa2 = ^5+作者简介:黄洪才(1963 -),男,湖南炎陵人,本科,中学特级教师,中学正高级教师,研究方向:中学物理学科教学.572021年3月Vol.39 No.05 中学物理走量採尧教具的幵发卖例—以“多功能圆锥摆”为例余杰1乐军20.浙江省舟山中学浙江舟山316000; 2.浙江省定海第一中学浙江舟山316000)摘要:针对教材给出的“圓锥摆粗略验证向心力公式”实验的不足,设计了可定量探究的教具.关键词:圆锥摆;教具;探究中图分类号:G633.7 文献标识码:B1现状的分析本文以人教版高中《物理(必修2 )》第五章第六 节“用圆锥摆粗略验证向心力公式”实验为例(如图 1).教材中的实验方案:构造一个圆锥摆,用手带动钢 球沿水平纸板上某一圆做匀速圆周运动,用秒表记录 运动周期7\再通过纸板上的圆测定运动半径《,用天 平测出球质量再通过受力分析,验证公式mgtan0 (其中taM= f)是否成立.此方案从理论上分析确实可行,可是在实践中不仅操作难度大,而 且误差大,教学中的实操性几乎为零,以至于很少有 老师会在课堂中对此实验进行演示.文章编号:1〇〇8 -4134(2021)05 -0058 -03賴_觀额祕力的表达式_线下由患桂-个钢球,切线上端B定在铁架台上•将i着几个R心《的白纸1于水平臬I I上,使供球许止时正好t于■心•用手辛动钢球,设法使它沿纸上的茱个■历运动85.6-1).用秒表或手表记象鋼球运动芳干曲的时间,再逼过炊上的明测出供球欽勺速®内运动的半这样就t算出供球的找速度•铜球的肩董1!■以由天平相出•于是,用⑴式就能算出你m受的句心力.图1圆锥摆粗略验证向心力公式分析此方案不难得出以下几个缺点:(1)摆球空 间位置的精确测定难;(2 )圆锥摆摆动的稳定性差,不0S各丨用脱心力的»达式作者简介:余杰(1977 -),男,浙江舟山人,本科,中学高级教师,研究方向:教学艺术和演示实验创新;乐军(1985 -),男,浙江舟山人,本科,中学一级教师,研究方向:中学物理自制教具.A fl3-Ax4 +2A^+2Arc+2A^D+2A%+2A^3f2(xa -2xb +2xc -2xd +2xe -2xf +x g)AT3f为方便起见,作为估算,假设Ax,, = Axf l = = A xd= A xe= ^xF = Axc = 0.2mm,T= 0.Is, AT= 0,PJ 方法2和方法3计算出的加速度的不确定度分别为Aa2 =4 x2 x10~49 x0.I2m/ s2:9 x10 m/s*"A a3 =12 x2 x l O~3 x O.I2*m/ s2=8 x10 "2m/s2显然,方法3算出的加速度的不确定度比方法2 算出的加速度的不确定度大•.在中学物理实验中,物 体的加速度通常是I -2m/S2,上述两种方法因读数引 起的误差都在误差允许的范围内.58 4究竟采用哪种方法好教辅资料给出的方法都是方法2.笔者认为,物理学是一门以实验为基础的学科,探究客观事物的真实规律是基于核心素养物理教学的基本要求.虽然方法3可能比方法2存在更大的偶然误差,但由于方法3算出的结果可信度高,更能真实地反映物体的运动情 况,而且实验误差在允许的范围内,所以采用方法3计算物体的加速度比方法2要更加合理.参考文献:[1] 人民教育出版社,课程教材研究所,物理课程教材研 究开发中心.普通高中教科书物理(必修第二册)[M].北京:人民教育出版社,2019.[2] 周久波.关于用逐差法计算纸带加速度合理性的讨论 [J].中学物理,2016,34(23) :79.(收稿日期:2020-11 -10)。

纸带加速度计算公式逐差法
纸带加速度计算公式使用逐差法。
逐差法是一种通过计算相邻数
据之差来估算连续变化的方法。
在纸带加速度计中,通过记录在一段
时间内物体的运动情况,可以获得该物体的平均加速度。
使用逐差法,可以计算出物体在一段时间内的瞬时加速度,即使加速度不是恒定的。
公式如下:
a = (v2 - v1) / (t2 - t1)
其中,a表示瞬时加速度,v2表示结束速度,v1表示起始速度,
t2表示结束时间,t1表示起始时间。
通过逐差法,可以计算出物体在不同时间段内的瞬时加速度,并
绘制出加速度-时间曲线,以更加准确地分析物体的运动情况。

提高学生高考物理实验解题能力以实验 纸带求加速度 为例方法归纳㊁错误分析鲁同心(江苏省清浦中学㊀223001)摘㊀要:近几年高考物理实验的得分普遍较低ꎬ学生的动手实践能力较差ꎬ解决具体问题思路不清晰.本文以高一物理实验案例为基础ꎬ尝试通过方法归纳ꎬ错题分析.精讲精练等方式入手ꎬ努力提高学生的解题能力.根据打点计时器在打在纸带上的点计算物体的瞬时速度和加速度是高中物理实验的常见问题.如何准确㊁快速的计算出加速度?笔者对如何处理加速度做了进一步的探讨ꎬ并统计了学生在习题中容易出现的错误.关键词:纸带ꎻ加速度ꎻ逐差法ꎻ两段法中图分类号:G632㊀㊀㊀㊀㊀㊀文献标识码:A㊀㊀㊀㊀㊀㊀文章编号:1008-0333(2020)31-0084-02收稿日期:2020-08-05作者简介:鲁同心(1982.10-)ꎬ男ꎬ江苏省淮安人ꎬ本科ꎬ中学一级教师ꎬ从事高中物理教学研究.㊀㊀在 探究小车速度随时间变化的规律 的实验中ꎬ要求学生通过对纸带打出点的数据处理ꎬ测量小车瞬时速度和小车运动的加速度.这已经成为考试的热点之一.㊀㊀一㊁方法归纳笔者对加速度计算的方法做如下归纳:为了有效减少测量加速度时的偶然误差ꎬ应用该公式进行数据处理.选择合适的计算方法ꎬ真正减少实验误差.常见方法如下:方法1㊀运用公式Δx=aT2计算.Δx=x2-x1=x3-x2= =aT2ꎬ即任意两个相邻相等的时间T内的位移之差Δx=aT2.利用xm-xn=m-n()aT2求解ꎬ如果纸带给出的数据不是连续的两段位移ꎬ如目前只知道x2和x5ꎬ则可以有x5-x2=3aT2.方法2㊀利用 逐差法 或 两段法 计算.逐差法:a1=x4-x13T2ꎬa2=x5-x23T2ꎬa3=x6-x33T2ꎬa-=a1+a2+a33=(x6+x5+x4)-(x3+x2+x1)9T2.由于采用将打点纸带分成两大段来处理即 两段法 求运动物体的加速度会更准确ꎬ计算也较简便ꎬ建议教师在教学过程多介绍 两段法 即ꎬxⅡ-xⅠ=at2(其中t=3T).无论从实际的实验操作时的数据采集ꎬ还是从减小误差的角度ꎬ或者从数据处理的方便ꎬ 两段法 均为最佳方法.㊀㊀二㊁学生常见错误类型统计加速度的计算成为考试中的经典ꎬ学生也能掌握一定的处理方法.但仍然很容易出错.笔者对历次考试中不同类型的学生 纸带的加速度计算 错误类型做了统计如下:㊀1.时间间隔T没有判断正确ꎬ每段位移的间隔一般为T=0.1s或者T=0.02s.2.计算时未将数值换算为国际制单位m.3.有些题目物体做匀减速直线运动ꎬ学生定向思维ꎬ未考虑加速度为负.4.未按题目要求选取有效数字的位数.5.计算的方法并没有准确掌握.㊀㊀三㊁几种典型情况1.直接利用公式求解例1㊀在«探究小车的速度随时间变化的规律»的实验中ꎬ给出了这次实验中的一条纸带ꎬ如图2所示ꎬ其中0㊁1㊁2㊁3㊁4㊁5㊁6都为计数点.从0点开始ꎬ每相邻两个计数点之间的时间间隔为0.1sꎬ测得:x1=1.40cmꎬx2=482.00cmꎬx3=2.60cmꎬx4=3.20cmꎬx5=3.80cmꎬx6=4.40cm.则小车的加速度为m/s2.答案:0.6m/s2.点评㊀此类题型由于连续相等时间间隔内的位移差均相等ꎬ所以直接利用方法一计算即可.例2㊀在«研究匀变速直线运动»的实验中ꎬ得到一条纸带如图3所示ꎬA㊁B㊁C㊁D㊁E㊁F㊁G为相邻的7个计数点ꎬ已知相邻计数点间的时间间隔为0.10sꎬ则利用图中标明的数据(单位:cm)可得小车的加速度为m/s2ꎬ在打点计时器打出D点时ꎬ小车的瞬时速度为m/s.答案:1.57m/s2.点评㊀此题已知的位移不是相邻的ꎬ计算时要注意公式的正确运用.例3㊀小球作直线运动时的频闪照片如图4所示.已知频闪周期T=0.1sꎬ小球相邻位置间距(由照片中的刻度尺量得)分别为OA=6.51cmꎬAB=5.59cmꎬBC=4.70cmꎬCD=3.80cmꎬDE=2.89cmꎬEF=2.00cm.小球在位置A时速度大小vA=m/sꎬ小球运动的加速度为m/s2.答案:0.605m/sꎬ-0.901m/s2.点评㊀此题是小球做匀减速运动ꎬ计算的加速度应为负值.相邻时间间隔的位移差都不完全相等ꎬ计算需要使用 逐差法 或 两段法 .本题直接运用 两段法 计算简单又容易理解.另外学生在做题时容易定向思维将加速度写成0.9m/s2ꎬ漏掉负号.2.利用 逐差法 或 两段法 求解对比例4㊀某同学在做 测定匀变速直线运动的加速度 实验时ꎬ从打下的若干纸带中选出了如图5所示的一条(每两点间还有4个点没有画出来)ꎬ图5中上部的数值为相邻两个计数点间的距离.打点计时器的电源频率为50Hz.由这些已知数据计算:(1)该匀变速直线运动的加速度a=m/s2.(2)与纸带上D点相对应的瞬时速度v=m/s.(答案均要求保留3位有效数字.)解析㊀相邻计数点间的时间间隔为T=0.10s.方法1㊀利用逐差法a1=x4-x13T2ꎬa2=x5-x23T2ꎬa3=x6-x33T2ꎬa-=a1+a2+a33ꎬa-=(x6+x5+x4)-(x3+x2+x1)9T2=1.93m/s2.方法2㊀利用 两段法将OC段看成xⅠꎬCF段看成xⅡꎬ由xⅡ-xⅠ=at2ꎬ(其中t=3T)ꎬa=xⅡ-xⅠ3T2()=(15.10+12.70+10.81)-(9.10+7.10+5.00)(3ˑ0.1)2cm/s2=1.93m/s2.点评㊀本题中如果是奇数段位移ꎬ可考虑去掉前面较短的位移ꎬ然后在用上述方法处理.两种方法从数学计算上看貌似一样.但细想一下:在实验数据处理时用 逐差法 原理变得较难理解ꎬ实验误差更大ꎬ计算也更复杂.将纸带分成六段ꎬ有的甚至更多ꎬ这样做必然使被测量的长度变短ꎬ增大了测量的相对误差ꎬ这不可能减小实验误差.此题用 两段法 可以达到同样目的.将打点纸带分成较长的两段来处理ꎬ便于数据的测量ꎬ公式的理解ꎬ结果的计算.此法减小了误差ꎬ达到了更好的实验效果.教材中介绍的 逐差法 可以简化为 两段法 .教师在平时的教学中多找出学生出错的主要原因ꎬ将一类题型整合在一起理解ꎬ能帮助学生提高解决物理问题的能力ꎬ可以起到化难为易ꎬ化繁为简ꎬ事半功倍的效果.㊀㊀参考文献:[1]齐春法.对 逐差法 与 二段法 求加速度所引起误差的探讨[J].物理教学探讨ꎬ2006ꎬ24(271):26.[2]刘晓红.几种由纸带求加速度的实验数据处理方法的比较[J].物理教师ꎬ2004ꎬ25(5):34-35.[责任编辑:李㊀璟]58。

如何利用纸带数据计算匀变速直线运动的速度和加速度如何利用纸带数据计算出加速度,较多同学没有弄明白逐差法求加速度的实质,因而难于记住相关的公式以至于考试时无法求解。
本文厘清了逐差法求加速度的实质是两段法。
也演示了怎样用两段法求加速度。
一、准备知识㈠.由纸带数据求运动物体速度的方法――替代法。
根据匀变速直线运动某段时间中间时刻的瞬时速度等于这段时间内的平均速度v n =(x n +x n +1)/2T . ㈡.由纸带数据求运动物体加速度的方法――图象法和逐差法(下面重点认识逐差法)。
1、图像法:先求出打各个计数点时物体的瞬时速度,再作出v -t 图像,图像的斜率即为物体做匀变速直线运动的加速度.2、逐差法【引题】(有6小段)如图1所示小车匀加速运动时用打点计时器打出的一条纸带,图中的各点是计数点且其计数周期为T(即相邻两计数点之间的时间间隔是T),各计数点之间的距离分别是x 1、x 2、x 3、x 4、x 5、x 6…。
已知拉动纸带的小车做匀加速直线运动,求小车运动的加速度大小(用字母表示,要求多次测量求平均值)。
解法A :由21363T a x x =-得213T x x a 36-=由22253T a x x =-得223Tx x a 25-= 由23143T a x x =-得233Tx x a 14-= ()()232165432193T x x x x x x a a a a ++-++=++=∴ ()()()23216543T x x x x x x a ++-++=∴ 或写成:(x 4+x 5+x 6)-(x 1+x 2+x 3)=a(3T)2……………………公式1对上式你怎么理解?类比推理,如果只有4小段,公式又如何?(x 3+x 4)-(x 1+x 2)=a(2T)2………………………………公式2说明:这种计算加速度的方法叫逐差法或叫隔差法。
(1)为什么要用逐差法求加速度?逐差法求加速度的实质是什么?请再看解法B :2112T a x x =-, 2223T a x x =-,2334T a x x =-, 2445T a x x =- 2556T a x x =- 2165432155T x x a a a a a a -=++++=∴比较一下:解法B 的实质只用了(x 1 、 x 6)两小段,解法A 的实质是使用了(x 1、x 2、x 3、x 4、x 5、x 6)六小段,能有效的减少偶然误差,所以要用逐差法求加速度。

专题:纸带问题求加速度与速度分析纸带问题的核心公式◆21aT s s sn n =-=∆- 求加速度a◆V t/ 2 =V =s t=T S S N N 21++ 求某点瞬时速度v分析纸带时要做的工作一般有:1.判定物体的运动性质(1)若纸带上各相邻点间距相等,则物体做匀速运动.(2)若相邻计数点时间间隔为T ,计算各个连续相等时间内位移的差Δx ,若Δx =aT 2(恒量),则物体做匀变速直线运动. 2.某点瞬时速度的计算根据在匀变速直线运动中,某段时间内的平均速度等于该段时间中点时刻的瞬时速度:v n =Tx x n n 21++即n 点的瞬时速度等于(n -1)点和(n +1)点间的平均速度. 3.加速度的计算由于物体做匀变速运动,所以满足在连续相等的时间间隔内位移差相等,即Δx =aT 2可得a =2Tx ∆.但利用一个Δx 求得的加速度偶然误差太大,为了减小实验中的偶然误差,分析纸带时,纸带上的各段位移最好都用上,方法如下:如果纸带上测得连续6个相同时间T 内的位移s 1、s 2、s 3、s 4、s 5、s 6,如图2-2所示.,求加速度a解:(1)由于2213243x x x x x x aT -=-=-=所以,2413x x aT -=;同理得,2523x x aT -=,2633x x aT -= 因此,6543212()33x x x x x x a aT ++-++=⋅(2)以时间间隔为3T 考虑,有2654321()()(3)x x x x x x a T ++-++= 所以,6543212()()(3)x x x x x x a a T ++-++=1、某学生用打点计时器研究小车的匀变速直线运动.他将打点计时器接到频率为50 Hz的交流电源上,实验时得到一条纸带如图实-1-10所示.他在纸带上便于测量的地方选取第一个计数点,在这点下标明A,第六个点下标明B,第十一个点下标明C,第十六个点下标明D,第二十一个点下标明E.测量时发现B点已模糊不清,于是他测得AC长为14.56 cm,CD长为11.15 cm,DE长为13.73 cm,则1,打C点时小车的瞬时速度大小为________ m/s,2,小车运动的加速度大小为________ m/s2,3,AB的距离应为________ cm2. 在“测定匀变速直线运动的加速度”的实验中,用打点计时器记录纸带运动的时间。

纸带问题求加速度与速度分析纸带问题的核心公式
◆
2
1
aT
s
s
s
n
n
=
-
=
∆
-求加速度a ◆=
V
=
s
t=T
S
S
N
N
2
1
+
+
求某点瞬时速度v
2,在“测定匀变速直线运动的加速度”的实验中,用打点计时器记录纸带运动的时间。
计时器所用电源的频率为50Hz,图为一次实验得到的一条纸带,纸带上每相邻的两计数点间都有四个点未画出,按时间顺序取0、1、2、3、4、5六个计数点,用米尺量出1、2、3、4、5点到0点的距离如图所示(单位:cm)。
由纸带数据计算可得
1,计数点4所代表时刻的瞬时速度大小v4=________m/s,
小车的加速度大小a=________m/s2。
3,研究小车的匀变速运动,记录纸带如图所示,图中两计数点间有四个点未画出。
已知打点计时器所用电源的频率为50Hz,则小车运动的加速度a = m/s
4,研究匀变速直线运动的实验中,如图示为一次记录小车运动情况的纸带,图中A、B、C、D、E、F、G为相邻的计数点,相邻计数点的时间间隔T=0.1S,AB、AC的位移大小分别为S1=1.30cm,S2=3.10cm,
求加速度的公式为a=______________,加速度大小为______________ m/s2。

求纸带的加速度及速度一、公式:S 1-S 2=△X=aT 2注意;△X 指的是两段位移的差值,T 代表每段时间,以为每段时间只能是相等的。
同理可得,S m -S n =(m-n )aT 2 二、某段时间内中间时刻的瞬时速度等于这段时间内的平均速度:。
证明:由v t =v 0+at 可知,经后的瞬时速度为:1、某同学用如图10所示的装置测量重力加速度g ,打下如图11所示的纸带.如果在所选纸带上取某点为0号计数点,然后每隔4个点取一个计数点,相邻计数点之间的距离记为x1、x2、x3、x4、x5、x6。
图10图11(1)实验时纸带的 端应和重物相连接。
(选填“A”或“B”)(2)该同学用两种方法处理数据(T 为相邻两计数点间的时间间隔):方法A:由g1=错误!,g2=错误!,…,g5=错误!取平均值g =9.767 m/s2;方法B:由g1=x4-x13T2,g2=错误!,g3=错误! 取平均值g =9。
873 m/s2。
从数据处理方法看,在x1、x2、x3、x4、x5、x6中,对实验结果起作用的数据,方法A 中有 ;方法B 中有 。
因此,选择方法 (填“A”或“B”)更合理。
2、在“研究匀变速直线运动的规律”实验中,小车拖纸带运动,打点计时器在纸带上打出一系列点, 从中确定五个记数点,每相邻两个记数点间的时间间隔是0。
1s,用米尺测量出的数据如图12所示. 则小车在C点的速度V C = m/s,小车在D点的速度V d = m/s,小车运动的加速度a =______________m/s2.3、在做“研究匀变速直线运动"的实验中,取下一段如图所示的纸带研究其运动情况.设O 点为计数的起始点,在四个连续的计数点中,相邻两计数点间的时间间隔为0。
1 s,若物体做理想的匀加速直线运动,则计数点A与起始点O之间的距离x1为 cm,打计数点O时物体的瞬时速度为 m/s,物体的加速度为 m/s2(结果均保留三位有效数字)。

高中物理实验——测定物体的速度及加速度(含逐差法) 一、通过纸带测算速度:通过纸带求速度有两种方法,公式法和位移—时间图象法。
(1)公式法:02t v v v +==总位移总时间;(2)位移—时间图象法:习题1. 如图为某次实验时打出的纸带,打点计时器每隔0.02s 打一个点,图中O 点为第一个点,A 、B 、C 、D 为每隔两点选定的计数点。
根据图中标出的数据,求:(1)打A 、D 点时间内纸带的平均速度有多大;(2)打B 和C 点时刻纸带的瞬时速度有多大。
解析:(1)AD 段的平均速度/(43.2515.50)/(0.0233)/ 1.54/AD AD v AD t cm s m s ==-⨯⨯=;(2)可以用平均速度代替/(32.5015.50)/(0.0232)/ 1.42/B AC v AC t cm s m s ==-⨯⨯= 。
/(43.2523.25)/(0.0232) 1.67/C BD v BD t m s ==-⨯⨯= 。
二、通过纸带测算加速度:通常有3种方法,即公式法、v t -图象法、2x t -图象法。
1、公式法:主要运用公式2x at ∆=。
涉及两种情况:①每n 个时间段为一组,则2()x a nt ∆=;②另一种情况中间跨过n 个时间段,则2x nat ∆=。
习题2. 在“研究匀变速直线运动”的实验中,小车拖着纸带运动,打点计时器每隔0.02s 打一个点,打出的纸带如图,选出A 、B 、C 、D 、E 共5个计数点,每相邻两点间还有四个实验点(图中未画出),以A 点为起点量出的到各点的位移已标在图上。
由此可求得小车运动的加速度a = 2/m s ,打A 点时小车运动的速度为A v = /m s 。
答案:0.05,0.075。
提示:0.085/c v m s =。
习题3. 在“研究匀变速直线运动”的实验中,小车拖着纸带运动,打点计时器每隔0.02s 打一个点,打出的纸带如图,选出A 、B 、C 、D 、E 共5个计数点,每相邻两点间还有四个实验点(图中未画出),以A 点为起点量出的到各点的位移已标在图上。

通过纸带求加速度的两种方法在学完第二章《匀变速直线运动的研究》内容以后,老师布置这样一道题:某同学在做“测定匀变速直线运动的加速度”实验时,从打下的若干纸带中选出了如图所示的一条(每两点间还有4个点没有画出来),图中上部的数字为相邻两个计数点间的距离。
打点计时器的电源频率为50Hz 。
由这些已知数据计算:(1)求下列各点的瞬时速度:1v = m/s ;2v = m/s ;3v = m/s ;4v = m/s ;5v = m/s 。
(2)思考:如何得出O v = m/s ; v 6= m/s 。
(3)根据提供的数据你能用几种方法求出该匀变速直线运动的加速度a =___m/s 2。
(答案均要求保留3位有效数字)由于两个相邻记数点间的时间间隔为T=0.1s,利用匀变速直线运动的中间时刻瞬时速度等于这一段时间的平均速度同学们很快得出了V 1、、V 2、V 3、V 4、V 5分别为0.605m/s 、0.810m/s 、1.01m/s 、1.21m/s 、1.42m/s.同样道理由于01v =S 1/ T=( V O +V 1)/2, 56v == S 6/T=(V 5+V 6)/2,可得V O 、、V 6为0.395m/s 、1.60m/s .对于第三个问题,同学们展开了热烈的讨论,经过一段时间的讨论与演练,同学共提出了几种不同的方法,老师让几位同学在黑板上板演了自己的做法。
一位同学解法:△S 1=S 2-S 1=2.10cm, △S 2=S 3-S 2=2.00cm, △S 3=S 4-S 3=1.90cm, △S 4=S 5-S 4=2.20cm, △S 5=S 6-S 5=1.90cm,由于△S 不等,所以s ∆=(△S 1+△S 2+△S 3+△S 4+△S 5)/5=2.02 cm.a =s ∆ /T 2=2.02m/s 2另一位同学利用坐标纸,根据得出的V 1、、V 2、V 3、V 4、V 5的大小作出V-t 图象,通过求图象的斜率△V /△t 求加速度a 。

如何快速、准确地处理“研究匀变速运动”纸带有关“研究匀变速运动”的实验目的、实验原理、实验器材、实验步骤和注意事项在这里就不再赘述,现在主要研讨对已打出“研究匀变速运动”的纸带,如何快速、准确地求出匀变速运动的加速度a 值和纸带上任意一点的速度V 值,使求得的加速度a 值和速度V 值的误差更小。
一般为了减小误差,在处理纸带时多用逐差法处理,但计算处理不简捷。
逐差法处理是这样的:如下图所示:相邻计数点间的距离分别为,两计数点间的时间间隔为为T ,根据ΔS =aT 2有:S 4-S 1=(S 4-S 3)+(S 3-S 2)+(S 2-S 1)=3aT 2同理:S 5-S 2=S 6-S 3=3aT 2 求出21413T s s a -=, 22513T s s a -=, 23633T s s a -= 再算出a 1、a 2、a 3的平均值:236251432133)()()(3Ts s s s s s a a a a ⨯-+-+-=++= 以上方法比较麻烦,若给出的段数为3段、5段或7段时,就不便计算加速度的平均值,可把以上方法略作变形,加以总结推广如下: 由上式得:2321654)3()()(T s s s s s s a ++-++= 即若给出6段,则用后三段之和减去前三段之和,再除以三段的时间的平方,即为所求的加速度的值。
总结推广:(1)、若给出的段数为3段、5段、7段或9段的奇数段,则去掉最小的一段,再按段数平分为两大段,用后一大段的总长度减去前一大段的总长度,然后除以相应的一大段所对应的时间的平方,即为所求的加速度a 的值。
去掉最小段的原理是:我们在打点计时器打出的纸带上取计数点的目的就是为了增大测量段的长度,以减小测量长度时带来的误差,所以可去掉最小的一段。
(2)若给出的段数为偶数段,直接把总段数分成段数相等的两大段,用后一段的总长度减去前一大段的总长度,再除以一大段的时间的平方,即为所求的加速度a 值。

匀变速直线运动纸带实验匀变速直线运动纸带实验是一种常见的物理实验,用于研究物体的匀变速直线运动规律。
以下是该实验的详细步骤和注意事项。
一、实验准备1.实验器材准备:准备好必要的实验器材,如打点计时器、纸带、刻度尺、电源等。
打点计时器是一种能够在纸带上打点的计时仪器,是实验中重要的测量工具。
2.实验场地与环境:选择一个安静、平稳的实验场地,确保实验过程中没有干扰因素。
二、实验步骤1.安装纸带:将纸带穿过打点计时器的限位孔,并挂在支架上。
将纸带的一端固定在物体上,另一端通过打点计时器与纸带磨砂面接触。
2.启动与暂停:接通电源后启动打点计时器,打点计时器将在纸带上打下一个点。
当物体运动到预定位置时,关闭打点计时器并暂停纸带运动。
3.测量距离:用刻度尺测量纸带上两个点之间的距离,即为物体在两点间运动的位移。
重复此步骤,在不同位置测量多个位移数据。
4.数据记录:将测量数据记录在表格中,包括起始位置、终止位置、位移量等。
可以用公式计算物体的速度、加速度等物理量。
5.清理实验场地:实验结束后,关闭电源并清理实验场地。
三、注意事项1.打点计时器的使用:使用打点计时器时要注意调整纸带的张力,确保纸带在运动过程中不会偏离或断裂。
同时,要确保打点计时器的打点针头与纸带面接触良好,以保证在纸带上打下清晰的点迹。
2.测量准确性:为了提高测量准确性,可以在不同位置多次测量位移数据,并将结果取平均值。
同时,要使用精确的刻度尺,确保测量位移时的读数准确。
3.误差来源:匀变速直线运动纸带实验的误差主要来源于人为因素和环境因素。
例如,测量位移时的读数误差、打点计时器的计时误差等。
为了减小误差,可以通过多次测量取平均值或使用更精确的测量工具等方式进行改进。
4.实验重复性:为了验证实验结果的可靠性,可以多次进行匀变速直线运动纸带实验,并比较各次实验的测量结果。
如果测量结果一致,说明实验具有较好的重复性。
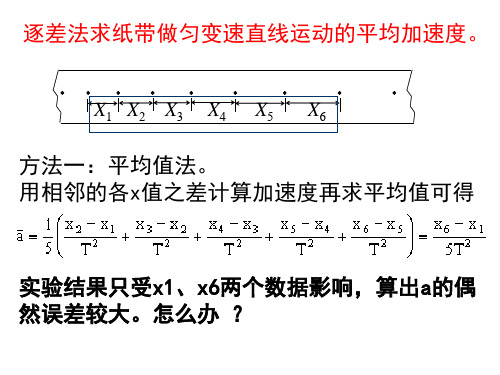
5.安全问题:在实验过程中要注意安全问题,例如接通电源前要检查电源是否正常、关闭电源后才能移动纸带等。


匀变速直线运动纸带的处理——处理纸带数据计算加速度方法归纳徐卫兵江苏木并茶高级中学,江苏省南通市226406利用电磁打点计时器打出的纸带测物体做匀变速运动的加速度,是高中阶段的一个重要实验。
实验操作完后从三条纸带中选择一条比较理想的,舍掉开头比较密集的点子,在后边便于测量的地方找一个开始点,我们把每打五次点的时间作为时间的单位,也就是T=0.02×5=0.1 s,在选好的开始点下面标明0,在第六点下面标明1,在第十一点下面标明2,在第十六点下面标明3……标明的点0,1,2,3……叫做记数点,如图1所示,两个相邻记数点间的距离分别是s 1、s 2、s 3……本文拟谈谈如何利用这些数据求物体的加速度。
1 逐差法及演绎1.1 逐差法物体做匀加速直线运动时的初速度是v 0,加速度是a,在两个连续相等的时间T 里的位移分别是s 1和s 2,由于s 1=v o T=aT v v aT T v s aT o +=+=121222121,又因为,所以△s=s 2-s 1=aT 2所以我们可以由测得的各段位移s 1、s 2、s 3……,求出,,再求出、、3333321236322522321a a a T s s a T s s a T a a a a ++-=-=++=-这就是要测定的匀变速直线运动的加速度,这种方法就叫“逐差法”。
(1)逐差法进行数据处理的优点实验测定中,尽量减小误差是根本原则,按逐差法处理数据,则加速度的平均值3321a a a ++=31(+-2143T s s 2253T s s -+ 2363T s s -)=23216549)()(Ts s s s s s ++-++ ① 这样一来,能将全部测量数据s 1、s 2、s3、s 4、s 5、s 6都加以充分利用,并通过取平均值减小了偶然误差。
如果不按逐差法,而用相邻的各s 值之差计算加速度,即,,则,,2165432125652232212155Ts s a a a a a a T s s a T s s a T s s a -=++++=-=⋯⋯-=-=- 由此看出,此法在取平均值的表象下,实际上只有s 1和s 6两个数据被利用,其余的数据s 2、s 3、s 4、s 5都没有用,因而失去了多个数据正负偶然误差互相抵消的作用,算出的结果-a 的误差较大。

对由纸带求加速度的实验方法的探讨摘要:结合常见试题对“测定匀变速直线运动的加速度”的实验方法进行探讨,提出采用直接读取每个计数点位置坐标值的方法采集数据,然后采用“二段法”处理数据。
关键词:匀变速直线运动加速度逐差法二段法物理学是一门实验科学,准确采集并正确处理实验数据在实验教学中具有重要意义。
在高中物理教学中,学生使用打点计时器“测定匀变速直线运动的加速度”的实验在处理数据时常用隔项逐差法(即下述“方法一”)求加速度,也有教师提出其它方法,如下述“方法二”[1]。
设物体以加速度做匀加速直线运动,取六段连续相等的时间内的位移、、……【方法一】根据常用的隔项逐差法,加速度的表达式为:①【方法二】其改进后的实验原理如下:,,则,,。
再计算平均值得②文章作者认为,“方法二”的结果“既应用了6个数据,又对6个数据间隔使用,起到进一步减小误差的作用”,实则不然。
一、对两种方法的误差分析当用公式计算时,测量值的相对误差为③由于一般使用最小刻度为1mm的刻度尺来测量长度,故测量值、的最大绝对误差为=0.5mm+0.5mm=1.0mm的绝对误差=0将该误差分析应用到①②两式分别为因为>,所以<,故从减小实验误差的角度看,“方法一”更为合理。
二、对实验方法的进一步探讨应用“方法一”测量各相邻计数点之间的位移的方法并不好,因为用一把刻度尺测量某一段长度时,读数的偶然误差并不只是由于末端读数估计值而产生的,起始端与刻度尺的某刻度线是否对齐也是估计的。
在实际操作时,往往要多次移动刻度尺的位置,每次都要读取刻度尺两端的数据,这样既不方便,又会引入较大的误差,甚至发生读数错误。
笔者认为,采用下述“方法三”无论从误差理论分析,还是从实际操作考虑,都更为合理。
【方法三】如果把作为,把作为,连续相等时间为3,则有可得加速度大小为④该测量值的相对误差为可见,该方法的相对误差更小,并且实验操作中只需测量两段较长的长度,计算简便,也不容易发生错误,笔者称之为“二段法”。