材料力学实验指导书(矩形截面梁纯弯曲正应力的电测实验)

单一材料梁的弯曲正应力实验一、实验目的1．用电测法测量单一材料的矩形截面梁在纯弯曲状态时其横截面上正应力的大小及分布规律，并与理论计算值比较，从而验证梁的弯曲正应力理论公式。

2．初步掌握电测法原理和静态电阻应变仪的使用方法。

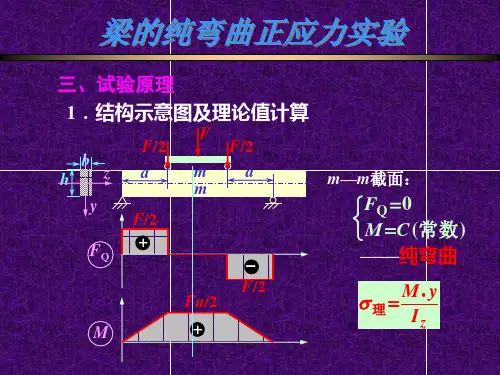
二、预习思考要点1．本实验装置是如何实现使梁的某一区段处于纯弯曲状态的？2．梁处于纯弯曲状态时其内力分布有何特征？3．梁处于纯弯曲状态时，若要测取其上某一点的线应变为何只需在该点布设一枚应变计，且平行于梁的轴线方向？三、实验装置和仪器1．纯弯曲实验装置本实验采用低碳钢或中碳钢制成的矩形截面梁，测试其正应力分布规律的实验装置如图1-26（a）所示，所加的砝码重量通过杠杆以一定的放大比例作用于加载辅梁的中央，设作用于辅梁中央的载荷为F，由于载荷对称，支承条件对称，则通过两个挂杆作用于待测梁上C、D处的载荷各为F/2。

由待测梁的内力图可知CD段上的剪力Q=0，弯矩为一常量M=2aF ，即梁的CD段处于纯弯曲状态。

图1-26 弯曲正应力实验装置及试样贴片位置图2．静态电阻应变仪3．游标卡尺、钢直尺四、实验原理由于矩形截面梁的CD段处于纯弯曲状态，当梁发生变形其横截面保持平面的假设成立，又可将梁视作由一层一层的纵向纤维叠合而成且假设纵向纤维间无挤压作用，此时纯弯曲梁上的各点处于单向应力状态，且弯曲正应力的方向平行于梁的轴线方向，所以若要测量纯弯曲状态下梁的横截面上的正应力的分布规律，可在梁的CD 段任一截面上沿不同高度处平行于梁的轴线方向布设若干枚电阻应变计，为简便计算，本实验的布片方案如图1-26（b ）所示，一枚布设在梁的中性层上，其余四枚分别布设在距中性层h/4或h/2处（h 为梁矩形截面的高度），此外还布设了一枚温度补偿片。

当梁受载后，电阻应变计随梁的弯曲变形而产生伸长或缩短，使自身的电阻改变。

通过力学量的电测法原理，利用电阻应变仪即可测出梁横截面上各测点的应变值ε实。

由于本实验梁的变形控制在线弹性范围内，所以依据单向虎克定律即可求解相应各测点的应力值，即σ实=E ·ε实，E 为梁材料的弹性模量。

实验三 直梁弯曲正应力测定实验指导书一、实验目的1、用电测法测定直梁纯弯曲时的正应力分布，并与理论计算结果进行比较，以验证弯曲正应力公式。

2、了解电阻应变测量的原理，初步掌握静态电阻应变仪的使用方法。

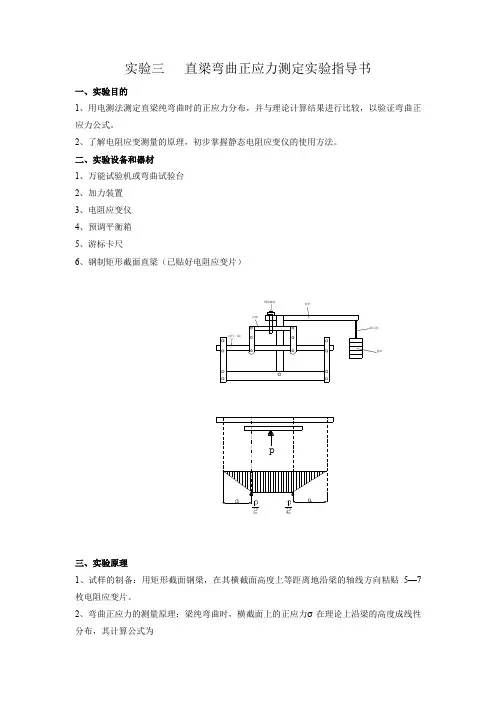
二、实验设备和器材 1、万能试验机或弯曲试验台 2、加力装置3、电阻应变仪4、预调平衡箱5、游标卡尺6、钢制矩形截面直梁（已贴好电阻应变片）试件（梁）付梁蝶形螺母杠杆砝码砝码托三、实验原理1、试样的制备：用矩形截面钢梁，在其横截面高度上等距离地沿梁的轴线方向粘贴5—7枚电阻应变片。

2、弯曲正应力的测量原理：梁纯弯曲时，横截面上的正应力σ在理论上沿梁的高度成线性分布，其计算公式为z I y M ⋅=σ式中，σ的单位为MPa ；M 为梁横截面上的弯矩，单位为N ·mm ；y 为应力σ所在的点到中性轴的距离，单位为mm ；I z 为横截面对中性轴z 的面积二次矩，单位为mm 4。

面积二次矩对于矩形截面按下式计算123bh I z =式中，b 为梁横截面的宽度，单位为mm ；h 为梁横截面的高度，单位为mm 。

令使载荷P 对称地加在矩形截面直梁上（如图所示）。

这时，梁的中段将产生纯弯曲。

若载荷每增加一级p ∆（用增量法），则可由电阻应变仪测出梁中段所贴应变片各点的纵向应变增量ε∆，根据虎克定律求出各点实测正应力增量σ实为σ实=E ε∆此值与理论公式计算出的各点正应力的增量即σ理＝ZI My∆ 进行比较，就可验证弯曲正应力公式。

这里，弯矩增量2paM ∆=∆。

梁上各点的应变测量，采用半桥接线，各工作应变片共用一个温度补偿块。

四、实验步骤1．准备试样。

如图所示，测量试样的高度h 、宽度b ，以及试样各测量点的坐标y ；。

将试样放在试验机活动台的支座上，布置成纯弯曲梁，测量梁的跨度l 及加载梁的支点到支座的距离a 。

2．准备应变仪。

把梁上各测量点的应变片（工作应变片）按编号逐点接到预调平衡箱A 、B 接线柱上，将温度补偿片接到预调平衡箱上任一工作应变片所在列的B 、C 接线柱上作公共补偿，此时C 排接线柱应用金属连接片或导线连接起来。

第一节矩形截面梁的纯弯曲实验一、实验目的1.学习电测法的基本原理和静态电阻应变仪的使用方法。

2.学习电测法中的1/4桥、1/2桥和全桥的测量方法。

3.测量矩形截面梁在纯弯曲段中测点沿轴线方向的线应变，画出该线应变沿梁高度方向的变化规律，验证平面截面假设。

4.根据上述测量结果计算测点的正应力，并与理论计算值进行比较。

二、实验设备和仪器1.多用电测实验台。

2.DH-3818型静态电阻应变仪。

3.SDX-I型载荷显示仪。

三、实验原理及方法实验装置如图2-1所示，矩形截面梁采用低碳钢制成，其弹性模量GPa=E，210梁的尺寸为mmb，m m40h。

在发生纯弯曲变形的梁段上，沿=20100=a，m m=梁的沿轴线方向粘贴有5个应变片（其中应变片1位于梁的上表面，应变片2位于梁的上表面与中性层的中间，应变片3位于梁的中性层上，应变片4位于梁的中性层与下表面的中间，应变片5位于梁的下表面），另外在梁的支撑点以外粘贴有一个应变片作为温度补偿片。

应变片的灵敏系数08K。

=.21.应变测量3种测量桥路的接线方法如下：图2-1 矩形截面梁的纯弯曲(1) 1/4桥测量方法将5个工作片和温度补偿片按1/4桥形式分别接入电阻应变仪的5个通道中，组成5个电桥。

具体接法：工作片的引线接在每个电桥的A、B端，温度补偿片接在电桥的B 、C 端。

当梁在载荷作用下发生弯曲变形时，工作片的电阻值将随着梁的变形而发生变化，电阻应变仪相应通道的输出应变为仪ε，于是测点的应变为仪实εε=(2) 1/2桥测量方法由于测点5与测点1的应变之间存在关系15实实εε-=测点4与测点2的应变之间存在关系24实实εε-=于是可将工作片5和1、4和2分别按1/2桥形式接入电阻应变仪的2个通道中，组成2个电桥。

具体接法：工作片5接到一个电桥的A 、B 端，工作片1接到该电桥的B 、C 端；工作片4接到另一个电桥的A 、B 端，工作片2接到相应电桥的B 、C 端。

纯弯曲正应力电测实验指导书一．实验作用和目的1．用电测法测定矩形截面简支梁受纯弯曲时横截面上弯曲正应力的大小及其、分布规律，并与理论值进行比较，以验证弯曲正应力公式正确性。

2．熟悉电测实验的基本原理和操作方法，掌握该方法在工程中的应用。

二．实验内容梁受纯弯曲时的正应力计算公式为：y I M Z=σ 式中 M —作用在横截面上的弯矩；I z —横截面对其中性轴Z 的惯性矩；y 一由欲求应力点到中性轴的距离。

本实验采用矩形截面直梁(或铝合金制成的箱形截面直梁)，实验装置如图1（a ）、图1(b)所示。

施加的砝码重量通过杠杆以一定比例作用于附梁。

通过两个挂杆作用于梁上C 、D 处的载荷各为F /2。

由该梁的内力图可知CD 段上的剪力Q F 等于零，弯矩M =F .a /2。

因此梁上CD 段处于纯弯曲状态。

图1纯弯曲正应力试验台1-试验机活动台；2-支座；3-试样；4-试验机压头；5-加力梁；6-电阻应变片在CD 段内任选的一个截面上，距中性层不同高度处，沿着平行于梁的轴线方向，等距离地粘贴七个电阻应变片，每片相距h /6，在梁不受载荷的自由端贴上温度补偿片。

试验时，采用半桥接法将各测点的工作应变片和温度补偿应变片连接在应变电桥的相邻桥臂上，按照电阻应变仪的操作规程将电桥预调平衡，加载后即可从电阻应变仪上读出实ε。

由于纤维之间不相互挤压，故可根据虎克定律求出弯曲正应力的实验值 实实εσ⋅=E a (1)式中E — 梁所用材料的弹性模量。

本实验采用“增量法”加载，每次增加等量的载荷F ∆并相应地测定各点的应变增量实ε∆。

取应变增量的平均值实ε∆，依次求出各点应力增量实σ∆。

实实εσ∆⋅=∆E (2)将实σ∆实值与理论公式算出的应力增量ZI y ⋅∆=∆M 理σ (3) 进行比较，计算出截面上各测点的应力增量实验值与理论值的误差。

其计算公式为%100⨯∆∆-∆=理实理σσση (4)以验证弯曲正应力公式的正确性。

材料力学实验指导书§5 梁弯曲正应力电测实验指导书1、概述梁是工程中常用的受弯构件。

梁受弯时，产生弯曲变形，在结构设计和强度计算中经常要涉及到梁的弯曲正应力的计算，在工程检验中，也经常通过测量梁的主应力大小来判断构件是否安全，也可采用通过测量梁截面不同高度的应力来寻找梁的中性层。

2、实验目的1、用应变电测法测定矩形截面简支梁纯弯曲时，横截面上的应力分布规律。

2、验证纯弯梁的弯曲正应力公式。

3、观察纯弯梁在双向交变加载下的应力变化特点。

3、实验原理梁纯弯曲时，根据平面假设和纵向纤维之间无挤压的假设，得到纯弯曲正应力计算公式为：Z I My=σ式中：M —弯矩 Z I —横截面对中性层的惯性矩 y —所求应力点的纵坐标（中性轴为坐标零点）。

由上式可知梁在纯弯曲时，沿横截面高度各点处的正应力按线性规律变化，根据纵向纤维之间无挤压的假设，纯弯梁中的单元体处于单纯受拉或受压状态，由单向应力状态的胡克定律E *εσ=可知，只要测得不同梁高处的ε，就可计算出该点的应力σ，然后与相应点的理论值进行比较，以验证弯曲正应力公式。

4、实验方案4.1实验设备、测量工具及试件：YDD-1型多功能材料力学试验机（图1.8）、150mm 游标卡尺、四点弯曲梁试件（图5.1）。

YDD-1型多功能材料力学试验机由试验机主机部分和数据采集分析两部分组成，主机部分由加载机构及相应的传感器组成，数据采集部分完成数据的采集、分析等。

图5.1实验中用到的纯弯梁，矩形截面，在梁的两端有支撑圆孔，梁的中间段有四个对称半圆形分配梁加载槽，加载测试时，两半圆型槽中间部分为纯弯段，在纯弯段中间不同梁高部位、在离开纯弯图5.1 四点弯曲梁试件段中间一定距离的梁顶及梁底、在加工有长槽孔部位的梁顶及梁底均粘贴电阻应变片。

4.2 装夹、加载方案安装好的试件如图5.2所示。

试验时，四点弯曲梁通过销轴安装在支座的长槽孔内，形成滚动铰支座。

梁向下弯曲时，荷载通过分配梁等量地分配到梁上部两半圆形加载槽，梁向上弯曲时，荷载通过分配梁等量地分配到梁下部两半圆形加载槽，分配梁的两个加载支滚，一个为滚动铰支座，一个为滑动铰支座，这样就可保证梁在弯曲加载时不产生其它附加荷载。

纯弯曲梁的正应力电测实验一、实验目的1．用电测法测量单一材料的矩形截面梁在纯弯曲状态时其横截面上正应力的大小及分布规律，并与理论计算值比较，从而验证梁的弯曲正应力理论公式。

2．初步掌握电测法原理和静态电阻应变仪的使用方法。

二、实验装置和仪器1．纯弯曲实验装置本实验采用低碳钢或中碳钢制成的矩形截面梁，测试其正应力分布规律的实验装置如图20（a）所示，所加的砝码重量通过杠杆以一定的放大比例作用于加载辅梁的中央，设作用于辅梁中央的载荷为F，由于载荷对称，支承条件对称，则通过两个挂杆作用于待测梁上C、D处的载荷各为F/2。

由待测梁的内力图可知CD段上的剪力Q=0，弯矩为一常量M=2aF ，即梁的CD段处于纯弯曲状态。

图20 弯曲正应力实验装置及试样贴片位置图2．静态电阻应变仪3．游标卡尺、钢直尺三、实验原理由于矩形截面梁的CD段处于纯弯曲状态，当梁发生变形其横截面保持平面的假设成立，又可将梁视作由一层一层的纵向纤维叠合而成且假设纵向纤维间无挤压作用，此时纯弯曲梁上的各点处于单向应力状态，且弯曲正应力的方向平行于梁的轴线方向，所以若要测量纯弯曲状态下梁的横截面上的正应力的分布规律，可在梁的CD段任一截面上沿不同高度处平行于梁的轴线方向布设若干枚电阻应变计，为简便计算，本实验的布片方案如图20（b）所示，一枚布设在梁的中性层上，其余四枚分别布设在距中性层h/4或h/2处（h 为梁矩形截面的高度），此外还布设了一枚温度补偿片。

当梁受载后，电阻应变计随梁的弯曲变形而产生伸长或缩短，使自身的电阻改变。

通过力学量的电测法原理，利用电阻应变仪即可测出梁横截面上各测点的应变值ε实。

由于本实验梁的变形控制在线弹性范围内，所以依据单向虎克定律即可求解相应各测点的应力值，即σ实=E ·ε实，E 为梁材料的弹性模量。

实验采用“等增量法”加载，即每增加等量的载荷ΔF ，测定一次各点相应的应变增量Δε实，并观察各点应变增量的线性程度。

实验二：梁的纯弯曲正应力试验一、实验目的1、测定矩形截面梁在只受弯矩作用的条件下，横截面上正应力的大小随高度变化的分布规律，并与理论值进行比较，以验证平面假设的正确性，即横截面上正应力的大小沿高度线性分布。

2、学习多点静态应变测量方法。

二：实验仪器与设备:①贴有电阻应变片的矩形截面钢梁实验装置 1台②DH3818静态应变测试仪 1件三、实验原理（1）受力图主梁材料为钢梁，矩形截面，弹性模量E=210GPa,高度h=40.0mm，宽度b=15.2mm。

旋动转轮进行加载，压力器借助于下面辅助梁和拉杆（对称分布）的传递，分解为大小相等的两个集中力分别作用于主梁的C、D截面。

对主梁进行受力分析，得到其受力简图，如图1所示。

（2）内力图分析主梁的受力特点，进行求解并画出其内力图，我们得到CD段上的剪力为零，而弯矩则为常值，因此主梁的CD段按理论描述，处于纯弯曲状态。

主梁的内力简图，如图2所示。

Page 1 of 10（3）弯曲变形效果图（纵向剖面）（4）理论正应力根据矩形截面梁受纯弯矩作用时，对其变形效果所作的平面假设，即横截面上只有正应力，而没有切应力（或0=τ），得到主梁纯弯曲CD 段横截面上任一高度处正应力的理论计算公式为zii I y M =理论σ其中，M 为CD 段的截面弯矩（常值），z I 为惯性矩，iy 为所求点至中性轴的距离。

（5）实测正应力测量时，在主梁的纯弯曲CD 段上取5个不同的等分高度处（1、2、3、4、5），沿着与梁的纵向轴线平行的方向粘贴5个电阻应变片，如图4所示。

在矩形截面梁上粘贴上如图5.3所示的2组电阻应变片，应变片1－5分别贴在横力弯曲区，6－10贴在纯弯曲区，同一组应变片之间的间隔距离相等。

Page 2 of 10Page 3 of 10Page 4 of 10Page 5 of 10Page 6 of 10Page 7 of 10b.σ–P曲线图在σ–P坐标系中，以σi实的值为横坐标，P的值为纵坐标，将各点的实测应力值分别绘出，然后进行曲线拟合，这样就得到了纯弯梁横截面上各点在不同载荷下的5条正应力分布曲线。

74实验四 纯弯曲梁正应力实验一、实验目的1、测定矩形截面梁在纯弯曲时的正应力分布规律，并验证弯曲正应力公式的正确性；2、学习多点静态应变测量方法。

二、仪器设备1、纯弯曲梁实验装置；2、YD-88型数字式电阻应变仪；3、游标卡尺。

三、试件制备与实验装置1、试件制备本实验采用金属材料矩形截面梁为实验对象。

为了测量梁横截面上正应力的大小和它沿梁高度的分布规律，在梁的纯弯段某一截面处，中性轴和以其为对称轴的上下1/4点、梁顶、梁底等5个测点沿高度方向均匀粘贴了五片轴向的应变计（如图4-4-1），梁弯曲后，其纵向应变可通过应变仪测定。

图4-4-12、实验装置如图4-4-2和图4-4-3所示，将矩形截面梁安装在纯弯曲梁实验装置上，逆时针转动实验装置前端的加载手轮，梁即产生弯曲变形。

从梁的内力图可以发现：梁的CD 段承受的剪力为0，弯矩为一常数，处于“纯弯曲”状态，且弯矩值M=21P •a ，弯曲正应力公式 σ=z yI ⋅M可变换为σ=y az⋅P ⋅I 2图4-4-2图4-4-37576四、实验原理实验时，通过转动手轮给梁施加载荷，各测点的应变值可由数字式电阻应变仪测量。

根据单向胡克定律即可求得σi 实=E ·εi 实(i=1,2,3,6,7)为了验证弯曲正应力公式σ=z y I ⋅M 或σ=y az⋅P ⋅I 2的正确性，首先要验证两个线性关系，即σ∝y 和σ∝P 是否成立:1、检查每级载荷下实测的应力分布曲线，如果正应力沿梁截面高度的分布是呈直线的，则说明σ∝y 成立；2、由于实验采用增量法加载，且载荷按等量逐级增加。

因此，每增加一级载荷，测量各测点相应的应变一次，并计算其应变增量，如果各测点的应变增量也大致相等，则说明σ∝P 成立。

最后，将实测值与理论值相比较，进一步可验证公式的正确性。

五、实验步骤1、试件准备用游标卡尺测量梁的截面尺寸（一般由实验室老师预先完成），记录其数值大小；将梁正确地放置在实验架上，保证其受力仅发生平面弯曲，注意将传感器下部的加力压杆对准加力点的缺口，然后打开实验架上测力仪背面的电源开关；2、应变仪的准备 a.测量电桥连接：图4-4-4如图4-4-4，为了简化测量电桥的连接，将梁上5个测点的应变计引出导线各取出其中一根并联成一根总的引出导线，并以不同于其他引出导线的颜色区别，所以，测量导线由原来的10根缩减为6根，连接测量电桥时，将颜色相同的具有编号1、2、3、6、7的五根线分别连接在仪器后面板上五个不同通道的A号接线孔内，并将具有特殊颜色的总引出导线连接在仪器后面板上的“公共补偿片BC”位置的B号接线孔内。

基 本 实 验 4矩形梁纯弯曲时正应力分布电测实验一、实验目的1．学习使用电阻应变仪，掌握测试技能。

2．测量纯弯曲梁上应变随高度的分布规律，验证平面假设的正确性。

二、仪器设备弯扭试验台、电阻应变仪。

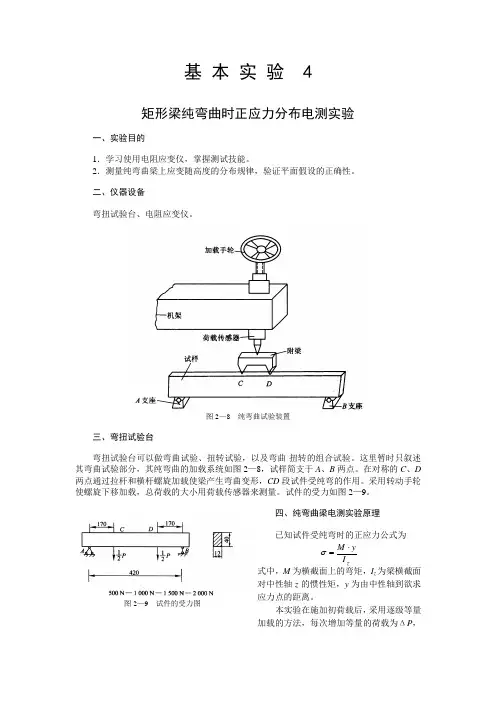
图2—8 纯弯曲试验装置三、弯扭试验台弯扭试验台可以做弯曲试验、扭转试验，以及弯曲-扭转的组合试验。

这里暂时只叙述其弯曲试验部分，其纯弯曲的加载系统如图2—8，试样简支于A 、B 两点。

在对称的C 、D 两点通过拉杆和横杆螺旋加载使梁产生弯曲变形，CD 段试件受纯弯的作用。

采用转动手轮使螺旋下移加载，总荷载的大小用荷载传感器来测量。

试件的受力如图2—9。

四、纯弯曲梁电测实验原理已知试件受纯弯时的正应力公式为z I y M ⋅=σ 式中，M 为横截面上的弯矩，I z 为梁横截面对中性轴z 的惯性矩，y 为由中性轴到欲求应力点的距离。

本实验在施加初荷载后，采用逐级等量加载的方法，每次增加等量的荷载为ΔP，图2—9 试件的受力图测定各点相应的应变增量一次，分别取应变增量的平均值。

，求出各点应力增量实实平σεz I yM E ⋅=⋅=∆σεσ理实平实，把实σ与理论公式算出的应力增量理σ加以比较，从而可验证公式的正确性，上述理论公式的ΔM 按下式求出：)17021mm N P M ⋅⨯=（∆∆五、电阻应变片的粘贴位置电阻应变片及电阻应变仪的有关说明请参看指导书的第一部分。

为了测量应变随试件截面高度的分布规律，应变片的粘贴位置如图2—10。

这样可以测量试件上下边缘处的最大应变和中性层无应变的特殊点，及其它中间点便于了解应变沿截面高度变化的规律。

六、SY-Ⅲ型数字应变仪及DSP-10型平衡箱操作使用方法应变仪的使用方法见第一章有关内容。

七、试验结果的整理1．求出各测量点在等量荷载作用下，应变增量的平均值。

2．以各测点位置为纵座标，以应变增量为横坐标，画出应变随试件高度变化曲线。

3．根据各测点应变增量的平均值，可计算出测量的应力值。

材料力学实验指导书目录序言0 实验一金属材料拉伸实验 2 实验二金属材料扭转实验9 实验三纯弯曲梁正应力电测实验16 附件：1、实验报告册封面2、材料力学实验要求3、实验报告要求序言材料力学实验是材料力学的重要支柱之一。

材料力学从理论上研究工程结构构件的应力分析和计算，并对构件的强度、刚度和稳定性进行设计或校核其可靠性。

材料力学实验从实验角度为材料力学理论和应用提供实验支持。

一、材料力学实验由三部分组成：1、材料的力学性能测定。

材料的力学性能是指在力的作用下，材料的变形、强度等方面表现出的一些特征，如弹性模量、弹性极限、屈服极限、强度极限、疲劳极限、冲击韧度等。

这些强度指标或参数是构件强度、刚度和稳定性计算的依据，而他们一般通过实验来测定。

此外，材料的力学性能测定又是检验材质、评定材料热处理工艺、焊接工艺的重要手段。

随着材料科学的发展，各种新型材料不断涌现，力学性能测定是研究新型材料的重要手段。

材料的力学性能测定一般是通过对标准试样加载至破坏，记录其应力-应变关系曲线（扭转破坏时记录其扭矩-扭转角或剪应力-剪应变曲线），测定材料的一些力学性能特征指标，如弹性模量、弹性极限、屈服极限、强度极限、冲击韧度等；因此，学会记录材料的应力-应变关系曲线成为材料力学性能实验的一项重要任务。

2、验证已建立的理论。

材料力学的一些理论是以某些假设为基础的，例如杆件的弯曲理论是以平面假设为基础。

用实验验证这些理论的正确性和适用范围，有助于加深对理论的认识和理解。

实验是验证、修正、发展理论的必要手段，是揭示材料受力、变形过程本质的重要方法。

3、应力分析实验。

某些情况下，如因构件形状不规则、受力复杂或精确地边界条件难以确定等，应力分析计算难以获得准确结果。

这时，采用如电测实验应力分析方法可以直接测定构件的应力。

应力分析实验主要是对构件形状不规则、受力复杂或边界条件很难确定、计算法难以得到准确结果的情况，用实验方法测定构件的应力。

梁的纯弯曲正应力实验电测法是应力应变测量最常用的方法，其方法简便，技术成熟，已经成为工程中不可缺少的测量手段。

纯弯曲时正应力在横截面上线性分布，是弯曲中最简单的应力情况。

用电测法测定纯弯曲梁上的正应力，不仅可以验证材料力学理论，也可以熟悉电测法测量的原理、操作方法和注意的问题，为复杂的实验应力分析打下基础。

一、预习要求1、YJ—5电阻应变仪测量前如何进行预调平衡？2、采用半桥接法进行弯曲正应力测量时，如何进行温度补偿？说明原理。

二、实验目的1、初步掌握电测应力分析方法，学习电测接线方法、仪器调试使用方法。

2、测定梁在纯弯曲下的弯曲正应力及分布规律，验证理论公式。

三、实验设备1、纯弯曲正应力试验台。

2、电阻应变仪及预调平衡箱。

3、矩形截面钢梁。

四、实验原理及方法纯弯曲梁如图1a所示。

在载荷P作用下，梁的CD段为纯弯曲变形。

沿梁横截面的高度方向每隔4h高度粘贴平行于轴线的测量应变片，共五片，其中第三片在中性层上。

另外在梁外安置温度补偿块，其上贴一公共温度补偿应变片。

每一测量应变片与公共温度补偿片按图1b接法接为半桥测量系统。

梁受到P力作用后，产生弯曲变形。

通过电阻应变仪测出载荷作用下五个点处的应变，由于是单向拉压变形，由虎克定律εσE=即可算出各点的应力值。

另一方面，由弯曲正应力理论公式zIMy=σ，可算出各点的应力理论值。

于是可将实测值和理论值进行比较，验证理论公式的正确性。

实验时，载荷由砝码经过20倍杠杆放大施加。

加载分四级，每增加一个砝码，产生P图1 纯弯曲实验装置示意图力的增量ΔP。

每加一级后测出五个点的应变，最后取力和应变的增量平均值计算理论值和实验值。

该实验也可用万能试验机加载进行测量。

五、实验步骤1、检查调整纯弯曲梁、电阻应变仪，使各部件和旋钮在正确位置，并打开应变仪进行预热。

2、接桥练习。

参照表1组桥，每种方式下按应变仪的使用方法进行预调平衡，平衡后加一个砝码读取应变。

读数方法为，当加载后应变仪的指针发生偏转，根据应变的大小选择并调节微调、中调、粗调读数盘使电表指针回零，这时各读数盘所指读数的代数和即是所测点的应变值。

实验五纯弯曲梁的正应力测量一、实验目的1、测定梁在纯弯曲时横截面上正应力的大小和分布规律。

2、验证纯弯曲梁的正应力计算公式。

二、实验设备材料力学多功能实验台（见图1）、力/应变综合参数测试仪、游标卡尺、钢板尺图1 材料力学多功能实验台三、试件制备试件是一个横截面为矩形b×h的长条形钢块。

在其顶面、底面和侧面均匀、对称、平行地贴着五个应变片，其中应变片3#应在中性层的位置上（见图2）。

图2 应变片在梁中的位置四、实验原理如图1所示，在材料力学多功能实验台上顺时针转动手轮可对下横梁加力，下横梁再带动其两侧的拉杆机构对实验台的上横梁两侧对称地施加压力。

从而在上横梁的中间段形成一个纯弯曲梁。

在纯弯曲条件下，梁横截面上任一点的正应力的理论计算公式为zI My =σ理式中M 为弯矩，Iz 为横截面对中性轴的惯性矩，y 为所求应力点至中性轴的距离。

弯矩可按公式M = ΔF/2×a 求出，惯性矩可按公式Iz = bh3/12求出。

仍采用1/4桥方法（单臂测量方式）测量各纵向应变ε，其原理图及接线示意图参照实验三的图4、5、6。

加载采用增量法，即每增加等量的载荷ΔF ，测出各点的应变增量Δε，然后分别取各点应变增量的平均值Δε平均，可按以下公式依次求出各点的实测正应力值。

平均实ε∆=σE将实测应力值与理论应力值进行比较，可验证上述的纯弯曲正应力计算公式。

五、实验步骤1、用游标卡尺和钢板尺分别测量梁横截面的宽度b 和高度h 、梁的跨度L 、力作用点位置a 以及各应变片到中性层的距离y 。

2、按1/4桥方法接线。

在接线中应确定所采用的测量应变片在梁上的位置以及所引出的导线的颜色。

另外应确定所采用的通道号。

3、打开力/应变综合参数测试仪电源开关，将加力手柄摇到使试件完全放松的位置。

然后在力的测试面板上清零，再在应变的测试面板上进行所有通道的自动平衡。

4、按下通道按钮选择所采用的通道号，准备开始试验。

矩形截面梁的纯弯曲实验一、实验目的1、测定梁在纯弯曲时横截面上正应力大小和分布规律2、验证纯弯曲梁的正应力计算公式二、实验仪器设备和工具1、组合实验台中纯弯曲梁实验装置2、XL2118系列力＆应变综合参数测试仪3、游标卡尺、钢板尺三、实验原理及方法其装置如图1（a ）所示，该装置附有弯曲梁两根，高度25mm 的一根 用于电阻应变片灵敏系数的标定实验，见图1（b ）；另一根高度40mm 的用于纯1.弯曲梁2.支座3.加载杆4.手轮5.实验台后片架6.可调节底盘7.承力下梁 8.压头 9.传感器 10.蜗杆升降机构 11.定位标尺（a ）（c ） （b ）在纯弯曲条件下，根据平面假设和纵向纤维间无挤压的假设，可得到梁横截面上任一点的正应力，计算公式为σ= My / I z式中M 为弯矩，I z 为横截面对中性轴的惯性矩；y 为所求应力点至中性轴的距离。

为了测量梁在纯弯曲时横截面上正应力的分布规律，在梁的纯弯曲段沿梁侧面不同高度，平行于轴线贴有应变片（如图3-1）。

图 3-1 应变片在梁中的位置实验可采用半桥单臂、公共补偿、多点测量方法。

加载采用增量法，即每增加等量的载荷△P ，测出各点的应变增量△ε，然后分别取各点应变增量的平均值△ε实i ，依次求出各点的应变增量σ实i =E △ε实i将实测应力值与理论应力值进行比较，以验证弯曲正应力公式。

四、实验步骤1、设计好本实验所需的各类数据表格。

2、测量矩形截面梁的宽度b 和高度h 、载荷作用点到梁支点距离a 及各应变片到中性层的距离y i 。

见附表13、拟订加载方案。

先选取适当的初载荷P 0（一般取P 0 =10％P max 左右），估算P max （该实验载荷范围P max ≤6000N ），分4～6级加载。

4、根据加载方案，调整好实验加载装置。

5、按实验要求接好线，调整好仪器，检查整个测试系统是否处于正常工作状态。

6、加载。

均匀缓慢加载至初载荷P 0，记下各点应变的初始读数；然后分级等增量加载，每增加一级载荷，依次记录各点电阻应变片的应变值εi ，直到最终载荷。

梁的弯曲实验梁的弯曲实验大纲1．通过弯曲正应力的电测实验，了解电阻应变计的测量原理，验证平面假设测定弯曲正应力的分布规律。

2. 通过实验初步了解电测法中全桥和半桥桥路的接法，掌握电阻应变仪的使用操作方法。

3. 主要设备：多功能电测实验装置；主要耗材：电阻应变片，每次实验8片。

梁的弯曲实验指导书一、实验目的1、初步掌握电测方法和多点应变测量技术。

2、用电测方法测定矩形截面梁在承受纯弯曲作用时横截面高度方向上正应力的 分布规律。

3、验证纯弯曲梁横截面上正应力理论计算公式。

4、测量梁在载荷作用下的最大挠度，验证梁的挠度理论计算公式的正确性。

二、实验设备1、多功能电测实验装置2、智能全数字式静态应变仪3、游标卡尺、钢尺4、千分表及表座三、实验原理矩形截面纯弯曲钢梁的试验装置如图3-7所示。

本实验采用四点弯曲实验，加载后，梁在两个加力点间段承受纯弯曲。

根据平面假设和纵向纤维间无挤压的假设，可以得到纯弯曲梁横截面的正应力的理论计算公式为：I yM ⋅=σ （3-10）式中 M ：横截面弯矩I ：横截面对形心主轴（即中性轴）的惯性矩 y ：所求应力点到中性轴的距离由式（3-10）可知沿横截面高度正应力按线性规律变化。

实验采用半桥接线，粘贴在矩形截面梁上两个加力点之间的上、下表面、中性轴和离上、下表面1/4h 的5个应变计作为工作片（见图3-8），应变计的两个引出导线分别接到应变仪上5 个通道的A 、B 接线柱上，用一个不受力的应变计作为温度补偿片，接到应变仪上相应通道的B 、C 接线柱上，测出载荷作用下各测点的应变ε，由虎克定律知实实εσE = （3-11）式中E 为材料的弹性模量中性轴M=P/2 a Nmm图3-7 多功能电测实验装置 图3－8 纯弯曲梁实验装置及弯矩图四、实验方法实验采用手动加载，转动螺旋手柄，使压头压迫梁进行加载（见图3-7），载 荷的大小由智能全数字式静态应变仪右边窗口显示的数字所控制。