三角函数正余弦函数的图像及性质复习汇总

考点十七 三角函数的图象和性质知识梳理1．正弦函数、余弦函数、正切函数的图象与性质2．正弦函数y ＝sin x ，x ∈[0，2π]的图象中，五个关键点是：(0，0)，(π2，1)，(π，0)，(3π2，－1)，(2π，0)．余弦函数y ＝cos x ，x ∈[0，2π]的图象中，五个关键点是：(0，1)，(π2，0)，(π，－1)，(3π2，0)，(2π，1)．3. 三角函数的周期性正弦函数、余弦函数都是周期函数，周期均为2k π，k ∈Z ，最小正周期均为2π；正切函数也是周期函数，周期为k π，k ∈Z ，最小正周期为π．典例剖析题型一 三角函数的定义域和值域 例1 函数y ＝cos x －32的定义域为________. 答案 ⎣⎡⎦⎤2k π－π6，2k π＋π6(k ∈Z ) 解析 ∵cos x －32≥0，得cos x ≥32，∴2k π－π6≤x ≤2k π＋π6，k ∈Z . 变式训练 函数y ＝sin x －cos x 的定义域为________.答案 ⎩⎨⎧⎭⎬⎫x |2k π＋π4≤x ≤2k π＋5π4，k ∈Z解析 要使函数有意义，必须有sin x －cos x ≥0，即sin x ≥cos x ，同一坐标系中作出y ＝sin x ，y ＝cos x ，x ∈[0，2π]的图象如图所示． 结合图象及正、余弦函数的周期是2π知，函数的定义域为⎩⎨⎧⎭⎬⎫x |2k π＋π4≤x ≤2k π＋5π4，k ∈Z .例2 (1) 函数y ＝2sin x ⎝⎛⎭⎫π6≤x ≤2π3的值域是________．(2) 函数f (x )＝sin ⎝⎛⎭⎫2x －π4在区间⎣⎡⎦⎤0，π2上的最小值为________. 答案 (1) [1，2] (2) －22解析 (1) 根据正弦函数图象，可知x ＝π6时，函数取到最小值1；x ＝π2时，函数取到最大值2.(2) ∵x ∈⎣⎡⎦⎤0，π2，∴－π4≤2x －π4≤3π4，令y ＝2x －π4，则sin ⎝⎛⎭⎫2x －π4＝sin y 在y ∈⎣⎡⎦⎤－π4，3π4上的最小值为sin ⎝⎛⎭⎫－π4＝－22. 变式训练 求函数y ＝cos 2x ＋sin x ⎝⎛⎭⎫|x |≤π4的最大值与最小值． 解析 令t ＝sin x ，∵|x |≤π4，∴t ∈⎣⎡⎦⎤－22，22.∴y ＝－t 2＋t ＋1＝－⎝⎛⎭⎫t －122＋54， ∴当t ＝12时，y max ＝54，当t ＝－22时，y min ＝1－22.∴函数y ＝cos 2x ＋sin x ⎝⎛⎭⎫||x ≤π4的最大值为54，最小值为1－22. 解题要点 1．三角函数定义域的求法求三角函数定义域实际上是构造简单的三角不等式(组)，常借助三角函数线或三角函数图象来求解．2．三角函数值域的不同求法 (1)利用sin x 和cos x 的值域直接求；(2)把所给的三角函数式变换成y ＝A sin(ωx ＋φ)的形式求值域；(3)把sin x 或cos x 看作一个整体，通过换元，令t ＝sin x (或t ＝cos x )，转换成二次函数求值域；(4)利用sin x ±cos x 和sin x cos x 的关系通过换元，令t =sin x +cos x ,转换成二次函数求值域． 题型二 三角函数的单调性例3 (1)函数y ＝cos ⎝⎛⎭⎫π4－2x 的单调减区间为________． (2) 函数f (x )＝tan ⎝⎛⎭⎫2x －π3的单调递增区间是____________________． 答案 (1) ⎣⎡⎦⎤k π＋π8，k π＋5π8(k ∈Z ) (2) ⎝⎛⎭⎫k π2－π12，k π2＋5π12(k ∈Z ) 解析 (1)由y ＝cos ⎝⎛⎭⎫π4－2x ＝cos ⎝⎛⎭⎫2x －π4，得2k π≤2x －π4≤2k π＋π(k ∈Z )， 故k π＋π8≤x ≤k π＋5π8(k ∈Z )．所以函数的单调减区间为⎣⎡⎦⎤k π＋π8，k π＋5π8(k ∈Z )． (2) 由k π－π2<2x －π3<k π＋π2(k ∈Z )，得k π2－π12<x <k π2＋5π12(k ∈Z )，所以函数f (x )＝tan ⎝⎛⎭⎫2x －π3的单调递增区间为⎝⎛⎭⎫k π2－π12，k π2＋5π12(k ∈Z ).变式训练 若函数f (x )＝－cos 2x ，则f (x )的一个递增区间为________． 答案 ⎝⎛⎭⎫0，π2 解析 由f (x )＝－cos 2x 知递增区间为⎣⎡⎦⎤k π，k π＋π2，k ∈Z ，故只有B 项满足． 解题要点 1.求函数的单调区间应遵循简单化原则，将解析式先化简，并注意复合函数单调性规律“同增异减”；2.求形如y ＝A sin(ωx ＋φ)或y ＝A cos(ωx ＋φ)(其中ω>0)的单调区间时，要视“ωx ＋φ”为一个整体，通过解不等式求解．但如果ω<0，那么一定先借助诱导公式将ω化为正数，防止把单调性弄错． 题型三 三角函数的周期性例4 函数f (x )＝3sin ⎝⎛⎭⎫x 2－π4，x ∈R 的最小正周期为________． 答案 4π解析 函数f (x )＝3sin ⎝⎛⎭⎫x 2－π4的最小正周期为T ＝2π12＝4π. 当堂练习1．函数f (x )＝sin ⎝⎛⎭⎫2x －π4在区间⎣⎡⎦⎤0，π2上的最小值为________． 答案 －22解析 因为x ∈⎣⎡⎦⎤0，π2，所以2x －π4∈⎣⎡⎦⎤－π4，3π4，当2x －π4＝－π4，即x ＝0时，f (x )取得最小值－22. 2．如果函数f (x )＝sin(ωx ＋π6)(ω>0)的两个相邻零点之间的距离为π12，则ω的值为________．答案 12解析 T ＝π6，ω＝2πT ＝12．3. 函数y ＝cos x －12的定义域为________．答案 ⎣⎡⎦⎤2k π－π3，2k π＋π3，k ∈Z 解析 ∵cos x －12≥0，得cos x ≥12，∴2k π－π3≤x ≤2k π＋π3，k ∈Z .4．y ＝sin(x －π4)的图象的一个对称中心是________．答案 (－3π4，0)解析 令x －π4＝k π，k ∈Z 得x ＝π4＋k π，k ∈Z ，于是(－3π4，0)是y ＝sin(x －π4)的图象的一个对称中心.5．函数f (x )＝cos(2x ＋3π2)(x ∈R )，下面结论不正确的是________．(填序号)① 函数f (x )的最小正周期为π ② 函数f (x )的对称中心是(π2，0)③ 函数f (x )的图象关于直线x ＝π4对称④ 函数f (x )是偶函数 答案 ④解析 ∵f (x )＝cos(2x ＋3π2)＝sin2x (x ∈R )，∴最小正周期T ＝2π2＝π，选项①正确；由2x ＝k π得x ＝k π2，k ∈Z ，∴函数f (x )的对称中心为(k π2，0)，∴取k ＝1得选项②正确；由2x ＝k π＋π2得x ＝k π2＋π4，k ∈Z ，∴取k ＝0得函数f (x )的对称轴为x ＝π4，∴选项③正确；∵f (x )＝sin2x (x ∈R )，∴f (－x )＝－f (x )，f (x )为奇函数， ∴选项④不正确．课后作业一、 填空题1．若函数f (x )＝sin x ＋φ3(φ∈[0,2π]) 是偶函数，则φ＝________．答案3π2解析 ∵f (x )为偶函数，关于y 轴对称，x ＝0为其对称轴． ∴x ＋φ3＝π2＋k π，令x ＝0，φ＝3k π＋32π，当k ＝0时，φ＝32π．2．如果函数y ＝3cos(2x ＋φ)的图象关于点⎝⎛⎭⎫4π3，0中心对称，那么|φ|的最小值为________． 答案 π6解析 由题意得3cos ⎝⎛⎭⎫2×4π3＋φ＝3cos ⎝⎛⎭⎫2π3＋φ＋2π＝3cos ⎝⎛⎭⎫2π3＋φ＝0， ∴2π3＋φ＝k π＋π2，k ∈Z ， ∴φ＝k π－π6，k ∈Z ，取k ＝0，得|φ|的最小值为π6.3．函数y ＝cos 2x ，周期为_____，且在⎣⎡⎦⎤0，π2上是________（填“增函数”或“减函数”）． 答案 π，减函数解析 因为y ＝cos 2x 的周期T ＝2π2＝π，而2x ∈[0，π]，所以y ＝cos 2x 在⎣⎡⎦⎤0，π2上为减函数. 4．函数f (x )＝tan ⎝⎛⎭⎫2x －π3的单调递增区间是________． 答案 ⎝⎛⎭⎫k π2－π12，k π2＋5π12(k ∈Z )解析 由k π－π2＜2x －π3＜k π＋π2(k ∈Z )得，k π2－π12＜x ＜k π2＋5π12(k ∈Z )，所以函数f (x )＝tan ⎝⎛⎭⎫2x －π3的单调递增区间为⎝⎛⎭⎫k π2－π12，k π2＋5π12(k ∈Z ).5．已知ω＞0,0＜φ＜π，直线x ＝π4和x ＝5π4是函数f (x )＝sin(ωx ＋φ)图象的两条相邻的对称轴，则φ＝________． 答案 π4解析 由题意得周期T ＝2⎝⎛⎭⎫54π－14π＝2π，∴2π＝2πω，即ω＝1，∴f (x )＝sin(x ＋φ)，∴f ⎝⎛⎭⎫π4＝sin ⎝⎛⎭⎫π4＋φ＝±1，f ⎝⎛⎭⎫5π4＝sin ⎝⎛⎭⎫5π4＋φ＝±1.∵0＜φ＜π，∴π4＜φ＋π4＜54π，∴φ＋π4＝π2，∴φ＝π4.6．函数f (x )＝sin ⎝⎛⎭⎫2x －π4在区间⎣⎡⎦⎤0，π2上的最小值为________． 答案 －22解析 由已知x ∈⎣⎡⎦⎤0，π2，得2x －π4∈⎣⎡⎦⎤－π4，3π4，所以sin ⎝⎛⎭⎫2x －π4∈⎣⎡⎦⎤－22，1，故函数f (x )＝sin ⎝⎛⎭⎫2x －π4在区间⎣⎡⎦⎤0，π2上的最小值为－22.7．(2015四川文)下列函数中，最小正周期为π的奇函数是________．(填序号) ①y ＝sin ⎝⎛⎭⎫2x ＋π2 ②y ＝cos ⎝⎛⎭⎫2x ＋π2 ③y ＝sin 2x ＋cos 2x ④y ＝sin x ＋cos x 答案 ②解析 ①项，y ＝sin ⎝⎛⎭⎫2x ＋π2＝cos 2x ，最小正周期为π，且为偶函数，不符合题意； ②项，y ＝cos ⎝⎛⎭⎫2x ＋π2＝－sin 2x ，最小正周期为π，且为奇函数，符合题意； ③项，y ＝sin 2x ＋cos 2x ＝2sin ⎝⎛⎭⎫2x ＋π4，最小正周期为π，为非奇非偶函数，不符合题意； ④项，y ＝sin x ＋cos x ＝2sin ⎝⎛⎭⎫x ＋π4，最小正周期为2π，为非奇非偶函数，不符合题意． 8．函数f (x )＝3sin ⎝⎛⎭⎫2x －π6在区间⎣⎡⎦⎤0，π2上的值域为________． 答案 ⎣⎡⎦⎤－32，3 解析 当x ∈⎣⎡⎦⎤0，π2时，2x －π6∈⎣⎡⎦⎤－π6，5π6，sin ⎝⎛⎭⎫2x －π6∈⎣⎡⎦⎤－12，1， 故3sin ⎝⎛⎭⎫2x －π6∈⎣⎡⎦⎤－32，3， 即此时函数f (x )的值域是⎣⎡⎦⎤－32，3. 9．函数y ＝3sin(2x ＋π4)的最小正周期为________．答案 π 解析 T ＝2π2＝π.10．函数f (x )＝cos(2x －π4)＋3在[－π2，π2]上的单调递减区间为________．答案 [－π2，－3π8]∪[π8，π2]解析 由2k π≤2x －π4≤2k π＋π得k π＋π8≤x ≤k π＋5π8，k ∈Z .∵x ∈[－π2，π2]，∴取k ＝0得f (x )在[－π2，π2]上的单调递减区间为[π8，π2]；取k ＝－1得f (x )在[－π2，π2]上的单调递减区间为[－π2，－3π8]．∴f (x )在[－π2，π2]上的单调递减区间为[－π2，－3π8]和[π8，π2]． 11．函数y ＝sin(x ＋π4)的对称中心为________．答案 (k π－π4，0)，k ∈Z二、解答题12．已知函数f (x )＝4cos ωx ·sin ⎝⎛⎭⎫ωx ＋π4(ω＞0)的最小正周期为π. (1)求ω的值；(2)讨论f (x )在区间⎣⎡⎦⎤0，π2上的单调性． 解析 (1)f (x )＝4cos ωx ·sin ⎝⎛⎭⎫ωx ＋π4 ＝22sin ωx ·cos ωx ＋22cos 2ωx ＝2(sin2ωx ＋cos2ωx )＋ 2 ＝2sin ⎝⎛⎭⎫2ωx ＋π4＋ 2. 因为f (x )的最小正周期为π，且ω＞0， 从而有2π2ω＝π，故ω＝1.(2)由(1)知，f (x )＝2sin ⎝⎛⎭⎫2x ＋π4＋ 2. 若0≤x ≤π2，则π4≤2x ＋π4≤5π4.当π4≤2x ＋π4≤π2，即0≤x ≤π8时，f (x )单调递增； 当π2≤2x ＋π4≤5π4，即π8≤x ≤π2时，f (x )单调递减． 综上可知，f (x )在区间⎣⎡⎦⎤0，π8上单调递增，在区间⎣⎡⎦⎤π8，π2上单调递减．13．(2015北京文)已知函数f (x )＝sin x －23sin 2x2.(1)求f (x )的最小正周期；(2)求f (x )在区间⎣⎡⎦⎤0，2π3上的最小值． 解 (1)因为f (x )＝sin x ＋3cos x － 3.＝2sin ⎝⎛⎭⎫x ＋π3－ 3. 所以f (x )的最小正周期为2π.(2)因为0≤x ≤2π3时，所以π3≤x ＋π3≤π.当x ＋π3＝π，即x ＝2π3时，f (x )取得最小值．所以f (x )在区间⎣⎡⎦⎤0，2π3上的最小值为f ⎝⎛⎭⎫2π3＝－ 3.。

三角函数正余弦函数的图像及性质复习汇总(共8页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一、正弦函数和余弦函数的图象：正弦函数sin y x =和余弦函数cos y x =图象的作图方法：五点法：先取横坐标分别为0，3,,,222ππππ的五点，再用光滑的曲线把这五点连接起来，就得到正弦曲线和余弦曲线在一个周期内的图象。

二、正弦函数sin ()y x x R =∈、余弦函数cos ()y x x R =∈的性质：（1）定义域：都是R 。

（2）值域： 1、都是[]1,1-， 2、sin y x =，当()22x k k Z ππ=+∈时，y 取最大值1；当()322x k k Z ππ=+∈时，y 取最小值－1；3、cos y x =，当()2x k k Z π=∈时，y 取最大值1，当()2x k k Z ππ=+∈时，y 取最小值－1。

例：（1）若函数sin(3)6y a b x π=-+的最大值为23，最小值为21-，则=a __，=b ＿（答：1,12a b ==或1b =-）；z)(k k 223.k 22∈⎥⎦⎤⎢⎣⎡++πππz)(k 43k ,4k ∈⎥⎦⎤⎢⎣⎡++ππππz)(k 4k ,4k ∈⎥⎦⎤⎢⎣⎡+-ππππ⑵ 函数y=-2sinx+10取最小值时，自变量x 的集合是_________________________。

（3）周期性：①sin y x =、cos y x =的最小正周期都是2π；②()sin()f x A x ωϕ=+和()cos()f x A x ωϕ=+的最小正周期都是2||T πω=。

例：(1)若3sin)(xx f π=，则(1)(2)(3)(2003)f f f f ++++＝___（答：0）；⑵．下列函数中，最小正周期为π的是（ ）A.cos 4y x =B.sin 2y x =C.sin 2x y =D.cos 4xy =（4）奇偶性与对称性：1、正弦函数sin ()y x x R =∈是奇函数，对称中心是()(),0k k Z π∈，对称轴是直线()2x k k Z ππ=+∈；2、余弦函数cos ()y x x R =∈是偶函数，对称中心是(),02k k Z ππ⎛⎫+∈ ⎪⎝⎭，对称轴是直线()x k k Z π=∈（正(余)弦型函数的对称轴为过最高点或最低点且垂直于x 轴的直线，对称中心为图象与x 轴的交点）。

千里之行，始于足下。

三角函数及反三角函数图像性质、知识点总结三角函数及反三角函数是高中数学中重要的内容之一，它们的图像性质是我们学习和理解这些函数的基础。

下面是关于三角函数及反三角函数图像性质的知识点总结。

一、正弦函数的图像性质：1. 定义域：正弦函数的定义域为全体实数。

2. 值域：正弦函数的值域为闭区间[-1,1]。

3. 周期性：正弦函数的周期是2π，即在一个周期内，正弦函数的图像重复出现。

4. 奇偶性：正弦函数是奇函数，即sin(-x)=-sin(x)。

5. 对称轴：正弦函数的对称轴是y轴。

6. 最值点：正弦函数的最值点包括最大值1和最小值-1，最值点的横坐标为周期的整数倍。

二、余弦函数的图像性质：1. 定义域：余弦函数的定义域为全体实数。

2. 值域：余弦函数的值域为闭区间[-1,1]。

3. 周期性：余弦函数的周期是2π，即在一个周期内，余弦函数的图像重复出现。

4. 奇偶性：余弦函数是偶函数，即cos(-x)=cos(x)。

5. 对称轴：余弦函数的对称轴是x轴。

6. 最值点：余弦函数的最值点包括最大值1和最小值-1，最值点的横坐标为周期的半整数倍。

三、正切函数的图像性质：1. 定义域：正切函数的定义域为全体实数，除了临界点kπ（k为整数）。

第1页/共3页锲而不舍，金石可镂。

2. 值域：正切函数的值域为全体实数。

3. 周期性：正切函数的周期是π，即在一个周期内，正切函数的图像重复出现。

4. 奇偶性：正切函数是奇函数，即tan(-x)=-tan(x)。

5. 渐近线：正切函数有两条渐近线，分别是x=kπ+π/2（k为整数）和x=kπ（k为整数）。

6. 最值点：正切函数没有最值点。

四、反正弦函数的图像性质：1. 定义域：反正弦函数的定义域为闭区间[-1,1]。

2. 值域：反正弦函数的值域为闭区间[-π/2,π/2]。

3. 奇偶性：反正弦函数是奇函数，即arcsin(-x)=-arcsin(x)。

4. 递增性：反正弦函数在定义域内是递增的。

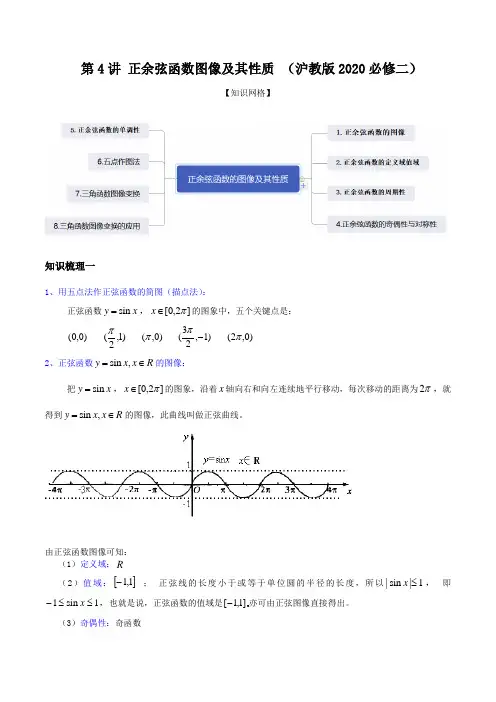
第4讲 正余弦函数图像及其性质 （沪教版2020必修二）【知识网格】知识梳理一1、用五点法作正弦函数的简图（描点法）：正弦函数x y sin =，]2,0[π∈x 的图象中，五个关键点是：)0,0( )1,2(π)0,(π )1,23(-π )0,2(π2、正弦函数R x x y ∈=,sin 的图像：把x y sin =，]2,0[π∈x 的图象，沿着x 轴向右和向左连续地平行移动，每次移动的距离为π2，就得到R x x y ∈=,sin 的图像，此曲线叫做正弦曲线。

由正弦函数图像可知：（1）定义域：R（2）值域：[]1,1- ； 正弦线的长度小于或等于单位圆的半径的长度，所以1|sin |≤x ， 即1sin 1≤≤-x ，也就是说，正弦函数的值域是1,1[-亦可由正弦图像直接得出。

（3）奇偶性：奇函数由x x sin )sin(-=-可知：x y sin =为奇函数，正弦曲线关于原点O 对称 （4）单调递增区间：z k k k ∈⎥⎦⎤⎢⎣⎡+-,22,22ππππ； （5）单调递减区间：z k k k ∈⎥⎦⎤⎢⎣⎡++,232,22ππππ； （6）对称中心：（0,πk ）； （7）对称轴：2ππ+=k x（8）最值：当且仅当,22ππ+=k x y 取最大值1max =y ；当且仅当,232ππ+=k x y 取最小值1min -=y 。

（9）最小正周期：π2=T一般地，对于函数)(x f ，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有)()(x f T x f =+，那么函数)(x f 就叫做周期函数，非零常数T 叫做这个函数的周期由此可知)0(2,,4,2,2,4,≠∈--k z k k 且πππππ 都是这两个函数的周期对于一个周期函数)(x f ，如果在它所有的周期中存在一个最小的正数，那么这个最小正数就叫做)(x f 的最小正周期根据上述定义，可知：正弦函数、余弦函数都是周期函数，)0(2≠∈k z k k 且π都是它的周期，最小正周期是π2 注意：1.周期函数定义域M x ∈，则必有M T x ∈+, 且若0>T ，则定义域无上界；0<T 则定义域无下界；2.“每一个值”只要有一个反例，则)(x f 就不为周期函数;3.T 往往是多值的（如x y sin =中 ,4,2,2,4,ππππ--都是周期）周期T 中最小的正数叫做)(x f 的最小正周期（有些周期函数没有最小正周期） 5、余弦函数R x x y ∈=,cos 的图像：（1）定义域：R （2）值域：[]1,1- （3）奇偶性：偶函数（4）单调递增区间：[]πππk k 2,2-，Z k ∈ （5）单调递减区间：[]Z k k k ∈+,2,2πππ （6）对称中心：（0,2ππ+k ）（7）对称轴：πk x =（8）最值：当且仅当,2πk x =y 取最大值1max =y ； 当且仅当,2ππ+=k x y 取最小值1min -=y 。

高中数学三角函数及反三角函数图像性质、知识点总结高中数学中，三角函数及反三角函数是重要的内容之一。

在学习这一部分知识时，需要掌握其图像性质以及相关的知识点。

下面将对这些内容进行总结。

一、三角函数的图像性质1. 正弦函数（sin）的图像性质：- 周期性：sin函数的周期为2π，即在每个周期内，函数的图像重复出现；- 奇函数性质：sin函数关于原点对称；- 取值范围：sin函数的取值范围为[-1,1]，即函数的值始终在该区间内波动。

2. 余弦函数（cos）的图像性质：- 周期性：cos函数的周期为2π；- 偶函数性质：cos函数关于y轴对称；- 取值范围：cos函数的取值范围也为[-1,1]。

3. 正切函数（tan）的图像性质：- 周期性：tan函数的周期为π；- 奇函数性质：tan函数关于原点对称；- 无界性：tan函数的值域为实数集，即函数在某些点无界。

二、三角函数的知识点1. 基本正弦函数的性质：- 特殊角的正弦值：0°、90°、180°、270°和360°对应的正弦值分别为0、1、0、-1和0；- 正弦函数的增减性：在0°到180°的区间上，sin函数是单调递增的；- 正弦函数的奇偶性：sin(-x)=-sin(x)，即sin函数关于原点对称。

2. 基本余弦函数的性质：- 特殊角的余弦值：0°、90°、180°、270°和360°对应的余弦值分别为1、0、-1、0和1；- 余弦函数的增减性：在0°到180°的区间上，cos函数是单调递减的；- 余弦函数的奇偶性：cos(-x)=cos(x)，即cos函数关于y轴对称。

3. 基本正切函数的性质：- 特殊角的正切值：0°、90°、180°和270°对应的正切值分别为0、无穷大、0和无穷大；- 正切函数的周期性：tan(x+π)=tan(x)，即tan函数的周期是π。

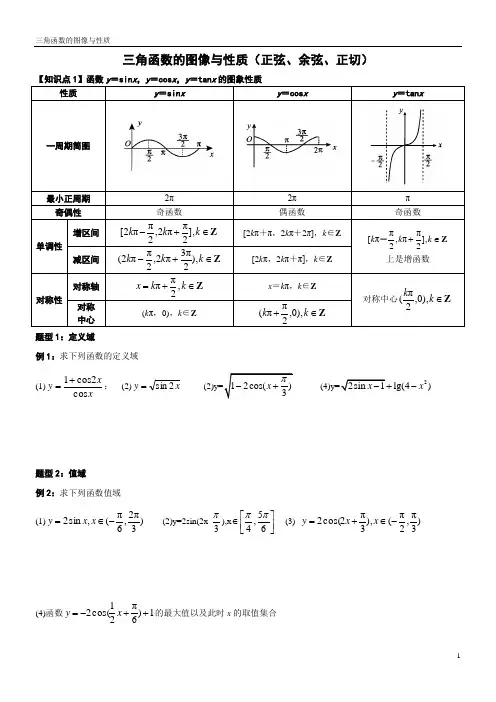
三角函数的图像与性质（正弦、余弦、正切）【知识点1】函数y ＝sin x ，y ＝cos x ，y ＝tan x 的图象性质题型1：定义域例1：求下列函数的定义域(1)xx y cos 2cos 1+=； (2)x y 2sin = 2lg(4)x -题型2：值域 例2：求下列函数值域 (1))3π2,6π(,sin 2-∈=x x y (2)y=2sin(2x-3π),x 5,46ππ⎡⎤∈⎢⎥⎣⎦(3) )3π,2π(),3π2cos(2-∈+=x x y(4)函数1)6π21cos(2++-=x y 的最大值以及此时x 的取值集合题型3：周期例3：求下列函数的周期： （1）f(x)=2sin2x (2)y=cos(123x π-) (3)y=tan(2x 4π-) （4）y=sin x 例4： 若函数()2sin(2)3f x kx π=+的最小正周期T 满足12T <<,则自然数k 的值为______.例5：若)10(sin 2)(<<=ϖϖx x f 在区间[0,]3π上的最大值是2，则ϖ=________.例6：使x y ωsin =（ω＞0）在区间[0，1]至少出现2次最大值，则ω的最小值为【 】A ．π25B ．π45C ．πD ．π23例7：设函数f(x)=2sin(25x ππ+),若对于任意的x R ∈,都有f(1x )2()()f x f x ≤≤成立，则12x x -的最小值是A.4B.2C.1D.12题型4：奇偶性 例8：函数y ＝sin （x ＋2π）（x ∈［－2π，2π］）是【 】A.增函数B.减函数C.偶函数D.奇函数例9：判断下列函数的奇偶性 (1)y=xsin(x π+) (2)y=cos 1sin x x+例10：已知函数f(x)=x 3cosx+1,若f(a)=11,则f(-a)=________ 题型5：单调性例11：函数y =21log sin(2x +4π)的单调递减区间是【 】 A.（k π－4π,k π］(k ∈Z ) B.（k π－8π,k π+8π］(k ∈Z ) C.（k π－83π,k π+8π］(k ∈ D.（k π+8π,k π+83π］(k ∈Z )例12：.求1cos()3412logx y π+=的单调区间例13：求下列函数的单调增区间(1))3π21cos(-=x y ; (2) ]0,π[),6π2sin(2-∈+=x x y ；(3))23πsin(2x y -=例14：（1）求函数y=2sin(2x-3π)的单调递减区间。

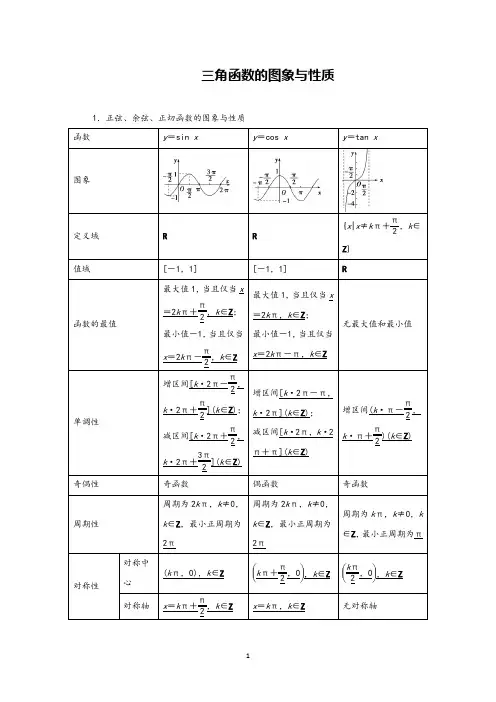
三角函数的图象与性质1．正弦、余弦、正切函数的图象与性质2.周期函数的定义对于函数f (x )，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有f (x ＋T )＝f (x )，那么函数f (x )就叫做周期函数，非零常数T 叫做这个函数的周期；函数y＝A sin(ωx ＋φ)和y ＝A cos(ωx ＋φ)的周期均为T ＝2π|ω|；函数y ＝A tan(ωx ＋φ)的周期为T ＝π|ω|. 3．对称与周期正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是四分之一个周期；正切曲线相邻的两个对称中心之间的距离是半个周期．判断正误(正确的打“√”，错误的打“×”) (1)y ＝cos x 在第一、二象限内是减函数．( ) (2)若y ＝k sin x ＋1，x ∈R ，则y 的最大值是k ＋1.( )(3)若非零实数T 是函数f (x )的周期，则kT (k 是非零整数)也是函数f (x )的周期．( ) (4)函数y ＝sin x 图象的对称轴方程为x ＝2k π＋π2(k ∈Z )．( )(5)函数y ＝tan x 在整个定义域上是增函数．( ) 答案：(1)× (2)× (3)√ (4)× (5)×函数y ＝tan 3x 的定义域为( ) A ．⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠3π2＋3k π，k ∈Z B ．⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠π6＋k π，k ∈ZC ．⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠－π6＋k π，k ∈ZD ．⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠π6＋k π3，k ∈Z解析：选D.由3x ≠π2＋k π(k ∈Z )，得x ≠π6＋k π3，k ∈Z .故选D.(2019·温州市十校联合体期初)下列函数中，最小正周期为π的是( ) A ．y ＝cos 4x B ．y ＝sin 2x C ．y ＝sin x 2D ．y ＝cos x4解析：选B.A.y ＝cos 4x 的周期T ＝2π4＝π2，本选项错误；B.y ＝sin 2x 的周期T ＝2π2＝π，本选项正确；C.y ＝sin x 2的周期为T ＝2π12＝4π，本选项错误；D.y ＝cos x4的周期为T＝2π14＝8π，本选项错误，则最小正周期为π的函数为y ＝sin 2x. (2019·金华十校联考)函数y ＝3－2cos ⎝⎛⎭⎪⎫x ＋π4的最大值为________，此时x ＝________．解析：函数y ＝3－2cos ⎝ ⎛⎭⎪⎫x ＋π4的最大值为3＋2＝5，此时x ＋π4＝π＋2k π(k ∈Z )，即x ＝3π4＋2k π(k ∈Z )．答案：53π4＋2k π(k ∈Z) 函数f (x )＝2sin ⎝⎛⎭⎪⎫x ＋π4，x ∈[0，π]的减区间为________．解析：当2k π＋π2≤x ＋π4≤2k π＋3π2，k ∈Z ，即2k π＋π4≤x ≤2k π＋5π4，k ∈Z 时，函数f (x )是减函数．又x ∈[0，π]，所以f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤π4，π.答案：⎣⎢⎡⎦⎥⎤π4，π三角函数的定义域和值域(1)(2017·高考全国卷Ⅱ)函数f (x )＝sin 2x ＋3cos x －34⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤0，π2的最大值是________．(2)函数y ＝lg(2sin x －1)＋1－2cos x 的定义域是________．【解析】 (1)依题意，f (x )＝sin 2x ＋3cos x －34＝－cos 2x ＋3cos x ＋14＝－⎝⎛⎭⎪⎫cos x －322＋1，因为x ∈⎣⎢⎡⎦⎥⎤0，π2，所以cos x ∈[0，1]，因此当cos x ＝32时，f (x )max ＝1.(2)要使函数y ＝lg(2sin x －1)＋1－2cos x 有意义，则⎩⎪⎨⎪⎧2sin x －1>0，1－2cos x ≥0， 即⎩⎪⎨⎪⎧sin x >12，cos x ≤12.解得2k π＋π3≤x <2k π＋5π6，k ∈Z .即函数的定义域为⎣⎢⎡⎭⎪⎫2k π＋π3，2k π＋5π6，k ∈Z .【答案】 (1)1 (2)⎣⎢⎡⎭⎪⎫2k π＋π3，2k π＋5π6，k ∈Z(1)三角函数定义域的求法求三角函数定义域实际上是构造简单的三角不等式(组)，常借助三角函数线或三角函数图象来求解．(2)三角函数值域的不同求法①利用sin x 和cos x 的值域直接求；②把所给的三角函数式变换成y ＝A sin(ωx ＋φ)的形式求值域；③(换元法)把sin x 或cos x 看作一个整体，转换成二次函数求值域；④(换元法)利用sin x ±cos x 和sin x cos x 的关系转换成二次函数求值域．1．函数f (x )＝3sin ⎝ ⎛⎭⎪⎫2x －π6在区间⎣⎢⎡⎦⎥⎤0，π2上的值域为( ) A ．⎣⎢⎡⎦⎥⎤－32，32B ．⎣⎢⎡⎦⎥⎤－32，3C ．⎣⎢⎡⎦⎥⎤－332，332D ．⎣⎢⎡⎦⎥⎤－332，3 解析：选B.当x ∈⎣⎢⎡⎦⎥⎤0，π2时，2x －π6∈⎣⎢⎡⎦⎥⎤－π6，5π6，sin ⎝ ⎛⎭⎪⎫2x －π6∈⎣⎢⎡⎦⎥⎤－12，1，故3sin ⎝ ⎛⎭⎪⎫2x －π6∈[－32，3]，即此时函数f (x )的值域是⎣⎢⎡⎦⎥⎤－32，3.2．(2019·温州市十校联合体期初)已知函数f (x )＝2cos x ·(sin x －cos x )，x ∈R ，则f ⎝ ⎛⎭⎪⎫π4＝________，f (x )的最大值是________． 解析：f (x )＝2cos x (sin x －cos x ) ＝2cos x sin x －2cos 2x ＝sin 2x －1－cos 2x＝2sin ⎝⎛⎭⎪⎫2x －π4－1. 当x ＝π4时，f ⎝ ⎛⎭⎪⎫π4＝2sin ⎝⎛⎭⎪⎫2×π4－π4－1＝0.由正弦函数的图象和性质可得，sin ⎝ ⎛⎭⎪⎫2x －π4的最大值为1.所以f (x )的最大值为2－1. 答案：02－1三角函数的单调性(高频考点)三角函数的单调性是每年高考命题的热点，题型既有选择题也有填空题，或解答题某一问出现，难度为中档题．主要命题角度有：(1)求已知三角函数的单调区间； (2)已知三角函数的单调区间求参数； (3)利用三角函数的单调性比较大小；(4)利用三角函数的单调性求值域(或最值)．(见本节例1(1)及跟踪训练T1)角度一 求已知三角函数的单调区间(2017·高考浙江卷)已知函数f (x )＝sin 2x －cos 2x －23sin x cos x (x ∈R )． (1)求f ⎝⎛⎭⎪⎫2π3的值；(2)求f (x )的最小正周期及单调递增区间．【解】 (1)由sin 2π3＝32，cos 2π3＝－12，f ⎝ ⎛⎭⎪⎫2π3＝⎝ ⎛⎭⎪⎫322－⎝ ⎛⎭⎪⎫－122－23×32×⎝ ⎛⎭⎪⎫－12，得f ⎝ ⎛⎭⎪⎫2π3＝2.(2)由cos 2x ＝cos 2x －sin 2x 与sin 2x ＝2sin x cos x 得f (x )＝－cos 2x －3sin 2x ＝－2sin ⎝⎛⎭⎪⎫2x ＋π6.所以f (x )的最小正周期是π.由正弦函数的性质得π2＋2k π≤2x ＋π6≤3π2＋2k π，k ∈Z ，解得π6＋k π≤x ≤2π3＋k π，k ∈Z ， 所以，f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤π6＋k π，2π3＋k π(k ∈Z )．角度二 已知三角函数的单调区间求参数函数f (x )＝sin(x ＋φ)在区间⎝ ⎛⎭⎪⎫π3，2π3上单调递增，则常数φ的值可能是( )A ．0B ．π2C ．πD ．3π2【解析】 法一：结合选项，当φ分别取选项中的值时，A ：f (x )＝sin x ；B ：f (x )＝cos x ；C ：f (x )＝－sin x ；D ：f (x )＝－cos x ．验证得D 选项正确．法二：⎝⎛⎭⎪⎫π3，2π3⊆f (x )的递增区间，⎝ ⎛⎭⎪⎫π3，2π3⊆⎝ ⎛⎭⎪⎫－π2－φ＋2k π，π2－φ＋2k π，⇒－5π6＋2k π≤φ≤－π6＋2k π(k ∈Z )，k ＝0，选项中无值符合；k ＝1，7π6≤φ≤11π6，φ＝3π2符合； k ＝2，19π6≤φ≤23π6，选项中无值符合．可知φ的可取值逐渐增大，故只有D 选项符合题意．【答案】 D角度三 利用三角函数的单调性比较大小已知函数f (x )＝2sin ⎝ ⎛⎭⎪⎫x ＋π3，设a ＝f ⎝ ⎛⎭⎪⎫π7，b ＝f ⎝ ⎛⎭⎪⎫π6，c ＝f ⎝ ⎛⎭⎪⎫π3，则a ，b ，c的大小关系是( )A ．a <c <bB ．c <a <bC ．b <a <cD ．b <c <a【解析】 a ＝f ⎝ ⎛⎭⎪⎫π7＝2sin 1021π，b ＝f ⎝ ⎛⎭⎪⎫π6＝2sin π2＝2，c ＝f ⎝ ⎛⎭⎪⎫π3＝2sin 2π3＝2sin π3， 因为y ＝sin x 在⎣⎢⎡⎦⎥⎤0，π2上递增，所以c <a <b .【答案】 B(1)求三角函数单调区间的两种方法①代换法：就是将比较复杂的三角函数含自变量的代数式整体当作一个角u (或t )，利用复合函数的单调性列不等式求解．②图象法：画出三角函数的正、余弦曲线，结合图象求它的单调区间．[提醒] 要注意求函数y ＝A sin(ωx ＋φ)的单调区间时ω的符号，若ω<0，那么一定先借助诱导公式将ω化为正数．同时切莫漏掉考虑函数自身的定义域．(2)利用单调性确定ω的范围的方法对于已知函数的单调区间的某一部分确定参数ω的范围的问题，首先，明确已知的单调区间应为函数的单调区间的子集，其次，要确定已知函数的单调区间，从而利用它们之间的关系可求解，另外，若是选择题利用特值验证排除法求解更为简捷．(3)利用单调性比较大小的方法首先利用诱导公式把已知角转化为同一区间内的角且函数名称相同，再利用其单调性比较大小．1．(2019·浙江宁波质检)已知函数f (x )＝2sin ωx 在区间⎣⎢⎡⎦⎥⎤－π3，π4上的最小值为－2，则ω的取值范围是( )A ．⎝ ⎛⎭⎪⎫－∞，－92∪[6，＋∞)B ．⎝ ⎛⎦⎥⎤－∞，－92∪⎣⎢⎡⎭⎪⎫32，＋∞C ．(－∞，－2]∪[6，＋∞)D ．(－∞，－2]∪⎣⎢⎡⎭⎪⎫32，＋∞解析：选D.当ω>0时，由题意知－π3ω≤－π2，即ω≥32；当ω<0时，由题意知π4ω≤－π2，所以ω≤－2.综上可知，ω的取值范围是(]－∞，－2∪⎣⎢⎡⎭⎪⎫32，＋∞.2．函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x －π4在区间⎣⎢⎡⎦⎥⎤0，π2上的最小值为 ( )A ．－1B ．－22C ．22D ．0解析：选B.由已知x ∈⎣⎢⎡⎦⎥⎤0，π2，得2x －π4∈⎣⎢⎡⎦⎥⎤－π4，3π4，所以sin ⎝ ⎛⎭⎪⎫2x －π4∈⎣⎢⎡⎦⎥⎤－22，1，故函数f (x )＝sin(2x －π4)在区间⎣⎢⎡⎦⎥⎤0，π2上的最小值为－22.3．函数y ＝sin ⎝⎛⎭⎪⎫－2x ＋π3的单调减区间为________． 解析：(同增异减法)y ＝－sin ⎝ ⎛⎭⎪⎫2x －π3，它的减区间是y ＝sin ⎝ ⎛⎭⎪⎫2x －π3的增区间．由2k π－π2≤2x －π3≤2k π＋π2，k ∈Z ，得k π－π12≤x ≤k π＋5π12，k ∈Z .故其单调减区间为⎣⎢⎡⎦⎥⎤k π－π12，k π＋5π12，k ∈Z .答案：⎣⎢⎡⎦⎥⎤k π－π12，k π＋5π12(k ∈Z )三角函数的奇偶性、周期性及对称性(1)设函数f (x )＝sin 2x ＋b sin x ＋c ，则f (x )的最小正周期( ) A ．与b 有关，且与c 有关 B ．与b 有关，但与c 无关 C ．与b 无关，且与c 无关 D ．与b 无关，但与c 有关(2)已知ω>0，f (x )＝1＋tan ωx 1－tan ωx ，f ⎝ ⎛⎭⎪⎫x ＋π3的图象与f (x )的图象关于点⎝ ⎛⎭⎪⎫π3，0对称，则ω的最小值为( )A ．12 B ．1 C ．32D ．2(3)已知函数f (x )＝sin(ωx ＋φ)＋cos(ωx ＋φ)(ω>0，0<φ<π)是奇函数，直线y ＝2与函数f (x )的图象的两个相邻交点的横坐标之差的绝对值为π2，则( )A ．f (x )在⎝ ⎛⎭⎪⎫0，π4上单调递减B ．f (x )在⎝ ⎛⎭⎪⎫π8，3π8上单调递减C ．f (x )在⎝ ⎛⎭⎪⎫0，π4上单调递增D ．f (x )在⎝ ⎛⎭⎪⎫π8，3π8上单调递增 【解析】 (1)由于f (x )＝sin 2x ＋b sin x ＋c ＝1－cos 2x 2＋b sin x ＋c .当b ＝0时，f (x )的最小正周期为π；当b ≠0时，f (x )的最小正周期为2π.c 的变化会引起f (x )图象的上下平移，不会影响其最小正周期．故选B.(2)因为f (x )＝1＋tan ωx 1－tan ωx ＝tan ⎝⎛⎭⎪⎫ωx ＋π4， 所以f ⎝ ⎛⎭⎪⎫x ＋π3＝tan ⎝⎛⎭⎪⎫ωx ＋ωπ3＋π4， 因为f ⎝ ⎛⎭⎪⎫x ＋π3的图象与f (x )的图象关于点⎝ ⎛⎭⎪⎫π3，0对称， 所以tan ⎝ ⎛⎭⎪⎫ωx ＋π4＋tan ⎝ ⎛ω2π3－ωx ＋ωπ3＋⎭⎪⎫π4＝0， 即tan ⎝ ⎛⎭⎪⎫ωx ＋π4＝tan ⎝⎛⎭⎪⎫ωx －ωπ－π4，所以π4＝－ωπ－π4＋k π，(k ∈Z )，ω＝－12＋k ，(k ∈Z )，因为ω>0，所以当k ＝1时，ω取最小值为12，故选A.(3)f (x )＝sin(ωx ＋φ)＋cos(ωx ＋φ)＝2sin(ωx ＋φ＋π4)，因为0<φ<π且f (x )为奇函数，所以φ＝3π4，即f (x )＝－2sin ωx ，又直线y ＝2与函数f (x )的图象的两个相邻交点的横坐标之差的绝对值为π2，所以函数f (x )的最小正周期为π2，由2πω＝π2，可得ω＝4，故f (x )＝－2sin 4x ，由2k π＋π2≤4x ≤2k π＋3π2，k ∈Z ，即k π2＋π8≤x ≤k π2＋3π8，k ∈Z ，令k ＝0，得π8≤x ≤3π8，此时f (x )在⎝ ⎛⎭⎪⎫π8，3π8上单调递增． 【答案】 (1)B (2)A (3)D三角函数的奇偶性、对称性和周期问题的解题思路(1)奇偶性的判断方法：三角函数中奇函数一般可化为y ＝A sin ωx 或y ＝A tan ωx 的形式，而偶函数一般可化为y ＝A cos ωx ＋b 的形式．(2)周期的计算方法：利用函数y ＝A sin(ωx ＋φ)(ω>0)，y ＝A cos(ωx ＋φ)(ω>0)的周期为2πω，函数y ＝A tan(ωx ＋φ)(ω>0)的周期为πω求解．(3)解决对称性问题的关键：熟练掌握三角函数的对称轴、对称中心．[提醒] 对于函数y ＝A sin(ωx ＋φ)，其对称轴一定经过图象的最高点或最低点，对称中心的横坐标一定是函数的零点，因此在判断直线x ＝x 0或点(x 0，0)是否是函数的对称轴或对称中心时，可通过检验f (x 0)的值进行判断．1．(2019·舟山市普陀三中高三期中)设函数f (x )＝sin(2x ＋φ)＋cos(2x ＋φ)⎝⎛⎭⎪⎫|φ|<π2为偶函数，则φ＝( )A ．π2B ．π3C ．π4D ．π6解析：选C.f (x )＝sin(2x ＋φ)＋cos(2x ＋φ)＝2sin ⎝ ⎛⎭⎪⎫2x ＋φ＋π4， 因为函数f (x )为偶函数，所以f (－x )－f (x )＝2sin ⎝ ⎛⎭⎪⎫－2x ＋φ＋π4－2sin ⎝ ⎛⎭⎪⎫2x ＋φ＋π4＝0，即sin ⎝ ⎛⎭⎪⎫－2x ＋φ＋π4＝sin ⎝⎛⎭⎪⎫2x ＋φ＋π4，所以－2x ＋φ＋π4＝2x ＋φ＋π4＋2k π，或－2x ＋φ＋π4＋2x ＋φ＋π4＝π＋k π，即x ＝－k π2，k ∈Z (舍)或φ＝π4＋k π2，k ∈Z . 因为|φ|<π2，所以φ＝π4.2．(2019·浙江省名校协作体高三联考)已知函数f (x )＝sin 2x ·(1－2sin 2x )＋1，则f (x )的最小正周期T ＝________，f (T )＝________．解析：由题意得，f (x )＝sin 2x cos 2x ＋1＝12sin 4x ＋1，所以最小正周期T ＝2π4＝π2，f (T )＝f ⎝ ⎛⎭⎪⎫π2＝1.答案：π213．已知函数f (x )＝sin x 的图象与直线kx －y －k π＝0(k >0)恰有三个公共点，这三个点的横坐标从小到大分别为x 1，x 2，x 3，则tan （x 2－x 3）x 1－x 3＝________．解析：如图所示，易知x 2＝π，x 1＋x 3＝2x 2＝2π，则k ＝sin x 3－0x 3－x 2＝sin x 312（x 3－x 1），又直线与y ＝sin x 相切于点A (x 3，sin x 3)， 则k ＝cos x 3， 则sin x 312（x 3－x 1）＝cos x 3⇒tan （x 2－x 3）x 1－x 3＝tan x 3x 3－x 1＝12，故答案为12.答案：12奇偶性对于y ＝A sin(ωx ＋φ)(A ≠0)，若为奇函数，则φ＝k π(k ∈Z )；若为偶函数，则φ＝π2＋k π(k ∈Z )．对于y ＝A cos(ωx ＋φ)(A ≠0)，若为奇函数，则φ＝π2＋k π(k ∈Z )；若为偶函数，则φ＝k π(k ∈Z )．对于y ＝A tan(ωx ＋φ)(A ≠0)，若为奇函数，则φ＝k π2(k∈Z )．函数图象的对称中心、对称轴(1)求形如y ＝A sin(ωx ＋φ)或y ＝A cos(ωx ＋φ)的函数图象的对称轴或对称中心时，都是先把“ωx ＋φ”看作一个整体，然后根据y ＝sin x 和y ＝cos x 图象的对称轴或对称中心进行求解． (2)在判断对称轴或对称中心时，用以下结论可快速解题：设y ＝f (x )＝A sin(ωx ＋φ)，g (x )＝A cos(ωx ＋φ)，x ＝x 0是对称轴方程⇔f (x 0)＝±A ，g (x 0)＝±A ；(x 0，0)是对称中心⇔f (x 0)＝0，g (x 0)＝0.易错防范(1)闭区间上最值或值域问题，首先要在定义域基础上分析单调性；含参数的最值问题，要讨论参数对最值的影响．(2)要注意求函数y ＝A sin(ωx ＋φ)的单调区间时A 和ω的符号，尽量化成ω>0时的情况，避免出现增减区间的混淆．[基础达标]1．最小正周期为π且图象关于直线x ＝π3对称的函数是( )A ．y ＝2sin ⎝⎛⎭⎪⎫2x ＋π3 B ．y ＝2sin ⎝ ⎛⎭⎪⎫2x －π6C ．y ＝2sin ⎝ ⎛⎭⎪⎫x 2＋π3D ．y ＝2sin ⎝⎛⎭⎪⎫2x －π3 解析：选B.由函数的最小正周期为π，可排除C.由函数图象关于直线x ＝π3对称知，该直线过函数图象的最高点或最低点，对于A ，因为sin ⎝⎛⎭⎪⎫2×π3＋π3＝sin π＝0，所以选项A 不正确．对于D ，sin ⎝ ⎛⎭⎪⎫2×π3－π3＝sin π3＝32，所以D 不正确，对于B ，sin ⎝ ⎛⎭⎪⎫2×π3－π6＝sin π2＝1，所以选项B 正确，故选B.2．(2019·合肥市第一次教学质量检测)函数y ＝sin(ωx ＋π6)在x ＝2处取得最大值，则正数ω的最小值为( )A ．π2B ．π3C ．π4D ．π6解析：选D.由题意得，2ω＋π6＝π2＋2k π(k ∈Z )，解得ω＝π6＋k π(k ∈Z )，因为ω>0，所以当k ＝0时，ωmin ＝π6，故选D.3．(2019·浙江省名校协作体高三联考)下列四个函数：y ＝sin|x |，y ＝cos|x |，y ＝|tanx |，y ＝－ln|sin x |，以π为周期，在⎝⎛⎭⎪⎫0，π2上单调递减且为偶函数的是( )A ．y ＝sin|x |B ．y ＝cos|x |C ．y ＝|tan x |D ．y ＝－ln|sin x |解析：选D.A.y ＝sin|x |在⎝ ⎛⎭⎪⎫0，π2上单调递增，故A 错误；B.y ＝cos|x |＝cos x 周期为T ＝2π，故B 错误；C.y ＝|tan x |在⎝ ⎛⎭⎪⎫0，π2上单调递增，故C 错误；D.f (x ＋π)＝－ln|sin(x ＋π)|＝－ln|sin x |，周期为π，当x ∈⎝ ⎛⎭⎪⎫0，π2时，y ＝－ln(sin x )是在⎝⎛⎭⎪⎫0，π2上单调递减的偶函数，故D 正确，故选D.4．(2017·高考全国卷Ⅲ)设函数f (x )＝cos(x ＋π3)，则下列结论错误的是( )A ．f (x )的一个周期为－2πB ．y ＝f (x )的图象关于直线x ＝8π3对称C ．f (x ＋π)的一个零点为x ＝π6D ．f (x )在(π2，π)单调递减解析：选D.根据函数解析式可知函数f (x )的最小正周期为2π，所以函数的一个周期为－2π，A 正确；当x ＝8π3时，x ＋π3＝3π，所以cos ⎝ ⎛⎭⎪⎫x ＋π3＝－1，所以B 正确；f (x ＋π)＝cos ⎝ ⎛⎭⎪⎫x ＋π＋π3＝cos ⎝⎛⎭⎪⎫x ＋4π3，当x ＝π6时，x ＋4π3＝3π2，所以f (x ＋π)＝0，所以C 正确；函数f (x )＝cos ⎝ ⎛⎭⎪⎫x ＋π3在⎝ ⎛⎭⎪⎫π2，23π上单调递减，在⎝ ⎛⎭⎪⎫23π，π上单调递增，故D 不正确．所以选D.5．若函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π6(ω>0)在区间(π，2π)内没有最值，则ω的取值范围是( )A ．⎝ ⎛⎦⎥⎤0，112∪⎣⎢⎡⎦⎥⎤14，23B ．⎝ ⎛⎦⎥⎤0，16∪⎣⎢⎡⎦⎥⎤13，23C ．⎣⎢⎡⎦⎥⎤14，23 D ．⎣⎢⎡⎦⎥⎤13，23 解析：选B.易知函数y ＝sin x 的单调区间为 [k π＋π2，k π＋3π2]，k ∈Z ，由k π＋π2≤ωx ＋π6≤k π＋3π2，k ∈Z ，得k π＋π3ω≤x ≤k π＋4π3ω，k ∈Z ，因为函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π6(ω>0)在区间(π，2π)内没有最值，所以f (x )在区间(π，2π)内单调，所以(π，2π)⊆⎣⎢⎢⎡⎦⎥⎥⎤k π＋π3ω，k π＋4π3ω，k ∈Z ， 所以⎩⎪⎨⎪⎧k π＋π3ω≤π，k π＋4π3ω≥2π，k ∈Z ，解得k ＋13≤ω≤k 2＋23，k ∈Z ，由k ＋13≤k 2＋23，得k ≤23，当k ＝0时，得13≤ω≤23；当k ＝－1时，得－23≤ω≤16.又ω>0，所以0<ω≤16.综上，得ω的取值范围是⎝ ⎛⎦⎥⎤0，16∪⎣⎢⎡⎦⎥⎤13，23.故选B. 6．已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π12，f ′(x )是f (x )的导函数，则函数y ＝2f (x )＋f ′(x )的一个单调递减区间是( )A ．⎣⎢⎡⎦⎥⎤π12，7π12B ．⎣⎢⎡⎦⎥⎤－5π12，π12C ．⎣⎢⎡⎦⎥⎤－π3，2π3D ．⎣⎢⎡⎦⎥⎤－π6，5π6解析：选A.由题意，得f ′(x )＝2cos ⎝ ⎛⎭⎪⎫2x ＋π12，所以y ＝2f (x )＋f ′(x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π12＋2cos ⎝ ⎛⎭⎪⎫2x ＋π12＝22sin ⎝ ⎛⎭⎪⎫2x ＋π12＋π4＝22sin ⎝ ⎛⎭⎪⎫2x ＋π3.由2k π＋π2≤2x ＋π3≤2k π＋3π2(k ∈Z )，得k π＋π12≤x ≤k π＋7π12(k ∈Z )，所以y ＝2f (x )＋f ′(x )的一个单调递减区间为⎣⎢⎡⎦⎥⎤π12，7π12，故选A.7．函数y ＝lg sin x ＋cos x －12的定义域为________．解析：要使函数有意义，则有⎩⎪⎨⎪⎧sin x >0，cos x －12≥0， 即⎩⎪⎨⎪⎧sin x >0，cos x ≥12，解得⎩⎪⎨⎪⎧2k π<x <π＋2k π，－π3＋2k π≤x ≤π3＋2k π(k ∈Z )， 所以2k π<x ≤π3＋2k π，k ∈Z .所以函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪2k π<x ≤π3＋2k π，k ∈Z .答案：⎩⎨⎧⎭⎬⎫x ⎪⎪⎪2k π<x ≤π3＋2k π，k ∈Z8．函数y ＝(4－3sin x )(4－3cos x )的最小值为________． 解析：y ＝16－12(sin x ＋cos x )＋9sin x cos x ， 令t ＝sin x ＋cos x ，则t ∈[－2，2]，且sin x cos x ＝t 2－12，所以y ＝16－12t＋9×t 2－12＝12(9t 2－24t ＋23)． 故当t ＝43时，y min ＝72.答案：729．(2019·温州市高中模考)已知函数y ＝sin x 的定义域为[a ，b ]，值域为⎣⎢⎡⎦⎥⎤－1，32，则b －a 的最大值和最小值之差等于________．解析：如图，当x ∈[a 1，b ]时，值域为⎣⎢⎡⎦⎥⎤－1，32且b －a 最大；当x ∈[a 2，b ]时，值域为⎣⎢⎡⎦⎥⎤－1，32，且b －a 最小，所以最大值与最小值之差为(b －a 1)－(b －a 2)＝a 2－a 1＝－π2－⎝ ⎛⎭⎪⎫－4π3＝5π6.答案：5π610．(2019·杭州学军中学质检)已知f (x )＝sin 2x －3cos 2x ，若对任意实数x ∈⎝⎛⎦⎥⎤0，π4，都有|f (x )|<m ，则实数m 的取值范围是________． 解析：因为f (x )＝sin 2x －3cos 2x ＝2sin ⎝ ⎛⎭⎪⎫2x －π3，x ∈⎝ ⎛⎦⎥⎤0，π4，所以⎝⎛⎭⎪⎫2x －π3∈⎝ ⎛⎦⎥⎤－π3，π6，所以2sin ⎝⎛⎭⎪⎫2x －π3∈(－3，1]，所以|f (x )|＝⎪⎪⎪⎪⎪⎪2sin ⎝ ⎛⎭⎪⎫2x －π3<3，所以m ≥ 3.答案：[3，＋∞)11．(2019·杭州市名校协作体高三下学期考试)已知0≤φ＜π，函数f (x )＝32cos(2x ＋φ)＋sin 2x .(1)若φ＝π6，求f (x )的单调递增区间；(2)若f (x )的最大值是32，求φ的值．解：(1)由题意f (x )＝14cos 2x －34sin 2x ＋12＝12cos ⎝⎛⎭⎪⎫2x ＋π3＋12，由2k π－π≤2x ＋π3≤2k π，得k π－2π3≤x ≤k π－π6.所以函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π－2π3，k π－π6，k ∈Z .(2)由题意f (x )＝⎝ ⎛⎭⎪⎫32cos φ－12cos 2x －32sin φsin 2x ＋12，由于函数f (x )的最大值为32，即⎝ ⎛⎭⎪⎫32cos φ－122＋⎝ ⎛⎭⎪⎫32sin φ2＝1，从而cos φ＝0，又0≤φ＜π，故φ＝π2.12．(2019·台州市高三期末评估)已知函数f (x )＝sin(ωx ＋φ)⎝ ⎛⎭⎪⎫ω＞0，|φ|≤π2的最小正周期为π，且x ＝π12为f (x )图象的一条对称轴．(1)求ω和φ的值；(2)设函数g (x )＝f (x )＋f ⎝⎛⎭⎪⎫x －π6，求g (x )的单调递减区间．解：(1)因为f (x )＝sin(ωx ＋φ)⎝ ⎛⎭⎪⎫ω＞0，|φ|≤π2的最小正周期为π，由T ＝2πω＝π，所以ω＝2，由2x ＋φ＝k π＋π2，k ∈Z ，所以f (x )的图象的对称轴为x ＝k π2＋π4－φ2，k ∈Z . 由π12＝k π2＋π4－φ2，得φ＝k π＋π3. 又|φ|≤π2，则φ＝π3.(2)函数g (x )＝f (x )＋f ⎝ ⎛⎭⎪⎫x －π6＝sin ⎝ ⎛⎭⎪⎫2x ＋π3＋sin 2x ＝12sin 2x ＋32cos 2x ＋sin 2x＝3sin ⎝⎛⎭⎪⎫2x ＋π6.所以g (x )的单调递减区间为⎣⎢⎡⎦⎥⎤k π＋π6，k π＋2π3，k ∈Z .[能力提升]1．(2019·湖州市高三期末考试)若α，β∈⎣⎢⎡⎦⎥⎤－π2，π2，且αsin α－βsin β＞0，则必有( )A ．α2＜β2B ．α2＞β2C ．α＜βD ．α＞β解析：选B.α，β∈⎣⎢⎡⎦⎥⎤－π2，π2，且αsin α－βsin β＞0，即αsin α＞βsin β，再根据y ＝x sin x 为偶函数，且在⎣⎢⎡⎦⎥⎤0，π2上单调递增，可得|α|＞|β|，即α2＞β2，故选B.2．若f (x )＝cos 2x ＋a cos ⎝ ⎛⎭⎪⎫π2＋x 在区间⎝ ⎛⎭⎪⎫π6，π2上是增函数，则实数a 的取值范围为( )A ．[－2，＋∞)B ．(－2，＋∞)C ．(－∞，－4)D ．(－∞，－4]解析：选D.f (x )＝1－2sin 2x －a sin x ，令sin x ＝t ，t ∈⎝ ⎛⎭⎪⎫12，1，则g (t )＝－2t 2－at＋1，t ∈⎝ ⎛⎭⎪⎫12，1，因为f (x )在⎝ ⎛⎭⎪⎫π6，π2上单调递增，所以－a 4≥1，即a ≤－4，故选D. 3．(2019·浙江“七彩阳光”联盟高三联考)已知函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎪⎫ω＞0，|φ|＜π2的图象过点⎝ ⎛⎭⎪⎫0，32，若f (x )≤f ⎝ ⎛⎭⎪⎫π6对x ∈R 恒成立，则ω的值为________；当ω最小时，函数g (x )＝f ⎝⎛⎭⎪⎫x －π3－22在区间[0，22]的零点个数为________．解析：由题意得φ＝π3，且当x ＝π6时，函数f (x )取到最大值，故π6ω＋π3＝π2＋2kπ，k ∈Z ，解得ω＝1＋12k ，k ∈N ，又因为ω＞0，所以ω的最小值为1，因此，g (x )＝f ⎝⎛⎭⎪⎫x －π3－22＝sin x －22的零点个数是8个． 答案：1＋12k (k ∈N ) 84．(2019·金华市东阳二中高三调研)设函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx －π6－2cos 2ω2x ＋1(ω>0)，直线y ＝3与函数f (x )图象相邻两交点的距离为π.(1)求ω的值；(2)在△ABC 中，角A 、B 、C 所对的边分别是a 、b 、c ，若点⎝ ⎛⎭⎪⎫B2，0是函数y ＝f (x )图象的一个对称中心，且b ＝3，求△ABC 面积的最大值．解：(1)函数f (x )＝sin ⎝⎛⎭⎪⎫ωx －π6－2cos 2ω2x ＋1＝sin ωx cos π6－cos ωx sin π6－2·1＋cos ωx2＋1＝32sin ωx －32cos ωx ＝3sin ⎝⎛⎭⎪⎫ωx －π3.因为f (x )的最大值为3，所以f (x )的最小正周期为π， 所以ω＝2.(2)由(1)知f (x )＝3sin ⎝ ⎛⎭⎪⎫2x －π3，因为3sin ⎝⎛⎭⎪⎫B －π3＝0⇒B ＝π3，因为cos B ＝a 2＋c 2－b 22ac ＝a 2＋c 2－92ac ＝12，所以ac ＝a 2＋c 2－9≥2ac －9，ac ≤9， 故S △ABC ＝12ac sin B ＝34ac ≤934.故△ABC 面积的最大值为934.5．已知a >0，函数f (x )＝－2a sin ⎝ ⎛⎭⎪⎫2x ＋π6＋2a ＋b ，当x ∈⎣⎢⎡⎦⎥⎤0，π2时，－5≤f (x )≤1. (1)求常数a ，b 的值；(2)设g (x )＝f ⎝⎛⎭⎪⎫x ＋π2且lg g (x )>0，求g (x )的单调区间．解：(1)因为x ∈⎣⎢⎡⎦⎥⎤0，π2，所以2x ＋π6∈⎣⎢⎡⎦⎥⎤π6，7π6. 所以sin ⎝ ⎛⎭⎪⎫2x ＋π6∈⎣⎢⎡⎦⎥⎤－12，1，所以－2a sin ⎝⎛⎭⎪⎫2x ＋π6∈[－2a ，a ]．所以f (x )∈[b ，3a ＋b ]，又因为－5≤f (x )≤1， 所以b ＝－5，3a ＋b ＝1，因此a ＝2，b ＝－5. (2)由(1)得，f (x )＝－4sin ⎝⎛⎭⎪⎫2x ＋π6－1，g (x )＝f ⎝ ⎛⎭⎪⎫x ＋π2＝－4sin ⎝⎛⎭⎪⎫2x ＋7π6－1＝4sin ⎝⎛⎭⎪⎫2x ＋π6－1， 又由lg g (x )>0，得g (x )>1，所以4sin ⎝ ⎛⎭⎪⎫2x ＋π6－1>1，所以sin ⎝⎛⎭⎪⎫2x ＋π6>12，所以2k π＋π6<2x ＋π6<2k π＋5π6，k ∈Z ，其中当2k π＋π6<2x ＋π6≤2k π＋π2，k ∈Z 时，g (x )单调递增，即k π<x ≤k π＋π6，k∈Z ，所以g (x )的单调增区间为⎝ ⎛⎦⎥⎤k π，k π＋π6，k ∈Z .又因为当2k π＋π2<2x ＋π6<2k π＋5π6，k ∈Z 时，g (x )单调递减，即k π＋π6<x <k π＋π3，k ∈Z .所以g (x )的单调减区间为⎝ ⎛⎭⎪⎫k π＋π6，k π＋π3，k ∈Z .。

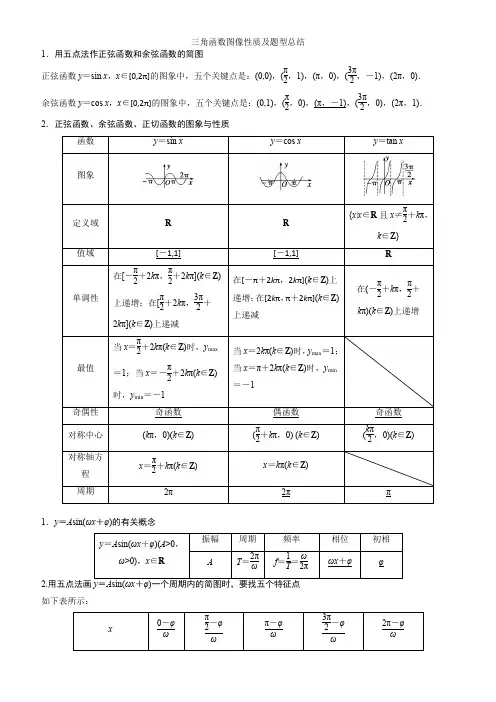
三角函数图像性质及题型总结1．用五点法作正弦函数和余弦函数的简图正弦函数y ＝sin x ，x ∈[0,2π]的图象中，五个关键点是：(0,0)，(π2，1)，(π，0)，(3π2，－1)，(2π，0)．余弦函数y ＝cos x ，x ∈[0,2π]的图象中，五个关键点是：(0,1)，(π2，0)，(π，－1)，(3π2，0)，(2π，1)．2．正弦函数、余弦函数、正切函数的图象与性质π1．y ＝A sin(ωx ＋φ)的有关概念2.用五点法画如下表所示：3.函数函数y ＝12sin x ，x ∈[－π，π]的单调性是( )A ．在[－π，0]上是增函数，在[0，π]上是减函数B ．在⎣⎡⎦⎤－π2，π2上是增函数，在⎣⎡⎦⎤－π，－π2和⎣⎡⎦⎤π2，π上都是减函数 C ．在[0，π]上是增函数，在[－π，0]上是减函数D ．在⎣⎡⎦⎤π2，π和⎣⎡⎦⎤－π，－π2上是增函数，在⎣⎡⎦⎤－π2，π2上是减函数 答案 B2．函数y ＝tan 2x 的定义域是( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π＋π4，k ∈ZB.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π2＋π8，k ∈Z C.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π＋π8，k ∈Z D.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π2＋π4，k ∈Z 答案 D解析 由2x ≠k π＋π2，k ∈Z ，得x ≠k π2＋π4，k ∈Z ，∴y ＝tan 2x 的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2＋π4，k ∈Z .已知函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ均为正的常数)的最小正周期为π，当x ＝2π3时，函数f (x )取得最小值，则下列结论正确的是( )A ．f (2)<f (－2)<f (0)B ．f (0)<f (2)<f (－2)C ．f (－2)<f (0)<f (2)D ．f (2)<f (0)<f (－2) 答案 A解析 由于f (x )的最小正周期为π，∴ω＝2，即f (x )＝A sin(2x ＋φ)， 又当x ＝2π3时，2x ＋φ＝4π3＋φ＝2k π－π2(k ∈Z )，∴φ＝2k π－11π6(k ∈Z )，又φ>0，∴φmin ＝π6，故f (x )＝A sin(2x ＋π6)．于是f (0)＝A sin π6，f (2)＝A sin ⎝⎛⎭⎫4＋π6 ＝A sin ⎣⎡⎦⎤π－⎝⎛⎭⎫4＋π6＝A sin ⎝⎛⎭⎫5π6－4， f (－2)＝A sin ⎝⎛⎭⎫－4＋π6＝A sin ⎝⎛⎭⎫13π6－4＝A sin ⎣⎡⎦⎤π－⎝⎛⎭⎫13π6－4＝A sin ⎝⎛⎭⎫4－7π6. 又∵－π2<5π6－4<4－7π6<π6<π2，又f (x )在⎝⎛⎭⎫－π2，π2上单调递增， ∴f (2)<f (－2)<f (0)，故选A.函数y ＝3－2cos ⎝⎛⎭⎫x ＋π4的最大值为________，此时x ＝__________________. 答案 53π4＋2k π(k ∈Z ) 解析 函数y ＝3－2cos ⎝⎛⎭⎫x ＋π4的最大值为3＋2＝5， 此时x ＋π4＝π＋2k π(k ∈Z )，即x ＝3π4＋2k π(k ∈Z )．函数f (x )＝tan ⎝⎛⎭⎫2x －π3的单调递增区间是( ) A.⎣⎡⎦⎤k π2－π12，k π2＋5π12(k ∈Z ) B.⎝⎛⎭⎫k π2－π12，k π2＋5π12(k ∈Z ) C.⎝⎛⎭⎫k π＋π6，k π＋2π3(k ∈Z ) D.⎣⎡⎦⎤k π－π12，k π＋5π12(k ∈Z ) 答案 B 解析由k π－π2＜2x －π3＜k π＋π2(k ∈Z )得，k π2－π12＜x ＜k π2＋5π12(k ∈Z )， 所以函数f (x )＝tan ⎝⎛⎭⎫2x －π3的单调递增区间为⎝⎛⎭⎫k π2－π12，k π2＋5π12(k ∈Z )，故选B.函数f (x )＝sin ⎝⎛⎭⎫－2x ＋π3的单调减区间为___________ 答案)⎣⎡⎦⎤k π－π12，k π＋512π 解析由已知函数为y ＝－sin ⎝⎛⎭⎫2x －π3， 欲求函数的单调减区间，只需求y ＝sin ⎝⎛⎭⎫2x －π3的单调增区间． 由2k π－π2≤2x －π3≤2k π＋π2，k ∈Z ，得k π－π12≤x ≤k π＋5π12，k ∈Z .故所给函数的单调减区间为⎣⎡⎦⎤k π－π12，k π＋5π12(k ∈Z )．在函数①y ＝cos|2x |，②y ＝|cos x |，③y ＝cos ⎝⎛⎭⎫2x ＋π6，④y ＝tan ⎝⎛⎭⎫2x －π4中，最小正周期为π的所有函数为( ) A ．①②③ B ．①③④ C ．②④ D ．①③答案 A解析 ①y ＝cos|2x |＝cos 2x ，最小正周期为π； ②由图象知y ＝|cos x |的最小正周期为π； ③y ＝cos ⎝⎛⎭⎫2x ＋π6的最小正周期T ＝2π2＝π； ④y ＝tan ⎝⎛⎭⎫2x －π4的最小正周期T ＝π2，因此选A. 已知函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω＞0，|φ|＜π2的最小正周期是π，若将f (x )的图象向右平移π3个单位后得到的图象关于原点对称，则函数f (x )的图象( )A ．关于直线x ＝π12对称B ．关于直线x ＝5π12对称C ．关于点⎝⎛⎭⎫π12，0对称D ．关于点⎝⎛⎭⎫5π12，0对称 答案B解析由题意知2πω＝π，∴ω＝2；又由f (x )的图象向右平移π3个单位后得到y ＝sin[2⎝⎛⎭⎫x －π3＋φ]＝sin ⎝⎛⎭⎫2x ＋φ－23π，此时关于原点对称， ∴－2π3＋φ＝k π，k ∈Z ，∴φ＝2π3＋k π，k ∈Z ，又|φ|＜π2，∴⎪⎪⎪⎪2π3＋k π＜π2，∴k ＝－1，φ＝－π3， ∴f (x )＝sin ⎝⎛⎭⎫2x －π3.当x ＝π12时，2x －π3＝－π6，∴A 、C 错误；当x ＝5π12时，2x －π3＝π2，∴B 正确，D 错误．(2015·四川)下列函数中，最小正周期为π且图象关于原点对称的函数是( ) A ．y ＝cos ⎝⎛⎭⎫2x ＋π2 B ．y ＝sin ⎝⎛⎭⎫2x ＋π2 C ．y ＝sin 2x ＋cos 2x D ．y ＝sin x ＋cos x 解析选项A 中，y ＝cos ⎝⎛⎭⎫2x ＋π2＝－sin 2x ，符合题意．函数f (x )＝cos(ωx ＋φ)的部分图象如图所示，则f (x )的单调递减区间为( )A.⎝⎛⎭⎫k π－14，k π＋34，k ∈Z B.⎝⎛⎭⎫2k π－14，2k π＋34，k ∈Z C.⎝⎛⎭⎫k －14，k ＋34，k ∈Z D.⎝⎛⎭⎫2k －14，2k ＋34，k ∈Z 解析由图象知，周期T ＝2×⎝⎛⎭⎫54－14＝2， ∴2πω＝2，∴ω＝π. 由π×14＋φ＝π2＋2k π，k ∈Z ，不妨取φ＝π4，∴f (x )＝cos ⎝⎛⎭⎫πx ＋π4. 由2k π<πx ＋π4<2k π＋π，k ∈Z ，得2k －14<x <2k ＋34，k ∈Z ，∴f (x )的单调递减区间为⎝⎛⎭⎫2k －14，2k ＋34，k ∈Z .故选D.对于函数f (x )＝sin ⎝⎛⎭⎫πx ＋π2，下列说法正确的是( ) A ．f (x )的周期为π，且在[0,1]上单调递增 B ．f (x )的周期为2，且在[0,1]上单调递减 C ．f (x )的周期为π，且在[－1,0]上单调递增D ．f (x )的周期为2，且在[－1,0]上单调递减 答案 B解析 因为f (x )＝sin ⎝⎛⎭⎫πx ＋π2＝cos πx ，则周期T ＝2，在[0,1]上单调递减，故选B. 2．函数y ＝2sin ⎝⎛⎭⎫πx 6－π3(0≤x ≤9)的最大值与最小值之和为( ) A ．2－ 3 B ．0 C ．－1 D ．－1－3 答案 A解析 ∵0≤x ≤9，∴－π3≤π6x －π3≤7π6，∴sin ⎝⎛⎭⎫π6x －π3∈⎣⎡⎦⎤－32，1. ∴y ∈[]－3，2，∴y max ＋y min ＝2－ 3.关于函数y ＝tan ⎝⎛⎭⎫2x －π3，下列说法正确的是( ) A ．是奇函数B ．在区间⎝⎛⎭⎫0，π3上单调递减 C.⎝⎛⎭⎫π6，0为其图象的一个对称中心 D ．最小正周期为π 答案 C解析 函数y ＝tan ⎝⎛⎭⎫2x －π3是非奇非偶函数，A 错误； 在区间⎝⎛⎭⎫0，π3上单调递增，B 错误； 最小正周期为π2，D 错误．∵当x ＝π6时，tan ⎝⎛⎭⎫2×π6－π3＝0， ∴⎝⎛⎭⎫π6，0为其图象的一个对称中心，故选C.函数y ＝cos 2x ＋sin 2x ，x ∈R 的值域是( ) A ．[0,1] B ．[12，1] C ．[－1,2] D ．[0,2]答案 A解析 y ＝cos 2x ＋sin 2x ＝cos 2x ＋1－cos 2x2＝1＋cos 2x2. ∵cos 2x ∈[－1,1]，∴y ∈[0,1]．函数f (x )＝sin(－2x )的单调增区间是___________________________________________． 答案 ⎣⎡⎦⎤k π＋π4，k π＋3π4(k ∈Z ) 解析 由f (x )＝sin(－2x )＝－sin 2x ， 2k π＋π2≤2x ≤2k π＋3π2 (k ∈Z )得k π＋π4≤x ≤k π＋3π4(k ∈Z )．函数y ＝tan ⎝⎛⎭⎫2x ＋π4的图象与x 轴交点的坐标是__________________． 答案 ⎝⎛⎭⎫k π2－π8，0(k ∈Z ) 解析 由2x ＋π4＝k π(k ∈Z )得，x ＝k π2－π8(k ∈Z )．∴函数y ＝tan ⎝⎛⎭⎫2x ＋π4的图象与x 轴交点的坐标是⎝⎛⎭⎫k π2－π8，0(k ∈Z )．把函数y ＝sin(x ＋π6)图象上各点的横坐标缩短到原来的12(纵坐标不变)，再将图象向右平移π3个单位长度，那么所得图象的一条对称轴方程为( ) A ．x ＝－π2 B ．x ＝－π4C ．x ＝π8D ．x ＝π4答案 A 解析将y ＝sin(x ＋π6)图象上各点的横坐标缩短到原来的12(纵坐标不变)，得到函数y ＝sin(2x ＋π6)；再将图象向右平移π3个单位长度，得到函数y ＝sin[2(x －π3)＋π6]＝sin(2x －π2)，故x ＝－π2是其图象的一条对称轴方程函数f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0，|φ|＜π)的部分图象如图所示，则函数f (x )的解析式为__________．答案f (x )＝2sin(2x ＋π3)解析 由题图可知A ＝2，T 4＝7π12－π3＝π4，所以T ＝π，故ω＝2，因此f (x )＝2sin(2x＋φ)，又⎝⎛⎭⎫712π，－2为最小值点，∴2×712π＋φ＝2k π＋3π2，k ∈Z ，∴φ＝2k π＋π3，k ∈Z ，又|φ|＜π，∴φ＝π3. 故f (x )＝2sin(2x ＋π3)．设函数f (x )＝3sin(ωx ＋φ)(ω>0，－π2<φ<π2)的图象关于直线x ＝2π3对称，它的周期是π，则下列说法正确的是________．(填序号)①f (x )的图象过点(0，32)；②f (x )在[π12，2π3]上是减函数；③f (x )的一个对称中心是(5π12，0)；④将f (x )的图象向右平移|φ|个单位长度得到函数y ＝3sin ωx 的图象．答案 ①③解析 ∵周期为π，∴2πω＝π⇒ω＝2，∴f (x )＝3sin(2x ＋φ)，f (2π3)＝3sin(4π3＋φ)，则sin(4π3＋φ)＝1或－1.又φ∈(－π2，π2)，4π3＋φ∈(5π6，116π)，∴4π3＋φ＝3π2⇒φ＝π6，∴f (x )＝3sin(2x ＋π6)．①：令x ＝0⇒f (x )＝32，正确．②：令2k π＋π2<2x ＋π6<2k π＋3π2，k ∈Z⇒k π＋π6<x <k π＋2π3，k ∈Z .令k ＝0⇒π6<x <2π3，即f (x )在(π6，2π3)上单调递减，而在(π12，π6)上单调递增，错误．③：令x ＝5π12⇒f (x )＝3sin π＝0，正确．④：应平移π12个单位长度，错误．已知函数f (x )＝23sin(x 2＋π4)·cos(x 2＋π4)－sin(x ＋π)．(1)求f (x )的最小正周期；(2)若将f (x )的图象向右平移π6个单位长度，得到函数g (x )的图象，求函数g (x )在区间[0，π]上的最大值和最小值．解 (1)f (x )＝23sin(x 2＋π4)·cos(x 2＋π4)－sin(x ＋π)＝3cos x ＋sin x [3分]＝2sin(x ＋π3)，[5分]于是T ＝2π1＝2π.[6分](2)由已知得g (x )＝f (x －π6)＝2sin(x ＋π6)，[8分]∵x ∈[0，π]，∴x ＋π6∈[π6，7π6]，∴sin(x ＋π6)∈[－12，1]，[10分]∴g (x )＝2sin(x ＋π6)∈[－1,2]．[11分]故函数g (x )在区间[0，π]上的最大值为2，最小值为－1.[12分]函数y ＝cos ⎝⎛⎭⎫2x －π3的部分图象可能是( )答案 D解析 ∵y ＝cos ⎝⎛⎭⎫2x －π3，∴当2x －π3＝0， 即x ＝π6时，函数取得最大值1，结合图象看，可使函数在x ＝π6时取得最大值的只有D.已知函数f (x )＝sin 2x －sin 2⎝⎛⎭⎫x －π6，x ∈R . (1)求f (x )的最小正周期；(2)求f (x )在区间⎣⎡⎦⎤－π3，π4上的最大值和最小值． 解 (1)由已知，有f (x )＝1－cos 2x2－1－cos ⎝⎛⎭⎫2x －π32＝12⎝⎛⎭⎫12cos 2x ＋32sin 2x －12cos 2x ＝34sin 2x －14cos 2x ＝12sin ⎝⎛⎭⎫2x －π6. 所以f (x )的最小正周期T ＝2π2＝π.(2)因为f (x )在区间⎣⎡⎦⎤－π3，－π6上是减函数，在区间⎣⎡⎦⎤－π6，π4上是增函数，且f ⎝⎛⎭⎫－π3＝－14， f ⎝⎛⎭⎫－π6＝－12，f ⎝⎛⎭⎫π4＝34，所以f (x )在区间⎣⎡⎦⎤－π3，π4上的最大值为34，最小值为－12.。

•正弦、余弦、正切函数图象和性质函数正弦函数y =sinx,x运R余弦函数y=cosx, x^R正切函数y = tanx, xHkr +上2有界性有界有界无界疋义域(^□0, +Xi)r 兀i2 x | x式k兀+—, Z ,I 2 J值域[-1,1]当X =3 +2kjl(k 乏Z)时，y max =〔2■JT当x =_二+2kir(k ^Z)时，2『min =-〔3,1]当X=2k H(k€Z)时，y max =1当x =兀+2k n(k€Z)时，『min = -1(^aC, ^C)周期性是周期函数，最小正周期T=2兀是周期函数，最小正周期T =2兀T =兀奇偶性奇函数，图象关于原点对称偶函数，图象关于y轴对称奇函数，图象关于原点对称单调性在［一生+2k兀，壬+2小］,(k € z)2 2上是单调增函数在［壬+2kn,竺+2阪］,(k乏Z)2 2上是单调减函数在［兀+2kir,2兀+2kn:］, (k 乏Z)上是单调增函数在［2k%兀+2kn］, (k^Z)上是单调减函数”H 兀在(_一+k兀，一+k兀),(k^ Z) 2 2上是单调增函数对称轴1Tx =k 兀+ = ,(k E Z)2x =kir, (k w Z)对称中心(也,0) (MZ)(k兀+ 匹,0) (k^Z)2k兀(三,0) (HZ)正弦函数、余弦函数、正切函数的图像三角函数的性质1定义域与值域 2、奇偶性(1) 基本函数的奇偶性 奇函数：y = sinx , y = tanx ；偶函数：y = cosx.(2),型三角函数的奇偶性(i) g ( x )=—二匚(x € R )g (x )为偶函数二T ■-匚「•匚O 虫血(曲+®)二虫sm (-蕊+©(XE R) n 迪欧刚片Q (応R) 8$少二 Oo®=fc?r+—优eZ)由此得同理，=虫迎(的物仃E 去)为奇函数sin = 0(p — k7l(k € Z).(丘).；'：.■. - ■ J .：!■, ■ /.'■■■.'■.I宀'-■■ : - ■■- - /'为偶函数---::1 ；：—上:-■■- - -；1 为奇函数 (圧 2) 2 .3、周期性1)基本公式(i)基本三角函数的周期 y = sinx , y = cosx 的周期为：•'； ; y = tanx , y = cotx的周期为匚.(ii)「V 」型三角函数的周期2JTy= 4$in(眾x+卩)+kj=i4coK 驱+©+上开y 二虫 tan (临+仍 +匕丁 二 Acot(@z+g) + 上 的周期为|少| . (2) 认知y=ta nxyiy；y=cotx II 丿 /f f / y1 /I112■ z n -2oJ2! , n 212x-JI2o恥312-込：—1 r [ ii f I\tI 1 1 i2 2-1y=cosx(i) 讨型函数的周期开尸恤in(处+©卩屮cos(曲+创的周期为0| ；7T》=|血购(亦+ ©卜=|乂嗽(倾+釧的周期为0 .(ii) 一：“」的周期严|加1伽+©+斗尸血o$伽+©+貝的周期为青；71尸|伽血+ ©+丽二血0t伽+© +上|的周期为0 .均同它们不加绝对值时的周期相同，即对+ 的解析式施加绝对值后，该函数的周期不变•注意这一点与(i)的区别•(ii) 若函数为「川型两位函数之和，则探求周期适于“最小公倍数法”.(iii) 探求其它“杂”三角函数的周期，基本策略是试验一一猜想一一证明(3)特殊情形研究7T(i) y = tanx —cotx的最小正周期为］;(ii) '的最小正周期为］;(iii) y = sin 4X + cos4x的最小正周期为 _ .由此领悟“最小公倍数法”的适用类型，以防施错对象.4、单调性(1)基本三角函数的单调区间(族)依从三角函数图象识证“三部曲”：①选周期：在原点附近选取那个包含全部锐角，单调区间完整，并且最好关于原点对称的一个周期；②写特解：在所选周期内写出函数的增区间(或减区间)；③获通解：在②中所得特解区间两端加上有关函数的最小正周期的整数倍，即得这一函数的增区间族(或减区间族)循着上述三部曲，便可得出课本中规范的三角函数的单调区间族.揭示：上述“三部曲”也适合于寻求简单三角不等式的解集或探求三角函数的定义域•(2)R 型三角函数的单调区间此类三角函数单调区间的寻求“三部曲”为①换元、分解：令u—二，将所给函数分解为内、外两层：y二f （u）, u… ；②套用公式：根据对复合函数单调性的认知，确定出f （u）的单调性，而后利用（1）中公式写出关于u的不等式；③还原、结论：将u=J「二代入②中u的不等式，解出x的取值范围，并用集合或区间形成结论•正弦、余弦、正切、余切函数的图象的性质：/y =s inx y =cosx y =ta nx y =cotxy = Asin®x+申)(A、⑷ > 0)定义域R R- 1 _x|x E R且x #冗岂兀k亡Z卩{x|x^R 且x^k jL k^z}R值域[_1,+1][_1,+1]R RL A, A】周期性2兀2兀312H看奇偶性奇函数偶函数奇函数奇函数当甲式0,非奇非偶当® =0,奇函数单调性n:[——+2kTi,2-+2^I]2上为增函数；TT[—+2kir,23兀丄—■ +2kn]2上为减函数( "Z )［（2k—1兀.2kn］上为增函数［2k 兀,（2k +1 対上为减函数（"Z ）+k ii,匹+k n〕1 2 2丿上为增函数（"Z ）(5, (k+1^ )上为减函数(k^Z ) 1[上■上兀 22kn:------- Q2( A)(A),12kn: +— n 一申2( A)（八丿_ 0 」二为增函数；2kn十匹一护(A),O2k兀+^3兀一半2 ( 八)（一八）. ⑷一二为减函数注意：①y =-sinx与y =sinx的单调性正好相反；y =-cosx与y =cosx的单调性也同样相反一般地，若y =f（x）在［a,b］上递增（减），则y=-f（x）在［a,b］上递减（增）②y =sin x与y =COSX的周期是二.③y =sin（灼x+巧或y=cos®x+®）（⑷芒0 ）的周期T =吾.y=tan x的周期为2兀（T=2L—T=2TT，如图，翻折无效）•2抄厂JT④y =sin（，x •「）的对称轴方程是- （k • Z ），对称中心（k二,0 ） ; y住x ）的对称轴方程是x=k二（Z），对称中心（k-）；y =a x :）的对称中心（—,0）.k 2 ,02原点对称> y - _cos( _2x) - _cos2xy =cos2x⑤当tan : tan 1 =1, : - -k (k Z)；ta n : tan 一- _1, ： - 一- k (k Z).2 2⑥y =cosx与y =sin i x 2k二是同一函数，而y=(.x・)是偶函数，贝UI 2 丿1y =( x ：T)二sin( x k - ) = cos( x).⑦函数yy=tanx为增函数，同样也是错误的］.⑧定义域关于原点对称是f （x）具有奇偶性的必要不充分条件.（奇偶性的两个条件：一是定义域关于原点对称（奇偶都要），二是满足奇偶性条件，偶函数：f（「x）=f（x），奇函数：f（_x）--f（x））奇偶性的单调性：奇同偶反.例如：y=tanx是奇函数，y =tan（x --）是非奇非偶.（定义域不3关于原点对称）奇函数特有性质：若x的定义域，则f （x）一定有f（o）=o. （O^x的定义域，贝U无此性质）⑨y =sinx不是周期函数；y = sin x为周期函数（T ★）;y .cosx是周期函数（如图）；y = cos x为周期函数（T二二）；y=cos2x』的周期为兀（如图），并非所有周期函数都有最小正周期, 2y、 /一：、X *例如：y =f (x) =5 =f (x k),k R.⑩ y =a cos* 亠bsin - - a2b2sin(x 亠门)cos =b有a2b2y .、形如y =Asin（「x •的函数:11、几个物理量：A—振幅；f二1—频率（周期的倒数）；「X •「一相位；‘一初相；2、函数y = Asin（）表达式的确定：A由最值确定；• •由周期确定；:由图象上的特殊点确定,如f（x）= Asgx +申"“妙＞0宀的图象如图所示,则 f (x)(答:f (x)二2sin^ x3.函数y 二Asin(・x ) B (其中 A 0, ，0)最大值是A最小正周期T十|y= cos|x| 图象yy=| cos2x+1/21图象Q JT频率是f ，相位是，初相是：;其图象的对称轴是直线•■x W：=k （k・Z），凡2兀2是该图象与直线y=B 的交点都是该图象的对称中心 4、 研究函数y =Asin （「x •「）性质的方法：类比于研究y =sin x 的性质，只需将y = Asin （ • x J 中的 看成y =si n x 中的x ，但在求y = A si n （・・x •「）的单调区间时，要特别注意 A 和• ‘的 符号，通过诱导公式先将•’化正。

1●高考明方向1.能画出y ＝sin x ，y ＝cos x ，y ＝tan x 的图象， 了解三角函数的周期性．2.理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、 最大值和最小值，图象与x 轴的交点等)，理解正切函数在区间⎝ ⎛⎭⎪⎫－π2，π2内的单调性．★备考知考情三角函数的周期性、单调性、最值等是高考的热点，题型既有选择题、填空题、又有解答题，难度属中低档，如2014课标全国Ⅱ14、北京14等；常与三角恒等变换交汇命题，在考查三角函数性质的同时，又考查三角恒等变换的方法与技巧，注重考查函数方程、转化化归等思想方法.《名师一号》P552二、例题分析： （一）三角函数的定义域和值域 例1．（1）《名师一号》P56 对点自测3函数y ＝lg(sin x )＋ cos x －12的定义域为____________解析 要使函数有意义必须有⎩⎪⎨⎪⎧ sin x >0，cos x －12≥0， 即⎩⎪⎨⎪⎧sin x >0，cos x ≥12，解得⎩⎪⎨⎪⎧2k π<x <π＋2k π，－π3＋2k π≤x ≤π3＋2k π (k ∈Z)．∴2k π<x ≤π3＋2k π，k ∈Z.∴函数的定义域为{x |2k π<x ≤π3＋2k π，k ∈Z}．3例1．（2）《名师一号》P56 高频考点 例1(1) 函数y ＝sin x －cos x 的定义域为________．解:(1)要使函数有意义，必须有sin x －cos x ≥0，即sin x ≥cos x ，同一坐标系中作出y ＝sin x ，y ＝cos x ，x ∈[0,2π]的图象如图所示．结合图象及正、余弦函数的周期是2π知，函数的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π＋π4≤x ≤2k π＋54π，k ∈Z .注意：《名师一号》P56 高频考点 例1 规律方法 (1)求三角函数的定义域实质就是解三角不等式（组）． 一般可用三角函数的图象或三角函数线确定 三角不等式的解．4例2．（1）《名师一号》P56 对点自测4函数y ＝2sin ⎝ ⎛⎭⎪⎫πx 6－π3(0≤x ≤9)的最大值与最小值之和为( )A ．2－ 3B ．0C ．－1D ．－1－3解:∵0≤x ≤9，∴－π3≤π6x －π3≤7π6.∴sin ⎝ ⎛⎭⎪⎫π6x －π3∈⎣⎢⎡⎦⎥⎤－32，1.∴y ∈[－3，2]，∴y max ＋y min ＝2－ 3. 注意：《名师一号》P56 高频考点 例1 规律方法2 求三角函数的值域的常用方法之一： 利用sin x 和cos x 的值域(图像)直接求；例2．（2）8月月考第17题(1)17．（满分12分）已知函数22()3cos 2cos sin sin f x x x x x =++．5（I ）当[0,]2x π∈时，求()f x 的值域；222()3cos 2cos sin sin 12cos sin 2f x x x x x x x =++=++………2分)2x =++ …………3分……4分即()f x 的值域为2]+. …………………6分注意：《名师一号》P56 高频考点 例1 规律方法2 求三角函数的值域的常用方法之二： 化为求sin()=++y A x b ωϕ的值域 如：①sin cos y a x b x =+合一变换6sin()y A x ϕ=+②22sin sin cos cos y a x b x x c x =++sin 2cos2y d x e x f =++sin(2)y A x b ϕ=++ 注意弦函数的有界性！变式:《名师一号》P58 特色专题 典例1若函数f (x )＝a sin x －b cos x 在x ＝π3处有最小值－2，则常数a ，b 的值是( )A ．a ＝－1，b ＝ 3B ．a ＝1，b ＝－3C ．a ＝3，b ＝－1D ．a ＝－3，b ＝1解:函数f (x )＝a sin x －b cos x 的最小值为－a 2＋b 2. f (x )＝a 2＋b 2sin(x －φ)⎝⎛⎭⎪⎫其中cos φ＝a a 2＋b 2，sin φ＝b a 2＋b 2，降幂 合一变换7则⎩⎨⎧－a 2＋b 2＝－2，f ⎝ ⎛⎭⎪⎫π3＝32a －12b ＝－2，解得⎩⎨⎧a ＝－3，b ＝1.【名师点评】 解答本题的两个关键：①引进辅助角，将原式化为三角函数的基本形式； ②利用正弦函数取最值的方法建立方程组．例2．(3)《名师一号》P56 高频考点 例1(2)当x ∈⎣⎢⎡⎦⎥⎤π6，7π6时，函数y ＝3－sin x －2cos 2x 的最小值是________，最大值是________．解:∵x ∈⎣⎢⎡⎦⎥⎤π6，7π6，∴sin x ∈⎣⎢⎡⎦⎥⎤－12，1.又y ＝3－sin x －2cos 2x ＝3－sin x －2(1－sin 2x )＝2⎝ ⎛⎭⎪⎫sin x －142＋78. ∴当sin x ＝14时，y min ＝78；当sin x ＝－12或sin x ＝1时，y max ＝2.8注意：《名师一号》P56 高频考点 例1 规律方法2 求三角函数的值域的常用方法之三：把sin x 或cos x 看作一个整体，转换成二次函数求值域．练习: (补充)（1）求函数22tan 1()tan 1x f x x -=+的值域【答案】[)1,1-（2）求函数22sin 1()0,sin 22x f x x x π+⎛⎫⎛⎫=∈ ⎪ ⎪⎝⎭⎝⎭的值域【答案】)+∞92222sin 13sin cos ()sin 22sin cos 3tan 1113tan 2tan 2tan 0,tan 0211()23tan 32tan x x x f x x x xx x x x x x f x x xπ++==+⎛⎫==+ ⎪⎝⎭⎛⎫∈∴> ⎪⎝⎭≥=注意：求三角函数的值域的常用方法之三：求三角函数的值域的常用方法： 化为求代数函数的值域注意约束条件----三角函数自身的值域！例2．（4）(补充)求函数()sin cos sin cos =+-f x x x x x 的值域【答案】12⎡⎤-+⎢⎥⎣⎦注意：求三角函数的值域的常用方法之四：10《名师一号》P56 问题探究 问题3 如何求三角函数的值域或最值？③形如y ＝a sin x cos x ＋b (sin x ±cos x )＋c 的三角函数，可先设t ＝sin x ±cos x ，化为关于t 的二次函数求值域(或最值)． 利用22sin cos 1x x +=转化为二次函数在指定区间 上的值域问题变式:求函数()sin cos sin cos +=+f x x x x x 的值域例2．（5）详见 第一章 第二讲函数值域 7．数形结合法： 例7(2)《名师一号》P14 问题探究 问题（6）当一个函数图象可作时，通过图象可求其值域和最值；或利用函数所表示的几何意义，借助于几何方法求出函数的值域．(补充)如两点间距离、直线斜率等等求函数4sin 12cos 4+=-x y x 的值域11解:()114sin sin 4422cos 2cos 2⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭==--x x y x x 可视作单位圆外一点12,4⎛⎫- ⎪⎝⎭P 与圆221+=x y 上的点()cos ,sin x x 所连线段斜率的2倍,设过点12,4⎛⎫- ⎪⎝⎭P 的点的直线方程为()12+=-y k x 即1204---=kx y k1=解得34=-k 或512=k答案：35,26⎡⎤-⎢⎥⎣⎦注意：求三角函数的值域的常用方法之五： 数形结合法练习：求函数[]cos 10,sin 2-=∈-x y x x π的值域12答案：40,3⎡⎤⎢⎥⎣⎦变式：求函数cos 1,sin 222-⎡⎤=∈-⎢⎥-⎣⎦x y x x ππ的值域答案：10,2⎡⎤⎢⎥⎣⎦拓展:8月月考第16题函数22)24()2cos x x xf x x xπ+++=+的最大值是M ，最小值是m ，则M m +的值是 .22222)2sin cos 2sin 4()12cos 2cos 2cos x x xx x x x x x f x x x x x x x π+++++++===++++，记2sin ()2cos x xg x x x+=+，则()g x 是奇函数且()1()f x g x =+，所以()f x 的最大值是max 1()M g x =+，13 最小值是min 1()m g x =+，因为()g x 是奇函数， 所以max min ()()0g x g x +=，所以max min 1()1()2M m g x g x +=+++=.（三）三角函数的周期性、奇偶性、对称性 例1．（1）《名师一号》P56 对点自测5设函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x －π2，x ∈R ，则f (x )是( )A.最小正周期为π的奇函数B.最小正周期为π的偶函数C.最小正周期为π2的奇函数D.最小正周期为π2的偶函数答案 B例1．（2）《名师一号》P57 高频考点 例3（2）(2014·新课标全国卷Ⅰ)在函数①y ＝cos|2x |，②y ＝|cos x |，③y ＝cos ⎝⎛⎭⎫2x ＋π6，④y ＝tan ⎝⎛⎭⎫2x －π4中，最小正周期为π的所有函数为( )A ．①②③B ．①③④C ．②④D ．①③解：由于y ＝cos|2x |＝cos2x ，所以该函数的周期为2π2＝π；由函14数y ＝|cos x |的图象易知其周期为π；函数y ＝cos ⎝⎛⎭⎫2x ＋π6的周期为2π2＝π；函数y ＝tan ⎝⎛⎭⎫2x －π4的周期为π2，故最小正周期为π的函数是①②③，故选A.注意：《名师一号》P56 问题探究 问题1 如何求三角函数的周期？ (1)利用周期函数的定义． (2)利用公式：y ＝A sin(ωx ＋φ)和y ＝A cos(ωx ＋φ)的最小正周期为2π|ω|， y ＝tan(ωx ＋φ)的最小正周期为π|ω|.例1．（3）《名师一号》P58 特色专题 典例2函数f(x)＝sin ⎝⎛⎭⎫ωx ＋π3＋sin ωx(ω>0)相邻两对称轴之间的距离为2，则ω＝________【规范解答】 相邻两对称轴之间的距离为2，即T ＝4.f(x)＝sin ⎝⎛⎭⎫ωx ＋π3＋sin ωx ＝12sin ωx ＋32cos ωx ＋sin ωx ＝32sin ωx15＋32cos ωx ＝3sin ⎝⎛⎭⎫ωx ＋π6，又因为f(x)相邻两条对称轴之间的距离为2，所以T ＝4，所以2πω＝4，即ω＝π2.注意：【名师点评】 函数f(x)＝A sin (ωx ＋φ)，f(x)＝A cos (ωx ＋φ)图象上一个最高点和它相邻的最低点的横坐标之差的绝对值是函数的半周期π|ω|，纵坐标之差的绝对值是2A .在解决由三角函数图象确定函数解析式的问题时，要注意使用好函数图象显示出来的函数性质、函数图象上特殊点的坐标及两个坐标轴交点的坐标等．练习:《加加练》P3 第11题例2．（1）《名师一号》P57 高频考点 例3（1）(1)若函数f (x )＝sin x ＋φ3(φ∈[0,2π])是偶函数，则φ＝( ) A.π2 B.2π3 C.3π2 D.5π3解： (1)∵f (x )＝sin x ＋φ3是偶函数，∴f (0)＝±1.16∴sin φ3＝±1，∴φ3＝k π＋π2(k ∈Z)．∴φ＝3k π＋3π2(k ∈Z)．又∵φ∈[0,2π]，∴当k ＝0时，φ＝3π2.故选C.变式：若函数f (x )＝sin x ＋φ3(φ∈[0,2π])是奇函数，则φ＝？例2．（2）《名师一号》P57 高频考点 例3（3）(3)如果函数y ＝3cos(2x ＋φ)的图象关于点⎝ ⎛⎭⎪⎫4π3，0中心对称，那么|φ|的最小值为( ) A.π6 B.π4 C.π3 D.π2解：(3)由题意得3cos ⎝⎛⎭⎫2×4π3＋φ＝3cos ⎝⎛⎭⎫2π3＋φ＋2π ＝3cos ⎝⎛⎭⎫2π3＋φ＝0，∴2π3＋φ＝k π＋π2，k ∈Z. ∴φ＝k π－π6，k ∈Z ，取k ＝0，得|φ|的最小值为π6.注意：【规律方法】(1)若f(x)＝A sin(ωx＋φ)为偶函数，则当x＝0时，f(x)取得最大或最小值，若f(x)＝A sin(ωx＋φ)为奇函数，则当x＝0时，f(x)＝0.(2)对于函数y＝A sin(ωx＋φ)，其对称轴一定经过图象的最高点或最低点，对称中心一定是函数的零点，因此在判断直线x＝x0或点(x0,0)是否是函数的对称轴或对称中心时，可通过检验f(x0)的值进行判断．《名师一号》P56 问题探究问题4如何确定三角函数的对称轴与对称中心？若f(x)＝A sin(ωx＋φ)为偶函数，则当x＝0时，f(x)取得最大值或最小值．若f(x)＝A sin(ωx＋φ)为奇函数，则当x＝0时，f(x)＝0.如果求f(x)的对称轴，只需令ωx＋φ＝π2＋kπ(k∈Z)，求x.(补充)结果写成直线方程！如果求f(x)的对称中心的横坐标，只需令ωx＋φ＝kπ(k∈Z)即可．(补充)结果写点坐标！同理对于y＝A cos(ωx＋φ)，可求其对称轴与对称中心，对于y＝A tan(ωx＋φ)可求出对称中心．1718练习1：《名师一号》P58 特色专题 典例3已知f(x)＝sin x ＋3cos x(x ∈R)，函数y ＝f (x ＋φ)⎝⎛⎭⎫|φ|≤π2为偶函数，则φ的值为________．【规范解答】 先求出f (x ＋φ)的解析式，然后求解．∵f (x )＝sin x ＋3cos x ＝2sin ⎝⎛⎭⎫x ＋π3. ∴f (x ＋φ)＝2sin ⎝⎛⎭⎫x ＋φ＋π3. ∵函数f (x ＋φ)为偶函数，∴φ＋π3＝π2＋k π，k ∈Z ，即φ＝π6＋k π(k ∈Z)．又∵|φ|≤π2，∴φ＝π6.练习2：《计时双基练》P247 第3题（四）三角函数的单调性 例1．（1）《名师一号》P56 对点自测6下列函数中，周期为π，且在⎣⎡⎦⎤π4，π2上为减函数的是( )19A ．y ＝sin ⎝⎛⎭⎫2x ＋π2B ．y ＝cos ⎝⎛⎭⎫2x ＋π2C ．y ＝sin ⎝⎛⎭⎫x ＋π2D ．y ＝cos ⎝⎛⎭⎫x ＋π2解析 由函数的周期为π，可排除C ，D.又函数在⎣⎡⎦⎤π4，π2上为减函数，排除B ，故选A.练习1：《计时双基练》P247 第7题函数y cos x π⎛⎫=- ⎪⎝⎭24的单调递减区间为练习2:《加加练》P1 第11题（2）《名师一号》P57 高频考点 例2已知函数f (x )＝4cos ωx ·sin ⎝⎛⎭⎫ωx ＋π4(ω>0)的最小正周期为π. (1)求ω的值；(2)讨论f (x )在区间⎣⎡⎦⎤0，π2上的单调性．20解：(1)f (x )＝4cos ωx ·sin ⎝⎛⎭⎫ωx ＋π4＝22sin ωx ·cos ωx ＋22cos 2ωx ＝2(sin2ωx ＋cos2ωx )＋2＝2sin ⎝⎛⎭⎫2ωx ＋π4＋ 2. 因为f (x )的最小正周期为π，且ω>0.从而有2π2ω＝π，故ω＝1.(2)由(1)知，f (x )＝2sin ⎝⎛⎭⎫2x ＋π4＋ 2. 若0≤x ≤π2，则π4≤2x ＋π4≤5π4.当π4≤2x ＋π4≤π2，即0≤x ≤π8时，f (x )单调递增； 当π2≤2x ＋π4≤5π4，即π8≤x ≤π2时，f (x )单调递减． 综上可知，f (x )在区间⎣⎡⎦⎤0，π8上单调递增， 在区间⎣⎡⎦⎤π8，π2上单调递减．注意：《名师一号》P56 问题探究 问题2 如何求三角函数的单调区间？(1)求函数的单调区间应遵循简单化原则，将解析式先化简，并注意复合函数单调性规律“同增异减”．(2)求形如y ＝A sin(ωx ＋φ)或y ＝A cos(ωx ＋φ)(其中，ω>0)的单调区间时，要视“ωx ＋φ”为一个整体，通过解不等式21求解．但如果ω<0，那么一定先借助诱导公式将ω化为正数，防止把单调性弄错．例2．《名师一号》P58 特色专题 典例4(2014·全国大纲卷)若函数f (x )＝cos2x ＋a sin x 在区间⎝ ⎛⎭⎪⎫π6，π2是减函数，则a 的取值范围是________．【规范解答】 先化简，再用换元法求解．f (x )＝cos2x ＋a sin x ＝1－2sin 2x ＋a sin x .令t ＝sin x ，∵x ∈⎝⎛⎭⎫π6，π2，∴t ∈⎝⎛⎭⎫12，1.∴g (t )＝1－2t 2＋at ＝－2t 2＋at ＋1⎝⎛⎭⎫12<t <1，由题意知－a 2×(－2)≤12，∴a ≤2. ∴a 的取值范围为(－∞，2]．22 课后作业一、计时双基练P247 基础1-11、课本P56变式思考1二、计时双基练P247培优1-4课本P56变式思考2、3预习 第五节练习：1、设函数f (x )＝2sin(2πx ＋5π)．若对任意x ∈R ，都有f (x 1)≤f (x )≤f (x 2)成立，则|x 1－x 2|的最小值为( )A ．4B ．2C ．1 D. 12分析：∵f (x )的最大值为2，最小值为－2，∴对∀x ∈R ，－2≤f (x )≤2.取到最值时x ＝2π＋k π，|x 1－x 2|取最小值，即f (x 1)为最小值，f (x 2)为最大值且(x 1，f (x 1))，(x 2，f (x 2))为相邻的最小(大)值点，即半个周期．解析：f (x )的周期T ＝4，|x 1－x 2|min ＝2T ＝2. 故选B.232、为了使函数)0(sin >=ωωx y 在区间]1,0[上至少出现50次最大值，求ω的最小值。

知识点总结归纳正余弦正弦和余弦函数的定义：正弦函数sin(x)是一个周期函数，它的定义域是实数集合，值域是[-1,1]。

正弦函数的图像是周期性的，其周期为2π，在每一个周期内，正弦函数的图像都呈现出一条W型的波浪线。

余弦函数cos(x)也是一个周期函数，它的定义域是实数集合，值域也是[-1,1]。

余弦函数的图像是周期性的，其周期同样为2π，在每一个周期内，余弦函数的图像都呈现出一条M 型的波浪线。

正弦和余弦函数的性质：1.周期性：正弦和余弦函数都是周期函数，其周期均为2π。

2.奇偶性：正弦函数是奇函数，即sin(-x)=-sin(x)，而余弦函数是偶函数，即cos(-x)=cos(x)。

3.正负性：正弦函数在第一、二象限为正，在第三、四象限为负；而余弦函数在第一、四象限为正，在第二、三象限为负。

4.关系：正弦函数和余弦函数是相互关联的，它们的图像呈现出相位差，即正弦函数与余弦函数的图像是互补的。

正弦和余弦函数的求解方法：1.利用单位圆：正弦和余弦函数可以通过单位圆来求解，单位圆的半径为1，利用三角形的性质可以求解出正弦和余弦函数的值。

2.利用三角恒等式：正弦和余弦函数可以通过三角恒等式来求解，通过三角恒等式可以将正弦和余弦函数与其他三角函数之间进行转换和关联。

正弦和余弦函数的应用领域：1.数学领域：正弦和余弦函数在数学领域中广泛应用于几何、三角形、圆等相关问题的解决中。

2.物理领域：正弦和余弦函数在物理领域中广泛应用于波动、振动、谐波等相关问题的解决中。

3.工程领域：正弦和余弦函数在工程领域中广泛应用于声音、光波、振动等相关问题的解决中。

总之，正弦和余弦函数是数学中的重要概念，它们具有广泛的应用价值，对于理解和应用正弦和余弦函数，可以提高我们在数学、物理、工程等领域中的分析和解决问题的能力。

希望本文的知识点总结可以帮助读者更好地理解和应用正弦和余弦函数。

专题18三角函数（知识梳理）一、知识点(一)角的概念的推广1、角：一条射线绕着端点从一个位置旋转到另一个位置所成的图形。

其中顶点，始边，终边称为角的三要素。

角可以是任意大小的。

(1)角按其旋转方向可分为：正角，零角，负角。

①正角：习惯上规定，按照逆时针方向旋转而成的角叫做正角；②负角：按照顺时针方向旋转而成的角叫做负角；③零角：当射线没有旋转时，我们也把它看成一个角，叫做零角。

(2)在直角坐标系中讨论角：①角的顶点在原点，始边在x 轴的非负半轴上，角的终边在第几象限，就说这个角是第几象限角。

②若角的终边在坐标轴上，就说这个角不属于任何象限，它叫轴线角。

(3)终边相同的角的集合：设α表示任意角，所有与α终边相同的角，包括α本身构成一个集合，这个集合可记为},360|{Z n n S ∈⋅+α=ββ= 。

集合S 的每一个元素都与α的终边相同，当0=k 时，对应元素为α。

2、弧度制和弧度制与角度制的换算(1)角度制：把圆周360等分，其中1份所对的圆心角是1度，用度作单位来度量角的制度叫做角度制。

(2)1弧度的角：长度等于半径长的圆弧所对的圆心角叫做1弧度的角。

规定：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零。

任一已知角α的弧度数的绝对值rl=α||，这种以“弧度”作为单位来度量角的制度叫做弧度制。

(3)角度制与弧度制的互化：π=2360，π=180；815730.571801'≈≈π= rad ；rad 01745.01801≈π= 。

3、特殊角的三角函数值30 45 60 90 120 135 150 18006π4π3π2π32π43π65ππsin 021222312322210cos 1232221021-22-23-1-tan3313⨯3-1-33-0210 225 240 270 300 315 330 36067π45π34π23π35π47π611ππ24、平面直角坐标系中特殊线表示的角的集合：其中：Z n ∈，Z k ∈；x 轴正半轴 360⋅n πk 2第一象限角平分线36045⋅+n π+πk 24x 轴负半轴360180⋅+n π+πk 2第二象限角平分线 360135⋅+n π+πk 243x 轴 180⋅n πk 第三象限角平分线360225⋅+n π+πk 245y 轴正半轴36090⋅+n π+πk 22第四象限角平分线 360315⋅+n π+πk 247y 轴负半轴 360270⋅+n π+πk 223第一、三象限角平分线18045⋅+n π+πk 4y 轴18090⋅+n π+πk 2第二、四象限角平分线 180135⋅+n π+πk 43坐标轴90⋅n 2πk 象限角平分线9045⋅+n 24π+πk 5、弧长及扇形面积公式：弧长公式：r l ⋅α=||扇形弧长，扇形面积公式：lr r S 21||212=⋅α=扇形，α是圆心角且为弧度制，r 是扇形半径。

[ 键入文字 ]课题 三角函数的图像及性质1.借助单位圆中的三角函数线推导出诱导公式（ π /2 ±α , 的π±α正弦、余弦、正切）2.利用单位圆中的三角函数线作出y sin x, x R 的图象，明确图象的形状；教学目标3.根据关系 cos xsin( x) ，作出 y cos x, x R 的图象；2重点、难点4.用“五点法”作出正弦函数、余弦函数的简图，并利用图象解决一些有关问题；1、正确地用三角函数线表示任意角的三角函数值2、作余弦函数的图象。

教学内容一、正弦函数和余弦函数的图象 ：y=sinxy-5-2 12-7o -4-3-2 -3 -2 -123 7 22 25 3422xy=cosxy-5- 2 1-32- -4-7-2 -3o 22-13 37 2225 422x正弦函数 ysin x 和余弦函数 ycos x 图象的作图方法：五点法：先取横坐标分别为 0，,,3, 222的五点，再用光滑的曲线把这五点连接起来，就得到正弦曲线和余弦曲线在一个周期内的图象。

二、正弦函数 y sin x(xR) 、余弦函数 y cos x(xR) 的性质 ：（ 1）定义域 ：都是 R 。

（ 2）值域 ： 1、都是 1,1 ，2、 ysin x ，当 x2kk Z 时， y 取最大值 1；当 x 2k3 Z 时， y 取最小值－ 1；k223、 y cos x ，当 x 2k k Z 时， y 取最大值 1，当 x 2kk Z 时， y 取最小值－ 1。

例：（ 1）若函数 y absin(3 x) 的最大值为 3 ，最小值为1，则 a __， b ＿1,b 1 或 b622（答： a1）；2[ 键入文字 ]⑵ 函数 y=-2sinx+10 取最小值时，自变量 x 的集合是。

（ 3）周期性 ：① y sin x 、 y cos x 的最小正周期都是 2 ；② f ( x)Asin( x) 和 f ( x)A cos( x) 的最小正周期都是2 。

高中数学知识点总结三角函数的变换与性质三角函数是高中数学中的重要部分，它在几何、物理、工程等领域中都有广泛的应用。

掌握三角函数的变换与性质对于解题和理解数学概念都具有重要的意义。

本文将对高中数学中的三角函数的变换与性质进行总结。

1. 正弦函数与余弦函数的图像变换正弦函数和余弦函数是最基本的三角函数之一，它们的图像变换具有以下特点：- 幅度变换：改变函数的幅度可以使得函数的振幅变大或变小。

当幅度为正数时，函数的振幅变大；当幅度为负数时，函数的振幅变小。

- 周期变换：改变函数的周期可以使得函数的图像在横轴上拉长或压缩。

周期为正数时，函数的图像在横轴上压缩；周期为负数时，函数的图像在横轴上拉长。

- 相位变换：改变函数的相位可以使得函数的图像在横轴上左移或右移。

相位为正数时，函数的图像在横轴上左移；相位为负数时，函数的图像在横轴上右移。

通过改变幅度、周期和相位，可以对正弦函数和余弦函数的图像进行灵活的变换，使其适用于不同的数学问题。

2. 正切函数与余切函数的图像变换正切函数和余切函数是三角函数中的另外两个重要函数，它们的图像变换具有以下特点：- 幅度变换：改变函数的幅度可以使得函数的振幅变大或变小。

当幅度为正数时，函数的振幅变大；当幅度为负数时，函数的振幅变小。

- 周期变换：改变函数的周期可以使得函数的图像在横轴上拉长或压缩。

周期为正数时，函数的图像在横轴上压缩；周期为负数时，函数的图像在横轴上拉长。

- 图像翻转：通过将函数的图像进行上下翻转或左右翻转，可以得到正切函数和余切函数的不同变换形式。

正切函数和余切函数的图像变换与正弦函数和余弦函数的变换类似，可以通过改变幅度、周期和图像翻转来得到不同形式的图像。

3. 三角函数的性质除了图像变换外，三角函数还具有以下重要的性质：- 周期性：正弦函数、余弦函数、正切函数和余切函数的周期都是360度或2π弧度。

这意味着这些函数的图像在一定角度范围内会重复出现，可以利用这一性质简化问题的求解。

专题4.7 三角函数的图象与性质-重难点题型精讲1．正弦函数与余弦函数的图象(1)正弦函数的图象①根据三角函数的定义，利用单位圆，我们可以得到函数y=,x∈[0,2π]的图象，如图所示.②五点法观察图，在函数y=,x∈[0,2π]的图象上，以下五个点：,1),( π,0),(-1),(2π,0)在确定图象形状时起关键作用.描出这五个点，函数y=,x∈[0,2π]的图象形状就基本确定了.因此，在精确度要求不高时，常先找出这五个关键点，再用光滑的曲线将它们连接起来，得到正弦函数的简图.这种作图的方法叫做“五点(画图)法”.(2)余弦函数的图象①图象变换法作余弦函数的图象由诱导公式六，我们知道，而函数x∈R的图象可以通过正弦函数y=,x∈R的图象向左平移个单位长度而得到.所以将正弦函数的图象向左平移个单位长度，就得到余弦函数的图象，如图所示.②五点法作余弦函数的图象类似于正弦函数图象的作法，从余弦函数y=,x∈R的图象可以看出，要作出函数y=在[0,2]上的图象，起关键作用的五个点是：(0,1),(,0),(,-1),(,0),(2,1).先描出这五个点，然后把这五个点用一条光滑的曲线连接起来就得到了函数y=在[0,2]上的简图，再通过左右平移(每次移动2个单位长度)即可得到余弦函数y=,x∈R的图象.(3)正弦曲线、余弦曲线正弦函数的图象和余弦函数的图象分别叫做正弦曲线和余弦曲线.它们是具有相同形状的“波浪起伏”的连续光滑曲线.2．正弦函数与余弦函数的性质(1)周期函数①定义：一般地，设函数f(x)的定义域为D，如果存在一个非零常数T，使得对每一个x∈D都有x+T∈D，且f(x+T)=f(x)，那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期.②最小正周期：如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期.(2)正弦函数与余弦函数的性质正弦函数与余弦函数的图象与性质如下表：3．正弦型函数的性质的性质4．正切函数的性质与图象(1)正切函数的图象及性质(2)三点两线法作正切曲线的简图类比于正、余弦函数图象的五点法，我们可以采用三点两线法作正切函数的简图.“三点”是指点(-,-1),(0,0),(,1);“两线”是指直线x=-和x=.在三点、两线确定的情况下,可以大致画出正切函数在区间(-上的简图.5．余切函数的图象及性质正切函数的图象及性质：的图象先向右平移个单位长度，再以x轴为对称轴上下翻折，可得的图象.余切函数的图象与性质如下表：【题型1 三角函数的定义域和值域（最值）】【方法点拨】求与三角函数有关的函数的值域(最值)的常用方法有：(1)借助三角函数的有界性、单调性求解；(2)转化为关于的二次函数求解.注意求三角函数的最值对应的自变量x的值时，要考虑三角函数的周期性.【例1】（2022·甘肃·高二开学考试）函数f(x)=tan(x+π4)的定义域为（）A．{x|x≠kπ+π4,k∈Z}B．{x|x≠2kπ+π4,k∈Z}C．{x|x≠kπ−π4,k∈Z}D．{x|x≠kπ,k∈Z}【解题思路】根据正切函数的定义域可得结果.【解答过程】因为x+π4≠kπ+π2,k∈Z，所以x≠kπ+π4,k∈Z.故f(x)的定义域为{x|x≠kπ+π4,k∈Z}.故选：A.【变式1-1】（2022·四川省高三阶段练习（理））若x∈[π4,2π3]，则函数f(x)=3sin x cos x+√3sin2x的值域为（ ） A ．[0,3√32]B ．[0,√32] C ．[0,√3]D ．[0,3+√3]【解题思路】利用二倍角公式和辅助角公式化简原式为f (x )=√3sin(2x -π6)+√32，结合正弦函数的图像和性质，求解即可. 【解答过程】由题意，f (x )=3sin x cos x +√3sin 2x =32sin2x +√32(1-cos2x )=√3×(√32sin2x -12cos2x )+√32=√3×(cos π6sin2x -sin π6cos2x )+√32=√3sin(2x -π6)+√32,当x ∈[π4,2π3]时，有2x -π6∈[π3,7π6]，当2x -π6=π2，即x =π3时，f (x )max =f (π3)=√3+√32=3√32； 当2x -π6=7π6，即x =2π3时，f (x )min =f (2π3)=0.即函数f (x )的值域为[0,3√32].故选：A.【变式1-2】（2022·福建省高二阶段练习）函数f (x )=sinx +cos (x +π6)的值域为（ ） A ．[−2,2]B ．[−√3,√3]C ．[−1,1]D ．[−√32,√32] 【解题思路】利用两角和的余弦公式和辅助角公式进行化简，即可得到答案 【解答过程】解：函数f (x )=sinx +cos (x +π6)=sinx +√32cosx −12sinx =√32cosx +12sinx =cos (x −π6)，∵x ∈R ，∴cos (x −π6)∈[−1,1]，∴函数的值域为[−1,1]， 故选：C ．【变式1-3】（2022·全国·高一单元测试）若x ∈[−π3,2π3]，则函数y =cos 2(x +π6)+sin (x +2π3)的最大值与最小值之和为（ ）A ．12B ．1C ．74D ．√2【解题思路】利用诱导公式可化简函数为y =(cos (x +π6)+12)2−14，根据余弦型函数值域的求法可求得cos(x+π6)∈[−√32,1]，结合二次函数最值的求法可求得y的最大值和最小值，加和即可求得结果.【解答过程】y=cos2(x+π6)+sin(x+2π3)=cos2(x+π6)+sin(π2+x+π6)=cos2(x+π6)+cos(x+π6)=(cos(x+π6)+12)2−14，当x∈[−π3,2π3]时，x+π6∈[−π6,5π6]，∴cos(x+π6)∈[−√32,1]，∴当cos(x+π6)=1时，y max=94−14=2；当cos(x+π6)=−12时，y min=−14；∴y max+y min=2−14=74.故选：C.【方法点拨】证明一个函数是否为周期函数或求函数周期的大小常用以下方法：(1)定义法：即对定义域内的每一个x值，看是否存在非零常数T使f(x+T)=f(x)成立，若成立，则函数是周期函数且T是它的一个周期.(2)公式法：利用三角函数的周期公式来求解.(3)图象法：画出函数的图象，通过图象直观判断即可.【例2】（2023·广东·高三学业考试）函数f(x)=sin(x2−π4)的最小正周期是（）A．π2B．πC．2πD．4π【解题思路】利用正弦函数的周期求解．【解答过程】f(x)的最小正周期为T=2π12=4π．故选：D．【变式2-1】（2023·广东·高三学业考试）函数f(x)=cos(12x+π6)的最小正周期为（）A．π2B．πC．2πD．4π【解题思路】利用余弦型函数的周期公式进行求解.【解答过程】∵f(x)=cos(12x+π6)，∴f(x)最小正周期T=2π12=4π．故A，B，C错误.故选：D.【变式2-2】（2022·甘肃临夏·高二期末（理））函数f(x)=cos(ωx+π6)(ω>0)的最小正周期为π，则f(π2)=（）A．−√32B．−12C．12D．√32【解题思路】由周期求出ω，从而可求出f(x)，进而可求出f(π2).【解答过程】因为函数f(x)的最小正周期为π，ω>0，所以ω=2ππ=2，得f(x)=cos(2x+π6)，所以f(π2)=cos(2×π2+π6)=−cosπ6=−√32．故选：A.【变式2-3】（2022·广东佛山·高三阶段练习）在下列函数中，最小正周期为π且在(0,π2)为减函数的是（）A．f(x)=sin|2x|B．f(x)=cos(2x+π6)C．f(x)=|cosx|D．f(x)=tan(2x−π4)【解题思路】根据三角函数的图像性质，逐个选项进行判断即可得出答案.【解答过程】对于A，f(x)=sin|2x|的图像关于y轴对称，在(0,π2)为增函数，不符题意，故A错；对于B，f(x)=cos(2x+π6)的最小正周期为π，x∈(0,π2),2x+π6∈(π6,7π6)，不是减函数，不符题意，故B错；对于C，f(x)=|cosx|的最小正周期为π，在(0,π2)为减函数，符合题意，故C对；对于D，f(x)=tan(2x−π4)的最小正周期为π2，不符题意，故D错；故选：C.【题型3 三角函数的奇偶性】【方法点拨】掌握正弦、余弦、正切函数的奇偶性相关知识，结合具体题目，灵活求解.【例3】（2022·广东·高三学业考试）若函数f(x)=sin(x+φ)是偶函数，则φ可取一个值为（）A．−πB．−π2C．π4D．2π【解题思路】根据偶函数的定义得φ=kπ+π2,k∈Z,结合选项可确定答案.【解答过程】∵函数f(x)=sin(x+φ)是偶函数，∴f(−x)=f(x)，即sin(−x+φ)=sin(x+φ).∴−x+φ=x+φ+2kπ或−x+φ+x+φ=π+2kπ,k∈Z.当−x+φ=x+φ+2kπ时，可得x=−kπ，不满足函数定义.当−x+φ+x+φ=π+2kπ时，φ=kπ+π2,k∈Z,若φ=kπ+π2=−π，解得k=−32∉Z，故A错误;若φ=kπ+π2=−π2，解得k =−1∈Z ，故B 正确; 若φ=kπ+π2=π4，解得k =−14∉Z ，故C 错误;若φ=kπ+π2=2π，解得k =32∉Z ，故D 错误;故选:B.【变式3-1】（2022·全国·高一）下列函数中，在其定义域上是偶函数的是（ ） A ．y =sinxB ．y =|sinx |C ．y =tanxD ．y =cos (x −π2)【解题思路】根据奇偶性定义，结合三角函数的奇偶性可直接得到结果.【解答过程】对于A ，∵y =sinx 定义域为R ，sin (−x )=−sinx ，∴y =sinx 为奇函数，A 错误；对于B ，∵y =|sinx |定义域为R ，|sin (−x )|=|−sinx |=|sinx |，∴y =|sinx |为偶函数，B 正确；对于C ，∵y =tanx 定义域为(kπ−π2,kπ+π2)(k ∈Z )，即定义域关于原点对称，tan (−x )=−tanx ，∴y =tanx 为奇函数，C 错误；对于D ，∵y =cos (x −π2)=sinx 定义域为R ，sin (−x )=−sinx ，∴y =cos (x −π2)为奇函数，D 错误. 故选：B.【变式3-2】（2022·北京高三阶段练习）函数f (x )=cos x +cos2x 是（ ） A ．奇函数，且最大值为2 B ．偶函数，且最小值为-98 C ．奇函数，且最小值为-98D ．偶函数，且最大值为98【解题思路】利用函数奇偶性的定义可判断出函数f (x )的奇偶性，利用二次函数的基本性质可求得函数f (x )的最值.【解答过程】函数f (x )的定义域为R ，f (-x )=cos (-x )+cos (-2x )=cos x +cos2x =f (x )， 故函数f (x )为偶函数，因为-1≤cos x ≤1，则f (x )=2cos 2x +cos x -1=2(cos x +14)2-98， 所以，f (x )min =-98，f (x )max =2+1-1=2.故选：B.【变式3-3】（2022·广西·模拟预测（理））若将函数f (x )=sin2x −√3cos2x 的图象向右平移m (m >0)个单位后，所得图象对应的函数为奇函数，则m 的最小值是（ ） A ．π6B ．π3C ．2π3D ．5π6【解题思路】首先对f (x )化简得到f (x )=2sin (2x −π3)，再写出平移后的解析式y =2sin (2x −2m −π3)，因为其为奇函数，则−2m −π3=k π,k ∈Z ，解出m 即可得到最小值.【解答过程】f (x )=sin2x −√3cos2x =2(12sin2x −√32cos2x)=2sin (2x −π3)，向右平移m(m >0)个单位后得到函数y =2sin [2(x −m )−π3]=2sin (2x −2m −π3)，由于是奇函数，因此，得−2m −π3=k π,k ∈Z ，m =−π6−k π2,k ∈Z.又∵m >0，则当k =−1时，m 的最小值是π3，故选：B.【方法点拨】掌握正弦、余弦、正切函数的对称性相关知识，结合具体题目，灵活求解.【例4】（2022·安徽·高三开学考试）函数f (x )=tan (2x −π3)的图象的一个对称中心为（ ） A ．(π12,0)B ．(7π12,0)C ．(−5π12,0)D ．(−π12,0)【解题思路】根据正切型函数的对称中心为(k π2,0) k ∈Z ，求解即可. 【解答过程】由2x −π3=k π2,k ∈Z ，可得x =k π4+π6,k ∈Z ，当k =0时，x =π6，当k =1时，x =π4+π6=5π12，当k =2时，x =8π12=23π， 当k =−1时，x =−π4+π6=−π12， 当k =−2时，x =−4π12=−13π， 当k =−3时，x =−7π12，所以(−π12,0)为f (x )图象的一个对称中心， 故选：D.【变式4-1】（2022·河南·高三阶段练习（理））已知函数f (x )=2cos (ωx −π6)(ω>0)在[0,2π]内恰有三条对称轴，则ω的取值范围是（ ） A ．[43,116)B ．(43,116]C ．[1312,1912)D ．(1312,1912]【解题思路】根据余弦函数的性质可得2π≤2ωπ−π6<3π，进而即得. 【解答过程】因为0≤x ≤2π， 所以−π6≤ωx −π6≤2ωπ−π6， 所以2π≤2ωπ−π6<3π， 解得1312≤ω<1912．故选：C.【变式4-2】已知函数f(x)=sin (12x −π6)，则结论正确的是（ ）A ．f (x )的图象关于点(5π3,0)中心对称B ．f (x )的图象关于直线x =−π3对称C ．f (x )在区间(−π,π)内有2个零点D ．f (x )在区间[−π2,0]上单调递增【解题思路】A 、B 应用代入法判断对称轴和对称中心；C 、D 根据给定区间求12x −π6的范围，结合正弦型函数的性质求零点和单调性. 【解答过程】A ：f(5π3)=sin (12×5π3−π6)=sin2π3≠0，故(5π3,0)不是对称中心，错误；B ：f(−π3)=sin[12×(−π3)−π6]=−sin π3≠±1，故x =−π3不是对称轴，错误；C ：在x ∈(−π,π)，则12x −π6∈(−2π3,π3)，故f(x)=0，可得12x −π6=0，所以x =π3为f (x )在(−π,π)内的唯一零点，错误；D ：在x ∈[−π2,0]，则12x −π6∈[−5π12,−π6]，故f(x)=sin (12x −π6)递增，正确. 故选：D.【变式4-3】（2022·贵州·高三阶段练习（文））已知函数f (x )=2cos (ωx +φ)（ω>0，0<φ<π）的相邻两条对称轴之间的距离为2π，且为奇函数，将f (x )的图象向右平移π3个单位得到函数g (x )的图象，则函数g (x )的图象（ ） A ．关于点(−5π3,0)对称B ．关于点(π2,0)对称 C ．关于直线x =−π3对称D ．关于直线x =π2对称【解题思路】两个相邻对称轴的为半个周期，奇函数可以确定f (x )为正弦函数，由此条件得出f (x )的解析式，再根据平移得出g (x )的解析式，根据解析式写出对称中心和对称轴的通式即可得出答案.【解答过程】由相邻两条对称轴之间的距离为2π可知T2=2π，即T =4π，ω=2πT ，ω=12, 因为f (x )为奇函数，根据0<φ<π可知φ=π2，f (x )=2sin 12x , g (x )=2sin (12(x −π3))=2sin (12x −π6),对称中心：12x −π6=k π(k ∈Z )，x =2k π+π3(k ∈Z )，故A 正确，B 错误;对称轴：12x −π6=π2+k π(k ∈Z )，x =2k π+4π3(k ∈Z )，故C 、D 错误;故选：A.【方法点拨】三角函数的单调性问题主要有：三角函数的单调区间的求解、比较函数值的大小、根据三角函数的单调性求参数；结合具体条件，根据三角函数的图象与性质进行求解即可.【例5】（2022·江西·高三阶段练习（理））函数y =sin (π6−2x)(x ∈[0,π])为增函数的区间是（ ） A ．[0,π3]B ．[π12,7π12]C ．[π3,5π6]D ．[5π6,π]【解题思路】根据三角函数单调性的求法求得正确答案. 【解答过程】y =sin (π6−2x)=−sin (2x −π6)，2k π+π2≤2x −π6≤2k π+3π2，k π+π3≤x ≤k π+5π6，k ∈Z ， 令k =0可的y =sin (π6−2x)(x ∈[0,π])的递增区间为[π3,5π6]. 故选：C.【变式5-1】（2022·河南信阳·一模（理））已知函数f (x )=2√3cos (x -π2)cos x -2sin 2x ，若f (x )在区间[m ,π4]上单调递减，则实数m 的取值范围（ ）A ．[π6,π4]B ．[π3,π2]C ．[π6,π4)D ．[π6,π3)【解题思路】利用三角恒等变换，化简三角函数，利用正弦型函数的单调性，建立不等式组，可得答案.【解答过程】f (x )=2√3cos (x -π2)cos x -2sin 2x =2√3sin x cos x -2·1-cos2x 2=√3sin2x -1+cos2x=2(√32sin2x +12cos2x)-1 =2sin (2x +π6)-1，由x ∈[m ,π4]，则2x +π6∈[2m +π6,2π3]，由题意，[2m +π6,2π3]⊆[π2,3π2]，则π2≤2m +π6<2π3，解得π6≤m <π4. 故选：C.【变式5-2】（2022·江苏·高三阶段练习）已知a =log 168，b =πln0.8，c =sin2.5，则a ，b ，c 的大小关系是（ ） A ．c <a <b B ．c <b <a C ．a <b <cD ．a <c <b【解题思路】由对数的运算法则求出a ，又πln0.8，sin2.5分别可看做y =πx ，y =sinx 的函数值，考虑构造指数函数和正弦函数，利用函数的单调性对其值进行估计，又因为ln0.8估值困难，故考虑利用与函数y =lnx 近似的有理函数y =1−1x 对其大小进行估值，最后求得答案.【解答过程】由题意，a =log 168=log 2423=34=0.75， 设f (x )=lnx +1x −1，则f ′(x )=1x −1x 2=x−1x 2，当0<x <1时，f ′(x )<0，函数f (x )在(0,1)上单调递减，当x >1时，f ′(x )>0，函数f (x )在(1,+∞)上单调递增，所以f (0.8)>f (1)，即ln0.8+54−1>0，所以ln0.8>−14，因为函数y =πx 在(−∞,+∞)上单调递增，所以πln0.8>π−14，又(π−14)−4=π，(34)−4=25681≈3.16，所以(34)−4>(π−14)−4，因为y =x−4在(0,+∞)单调递减，所以34<π−14，所以πln0.8>34，故b >a ， 因为3π4<2.5<5π6，函数y =sinx 在(π2,π)上单调递减，所以sin 5π6<sin2.5<sin3π4，所以12<sin2.5<√22，所以sin2.5<34，即c <a ，所以c <a <b ， 故选：A.【变式5-3】（2022·内蒙古·高三阶段练习（文））若函数f(x)=√2cos (ωx +π4)(ω>0)在(0,7π4)上单调递减，则ω的最大值为（ ）A ．37 B ．34C ．14D ．1【解题思路】由题知ωx +π4∈(π4,7π4ω+π4)，再根据函数y =√2cosx 在(0,π)上单调递减可得7π4ω+π4≤π，进而解不等式求解即可.【解答过程】解：因为函数f(x)=√2cos (ωx +π4)(ω>0)在(0,7π4)上单调递减，所以7π4≤12T =πω，解得0<ω≤47，因为x ∈(0,7π4)，所以ωx +π4∈(π4,7π4ω+π4)，因为函数y =√2cosx 在(0,π)上单调递减， 所以，函数f(x)=√2cos (ωx +π4)(ω>0)在(0,7π4)上单调递减，则有7π4ω+π4≤π，解得ω≤37，所以ω的取值范围是ω∈(0,37]，即ω的最大值为37. 故选：A.【方法点拨】解决正(余)弦型函数性质的综合应用问题的思路： (1)熟练掌握函数或的图象，利用基本函数法得到相应的函数性质，然后利用性质解题.(2)直接作出函数图象，利用图象形象直观地分析并解决问题. 【例6】已知函数f (x )=4sinxcos (x +π6)+1.(1)求f (x )的最小正周期及单调区间； (2)求f (x )在区间[−π6,π4]上的最大值与最小值.【解题思路】（1）先利用三角恒等变换化简得到f (x )=2sin (2x +π6)，从而利用T =2π|ω|求出最小正周期，再利用整体法求解函数的单调区间；（2）根据x ∈[−π6,π4]求出2x +π6∈[−π6,2π3]，从而结合函数图象求出最大值为2，最小值为−1.【解答过程】（1）因为f (x )=4sinx (cosxcos π6−sinxsin π6)+1=2√3sinxcosx −2sin 2x +1 =√3sin2x +cos2x =2sin (2x +π6) 所以f (x )的最小正周期T =2π2=π；令−π2+2k π≤2x +π6≤π2+2k π，k ∈Z ，解得：[−π3+k π,π6+k π]，k ∈Z ， 令π2+2k π≤2x +π6≤3π2+2k π，k ∈Z ，解得：[π6+k π,2π3+k π]，k ∈Z ，单调增区间为[−π3+k π,π6+k π]，k ∈Z ，单调减区间为[π6+k π,2π3+k π]，k ∈Z ；（2）已知x ∈[−π6,π4]，所以2x +π6∈[−π6,2π3]，当2x +π6=π2，即x =π6时，f (x )取得最大值，最大值为2， 当2x +π6=−π6，即x =−π6时，f (x )取得最小值，最小值为-1， 所以f (x )在区间[−π6,π4]上的最大值为2，最小值为−1.【变式6-1】（2022·陕西·高三阶段练习（文））已知函数f (x )=4sin (ωx +φ)（ω>0，|φ|<π2）图象的一条对称轴为直线x =−π12，这条对称轴与相邻对称中心之间的距离为π8．(1)求f (x )；(2)求f (x )在[−π24,π4]上的值域．【解题思路】（1）先求出周期，由此求出ω的值，利用对称轴方程求出φ，即可得到函数的解析式；（2）根据自变量的范围求得4x −π6∈[−π3,5π6]，根据正弦函数的取值求得函数的值域【解答过程】（1）因为函数f(x)图象的对称轴与相邻对称中心之间的距离为π8， 所以T =π2，故ω=2πT=4，又f(x)的图象的一条对称轴方程为x =−π12， 则4×(−π12)+φ=π2+k π，k ∈Z ，即φ=5π6+k π，k ∈Z ，又|φ|<π2，所以φ=−π6， 故f(x)=4sin (4x −π6)；（2）因为x ∈[−π24,π4]，所以4x −π6∈[−π3,5π6]，所以sin (4x −π6)∈[−√32,1]，所以4sin (4x −π6)∈[−2√3,4]， 故f (x )在[−π24,π4]上的值域为[−2√3,4].【变式6-2】（2021·天津·高一期末）已知函数f (x )=2√3cos 2(π2+x)-2sin(π+x )cos x -√3 (1)求f (x )的最小正周期及单调递减区间； (2)求f (x )在区间[π4,π2]上的最值；(3)若f (x 0-π6)=1013,x 0∈[3π4,π]，求sin2x 0的值．【解题思路】（1）根据三角恒等变换可得f (x )=2sin (2x -π3)，然后根据三角函数的性质即得；（2）根据正弦函数的性质即得；（3）由题可得sin (2x 0-2π3)=513，然后根据同角关系式及和差角公式即得. 【解答过程】（1）因为f (x )=2sin x cos x +2√3sin 2x -√3 =sin2x -√3cos2x =2sin (2x -π3)． 所以f (x )的最小正周期T =2π2=π，∵π2+2k π≤2x -π3≤3π2+2k π,k ∈Z ，∴5π12+k π≤x ≤11π12+k π，所以f (x )的单调递减区间为[5π12+k π,11π12+k π](k ∈Z)；（2）由（1）知f (x )的单调递减区间为[5π12+k π,11π12+k π](k ∈Z)，∵x ∈[π4,π2]，∴f (x )在[π4,5π12]上单调递增，在[5π12,π2]上单调递减，又f (5π12)=2sin π2=2,f (π4)=2sin π6=1,f (π2)=2sin2π3=√3，故f (x )min =1,f (x )max =2； 另解：∵x ∈[π4,π2]， ∴t =2x -π3∈[π6,2π3]，∵y =sin t 在t ∈[π6,π2]单调递增，在[π2,2π3]上单调递减， ∴当t =π2时，(sin t )max =1,f (x )max =2×1=2， ∴当t =π6时，(sin t )min =12,f (x )min =2×12=1； （3）∵f (x 0-π6)=1013，∴sin (2x 0-2π3)=513， 由x 0∈[3π4,π]，得2x 0-2π3∈[5π6,4π3]，∴cos (2x 0-2π3)=-1213， ∴sin2x 0=sin [(2x 0-2π3)+2π3]=sin (2x 0-2π3)cos2π3+cos (2x 0-2π3)sin 2π3=513×(-12)+(-1213)×√32=-5+12√326． 【变式6-3】（2022·黑龙江·高三阶段练习）已知函数f (x )=[(1+√2)sin x -cos x]⋅[(1-√2)sin x -cos x]. (1)求f (x )的最小正周期T 和单调递减区间；(2)四边形ABCD 内接于⊙O ，BD =2，锐角A 满足f (3A4)=-1，求四边形ABCD 面积S 的取值范围.【解题思路】（1）利用三角函数恒等变换公式对函数化简变形得f (x )=√2cos (2x +π4)，从而可求出最小正周期，再由2kπ≤2x +π4≤2kπ+π(k ∈Z )求出其单调区间，（2）由f (3A4)=-1，求得A =π3，再由圆的性质可得C =2π3，设AB =a ，AD =b ，BC =c ，CD =d ，分别在△ABD 和△CBD 中利用余弦定理结合基本不等式可得0<ab ≤4，0<cd ≤43，从而可求出四边形ABCD 面积S 的取值范围.【解答过程】（1）[(1+√2)sin x -cos x]⋅[(1-√2)sin x -cos x]=[(sin x -cos x )+√2sin x]⋅[(sin x -cos x )-√2sin x]=(sin x -cos x )2-2sin 2x =sin 2x -2sin x cos x +cos 2x -2sin 2x=1-2sin 2x -sin2x =cos2x -sin2x=√2cos (2x +π4)， ∴f (x )=√2cos (2x +π4) ∴T =π.由2kπ≤2x +π4≤2kπ+π(k ∈Z )，得kπ-π8≤x ≤kπ+3π8(k ∈Z )，所以f (x )单调递减区间为[kπ-π8,kπ+3π8](k ∈Z ). （2）由于f (3A4)=-1，根据（1）得√2cos (2×3A 4+π4)=-1，∵0<A <π2，∴A =π3，C =2π3.分别设AB =a ，AD =b ，BC =c ，CD =d .因BD =2，分别在△ABD 和△CBD 中由余弦定理得a 2+b 2-2ab cos π3=4，c 2+d 2-2cd cos2π3=4，∴a 2+b 2=4+ab ，c 2+d 2=4-cd .∵a 2+b 2≥2ab ，c 2+d 2≥2cd ，等号在a =b =2，c =d =2√33时成立，∴4+ab ≥2ab ，4-cd ≥2cd ，解得0<ab ≤4，0<cd ≤43. ∴0<ab +cd ≤163.等号在a =b =2，c =d =2√33时成立，∵S =12ab sin A +12cd sin C =√34(ab +cd )， 所以S 的取值范围是(0,4√33].。