2分压定律和分体积定律

道尔顿分压定律
道尔顿分压定律是一个关于气体的定律，在化学和物理学中有广泛的应用。

该定律源
于18世纪末期英国化学家约翰·道尔顿对气体分压的研究。

简介
在一个混合气体中，每种气体分别对总压的贡献被称为分压，这种分压与一个理想气
体的分压是相同的，被称为道尔顿分压。

该定律描述了混合气体中各种气体的分压的关
系。

内容
p=iP
其中，p表示每种气体的分压，i表示该气体所占气体总量的比例，P表示总压。

该定律的含义是，一个混合气体总压等于各个气体分别对总压的贡献之和。

推导
假设有一个容器，其中有两种气体A和B。

总压为P，其中气体A占据的比例为i，气体B占据的比例为1-i。

根据气体状态方程可以得到：
V=iV_A+(1-i)V_B
其中，V_A和V_B分别是气体A和气体B的体积。

p_A=iP=pV_A/V
同样地，气体B的分压为：
因此，根据分压的定义，总压等于两种气体分别的分压之和：
化简可得：
P=P
应用
道尔顿分压定律的应用非常广泛。

例如，在制备氧气时，可以使用分离技术将氮气和
氧气分离，并利用道尔顿分压定律计算出所需的氧气的分压。

另一个应用是在深水潜水中，
可以使用混合气体替代普通空气，使用道尔顿分压定律来计算各种气体在不同深度下的分压，以防止气体过多压缩导致人体出现问题。

结论
道尔顿分压定律是一个重要的气体定律，可以用于解释和预测混合气体中各种气体的分压。

该定律的应用非常广泛，特别是在气体分离、潜水和其他技术中。

气体的压强与分压定律在我们的日常生活中，气体无处不在，从我们呼吸的空气到充满气球的氦气，气体的性质和行为都与我们的生活息息相关。

而在研究气体的众多特性中，气体的压强和分压定律是非常重要的概念。

首先，让我们来了解一下什么是气体的压强。

简单来说，气体压强就是气体作用在单位面积上的压力。

想象一下，气体分子就像一群活跃的小精灵，在容器内不停地运动、碰撞。

当它们撞击容器壁时，就会产生压力。

而压强就是这种压力的强度表现。

气体压强的大小受到多种因素的影响。

其中，最主要的因素是气体的温度、体积和物质的量。

当温度升高时，气体分子的运动速度加快，撞击容器壁的力量增大，压强也就随之增大。

比如，夏天的时候，汽车轮胎内的气体压强往往会比冬天高，这就是因为温度升高导致的。

相反，当气体的体积减小时，单位体积内的气体分子数量增加，碰撞容器壁的频率增加，压强也会增大。

例如，给一个密封的气球不断压缩，气球内部的压强就会不断上升。

物质的量，也就是气体的摩尔数，也会影响压强。

在相同的温度和体积条件下，气体的摩尔数越多，压强就越大。

接下来，我们要探讨分压定律。

分压定律是描述混合气体中各组分气体压强关系的重要定律。

假设我们有一个装有多种气体的容器，比如氧气、氮气和二氧化碳。

那么，每种气体都会对容器壁产生一定的压强。

这个压强就叫做该气体的分压。

分压定律指出，在温度和体积一定的条件下，混合气体的总压强等于各组分气体的分压之和。

为了更好地理解分压定律，我们可以通过一个例子来说明。

假设一个容器中装有氧气和氮气，氧气的分压为 P₁，氮气的分压为 P₂，那么混合气体的总压强 P 总＝ P₁＋ P₂。

分压的大小与气体的物质的量成正比。

也就是说，在混合气体中，某种气体的物质的量占总物质的量的比例越大，它的分压就越大。

分压定律在实际生活中有很多应用。

比如在潜水时，我们需要了解氧气和氮气在呼吸气体中的分压，以确保潜水员的安全。

在化学实验中，分压定律也非常重要。

2008---2009学年第二学期第1周第1页（共5页）第二节理想气体混合物的两个定律复习回忆：1、理想气体状态方程的数学表达式；2 、理想气体微观模型的特征。

讲授新课:一、分压定律1、基本概念（1）道尔顿分压定律：低压下气体混合物的总压等于组成该气体混合物的各组分的分压力之和，这个定律称为道尔顿分压定律。

（2）分压力：所谓分压力是指气体混合物中任一组分B单独存在于气体混合物所处的温度、体积条件下所产生的压力P B。

2、道尔顿分压定律的数学表达式P（T,V） P A仃,V） P B仃,V） L或p P B（1-4）B对于理想气体混合物，在T、V 一定条件下，压力只与气体物质的量有关，根据理想气体状态方程，有PV ,n 门人n B n c LRTP A V P B V P c V LRT RT RT（P A P B P c L）V / RT故有P （P A P B P c L ）或P P BB适用范围：理想气体混合物或接近于理想气体性质的气体混合物。

3、气体物质的量分数与分压力的关系气体混合物中组分B的分压力与总压力之比可用理想气体状态方程得出P B n B RT /V n By BP nRT/V n即P B y B P （1-5）式中yB ――组分B的物质的量分数式（1-5 ）表明，混合气体中任一组分的分压等于该组分的物质的量分数与总压的乘积。

例题1-3某烃类混合气体的压力为100kPa,其中水蒸气的分压为20 kPa，求每100mol2008---2009学年第二学期第1周第2页（共5页）该混合气体中所含水蒸气的质量。

解：p=100kPa , p（H2O）=20kPa , n=100mol , M （H2O）=18 x10-3kg/molB2008---2009学年 第二学期 第1周第3页（共5页）y（H 2。

）営而。

2n(H 2。

) y(H 2O)n 0.2 100 20mol100mol 混合气体中水蒸气的质量 m （H 2。

分压力和分体积的定义分压力和分体积是化学中常用的概念，旨在描述气体和液体在不同条件下的物理性质。

本文将从深度和广度的角度对这两个概念进行全面评估，并对其定义和应用进行详细讨论。

我们将以从简到繁、由浅入深的方式来探讨这个主题，以便读者能更深入地理解并灵活应用。

一、分压力的定义及背景介绍1.1 压力的基础概念我们需要了解压力的基本概念。

在物理学中，压力定义为单位面积上的力的作用。

1.2 分压力的概念接下来，我们引入分压力的概念。

分压力是指气体混合物中每个组分对总压力的贡献。

根据道尔顿定律，气体混合物中每个组分的分压力等于该组分在混合气体中所占的体积分数乘以总压力。

1.3 分压力的应用分压力的概念在化学反应和气体收集中具有重要的应用。

在化学反应中，分压力可以用来确定反应的平衡常数和反应速率。

在气体收集中，通过将气体通入到一定体积的容器中，利用分压力可以计算出气体的体积。

二、分体积的定义及背景介绍2.1 体积的基本概念在继续探讨分体积之前，我们需要了解体积的基本概念。

在物理学和化学中，体积是指占据一定空间的物质所占的空间大小。

一般情况下，体积可以通过测量长度、宽度和高度来计算得出。

2.2 分体积的概念分体积是指液体混合物中每个组分所占据的体积。

根据混合物的成份不同，各组分占据的体积也会不同。

2.3 分体积的应用分体积在溶液浓度计算、溶解度和物理化学性质研究等方面有广泛的应用。

在溶液浓度计算中，通过测量溶液中每个组分所占据的体积可以计算出其浓度。

在溶解度和物理化学性质研究中，分体积可以用来确定溶质在溶液中的分布和相互作用程度。

三、分压力与分体积之间的关系通过以上的介绍，我们可以看到分压力和分体积在描述混合物中各组分的性质和分布时具有重要的作用。

然而，分压力和分体积并不是完全独立的概念，它们之间存在一定的关系。

在理想气体状态下，根据道尔顿定律和理想气体状态方程，可以得到分压力与分体积的关系式。

对于混合气体，每个组分的分压力可以通过浓度和总压力来计算。

道尔顿分压定律在热学中的应用-概述说明以及解释1.引言1.1 概述道尔顿分压定律是指在混合气体系统中，每种气体的分压等于该气体在混合气体中所占的体积比例与总压强的乘积。

它是由英国化学家约翰·道尔顿提出的气体定律之一，被广泛应用于热学领域。

该定律的基本原理是基于理想气体分子运动论的假设，假设气体分子之间无相互作用和体积，且分子速度服从麦克斯韦速度分布定律。

根据这个假设，道尔顿分压定律得出的结果可以近似地描述气体的行为。

在应用场景中，道尔顿分压定律常被用于混合气体的计算和分析。

例如，在化学反应过程中，混合气体的压强和分子的速度对于反应的进行起着重要作用。

通过使用道尔顿分压定律，可以计算出每种气体在混合气体中的分压，从而确定反应的方向和速率。

道尔顿分压定律在热学中也有广泛的应用。

在热力学研究中，研究气体的温度、压力和体积之间的关系非常重要。

通过运用道尔顿分压定律，可以分析和计算不同气体在给定条件下的温度、压力和体积的变化规律，从而推导出热力学方程，并进一步研究热力学系统的特性和行为。

然而，道尔顿分压定律也有其局限性。

它在假设气体分子之间无相互作用和体积的基础上，仅适用于理想气体的近似描述。

在高压或低温的条件下，气体分子之间的相互作用和体积不能忽略，道尔顿分压定律的适用性会受到限制。

总之，道尔顿分压定律是热学领域中一个重要的工具和理论基础。

它为我们理解和研究气体的特性和行为提供了一种简便的方法。

然而，在应用和推广该定律时，需要考虑其假设条件和局限性，以获得准确和可靠的结果。

1.2文章结构文章结构的部分内容可以如下编写：2. 正文2.1 道尔顿分压定律的基本原理2.2 道尔顿分压定律的应用场景2.3 道尔顿分压定律在热学中的应用2.4 道尔顿分压定律的局限性在本文的正文部分，我们将首先介绍道尔顿分压定律的基本原理，包括该定律的主要概念和数学表达方式。

接着，我们将探讨道尔顿分压定律在实际应用中的场景，例如化学反应、气体混合和气体溶解等领域，以展示其广泛的适用性和实用性。

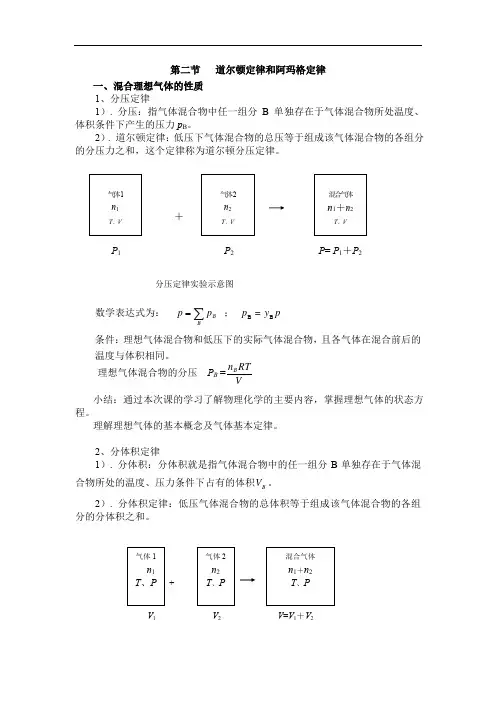
第二节 道尔顿定律和阿玛格定律 一、混合理想气体的性质
1、分压定律
1）. 分压：指气体混合物中任一组分B 单独存在于气体混合物所处温度、体积条件下产生的压力p B 。

2）. 道尔顿定律：低压下气体混合物的总压等于组成该气体混合物的各组分数学表达式为： ∑=B
B p p ； p y =p B B
条件：理想气体混合物和低压下的实际气体混合物，且各气体在混合前后的温度与体积相同。

理想气体混合物的分压 P B =
V
RT n B
小结：通过本次课的学习了解物理化学的主要内容，掌握理想气体的状态方程。

理解理想气体的基本概念及气体基本定律。

2、分体积定律
1）. 分体积：分体积就是指气体混合物中的任一组分B 单独存在于气体混合物所处的温度、压力条件下占有的体积B V 。

2）. 分体积定律：低压气体混合物的总体积等于组成该气体混合物的各组分的分体积之和。

+
V 1 V 2 V =V 1＋V 2
＋
P 1 P 2 P = P 1＋P 2
分压定律实验示意图
气体1 n 1
T 、P 气体2 n 2 T 、P 混合气体 n 1＋n 2 T 、P
气体 2 n 2 T 、V 混合气体 n 1＋n 2
T 、V
气体 1
n 1
T 、V。

第二节 理想气体混合物的两个定律复习回忆：1、理想气体状态方程的数学表达式；2、理想气体微观模型的特征。

讲授新课：一、分压定律1、基本概念（1）道尔顿分压定律：低压下气体混合物的总压等于组成该气体混合物的各组分的分压力之和，这个定律称为道尔顿分压定律。

（2）分压力：所谓分压力是指气体混合物中任一组分B 单独存在于气体混合物所处的温度、体积条件下所产生的压力p B 。

2、道尔顿分压定律的数学表达式(,)(,)(,)A B p T V p T V p T V =++L或 B B p p=∑ （1-4）对于理想气体混合物，在T 、V 一定条件下，压力只与气体物质的量有关，根据理想气体状态方程，有()/A B C C A B A B C pV n n n n RTp V p V p V RT RT RTp p p V RT ==+++=+++=+++L L L 故有 ()A B C p p p p =+++L 或 B B p p=∑适用范围：理想气体混合物或接近于理想气体性质的气体混合物。

3、气体物质的量分数与分压力的关系气体混合物中组分B 的分压力与总压力之比可用理想气体状态方程得出//B B B B p n RT V n y p nRT V n=== 即 B B p y p = （1-5） 式中 yB ——组分B 的物质的量分数式（1-5）表明，混合气体中任一组分的分压等于该组分的物质的量分数与总压的乘积。

例题1-3 某烃类混合气体的压力为100kPa ，其中水蒸气的分压为20 kPa ，求每100mol 该混合气体中所含水蒸气的质量。

解：p=100kPa ，p(H 2O)=20kPa ，n=100mol ，M （H 2O ）=18×10-3kg/mol由式（1-5）得22()20()0.2100p H O y H O p === 又 22()()n H O y H O n= 所以 22()()0.210020n H O y H O n mol ==⨯= 100mol 混合气体中水蒸气的质量m(H 2O)为3222()()()2018100.36m H O n H O M H O kg -==⨯⨯=课堂练习题1、某气柜内贮有气体烃类混合物，其压力p 为104364Pa ，气体中含水蒸气的分压力p(H 2O)为3399.72Pa 。

瓶装气体的基础知识——气体体积与温度、压力的关系2004-5-29瓶装气体的基础知识——气体体积与温度、压力的关系气体的体积、温度、压力是确定气体状态的三个基本参数。

要研究气体物理状态的变化，进行工程上的计算，就要研究这三个基本状态参数间的关系。

而表示其三个基本状态参数间的数学关系式就是气体状态方程式，其方程式又有理想气体状态方程式和真实气体状态方程式之分。

一、理想气体状态方程式所谓理想气体，是人们为了在研究气体状态方程式时，忽略气体某些性质对基本状态参数计算的影响，而提出的一种假想的气体。

此种气体的假设条件为：1．气体分子本身不占有体积；2．气体分子间没有引力。

当实际气体的压力很低、温度较高时，由于气体的密度很小，其分子本身所占的体积与气体的全部空间之比小到可以忽略不计，而气体分子间的作用力也由于分子间的距离较大亦可忽略时，即可近似地作为理想气体进行计算。

前人曾总结出一些联系压力(P)、体积(V)、温度(T)和物质的量(n)之间关系的经验规律，现分述如下：1，波义耳-马略特定律波义耳—马略特定律可表述为：一定量的气体在等温时的容积(V)与压力(P)成反比。

即：式中：V1，V2旷：分别是定量的气体在压力Pl、P2时的容积。

2．查理定律查理定律可表述为：一定量的气体在等容时的压力(P)与热力学温度(T)成正比。

即：式中P1，P2分别是定量的气体在热力学温度T1，T2时的压力。

3，盖—吕萨克定律盖—吕萨克定律可表述为：一定量的气体在等压时的容积(V)与热力学温度(T)成正比。

即：式中T1，T2分别是定量气体在容积V1，V2时的热力学温度。

4．阿伏加德罗定律阿伏加德罗定律可表述为：在一定的温度与压力下，同体积的任何气体的摩尔数(n)相同。

即：5，理想气体状态方程理想气体状态方程(克莱庇隆方程)：上述四个经验定律，总共涉及了四个变量P、V、T、n。

每一个定律反映了气体规律的一个侧面，即两参数间的关系。

综合上述四个定律，推导出P、V、T、n之间的数学关系式。

第二节 理想气体混合物的两个定律复习回忆：1、理想气体状态方程的数学表达式；2、理想气体微观模型的特征。

讲授新课：一、分压定律1、基本概念（1）道尔顿分压定律：低压下气体混合物的总压等于组成该气体混合物的各组分的分压力之和，这个定律称为道尔顿分压定律。

（2）分压力：所谓分压力是指气体混合物中任一组分B 单独存在于气体混合物所处的温度、体积条件下所产生的压力p B 。

2、道尔顿分压定律的数学表达式(,)(,)(,)A B p T V p T V p T V =++或 B B p p=∑ （1-4）对于理想气体混合物，在T 、V 一定条件下，压力只与气体物质的量有关，根据理想气体状态方程，有()/A B C C A B A B C pV n n n n RTp V p V p V RT RT RTp p p V RT ==+++=+++=+++ 故有 ()A B C p p p p =+++ 或 B Bp p =∑适用范围：理想气体混合物或接近于理想气体性质的气体混合物。

3、气体物质的量分数与分压力的关系气体混合物中组分B 的分压力与总压力之比可用理想气体状态方程得出//B B B B p n RT V n y p nRT V n=== 即 B B p y p = （1-5） 式中 yB ——组分B 的物质的量分数式（1-5）表明，混合气体中任一组分的分压等于该组分的物质的量分数与总压的乘积。

例题1-3 某烃类混合气体的压力为100kPa ，其中水蒸气的分压为20 kPa ，求每100mol 该混合气体中所含水蒸气的质量。

解：p=100kPa ，p(H 2O)=20kPa ，n=100mol ，M （H 2O ）=18×10-3kg/mol由式（1-5）得22()20()0.2100p H O y H O p === 又 22()()n H O y H O n= 所以 22()()0.210020n H O y H O n mol ==⨯= 100mol 混合气体中水蒸气的质量m(H 2O)为3222()()()2018100.36m H O n H O M H O kg -==⨯⨯=课堂练习题1、某气柜内贮有气体烃类混合物，其压力p 为104364Pa ，气体中含水蒸气的分压力p(H 2O)为3399.72Pa 。

瓶装气体的基础知识——气体体积与温度、压力的关系2004-5-29瓶装气体的基础知识——气体体积与温度、压力的关系气体的体积、温度、压力是确定气体状态的三个基本参数。

要研究气体物理状态的变化，进行工程上的计算，就要研究这三个基本状态参数间的关系。

而表示其三个基本状态参数间的数学关系式就是气体状态方程式，其方程式又有理想气体状态方程式和真实气体状态方程式之分。

一、理想气体状态方程式所谓理想气体，是人们为了在研究气体状态方程式时，忽略气体某些性质对基本状态参数计算的影响，而提出的一种假想的气体。

此种气体的假设条件为：1．气体分子本身不占有体积；2．气体分子间没有引力。

当实际气体的压力很低、温度较高时，由于气体的密度很小，其分子本身所占的体积与气体的全部空间之比小到可以忽略不计，而气体分子间的作用力也由于分子间的距离较大亦可忽略时，即可近似地作为理想气体进行计算。

前人曾总结出一些联系压力(P)、体积(V)、温度(T)和物质的量(n)之间关系的经验规律，现分述如下：1，波义耳-马略特定律波义耳—马略特定律可表述为：一定量的气体在等温时的容积(V)与压力(P)成反比。

即：式中：V1，V2旷：分别是定量的气体在压力Pl、P2时的容积。

2．查理定律查理定律可表述为：一定量的气体在等容时的压力(P)与热力学温度(T)成正比。

即：式中P1，P2分别是定量的气体在热力学温度T1，T2时的压力。

3，盖—吕萨克定律盖—吕萨克定律可表述为：一定量的气体在等压时的容积(V)与热力学温度(T)成正比。

即：式中T1，T2分别是定量气体在容积V1，V2时的热力学温度。

4．阿伏加德罗定律阿伏加德罗定律可表述为：在一定的温度与压力下，同体积的任何气体的摩尔数(n)相同。

即：5，理想气体状态方程理想气体状态方程(克莱庇隆方程)：上述四个经验定律，总共涉及了四个变量P、V、T、n。

每一个定律反映了气体规律的一个侧面，即两参数间的关系。

综合上述四个定律，推导出P、V、T、n之间的数学关系式。