梁的弯曲正应力电测实验

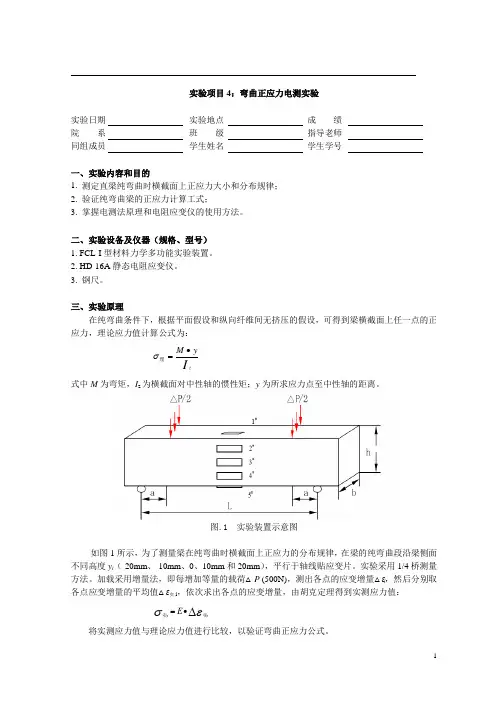
实验项目4：弯曲正应力电测实验实验日期 实验地点 成 绩 院 系 班 级 指导老师 同组成员 学生姓名 学生学号一、实验内容和目的1. 测定直梁纯弯曲时横截面上正应力大小和分布规律；2. 验证纯弯曲梁的正应力计算工式；3. 掌握电测法原理和电阻应变仪的使用方法。

二、实验设备及仪器（规格、型号） 1. FCL-I 型材料力学多功能实验装置。

2. HD-16A 静态电阻应变仪。

3. 钢尺。

三、实验原理在纯弯曲条件下，根据平面假设和纵向纤维间无挤压的假设，可得到梁横截面上任一点的正应力，理论应力值计算公式为：Izy M ∙=理σ式中M 为弯矩，I z 为横截面对中性轴的惯性矩；y 为所求应力点至中性轴的距离。

图.1 实验装置示意图如图1所示，为了测量梁在纯弯曲时横截面上正应力的分布规律，在梁的纯弯曲段沿梁侧面不同高度y i （-20mm 、-10mm 、0、10mm 和20mm ），平行于轴线贴应变片。

实验采用1/4桥测量方法。

加载采用增量法，即每增加等量的载荷△P (500N)，测出各点的应变增量△εi ，然后分别取各点应变增量的平均值△ε实i ，依次求出各点的应变增量，由胡克定理得到实测应力值： εσ∆∙=i iE 实实将实测应力值与理论应力值进行比较，以验证弯曲正应力公式。

四、实验步骤1. 设计好本实验所需的各类数据表格。

2. 拟订加载方案。

为减少误差，先选取适当的初载荷P0（一般P0=300N左右），估算P max，分级加载。

3. 根据加载方案，调整好实验加载装置。

测量矩形截面梁的宽度b、高度h、跨度L、载荷作用点到梁支点距离a及各应变片到中性层的距离y i。

4. 按实验要求接好线组成测量电桥后，调节应变仪的灵敏系数指针，并进行预调平衡。

观察几分钟看应变仪指针有无漂移，正常后即可开始测量。

5. 加载。

均匀缓慢加载至初载荷P0，记下各点应变的初始读数；然后分级等增量加载，每增加一级载荷，依次记录各点电阻应变片的应变值εi，直到最终载荷。

电测纯弯曲梁正应力实验教学大纲一、学时实验学时：2二、适用专业及年级所有开设工程力学的专业，2年级。

三、实验目的1.学习使用电阻应变仪测量应变以确定应力的基本原理和方法。

2.测定梁承受纯弯曲时的正应力分布，并与理论计算结果进行比较，以验证弯曲正应力公式。

四、实验仪器及设备1.纯弯曲梁实验装置一套2.应变片3.电阻应变仪五、实验原理低碳钢的矩形截面梁，在梁的纯弯曲部分，沿梁的侧面不同高度刻划平行于轴线的纵向线1-1、2-2、3-3、4-4、5-5， 3-3线位于梁的中性层上，1-1和5-5位于梁的上下两表面，2-2和4-4位于梁中性层和上下两表面之间，各距3-3线等远，其距离分别为y 1、y 2。

这些线段表示梁的纵向纤维。

梁受纯弯曲时，各层纤维处于单向拉伸或压缩状态，其长度将发生改变。

我们沿刻线方向粘贴电阻应变片，用电阻应变仪测出梁受力后各纤维层的应变ε实，由虎克定律求出实验应力σ实.实实εσ⨯=E （公式1） 式中：E 是梁所用材料的弹性模量。

实验时采用螺旋手柄加载，可以连续加载，载荷大小由拉压传感器通过应变仪读出。

当载荷增加ΔP 时，通过两根加载杆，使得测试梁两端的受力点分别增加ΔP/2，本实验采用“一次增载法”，既对钢梁先加一初载荷P 初，读出应变仪的初读数ε初，然后一次加载至额定载荷总P ，读出对应的应变值ε总，其应变增量△ε实=ε总-ε初。

如此重复三次。

计算出三次应变增量△ε实 的平均值实ε∆后，即可由虎克定律求出应力增量△σ实=E ×实ε∆ （公式2） 采用上式，可依次求出各层纤维的应力。

按纯弯曲理论，计算各层纤维应力增量的理论公式为 ZI y M ⨯∆=∆理σ （公式3） 式中：弯矩△M= △P ×a （△P —载荷增量，a －加力点到支座的距离）y 为各 纤维层至中性层的距离。

I z 为横截面对中性轴Z 的惯性矩，对于矩形截面3121bh I Z =六、实验步骤1.测量矩形截面梁的宽度b和高度h，载荷作用点到梁支点距离a，并推算出各应变计到中性层的距离y。

实验七 纯弯梁正应力分布电测实验实验内容一 纯弯梁正应力分布电测实验一、实验目的1、用电测法测定矩形截面梁在纯弯曲时的正应力的大小及其分布规律，并与理论值作比较。

2、初步掌握电测方法。

二、实验设备1、弯曲梁实验装置一台（见图7.2）2、YJ-4501A 静态数字电阻应变仪一台3、温度补偿片三、实验原理及方法试件选用矩形截面，荷载及测量点的布置如图7.1。

梁的材料为钢，其弹性模量a G E Ρ=210，转动实验装置上的加载手轮，可使梁受到如图7.1的荷载，梁的中段为纯弯曲段，荷载作用于纵向对称平面内，而且在弹性极限内进行实验，故为弹性范围内平面弯曲问题。

梁的正应力公式为y I M Z=σ式中：M --纯弯曲段梁截面上的弯矩Z I --横截面对中性轴的惯性矩y --截面上测点至中性轴的距离。

为了测量梁纯弯曲时横截面上应力分布规律，在梁的纯弯曲段沿梁的侧面各点沿轴线方向粘贴应变片，其分布如图（图7.1）应变片1#粘贴在中性层上，应变片2#、3#、应变片4#和应变片6#、7#分别粘贴在距离中性层为、和上下表面。

此外，在梁的上表面沿横向粘贴应变片8#，如果测得纯梁弯曲时沿横截面高度各点的轴向应变，则由单向应力状态的胡克定律公式4/h 8/3h εσE =，可求出各点处的应力实验值。

将应力实验值与应力理论值进行比较，可得出测量误差。

式中：ε—各测量点的线应变E —材料的弹性模量 σ--相应各测点正应力若由实验，测得的应变片7#和8#的应变7ε和8ε满足μεε=78，则证明 验采用等增量加载的方法测量应力的实验值及计算理论值，计算时均应以弯矩增量及应变增量的平均值代入。

4#图7.1图中：， mm c 150=mm h 40=mm b 20= ， mm l 620= 1#--8#所示应变片粘贴位置及方向。

四、实验步骤1、检查梁是否安放稳妥2、把梁上的应变片接在静态电阻应变仪的A 、B 接线柱上。

公共温度补偿片接在0通道接线柱B 、C 上。

实验六弯曲正应力电测实验
一、实验目的
1．学习使用应变片和电阻应变仪测定静态应力的基本原理和方法。

2．测定弯曲钢梁横截面不同位置的正应力。

3．观察梁纯弯曲段横截面正应力分布规律，验证弯曲正应力公式的适用范围
二、实验设备和仪器
1．微机控制电子万能试验机。

2．静态电阻应变仪。

三、实验数据及处理
数据记录
载荷和应变
横截面上应力分布比较（用蓝线代表实验值，用红线代表理论值）
四、问题讨论
沿梁截面高度，应变怎样分布？随载荷逐级增加，应变分布按什么规律变化？中性轴在横截面的什么位置？
1.沿梁截面的高度，应变从边界到中性轴逐渐变小，切关于中性轴大小相等，方向相反
2.随着载荷的增加应变也随着增加，两者增加成比例
3.横截面为矩形，中性轴在横截面的中心，也是矩形的对角线交点。

弯曲正应力电测实验原始试验数据记录2017年05月01日。

实验二、纯弯曲梁正应力电测实验一、 实验目的1、 电测法测定纯弯曲梁正应力分布规律。

2、验证纯弯曲梁正应力计算公式。

二、 实验装置与仪器1、 纯弯曲梁实验装置。

2、 数字式电阻应变仪。

三、 实验装置与实验原理1、实验装置弯曲梁试验装置如图1所示。

它有弯曲梁1，定位板2，支座3，试验机架4，加载系统5，两端带万向接头的加载杆6，加载压头（包括φ16钢珠）7，加载横梁8，载荷传感器9和测力仪10等组成。

该装置有已粘贴好应变片的钢梁（其弹性模量2210m GNE =）用来完成纯弯曲梁正应变分布规律试验。

纯弯曲梁正应变分布规律试验纯弯曲梁受力状态及有关尺寸见图2。

图 2在梁的纯弯曲段内已粘贴好两组应变片，每组8片，分别为1～8号片和1*～8*号片，各片距中心层的距离在图3中已标出。

当梁受力变形后，可由应变仪测出每片应变片产生的应变，这样就可得到实测的沿梁横截面高度的正应变分布规律。

根据材料力学中纯弯曲梁的平面假设，沿梁横截面高度的正应变分布规律应当是直线。

另外材料力学中还假设梁在纯弯曲段内是单向应力状态，为此，我们在梁的下表面粘贴有与7号片和7*号片垂直的8号片和8*号片，当梁受力变形后，可测得8ε和*8ε，根 据泊松比纵横εεμ=，可由78εε或**78εε计算得到 'μ，若'μ近似等于μ时，则证明梁纯弯曲段内近似于单向应力状态。

2、实验原理梁的纯弯曲段内，每片应变片所处状态是单向应力状态。

根据单向应力状态的虎克定律：σ = E ε可以计算出梁的纯弯曲段内每片应变片所处的应力。

注：该装置只允许加4KN 载荷，超载会损坏传感器。

一、实验目的1. 通过实验，了解梁在弯曲状态下的应力分布规律；2. 验证梁的弯曲正应力计算公式的准确性；3. 掌握应变电测法的基本原理和操作方法；4. 培养学生严谨的实验态度和科学的研究方法。

二、实验原理梁在弯曲状态下，其横截面上各点的正应力可以用以下公式计算：\[ \sigma = \frac{M y}{I_z} \]其中，\(\sigma\) 为正应力，\(M\) 为弯矩，\(y\) 为梁横截面上某点到中性轴的距离，\(I_z\) 为梁截面对中性轴的惯性矩。

实验中，通过测量梁横截面上不同位置的应变，根据虎克定律，可计算出相应位置的应力。

实验装置主要包括梁、应变片、静态数字电阻应变仪等。

三、实验仪器与设备1. 梁材料：矩形截面试件，尺寸为 \(b \times h\)；2. 应变片：电阻应变片，用于测量梁横截面上的应变；3. 静态数字电阻应变仪：用于测量应变片输出的电阻变化，从而计算出应变；4. 加载装置：用于对梁施加弯矩；5. 游标卡尺：用于测量梁的尺寸；6. 计算器：用于计算实验数据。

四、实验步骤1. 准备实验装置，包括梁、应变片、应变仪等；2. 将应变片粘贴在梁的预定位置，确保应变片与梁表面紧密贴合；3. 接通应变仪电源，调整应变仪的量程和灵敏度；4. 使用游标卡尺测量梁的尺寸，记录数据；5. 在梁上施加预定的弯矩，确保梁处于弯曲状态；6. 使用应变仪测量梁横截面上不同位置的应变，记录数据；7. 根据实验数据和应变片的位置，计算出梁横截面上不同位置的应力；8. 比较实验测得的应力与理论计算值，分析误差原因。

五、实验结果与分析1. 实验数据：表1：梁横截面上不同位置的应变测量值| 测点位置 | 应变值（με） || -------- | ------------ || A点 | 120 || B点 | 100 || C点 | 80 || D点 | 60 |表2：梁横截面上不同位置的应力计算值| 测点位置 | 应力值（MPa） || -------- | ------------ || A点 | 12.00 || B点 | 10.00 || C点 | 8.00 || D点 | 6.00 |2. 结果分析：通过实验数据与理论计算值的比较，可以看出，在梁的弯曲状态下，应力在梁横截面上呈线性分布。

实验六 纯弯曲梁正应力的测定一、实验目的1. 初步掌握电测法的基本原理和方法。

2. 测定梁在纯弯曲时横截面上正应力大小和分布规律；验证纯弯曲梁的正应力计算公式。

二、实验仪器、设备和工具1、组合实验台纯弯曲梁实验装置。

2、静态电阻应变仪。

3、游标卡尺、钢板尺。

三、实验原理梁受纯弯曲时，纯弯曲正应力计算公式为：ZI My=σ式中：M－弯矩－横截面对中性轴的惯矩Z I y－所求应力点到中性轴的距离由上述可知，梁在纯弯曲时，各点处的正应力沿横截面高度按直线规律分布。

如将电阻应变计粘贴在距中性层不等的位置上（见图），测得纯弯曲时沿横截面高度各点的纵向应变ε。

根据理论推导可知，各纵向纤维层只受简单拉伸或压缩，由单向应力状态的虎克定律εσE =，可求出各点处的实验应力实σ。

要测纯弯曲梁沿截面高度各点的应变值，可采用温补半桥组桥方法，见电阻应变片各种接桥方法(1)。

加载采用增量法，即每增加等量的载荷，测出各点的应变增量P ΔεΔ，然后分别取各点应变增量的平均值i εΔ，记录应变仪读数并填入表中，依次求出各点的应变增量实i εΔ.实实i E εσΔ=将实测应力值实σ与理论应力值理σ进行比较，以验证弯曲正应力公式。

四、实验步骤(一)、实验准备1、 按规定位置粘贴电阻应变计，焊线、防护（己由生产厂家准备好）。

2、 制定加载方案，四级加载：20Kg、40Kg、60Kg、80Kg。

3、 接通传感器和负荷显示器及电阻应变仪，预热10分钟。

4、 记录梁的截面尺寸，载荷作用点到支点距离及各应变计的位置。

见附表15、 加初载荷0P （一般取0P ＝10%max P 左右）估算max P ，记下初读数。

(二)、进行实验1、 均匀缓慢加载到初载荷0P ，记下各点应变的初始读数：后分级等量加载，每增加一级载荷，依次记录各点电阻应变片的应变值仪i ε，直到最终载荷。

实验至少重复两次。

见附表2 2、 按力值对照表分四级加载。

3、 做完实验后，卸掉载荷，仪器复原。

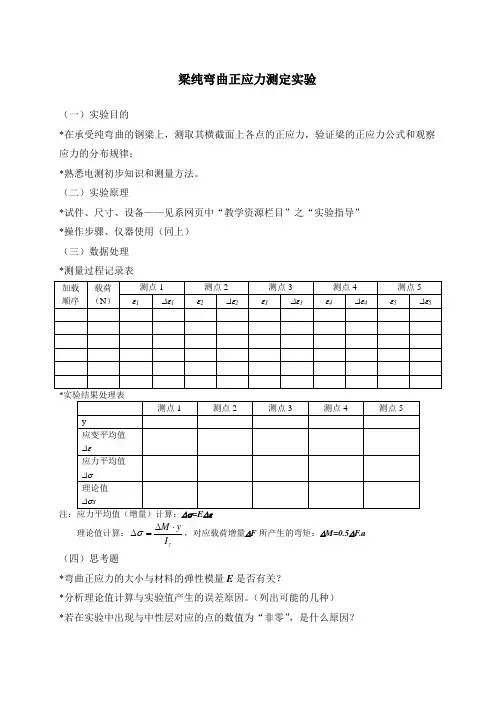
梁纯弯曲正应力测定实验（一）实验目的*在承受纯弯曲的钢梁上，测取其横截面上各点的正应力，验证梁的正应力公式和观察应力的分布规律；*熟悉电测初步知识和测量方法。

（二）实验原理*试件、尺寸、设备——见系网页中“教学资源栏目”之“实验指导” *操作步骤、仪器使用（同上） （三）数据处理 *测量过程记录表*注：应力平均值（增量）计算：=E 理论值计算：zM yI σ∆⋅∆=，对应载荷增量∆F 所产生的弯矩：∆M=0.5∆F .a （四）思考题*弯曲正应力的大小与材料的弹性模量E 是否有关？*分析理论值计算与实验值产生的误差原因。

（列出可能的几种） *若在实验中出现与中性层对应的点的数值为“非零”，是什么原因？临床实验室定量测定室内质量控制一术语和定义1偏倚 bias试验结果偏离可接受参考值的系统偏离（带有正负号）。

2不精密度 imprecision一组重复测定结果的随机离散，其值由统计量定量表示为标准差或变异系数。

3质量控制quality control质量管理的一部分，致力于满足质量要求。

[GB/T 19000-2000，]4 质量控制策略 quality control strategy质控品种类、每种检测频次、放置的位置，以及用于质控数据解释和确定分析批是在控还是失控的规则。

5 随机误差 random error测量结果与在重复性条件下对同一被测量进行无限多次测量所得结果的平均值之差。

6 系统误差 systematic error在重复性条件下，对同一被测量进行无限多次测量所得结果的平均值与被测量的真值之差。

7 可报告范围 reportable range在仪器、试剂盒或系统的测定响应之间的关系,显示是有效的期间内试验值范围。

8 标准差 standard deviation观察值或测定结果中不精密度的统计度量。

变异性/离散的度量是总体方差的正平方根。

二质量控制的目的质量控制方法是用来监测检验方法的分析性能，警告检验人员存在的问题。

纯弯曲正应力电测实验指导书一．实验作用和目的1．用电测法测定矩形截面简支梁受纯弯曲时横截面上弯曲正应力的大小及其、分布规律，并与理论值进行比较，以验证弯曲正应力公式正确性。

2．熟悉电测实验的基本原理和操作方法，掌握该方法在工程中的应用。

二．实验内容梁受纯弯曲时的正应力计算公式为：y I M Z=σ 式中 M —作用在横截面上的弯矩；I z —横截面对其中性轴Z 的惯性矩；y 一由欲求应力点到中性轴的距离。

本实验采用矩形截面直梁(或铝合金制成的箱形截面直梁)，实验装置如图1（a ）、图1(b)所示。

施加的砝码重量通过杠杆以一定比例作用于附梁。

通过两个挂杆作用于梁上C 、D 处的载荷各为F /2。

由该梁的内力图可知CD 段上的剪力Q F 等于零，弯矩M =F .a /2。

因此梁上CD 段处于纯弯曲状态。

图1纯弯曲正应力试验台1-试验机活动台；2-支座；3-试样；4-试验机压头；5-加力梁；6-电阻应变片在CD 段内任选的一个截面上，距中性层不同高度处，沿着平行于梁的轴线方向，等距离地粘贴七个电阻应变片，每片相距h /6，在梁不受载荷的自由端贴上温度补偿片。

试验时，采用半桥接法将各测点的工作应变片和温度补偿应变片连接在应变电桥的相邻桥臂上，按照电阻应变仪的操作规程将电桥预调平衡，加载后即可从电阻应变仪上读出实ε。

由于纤维之间不相互挤压，故可根据虎克定律求出弯曲正应力的实验值 实实εσ⋅=E a (1)式中E — 梁所用材料的弹性模量。

本实验采用“增量法”加载，每次增加等量的载荷F ∆并相应地测定各点的应变增量实ε∆。

取应变增量的平均值实ε∆，依次求出各点应力增量实σ∆。

实实εσ∆⋅=∆E (2)将实σ∆实值与理论公式算出的应力增量ZI y ⋅∆=∆M 理σ (3) 进行比较，计算出截面上各测点的应力增量实验值与理论值的误差。

其计算公式为%100⨯∆∆-∆=理实理σσση (4)以验证弯曲正应力公式的正确性。

纯弯曲梁的正应力电测实验一、实验目的1．用电测法测量单一材料的矩形截面梁在纯弯曲状态时其横截面上正应力的大小及分布规律，并与理论计算值比较，从而验证梁的弯曲正应力理论公式。

2．初步掌握电测法原理和静态电阻应变仪的使用方法。

二、实验装置和仪器1．纯弯曲实验装置本实验采用低碳钢或中碳钢制成的矩形截面梁，测试其正应力分布规律的实验装置如图20（a）所示，所加的砝码重量通过杠杆以一定的放大比例作用于加载辅梁的中央，设作用于辅梁中央的载荷为F，由于载荷对称，支承条件对称，则通过两个挂杆作用于待测梁上C、D处的载荷各为F/2。

由待测梁的内力图可知CD段上的剪力Q=0，弯矩为一常量M=2aF ，即梁的CD段处于纯弯曲状态。

图20 弯曲正应力实验装置及试样贴片位置图2．静态电阻应变仪3．游标卡尺、钢直尺三、实验原理由于矩形截面梁的CD段处于纯弯曲状态，当梁发生变形其横截面保持平面的假设成立，又可将梁视作由一层一层的纵向纤维叠合而成且假设纵向纤维间无挤压作用，此时纯弯曲梁上的各点处于单向应力状态，且弯曲正应力的方向平行于梁的轴线方向，所以若要测量纯弯曲状态下梁的横截面上的正应力的分布规律，可在梁的CD段任一截面上沿不同高度处平行于梁的轴线方向布设若干枚电阻应变计，为简便计算，本实验的布片方案如图20（b）所示，一枚布设在梁的中性层上，其余四枚分别布设在距中性层h/4或h/2处（h 为梁矩形截面的高度），此外还布设了一枚温度补偿片。

当梁受载后，电阻应变计随梁的弯曲变形而产生伸长或缩短，使自身的电阻改变。

通过力学量的电测法原理，利用电阻应变仪即可测出梁横截面上各测点的应变值ε实。

由于本实验梁的变形控制在线弹性范围内，所以依据单向虎克定律即可求解相应各测点的应力值，即σ实=E ·ε实，E 为梁材料的弹性模量。

实验采用“等增量法”加载，即每增加等量的载荷ΔF ，测定一次各点相应的应变增量Δε实，并观察各点应变增量的线性程度。

纯弯曲梁正应力电测实验报告纯弯曲梁正应力电测实验是一种常用的材料力学实验方法，用于测量梁在弯曲过程中的正应力分布情况。

本实验通过加载施加在金属横截面上的外力，测量由于弯曲产生的电势差，从而得到梁在各个截面上的正应力大小。

下面是一份纯弯曲梁正应力电测实验报告的参考内容。

实验目的：1. 理解材料在弯曲过程中的正应力分布特性；2. 掌握纯弯曲梁正应力电测实验的原理和方法；3. 学习使用实验仪器和数据处理软件。

实验仪器：1. 弯曲实验台；2. 弯曲应变计；3. 电压采集仪；4. 电压放大器；5. 计算机。

实验原理：在纯弯曲梁实验中，通过加载施加在梁上的外力，梁发生弯曲变形。

根据材料力学理论，梁在弯曲过程中会产生正应力。

实验中利用弯曲应变计测量梁在各个截面上的应变大小。

弯曲应变计通过压电效应将应变转化为电荷，产生电势差。

通过电压采集仪和电压放大器将电势差放大并记录下来，就可以得到梁在各个截面上的正应力大小。

实验步骤：1. 将要进行实验的梁固定在弯曲实验台上，调整梁的位置和姿态，使其能够正常受力并产生弯曲变形；2. 将弯曲应变计安装在梁的截面上，保证其能够准确测量应变；3. 连接弯曲应变计和电压采集仪，调整采集仪的参数，使其能够正常采集电势差；4. 将电压采集仪与电压放大器连接，调整放大器的增益，保证能够得到合适范围的电压信号；5. 开始加载外力，在加载过程中，实时记录电压采集仪采集到的电势差数据；6. 加载外力达到一定值后停止，记录下此时的电势差数据。

数据处理：1. 将采集到的电势差数据导入计算机；2. 对电势差数据进行处理，根据电压放大器的增益和弯曲应变计的灵敏度，将电势差数据转换为应变数据；3. 根据应变计的位置和梁的材料参数，计算出各个截面上的应变值；4. 利用梁的几何参数和材料参数，计算出各个截面上的正应力大小。

实验结果：根据数据处理的结果，可以得到梁在各个截面上的正应力大小的分布情况。

通过绘制应力-位置曲线，可以直观地观察梁在弯曲过程中正应力的变化趋势，并分析其特点和规律。

梁的纯弯曲正应力实验电测法是应力应变测量最常用的方法，其方法简便，技术成熟，已经成为工程中不可缺少的测量手段。

纯弯曲时正应力在横截面上线性分布，是弯曲中最简单的应力情况。

用电测法测定纯弯曲梁上的正应力，不仅可以验证材料力学理论，也可以熟悉电测法测量的原理、操作方法和注意的问题，为复杂的实验应力分析打下基础。

一、预习要求1、YJ—5电阻应变仪测量前如何进行预调平衡？2、采用半桥接法进行弯曲正应力测量时，如何进行温度补偿？说明原理。

二、实验目的1、初步掌握电测应力分析方法，学习电测接线方法、仪器调试使用方法。

2、测定梁在纯弯曲下的弯曲正应力及分布规律，验证理论公式。

三、实验设备1、纯弯曲正应力试验台。

2、电阻应变仪及预调平衡箱。

3、矩形截面钢梁。

四、实验原理及方法纯弯曲梁如图1a所示。

在载荷P作用下，梁的CD段为纯弯曲变形。

沿梁横截面的高度方向每隔4h高度粘贴平行于轴线的测量应变片，共五片，其中第三片在中性层上。

另外在梁外安置温度补偿块，其上贴一公共温度补偿应变片。

每一测量应变片与公共温度补偿片按图1b接法接为半桥测量系统。

梁受到P力作用后，产生弯曲变形。

通过电阻应变仪测出载荷作用下五个点处的应变，由于是单向拉压变形，由虎克定律εσE=即可算出各点的应力值。

另一方面，由弯曲正应力理论公式zIMy=σ，可算出各点的应力理论值。

于是可将实测值和理论值进行比较，验证理论公式的正确性。

实验时，载荷由砝码经过20倍杠杆放大施加。

加载分四级，每增加一个砝码，产生P图1 纯弯曲实验装置示意图力的增量ΔP。

每加一级后测出五个点的应变，最后取力和应变的增量平均值计算理论值和实验值。

该实验也可用万能试验机加载进行测量。

五、实验步骤1、检查调整纯弯曲梁、电阻应变仪，使各部件和旋钮在正确位置，并打开应变仪进行预热。

2、接桥练习。

参照表1组桥，每种方式下按应变仪的使用方法进行预调平衡，平衡后加一个砝码读取应变。

读数方法为，当加载后应变仪的指针发生偏转，根据应变的大小选择并调节微调、中调、粗调读数盘使电表指针回零，这时各读数盘所指读数的代数和即是所测点的应变值。

梁弯曲正应力测定一、实验目的1.用电测法测定直梁纯弯曲时的正应力分布，并与理论计算结果进行比较，以验证弯曲正应力公式。

2.了解电阻应变测量的原理，初步掌握静态电阻应变仪的使用方法。

二、实验设备名称及型号1.WSG-80型纯弯曲正应力试验台。

2.YE2538A 程控静态应变仪。

3.应变片、导线、接线端子等。

三、实验原理1.试样的制备：用矩形截面钢梁，在其横截面高度上等距离地沿梁的轴线方向粘贴5枚电阻应变片。

2.弯曲正应力的测量原理：梁纯弯曲时，横截面上的正应力σ在理论上沿梁的高度成线性分布，其计算公式为z I y M ⋅=σ式中，σ的单位为MPa ；M 为梁横截面上的弯矩，单位为N ·mm ；y 为应力σ所在的点到中性轴的距离，单位为mm ； I z 为横截面对中性轴z 的面积二次矩，单位为mm 4。

面积二次矩对于矩形截面按下式计算123bh I z =式中，b 为梁横截面的宽度，单位为mm ；h 为梁横截面的高度，单位为mm 。

令使载荷P 对称地加在矩形截面直梁上（如图4-1所示）。

这时，梁的中段将产生纯弯曲。

若载荷每增加一级p ∆（用增量法），则可由电阻应变仪测出梁中段所贴应变片各点的纵向应变增量ε∆，根据虎克定律求出各点实测正应力增量εσ∆=E 实图4-1此值与理论公式计算出的各点正应力的增量即ZI My∆=理σ 进行比较，就可验证弯曲正应力公式。

这里，弯矩增量2paM ∆=∆。

梁上各点的应变测量，采用1/4桥接线，各工作应变片共用一个温度补偿块。

四、实验步骤1.记录实验台参数，设计实验方法。

2.准备应变仪：把梁上各测量点的应变片（工作应变片）按编号逐点接到电阻应变仪A 、B 接线柱上，将温度补偿片接到电阻应变仪接线柱上作公共补偿。

3.进行实验：把砝码托挂在杠杆上、加初载荷、调节应变仪，使各测量点均为零。

加载，加一次砝码，各测量点读一次数，记下各点的应变值，直到加完砝码读数完毕为止。

弯曲正应力电测实验报告弯曲正应力电测实验报告引言：弯曲正应力电测实验是一种常用的材料力学实验方法，通过施加外力使材料产生弯曲变形，进而测量材料在不同位置上的正应力分布情况。

本实验旨在探究不同材料在弯曲过程中的应力分布特点，并通过电测方法进行准确测量。

实验原理：弯曲正应力电测实验基于梁的弯曲理论，根据材料的弯曲变形情况，可以推导出弯曲梁上不同位置的应力分布。

在实验中，通过施加外力使梁产生弯曲，然后利用电测方法测量不同位置上的电势差，从而得到该位置上的正应力数值。

实验装置：本实验采用了一台弯曲正应力电测仪，该仪器由弯曲梁、电测电路和数据采集系统组成。

弯曲梁通常采用金属材料，如钢材或铝材，其形状可以是矩形、圆形或其他几何形状。

电测电路通过电极与弯曲梁连接，测量弯曲梁上不同位置的电势差。

数据采集系统用于记录和分析实验数据。

实验步骤：1. 准备工作：根据实验要求选择合适的弯曲梁材料，并将其固定在实验台上。

2. 施加外力：通过调节实验台上的施力装置，施加合适的外力使弯曲梁产生弯曲变形。

3. 连接电测电路：将电测电路与弯曲梁连接，确保电极与梁表面接触良好。

4. 测量电势差：打开数据采集系统，记录不同位置上的电势差数值。

5. 数据分析：根据电势差数值，计算得到不同位置上的正应力数值，并绘制应力分布曲线。

实验结果与讨论：根据实验数据，我们可以得到弯曲梁上不同位置的正应力分布情况。

通常情况下，弯曲梁的上表面受到压应力，下表面受到拉应力，而中性轴附近的应力为零。

应力分布曲线呈现出一定的对称性，符合弯曲梁的力学性质。

不同材料的弯曲正应力分布特点也有所不同。

例如，钢材的弯曲梁上应力分布相对均匀，且强度较高；而铝材的应力分布相对不均匀，容易出现应力集中现象。

这些差异可以通过实验数据进行比较和分析，为材料选择和工程设计提供参考。

实验误差与改进：在实验过程中，由于实验条件和仪器精度的限制，可能会产生一定的误差。

例如，电极与弯曲梁之间的接触电阻、电测电路的灵敏度等因素都会对实验结果产生影响。

纯弯曲梁正应力电测实验报告一、实验目的本次实验旨在通过纯弯曲梁正应力电测实验，掌握梁的正应力计算方法以及电阻应变计的使用方法，并了解梁的受力特性和变形规律。

二、实验原理1.梁的受力特性当梁受到外力作用时，会产生内部应力和变形。

根据材料力学原理，内部应力可以分为正应力和剪应力。

在纯弯曲情况下，梁内部只存在正应力，且沿截面法线方向呈线性分布。

2.电阻应变计电阻应变计是一种常用的测量金属材料应变的仪器。

当金属材料发生形变时，其电阻值也会发生微小变化。

通过测量这种微小变化来计算金属材料的应变值。

3.纯弯曲梁正应力计算公式在纯弯曲情况下，梁内部只存在正应力。

根据受拉或受压状态下截面上某点处的正应力公式：σ = M*y/I其中，σ为该点处的正应力；M为作用于该点处剪跨截面上侧边缘的弯矩；y为该点到中性轴的距离；I为该截面的惯性矩。

三、实验器材和试件1.器材：纯弯曲梁实验台、电阻应变计、数字万用表等。

2.试件：长度为1.2m，宽度为20mm，厚度为2mm的钢板梁。

四、实验步骤1.将钢板梁放置在纯弯曲梁实验台上，并调整好实验台的支承距离。

2.将电阻应变计粘贴在梁上，保证其与梁表面紧密贴合，并接好电路。

3.通过旋钮调节实验台施加的力矩大小，使得钢板梁发生一定程度的弯曲变形，并记录下此时电阻应变计显示的电压值。

4.重复以上步骤，每次增加一定大小的力矩，直至达到最大载荷或者出现塑性变形等异常情况。

5.根据所得到的数据，计算出不同载荷下钢板梁各点处的正应力值，并绘制出正应力-距离曲线图和载荷-挠度曲线图。

五、实验结果分析1.正应力-距离曲线图通过计算所得到的正应力-距离曲线图，可以看出钢板梁内部正应力随着距离的增加而减小，且呈线性分布。

在最大载荷下，梁中心处的正应力最大，约为200MPa。

2.载荷-挠度曲线图通过实验数据计算得到的载荷-挠度曲线图，可以看出钢板梁的弯曲刚度随着载荷的增加而降低。

当达到最大载荷时，梁发生塑性变形并无法恢复原状。

实验四 梁弯曲正应力一、实验目的1．用电测法测定梁在纯弯曲时横截面上正应力分布规律，将实验值与理论计算结果进行比较以此验证弯曲正应力公式2．熟悉电测的基本原理和静态测量方法以及应变测试仪操作 3．学习误差分析 二 、实验设备1．DH3818静态电阻应变测试仪 2．梁弯曲实验装置 三、实验原理当矩形钢梁在承受四点弯曲时，在纯弯曲范围内任一横截面（远离载荷作用点，否则受力为复杂状态）以中心层为基准，上下对称至少取五层纤维层作为研究对象。

（如图1所示）用纯弯曲公式作为理论计算公式图1 矩形钢梁四点弯曲示意图y z M I σ=式中:yM 测点所在截面上的弯矩；y 测点至中性层的距离；z I 测点至中性轴的距离。

横截面各纤维层表面牢固的粘贴电阻应变片，使其成为一个整体。

当钢梁受力变形时应变片也跟随一起变形，此时粘贴在钢梁上的应变片的电阻值也发生改变，而电阻的改变量ΔR/R 与钢梁纤维（或应变片电阻丝）的变形量ΔL/L 成正比关系。

因此可通过应变测试仪分别测量出各点对应的实际变形量及应变值ε，然后根据单向虎克定律率，计算出相应的应力值。

实验公式E σε=式中：E 为钢梁的弹性模量 接桥方式如图2图2 电桥连接示意图四、实验步骤:1．准备：检查实验用矩形截面梁的加力点位置与支座位置是否正确。

记录有关参数。

2．根据有关参数确定其加载方案，即确定初载荷和最终载荷。

（因测力计原因最大载荷不得超过4KN,设备上显示为4.00）3．接线：根据实验要求，本试验选择1/4桥路形式及AB桥接工作片，BC桥路接温度补尝片。

3.1将被测应变片分别依次接在各工作电桥桥路B点（或vi+ 点）接线柱上。

被测应变片的另一端，一根不同颜色的导线（在引出导线时，已将所有被测应变片另一端引线全并连在一起）接在任一工作电桥桥路的A点（或eg点）接线柱上（因该设备各桥路A点（或eg 点）用一个导线全串在一起）3.2将温度补偿片的两端引线分别接到补偿电桥桥路中B点、C点(或vi+点、或0点)上。