中考数学方案设计试题分类汇编

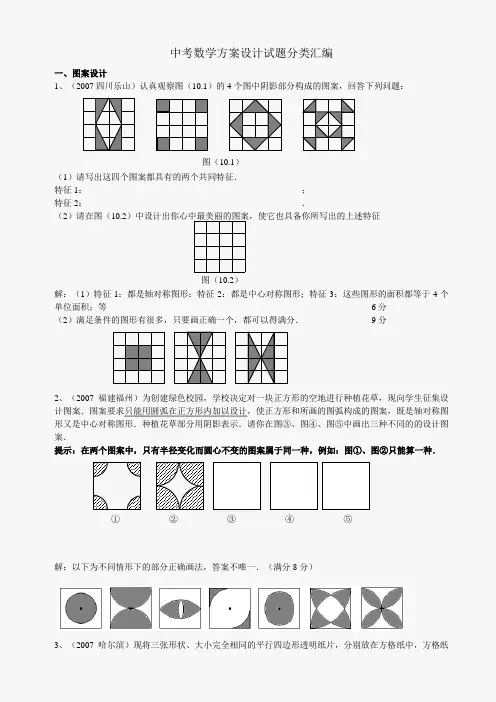
中考数学方案设计试题分类汇编一、图案设计1、（2007四川乐山）认真观察图（10.1）的4个图中阴影部分构成的图案，回答下列问题：（1）请写出这四个图案都具有的两个共同特征．特征1：_________________________________________________； 特征2：_________________________________________________．（2）请在图（10.2）中设计出你心中最美丽的图案，使它也具备你所写出的上述特征解：（1）特征1：都是轴对称图形；特征2：都是中心对称图形；特征3：这些图形的面积都等于4个单位面积；等 ··························································································· 6分 （2）满足条件的图形有很多，只要画正确一个，都可以得满分． ······················· 9分2、（2007福建福州）为创建绿色校园，学校决定对一块正方形的空地进行种植花草，现向学生征集设计图案．图案要求只能用圆弧在正方形内加以设计，使正方形和所画的图弧构成的图案，既是轴对称图形又是中心对称图形．种植花草部分用阴影表示．请你在图③、图④、图⑤中画出三种不同的的设计图案．提示：在两个图案中，只有半径变化而圆心不变的图案属于同一种，例如：图①、图②只能算一种．解：以下为不同情形下的部分正确画法，答案不唯一．（满分8分）3、（2007哈尔滨）现将三张形状、大小完全相同的平行四边形透明纸片，分别放在方格纸中，方格纸图（10.1） 图（10.2） ① ② ③ ④ ⑤中的每个小正方形的边长均为1，并且平行四边形纸片的每个顶点与小正方形的顶点重合（如图1、图2、图3）．分别在图1、图2、图3中，经过平行四边形纸片的任意一个顶点画一条裁剪线，沿此裁剪线将平行四边形纸片裁成两部分，并把这两部分重新拼成符合下列要求的几何图形． 要求：（1）在左边的平行四边形纸片中画一条裁剪线，然后在右边相对应的方格纸中，按实际大小画出所拼成的符合要求的几何图形；（2）裁成的两部分在拼成几何图形时要互不重叠且不留空隙； （3）所画出的几何图形的各顶点必须与小正方形的顶点重合．解：二、代数式中的方案设计4、（2007辽宁大连）某班级为准备元旦联欢会，欲购买价格分别为2元、4元和10元的三种奖品，每种奖品至少购买一件，共买16件，恰好用50元。

2021年全国(quán ɡuó)各地100份中考数学试卷分类汇编第41章方案设计三解答题1. 〔 2021江， 26，12分〕在“五个〞建立中,为了进步民的宜居环境,某区规划修建一个文化(平面图形如下图),其中四边形ABCD是矩形,分别以AB、BC、CD、DA边为直径向外作半圆,假设整个的周长为628米,高矩形的边长AB=y米,BC=x米.(注:取π=3.14)(1)试用含x的代数式表示y;(2)现方案在矩形ABCD区域上种植花草和铺设鹅卵石等,平均每平方米造价为428元,在四个半圆的区域上种植草坪及铺设花岗岩,平均每平方米造价为400元;①设该工程的总造价为W元，求W关于x的函数关系式；②假设该工程政府投入1千万元，问能否完成该工程的建立任务？假设能，请列出设计方案，假设不能，请说明理由？③假设该工程在政府投入1千万元的根底上，又增加企业募捐资金64·82万元，但要求矩形的边BC的长不超过AB长的三分之二，且建立恰好用完所有资金，问：能还完成该工程的建立任务？假设能，请列出所有可能的设计方案，假设不能，请说明理由·【答案(dá àn)】〔1〕 由题意得 y+πx=6·28∵π=3.14 ∴3.14y+3.14x=628. ∴x+y=200.那么 y=200-x; (2) ①w=428xy+400π()2+400π()2 =428x(200-x)+400××+400××=200x 2-40000x+12560000;②仅靠政府投入的1千万不能完成该工程的建立任务，其理由如下：由①知 w=200(x-100)2×107＞107, 所以不能； ③由题意得 x ≤y, 即x ≤32(200-x) 解之得 x ≤80 ∴0≤x ≤80.又根据题意得 w=200(x-100)2×107=107×105整理得 (x-100)2=441 解之得 x 1=79, x 2=121 〔不合题意舍去〕 ∴只能取 x=79， 那么y=200-79=121所以设计的方案是： AB 长为121米，BC 长为79米，再分别以各边为直径向外作半圆·2. (2021綦江，25，10分)为了保护环境，某化工厂一期工程完成后购置了3台甲型和2台乙型污水处理设备，一共花费资金54万元，且每台乙型设备的A BC D 第26价格是每台甲型设备价格的75%，实际运行中发现，每台甲型设备每月能处理污水200吨，每台乙型设备每月能处理污水160吨，且每年用于每台甲型设备的各种维护费和电费为1万元，每年用于每台乙型设备的各种维护费和电费为1.5万元.今年该厂二期工程即将完成，产生的污水将大大增加，于是该厂决定再购置甲、乙两型设备一共8台用于二期工程的污水处理，预算本次购置资金不超过．．．84万元，预计二期工程完成后每月将产生不．少于．．1300吨污水.〔1〕请你计算每台甲型设备和每台乙型设备的价格(jiàgé)各是多少元？〔2〕请你求出用于二期工程的污水处理设备的所有购置方案；〔3〕假设两种设备的使用年限都为10年，请你说明在〔2〕的所有方案中，哪种购置方案的总费用最少？〔总费用＝设备购置费＋各种维护费和电费〕【答案】：25. 解：〔1〕设一台甲型设备的价格为x万元，由题，解得x＝12，∵ 12×75%＝9 ，∴一台甲型设备的价格为12万元，一台乙型设备的价格是9万元(2)设二期工程中,购置甲型设备a台,由题意有，解得：由题意a为正整数,∴a＝1,2,3,4 ∴所有购置方案有四种,分别为方案一:甲型1台,乙型7台；方案二:甲型2台,乙型6台方案三:甲型3台,乙型5台；方案四:甲型4台,乙型4台(3)设二期工程10年用于治理污水的总费用为W万元化简得: －2a ＋192,∵W 随a 的增大(zēnɡ dà)而减少 ∴当a ＝4时, W 最小〔逐一验算也可〕 ∴按方案四甲型购置4台,乙型购置4台的总费用最少.3. 〔2021凉山州，24，9分〕我州鼓苦荞茶、青花椒、野生蘑菇，为了让这些珍宝走出大山，走向世界，州政府决定组织21辆汽车装运这三种土特产一共120吨，参加全国农产品博览会。

方案设计一、解答题1. (2016·四川资阳)某大型企业为了保护环境，准备购买A、B两种型号的污水处理设备共8台，用于同时治理不同成分的污水，若购买A型2台、B 型3台需54万，购买A型4台、B型2台需68万元．（1）求出A型、B型污水处理设备的单价；（2）经核实，一台A型设备一个月可处理污水220吨，一台B型设备一个月可处理污水190吨，如果该企业每月的污水处理量不低于1565吨，请你为该企业设计一种最省钱的购买方案．【考点】一元一次不等式的应用；二元一次方程组的应用．【分析】（1）根据题意结合购买A型2台、B型3台需54万，购买A型4台、B型2台需68万元分别得出等式求出答案；（2）利用该企业每月的污水处理量不低于1565吨，得出不等式求出答案．【解答】解：（1）设A型污水处理设备的单价为x万元，B型污水处理设备的单价为y万元，根据题意可得：，解得：．答：A型污水处理设备的单价为12万元，B型污水处理设备的单价为10万元；（2）设购进a台A型污水处理器，根据题意可得：220a+190（8﹣a）≥1565，解得：a≥1.5，∵A型污水处理设备单价比B型污水处理设备单价高，∴A型污水处理设备买越少，越省钱，∴购进2台A型污水处理设备，购进6台B型污水处理设备最省钱．2．（2016.山东省泰安市）某学校是乒乓球体育传统项目学校，为进一步推动该项目的开展，学校准备到体育用品店购买直拍球拍和横拍球拍若干副，并且每买一副球拍必须要买10个乒乓球，乒乓球的单价为2元/个，若购买20副直拍球拍和15副横拍球拍花费9000元；购买10副横拍球拍比购买5副直拍球拍多花费1600元．（1）求两种球拍每副各多少元？（2）若学校购买两种球拍共40副，且直拍球拍的数量不多于横拍球拍数量的3倍，请你给出一种费用最少的方案，并求出该方案所需费用．【分析】（1）设直拍球拍每副x元，横拍球每副y元，根据题意列出二元一次方程组，解方程组即可；（2）设购买直拍球拍m副，根据题意列出不等式，解不等式求出m的范围，根据题意列出费用关于m的一次函数，根据一次函数的性质解答即可．【解答】解：（1）设直拍球拍每副x元，横拍球每副y元，由题意得，，解得，，答：直拍球拍每副220元，横拍球每副260元；（2）设购买直拍球拍m副，则购买横拍球（40﹣m）副，由题意得，m≤3（40﹣m），解得，m≤30，设买40副球拍所需的费用为w，则w=（220+20）m+（260+20）（40﹣m）=﹣40m+11200，∵﹣40＜0，∴w随m的增大而减小，∴当m=30时，w取最大值，最大值为﹣40×30+11200=10000（元）．答：购买直拍球拍30副，则购买横拍球10副时，费用最少．【点评】本题考查的是列二元一次方程组、一元一次不等式解实际问题，正确列出二元一次方程组和一元一次不等式并正确解出方程组和不等式是解题的关。

中考数学方案设计试题分类汇编六、不等式中的方案设计1、（2007山东青岛）某饮料厂开发了 A、B两种新型饮料，主要原料均为甲和乙，每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产，计划生产A、B两种饮料共100 瓶.设生产A种饮料x瓶，解答下列问题：（1）有几种符合题意的生产方案？写出解答过程；（2）如果A种饮料每瓶的成本为2. 60兀，B种饮料每瓶的成本为2. 80兀，这两种饮料成本总额为y兀，请写出y与x之间的关系式，并说明x取何值会使成本总额最低？名称饮料名"甲乙A 20克40克B 30克20克2、（2007重庆）我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售。

按计划, 20辆汽车都要装运，每辆汽车只能装运同一种脐橙，旦必须装满。

根据下表提供的信息，解答以下可题:脐橙品种 A B C每辆汽车运载量（吨）6 5 4每吨脐橙获得（百兀）12 16 10（1）设装运A种脐橙的车辆数为x,装运B种脐橙的车辆数为y,求y与x之间的函数关系式;（2）如果装运每种脐橙的车辆数都不少于4辆，那么车辆的安排方案有几种？并写出每种安排方案；（3）若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润的值。

3、（2007南充）某商店需要购进一批电视机和洗衣机，根据市场调查，决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表：类别电视机洗衣机进价（元/台）1800 1500售价（元/台）2000 1600计划购进电视机和洗衣机共100台，商店最多可筹集资金161 800兀.（1）请你帮助商店算一算有多少种进货方案？（不考虑除进价之外的其它费用）（2）哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多？并求出最多利润.（利润=售价一进价） 4、（2007四川眉山）某县响应“建设环保节约型社会”的号召，决定资助部分付镇修建一批沼气池，使农民用到经济、环保的沼气能源.幸福村共有264户村民，政府补助村里34万兀，不足部分由村民集资.修建A型、B型沼气池共20个.两种型号沼气池每个修建费用、可供使用户数、修建用地情况如下表：沼气池修建费用（万元/个）可供使用户数（户/个）占地面积成/个）A型 3 20 48 B型 2 3 6 门批给该村沼气池修建用地型沼气池X个，修建两种型号 y万元.政府相关部708m2,设修建A沼气池共需费用（1）求y与x之间的函数关系式；（2）不超过政府批给修建沼气池用地面积，又要使该村每户村民用上沼气的修建方案有几种；（3）若平均每户村民集资700兀，能否满足所需费用最少的修建方案.5、（2007山东临沂）某工程机械厂根据市场需求，计划生产，、方两种型号的大型挖掘机共100 台，该厂所筹生产资金不少于羽以。

方案设计制卷人：歐陽文化、歐陽理複；制卷時間：二O二二年二月七日1. 〔2021•A 卷•10 分〕如图，在足够大的空地上有一段长为a 米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园 ABCD，其中 A D≤MN，矩形菜园的一边靠墙，另三边一一共用了 100 米木栏．〔1〕假设a=20，所围成的矩形菜园的面积为450 平方米，求所利用旧墙AD 的长；〔2〕求矩形菜园 ABCD 面积的最大值．【分析】〔1〕设AB=xm，那么BC=〔100﹣2x〕m，利用矩形的面积公式得到x〔100﹣2x〕=450，解方程得x1=5，x2=45，然后计算100﹣2x 后与20 进展大小比拟即可得到AD 的长；〔2〕设AD=xm，利用矩形面积得到S=12x〔100﹣x〕，配方得到S=﹣12〔x﹣50〕2+1250，讨论：当a≥50 时，根据二次函数的性质得S 的最大值为1250；当0＜a＜50 时，那么当0＜x≤a时，根据二次函数的性质得 S 的最大值为 50a﹣12a2．【解答】解：〔1〕设AB=xm，那么BC=〔100﹣2x〕m，根据题意得 x〔100﹣2x〕=450，解得x1=5，x2=45，当x=5 时，100﹣2x=90＞20，不合题意舍去；当x=45 时，100﹣2x=10，答：AD的长为10m；〔2〕设AD=xm，∴S=12x〔100﹣x〕=﹣12〔x﹣50〕2+1250，当 a≥50 时，那么 x=50 时，S 的最大值为1250；当0＜a＜50 时，那么当0＜x≤a时，S 随x 的增大而增大，当x=a 时，S 的最大值为50a﹣12a2，综上所述，当a≥50时，S 的最大值为1250；当0＜a＜50 时，S 的最大值为50a﹣12a2．【点评】此题考察了二次函数的应用：解此类题的关键是通过几何性质确定出二次函数的解析式，然后确定其最大值，实际问题中自变量x 的取值要使实际问题有意义，因此在求二次函数的最值时，一定要注意自变量x 的取值范围．2.〔2021•B 卷•10 分〕空地上有一段长为a 米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，木栏总长为100 米．〔1〕a=20，矩形菜园的一边靠墙，另三边一一共用了100 米木栏，且围成的矩形菜园面积为450 平方米．如图1，求所利用旧墙AD 的长；〔2〕0＜α＜50，且空地足够大，如图2．请你合理利用旧墙及所给木栏设计一个方案，使得所围成的矩形菜园ABCD 的面积最大，并求面积的最大值．图1 图2【分析】〔1〕按题意设出AD，表示AB 构成方程；〔2〕根据旧墙长度a 和AD 长度表示矩形菜园长和宽，注意分类讨论s 与菜园边长之间的数量关系．【解答】解：〔1〕设AD=x 米，那么AB=1002x-米依题意得，(100)4502x x-=解得x1=10，x2=90∵a=20，且 x ≤a∴x=90 舍去∴利用旧墙 AD 的长为 10 米．〔2〕设 AD=x 米，矩形 ABCD 的面积为 S 平方米①假如按图一方案围成矩形菜园，依题意 得： S=2(100)1(50)125022x x x -=--+，0＜x ＜a ∵0＜α ＜50∴x＜a ＜50 时，S 随 x 的增大而增大 当 x=a 时，S 最大=50a ﹣213a②如按图 2 方案围成矩形菜园，依题意得 S=22(1002)[(25)](25)244x a x a a x +-=---++，a ≤x＜50+2a当 a ＜25+4a ＜50 时，即 0＜a ＜1003时， 那么 x=25+4a 时， S 最大=〔25+4a 〕2=21000020016a a ++ 当 25+4a ≤a，即100503a ≤时，S 随 x 的增大而减小∴x=a 时，S 最大=(1002)2a a a +-=21502a a - 综合①②，当 0＜a ＜1003时， 21000020016a a ++﹣〔21502a a -〕=2(3100)016a - 21000020016a a ++＞21502a a -，此时，按图 2 方案围成矩形菜园面积最大，最大面积为21000020016a a ++平方米 当100503a ≤时，两种方案围成的矩形菜园面积最大值相等．∴ 当 0 ＜ a ＜1003 时 ，围成长 和宽均为 〔 25+4a 〕米的 矩形菜园 面积最 大，最 大面积 为 21000020016a a ++平方米； 当100503a ≤时，围成长为 a 米，宽为〔50﹣2a 〕米的矩形菜园面积最大，最大面积为〔21502a a -〕平方米． 【点评】此题以实际应用为背景，考察了一元二次方程与二次函数最值的讨论，解得时注意分类 讨论变量大小关系．3.〔2021··10 分〕某积极响应“三城同创〞的号召，绿化校园，方案购 进 A ，B 两种树苗，一共 21 棵， A 种树苗每棵 90 元，B 种树苗每棵 70 元．设购置 A 种树苗 x棵，购置两种树苗所需费用为y 元．〔1〕求 y 与 x 的函数表达式，其中0≤x≤21；〔2〕假设购置B 种树苗的数量少于A 种树苗的数量，请给出一种费用最的方案，并求出该方案所需费用．【分析】〔1〕根据购置两种树苗所需费用=A 种树苗费用+B 种树苗费用，即可解答；〔2〕根据购置 B 种树苗的数量少于 A 种树苗的数量，列出不等式，确定 x 的取值范围，再根据〔1〕得出的y 与x 之间的函数关系式，利用一次函数的增减性结合自变量的取值即可得出更合算的方案．【解答】解：〔1〕根据题意，得：y=90x+70〔21﹣x〕=20x+1470，所以函数解析式为：y=20x+1470；〔2〕∵购置B 种树苗的数量少于 A 种树苗的数量，∴21﹣x＜x，解得：x＞10.5，又∵y=20x+1470，且x 取整数，∴当x=11 时，y 有最小值=1690，∴使费用最的方案是购置 B 种树苗 10 棵，A 种树苗 11 棵，所需费用为1690 元．【点评】此题考察的是一元一次不等式及一次函数的应用，解决问题的关键是读懂题意，找到关键描绘语，进而找到所求的量的等量关系和不等关系．4.〔2021 年〕两种型号的垃圾处理设备一共 10 台．每台 A 型设备日处理才能为 12 吨；每台B 型设备日处理才能为15 吨；购回的设备日处理才能不低于140 吨．〔1〕请你为该景区设计购置两种设备的方案；〔2〕每台A 型设备价格为3 万元，每台B 型设备价格为万元．厂家为了促销产品，规定货款不低于40 万元时，那么按9 折优惠；问：采用〔1〕设计的哪种方案，使购置费用最少，为什么？【分析】〔1〕设购置A 种设备x 台，那么购置B 种设备〔10﹣x〕台，根据购回的设备日处理才能不低于140 吨列出不等式12x+15〔10﹣x〕≥140，求出解集，再根据x 为正整数，得出x=1，2，3．进而求解即可；〔2〕分别求出各方案实际购置费用，比拟即可求解．【解答】解：〔1〕设购置A 种设备x 台，那么购置B 种设备〔10﹣x〕台，根据题意，得12x+15〔10﹣x〕≥140，解得x≤31，3∵x为正整数，∴x=1，2，3．制卷人：歐陽文化、歐陽理複；制卷時間：二O二二年二月七日∴该景区有三种设计方案：方案一：购置 A 种设备 1 台，B 种设备 9 台；方案二：购置 A 种设备 2台，B 种设备8 台；方案三：购置A种设备3 台，B 种设备7 台；〔2〕各方案购置费用分别为：方案一：3×1+4.4×9=42.6＞40，实际付款：42.6×0.9=38.34〔万元〕；方案二：3×2+4.4×8=41.2＞40，实际付款：41.2×0.9=37.08〔万元〕；方案三：3×3+4.4×7=39.8＜40，实际付款：39.8〔万元〕；∵37.08＜34＜39.8，∴采用〔1〕设计的第二种方案，使购置费用最少．【点评】此题考察了一次函数的应用，一元一次不等式的应用，分析题意，找到适宜的不等关系是解决问题的关键．5.〔2021 湘西州 12.00 分〕某商店销售A 型和B 型两种电脑，其中 A 型电脑每台的利润为400 元，B 型电脑每台的利润为 500 元．该商店方案再一次性购进两种型号的电脑一共100 台，其中B 型电脑的进货量不超过A 型电脑的2 倍，设购进A 型电脑x 台，这100 台电脑的销售总利润为y 元．〔1〕求 y 关于 x 的函数关系式；〔2〕该商店购进A 型、B 型电脑各多少台，才能使销售总利润最大，最大利润〔3〕实际进货时，厂家对 A 型电脑出厂价下调 a〔0＜a＜200〕元，且限定商店最多购进A 型电脑 60 台，假设商店保持同种电脑的售价不变，请你根据以上信息，设计出使这100 台电脑销售总利润最大的进货方案．【分析】〔1〕根据“总利润=A 型电脑每台利润×A电脑数量+B 型电脑每台利润×B电脑数量〞可得函数解析式；〔2〕根据“B型电脑的进货量不超过A 型电脑的2 倍且电脑数量为整数〞求得x 的范围，再结合〔1〕所求函数解析式及一次函数的性质求解可得；〔3〕据题意得 y=〔400+a〕x+500〔100﹣x〕，即 y=〔a﹣100〕x+50000，分三种情况讨论，①当0＜a＜100 时，y 随x 的增大而减小，②a=100 时，y=50000，③当100＜m＜200 时，a﹣100＞0，y 随 x 的增大而增大，分别进展求解．【解答】解：〔1〕根据题意，y=400x+500〔100﹣x〕=﹣100x+50000；〔2〕∵100﹣x≤2x，∴x≥1003，∵y=﹣100x+50000 中 k=﹣∴y随x 的增大而减小，∵x为正数，∴x=34 时，y 获得最大值，最大值为46600，答：该商店购进A 型34 台、B 型电脑66 台，才能使销售总利润最大，最大利润是46600 元；〔3〕据题意得，y=〔400+a〕x+500〔100﹣x〕，即y=〔a﹣100〕x+50000，1333≤x≤60①当0＜a＜100 时，y 随x 的增大而减小，∴当x=34 时，y 取最大值，即商店购进34 台A 型电脑和66 台B 型电脑的销售利润最大．②a=100 时，a﹣100=0，y=50000，即商店购进A 型电脑数量满足1333≤x≤60的整数时，均获得最大利润；③当100＜a＜200 时，a﹣100＞0，y 随x 的增大而增大，∴当x=60 时，y 获得最大值．即商店购进60 台A 型电脑和40 台B 型电脑的销售利润最大．【点评】题主要考察了一次函数的应用及一元一次不等式的应用，解题的关键是根据一次函数x值的增大而确定y 值的增减情况．6.〔2021••7分〕绿水青山就是金山银山〞，为保护生态环境，A，B 两村准备各自清理所属区域养鱼网箱和捕鱼网箱，每村参加清理人数及总开支如下表：人均支出费用各是多少元；〔2〕在人均支出费用不变的情况下，为节约开支，两村准备抽调 40 人一共同清理养鱼网箱和捕鱼网箱，要使总支出不超过 102000 元，且清理养鱼网箱人数小于 清理捕 鱼网箱人数，那么有哪几种分配清理人员方案？【解答】解：〔1〕设清理养鱼网箱的人均费用为 x 元，清理捕鱼网箱的人均费用 为y 元，根据题意，得1595700010+1668000x y x y +=⎧⎨=⎩，解得：20003000x y =⎧⎨=⎩， 答：清理养鱼网箱的人均费用为2000 元，清理捕鱼网箱的人均费用为3000 元；〔2〕设m 人清理养鱼网箱，那么〔40﹣m 〕人清理捕鱼网箱，根据题 意，得：20003000(40)1020040m m m m +-≤⎧⎨-⎩， 解得：18≤m＜20，∵m 为整数，∴m=18 或者m=19，那么分配清理人 员方案有两种：方案一：18 人清理养鱼网箱，22 人清理捕鱼网箱；方 案二：19 人清理养鱼网箱，21 人清理捕鱼网箱．7.〔2021··10 分〕某为改善办学条件，方案采购 A.B 两种型号的空调， 采购 3 台 A 型空调和 2 台 B 型空调，需费用 39000 元；4 台 A 型空调比 5 台 B 型空调的 费用多 6000：元．〔1〕求 A 型空调和B 型空调每台各需多少元；〔2〕假设方案采购两种型号空调一共30 台，且A 型空调的台数不少于B 型空调的一半，两种型号空调的采购总费用不超过217000 元，该校一共有哪几种采购方案？〔3〕在〔2〕的条件下，采用哪一种采购方案可使总费用最低，最低费用是多少元？【分析】〔1〕根据题意可以列出相应的方程组，从而可以解答此题；〔2〕根据题意可以列出相应的不等式组，从而可以求得有几种采购方案；〔3〕根据题意和〔2〕中的结果，可以解答此题．【解答】解：〔1〕设A 型空调和B 型空调每台各需x 元、y元，3239000456000x y x y +=⎧⎨-=⎩，解得，90006000x y =⎧⎨=⎩ ，答：A 型空调和 B 型空调每台各需 9000 元、6000元；〔2〕设购置 A 型空调 a 台，那么购置 B 型空调〔30﹣a 〕台，90006000(30)217001(30)2a a a a +-≤⎧⎪⎨≤-⎪⎩ ， 解得，10≤a≤1213，∴a=10.11.12，一共有三种采购方案，方案一：采购 A 型空调 10 台，B 型空调 20台， 方案二：采购 A 型空调 11 台，B 型空调19 台， 方案三：采购 A 型空调 12 台，B 型空调 18 台；〔3〕设总费用为 w元，w=9000a+6000〔30﹣a 〕=3000a+180000，∴当 a=10 时，w 获得最小值，此时w=210000，即采购 A 型空调 10 台，B 型空调 20 台可使总费用最低，最低费用是 210000 元．【点评】此题考察一次函数的应用、一元一次不等式组的应用、二元一次方程组的应用，解答此题的关键是明确题意，找出所求问题需要的条件，利用函数和不等式的思想解答．8.〔2021••12 分〕准备购进一批甲、乙两种办公桌假设干张，并且每买 1 张办公桌必须买2 把椅子，椅子每把100 元，假设购进20 张甲种办公桌和15 张乙种办公桌一共花费24000 元；购置10 张甲种办公桌比购置5 张乙种办公桌多花费2000 元．〔1〕求甲、乙两种办公桌每张各多少元？〔2〕假设购置甲乙两种办公桌一共 40 张，且甲种办公桌数量不多于乙种办公桌数量的3倍，请你给出一种费用最少的方案，并求出该方案所需费用．【分析】〔1〕设甲种办公桌每张x 元，乙种办公桌每张y 元，根据“甲种桌子总钱数+乙种桌子总钱数+所有椅子的钱数=24000、10 把甲种桌子钱数﹣5 把乙种桌子钱数+多出 5 张桌子对应椅子的钱数=2000〞列方程组求解可得；〔2〕设甲种办公桌购置a 张，那么购置乙种办公桌〔40﹣a〕张，购置的总费用为y，根据“总费用=甲种桌子总钱数+乙种桌子总钱数+所有椅子的总钱数〞得出函数解析式，再由“甲种办公桌数量不多于乙种办公桌数量的3 倍〞得出自变量a 的取值范围，继而利用一次函数的性质求解可得．【解答】解：〔1〕设甲种办公桌每张x 元，乙种办公桌每张y元，根据题意，得：2015700024000 10510002000x yx y++=⎧⎨-+=⎩，解得：400600 xy=⎧⎨=⎩，答：甲种办公桌每张400 元，乙种办公桌每张600 元；〔2〕设甲种办公桌购置a 张，那么购置乙种办公桌〔40﹣a〕张，购置的总费用为y，那么y=400a+600〔40﹣a〕+2×40×100=﹣200a+32000，∵a≤3〔40﹣a〕，∴a≤30，∵﹣200＜0，∴y随a 的增大而减小，∴当a=30 时，y 获得最小值，最小值为26000 元．制卷人：歐陽文化、歐陽理複；制卷時間：二O二二年二月七日。

中考数学试题中的方案问题归类（一）利用不等式组解决方案问题[2020·邵阳]2020年5月，全国“两会”召开以后，应势复苏的“地摊经济”带来了市场新活力，小丹准备购进A 、B 两种类型的便携式风扇到地摊一条街出售．已知2台A 型风扇和5台B 型风扇进价共100元，3台A 型风扇和2台B 型风扇进价共62元．（1）求A 型风扇、B 型风扇进货的单价各是多少元？（2）小丹准备购进这两种风扇共100台，根据市场调查发现，A 型风扇销售情况比B 型风扇好，小丹准备多购进A 型风扇，但数量不超过B 型风扇数量的3倍，购进A 、B 两种风扇的总金额不超过1170元．根据以上信息，小丹共有哪些进货方案？解：（1）设A 型风扇进价为每台x 元，B 型风扇进价为每台y 元，则241003262x y x y += ⎧⎨+= ⎩①②①3⨯-②×2得：11176y =， ∴16y =，把16y =代入①得：10x = ∴1016x y =⎧⎨=⎩答：A 型风扇、B 型风扇进货的单价各是10元、16元；（2）由题意得： A 型风扇进了a 个，则B 型风扇进了()100a -个，所以：()31001016(100)1170a a a a ≤- ⎧⎪⎨+-≤⎪⎩①② ∴解不等式①，得75a ≤，解不等式②，得2713a ≥ 所以不等式组的解集为：271753a ≤≤ 其中a 为正整数，所以72,73,74,75a =． ∴小丹的进货方案如下：∴或：小丹共有4种进货方案，方案1：购进A 型风扇72台，B 型风扇28台；方案2：购进A 型风扇73台，B 型风扇27台；方案3：购进A 型风扇74台，B 型风扇26台；方案4：购进A 型风扇75台，B 型风扇25台．（二）利用一次函数性质解决方案问题[2020·遵义]为倡导健康环保，自带水杯已成为一种好习惯，某超市销售甲，乙两种型号水杯，进价和售价均保持不变，其中甲种型号水杯进价为25元/个，乙种型号水杯进价为45元/个，下表是前两月两种型号水杯的销售情况：（1）求甲、乙两种型号水杯的售价；（2）第三月超市计划再购进甲、乙两种型号水杯共80个，这批水杯进货的预算成本不超过2600元，且甲种型号水杯最多购进55个，在80个水杯全部售完的情况下设购进甲种号水杯a 个，利润为w 元，写出w 与a 的函数关系式，并求出第三月的最大利润． 解：（1）设甲种型号的水杯的售价为每个x 元，乙种型号的水杯每个y 元，则 228110038242460x y x y +=⎧⎨+=⎩①② ①3⨯-②得：28840,x = 30,x ∴=把30x =代入①得：55,y =30,55x y =⎧∴⎨=⎩答：甲、乙两种型号水杯的销售单价分别为30元、55元；（2）由题意得：甲种水杯进了a 个，则乙种水杯进了()80a -个，所以：()()()30255545805800,W a a a =-+--=-+又()254580260055a a a ⎧+-≤⎨≤⎩①② 由①得：50a ≥，所以不等式组的解集为：5055,a ≤≤其中a 为正整数，所以50,51,52,53,54,55.a =∵k=-5＜0,W ∴随a 的增大而减小，当50a =时，第三月利润达到最大，最大利润为：550800550W =-⨯+=元．（三）利用二次函数解决方案问题[2020·营口]某超市销售一款“免洗洗手液”，这款“免洗洗手液”的成本价为每瓶16元，当销售单价定为20元时，每天可售出80瓶．根据市场行情，现决定降价销售．市场调查反映：销售单价每降低0.5元，则每天可多售出20瓶（销售单价不低于成本价），若设这款“免洗洗手液”的销售单价为x （元），每天的销售量为y （瓶）．（1）求每天的销售量y （瓶）与销售单价x （元）之间的函数关系式；（2）当销售单价为多少元时，销售这款“免洗洗手液”每天的销售利润最大，最大利润为多少元？解：（1）由题意得：y ＝80+20×，∴y ＝﹣40x +880；（2）设每天的销售利润为w 元，则有：w ＝（﹣40x +880）（x ﹣16）＝﹣40（x ﹣19）2+360，∵a ＝﹣40＜0，∴二次函数图象开口向下，∴当x ＝19时，w 有最大值，最大值为360元．答：当销售单价为19元时，销售这款“免洗洗手液”每天的销售利润最大，最大利润为880元．（四）利用分段函数解决方案问题[2020·黄冈] 网络销售已经成为一种热门的销售方式为了减少农产品的库存，我市市长亲自在某网络平台上进行直播销售大别山牌板栗．为提高大家购买的积极性，直播时，板栗公司每天拿出2000元现金，作为红包发给购买者．已知该板栗的成本价格为6元/kg ，每日销售量(kg)y 与销售单价x （元/kg ）满足关系式：1005000y x =-+．经销售发现，销售单价不低于成本价格且不高于30元/kg ．当每日销售量不低于4000kg 时，每千克成本将降低1元设板栗公司销售该板栗的日获利为W （元）．（1）请求出日获利W 与销售单价x 之间的函数关系式（2）当销售单价定为多少时，销售这种板栗日获利最大？最大利润为多少元？（3）当40000W ≥元时，网络平台将向板栗公可收取a 元/kg(4)a <的相关费用，若此时日获利的最大值为42100元，求a 的值．解：（1）当4000y ≥，即10050004000x -+≥，10x ∴≤．∴当610x ≤≤时，(61)(1005000)2000w x x =-+-+-2100550027000x x =-+-当1030x <≤时，(6)(1005000)2000w x x =--+-2100560032000x x =-+-．22100550027000(610)100560032000(1030)x x x w x x x ⎧-+-≤≤∴=⎨-+-<≤⎩ （2）当610x ≤≤时，2100550027000w x x =-+-． ∵对称轴为5500551022(100)2b x a =-=-=>⨯-， ∴当10x =时，max 54000200018000w =⨯-=元．当1030x <≤时，2100560032000w x x =-+-． ∵对称轴为56002822(100)b x a =-=-=⨯-， ∴当28x =时，max 222200200046400w =⨯-=元．4640018000>∴综合得，当销售单价定为28元时，日获利最大，且最大为46400元．（3）4000018000>，1030x ∴<≤，则2100560032000w x x =-+-． 令40000w =，则210056003200040000x x -+-=． 解得：1220,36x x ==．在平面直角坐标系中画出w 与x 的数示意图． 观察示意图可知：40000,2036w x ≥≤≤．又1030x <≤，2030x ∴≤≤．1(6)(1005000)2000w x a x ∴=---+-2100(5600100)320005000x a x a =-++--． 对称轴为560010012822(100)2b a x a a +=-=-=+⨯- 4a <，∴对称轴128302x a =+<． ∴当1282x a =+时，max 42100w =元． 1128610028500020004210022a a a ⎡⎤⎛⎫⎛⎫∴+---++-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦2881720a a ∴-+=，122,86a a ∴==．又4a <，2a ∴=．。

方案设计
一、选择题
二.填空题
三.解答题
1．（2014•浙江宁波，第26题14分）木匠黄师傅用长AB=3，宽BC=2的矩形木板做一个尽可能大的圆形桌面，他设计了四种方案：
方案一：直接锯一个半径最大的圆；
方案二：圆心O1、O2分别在CD、AB上，半径分别是O1C、O2A，锯两个外切的半圆拼成一个圆；
方案三：沿对角线AC将矩形锯成两个三角形，适当平移三角形并锯一个最大的圆；
方案四：锯一块小矩形BCEF拼到矩形AFED下面，利用拼成的木板锯一个尽可能大的圆．
（1）写出方案一中圆的半径；
（2）通过计算说明方案二和方案三中，哪个圆的半径较大？
（3）在方案四中，设CE=x（0＜x＜1），圆的半径为y．
①求y关于x的函数解析式；
②当x取何值时圆的半径最大，最大半径为多少？并说明四种方案中哪一个圆形桌面的半径最大．
度．则选择最小跨度，取其，即为半径．由）
=．
，。

中考数学方案题篇一：中考数学方案设计试题分类汇编中考数学方案设计试题分类汇编算一种．一、图案设计1、（XX四川乐山）认真观察图（）的4个图中阴影部分构成的图案，回答下列问题：①②③④、（XX哈尔滨）现将三张形状、大小完全相图（）（1）请写出这四个图案都具有的两个共同特征．方格纸中的每个小正方形的边长均为1，并且平特征1：______________________；行四边形纸片的每个顶点与小正方形的顶点重特征2：____________________．合（如图1、图2、图3）．（2）请在图（）中设计出你心中最美丽的分别在图1、图2、图3中，经过平行四边形纸图案，使它也具备你所写出的上述特征片的任意一个顶点画一条裁剪线，沿此裁剪线将平行四边形纸片裁成两部分，并把这两部分重新拼成符合下列要求的几何图形．要求：（1）在左边的平行四边形纸片中画一条裁剪线，图（）（2）满足条件的图形有很多，只要画正确一个，然后在右边相对应的方格纸中，按实际大小画出都可以得满分．··················所拼成的符合要求的几何图形； 9分（2）裁成的两部分在拼成几何图形时要互不重叠且不留空隙；（3）所画出的几何图形的各顶点必须与小正方形的顶点重合．2、（XX福建福州）为创建绿色校园，学校决定对一块正方形的空地进行种植花草，现向学生征集设计图案．图案要求只能用圆弧在正方形内加以设计，使正方形和所画的图弧构成的图案，既是轴对称图形又是中心对称图形．种植花草部分用阴影表示．请你在图③、图④、图⑤中画出三种不同的的设计图案．提示：在两个图案中，只有半径变化而圆心不变的图案属于同一种，例如：图①、图②只能⑤图1 A处测得对岸岸边的一根标杆B在它的正北方向，测量员从A点开始沿岸边向正东方向前进100米到达点C处，测得?ACB?68?.矩形（非正方形）图2 正方形图3 有一个角是135°的三角形（第3题图）二、代数式中的方案设计4、（XX辽宁大连）某班级为准备元旦联欢会，欲购买价格分别为2元、4元和10元的三种奖品，每种奖品至少购买一件，共买16件，恰好用50元。

中考方案设计专题八、方案设计一（10）1.（原创）丹江中学在商场购买甲、乙两种足球，用2000元购买甲种足球的数量等于用1400元购买乙种足球数量的2倍，且购买一个乙种足球比购买一个甲种足球多花20元.请解答下列问题：（1）求购买一个甲种足球、一个乙种足球各需要多少钱？（2）为响应习总书记“足球进校园”的号召，学校决定购买50个足球，此次购买甲、乙两种足球总费用超过3000元，且甲种足球最少买19个，求学校共有几种购买方案？（3）在（2）的条件下，学校又同时购买了甲、乙两种足球共6个，学校把全部足球平均分给7个足球队.每队分得两种足球数量分别相等，且每队甲种足球超过3个.直接写出这6个足球的购买方案.解：（1）设购买一个甲种足球需要x 元，一个乙种足球需要(x +20)元.则20214002000+×=x x . 解得x =50 , x +20=70,经检验x =50是原分式方程的解.答：购买一个甲种足球需要50元，一个乙种足球需要70元.（2）设学校购买甲种足球m 个，则购买乙种足球（50-m ）个.50m+70(50-m)>3000解得 m <25, ∴19≤m <25.∴m 的整数值为19、20、21、22、23、24.∴学校共有6种购买方案.（3）购买甲种足球4个，乙种足球2个；购买甲种足球5个，乙种足球1个.2．（原创）某商场销售A ，B 两种商品，售出1件A 种商品比售出1件B 种商品所得利润多100元，售出A 种商品获利30000元的件数是售出B 种商品利20000元的件数的43． （1）求每件A 种商品和每件B 种商品售出后所得利润分别为多少元； （2）由于需求量大，A 、B 两种商品很快售完，商场决定再一次购进A 、B 两种商品共34件．如果将这34件商品全部售完后所得利润不低于4000元，且A 种商品至多购进8件，求商场有哪几种购进方案；（3）在（2）的条件下，若每件A 种商品售价500元，每件B 种商品售价220元，用（2）中获得的最大利润全部用于再购进A,B两种商品，直接写出再次进货售出后所获得的利润.解：（1）设每件A种商品售出后所得利润为x元，则每件B种商品售出后所得利润为（x-100）元．由题意，得3000032000041x x=-，解得x=200 , x-100=100，经检验x=200是原分式方程的解.答：每件A种商品售出后所得利润为200元，每件B种商品售出后所得利润为100元．（2）设购进A种商品a件，则购进B种商品（34﹣a）件．由题意，得200a+100（34﹣a）≥4000，解得：6≤a≤8，∴a的整数值为6、7、8，∴34-a=28,27,26.∴商场有三种购进方案：方案一：购进A种商品6件，B种商品28件；方案二：购进A种商品7件，B种商品27件；方案三：购进A种商品8件，B种商品26件.（3）300元.3.（原创）“一带一路”的战略构想为国内许多企业的发展带来了新的机遇.某公司生产A，B两种机械设备，每台B种设备的成本是A种设备的1.5倍.公司若投入16万元生产A种设备，36万元生产B 种设备，则可生产两种设备共10台.请解答下列问题：（1）A,B两种设备每台的成本分别是多少万元；（2）若A,B两种设备每台的售价分别是6万元、10万元，公司决定生产两种设备共60台，计划销售后获利不低于126万元，且A种设备至少生产53台.求该公司有几种生产方案；（3）在(2)的条件下，销售前公司决定从这批设备中拿出一部分，赠送给“一带一路”沿线的甲国，剩余设备全部售出，公司仍获利44万元.赠送的设备采用水路运输和航空运输两种方式，共运输4次，水路运输每次运4台A种设备，航空运输每次运2台B种最备（运输过程中产生的费用由甲国承担）.直接写出水路运输的次数.（3）水路运输2次.4．（原创题）某商场计划购进一批甲、乙两种玩具，已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元，用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同．（1）求每件甲种、乙种玩具的进价分别是多少元？（2）商场计划购进甲、乙两种玩具共48件，其中甲种玩具的件数少于乙种玩具的件数，商场决定此次进货的总资金不超过1000元，求商场共有几种进货方案？（3）在(2)的条件下，若甲种玩具每件售价40元，乙种玩具每件售价55元，商场为扩大销量，推出“买一赠一”活动，顾客从这两种玩具中任购一件，就可以从两种玩具任选一件作为赠品，这批玩具全部售出后，共获利280元.直接写出（2）问中商场的进货方案.解：设甲种玩具进价x元/件，则乙种玩具进价为（40﹣x）元/件，x=15，经检验x=15是原方程的解．∴40﹣x=25．∴甲，乙两种玩具分别是15元/件，25元/件；（2）设购进甲种玩具y件，则购进乙种玩具（48﹣y）件，解得20≤y＜24．因为y是整数，甲种玩具的件数少于乙种玩具的件数，∴y取20，21，22，23，共有4种方案．（3）购进甲种玩具23件，则购进乙种玩具25件.5.（原创题）朱彤同学准备购买笔和本子送给农村希望小学的同学.在某文具店了解到某种本子的单价比某种笔的单价少4元，且用30元买这种本子的数量与用50元买这种笔的数量相同.（1）求这种笔和这种本子的单价；（2）朱彤同学打算用自己的100元压岁钱在该文具店购买这种笔和这种本子，计划100元钱刚好用完，并且笔和本子都要买，请列出所有购买的方案.（3）在（2）条件下，文具店店主了解到朱彤同学购买笔和本子要送给农村希望小学的同学，于是就又赠送给朱彤同学笔和本子共7件，这样朱彤同学购买的笔相当于打8折，购买的本子相当于打6.25折，直接写出（2）问中的购买方案.（3）购买4支笔，10个本子.6．（原创题）某市为创建全国文明城市，开展“美化绿化城市”活动，计划经过若干年使城区绿化总面积新增360万平方米．自2015年初开始实施后，实际每年绿化面积是原计划的1.6倍，这样可提前4年完成任务．（1）问实际每年绿化面积多少万平方米？（2）求城区实际绿化总面积新增y 万平方米与绿化时间x 年之间的函数解析式（不需要写出自变量的取值范围）；（3）为加大创城力度，市政府决定从2017年起加快绿化速度，要求不超过2年完成，平均每年绿化面积增加不超过74万平方米，那么实际平均每年绿化面积要增加多少万平方米？（结果以“万平方米”为单位，且为整数）解：（1）设原计划每年绿化面积为x 万平方米，则实际每年绿化面积为1.6x 万平方米，根据题意，得﹣=4解得：x=33.75，经检验x=33.75是原分式方程的解，则1.6x=1.6×33.75=54（万平方米）．答：实际每年绿化面积为54万平方米；（2）y=54x（3）设平均每年绿化面积增加a 万平方米，根据题意得54×2+2（54+a ）≥360 解得：72≤a ≤74．∴a 的整数值为72、73、74.∴每年平均增加72、73、74万平方米．7.（改编题）某校为了更好地开展球类运动，体育组决定购进一批足球、篮球，若用2400元购进篮球的数量比购进足球的数量少10个，并且足球的单价是篮球单价的43．请解答下列问题： (1)求出足球和篮球的单价；(2)若学校欲用不超过3240元，且不少于3200元购进两种球共50个，求出有哪几种购买方案？(3)在(2)的条件下，若已知足球的进价为50元，篮球的进价为65元，则在这次购买方案中，哪种方案商家获利最多？解：(1)设篮球的单价为x 元，则足球的单价为x 43元．根据题意，得 102400432400+=x x ， 解得，x=80， 经检验x=80是原分式方程的解，答：篮球和足球的单价分别为80元和60元．(2)设再次购买足球 m 个，则篮球(50-m )个．根据题意，得 ()()⎩⎨⎧≤-+≥-+．，32405080603200508060m m m m 解得，4038≤≤m ，且m 为正整数．∴m 可以取38，39或40．∴ 有三种方案：方案一：购买足球40个，篮球10个；方案二：购买足球39个，篮球11个；方案三：购买足球38个，篮球12个．(3)设购买足球m 个，篮球（50-m ）个时，总利润为W 元．W=(60-50)m + (80-65)(50-m )= -5m +750．∵-5＜0 ，∴W 随m 的增大而减小，当m =38时W 最大．∴购买足球38个，篮球12个时，商家获利最多．8.（改编题）夏季来临，商场准备购进甲、乙两种空调.已知甲种空调每台进价比乙种空调多500元，用80000元购进甲种空调的数量与用60000元购进乙种空调的数量相同.请解答下列问题：(1)求甲、乙两种空调每台的进价；(2)若甲种空调每台售价2500元，乙种空调每台售价1800元，商场欲同时购进两种 空调20台，且全部售出，请写出所获利润y (元)与甲种空调x (台)之间的函数关系式；(3)在(2)的条件下，若商场计划用不超过36000元购进空调，且甲种空调至少购进10台，并将所获得的最大利润全部用于为某敬老院购买1100元/台的A 型按摩器和700元/台的B 型按摩器．直接写出购买按摩器的方案.解：（1）设甲种空调每台进价x 元，则乙种空调每台进价（x -500）元.500-6000080000x x =， 解得x =2000经检验x =2000是原方程的解.∴x -500=1500.∴甲种空调每台进价2000元，乙种空调每台进价1500元.（2）y =200x +6000.（3）方案一：购买7台A 型按摩器，1台B 型按摩器；方案二：购买12台B 型按摩器.9.10.（原创）某商店用1000元人民币购进水果销售，过了一段时间，又用2400元人民币购进这种水果，所购数量是第一次购进数量的2倍，但每千克的价格比第一次购进的贵了2元。

方案设计一、填空题1. （2018•湖南省永州市•4分）现有A、B两个大型储油罐，它们相距2km，计划修建一条笔直的输油管道，使得A、B两个储油罐到输油管道所在直线的距离都为0.5km，输油管道所在直线符合上述要求的设计方案有 4 种．【分析】根据点A、B的可以在直线的两侧或异侧两种情形讨论即可；【解答】解：输油管道所在直线符合上述要求的设计方案有4种，如图所示；故答案为4．【点评】本题考查整体﹣应用与设计，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．二、解答题(要求同上一)1. （2018·天津·10分）某游泳馆每年夏季推出两种游泳付费方式.方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费5元；方式二：不购买会员证，每次游泳付费9元.设小明计划今年夏季游泳次数为（为正整数）.（Ⅰ）根据题意，填写下表：（Ⅱ）若小明计划今年夏季游泳的总费用为270元，选择哪种付费方式，他游泳的次数比较多？（Ⅲ）当时，小明选择哪种付费方式更合算？并说明理由.【答案】（Ⅰ）200，，180，.（Ⅱ）小明选择方式一游泳次数比较多. （Ⅲ）当时，有，小明选择方式二更合算；当时，有，小明选择方式一更合算.【解析】分析：（Ⅰ）根据题意得两种付费方式，进行填表即可；（Ⅱ）根据（1）知两种方式的关系，列出方程求解即可；（Ⅲ）当时，作差比较即可得解.详解：（Ⅰ）200，，180，.（Ⅱ）方式一：，解得.方式二：，解得.∵，∴小明选择方式一游泳次数比较多.（Ⅲ）设方式一与方式二的总费用的差为元.则，即.当时，即，得.∴当时，小明选择这两种方式一样合算.∵，∴随的增大而减小.∴当时，有，小明选择方式二更合算；当时，有，小明选择方式一更合算.点睛：本题考查一次函数的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用一次函数的性质解答．2.（2018•湖北恩施•10分）某学校为改善办学条件，计划采购A、B两种型号的空调，已知采购3台A型空调和2台B型空调，需费用39000元；4台A型空调比5台B型空调的费用多6000元．（1）求A型空调和B型空调每台各需多少元；（2）若学校计划采购A、B两种型号空调共30台，且A型空调的台数不少于B型空调的一半，两种型号空调的采购总费用不超过217000元，该校共有哪几种采购方案？（3）在（2）的条件下，采用哪一种采购方案可使总费用最低，最低费用是多少元？【分析】（1）根据题意可以列出相应的方程组，从而可以解答本题；（2）根据题意可以列出相应的不等式组，从而可以求得有几种采购方案；（3）根据题意和（2）中的结果，可以解答本题．【解答】解：（1）设A型空调和B型空调每台各需x元、y元，，解得，，答：A型空调和B型空调每台各需9000元、6000元；（2）设购买A型空调a台，则购买B型空调（30﹣a）台，，解得，10≤a≤12，∴a=10、11、12，共有三种采购方案，方案一：采购A型空调10台，B型空调20台，方案二：采购A型空调11台，B型空调19台，方案三：采购A型空调12台，B型空调18台；（3）设总费用为w元，w=9000a+6000（30﹣a）=3000a+180000，∴当a=10时，w取得最小值，此时w=210000，即采购A型空调10台，B型空调20台可使总费用最低，最低费用是210000元．【点评】本题考查一次函数的应用、一元一次不等式组的应用、二元一次方程组的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用函数和不等式的思想解答．3.（2018·广东广州·12分）友谊商店A型号笔记本电脑的售价是a元/台，最近，该商店对A型号笔记本电脑举行促销活动，有两种优惠方案，方案一：每台按售价的九折销售，方案二：若购买不超过5台，每台按售价销售，若超过5台，超过的部分每台按售价的八折销售，某公司一次性从友谊商店购买A型号笔记本电脑x台。

中考数学方案设计试题分类汇编一、图案设计1、（2007四川乐山）认真观察图（10.1）的4个图中阴影部分构成的图案，回答下列问题：（1）请写出这四个图案都具有的两个共同特征．特征1：_________________________________________________； 特征2：_________________________________________________．（2）请在图（10.2）中设计出你心中最美丽的图案，使它也具备你所写出的上述特征解：（1）特征1：都是轴对称图形；特征2：都是中心对称图形；特征3：这些图形的面积都等于4个单位面积；等 ····························· 6分 （2）满足条件的图形有很多，只要画正确一个，都可以得满分． ······· 9分2、（2007福建福州）为创建绿色校园，学校决定对一块正方形的空地进行种植花草，现向学生征集设计图案．图案要求只能用圆弧在正方形内加以设计，使正方形和所画的图弧构成的图案，既是轴对称图形又是中心对称图形．种植花草部分用阴影表示．请你在图③、图④、图⑤中画出三种不同的的设计图案．提示：在两个图案中，只有半径变化而圆心不变的图案属于同一种，例如：图①、图②只能算一种．解：以下为不同情形下的部分正确画法，答案不唯一．（满分8分）3、（2007哈尔滨）现将三张形状、大小完全相同的平行四边形透明纸片，分别放在方格纸中，方格纸中的每个小正方形的边长均为1，并且平行四边形纸片的每个顶点与小正方形的顶点重合（如图1、图2、图（10.1） 图（10.2） ① ② ③ ④ ⑤图3）．分别在图1、图2、图3中，经过平行四边形纸片的任意一个顶点画一条裁剪线，沿此裁剪线将平行四边形纸片裁成两部分，并把这两部分重新拼成符合下列要求的几何图形．要求：（1）在左边的平行四边形纸片中画一条裁剪线，然后在右边相对应的方格纸中，按实际大小画出所拼成的符合要求的几何图形；（2）裁成的两部分在拼成几何图形时要互不重叠且不留空隙；（3）所画出的几何图形的各顶点必须与小正方形的顶点重合．解：二、代数式中的方案设计4、（2007辽宁大连）某班级为准备元旦联欢会，欲购买价格分别为2元、4元和10元的三种奖品，每种奖品至少购买一件，共买16件，恰好用50元。

中考数学方案设计一、选择题二.填空题三.解答题1．（2014•浙江宁波，第26题14分）木匠黄师傅用长AB=3，宽BC=2的矩形木板做一个尽可能大的圆形桌面，他设计了四种方案：方案一：直接锯一个半径最大的圆；方案二：圆心O1、O2分别在CD、AB上，半径分别是O1C、O2A，锯两个外切的半圆拼成一个圆；方案三：沿对角线AC将矩形锯成两个三角形，适当平移三角形并锯一个最大的圆；方案四：锯一块小矩形BCEF拼到矩形AFED下面，利用拼成的木板锯一个尽可能大的圆．（1）写出方案一中圆的半径；（2）通过计算说明方案二和方案三中，哪个圆的半径较大？（3）在方案四中，设CE=x（0＜x＜1），圆的半径为y．①求y关于x的函数解析式；②当x取何值时圆的半径最大，最大半径为多少？并说明四种方案中哪一个圆形桌面的半径最大．度．则选择最小跨度，取其，即为半径．由）解得r=．方案三：设半径为r，在△AOM和△OFN中，，∴△AOM∽△OFN，∴，∴，解得r=．比较知，方案三半径较大．（3）方案四：①∵EC=x，∴新拼图形水平方向跨度为3﹣x，竖直方向跨度为2+x．类似（1），所截出圆的直径最大为3﹣x或2+x较小的．1．当3﹣x＜2+x时，即当x＞时，r=（3﹣x）；2．当3﹣x=2+x时，即当x=时，r=（3﹣）=；3．当3﹣x＞2+x时，即当x＜时，r=（2+x）．②当x＞时，r=（3﹣x）＜（3﹣）=；当x=时，r=（3﹣）=；当x＜时，r=（2+x）＜（2+）=，∴方案四，当x=时，r最大为．∵1＜＜＜，∴方案四时可取的圆桌面积最大．点评：本题考查了圆的基本性质及通过勾股定理、三角形相似等性质求解边长及分段函数的表示与性质讨论等内容，题目虽看似新颖不易找到思路，2. （2014•湘潭，第21题）某企业新增了一个化工项目，为了节约资源，保护环境，该企业决定购买A、B两种型号的污水处理设备共8台，具体情况如下表：经预算，企业最多支出89万元购买设备，且要求月处理污水能力不低于1380吨．（1）该企业有几种购买方案？（2）哪种方案更省钱，说明理由．3. （2014•益阳，第19题，10分）某电器超市销售每台进价分别为200元、170元的A、B 两种型号的电风扇，下表是近两周的销售情况：（进价、售价均保持不变，利润=销售收入﹣进货成本）（1）求A、B两种型号的电风扇的销售单价；（2）若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台，求A种型号的电风扇最多能采购多少台？（3）在（2）的条件下，超市销售完这30台电风扇能否实现利润为1400元的目标？若能，请给出相应的采购方案；若不能，请说明理由．依题意得：，解得：4.（2014•济宁，第20题8分）在数学活动课上，王老师发给每位同学一张半径为6个单位长度的圆形纸板，要求同学们：（1）从带刻度的三角板、量角器和圆规三种作图工具中任意选取作图工具，把圆形纸板分成面积相等的四部分；（2）设计的整个图案是某种对称图形．王老师给出了方案一，请你用所学的知识再设计两种方案，并完成下面的设计报告．。