当前位置：文档之家 › 2019年MBA数学真题及答案

2019年MBA数学真题及答案

  • 格式：doc
  • 大小：2.82 MB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

2019年管理类MBA综合考试数学真题及详细答案解析(word版)

2019年管理类MBA综合考试数学真题及详细答案解析(word版)

2019年管理类MBA综合考试数学真题及详细答案解析一、问题求解：第1～15小题，每小题3分，共45分。

下列每题给出A、B、C、D、E五个选项中，只有一项是符合试题要求的。

请在答题卡上将所选项字母涂黑。

1. 学科竞赛设一等奖、二等奖和三等奖，比例为1：3：8，获奖率为30%，已知10人获得一等奖，则参加竞赛的人数为（）A．300 B. 400 C. 500 D. 550 E. 600解析：（B）解法1：由一等奖：二等奖：三等奖=1：3：8，且一等奖10人，可推出二等奖、三等奖分别为30人和80人，所以获奖人数为10+30+80=120人，所以参加竞赛人数为12030%=400÷人。

解法2：设参加竞赛的人数为x，根据题意有130%10400138x x=⇒=++。

2. 为了解某公司员工的年龄结构，按男、女人数的比例进行了随机抽样，结果如下：A. 32, 30B. 32, 29.5C. 32, 27D. 30, 27E. 29.5, 27解析：（A）23+26+28+30+32+34+36+38+41==329x男23+25+27+27+29+31==276x 女329+276==3015x⨯⨯总3. 某单位采取分段收费的方式收取网络流量(单位: GB)费用，每月流量20(含)以内免费，流量20到30(含)的每GB收费1元，流量30到40(含)的每GB收费3元，流量40以上的每GB收费5元，小王这个月用了45GB的流量，则他应该交费（）A. 45元B. 65元C. 75元D. 85元E. 135元解析：（B）各个流量段所需缴费数额见下表：所以小王应该缴费0+10+30+25=65元。

4. 如图，圆O 是三角形ABC 的内切圆，若三角形ABC 的面积与周长的大小之比为1:2，则圆O 的面积为( ) A. π B.2π C. 3π D. 4π E. 5π解析：（A ）解法1：设三角形边长分别为,,a b c ，内切圆O 的半径为r ，则三角形周长L a b c =++，三角形面积12S Lr =(最好记住该结论)。

2019年MBA联考综合能力真题及答案解析

2019年MBA联考综合能力真题及答案解析
下列每题给出的A、B、C、D、E五个选项中，只有一个选项符合试题要求．
第14题
某中学的5个学科各推荐2名教师作为支教候选人，若从中选派来自不同学科的2人参加支教工作，则不同的选派方案有______
A.20种
B.24种
C.30种
D.40种
E.45种
上一题下一题
(15/15)一、问题求解
下列每题给出的A、B、C、D、E五个选项中，只有一个选项符合试题要求．
第15题
设数列{an}满足a1=0，an+1-2an=1，则a100=______
A.299-1
B.299
C.299+1
D.2100-1
E.2100+1
上一题下一题
(16~25/共10题)二、条件充分性判断
要求判断每题给出的条件(1)和(2)能否充分支持题干所陈述的结论．A、B、C、D、E五个选项为判断结果，请选择一项符合试题要求的判断．
A.条件(1)充分，但条件(2)不充分。B.条件(2)充分，但条件(1)不充分。C.条件(1)和条件(2)单独都不充分，但条件(1)和条件(2)联合起来充分。D.条件(1)充分，条件(2)也充分。E.条件(1)和条件(2)单独都不充分，条件(1)和条件(2)联合起来也不充分。
第16题
甲、乙、丙三人各自拥有不超过10本图书，甲再购入2本图书后，他们拥有图书的数量能构成等比数列。则能确定甲拥有图书的数量。
C.(x-3)2+(y+4)2=2
D.(x+3)2+(y+4)2=2
E.(x+3)2+(y-4)2=2
上一题下一题
(6/15)一、问题求解
下列每题给出的A、B、C、D、E五个选项中，只有一个选项符合试题要求．

2019年管理类MBA综合考试数学真题及详细答案解析(pdf版)

2019年管理类MBA综合考试数学真题及详细答案解析(pdf版)

2019年管理类MBA 综合考试数学真题及详细答案解析一、问题求解：第1～15小题，每小题3分，共45分。

下列每题给出的A 、B 、C 、D 、E五个选项中，只有一项是符合试题要求的。

请在答题卡上将所选项的字母涂黑。

1. 某车间计划10天完成一项任务，工作了3天后因故停工2天，若要按原计划完成任务，则工作效率需要提高（ ）.A ．20% B. 30% C. 40% D. 50% E. 60%解析：（C ）解法1：将整个任务的工作量看作单位“1”，则原计划的工作效率为110.工作3天后因故停工2天，余下的工作量为17131010-⨯=，需要5天完成，则工作效率为7751050÷=，工作效率提高了71501040%10-=.解法2：工作3天后因故停工2天,若要按原计划完成任务，就要在剩余的5天内完成原计划7天的工作量，则工作效率需要提高11757100%1100%40%157⎛⎫- ⎪⎛⎫⨯=-⨯= ⎪ ⎪⎝⎭ ⎪⎝⎭。

2. 设函数2()2(0)af x x a x=+>在(0,)+∞内的最小值为0()12f x =，则0x =( ).A. 5B. 4C. 3D. 2E. 1解析：（B ）利用三个数的均值定理求最值：a b c ++≥，且“=”只在a b c ==时取到。

322()231264a a f x x x x x x a a x x =+=++≥==⇒=， 此时有2644x x x x==⇒= 注：本解法中2x 一定要拆成两个相等的数相加，即x x +，如果拆成其它形式(如0.5 1.5x x +)，则不等式取等号的条件就不满足了。

3. 某影城统计了一季度的观众人数，如图，则一季度的男性观众人数与女性观众之比为( ) A. 3:4 B. 5:6 C. 12:13 D. 13:12 E. 4:3 解析：（C ）由图可得一季度男女观众人数分别为：男：54312++=万人； 女：63413++=万人因此一季度男女人数比为：12:134. 设实数,a b 满足6,6ab a b a b =++-=，则22a b +=( ). A. 10 B. 11 C. 12 D. 13 E. 14解析：（D ）解法1：想办法去掉绝对值，由60ab =>知,a b 同号，若同正，不妨设0a b >>，此时263a b a b a b a b a a ++-=++-==⇒=，进而62b a==，代入得2213a b +=；若同负，不妨设0a b <<，此时263a b a b a b a b a a ++-=---+=-=⇒=-，进而62b a==-，代入得2213a b +=。

2019全国MBA联考综合能力真题及答案

2019全国MBA联考综合能力真题及答案

1、某车间计划10天完成一项任务，工作3天后事故停工2天，若仍要按原计划完成任务，则工作效率要提高( )% % % % E. 60%[参考答案]C[详解]整个工程看做单位"1"，原计划的工作效率为1/10，实际的工作效率为(1-1/10x3)/( 10-3-2) =7/50，因此工作效率提高了(7/50-1/10)/(1/10)=40%，选C。

2、函数f(x)=2x+a/π²(a﹥0)，在(0，+∞)内最小值为f(x0)=12，则x0=[参考答案]B[详解]利用三个数的均值定理求最值：a+b+c≥33√abc。

f(x)=2x+a/x2=x+x+a/x2≥33√x*x*a/x2，因此最小值为33√a=12→a=64，因此x=x=64/x2→x=4，选B。

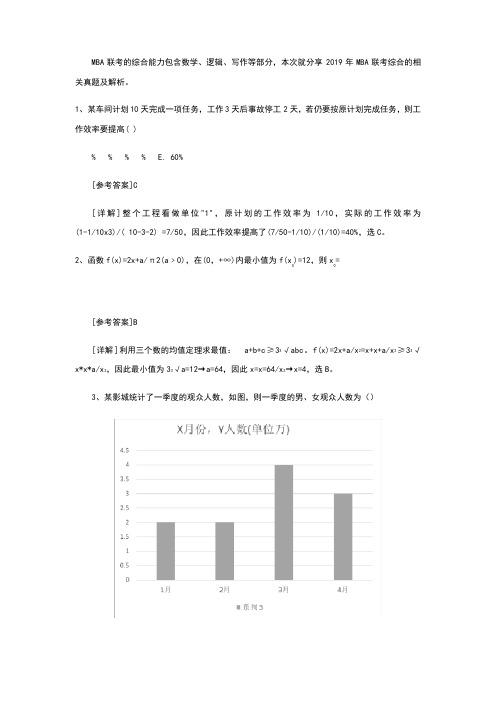
（3、某影城统计了一季度的观众人数，如图，则一季度的男、女观众人数为（）:4 :6 :13 :12 :3[参考答案]C[详解]如图可得：一季度男女观众人数分別为:男: 5w+ 4w+ 3w= 12w女: 6w+ 3w+ 4w= l3w故一季度男女人数比的: 12:13，选C。

4、;2+b2=( )5、没实数a,b満足ab=6，|a+b| +|a-b|=6，则aE. 14[参考答案]D[解析] : ab=6,特值法a=2，b=3満足条件，a2+b2=4+9=13，选D。

6、设圆C与圆(x-5)2+y2=2，关于y=2x时称，则圆C方程为( )A.(x-3)2+(y-4)2=2B.(x+4)2+(y-3)2=2B.(x-3)2+(y+4)2=2 D.(x+3)2+(y+4)2=2E.(x+3)2+(y-4)2= 2…[参考答案]E7、将一批树苗种在应该正方形花园边上，四角都种，如果每隔3米种一棵，那么剩下10课树苗,如果每隔2米种一棵那么种满正方形的3条边,则这批树苗有( ) 棵A、54B、60C、70D、82E、94[参考答案]D[详解]设正方形的边长为x，由已知可得方程4x/3+10=3x/2+1，求解得x=54故树苗有(54x4)/3+10=82，选D。

2019管综数学题

2019管综数学题

2019管综数学题2019年全国硕士研究生招生考试管理类联考综合能力试题（数学部分）一、问题求解：1. 某单位组织出游，36人排成两行，每行相邻两员工的距离相等，第一个员工在队头，从第二个员工起到队尾，每个员工所占的距离是前一个员工的倍。

求第一个员工所占的距离。

2. 甲、乙、丙三人进行象棋比赛，每两人赛一盘，规定：赢一盘得2分，输得0分，打平各得1分。

全部比赛的三盘棋下完后，甲得3分，乙得1分，那么丙得多少分。

3. 某项密码破译工作需甲、乙、丙、丁四人完成，已知每人独立译出密码的概率为，若二人合为一组则该组破译的概率为，若三人合为一组则该组破译的概率为，若四人合作则破译的概率提升到。

为完成此项工作，现有四种方案，方案1：四人独立翻译；方案2：分为两组每组两人，两组独立翻译；方案3：分为两组，一组三人、一组一人，两组独立翻译；方案4：四人一组合作翻译。

则密码能被译出的概率最大的是（）。

A.方案1B.方案2C.方案3D.方案44. 甲、乙、丙三人按任意次序站成一排，对于任何一种站法，甲都不站在两端的概率是（）A. 1/4B. 1/3C. 1/2D. 2/35. 小张用40元钱去买5元一张的电影票和2元一张的小食品，要求小食品的数量不少于电影票数量的2倍，且电影票数量不少于两张。

则不同的购买方式有（）种。

A. 3B. 4C. 5D. 6二、条件充分性判断：1. 在三角形ABC中，AB = AC，∠BAC = 120°，若AC为直径的圆O与AB相切于点D，问切线长AD与半径OC的比值是多少？（1）作过点A与BC平行的直线AM与直线BC相交于点M，且与半径OC相交于点D。

（2）连接BD、CD、AO。

A. 仅条件（1）充分B. 仅条件（2）充分C. 条件（1）（2）单独都不充分D. 条件（1）（2）联合起来充分2. 一个盒子中装有大小相同的红球、黄球和蓝球共100个，已知从盒中任意摸出n个球时，摸到红球的概率为(n-2)/3n(n∈N)。

2019年MBA联考综合真题及答案

2019年MBA联考综合真题及答案

语文成绩: 90、92、94、88、86、85、87、89、91、93
数学成绩: 94、88、96、93、90、85、84、80、82、98
语文和数学成绩的均値分别为 E1 和 E2,柝准差分别为&1 和&2，则
>E2, &1>&2 >E2, &1<&2
>E2, &1=&2
<E2, &1>&2 <E2, &1<&28
E. 14 [参考答案]D [解析] : ab=6,特值法 a=2，b=3 満足条件，a2+b2=4+9=13，选 D。 5、设圆 C 与圆(x-5)2+y2=2，关于 y=2x 时称，则圆 C 方程为( ) A. (x-3)2+(y-4)2=2 B.(x+4)2+(y-3)2=2 B. (x-3)2+(y+4)2=2 D.(x+3)2+(y+4)2=2 E. (x+3)2+(y-4)2= 2 [参考答案]E 6、将一批树苗种在应该正方形花园边上，四角都种，如果每隔 3 米种一棵，那么剩下 10 课树苗,如果每隔 2 米种一棵那么种满正方形的 3 条边,则这批树苗有( ) 棵 A、54B、60 C、70D、82 E、94 [参考答案]D [详解]设正方形的边长为 x，由已知可得方程 4x/3+10=3x/2+1，求解得 x=54 故树苗有(54x4)/3+10=82，选 D。
2、函数 f(x)=2x+a/π2(a﹥0)，在(0，+∞)内最小值为 f(x )=12，则 x =

MBA联考数学分类模拟题2019年(3)_真题(含答案与解析)-交互

MBA联考数学分类模拟题2019年(3)_真题(含答案与解析)-交互

MBA联考数学分类模拟题2019年(3)(总分107.5, 做题时间90分钟)一、问题求解1.如果0＜p<15，那么代数式|x-p|+|x-15|+|x-p-15|在p≤x≤15的最小值是______。

•**•**•**•**E.一个与p有关的代数式SSS_SIMPLE_SINA B C D E分值: 3答案:C因为p≤x≤15，所以x-p≥0，x-15≤0，x-p-15≤0，故而|x-p|+|x-15|+|x-p-15|=x-p+(15-x)+(-x+p+15)=x-p+15-x-x+p+15=-x+30，又因为p≤x≤15，所以x最大可取15，即x=15，故而-x+30=-15+30=15，应选C。

2.在数字0，1，2，…，9中任取4个(不重复)，排成一个四位偶数，这样的偶数有______．•**个•**个•**个•**个**个SSS_SIMPLE_SINA B C D E分值: 3答案:A当此四位偶数个位数为0时，前三个数字有种取法．当个位数字为2，4，6，8之一时，这样的四位偶数的千位数有8种取法；百位数有8种取法；十位数有7种取法．所以，这样的四位偶数共有故本题应选A．3.等式|2a-1|=|3a+5|-|a+6|成立，则实数a的取值范围为______．A．B．(-1，+∞)C．D．E．SSS_SIMPLE_SINA B C D E分值: 3答案:E求解绝对值方程和不等式原式可化为|a+6|+|2a-1|=|3a+5|，由三角不等式，有|2a-1|+|a+6|≥|(2a-1)+(a+6)|≥|3a+5|，当且仅当(2a-1)(a+6)≥0时，上式取等号，解得a≤-6或4.设＝4:5:6，求使x+y+z＝74成立的y值为( )．•**•**•**•****、B、C、D都不正确SSS_SIMPLE_SINA B C D E分值: 3答案:A由于＝4：5：6，因此设则代入x+y+z=74，得故正确答案为(A)．5.甲、乙、丙三人都在银行存款，乙的存款数比甲的存款数的2倍少100元，丙的存款数比甲、乙两人的存款数之和少300元，甲的存款是丙的，那么甲、乙、丙共有的存款数额是元．•** 000•** 300•** 300•** 500E.以上结论均不正确SSS_SIMPLE_SINA B C D E分值: 3答案:B设甲、乙、丙的存款额分别为x，y，z，．6.设事件A1，A2，A3相互独立，且P(Ai)=p(i=1，2，3；0＜p＜1)，则这三个事件不全发生的概率为．• A.(1-p)3•**(1-p)C.(1-p)3+3p(1-p)•**(1-p)2+3p2(1-p)**(1-p)2SSS_SIMPLE_SINA B C D E分值: 3答案:CA 1，A2，A3三个事件不全发生，即至少有一个事件不发生，故所求概率为只有选项(C) 中(1-p)3+3p(1-p)=1-p3．故选(C)．7.底半径相等的等边圆柱(轴截面是正方形)和等边圆锥(轴截面是正三角形)表面积之比为．•**:1•**:1•**:1•**:1**:1SSS_SIMPLE_SINA B C D E分值: 3答案:D8.甲、乙、丙三人参加射击训练，已知三人命中目标的概率分别为，若每人射击一次，则至少一人命中目标的概率为______．A．B．C．D．E．SSS_SIMPLE_SINA B C D E分值: 3答案:E独立事件概率三人射击相互独立，从反面求解，故9.如下图所示，已知梯形ABCD中，AB∥CD，∠A=90°，∠DBC=90°，AB=1，BC=3AD，则梯形ABCD的面积为______．A．B．C．D．E．SSS_SIMPLE_SINA B C D E分值: 3答案:A设AD=x，则根据题意，有：．所以BD=3，，DC=9．那么．或者．10.不等式的解为______．A．B．C．1＜x＜4D．2＜x＜4E．以上结论均不正确SSS_SIMPLE_SINA B C D E分值: 3答案:A设，则有所以有t＞3，即有．所以其解集为．故选A．11.从甲地到乙地，水路比公路近40公里．上午10时，一艘轮船从甲地驶往乙地，下午1时，一辆汽车从甲地开往乙地，最后船、车同时到达乙地．若汽车的速度是每小时40公里，轮船的速度是汽车的，则甲、乙两地的公路长为______．•**公里•**公里•**公里•**公里**公里SSS_SIMPLE_SINA B C D E分值: 3答案:C设甲、乙两地公路长x公里，由题意，有解得x=280(公里)．故本题应选C．12.甲、乙两仓库储存的粮食重量之比为4:3，现从甲库中调出10万吨粮食，则甲、乙两仓库存粮吨数之比为7:6．甲仓库原有粮食的万吨数为______．•**•**•**•**E.以上结论均不正确SSS_SIMPLE_SINA B C D E分值: 3答案:C设原来甲、乙粮食库存分别为4x、3x，则解得x=20，故甲原有粮食为4x=80万吨，因此选C．13.将放有乒乓球的577个盒子从左到右排成一行，如果最左边的盒子里放了6个乒乓球，且每相邻的四个盒子里共有32个乒乓球，那么最右边的盒子里的乒乓球个数为______．•**•**•**•**E.以上结论均不正确SSS_SIMPLE_SINA B C D E分值: 3答案:A设从左到右的盒内所放乒乓球个数为6，a2，a3，…，a577，由题意，有6+a2+a3+a4=32，a2+a3+a4+a5=32．二式相减，得a5=6，同理可得a9=6=a13=…=a4k+1=a577=6．故本题应选A．14.若，则•**•**•**D.-3• E.-2SSS_SIMPLE_SINA B C D E分值: 3答案:C将已知条件化简后a:b=4:3，则二、条件充分性判断• A.条件(1)充分，但条件(2)不充分。

2019年MBA综合能力数学真题+答案详解

2019年MBA综合能力数学真题+答案详解
2019 综合能力数学 -2-（共 5页）
16. 甲、乙、丙三人各自拥有不超过 10 本图书，甲再购入 2 本图书后，他们拥有图书的数
量构成等比数列，则能确定甲拥有图书的数量 .
（1）已知乙拥有图书的数量 .
（2）已知丙拥有图书的数量 .
17. 有甲、乙两袋奖券，获奖率分别为 p 和 q ，某人从两袋中各随机抽取 1 张奖券，则此
（1） = 2 + 2 ， = 1,2,3 ⋯ .
（2） = 2 + 2 + 1 ， = 1,2,3 ⋯ .
25. 设三角形区域 D 由直线 x + 8 y − 56 = 0 ，x − 6 y + 42 = 0 与 kx − y + 8 − 6k = 0(k < 0) 围成，则对
行驶时间 的关系如图所示，则 0 =（ ）.
A.72
B.80
D.95
E.100
C.90
14. 某中学的五个学科各推荐了 2 名教师作为支教候选人，若从中派来自不同学科的 2 人
参加支教工作，则不同的选派方式有（ ）.
A.20 种
B.24 种
C.30 种
0a,na+1n−
−a2na=n 1= 1 ，则 a100 =（ ）.
D. ( x + 3) 2 + ( x + 4) 2 = 2
E. ( x + 3) 2 + ( x − 4) 2 = 2
C. ( x − 3) 2 + ( x + 4) 2 = 2
5. 设实数 a, b 满足 ab = 6 ， | a + b | + | a − b |= 6 , 则 a 2 + b 2 = （ ）.

2015-2019管理类联考MBA数学真题+答案

2015-2019管理类联考MBA数学真题+答案
— 2 —
１６．
已知
ｐ，ｑ
为非零实数．
则能确定ｑ（ ｐ
ｐ －
１）
的值．
（１） ｐ ＋ ｑ ＝ １．
（２）
１ ｐ
＋
１ ｑ
＝ １．
１７． 信封中装有 １０ 张奖券，只有 １ 张有奖． 从信封中同时抽取 ２ 张奖券，中奖的概率记为 Ｐ；从信封 中每次抽取 １ 张奖券后放回，如此重复抽取 ｎ 次，中奖的概率记为 Ｑ． 则 Ｐ ＜ Ｑ． （１）ｎ ＝ ２． （２）ｎ ＝ ３．
为（ ）
Ａ． ３０ 千米
Ｂ． ４３ 千米
Ｃ． ４５ 千米
Ｄ． ５０ 千米
Ｅ． ５７ 千米
４． 在分别标记了数字 １，２，３，４，５，６ 的 ６ 张卡片中随机抽取 ３ 张， 其上数字之和等于 １０ 的概率
是（ ）
Ａ． ０． ０５
Ｂ． ０． １
Ｃ． ０． １５
Ｄ． ０． ２
Ｅ． ０． ２５
５． 某商场将每台进价为 ２０００ 元的冰箱以 ２４００ 元销售时，每天售出 ８ 台． 调研表明，这种冰箱的售价
Ａ． （ － ３，２）
Ｂ． （３， － ２）
Ｃ． （６，４）
Ｄ． （ － ６，４）
Ｅ． （６， － ４）
１１． 如图 ４，点 Ａ，Ｂ，Ｏ 的坐标分别为（４，０） ，（０，３） ，（０，０） ． 若（ ｘ，ｙ） 是 △ＡＯＢ 中的点，则 ２ｘ ＋ ３ｙ 的最大值为（ ） Ａ． ６ Ｂ． ７ Ｃ． ８ Ｄ． ９ Ｅ． １２
１２． 设抛物线 ｙ ＝ ｘ２ ＋ ２ａｘ ＋ ｂ 与 ｘ 轴相交于 Ａ，Ｂ 两点，点 Ｃ 坐标为（０，２） ． 若
△ＡＢＣ 的面积等于 ６，则（ ）
Ａ． ａ２ － ｂ ＝ ９

(时光朋解析)2019年管理类专业学位联考数学真题解析

(时光朋解析)2019年管理类专业学位联考数学真题解析

工时费共计（ ）万元.
A. 2.25
B. 2.35
C. 2.4
D. 2.45
E. 2.5
解：选
E.设每天甲、乙工时费分别为
x
、
y
万元，则
6x 4x

6 9
y y

2.4 2.35
，得
x 0.25

y

0.15
.
设单独完成工作各需
a，b
天，则
1

a 4
a

）.
A. x 32 y 42 2
B. x 42 y 32 2
B. x 32 y+42 2
D. x 32 y 42 2
E. x 32 y 42 2
解：选
E. 设 圆
C
的圆心为
a, b
1 b 9 b
1 6
1
，得
a

10
.
则甲单独完成工时费需10 0.25 2.5 .
12.如图，六边形 ABCDEF 是平面与棱长为 2 的正方体所截到的，若 A, B, D, E 分别为相
应棱的中点，则六边形 ABCDEF 的面积为（
）.
A. 3 2
B. 3
C. 2 3
D. 3 3
E. 4 3
加支教工作，则不同的选择方式有（
）种.
A. 20 C. 30 E. 45
B. 24 D. 40
解：选 D. 考虑反面：总数减去 2 人来自同一学科，则 N C120 5 45 5 40 .
或 5 个学科选 2 个学科，每个学科的人有 2 种选法，则 N C52C21C21 40 满足.

2018-2019-mba数学word版本 (8页)

2018-2019-mba数学word版本 (8页)

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==mba数学篇一：201X年全国MBA联考数学真题解析201X年全国MBA联考数学真题解析篇二：201XMBA数学真题答案详解201XMBA数学真题答案详解1. 解析：增长率问题，实际提前两天完成，即8天完成，设工作总量为a,则计划每天的工作总量为,实际每天的工作总量为a/8,设每天的产量比计划提高了x，则a/10(1+x)=a/8,解得x=25%答案 C2. 解析：工程问题，设乙丙两公司单独完成分别需要x,y天，由甲、乙两公司共同承保需28天完成可得(1/60+1/x)×28=1,同理(1/x+1/y)×35=1,解得y=105答案：E3.解析：设低于60分以下的人数最多有x人，则高于90分的人数为3x，又因为总人数为30，所以x+3x≤30，解得x≤7.5所以60分一下的人数最多为7人答案B4.解析：由于乙行走一圈需要8分钟，乙一共走了25分钟，所以乙走的圈数是25÷8=3.125(圈)甲比乙多走一圈即甲走了4.25圈。

用甲行走的路程除以甲行走的时间得出甲的速度为66答案C5.二元一次方程的应用，设甲乙两商店的进货量分别为x,y。

由题意得：(x-15):(y-10)=8:7，(x-15)-(y-10)=5联立方程解得x=55,y=45。

所以甲乙两店的总进货量为100。

6.解析：考察最基本的列项公式答案为E 的运用7.解析：考察两个相似三角形的面积和边长的关系，面积比等于相似比的平方，由题意得：△ADE∽△ABC，利用这两个相似三角形可以求出DE的长答案：D8.解析：如果点A,B关于直线ax+bx+c=0对称，则经过这两点的直线与直线ax+bx+c=0垂直，并且A,B两点到直线ax+bx+c=0的距离相等。

根据点到直线的距离公式和两直线垂直斜率的关系可以得到答案。

2019年MBA管理类联考数学真题及解析

2019年MBA管理类联考数学真题及解析

2017年管理类专业联考综合能力数学试题及解析一、问题求解：第1~15小题，每小题3分，共45分。

下列每题给出的A ．B ．C ．D ．E 五个选项中，只有一项是符合试题要求的，请在答题卡上将所选项的字母涂黑。

1、某品牌的电冰箱连续两次降价10%后的售价是降价前的（） %%%%%2、甲、乙、丙三种货车的载重量成等差数列，2辆甲种车和1辆乙种车满载量为95吨，1辆甲种车和3辆丙种车满载量为150吨。

则用甲、乙、丙各1辆车一次最多运送货物（）吨3、张老师到一所中学进行招生咨询，上午接受了45名同学的咨询，其中的9名同学下午又咨询了张老师，占张老师下午咨询学生的10%。

一天中向张老师咨询的学生人数为（）4、某种机器人可搜索到的区域是半径为1米的圆，若该机器人沿直线行走10米。

其搜索过的区域的面积（单位：平方米）为（） A.102π+B.10π+C.202π+D.20π+E.10π5、不等式12x x -+≤的解集为（） A.(],1-∞B.3,2⎛⎤-∞ ⎥⎝⎦C.31,2⎡⎤⎢⎥⎣⎦D.[)1,+∞E.3,2⎡⎫+∞⎪⎢⎣⎭6、在1与100之间，能被9整除的整数的平均值为（）7、某试卷由15道选择题组成，每道题有4个选项，只有一项是符合试题要求的，甲有6道题能确定正确选项，有5道题能排除2个错误选项，有4道题能排除1个错误选项。

若从每题排除后剩余的选项中选1个作为答案，则甲能得满分的概率为（）A.451123⋅B.541123⋅C.541123+D.541324⎛⎫⋅ ⎪⎝⎭E.541324⎛⎫+ ⎪⎝⎭8、某公司用1万元购买了价格分别是1750元和950元的甲、乙两种办公设备，则购买的甲、乙办公设备的件数分别为（） ,5,3,4,6,29、如图1，在扇形AOB 中，,1,4AOB OA AC OB π∠==⊥，则阴影部分的面积为（）A.184π- B.188π- C.142π-图1D.144π- E.148π- 10、老师问班上50名同学周末复习的情况，结果有20人复习过数学，30人复习过语文，6人复习过英语，且同时复习了数学和语文的有10人，语文和英语的有2人，英语和数学的有3人。

2019年管理类MBA综合考试数学真题及详细答案解析(word版)

2019年管理类MBA综合考试数学真题及详细答案解析(word版)

2019年管理类MBA综合考试数学真题及详细答案解析一、问题求解：第1～15小题，每小题3分，共45分。

下列每题给出A、B、C、D、E五个选项中，只有一项是符合试题要求的。

请在答题卡上将所选项字母涂黑。

1. 学科竞赛设一等奖、二等奖和三等奖，比例为1：3：8，获奖率为30%，已知10人获得一等奖，则参加竞赛的人数为（）A．300 B. 400 C. 500 D. 550 E. 600解析：（B）解法1：由一等奖：二等奖：三等奖=1：3：8，且一等奖10人，可推出二等奖、三等奖分别为30人和80人，所以获奖人数为10+30+80=120人，所以参加竞赛人数为12030%=400÷人。

解法2：设参加竞赛的人数为x，根据题意有130%10400138x x=⇒=++。

2. 为了解某公司员工的年龄结构，按男、女人数的比例进行了随机抽样，结果如下：A. 32, 30B. 32, 29.5C. 32, 27D. 30, 27E. 29.5, 27解析：（A）23+26+28+30+32+34+36+38+41==329x男23+25+27+27+29+31==276x 女329+276==3015x⨯⨯总3. 某单位采取分段收费的方式收取网络流量(单位: GB)费用，每月流量20(含)以内免费，流量20到30(含)的每GB收费1元，流量30到40(含)的每GB收费3元，流量40以上的每GB收费5元，小王这个月用了45GB的流量，则他应该交费（）A. 45元B. 65元C. 75元D. 85元E. 135元解析：（B）各个流量段所需缴费数额见下表：所以小王应该缴费0+10+30+25=65元。

4. 如图，圆O 是三角形ABC 的内切圆，若三角形ABC 的面积与周长的大小之比为1:2，则圆O 的面积为( ) A. π B.2π C. 3π D. 4π E. 5π解析：（A ）解法1：设三角形边长分别为,,a b c ，内切圆O 的半径为r ，则三角形周长L a b c =++，三角形面积12S Lr =(最好记住该结论)。

MBA联考数学模拟题2019年(15)_真题(含答案与解析)-交互

MBA联考数学模拟题2019年(15)_真题(含答案与解析)-交互

MBA联考数学模拟题2019年(15)(总分75, 做题时间180分钟)一、问题求解1.如图所示，ABCD是边长为8的正方形，都是半径为4的圆弧，且分别与AB、AD、BC、DC相切，则阴影部分的面积为______．•**•**•**•****SSS_SIMPLE_SINA B C D E该问题分值: 3答案:E连接EH、HG、GF、EF、HF、EG，则阴影部分的面积等于正方形EFGH的面积，综上所述，答案选择E．2.在梯形ABCD中，若AE∥CD，S△ABE =15，则S△BCF=______．•**•**•**•****SSS_SIMPLE_SINA B C D E该问题分值: 3答案:B连接DE，S△ABE =S△DBE，故S△ABF=S△DEF．三角形DEF与三角形CEF共底等高，故S△DEF =S△CEF，所以S△ABF=S△CEF．所以S△BCF = S△ABE=15．综上所述，答案选择B．3.如图所示，在梯形ABCD中，AB∥CD，点E为BC的中点，设△DEA的面积为S 1，梯形ABCD的面积为S2，则S1与S2的关系为______．A．B．C．D．E．SSS_SIMPLE_SINA B C D E该问题分值: 3答案:D延长DE交AB延长线于点F．△CDE≌△BFE，故S△CDE =S△BFE，所以S梯形ABCD=S△ADF．△ADE与△AEF等底同高，故S△ADE =S△AFE．综上所述，答案选择D．4.如图所示，在四边形ADEF中，EC⊥AD于C，FB⊥AD于B，已知AC=10，BD=8，FB=5，EC=6，则四边形ADEF的面积为______．•**•**•**•****SSS_SIMPLE_SINA B C D E该问题分值: 3答案:C设AB=10-x，BC=x，CD=8-x综上所述，答案选择C．5.如图所示，在梯形ABCD中，AD平行BC，AD:BC=1:2，若△ABO的面积是2，则梯形ABCD的面积是______．•**•**•**•****SSS_SIMPLE_SINA B C D E该问题分值: 3答案:C设S△ADO =x，由AD:CB=AO:CO=S△ADO:S△CDO=1:2，得S△CDO =2x，同理S△ABO=2x，S△CBO=4x，故x=1，所以梯形ABCD的面积是9．综上所述，答案选择C．6.如图所示，已知M是平行四边形ABCD的AB边的中点，CM交BD于点E，则图中阴影部分面积与四边形ABCD面积之比为______．A．B．C．D．E．SSS_SIMPLE_SINA B C D E该问题分值: 3答案:B设平行四边形ABCD的面积为S，每个小阴影部分的面积为S'△EMB与△ECD的相似比为，则．综上所述，答案选择B．7.如图所示，AB，CD是⊙O的两条互相垂直的直径，且AB=2，以点B为圆心，BA为半径画弧AE交CD延长线于点E，又四边形EFGO为正方形，则阴影部分的面积为______．A．B．C．D．E．SSS_SIMPLE_SINA B C D E该问题分值: 3答案:EBA=BE，且EO垂直平分AB，故△ABE为正三角形，∠ABE=60°，综上所述，答案选择E．8.如图所示，若△ABC的面积为1，△AEC，△DEC，△BED的面积相等，则△AED的面积=______．A．B．C．D．E．SSS_SIMPLE_SINA B C D E该问题分值: 3答案:B法一：据三角形共底等高定理，得BD=DC，则法二：S△AED =S四边形AEDC-S△ACD=S△CDE +S△ACE-S△ACD综上所述，答案选择B．9.如图所示，直角△ABC，AB =20，以AB为直径作圆O，若面积Ⅰ比面积Ⅱ大7，那么△ABC的面积等于______．•**π•**π•**π+7•**π-7**π-7SSS_SIMPLE_SINA B C D E该问题分值: 3答案:DS Ⅰ-SⅡ=7，可得SⅢ+SⅡ=50π-7．综上所述，答案选择D．10.两块等腰直角三角板，如图所示那样重合(单位为cm)，则重合部分(即阴影部分)的面积是______ cm2．•**•**•**•****SSS_SIMPLE_SINA B C D E该问题分值: 3答案:E已知△ABC，△BDE是等腰直角三角形，所以∠EBC=45°，∠ACB=45°，由此得出∠BFC=180°-45°-45°=90。

2019年MBA联考综合真题及答案

2019年MBA联考综合真题及答案

MBA联考的综合能力包含数学、逻辑、写作等部分，本次就分享2019年MBA联考综合的相关真题及解析。

1、某车间计划10天完成一项任务，工作3天后事故停工2天，若仍要按原计划完成任务，则工作效率要提高( )% % % % E. 60%[参考答案]C[详解]整个工程看做单位"1"，原计划的工作效率为1/10，实际的工作效率为(1-1/10x3)/( 10-3-2) =7/50，因此工作效率提高了(7/50-1/10)/(1/10)=40%，选C。

2、函数f(x)=2x+a/π2(a﹥0)，在(0，+∞)内最小值为f(x0)=12，则x0=[参考答案]B[详解]利用三个数的均值定理求最值：a+b+c≥33√abc。

f(x)=2x+a/x2=x+x+a/x2≥33√x*x*a/x2，因此最小值为33√a=12→a=64，因此x=x=64/x2→x=4，选B。

3、某影城统计了一季度的观众人数，如图，则一季度的男、女观众人数为（）:4 :6 :13 :12 :3[参考答案]C[详解]如图可得：一季度男女观众人数分别为:男: 5w+ 4w+ 3w= 12w女: 6w+ 3w+ 4w= l3w故一季度男女人数比的: 12:13，选C。

4、没实数a,b満足ab=6，|a+b| +|a-b|=6，则a2+b2=( )E. 14[参考答案]D[解析] : ab=6,特值法a=2，b=3満足条件，a2+b2=4+9=13，选D。

5、设圆C与圆(x-5)2+y2=2，关于y=2x时称，则圆C方程为( )A.(x-3)2+(y-4)2=2B.(x+4)2+(y-3)2=2B.(x-3)2+(y+4)2=2 D.(x+3)2+(y+4)2=2E.(x+3)2+(y-4)2= 2[参考答案]E6、将一批树苗种在应该正方形花园边上，四角都种，如果每隔3米种一棵，那么剩下10课树苗,如果每隔2米种一棵那么种满正方形的3条边,则这批树苗有( ) 棵A、54B、60C、70D、82E、94[参考答案]D[详解]设正方形的边长为x，由已知可得方程4x/3+10=3x/2+1，求解得x=54故树苗有(54x4)/3+10=82，选D。

2019管理类联考数学真题-张全军

2019管理类联考数学真题-张全军

2019届(2018年12月)管理类联考数学真题-张全军张全军 整理一、问题求解1.某车间计划10天完成一项任务，工作3天后因故停工2天，但仍需要按计划完成任务，则工作效率需要提高( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)20%(B)30%(C)40%(D)50%(E)60%2.设函数2()2(0)af x x a x=+> 在(0,)+∞的最小值为0()12f x =，则0x =( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)5(B)4(C)3(D)2(E)13.某影城统计了一季度的观众人数，如图1，则一季度的男女观众人数之比为( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)3:4(B) 5:6(C) 12:13(D)13:12(E) 4:34.设实数,a b 满足6,||||6ab a b a b =++−=，则22a b += ( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学. (A)10 (B)11 (C)12 (D)13 (E)145.设圆C 与圆22(5)2x y −+=关于2y x =对称，则圆C 的方程为( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)22(3)(4)2x y −+−= (B)22(4)(3)2x y ++−= (C)22(3)(4)2x y −++= (D)22(3)(4)2x y +++= (E)22(3)(4)2x y ++−=6.将一批树苗种在一个正方形花园边上，四角都种，如果每隔3m 种一棵树，那么剩下10棵树苗，如果每隔2m 种一棵，那么恰好种满正方形3条边，则这批树苗有( )棵. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)54(B)60(C)70(D)82(E)947.在分别标记1、2、3、4、5、6的6张卡片里，甲抽取1张，乙从余下的卡片中再抽取2张，乙的卡片的数字之和大于甲的卡片数字的概率为( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)1160(B)1360(C)4360(D)4760(E)49608.十名同学的语文和数学成绩如下：1212号“MBAliankaoshuxue”MBA联考数学.(A)E1>E2, δ1>δ2(B)E1>E2, δ1<δ2(C)E1>E2, δ1=δ2(D)E1<E2, δ1>δ2(E)E1<E2,δ1<δ29.如图，正方体于半径为3m球内，且一面位于球的大圆上，则正方体的表面积最大为( ). 解析请关注公众号“MBAliankaoshuxue”MBA联考数学.(A)12(B)18(C)24(D)30(E)3610.在三角形ABC中，AB=4，AC=6，BC=8，D为BC的中点，则AD=( ). 解析请关注公众号“MBAliankaoshuxue”MBA联考数学.(C)3(D)11.某单位要铺设草坪，若甲乙两公司合作需6天完成，工时费共2.4万元；若甲公司单独做4天后由乙公司接着做9天完成，工时费共计2.35万元；若由甲公司单独完成该项目，则工时费共计( )万元. 解析请关注公众号“MBAliankaoshuxue”MBA联考数学.(A)2.25(B)2.35(C)2.4(D)2.45(E)2.512.如下图，六边形ABCDEF 是平面与棱长为2的正方体所截得到的，若A 、B 、D 、E 分别为相应棱的中点，则六边形ABCDEF 的面积为( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)2(C)(D)(E)13.火车行驶72千米用时1小时，其速度v 与行驶时间t 的关系如图所示，则v 0= ( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)72(B)80(C)90(D)95(E)9614.某中学的5个学科各推荐2名教师作为支教候选人，若从中选派来自不同学科的2人参加支教工作，则不同的选派方式有( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)20(B)24(C)30(D)40(E)4515.设数列{}n a 满足110,21n n a a a +=−=，则100a = ( ). 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(A)9921−(B)992(C)9921+(D)10021−(E)10021+二、条件充分性判断：16.甲、乙、丙三人各自拥有不超过10本图书，甲丙购入2本图书后，他们拥有的图书数量构成等比数列，则能确定甲拥有图书的数量. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)已知乙拥有的图书数量.(2)已知丙拥有的图书数量.17.有甲、乙两袋奖券，获奖率分别为p 和q ，某人从两袋中各随机抽取1张奖券，则此人获奖的概率不小于34.解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学. (1)已知p +q =1. (2)已知14pq =.18.直线y kx =与圆22430x y x +−+=有两个交点.解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)03k −<<.(2)02k <<.19.能确定小明年龄. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)小明年龄是完全平方数.(2)20年后小明年龄是完全平方数.20.关于x 的方程210x ax b ++−=有实根. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)0a b +=.(2)0a b −=.21.如图，已知正方形ABCD 面积，O 为BC 上一点，P 为AO 的中点，Q 为DO 上一点，则能确定三角形PQD 面积. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)O 为BC 的三等分点.(2)Q 为DO 的三等分点.22.设n 为正整数，则能确定n 除以5的余数. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)已知n 除以2的余数. (2)已知n 除以3的余数.23.某校理学院五个系每年的录取人数如下表：“MBAliankaoshuxue ”MBA 联考数学.(1)数学系录取平均分提高了3分，生物系录取平均分降低了2分. (2)化学系录取平均分提高了1分，地学系录取平均分降低了4分.24.设{}n a 的前n 项和为n S ，则数列{}n a 为等差数列. 解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学. (1)2=2,1,2,3,n S n n n +=.(2)2=21,1,2,3,n S n n n ++=.25.设三角形区域D 由直线8560x y +−=，6420x y −+=与860kx y k −+−=(0)k <组成，则对于任意的(,)x y D ∈，22lg()2x y +≤.解析请关注公众号“MBAliankaoshuxue ”MBA 联考数学.(1)(,1]k ∈−∞−.(2)1[1,)8k ∈−−.。

2019年管理类联考数学第8题

2019年管理类联考数学第8题

2019年管理类联考数学第8题
【实用版】
目录
1.题目概述
2.题目解析
3.题目答案
正文
【1.题目概述】
本文将以 2019 年管理类联考数学第 8 题为例，进行分析和解答。

这是一道典型的数学应用题，考察的是考生的逻辑思维能力和数学运算能力。

【2.题目解析】
2019 年管理类联考数学第 8 题的具体题目为：“某公司有 10 名员工，他们的月工资分别为：5000 元，5500 元，6000 元，6500 元，7000 元，7500 元，8000 元，8500 元，9000 元，9500 元。

现将这 10 名员工的工资按照从小到大的顺序排列，请问，排列后的第 5 个员工的工资是多少？”
该题主要考察了排序和逻辑思维能力。

我们可以通过以下步骤来解答这道题：
步骤一：将所有员工的工资按照从小到大的顺序排列。

步骤二：找出排列后的第 5 个员工，即可得到其工资。

【3.题目答案】
根据题目解析，我们可以得出排列后的第 5 个员工的工资为 7000 元。

【结语】
通过对 2019 年管理类联考数学第 8 题的解析，我们可以看出，这道题目虽然看起来复杂，但实际上只需要简单的排序和逻辑思维能力就可以解答出来。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2014年全国MBA联考数学真题解析2013年MBA 数学全国联考真题详解编辑：邓赐贤说明：由于试题为一题多卷，因此现场试卷中的选择题部分，不同考生有不同顺序。

请在核对答案时注意题目和选项的具体内容。

一、问题求解：第1~15题，每小题3分，共45分。

下列每题给出的A 、B 、C 、D 、E五个选项中，只有一项是符合试题要求的。

请在答题卡上将所选项的字母徐黑。

1. 某工厂生产一批零件，计划10天完成，实际提前2天完成，则每天生产量比计划平均提高了 （A ）、15% （B ）、20% （C ）、25% （D ）、30% （E ）、35% 解：选C11=(1)810x +⇒25%x =2.某工程由甲公司承包需60天，甲、乙共同承包需28天，由乙、丙两公司共同承包需35天完成，则由丙公司承包完成该工程所需的天数为 （A ）、85 （B ）、90 （C ）、95 （D ）、100 （E ）、105 解：选E设乙、丙各需x 、y 天，则111602811135x x y ⎧+=⎪⎪⎨⎪+=⎪⎩⇒105y =3.甲班有30名学生，在一次满分为100分的考试中，全班的平均成绩为90分，则成绩低于60分的学生最多有 （A ）、8名 （B ）、7名 （C ）、6名 （D ）、5名 （E ）、4名 解：选B设x 人，则3090100(30)59x x ⨯=-+⋅⇒3007.3141x =≈4.甲、乙两人同时从A 点出发，沿400米跑道同向匀速行走，25分钟后乙比甲少走了一圈，若乙行走一圈需要8分钟，则甲的速度是（单位：米/分钟） （A ）、62 （B ）、65 （C ）、66 （D ）、67 （E ）、69 解：选C设甲的速度为x ，则400()254008x -⋅=⇒66x =5.甲、乙两商店同时购进了一批某品牌的电视机，当甲店售出15台时乙售出了10台，此时两店的库存之比为8:7，库存之差为5，甲、乙两商店的总的进货量为？ （A ）、75 （B ）、80 （C ）、85 （D ）、100 （E ）、125 解：选D设甲、乙两商店的进货量分别为x 、y ，则158107(15)(10)5x y x y -⎧=⎪-⎨⎪---=⎩⇒5545x y =⎧⎨=⎩ ∴100x y +=6．已知111()...(1)(2)(2)(3)(9)(10)f x x x x x x x =+++++++++，则(8)f =（A ）、19 （B ）、110 （C ）、116 （D ）、117 （E ）、118 解：选E根据1111()n n n n n na b b a a b =-- 11()(12f x x x =-++1)(2x ++13x -+1)(9x +++111)10110x x x -=-+++ ∴111(8)91818f =-= 7.如图1，在直角三角形ABC 中，4,3AC BC ==，DE BC BCEDDE1421223162ADE ABC DE S S BC∆∆===⇒2DE =(0,4)关于直线210x y ++=的对称点为（ ） （A ）、()2,0 （B ）、()3,0-（C ）、()6,1-（D ）、()4,2（E ）、()4,2-解：选E设对称点为(,)x y ，则4(2)100421022y x x y -⎧⋅-=-⎪⎪-⎨++⎪⋅++=⎪⎩⇒42x y =-⎧⎨=⎩ 9将体积为34cm π和332cm π的两个实心金属球溶化后铸成一个实心大球，则大球的表面积是（ ）（A ）、232cm π （B ）、236cm π （C ）、238cm π （D ）、240cm π （E ）、242cm π 解：选B设实心大球的半径为R ，则344323R πππ=+⇒3R =，2=436S R ππ⋅=表10.在25(31)x x ++的展开式中，2x 的值（ ）（A ）、5 （B ）、10 （C ）、45 （D ）、90 （E ）、95解：选E25(31)x x ++=222222(31)(31)(31)(31)(31)(31)x x x x x x x x x x x x ++++++++++++其中一个因式取2x ，另4个因式各取1，共有1515C ⋅=其中两个因式取3x ，另2个因式各取1，共有225(3)190C x ⨯=∴一共9511已知10件商品中有4件一等品，从中任取2件，至少有1件为一等品的概率（ ） （A ）、1/3 （B ）、2/3 （C ）、2/15 （D ）、8/15 （E ）、13/15 解：选B11246421023C C C C +=12．有一批水果要装箱，一名熟练工单独装箱需要10天，每天报酬为200元；一名普通工单独装箱需要15天，每天报酬为120元，由于场地限制，最多可同时安排12人装箱，若要求在一天内完成装箱任务，则支付的最少报酬为（ ） （A ）、1800元 （B ）、1840元 （C ）、1920元 （D ）、1960元 （E ）、2000元 解：选C则111101512x y x y ⎧+=⎪⎨⎪+≤⎩⇒根据选项，满足题意的6x y ==，∴选C13.已知{}n a 等差，2a 和10a 是21090x x --=的两个根，则57a a += （A ）、10- （B ）、9- （C ）、9 （D ）、10 （E ）、12解：选D5721010a a a a +=+=14.已知抛物线2y x bx c =++的对称轴为1x =，且过点(1,1)-，则（ ）（A ）、2,2b c =-=- （B ）、2,2b c == （C ）、2,2b c =-= （D ）、1,1b c =-=- （E ）、1b =，1c = 解：选A依题意：212(1)(1)1bb c ⎧-=⎪⎨⎪-+⨯-+=⎩⇒22b c =-⎧⎨=-⎩15.确定两人从A 地出发经过B,C,沿逆时针方向行走一圈回到 A 的方案（如图2）。

若从A 地出发时每人均可选大路或山道， 经过B,C 时，至多有一人可以更改道路，则不同的方案有 （A ）、16种 （B ）、24种 （C ）、36种 （D ）、48种 （E ）、64种 解：选C433=36A B C A→→→⨯⨯二、条件充分性判断：第16—25小题，每小题3分，共30分。

要求判断每题给出的条件（1）和条件（2）能否充分支持题干所陈述的结论。

A 、B 、C 、D 、E 五个选项为判断结果，请选择一项符合试题要求的判断，在答题卡上将所选字母涂黑。

(A)条件（1）充分，但条件（2）不充分。

(B)条件（2）充分，但条件（1）不充分。

(C)条件（1）和条件（2）单独都不充分，但条件（1）和条件（2）联合起来充分。

(D)条件（1）充分，条件（2）也充分。

(E)条件（1）和条件（2）单独都不充分，条件（1）和条件（2）联合起来也不充分。

16.已知二次函数()2f x ax bx c =++,则方程()0f x =有两个不同实根。

（1）0a c +=（2）0a b c ++=解：选A前提：二次函数意味着0a ≠（1）0a c +=⇒c a =-，∴222440b ac b a ∆=-=+>（2）0a b c ++=⇒b a c =--，∴2224()4()0b ac a c ac a c ∆=-=---=-≥17.ABC ∆的边长分别为,,a b c ，则ABC ∆为直角三角形，（1）22222()()0c a b a b ---=（2）ABC ∆的面积为12ab 解：选B（1）222c a b =+或22=a b ，直角或等腰（2）11sin 22ABC S ab C ab ∆==⇒sin 1C =，∴90C =18.+1p mq =为质数。

（1）m 为正整数，q 为质数。

（2）,m q 均为质数。

解：选E（1）取4m =，2q =，则4219p =⨯+=，合数（2）取3m =，5q =，则35116p =⨯+=，合数19.已知平面区域(){}221=,9,D x y x y +≤()()(){}22200,9D x y x x y y =-+-≤，12,D D 覆盖区域的边界长度为8π（1）22009x y +=（2）003x y +=.解：选A28ππ （2）如图：无法确定20.三个科室的人数分别为6,3和2，因工作需要，每晚要安排3人值班，则在两个月中可以使每晚的值班人员不完全相同。

（1）值班人员不能来自同一科室（2）值班人员来自三个不同科室解：选A（1）333116314462C C C --=>天（2）1116323662C C C =<天21.档案馆在一个库房中按装了n 个烟火感应报警器，每个报警器遇到烟火成功报警的概率均为p ，该库房遇烟火发出警报的概率达到（1）3,0.9n p ==(2)2,0.97n p ==解：选D ，三个烟火独立（1）33()1()10.10.999P A A A P A ++=-=-=（2）22()1()10.030.9991P A A P A +=-=-=22.已知,a b 是实数，则1a ≤，1b ≤（1）1a b +≤，（2）1a b -≤，解：选C显然（1）和（2）单独不成立，联立，则11a b a b ⎧+≤⎪⎨-≤⎪⎩⇒22()1()1a b a b ⎧+≤⎪⎨-≤⎪⎩ ①② ①+②⇒221a b +≤∴1a ≤，1b ≤23.某单位年终共发了100万元奖金，奖金金额分别是一等奖万元，二等奖1万元，三等奖万元，则该单位至少有100人（1）得二等奖的人数最多（2）得三等奖的人数最多解：选B设一、二、三等奖的人数分别为x ，y 、z 则（1） 1.50.5100x y z y x y z ++=⎧⎪≥⎨⎪≥⎩，任取30x =，50y =，10z =，不符合题意 （2） 1.50.5100x y z z x z y ++=⎧⎪≥⎨⎪≥⎩⇒(1.510.5)100z ++>⇒1003z >，∴34z ≥， L x y z =++，由于z 的系数最小，权重也最小，x 的系数最大，权重也最大，所以z 越小，L 越小，令34z =，34y =，则49981.53x ==， 98302343410033x y z ++=++=>24.设,,x y z 为非零实数，则23412x y z x y z+-=-+-. （1）320x y -=（2）20y z -=解：选C 显然单独不成立，联立则232x y z y⎧=⎪⎨⎪=⎩，不妨令3y =，则2x =，3y =，6z =代入即可25.设12111,,(2)n n n a a k a a a n +-===-≥.则1001011022a a a ++=.（1） 2.k =（2）是小于20的正整数.解：选D（1）当2k =时11a =，22a =，3451,1,0a a a ===，6781,1,0a a a ===，，991001011,1,0a a a ===，1021a =，∴1001011022a a a ++=（2）①当1k =时1231,1,0a a a ===，4561,1,0a a a ===，，1001011021,1,0a a a ===，∴1001011022a a a ++=②当2k =时，同（1）③当3k =时11a =，23a =，32a =，4561,1,0a a a ===，7891,1,0a a a ===，， 1001011021,1,0a a a ===，∴1001011022a a a ++=⒆当19k =时11a =，219a =，318a =，41a =，517a =，616a =，，2829301,1,0a a a ===，1001011021,1,0a a a ===，∴1001011022a a a ++=2012年1月（秋季）MBA 联考数学真题答案解析参考答案：(学苑教育)2012年MBA管理类联考真题数学参考答案1、（C） 128元2、（A） a=b+c3、（C）万元4、（B） 1/65、（B） 3003次6、（E）丙、乙、甲7、（E）8、（A） M/37元9、（C）9（3 -π/4 ）10、（D）15棵11、（A）12种12、（D）a=-10,b=813、（B）2600元14、E15、（B）200参考答案：（华章）1-5 CACBB 6-10 EEACD11-15 ADBEB 16-20 D?ABD21-25 EDDCA2011年管理类联考综合真题及答案一、问题求解：第1~15小题，每小题3分，共45分。

相关主题