小学数学几何专题
- 格式:doc
- 大小:63.50 KB
- 文档页数:4
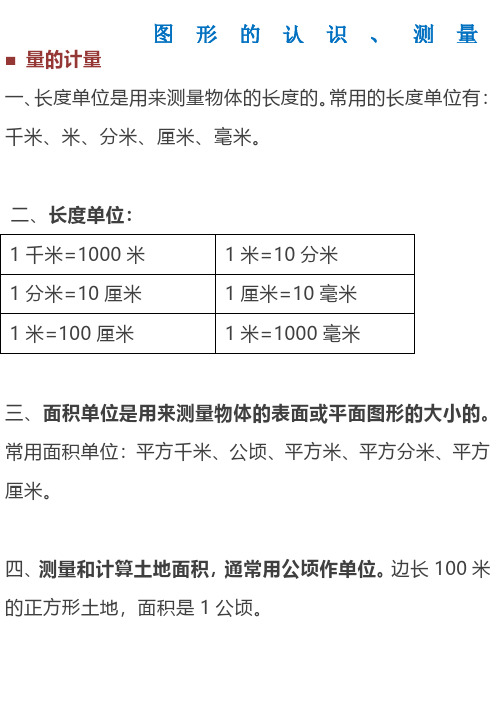
图形的认识、测量■量的计量一、长度单位是用来测量物体的长度的。
常用的长度单位有:千米、米、分米、厘米、毫米。
三、面积单位是用来测量物体的表面或平面图形的大小的。
常用面积单位:平方千米、公顷、平方米、平方分米、平方厘米。
四、测量和计算土地面积,通常用公顷作单位。
边长100米的正方形土地,面积是1公顷。
五、测量和计算大面积的土地,通常用平方千米作单位。
边长1000米的正方形土地,面积是1平方千米。
七、体积单位是用来测量物体所占空间的大小的。
常用的体积单位有:立方米、立方分米(升)、立方厘米(毫升)。
九、常用的质量单位有:吨、千克、克。
十、质量单位:十一、常用的时间单位有:世纪、年、季度、月、旬、日、时、分、秒。
十三、高级单位的名数改写成低级单位的名数应该乘以进率;低级单位的名数改写成高级单位的名数应该除以进率。
十四、常用计量单位用字母表示:■平面图形【认识、周长、面积】一、用直尺把两点连接起来,就得到一条线段;把线段的一端无限延长,可以得到一条射线;把线段的两端无限延长,可以得到一条直线。
线段、射线都是直线上的一部分。
线段有两个端点,长度是有限的;射线只有一个端点,直线没有端点,射线和直线都是无限长的。
二、从一点引出两条射线,就组成了一个角。
角的大小与两边叉开的大小有关,与边的长短无关。
角的大小的计量单位是(°)。
三、角的分类:小于90度的角是锐角;等于90度的角是直角;大于90度小于180度的角是钝角;等于180度的角是平角;等于360度的角是周角。
四、相交成直角的两条直线互相垂直;在同一平面不相交的两条直线互相平行。
五、三角形是由三条线段围成的图形。
围成三角形的每条线段叫做三角形的边,每两条线段的交点叫做三角形的顶点。
六、三角形按角分,可以分为锐角三角形、直角三角形和钝角三角形。
按边分,可以分为等边三角形、等腰三角形和任意三角形。
七、三角形的内角和等于180度。
八、在一个三角形中,任意两边之和大于第三边。

小学数学空间与图形专题(试题+答案) 图形与几何试题一、填空题(19分)1.从直线外一点到这条直线可以画无数条线段,其中最短的是与这条直线垂直的线段。
2.半圆的直径是10厘米,它的周长是π×10厘米。
3、圆柱的体积比与它等底等高的圆锥的体积大π:3.4.一个三角形中,最小的角是46°,按角分类,这个三角形是锐角三角形。
5.用百分数表示以下阴影部分是整个图形面积的百分之几。
6.把一个底面直径2分米的圆柱体截去一个高1分米的圆柱体,原来的圆柱体表面积减少π平方分米。
7.“∠ABC=60°”和“∠DEF=120°”的周长之比是2:1,面积之比是1:4.8.画一个周长25.12厘米的圆,圆规两脚间的距离是12.56厘米,画成的圆的面积是100π平方厘米。
9.一个梯形,上底长a厘米,下底长b厘米,高h厘米。
它的面积是(a+b)h/2平方厘米。
如果a=b,那么这个图形就是一个菱形。
10.在一块边长是20厘米的正方形木板上锯下一个最大的圆,这个圆的面积是100π平方厘米,剩下的边料是(400-100π)平方厘米。
11.5个棱长为30厘米的正方体木箱堆放在墙角(如下图),露在外面的表面积是1500平方厘米。
12、如图所示,把底面周长18.84厘米、高1分米的圆柱切成若干等分,拼成一个近似的长方体。
这个长方体的右侧面积是π平方厘米。
二、判断题(7分)1.小于18°的角是锐角。
(错)2.用一副三角板可以拼成105°的角。
(对)3.只要有一个角是直角的平行四边形,就是长方形或正方形。
(错)4.如果圆柱的底面周长和高相等,则它的侧面展开一定是个长方形。
(错)5.把一个长方形拉成一个平行四边形后,保持不变的是面积。
(对)6.一个正方形的边长与一个圆的直径相等,那么这个正方形的周长一定大于圆的周长。
(错)7.长6厘米的正方体,表面积和体积相等。
(错)三、选择题(每题1.5分共18分)1.有2cm,3cm,4cm,6cm长的小棒各1根,选其中的3根小棒围成三角形,最多可以围成4个。
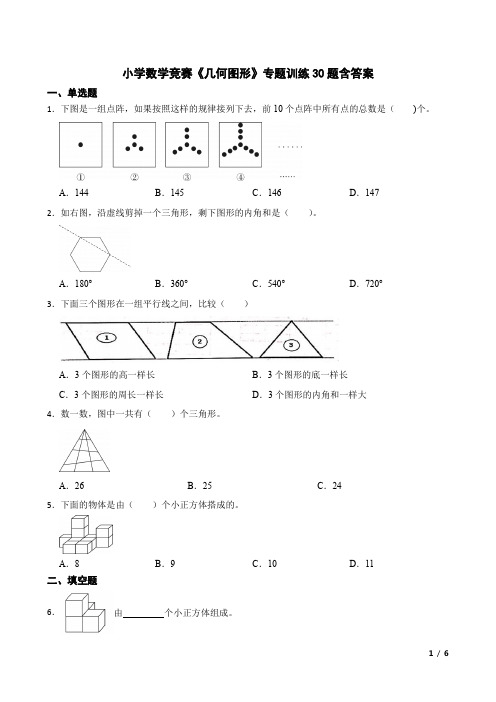
小学数学竞赛《几何图形》专题训练30题含答案一、单选题1.下图是一组点阵,如果按照这样的规律接列下去,前10个点阵中所有点的总数是()个。
A.144B.145C.146D.1472.如右图,沿虚线剪掉一个三角形,剩下图形的内角和是()。
A.180°B.360°C.540°D.720°3.下面三个图形在一组平行线之间,比较()A.3个图形的高一样长B.3个图形的底一样长C.3个图形的周长一样长D.3个图形的内角和一样大4.数一数,图中一共有()个三角形。
A.26B.25C.245.下面的物体是由()个小正方体搭成的。
A.8B.9C.10D.11二、填空题6.由个小正方体组成。
由个小正方体组成。
由个小正方体组成。
7.左图是由个正方体搭成的。
8.数一数。
(1)一共有个三角形。
(2)一共有个长方形。
9.小明用两个完全相同的三角形拼成了一个平行四边形,拼成的平行四边形的内角和是°、如果用这两个三角形拼成一个大三角形,它的内角和是°。
10.找规律,填数:10,14,38,70,,。
11.某小学有一块长方形空地,总面积50平方米,种上两种不同的植物,阴影部分种草,空白地方种菊花。
种草的面积是平方米。
12.数一数,下图有个三角形。
13.把一个棱长为4dm的正方体木块外面涂上红色,然后切割成棱长是1dm的小正方体,一面涂红色的小正方体有块,两面涂红色的小正方体有块。
14.下面每幅图分别是由几个小正方体组成的?数一数,写一写。
个个个个三、作图题15.下面是一个正方形,共16个方格。
其中有4个方格中分别画了一只小兔,请你把这个正方形分成大小、形状完全相同的4块,使每一块中都有1只小兔应怎样分割?(画粗线)16.下面的长方形中,共有28个小方格,其中有4个小方格中分别写了“我”“爱”“数”“学”四个字,请你把这个长方形沿着格线剪成大小相等的四块,而且每块中要有1个字。

专题六立体图形类型一正方体【知识讲解】一、正方体的认识:1. 特征:正方体有6个面,每个面都是正方形,所有的面都完全相同,有12条棱,所有的棱都相等,有8个顶点。
2. 正方体的棱长总和=棱长×12用字母表示:12a二、正方体表面积的计算1. 表面积:正方体6个面的总面积叫做它的表面积。
2. 正方体的表面积=棱长×棱长×6用字母表示:S=6a2三、正方体体积的计算1. 物体所占空间的大小叫做物体的体积。
2. 正方体的体积=棱长×棱长×棱长或底面积×高用字母表示: V= a3 或Sh【典例精讲】计算下面图形的表面积和体积。
【答案】表面积是54平方分米,体积是27立方分米.【解析】根据正方体的体积=棱长×棱长×棱长,表面积=棱长×棱长×6,列式计算即可。
解:3×3×6=54(平方分米);3×3×3=27(立方分米);答:正方体的表面积是54平方分米,体积是27立方分米。
【点评】此题主要考查正方体的表面积和体积公式及其计算。
【巩固练习】一、选择题。
1.下列图形中,()是正方体的展开图。
2.正方体的棱长扩大3倍,则体积扩大()倍。
A.2B.4C.27D.83.一个正方体每个面的面积都是9cm2,它的棱长是()cm。
A.9 B.54 C.34.一个正方体的棱长总和是96dm,它的表面积是()dm2。
A.384 B.1536 C.9516 D.5125.一个正方体的棱长是6dm,它的表面积和体积相比较,()A.体积大 B.表面积大 C.同样大 D.无法比较6.用棱长2厘米的正方体木块拼成一个较大的正方体,至少需要()块。
A.4B.8C.9D.647.把一个棱长为6分米的正方体切成棱长为2分米的小正方体,可以得到()小正方体。
A.27个 B.81个 C.9个8.如图是几个相同小正方体拼成的大正方体,由AB向C点斜切,没被切掉的小正方体有()个。

几何的初步知识1、平面图形的分类及概念类别概念图示线直线:没有端点、它是无限长的。
线段:有两个端点、它的长度是有限的。
射线:有一个端点,它的长度是无限的。
弧线:圆上A、B两点间的部分叫做弧。
角(由一点引出的两条射线所围成的图形)锐角:大于0°,小于90°的角。
钝角:大于90°,小于180°的角。
直角:等于90°的角。
平角:等180°的角。
周角:等于360°的角。
垂直在同一平面内相交成直角的两条直线叫做互相垂直。
平行在同一平面内不相交成直角的两条直线叫做平行。
三角形(由三条边围成的平面图形)按边分不等边三角形:三条边都不相等。
等腰三角形:有两条边相等。
等边三角形:三条边不相等。
按角分锐角三角形:三个角都是锐角。
直角三角形:有一个角都是直角。
钝角三角形:三个角都是钝角。
四边形(由四条边围成的平面图形)平行四边形(两组对边平行)→长方形(有一个角是直角)梯形(只有一组对边平行)直角梯形:有一个角是直角。
等腰梯形:两条腰相等。
圆形一条线段围绕其中一个端点旋转一圈所形成的图形叫做圆形。
扇形由两条半径和弧AB所围成的图形叫做扇形。
2、 立体图形的分类及概念 类别 概念图示正方体由6个正方形围成的立体图形,有8个顶点,12条棱。
长方体由6个长方形围成的立体图形,有8个顶点,12条棱。
圆柱体由完全相同的两个圆和一个曲面所围成的图形叫做圆柱体。
圆锥体由一个圆和一个扇形所围成的图形叫做圆锥体。
3、 平面图形的周长、面积计算公式表 图形名称 周长公式(C) 面积公式(S) 备注 长方形 (长+宽)×2即:长×宽 即: S=a ×b 用字母“a ”、“b ”分别表示长、正方形 边长×4 即:C=a ×4 边长×边长 即: S=a ×a 用字母“a ”表示边长。
平行四边形 底长×高 即:S=a ×h 用字母“a ”、“h ”分别表示底长、梯形(上底长下底长)×高÷2 用字母“a ”、“b ”、“h ” 分别三角形底长×高÷2即:S=a ×h ÷2 用字母“a ”“h ”表示底长、高。

01几何易错知识点2. 三角形具有稳定的特性,三角形两边之和大于第三边,三角形两边之差小于第三边。
3. 任何三角形都有三条高。
4. 直角三角形两个锐角的和是90度。
5. 两个三角形等底等高,则它们面积相等。
6. 面积相等的两个三角形,形状不一定相同。
三、正方形面积1. 正方形面积:边长×边长2. 正方形面积:两条对角线长度的积÷2四、三角形、四边形的关系1. 两个完全一样的三角形能组成一个平行四边形。
2. 两个完全一样的直角三角形能组成一个长方形。
3. 两个完全一样的等腰直角三角形能组成一个正方形。
4. 两个完全一样的梯形能组成一个平行四边形。
五、圆把一个圆割成一个近似的长方形,割拼成的长方形的长相当于圆周长的一半,宽相当于圆的半径。
则长方形的面积等于圆的面积,长方形的周长比圆的周长增加r×2。
半圆的周长等于圆的周长的一半加直径。
半圆的周长公式:C=pd¸2+d或C=pr+2r 在同一个圆里,半径扩大或缩小多少倍,直径和周长也扩大或缩小相同的倍数。
而面积扩大或缩小以上倍数的平方倍。
02几何图形的九大解法▌例2:下列两个正方形边长分别为8厘米和5厘米,求阴影部分面积。
解:将图形分割成3个三角形。
S=5×5÷2+5×8÷2+(8-5)×5÷2=12.5+20+7.5=38(平方厘米)▌例3:左图中两个正方形边长分别为8厘米和6厘米。
求阴影部分面积。
解:将阴影部分分割成两个三角形。
S阴=8×(8+6)÷2+8×6÷2=56+24=80(平方厘米)添辅助线▌例1:已知正方形边长4厘米,A、B、C、D是正方形边上的中点,P是任意一点。
求阴影部分面积。
解:从P点向4个定点添辅助线,由此看出,阴影部分面积和空白部分面积相等。
S阴=4×4÷2=8(平方厘米)。

小升初数学专项复习:几何的初步知识一、例题:1. 通过放大10倍的放大镜来看一个60∘的角,这个角是多少度?2. 王小明家把一块长15米,宽12米5分米的长方形草场围上篱笆,求篱笆有多长?3. 有一块正方形实验田,周长24米,它的面积是多少平方米?4. 用10.28厘米的铁丝围成一个半圆形,半圆形的面积是多少平方厘米?5. 一个长方形和一个三角形等底等高,已知三角形的面积是30平方厘米,长方形的面积是多少?6. 一块梯形棉田,上底长85米,下底长160米,高70米;在这块棉田里共收籽棉1845千克,每平方米产籽棉多少千克?二、填空题在同一平面内不相交的两条直线叫________.12个正方形可以摆成________种不同形式的长方形。
在等腰三角形中,如果顶角为124∘,底角各是________,这个三角形是________角三角形。
把两个边长都是2厘米的正方形拼成一个长方形,这个长方形的周长是________,面积是________.一个平行四边形,底是24厘米,高2分米,面积是________.一个等边三角形,周长是12.6厘米,它的边长是________厘米。
周长是28厘米的长方形,长是10厘米,面积是________.一个梯形的面积是10平方分米,高是4分米,上底是2.2分米,下底是________分米。
一个圆,周长是6.28分米,它的面积是________.圆心角是1∘的扇形的面积是________.三、判断小明画了一条25厘米长的直线。
________.(判断对错)等边三角形和等腰三角形都是锐角三角形。
________.两个面积相等的三角形一定能拼成平行四边形。
________(判断对错)平行四边形和长方形的周长相等,它们的面积也相等。
________.(判断对错)半径是2厘米的圆,它的周长和面积相等。
________.(判断对错)半圆的周长是和它相等半径的圆周长的一半。
________.(判断对错)平行四边形不是对称图形,没有对称轴。

小升初七大专题:图形与几何(专项突破)-小学数学六年级下册人教版一、选择题1.一个圆锥的体积是24cm3,底面积是8cm2,高是()cm。
A.3B.6C.9D.52.小刚有一个圆柱形的水杯,从里面量,底面直径是5cm,高是10cm。
有资料显示:“每人每天的正常饮水量大约是1L。
”小刚一天大约要喝()杯水。
A.4B.5C.3D.83.一张长方形铁皮(如图),配上底面刚好可以做一个圆柱形盒子(接头不计)。
现有A、B两种不同型号的圆片,直径分别是2分米、3分米,每种圆片各有两块。
做成的盒子体积是()立方分米。
A.108πB.9πC.12π×6.28D.1.52π×6.284.两个正方体的棱长比是2∶3,它们的体积比是()。
A.2∶3B.4∶9C.8∶27D.8∶95.如图,下面关于圆的周长的说法,正确的是()。
A.大圆的周长大于两个小圆周长的和B.大圆的周长小于两个小圆周长的和C.大圆的周长等于两个小圆周长的和D.没有数据,无法比较6.一个圆锥沿高切成相等的两部分,切面如图。
这个圆锥的体积是()立方厘米。
A.36πB.24πC.12πD.9π7.一个圆柱的底面半径是2厘米,侧面展开是一个正方形,它的高是()厘米。
A.2B.4C.12.56D.25.128.将一个圆柱削成一个最大的圆锥,削去部分为24立方厘米。
这个圆锥的体积是()立方厘米,原来圆柱的体积是()立方厘米。
A.8;24B.12;36C.24;8D.36;12二、填空题9.一个圆柱的底面半径是2米,若高增加2米,底面积不变,则表面积会增加( )平方米。
10.一根圆柱形木料的长是3米,把它截成三段小圆柱,表面积增加50.24平方米,这根木料的体积是( )立方米。
11.如下图所示,一个球的体积是( )立方厘米,两个球大小相同。
(单位:厘米)12.用一块轻黏土正好可以捏成一个底面积是12cm2,高是5cm的长方体。
如果把这块轻黏土捏成底面积是6cm2的圆柱,这个圆柱的高是( )cm。

几何问题1.问题:一个正方形的边长为5厘米,它的面积是多少平方厘米?2.问题:一个矩形的长为8厘米,宽为4厘米,它的周长是多少厘米?3.问题:一个三角形的底边长为6厘米,高为4厘米,它的面积是多少平方厘米?4.问题:一个圆的半径为3厘米,它的周长是多少厘米?5.问题:一个正方形的周长为20厘米,它的边长是多少厘米?6.问题:一个梯形的上底长为5厘米,下底长为9厘米,高为6厘米,它的面积是多少平方厘米?7.问题:一个圆的直径为10厘米,它的周长是多少厘米?8.问题:一个正方形的面积为36平方厘米,它的边长是多少厘米?9.问题:一个矩形的周长为16厘米,长为6厘米,它的宽是多少厘米?10.问题:一个三角形的底边长为10厘米,高为8厘米,它的面积是多少平方厘米?11.问题:一个圆的半径为5厘米,它的面积是多少平方厘米?12.问题:一个正方形的周长为24厘米,它的面积是多少平方厘米?13.问题:一个梯形的上底长为8厘米,下底长为12厘米,高为5厘米,它的面积是多少平方厘米?14.问题:一个圆的直径为6厘米,它的面积是多少平方厘米?15.问题:一个正方形的面积为64平方厘米,它的周长是多少厘米?16.问题:一个矩形的周长为20厘米,长为8厘米,它的宽是多少厘米?17.问题:一个三角形的底边长为12厘米,高为10厘米,它的面积是多少平方厘米?18.问题:一个圆的半径为4厘米,它的周长是多少厘米?19.问题:一个正方形的周长为28厘米,它的边长是多少厘米?20.问题:一个梯形的上底长为10厘米,下底长为14厘米,高为7厘米,它的面积是多少平方厘米?21.问题:一个圆的直径为8厘米,它的周长是多少厘米?22.问题:一个正方形的面积为81平方厘米,它的边长是多少厘米?23.问题:一个矩形的周长为24厘米,长为9厘米,它的宽是多少厘米?24.问题:一个三角形的底边长为15厘米,高为12厘米,它的面积是多少平方厘米?25.问题:一个圆的半径为6厘米,它的面积是多少平方厘米?26.问题:一个正方形的周长为32厘米,它的面积是多少平方厘米?27.问题:一个梯形的上底长为12厘米,下底长为16厘米,高为8厘米,它的面积是多少平方厘米?28.问题:一个圆的直径为10厘米,它的周长是多少厘米?29.问题:一个正方形的面积为100平方厘米,它的周长是多少厘米?30.问题:一个矩形的周长为30厘米,长为12厘米,它的宽是多少厘米?答案1.25平方厘米2.24厘米3.12平方厘米4.6π厘米5.5厘米6.35平方厘米7.10π厘米8.6厘米9.2厘米10.40平方厘米11.25π平方厘米12.36平方厘米13.50平方厘米14.9π平方厘米15.16厘米16.2厘米17.60平方厘米18.8π厘米19.7厘米20.48平方厘米21.8π厘米22.9厘米23.3厘米24.90平方厘米25.36π平方厘米26.64平方厘米27.100平方厘米28.10π厘米29.20厘米30.3厘米。

小学数学图形与几何一、图形的认识和测量1、图形知识大盘点(1)点、线、角○1从一点出发可以画无数条射线,过一点可以画无数条直线,过两点只能画一条直线○2直线没有端点,可以向两端无限延伸,所以直线长度无法测量。
射线有一个端点,可以向一端无限延伸,所以直线长度无法测量。
线段有两个端点,长度可以测量。
○3从一点引出两条射线,就组成了一个角。
角的大小和角两边的长短无关。
(2)平面图形○1三角形三角形具有稳定性三角形任意两条边之和大于第三条边。
任意两条边之差都小于第三条边。
三条线段,如果两条短的线段长度之和小于第三条,则一定能围城三角形。
三角形的内角和是180度。
一个三角形,至少有2个锐角。
三角形的三个内角中,有一个角是直角的三角形叫做直角三角形;有一个角是钝角的三角形叫做钝角三角形。
三个角都是锐角的三角形叫做锐角三角形。
○2四边形两组对边分别平行四边形叫做平行四边形。
平行四边形具有不稳定性,容易变形。
只有一组对边平行的四边形叫做梯形。
两组对边分别平行且相等,四个角都是直角的四边形是长方形。
有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
四条边都相等的长方形是正方型。
长方形是特殊的平行四边形正方形是特殊的长方形、平行四边形。
○3圆圆是曲线图形在同一个圆内,所有的半径都相等,所有的直径都相等。
○4平面图形的面积和周长计算公式(3)立体图形○1长方体和正方体长方体是由6个长方形围成的立体图形。
在一个长方体中,相对的面完全相等。
(特殊情况是有两个相对的面是正方形,其它四个面都是长方形,且完全相等)长方体有12条棱,相对的棱长度相等。
可分为三组,每一组有4条棱。
长方体有8个顶点。
每个顶点连接三条棱。
长方体相邻的两条棱互相(相互)垂直。
正方体是由6个完全相同的正方形围成的立体图形。
在一个正方体中,6个面完全相等。
○2圆柱和圆锥圆柱的两个圆面叫做地面,周围的面叫做侧面;两个底面之间的距离叫做高。
圆柱的侧面是曲面,展开后可能是长方形,也可能是正方形,还可能是平行四边形。

几何图形—专题03《巧算周长》一.选择题1.(2018秋•海淀区期末)一只小蚂蚁沿着甲、乙两图分别行走一周(如图),它行走的路线( )A .一样长B .甲长C .乙长D .不确定【解答】解:根据题干分析可得,一只小蚂蚁沿着甲、乙两图分别行走一周(如图),它行走的路线都等于长5、宽2的长方形的周长,即(52)214+⨯=,答:它行走的路线一样长.故选:A .2.(2019春•上海月考)分别以一个边长为2厘米的等边三角形的三个顶点为圆心,以2厘米为半径画弧,得到如图.那么,阴影部分的周长是( )厘米.(π取3.14)A .12.56B .18.84C .15.7D .20 【解答】解:如图所示,此时60n =︒,2r =, 一条弧长602223603ππ=⨯⨯⨯=, 所以阴影图形的周长是26412.563ππ⨯==(厘米)答:阴影部分的周长是12.56厘米.故选:A .3.(2019•郴州模拟)如图,方格纸上的每个小正方形的边长都是1厘米.哪个图形的周长最长?()A.图①B.图②C.三个周长一样⨯+=厘米,【解答】解:图①的周长:2(23)10+⨯+=厘米;图②的周长:22(22)10⨯++=厘米.图③的周长:2(13)210故选:C.4.(2018春•滨湖区期末)图中图形的周长()A.等于22cm B.大于22cm C.小于22cm+⨯【解答】解:(47)2=⨯112=(米)22答:这个图形的周长是22米.故选:A.5.(2018春•江宁区期末)一个木匠有32米围栏材料,要把一块花园地围起来,下面能正好围起来的有( )种.A.1 B.2 C.3 D.4+⨯=⨯=(米)【解答】解:图一:(106)216232图二:平行四边形的斜边大于6米,周长大于32米;+⨯=⨯=(米)图三:(106)216232+⨯=⨯=(米)图四:(106)216232所以,能正好围起来的有3种.故选:C.6.计算如图的周长,至少要量()条边.A.8 B.5 C.2 D.3 【解答】解:如图所示:测量出线段①②③的长度即可求得图形的周长.故选:D.7.图中阴影部分是一个正方形,那么最大长方形的周长是()厘米.A.26 B.28 C.24 D.25+⨯【解答】解:(68)2=⨯142=(厘米)28答:最大长方形的周长是28厘米.故选:B.二.填空题8.(2018秋•长阳县期末)一个平行四边形的一条边是25厘米,它的邻边和它相差4厘米,这个平行四边形的周长是92或108厘米.【解答】解:①25421-=(厘米)+⨯(2521)2=⨯462=(厘米)22②25429+=(厘米)+⨯(2529)2=⨯542=(厘米)108答:这个平行四边形的周长是92厘米或108厘米.故答案为:92或108.9.(2019春•海淀区月考)如图,将一些宽9厘米、长18厘米的长方形按如图规律摆放,共摆10层,则一共有55个长方形,这10层构成的整个图形的周长为厘米.【解答】解:一共有:+⨯÷(110)102=⨯÷111021102=÷=(个),55周长为⨯+⨯⨯(1810910)2=⨯2702=cm540()答:一共有55个长方形,这10层构成的整个图形的周长为540cm.故答案为:55,540.10.(2018秋•西城区期末)下面是某楼房从一层到二层的楼梯示意图.每层台阶高0.172米.【解答】解:楼梯一共10个台阶,÷=(米)每层高度是:1.72100.172故答案是:0.172.11.(2019•保定模拟)图中每个正方形边长为1厘米,这个组合图形的周长12厘米.⨯⨯=(厘米);【解答】解:13412答:这个组合图形的周长是12厘米.故答案为:12.12.(2018秋•长沙月考)一个长10厘米、宽6厘米的长方形,沿对角线对折后,得到如图所示几何图形,阴影部分周长是32厘米.+⨯【解答】解:(106)2=⨯162=(厘米);32答:阴影部分周长是32厘米.故答案为:32.13.(2018•浙江模拟)把长2cm、宽1cm的长方形如图这样拼,如果拼5层,图形的周长是30cm;如果图形周长是120cm,共拼了层.+⨯⨯【解答】解:(21)25=⨯⨯32530()=;cm÷÷=(层)1202320拼5层,图形的周长是30cm;如果图形周长是120cm,共拼了20层.故答案为:30;20.14.(2012•台州校级自主招生)如图是从一个大正方形中剪去一个边长为4.8厘米的小正方形后形成的图形,已知阴影部分的周长是52厘米,那么原来大正方形的边长是10.6厘米.-⨯,【解答】解:52 4.82=-,529.642.4=(厘米);42.4410.6÷=厘米;答:原来大正方形的边长是10.6厘米.15.(2003•广州自主招生)在长方形ABCD 中,EFGH 是正方形.如果12AG =厘米,9EC = 厘米,那么长方形ABCD 的周长是 42 厘米.【解答】解:根据图形可得:12BF AG ==厘米,所以12921BF EC +=+=(厘米),即21BE EF EC BC EF ++=+=厘米,又因为EF AB =,所以可得:21AB BC +=厘米,所以长方形ABCD 的周长为:21242⨯=(厘米);答:长方形ABCD 的周长为42厘米.故答案为:42.16.(1998•广州自主招生)把长2厘米,宽1厘米的长方形如下图那样拼摆:第一层放一个,第二层放二个,第三层放三个⋯如果照这样摆下去,当摆成2008层图形时,周长是 12048 厘米.【解答】解:根据题干分析可得:摆成n 层时,图形的周长为:42n n +,当2008n =时:420082*********⨯+⨯=(厘米),答:周长为12048厘米.故答案为:12048.17.如图,等边ABC ∆的边长是5,D ,E 分别是边AB ,AC 上的点,将ADE ∆沿直线DE 折叠,点A 落在A '处,且点A '在ABC ∆外部,则阴影图形的周长等于 15 .【解答】解:阴影图形的周长是A D DB BC CE EA ''++++的总和,又根据折叠可知,ADE ∆与△A DE '关于直线DE 轴对称,即线段A D AD '=,EA EA '=.所以阴影图形的周长A D DB BC CE EA ''=++++()()AD DB BC CE EA AD DB BC CE EA =++++=++++AB BC CA =++ABC =∆的周长53=⨯15=.故答案为:15.三.判断题18.(2008•南海区校级自主招生)如图,大圆的周长与四个小圆的周长和相等. 正确 .(判断对错)【解答】解:大圆的周长与四个小圆的周长和相等,正确;故答案为:正确.四.计算题19.(2018秋•海陵区校级期末)求下面各图形的周长.(每个小正方形边长是1厘米)【解答】解:如图:(1)(43)2+⨯=⨯72=(厘米)14答:该图形的周长是14厘米.(2)(43)2+⨯=⨯72=(厘米)14答:该图形的周长是14厘米.20.(2018秋•盘龙区期末)下列图形都是用6个边长1厘米的小正方形拼成的,求出每个图形的周长.【解答】解:图A通过平移转化为长是4厘米、宽是2厘米的长方形,再加上2厘米,周长是:+⨯+(42)22122=+=(厘米);14图B通过平移转化为长是4厘米、宽是2厘米的长方形,周长是:+⨯(42)2=⨯62=(厘米);12图C通过平移转化为长是4厘米、宽是2厘米的长方形,周长是:+⨯(42)2=⨯62=(厘米).12如图:故答案为:14厘米、12厘米、12厘米.21.(2017秋•英山县期末)巧求周长.⨯=(厘米)【解答】解:(1)1054420答:这个图形的周长是420厘米.+⨯(2)(4832)2=⨯802160=(分米)答:这个图形的周长是160分米.22.(2018春•泰兴市期末)计算阴影部分的周长.⨯++⨯÷【解答】解:1528 3.1482=++÷30825.122=+3812.56=(厘米)50.56答:阴影部分的周长是50.56厘米.五.应用题23.(2018秋•新华区期末)小蚂蚁从A点出发,沿着这个图形的边爬行,它要爬多少厘米才能回到起点?【解答】解:354140⨯=(厘米)答:它要爬140厘米才能回到起点.24.用长9cm、宽5cm的长方形摆成如图所示形状,最上层是一个长方形,以下每层多一个长方形,得到的图形的周长是多少厘米?⨯+⨯⨯【解答】解:(4945)2=+⨯(3620)2=⨯562=(厘米)112答:这个图形的周长为112厘米.25.如图,在一个长为8厘米、宽为6厘米的长方形纸片上剪去一个边长为3厘米的正方形.(1)如果剪去的正方形在右上角那么剩下的图形周长是多少厘米?(2)如果剪去的正方形在右边那么剩下的图形周长是多少厘米+⨯【解答】解:(1)(86)2=⨯142=(厘米)28答:剩下的图形周长是28厘米.+⨯+⨯(2)(86)232=⨯+1426286=+=(厘米)34答:剩下的图形周长是34厘米.26.如图是由6个周长为24厘米的正方形拼成的图形,小蚂蚁沿着外围爬一圈,一共爬了多少厘米?÷=(厘米)【解答】解:24466424⨯=(厘米)⨯=(厘米)6212+⨯(2412)2=⨯362=(厘米)72答:小蚂蚁沿着外围爬一圈,一共爬了72厘米.27.下面的图形是由1个大的半圆和6个小的半圆围成的.已知最大的半圆的直径为1,求这个图形的周长是多少.(圆周率用π表示.)【解答】解:1212ππ⨯÷+⨯÷0.50.5ππ=+π=答:这个图形的周长是10π.28.在长方形中,4AB cm =,3BC cm =,5AC cm =,从图的位置开始,在直线上不滑动地每次翻滚90度.当A 点第一次落到直线上时,A 点经过的路程是多少?【解答】解:(1)在图上画出A 点旋转时的运动路线(下图红色虚线部分):(2)1112 3.1442 3.1452 3.143444⨯⨯⨯+⨯⨯⨯+⨯⨯⨯ 6.287.85 4.71=++18.84=(厘米)答:A 点经过的路程是18.84厘米.六.操作题29.在一张长8厘米、宽6厘米的长方形纸中,剪去一个边长3厘米的正方形.小林的剪法如图,请你算一算:剩下部分的周长是多少?剩下部分的面积是多少?【解答】解:(86)232+⨯+⨯=+28634=(厘米)⨯-⨯8633489=-=(平方厘米)391答:剩下部分的周长是34厘米,剩下部分的面积是391平方厘米.七.解答题30.(2019•山西模拟)已知50AB cm=,求图中三个圆的周长总和.【解答】解:3.1450157⨯=(厘米)答:这三个圆的周长总和是157厘米.31.(2018秋•南京期末)数一数,算一算,下面图形的周长各是多少厘米?⨯⨯=(厘米)【解答】解(1)52440+++++++++++⨯(2)(454321112331)2=⨯302=(厘米)60(3)(27164)2⨯+⨯+⨯(1464)2=++⨯242=⨯48=(厘米)答:三个图形的周长分别是10厘米,60厘米,48厘米.32.(2018•南京)已知50AB=厘米,则图中各圆的周长之和是157厘米.【解答】解:3.1450157⨯=(厘米);答:这几个圆的周长和是157厘米.故答案为:157.33.(2015春•海安县期中)图形计算(1)求下面图形的周长.(2)将一个三角形的小旗绕旗杆旋转一周,可以形成一个形体.这个形体的体积是多少立方厘米?(单位:厘米)【解答】解:(1)(1210)2+⨯222=⨯44=(厘米);答:这个图形的周长是44厘米.(2)三角形小旗绕着轴旋转一周可得到一个圆锥体,圆锥的体积为:213.14683⨯⨯⨯,1=⨯⨯⨯3.143683=(立方厘米).301.44答:这个形体的体积是301.44立方厘米.34.(2013秋•郧西县期中)算出各图形的周长.+⨯【解答】解:①(32)2=⨯52=;10+⨯②(43)2=⨯72=;14⨯++⨯③14(21)2=+46=;10+⨯④(43)2=⨯72=.1435.(2015秋•成都期末)求下面各图形的周长.(单位:厘米)+++=(厘米)【解答】解:(1)252530888答:图形的周长是88厘米.+⨯(2)(1537)2522=⨯=(厘米)104⨯=(厘米)2612+=(厘米)10412116答:图形的周长是116厘米.36.(2015秋•梁平县期中)如图,圆的面积和长方形OABC的面积相等,求阴影部分的周长.⨯⨯=(厘米),【解答】解:圆的周长:2 3.14425.12阴影部分的周长:1+⨯25.1225.12425.12 6.28=+31.4=(厘米);答:阴影部分的周长是31.4厘米.37.(2013秋•凉州区校级期末)爸爸汪英要为新居的楼梯铺上地毯(如图).请你帮汪英想一想,爸爸至少要买多长的地毯?【解答】解:538+=(米).答:爸爸至少要买8米多长的地毯. 38.(2013•石家庄)将两个半径分别是6厘米和9厘米的半圆如图放置,求阴影部分的周长.(结果保留到)π【解答】解:6992ππ⨯+⨯+⨯6918ππ=++1518π=+(厘米) 答:阴影部分的周长是(1518)π+厘米.。

小学数学几何专题Prepared on 21 November 2021小学数学几何专题平行四边形概念:两组对边分别平行的四边形叫做平行四边形。
性质:平行四边形的对边相等,对角相等。
面积公式:面积=底×高,S=ah三角形面积公式:面积=底×高÷2,S=ah÷2梯形概念:只有一组对边互相平行的四边形叫梯形。
有一个角是直角的梯形叫做直角梯形。
两腰相等的梯形叫做等腰梯形。
面积公式:面积=(上底+下底)×高÷2=中位线×高S=(a+b)h÷2平面图形面积公式汇总常见平面图形的面积公式汇总⑴求四边形ABCD的面积。
5D(单位:厘米)A45°B7 C⑴求四边形ABCD的面积。
D(单位:厘米)A445°B7 CAED⑵已知正方形EFGH的边长为7厘米,求正方形ABCDFH 的面积。
BGC⑶如图,一个正方形分5成五部分,中间是一个小正方形,其余四个是相同的图形,每一个都是等腰直角三角形缺了一个角,⑷求阴影部分的面积。
5∠C=90°,ADBAC=BC,CD=AD=DB=AB÷2,四个完全相同的等腰直角三角形可以拼成一个以等腰直角三角形的斜边为边长的正方形。
面积计算:S=直角边2÷2S=AC2÷2=斜边2÷4=AB2÷4⑵割补法:将一个较复杂的图形,分割或补成一个或多个简单的可计算的图形,计算出这几个简单图形的面积之后,再相加或相减。
例:右图中,和DEFG 都是正方形, 求△BDF 的面积。
GF (单位:厘米)4 解:由于△BDF 的底CDE和高都是未知的,因此,表面上我们无法直接运用公式计算面积。
为此,我们可以运用割补法,将△BDF 分割成△BDG 、△DFG 和△BGF ,先分别求出这三个小三角形的面积,再相加得到△BDF 的面积。
S △BDG =DG ×AB ÷2=4×7÷2=14(厘米2) S △DFG =DG ×GF ÷2=4×4÷2=8(厘米2) S △BGF =GF ×AG ÷2=4×(7-4)÷2=6(厘米2) S △BDF =14+8+6=28(厘米2) 答。

几何图形—专题02《长度比较问题》一.选择题1.(2019秋•迎江区期末)如图,一个正方形被分成甲和乙两部分,两部分的周长相比,甲的周长()乙的周长.A.大于B.等于C.小于【解答】解:解:因为围成甲和乙的分别是正方形的两个边长和公共曲线段,则它们的周长相等.故选:B.2.(2019秋•灵武市期末)如图图形中,周长最长的是()A.B.C.【解答】解:把图形B凹进去的线段向外平移,与图形A的周长;而图形C的周长,等于这个长方形的周长 竖着的两条较短的边长;所以周长最长的是图形C.故选:C.3.(2019秋•朝阳区期末)如图的正方形分成甲和乙两个部分,那么甲和乙的周长相比,()A.甲长B.乙长C.一样长【解答】解:因为甲的周长=长方形的长和宽和+中间的曲线的长,乙的周长=长方形的长和宽的和+中间的曲线的长所以甲的周长=乙的周长;故选:C.4.(2019秋•西城区期末)下面如图所示的四个图形中、周长相等的两个图形是()A.①和④B.②和③C.②和④D.③和④【解答】解:设每个方格的边长为1,图①阴影部分的周长为:(43)23220+⨯+⨯=;图②阴影部分的周长为:(43)214+⨯=;图③阴影部分的周长为:(43)214+⨯=;图④阴影部分的周长为:(43)21216+⨯+⨯=;故周长相等的两个图形是②和③.故选:B.5.(2019秋•隆昌市期末)下面图形的周长()A.乙最长B.丙最长C.甲乙丙一样长【解答】解:观察上图,发现:甲的周长是长10,宽6的长方形的周长; 乙的周长是长10,宽6的长方形的周长;丙的周长是长10,宽6的长方形的周长,再加上两条线段a 的长度; 所以丙的周长最长; 故选:B .6.(2019秋•成华区期末)如图,关于甲、乙两个图形的说法,正确的是( )A .它们周长、面积分别相等B .甲周长稍短,但甲的面积稍大C .乙周长稍长,但甲、乙面积相等 【解答】解:甲的长=乙的底 甲的宽=乙的高 面积:甲的面积=长⨯宽6318=⨯= 乙的面积=底⨯高6318=⨯= 所以甲乙的面积相等; 周长:甲的周长=长2⨯+宽2⨯ 乙的周长=底22a ⨯+⨯ 由于长=底,a >宽所以:底22a ⨯+⨯>长2⨯+宽2⨯即:乙的周长稍长,但是它们的面积相等.故选:C.7.下列图形中,图形甲与图形乙的周长不相等的是()A.B.C.D.【解答】解:观察图形A和C、D可知,可得图形甲与图形乙的周长都等于长方形的周长的一半与中间曲线(或直线)的和,所以它们的周长相等.B图很明显甲的周长大于乙的周长,所以它们的周长相等.故选:B.二.填空题8.(2019春•北京月考)如图,路线1是以AB为直径的半圆,路线2是四个半圆组成的曲线,一只蚂蚁要从A爬到B,则沿路线1和沿路线2所走的路程C.(A)路线1少(B)路线2少(C)路线1和路线2一样(D)无法确定【解答】解:设4个小圆的直径分别是1d ,2d ,3d ,4d , 则大圆的直径为1234()d d d d +++ 路线1的路程1234()2d d d d π=+++÷,路线2的路程12341234()2()2d d d d d d d d πππππ=+++÷=+++÷. 所以路线1和路线2的路程一样长. 故选:C .9.(2019春•简阳市 期中)一块玻璃被打碎成两块(如图)那么甲的面积 A 乙的面积,甲的周长 乙的周长.A 、大于B 、小于C 、等于【解答】解:如图可知:甲的面积明显大于乙的面积; 甲的周长是两条边长与裂纹长度之和, 乙的周长也是两条边长与裂纹长度之和, 所以周长相等. 故选:A ;C .10.(2018秋•庐江县月考)图形中周长最大的是 C ,最小的是 .【解答】解:根据题干分析可得: 设每个方格的边长为1, 图A 的周长为:(32)210+⨯=, 图B 的周长为:(42)212+⨯=, 图C 的周长为:(52)214+⨯=, 所以最大的是C ,最小的是A .故选:C ;A .11.(2017•太原模拟)如图,从边长是20cm 的正方形中剪去等边三角形B 和C 后剩下了图形A ,图形A 的周长是 100 cm .【解答】解:20312282⨯+⨯+⨯ 602416=++100()cm =答:图形A 的周长是100cm . 故答案为:100.12.(2015秋•彭州市期末)甲的周长与乙的周长 一样 长.(如图所示)【解答】解:甲的周长=长方形的一组邻边的和+中间的曲线的长, 乙的周长=长方形的另一组邻边的和+中间的曲线的长, 因为长方形对边相等,所以甲的周长与乙的周长 一样长. 故答案为:一样.13.今有长度分别为1厘米、2厘米、3厘米、⋯、9厘米长的木棍各一根(规定不许折断),从中选用若干根组成正方形,可有 9 种不同方法. 【解答】解:12945++⋯+=,小于45的4的倍数有,4,8,12,16,20,24,28,32,36,40,44,所以相对应的正方形的边长应为1厘米,2厘米,3厘米,4厘米,5厘米,6厘米,7厘米,8厘米,9厘米,10厘米,11厘米.根据题意分析可得,利用题干中的小棒能拼出的正方形只有边长为7厘米;8厘米;9厘米;10厘米,11厘米,1、边长是10厘米的正方形,边长分别为:91+,82+,73+,64+,2、边长是11的正方形,边长分别为:92+,83+,74+,65+,3、边长是9的正方形五种:边长分别为:9,81+,72+,63+;9,81+,72+,54+;9,81+,63+,54+;9,81+,72+,54+;81+,72+,63+,54+;4、边长是8的正方形,边长分别为:8,71+,62+,53+5、边长是7的正方形,边长分别为:7,61+,52+,43+; 故答案为:9. 三.判断题14.(2019秋•兴国县期末)甲、乙两只蚂蚁分别沿着边长为2cm 正方形和直径为2cm 的圆走一圈,它们的速度一样,甲先爬行完一圈. ⨯ (判断对错) 【解答】解:248⨯=(厘米) 3.142 6.28⨯=(厘米) 8 6.28>所以乙先爬完一圈,原题说法错误. 故答案为:⨯.15.(2019秋•郓城县期末)从长方形的一角剪掉一个小长方形.剩下图形和原长方形比,周长不变. √ (判断对错)【解答】解:减去一个正方形后,面积是减少了一个小正方形的面积,所以面积减少了; 因为减去一个正方形后,围成长方形的线段的和没变,所以图形的周长不变; 原题说法正确. 故答案为:√.16.(2019秋•保定期末)甲、乙两图的周长一样长. 正确 .(判断对错)【解答】解:因为长方形对边相等,即长方形两组邻边的长度和相等,甲图形的周长=长方形一组邻边的长度和+中间的曲线,乙图形的周长=长方形另一组邻边的长度和+中间的曲线,所以甲图形的周长=乙图形的周长;故答案为:正确.17.(2018秋•正定县期末)长方形中,图形A与图形B的周长相等.√(判断对错)【解答】解:A的周长=长方形的两条邻边的和+中间的曲线的长,B的周长=长方形的两条邻边的和+中间的曲线的长,所以A的周长等于B的周长;所以原题说法正确.故答案为:√.四.应用题18.从下面的正方形中剪去一个小长方形,剩下的图形面积和周长有什么变化?【解答】解:①先看面积,从正方形中剪去一个小长方形,剩下的图形面积为正方形的面积-小长方形的面积,因此剩下的图形面积减少;②再看周长,把小长方形左边的宽平移到右边,正好补成一个正方形,因此剩下的图形周长等于正方形的周长+小长方形的2个长,所以剩下的图形周长增加.答:剩下的图形面积减少,周长增加.19.如图,三只蜗牛分别沿等边三角形、正方形和圆形爬一圈,哪只蜗牛爬的路线最长?⨯=(厘米)【解答】解:339⨯=(厘米)3412⨯=(厘米)3.1439.42>>129.429答:第二只蜗牛爬的路线最长.20.如图,从小明家去外婆家有两条路可以走,走哪条路近呢?为什么?【解答】解:如图:第①条路线的长度=长方形的一条长边+一条宽边,第②条路线的长度=长方形的一条长边+一条宽边,所以两条路线同样近.五.操作题21.(2018秋•西湖区期末)用圆规和三角尺画美丽的图案.要求:在右边方框内设计2个图案,使得这2个图案阴影部分的周长与左边图例中阴影部分周长相同.【解答】解:如图所示:22.把周长相同的图形用线连起来.【解答】解:第一个图形的周长等于长方形的周长加上2条短宽边,下面第1、2个图形的周长也等于长方形的周长加上2条短宽边;第二个图形是标准的长方形,下面第3个图形经过平移可得,周长相等;连线如图:23.描一描,想一想.(1)描一描:从A到B有6条路可以走.(2)想一想:这几条路一样长吗?【解答】解:(1)如图所示:(2)上图中第一、二两种走法的路线长度为大圆的周长的一半:122C rπ=大圆.图中第三、四、五、六种走法的路线长度为:小圆的周长:2C rπ=小圆.路线长度相等.答:这几种走法路一样长.24.每组两个图形的周长是否相等?相等的打“√”,否则画“⨯”.【解答】解:故答案为:√,⨯.25.如图是两个完全一样的正方形,请你从中剪去一块(必须是长方形),使剩下部分的周长:要求:A图比原来的正方形周长增大.B图与原来的长方形周长相等.(根据要求,将剪去的部分分别在这两个图中画出来,并用阴影表示.)【解答】解:由分析可得:图A的周长多了2a的长度,图B的周长不变.六.解答题26.(2019秋•朝阳区期末)谁家离学校近?用你喜欢的方式说明理由.【解答】解:小东家到学校的路程:400300700+=(米)小立家到学校的路程:400300700+=(米)700米700=米答:两人家离学校同样近.27.(2016秋•莱阳市期末)巧算周长.【解答】解:仔细观察可看出,左上方的阶梯的水平方向的线段向上平移,垂直方向的线段向右平移.则平移后,正好围成一个长5米,宽4米的长方形,+⨯所以周长是:(45)2=⨯92=(米).18答:这个图形的周长是18米.28.(2016春•利川市月考)在一个边长是5厘米的正方形中,剪去一个长3厘米,宽2厘米的长方形,有以下三种不同的剪法.这三种剪法是面积减少周长不变的在括号里画上〇,是面积减少周长增大的在括号里画上△.【解答】解:三种剪法面积都是减少的,第一种剪法周长不变;第二种剪法周长增大,多了两个2厘米;第三种剪法周长增大,多了两个3厘米.故答案为:〇,△,△.29.(2014秋•淄川区期末)哪根绳子最长?最长的画√.【解答】解:由分析可得:30.(2014秋•遵义县校级期末)小狗和小猴进行跑步比赛.小狗从点A 出发,沿1号箭头所表示的路线跑到点B .小猴从点A 出发,沿2号箭头所表示的路线跑到点B .比赛结束后,小狗输了,可它不服气,说比赛不公平,它跑的路线比小猴的长.你认为呢?为什么?【解答】解:设小半圆的半径为1r ,2r ,3r ,则大半圆的半径为12(r r +,3)r +小狗所爬的弧长12(n r r π=+,3)r +,小猴所爬的弧长123n r n r n r πππ=++, 所以它们跑的路线一样长.。

1-6年级数学几何问题(一)图形的认识、测量量的计量一、长度单位是用来测量物体的长度的。
常用的长度单位有:千米、米、分米、厘米、毫米。
二、长度单位:1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米1米=100厘米1米=1000毫米三、面积单位是用来测量物体的表面或平面图形的大小的。
常用面积单位:平方千米、公平顷方、米、平方分米、平方厘米。
四、测量和计算土地面积,通常用公顷作单位。
边长100米的正方形土地,面积是1公顷。
五、测量和计算大面积的土地,通常用平方千米作单位。
边长1000米的正方形土地,面积是1平方千米。
六、面积单位:(100)1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米七、体积单位是用来测量物体所占空间的大小的。
常用的体积单位有:立方米、立方分米(升)、立方厘米(毫升)八。
、体积单位:(1000)1立方米=1000立方分米1立方分米=1000立方厘米1升=1000毫升九、常用的质量单位有:吨、千克、克。
十、质量单位:十三、高级单位的名数改写成低级单位的名数应该乘以进率;低级单位的名数改写成高级位单的名数应该除以进率。
十四、常用计量单位用字母表示:千米:km 米:m 分米:dm 厘米:cm 毫米:mm 吨:t 千克:kg 克:g 升:l 毫升:ml平面图形【认识、周长、面积】一、用直尺把两点连接起来,就得到一条线段;把线段的一端无限延长,可以得到一条射把线线;段的两端无限延长,可以得到一条直线。
线段、射线都是直线上的一部分。
线段有两个端点,长度是有限的;射线只有一个端点,直线没有端点,射线和直线都是无限长的。
二、从一点引出两条射线,就组成了一个角。
角的大小与两边叉开的大小有关,与边的长无短关。
角的大小的计量单位是(°)。
三、角的分类:小于90度的角是锐角;等于90度的角是直角;大于90度小于180度的角1吨=1000千克十一、常用的时间单位有:世纪、年、季度、月、旬、十二、时间单位:(60)1世纪=100年 1年=4个季度 1个月=3旬小月=30天 闰年二月=29天1小时=60分1千克=1000克日、时、分、秒。

三、面积单位是用来测量物体的表面或平面图形的大小的。
常七、体积单位是用来测量物体所占空间的大小的。
常用的体积单位有:立方米、立方分米(升)、立方厘米(毫升)。
八、体积单位:(1000)十一、常用的时间单位有:世纪、年、季度、月、旬、日、时、十三、高级单位的名数改写成低级单位的名数应该乘以进率;平面图形【认识、周长、面积】一、用直尺把两点连接起来,就得到一条线段;把线段的一端无限延长,可以得到一条射线;把线段的两端无限延长,可以得到一条直线。
线段、射线都是直线上的一部分。
线段有两个端点,长度是有限的;射线只有一个端点,直线没有端点,射线和直线都是无限长的。
二、从一点引出两条射线,就组成了一个角。
角的大小与两边叉开的大小有关,与边的长短无关。
角的大小的计量单位是(°)。
三、角的分类:小于90度的角是锐角;等于90度的角是直角;大于90度小于180度的角是钝角;等于180度的角是平角;等于360度的角是周角。
四、相交成直角的两条直线互相垂直;在同一平面不相交的两条直线互相平行。
五、三角形是由三条线段围成的图形。
围成三角形的每条线段叫做三角形的边,每两条线段的交点叫做三角形的顶点。
六、三角形按角分,可以分为锐角三角形、直角三角形和钝角三角形。
按边分,可以分为等边三角形、等腰三角形和任意三角形。
七、三角形的内角和等于180度。
八、在一个三角形中,任意两边之和大于第三边。
九、在一个三角形中,最多只有一个直角或最多只有一个钝角。
十、四边形是由四条边围成的图形。
常见的特殊四边形有:平行四边形、长方形、正方形、梯形。
十一、圆是一种曲线图形。
圆上的任意一点到圆心的距离都相等,这个距离就是圆的半径的长。
通过圆心并且两端都在圆的线段叫做圆的直径。
十二、有一些图形,把它沿着一条直线对折,直线两侧的图形能够完全重合,这样的图形就是轴对称图形。
这条直线叫做对称轴。
十三、围成一个图形的所有边长的总和就是这个图形的周长。

几何计数例题讲解板块一:基础题型1.如图,线段AB、BC、CD、DE的长度都是3厘米.请问:图中一共有多少条线段?这些线段的长度之和是多少厘米?解:1,4+3+2+1=10段2,4×1+3×2+2×3+1×4=20厘米2.小明把巧克力棒摆成了如图所示的形状,其中每一条小短边代表一个巧克力棒.请问:(1)一共有多少个巧克力棒?(2)这些巧克力棒共构成了多少个三角形?(3)嘴馋的小明吃掉一个巧克力棒后(图中两端带有箭头的小边),剩下的图形中还有多少个三角形?解:1,(1+2+3+4)×3=30根2,(1+3+5+7)+(1+2+3+1)+(1+2)+1=27个3,27-2-2-1=22个3.如图,它是由18个大小相同的小正三角形拼成的四边形,其中某些相邻的小正三角形可以拼成较大的正三角形,图中包含“冰”的各种大小的正三角形一共有多少个?解:1+4+1=6个4.如图,数一数,两个图形中分别有多少个三角形?解:5+4+1+1+1=12个6×2+10×2=28个5.如图,在一个4x4的方格表中,共有多少个正方形?解:42+32+22+12=30个6.如图,数一数图中一共有多少条线段?多少个矩形?解:C53×4+C42×5=70条C52×C42=60个7.如图,AB、CD、EF、MN互相平行,则图中梯形个数与三角形个数的差是多少?解:C52×C42-C52×4=208.如图,125个黑色与白色小立方体相间排列拼成了一个大立方体,其中露在表面上的黑色小立方体有多少个?解:4×6+2×12=48个9.如图,木板上钉着12枚钉子,排成三行四列的长方阵.用橡皮筋一共可以套出多少个不同的三角形?解:C123-4×3-4-4=200个10.如图,在2x3的长方形中,每个小正方形的面积都是1.请问:以A、B、C、D、E、F、G为顶点且面积为1的三角形共有多少个?解:3×2+4+2+1=13个板块二:中档题型1.如图,数一数,图中有多少个三角形?解:25+10+6+3+1+3=48个2.如图,数一数下面的三个图形中分别有多少个三角形.解:10+4×5+5=35个35-6=29个35+6×2=47个3.如图,数一数,图中有多少个三角形?解:35×2+3×5=85个4.如图,数一数.,图中共有多少个长方形?(正方形是一种特殊的长方形)解:7+2+2+2+3+1=17个5.如图,四条边长度都相等的四边形称为菱形,用16个同样大小的菱形组成如图的一个大菱形.数一数,图中共有多少个菱形?解:4×4+3×3+2×2+1×1=30个6.如图,这是一个长为9,宽为4的网格,每一个小格都是一个正方形.请问:(1)从中可以数出多少个长方形?(2)从中可以数出包含黑点的长方形有多少个?解:C102×C52=450个2×3×4×6=144个7.如图,数一数,图中共有多少个长方形?解:15×6+21×3-6×3=135个8.如图,数一数,图中共有多少个平行四边形?解:6×3+15+3×2+3+3=45个9.如图,18个大小相同的小正三角形拼成了一个平行四边形,数一数,图中共有多少个梯形?解12×2+4×2+6×2+2+8+2=5610.如图,方格纸上放了20枚棋子,以这些棋子为顶点,可以连出多少个正方形?解:9+4×2+2×2=21个11.一个平面封闭图形,只要组成它的边中有一条边不是直线段,就将这个图形称为曲边形,例如圆、半圆、扇形等都是曲边形.在图中,共有多少个不同的曲边形?解:10+10+10+5+1=36个12.如图,一个2×3的网格中,每个小正方形的面积都是1.以这些格点为顶点,可以连成多少个面积为l的三角形?解:6×7+8×2+8+4=70个板块三:拔高题型1.图中是一个等边三角形的点阵.以这些点为顶点,可以画出多少个等腰三角形(包括等边三角形)?解:等边有:9+3+1+2=15个等腰有:3+2×6+6+3=24个共39个2.如图,数一数,图中共有多少个三角形?解:C72×2+C31×2×4+1=67个3.如图,这是一个4x8的矩形网格,每一个小格都是一个正方形.请问:(1)包含有两个“★”的矩形共有多少个?(2)至少包含一个“★”的矩形有多少个?解:2×1×3×5=30个3×4×6+4×2×5×3-3×2×5=162个4.如图,在图中的3×3正方形格子中,格线的交点称为格点.例如:A,B,C这3个点都是格点,那么,以格点为顶点,且完全覆盖了阴影部分小方格的三角形共有多少个?解:4×4=16个5.如图,用12个点将圆周12等分,以这些点为顶点的梯形共有多少个?解:12×(4+3+2+1)=120个6.一个平面封闭图形,只要组成它的边中有一条边不是直线段,就将这个图形称为曲边形,例如圆、半圆、扇形等都是曲边形,在图10-29中,共有多少个不同的曲边形?解:4×8+4×4+2×3+4×2+1=63个7.如图,木板上钉着16枚钉子,排成四行四列的方阵.用橡皮筋一共可以套出多少个不同的等腰三角形?解:4×6+8×(3+1+3+1)+4×(3+3+2+5+2)=148个8.如图,在3×3的方格表内,每个小正方形的面积均为1.请问:(1)以格点为顶点共可以连出多少个面积为4的三角形?(2)以格点为顶点共可以连出多少个面积为3的三角形?(3)以格点为顶点共可以连出多少个面积为1.5的三角形?解:(1)4个(2)4×10+2×4=48个(3)6×8+4×4+8+4×4+4=92个。

【精品】小学数学几何精讲精析专题2 平面图形-类型2三角形专题2 平面图形类型2 三角形【知识讲解】1.三角形的特征(1)由三条线段围成的封闭图形。
(2)三角形的内角和是180度。
(3)三角形具有稳定性。
(4)三角形有三条高。
2. 三角形的三边关系任意两边之和大于第三边,任意两边之差小于第三边。
3. 三角形的分类锐角三角形:三个角都小于90度(都是锐角)按角分直角三角形:有一个角等于90度(一个直角,两个锐角)三钝角三角形:有一个角大于90度(一个钝角,两个锐角)角等边三角形:三条边全相等(三个角也相等,都是60度)形按边分等腰三角形:只有两条边相等(两个底角相等)不等边三角形:三条边都不相等4.三角形的面积公式三角形的面积=底×高÷2【典例精讲】看图计算下列各角的度数。
【答案】15°;55°.【解析】因为三角形的内角和是180°,知道两个角的度数求另一个角的度数,用180度分别减去知道的两个角的度数即可。
解:180°﹣40°﹣125°=140°﹣125°=15°180°﹣90°﹣35°=90°﹣35°=55°【点评】知道三角形内角和为180度,是解答此题的关键。
【巩固练习】一、选择题1.小猴要给一块地围上篱笆,你认为()的围法更牢固些。
2.下面三组小棒,不能围成三角形的是()3.画△ABC中AB边上的高,下列画法中正确的是()。
4.只看三角形的一个角,()判断出它是什么三角形。
A. 能B. 不能C. 不一定能D. 肯定不能5.不管是什么三角形,至少有()个锐角。
A.1 B.2 C.36.把一个三角形纸片剪成两个小三角形,每个小三角形的内角和()180度。
A.大于 B.小于 C.等于7.下面三组线段能围成三角形的是()。
A. 0.5cm,1cm,1.8cmB. 1dm,ldm,ldmC. 2cm,2cm,4cm8.三角形中最小的一个角是50°,按角分类这是一个()三角形。

专题六立体图形类型一正方体【知识讲解】一、正方体的认识:1. 特征:正方体有6个面,每个面都是正方形,所有的面都完全相同,有12条棱,所有的棱都相等,有8个顶点。
2. 正方体的棱长总和=棱长×12用字母表示:12a二、正方体表面积的计算1. 表面积:正方体6个面的总面积叫做它的表面积。
2. 正方体的表面积=棱长×棱长×6用字母表示:S=6a2三、正方体体积的计算1. 物体所占空间的大小叫做物体的体积。
2. 正方体的体积=棱长×棱长×棱长或底面积×高用字母表示: V= a3 或Sh【典例精讲】计算下面图形的表面积和体积。
【答案】表面积是54平方分米,体积是27立方分米.【解析】根据正方体的体积=棱长×棱长×棱长,表面积=棱长×棱长×6,列式计算即可。
解:3×3×6=54(平方分米);3×3×3=27(立方分米);答:正方体的表面积是54平方分米,体积是27立方分米。
【点评】此题主要考查正方体的表面积和体积公式及其计算。
【巩固练习】一、选择题。
1.下列图形中,()是正方体的展开图。
2.正方体的棱长扩大3倍,则体积扩大()倍。
A.2B.4C.27D.83.一个正方体每个面的面积都是9cm2,它的棱长是()cm。
A.9 B.54 C.34.一个正方体的棱长总和是96dm,它的表面积是()dm2。
A.384 B.1536 C.9516 D.5125.一个正方体的棱长是6dm,它的表面积和体积相比较,()A.体积大 B.表面积大 C.同样大 D.无法比较6.用棱长2厘米的正方体木块拼成一个较大的正方体,至少需要()块。
A.4B.8C.9D.647.把一个棱长为6分米的正方体切成棱长为2分米的小正方体,可以得到()小正方体。
A.27个 B.81个 C.9个8.如图是几个相同小正方体拼成的大正方体,由AB向C点斜切,没被切掉的小正方体有()个。

小学一年级数学几何题数学对于小学生来说是一门非常重要的学科,数学几何题是其中的一部分,它让孩子们学会观察、分析和解决问题的能力。
下面是一些适合小学一年级的数学几何题,帮助孩子们学习并提升他们的数学思维能力。
问题一:图形辨认请根据以下描述,在每个方框内画出对应的图形。
1. 一个有四条边的图形,两边长,两边短,四个角是直角。
2. 一个有三条边的图形,三个边都一样长,三个角都是锐角。
3. 一个有三条边的图形,两边短,一边长,三个角都是锐角。
4. 一个有四条边的图形,四个角都是锐角,没有相等的边。
问题二:选择正确的图形从下面的A、B、C、D四个选项中选择与描述相符的图形。
1. 这个图形有四条边,两条边相等,四个角都是直角。
A. 正方形B. 三角形C. 长方形D. 圆形2. 这个图形有三条边,三个角都是锐角。
A. 正方形B. 三角形C. 长方形D. 圆形3. 这个图形有三条边,两个角是锐角,一个角是直角。
A. 正方形B. 三角形C. 长方形D. 圆形4. 这个图形有四条边,四个角都是锐角,没有相等的边。
A. 正方形B. 三角形C. 长方形D. 圆形问题三:用图形填空请在空格内选择正确的图形,使得等式成立。
1. □ + □ = 72. □ - □ = 43. □ + □ = 94. □ - □ = 3问题四:几何图案下面是一些几何图案,请根据图案的特点,找出规律并选择正确的选项,将图案填入空格中。
1. 规律:每个图案都是一个三角形。
□ □ □ □ □□ □ △ □ □□ △△△ □△△△△△□ □ □ □ □A. ▲B. □C. △2. 规律:每个图案都是一个正方形。
□ □ □ □ □□ □ ■ □ □□ ■ ■ ■ □□ □ ■ □ □□ □ □ □ □A. ■B. □C. △以上就是适合小学一年级的数学几何题,通过解答这些问题,孩子们可以培养他们的观察力、逻辑思维和图形辨认能力。
希望孩子们能够喜欢数学,并在解题的过程中不断提升自己的数学水平。
小学数学几何专题
平行四边形
概念:两组对边分别平行的四边形叫做平行四边形。
性质:平行四边形的对边相等,对角相等。
面积公式:面积= 底×高,S=ah
三角形
面积公式:面积= 底×高÷2,S=ah÷2
梯形
概念:只有一组对边互相平行的四边形叫梯形。
有一个角是直角的梯形叫做直角梯形。
两腰相等的梯形叫做等腰梯形。
面积公式:面积=(上底+下底)×高÷2
=中位线×高
S=(a+b)h÷2
平面图形面积公式汇总
常见平面图形的面积公式汇总
⑴求四边形ABCD的面积。
5 D
(单位:厘米) A
45°
B 7
C ⑴求四边形ABCD的面积。
D
(单位:厘米) A
4 45°
B 7 C
A D
⑵已知正方形EFGH的边长
为7厘米,求正方形ABCD H 的面积。
B G C
⑶如图,一个正方形分
成五部分,中间是一个小
正方形,其余四个是相同
的图形,每一个都是等腰
直角三角形缺了一个角,
⑷求阴影部分的面积。
5
(单位:厘米)
3 平面图形面积计算的基本方法
∠C=90°, A D B AC=BC ,
CD=AD=DB=AB ÷2,
四个完全相同的等腰直角三角形可以拼成一个以等腰直角三角形的斜边为边长的正方形。
面积计算:
S=直角边2÷2 S=AC 2÷2 =斜边2÷4 =AB 2÷4
⑵割补法:将一个较复杂的图形,分割或补成一个或多个简单的可计算的图形,计算出这几个简单图形的面积之后,再相加或相减。
例:右图中,ABCD 和DEFG 都是正方形,
求△BDF 的面积。
(单位:厘米) 4 解:由于△BDF 的底 C D E 和高都是未知的,因此,表面上我们无法直接运用公式计算面积。
为此,我们可以运用割补法,将△BDF 分割成△BDG 、△DFG 和△BGF ,先分别求出这三个小三角形的面积,再相加得到△BDF 的面积。
S △BDG =DG ×AB ÷2=4×7÷2=14(厘米2) S △DFG =DG ×GF ÷2=4×4÷2=8(厘米2) S △BGF =GF ×AG ÷2=4×(7-4)÷2=6(厘米2) S △BDF =14+8+6=28(厘米2) 答。
⑸把长方形纸折成 如图形状,求阴影
部分的面积。
18 (单位:厘米) 8
22
⑹如图,直角三角形中 4 有一个矩形,求矩形的 面积。
(单位:厘米)
6
⑺如图,ABCD 是直角 A 3 D 梯形,求阴影部分的面 积和。
(单位:厘米)
B E 6 C
⑻如图,把△ABC 的底边四 A 等分,那么,甲、乙两个三 角形的面积谁大,为什么
甲 乙 B C
⑶等积法:当两个三角形或平行四边形的底、高分别相等时,它们的面积相等。
例:如图,在直角三角形ABC 中,
D 、
E 分别是AB 、AC 的中点,如果
B △
AED 的面积是30平方厘米。
D 求△ABC 的面积。
解:此题已知的值仅有 △AED 的面积,一般这种情况下,我们通常要用两个三角形等底等高面积相等的性质来求解。
连接BE ,因为D 是AB 中点,所以△AED 和△BED 面积相等;因为E 是AC 的中点,所以△ABE 和△CBE 面积相等。
S △BED = S △AED =30(厘米2); S △ABE = S △AED +S △BED =60(厘米2); S △CBE = S △ABE =60(厘米2);
S △ABC = S △ABE +S △CBE =120(厘米2)。
答。
⑷倍比法:当两个三角形或平行四边形的底或高相等,若它们的高或底成倍数关系,则它们的面积也成同样的倍数关系,反之亦然。
例:如图,一个矩形被 分成A 、B 、C 、D 四个矩
形,已知A 的面积是4平 方厘米,B 的面积是8平方厘米,C 的面积是14平方厘米。
求原来整个矩形的面积是多少 解:通过观察可知,A 和B 的宽相等,B 的面积是A 的2倍,所以,B 的长必是A 的长的2倍; 再观察C 和D ,由上可知D 的长也是C 的长的2倍,而它们的宽相等,因此,D 的面积也是C 的面积的2倍。
长方形D 的面积为:14×(8÷4)=28(厘米2
); 整个长方形的面积为:4+8+14+28=54(厘米2
)。
答。
⑼如图,在△ABC 中, A BE=2EC ,AD=BD , D 已知△ABC 的面积是
18平方厘米。
求四边 B E C 形ADEC 的面积。
⑽一个梯形与一个三角形等高,梯形下底的长是上底的2倍,梯形上底的长又是三角形底长的2倍,这个梯形的面积是三角形面积的多少倍
⑾将△ABC 的各条边都延长一倍至 A ’ A’、B’、C ’,连接这些点得到一个 新的△A ’B ’C ’。
若△ABC 的 A 面积为1,求△A ’B ’C ’ B C 的面积。
B’ ’
⑿在平行四边形ABCD 中, E 、F 分别是AB 、BC 的中 点。
如果△BEF 的面积是1则平行四边形ABCD 的面 B F C 积是多少
⑸置换法:用一个可以求得的面积置换另一个相等或知道相差数的面积。
例:如图,正方形 ABCD 边长8厘米,△
CEF的面积比△ABE E
的面积小12平方厘米。
△ACF的面积是多少D C F 解:S△ABC=S□ABCD÷2
=8×8÷2=32(厘米2)
已知S△CEF= S△ABE-12
等式两边各加上△ACE的面积,得:
S△ACF = S△ABC-12
=32-12=20 (厘米2) 答。
⑵逆推法:从要求的数量出发,反向思考,找出解题所必要的条件。
例:如图,AD的长 A D
12厘米,AB长10厘米,
△CDE的面积是24平方
厘米。
求梯形的面积。
解:要求梯形的面积,
目前已知梯形的高和上底,只需求出下底的长度,就能计算梯形的面积。
由于AD=BF,因此需要计算FC的长度。
S△ADC=AD×AB÷2=12×10÷2=60(厘米2);
由于S△CDE=24(厘米2),
S△ADE= S△ADC-S△CDE=60-24
=36(厘米2);
DE= S△ADE÷AD×2=6(厘米)
FC= S△CDE÷DE×2=8(厘米)
梯形的面积:(12+12+8)×10÷2=160(厘米2)
答。
⒀如图,将图中的四边A’
形ABCD的各边都延长
一倍至A’B’C’D’,连接 A D D’这些点得到一个新的四B’ B C
边形A’B’C’D’。
若四边形ABCD的面积是1,C’
求四边形A’B’C’D’的面积。
⒁如图,已知正方形
ABCD的边长为8分
米,三角形ABF的面
积比三角形CEF的面
积大80平方分米。
求 D C E CE的长度。
A B C
⒂如图,四边形
ACEH是梯形, D ACEG是平行四 E 边形,ABGH是H G F 正方形,CDFG是长方形。
已知AC=6厘米,HE=10厘米。
求阴影部分的面积。