无机材料科学基础答案第十章

第六章6-4 什么是吉布斯相律？它有什么实际意义？解：相律是吉布斯根据热力学原理得出的相平衡基本定律，又称吉布斯相律，用于描述达到相平衡时系统中自由度数与组分数和相数之间的关系。

一般形式的数学表达式为F＝C－P＋2。

其中F为自由度数，C为组分数，P为相数，2代表温度和压力两个变量。

应用相率可以很方便地确定平衡体系的自由度数。

6-6 根据Al2O3－SiO2系统相图说明：（1）铝硅质耐火材料：硅砖（含SiO2＞98％）、粘土砖（含Al2O335％～50％）、高铝砖（含Al2O360％～90％）、刚玉砖（含Al2O3＞90％）内，各有哪些主要的晶相？（2）为了保持较高的耐火度，在生产硅砖时应注意什么？（3）若耐火材料出现40％的液相便软化不能使用，试计算含40mol％Al2O3的粘土砖的最高使用温度。

解：（1）硅砖（含SiO2>98%）主要晶相： SiO2、2Al2O3·2SiO3固溶体（莫来石），粘土砖（含Al20335 ～50%）主要晶相：SiO2、A3S2，高铝砖（含Al20360 ～90%）主要晶相：60～72%A3S2 72 ～90% Al2O3、A3S2。

（2）为了保持硅砖的耐火度，要严格防止原料中混如Al203。

SiO2熔点为1723 ℃，SiO2液相很陡，加入少量的Al203后，硅砖中会产生大量的液相，SiO2的熔点剧烈下降。

如加入1wt% Al203，在低共熔点（1595 ℃）时产生的液相量为1/5.5=18.2% ，会使硅砖的耐火度大大下降；（3）根据相图，当出现40%液相时，由杆杠规则可知，，得x=0.1, 在相图中作出析晶路线，可以估计出粘土砖的最高温度约为1670 ℃。

6-9图6-15为生成2个一致熔融二元化合物的三元系统，据图回答下列问题：（l）可将其划分为几个副三角形？（2）标出图中各边界及相区界线上温度下降方向。

（3）判断各无变量点的性质，并写出相平衡关系式。

1.1 名词解释：等同点、结点、空间点阵、晶体、对称、对称型、晶系、晶类、布拉菲格子、晶胞、晶胞参数、晶体定向、晶面指数、晶向指数、晶带轴定律1.2 略述从一个晶体结构中抽取点阵的意义和方法？空间点阵与晶体结构有何对应关系？1.3 什么叫对称性？晶体的对称性有何特点，为什么？1.4 晶体中有哪些对称要素，用国际符号表示。

1.5 试找出正四面体、正八面体和立方体中的所有对称元素，并确定其所属点群、晶系。

1.6 根据什么将14种布拉维点阵分成七个晶系？各晶系特点如何？为什么14种布拉维点阵中有正交底心而无四方底心和立方底心点阵型式？以图说明。

说明七个晶系的对称特点及晶体几何常数的关系。

1.7 什么叫单位平行六面体（或单位）？在三维点阵中选取单位平行六面体应遵循哪些原则？为什么？1.8 a≠b≠c, α=β=γ=90℃的晶体属于什么晶系？a≠b≠c, α≠β≠γ≠90°的晶体属什么晶系？能否据此确定这二种晶体的布拉维点阵？1.9 一个四方晶系晶体的晶面，其上的截距分别为3a、4 a，6c，求该晶面的晶面指数。

1.10 四方晶系晶体a＝b，c＝1/2a。

一晶面在X、Y、Z轴上的截距分别为2a, 3b和6c。

给出该晶面的密勒指数。

1.11 某一晶面在x、y、z三个坐标轴上的截距分别为1a，∞b,3c，求该晶面符号。

1.12 在正交简单点阵、底心点阵、体心点阵、面心点阵中分别标出（110）、（011）、（101）三组晶面，并指出每个晶面上的结点数。

1.13 在立方晶系中画出下列晶面：a）（001）；b）（110）；c）（111）。

在所画的晶面上分别标明下列晶向：a）[210]；b）[111]；c）[101]。

1.14 试说明在等轴晶系中，（111）、（111）、（222）、（110）与（111）面之间的几何关系。

1.15 在立方晶系晶胞中画出下列晶面指数和晶向指数：（001）与[210]，(111)与[112]，(110)与[111]，（322）与[236]，(257)与[111]，(123)与[121]，(102)，(112)，(213)，[110]，[111]，[120]，[ 321]。

6-1 略。

6-2 什么是吉布斯相律？它有什么实际意义？解：相律是吉布斯根据热力学原理得出的相平衡基本定律，又称吉布斯相律，用于描述达到相平衡时系统中自由度数与组分数和相数之间的关系。

一般形式的数学表达式为F＝C－P＋2。

其中F为自由度数，C 为组分数，P为相数，2代表温度和压力两个变量。

应用相率可以很方便地确定平衡体系的自由度数。

6-3 固体硫有两种晶型，即单斜硫、斜方硫，因此，硫系统可能有四个相，如果某人实验得到这四个相平衡共存，试判断这个实验有无问题？解：有问题，根据相律，F=C-P+2=1-P+2=3-P，系统平衡时，F=0 ，则P=3 ，硫系统只能是三相平衡系统。

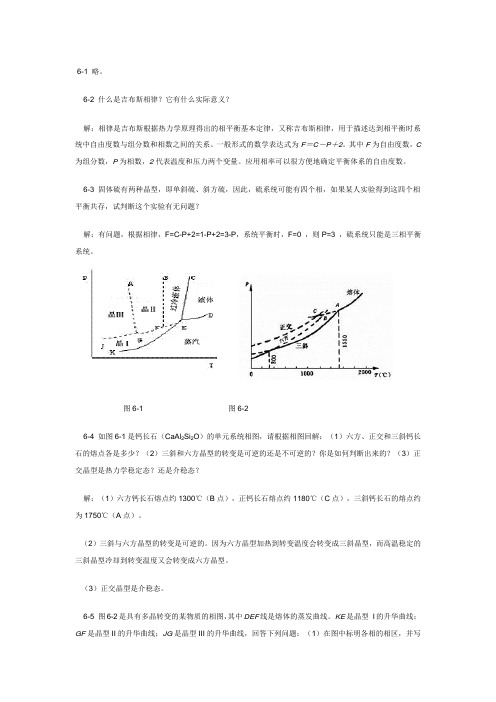
图6-1 图6-26-4 如图6-1是钙长石（CaAl2Si2O）的单元系统相图，请根据相图回解：（1）六方、正交和三斜钙长石的熔点各是多少？（2）三斜和六方晶型的转变是可逆的还是不可逆的？你是如何判断出来的？（3）正交晶型是热力学稳定态？还是介稳态？解：（1）六方钙长石熔点约1300℃（B点），正钙长石熔点约1180℃（C点），三斜钙长石的熔点约为1750℃（A点）。

（2）三斜与六方晶型的转变是可逆的。

因为六方晶型加热到转变温度会转变成三斜晶型，而高温稳定的三斜晶型冷却到转变温度又会转变成六方晶型。

（3）正交晶型是介稳态。

6-5 图6-2是具有多晶转变的某物质的相图，其中DEF线是熔体的蒸发曲线。

KE是晶型I的升华曲线；GF是晶型II的升华曲线；JG是晶型III的升华曲线，回答下列问题：（1）在图中标明各相的相区，并写出图中各无变量点的相平衡关系；（2）系统中哪种晶型为稳定相？哪种晶型为介稳相？（3）各晶型之间的转变是可逆转变还是不可逆转变？解：（1）KEC为晶型Ⅰ的相区，EFBC 过冷液体的介稳区，AGFB晶型Ⅱ的介稳区，JGA晶型Ⅲ的介稳区，CED是液相区，KED是气相区；（2）晶型Ⅰ为稳定相，晶型Ⅱ、Ⅲ为介稳相；因为晶型Ⅱ、Ⅲ的蒸汽压高于晶型Ⅰ的，即它们的自由能较高，有自发转变为自由能较低的晶型Ⅰ的趋势；（3）晶型Ⅰ转变为晶型Ⅱ、Ⅲ是单向的，不可逆的，多晶转变点的温度高于两种晶型的熔点；晶型Ⅱ、Ⅲ之间的转变是可逆的，双向的，多晶转变点温度低于Ⅱ、Ⅲ的熔点。

《无机材料科学基础》习题和思考题第一章晶体1.球体按立方最紧密堆积方式堆积，取出立方晶胞，画出立方晶胞中的四面体空隙和八面体空隙的位置分布图。

2.用鲍林规则分析氧化镁晶体结构。

已知镁离子半径为0.65Å，氧离子半径为1.40Å。

（1）确定晶胞中质点的位置坐标；（2）计算每个晶胞中含氧化镁“分子”数，（3）已知晶胞常数a=4.20 Å，求氧化镁堆积系数和密度，（4）氧化镁晶体中最邻近的两个镁离子中心距为多少？次邻近的两个镁离子中心距为多少？最邻近和次邻近的两个氧离子中心距为多少？（5）画出氧化镁晶胞的（111）、（110）、（100）面的质点分布图并在图上标出氧离子的密排方向，求个面的面密度。

3．已知纤锌矿结构中存在两套硫离子和两套锌离子的六方底心格子，并已知锌离子填充在硫离子最紧密堆积体的四面体空隙中，现以一套硫离子的等同点为基准取六方晶胞，画出晶胞中的质点分布图，计算晶胞中所含式量分子数。

4．完成下表5. 六方最紧密堆积与四方最紧密堆积的堆积密度相同，为什么许多氧化物是以氧离子的立方最紧密堆积为基础，而较少以六方最紧密堆积为基础？6. 用鲍林规则分析镁橄榄石的结构：P48 图2-18（1）标记为50的Mg2+与哪几个氧离子配位形成[MgO6]八面体？写出O2+的标高；（2）标记为25的两个O2+与哪几个镁离子配位？写出Mg2+离子的标高；（3）标记为75的O2+离子与哪几个镁离子配位？写出Mg2+离子的标高；（4）标记为0和50的两个Mg2+的[MgO6] 八面体共用几个顶点？写出O2+的标高；（5）[SiO4] 和 [MgO6] 之间、[MgO6]和[MgO6] 八面体之间有那些连接方式？（6）镁橄榄石的晶胞是什么形状？计算晶胞中含有的式量分子数。

第二章晶体缺陷1.氧化镁为氯化钠型结构，氧化锂为反萤石型结构，在两种结构中氧离子都作立方最紧密堆积，为什么在氧化镁中主要的热缺陷是肖特基型，而在氧化锂中却是弗伦克尔型？萤石型结构的氧化物晶体中常见的热缺陷估计主要是什么类型？为什么？2.已知氯化钠晶体中肖特基缺陷形成焓为2.2ev，而氧化镁晶体中肖特基缺陷形成焓为6ev，试分别计算400℃时氯化纳晶体与氧化镁晶体中肖特基缺陷的浓度。

无机材料科学基础试卷一、名词解释液相独立析晶：是在转熔过程中发生的，由于冷却速度较快，被回收的晶相有可能会被新析出的固相包裹起来，使转熔过程不能继续进行，从而使液相进行另一个单独的析晶过程，就是液相独立析晶。

二次再结晶：少数巨大晶粒在细晶消耗时成核长大过程。

晶粒生长：平衡晶粒尺寸在不改变其分布的情况下，连续增大的过程。

本征扩散：是指空位来源于晶体结构中本征热缺陷而引起质点的迁移。

非本征扩散：受固溶引入的杂质离子的电价和浓度等外界因素所控制的扩散。

或由不等价杂质离子取代造成晶格空位，由此而引起的质点迁移。

一级相变：体系由一相变为另一相时，如两相的化学势相等但化学势的一级偏微商(一级导数)不相等的称为一级相变二级相变：相变时两相化学势相等，其一级偏微商也相等，但二级偏微商不等的称为二级相变。

液相烧结：凡有液相参加的烧结过程称为液相烧结。

固相烧结：固态粉末在适当的温度、压力、气氛和时间条件下，通过物质与气孔之间的传质，变为坚硬、致密烧结体的过程。

均匀成核：晶核从均匀的单相熔体中产生的过程。

非均匀成核：是指借助于表面、界面、微粒裂纹器壁以及各种催化位置等而形成晶核的过程稳定扩散：若扩散物质在扩散层dx内各处的浓度不随时间而变化，即dc/dt=0。

这种扩散称稳定扩散。

不稳定扩散：扩散物质在扩散层dx内的浓度随时间而变化，即dc/dt≠0。

这种扩散称为不稳定扩散。

三角形规则：原始熔体组成点所在副三角形的三个顶点表示的物质即为其结晶产物；与这三个物质相应的初初晶区所包围的三元无变量点是其结晶结束点。

连线规则：将一界线（或其延长线）与相应的连线（或其延长线）相交，其交点是该界线上的温度最高点。

一致熔融化合物：是一种稳定的化合物。

它与正常的纯物质一样具有固定的熔点，熔化时，所产生的液相与化合物组成相同，故称一致熔融化合物。

不一致熔化合物：是一种不稳定的化合物，加热到一定温度会发生分解，分解产物是一种液相和一种固相，液相和固相的组成与化合物组成都不相同。

1，（a ）在MgO 晶体中，肖特基缺陷的生成能为6ev ，计算在25℃和1600℃时热缺陷的浓度。

℃时热缺陷的浓度。

（b ）如果MgO 晶体中，晶体中，含有百万分之一含有百万分之一mol 的Al2O3杂质，杂质，则在则在1600℃时，MgO 晶体中是热缺陷占优势还是杂质缺陷占优势？说明原因。

质缺陷占优势？说明原因。

解：（a ）根据热缺陷浓度公式：）根据热缺陷浓度公式：exp （－） 由题意由题意△G=6ev=6×G=6ev=6×1.602×1.602×1.602×10-19=9.612×10-19=9.612×10-19=9.612×10-19J 10-19J K=1.38×K=1.38×10-23 J/K 10-23 J/K T1=25+273=298K T2=1600+273=1873K298K ：exp =1.92×10-511873K ： exp =8×10-9（b ）在MgO 中加入百万分之一的Al2O3杂质，缺陷反应方程为：杂质，缺陷反应方程为：此时产生的缺陷为[ ]杂质。

杂质。

而由上式可知：[Al2O3]=[]杂质杂质 ∴当加入10-6 Al2O3时，杂质缺陷的浓度为时，杂质缺陷的浓度为[ ]杂质=[Al 2O 3]=10-6由（a ）计算结果可知：在1873 K ，[]热=8×=8×10-9 10-9显然：显然：[ ]杂质＞[ ]热，所以在1873 K 时杂质缺陷占优势。

时杂质缺陷占优势。

2，非化学计量化合物FexO 中，Fe3+/Fe2+=0.1，求FexO 中的空位浓度及x 值。

值。

解：解： 非化学计量化合物Fe x O ，可认为是α(mol)的Fe 2O 3溶入FeO 中，缺陷反应式为：中，缺陷反应式为：Fe 2O 32Fe + V +3O Oα 2α α此非化学计量化合物的组成为：此非化学计量化合物的组成为：FeFe O 已知：Fe 3+/Fe 2+＝0.1 则：∴ α ＝ 0.044 ∴x ＝2α+(1－3α)＝1－α＝0.956又：∵[V 3+]＝α ＝0.044 正常格点数N ＝1+x ＝1+0.956＝1.956∴空位浓度为3，试写出少量MgO 掺杂到Al 2O 3中和少量YF 3掺杂到CaF 2中的缺陷方程。

名师整理优秀资源4.1 名词解释（a）弗伦克尔缺陷与肖特基缺陷；（b）刃型位错和螺型位错解：（a）当晶体热振动时，一些能量足够大的原子离开平衡位置而挤到晶格点的间隙中，形成间隙原子，而原来位置上形成空位，这种缺陷称为弗伦克尔缺陷。

如果正常格点上原子，热起伏后获得能量离开平衡位置，跃迁到晶体的表面，在原正常格点上留下空位，这种缺陷称为肖特基缺陷。

（b）滑移方向与位错线垂直的位错称为刃型位错。

位错线与滑移方向相互平行的位错称为螺型位错。

4.2试述晶体结构中点缺陷的类型。

以通用的表示法写出晶体中各种点缺陷的表示符号。

试举例写出CaCl2中Ca2+置换KCl中K+或进入到KCl间隙中去的两种点缺陷反应表示式。

解：晶体结构中的点缺陷类型共分：间隙原子、空位和杂质原子等三种。

在MX晶体中，间隙原子的表示符号为MI或XI；空位缺陷的表示符号为：VM或VX。

如果进入MX晶体的杂质原子是A，则其表示符号可写成：AM或AX（取代式）以及Ai（间隙式）。

当CaCl2中Ca2+置换KCl中K+而出现点缺陷，其缺陷反应式如下：++2Cl CaCl Cl2CaCl2中Ca2+进入到KCl间隙中而形成点缺陷的反应式为：+2CaCl+2Cl Cl24.3在缺陷反应方程式中，所谓位置平衡、电中性、质量平衡是指什么？解：位置平衡是指在化合物MaXb中，M格点数与X格点数保持正确。

电中性是指在方程式两边应具有相同的b：X=a：M的比例关系，即．名师整理优秀资源有效电荷。

质量平衡是指方程式两边应保持物质质量的守恒。

4.4（a）在MgO晶体中，肖特基缺陷的生成能为6ev，计算在25℃和1600℃时热缺陷的浓度。

（b）如果MgO晶体中，含有百万分之一mol的Al2O3杂质，则在1600℃时，MgO晶体中是热缺陷占优势还是杂质缺陷占优势？说明原因。

解：（a）根据热缺陷浓度公式：（－）exp由题意△G=6ev=6×1.602×10-19=9.612×10-19JK=1.38×10-23 J/KT1=25+273=298K T2=1600+273=1873K-5110=1.92：×exp 298K-9×10=8exp1873K：（b）在MgO中加入百万分之一的Al2O3杂质，缺陷反应方程为：[ ]杂质。

材料科学基础西南科技大学智慧树知到答案2024年第一章测试1.选用材料应该遵循（）原则。

A:工艺性能 B:使用性能 C:环境协调性 D:经济性答案:ABCD2.耐火材料是指耐火度不低于（）℃的无机非金属材料。

A:1300 B:1000 C:1800 D:1580答案:D3.材料按其化学作用（或基本组成）分为：A:无机非金属材料 B:复合材料 C:金属材料 D:高分子材料（聚合物）答案:ABCD4.传统的无机非金属材料主要是指由ＳｉＯ２及其硅酸盐化合物为主要成分制成的材料，包括：A:陶瓷 B:耐火材料 C:水泥 D:玻璃答案:ABCD第二章测试1.如果等大球体在空间形成密排六方结构，则按如下方式（）的层序堆积。

A:ABBABB•••••• B:AABAAB•••••• C:ABCABC•••••• D:ABAB••••••答案:D2.在一个面心立方晶胞中，共存在（）。

A:4个四面体空隙，8个八面体空隙 B:8个四面体空隙，4个八面体空隙C:8个四面体空隙，8个八面体空隙 D:4个四面体空隙，4个八面体空隙答案:B3.在一个密排六方晶胞中，晶胞的质点数为（）。

A:2 B:8 C:6 D:4答案:C4.当6个等大的球体作面心立方堆积时，每个球周围形成的四面体空隙个数为( )。

A:12 B:6 C:2 D:18答案:C5.离子晶体的配位数决定主要取决于正、负离子半径比，当配位多面体为八面体时，正负离子的半径比（）。

A:正负离子半径比应处于0.155~0.225范围 B:正负离子半径比应处于0.732~1.0范围 C:正负离子半径比应处于0.225~0.414范围 D:正负离子半径比应处于0.414~0.732范围答案:D6.在某MX离子晶体中，若其中的阴离子易被极化，则下列说法正确的是：（）。

A:阴阳离子间距增大、配位数增加。

B:阴阳离子间距增大、配位数降低。

C:阴阳离子间距降低、配位数降低。

D:阴阳离子间距降低、配位数增加。

第一章晶体几何基础1-1 解释概念：等同点：晶体结构中，在同一取向上几何环境和物质环境皆相同的点。

空间点阵：概括地表示晶体结构中等同点排列规律的几何图形。

结点：空间点阵中的点称为结点。

晶体：部质点在三维空间呈周期性重复排列的固体。

对称：物体相同部分作有规律的重复。

对称型：晶体结构中所有点对称要素（对称面、对称中心、对称轴和旋转反伸轴）的集合为对称型，也称点群。

晶类：将对称型相同的晶体归为一类，称为晶类。

晶体定向：为了用数字表示晶体中点、线、面的相对位置，在晶体中引入一个坐标系统的过程。

空间群：是指一个晶体结构中所有对称要素的集合。

布拉菲格子：是指法国学者A.布拉菲根据晶体结构的最高点群和平移群对称及空间格子的平行六面体原则，将所有晶体结构的空间点阵划分成14种类型的空间格子。

晶胞：能够反应晶体结构特征的最小单位。

晶胞参数：表示晶胞的形状和大小的6个参数（a、b、c、α 、β、γ ）.1-2 晶体结构的两个基本特征是什么？哪种几何图形可表示晶体的基本特征？解答：⑴晶体结构的基本特征：①晶体是部质点在三维空间作周期性重复排列的固体。

②晶体的部质点呈对称分布，即晶体具有对称性。

⑵14种布拉菲格子的平行六面体单位格子可以表示晶体的基本特征。

1-3 晶体中有哪些对称要素，用国际符号表示。

解答：对称面—m，对称中心—1，n次对称轴—n，n次旋转反伸轴—n螺旋轴—ns ，滑移面—a、b、c、d1-5 一个四方晶系的晶面，其上的截距分别为3a、4a、6c，求该晶面的晶面指数。

解答：在X、Y、Z轴上的截距系数：3、4、6。

截距系数的倒数比为：1/3:1/4:1/6=4:3:2晶面指数为：（432）补充：晶体的基本性质是什么？与其部结构有什么关系？解答：①自限性：晶体的多面体形态是其格子构造在外形上的反映。

②均一性和异向性：均一性是由于部质点周期性重复排列，晶体中的任何一部分在结构上是相同的。

异向性是由于同一晶体中的不同方向上，质点排列一般是不同的，因而表现出不同的性质。

无机材料科学基础习题与解答2、 晶体的结构类型：形成连续固溶体的两个组分必须具有完全相同的晶体结构。

结构不同最多只能生成有限固溶体。

3、 离子的电价因素：只有离子价相同或复合替代离子价总和相同时，才可能形成连续置换型固溶体。

4、电负性因素：电负性相近，有利于固溶体的生成。

4.1名词解释（a ）弗伦克尔缺陷与肖特基缺陷；（b ）刃型位错和螺型位错 （c ）类质同象与同质多晶解：（a ）当晶体热振动时，一些能量足够大的原子离开平衡位置而挤到晶格点的间隙中，形成间隙原子，而原来位置上形成空位，这种缺陷称为弗伦克尔缺陷。

如果正常格点上原子，热起伏后获得能量离开平衡位置，跃迁到晶体的表面，在原正常格点上留下空位，这种缺陷称为肖特基缺陷。

（ b ）滑移方向与位错线垂直的位错称为刃型 位错。

位错线与滑移方向相互平行的位错称为螺型位错。

（c ）类质同象：物质结晶时，其晶体结构中部分原有的离子或原子位置被性质相似的其它离 子或原子所占有，共同组成均匀的、呈单一相的晶体，不引起键性和晶体结构变化的现象。

同质多晶：同一化学组成在不同热力学条件下形成结构不同的晶体的现象。

6-3名词解释（并比较其异同）⑴晶子学说：玻璃内部是由无数 晶子”组成，微晶子是带有晶格变形的有序区域。

它们分散在无定形介中质，晶子向无定形部分过渡是逐渐完成时,二者没有明显界限。

无规则网络学说：凡是成为玻璃态的物质和相应的晶体结构一样，也是由一个三度空间网络所构成。

这种网络是由离子多面体（三角体本或四 面体）构筑起来的。

晶体结构网是由多面体无数次有规律重复构成，而玻璃中结构多面体的重复没有规律性。

⑵单键强：单键强即为各种化合物分解能与该种化合物配位数的商。

⑶分化过程：架状［SiO 』断裂称为熔融石英的分化过程。

缩聚过程：分化过程产生的低聚化合物相互发生作用，形成级次较高的聚合物，次过程为缩聚过程。

⑷网络形成剂：正离子是网络形成离子，对应氧化物能单独形成玻璃。

第一章晶体几何基础1-1 解释概念：等同点：晶体结构中，在同一取向上几何环境和物质环境皆相同的点。

空间点阵：概括地表示晶体结构中等同点排列规律的几何图形。

结点：空间点阵中的点称为结点。

晶体：内部质点在三维空间呈周期性重复排列的固体。

对称：物体相同部分作有规律的重复。

对称型：晶体结构中所有点对称要素（对称面、对称中心、对称轴和旋转反伸轴）的集合为对称型，也称点群。

晶类：将对称型相同的晶体归为一类，称为晶类。

晶体定向：为了用数字表示晶体中点、线、面的相对位置，在晶体中引入一个坐标系统的过程。

空间群：是指一个晶体结构中所有对称要素的集合。

布拉菲格子：是指法国学者A.布拉菲根据晶体结构的最高点群和平移群对称及空间格子的平行六面体原则，将所有晶体结构的空间点阵划分成14种类型的空间格子。

晶胞：能够反应晶体结构特征的最小单位。

晶胞参数：表示晶胞的形状和大小的6个参数（a、b、c、α、β、γ）.1-2 晶体结构的两个基本特征是什么？哪种几何图形可表示晶体的基本特征？解答：⑴晶体结构的基本特征：①晶体是内部质点在三维空间作周期性重复排列的固体。

②晶体的内部质点呈对称分布，即晶体具有对称性。

⑵14种布拉菲格子的平行六面体单位格子可以表示晶体的基本特征。

1-3 晶体中有哪些对称要素，用国际符号表示。

解答：对称面—m，对称中心—1，n次对称轴—n，n次旋转反伸轴—n螺旋轴—ns ，滑移面—a、b、c、d1-5 一个四方晶系的晶面，其上的截距分别为3a、4a、6c，求该晶面的晶面指数。

解答：在X、Y、Z轴上的截距系数：3、4、6。

截距系数的倒数比为：1/3:1/4:1/6=4:3:2晶面指数为：（432）补充：晶体的基本性质是什么？与其内部结构有什么关系？解答：①自限性：晶体的多面体形态是其格子构造在外形上的反映。

②均一性和异向性：均一性是由于内部质点周期性重复排列，晶体中的任何一部分在结构上是相同的。

异向性是由于同一晶体中的不同方向上，质点排列一般是不同的，因而表现出不同的性质。

1. 解释下列名词：凝聚系统，介稳平衡，低共熔点，双升点，双降点，马鞍点，连线规则，切线规则，三角形规则，重心规则。

解：凝聚系统：不含气相或气相可以忽略的系统。

介稳平衡：即热力学非平衡态，能量处于较高状态，经常出现于硅酸盐系统中。

低共熔点：是一种无变量点，系统冷却时几种晶相同时从熔液中析出，或加热时同时融化。

双升点：处于交叉位的单转熔点。

双降点：处于共轭位的双转熔点。

马鞍点：三元相图界线上温度最高点，同时又是二元系统温度的最低点。

连线规则：将一界线（或其延长线）与相应的连线（或其延长线）相交，其交点是该界线上的温度最高点。

切线规则：将界线上某一点所作的切线与相应的连线相交，如交点在连线上，则表示界线上该处具有共熔性质；如交点在连线的延长线上，则表示界线上该处具有转熔性质，远离交点的晶相被回吸。

三角形规则：原始熔体组成点所在副三角形的三个顶点表示的物质即为其结晶产物；与这三个物质相应的初初晶区所包围的三元无变量点是其结晶结束点。

重心规则：如无变点处于其相应副三角形的重心位，则该无变点为低共熔点：如无变点处于其相应副三角形的交叉位，则该无变点为单转熔点；如无变点处于其相应副三角形的共轭位，则该无变点为双转熔点。

2. 从SiO2的多晶转变现象说明硅酸盐制品中为什么经常出现介稳态晶相？解：在573℃以下的低温，SiO2的稳定晶型为b －石英，加热至573℃转变为高温型的a －石英，这种转变较快；冷却时在同一温度下以同样的速度发生逆转变。

如果加热速度过快，则a －石英过热而在1600℃时熔融。

如果加热速度很慢，则在870℃转变为a －鳞石英。

a －鳞石英在加热较快时，过热到1670℃时熔融。

当缓慢冷却时，在870℃仍可逆地转变为a －石英；当迅速冷却时，沿虚线过冷，在163℃转变为介稳态的b －鳞石英，在117℃转变为介稳态的g －鳞石英。

加热时g －鳞石英仍在原转变温度以同样的速度先后转变为b －鳞石英和a －鳞石英。

第一章答案20、（1）略；（2）四面体空隙数/O2-数=2:1，八面体空隙数/O2-数=1:1；（3）(a)CN=4，z+/4×8=2，z+=1，Na2O，Li2O；(b)CN=6，z+/6×6=2，z+=2，FeO，MnO；（c）CN=4，z+/4×4=2，z+=4，ZnS，SiC；(d)CN=6，z+/6×3=2，z+=4，MnO2。

21、解：岛状；架状；单链；层状（复网）；组群（双四面体）。

22、解：（1）有两种配位多面体，[SiO4]，[MgO6]，同层的[MgO6]八面体共棱，如59[MgO6]和49[MgO6]共棱75O2-和27O2-，不同层的[MgO6]八面体共顶，如1[MgO6]和51[MgO6]共顶是22O2-，同层的[MgO6]与[SiO4]共顶，如T[MgO6]和7[SiO4]共顶22O2-，不同层的[MgO6]与[SiO4]共棱，T[MgO6]和43[SiO4]共28O2-和28O2-；（3）z=4；（4）Si4+占四面体空隙=1/8，Mg2+占八面体空隙=1/2。

23、解：透闪石双链结构，链内的Si-O键要比链5的Ca-O、Mg-O键强很多，所以很容易沿链间结合力较弱处劈裂成为纤维状；滑石复网层结构，复网层由两个[SiO4]层和中间的水镁石层结构构成，复网层与复网层之间靠教弱的分之间作用力联系，因分子间力弱，所以易沿分子间力联系处解理成片状。

24、解：石墨中同层C原子进行SP2杂化，形成大Π键，每一层都是六边形网状结构。

由于间隙较大，电子可在同层中运动，可以导电，层间分子间力作用，所以石墨比较软。

25、解：（1）Al3+可与O2-形成[AlO4]5-；Al3+与Si4+处于第二周期，性质类似，易于进入硅酸盐晶体结构中与Si4+发生同晶取代，由于鲍林规则，只能部分取代；（2）Al3+置换Si4+是部分取代，Al3+取代Si4+时，结构单元[AlSiO4][ASiO5]，失去了电中性，有过剩的负电荷，为了保持电中性，将有一些半径较大而电荷较低的阳离子如K+、Ca2+、Ba2+进入结构中；（3）设Al3+置换了一半的Si4+，则O2-与一个Si4+一个Al3+相连，阳离子静电键强度=3/4×1+4/4×1=7/4，O2-电荷数为-2，二者相差为1/4，若取代超过一半，二者相差必然>1/4，造成结构不稳定。

第一章晶体几何基础欧阳家百（2021.03.07）1-1 解释概念：等同点：晶体结构中，在同一取向上几何环境和物质环境皆相同的点。

空间点阵：概括地表示晶体结构中等同点排列规律的几何图形。

结点：空间点阵中的点称为结点。

晶体：内部质点在三维空间呈周期性重复排列的固体。

对称：物体相同部分作有规律的重复。

对称型：晶体结构中所有点对称要素（对称面、对称中心、对称轴和旋转反伸轴）的集合为对称型，也称点群。

晶类：将对称型相同的晶体归为一类，称为晶类。

晶体定向：为了用数字表示晶体中点、线、面的相对位置，在晶体中引入一个坐标系统的过程。

空间群：是指一个晶体结构中所有对称要素的集合。

布拉菲格子：是指法国学者 A.布拉菲根据晶体结构的最高点群和平移群对称及空间格子的平行六面体原则，将所有晶体结构的空间点阵划分成14种类型的空间格子。

晶胞：能够反应晶体结构特征的最小单位。

晶胞参数：表示晶胞的形状和大小的6个参数（a、b、c、α 、β、γ ）.1-2 晶体结构的两个基本特征是什么？哪种几何图形可表示晶体的基本特征？解答：⑴晶体结构的基本特征：① 晶体是内部质点在三维空间作周期性重复排列的固体。

②晶体的内部质点呈对称分布，即晶体具有对称性。

⑵14种布拉菲格子的平行六面体单位格子可以表示晶体的基本特征。

1-3 晶体中有哪些对称要素，用国际符号表示。

解答：对称面—m，对称中心—1，n次对称轴—n，n次旋转反伸轴—n螺旋轴—ns ，滑移面—a、b、c、d1-5 一个四方晶系的晶面，其上的截距分别为3a、4a、6c，求该晶面的晶面指数。

解答：在X、Y、Z轴上的截距系数：3、4、6。

截距系数的倒数比为：1/3:1/4:1/6=4:3:2晶面指数为：（432）补充：晶体的基本性质是什么？与其内部结构有什么关系？解答：①自限性：晶体的多面体形态是其格子构造在外形上的反映。

②均一性和异向性：均一性是由于内部质点周期性重复排列，晶体中的任何一部分在结构上是相同的。

第二章答案2-1略。

2-2〔1〕一晶面在x、y、z轴上的截距分别为2a、3b、6c，求该晶面的晶面指数；〔2〕一晶面在x、y、z轴上的截距分别为a/3、b/2、c，求出该晶面的晶面指数。

答：〔1〕h:k:l==3:2:1,∴该晶面的晶面指数为〔321〕；〔2〕h:k:l=3:2:1，∴该晶面的晶面指数为〔321〕。

2-3在立方晶系晶胞中画出以下晶面指数和晶向指数：〔001〕与[]，〔111〕与[]，〔〕与[111]，〔〕与[236]，〔257〕与[]，〔123〕与[]，〔102〕，〔〕，〔〕，[110]，[]，[]答：2-4定性描述晶体构造的参量有哪些.定量描述晶体构造的参量又有哪些.答：定性：对称轴、对称中心、晶系、点阵。

定量：晶胞参数。

2-5依据结合力的本质不同，晶体中的键合作用分为哪几类.其特点是什么.答：晶体中的键合作用可分为离子键、共价键、金属键、范德华键和氢键。

离子键的特点是没有方向性和饱和性，结合力很大。

共价键的特点是具有方向性和饱和性，结合力也很大。

金属键是没有方向性和饱和性的的共价键，结合力是离子间的静电库仑力。

范德华键是通过分子力而产生的键合，分子力很弱。

氢键是两个电负性较大的原子相结合形成的键，具有饱和性。

2-6等径球最严密堆积的空隙有哪两种.一个球的周围有多少个四面体空隙、多少个八面体空隙.答：等径球最严密堆积有六方和面心立方严密堆积两种，一个球的周围有8个四面体空隙、6个八面体空隙。

2-7n个等径球作最严密堆积时可形成多少个四面体空隙、多少个八面体空隙.不等径球是如何进展堆积的.答：n个等径球作最严密堆积时可形成n个八面体空隙、2n个四面体空隙。

不等径球体进展严密堆积时，可以看成由大球按等径球体严密堆积后，小球按其大小分别填充到其空隙中，稍大的小球填充八面体空隙，稍小的小球填充四面体空隙，形成不等径球体严密堆积。

2-8写出面心立方格子的单位平行六面体上所有结点的坐标。

答：面心立方格子的单位平行六面体上所有结点为：〔000〕、〔001〕〔100〕〔101〕〔110〕〔010〕〔011〕〔111〕〔0〕〔0〕〔0〕〔1〕〔1〕〔1〕。