一维单原子链
- 格式:pdf
- 大小:286.83 KB
- 文档页数:6

一维单原子链推导
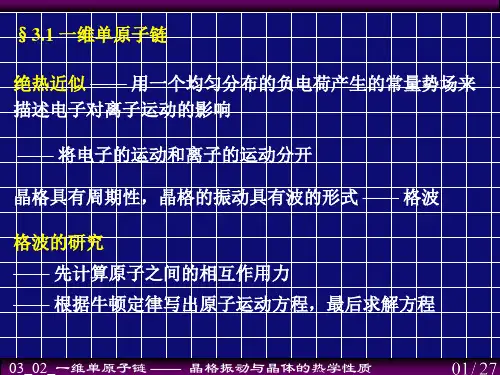
一维单原子链是指一维无限长的单原子链,其中原子质量为m,原子间距为a。
热运动使得原子离开平衡位置,假设第n个原子离开平衡位置的位移为μn,它相对于a是一个很小的量,第n个原子到第n+1个原子间相对位移为δ,则:$\delta=μn+1-μn$。
当原子m在平衡位置时,两个原子相互作用势为$V(a)$;相对位移为$\delta$时,两个原子相互作用势为$V(a+\delta)$。
将$V(a+\delta)$在平衡位置用泰勒级数展开,可得:$\cdots(21)(222=+++=aaδaδdrdVaVdrVddrdVaVaVrVδ$。
由于考虑的是微振动,即$\delta$很小,展开式可以近似保留到$\delta^2$项,可得:$10(\cdots)!(\cdots)!2)(\cdots)('\theta'\theta'\theta'\theta'\theta'\approx++++ +++2222\delta\delta\delta$。
只考虑最近邻原子间的相对位移的二次项对系统总势能的贡献,则总势能写为:$\cdots212)(μ221−−=≈∑nnnVμββδ$。
第n个原子所受的力为:$\cdots2(11+−−−−=−≈∂δ∂−=nnnnVfμμμββδβ$,其中β是相邻原子间准弹性力的力常数,它直接由两个原子间的相互作用势能所决定,$a$是两个原子间的平衡间距。
若只考虑最近邻原子间的相互作用,则作用在第n个原子上的力为来自左边弹簧的张力β$(μn-μn-1)$与来自右边弹簧的张力β$(μn+1-μn)$之和。


一维单原子链的频率分布一维单原子链是指由相同类型的原子按照一定的规则排列成的链状结构。
频率分布是指在单原子链中各个振动模式的频率出现的分布情况。
本文将从单原子链的基本特征、频率的计算方法以及频率分布的特点三个方面来详细探讨一维单原子链的频率分布。
一、单原子链的基本特征一维单原子链是凝聚态物理中常见的模型系统,它具有以下基本特征:1. 原子之间的相互作用力:在单原子链中,相邻原子之间存在着弹性力和相互作用力,这些力决定了原子在链中的振动行为。
2. 间距和质量的均匀性:单原子链中的原子间距相等,原子质量也相等,这使得单原子链具有均质性,便于分析和计算。
3. 边界条件:单原子链的两端通常会施加边界条件,如固定边界条件或周期性边界条件,以模拟实际情况中的约束条件。
二、频率的计算方法在一维单原子链中,原子的振动可以通过离散化简化为谐振子模型,通过求解谐振子的本征值问题可以得到振动频率。
对于一维单原子链,振动频率的计算方法如下:1. 利用牛顿第二定律:应用牛顿第二定律,可以得到原子的运动方程。
通过求解运动方程可以得到振动频率。
2. 应用弹性势能:利用弹性势能的定义,可以将原子的振动视为在势能函数中寻找最小值的过程。
通过求解势能函数的最小值问题,可以得到振动频率。
3. 应用量子力学:在一维单原子链中,可以将原子的振动量子化,利用量子力学的方法求解振动频率。
具体的计算方法可以通过哈密顿算符的对角化来实现。
三、频率分布的特点在一维单原子链中,频率分布具有以下特点:1. 频率的离散性:由于单原子链的离散结构,振动频率呈现出离散的特点。
频率分布通常由一系列离散的振动模式组成,每个模式对应一个特定的频率。
2. 频率的对称性:对于一维周期性边界条件的单原子链,频率分布具有对称性。
即频率分布在频率为零的点处对称,且对称轴上的频率相等。
3. 频率的分布范围:频率分布的范围取决于原子之间的相互作用力和边界条件。
不同的相互作用力和边界条件将导致不同的频率分布范围。


一维单原子链有支格波,且是波(光学或声学)一维单原子链是指所有原子都位于同一条直线上的晶格结构。
在这样的结构中,支格波是一种特殊的波动形式,它在晶格内传播,由于晶格的周期性结构而呈现出特定的性质。
支格波可以分为光学支格波和声学支格波两种类型,它们分别对应着不同的波动性质和传播特点。
在一维单原子链中,光学支格波是指在晶格中原子的振动与电磁波的耦合现象。
这种耦合导致了支格波在晶格中的传播,其频率范围通常高于声学支格波。
光学支格波的频率与晶格的结构有关,通常在布里渊区的边界处出现,对应着晶格的高频振动模式。
光学支格波通常具有较高的能量和传播速度,其在晶体中传播时能够产生材料的光学性质变化,例如光学吸收、光学色散等现象。
另声学支格波是指晶格中原子的振动与物质的机械性质耦合所形成的波动现象。
声学支格波的频率范围通常低于光学支格波,对应着晶格的低频振动模式。
声学支格波在晶格中的传播速度通常较慢,且具有较低的能量。
它们在晶体中的传播会导致声学性质的变化,例如声子散射、声子导热等现象。
对于一维单原子链中的支格波,其理论描述和实验观测都具有重要意义。
从理论上讲,通过研究支格波的频谱和传播特性,可以深入理解晶格动力学和固体材料的特性。
从实验上讲,通过光学或声学手段观测支格波的传播行为,可以验证理论模型,并且为材料科学和物理学的研究提供重要数据。
一维单原子链中的支格波是一种具有特殊传播性质的波动现象,包括光学支格波和声学支格波两种类型。
它们对应着晶格中的不同振动模式,具有重要的理论和实验意义。
通过深入研究支格波的特性,可以更好地理解固体材料的性质和行为,为材料科学和物理学的发展贡献重要的理论和实验成果。
在我看来,一维单原子链中的支格波是固体物理学中非常有趣且具有挑战性的研究课题。
通过对支格波的深入探索,我们可以揭示材料的微观结构和性质,为材料设计和应用提供新的思路和方法。
支格波的研究也可以深化我们对波动理论和晶格动力学的理解,拓展物理学的研究领域。



第n-2个原子第n-1个原子第n+1个原子第n+2个原子第n个原子maµn-2µn-1µnµn+1µn+2第n-2个原子第n-1个原子第n+1个原子第n+2个原子第n个原子maµn-2µn-1µnµn+1µn+2a一维晶格仅考虑最近邻原子间相互作用时的色散关系qv p ω=2.21∑=qqQ 221∑⎟⎠⎞⎜⎝⎛=•n n m T μ∑••=qiqna q n t Q Nmt ,)e (1)(μ∑∑∑′−′−′=nq qinaq q .q ina q .,t Q t QN T )e ()e (21∑∑∑′+′−′=q nq q ina qq .q .,Nt Q t Q)(e1)()(21∑∑′−′′=q qqq qq t Qt Q,)()(21,..δ∑−=qqqt Qt Q)()(21..∑=qqqt Qt Q)()(21.*.)()(*t Q t Q q q =−动能的正则坐标表示:势能∑−=qinaqq n eQ Nm 1μ∑−−−='')1('11q aq n i q n e QNm μ∑−−=nn n U 21)(21μμβ1(')'(')','1{[1]}()2N ia q q iaq iaq ina q q q q q q n U Q Q e e e emNβ−++==+−−∑∑}2{2∑−−−−=qiaq iaq qq e e Q Q mβ{1cos()}q qqQ Qaq mβ−=−∑代入上式,得:*{1cos()}qqqU Q Q aq mβ=−∑利用)}cos(1{22aq mq −=βω2*12q q q qU Q Q ω=∑2221∑=qq q Q U ω系统势能所以2221∑=qq q Q U ω哈密顿量2221()2q q qqH T U Q Q ω=+=+∑ ——系统复数形式的简正坐标ti q q q eA Nm Q ω=势能动能∑=qq Q T 221 1()[()()]2Q q a q ib q =+)]()([21)(*q ib q a q Q −=∑=qq Q T 2212221∑=qq q Q U ω∑>+=22)]()([21q q b q a T 实数形式的简正坐标令∑>+=222)]()([21q q q b q a U ω能量本征值qq n n qωε=)21(+=2()/exp()()2qq n q q n Q H ξϕωξ=−=本征态函数一个简正坐标对应一个谐振子方程,波函数是以简正坐标为宗量的谐振子波函数。
一维单原子链
一维单原子链,是由单个原子组成的一条直线结构。
这样的结构
具有稳定性和强的原子间作用力,因此一维单原子链在纳米科学领域
中被广泛应用。
一维单原子链的材料种类多样,通常包括金属、半导体和氧化物等。
在制备一维单原子链时,需要使用类似于扫描隧道显微镜等高技
术仪器,将原子逐个逐个地排列在一起,制成精细的结构。
利用一维单原子链,可以制作出具有独特性能的纳米器件。
例如,在光学应用方面,可以通过改变单原子链的排列方式,来控制其吸收、反射和透射等特性,进而实现光学信息存储、光伏电池和量子计算等
方面的研究。
在电子学应用方面,一维单原子链可以用于制作高性能
电子器件,例如纳米电缆、纳米场效应晶体管和纳米传感器等。
此外,一维单原子链的制备也为物理学和化学学科的发展带来了
新的思想和方法。
例如,在材料科学和固体物理学领域,研究人员可
以利用单原子链构建的新型组织结构,来探索材料的独特性能和物理
行为;在化学领域,通过单原子链的构建,可以实现对反应过程的控
制和调节,从而开发新型化学反应催化剂等。
总的来说,一维单原子链的制备和应用具有非常广泛的前景和重
要的意义,对于人类社会的发展和科学技术的进步都将发挥重要的作用。
一维单原子链,原子间距为a,但力常数交错一维单原子链是由一排原子组成的链状结构,原子间的距离为a。
在这个链中,每个原子之间存在一种交错的力常数关系。
本文将探讨这种交错力常数的特性及其在物理学中的应用。
我们来解释什么是力常数。
力常数是描述物体在受力时的刚度或弹性的物理量。
在一维单原子链中,原子之间的力常数交错意味着相邻原子之间的刚度或弹性不完全相同。
原子链中的力常数交错可以由两个方面来实现:原子的质量和原子之间的键强度。
首先,原子的质量会影响其惯性和受力后的振动频率。
较重的原子会具有较高的力常数,而较轻的原子则会具有较低的力常数。
其次,原子之间的键强度也会影响力常数。
键强度较高的原子之间会具有较高的力常数,而键强度较低的原子之间则会具有较低的力常数。
在物理学中,一维单原子链的力常数交错现象可以应用于多个领域。
首先,它在固体力学中起着重要作用。
通过研究力常数交错的原子链,我们可以了解固体的弹性特性和变形行为。
这对于材料工程师来说是非常重要的,因为他们可以根据这些特性来设计具有特定弹性和刚度的材料。
力常数交错的原子链在纳米科学和纳米技术中也有广泛的应用。
纳米材料是由纳米尺度的原子或分子构成的材料。
通过控制一维单原子链中的力常数交错,科学家可以设计出具有特定性质和功能的纳米材料,如纳米传感器、纳米机器人等。
这些纳米材料在医学、环境监测和信息技术等领域有着广泛的应用前景。
力常数交错的原子链还可以用于研究声子晶体。
声子晶体是一种具有特殊声学性质的材料,其声子频率的禁带结构可以通过调节原子链中的力常数交错来实现。
这种材料在声学隔离、声波传感和声子学器件等领域有着重要的应用潜力。
一维单原子链中的力常数交错是一种重要的物理现象,具有广泛的应用前景。
通过研究和控制这种交错,我们可以深入了解材料的弹性特性和变形行为,并设计出具有特定功能和性质的纳米材料。
此外,力常数交错还可以用于研究声子晶体,为声学隔离和声波传感等领域提供新的解决方案。
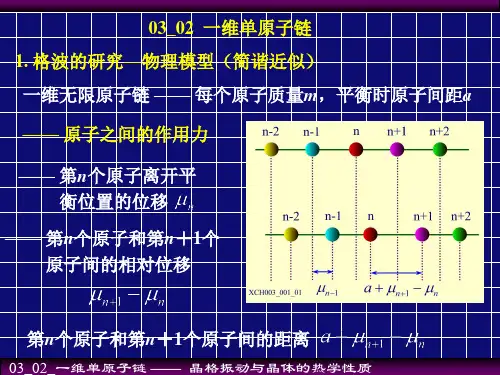
第九讲:晶体振动上一维单原子链简谐近似和简正坐标布拉伐晶格晶体中的格点表示原子的平衡位置,原子在格点附近作热振动,由于晶体内原子之间存在相互作用力,各个原子的振动不是孤立的,而是相互联系在一起的,因此在晶体中形成各种模式的波,称为格波。
只有当振动非常微弱时,原子间的相互作用可以认为是简谐的,非简谐的相互作用可以忽略,在简谐近似下,振动模式才是独立的。
由于晶体的平移对称性,振动模式所取的能量值不是连续的,而是分立的。
通常用一系列独立的简谐振子来描述这些独立的振动模,它们的能量量子称为声子。
势能和动能函数设简单晶格晶体包含N 个原子,平衡位置为R n ,偏离平衡位置的位移矢量为µn (t ),则原子的位置为()()R R n n n t t '=+µ。
将位移矢量µn (t )用分量表示,写成µi ( i = 1, 2, ..., 3N )。
N 个原子体系的势能函数可以在平衡位置附近展开成泰勒级数:⋅⋅⋅++ +=∑∑==j i N i N j i j i i i V V V V µµ∂µ∂µ∂µ∂µ∂03131,20021 (3-1) 下标0表示为在平衡位置时所具有的值。
可以设V 0 = 0,而且在平衡位置相互作用力为零:0 0=i V ∂µ∂ (3-2) 忽略二阶以上的非简谐项可得:j i N j i ji V V µµ∂µ∂µ∂031,221∑==(3-3) N 个原子体系的动能函数为:∑==Ni ii m T 31221µ(3-4)简正坐标 为了使问题简化,引入简正坐标N Q Q Q 321 , , ,⋅⋅⋅简正坐标和原子的位移坐标 µi 之间通过正交变换相互联系:∑==Nj jij i i Qa m 31µ (3-5)引入简正坐标后体系的势能函数和动能函数为:∑==Ni iQT 31221(3-6)∑==N i ii QV 312221ω (3-7)由于动能函数T 是正定的,根据线性代数的理论,总可以找到这样的正交变换,使势能函数和动能函数同时化为平方项之和。
第n-2个原子第n-1个原子第n+1个原子第n+2个原子
第n个原子
m
a
µn-2µn-1µnµn+1µn+2
第n-2个原子第n-1个原子第n+1个原子第n+2个原子
第n个原子
m
a
µn-2µn-1µnµn+1µn+2
a
一维晶格仅考虑最近邻原子间相互作用时的色散关系
q
v p ω=
2
.
2
1∑=q
q
Q 2
21∑⎟
⎠
⎞⎜⎝⎛=•n n m T μ∑
•
•
=
q
iqna q n t Q Nm
t ,
)e (1)(μ∑∑∑′−′−′
=n
q q
inaq q .
q ina q .
,
t Q t Q
N T )e ()e (21∑∑∑′
+′−′
=
q n
q q ina q
q .
q .,
N
t Q t Q
)
(e
1)
()(2
1∑∑′
−′′
=q q
q
q q
q t Q
t Q
,
)()(21,.
.
δ
∑−=
q
q
q
t Q
t Q
)
()(2
1.
.
∑
=q
q
q
t Q
t Q
)
()(2
1
.
*.)
()(*
t Q t Q q q =−动能的正则坐标表示:
势能∑−=
q
inaq
q n e
Q N
m 1μ∑−−−=
'
'
)1('
11q aq n i q n e Q
N
m μ∑−−=
n
n n U 21)(21
μμβ1
(')'(')
','
1{[1]}(
)
2N ia q q iaq iaq ina q q q q q q n U Q Q e e e e
m
N
β
−++==
+−−∑∑}2{2∑−−−−=
q
iaq iaq q
q e e Q Q m
β
{1cos()}
q q
q
Q Q
aq m
β
−=
−∑代入上式,得:
*{1cos()}q
q
q
U Q Q aq m
β
=
−∑利用
)}cos(1{22aq m
q −=
β
ω2*
12q q q q
U Q Q ω=
∑2
221∑=
q
q q Q U ω系统势能所以
2
2
21∑=
q
q q Q U ω哈密顿量
2221()2q q q
q
H T U Q Q ω=+=
+∑ ——系统复数形式的简正坐标
t
i q q q e
A Nm Q ω=势能
动能
∑=
q
q Q T 2
21 1
()[()()]2
Q q a q ib q =
+)]()([2
1
)(*q ib q a q Q −=
∑=
q
q Q T 2
21
2
2
21∑=
q
q q Q U ω∑>+=
22)]()([21q q b q a T 实数形式的简正坐标令∑>+=
222
)]()([21q q q b q a U ω能量本征值
q
q n n q
ωε=)2
1
(+=2
()/exp()()
2
q
q n q q n Q H ξϕωξ=−
=本征态函数
一个简正坐标对应一个谐振子方程,波函数是以简正
坐标为宗量的谐振子波函数。
哈密顿量:
2222200
11[()()][()()]22q q q H a q b q a q b q ω>>=
+++∑∑
声子系综是无相互作用的声子气组成的系统,每个振动模式在简谐近似条件下都是独立的,晶格振动的问题转化为声子系统问题的研究。
9.声子
晶格振动的能量量子;或格波的能量量子。
一个格波也就是一种振动模式,称为一种声子。
当这种振动模处于时,说明有个声子。
q q n ω=)2
1
(+q n q ω=声子具有能量
、准动量
,可以看作是准粒子,
声子是一种元激发,可与电子或光子发生作用。
q
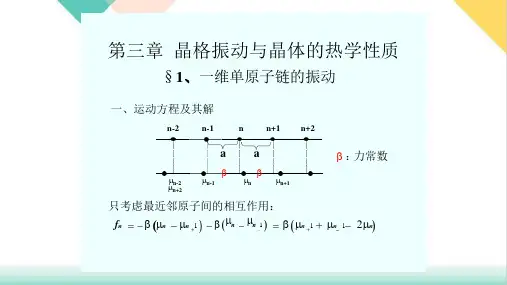
G =模型运动方程试探解
色散关系
波矢q 范围
一维无限长原子链,m ,a ,β晶格振动波矢的数
目=晶体的原胞数
B--K 条件波矢的数目
()()
11..
+−−−−−=n n n n n m μμβμμβμ()
naq t i n A −=ωμe 2sin
2
aq m
β
ω=a
q a π
π≤<−
N
n n +=μμn -2n
n +1
n +2
n -1a
m m
o a π−a
πω
m
2
β总结:本节研究思路。