一维单原子链

第n-2个原子第n-1个原子第n+1个原子第n+2个原子第n个原子maµn-2µn-1µnµn+1µn+2第n-2个原子第n-1个原子第n+1个原子第n+2个原子第n个原子maµn-2µn-1µnµn+1µn+2a一维晶格仅考虑最近邻原子间相互作用时的色散关系qv p ω=2.21∑=qqQ 221∑⎟⎠⎞⎜⎝⎛=•n n m T μ∑••=qiqna q n t Q Nmt ,)e (1)(μ∑∑∑′−′−′=nq qinaq q .q ina q .,t Q t QN T )e ()e (21∑∑∑′+′−′=q nq q ina qq .q .,Nt Q t Q)(e1)()(21∑∑′−′′=q qqq qq t Qt Q,)()(21,..δ∑−=qqqt Qt Q)()(21..∑=qqqt Qt Q)()(21.*.)()(*t Q t Q q q =−动能的正则坐标表示：势能∑−=qinaqq n eQ Nm 1μ∑−−−='')1('11q aq n i q n e QNm μ∑−−=nn n U 21)(21μμβ1(')'(')','1{[1]}()2N ia q q iaq iaq ina q q q q q q n U Q Q e e e emNβ−++==+−−∑∑}2{2∑−−−−=qiaq iaq qq e e Q Q mβ{1cos()}q qqQ Qaq mβ−=−∑代入上式，得：*{1cos()}qqqU Q Q aq mβ=−∑利用)}cos(1{22aq mq −=βω2*12q q q qU Q Q ω=∑2221∑=qq q Q U ω系统势能所以2221∑=qq q Q U ω哈密顿量2221()2q q qqH T U Q Q ω=+=+∑ ——系统复数形式的简正坐标ti q q q eA Nm Q ω=势能动能∑=qq Q T 221 1()[()()]2Q q a q ib q =+)]()([21)(*q ib q a q Q −=∑=qq Q T 2212221∑=qq q Q U ω∑>+=22)]()([21q q b q a T 实数形式的简正坐标令∑>+=222)]()([21q q q b q a U ω能量本征值qq n n qωε=)21(+=2()/exp()()2qq n q q n Q H ξϕωξ=−=本征态函数一个简正坐标对应一个谐振子方程，波函数是以简正坐标为宗量的谐振子波函数。

一维单原子链推导
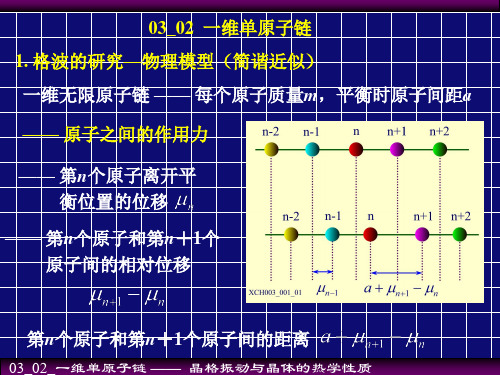
一维单原子链是指一维无限长的单原子链，其中原子质量为m，原子间距为a。

热运动使得原子离开平衡位置，假设第n个原子离开平衡位置的位移为μn，它相对于a是一个很小的量，第n个原子到第n+1个原子间相对位移为δ，则：$\delta=μn+1-μn$。

当原子m在平衡位置时，两个原子相互作用势为$V(a)$；相对位移为$\delta$时，两个原子相互作用势为$V(a+\delta)$。

将$V(a+\delta)$在平衡位置用泰勒级数展开，可得：$\cdots(21)(222=+++=aaδaδdrdVaVdrVddrdVaVaVrVδ$。

由于考虑的是微振动，即$\delta$很小，展开式可以近似保留到$\delta^2$项，可得：$10(\cdots)!(\cdots)!2)(\cdots)('\theta'\theta'\theta'\theta'\theta'\approx++++ +++2222\delta\delta\delta$。

只考虑最近邻原子间的相对位移的二次项对系统总势能的贡献，则总势能写为：$\cdots212)(μ221−−=≈∑nnnVμββδ$。

第n个原子所受的力为：$\cdots2(11+−−−−=−≈∂δ∂−=nnnnVfμμμββδβ$，其中β是相邻原子间准弹性力的力常数，它直接由两个原子间的相互作用势能所决定，$a$是两个原子间的平衡间距。

若只考虑最近邻原子间的相互作用，则作用在第n个原子上的力为来自左边弹簧的张力β$(μn-μn-1)$与来自右边弹簧的张力β$(μn+1-μn)$之和。

一维单原子链的频率分布一维单原子链是指由相同类型的原子按照一定的规则排列成的链状结构。

频率分布是指在单原子链中各个振动模式的频率出现的分布情况。

本文将从单原子链的基本特征、频率的计算方法以及频率分布的特点三个方面来详细探讨一维单原子链的频率分布。

一、单原子链的基本特征一维单原子链是凝聚态物理中常见的模型系统，它具有以下基本特征：1. 原子之间的相互作用力：在单原子链中，相邻原子之间存在着弹性力和相互作用力，这些力决定了原子在链中的振动行为。

2. 间距和质量的均匀性：单原子链中的原子间距相等，原子质量也相等，这使得单原子链具有均质性，便于分析和计算。

3. 边界条件：单原子链的两端通常会施加边界条件，如固定边界条件或周期性边界条件，以模拟实际情况中的约束条件。

二、频率的计算方法在一维单原子链中，原子的振动可以通过离散化简化为谐振子模型，通过求解谐振子的本征值问题可以得到振动频率。

对于一维单原子链，振动频率的计算方法如下：1. 利用牛顿第二定律：应用牛顿第二定律，可以得到原子的运动方程。

通过求解运动方程可以得到振动频率。

2. 应用弹性势能：利用弹性势能的定义，可以将原子的振动视为在势能函数中寻找最小值的过程。

通过求解势能函数的最小值问题，可以得到振动频率。

3. 应用量子力学：在一维单原子链中，可以将原子的振动量子化，利用量子力学的方法求解振动频率。

具体的计算方法可以通过哈密顿算符的对角化来实现。

三、频率分布的特点在一维单原子链中，频率分布具有以下特点：1. 频率的离散性：由于单原子链的离散结构，振动频率呈现出离散的特点。

频率分布通常由一系列离散的振动模式组成，每个模式对应一个特定的频率。

2. 频率的对称性：对于一维周期性边界条件的单原子链，频率分布具有对称性。

即频率分布在频率为零的点处对称，且对称轴上的频率相等。

3. 频率的分布范围：频率分布的范围取决于原子之间的相互作用力和边界条件。

不同的相互作用力和边界条件将导致不同的频率分布范围。

一维单原子链有支格波,且是波(光学或声学)一维单原子链是指所有原子都位于同一条直线上的晶格结构。

在这样的结构中，支格波是一种特殊的波动形式，它在晶格内传播，由于晶格的周期性结构而呈现出特定的性质。

支格波可以分为光学支格波和声学支格波两种类型，它们分别对应着不同的波动性质和传播特点。

在一维单原子链中，光学支格波是指在晶格中原子的振动与电磁波的耦合现象。

这种耦合导致了支格波在晶格中的传播，其频率范围通常高于声学支格波。

光学支格波的频率与晶格的结构有关，通常在布里渊区的边界处出现，对应着晶格的高频振动模式。

光学支格波通常具有较高的能量和传播速度，其在晶体中传播时能够产生材料的光学性质变化，例如光学吸收、光学色散等现象。

另声学支格波是指晶格中原子的振动与物质的机械性质耦合所形成的波动现象。

声学支格波的频率范围通常低于光学支格波，对应着晶格的低频振动模式。

声学支格波在晶格中的传播速度通常较慢，且具有较低的能量。

它们在晶体中的传播会导致声学性质的变化，例如声子散射、声子导热等现象。

对于一维单原子链中的支格波，其理论描述和实验观测都具有重要意义。

从理论上讲，通过研究支格波的频谱和传播特性，可以深入理解晶格动力学和固体材料的特性。

从实验上讲，通过光学或声学手段观测支格波的传播行为，可以验证理论模型，并且为材料科学和物理学的研究提供重要数据。

一维单原子链中的支格波是一种具有特殊传播性质的波动现象，包括光学支格波和声学支格波两种类型。

它们对应着晶格中的不同振动模式，具有重要的理论和实验意义。

通过深入研究支格波的特性，可以更好地理解固体材料的性质和行为，为材料科学和物理学的发展贡献重要的理论和实验成果。

在我看来，一维单原子链中的支格波是固体物理学中非常有趣且具有挑战性的研究课题。

通过对支格波的深入探索，我们可以揭示材料的微观结构和性质，为材料设计和应用提供新的思路和方法。

支格波的研究也可以深化我们对波动理论和晶格动力学的理解，拓展物理学的研究领域。

一维单原子链
一维单原子链，是由单个原子组成的一条直线结构。

这样的结构
具有稳定性和强的原子间作用力，因此一维单原子链在纳米科学领域
中被广泛应用。

一维单原子链的材料种类多样，通常包括金属、半导体和氧化物等。

在制备一维单原子链时，需要使用类似于扫描隧道显微镜等高技
术仪器，将原子逐个逐个地排列在一起，制成精细的结构。

利用一维单原子链，可以制作出具有独特性能的纳米器件。

例如，在光学应用方面，可以通过改变单原子链的排列方式，来控制其吸收、反射和透射等特性，进而实现光学信息存储、光伏电池和量子计算等
方面的研究。

在电子学应用方面，一维单原子链可以用于制作高性能
电子器件，例如纳米电缆、纳米场效应晶体管和纳米传感器等。

此外，一维单原子链的制备也为物理学和化学学科的发展带来了
新的思想和方法。

例如，在材料科学和固体物理学领域，研究人员可
以利用单原子链构建的新型组织结构，来探索材料的独特性能和物理
行为；在化学领域，通过单原子链的构建，可以实现对反应过程的控
制和调节，从而开发新型化学反应催化剂等。

总的来说，一维单原子链的制备和应用具有非常广泛的前景和重
要的意义，对于人类社会的发展和科学技术的进步都将发挥重要的作用。

一维单原子链费米半径费米半径是描述一维单原子链中费米子行为的一个重要概念。

在固体物理学中，费米子是具有半整数自旋的粒子，如电子，中子等。

费米子遵循费米-狄拉克统计，根据泡利不相容原理，同一量子态最多只能容纳一个费米子。

费米半径则是描述费米子在动量空间中占据态密度的临界值，低于费米半径的态密度被称为占据态密度，高于费米半径的态密度被称为非占据态密度。

一维单原子链是一种理想化的模型系统，在实际物理体系中也具有一定的现实意义。

研究一维单原子链费米半径可以揭示费米子在一维结构中的特殊行为，对于理解低维系统的物理性质具有重要意义。

为了理解一维单原子链费米半径的概念和其物理意义，首先需要了解费米子的本质和费米-狄拉克统计方法。

费米子是半整数自旋粒子，其运动状态由哈密顿量描述。

费米子具有泡利不相容原理，该原理指出相同自旋的费米子之间不能处于同一量子态。

因此，费米子分布在动量空间中的态密度被分为占据态密度和非占据态密度。

费米子的动量分布由费米-狄拉克分布函数给出。

一维单原子链是一种理想化的模型系统，其由无限长的原子线依次排列而成。

在一维单原子链中，费米子受限于维度的约束，其态密度的形态将会与三维情况有所不同。

费米-狄拉克分布函数可以用来描述一维单原子链费米子的动量分布。

费米-狄拉克分布函数给出了费米子在不同动量处占据态密度的概率分布。

在一维单原子链中，费米子的能量和动量之间的关系由能带结构决定。

在低温下，费米子的动量分布将呈现两个尖峰，分别对应于占据态密度和非占据态密度。

费米半径的确定通过占据态密度和非占据态密度尖峰之间的交叉点得到。

费米半径对于理解一维单原子链中费米子的行为至关重要。

由于一维结构的约束，费米半径相较于三维情况更加复杂。

一维单原子链中费米半径的计算可以通过数值方法或理论推导得到。

在具体的一维单原子链模型中，费米半径可能会受到外界因素的影响，如温度、相互作用等。

研究一维单原子链费米半径的物理意义在于理解低维系统中的费米子行为。

一维单原子链和一维双原子链的色散关系下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!一维单原子链和一维双原子链是凝聚态物理领域中常见的研究对象，它们的色散关系对于理解材料的光学和电学性质具有重要意义。

第n-2个原子第n-1个原子第n+1个原子第n+2个原子第n个原子maµn-2µn-1µnµn+1µn+2第n-2个原子第n-1个原子第n+1个原子第n+2个原子第n个原子maµn-2µn-1µnµn+1µn+2a一维晶格仅考虑最近邻原子间相互作用时的色散关系qv p ω=2.21∑=qqQ 221∑⎟⎠⎞⎜⎝⎛=•n n m T μ∑••=qiqna q n t Q Nmt ,)e (1)(μ∑∑∑′−′−′=nq qinaq q .q ina q .,t Q t QN T )e ()e (21∑∑∑′+′−′=q nq q ina qq .q .,Nt Q t Q)(e1)()(21∑∑′−′′=q qqq qq t Qt Q,)()(21,..δ∑−=qqqt Qt Q)()(21..∑=qqqt Qt Q)()(21.*.)()(*t Q t Q q q =−动能的正则坐标表示：势能∑−=qinaqq n eQ Nm 1μ∑−−−='')1('11q aq n i q n e QNm μ∑−−=nn n U 21)(21μμβ1(')'(')','1{[1]}()2N ia q q iaq iaq ina q q q q q q n U Q Q e e e emNβ−++==+−−∑∑}2{2∑−−−−=qiaq iaq qq e e Q Q mβ{1cos()}q qqQ Qaq mβ−=−∑代入上式，得：*{1cos()}qqqU Q Q aq mβ=−∑利用)}cos(1{22aq mq −=βω2*12q q q qU Q Q ω=∑2221∑=qq q Q U ω系统势能所以2221∑=qq q Q U ω哈密顿量2221()2q q qqH T U Q Q ω=+=+∑ ——系统复数形式的简正坐标ti q q q eA Nm Q ω=势能动能∑=qq Q T 221 1()[()()]2Q q a q ib q =+)]()([21)(*q ib q a q Q −=∑=qq Q T 2212221∑=qq q Q U ω∑>+=22)]()([21q q b q a T 实数形式的简正坐标令∑>+=222)]()([21q q q b q a U ω能量本征值qq n n qωε=)21(+=2()/exp()()2qq n q q n Q H ξϕωξ=−=本征态函数一个简正坐标对应一个谐振子方程，波函数是以简正坐标为宗量的谐振子波函数。