工程力学 第十一章-能量法
- 格式:ppt
- 大小:1.06 MB
- 文档页数:35


12 能量法1、外力的功、应变能、比能等的有关概念,外力的功应变能比能2、基本变形杆件应变能计算和组合变形杆件应变能计算对于线弹范围内的等直拉压杆的应变能梁横力弯曲的剪切应变能为(常忽略)当扭矩Mt沿杆轴变化时,圆轴的扭转应变能横力弯曲时,不计剪切能,,弯矩沿截面变化,梁的应变能为3、功能原理、功的互等定理和位移互等定理4、余能概念5、卡氏第一和第二定理解题范例12.1具有中间铰的线弹性材料梁,受力如图12.1(a)所示,两端梁的弯曲刚度均为EI。
用莫尔法确定中间铰两侧界面的相对转角有下列四种分段方法,使判断哪一种是正确的。
(A)按图(b)所示施加一对单位力偶,积分时不必分段;(B)按图(b)所示施加一对单位力偶,积分时必须分段;(C)按图(c)所示施加一对单位力偶,积分时不必分段;(D)按图(c)所示施加一对单位力偶,积分时必须分段;图12.1答案:(A)12.2图12.2示简支梁中点只承受集中力F时,最大转角为,应变能为;中点只承受集中力偶M时,最大挠度是、梁的应变能为。
当同时在中点施加F和M时,梁的应变能有以下四种答案,试判断哪一种是正确的。
(A)+;(B)++M;(C)++F;(D)++( M+F);图12.2[解] 因为对于线性弹性结构,先加F时梁内的应变能为:=F f F在加M时,由于反对称载荷,梁中点的挠度仍是f F,所以梁内应变能将增加:M=当同时施加F和M时的应变能,等于先加F再加M时的应变能,即+故答案(A)正确。
12.3 用卡氏第二定理求图12.3所示刚架A截面的位移和B截面的转角。
略去剪力Q和轴力N的影响,EⅠ为已知.LLⅠ2Ⅰ图 12.3[解] (1)A截面的位移AB段弯矩:M(x)=-Px (0x)∂M(x) /∂P=-x在A 处虚加一水平力向右的力Q,之后,再令其为0.那么,BC段弯矩:M(y)=-2P- Q+(P+Q)y∂M(y) /∂P=-2+y ∂M(y) /∂ Q=-+yA截面的竖直位移:A截面的水平位移:积分,令Q=0得(2)B截面的转角在B处虚加一力偶M B,AB段弯矩:M(x)=-Px (0x<)BC段弯矩:M(y)=-2P-+P y (0<y<)∂M(x) /∂M B=0 ∂M(y) /∂M B =-1习题解析12.1用卡氏第二定理求图12.4示的A截面的位移和B截面的转角。
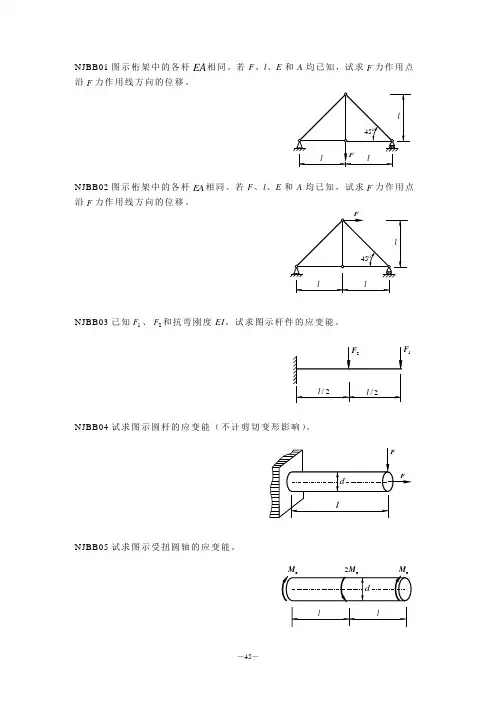
NJBB01图示桁架中的各杆EA 相同。
若F 、l 、E 和A 均已知,试求F 力作用点沿F 力作用线方向的位移。
NJBB02图示桁架中的各杆EA 相同。
若F 、l 、E 和A 均已知,试求F 力作用点沿F 力作用线方向的位移。
NJBB03已知1F 、2F 和抗弯刚度EI 。
试求图示杆件的应变能。
NJBB04试求图示圆杆的应变能(不计剪切变形影响)。
NJBB05试求图示受扭圆轴的应变能。
1FMNJBB06求图示受扭圆轴的应变能(125.1d d =)。
NJBB07图示等截面杆受轴向力1F 和2F 的作用,横截面面积为A ,弹性模量为E 。
试求杆的应变能。
NJBB08试求图示结构C 点的铅垂位移。
EI 、l 和F 均为已知。
NJBB09图示由等截面直杆AB 和AC 组成的桁架,若二杆的抗拉(压)刚度相等,且F 、l 、α、E 和A 为已知。
试求力F 作用点的铅垂位移。
NJBB10图示悬臂梁受集中力偶e M 作用。
若EI 和l 已知,试用能量法求B 截面的转角。
NJBB11试求图示阶梯形梁B 点的挠度。
E 、I 、a 和F 均为已知。
NJBB12图示用同样材料制成的两根圆截面直杆。
试比较二杆的应变能,并求二杆的伸长。
NJBB13试利用功能原理求图示阶梯轴B 截面相对于A 截面的扭转角。
已知切变模量为G ,125.1d d =。
NJBB14试证明矩形截面简支梁跨中受集中力F 作用时的应变能为)9/()2/(2Al E U ⋅=σ,其中A 为横截面面积,σ为梁中最大应力。
(a)(b)NJBB15已知图示(a )情况下梁的应变能为1U 。
试求图(b )情况下梁的应变能。
NJBB16试求图示梁B 点的挠度。
NJBB17试求图示梁B 点的挠度。
NSBB18试求图示悬臂量自由端A 点的挠度A y 和转角A 。
NSBB19试求图示悬臂量自由端A 点的挠度A y 。
(a)(b)BFCFNSBB20试求图示悬臂梁自由端的水平位移和铅垂位移。








材料力学能量法知识点总结材料力学是工程力学的重要分支之一,研究材料在受力作用下的变形与破坏行为。
能量法是材料力学的基础理论之一,通过利用能量守恒原理,分析和求解材料的力学问题,具有重要的理论和实践价值。
本文将对材料力学能量法的基本概念、原理和应用进行总结。
1. 弹性势能与弹性应变能材料在受力作用下产生的变形能够存储为弹性势能,其中最常用的势能是弹性应变能。
弹性应变能是由于材料的弹性变形而储存的能量,可表示为弹性应变能密度。
2. 弹性势能的计算方法弹性应变能的计算方法主要有两种:一是通过力学平衡方程和材料力学性质的函数关系进行积分计算;二是通过应力-应变关系和应变能密度公式进行计算。
3. 弹性势能的应用弹性势能的应用涉及材料的变形、破裂、接头设计等问题。
通过计算弹性势能可以判断材料是否会发生破裂,并可用于材料的优化设计。
4. 塑性势能与塑性应变能材料在塑性变形时会产生塑性势能,塑性势能是由于材料的塑性变形而储存的能量。
塑性应变能可表示为塑性应变能密度。
5. 塑性势能的计算方法塑性势能的计算方法适用于材料的非弹性变形过程,常用的方法有等效应力法和Mises准则。
通过计算塑性势能可以估计材料在受力作用下的变形程度和破坏形式。
6. 塑性势能的应用塑性势能的应用主要涉及材料的变形、强度分析和塑性成形工艺等问题。
通过计算塑性势能可以评估材料的强度和变形能力,并可用于材料的成形优化。
7. 总势能与变分原理材料受到多种因素的叠加作用时,总势能是各种势能的代数和。
变分原理是能量法的基本原理之一,通过对总势能进行变分,得到材料力学问题的基本方程。
8. 总势能的应用总势能的应用主要涉及材料的稳定性分析和振动问题。
通过计算总势能可以判断材料的稳定性,预测振动频率和振动模式。
9. 耗散能与损伤模型材料在受力作用下会发生能量损耗,产生耗散能。
通过建立耗散能与应变的关系,可以描述材料的损伤行为,并建立损伤模型进行应力-应变分析。