平行线等分线段定理练习及答案
- 格式:doc
- 大小:269.50 KB
- 文档页数:8

平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111cab=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题【例4】(2007年北师大附中期末试题) (1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( )A.52B.1C.32D.2(1)MEDC BA(2)F ED CBA【例5】 (2001年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD 的值;(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.【例6】 (2003年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是ADED CAO上的一点,且BE AC =,延长BE 交AC 于F 。

平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=.2. 平行线分线段成比例定理的推论:如图,在三角形中, 如果DE BC ∥,则AD AE DEAB AC BC==3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
1、如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
2、 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.3、如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=.4、如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.l 3l 2l 1FE D CB A ABCDEE DC B AEDCBAFE DCBAFEDCBAECA5、如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作 EF CD ∥交AD BC ,于E F ,,求EF 的长。
6、(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
7、(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =,连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( ) A.52 B.1 C.32D.28、如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD于点O . (1)当1A 2AE C =时,求AOAD 的值; (2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.9、如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.10、如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。

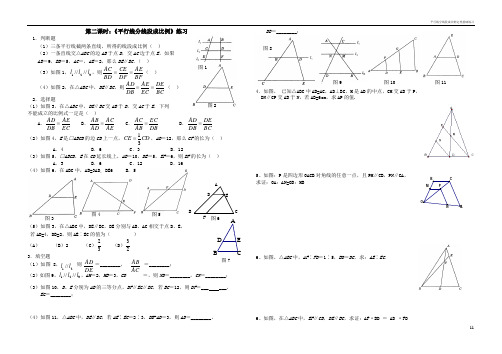
平行线分线段成比例定理基础练习第二课时:《平行线分线段成比例》练习1.判断题(1)三条平行线截两条直线,所得的线段成比例( )(2)一条直线交△ABC 的边AB 于点D ,交AC 边于点E ,如果 AB =9,BD =5,AC =,AE =2,那么DE ∥BC .( )(3)如图1,321////l l l ,则BFAE DF CE BD AC ==( ) (4)如图2,在△ABC 中,DE ∥BC ,则BC DEEC AE DB AD ==( ) 2.选择题(1)如图3,在△ABC 中,DE ∥BC 交AB 于D ,交AC 于E ,下列 不能成立的比例式一定是( ) A .EC AE DB AD = B .AE AC AD AB = C .DB EC AB AC = D .BCDEDB AD =(2)如图4,E 是□ABCD 的边CD 上一点,CD CE 31=,AD =12,那么CF 的长为( )A .4B .6C .3D .12(3)如图5,□ABCD ,E 在CD 延长线上,AB =10,DE =5,EF =6,则BF 的长为( )A .3B .6C .12D .16(4)如图6,在ABC 中,AB=3AD, DE6 B. 5 C. 4 D. 3(5)如图3,在△ABC 中,DE ∥BC ,DE 分别与AB 、AC 相交于点D 、E ,若AD=4,DB=2,则AE ︰EC 的值为( ) (A ) (B )2 (C )32 (D )23 3.填空题(1)如图8, 则=________, =________; (2)如图9,321////l l l ,AM =2,MB =3,CD =,则ND =________,CN =________;(3)如图10,D 、E 分别为AB 的三等分点,DF ∥EG ∥BC ,若BC =12,则DF =___ ___,EG =________;(4)如图11,△ABC 中,DE ∥BC ,若AE ∶EC =2∶3,DB -AD =3,则AD =________,DB =________;4.如图, 已知△ABC 中AB=AC ,AD ⊥BC ,M 是AD 的中点,CM 交AB 于P , DN ∥CP 交AB 于N ,若AB=6cm ,求AP 的值.5、如图:P 是四边形OACB 对角线的任意一点,且PM ∥CB ,PN ∥CA , 求证:OA :AN=OB :MB6、如图,△ABC 中,AF ∶FD =1∶5,BD =DC ,求:AE ∶EC .6、如图,在△ABC 中,EF ∥CD ,DE ∥BC ,求证:AF ·BD = AD ·FDOPN MCB A21//l l DE AD ACAB 图6 B A C F D E图7E D CBA 图1 图2图3 图4 图5 图11图10 图9 图8平行线分线段成比例定理基础练习(如图2-2)已知直线截△ABC 三边所在的直线分别于E 、F 、D 三点 且AD=BE. 求证:EF :FD=CA :CB.练习1.两地实际距离是3500米,画在图上距离是5厘米,则比例尺为______. 若在地图上量得为6厘米,实际距离为______米. 2.已知:,346x y z 那么3242x yz x=______. 3.若a 、b 、c 表示三条线段,且a =2511, b =25+11, c 是a 、b 的比例中项,则c =______.4.若(a -b ) : b =2 : 3. 则a : b =______.5.如图,BE 平分∠ABC ,DE ∥BC 交AB 于D ,BC =6,AB =9,求DE .6.已知:如图,若AB ∥A ′B ′, BC ∥B ′C ′. 求证:AC ∥A ′C ′.一.相似的图形1、 相同, 不一定相同的图形叫相似图形。




例01.如图,在ABC ∆中,AD 是BC 边上的中线,M 是AD 的中点,BM 的延长线交AC 于N .求证:.21CN AN =证明:过点D 作BN DE //,交AC 于E . ∵D 为BC 中点, ∴EC NE =.∵M 为AD 中点,DN MN //, ∴NE AN =.∴EC NE AN ==, 即CN AN 21=说明:本题考查平行线等分线段定理的推论,解题关键是过中点D 作BN 的平行线DE 交AC 于E ,证出E 是NC 的中点.例02.如图,已知:在梯形ABCD 中,BC AD //,BE AE =,BC EF //交DC 于F ,AF 、BC 延长线交于点G .求证:BC AD BG +=.分析:因为CG BC BG +=,所以为了证明BC AD BG +=只需证明CG AD =就可以了. 那么由GCF ADF ∆≅∆很容易得到这点.证明 ∵BC EF BC AD //,//(已知),∴ BC EF AD ////(如果两条直线都平行于第三条直线,则这两条直线平行) 又∵ BE AE =(已知)∴ FG AF =(经过三角形一边的中点与另一边平行的直线必平分第三边) FC DF =(经过梯形一腰的中点与底平行的直线,必平分另一腰) 又∵GFC AFD ∠=∠, ∴ GCF ADF ∆≅∆ ∴GC AD =∴ AD BC CG BC BG +=+=例03.如图,已知:在矩形ABCD 中,E 、F 分别是AD 、BC 的中点,连结BE 、DF 交AC 于G 、H 两点.求证:HC GH AG ==.分析:图中E 、F 是线段的中点,而求证中,G 应该为AH 中点,而H 应该是CG 的中点,因此,我们分析后判断,可能与平行线等分线段定理有一定联系.证明:∵四边形ABCD 是矩形, ∴BC AD //且BC AD =又∵E 、F 分别为AD 、BC 中点, ∴BF ED =,且BF ED //∴四边形BFDE 是平行四边形. ∴FD BE //. ∵DE AE =,∴ GH AG =(经过三角形一边中点与另一边平行的直线平分第三边) 同理,∵FC BF =, ∴HC GH =. ∴HC GH AG ==说明 无论平行线出现三条、四条或更多条,截得的线段如果相等,在另一条直线上截得的各条线段也相等,两条平行线的出现往往关系到推论.例04.如图,已知:在梯形ABCD 中,BC AD //,BC DC ⊥,E 为AB 的中点. 求证:ED EC =.分析:要证ED EC =,实际上只要证E 点在CD 的垂直平分线上,故过E 点作CD EF ⊥,因为CD BC ⊥,所以BC EF //. 由E 为AB 的中点. 根据平行线等分线段定理的推论可证出F 是CD 的中点. EF 是线段CD 的垂直平分线,从而有ED EC =.证明:过点E 作CD EF ⊥,垂足为F , ∵CD BC ⊥, ∴EF BC //∵E 为梯形ABCD 的腰AB 的中点, ∴EF 平分CD .∴EF 是CD 的垂直平分线. ∴ED EC =例05.如图,AB CB AB DA ⊥⊥,,M 是DC 的中点. 求证:MB MA =.证法1 作AB MN ⊥于N. ∵AB CB AB DA ⊥⊥,, ∴BC MN AD //// ∵MC DM =, ∴BN AN =.∴MN 垂直平分AB , 故MB AM =证法2 如图,延长BM 交AD 于P . ∵AB CB AB DA ⊥⊥,, ∴CB DA //. ∴C D ∠=∠∵CMB DMP CM DM ∠=∠=,,∴CMB DMP ∆≅∆. ∴MB PM =∴AM 是PAB Rt ∆斜边PB 的中线. ∴MB MA =.说明 证法1是运用平分线等分线段定理证明的,证法2则是用补全基本图形的方法运用直角三角形斜边中线等于斜边一半证明的.例06.如图,梯形ABCD 中,BC AD //,BC DC ⊥,︒=∠60B ,BC AB =,E 为AB 的中点.求证:ECD ∆为等边三角形.证明 过点E 作AD EF //. ∵BC AD //, ∴BC EF AD //// ∵E 为AB 的中点, ∴F 为CD 的中点.∵BC DC ⊥,BC EF //, ∴CD EF ⊥ ∴EC ED = ∵︒=∠=60,B BC AB ,∴ABC ∆为等边三角形. ∴︒=∠60ACB ∵E 为AB 的中点,∴︒=∠=∠30ECA BCE ∴︒=∠30DCA ∴ ︒=∠60ECD ∵EC ED =,∴ECD ∆为等边三角形.说明 本题综合考查了平行线等分线段定理的推论及等边三角形的判定与性质,解题关键是作辅助线.例07.如图,有一块直角三角形菜地,分配给张、王、李三家农户耕地. 已知张、王、李三家人口分别为2人,4人,6人,菜地分配方法要按人口比例,并要求每户土地均有一部分紧靠水渠AB . P 点处是三家合用的肥料仓库,所以P 点必须是三家地的交界处. 已知PAB Rt ∆的︒=∠90P ,20=PA 米,︒=∠60PAB . (1)计算出每家应分配的菜地面积;(2)用尺规在图中作出各家菜地的分界线(保留痕迹,不写作法,标出户名).解答:(1)在PAB Rt ∆中, ∵︒=∠60PAB , ∴︒=∠30PBA .∴402==PA AB (米) ∴32020402222=-=-=PA AB PB (米)3200320202121=⨯⨯=⋅=∆PB PA S PAB (米) ∵3:2:16:4:2::==李王张S S S ∴33100320061=⨯=张S (2米) 33200320062=⨯=王S (2米)3100320063=⨯=李S (2米)(2)运用平行线等分线段的方法作出图形如图. 说明:本题考查了平行线等分线段定理的应用,解题的易错点是忽视运用︒30的直角三角形的性质,关键是运用平行线等分线段定理的作图.选择题1.下列用平行线等分线段的图形中,错误的是( )2.如图,在线段AB 上取一点C ,使BC AC 32=. 作法正确的是( )3.(福州市,2001)下列四个命题中错误的是( ) A .两条对角线互相垂直且相等的四边形是正方形B .菱形的一条对角线平分一组对角C .顺次连结四边形的各边中点所得的四边形是平行四边形D .等腰梯形的两条对角线相等 4.(北京市朝阳区,2001)顺次连结任意四边形各边中点所得的四边形是( ) A .平行四边形 B .矩形 C .菱形 D .正方形5.如图,EF CD AB ////,且OF OD AO ==,6=OE ,则=BE ( )A .9B .10C .11D .126.AD 是锐角ABC ∆的高,BD DC 31=,M ,N 在AB 上,且NB MN AM ==,BC ME ⊥于E ,BC NF ⊥于F ,则=FC ( )A .BC 32B .BD 32C .BC 43D .BD 437.(哈尔滨市,2001)直角三角形的两条直角边长分别为cm 6和cm 8,则连结这两条直角边中点线段的长为( )A .3cmB .4cmC .5cmD .12cm 8.(绍兴市,2001)如图,ABC ∆中,D 、E 分别是边BC 、AC 的中点,若3=ED ,则AB 等于( )A .23 B .6 C .9 D .49 9.等腰ABC ∆的底边BC 是周长的41,自底边上任意一点P 引平行于两腰的直线,分别交两腰于E ,F ,则四边形AEPF 的周长与ABC ∆的周长之比为()A .41B .32C .43D .54参考答案:1.C 2.D 3.A 4.A 5.A 6.A 7.C 8.B 9.C填空题1.如图,54321///////l l l l l ,11111111E D D C C B B A ===,则=22B A _____=___=_____,=22C A ______=______.2.如图,已知EF CD AB ////,AF ,BE 交于O ,若DF OD AO ==,cm BE 10=,则=BO _______.3.(北京市西城区,2001)以长为8,宽为6的矩形各边中点为顶点的四边形的周长为______.4.(厦门市,2001)如图,梯形ABCD 中,BC AD //,且5:3:=BC AD ,梯形ABCD 的面积是28cm ,点M 、N 分别是AD 和BC 上一点,E 、F 分别是BM 、CM 的中点,则四边形MENF 的面积是______ 2cm .5.(盐城市,2001)已知三角形的周长是cm 12,则以它的三条边中点为顶点所构成的三角形周长是______ cm .参考答案:1.22C B ,22D C ,22E D ,22D B 2.cm 310 3.20 4.25 5.6解答题1.把线段AB 五等分.2.如图,在ABC ∆中,AD 为BC 边中线,F 为AC 上一点,AC AF 31=,连结BF 交AD 于E ,cm EF 6=. 求BF 的长.3.如图,直角梯形ABCD 中,BC AD //,BC AB ⊥,M 是CD 的中点. 求证:MB MA =.4.用两种方法证明:如图,MN 过ABC ∆顶点A ,过B ,C 分别作MN BE ⊥于E ,MN CF ⊥于F ,D 为BC 中点.求证:DF DE =.5.如图,已知四边形ABCD 为平行四边形,E 是AD 上一点,且CE 平分BCD ∠,CE BE ⊥.求证:CD BC 2=.6.(聊城市,2001)已知:如图,ABC Rt ∆中,︒=∠90ACB ,D 、E 分别为AB 、BC 的中点,点F 在AC 的延长线上,B FEC ∠=∠.(1)求证:DE CF =;(2)若6=AC ,10=AB ,求四边形DCFE 的面积.7.如图,M ,N 分别是ABCD 中AB ,CD 的中点.求证:FD EF BE ==.8.如图,ABC ∆中,CH 是ACB ∠的平分线,CH AD ⊥于D ,BC DE //交AB 于E . 求证:EB AE =.9.如图,等腰直角ABC ∆,︒=∠90ACB ,CD CE =,BD EF ⊥交AB 于F ,BD CG ⊥交AB 于G .求证:GF AG =.10.如图,ABCD 为梯形,DC AB //,ADBE 是平行四边形,AB 的延长线交EC 于F . 求证:FC EF =.11.已知:如图,AD 平分BAC ∠,AD CD ⊥,垂足为D ,AB DE //并AC 于E . 求证:AC DE 21=.12.如图,F 为AB 的中点,四边形CGFE 为菱形,FCG ∠=∠=∠21. 求证:D ,F ,H 为线段AB 的四等分点.13.垂直放在地面上的镜子要多高,你就可以站在镜子前看到你的全身像?参考答案: 1.略2.过D 作BF DM //交FC 于M . cm BF 24=. 3.证明:过点M 作BC MN //交AB 于点N . ∴BN AN =∵BC AB ⊥, ∴ AB MN ⊥.∴)(SAS BMN AMN ∆≅∆ ∴MB MA =4.证法1:过D 作EF DG ⊥于G ;用平行线等分线段定理证明;证法2:延长FD 交EB 的延长线于H .;用直角三角形斜边的中线等于斜边的一半证明. 5.证法1:取BC 的中点M ,连EM ,则EM 是BEC Rt ∆斜边上的中线.∴BM BC EM ==21. ∴MCE MEC ∠=∠ ∵ECD ECM ∠=∠. ∴CD EM //∵CM ED //,∴ 四边形EMCD 是平行四边形.∴CD EM =. ∴BC CD 21= ∴CD BC 2=证法2:如图,延长BE 交CD 的延长线于F . ∵CE BE ⊥,CE 平分BCF ∠,∴ EF BE = ∵BC ED //,∴DC FD =.∵CF BC =,∴BC DC 21=. 6.(1)证DBE FEC ∆≅∆;(2)127.易证CM AN //,EB FE FE DF ==,8.延长AD 交BC 于F ,可证DF AD =. 因为BC DE //,∴BE AE =9.延长BC 到H ,使CD CH =,连AH ,则BCD ACH ∆≅∆,∴BDC H ∠=∠∵BEF BDC ∠=∠,∴BEF H ∠=∠. ∴HA CG EF //// ∵CH CD EC ==,∴AG FG =10.连结DE 并交AB 于O . EO DO =,CD AF //,∴ FC EF =11.证明:延长CD 交AB 于F . 在ADC ∆和ADF ∆中,∵FAD CAD ∠=∠,AD AD =,ADF ADC ∠=∠,∴ADF ADC ∆≅∆,∴DF CD =又∵AF DE //,∴ EA CE =又∵︒=∠90ADC ,∴AC DE 21=. 12.∵F 是AB 中点,BC FG //,∴G 为A 中点. 同理E 为BC 中点. 因AC FE //,则FC DE EFC FCG //2⇒∠=∠=∠. 同理FC GH //. 由E ,G 为中点,可得D 为BF 中点,H 为AF 中点13.当镜子高度为一个人高度的一半。


北师大版九年级数学上册3.2平行线分线段成比例同步练习一、选择题1.如图,直线123l l l ∥∥,直线AC 分别交1l ,2l ,3l 于点A ,B ,C ,直线DF 分别交1l ,2l ,3l 于点D ,E ,F ,AC 与DF 相交于点G ,且AG =2,GB =1,BC =5,则DE EF 的值为( )A .12B .2C .25D .35答案:D解析:解答:∵AG =2,GB =1,∴3AB AG BG =+=,∵直线123l l l ∥∥,∴35DEABEF BC ==,故选:D .分析:根据平行线分线段成比例可得DE ABEF BC =,代入计算,可求得答案.2.如图,在△ABC 中,DE ∥BC ,AD =6,DB =3,AE =4,则EC 的长为()A .1B .2C .3D .4答案:B解析:解答:∵DE∥BC,∴AD AE DB EC=,即643EC =,解得:EC=2,故选:B.分析:根据平行线分线段成比例可得AD AEDB EC=,代入计算即可解答.3.如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则DEBC的值为()A.2 3B.1 4C.1 3D.1 2答案:C解析:解答:∵DE∥BC,∴△ADE∽△ABC,∴11123 DE AD ADBC AB AD DB===++=.故选C.分析:根据平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似,再根据相似三角形的对应边成比例解则可.4.如图,在△ABC中,DE∥BC,12ADDB=,DE=4,则BC的长是()A .8B .10C .11D .12答案:D解析:解答:∵12AD DB =,12AD DB = ∴13AD AB =, ∵在△ABC 中,DE ∥BC ,∴13DE AD BC AB ==, ∵4DE =,∴312BC DE ==.故选D .分析:由在△ABC 中,DE ∥BC ,根据平行线分线段成比例定理,即可得DE BC AD AB =::,又由12AD DB =,DE =4,即可求得BC 的长. 5.如图,已知AB ∥CD ,AD 与BC 相交于点O ,AO :DO =1:2,那么下列式子正确的是( )A .BO :BC =1:2B .CD :AB =2:1C .CO :BC =1:2D .AD :DO =3:1答案:B解析:解答:∵AB ∥CD ,∴△AOB ∽△DOC ,∴AB :CD=AO :DO =1:2,∴CD:AB=2:1,故选B.分析:证明△AOB∽△DOC,得到AB:CD=AO:DO=1:2,即可解决问题.6.如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是()A.AD AE BD EG=B.DE DF CG CF=C.AE DE AG BC=D.AD DE AB BG=答案:C解析:解答:∵DE∥BC交GA于点E,∴AD AEBD EG=,DE DFCG CF=,AD DEAB BG=,A,B,D正确,故选C.分析:利用平行线分线段成比例定理即可得到答案.7.如图,△ABC中,D、E分别为边AB、AC上的点,且DE∥BC,下列判断错误的是()A.AD AE DB EC=B.AD DE DB BC=C.AD AE AB AC=D.AD DE AB BC=答案:B解析:解答:如图,∵DE∥BC,∴△ADE∽△ABC,∴AD DE AE AB BC AC==,∴C、D正确.∵DE∥BC,∴AD AE DE DB EC BC≠=,故选B.分析:如图,证明△A DE∽△ABC,得到AD DE AEAB BC AC==;证明AD AE DEDB EC BC≠=,即可解决问题.8.如图,DE∥BC,分别交△ABC的边AB、AC于点D、E,13ADAB=,若AE=5,则EC的长度为()A.10B.15C.20D.25答案:A解析:解答:∵DE∥BC,∴AD AE AB AC=,∴513AC =, ∴AC =15.∴15510EC AC AE =-=-=.故选A . 分析:根据平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例,由DE ∥BC 得到AD AE AB AC=,于是可计算出AC 的长,然后利用EC AC AE =-进行计算即可.9.如图,AD ∥BE ∥CF ,直线1l 、2l 与这三条平行线分别交于点A 、B 、C 和点D 、E 、F ,若AB =2,AC=6,DE =1.5,则DF 的长为( )A .7.5B .6C .4.5D .3答案:C解析:解答:∵AD ∥BE ∥CF ,∴AB DE AC DF=,即2 1.56DF =, ∴DF =4.5.故选C .分析:根据平行线分线段成比例,由AD ∥BE ∥CF 得到2 1.56DF=,然后根据比例性质求DF . 10.如图,AB ∥CD ∥EF ,AC 与BD 相交于点E ,若CE =5,CF =4,AE =BC ,则CD AB 的值是( )A .23B .12C .13D .14答案:D解析:解答:设AE =x ,则BC =x ,∵EF ∥AB ,∴CE CF CA CB =,即545x x=+,解得x =20, 即AE =20,∵CD ∥AB ,∴△ECD ∽△EAB ,∴51204CD CE AB AE ===. 故选D .分析:设AE =x ,则BC =x ,根据平行线分线段成比例定理,由EF ∥AB 得到545x x=+,解得x=20,再根据如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边,由CD ∥AB 得到△ECD ∽△EAB ,所以51204CD CE AB AE ===. 11.如图,已知在△ABC 中,点D ,E ,F 分别是边AB ,AC ,BC 上的点,DE ∥BC ,EF ∥AB ,且AD :DB =4:7,那么CF :CB 等于( )A.7:11B.4:8C.4:7D.3:7答案:A解析:解答:如图,∵DE∥BC,且AD:DB=4:7,∴AE:CE=AD:DB=4:7,∴CE:AC=7:11;∵EF∥AB,∴CF:CB=CE:CA=7:11,故选A.分析:如图,首先运用平行线的性质证明CE:AC=7:11,这是解决问题的关键性结论;再次运用平行线的性质证明CE:AC=CF:CB,即可解决问题.12.如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则CE的长为()A.9B.15C.12D.6答案:A解析:解答:∵DE∥FG∥BC,∴AF AG DB EC=,而AD:DF:FB=3:2:1,∴53 AFDB=,∴1553 EC=,∴EC=9.故选A.分析:根据平行线分线段成比例定理得到AF AGDB EC=,再利用比例性质由AD:DF:FB=3:2:1得53AFDB=,则1553EC=,然后把AG=15代入计算即可.13.如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于()A.36 5B.24 5C.15 2D.9 2答案:B解析:解答:∵AB∥CD∥EF,∴BC ADBE AF=,即3125BC=,∴365 BC=,∴36241255 CE BE BC=-=-=.故选B.分析:根据平行线分线段成比例得到3125BC=,然后利用比例性质计算出365BC=,然后利用计算BE BC-即可.14.如图,已知D为△ABC边AB上一点,AD=2BD,DE∥BC交AC于E,AE=6,则EC=()A.1B.2C.3D.4答案:C解析:解答:∵DE∥BC,∴AD AEBD EC=,即26BDBD EC=,∴EC=3.故选C.分析:根据平行线分线段成比例得到AD AEBD EC=,即26BDBD EC=,然后利用比例性质计算EC的长.15.如图,在△ABC中,点D、E分别在AB、A C边上,DE∥BC,若AD=6,BD=2,AE=9,则EC的长是()A.8B.6C.4D.3答案:D解析:解答:∵AD=6,BD=2,∴AB=AD+BD=8;又∵DE∥BC,AE=9,∴AD AE AB AC =, ∴AC =12, ∴1293EC AC AE =-=-=;故选:D .分析:根据题意知两平行线DE ∥BC 间的线段成比例AD AE AB AC=,据此可以求得AC 的长度,所以EC AC AE =-.二、填空题 16.如图,AD ∥BE ∥CF ,直线1l ,2l 与这三条平行线分别交于点A ,B ,C 和点D ,E ,F ,23AB BC =,DE =6,则EF =______.答案:9解析:解答:∵AD ∥BE ∥CF ,∴AB DE BC EF =,即263EF=, ∴EF =9.故答案为9.分析:根据平行线分线段成比例定理得到AB DE BC EF =,即263EF=,然后根据比例性质求EF . 17.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A 、B 、C 都在横格线上.若线段AB =4cm ,则线段BC =______cm .答案:12解析:解答:如图,过点A作AE⊥CE于点E,交BD于点D,∵练习本中的横格线都平行,且相邻两条横格线间的距离都相等,∴AB AD BC DE=,即426 BC=,∴BC=12cm.故答案为:12.分析:过点A作AE⊥CE于点E,交BD于点D,根据平行线分线段成比例可得AB AD BC DE=,代入计算即可解答.18.如图,在△ABC中,若DE∥BC,12ADDB=,DE=4cm,则BC的长为______.答案:12cm解析:解答:∵DE∥BC,∴DE AD BC AB=,又∵12 ADDB=,∴13 ADAB=,∴413 BC=,∴BC=12cm.故答案为:12cm.分析:因为DE∥BC,可利用平行线分线段成比例定理求出BC的长.19.如图,已知D,E分别是△ABC的边BC和AC上的点,AE=2,CE=3,要使DE∥AB,那么BC:CD应等于______.答案:5 3解析:解答:∵DE∥AB,∴23533 BC AC AE CECD CE CE++====.故答案为53.分析:直接根据平行线分线段成比例进行计算.20.如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC=______.答案:14 3解析:解答:∵DE∥BC,∴AD AEDB EC=,即324EC=,解得83 EC=,∴814233 AC AE EC=+=+=,故答案为:143.分析:由平行可得到AD AEDB EC=,代入可求得EC,再利用线段的和可求得AC.三、解答题21.如图,△ABC的顶点A是线段PQ的中点,PQ∥BC,连接PC、QB,分别交AB、AC于M、N,连接MN,若MN=1,BC=3,求线段PQ的长.答案:解答:∵PQ∥BC,∴13 AM MNAB BC==,∴12 AMBM=,∴12AP AMBC BM==,1322AP BC==,∵AP=AQ,∴PQ=3.解析:分析:根据PQ∥BC可得AM MNAB BC=,进而得出AP AMBC BM=,再解答即可.22.如图所示,D,E是△ABC的边AB,AC上的两点,AE:AC=2:3,且AD=10,AB=15,DE=8,求BC的长.答案:解答:∵AD=10,AB=15,∴AD:AB=10:15=2:3,而AE:AC=2:3,∴AE:AC=AD:AB,∴DE∥BC,∴DE AEBC AC=,即823BC=,∴BC=12.解析:分析:先计算出AD:AB=2:3,加上AE:AC=2:3,由于根据如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边,所以DE∥BC,然后根据平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例得到DE AEBC AC=,再利用比例性质计算BC的长.23.如图,在△ABC中,EF∥CD,DE∥BC.求证:AF:FD=AD:DB.答案:证明:∵EF∥CD,DE∥BC,∴AF AEFD EC=,AD AEDB EC=,∴AF AD FD DB=,即AF:FD=AD:DB.解析:分析:根据平行线分线段成比例定理得出AF AEFD EC=,AD AEDB EC=,推出AF ADFD DB=即可.24.如图,F为平行四边形ABCD的边AD的延长线上的一点,B F分别交于CD、AC于G、E,若EF=32,GE=8,求BE.答案:解答:设BE=x,∵EF=32,GE=8,∴32824FG=-=,∵AD∥BC,∴△AFE ∽△CBE , ∴EF AF EB BC =, ∴则321DF AD DF x BC BC +==+① ∵DG ∥AB ,∴△DFG ∽△CBG , ∴248DF BC x=+代入① 322418x x=++, 解得:x=±16(负数舍去), 故BE =16. 解析:分析:利用平行四边形的性质得出相似三角形,进而利用相似三角形的性质得出答案.25.如图所示,已知AB ∥EF ∥CD ,AC 、BD 相交于点E ,AB =6cm ,CD =12cm ,求EF .答案:解答:∵AB ∥CD ,∴1226CE CD AE AB ===, ∴22123CE CE AC AE CE ===++, ∵AB ∥EF ,∴EF CE AB AC =, 即263EF =, 解得EF =4cm .解析:分析:根据平行线分线段成比例定理可得CE CD AE AB =,然后求出CE AC,再利用平行线分线段成比例定理解答即可.。

平行线分线段成比例阅读与思考平行线分线段成比例定理是证明比例线段的常用依据之一,是研究比例线段及相似形的最基本、最重要的理论.运用平行线分线段成比例定理解题的关键是寻找题中的平行线.若无平行线,需作平行线,而作平行线要考虑好过哪一个点作平行线,一般是由成比例的两条线段启发而得.此外,还要熟悉并善于从复杂的图形中分解出如下的基本图形:例题与求解【例1】如图,在梯形ABCD 中,AD ∥BC ,AD =a ,BC =b ,E ,F 分别是AD ,BC 的中点,且AF 交BE 于P ,CE 交DF 于Q ,则PQ 的长为____.(上海市竞赛试题)解题思路:建立含PQ 的比例式,为此,应首先判断PQ 与AD (或BC )的位置关系,关键是从复杂的图形中分解出基本图形,并能在多个成比例线段中建立联系.【例2】如图,在△ABC 中,D ,E 是BC 的三等分点,M 是AC 的中点,BM 交AD ,AE 于G ,H ,则BG ︰GH :HM 等于( )A .3︰2︰1B .4︰2︰1C .5︰4︰3D .5︰3︰2(“祖冲之杯”邀请赛试题)解题思路:因题设条件没有平行线,故须过M 作BC 的平行线,构造基本图形.A BCDEGH MQA BCDEFP【例3】如图,□ABCD中,P为对角线BD上一点,过点P作一直线分别交BA,BC的延长线于Q,R,交CD,AD于S,T.求证:PQ•PT=P R•PS.(吉林省中考试题)解题思路:要证PQ•PT=P R•PS,需证PQPS=PRPT,由于PQ,PT,P R,PS在同一直线上,故不能直接应用定理,需观察分解图形.【例4】梯形ABCD中,AD//BC,AB=DC.(1)如图1,如果P,E,F分别是BC,AC,BD的中点,求证:AB=PE+PF;(2)如图2,如果P是BC上的任意一点(中点除外),PE∥AB,PF∥DC,那么AB=PE+PF这个结论还成立吗?如果成立,请证明;如果不成立,说明理由.(上海市闵行区中考试题)解题思路:(1)不难证明;对于(2),先假设结论成立,从平行线出发证明AB=PE+PF,即要证明PEAB+PFAB=1,将线段和差问题的证明转化为与成比例线段相关问题的证明.AB CDEFP图2AB CDEFP图1QARBCDSP【例5】如图,已知AB ∥CD ,AD ∥CE ,F ,G 分别是AC 和FD 的中点,过G 的直线依次交AB ,AD ,CD ,CE 于点M ,N ,P ,Q .求证:MN +PQ =2PN .解题思路:考虑延长BA ,EC 构造平行四边形,再利用平行线设法构造有关的比例式.(浙江省竞赛试题)【例6】已知:△ABC 是任意三角形.(1)如图1,点M ,P ,N 分别是边AB ,BC ,CA 的中点,求证:∠MPN =∠A ; (2)如图2,点M ,N 分别在边AB ,AC 上,且AM AB =13,AN AC =13,点P 1,P 2是 边BC 的三等分点,你认为∠MP 1N +∠MP 2N =∠A 是否正确?请说明你的理由;(3)如图3,点M ,N 分别在边AB ,AC 上,且P 1,P 2,…,P 2009是边BC 的2010等分点,则∠MP 1N +∠MP 2N +…+∠MP 2009N =____.(济南市中考试题)解题思路:本题涉及的考点有三角形中位线定理、平行四边形的判定、相似三角形的判定与性质.ABCM NP图1A BC MN1P 2P 图2A MNBC1P 2P 2009P 图3QABCDEFGMNP能力训练A 级1.设K =a b c c +-=a b c b -+=a b ca-++,则K =____. (镇江市中考试题)2.如图,AD ∥EF ∥BC ,AD =15,BC =21,2AE =EB ,则EF =____.3.如图,在△ABC 中,AM 与BN 相交于D ,BM =3MC ,AD =DM ,则BD ︰DN =____.(杭州市中考试题)4.如图,ABCD 是正方形,E ,F 是AB ,BC 的中点,连结EC 交DB ,交DF 于G ,H ,则EG ︰GH ︰HC =____.(重庆市中考试题)5.如图,在正△ABC 的边BC ,CA 上分别有点E ,F ,且满足BE =CF =a ,EC =F A =b (a >b ),当BF 平分AE 时,则ab 的值为( ) ABCD6.如图,△ABC 中,AD 是BC 边上的中线,F 是AD 上的一点,且AF ︰FD =1︰5,连结CF 并延长交AB 于E ,则AE ︰EB 等于( )A .1︰10B .1︰9C .1︰8D .1︰77.如图,PQ ∥AB ,PQ =6,BP =4,AB =8,则PC 等于( ) A .4B .8C .12D .168.如图,EF ∥BC ,FD ∥AB ,BD =35BC ,则BE ︰EA 等于( )A .3︰5B .2︰5C .2︰3D .3︰2A BCD E F 第2题ABCD M N第3题ABCDEFGH 第4题A BCEFG第5题ABCDE F第6题QABCP第7题AB CDEF 第8题9.(1)阅读下列材料,补全证明过程.已知,如图,矩形ABCD 中,AC ,BD 相交于点O ,OE ⊥BC 于E ,连结DE 交OC 于点F ,作FG ⊥BC 于G .求证:点G 是线段BC 的一个三等分点.(2)请你依照上面的画法,在原图上画出BC 的一个四等分点.(要求:保留画图痕迹,不写画法及证明过程)(山西中考试题)10.如图,已知在□ABCD 中,E 为AB 边的中点,AF =12FD ,FE 与AC 相交于G . 求证:AG =15AC .11.如图,梯形ABCD 中,AD ∥BC ,EF 经过梯形对角线的交点O ,且EF ∥AD . (1)求证:OE =OF ; (2)求OE AD +OEBC的值; (3)求证:1AD +1BC =2EF. (宿迁市中考试题)ABCDE FGO第9题ABCDEG第10题ABCD EFO第11题12.如图,四边形ABCD 是梯形,点E 是上底边AD 上的一点,CE 的延长线与BC 的延长线交于点F ,过点E 作BA 的平行线交CD 的延长线于点M ,MB 与AD 交于点N .求证:∠AFN =∠DME .(全国初中数学联赛试题)B 级1.如图,工地上竖立着两根电线杆AB ,CD ,它们相距15cm ,分别自两杆上高出地面4m ,6m 的A ,C 处,向两侧地面上的E ,D 和B ,F 点处,用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD 与BC 的交点P 离地面的高度为____m .(全国初中数学联赛试题)2.如图,□ABCD 的对角线交于O 点,过O 任作一直线与CD ,BC 的延长线分别交于F ,E 点.设BC =a ,CD =b ,CF =c ,则CE =____.(黑龙江省中考试题)3.如图,D ,F 分别是△ABC 边AB ,AC 上的点,且AD ︰DB =CF ︰F A =2︰3,连结DF 交BC 边的延长线于点E ,那么EF ︰FD =____.(“祖冲之杯”邀请赛试题)4.如图,设AF =10,FB =12,BD =14,DC =6,CE =9,EA =7,且KL ∥DF ,LM ∥FE ,MN ∥ED ,则EF ︰FD =____.(江苏省竞赛试题)ABCDEF M NP ABCDEF O第2题ABCD EF 第3题QABCD EF 第1题5.如图,AB ∥EF ∥CD ,已知AB =20,CD =80,那么EF 的值是( ) A .10B .12C .16D .18(全国初中数学联赛试题)6.如图,CE ,CF 分别平分∠ACB ,∠ACD ,AE ∥CF ,AF ∥CE ,直线EF 分别交AB ,AC 于点M ,N .若BC =a ,AC =b ,AB =c ,且c >a >b ,则EM 的长为( )A .2c a- B .2a b- C .2c b- D .2a b c+- (山东省竞赛试题)7.如图,在□ABCD 的边AD 延长线上取一点F ,BF 分别交AC 与CD 于E ,G .若EF =32,GF =24,则BE 等于( )A .4B .8C .10D .12E .16(美国初中数学联赛试题)8.如图,在梯形ABCD 中,AB ∥CD ,AB =3CD ,E 是对角线AC 的中点,直线BE 交AD 于点F ,则AF ︰FD 的值是( )A .2B .53C .32D .1(黄冈市竞赛试题)9.如图,P 是梯形ABCD 的中位线MN 所在直线上的任意一点,直线AP ,BP 分别交直线CD 于E ,F .求证:MN NP =1()2AE BFEP FP+. (宁波市竞赛试题)ABCD EFG第7题ABCDE F第8题A BCD E F MNP第9题A BCDE F第5题AB CD E F LKMN第4题AB CDEFM第6题10.如图,在四边形ABCD 中,AC 与BD 相交于O ,直线l 平行于BD 且与AB ,DC ,BC ,AD 及AC 的延长线分别交于点M ,N ,R ,S 和P .求证:PM ·PN =P R ·PS .(山东省竞赛试题)11.如图,AB ⊥BC ,CD ⊥BC ,B ,D 是垂足,AD 和BC 交于E ,EF ⊥BD 于F .我们可以证明:11AB CD +=1EF 成立(不要求证出).以下请回答:若将图中垂直改为AB ∥CD ∥EF ,那么, (1)11AB CD+=1EF 还成立吗?如果成立,请给出证明;如果不成立,请说明理由. (2)请找出S △ABD ,S △BED 和S △BDC 的关系式,并给出证明.(黄冈市竞赛试题)ABCDEF第11题SA R BC DMN OPl第10题12.在Rt△ABC中,∠BAC=90°,AD平分∠BAC,过D点的直线PQ交边AC于点P,交边AB 的延长线于点Q.(1)如图1,当PQ⊥AC时,求证:11AQ AP+;(2)如图2,当PQ不与AD垂直时,(1)的结论还成立吗?证明你的结论;(3)如图3,若∠BAC=60°,其它条件不变,且11AQ AP+=nAD,则n=____(直接写出结果)AQ B CDP图1AQB CDP图2AQB CDP图3专题14 平行线分线段成比例例1aba b+ 提示:由AP DQ a PF QF b ==,推得PQ ∥AD 。

平行线分线段成比例知识梳理平行线分线段成比例定理及其推论1.平行线分线段成比例定理如下图,如果h // I2 // I3,则BCACABDEACDF2.平行线分线段成比例定理的推论:3.平行的判定定理:AB DEAC12DF,EFDF如图,在三角形中,如果ADDE // BC,贝U --ABAEACDEBC 如上图,如果有ADABAEACDEBC,那么DE // BC专题讲解专题一、平行线分线段成比例定理及其推论基本应用【例1】如图,DE // BC,且DB AE,若AB 5, AC 10,求AE的长。
【例2】如图,已知AB//EF//CD,若AB a , CD b , EF c ,求证:111. cab 【巩固】如图,AB BD,CD BD,垂足分别为B、D,AC和【巩固】如图,找出S ABD、S BED、S BCD之间的关系,并证明你的结论BD相交于点E,EF BD,垂足为F .证明:1 1AB CD1EFA连接EM 并延长,交BC 的延长线于D , 则CC (2)如图(2),已知 ABC 中,AE:EB 1:3,BD :DC 2:1,AD 与CE 相交于F ,则EF FCAF FD的值为()A.|B.1C.【例5】(2001年河北省中考试题)如图,在 AC 边上的任意一点,BE 交AD 于点O .【例3】如图,在梯形ABCD 中,AB // CD , AB 12 , CD 9,过对角线交点0作EF // CD 交 AD , BC 于 E , F ,求 EF 的长。
【巩固】(上海市数学竞赛题)如图,在梯形 ABCD 中,AD // BC ,AD a ,BC b ,E ,F 分别 是AD ,BC 的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
专题二、定理及推论与中点有关的问题 【例4】(2007年北师大附中期末试题)1(1)如图(1),在 ABC 中,M 是AC 的中点,E 是AB 上一点,且AE - AB ,43 2D.2A(1)当AE-时,求AO的值;AC2AD(2)当AE 1 1 口」、—求A0的值;AC 3 4AD(3)试猜想AE 1AC n 1时A0的值,并证明你的猜想AD【例6】(2003年湖北恩施中考题)如图,AD是ABC的中线,点E在AD上,F 是BE延长线与AC的交点.(1)如果E是AD的中点,求证:圧 -;FC 2(2)由(1)知,当E是AD中点时,圧-成立,若E是AD上任意一点(E与A、DFC 2 ED不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.【巩固】(天津市竞赛题)如图,已知ABC中,AD是BC边上的中线,E是AD 上的一点,且BE AC,延长BE交AC于F。

第1课时 平行线等分线段定理
习题1.1 (第5页)
1.解 如图所示,设AB 为待7等分的长为6厘米的线段.
作法 (1)过点A 作射线AC ;
(2)在射线AC 上以适当的长度顺次截取AD =DE =EF =FG =GH =HK =KM ;
(3)连接BM ;
(4)过D 、E 、F 、G 、H 、K 做BM 的平行线,分别交AB 于点D ′、E ′、F ′、G ′、H ′、K ′,则D ′、E ′、F ′、G ′、H ′、K ′即为线段AB 的7等分点.
2.解 猜想:BE =EF =FD .
证明:∵M 是AB 的中点,N 是DC 的中点,四边形ABCD 是平行四边形,∴AM ∥CN ,且AM =CN ,
∴四边形ANCM 是平行四边形.
∴MC ∥AN ,∴ME 平分BF ,即BE =EF ,
同理可证FD =EF ,∴BE =EF =FD .
3.证明 ∵E 、F 分别是梯形ABCD 中AB 、DC 边上的中点,
∴EF ∥AD ∥BC .
∴G 、H 分别是梯形对角线BD 、AC 的中点.
∴EG =12AD ,FH =12AD ,EH =12BC ,FG =12
BC . 又∵GH =EH -EG ,GH =FG -FH ,
∴2GH =EH +FG -(EG +FH )
=12BC +12BC -⎝ ⎛⎭
⎪⎫12AD +12AD =BC -AD ,∴GH =12
(BC -AD ).。

二平行线分线段成比例定理课后篇巩固探究一、A组1.若,则下列各式一定成立的是()A. B.D.,得ad=bc,而由,得ac=bd,故A不正确;由,得ad=bc,故B正确;同均不正确.ABC中,点D,E分别在AB,AC上,下列条件不能判定DE∥BC的是()A.AD=5,AB=8,AE=10,AC=16B.BD=1,AD=3,CE=2,AE=6C.AB=7,BD=4,AE=4,EC=39,AD=AE=8C项中,,故DE与BC不平行.,AD是△ABC的中线,E是CA边的三等分点,BE交AD于点F,则AF∶FD等于()A.2∶1B.3∶1D.5∶1D是BC的中点,过点D作DG∥AC交BE于点G,所以DG=EC.又AE=2EC,所以AF∶FD=AE∶DG=2EC∶EC=4∶1.如图,DE∥AB,DF∥BC.若AF∶FB=m∶n,BC=a,则CE=()A. B.D.DF∥BC,∴.∵DE∥AB,∴.EC=.如图,在梯形ABCD中,AD∥BC,E是DC的延长线上一点,AE分别交BD,BC于点G,F,有下列结论:①;②;③;④.其中正确的个数是()B.2C.3D.4解析:在△ADE中,CF∥AD,故①和④正确;BF∥AD,得②正确;BF∥AD,得,故③不正确.答案:C,在△ABC中,MN∥DE∥BC.若AE∶EC=7∶3,则DB∶AB的值为.解析:由AE∶EC=7∶3,得EC∶AC=3∶10.MN∥DE∥BC,得DB∶AB=EC∶AC,DB∶AB=3∶10.答案:3∶10,l1∥l2∥l3.若CH=4.5 cm,AG=3 cm,BG=5 cm,EF=12.9 cm,则DH=,EK=.解析:由l1∥l2∥l3,得,故DH==7.5(cm).同理可得EK的长度为34.4 cm.答案:7.5 cm34.4 cm,∠ACB=90°,以BC为边作正方形BEDC,连接AE交BC于点F,过点F作FG∥AC,交AB于点G.求证:FC=FG.证明:∵FG∥AC∥BE,∴.∵FC∥DE,∴.∴.又BE=DE,∴FC=FG.9.如图,在△ABC中,AE∶EB=1∶3,BD∶DC=2∶1,AD与CE相交于点F.求的值.解:过点D作DG∥AB交EC于点G,则,而,即,所以AE=DG,从而AF=DF,EF=FG=CG,故+1=.10.如图,AD为△ABC的中线,在AB上取点E,AC上取点F,使AE=AF.求证:.,过点C作CM∥EF,交AB于点M,交AD于点N.∵AE=AF,∴AM=AC.∵AD为△ABC的中线,∴BD=CD.延长AD到G,使得DG=AD,连接BG,CG,则四边形ABGC为平行四边形,∴AB=GC.∵CM∥EF,∴,∴.又AB∥GC,AM=AC,GC=AB,∴.∴.二、B组1.如图,BD,CE是△ABC的中线,P,Q分别是BD,CE的中点,则等于()B. C. D.QP交AB于点M,连接ED.因为P,Q分别是BD,CE的中点,所以M是BE的中点.所以MQ=BC,MP=ED=BC.所以PQ=MQ-MP=BC-BC=BC,.答案:B如图,在▱ABCD中,N是AB延长线上一点,则的值为()A. B. C.1 D.解析:∵DC∥BN,∴.又BM∥AD,∴.=1.答案:C导学号52574006如图,D是△ABC中BC边上一点,点E,F分别是△ABD,△ACD的重心,EF与AD交于点M,则=.解析:连接AE,AF,并分别延长交BC于点G,H.因为点E,F分别是△ABD,△ACD的重心,所以=2,所以EF∥GH,所以=2.答案:24.如图,E,F分别是梯形ABCD的腰AD,BC上的点,其中CD=2AB,EF∥AB.若,则=.解析:过A作AH∥BC,交EF,CD于点G,H.设AB=a,则CD=2a.由,得EF= a.由EF∥AB∥CD,得-1.又AD=AE+ED,故-1,得.答案:5.导学号52574007如图,AC∥BD,AD,BC相交于点E,EF∥BD.求证:.AC∥EF∥BD,∴.两式相加,得=1,即.6.如图,在▱ABCD中,E是AB延长线上一点,DE交AC于点G,交BC于点F.求证:(1)DG2=GE·GF;.∵CD∥AE,∴.又AD∥CF,∴.∴,即DG2=GE·GF.(2)∵BF∥AD,∴.又CD∥BE,∴.∴.。

【金版学案】2015-2016学年高中数学1.1平行线等分线段定理练习
新人教A版选修4-1
1.平行线等分线段定理:如果一组________在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.
2.推论1:经过三角形一边的中点与另一边平行的直线必________第三边.
3.推论2:经过梯形一腰的中点,且与底边平行的直线________另一腰.
4.如图所示,D、E、F分别△ABC三边的中点,则与△DEF全等的三角形有________个.
预习导学
1.平行线
2.平分
3.平分
4.3
►一层练习
1.下列用平行线等分线段的图形中,错误的是( )
1.C
2.如图所示,l1∥l2∥l3,直线AB与l1、l2、l3相交于点A、E、B,直线CD与l1、l2、l3相交于点C、E、D,AE=EB,则有( )
A .AE =CE
B .BE =DE
C .CE =DE
D .C
E >DE 2.C
3.如图所示,AB ∥CD ∥EF ,且AO =OD =DF ,BC =6,则BE 为( )
A .9
B .10
C .11
D .12 3.A
4.如图所示,已知a ∥b ∥c ,直线m 、n 分别与直线a 、b 、c 交于点A 、B 、C 和点A ′、
B ′、
C ′,如果AB =BC =1,A ′B ′=32
,则B ′C ′=________.
4.32
5.如上图所示,AB =AC ,AD ⊥BC 于点D ,点M 是AD 的中点,CM 交AB 于点P ,
DN ∥CP .若AB =6 cm ,则AP =________;若PM =1 cm ,则PC =________.
5.2 cm 4 cm ►二层练习
6.AD 是△ABC 的高,DC =1
3
BD ,M ,N 在AB 上,且AM =MN =NB ,ME ⊥BC 于
E ,N
F ⊥BC 于F ,则FC =( )
A.23BC
B.23BD
C.34BC
D.34BD 6.C
7.在梯形ABCD 中,点M 、N 分别是腰AB 与腰CD 的中点,且AD =2,BC =4,则
MN 等于( )
A .2.5
B .3
C .3.5
D .不确定 7.B
8.顺次连接梯形各边中点的连线所围成的四边形是________. 8.平行四边形
9.梯形中位线长10 cm ,一条对角线将中位线分成的两部分之差是3 cm ,则该梯形中的较大的底是________cm.
9.13
10.如图,F 是AB 的中点,FG ∥BC ,EG ∥CD ,则AG =________,AE =________.
10.GC ED ►三层练习
11.如上图,在直角梯形ABCD 中,DC ∥AB ,CB ⊥AB ,AB =AD =a ,CD =a
2
,点E ,
F 分别是线段AB ,AD 的中点,则EF =________.
11.解析:连接DE ,由于点E 是AB 的中点,故BE =a 2.又CD =a
2,AB ∥DC ,CB ⊥AB ,
∴四边形EBCD 是矩形.
在Rt △ADE 中,AD =a ,点F 是AD 的中点,故EF =a
2. 答案:a
2
12.如图所示,在△ABC 中,E 是AB 的中点,EF ∥BD ,EG ∥AC 交BD 于G ,CD =
1
2
AD ,若EG =5 cm ,则AC =________;若BD =20 cm ,则EF =________.
12.解析:E 为AB 中点,EF ∥BD ,则AF =FD =1
2AD ,
即AF =FD =CD . 又EF ∥BD ,EG ∥AC
∴四边形EFDG 为平行四边形,FD =5(cm). ∴AC =AF +FD +CD =15(cm). ∵EF =1
2BD ,
∴EF =10 cm. 答案:15 cm 10 cm
13.如图,在▱ABCD 中,E 、F 分别为AD 、BC 的中点,连BE 、DF 交AC 于G 、H 点.求证:AG =GH =HC .
13.证明:在△ACD中,EG∥DH,E是AD的中点,∴AE
ED=AG
GH=1,得
AG=GH,同理在△ABC中,GH=HC,得AG=GH=HC.
14.如图所示,在等腰梯形ABCD中,AB∥CD,AD=12 cm,AC交梯形中位线EG于点F.若EF=4 cm,FG=10 cm,求梯形ABCD的面积.
14.解析:作高DM、CN,则四边形DMNC为矩形.
∵EG是梯形ABCD的中位线,
∴EG∥DC∥AB.
∴点F是AC的中点.
∴DC=2EF=8 cm,AB=2FG=20 cm,MN=DC=8 cm.
在Rt△ADM和Rt△BCN中,
AD=BC,∠DAM=∠CBN,∠AMD=∠BNC,
∴△ADM≌△BCN.
∴AM=BN=1
2
(20-8)=6(cm).
∴DM=AD2-AM2=122-62=63(cm),∴S梯形=EG·DM=14×63=843(cm2).
1.应用平行线等分线段定理要注意其条件是:a、b、c互相平行,构成一组平行线,m 与n可以平行,也可以相交,但它们必须与已知的平行线a、b、c相交,即被平行线a、b、c所截.
2.利用平行线等分线段定理解题要注意弄清题目所给的条件,常见的题型多与三角形中位线、梯形中位线有关,因此取中点、作平行线是常用技巧.另外,要注意灵活运用三角形、平行四边形、等腰梯形的有关定理及性质.
3.注意证明线段的和、差时,通常采用的方法是作辅助线截取的方法.
4.平行线等分线段定理应在有线段的中点时应用,在没有线段的中点时构造线段的中
点来应用.
【习题1.1】
1.解析:如图所示,线段AB的长为6 cm.①过点A作射线AC.②在射线AC上以适当的长度顺次截取AD=DE=EF=FG=GH=HK=KM.③连接BM.④过点D,E,F,G,H,K分别作BM的平行线,分别交AB于点D′,E′,F′,G′,H′,K′,则D′,E′,F′,G′,H′,K′即为线段AB的7等分点.
2.解析:猜想BE=EF=FD.证明如下:如图所示,∵M是AB的中点,N是DC的中点,四边形ABCD是平行四边形,∴AM∥CN,且AM=CN,∴四边形ANCM 是平行四边形,∴MC∥AN,∴点E平分BF,即BE=EF.同理可证FD=EF.∴BE=EF =FD.
3.证明:如图所示,∵E ,F 分别是梯形ABCD 的边AB ,DC 的中点,∴EF ∥AD ,EF ∥BC ,∴EG =12AD ,FH =12AD ,EH =12BC ,FG =1
2BC ,又∵GH =EH -EG ,GH =FG -FH ,
∴2GH =EH +FG -(EG +FH )=12BC +12BC -⎝ ⎛⎭⎪⎫1
2
AD +12AD =BC -AD ,∴GH =12(BC -AD ).。