当前位置：文档之家 › 线性系统理论第二章 系统状态空间模型

线性系统理论第二章 系统状态空间模型

  • 格式：ppt
  • 大小：1.45 MB
  • 文档页数：66

下载文档原格式

  / 66

合集下载

第二章 线性系统的状态空间描述-wyz

第二章 线性系统的状态空间描述-wyz

确定性系统：
参数、动态等都是确定的或随时间变化的确定性函数
非确定性系统：系统含有不确定性成分，如 参数未知（摄动）， 外部未知干扰， 未建模动态（动态摄动）， 输入和扰动随机变量（随机系统）
2013-7-21
35
2.4 由系统的输入输出导出状态空间方程 （SISO系统）
1、由输入输出描述（含传递函数）导出状态空间方程 2、由方块图导出状态空间方程
2013-7-21
a1n a2 n , , 系 n n维系统矩阵 表征各状态变量间的关 ann b1 p b2 p n p维输入矩阵 表征输入对每个变量的 , 作用 , bnp
17
输出方程： 通式为：
y1 c11 x1 c12 x2 c1n xn d11u1 d12u2 d1r ur y2 a21 x1 a22 x2 c2 n xn d 21u1 d 22u2 d 2 r ur ym cm1 x1 cm 2 x2 cmn xn bm1u1 d m 2u2 d mr ur
f1 ( x, u, t ) , f ( x, u , t ) f n ( x, u , t ) 均为向量函数。
2013-7-21 32
g1 ( x, u, t ) g ( x, u , t ) g q ( x, u , t )
第2章 线性系统的状态空间描述
2.1 状态和状态空间 2.2 线性系统的状态空间描述 2.3 连续变量动态系统按状态空间分类 2.4 由输入输出描述导出状态空间描述 2.5 线性系统的特征结构 2.6 状态方程的约当规范形 2.7 由状态空间描述导出传递函数矩阵

线性系统理论课件02-第二章状态空间描述-2.1系统的状态空间描述2.2系统的状态空间表达式的分类

线性系统理论课件02-第二章状态空间描述-2.1系统的状态空间描述2.2系统的状态空间表达式的分类

上式即为图2-1所示电路的状态方程，并将其写成 向量-矩阵形式，即
du c (t ) dt 0 di(t ) 1 dt L 1 0 u ( t ) c C 1 u (t ) R i(t ) L L
(3)状态向量 设x1(t),x2(t),…,xn(t)是系统的一组状态变量，把这 些状态变量看作向量x(t)的分量，则x(t)就称为状态 向量，记为
x1 (t ) x (t ) x n (t )
(4)状态空间 以x1(t),x2(t),…,xn(t)为坐标轴构成的一个n维欧氏空 间，称为状态空间。
(5)状态方程 描述系统状态变量间或状态变量与系统输入变量 间关系的一个一阶微分方程组(连续系统)或一阶 差分方程组（离散系统），称为状态方程。
Ax Bu x
x(k 1) Gx(k ) Hu (k )
【例2-2】建立图2－1所示RLC电路的状态方程。 取电容上的电压uC (t)和电感中的电流i(t)作为状态 变量，根据电路原理有
不表征系统的内部结构和内部变量，只反映外部 变量间的因果关系，即输出和输入间的因果关系。
例：线性定常、单输入—单输出系统，外部描述为线 性常系数微分方程
y (n) an1 y (n1) a1 y (1) a0 y bn1u (n1) b1u (1) b0u
并非所有电路中的电容器电压和电感器电流都是独立 变量
假定电容器初始电压值均为0，有
c3 x2 x1 c 2 c3
因此，只有一个变量是独立的，状态变量只能选其 中一个，即用其中的任意一个变量作为状态变量便可以 确定该电路的行为。实际上，三个串并联的电容可以等 效为一个电容。

状态空间模型

状态空间模型

状态空间模型状态空间模型是一种用于描述动态系统行为的数学模型。

在状态空间模型中，系统的行为由状态方程和观测方程确定。

状态方程描述系统状态如何随时间演变，而观测方程则描述系统状态如何被观测。

通过利用状态空间模型，我们可以对系统进行建模、预测和控制。

状态空间模型的基本概念状态空间模型通常由以下几个要素构成：1.状态变量（State Variables）：描述系统状态的变量，通常用向量表示。

状态变量是系统内部的表示，不可直接观测。

2.观测变量（Observation Variables）：直接观测到的系统状态的变量，通常用向量表示。

3.状态方程（State Equation）：描述状态变量如何随时间演变的数学方程。

通常表示为状态向量的一阶微分方程。

4.观测方程（Observation Equation）：描述观测变量与状态变量之间的关系的数学方程。

状态空间模型的应用状态空间模型在许多领域都有着广泛的应用，包括控制系统、信号处理、经济学和生态学等。

其中，最常见的应用之一是在控制系统中使用状态空间模型进行系统建模和控制设计。

在控制系统中，状态空间模型可以用于描述系统的动态行为，并设计控制器来实现系统性能的优化。

通过对状态方程和观测方程进行数学分析，可以确定系统的稳定性、可控性和可观测性，并设计出满足特定要求的控制器。

状态空间模型的特点状态空间模型具有以下几个特点：1.灵活性：可以灵活地描述各种复杂系统的动态行为，适用于各种不同的应用领域。

2.结构化：将系统分解为状态方程和观测方程的结构使得系统的分析更加清晰和系统化。

3.预测性：通过状态空间模型，可以进行系统状态的预测和仿真，帮助决策者做出正确的决策。

4.优化性：可以通过状态空间模型设计出有效的控制器，优化系统的性能指标。

在实际应用中，状态空间模型可以通过参数估计和参数辨识等方法进行模型的训练和调整，以适应实际系统的特性。

结语状态空间模型是一种强大的数学工具，可以帮助我们理解和分析动态系统的行为。

第1-2章线性系统状态空间描述

第1-2章线性系统状态空间描述

• 线性系统理论的主要流派： • 状态空间法 （线性代数、矩阵变换） 属于时间域方法 流派代表人：R. E. Kalman (1960s) • 几何理论 （矩阵计算） 将线性系统转换为状态空间的几何问题，采用几何语言对系统 进行描述、分析和综合 流派代表人：W.M. Wonham (1970s) • 代数理论 （模论、群、环、泛代数、集合等） 采用抽象代数工具标志和研究线性系统 流派代表人：R. E. Kalman (1960-70s) • 多变量频域方法 以状态空间法为基础，采用频率域系统描述和计算方法 流派代表人：H.H.Rosenbrock，A.G.J.MacFalance W.A.Wolovich （多项式矩阵，1970s）
• 动态系统的类型 • 连续时间线性系统 • 离散时间系统系统 对应的分析和综合问题
• 线性系统 线性系统是最简单和最基本的动态系统。 线性系统理论是系统控制理论研究最充分、发展最成熟、应用 最广泛的分支。 • 线性系统的基本特征： 满足叠加原理） 模型方程具有线性属性 （满足叠加原理） L(c1u1 + c2u2) = cl L(u1) + c2 L(u2) • 基于叠加原理的定义严格性 • 叠加原理的限制：不能推广到无穷项的和 • 叠加原理导致研究的简便性 • 线性系统的现实性 • 实际系统能否按线性系统处理的判断准则
1.2 线性系统理论概貌
线性系统理论是一门以研究线性系统的分析和综合的理论和方法为 基本任务的学科。 其目的是认识和避免线性系统中可能发生的有害运动行为，了解和 掌握线性系统所期望的方法和手段。 • 线性系统理论的主要内容： • 线性系统分析理论 定量分析：建立系统状态或输出相对于输入的因果关系一般表 达式，作为分析系统的响应或性能基础。 定性分析：研究对系统性能和控制具有重要意义的基本结构特 性，包括稳定性、能控性与能观性、互质性等。 • 线性系统综合理论 同时基于系统模型和期望性能指标确定满足综合要求的控制器。 目的是使系统性能达到期望的指标或实现最优化。 三个问题：可综合性问题、综合算法、综合的工程化问题

线性系统理论(第2章)2[1].1

线性系统理论(第2章)2[1].1

2、对于线性定常系统情况
系数矩阵 A 和 B 均为常阵，只要其元的值为有限值，则条件 满足，解存在且唯一。
3
2010-10-08
三、零输入响应和零状态响应
线性系统满足叠加原理。 即线性系统在初始状态和输入向量作用下的运动，可分解为两 个单独的分运动： 初始状态作用 → 自由运动 输入向量作用 → 强迫运动
Φ ( t ) = e A(t) , t 0 Φ (t t0 ) = e A(t t0 ) , t t0
则系统零输入响应可表达式为：
φ(t;0, x0 ,0) = Φ(t) x0 , t 0 φ (t; t0 , x0 ,0) = Φ(t t0) x0 , t t0
物理意义： Φ(t t0 ) 就是将时刻 t 0 之状态 x0 映射到时刻 t 之状态 x 的一个线性变换。
12 22
1n 1 e t 2n 1 e t
1 2
n2
n 1 n t n e
④ 对给定 n n 常阵 A ，先求出预解矩阵：
(sI - A)-1
则有
e At = L-1 (sI - A)-1
二、零状态响应
给定初始状态为零的线性定常系统的强迫方程：
& = Ax + Bu, x (0) = 0, t 0 x
其中，x 为 n 维状态向量，u为p 维输入向量，A和B 分别为 n ×n 和 n × p 常阵。
8
2010-10-08
结论 2 ： 零状态响应的表达式为：
(t;0,0, u) = e A(t ) Bu( )d ,
第2 章
线性系统的运动分析
2.1 引言
一、运动分析的实质

线性系统理论(郑大忠)第2章

线性系统理论(郑大忠)第2章
基此，选取电容端电压uc和流经电感的电流iL作 为电路状态变量组。 显然，uc和iL必满足状态变量定义中所指出的线 性无关极大组属性。
2013/11/22
线性系统理论
23
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
1、电路系统状态空间描述的列写示例
R1 C + uC iL R2 iC + -
由此，得 和，
X QX
X PX PQX
X QX QPX
显然， PQ QP I
即矩阵P和Q互逆。
结论：系统的任意选取的两个状态X和 X 之间 为线性非奇异变换的关系。
2013/11/22
线性系统理论
18
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
2013/11/22
线性系统理论
2
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
一、状态和状态空间
1、系统动态过程的两类数学描述 2、状态和状态空间的定义
2013/11/22
线性系统理论
3
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
1、系统动态过程的两类数学描述
线性系统理论
21
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
1、电路系统状态空间描述的列写示例
电路系统如图所示，设各组元件的参数值为已 知，取电压源e(t)为输入变量，电阻R2端电压uR2为输 出变量。 C
R1 iC + e (t ) -
L
+ uC iL R2

线性控制系统的状态空间描述

线性控制系统的状态空间描述

§3.3 Matlab 实验
1. 状态空间模型脉冲响应、阶跃响应和任意输入响
应
(1) [y,x,t]=impulse(a,b,c,d)
(2) [y,x,t]=step(a,b,c,d)，其中y、x 和t 是输出、
状态向量和仿真时间。

(3) [y,x]=lsim(a,b,c,d,u,t,x0)。

例求管亠[0* x c£，为
u(t) =sint的状态输出值。

解程序和结果如下
-0.2
-0.4
2. 离散系统的脉冲响应、阶跃响应、任意输入响应
⑴[y, x]=dimpulse(sys);
(2) [y, x] = dstep( nu m,de n);
(3) [y, x]=dlsim(sys,u); 47y、x 和u 分别为输出、
状态和输入，sys可以是num,den或a,b,c,d,不绘图，当无y, x时直接绘图。

3 •连续和离散状态模型的零输入响应(只对初态x0 响应)
(1) [y,x,t]=i nitial(a,b,c,d,xO)
⑵[y,x,t]=dinitial(a,b,c,d,x0) ，y 为输出，x 为状态，
t为指定输出时间。

当不带y、x和t时，直接绘图。

4 •连续系统离散化
(1) [da,db,dc,dd]=c2dm(a,b,c,d,Ts)
⑵[dnum,dden]=c2d(num,den,Ts) , Ts 是采样周期。

5.矩阵指数
expm(a*t)，其中t可为符号变量，也可为实值。

0 1
例如设A = 0'，则求e At的命令和结果如下:
||-4 -4。

第2章 控制系统的状态空间模型

第2章 控制系统的状态空间模型

一.输入项中不含有导数项：
假设单输入单输出线性系统的微分方程为：
D-E
y ( n ) a1 y ( n1) a n1 y a n y bu
x Ax bu S-E：状态空间表达式为： Y Cx Du
n阶系统要设n个状态变量，并且已知y (0), y (0), y n 1 (0). 以及输入u,就能惟一确定状态，故按状态变量的定义， 可直接按已知初始条件选状态变量--称为相变量
x1 x2 x y x x 1 3 2 x2 y 令 n 2 xn 1 xn xn 1 y x y n a y n 1 a y a y bu n n 1 n 1 n 1 x y n =-an x1 an 1 x2 a1 xn bu
引入状态矢量后，则状态矢量的端点就表示了 系统在某时刻的状态。 4.状态轨线： 定义：系统状态矢量的端点在状态空间中所 移动的路径，称为系统的状态轨线，代表了状态 随时间变化的规律。 例如：三阶系统应是三维状态空间，初始状 态是x10,x20,x30 。在u(t)作用下 ，系统的状态开 始变化，运动规律如下：
﹡完全描述：若给定 t=t0 时刻这组变量的值（初 始状态）又已知t≥t0 时系统的输入u(t)，则系 统在 t≥t0 时，任何瞬时的行为就完全且唯一 被确定。 ﹡最小变量组：即这组变量应是线性独立的。
2. 状态空间： 定义：由系统的n个状态变量x1(t),x2(t),…,xn(t) 为坐标轴，构成的n维欧氏空间，称为n维状态空间。 引入状态空间，即可把n个状态变量用矢量形式表 示出来，称为状态矢量 x1 ( t ) x (t ) x( t ) 2 xn ( t ) n1 又表示为：x(t) ∈Rn [x(t) 属于n维状态空间 ]

现代控制理论 第二章 线性系统的状态空间描述PPT课件

现代控制理论 第二章 线性系统的状态空间描述PPT课件
为系统两状态变量，则原方程可化成:
xx121RL L01C xx12L10u
y 0
1 x1
C
x2
19
由上可见,状态变量的选取有许多方法。因此同一个系 统有许多不同的状态空间表达式来描述。状态变量的 不同选取，其实是状态向量的一种线性变换。
, 设: x1i x2C 1id;tx1i , x2idt
x2
状 态 轨迹
A
( x1 (t0 ), x2 (t0 ))
0
x1
( x1 (t1 ), x2 (t1 ))
B
t
x(t)
x1(t)
x
2
(
t
)
8
6.状态方程：状态变量的一阶导数与状态变量、 输入变量间的数学表达式称为状态方程。
x (t)f[x(t)u ,(t)t,], x (tk 1 )f[x (tk)u ,(tk)tk ,]
0
0
0
1
a0 a1 a2 an1
30
0
0
b
0
0
C 10 0
31
u 0
x n 1 x n 1 x n 1 x 2 1
s
s
s
x1 y
a n1
a
n
2
a1
a0
状态变量结构图
32
例1:
设 y 5y8y6y 3u
求（A，B，C，D）
解：选 x1 y x2 y
x3 y
微分方程、传递函数、结构图求 {A，B，C，D}
1. 由系统微分方程建立状态空间表达式
1）系统输入量中不含导数项
y ( n ) a n 1 y ( n 1 ) a n 2 y ( n 2 ) a 1 y a 0 y 0 u

第二章系统的状态空间描述

第二章系统的状态空间描述

x1 x x 2 xn
a11 a12 a1n a a a 2n 21 22 A an1 an 2 ann
b1 b2 b bn
2009-08 CAUC--空中交通管理学院 15
§2-2.1 由控制系统的结构图求系统动态方程
【例2.2.2】某控制系统的结构图如图2－3（a）所示，试求出其动态方程。
图2-3 控制系统结构图
，
（a）
，
解: 该系统主要有一个一阶惯性环节和一个积分器组成。 对于一阶惯性环节，我们可以通过等效变换，转化为一个前向通道为一 标准积分器的反馈系统。 图2-3（a）所示结构图经等效变换后如图2-3（b）所示
其向量—矩阵形式为：
y(t ) cx(t ) du(t )
2009-08
CAUC--空中交通管理学院
6
§2-1 状态空间的基本概念
7、状态空间表达式：状态方程与输出方程的组合称为状态空间 表达式，又称为动态方程。它是对系统的一种完全的描述。 例：SISO系统状态空间表达式：
x Ax bu y cx du
图2-1 动力学系统结构示意图
与输入—输出描述不同，状态空间描述把系统动态过程 的描述考虑为一个更为细致的过程：输入引起系统状态的变 化，而状态和输入则决定了输出的变化。
2009-08
CAUC--空中交通管理学院
3
§2-1 状态空间的基本概念
5、状态方程：状态变量的一阶导数与状态变量、输入量的关系， 称为系统的状态方程。
2009-08
x1 8 x1 x 2 x 64 x x 2 1 3 x3 3x3 x 4 x1 u x1 3x3 x 4 u x 4 2 x 4 x1 u x1 2 x 4 u

线性系统理论(xue)

线性系统理论(xue)

线性系统理论Linear System Theory 1-1 状态空间的基本概念例1-1 图示RLC 网络。

设：u i 为输入变量；u o =u c 为输出变量。

2 状态空间描述中常用的基本概念例1-1 图示RLC 网络。

设：u i 为输入变量；u o =u c 为输出变量。

用矩阵表示状态空间表达式：⎪⎨+−−=u x R x x 11&1-2 线性连续系统状态空间表达式的建立1......)((b s b s b s b s Y G n n ++++−1 N(s)/D(s)的串联分解——可控标准型实现x&x x⎤⎡⎡00010L &状态变量图例1-5 已知系统微分方程：u u T y y y +=ω+ωζ+试求系统的状态空间表达式，并绘制该系统的状态变量图。

21u x x x+ζω−ω−=22&2 可观测标准型实现设可控标准型实现为例1-6 已知系统微分方程：试求可观测标准型实现，并绘制其状态变量图。

3 并联分解——Jordan标准型实现⎤⎡−s L 0001ss s s U s G 89)()(23++==例1-7 已知某系统传递函数:⎡1⎤4 矩阵的特征方程、特征值1）方阵2 线性定常连续系统状态方程的求解2-1 齐次状态方程的解⎢⎣⎥⎦⎢⎣−−=⎥⎦⎢⎣22x 32x &解：用拉氏变换的方法:例2-1 求已知状态方程的状态转移矩阵。

2-2 状态转移矩阵的性质例2-2 已知状态转移矩阵，求Φ-1和系统矩阵A。

性质9 若例2-3已知系统矩阵，求状态转移矩阵及其状态转移矩阵的逆。

非齐次状态方程：例2-4 已知状态空间描述及零初始条件，输入为单位阶跃，求状态方程的解SISO系统：例9-29 已知系统动态方程，试求系统的传递矩阵。

⎡x&9-4-2开环与闭环传递矩阵MIMOU(s)E(s)Y(s)由图可知：3-1 线性系统的可控性与可观性3-1-1 问题的提出例3-2 已知系统状态空间表达式，⎧3-2 可控性问题基本概念考虑线性系统：3-3 可观测性的基本概念3-4 线性定常系统可控性判据考虑线性定常系统：例3-3 判断已知系统的可控性。

第2章线性系统的状态空间描述

第2章线性系统的状态空间描述
第2章 状态空间描述
➢ 2.1 状态和状态空间 ➢ 2.2 线性系统的状态空间描述 ➢ 2.3 由输入-输出描述导出状态空间描述 ➢ 2.4 线性时不变系统的特征结构 ➢ 2.5 状态方程的规范型 ➢ 2.6 由状态空间描述导出传递函数矩阵 ➢ 2.7 组合系统的状态空间描述和传递函
数矩阵
2.1 状态和状态空间 ➢系统动态过程数学描述的两种基本类型
数矩阵
2.2 线性系统的状态空间描述
分析方法 建立系统的状态空间描述
辩识方法
▪ 分析方法适用于结构和模型参数为已知的 系统。
▪ 辩识方法适用于结构和系统参数不清楚的 系统，需要通过实验的手段取得输入-输出 数据，导出相应的系统状态空间描述。
2.2 线性系统的状态空间描述
例2.1 考察下图所示的简单电路，电路各组成元 件的参数为已知，输入变量取为电压源 e(t) ，输出 变量取为电阻 R2 两端的电压 uR2
2. 系统的内部描述（状态空间描述）
2.1 状态和状态空间
3. 外部描述与内部描述之间的关系
▪ 外部描述通常是一种不完全描述，它不能反 映系统内部结构的不能控和不能观测的部分；
▪ 内部描述则是对系统的完全描述，能够完全 表征系统内部结构的一切，能够体现系统所 有的动力学特性；
▪ 只有在满足一定的条件下，系统的外部描述 与内部描述才具有等价关系。
R1R2 (R1 R2
)C )L
uC iL
( (
R1 R1
1 R2 R2 R2
)C )L
e(t
)
A
B
uR2
(
R1
R2 R2
)
(
R1R2 R1 R2
)
uC iL

现代控制理论_2-1_线性系统的状态空间描述

现代控制理论_2-1_线性系统的状态空间描述

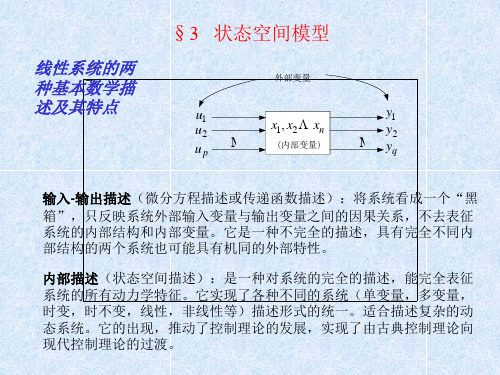
第二章 线性系统的状态空间分析法c§1 线性系统的状态空间描述§2 线性定常连续系统的分析e a第二章 线性系统的状态空间分析法§3 线性定常离散系统的分析 §4 系统的传递函数矩阵ty cc§1 线性系统的状态空间描述§2 线性定常连续系统的分析e a§3 线性定常离散系统的分析 §4 系统的传递函数矩阵ty c叠加 原理一、系统描述的基本概念 一、系统描述的基本概念1，输入、输出2，松弛性：若系统的输出y[t0,∞) 由输入u[t0,∞)唯一确定，则称系统在t0时刻是松弛的。

系统在t0 时刻不存储能量，初始条件为零！ce a4，线性: H (u1 + u 2 ) = Hu1 + Hu2 可加性5，定常性： Qa 为位移算子y = Hu算子，如传递函数3，因果性：系统在t 时刻的输出仅取决于t时刻和t 时刻之前的输入，与t 时刻之后的输入无关。

ty cy1 y2 yq输入延迟输出相应延迟 y = Hu = HQa u = Qa Hu = Qa y = y (t − a )u (t ) y (t ) u (t ) y (t )cH (αu1 ) = αH (u1 )e at齐次性a为实数u (t ) = Qa u (t ) = u (t − a )ty ct系统 数学描述cu1 u2 up外部描述（输入—输出描述）不完全描述微分方程、传递函数e aM二、状态空间的基本概念 二、状态空间的基本概念Mx 例：机械位移系统 依据牛顿定律： ∑ F = m&&(t )系 统x1 , x2 , L , xn内部描述（状态空间描述）状态方程＋输出方程ty c完全描述ckmF (t )e ax (t )& ∴ F (t ) − kx(t ) − fx(t ) = m&&(t ) x微分方程：& m&&(t ) + fx(t ) + kx(t ) = F (t ) xf传递函数：X (s ) 1 = (s ) ms 2 + fs + k F经典控制理论中的数学模型（外部描述），反映 了输入输出的关系，不能反映内部变量的关系。

状态空间模型

状态空间模型
这时，状态方程不变（同上），而输出方程变为：
y (t ) = [b0 bn a0 , b1 bn a1, L, bn 1 bn an 1 ]X (t ) + bnu (t )
Example
分别求传递函数
和 2）
4 s 2 + 3s 3 G(s) = 2 s + 7s + 5
s 3 G(s) = 2 1） s + 3s + 2
Example
设一线性系统的状态表示为
dx1 dt = x1 + x2 + u dx 2 = x2 u dt y = x1 x2 + 2u
{A, B, C , D}
试求其输入-输出微分方程.
解:
1 2 1 , , [1 1],2, = 0 1 1
1
代入公式(3)得
的状态模型表示。 解：1） m=1,n=2且 a0 = 2, a1 = 3, b0 = 3, b1 = 1.
0 A= a0 1 0 1 0 B = , = , a1 2 3 1 C = [b0 b1 ] = [ 3 1], D = 0
状态模型为：
1 x1 (t ) 0 d x1 (t ) 0 = + u (t ) dt x2 (t ) 2 3 x2 (t ) 1 x1 (t ) y (t ) = [ 3 1] x2 (t )
其中 H i 为待定向量,维数与 X 相同. 显然,由初始条件X (0) = X 0 可得 H 0 = X 0 , 并将(3)式代入(2)式得:
H1 + 2 H 2t + L + nH nt n 1 + L = AH 0 + AH1t + L + AH nt n + L

第二章 系统的状态空间模型

第二章 系统的状态空间模型

+
• 0
(β
+ a β + a β )u
1 1 2
( n −2)
(β
0
+ L + (β
n −1
n −1
+ a1 β
1
+ L + an − 2 β + an −1
0
n
+ a1 β
( n)
+ L + an −1 β + an β
( n −1) •
)u }=
1
β )u +
bu
0
（ k）
+ b1 u
+ L + bn −1 u + bn u
+ B (t ) u
y = C (t )X + D(t )u
► 在经典控制理论中，通常控制系统的时域模
型表征为输出和输入间的一个单变量高阶微 分方程，它具有如下一般形式
y
(n)
+ a1 y
( n −1)
+ L + an −1 y + an y = b0 u
•
(n)
+ b1 u
( n −1)
+ L + bn −1 u + bn u
的关系式
2.导出状态变量的一阶微分方程组和输出关系 2.导出状态变量的一阶微分方程组和输出关系 式
•
x
•
1
=
=
y−β u = x +β u
0 2 1
••
•
•
x
•
Байду номын сангаас
2

线性系统理论-郑大钟(第二版)(2013)

线性系统理论-郑大钟(第二版)(2013)

状态空间： 状态空间定义为状态向量的一个集合，状态空间的维数等同于状态 的维数
几点解释 （1）状态变量组对系统行为的完全表征性
只要给定初始时刻 t0 的任意初始状态变量组 x1 (t0 ), x2 t0 ,, xn (t0 )
和t≥t0 各时刻的任意输入变量组 u1 (t ),u2 t ,, u p (t ) 那么系统的任何一个内部变量在t≥t0各时刻的运动行为也就随之而完全确定
R1
C
iC
duc di L u c R 2C L 0 dt dt duc di L R1i L R1C L e dt dt
1 uc ( R1 R2 )C i R1 L L( R1 R2 ) R2 u R2 R1 R2
x Ax Bu y Cx Du
机电系统状态空间描述的列写示例
R a i a La
dia c e e dt d c M i a f J dt c Ra e 1 ia La ia La L e f a cM 0 J J i
第二章 线性系统的状态空间描述
2.1 状态和状态空间
系统动态过程的两类数学描述
u1
y1
u2
up
x1, x2 ,, xn
y2
yq
(1) 系统的外部描述 外部描述常被称作为输出—输入描述 例如.对SISO线性定常系统:时间域的外部描述:
u1
y1
u2
up
x1, x2 ,, xn
y2
yq
y ( n) an1 y ( n1) a1 y (1) a0 y bn1u ( n1) b1u (1) b0u

状态空间模型

状态空间模型

所以 D 4
a0 5,a1 1,b0 23,b1 3.
所以
0 A a0
1 a1
0 5
11,
B 10,
C b0 b1 23 3,
状态模型为：
d dt
x1(t ) x2 (t )
0 5
1 1
x1(t ) x2 (t )
10u(t
)
y(t) 23
3
x1(t ) x2 (t )
dt 3. e At1 e At2 e A(t1t2 );
4. eAt 1 eAt ;
5. AB BA e At eBt e( AB)t ;
6. M 1e At M eM 1AMt;
1
7.
A
e1t
e At
;
n
ent
状态方程的解
对方程
d dt
X
(t)
AX
(t)
BU
C
c21
c22
c2n
cq1
cq 2
cqn
（输出矩阵）
d11 d12 d1p
D
d21
d22
d
2
p
dq1
dq2
dqp
（输出-输入矩阵）
状态模型的矩阵表示为：
d dt
X
(t)
AX
(t)
BU
(t),
X
(0)
X
0
Y (t) CX (t) DU (t).
显然，该系统完全由矩阵 A, B,C, D 所确定。以后我们以{ A, B,C, D }形 式来简记该系统。
得状态方 程：
dx1 dt
y'
x2
dx2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

15
第2章 线性系统的状态空间描述
2.1 系统的状态空间描述
2.2
系统按其状态空间描述的分类
2.3 化输入-输出描述为状态空间描述
2.4 状态方程的对角线规范型和约当规范型
2.5 由状态空间描述导出传递函数矩阵
2.6 线性系统在坐标变换下的特性
2.7 组合系统的状态空间描述
2
2.1 系统的状态空间描述
系统的状态和状态空间
系统动态过程的数学描述
u1
yq
u2
up
x1 , x2 , , xn
y2
yq
考察一个系统由一些相互制约的部分构成整体，可用上图所示的一个方 块来表示。方块以外的部分为系统环境，环境对系统的作用为系统输入， 系统对环境的作用为系统输出，两者分别用 u 和 y 表示，称其为系统外 部变量。用以刻画系统在每个时刻所处状况的变量为系统的内部变量， 用 来表征，这些变量随着时间的变化体现了系统的行为。系统的数学描 述就是反映系统变量间因果关系和变换关系的一种数学模型。
19
第2章 线性系统的状态空间描述
2.1 系统的状态空间描述
2.2 系统按其状态空间描述的分类
2.3
化输入-输出描述为状态空间描述
2.4 状态方程的对角线规范型和约当规范型
2.5 由状态空间描述导出传递函数矩阵
2.6 线性系统在坐标变换下的特性
2.7 组合系统的状态空间描述
12
2.1 系统的状态空间描述
离散时间线性系统的状态空间描述
状态空间描述形式 离散时间线性时不变系统
X (k 1) Gx(k ) Hu (k ) Y (k ) Cx(k ) Du (k )
n n阵G : 系统矩阵 n p阵H : 输入矩阵 q n阵C : 输出矩阵 q p阵D : 传输矩阵
写成矩阵形式
x1 (k 1) 0.9696 x (k 1) 0.0404 2 0.0202 x1 (k ) 5.05 104 u (k ) 4 0.9898 x2 (k ) 5.05 10
x1 (k ) y (k ) 1 1 x2 (k )
线性系统理论
第二章 系统状态空间模型
重庆大学 自动化学院 柴毅 魏善碧
第2章 线性系统的状态空间描述
2.1
系统的状态空间述
2.2 系统按其状态空间描述的分类
2.3 化输入-输出描述为状态空间描述
2.4 状态方程的对角线规范型和约当规范型
2.5 由状态空间描述导出传递函数矩阵 2.6 线性系统在坐标变换下的特性 2.7 组合系统的状态空间描述
状态空间：状态空间定义为状态向量的一个集合，状态空间的维数等
同于状态的维数
6
2.1 系统的状态空间描述
系统的状态和状态空间
几点解释
(1) 状态变量组对系统行为的完全表征性
(2) 状态变量组最小性的物理特征 (3) 状态变量组最小性的数学特征 (4) 状态变量组的不唯一性 (5) 系统任意两个状态变量组之间的关系 (6) 有穷维系统和无穷维系统 (7) 状态空间的属性
AX Bu X Y CX Du
R1R2 uc R2 e R1 R2 iL R1 R2
9
2.1 系统的状态空间描述
机电系统状态空间描述的示例
R a i a La dia c e e dt d c M i a f J dt ce Ra 1 &a L i i La a e a La c f & M 0 J J i 0 1 a
离散时间线性时变系统
X (k 1) G(k ) x(k ) H (k )u (k ) Y (k ) C (k ) x(k ) D(k )u (k )
13
2.1 系统的状态空间描述
状态空间描述的特点
状态方程形式上的差分型属性
描述方程的线性属性
变量取值时间的离散属性
D( k )
连续时间系统和离散时间系统
当且仅当系统的输入变量，状态变量和输出变量取值于连续时间点， 反映变量间因果关系的动态过程为时间的连续过程，该系统称为连续 时间系统
& AX Bu X Y CX Du
& A(t ) X B (t )u X Y C (t ) X D (t )u
7
2.1 系统的状态空间描述
系统的状态和状态空间
线性系统的状态空间描述
系统的状态空间表达式（动态方程或运动方程）:描述系统输入、输出和
状态变量之间关系的方程组 • 状态方程（描述输入和状态变量之间的关系）
• 输出方程（描述输出和输入、状态变量之间的关系）。
A(t ) x B(t )u, t t0 x y C (t ) x D(t )u
3
2.1 系统的状态空间描述
系统的状态和状态空间
(1) 系统的外部描述
外部描述常被称作为输出—输入描述 例如:对SISO线性定常系统:时间域的外部描述:
y ( n ) an 1 y ( n 1) a1 y (1) a0 y bn1u ( n 1) b1u (1) b0u
若f(x,u,t)，g(x,u,t)的全部或至少一 个组成元为x、u的非线性函数,该 系统称为非线性系统 非线性系统可以用泰勒展开方 法化为线性系统
若f(x,u,t),g(x,u,t)的全部组成元为x、u 的线性函数,该系统称为线性系统
对于线性系统
& A(t ) X B (t )u X Y C (t ) X D (t )u
17
2.2 系统按其状态空间描述的分类
时变系统和时不变系统
f f ( x, u ) 该系统称为时不变系统 若向量 f，g不显含时间变量 t，即 g g ( x, u )
f f ( x, u , t ) 该系统称为时变系统 若向量 f，g显含时间变量 t，即 g g ( x, u , t )
16
2.2 系统按其状态空间描述的分类
线性系统和非线性系统
f ( x, u , t ) x 设系统的状态空间描述为 y g ( x, u , t )
g1 ( x, u , t ) f1 ( x , u , t ) g ( x, u , t ) f ( x, u , t ) 2 ，g ( x, u , t ) 2 向量函数 f ( x, u , t ) g ( x , u , t ) f ( x , u , t ) q n
当且仅当系统的输入变量，状态变量和输出变量只取值于离散时间 点，反映变量间因果关系的动态过程为时间的不连续过程，该系统称 为离散时间系统。
X (k 1) Gx (k ) Hu (k ) Y (k ) Cx(k ) Du (k )
X (k 1) G (k ) x(k ) H (k )u (k )
bn 1 s n 1 b1 s b0 y( s) n 复频率域描述即传递函数描述 g ( s ) u ( s ) s an 1 s n 1 a1 s a0
u1
yq
u2
up
x1 , x2 ,, xn
y2
yq
4
2.1 系统的状态空间描述
系统的状态和状态空间
Ra
i f const
J, F
e(t )
La
AX Bu X 上式可表为形如 Y CX Du
10
2.1 系统的状态空间描述
连续时间线性系统的状态空间描述
动态系统的结构
u1
u2
x1 x2
y1 y2

up
动力学部件

xn
输出部件

yq
连续时间线性系统的状态空间描述
线性时不变系统
8
2.1 系统的状态空间描述
电路系统状态空间描述的列写示例
R1
duc diL u R C L 0 2 c dt dt duc di R1iL R1C L L e dt dt
1 & ( R R )C u c 1 2 & R1 iL L( R1 R2 ) u R2 R2 R1 R2
2.1 系统的状态空间描述
系统的状态和状态空间
状态：一个动力学系统的状态定义为由其状态变量组 状态变量组：一个动力学系统的状态变量组定义为能完全表征其时 间域行为的一个最小内部变量组
x1 (t ), x2 t ,, xn (t ) x1 (t ) x (t ) 2 x ( t ) 所组成的一个列向量 x ( t ) n
x1 (k 1) 1.01 (1 0.04) x1 (k ) 1.01 0.02 x 2 (k ) 1.01 5 10 4 u (k ) x 2 (k 1) 1.01 (1 0.02) x 2 (k ) 1.01 0.04 x1 (k ) 1.01 5 10 4 u (k )
H (k )
x(k 1)

单位延迟
x(k )

C (k )
u (k )

y (k )
G (k )
离散时间线性系统的方块图
14
2.1 系统的状态空间描述
人口分布问题状态空间描述的列写示例
假设某个国家，城市人口为107,乡村人口为9x107，每年4%的城市人 口迁移去乡村，2%的乡村人口迁移去城市，整个国家的人口的自然增长 率为1% 设k为离散时间变量， x1(k)、x2(k)为第k年的城市人口和乡村人口, u(k) 为第k年所采取的激励性政策控制手段,设一个单位正控制措施可激励 5×104城市人口迁移乡村,而一个单位负控制措施会导致5×104乡村人口 去城市, y(k)为第k年全国人口数