高等代数论文 个人 绝对直接可用
- 格式:doc
- 大小:142.35 KB
- 文档页数:7

高等代数实践小论文代数在讨论任意多个未知数的一次方程组,也叫线性方程组的同时还研究次数更高的一元方程组。
发展到这个阶段,就叫做高等代数。
高等代数是代数学发展到高级阶段的总称,它包括许多分支。
《高等代数I 》主要介绍了多项式、行列式、矩阵以及线性方程组的相关知识并建立了联系。
其相关具有代表性的习题如下:1.设a,b 为两个不相等的常数,则多项式f(x)被(x-a)(x-b)除所得余式为_____.解答:设r(x)=cx+d,其中∂(r(x))<2.f(x)=(x-a)(x-b)g(x)+cx+d,f(a)=ca+d,f(b)=cb+d,联立可解得c=f (a )−f(b)a−b ,d=f(a)-a f (a )−f(b)a−b 故r(x)= f (a )−f(b)a−b x + f(a)-a f (a )−f(b)a−b .Thoughts of mine:已知除式为2次则可由余式的次数小于除式得到余式的次数,进而带入已知数求解。
2.设f(x)=3x 4-41x 3-53x 2-101x+7,求f(15).解答:由余数定理,f(15)即为f(x)除以15所得的余数.做综合除法可得f(15)=67.Thoughts of mine:余数定理即可得此时的值,没有必要将15代入求解.3.求f(x)=x 7+2x 6-6x 5-8x 4+17x 3+6x 2-20x+8的根.解答:f ’(x)= 7x 6+12x 5-30x 4-32x 3+51x 2+12x-20.则(f(x),f ’(x))= x 5+x 4-5x 3-x 2+8x-4.f(x)((f (x ),f ′(x ))=x 2+x-2=(x+2)(x-1). 根据f(x)的常数项可以得到,f(x)=(x +2)3(x −1)4.故f(x)的根为1,-2.Thoughts of mine:对于有些多项式来说,单看公因子判别是否为有理根的情况很多且很复杂,先去掉次数的方法相对容易.4.已知f(x)=x 3+a x 2+bx+c,a,b,c ∈Z.求证:若ac+bc 为奇数,则f(x)无整数根.证:假设f(x)有整数根α,则有α|c.由于(a+b)c 为奇数,故a+b,c 均为奇数,故α也为奇数.则x-α|f(x),设f(x)=(x-α)q(x),其中q(x)为整系数多项式.f(1)=(1-α)q(1)=1+a+b+c,而1+a+b+c 为奇数,但1-α为偶数,矛盾. 故f(x)无整数根.Thoughts of mine:奇偶矛盾是反证法常用的一种矛盾,不管是次数矛盾还是根的奇偶都容易得到,也就容易推出矛盾.5.已知x+y+z=0,xyz ≠0,,求x 2yz +y 2xz +z 2xy 的值.解答: x 2yz +y 2xz +z 2xy =x 3+y 3+z 3xyz .令f(x,y,z)=x 3+y 3+z 3,首项为x 3.故f(x,y,z)=σ13+a σ1σ2+b σ3,其中σ1= x+y+z=0.故f(x,y,z)=x 3+y 3+z 3=-6=-2b,故b=3.则x 2yz +y 2xz +z 2xy =x 3+y 3+z 3xyz =3σ3σ3=3.Thoughts of mine:表成初等对称多项式可以解决很多对称多项式的求值问题或求方程组的解的问题.例如:解方程组{x +y +z =2,(x −y)2+(y −z)2+(z −x)2=14,x 2y 2z +x 2yz 2+xy 2z 2=2.解答:σ1=x+y+z=2=-a 1,对方程组作加减变换,可得x 2+y 2+z 2-(xy+xz+yz)=7,xyz(xy+yz+xz)=2,x 2+y 2+z 2+2(xy+xz+yz)=4,故xy+xz+yz=σ2=-1=a 2,xyz=σ3=-2=-a 3.故x,y,z 为方程f(x)=x 3-2x 2-x+2的三个根,易得x=1为一个有理根. 用综合除法可得f(x)=(x-1)(x+1)(x-2),故f(x)的三个根为1,-1,2.6.已知5阶行列式5123452221127312451112243150D ==.求414243A A A ++ 和4445A A +.解答:设x=414243A A A ++,y=4445A A +则D 5=414243A A A +++2(4445A A +)=x+2y=27,若将第四行换成与第二行相同的数字,则有D′5=|1 2 3 4 52 2 2 1 13 1 24 52 2 2 1 14 3 15 1|=0,则D′5=2x+y=0.联立可解得x=-9,y=18.Thoughts of mine:因为A ij 为代数余子式,故可看成按某一行全为1或2展开即行列式的值.类似地,还有| 2 1 5 41 2 3 1−1 0 2 3 3 1 0 −1|,求M 13-M 23-2M 43的值.简解: M 13-M 23-2M 43=1∙A 13+1∙A 23+0∙A 33+2∙A 43=| 2 1 1 41 2 1 1−1 0 0 33 1 2 −1|,即将第三列元素换为代数余子式前的系数.7.求行列式的值:|1 1 1a b c a 3 b 3 c 3|.解答:|A |=| 1 1 1 1a b c y a 2 b 2 c 2 y2a 3 b 3 c 3 y 3|,原行列式的值即为该行列式求值后y 2的系数的相反数.显然,|A |是Vandermonde 行列式, |A |=(y-a)(y-b)(y-c)(b-a)(c-a)(c-b), 由根与系数的关系可得y 2的系数为-(a+b+c)(b-a)(c-a)(c-b),故所求原行列式的值为(a+b+c)(b-a)(c-a)(c-b)= a 2+ b 2+c 2.Thoughts of mine:与Vandermonde 行列式类似的情形可转化为Vandermonde 行列式,根据根与系数的关系求解.8. R 是实数域,对任意正整数m n ≥,证明:在n R 中存在m 个向量12,,,m ααα,使其中任意n 个向量线性无关.解答:令α1=(1,1,1,⋯,1),α2=(1,2,22,⋯,2n−1),⋯,αm =(1,m,m 2,⋯,m n−1),将其排成列矩阵,A=[1⋯1⋮⋱⋮1 ⋯m n−1],任意取其中n 列都可能到一个方阵,且这个方阵取行列式为Vandermonde 行列式.由于1,2,⋯,m 各不相等,故|A |≠0,即其中任意n 个向量线性无关.Thoughts of mine:Vandermonde 行列式的值易求得,且容易构造,所以取特殊情况构造时可以选择Vandermonde 行列式.9. 百鸡术:母鸡每只5钱,公鸡每只3钱,小鸡3只1钱,百钱买百鸡,各买几何?解答:设买母鸡、公鸡、小鸡数分别为x,y,z.则可得线性方程组和约束条件:{x +y +z =100,5x +3y +13z =100且100≥x ,y,z ≥0,3|z.A̅=[1 1 11005 3 13100]→[1 0 −43−1000 1 73200],故{x=43z−100,y=−73z+200根据约束条件z=75,78,81,84,故可以得到四组解{x=0,y=25,z=75.{x=4,y=18,z=78.{x=8,y=11,z=81.{x=12,y=4,z=84.Thoughts of mine:可用线性方程组解决实际问题,但应注意的是,在用线性方程组解决实际问题时要注意实际问题的约束条件.类似的还有, 将军点兵,三三数之剩二,五五数之剩三,七七数之剩二,问兵几何?(求在500至1000范围内的解)10.已知A是方阵,A2-A-2E=0,则A−1=_______,(A+2E)−1=__________.解答:A2-AE-2E=0,A(A-E)=2E,所以A−1=A−E2.(A+2E)(A-3E)=-4E,所以(A+2E)−1=-A−3E4.Thoughts of mine:求A−1需要对已知的式子进行变形,得到A A−1=E,从而得到所求结果.。

经济学中高等代数的应用-经济学论文-经济论文——文章均为WORD文档,下载后可直接编辑使用亦可打印——摘要:高等代数是研究经济学的基础工具之一,同时也是最为重要的工具之一。
本文探讨了经济学中应用高等代数的策略,总结了经济学应用高等代数的意义。
关键词:经济学;高等代数;策略高等代数在经济学中的应用较为常见,如微分、积分、函数、数列等,这些数学方法被应用到经济学的研究中,始于法国经济学家古诺。
自古诺之后,大量的经济学家开始纷纷采用数学方法来研究经济学问题,使经济学的研究更加的理性,推动了经济学的发展,使人们对经济学的规律有了更为深入的认识。
本文分析了经济学应用高等代数的具体表现,研究了经济学应用高等代数的策略。
一、经济学中应用高等代数的策略经济学中应用高等代数,其策略主要是应用高等代数的基本概念、性质、模型、数学思想等,具体则可以分为两类,即直接应用与间接应用两类,分析如下:第一,经济学中直接应用高等代数。
高等代数在经济学中的直接应用,往往是着眼于直接计算相应的结果,如微分计算边际成本问题、最优化问题、弹性分析问题,积分计算总函数、函数计算需求函数、供给函数、总成本函数、销售收入函数、总利润函数等,这些经济概念,主要是集中在经济管理中,都是利用高等代数的概念、性质、模型等,从而解决经济管理中的一些常见问题[1]。
经济学中直接应用高等代数,这种应用较为普遍,同时也可以看出经济学家在研究经济现象时对高等代数的依赖,同时,利用高等代数解决经济学中这些问题,也更为的科学、理性,也能够为经济管理提供最正确的决策支持。
更为重要的一点是,高等代数应用在经济学中,使得经济学的研究更加准确,特别是对企业生产来说,更是能够找到理论依据,不至于盲目生产,造成经济损失。
如企业对需求函数、供给函数、总成本函数、销售收入函数、总利润函数等使用,举例来说,设某厂准备了生产经费1000元,其可变资本为4元,销售单价为8元,则该商品的总成本、单位成本、销售收入、利润函数是什么[2]。

莆田学院毕业论文题目数学归纳法及其在图论中的应用学生姓名余晶晶学号510401425专业数学与应用数学班级数本054指导教师陈梅香二00九年五月十日目录0引言 (1)1数学归纳法的理论基础 (2)1.1数学归纳法的理论基础是Peano公理 (2)1.2第一数学归纳法 (2)2数学归纳法的基本步骤 (2)2.1n的取值 (2)2.2验证初值 (3)3数学归纳法的其他形式 (4)3.1第二数学归纳法 (4)3.2跳跃数学归纳法 (4)3.3反向数学归纳法 (6)3.4二重数学归纳法 (7)4数学归纳法原理在图论中的应用 (8)4.1对顶点数进行归纳证明 (8)4.2 对边数进行归纳证明 (9)4.3 对顶点集(或边集)的子集中的元素个数进行归纳证明 (9)4.4图论中其他与自然数有关命题的归纳证明 (10)结束语 (12)致谢 (13)参考文献 (13)数学归纳法及其在图论中的应用余晶晶(数学与应用数学指导老师:陈梅香)摘要:本文介绍了数学归纳法原理的两个基本步骤,以及由它的基本原理推导出的数学归纳法的其他四种形式,包括:第二数学归纳法、跳跃数学归纳法、反向数学归纳法、二重数学归纳法,并给出这四个数学归纳法及其应用,并应用数学归纳法、证明图论中的图的顶点数、边数、顶点集或边集、距离、途径等等各个方面与自然数n有关的命题。
关键词:数学归纳法形式归纳假设基本步骤图论Abstract:This paper introduces the principle of mathematical induction of the two basic steps, as well as thebasic principles of it deduce the mathematical induction of the other four forms, including: Second mathematicalinduction, jumping mathematical induction , reverse mathematical induction, double mathematical induction,and gives the theorem of the four mathematical induction and its applications, and prove some proposition aboutnatural number n by mathematical induction in graph theory, such as the proposition about vertices of thegraph, edge, vertex set or edge set, distance, and so on in graph theory.Keywords: mathematical induction form inductive assumption basic step graph theory0引言()的一种推理方法。

高等代数教学中的几点感悟文宋雪丽摘要在大学数学课程中,高等代数是其中一门十分重要的科目。
结合教学实践,谈了一些感悟。
关键词内容;概念;方法高等代数是大学数学课程中一门重要的专业基础课程,为后继课程提供必不可少的数学理论基础知识,一般都在大学一年级开设。
由于该课程是学习大学后继相关课程的基石,同时也是研究其他学科的工具,许多高等院校都将高等代数列为研究生招生考试课程,因此,该课程在整个专业课程体系中地位很高。
由于该课程的抽象性和枯燥性,许多初学者往往觉得学起来很困难。
因此,作为高校教师,如何培养学生对高等代数的学习兴趣,提高高等代数的课堂教学质量显得尤为重要。
结合多年的教学实践经验,下面我谈谈在《高等代数》教学中的一些感悟。
一、尽量与中学数学内容相联系高等代数课程中的许多教学内容与中学数学有着紧密的联系。
例如数与数域,中学教材中有整数、有理数、实数及复数。
高等代数中介绍了数域的概念;多项式,在中学数学教材中就有多项式的加、减、乘、除四则运算法则。
在高等代数中严格定义了多项式的次数及加法、减法、乘法运算,介绍了多项式的整除理论及最大公因式理论;方程,中学教材中有一元一次方程、一元二次方程的求解方法、一元二次方程根与系数的关系。
高等代数中介绍一元次方程根的定义、复数域上一元次方程根与系数的关系及根的个数、实系数一元次方程根的特点、有理数一元次方程根的性质及其求法;方程组,中学教材中有二元一次方程组、三元一次方程组的消元解法。
高等代数中有元一次线性方程组的行列式解法克拉默法则和矩阵消元解法、线性方程族解的判定及解与解之间的关系;空间与图形,中学教材中有平面与空间向量的长度与夹角,高等代数中有欧式空间向量的长度和夹角。
通过以上分析,高等代数与中学数学在内容上有很多相关联的地方。
不同的是中学数学知识比较浅显,面也比较窄,而高等代数将中学数学的内容拓宽了许多,同时也抽象了许多。
因此作为老师,要正确地引导学生以较高的观点去认识中学教学内容。

摘要:线性方程组的求解在高等代数学的是一个很重要组成分,因此对于对线性方程组解的广泛应用于数学与其他科学领域,因此对于线性方程组有解的判别定理和线性方程组解的结构我们必须进行认真的研究,搞清楚他们之间的关系。
本文对线性方程组的解和判定进行了全面的分析与研究。
关键字:线性方程组;解结构;矩阵;解的判定目录线性方程组解的判定与结构 .............................. 错误!未定义书签。
引言 (1)1 线性方程组解的判别定理 (1)2 齐次线性方程组的解的结构 (2)3 一般线性方程组的解的结构 (3)致谢 (7)参考文献: (7)引言线性方程组是线性代数的主要内容,包括线性方程组有解性的判定、消元法解线性方程组和线性方程组解的结构以及他们的基础解系。
它与矩阵、向量还有行列式、方程组、秩、克拉默法则的内容密切相关,与矩阵、向量组相关的许多重要结论都是线性方程组有关结论的应用和推广,对此本论文紧紧围绕线性方程组与解的结构进行展开,这也对我们以后学习线性方程组的解结构与解判别定理有很大帮助。
下面我就分几大板块来介绍关于线性方程解的判定与结构。
1 线性方程组解的判别定理线性方程组是否有解,我们有没有其他办法来解决?当然有,那就是通过用系数矩阵和增广矩阵的秩来进行刻划,下面我们对此介绍几个相关的定理:定理 1 线性方程组AX=b 有解的充分必要条件是它的系数矩阵的秩和增广矩阵的秩相等,即 秩(A )=秩(A ')。
证明 线性方程组(1)有解,就是说β可以经向量组12,,n ααα线性表出,由此立即推出,向量组12,,n ααα与向量组12,,,n αααβ等价,因而有相同的秩。
这两个向量组分别是矩阵A 与A '的列向量组,因此矩阵A 与A '有相同的秩定理2若线性方程组AX=b 有满足 秩(A )=秩(A ')=r ,则当r=n 时,线性方程组有解且只有唯一解;当r<n 时,线性方程组有无穷多解。

高等代数教学中的一些想法的论文高等代数教学中的一些想法的论文一、引言高等代数[1]是理工科大学生的基础课, 对数学系的学生尤其重要.它的教学质量的高低直接关系到理工科大学生的专业基础和后继课程的学习, 提高其教学质量对培养高层次人才具有重要意义[2].高等代数包括多项式、行列式、线性方程组、矩阵、二次型、线性空间、线性变换、λ-矩阵、欧式空间、双线性函数与辛空间等内容, 对理工科的大学生来说课程内容量多, 教学课时紧, 理解难度较大, 学生普遍感觉学习比较吃力.笔者近年来主要在数学系从事高等代数的教学工作, 针对学生在学习这门课程中存在的上述问题, 总结归纳了几个方面, 期望对学生的学习和同行教师的教学有所帮助, 共同改进和提高高等代数的教学质量.二、具体问题 (注:本文中的教材均指参考文献[1], 以后不再详细赘述)1. 关于"阶梯形矩阵"的理解和运用.教材P72给出了"阶梯形矩阵"的文字定义, 但学生普遍反映该定义较抽象, 理解难度较大, 笔者建议学生可同时参看另一本书[3]给出的相关内容.在[3]中不仅给出了"阶梯形矩阵"具体数学表达式的定义, 还给出了什么是"阶梯头", 以及一类特殊的阶梯形矩阵---约化阶梯形矩阵(也称为行最简形) .实践证明, 学生若理解阶梯头的概念和约化阶梯形矩阵, 对其解题帮助甚多.对此类问题, 可用两种方法求解.分析:方法1是教材上给出的传统解法, 也是大多数教师在讲解第三章内容时所用的方法;方法2是笔者将方法1解答过程中得到的阶梯形矩阵利用初等行变换进一步化为约化阶梯形矩阵, 进而求解方程组.表面上看, 两种方法复杂程度相当, 实际上方法2比方法1快捷, 因为化为约化阶梯形矩阵以后, 每个阶梯头都是1, 该列其余所有的元素均为0, 因此与原方程组等价同解的方程组(如上述方程组(*) ) 就非常容易求解, 其解一目了然.[4]2. 教材P188给出引理:对一个s×n矩阵A作一初等行变换就相当于在A的左边乘上相应的s×s初等矩阵, 对A作一初等列变换就相当于在A的'右边乘上相应的n×n的初等矩阵, 我们不妨简记为"左乘行变, 右乘列变", P191给出定理6:n级矩阵A为可逆的充分必要条件是它能表成一些初等矩阵的乘积:A=Q1Q2…Qm,利用该引理和定理6, 笔者给出教材P180定理4的另一种简单证明方法.定理4 A是一个s×n矩阵, 如果P是s×s可逆矩阵, Q是n×n可逆矩阵, 那么证明:因为P是可逆矩阵, 根据定理6, 它能表成一些初等矩阵的乘积:根据引理, 矩阵X1X2…XmA (即PA) 相当于对矩阵A作m次的初等行变换, 由于初等变换不改变矩阵的秩, 故秩 (A) =秩 (P A) .另一个等式可同样证明.3. 分块矩阵的分块原则.教材第三章第五节讲到了"矩阵的分块", 但是并没有很直接地说明相关问题, 比如是否对每一个矩阵的计算都适合用分块的方法, 以及分块时如何去进行.首先需要明确:并不是所有的矩阵都适合用分块的方法去计算.总结讲解高等代数的相关书籍, 我们会发现下面的规律:对于一般矩阵而言, 只有将其分块以后能分出诸如零矩阵、单位矩阵、数量矩阵、对角矩阵等特殊的子矩阵, 我们一般才考虑用分块的方法去计算.这样的例子有很多, 如教材P181所给的例子:按照教材上的分块方法, 矩阵A分成的四个子矩阵中, 包括两个2级单位矩阵和一个2级零矩阵.当然上述规律也不尽然, 对一些特别的矩阵, 可能分块以后并没有上面提到的一些特殊子矩阵, 但是实践证明也较适用分块的方法.读者可参看教材P203第28题, 对于矩阵A,本题要求用两种方法求逆矩阵, 一是初等变换, 二是矩阵分块.读者通过用两种方法分别计算可知, 本题用第二种方法较为简便.4. 向量组的极大线性无关组P125:定义13一向量组的一个部分组称为一个极大线性无关组, 如果这个部分组本身是线性无关的, 并且从这向量组中任意添加一个向量(如果还有的话) , 所得的部分向量组都线性相关.齐次线性方程组的基础解系P142:定义17齐次线性方程组(1) (见教材P141) 的一组解η1, η2, …, ηt称为它的基础解系, 如果 (1) (1) 的任一个解都能表成η1, η2, …, ηt 的线性组合; (2) η1, η2, …, ηt线性无关.线性空间的一组基P249:定义6在n维线性空间V中, n个线性无关的向量ε1, ε2, …, εn称为V的一组基.设α是V中任一向量, 于是ε1, ε2, …, εn, α线性相关, 因此α可以被基ε1, ε2, …, εn线性表出:α=a1ε1+a2ε2+…anεn.三者的区别与联系:区别是很明显的, 无须多言.联系在于:齐次线性方程组的任一个解本质上都是一个解向量, 因此从定义上可看出, 齐次线性方程组的一个基础解系即是它所有解构成的解向量组的一个极大线性无关组.同样的道理可知, 线性空间的一组基也为该空间中所有向量组成向量组的一个极大线性无关组.又向量本质上为矩阵, 故对三者的各类求解问题, 虽然表面差别很大, 但实质都是考察矩阵的行 (列) 初等变换、化为阶梯形矩阵、秩、找出极大线性无关组等问题, 殊途同归.具体例子请参看教材P271第17题.5. 对矩阵秩r的全面理解.教材P134定理6:一矩阵的秩为r的充分必要条件为矩阵中有一个r级子式不为零, 同时所有r+1级子式全为零.这里补充注意两个问题:(1) 对该矩阵A而言, 其所有的k (≤r-1) 级子式均不全为零.因为由行列式按一行展开的公式可知, 如果矩阵A的k (≤r-1) 级子式全为零, 则矩阵A的k+1级子式全为零, 从而A的所有级数大于k的子式全为零.显然r≥k+1, 故A的所有级数为r的子式全为零, 与定理条件"有一个r级子式不为零"相矛盾.(2) 同 (1) 分析可知, 若矩阵A的k+1级子式全为零, 则A的所有级数大于k+1的子式也必然全为零, 从而可以说:此时, A的所有级数大于k的子式全为零.综合以上两点, 可将定理6换一种定义说法, 即:一矩阵的秩为r的充分必要条件为矩阵的非零子式的最高级数为r级.三、总结高等代数是理工科大学生一门非常重要的专业基础课.本文总结了高等代数教学过程中几个容易被忽视而对整个知识体系的理解又非常关键的问题, 旨在帮助学生们更好地把握整个代数知识框架的脉络, 同时也期望为从事这门课程教学的教师同行们提供积极的教学参考.参考文献[1]北京大学数学系前代数小组.高等代数[M].第4版.北京:高等教育出版社, 2013.[2]张华民, 殷红彩.高等代数教学中的几点思考[J].安庆师范学院学报:自然科学版, 2014, 20 (1) :90-93.[3]陈维新.线性代数[M].第2版.北京:科学出版社, 2005.[4]张盛祝, 蔡礼明, 胡余旺.高等代数内容、方法及典型问题[M].北京:中国石化出版社, 2014.。

莆田学院数学与应用数学系“高等代数选讲”课程论文题目:小论矩阵的对角化姓名:刘文娟学号:410401210莆田学院数学与应用数学系数学与应用数学专业2004级2007年6 月22 日小论矩阵的对角化刘文娟 042数本 410401210摘要:对角矩阵可以认为是矩阵中最简单的一种,这里讨论n 阶矩阵对角化的一些判定条件(充要条件)及几种常用矩阵的对角化问题。
关键词:可对角化 特征值 特征向量 不变因子 初等因子 最小多项式 矩阵的秩特征多项式 循环矩阵定义:数域F 上方阵A ,如果能与一个F 上的对角方阵相似,则A 在F 可对角化。
判定1:A 可对角化的充要条件是:有n 个线性无关的特征向量。
判定2:设n 方阵A 的全部不同的特征根为12,,,m λλλ而()12,,1,2,i i isi i m ααα=为()0i E A X λ-=的一个基础解系(从而是属于i λ的一极大无关特征向量组),A 可对角化的充要条件是:12m s s s n ++=判定3:设12,,,m λλλ为n 方阵A 的全部不同的特征根,且分别为12,,m s s s 重根,A 可对角化的充要条件是: 对每个()1,2,i i m =都有:()i i r E A n s λ-=- 证明:充分性 设()i i r E A n s λ-=-, ()1,2,i m =则齐次线性方程组()0i E A X λ-=的基础解系含()i i n n s s --=个向量,但由于12,,,m λλλ分别为12,,m s s s 重根,从而12m s s s n ++=故A 可对角化。
必要性 设A 必有n 个线性无关的特征向量,但由于12m s s s n ++=,故每个次线性方程组()0i E A X λ-=的基础解系必含i s 个向量,从而()i i r E A n s λ-=-, ()1,2,i m =判定4:数域F 上n 方阵A 与对角矩阵相似的充要条件是:A 的最小多项式是F 上互素的一次因式的乘积。

数统学院数学与应用数学系“高等代数”课程论文题目:n维线性空间的线性变换的核与值域的性质及应用姓名:郑某某学号:20111010xxx数统学院数学与应用数学系数学与应用数学专业2011级2013年2 月26 日摘要:本文先从n 维线性空间上的线线变换的核与值域出发,引出它们的一些性质。
通过几种类型的例题来加深对这些性质的理解。
由解题的过程,可以总结出解决n 维线新空间的线新变幻的核与值域的一般方法与思想。
关键词:n 维线新空间 线新变换 值域 核一.相关定义及性质。
文[1][2]给出了具体的关于n 维线性空间的线性变换的相关定义及性质。
下面是性质的一个补充。
我们知道:若σ的n 维线性空间V 的线性变换,则σ(V )和1(0)σ-是σ的不变子空间。
若τ也是V 的一个线性变换,且τ与σ可交换,那么τ的值域和核是不是也是σ的不变子空间?命题一:若线性变换,στ是n 维线性空间V 的线性变换,且σ,τ可交换,则τ的核和值域都是σ-子[3]空间。
证明:ξ∀∈1(0)σ-,则有τ(σ(ξ)) =τσ(ξ)=σ(0)=0 ∴σ(ξ)∈1(0)σ-∀τ(η)()V τ∈,σ(τ(η))=τ(σ(η))()V τ∈ ()V τ∴也是A-子空间。
二.有关核与值域的维数问题。
例一:设F 为数域,V=n F ,证明:1)T(12,,,n x x x )=(1210,,,,n x x x - )是线性空间V 的一个线性变换,且n T =02)求T 的核与值域TV 的维数。
证明:设α=(12n ααα+++ ),V β∈=(12n βββ+++ )V ∈。
T(αβ+)=(0,112211,,,n n αβαβαβ--+++ )=(1210,,,,n ααα- )+(1210,,,,n βββ- )=T α+T β k F ∀∈,则T (k α)=(1210,,,,n k k k ααα- )=k (1210,,,,n ααα- )=kT α,∴T 为线性空间V 的线性变换。

高等代数论文矩阵在生产生活方面的应用指导老师李思泽运输1512 崔粲 15251169知行1501 徐鹏宇 15291200目录【摘要】 (2)【关键词】 (2)【Abstract】 (2)【Key words】..................................... 错误!未定义书签。
【实际应用举例】 (3)1. 计算网络中的流 (3)1.1 交通流分析 (3)1.2 程序运行代码 (5)1.3 程序运行截图 (8)1.4 程序运行代码(2) (9)1.5程序运行截图(2) (13)2.电路分析 (13)2.2程序运行代码 (15)2.3 程序运行截图 (18)【论文总结】...................................... 错误!未定义书签。
【参考文献】...................................... 错误!未定义书签。
摘要近二十年来,随着计算机技术的蓬勃发展,利用计算机的符号计算系统对代数中可计算问题形成了计算代数这个新的方向,本文主要通过对于矩阵的应用实例来说明代数在实际生活中的应用。
随着科学技术的发展,数学也越来越贴近我们的生活,可以说是息息相关。
我们在学习数学知识的同时,也不能忘记将数学知识应用于生活。
在学习高等代数的过程中,我们发现代数在生活和实践中都有不可缺少的的位置。
本篇论文中,我们就对代数中的矩阵在交通流量分析,电路分析的应用进行了探究并编写了相关程序。
【关键词】高等代数,矩阵,实际,应用,电路分析,交通流AbstractIn recent twenty years, with the rapid development of computer technology, using computer symbol computing system of algebra computational problems form the computational algebra in this new direction. This paper mainly through the matrix of the application examples to illustrate the application of algebra in real life. With the development of science and technology, mathematics is more and more close to our life, it can be said that it is closely related to the development of science and technology. At the same time, we can not forget to apply mathematical knowledge to life. In the course of learning advanced algebra, we found that the algebra has an indispensable position in life and practice. In this thesis, we study the application of the matrix in theanalysis of the traffic flow and the application of the circuit analysis.【Key words】Higher algebra,Practical,Matrix,Application,Circuit analysis,Traffic flow【实际应用举例】1.计算网络中的流在这一部分中,我们将介绍网络以及确定网络中流量的方法,网络的一个应用就是如图所示的单行道系统网络包括分支和节点,对于图1所示的单行道网络,分支是道路,节点是交叉路口,我们假定对于一个网络,进入一个节点的总流等于离开该节点的总流。

向量组线性相关的证明方法内容提要向量组的现行相关性是高等代数理论中的一块基石,在它的基础上我们可以衍生出许多其他理论,所以熟练地掌握判定向量组线性相关的方法可以更好地帮助我们理解其他理论的知识。
本文从理解向量组线性相关性的定义入手,论述了若干证明向量组线性相关的方法,例如利用线性相关的定义,行列式的值,矩阵的秩,齐次线性方程组的解等知识判定向量组线性相关性的判定,并且比较了不同种证明方法的适用范围和条件。
向量组线性相关性的证明理论在现实生活当中有着广泛的应用。
因此学好这一块的理论知识,掌握证明方法是很重要的。
第一章 绪论线性相关性的理论在数学专业许多课程中都有体现,如解析几何,高等代数和常微分方程中等等,它是线性代数理论当中的基本概念,它与向量空间和子空间的概念有着密切的联系,同时在解析几何以及常微分方程中有广泛的应用,因此掌握向量组线性相关性这个概念有着十分重要的意义,也是解决问题重要的理论依据。
向量组的线性相关和线性无关可以推广到函数组的线性相关和线性无关。
在线性代数中,向量组的线性相关性占到了举足轻重的作用。
它可以将线性代数中的矩阵,行列式,二次型的知识联系起来,如果能熟练掌握线性相关性则能更好地理解线性代数当中的其他知识,,理清线性代数的框架,做到融会贯通。
本文主要研究的是向量组的线性相关性的判定方法,从定义和性质下手,熟悉了一些重要的理论,熟悉了定义我们就能更好地把握线性相关性的本质。
而本文的第三章就并提出了几种线性相关性的证明方法,比较了不同种证明方法的适用范围和优势劣势,并给出了详细地证明过程和例题,从而更加深入地理解线性相关性的理论知识。
最后是关于这部分理论的展望和本文参考的具体文献。
第二章 向量组线性相关性的定义和性质2.1.1线性相关的概念定义1设m 21,,,ααα 是F 上向量空间V 的m 个向量.如果存在F 中一组不全为零的数,,,,21m k k k 使得0m 2211=+++αααm k k k (1)那么就称向量m 21,,,ααα 线性相关.如果不存在不全为零的数,,,,m 21k k k 使(1)式成立,或者说,只有当0m 21====k k k 时,(1)式才成立,那么就称m 21,,,ααα 线性无关.定义 2 若向量组A 中每一个向量i α(t i ,,2,1 =)都可由向量组B ={s ββ,,1 }线性表示,则称A 可由B 线性表示.若两个向量组可互相线性表示,则称这两个向量组等价.性质1 向量组的等价具有1)反射性;2)对称性;3)传递性.定义 3 设向量组{r i i i ααα,,,21 }是向量组{s ααα,,,21 }的部分组.称{r i i i ααα,,,21 }是{s ααα,,,21 }的极大无关组,如果1)向量组{r i i i ααα,,,21 }线性无关;2){s ααα,,,21 }中的任意1+r 个向量(如果有的话)构成的向量组总是线性相关的.定义 4 向量组{s ααα,,,21 }的极大无关组所含向量的个数称为该向量组的秩. 记为秩(s ααα,,,21 ).性质2 向量组{r αα,,1 }线性无关⇔秩{r αα,,1 } =r .向量组{r αα,,1 }线性相关⇔{r αα,,1 }秩<r .2.1.2线性相关的性质性质(1) 含零向量的向量组必线性相关,即{s αα,,,01 }线性相关.性质(2) 一个向量组若有部分向量线性相关,则此向量组线性相关.性质(3) 若一个向量组线性无关,则它的每个非空部分向量组也线性无关. 性质(4) {α}线性相关0=⇔α.性质(5) {βα,}线性相关λβα=⇔)(P ∈λ.性质(6) n P 中单位向量组线性无关.性质(7) 向量组i α=),,,(21in i i a a a ),,2,1(s i =线性相(无)关⇔齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++000221122221121221111s sn n n s s s s x a x a x a x a x a x a x a x a x a(2) 有(无)非零解.性质(8) 设向量组{r ααα,,,21 }线性无关,而向量组{r ααα,,,21 ,β}线性相关,则β一定可由r ααα,,,21 唯一的线性表示.性质(9) 向量组{r ααα,,,21 }(r 2≥)线性相关的充要条件是其中某一个向量是其余向量的线性组合.性质(10) 设s ααα,,,21 是向量空间V 中的向量,A 是t s ⨯矩阵,B 是r t ⨯矩阵.则有((s ααα,,,21 )A )B =(s ααα,,,21 )AB (3)性质(11) 设向量组{p γγγ ,,21}可以由向量组{t βββ,,,21 }线性表示,向量组{t βββ,,,21 }可以由向量组{s ααα,,,21 }线性表示,则向量组{p γγγ ,,21}可以由向量组{s ααα,,,21 }线性表示.性质(12) 设向量组{r ααα,,,21 }线性无关,且可由向量组{s βββ,,,21 }线性表示.则s r ≤.必要时对向量组{s βββ,,,21 }中的元素重新排序,使得用r ααα,,,21 替换s βββ,,,21 后,所得向量组},,,,,{121s r r ββααα +与{s βββ,,,21 }等价. 性质(13) (1)若向量组{t βββ,,,21 }可由向量组{s ααα,,,21 } 线性表示,并且s t >,则向量组{t βββ,,,21 }线性相关;(2) 设向量组{t βββ,,,21 }线性无关,t s <,则向量组{t βββ,,,21 }不能由含s 个向量的向量组线性表示.性质(14) 两个等价的线性无关的向量组含有相同个数的向量.性质(15) 任意1+n 个n 维向量必线性相关.性质(16) 若{s ααα,,,21 }和{t βββ,,,21 }是两个等价的线性无关的向量组,则t s =,且存在s 阶可逆矩阵A 使得(s ααα,,,21 )=(t βββ,,,21 )A (4)性质(17) 设向量组{r i i i ααα,,,21 }是向量组{s ααα,,,21 }的一个部分组,则{r i i i ααα,,,21 }是极大线性无关组的充要条件为1)向量组{r i i i ααα,,,21 }线性无关;2)每一个j α(s j ,,2,1 =)都可由r i i i ααα,,,21 线性表示.性质(18) 向量组的任意一个极大无关组都与向量组本身等价.性质(19) 一个向量组的任意两个极大无关组含有相同个数的向量.性质(20) 两个等价的向量组有相同的秩.性质(21)设向量组(s ααα,,,21 )线性无关,A 是一个t s ⨯矩阵,令(t βββ,,,21 )=(s ααα,,,21 )A ,则 A R t =),,,(21βββ .性质(22)如果向量函数)(,),(),(21t x t x t x m 在区间b t a ≤≤上线性相关,则它们的朗斯基行列式0)(=t W .性质(23) 如果向量函数)(,),(),(21t x t x t x m 在区间d t ≤≤c 上线性无关,则它们的朗斯基行列式0)(≠t W .第三章 向量组线性相关性的证明方法3.1定义法这是判定向量组线性相关的基本方法.定义法既适用于分量没有具体给出的抽象向量组,也适用于分量已经给出的具体向量组.其定义是,设m 21,,,ααα 是F 上向量空间V 的m 个向量.如果存在F 中一组不全为零的数,,,,m 21k k k 使得0m 2211=+++αααm k k k ,那么就称向量m 21,,,ααα 线性相关,否则称它是线性无关的. 例1设有两个n 维向量组,,,s 12 ααα、,,,s 12 βββ,若存在两组不全为零的数12,,,s k k k ;12,,,s λλλ ,使111111()()()()s s s s s s k k k k λλλλ+++++-++-= 0ααββ;则 .证明111111()()()()s s s s s s k k k k λλλλ+++++-++-= ααββ0,111111()()()()s s s s s s k k λλ-++-+++++= αβαβαβαβ0,所以1111,,,,,s s s s --++ αβαβαβαβ线性相关.例2 设A 是n 阶矩阵,若存在正整数k ,使线性方程组x A k 0=有解向量α,且01≠-αk A .证明向量组ααα1,,,-k A A 线性无关.证明 设有实数,,,21k λλλ 使得0121=+++-αλαλαλk k A A (9) 则有)(1211=+++--αλαλαλk k k A A A . (10)从而011=-αλk A 由于01≠-αk A ,所以,01=λ.把01=λ代入(*)式再左乘2-k A 可得012=-αλk A ,由01≠-αk A ,得02=λ.类似可证得043====k λλλ故向量组ααα1,,,-k A A 线性无关.我们还可以利用向量组内向量之间的线性关系判定.即向量组A :12,,m ααα⋅⋅⋅线性相关的充要条件是向量组A 中至少有一个向量可由其余线性表示.比如例1,取1k =3k =1,2k =4k =-1,则1β=2β-3β+4β,即1β可由2β,3β,4β三个向量线性表示,所以向量组1β,2β,3β,4β线性相关.3.2根据齐次线性方程组的解进行判定在应用定义法解一个齐次线性方程组,需由该方程组是否有非零解来判定向量组的线性相关性.即应用定义法的同时也就应用了齐次线性方程组的解进行了线性相关性的判定.于是我们可以利用结论[1]进行判定.结论[1] 向量组i α=),,,(21in i i a a a ),,2,1(m i =线性相(无)关⇔齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++000221122221121221111m mn n n m m m m x a x a x a x a x a x a x a x a x a (11) 有(无)非零解.例3[7] 证明向量组1α=(2,1,0,5),2α=(7,-5,4,-1),3α=(3,-7,4,-11)线性相关.证明 以1α,2α,3α为系数向量的齐次线性方程组是1x 1α+2x 2α+3x 3α=0,即⎪⎪⎩⎪⎪⎨⎧=--=+=--=++0115044075037232132321321x x x x x x x x x x x (12) 利用矩阵的行初等变换将方程组的系数矩阵转化为阶梯型矩阵,即→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----110110110751242404401717075111154403727511115440751372 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--000000110751 由行阶梯型矩阵可知,()R A =32<.即齐次线性方程组有非零解,所以向量组1α,2α,3α线性相关.3.3利用矩阵的秩进行判定结论[5] 设向量组A :12,,m ααα⋅⋅⋅是由m 个n 维列向量所组成的向量组,则向量组A 的线性相关性可由向量组A 所构成的矩阵A =(12,,m ααα⋅⋅⋅)的秩的大小来进行判定.即(i) 当R(A )= m 时,则向量组A :12,,m ααα⋅⋅⋅是线性无关的.(ii) 当R(A )<m 时,则向量组A :12,,m ααα⋅⋅⋅是线性相关的.例4 设1α=T )1,1,1(,2(1,2,3)T α=,3(1,3,5)T α=问向量组1α,2α,3α是否线性相关.解 因为⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛=000210111420210111531321111A3)(<A R ,所以向量组1α,2α,3α线性相关.例5[4] 试讨论n 维单位向量组的相关性.解 因为),,,(21n e e e E =的行列式01≠=E , 即n E R =)(,所以,n 维单位向量组线性相关.利用矩阵的秩与利用齐次线性方程组的解进行判定的出发点不同,但实质上是一样的,都是要利用矩阵的初等行变换将相应的系数矩阵化简为行阶梯形矩阵,从而求出向量组的秩,即系数矩阵的秩,然后再作出判定.3.4利用行列式值进行判定行列式值的判定实质上是根据克莱姆法则判定以向量组作为系数向量的齐次线性方程组是否有非零解,然后再对向量组的线性相关性作出判定,所以能应用行列式值进行判定的向量组,也可以应用矩阵的秩和齐次线性方程组是否有非零解的方法来进行判定.结论 [3] 若向量组A :12,,m ααα⋅⋅⋅ 是由m 个m 维列向量所组成的向量组,且向量组A 所构成的矩阵A =(12,,m ααα⋅⋅⋅),即A 为m 阶方阵,则(i) 当A =0时,则向量组A :12,,m ααα⋅⋅⋅是线性相关的.(ii) 当A ≠0时,则向量组A :12,,m ααα⋅⋅⋅是线性无关的.例6设向量组4321,,,αααα线性无关,判断向量组12,αα+23,αα+34,αα+ 41αα-是线性相关还是线性无关.解 设存在4个数4321,,,k k k k ,使得)()()()(144433322211=-++++++ααααααααk k k k ,(13)拆项重组为 0)()()()(443332221141=++++++-ααααk k k k k k k k ,(14)由4321,,,αααα线性无关知 ⎪⎪⎩⎪⎪⎨⎧=+=+=+=-000043322141k k k k k k k k (15)由于系数行列式021100011000111001≠=- (16)所以,齐次线性方程组(1)只有零解,即04321====k k k k .因此向量组14433221,,,αααααααα-+++线性无关.3.5反证法在有些题目中,直接证明结论常常比较难,但从结论的反面入手却很容易推出一些与已知条件相悖的结果,近而得出结论.例7[5] 设向量组12,,,m ααα 中任一向量i α不是它前面1i -个向量的线性组合,且i α≠0,证明向量组12,,,m ααα 线性无关.证明 (反证法)假设向量组12,,,m ααα 线性相关,则存在不全为零的数21,k k m k ,使得11k α+22m m k k αα++ =0 (17)由此可知,0=m k ,否则由上式可得112211------=m m m m m m k k k k k k αααα ,(18) 即m α可由它前面1m -个向量线性表示,这与提设矛盾,因此0=m k , 于是(17)式转化为1k 1α+22k α+ +11m m k α--=0.类似于上面的证明,同样可得01221=====--k k k k m m ,这与m k k k ,,,21 不全为零的假设矛盾,因此,向量组12,,,m ααα 线性无关.3.6 数学归纳法有些题中,我们还可以利用数学归纳法,如下例. 例8[9] 设线性无关的向量组r γγγ ,,21①可由向量组t βββ,,,21 ②线性表示,且t r ≤,则可从{t βββ,,,21 }中选出)(m t -个向量组)(21,,,m t j j j -βββ , 使得向量组m γγγ ,,21,)(21,,,m t j j j -βββ ③与向量组②等价.证明:用数学归纳法(1)当1=r 时,有t r ≤,由于∑==tj j j k 11βγ,且01≠γ,则t k k k ,,,21 不全为0,在②中,设01≠k t t k k k k k ββγβ12121111---= ,故t r ββ,,,11 与t βββ,,,21 等价 (2)设1-=s r 时结论成立,推证s r =时结论成立. 由于121,,-s γγγ ,t βββ,,,21 与向量组②等价,而s γ又可由向量组t βββ,,,21 线性表示故有tt s s s s s h h h h h βγγγγγ++++++=-- 112211 , (19)而题设s γγγ,,,21 线性无关,必有t s s h h h ,,,1 +不全为0,设0≠s h ,则 t s t s s s s s s s s s s h h h h h h h h h ββγγγβ-+-+--=++-- 1111111 (20) 因此,s γγγ,,,21 ,t β与121,,,-s γγγ ,t s ββ,, 等价,由上分析可知,当t s ≤,s r =时结论成立.由数学归纳法知命题成立.3.7利用线性微分方程组的相关理论判定结论[8] 一组1-n 次可微的纯量函数)(,),(),(21t x t x t x m 线性相关的充要条件是向量函数⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'---)()()(,,)()()(,)()()()1()1(222)1(111t x t x t x t x t x t x t x t x t x n mmm n n (21) 线性相关.证明:事实上,如果)(,),(),(21t x t x t x m 线性相关,则存在不全为零的常数m c c c ,,,21 使得0)()()(2211=+++t x c t x c t x c m m .将上式对t 微分一次,二次,…,1-n 次,得到,0)()()(,0)()()(,0)()()()1()1(22)1(1122112211=+++=''+''+''='+'+'---t x c t x c t x c t x c t x c t x c t x c t x c t x c n m m n n m m m m(22)即有,0)()()()()()()()()()1()1(2222)1(1111=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'++⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'---t x t x t x c t x t x t x c t x t x t x c n mm m m n n (23)这就是说,向量函数组(22)式是线性相关的.反之,如果向量函数(22)线性相关,则存在不全为零的常数使m c c c ,,,21 得(23)成立,当然有0)()()(2211=+++t x c t x c t x c m m ,这就表明)(,),(),(21t x t x t x m 线性相关.例9若函数)(,),(),(21t x t x t x m 在区间b t a ≤≤上线性相关,则它们的朗斯基行列式0)(=t W .证明 据结论[8] 和纯量函数朗斯基行列式的概念知,存在一组不全为零的常数m c c c ,,,21 ,使得,0)()()()()()()()()()1()1(2222)1(1111=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'++⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'---t x t x t x c t x t x t x c t x t x t x c n mm m m n n (24) 上式可以看成是关于m c c c ,,,21 的齐次线性代数方程组,它的系数行列式就是)](,),(),([21t x t x t x W m ,于是由线性代数理论知,要此方程组存在非零解,则它的系数行列式必为零,即0)(=t W .结束语以上归纳了判断向量组线性相关性的几种方法,只要我们熟练掌握并能灵活的运用,将会在研究线性方程组解之间的关系,或者说研究线性方程组解的结构问题时带来很大的方便.参考文献[1]刘仲奎等.高等代数[M].北京:高等教育出版社,2005.[2]北京大学数学力学系几何和代数教研室代数小组.高等代数[M].北京:人民教育出版社,2003.[3]张禾瑞,郝炳新.高等代数[M].北京:高等教育出社,2005.[4]王品超.高等代数新方法[M].北京:中国矿业大学出版社,2002.[5]王萼方.高等代数题解[M].北京:北京大学出版社,2002.[6]邱森.高等代数[M].武汉:武汉大学出版社,2008.[7]西北工业大学高等代数编写组.高等代数[M].北京:科学出版社,2008.[8]王高雄等.常微分方程[M].北京:高等教育出版社,2006.[9]栾召平.证明向量组线性相关性的几种方法[J].山东电大学报,2002,(2):61-62.致谢在本次论文设计过程中,白永强老师对该论文从选题、构思到最后定稿的各个环节都给予细心指引与教导,使我得以最终完成毕业论文设计.在学习中,老师渊博的专业知识、深厚的学术素养、严谨的治学态度、精益求精的工作作风、诲人不倦的高尚师德对我影响深远,也是我永远学习的榜样,并将积极影响我今后的学习和工作,使我终身受益.在此,谨向陈老师表示崇高的敬意和衷心的感谢!这四年中还得到众多老师的关心、支持和帮助.在此,向他们表示我深深的谢意!最后,向在百忙中抽出时间对本文进行评审并提出宝贵意见的各位老师表示衷心地感谢!。

⾼等代数课程论⽂(⽰例)⾼等代数有关理论的⼏何描述探讨信息与计算科学04-01班⽑维东内容摘要:⾸先通过对线性空间理论的基本阐述,重点讨论了线性空间元素向量的运算、相关性和向量内积的⼏何意义。
其次分析了线性⽅程组的解在⼏何上如何⽤线或者⾯的关系来表⽰,并⽤实例说明解的情况与⼏何图形的关系,并对解得关系进⾏了图形描述;再通过矩阵对实际计算机图形中的变化进⾏研究,得出图形变化后的坐标矩阵;最后,通过对⼆次型的基本概念与基本理论的阐述,重点讨论了正定⼆次型、负定⼆次型,并通过具体的实例给出了分类问题的⼏何描述,与此同时,分析并列举了⼆次型标准型在⼆次曲⾯分类上的应⽤,由此得到了常见的⼏种⼆次曲⾯标准⽅程,并对典型⽅程给出了图形描述。
在问题的研究中,采⽤理论分析与实例应⽤相结合,充分发挥数学应⽤软件的优势,将代数理论的内涵形象、直观、清晰地给予展现。
关键字:线性空间;向量;矩阵;⼆次型;⼏何描述1 导⾔对于在数学内容上是否应将代数与⼏何统⼀处理, ⼈们对此有不同的意见和做法。
从国内来看, 在许多院校试⾏了将线性代数与解析⼏何统⼀的课程改⾰,有的将线性代数与解析⼏何统⼀课程作为⾼等院校理⼯、经管、数学专业学科的教材,也有⼀些⾼校将线性代数与解析⼏何作为不同的学科分开教学。
从国际来看, 早已出现了⼤量将线性代数与解析⼏何统⼀在⼀个学科内的教材。
对于是否统⼀的问题各⼈持有不同的观点:反对代数与⼏何统⼀的⼀些⼈认为, 这是在消灭⼏何,⽽历史上忽视⼏何的做法起码在教学上效果不好;赞同代数与⼏何统⼀的⼈认为, 代数与⼏何本来就是统⼀的,⼈为的割裂使学⽣不能从整体上理解数学,迄今为⽌分裂代数与⼏何的做法起码在实践上的效果并不好,⼜由于理论数学分⽀, 如代数⼏何、解析数论、拓扑结构等都是代数与⼏何的统⼀体,因此在学习的初级阶段, 让学⽣更⾃觉地体会⼏何与代数的统⼀性是必要的。
代数与⼏何是两门相互依赖、紧密相联的学科。
由于代数学科概念的⾼度抽象性、定理的⾼度概括性和⼏何学科的具体直观性,使“数”“形”结合问题受到越来越多的关注。

高等代数心得体会及感悟(实用17篇)(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如职场文书、公文写作、党团资料、总结报告、演讲致辞、合同协议、条据书信、心得体会、教学资料、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, this store provides various types of classic sample essays for everyone, such as workplace documents, official document writing, party and youth information, summary reports, speeches, contract agreements, documentary letters, experiences, teaching materials, other sample essays, etc. If you want to learn about different sample formats and writing methods, please pay attention!高等代数心得体会及感悟(实用17篇)心得体会是通过实践和经验总结得出的有关某个问题或事物的深刻认识和领悟。

高等代数期末论文学习总结LELE was finally revised on the morning of December 16, 2020高等代数学习总结摘要:两学期的高等代数已经接近尾声了,高等代数作为数学专业的基础学科之一。
本文主要讲述本人两学期下来学习高等代数的一些知识总结和学习体会。
关键词:行列式矩阵二次型正文:《高等代数》是数学学科的一门传统课程。
在当今世界的数学内部学科趋于统一性和数学在其他学科的广泛应用性的今天,《高等代数》以其追求内容结构的清晰刻画和作为数学应用的基础,是大学数学各个专业的主干基础课程。
它是数学在其它学科应用的必需基础课程,又是数学修养的核心课程。
高等代数是代数学发展到高级阶段的总称,它包括许多分支。
它是在初等代数的基础上研究对象进一步的扩充,引进了许多新的概念以及与通常很不相同的量,比如最基本的有集合、向量和向量空间等。
这些量具有和数相类似的运算的特点,不过研究的方法和运算的方法都更加繁复。
通过学习后,我们知道,不仅是数,还有矩阵、向量、向量空间的变换等,对于这些对象,都可以进行运算,虽然也叫做加法或乘法,但是关于数的基本运算定律,有时不再保持有效。
因此代数学的内容可以概括称为带有运算的一些集合,在数学中把这样的一些集合,叫做代数系统。
在学习之前,我一直认为高等代数就是把线性代数重学一遍,因为大一的时候线性代数学得不深,而且也没有学完。
经过两学期的学习后,我发现,这两者之间区别还是挺大的。
高等代数数学专业开设的专业课,更注重理论的分析,需要搞懂许多概念是怎么来的,而线性代数,只是一种运算工具,是供工科和部分医科专业开设的课程,只注重应用。
经过两学期的学习,我对高等代数里面的知识有了个初步的认识和接触,特别是代数的一些思想,也从中收获不少。
下面就对两学期的学习做一个回顾和总结。
行列式行列式是代数学中的一个基本概念,它不仅是讨论线性方程组理论的有力工具,而且还广泛的应用于数学及其他科学技术领域定义:设A=()为数域F上的n n矩阵,规定A的行列式为其中,为1,2,…,n的一个排列。
正交变换与群问题探(莆田学院数学系02级1班 林月娥、连涵生)[摘要]主要探讨: (i )正n 边形保形运动的存在情况及分类;(ii )保形运动构成一个群;(iii )运用到南开大学2004年研究生入学考试试题第5题。
[关键词] 正n 边形;正交变换;保形运动;群说明:以下我们用①2R 表示平面运动的标准度量;②k ρ表示图形绕中心旋转,01k n ≤≤-;③k π表示沿对称轴翻转,01k n ≤≤-;④ n D 表示由k ρ和kπ的所有正交变换的集合;⑤实线表示图形原来位置,虚线表示图形运动后位置。
⑥ 以下均以正方形代表正n 边形来作图。
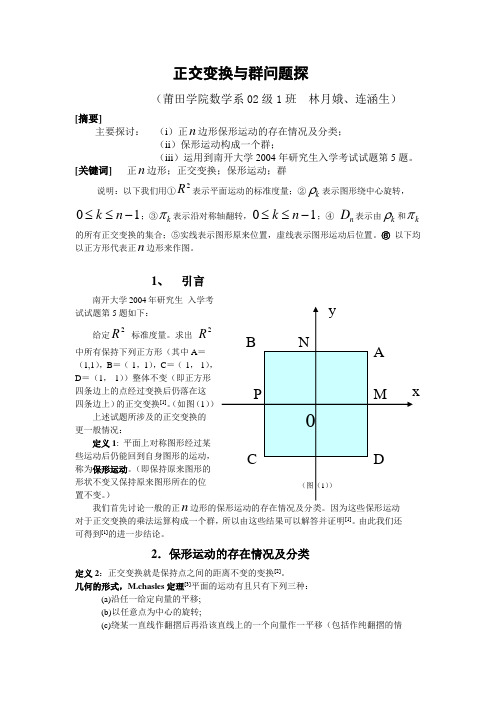
1、 引言南开大学2004年研究生 入学考试试题第5题如下: 给定2R标准度量。
求出2R 中所有保持下列正方形(其中A =(1,1),B =(-1,1),C =(-1,-1),D =(1,-1))整体不变(即正方形四条边上的点经过变换后仍落在这四条边上)的正交变换[1]。
(如图(1))上述试题所涉及的正交变换的更一般情况:定义1: 平面上对称图形经过某些运动后仍能回到自身图形的运动,称为保形运动。
(即保持原来图形的形状不变又保持原来图形所在的位置不变。
)我们首先讨论一般的正n 边形的保形运动的存在情况及分类。
因为这些保形运动对于正交变换的乘法运算构成一个群,所以由这些结果可以解答并证明[1]。
由此我们还可得到[1]的进一步结论。
2.保形运动的存在情况及分类定义2:正交变换就是保持点之间的距离不变的变换[2]。
几何的形式,M.chasles 定理[3]平面的运动有且只有下列三种:(a)沿任一给定向量的平移; (b)以任意点为中心的旋转;(c)绕某一直线作翻摺后再沿该直线上的一个向量作一平移(包括作纯翻摺的情况)。
由M.chasles 定理,对于一个给定的正n 边形,适当选取坐标系,不妨选其中心为坐标原点O ,则它在平面上的保形运动的存在情况可通过以下分析得到:(1)由M.chasles 定理的(a),我们可以通过简单的正n 边形沿某一个定向量平移知平移后图形不可能回到自身上去。

高等代数的应用论文代数在经济管理中的应用目录摘要.................................................................. 3 问题提出............................................................ 4 实际应用举例...................................................... 4 论文总结............................................................ 10 参考文献 (11)2【摘要】科学技术的开展使我们的生活水平有了很大的提高,也促进了整体的经济水平和管理层次的提升。
我们所学的知识源于生活,同时这些知识也最终会效劳于生活,在高等代数的学习过程中,我们发现代数在经济管理中有着很多用途,为经济管理等方面的计算提供了便利。
本篇论文中,我们就对代数在经济学和管理学方面的应用进行了探究。
【关键词】高等代数,经济管理,实际,应用【Abstract】The development of science and technology not only make our living standard greatly improved, but also promote the whole economic level and management level. We learned lots of knowledge from life, at the same time this knowledge will eventually serve in life. In the learning process of the advanced algebra, we found that the algebra in economic and management has many uses. It provide Economic and management convenience. In this thesis, we do research on the algebra about the economics and management. 【Key words】3Advanced Algebra, Economic and management, Practical, Application 【问题提出】学习高等代数已经两个学期,马上就要结束这门课程了。

莆田学院毕业论文题目n阶行列式的计算方法学生姓名张文才学号510401424专业数学与应用数学班级数学054指导教师陈梅香二00九年五月十日目录0引言 (1)1常见一般阶行列式计算方法 (1)1.1定义法 (1)1.2利用行列式的性质 (2)1.3化三角行列式 (3)1.4按行列式某行或某列展开 (4)1.5升阶法 (5)1.6递推方法 (6)1.7数学归纳法 (7)1.8范德蒙行列式 (8)1.9拉普拉斯定理 (8)1.10辅助行列式法 (9)1.11析因法 (10)2一些计算阶抽象行列式的方法 (11)2.1利用行列式性质 (11)2.2利用正交矩阵的性质 (12)2.3利用方阵的特征值的性质及矩阵相似 (12)结束语 (13)致谢 (13)参考文献 (13)n 阶行列式的计算方法张文才(莆田学院数学系 指导教师:陈梅香)摘要:行列式的计算是大学高等代数的重要内容之一,也是学习的一个难点。
本文第一部分主要探讨常见一般n 阶行列式计算方法,第二部分讨论一类n 阶抽象行列式的计算方法。
关键词:行列式 矩阵 计算方法Abstract :Computing the determinant is an important part of advanced algebra in university, and is also thedifficulty in learning. In the first part, calculation methods of the n-order determinant were discussed; second is the methods of computing a class of n-order abstract determinant.Keywords :determinant matrix calculation method0 引言一般n 阶行列式的计算问题是数学系高等代数教学的一个重要内容,同时也是一个难点。

2024年高等代数学习心得模版一、将三门基础2113课作为一个整体去学,摒弃孤立5261的学习,提倡综合4102的思考恩格斯曾经说1653过:“数学是研究数和形的科学。
”这位先哲对数学的这一概括,从现代数学的发展来看,已经远远不够准确了,但这一概括却点明了数学最本质的研究对象,即为“数”与“形”。
比如说,从“数”的研究衍生出数论、代数、函数、方程等数学分支;从“形”的研究衍生出几何、拓扑等数学分支。
____世纪以来,这些传统的数学分支相互渗透、相互交叉,形成了现代数学最前沿的研究方向,比如说,代数数论、解析数论、代数几何、微分几何、代数拓扑、微分拓扑等等。
可以说,现代数学正朝着各种数学分支相互融合的方向继续蓬勃地发展下去。
数学分析、高等代数、空间解析几何这三门基础课,恰好是数学最重要的三个分支--分析、代数、几何的最重要的基础课程。
根据课程的特点,每门课程的学习方法当然各不相同,但是如果不能以一种整体的眼光去学习和思考,即使每门课都得了A,也不见得就学的很好。
学院的资深教授曾向我们抱怨:“有的问题只要画个图,想一想就做出来了,怎么现在的学生做题,拿来就只知道死算,连个图也不画一下。
”当然,造成这种不足的原因肯定是多方面的。
比如说,从教的角度来看,各门课程的教材或授课在某种程度上过于强调自身的特点,很少以整体的眼光去讲授课程或处理问题,课程之间的相互联系也涉及的较少;从学的角度来看,学生们大都处于孤立学习的状态,也就是说,孤立在某门课程中学习这门课程,缺乏对多门课程的整体把握和综合思考。
根据我的经验,将高等代数和空间解析几何作为一个整体去学,效果肯定比单独学好,因为高等代数中最核心的概念是“线性空间”,这是一个几何对象;而且高等代数中的很多内容都是空间解析几何自然的延续和推广。
另外,高等代数中还有很多分析方面的技巧,比如说“摄动法”,它是一种分析的方法,可以让我们把问题从一般矩阵化到非异矩阵的情形。

莆田学院数学与应用数学系“高等代数”课程论文题目:四分块矩阵的初等变换的性质及应用姓名:黄俊艺学号:410401338莆田学院数学与应用数学系数学与应用数学专业043数本2007年6月24号四分块矩阵的初等变换的性质及应用摘要:给出四分块矩阵初等变换及其性质;论述它们在矩阵秩,等式,不等式证明及求解矩阵行列式,求矩阵逆的应用。
关键词:四分块矩阵,初等变换,矩阵秩,矩阵行列式,矩阵逆正文:预备知识:定义1 初等矩阵:由单位矩阵经过一次初等变换(初等行或初等列变换)所得到的矩阵。
初等矩阵共分3类:(1)(),P i j ——变换E 的第i 行与第j 行(或第i 列与第列)得到的矩阵(2)()()P i k ——用数域P 中的非零数k 乘以E 的第i 行(或第j 列)得到的矩阵 (3)(),()P i j k ——把E 的第j 行的k 倍加到第i 行(或第j 列的k 倍加到第i 列)得到的矩阵定义2 分块初等矩阵分块初等矩阵共分3类:()1 ()01,2E0n m E P ⎛⎫⎪⎝⎭()2 ()()01,20n M P M E ⎛⎫ ⎪⎝⎭ ,()()01,20mE P M M ⎛⎫⎪⎝⎭,其中M 可逆. ()3 ()()1,20mn E M P M E ⎛⎫⎪⎝⎭, ()()01,2m n E P M ME ⎛⎫⎪⎝⎭性质1:分块初等矩阵均是可逆矩阵 性质2:分块初等矩阵左(右)乘A B C D ⎛⎫⎪⎝⎭(要可乘,可加)相当于对其作相应的分块初等行(列)变换性质3:分块初等变换不改变矩阵的秩一 四分块矩阵极其初等变换在证明矩阵秩等式与不等式的应用例1 SyWester 公式:设,s nn m A PB P ⨯⨯∈∈证明: ()()()r A r B n r AB +-≤证明:利用分块初等矩阵相关性质00000n nn ns m E E B E B E A E E A AB -⎛⎫⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭ 由性质3得:()()()000n n E B E r r r A r AB n r AB A AB ⎛⎫⎛⎫==+-=+ ⎪ ⎪-⎝⎭⎝⎭()1,20P n n AO E B E B A⎛⎫⎛⎫−−−→ ⎪ ⎪⎝⎭⎝⎭故()()0nnA O EB r r r A r B E B A⎛⎫⎛⎫=≥+ ⎪⎪⎝⎭⎝⎭ 所以()()()00nnA EB n r AB r r r A r B E B A⎛⎫⎛⎫+==≥+ ⎪ ⎪⎝⎭⎝⎭因此()()()r A r B n r AB +-≤例2 Frobenius 不等式设,,ABC AB BC 存在证明:()()()()r ABC r AB r BC r B ≥+-证明:对于四分块矩阵00ABC B ⎛⎫⎪⎝⎭()()()()1,21,21,200000P C P P ABC ABCAB AB AB B B BCB B BC -⎛⎫⎛⎫⎛⎫⎛⎫−−−→−−−−→−−−→ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭由性质3得:()()()()000ABC AB r ABC r B r r r AB r BC B B BC ⎛⎫⎛⎫+==≥+⎪ ⎪⎝⎭⎝⎭所以 ()()()()r ABC r AB r BC r B ≥+- 例3 设A 为n n ⨯矩阵证明: ()()2A E r A E r A E n =⇔++-=证明:对于四分块矩阵00A E A E -⎛⎫⎪+⎝⎭()()()()()()()()()()()1,21,21221,22121,220002111222201020P A E P E P E P A E P A E A E A EA EE A A E A EA E A EE A EE A A E E A A EE E A E E --⎛⎫⎛⎫ ⎪ ⎪-⎝⎭⎝⎭⎛⎫⎡⎤- ⎪⎢⎥⎣⎦⎝⎭----⎛⎫⎛⎫⎛⎫−−−−−→−−−−→ ⎪ ⎪ ⎪+-+-⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫-----⎪ ⎪−−−−→−−−−−→⎪ ⎪-⎝⎭⎝⎭⎛⎫-- ⎪−−−−−−→ ⎪⎝⎭由性质3得:()()()()222100200A EA E r r r A E r E r A E n A E E ⎛⎫---⎛⎫ ⎪==-+=-+ ⎪ ⎪+⎝⎭⎝⎭又 ()()00A Er r A E r A E A E -⎛⎫=-++⎪+⎝⎭故 ()()()2r A E r AE rA E n-++=-+则 ()()()220r A E r A E n r A E A E -++=⇔-=⇔=例4 设,A B 分别为,n m m n ⨯⨯矩阵,且1ABA B -= 证明: ()()r E A B r E A B n-++= 证明: 对于四分块矩阵 00E ABE AB -⎛⎫⎪+⎝⎭因为1ABA B -=,则()1ABA B B B E -==()()()()()12,11,21,2212,120002000202P E P E P E P AB E E AB E AB E AB E AB E AB E AB E AB E AB E E AB E AB E E ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎡⎤- ⎪⎢⎥⎣⎦⎝⎭----⎛⎫⎛⎫⎛⎫−−−−→−−−−→−−−−→⎪ ⎪ ⎪+-+-⎝⎭⎝⎭⎝⎭--⎛⎫⎛⎫−−−−−−→ ⎪ ⎪-⎝⎭⎝⎭由性质3得000002E AB r n E AB E r -⎛⎫⎛⎫== ⎪ ⎪+⎝⎭⎝⎭又()()00E ABr E AB r E AB E A r B -⎛⎫=-++⎪+⎝⎭所以()()r E AB r E AB n -++= 例5 设A 为n n ⨯矩阵证明:()()()()()3222A A r A r E A n r A r A A r A A =⇔+-=⇔=-++ 证明:先证:()()32A A r A r E A n =⇔+-=对于四分块200AE A ⎛⎫⎪-⎝⎭()()()()()()()()221,22,1223231,21,200000P A P A P A P A AA A A E A A E A A E A AA A A E E ---⎛⎫⎛⎫⎛⎫−−−−→−−−−→ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫--−−−−→−−−−→⎪ ⎪⎝⎭⎝⎭由性质3知()3320000AA A r r r A A n E A E ⎛⎫-⎛⎫==-+ ⎪ ⎪-⎝⎭⎝⎭而()()2200Ar r A r E A E A ⎛⎫=+-⎪-⎝⎭故()()()2330r A r E A n r A A A A +-=⇔-=⇔= 现证:()()()322A A r A r A A r A A =⇔=-++对于四分块矩阵()()()()()()()()()2221,21,22221132221,21,22221312,220001*********P A A P E P A E P A E P E E A A A A A A A A A A A A A A A A A A A AA A A A A -⎛⎫⎛⎫⎛⎫⎛⎫-- ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫--−−−−−→−−−−→ ⎪ ⎪+-+⎝⎭⎝⎭⎛⎫⎛⎫---- ⎪−−−−−−→−−−−−−→ ⎪ ⎪-⎝⎭⎝⎭⎛⎫- ⎪−−−−→ ⎪⎝⎭300A A A ⎛⎫-−−⎪⎝⎭由性质3得:()()23320000A A A A r r r A A r A A A A ⎛⎫⎛⎫--==-+ ⎪ ⎪+⎝⎭⎝⎭而()()2222A A r r A A r A A A A ⎛⎫-=-++⎪+⎝⎭ 故()()()()22330r A A r A A r A r A A A A -++=⇔-=⇔=小结: 分块初等变换不改变矩阵的秩,这一性质在求矩阵的秩,特别是分块矩阵的秩是很方便的,很常见的,很重要的。

高数论文(五篇)第一篇:高数论文高数论文短短一个学期的高数的学习就结束了,感觉过的好快有好慢,总得来说收获还是很大,收获了不仅是知识、还有学习知识的方法、研究问题的方法,还有学习的态度。
相比较上个学期,这个学期高数的学习我个人认为难度加大了不少。
在这个学期我们主要学习的是高等数学下册的知识,这本书的基础就是上学期学习的微积分。
学习了向量代数与空间解析几何、多元函数微分学、重积分、曲线积分与曲面积分,无穷级数。
在向量代数与空间解析几何这一章,我们学习了向量代数的基本知识,空间曲线,曲面及方程,空间平面与直线等,总得来说这一章需要一定的空间想象能力。
在多元函数微分学这一章,我觉得有些地方掌握的不好,隐函数的求导显得很生疏,对于多元函数的隐函数的求导感觉掌握不是很好。
另外,全微分,多元函数微分学也是这一章的重点。
在重积分这一章,不管是几重积分,这都是建立在一元函数的积分的基础之上的,在这一章,化归的思想体现的很是淋漓尽致,这一思想不仅在数学上体现的很明显,在很多领域都有体现。
在积分这一块都采用分割,近似,求和,取极限四个步骤。
此外三重积分的计算,主要从直角坐标系,柱面坐标系,球面坐标系三种坐标系下计算。
另外重积分也应用于物理方面,如运用重积分求物体的质心,转动惯量及引力。
在曲线积分与曲面积分这一章当中,化归的思想继续在体现。
这一章的逻辑性很强,在这一章我们学习了4种积分,对弧长的曲线积分,对坐标的曲线积分,对面积的曲面积分,对坐标的曲面积分。
学完这一章,加上之前学习的一元函数的积分,二重积分,三重积分,我们就学习了七种积分。
在这一章还有一个重要的结论,那就是在对曲面的积分时,偶倍奇零不再是什么时候都是用了,在这里用偶倍奇零需要认真考虑,因为有时是偶零奇倍。
最后一章的无穷级数,很大程度上和数列有很多类似的地方,而且这一章的定理很多,很多东西容易混淆,很多结论都有自己的前提,这是这一章的重点之处,定理成为这一章很重要的解题根据。