当前位置：文档之家 › 第十三讲-弯曲切应力与强度条件

第十三讲-弯曲切应力与强度条件

  • 格式：ppt
  • 大小：1.82 MB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

弯曲正应力强度条件

弯曲正应力强度条件

弯曲正应力强度条件弯曲正应力强度条件，是指在材料发生弯曲加载时，使材料内部产生的正应力不超过其破坏强度的条件。

在工程设计和结构分析中，了解和应用弯曲正应力强度条件十分重要，因为它可以帮助我们确定结构的合理尺寸和材料的选择，以确保结构的安全可靠。

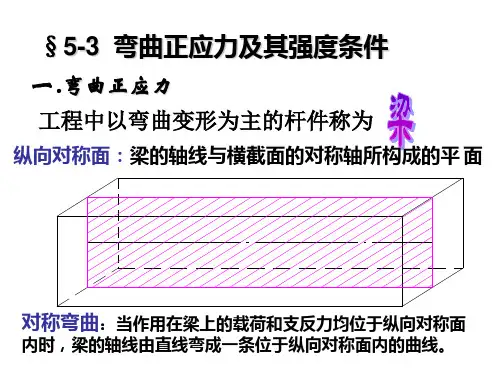
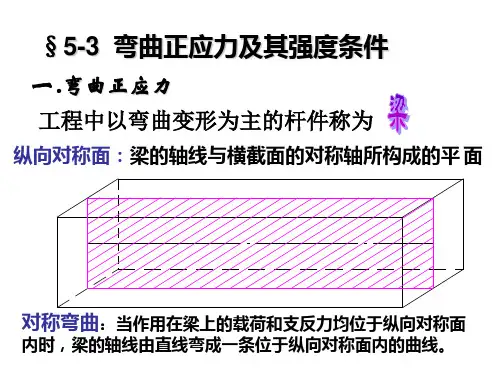
弯曲是指外加力矩或弯矩作用下，材料发生弯曲变形。

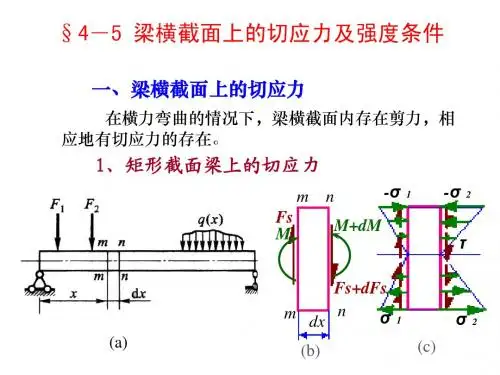
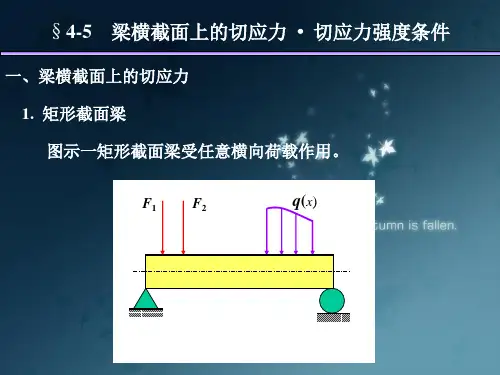
当材料受到弯矩作用时，其横截面上会产生正应力和剪应力。

其中，弯曲正应力是指与弯曲轴垂直的方向上的应力，其计算公式为σ = M * y / I，其中M是弯矩，y是距离弯曲轴的垂直距离，I是截面惯性矩。

弯曲正应力会导致材料发生弯曲破坏，因此我们需要控制这一应力。

对于材料的弯曲正应力强度条件，常见的有屈服强度条件和疲劳强度条件。

屈服强度条件是指弯曲正应力不应超过材料的屈服强度。

材料的屈服强度是指在特定的加载条件下，材料产生塑性变形的临界应力。

在设计中，我们通常选择使弯曲正应力小于等于材料的屈服强度，以确保材料在加载过程中不会发生塑性变形。

疲劳强度条件是指材料在循环加载下，弯曲正应力不应超过材料的疲劳强度。

材料在长时间的循环加载下容易发生疲劳破坏，因此我们需要控制弯曲正应力，以避免疲劳破坏的发生。

疲劳强度通常通过材料的疲劳寿命曲线来表示，我们需要使弯曲正应力小于等于材料对应寿命下的疲劳强度。

为了满足弯曲正应力强度条件，我们可以通过合理的结构设计、材料选择和工艺控制来实现。

首先，结构设计应考虑材料的弯曲特性，避免产生过大的弯矩和应力集中现象。

合理选择结构截面形状和尺寸，以增加结构的承载能力和抗弯性能。

其次，材料的选择应根据力学性能和使用环境来确定。

不同材料的弯曲正应力强度条件有所不同，我们需要选择具有足够强度和韧性的材料，以确保结构的安全工作。

最后，工艺控制也是实现弯曲正应力强度条件的关键。

合理的工艺控制可以提高材料的力学性能和强度，如控制材料的冷加工、热处理和表面处理等。

总之，了解和应用弯曲正应力强度条件对于工程设计和结构分析至关重要。

弯曲正应力强度条件的内容

弯曲正应力强度条件的内容

弯曲正应力强度条件弯曲应力与弯曲正应力在工程力学中，弯曲是指物体在受到外部力矩作用下发生形变的过程。

当物体受到外部力矩作用时，会产生内部的弯曲应力。

弯曲应力是指材料内部由于受到外部力矩作用而产生的应力。

弯曲应力可以分为正应力和剪应力两个分量。

其中，正应力是垂直于截面的应力分量，剪应力则是平行于截面的应力分量。

本文将重点讨论弯曲正应力的强度条件。

弯曲正应力的定义弯曲正应力是指与截面法线方向相同的剖面上所受到的垂直于该剖面方向的拉伸或压缩效果产生的内部正应力。

弯曲正应力强度条件在设计工程结构时，需要保证结构在使用过程中不发生断裂或失效。

为了满足这一要求，需要对结构进行合理设计，并保证其满足一定的强度条件。

对于弯曲结构而言，其强度条件主要包括抗拉和抗压两个方面。

在弯曲结构中，正应力最大的位置往往出现在截面的远离中性轴的位置，因此我们需要对这一位置的正应力进行分析和计算。

根据弯曲理论，弯曲正应力的大小与弯矩、截面形状和材料性质有关。

在设计过程中，我们通常采用强度理论来确定结构是否满足弯曲正应力的要求。

常用的强度理论包括极限平衡法、变形能法和应变能密度法等。

这些方法都是通过建立结构受力平衡方程、变形能方程或应变能密度方程来判断结构是否满足强度条件。

极限平衡法极限平衡法是一种常用的判断结构强度的方法。

该方法基于平衡条件，通过假设截面内部存在一个平衡状态来分析结构受力情况。

在弯曲结构中，我们可以假设截面内部存在一个剖面，使得该剖面上各点处的正应力达到最大值。

然后根据受力平衡条件，在该剖面上建立受力平衡方程。

根据极限平衡法得到的受力平衡方程，我们可以计算出弯曲正应力的最大值，并与材料的抗拉或抗压强度进行比较，从而判断结构是否满足强度条件。

变形能法变形能法是另一种常用的判断结构强度的方法。

该方法基于变形能原理，通过假设截面内部存在一个平衡状态来分析结构受力情况。

在弯曲结构中，我们可以假设截面内部存在一个剖面，使得该剖面上各点处的正应力达到最大值。

材料力学-弯曲应力分析与强度计算幻灯片

材料力学-弯曲应力分析与强度计算幻灯片

111
MPa
B点
B

M1 yB Iz

300 10 103 4.05 104 1012
71.1 MPa
C点
C

M1 yC Iz

300 0 4.05 104 1012
0
MPa
求得的A点的应力为正值，表明该点为拉应力，B点的应力
为负值，表明该点为压应力，C点无应力。当然，求得的正应
通常取梁的轴线来代替梁。 2. 载荷简化
作用于梁上的载荷（包括支座反力）可简化为三种类型： 集中力、集中力偶和分布载荷。 3. 支座简化
10
① 固定铰支座 2个约束，1个自由度。
如：桥梁下的固定支座，止 推滚珠轴承等。
② 可动铰支座 1个约束，2个自由度。
如：桥梁下的辊轴支座，滚 珠轴承等。
11
③ 固定端
x dx
图a y
M(x)
Q(x)+d Q(x)
图b
Q(x) dx M(x)+d M(x)
z
1
x

1 图c
y
1、两点假设： ① 剪应力与剪力平行； ② 矩中性轴等距离处，剪应 力相等。
2、研究方法：分离体平衡。
① 在梁上取微段如图b； ② 在微段上取一块如图c,平衡
X

N2
N1
1b(dx)
动，距中性轴等高处，变形相等。
横截面上只有正应力。 （可由对称性及无限分割法证明）
28
4.几何条件
dq
a
b
A c
B d
O A1
) ))
)
x

A1B1 AB AB

弯曲(6)弯曲切应力

弯曲(6)弯曲切应力

F ，在右端截面上有法向的合内力
∗ N1
∗ 。 FN 2
§4―5 梁横截面上的切应力及强度条件
§4―5 梁横截面上的切应力及强度条件
' 在AA1BB1面上有合力 dFS 。其大小为
My1 M F = ∫ ∗ σ 1dA = ∫ ∗ dA = A A Iz Iz
∗ N1
M ∗ ∫A∗ y1dA = I z S z
§4―5 梁横截面上的切应力及强度条件
一、梁横截面上的切应力
在横力弯曲的情况下，梁横截面内存在剪力，相 应地有切应力的存在。
1、矩形截面梁上的切应力
m Fs M n M+dM -σ1 -σ2
τ
m (a)
dx (b)
Fs+dFs n σ1 (c)
σ2
§4―5 梁横截面上的切应力及强度条件
如上图a所示，用m—m、n—n两截面假想地从梁中 取出长为dx的微段。该段两端横截面上的内力如图b所 示；两端截面上正应力的大小和方向可由正应力公式求 出；其切应力的方向如图c所示，大小未知。 为求得切应力τ 的大小，在上述微段上用平行于中 性层且离中性层距离为y的位置，截取体积元素B1m， 如下图a 所示。由切应力互等定律，除在两端面上有正 应力和切应力外，在A1AB1B面上也在切应力，且切应 力大小与y位置处的切应力相等。将体积元素B1m作为 脱离体进行受力分析（图b)，在左端截面上有法向合内 力
§4―5 梁横截面上的切应力及强度条件
例题4 23 例题4—23 如下
图a所示为一简易起重设 备。起重机（包含电葫 芦自重）P = 30kN ,跨 长l = 5m 。吊车大梁AB 由20a工字钢制成，其许 用弯曲正应力〔σt〕 =30MPa ，许用切应力 〔τ〕=30MPa 。试校核 梁的强度。

(弯曲正应力强度条件).

(弯曲正应力强度条件).

1. 由t,max ≤[t] 确定[F ]。
( F1 / 2 2m)(86103 m) t,max 5493108 m 4 30106 Pa
F1≤19200N=19.2kN
材 料 力 学 Ⅰ 电 子 教 案
2. 由c，max ≤[c] 确定[F ]。
( F2 / 4 2m)(134103 m) c,max 5493108 m 4 90106 Pa
F2≤36893N=36.893kN 3.结果：取较小者[F]=19.2kN， 可见梁的强度由拉应力确定。
1 / 2 Fb 最大拉应力分别为 tB 86 ， ,max
tC,max
1 / 4Fb 134 。可见全梁的最大拉 Iz
Iz
应力为 t ,max tB ,max 。全梁最大压 应力显然
c ,max
1 / 4Fb 134 Iz
。
材 料 力 学 Ⅰ 电 子 教 案
d

o
y dA
z
z
y
而由图可见，ρ2=y2+z2 , 从而知
4 π d Ip 2 d A y2 d A z2 d A I z I y A A A 32
7
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
根据对称性可知，圆截面对于形心轴z和y的惯性矩Iz 和Iy是相等的，Iz= Iy，于是得
(a)
(b)
13
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
解：在不计梁的自重的情况下，弯矩图如图所示
M max 375 kN m
14
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力

梁的弯曲强度

梁的弯曲强度
目录
弯曲应力\梁的弯曲强度 例如宽为b、高为h（h＞b）的矩形截面梁，如将截面竖置 (图a)，
则Wz1=bh2/6，而将截面横置 (图b)，则Wz2=hb2/6。因为h>b，所以 Wz1>Wz2。说明矩形截面竖置时，较多材料远离中性轴，弯曲截面 系数较大，而横置时，多数材料都在中性轴附近，弯曲截面系数较 小。显然，竖置比横置合理。
cmax 46.1MPa [c ] 90MPa
因此，该梁满足正应力强度条件。
由本例可以看出，当材料的[t] [c] 、截面不对称于中性轴、
且弯矩图有正和负时，梁的危险截面将分别是最大正弯矩和最大负 弯矩所在的横截面，梁的正应力强度计算应对这两个横截面上的危 险点分别进行。
目录
弯曲应力\梁的弯曲强度 【例5.6】 图示为支承在墙上的木栅的计算简图。已知材料的
目录
弯曲应力\梁的弯曲强度
【例5.5】已知图示T形截面梁最大拉、压应力分别为 tmax=tC=28.8MPa ，cmax=cB=46.1MPa。若材料的许用拉应力，许 用压应力，试校核该梁的正应力强度。 【解】 校核梁的正应力强度。 在C截面的下边缘各点处应力为
tmax 28.8MPa [t ] 30MPa 在B截面下边缘各点处的应力为
0.45MPa [ ] 1.2MPa
可见梁也满足切应力强度条件。
目录
弯曲应力\梁的弯曲强度
【例5.7】 图a所示工字形截面外伸梁，已知材料的许用应力
［］=160MPa,［τ］=100ΜPa。试选择工字钢型号。
【解】 1)绘制剪力图和弯矩图。 梁的剪力图和弯矩图分别如图b、 c所示。由图可知，最大剪力和 最大弯矩分别为
目录
弯曲应力\梁的弯曲强度 若将竖置矩形横截面(图a)中性轴附近材料取出，移置到距中性

材料力学 弯曲应力与强度条件

材料力学 弯曲应力与强度条件
3 3
2 0
y1
Z
I ZC 2
b2 h2 20 120 3 a22 ( yC y2 ) 2 20 120 4.3 10 6 mm 4 12 12
I ZC I ZC1 I ZC 2 3.4 10 6 4.3 10 6 7.66 10 6 mm 4
y=0,中性轴上各点σ=0
三、横截面上正应力分布状态及
max
max ,
截面关于中性轴对称 （塑性材料） M max max ymax IZ
M IZ (其中WZ ), WZ ymax WZ : 为横截面的抗弯截面系数
截面关于中性轴不对称 （脆性材料）

∴危险截面在=1.56m处。
15 3.75
kN
2、由梁的强度条件确定工字钢型号
28.1


kNm
WZ
M max

13 .16 10 6 61209 .3mm 3 61 .2cm3 215
查型钢表（附录表B3)P280页
13.16
N M max截面 0 12.6工字钢

WZ=77.5cm3
1.02 108 mm4
例题
A
y 铸铁制作的悬臂梁，尺寸及受力如图示，图中F＝20kN。梁 的截面为T字形，形心坐标yc=96.4mm。已知材料的拉伸许用应 150 力和压缩许用应力分别为[σ]+＝40MPa， [σ]－＝100MPa。试 校核梁的强度是否安全。 F 50 96 .4
B
C
B
A
平面弯曲为拉应力下边缘各点为压应力上边缘各点为压应力下边缘各点为拉应力上边缘各点三横截面上正应力分布状态及截面关于中性轴对称塑性材料截面关于中性轴不对称脆性材料maxmaxmax为横截面的抗弯截面系其中maxmaxmaxmax四惯性矩抗弯截面系数的计算一简单截面惯性矩与抗弯截面系数的计算1矩形截面惯性矩与抗弯截面系数的计算12123264二组合截面的惯性矩平行移轴公式zi1组合截面的惯性矩2平行移轴公式空心水泥板截面如图示已知bh和d试求阴影线部分对y轴惯性矩

材料力学课件第十三章弯曲的几个补充问题

材料力学课件第十三章弯曲的几个补充问题

（2） 绘制弯矩图 绘出 Mz (x)图 绘出 My(x) 图
A截面为梁的危险截面
y
F1=1kN
0.5m 0.5m
A z
B
C
x
F2=2kN
x
Mz = 1 kN·m
1kN·m
My= 1 kN·m
1kN·m
Mz使A截面上部受拉，下部受压
My使A截面前部受拉，后部受压
Mz(x)图
x My(x)图
（3） 应力分析
1.分解(Resolution) 将外载沿横截面的两个形心主轴分解，于是得到两个正交的
平面弯曲 2.叠加(Superposition)
对两个平面弯曲进行研究，然后将计算结果叠加起来
Fz
z
j
Fy F
y
A
z y
Bx
Fz
Fy
F
垂直纵向对称面
梁在垂直纵向对 称面 xy 面内发 生平面弯曲 。 z轴为中性轴
' My z
Iy
2.与 Mz 相应的正应力为(The bending normal stress corresponding to Mz)
'' M z y
Iz
C 点处的正应力(The normal stress at point C)
' '' M y z Mz y
Iy
Iz
m
z C ( y,z )
Fy 与均布荷载 q使梁在 xy平面内产生弯曲(z为中性轴)
Fz 使梁在 xz平面内产生弯曲(y为中性轴)
q
F 40° Fy
z
A
C
Fz B
a
a
y
（1） 画弯矩图

材料力学 弯曲正应力及其强度条件

材料力学 弯曲正应力及其强度条件

l 1m
由强度条件
max
Mmax Wz
W zM m a x1 2 4 0 0 1 1 0 0 3 6m 3143 cm 3
P l
(3)工字形
(1)矩形
Wz
bh2 6
b=6cm A172cm2 h=12cm
(2)圆形
Wz
d3
32
d≈11.3cm A2100cm2
查型钢表，取16号工字钢 Wz 141cm3 A326.1cm2
dh b
解： b2h2d2
Wz
bh2 6
b(d2 b2) 6
Wz d2 b2 0 b 6 2
由此得 b d
3 h d2b2 2d
3
h 2 ≈3:2
d
dh b
例23:跨长l=2m的铸铁梁受力如图示，已知材料
许用拉、压应力分别为 30M Pa和90M Pa
试根据截面最为合理的要求，确定T形梁横截面的
对于横力弯曲，由于剪力的存在，横截面产生剪切变形，
使横截面发生翘曲，不再保持为平面。
弹性力学精确分析结果指出：当梁的跨高比大于5时，剪应
力和挤压应力对弯曲正应力的影响甚小，可以忽略不计。因此
由纯弯曲梁导出的正应力计算公式，仍可以应用于横力弯曲的
梁中，误差不超过1%。
横力弯曲时，弯矩不再是常量。
M (x) Iz
2
2
ql2 qlaqa2 取有效值 a0.207l
82 2
二.梁的正应力强度条件
强度条件： max
等直梁强度条件
max
Mmax Wz
对于铸铁等脆性材料，抗拉和抗压能力不同，所以有许用 弯曲拉应力和许用弯曲压应力两个数值。强度条件为：

材料力学弯曲切应力ppt课件

材料力学弯曲切应力ppt课件
m
F*
B N2 n
dFs
FN*2
FN*1
dM Iz
S
* z
3 求纵截面 AB1 上的切应力 ’
S dFs 1 dM *
b dx bI z dx z
Fs
S
* z
bI z
z x
y
A1
FN*1
m
B1 dFs
A
n
bm
dx
B FN*2 n
Fs
S
* z
bI z
4 横截面上距中性轴为任意 y 的点，其切应力 的计 算公式。
*
z max [ ]
I zb
式中 ：[] 为材料在横力弯曲时的许用切应力。
S* z max
为中性轴任一边的半个横截面面积对中性轴的静矩
F S s,max
*
z max [ ]
I zb
在选择梁的截面时，通常先按正应力选出截面， 再按切应力进行强度校核。
例题3 ： 简支梁受均布荷载作用，其荷载集度 q 3.6 kN m
Fs,max 所在的横截面上，而且一般说是位于该截面的中性轴上。 全梁各横截面中最大切应力可统一表达为
S Fsmax
* z max
max
Izb
S Fsmax
* z max
max
Izb
S* z max
—— 中性轴一侧的横截面面积对中性轴的静矩
b —— 横截面在中性轴处的宽度
Fs max —— 全梁的最大剪力
q
m
C
E
G
H D
m
l 2
l
Fs 图 F
M图
ql 2
ql 2 8
E
τ max

材料力学--弯曲正应力及其强度条件

材料力学--弯曲正应力及其强度条件

C
E
15 106 200 109
7.5 105
q 40 kN / m
A
C
1.5 m
1.5 m
B 300 200
例21：图示木梁，已知下边缘纵向总伸
长为 10 mm，E=10GPa，求载荷P的大小。
P
300
A
C
B 200
2m
2m
解： AC
l/2
(x) dx
0
l/2 (x) d x l/2 M ( x) d x
1m
例20：简支梁受均布荷载，在其Ｃ截面
的下边缘贴一应变片，已知材料的 E=200GPa，试问该应变片所测得的应变 值应为多大？
q 40 kN / m
A
C
1.5 m
1.5 m
B 300 200
解：C截面的弯矩
ql2 MC 8 45kN m
C截面下边缘的应力 C
MC Wz
15MPa
应变值
P
y1
y2
Cz
解：
max
M max y1 Iz
[ ]
(1)
max
M max y2 Iz
[ ]
(2)
(1) 得： y1 [ ]
(2)
y2 [ ]
例16：图示外伸梁，受均布载荷作用，
材料的许用应力［σ］=160 MPa，校核 该梁的强度。
10 kN / m
2m
4m
200 100
10 kN / m
变形几何关系 从三方面考虑： 物理关系
静力学关系
1、变形几何关系
m
mn
m
aa
bb
mn
m
m
观察到以下变形现象: (1)aa、bb弯成弧线，aa缩短，bb伸长 (2)mm、nn变形后仍保持为直线，且仍与变为

梁的弯曲应力与强度计算ppt课件

梁的弯曲应力与强度计算ppt课件

bh 2 6
对于直径为 D 的圆形截面
Wz
Iz y max
D 4 / 64 D 3
D / 2 32
对于内外径分别为 d 、D 的空心圆截面
Wz
Iz y max
D4(14)/64 D3 (14)
D/2
32
14
8 梁的弯曲应力与强度计算
8.2 弯曲正应力的强度条件
如果梁的最大工作应力，不超过材料的许用弯曲应力，梁就是安全的。因此，梁弯曲时的正 应力强度条件为
(3) 经焊接、铆接或胶合而成的组合梁，一般需对焊缝、铆钉或胶合面进行剪应力强度校核。
29
8 梁的弯曲应力与强度计算
8.3 梁的剪应力及其强度条件
例：已知：F=58kN，a=0.15m，l=1m，试选择工字钢的型号。
解： （1）计算支反力
FA
(1
a)F l
FB
a l
F
FA
FB （2）作剪力图和弯矩图
8.1 梁弯曲时横截面上的正应力
静力学关系
FN
dA
A
My
zdA
A
Mz
ydA
A
FN
dA0
A
(c)
My AzdA0
(d)
将式 E代入y式(c)，得
Mz AydAMe
(e)
AdAAEydA0
E ＝常量，
E
y dA 0
A
Sz 0
z 轴（中性轴）通过截面形 心。
梁的轴线在中性层内，其长度不变。
8
8 梁的弯曲应力与强度计算
8.1 梁弯曲时横截面上的正应力
E y
(b)
将式(b)代入式(d)，得

梁的切应力及其强度条件

梁的切应力及其强度条件
FS S z 66103 462102 ta 26.5MPa 4 dIz 10115210
4) 求d点的切应力
10 220 d 103 47
FSD C y
td ta
140
10
C y 10
tmax
3 3 S z 15010 [103 (150/ 2)] 4210 mm
10 320 10 50kN 50kN 50kN
Байду номын сангаас
100
9.5
F1
F2
C B A 1.5 m 1.5 m 1.5 m 1.5 m FA FB
y
解 1）求内力
FA 75kN
FB 75kN
10 320 10
50kN 50kN 50kN
100
F1
F2
9.5
C B A 1.5 m 1.5 m 1.5 m 1.5 m FA FB
y
dA
tmax
* FS S z t bI z
h
z
y
h h/2 y S b y 2 2
* z
y
b
2
b h2 2 y 2 4
FS h 2 FS b h 2 2 y t y 4 2I 4 I zb 2 z 2 2 3 FS 3FS FSh FSh t max 3 8I z 8 bh 12 2 bh 2 A
y
2、翼缘上的切应力

F
* N2

d h
O
t
y
F t
* 1 N1
t1'
d F S t 1 d x
* FS S z t 1 I z

弯曲正应力强度条件的内容

弯曲正应力强度条件的内容

弯曲正应力强度条件的内容弯曲正应力强度条件的内容一、弯曲正应力强度条件的定义弯曲正应力强度条件是指在材料受到弯曲时，其最大正应力不能超过该材料的屈服极限。

这个条件是一种基本的材料设计原则，它可以用来保证材料在使用过程中不会发生破坏。

二、弯曲正应力强度条件的计算公式在进行弯曲试验时，我们通常会测量出受试样件上的最大正应力。

这个最大正应力可以通过下面的公式来计算：σ = M*y/I其中，σ表示最大正应力；M表示试样受到的最大弯矩；y表示试样截面上离中性轴距离最远的点到中性轴距离；I表示试样截面对中性轴的惯性矩。

三、弯曲正应力强度条件与屈服极限之间的关系根据材料学理论，屈服极限是指材料在受到外部载荷作用下开始发生塑性变形并且无法恢复原来形态时所承受的最大载荷。

因此，在进行材料设计时，我们需要确保所选用的材料的屈服极限大于或等于试样受到的最大正应力。

四、弯曲正应力强度条件的应用弯曲正应力强度条件是一种非常重要的材料设计原则，它可以用来保证材料在使用过程中不会发生破坏。

这个原则在许多不同领域都有广泛的应用，例如：1. 桥梁设计：在桥梁设计中，我们需要确保桥梁所使用的材料能够承受车辆和行人的重量。

因此，在进行桥梁设计时，我们需要计算出桥梁受到最大荷载时所承受的最大正应力，并且确保该正应力小于所选用材料的屈服极限。

2. 航空航天工业：在航空航天工业中，我们需要确保飞机和火箭等载具所使用的材料能够承受高速飞行时产生的巨大载荷。

因此，在进行航空航天工业设计时，我们需要计算出载具受到最大荷载时所承受的最大正应力，并且确保该正应力小于所选用材料的屈服极限。

3. 机械制造业：在机械制造业中，我们需要确保机械零件所使用的材料能够承受工作时所产生的载荷。

因此，在进行机械设计时，我们需要计算出机械零件受到最大荷载时所承受的最大正应力，并且确保该正应力小于所选用材料的屈服极限。

五、弯曲正应力强度条件的局限性尽管弯曲正应力强度条件是一种非常重要的材料设计原则，但是它仍然存在一些局限性。

弯曲应力-材料力学

弯曲应力-材料力学
已知：弯矩M、横截面的惯性矩Iz、许用应力[]。求：判断不等号。
max
Mymax Iz
工程力学 Engineering Mechanics
典型例题
例1 图示矩形截面梁，梁上载荷q=100kN/m，梁跨度l=6m，截面尺寸：
b=400mm，h=600mm，材料许用应力[]=100MPa，试判断该梁是否安全。
弹性力学精确分析表明，当跨度l与横截面高度h之比l/h>5（细长梁）时， 纯弯曲正应力公式对于横力弯曲近似成立。
横力弯曲最大正应力
max
M max ymax Iz
弯曲正应力适用范围 细长梁的纯弯曲或横力弯曲 横截面惯性积Iyz=0 弹性变形阶段
工程力学 Engineering Mechanics
YA
2m
2m YB
B 2m
20 b
90
c
z
a
50
解：（3）求解正应力
My Iz
惯性矩
Iz
1 12
50 903
3.0375106 mm4
弯矩
M 10kN.m
典型例题
例1 求图示矩形截面梁指定截面上对应点的正内力。
10kN
1
A
YA
2m
2m YB
B 2m
20 b
90
c
z
a
50
解：（3）求解正应力
M max
1 8
ql 2
1 8
q
62
q
533.3kN/m
练习1
受均布载荷作用的简支梁如图，求 ① 1-1截面上1、2两点的正应力； ② 1-1截面上的最大正应力； ③ 全梁的最大正应力； ④ 已知E=200GPa，求1-1截面的曲率半径。

材料力学__弯曲正应力及其强度条件

材料力学__弯曲正应力及其强度条件

a
⊕
qa 2
2
ql 2 qla qa 2 8 2 2
qa 2 2
取有效值
a 0.207 l
二.梁的正应力强度条件
强度条件：
等直梁强度条件
max
max
M max Wz
对于铸铁等脆性材料，抗拉和抗压能力不同，所以有许用 弯曲拉应力和许用弯曲压应力两个数值。强度条件为：
由 max 1 max 2 [ ] 得:
例13：矩形截面梁当横截面的高度增加一倍，宽度
减小一半时，从正应力强度条件考虑，该梁 的承载能力将是原来的多少倍？
解： 由公式
max
M max M max 2 Wz bh 6
可以看出， 该梁的承载能力将是原来的 2 倍。
例14：主梁AB，跨度为L，采用加副梁
由
M max AB M max CD
得
Pa P (l a ) 4 4
l a 2
例15：图示梁的截面为T形，材料的许用拉
应力和许用压应力分别为［σ+］和［ σ-］， 则 y1 和 y2 的最佳比值为多少? (Ｃ为截面形心)
P
y1
y2
C
z
解：


max
M max y1 [ ] Iz
2 3 3
M max max Wz
2b A1 b
a
A2
A3
d
a
例18：图示铸铁梁，许用拉应力[σ+ ]=30MPa，
许用压应力[σ- ]=60MPa,Ｉz=7.63×10-6m4，试 校核此梁的强度。
A
4 kN 52 B C D 88 1m 1m 1m

弯曲正应力切应力与强度条件

弯曲正应力切应力与强度条件
Z
C
Z
中性轴
中性轴
拉
y
y
压
中性轴将横截面分为 受拉 和 受压 两部分。
第三十二页，课件共有154页
My
A z (dA)
E
A
z
y
dA
E
I
yz
0
I yz 0
因为 y 轴是横截面的对称轴，所以 Iyz 一定为零。 该式自动满足
中性轴是横截面的形心主惯性轴
第三十三页，课件共有154页
MZ
A
y (dA)
第四十九页，课件共有154页
Cmax
σ c max
yc max
yt max
M
z
y
tmax
σ t max
σ t max M yt max
IZ
σ c max M yc max
IZ
第五十页，课件共有154页
例题：T形截面铸铁梁的荷载和截面尺寸如图所示。求横截面最大 拉应力 t，max ，和最大压应力 C，max ，已知 ，Iz = 290. 610-8 mm4
第三页，课件共有154页
一，纯弯曲梁横截面上的正应力
RA
P
C a
P
+
P RB D
a
+
P
+
Pa
第四页，课件共有154页
P
C
a
P
+
P
D
a
+
P
横力弯曲
梁的横截面上同时有弯
矩和剪力的弯曲。
纯弯曲
梁的横截面上只有弯矩 没有剪力的弯曲。
横截面上只有正应
力而无切应力。
+
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
FS bh 1 h2 qw ( y) y 2 Iz 2 24
y
翼缘中心线高度。 与腹板高度、梁高 度给出的结果有何 差别？
14
3. 剪流方向判断
dF2 0
w 与 FS 同向
FS 0 dM 0
dF1 0
f 指向腹板
§4 梁的强度条件
梁危险点处的应力状态
梁的强度条件 强度条件的应用 例题
25
梁危险点处的应力状态
实心与非薄壁截面梁
a, c 点处－单向应力
b 点处－纯剪切
26
薄壁截面梁
d
a 点处－纯剪切
c , d 点处－单向应力
b 点处－ , 联合作用
27
梁的强度条件
弯曲正应力强度条件：
0 z
A1
A2 y
Sz S
( 整) z
S
( 孔) z
负面积法
S z( 整 ) S z( 孔) y c ( 整) A A( 孔)
3
弯曲正应力的另一种推导方法
根据平面假设，令
a by
y

A
dA 0

A
y dA M
0
M ( y) y Iz
15
4. 剪流分布图
qw,max FS h(4b h 1 ) 8Iz

下翼缘的剪流均指
向腹板；上翼缘的剪流 均背离腹板


腹板上的剪流与剪
“视”截面如管道，
力 FS 同向
“视”剪流如管流，连 续流动；由qw推及其他
16
盒形薄壁梁弯曲切应力

FS Sz ( ) FS ( y) b( h02 - h2 ) 2 ( h2 - 4 y 2 ) I z 2 16 I z
22
例 3-4 已知梁段剪力FS，试分析铆钉之受力
解：
2F'S F2 F1
23
2F'S F2 F1
F2 F1 F'S 2 M Sz F1 1 Iz
F2 M2 S z Iz
M 2 M 1 FS e
F'S FS e S z 2I z
24
S z －上翼板对 中性轴 z 的静矩
抗弯截 面系数
41
max [ ]
短而高梁、薄壁梁、 M 小 FS大的梁
max [ ]
max [ ]
考虑 , 联合作用的强度条件
29
例 题
例 4-1 简易吊车梁，F =20 kN，l = 6 m，[] = 100 MPa ， [] = 60 MPa，选择工字钢型号
解：1. 内力分析
M （I z －惯性矩） 中性层曲率： EI z （EI z －截面弯曲刚度） M My max 正应力公式： ( y ) Wz Iz
（Wz －抗弯截面系数）
应用条件： max p 对称弯曲 , 纯弯与非纯弯
2
截面几何性质
• 截面形心、静矩 • 惯性矩 • 组合公式，平行移轴定理
FS Sz ( ) ( s) I z ( s )
Sz-截面 对 z 轴的静矩
Iz- 整个截面对 z 轴的惯性矩
21
例 题
例 FS = 15 kN，Iz = 8.8410-6 m4， b = 120 mm， 20 mm， yC = 45 mm，求 max、腹板与翼缘交接处 切应力 a 解：
max
3 FS 2 A
10
截面翘曲与非纯弯推广 切应力非均布 切应变非均布 截面翘曲
当FS=常数时， ab = a'b' ，弯曲 仍保持线性分布

当梁上作用横向分布载荷时，各截面翘曲量不同，
对 有影响；只要 l > 5h，纯弯 公式仍足够精确 矩形截面简支梁受均布载荷，根据弹性理论，
9

( y)
FS Sz ( ) I zb
h 1 h Sz ( ) b y y 2 2 2
可否取上部 计算，结论是 否相同？
b h2 2 y 2 4
bh3 Iz 12
3FS 4 y 2 ( y) 1 2 2bh h
FS S M y y2 3 y q 4 , 2 I bh h 5 It 2 2 2 q 3 l 1 3 ql 4 h 1 max b 4 h2 5 4bh2 15 l
6
矩形截面梁弯曲切应力
儒拉夫斯基（Jourawski）的贡献
1842年毕业于圣彼得堡交通工 程学院；1844年负责设计并制 造横跨维列比亚河的大桥，9
跨，每跨180英尺，距水面170
英尺，采用高度很大的木梁， 木组合梁。
判断：梁内切应力非常重要，
不能忽略。
T
max bh
4
3Ql 2h
第6章 弯曲应力 本章主要研究： 梁的弯曲正应力 梁的弯曲切应力 梁的强度分析与设计 对称与非对称弯曲
1
弯曲正应力回顾
表面变形观察 平面假设 单向受力假设

y

( y) E
y

(a)
AdA 0 (b)
1
A ydA M (c)
中性轴位置： 中性轴过截面形心
max [ ]
max 最大弯曲正应力
材料单向应力许用应力 弯曲切应力强度条件：
max [ ]
max 最大弯曲切应力
材料纯剪切许用应力
, 联合作用强度条件 （详见第九章强度理论）
28
梁强度条件的选用
细长非薄壁梁
max max
30
FS ( )
FS, max
( l )F l FS (0) F
M ( ) F 1 l Fl M max 4
2. 按弯曲 条件选截面
Fl 3.0 104 m4 Wz 4[ ]
选 №22a, Wz=3.09×10-4 m4
Sz ,max
( b yC ) 2
Sz ,a
2 FS Sz ,max max 7.66 MPa I z b b ( - yC ) 8.40 10-5 m3 2 FS Sa a 7.13 MPa I z
9.03 105 m3
max
6Ql bh2
断定：固定端mn上法向应力有使OO 面产生剪切的趋势。
T 3 Q lb 2 bh
7
矩形截面梁弯曲切应力
问题 狭窄矩形截面梁(h>b)，分析其弯曲切应力分布
假设 思路
(y) // 截面侧边，并沿截面宽度均匀分布
由正应力的差确定切应力
8
矩形截面梁弯曲切应力
ql 2 bh3 若 M l 5,h, I 8 12 2 2
max
3ql ql 6 4bh2 8 bh2
11
薄壁梁弯曲切应力公式
y、z 轴－主形心轴
假设
切应力平行于中心线切线
切应力沿壁厚均匀分布
12
弯曲切应力公式
由正应力的差确定切应力
推导 详见
FS Sz ( ) ( s) I z ( s )
ydA A yC 0 A
(a)(b)
E
(a)(c)
y dA M A
2
I z A y 2dA－惯性矩
1 M EI z
(d)
(d)(a) max
My ( y) Iz
Mymax M Iz Iz ymax
max
M Wz
Iz Wz ymax
t,max c 33.6 MPa t
33
§5 梁的合理强度设计
梁的合理截面形状
变截面梁与等强度梁 梁的合理受力
34
梁的合理截面形状 将较多材料放置在远离中性轴的位置，并注意塑性
与脆性材料的差异
塑性材料梁
脆性材料梁
上下对称
yc [ c ] yt [ t ]
17
例 确定闭口薄壁圆截面梁的切应力分布
解：1. 问题分析 2. 切应力分析
切应力分布对称于 y 轴，A 处切 应力为零,等价于开口薄壁截面
( )
FS Sz ( ) I z
18
I z R03

0
Sz ( ) ydA

Sz ( ) R0cos R0d R02sin
32
截面B
截面D
MD MB ,
ya yd

a d
危险点－ a, b, c
M D y2 -59.8 MPa a Iz
M D y1 28.3 MPa b Iz M B y2 33.6 MPa c Iz
c,max a 59.8 MPa c
35
注重弯曲强度，兼顾腹板的剪切强度与稳定性
腹板不能过薄，以避免剪切破坏与失稳
36
变截面梁与等强度梁
M ( x) [ ] －弯曲等强条件 W ( x) bh2 ( x ) M ( x ) Fx W ( x ) 6 6Fx h( x ) b[ ]
3FS ( x ) [ ] －剪切等强条件 2bh( x )
当 l >> h 时，max >> max
20
Fx 0, ( s) ( s)dx dF
1 dF ( s ) dx MS z ( ) My F dA dA Iz Iz 1 dM Sz ( ) ( s) ( s) dx I z