最新文档
-
饭店包间名字大全页数:1
-
自行车健身比赛开幕式讲话词页数:2
-
2018乡村医生个人工作总结页数:16
-
MySQL测试题 SQL页数:10
-
合勤NXC5200页数:14
-
铁路集中箱空箱调度优化建模案例(案例2)页数:4
-
微分几何教学大纲-复旦大学数学科学学院页数:3
-
(整容后办护照用)医院整容证明页数:1
-
危险废物管理台账页数:31
-
2017年终大会会场物料设计方案页数:6
-
军队现状浅析页数:1
-
浅析医学信息系统的应用页数:1
-
网络故障排除硬件和软件工具调查报告页数:3




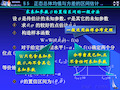




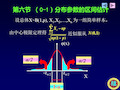





![置信区间的概念[1]](https://img.taocdn.com/s1/s/703fd06dcfc789eb172dc882.jpg)