代数几何综合题含答案

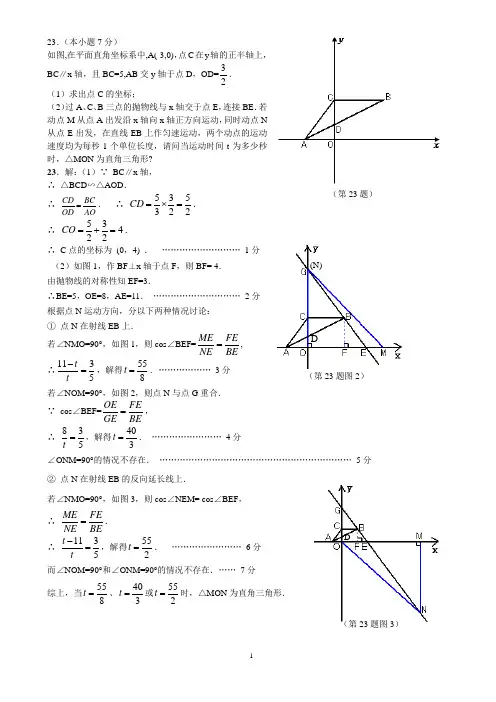
23．（本小题7分）如图,在平面直角坐标系中,A(-3,0)，点C 在y 轴的正半轴上，BC ∥x 轴，且BC=5,AB 交y 轴于点D ，OD=23． （1）求出点C 的坐标； （2）过A 、C 、B 三点的抛物线与x 轴交于点E ，连接BE ．若动点M 从点A 出发沿x 轴向x 轴正方向运动，同时动点N 从点E 出发，在直线EB 上作匀速运动，两个动点的运动速度均为每秒1个单位长度，请问当运动时间t 为多少秒时，△MON 为直角三角形? 23．解：（1）∵ BC ∥x 轴， ∴ △BCD ∽△AOD ．∴ CD BC OD AO=． ∴ 535322CD =⨯=．∴ 53422CO =+=． ∴ C 点的坐标为 (0，4) ． ……………………… 1分 （2）如图1，作BF ⊥x 轴于点F ，则BF= 4． 由抛物线的对称性知EF=3．∴BE=5，OE=8，AE=11． ………………………… 2分 根据点N 运动方向，分以下两种情况讨论： ① 点N 在射线EB 上．若∠NMO=90°，如图1，则cos ∠BEF=ME FENE BE=, ∴1135t t -=，解得558t =．……………… 3分 若∠NOM=90°，如图2，则点N 与点G 重合．∵ cos ∠BEF=OE FEGE BE=， ∴ 835t =，解得403t =． …………………… 4分∠ONM=90°的情况不存在． ………………………………………………………… 5分 ② 点N 在射线EB 的反向延长线上．若∠NMO=90°，如图3，则cos ∠NEM= cos ∠BEF ，∴ME FENE BE =． ∴ 1135t t -=，解得552t =． …………………… 6分 而∠NOM=90°和∠ONM=90°的情况不存在．…… 7分 综上，当558t =、403t =或552t =时，△MON 为直角三角形．（第23题图2）D(N)（第23题图3）D（第23题）25.（7分）已知，抛物线22y ax bx =+-与x 轴的两个交点分别为A （1,0），B （4，0），与y 轴的交点为C ． （1）求出抛物线的解析式及点C 的坐标；（2）点P 是在直线x=4右侧的抛物线上的一动点，过P 作PM x ⊥轴，垂足为M ，是否存在P 点，使得以A ，P ，M 为顶点的三角形与△OCB 相似？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由． 25．（7分）解：（1）据题意，有0164202a b a b =+-⎧⎨=+-⎩，　． 解得 1252a b ⎧=-⎪⎪⎨⎪=⎪⎩，　． ∴抛物线的解析式为：215222y x x =-+-．点C 的坐标为：（0，-2）． ………………………（2）答：存在点P （x ，215222x x -+-），使以A ，P ，M ∵∠COB =∠AMP =90°，∴①当OC OBMP MA =时，△OCB ∽△MAP ． ②当OC OB MA MP=时，△OCB ∽△MP A ． ①OC MP OB MA =，∴215222241x x x -+=-． 解得：x 1=8，x 2=1（舍）． ②OC MA OB MP =，∴221154222x x x -=-+． 解得：x 3=5，x 4=1（舍）．综合①，②知，满足条件的点P 为：P 1（8，-14），P 2（5，-2）． ……………………… 7分24. 在△ABC 中，∠A =∠B =30°，AB=．把△ABC 放在平面直角坐标系中，使AB 的中点位于坐标原点O (如图)，△ABC 可以绕点O 作任意角度的旋转．(1) 当点BB 的横坐标；(2) 如果抛物线2y ax bx c =++(a ≠0)的对称轴经过点C ，请你探究：当a =，12b =-，c =A ，B 两点是否都在这条抛物线上？并说明理由。

一次函数代几综合问题一．填空题（共6小题）1．如图，直线和x轴、y轴分别交于点A、B．若以线段AB为边作等边三角形ABC，则点C的坐标是．2．一次函数y=x+4分别交x轴、y轴于A、B两点，在x轴上取一点，使△ABC为等腰三角形，则这样的点C的坐标为．3．如图，平面直角坐标系中，已知直线y=x上一点P（1，1），C为y轴上一点，连接PC，线段PC绕点P顺时针旋转90°至线段PD，过点D作直线AB⊥x轴，垂足为B，直线AB与直线y=x交于点A，且BD=2AD，连接CD，直线CD与直线y=x交于点Q，则点Q的坐标为．4．如图，已知直线l：y=x，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2；…；按此作法继续下去，则点A4的坐标为．5．在直角坐标系中，正方形A1B1C1O1、A2B2C2C1、…、A n B n C n C n﹣1按如图所示的方式放置，其中点A1、A2、A3、…、A n均在一次函数y=kx+b的图象上，点C1、C2、C3、…、C n均在x轴上．若点B1的坐标为（1，1），点B2的坐标为（3，2），则点A n的坐标为．6．如图，直线1：与x轴、y轴分别相交于点A、B，△AOB与△ACB关于直线l对称，则点C的坐标为．二．解答题（共24小题）7．已知一次函数y=2x﹣4的图象与x轴、y轴分别相交于点A、B，点P在该函数的图象上，P到x轴、y 轴的距离分别为d1、d2．（1）当P为线段AB的中点时，求d1+d2的值；（2）直接写出d1+d2的范围，并求当d1+d2=3时点P的坐标；（3）若在线段AB上存在无数个P点，使d1+ad2=4（a为常数），求a的值．8．在平面直角坐标系xOy中，边长为6的正方形OABC的顶点A，C分别在x轴和y轴的正半轴上，直线y=mx+2与OC，BC两边分别相交于点D，G，以DG为边作菱形DEFG，顶点E在OA边上．（1）如图1，当CG=OD时，直接写出点D和点G的坐标，并求直线DG的函数表达式；（2）如图2，连接BF，设CG=a，△FBG的面积为S．①求S与a的函数关系式；②判断S的值能否等于等于1？若能，求此时m的值，若不能，请说明理由；（3）如图3，连接GE，当GD平分∠CGE时，m的值为．9．认真阅读材料，然后回答问题：我们知道，在数轴上，x=1表示一个点．而在平面直角坐标系中，x=1表示一条直线；我们还知道，以二元一次方方程2x﹣y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象，它也是一条直线，如图1可以得出：直线x=1与直线y=2x+1的交点P的坐标（1，3）就是方程组在直角坐标系中，x≤1表示一个平面区域，即直线x=1以及它左侧的部分，如图2；y≧2x+1也表示一个平面区域，即直线y=2x+1以及它上方的部分，如图3．回答下列问题：请你自己作一个直角坐标系，并在直角坐标系中（1）用作图象的方法求出方程组的解．（2）用阴影表示，所围成的区域．10．如图，直线l1的解析表达式为：y=3x﹣3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．（1）求△ADC的面积；（2）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，则点P的坐标为；（3）若点H为坐标平面内任意一点，在坐标平面内是否存在这样的点H，使以A、D、C、H为顶点的四边形是平行四边形？若存在，请直接写出点H的坐标；若不存在，请说明理由．11．如图，在平面直角坐标系中，已知直线l1和l2相交于点A，它们的解析式分别为l1：y=x，l2：y=﹣x+．直线l2与两坐标轴分别相交于点B和点C，点P在线段OB上从点O出发．以每秒1个单位的速度向点B运动，同时点Q从点B出发以每秒4个单位的速度沿B→O→C→B的方向向点B运动，过点P作直线PM⊥OB分别交l1，l2于点M，N．连接MQ．设点P，Q运动的时间是t秒（t＞0）（1）求点A的坐标；（2）点Q在OC上运动时，试求t为何值时，四边形MNCQ为平行四边形；（3）试探究是否存在某一时刻t，使MQ∥OB？若存在，求出t的值；若不存在，请说明理由．12．已知，将边长为5的正方形ABCO放置在如图所示的直角坐标系中，使点A在x轴上，点C在y轴上．点M（t，0）在x轴上运动，过A作直线MC的垂线交y轴于点N．（1）当t=1时，求直线MC的解析式；（2）设△AMN的面积为S，求S关于t的函数解析式并写出相应t的取值范围；（3）在该平面直角坐标系中，第一象限内取点P（2，y），是否存在以M、N、C、P为顶点的四边形是直角梯形？若存在，直接写出点P的坐标；若不存在，请说明理由．13．如图①，以四边形AOCD的顶点O为原点建立直角坐标系，点A、C、D的坐标分别为（0，2）、（2，0）、（2，2），点P（m，0）是x轴上一动点，m是大于0的常数，以AP为一边作正方形APQR（QR落在第一象限），连接CQ．（1）请判断四边形AOCD的形状，并说明理由：（2）连接RD，请判断△ARD的形状，并说明理由：（3）如图②，随着点P（m，0）的运动，正方形APQR的大小会发生改变，若设CQ所在直线的表达式为y=kx+b（k≠0），求k的值．14．如图，将边长为4的正方形纸片，置于平面直角坐标系内，顶点A在坐标原点，AB在x轴正方向上，E、F分别是AD、BC的中点，M在DC上，将△ADM沿折痕AM折叠，使点D折叠后恰好落在EF上的P点处．（1）求点M、P的坐标；（2）求折痕AM所在直线的解析式；（3）设点H为直线AM上的点，是否存在这样的点H，使得以H、A、P为顶点的三角形为等腰三角形？若存在，请直接写出点H的坐标；若不存在，请说明理由．15．如图①，在平面直角坐标系中，A点坐标为（3，0），B点坐标为（0，4）．动点M从点O出发，沿OA方向以每秒1个单位长度的速度向终点A运动；同时，动点N从点A出发沿AB方向以每秒个单位长度的速度向终点B运动．设运动了x秒．（1）点N的坐标为（，）；（用含x的代数式表示）（2）当x为何值时，△AMN为等腰三角形；（3）如图②，连接ON得△OMN，△OMN可能为正三角形吗？若不能，点M的运动速度不变，试改变点N的运动速度，使△OMN为正三角形，并求出点N的运动速度．16．已知直线y=﹣x+4与x轴和y轴分别交与B、A两点，另一直线经过点B和点D（11，6）．（1）求AB、BD的长度，并证明△ABD是直角三角形；（2）在x轴上找点C，使△ACD是以AD为底边的等腰三角形，求出C点坐标；（3）一动点P速度为1个单位/秒，沿A﹣﹣B﹣﹣D运动到D点停止，另有一动点Q从D点出发，以相同的速度沿D﹣﹣B﹣﹣A运动到A点停止，两点同时出发，PQ的长度为y（单位长），运动时间为t（秒），求y关于t的函数关系式．17．如图：直线y=kx+3与x轴、y轴分别交于A、B两点，，点C（x，y）是直线y=kx+3上与A、B不重合的动点．（1）求直线y=kx+3的解析式；（2）当点C运动到什么位置时△AOC的面积是6；（3）过点C的另一直线CD与y轴相交于D点，是否存在点C使△BCD与△AOB全等？若存在，请求出点C的坐标；若不存在，请说明理由．18．如图，在平面直角坐标系中，已知O为原点，四边形ABCD为平行四边形，A、B、C的坐标分别是A（﹣5，1），B（﹣2，4），C（5，4），点D在第一象限．（1）写出D点的坐标；（2）求经过B、D两点的直线的解析式，并求线段BD的长；（3）将平行四边形ABCD先向右平移1个单位长度，再向下平移1个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少？并求出平行四边形ABCD与四边形A1B1C1D1重叠部分的面积．19．如图1，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是（0，4），点B在第一象限，点P是x轴上的一个动点，连接AP，并把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，得到△ABD．（1）求直线AB的解析式；（2）当点P运动到点（，0）时，求此时DP的长及点D的坐标；（3）是否存在点P，使△OPD的面积等于？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．20．已知，直线y=﹣x+1与x轴，y轴分别交于点A、B，以线段AB为直角边在第一象限内作等腰Rt△ABC，∠BAC=90度．且点P（1，a）为坐标系中的一个动点．（1）求三角形ABC的面积S△ABC；（2）证明不论a取任何实数，三角形BOP的面积是一个常数；（3）要使得△ABC和△ABP的面积相等，求实数a的值．21．如图，在直角坐标系xoy中，一次函数的图象与x轴交于点A，与y轴交于点B．（1）已知OC⊥AB于C，求C点坐标；（2）在x轴上是否存在点P，使△PAB为等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．22．如图1，在正方形ABOC中，BD平分∠OBC，交OA于点D．（1）若正方形ABOC的边长为2，对角线BC与OA相交于点E．则：①BC的长为；②DE的长为；③根据已知及求得的线段OB、BC、DE的长，请找出它们的数量关系？（2）如图2，当直角∠BAC绕着其顶点A顺时针旋转时，角的两边分别与x轴正半轴、y轴正半轴交于点C1和B1，连接B1C1交OA于P．B1D平分∠OB1C1，交OA于点D，过点D作DE⊥B1C1，垂足为E，请猜想线段OB、B1C1、DE三者之间的数量关系，并证明你的猜想；（3）在（2）的条件下，当B1E=6，C1E=4时，求直线B1D的解析式．23．如图，一次函数的函数图象与x轴、y轴分别交于点A、B，以线段AB为直角边在第一象限内作Rt△ABC，且使∠ABC=30°；（1）如果点P（m，）在第二象限内，试用含m的代数式表示四边形AOPB的面积，并求当△APB与△ABC面积相等时m的值；（2）如果△QAB是等腰三角形并且点Q在坐标轴上，请求出点Q所有可能的坐标；（3）是否存在实数a，b使一次函数和y=ax+b的图象关于直线y=x对称？若存在，求出的值；若不存在，请说明理由．24．一次函数的图象与x轴、y轴分别交于点A（8，0）和点B（0，6）．（1）确定此一次函数的解析式．（2）求坐标原点O到直线AB的距离．（3）点P是线段AB上的一个动点，过点P作PM垂直于x轴于M，作PN垂直于y轴于N，记L=PM+PN，问L是否存在最大值和最小值？若存在，求出此时P点到原点O的距离，若不存在请说明理由．25．已知直线y=2x+4与x轴交于点A，与y轴交于点B，点P在坐标轴上，且PO=2AO．求△ABP的面积．26．已知A（1，5），B（3，﹣1）两点，在x轴上取一点M，使AM﹣BM取得最大值时，则M的坐标为．27．如图，在平面直角坐标系中，直线分别交于x轴，y轴于B、A两点，D、E分别是OA、OB的中点，点P从点D出沿DE方向运动，过点P作PQ⊥AB于Q，过点Q作QR∥OA交OB于R，当点Q与B点重合时，点P停止运动．（1）求A、B两点的坐标；（2）求PQ的长度；（3）是否存在点P，使△PQR为等腰三角形？若存在，请求出所有满足要求的点R的坐标；若不存在，请说明理由．28．如图，直线y=﹣2x+2与x轴、y轴分别交于A、B两点，将△OAB绕点O逆时针方向旋转90°后得到△OCD．（1）填空：点C的坐标是（，），点D的坐标是（，）；（2）设直线CD与AB交于点M，求线段BM的长；（3）在y轴上是否存在点P，使得△BMP是等腰三角形？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．29．已知△ABC，∠BAC=90°，AB=AC=4，BD是AC边上的中线，分别以AC，AB所在直线为x轴，y 轴建立直角坐标系（如图）．（1）在BD所在直线上找出一点P，使四边形ABCP为平行四边形，画出这个平行四边形，并简要叙述其过程；（2）求直线BD的函数关系式；（3）直线BD上是否存在点M，使△AMC为等腰三角形？若存在，求点M的坐标；若不存在，说明理由．30．如图，一次函数的图象与x轴、y轴交于点A、B，以线段AB为边在第一象限内作等边△ABC，（1）求△ABC的面积；（2）如果在第二象限内有一点P（a，）；试用含有a的代数式表示四边形ABPO的面积，并求出当△ABP的面积与△ABC的面积相等时a的值；（3）在x轴上，是否存在点M，使△MAB为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．。

人教版数学中考专题：代数几合综合问题含答案 Revised by BETTY on December 25,2020中考数学专题：代数几何综合问题一、填空题1. 在平面直角坐标系中，点A的坐标为(4，0)，点B的坐标为(4，10)，点C在y轴上，且△ABC是直角三角形，则满足条件的 C点的坐标为______________．2.如图，在坐标轴上取点A1（2，0），作x轴的垂线与直线y=2x交于点B1，作等腰直角三角形A1B1A2；又过点A2作x轴的垂线交直线y=2x交于点B2，作等腰直角三角形A2B2A3；…，如此反复作等腰直角三角形，当作到An（n为正整数）点时，则An的坐标是______．二，选择题3.如图，O是边长为4cm的正方形ABCD的中心，M是BC的中点，动点P由A开始沿折线A﹣B﹣M方向匀速运动，到M时停止运动，速度为1cm/s．设P点的运动时间为t（s），点P的运动路径与OA、OP所围成的图形面积为S（cm2），则描述面积S（cm2）与时间t（s）的关系的图象可以是（）A． B．B． D．C．D． 4. 如图，夜晚，小亮从点A经过路灯C的正下方沿直线走到点B，他的影长y随他与点A之间的距离x的变化而变化，那么表示y与x之间函数关系的图象大致为（）E．F．G．三、解答题H． 5. 如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=5cm，点D在BC上，且CD=3cm，现有两个动点P，Q分别从点A和点B同时出发，其中点P以1厘米/秒的速度沿AC向终点C运动；点Q以厘米/秒的速度沿BC向终点C运动．过点P作I．PE∥BC交AD于点E，连接EQ．设动点运动时间为t秒（t＞0）．J．（1）连接DP，经过1秒后，四边形EQDP能够成为平行四边形吗请说明理由；K．（2）连接PQ，在运动过程中，不论t取何值时，总有线段PQ与线段AB平行．为什么L．（3）当t为何值时，△EDQ为直角三角形．M．N．6．如图，在平面直角坐标系中，四边形OABC是梯形，OA∥BC，点A的坐标为（6，0），点B的坐标为（3，4），点C在y轴的正半轴上．动点M在OA上运动，从O点出发到A点；动点N在AB上运动，从A点出发到B点．两个动点同时出发，速度都是每秒1个单位长度，当其中一个点到达终点时，另一个点也随即停止，设两个点的运动时间为t（秒）O．（1）求线段AB的长；当t为何值时，MN∥OC？P．（2）设△CMN的面积为S，求S与t之间的函数解析式，并指出自变量t的取值范围；S是否有最小值若有最小值，最小值是多少Q．R．7. 条件：如下图，A、B是直线l同旁的两个定点．S．T．问题：在直线l上确定一点P，使PA+PB的值最小．U．方法：作点A关于直线l的对称点A′，连接A′B交l于点P，则PA+PB=A′B的值最小（不必证明）．V．模型应用：W．（1）如图1，正方形ABCD的边长为2，E为AB的中点，P是AC上一动点．连接BD，由正方形对称性可知，B与D关于直线AC对称．连接ED交AC于P，则PB+PE的最小值是______；X．（2）如图2，⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC=60°，P是OB上一动点，求PA+PC的最小值；Y．（3）如图3，∠AOB=45°，P是∠AOB内一点，PO=10，Q、R分别是OA、OB 上的动点，求△PQR周长的最小值．Z．8.如图，四边形OABC是一张放在平面直角坐标系的矩形纸片，O为原点，点A在x 轴上，点C在y轴上，OA=15，OC=9，在AB上取一点M，使得△CBM沿CM翻折后，点B落在x轴上，记作N点．9.（1）求N点、M点的坐标；10.（2）将抛物线y=x2﹣36向右平移a（0＜a＜10）个单位后，得到抛物线l，l经过点N，求抛物线l的解析式；11.（3）①抛物线l的对称轴上存在点P，使得P点到M、N两点的距离之差最大，求P点的坐标；12.②若点D是线段OC上的一个动点（不与O、C重合），过点D作DE∥OA交CN于E，设CD的长为m，△PDE的面积为S，求S与m之间的函数关系式，并说明S 是否存在最大值？若存在，请求出最大值；若不存在，请说明理由．13.14.9. 如图，直线y=kx﹣1与x轴、y轴分别交于B、C两点，tan∠OCB=．（1）求B点的坐标和k的值；（2）若点A（x，y）是第一象限内的直线y=kx﹣1上的一个动点．当点A运动过程中，试写出△AOB的面积S与x的函数关系式；（3）探索：在（2）的条件下：①当点A运动到什么位置时，△AOB的面积是；②在①成立的情况下，x轴上是否存在一点P，使△POA是等腰三角形？若存在，请写出满足条件的所有P点的坐标；若不存在，请说明理由．10. （2018成都）如图，在平面直角坐标系xOy中，抛物线y=ax2﹣2ax﹣3a（a ＜0）与x轴交于A，B两点（点A在点B的左侧），经过点A的直线l：y=kx+b与y 轴交于点C，与抛物线的另一个交点为D，且CD=4AC．（1）直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；（2）点E是直线l上方的抛物线上的一点，若△ACE的面积的最大值为，求a 的值；（3）设P是抛物线对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．11. 如图，已知等边三角形ABC中，点D，E，F分别为边AB，AC，BC的中点，M 为直线BC上一动点，△DMN为等边三角形（点M的位置改变时，△DMN也随之整体移动）．（1）如图①，当点M在点B左侧时，请你判断EN与MF有怎样的数量关系点F 是否在直线NE上请直接写出结论，不必证明或说明理由；（2）如图②，当点M在BC上时，其它条件不变，（1）的结论中EN与MF的数量关系是否仍然成立？若成立，请利用图2证明；若不成立，请说明理由；（3）若点M在点C右侧时，请你在图③中画出相应的图形，并判断（1）的结论中EN与MF的数量关系是否仍然成立？若成立，请直接写出结论，不必证明或说明理由．【答案与解析】一、填空题1.【答案】（0，0），（0，10），（0，2），（0，8）2.【答案】（2×3n﹣1，0）.【解析】∵点B1、B2、B3、…、Bn在直线y=2x的图象上，∴A1B1=4，A2B2=2×（2+4）=12，A3B3=2×（2+4+12）=36，A4B4=2×（2+4+12+36）=108，…，∴An Bn=4×3n﹣1（n为正整数）．∵OAn =AnBn，∴点An的坐标为（2×3n﹣1，0）．故答案为：（2×3n﹣1，0）．二、选择题3.【答案】A.【解析】分两种情况：①当0≤t＜4时，作OG⊥AB于G，如图1所示：∵四边形ABCD是正方形，∴∠B=90°，AD=AB=BC=4cm，∵O是正方形ABCD的中心，∴AG=BG=OG=AB=2cm，∴S=APOG=×t×2=t（cm2），②当t≥4时，作OG⊥AB于G，如图2所示：S=△OAG的面积+梯形OGBP的面积=×2×2+（2+t﹣4）×2=t（cm2）；综上所述：面积S（cm2）与时间t（s）的关系的图象是过原点的线段，故选A．4.【答案】A.三、解答题5.【答案与解析】解：（1）能，如图1，∵点P以1厘米/秒的速度沿AC向终点C运动，点Q以厘米/秒的速度沿BC向终点C运动,t=1秒∴AP=1，BQ=，∵AC=4，BC=5，点D在BC上，CD=3，∴PC=AC-AP=4-1=3，QD=BC-BQ-CD==，∵PE∥BC，解得PE=，∵PE∥BC，PE=QD，∴四边形EQDP是平行四边形；（2）如图2，∵点P以1厘米/秒的速度沿AC向终点C运动，点Q以厘米/秒的速度沿BC向终点C运动，∴PC=AC-AP=4-t，QC=BC-BQ=，∴∴PQ∥AB；（3）分两种情况讨论：①如图3，当∠EQD=90°时，显然有EQ=PC=4-t，又∵EQ∥AC，∴△EDQ∽△ADC∴，∵BC=5，CD=3，∴BD=2，∴DQ=，∴解得t=（秒）；②如图4，当∠QED=90°时，作EM⊥BC于M，CN⊥AD于N，则EM=PC=4-t，在 Rt△ACD中，∵AC=4，CD=3，∴AD=，∵∠CDA=∠EDQ，∠QED=∠C=90°，∴△EDQ∽△CDA，∴ t=（秒）．综上所述，当 t=秒或t=秒时，△EDQ为直角三角形．6.【答案与解析】解：（1）过点B作BD⊥OA于点D，则四边形CODB是矩形，BD=CO=4，OD=CB=3，DA=3在Rt△ABD中，．当时，，，．∵，，∴，即（秒）．（2）过点作轴于点，交的延长线于点，∵，∴，．即，．，．，∴．即（）．由，得．∴当时，S有最小值，且7.【答案与解析】解：（1）∵四边形ABCD是正方形，∴AC垂直平分BD，∴PB=PD，由题意易得：PB+PE=PD+PE=DE，在△ADE中，根据勾股定理得，DE=；（2）作A关于OB的对称点A′，连接A′C，交OB于P，PA+PC的最小值即为A′C的长，∵∠AOC=60°∴∠A′OC=120°作OD⊥A′C于D，则∠A′OD=60°∵OA′=OA=2∴A′D=∴；（3）分别作点P关于OA、OB的对称点M、N，连接OM、ON、MN，MN交OA、OB于点Q、R，连接PR、PQ，此时△PQR周长的最小值等于MN．由轴对称性质可得，OM=ON=OP=10，∠MOA=∠POA，∠NOB=∠POB，∴∠MON=2∠AOB=2×45°=90°，在Rt△MON中，MN===10．即△PQR周长的最小值等于10．8.【答案与解析】解：（1）∵CN=CB=15，OC=9，∴ON==12，∴N（12，0）；又∵AN=OA﹣ON=15﹣12=3，设AM=x∴32+x2=（9﹣x）2，∴x=4，M（15，4）；（2）解法一：设抛物线l为y=（x﹣a）2﹣36则（12﹣a）2=36∴a1=6或a2=18（舍去）∴抛物线l：y=（x﹣6）2﹣36 解法二：∵x2﹣36=0，∴x1=﹣6，x2=6；∴y=x2﹣36与x轴的交点为（﹣6，0）或（6，0）由题意知，交点（6，0）向右平移6个单位到N点，所以y=x2﹣36向右平移6个单位得到抛物线l：y=（x﹣6）2﹣36；（3）①由“三角形任意两边的差小于第三边”知：P点是直线MN与对称轴x=6的交点，设直线MN的解析式为y=kx+b，则，解得，∴y=x﹣16，∴P（6，﹣8）；②∵DE∥OA，∴△CDE∽△CON，∴；∴S=∵a=﹣＜0，开口向下，又m=﹣∴S有最大值，且S=﹣．最大9.【答案与解析】解：（1）∵y=kx﹣1与y轴相交于点C，∴OC=1；∵tan∠OCB=，∴OB=；∴B点坐标为:；把B点坐标为：代入y=kx﹣1得：k=2；（2）∵S=，y=kx﹣1，∴S=×|2x﹣1|；∴S=|x﹣|；（3）①当S=时，x﹣=，∴x=1，y=2x﹣1=1；∴A点坐标为（1，1）时，△AOB的面积为；②存在．满足条件的所有P点坐标为：P1（1，0），P2（2，0），P3（，0），P4（，0）．10.【答案与解析】解：（1）令y=0，则ax2﹣2ax﹣3a=0，解得x1=﹣1，x2=3∵点A在点B的左侧，∴A（﹣1，0），如图1，作DF⊥x轴于F，∴DF∥OC，∴=，∵CD=4AC，∴==4，∵OA=1，∴OF=4，∴D点的横坐标为4，代入y=ax2﹣2ax﹣3a得，y=5a，∴D（4，5a），把A、D坐标代入y=kx+b得，解得，∴直线l的函数表达式为y=ax+a．（2）设点E（m，a（m+1）（m﹣3）），yAE =k1x+b1，则，解得：，∴yAE=a（m﹣3）x+a（m﹣3），∴S△ACE=（m+1）[a（m﹣3）﹣a]=（m﹣）2﹣a，∴有最大值﹣a=，∴a=﹣；（3）令ax2﹣2ax﹣3a=ax+a，即ax2﹣3ax﹣4a=0，解得x1=﹣1，x2=4，∴D（4，5a），∵y=ax2﹣2ax﹣3a，∴抛物线的对称轴为x=1，设P1（1，m），①若AD是矩形的一条边，由AQ∥DP知xD ﹣xP=xA﹣xQ，可知Q点横坐标为﹣4，将x=﹣4带入抛物线方程得Q（﹣4，21a），m=yD +yQ=21a+5a=26a，则P（1，26a），∵四边形ADPQ为矩形，∴∠ADP=90°，∴AD2+PD2=AP2，∵AD2=[4﹣（﹣1）]2+（5a）2=52+（5a）2，PD2=[4﹣（﹣1）]2+（5a）2=52+（5a）2，∴[4﹣（﹣1）]2+（5a）2+（1﹣4）2+（26a﹣5a）2=（﹣1﹣1）2+（26a）2，即a2=，∵a＜0，∴a=﹣，∴P1（1，﹣）．②若AD是矩形的一条对角线，则线段AD的中点坐标为（，），Q（2，﹣3a），m=5a﹣（﹣3a）=8a，则P（1，8a），∵四边形ADPQ为矩形，∴∠APD=90°，∴AP2+PD2=AD2，∵AP2=[1﹣（﹣1）]2+（8a）2=22+（8a）2，PD2=（4﹣1）2+（8a﹣5a）2=32+（3a）2，AD2=[4﹣（﹣1）]2+（5a）2=52+（5a）2，∴22+（8a）2+32+（3a）2=52+（5a）2，解得a2=，∵a＜0，∴a=﹣，∴P2（1，﹣4）．综上可得，P点的坐标为P1（1，﹣4），P2（1，﹣）．11.【答案与解析】解：（1）判断：EN与MF相等（或EN=MF），点F在直线NE上.（2）成立．证明：连结DE，DF．∵△ABC是等边三角形，∴AB=AC=BC．又∵D，E，F是三边的中点，∴DE，DF，EF为三角形的中位线．∴DE=DF=EF，∠FDE=60°．又∠MDF+∠FDN=60°，∠NDE+∠FDN=60°，∴∠MDF=∠NDE．在△DMF和△DNE中，DF=DE，DM=DN，∠MDF=∠NDE，∴△DMF≌△DNE．∴MF=NE．（3）画出图形（连出线段NE），MF与EN相等的结论仍然成立（或MF=NE成立）．。

代数几何综合课后练习题一：如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于A（-1，0）、B（3，0）两点，与y轴交于点C （0，3）．（1）求抛物线的解析式及顶点M坐标；（2）在抛物线的对称轴上找到点P，使得△PAC的周长最小，并求出点P的坐标.题二：如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于点A（-4，0），B（1，0），与y轴交于点D（0，4），点C（-2，n）也在此抛物线上．（1）求此抛物线的解析式及点C的坐标；（2）设BC交y轴于点E，连接AE，AC请判断△AC E的形状，并说明理由.C的横坐标)（代数几何综合课后练习参考答案题一： （1）y=214x --+（），M （1，4）；（2）P （1，2）. 详解：（1）∵抛物线y =ax 2+bx+c （a≠0）过A （-1，0）、B （3，0）， C （0，3）三点，∴93003a b c a b c c ++=⎧⎪-+=⎨⎪=⎩，解得12c=3a b =-⎧⎪=⎨⎪⎩.[来源:Zxx k.Com]故抛物线的解析式为222314y x x x =-++=--+（），故顶点M 为（1，4）； （2）如图1，∵点A 、B 关于抛物线的对称轴对称，∴连接BC 与抛物线对称轴交于一点，即为所求点P ．设对称轴与x 轴交于点H ， 题二： （1）y=-x 2-3x+4，C （-2，6）；（2）△ACE 为等腰直角三角形.详解：（1）∵抛物线经过A 、B 、D 三点，∴代入抛物线解析式可得164004a b c a b c c -+⎧⎪++⎨⎪⎩＝＝＝，解得134a b c -⎧⎪-⎨⎪⎩＝＝＝，∴抛物线的解析式为 y=-x 2-3x+4，∵点C （-2，n ）也在此抛物线上，∴n=-4+6+4=6，∴C 点坐标为（-2，6）；∴AE2+CE2=20+20=40=AC 2，且AE=CE，∴△ACE为等腰直角三角形.详解：（1）①连接OB，过点B作轴的交点，），．详解：（1）①如图1所示，过点E作⊙O ∴∠OE R=30°，的关联点，则需点H=60°，可得点2019-2020学年数学中考模拟试卷一、选择题1．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（）A．30°B．25°C．20°D．15°2．小明骑自行车去上学途中，经过先上坡后下坡的一段路，在这段路上所骑行的路程S(米)与时间t(分钟)之间的函数关系如图所示.下列结论:①小明上学途中下坡路的长为1800米;②小明上学途中上坡速度为150米/分，下坡速度为200米/分;③如果小明放学后按原路返回，且往返过程中，上、下坡的速度都相同，则小明返回时经过这段路比上学时多用1分钟;④如果小明放学后按原路返回，返回所用时间与上学所用时间相等，且返回时下坡速度是上坡速度的1.5倍，则返回时上坡速度是160米/分其中正确的有（）A.①④B.②③C.②③④D.②④3．某游客为爬上3千米高的山顶看日出，先用1小时爬了1千米，休息0.5小时后，再用1.5小时爬上山顶．游客爬山所用时间l与山高h间的函数关系用图形表示是（）A. B.C. D.4．我们探究得方程x+y＝2的正整数解只有1组，方程x+y＝3的正整数解只有2组，方程x+y＝4的正整数解只有3组，……，那么方程x+y+z＝10的正整数解得组数是（）A．34 B．35 C．36 D．375．实数在数轴上对应点的位置如图所示，则正确的结论是（）A. B. C. D.6．在半径为8cm 的圆中，垂直平分半径的弦长为( )A ．4cmB ．C ．8cmD ．7．如图，在平面直角坐标系xOy 中，以原点O 为圆心的圆过点A(13,0)直线y=kx-3k+4与交于B 、C 两点，则弦BC 的长的最小值为( )A ．22B ．24C ．D ． 8．如图，抛物线2y ax bx c =++与x 轴相交于A 、B 两点，点A 在点B 左侧，顶点在折线M-P-N 上移动，它们的坐标分别为(1,4)M -、(3,4)P 、(3,1)N .若在抛物线移动过程中，点A 横坐标的最小值为-3，则a b c -+的最小值是（ ）A ．-15B ．-12C ．-4D ．-29．如图，点P 是∠AOB 内任意一点，∠AOB ＝30°，OP ＝8，点M 和点N 分别是射线OA 和射线OB 上的动点，则△PMN 周长的最小值为（ ）A ．5B ．6C ．8D ．1010．如图，在四边形ABCD 中，对角线AC ⊥BD ，垂足为点O ，顺次连接四边形ABCD 各边中点E ，F ，G ，H ，则所得四边形EFGH 的形状为（ ）A.对角线不相等的平行四边形B.矩形C.菱形D.正方形11．下列图案中，既是轴对称图形，又是中心对称图形的是（ ）A ．B ．C ．D ．12．已知二次函数()2y x h =-+（h 为常数），当自变量x 的值满足25x ≤≤时，其对应对的函数值y 的最大值为1-，则h 的值为（ ） A.3-或6- B.1-或6-C.1-或3-D.4-或6-二、填空题13．如图，AB ∥CD ．若∠ACD=82°，∠CED=29°，则∠ABD 的大小为______度．14．一次函数y=ax+b 和反比例函数y=bx在同一坐标系内的大致图象如上图所示，则a___0，b___0.15．如图，AB 、BC 是⊙O 的弦，OM ∥BC 交AB 于点M ，若∠AOC=100°，则∠AMO=___.16．36的算术平方根是 ．17．《算法统宗》是中国古代数学名著，作者是明代著名数学家程大位．在其中有这样的记载“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”译文：有100名和尚分100个馒头，正好分完．如果大和尚一人分3个，小和尚3人分一个，试问大、小和尚各有几人？设有大和尚x 人，小和尚y 人，可列方程组为______．18．某校抽查50名九年级学生对艾滋病三种主要传授途径的知晓情况，结果如表估计该校九年级600名学生中，三种传播途径都知道的有_____人．三、解答题19．如图，在▱ABCD中，E是对角线BD上的一点，过点C作CF∥BD，且CF＝DE，连接AE，BF，EF．（1）求证：△ADE≌△BCF．（2）若∠BFC﹣∠ABE＝90°，sin∠ABE＝23，BF＝4，求BE的长．20．如图，点P是AB所对弦AB上一动点，点Q是AB与弦AB所围成的图形的内部的一定点，作射线PQ交AB于点C，连接BC．已知AB＝6cm，设A，P两点间的距离为xcm，P，C两点间的距离为y1cm，B，C两点间的距离为y2cm．（当点P与点A重合时，x的值为0）．小平根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．下面是小平的探究过程，请补充完整：（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了y与x的几组对应值；x/经测量m的值是（保留一位小数）．（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），（x，y2），并画出函数y1，y2的图象；（3）结合函数图象，解决问题：当△BCP为等腰三角形时，AP的长度约为cm．21．为丰富学生的课余生活，学校准备购买部分体育器材，以满足学生们的需求．学校对“我最喜爱的体育运动”进行了抽样调查（每个学生只选一次），根据调查结果绘成如图所示的两幅不完整统计图，请你根据统计图提供的信息解答下列问题．（1）求m、n的值；（2）若该校有2000名学生，请你根据样本数据，估算该校喜欢踢足球的学生人数是多少？22．消费者在网店购物后，将从“好评、中评、差评”中选择一种作为对卖家的评价，假设这三种评价是等可能的，若小明、小亮在某网店购买了同一商品，且都给出了评价，则两人中至少有一个给“好评”的概率为( )A．13B．49C．59D．2323．一只不透明的袋子中装有1个蓝球和2个红球，这些球除颜色外都相同．(1)搅匀后从中任意摸出1个球，摸到蓝球的概率为；(2)搅匀后从中任意摸出1个球，记录颜色后放回、搅匀，再从中任意摸出1个球，求至少有1次摸到红球的概率．24．如图，在△ABC中，以AC为直径的⊙O与边AB交于点D，点E为⊙O上一点，连接CE并延长交AB于点F，连接ED．（1）若BC是⊙O的切线，求证：∠B+∠FED＝90°；（2）若FC＝6，DE＝3，FD＝2．求⊙O的直径．25．“扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售y（件）与销售单价x（元）之间存在一次函数关系，如图所示.（1）求y与x之间的函数关系；（2）如果规定每天漆器笔筒的销售量不低于260件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？（3）该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3490元，试确定该漆器笔筒销售单价的范围.【参考答案】***一、选择题二、填空题13．5314．< >15．5016．17．100131003x yx y+=⎧⎪⎨+=⎪⎩18．300三、解答题19．（1）见解析（2）6【解析】【分析】（1）根据平行四边形的性质和全等三角形的判定证明即可；（2）想证明四边形ABFE是平行四边形，得出AE=BF=4，由△ADE≌△BCF，得出∠AED=∠BFC，由三角形的外角性质证出∠BAE=90°，再由三角函数定义即可求出BE的长．【详解】（1）证明：∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，∴∠ADB＝∠DBC，∵CF∥DB，∴∠BCF＝∠DBC，∴∠ADB＝∠BCF在△ADE与△BCF中，DE CFADE CBF AD BC=⎧⎪∠=∠⎨⎪=⎩，∴△ADE≌△BCF（SAS）．（2）解：∵CF∥DB，且CF＝DE，∴四边形CFED是平行四边形，∴CD＝EF，CD∥EF，∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∴AB＝EF，AB∥EF，∴四边形ABFE是平行四边形，∴AE＝BF＝4，∵△ADE≌△BCF，∴∠AED＝∠BFC，∵∠BFC﹣∠ABE＝90°，∴∠AED﹣∠ABE＝90°，∵∠AED＝∠ABE+∠BAE，∴∠BAE＝90°，∵sin∠ABE＝AEBE＝23，∴BE＝32BE＝6．【点睛】此题考查平行四边形的性质与判定、全等三角形的判定与性质、三角形的外角性质、三角函数等知识；熟练掌握平行四边形的性质和判定，和全等三角形的判定以及菱形的判定解答．20．（1）3；（2）详见解析；（3）1.2或1.6或3.0．【解析】【分析】（1）利用圆的半径相等即可解决问题；（2）利用描点法画出图象即可．（3）图中寻找PB长关于x的函数：直线y=-x+6与两个函数的交点的横坐标以及y1与y2的交点的横坐标即可.【详解】解：（1）（1）∵PA＝0时，点P与点A重合，AB＝6，PC＝AC＝5.37，BC＝2.68，∴AB2＝PC2+BC2，∴∠ACB＝90°，∴AB是直径．当x＝3时，PA＝PB＝PC＝3，∴y1＝3，故答案为3．（2）如图；（3）观察图象可知：当x＝y，即当PB＝PC或PB＝BC时，x＝3或1.2，当y1＝y2时，即PC＝BC时，x＝1.6，或x＝6（与P重合，△BCP不存在）综上所述，满足条件的x的值为1.2或1.6或3，．故答案为1.2或1.6或3.0．【点睛】本题考查动点问题函数图象、圆的有关知识，解题的关键是学会利用图象法解决问题，属于中考常考题型．21．（1）m＝40，n＝60；（2）该校喜欢踢足球的学生人数是400人．【解析】【分析】（1）根据喜爱篮球的人数÷其所占的百分比得到总人数，再由总人数乘以喜爱排球的人数所占百分比得到n，用总人数-喜爱篮球人数-喜爱排球的人数-喜爱其他人数，即可确定出m的值；（2）求出喜欢踢足球的学生人数所占的百分比，乘以2000即可得到结果．【详解】（1）70÷35%＝200（人）n＝200×30%＝60，m＝200﹣70﹣60﹣40＝40；（2）2000×40200＝400 （人）答：该校喜欢踢足球的学生人数是400人．【点睛】此题考查了条形统计图，扇形统计图，以及用样本估计总体，弄清题意是解本题的关键．22．C【解析】【分析】画树状图展示所有9种等可能的结果数，找出两人中至少有一个给“好评”的结果数，然后根据概率公式求解．【详解】画树状图为：共有9种等可能的结果数，两人中至少有一个给“好评”的结果数为5，所以两人中至少有一个给“好评”的概率＝59．故选C．【点睛】本题考查了列表法与树状图法：利用列表法或树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式计算事件A或事件B的概率．23．(1)13;(2)89.【解析】【分析】（1）由共有3种等可能结果，其中摸到蓝球可能的结果有1种，根据概率公式求解可得；（2）画树状图列出所有等可能结果，再根据概率公式求解可得．【详解】解：（1）∵袋中共有3个球，∴共有3种等可能结果，其中摸到蓝球可能的结果有1种．∴P（摸到蓝球）=13，故答案为：13；（2）将2个红球编号为红球1，红球2，用树状图表示出所有可能出现的结果，由树状图知，共有9种等可能结果，其中至少有一次摸到红球可能的结果有8种．∴P （至少有1次摸到红球）=89． 【点睛】本题考查了列表法与树状图法求概率：通过列表法或树状图法展示所有等可能的结果求出n ，再从中选出符合事件A 或B 的结果数目m ，然后根据概率公式求出事件A 或B 的概率． 24．（1）见解析；（2）⊙O 的直径为9． 【解析】 【分析】（1）利用圆内接四边形对角互补以及邻补角的定义得出∠FED=∠A ，进而得出∠B+∠A=90°，求出答案； （2）利用相似三角形的判定与性质首先得出△FED ∽△FAC ，进而求出即可． 【详解】（1）证明：∵∠A+∠DEC ＝180°，∠FED+∠DEC ＝180°， ∴∠FED ＝∠A ， ∵BC 是⊙O 的切线， ∴∠BCA ＝90°， ∴∠B+∠A ＝90°， ∴∠B+∠FED ＝90°；（2）解：∵∠CFA ＝∠DFE ，∠FED ＝∠A ， ∴△FED ∽△FAC ，∴DE DFAC FC =， ∴326AC =， 解得：AC ＝9，即⊙O 的直径为9． 【点睛】此题主要考查了相似三角形的判定与性质以及切线的性质等知识，得出△FED ∽△FAC 是解题关键．25．（1）10700y x =-+；（2）销售单价为44元时，每天获取的利润最大，3640W =最大元；（3）4456x ≤≤.【解析】 【分析】（1）可用待定系数法来确定y 与x 之间的函数关系式；（2）根据利润=销售量×单件的利润，然后将（1）中的函数式代入其中，求出利润和销售单件之间的关系式，然后根据其性质来判断出最大利润；（3）首先得出w 与x 的函数关系式，进而利用所获利润等于3490元时，对应x 的值，根据增减性，求出x 的取值范围． 【详解】（1）设y kx b =+y=k x+b ∴ 经过点(40,300),(55,150)4030055150k b k b +=⎧∴⎨+=⎩ 解得10700k b =-⎧⎨=⎩故y 与x 的关系式为：10700y x =-+ （2）30＜44x ≤设利润为(30)(30)(10700)w x y x x =-⋅=--+221010002100010(50)4000w x x x =-+-=--+100-<∴x<50时，w 随x 的增大而增大， ∴当44x =时，3640W =最大 （2）由题意，得 -10x+700≥260， 解得x≤44， ∴30＜x≤44，设利润为w=（x-30）•y=（x-30）（-10x+700）， w=-10x 2+1000x-21000=-10（x-50）2+4000， ∵-10＜0，∴x ＜50时，w 随x 的增大而增大，∴x=44时，w 最大=-10（44-50）2+4000=3640，答：当销售单价为44元时，每天获取的利润最大，最大利润是3640元； （3）w-150=-10x 2+1000x-21000-150=3490， -10（x-50）2=-360， x-50=±6， x 1=56，x 2=44， 如图所示，由图象得：当44≤x≤56时，捐款后每天剩余利润不低于3490元．【点睛】此题主要考查了二次函数的应用、一次函数的应用和一元二次方程的应用，利用函数增减性得出最值是解题关键，能从实际问题中抽象出二次函数模型是解答本题的重点和难点．2019-2020学年数学中考模拟试卷一、选择题1．若x+y＝3且xy＝1，则代数式（1+x）（1+y）的值等于（）A.5B.﹣5C.3D.﹣32．下列图形既是轴对称图形，又是中心对称图形的是（）A．三角形 B．菱形 C．角 D．平行四边形3．如图，是由几个大小相同的小立方块所搭几何体的俯视图，其中小正方形中的数字表示在该位置的小立方块的个数，则这个几何体的主视图是（）A．B．C．D．4．在一次数学课上，张老师出示了一个题目：“如图，▱ABCD的对角线相交于点O，过点O作EF垂直于BD交AB，CD分别于点F，E，连接DF，BE．请根据上述条件，写出一个正确结论．”其中四位同学写出的结论如下：小青：OE=OF；小何：四边形DFBE是正方形；小夏：S四边形AFED=S四边形FBCE；小雨：∠ACE=∠CAF．这四位同学写出的结论中不正确的是（）A.小青B.小何C.小夏D.小雨5．如图，八个完全相同的小长方形拼成一个正方形网格，连结小长方形的顶点所得的四个三角形中是相似三角形的是（）A．①和②B．②和③C．①和③D．①和④6．已知二次函数y＝ax2+（a+2）x﹣1（a为常数，且a≠0），（）A．若a＞0，则x＜﹣1，y随x的增大而增大B．若a＞0，则x＜﹣1，y随x的增大而减小C．若a＜0，则x＜﹣1，y随x的增大而增大D．若a＜0，则x＜﹣1，y随x的增大而减小7．已知圆锥的侧面积是8πcm2，若圆锥底面半径为R（cm），母线长为l（cm），则R关于l的函数图象大致是（ ）A ．B ．C ．D ．8 （ ） A ．16的平方根B ．16的算术平方根C ．±4D ．±29．下列运算正确的是( ) A ．3x 2•4x 2＝12x 2B ．x 3+x 5＝x 8C ．x 4÷x＝x 3D ．(x 5)2＝x 710．如图，在△ABC 中，点D 在AB 边上，点E 在AC 边上DE ∥BC ，点B 、C 、F 在一条直线上，若∠ACF ＝140°，∠ADE ＝105°，则∠A 的大小为（ ）A ．75°B ．50°C ．35°D ．30°11．在同一直角坐标平面内，如果直线y ＝k 1x 与双曲线2k y x=没有交点，那么k 1和k 2的关系一定是（ ） A.k 1+k 2＝0B.k 1•k 2＜0C.k 1•k 2＞0D.k 1＝k 212．如图，已知圆锥的母线长为6，圆锥的高与母线所夹的角为θ，且sin θ=13，则该圆锥的侧面积是（ ）A ．B ．24πC ．16πD ．12π二、填空题 13．反比例函数y ＝kx与一次函数y ＝kx+m 的图象有一个交点是（﹣2，1），则它们的另一个交点的坐标是_____．14．从1,2,3,4四个数中任取一个数作为AC的长度，又从4,5中任取一个数作为BC的长度，6AB ，则AB AC BC、、能构成三角形的概率是_____．15．二次函数y＝x2﹣2x﹣5的最小值是______．16﹣|﹣2|＝_____．17．已知⊙O的半径为2cm，弦AB长为，则这条弦的中点到弦所对劣弧中点的距离为_____cm．18．当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为100°，那么这个“特征三角形”的最小内角的度数为_______．三、解答题19．从甲地到乙地有A，B，C三条不同的公交线路．为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况，在每条线路上随机选取了500个班次的公交车，收集了这些班次的公交车用时（单位：分钟）的数据，统计如下：（1）将上面表格补充完整；（2）某天王先生和李女士从甲地到乙地，试用树状图或列表法求在早高峰期间刚好都坐同一条线路的概率；（3）小张从甲地到乙地，早高峰期间用时不超过45分钟，请问小张应该选择哪条线路？请说明理由．20．(1)阅读理解利用旋转变换解决数学问题是一种常用的方法．如图1，点P是等边三角形ABC内一点，PA＝1，PB，PC＝2．求∠BPC的度数．为利用已知条件，不妨把△BPC绕点C顺时针旋转60°得△AP′C，连接PP′，则PP′的长为_____；在△PAP′中，易证∠PAP′＝90°，且∠PP′A的度数为_____，综上可得∠BPC的度数为_____；(2)类比迁移如图2，点P是等腰Rt△ABC内的一点，∠ACB＝90°，PA＝2，PB，PC＝1，求∠APC的度数；(3)拓展应用如图3，在四边形ABCD中，BC＝3，CD＝5，AB＝AC＝12AD．∠BAC＝2∠ADC，请直接写出BD的长．21．计算：020194sin60|2|(1)--+-．22．解不等组533(1)131922x xx x->+⎧⎪⎨-<-⎪⎩并求出其整数解．23．某汽车专卖店销售甲，乙两种型号的新能源汽车，上周售出甲型汽车和乙型汽车各2辆，销售额为88万元；本周售出3辆甲型汽车和1辆乙型汽车，两周的销售额为184万元.（1）求每辆甲型汽车和乙型汽车的售价；（2）某公司拟向该店购买甲，乙两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元.则有哪几种购车方案？24．已知O的直径为10，点A，B，C在O上，CAB∠的平分线交O于点D.（I）如图①，当BC为OO的直径时，求BD的长；（Ⅱ）如图②，当BD=5时，求∠CDB的度数。

代数几何综合1、〔2021年潍坊市压轴题〕如图，抛物线c bx ax y ++=2关于直线1=x 对称，与坐标轴交于C B A 、、三点，且4=AB ,点⎪⎭⎫ ⎝⎛232，D 在抛物线上，直线是一次函数()02≠-=k kx y 的图象，点O 是坐标原点.〔1〕求抛物线的解析式；〔2〕假设直线平分四边形OBDC 的面积，求k 的值.〔3〕把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线与直线交于N M 、两点，问在y 轴正半轴上是否存在一定点P ，使得不管k 取何值，直线PM 与PN 总是关于y 轴对称？假设存在，求出P 点坐标；假设不存在，请说明理由.答案：〔1〕因为抛物线关于直线x=1对称，AB=4，所以A(-1，0),B(3，0), 由点D(2，1.5)在抛物线上，所以⎩⎨⎧=++=+-5.1240c b a c b a ，所以3a+3b=1.5,即a+b=0.5,又12=-a b ，即b=-2a,代入上式解得a =-0.5,b =1,从而c=1.5,所以23212++-=x x y . 〔2〕由〔1〕知23212++-=x x y ，令x=0,得c(0,1.5),所以CD//AB,令kx -2=1.5,得l 与CD 的交点F(23,27k )，令kx -2=0，得l 与x 轴的交点E(0,2k)，根据S 四边形OEFC =S 四边形EBDF 得：OE+CF=DF+BE,即：,511),272()23(272=-+-=+k k k k k 解得 〔3〕由〔1〕知,2)1(21232122+--=++-=x x x y所以把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线的解析式为221x y -= 假设在y 轴上存在一点P(0，t)，t ＞0，使直线PM 与PN 关于y 轴对称，过点M 、N 分别向y 轴作垂线MM 1、NN 1，垂足分别为M 1、N 1，因为∠MPO=∠NPO,所以Rt △MPM 1∽Rt △NPN 1,所以1111PN PM NN MM =,………………(1) 不妨设M(x M ,y M )在点N(x N ,y N )的左侧，因为P 点在y 轴正半轴上， 那么〔1〕式变为NMN M y t y t x x --=-,又y M =k x M -2, y N =k x N -2, 所以〔t+2〕(x M +x N )=2k x M x N,……(2) 把y=kx-2(k ≠0)代入221x y -=中，整理得x 2+2kx-4=0, 所以x M +x N =-2k, x M x N =-4,代入〔2〕得t=2,符合条件，故在y 轴上存在一点P 〔0,2〕，使直线PM 与PN 总是关于y 轴对称.考点：此题是一道与二次函数相关的压轴题，综合考查了考查了二次函数解析式确实定，函数图象交点及图形面积的求法，三角形的相似，函数图象的平移，一元二次方程的解法等知识，难度较大.点评：此题是一道集一元二次方程、二次函数解析式的求法、相似三角形的条件与性质以及质点运动问题、分类讨论思想于一体的综合题，能够较好地考查了同学们灵活应用所学知识，解决实际问题的能力。

代数几何综合问题题1、（北京丰台）如图，已知平面直角坐标系中三点A （2，0），B （0，2），P （x ，0）)0(<x ，连结BP ，过P 点作PC PB ⊥交过点A 的直线a 于点C （2，y ） （1）求y 与x 之间的函数关系式；（2）当x 取最大整数时，求BC 与PA 的交点Q 的坐标。

解：（1） PC PB BO PO ⊥⊥, ∴∠+∠=︒∠+∠=︒∴∠=∠CPA OPB PBO OPB CPA PBO 9090, A （2，0），C （2，y ）在直线a 上 ∴∠=∠=︒BOP PAC 90 ∴∆∆B O P PAC ~∴=PO AC BO PA ，∴=+||||||x y x 22， x y x y x <<∴=-0022，，∴=-+y x x 122 （2） x <0，∴x 的最大整数值为-1 , 当x =-1时，y =-32，∴=CA 32BO a BOQ CAQ OQ AQ BOCA//~,，∴∴=∆∆ 设Q 点坐标为()m ，0，则AQ m =-2∴-=∴=m m m 223287， ∴Q 点坐标为()870，说明：利用数形结合起来的思想，考查了相似三角形的判定及应用。

关键是搞清楚用坐标表示的数与线段的长度的关系。

题2、（2006、徐州）在平面直角坐标系中，已知矩形ABCD 中，边2AB =，边1AD =，且AB 、AD 分别在x 轴、y 轴的正半轴上，点A 与坐标原点重合．将矩形折叠，使点A 落在边DC 上，设点A '是点A 落在边DC 上的对应点．（1）当矩形ABCD 沿直线12y x b =-+折叠时（如图1），求点A '的坐标和b 的值；（2）当矩形ABCD 沿直线y kx b =+折叠时，① 求点A '的坐标（用k 表示）；求出k 和b 之间的关系式； ② 如果我们把折痕所在的直线与矩形的位置分 为如图2、3、4所示的三种情形， 请你分别写出每种情形时k 的取值范围． （将答案直接填在每种情形下的横线上）k 的取值范围是 ； k 的取值范围是 ；k 的取值范围是 ；【分析：】1、对折是一个操作性名词，它的数学实质就是轴对称。

代数综合题一：对于实数a, b,我们用符号min{a, b}表示a, b两数中较小的数,如min{3, 5}=3 ,因此，min{ —1, — 2}=; 若min {(x+1)2,x2} = 4 ,则x=.题二：对于实数c, d,我们用符号max{c, d}表示c, d两数中较大的数，如max{3 , 5}=5 ,因此，max{—1, —1}= ;若max1x2+2x + 2,x2} = 2 ,贝U x= .2 3 ----------- -----------------------------------------------------2题三：如图，平行于x轴的直线AC分别交抛物线y i=x2(x>)与y2=上(xA)3于B、C两点，过点C作y轴的平行线交y1于点D,直线DE//AC,交y2于点E,则匹=BC ----------题四：在平面直角坐标系中，点P(0, m2)(m>0)在y轴正半轴上，过点P作2 2 平行于x轴的直线，分别交抛物线C I： y=工于点A、B,交抛物线C2： y=上49 于点C、D.(1)如图①，原点O关于直线AB的对称点为点Q,分别连接OA, OB, QC 和QD,求》OB与笈QD面积比为.(2)如图②过点A作y轴的平行线交抛物线C2于点E,过点D作y轴的平行线交抛物线C I于点F,在y轴上任取一点M,连接MA、ME、MD和MF, 则/IMAE与Z1MDF 面积的比值为.题五：如图，点E、F在函数y=上(k>0)的图象上，直线EF分别与x轴、y x 轴交于点A、B,且BE: BF=1: 4,过点E作EP，y轴于P,已知—EP的面积为2.⑴求反比例函数的解析式；(2)计算为EF的面积.题六：如图，点A(1, 6)和点M(m, n)都在反比例函数y" (k>0)的图象上. x⑴求反比例函数的解析式；(2)当m=3时，求直线AM的解析式，并求出BOM的面积.「2 ’“题七：设函数v=' x ,若互不相等的实数Xi, X2, X3,满足Vl=V2=/3, 3X +1, X <0求X1 + X2+X3的取值范围.题八：在平面直角坐标系xOy中，抛物线y=x2+4x+3与x轴交于点A、B（点A在点B的左侧），与y轴交于点C.（1）求直线AC的表达式；（2）在x轴下方且垂直于y轴的直线l与抛物线交于点P（X1,必），Q（X2, 丫2）, 与直线AC交于点N（x3, y3）,若x1>x2>x3,结合函数的图象，求与+&+期的取值范围.参考答案题一：一2, —3或 2.详解：.. 一 2<—1,「.min{ —1, —2}=—2,: min{(x+1)2,x 2} = 4 ,当(x+1)2=x 2时，解得：x= —0.5, (x+1)2=x 2=0.25,这时不可能得出最小值为4,当 x> —0.5, (x+1)2>x 2,则 x 2=4,解得 ％=2 或 M = —2(舍去)， 当 x< —0.5, (x+1)2<x 2,则(x+1)2=4,解得 x 1二 —3 或 x 2=1(舍去)，• . x= - 3 或 x=2.题二:详解：- 3>-》「.maxL 12 : max{x 2+2x +2,x 2} = 2 ,2,当 x>—1, x 2+2x+2>x 2,则 x 2+2x+2=2,解得 x 1=0 或 x 2= —2（舍去）， 当 x<—1, x 2+2x+2<x 2,则 x 2=2,解得 x 1 二 —后或 x 2=我 （舍去），• . x=—五或 x=0.题三：V 3 .详解：设A 点坐标为（0, a ）, （a>0）,则x 2=a,解得x= a a ，.二点B （4 , a ）,2____ _.解得—，，点C （肖明」.B —公•「C D //y轴，-3｝二，当 x 2+2x+2=x 2 时,解得：x= — 1, x 2+2x+2=x 2=1,这时不可能得出最大值为•••点D的横坐标与点C的横坐标相同均为怎,• - y1=（v13a）2=3a,题五:(1)y=4, (2)15 .占 八、D 的坐标为（痣,占 八、E 的纵坐标为3a,3a), 「DE//AC,2——=3a, • . x=3 v 1 a , 3 占八、E 的坐标为（3 v,a ,3a), •.DE=3Va —痘，「 DE 3, a 7 3a1八A— AB PO,cS AOB _ 2- 4m-2••.E 点的横坐标为一2m, F 点的横坐标为 3m, .•.y E =l^-2m)2=4m99222 4m _ 5m9 ・ 9，AE=m 2，y F =1x (3m)2=也, 4 422DF=9m- - m 2=-5m-44 5m 3E(—2m,当 SA AEM =1292X 5m 2-)F(3m,耳),4SA DFM = 12① X5m= 15m 3一S DFM15m 3278详解：(1)作EC ，x 轴于C, FD ，x 轴于D, FH ，y 轴于H,如图，•••△OEP 的面积为2,：|k|=2,而k>0,k=4, •••反比例函数解析式为 y=4; x(2) 「EPLy 轴,FH ，y 轴,「.EP//FH, /. A BPE^A BHF ,即HF=4PE,设E 点坐标为(t,，)，则F 点的坐标为(4t,，)， t 4t ・ S ^OEF +S* AQFD = S AQEC +S 梯形ECDF ， 而 S AQFD =S 8EC =2 ,题六：(1)y=6; (2)y=—2x+8, 8. x・「y=x 2_4x+2(x 刃)的对称轴为 x=2, y i =y 2, ：x 2+x 3=4,・•・y=x 2—4x+2(x 冷)的顶点坐标为(2, —2),令 y= —2,代入 y=3x+1,解得：x=—1,「•—1<x 1<0, 贝U x i +x 2+x 3 的取值范围是：-1+4<x 1+x 2+x 3<0+4,3<x 1+x 2+x 3<4.题八：(1)y=x+3; (2) - 8<x 1+x 2+x 3< - 7.PE BE _ 1 =-- , IM ，详解：先作出函数y=」x2-4x '2,* * ** x -0的图象，如图，不妨设X 1VX 2VX 3,勺+…可详解:(1)由y=x2+4x+3得至U： y=(x+3)(x+1), C(0, 3),• .A(—3, 0), B(—1, 0),设直线AC 的表达式为:y=kx+b(k?・•. ：3k：b=°,解得：；k=：，所以直线AC的表达式为y=x+3, b =3 b =3(2)由y=x2+4x+3得至U：y=(x+2)2—1, ••・抛物线y=x2+4x+3的对称轴是x= —2, 顶点坐标是(一2, —1), •. y1=y2,「-2=—4,令y= —1,代入y=x+3,解得：x= — 4,: x1 >x2>x3, •二—4<x3<—3, •二一4 — 4<x1 +x2+x3< — 3 — 4,「•一8<必+垣+&< 一7.代数几何综合题一：如图，已知抛物线y=ax2+bx+c (a?0与x轴交于A (-1, 0)、B (3, 0)两点，与y轴交于点C (0, 3).(1)求抛物线的解析式及顶点M坐标；(2)在抛物线的对称轴上找到点P,使得APAC的周长最小，并求出点P 的坐标.题二：如图，已知抛物线y=ax2+bx+c (a?0与x轴交于点A (-4, 0), B (1,0),与y轴交于点D (0, 4),点C (-2, n)也在此抛物线上.(1)求此抛物线的解析式及点C的坐标；(2)设BC交y轴于点E,连接AE, AC请判断△ ACE的形状，并说明理由.题三：在平面直角坐标系xOy中，给出如下定义：若点P在图形M上，点Q在图形N上，称线段PQ长度的最小值为图形M, N的密距，记为d (M, N).特别地，若图形M, N有公共点，规定d (M, N) =0.(1)如图1, OO的半径为2,①点A (0, 1) , B (4, 3),则d (A, OO) =, d (B, OO) =.②已知直线l： y=3x + b与。

代数几何综合题代数几何综合题是初中数学中覆盖面最广、综合笥最强的题型，近几年的中考试题很多以代数几何综合题的形式出现，其命题的主要结合点是方程与几何、函数与几何等，解代数几何综合题最常用的数学方法是数形结合，由形导数，以数促形。

例1、如图，已知平面直角坐标系中三点A （2，0），B （0，2），P （x ，0）()x <0，连结BP ，过P 点作PC PB ⊥交过点A 的直线a 于点C （2，y ） （1）求y 与x 之间的函数关系式；（2）当x 取最大整数时，求BC 与PA 的交点Q 的坐标。

解：（1） PC PB BO PO ⊥⊥,∴∠+∠=︒∠+∠=︒∴∠=∠CPA OPB PBO OPB CPA PBO 9090, A （2，0），C （2，y ）在直线a 上 ∴∠=∠=︒BOP PAC 90∴∆∆BOP PAC ~∴=PO AC BOPA，∴=+||||||x y x 22， x y x y x<<∴=-0022，，∴=-+y x x 122（2） x <0，∴x 的最大整数值为-1 ,当x =-1时，y =-32，∴=CA 32BO a BOQ CAQ OQ AQ BOCA//~,，∴∴=∆∆ 设Q 点坐标为()m ，0，则AQ m =-2∴-=∴=m m m 223287，Q 点坐标为()870，说明:利用数形结合起来的思想，考查了相似三角形的判定及应用。

关键是搞清楚用坐标表示的数与线段的长度的关系。

练习1．如图，从⊙O 外一点A 作⊙O 的切线AB 、AC ，切点分别为B 、C ，⊙O 的直径BD 为6，连结CD 、AO.(1)求证：CD ∥AO ；（3分）(2)设CD ＝x ，AO ＝y ，求y 与x 之间的函数关系式，并写出自变量x 的取值范围；（3分） (3)若AO ＋CD ＝11，求AB 的长。

（4分）B2．如图，A、B两点的坐标分别是(x1，0)、(x2，O)，其中x1、x2是关于x的方程x2+2x+m-3=O 的两根，且x1<0<x2．(1)求m的取值范围；(2)设点C在y轴的正半轴上，∠ACB=90°，∠CAB=30°，求m的值；(3)在上述条件下，若点D在第二象限，△DAB≌△CBA，求出直线AD的函数解析式.3．一张矩形纸片OABC 平放在平面直角坐标系内，O 为原点，点A 在x 的正半轴上，点C 在y 轴的正半轴上，OA ＝5，OC ＝4。

中考数学模拟题《代数几何综合问题》专项检测题(附答案) 学校:___________班级：___________姓名：___________考号：___________两圆一中垂模型讲解【模型】已知点A，B是平面内两点，再找一点C，使得△ABC为等腰三角形.【结论】分类讨论：若AB=AC,，则点 C 在以点 A 为圆心，线段 AB 的长为半径的圆上若BA=BC,，则点 C 在以点 B 为圆心，线段 AB 的长为半径的圆上若CA=CB 则点 C在线段AB 的垂直平分线PQ 上.以上简称“两圆一中垂”.“两圆一中垂”上的点能构成等腰三角形，但是要除去原有的点A，B，还要除去因共线无法构成三角形的点M，N以及线段AB 中点E(共除去5个点)，需要注意细节.典例秒杀典例1如图平面直角坐标系中已知A(2 2) B(4 0) 若在x轴上取点 C 使. △ABC为等腰三角形，则满足条件的点C 有( ).A.1个B.2 个C.3个D.4个【答案】D【解析】∵点 A B的坐标分别为(2 2) B(4 0) ∴AB=2√2.①若AC=AB 以 A为圆心 AB长为半径画弧与x 轴有2个交点(含 B点) 即(0 0) (4 0)(舍去)∴满足△ABC是等腰三角形的点C 有1个②若 BC=AB 以B为圆心 BA长为半径画弧与x 轴有2个交点，即满足△ABC是等腰三角形的点C 有2个③若CA=CB，作线段AB的垂直平分线与x轴有 1个交点，即满足△ABC是等腰三角形的点C有1个.综上所述，满足条件的点C共有 4个.故选 D.典例2图象上的一点，连接AO并延长交双曲线的另一分支于点B，P 是x 如图，已知点 A(1，2)是反比例函数y=kx轴上一动点.若△PAB是等腰三角形，则点 P的坐标是 .【答案】(-3 0)或(5 0)或(3 0)或(-5 0)的图象关于原点对称【解析】∵反比例函数y=kx∴A，B两点关于点O对称∴O为AB 的中点且 B(-1 -2)∴当△PAB为等腰三角形时，只有. PA=AB或PB=AB两种情况.设点 P 的坐标为(x 0)∵A(1 2) B(-1 -2)∴AB=√[1−(−1)]2+[2−(−2)]2=2√5,PA=√(x−1)2+22,PB=√(x+1)2+(−2)2故当 PA=AB时√(x−1)2+22=2√5,解得x=--3 或x=5 此时 P点坐标为(-3 0)或(5 0);当 PB=AB 时√(x+1)2+(−2)2=2√5,解得 x=3 或x=-5 此时P点坐标为(3 0)或(-5 0).综上可知点 P的坐标为(-3 0)或(5 0)或(3 0)或(-5 0).典例3如图，抛物线y=x²−2x−3与y轴交于点C，点 D的坐标为(0，-1)，抛物线在第四象限内有一点 P，若△PCD 是以CD 为底边的等腰三角形，则点 P 的横坐标为( ).A.1+√2B.1−√2C.√2−1D.1−√2或1+√2【答案】A【解析】令x=0 则y=-3∴点C的坐标为( (0,−3).∵点 D的坐标为(0 -1)×(−1−3)=−2.∴线段CD的中点的纵坐标为12∵△PCD是以CD 为底边的等腰三角形∴点 P 只能在线段CD 的垂直平分线上∴点 P 的纵坐标为-2∴x²−2x−3=−2,解得x1=1−√2,x2=1+√2.∵点 P 在第四象限∴点 P 的横坐标为1+√2.故选 A.小试牛刀1.(★★☆☆☆)如图在平面直角坐标系中AB=2OB,在坐标轴上取一点 P，使得△ABP为等腰三角形，则符合条件的点 P共有( ).A.4个B.5 个C.6个D.7个2.(★★☆☆☆)如图点 A的坐标是(2 2) 若点 P 在x 轴上且△APO是等腰三角形，则点 P的坐标不可能是( ).A.(4 0)B.(1 0)C.(−2√2,0)D.(2 0)(x−√3)2+4上则能3.(★★☆☆☆)已知直线y=−√3x+3与坐标轴分别交于点A B 点 P 在抛物线y=−13使△ABP为等腰三角形的点 P 有( ).A.3个B.4个C.5个D.6 个直击中考的图象交于A(3 4) B(n -1)两点.1.如图所示，一次函数y=kx+b的图象与反比例函数y=mx(1)求反比例函数和一次函数的解析式.(2)在x轴上存在一点C，使△AOC为等腰三角形，求此时点C的坐标.(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.2.已知抛物线y=ax²+bx+c(a≠0)与x轴交于A，B两点(点 A 在点B 的左边)，与y轴交于点C(0,−3),顶点 D 的坐标为( (1,−4).(1)求抛物线的解析式.(2)在y轴上找一点E，使得. △EAC为等腰三角形，请直接写出点 E 的坐标.两垂一圆模型讲解【模型】平面内有两点A，B，再找一点C，使得△ABC为直角三角形.【结论】分类讨论：若∠A=90°,则点 C在过点 A 且垂直于 AB 的直线上(除点 A 外);若∠B=90°,则点 C 在过点 B 且垂直于 AB 的直线上(除点 B 外);若∠C=90°,则点 C在以 AB为直径的圆上(除点 A B外).以上简称“两垂一圆”.“两垂一圆”上的点能构成直角三角形，但要除去A，B两点.典例秒杀典例1如图已知点A(-8 0) B(2 0) 点 C在直线y=−3x+4上，则使△ABC是直角三角形的点C 的个数为( ).4A.4B.3C.2D.1【答案】B【解析】如图所示，有三个点满足条件.典例2的图象上，若△PAB为直角三角形，则满足已知抛物线y=x²−9与x轴交于A，B两点，点 P 在函数y=√3x条件的点 P 的个数为( ).A.2B.3C.4D.6【答案】D【解析】令x²−9=0,解得x₁=3,x₂=−3,不妨设A(-3 0) B(3 0)若AB为斜边，则以 O为圆心，OA长为半径作圆，如图1.的图象的交点即为满足条件的点，这样的点有4个，分别是P₁,P₂,P₃,P₄;圆O与y=√3x的图象于点P₆，P₅，交点即为满足条件的点，若以AB为一直角边，则分别过A，B作x轴的垂线，交y=√3x如图2，这样的点有2个.综上所述，满足条件的点 P 有 6 个.故选 D.典例3如图，在平面直角坐标系中，二次函数y=x²+bx+c的图象的对称轴为经过点(1，0)的直线，其图象与x轴交于点A，B，且过点 C(0，−3),，其顶点为 D，在 y轴上有一点 P(点 P 与点 C 不重合)，使得△APD是以点 P 为直角顶点的直角三角形，则点 P 的坐标为( ).A.(0 3)B.(0,−3)C.(0 -1)D.(0,−1)或(0,−3)【答案】C【解析】由题意得二次函数图象的对称轴为直线. x=1,则−b=1,b=-22又二次函数的图象过点 C(0，-3)∴--3=c 即c=-3∴二次函数的解析式为y=x²−2x−3.由y=x²−2x−3=(x−1)²−4,得顶点 D的坐标为(1 -4).令x²−2x−3=0,得x₁=3,x₂=−1,则 A(3 0).设 P(0 m)(m≠-3) 由题意得PA=√9+m2,PD=√1+(m+4)2,AD=2√5.∵∠APD=90°∴PA²+PD²=AD²,即(√9+m2)2+(√1+(m+4)2)2=(2√5)2.解得m₁=−1,m₂=−3(不合题意，舍去).∴P(0 -1).故选 C.1.(★★★☆☆)如图所示已知 A(2 6) B(8 -2) C为坐标轴上一点且△ABC是直角三角形，则满足条件的点 C 有( ).A.6 个B.7 个C.8个D.9 个2.(★★★☆☆)已知点 P 为二次函数y=x²−2x−3图象上一点，设这个二次函数的图象与x轴交于A，B两点(A 在B 的右侧)，与y轴交于C 点，若△APC为直角三角形且 AC 为直角边，则点 P 的横坐标的值为 .直击中考1.如图 1，抛物线y=ax²+bx+6与 x轴交于点A(-2 0) B(6 0) 与y轴交于点C 顶点为 D 直线AD交y轴于点E.(1)求抛物线的解析式.(2)如图2 将△AOE沿直线AD 平移得到△NMP.①当点 M落在抛物线上时，求点 M的坐标②在△NMP 移动过程中，存在点 M使△MBD为直角三角形，请直接写出所有符合条件的点 M的坐标.胡不归模型讲解从前，有一个小伙子在外地当学徒，当他获悉在家乡的老父亲病危的消息后，便立即启程日夜赶路.由于思念心切，他选择了全是沙砾地带的直线路径A-B(如图所示，A是出发地，B是目的地，AC是一条驿道，而驿道靠近目的地的一侧全是沙砾地带)，当他气喘吁吁地赶到家时，老人刚刚咽了气，小伙子不觉失声痛哭，邻居劝慰小伙子时告诉说，老人在弥留之际不断喃喃地念叨着“胡不归? 胡不归? ……”这个古老的传说，引起了人们的思索，小伙子要提前到家是否有可能呢?倘若有可能，他应该选择怎样的路线呢?这就是风靡千年的“胡不归问题”.【模型】由于在驿道和沙砾地带的行走速度不一样，那么，小伙子有没有可能先在驿道上走一段路程后，再走沙砾地带，虽然多走了路，但反而总用时更短呢?如果存在这种可能，那么要在驿道上行走多远才最省时?【解析】设在沙砾地带的行驶速度为v₁，在驿道上的行驶速度为v₂显然v₁<v₂.不妨假设从 C处进入沙砾地带.设总用时为t，则t=BCv1+ACv2=1v1(BC+v1v2AC).因为 v₁，v₂是确定的，所以只要BC+v1v2AC的值最小，用时就最少.问题就转化为求BC+v1v2AC的最小值.我们可以作一条以C为端点的线段，使其等于v1v2AC,并且与线段CB位于AM 两侧，然后根据两点之间线段最短，不难找到最小值点.怎么作呢?由三角函数的定义，过A点，在 AM的另一侧以A 为顶点，以AM为一边作∠MAN=α,sinα=v1v2,然后作CE⊥AN 则CE=v1v2AC.故当点 B，C，E在一条直线上时，BC+CE的值最小即BC+v1v2AC的值最小，即总用时最少.【问题解决】求形如“PA+kPB”的最值问题，构造射线 AD，使得sin∠DAN=k,即CHAC=k,CH=kAC.将问题转化为求BC+CH 的最小值过 B 点作BH⊥AD交MN于点C 交 AD 于点H 此时BC+CH 取到最小值即BC+kAC的值最小.典例秒杀典例1如图菱形 ABCD中∠ABC=60° 边长为3 P是对角线BD 上的一个动点，则12BP+PC的最小值是( ).A. √3B.32√3 C.3 D.√3+32【答案】B【解析】如图作 PM⊥AB于点M CH⊥AB 于点H.∵四边形ABCD是菱形∴∠PBM=12∠ABC=30∘,∴PM=12PB,∴12PB+PC=PC+PM,根据垂线段最短可知CP+PM的最小值为CH 的长在 Rt△CBH中CH=BC⋅sin60∘=3√32,∴12PB+PC的最小值为3√32,故选 B.典例2如图，△ABC在平面直角坐标系内，点A(0，3 √3) C(2 0).点 B为y 轴上的动点，则12AB+BC的最小值为( ).A.2√3B.52√3C.3√3D.72√3【答案】B【解析】如图，取. D(−3,0),连接AD 作. BE⊥AD,CE′⊥AD交AD于点E′,交 y轴于点B′.∵A(0,3√3),C(2,0),D(−3,0),∴OD=3,OA=3√3,OC=2,CD=5,∴tan∠DAO=ODOA =√33,∴∠DAO=30°,∴EB=12AB,∠ADO=60∘,∴12AB+BC=EB+CB,∴当 E 与E′重合，B与B′重合时，EB+BC的值最小，即最小值为CE'的长.在 Rt△CDE'中 ( CE′=CD⋅sin60∘=5√32,∴12AB+BC的最小值为5√32.故选 B.典例3如图，△ABC中AB=AC=10,tanA=2,BE⊥AC于点 E D 是线段BE 上的一个动点，则CD+√55BD的最小值是( ).A.2√5B.4√5C.5√3D.10【答案】B【解析】如图，作DH⊥AB于点H ( CM⊥AB于点M.∵BE⊥AC,∴∠AEB=90°.∵tanA=BEAE=2,∴设AE=a BE=2a则100=a²+4a²,∴a²=20,解得a=2√5或a=−2√5(舍去)∴BE=2a=4√5.∵AB=AC BE⊥AC CM⊥AB∴CM=BE=4√5(等腰三角形两腰上的高相等).∵∠DBH=∠ABE,∠BHD=∠BEA,∴sin∠DBH=DHBD =AEAB=√55,∴DH=√55BD,∴CD+√55BD=CD+DH,∴CD+DH≥CM,∴CD+√55BD≥4√5,∴CD+√55BD的最小值为4√5.故选 B.小试牛刀1.(★★★☆☆)如图 △ABC 在平面直角坐标系中 AB=AC A(0 2 √2) C(1 0) D 为射线AO 上一点，一动点 P 从点 A 出发，运动路径为A→D→C ，点 P 在AD 上的运动速度是在CD 上的3倍，要使整个运动时间最少，则点 D 的坐标为( ).A.(0 √2 )B.(0,√22)C.(0,√23)D.(0,√24)2.(★★★☆☆)如图 在△ABC 中 ∠A=90° ∠B=60° AB=2 若 D 是BC 边上的动点 则2AD+CD 的最小值为 .直击中考1.已知抛物线 y =ax²+bx +c 与 x 轴交于A(-1 0) B(5 0)两点 C 为抛物线的顶点 抛物线的对称轴交 x 轴于点D ，连接 BC ，且 tan∠CBD =43,如图所示.(1)求抛物线的解析式.(2)设 P 是抛物线的对称轴上的一个动点.①过点 P 作x 轴的平行线交线段BC 于点 E 过点 E 作EF ⊥PE 交抛物线于点F ，连接FB ，FC ，求△BCF 的面积的最大值 ②连接PB 求 35PC +PB 的最小值.阿氏圆问题模型讲解“阿氏圆”又称为“阿波罗尼斯圆”，如图，已知A，B两点，点P 满足PA : PB=k(k≠1) 则点 P 的轨迹为圆.这个轨迹最早由古希腊数学家阿波罗尼斯发现，故称“阿氏圆”.【模型】如图所示⊙O的半径为R 点A B都在⊙O外 P为⊙O上一动点，已知K=25OB,连接PA PB 则当102:25/4B的值最小时，P点的位置如何确定?【解析】如图，在线段OB上截取OC 使OC=25R,连接PO PC 则可说明△BPO与△PCO相似，则有25PB=PC.故本题求PA+25PB的最小值可以转化为求PA+PC的最小值，其中A与C 为定点，P 为动点，故当A，P，C 三点共线时，PA+PC的值最小.典例秒杀典例1如图，正方形ABCD的边长为4，⊙B的半径为2，P 为⊙B上的动点，则PD+12PC的最小值等于( ).A.3B.4C.5D.6【答案】C【解析】如图，在 BC上截取BE=1,连接BP PE DE.∵正方形ABCD的边长为4 ⊙B的半径为2∴BC=CD=4,BP=2,∴EC=3,∴BPBC =BEBP=12,又∠PBE=∠PBE,∴PBECBP,∴PEPC =BEBP=12,∴PE=12PC,∴PD+12PC=PD+PE,∴当D P E三点共线时 PD+PE取得最小值即PD+12PC取得最小值∴PD+12PC的最小值为DE=√DC2+CE2=5.故选 C.典例2问题提出:如图1 在 Rt△ABC中∠ACB=90° CB=4 CA=6 ⊙C的半径为2 P 为圆上一动点连接AP BP 求AP+12BP的最小值.(1)尝试解决：为了解决这个问题，下面给出一种解题思路：如图2 连接CP 在CB 上取点D 使CD=1 连接 PD 则有CDCP =CPCB=12.又∵∠PCD=∠BCP ∴△PCD∽△BCP.∴PDBP =PCBC=12,∴PD=12BP,∴AP +12BP =AP +PD.请你完成余下的思考，并直接写出答案： AP +12BP 的最小值为(2)自主探索：在“问题提出”的条件不变的情况下， 13AP +BP 的最小值为 .(3)拓展延伸:如图3 已知扇形 COD 中 ∠COD =90°,OC =6, OA =3,OB =5,点 P 是 ⌢CD 上一点，求2 2PA +PB 的最小值.【解析】(1)如图 连接AD. ∵AP +12BP =AP +PD,∴要使 AP +12BP 最小，即AP+PD 最小 则点A P D 在同一条直线上 ∴AP +12BP 的最小值为AD 的长，在 Rt △ACD 中 CD=1 AC=6 ∴AD =√AC 2+CD 2=√37, ∴AP +12BP 的最小值为 √37.(2)如图 在 CA 上取点 D 连接 BD 使 CD =23, ∴CD CP=CP CA=13.∵∠PCD=∠ACP ∴△PCD ∽△ACP ∴PD AP =CP CA=13,∴PD =13AP,∴13AP +BP =PD +BP,同(1)的方法得 13AP +BP 的最小值为 BD =√BC 2+CD 2= 23√37.(3)如图 延长OC 到点E 使CE=6 则OE=OC+CE=12 连接 PE OP∵OA =3,∴OAOP =OPOE =12. ∵∠AOP =∠EOP,∴△OAPO △OPE, ∴APEP =OAOP =12,∴EP =2PA,∴2PA +PB =EP +PB,∴当E P B 三点共线时 2PA +PB 取得最小值，为 BE = √OB 2+OE 2=13.小试牛刀1.(★★☆☆☆)如图在Rt△ABC中∠ACB=90°,CB=7,AC=9,，以C为圆心 3为半径作⊙C，P 为⊙C上一动点，连接AP BP 则1AP+BP的最小值为( ).3A.7B.5√2C.4+√10D.2√132.(★★☆☆☆)如图所示已知正方形 ABCD 的边长为4 ⊙B的半径为2，点 P是⊙B上的一个动点，则PD−1PC的最大值为( ).2A.3B.4C.5D.6PA+PB的3.(★★☆☆☆)如图在平面直角坐标系中点A(4 0) B(4 4) 点 P 在半径为 2 的圆 O 上运动，则12最小值是 .直击中考1.如图1，在平面直角坐标系中，直线y=-5x+5与x轴 y轴分别交于A C两点抛物线y=x²+bx+c经过A，C两点，与x轴的另一交点为B.(1)求抛物线解析式及B点坐标(2)若点M为x轴下方抛物线上一动点，连接MA，MB，BC，当点 M运动到某一位置时，四边形AMBC的面积最大，求此时点 M的坐标及四边形AMBC的面积PA的值最小，(3)如图2 若 P点是半径为2的⊙B上一动点连接PC PA 当点 P 运动到某一位置时，PC+12请求出这个最小值，并说明理由.等分面积模型讲解【模型】三角形中的中线等分面积很常见，如图，在△ABC中，取BC的中点D，连接AD，由于左右两个三角形等底同高，故它们的面积相等，即S ABD=AGD,如果在AC边上取一点P，那么如何作线平分面积呢?¯【作法】因为 D 是 BC 的中点S ABD=S ACD,所以要想平分三角形的面积，可作. AE‖PD,连接PE 如图.比较S ABD=S ACD,AED可等量替换为△AEP,因此，得S=S EPC,即完成了面积平分.四边形ABEP典例秒杀典例1已知平面上点O(0 0) A(3 2) B(4 0) 直线. y=mx−3m+2将△OAB分成面积相等的两部分，则m的值为( ).A.1B.2C.3D.4【答案】B【解析】y=mx--3m+2=m(x-3)+2当x=3时 y=2则直线y=mx--3m+2一定过点A(3 2)因为直线 y=mx--3m+2 将△OAB分成面积相等的两部分所以直线y=mx-3m+2一定过OB的中点(2 0)把x=2 y=0代入y=mx-3m+2得0=2m--3m+2解得m=2.故选 B.典例2如图 AB∥DC ED∥BC AE∥BD 那么图中与△ABD面积相等的三角形(不包括△ABD)有( ).A.1个B.2个C.3 个D.4 个【答案】B【解析】∵AB∥DC∴△ABC与△ABD的面积相等.∵AE∥BD∴△BED 与△ABD的面积相等.∵ED∥BC找不到与△ABD等底等高的三角形∴与△ABD面积相等的三角形有△ABC △BED 共2个.故选 B.典例3(1)如图1 梯形 ABCD的对角线交于点O AB∥CD 请写出图中面积相等的三角形(2)如图 2，在平面直角坐标系中，O 是坐标原点，点 A(—2，3) B(2 1).①求点 C的坐标及三角形 AOC 和三角形BOC 的面积②请利用(1)的结论解决如下问题：D 是边OA 上一点，过点 D 作直线DE 平分三角形ABO的面积，并交AB 于点E(要有适当的作图说明).【解析】(1)∵AB∥DC∴S ABD=S ABC,S ADC=S BDC,∴S AOD=S BOC.(2)①∵点 A(-2 3) B(2 1)∴直线AB的解析式为y=−12x+2,∴C(0 2)∴S AOC=12×2×2=2,S Bx=12×2×2=2.②由①可知点 C是线段AB 的中点，则S CA=S OBC.连接CD 过点O作( OE‖CD交AB 于点E 连接DE 则直线DE就是所求作的直线.小试牛刀1.(★★★☆☆)操作体验.(1)如图 1 已知△ABC,请画出△ABC的中线AD，并判断△ABD与△ACD面积的大小关系.(2)如图2，在平面直角坐标系中，△ABC的边 BC 在 x 轴上已知点A(2 4) B(-1 0) C(3 0) 试确定过点 A 的一条直线l 平分△ABC的面积，请写出直线l的表达式.(3)如图3 在平面直角坐标系中若A(1 4) B(3 2) 则在直线y=−4x+20上是否存在一点C，使直线OC 恰好平分四边形OACB 的面积?若存在，请计算点 C的坐标若不存在，请说明理由.2.(★★★☆☆)已知在梯形ABCD中AB‖CD.(1)如图1 若点 E 为AD 的中点 BE 的延长线交 CD 的延长线于点F，求证：(2)如图2，请过点 B画一条直线将梯形ABCD 的面积平分，并简单说出画法.x+m的图象与x 轴交于点A(−6,0),交 y轴于点 B.3.(★★★☆☆)如图已知一次函数y=43(1)求m的值与点 B 的坐标.(2)在x轴上是否存在点C，使得. △ABC的面积为 16?若存在，求出点C的坐标若不存在，说明理由.(3)一条经过点 D(0，2)和直线AB上一点的直线将△AOB分成面积相等的两部分，请求出这条直线的函数表达式.直击中考1.在学习三角形中线的知识时，小明了解到：三角形的任意一条中线所在的直线可以把该三角形分为面积相等的两部分.进而，小明继续研究，过四边形的某一顶点的直线能否将该四边形分为面积相等的两部分?他画出了如下示意图(如图1)，得到了符合要求的直线AF.小明的作图步骤如下：第一步，连接AC第二步过点 B作BE∥AC交DC 的延长线于点E;第三步，取ED的中点F，作直线AF则直线 AF即为所求.请参考小明思考问题的方法，解决问题：如图2 五边形 ABOCD各顶点坐标为A(3 4) B(0 2) O(0 0) C(4 0) D(4 2).请你构造一条经过顶点 A 的直线将五边形 ABOCD分为面积相等的两部分，并求出该直线的解析式.第 21 页共 21 页。

8.9 代数与几何综合一、选择题1. (2016 广西玉林市) 如图，已知正方形ABCD边长为1，∠EAF=45°，AE=AF，则有下列结论：①∠1=∠2=22.5°；②点C到EF的距离是；③△ECF的周长为2；④BE+DF＞EF．其中正确的结论是．（写出所有正确结论的序号）2. (2019 重庆市綦江县) （4分）如图，在△ABC中，∠ABC＝45°，AB＝3，AD ⊥BC于点D，BE⊥AC于点E，AE＝1．连接DE，将△AED沿直线AE翻折至△ABC所在的平面内，得△AEF，连接DF．过点D作DG⊥DE交BE于点G．则四边形DFEG的周长为（）A．8 B．4 C．2+4 D．3+23. (2019 四川省遂宁市) （4分）如图，四边形ABCD是边长为1的正方形，△BPC 是等边三角形，连接DP并延长交CB的延长线于点H，连接BD交PC于点Q，下列结论：①∠BPD＝135°；②△BDP∽△HDB；③DQ：BQ＝1：2；④S△BDP＝．其中正确的有（）A．①②③B．②③④C．①③④D．①②④１２二、填空题4. (2019 浙江省台州市) （5分）如图，直线l 1∥l 2∥l 3，A ，B ，C 分别为直线l 1，l 2，l 3上的动点，连接AB ，BC ，AC ，线段AC 交直线l 2于点D ．设直线l 1，l 2之间的距离为m ，直线l 2，l 3之间的距离为n ，若∠ABC ＝90°，BD ＝4，且＝，则m +n 的最大值为 ．5. (2019 广西防城港市) （3分）如图，AB 与CD 相交于点O ，AB CD =，60AOC ∠=︒，210ACD ABD ∠+∠=︒，则线段AB ，AC ，BD之间的等量关系式为 ．三、应用题6. (2012 福建省莆田市) (1)如图①，在Rt ABC △中，90ABC ∠=°，BD AC ⊥于点D ．求证：2AB AD AC =•；(2)如图②，在Rt ABC △中，90ABC ∠=°，点D 为BC 边上的点，BE AD ⊥于点E ，延长BE 交AC 于点F ．若1AB BD BC DC ==，求AFFC的值； (3)在Rt ABC △中，90ABC ∠=°，点D 为直线．．BC 上的动点．．(点D 不与B 、C 重合)，直线BE AD ⊥于点E ，交直线AC 于点F ．若AB BD n BC DC ==，请探究并直接写出AFFC所有可能的值(用含n 的式子表示)，不必证明．7. (2014 福建省漳州市)阅读材料：如图1，在△AOB中，∠O=90°，OA=OB，点P在AB边上，PE⊥OA于点E，PF⊥OB于点F，则PE+PF=OA．（此结论不必证明，可直接应用）（1）理解与应用如图2，正方形ABCD的边长为2，对角线AC，BD相交于点O，点P在AB边上，PE⊥OA于点E，PF⊥OB于点F，则PE+PF的值为．（2）类比与推理如图3，矩形ABCD的对角线AC， BD相交于点O，AB=4，AD=3，点P在AB边上，PE∥OB交AC于点E，PF∥OA交BD于点F，求PE+PF的值；（3）拓展与延伸如图4，⊙O的半径为4，A，B，C， D是⊙O上的四点，过点C，D的切线CH，DG相交于点M，点P在弦AB上，PE∥BC交AC于点E，PF∥AD于点F，当∠ADG=∠BCH=30°时，PE+PF是否为定值？若是，请求出这个定值；若不是，请说明理由．３４8. (2015 四川省绵阳市) 如图，在边长为2的正方形ABCD 中，G 是AD 延长线时的一点，且DG=AD ，动点M 从A 点出发，以每秒1个单位的速度沿着A →C →G 的路线向G 点匀速运动（M 不与A ，G 重合），设运动时间为t 秒，连接BM 并延长AG 于N ．（1）是否存在点M ，使△ABM 为等腰三角形？若存在，分析点M 的位置；若不存在，请说明理由；（2）当点N 在AD 边上时，若BN ⊥HN ，NH 交∠CDG 的平分线于H ，求证：BN=HN ； （3）过点M 分别作AB ，AD 的垂线，垂足分别为E ，F ，矩形AEMF 与△ACG 重叠部分的面积为S ，求S 的最大值．9. (2015 四川省自贡市) 在△ABC 中，,cos 3AB AC 5ABC 5==∠=,将△ABC 绕点C 顺时针旋转，得到△11A B C .⑴.如图①，当点1B 在线段BA 延长线上时. ①.求证：11BB CA P ；②.求△1AB C 的面积；⑵. 如图②，点E 是BC 上的中点，点F 为线段AB 上的动点，在△ABC 绕点C 顺时针旋转过程中，点F 的对应点是1F ，求线段1EF 长度的最大值与最小值的差.A 1B 1ACB①F 1A 1B 1ACBF ②10. (2015 浙江省衢州市) 如图，在△ABC中，AB=5，AC=9，S△ABC=，动点P从A 点出发，沿射线AB方向以每秒5个单位的速度运动，动点Q从C点出发，以相同的速度在线段AC上由C向A运动，当Q点运动到A点时，P、Q两点同时停止运动，以PQ为边作正方形PQEF（P、Q、E、F按逆时针排序），以CQ为边在AC上方作正方形QCGH．（1）求tanA的值；（2）设点P运动时间为t，正方形PQEF的面积为S，请探究S是否存在最小值？若存在，求出这个最小值，若不存在，请说明理由；（3）当t为何值时，正方形PQEF的某个顶点（Q点除外）落在正方形QCGH的边上，请直接写出t的值．11. (2016 广西贵港市) 如图1，在正方形ABCD内作∠EAF=45°，AE交BC于点E，AF交CD于点F，连接EF，过点A作AH⊥EF，垂足为H．（1）如图2，将△ADF绕点A顺时针旋转90°得到△ABG．①求证：△AGE≌△AFE；②若BE=2，DF=3，求AH的长．５６（2）如图3，连接BD 交AE 于点M ，交AF 于点N ．请探究并猜想：线段BM ，MN ，ND 之间有什么数量关系？并说明理由．四、复合题12. (2012 新疆乌鲁木齐) 如图，已知点(120)A -，，(30)B ，，点C 在y 轴的正半轴上，且90ACB ∠=°． （1）求点C 的坐标；（2）求Rt ACB △的角平分线CD 所在直线l 的解析式； （3）在l 上求出满足12PBC ACB S S =△△的点P 的坐标； （4）已知点M 在l 上，在平面内是否存在点N ，使以O C M N 、、、为顶点的四边形是菱形．若存在，请直接写出点N 的坐标；若不存在，请说明理由．13. (2013 湖北省荆门市) 如图1，正方形ABCD 的边长为2，点M 是BC 的中点，７P 是线段MC 上的一个动点(不与M ，C 重合)，以AB 为直径作⊙O ，过点P 作⊙O的切线，交AD 于点F ，切点为E ． (1)求证：OF ∥BE ；(2)设BP ＝x ，AF ＝y ，求y 关于x 的函数解析式，并写出自变量x 的取值范围； (3)延长DC ，FP 交于点G ，连接OE 并延长交直线DC 于H (图2)，问是否存在点P ，使△EFO ∽△EHG (E ，F ，O 分别与E ，H ，G 为对应点)，如果存在，试求(2)中x 和y 的值，如果不存在，请说明理由．14. (2017 吉林省长春市) 如图，在Rt △ABC 中，∠ACB=90°，∠A=45°，AB=4cm ．点P 从点A 出发，以2cm/s 的速度沿边AB 向终点B 运动．过点P 作PQ ⊥AB 交折线ACB 于点Q ，D 为PQ 中点，以DQ 为边向右侧作正方形DEFQ ．设正方形DEFQ 与△ABC 重叠部分图形的面积是y （cm 2），点P 的运动时间为x （s ）．（1）当点Q在边AC上时，正方形DEFQ的边长为cm（用含x的代数式表示）；（2）当点P不与点B重合时，求点F落在边BC上时x的值；（3）当0＜x＜2时，求y关于x的函数解析式；（4）直接写出边BC的中点落在正方形DEFQ内部时x的取值范围．15. (2017 山东省日照市) 如图所示，在平面直角坐标系中，⊙C经过坐标原点O，且与x轴，y轴分别相交于M（4，0），N（0，3）两点．已知抛物线开口向上，与⊙C交于N，H，P三点，P为抛物线的顶点，抛物线的对称轴经过点C且垂直x轴于点D．（1）求线段CD的长及顶点P的坐标；（2）求抛物线的函数表达式；（3）设抛物线交x轴于A，B两点，在抛物线上是否存在点Q，使得S四边形OPMN=8S△QAB，且△QAB∽△OBN成立？若存在，请求出Q点的坐标；若不存在，请说明理由．８16. (2018 四川省达州市) （11分）阅读下列材料：已知：如图1，等边△A1A2A3内接于⊙O，点P是上的任意一点，连接PA1，PA2，PA3，可证：PA1+PA2=PA3，从而得到：是定值．（1）以下是小红的一种证明方法，请在方框内将证明过程补充完整；证明：如图1，作∠PA1M=60°，A1M交A2P的延长线于点M．∵△A1A2A3是等边三角形，∴∠A3A1A2=60°，∴∠A3A1P=∠A2A1M又A3A1=A2A1，∠A1A3P=∠A1A2P，∴△A1A3P≌△A1A2M∴PA3=MA2=PA2+PM=PA2+PA1．９∴，是定值．（2）延伸：如图2，把（1）中条件“等边△A1A2A3”改为“正方形A1A2A3A4”，其余条件不变，请问：还是定值吗？为什么？（3）拓展：如图3，把（1）中条件“等边△A1A2A3”改为“正五边形A1A2A3A4A5”，其余条件不变，则= （只写出结果）．17. (2018 浙江省温州市) （14分）如图，已知P为锐角∠MAN内部一点，过点P 作PB⊥AM于点B，PC⊥AN于点C，以PB为直径作⊙O，交直线CP于点D，连接AP，BD，AP交⊙O于点E．（1）求证：∠BPD=∠BAC．（2）连接EB，ED，当tan∠MAN=2，AB=2时，在点P的整个运动过程中．①若∠BDE=45°，求PD的长．②若△BED为等腰三角形，求所有满足条件的BD的长．（3）连接OC，EC，OC交AP于点F，当tan∠MAN=1，OC∥BE时，记△OFP的面积为S1，△CFE的面积为S2，请写出的值．１０五、开放题18. (2013 黑龙江省大庆市) 如图所示，在直角梯形ABCD 中，AB 为垂直于底边的腰，AD =1，BC =2，AB =3，点E 为CD 上异于C 、D 的一个动点，过点E 作AB 的垂线，垂足为F ，△ADE 、△AEB 、△BCE 的面积分别为1S 、2S 、3S . （1）设AF x =，试用x 表示1S 与3S 的乘积1S 3S ，并求1S 3S 的最大值； （2）设AFt FB=，试用t 表示EF 的长； （3）在（2）的条件下，当t 为何值时，22134S S S =.六、动态几何19. (2019 浙江省温州市) （14分）如图，在平面直角坐标系中，直线y ＝﹣x +4分别交x 轴、y 轴于点B ，C ，正方形AOCD 的顶点D 在第二象限内，E 是BC 中点，OF ⊥DE 于点F ，连结OE ．动点P 在AO 上从点A 向终点O 匀速运动，同时，动点Q 在直线BC 上从某一点Q 1向终点Q 2匀速运动，它们同时到达终点．（1）求点B 的坐标和OE 的长 （2）设点Q 2为（m ，n ），当＝tan ∠EOF 时，求点Q 2的坐标．（3）根据（2）的条件，当点P运动到AO中点时，点Q恰好与点C重合．①延长AD交直线BC于点Q3，当点Q在线段Q2Q3上时，设Q3Q＝s，AP＝t，求s 关于t的函数表达式．②当PQ与△OEF的一边平行时，求所有满足条件的AP的长．七、阅读理解与信息迁移20. (2014 江西省抚州市) 试题背景已知：l∥m∥n∥k，平行线l与m、m与n、n与k之间的距离分别为d1、d2、d3，且d1 =d3 = 1，d2 = 2 . 我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”.探究1 ⑴如图1，正方形ABCD为“格线四边形”，BE l⊥于点E,BE的反向延长线交直线于点F. 求正方形ABCD的边长.探究2 ⑵矩形ABCD为“格线四边形”，其长：宽 = 2 ：1 ，则矩形ABCD的宽为 . (直接写出结果即可)探究3 ⑶如图2，菱形ABCD为“格线四边形”且∠ADC=60°，△AEF是等边三角形，AE⊥k于点E，∠AFD=90°，直线DF分别交直线、于点G、M. 求证：EC DF=.拓展⑷如图3，l∥k，等边三角形ABC的顶点A、B分别落在直线l、k上，AB⊥k于点B，且AB=4 ，∠ACD=90°，直线CD分别交直线l、k于点G、M，点D、E分别是线段GM、BM上的动点，且始终保持AD=AE，DH l⊥于点H.猜想：DH在什么范围内，BC∥DE？并说明此时BC∥DE的理由.参考答案一、选择题1. 考点四边形综合题．分析先证明Rt△ABE≌Rt△ADF得到∠1=∠2，易得∠1=∠2=∠22.5°，于是可对①进行判断；连结EF、AC，它们相交于点H，如图，利用Rt△ABE≌Rt△ADF 得到BE=DF，则CE=CF，接着判断AC垂直平分EF，AH平分∠EAF，于是利用角平分线的性质定理得到EB=EH，FD=FH，则可对③④进行判断；设BE=x，则EF=2x，CE=1﹣x，利用等腰直角三角形的性质得到2x=（1﹣x），解得x=﹣1，则可对④进行判断．解答解：∵四边形ABCD为正方形，∴AB=AD，∠BAD=∠B=∠D=90°，在Rt△ABE和Rt△ADF中，∴Rt△ABE≌Rt△ADF，∴∠1=∠2，∵∠EAF=45°，∴∠1=∠2=∠22.5°，所以①正确；连结EF、AC，它们相交于点H，如图，∵Rt△ABE≌Rt△ADF，∴BE=DF，而BC=DC，∴CE=CF，而AE=AF，∴AC垂直平分EF，AH平分∠EAF，∴EB=EH，FD=FH，∴BE+DF=EH+HF=EF，所以④错误；∴△ECF的周长=CE+CF+EF=CED+BE+CF+DF=CB+CD=1+1=2，所以③正确；设BE=x，则EF=2x，CE=1﹣x，∵△CEF为等腰直角三角形，∴EF=CE，即2x=（1﹣x），解得x=﹣1，∴EF=2（﹣1），∴CH=EF=﹣1，所以②正确．故答案为①②③．2.分析先证△BDG≌△ADE，得出AE＝BG＝1，再证△DGE与△EDF是等腰直角三角形，在直角△AEB中利用勾股定理求出BE的长，进一步求出GE的长，可通过解直角三角形分别求出GD，DE，EF，DF的长，即可求出四边形DFEG的周长．解答解：∵∠ABC＝45°，AD⊥BC于点D，∴∠BAD＝90°﹣∠ABC＝45°，∴△ABD是等腰直角三角形，∴AD＝BD，∵BE⊥AC，∴∠GBD+∠C＝90°，∵∠EAD+∠C＝90°，∴∠GBD＝∠EAD，∵∠ADB＝∠EDG＝90°，∴∠ADB﹣∠ADG＝∠EDG﹣∠ADG，即∠BDG＝∠ADE，∴△BDG≌△ADE（ASA），∴BG＝AE＝1，DG＝DE，∵∠EDG＝90°，∴△EDG为等腰直角三角形，∴∠AED＝∠AEB+∠DEG＝90°+45°＝135°，∵△AED沿直线AE翻折得△AEF，∴△AED≌△AEF，∴∠AED＝∠AEF＝135°，ED＝EF，∴∠DEF＝360°﹣∠AED﹣∠AEF＝90°，∴△DEF为等腰直角三角形，∴EF＝DE＝DG，在Rt△AEB中，BE＝＝＝2，∴GE＝BE﹣BG＝2﹣1，在Rt△DGE中，DG＝GE＝2﹣，∴EF＝DE＝2﹣，在Rt△DEF中，DF＝DE＝2﹣1，∴四边形DFEG的周长为：GD+EF+GE+DF＝2（2﹣）+2（2﹣1）＝3+2，故选：D．点评本题考查了等腰直角三角形的判定与性质，全等三角形的判定与性质，勾股定理，解直角三角形等，解题关键是能够灵活运用等腰直角三角形的判定与性质．3.分析由等边三角形及正方形的性质求出∠CPD＝∠CDP＝75°、∠PCB＝∠CPB ＝60°，从而判断①；证∠DBP＝∠DPB＝135°可判断②；作QE⊥CD，设QE＝DE＝x，则QD＝x，CQ＝2QE＝2x，CE＝x，由CE+DE＝CD求出x，从而求得DQ、BQ的长，据此可判断③，证DP＝DQ＝，根据S△BDP＝BD•PD sin∠BDP 求解可判断④．解答解：∵△PBC是等边三角形，四边形ABCD是正方形，∴∠PCB＝∠CPB＝60°，∠PCD＝30°，BC＝PC＝CD，∴∠CPD＝∠CDP＝75°，则∠BPD＝∠BPC+∠CPD＝135°，故①正确；∵∠CBD＝∠CDB＝45°，∴∠DBP＝∠DPB＝135°，又∵∠PDB＝∠BDH，∴△BDP∽△HDB，故②正确；如图，过点Q作QE⊥CD于E，设QE＝DE＝x，则QD＝x，CQ＝2QE＝2x，∴CE＝x，由CE+DE＝CD知x+x＝1，解得x＝，∴QD＝x＝，∵BD＝，∴BQ＝BD﹣DQ＝﹣＝，则DQ：BQ＝：≠1：2，故③错误；∵∠CDP＝75°，∠CDQ＝45°，∴∠PDQ＝30°，又∵∠CPD＝75°，∴∠DPQ＝∠DQP＝75°，∴DP＝DQ＝，∴S△BDP＝BD•PD sin∠BDP＝×××＝，故④正确；故选：D．点评本题主要考查相似三角形的判定与性质，解题的关键是熟练掌握等边三角形和正方形的性质、等腰三角形的判定与性质及相似三角形的判定等知识点．二、填空题4. 解答解：过B作BE⊥l1于E，延长EB交l3于F，过A作AN⊥l2于N，过C作CM⊥l2于M，设AE＝x，CF＝y，BN＝x，BM＝y，∵BD＝4，∴DM＝y﹣4，DN＝4﹣x，∵∠ABC＝∠AEB＝∠BFC＝∠CMD＝∠AND＝90°，∴∠EAB+∠ABE＝∠ABE+∠CBF＝90°，∴∠EAB＝∠CBF，∴△ABE∽△BFC，∴，即＝，∴xy＝mn，∵∠ADN＝∠CDM，∴△CMD∽△AND，∴＝，即＝，∴y＝﹣x+10，∵＝，∴n＝m，∴（m +n ）最大＝m ，∴当m 最大时，（m +n ）最大＝m ，∵mn ＝xy ＝x （﹣x +10）＝﹣x 2+10x ＝m 2， ∴当x ＝﹣＝时，mn 最大＝＝m 2，∴m 最大＝，∴m +n 的最大值为×＝．故答案为：．5. 分析过点A 作//AE CD ，截取AE CD =，连接BE 、DE ，则四边形ACDE 是平行四边形，得出DE AC =，ACD AED ∠=∠，证明ABE ∆为等边三角形得出BE AB =，求得360()90BDE AED ABD EAB ∠=︒-∠+∠-∠=︒，由勾股定理得出222BE DE BD =+，即可得出结果．解答解：过点A 作//AE CD ，截取AE CD =，连接BE 、DE ，如图所示： 则四边形ACDE 是平行四边形，DE AC ∴=，ACD AED ∠=∠， 60AOC ∠=︒Q ，AB CD =， 60EAB ∴∠=︒，CD AE AB ==，ABE ∴∆为等边三角形，BE AB ∴=，210ACD ABD ∠+∠=︒Q ，210AED ABD ∴∠+∠=︒，360()3602106090BDE AED ABD EAB ∴∠=︒-∠+∠-∠=︒-︒-︒=︒，222BE DE BD ∴=+，222AB AC BD ∴=+；故答案为：222AB AC BD =+．点评本题考查了勾股定理、平行四边形的判定与性质、等边三角形的判定与性质、平行线的性质、四边形内角和等知识，熟练掌握平行四边形的性质、通过作辅助线构建等边三角形与直角三角形是解题的关键．三、应用题6. 1）证明：如图①，∵BD AC ⊥，90ABC ∠=°，∴∠ADB ＝∠ABC.又∵ ∠A ＝∠A ，∴△ADB ∽△ABC ．∴ AB AD AC AB=，∴ 2AB AD AC =•．（2）解：方法一：如图②，过点C 作CG AD ⊥交AD 的延长线于点G ．∵BE AD ⊥，∴ 90CGD BED ∠=∠=°，CG BF ∥．又∵1AB BD BC DC== ∴22AB BC BD DC ===，BD DC =．又∵BDE CDG ∠=∠，∴BDE CDG △≌△．∴12ED GD EG ==．由（1）可得：2AB AE AD =•，2BD DE AD =•．∴ 2222(2)4AE AB BD DE BD BD === ，∴4AE DE =， ∴422AE DE EG DE ==． 又∵CG BF ∥，2AF AE FC EG==． 方法二：如图③，过点D 作DG BF ∥交AC 于点G ． ∴1AB BD BC DC ==， 12BD DC BC ==，AB BC =． ∵DG BF ∥，∴2FC BC FG BD ==，2FC FG =．由（1）可知： 2AB AE AD =•，2BD DE AD =•．∴22224AE AB BC DE BD BD ===． ∵DG BF ∥，∴4AF AE FG ED ==，∴22AF AF FC FG==． （3） ①当点D 在BC 边上时，AF FC的值为2n n +. ②当点D 在BC 延长线上时，AF FC的值为2n n -． ③当点D 在BC 延长线上时，AF FC 的值为2n n -． （注：写对一种得1分，写对二种得3分，写对三种得5分）7.解：（1）如图2，∵四边形ABCD是正方形，∴OA=OB=OC=OD，∠ABC=∠AOB=90°．∵AB=BC=2，∴AC=2．∴OA=．∵OA=OB，∠AOB=90°，PE⊥OA，PF⊥OB，∴PE+PF=OA=．（2）如图3，∵四边形ABCD是矩形，∴OA=OB=OC=OD，∠DAB=90°．∵AB=4，AD=3，∴BD=5．∴OA=OB=OC=OD=．∵PE∥OB，PF∥AO，∴△AEP∽△AOB，△BFP∽△BOA．∴，．∴==1．∴+=1．∴EP+FP=．∴PE+PF的值为．（3）当∠ADG=∠BCH=30°时，PE+PF是定值．理由：连接OA、OB、OC、OD，如图4．∵DG与⊙O相切，∴∠GDA=∠ABD．∵∠ADG=30°，∴∠ABD=30°．∴∠AOD=2∠ABD=60°．∵OA=OD，∴△AOD是等边三角形．∴AD=OA=4．同理可得：BC=4．∵PE∥BC，PF∥AD，∴△AEP∽△ACB，△BFP∽△BDA．∴，．∴==1．∴=1．∴PE+PF=4．∴当∠ADG=∠BCH=30°时，PE+PF=4．8.分析：(1）四种情况：当点M为AC的中点时，AM=BM；当点M与点C重合时，AB=BM；当点M在AC上，且AM=2时，AM=AB；当点M为CG的中点时，AM=BM；△ABM为等腰三角形；（2）在AB上截取AK=AN，连接KN；由正方形的性质得出∠ADC=90°，AB=AD，∠CDG=90°，得出BK=DN，先证出∠BKN=∠NDH，再证出∠ABN=∠DNH，由ASA证明△BNK≌△NHD，得出BN=NH即可；（3）①当M在AC上时，即0＜t≤2时，△AMF为等腰直角三角形，得出AF=FM=t，求出S=AF•FM=t2；当t=2时，即可求出S的最大值；②当M在CG上时，即2＜t＜4时，先证明△ACD≌△GCD，得出∠ACD=∠GCD=45°，求出∠ACM=90°，证出△MFG为等腰直角三角形，得出FG=MG•cos45°=4﹣t，得出S=S△ACG﹣S△CMJ﹣S△FMG，S为t的二次函数，即可求出结果．解答：（1）解：存在；当点M为AC的中点时，AM=BM，则△ABM为等腰三角形；当点M与点C重合时，AB=BM，则△ABM为等腰三角形；当点M在AC上，且AM=2时，AM=AB，则△ABM为等腰三角形；当点M为CG的中点时，AM=BM，则△ABM为等腰三角形；（2）证明：在AB上截取AK=AN，连接KN；如图1所示：∵四边形ABCD是正方形，∴∠ADC=90°，AB=AD，∴∠CDG=90°，∵BK=AB﹣AK，ND=AD﹣AN，∴BK=DN，∵DH平分∠CDG，∴∠CDH=45°，∴∠NDH=90°+45°=135°，∴∠BKN=180°﹣∠AKN=135°，∴∠BKN=∠NDH，在Rt△ABN中，∠ABN+∠ANB=90°，又∵BN⊥NH，即∠BNH=90°，∴∠ANB+∠DNH=180°﹣∠BNH=90°，∴∠ABN=∠DNH，在△BNK和△NHD中，，∴△BNK≌△NHD（ASA），∴BN=NH；（3）解：①当M在AC上时，即0＜t≤2时，△AMF为等腰直角三角形，∵AM=t，∴AF=FM=t，∴S=AF•FM=×t×t=t2；当t=2时，S的最大值=×（2）2=2；②当M在CG上时，即2＜t＜4时，如图2所示：CM=t﹣AC=t﹣2，MG=4﹣t，在△ACD和△GCD中，，∴△ACD≌△GCD（SAS），∴∠ACD=∠GCD=45°，∴∠ACM=∠ACD+∠GCD=90°，∴∠G=90°﹣∠GCD=45°，∴△MFG为等腰直角三角形，∴FG=MG•cos45°=（4﹣t）•=4﹣t，∴S=S△ACG﹣S△CMJ﹣S△FMG=×4×2﹣×CM×CM﹣×FG×FG =4﹣（t﹣2）2﹣（4﹣）2=﹣+4t﹣8=﹣（t﹣）2+，∴当t=时，S的最大值为．点评：本题是相似形综合题目，考查了等腰三角形的判定、正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、三角函数以及三角形面积的计算等知识；本题难度较大，综合性强，特别是（3）中，需要进行分类讨论，通过证明三角形全等和等腰直角三角形才能得出结果．9.分析：（1）①根据旋转的性质和平行线的性质证明；②过A作AF⊥BC于F，过C作CE⊥AB于E，根据三角函数和三角形的面积公式解答；（2）过C作CF⊥AB于F，以C为圆心CF为半径画圆交BC于F1，和以C为圆心BC为半径画圆交BC的延长线于F1，得出最大和最小值解答即可．解答：解：（1）①证明：∵AB=AC，B1C=BC，∴∠1=∠B，∠B=∠ACB，∵∠2=∠ACB（旋转角相等），∴∠1=∠2，∴BB1∥CA1；②过A作AF⊥BC于F，过C作CE⊥AB于E，如图①：∵AB=AC，AF⊥BC，∴BF=CF，∵cos∠ABC=，AB=5，∴BF=3，∴BC=6，∴B1C=BC=6，∵CE⊥AB，∴BE=B1E=，∴BB1=，CE=，∴AB1=，∴△AB1C的面积为：；（2）如图2，过C作CF⊥AB于F，以C为圆心CF为半径画圆交BC于F1，EF1有最小值，此时在Rt△BFC中，CF=，∴CF1=，∴EF1的最小值为；如图，以C为圆心BC为半径画圆交BC的延长线于F1，EF1有最大值；此时EF1=EC+CF1=3+6=9，∴线段EF1的最大值与最小值的差为．点评：此题考查几何变换问题，关键是根据旋转的性质和三角形的面积公式进行解答．10.分析：（1）如图1，过点B作BM⊥AC于点M，利用面积法求得BM的长度，利用勾股定理得到AM的长度，最后由锐角三角函数的定义进行解答；（2）如图2，过点P作PN⊥AC于点N．利用（1）中的结论和勾股定理得到PN2+NQ2=PQ2，所以由正方形的面积公式得到S关于t的二次函数，利用二次函数的顶点坐标公式和二次函数图象的性质来求其最值；（3）需要分类讨论：当点E在边HG上、点F在边HG上、点P边QH（或点E在QC上）、点F边C上时相对应的t的值．解答：解：（1）如图1，过点B作BM⊥AC于点M，∵AC=9，S△ABC=，∴AC•BM=，即×9•BM=，解得BM=3．由勾股定理，得AM===4，则tanA==；（2）存在．如图2，过点P作PN⊥AC于点N．依题意得AP=CQ=5t．∵tanA=，∴AN=4t，PN=3t．∴QN=AC﹣AN﹣CQ=9﹣9t．根据勾股定理得到：PN2+NQ2=PQ2，S正方形PQEF=PQ2=（3t）2+（9﹣9t）2=90t2﹣162t+81（0＜t＜）．∵﹣==在t的取值范围之内，∴S最小值===；（3）①如图3，当点E在边HG上时，t1=；②如图4，当点F在边HG上时，t2=；③如图5，当点P边QH（或点E在QC上）时，t3=1④如图6，当点F边C上时，t4=．点评：本题考查了四边形综合题．其中涉及到了三角形的面积公式，正方形的性质，勾股定理以及二次函数的最值的求法．其中，解答（3）题时，要分类讨论，做到不重不漏，结合图形解题，更形象、直观．11.考点四边形综合题．分析（1）①由旋转的性质可知：AF=AG，∠DAF=∠BAG，接下来在证明∠GAE=∠FAE，然后依据SAS证明△GAE≌△FAE即可；②由全等三角形的性质可知：AB=AH，GE=EF=5．设正方形的边长为x，接下来，在Rt△EFC中，依据勾股定理列方程求解即可；（2）将△ABM逆时针旋转90°得△ADM′．在△NM′D中依据勾股定理可证明NM′2=ND2+DM′2，接下来证明△AMN≌△ANM′，于的得到MN=NM′，最后再由BM=DM′证明即可．解答解：（1）①由旋转的性质可知：AF=AG，∠DAF=∠BAG．]∵四边形ABCD为正方形，∴∠BAD=90°．又∵∠EAF=45°，∴∠BAE+∠DAF=45°．∴∠BAG+∠BAE=45°．∴∠GAE=∠FAE．在△GAE和△FAE中，∴△GAE≌△FAE．②∵△GAE≌△FAE，AB⊥GE，AH⊥EF，∴AB=AH，GE=EF=5．设正方形的边长为x，则EC=x﹣2，FC=x﹣3．在Rt△EFC中，由勾股定理得：EF2=FC2+EC2，即（x﹣2）2+（x﹣3）2=25．解得：x=6．∴AB=6．∴AH=6．（3）如图所示：将△ABM逆时针旋转90°得△ADM′．∵四边形ABCD为正方形，∴∠ABD=∠ADB=45°．由旋转的性质可知：∠ABM=∠ADM′=45°，BE=DM′．∴∠NDM′=90°．∴NM′2=ND2+DM′2．∵∠EAM′=90°，∠EAF=45°，∴∠EAF=∠FAM′=45°．在△AMN和△ANM′中，，∴△AMN≌△ANM′．∴MN=NM′．又∵BM=DM ′， ∴MN 2=ND 2+BM 2．四、复合题12. 解：（1）由AOC COB △∽△，可得236OC OA OB =⨯=，6OC ∴= 又点C 在y 轴的正半轴上，故点C 的坐标是(06)，； （2）过点D 作DE BC ⊥于点E ，设DB 的长为m ，在Rt DEB △中，sin 5AC DE DB B m m AB =•=•=，cos 5BE DB B m =•=在Rt DEC △中，45DCE ∠=°，于是，5CE DE m ==由CE BE BC +=m +=5m = 又由OA OB >，知点D 在线段OA 上，3OB =，所以2OD =，故点(20)D -，； 设直线l 的解析式为：y kx b =+，把(06)C ，和(20)D -，代入y kx b =+中， 得620b k b =⎧⎨-+=⎩，解之，得36k b =⎧⎨=⎩，故直线l 的解析式为：36y x =+；（3）①取AB 的中点( 4.50)F -，，过点F 作BC 的平行线交直线l 于点1P ，连接CF ．易知112P BC FBC ACB S S S ==△△△，∴点1P 为符合题意的点．直线1P 可由直线BC 向左平移BF 个单位得到（即向左平移7.5个单位）而直线BC 的解析式为26y x =-+，直线1P F 的解析式为2(7.5)6y x =-++即29y x =--，由2936y x y x =--⎧⎨=+⎩得到点1(33)P --，②在直线l 上取点2P 使21P C PC =，此时有2112P BC P BC ACB S S S ==△△△，∴点2P 符合题意．由21P C PC =，可得2P 的坐标为(315)，， ∴点(33)P --，或(315)P ，可使12PBC ACB S S =△△；（4）点N 分别为(13)，，18655⎛⎫- ⎪⎝⎭，，55⎛⎫-- ⎪ ⎪⎝⎭，55⎛⎫⎪ ⎪⎝⎭，13. (1)证明：连接OE ．∵FE ，FA 是⊙O 的切线，∴∠OAF ＝∠OEF ＝90°． 又∵FO ＝FO ，OA ＝OE ．∴△FAO ≌△FEO ． ∴∠AOF ＝∠EOF ＝12∠AOE ． ∵∠ABE ＝12∠AOE ，∴∠AOF ＝∠ABE ． ∴OF ∥BE ．(2)过F 作FQ ⊥BC 于Q ，∴PQ ＝BP －AF ＝x －y ，PF ＝PE ＋EF ＝x ＋y ． 在Rt △PFQ 中，FQ 2＋PQ 2＝PF 2． ∴22＋(x －y )2＝(x ＋y )2． 化简得y ＝1x (1＜x ＜2)． (3)存在这样的P 点．∠EOF ＝∠AOF ，∴∠EHG ＝∠EOA ＝2∠EOF ． ∵OH ⊥FG ，∴∠OEF ＝∠HEG ＝90°．当∠EFO＝∠EHG＝2∠EOF时，即∠EOF＝30°时，△EFO∽△EHG．此时Rt△AFO中，y＝AF＝OA·tan30°＝3．∴x＝1y＝3．∴当x＝3，y＝3时，△EFO∽△EHG．14.答案（1）x；（2）x=45；（3）见解析；（4）1＜x＜32．（3）如图②，当0＜x≤45时，根据正方形的面积公式得到y=x2；如图③，当45＜x≤1时，过C作CH⊥AB于H，交FQ于K，则CH=12AB=2，根据正方形和三角形面积公式得到y=﹣232x2+20x﹣8；如图④，当1＜x＜2时，PQ=4﹣2x，根据三角形的面积公式得到结论；（4）当Q与C重合时，E为BC的中点，得到x=1，当Q为BC的中点时，2得到x=32，于是得到结论．试题解析：（1）∵∠ACB=90°，∠A=45°，PQ⊥AB，∴∠AQP=45°，∴PQ=AP=2x，∵D为PQ中点，∴DQ=x，∵D为PQ中点，∴DQ=x，∴GP=2x，∴2x+x+2x=4，∴x=45；（3）如图②，当0＜x≤45时，y=S正方形DEFQ=DQ2=x2，∴y=x2；如图③，当45＜x≤1时，过C作CH⊥AB于H，交FQ于K，则CH=12AB=2，∵PQ=AP=2x，CK=2﹣2x，∴MQ=2CK=4﹣4x，FM=x﹣（4﹣4x）=5x﹣4，∴y=S正方形DEFQ﹣S△MNF=DQ2﹣12FM2，∴y=x2﹣12（5x﹣4）2=﹣232x2+20x﹣8，∴y=﹣232x2+20x﹣8；∴DQ=2﹣x，∴y=S△DEQ=12DQ2，∴y=12（2﹣x）2，∴y=12x2﹣2x+2；（4）当Q与C重合时，E为BC的中点，即2x=2，∴x=1，当Q为BC的中点时，2，PB=1，∴AP=3，∴2x=3，∴x=3，2∴边BC的中点落在正方形DEFQ内部时x的取值范围为：1＜x＜3．2考点：四边形综合题．15.答案(1) CD=3， P（2，﹣1）；(2) y=x2﹣4x+3；(3) 存在满足条件的点Q，2其坐标为（2，﹣1）．试题分析：（1）连接OC，由勾股定理可求得MN的长，则可求得OC的长，由垂径定理可求得OD的长，在Rt△OCD中，可求得CD的长，则可求得PD的长，可求得P点坐标；（2）可设抛物线的解析式为顶点式，再把N点坐标代入可求得抛物线解析式；（3）由抛物线解析式可求得A、B的坐标，由S四边形OPMN=8S△QAB可求得点Q到x轴的距离，且点Q只能在x轴的下方，则可求得Q点的坐标，再证明△QAB∽△OBN即可．试题解析：（1）如图，连接OC，∵M（4，0），N（0，3），∴OM=4，ON=3，∴MN=5，∴OC=12MN=52，∵CD为抛物线对称轴，∴OD=MD=2，在Rt△OCD中，由勾股定理可得=32，∴PD=PC﹣CD=52﹣32=1，∴P（2，﹣1）；（2）∵抛物线的顶点为P（2，﹣1），∴设抛物线的函数表达式为y=a（x﹣2）2﹣1，∵抛物线过N（0，3），∴3=a（0﹣2）2﹣1，解得a=1，∴抛物线的函数表达式为y=（x﹣2）2﹣1，即y=x2﹣4x+3；（3）在y=x2﹣4x+3中，令y=0可得0=x2﹣4x+3，解得x=1或x=3，∴A（1，0），B（3，0），∴AB=3﹣1=2，∵ON=3，OM=4，PD=1，∴S四边形OPMN=S△OMP+S△OMN=12OM•PD+12OM•ON=12×4×1+12×4×3=8=8S△QAB，∴S△QAB=1，设Q点纵坐标为y，则12×2×|y|=1，解得y=1或y=﹣1，当y=1时，则△QAB为钝角三角形，而△OBN为直角三角形，不合题意，舍去，当y=﹣1时，可知P点即为所求的Q点，∵D为AB的中点，∴AD=BD=QD，∴△QAB为等腰直角三角形，∵ON=OB=3，∴△OBN为等腰直角三角形，∴△QAB∽△OBN，学-科网综上可知存在满足条件的点Q，其坐标为（2，﹣1）．考点：二次函数综合题．16.分析（2）结论：是定值．在A4P上截取AH=A2P，连接HA1．想办法证明PA 4=A4+PH=PA2+PA1，同法可证：PA3=PA1+PA2，推出（+1）（PA1+PA2）=PA 3+PA4，可得PA1+PA2=（﹣1）（PA3+PA4），延长即可解决问题；（3）结论：则=．如图3﹣1中，延长PA1到H，使得A1H=PA2，连接A4H，A4A2，A4A1．由△HA4A1≌△PA4A2，可得△A4HP是顶角为36°的等腰三角形，推出PH=PA4，即PA1+PA2=PA4，如图3﹣2中，延长PA5到H，使得A5H=PA3．同法可证：△A4HP是顶角为108°的等腰三角形，推出PH=PA4，即PA5+PA3=PA4，延长即可解决问题；解答解：（1）如图1，作∠PA1M=60°，A1M交A2P的延长线于点M．∵△A1A2A3是等边三角形，∴∠A3A1A2=60°，∴∠A3A1P=∠A2A1M又A3A1=A2A1，∠A1A3P=∠A1A2P，∴△A1A3P≌△A1A2M∴PA3=MA2，∵PM=PA1，∴PA3=MA2=PA2+PM=PA2+PA1．∴，是定值．（2）结论：是定值．理由：在A4P上截取AH=A2P，连接HA1．∵四边形A1A2A3A4是正方形，∴A4A1=A2A1，∵∠A1A4H=∠A1A2P，A4H=A2P，∴△A1A4H=△A1A2P，∴A1H=PA1，∠A4A1H=∠A2A1P，∴∠HA1P=∠A4A1A2=90°∴△HA1P的等腰直角三角形，∴PA 4=A4+PH=PA2+PA1，同法可证：PA 3=PA1+PA2，∴（+1）（PA1+PA2）=PA3+PA4，∴PA1+PA2=（﹣1）（PA3+PA4），∴=．（3）结论：则=．理由：如图3﹣1中，延长PA1到H，使得A1H=PA2，连接A4H，A4A2，A4A1．由△HA4A1≌△PA4A2，可得△A4HP是顶角为36°的等腰三角形，∴PH=PA4，即PA1+PA2=PA4，如图3﹣2中，延长PA5到H，使得A5H=PA3．同法可证：△A4HP是顶角为108°的等腰三角形，∴PH=PA4，即PA5+PA3=PA4，∴=．故答案为．17.分析（1）由PB⊥AM、PC⊥AN知∠ABP=∠ACP=90°，据此得∠BAC+∠BPC=180°，根据∠BPD+∠BPC=180°即可得证；（2）①由∠APB=∠BDE=45°、∠ABP=90°知BP=AB=2，根据tan∠BAC=tan∠BPD==2知BP=PD，据此可得答案；②根据等腰三角形的定义分BD=BE、BE=DE 及BD=DE三种情况分类讨论求解可得；（3）作OH⊥DC，由tan∠BPD=tan∠MAN=1知BD=PD，据此设BD=PD=2a、PC=2b，从而得出OH=a、CH=a+2b、AC=4a+2b，证△ACP∽△CHO得=，据此得出a=b 及CP=2a、CH=3a、OC=a，再证△CPF∽△COH，得=，据此求得CF=a、OF=a，证OF为△PBE的中位线知EF=PF，从而依据=可得答案．解答解：（1）∵PB⊥AM、PC⊥AN，∴∠ABP=∠ACP=90°，∴∠BAC+∠BPC=180°，又∠BPD+∠BPC=180°，∴∠BPD=∠BAC；（2）①如图1，∵∠APB=∠BDE=45°，∠ABP=90°，∴BP=AB=2，∵∠BPD=∠BAC，∴tan∠BPD=tan∠BAC，∴=2，∴BP=PD，∴PD=2；②当BD=BE时，∠BED=∠BDE，∴∠BPD=∠BPE=∠BAC，∴tan∠BPE=2，∵AB=2，∴BP=，∴BD=2；当BE=DE时，∠EBD=∠EDB，∵∠APB=∠BDE、∠DBE=∠APC，∴∠APB=∠APC，∴AC=AB=2，过点B作BG⊥AC于点G，得四边形BGCD是矩形，∵AB=2、tan∠BAC=2，∴AG=2，∴BD=CG=2﹣2；当BD=DE时，∠DEB=∠DBE=∠APC，∵∠DEB=∠DPB=∠BAC，∴∠APC=∠BAC，设PD=x，则BD=2x，∴=2，∴，∴x=，∴BD=2x=3，综上所述，当BD=2、3或2﹣2时，△BDE为等腰三角形；（3）如图3，过点O作OH⊥DC于点H，∵tan∠BPD=tan∠MAN=1，∴BD=PD，设BD=PD=2a、PC=2b，则OH=a、CH=a+2b、AC=4a+2b，∵OC∥BE且∠BEP=90°，∴∠PFC=90°，∴∠PAC+∠APC=∠OCH+∠APC=90°，∴∠OCH=∠PAC，∴△ACP∽△CHO，∴=，即OH•AC=CH•PC，∴a（4a+2b）=2b（a+2b），∴a=b，即CP=2a、CH=3a，则OC=a，∵△CPF∽△COH，∴=，即=，则CF=a，OF=OC﹣CF=a，∵BE ∥OC 且BO=PO ， ∴OF 为△PBE 的中位线， ∴EF=PF ， ∴==．五、开放题18. 解：（1）∵11122S AD AF x ==g ，3112(3)322S BC BF x x ==⨯⨯-=-g . ∴131(3)2S S x x =-=221139(3)()2224x x x ⎡⎤-+=--+⎢⎥⎣⎦2139()(03)228x x =--+<<. 当32x =时，13S S 取最大值98（不写03x <<，扣1分）. （2）作DM ⊥BC ，垂足为M ，DM 与EF 交于点N .∵AFt FB=，∴AF tFB =. 又∵BM =MC =AD =1，∴1NE DN AF AF tFB tMC DM AB AF FB tFB FB t =====+++. ∴1tNE t =+.∴EF =FN +NE =21111t t t t ++=++. （3）∵AB =AF +FB =（t +1）FB =3， ∴31FB t =+. ∴31t AF tFB t ==+. ∴111332212(1)t tS AD AF t t ==⨯=++g ， 3113322211S BC FB t t ==⨯⨯=++g ，211213(21)32212(1)t t S AB FE t t ++==⨯⨯=++g . ∴221322299(21)2(1)4(1)t t S S S t t +==++，，∴2229(21)944(1)2(1)t t t t +=⨯++， 化简得24410t t -+=，解得12t =.（第（3）问，由13ABCD S S S --梯形得到2S ，可酌情给分）六、动态几何19. 分析（1）令y ＝0，可得B 的坐标，利用勾股定理可得BC 的长； （2）如图1，作辅助线，证明△CDN ∽△MEN ，得CN ＝MN ＝1，计算EN 的长，根据面积法可得OF 的长，利用勾股定理得OF 的长，由＝tan ∠EOF 和n ＝﹣m +4，可得结论；（3）①先设s 关于t 成一次函数关系，设s ＝kt +b ，根据当点P 运动到AO 中点时，点Q 恰好与点C 重合，得t ＝2时，CD ＝4，DQ 3＝2，s ＝2，根据Q 3（﹣4，6），Q 2（6，1），可得t ＝4时，s ＝5，利用待定系数法可得s 关于t 的函数表达式； ②分三种情况：（i ）当PQ ∥OE 时，如图2，根据cos ∠QBH ＝＝＝＝，表示BH 的长，根据AB ＝12，列方程可得t 的值；（ii ）当PQ ∥OF 时，如图3，根据tan ∠HPQ ＝tan ∠CDN ＝，列方程为2t ﹣2＝，可得t 的值．（iii ）由图形可知PQ 不可能与EF 平行． 解答解：（1）令y ＝0，则﹣x +4＝0，∴x＝8，∴B（8，0），∵C（0，4），∴OC＝4，OB＝8，在Rt△BOC中，BC＝＝4；（2）如图1，作EM⊥OC于M，则EM∥CD，∵E是BC的中点∴M是OC的中点∴EM＝OB＝4，OE＝BC＝2∵∠CDN＝∠NEM，∠CND＝∠MNE∴△CDN∽△MEN，∴＝1，∴CN＝MN＝1，∴EN＝＝，∵S△ONE＝EN•OF＝ON•EM，∴OF＝＝，由勾股定理得：EF＝＝＝，。

代数几何综合题Ⅰ、综合问题精讲：代数几何综合题是初中数学中覆盖面最广、综合性最强的题型，近几年中考试题中的综合题大多以代数几何综合题的形式出现，其解题关键点是借助几何直观解题，运用方程、函数的思想解题，灵活运用数形结合，由形导数，以数促形，综合运用代数和几何知识解题．Ⅱ、典型例题剖析【例1】（2005，温州，12分）如图，已知四边形ABCD 内接于⊙O，A 是 BD C 的中点，AE⊥AC 于A ，与⊙O 及CB 的延长线分别交于点F 、E ，且 BF AD =，EM 切⊙O 于M 。

⑴ △ADC∽△EBA ;⑵ AC2＝12 BC·CE；⑶如果AB ＝2，EM ＝3，求cot∠CAD 的值。

解:⑴∵四边形ABCD 内接于⊙O，∴∠CDA＝∠ABE， ∵ BF AD =，∴∠DCA＝∠BAE，∴△CAD∽△AEB⑵ 过A 作AH⊥BC 于H(如图)∵A 是 BD C 中点，∴HC＝HB ＝12BC ， ∵∠CAE＝900，∴AC 2＝CH·CE＝12BC·CE⑶∵A 是 BD C 中点，AB ＝2，∴AC＝AB ＝2， ∵EM 是⊙O 的切线，∴EB·EC＝EM 2 ① ∵AC 2＝12 BC·CE，BC·CE＝8 ②①＋②得：EC(EB ＋BC)＝17，∴EC 2＝17 ∵EC 2＝AC 2＋AE 2，∴AE＝17－22＝13 ∵△CAD∽△ABE，∴∠CAD＝∠AEC， ∴cot∠CAD＝cot∠AEC＝AE AC ＝132点拨：此题的关键是树立转化思想，将未知的转化为已知的．此题表现的非常突出．如，将∠CAD 转化为∠AEC 就非常关键.【例2】（2005，自贡）如图 2－5－2所示，已知直线y=2x+2分别与x 轴、y 轴交于点A 、B ，以线段AB 为直角边在第一象限内作等腰直角△ABC ，∠BAC=90○。

过C 作CD ⊥x 轴，D 为垂足． （1）求点 A 、B 的坐标和AD 的长；（2）求过B 、A 、C 三点的抛物线的解析式。

代数几何综合题1、如图，已知平面直角坐标系中三点A （2，0），B （0，2），P （x ，0）()x <0，连结BP ，过P 点作PC PB ⊥交过点A 的直线a 于点C （2，y ） （1）求y 与x 之间的函数关系式；（2）当x 取最大整数时，求BC 与PA 的交点Q 的坐标。

2．如图，从⊙O 外一点A 作⊙O 的切线AB 、AC ，切点分别为B 、C ，⊙O 的直径BD 为6，连结CD 、AO.(1)求证：CD ∥AO ；(2)设CD ＝x ，AO ＝y ，求y 与x 之间的函数关系式，并写出自变量x 的取值范围； (3)若AO ＋CD ＝11，求AB 的长.3．如图，A 、B 两点的坐标分别是(x 1，0)、(x 2，O)，其中x 1、x 2是关于x 的方程x 2+2x+m -3=O 的两根，且x 1<0<x 2． (1)求m 的取值范围；(2)设点C 在y 轴的正半轴上，∠ACB=90°，∠CAB=30°，求m 的值；(3)在上述条件下，若点D 在第二象限，△DAB ≌△CBA ，求出直线AD 的函数解析式.4.一张矩形纸片OABC 平放在平面直角坐标系内，O 为原点，点A 在x 的正半轴上，点C 在y 轴的正半轴上，OA ＝5，OC ＝4。

①求直线AC 的解析式；②若M 为AC 与BO 的交点，点M 在抛物线285y x kx=-+上，求k 的值；③将纸片沿CE 对折，点B 落在x 轴上的点D 处，试判断点D 是否在②的抛物线上，并说明理由。

1、已知抛物线)0(22>--=m m x x y 与y 轴的交于C 点，C 点关于抛物线对称轴的对称点为C ′。

（1）求抛物线的对称轴及C 、C ′的坐标（可用含m 的代数式表示）；（2）如果点Q 在抛物线的对称轴上，点P 在抛物线上，以点C 、C ′、P 、Q 为顶点的四边形是平行四边形，求Q 点和P 的坐标（可用含m 的代数式表示）； （3）在（2）的条件下，求出平行四边形的周长。

中考代数几何综合题代几综合题是初中数学中覆盖面最广、综合性最强的题型．近几年的中考压轴题多以代几综合题的形式出现．解代几综合题一般可分为“认真审题、理解题意；探求解题思路；正确解答”三个步骤,解代几综合题必须要有科学的分析问题的方法．数学思想是解代几综合题的灵魂，要善于挖掘代几综合题中所隐含的重要的转化思想、数形结合思想、分类讨论的思想、方程（不等式）的思想等，把实际问题转化为数学问题，建立数学模型，这是学习解代几综合题的关键．题型一般分为：（1）方程与几何综合的问题；（2）函数与几何综合的问题；（3）动态几何中的函数问题；（4）直角坐标系中的几何问题；（5）几何图形中的探究、归纳、猜想与证明问题.题型特点：一是以几何图形为载体，通过线段、角等图形寻找各元素之间的数量关系，建立代数方程或函数模型求解；二是把数量关系与几何图形建立联系，使之直观化、形象化，从函数关系中点与线的位置、方程根的情况得出图形中的几何关系.以形导数，由数思形，从而寻找出解题捷径. 解代几综合题要灵活运用数形结合的思想进行数与形之间的相互转化，关键是要从题目中寻找这两部分知识的结合点，从而发现解题的突破口.方法点拨方程与几何综合问题是中考试题中常见的中档题，主要以一元二次方程根的判别式、根与系数的关系为背景，结合代数式的恒等变形、解方程（组）、解不等式（组）、函数等知识．其基本形式有：求代数式的值、求参数的值或取值范围、与方程有关的代数式的证明．函数型综合题主要有：几何与函数结合型、坐标与几何、方程与函数结合型问题，是各地中考试题中的热点题型．主要是以函数为主线，建立函数的图象，结合函数的性质、方程等解题．解题时要注意函数的图象信息与方程的代数信息的相互转化．例如函数图象与x 轴交点的横坐标即为相应方程的根；点在函数图象上即点的坐标满足函数的解析式等．函数是初中数学的重点，也是难点，更是中考命题的主要考查对象，由于这类题型能较好地考查学生的函数思想、数形结合思想、分类讨论思想、转化思想，能较全面地反映学生的综合能力，有较好的区分度，因此是各地中考的热点题型．几何综合题考查知识点多、条件隐晦，要求学生有较强的理解能力，分析能力，解决问题的能力，对数学知识、数学方法有较强的驾驭能力，并有较强的创新意识与创新能力．1．几何型综合题，常以相似形与圆的知识为考查重点，并贯穿其他几何、代数、三角等知识，以证明、计算等题型出现．2．几何计算是以几何推理为基础的几何量的计算，主要有线段和弧长的计算，角的计算，三角函数值的计算，以及各种图形面积的计算等．3．几何论证题主要考查学生综合应用所学几何知识的能力．4．解几何综合题应注意以下几点：（1）注意数形结合，多角度、全方位观察图形，挖掘隐含条件，寻找数量关系和相等关系；（2）注意推理和计算相结合，力求解题过程的规范化；（3）注意掌握常规的证题思路，常规的辅助线作法；（4）注意灵活地运用数学的思想和方法．类型一、方程与几何综合的问题1.如图，在梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3．问：线段AB上是否存在点P，使得以P、A、D为顶点的三角形与以P、B、C为顶点的三角形相似？若存在，这样的总共有几个？并求出AP的长；若不存在，请说明理由．【思路点拨】由于以P、A、D为顶点的三角形与以P、B、C为顶点的三角形相似时的对应点不能确定，故应分两种情况讨论．【答案与解析】解：存在．∵AD∥BC，∠A=90°，∴∠B=90°，当△PAD∽△PBC时，∵AD=2，BC=3，设AP=x，PB=7-x，则∴．①当△ADP∽△BPC时，AD=2，BC=3，设设AP=x，PB=7-x，则∴AP=1或AP=6．②由①②可知，P点距离A点有三个位置：，AP=1，AP=6．【总结升华】本题考查的是相似三角形的判定，解答此题时要注意分类讨论，不要漏解．【变式】有一张矩形纸片ABCD，已知AB=2，AD=5．把这张纸片折叠，使点A落在边BC上的点E处，折痕为MN，MN交AB于M，交AD于N．（1）若BE=，试画出折痕MN的位置，并求这时AM的长；（2）点E在BC上运动时，设BE=x，AN=y，试求y关于x的函数解析式，并写出x 的取值范围；（3）连接DE，是否存在这样的点E，使得△AME与△DNE相似？若存在，请求出这时BE的长；若不存在，请说明理由．【答案】（1）画出正确的图形．（折痕MN必须与AB、AD相交）．设AM=t，则ME=t，MB=2-t，由BM2+BE2=ME2，得t=，即AM=．（2）如图（a），∵BE=x，设BM=a，则a2+x2=（2-a）2，a2+x2=4-4a+a2，∴a=，AM=2-BM=2-=．由△AMN∽△BEA，得，∴y=，∵0＜x≤2，0＜y≤5，x的取值范围为：，故x=1．（3）如图（b），若△AME与△DNE相似，不难得∠DNE=∠AME．又∵AM=ME，∴DN=NE=NA=，∴＝解得：x=1或x=4．又∵，故x=1．或者由∠DEN=∠AEM，得∠AED=90°，推出△ABE∽△ECD，从而得BE=1类型二、函数与几何综合问题2.如图，在平面直角坐标系中，点P从原点O出发，沿x轴向右以每秒1个单位长的速度运动t（t＞0）秒，抛物线y=x2＋bx＋c经过点O和点P．已知矩形ABCD的三个顶点为A （1，0）、B（1，－5）、D（4，0）．⑴求c、b（可以用含t的代数式表示）；⑵当t>1时，抛物线与线段AB交于点M．在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；⑶在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”．若抛物线将这些“好点”分成数量相等的两部分，请直接写出t的取值范围．答案与解析【思路点拨】（1）由抛物线y=x2+bx+c经过点O和点P，将点O与P的坐标代入方程即可求得c，b；（2）当x=1时，y=1-t，求得M的坐标，则可求得∠AMP的度数；（3）根据图形，可直接求得答案．【答案与解析】解：（1）把x=0，y=0代入y=x2+bx+c，得c=0，再把x=t，y=0代入y=x2+bx，得t2+bt=0，∵t＞0，∴b=-t；（2）不变．∵抛物线的解析式为：y=x2-tx，且M的横坐标为1，∴当x=1时，y=1-t，∴M（1，1-t），∴AM=|1-t|=t-1，∵OP=t，∴AP=t-1，∴AM=AP，∵∠PAM=90°，∴∠AMP=45°；（3）＜ｔ＜．①左边4个好点在抛物线上方，右边4个好点在抛物线下方：无解；②左边3个好点在抛物线上方，右边3个好点在抛物线下方：则有 -4＜y2＜-3，-2＜y3＜-1，即-4＜4-2t＜-3，-2＜9-3t＜-1，∴＜ｔ＜４且＜ｔ＜，解得＜ｔ＜；③左边2个好点在抛物线上方，右边2个好点在抛物线下方：无解；④左边1个好点在抛物线上方，右边1个好点在抛物线下方：无解；⑤左边0个好点在抛物线上方，右边0个好点在抛物线下方：无解；综上所述， t的取值范围是：＜ｔ＜．【总结升华】此题考查了二次函数与点的关系．此题综合性很强，难度适中，解题的关键是注意数形结合与方程思想的应用类型三、动态几何中的函数问题3. 如图，在平面直角坐标系中，已知二次函数的图像与轴交于，与轴交于A、B两点，点B的坐标为（1）求二次函数的解析式及顶点D的坐标；（2）点M是第二象限内抛物线上的一动点，若直线OM把四边形ACDB分成面积为1:2的两部分，求出此时点的坐标；（3）点P是第二象限内抛物线上的一动点，问：点P在何处时△的面积最大？最大面积是多少？并求出此时点P的坐标.答案与解析举一反三【思路点拨】（1）抛物线的解析式中只有两个待定系数，因此只需将点B、C的坐标代入其中求解即可．（2）先画出相关图示，连接OD后发现：S△OBD：S四边形ACDB=2：3，因此直线OM必须经过线段BD才有可能符合题干的要求；设直线OM与线段BD的交点为E，根据题干可知：△OBE、多边形OEDCA的面积比应该是1：2或2：1，即△OBE的面积是四边形ACDB面积的，所以先求出四边形ABDC的面积，进而得到△OBE的面积后，可确定点E的坐标，首先求出直线OE（即直线OM）的解析式，联立抛物线的解析式后即可确定点M的坐标（注意点M的位置）．（3）此题必须先得到关于△CPB面积的函数表达式，然后根据函数的性质来求出△CPB 的面积最大值以及对应的点P坐标；通过图示可发现，△CPB的面积可由四边形OCPB的面积减去△OCB的面积求得，首先设出点P的坐标，四边形OCPB的面积可由△OCP、△OPB的面积和得出．【答案与解析】解：（1）由题意，得：解得：所以，二次函数的解析式为：，顶点D的坐标为（-1，4）.（2）画图由Ａ、Ｂ、Ｃ、Ｄ四点的坐标，易求四边形ACDB的面积为9.直线BD的解析式为y=2x+6.设直线OM与直线BD 交于点E，则△OBE的面积可以为3或6.①当时，如图，易得E点坐标（-2，-2），直线OE的解析式为y=-x.设M 点坐标（x，-x），∴②当时，同理可得M点坐标．∴ M 点坐标为（-1，4）．（3）如图，连接，设P点的坐标为，∵点P在抛物线上，∴，∴∵，∴当时，. △的面积有最大值∴当点P的坐标为时，△的面积有最大值，且最大值为【总结升华】此题主要考查了二次函数解析式的确定、图形面积的解法以及二次函数的应用等知识；（2）问中，一定先要探究一下点M的位置，以免出现漏解的情况．【变式】如图所示，四边形OABC是矩形，点A、C的坐标分别为（3，0），（0，1），点D是线段BC上的动点（与端点B、C不重合），过点D作直线＝－＋交折线OAB 于点E．（1）记△ODE的面积为S，求S与的函数关系式；（2）当点E在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形OA1B1C1，试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化，若不变，求出该重叠部分的面积；若改变，请说明理由.【答案】（1）由题意得B（3，1）．若直线经过点A（3，0）时，则b＝若直线经过点B（3，1）时，则b＝若直线经过点C（0，1）时，则b＝1.①若直线与折线OAB的交点在OA上时，即1＜b≤，如图1，此时点E（2b，0）.∴S＝OE·CO＝×2b×1＝b.②若直线与折线OAB的交点在BA上时，即＜b＜，如图2，此时点E（3，），D（2b－2，1）.∴S＝S矩－(S△OCD＋S△OAE ＋S△DBE )＝3－[(2b－1)×1＋×(5－2b)•()＋×3()]（2）如图3，设O1A1与CB相交于点M，C1B1与OA相交于点N，则矩形O1A1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积．由题意知，DM∥NE，DN∥ME，∴四边形DNEM为平行四边形,根据轴对称知，∠MED＝∠NED,又∠MDE＝∠NED，∴∠MED＝∠MDE，MD＝ME，∴平行四边形DNEM为菱形．过点D作DH⊥OA，垂足为H，设菱形DNEM的边长为a，由题可知，D（2b-2，1），E（2b，0），∴DH=1，HE=2b-（2b-2）=2，∴HN=HE-NE=2-a，则在Rt△DHM中，由勾股定理知：，∴a=.∴S四边形DNEM＝NE·DH＝．∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化，面积始终为．类型四、直角坐标系中的几何问题4. 如图所示，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA＝3，OC＝2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．（1）直接写出点E、F的坐标；（2）设顶点为F的抛物线交y轴正半轴于点P，且以点E、F、P为顶点的三角形是等腰三角形，求该抛物线的解析式；（3）在x轴、y轴上是否分别存在点M、N，使得四边形MNFE的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．答案与解析【思路点拨】（1）由轴对称的性质，可知∠FBD=∠ABD，FB=AB，可得四边形ABFD是正方形，则可求点E、F的坐标；（2）已知抛物线的顶点，则可用顶点式设抛物线的解析式. 因为以点E、F、P为顶点的等腰三角形没有给明顶角的顶点，而顶角和底边都是唯一的，所以要抓住谁是顶角的顶点进行分类，可分别以E、F、P为顶角顶点；（3）求周长的最小值需转化为利用轴对称的性质求解.【答案与解析】解：（1）E(3,1)；F(1,2)；（2）连结EF，在Rt△EBF中,∠B=90°，∴EF=.设点P的坐标为(0,n),n＞0,∵顶点F(1,2), ∴设抛物线的解析式为y=a(x-1)2+2，(a≠0)．①如图1，当EF=PF时，EF2=PF2，∴12+(n-2)2=5，解得n1=0(舍去)，n2=4.∴P(0，4)，∴4=a(0-1)2+2，解得a=2，∴抛物线的解析式为y=2(x-1)2+2．②如图2，当EP=FP时，EP2=FP2，∴(2-n)2+1=(1-n)2+9，解得n=－(舍去)③当EF=EP时，EP=＜3，这种情况不存在.综上所述，符合条件的抛物线为y=2(x-1)2+2．（3）存在点M、N，使得四边形MNFE的周长最小．如图3，作点E关于x轴的对称点E′，作点F关于y轴的对称点F′，连结E′F′，分别与x轴、y轴交于点M、N，则点M、N就是所求. 连结NF、ME.∴E′(3，-1)、F′(-1，2)，NF=NF′，ME=ME′. ∴BF′=4，BE′=3.∴FN+NM+ME=F′N+NM+ME′=F′E′==5.又∵EF=，∴FN+MN+ME+EF=5+，此时四边形MNFE的周长最小值为5+.【总结升华】本题考查了平面直角坐标系、等腰直角三角形、抛物线解析式的求法、利用轴对称求最短距离以及数形结合、分类讨论等数学思想. 分类讨论的思想要依据一定的标准，对问题分类、求解，要特别注意分类原则是不重不漏，最简分类常见的依据是：一是依据概念分类，如判断直角三角形时明确哪个角可以是直角，两个三角形相似时分清哪两条边是对应边；二是依运动变化的图形中的分界点进行分类，如一个图形在运动过程中，与另一个图形重合部分可以是三角形，也可以是四边形、五边形等. 几何与函数的综合题是中考常见的压轴题型，解决这类问题主要分为两步：一是利用线段的长确定出几何图形中各点的坐标；二是用待定系数法求函数关系式．类型五、几何图形中的探究、归纳、猜想与证明问题5. 如图所示，以等腰三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA，再以等腰直角三角形ABA的斜边为直角边向外作第3个等腰直角三角形A BB，……，如此作下去，若OA=OB=1，则第n个等腰直角三角形的面积Ｓ＝ ________（n为正整数）．答案与解析举一反三【思路点拨】本题要先根据已知的条件求出S1、S2的值，然后通过这两个面积的求解过程得出一般性的规律，进而可得出S n的表达式．【答案与解析】根据直角三角形的面积公式，得S1=；根据勾股定理，得：AB=，则S2=1=20；A1B=2，则S3=21，依此类推，发现：=．【总结升华】本题要先从简单的例子入手得出一般化的结论，然后根据得出的规律去求特定的值．【变式】阅读下面的文字，回答后面的问题．求 3+32+33+…+3100的值．解：令 S=3+32+33+…+3100（1），将等式两边提示乘以3得到：3S=32+33+34+…+3101（2），（2）-（1）得到：2S=3101-3∴S=∴3+32+33+ (3100)问题：（1）2+22+…+22011的值为__________________；（直接写出结果）（2）求4+12+36+…+4×350的值；（3）如图，在等腰Rt△OAB中，OA=AB=1，以斜边OB为腰作第二个等腰Rt△OBC，再以斜边OC为腰作第三个等腰Rt△OCD，如此下去…一直作图到第8个图形为止．求所有的等腰直角三角形的所有斜边之和．（直接写出结果）．答案与解析【答案】解：（1）22012-2．（2）令S=4+12+36+…+4×350①，将等式两边提示乘以3得到：3S=12+36+108+…+4×351②，②-①得到：2S=4×341-4∴S=2×351-2∴4+12+36+…+4×350=2×351-2．（3）．一、选择题1. 如图，正方形ABCD的边长为2, 将长为2的线段QF的两端放在正方形相邻的两边上同时滑动．如果点Q从点A出发，沿图中所示方向按滑动到点A为止，同时点F从点B出发，沿图中所示方向按滑动到点B为止那么在这个过程中线段QF的中点M所经过的路线围成的图形的面积为（）A. 2B. 4－C．D．2. 如图，夜晚，小亮从点A经过路灯C的正下方沿直线走到点B，他的影长y随他与点A之间的距离x的变化而变化，那么表示y与x之间函数关系的图象大致为（）二、填空题3. 在平面直角坐标系中，点A的坐标为(4，0)，点B的坐标为(4，10)，点C在y轴上，且△ABC是直角三角形，则满足条件的C点的坐标为______________．4. 如图，(n+1)个边长为2的等边三角形有一条边在同一直线上，设△B2D1C1的面积为S1，△B3D2C2的面积为S2，…，△B n+1D n C n的面积为S n，则S2=______________；S n=__________________(用含的式子表示）．三、解答题5. 如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=5cm，点D在BC上，且CD=3cm，现有两个动点P，Q分别从点A和点B同时出发，其中点P以1厘米/秒的速度沿AC向终点C运动；点Q以1.25厘米/秒的速度沿BC向终点C运动．过点P作PE∥BC交AD于点E，连接EQ．设动点运动时间为t秒（t＞0）．（1）连接DP，经过1秒后，四边形EQDP能够成为平行四边形吗？请说明理由；（2）连接PQ，在运动过程中，不论t取何值时，总有线段PQ与线段AB平行．为什么？（3）当t为何值时，△EDQ为直角三角形．6．如图，在平面直角坐标系中，四边形OABC是梯形，OA∥BC，点A的坐标为（6，0），点B的坐标为（3，4），点C在y轴的正半轴上．动点M在OA上运动，从O点出发到A点；动点N在AB上运动，从A点出发到B点．两个动点同时出发，速度都是每秒1个单位长度，当其中一个点到达终点时，另一个点也随即停止，设两个点的运动时间为t（秒）（1）求线段AB的长；当t为何值时，MN∥OC？（2）设△CMN的面积为S，求S与t之间的函数解析式，并指出自变量t的取值范围；S是否有最小值？若有最小值，最小值是多少？7. 条件：如下图，A、B是直线l同旁的两个定点．问题：在直线l上确定一点P，使PA+PB的值最小．方法：作点A关于直线l的对称点A′，连接A′B交l于点P，则PA+PB=A′B的值最小（不必证明）．模型应用：（1）如图1，正方形ABCD的边长为2，E为AB的中点，P是AC上一动点．连接BD，由正方形对称性可知，B与D关于直线AC对称．连接ED交AC于P，则PB+PE的最小值是______；（2）如图2，⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC=60°，P是OB上一动点，求PA+PC的最小值；（3）如图3，∠AOB=45°，P是∠AOB内一点，PO=10，Q、R分别是OA、OB上的动点，求△PQR周长的最小值．8. 如图，四边形OABC是一张放在平面直角坐标系的矩形纸片，O为原点，点A在x 轴上，点C在y轴上，OA=15，OC=9，在AB上取一点M，使得△CBM沿CM翻折后，点B落在x轴上，记作N点．（1）求N点、M点的坐标；（2）将抛物线y=x2﹣36向右平移a（0＜a＜10）个单位后，得到抛物线l，l经过点N，求抛物线l的解析式；（3）①抛物线l的对称轴上存在点P，使得P点到M、N两点的距离之差最大，求P 点的坐标；②若点D是线段OC上的一个动点（不与O、C重合），过点D作DE∥OA交CN于E，设CD的长为m，△PDE的面积为S，求S与m之间的函数关系式，并说明S是否存在最大值？若存在，请求出最大值；若不存在，请说明理由．9. 如图，直线y=kx﹣1与x轴、y轴分别交于B、C两点，tan∠OCB=．（1）求B点的坐标和k的值；（2）若点A（x，y）是第一象限内的直线y=kx﹣1上的一个动点．当点A运动过程中，试写出△AOB的面积S与x的函数关系式；（3）探索：在（2）的条件下：①当点A运动到什么位置时，△AOB的面积是；②在①成立的情况下，x轴上是否存在一点P，使△POA是等腰三角形？若存在，请写出满足条件的所有P点的坐标；若不存在，请说明理由．10. 如图，已知抛物线y=ax2+bx+3经过点B（-1，0）、C（3，0），交y轴于点A，将线段OB绕点O顺时针旋转90°，点B的对应点为点M，过点A的直线与x轴交于点D（4，0）．直角梯形EFGH的上底EF与线段CD重合∠FEH=90°，EF∥HG，EF=EH=1．直角梯形EFGH从点D开始，沿射线DA方向匀速运动，运动的速度为1个长度单位/秒，在运动过程中腰FG与直线AD始终重合，设运动时间为t秒．（1）求此抛物线的解析式；（2）当t为何值时，以M、O、H、E为顶点的四边形是特殊的平行四边形；（3）作点A关于抛物线对称轴的对称点A′，直线HG与对称轴交于点K，当t为何值时，以A、A′、G、K为顶点的四边形为平行四边形？请直接写出符合条件的t值．11. 如图，已知等边三角形ABC中，点D，E，F分别为边AB，AC，BC的中点，M 为直线BC上一动点，△DMN为等边三角形（点M的位置改变时，△DMN也随之整体移动）．（1）如图①，当点M在点B左侧时，请你判断EN与MF有怎样的数量关系？点F是否在直线NE上？请直接写出结论，不必证明或说明理由；（2）如图②，当点M在BC上时，其它条件不变，（1）的结论中EN与MF的数量关系是否仍然成立？若成立，请利用图2证明；若不成立，请说明理由；（3）若点M在点C右侧时，请你在图③中画出相应的图形，并判断（1）的结论中EN 与MF的数量关系是否仍然成立？若成立，请直接写出结论，不必证明或说明理由．【答案与解析】一、选择题1.【答案】B.2.【答案】A.三、填空题3.【答案】（0，0），（0，10），（0，2），（0，8）4.【答案】；；【解析】由于各三角形为等边三角形,且各边长为2,过各三角形的顶点B1、B2、B3…向对边作垂线，垂足为M1、M2、M3∵△AB1C1是等边三角形，∴AD1=AC1.sin60°=2×=，∵△B1C1B2也是等边三角形，∴C1B1是∠AC1B2的角平分线，∴AD1=B2D1=，故S1=S△B2C1A﹣S△AC1D1=×2×﹣×2×=；S2=S△B3C2A﹣S△AC2D2=×4×﹣×4×=；作AB∥B1C1，使AB=AB1，连接BB1，则B2，B3，…B n在一条直线上．∵B n C n∥AB，∴==，∴B n D n=.AD=，则D n C n=2﹣B n D n=2﹣=．△B n C n B n+1是边长是2的等边三角形，因而面积是：．△B n+1D n C n面积为S n=.=.=．即第n个图形的面积S n=．三、解答题5.【答案与解析】解：（1）能，如图1，∵点P以1厘米/秒的速度沿AC向终点C运动，点Q以1.25厘米/秒的速度沿BC向终点C运动,t=1秒∴AP=1，BQ=1.25，∵AC=4，BC=5，点D在BC上，CD=3，∴PC=AC-AP=4-1=3，QD=BC-BQ-CD=5-1.25-3=0.75，∵PE∥BC，解得PE=0.75，∵PE∥BC，PE=QD，∴四边形EQDP是平行四边形；（2）如图2，∵点P以1厘米/秒的速度沿AC向终点C运动，点Q以1.25厘米/秒的速度沿BC向终点C运动，∴PC=AC-AP=4-t，QC=BC-BQ=5-1.25t，∴∴PQ∥AB；（3）分两种情况讨论：①如图3，当∠EQD=90°时，显然有EQ=PC=4-t，又∵EQ∥AC，∴△EDQ∽△ADC∴，∵BC=5，CD=3，∴BD=2，∴DQ=1.25t-2，∴解得t=2.5（秒）；②如图4，当∠QED=90°时，作EM⊥BC于M，CN⊥AD于N，则EM=PC=4-t，在Rt△ACD中，∵AC=4，CD=3，∴AD=，∵∠CDA=∠EDQ，∠QED=∠C=90°，∴△EDQ∽△CDA，∴t=3.1（秒）．综上所述，当t=2.5秒或t=3.1秒时，△EDQ为直角三角形．6.【答案与解析】解：（1）过点B作BD⊥OA于点D，则四边形CODB是矩形，BD=CO=4，OD=CB=3，DA=3在Rt△ABD中，．当时，，，．∵，，∴，即（秒）．（2）过点作轴于点，交的延长线于点，∵，∴，．即，．，．，∴．即（）．由，得．∴当时，S有最小值，且7.【答案与解析】解：（1）∵四边形ABCD是正方形，∴AC垂直平分BD，∴PB=PD，由题意易得：PB+PE=PD+PE=DE，在△ADE中，根据勾股定理得，DE=；（2）作A关于OB的对称点A′，连接A′C，交OB于P，PA+PC的最小值即为A′C的长，∵∠AOC=60°∴∠A′OC=120°作OD⊥A′C于D，则∠A′OD=60°∵OA′=OA=2∴A′D=∴；（3）分别作点P关于OA、OB的对称点M、N，连接OM、ON、MN，MN交OA、OB于点Q、R，连接PR、PQ，此时△PQR周长的最小值等于MN．由轴对称性质可得，OM=ON=OP=10，∠MOA=∠POA，∠NOB=∠POB，∴∠MON=2∠AOB=2×45°=90°，在Rt△MON中，MN===10．即△PQR周长的最小值等于10．8.【答案与解析】解：（1）∵CN=CB=15，OC=9，∴ON==12，∴N（12，0）；又∵AN=OA﹣ON=15﹣12=3，设AM=x∴32+x2=（9﹣x）2，∴x=4，M（15，4）；（2）解法一：设抛物线l为y=（x﹣a）2﹣36则（12﹣a）2=36∴a1=6或a2=18（舍去）∴抛物线l：y=（x﹣6）2﹣36解法二：∵x2﹣36=0，∴x1=﹣6，x2=6；∴y=x2﹣36与x轴的交点为（﹣6，0）或（6，0）由题意知，交点（6，0）向右平移6个单位到N点，所以y=x2﹣36向右平移6个单位得到抛物线l：y=（x﹣6）2﹣36；（3）①由“三角形任意两边的差小于第三边”知：P点是直线MN与对称轴x=6的交点，设直线MN的解析式为y=kx+b，则，解得，∴y=x﹣16，∴P（6，﹣8）；②∵DE∥OA，∴△CDE∽△CON，∴；∴S=∵a=﹣＜0，开口向下，又m=﹣∴S有最大值，且S最大=﹣．9.【答案与解析】解：（1）∵y=kx﹣1与y轴相交于点C，∴OC=1；∵tan∠OCB=，∴OB=；∴B点坐标为:；把B点坐标为：代入y=kx﹣1得：k=2；（2）∵S=，y=kx﹣1，∴S=×|2x﹣1|；∴S=|x﹣|；（3）①当S=时，x﹣=，∴x=1，y=2x﹣1=1；∴A点坐标为（1，1）时，△AOB的面积为；②存在．满足条件的所有P点坐标为：P1（1，0），P2（2，0），P3（，0），P4（，0）．10.【答案与解析】解：（1）∵抛物线y=ax2+bx+3经过点B（﹣1，0）、C（3，0），∴，解得a=﹣1，b=2，∴抛物线的解析式为：y=﹣x2+2x+3．（2）在直角梯形EFGH运动的过程中：①四边形MOHE构成矩形的情形，如图1所示：此时边GH落在x轴上时，点G与点D重合．由题意可知，EH，MO均与x轴垂直，且EH=MO=1，则此时四边形MOHE构成矩形．此时直角梯形EFGH平移的距离即为线段DF的长度．过点F作FN⊥x轴于点N，则有FN=EH=1，FN∥y轴，∴，即，解得DN=．在Rt△DFN中，由勾股定理得：DF===，∴t=；②四边形MOHE构成正方形的情形．由图1可知，OH=OD﹣DN﹣HN=4﹣﹣1=，即OH≠MO，所以此种情形不存在；③四边形MOHE构成菱形的情形，如图2所示：过点F作FN⊥x轴于点N，交GH于点T，过点H作HR⊥x轴于点R．易知FN ∥y轴，RN=EF=FT=1，HR=TN．设HR=x，则FN=FT+TN=FT+HR=1+x；∵FN∥y轴，∴，即，解得DN=（1+x）．∴OR=OD﹣RN﹣DN=4﹣1﹣（1+x）=﹣x．若四边形MOHE构成菱形，则OH=EH=1，在Rt△ORH中，由勾股定理得：OR2+HR2=OH2，即：（﹣x）2+x2=12，解得x=，∴FN=1+x=，DN=（1+x）=．在Rt△DFN中，由勾股定理得：DF===3．由此可见，四边形MOHE构成菱形的情形存在，此时直角梯形EFGH平移的距离即为线段DF的长度，∴t=3．综上所述，当t=s时，四边形MOHE构成矩形；当t=3s时，四边形MOHE构成菱形．（3）当t=s或t=s时，以A、A′、G、K为顶点的四边形为平行四边形．简答如下：（注：本题并无要求写出解题过程，以下仅作参考）由题意可知，AA′=2．以A、A′、G、K为顶点的四边形为平行四边形，则GK ∥AA′，且GK=AA′=2．①当直角梯形位于△OAD内部时，如图3所示：过点H作HS⊥y轴于点S，由对称轴为x=1可得KS=1，∴SG=KS+GK=3．由SG∥x轴，得，求得AS=，∴OS=OA﹣AS=，∴FN=FT+TN=FT+OS=，易知DN=FN=，在Rt△FND中，由勾股定理求得DF=；②当直角梯形位于△OAD外部时，如图4所示：设GK与y轴交于点S，则GS=SK=1，AS=，OS=OA+AS=．过点F作FN⊥x轴，交GH于点T，则FN=FT+NT=FT+OS=．在Rt△FGT中，FT=1，则TG=，FG=．由TG∥x轴，∴，解得DF=．由于在以上两种情形中，直角梯形EFGH平移的距离均为线段DF的长度，则综上所述，当t=s或t=s时以A、A′、G、K为顶点的四边形为平行四边形．11.【答案与解析】解：（1）判断：EN与MF相等（或EN=MF），点F在直线NE上.（2）成立．证明：连结DE，DF．∵△ABC是等边三角形，∴AB=AC=BC．又∵D，E，F是三边的中点，∴DE，DF，EF为三角形的中位线．∴DE=DF=EF，∠FDE=60°．又∠MDF+∠FDN=60°，∠NDE+∠FDN=60°，∴∠MDF=∠NDE．在△DMF和△DNE中，DF=DE，DM=DN，∠MDF=∠NDE，∴△DMF≌△DNE．∴MF=NE．（3）画出图形（连出线段NE），MF与EN相等的结论仍然成立（或MF=NE成立）．。

专题71 代数与几何综合（1）【典例分析】例1、如图，四边形OABC为长方形，其中O为原点，A、C两点分别在x轴和y轴上，B 点的坐标是(4,6)，将长方形沿直线DE折叠，使点C落在AB边上点F处，折痕分别交OC，BC于点E、D，且D点坐标是(52,6)．(1)求F点的坐标；(2)如图2，P点在第二象限，且△PDE≌△CED，求P点的坐标；(3)若M点为x轴上一动点，N点为直线DE上一动点，△FMN为以FN为底边的等腰直角三角形，求N点的坐标．【答案】解：(1)∵点D坐标是(52,6)，B点的坐标是(4,6)，四边形OABC为矩形，∴BC=AO=4，OC=AB=6，CD=52，BD=BC−CD=32，∵将矩形沿直线DE折叠，∴DF=CD=52，∴BF=√DF2−DB2=√254−94=2，∴AF=6−2=4，∴点F(4,4)；(2)如图2中，连接PF交DE于J．当四边形EFDP是矩形时，△PDE≌△FED≌△CED，∵C(0,6)，F(4,4)，∴直线CF的解析式为y=−12x+6，∵DE垂直平分线段CF，∴直线DE的解析式为y=2x+1，∴E(0,1)，D(52,6)，∵DJ=JE，∴J(54,72 )，∵PJ=JF，∴P(−32,3)；(3)如图3中，连接FN，以FN为对角线构造正方形NMFM′，连接MM′交FN于K．设N(m,2m+1)，则K(m+42,2m+52)，M(7−m2,3m+12)，M′(3m+12,m+92)，当点M落在x轴上时，3m+12=0，解得m=−13，当点M′落在X轴上时，m+92=0，解得m=−9，∴满足条件的点N的坐标为(−13,13)或(−9,−17)．【解析】【试题解析】(1)由折叠的性质可得DF=CD=5，由勾股定理可求BF的长，即可求解；2(2)如图2中，连接PF交DE于J.当四边形EFDP是矩形时，△PDE≌△FED≌△CED，构建一次函数求出点E，点D坐标，求出点J的坐标即可解决问题．(3)如图3中，连接FN，以FN为对角线构造正方形NMFM′，连接MM′交FN于K.用m的代数式表示出点M，M′的坐标，根据点M，M′在x轴上时，纵坐标为0构建方程求解即可．本题属于四边形综合题，考查了矩形的性质，翻折变换，一次函数的应用等知识，解题的关键是学会构建一次函数解决问题，学会利用参数解决问题，属于中考压轴题．【好题演练】一、选择题1.在平面直角坐标系xOy中，点A(0,2)，B(a,0)，C(m,n)，其中m>a，a<1，n>0，若△ABC是等腰直角三角形，且AB=BC，则m的取值范围是A. 0<m<2B. 2<m<3C. m<3D. m>3【答案】B【解析】【分析】本题考查了坐标于图形的性质，等腰直角三角形的性质和全等三角形的判定和性质，不等式(组)的解集等有关知识，关键是知识的综合，利用数形结合思想解决问题．先由已知条件判定ΔAOB≌ΔBDC，故得OB=CD，OA=BD，再结合已知和点的坐标，得到不等式m−2<1和m−2>0，最后解不等式(组)即可求解．【解答】解：过点C作CD⊥x轴于点D，∴∠BDC=90°，∵∠ABC=90°，∴∠1+∠2=90°，∵∠AOB=90°，∴∠3+∠2=90°，∴∠1=∠3，∵∠AOB=∠BDC=90°，AB=BC，∴ΔAOB≌ΔBDC(AAS)，∴OB=CD，OA=BD，即a=n，m−a=2，∴a=n=m−2，∵a<1，∴m−2<1，即m<3;∵n>0，∴m−2>0，即m>2;∴m的取值范围是2<m<3．故答案为B．二、填空题2.如图A,E为反比例函数y=2x (x>0)上的两点，B、D为反比例函数y=kx(x>0)上的两点，AB//DE//y轴，连结DA并延长交y轴于点C且CD轴，若SΔABC−SΔADE=19，则k=__________．【答案】94【解析】【分析】本题主要考查的是反比例函数与几何综合，解题的关键是根据题意写出各点坐标．设点A(a,2a)，根据反比例函数及其图象的特点依次表示出B、C、D的坐标，再根据SΔABC−SΔADE=19即可得出结果．【解答】解：∵点A在反比例函数y=2x(x>0)上，设点A(a,2a)，∵AB//DE//y轴，∴B点的横坐标为a，C、D点纵坐标为2a，∴B(a,ka )，C(0,2a)，D(ak2,2a)，∴E点的横坐标为ak2，∵点E在反比例函数y=2x(x>0)上，∴E(ak2,4ak)，∵SΔABC−SΔADE=19，∴12⋅AC⋅AB−12AD⋅DE=19，∴12×a×(ka−2a)−12×(ak2−a)×(2kak−4ak)=19，∴k=94．故答案为：94．3.如图，矩形硬纸片ABCD的顶点A在y轴的正半轴上滑动，顶点B在x轴的正半轴上滑动，点E为AB的中点，AB=24，BC=5.当OD最大时，直线OD的表达式为________．【答案】y=5x【解析】【分析】本题主要考查代数与几何的综合.待定系数法，相似三角形的判定与性质等知识．求直线OD解析式.需要先求出D点坐标，用到相似三角形的判定与性质求D点的横坐标，纵坐标，代入计算即可．【解答】解：如图，当O 、E 、D 三点共线时，OD 最大，过点D 作DF ⊥y 轴于点F ，∵AD =BC =5，AE =12AB =12， ∴DE =√AD 2+AE 2=√52+122=13， ∴OD =DE +OE =13+12=25， 设DF =x ，∴OF =√OD 2−DF 2=√252−x 2， ∵四边形ABCD 是矩形， ∴∠DAB =90∘， ∵∠DFA =∠AOB =90°，∴∠DAF +∠ADF =∠DAF +∠OAB ， ∴ADF =∠OAB ，又Rt △OAB 中，E 为AB 中点， ∴EO =EA =EB ，∴∠OAE =∠AOE ， ∴∠ADF =FOD ， 又∠AFD =∠OFD ， ∴△FOD∽△FDA ， ∴OD AD =OFDF ， 即255=√252−x 2x，解得x =25√2626，或x =−25√2626(舍去)， ∴OF =125√2626，∴D(25√2626,125√2626).令直线OD的表达式：y=kx，把点D坐标代入得k=5，∴y=5x．故答案为：y=5x．三、解答题4.如图，直线l：y=x−2分别交x，y轴于A、B两点，C、D是直线l上的两个动点，点C在第一象限，点D在第三象限．且始终有∠COD=135∘．(1)求证：ΔOAC∽△DBO；(2)若点C、D都在反比例函数y=kx的图象上，求k的值；(3)记▵OBD的面积为S1，▵AOC的面积为S2，且S1S2=12，二次函数y=ax2+bx+c满足以下两个条件：①图象过C、D两点；②当S1≤x≤S2时，y有最大值2，求a的值．【答案】解：(1)证明：∵∠DOC=135°，∴∠BOD+∠AOC=45°，∵A，B分别是直线y=x−2与x轴，y轴的交点，∴OA=OB=2，∴∠OAB=∠OBA=45°，∴∠AOC +∠ACO =45°， ∴∠BOD =∠ACO ， ∵∠OBD =∠OAC ， ∴▵OAC ∽▵DBO ；(2)由(1)得▵OAC ∽▵DBO ， ∴ACBO =AOBD ， ∴AC ·BD =4， 设C(x C ,y C )，D(x D ,y D )，过点C 作CE ⊥OA 于点E ，过点D 作DF ⊥OB 于点F ，则BD =√2DF =−√2x D ，AC =√2CE =√2y C ． ∴−√2x D ·√2y C =4， ∴x D ·y C =−2， 即k·x D x C=−2，联立{y =x −2y =k x，消去y 得x 2−2x −k =0，∴x D ·x C =−k ，∴x D 2=2，∴x D =−√2， ∴y D =2−√2， ∴k =2√2+2；(3)由(1)知▵OAC ∽▵DBO ，∴S 1S 2=(OB AC )2=(BD OA )2=12，∴AC =2√2，BD =√2， ∴C(4,2)，D(−1,−3)， ∴S 1=1,S 2=2，把C ，D 代入二次函数解析式得： {16a +4b +c =2a −b +c =−3, 解得{b =1−3ac =−2−4a, ∴y =ax 2+(1−3a)x +(−2−4a)， 对称轴为x =−1−3a 2a=32−12a，①当a >0时， ∵x =32−12a <32，∴2到对称轴的距离大于1到对称轴的距离，∴当x =2时，二次函数取最大值为4a +2−6a −2−4a =2． ∴a =−13(舍去)，这种情况，不存在a 的值使二次函数的最大值为2； ②当−1≤a <0时，x =32−12a ≥2，∴二次函数y =ax 2+(1−3a)x +(−2−4a)在1≤x ≤2上是随着x 的增大而增大的， ∴当x =2时，二次函数取最大值为4a +2−6a −2−4a =2， 解得：a =−13； ③当a <−1时，32<x =32−12a <2，∴当x =32−12a 时，二次函数取最大值为−(3a−1)24a−2−4a =2，解得a =−15(舍去)， 综上可得a 的值为−13．【解析】本题主要考查的是相似三角形的判定和性质，一次函数的图象上点的坐标特征，等腰三角形的判定，二次函数的应用的有关知识．(1)根据∠DOC=135°，得到∠BOD+∠AOC=45°，根据A，B分别是直线y=x−2与x轴，y轴的交点，得到OA=OB=2，进而得到∠OAB=∠OBA=45°，从而有∠BOD=∠ACO，根据∠OBD=∠OAC，得到▵OAC∽▵DBO；(2)由相似三角形的性质得到AC·BD=4，设C(x C,y C)，D(x D,y D)，过点C作CE⊥OA于点E，过点D作DF⊥OB于点F，则BD=√2DF=−√2x D，AC=√2CE=√2y C.进而求出k·x Dx C=−2，联立{y=x−2y=kx，消去y得x2−2x−k=0，求出x D=−√2，y D=2−√2，进而求出k；(3)利用相似三角形的性质得到S1S2=(OBAC)2=(BDOA)2=12，求出点C，D的坐标，再代入二次函数的解析式求出y=ax2+(1−3a)x+(−2−4a)，求出对称轴为x=−1−3a2a =32−12a，再分①当a>0时，②当−1≤a<0时，③当a<−1时，讨论求解即可．5.如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y=kx(x>0)的图像上，点D的坐标为(4,3)．(1)求k的值．(2)设点M在反比例函数图像上，连接AM，DM，若△AMD的面积与菱形ABCD的面积相等，求点M的坐标．【答案】解：(1)延长AD交x轴于E，∵点D的坐标为(4,3)，∴OE=4，DE=3，由勾股定理得，OD=5，则AE=8，∴点A的坐标为(4,8)，∴k=4×8=32，答：k的值为32;(2)菱形ABCD的面积为5×4=20，∵△AMD的面积与菱形ABCD的面积相等，∴点M到AD的距离为20×25=8，∴点M的横坐标为4+8=12，y=3212=83，点M的坐标为(12,83).【解析】本题考查的是反比例函数系数k的几何意义、求反比例函数的解析式，勾股定理，三角形的面积，反比例函数的图象上点的坐标特征的有关知识，菱形的性质，掌握菱形的性质、反比例函数系数k=xy是解题的关键．(1)延长AD交的轴于E，根据勾股定理求出菱形的边长，确定A的坐标，代入反比例函数解析式求出k的值;(2)根据题意求出菱形的面积，根据题意求出点M到AD的距离，求出点M的横坐标，代入求值即可．6.如图，在平面直角坐标系xOy中，直线y=mx+1与双曲y=kx(k>0)相交于点A、B，点C在x轴正半轴上，点D(1,−2)，连结OA、OD、DC、AC，四边形AODC为菱形．(1)求k和m的值；(2)根据图象写出反比例函数的值小于2时x的取值范围；(3)设点P是y轴上一动点，且S△OAP=S菱形OACD，求点P的坐标．【答案】解：(1)∵四边形AODC是菱形，O、C在x轴上，∴A、D关于x轴对称，∵D(1,−2)，∴A(1,2)，将A(1,2)代入直线y=mx+1可得m+1=2，解得m=1，将A(1,2)代入反比例函数y=kx，可求得k=2．(2)∵当x=1时，反比例函数的值为2，∴当反比例函数图象在A点下方时，对应的函数值小于2，此时x的取值范围为：x<0或x>1；(3)连接AD交x轴于E，∵OC=2OE=2，AD=2DE=4，∴S菱形OACD =12OC⋅AD=4，S△OAP=S菱形OACD，∴S△OAP=4，设P点坐标为(0,y)，则OP=|y|，∴12×|y|×1=4，即|y|=8，解得y=8或y=−8，∴P点坐标为(0,8)或(0,−8)【解析】本题考查的是反比例函数的解析式，菱形的性质，三角形的面积有关知识．(1)由菱形的性质可知A、D关于x轴对称，可求得A点坐标，把A点坐标分别代入两函数函数解析式可求得k和m值；(2)由(1)可知A点坐标为(1,2)，结合图象可知在A点的下方时，反比例函数的值小于2，可求得x的取值范围；(3)根据菱形的性质可求得C点坐标，可求得菱形面积，设P点坐标为(0,y)，根据条件可得到关于y的方程，可求得P点坐标．7.抛物线y=ax2+bx+c的图象经过点A(−1,0)，B(3,0)，交y轴负半轴于点C且OC=OA．(1)求抛物线的解析式；(2)如图1，在第四象限内的抛物线上是否存在一点P，连接AP，直线AP将四边形ACPB的面积分为1：2的两部分？若存在，求出点P的坐标；若不存在，请说明理由；(3)如图2，以AB为直径向x轴上方画半圆，交y轴正半轴于点D，点Q是弧BD上的动点，M是弧DQ的中点，连接AQ、DQ，AM，设∠CDQ的角平分线交AM于点N，当点Q沿半圆从点D运动至点B时，求N点的运动路径长．【答案】解：(1)∵抛物线图象经过点A(−1,0)、点B(3,0)且OC=OA∴点C(0,−1)，设抛物线解析式为y=a(x+1)(x−3)，把点C(0,−1)代入，得a =13，∴设抛物线解析式为y =13(x +1)(x −3)， 即y =13x 2−23x −1；(2)连接BC 交AP 于点E ，过点C 作CG ⊥AP 垂足为点G 、过点B 作BH ⊥AP 交AP 的延长线于点H ，过点E 作EF ⊥AB ，垂足为点F ， 如图 ①若S △APC ：S △APB =1:2，则CG:BH =1:2，∵△CGE∽△BHE ， ∴CE:BE =CG:BH =1:2， 易证△BEF∽△BOC ， ∴BF BO=BE BC=EF OC =23， ∴E(1,−23)，∴AE 的解析式为y =−13(x +1)，令，解得{x 1=−1y 1=0(舍);{x 2=2y 2=−1，∴点P(2,−1) ；②如图若S △APC ：S △APB =2:1，则CG:BH =2:1，∵△CGE∽△BHE ∴CE:BE =CG:BH =2:1， 易证△BEF∽△BCO ， ∴，∴E(2,−13)，∴AE 的解析式为y =−19(x +1)， 令{y =−19(x +1),y =13(x +1)(x −3).解得∴点P(83,−1127)，综上所述点P(2,−1)或(83,−1127).(3)如图连接AD ，易知AB =4，OD =√3，∠AQD =∠ABD =30°，∴∠DAO =60°，∠ADO =30°，不妨设∠QAO=x，∴∠DAQ=60°−x，∵点M是弧DQ的中点，∴∠DAM=∠MAQ=12(60°−x)，∵∠QAO+∠DOA=∠ODQ+∠AQD，∴∠ODQ=x+90°−30°=60°+x，∵DN平分∠ODQ，∴∠ODN=12∠ODQ=12(60°+x)，∴∠ADN=∠ADO+∠ODN=30°+12(60°+x)=60°+12x，∴∠AND=180°−(∠DAN+∠ADN)=90°，如图∴点N在以AD为直径的圆上运动，起点为点D，终点为N′，取AD的中点S，连接SN′，当点Q运动到点B时，即∠QAO=x=0°，∴∠DAN=30°，则∠DSN=60°，∵AD=2∴SD=1，∴点N运动的路径长为60⋅π⋅12180=π3．【解析】本题考查二次函数与相似三角形和圆的有关知识的综合，并要具备分类讨论的思想、数形结合思想，需要很强的逻辑推理能力；要有很强的计算能力，熟记计算公式是关键；本道题是一道比较困难的综合题。